| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Необратимые процессы и общие условия равновесия
Для необратимого процесса второе начало термодинамики можно записать в следующем виде:

где  положительная величина.
положительная величина.
Из уравнения (33,4) видно, что энтропия системы при необратимом процессе может изменять свое значение в зависимости от следующих причин:
1) от поглощения системой теплоты извне или от потери ею теплоты;
2) при необратимых внутренних изменениях в системе: химических реакциях, диффузии, трении, излучении и т. д.
Рассмотрим изменение энтропии при разных процессах.
Для адиабатного процесса при  уравнение (33,4) переходит в равенство:
уравнение (33,4) переходит в равенство:

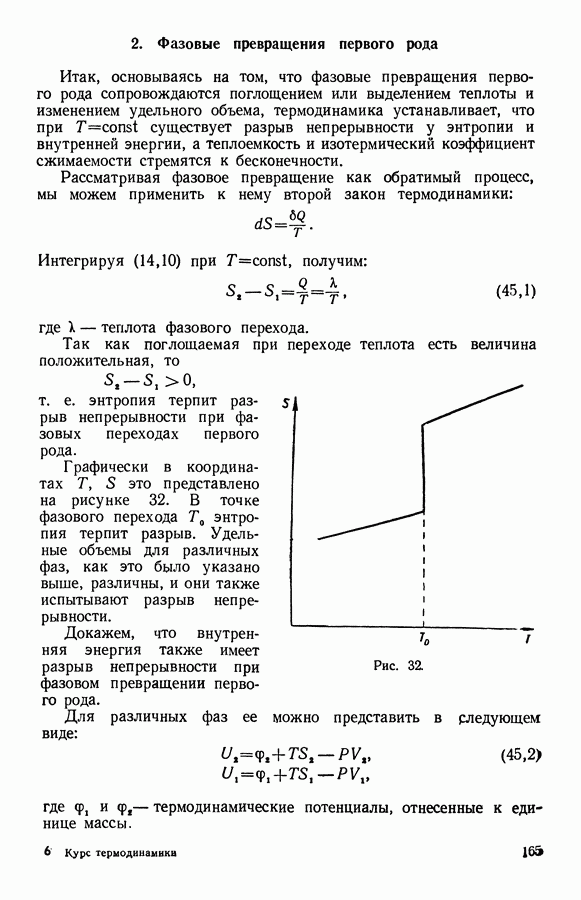
показывающее нам направление, в котором происходит изменение энтропии в системе. Энтропия будет изменяться до тех пор, пока система не придет в равновесие.
При равновесии системы изменение энтропии выражается так:

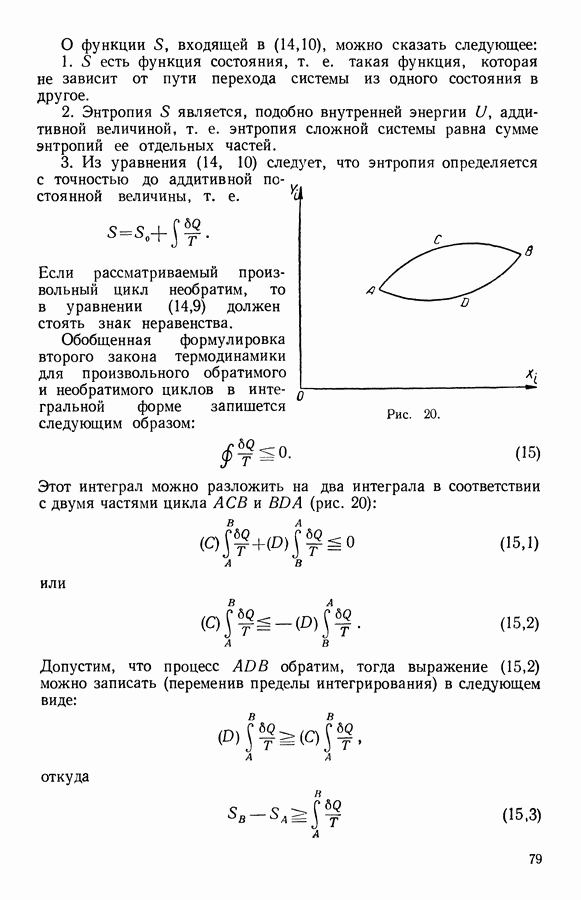
Уравнение (33,6) является условием максимума или минимума энтропии. Спрашивается, какое же значение принимает энтропия, когда система достигла равновесия? Так как член  всегда положителен, то энтропия при адиабатном необратимом процессе может только возрастать до тех пор, пока вся система не придет в равновесие.
всегда положителен, то энтропия при адиабатном необратимом процессе может только возрастать до тех пор, пока вся система не придет в равновесие.
Значит, при равновесии в системе

Итак, при адиабатном необратимом процессе энтропия характеризует его направление: оно таково, что энтропия увеличивается и в условиях равновесия принимает максимальное значение.
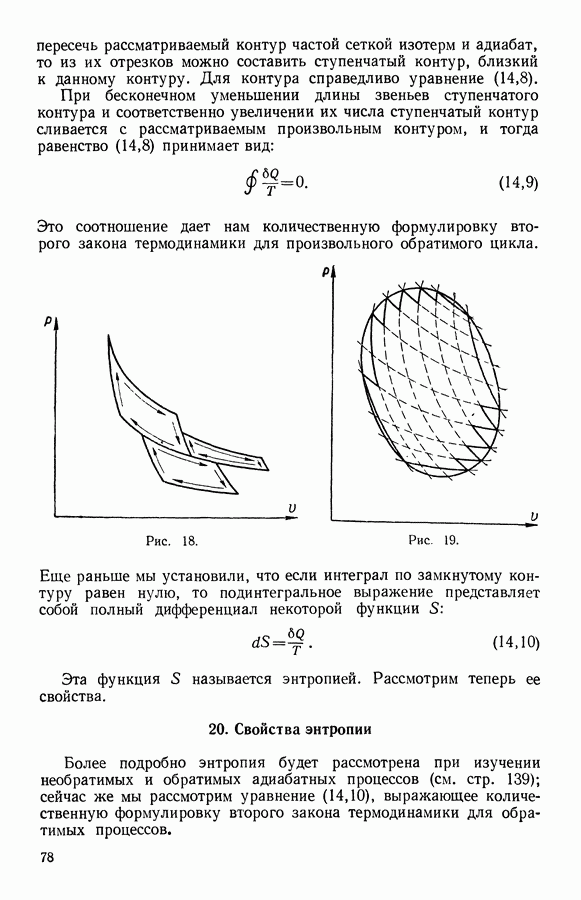
В общем случае энтропия системы может убывать, возрастать или оставаться постоянной в зависимости от того, какой процесс совершается в системе. Если система не адиабатна, энтропия будет возрастать, когда в систему поступает теплота, и уменьшаться, когда из системы теплота будет уходить. Если процесс адиабатный, но обратимый, то из уравнения (14,10) при  вытекает, что
вытекает, что

Найдем значения, к которым стремятся внутренняя энергия, энтальпия, свободная энергия и термодинамический потенциал в условиях равновесия системы.
Подставив в  можно получить, что
можно получить, что

или

где  выражено через
выражено через  При постоянных энтропии и обобщенной координате
При постоянных энтропии и обобщенной координате

Если энтропия и обобщенная координата остаются постоянными, то находящиеся в системе тела изменяются так, что внутренняя энергия достигает своего минимума, т. е.

Так как член —  всегда отрицателен, то внутренняя энергия при постоянных
всегда отрицателен, то внутренняя энергия при постоянных  их может только убывать, и в состоянии равновесия
их может только убывать, и в состоянии равновесия

Энтальпия в условиях равновесия также принимает минимальное значение. Изменение энтальпии для необратимого процесса можно вывести из уравнения (33,10), если прибавить к правой и левой частям этого уравнения по  т. е.
т. е.

или

где  выражено через
выражено через 
При постоянных 

В условиях равновесия

Вследствие того, что энтальпия при необратимом процессе и постоянных  уменьшалась с приближением системы к равновесию, по его достижении она принимает минимальное значение:
уменьшалась с приближением системы к равновесию, по его достижении она принимает минимальное значение:

В практических расчетах обычно пользуются характеристическими функциями системы, являющимися функциями температуры и обобщенной координаты или температуры и обобщенной силы. Как уже было показано выше, этими функциями являются свободная энергия и термодинамический потенциал.
Для необратимого процесса изменение свободной энергии можно получить из уравнения (33,10). Действительно, если вычесть из правой и левой частей уравнения (33,10) по  то получится:
то получится:

или

Здесь изменение свободной энергии выражено через  . В случае изотермического процесса из уравнения (34,6) находим, что
. В случае изотермического процесса из уравнения (34,6) находим, что

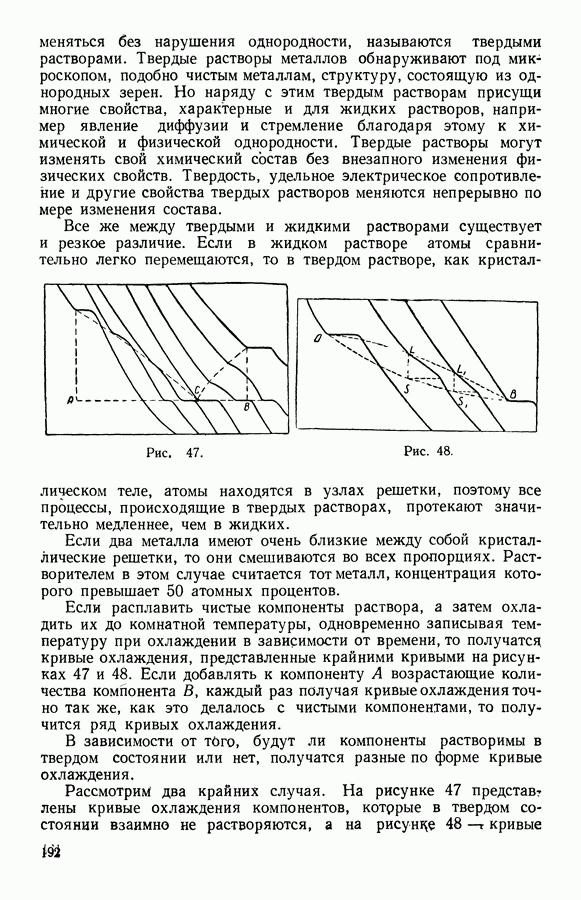
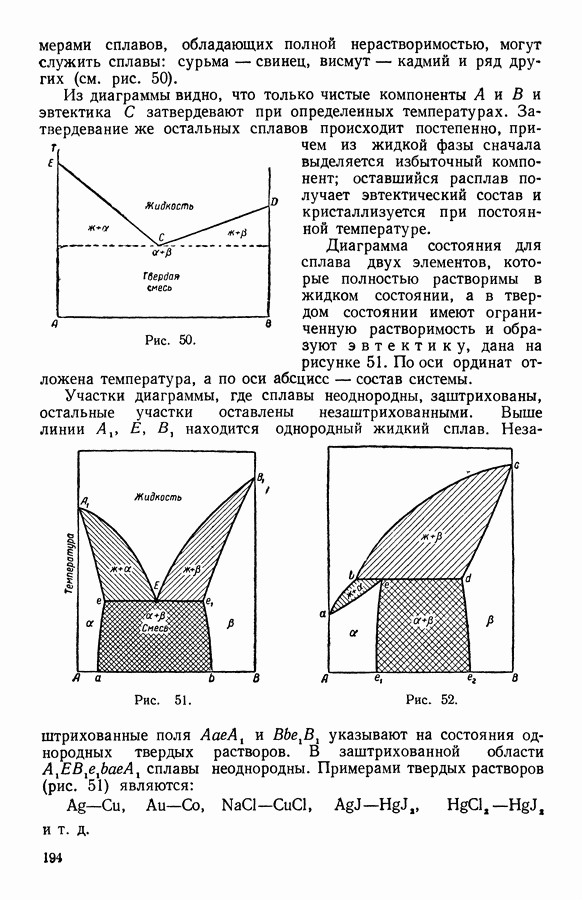
Сравнивая работу при изотермическом обратимом и необратимом процессах [уравнения (15,10) и (34,7)], видим, что работа при необратимом процессе меньше, чем при обратимом.
При изотермическом обратимом процессе работа равна изменению свободной энергии:

и является максимальной.
При постоянных температуре и обобщенной координате уравнение (34,6) принимает вид:

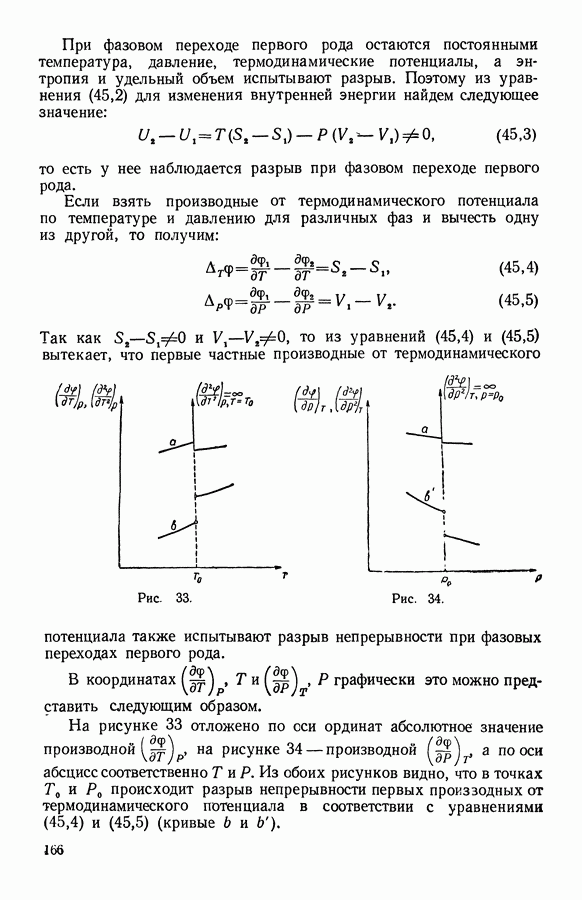
Уравнение (34,9) при необратимом процессе показывает то направление, в котором происходит изменение свободной энергии в системе. Так как член —  всегда отрицателен, то свободная энергия при
всегда отрицателен, то свободная энергия при  может только убывать. При равновесии системы изменение свободной энергии:
может только убывать. При равновесии системы изменение свободной энергии:

а сама свободная энергия принимает минимальное значение

Итак, при необратимом процессе и постоянных Тих свободная энергия характеризует направление происходящего в системе процесса: оно таково, что свободная энергия уменьшается и в условиях равновесия принимает минимальное значение.
Если в рассматриваемой термодинамической системе независимыми параметрами являются температура и обобщенная сила, то характеристической функцией, как показано выше, является термодинамический потенциал. Его вид для необратимого процесса можно получить из уравнения (34,6) путем прибавления к правой и левой частям по 

или

где изменение  выражено через
выражено через 
Когда температура и обобщенная сила постоянны, уравнение (35,2) принимает следующий вид:

Это уравнение показывает направление, по которому происходит изменение термодинамического потенциала в системе при необратимом процессе. Так как член  всегда отрицателен, то термодинамический потенциал при
всегда отрицателен, то термодинамический потенциал при  может только убывать. При равновесии системы
может только убывать. При равновесии системы

а сам термодинамический потенциал принимает минимальное значение:

Следовательно, как свободная энергия, так и термодинамический потенциал определяют направление процесса в системе и полностью характеризуют условие равновесия. Уравнения (33,6), (34,1), (34,5), (34,10) и (35,4) выражают общие условия равновесия в системе.
Выбор того или иного уравнения для изучения равновесия системы зависит от того, какими параметрами характеризуется система.

| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ ПОНЯТИЯ
- 1. Макроскопическая система
- 2. Состояние макроскопической система
- 3. Термодинамический процесс
- 4. Равновесное состояние
- 5. Функция состояния
- 6. Закон сохранения и превращения энергии
- 7. Внутренняя энергия системы
- 8. Количество теплоты
- 9. Температура
- 10. Работа
- 11. Условие полного дифференциала
- ГЛАВА ВТОРАЯ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 1. Внутренняя энергия как функция состояния системы
- 2. Аддитивность внутренней энергии
- 3. Количественная формулировка первого закона для различных термодинамических систем
- 4. Определение теплоемкости
- 5. Применение первого закона термодинамики к некоторым простейшим процессам
- 6. Идеальный газ
- 7. Уравнение Майера для идеального газа
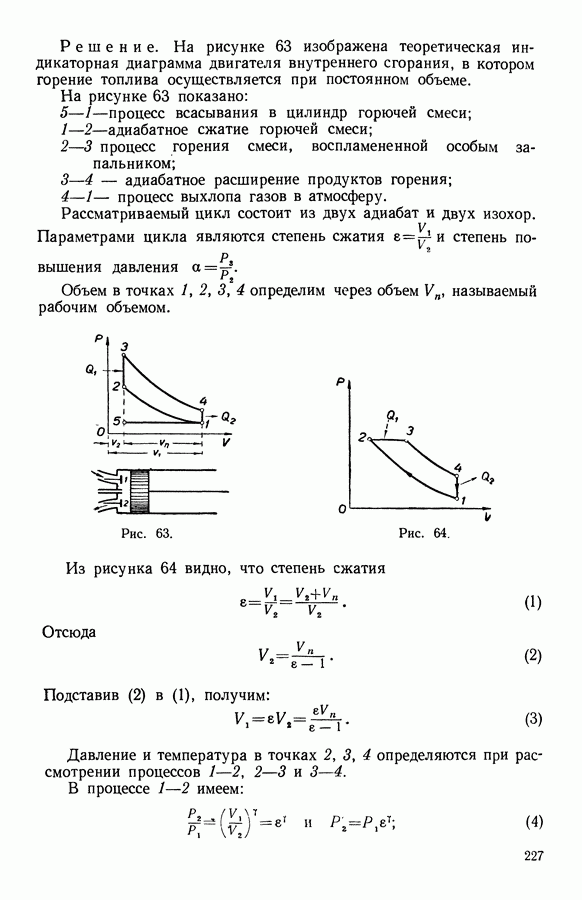
- 8. Адиабатный процесс
- 9. Уравнение адиабаты для идеального газа
- 10. Политропические процессы
- 11. Уравнение адиабаты для общего случая
- 12. Связь между модулями упругости и отношением теплоемкостей …
- 13. Связь отношения теплоемкостей со скоростью звука
- 14. Теплота процесса
- 15. Закон Гесса
- 16. Уравнение Кирхгофа
- ГЛАВА ТРЕТЬЯ. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
- 1. Необратимые процессы
- 2. Равновесные (обратимые) процессы
- 3. Значение равновесных (обратимых) процессов
- 4. Формулировка Клаузиуса
- 5. Формулировка Томсона
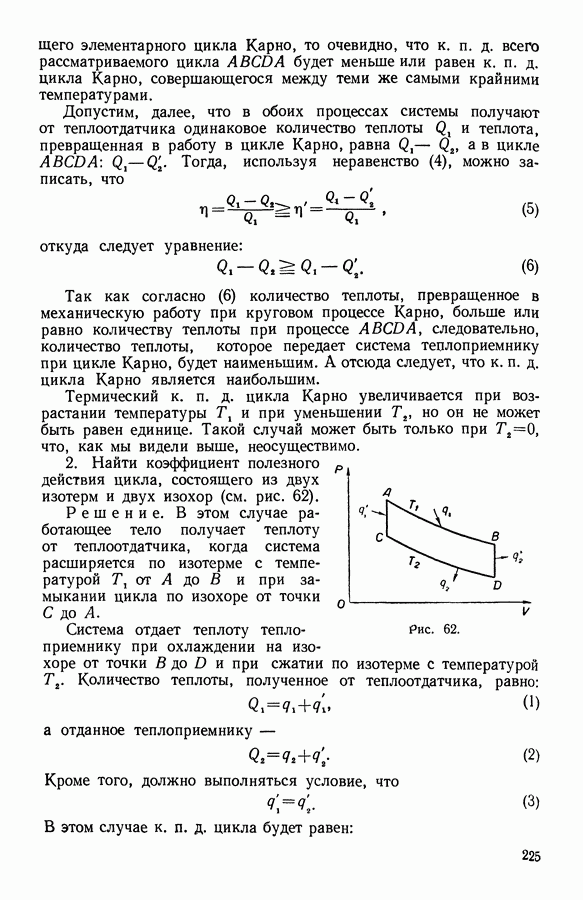
- 6. Циклы
- 7. Обратимый цикл Карно
- 8. Обратимый цикл Карно с идеальным газом
- 9. Эквивалентность формулировок Клаузиуса и Томсона
- 10. Теорема Карно
- 11. Количественная формулировка второго закона
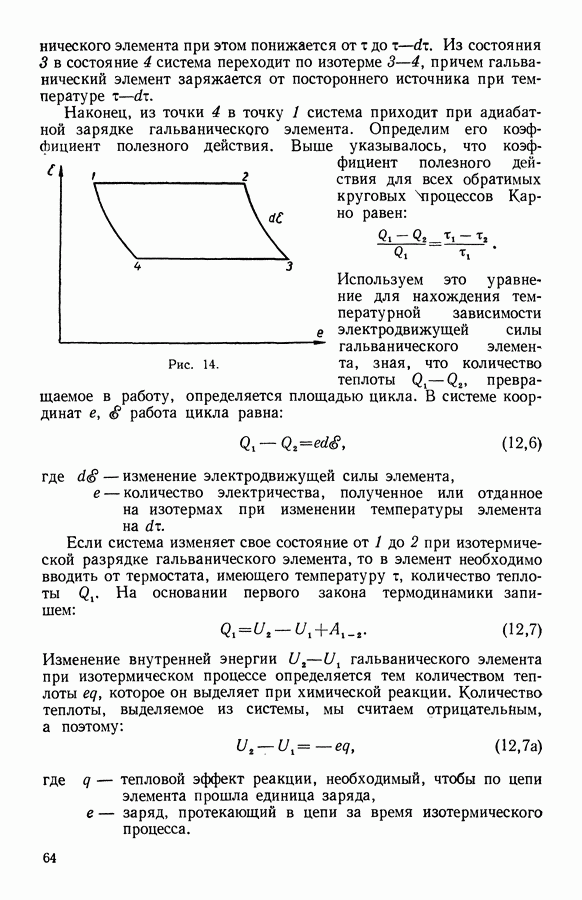
- 12. Зависимость электродвижущей силы гальванического элемента от температуры
- 13. Температурная шкала
- 14. Разнообразие шкал
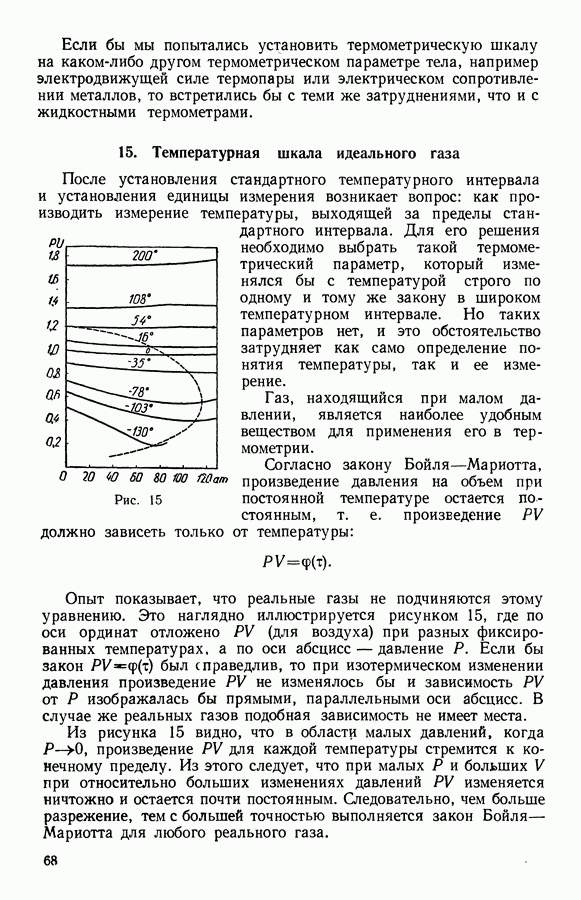
- 15. Температурная шкала идеального газа
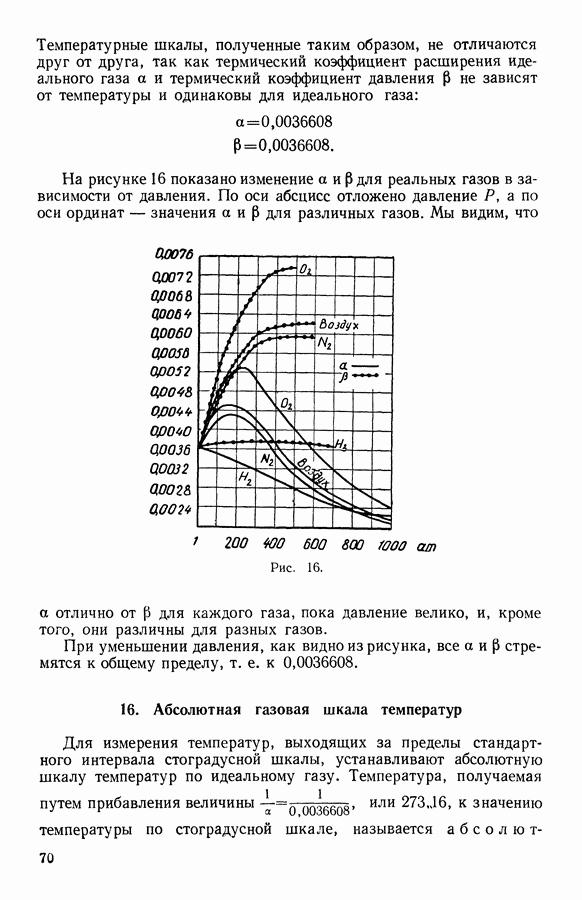
- 16. Абсолютная газовая шкала температур
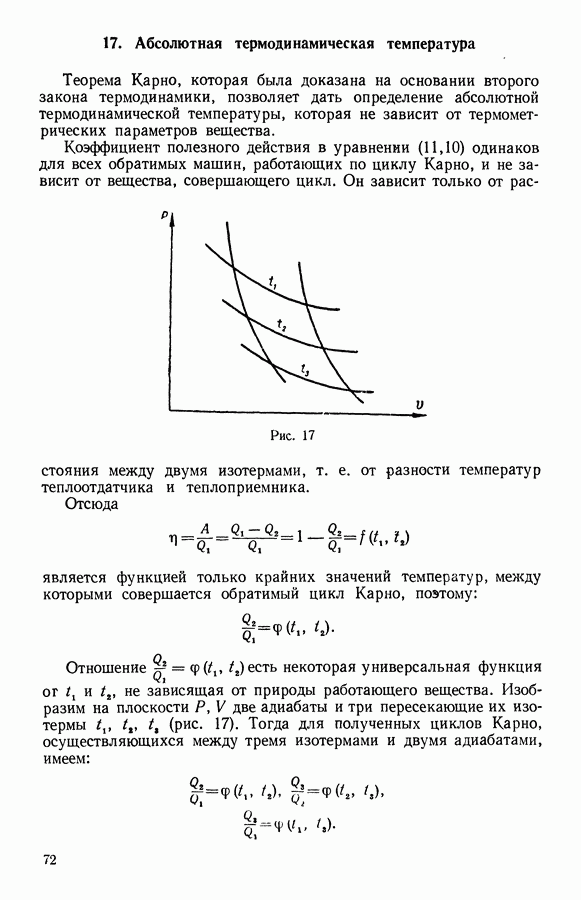
- 17. Абсолютная термодинамическая температура
- 18. Тождество шкалы идеального газа и газа, подчиняющегося уравнению Ван-дер-Ваальса, с термодинамической шкалой
- 19. Обобщение количественной формулировки второго закона термодинамики
- 20. Свойства энтропии
- 21. Аксиоматика второго закона термодинамики для равновесных (обратимых) процессов
- 22. Статистический характер второго закона термодинамики
- ГЛАВА ЧЕТВЕРТАЯ. ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ
- 2. Внутренняя энергия
- 3. Энтальпия
- 4. Свободная энергия
- 5. Термодинамический потенциал
- ГЛАВА ПЯТАЯ. РЕШЕНИЕ КОНКРЕТНЫХ ЗАДАЧ С ПОМОЩЬЮ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ
- 1. Вычисление энтропии при изменении агрегатного состояния при изотермическом процессе
- 2. Уравнение Клапейрона — Клаузиуса
- 3. Зависимость поверхностного натяжения от температуры
- 4. Энтропия как функция Т и x
- 5. Энтропия как функция T и Y
- 6. Энтропия как функция x и Y
- 7. Вычисление Cy-Cx
- 8. Связь теплоемкостей со скоростью звука
- 9. Зависимость Cv от объема
- 10. Зависимость Ср от давления
- 11. Изменение температуры в адиабатных системах
- 12. Уравнение адиабаты для газа, подчиняющегося уравнению Ван-дер-Ваальса
- 13. Уравнение Гиббса — Гельмгольца
- 14. Уравнение максимальной работы
- 15. Поверхностная энергия чистой жидкости
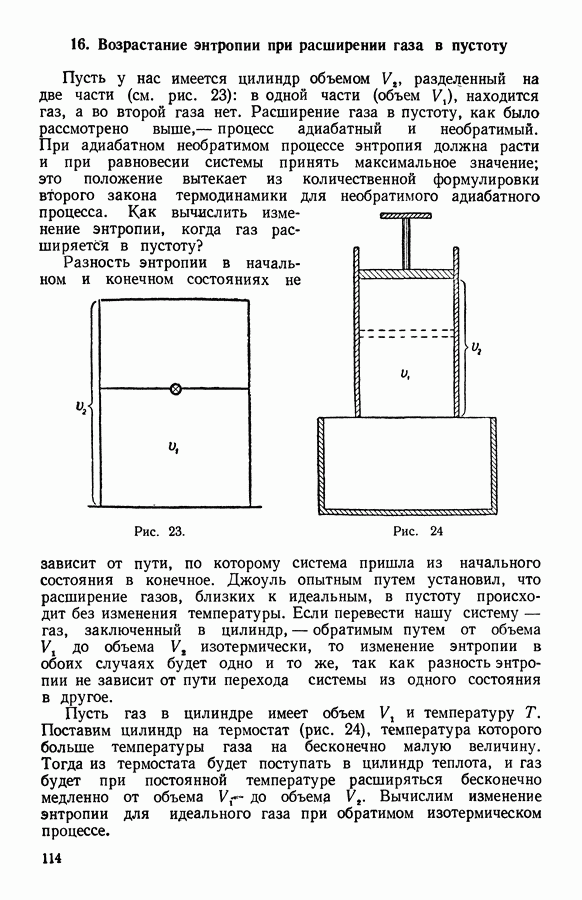
- 16. Возрастание энтропии при расширении газа в пустоту
- 17. Явление Джоуля — Томсона (дроссельный эффект)
- 18. Изотермическое дросселирование
- 19. Методы определения дифференциального и интегрального адиабатного дроссельного эффекта
- 20. Задачи
- ГЛАВА ШЕСТАЯ. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ
- 1. Тепловое излучение
- 2. Закон Кирхгофа
- 3. Световое давление
- 4. Закон Стефана — Больцмана
- 5. Формула и закон смещения Вина
- ГЛАВА СЕДЬМАЯ. ТЕРМОДИНАМИЧЕСКОЕ УЧЕНИЕ О РАВНОВЕСИИ
- 2. Гетерогенная и гомогенная системы
- 3. Компоненты
- 4. Необратимые процессы и общие условия равновесия
- 5. Химический потенциал
- 6. Идеальные газовые смеси
- 7. Свободная энергия системы идеальных газов до смешения
- 8. Свободная энергия идеальных газов после смешения
- 9. Химический потенциал компонента идеального газа
- 10. Термодинамический вывод закона действующих масс
- 11. Термодинамический вывод уравнения работы химической реакции
- 12. Зависимость константы равновесия от температуры
- 13. Зависимость константы равновесия Ky от давления
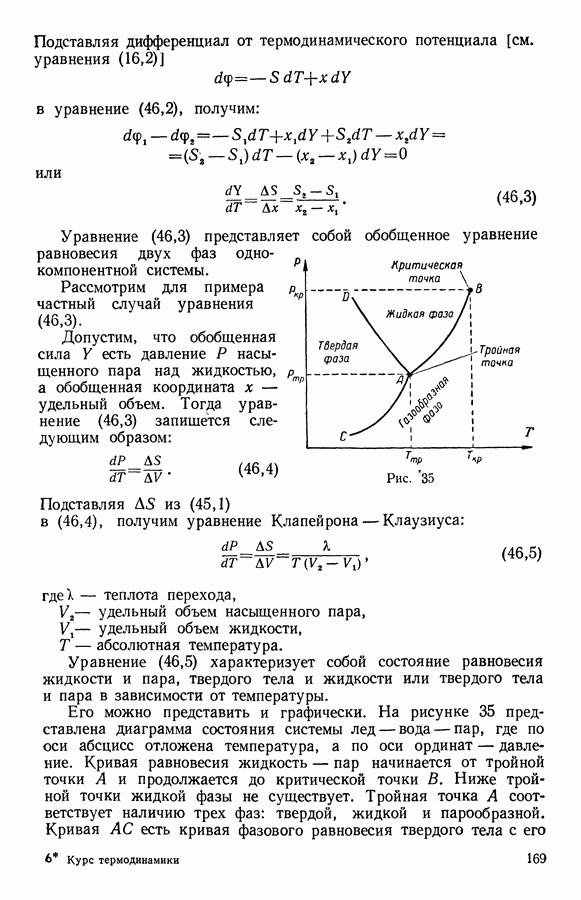
- 14. Условие равновесия в гетерогенной системе
- 14. Правило фаз
- ГЛАВА ВОСЬМАЯ. ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
- 1. Фазовые превращения в однокомпонентных системах
- 2. Фазовые превращения первого рода
- 3. Общее уравнение равновесия двух фаз однокомпонентной системы
- 4. Фазовые превращения второго рода
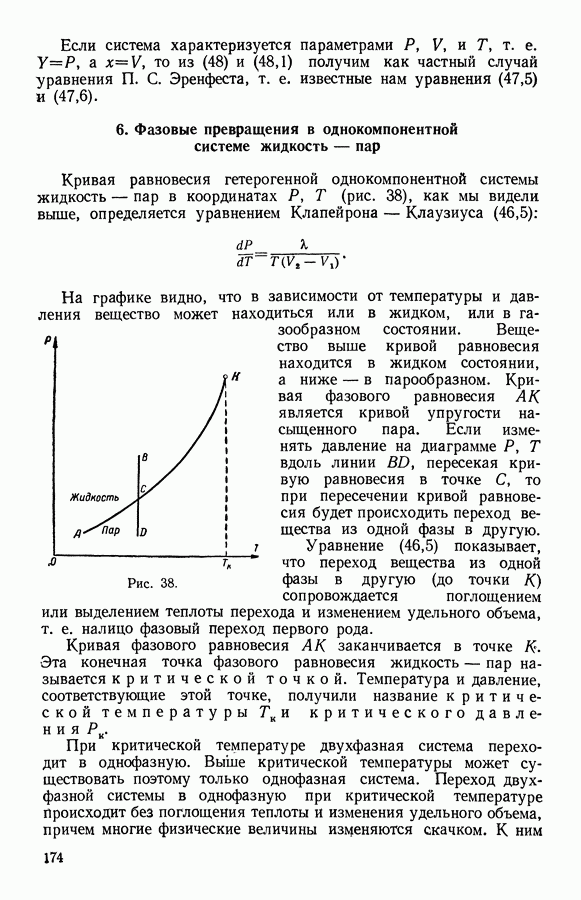
- 5. Термодинамическая теория фазовых превращений второго рода
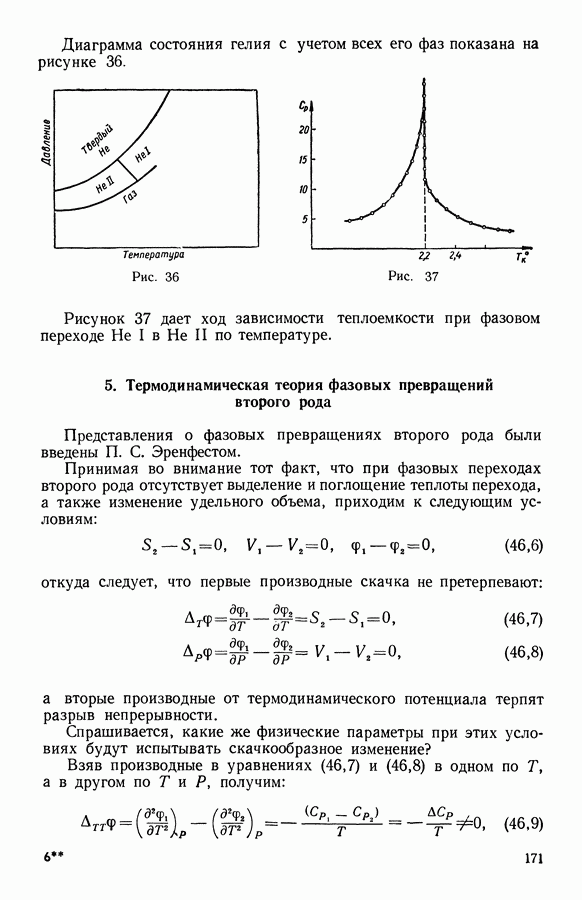
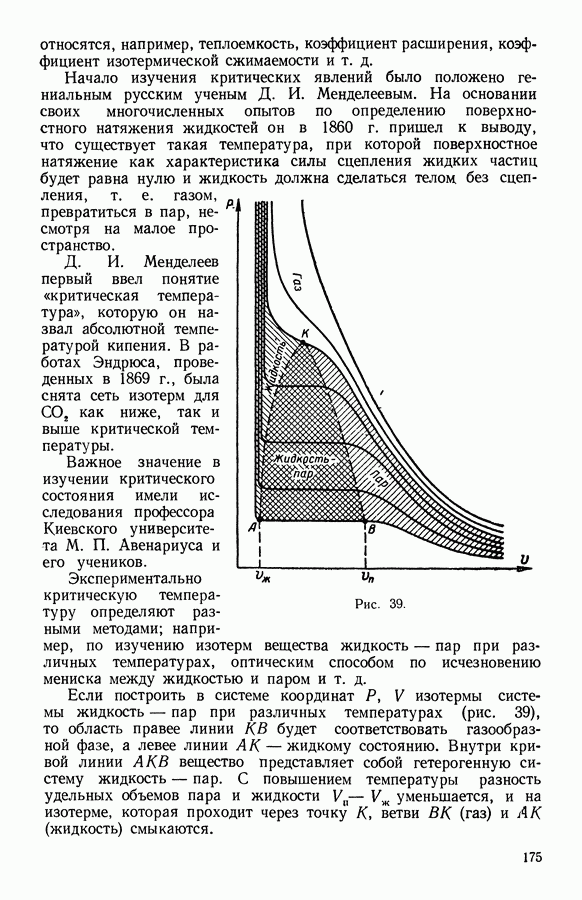
- 6. Фазовые превращения в однокомпонентной системе жидкость — пар
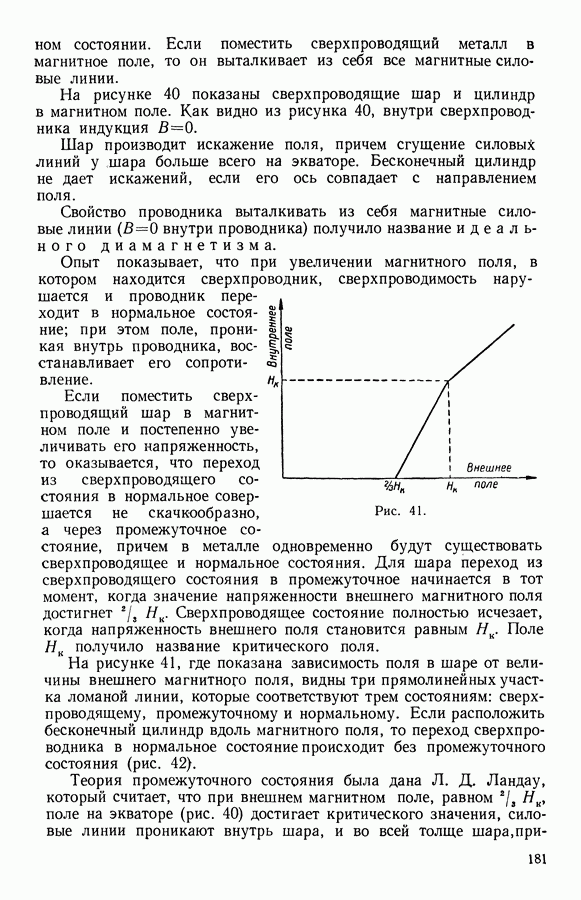
- 7. Термодинамическое условие равновесия системы жидкость — пар в критическом состоянии
- 8. Определение … из уравнения Ван-дер-Ваальса
- 9. Сверхпроводящее состояние металлов
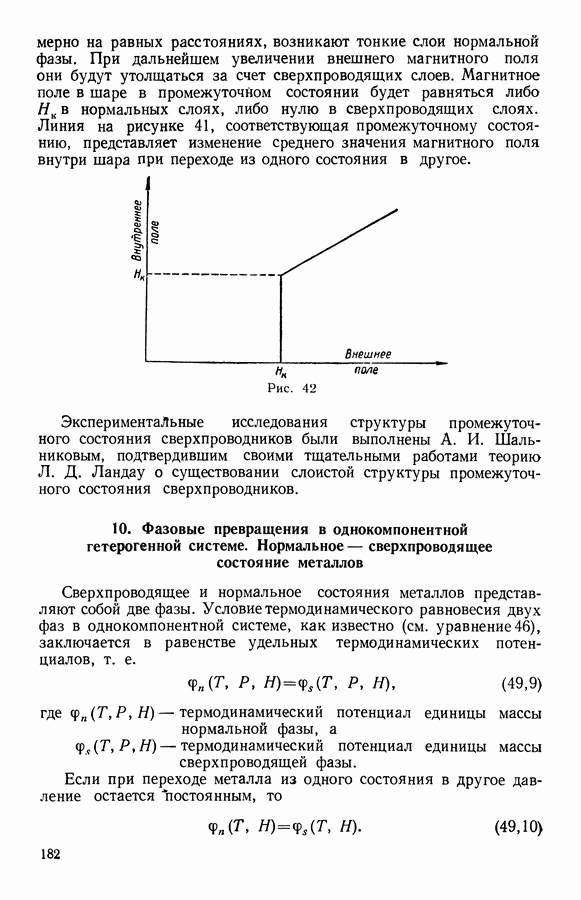
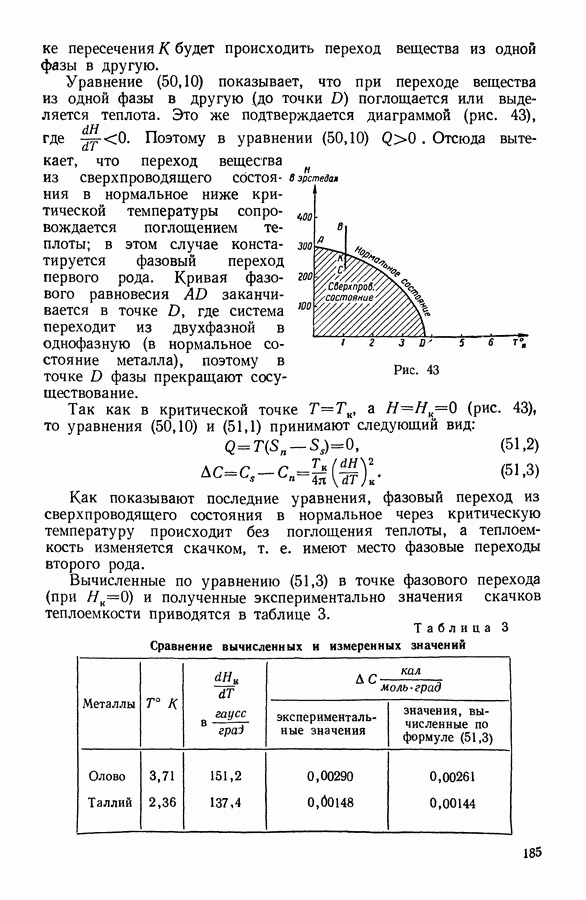
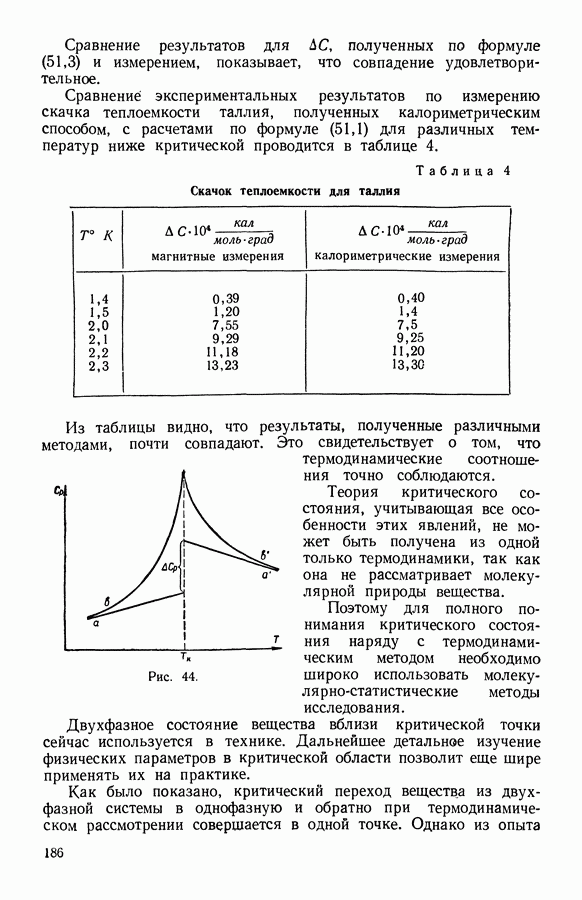
- 10. Фазовые превращения в однокомпонентной гетерогенной системе. Нормальное — сверхпроводящее состояние металлов
- 11. Бинарные системы
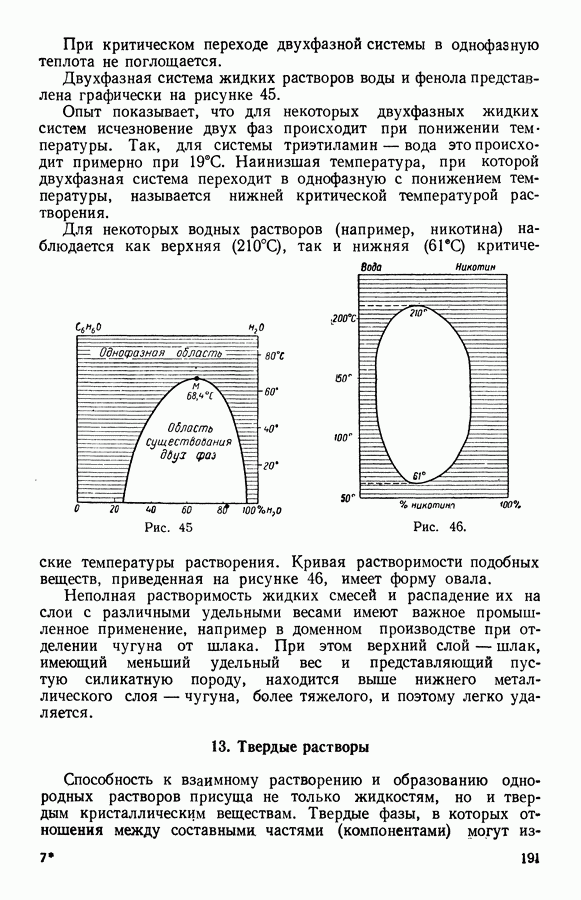
- 12. О взаимной растворимости жидкостей
- 13. Твердые растворы
- 14. Уравнение Ван-дер-Ваальса для бинарных смесей
- 15. Разбавленные растворы
- 16. Растворимость газа в жидкости
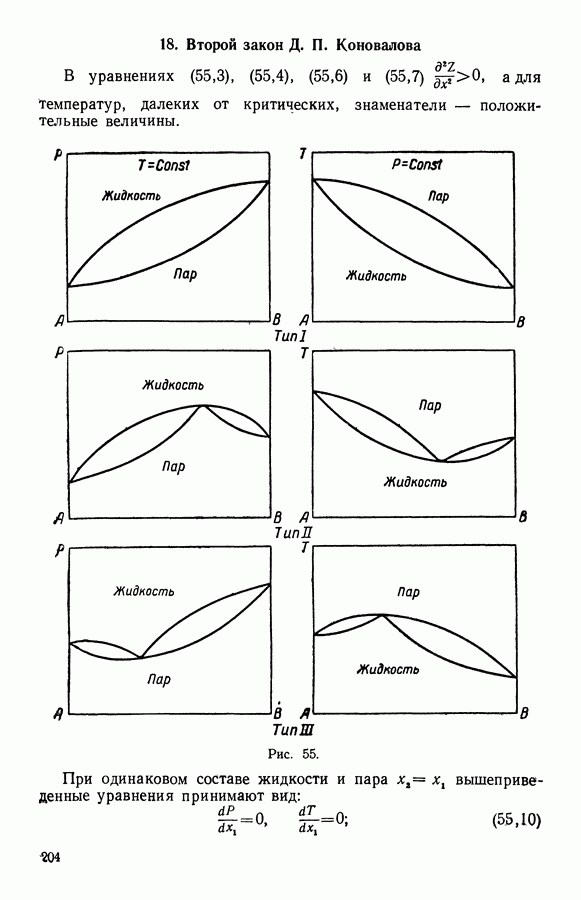
- 17. Первый закон Д. П. Коновалова
- 18. Второй закон Д. П. Коновалова
- 19. Температура кипения раствора и дистилляция двойных смесей
- ГЛАВА ДЕВЯТАЯ. НИЗКИЕ ТЕМПЕРАТУРЫ
- 1. Получение низких температур, их значение для техники и научных исследований
- 2. Каскадный метод
- 3. Метод дросселирования
- 4. Получение низких температур при расширении сжатого газа с отдачей внешней работы
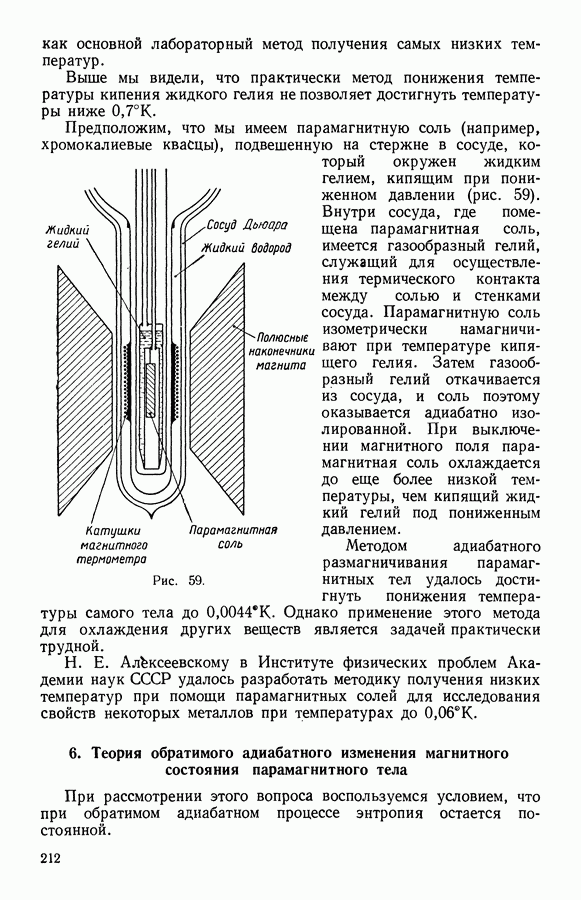
- 5. Охлаждение методом адиабатного размагничивания
- 6. Теория обратимого адиабатного изменения магнитного состояния парамагнитного тела
- 7. Тепловая теорема Нернста
- 8. О третьем законе термодинамики
- 9. Свойства вещества вблизи абсолютного нуля
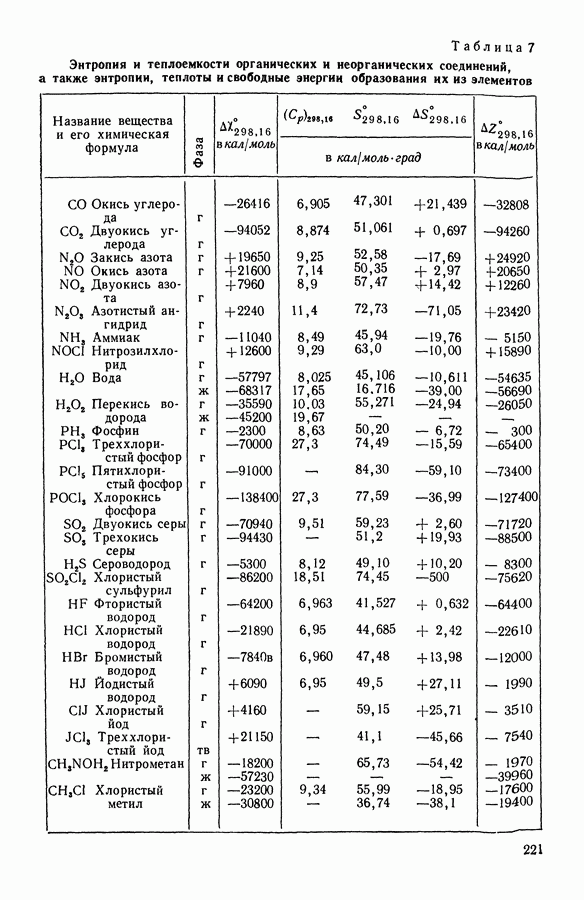
- 10. Стандартные таблицы термодинамических функций
- 11. Вычисление стандартных величин при изменении температуры
- 12. Вычисление стандартных величин при изменении давления
- 13. Применение стандартных таблиц
- 14. Вычисление стандартных величин
- 15. Задачи для всех разделов курса