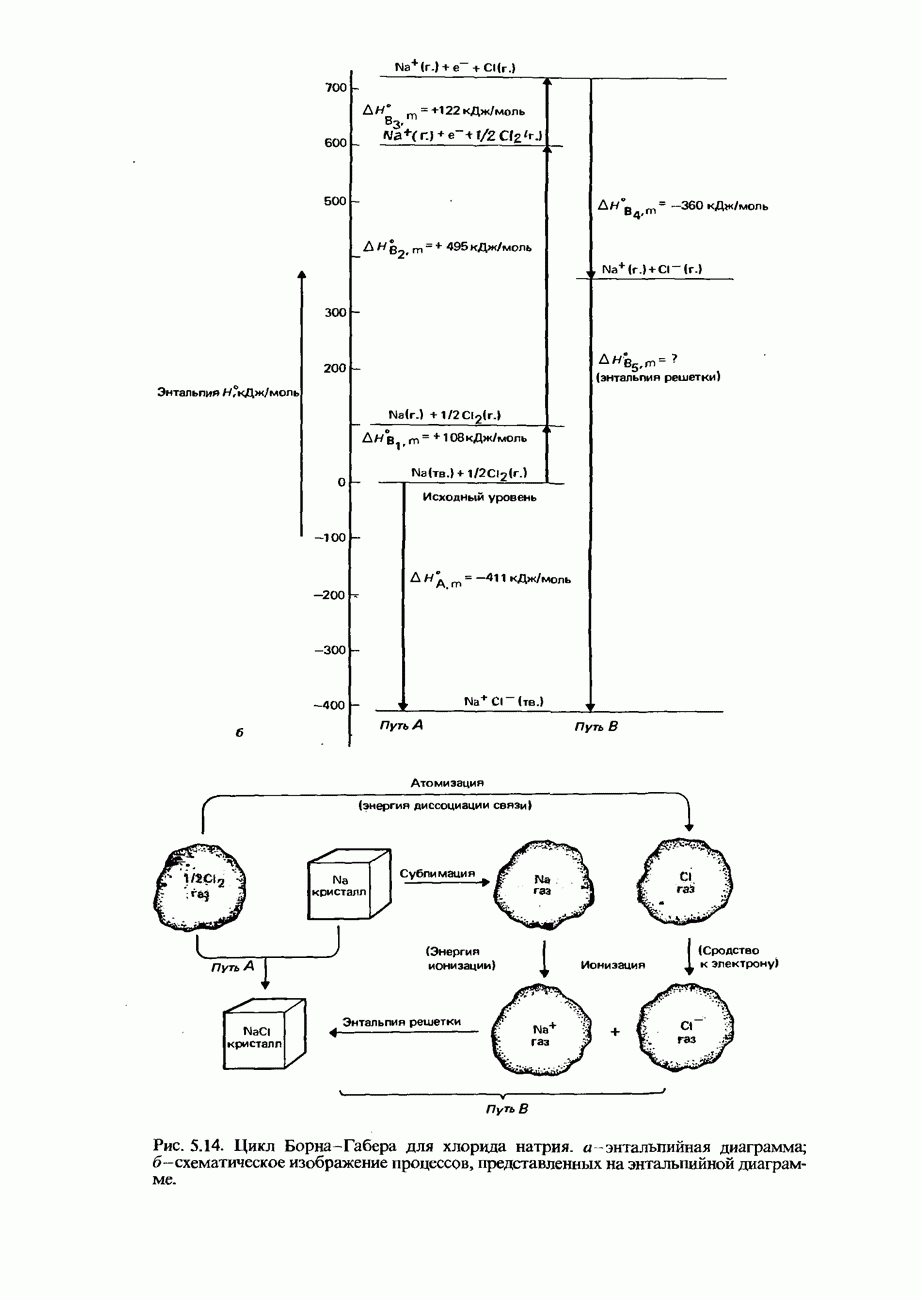
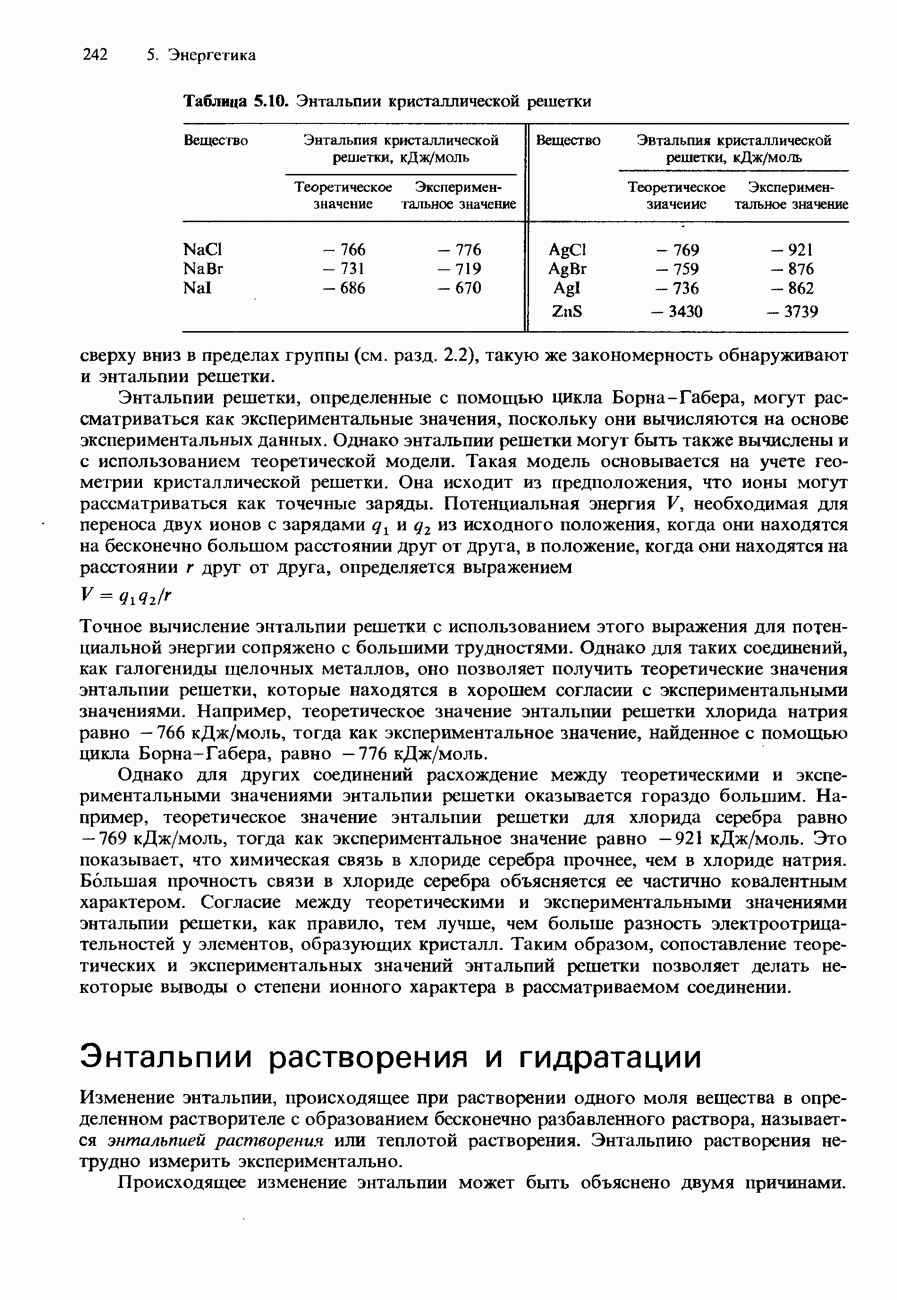
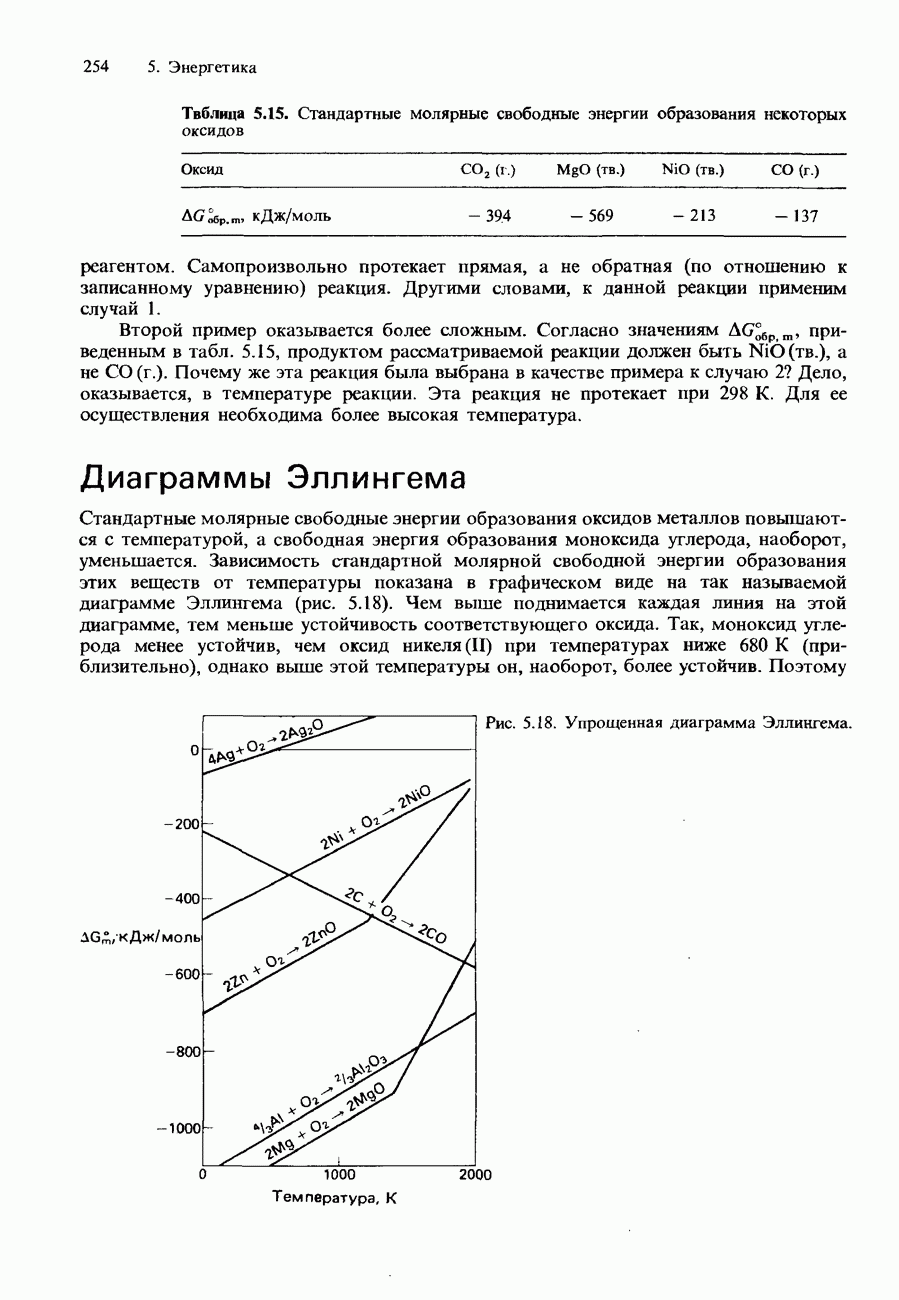
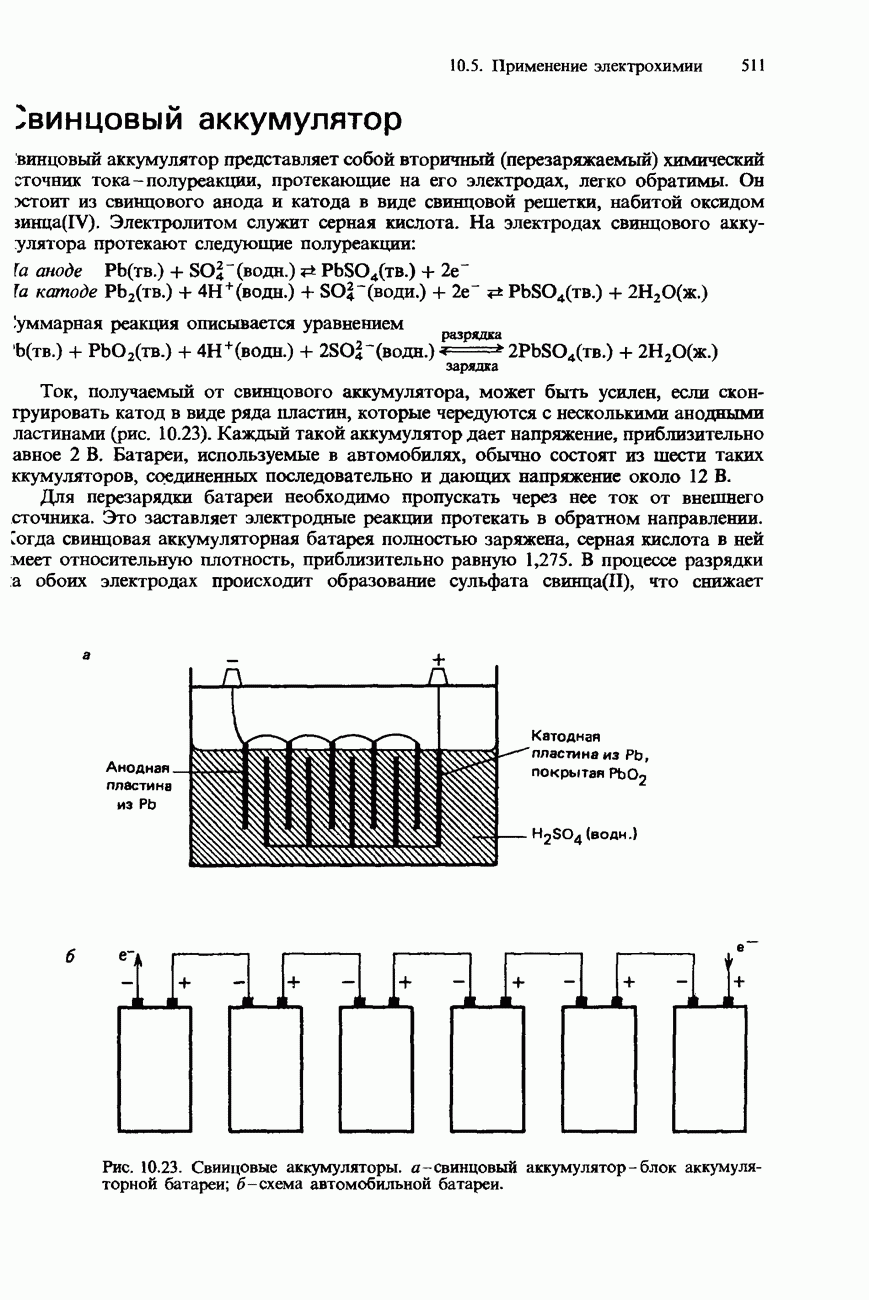
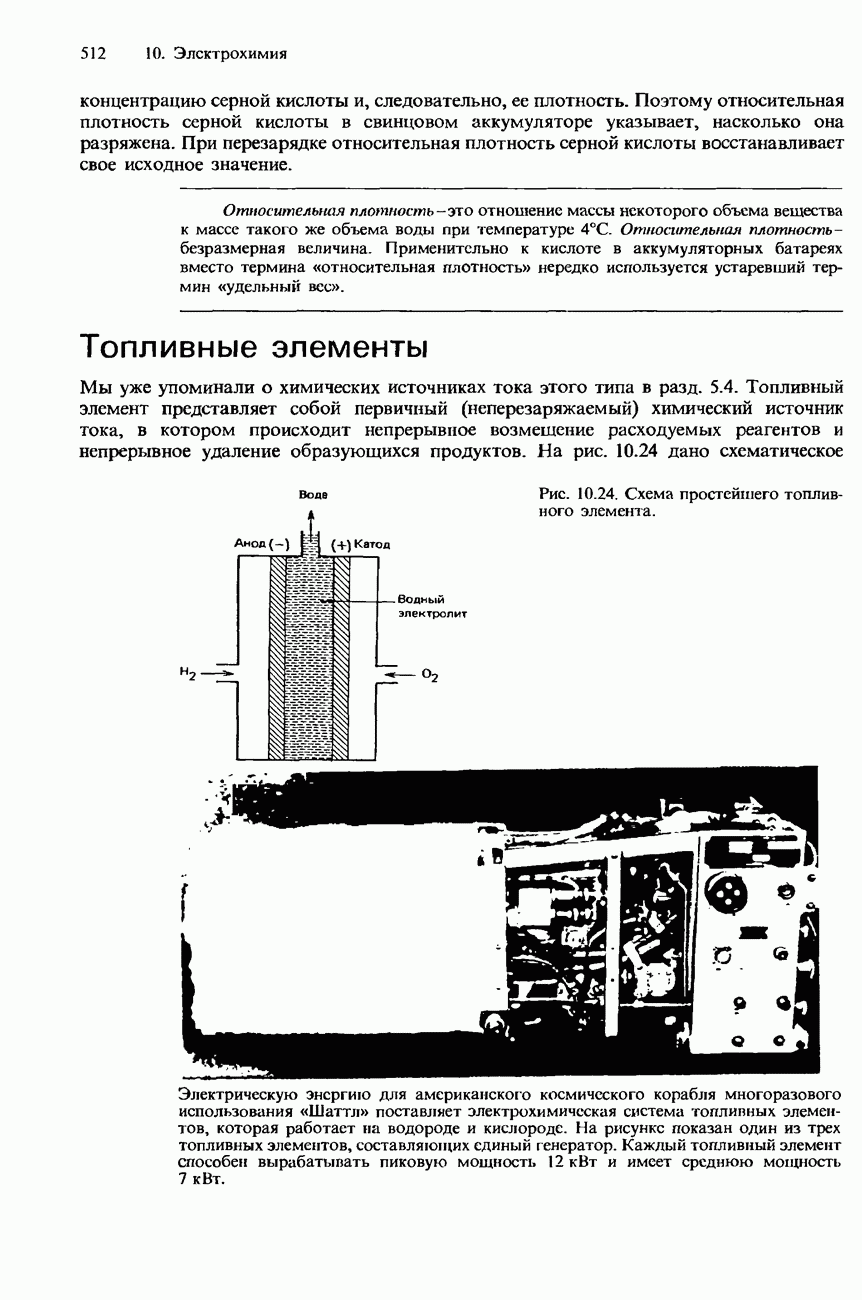
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
СВОБОДНАЯ ЭНЕРГИЯ ГИББСА
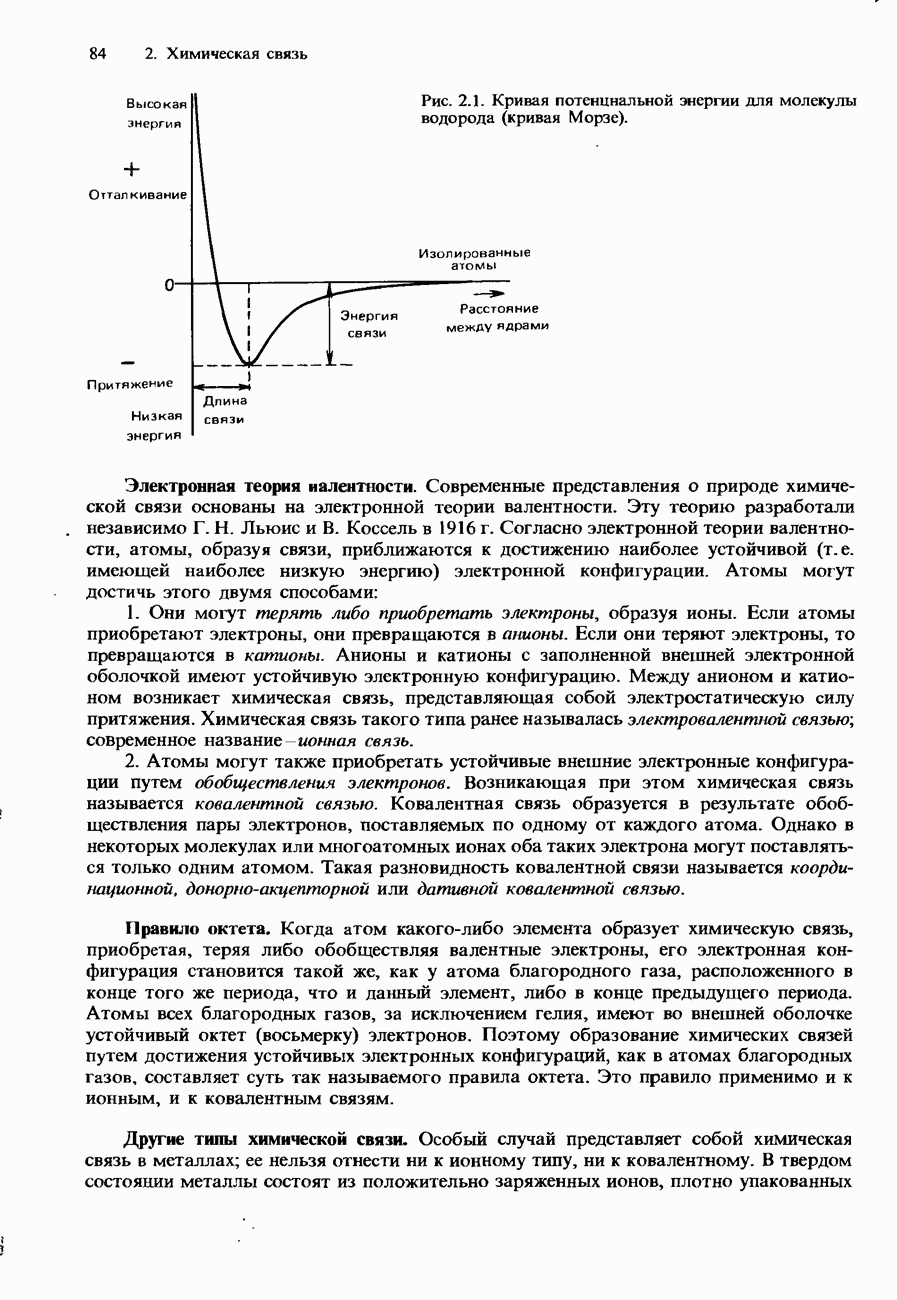
Согласно сказанному выше, для того чтобы судить о возможности самопроизвольного протекания реакции, следует учитывать два фактора-энергию и энтропию.
1. Энергия. Все материальные системы обнаруживают тенденцию к достижению минимума своей потенциальной энергии. Например, если поместить мяч на вершине холма, он будет скатываться вниз. Мяч теряет потенциальную энергию до тех пор, пока она не достигнет минимума у подножия холма. В химических системах при протекании реакции в условиях постоянного давления изменение энергии определяется изменением энтальпии. В экзотермических реакциях система теряет энергию до тех пор, пока полная энтальпия системы не достигнет минимума.
2. Энтропия. Все материальные системы обнаруживают тенденцию к достижению максимального беспорядка. Если обратиться к приведенному выше примеру с горением метана, то мы убедимся, что изменение энтальпии намного превышает изменение энтропии. Таким образом, движущей силой рассматриваемой реакции является изменение энтальпии. Однако в эндотермических реакциях преобладающую роль играет изменение энтропии. Эти реакции протекают самопроизвольно, несмотря на то что система поглощает энергию.
Каким же образом следует сбалансировать между собой оба указанных выше фактора, т. е. учесть одновременно действие каждого из них? Это позволяет сделать особая термодинамическая функция состояния, которая называется свободной энергией или функцией Гиббса и обозначается буквой G. Функция Гиббса определяется с помощью уравнения (21), которое в более общем виде записывается так:

Если умножить последнее уравнение на —Т, получится

Член  определяет изменение свободной энергии реакционной системы:
определяет изменение свободной энергии реакционной системы:

Это определение позволяет записать уравнение (22) в виде

где  относятся к реакционной системе.
относятся к реакционной системе.
Таким образом, изменение свободной энергии Гиббса учитывает изменение энтальпии и изменение энтропии реакционной системы. Отметим, что энтропийный член включает в качестве множителя абсолютную температуру. Этот множитель позволяет учесть, что при высоких температурах материальные системы более разупорядочены, чем при низких температурах.
Из второго закона термодинамики следует, что для самопроизвольного протекания реакции требуется, чтобы полное изменение энтальпии в реакционной системе и ее окружении  было положительным. Поскольку абсолютная температура всегда принимает только положительные значения, из уравнения (23) следует, что для самопроизвольной реакции изменение свободной энергии
было положительным. Поскольку абсолютная температура всегда принимает только положительные значения, из уравнения (23) следует, что для самопроизвольной реакции изменение свободной энергии  должно иметь отрицательное значение
должно иметь отрицательное значение  . Другими словами, если самопроизвольная реакция протекает при постоянной температуре и постоянном давлении, свободная энергия системы должна уменьшаться.
. Другими словами, если самопроизвольная реакция протекает при постоянной температуре и постоянном давлении, свободная энергия системы должна уменьшаться.
Стандартной молярной свободной энергией образования называется изменение свободной энергии Гиббса, которым сопровождается образование одного моля вещества из входящих в него элементов в их стандартных состояниях. Свободная энергия Гиббса измеряется в тех же единицах, что и обычная энергия; размерность молярной свободной энергии: кДж/моль.
В табл. 5.13 указаны стандартные молярные свободные энергии образования некоторых соединений. Обращает на себя внимание тот факт, что свободные энергии образования для твердых веществ имеют намного большие значения, чем для газов. Ранее в этой главе отмечалось, что энтальпия образования является мерой устойчивости соединения. Однако об устойчивости соединения гораздо правильнее судить по его свободной энергии образования. Она характеризует работу, которую необходимо выполнять, чтобы возвратить входящие в соединение элементы в их стандартные состояния. И, подобно энтальпиям образования, стандартные свободные энергии образования элементов в их стандартном состоянии равны нулю.
Стандартное изменение свободной энергии для химической реакции, или короче, стандартную свободную энергию реакции, можно вычислить двумя способами. Во-первых, ее можно вычислить по свободным энергиям образования продуктов и реагентов с
Таблвца 5.13. Стандартные молярные свободные энергии образования

помощью следующего уравнения:

Во-вторых, ее можно вычислить по стандартным изменениям молярных энтальпии и энтропии для рассматриваемой реакции с помощью уравнения (24).
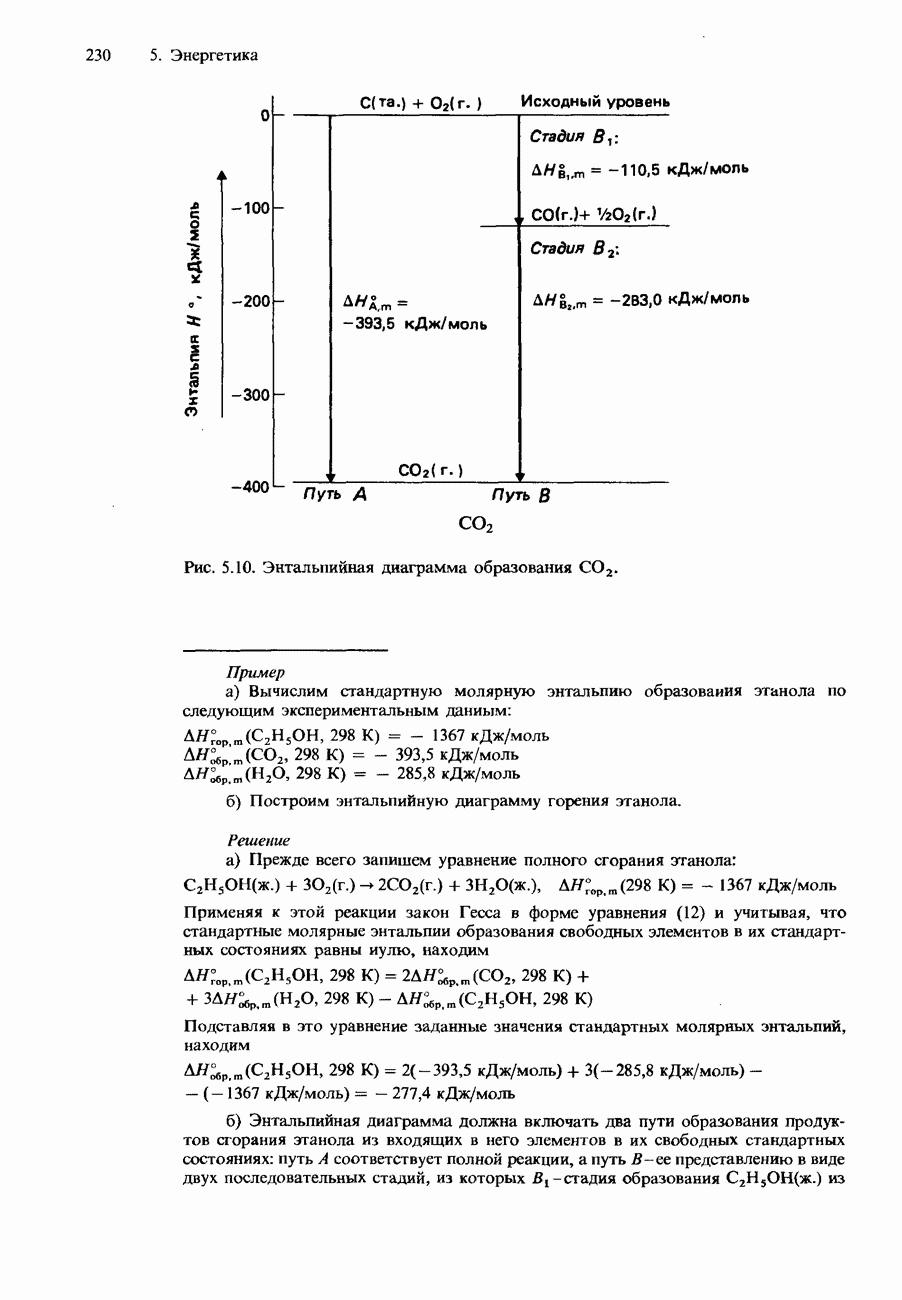
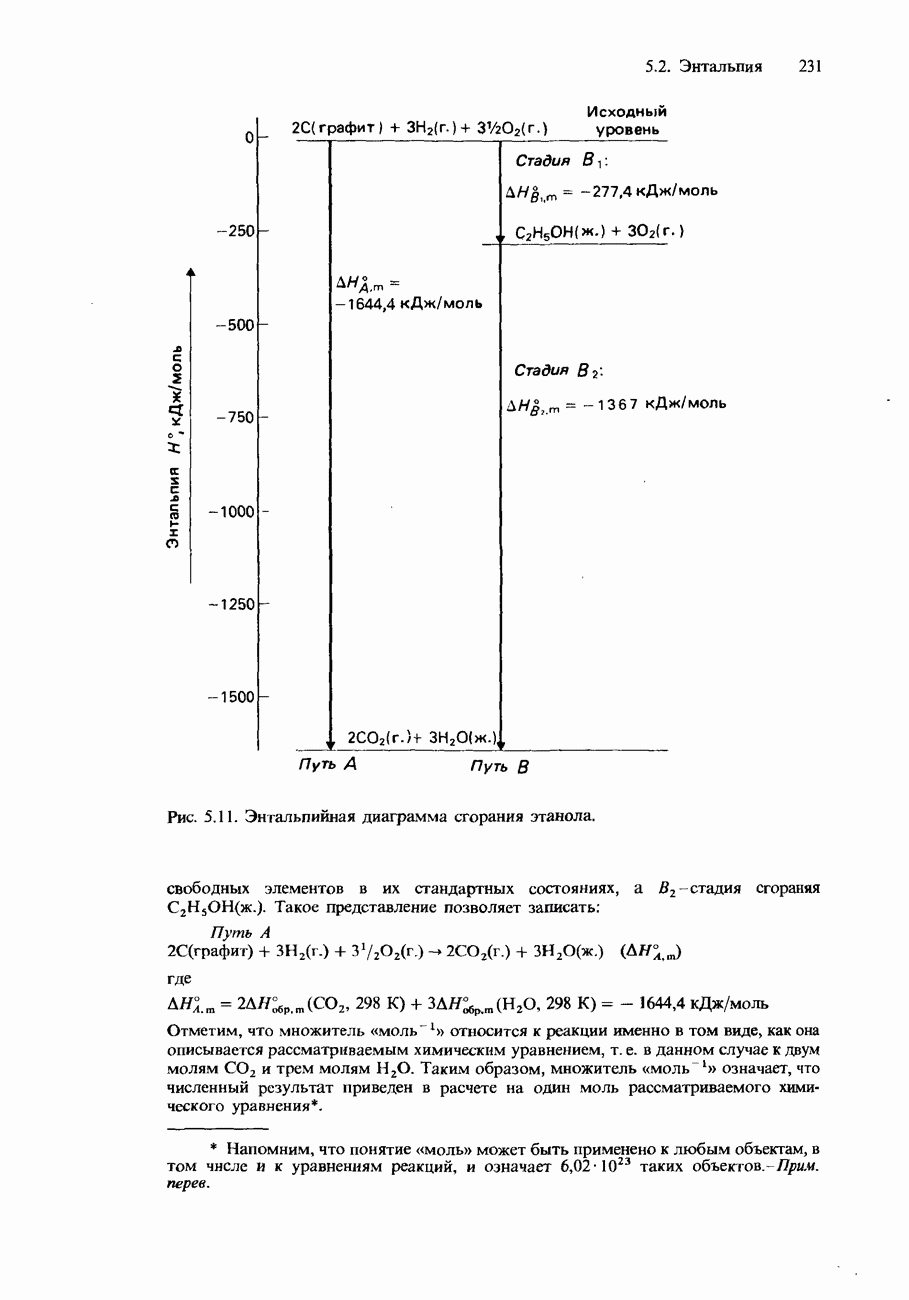
Пример
а) Вычислим стандартное изменение свободной энергии Гиббса при 25°С для реакции термического разложения карбоната кальция, если известно, что для этой реакции  .
.
б) Может ли протекать самопроизвольно эта реакция при 25°С?
в) При какой температуре становится возможным самопроизвольное протекание этой реакции, если предположить, что значения  не зависят от температуры?
не зависят от температуры?
Решение
Стехиометрическое уравнение рассматриваемой реакции имеет вид

а) Для вычисления  воспользуемся уравнением (24). Получим
воспользуемся уравнением (24). Получим

б) Поскольку при 25°С (298 К) величина  имеет положительное значение, реакция не должна протекать самопроизвольно при этой температуре,
имеет положительное значение, реакция не должна протекать самопроизвольно при этой температуре,
в) Реакция может протекать самопроизвольно при условии, что

Последнее неравенство можно преобразовать к виду

В рассматриваемом случае температура, начиная с которой становится возможным самопроизвольное протекание реакции, определяется неравенством

Таким образом, реакция будет протекать самопроизвольно при температурах выше 1106 К.
В табл. 5.14 указаны стандартные свободные энергии Гиббса для четырех реакций. Реакции (а), (б) и  являются самопроизвольными, поскольку характеризуются отрицательными значениями
являются самопроизвольными, поскольку характеризуются отрицательными значениями  . Реакция (в) не может протекать самопроизвольно, поскольку она характеризуется положительным значением
. Реакция (в) не может протекать самопроизвольно, поскольку она характеризуется положительным значением 
Таблица 5.14. Стандартные свободные энергии некоторых реакций (кДж/моль)

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ ПЕРЕВОДЧИКА
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ
- 1. СТРОЕНИЕ АТОМА
- 1.1. Субатомные частицы
- Модели атома
- Новые элементарные частицы
- МАССА АТОМА
- МАСС-СПЕКТРОМЕТРИЯ
- 1.2 Электронное строение атомов
- Связь между спектральными линиями и электронами (открытие Бора)
- Применение возбуждения электронов на практике
- Атомный спектр испускания водорода
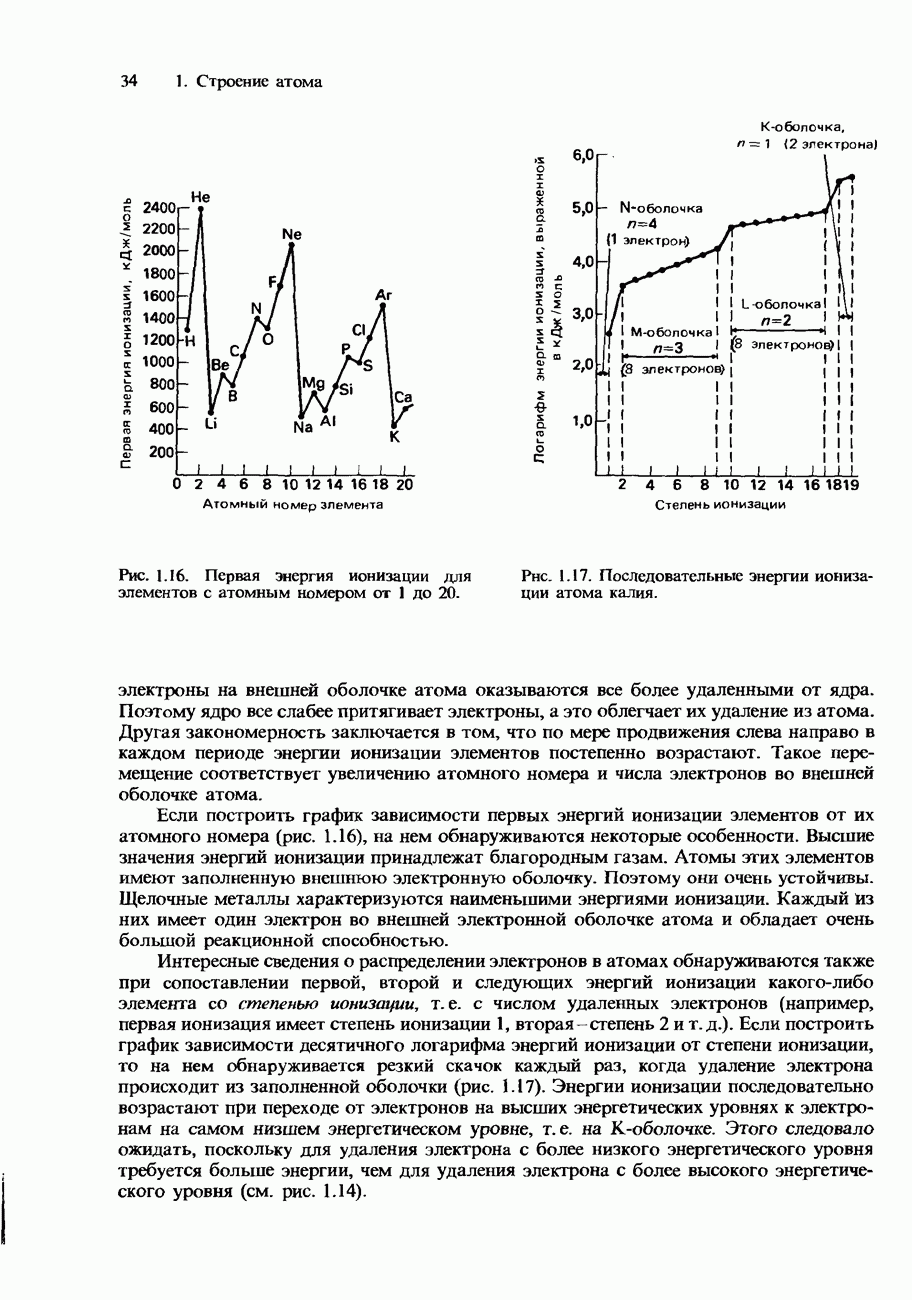
- ЭНЕРГИИ ИОНИЗАЦИИ
- Рассмотрение энергий ионизации в рамках модели атома, предложенной Бором
- ВОЛНОВАЯ ПРИРОДА ЭЛЕКТРОНА
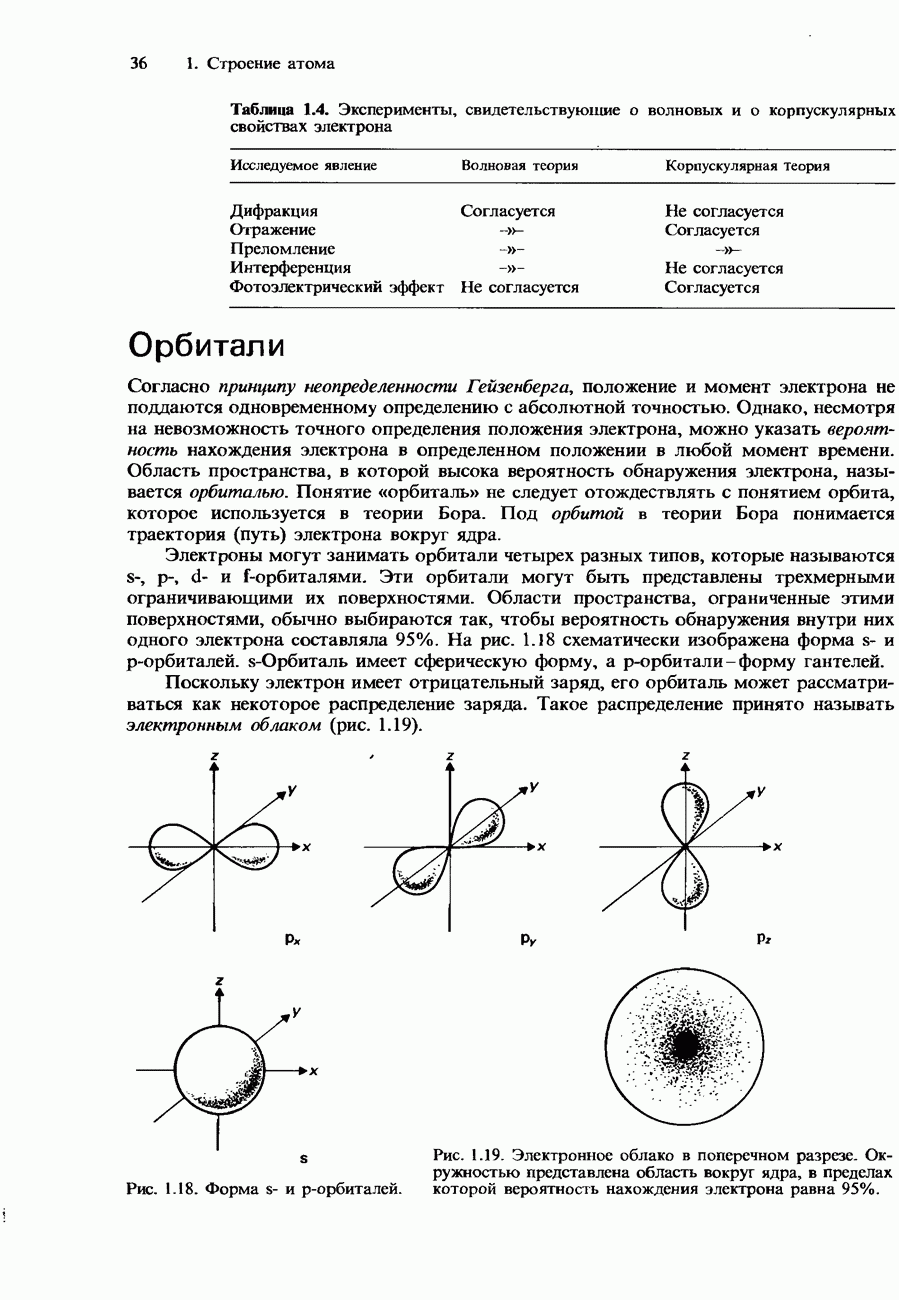
- Орбитали
- КВАНТОВЫЕ ЧИСЛА
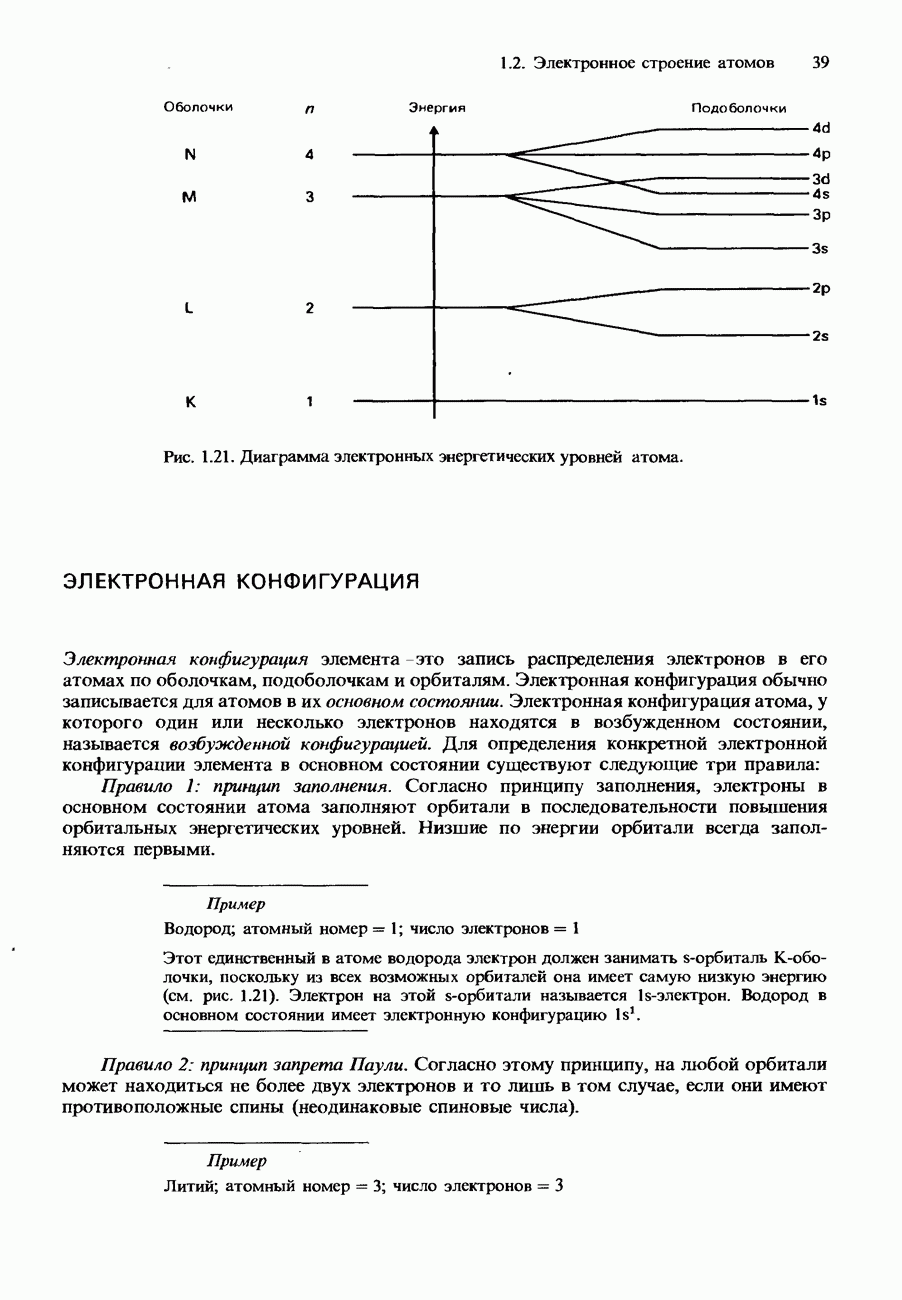
- ЭЛЕКТРОННАЯ КОНФИГУРАЦИЯ
- 1.3 Радиоактивность
- ИОНИЗИРУЮЩЕЕ ИЗЛУЧЕНИЕ
- Обнаружение и измерение радиоактивности
- УСТОЙЧИВЫЕ И НЕУСТОЙЧИВЫЕ ИЗОТОПЫ
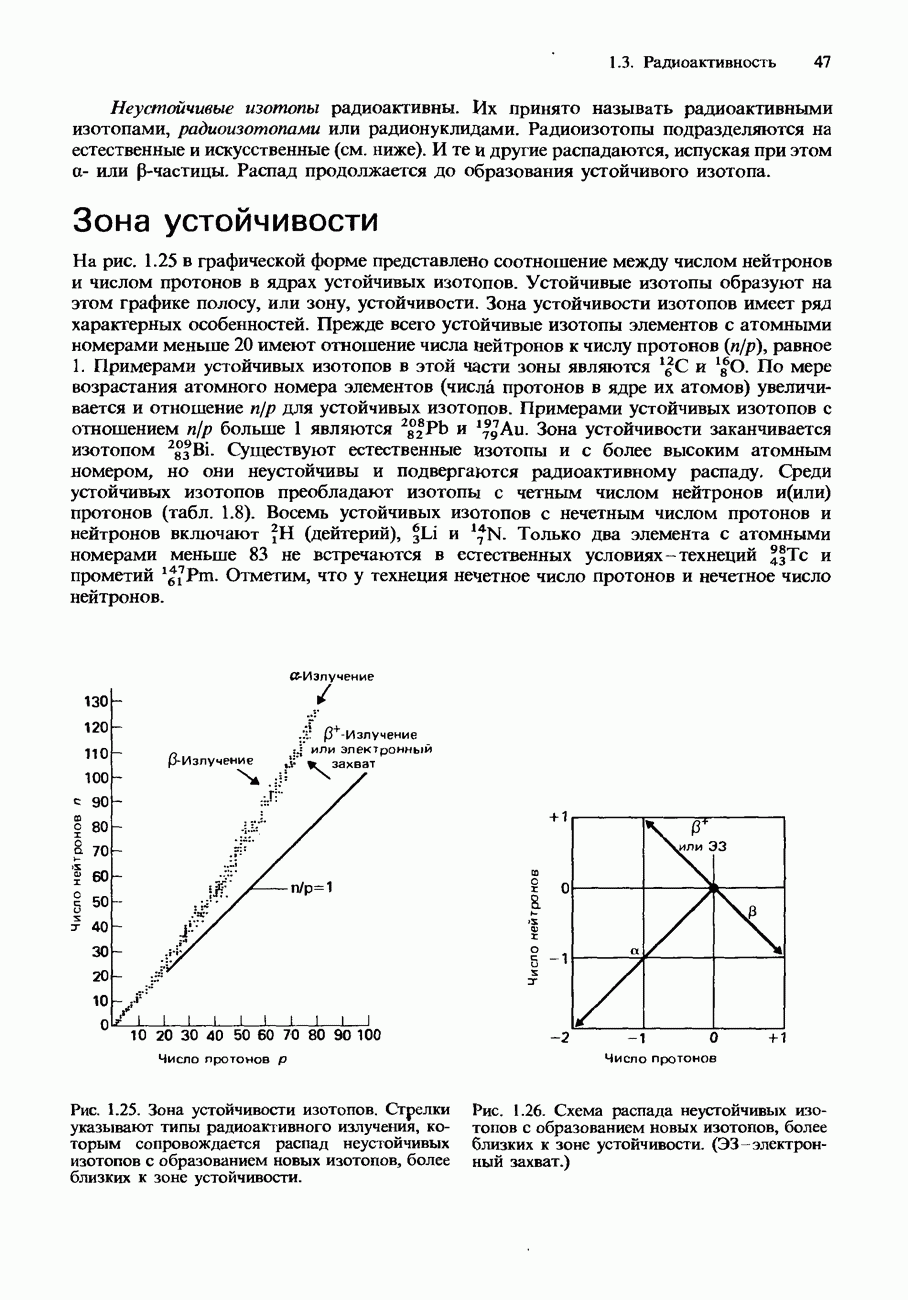
- Зона устойчивости
- Период полураспада
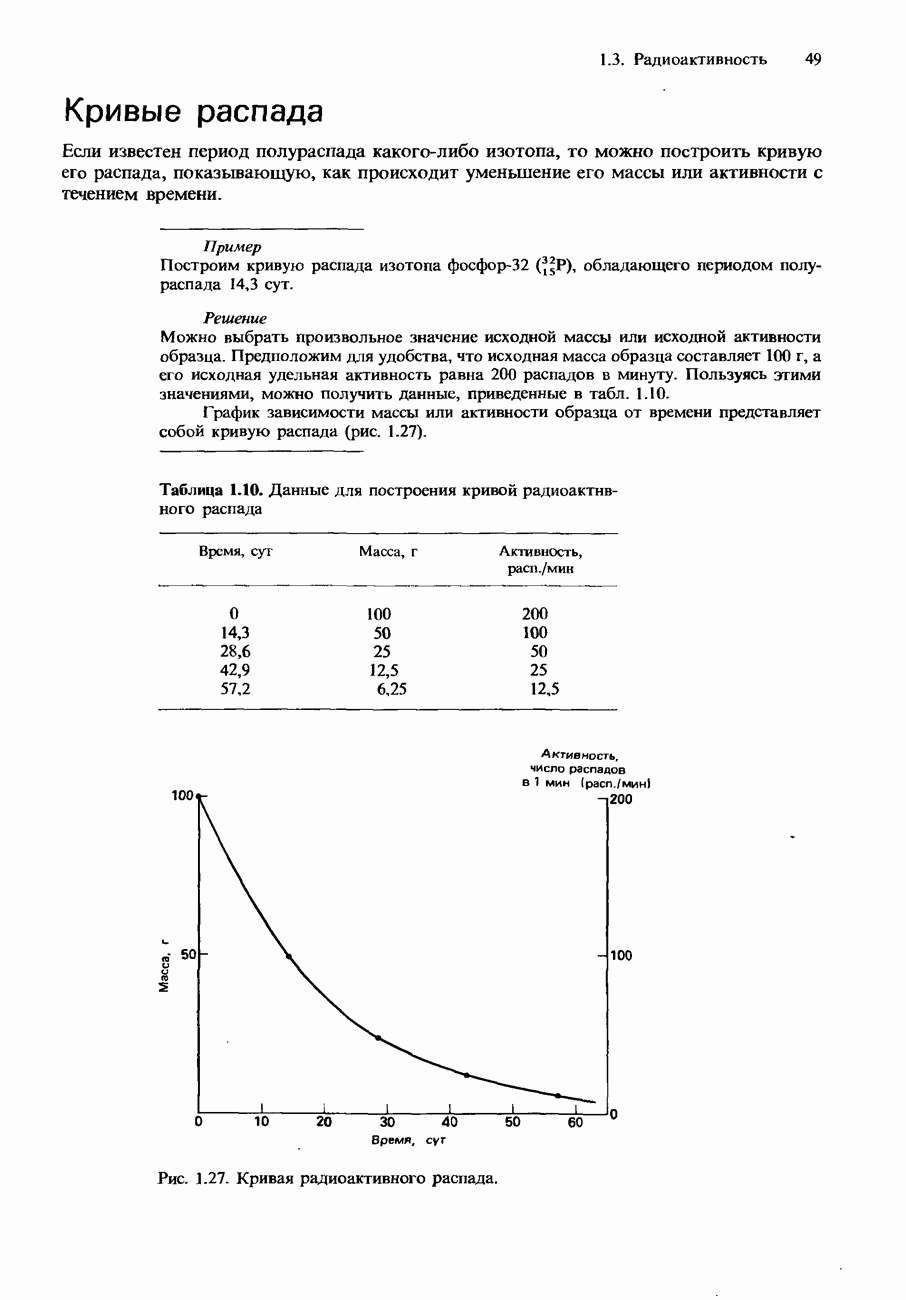
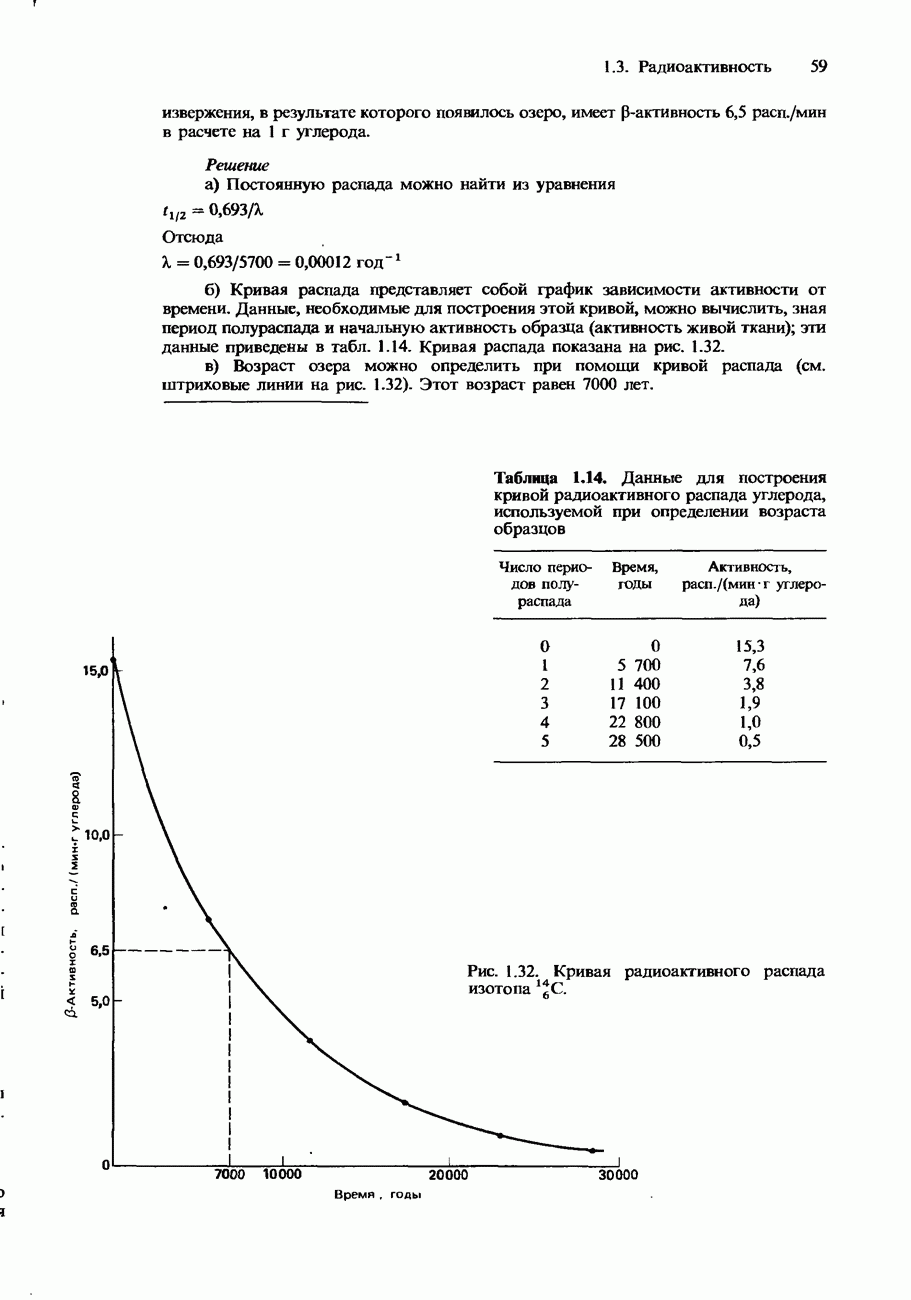
- Кривые распада
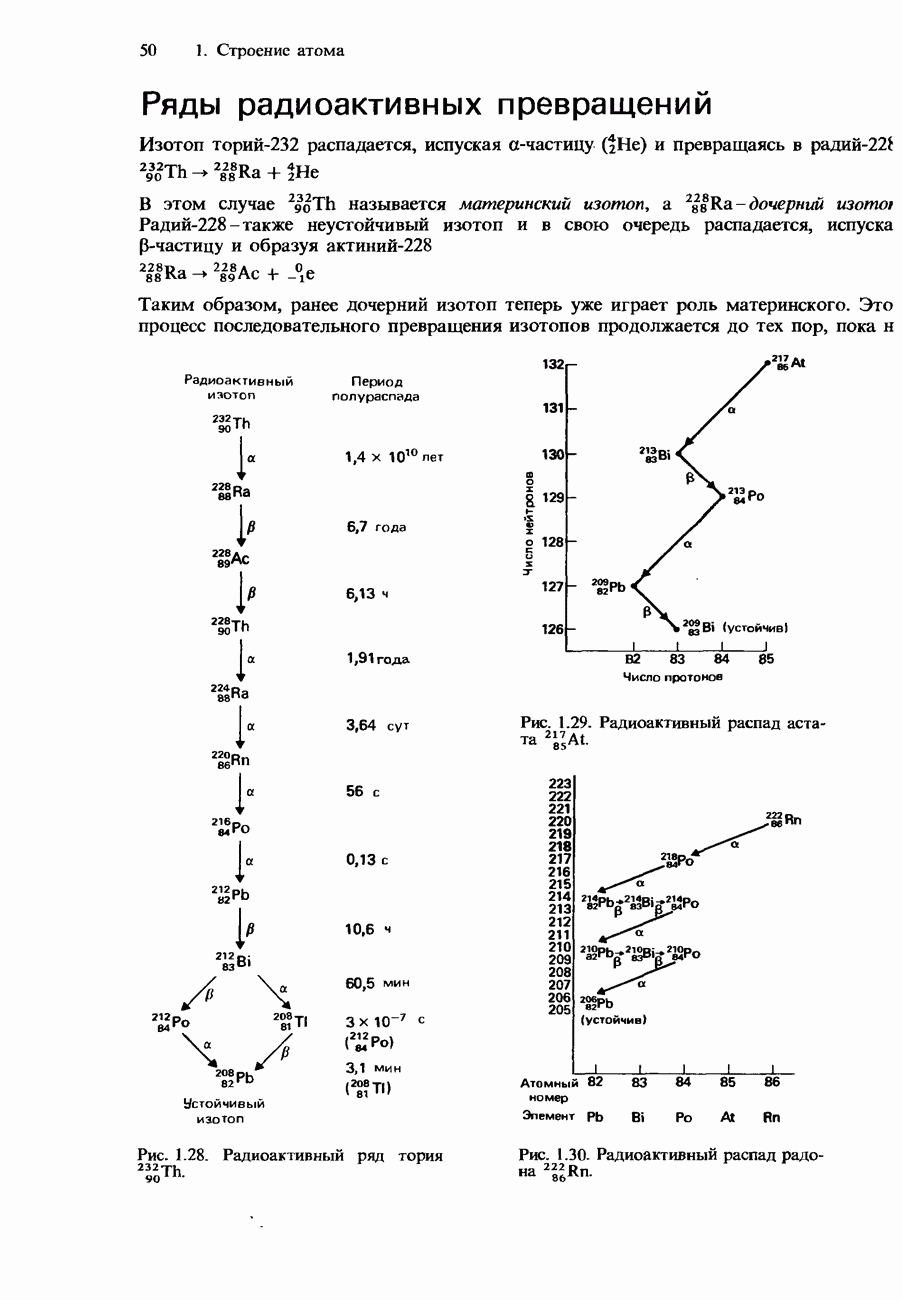
- Ряды радиоактивных превращений
- Естественные радиоизотопы
- ИСКУССТВЕННЫЕ ЯДЕРНЫЕ ПРЕВРАЩЕНИЯ
- Ускорители элементарных частиц
- Трансурановые элементы
- ПРИМЕНЕНИЯ ИЗОТОПОВ
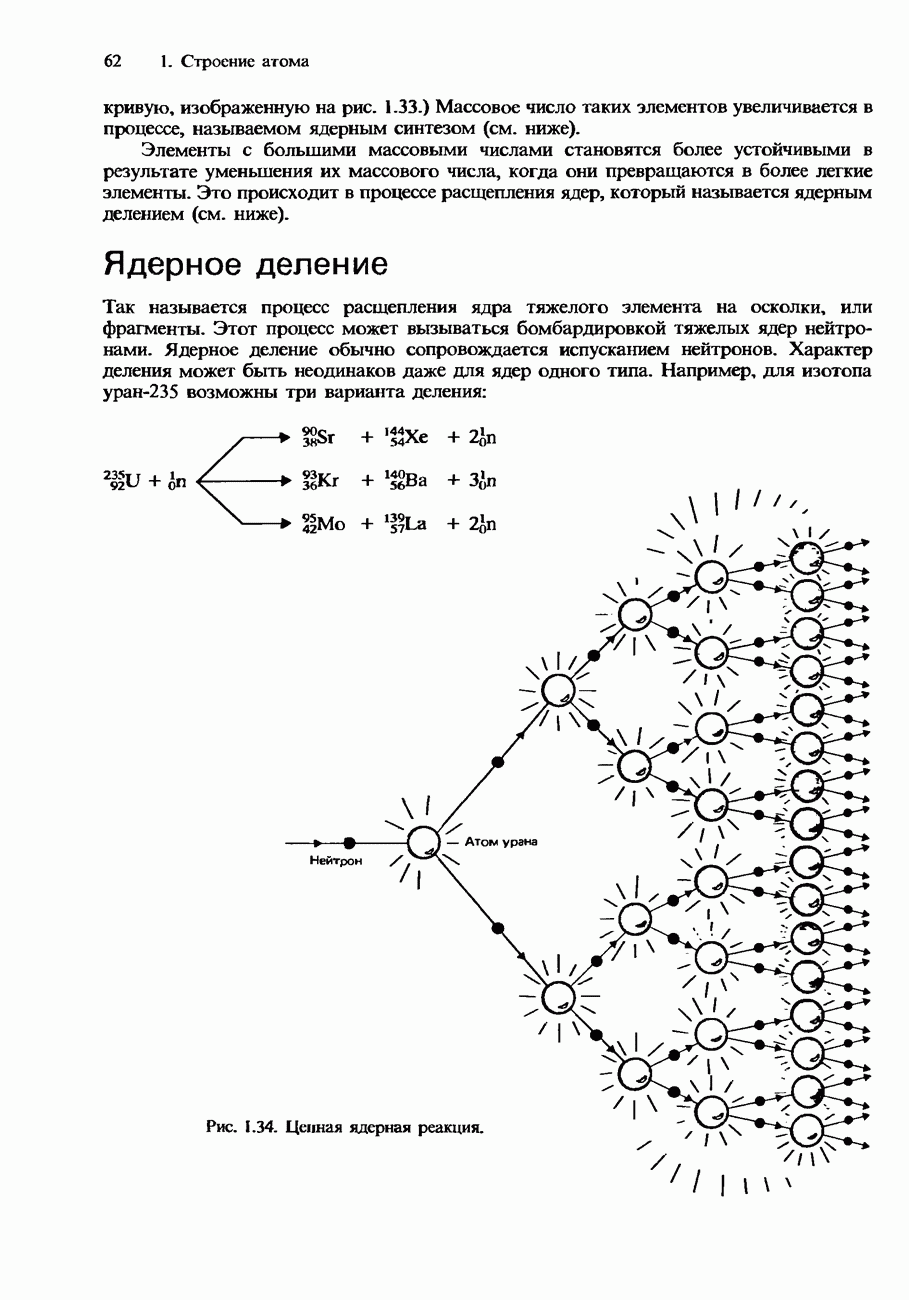
- ЯДЕРНОЕ ДЕЛЕНИЕ И ЯДЕРНЫЙ СИНТЕЗ
- Ядерное деление
- Ядерный синтез
- Ядерный синтез в звездах
- ЯДЕРНАЯ ЭНЕРГИЯ
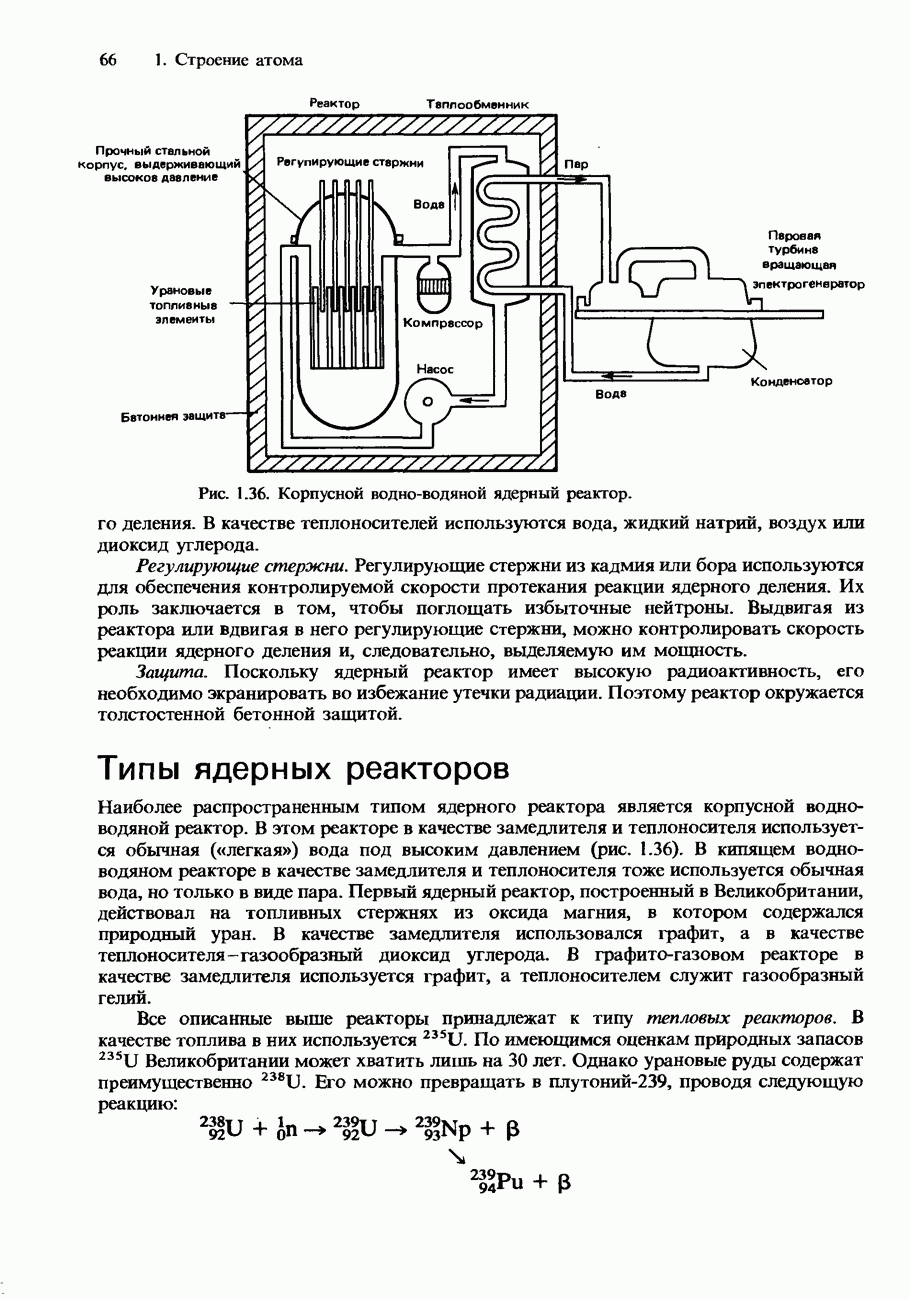
- Типы ядерных реакторов
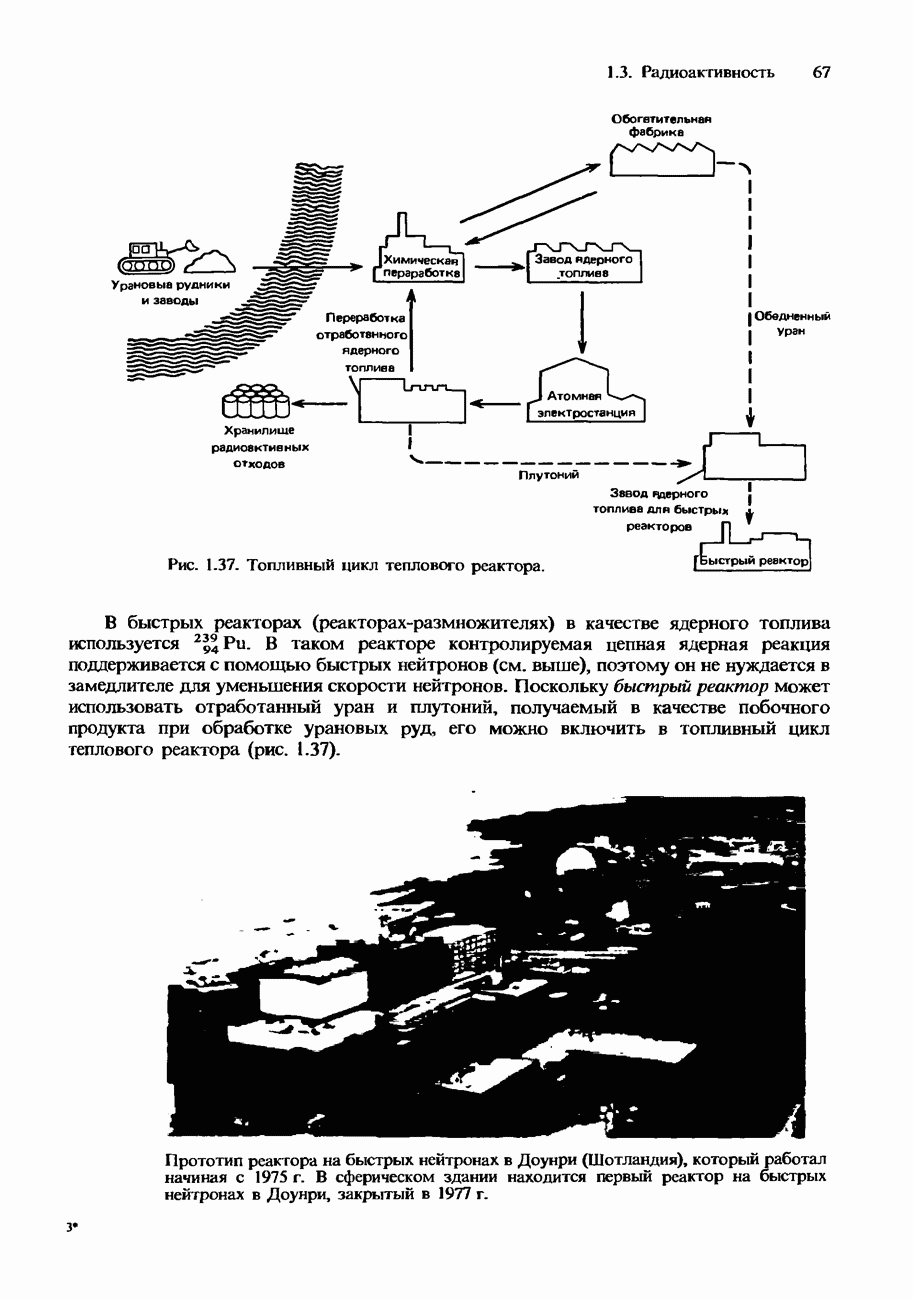
- Радиоактивные ядерные отходы и их переработка
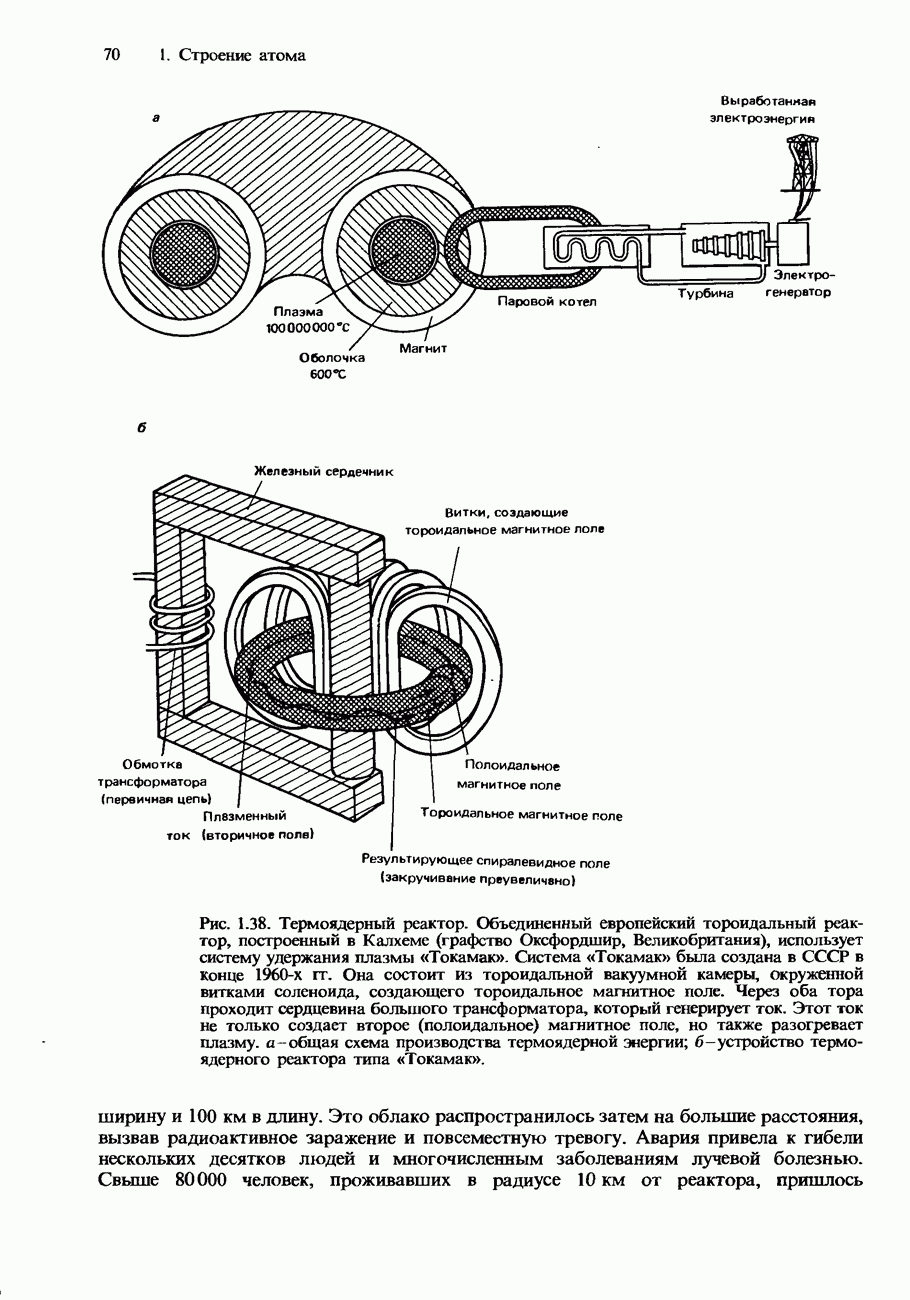
- Термоядерные реакторы
- Аргументы против использования ядерной энергии
- ЯДЕРНОЕ ОРУЖИЕ
- Ядерное разоружение
- ИСТОЧНИКИ РАДИАЦИИ И ЕЕ ВОЗДЕЙСТВИЕ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 2. ХИМИЧЕСКАЯ СВЯЗЬ
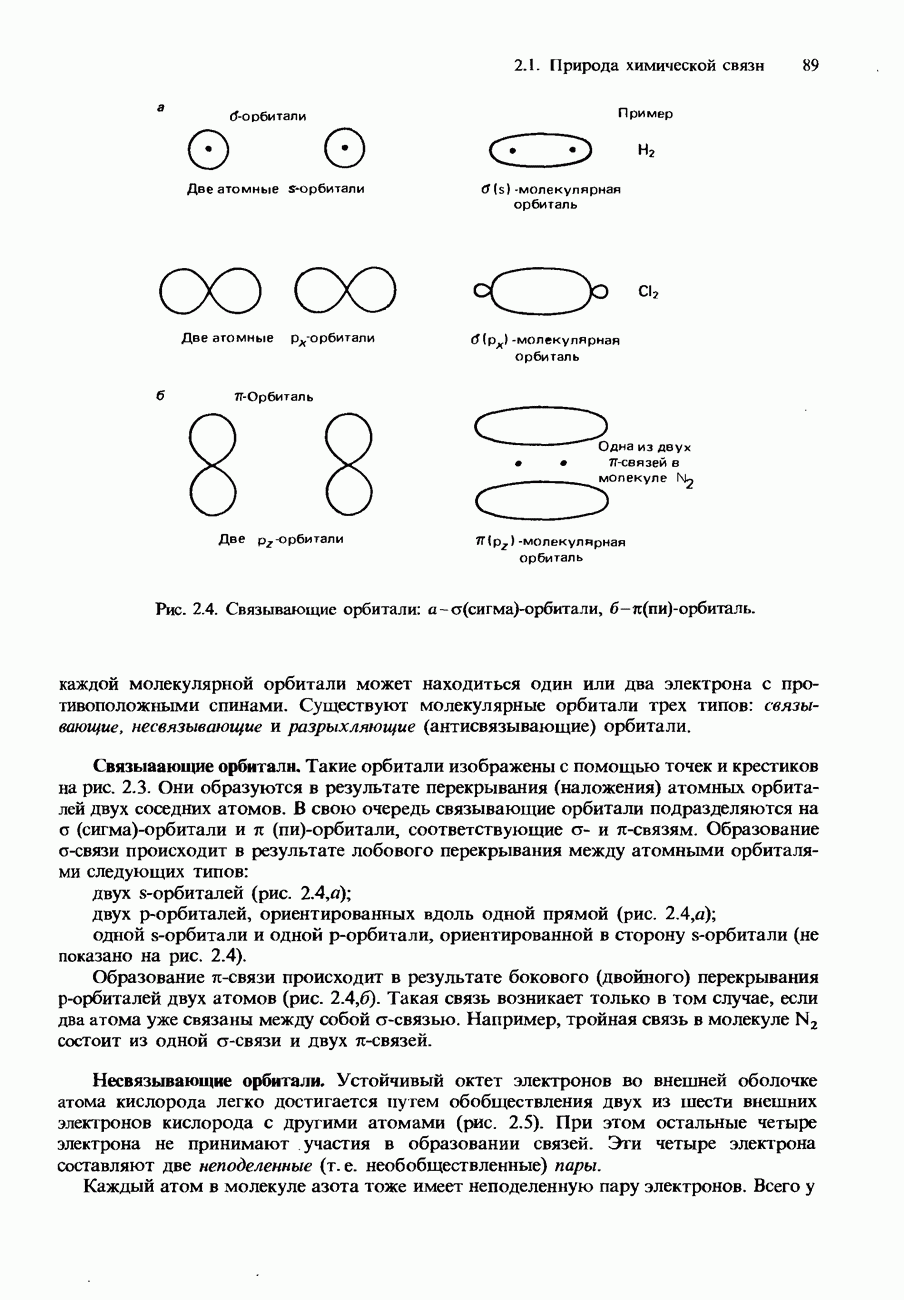
- 2.1. Природа химической связи
- ИОННАЯ СВЯЗЬ
- Устойчивость ионных соединений
- КОВАЛЕНТНАЯ СВЯЗЬ
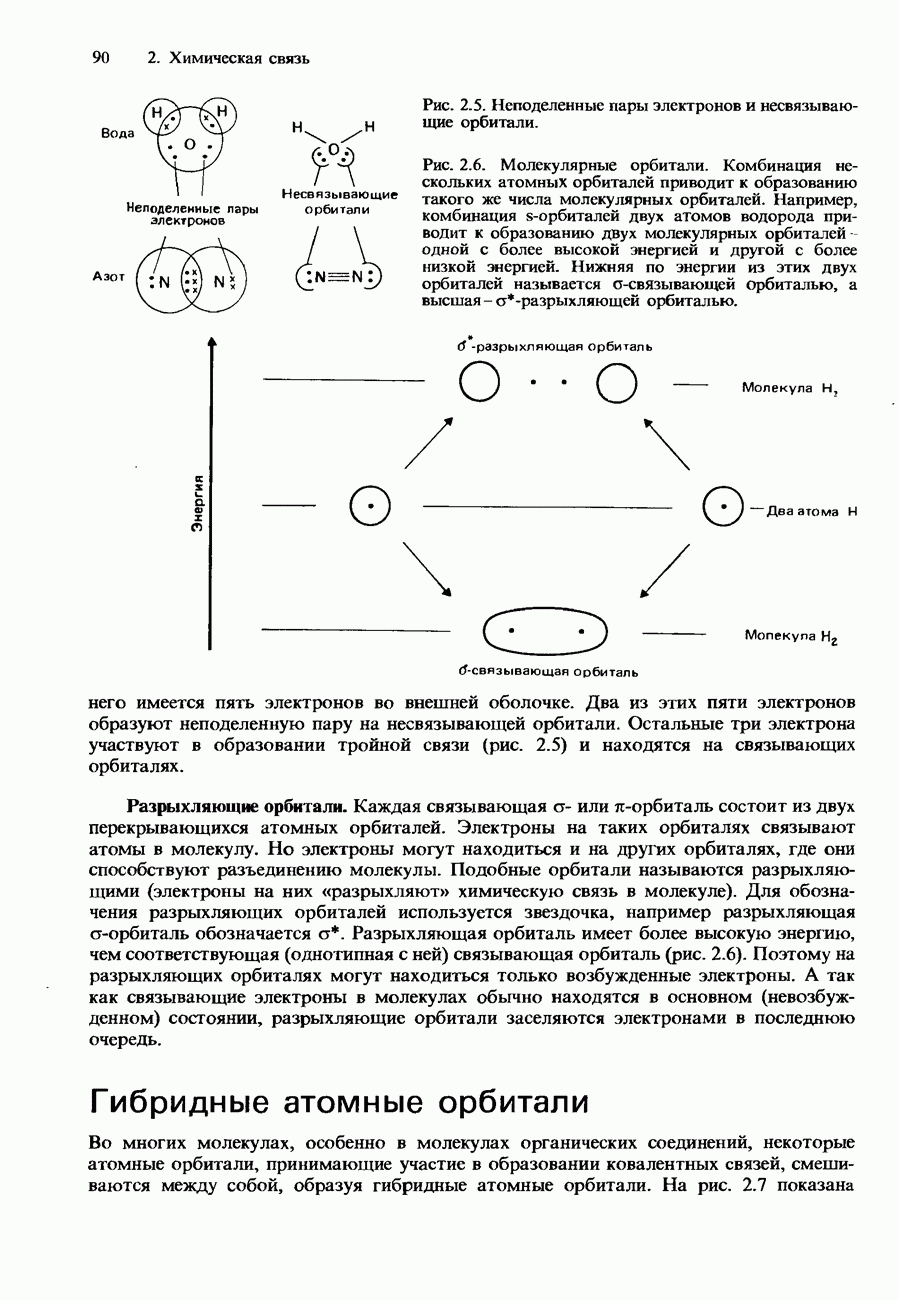
- Молекулярные орбитали
- Гибридные атомные орбитали
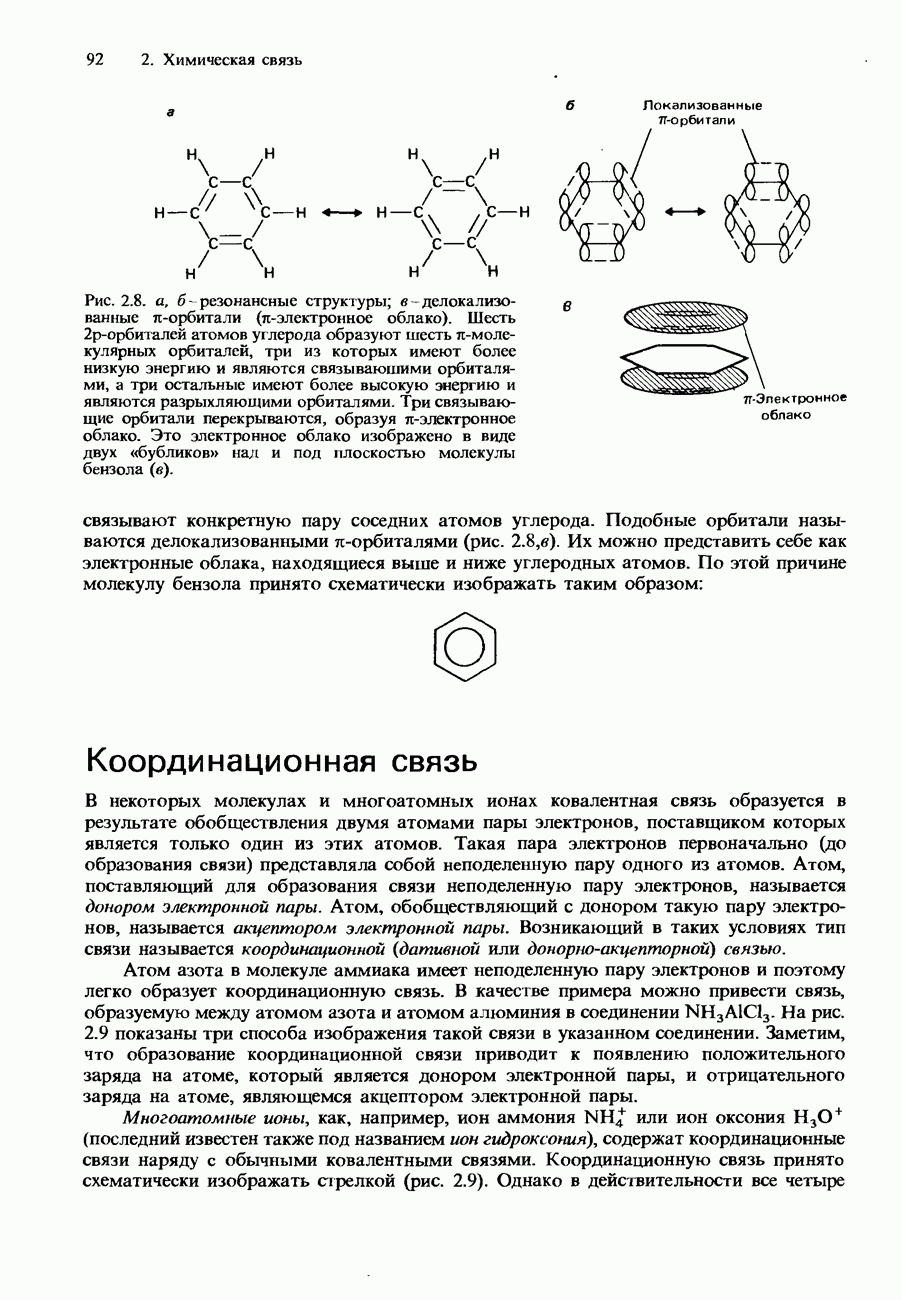
- Делокализованные орбитали
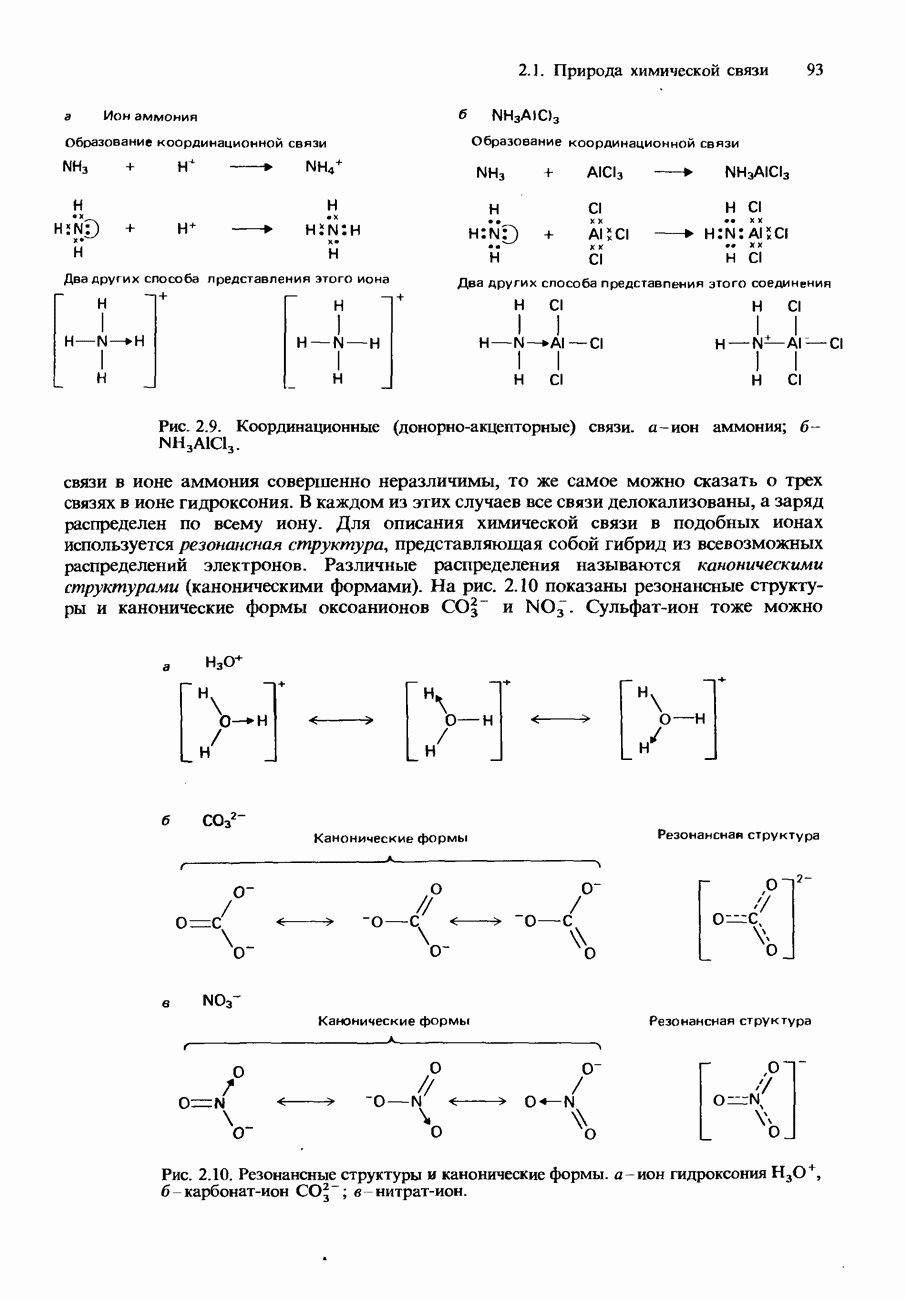
- Координационная связь
- ИОННЫЙ И КОВАЛЕНТНЫЙ ХАРАКТЕР СВЯЗИ
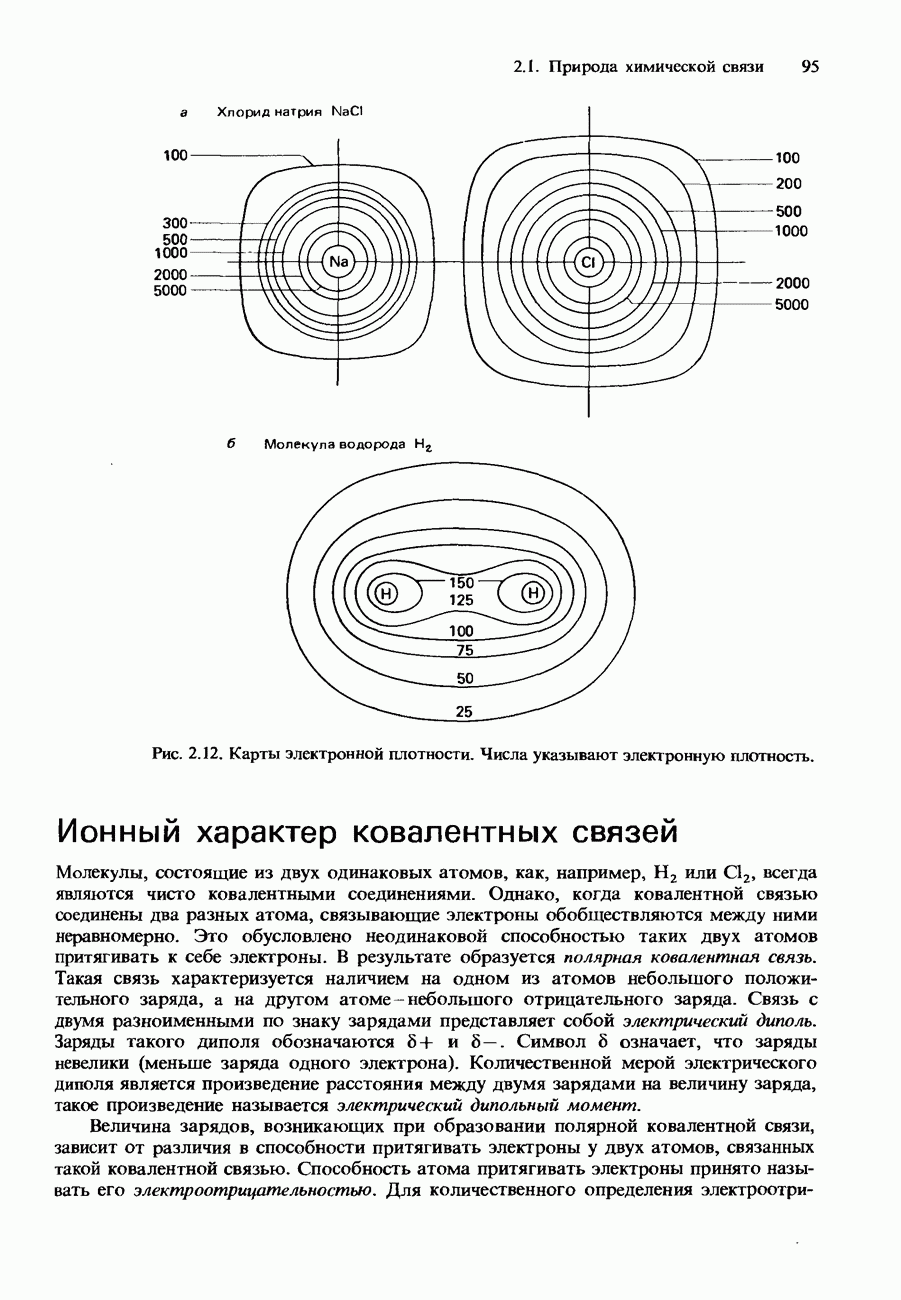
- Ионный характер ковалентных связей
- Ионные и ковалентные соединения
- МЕТАЛЛИЧЕСКАЯ СВЯЗЬ
- Валентная зона и зона проводимости
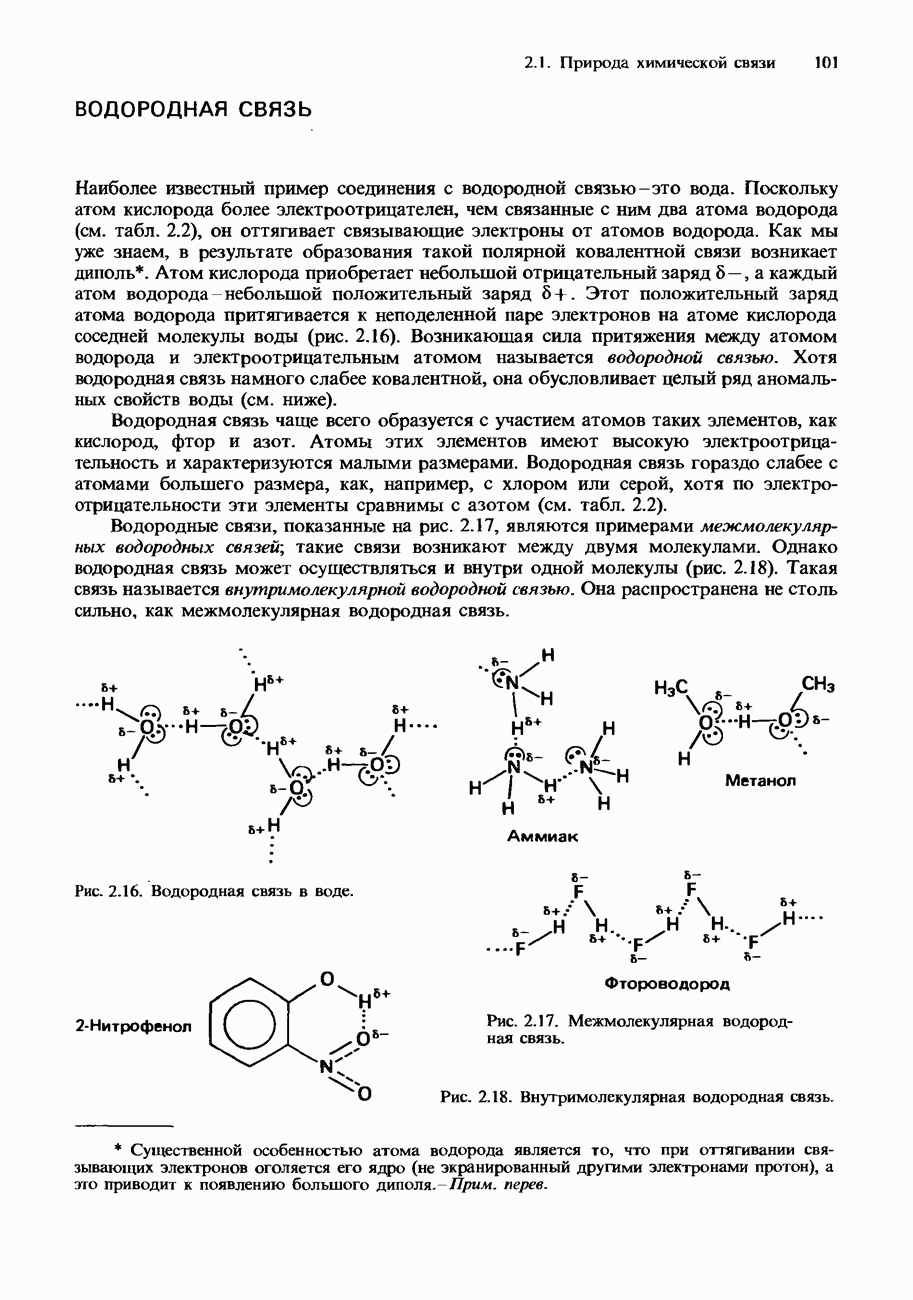
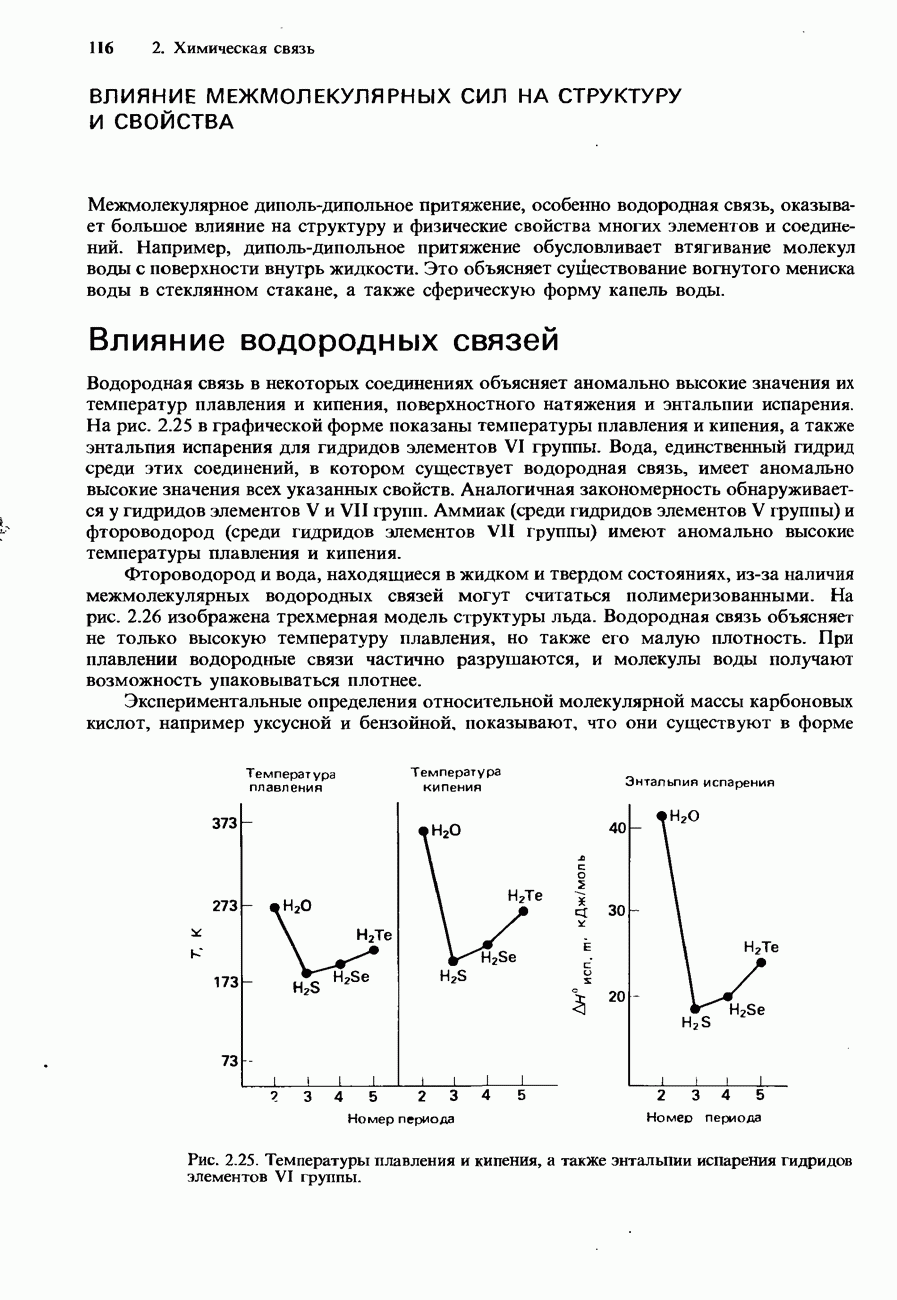
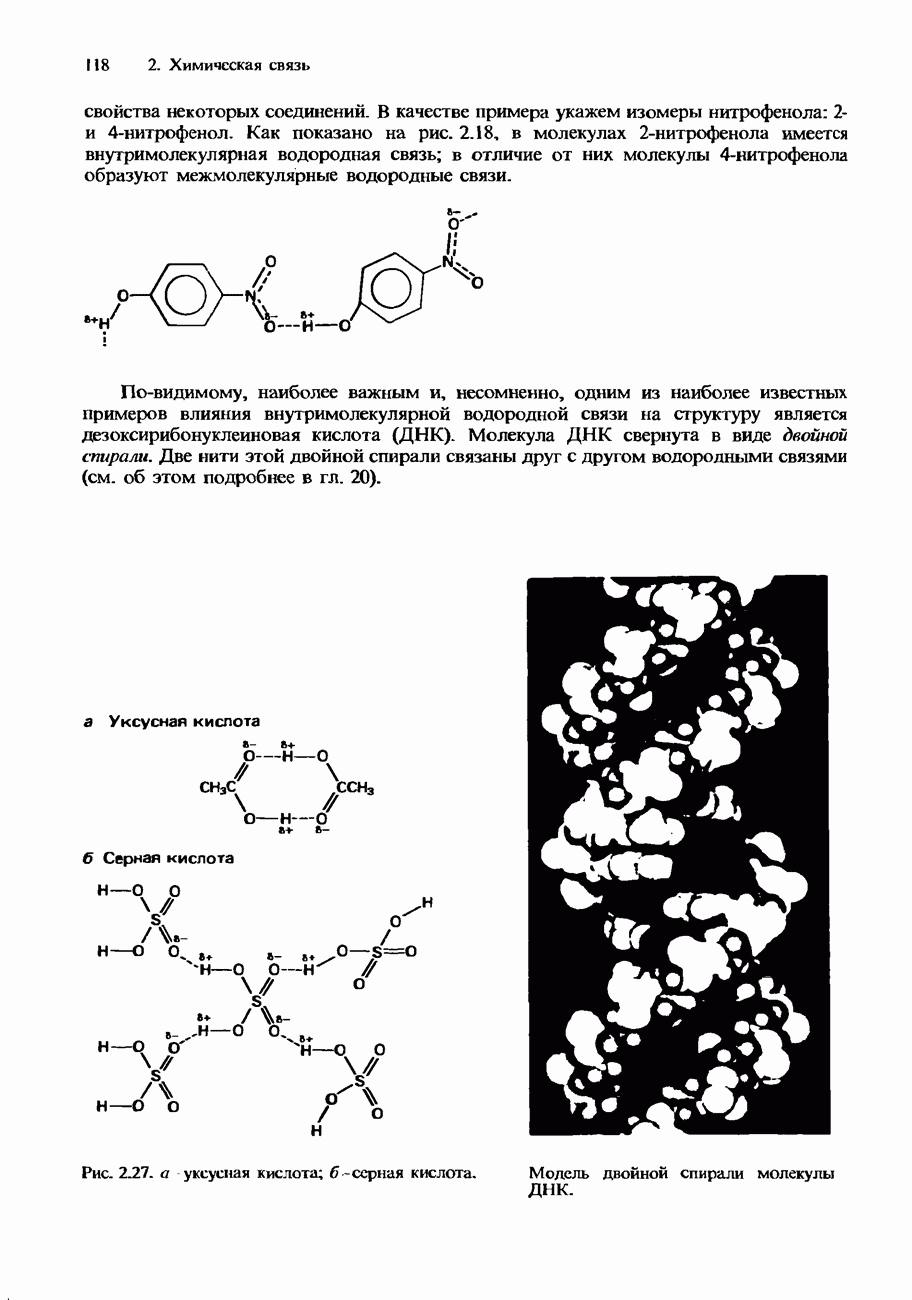
- ВОДОРОДНАЯ СВЯЗЬ
- ВАНДЕРВААЛЬСОВЫ СИЛЫ
- Притяжение типа диполь-индуцированный диполь (индукционное)
- Что понимается под вандерваальсовыми силами
- 2.2. Влияние химической связи на свойства соединений
- Атомные радиусы
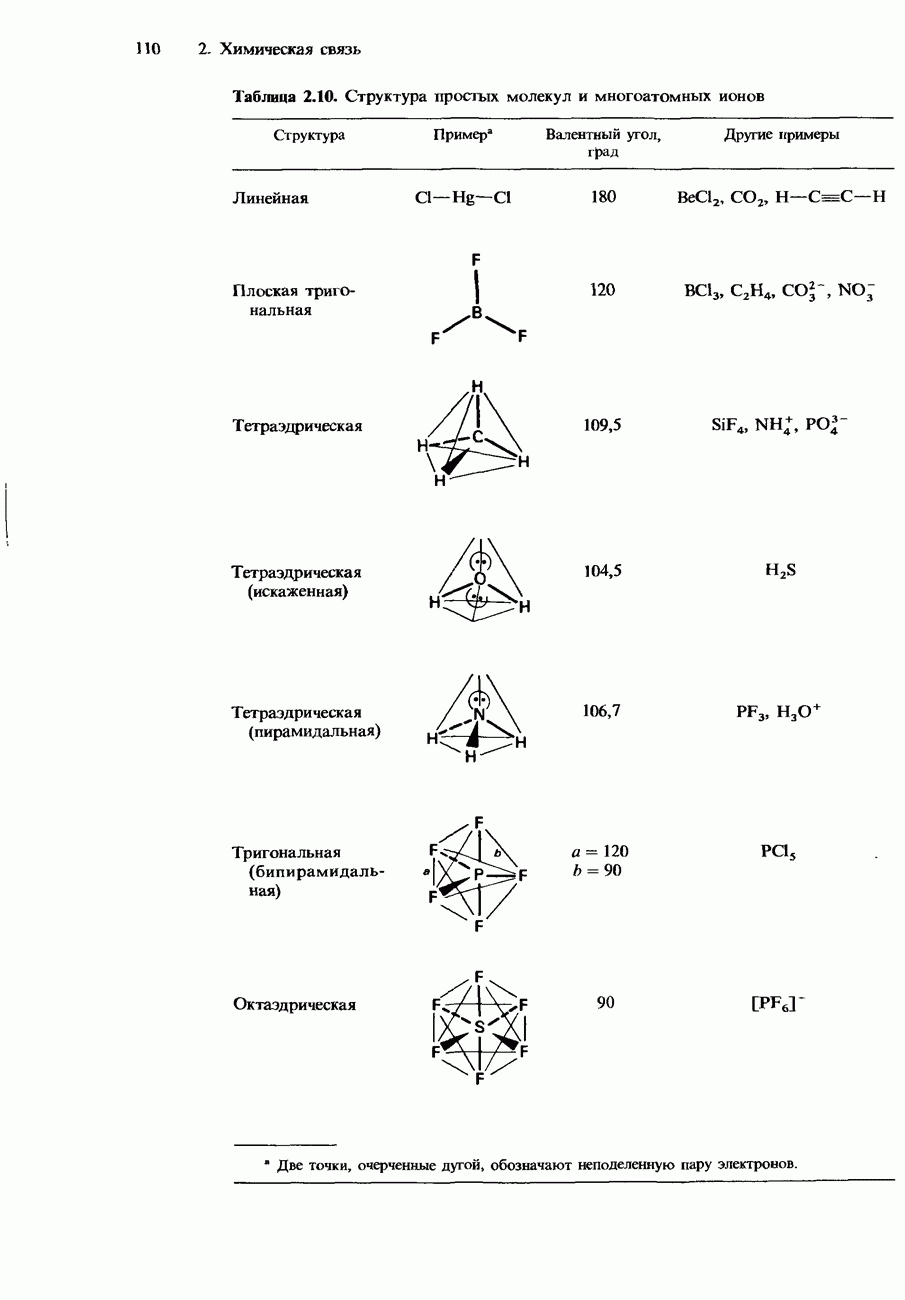
- ФОРМА ПРОСТЫХ МОЛЕКУЛ И МНОГОАТОМНЫХ ИОНОВ
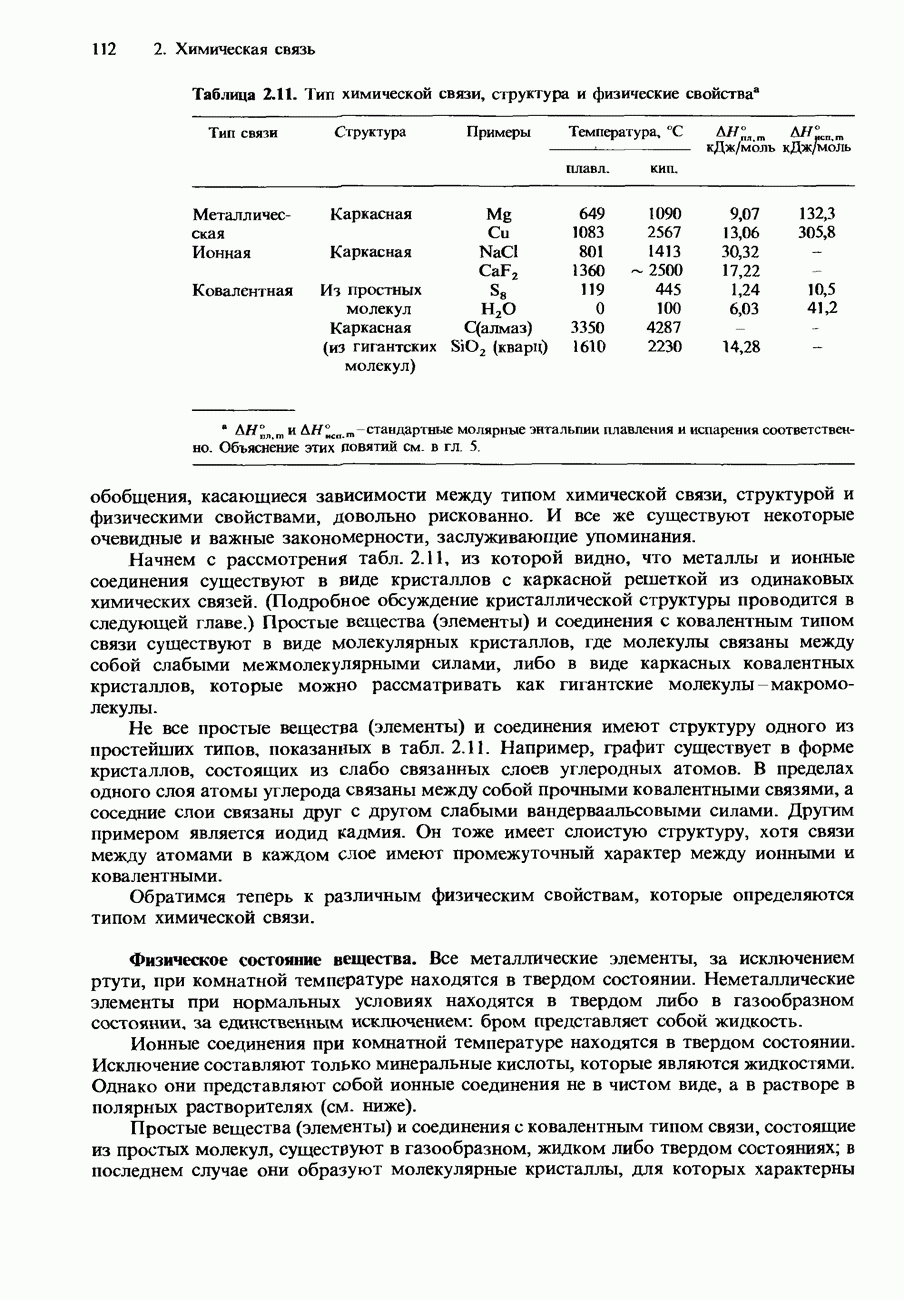
- ТИП ХИМИЧЕСКОЙ СВЯЗИ, СТРУКТУРА И ФИЗИЧЕСКИЕ СВОЙСТВА
- ТИП СВЯЗИ И ХИМИЧЕСКИЕ СВОЙСТВА
- ВЛИЯНИЕ МЕЖМОЛЕКУЛЯРНЫХ СИЛ НА СТРУКТУРУ И СВОЙСТВА
- ВЛИЯНИЕ ВАНДЕРВААЛЬСОВЫХ СИЛ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 3 ГАЗЫ, ЖИДКОСТИ И ТВЕРДЫЕ ВЕЩЕСТВА
- 3.1. Газы и жидкости
- ГАЗОВЫЕ ЗАКОНЫ
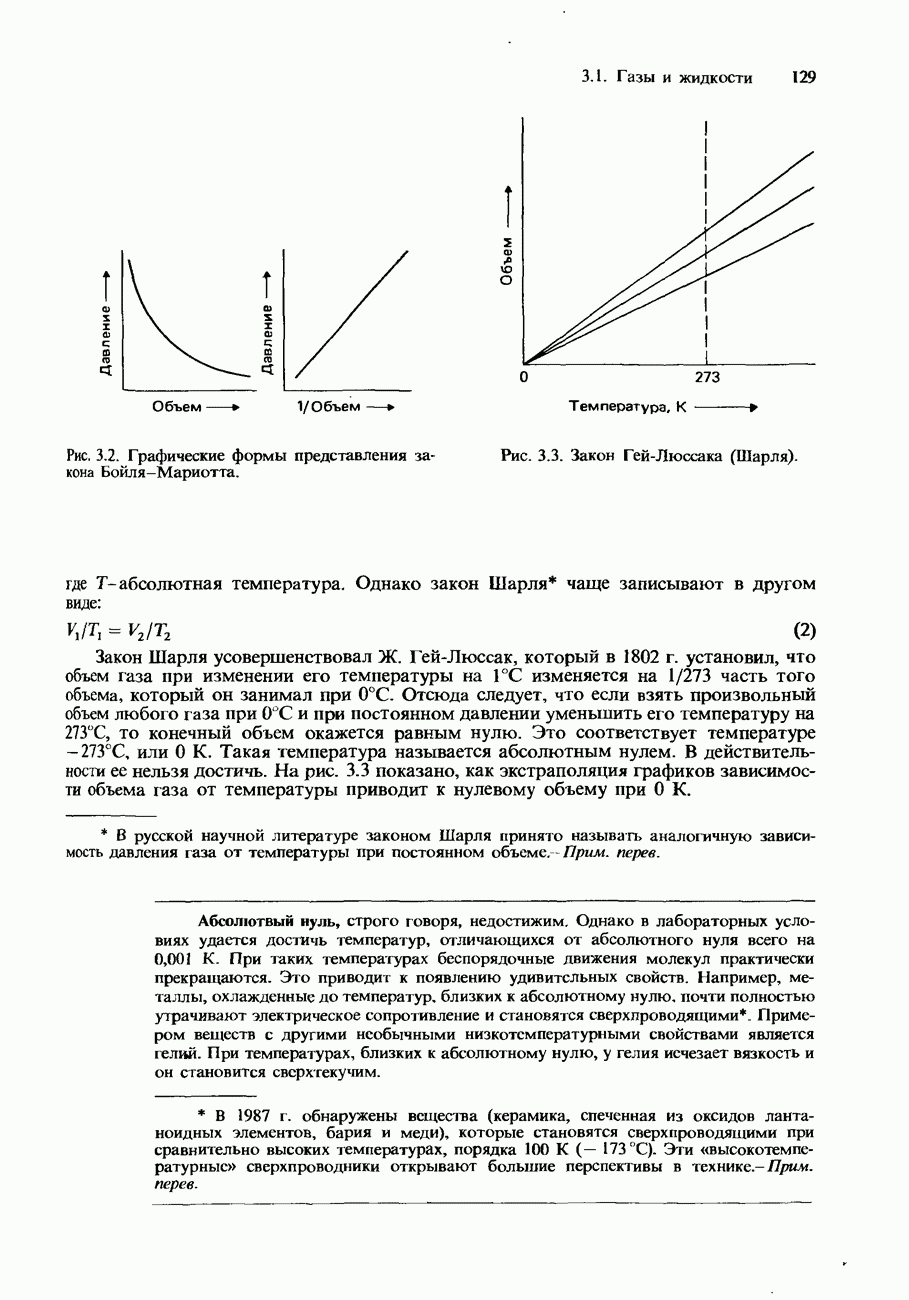
- Закон Бойля-Мариотта
- Закон Гей-Люссака (закон Шарля)
- Объединенный газовый закон
- Закон Авогадро
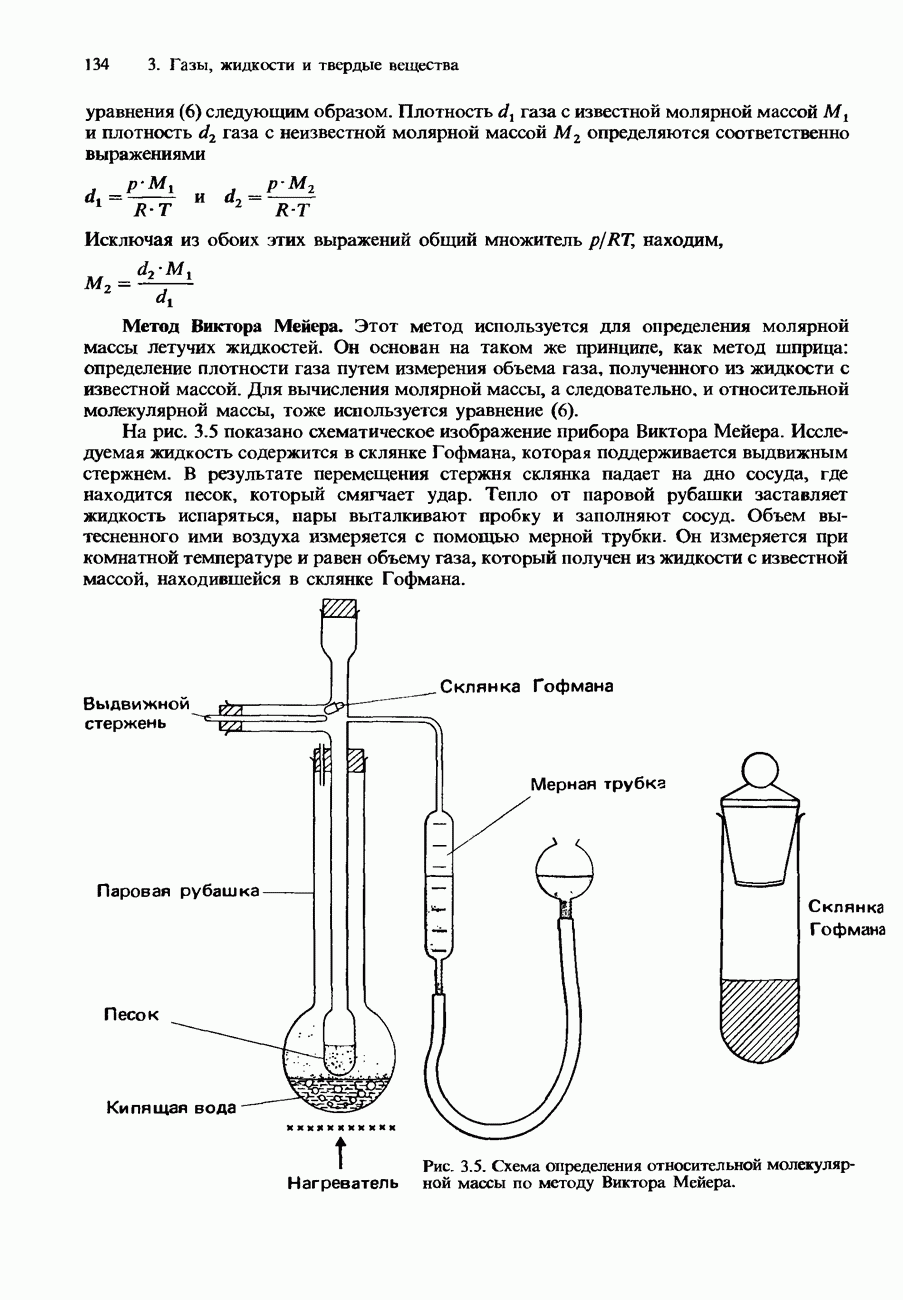
- Экспериментальное определение относительной молекулярной массы
- Закон парциальных давлений газов (закон Дальтона)
- Законы Грэхема
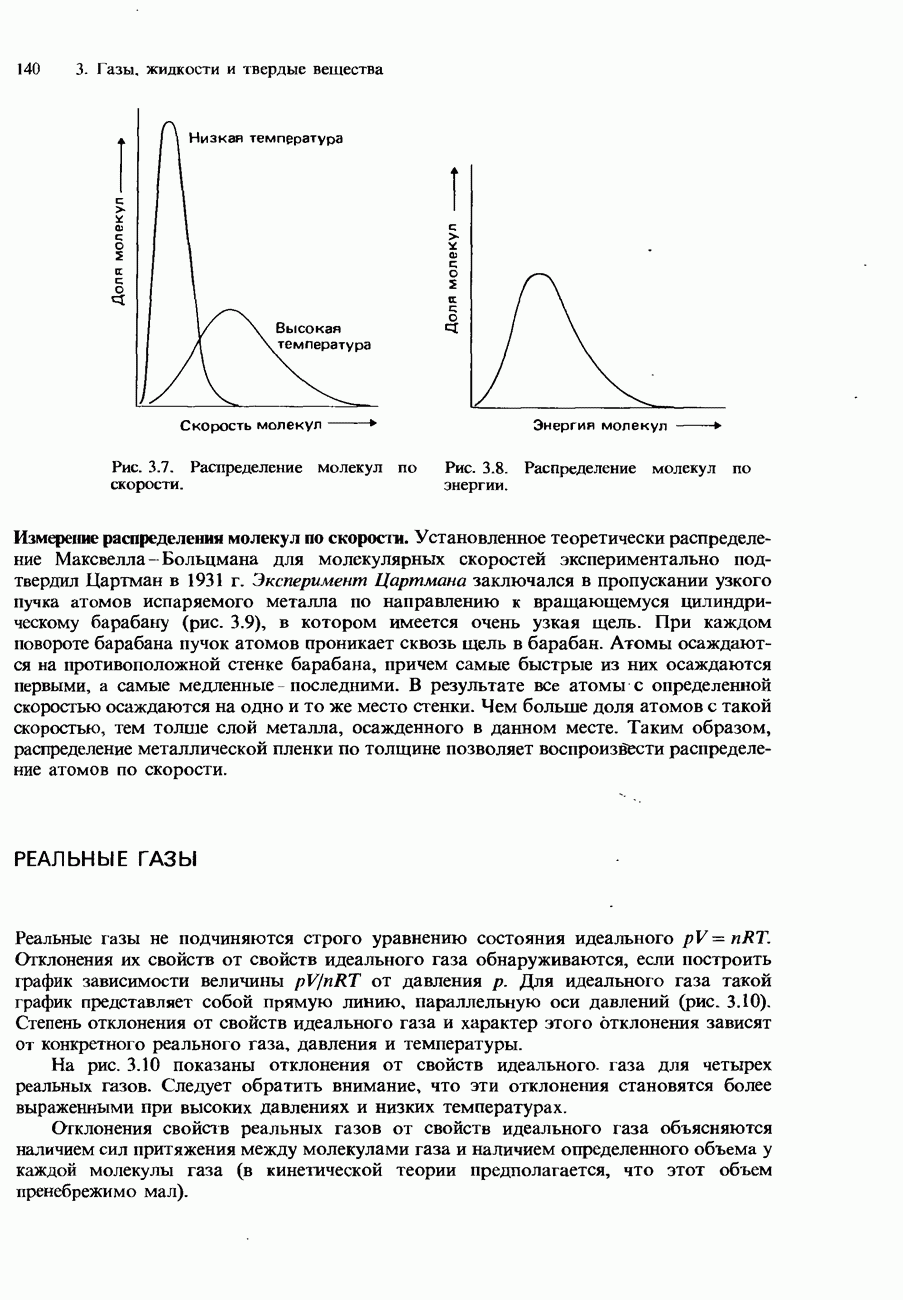
- КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- Скорости молекул
- Распределение Максвелла-Больцмана
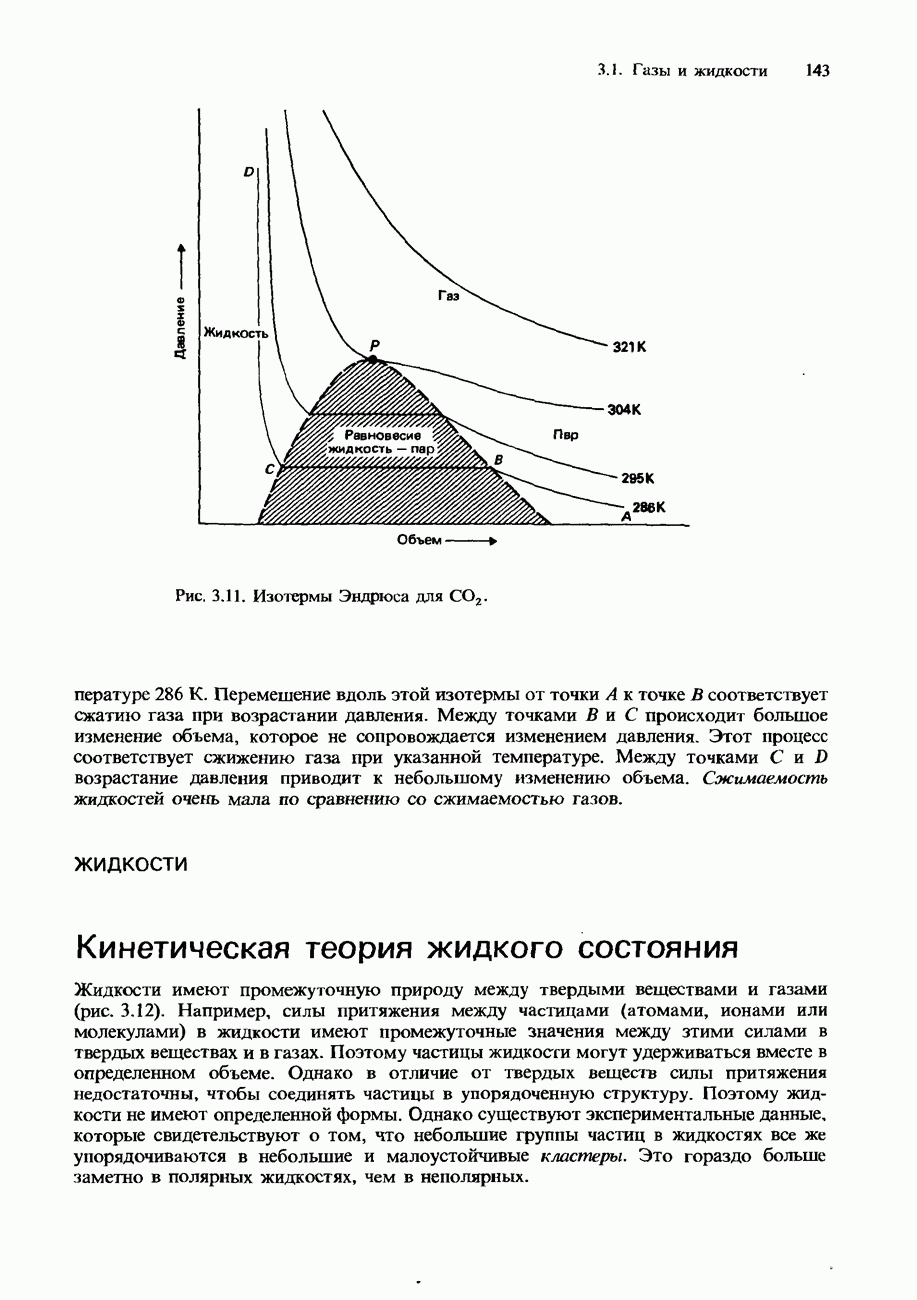
- РЕАЛЬНЫЕ ГАЗЫ
- Уравнение Ван-дер-Ваальса
- Сжижение газов
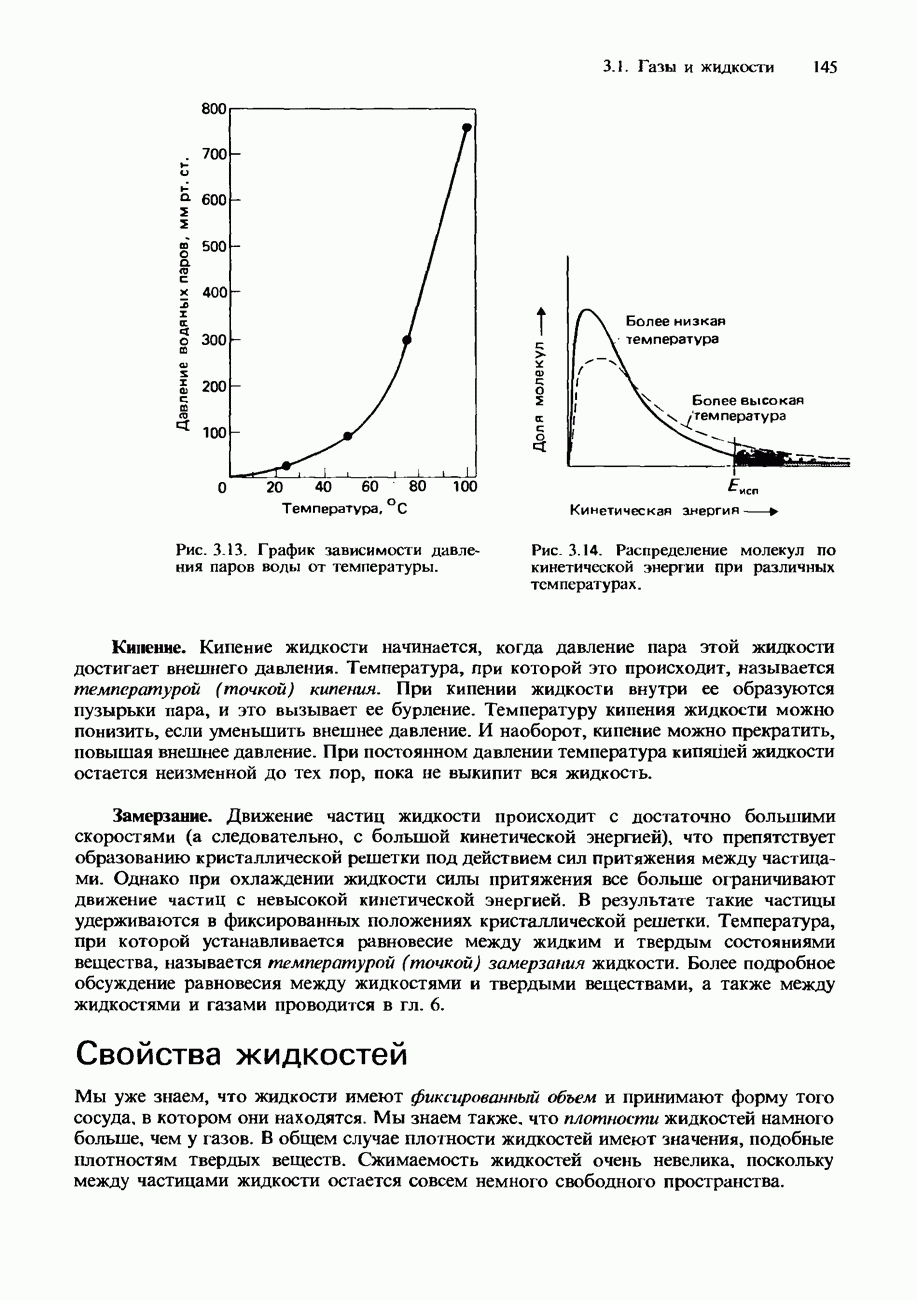
- ЖИДКОСТИ
- Свойства жидкостей
- 3.2. Твердые вещества
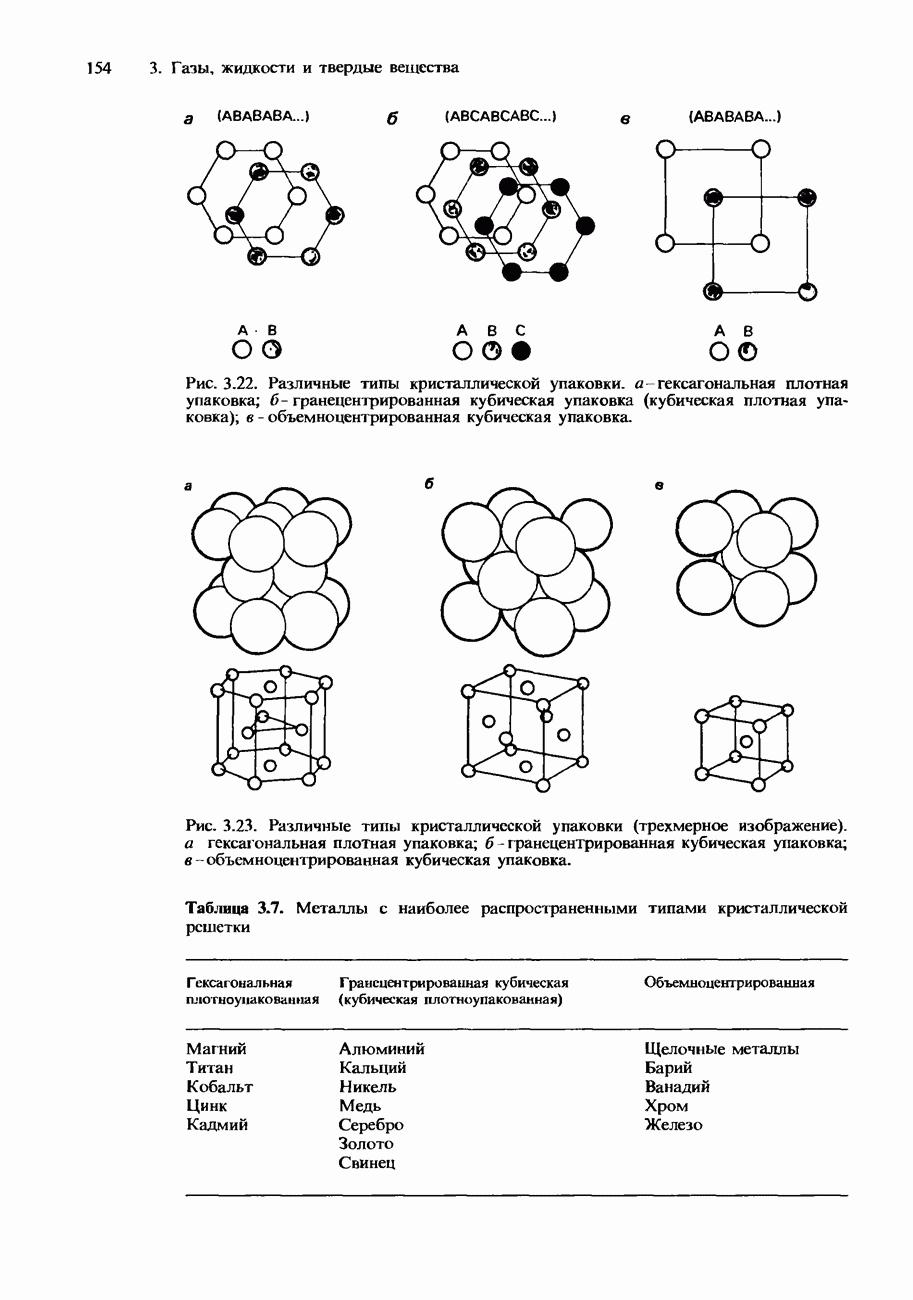
- КРИСТАЛЛИЧЕСКАЯ СТРУКТУРА
- Металлические кристаллы
- Ионные кристаллы
- Ковалентные кристаллы
- ИЗОМОРФИЗМ. ПОЛИМОРФИЗМ И АЛЛОТРОПИЯ
- СВОЙСТВА ТВЕРДЫХ ВЕЩЕСТВ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 4. СТЕХИОМЕТРИЯ
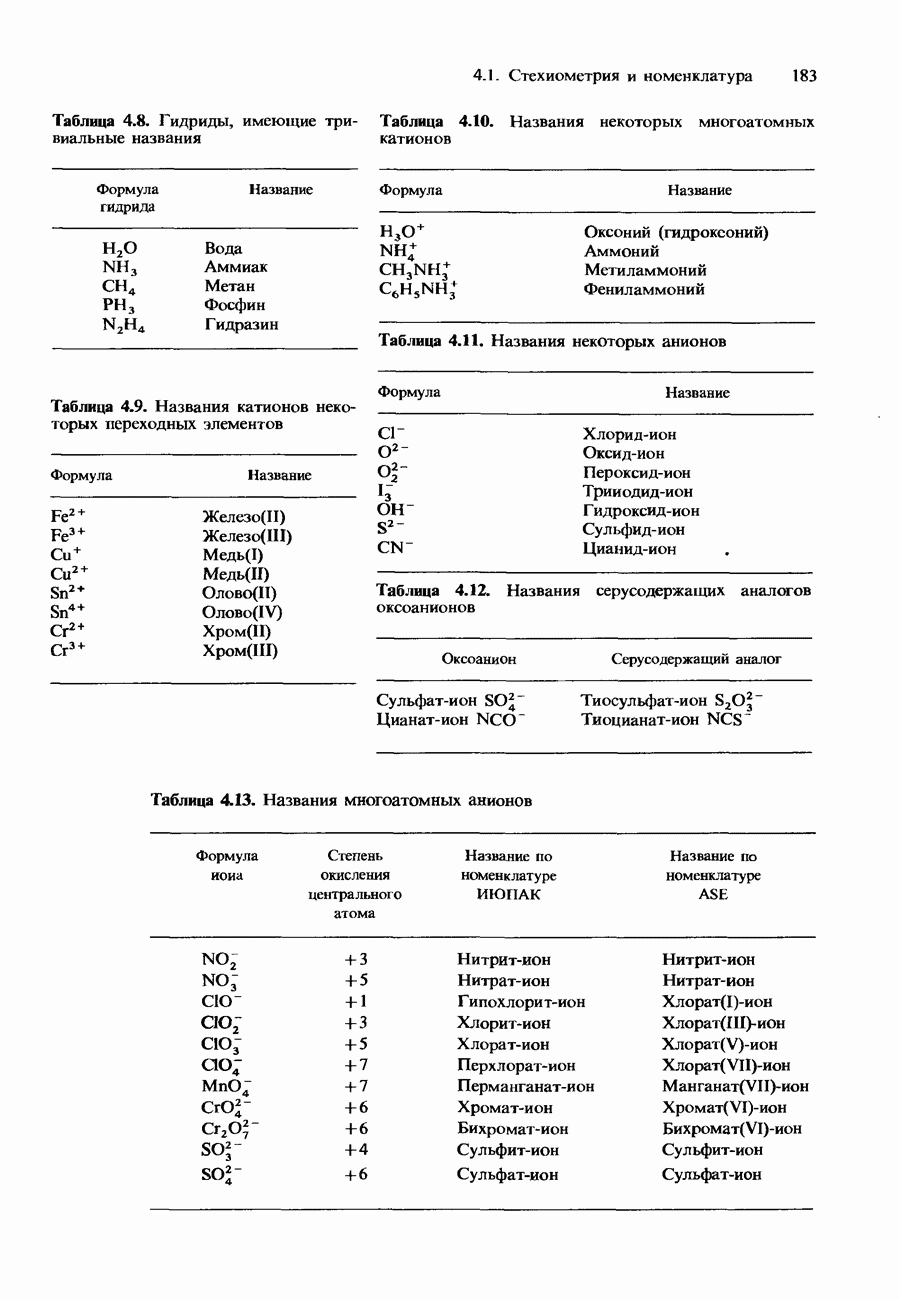
- 4.1. Стехиометрия и номенклатура
- Химические вещества
- Количественные законы химии
- Вес и масса
- НАЗВАНИЯ И ФОРМУЛЫ ХИМИЧЕСКИХ СОЕДИНЕНИЙ
- Химические формулы
- НОМЕНКЛАТУРА НЕОРГАНИЧЕСКИХ СОЕДИНЕНИЙ
- Степень окисления (состояние окисления)
- Элементы
- Бинарные соединения
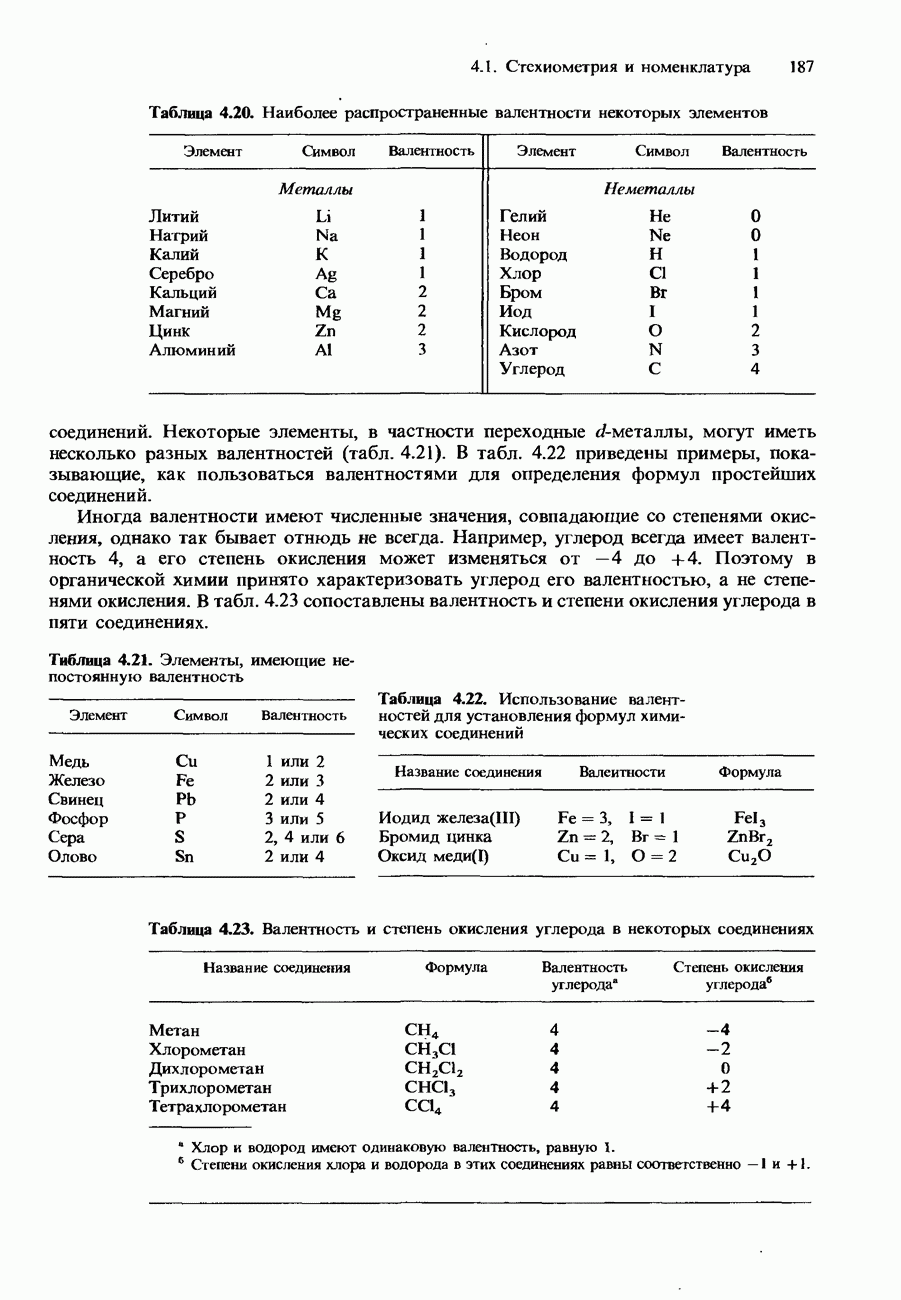
- 4.2 Стехиометрические вычисления
- Молярная масса
- Число частиц вещества
- Процентный состав соединения
- Эмпирическая формула соединения
- Молярные постоянные и молярные величины
- Состав гомогенных смесей
- ХИМИЧЕСКИЕ УРАВНЕНИЯ
- ВЫХОД РЕАКЦИИ
- ПРОМЫШЛЕННАЯ СТЕХИОМЕТРИЯ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 5. ЭНЕРГЕТИКА
- 5.1. Термодинамика
- ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 5.2. Энтальпия
- СТАНДАРТНЫЕ ИЗМЕНЕНИЯ ЭНТАЛЬПИИ
- ДРУГИЕ ИЗМЕНЕНИЯ ЭНТАЛЬПИИ
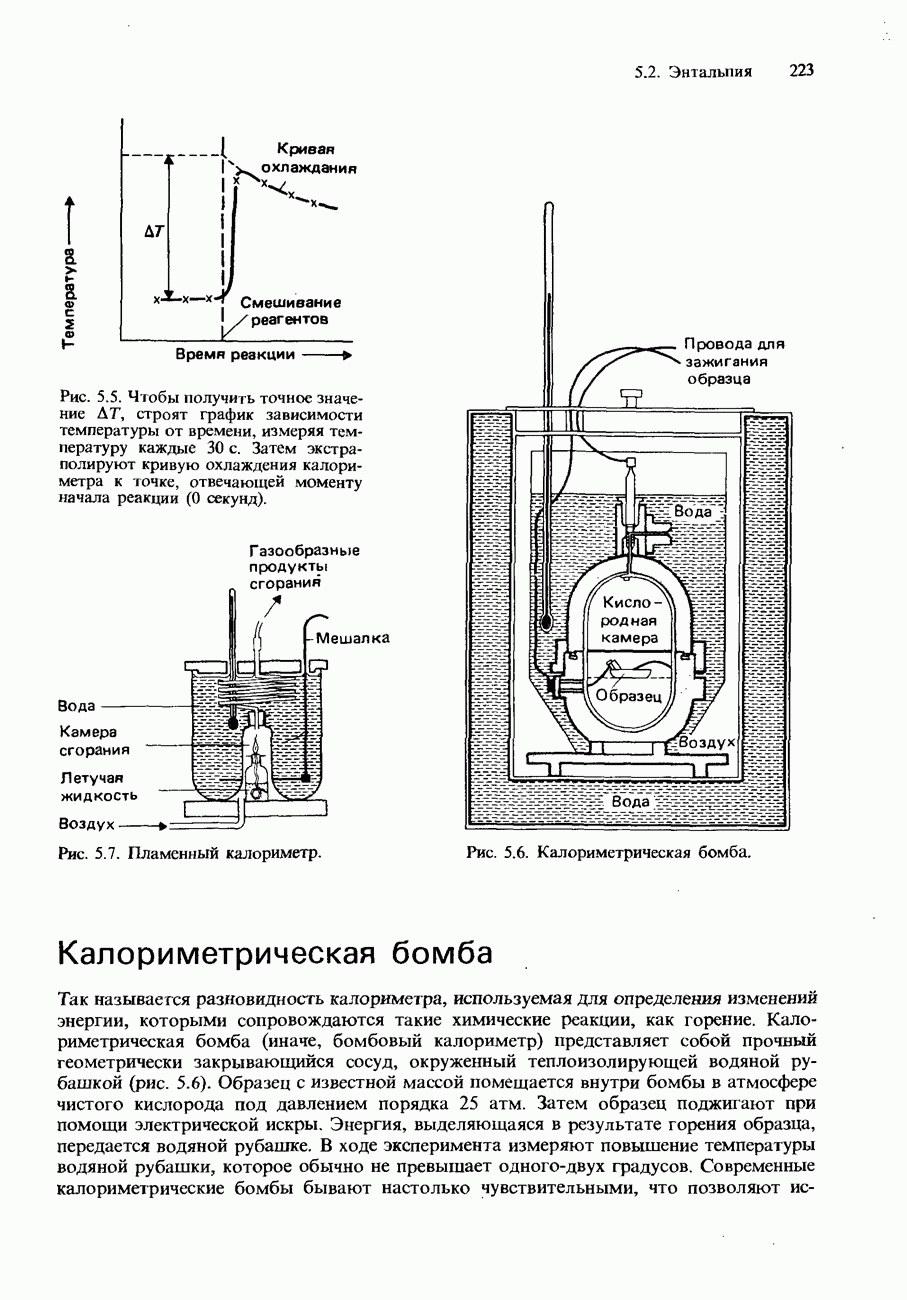
- КАЛОРИМЕТРИЯ
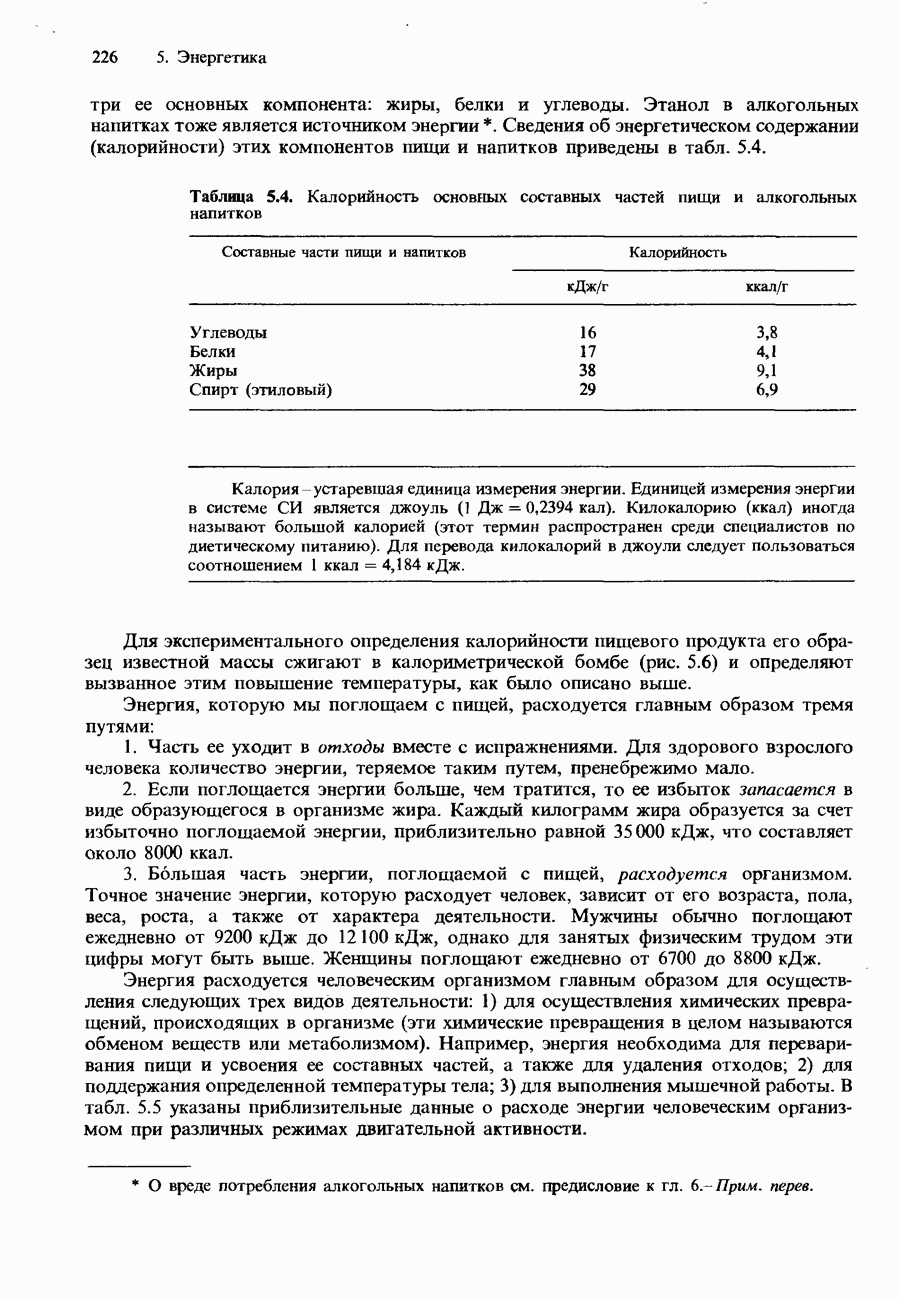
- КАЛОРИЙНОСТЬ ПИЩИ
- ЗАКОН ГЕССА
- 5.3 Энергия и структура
- ЭНТАЛЬПИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Энтальпии растворения и гидратации
- ЭНТРОПИЯ
- СВОБОДНАЯ ЭНЕРГИЯ ГИББСА
- О ЧЕМ ПОЗВОЛЯЕТ СУДИТЬ ИЗМЕНЕНИЕ СВОБОДНОЙ ЭНЕРГИИ СИСТЕМЫ
- 5.4. Источники энергии
- НЕТРАДИЦИОННЫЕ ИСТОЧНИКИ ЭНЕРГИИ
- ЗАПАСАНИЕ ЭНЕРГИИ
- ПОТРЕБЛЕНИЕ ЭНЕРГИИ В ПРОШЛОМ, НАСТОЯЩЕМ И БУДУЩЕМ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 6. ФАЗОВЫЕ РАВНОВЕСИЯ
- 6.1. Равновесия и фазы
- ФАЗЫ И КОМПОНЕНТЫ
- Фазы
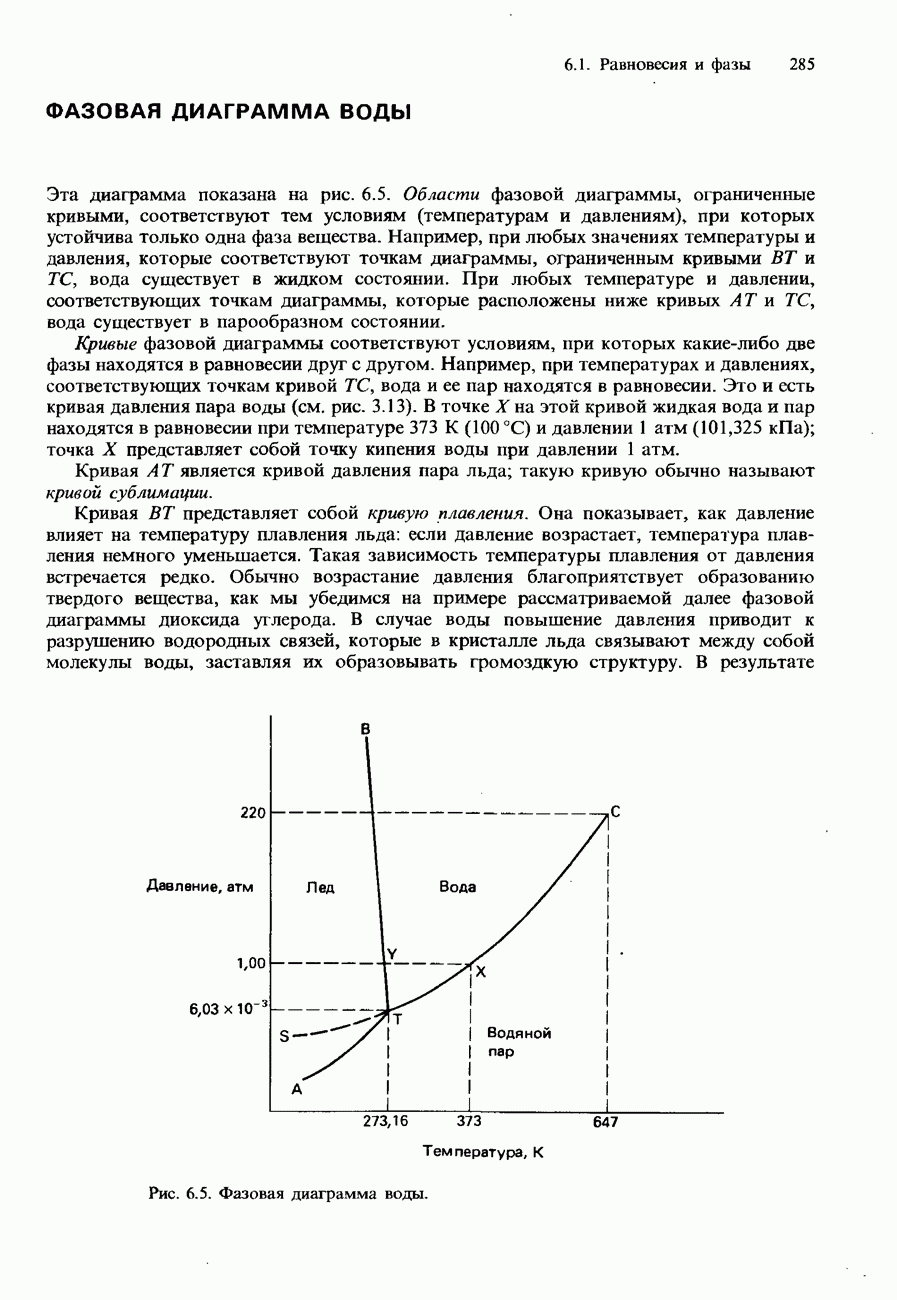
- ФАЗОВАЯ ДИАГРАММА ВОДЫ
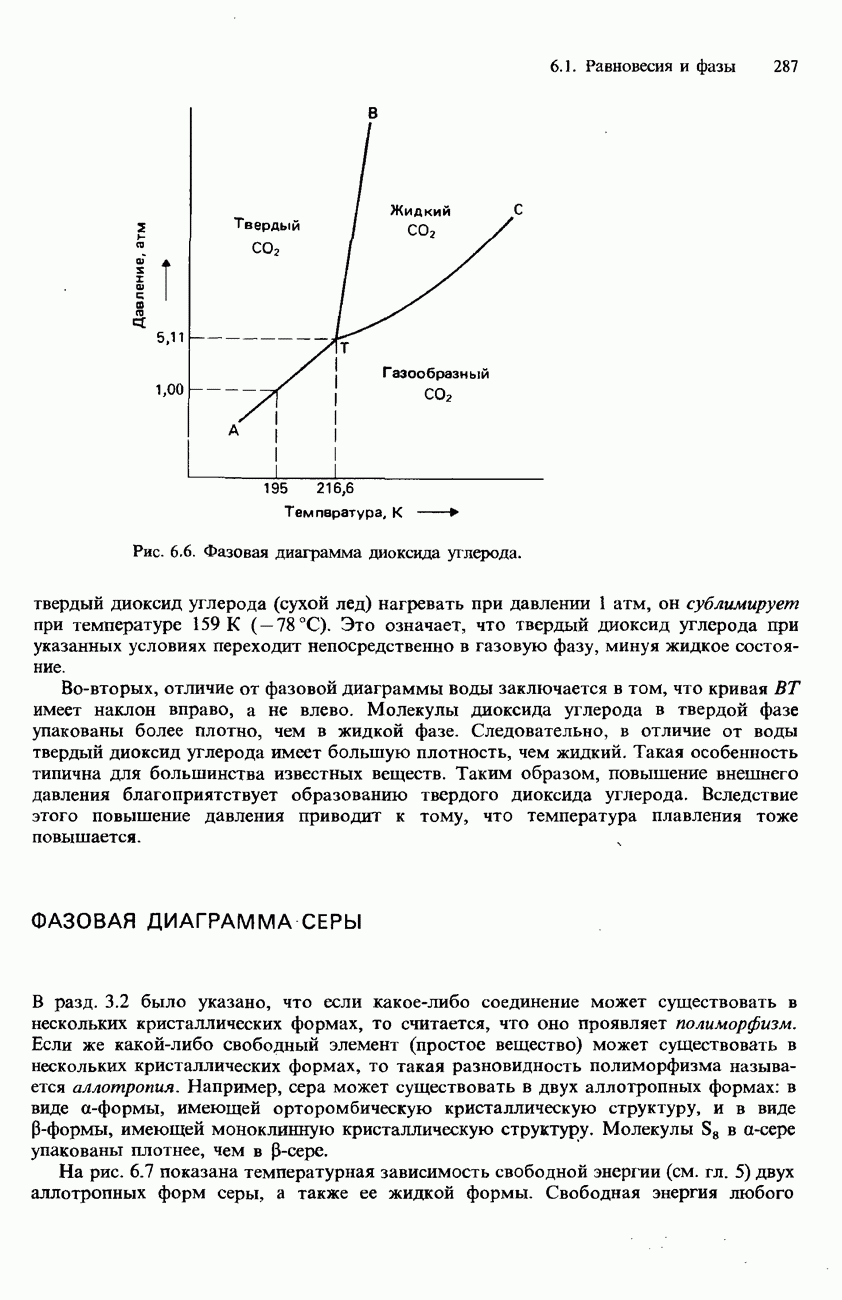
- ФАЗОВАЯ ДИАГРАММА ДИОКСИДА УГЛЕРОДА
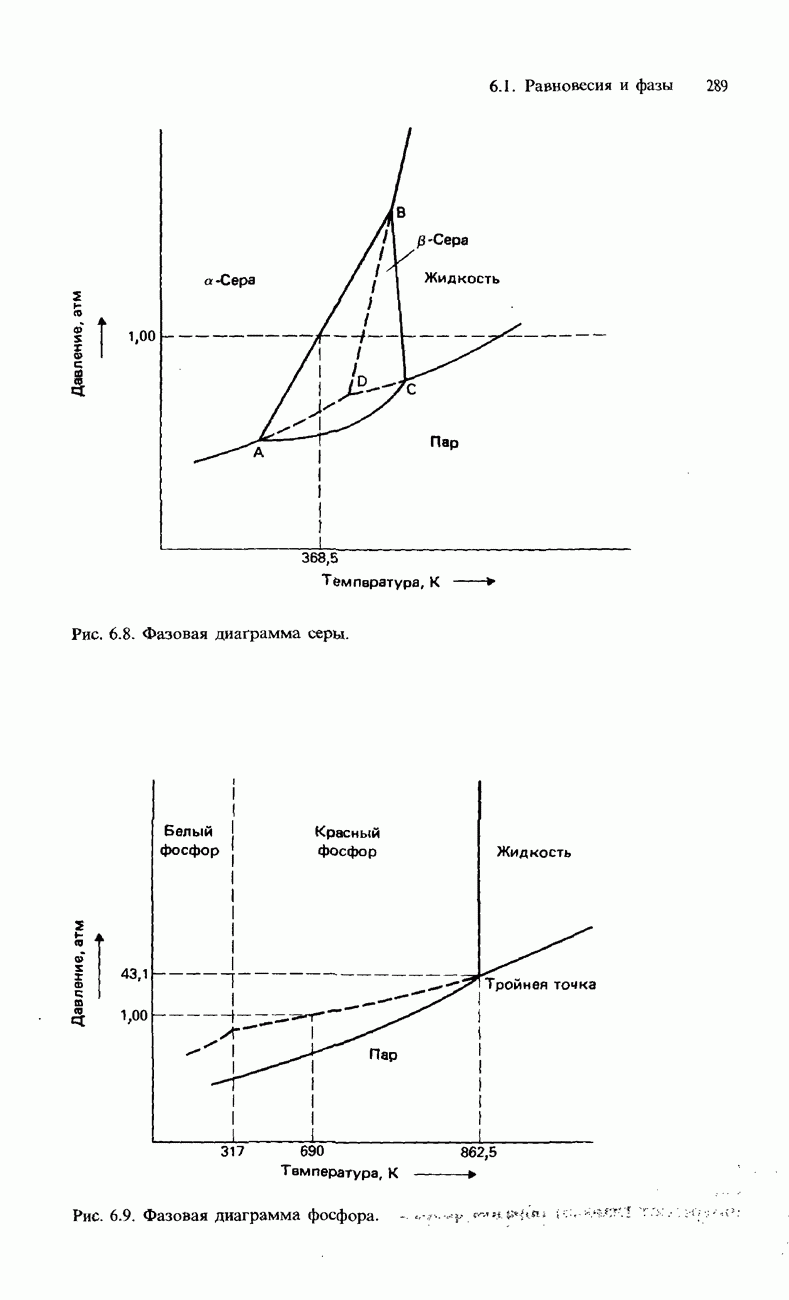
- ФАЗОВАЯ ДИАГРАММА СЕРЫ
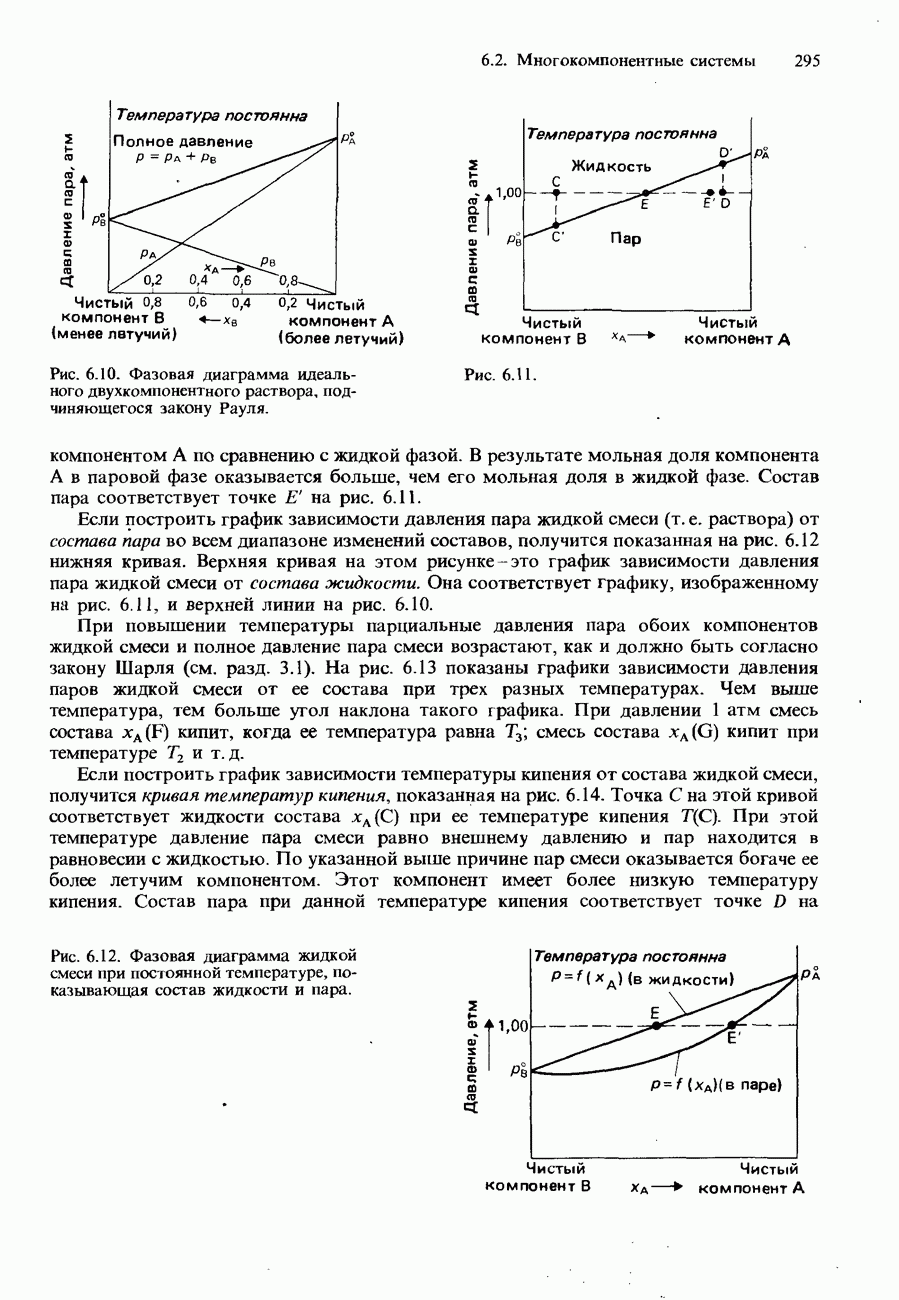
- ФАЗОВАЯ ДИАГРАММА ФОСФОРА
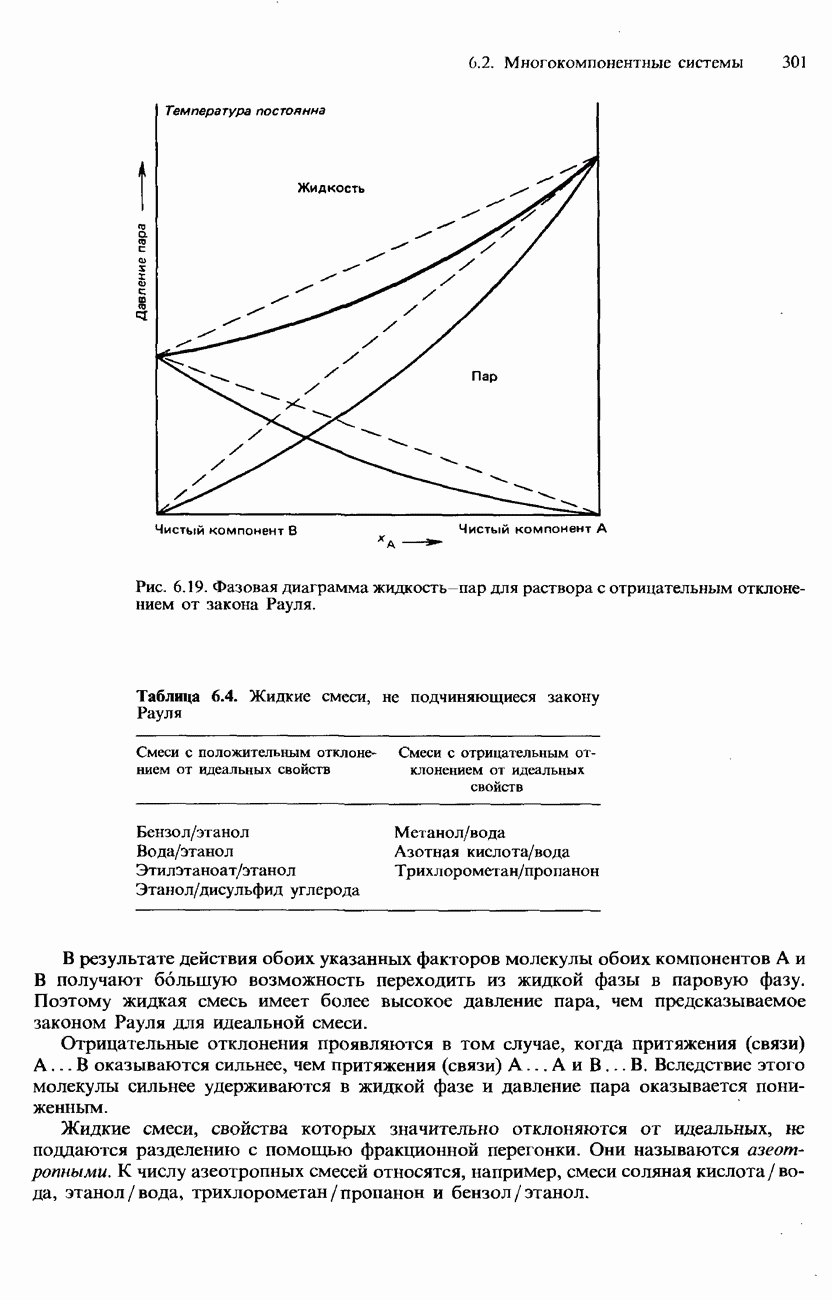
- 6.2. Многокомпонентные системы
- ДВУХКОМПОНЕНТНЫЕ ЖИДКИЕ СМЕСИ
- ПОЛНОСТЬЮ СМЕШИВАЮЩИЕСЯ ЖИДКОСТИ
- Фазовые диаграммы полностью смешивающихся жидкостей
- Фракционная перегонка
- Неидеальные растворы
- ЧАСТИЧНО СМЕШИВАЮЩИЕСЯ ЖИДКОСТИ
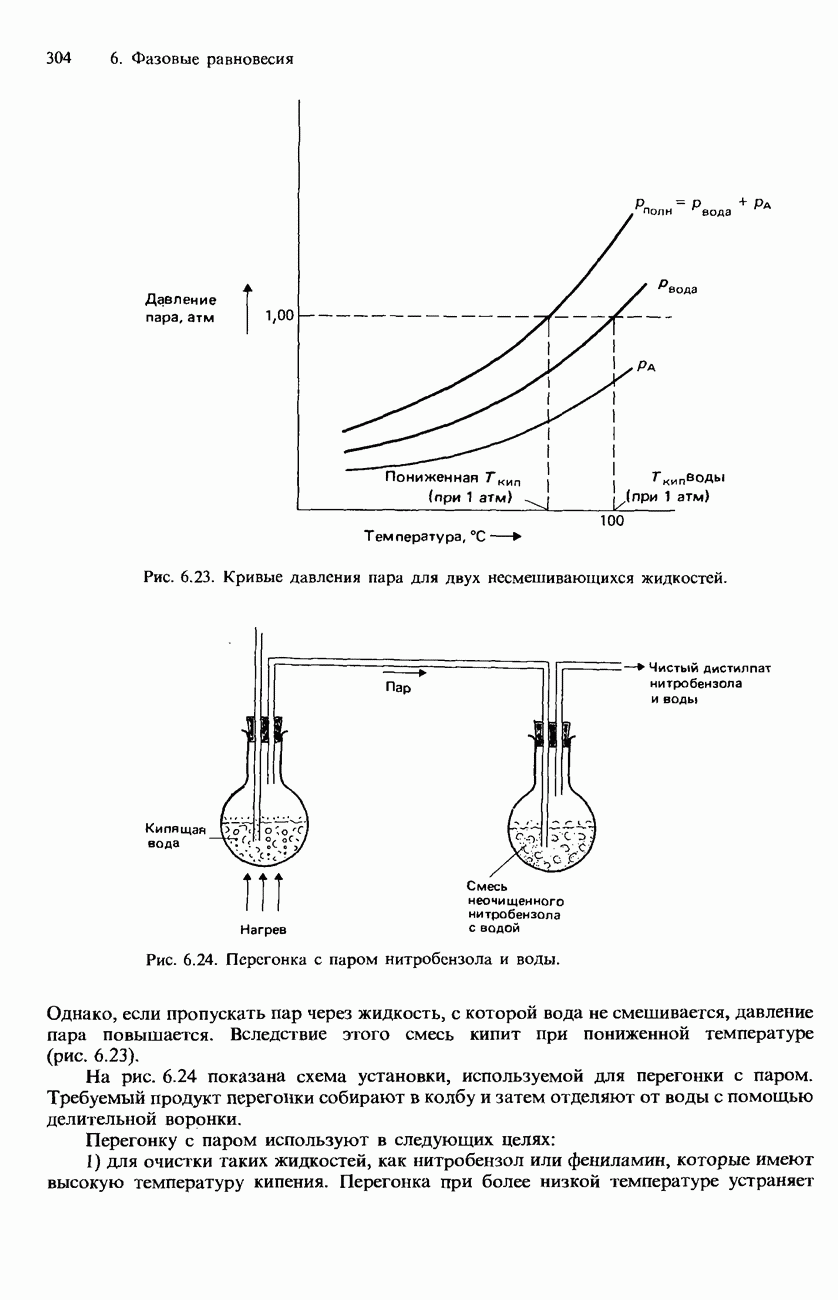
- НЕСМЕШИВАЮЩИЕСЯ ЖИДКОСТИ
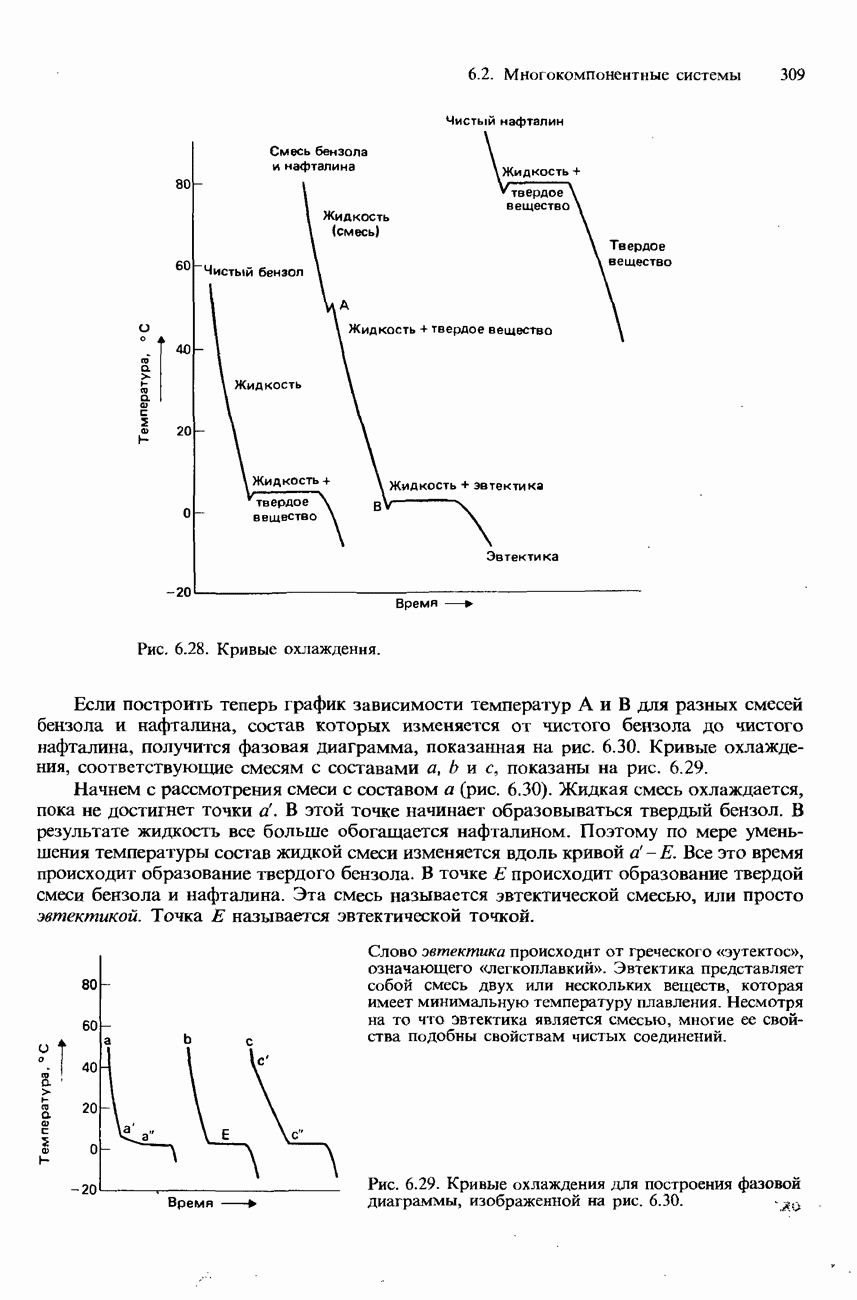
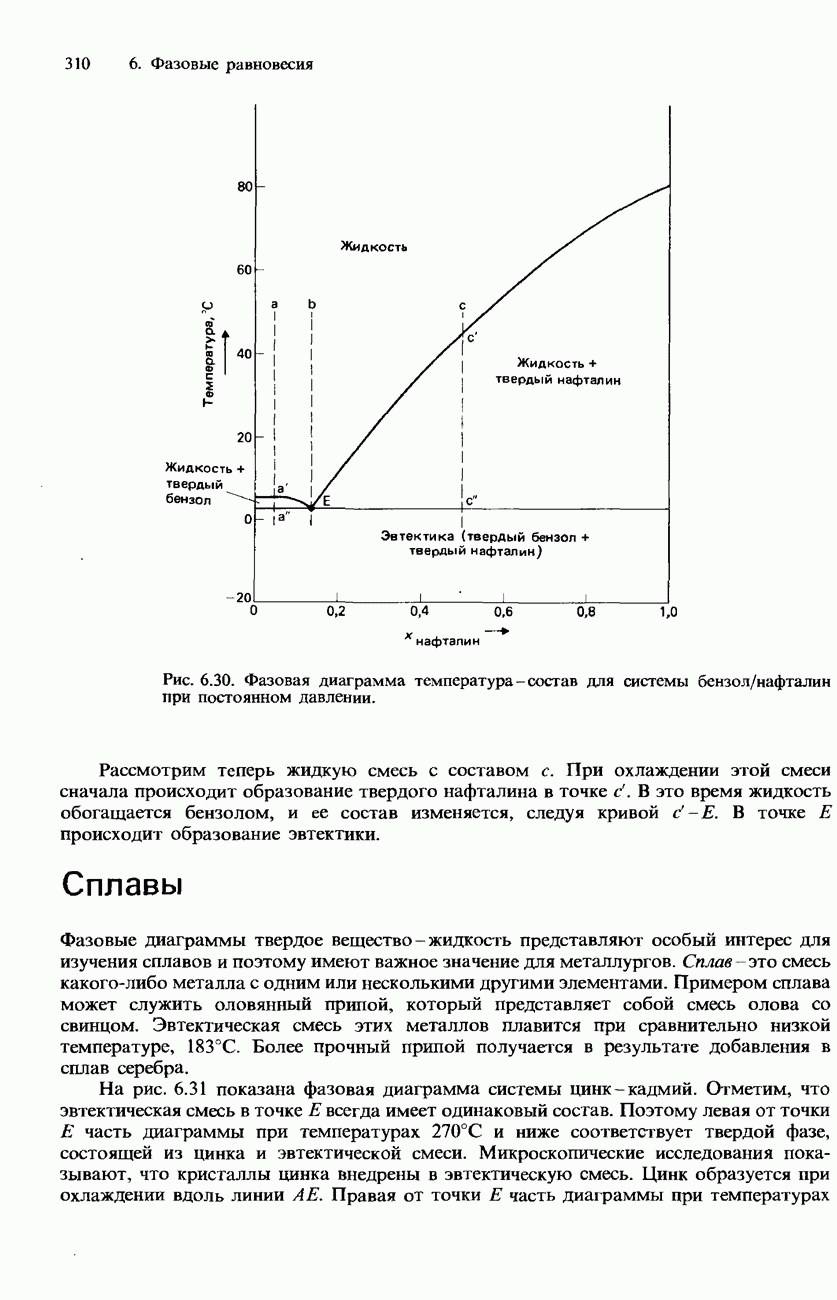
- РАВНОВЕСИЯ ТВЕРДОЕ ВЕЩЕСТВО-ЖИДКОСТЬ
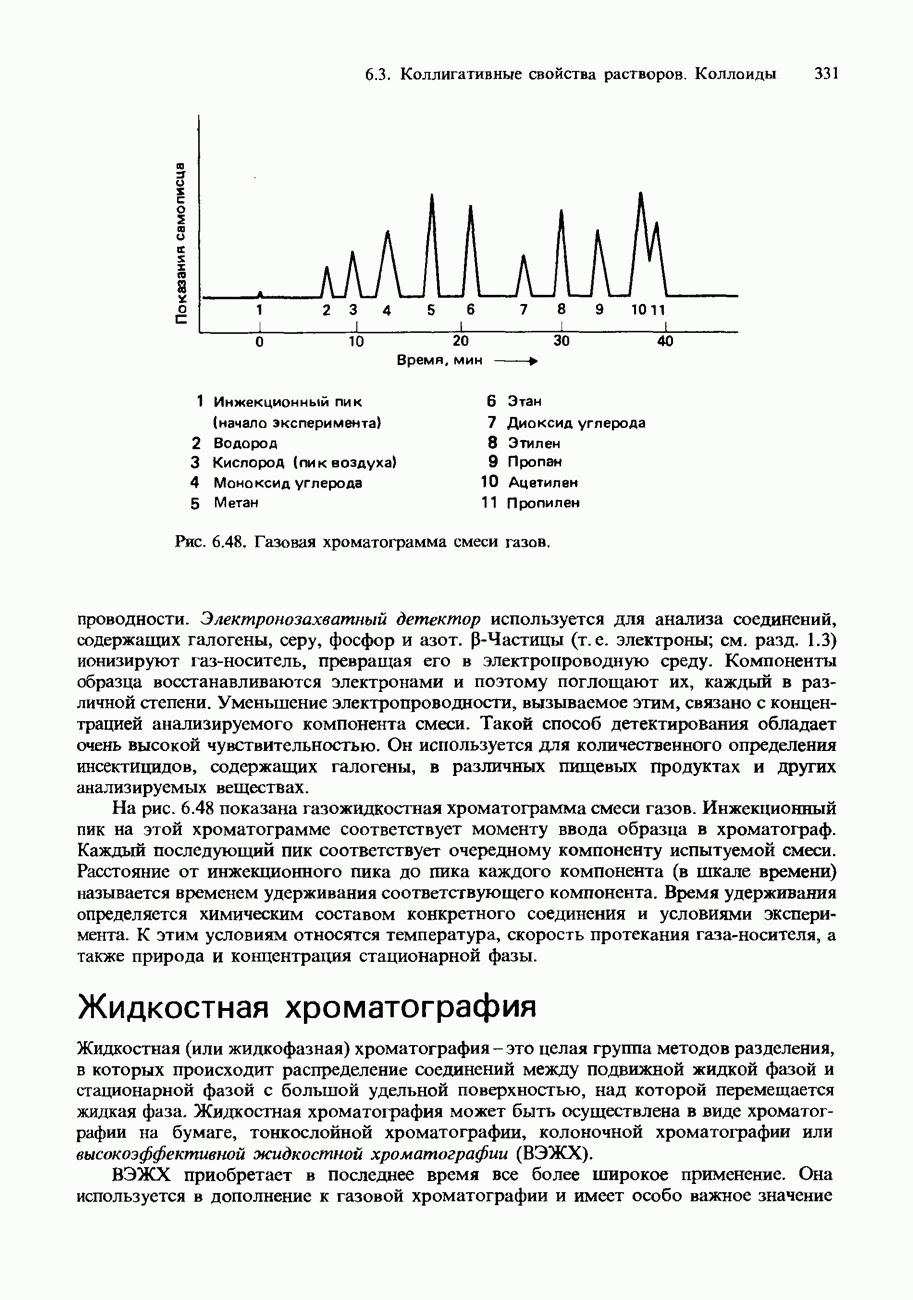
- 6.3. Коллигативные свойства растворов. Коллоиды Хроматография
- КОЛЛОИДЫ
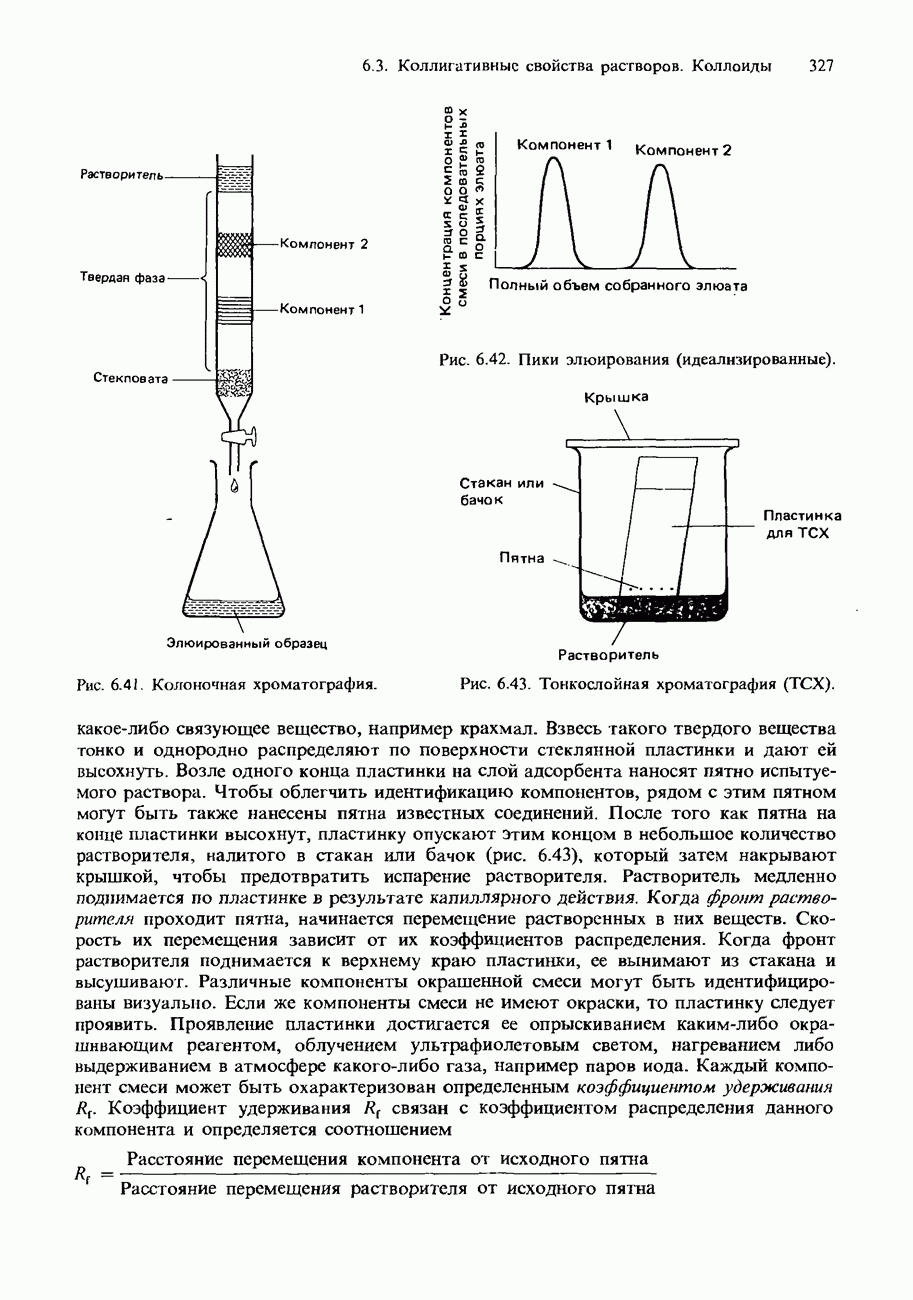
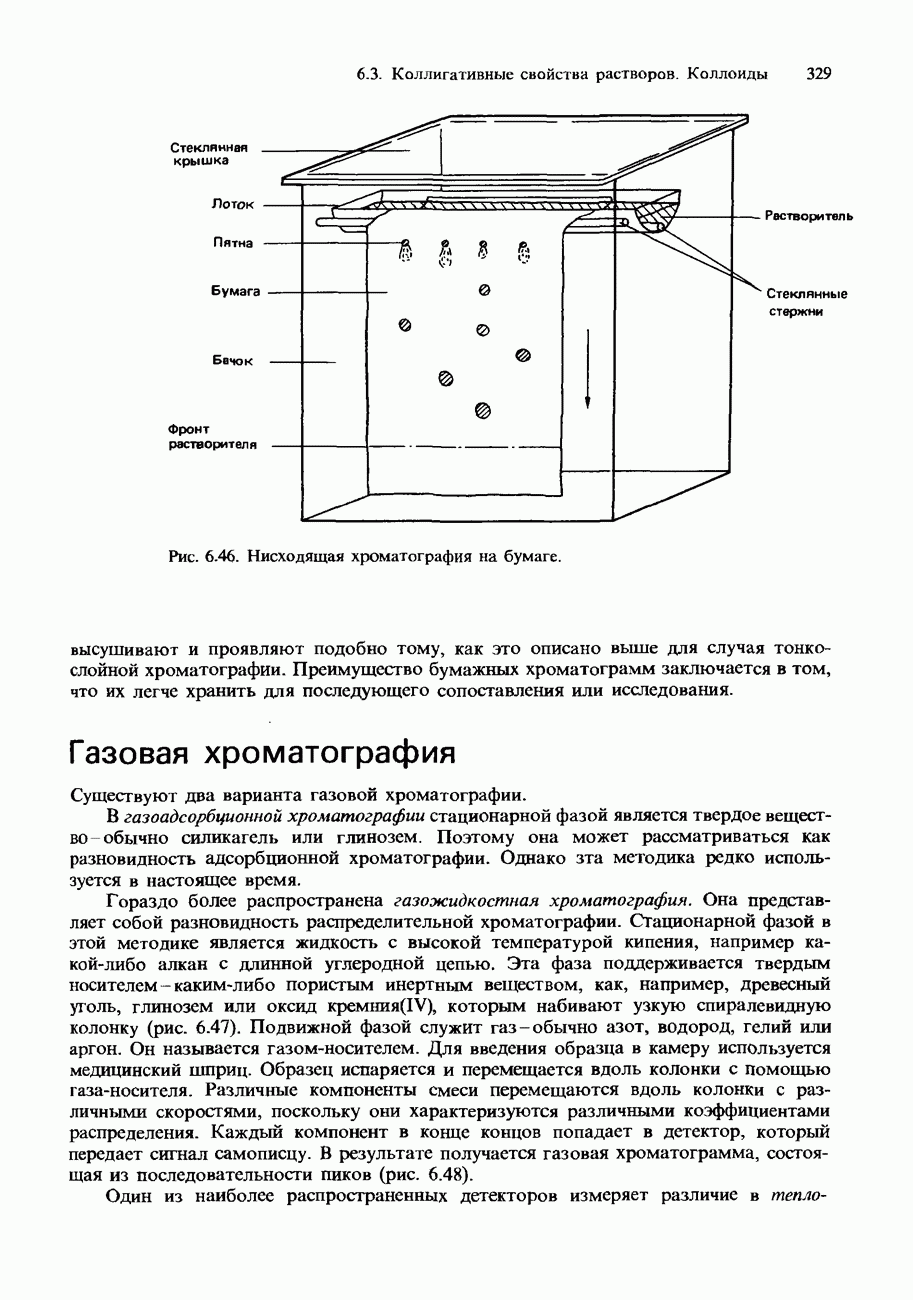
- ХРОМАТОГРАФИЯ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 7. ХИМИЧЕСКОЕ РАВНОВЕСИЕ
- 7.1. Константа равновесия
- ЗАКОН ДЕЙСТВУЮЩИХ МАСС
- ВЛИЯНИЕ УСЛОВИЙ ПРОТЕКАНИЯ РЕАКЦИИ НА ПОЛОЖЕНИЕ РАВНОВЕСИЯ
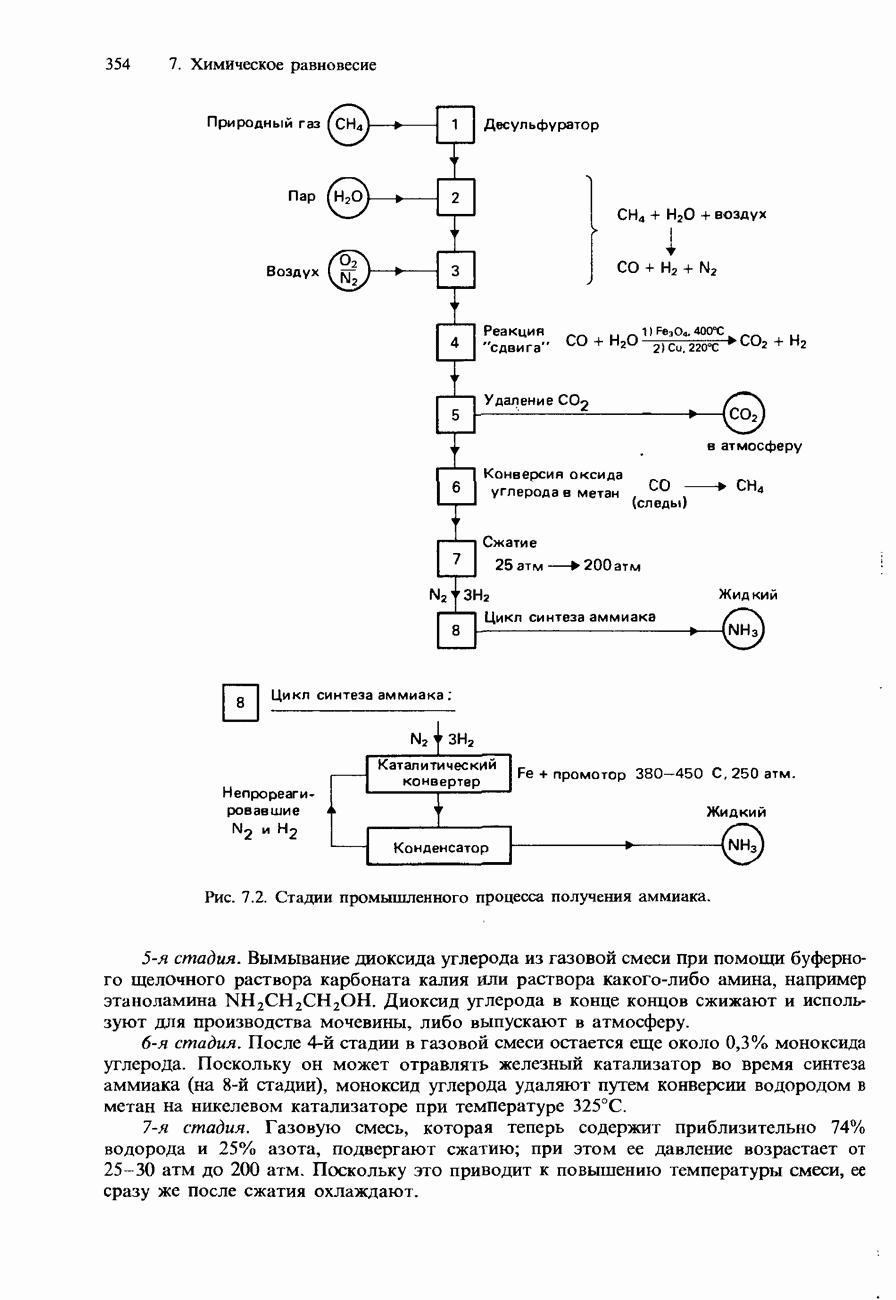
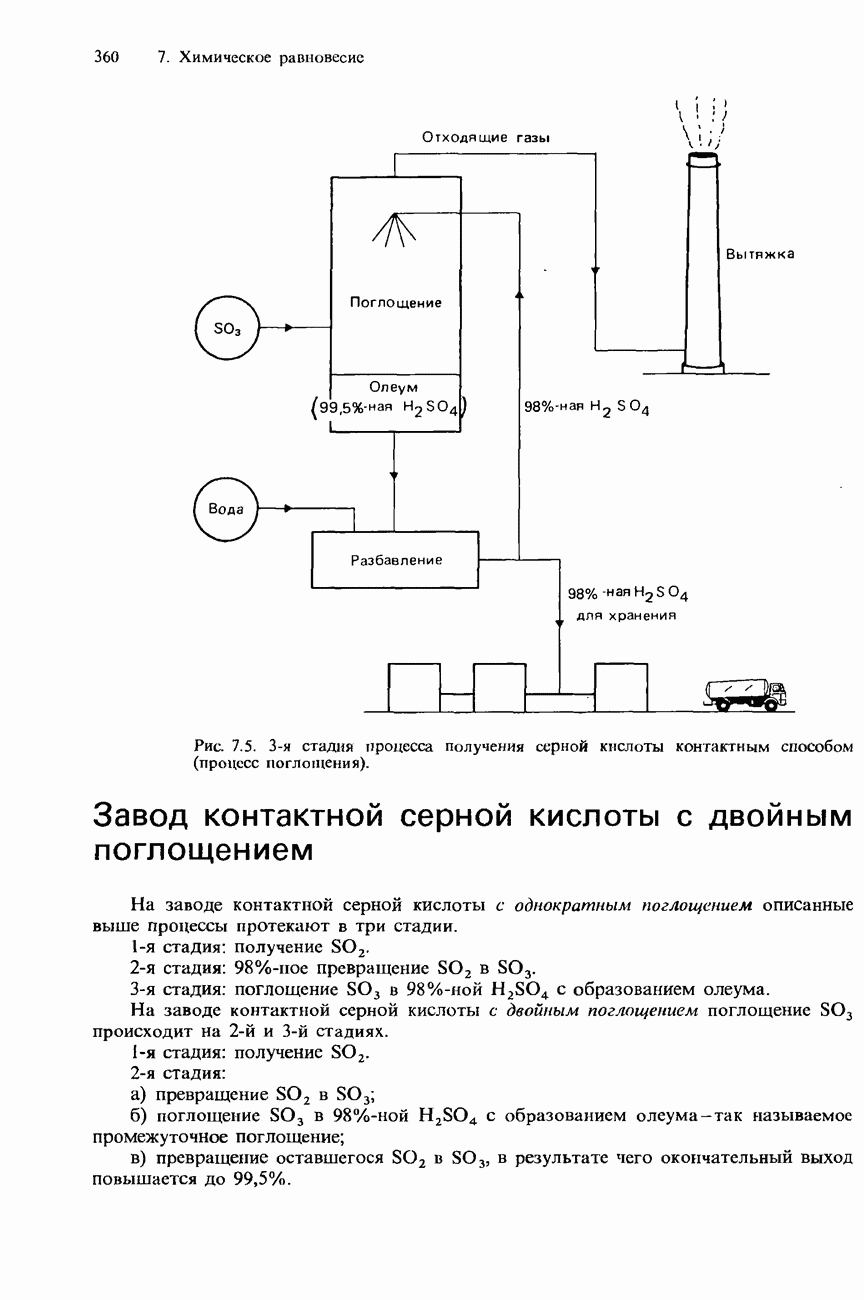
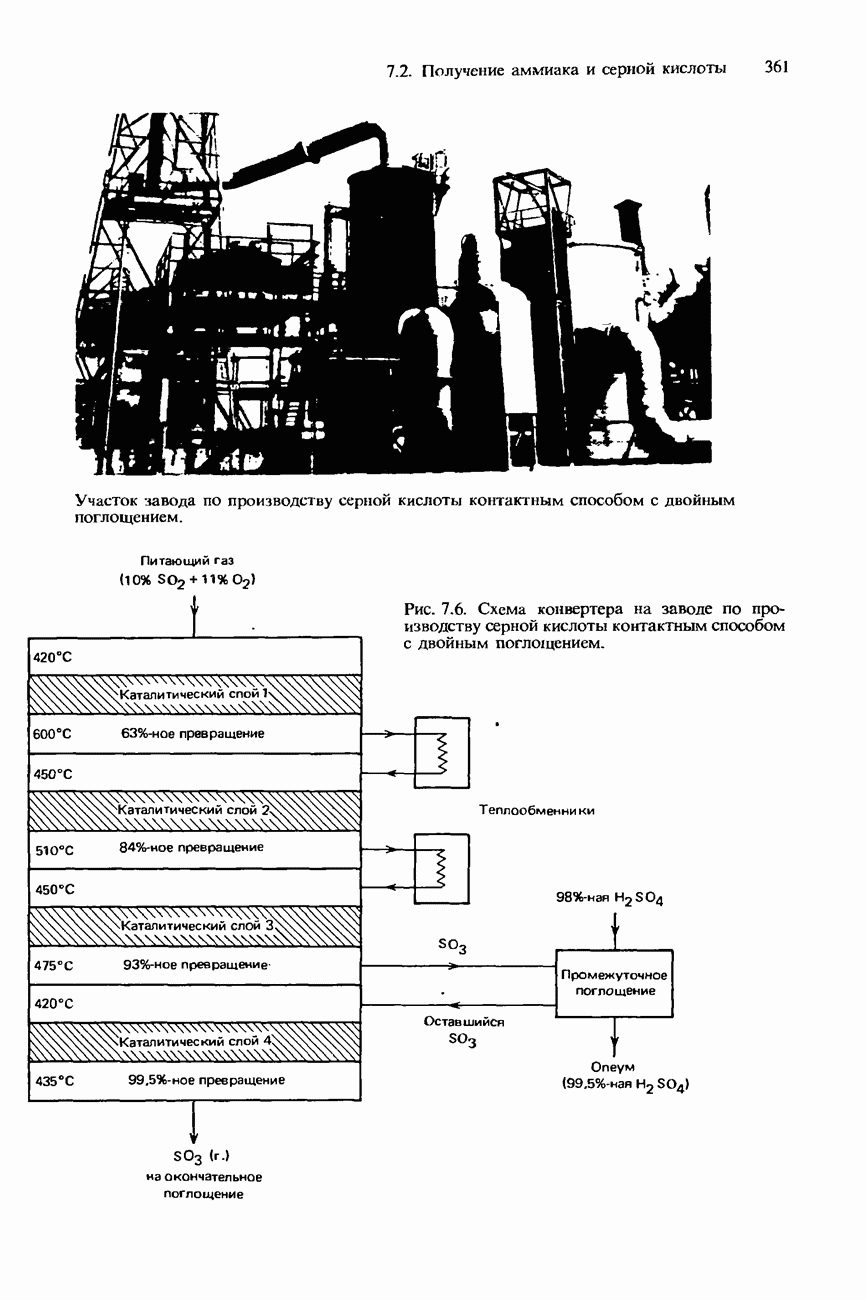
- 7.2. Получение аммиака и серной кислоты
- ПРОМЫШЛЕННОЕ ПОЛУЧЕНИЕ СЕРНОЙ КИСЛОТЫ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 8. ИОНЫ
- 8.1. Кислоты и основания
- ЭЛЕКТРОЛИТЫ
- КИСЛОТЫ И ОСНОВАНИЯ
- КОНСТАНТЫ ДИССОЦИАЦИИ
- ВОДОРОДНЫЙ ПОКАЗАТЕЛЬ pH ШКАЛА ЕГО ЗНАЧЕНИЙ
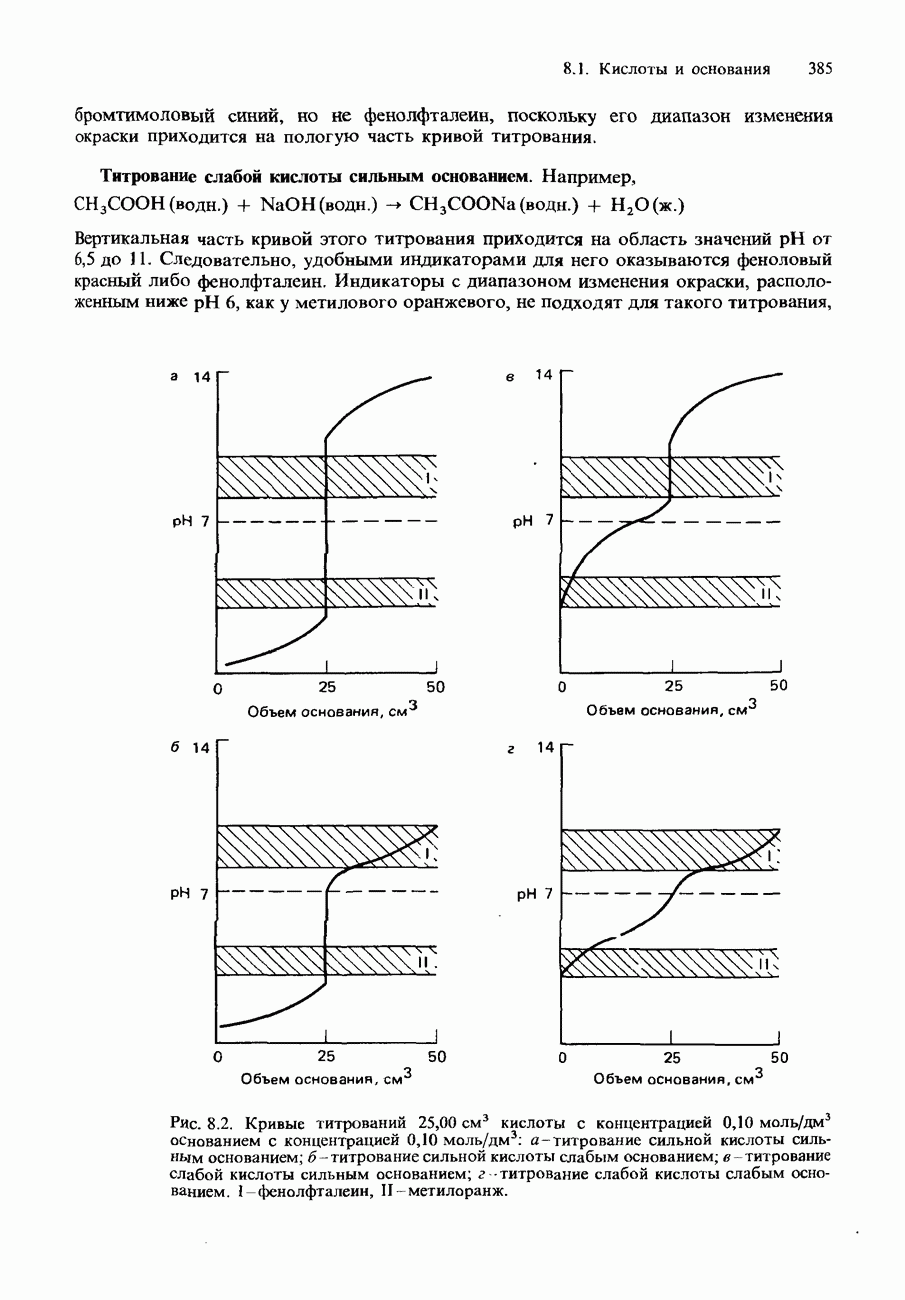
- КИСЛОТНО-ОСНОВНЫЕ ИНДИКАТОРЫ И ТИТРОВАНИЕ
- 8.2. Соли, растворимость и устойчивость
- БУФЕРНЫЕ РАСТВОРЫ
- РАСТВОРИМОСТЬ
- РАВНОВЕСИЯ С УЧАСТИЕМ КОМПЛЕКСНЫХ ИОНОВ
- ИОННЫЙ ОБМЕН
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 9. ХИМИЧЕСКАЯ КИНЕТИКА
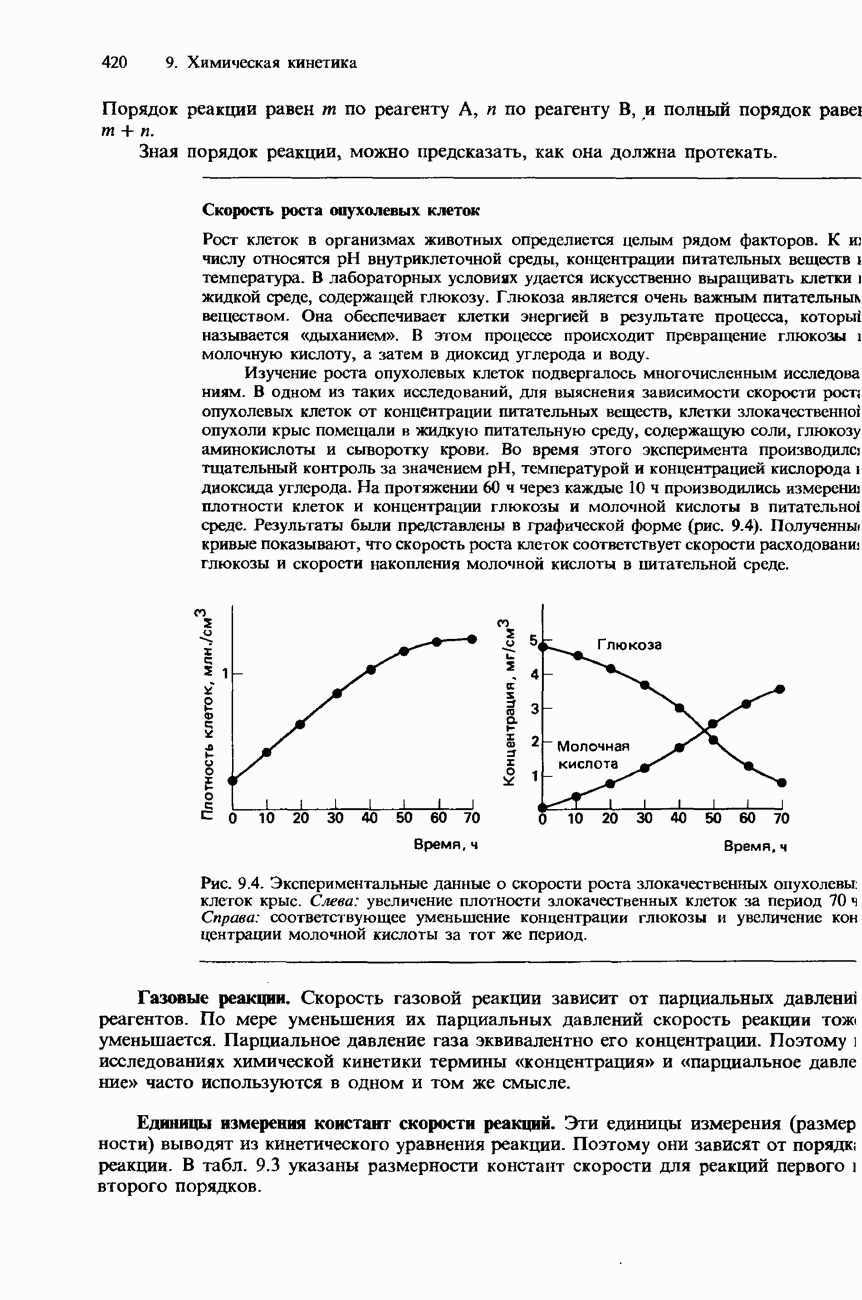
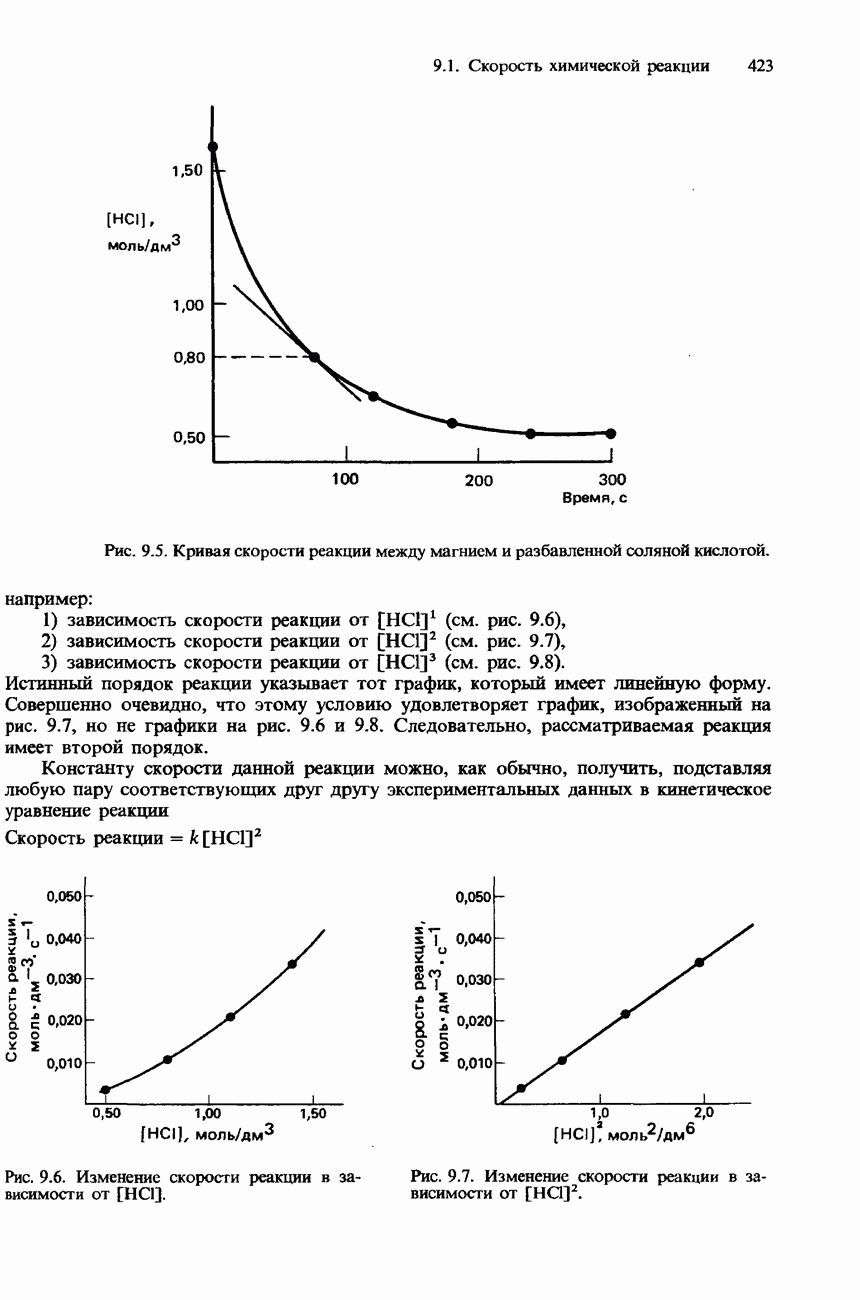
- 9.1. Скорость химической реакции
- МЕТОДЫ ИЗМЕРЕНИЯ СКОРОСТИ РЕАКЦИЙ
- СКОРОСТЬ РЕАКЦИИ И КОНЦЕНТРАЦИИ РЕАГЕНТОВ
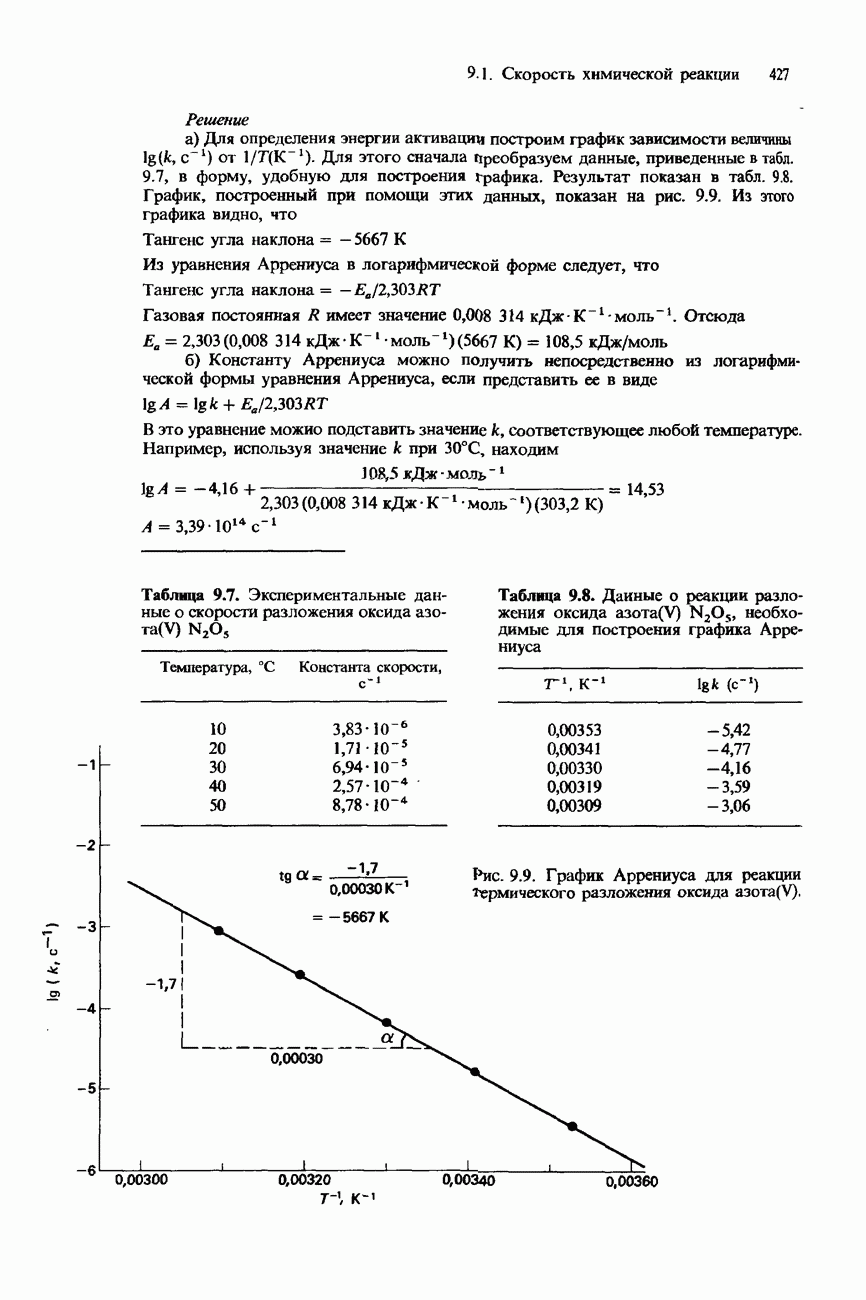
- ЗАВИСИМОСТЬ КОНСТАНТЫ СКОРОСТИ ОТ ТЕМПЕРАТУРЫ УРАВНЕНИЕ АРРЕНИУСА
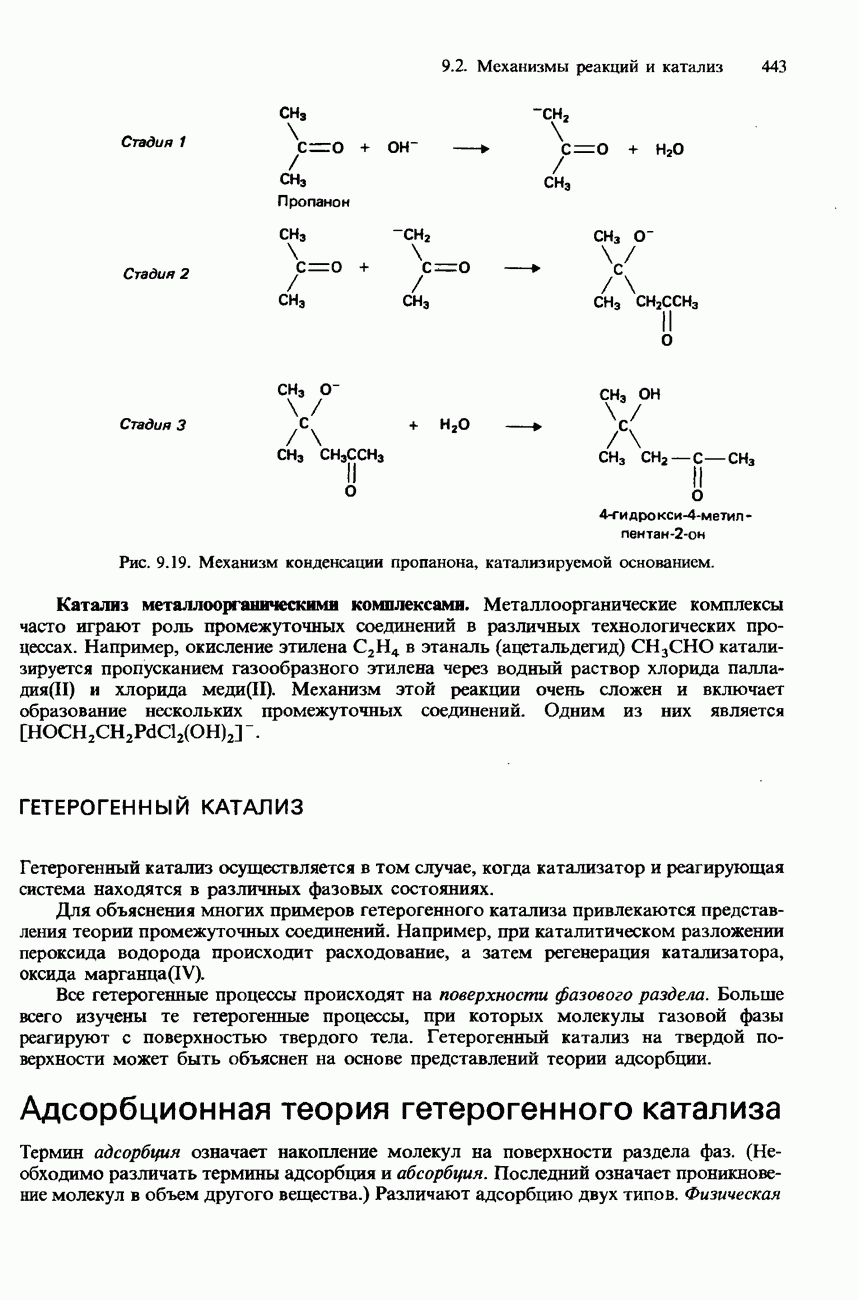
- 9.2. Механизмы реакций и катализ
- ТЕОРИЯ СТОЛКНОВЕНИЙ
- ТЕОРИЯ ПЕРЕХОДНОГО СОСТОЯНИЯ
- ЦЕПНЫЕ РЕАКЦИИ
- КАТАЛИЗ
- ТИПЫ КАТАЛИЗАТОРОВ
- ГОМОГЕННЫЙ КАТАЛИЗ
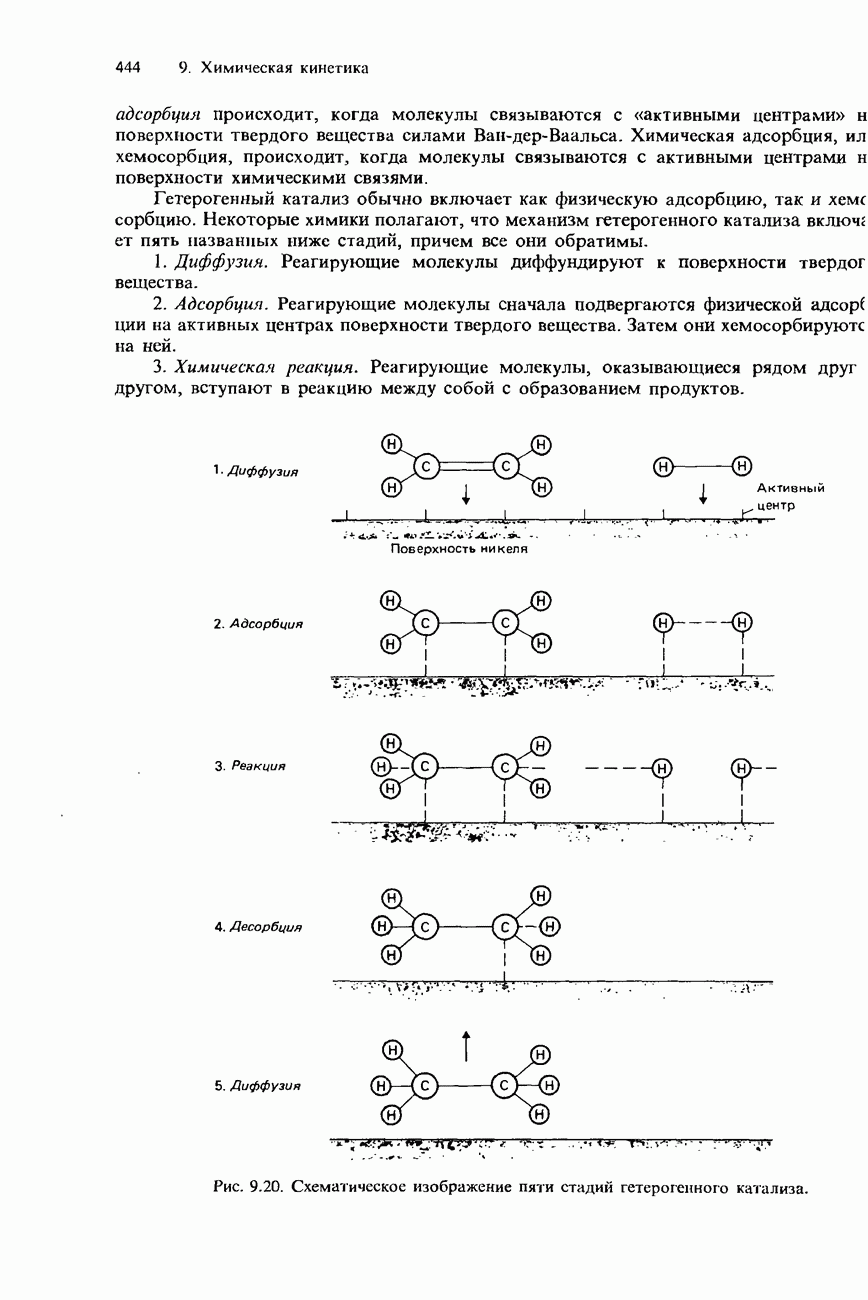
- ГЕТЕРОГЕННЫЙ КАТАЛИЗ
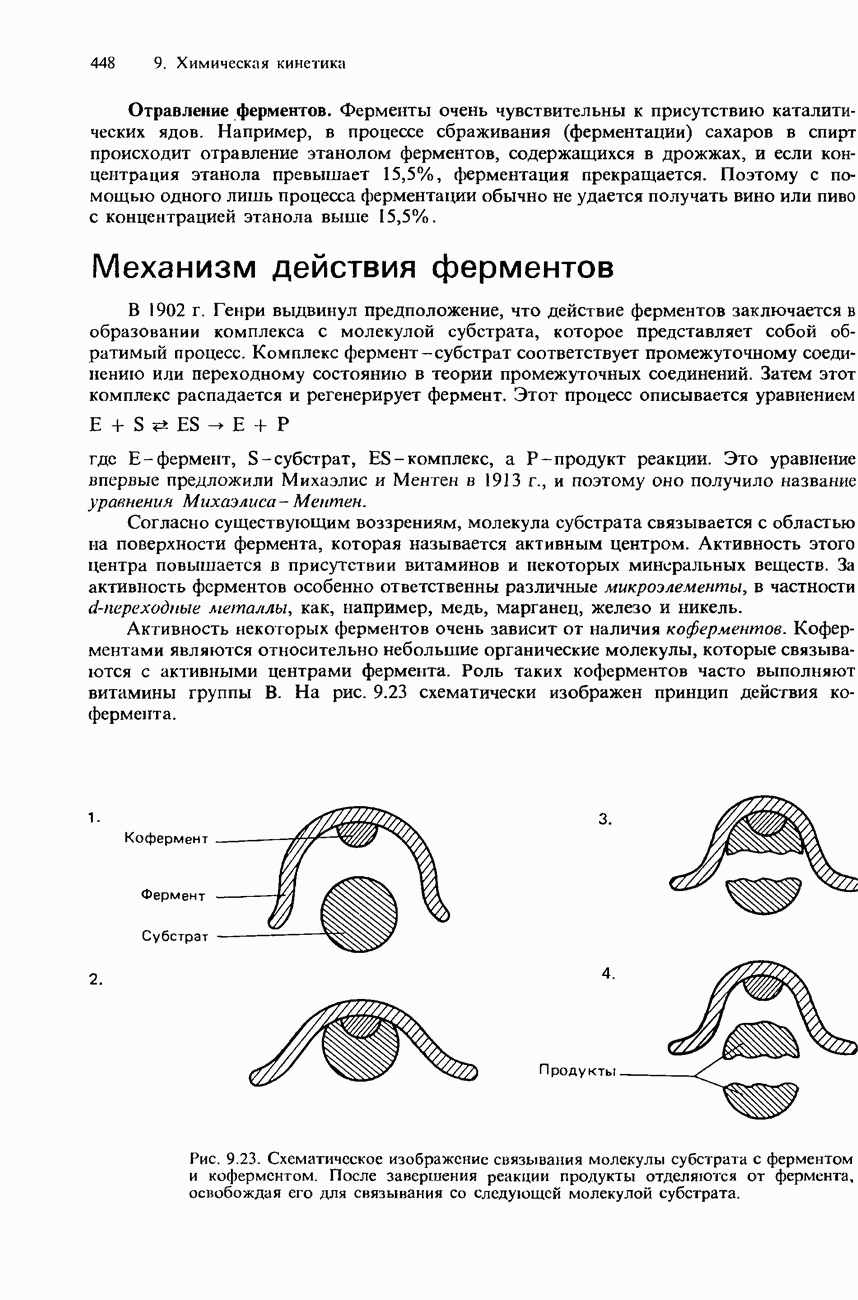
- ФЕРМЕНТАТИВНЫЙ КАТАЛИЗ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 10. ЭЛЕКТРОХИМИЯ
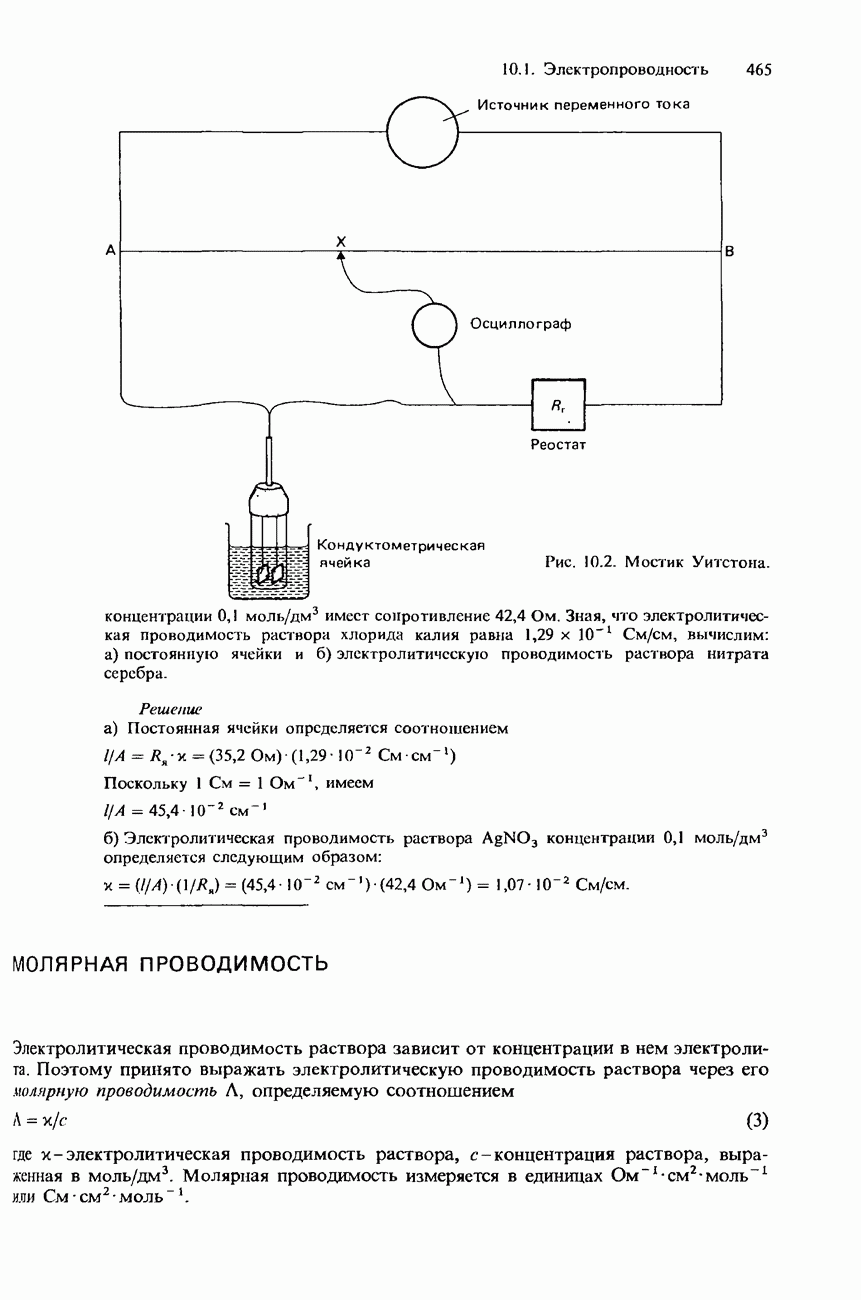
- 10.1. Электропроводность
- ПРОВОДНИКИ ЭЛЕКТРИЧЕСКОГО ТОКА И ЭЛЕКТРОПРОВОДНОСТЬ
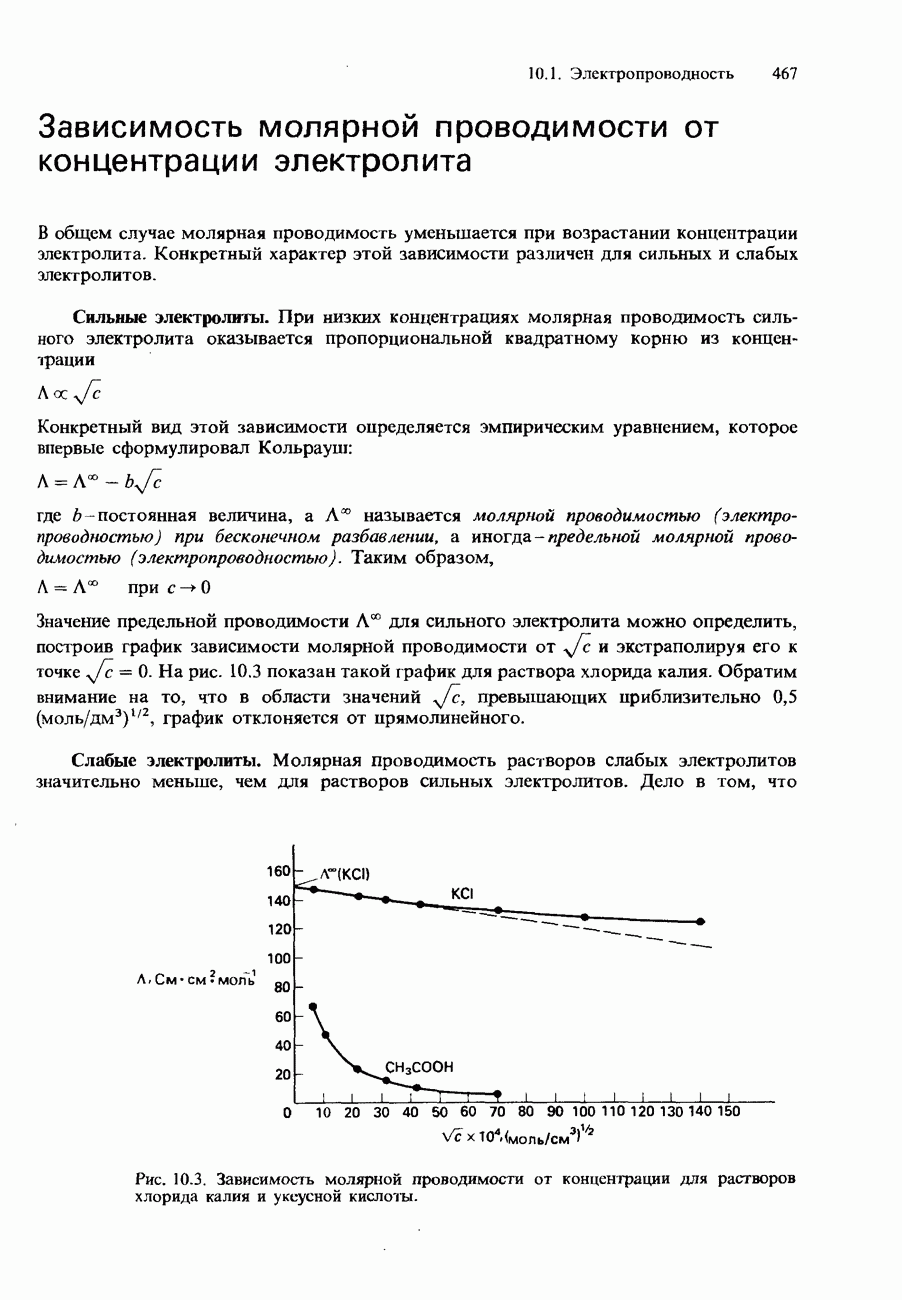
- МОЛЯРНАЯ ПРОВОДИМОСТЬ
- КОНДУКТОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- 10.2. Окислительно-восстановительные процессы
- ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫЕ РЕАКЦИИ
- ОПРЕДЕЛЕНИЕ СТЕХИОМЕТРИЧЕСКИХ КОЭФФИЦИЕНТОВ
- СТЕПЕНЬ ОКИСЛЕНИЯ
- ОКИСЛИТЕЛИ
- ВОССТАНОВИТЕЛИ
- ОКИСЛИТЕЛИ И ВОССТАНОВИТЕЛИ
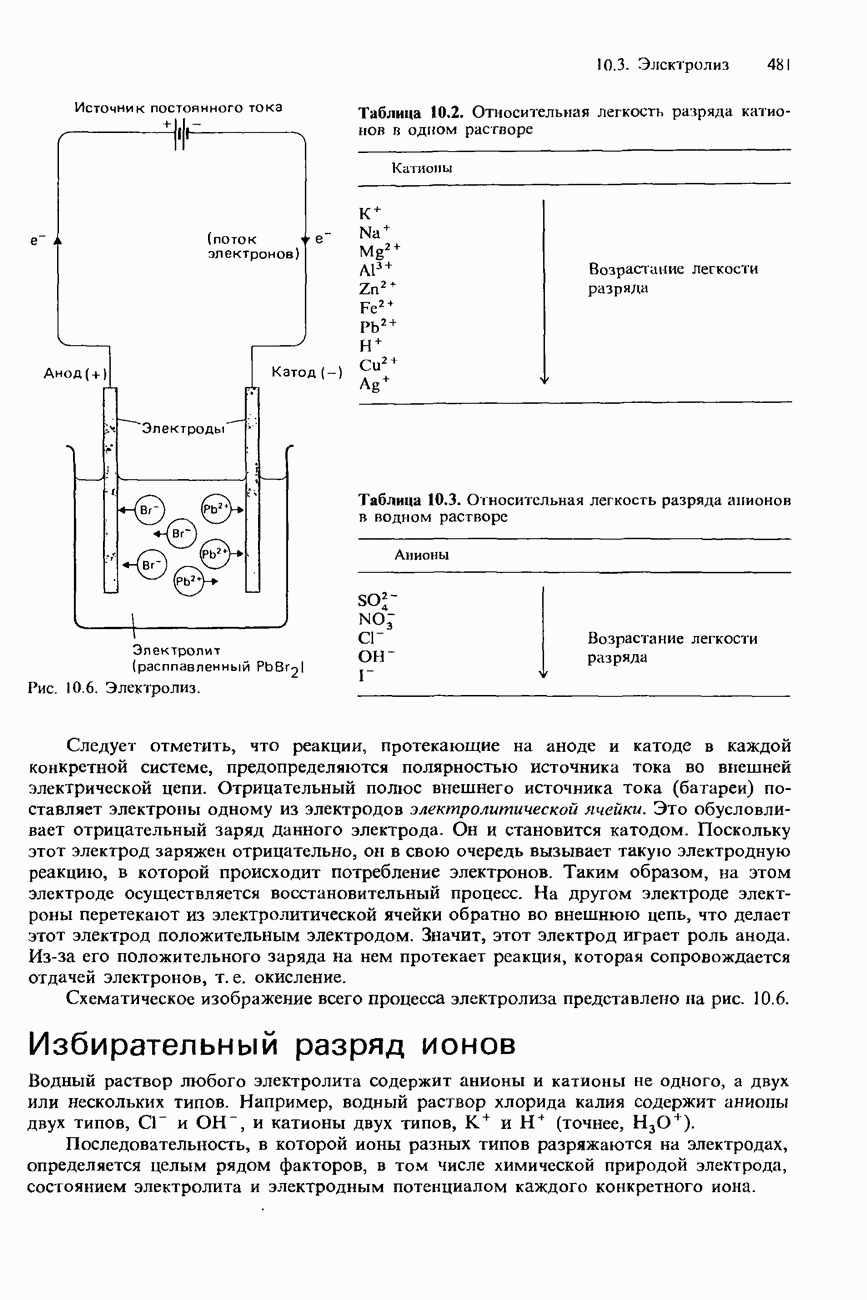
- 10.3. Электролиз
- ЗАКОНЫ ЭЛЕКТРОЛИЗА ФАРАДЕЯ
- ПРОМЫШЛЕННЫЕ ПРИМЕНЕНИЯ ЭЛЕКТРОЛИЗА
- 10.4. Химические источники тока
- СХЕМЫ ХИМИЧЕСКИХ ИСТОЧНИКОВ ТОКА
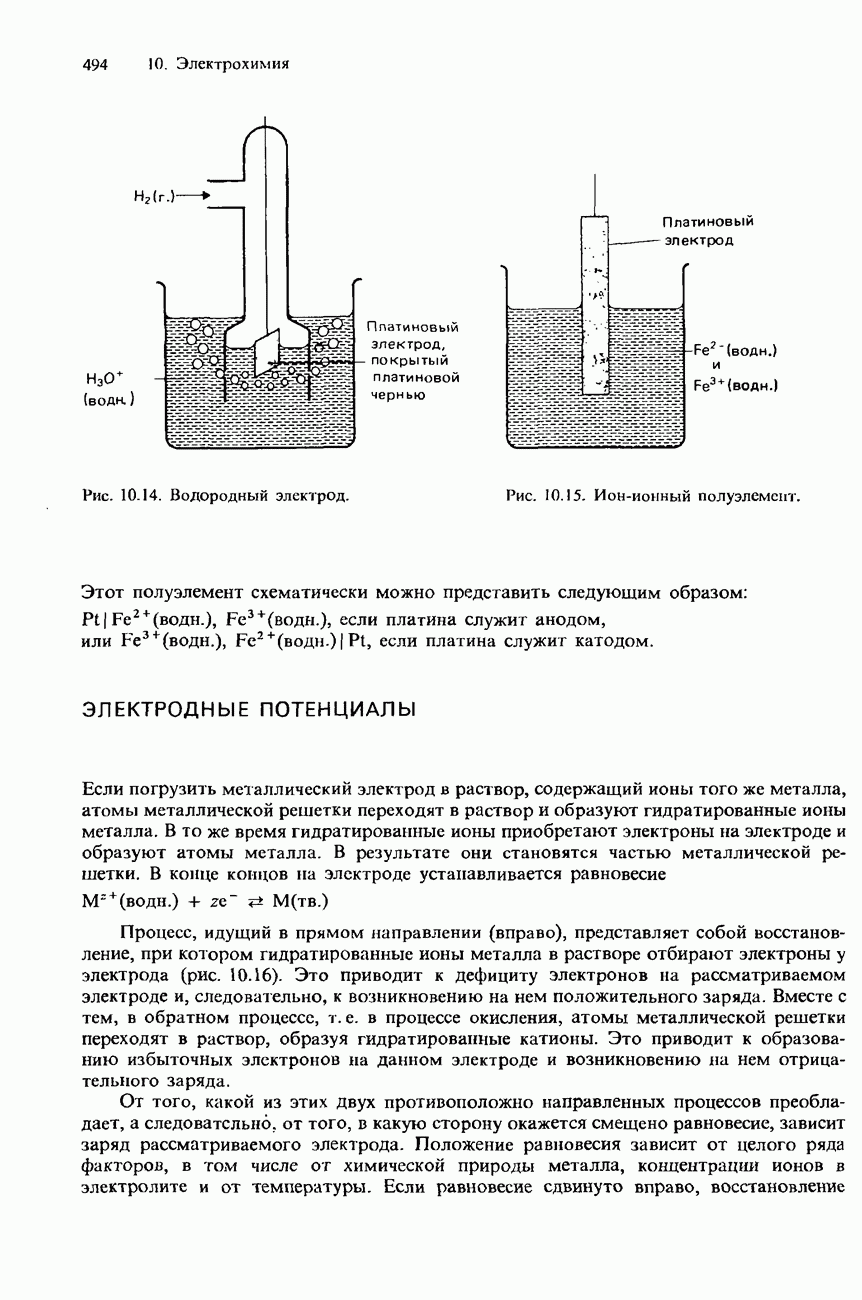
- ТИПЫ ПОЛУЭЛЕМЕНТОВ
- ЭЛЕКТРОДНЫЕ ПОТЕНЦИАЛЫ
- ЭЛЕКТРОДВИЖУЩАЯ СИЛА ХИМИЧЕСКИХ ИСТОЧНИКОВ ТОКА
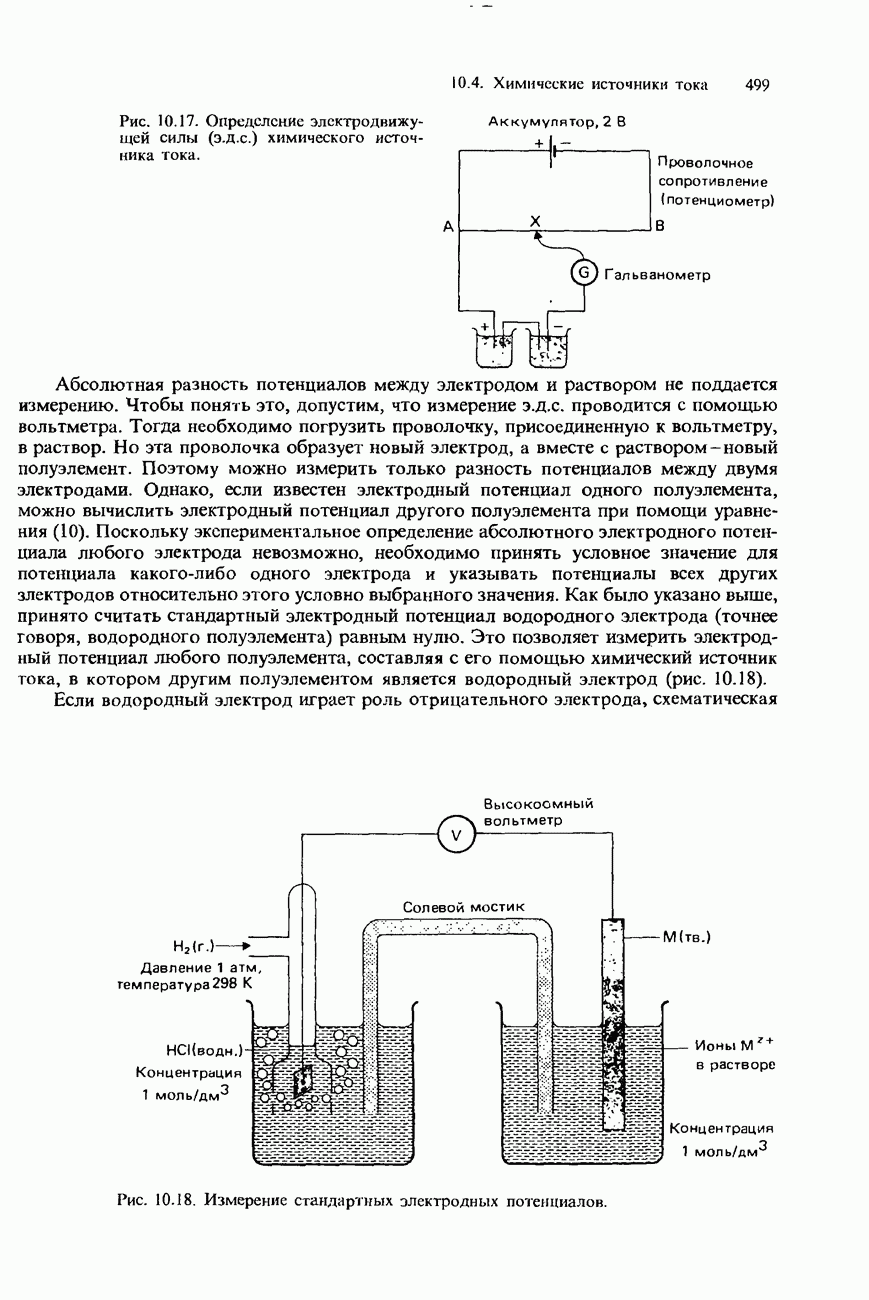
- ИЗМЕРЕНИЕ Э.Д.С. ХИМИЧЕСКИХ ИСТОЧНИКОВ ТОКА И ЭЛЕКТРОДНЫХ ПОТЕНЦИАЛОВ
- 10.5. Применения электрохимии
- ВЫЧИСЛЕНИЕ КОНСТАНТ РАВНОВЕСИЯ ДЛЯ ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫХ РЕАКЦИЙ
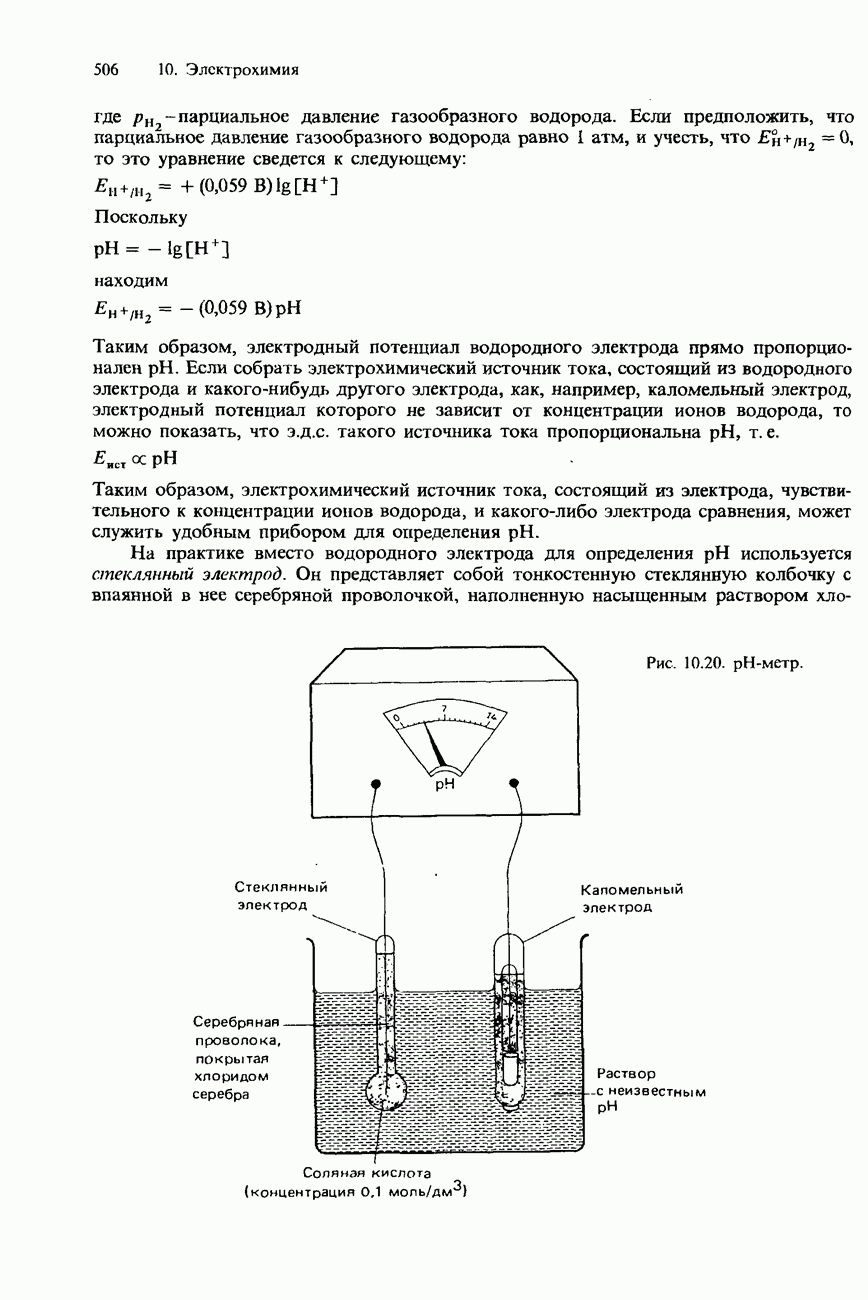
- ОПРЕДЕЛЕНИЕ pH РАСТВОРА
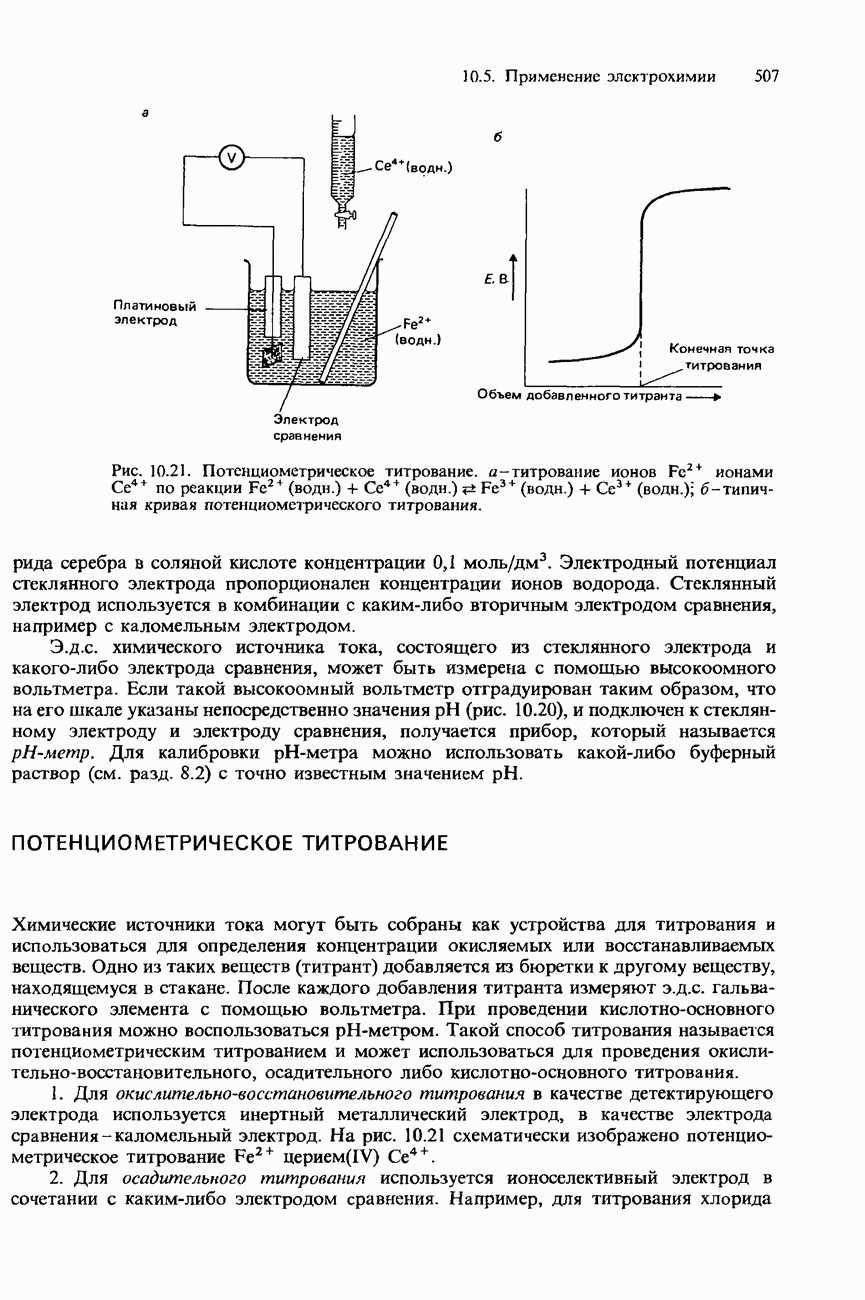
- ПОТЕНЦИОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- ОСУЩЕСТВИМОСТЬ ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫХ РЕАКЦИЙ
- ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ AG
- БАТАРЕИ И ПРОМЫШЛЕННЫЕ ИСТОЧНИКИ ТОКА
- МЕТАЛЛУРГИЯ
- КОРРОЗИЯ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ