| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
МОЛЯРНАЯ ПРОВОДИМОСТЬ
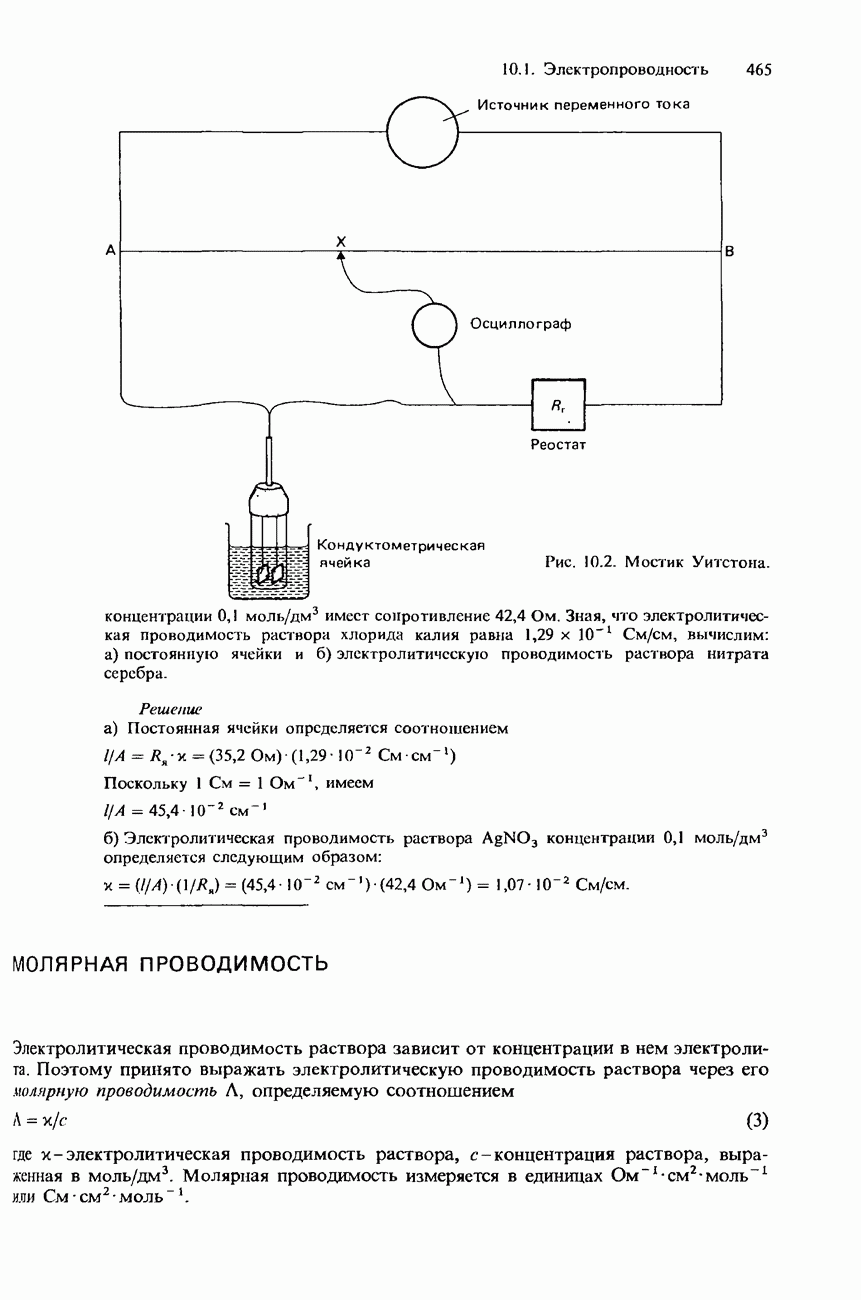
Электролитическая проводимость раствора зависит от концентрации в нем электролита. Поэтому принято выражать электролитическую проводимость раствора через его молярную проводимость А, определяемую соотношением

где  — электролитическая проводимость раствора, с - концентрация раствора, выраженная в моль/дм3. Молярная проводимость измеряется в единицах
— электролитическая проводимость раствора, с - концентрация раствора, выраженная в моль/дм3. Молярная проводимость измеряется в единицах 
Пример
Раствор хлорида калия концентрации 0,20 моль/дм3 имеет при 298 К электролитическую проводимость  См/см. Вычислим его молярную проводимость.
См/см. Вычислим его молярную проводимость.
Решение
Пользуясь уравнением (3), находим

Поскольку  то
то

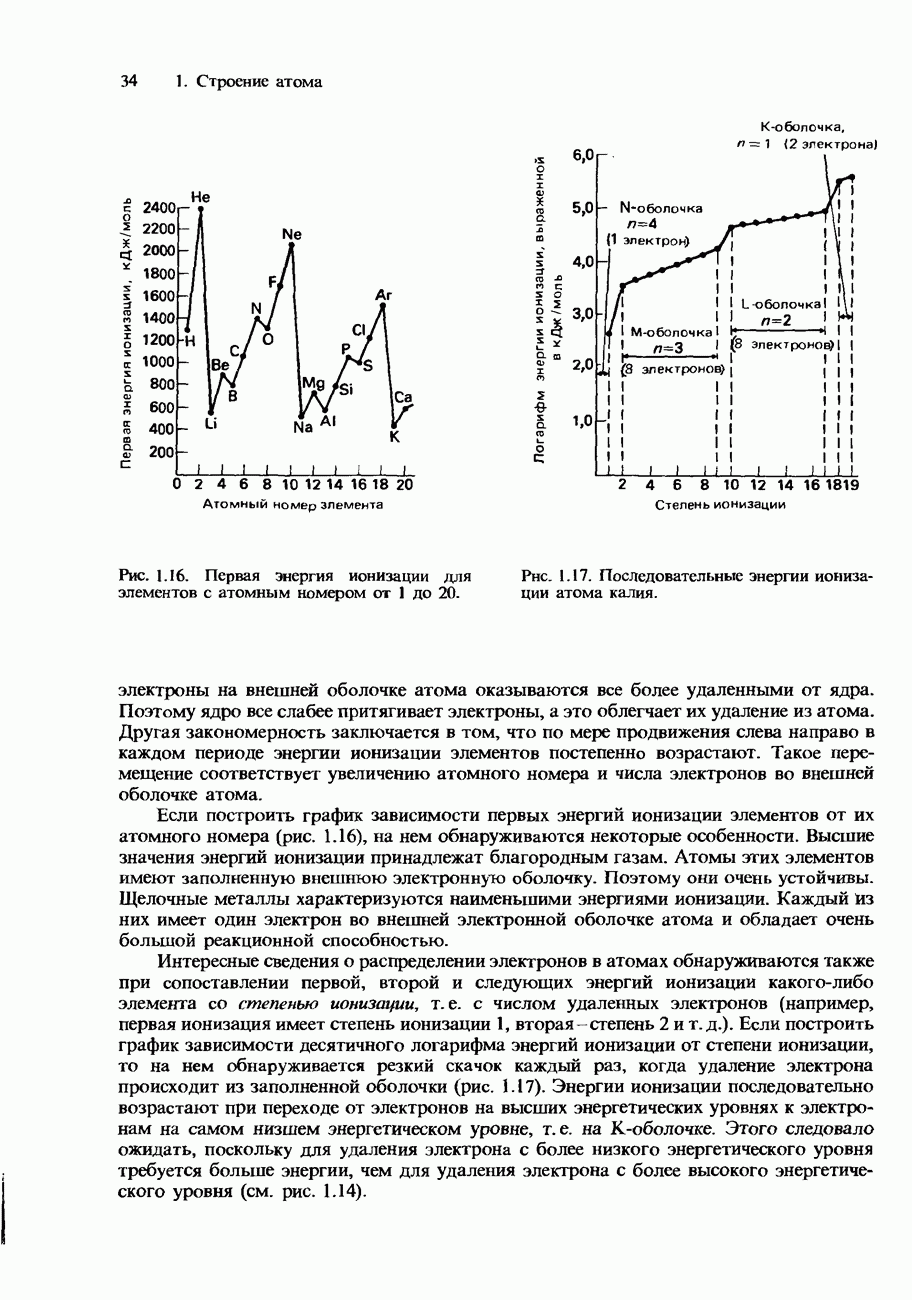
Зависимость молярной проводимости от концентрации электролита
В общем случае молярная проводимость уменьшается при возрастании концентрации электролита. Конкретный характер этой зависимости различен для сильных и слабых электролитов.
Сильные электролиты. При низких концентрациях молярная проводимость сильного электролита оказывается пропорциональной квадратному корню из концентрации

Конкретный вид этой зависимости определяется эмпирическим уравнением, которое впервые сформулировал Кольрауш:

где  - постоянная величина, а
- постоянная величина, а  называется молярной проводимостью (электропроводностью) при бесконечном разбавлении, а иногда - предельной молярной проводимостью (электропроводностью). Таким образом,
называется молярной проводимостью (электропроводностью) при бесконечном разбавлении, а иногда - предельной молярной проводимостью (электропроводностью). Таким образом,

Значение предельной проводимости  для сильного электролита можно определить, построив график зависимости молярной проводимости от
для сильного электролита можно определить, построив график зависимости молярной проводимости от  и экстраполируя его к точке
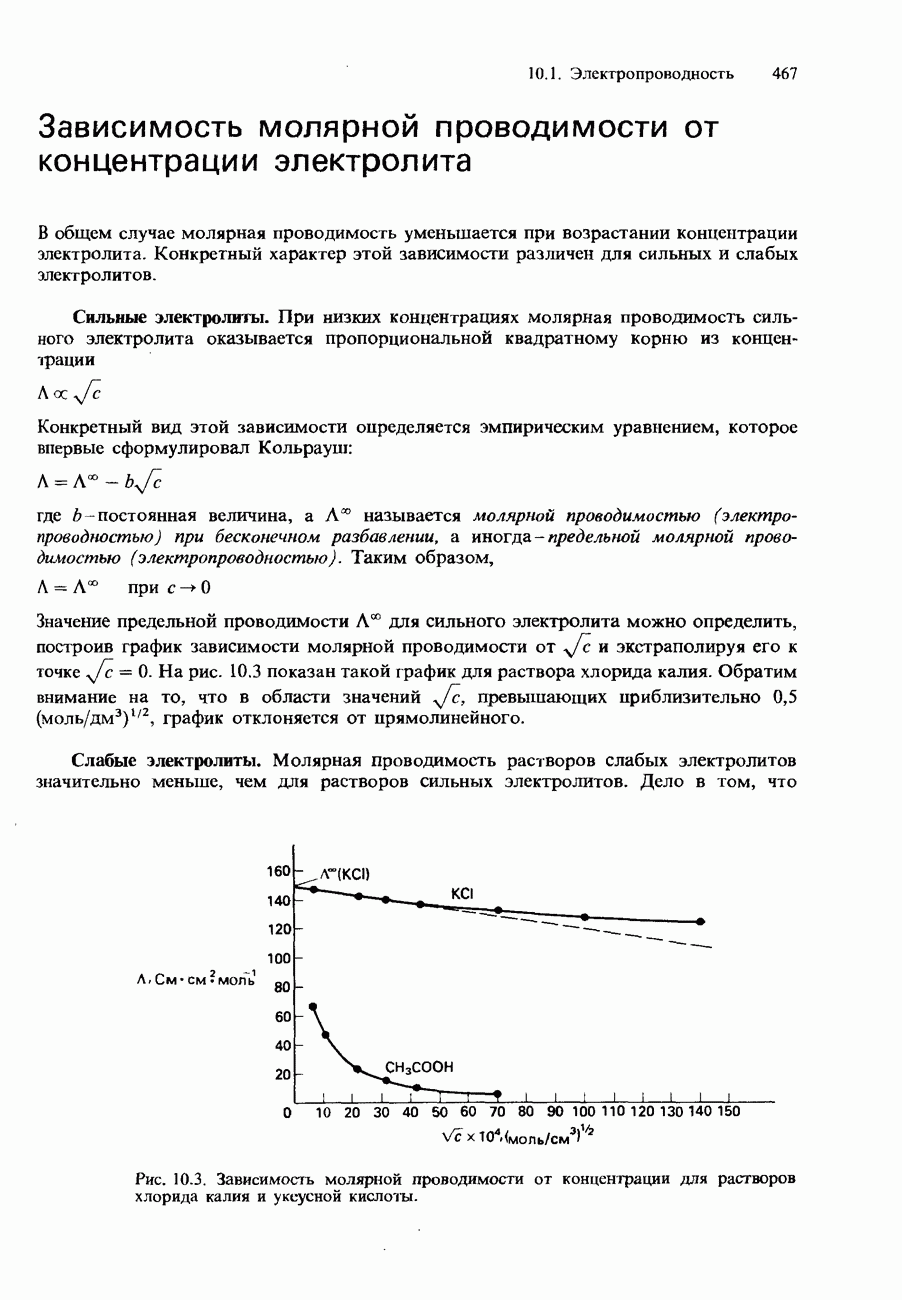
и экстраполируя его к точке  . На рис. 10.3 показан такой график для раствора хлорида калия. Обратим внимание на то, что в области значений
. На рис. 10.3 показан такой график для раствора хлорида калия. Обратим внимание на то, что в области значений  превышающих приблизительно
превышающих приблизительно  график отклоняется от прямолинейного.
график отклоняется от прямолинейного.
Слабые электролиты. Молярная проводимость растворов слабых электролитов значительно меньше, чем для растворов сильных электролитов. Дело в том, что

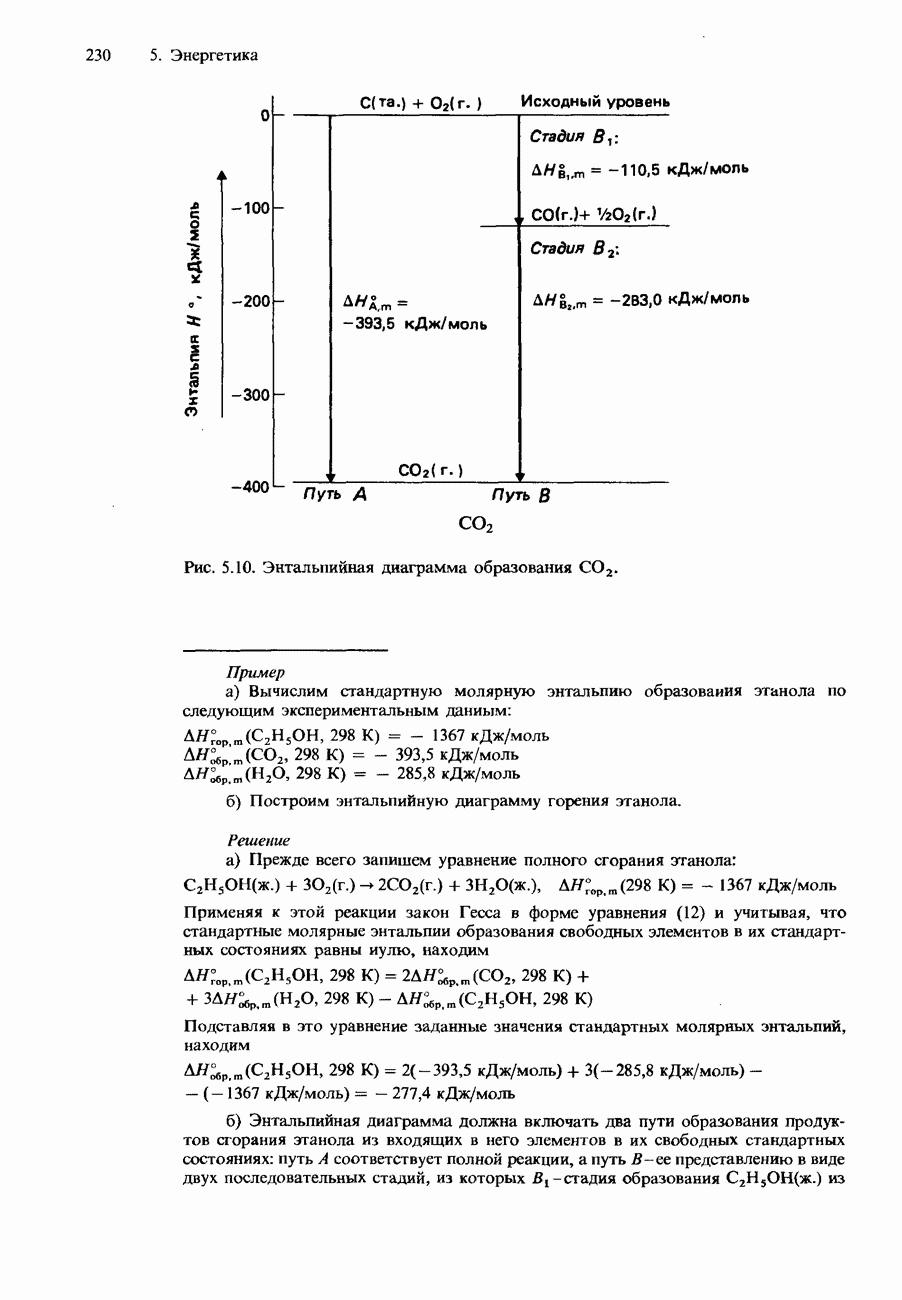
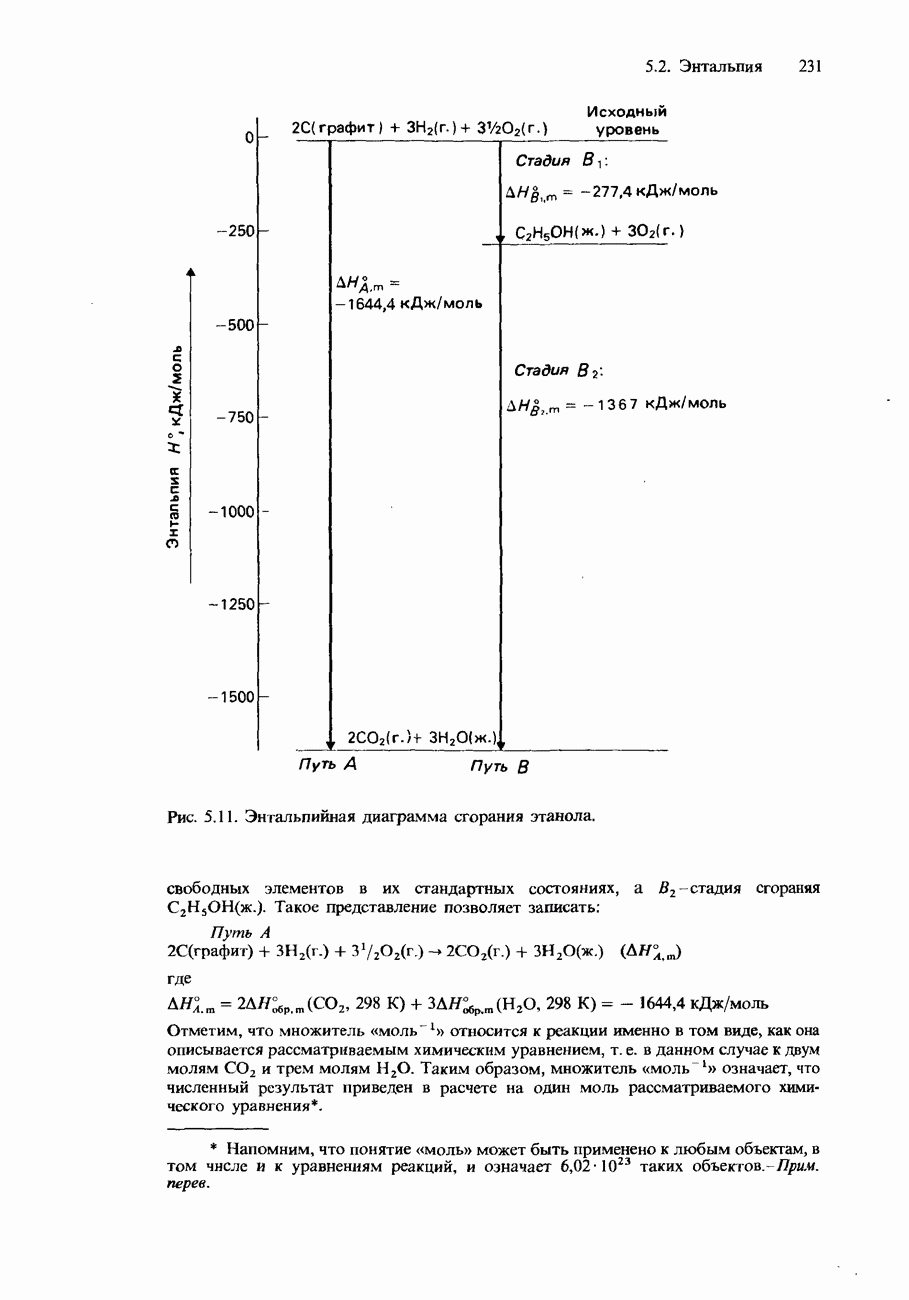
Рис. 10.3. Зависимость молярной проводимости от концентрации для растворов хлорида калия и уксусной кислоты.
Таблица 10.1. Молярные проводимости при бесконечном разбавлении для пар сильных электролитов с общим ионом

молярная проводимость раствора зависит от количества присутствующих в нем ионов. Слабые электролиты даже при низких концентрациях характеризуются малой степенью диссоциации. Но все же, когда концентрация слабого электролита становится очень Низкой, степень его ионизации резко возрастает. Это приводит к соответственному возрастанию молярной проводимости. На рис. 10.3 показан график зависимости молярной проводимости от квадратного корня из концентрации уксусной кислоты. Этот график имеет нелинейный характер и показывает, что слабые электролиты не подчиняются уравнению Кольрауша.
Ионная подвижность. В 1875 г. Кольрауш проводил сопоставление молярных проводимостей при бесконечном разбавлении для пары сильных электролитов, имеющих общие ионы. Он установил, что разность молярных проводимостей между членами каждой пары с общими ионами оказывается постоянной (табл. 10.1). На этом основании Кольрауш сформулировал закон аддитивности (независимости) ионных подвижностей, названный впоследствии его именем. Закон Кольрауша гласит, что молярная проводимость электролита при бесконечном разбавлении представляет собой сумму подвижностей ионов, образующих электролит, и что эти подвижности не зависят от других ионов.
Ионная подвижность связана с молярной проводимостью данного иона при бесконечном разбавлении. Для электролита состава 1:1 (иначе, для 1:1 - электролита) типа  закон Кольрауша математически записывается так:
закон Кольрауша математически записывается так:

Здесь  - ионная подвижность катиона, а
- ионная подвижность катиона, а  - ионная подвижность аниона.
- ионная подвижность аниона.
Ионная подвижность является мерой скорости, с которой данный ион перемещается через раствор. Вообще говоря, ионы с малыми ионными радиусами перемещаются медленнее, чем ионы с большими ионными радиусами. Это объясняется тем, что ион меньшего размера имеет более высокую плотность заряда и поэтому сильнее сольватируется растворителем (см. разд. 2.2). Его гидратная оболочка и, следовательно, его эффективный размер оказывается больше, чем у иона с большим ионным
радиусом. Большой эффективный заряд такого иона обусловливает его малую подвижность в растворе.
Двухзарядные или трехзарядные ионы, как правило, имеют более высокую ионную подвижность, чем однозарядные ионы. Исключение составляют ионы гидроксония  и гидроксильные ионы
и гидроксильные ионы  которые имеют самые высокие ионные подвижности из всех ионов. Это объясняется быстрым переносом протонов между ионами в растворе.
которые имеют самые высокие ионные подвижности из всех ионов. Это объясняется быстрым переносом протонов между ионами в растворе.
Вычисление ... для слабых электролитов
Если построить график зависимости молярной проводимости для слабого электролита от концентрации, получится кривая такого типа, как показано на рис. 10.3 для  . Поскольку эта кривая не пересекается с вертикальной осью координат, нельзя определить Л” для слабого электролита экстраполяцией графика к нулевой концентрации. Однако эту величину можно найти, применяя к слабому электролиту закон Кольрауша об аддитивности ионных подвижностей для сильных электролитов.
. Поскольку эта кривая не пересекается с вертикальной осью координат, нельзя определить Л” для слабого электролита экстраполяцией графика к нулевой концентрации. Однако эту величину можно найти, применяя к слабому электролиту закон Кольрауша об аддитивности ионных подвижностей для сильных электролитов.
Пример
Вычислим  для уксусной кислоты, пользуясь следующими данными:
для уксусной кислоты, пользуясь следующими данными:

Решение
Уксусная кислота - слабый электролит. Соляная кислота, хлорид натрия и ацетат натрия - сильные электролиты. Применяя закон Кольрауша к сильным электролитам, находим

Для слабого электролита можно записать

Степень диссоциации
Выше было показано, что молярная проводимость электролита зависит от относительного количества ионов, присутствующих в растворе, а следовательно, от степени диссоциации электролита. Аррениус выдвинул предположение, что молярная проводимость электролита связана с его степенью диссоциации следующим соотношением:

При концентрациях, близких к нулю, т. е. при бесконечном разбавлении  и, следовательно,
и, следовательно, 

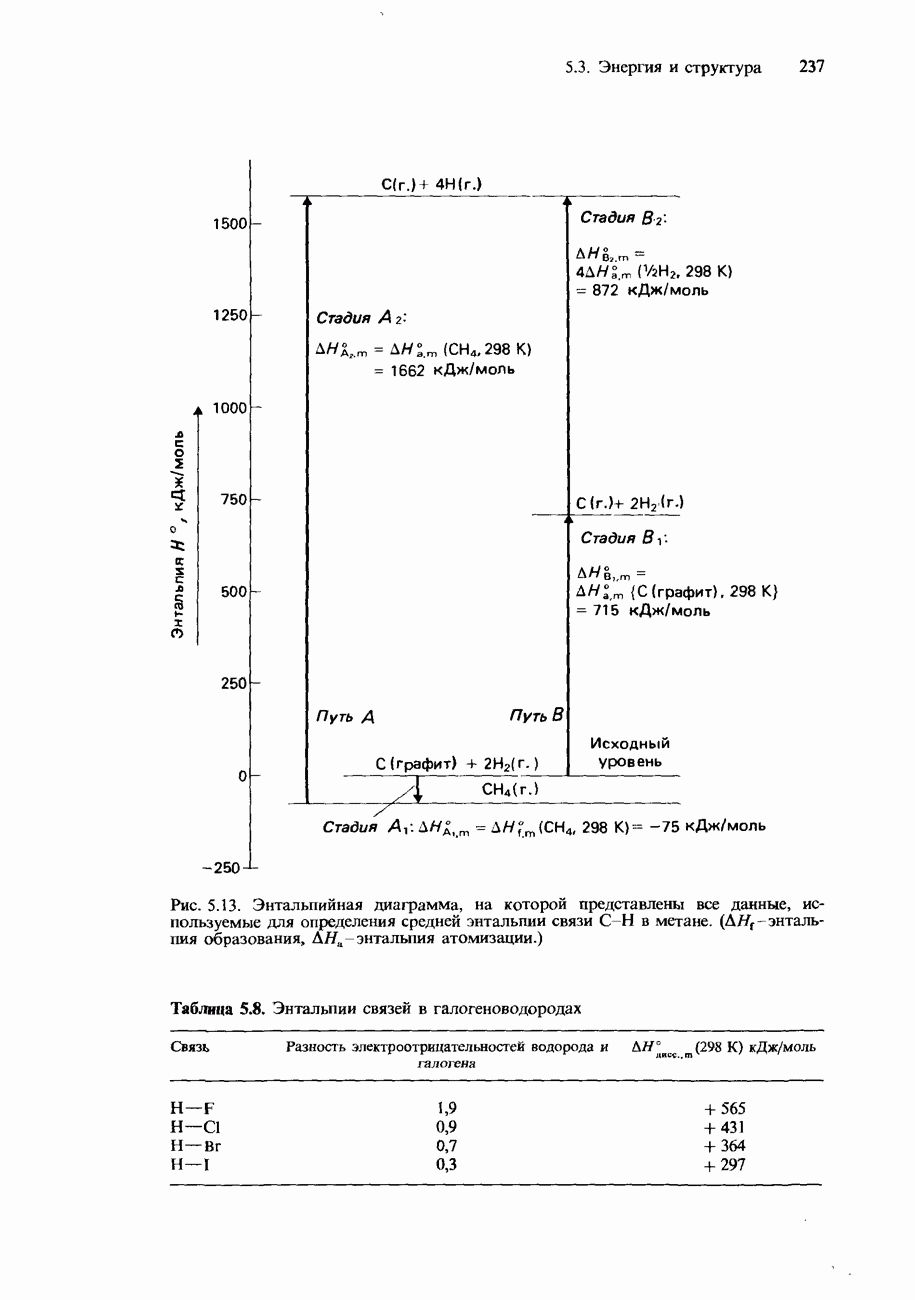
Рис. 10.4. Кондуктометрическое титрование.

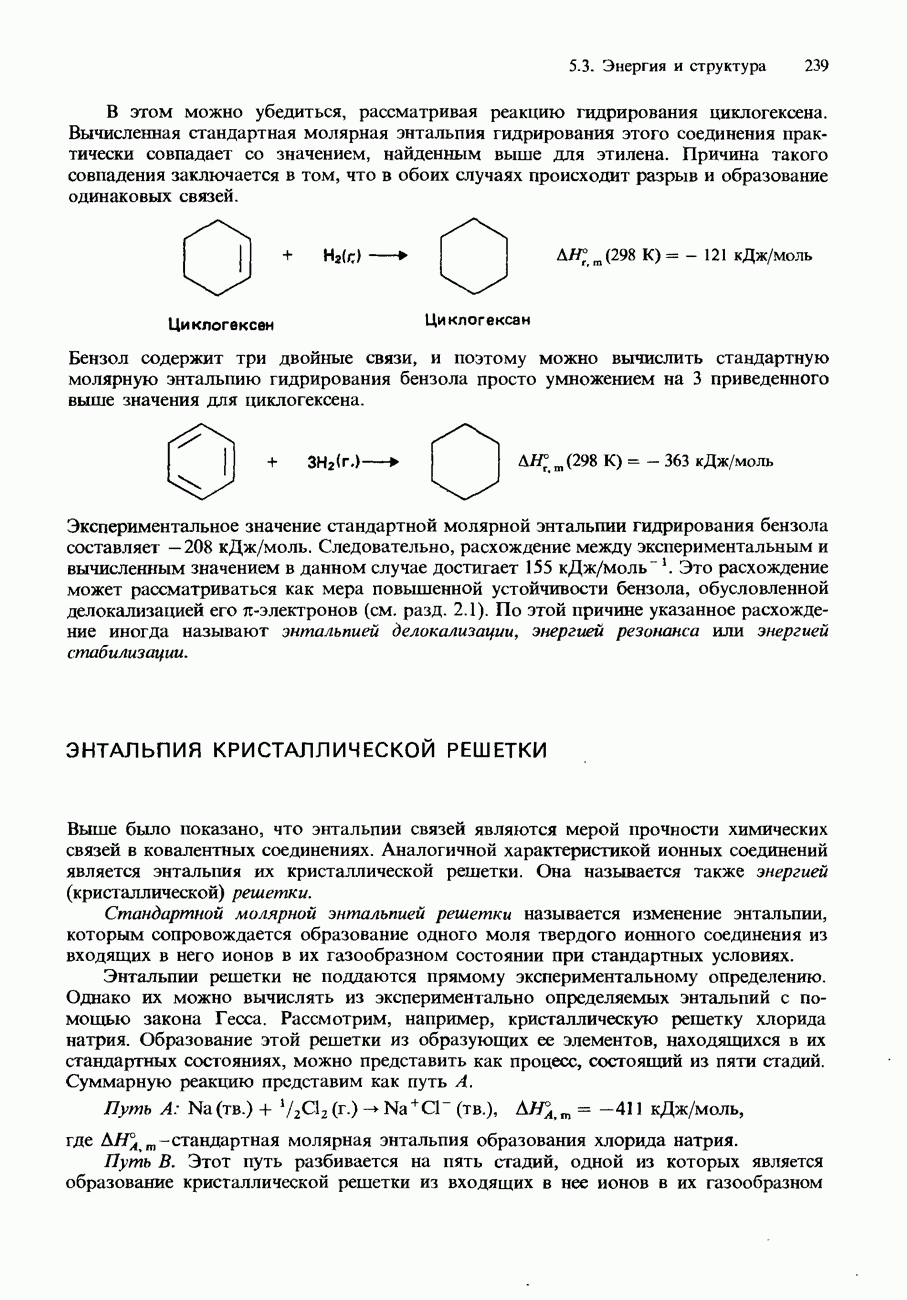
Рис. 10.5. Кривые кондуктометрическо-го титрования сильной и слабой кислоты сильным основанием.
Уравнение (4) вместе с законом разбавления Оствальда (см. разд. 8.1) может использоваться для вычисления константы диссоциации слабого электролита по экспериментально установленным молярным проводимостям. Действительно, подставляя выражение (4) в выражение закона разбавления Оствальда

находим

| << Предыдущий параграф | Следующий параграф >> |
- ОТ ПЕРЕВОДЧИКА
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ
- 1. СТРОЕНИЕ АТОМА
- 1.1. Субатомные частицы
- Модели атома
- Новые элементарные частицы
- МАССА АТОМА
- МАСС-СПЕКТРОМЕТРИЯ
- 1.2 Электронное строение атомов
- Связь между спектральными линиями и электронами (открытие Бора)
- Применение возбуждения электронов на практике
- Атомный спектр испускания водорода
- ЭНЕРГИИ ИОНИЗАЦИИ
- Рассмотрение энергий ионизации в рамках модели атома, предложенной Бором
- ВОЛНОВАЯ ПРИРОДА ЭЛЕКТРОНА
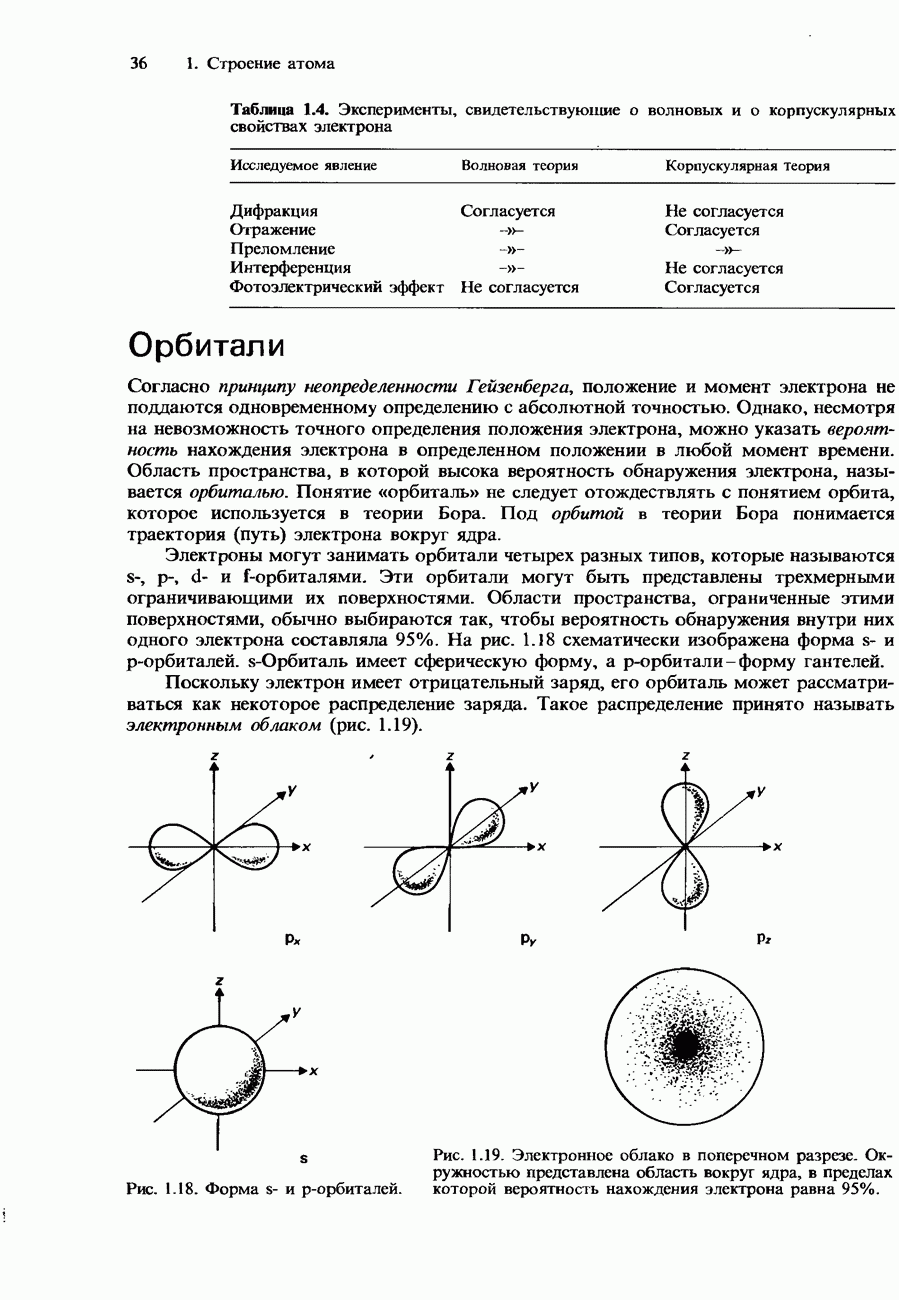
- Орбитали
- КВАНТОВЫЕ ЧИСЛА
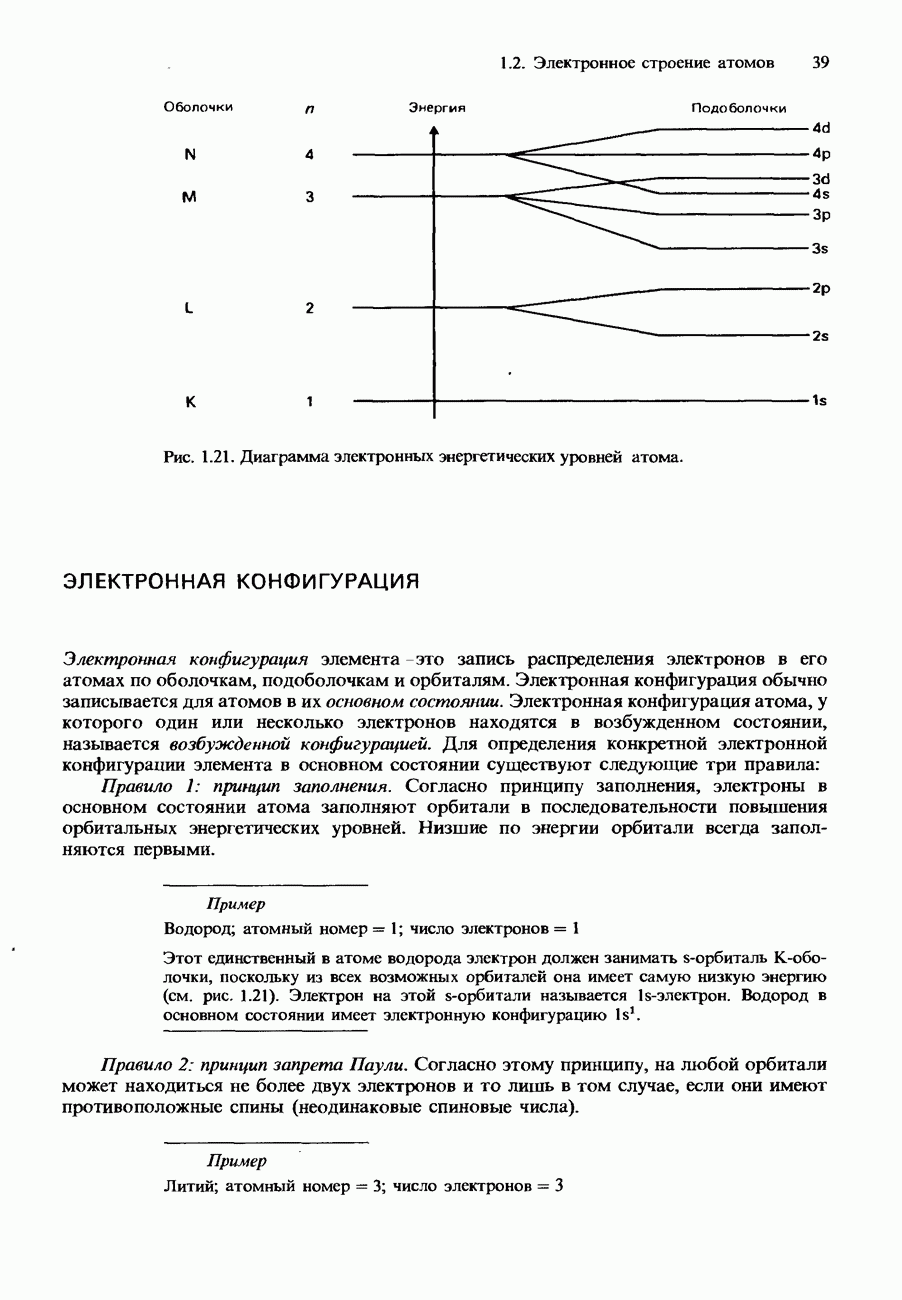
- ЭЛЕКТРОННАЯ КОНФИГУРАЦИЯ
- 1.3 Радиоактивность
- ИОНИЗИРУЮЩЕЕ ИЗЛУЧЕНИЕ
- Обнаружение и измерение радиоактивности
- УСТОЙЧИВЫЕ И НЕУСТОЙЧИВЫЕ ИЗОТОПЫ
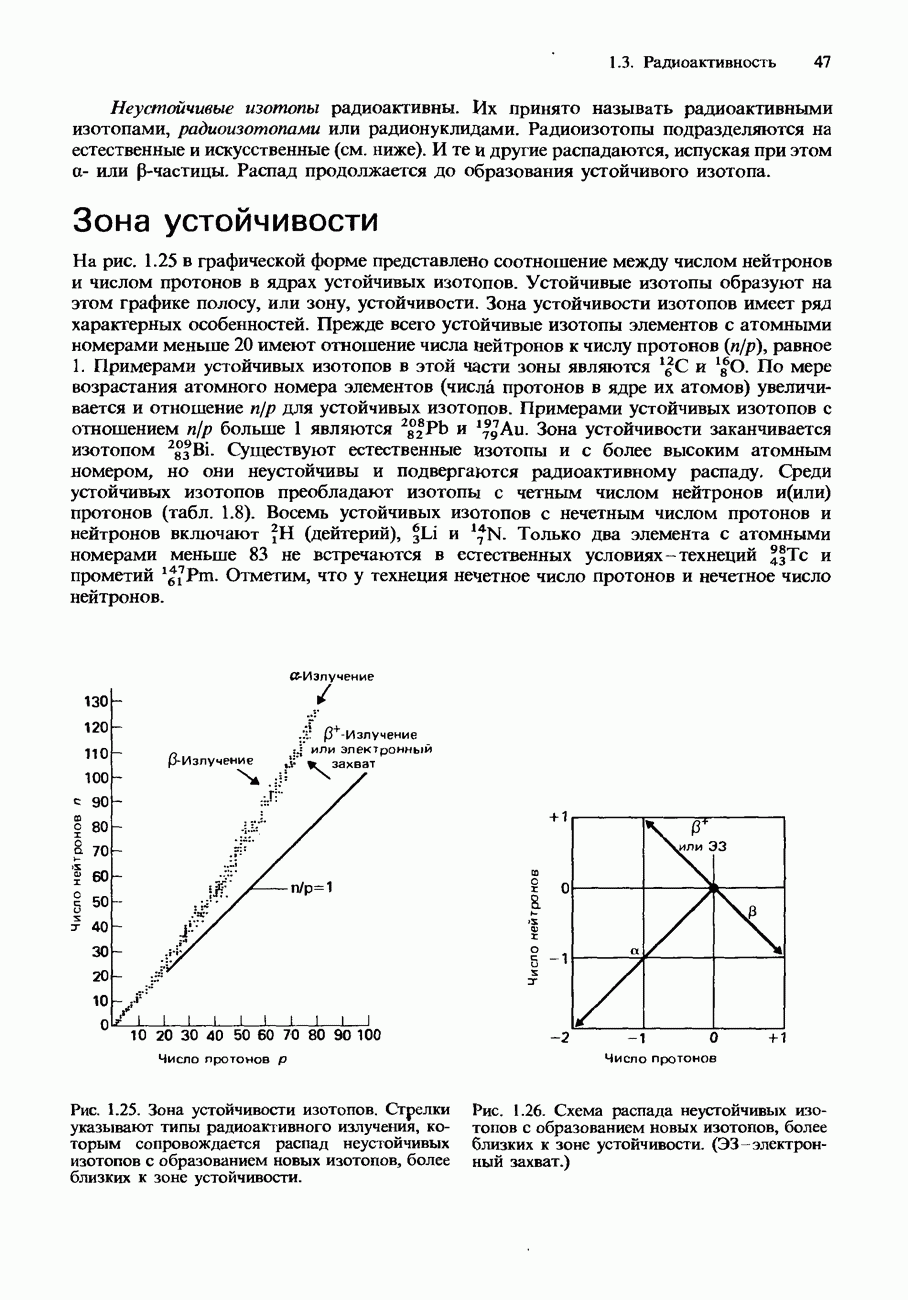
- Зона устойчивости
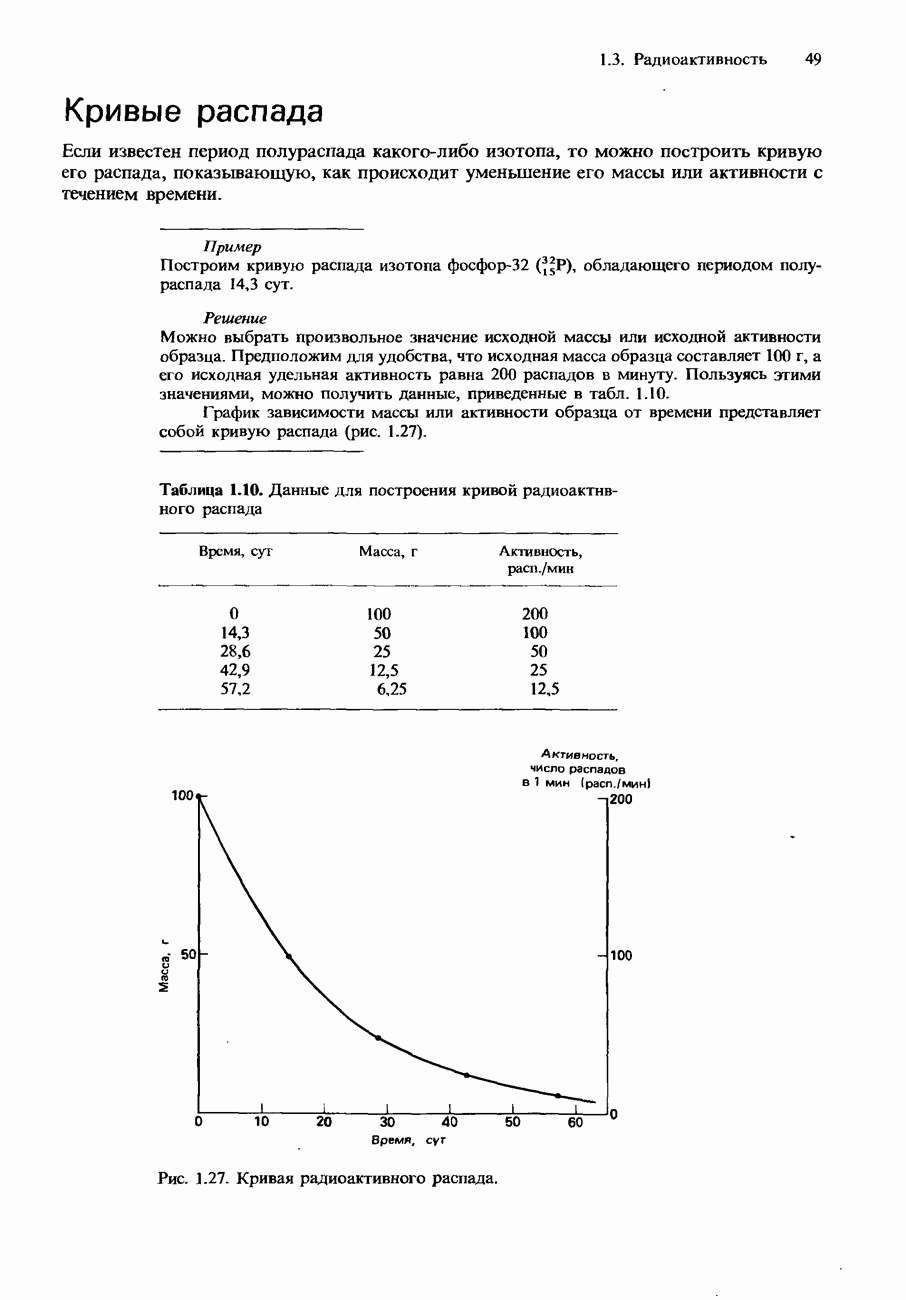
- Период полураспада
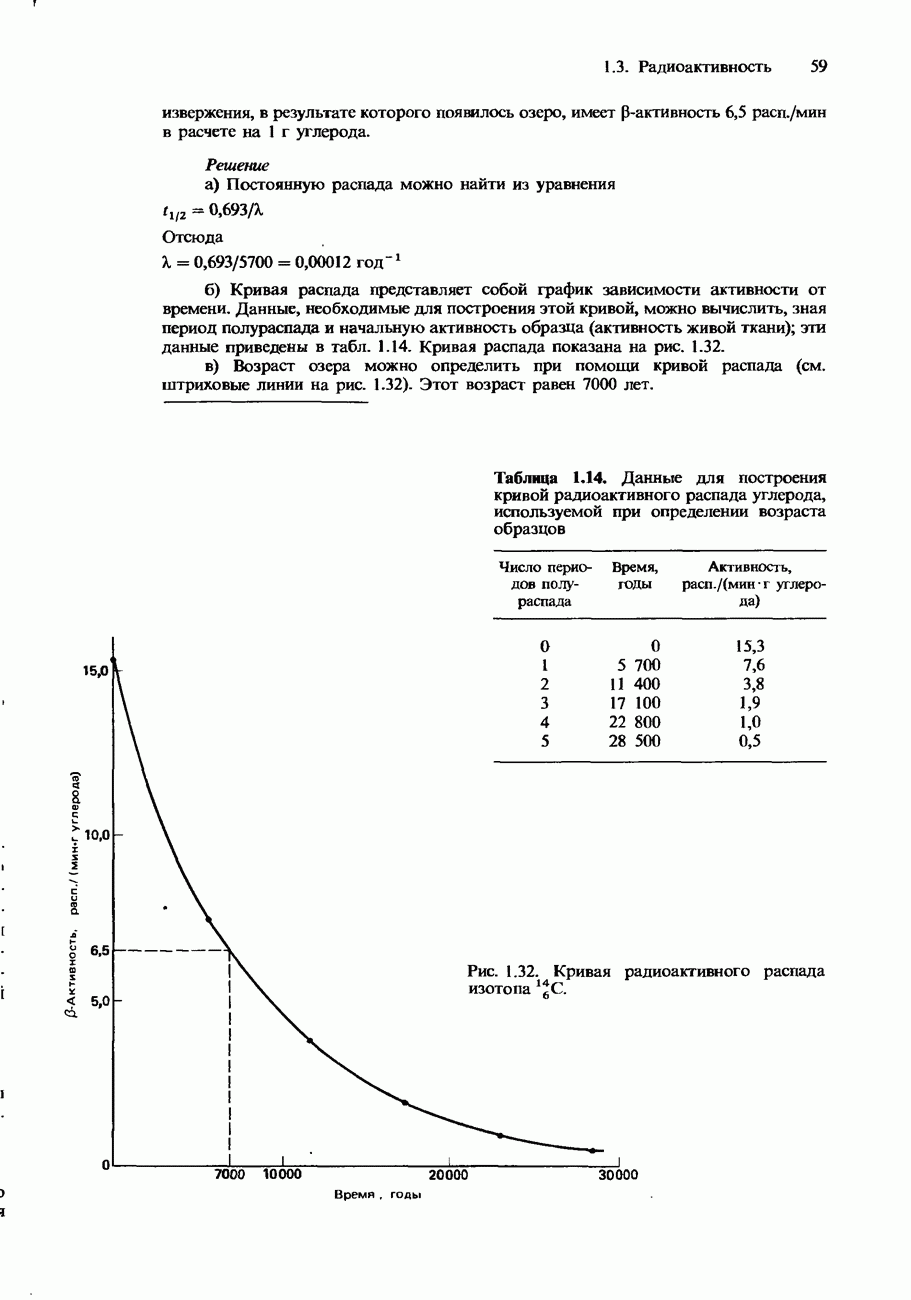
- Кривые распада
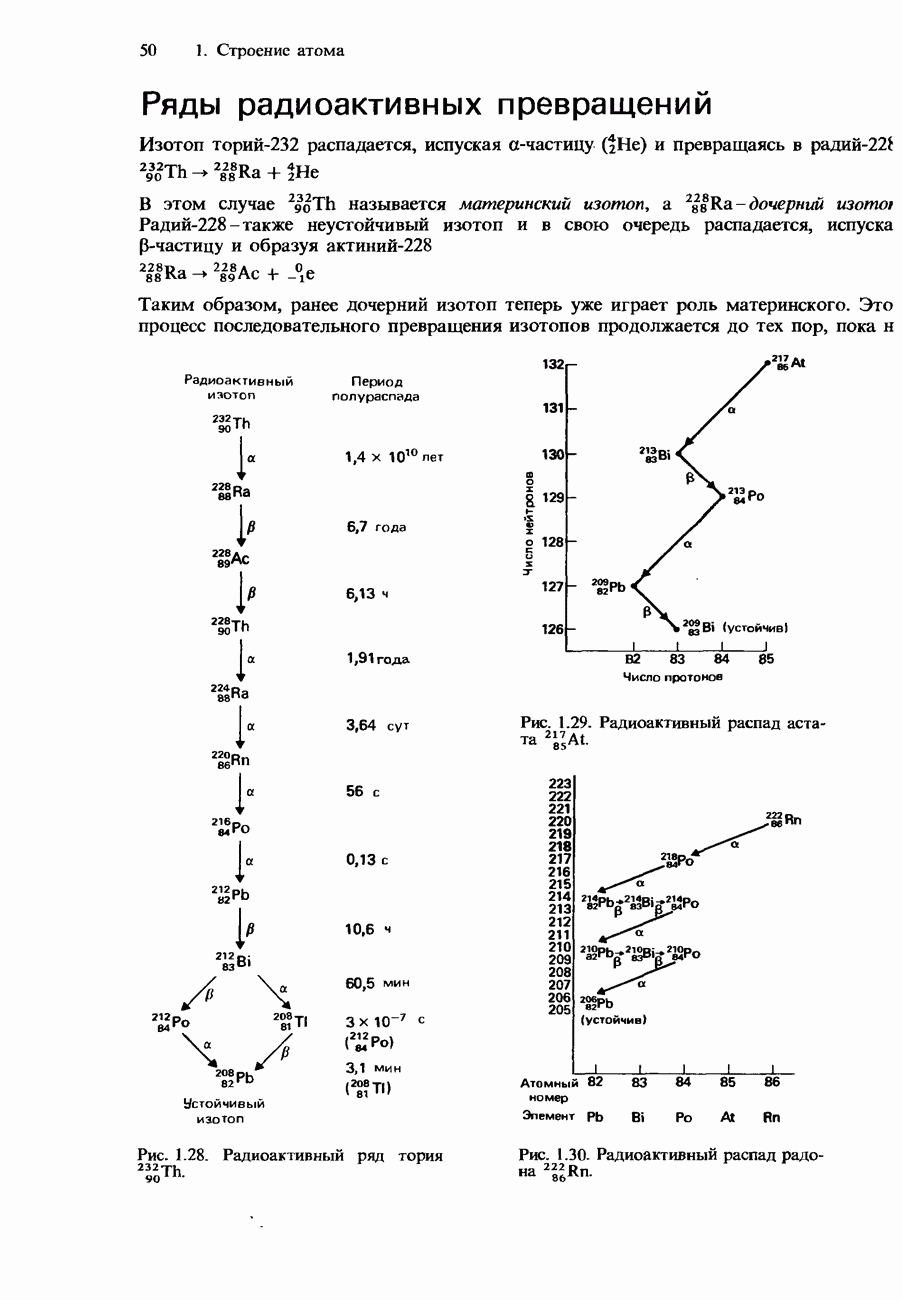
- Ряды радиоактивных превращений
- Естественные радиоизотопы
- ИСКУССТВЕННЫЕ ЯДЕРНЫЕ ПРЕВРАЩЕНИЯ
- Ускорители элементарных частиц
- Трансурановые элементы
- ПРИМЕНЕНИЯ ИЗОТОПОВ
- ЯДЕРНОЕ ДЕЛЕНИЕ И ЯДЕРНЫЙ СИНТЕЗ
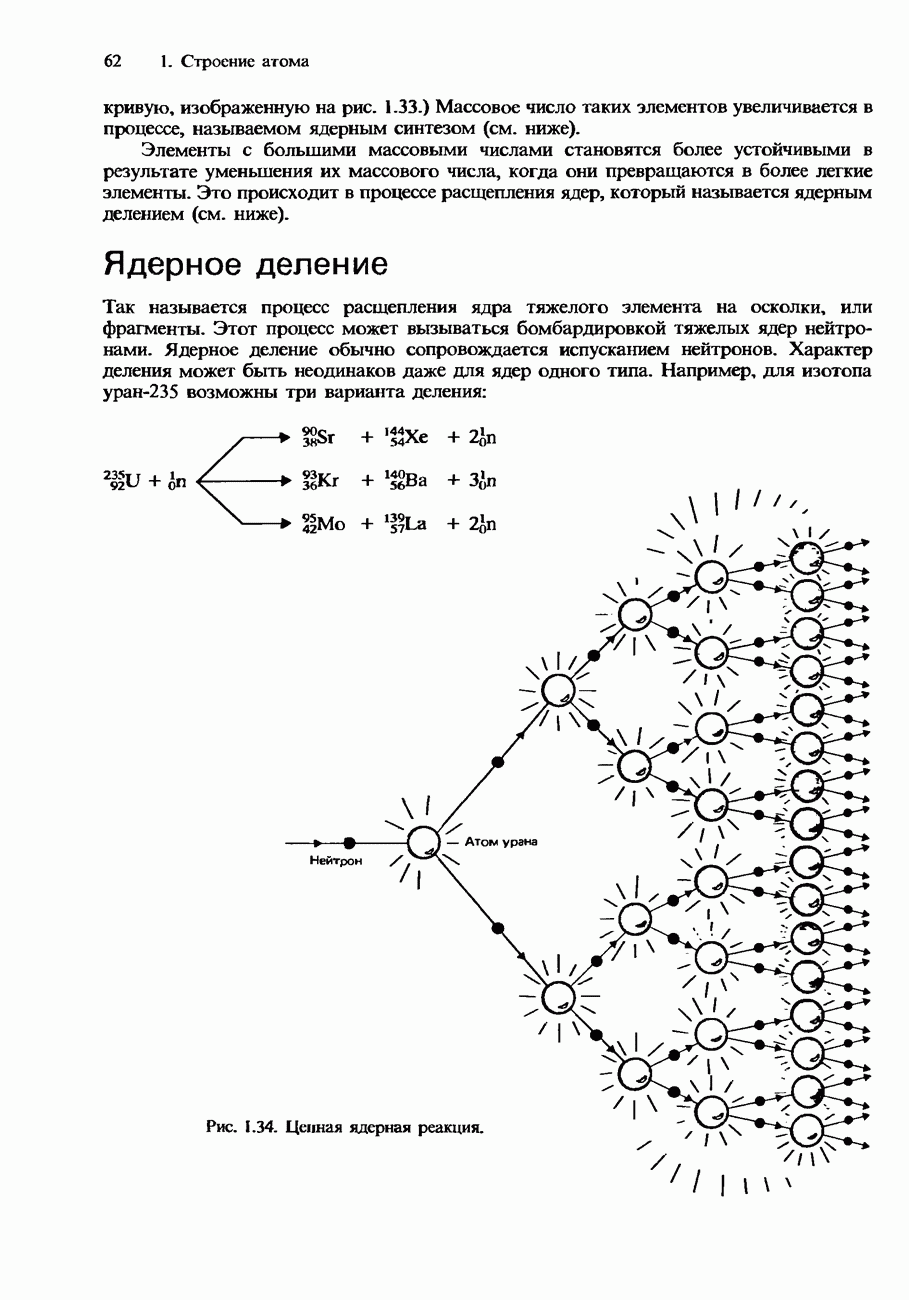
- Ядерное деление
- Ядерный синтез
- Ядерный синтез в звездах
- ЯДЕРНАЯ ЭНЕРГИЯ
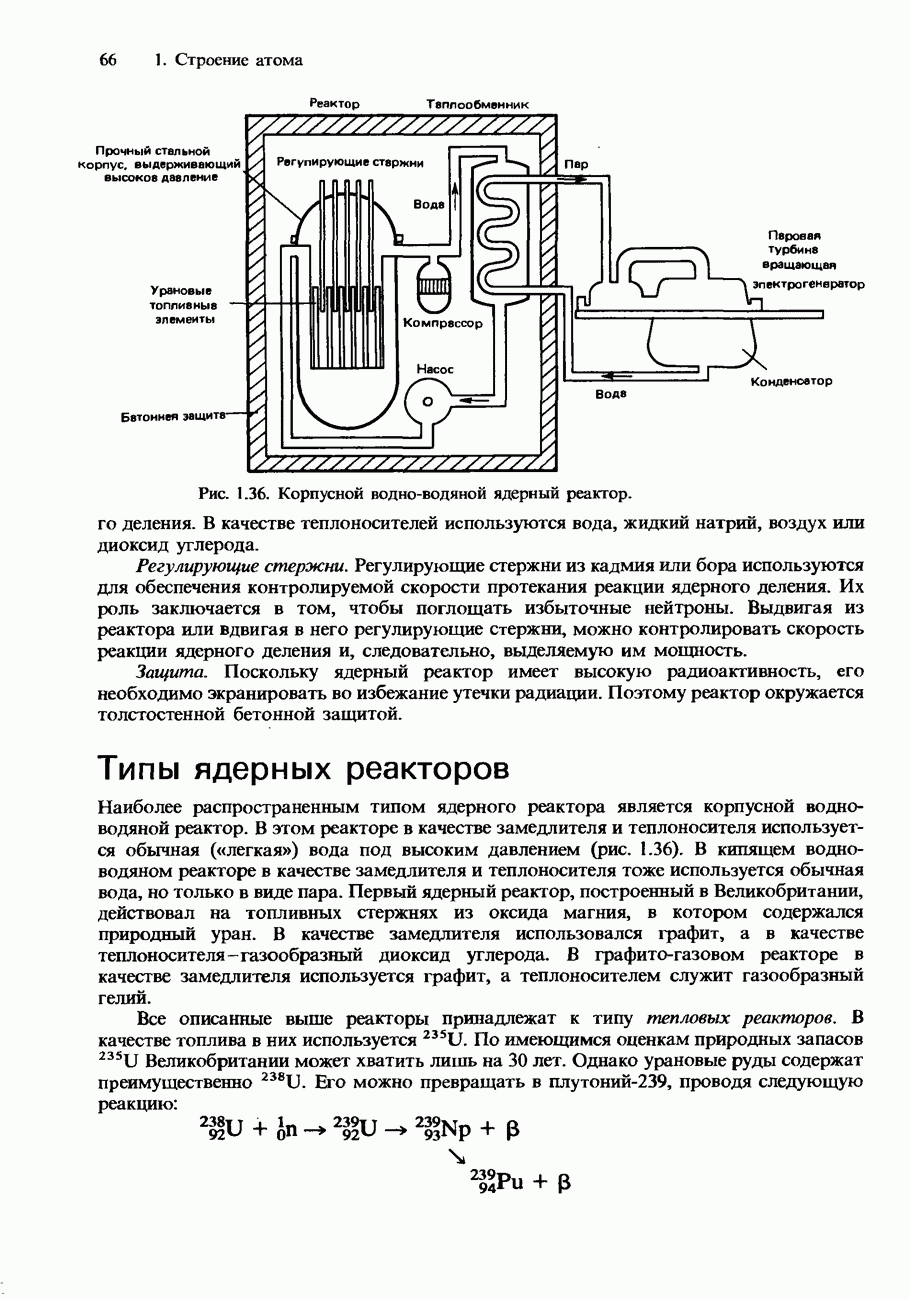
- Типы ядерных реакторов
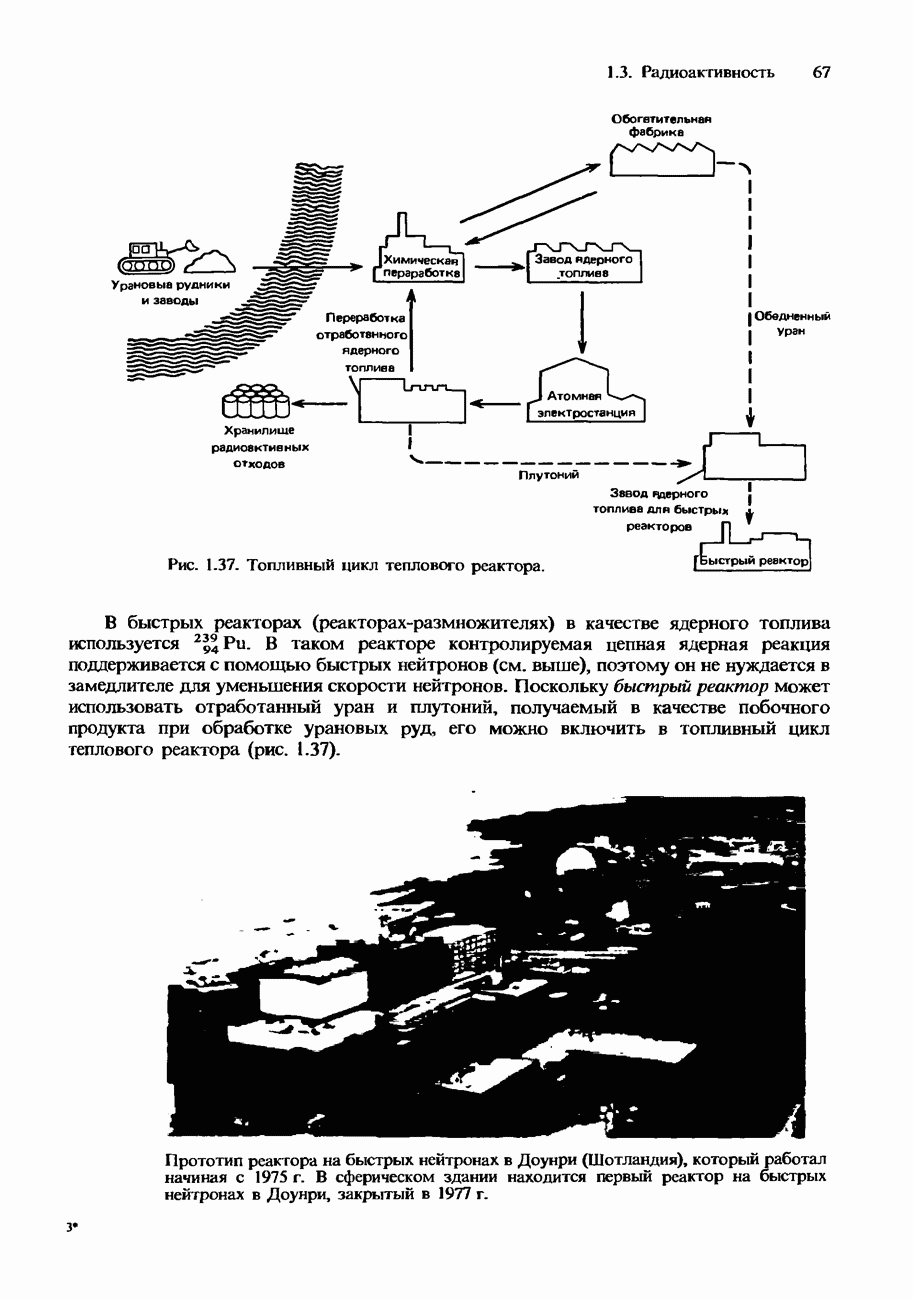
- Радиоактивные ядерные отходы и их переработка
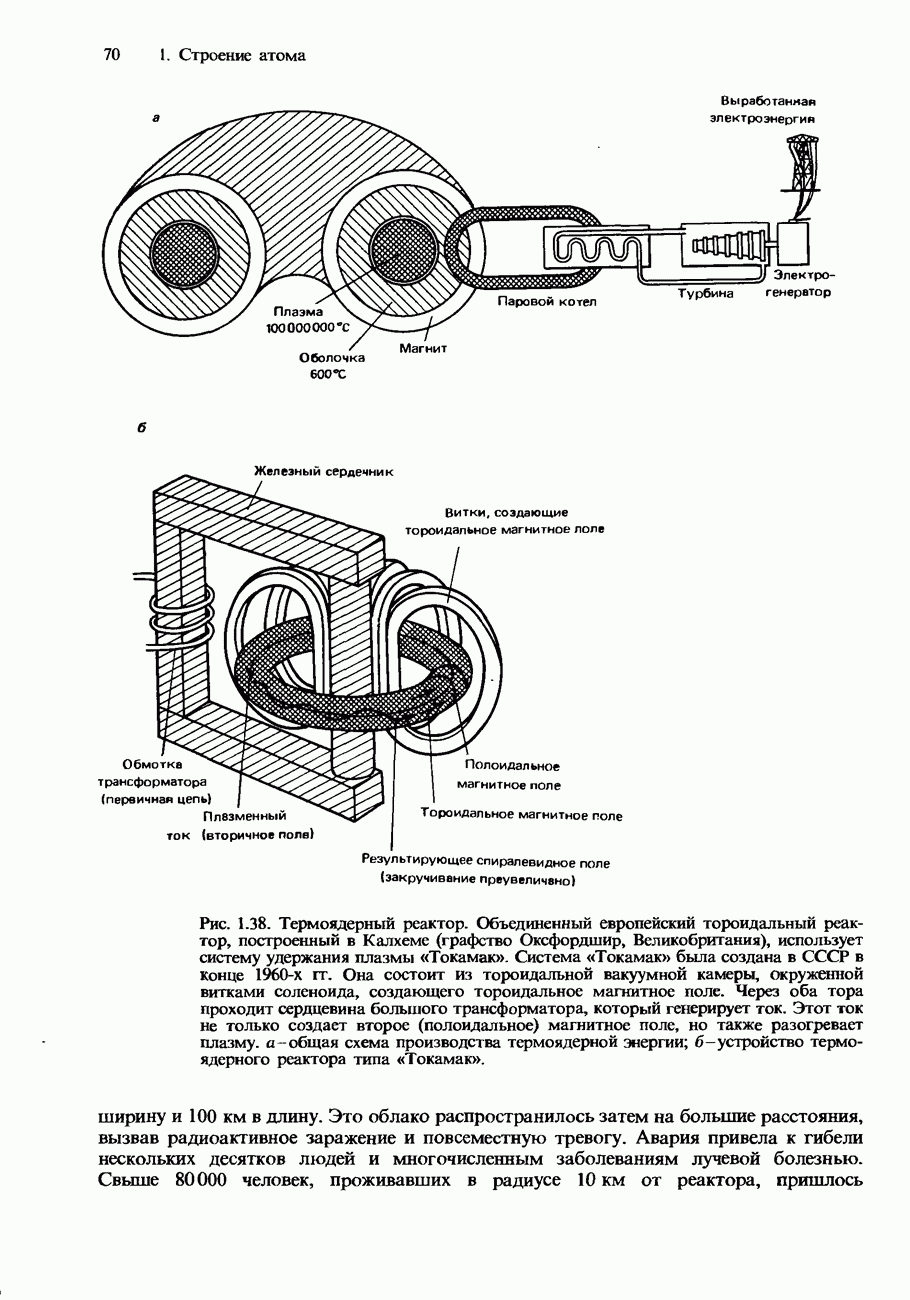
- Термоядерные реакторы
- Аргументы против использования ядерной энергии
- ЯДЕРНОЕ ОРУЖИЕ
- Ядерное разоружение
- ИСТОЧНИКИ РАДИАЦИИ И ЕЕ ВОЗДЕЙСТВИЕ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 2. ХИМИЧЕСКАЯ СВЯЗЬ
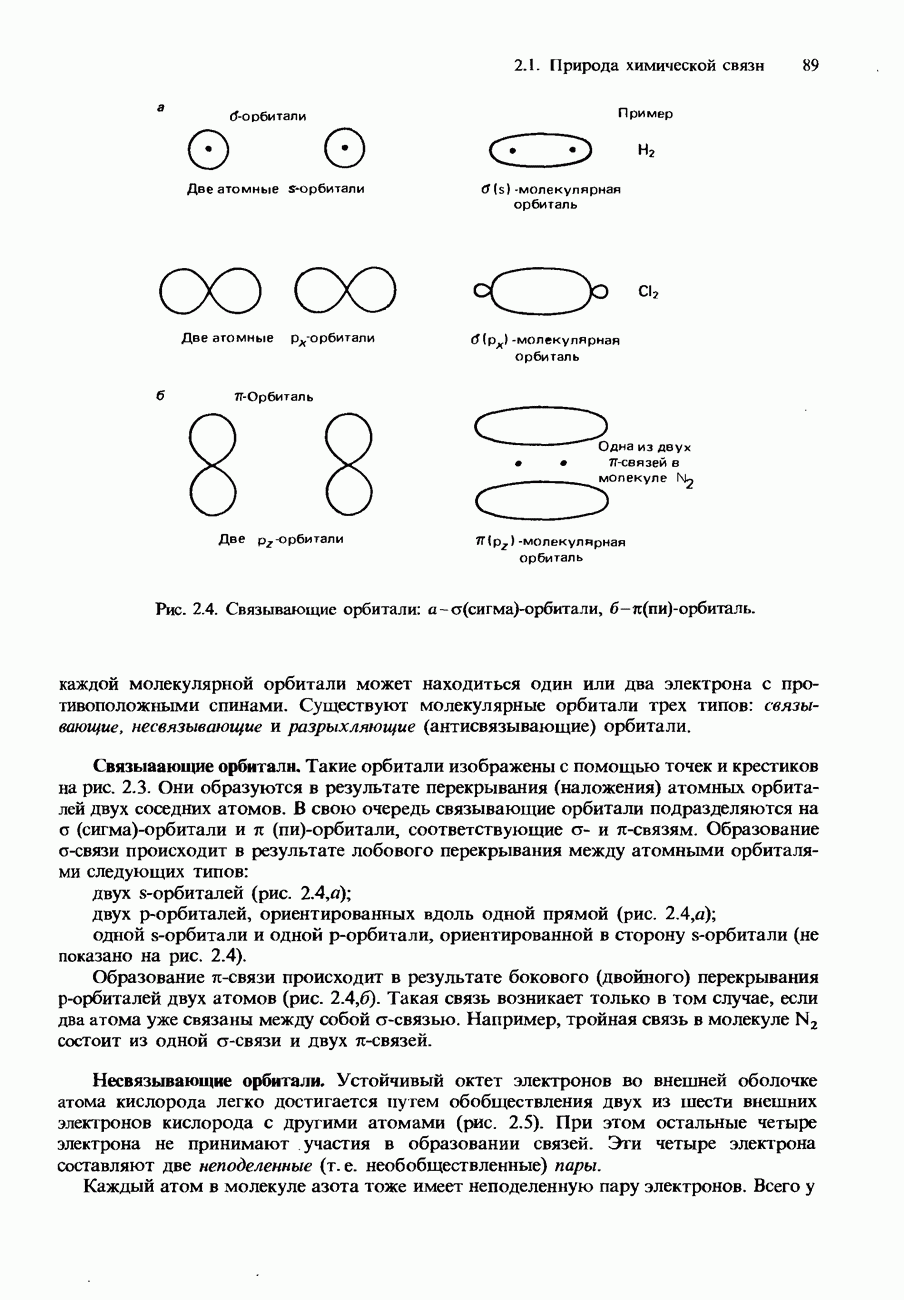
- 2.1. Природа химической связи
- ИОННАЯ СВЯЗЬ
- Устойчивость ионных соединений
- КОВАЛЕНТНАЯ СВЯЗЬ
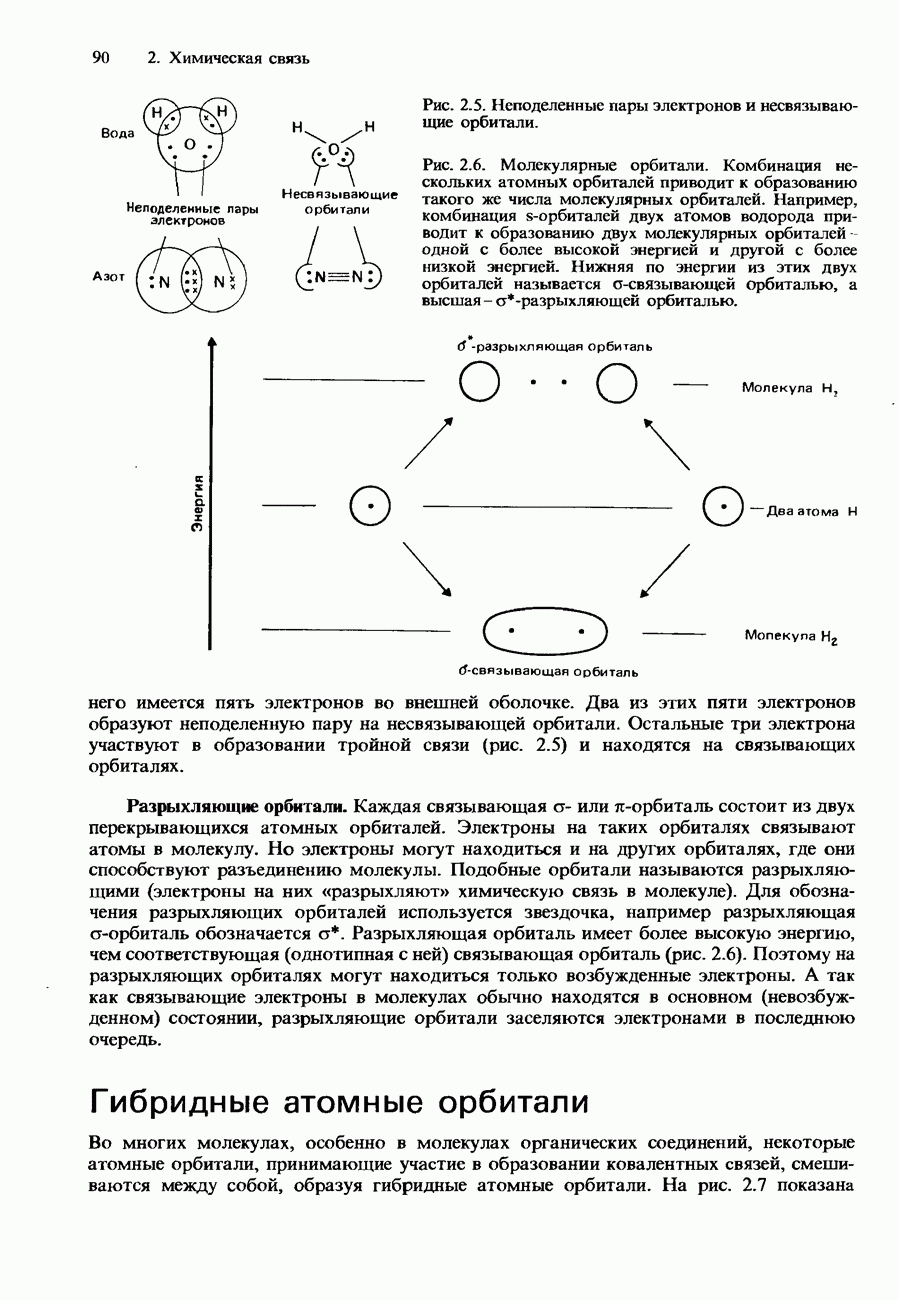
- Молекулярные орбитали
- Гибридные атомные орбитали
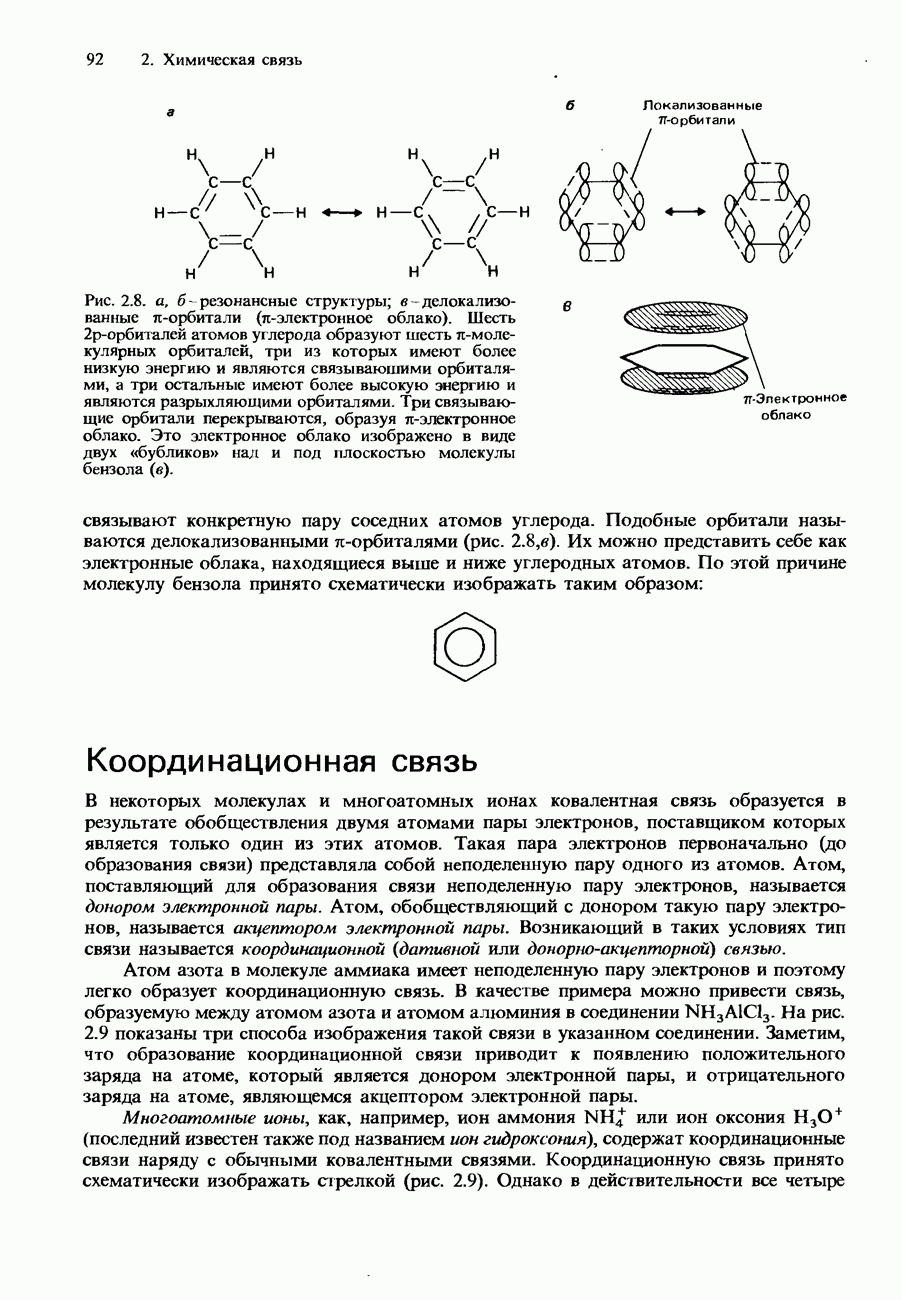
- Делокализованные орбитали
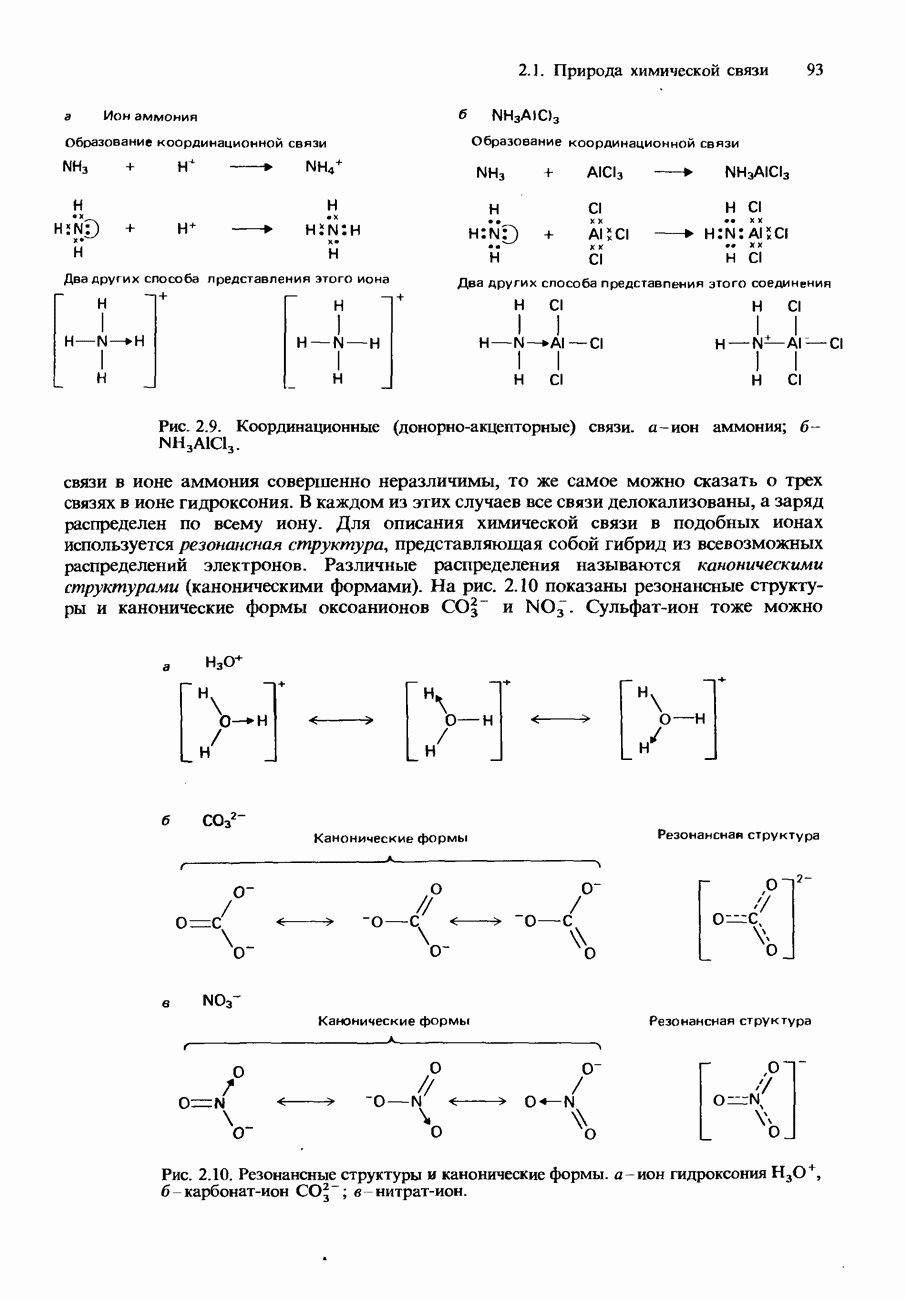
- Координационная связь
- ИОННЫЙ И КОВАЛЕНТНЫЙ ХАРАКТЕР СВЯЗИ
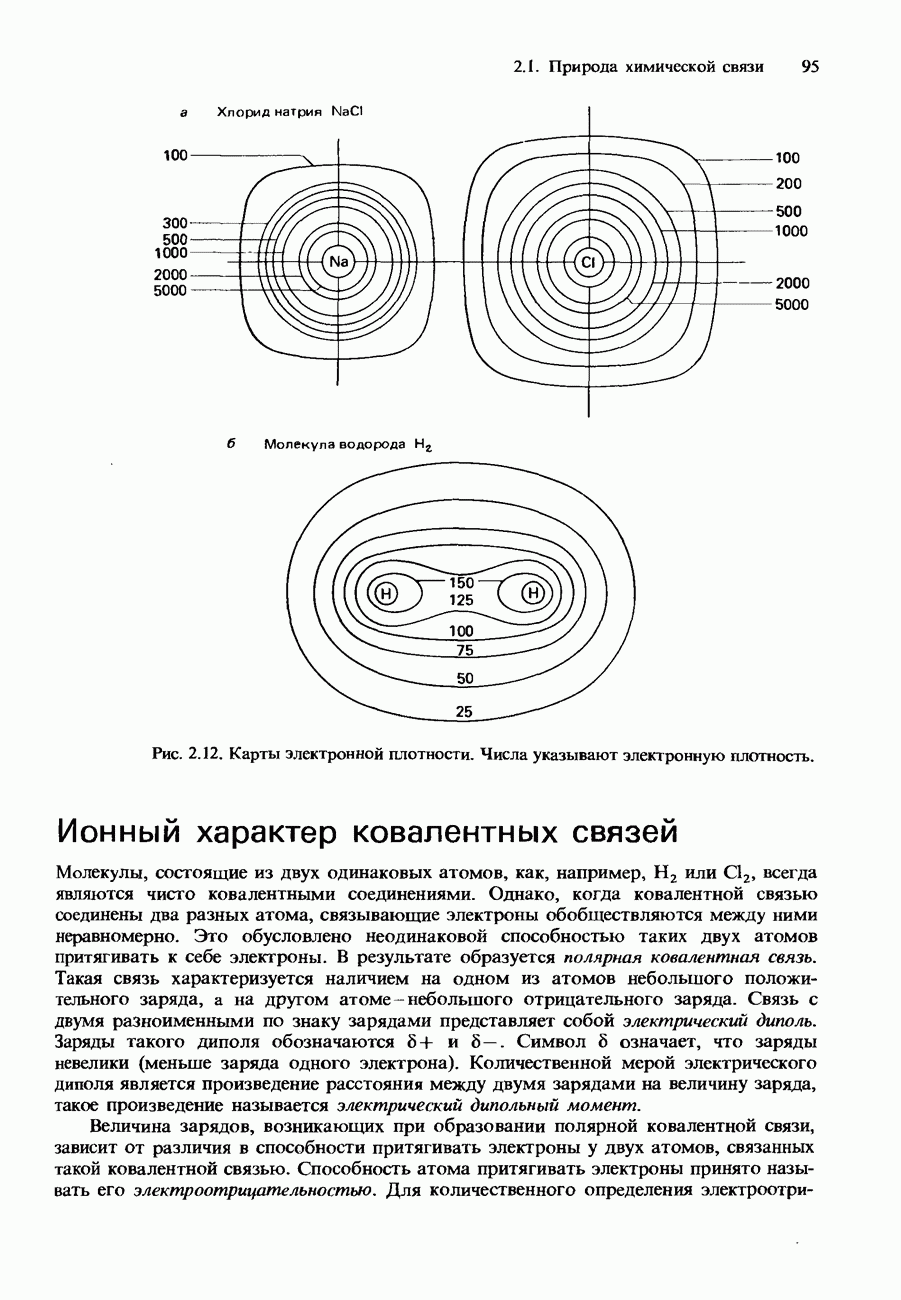
- Ионный характер ковалентных связей
- Ионные и ковалентные соединения
- МЕТАЛЛИЧЕСКАЯ СВЯЗЬ
- Валентная зона и зона проводимости
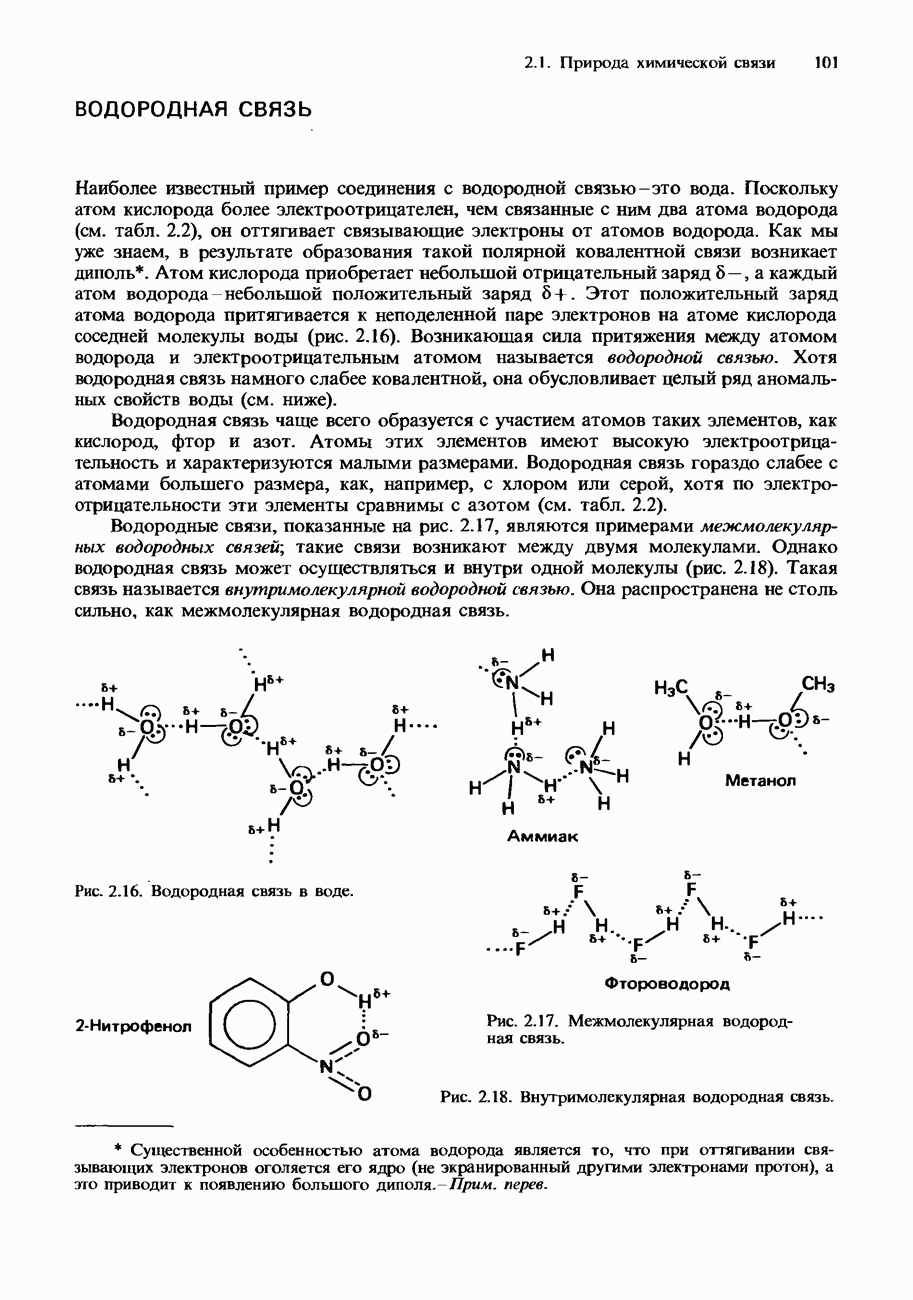
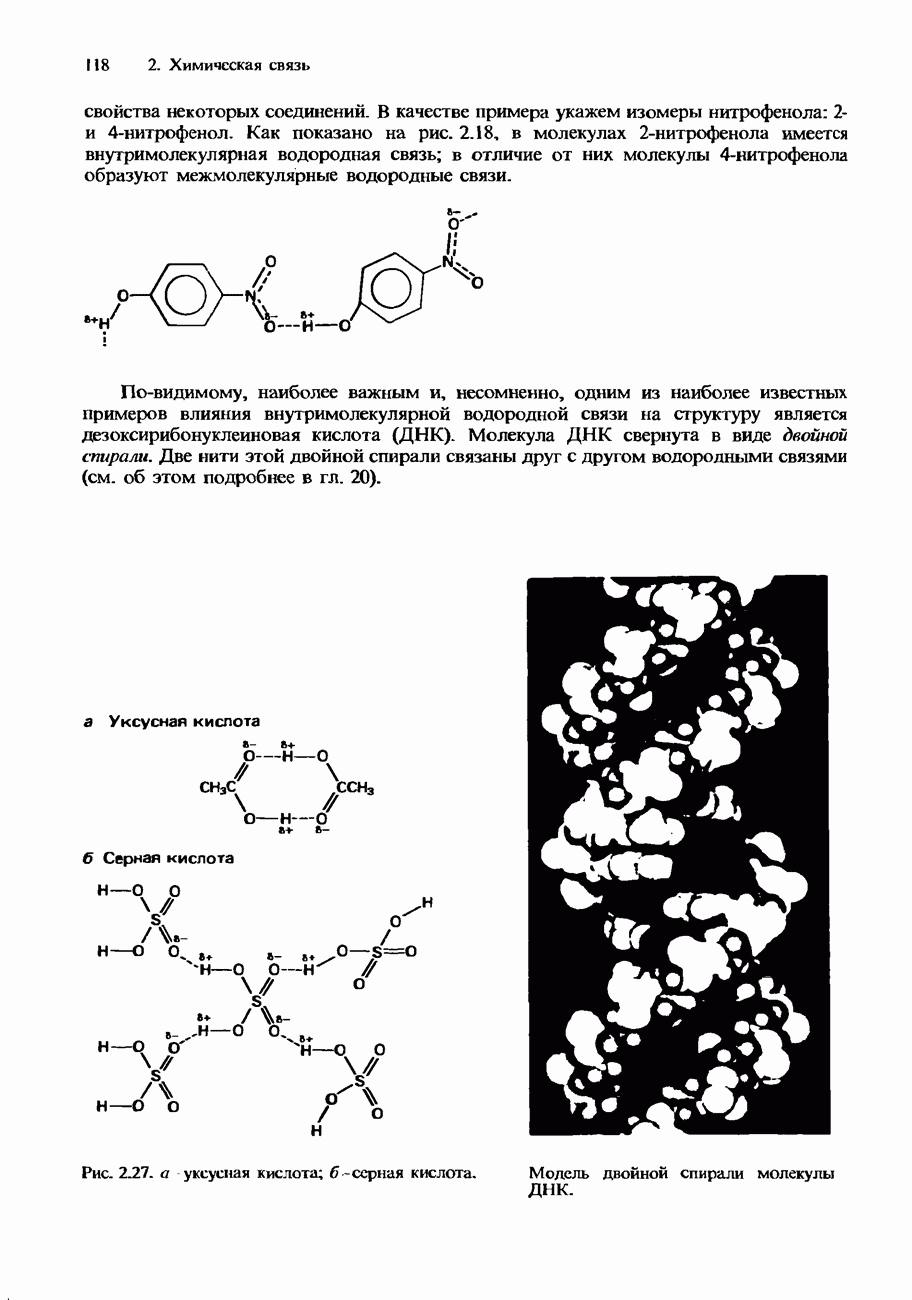
- ВОДОРОДНАЯ СВЯЗЬ
- ВАНДЕРВААЛЬСОВЫ СИЛЫ
- Притяжение типа диполь-индуцированный диполь (индукционное)
- Что понимается под вандерваальсовыми силами
- 2.2. Влияние химической связи на свойства соединений
- Атомные радиусы
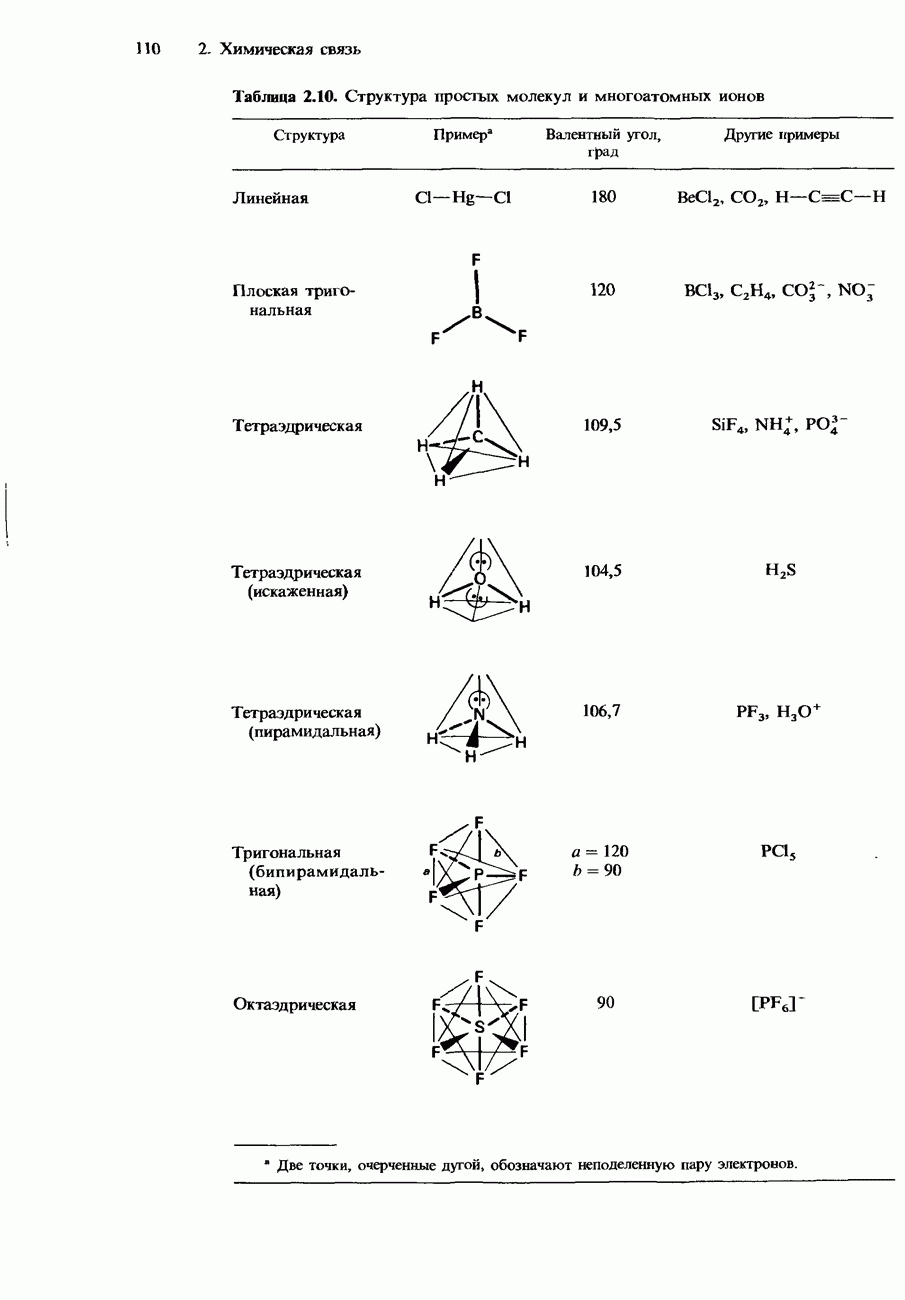
- ФОРМА ПРОСТЫХ МОЛЕКУЛ И МНОГОАТОМНЫХ ИОНОВ
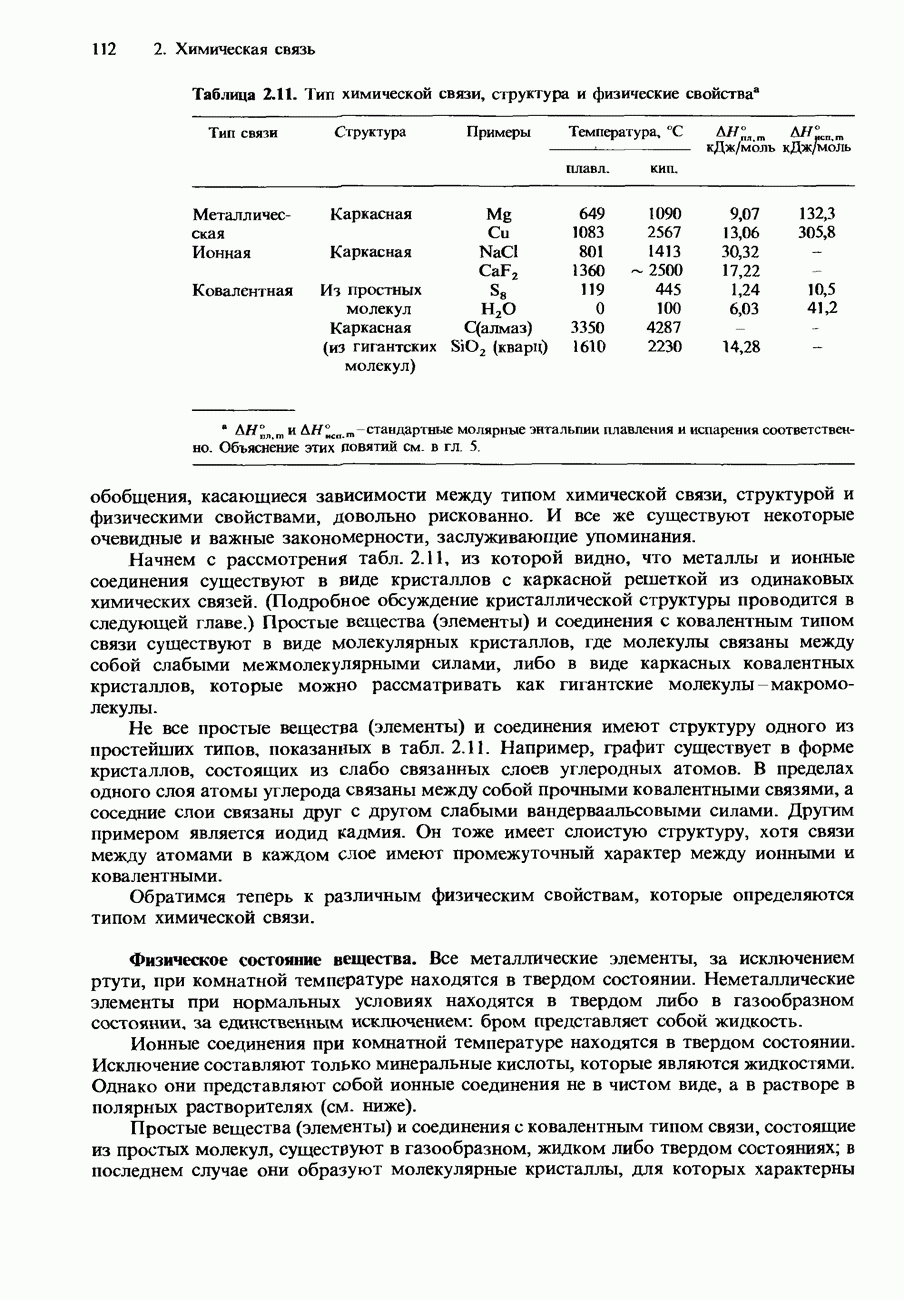
- ТИП ХИМИЧЕСКОЙ СВЯЗИ, СТРУКТУРА И ФИЗИЧЕСКИЕ СВОЙСТВА
- ТИП СВЯЗИ И ХИМИЧЕСКИЕ СВОЙСТВА
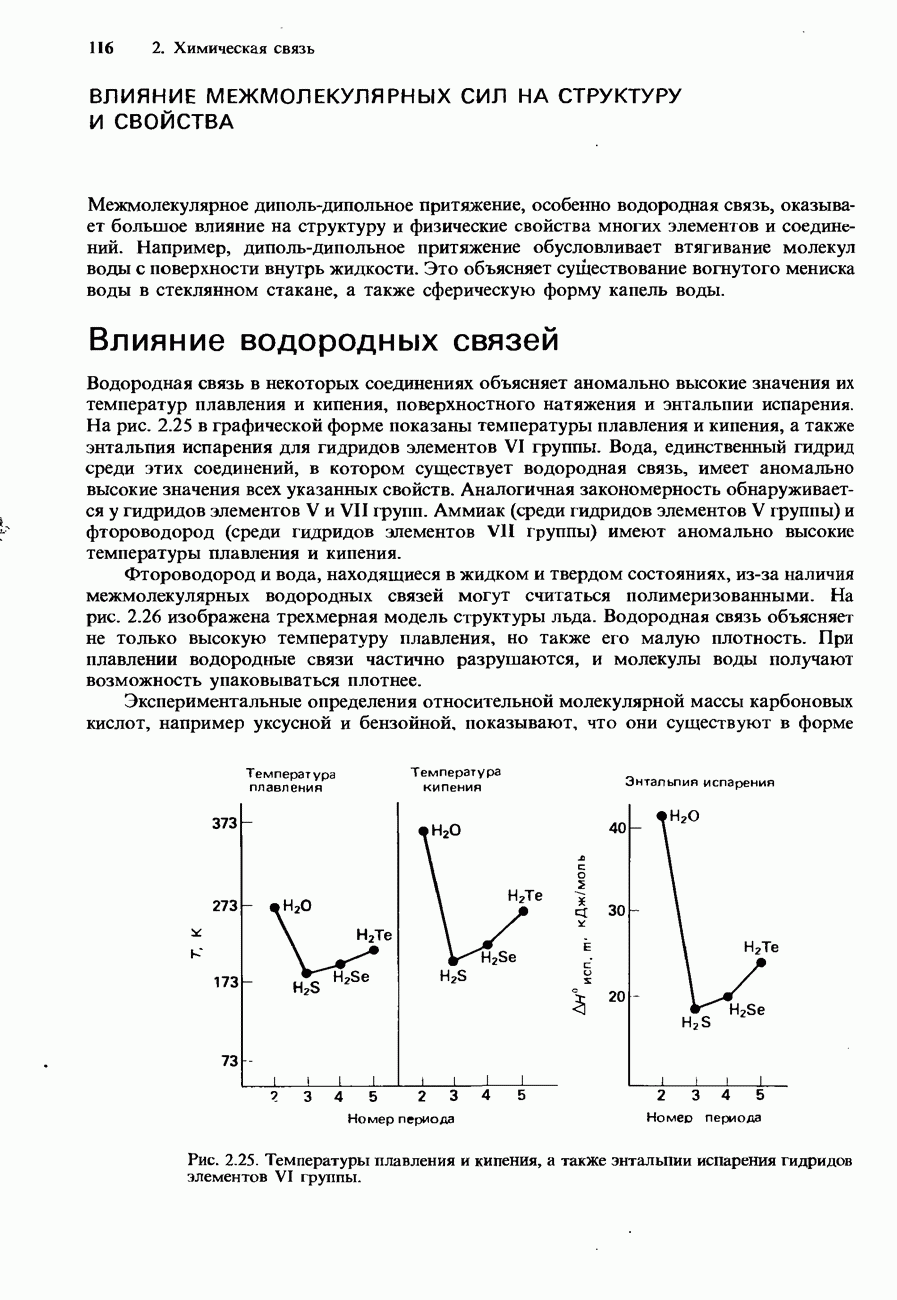
- ВЛИЯНИЕ МЕЖМОЛЕКУЛЯРНЫХ СИЛ НА СТРУКТУРУ И СВОЙСТВА
- ВЛИЯНИЕ ВАНДЕРВААЛЬСОВЫХ СИЛ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 3 ГАЗЫ, ЖИДКОСТИ И ТВЕРДЫЕ ВЕЩЕСТВА
- 3.1. Газы и жидкости
- ГАЗОВЫЕ ЗАКОНЫ
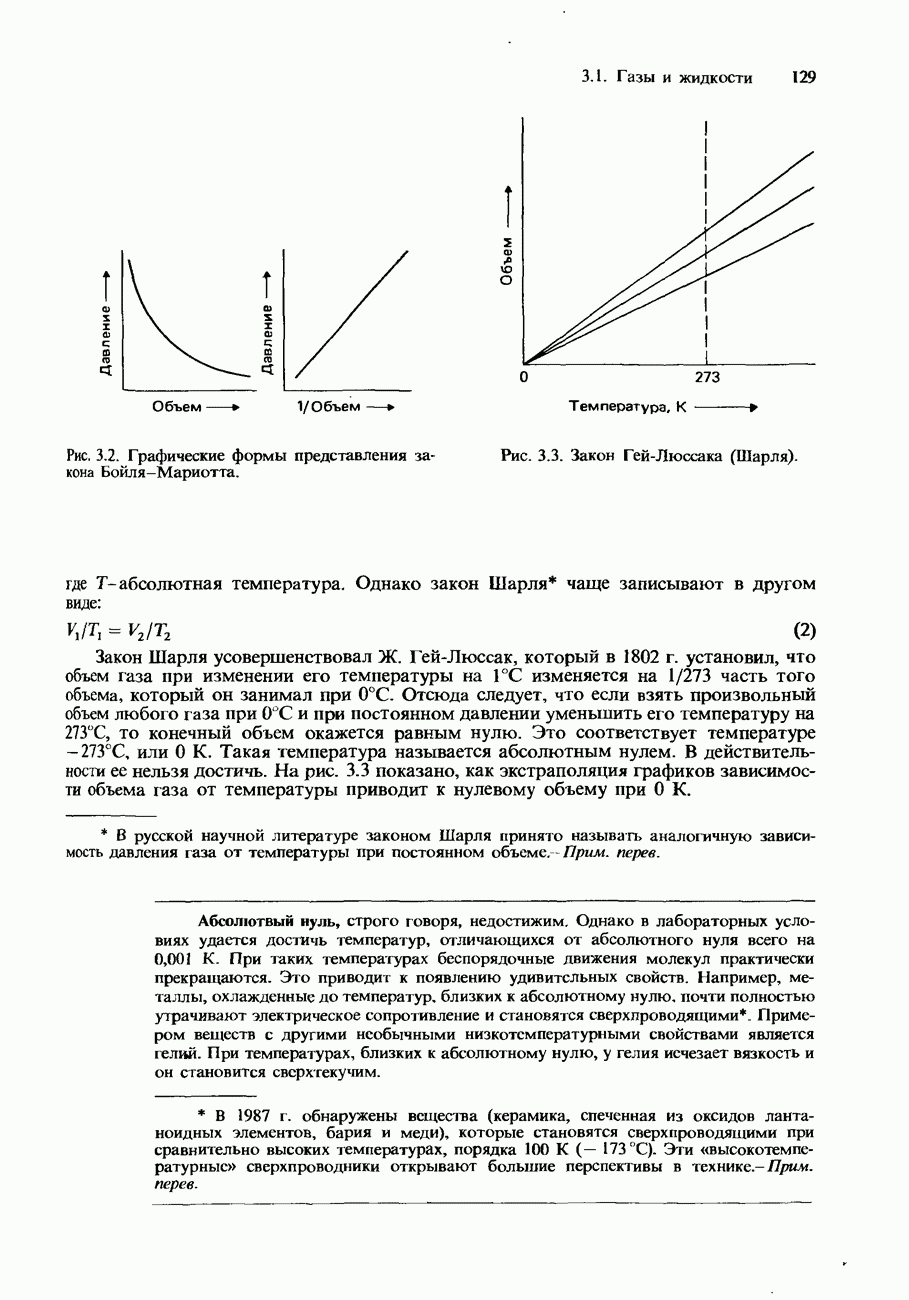
- Закон Бойля-Мариотта
- Закон Гей-Люссака (закон Шарля)
- Объединенный газовый закон
- Закон Авогадро
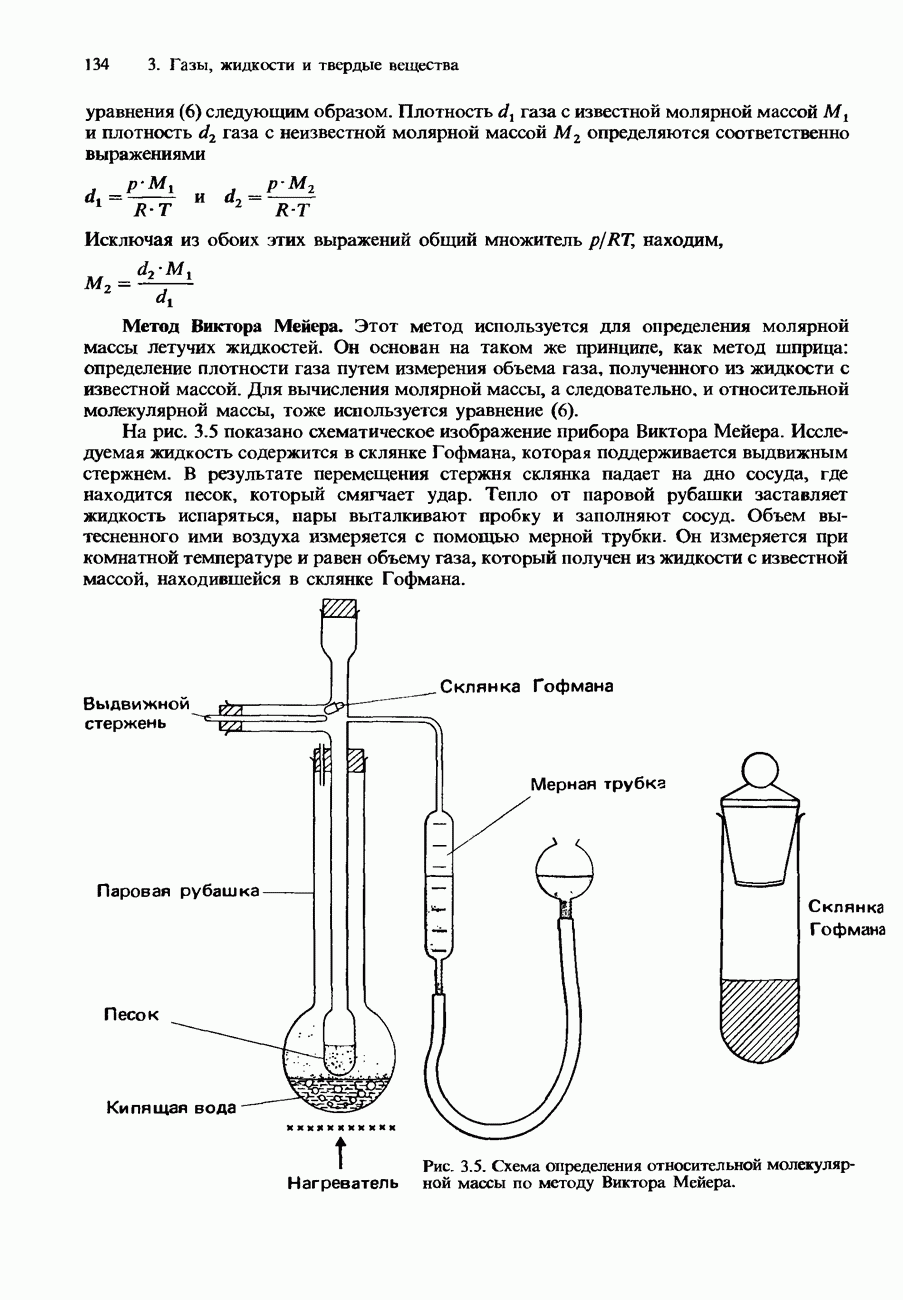
- Экспериментальное определение относительной молекулярной массы
- Закон парциальных давлений газов (закон Дальтона)
- Законы Грэхема
- КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
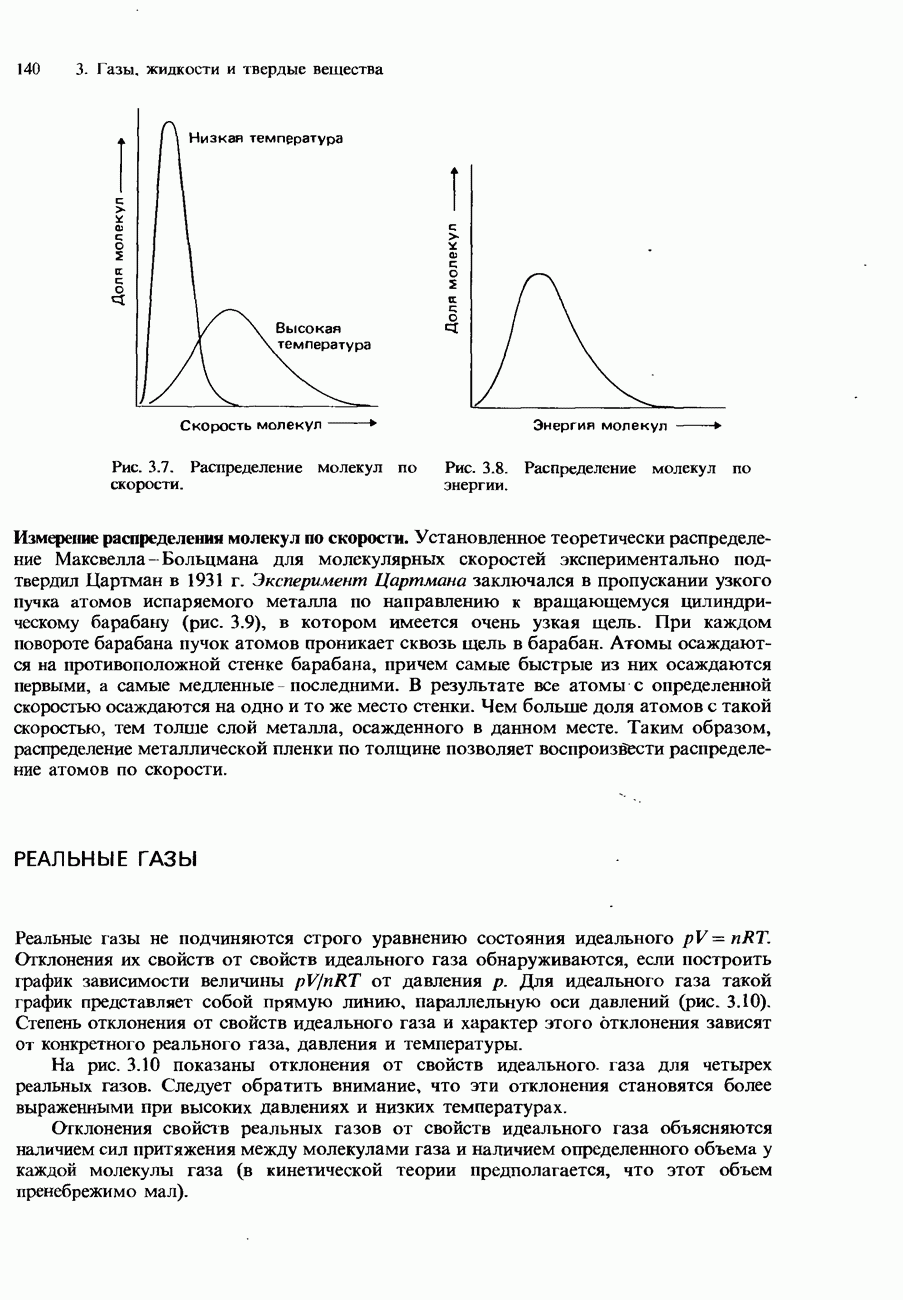
- Скорости молекул
- Распределение Максвелла-Больцмана
- РЕАЛЬНЫЕ ГАЗЫ
- Уравнение Ван-дер-Ваальса
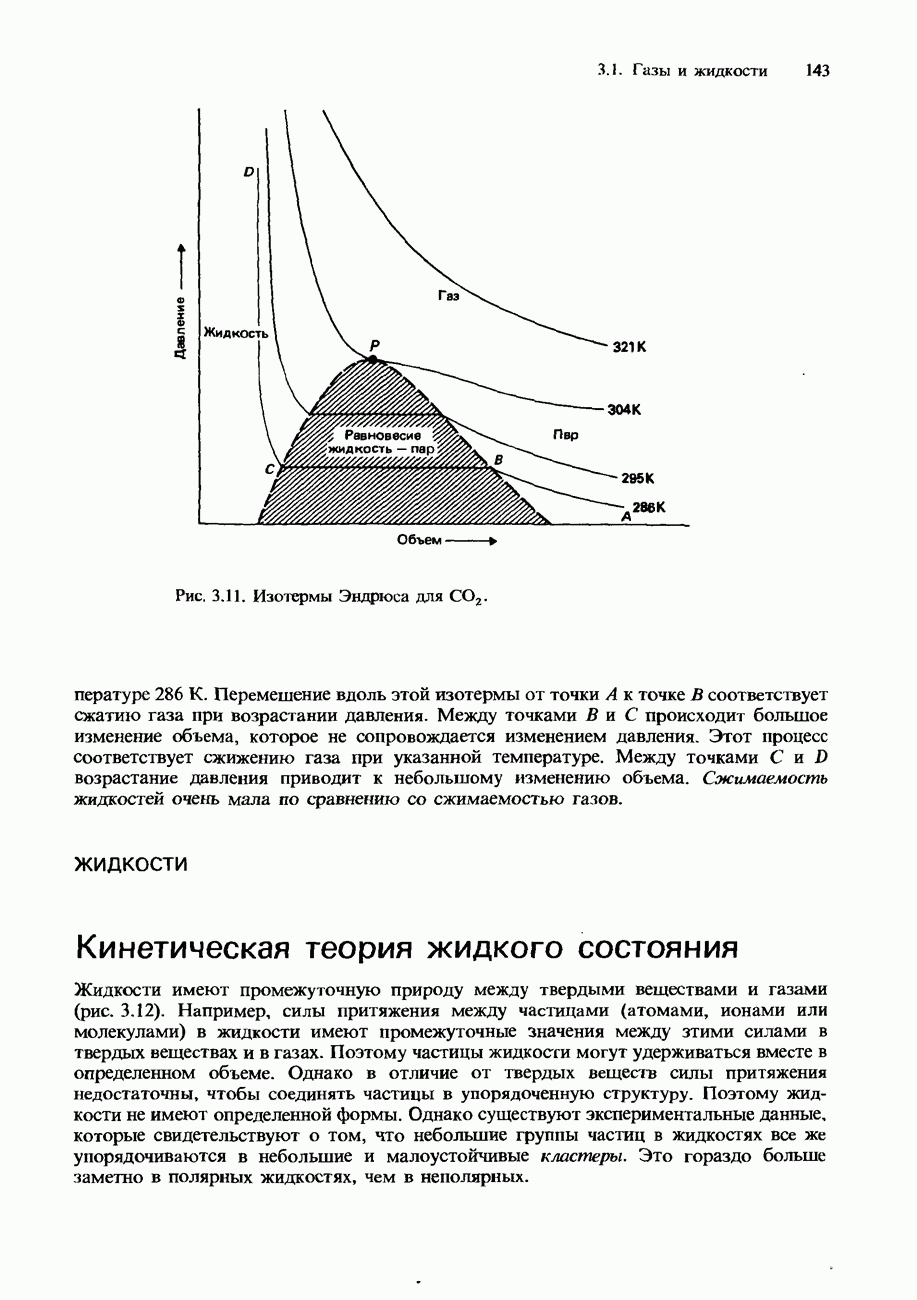
- Сжижение газов
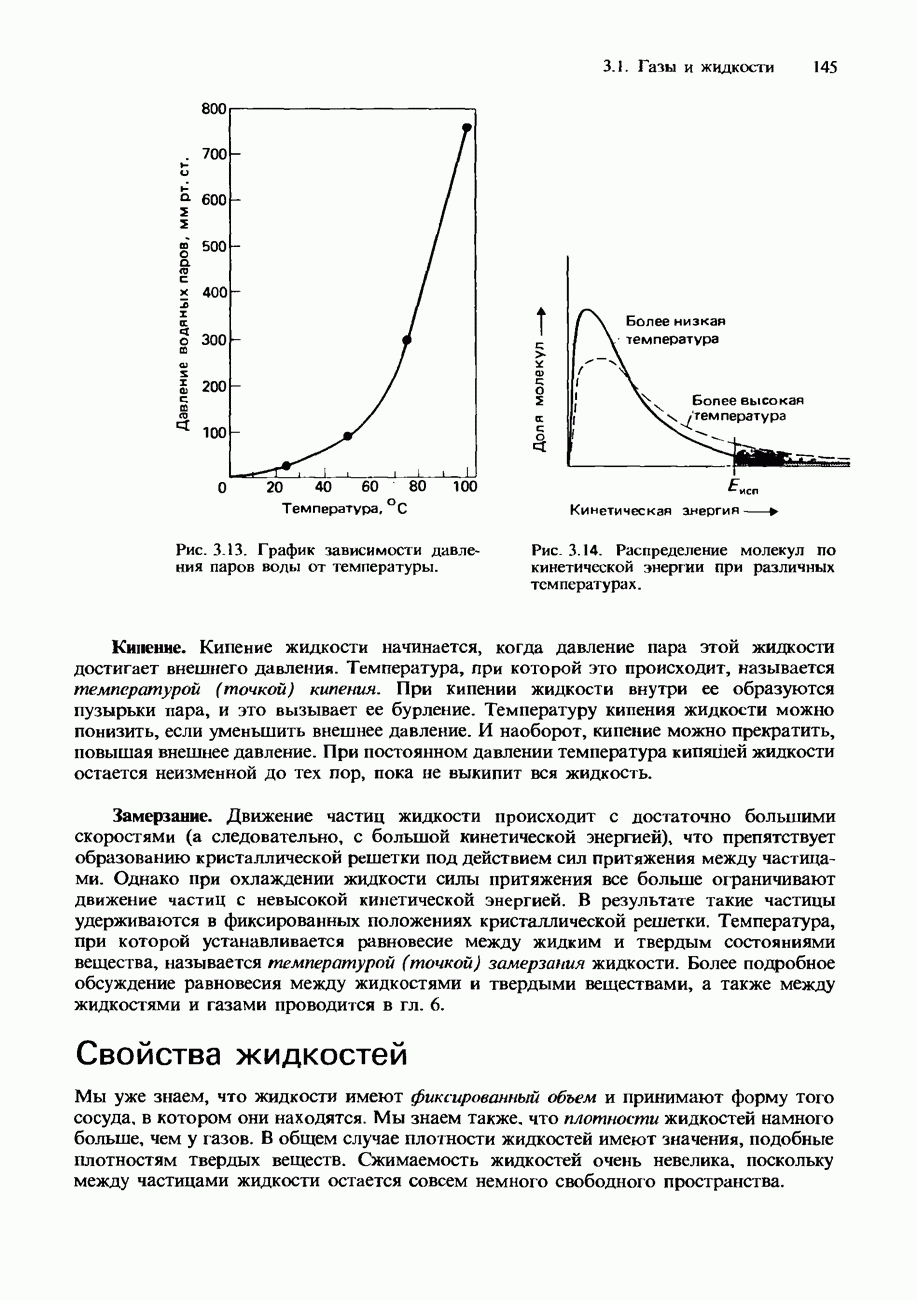
- ЖИДКОСТИ
- Свойства жидкостей
- 3.2. Твердые вещества
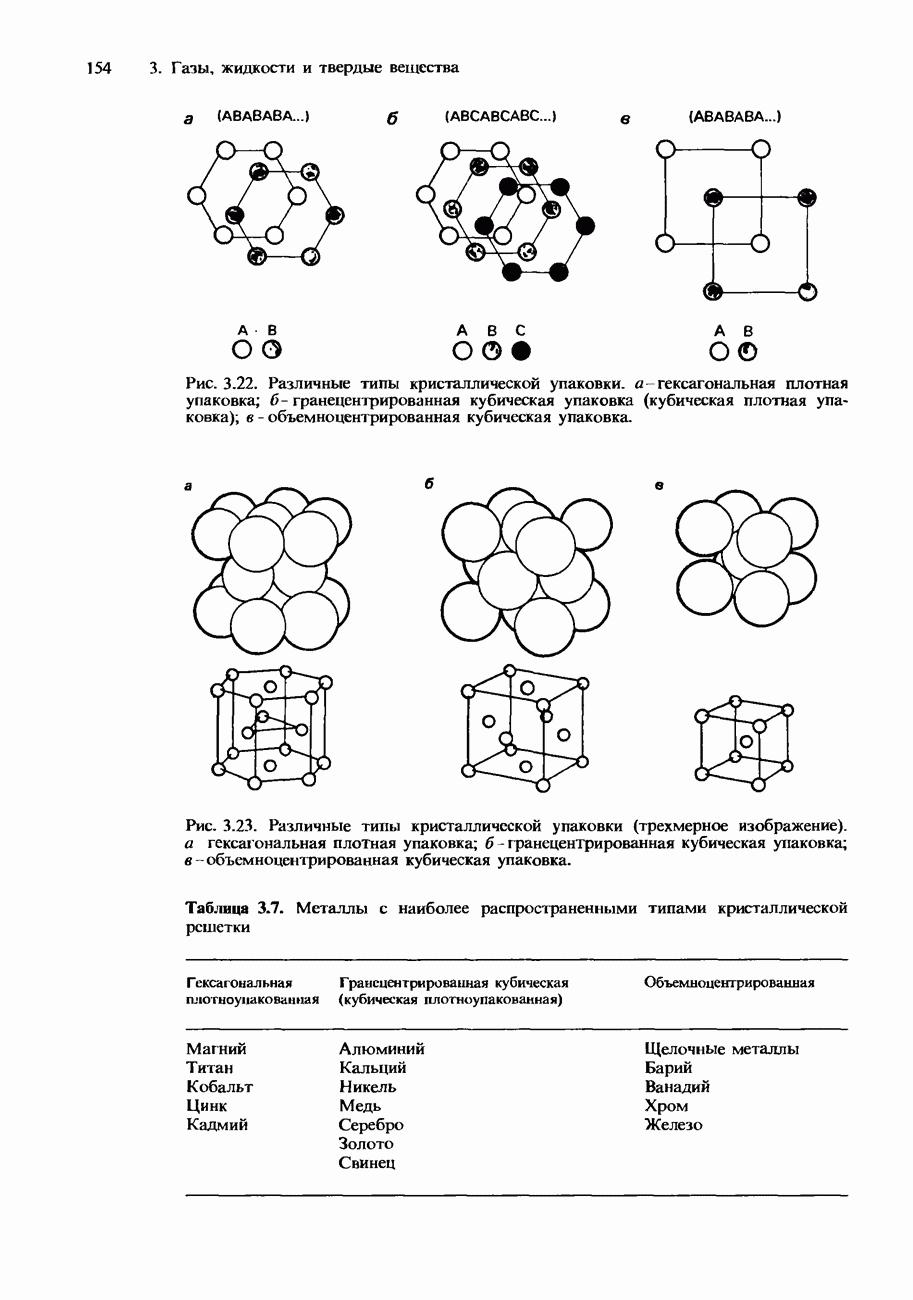
- КРИСТАЛЛИЧЕСКАЯ СТРУКТУРА
- Металлические кристаллы
- Ионные кристаллы
- Ковалентные кристаллы
- ИЗОМОРФИЗМ. ПОЛИМОРФИЗМ И АЛЛОТРОПИЯ
- СВОЙСТВА ТВЕРДЫХ ВЕЩЕСТВ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 4. СТЕХИОМЕТРИЯ
- 4.1. Стехиометрия и номенклатура
- Химические вещества
- Количественные законы химии
- Вес и масса
- НАЗВАНИЯ И ФОРМУЛЫ ХИМИЧЕСКИХ СОЕДИНЕНИЙ
- Химические формулы
- НОМЕНКЛАТУРА НЕОРГАНИЧЕСКИХ СОЕДИНЕНИЙ
- Степень окисления (состояние окисления)
- Элементы
- Бинарные соединения
- 4.2 Стехиометрические вычисления
- Молярная масса
- Число частиц вещества
- Процентный состав соединения
- Эмпирическая формула соединения
- Молярные постоянные и молярные величины
- Состав гомогенных смесей
- ХИМИЧЕСКИЕ УРАВНЕНИЯ
- ВЫХОД РЕАКЦИИ
- ПРОМЫШЛЕННАЯ СТЕХИОМЕТРИЯ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 5. ЭНЕРГЕТИКА
- 5.1. Термодинамика
- ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 5.2. Энтальпия
- СТАНДАРТНЫЕ ИЗМЕНЕНИЯ ЭНТАЛЬПИИ
- ДРУГИЕ ИЗМЕНЕНИЯ ЭНТАЛЬПИИ
- КАЛОРИМЕТРИЯ
- КАЛОРИЙНОСТЬ ПИЩИ
- ЗАКОН ГЕССА
- 5.3 Энергия и структура
- ЭНТАЛЬПИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Энтальпии растворения и гидратации
- ЭНТРОПИЯ
- СВОБОДНАЯ ЭНЕРГИЯ ГИББСА
- О ЧЕМ ПОЗВОЛЯЕТ СУДИТЬ ИЗМЕНЕНИЕ СВОБОДНОЙ ЭНЕРГИИ СИСТЕМЫ
- 5.4. Источники энергии
- НЕТРАДИЦИОННЫЕ ИСТОЧНИКИ ЭНЕРГИИ
- ЗАПАСАНИЕ ЭНЕРГИИ
- ПОТРЕБЛЕНИЕ ЭНЕРГИИ В ПРОШЛОМ, НАСТОЯЩЕМ И БУДУЩЕМ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 6. ФАЗОВЫЕ РАВНОВЕСИЯ
- 6.1. Равновесия и фазы
- ФАЗЫ И КОМПОНЕНТЫ
- Фазы
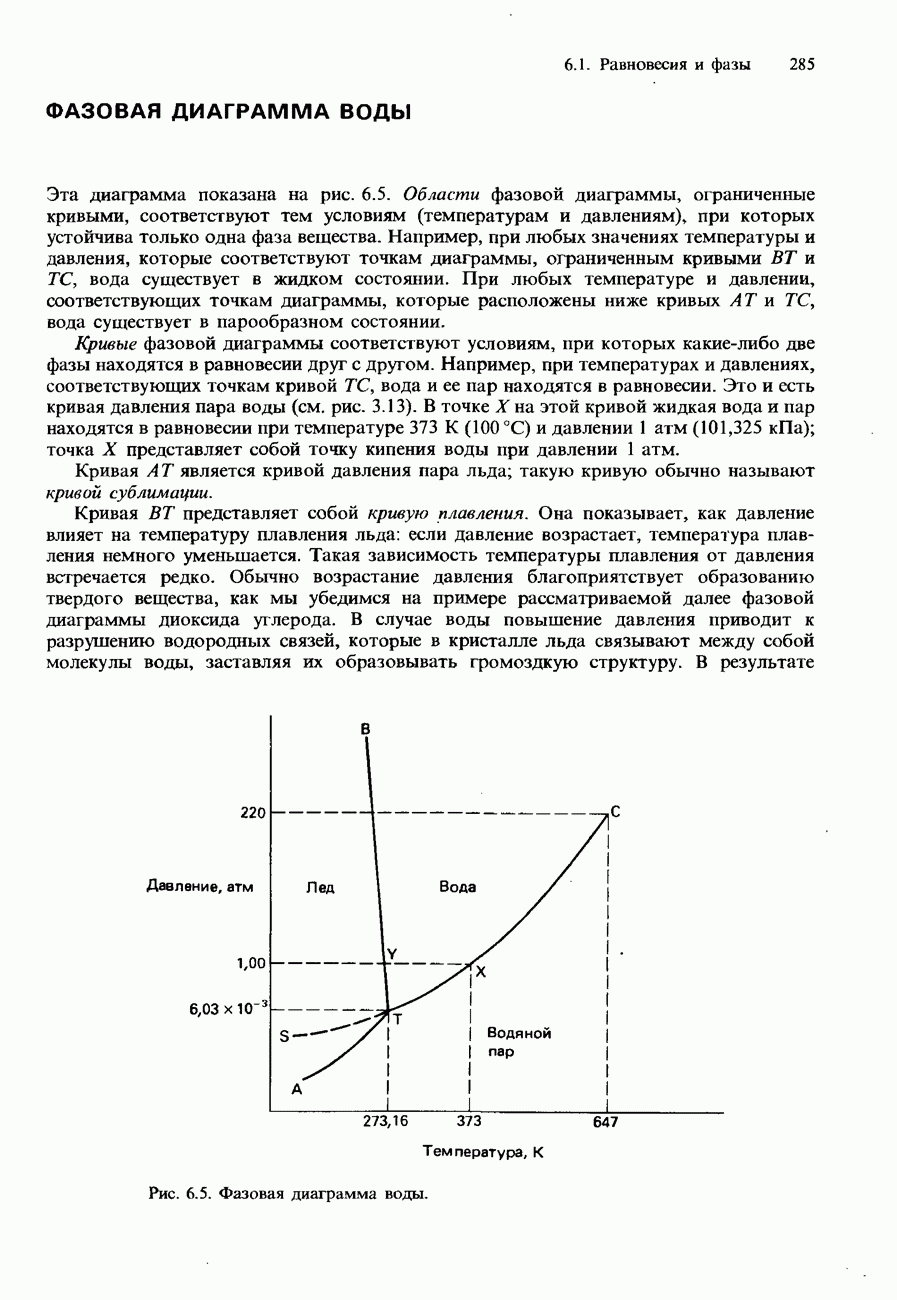
- ФАЗОВАЯ ДИАГРАММА ВОДЫ
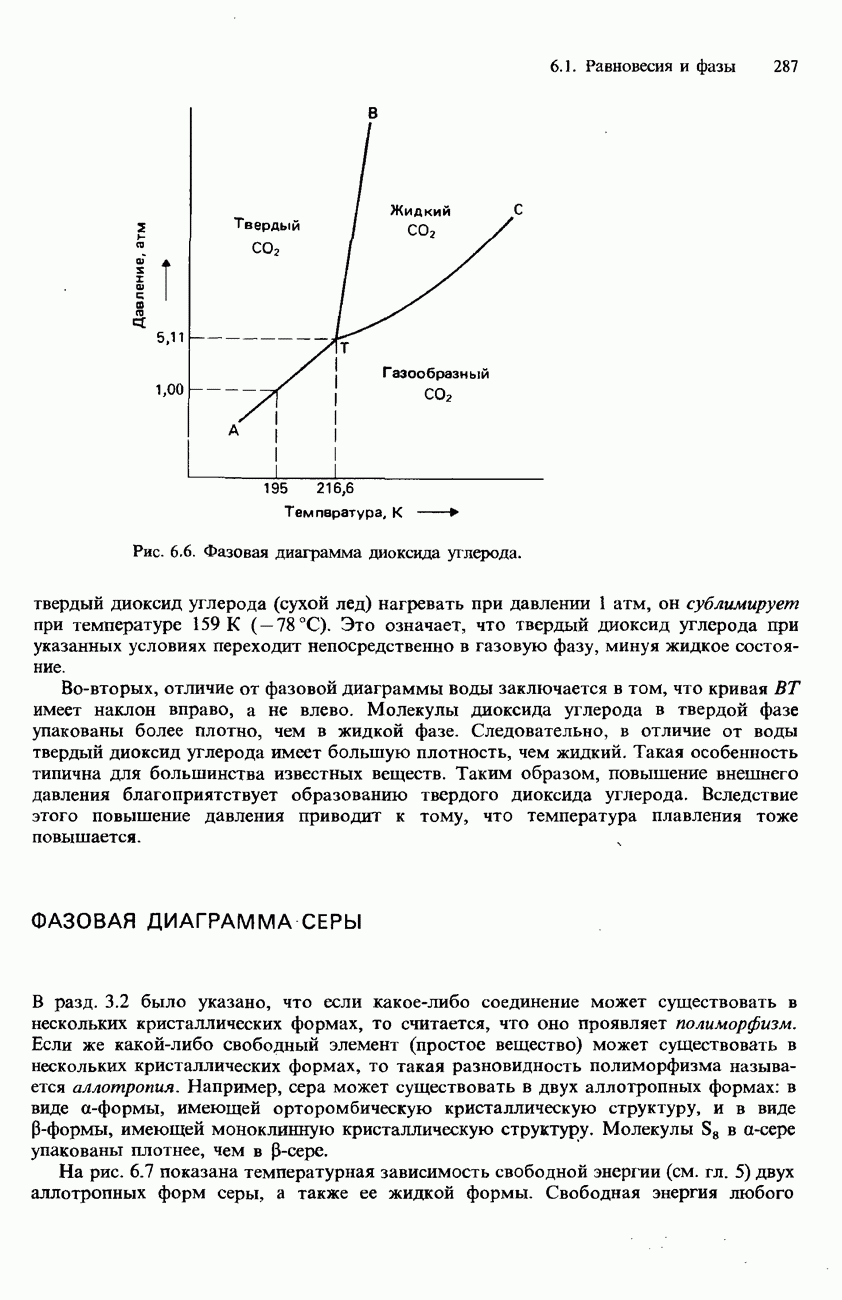
- ФАЗОВАЯ ДИАГРАММА ДИОКСИДА УГЛЕРОДА
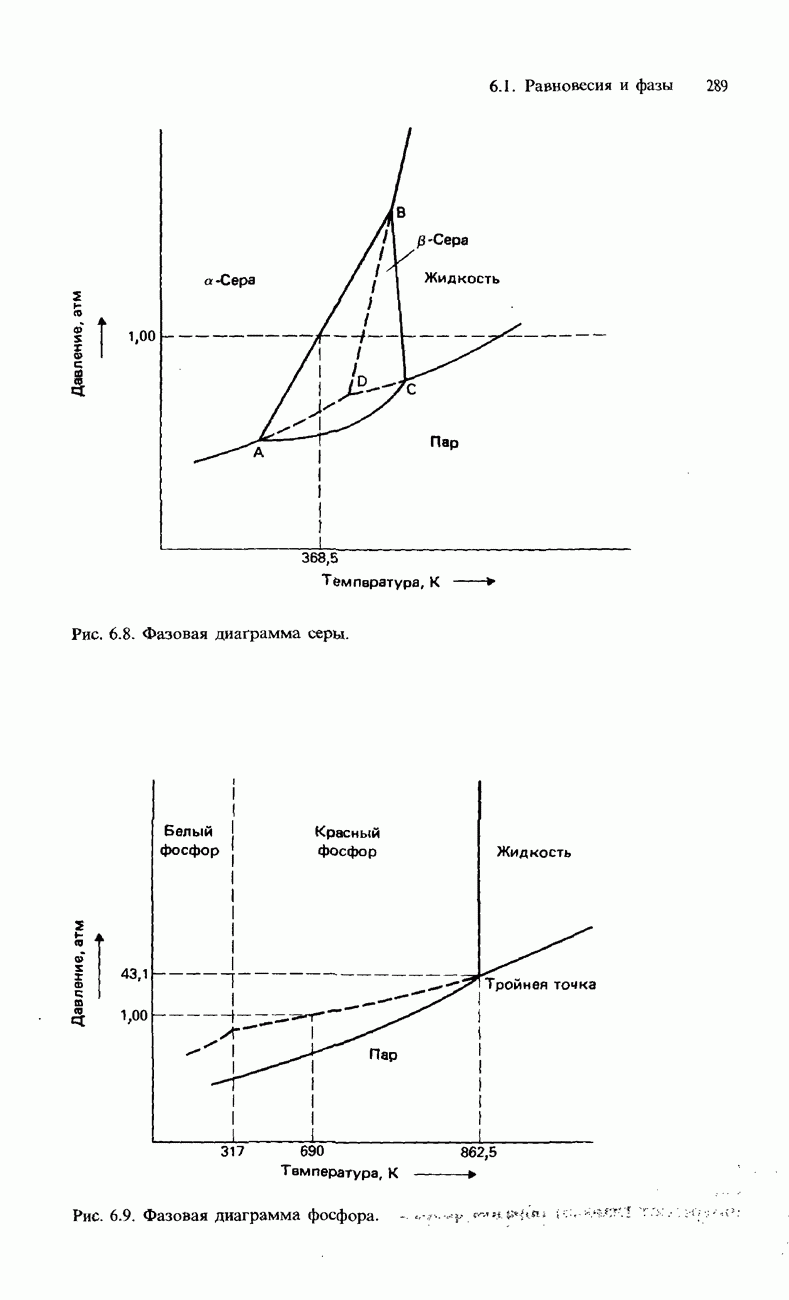
- ФАЗОВАЯ ДИАГРАММА СЕРЫ
- ФАЗОВАЯ ДИАГРАММА ФОСФОРА
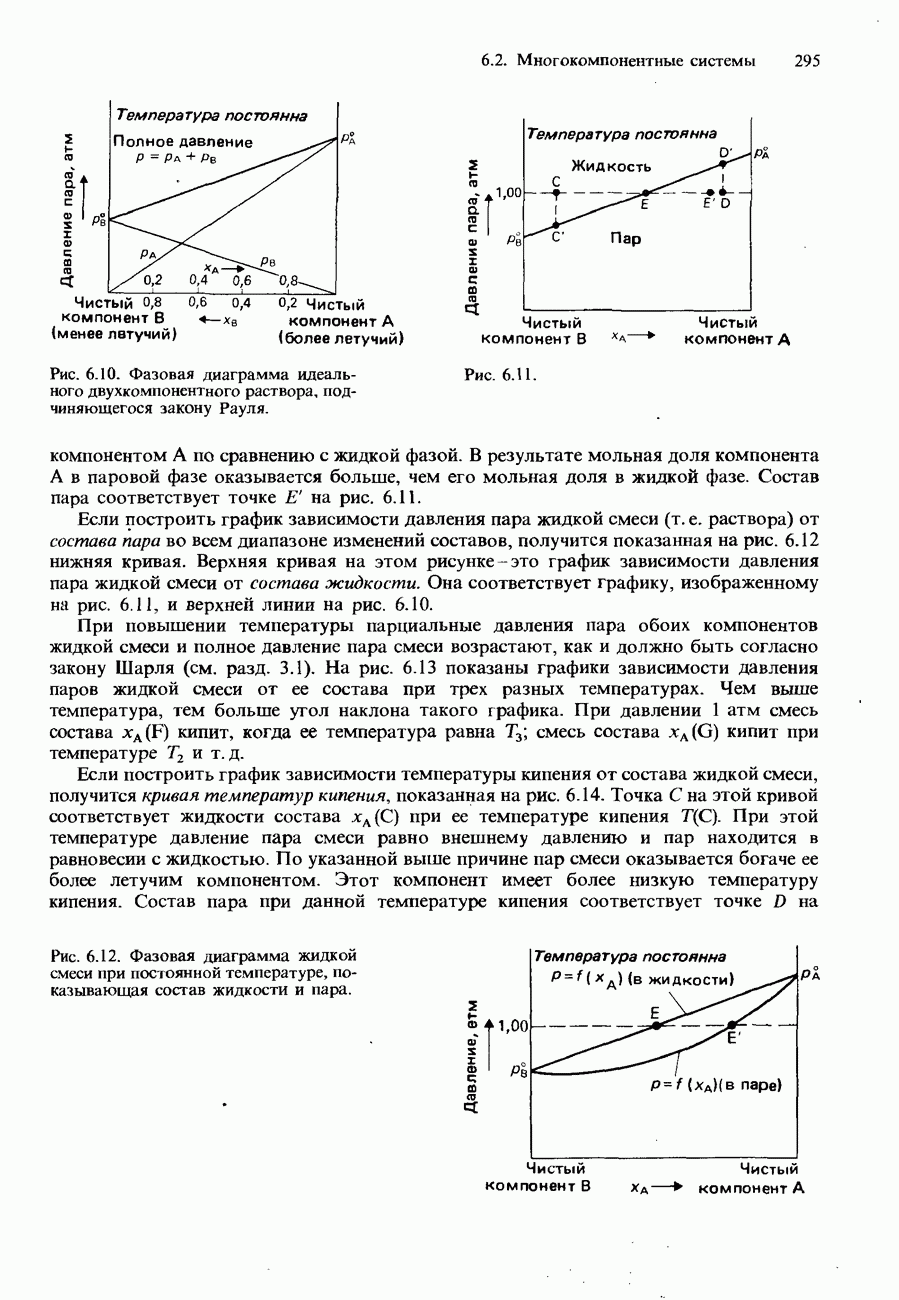
- 6.2. Многокомпонентные системы
- ДВУХКОМПОНЕНТНЫЕ ЖИДКИЕ СМЕСИ
- ПОЛНОСТЬЮ СМЕШИВАЮЩИЕСЯ ЖИДКОСТИ
- Фазовые диаграммы полностью смешивающихся жидкостей
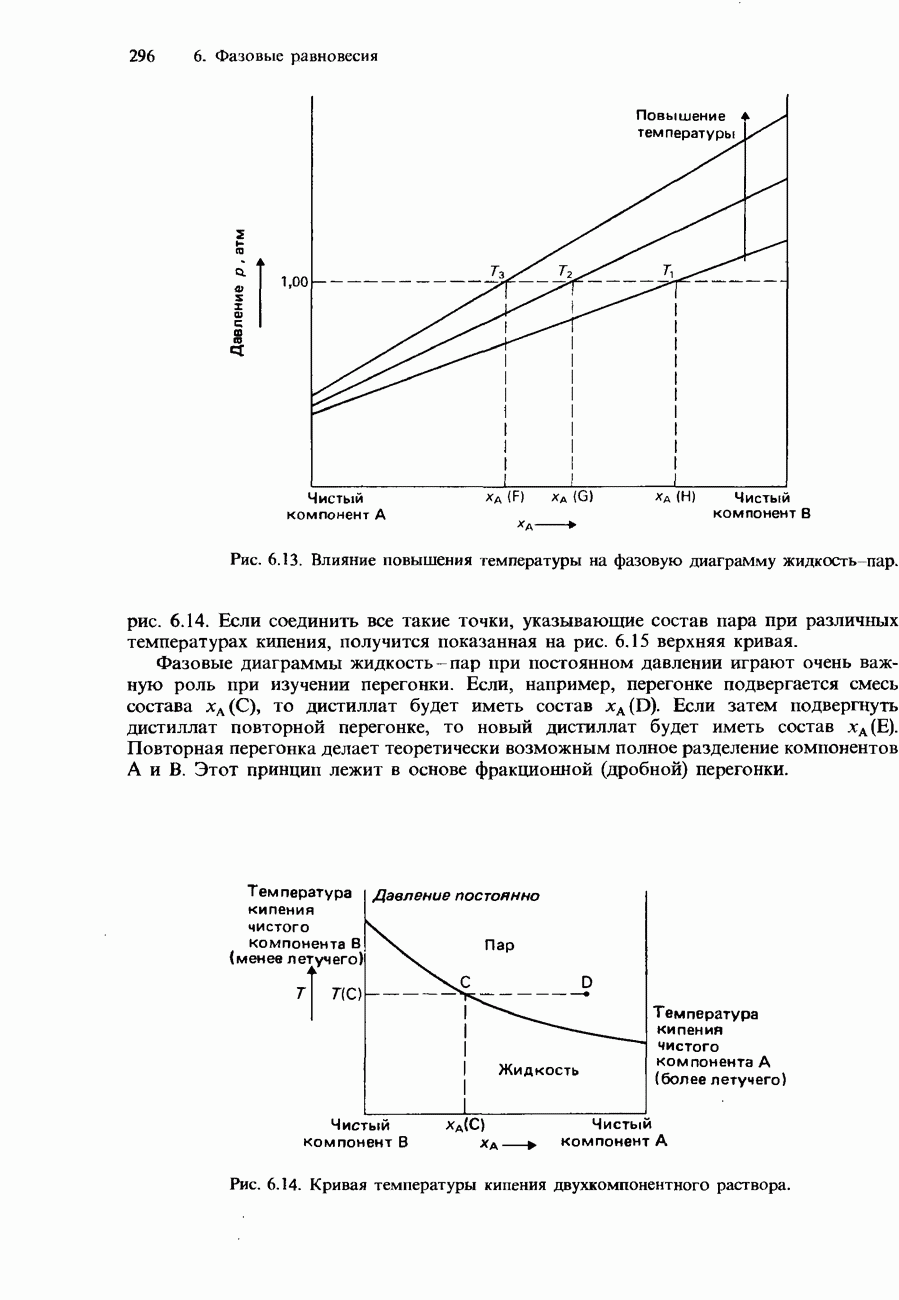
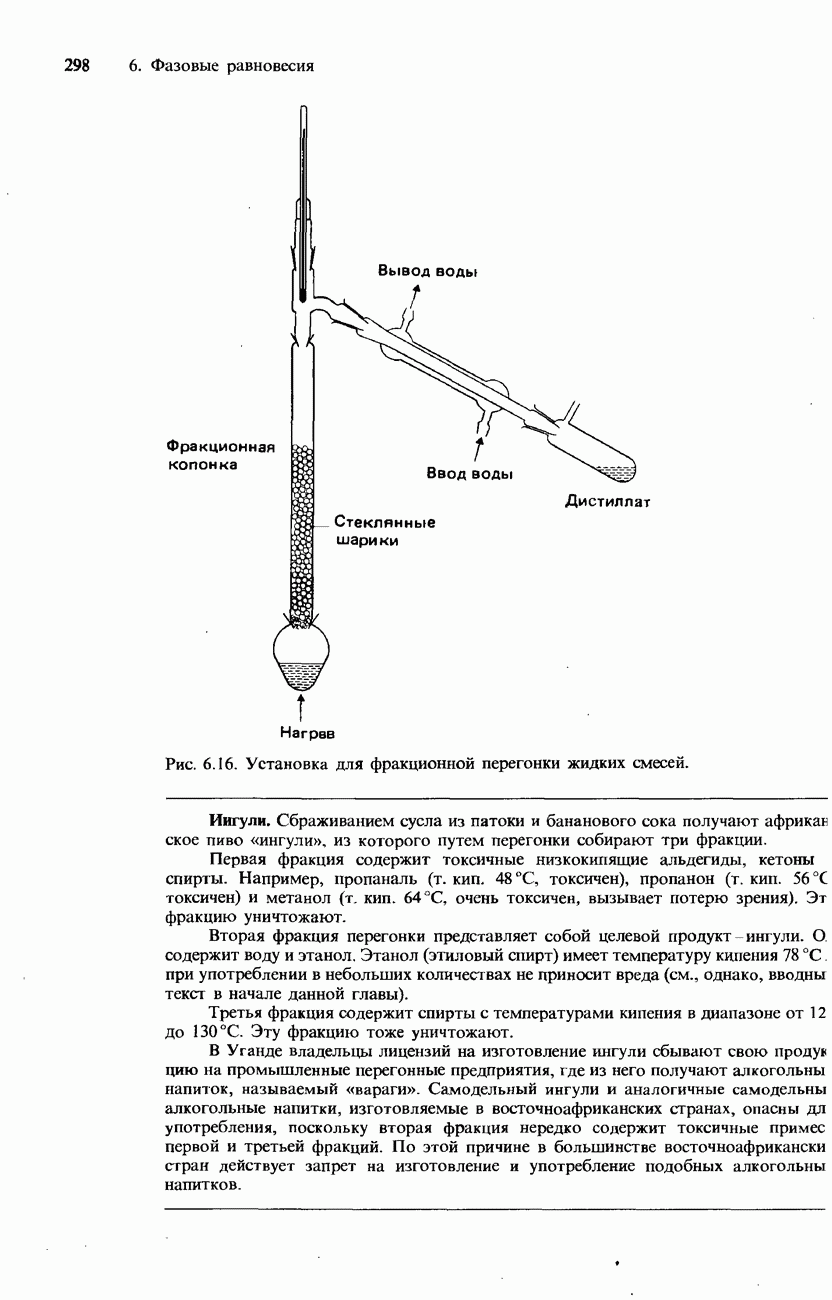
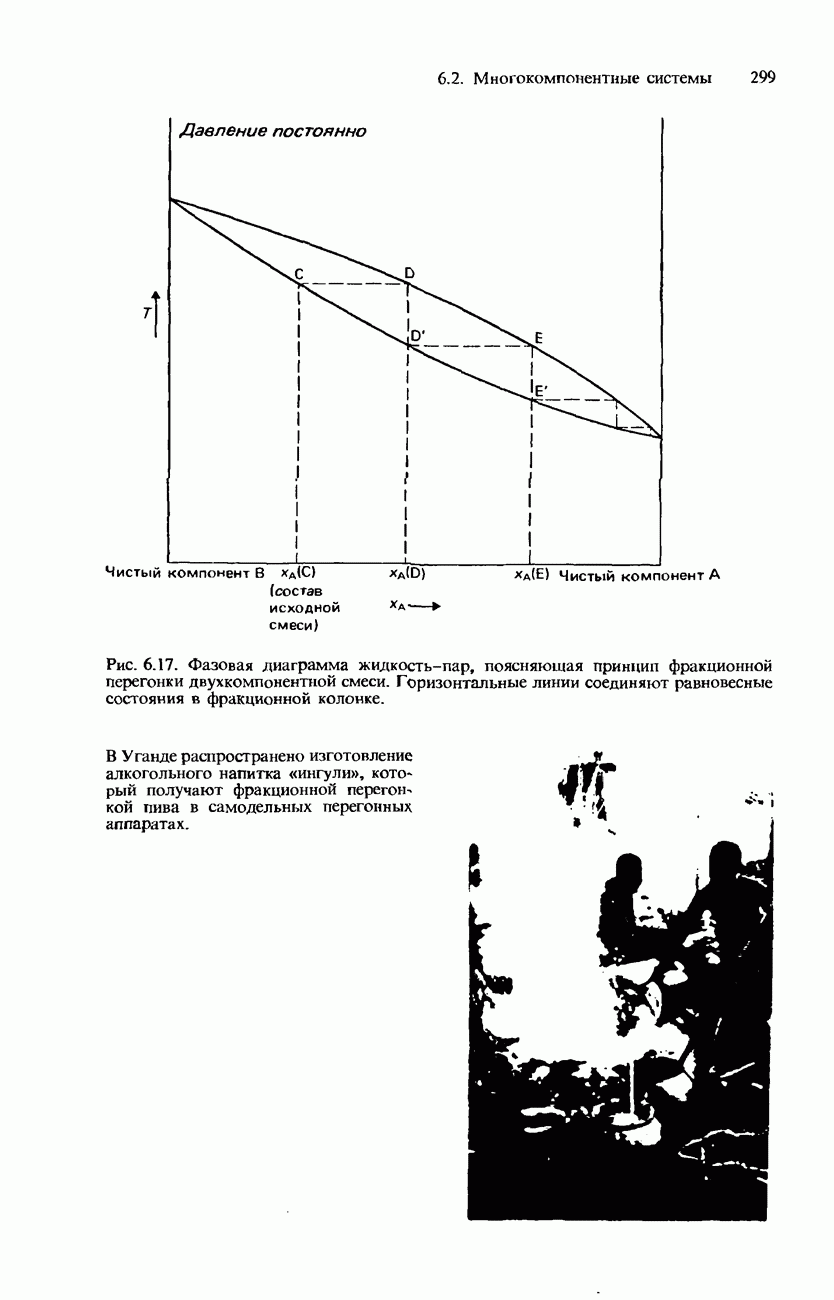
- Фракционная перегонка
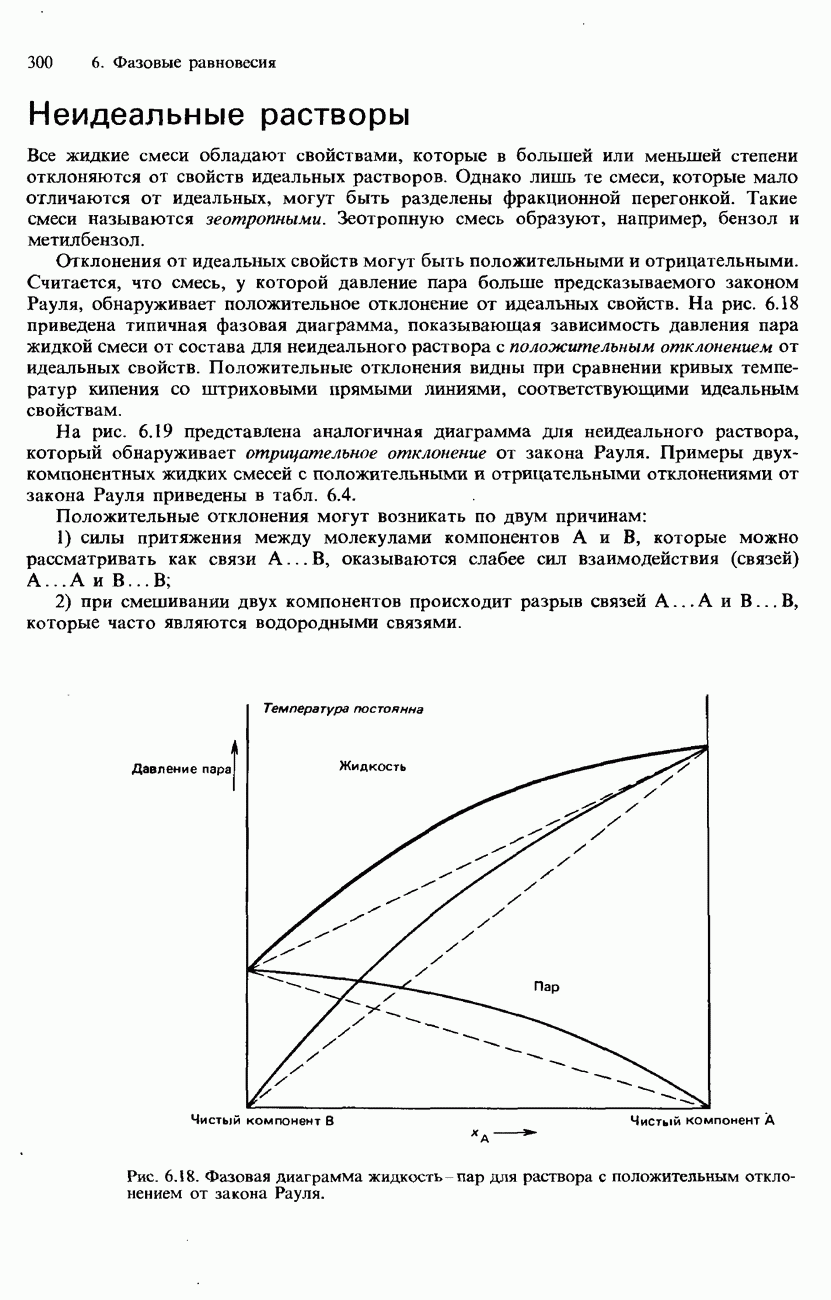
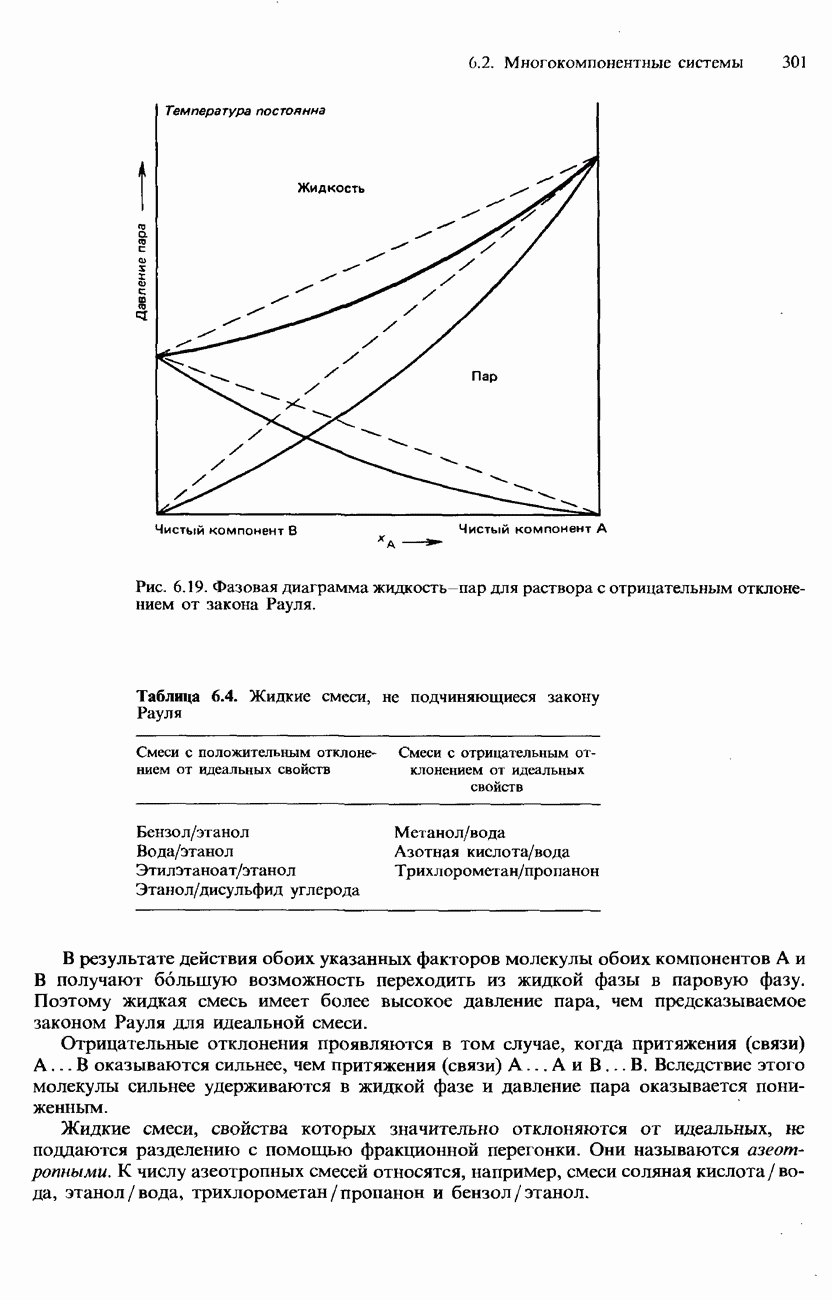
- Неидеальные растворы
- ЧАСТИЧНО СМЕШИВАЮЩИЕСЯ ЖИДКОСТИ
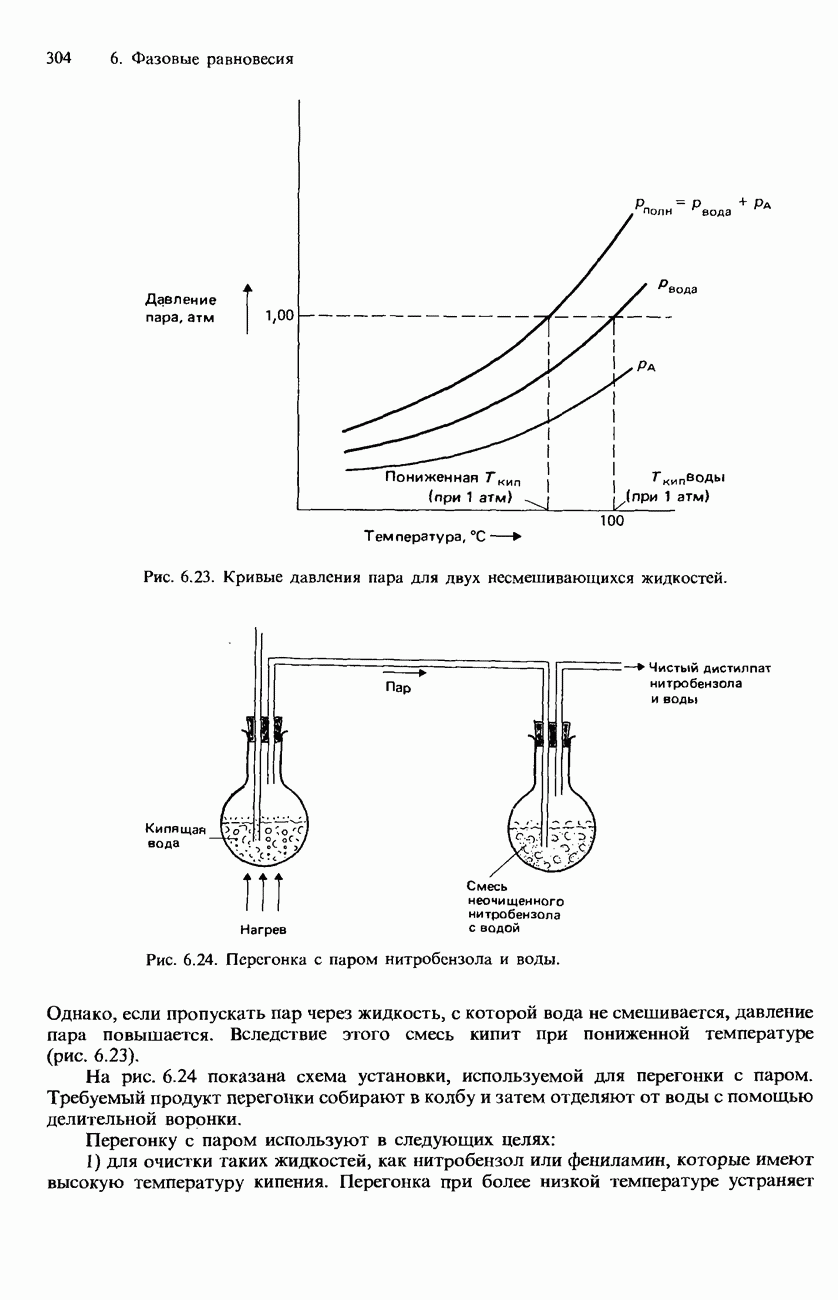
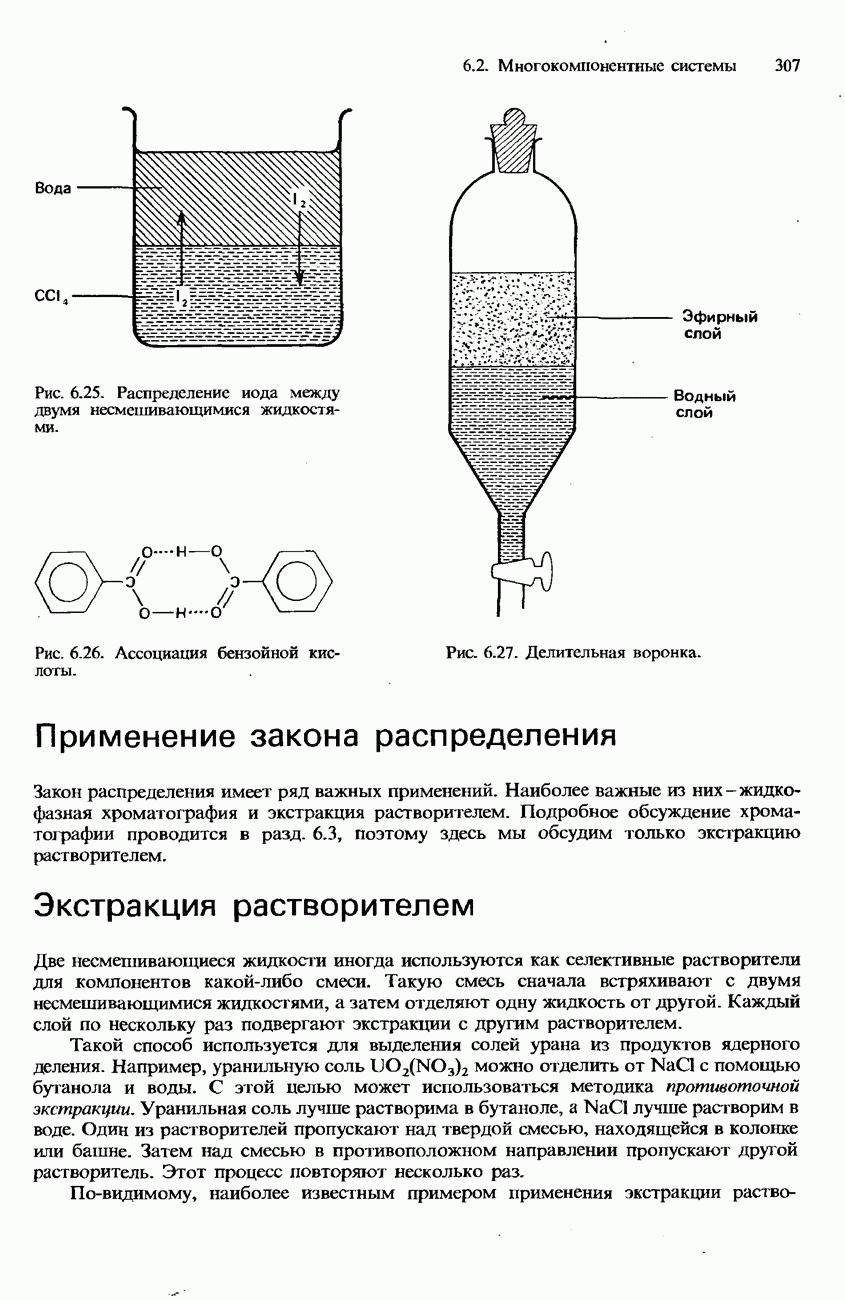
- НЕСМЕШИВАЮЩИЕСЯ ЖИДКОСТИ
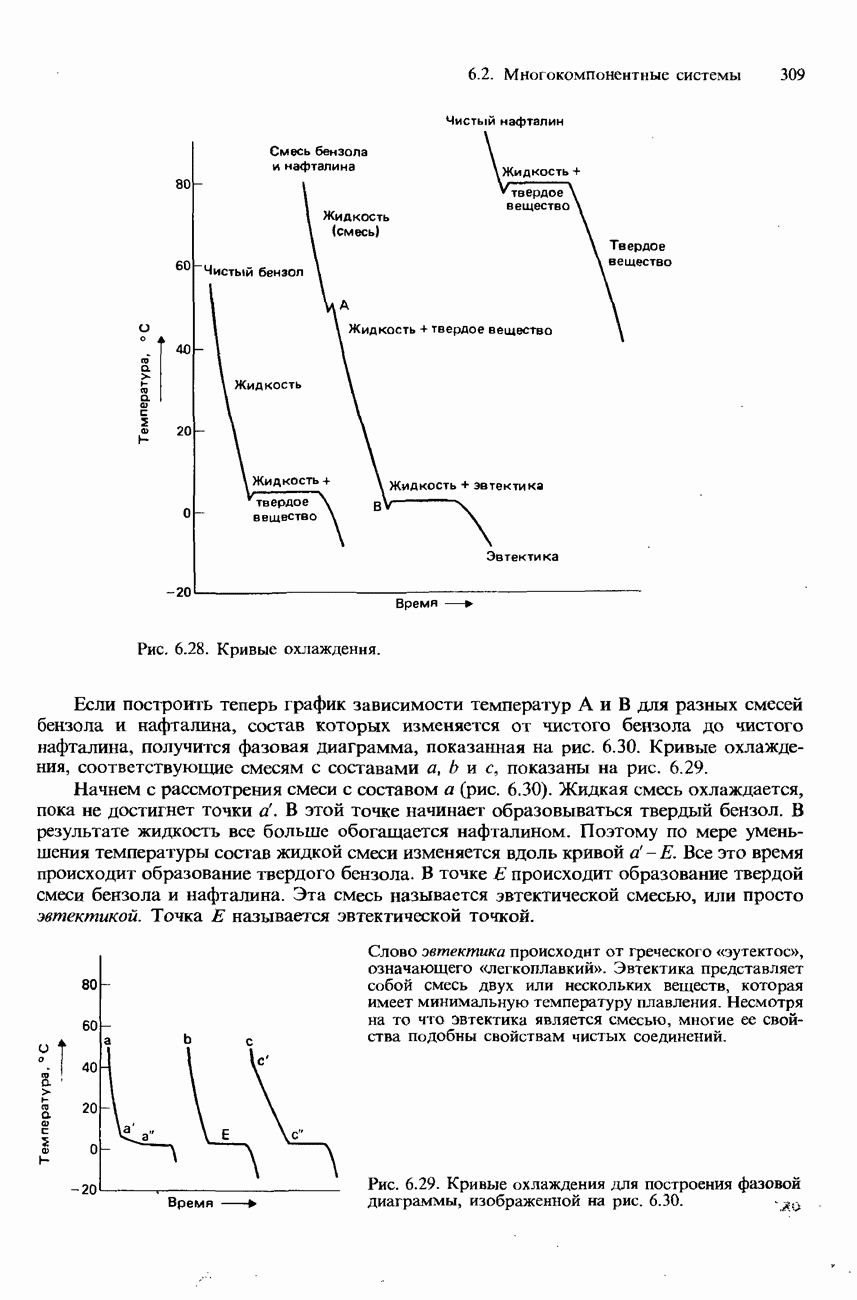
- РАВНОВЕСИЯ ТВЕРДОЕ ВЕЩЕСТВО-ЖИДКОСТЬ
- 6.3. Коллигативные свойства растворов. Коллоиды Хроматография
- КОЛЛОИДЫ
- ХРОМАТОГРАФИЯ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 7. ХИМИЧЕСКОЕ РАВНОВЕСИЕ
- 7.1. Константа равновесия
- ЗАКОН ДЕЙСТВУЮЩИХ МАСС
- ВЛИЯНИЕ УСЛОВИЙ ПРОТЕКАНИЯ РЕАКЦИИ НА ПОЛОЖЕНИЕ РАВНОВЕСИЯ
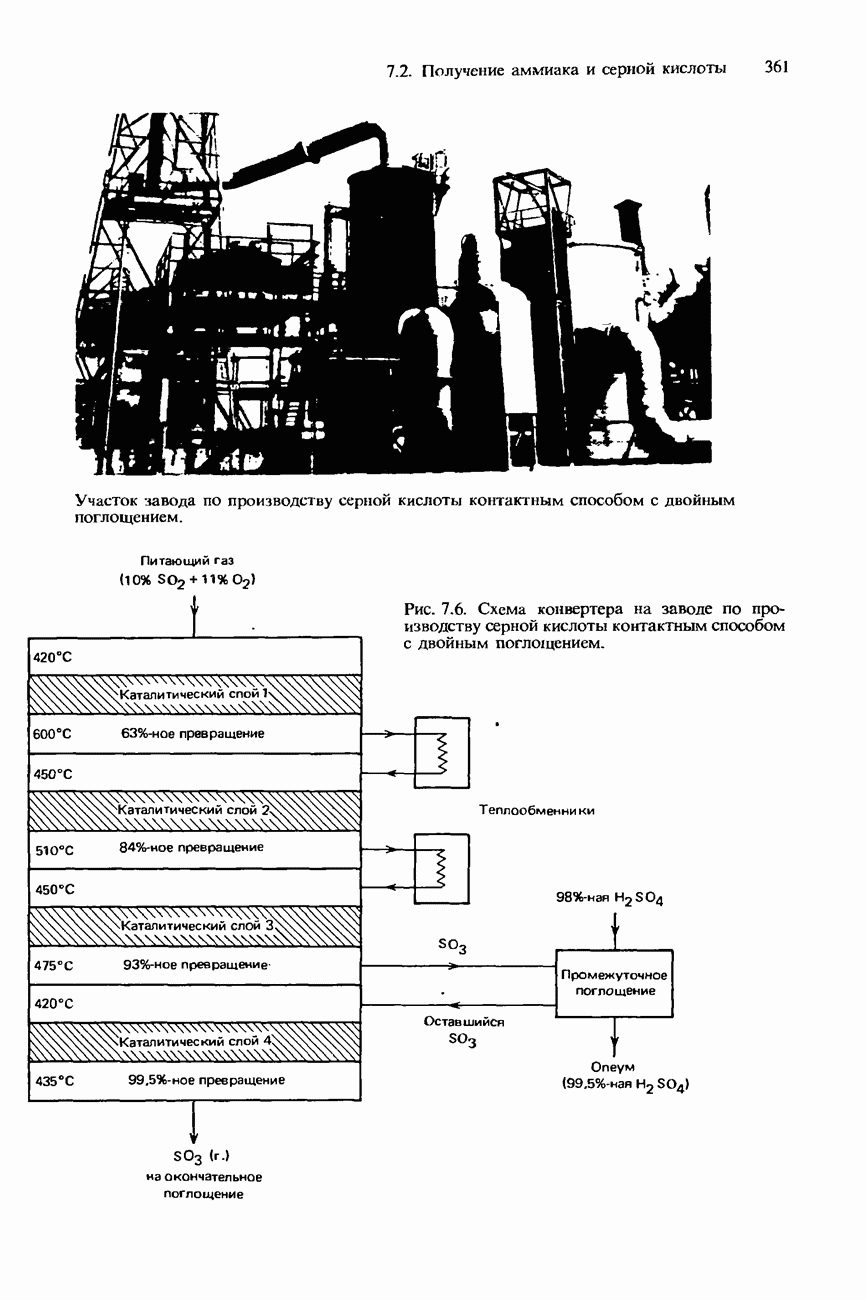
- 7.2. Получение аммиака и серной кислоты
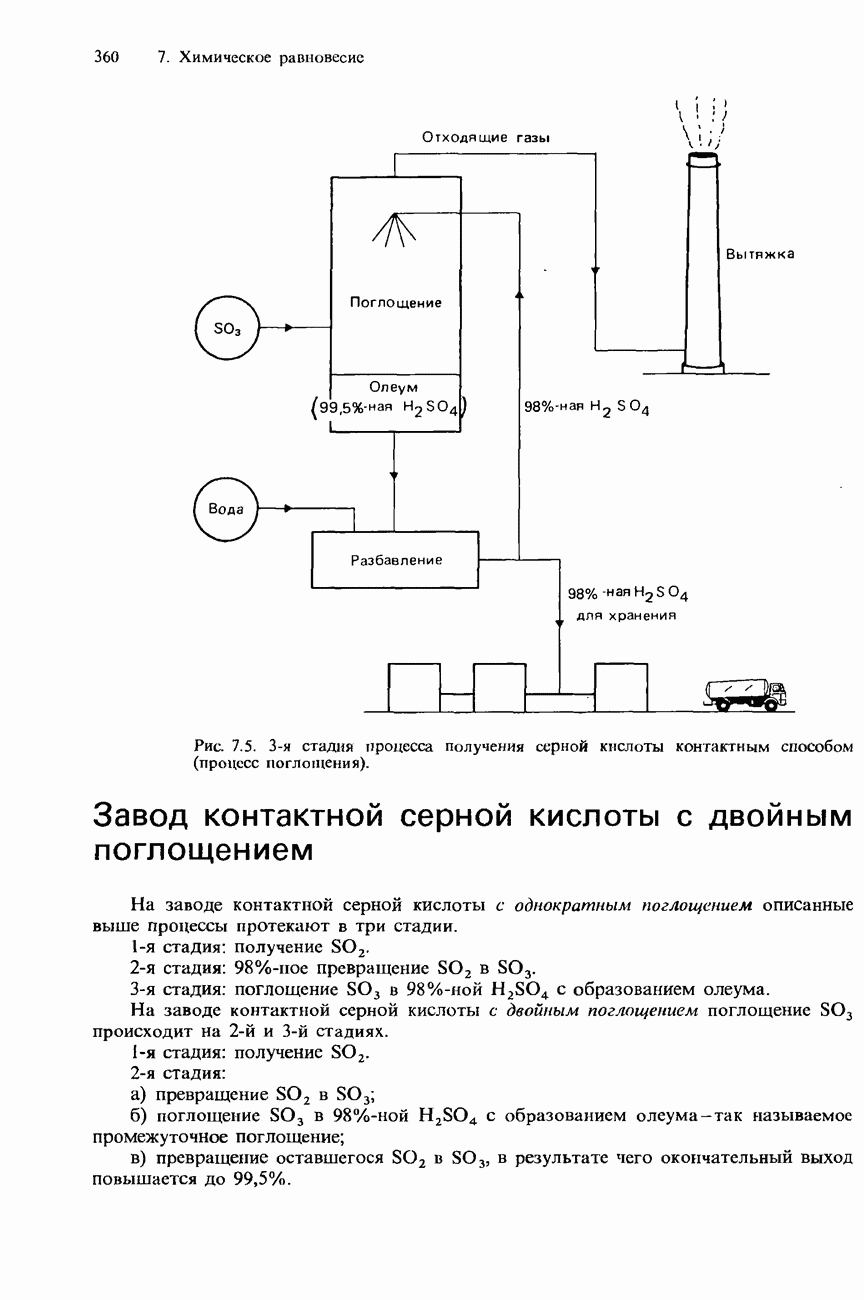
- ПРОМЫШЛЕННОЕ ПОЛУЧЕНИЕ СЕРНОЙ КИСЛОТЫ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 8. ИОНЫ
- 8.1. Кислоты и основания
- ЭЛЕКТРОЛИТЫ
- КИСЛОТЫ И ОСНОВАНИЯ
- КОНСТАНТЫ ДИССОЦИАЦИИ
- ВОДОРОДНЫЙ ПОКАЗАТЕЛЬ pH ШКАЛА ЕГО ЗНАЧЕНИЙ
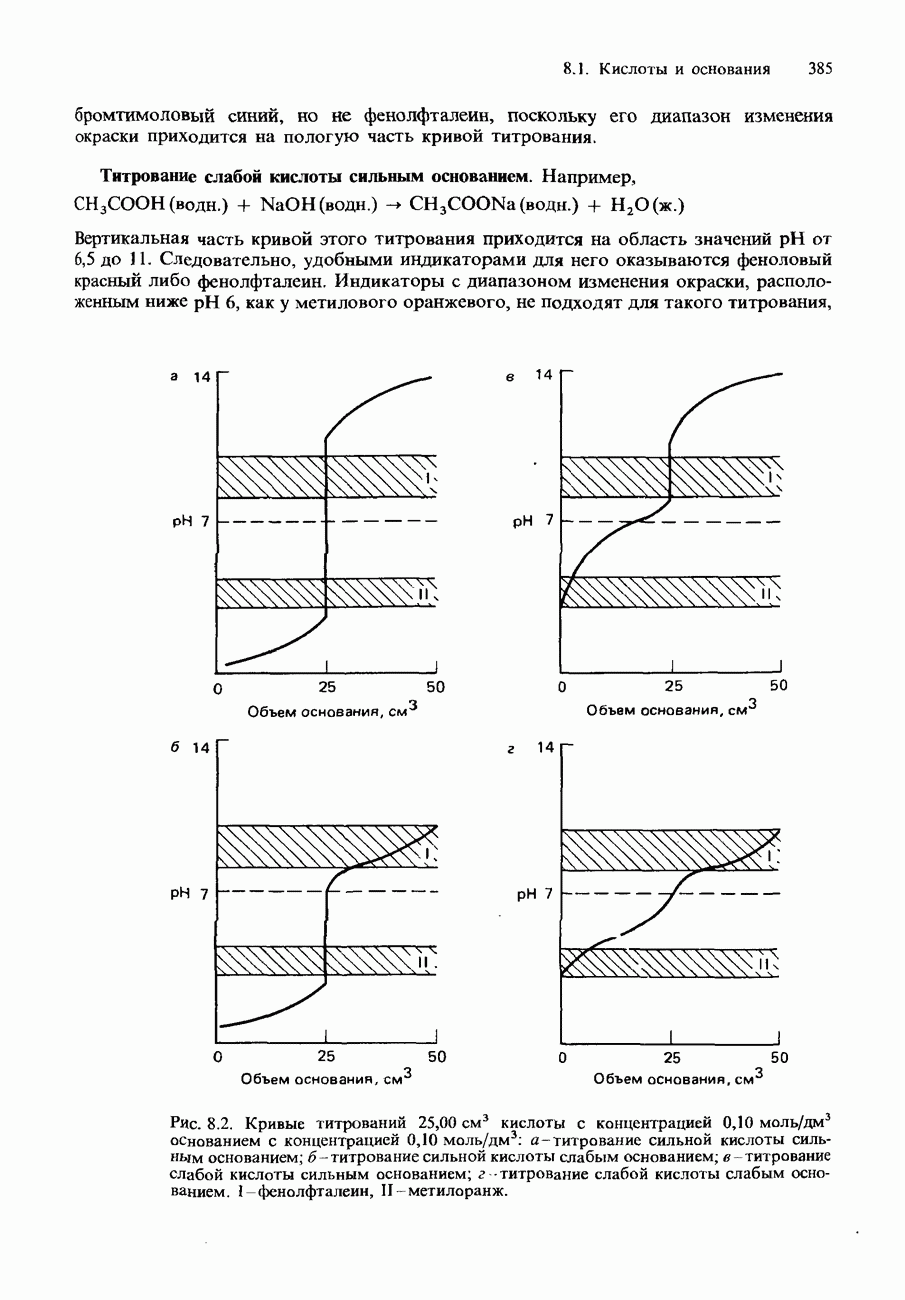
- КИСЛОТНО-ОСНОВНЫЕ ИНДИКАТОРЫ И ТИТРОВАНИЕ
- 8.2. Соли, растворимость и устойчивость
- БУФЕРНЫЕ РАСТВОРЫ
- РАСТВОРИМОСТЬ
- РАВНОВЕСИЯ С УЧАСТИЕМ КОМПЛЕКСНЫХ ИОНОВ
- ИОННЫЙ ОБМЕН
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 9. ХИМИЧЕСКАЯ КИНЕТИКА
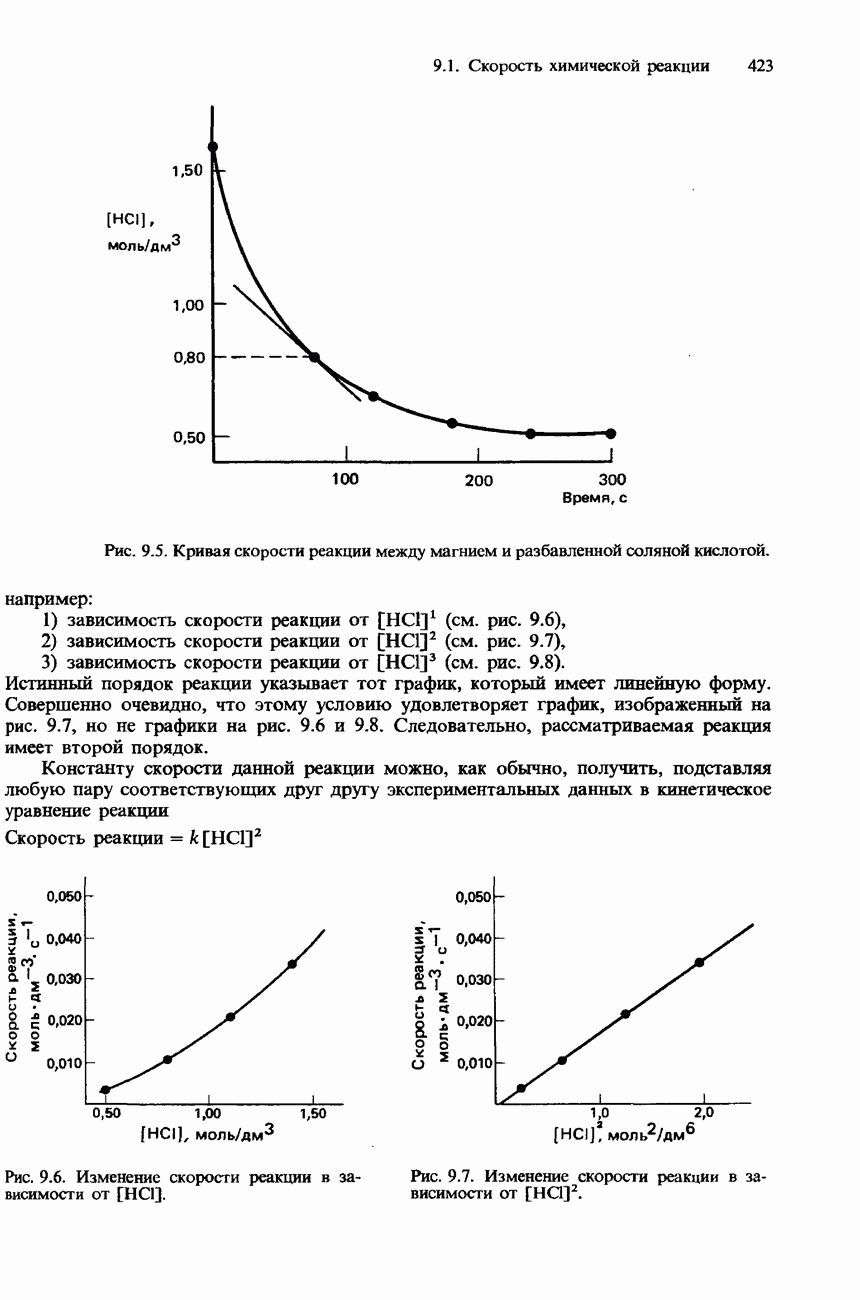
- 9.1. Скорость химической реакции
- МЕТОДЫ ИЗМЕРЕНИЯ СКОРОСТИ РЕАКЦИЙ
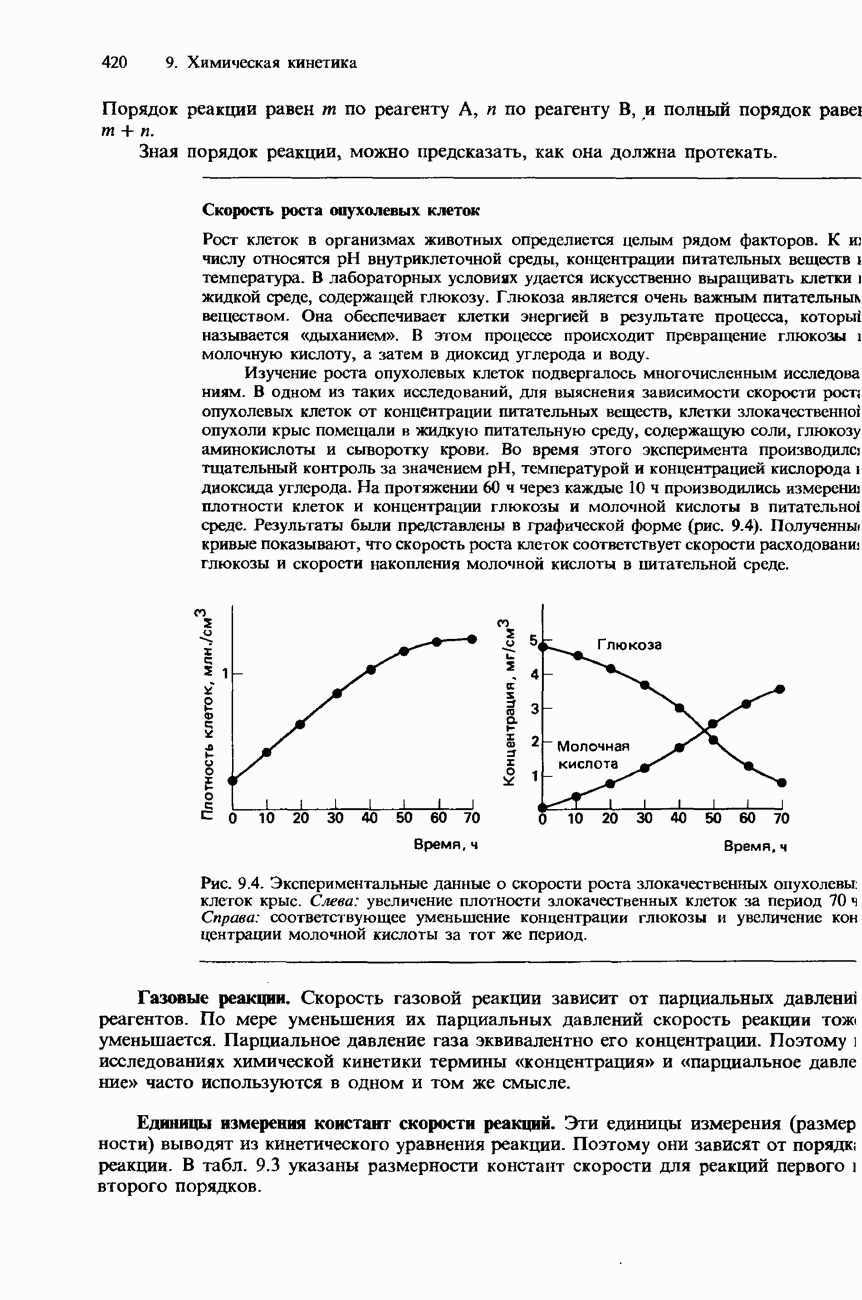
- СКОРОСТЬ РЕАКЦИИ И КОНЦЕНТРАЦИИ РЕАГЕНТОВ
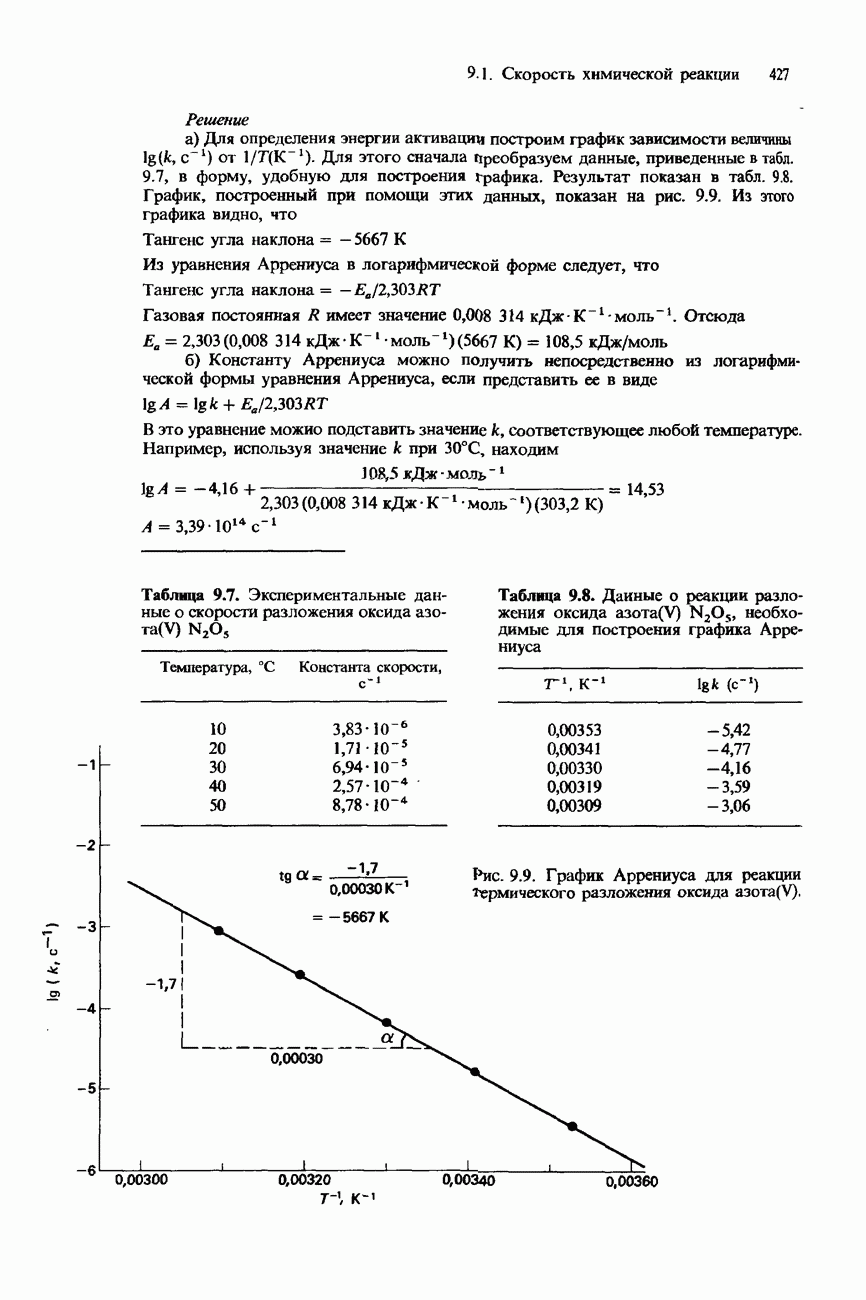
- ЗАВИСИМОСТЬ КОНСТАНТЫ СКОРОСТИ ОТ ТЕМПЕРАТУРЫ УРАВНЕНИЕ АРРЕНИУСА
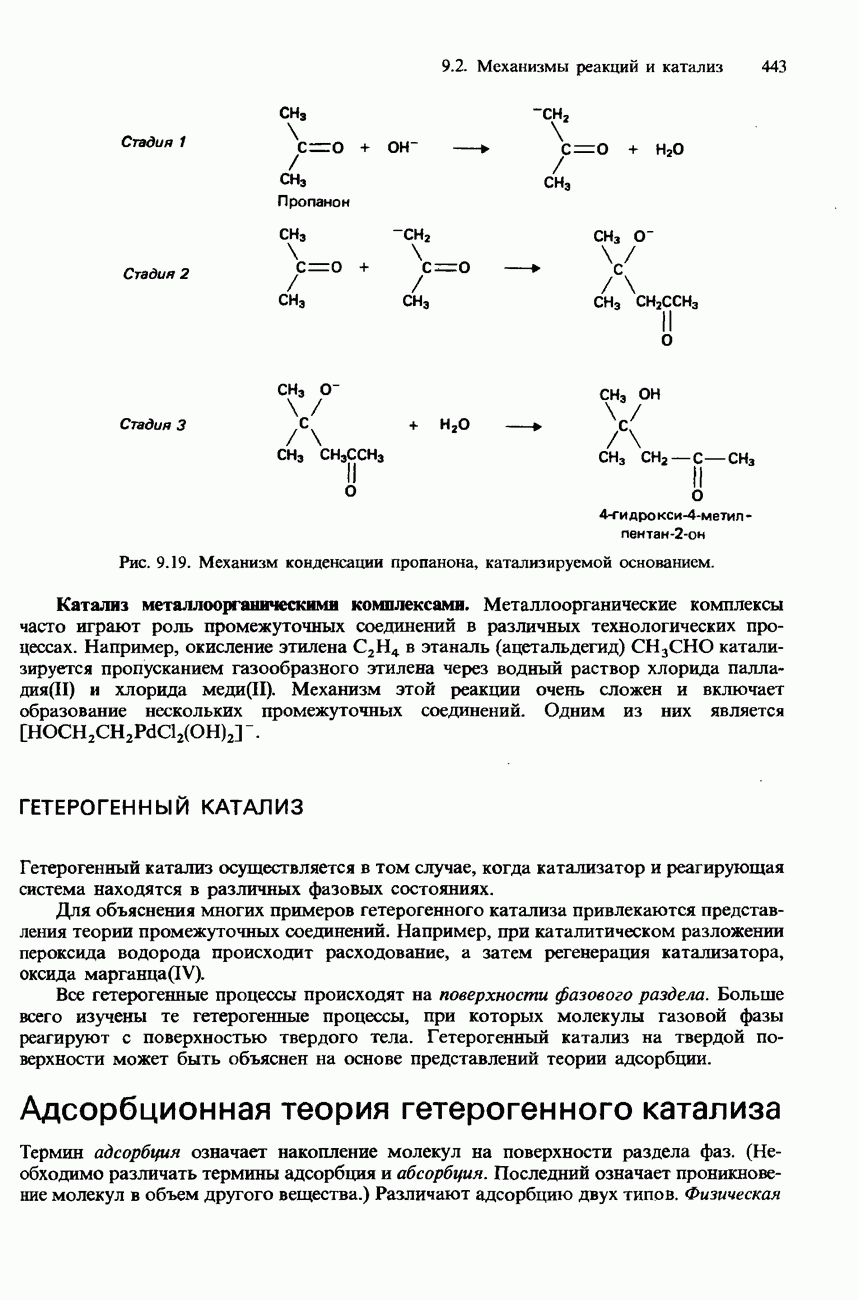
- 9.2. Механизмы реакций и катализ
- ТЕОРИЯ СТОЛКНОВЕНИЙ
- ТЕОРИЯ ПЕРЕХОДНОГО СОСТОЯНИЯ
- ЦЕПНЫЕ РЕАКЦИИ
- КАТАЛИЗ
- ТИПЫ КАТАЛИЗАТОРОВ
- ГОМОГЕННЫЙ КАТАЛИЗ
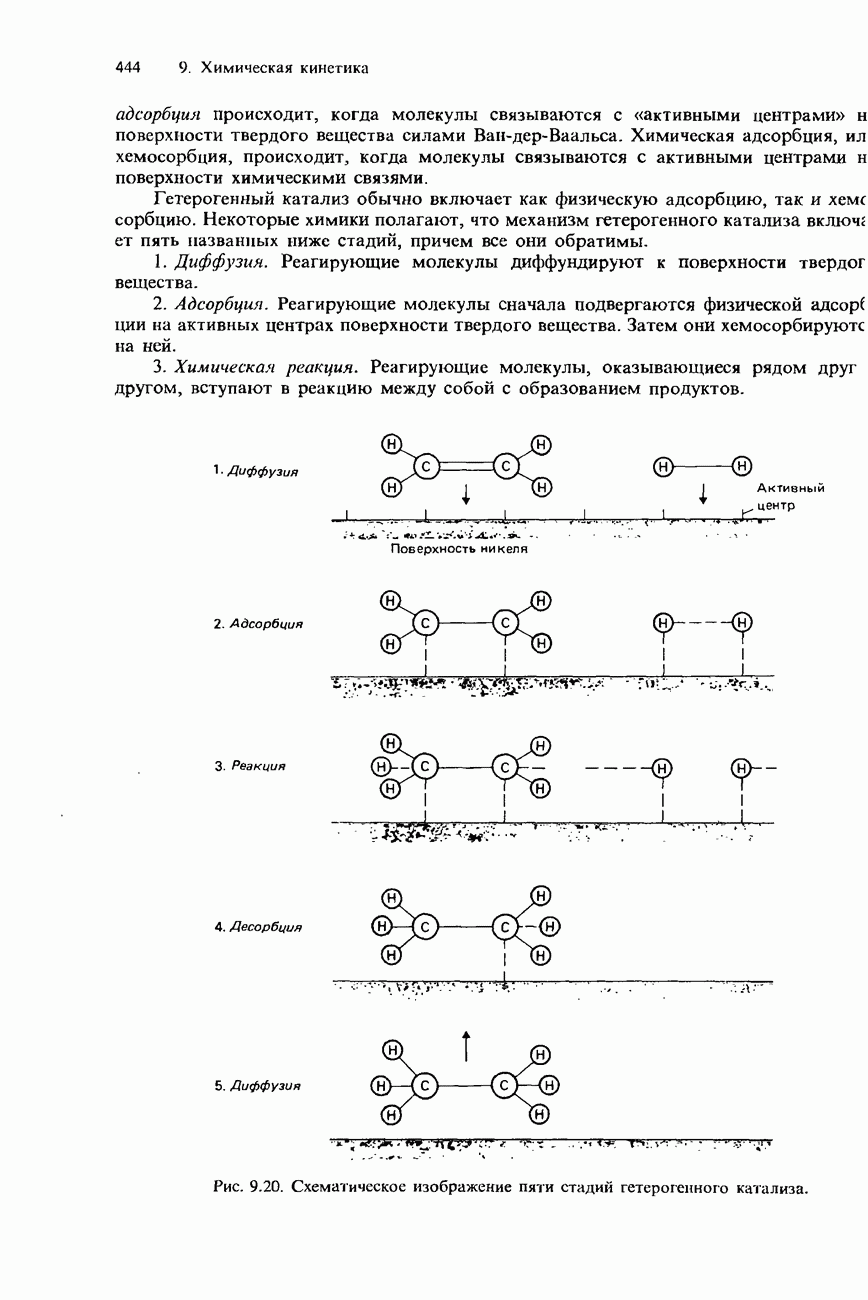
- ГЕТЕРОГЕННЫЙ КАТАЛИЗ
- ФЕРМЕНТАТИВНЫЙ КАТАЛИЗ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 10. ЭЛЕКТРОХИМИЯ
- 10.1. Электропроводность
- ПРОВОДНИКИ ЭЛЕКТРИЧЕСКОГО ТОКА И ЭЛЕКТРОПРОВОДНОСТЬ
- МОЛЯРНАЯ ПРОВОДИМОСТЬ
- КОНДУКТОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- 10.2. Окислительно-восстановительные процессы
- ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫЕ РЕАКЦИИ
- ОПРЕДЕЛЕНИЕ СТЕХИОМЕТРИЧЕСКИХ КОЭФФИЦИЕНТОВ
- СТЕПЕНЬ ОКИСЛЕНИЯ
- ОКИСЛИТЕЛИ
- ВОССТАНОВИТЕЛИ
- ОКИСЛИТЕЛИ И ВОССТАНОВИТЕЛИ
- 10.3. Электролиз
- ЗАКОНЫ ЭЛЕКТРОЛИЗА ФАРАДЕЯ
- ПРОМЫШЛЕННЫЕ ПРИМЕНЕНИЯ ЭЛЕКТРОЛИЗА
- 10.4. Химические источники тока
- СХЕМЫ ХИМИЧЕСКИХ ИСТОЧНИКОВ ТОКА
- ТИПЫ ПОЛУЭЛЕМЕНТОВ
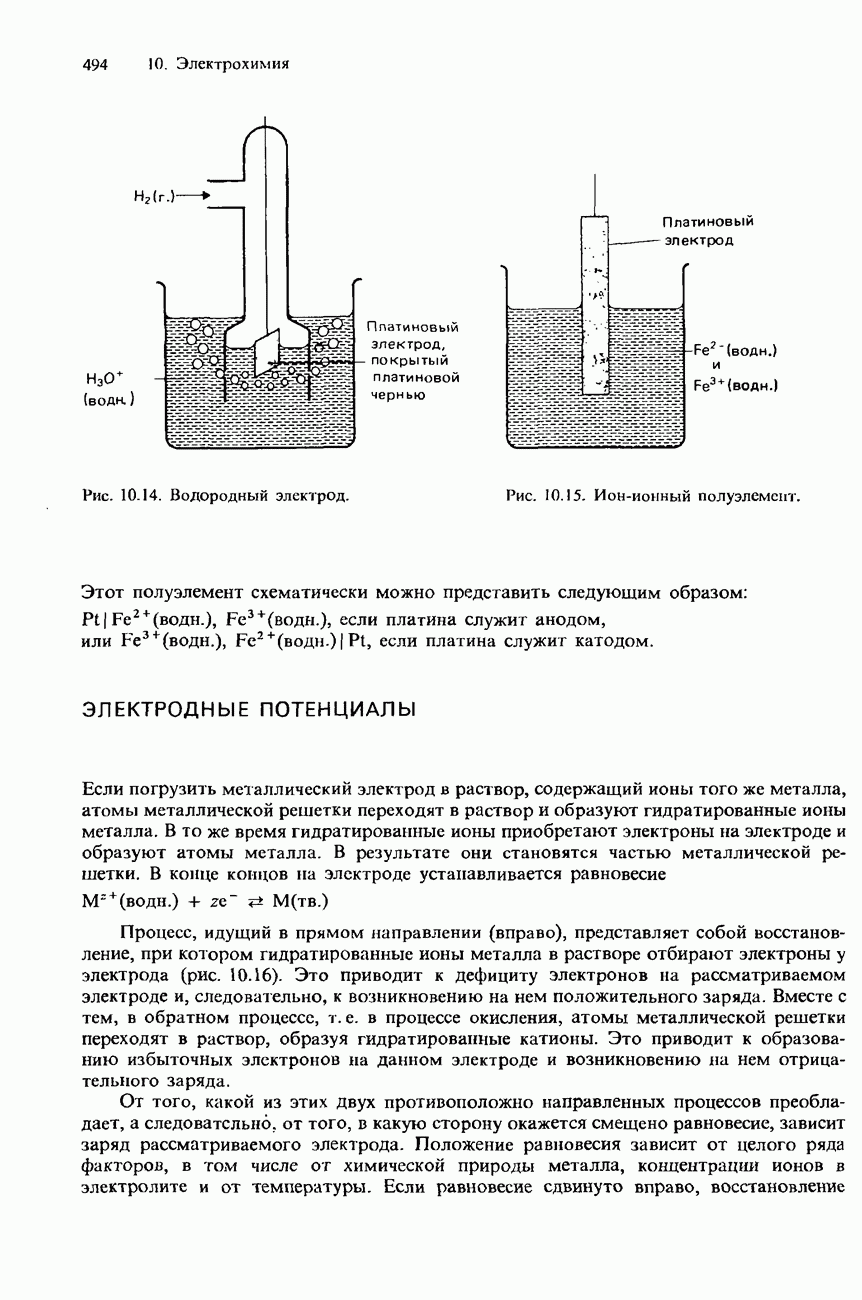
- ЭЛЕКТРОДНЫЕ ПОТЕНЦИАЛЫ
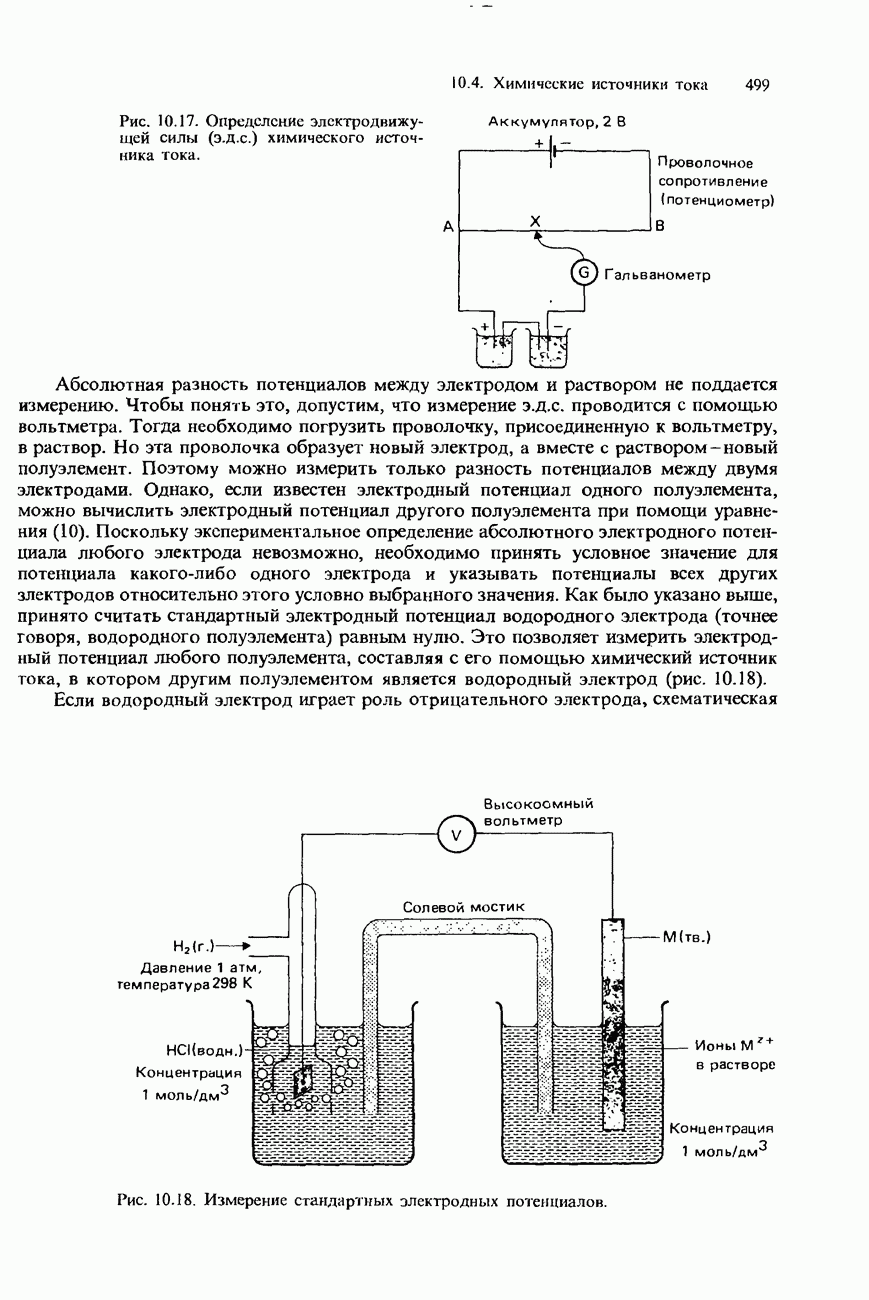
- ЭЛЕКТРОДВИЖУЩАЯ СИЛА ХИМИЧЕСКИХ ИСТОЧНИКОВ ТОКА
- ИЗМЕРЕНИЕ Э.Д.С. ХИМИЧЕСКИХ ИСТОЧНИКОВ ТОКА И ЭЛЕКТРОДНЫХ ПОТЕНЦИАЛОВ
- 10.5. Применения электрохимии
- ВЫЧИСЛЕНИЕ КОНСТАНТ РАВНОВЕСИЯ ДЛЯ ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫХ РЕАКЦИЙ
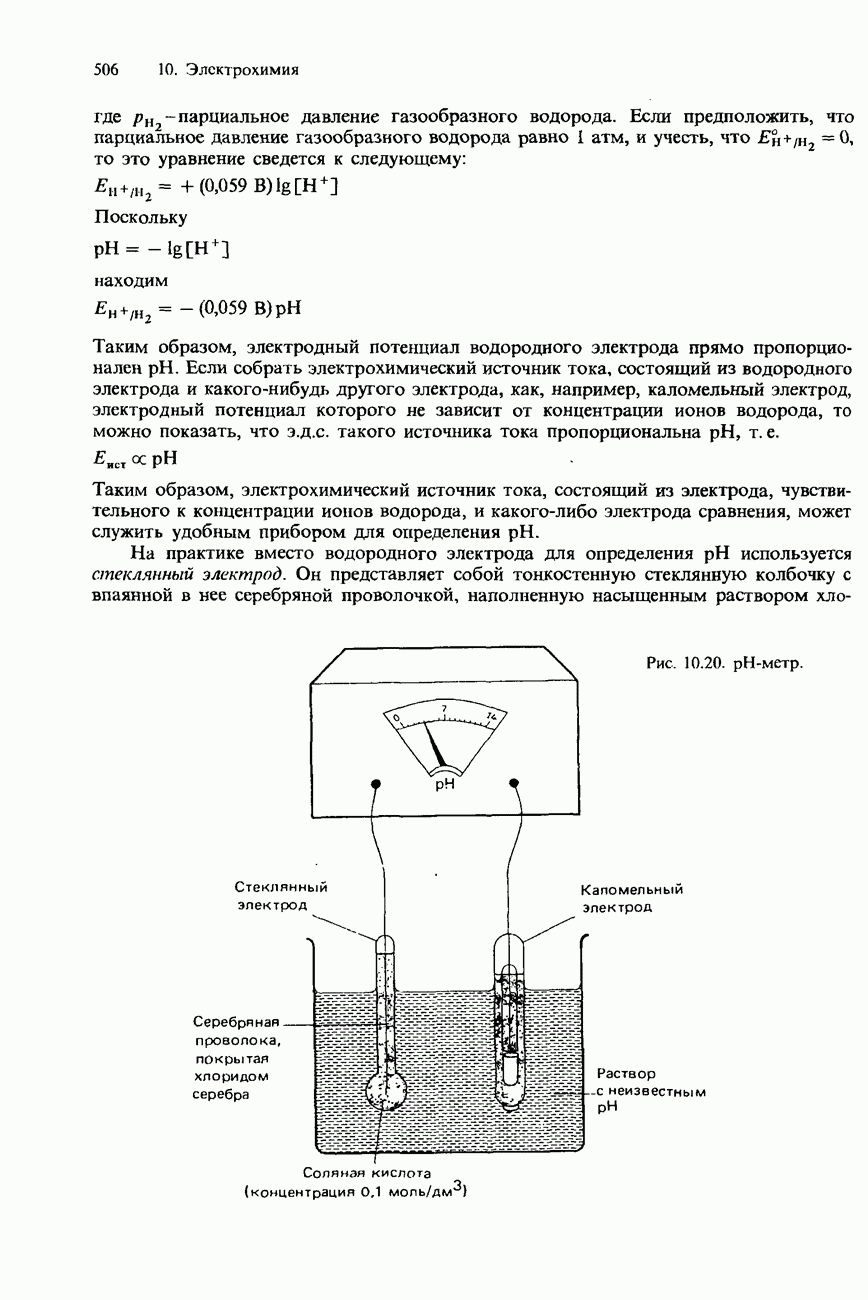
- ОПРЕДЕЛЕНИЕ pH РАСТВОРА
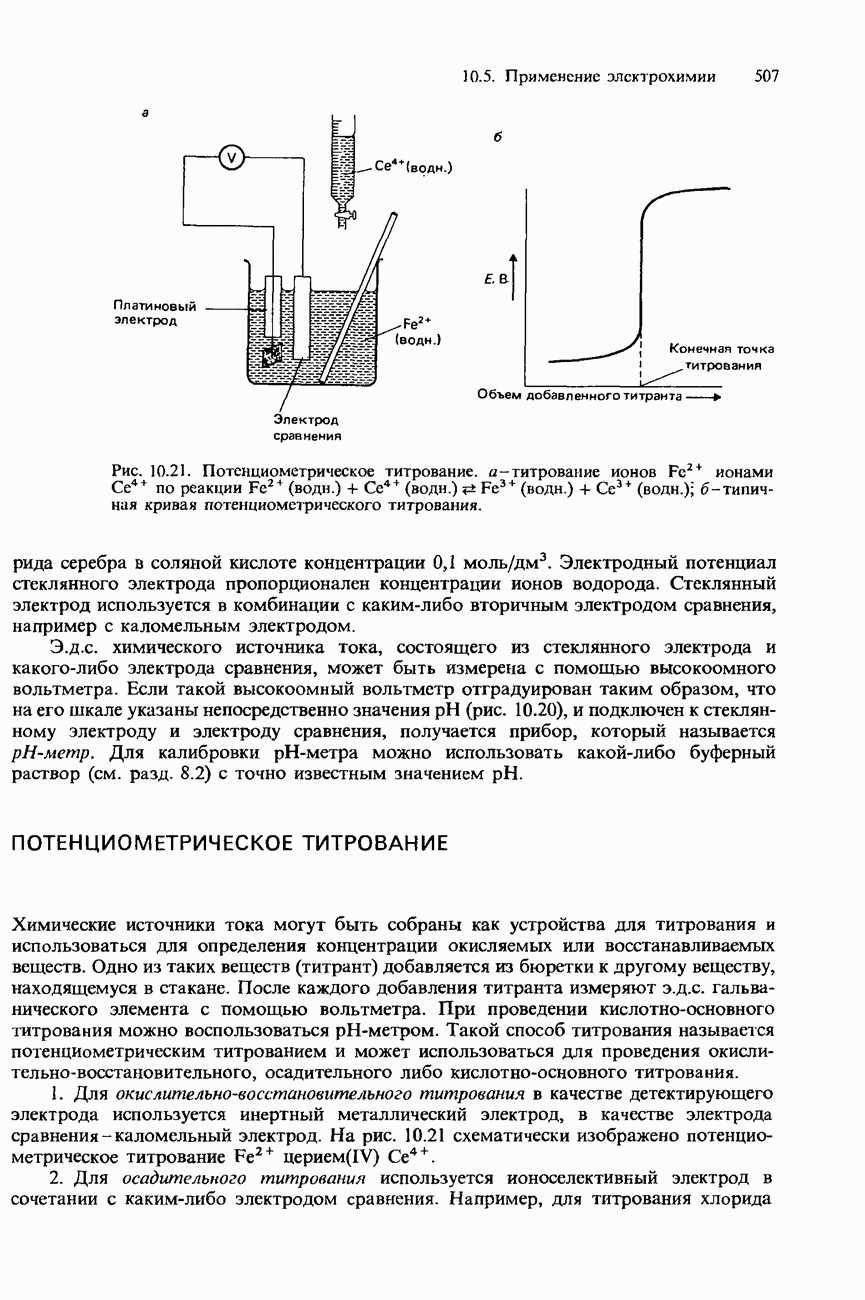
- ПОТЕНЦИОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- ОСУЩЕСТВИМОСТЬ ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫХ РЕАКЦИЙ
- ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ AG
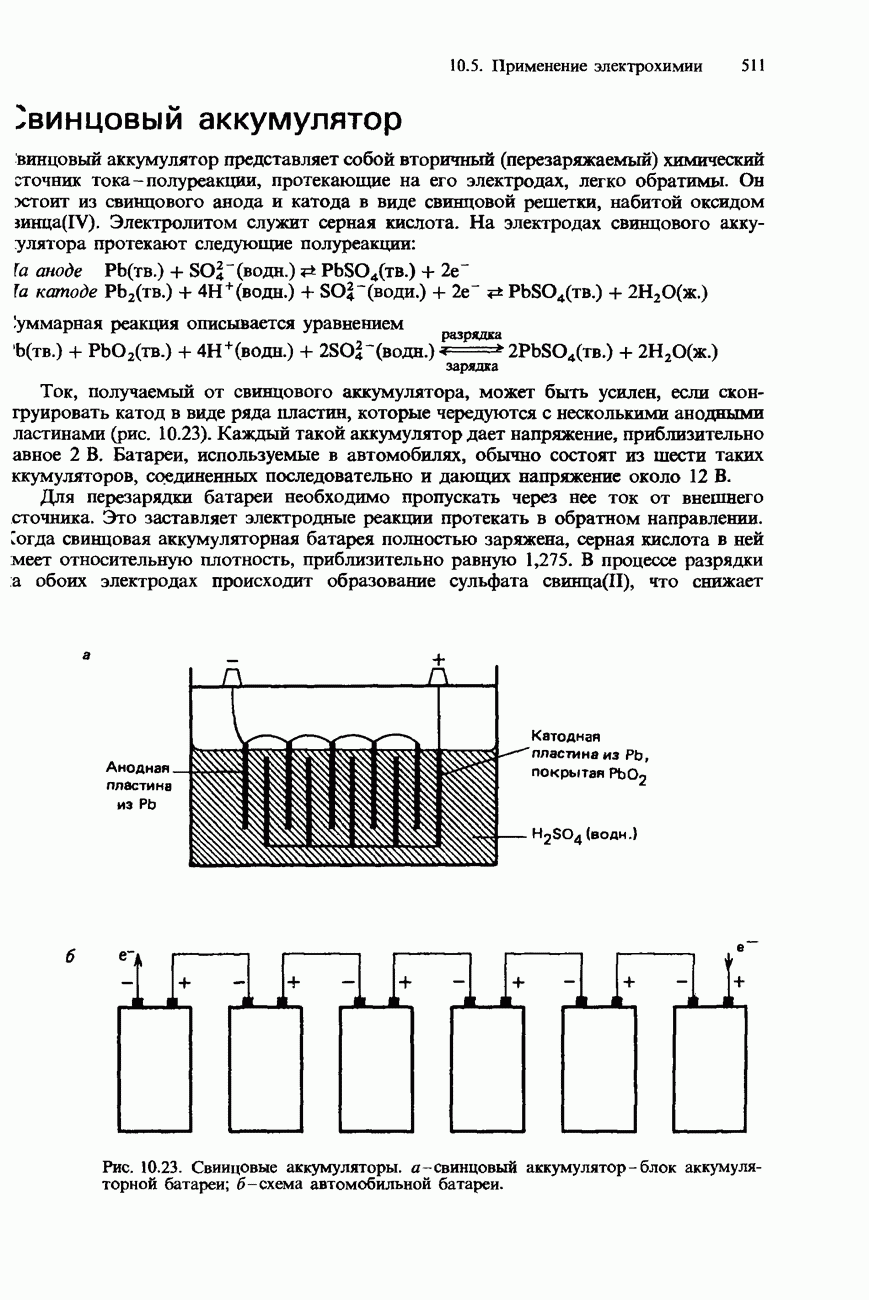
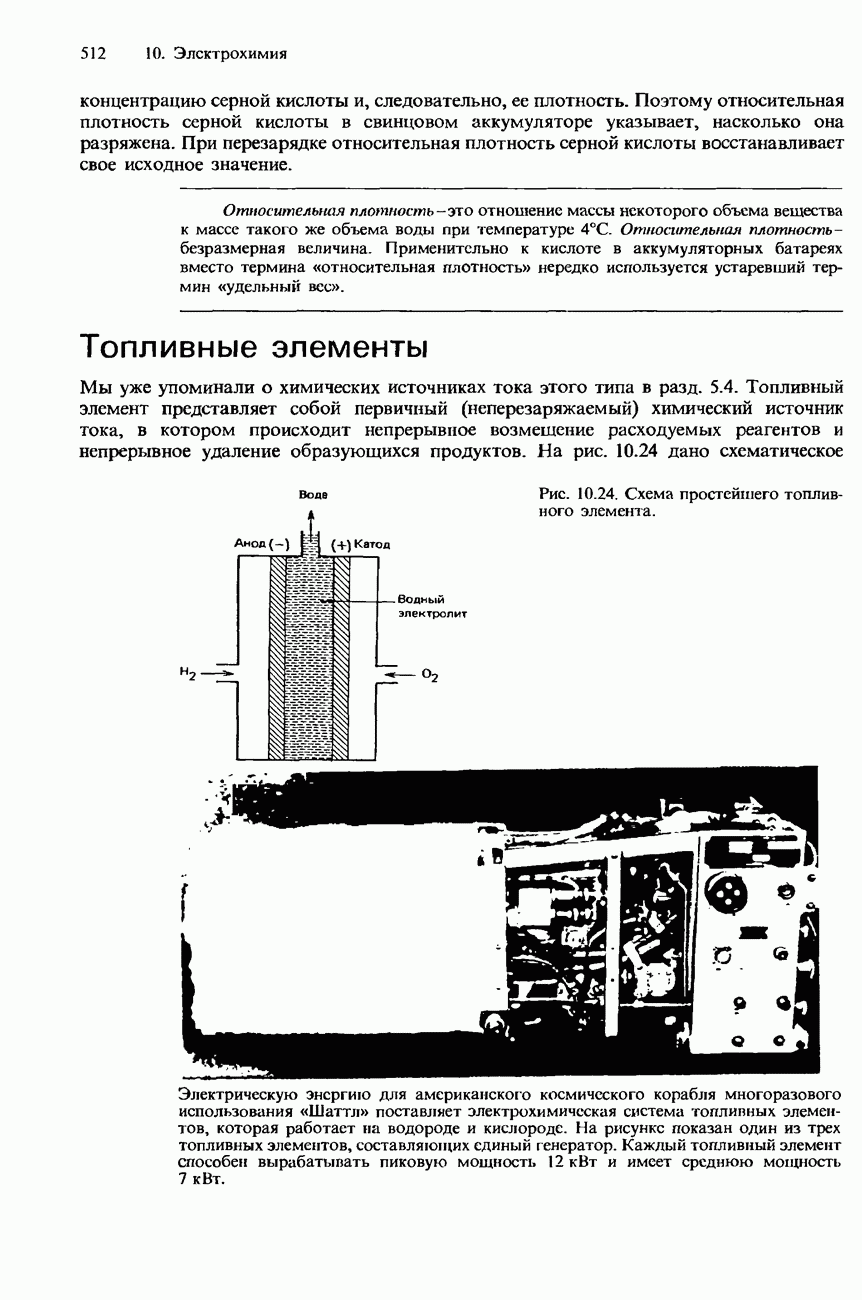
- БАТАРЕИ И ПРОМЫШЛЕННЫЕ ИСТОЧНИКИ ТОКА
- МЕТАЛЛУРГИЯ
- КОРРОЗИЯ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ