| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Объединенный газовый закон
Объединяя законы Бойля - Мариотта и Гей-Люссака (уравнения 1 и 2), можно получить следующее уравнение:

которое является математическим выражением объединенного газового закона, или закона состояния газов. Он позволяет вычислить, например, объем газа при определенных температуре и давлении, если известен его объем при других значениях температуры и давления.
Объединенный газовый закон можно также записать в другой форме:

Точное значение постоянной в правой части этого уравнения зависит от количества газа. Если количество газа равно одному молю (см. гл. 4), то соответствующая постоянная обозначается буквой R и называется молярная газовая постоянная, или просто газовая постоянная. Если давление выражено в атмосферах, постоянная R имеет значение

В системе СИ она равна

Объединенный газовый закон для одного моля газа приобретает вид

где  объем одного моля газа. Для
объем одного моля газа. Для  молей газа получается уравнение pV
молей газа получается уравнение pV

В такой форме объединенный газовый закон называется уравнением состояния идеального газа. Уравнение состояния это уравнение, связывающее между собой параметры состояния газа-давление, объем и температуру.
Газ, который полностью подчиняется уравнению состояния идеального газа, называется идеальный газ. Такой газ не существует в действительности. Реальные газы хорошо подчиняются уравнению состояния идеального газа при низких давлениях и высоких температурах. Отклонения в поведении реальных газов от предписываемых уравнением состояния идеального газа подробно обсуждаются ниже.
Вычисление относительной молекулярной массы с помощью уравнения состояние идеального газа.
Уравнение состояния идеального газа позволяет проводить прямые вычисления относительной молекулярной массы газа  Введем понятие относительной молекулярной массы, основываясь на уже знакомом нам (из гл. 1) определении относительной атомной массы АТ. Для газа, состоящего из простых молекул, относительная молекулярная масса представляет собой сумму относительных атомных масс всех атомов, входящих в молекулу. Например, для диоксида углерода
Введем понятие относительной молекулярной массы, основываясь на уже знакомом нам (из гл. 1) определении относительной атомной массы АТ. Для газа, состоящего из простых молекул, относительная молекулярная масса представляет собой сумму относительных атомных масс всех атомов, входящих в молекулу. Например, для диоксида углерода

Относительная молекулярная масса, выраженная в граммах на моль, называется молярной массой (см. гл. 4). Следовательно, молярная масса  равна 44 г/моль. Два моля
равна 44 г/моль. Два моля  имеют массу 88 г, а и молей - массу
имеют массу 88 г, а и молей - массу  . В общем случае можно записать
. В общем случае можно записать

где  - количество вещества в молях (т.е. число молей данного вещества),
- количество вещества в молях (т.е. число молей данного вещества),  - масса вещества в граммах, а М - его молярная масса.
- масса вещества в граммах, а М - его молярная масса.
Подстановка полученного выражения для  в уравнение состояния идеального газа (4) дает
в уравнение состояния идеального газа (4) дает

Это уравнение позволяет, зная массу и объем газа при определенных температурю и давлении, вычислить его молярную массу М. А поскольку

полученный результат непосредственно дает относительную молекулярную массу М.
Пример
Образец газа массой 1,236 г имеет при температуре  и давлении 1 атм объем
и давлении 1 атм объем  Необходимо вычислить относительную молекулярную массу этого газа. (Напомним, что
Необходимо вычислить относительную молекулярную массу этого газа. (Напомним, что 
Решение
Для вычисления искомого значения  сначала переведем все заданные величины в единицы системы СИ (см. приложение I):
сначала переведем все заданные величины в единицы системы СИ (см. приложение I):

Подставляя эти данные в уравнение (5), находим

Следовательно, 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ ПЕРЕВОДЧИКА
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ
- 1. СТРОЕНИЕ АТОМА
- 1.1. Субатомные частицы
- Модели атома
- Новые элементарные частицы
- МАССА АТОМА
- МАСС-СПЕКТРОМЕТРИЯ
- 1.2 Электронное строение атомов
- Связь между спектральными линиями и электронами (открытие Бора)
- Применение возбуждения электронов на практике
- Атомный спектр испускания водорода
- ЭНЕРГИИ ИОНИЗАЦИИ
- Рассмотрение энергий ионизации в рамках модели атома, предложенной Бором
- ВОЛНОВАЯ ПРИРОДА ЭЛЕКТРОНА
- Орбитали
- КВАНТОВЫЕ ЧИСЛА
- ЭЛЕКТРОННАЯ КОНФИГУРАЦИЯ
- 1.3 Радиоактивность
- ИОНИЗИРУЮЩЕЕ ИЗЛУЧЕНИЕ
- Обнаружение и измерение радиоактивности
- УСТОЙЧИВЫЕ И НЕУСТОЙЧИВЫЕ ИЗОТОПЫ
- Зона устойчивости
- Период полураспада
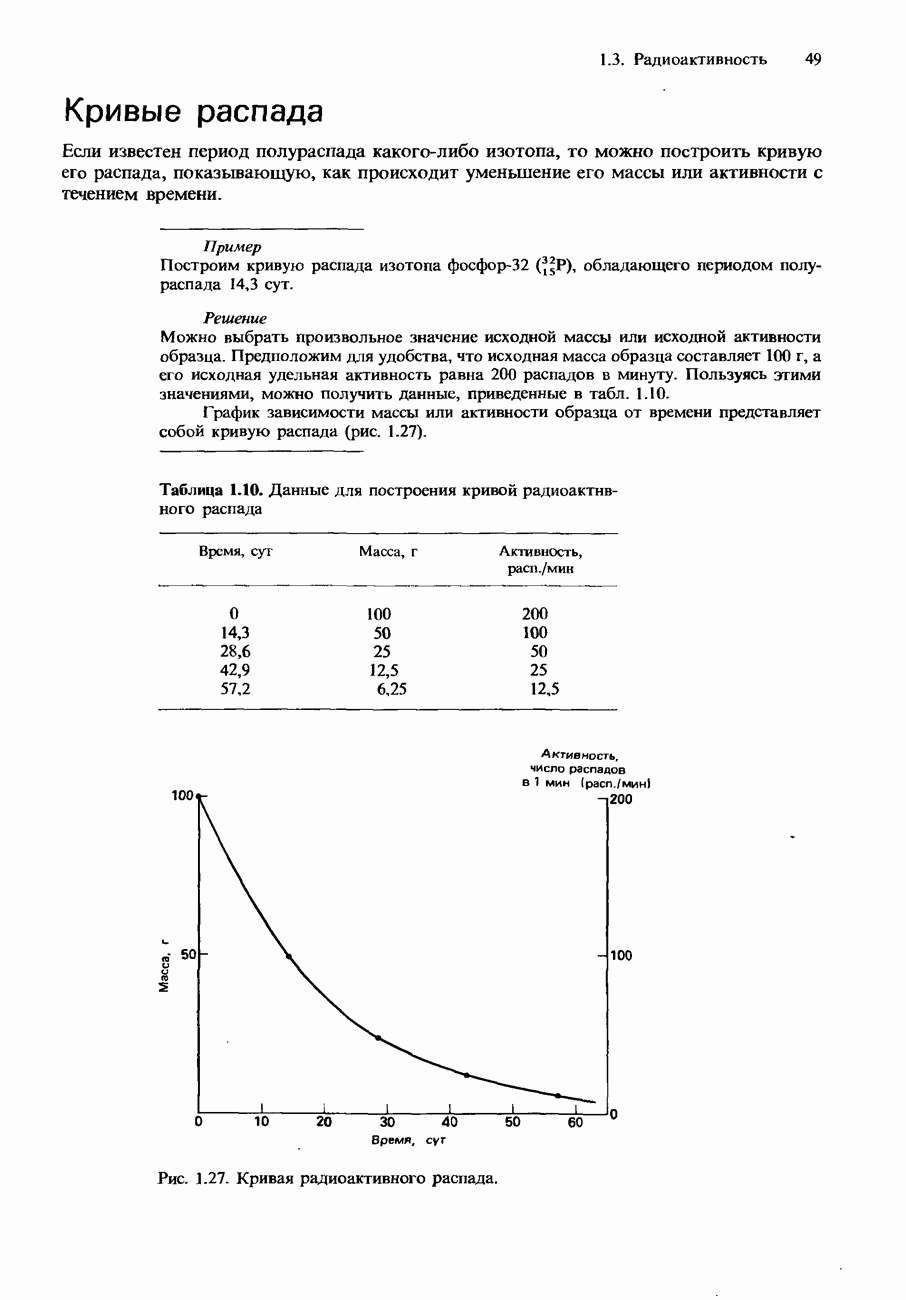
- Кривые распада
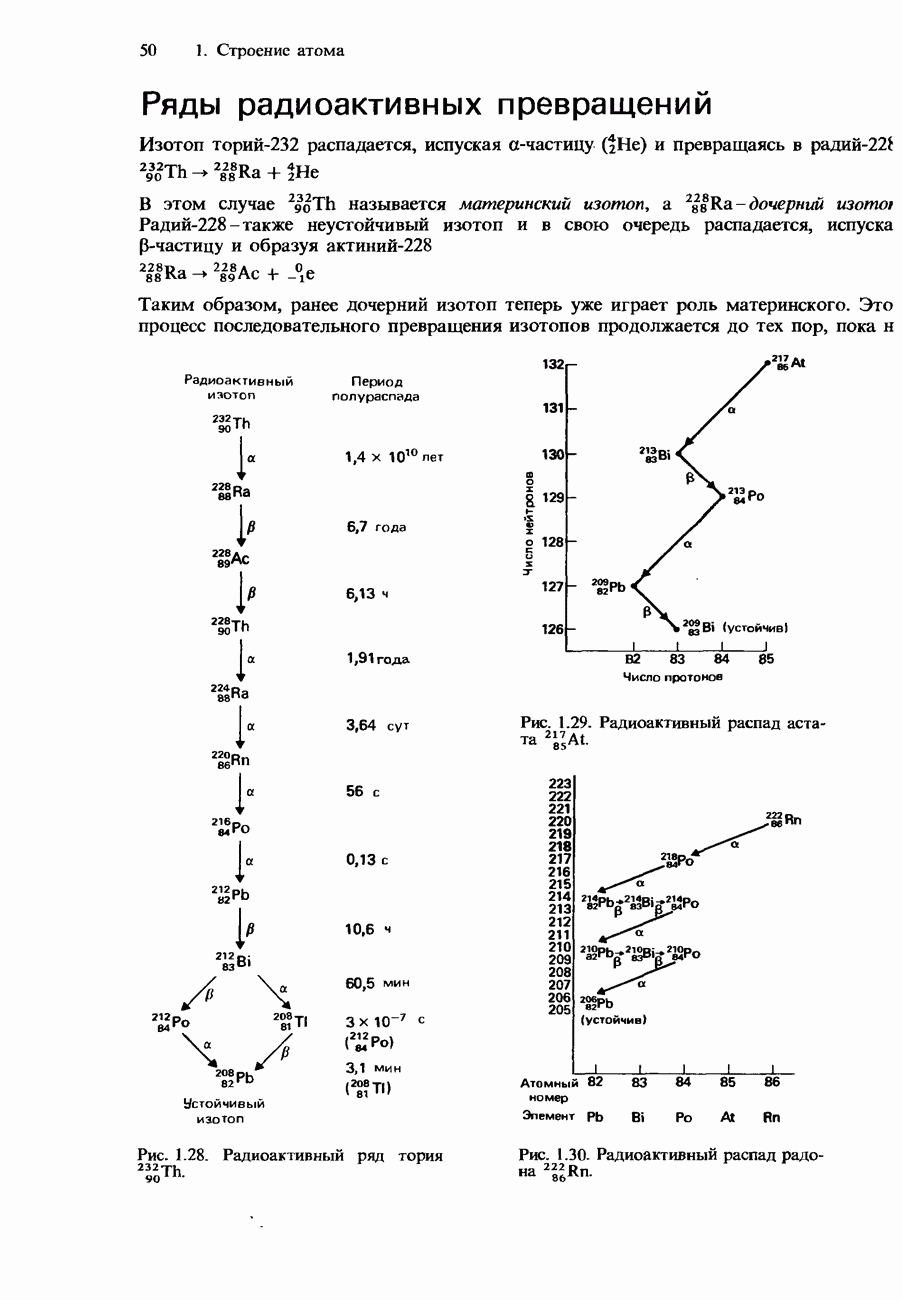
- Ряды радиоактивных превращений
- Естественные радиоизотопы
- ИСКУССТВЕННЫЕ ЯДЕРНЫЕ ПРЕВРАЩЕНИЯ
- Ускорители элементарных частиц
- Трансурановые элементы
- ПРИМЕНЕНИЯ ИЗОТОПОВ
- ЯДЕРНОЕ ДЕЛЕНИЕ И ЯДЕРНЫЙ СИНТЕЗ
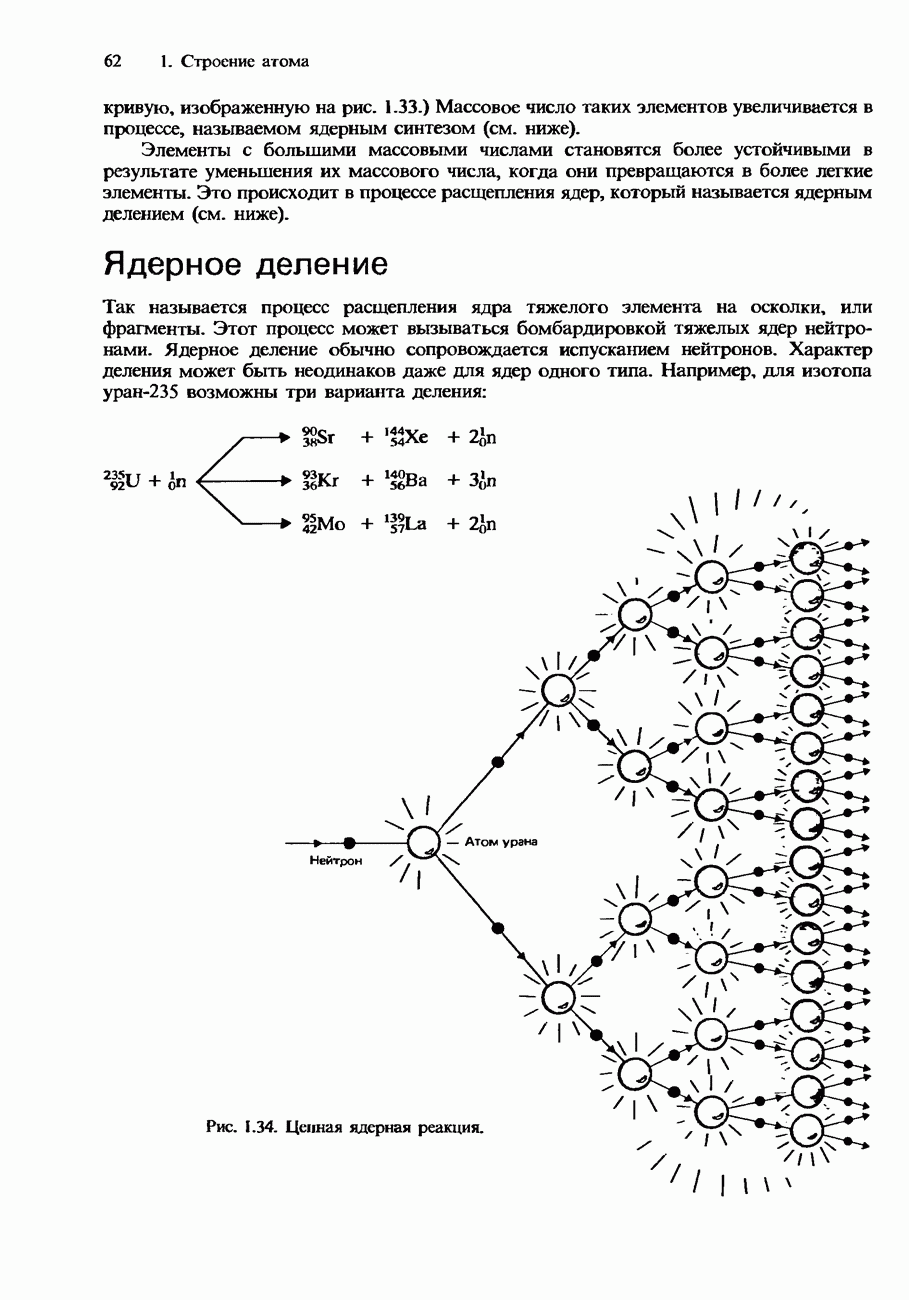
- Ядерное деление
- Ядерный синтез
- Ядерный синтез в звездах
- ЯДЕРНАЯ ЭНЕРГИЯ
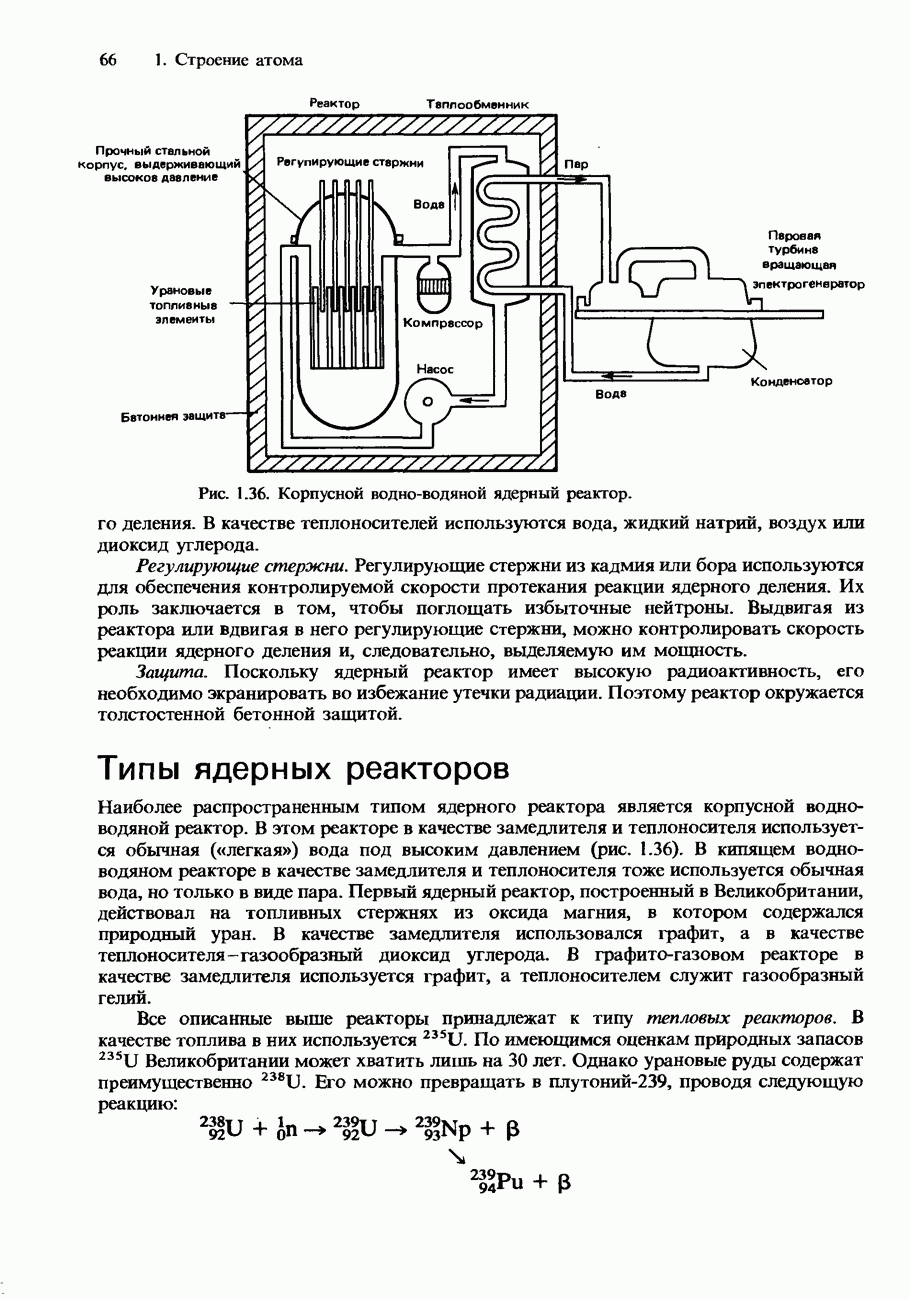
- Типы ядерных реакторов
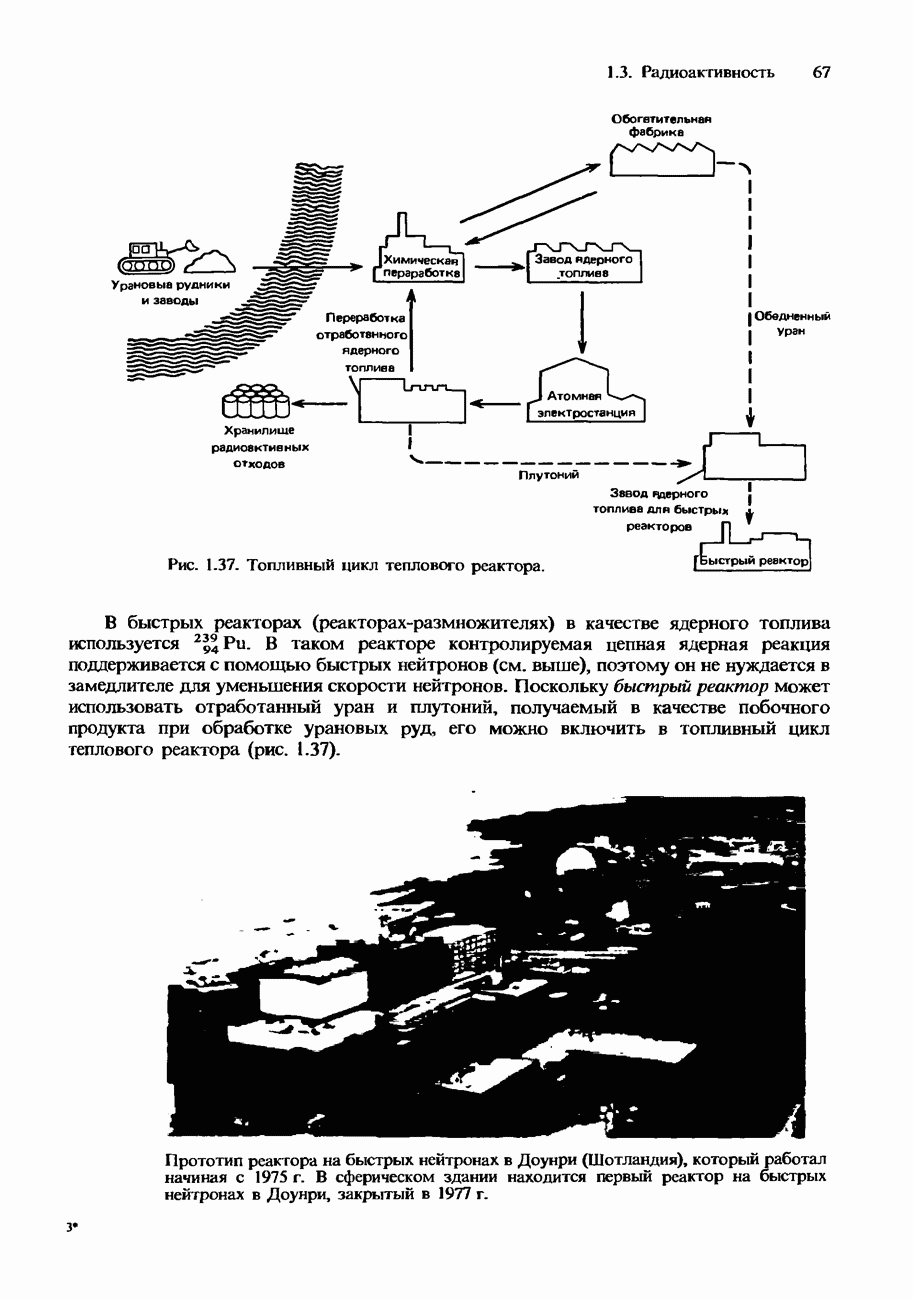
- Радиоактивные ядерные отходы и их переработка
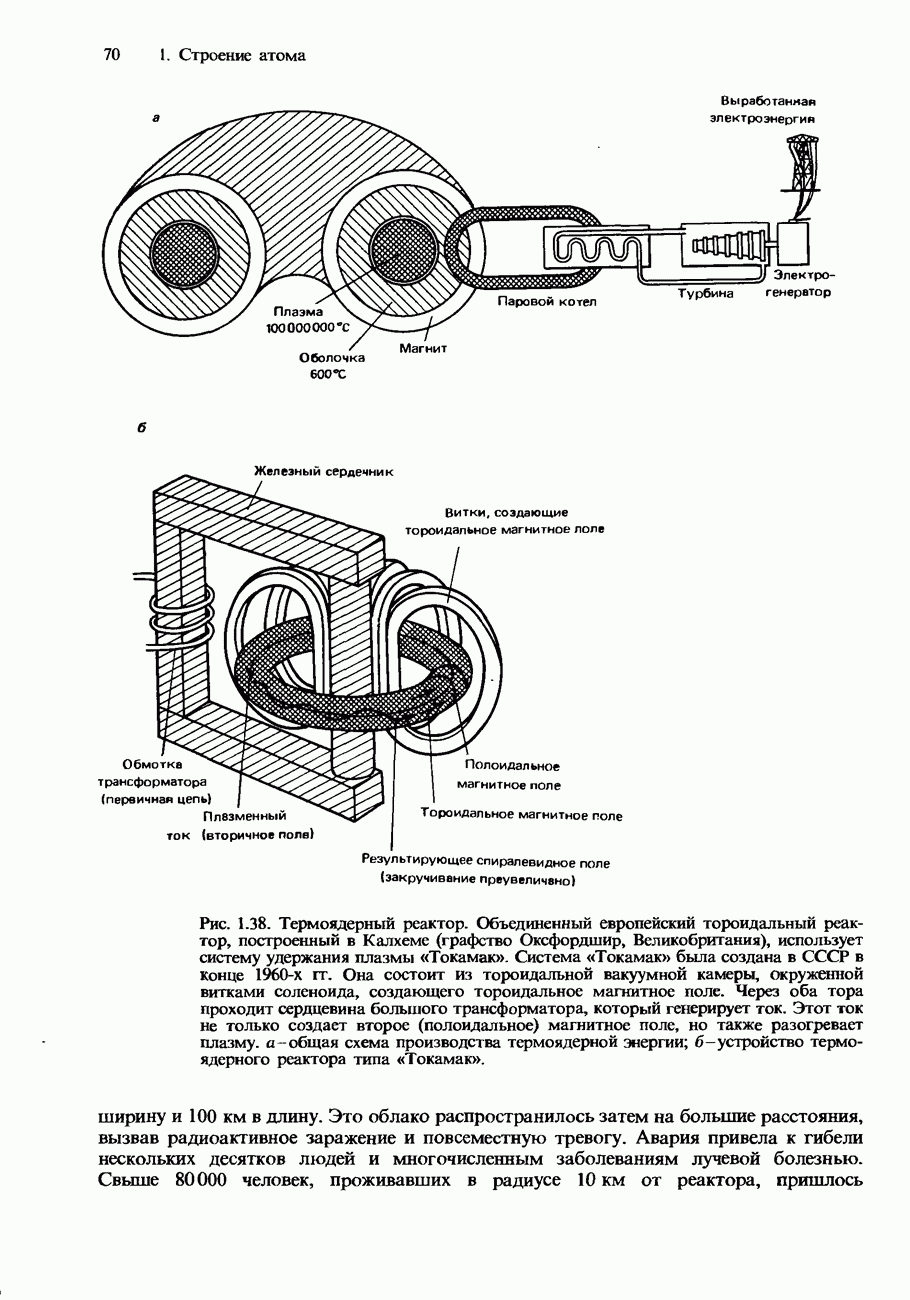
- Термоядерные реакторы
- Аргументы против использования ядерной энергии
- ЯДЕРНОЕ ОРУЖИЕ
- Ядерное разоружение
- ИСТОЧНИКИ РАДИАЦИИ И ЕЕ ВОЗДЕЙСТВИЕ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 2. ХИМИЧЕСКАЯ СВЯЗЬ
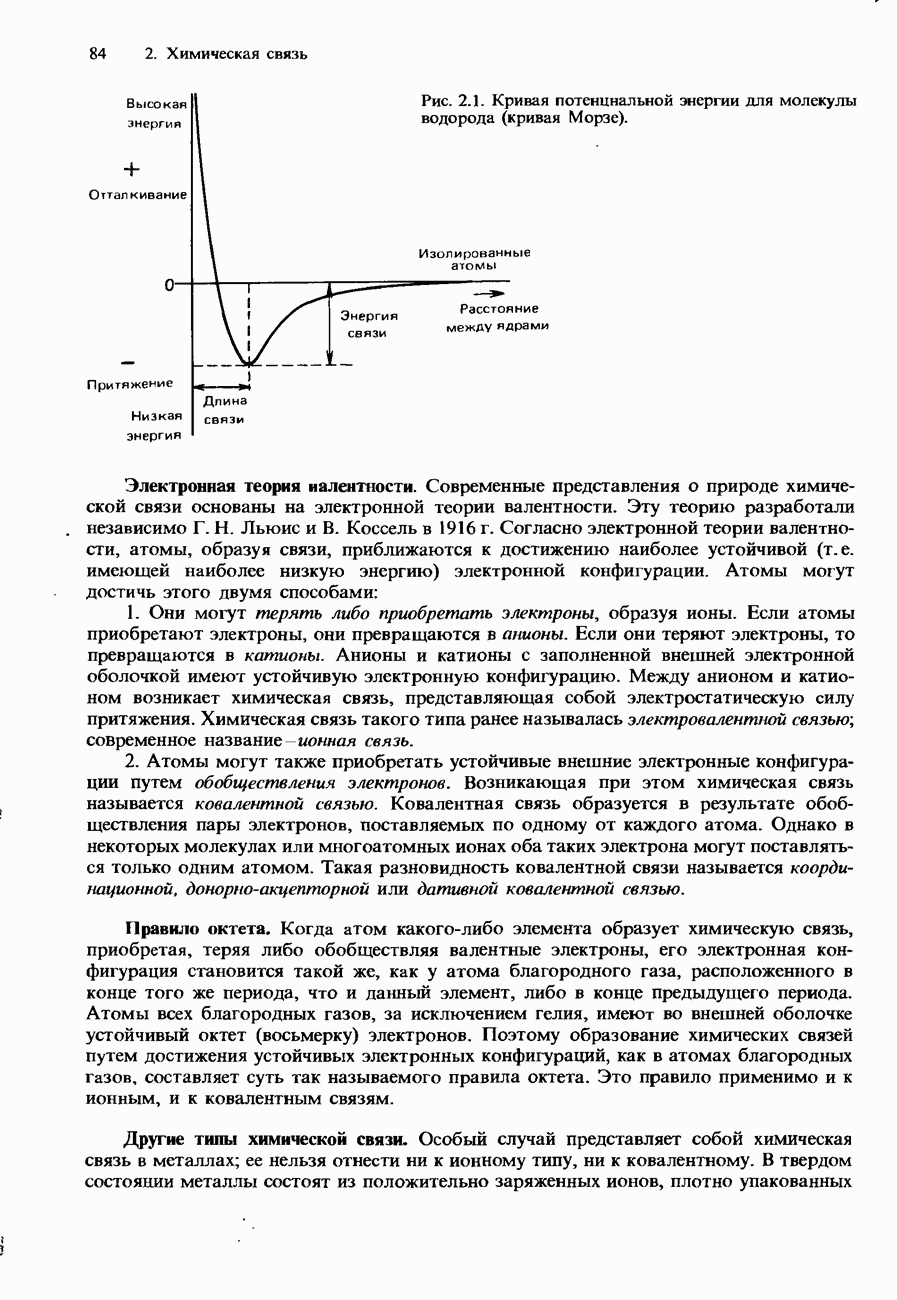
- 2.1. Природа химической связи
- ИОННАЯ СВЯЗЬ
- Устойчивость ионных соединений
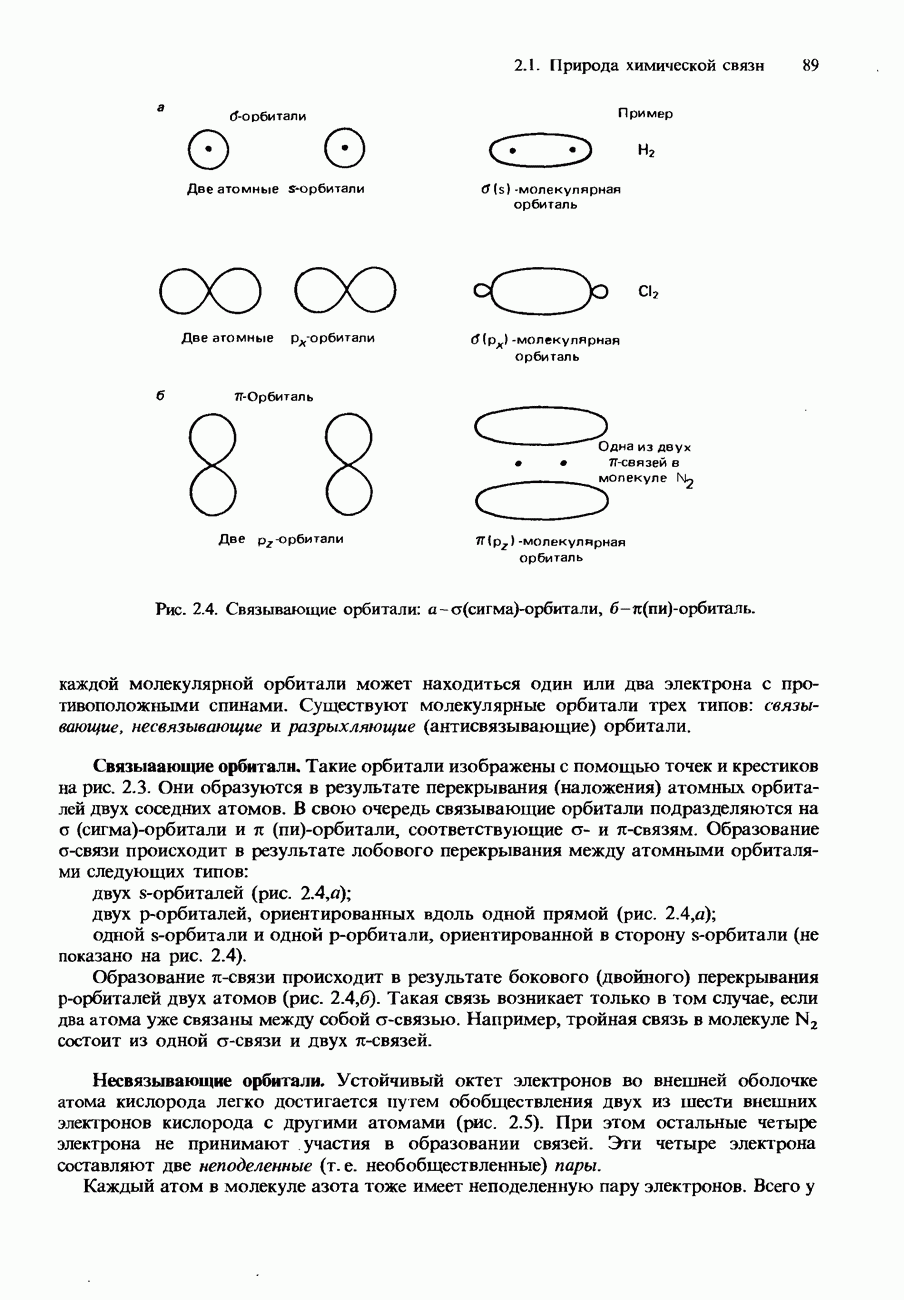
- КОВАЛЕНТНАЯ СВЯЗЬ
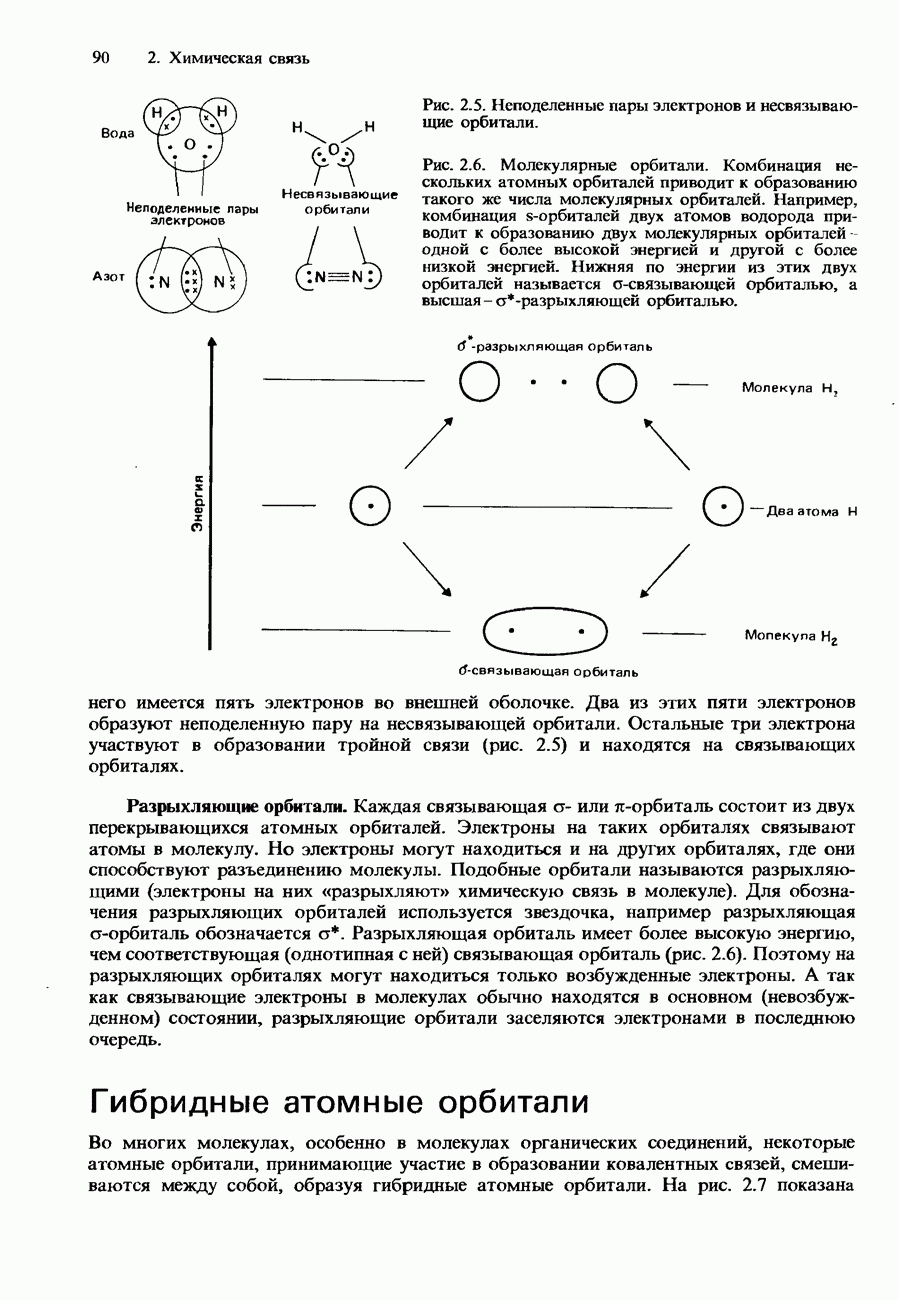
- Молекулярные орбитали
- Гибридные атомные орбитали
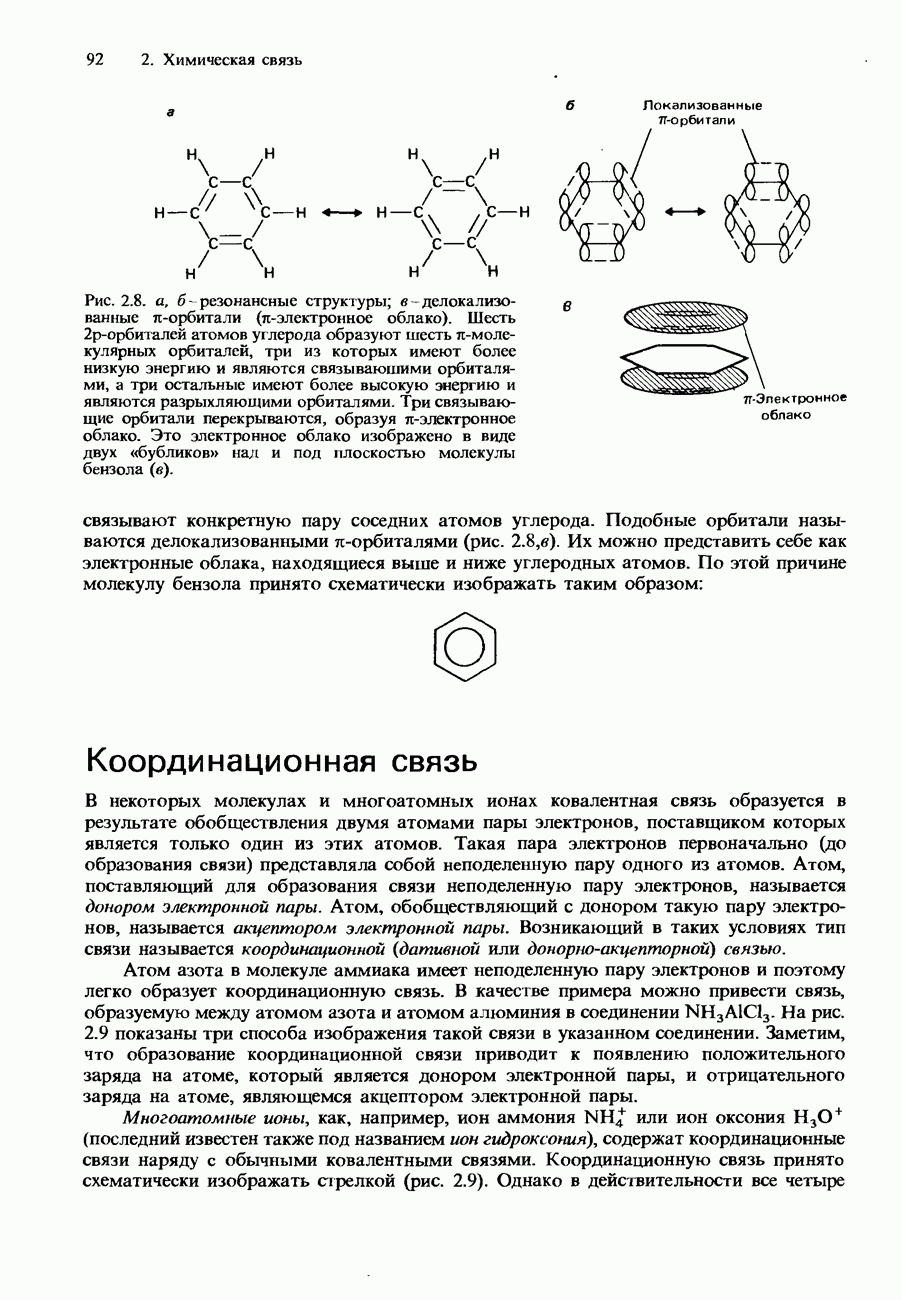
- Делокализованные орбитали
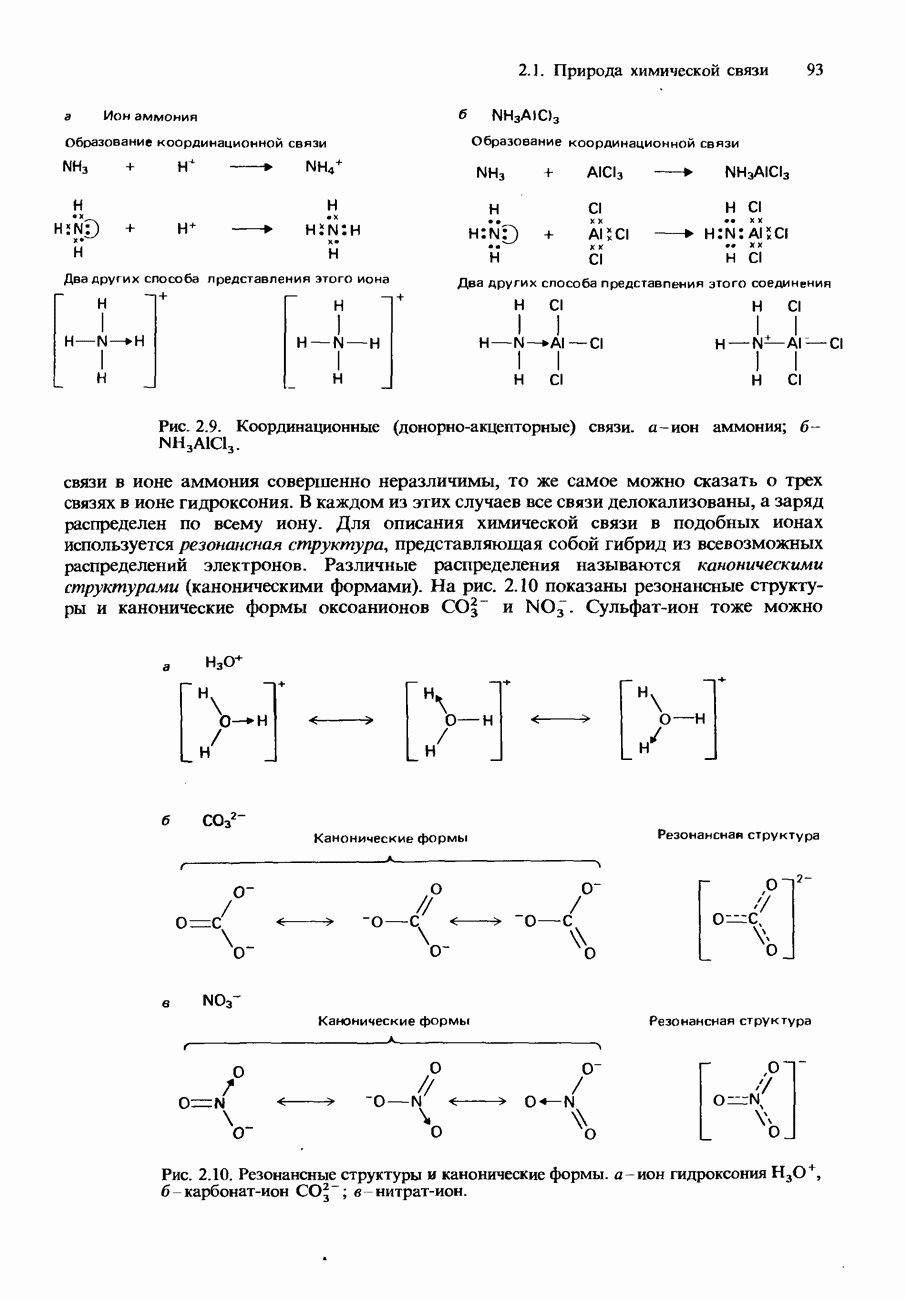
- Координационная связь
- ИОННЫЙ И КОВАЛЕНТНЫЙ ХАРАКТЕР СВЯЗИ
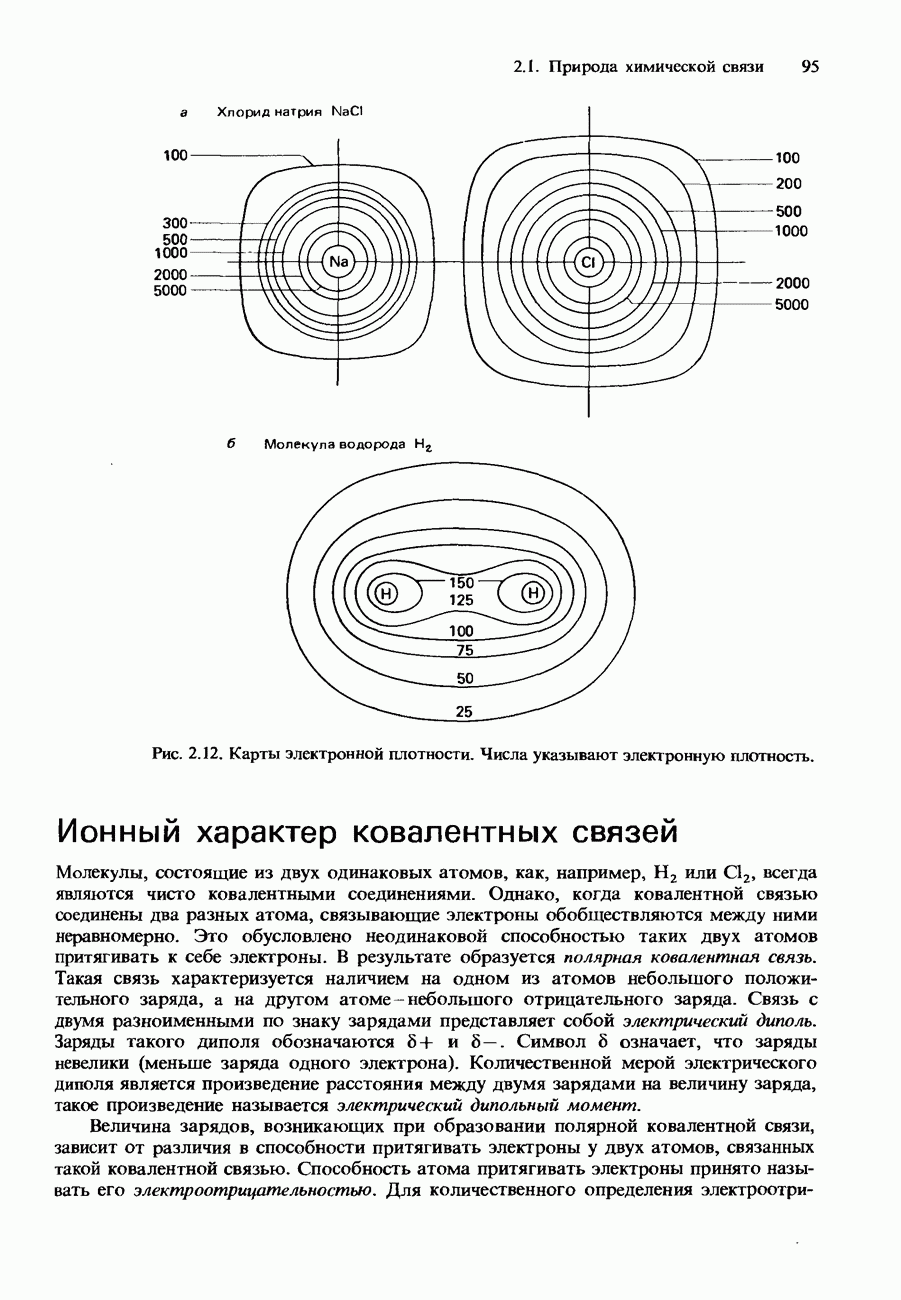
- Ионный характер ковалентных связей
- Ионные и ковалентные соединения
- МЕТАЛЛИЧЕСКАЯ СВЯЗЬ
- Валентная зона и зона проводимости
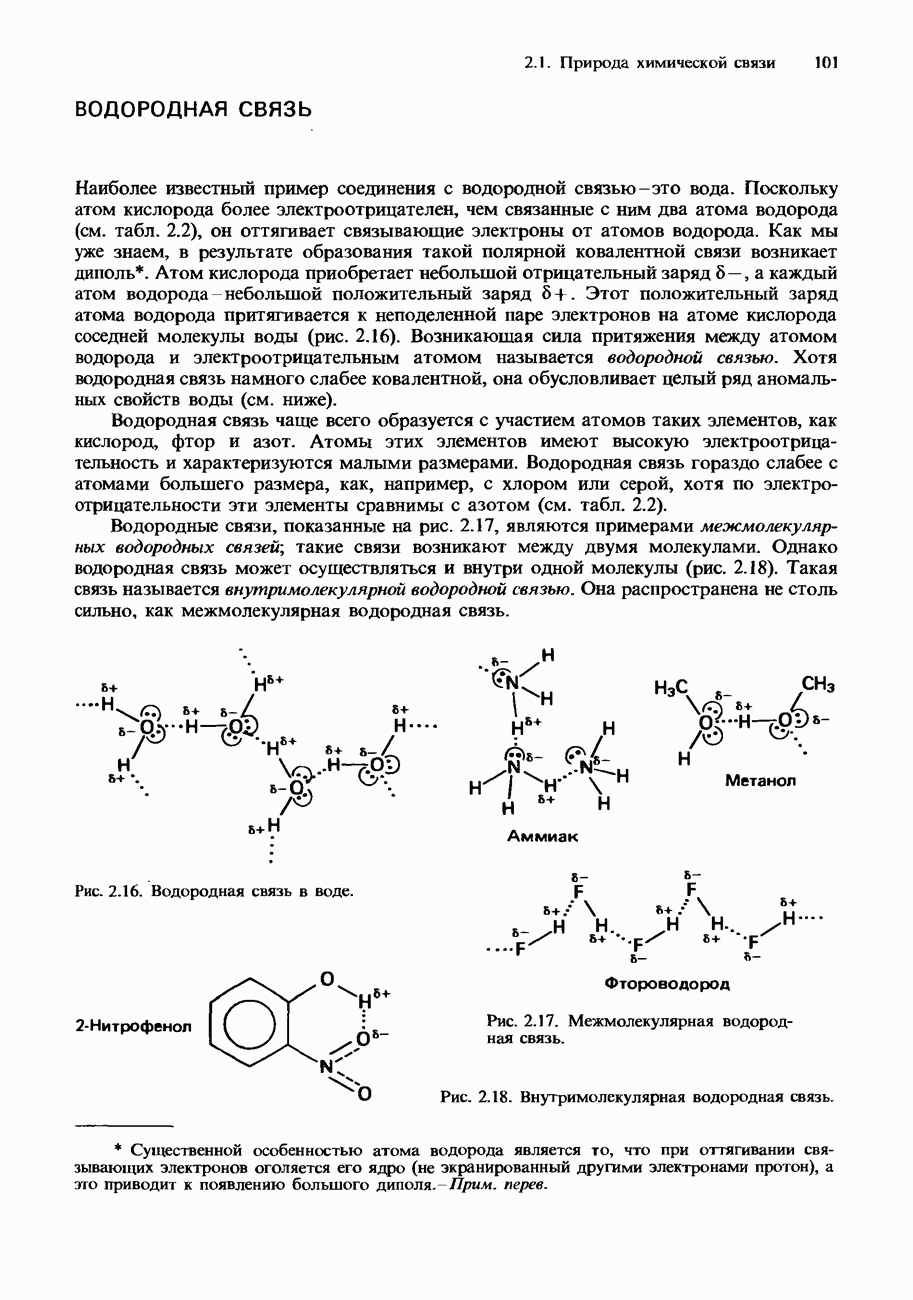
- ВОДОРОДНАЯ СВЯЗЬ
- ВАНДЕРВААЛЬСОВЫ СИЛЫ
- Притяжение типа диполь-индуцированный диполь (индукционное)
- Что понимается под вандерваальсовыми силами
- 2.2. Влияние химической связи на свойства соединений
- Атомные радиусы
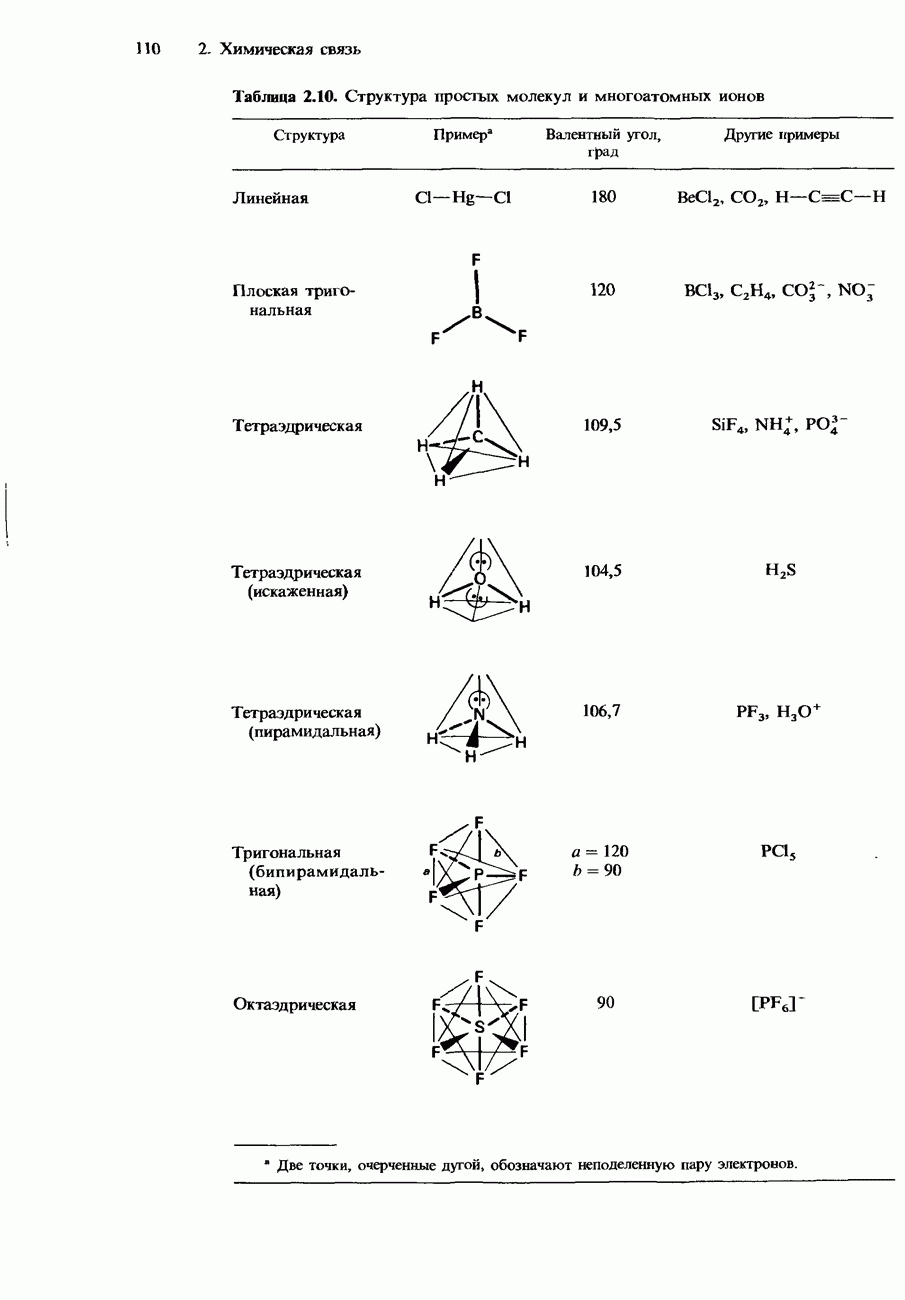
- ФОРМА ПРОСТЫХ МОЛЕКУЛ И МНОГОАТОМНЫХ ИОНОВ
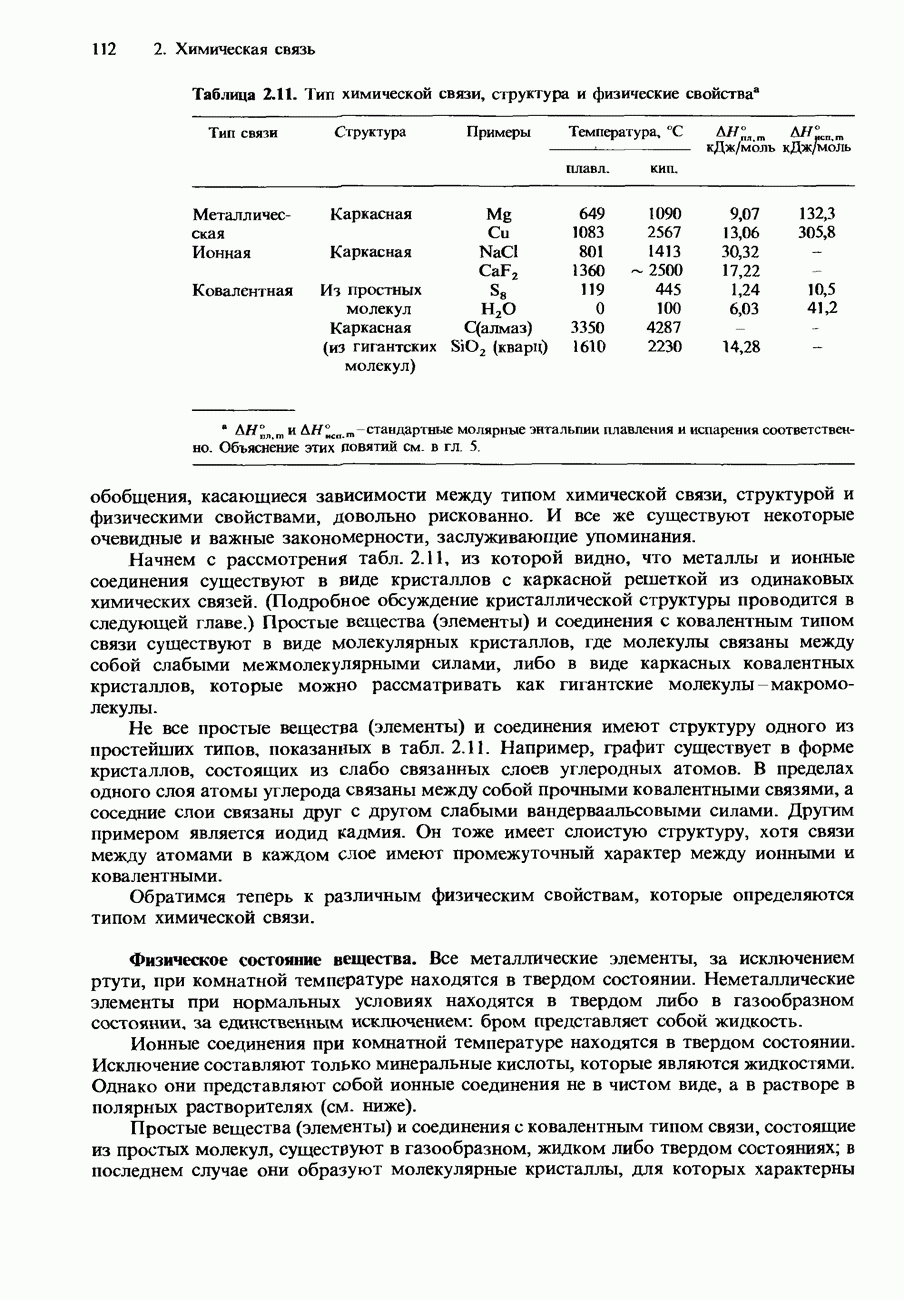
- ТИП ХИМИЧЕСКОЙ СВЯЗИ, СТРУКТУРА И ФИЗИЧЕСКИЕ СВОЙСТВА
- ТИП СВЯЗИ И ХИМИЧЕСКИЕ СВОЙСТВА
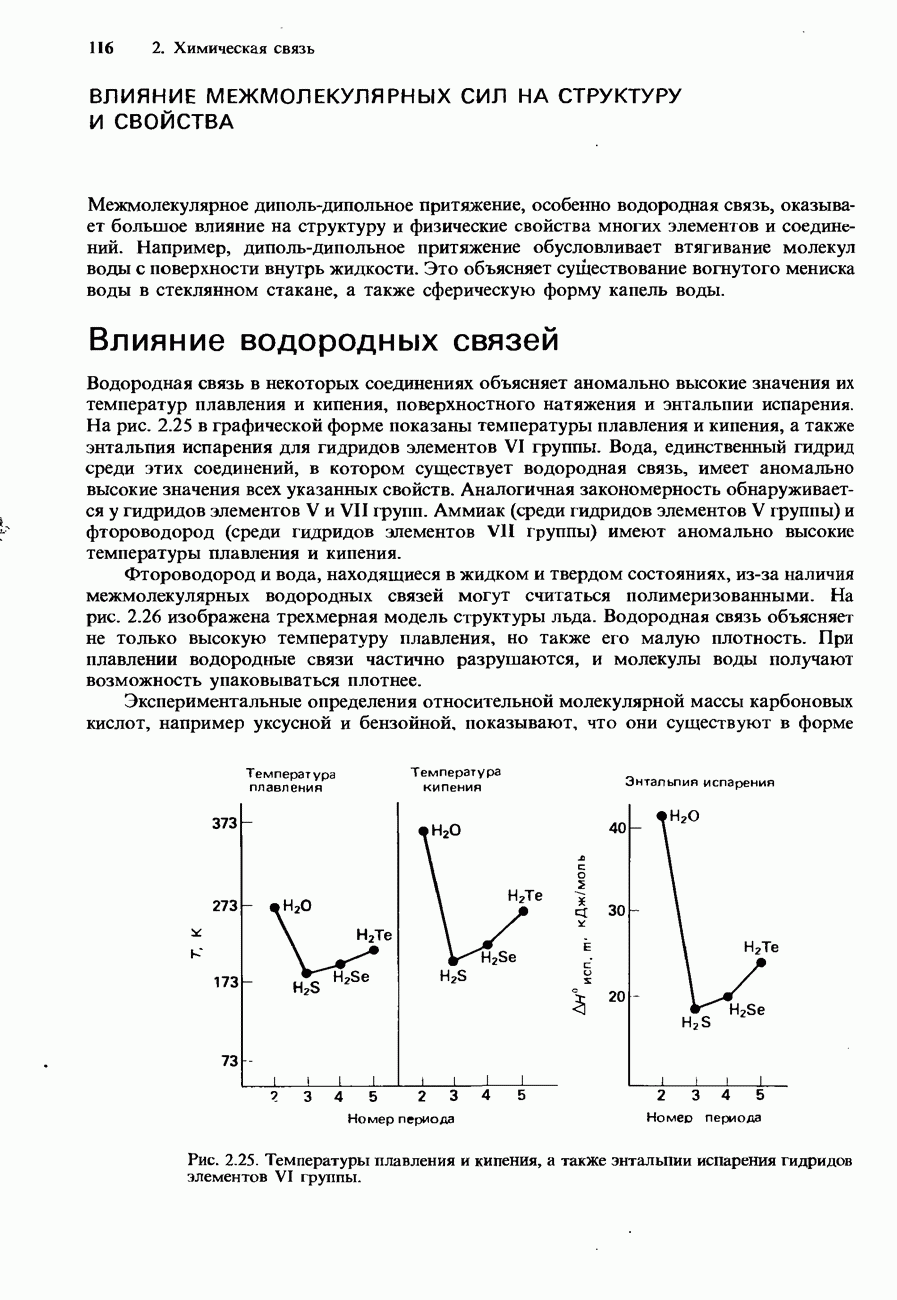
- ВЛИЯНИЕ МЕЖМОЛЕКУЛЯРНЫХ СИЛ НА СТРУКТУРУ И СВОЙСТВА
- ВЛИЯНИЕ ВАНДЕРВААЛЬСОВЫХ СИЛ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 3 ГАЗЫ, ЖИДКОСТИ И ТВЕРДЫЕ ВЕЩЕСТВА
- 3.1. Газы и жидкости
- ГАЗОВЫЕ ЗАКОНЫ
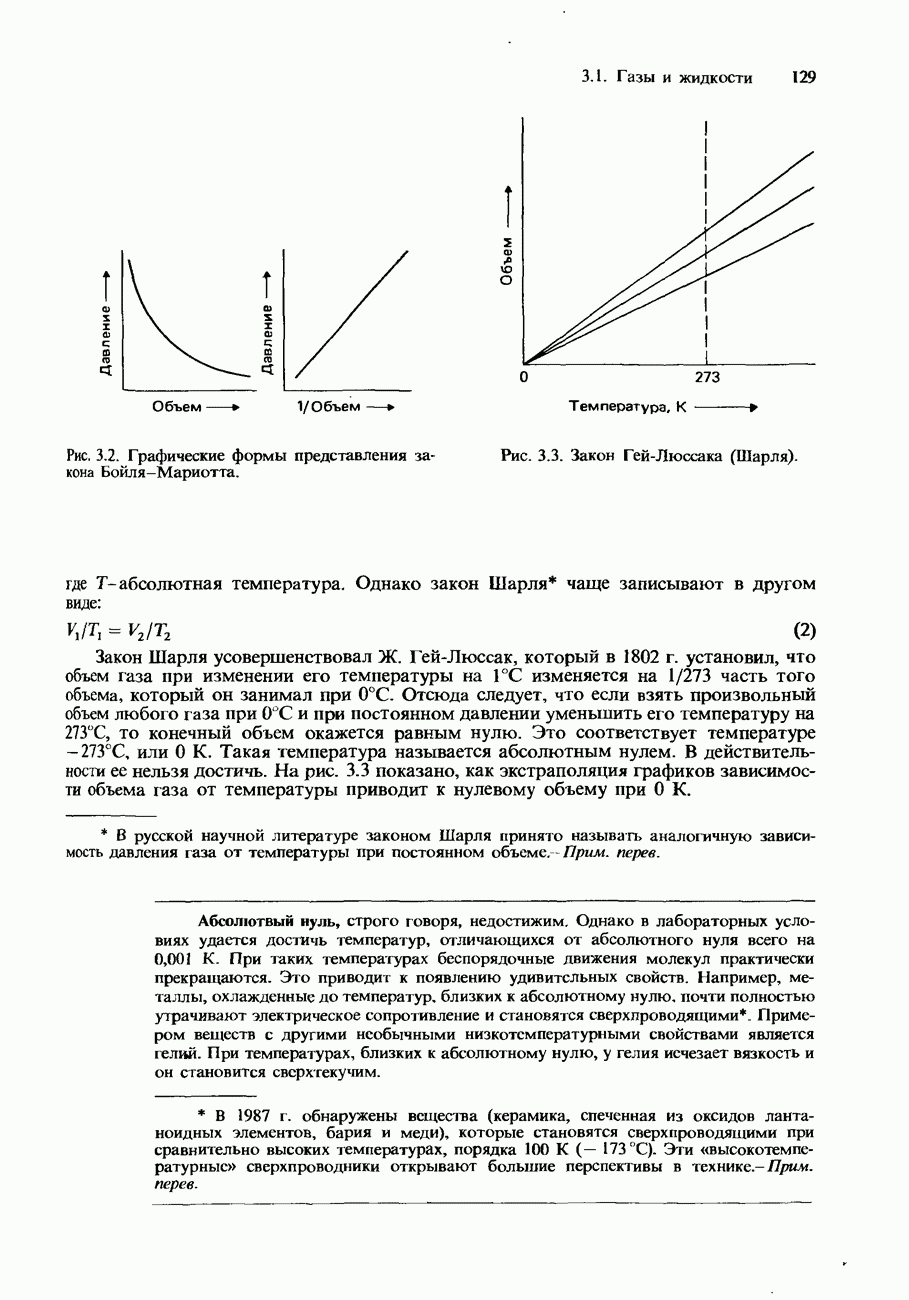
- Закон Бойля-Мариотта
- Закон Гей-Люссака (закон Шарля)
- Объединенный газовый закон
- Закон Авогадро
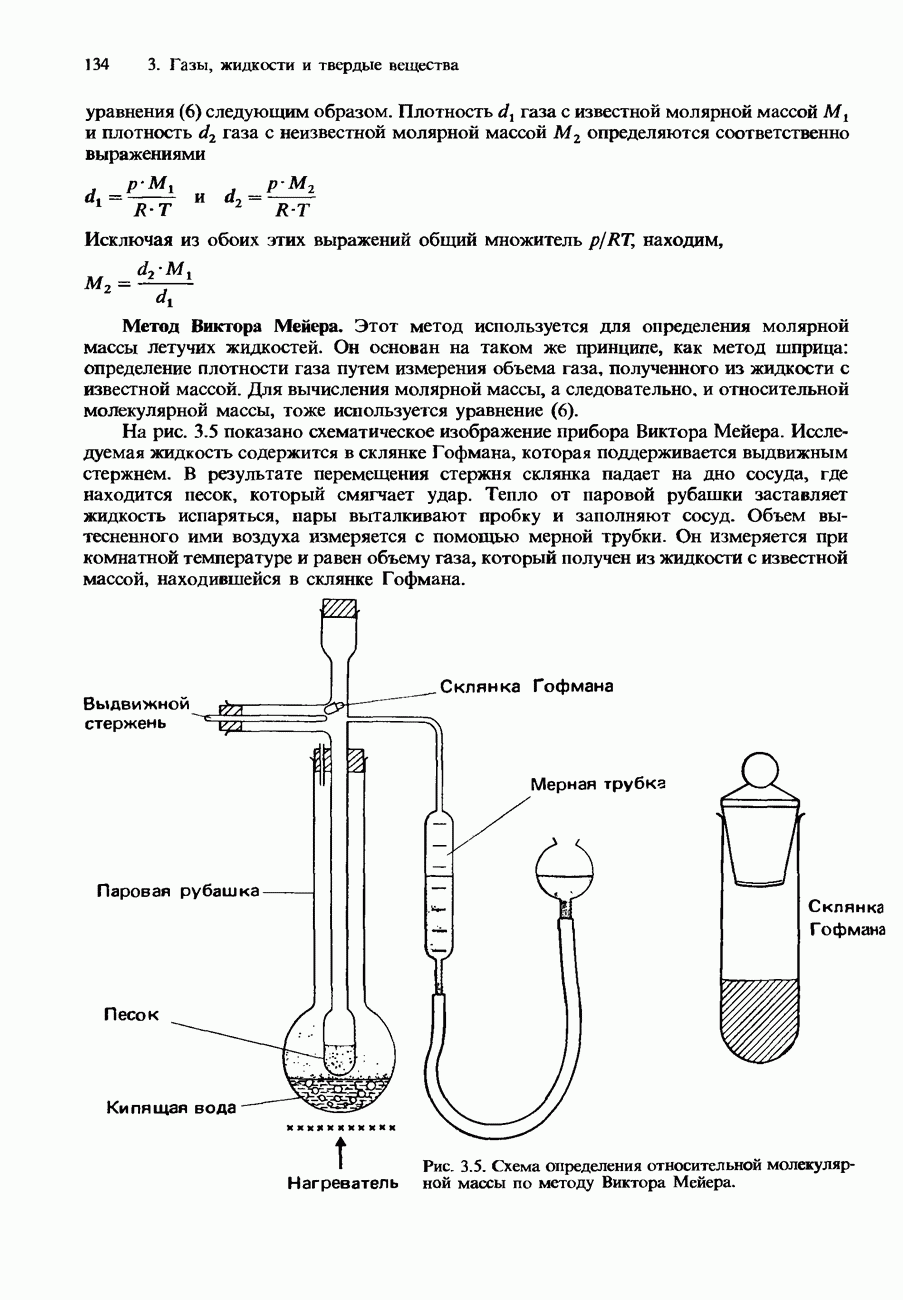
- Экспериментальное определение относительной молекулярной массы
- Закон парциальных давлений газов (закон Дальтона)
- Законы Грэхема
- КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- Скорости молекул
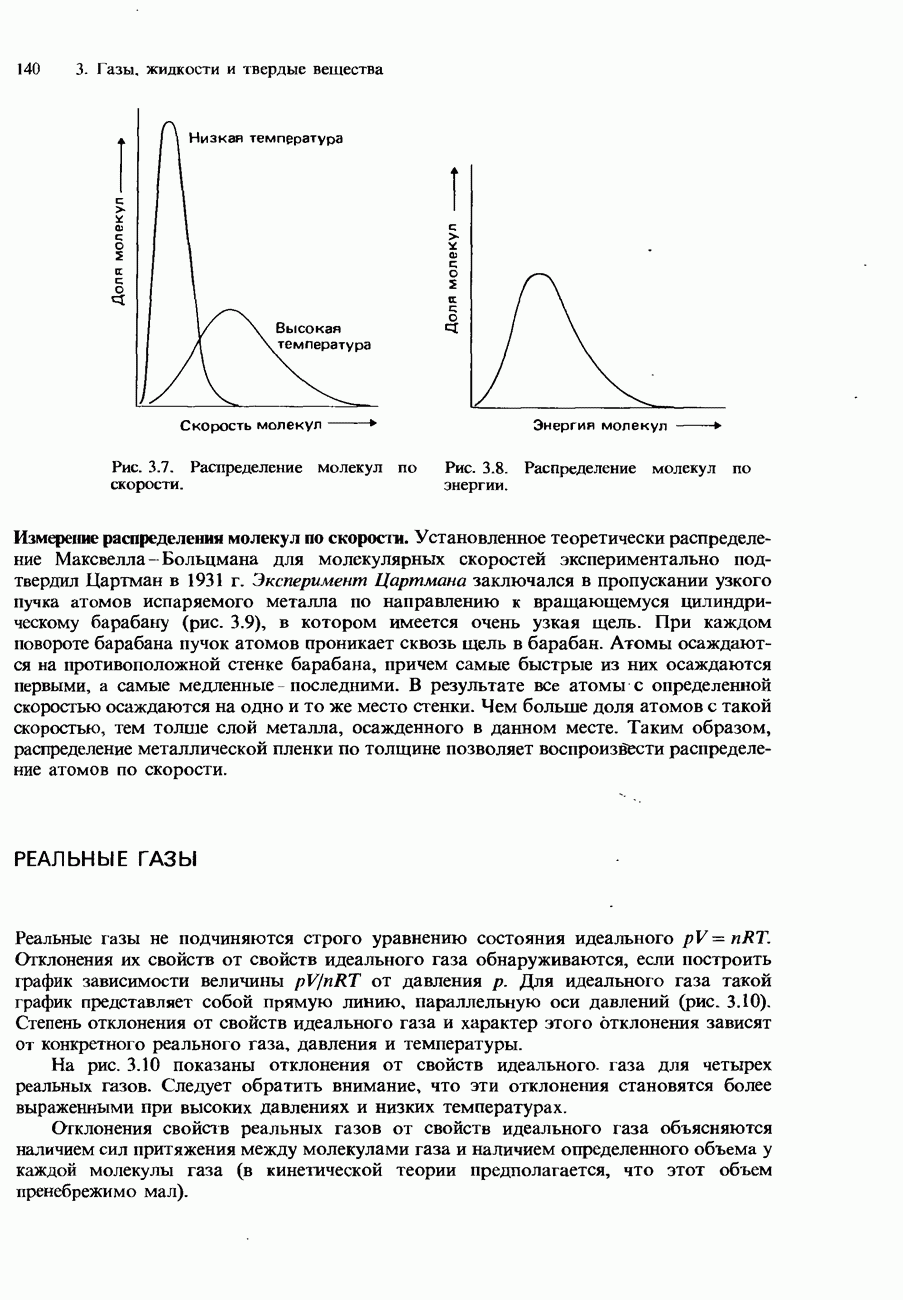
- Распределение Максвелла-Больцмана
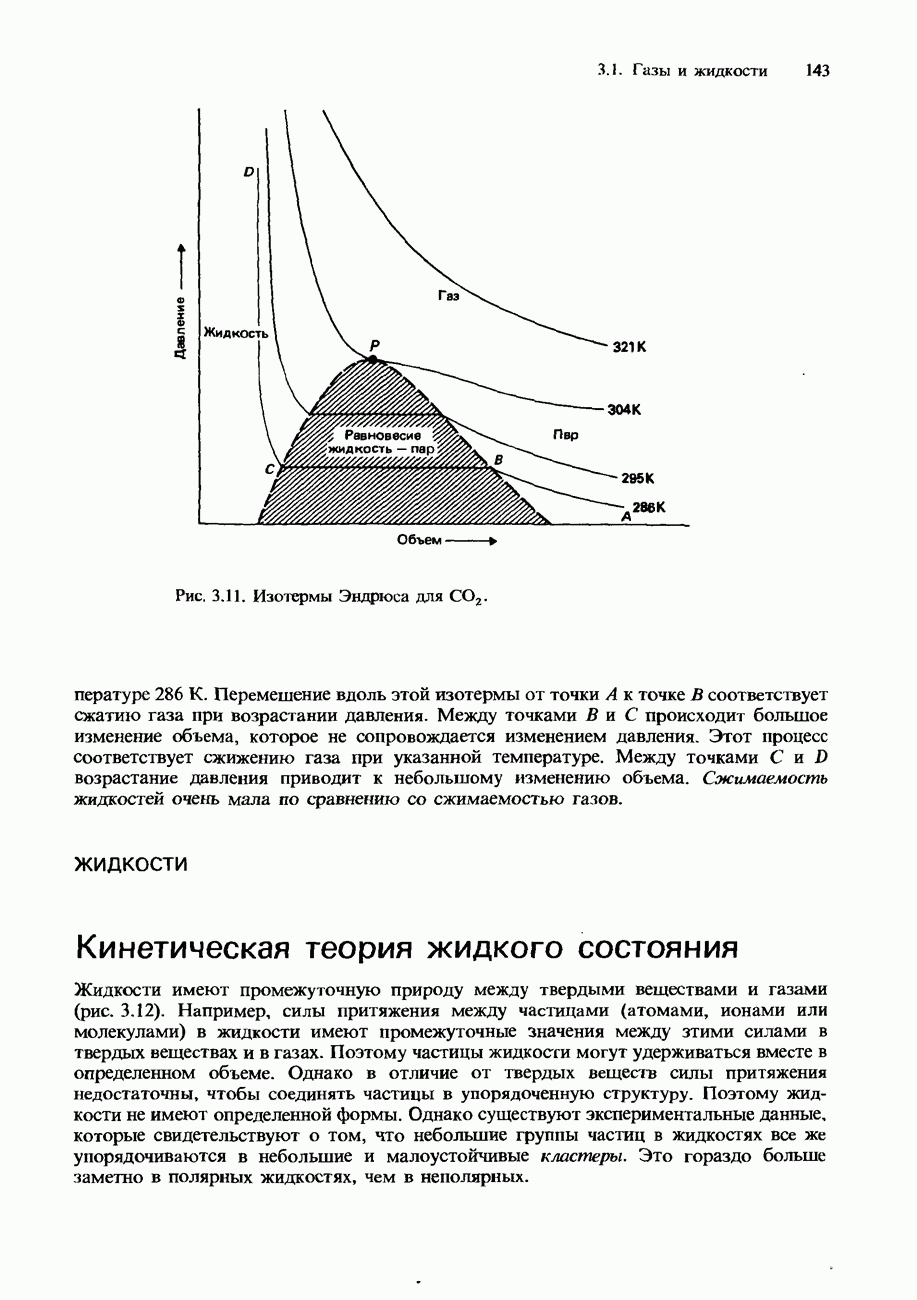
- РЕАЛЬНЫЕ ГАЗЫ
- Уравнение Ван-дер-Ваальса
- Сжижение газов
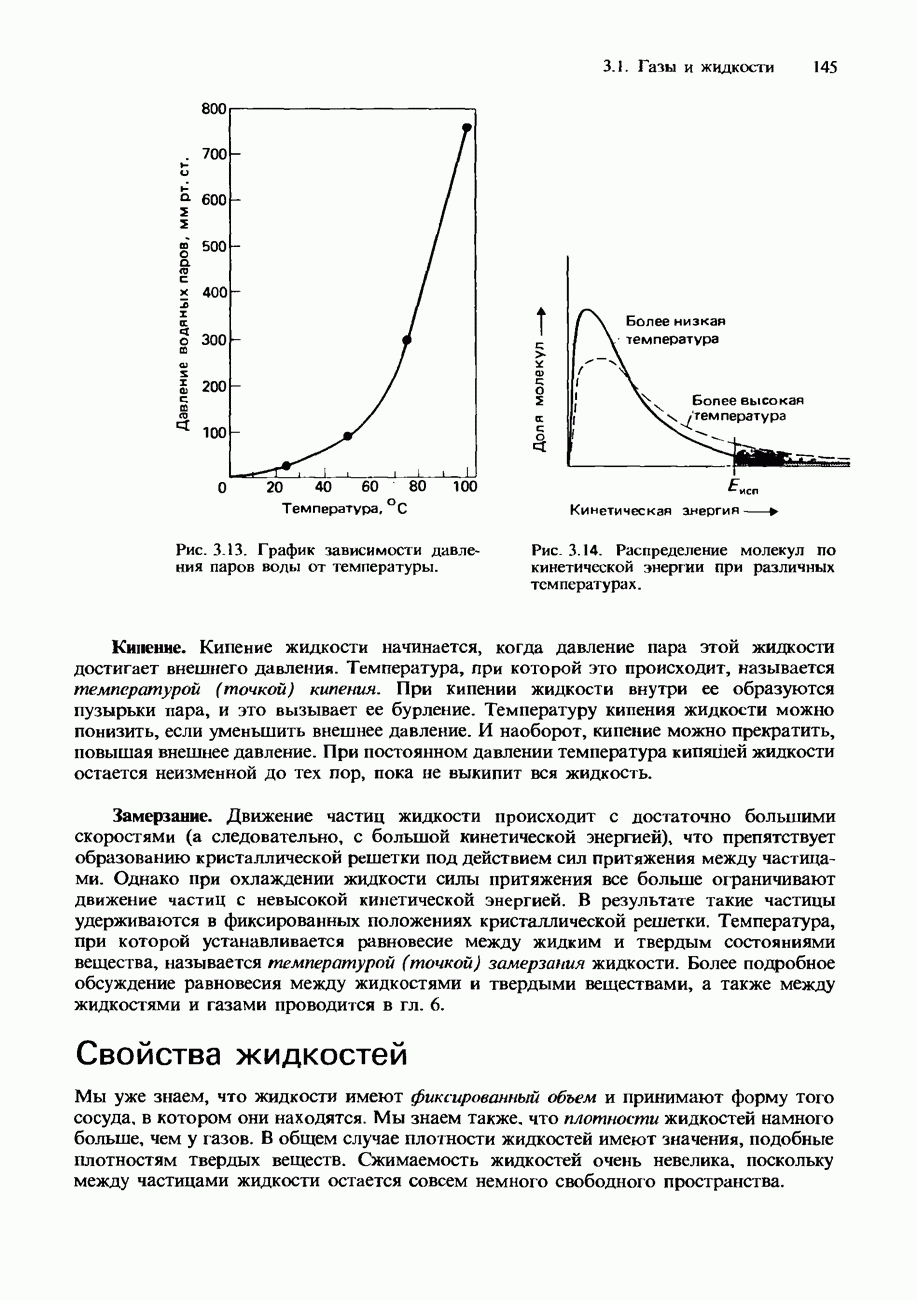
- ЖИДКОСТИ
- Свойства жидкостей
- 3.2. Твердые вещества
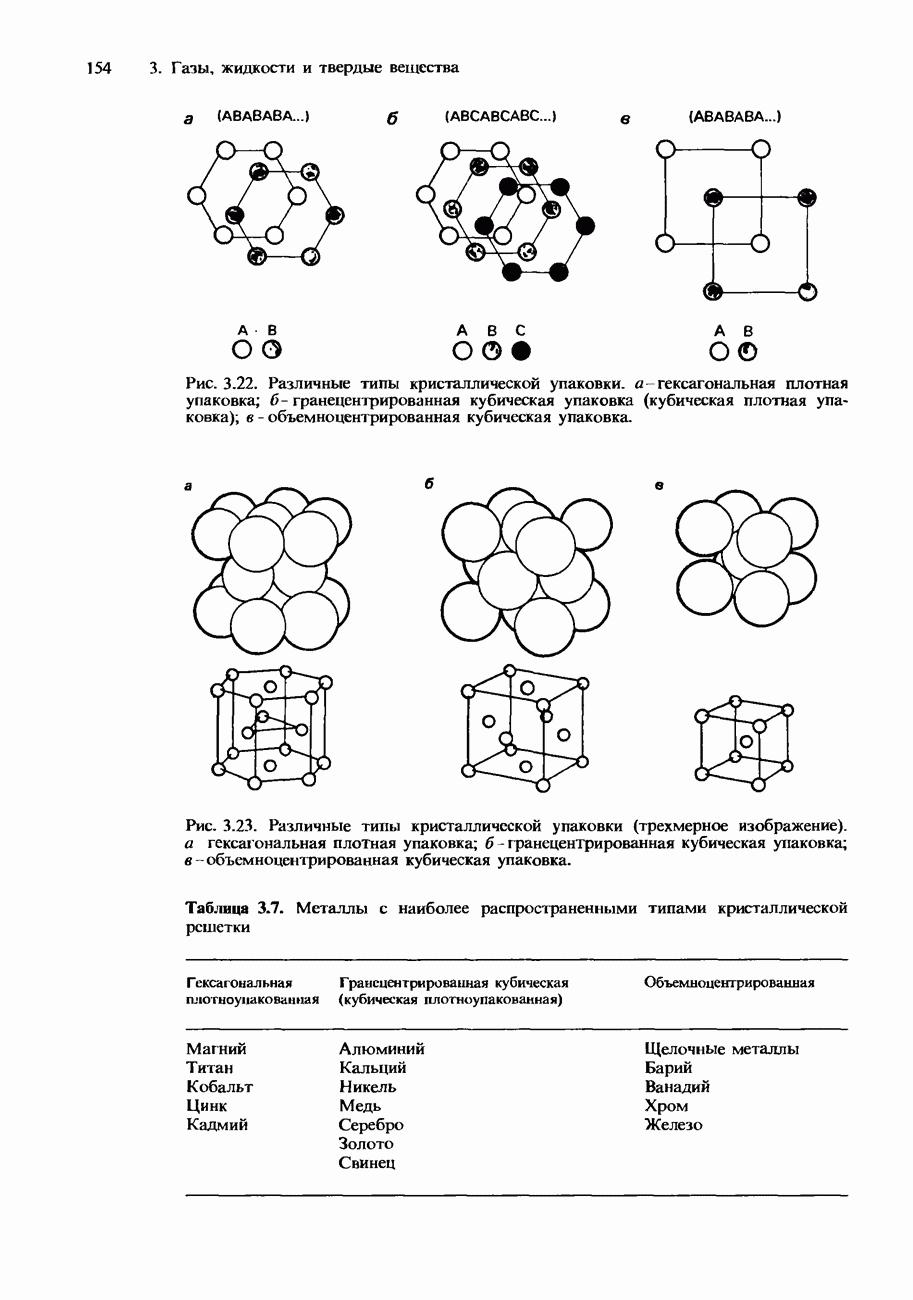
- КРИСТАЛЛИЧЕСКАЯ СТРУКТУРА
- Металлические кристаллы
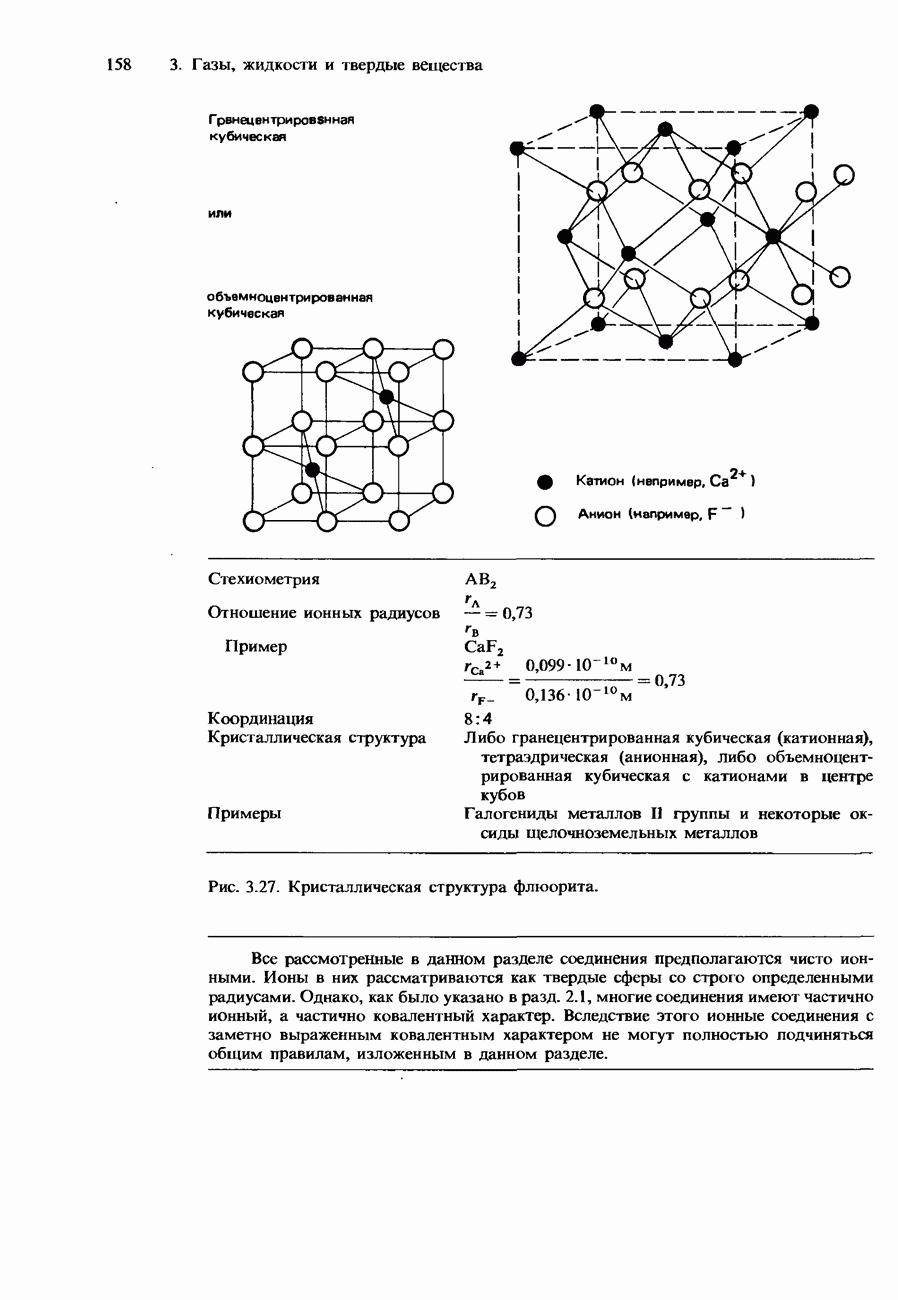
- Ионные кристаллы
- Ковалентные кристаллы
- ИЗОМОРФИЗМ. ПОЛИМОРФИЗМ И АЛЛОТРОПИЯ
- СВОЙСТВА ТВЕРДЫХ ВЕЩЕСТВ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 4. СТЕХИОМЕТРИЯ
- 4.1. Стехиометрия и номенклатура
- Химические вещества
- Количественные законы химии
- Вес и масса
- НАЗВАНИЯ И ФОРМУЛЫ ХИМИЧЕСКИХ СОЕДИНЕНИЙ
- Химические формулы
- НОМЕНКЛАТУРА НЕОРГАНИЧЕСКИХ СОЕДИНЕНИЙ
- Степень окисления (состояние окисления)
- Элементы
- Бинарные соединения
- 4.2 Стехиометрические вычисления
- Молярная масса
- Число частиц вещества
- Процентный состав соединения
- Эмпирическая формула соединения
- Молярные постоянные и молярные величины
- Состав гомогенных смесей
- ХИМИЧЕСКИЕ УРАВНЕНИЯ
- ВЫХОД РЕАКЦИИ
- ПРОМЫШЛЕННАЯ СТЕХИОМЕТРИЯ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 5. ЭНЕРГЕТИКА
- 5.1. Термодинамика
- ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 5.2. Энтальпия
- СТАНДАРТНЫЕ ИЗМЕНЕНИЯ ЭНТАЛЬПИИ
- ДРУГИЕ ИЗМЕНЕНИЯ ЭНТАЛЬПИИ
- КАЛОРИМЕТРИЯ
- КАЛОРИЙНОСТЬ ПИЩИ
- ЗАКОН ГЕССА
- 5.3 Энергия и структура
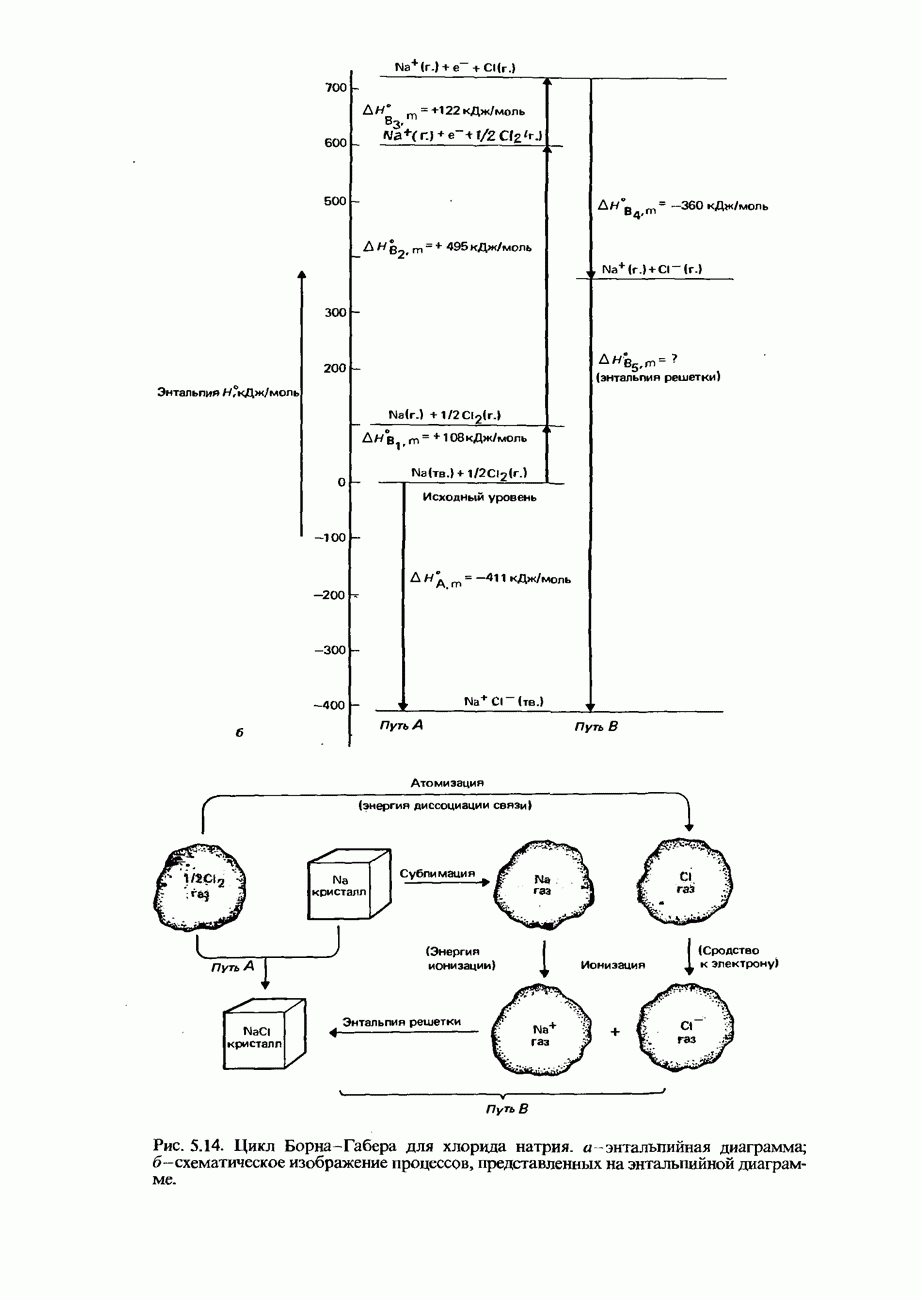
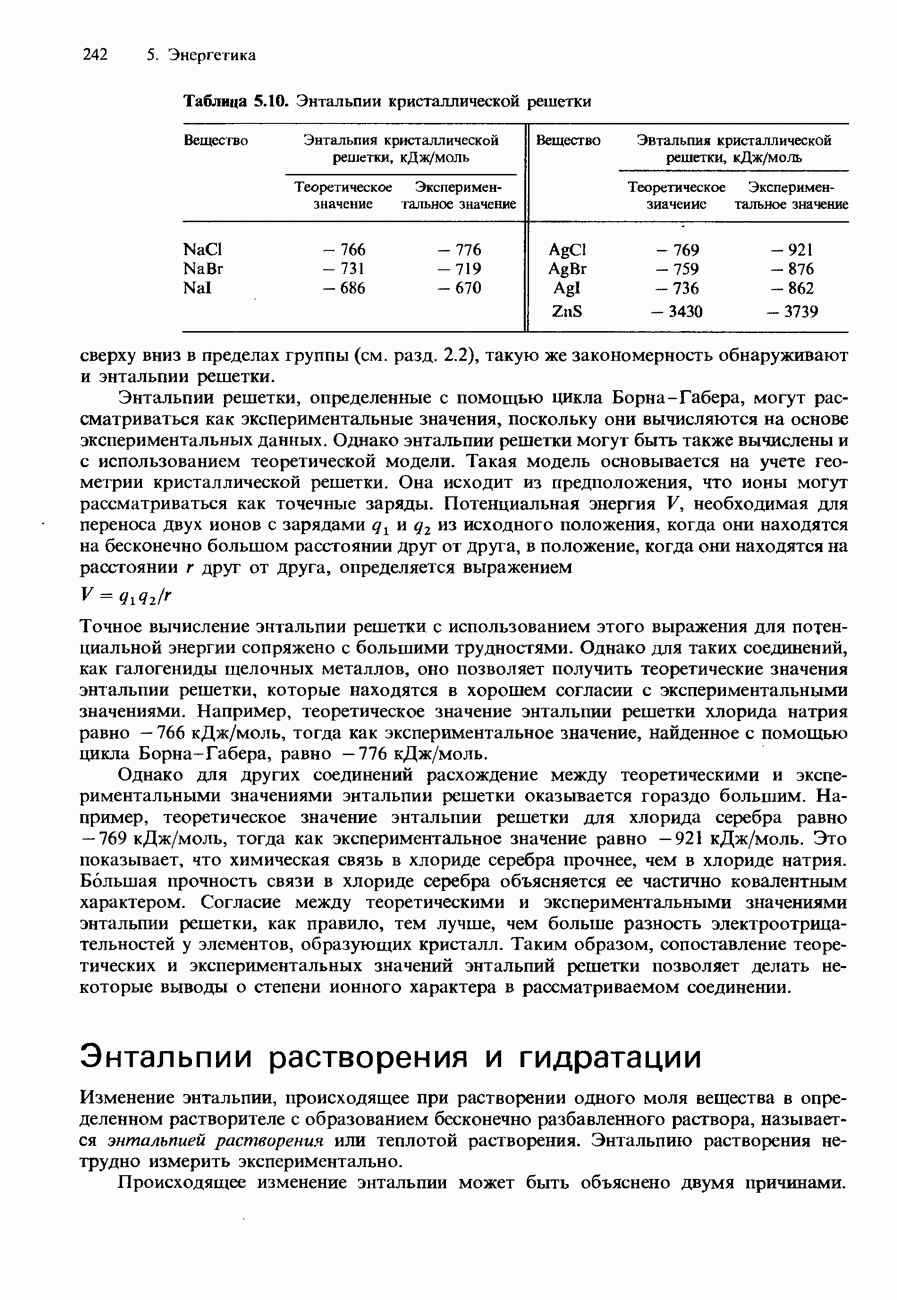
- ЭНТАЛЬПИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Энтальпии растворения и гидратации
- ЭНТРОПИЯ
- СВОБОДНАЯ ЭНЕРГИЯ ГИББСА
- О ЧЕМ ПОЗВОЛЯЕТ СУДИТЬ ИЗМЕНЕНИЕ СВОБОДНОЙ ЭНЕРГИИ СИСТЕМЫ
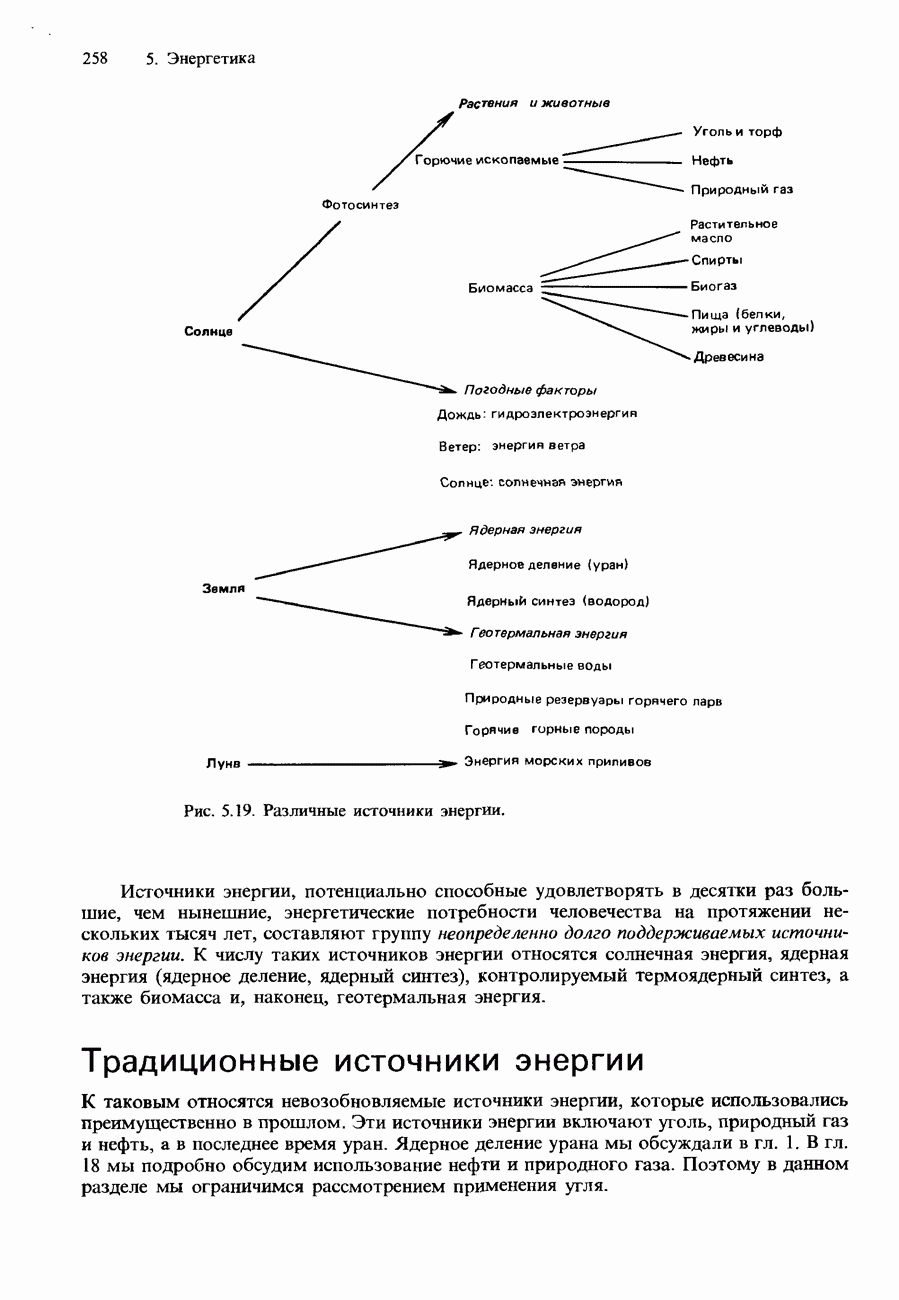
- 5.4. Источники энергии
- НЕТРАДИЦИОННЫЕ ИСТОЧНИКИ ЭНЕРГИИ
- ЗАПАСАНИЕ ЭНЕРГИИ
- ПОТРЕБЛЕНИЕ ЭНЕРГИИ В ПРОШЛОМ, НАСТОЯЩЕМ И БУДУЩЕМ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 6. ФАЗОВЫЕ РАВНОВЕСИЯ
- 6.1. Равновесия и фазы
- ФАЗЫ И КОМПОНЕНТЫ
- Фазы
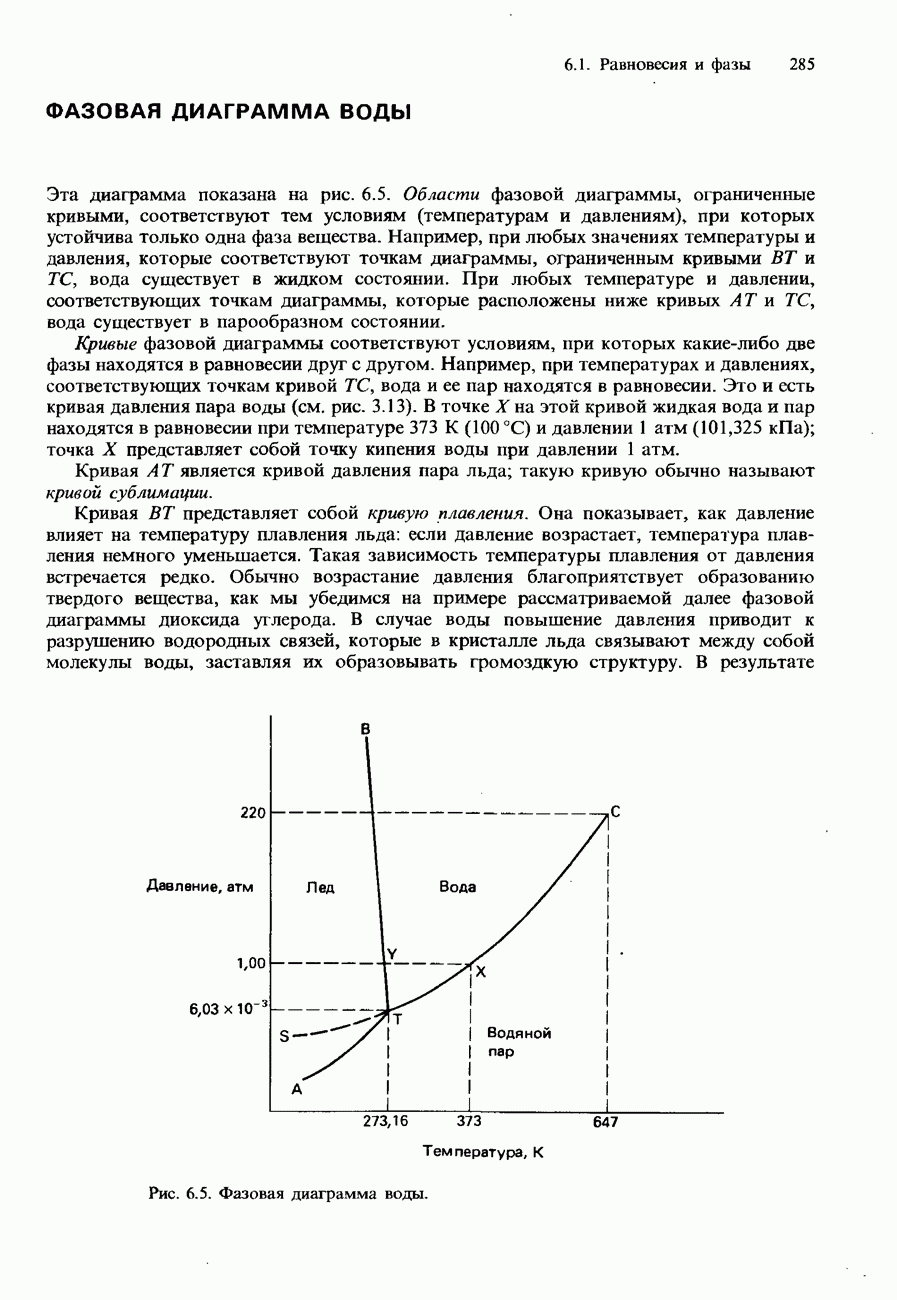
- ФАЗОВАЯ ДИАГРАММА ВОДЫ
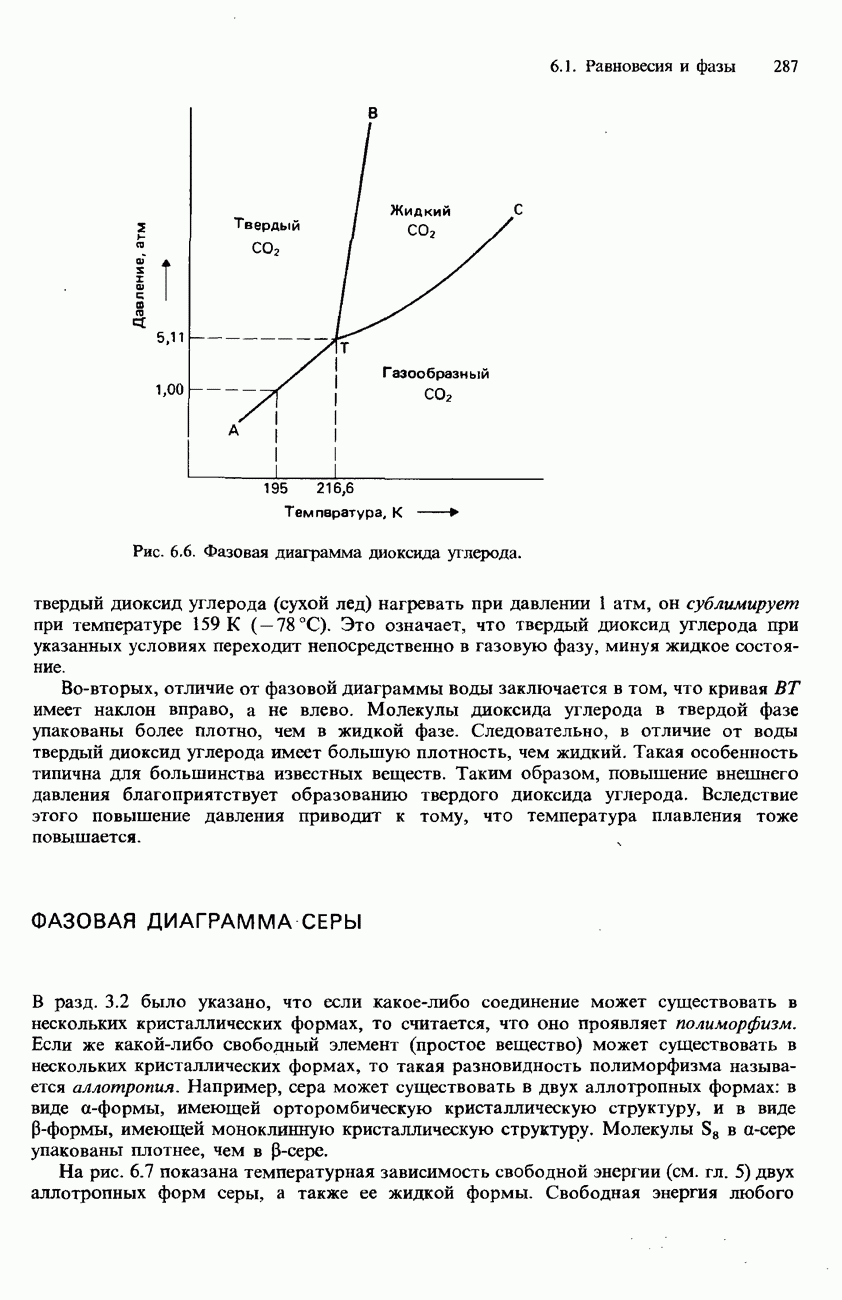
- ФАЗОВАЯ ДИАГРАММА ДИОКСИДА УГЛЕРОДА
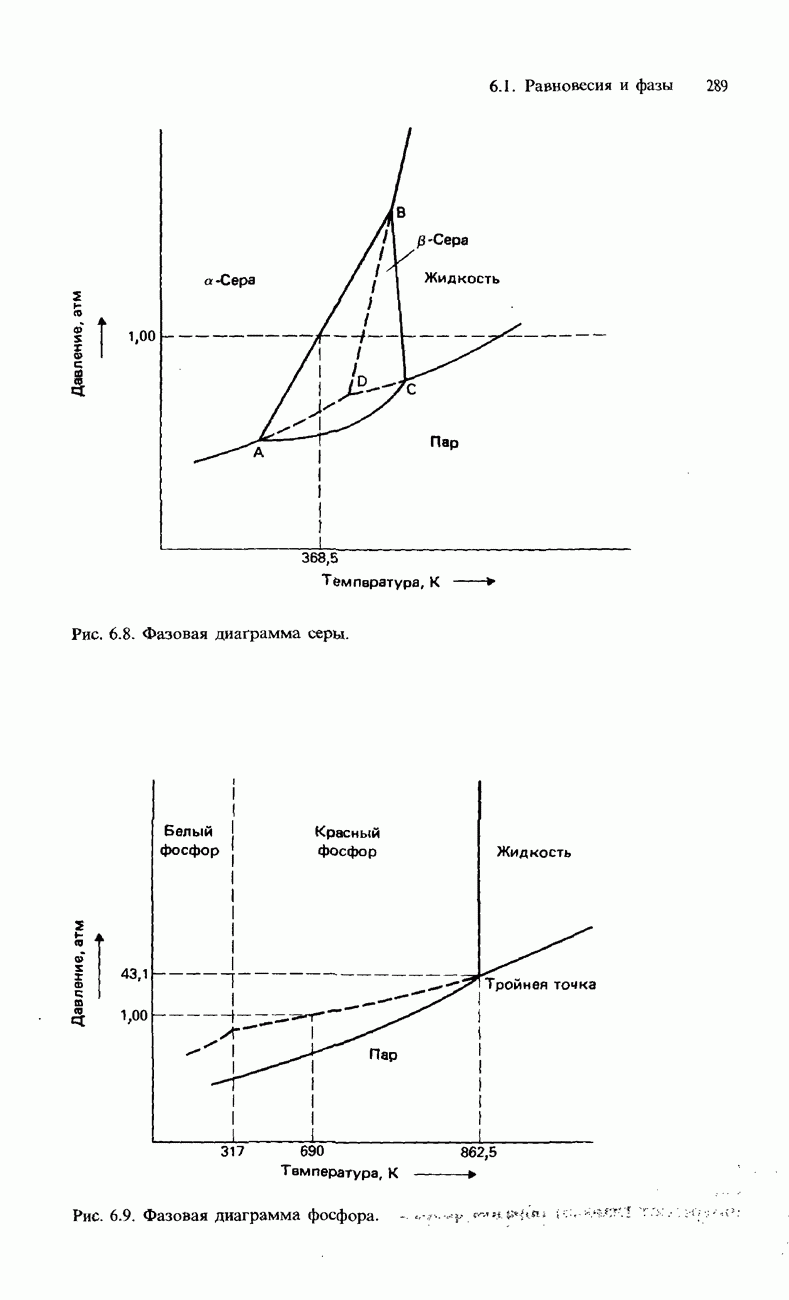
- ФАЗОВАЯ ДИАГРАММА СЕРЫ
- ФАЗОВАЯ ДИАГРАММА ФОСФОРА
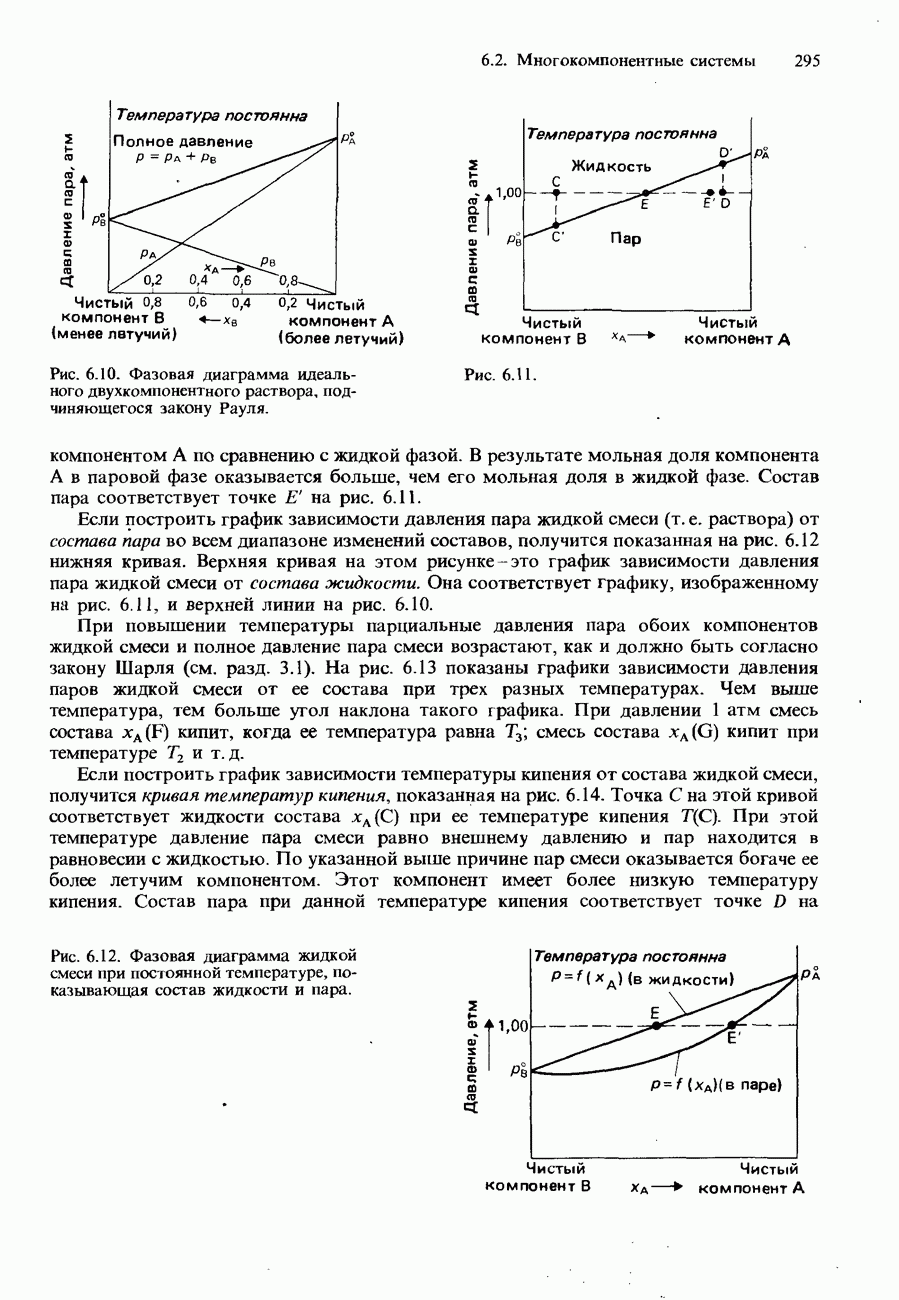
- 6.2. Многокомпонентные системы
- ДВУХКОМПОНЕНТНЫЕ ЖИДКИЕ СМЕСИ
- ПОЛНОСТЬЮ СМЕШИВАЮЩИЕСЯ ЖИДКОСТИ
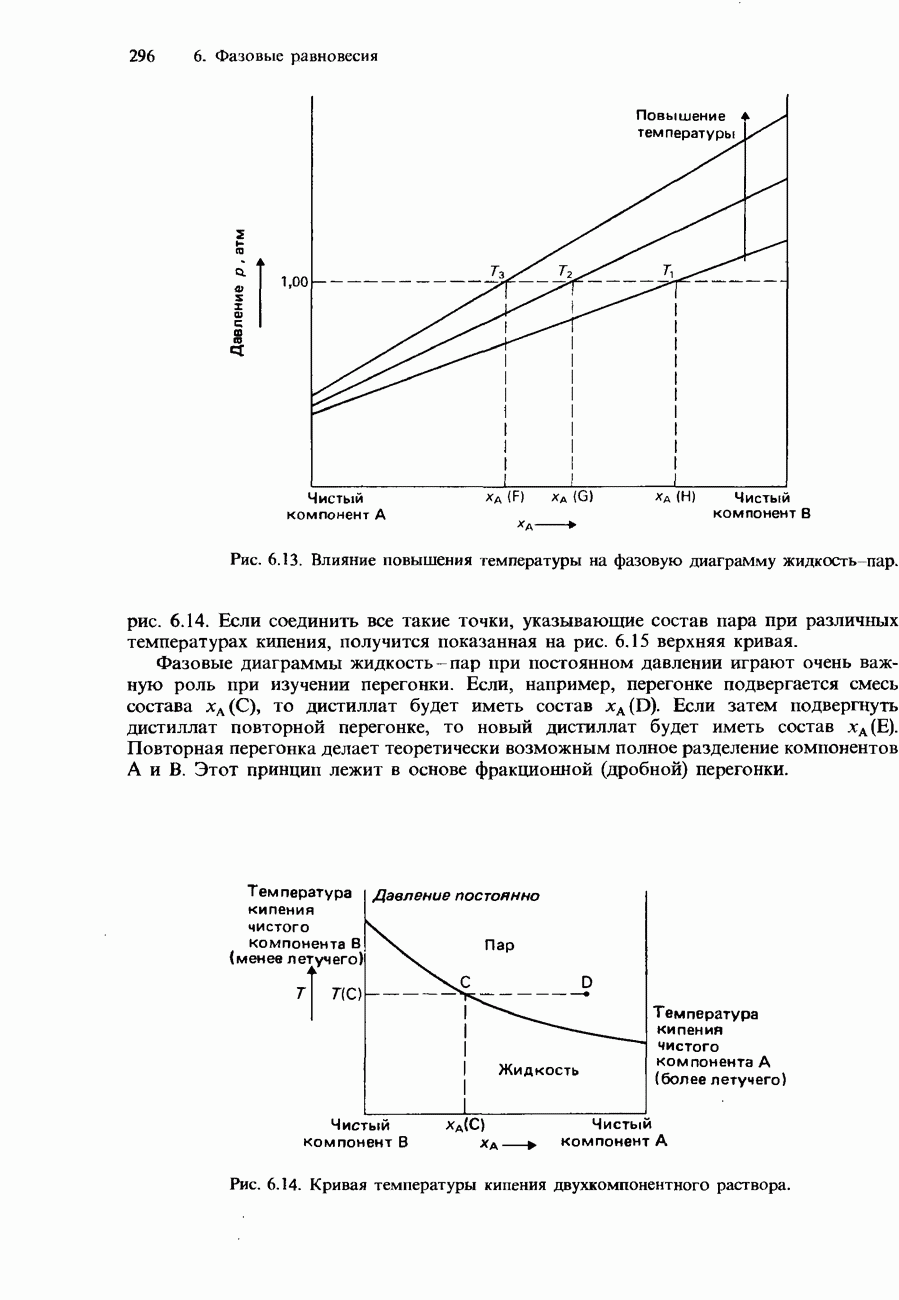
- Фазовые диаграммы полностью смешивающихся жидкостей
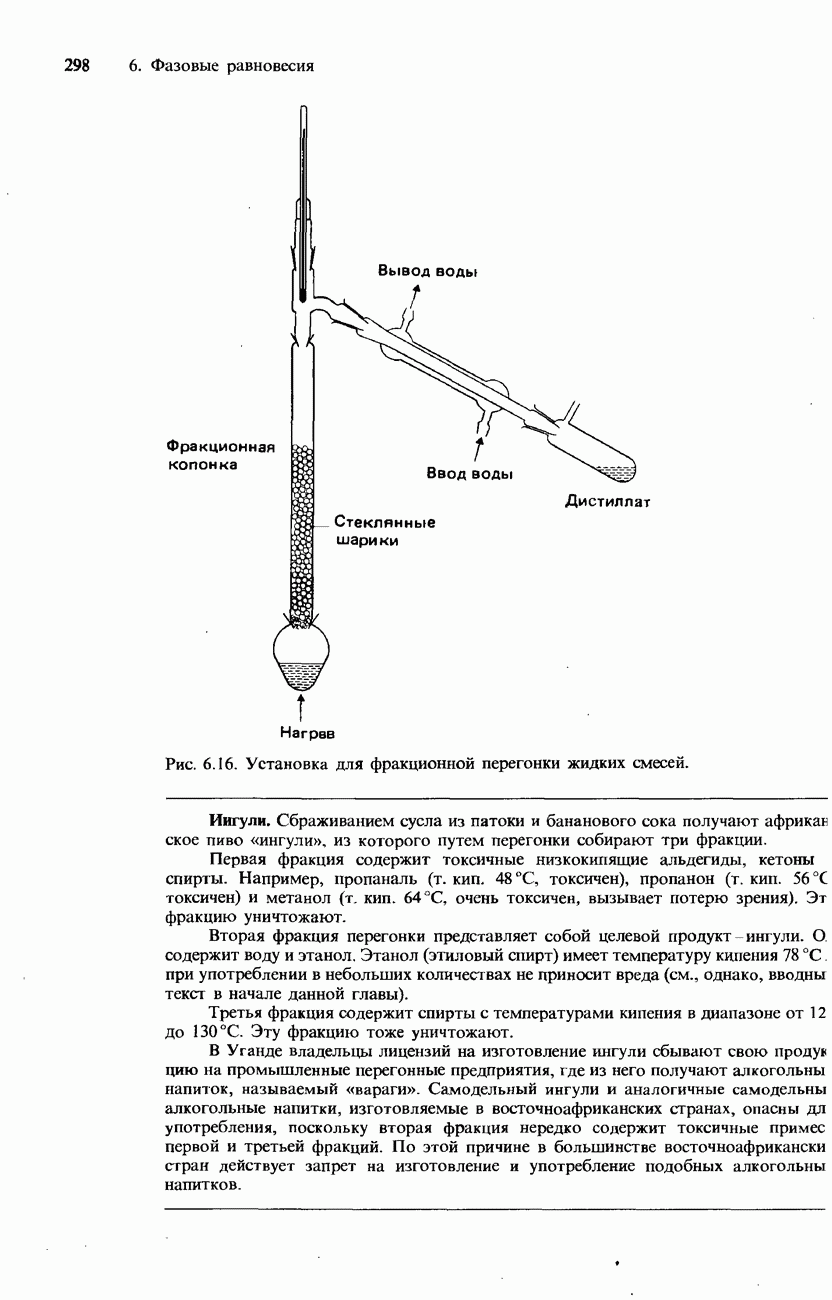
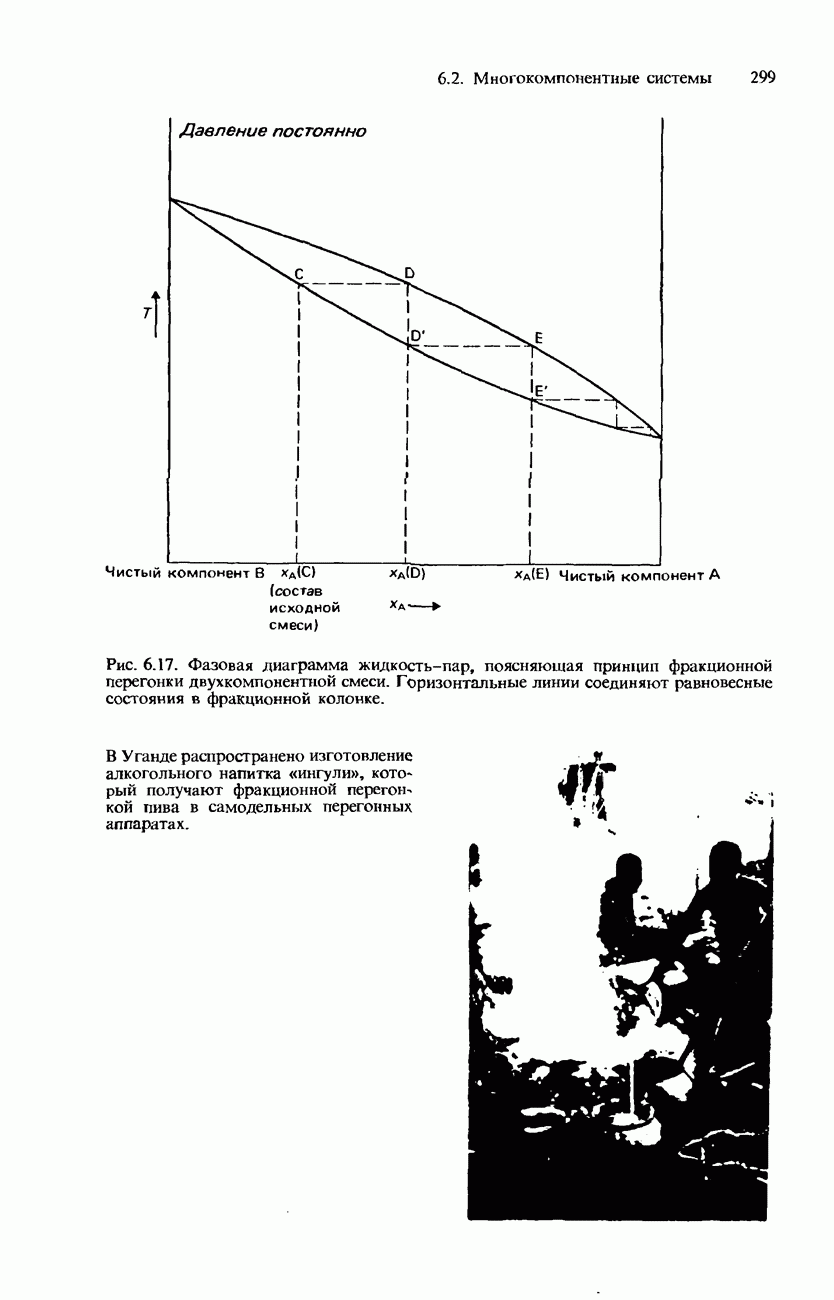
- Фракционная перегонка
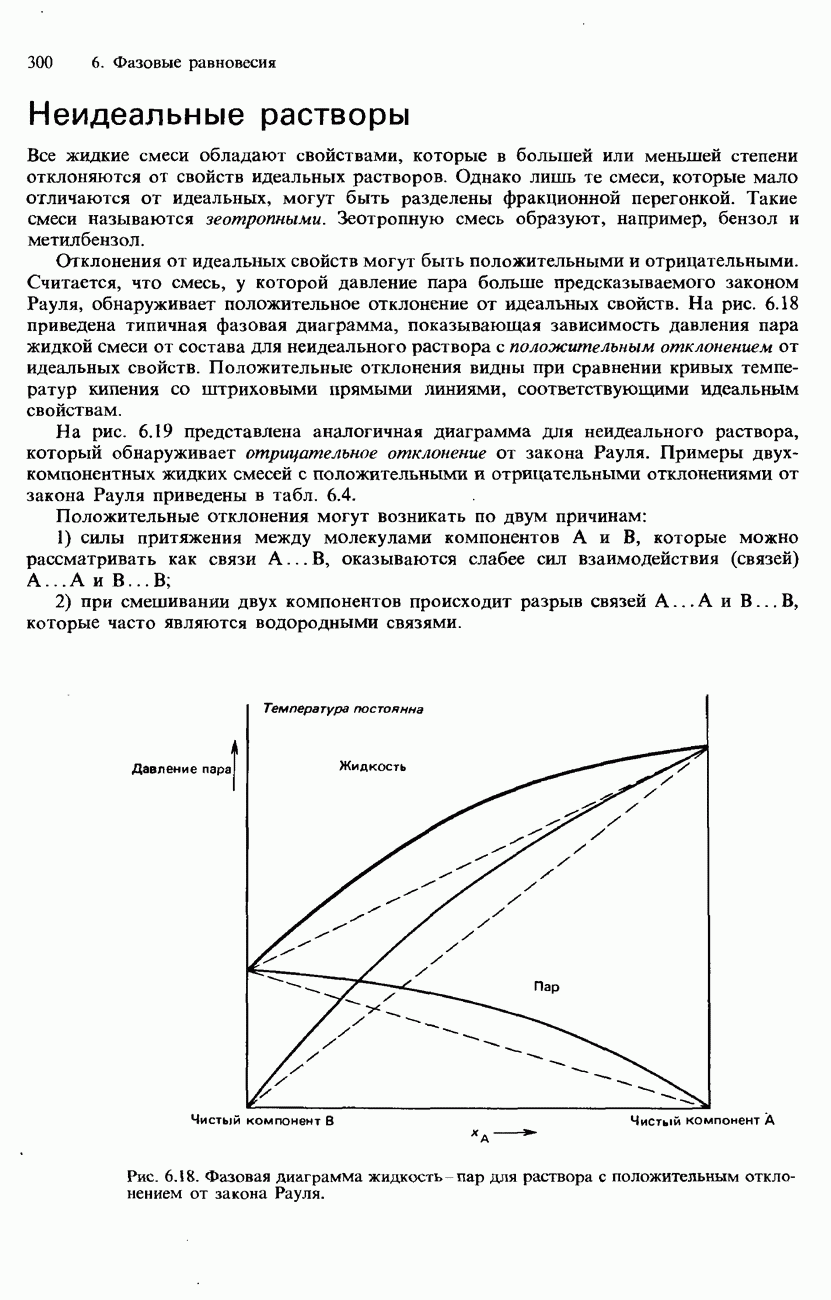
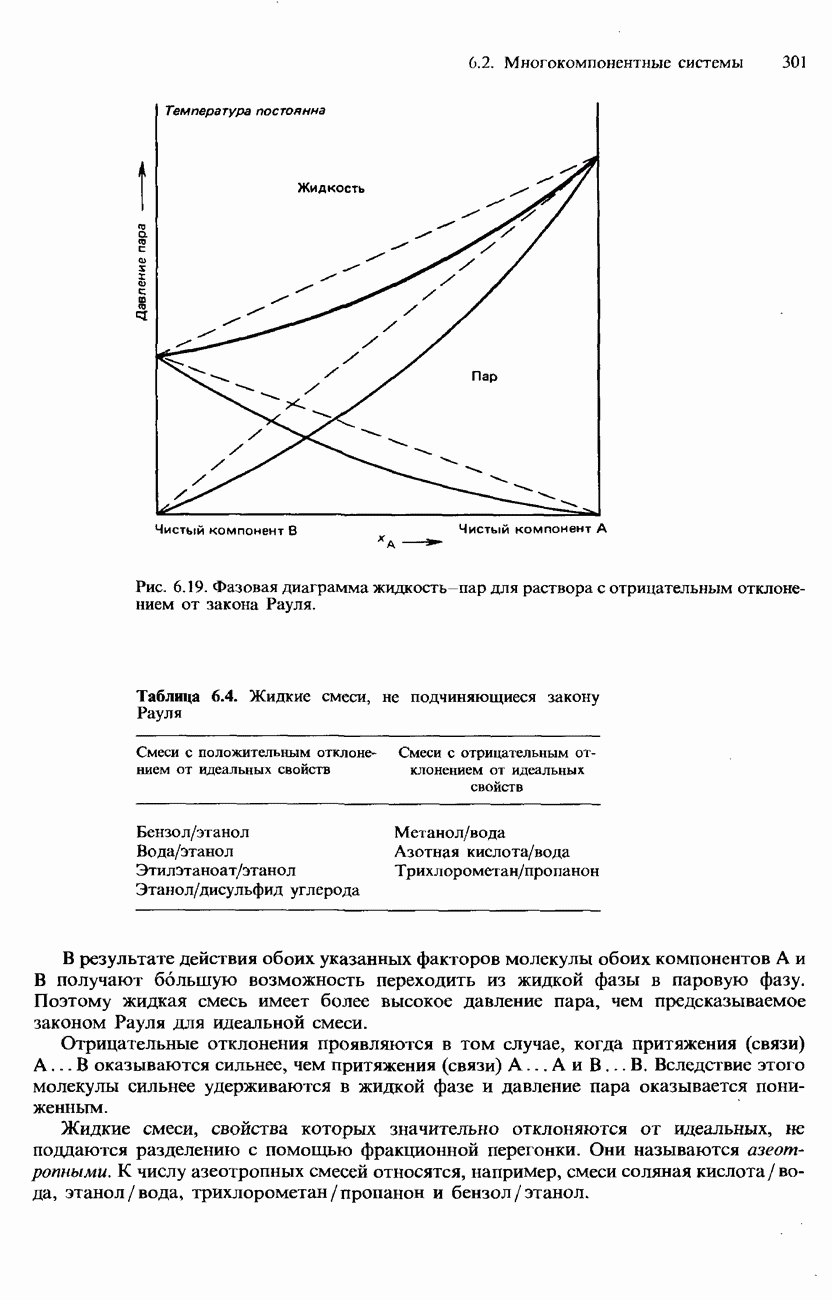
- Неидеальные растворы
- ЧАСТИЧНО СМЕШИВАЮЩИЕСЯ ЖИДКОСТИ
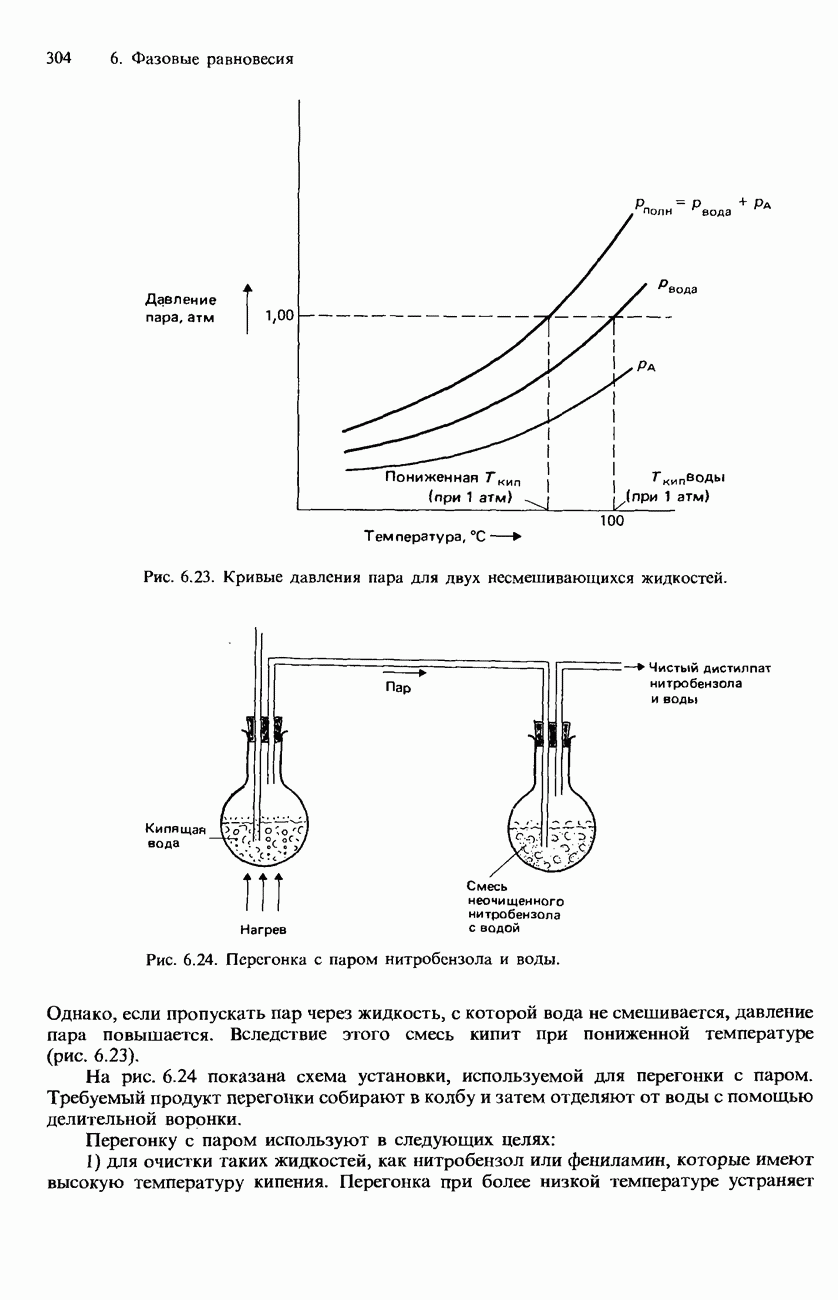
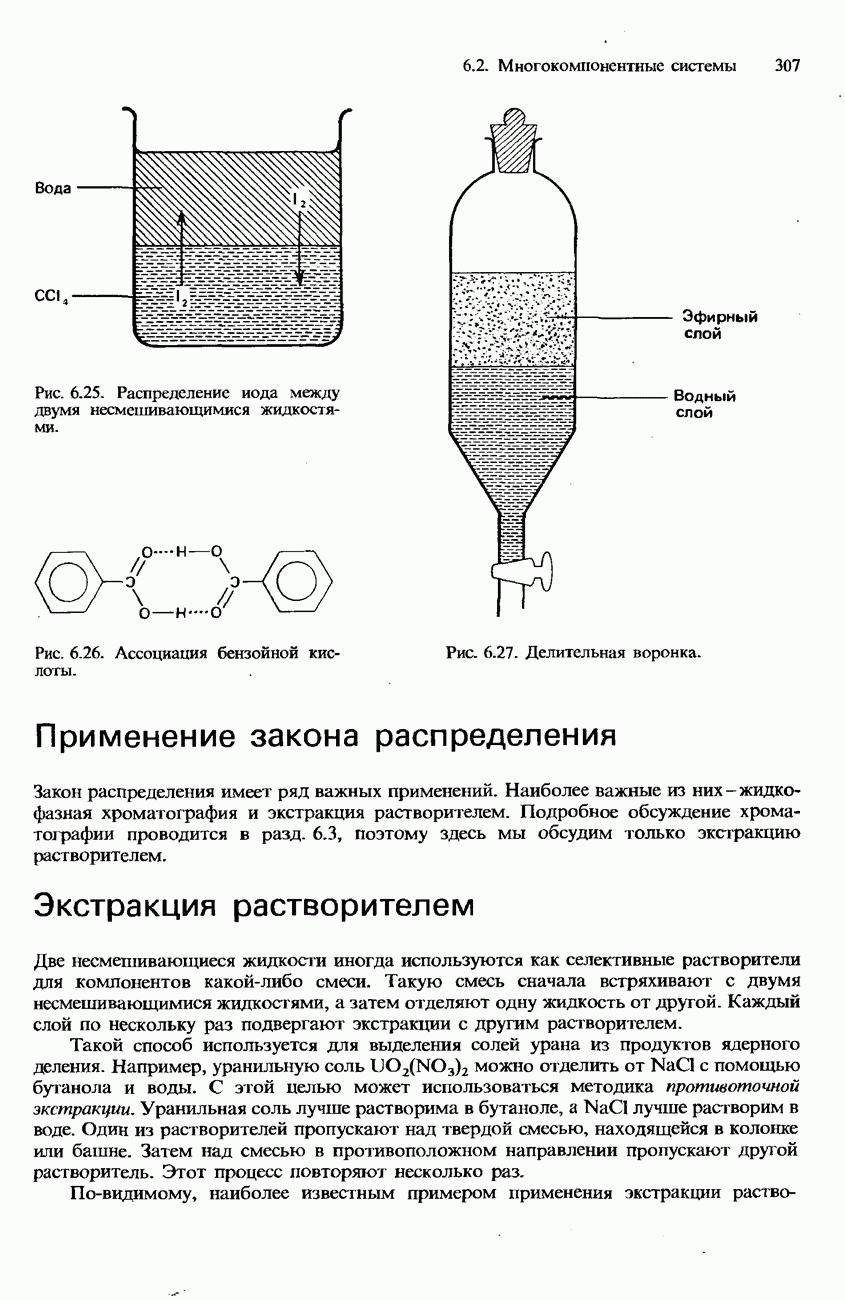
- НЕСМЕШИВАЮЩИЕСЯ ЖИДКОСТИ
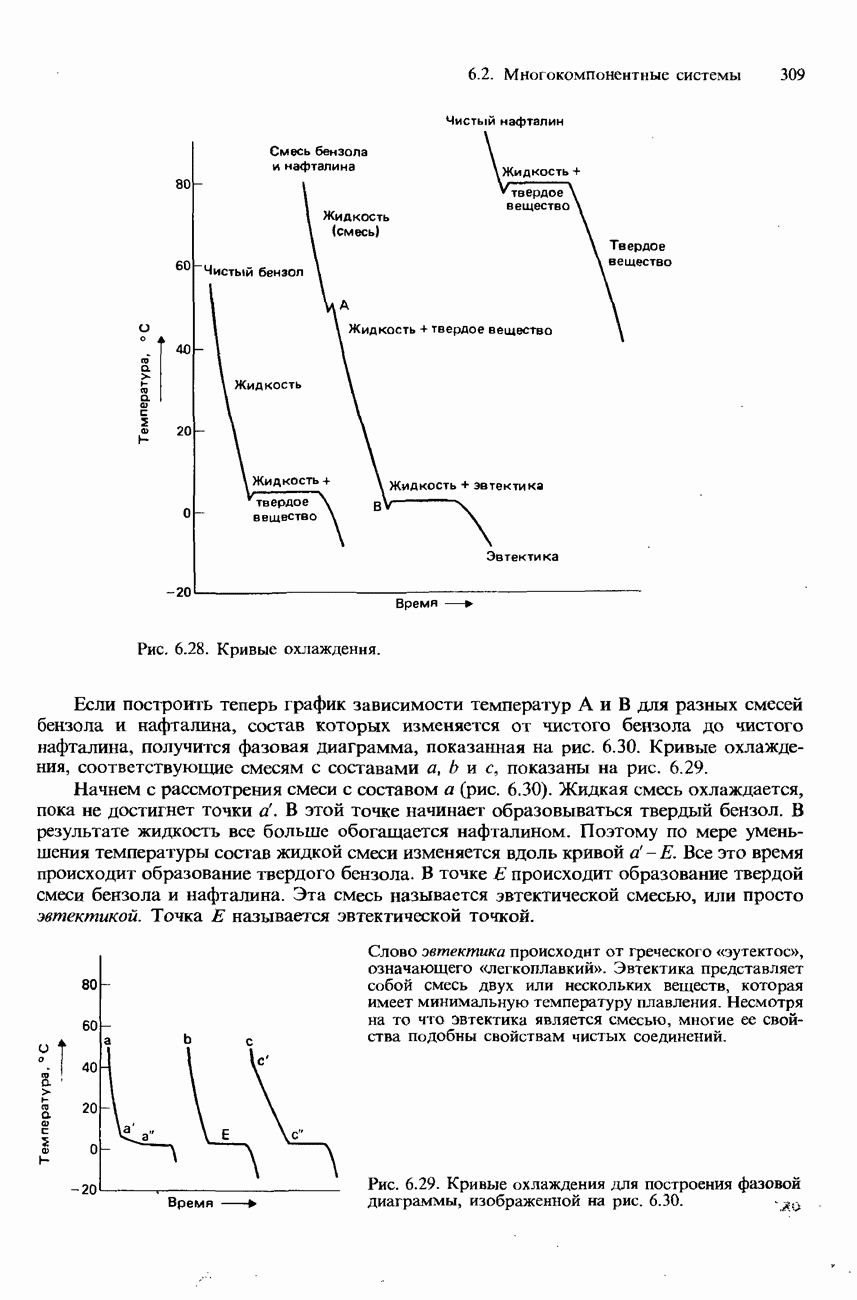
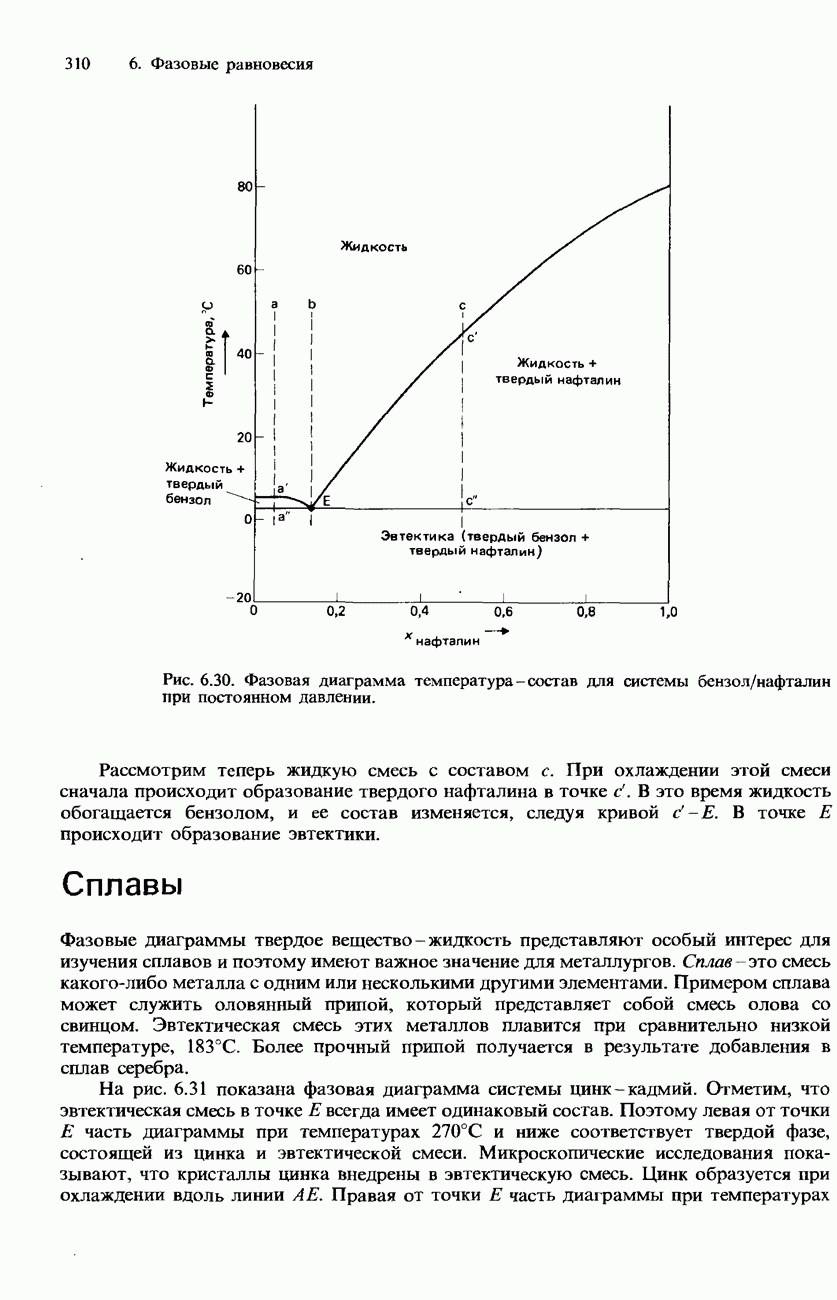
- РАВНОВЕСИЯ ТВЕРДОЕ ВЕЩЕСТВО-ЖИДКОСТЬ
- 6.3. Коллигативные свойства растворов. Коллоиды Хроматография
- КОЛЛОИДЫ
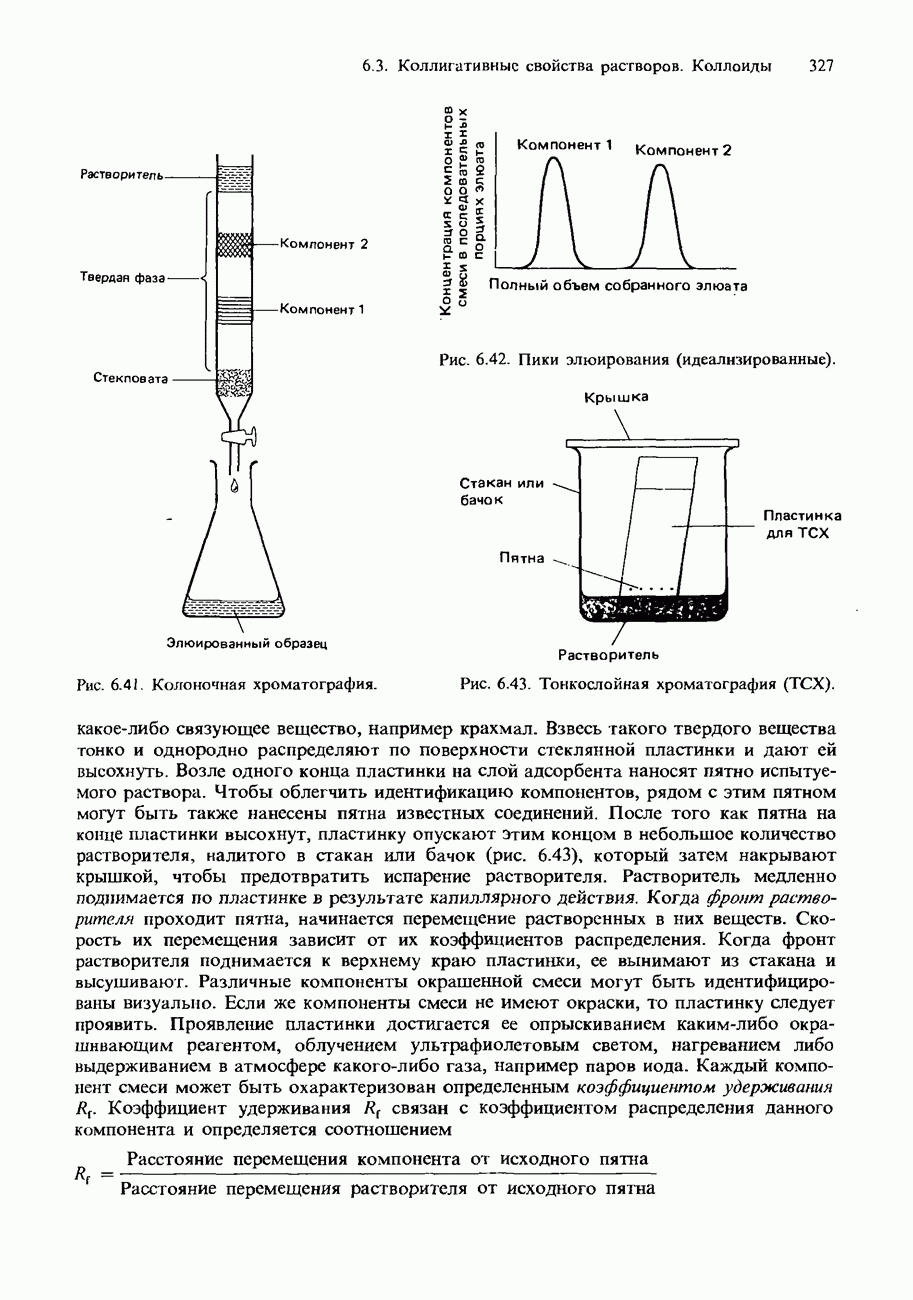
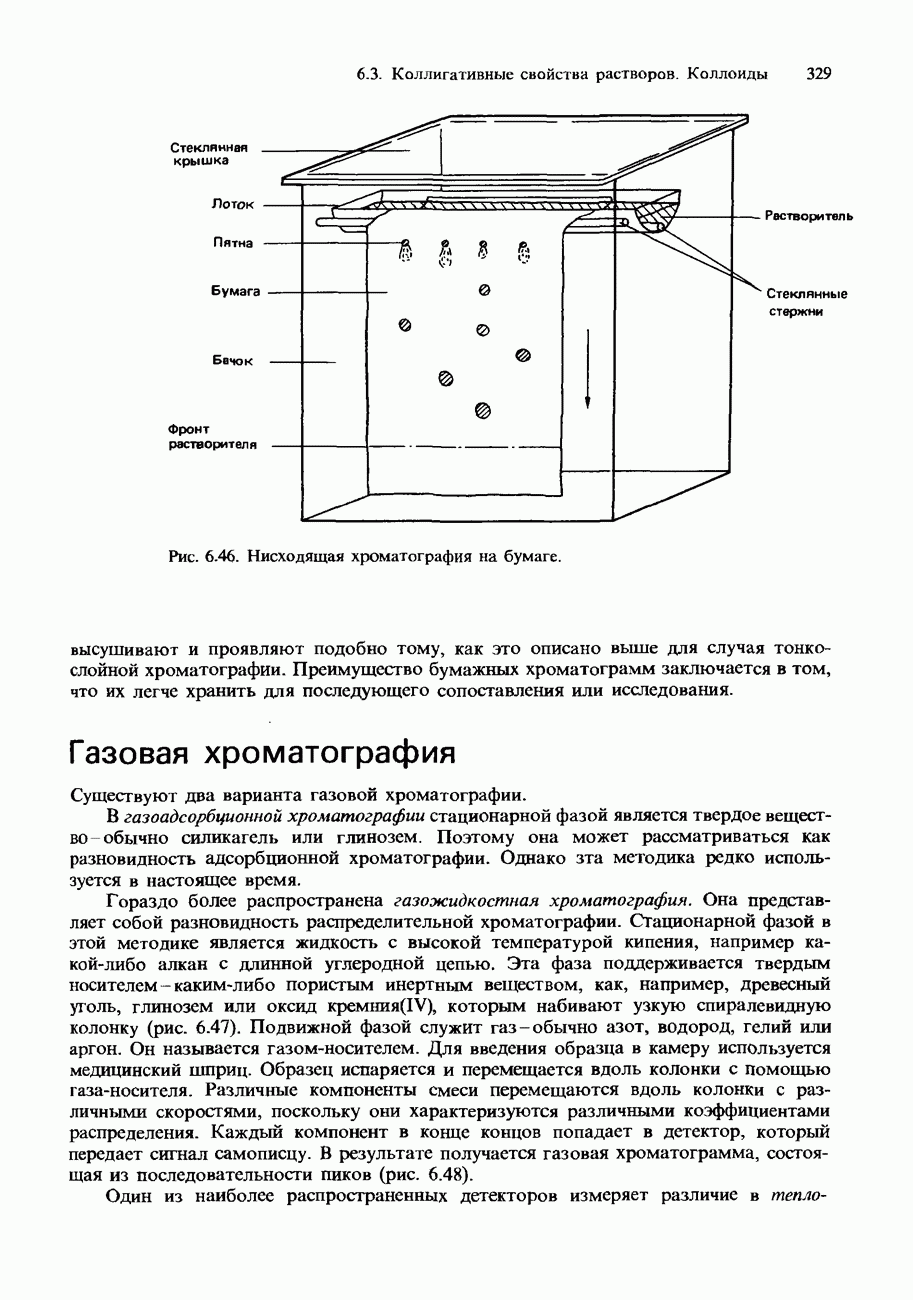
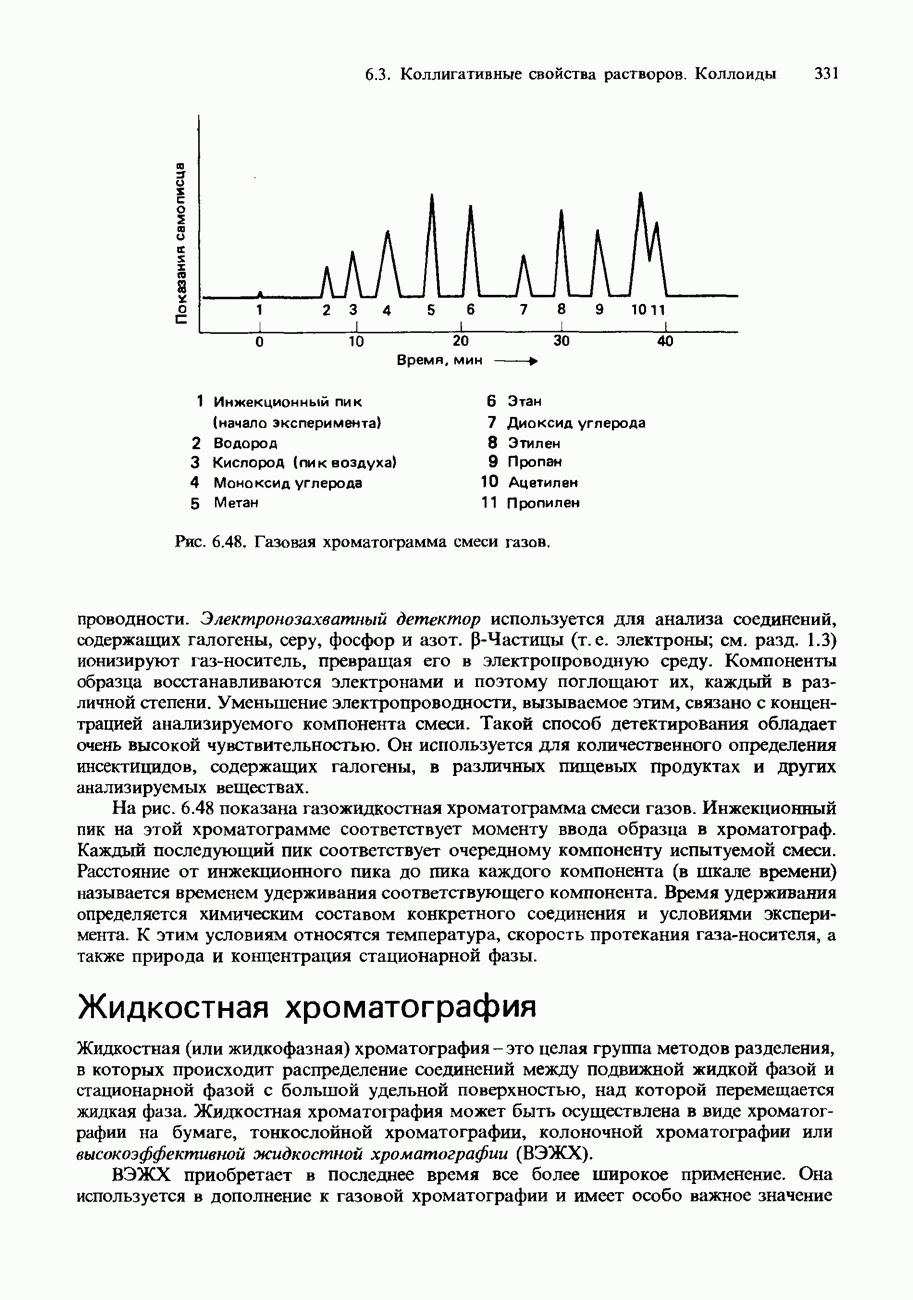
- ХРОМАТОГРАФИЯ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 7. ХИМИЧЕСКОЕ РАВНОВЕСИЕ
- 7.1. Константа равновесия
- ЗАКОН ДЕЙСТВУЮЩИХ МАСС
- ВЛИЯНИЕ УСЛОВИЙ ПРОТЕКАНИЯ РЕАКЦИИ НА ПОЛОЖЕНИЕ РАВНОВЕСИЯ
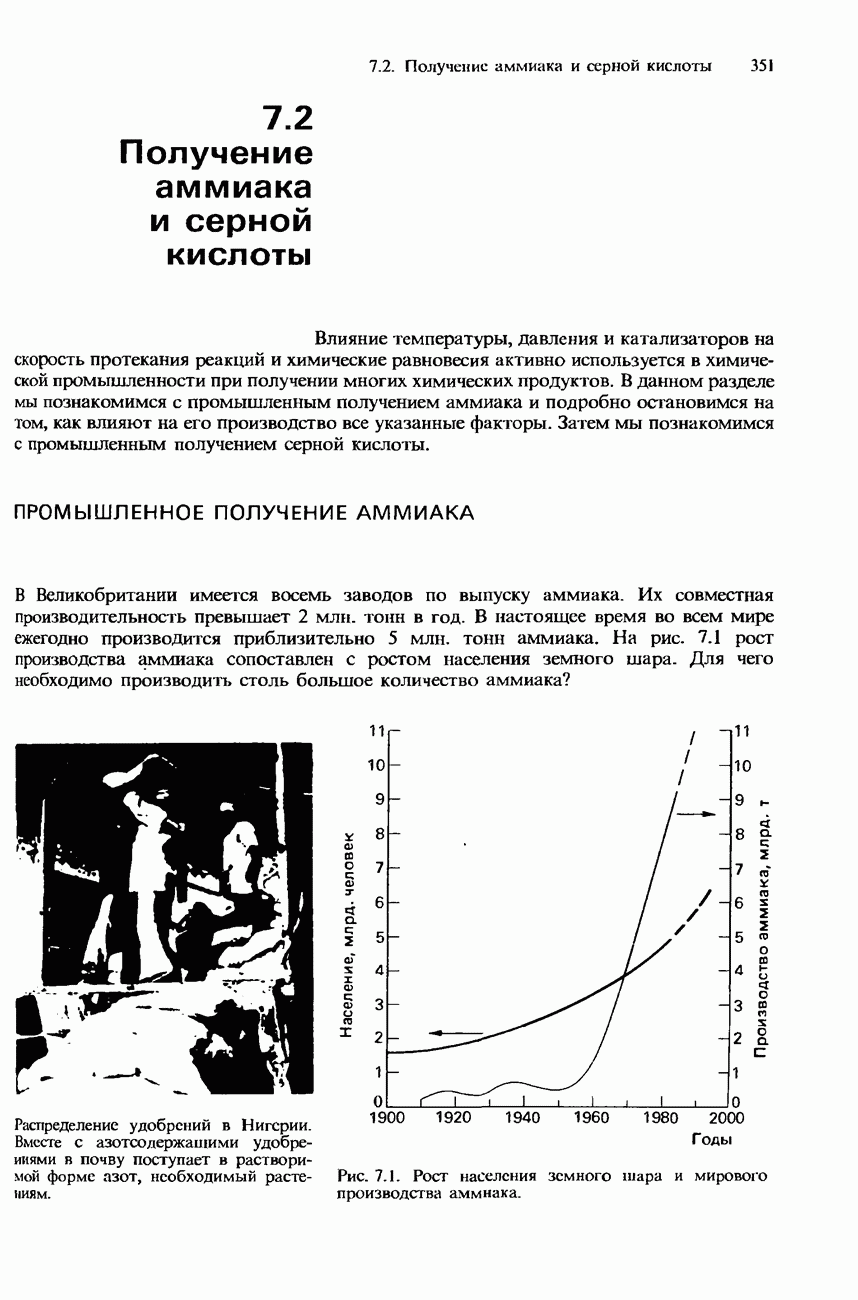
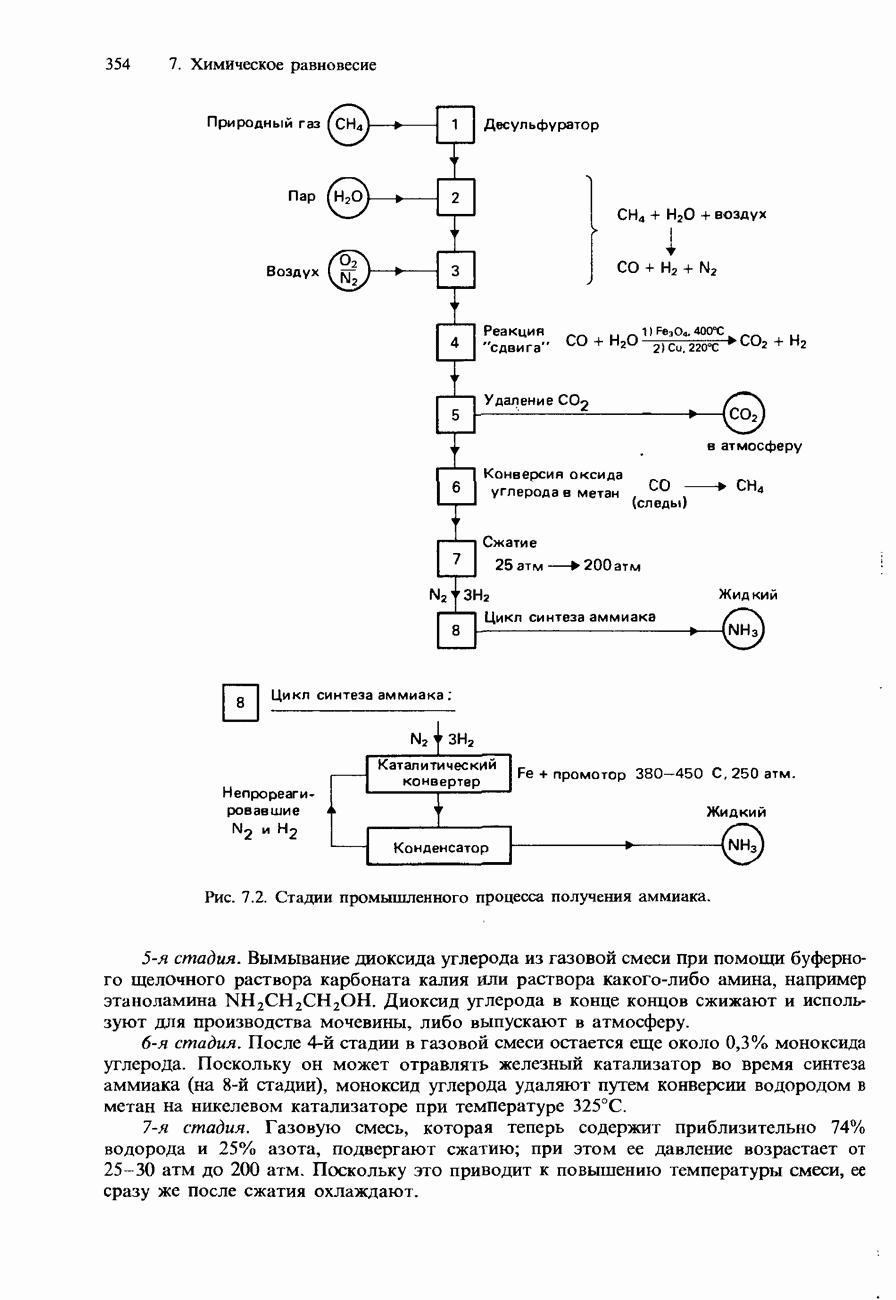
- 7.2. Получение аммиака и серной кислоты
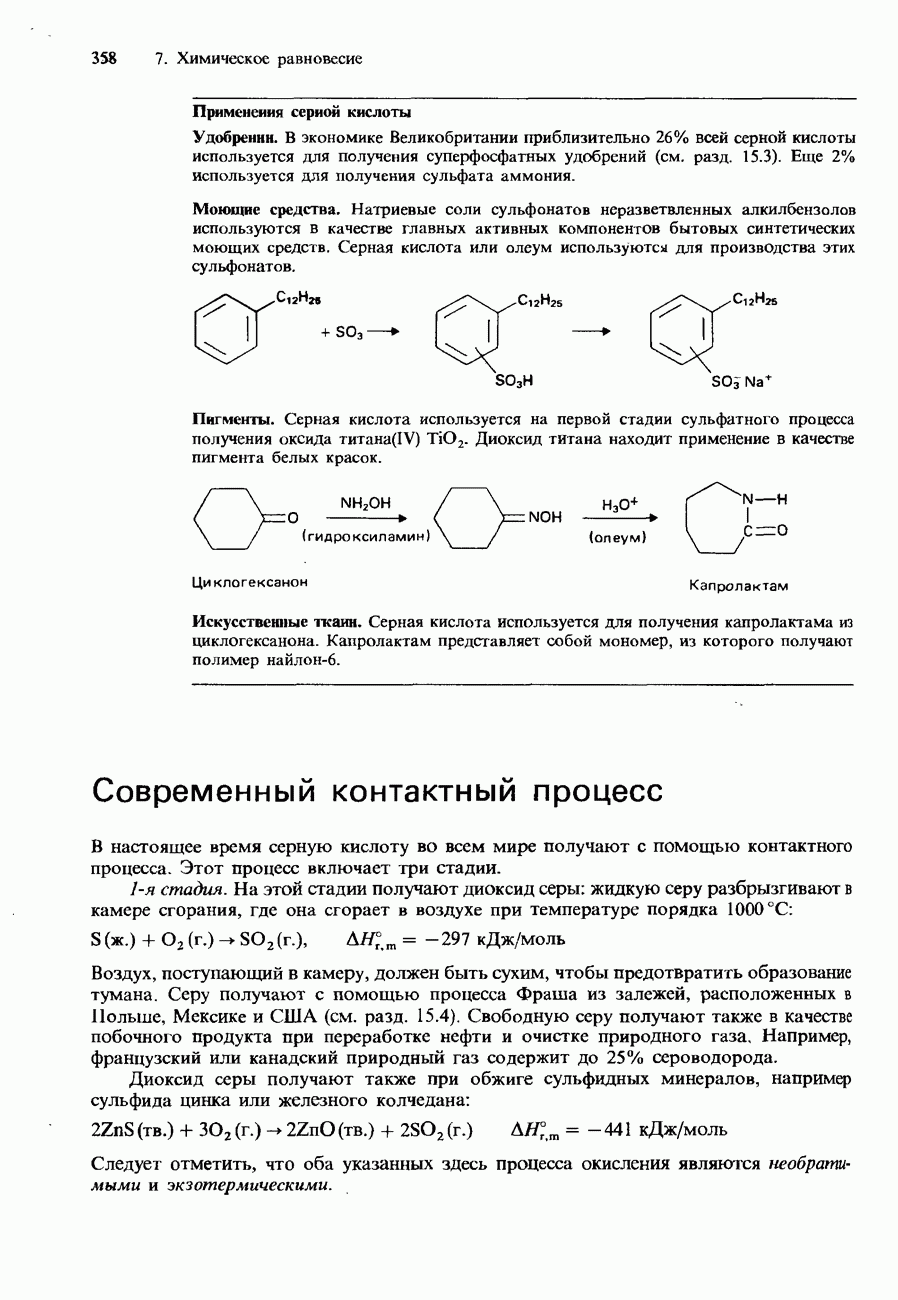
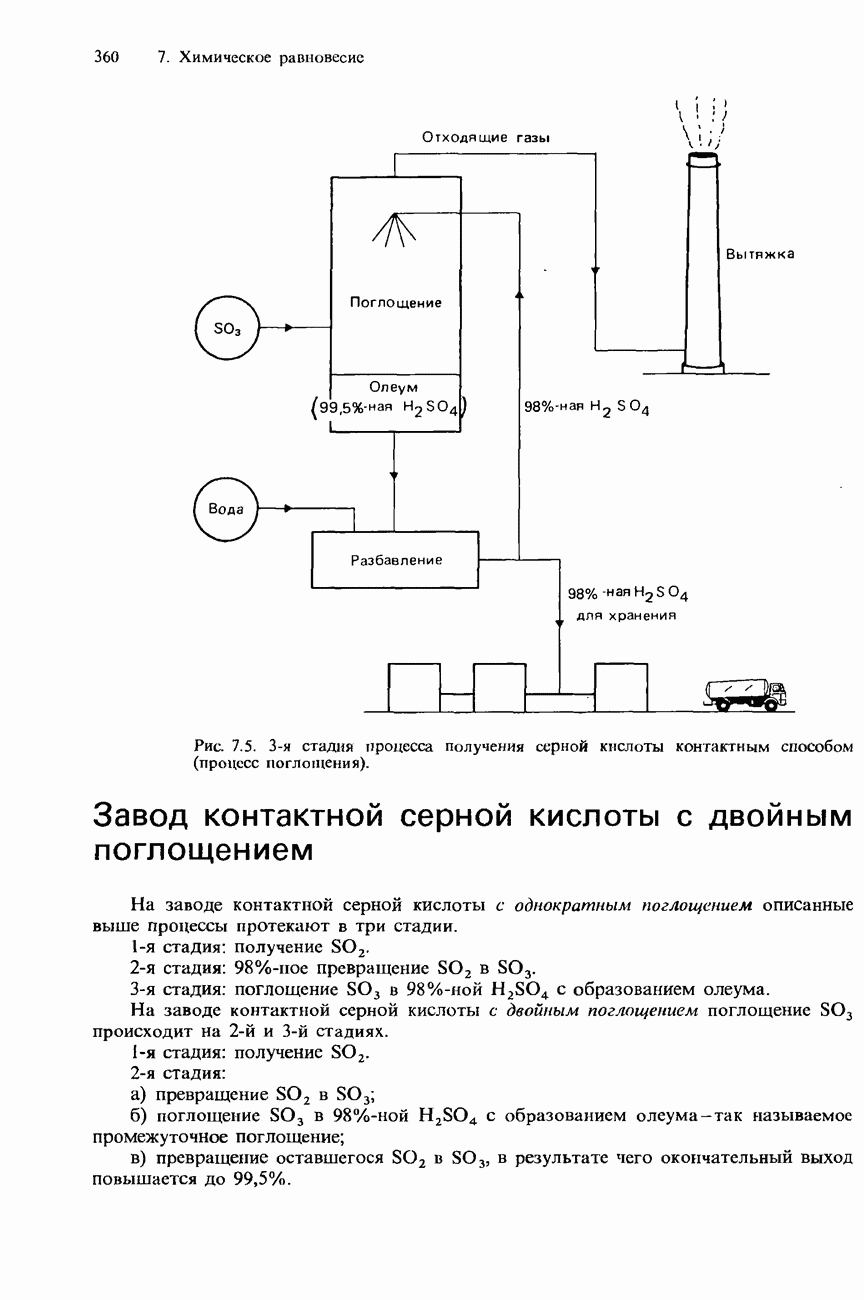
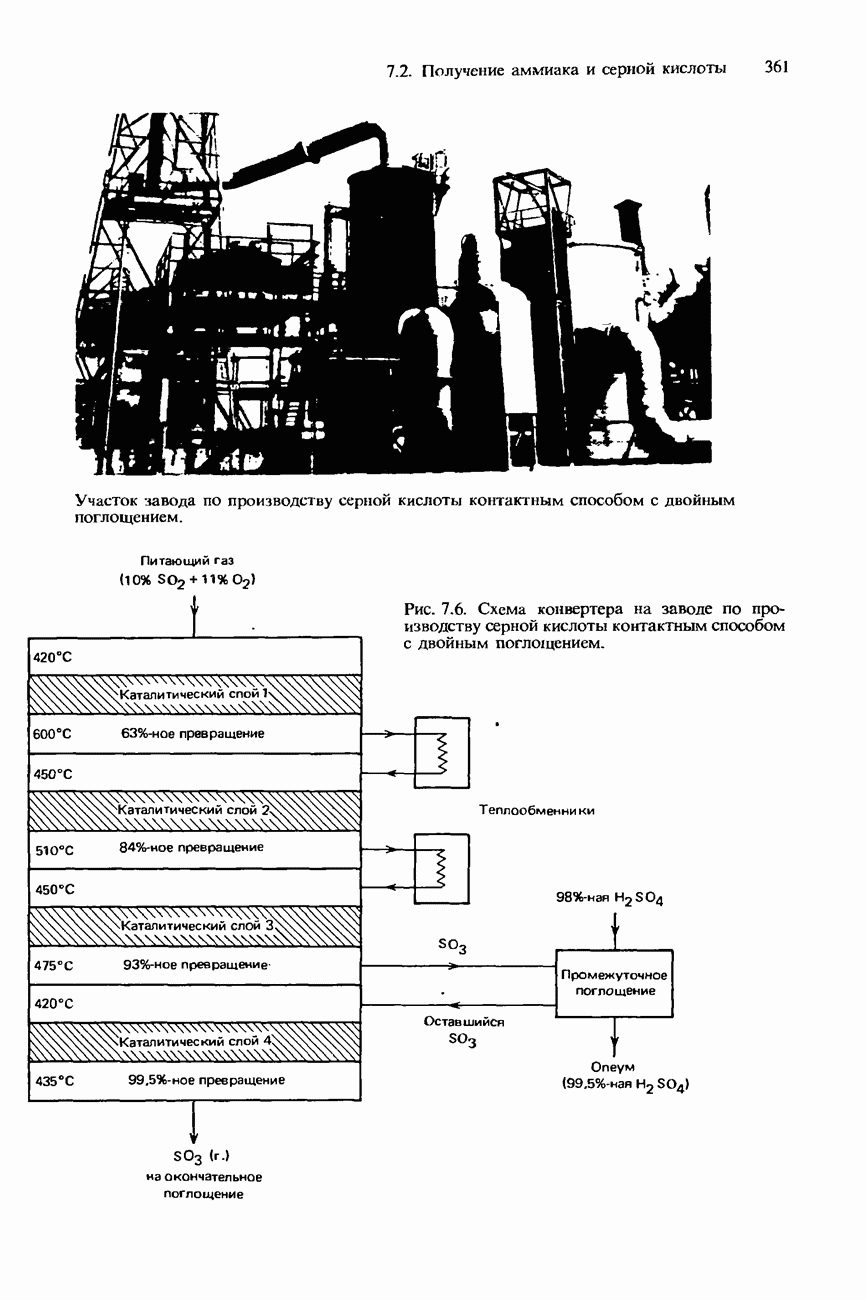
- ПРОМЫШЛЕННОЕ ПОЛУЧЕНИЕ СЕРНОЙ КИСЛОТЫ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 8. ИОНЫ
- 8.1. Кислоты и основания
- ЭЛЕКТРОЛИТЫ
- КИСЛОТЫ И ОСНОВАНИЯ
- КОНСТАНТЫ ДИССОЦИАЦИИ
- ВОДОРОДНЫЙ ПОКАЗАТЕЛЬ pH ШКАЛА ЕГО ЗНАЧЕНИЙ
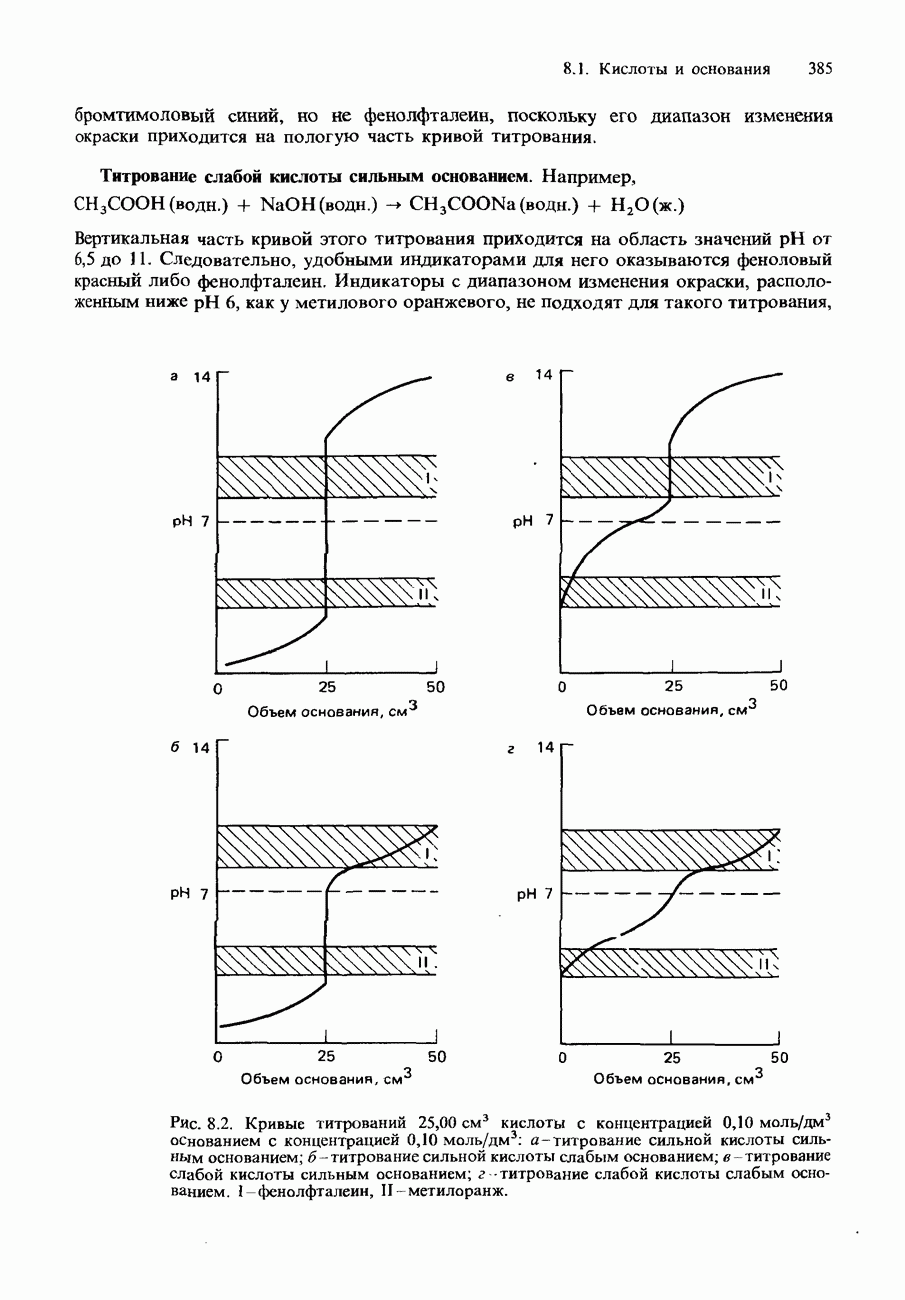
- КИСЛОТНО-ОСНОВНЫЕ ИНДИКАТОРЫ И ТИТРОВАНИЕ
- 8.2. Соли, растворимость и устойчивость
- БУФЕРНЫЕ РАСТВОРЫ
- РАСТВОРИМОСТЬ
- РАВНОВЕСИЯ С УЧАСТИЕМ КОМПЛЕКСНЫХ ИОНОВ
- ИОННЫЙ ОБМЕН
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 9. ХИМИЧЕСКАЯ КИНЕТИКА
- 9.1. Скорость химической реакции
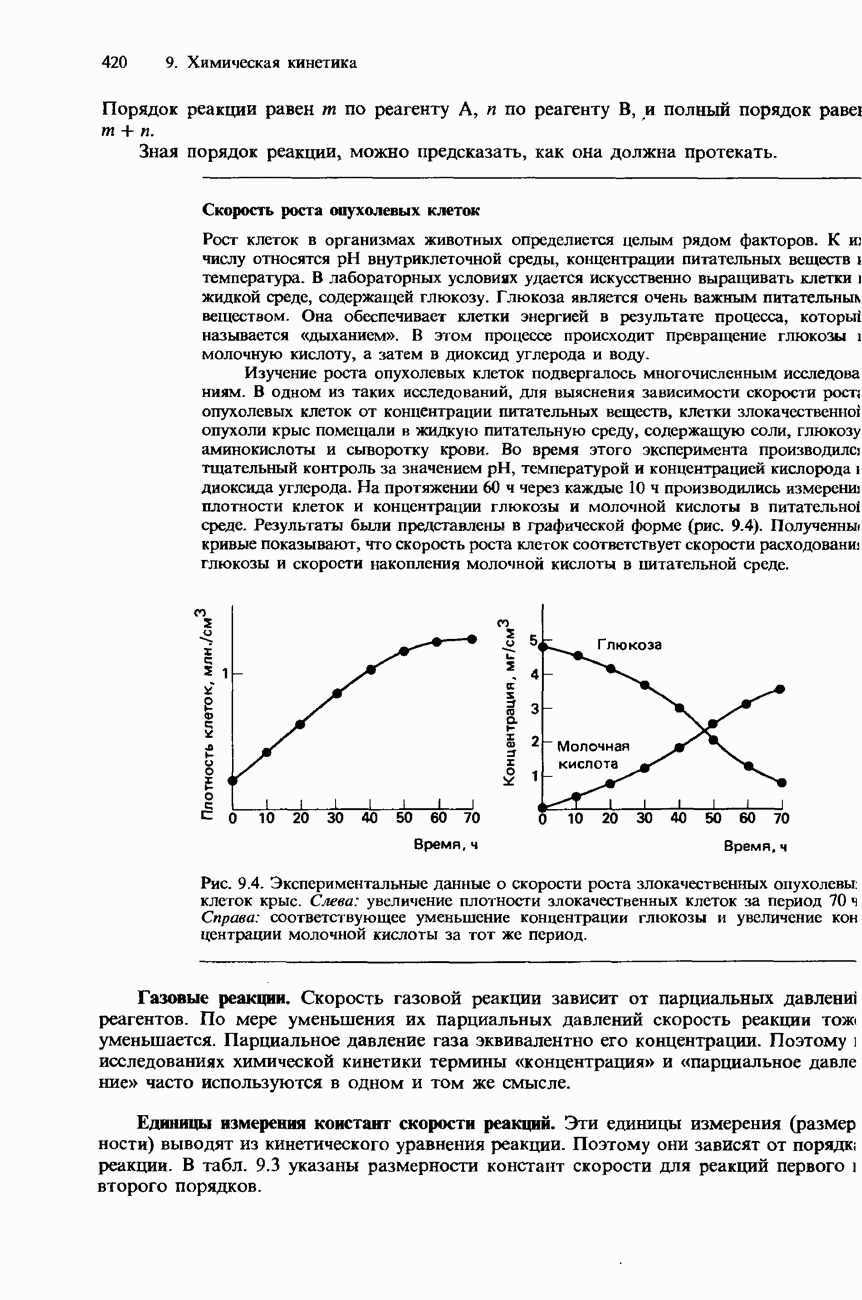
- МЕТОДЫ ИЗМЕРЕНИЯ СКОРОСТИ РЕАКЦИЙ
- СКОРОСТЬ РЕАКЦИИ И КОНЦЕНТРАЦИИ РЕАГЕНТОВ
- ЗАВИСИМОСТЬ КОНСТАНТЫ СКОРОСТИ ОТ ТЕМПЕРАТУРЫ УРАВНЕНИЕ АРРЕНИУСА
- 9.2. Механизмы реакций и катализ
- ТЕОРИЯ СТОЛКНОВЕНИЙ
- ТЕОРИЯ ПЕРЕХОДНОГО СОСТОЯНИЯ
- ЦЕПНЫЕ РЕАКЦИИ
- КАТАЛИЗ
- ТИПЫ КАТАЛИЗАТОРОВ
- ГОМОГЕННЫЙ КАТАЛИЗ
- ГЕТЕРОГЕННЫЙ КАТАЛИЗ
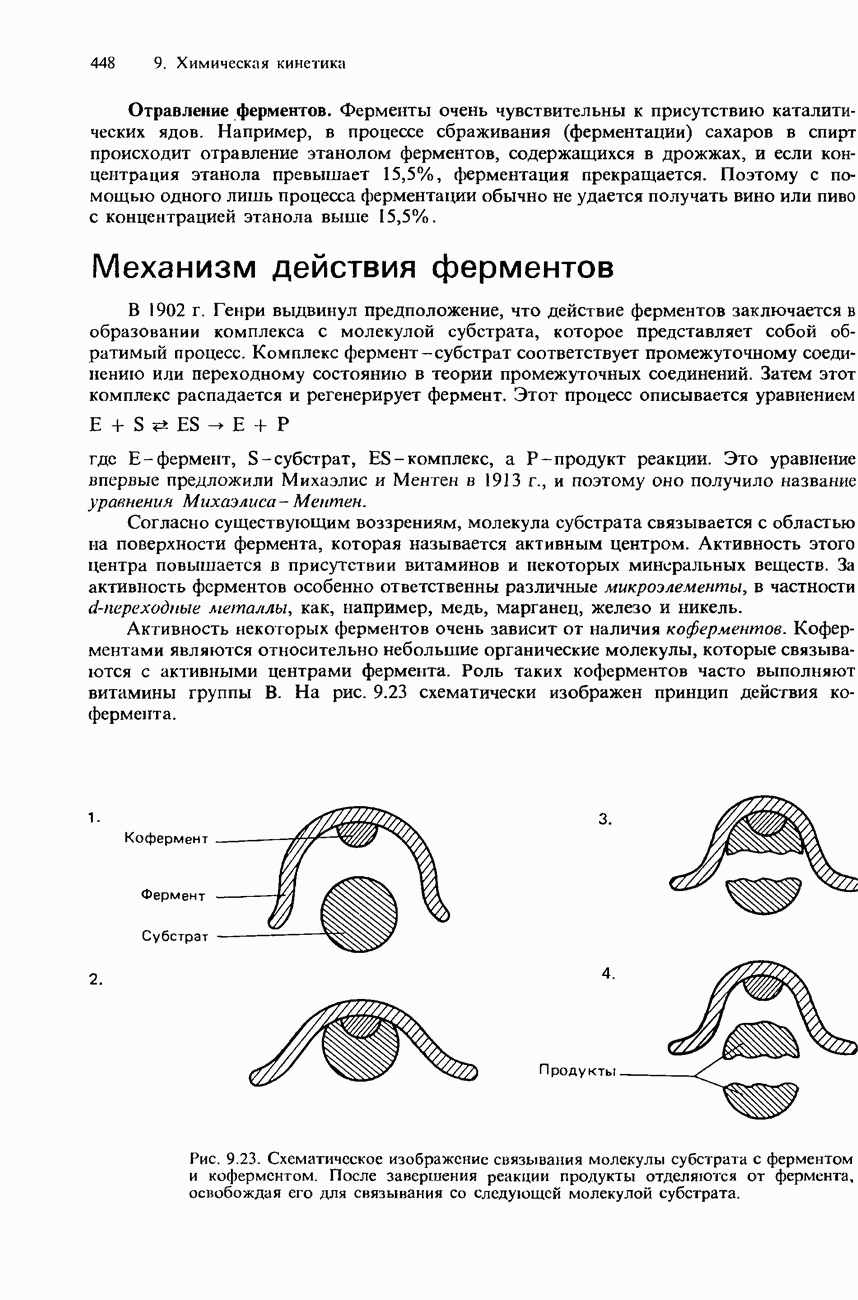
- ФЕРМЕНТАТИВНЫЙ КАТАЛИЗ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 10. ЭЛЕКТРОХИМИЯ
- 10.1. Электропроводность
- ПРОВОДНИКИ ЭЛЕКТРИЧЕСКОГО ТОКА И ЭЛЕКТРОПРОВОДНОСТЬ
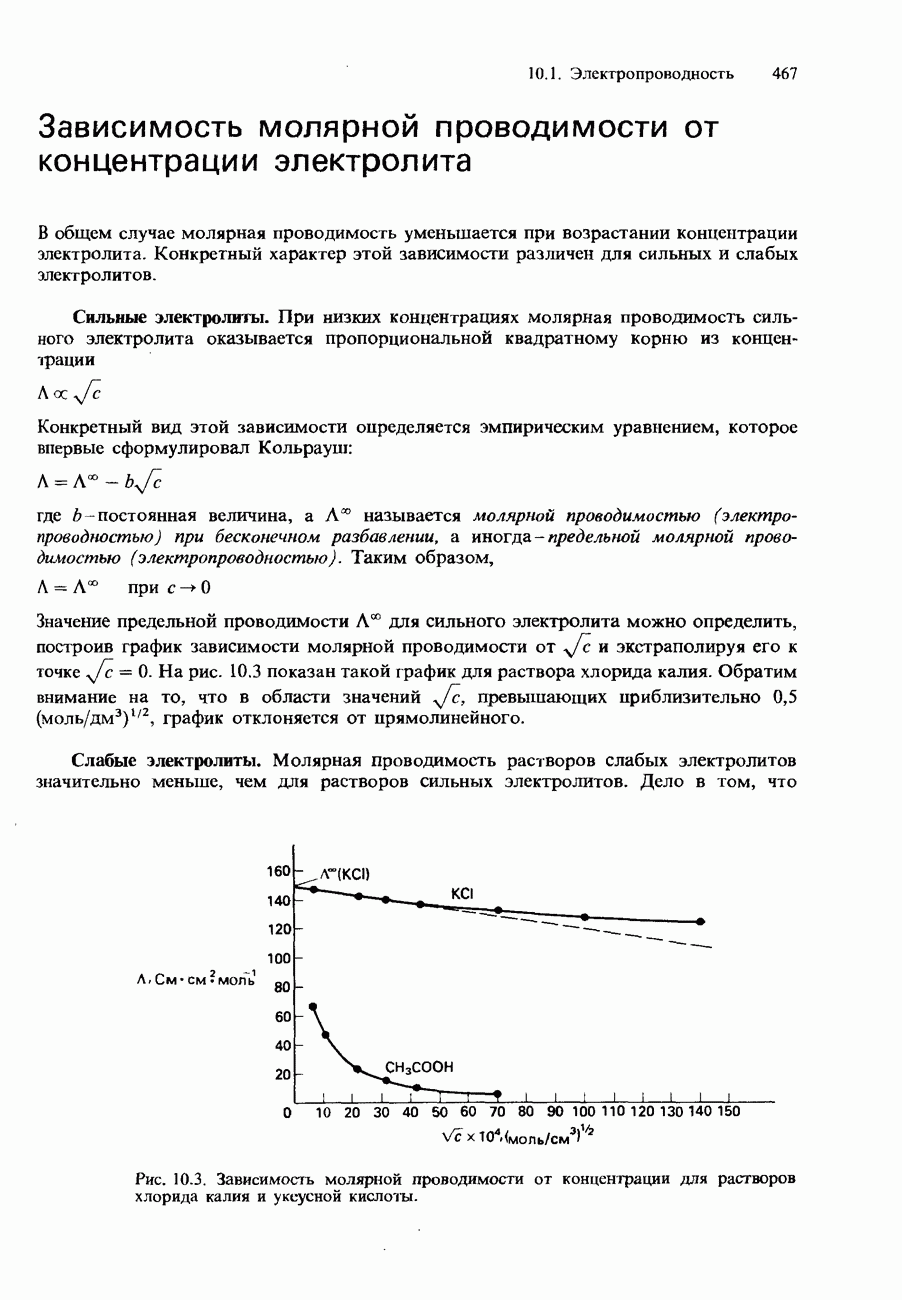
- МОЛЯРНАЯ ПРОВОДИМОСТЬ
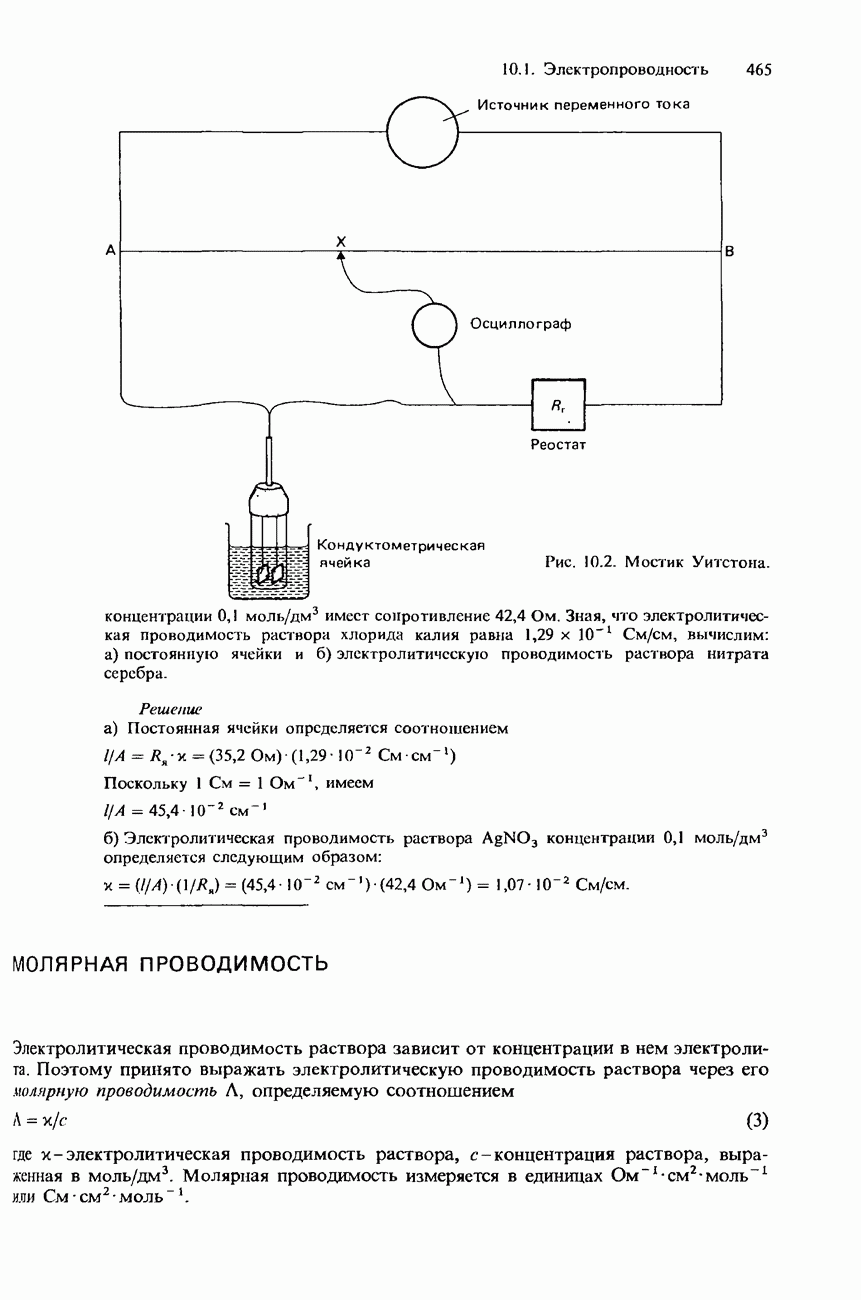
- КОНДУКТОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- 10.2. Окислительно-восстановительные процессы
- ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫЕ РЕАКЦИИ
- ОПРЕДЕЛЕНИЕ СТЕХИОМЕТРИЧЕСКИХ КОЭФФИЦИЕНТОВ
- СТЕПЕНЬ ОКИСЛЕНИЯ
- ОКИСЛИТЕЛИ
- ВОССТАНОВИТЕЛИ
- ОКИСЛИТЕЛИ И ВОССТАНОВИТЕЛИ
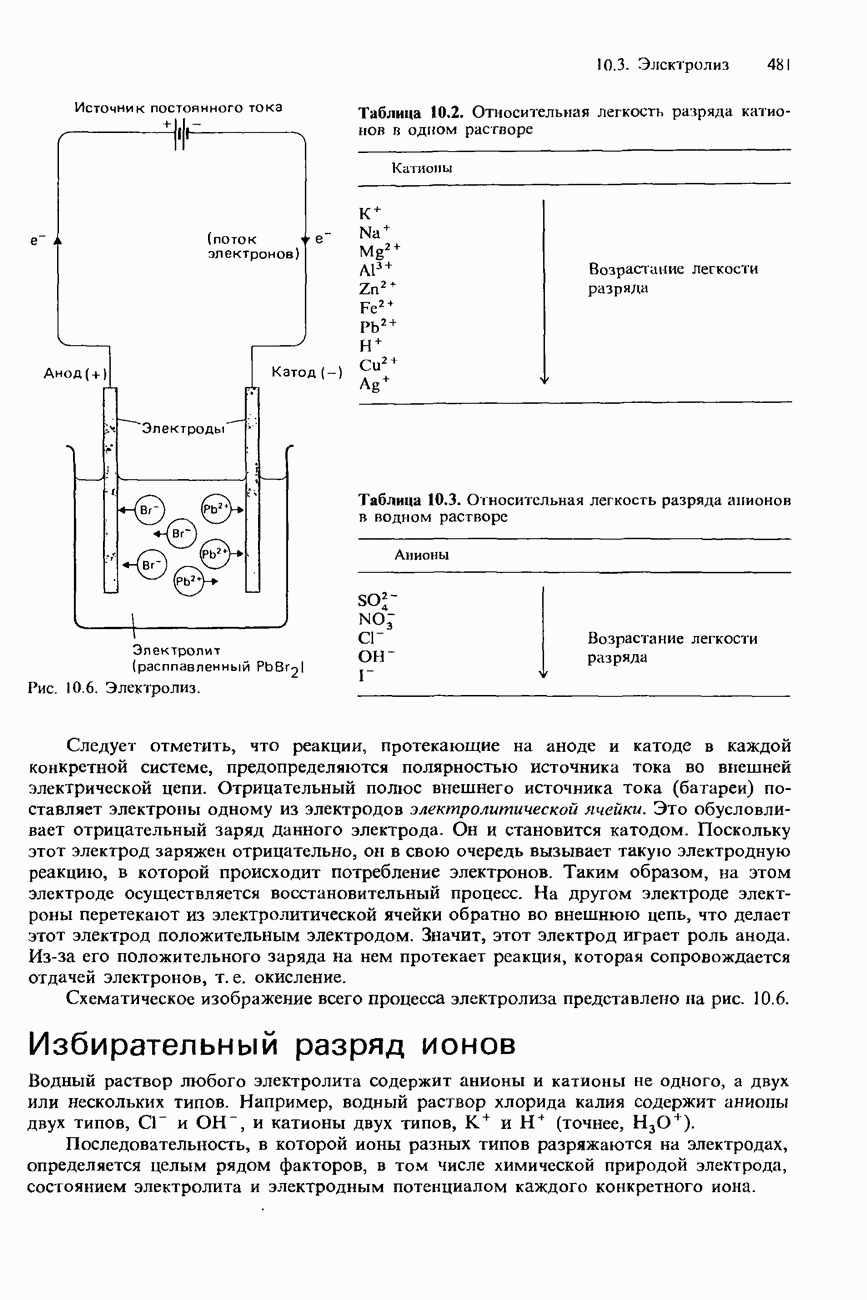
- 10.3. Электролиз
- ЗАКОНЫ ЭЛЕКТРОЛИЗА ФАРАДЕЯ
- ПРОМЫШЛЕННЫЕ ПРИМЕНЕНИЯ ЭЛЕКТРОЛИЗА
- 10.4. Химические источники тока
- СХЕМЫ ХИМИЧЕСКИХ ИСТОЧНИКОВ ТОКА
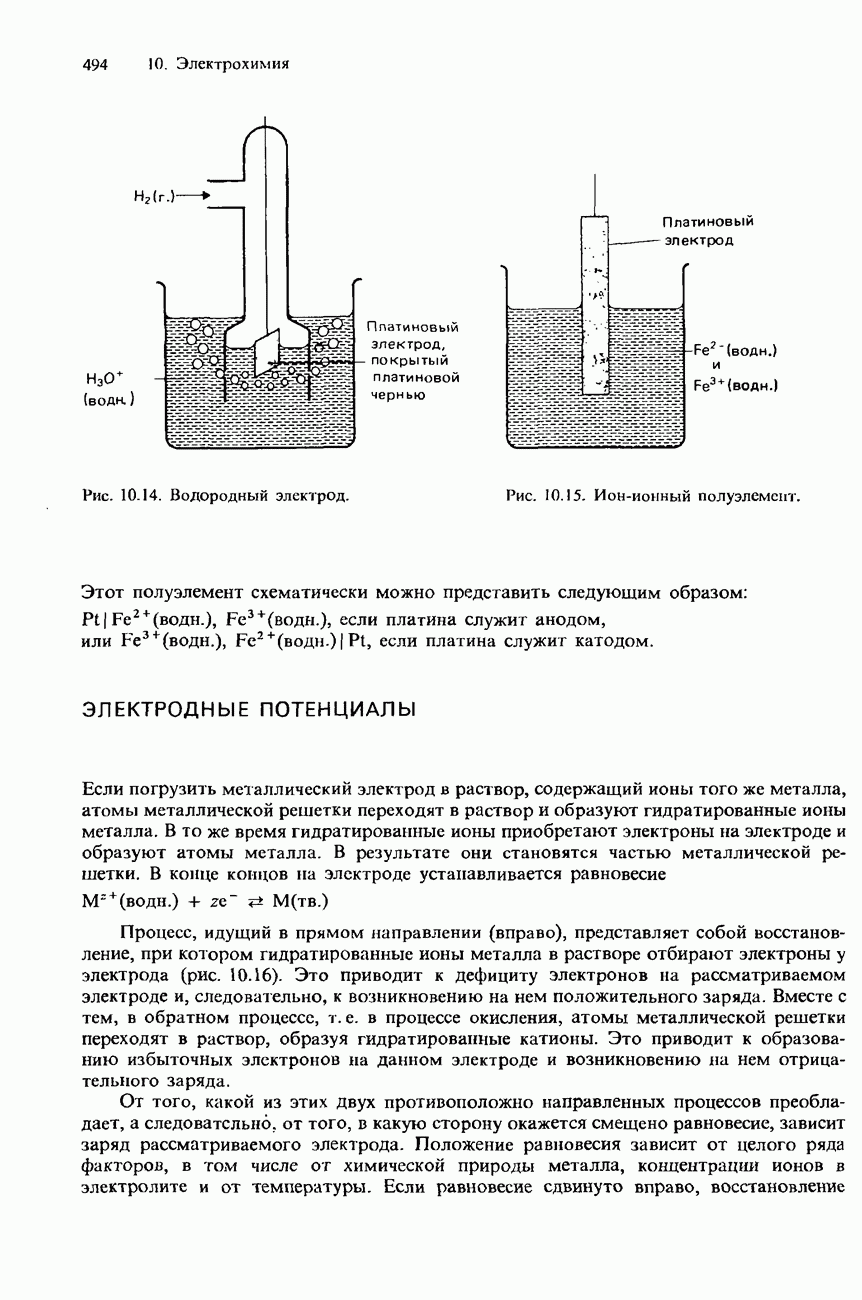
- ТИПЫ ПОЛУЭЛЕМЕНТОВ
- ЭЛЕКТРОДНЫЕ ПОТЕНЦИАЛЫ
- ЭЛЕКТРОДВИЖУЩАЯ СИЛА ХИМИЧЕСКИХ ИСТОЧНИКОВ ТОКА
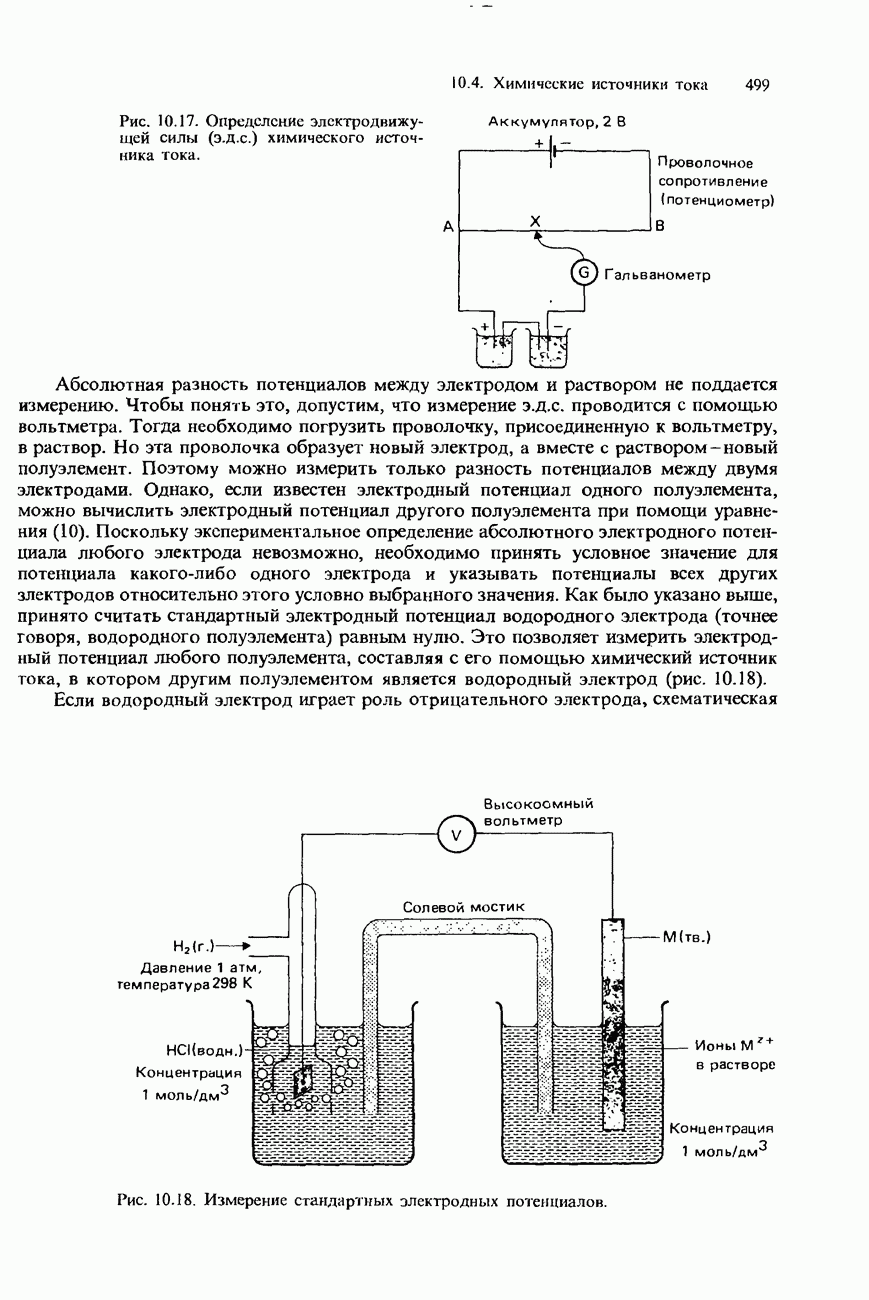
- ИЗМЕРЕНИЕ Э.Д.С. ХИМИЧЕСКИХ ИСТОЧНИКОВ ТОКА И ЭЛЕКТРОДНЫХ ПОТЕНЦИАЛОВ
- 10.5. Применения электрохимии
- ВЫЧИСЛЕНИЕ КОНСТАНТ РАВНОВЕСИЯ ДЛЯ ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫХ РЕАКЦИЙ
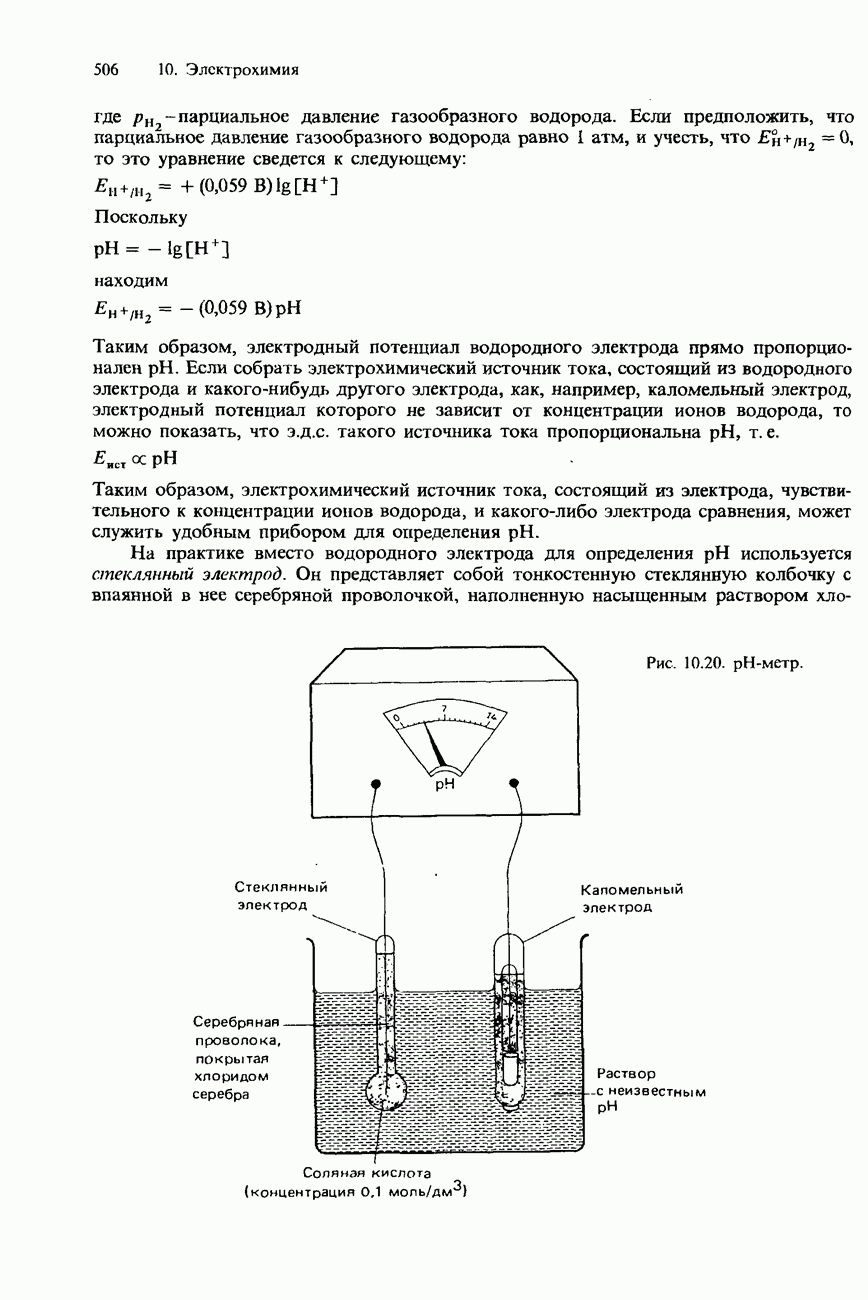
- ОПРЕДЕЛЕНИЕ pH РАСТВОРА
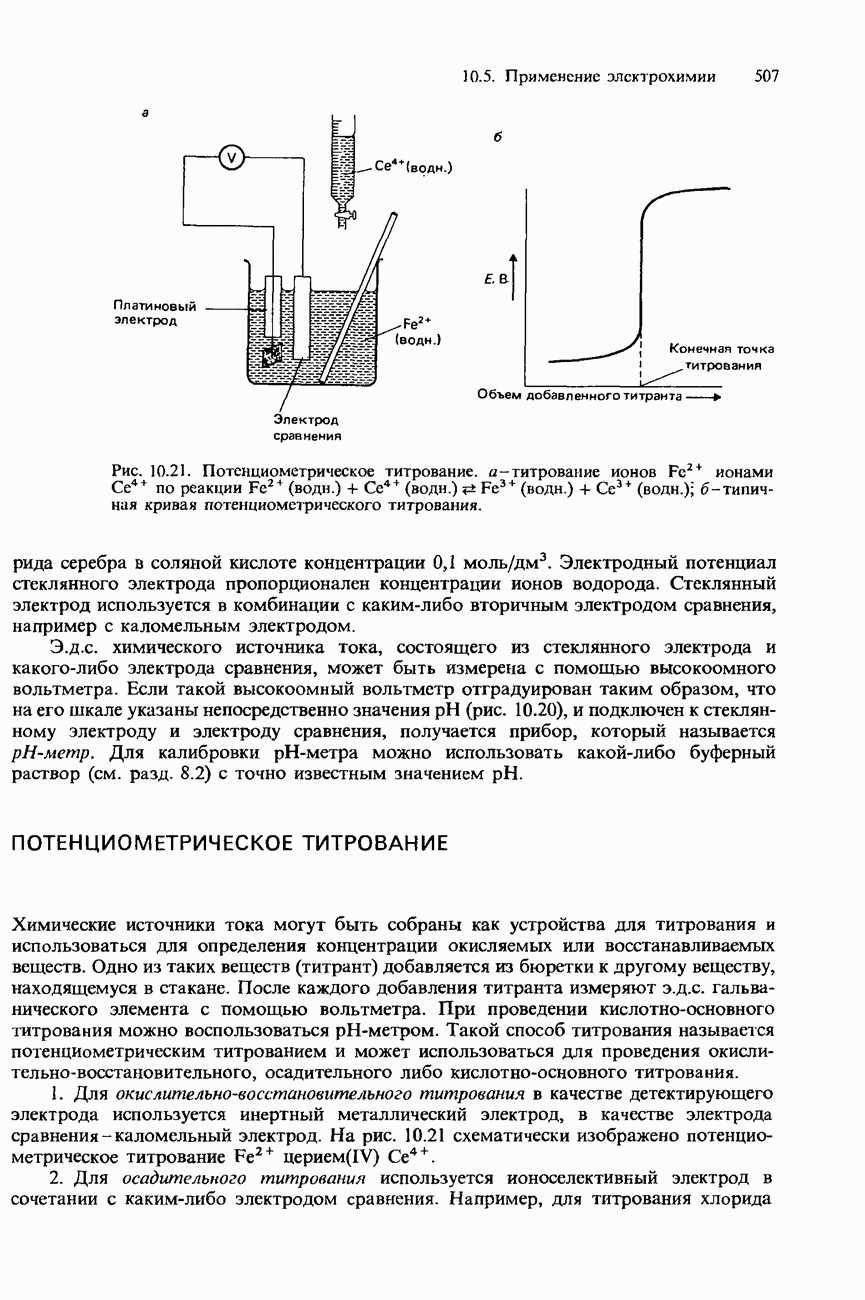
- ПОТЕНЦИОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- ОСУЩЕСТВИМОСТЬ ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫХ РЕАКЦИЙ
- ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ AG
- БАТАРЕИ И ПРОМЫШЛЕННЫЕ ИСТОЧНИКИ ТОКА
- МЕТАЛЛУРГИЯ
- КОРРОЗИЯ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ