| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
Кинетическая теория газов - это математическая модель идеального газа, которая позволяет дать объяснение описанным выше газовым законам.
Исходные предположения.
Кинетическая теория газов основывается на следующих упрощающих предположениях:1) газ состоит из частиц пренебрежимо малого объема,
2) эти частицы находятся в непрерывном беспорядочном движении,
3) частицы газа не притягиваются друг к другу,
4) частицы газа являются идеально упругими, поэтому их столкновения не сопровождаются потерей кинетической энергии,
5) средняя кинетическая энергия частиц газа пропорциональна его абсолютной температуре.
Основное уравнение кинетической теории.
Сформулированные выше предположения о свойствах идеального газа позволяют вывести следующее уравнение, которое служит основой кинетической теории газов:
где  - число частиц газа,
- число частиц газа,  масса частицы, а
масса частицы, а  - средний квадрат скорости частицы, т.е. среднее значение квадрата ее скорости
- средний квадрат скорости частицы, т.е. среднее значение квадрата ее скорости  .
.
Обоснование газовых законов.
Основное уравнение (12) кинетической теории позволяет обосновать описанные выше газовые законы, а именно: уравнение состояния идеального газа, закон Бойля - Мариотта, закон Гей-Люссака (Шарля), закон Авогадро, закон парциальных давлений Дальтона и законы диффузии и эффузии Грэхема. Ограничимся всего двумя примерами.Обоснование уравнения состояния идеального газа. Пятое предположение кинетической теории можно сформулировать в математическом виде следующим образом:

где  - средняя кинетическая энергия частицы газа,
- средняя кинетическая энергия частицы газа,  средняя кинетическая энергия N частиц.
средняя кинетическая энергия N частиц.
Сравнивая уравнения (12) и (13), находим, что

и, следовательно,

Как мы уже знаем, из уравнения (14) можно вывести уравнение состояния идеального газа.
Обоснование закона Бойля-Мариотта. Для определенной массы газа число N постоянно. При заданной температуре газа величина  тоже постоянна. Таким образом, из уравнения (12) следует, что
тоже постоянна. Таким образом, из уравнения (12) следует, что

Как мы уже знаем, в такой форме может быть сформулирован закон Бойля-Мариотта.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ ПЕРЕВОДЧИКА
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ
- 1. СТРОЕНИЕ АТОМА
- 1.1. Субатомные частицы
- Модели атома
- Новые элементарные частицы
- МАССА АТОМА
- МАСС-СПЕКТРОМЕТРИЯ
- 1.2 Электронное строение атомов
- Связь между спектральными линиями и электронами (открытие Бора)
- Применение возбуждения электронов на практике
- Атомный спектр испускания водорода
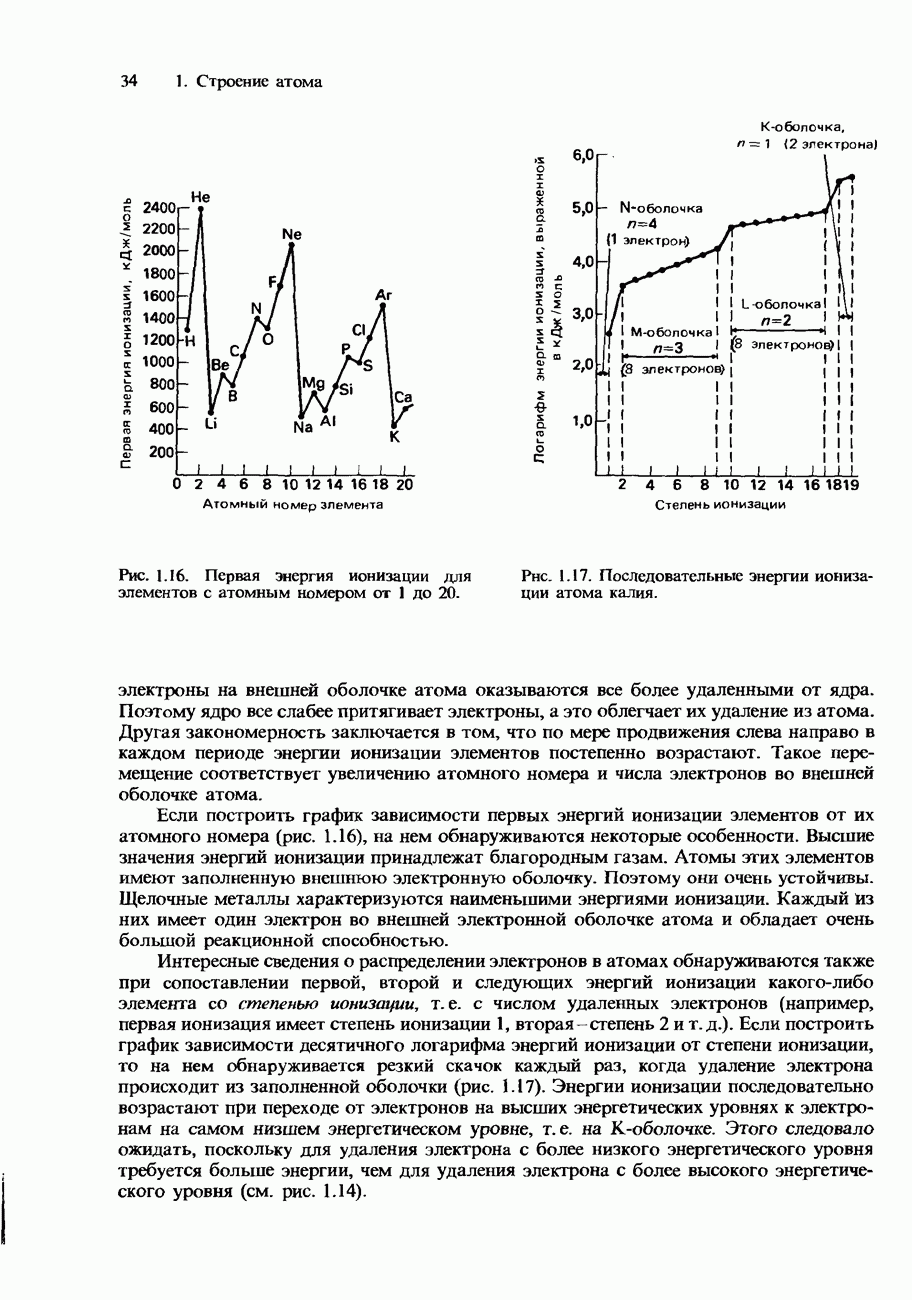
- ЭНЕРГИИ ИОНИЗАЦИИ
- Рассмотрение энергий ионизации в рамках модели атома, предложенной Бором
- ВОЛНОВАЯ ПРИРОДА ЭЛЕКТРОНА
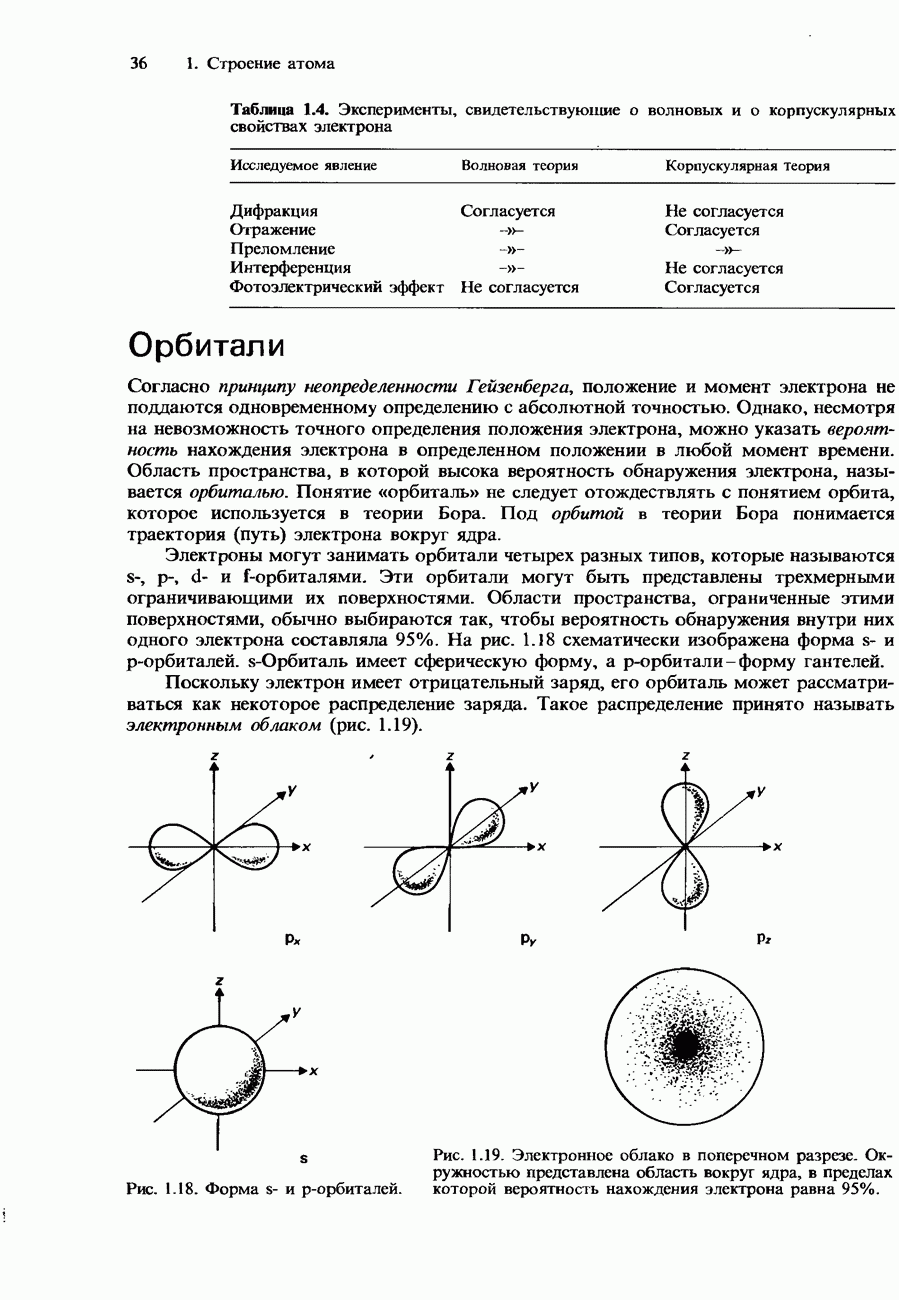
- Орбитали
- КВАНТОВЫЕ ЧИСЛА
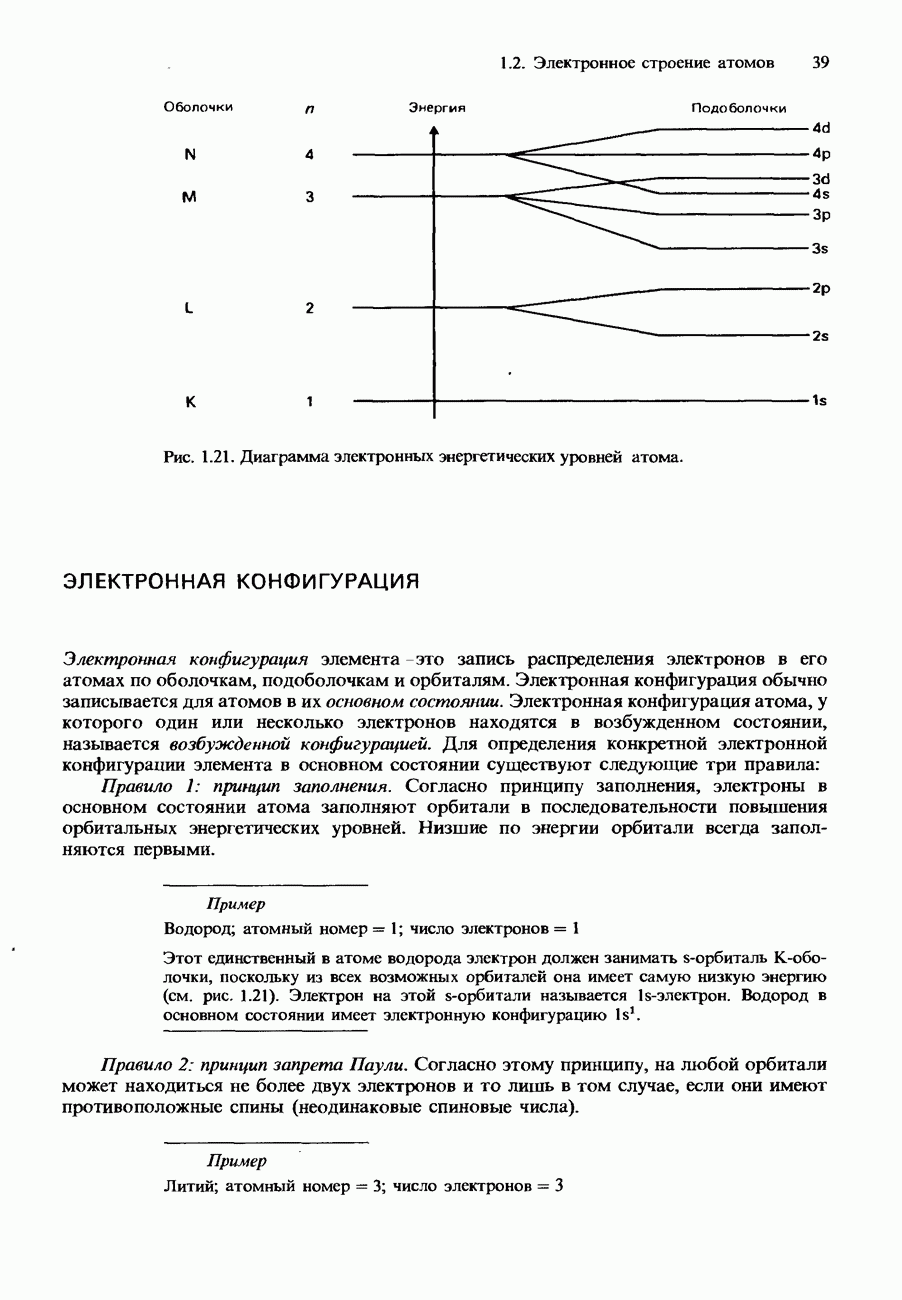
- ЭЛЕКТРОННАЯ КОНФИГУРАЦИЯ
- 1.3 Радиоактивность
- ИОНИЗИРУЮЩЕЕ ИЗЛУЧЕНИЕ
- Обнаружение и измерение радиоактивности
- УСТОЙЧИВЫЕ И НЕУСТОЙЧИВЫЕ ИЗОТОПЫ
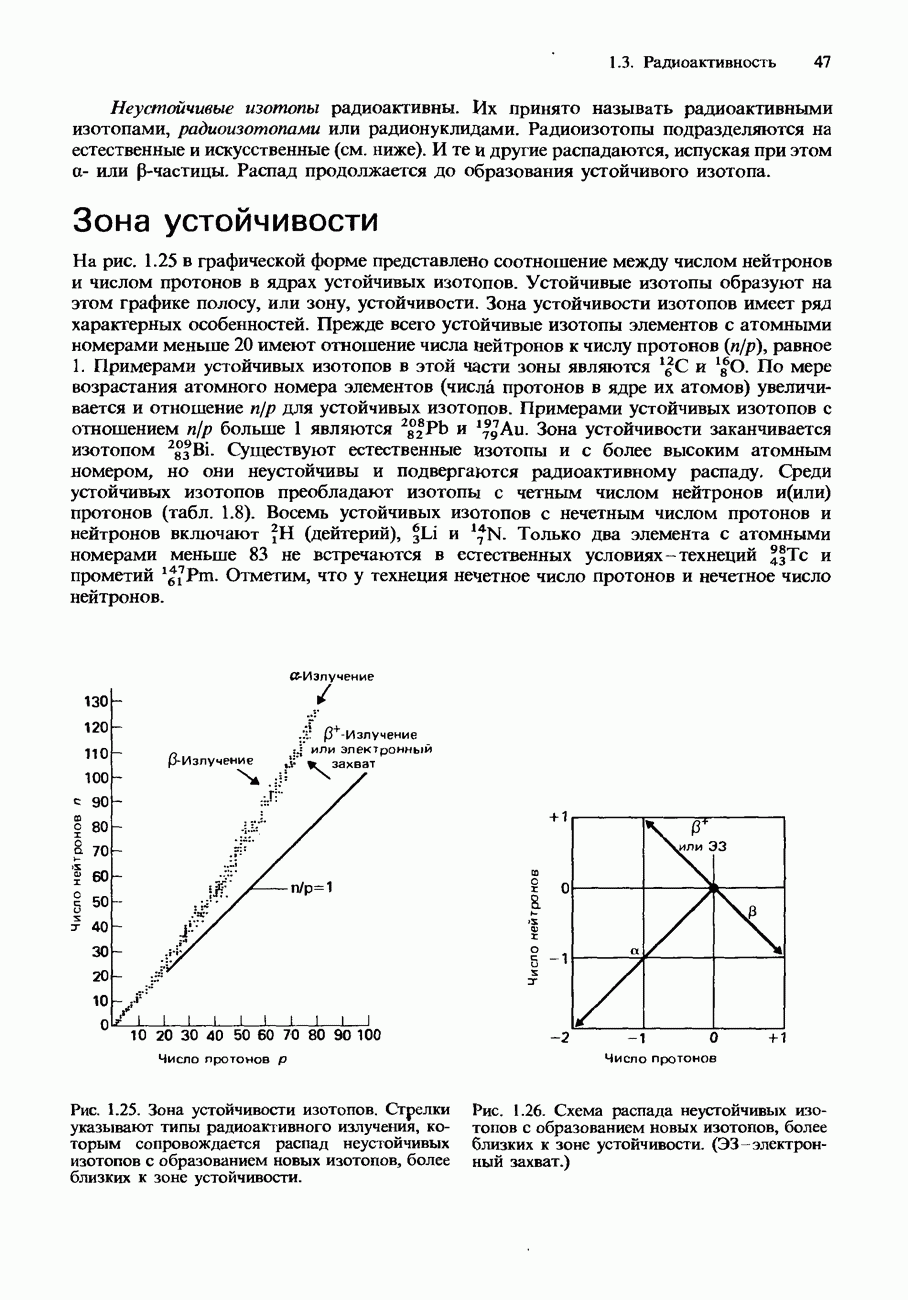
- Зона устойчивости
- Период полураспада
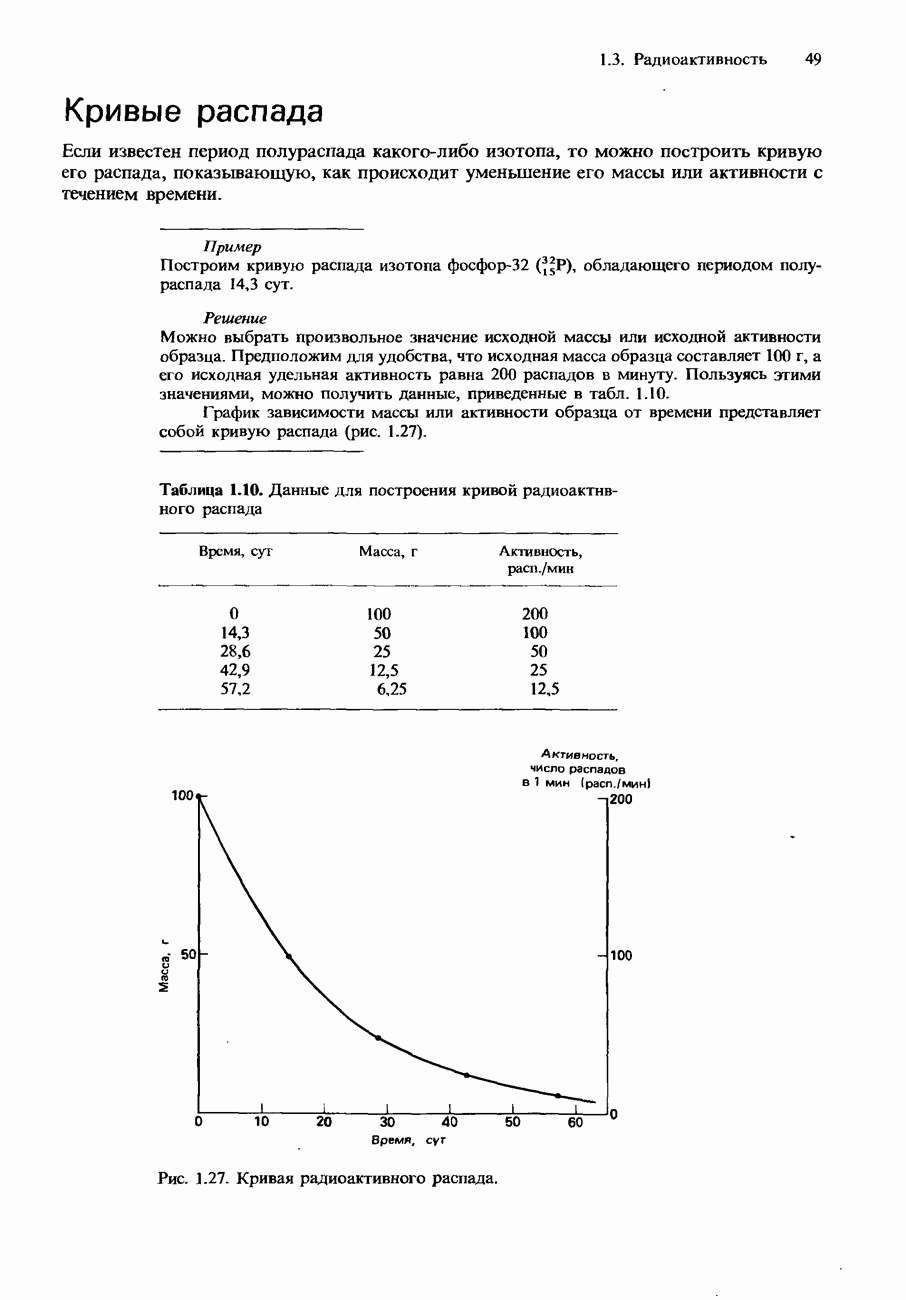
- Кривые распада
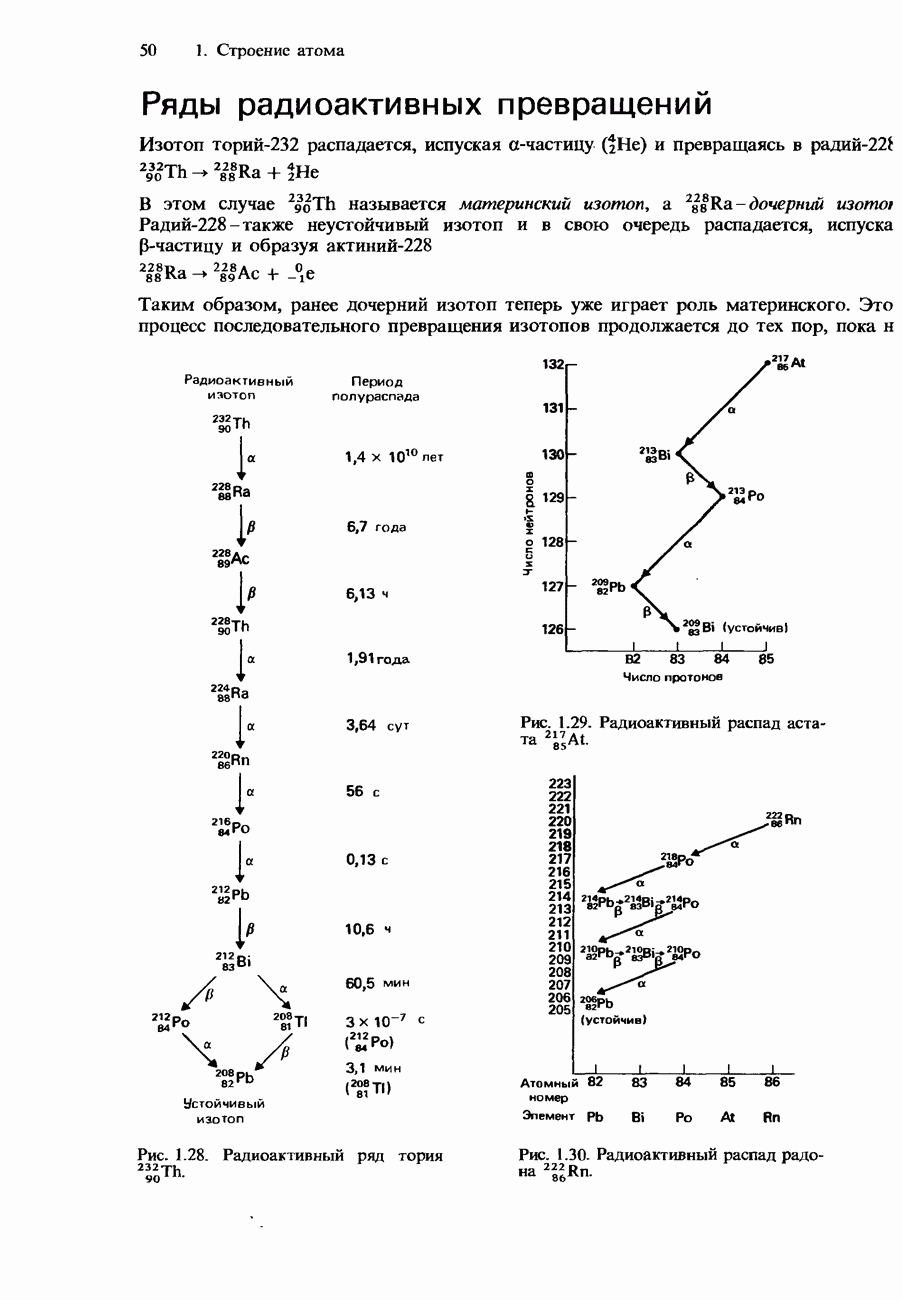
- Ряды радиоактивных превращений
- Естественные радиоизотопы
- ИСКУССТВЕННЫЕ ЯДЕРНЫЕ ПРЕВРАЩЕНИЯ
- Ускорители элементарных частиц
- Трансурановые элементы
- ПРИМЕНЕНИЯ ИЗОТОПОВ
- ЯДЕРНОЕ ДЕЛЕНИЕ И ЯДЕРНЫЙ СИНТЕЗ
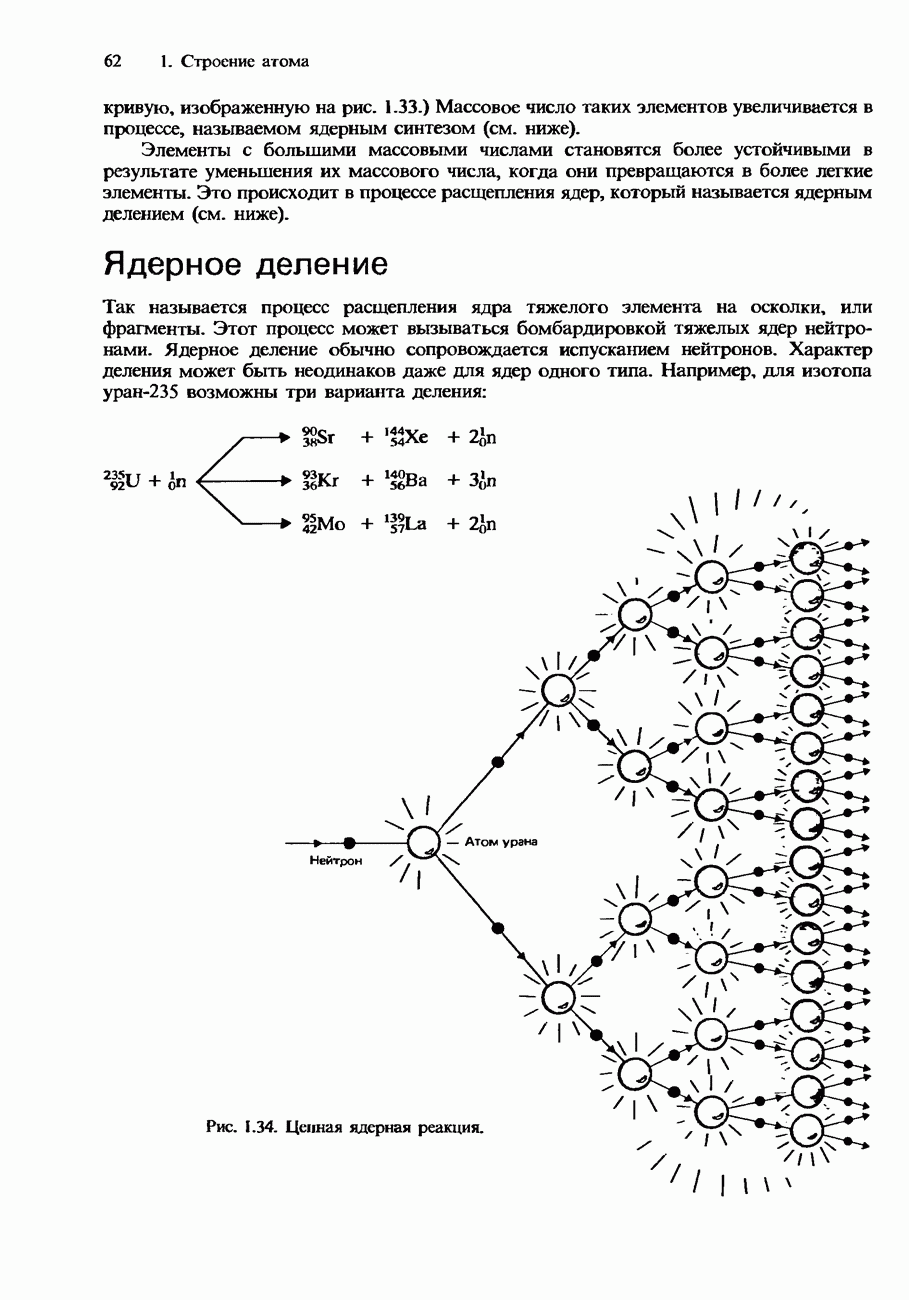
- Ядерное деление
- Ядерный синтез
- Ядерный синтез в звездах
- ЯДЕРНАЯ ЭНЕРГИЯ
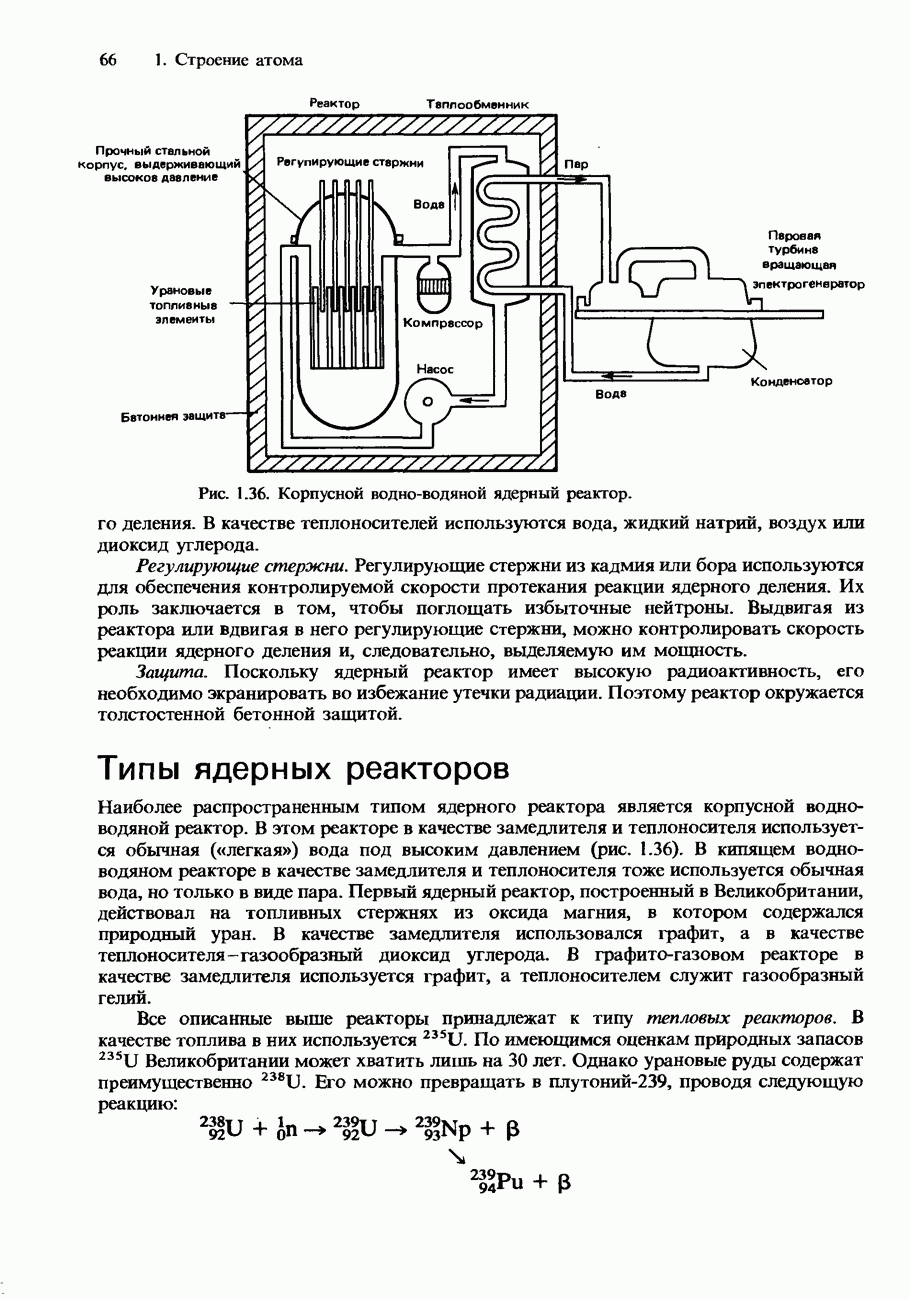
- Типы ядерных реакторов
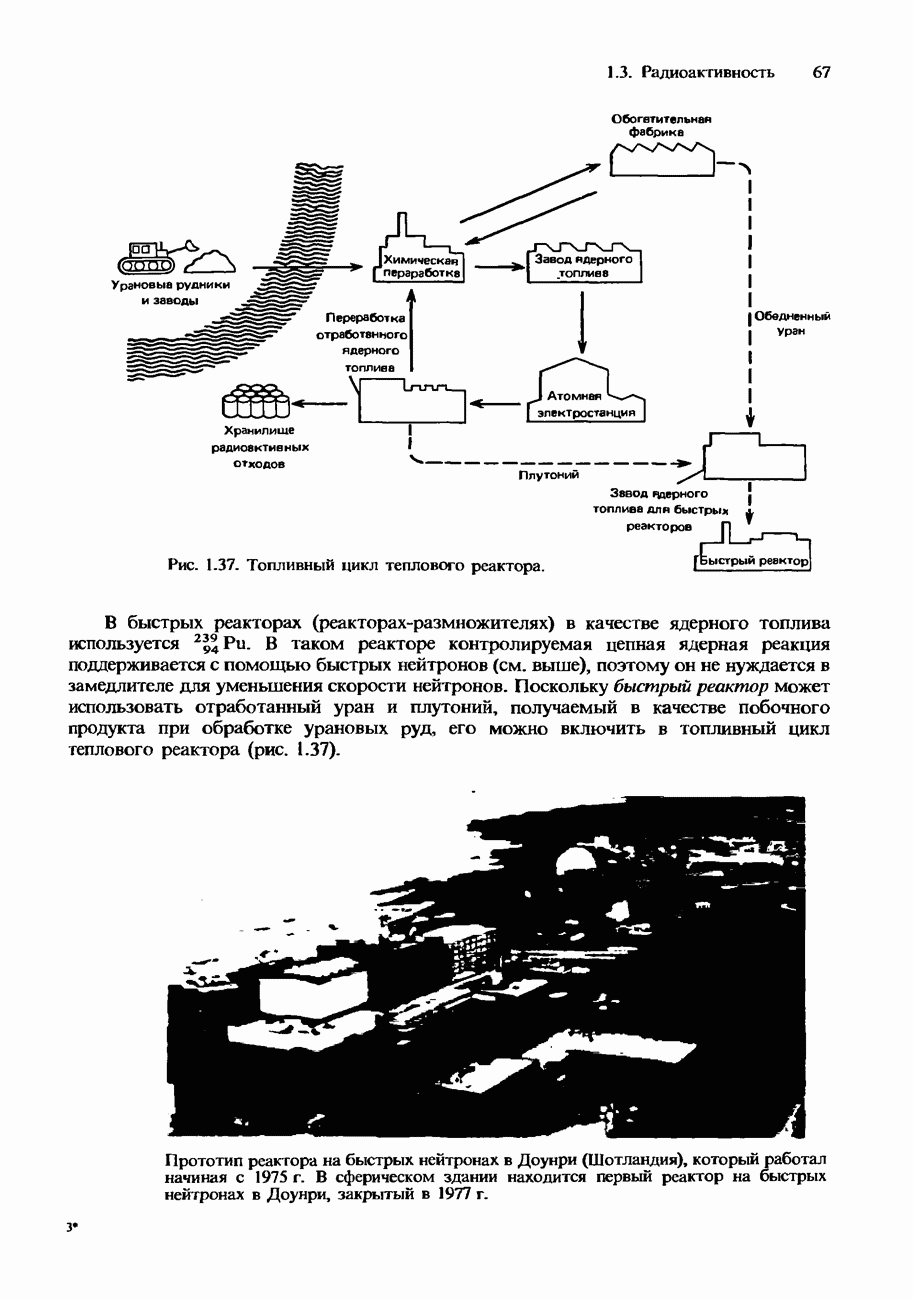
- Радиоактивные ядерные отходы и их переработка
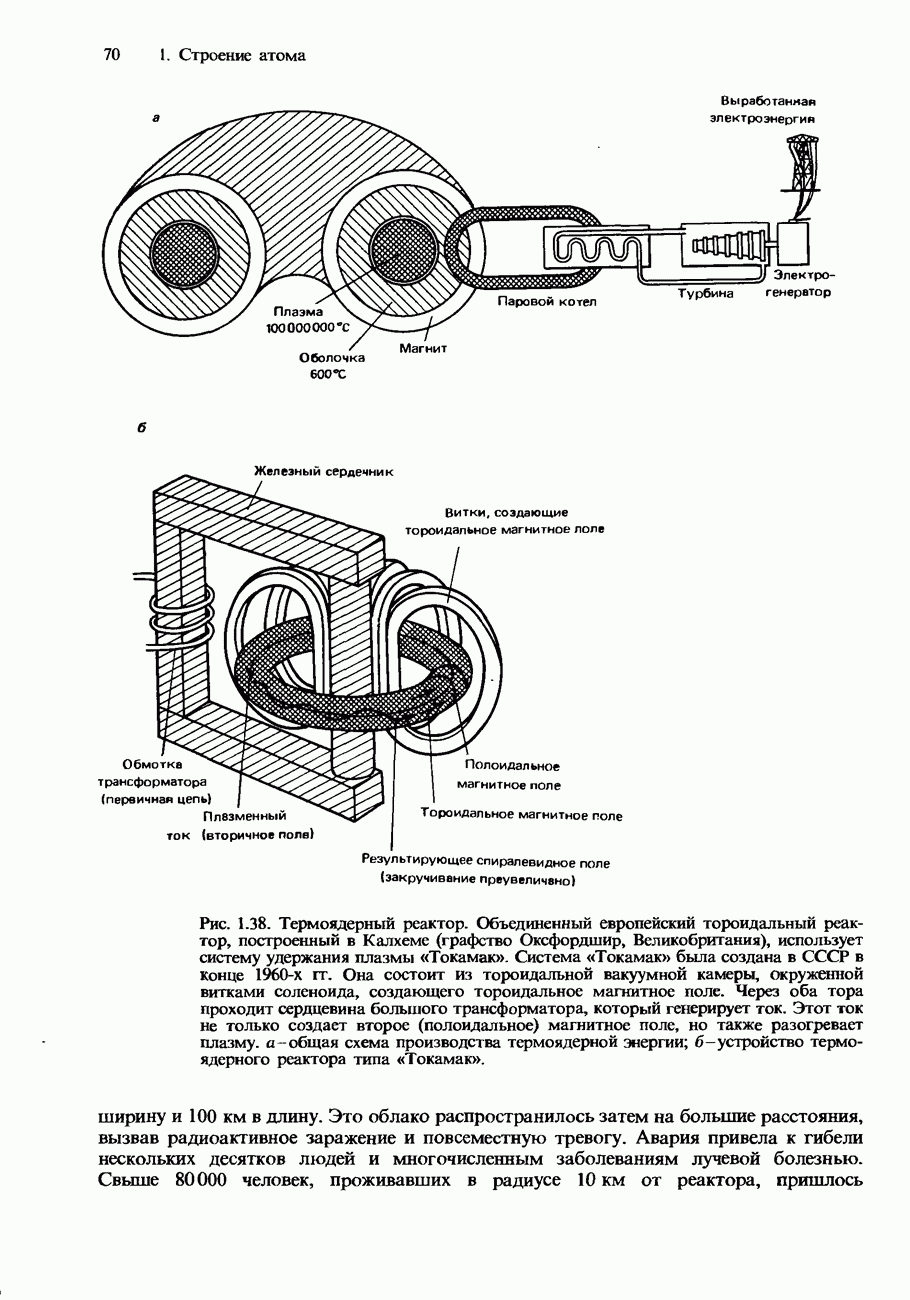
- Термоядерные реакторы
- Аргументы против использования ядерной энергии
- ЯДЕРНОЕ ОРУЖИЕ
- Ядерное разоружение
- ИСТОЧНИКИ РАДИАЦИИ И ЕЕ ВОЗДЕЙСТВИЕ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 2. ХИМИЧЕСКАЯ СВЯЗЬ
- 2.1. Природа химической связи
- ИОННАЯ СВЯЗЬ
- Устойчивость ионных соединений
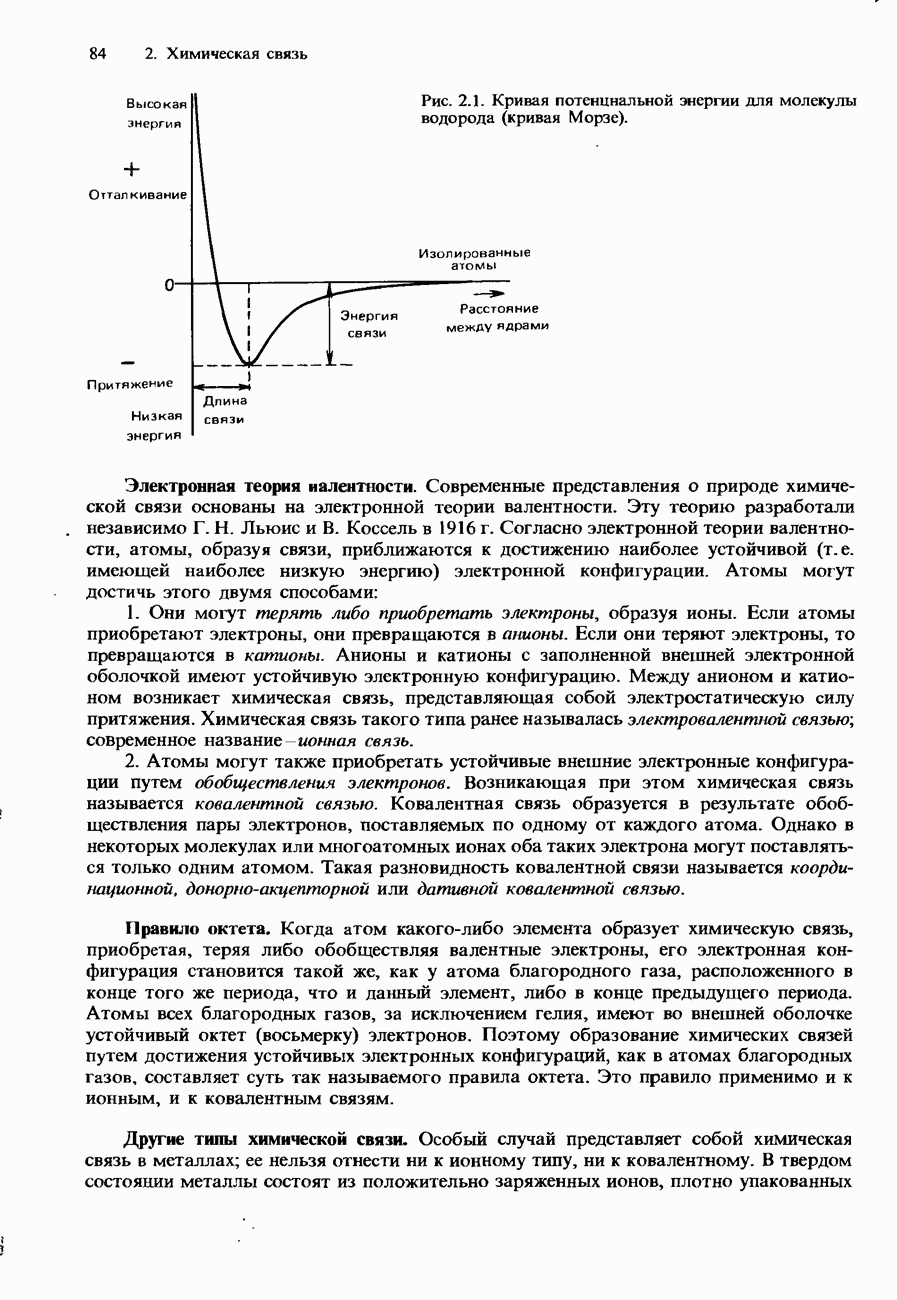
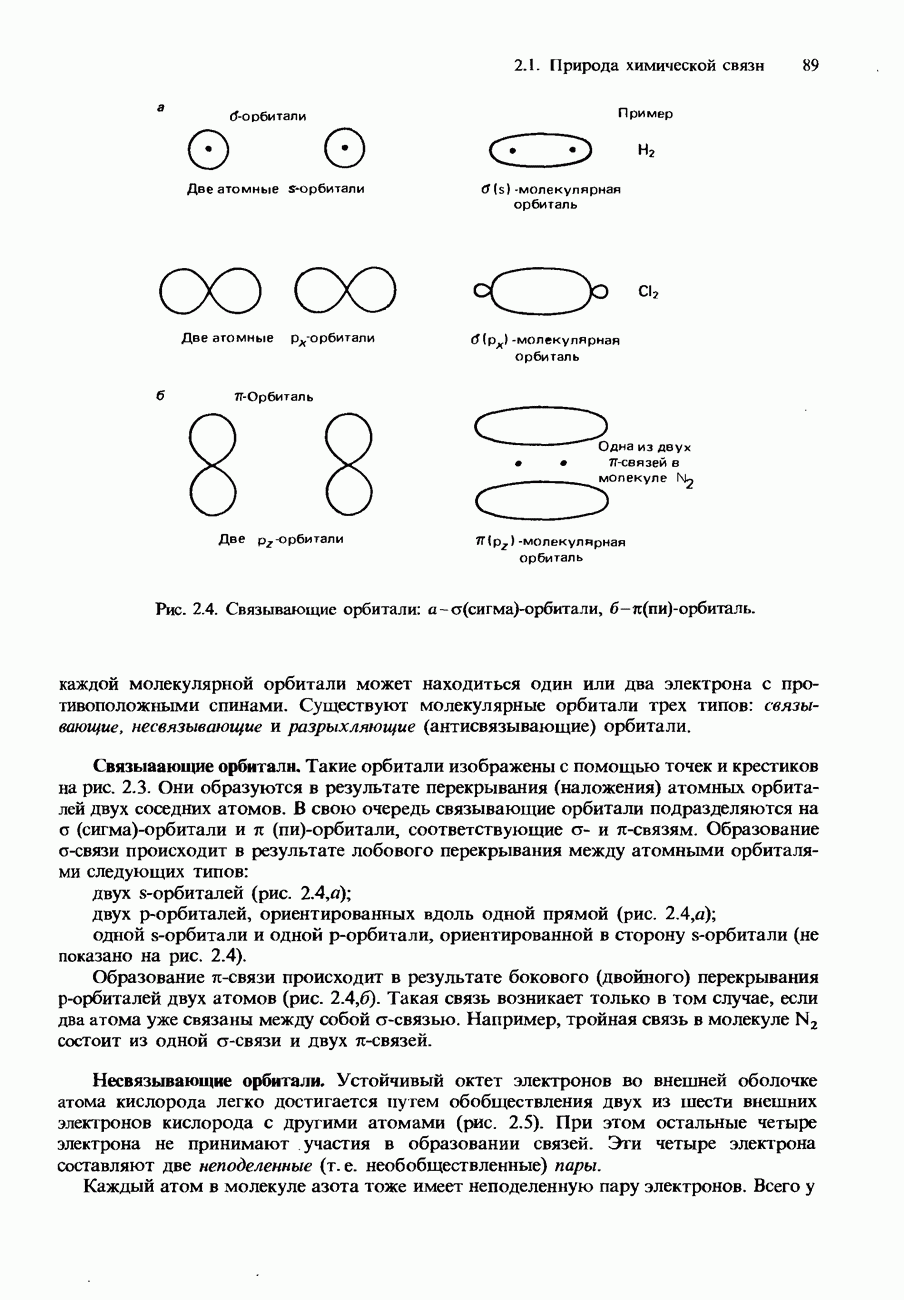
- КОВАЛЕНТНАЯ СВЯЗЬ
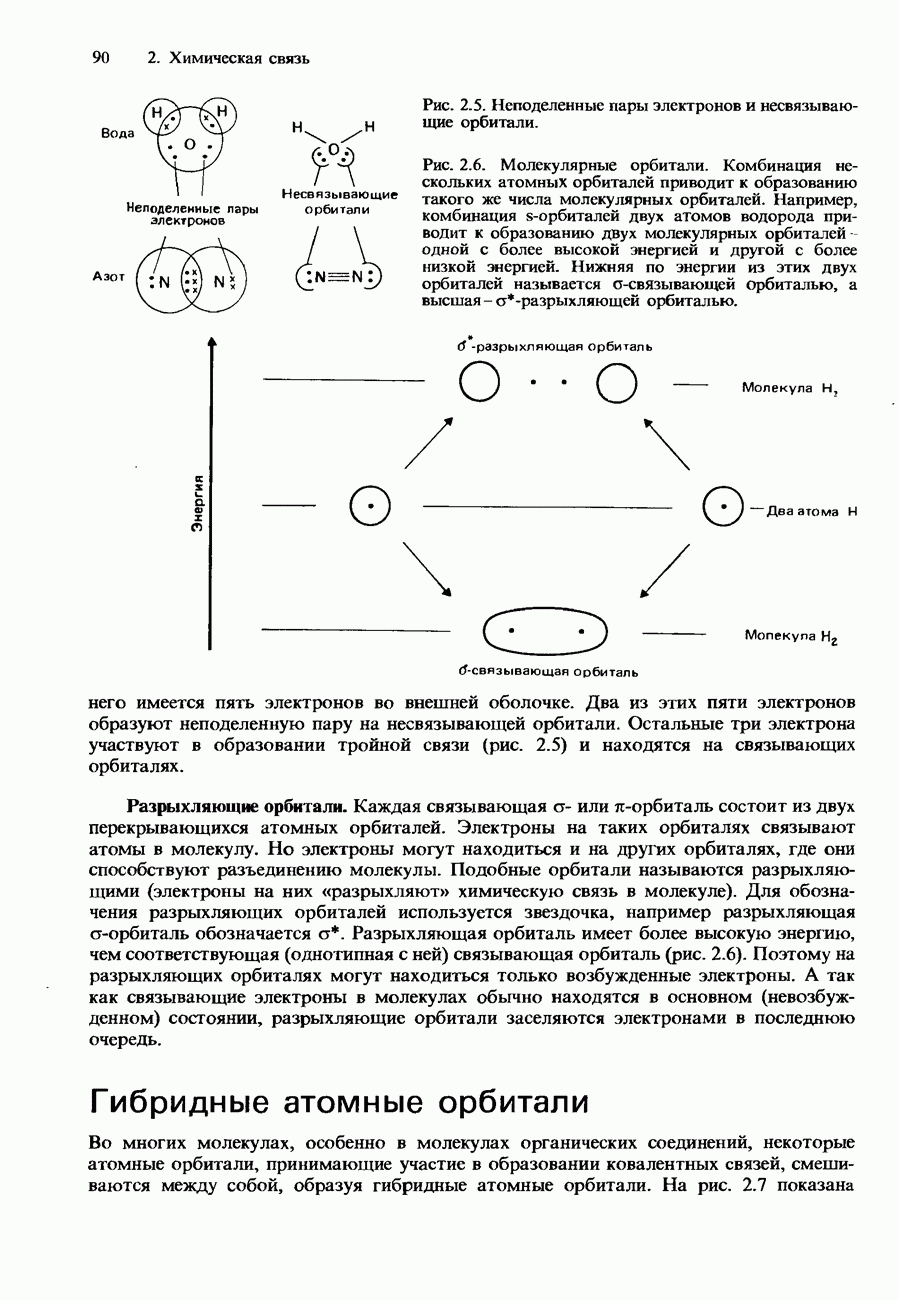
- Молекулярные орбитали
- Гибридные атомные орбитали
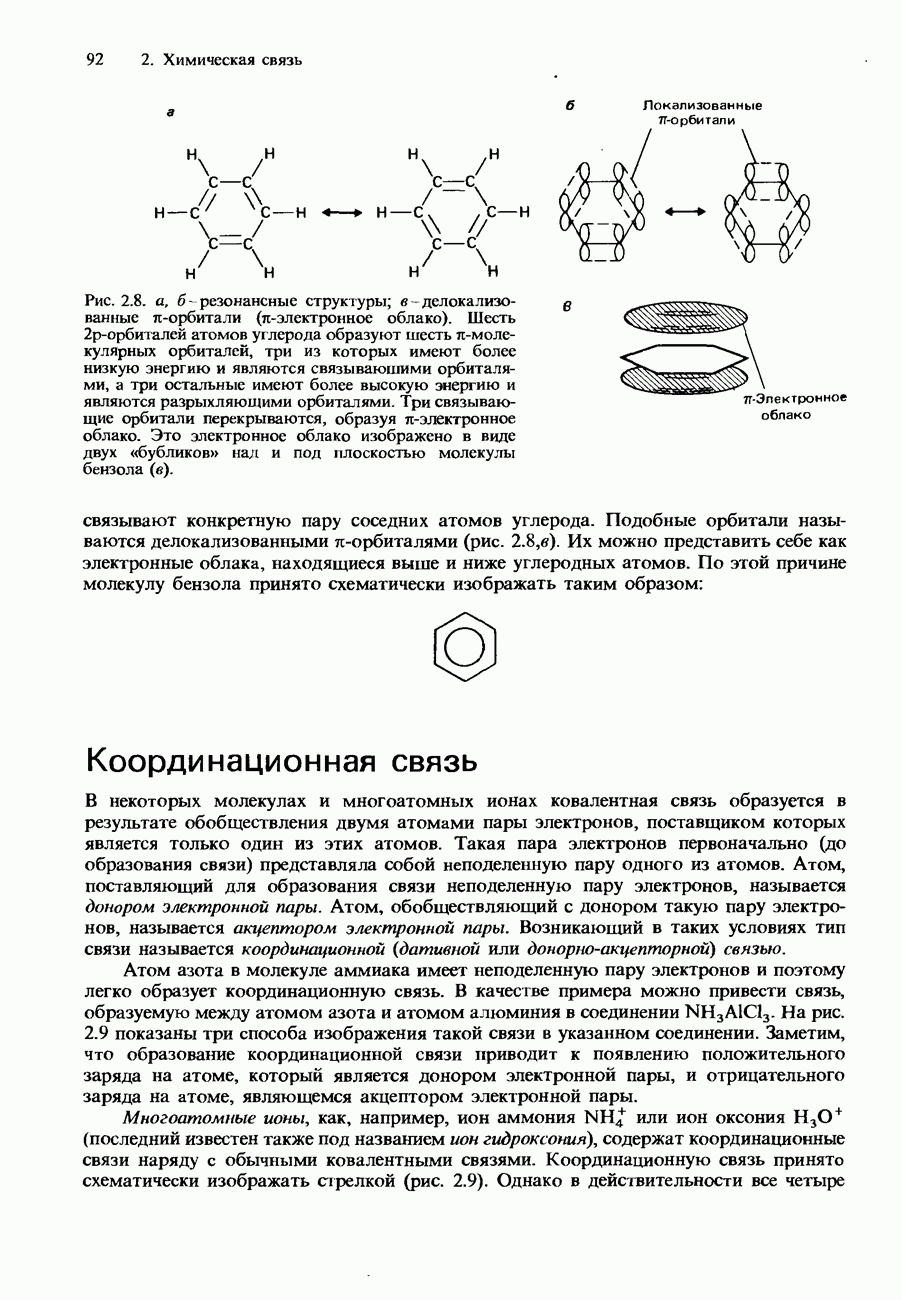
- Делокализованные орбитали
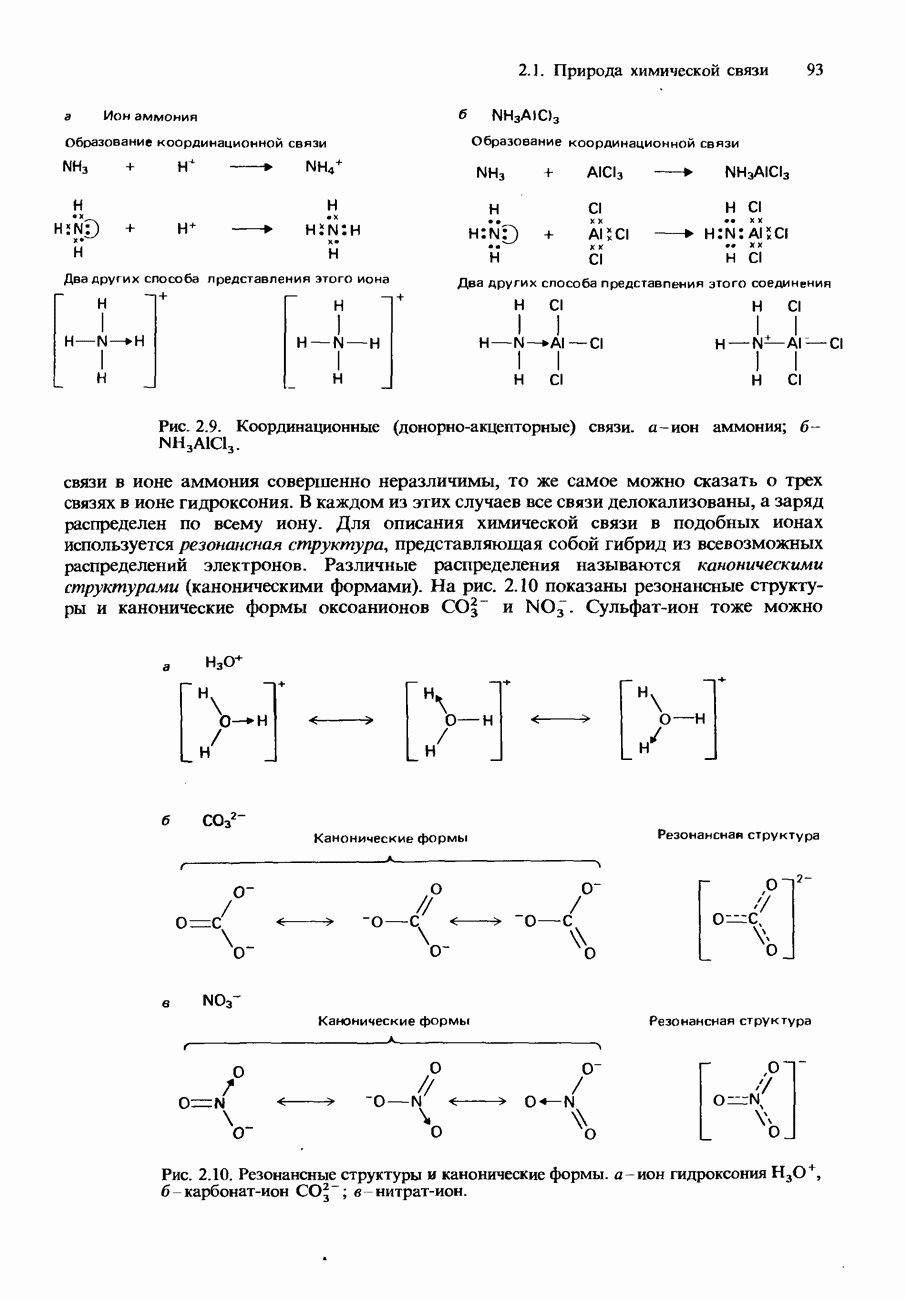
- Координационная связь
- ИОННЫЙ И КОВАЛЕНТНЫЙ ХАРАКТЕР СВЯЗИ
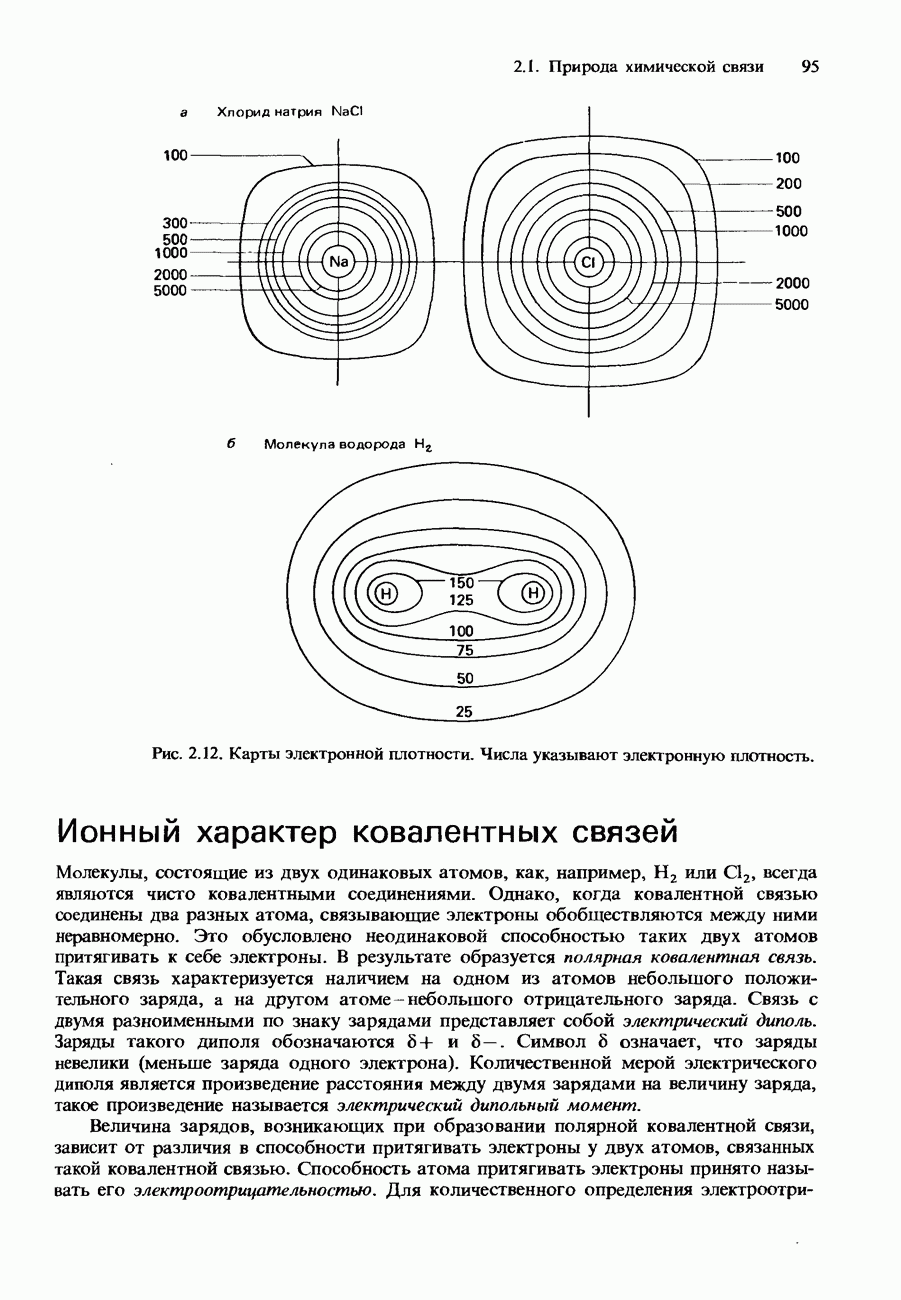
- Ионный характер ковалентных связей
- Ионные и ковалентные соединения
- МЕТАЛЛИЧЕСКАЯ СВЯЗЬ
- Валентная зона и зона проводимости
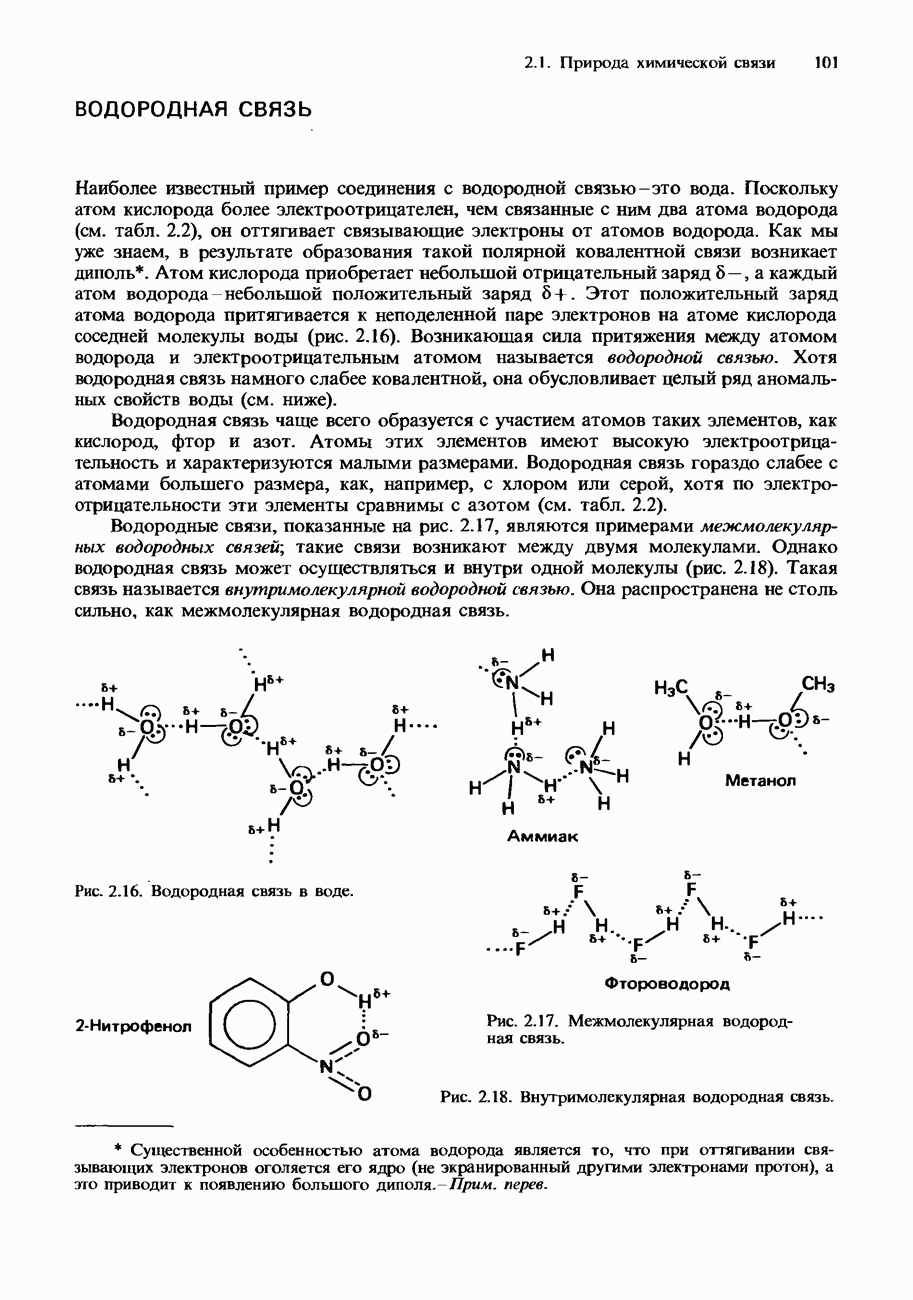
- ВОДОРОДНАЯ СВЯЗЬ
- ВАНДЕРВААЛЬСОВЫ СИЛЫ
- Притяжение типа диполь-индуцированный диполь (индукционное)
- Что понимается под вандерваальсовыми силами
- 2.2. Влияние химической связи на свойства соединений
- Атомные радиусы
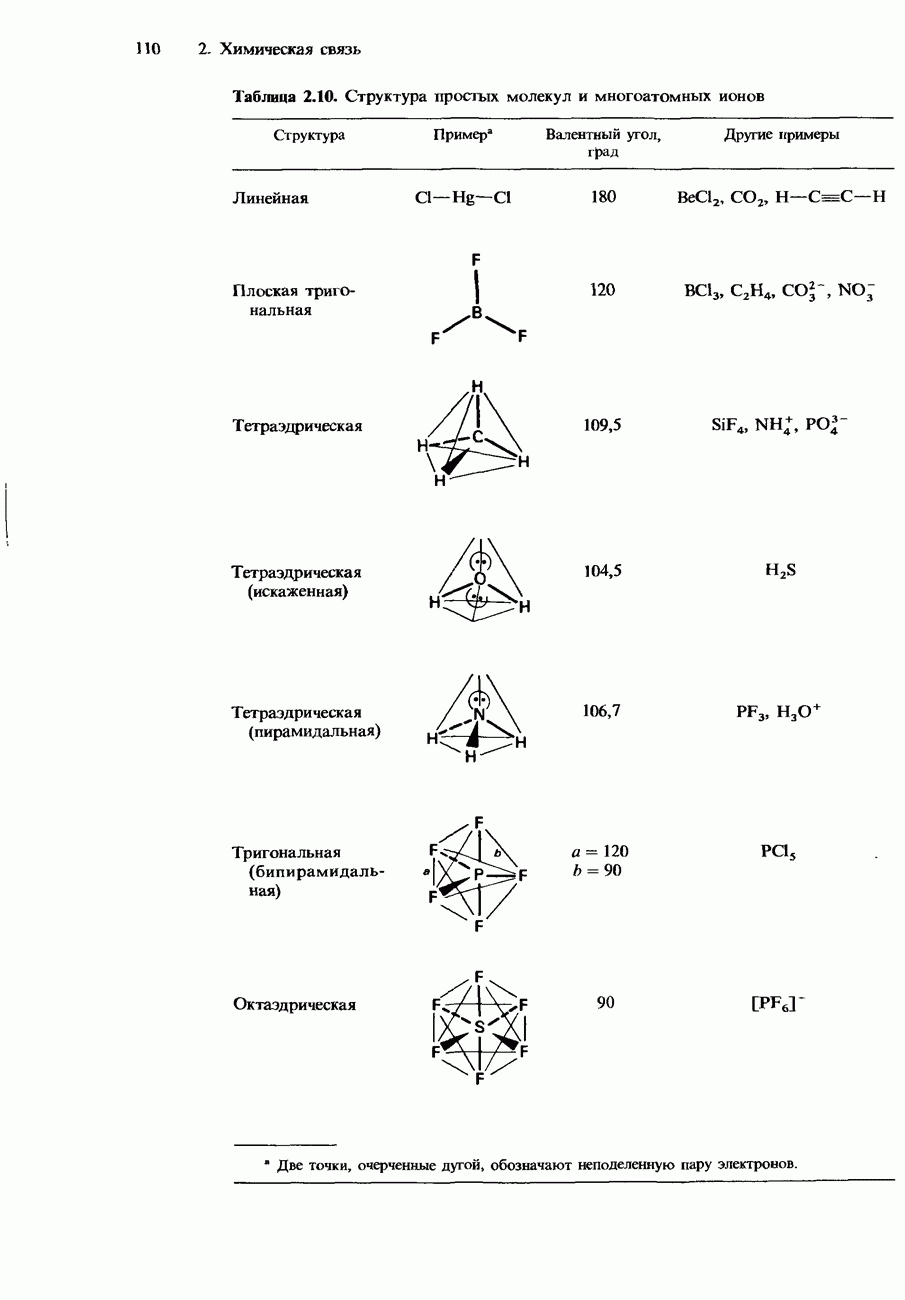
- ФОРМА ПРОСТЫХ МОЛЕКУЛ И МНОГОАТОМНЫХ ИОНОВ
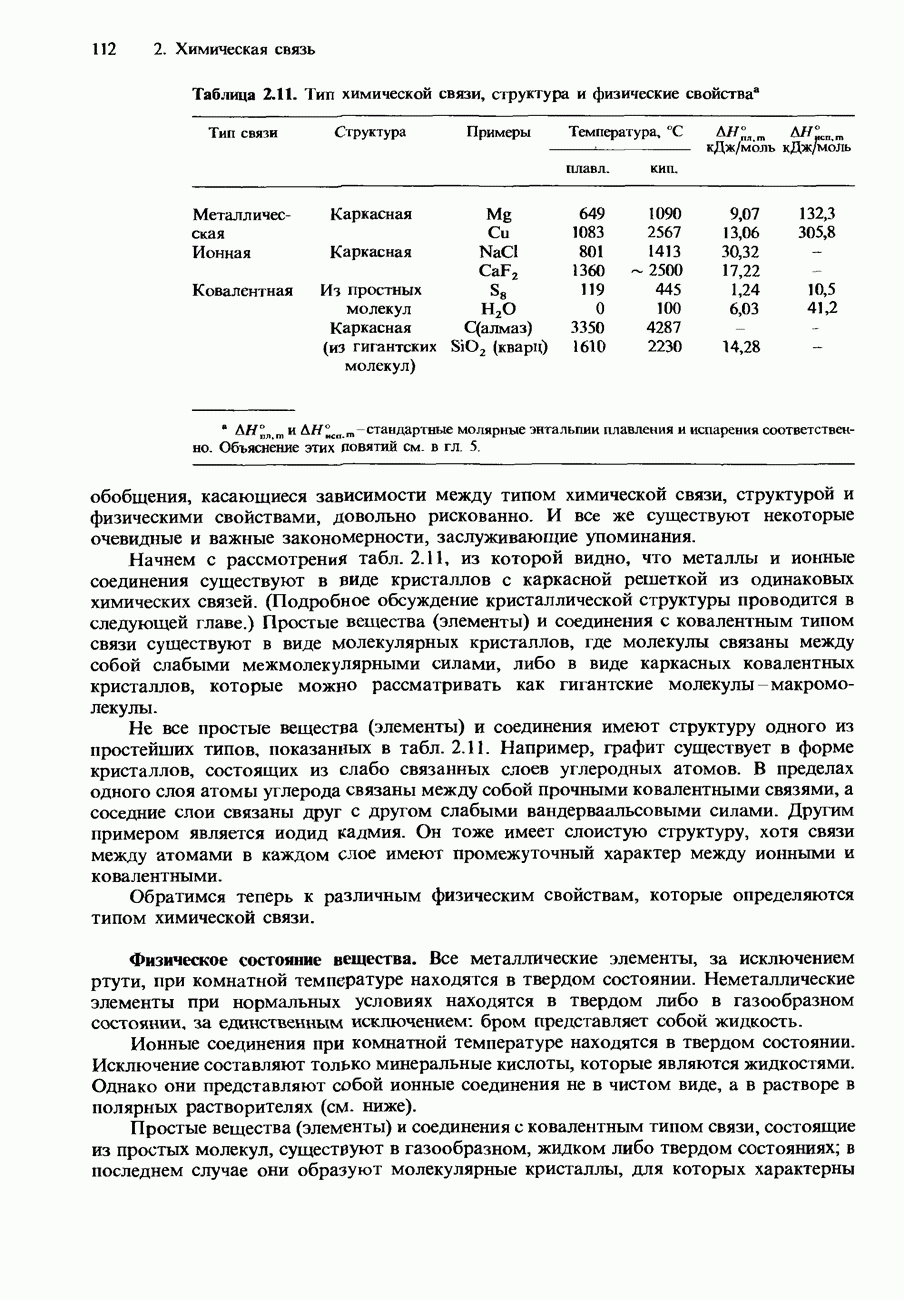
- ТИП ХИМИЧЕСКОЙ СВЯЗИ, СТРУКТУРА И ФИЗИЧЕСКИЕ СВОЙСТВА
- ТИП СВЯЗИ И ХИМИЧЕСКИЕ СВОЙСТВА
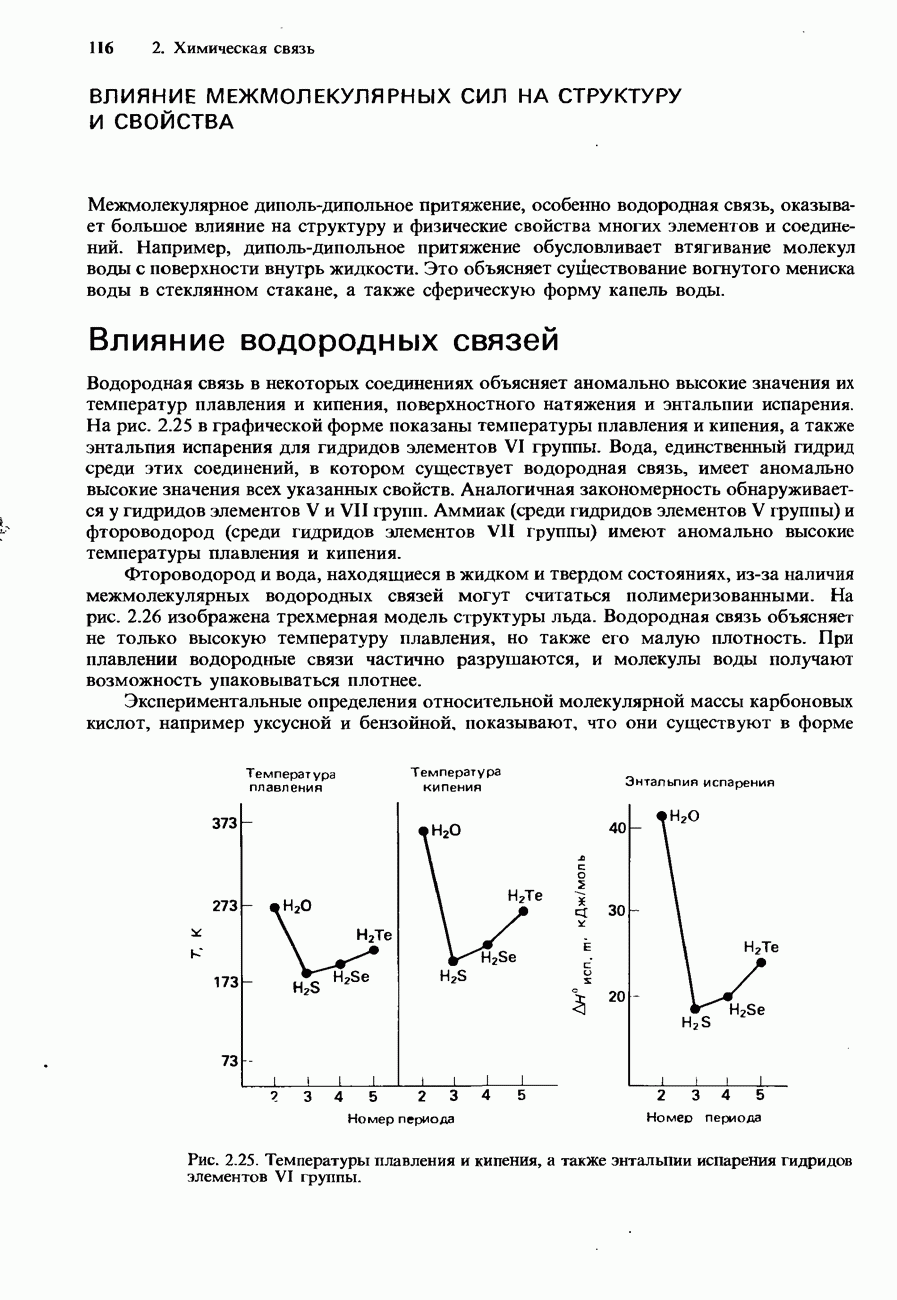
- ВЛИЯНИЕ МЕЖМОЛЕКУЛЯРНЫХ СИЛ НА СТРУКТУРУ И СВОЙСТВА
- ВЛИЯНИЕ ВАНДЕРВААЛЬСОВЫХ СИЛ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 3 ГАЗЫ, ЖИДКОСТИ И ТВЕРДЫЕ ВЕЩЕСТВА
- 3.1. Газы и жидкости
- ГАЗОВЫЕ ЗАКОНЫ
- Закон Бойля-Мариотта
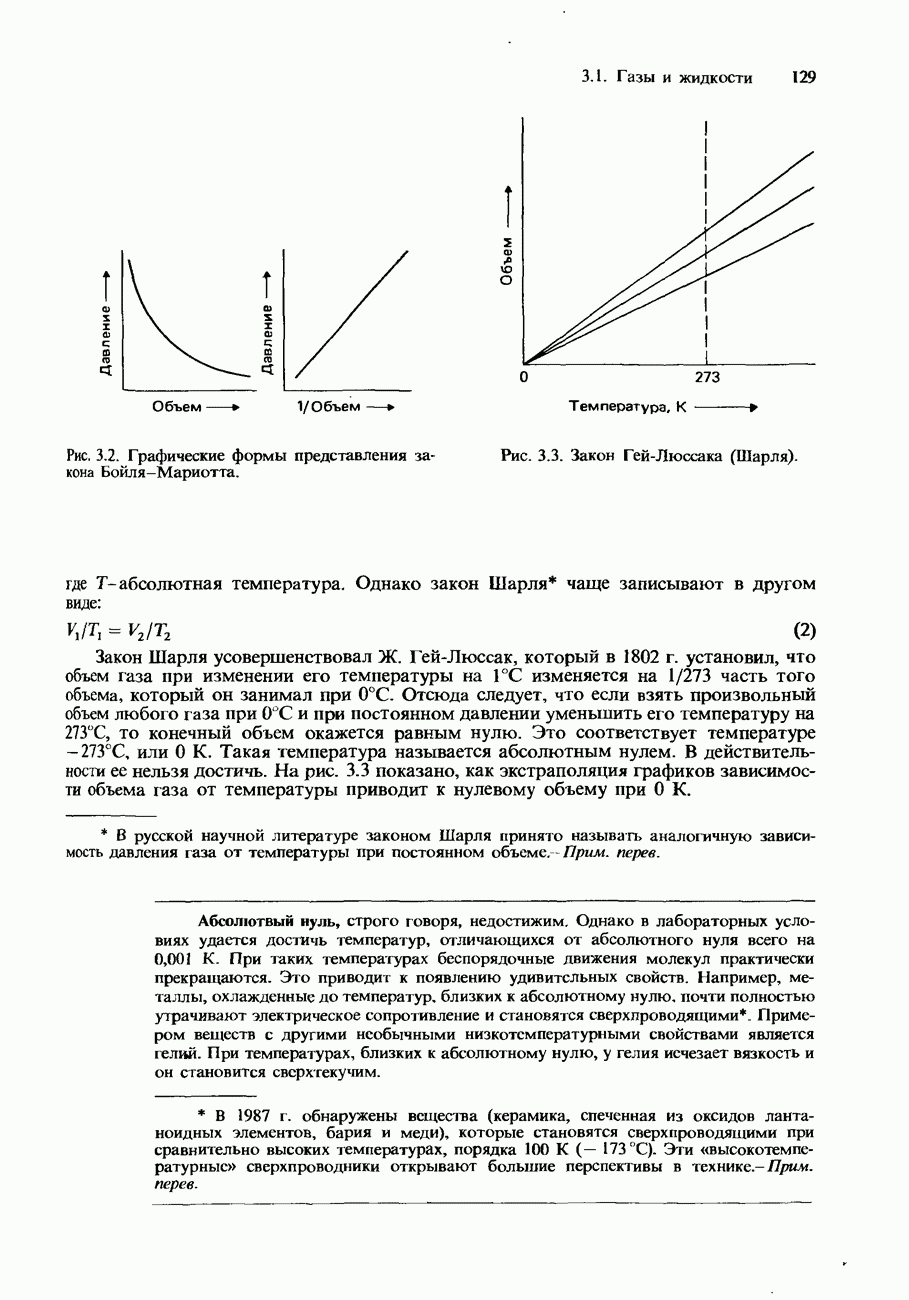
- Закон Гей-Люссака (закон Шарля)
- Объединенный газовый закон
- Закон Авогадро
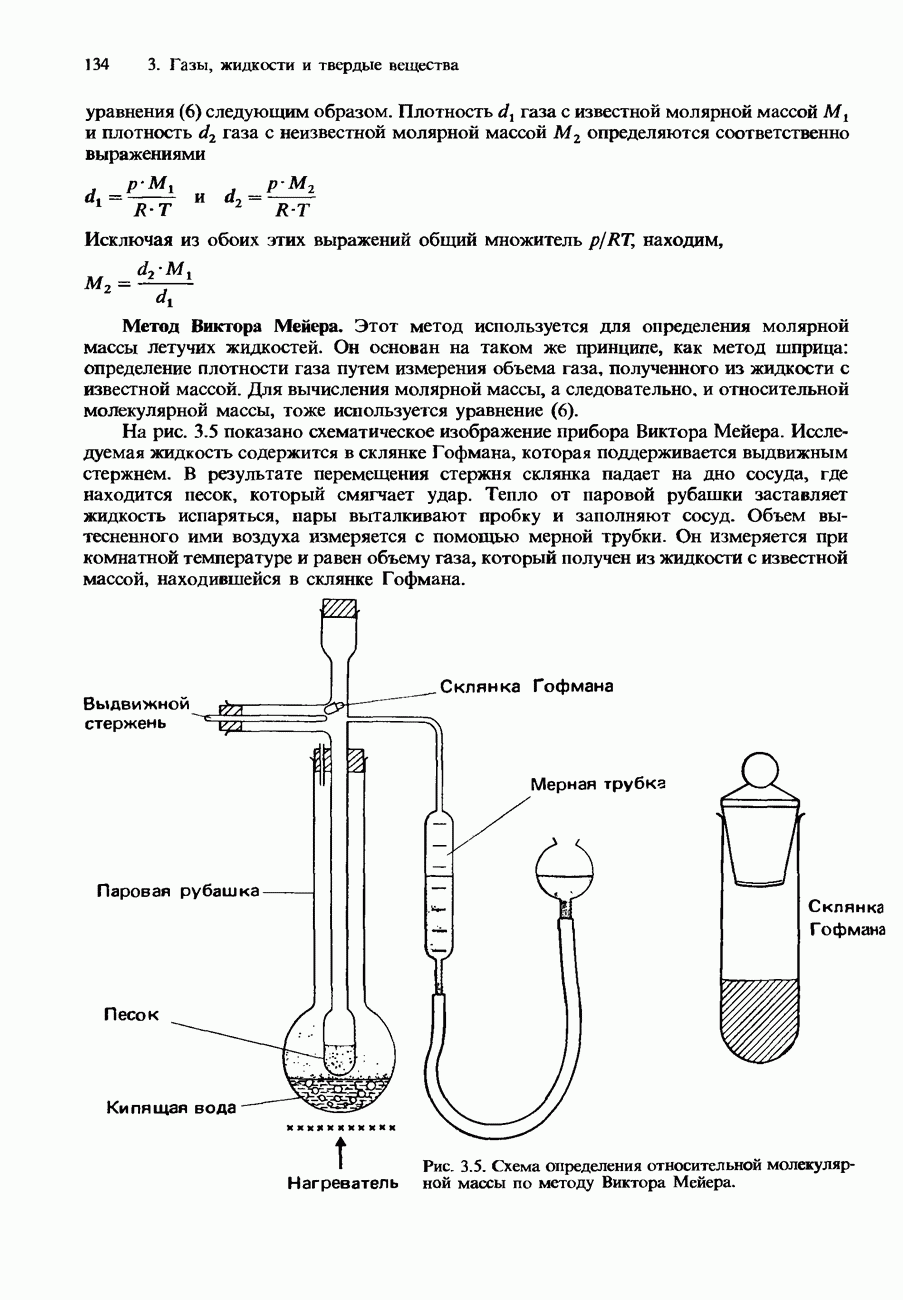
- Экспериментальное определение относительной молекулярной массы
- Закон парциальных давлений газов (закон Дальтона)
- Законы Грэхема
- КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
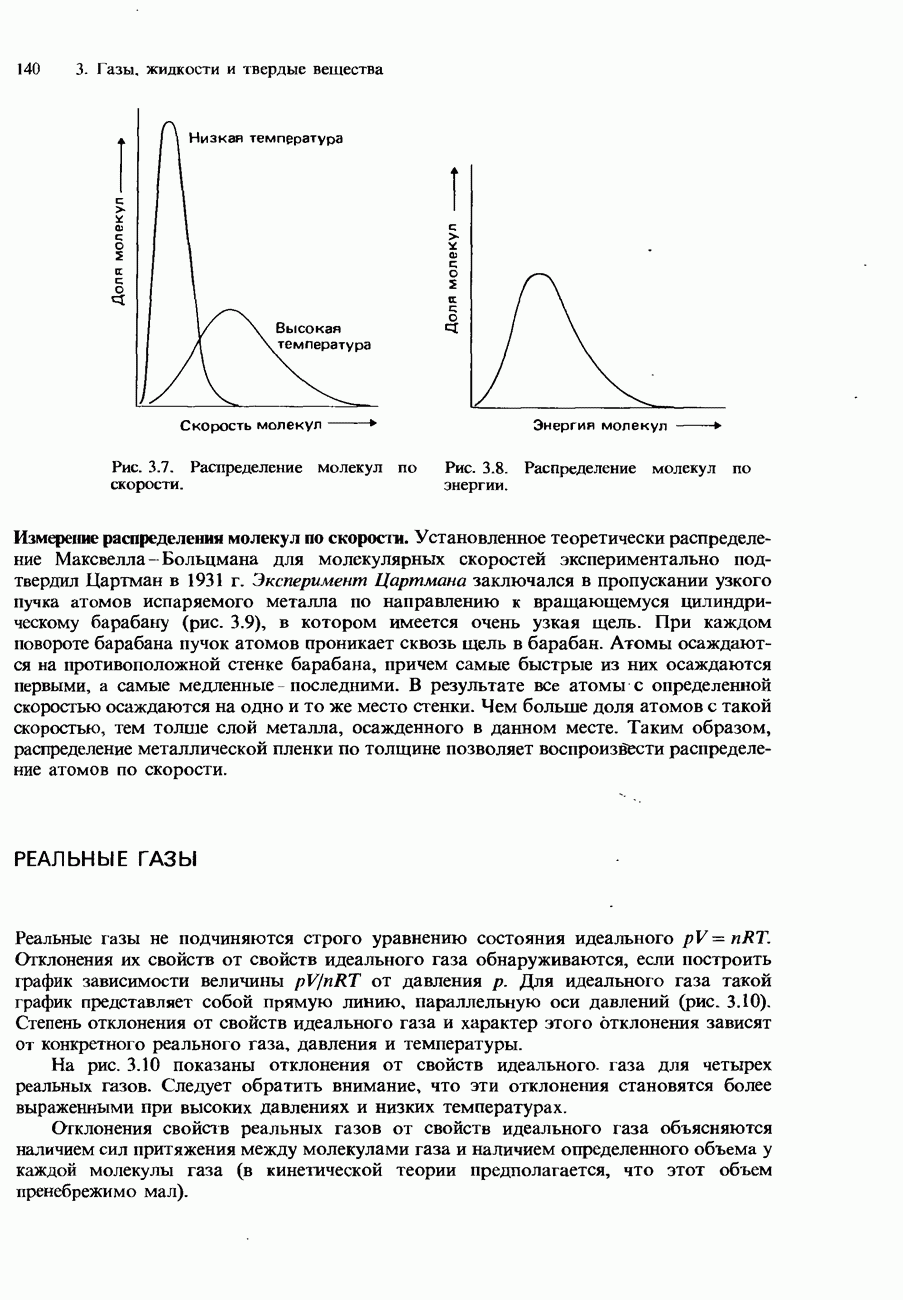
- Скорости молекул
- Распределение Максвелла-Больцмана
- РЕАЛЬНЫЕ ГАЗЫ
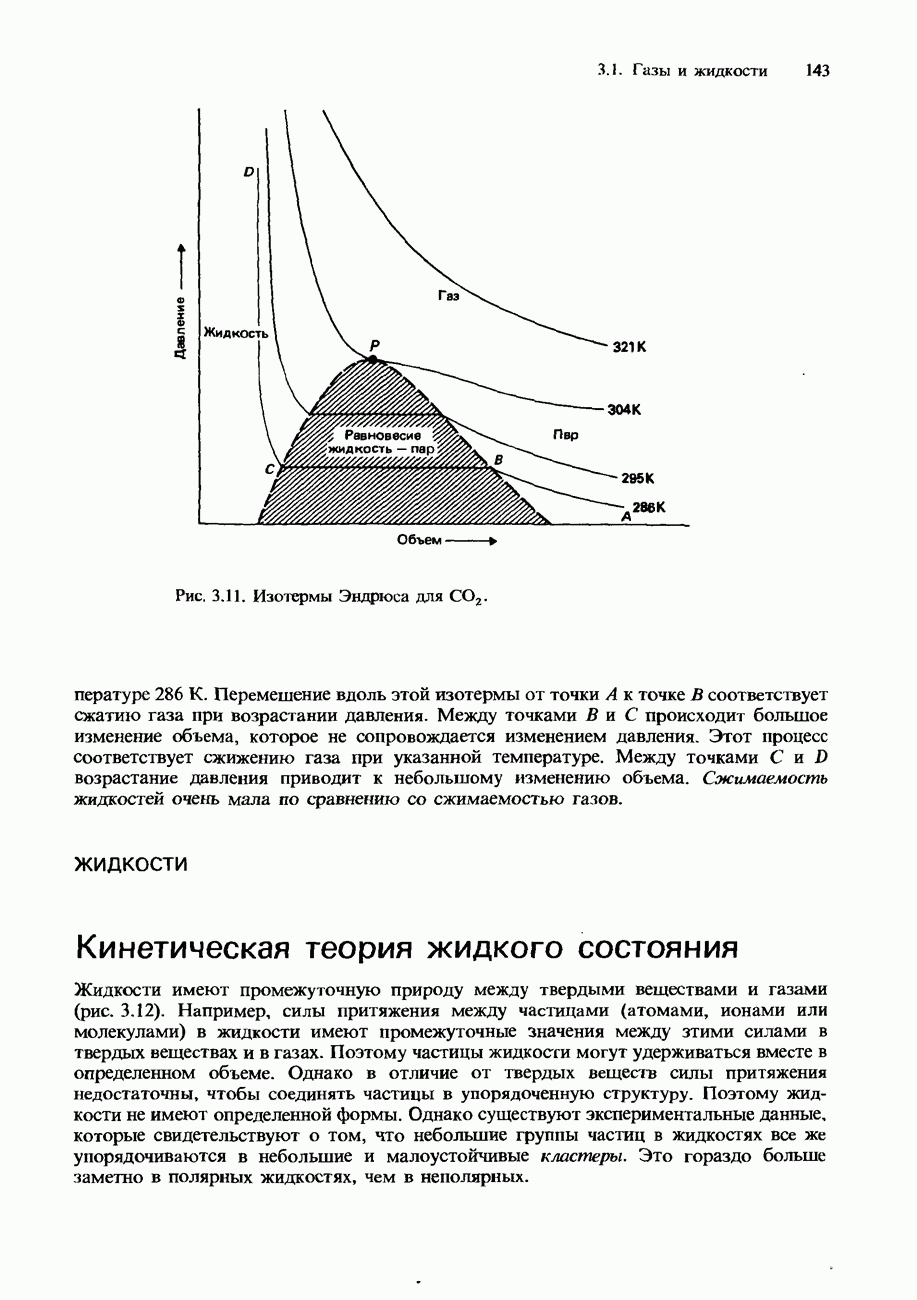
- Уравнение Ван-дер-Ваальса
- Сжижение газов
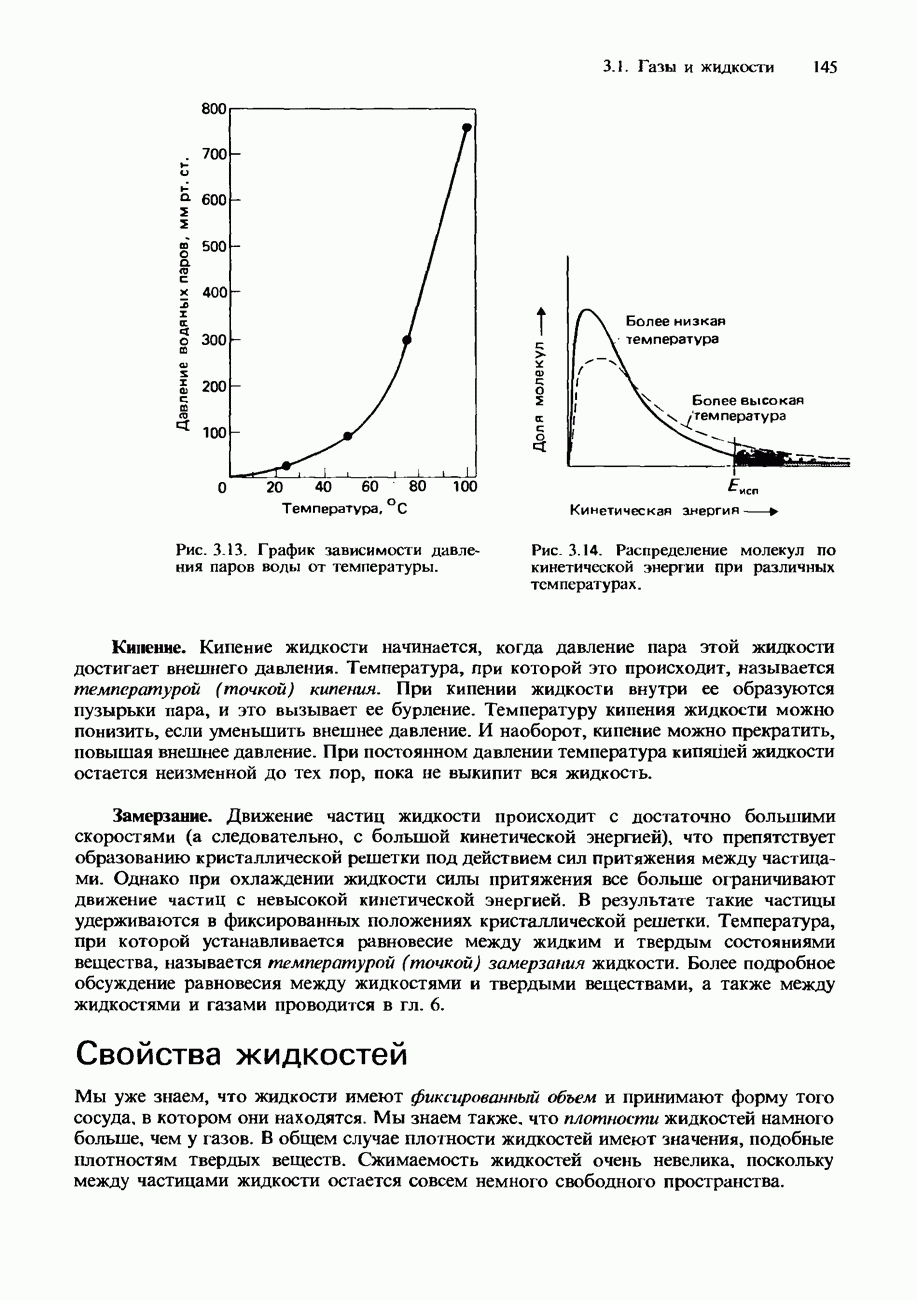
- ЖИДКОСТИ
- Свойства жидкостей
- 3.2. Твердые вещества
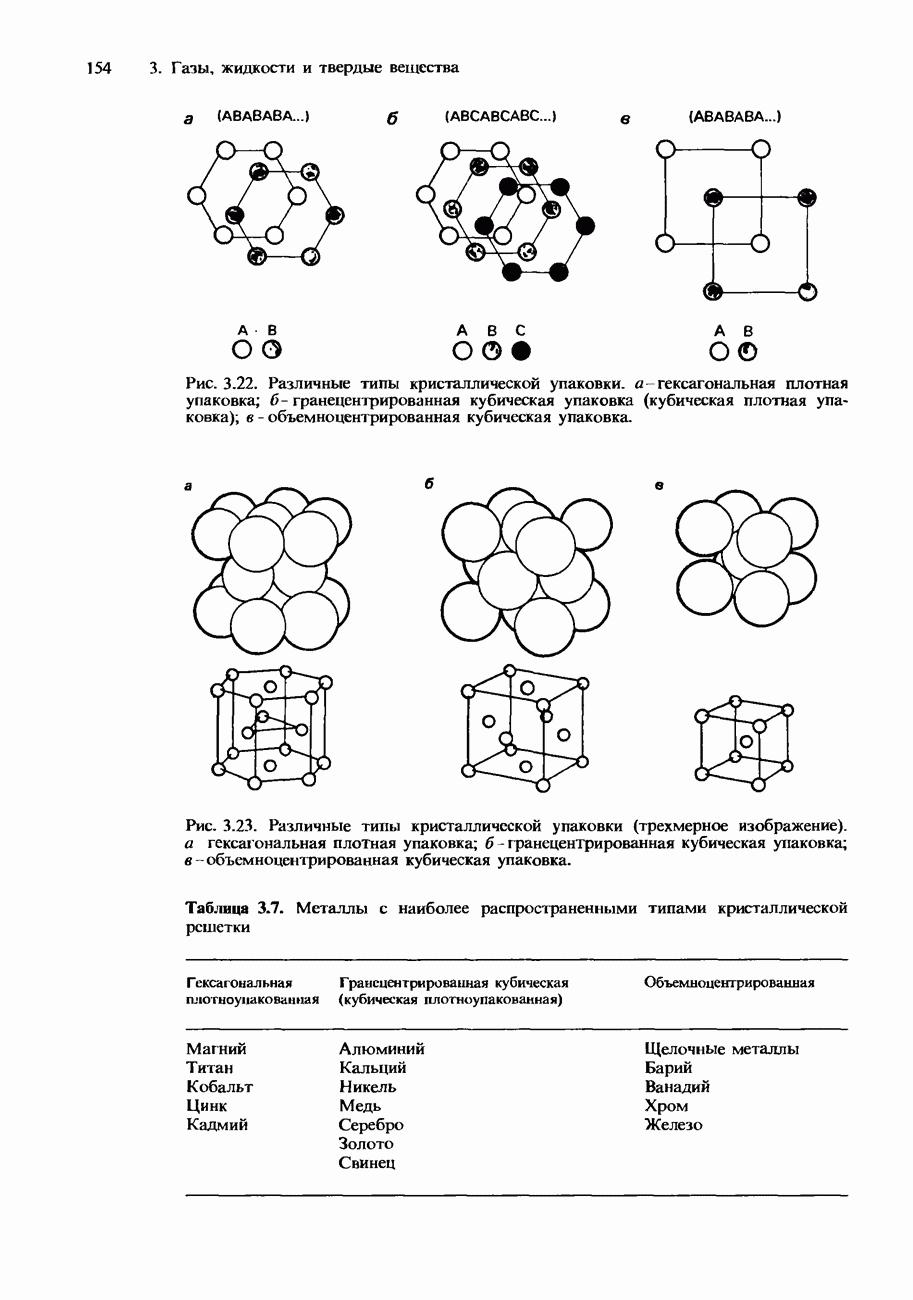
- КРИСТАЛЛИЧЕСКАЯ СТРУКТУРА
- Металлические кристаллы
- Ионные кристаллы
- Ковалентные кристаллы
- ИЗОМОРФИЗМ. ПОЛИМОРФИЗМ И АЛЛОТРОПИЯ
- СВОЙСТВА ТВЕРДЫХ ВЕЩЕСТВ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 4. СТЕХИОМЕТРИЯ
- 4.1. Стехиометрия и номенклатура
- Химические вещества
- Количественные законы химии
- Вес и масса
- НАЗВАНИЯ И ФОРМУЛЫ ХИМИЧЕСКИХ СОЕДИНЕНИЙ
- Химические формулы
- НОМЕНКЛАТУРА НЕОРГАНИЧЕСКИХ СОЕДИНЕНИЙ
- Степень окисления (состояние окисления)
- Элементы
- Бинарные соединения
- 4.2 Стехиометрические вычисления
- Молярная масса
- Число частиц вещества
- Процентный состав соединения
- Эмпирическая формула соединения
- Молярные постоянные и молярные величины
- Состав гомогенных смесей
- ХИМИЧЕСКИЕ УРАВНЕНИЯ
- ВЫХОД РЕАКЦИИ
- ПРОМЫШЛЕННАЯ СТЕХИОМЕТРИЯ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 5. ЭНЕРГЕТИКА
- 5.1. Термодинамика
- ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 5.2. Энтальпия
- СТАНДАРТНЫЕ ИЗМЕНЕНИЯ ЭНТАЛЬПИИ
- ДРУГИЕ ИЗМЕНЕНИЯ ЭНТАЛЬПИИ
- КАЛОРИМЕТРИЯ
- КАЛОРИЙНОСТЬ ПИЩИ
- ЗАКОН ГЕССА
- 5.3 Энергия и структура
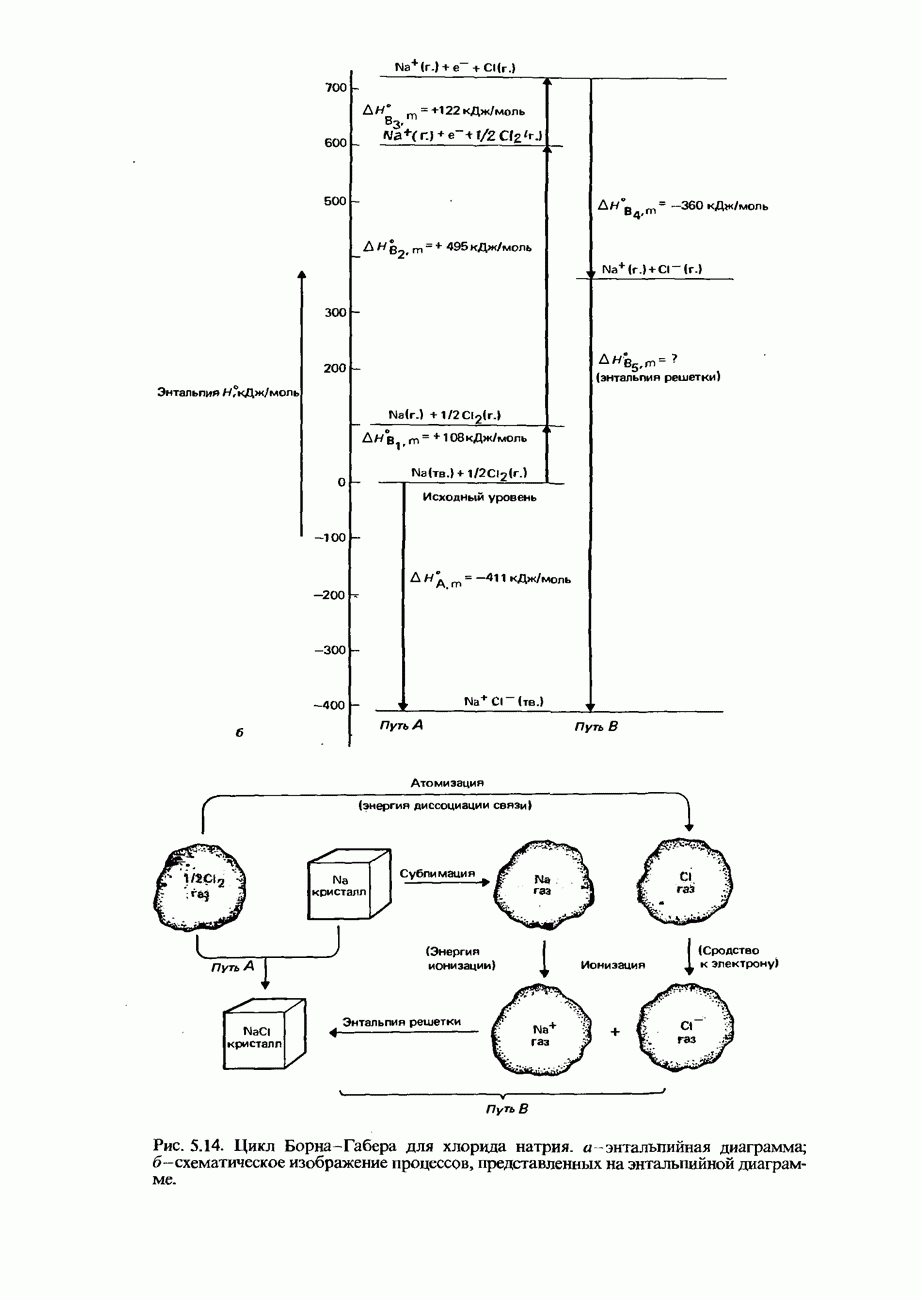
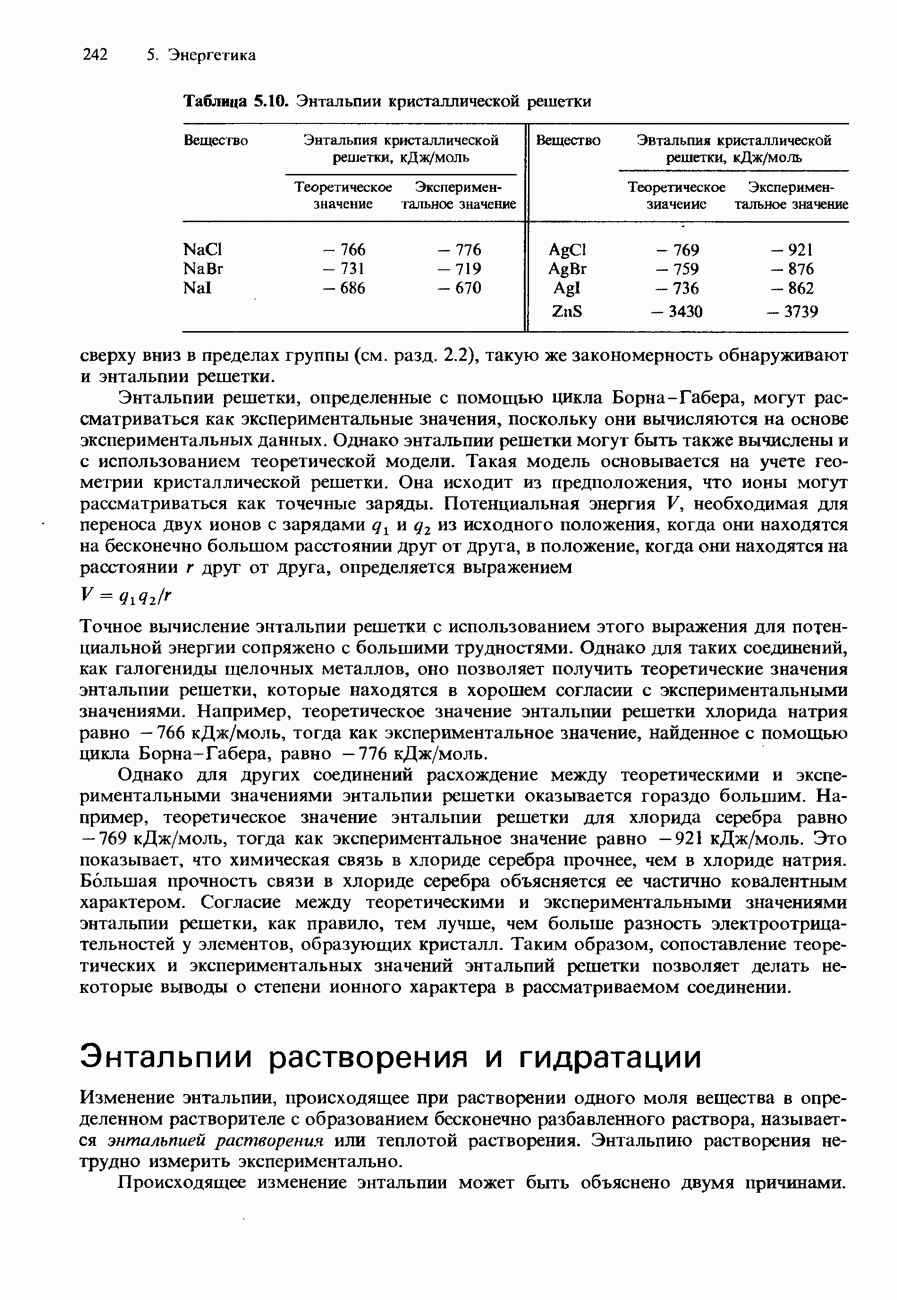
- ЭНТАЛЬПИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
- Энтальпии растворения и гидратации
- ЭНТРОПИЯ
- СВОБОДНАЯ ЭНЕРГИЯ ГИББСА
- О ЧЕМ ПОЗВОЛЯЕТ СУДИТЬ ИЗМЕНЕНИЕ СВОБОДНОЙ ЭНЕРГИИ СИСТЕМЫ
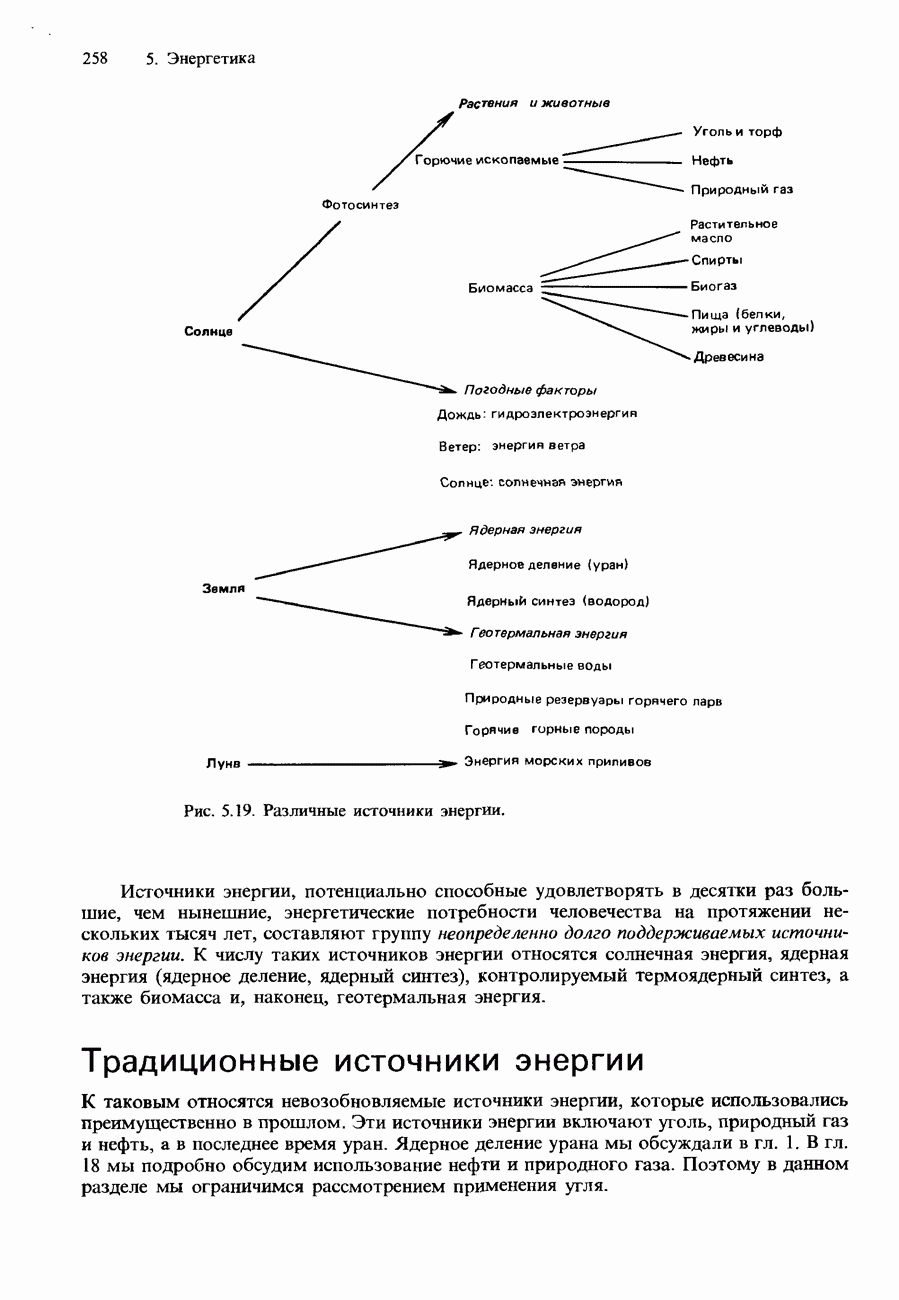
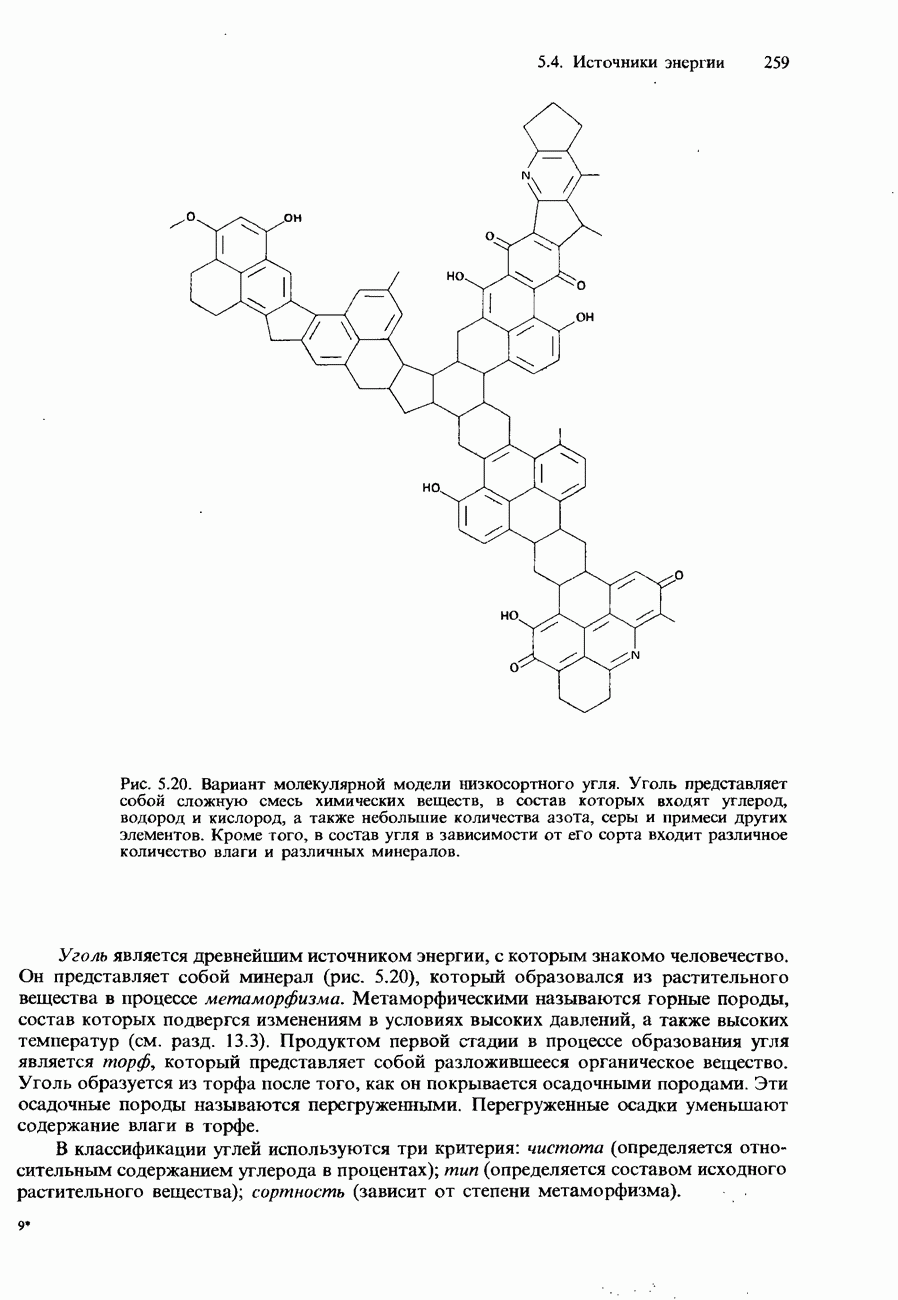
- 5.4. Источники энергии
- НЕТРАДИЦИОННЫЕ ИСТОЧНИКИ ЭНЕРГИИ
- ЗАПАСАНИЕ ЭНЕРГИИ
- ПОТРЕБЛЕНИЕ ЭНЕРГИИ В ПРОШЛОМ, НАСТОЯЩЕМ И БУДУЩЕМ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 6. ФАЗОВЫЕ РАВНОВЕСИЯ
- 6.1. Равновесия и фазы
- ФАЗЫ И КОМПОНЕНТЫ
- Фазы
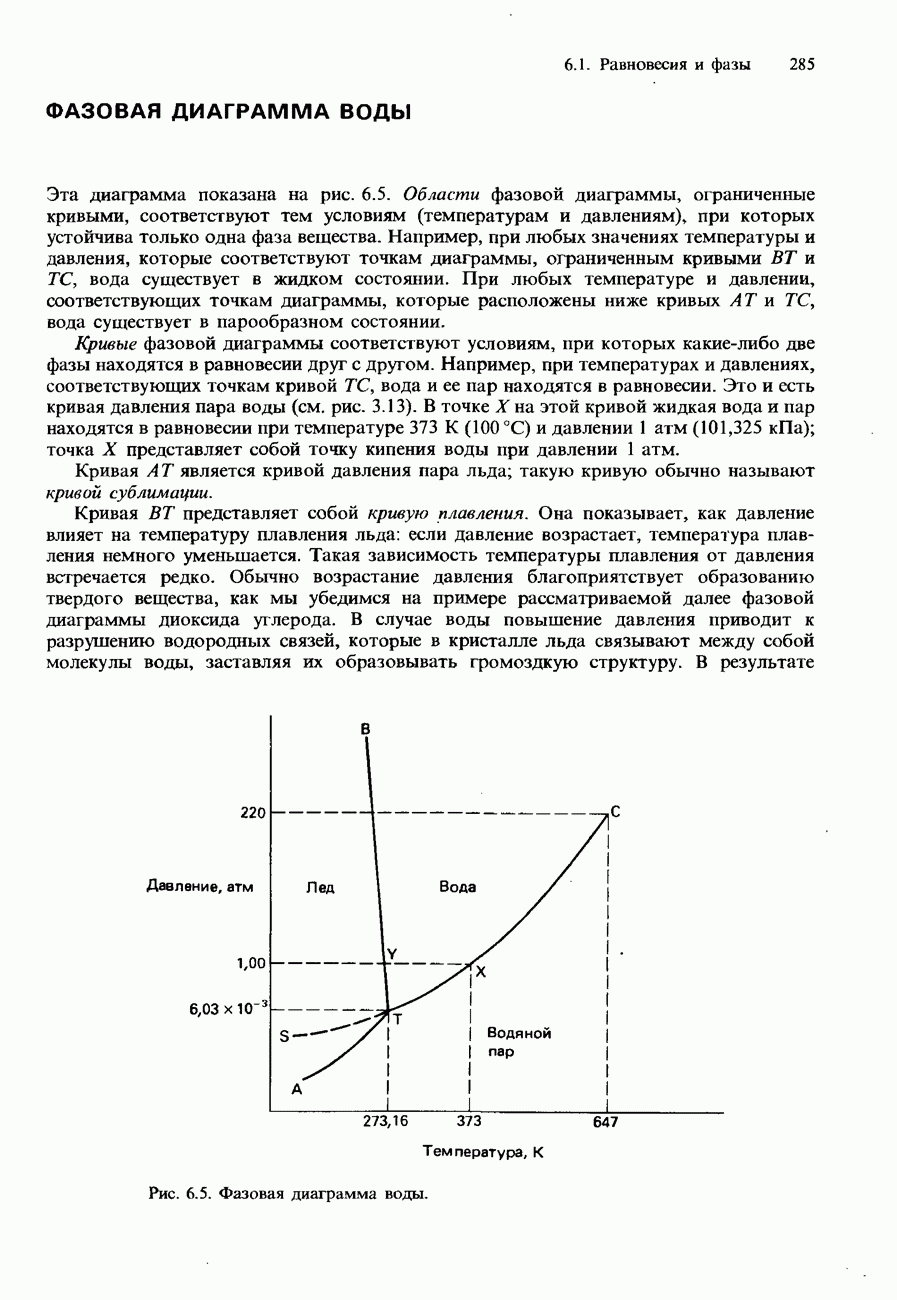
- ФАЗОВАЯ ДИАГРАММА ВОДЫ
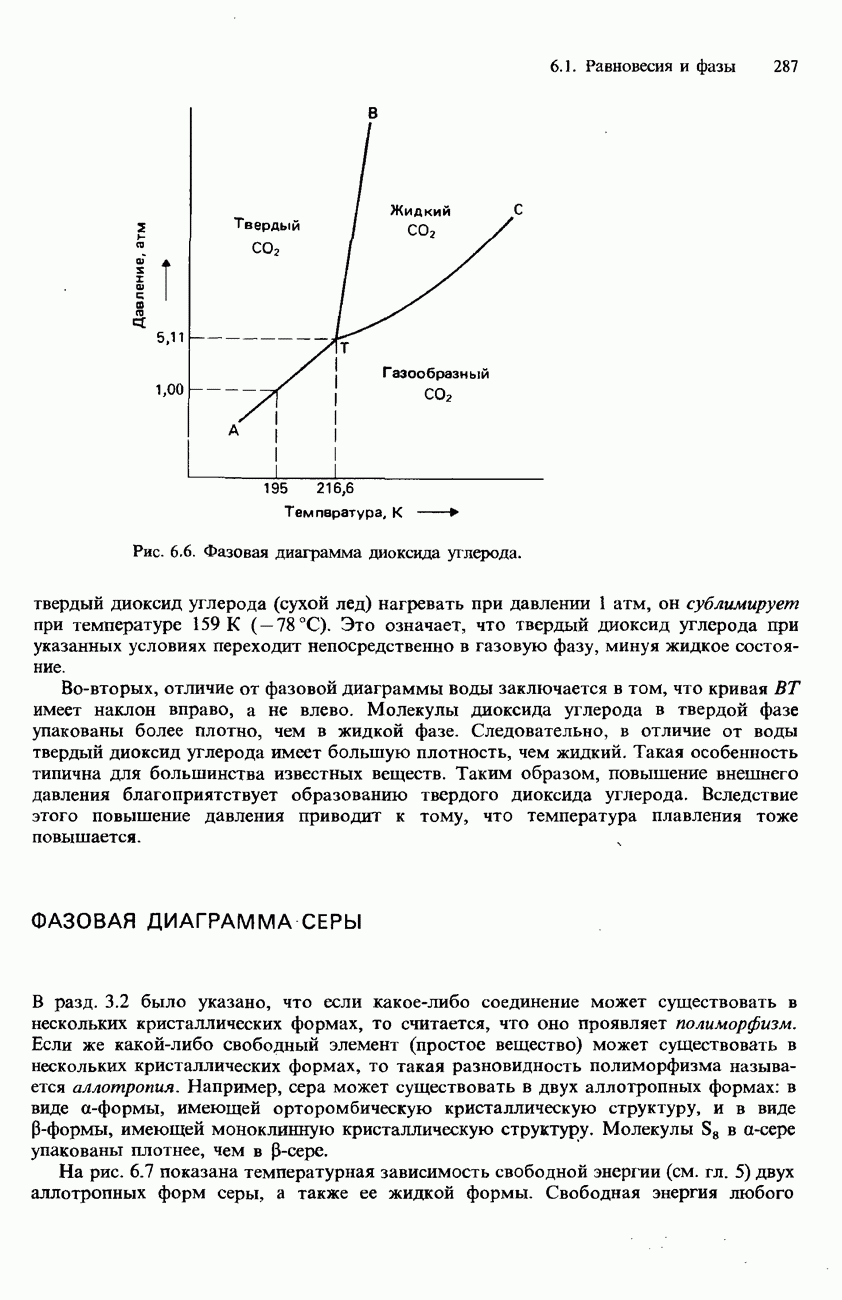
- ФАЗОВАЯ ДИАГРАММА ДИОКСИДА УГЛЕРОДА
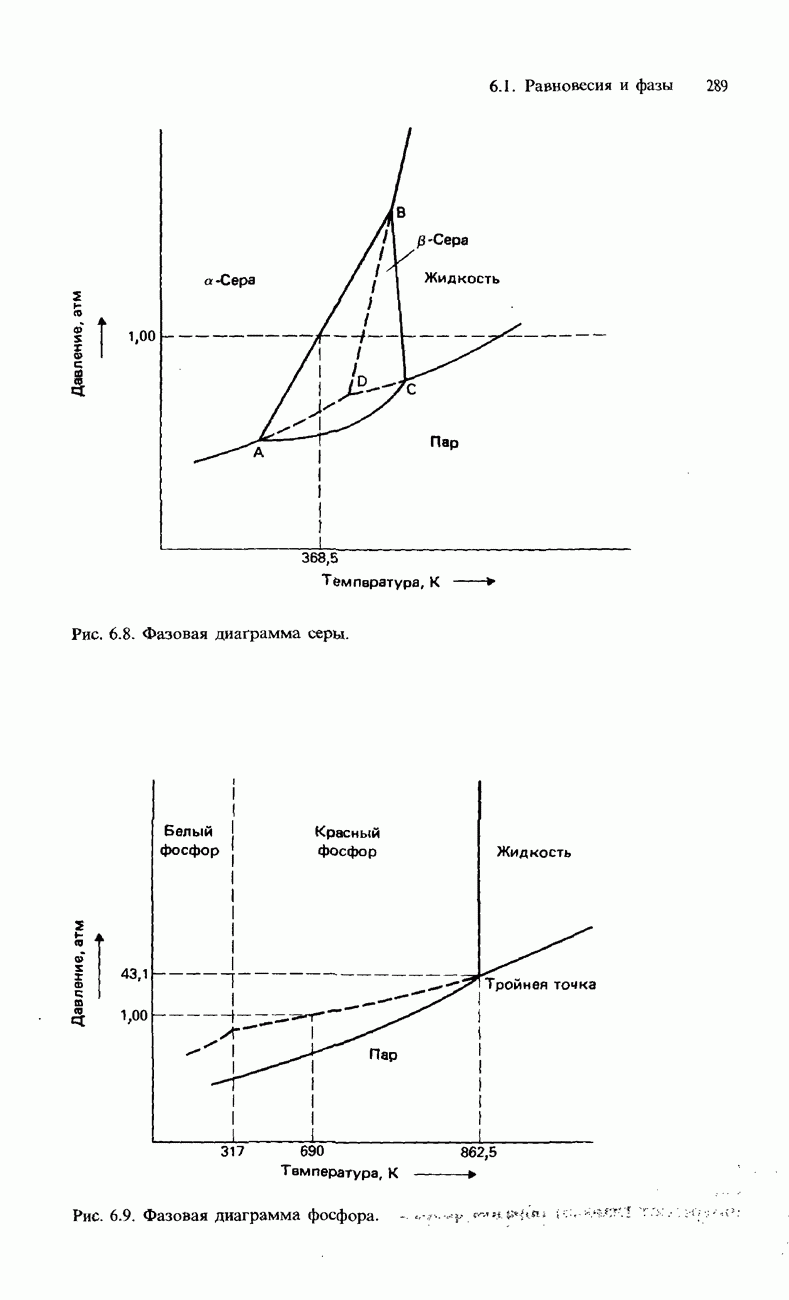
- ФАЗОВАЯ ДИАГРАММА СЕРЫ
- ФАЗОВАЯ ДИАГРАММА ФОСФОРА
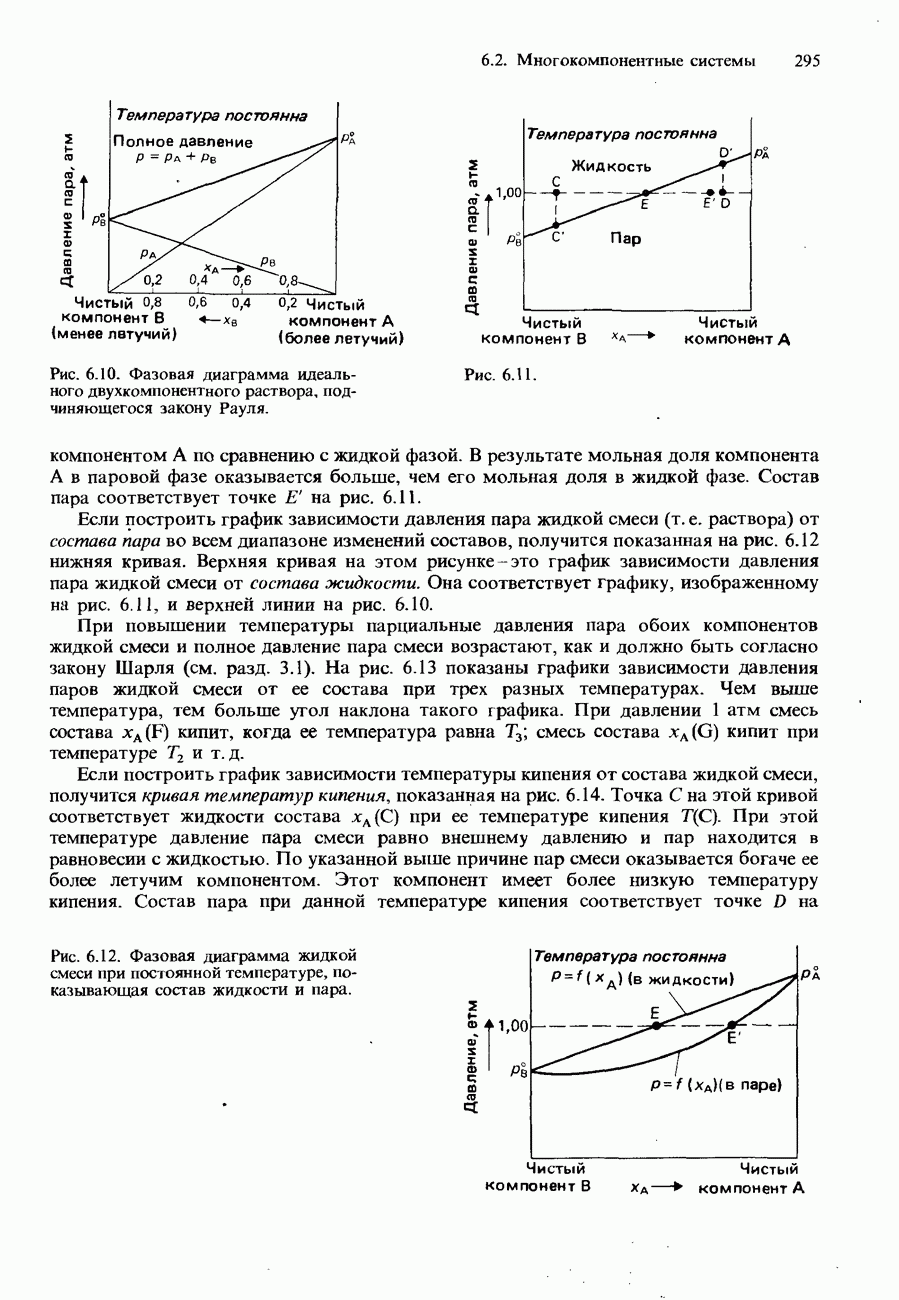
- 6.2. Многокомпонентные системы
- ДВУХКОМПОНЕНТНЫЕ ЖИДКИЕ СМЕСИ
- ПОЛНОСТЬЮ СМЕШИВАЮЩИЕСЯ ЖИДКОСТИ
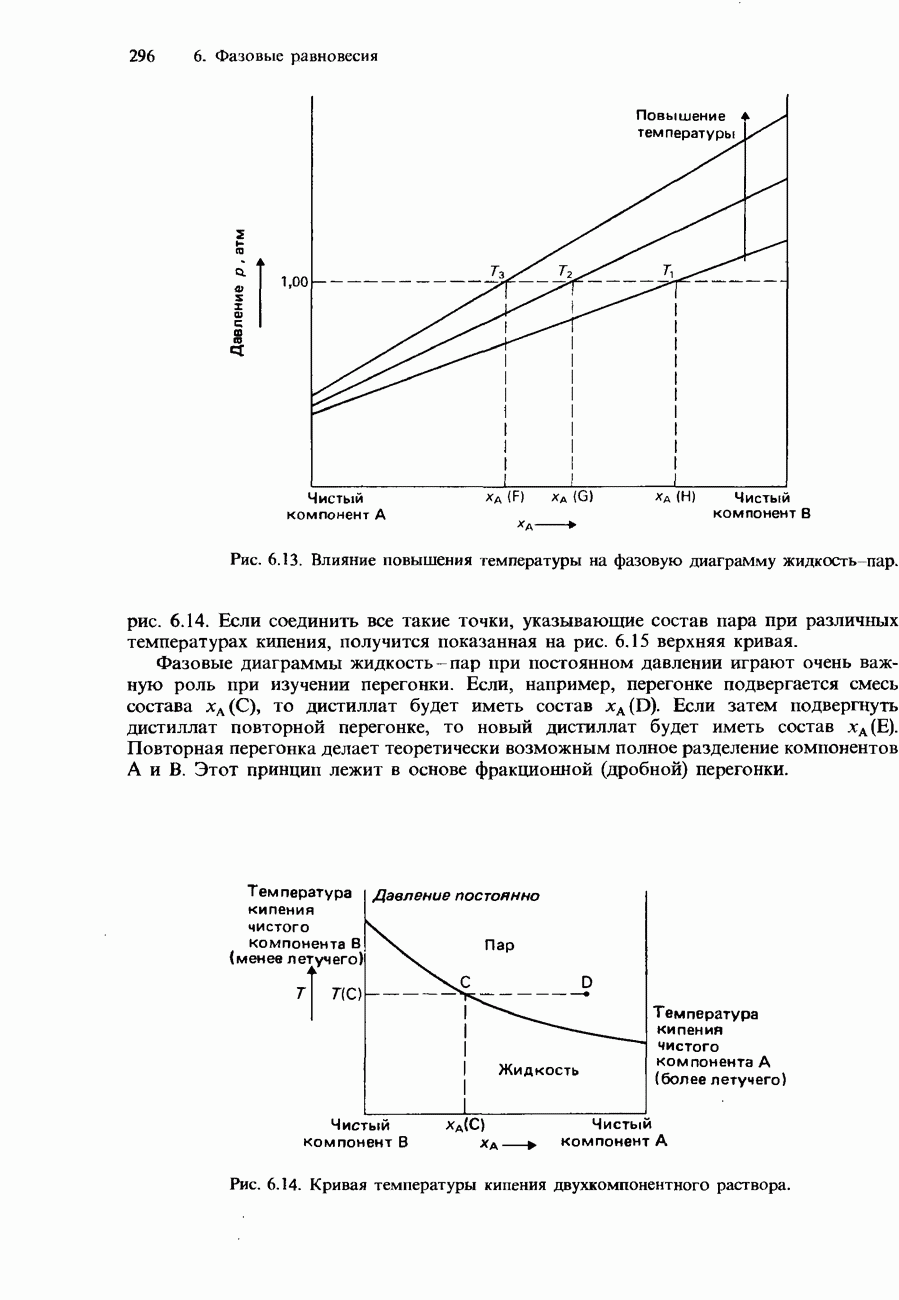
- Фазовые диаграммы полностью смешивающихся жидкостей
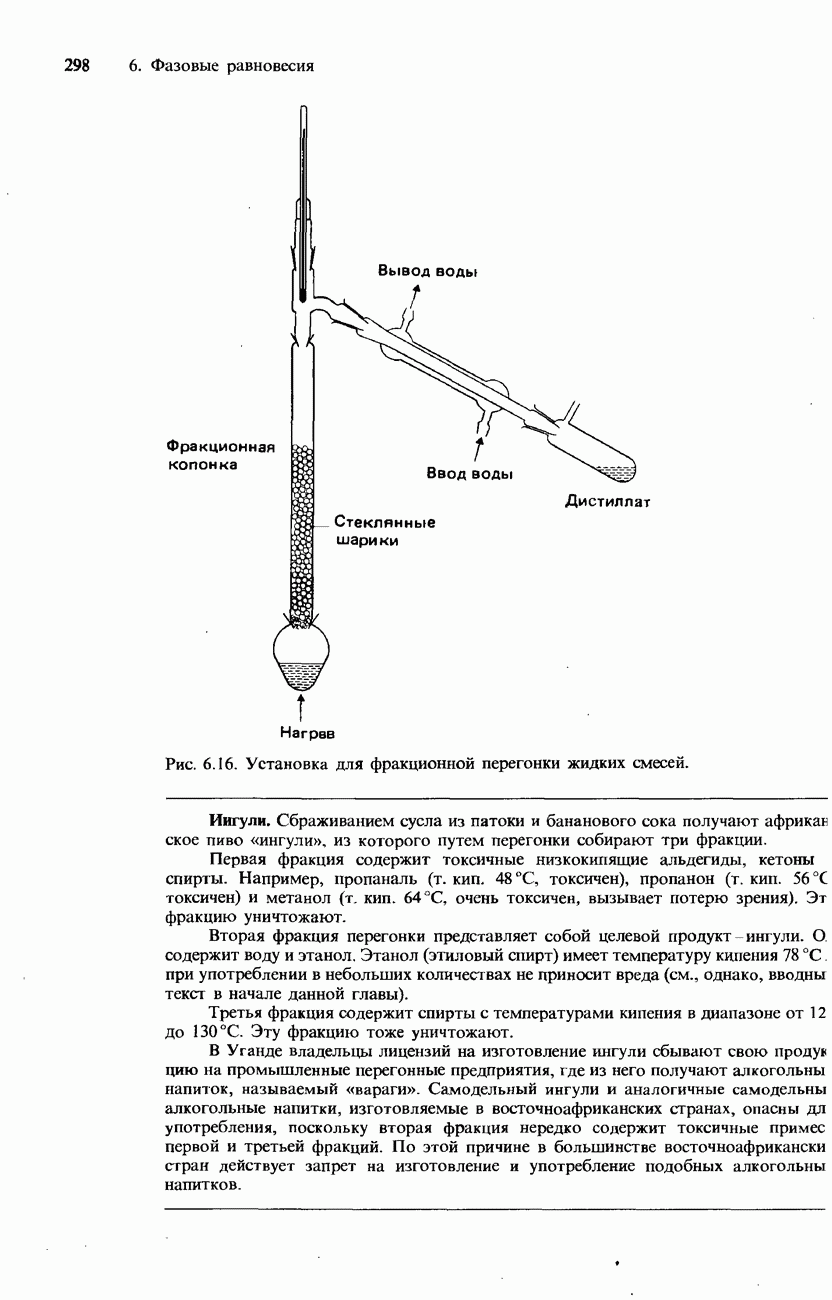
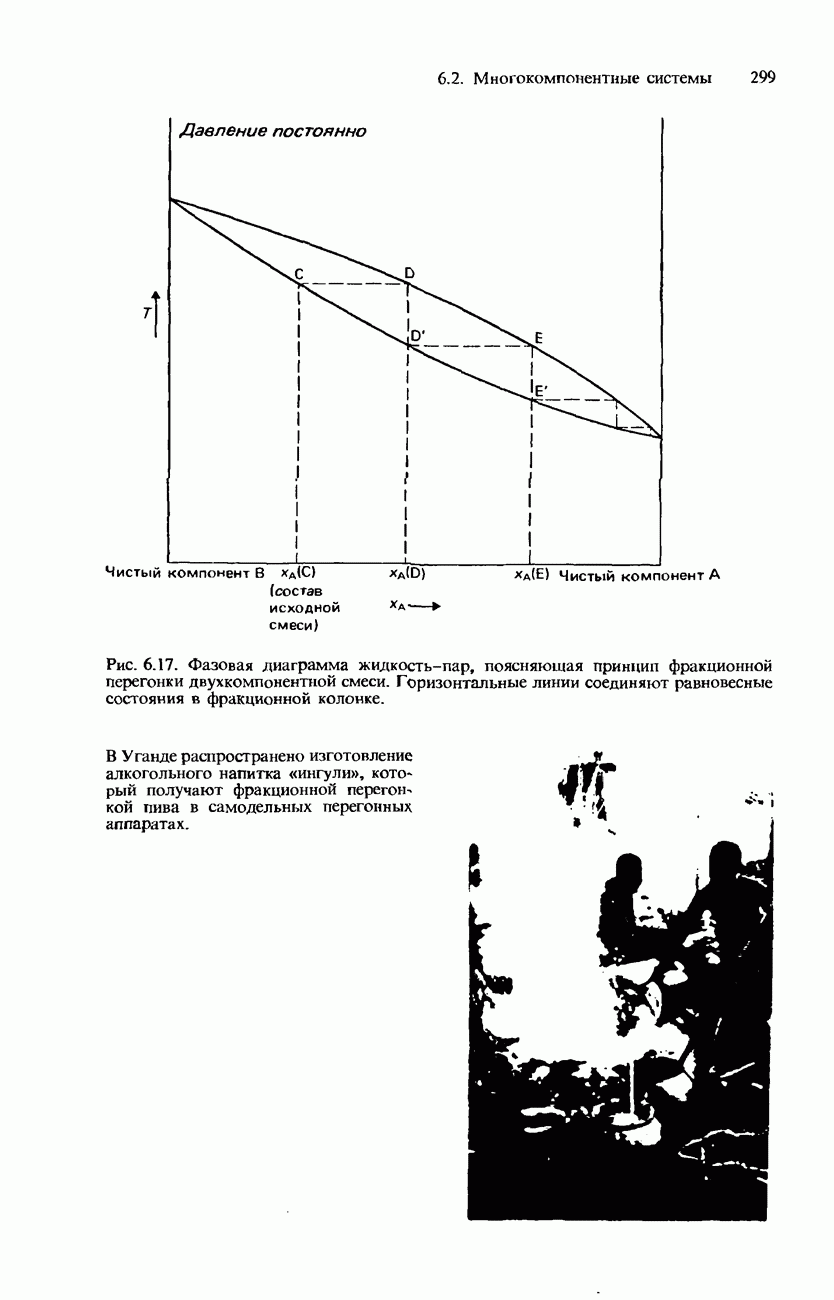
- Фракционная перегонка
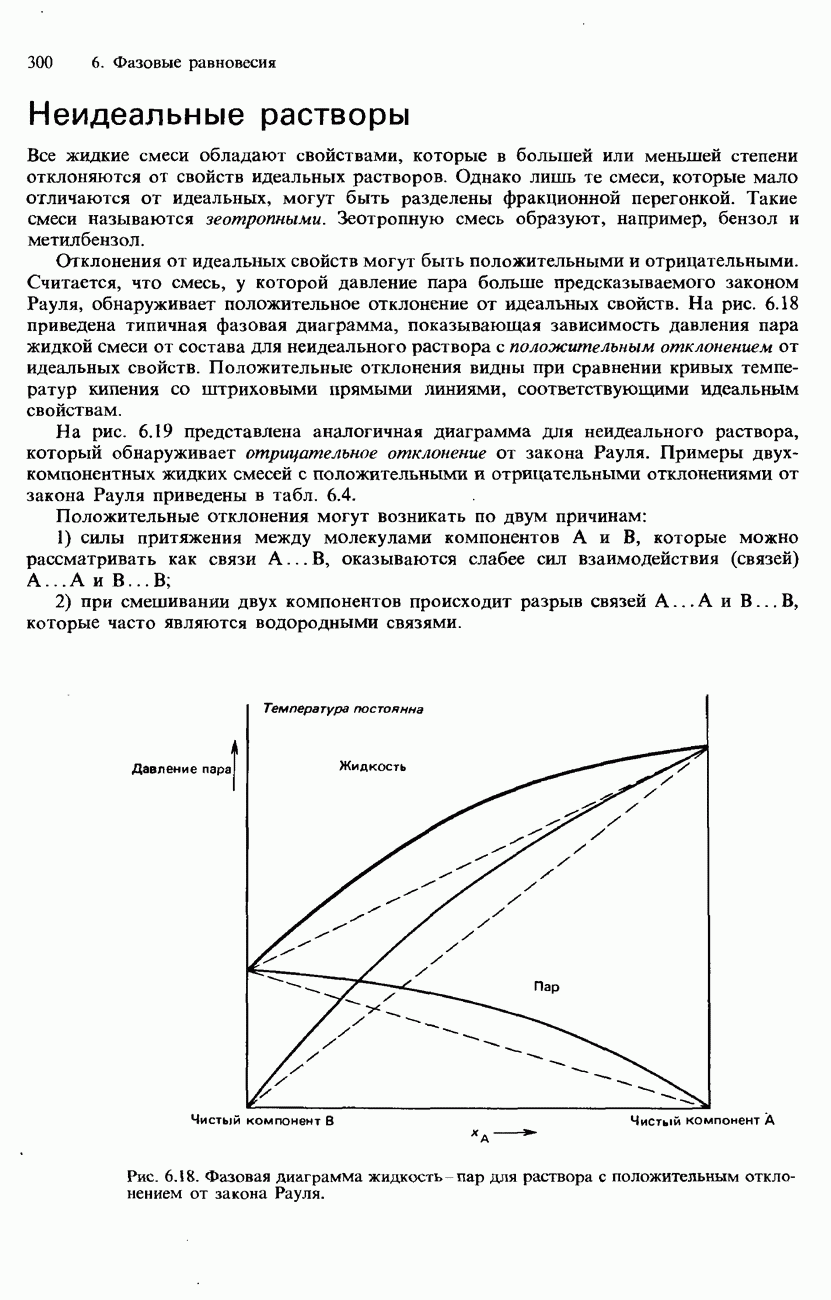
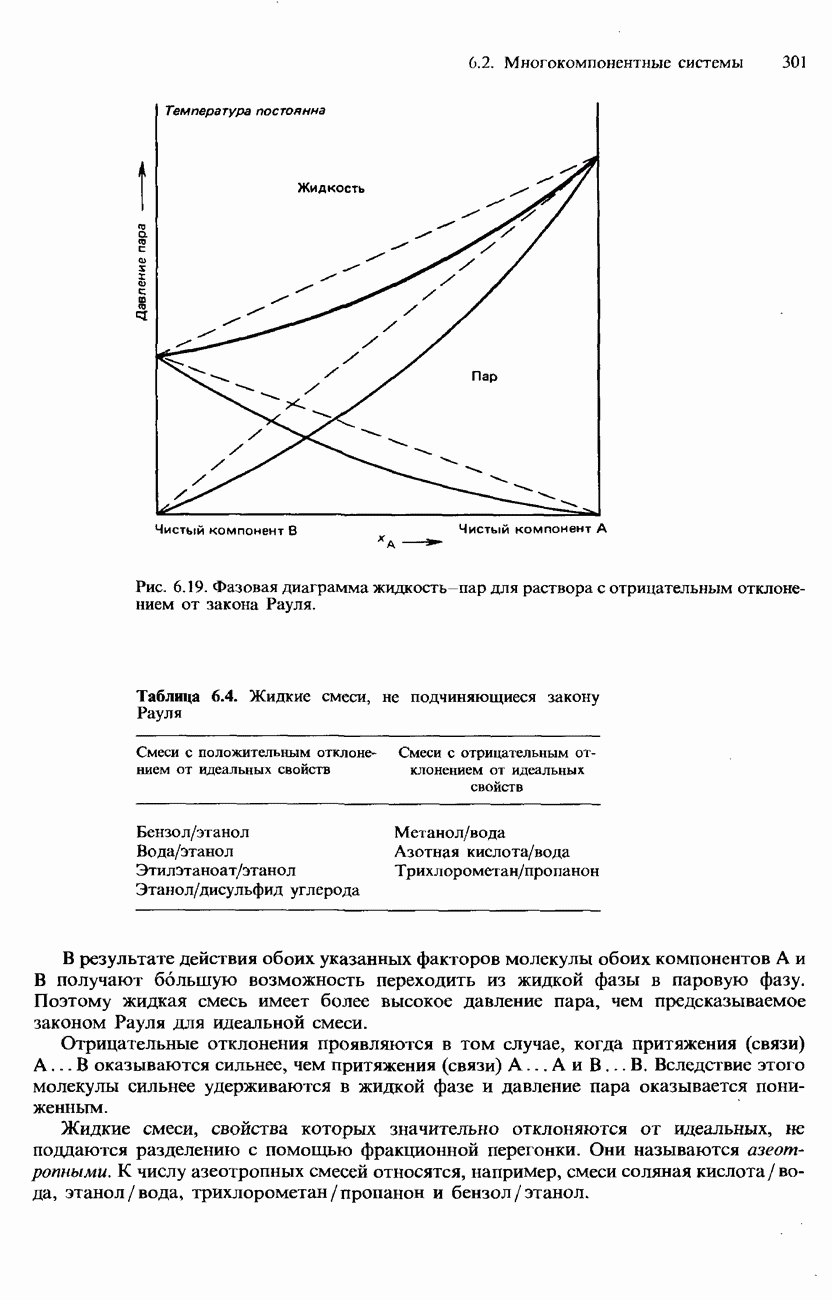
- Неидеальные растворы
- ЧАСТИЧНО СМЕШИВАЮЩИЕСЯ ЖИДКОСТИ
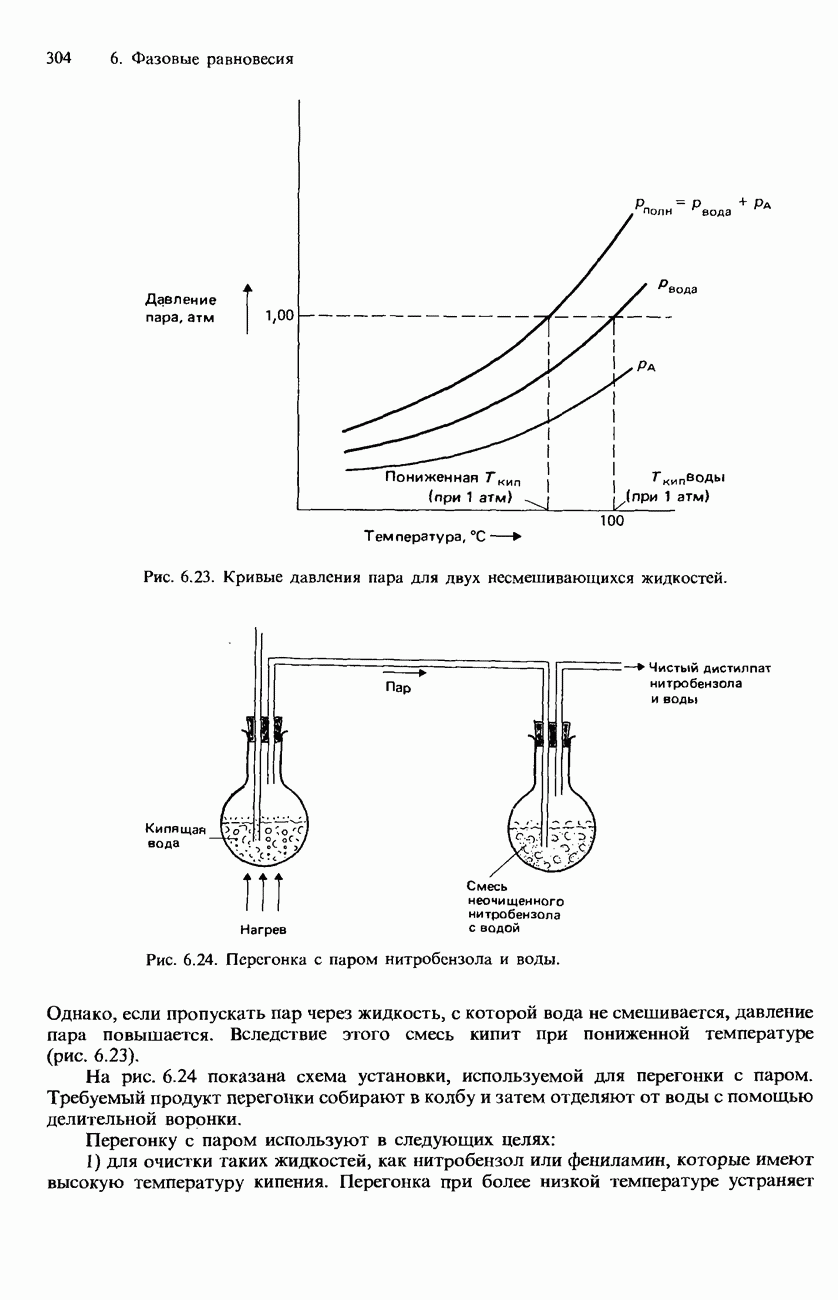
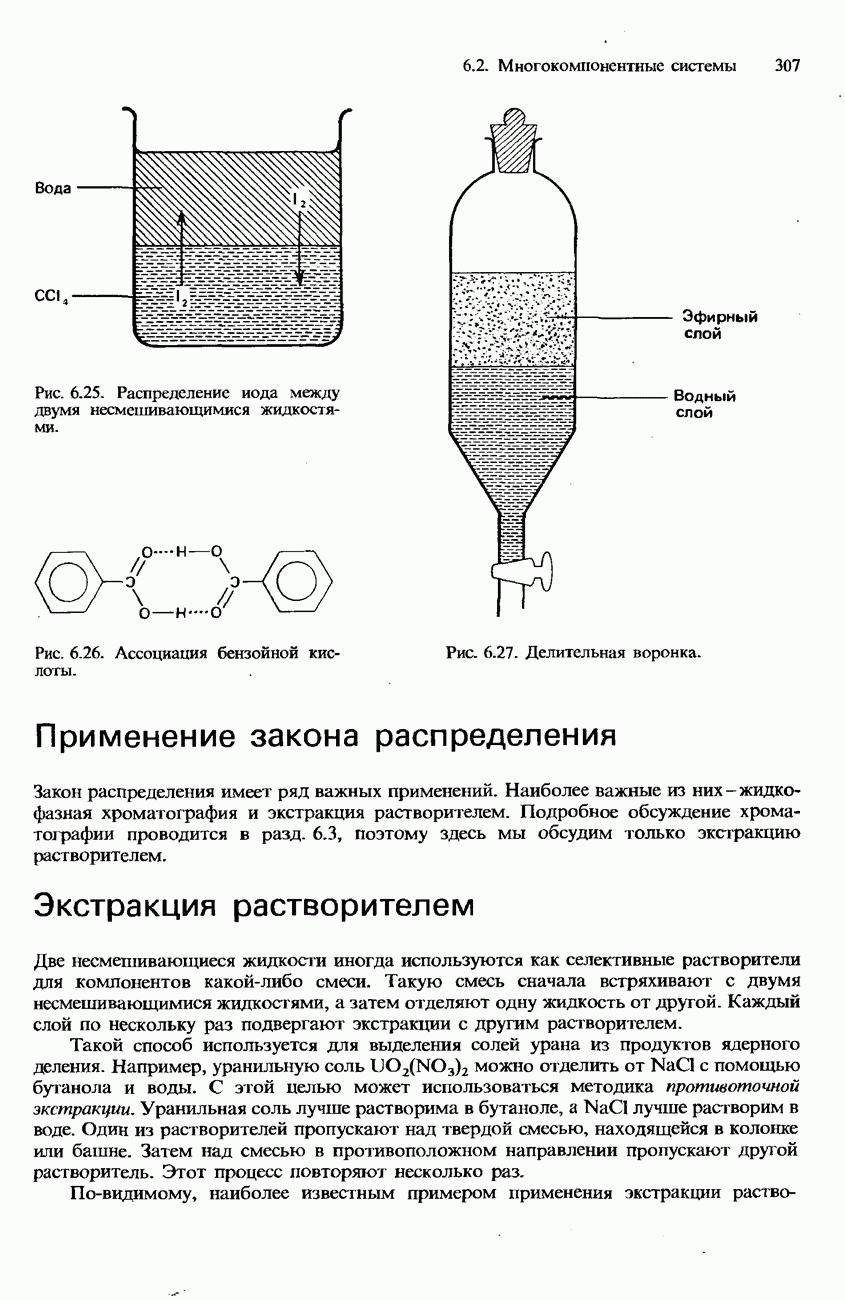
- НЕСМЕШИВАЮЩИЕСЯ ЖИДКОСТИ
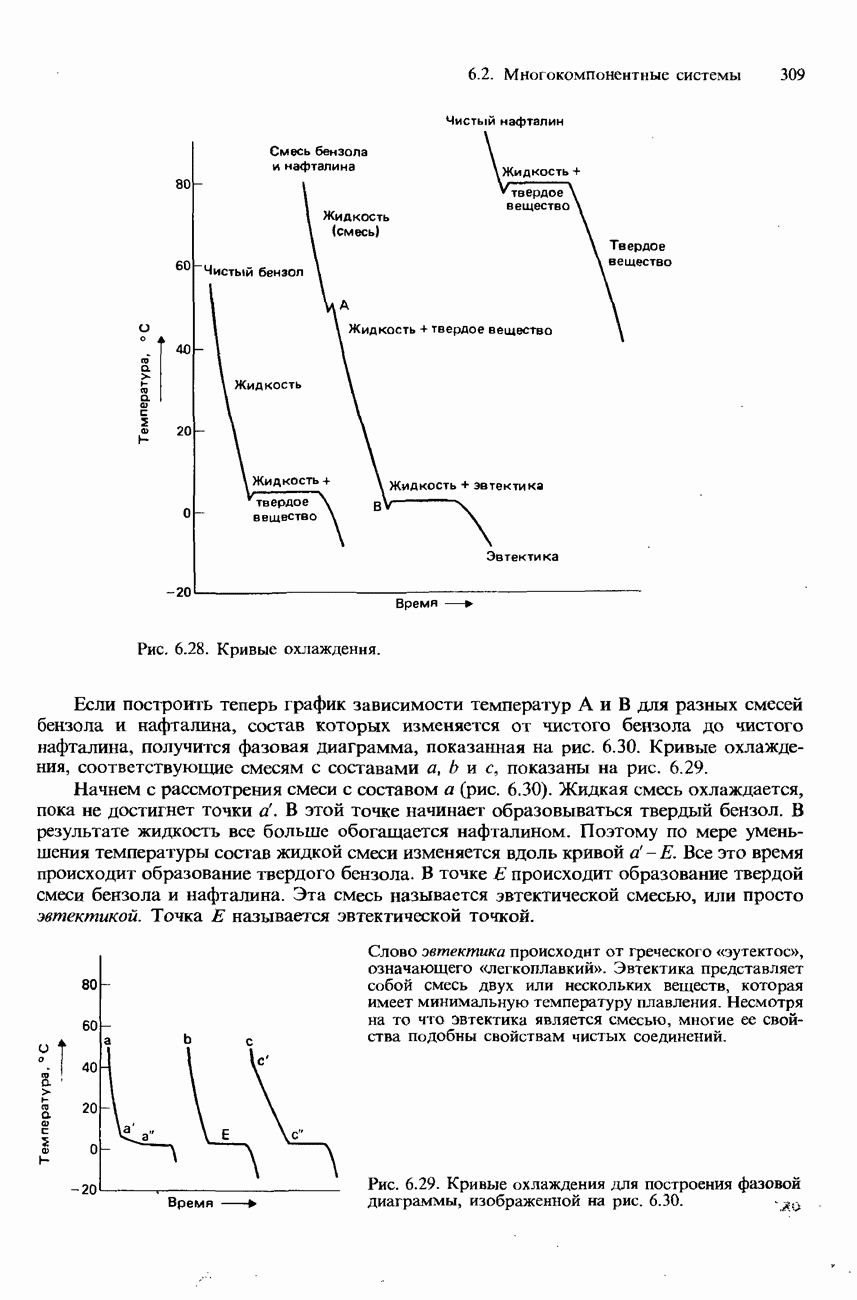
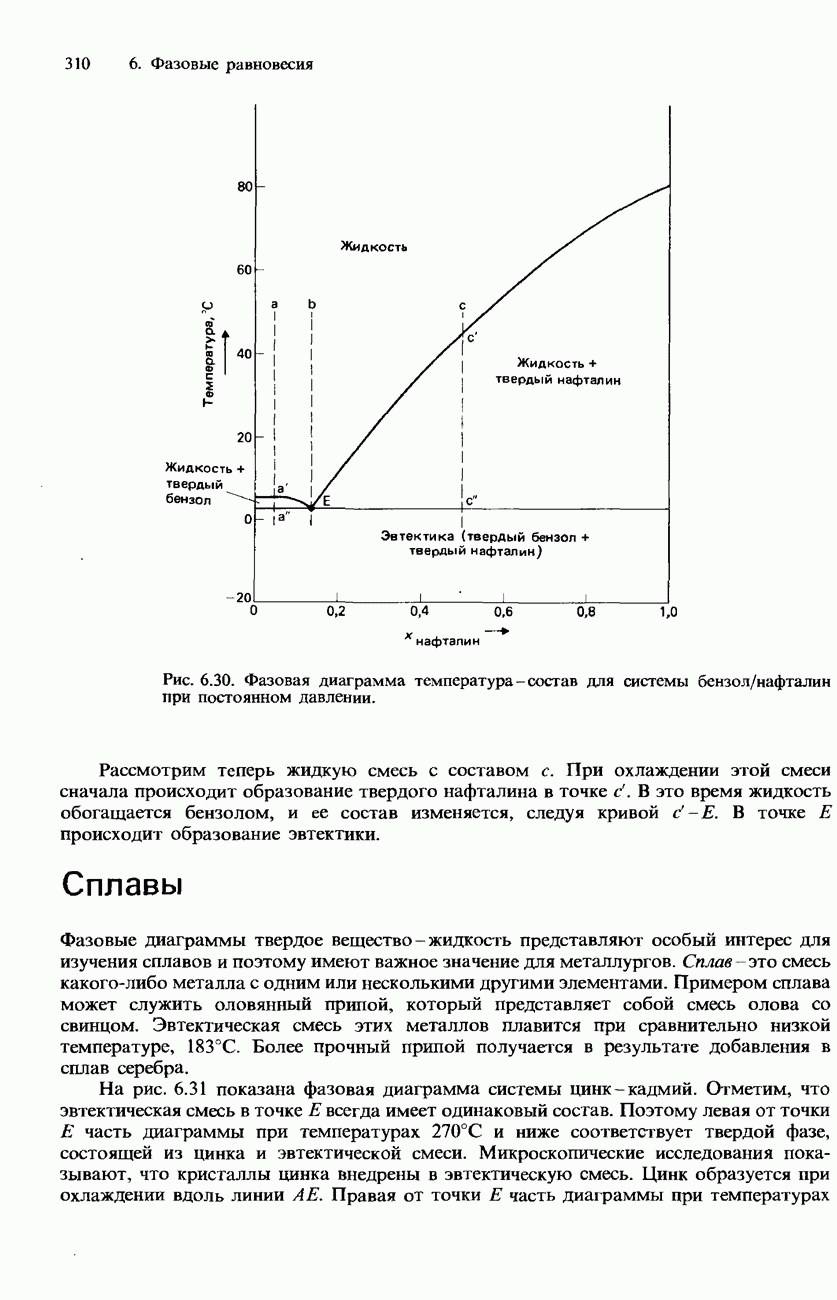
- РАВНОВЕСИЯ ТВЕРДОЕ ВЕЩЕСТВО-ЖИДКОСТЬ
- 6.3. Коллигативные свойства растворов. Коллоиды Хроматография
- КОЛЛОИДЫ
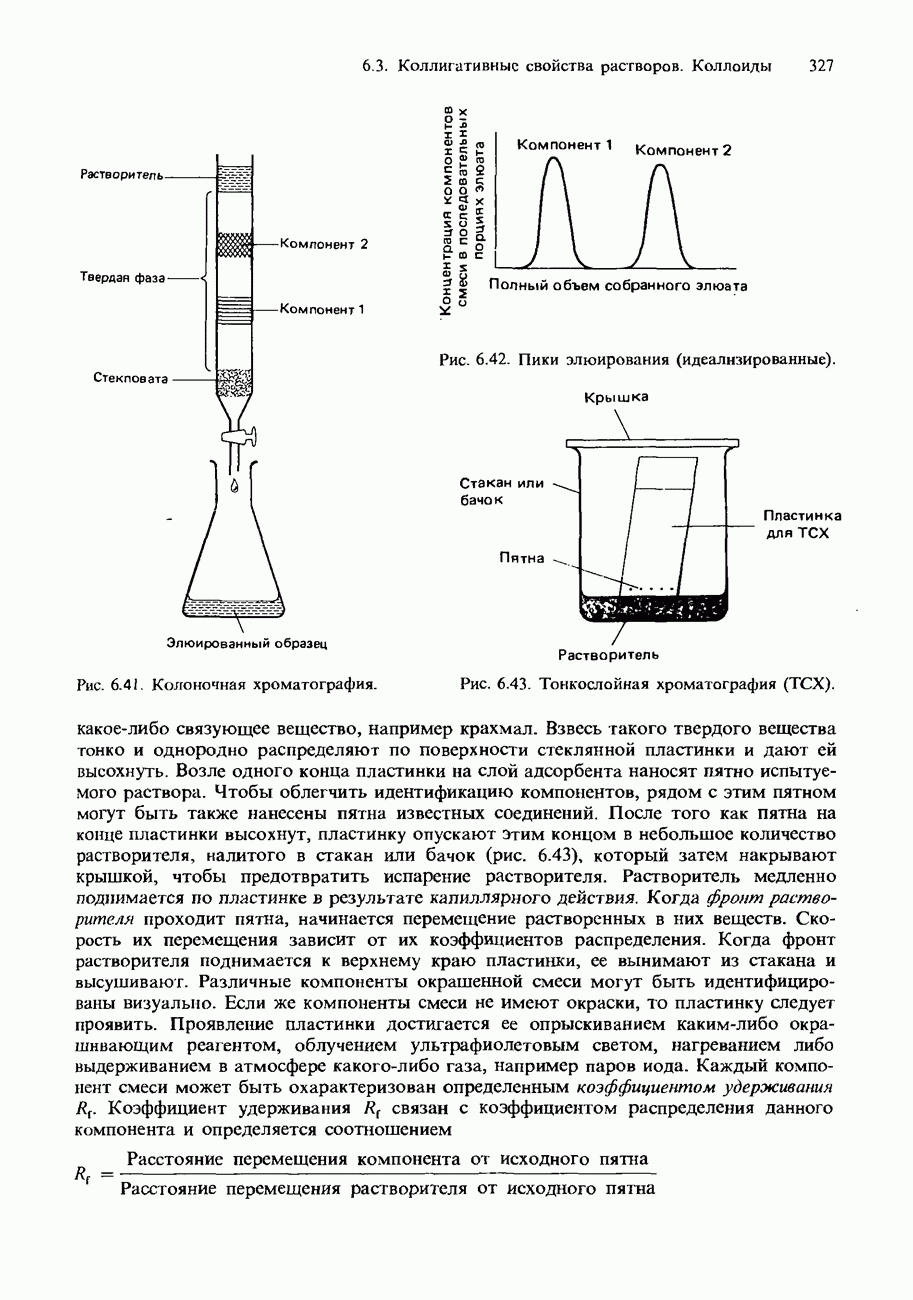
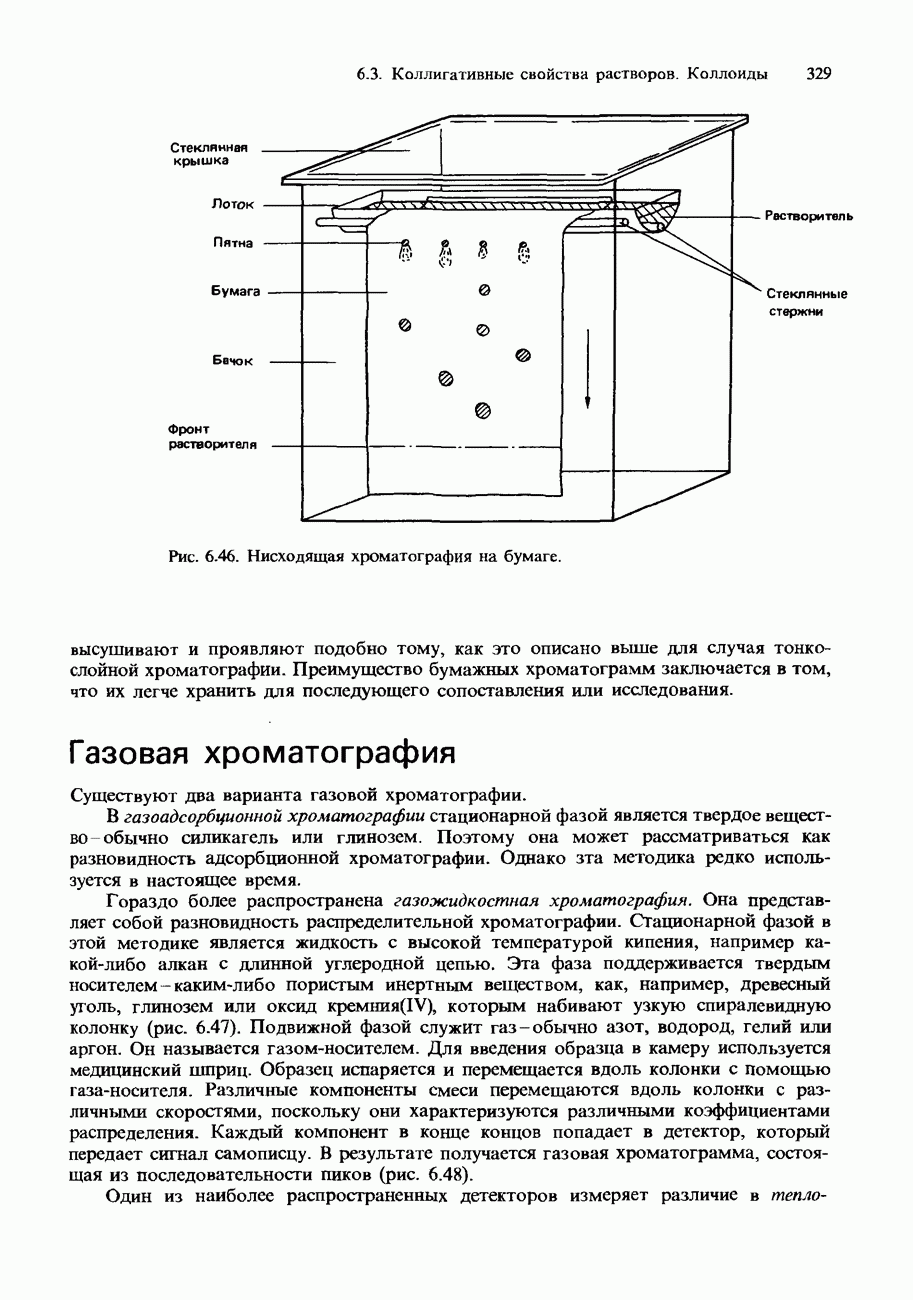
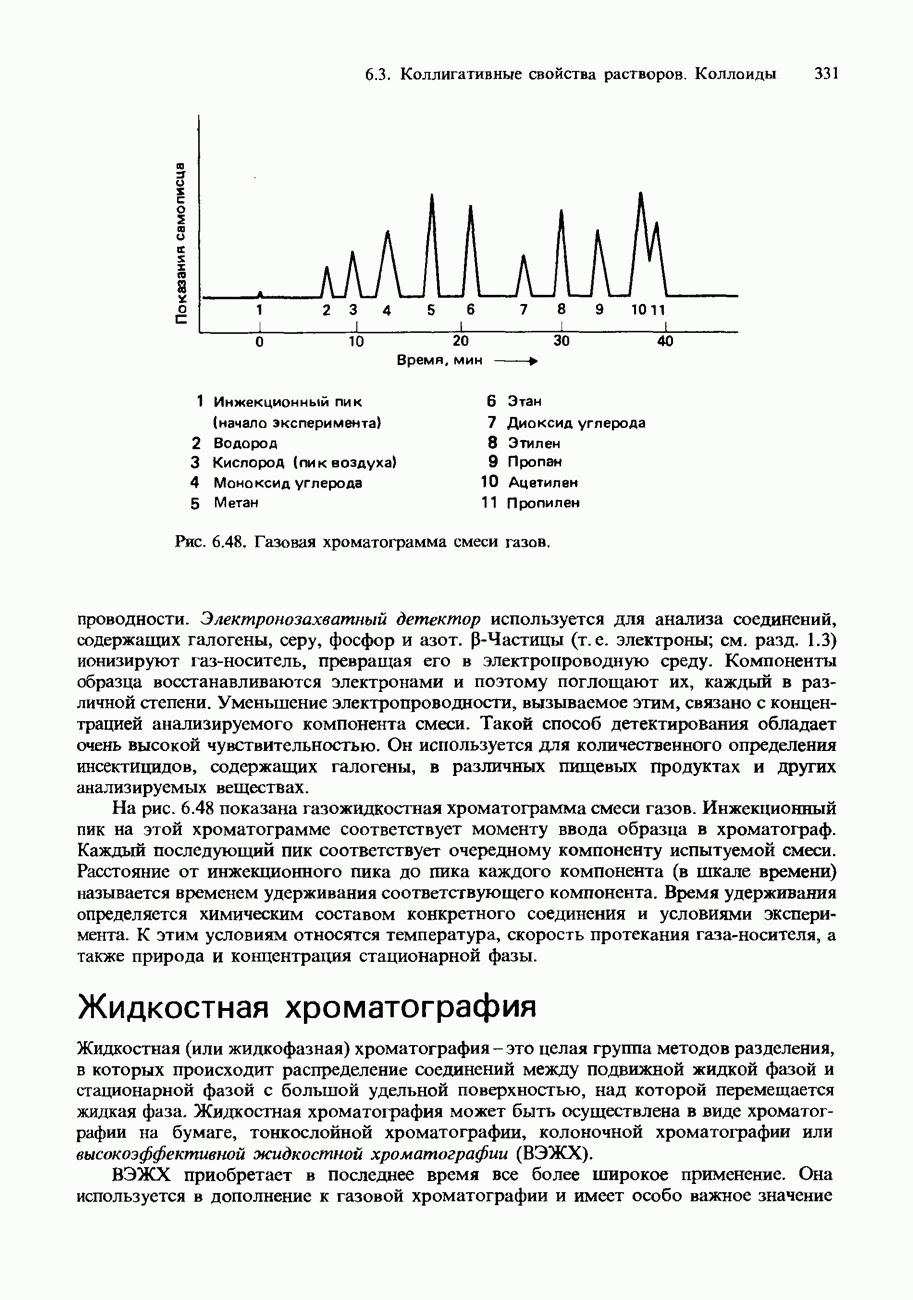
- ХРОМАТОГРАФИЯ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 7. ХИМИЧЕСКОЕ РАВНОВЕСИЕ
- 7.1. Константа равновесия
- ЗАКОН ДЕЙСТВУЮЩИХ МАСС
- ВЛИЯНИЕ УСЛОВИЙ ПРОТЕКАНИЯ РЕАКЦИИ НА ПОЛОЖЕНИЕ РАВНОВЕСИЯ
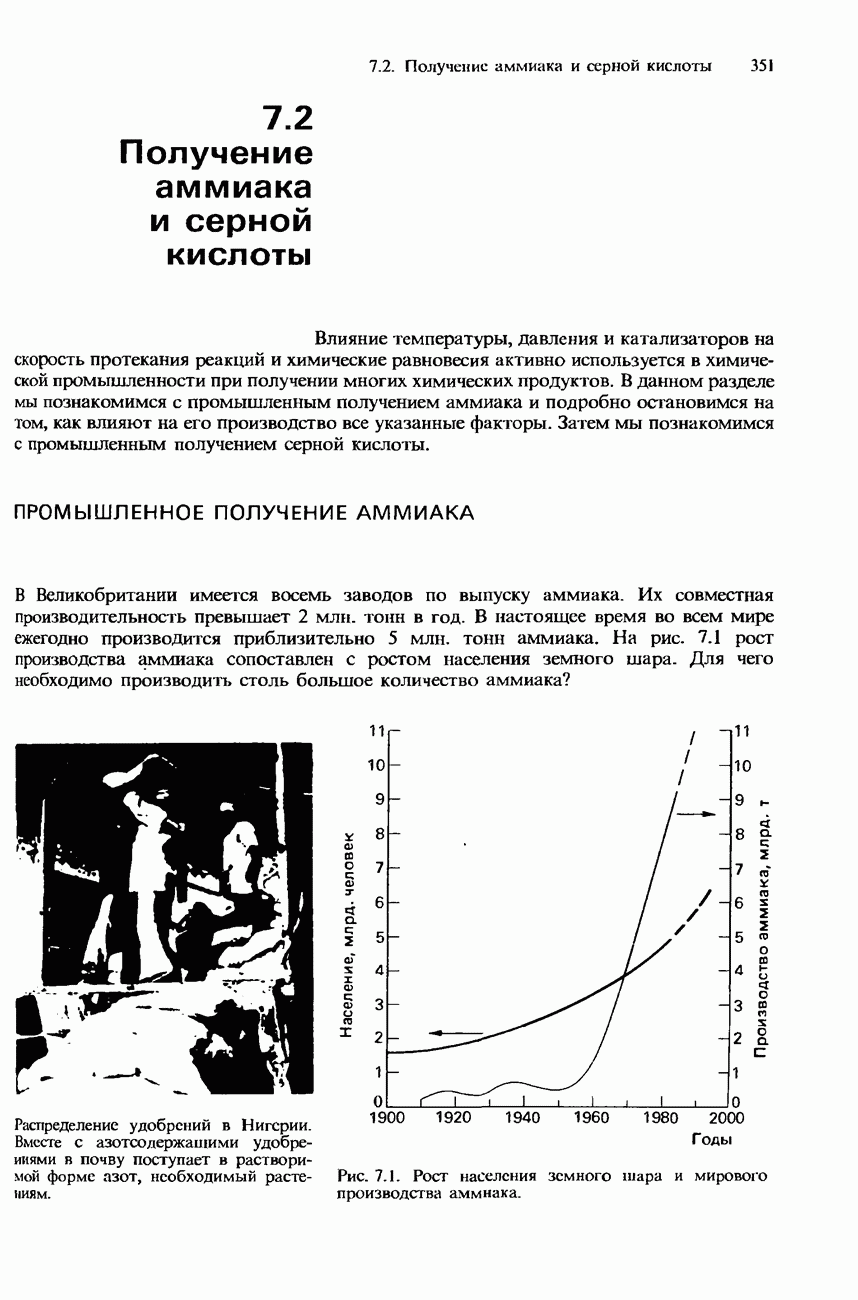
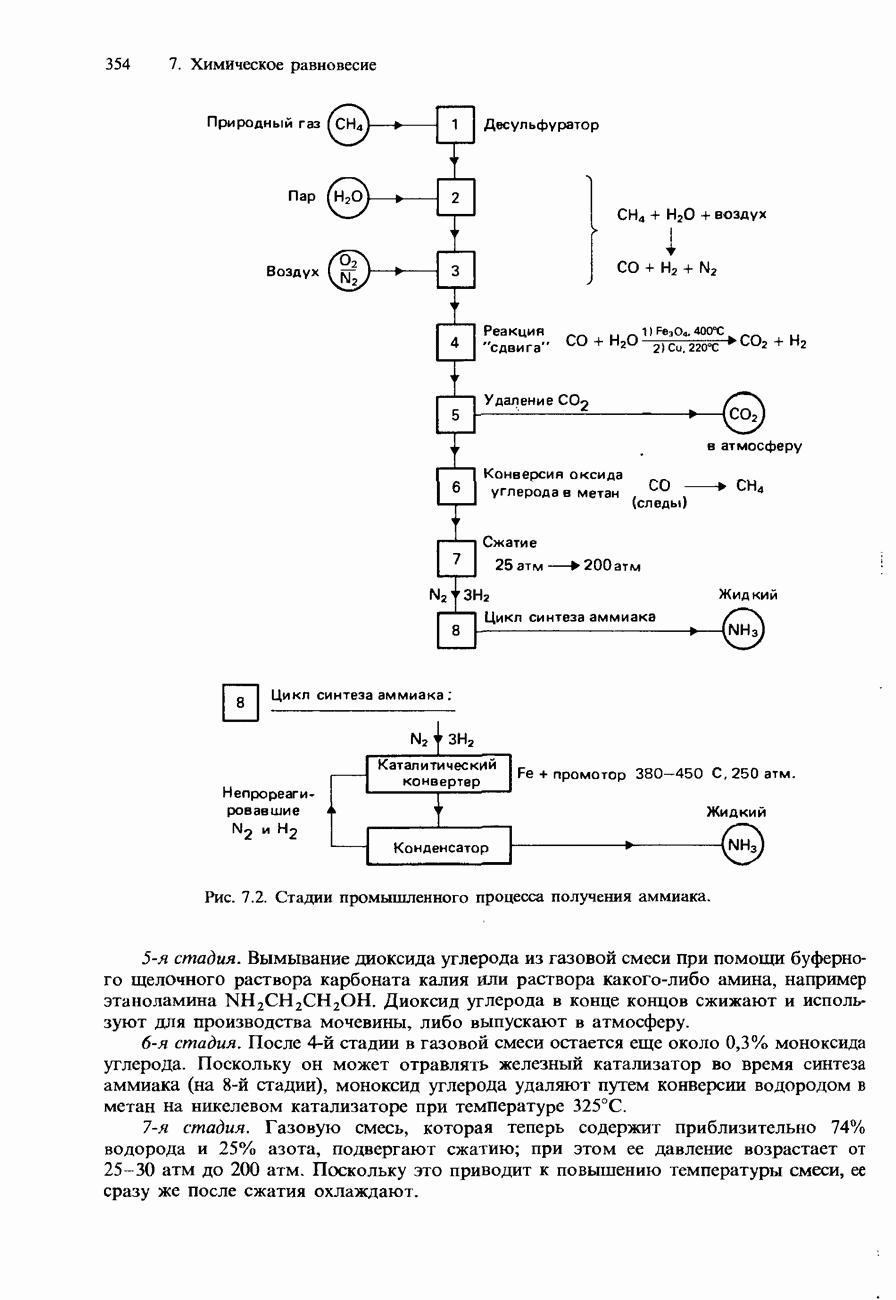
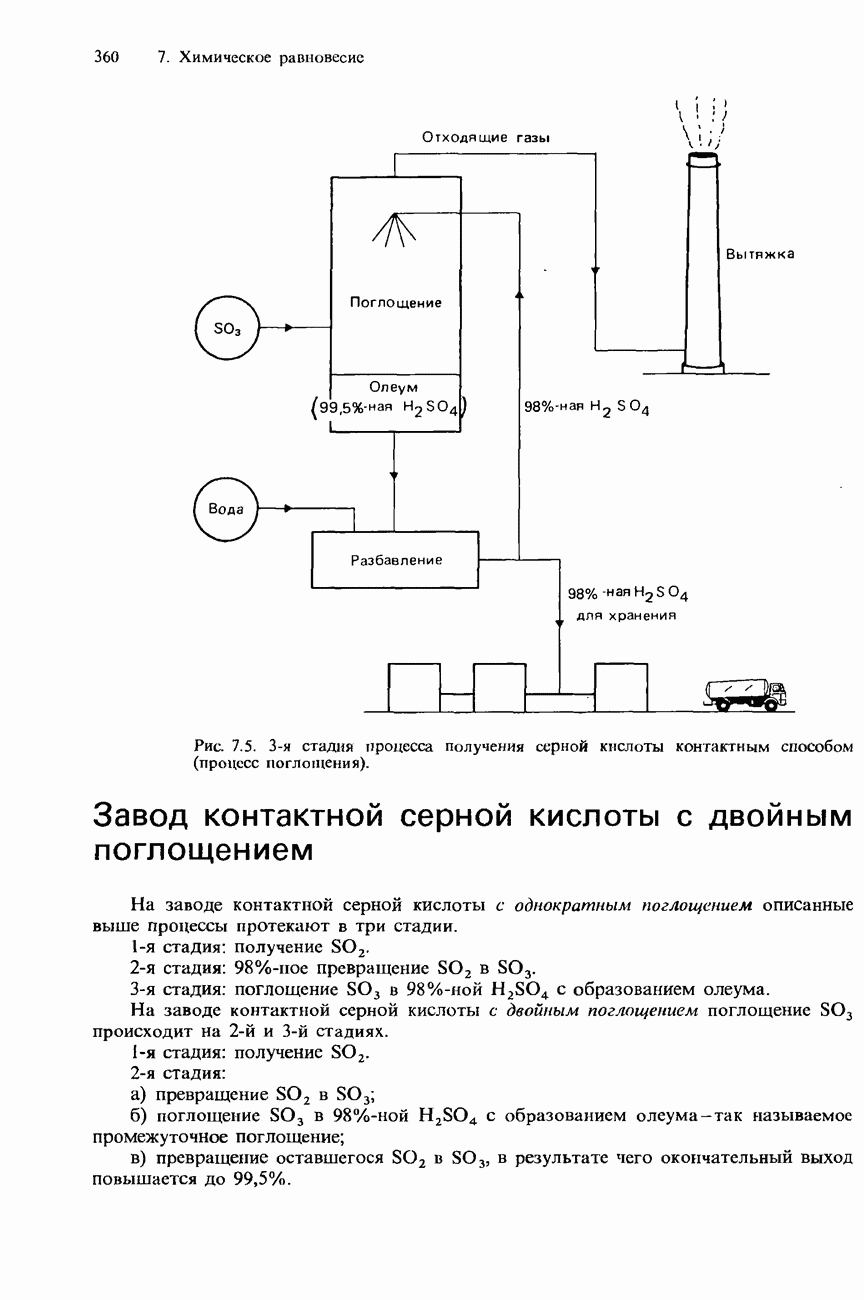
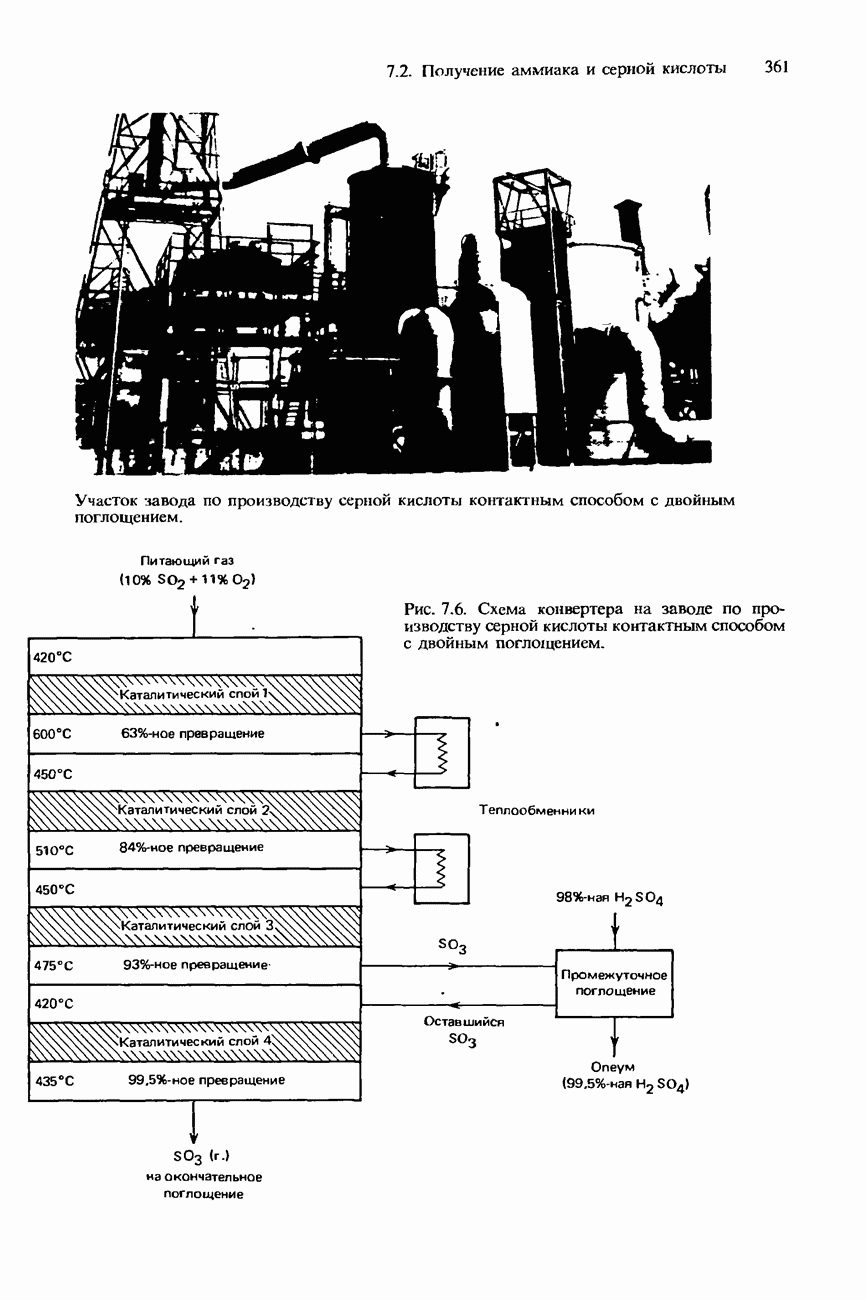
- 7.2. Получение аммиака и серной кислоты
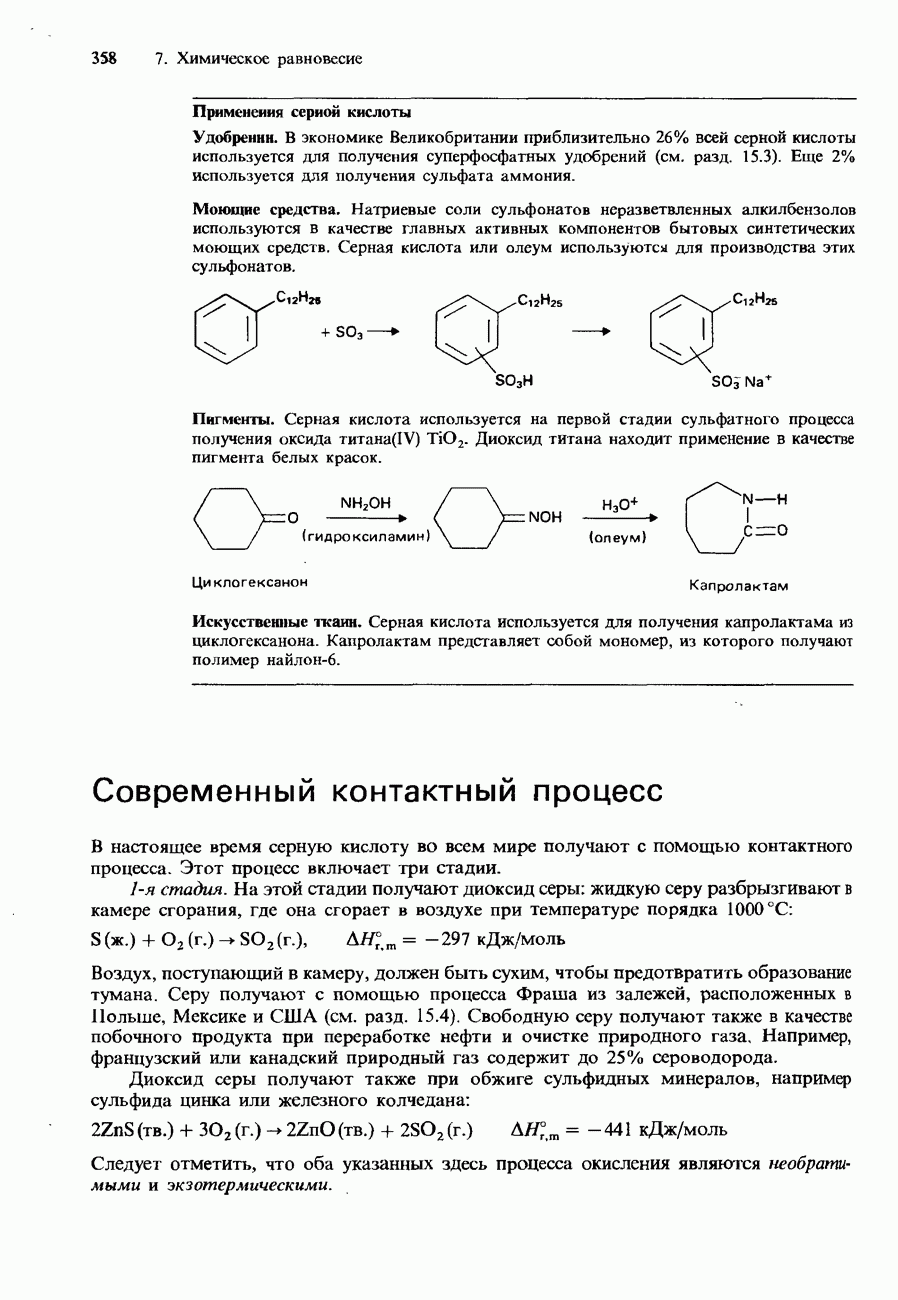
- ПРОМЫШЛЕННОЕ ПОЛУЧЕНИЕ СЕРНОЙ КИСЛОТЫ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 8. ИОНЫ
- 8.1. Кислоты и основания
- ЭЛЕКТРОЛИТЫ
- КИСЛОТЫ И ОСНОВАНИЯ
- КОНСТАНТЫ ДИССОЦИАЦИИ
- ВОДОРОДНЫЙ ПОКАЗАТЕЛЬ pH ШКАЛА ЕГО ЗНАЧЕНИЙ
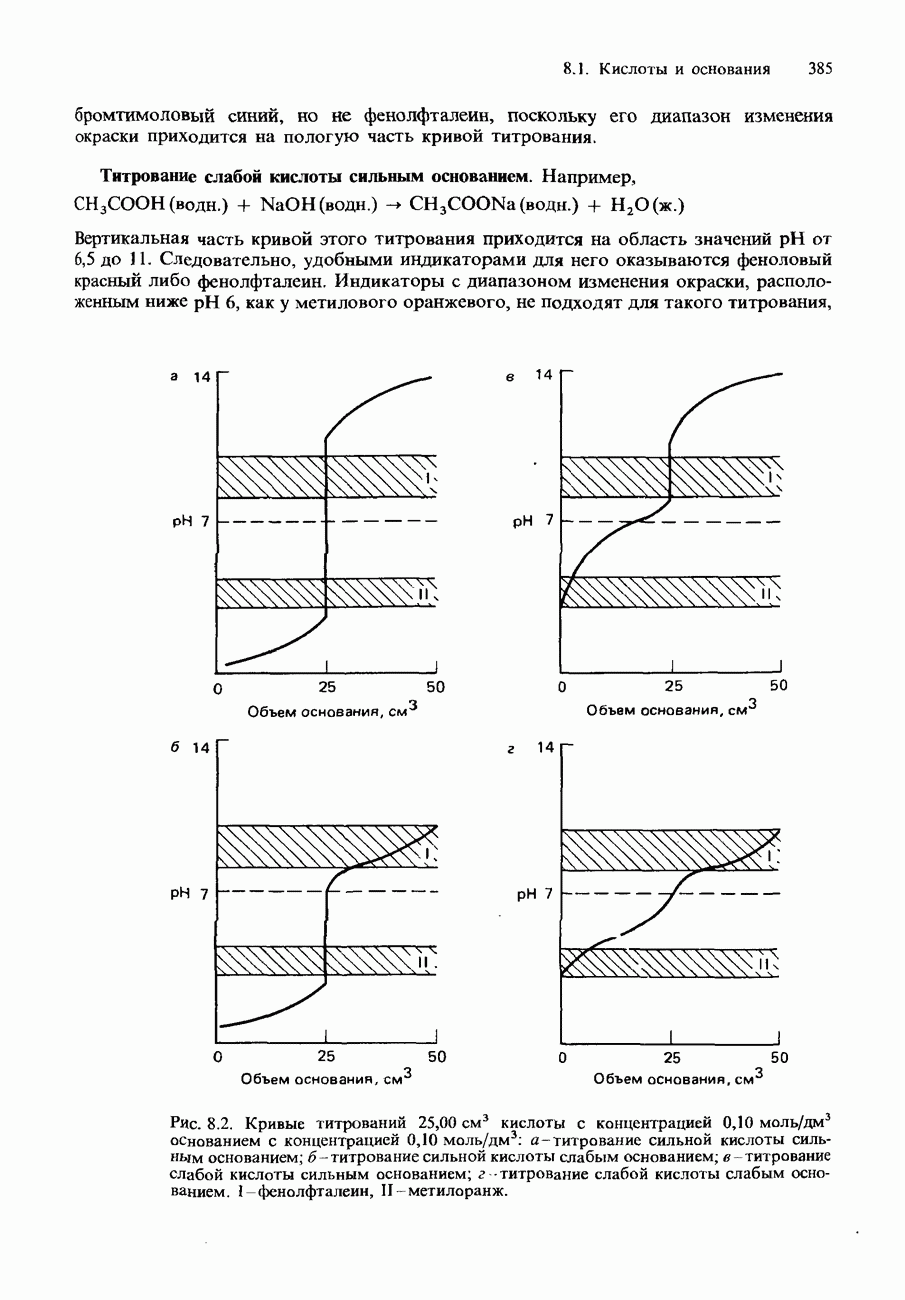
- КИСЛОТНО-ОСНОВНЫЕ ИНДИКАТОРЫ И ТИТРОВАНИЕ
- 8.2. Соли, растворимость и устойчивость
- БУФЕРНЫЕ РАСТВОРЫ
- РАСТВОРИМОСТЬ
- РАВНОВЕСИЯ С УЧАСТИЕМ КОМПЛЕКСНЫХ ИОНОВ
- ИОННЫЙ ОБМЕН
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 9. ХИМИЧЕСКАЯ КИНЕТИКА
- 9.1. Скорость химической реакции
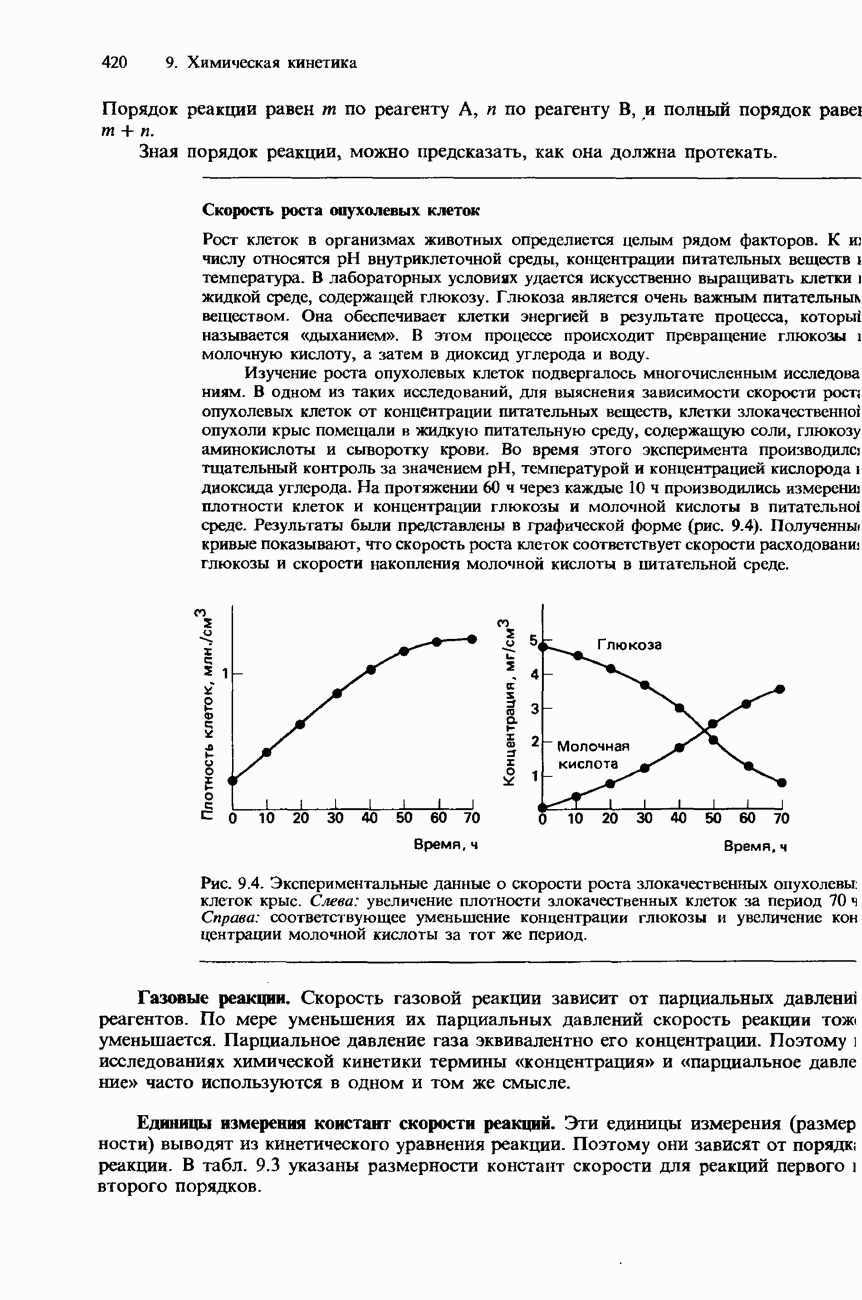
- МЕТОДЫ ИЗМЕРЕНИЯ СКОРОСТИ РЕАКЦИЙ
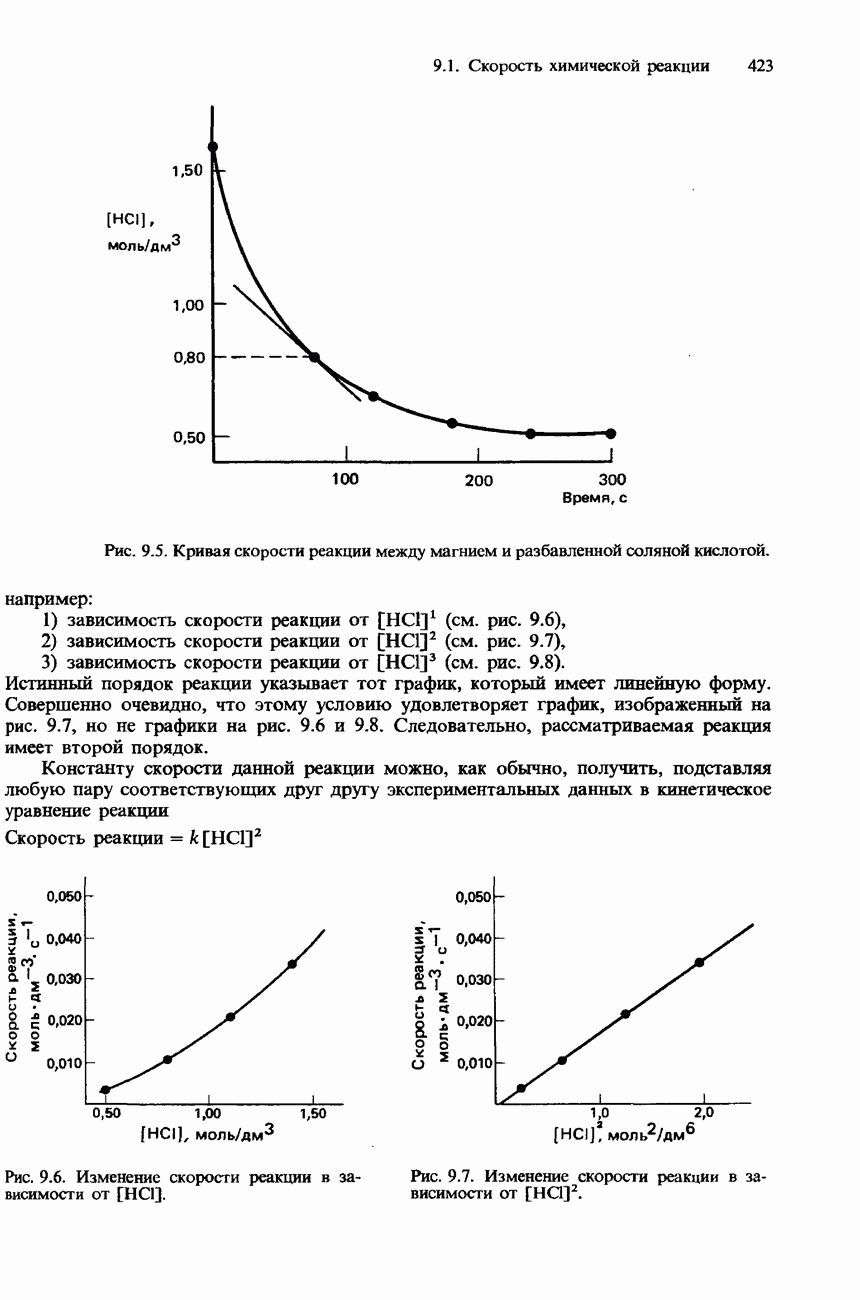
- СКОРОСТЬ РЕАКЦИИ И КОНЦЕНТРАЦИИ РЕАГЕНТОВ
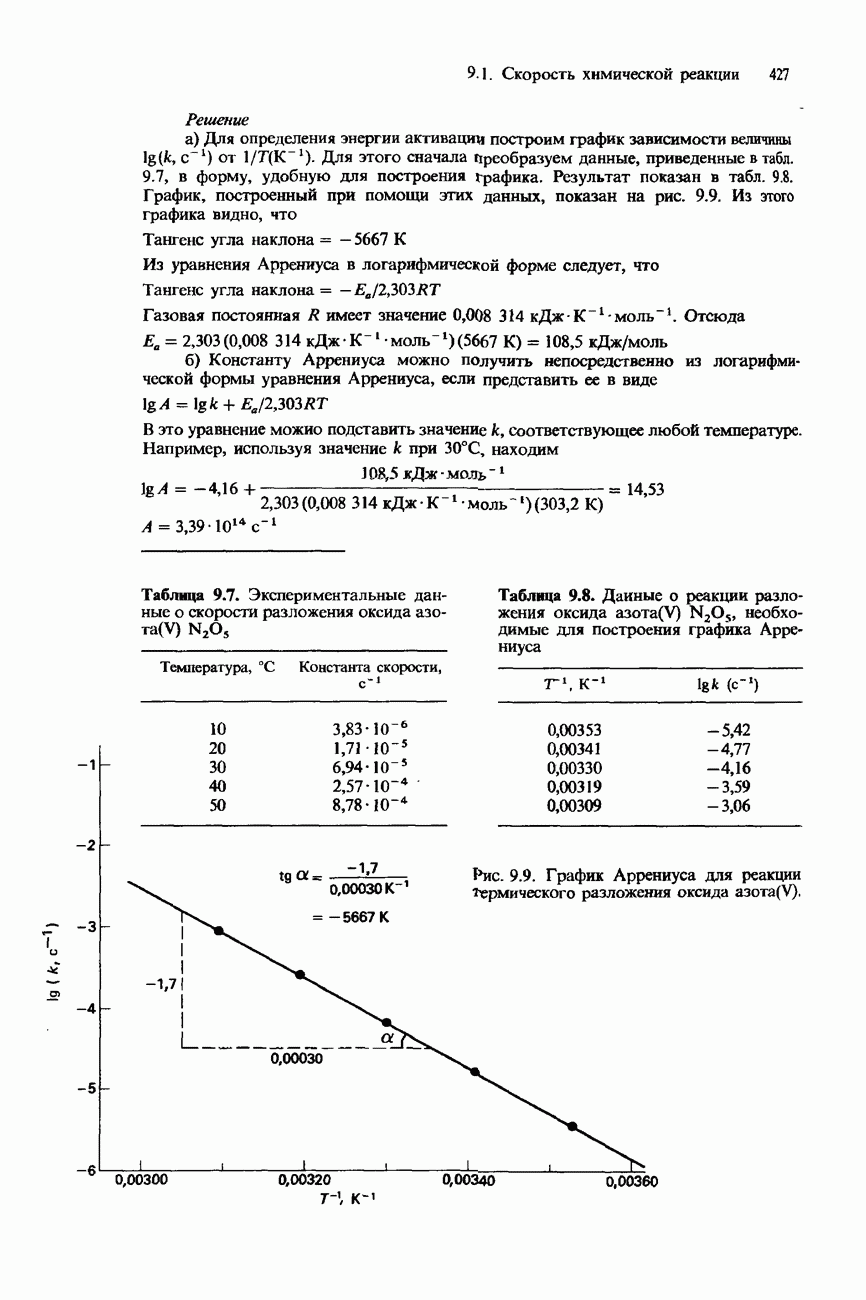
- ЗАВИСИМОСТЬ КОНСТАНТЫ СКОРОСТИ ОТ ТЕМПЕРАТУРЫ УРАВНЕНИЕ АРРЕНИУСА
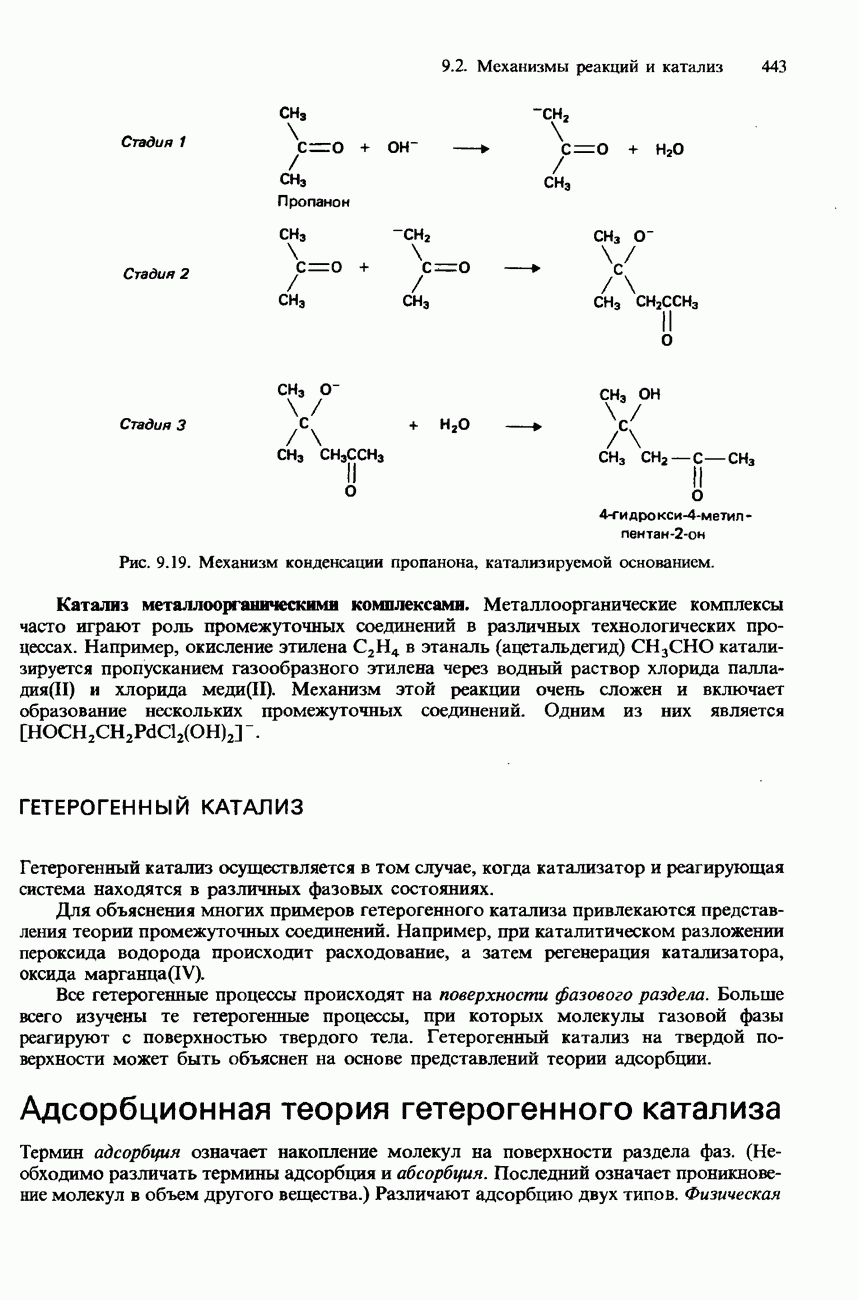
- 9.2. Механизмы реакций и катализ
- ТЕОРИЯ СТОЛКНОВЕНИЙ
- ТЕОРИЯ ПЕРЕХОДНОГО СОСТОЯНИЯ
- ЦЕПНЫЕ РЕАКЦИИ
- КАТАЛИЗ
- ТИПЫ КАТАЛИЗАТОРОВ
- ГОМОГЕННЫЙ КАТАЛИЗ
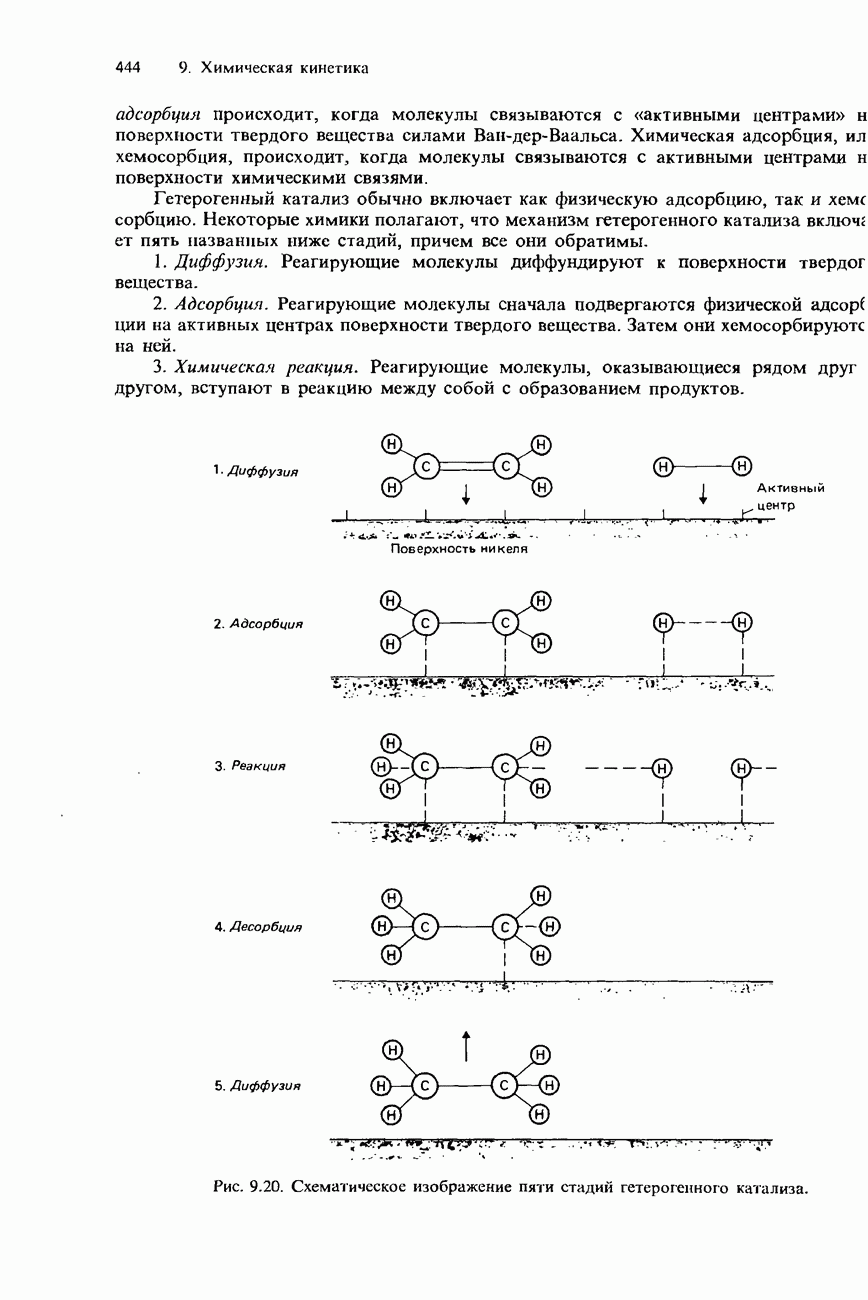
- ГЕТЕРОГЕННЫЙ КАТАЛИЗ
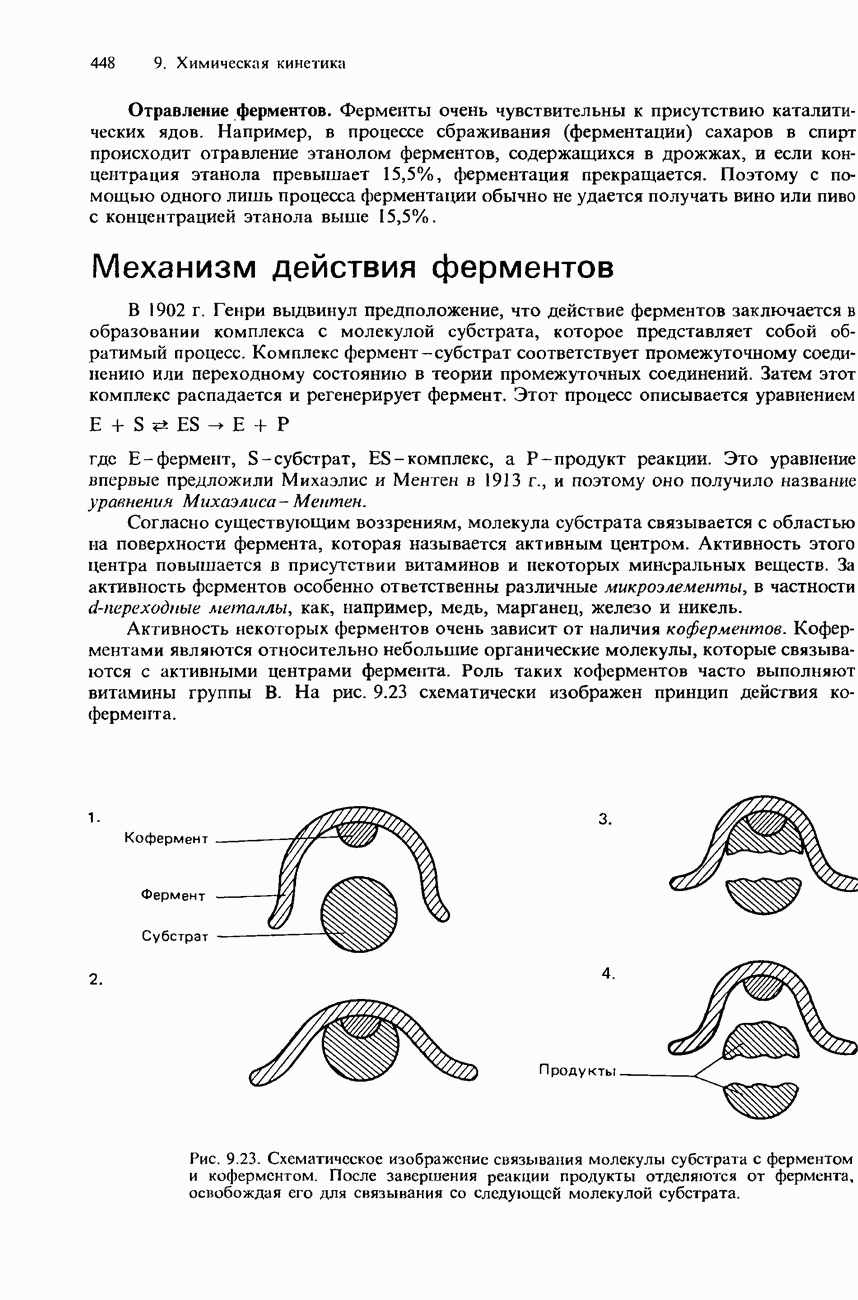
- ФЕРМЕНТАТИВНЫЙ КАТАЛИЗ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ
- 10. ЭЛЕКТРОХИМИЯ
- 10.1. Электропроводность
- ПРОВОДНИКИ ЭЛЕКТРИЧЕСКОГО ТОКА И ЭЛЕКТРОПРОВОДНОСТЬ
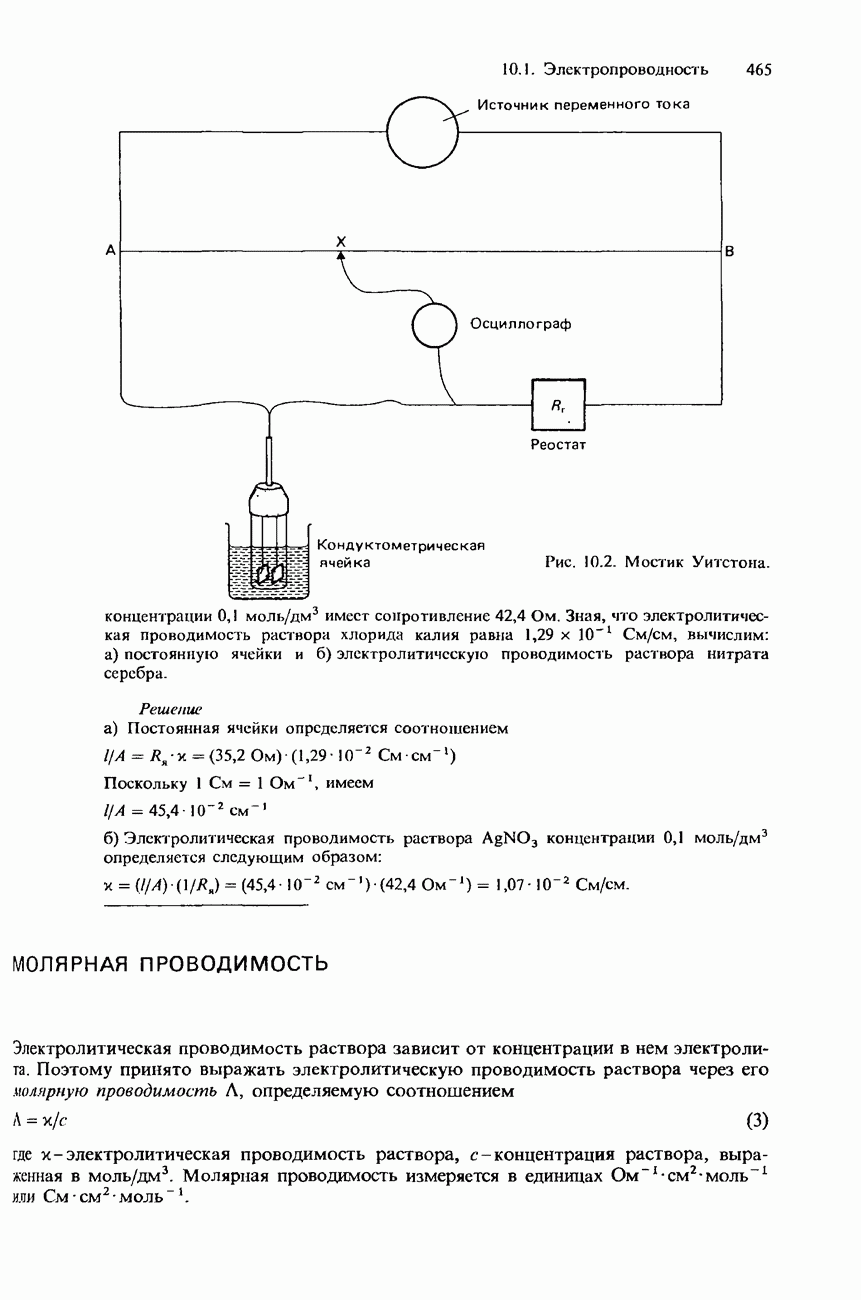
- МОЛЯРНАЯ ПРОВОДИМОСТЬ
- КОНДУКТОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- 10.2. Окислительно-восстановительные процессы
- ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫЕ РЕАКЦИИ
- ОПРЕДЕЛЕНИЕ СТЕХИОМЕТРИЧЕСКИХ КОЭФФИЦИЕНТОВ
- СТЕПЕНЬ ОКИСЛЕНИЯ
- ОКИСЛИТЕЛИ
- ВОССТАНОВИТЕЛИ
- ОКИСЛИТЕЛИ И ВОССТАНОВИТЕЛИ
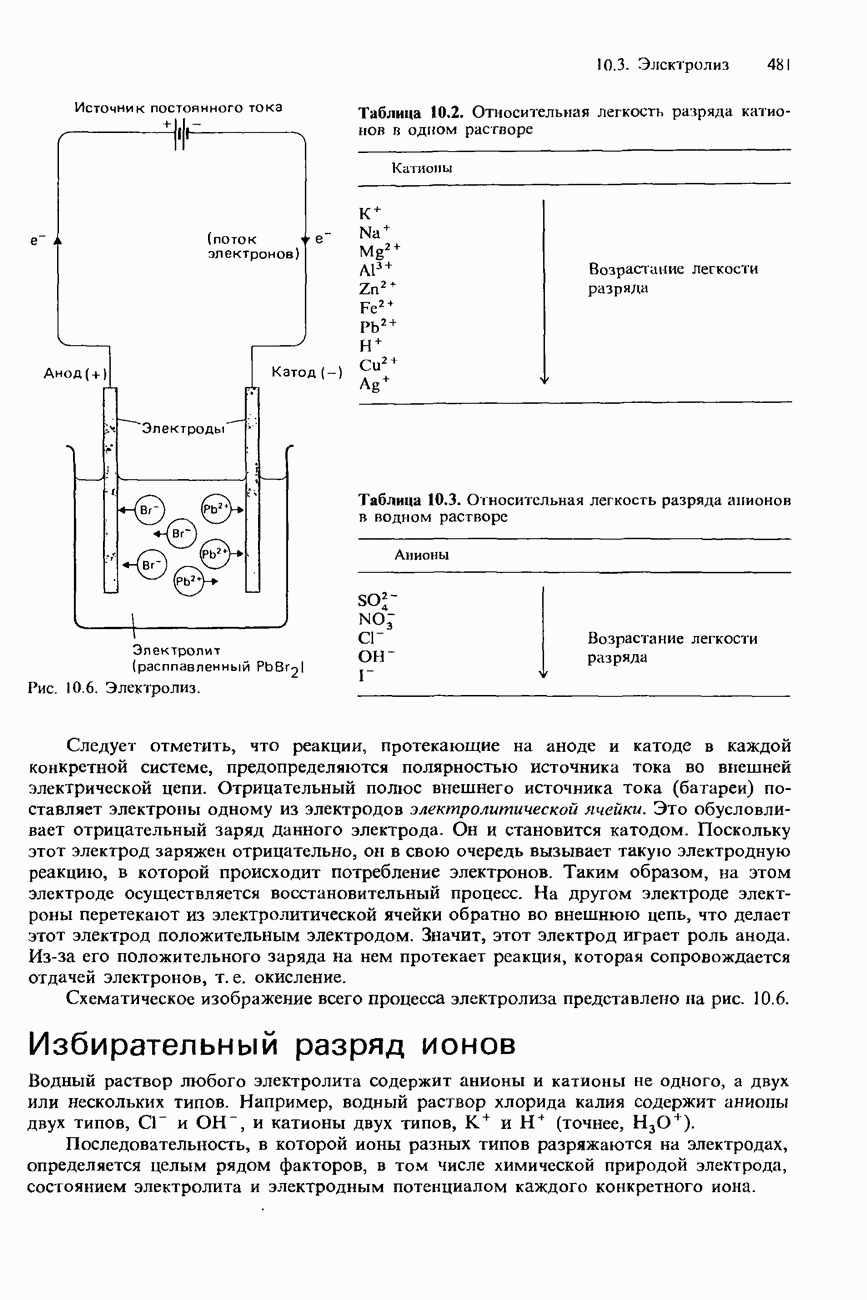
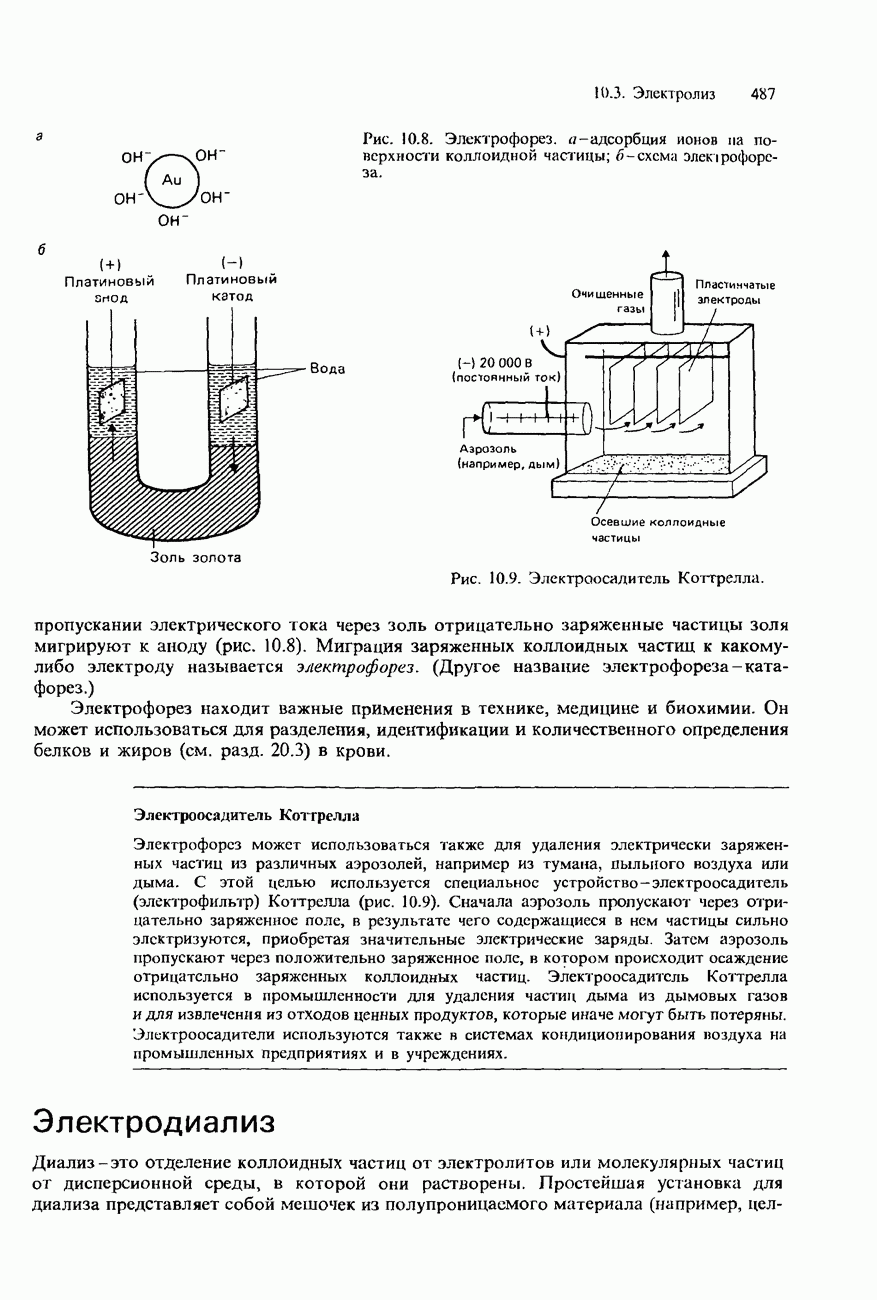
- 10.3. Электролиз
- ЗАКОНЫ ЭЛЕКТРОЛИЗА ФАРАДЕЯ
- ПРОМЫШЛЕННЫЕ ПРИМЕНЕНИЯ ЭЛЕКТРОЛИЗА
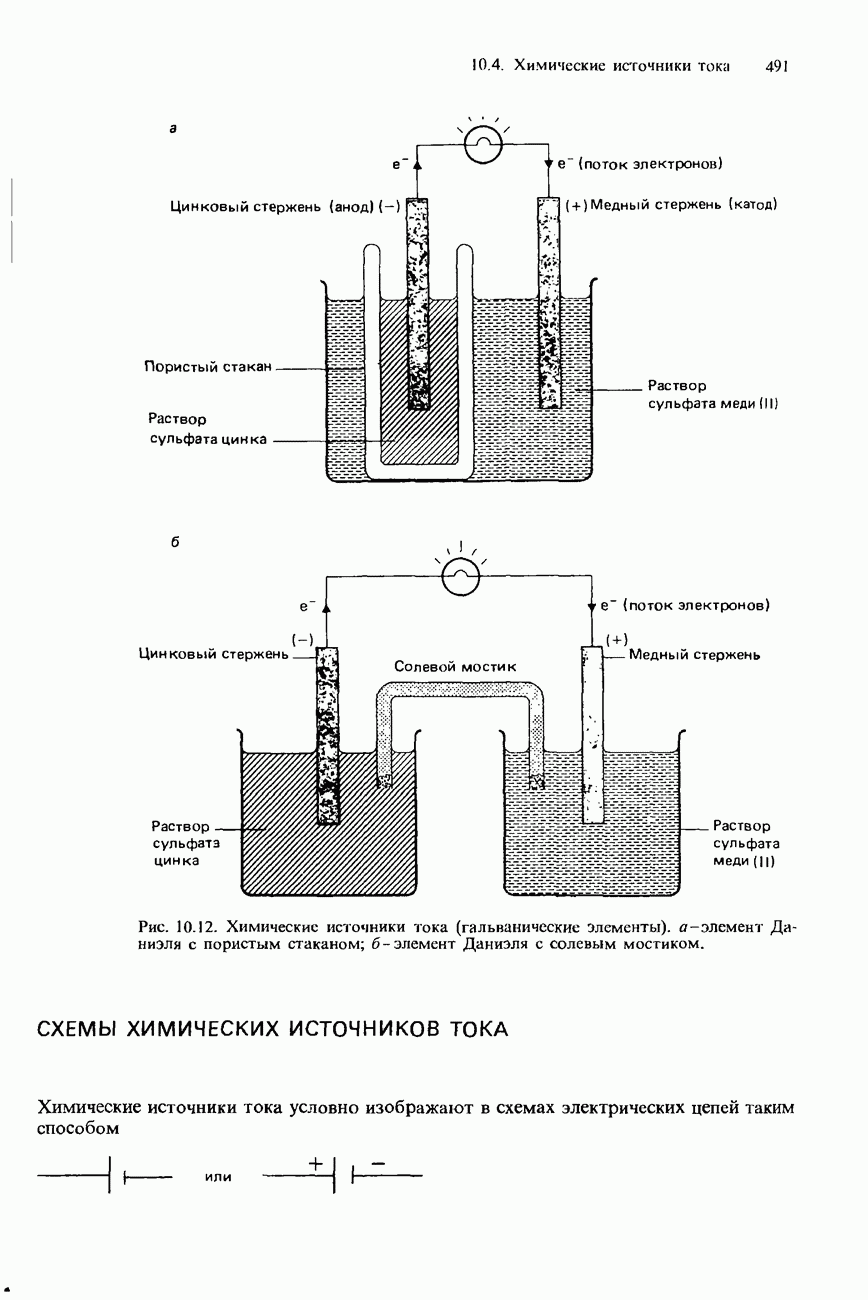
- 10.4. Химические источники тока
- СХЕМЫ ХИМИЧЕСКИХ ИСТОЧНИКОВ ТОКА
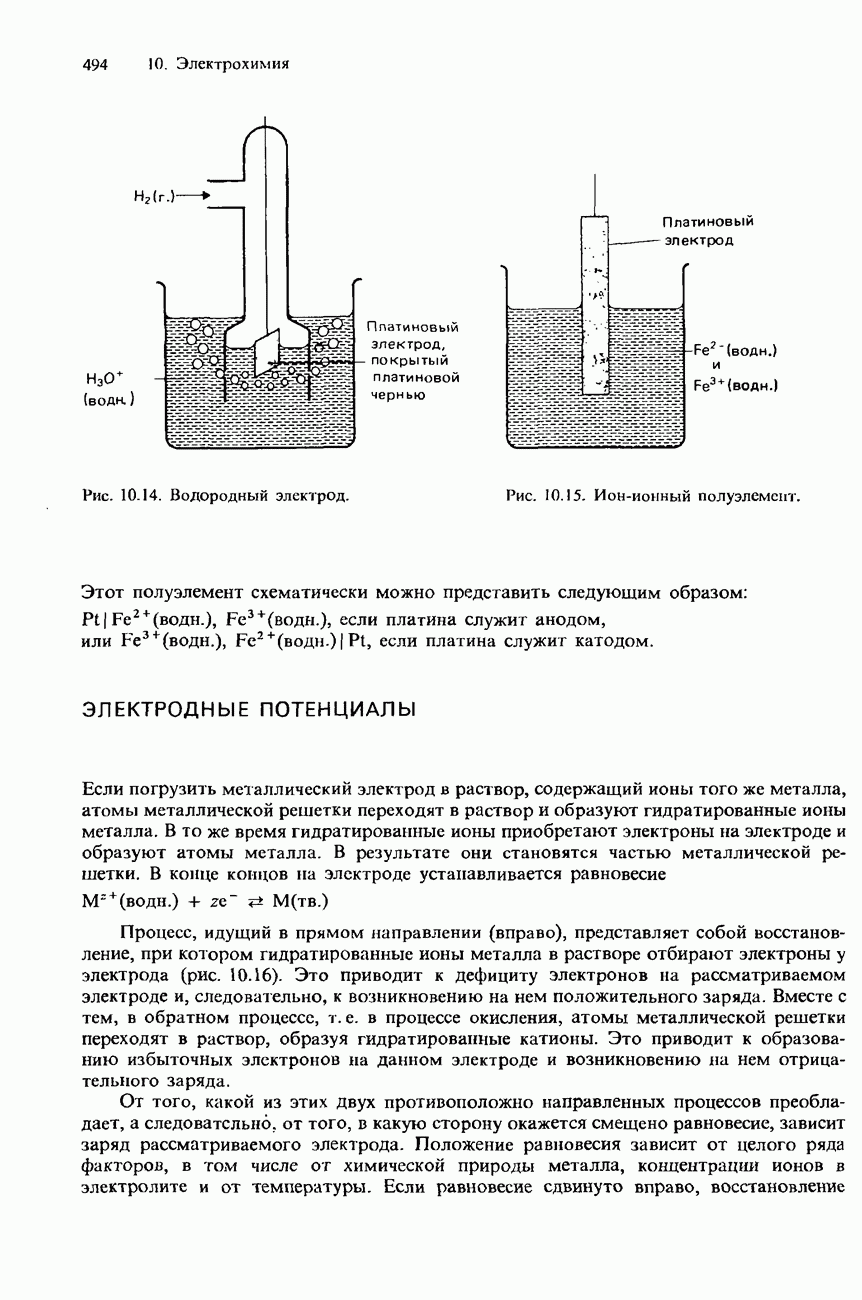
- ТИПЫ ПОЛУЭЛЕМЕНТОВ
- ЭЛЕКТРОДНЫЕ ПОТЕНЦИАЛЫ
- ЭЛЕКТРОДВИЖУЩАЯ СИЛА ХИМИЧЕСКИХ ИСТОЧНИКОВ ТОКА
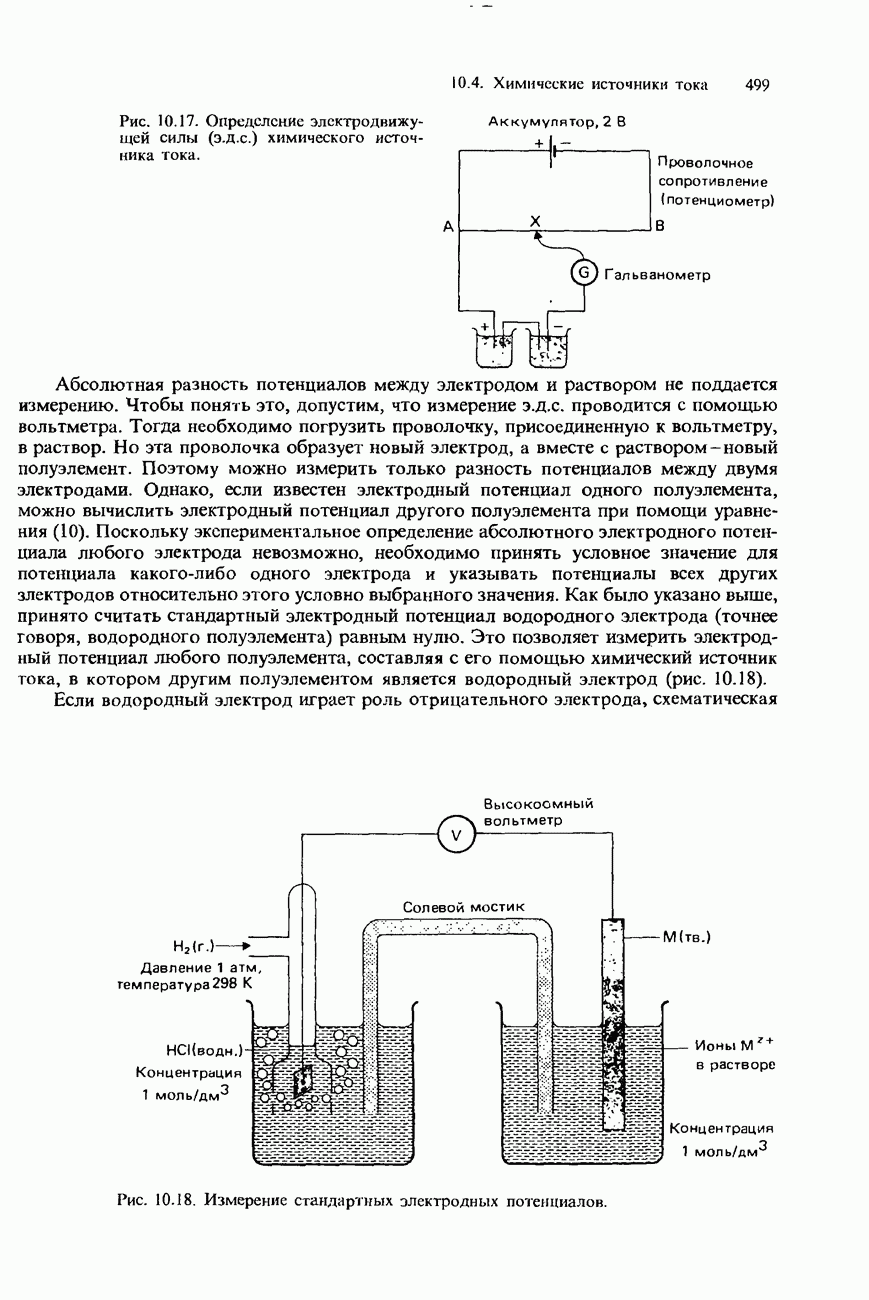
- ИЗМЕРЕНИЕ Э.Д.С. ХИМИЧЕСКИХ ИСТОЧНИКОВ ТОКА И ЭЛЕКТРОДНЫХ ПОТЕНЦИАЛОВ
- 10.5. Применения электрохимии
- ВЫЧИСЛЕНИЕ КОНСТАНТ РАВНОВЕСИЯ ДЛЯ ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫХ РЕАКЦИЙ
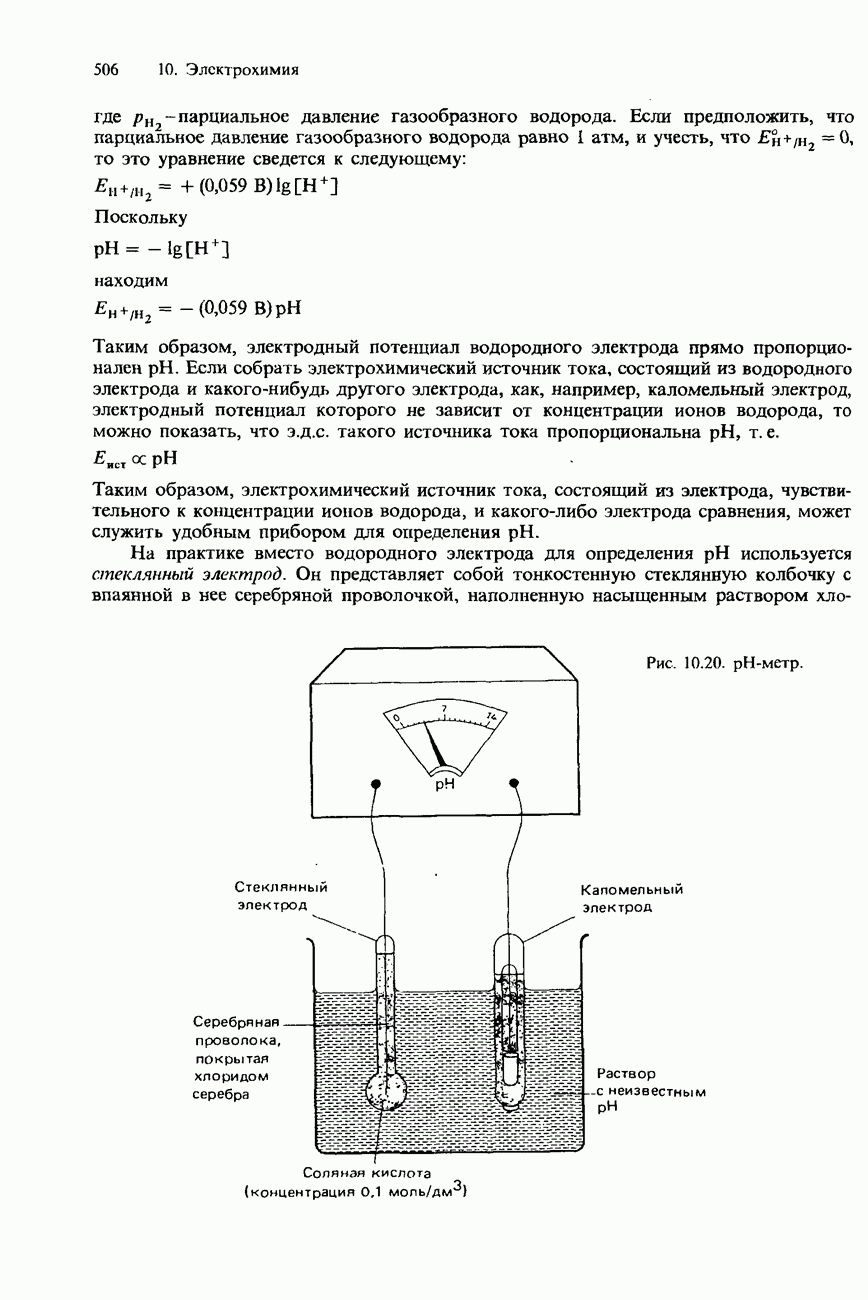
- ОПРЕДЕЛЕНИЕ pH РАСТВОРА
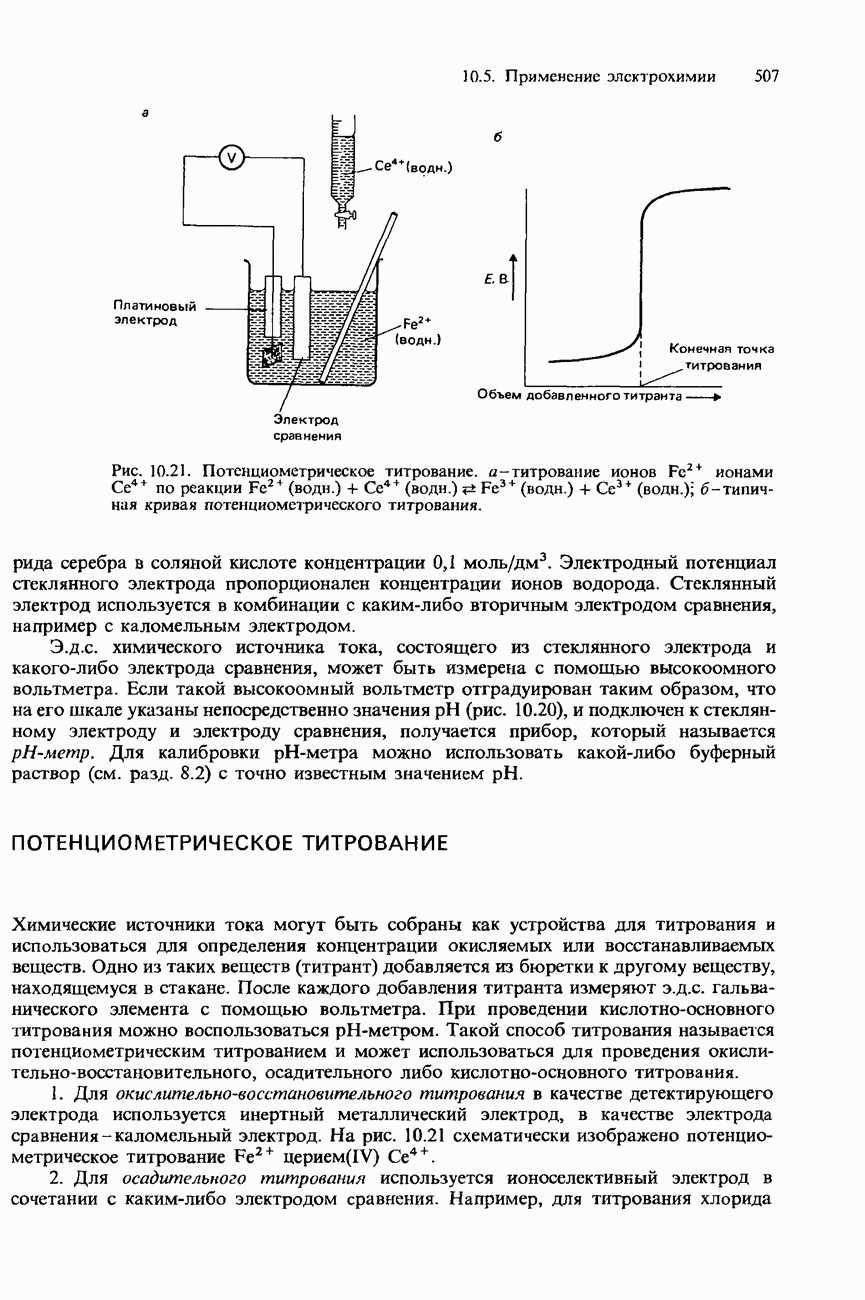
- ПОТЕНЦИОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- ОСУЩЕСТВИМОСТЬ ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫХ РЕАКЦИЙ
- ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ AG
- БАТАРЕИ И ПРОМЫШЛЕННЫЕ ИСТОЧНИКИ ТОКА
- МЕТАЛЛУРГИЯ
- КОРРОЗИЯ
- ВОПРОСЫ ДЛЯ ПРОВЕРКИ