| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
76. Электронейтральность и уравнение Лапласа
Условие электронейтральности (69-4) нельзя считать фундаментальным законом природы. Более точным является уравнение Пуассона, которое для среды с постоянной диэлектрической проницаемостью имеет вид [уравнение (22-8)]

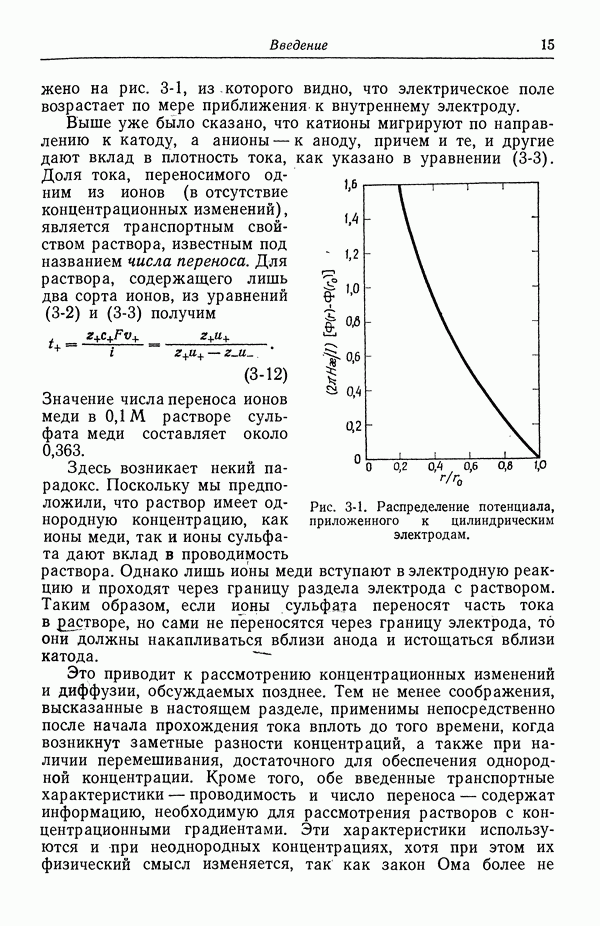
Уравнение (76-1) связывает плотность электрического заряда с лапласианом электрического потенциала. Коэффициентом пропорциональности в этом уравнении является постоянная Фарадея F, поделенная на диэлектрическую проницаемость е. Численное значение коэффициента пропорциональности довольно велико  для относительной диэлектрической постоянной 78,303), так что малые (в концентрационных единицах) отклонения от электронейтральности приводят к значительным отклонениям от уравнения Лапласа.
для относительной диэлектрической постоянной 78,303), так что малые (в концентрационных единицах) отклонения от электронейтральности приводят к значительным отклонениям от уравнения Лапласа.
То же самое можно сказать иными словами: отношение  настолько велико, что заметное разделение заряда потребовало бы преодоления чрезвычайно больших электрических сил. Другим фактором, способствующим электронейтральности, является большая проводимость, за счет которой любая начальная плотность заряда очень быстро нейтрализуется или заряд быстро уйдет на границы раствора.
настолько велико, что заметное разделение заряда потребовало бы преодоления чрезвычайно больших электрических сил. Другим фактором, способствующим электронейтральности, является большая проводимость, за счет которой любая начальная плотность заряда очень быстро нейтрализуется или заряд быстро уйдет на границы раствора.
Приведенных в разд. 69 уравнений вместе с соответствующими краевыми условиями достаточно для описания процессов переноса в растворах электролитов. Поэтому совместное использование уравнения Пуассона и условия электронейтральности было бы несостоятельным. Правильный способ действий состоит
в замене уравнения Пуассона условием электронейтральности (69-4) исходя из большой величины  . Таким образом, электронейтральность не предполагает справедливости уравнения Лапласа для потенциала
. Таким образом, электронейтральность не предполагает справедливости уравнения Лапласа для потенциала

что было бы неверно. Конечно, можно сохранить уравнение Пуассона и отказаться от предположения об электронейтральности при описании электрохимических систем. Однако то, что в растворах электролитов условие электронейтральности выполняется с высокой степенью точности, а математические расчеты конкретных систем, основанные на этом приближении, значительно упрощаются, оправдывает такой подход. Анализ явлений вблизи электрода, проведенный методами теории возмущений на основе уравнения Пуассона, можно найти в работах [3, 4].
Электронейтральность и уравнение Лапласа — понятия, хорошо устоявшиеся в электрохимии, тем не менее предположение об электронейтральности не означает, что для потенциала справедливо уравнение Лапласа. Во многих случаях распределение потенциала и тока в ячейках различной формы определяется по уравнению Лапласа, записанному для потенциала, и по закону Ома

записанному для тока. Такой подход оправдан в тех случаях, когда ток не лимитируется заметно за счет переноса реагентов к электродам. Тогда концентрации практически постоянны и уравнение (76-3) применяется с практически постоянной проводимостью. При этом из сохранения заряда следует уравнение Лапласа для потенциала [уравнения (71-2) — (71-4)]. Такое обоснование уравнения Лапласа значительно отличается от утверждения о том, что уравнение Лапласа возникает из условия электронейтральности. Можно ожидать, что описанная здесь процедура приведет к некоторым несогласованностям, если в дальнейшем пытаться исследовать детальное поведение каждого типа компонентов в растворе вблизи электродов.
Нужно отметить, что нельзя пренебрегать плотностью заряда в приэлектродном двойном слое, так как в этой области электрическое поле в действительности велико. Эта область, рассмотренная в разд. 52, может иметь толщину 10—100 А. Двойной слой разумно рассматривать как часть границы раздела фаз, а не часть раствора. В крайне разбавленных растворах плотность заряда также может быть значительной по сравнению с полной ионной концентрацией.
Проиллюстрируем на одном примере справедливость предположения об электронейтральности. Рассмотрим ячейку, в которой
бинарный электролит используется для осаждения катиона на катоде, тогда как анод растворяется и пополняет раствор. Упростим далее задачу, считая, что система одномерна и в ней установилось стационарное состояние без конвекции. Такие допущения обычно не принимаются при описании общей системы, здесь же они сделаны лишь с целью проверки предположения об электронейтральности. Рассмотрим одно-одновалентный электролит типа нитрата серебра и воспользуемся соотношением Нернста—Эйнштейна (75-1).
Наш метод состоит в решении задачи с использованием условия электронейтральности, из которого затем можно определить отклонение от электронейтральности с помощью уравнения Пуассона (76-1). Поскольку поток анионов равен нулю, уравнение (69-1) дает

Уравнение (72-7) приобретает вид

При интегрировании этого уравнения получается стационарная концентрация, выраженная через плотность тока:

где  — средняя концентрация в ячейке,
— средняя концентрация в ячейке,  расстояние, измеряемое от одного из электродов, и L — расстояние между электродами.
расстояние, измеряемое от одного из электродов, и L — расстояние между электродами.
Теперь при условии

концентрация на одном из электродов упадет до нуля, и достигается предельный ток. Более высокий ток можно пропустить лишь при протекании другой электродной реакции. Будем работать при токе, равном половине предельного, так что

Уравнение (76-4) дает

Если бы одновременно выполнялись условие электронейтральности и уравнение Пуассона, то вторая производная потенциала
равнялась бы нулю, что не имеет места. Следовательно, эти соотношения несовместимы.
Проверим предположение об электронейтральности, вычисляя плотность заряда и разность концентраций анионов и катионов, которая дает нужную величину 

При  и относительной диэлектрической постоянной 78,303 имеем
и относительной диэлектрической постоянной 78,303 имеем  экв/см. Отсюда при
экв/см. Отсюда при  мм и
мм и  мм получаем
мм получаем

и

Это свидетельствует о том, что предположение об электронейтральности в электрохимических системах выполняется очень хорошо.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
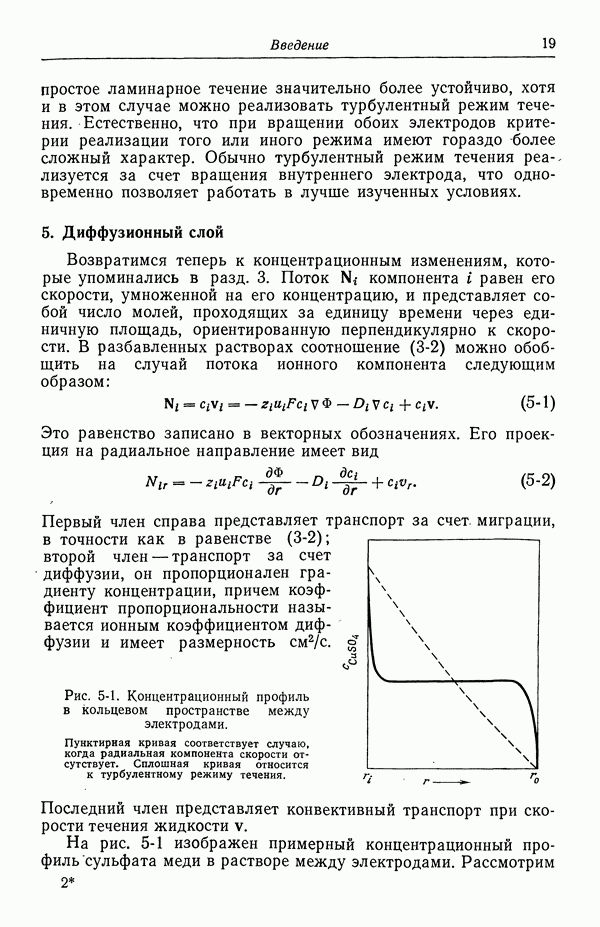
- 5. Диффузионный слой
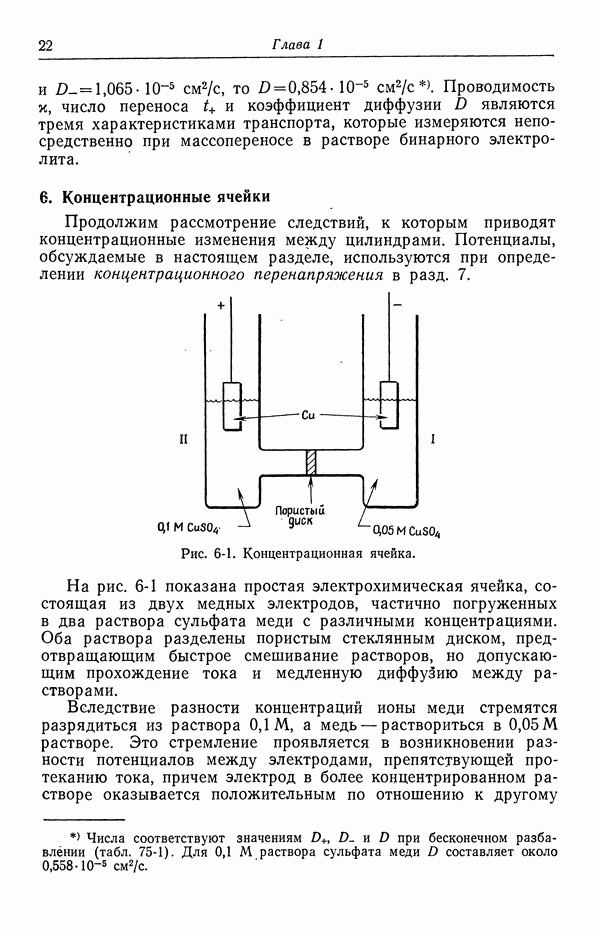
- 6. Концентрационные ячейки
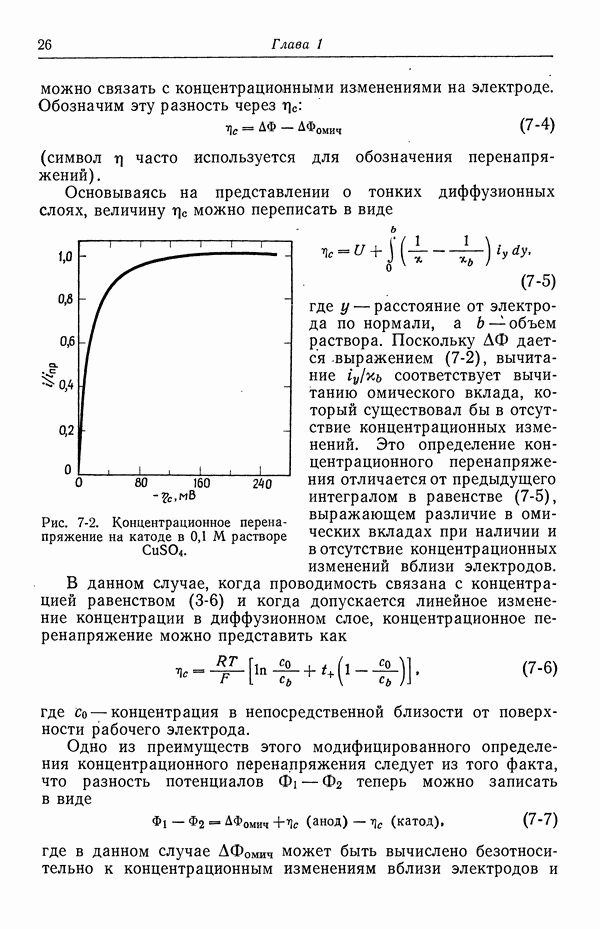
- 7. Концентрационное перенапряжение
- 8. Поверхностное перенапряжение
- 9. Потенциал ячейки
- 10. Фоновый электролит
- 11. Свободная конвекция
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая—Хюккеля
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 49. Качественное описание двойных слоев
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод — раствор
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 66. Динамика границы раздела
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 69. Законы переноса
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 78. Законы переноса
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 92. Интегральные коэффициенты диффузии
- ЗАДАЧА
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
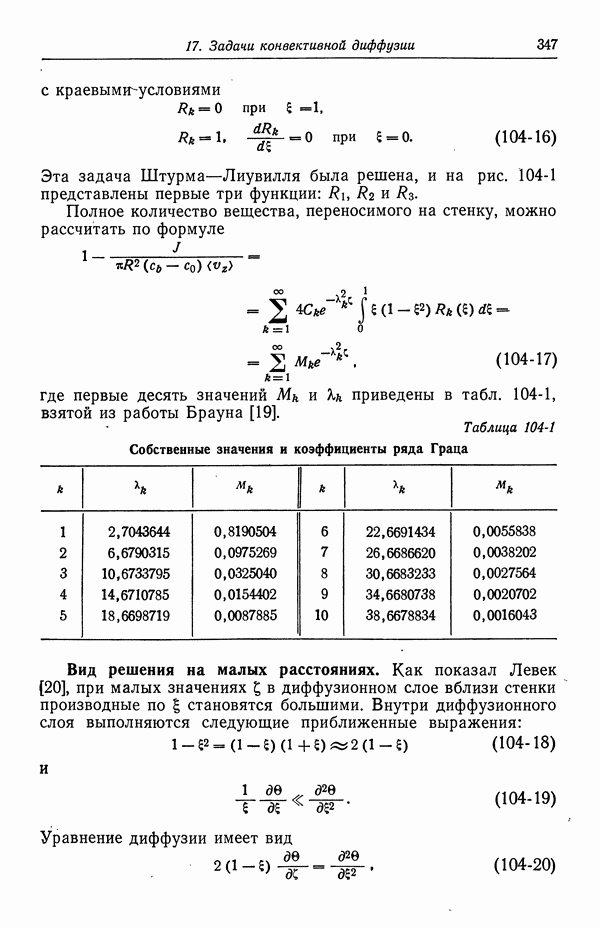
- 104. Задача Граца
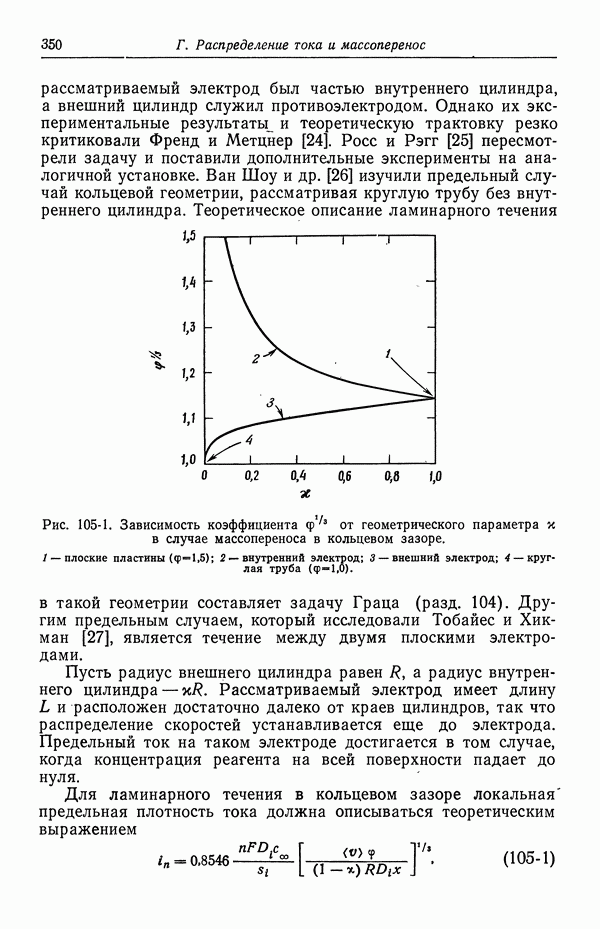
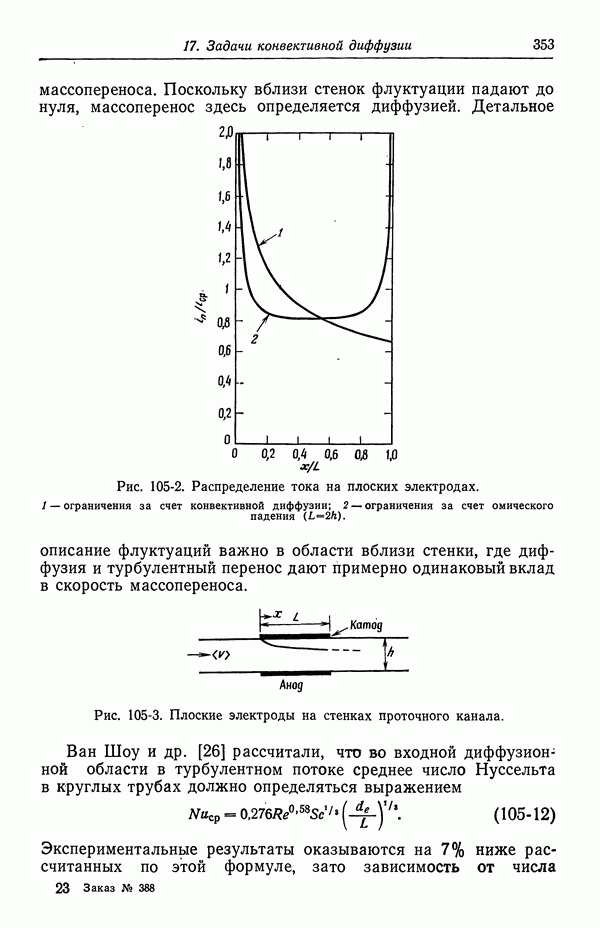
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 111. Свободная конвекция
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- СПИСОК ОБОЗНАЧЕНИЙ
- ГЛАВА 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 119. Решение задачи
- 120. Поправочный множитель в случае предельных токов
- 121. Изменение концентрации фонового электролита
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ