| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
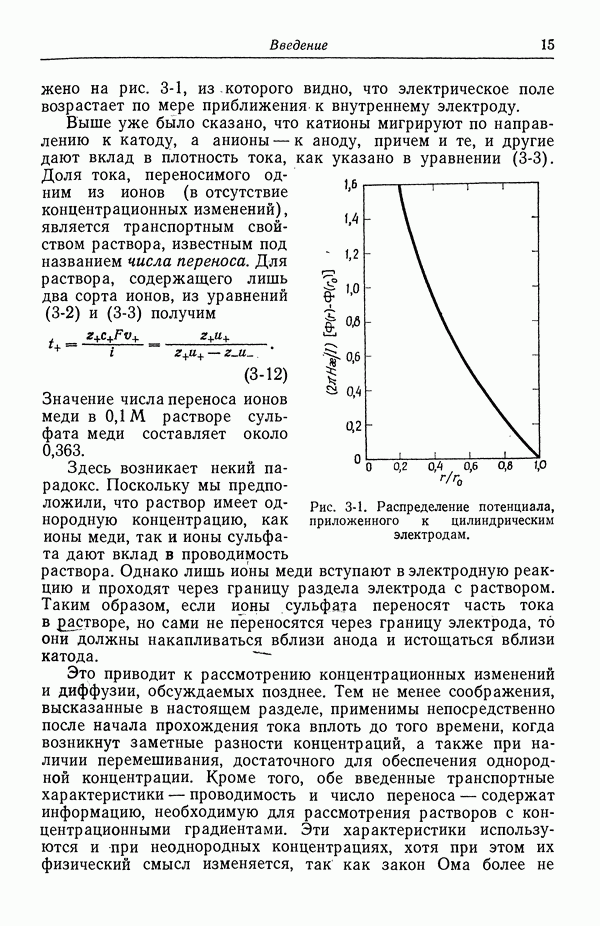
В предыдущей главе мы обсуждали термодинамику электрохимических ячеек, не вводя электрических потенциалов, за исключением разности потенциалов между двумя фазами одинакового состава, а именно между клеммами ячейки. В большей части электрохимической литературы фигурируют электрические потенциалы различных типов; поэтому следует остановиться на этом вопросе и выяснить, как потенциалы могут быть использованы в электрохимии. Многие недоразумения в электрохимии возникают в связи с неоднозначностью этих величин.
22. Электростатический потенциал
В электростатической теории рассматриваются чисто электрические силы взаимодействия между телами и вовсе не рассматриваются какие-либо специфические химические силы типа тех, которые действуют между молекулами. Обсуждаемые в этой теории системы обычно являются макроскопическими телами, разделенными вакуумом, так что специфические силы несущественны. Поэтому развиваемые в электростатической теории представления нельзя прямо перенести на энергетические соотношения в конденсированных фазах.
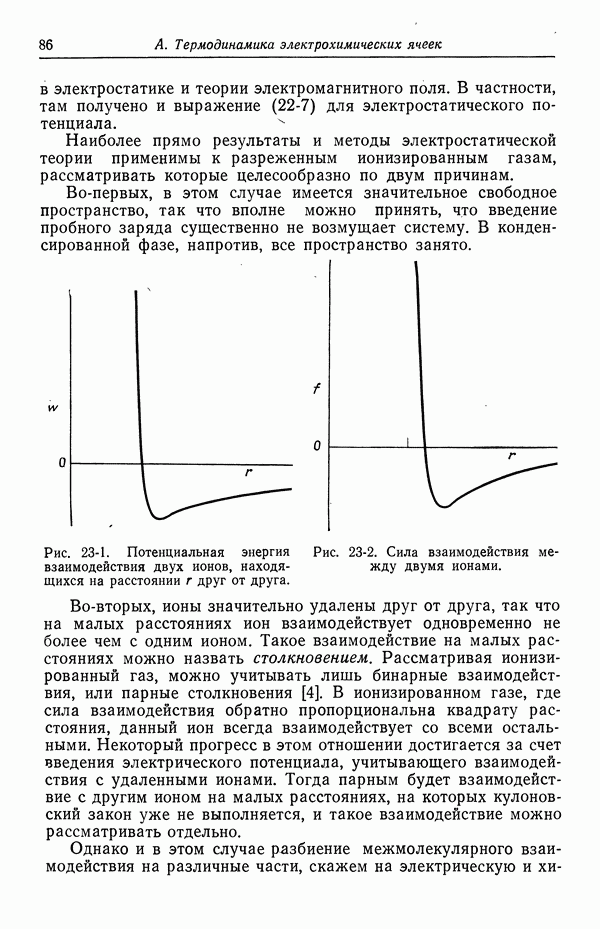
Электрическая сила f, действующая между двумя телами с зарядами  находящимися на расстоянии
находящимися на расстоянии  друг от друга, определяется законом Кулона
друг от друга, определяется законом Кулона

где  — диэлектрическая проницаемость среды, окружающей тела. Сила направлена вдоль линии, соединяющей тела, и является отталкивающей, если оба заряда имеют одинаковые знаки; если заряды имеют разные знаки, то эта сила является силой притяжения.
— диэлектрическая проницаемость среды, окружающей тела. Сила направлена вдоль линии, соединяющей тела, и является отталкивающей, если оба заряда имеют одинаковые знаки; если заряды имеют разные знаки, то эта сила является силой притяжения.
Диэлектрическая проницаемость вакуума  равна
равна  , или
, или  . Если тела погружены в диэлектрическую среду, состоящую из поляризующегося вещества, то силы, действующие между телами в такой среде, будут другими по сравнению с вакуумом. Отношение
. Если тела погружены в диэлектрическую среду, состоящую из поляризующегося вещества, то силы, действующие между телами в такой среде, будут другими по сравнению с вакуумом. Отношение  называется
называется
относительной диэлектрической постоянной среды. Для воды при 25° С это отношение равно 78,303.
На тело действует результирующая всех сил, приложенных к нему всеми другими телами системы. Для изложения теории удобно ввести электрическое поле Е, определенное так, что сила, действующая на заряд а, равна

Электрическое поле во всех точках среды определяется при допущении, что можно ввести пробный заряд, не нарушающий положения других зарядов системы. Измеряя силу, действующую на пробный заряд, электрическое поле можно найти с помощью соотношения (22-2).
Таким способом можно получить дифференциальные уравнения, описывающие изменение электрического поля. Например, ротор электрического поля равен нулю:

Это обстоятельство позволяет ввести электростатический потенциал Ф, так что электрическое поле можно выразить в виде градиента этой скалярной величины, взятого с обратным знаком:

Это допустимо, поскольку ротор градиента любого скалярного поля равен нулю:

Изменение электрического поля связано также с распределением заряда в системе уравнением Пуассона

где  — плотность электрического заряда. Для среды с постоянной диэлектрической проницаемостью последнее уравнение эквивалентно выражению электростатического потенциала через заряды
— плотность электрического заряда. Для среды с постоянной диэлектрической проницаемостью последнее уравнение эквивалентно выражению электростатического потенциала через заряды

где суммирование проводится по всем зарядам системы.
Уравнение (22-6) является дифференциальным уравнением для определения электростатического потенциала по распределению зарядов. Для среды с постоянной диэлектрической проницаемостью это уравнение приобретает вид

а в среде, не содержащей свободных зарядов, оно сводится к уравнению Лапласа

На поверхности, разделяющей две фазы, тангенциальная составляющая электрического поля непрерывна. Связь между нормальными составляющими электрического поля можно получить, применяя уравнение (22-6) к прямоугольному элементу объема, содержащему часть поверхности раздела (рис. 22-1). Мы допускаем возможность существования ненулевой поверхностной плотности заряда.

Рис. 22-1. Нормальные составляющие электрического поля на межфазной границе, единица площади которой может нести заряд а.
С помощью теоремы о дивергенции равенство (22-6) можно записать через поверхностный и объемный интегралы по произвольной области:

Это равенство выражает теорему Гаусса, согласно которой поверхностный интеграл от проекции ее на внешнюю нормаль к поверхности равен заряду области, ограниченной этой поверхностью. Применение теоремы Гаусса к поверхности, изображенной на рис. 22-1, дает связь между нормальными составляющими электрического поля:

где а — заряд единицы площади поверхности.
Электростатическая теория развивалась [1—3] в значительной мере в связи с решением уравнений (22-8) и (22-9) для систем с различной геометрией и различными краевыми условиями [6, 7]. Мы не обсуждали магнитных эффектов, возникающих при изменении электрического поля во времени и при наличии электрических токов.
Настоящий раздел мы завершим одним примером. Рассмотрим две металлические сферы радиусом 1 см каждая, расположенные на расстоянии 10 см между их центрами (рис. 22-2). Допустим, что мы хотим зарядить каждую сферу до  путем переноса
путем переноса  или
или  молей электронов с одной сферы на другую. Емкость этой системы составляет
молей электронов с одной сферы на другую. Емкость этой системы составляет  . Следовательно, разность потенциалов будет равна
. Следовательно, разность потенциалов будет равна  .
.
Этот пример показывает, что для разнесения электрических зарядов хотя бы на небольшие расстояния требуются огромные потенциалы.

Рис. 22-2. Разность потенциалов между двумя металлическими сферами при средней плотности заряда
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
- 5. Диффузионный слой
- 6. Концентрационные ячейки
- 7. Концентрационное перенапряжение
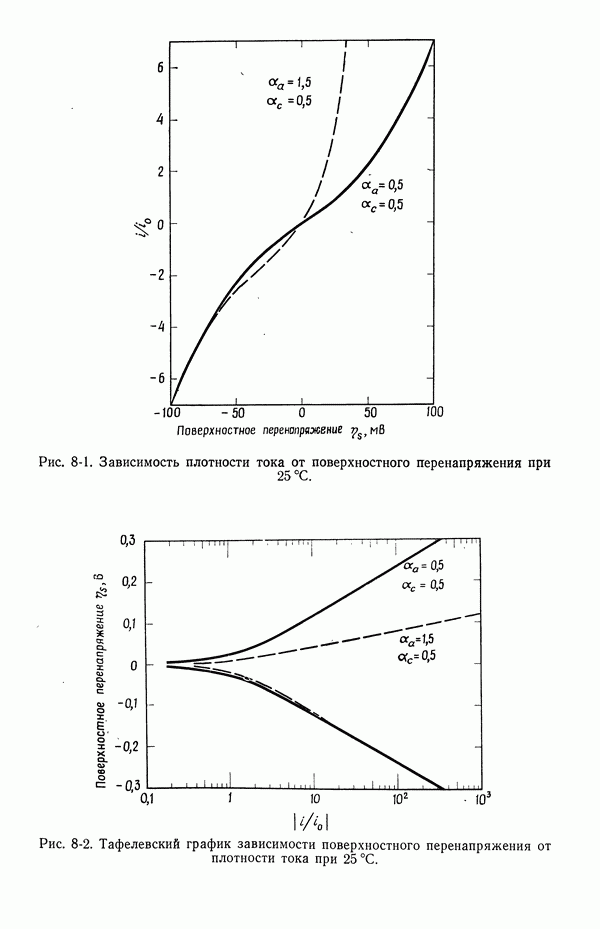
- 8. Поверхностное перенапряжение
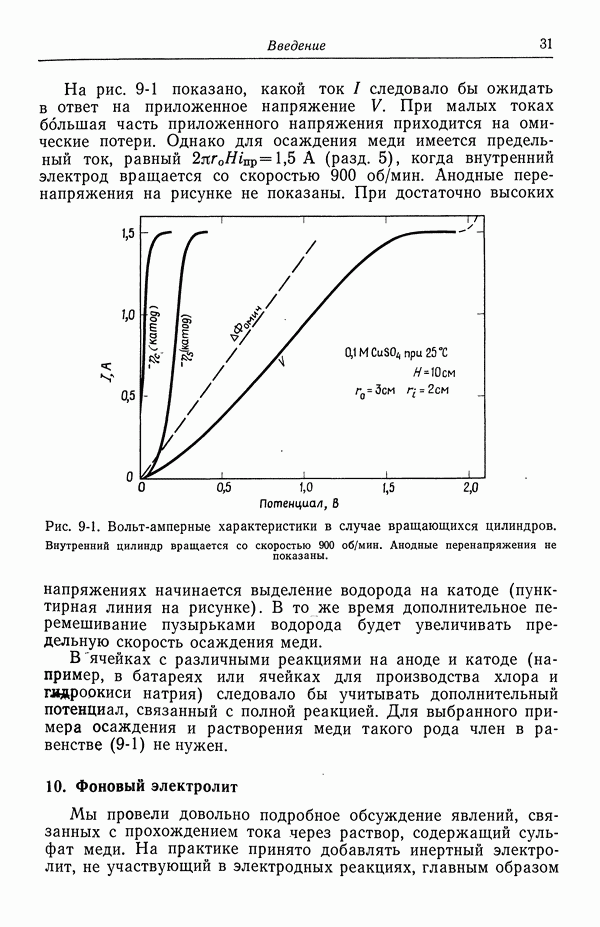
- 9. Потенциал ячейки
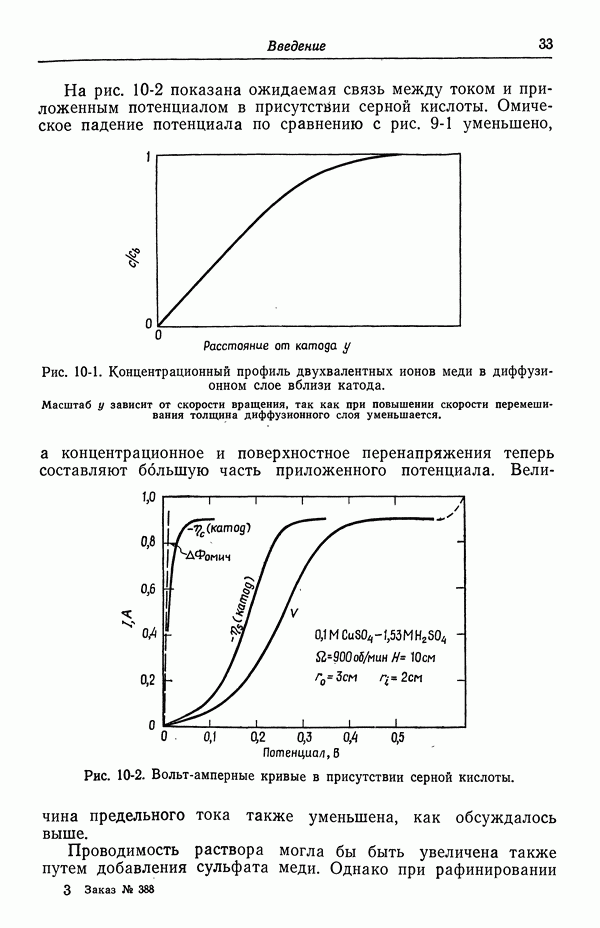
- 10. Фоновый электролит
- 11. Свободная конвекция
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая—Хюккеля
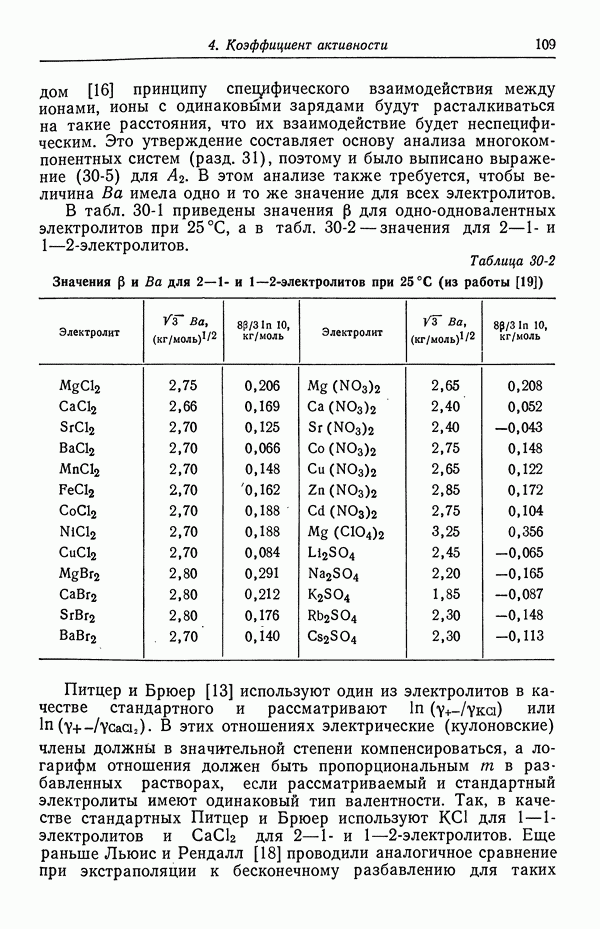
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
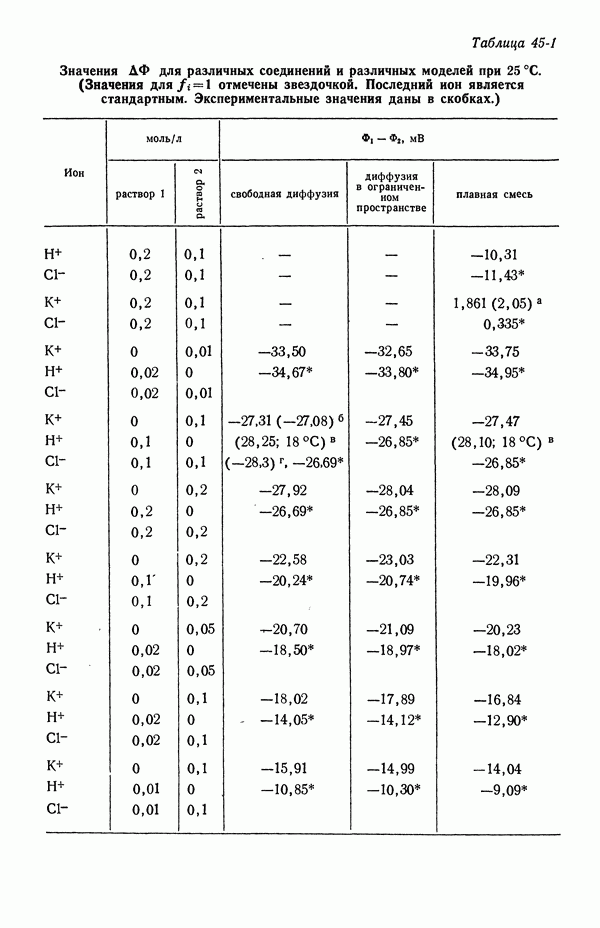
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 49. Качественное описание двойных слоев
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод — раствор
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 66. Динамика границы раздела
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 69. Законы переноса
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 78. Законы переноса
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 92. Интегральные коэффициенты диффузии
- ЗАДАЧА
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
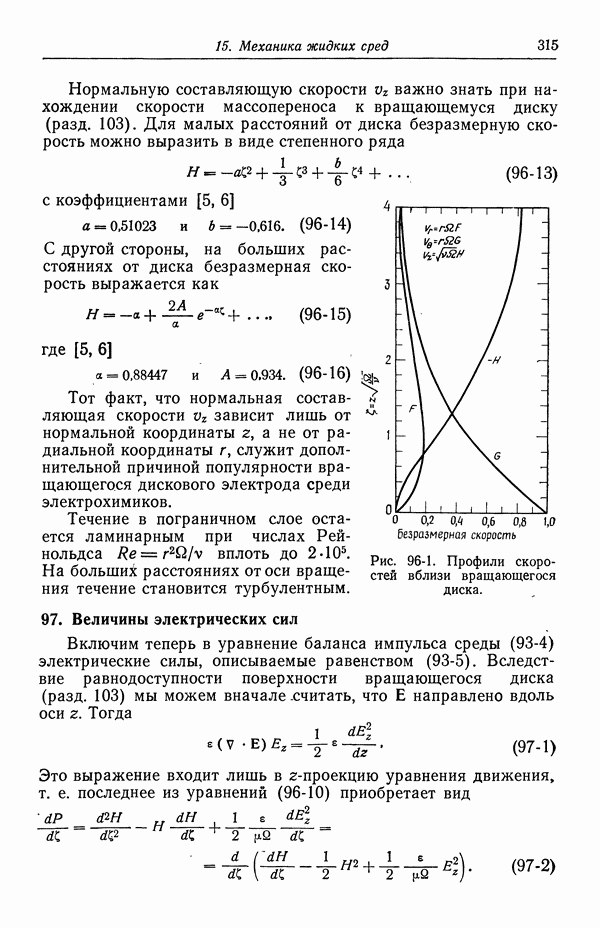
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
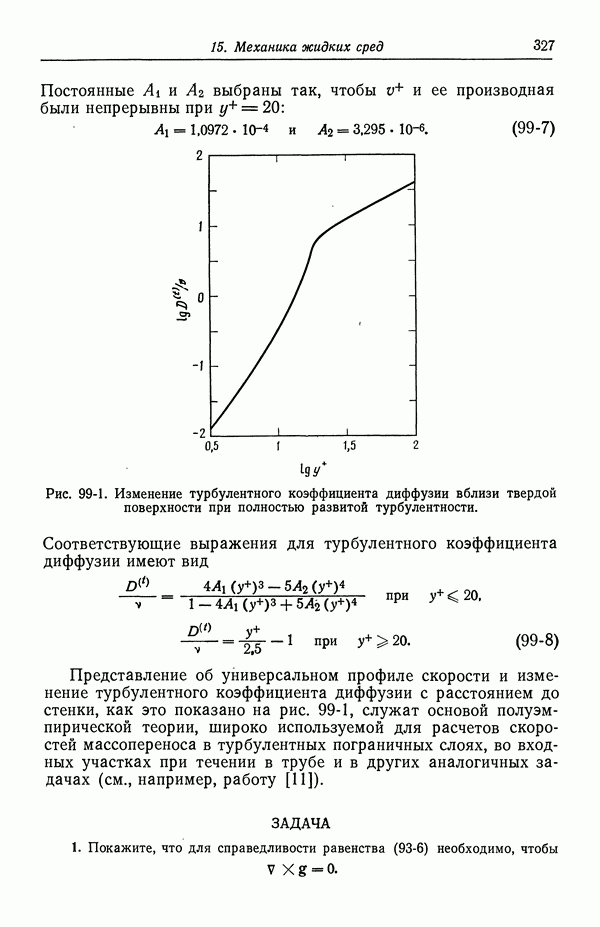
- 99. Массоперенос в турбулентном потоке
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
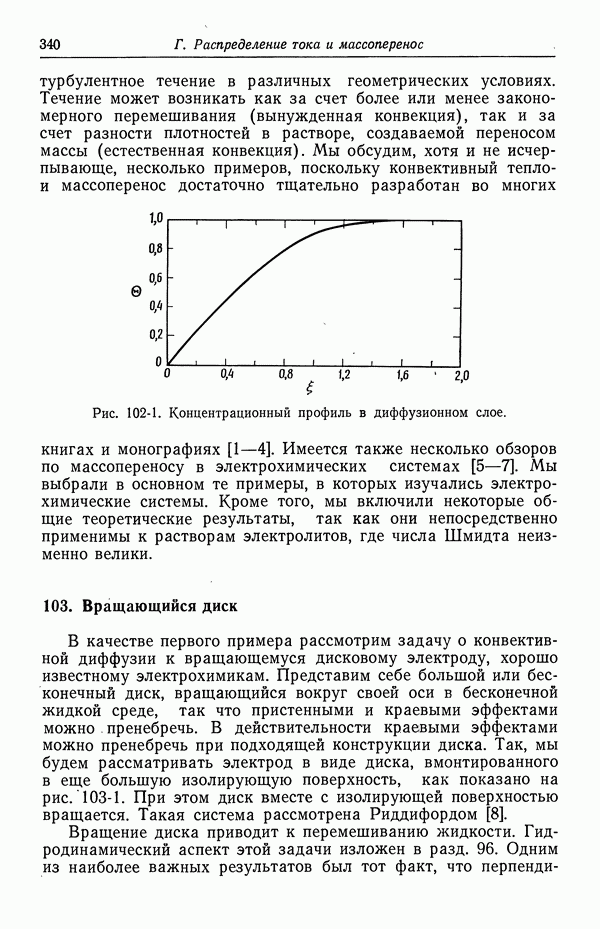
- 102. Упрощенное описание конвективной диффузии
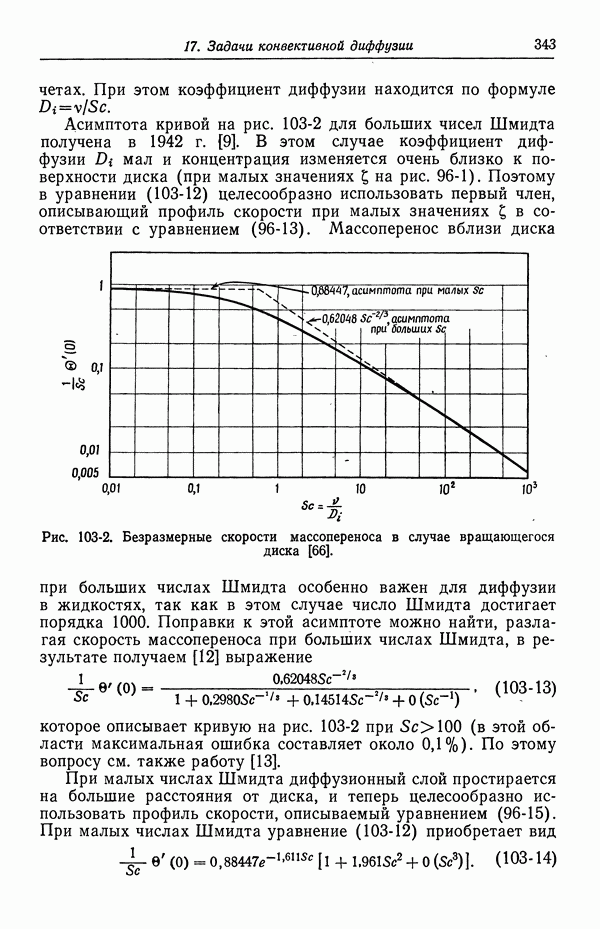
- 103. Вращающийся диск
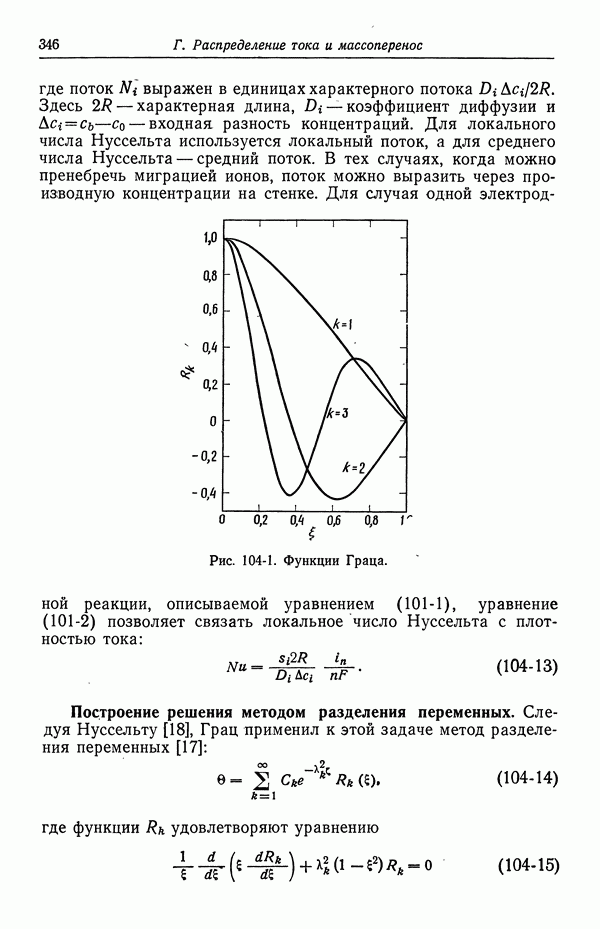
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 111. Свободная конвекция
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- СПИСОК ОБОЗНАЧЕНИЙ
- ГЛАВА 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 119. Решение задачи
- 120. Поправочный множитель в случае предельных токов
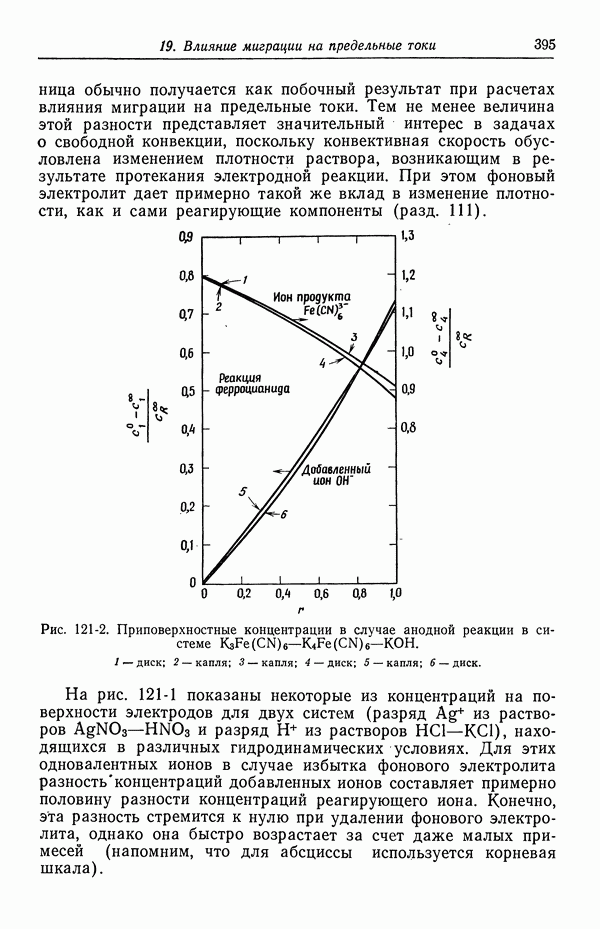
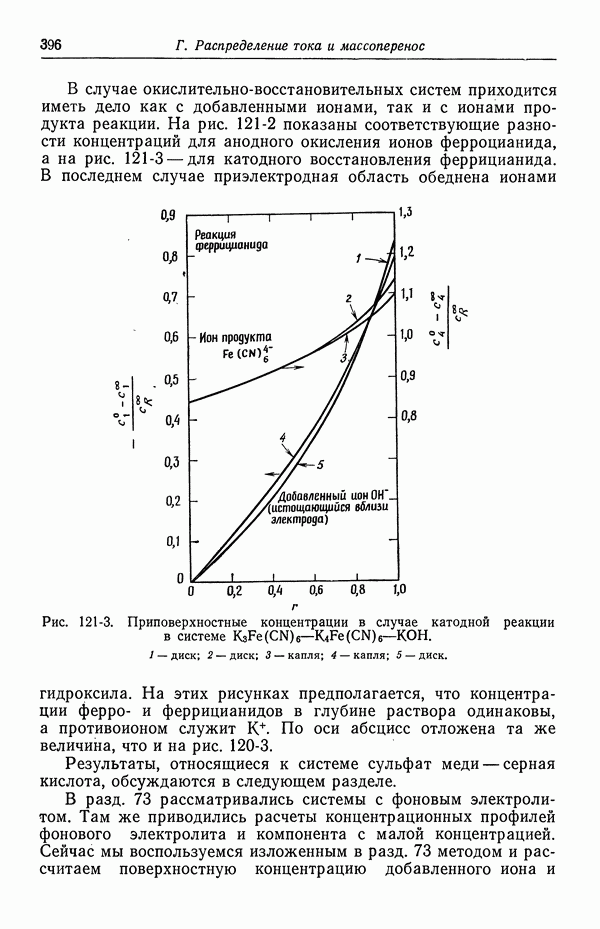
- 121. Изменение концентрации фонового электролита
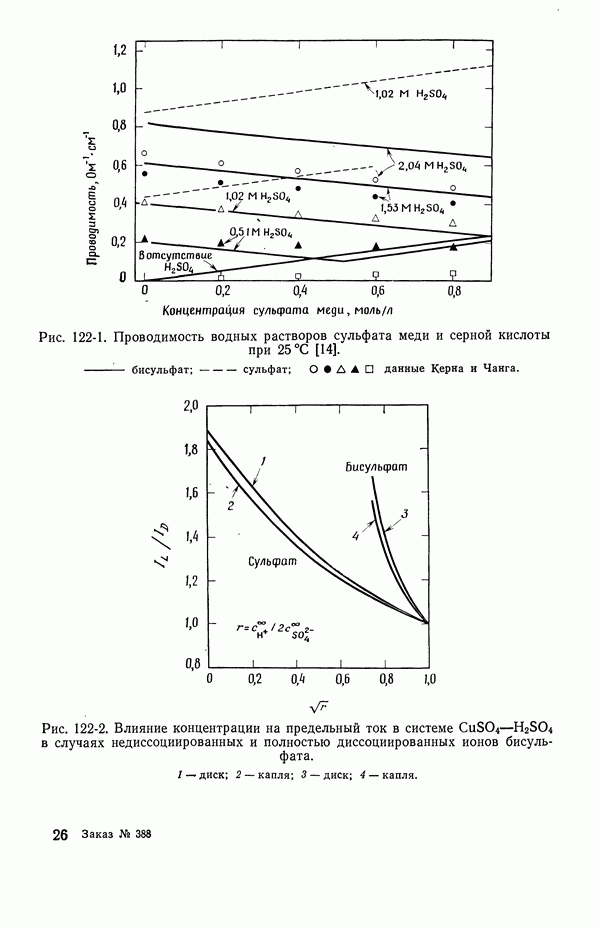
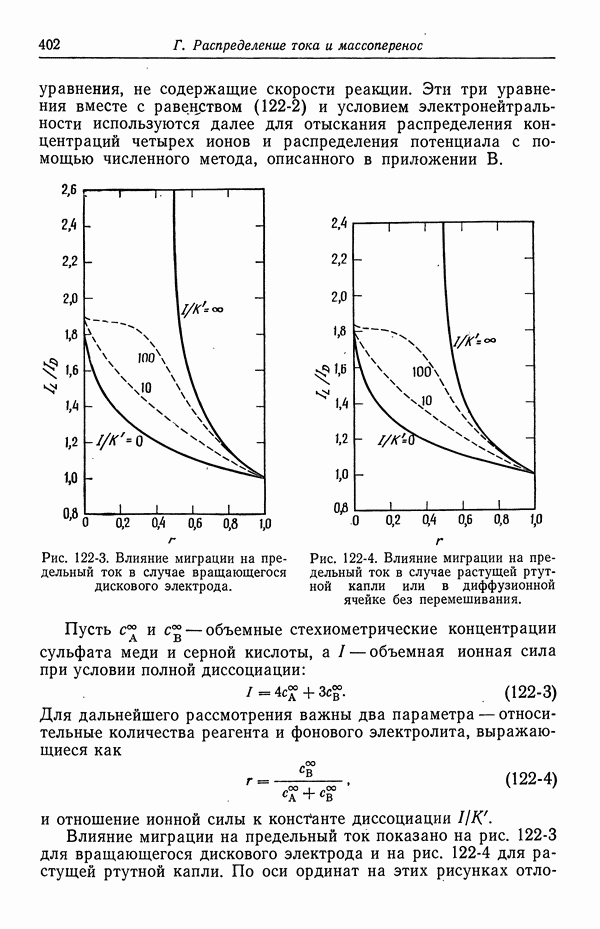
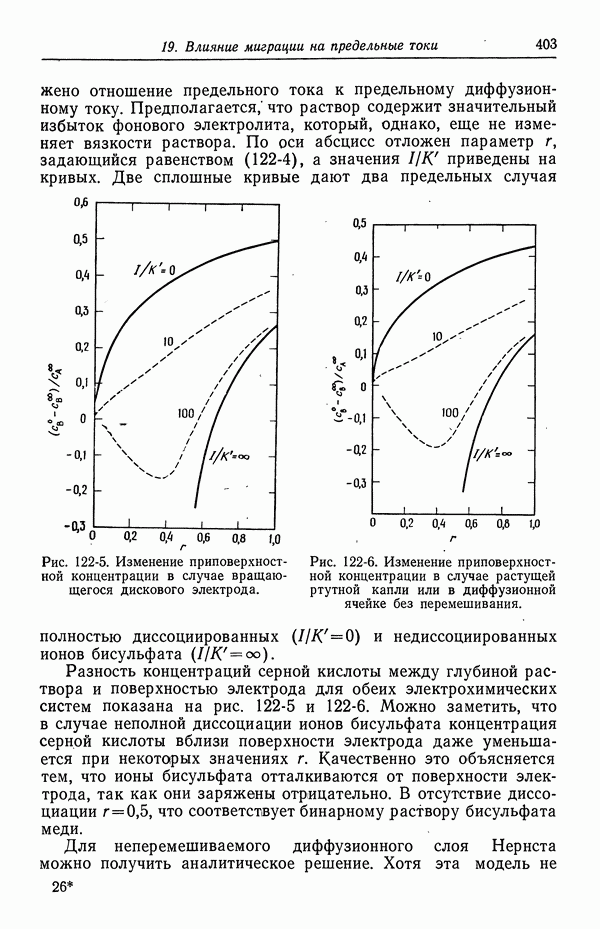
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
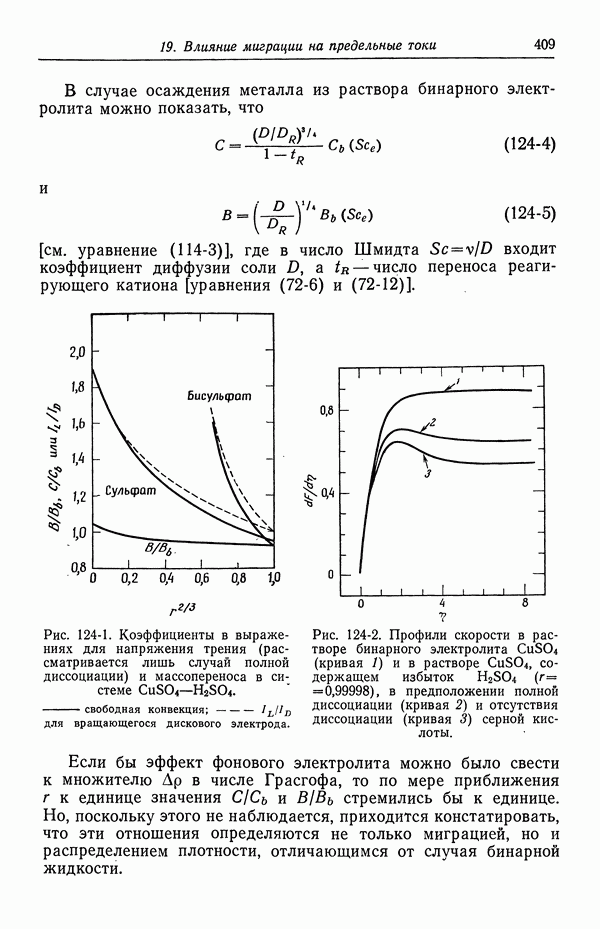
- 124. Предельные токи в случае свободной конвекции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ