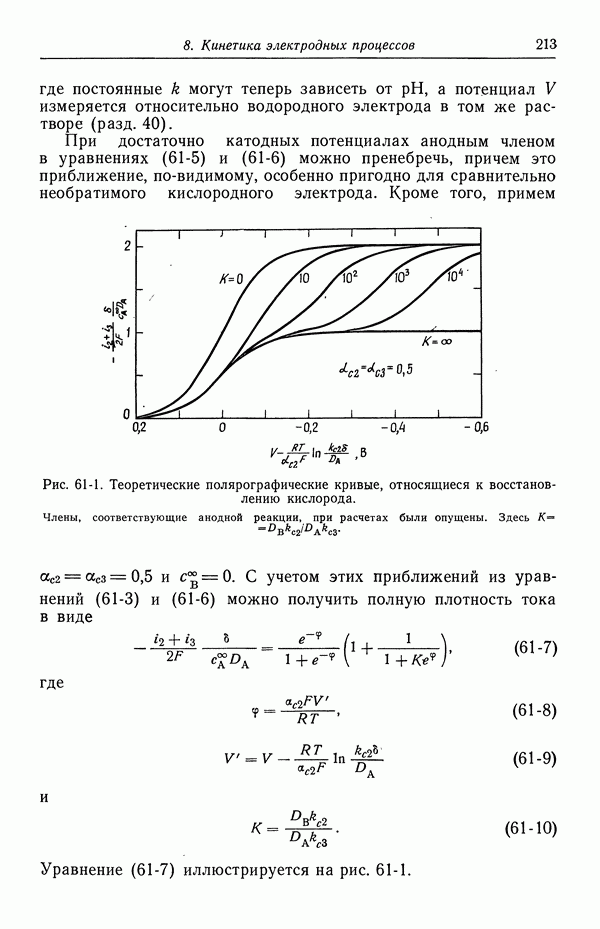
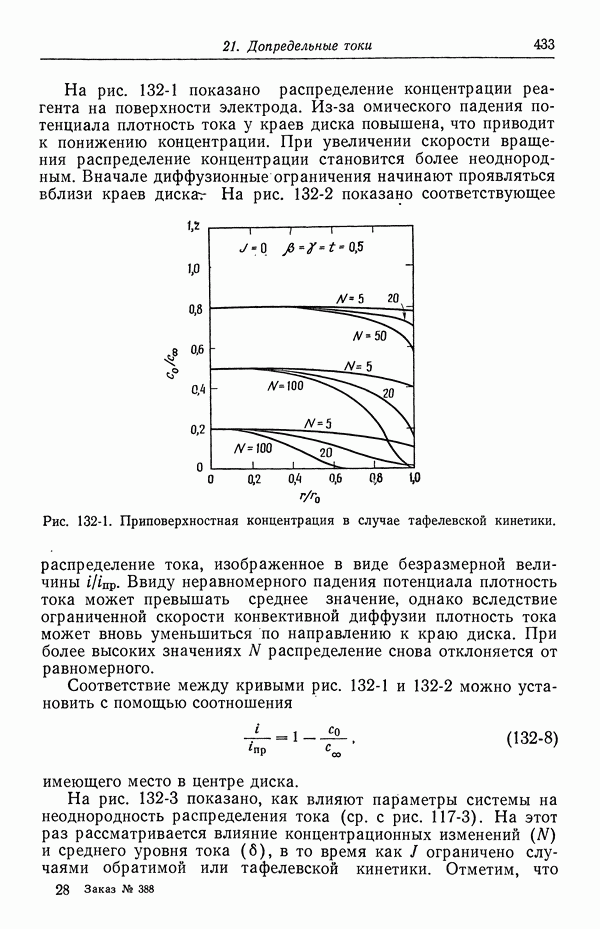
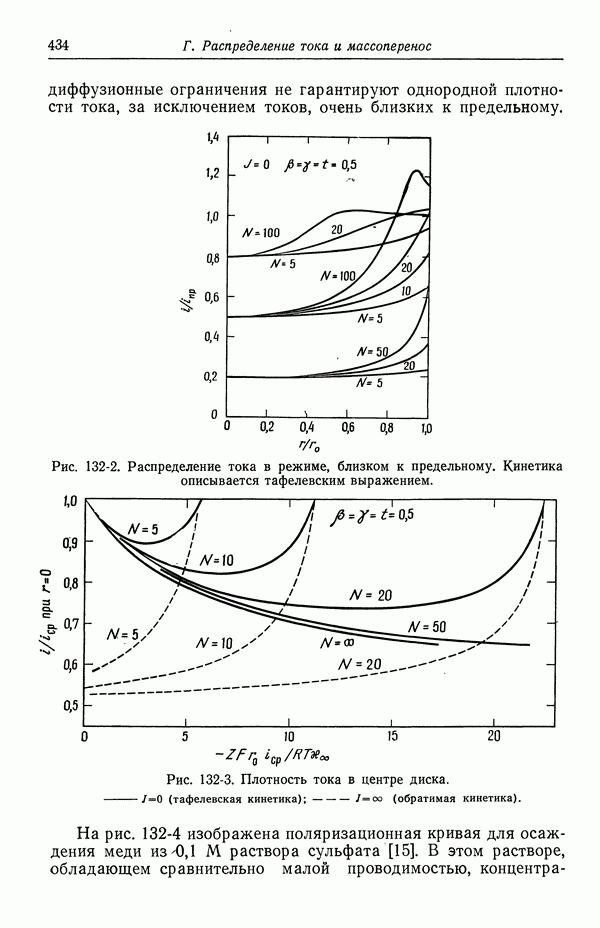
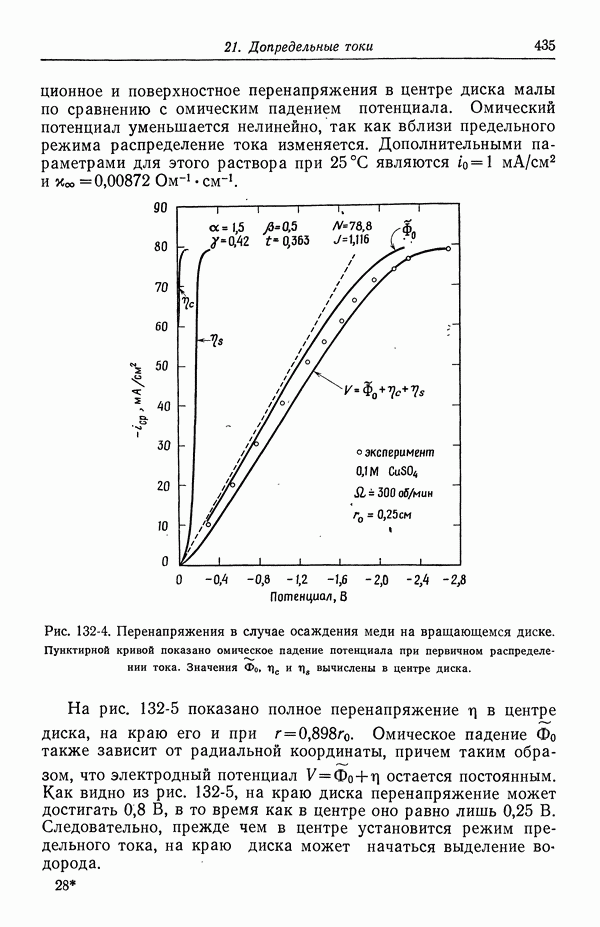
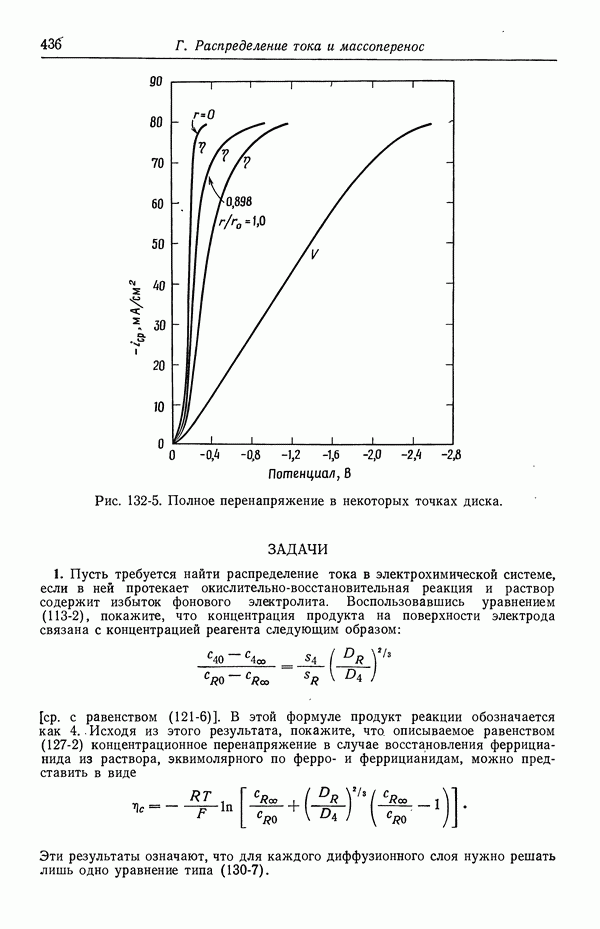
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
В этой главе рассматриваются эффекты, наблюдаемые при взаимодействии диффузного двойного слоя и внешнего электрического поля в связи с гидродинамическим течением. Тангенциальное электрическое поле может вызвать малое изменение скорости на незначительной толщине двойного слоя, а напряжение сдвига или градиент скорости на поверхности может создавать электрические эффекты.
Этот вопрос весьма важен при изучении коллоидов. Его решение дает также некоторую информацию о строении электрического двойного слоя на границе раздела твердого тела с раствором, которую невозможно получить при помощи поверхностного натяжения. Здесь представлено неполное изложение, что в особенности относится к экспериментальным результатам для конкретных границ раздела, и пдэтому читателю можно рекомендовать соответствующую литературу [1—3, 7].
62. Разрывная скорость на границе раздела
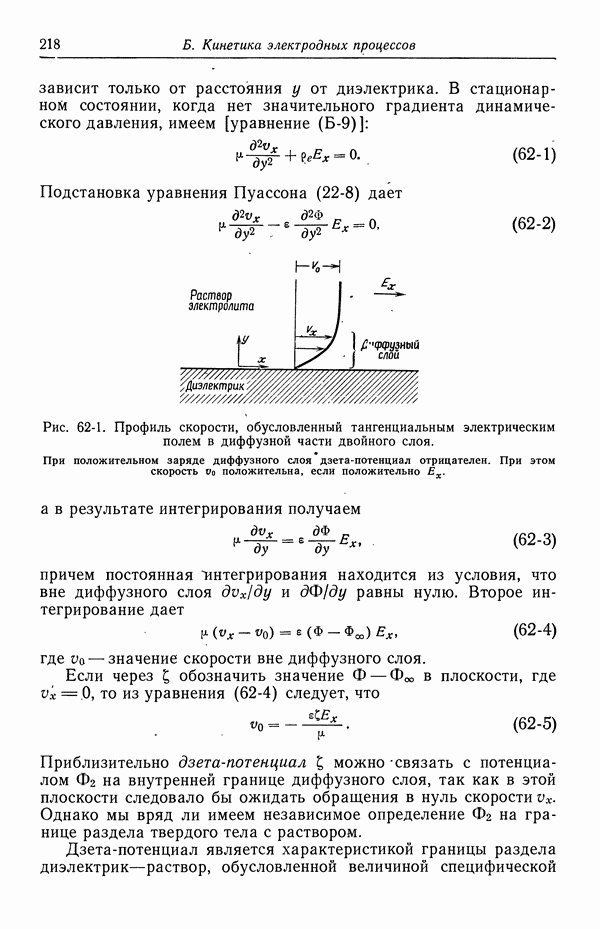
Допустим, что мы имеем плоский твердый диэлектрик в контакте с раствором электролита и что существует некоторое тангенциальное электрическое поле (рис. 62-1). В результате специфической адсорбции ионов на поверхности может существовать двойной слой, а это означает, что в диффузном слое будет находиться компенсирующий заряд. Строение диффузного слоя обсуждалось в разд. 52. Благодаря тангенциальному электрическому полю на заряд диффузного слоя действует некоторая сила. Поскольку этот слой является частью раствора, он подвижен, и можно ожидать, что под действием приложенной силы возникнет движение относительно твердого тела.
Тангенциальное поле считается однородным во всем диэлектрике и в растворе. Тогда строение двойного слоя не будет отличаться от рассмотренного в разд. 52. Результирующее движение раствора будет описываться уравнением Навье—Стокса (94-4), в которое включена электрическая сила [уравнение (93-5)]. Это уравнение упрощается благодаря тому обстоятельству, что скорость имеет лишь составляющую вдоль оси х и
зависит только от расстояния у от диэлектрика. В стационарном состоянии, когда нет значительного градиента динамического давления, имеем [уравнение (Б-9)]:

Подстановка уравнения Пуассона (22-8) дает

а в результате интегрирования получаем

причем постоянная интегрирования находится из условия, что вне диффузного слоя  равны нулю. Второе интегрирование дает
равны нулю. Второе интегрирование дает

где и» — значение скорости вне диффузного слоя.
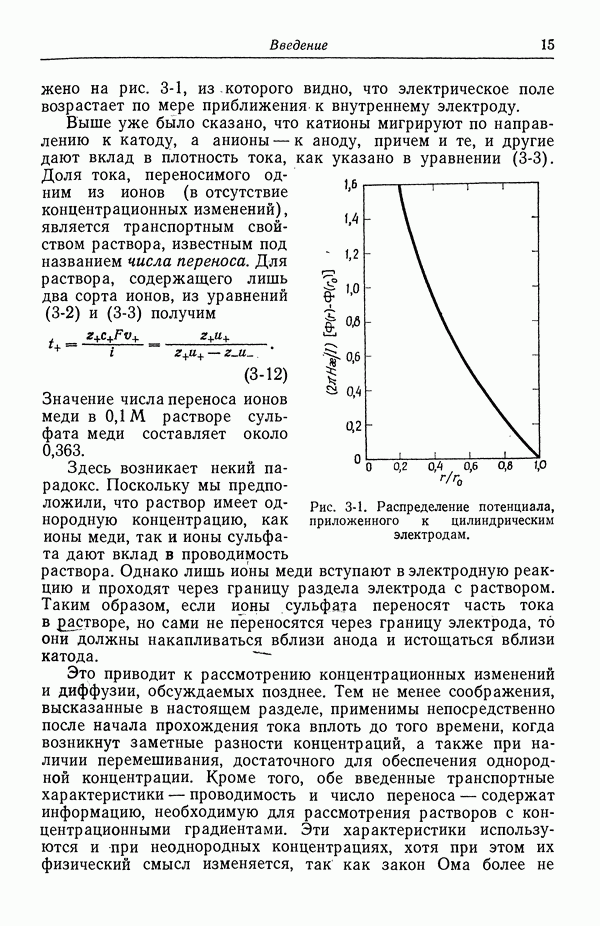
Если через  обозначить значение
обозначить значение  в плоскости, где
в плоскости, где  то из уравнения (62-4) следует, что
то из уравнения (62-4) следует, что


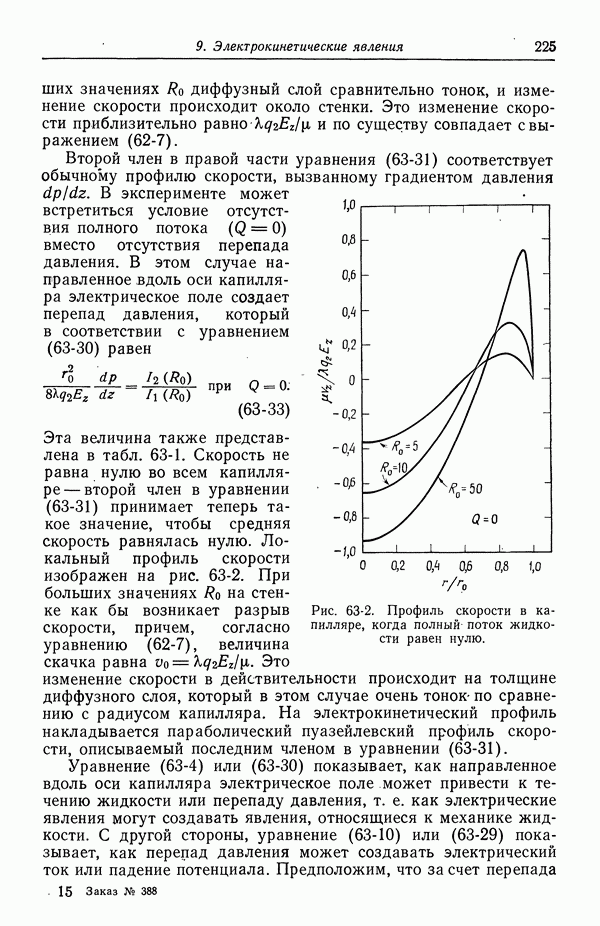
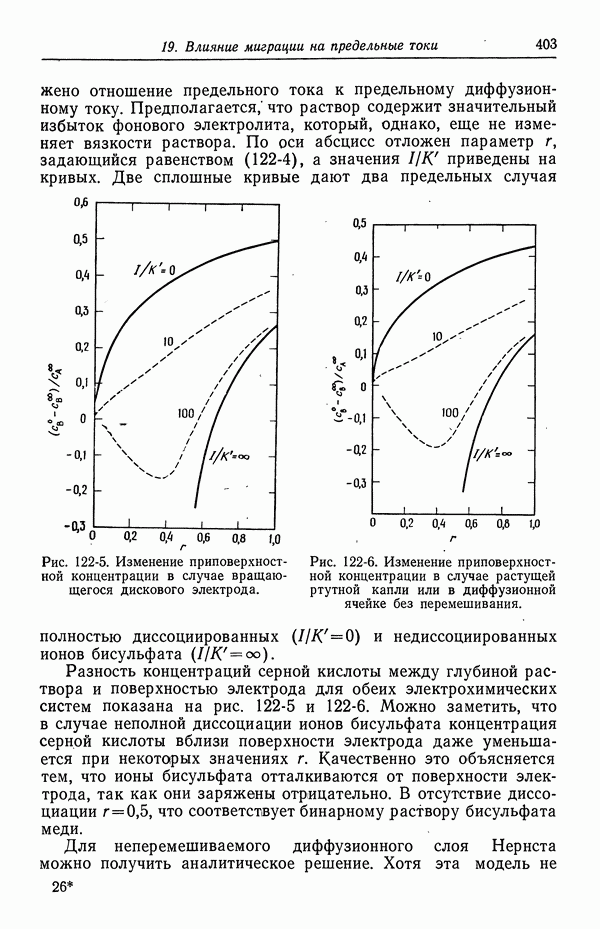
Рис. 62-1. Профиль скорости, обусловленный тангенциальным электрическим полем в диффузной части двойного слоя.
При положительном заряде диффузного слоя дзета-потенциал отрицателен. При этом скорость  положительна, если положительно
положительна, если положительно 
Приблизительно дзета-потенциал  можно связать с потенциалом
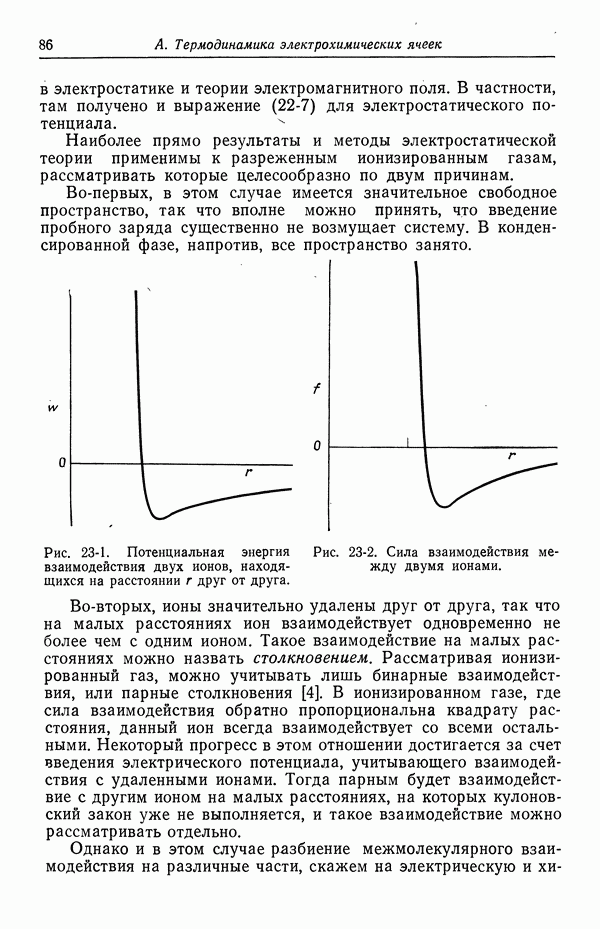
можно связать с потенциалом  на внутренней границе диффузного слоя, так как в этой плоскости следовало бы ожидать обращения в нуль скорости
на внутренней границе диффузного слоя, так как в этой плоскости следовало бы ожидать обращения в нуль скорости  Однако мы вряд ли имеем независимое определение
Однако мы вряд ли имеем независимое определение  на границе раздела твердого тела с раствором.
на границе раздела твердого тела с раствором.
Дзета-потенциал является характеристикой границы раздела диэлектрик—раствор, обусловленной величиной специфической
адсорбции. Поскольку маловероятно, чтобы  были постоянными в диффузном слое, величину
были постоянными в диффузном слое, величину  нужно рассматривать скорее как макроскопическую переменную, связывающую скорость
нужно рассматривать скорее как макроскопическую переменную, связывающую скорость  с тангенциальным электрическим полем
с тангенциальным электрическим полем  и поэтому ее связь с потенциалом
и поэтому ее связь с потенциалом  становится более слабой.
становится более слабой.
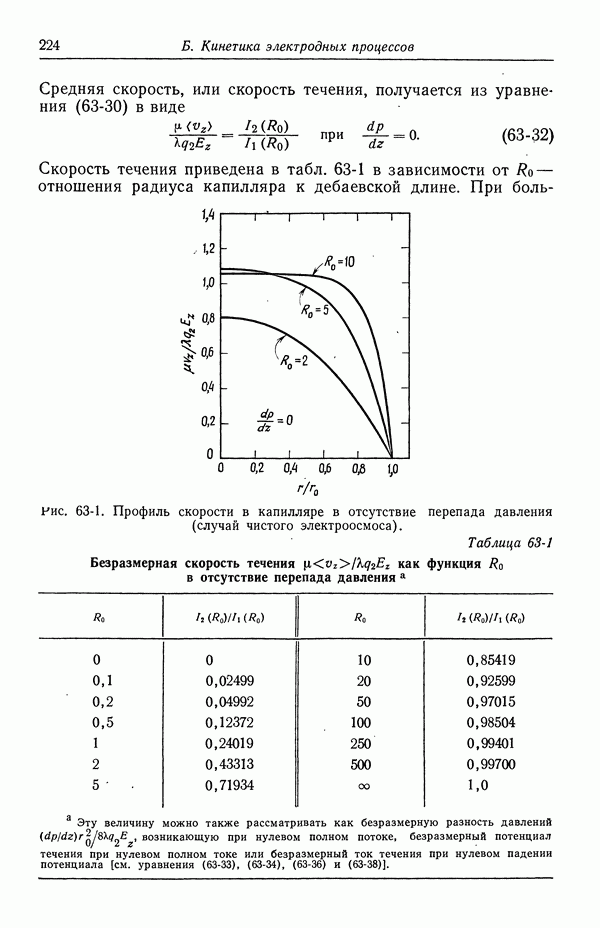
Поскольку диффузный слой тонок по сравнению с макроскопическими размерами, уравнение (62-5) можно рассматривать как связь между локальной скоростью скольжения  и локальным тангенциальным полем Ей даже если граница раздела диэлектрик—раствор не плоская, тангенциальное электрическое поле неоднородно и градиент динамического давления не равен нулю. Мы попытаемся пояснить смысл такого приближения на примере прямого капилляра в диэлектрическом материале. Это приближение будет использоваться при рассмотрении электрофоретических скоростей и потенциалов осаждения в случае сферических коллоидных частиц.
и локальным тангенциальным полем Ей даже если граница раздела диэлектрик—раствор не плоская, тангенциальное электрическое поле неоднородно и градиент динамического давления не равен нулю. Мы попытаемся пояснить смысл такого приближения на примере прямого капилляра в диэлектрическом материале. Это приближение будет использоваться при рассмотрении электрофоретических скоростей и потенциалов осаждения в случае сферических коллоидных частиц.
Маленькие частицы металла во многом сходны с небольшими диэлектрическими частицами, если металл ведет себя как идеально поляризуемый электрод (разд. 49). Электрическое поле внутри металла равно нулю, а локальная поляризация изменяется благодаря тангенциальному электрическому полю. Если только поляризация не становится настолько большой, чтобы нарушилось условие идеальной поляризуемости, то для связи локальной скорости скольжения  с локальным тангенциальным полем
с локальным тангенциальным полем  можно применять уравнение (62-5). В случае частиц металла имеется возможность изменять плотность заряда на металлической стороне границы раздела.
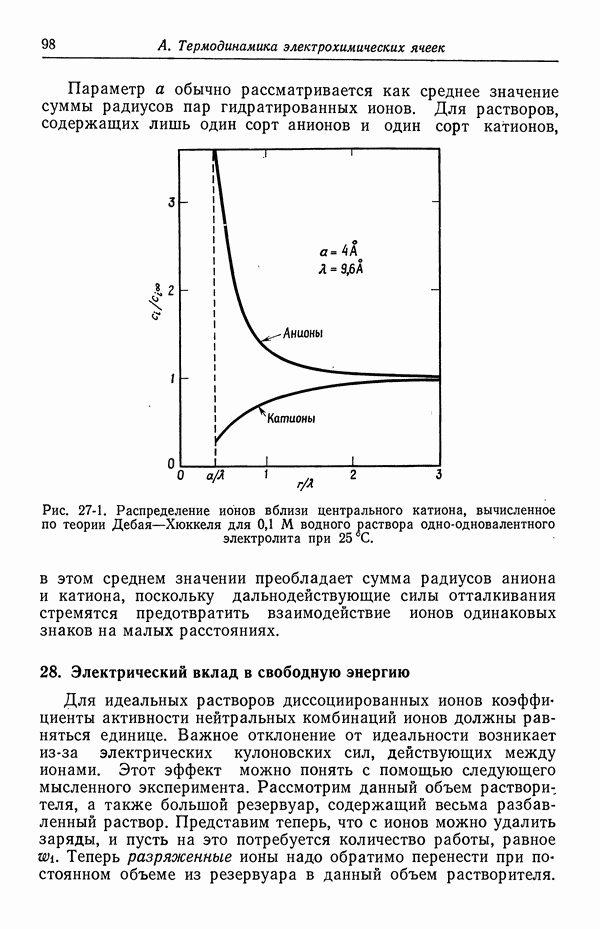
можно применять уравнение (62-5). В случае частиц металла имеется возможность изменять плотность заряда на металлической стороне границы раздела.
Автор работы [4] предпочитает заменять дзета-потенциал плотностью заряда  в диффузном слое. В приближении Дебая—Хюккеля величины
в диффузном слое. В приближении Дебая—Хюккеля величины  можно связать соотношением
можно связать соотношением

(задача 7-6), так что уравнение (62-5) приобретает вид

Дзета-потенциал может быть порядка 0,1 В. При относительной диэлектрической постоянной  равной 78,3, вязкости
равной 78,3, вязкости  и электрическом поле 10 В/см уравнение (62-5) дает
и электрическом поле 10 В/см уравнение (62-5) дает

Это сравнительно малая величина, и во многих приложениях ею можно пренебречь.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
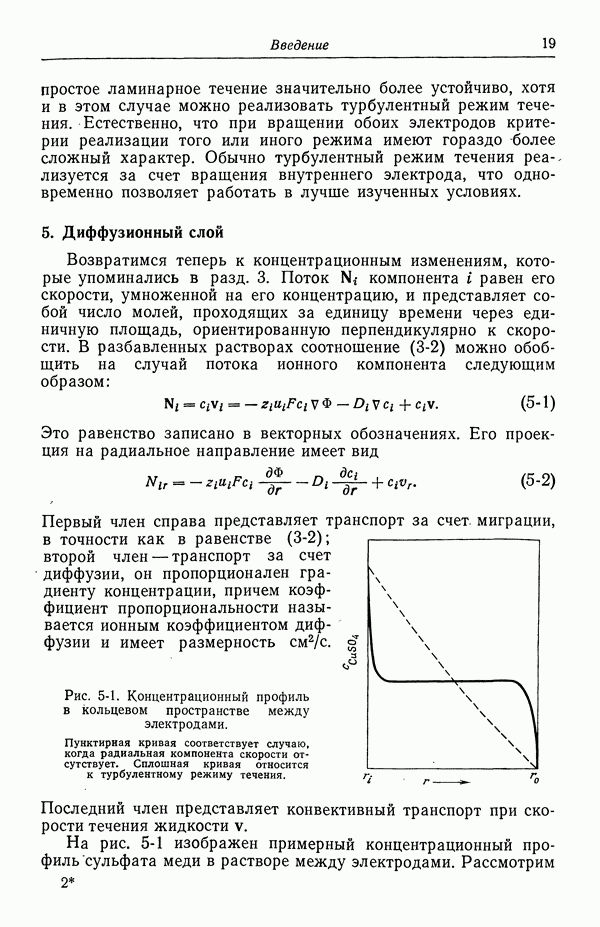
- 5. Диффузионный слой
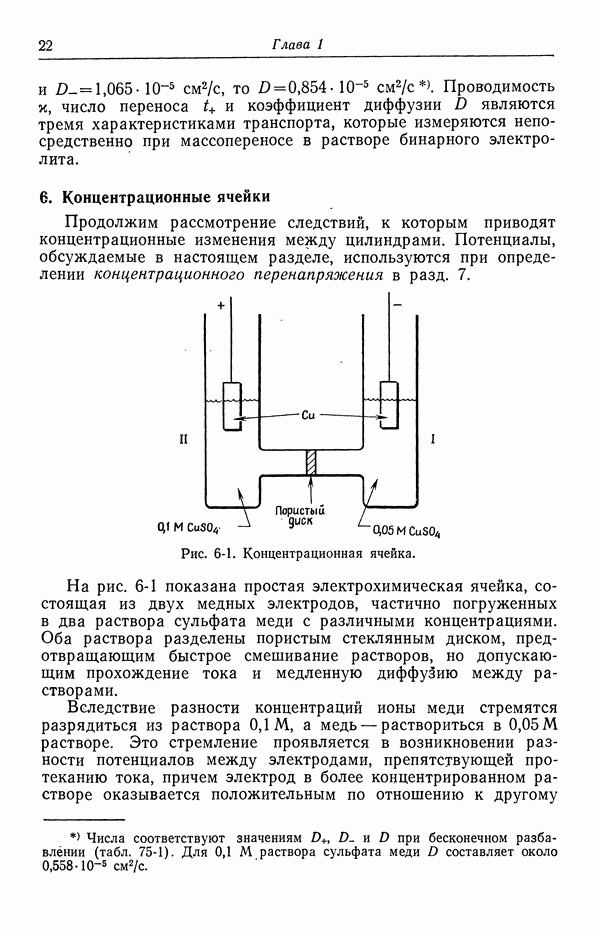
- 6. Концентрационные ячейки
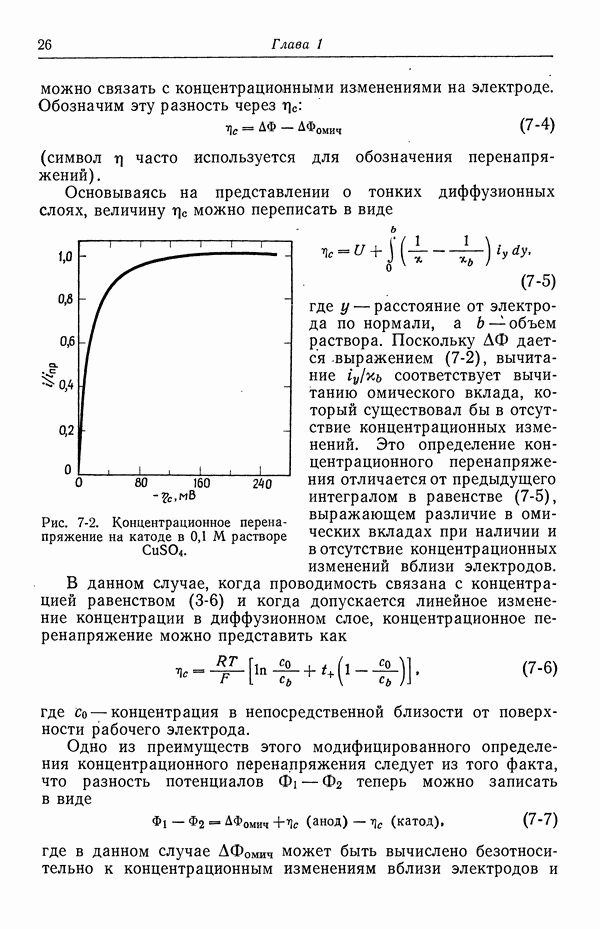
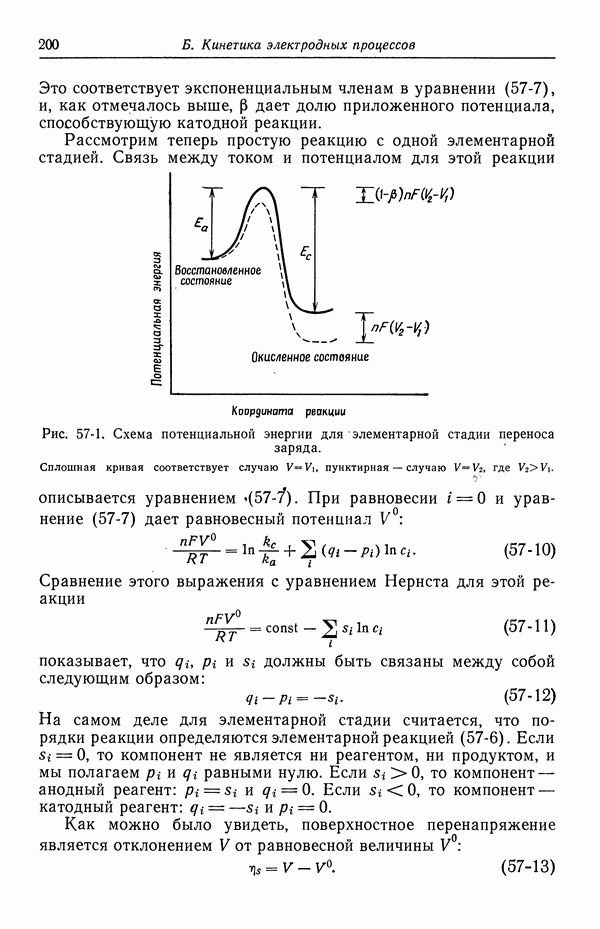
- 7. Концентрационное перенапряжение
- 8. Поверхностное перенапряжение
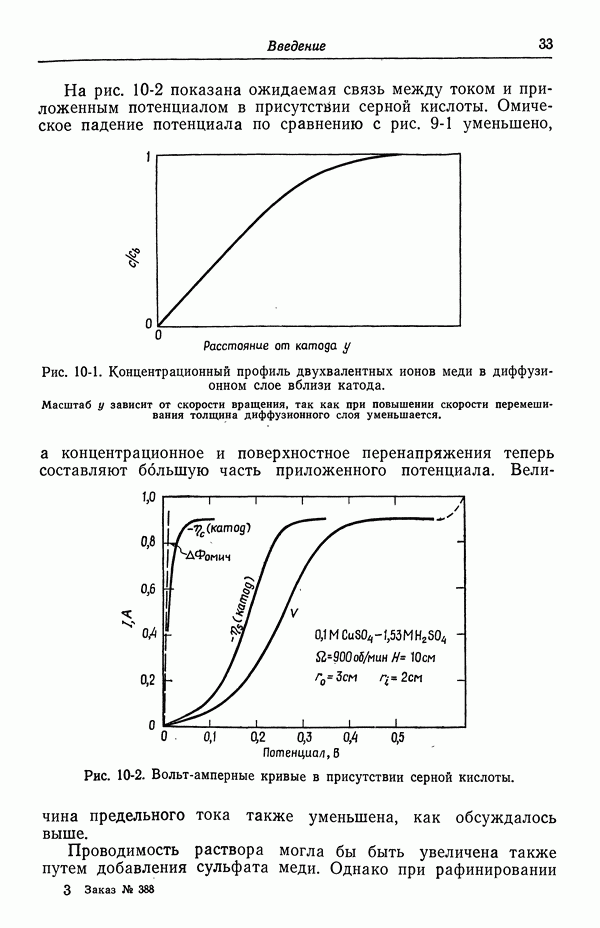
- 9. Потенциал ячейки
- 10. Фоновый электролит
- 11. Свободная конвекция
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
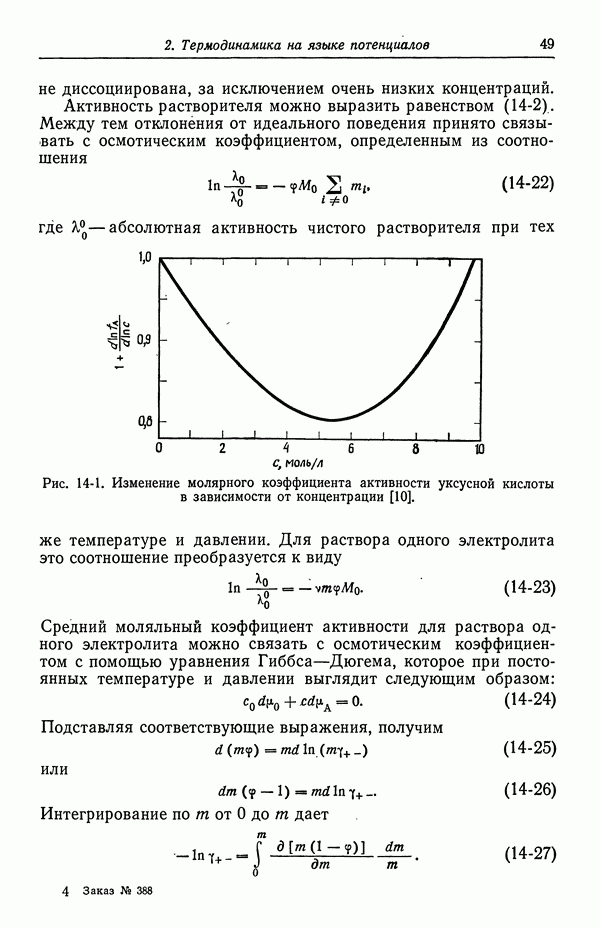
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая—Хюккеля
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
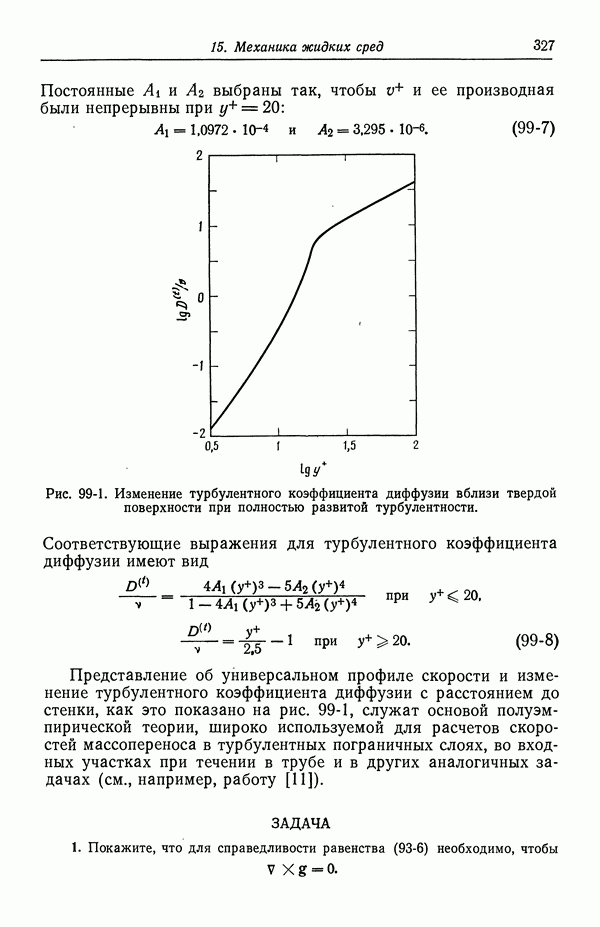
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
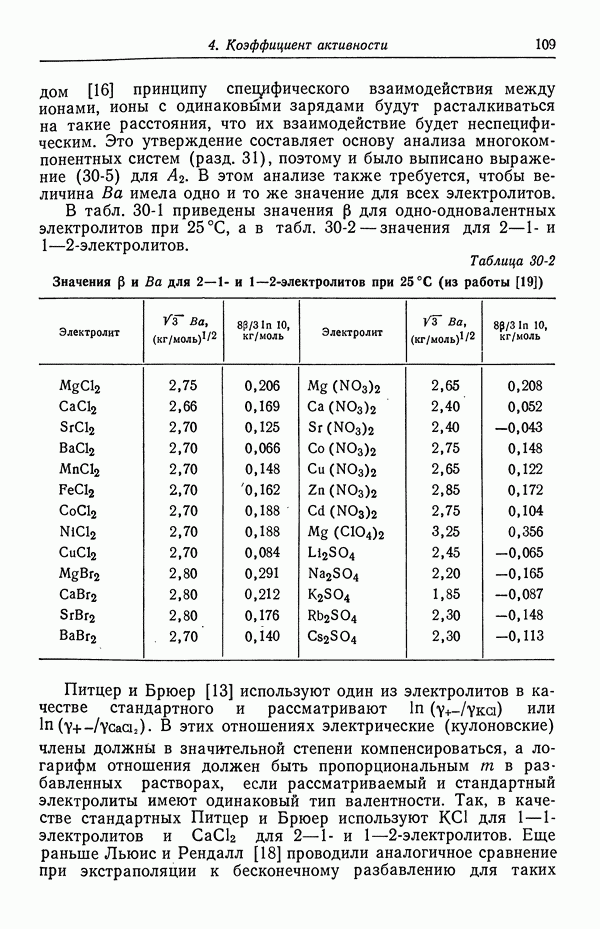
- 44. Определение концентрационных профилей
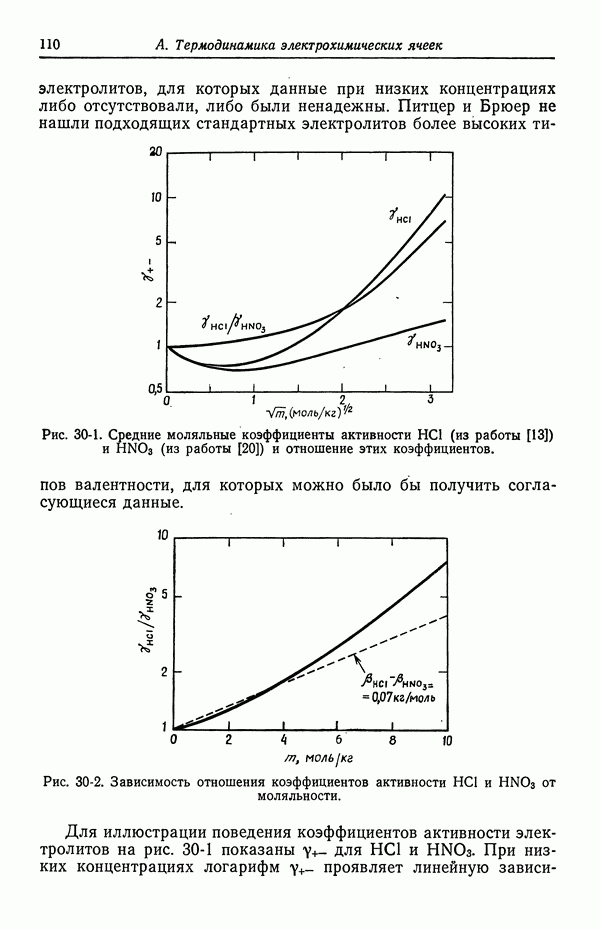
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
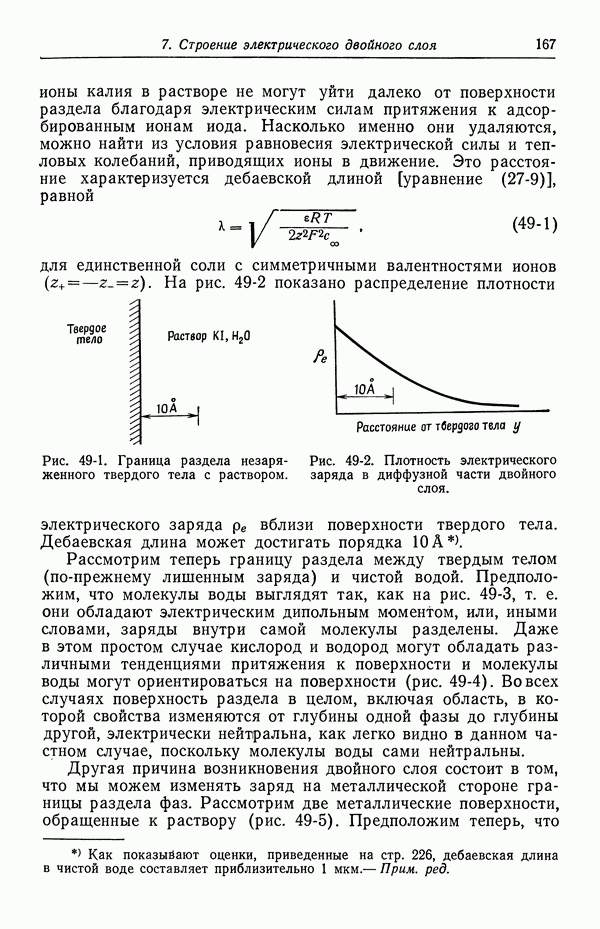
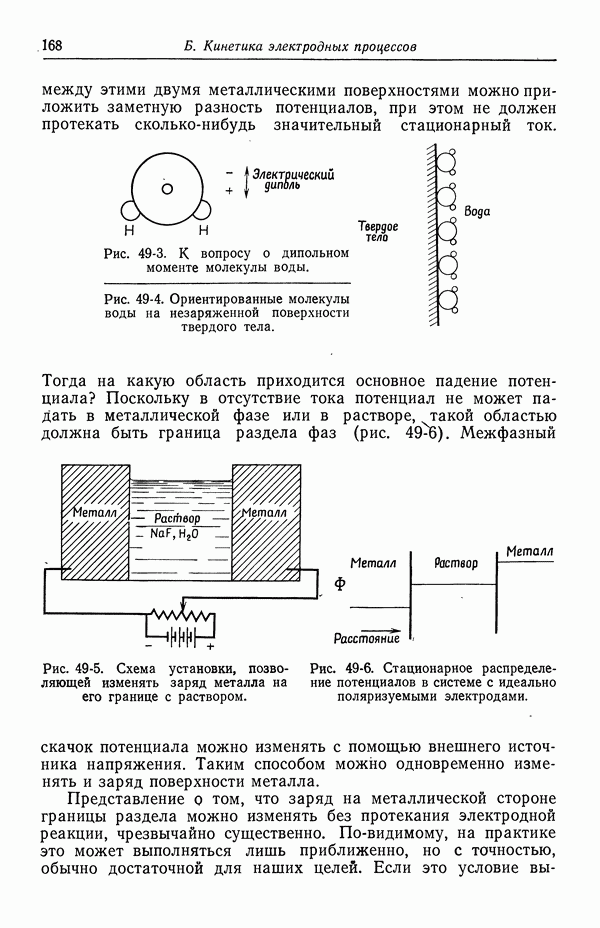
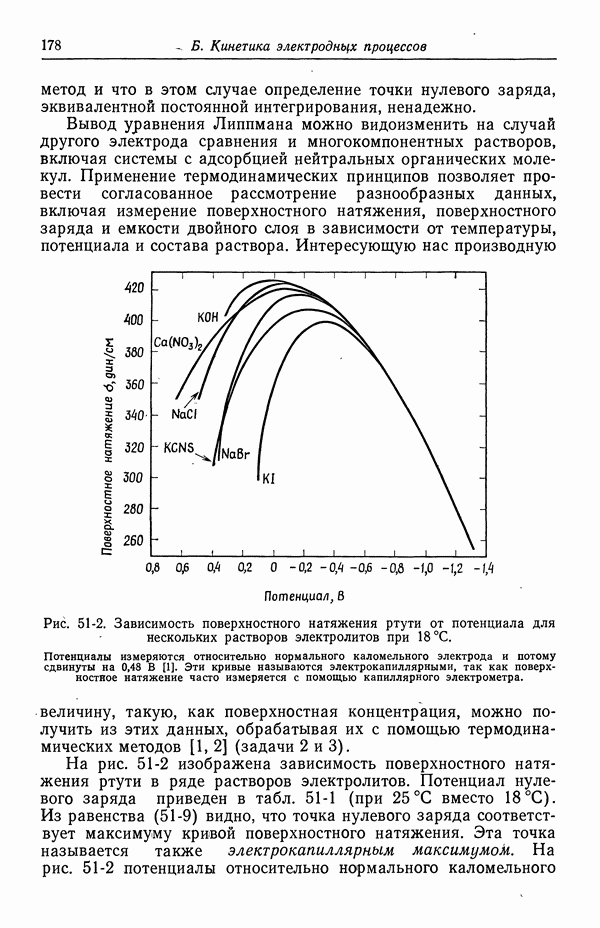
- 49. Качественное описание двойных слоев
- 50. Изотерма адсорбции Гиббса
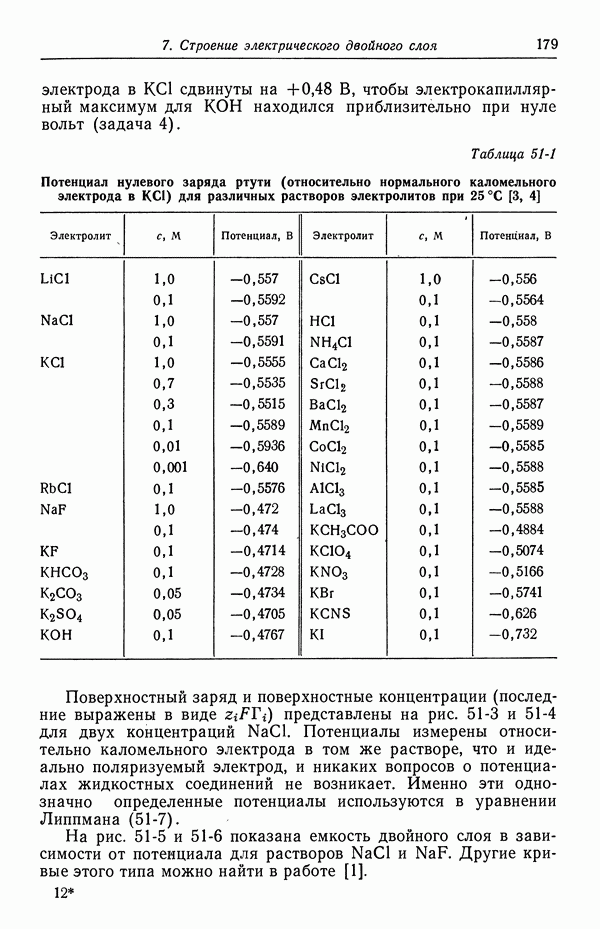
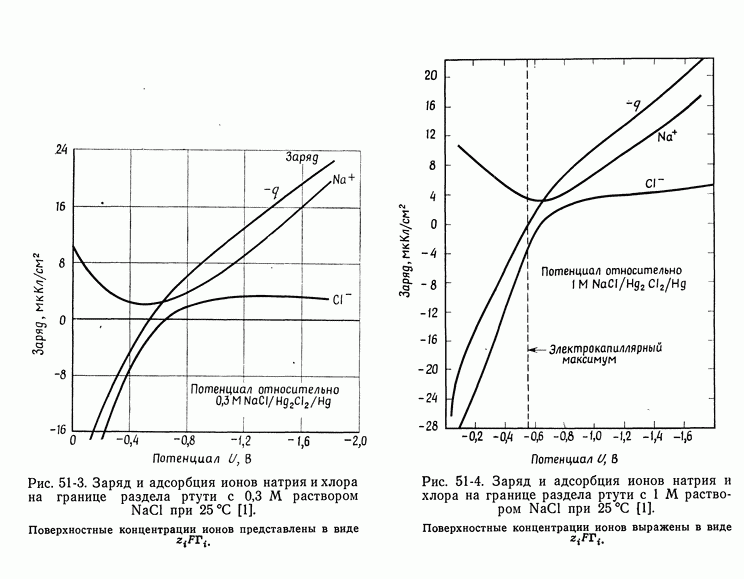
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
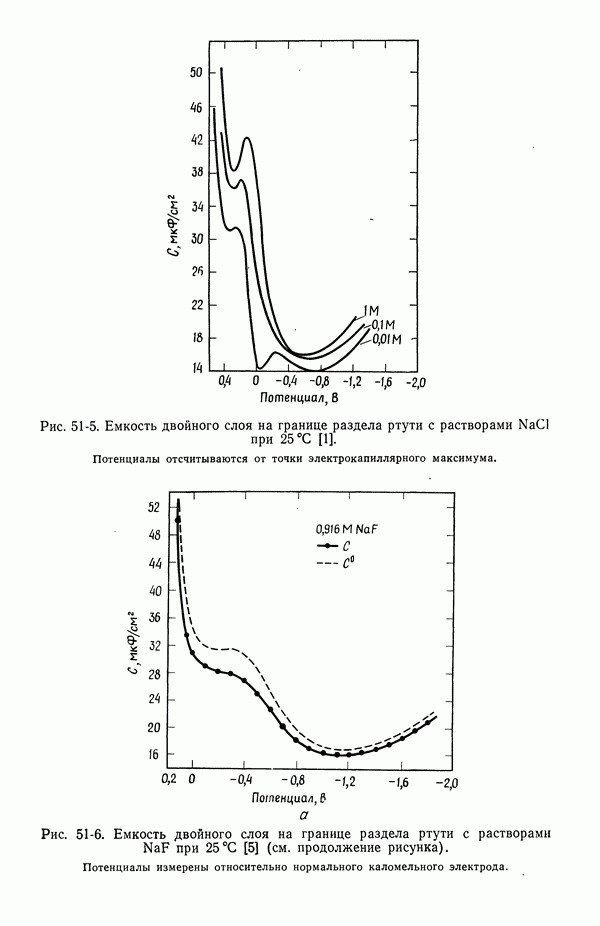
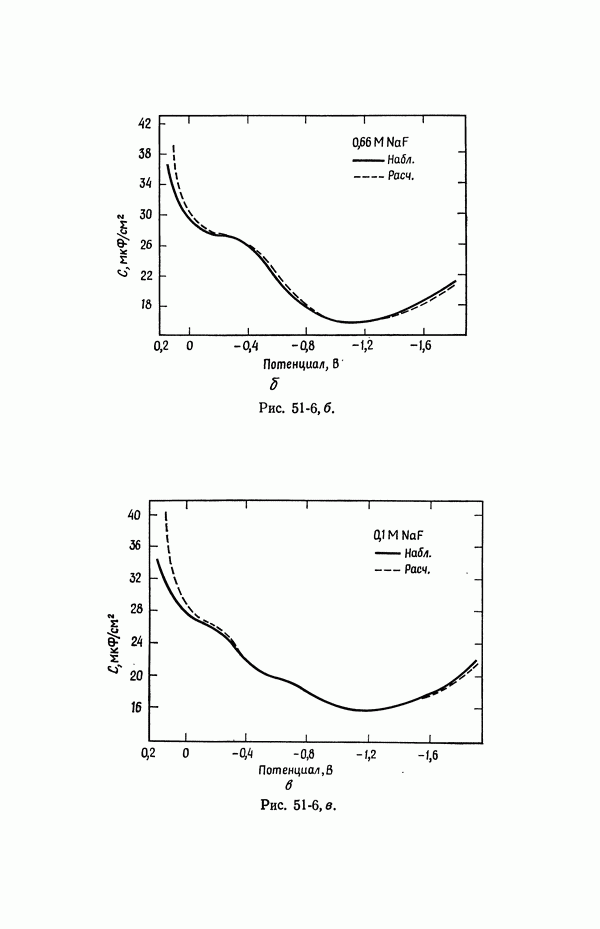
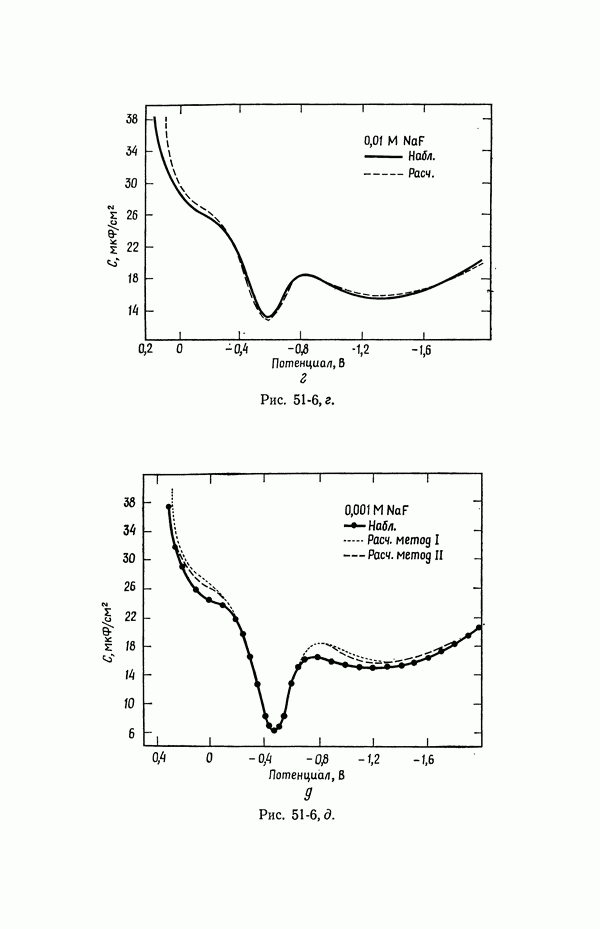
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод — раствор
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
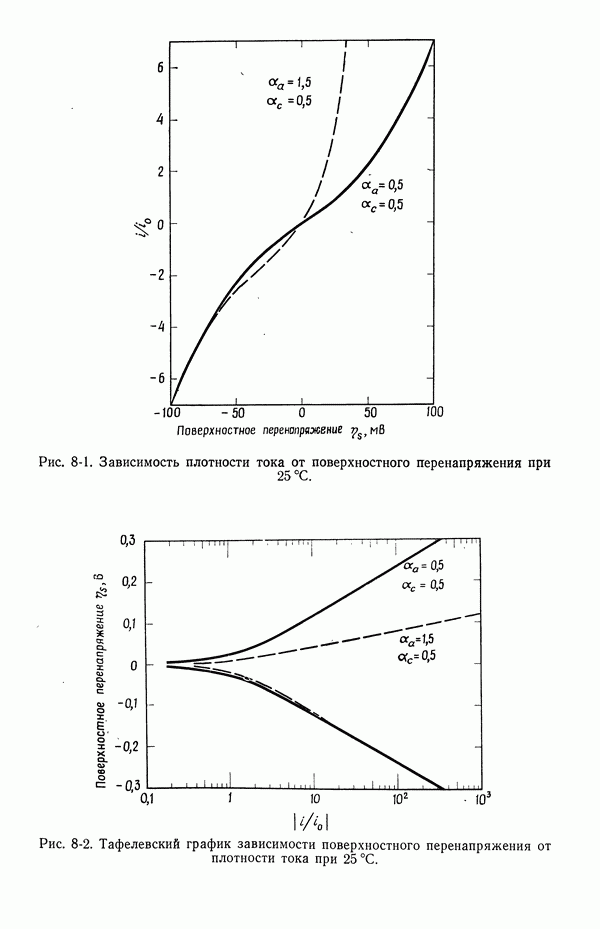
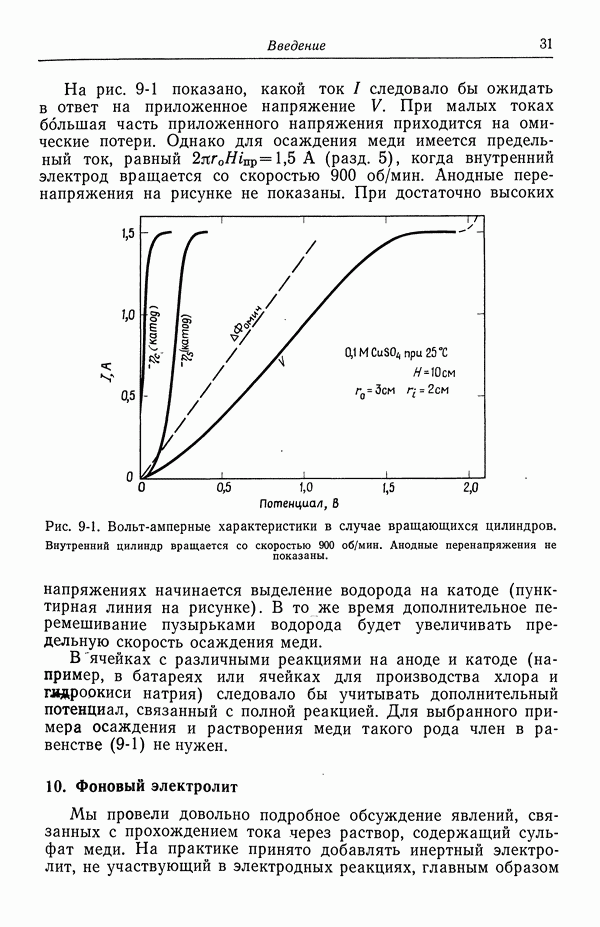
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 66. Динамика границы раздела
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 69. Законы переноса
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
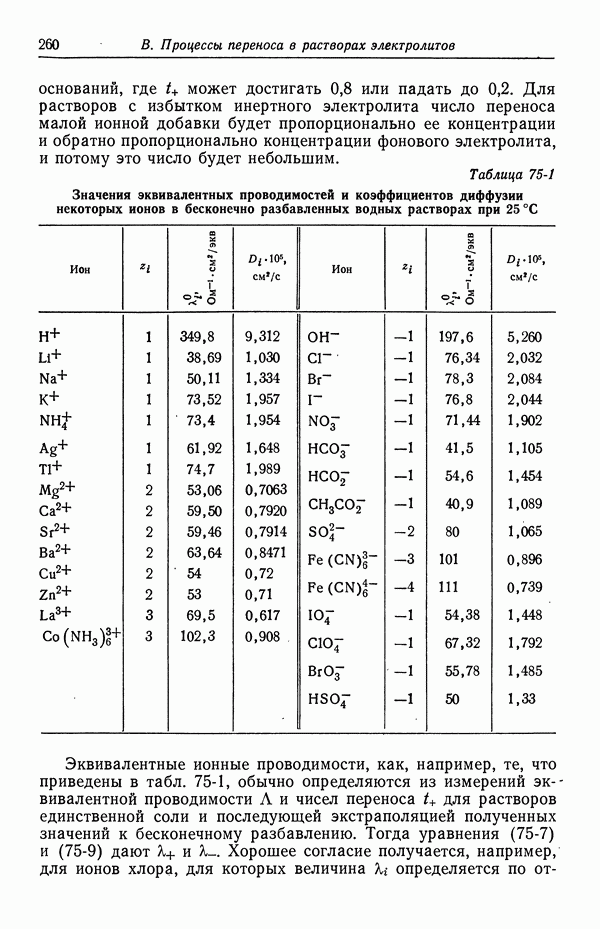
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 78. Законы переноса
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
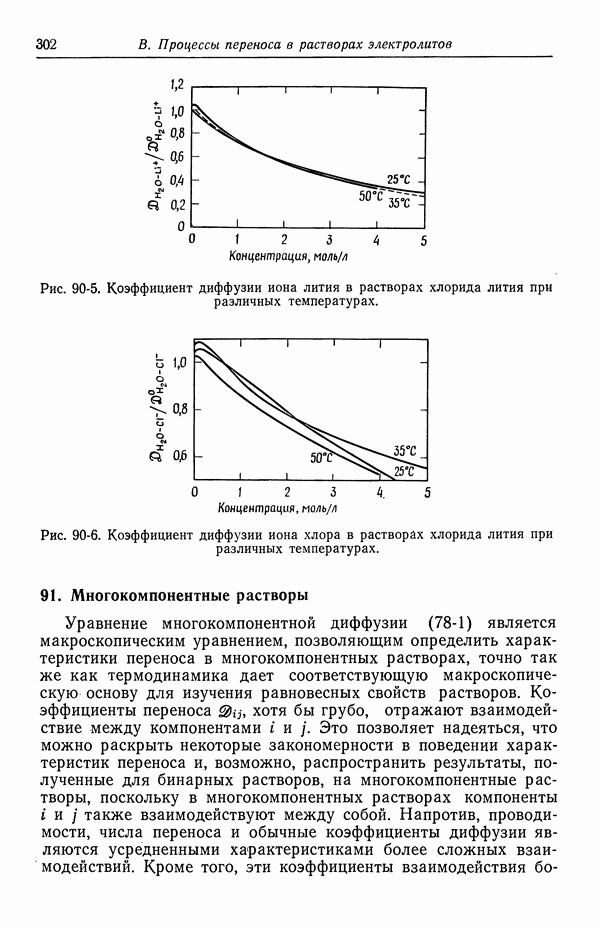
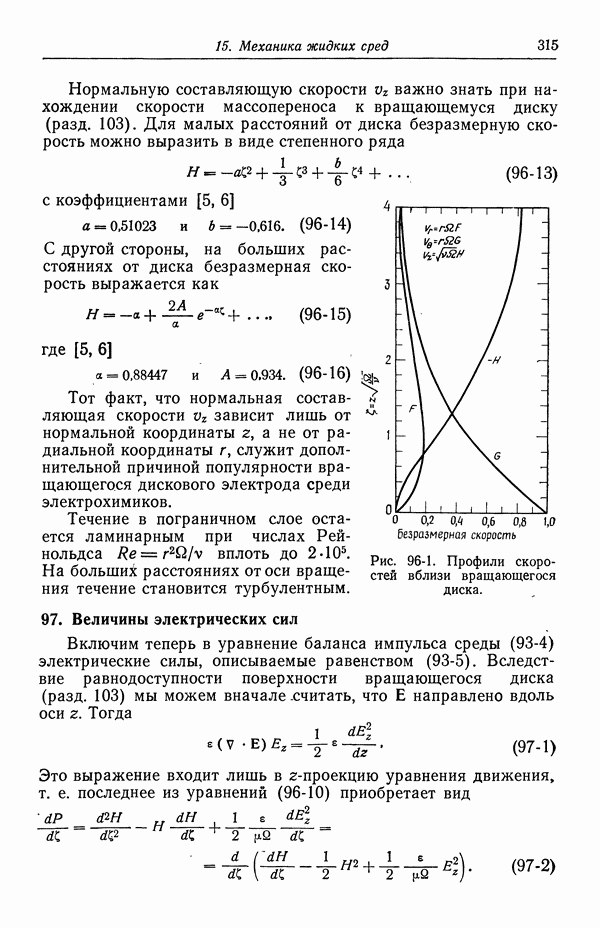
- 90. Растворы, содержащие одну соль
- 92. Интегральные коэффициенты диффузии
- ЗАДАЧА
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
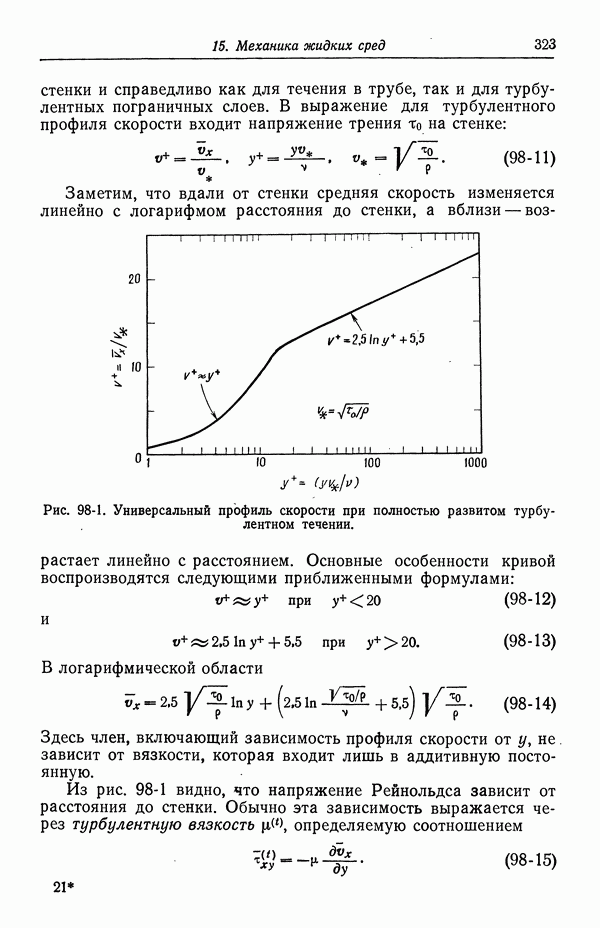
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
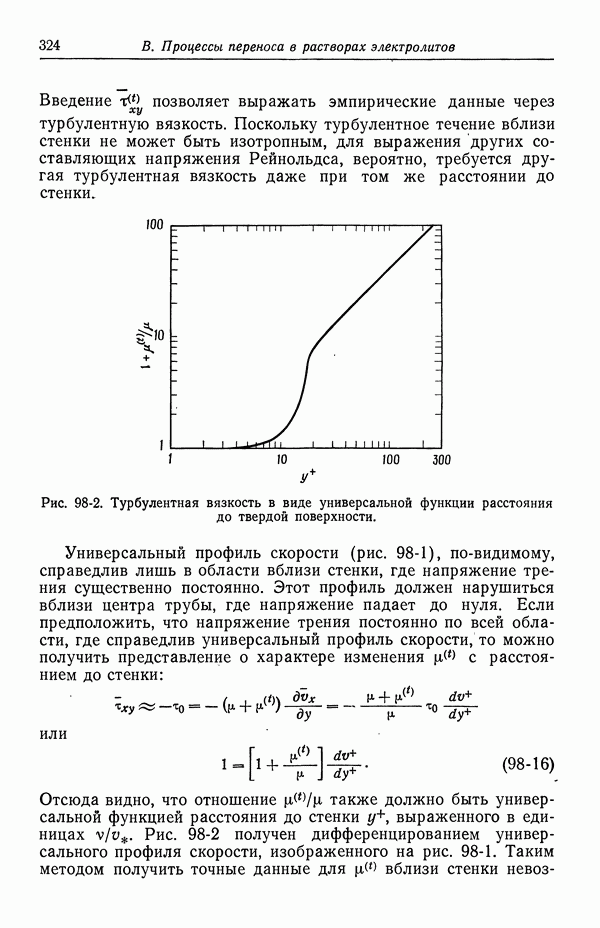
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
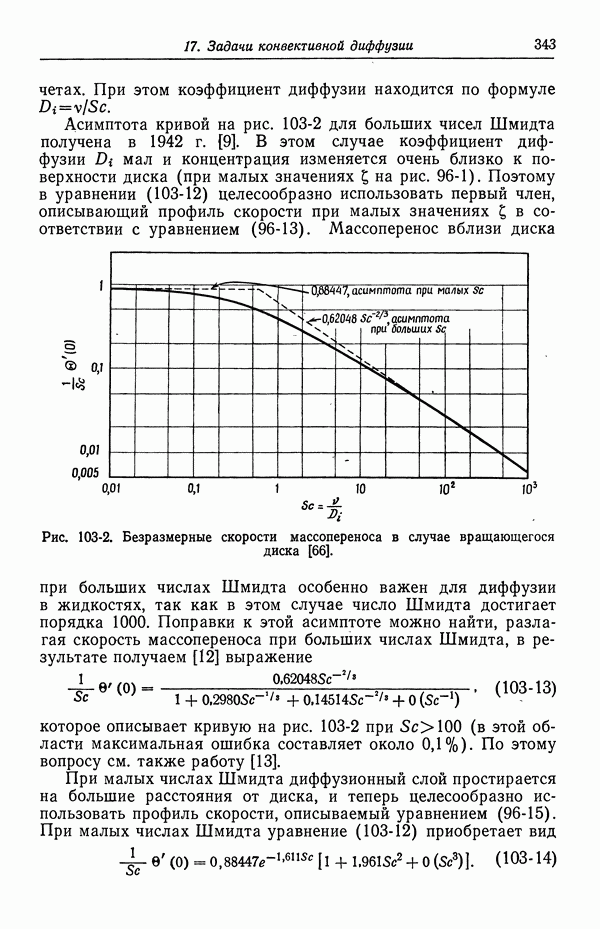
- 103. Вращающийся диск
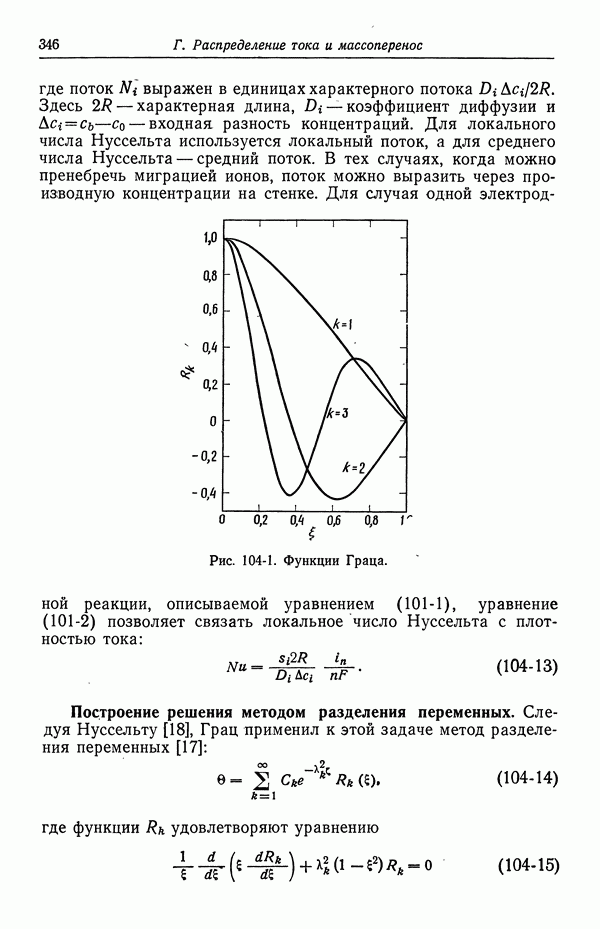
- 104. Задача Граца
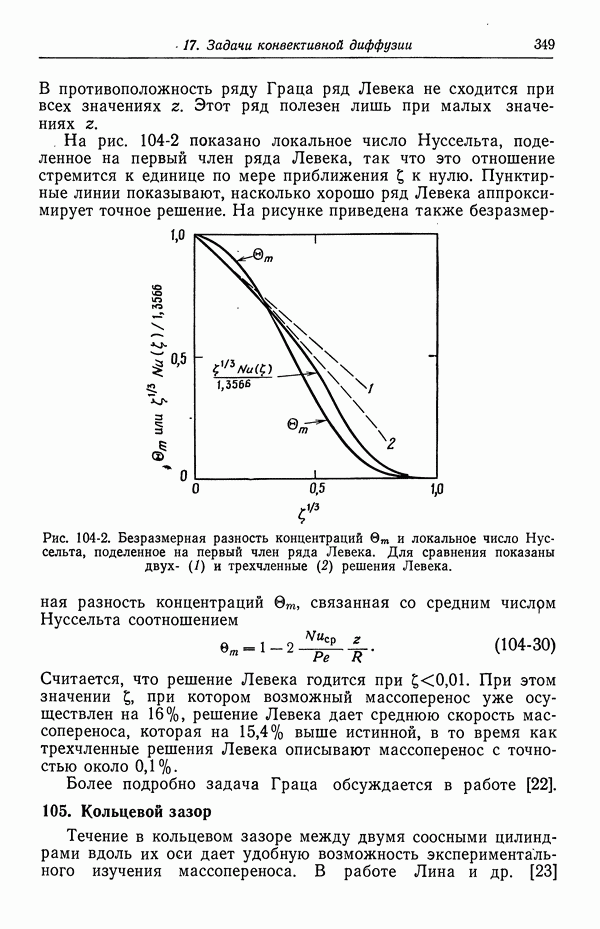
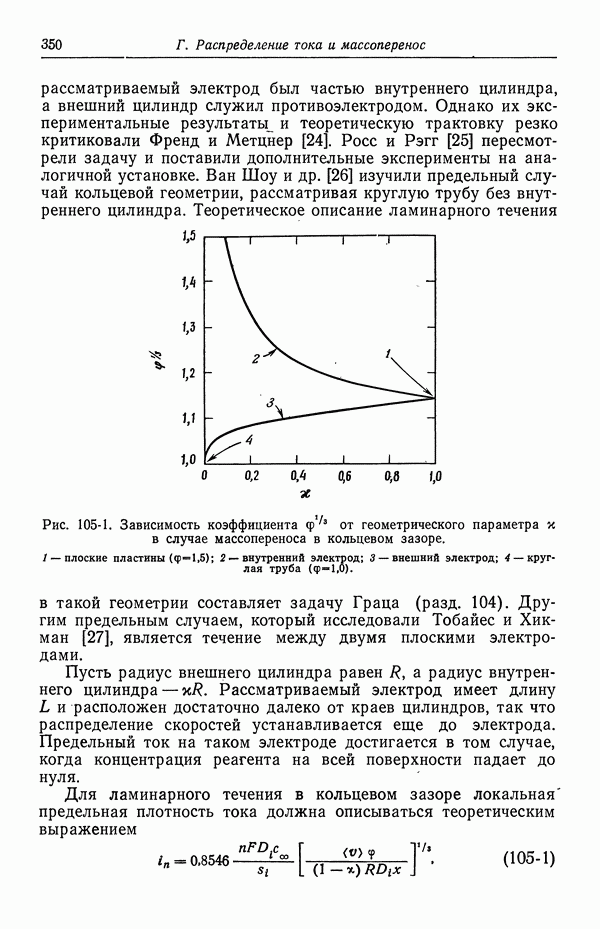
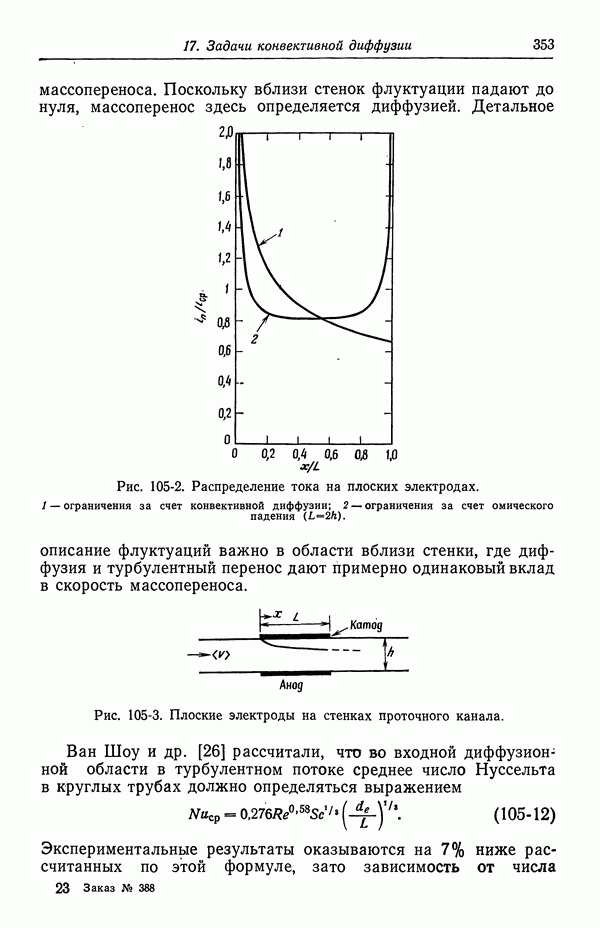
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 111. Свободная конвекция
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
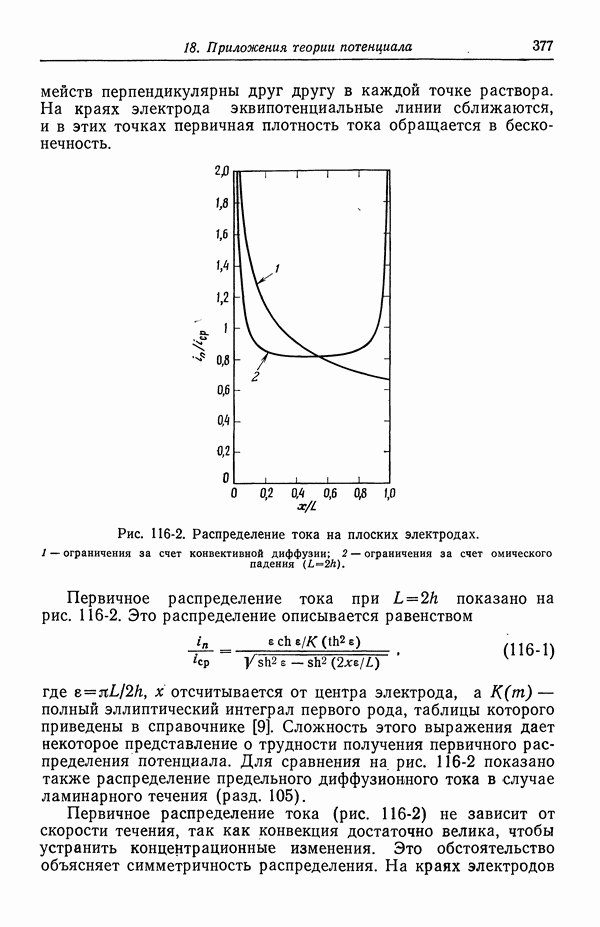
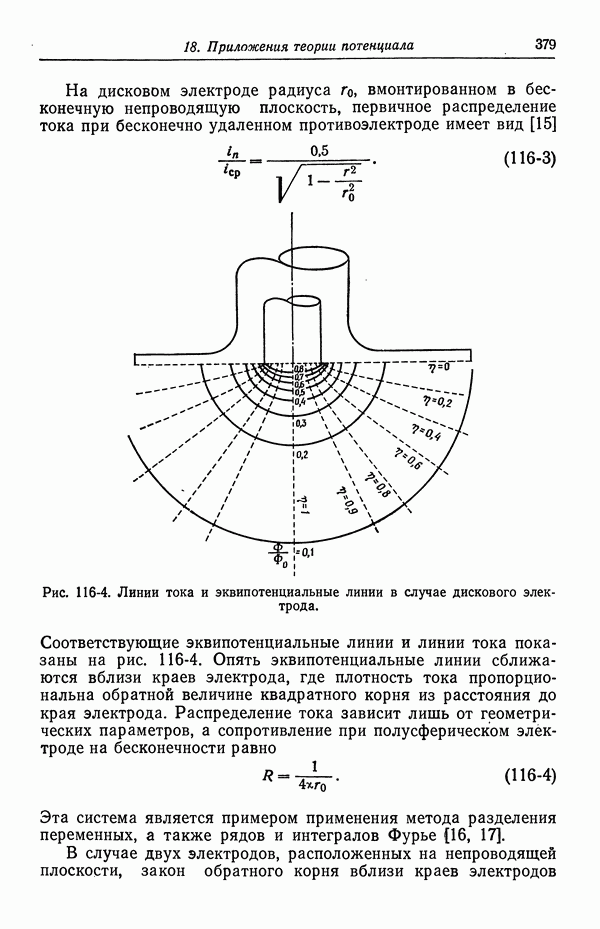
- 116. Первичное распределение тока
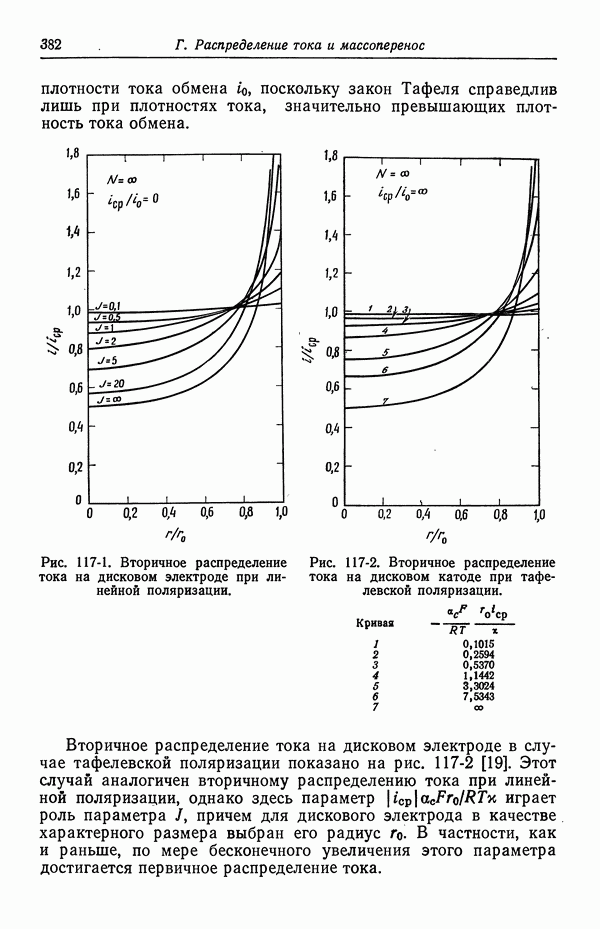
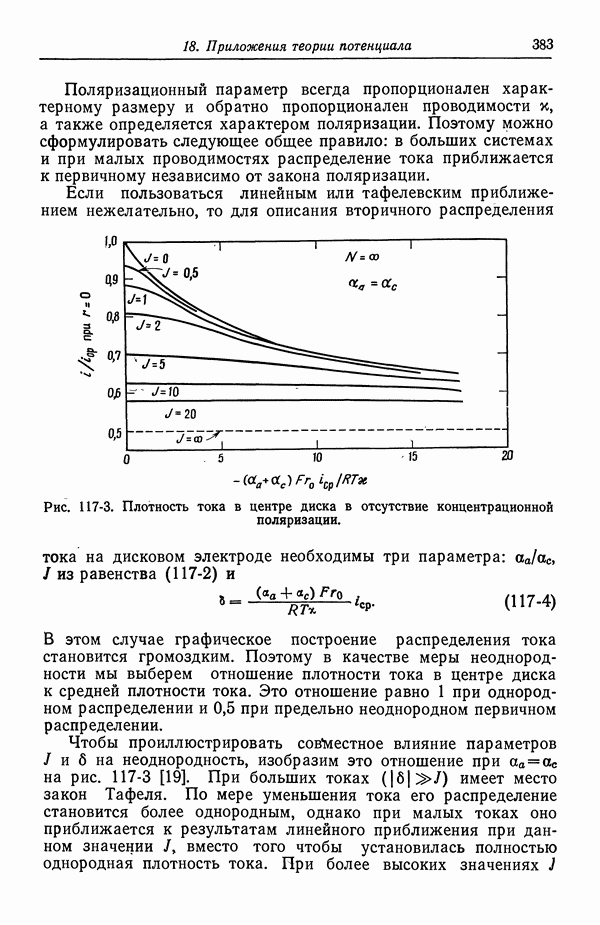
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- СПИСОК ОБОЗНАЧЕНИЙ
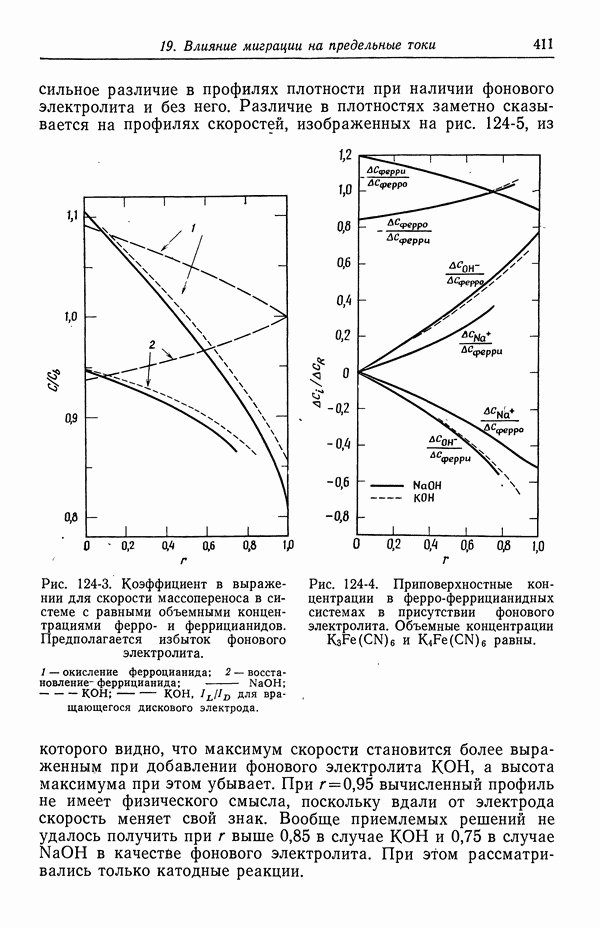
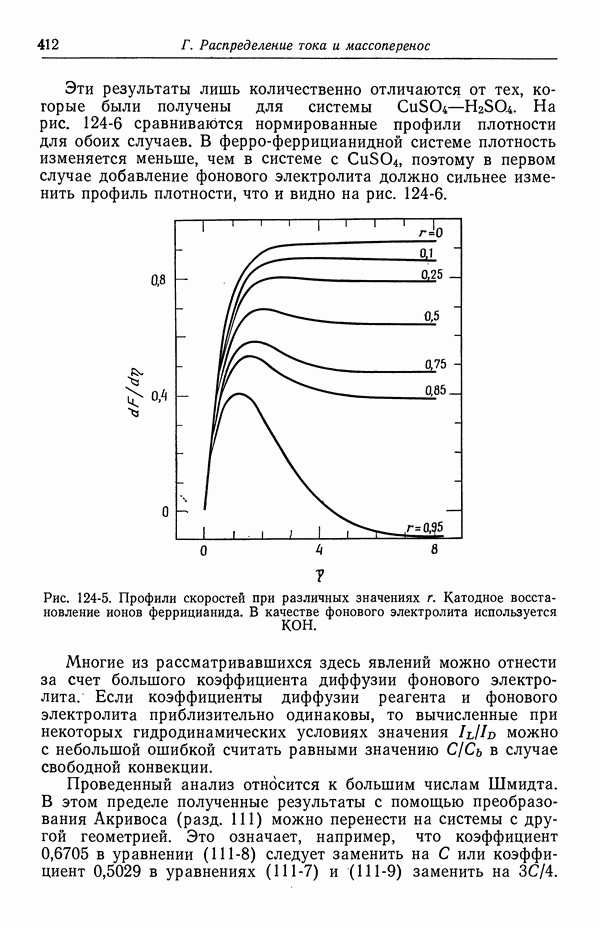
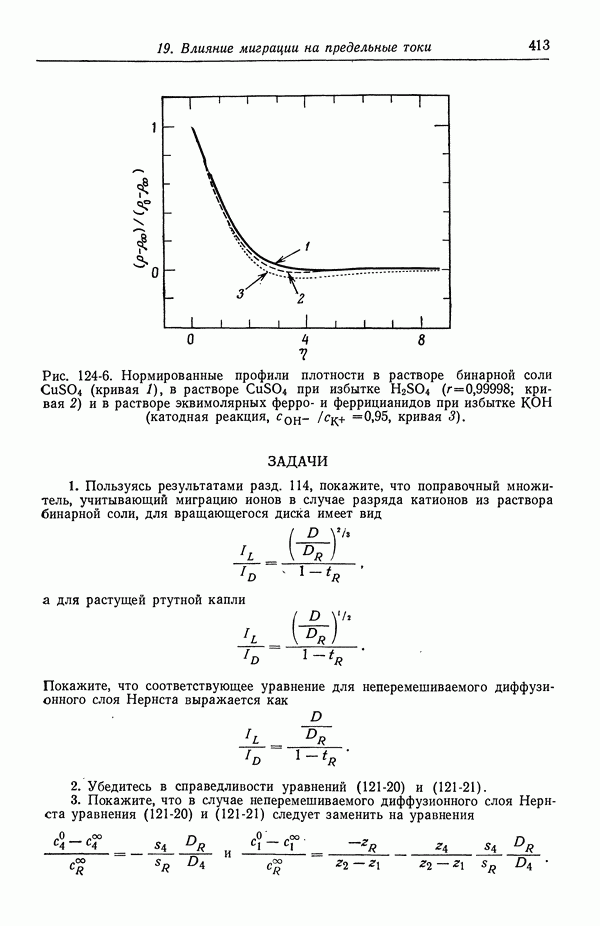
- ГЛАВА 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 119. Решение задачи
- 120. Поправочный множитель в случае предельных токов
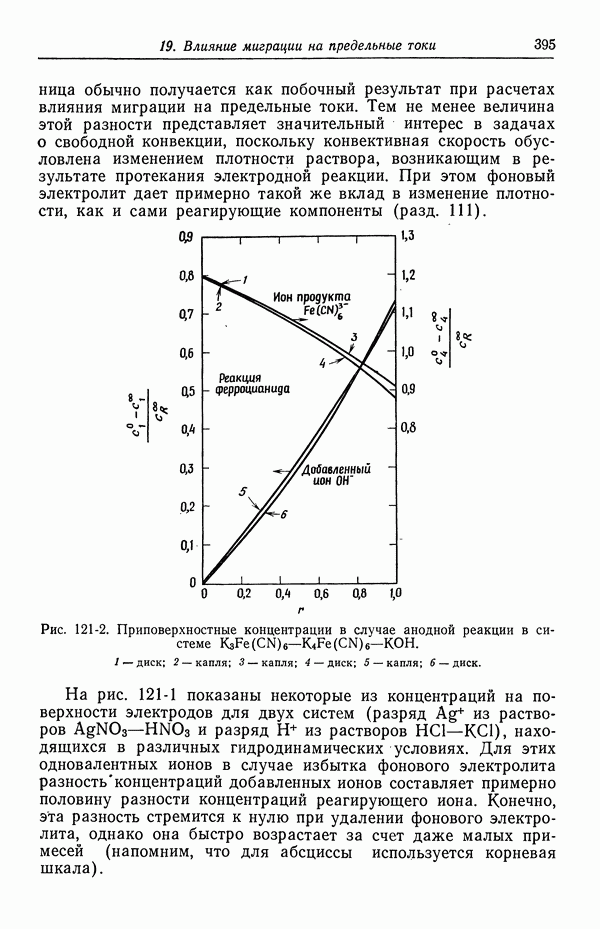
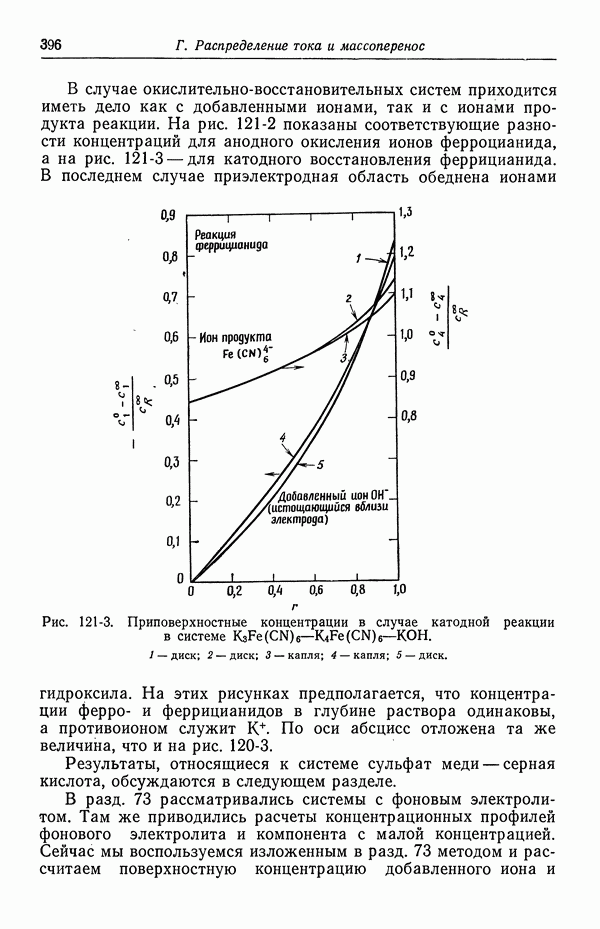
- 121. Изменение концентрации фонового электролита
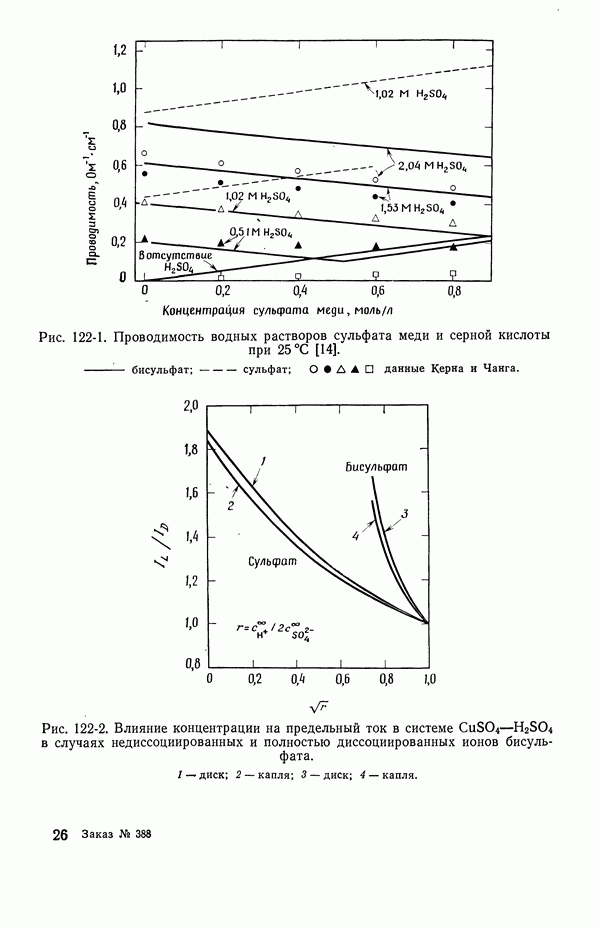
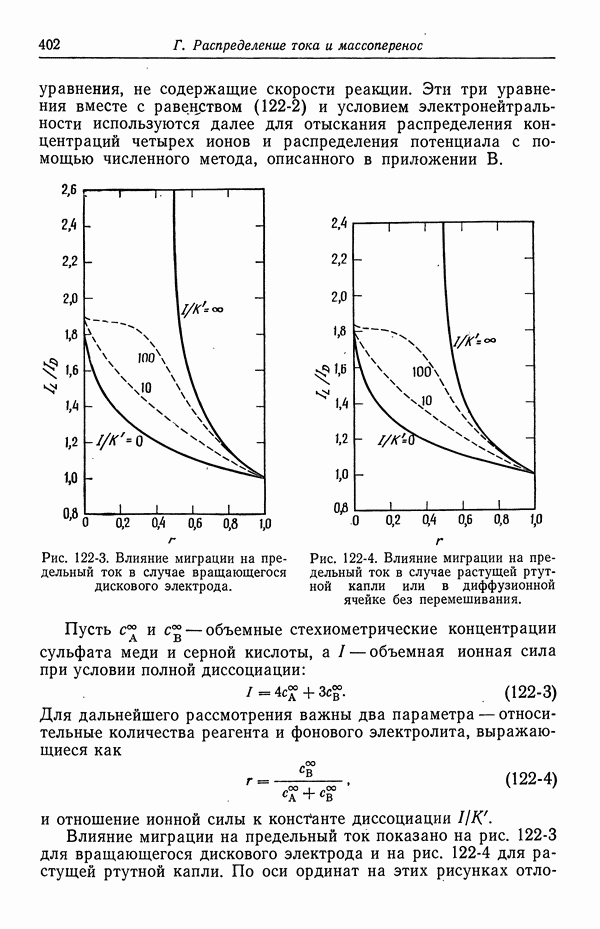
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
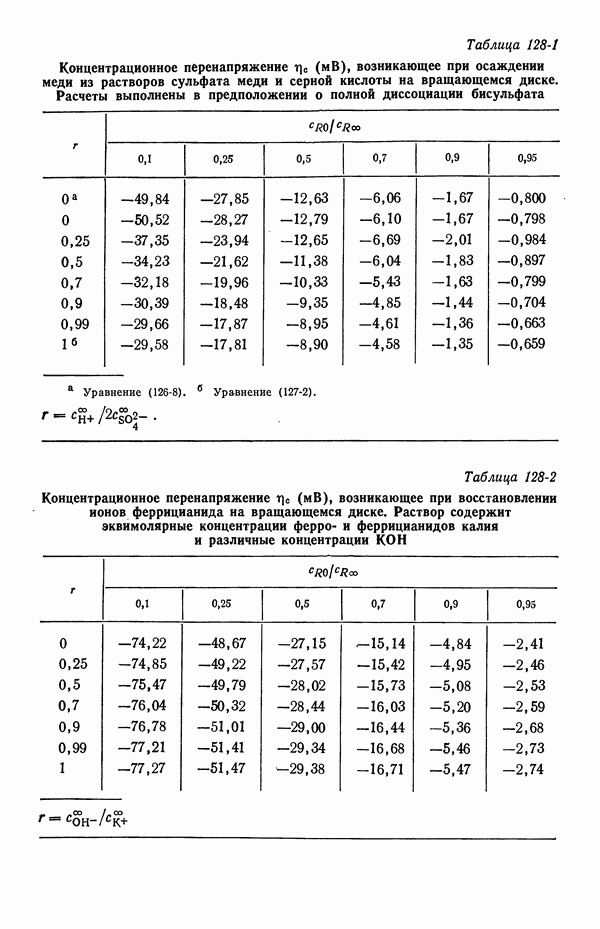
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ