| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
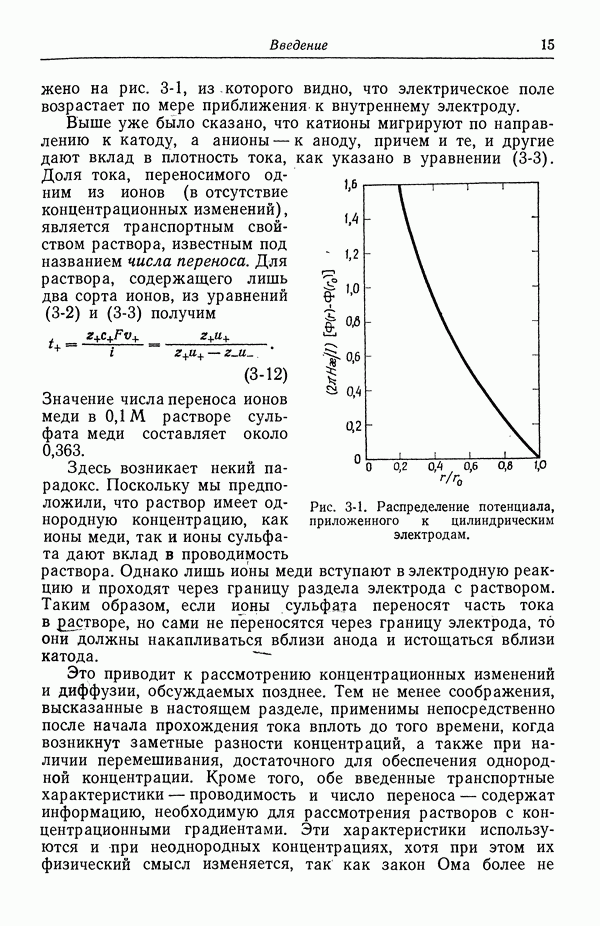
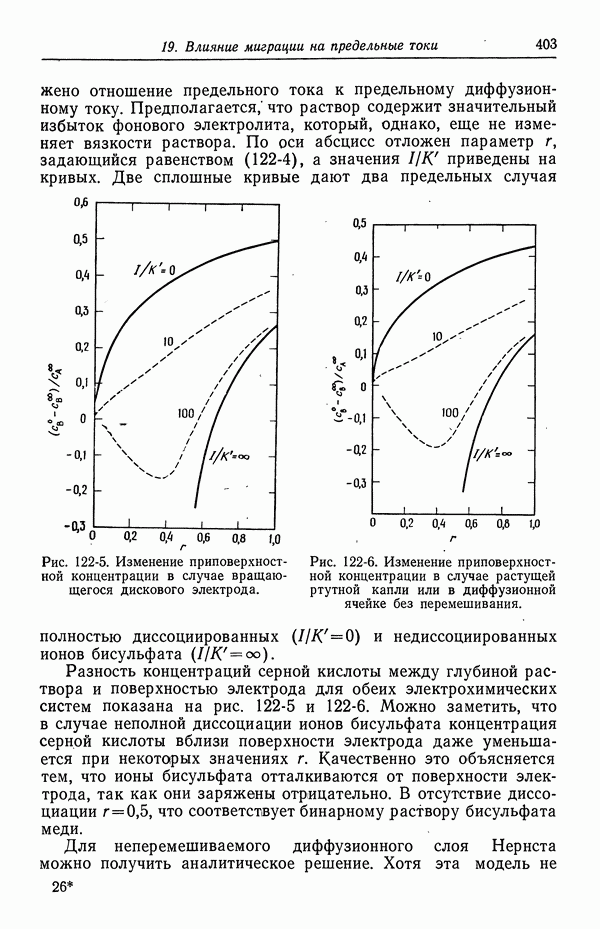
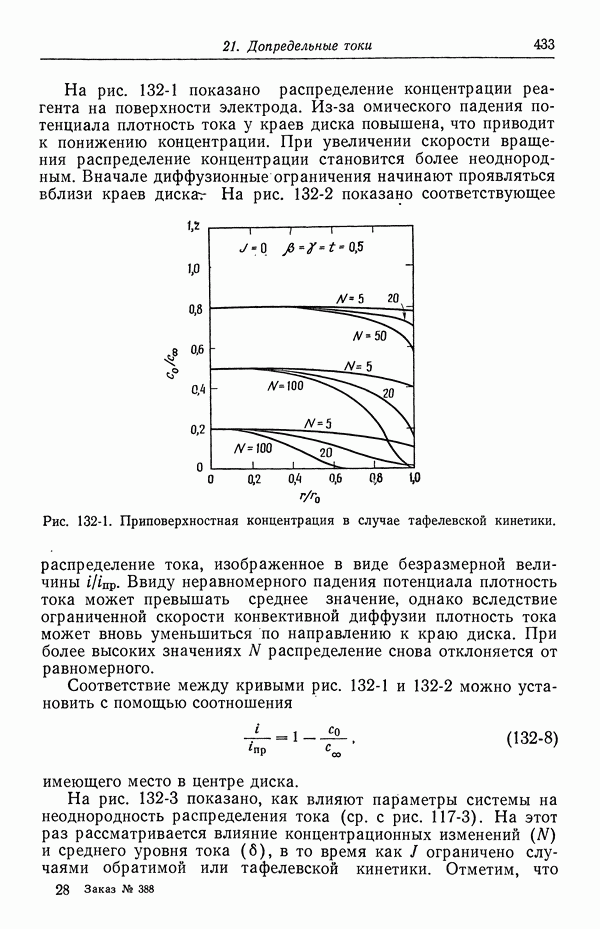
Хотя материал гл. 11 вполне успешно использовался при анализе электрохимических задач, здесь мы хотим привести более общее описание процессов переноса.
78. Законы переноса
Теория массопереноса в растворах электролитов включает описание движения подвижных ионов [уравнение (69-1) или (77-2)], материального баланса [уравнение (69-3)], тока [уравнение (69-2)], электронейтральности [уравнение (69-4)] и механики жидких сред (гл. 15). Уравнения для материального баланса, тока и электронейтральности, приведенные в разд. 69, верны и в случае концентрированных растворов, однако уравнение для потока требует уточнения.
Уравнения для потоков, рассматривавшиеся ранее, неверны даже для тернарных растворов неэлектролитов, поскольку в таких растворах имеется два независимых концентрационных градиента и на диффузионный поток каждого типа компонентов могут влиять оба концентрационных градиента.
Во избежание трудностей, упоминавшихся в разд. 69, уравнение (69-1) можно заменить уравнением многокомпонентной диффузии

где  — электрохимический потенциал компонентов i, а
— электрохимический потенциал компонентов i, а  — коэффициенты трения или коэффициенты взаимодействия. Величина
— коэффициенты трения или коэффициенты взаимодействия. Величина  представляет скорость компонентов i, точнее, среднюю скорость этих компонентов, но не ее мгновенное значение для отдельных молекул. Так, поток компонентов i равен
представляет скорость компонентов i, точнее, среднюю скорость этих компонентов, но не ее мгновенное значение для отдельных молекул. Так, поток компонентов i равен  Полная концентрация равна
Полная концентрация равна

где сумма включает растворитель, а  — коэффициенты диффузии, описывающие взаимодействие компонентов i и
— коэффициенты диффузии, описывающие взаимодействие компонентов i и  Здесь
Здесь
эти коэффициенты являются просто параметрами, которые могут заменить коэффициенты трения 

Член  в уравнении (78-1) можно рассматривать как движущую силу на единицу объема, действующую на компоненты i и заставляющую их двигаться по отношению к окружающей жидкости. Сила на единицу объема, приложенная компонентами
в уравнении (78-1) можно рассматривать как движущую силу на единицу объема, действующую на компоненты i и заставляющую их двигаться по отношению к окружающей жидкости. Сила на единицу объема, приложенная компонентами  к компонентам i в результате их относительного движения, выражена как
к компонентам i в результате их относительного движения, выражена как  , т. е. она пропорциональна разности скоростей компонентов обоих типов. Согласно третьему закону Ньютона (сила действия равна силе противодействия)
, т. е. она пропорциональна разности скоростей компонентов обоих типов. Согласно третьему закону Ньютона (сила действия равна силе противодействия)  находим, что
находим, что  или
или

Таким образом, уравнение (78-1) выражает баланс между движущей силой и полной силой трения, приложенной со стороны остальных компонентов.
Число независимых уравнений вида (78-1) на единицу меньше числа разных типов компонентов. Суммирование этих уравнений по i дает

Левая часть этого уравнения равна нулю ввиду соотношения Гиббса—Дюгема (при постоянных температуре и давлении), а правая часть равна нулю, поскольку 
Уравнение (78-1) свободно от трудностей, упоминавшихся в разд. 69 в связи с уравнением (69-1). Как и в разд. 77, в качестве движущей силы для диффузии и миграции использовался градиент электрохимического потенциала. Это разрешает вопрос об электрическом потенциале и коэффициентах активности отдельных ионов. Использование разности скоростей в уравнении (78-1) позволяет избежать или отложить на будущее обсуждение вопроса о точке отсчета скорости, или средней скорости, относительно которой определены диффузионный и миграционный потоки. Уравнение многокомпонентной диффузии является более общим, чем уравнение (69-1), так как оно связывает движущую силу с линейной комбинацией сопротивлений вместо одного лишь сопротивления растворителя. Число характеристик переноса  входящих в уравнение (78-1), равно
входящих в уравнение (78-1), равно  где — число компонентов разных типов. Такое выражение объясняется связью
где — число компонентов разных типов. Такое выражение объясняется связью  и неопределенностью величин
и неопределенностью величин  Это число отличается от числа характеристик переноса,
Это число отличается от числа характеристик переноса,  определенных уравнением (69-1), независимо от того, используется ли
определенных уравнением (69-1), независимо от того, используется ли
соотношение Нернста—Эйнштейна (75-1). Так, для компонентов трех типов (например, два иона и растворитель) имеются три транспортные характеристики, определенные уравнением (78-1), а для четырех компонентов (например, три иона и растворитель) — шесть транспортных характеристик.
Уравнение (78-1) аналогично уравнению Стефана—Максвелла (см. ссылку [1], стр. 570) и эквивалентно уравнению, выведенному Онзагером (уравнение 14 на стр. 245 в работе [2]). Уравнения Стефана—Максвелла применяются к диффузии в разреженных газовых смесях и выражают движущую силу через градиент мольной доли или градиент парциального давления вместо градиента электрохимического потенциала. Уравнение (78-4) эквивалентно соотношению взаимности Онзагера. Величины, обратные коэффициентам  можно рассматривать как коэффициенты трения, аналогично тому, как это делалось Лейти [3, 4] и Клеймом [5, 6] при описании переноса в ионных растворах и расплавах. Этот же прием использовал Бюргере [7] при рассмотрении проводимости ионизированных газов, а Лайтфут и др. [8] применяли уравнение (78-1) к жидким растворам. Справедливость доводов в пользу равенства
можно рассматривать как коэффициенты трения, аналогично тому, как это делалось Лейти [3, 4] и Клеймом [5, 6] при описании переноса в ионных растворах и расплавах. Этот же прием использовал Бюргере [7] при рассмотрении проводимости ионизированных газов, а Лайтфут и др. [8] применяли уравнение (78-1) к жидким растворам. Справедливость доводов в пользу равенства  обсуждал Трусделл [9] (см. также работу Лэмма [10]).
обсуждал Трусделл [9] (см. также работу Лэмма [10]).
Обобщение уравнения (78-1) на случай неизотермических сред будет проведено в разд. 85.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
- 5. Диффузионный слой
- 6. Концентрационные ячейки
- 7. Концентрационное перенапряжение
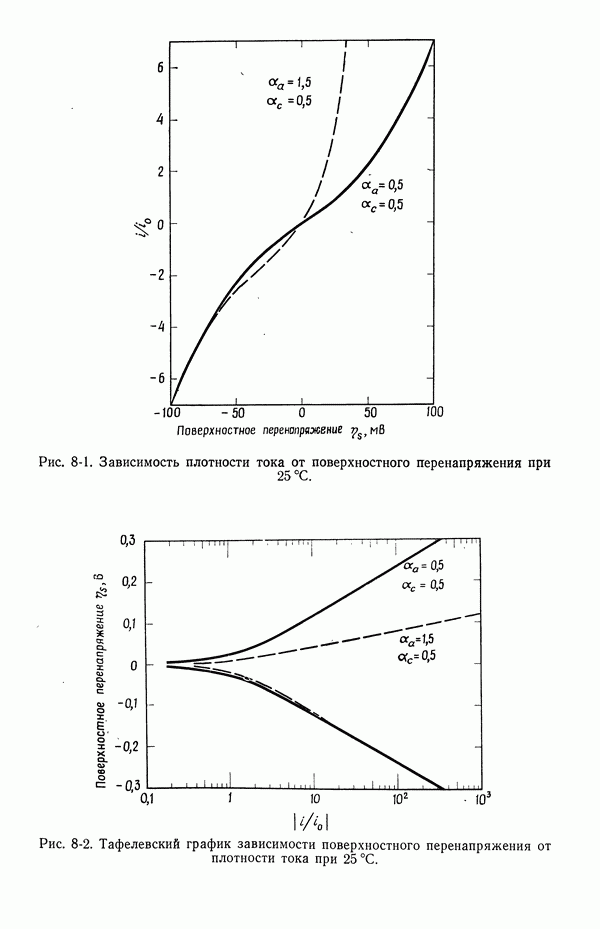
- 8. Поверхностное перенапряжение
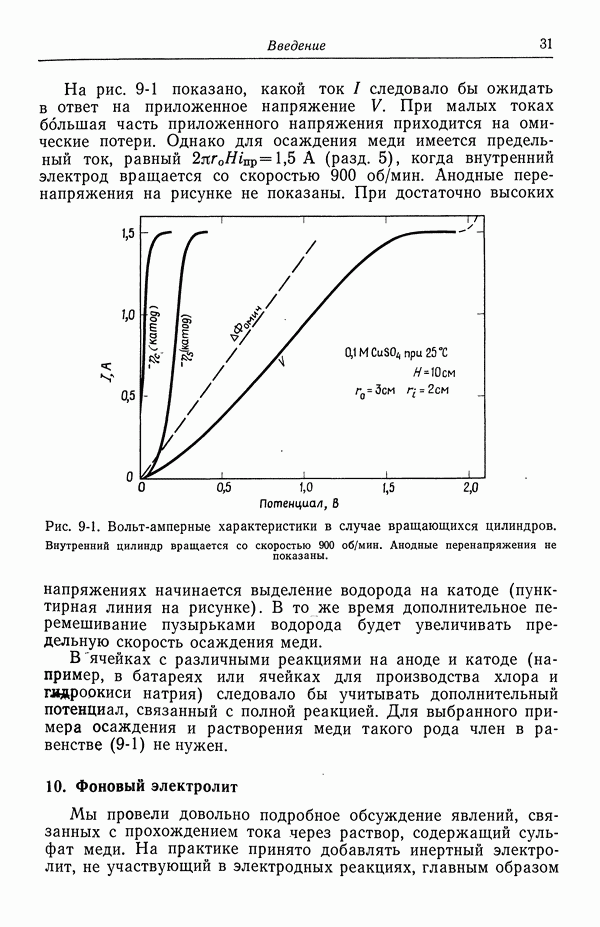
- 9. Потенциал ячейки
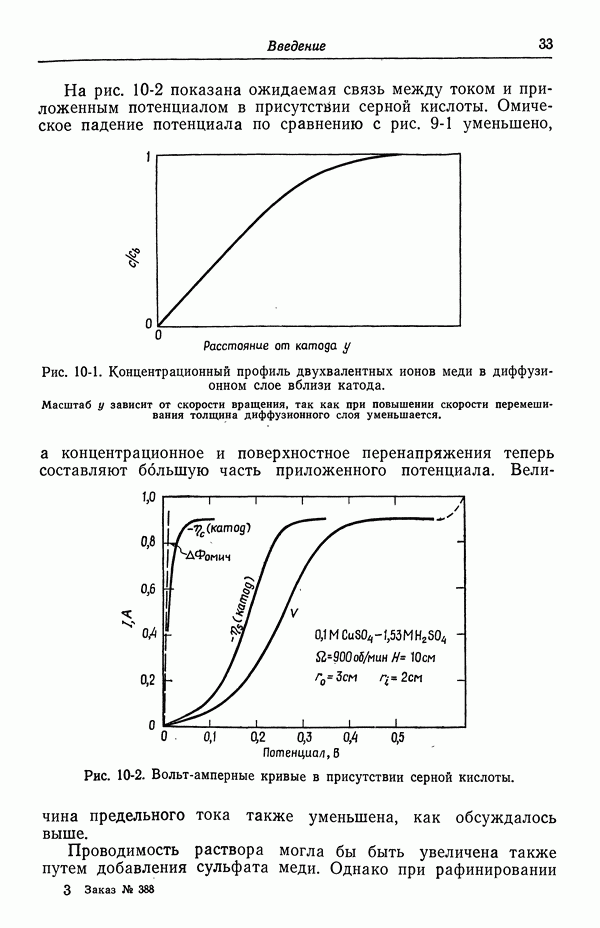
- 10. Фоновый электролит
- 11. Свободная конвекция
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
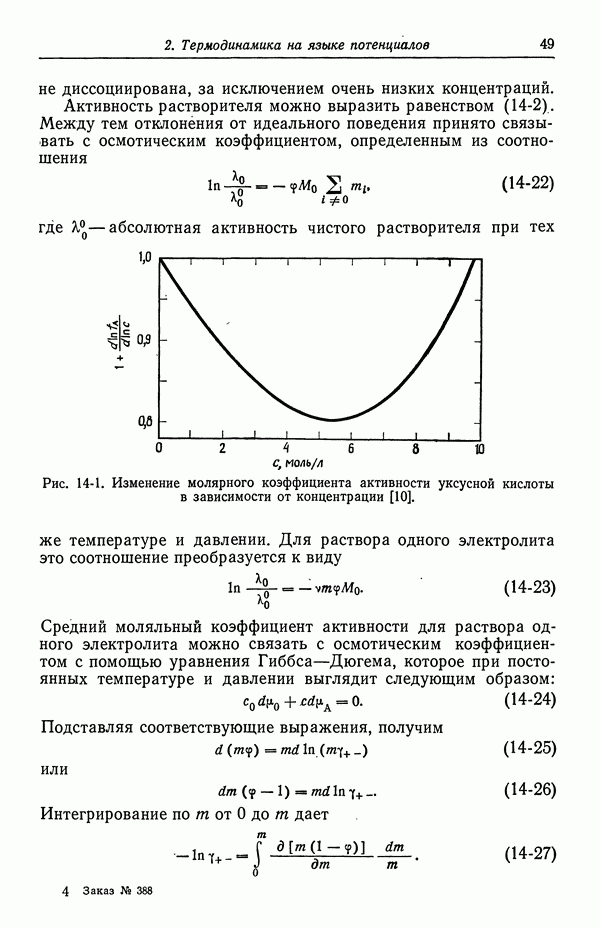
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая—Хюккеля
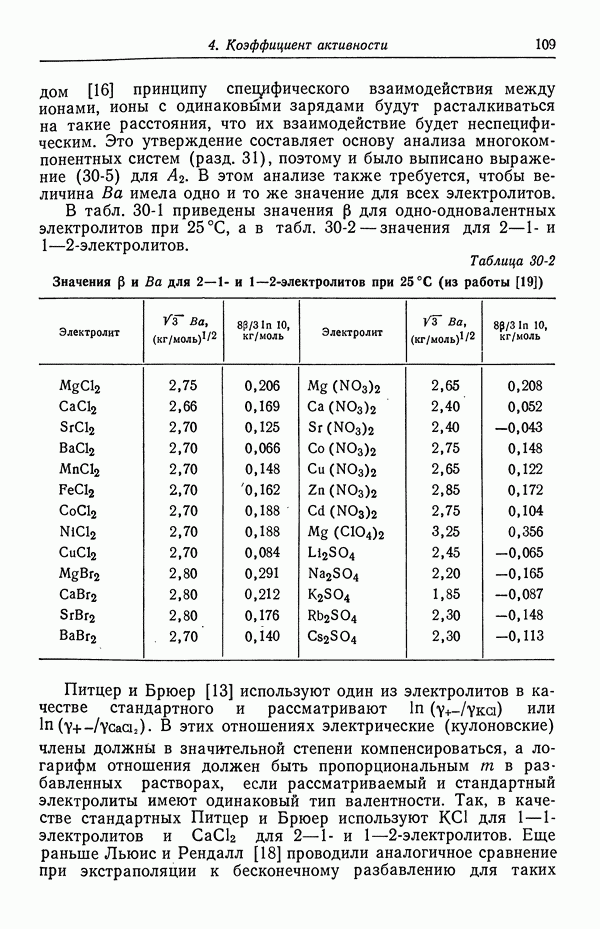
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
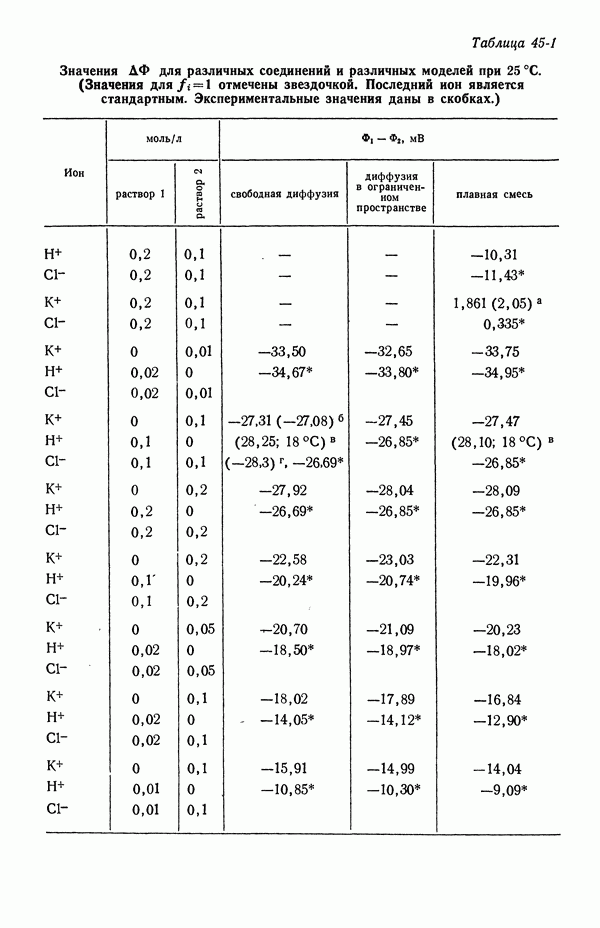
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 49. Качественное описание двойных слоев
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод — раствор
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 66. Динамика границы раздела
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 69. Законы переноса
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 78. Законы переноса
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 92. Интегральные коэффициенты диффузии
- ЗАДАЧА
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
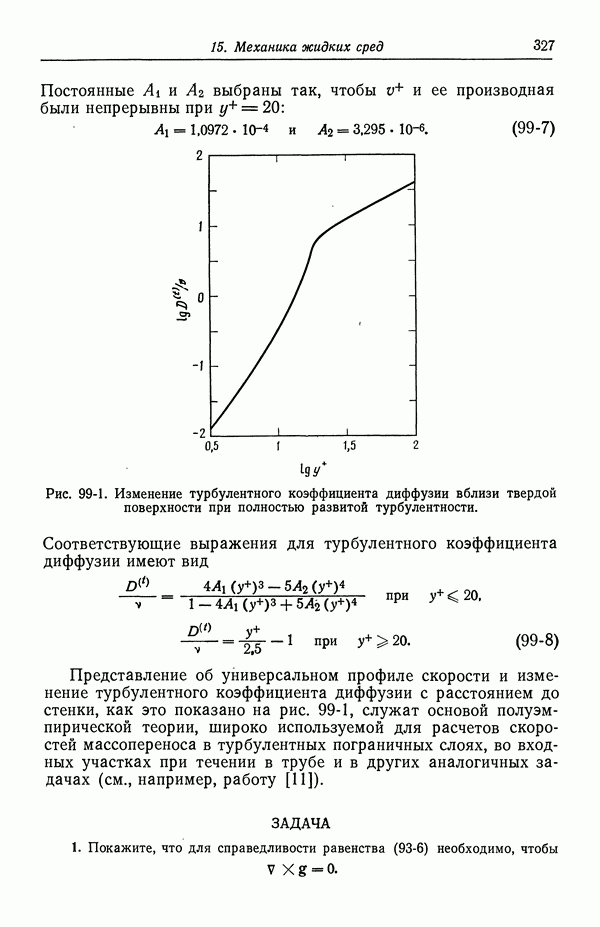
- 99. Массоперенос в турбулентном потоке
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
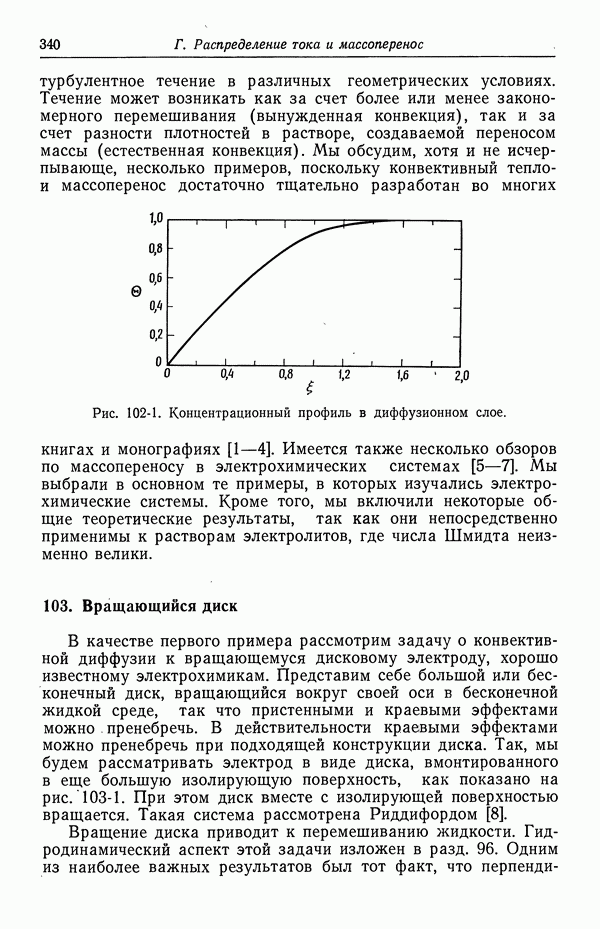
- 102. Упрощенное описание конвективной диффузии
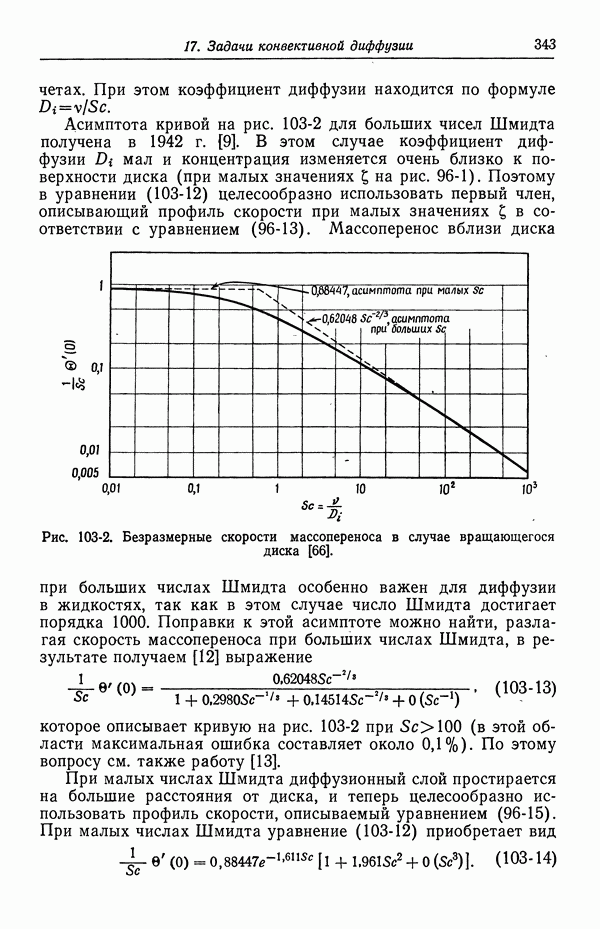
- 103. Вращающийся диск
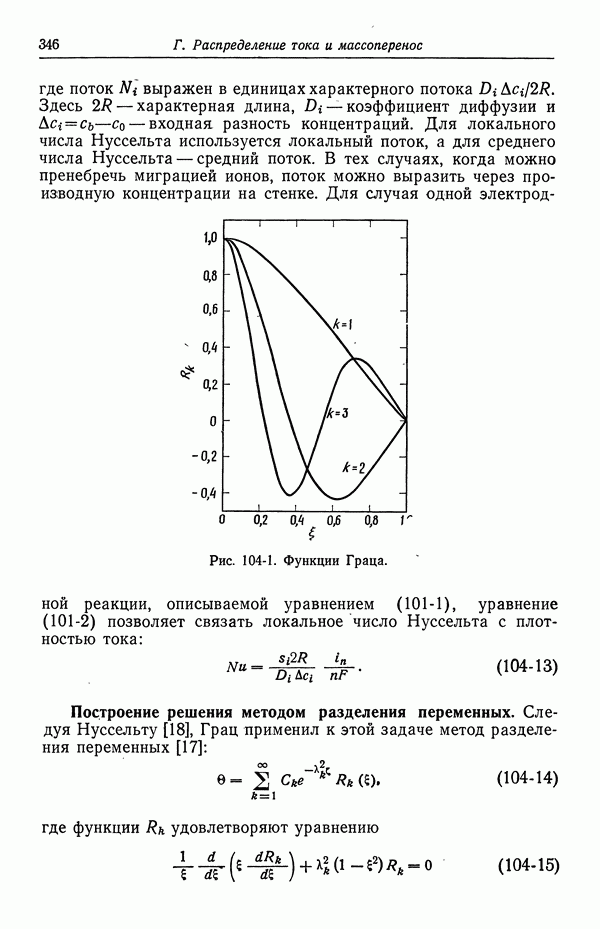
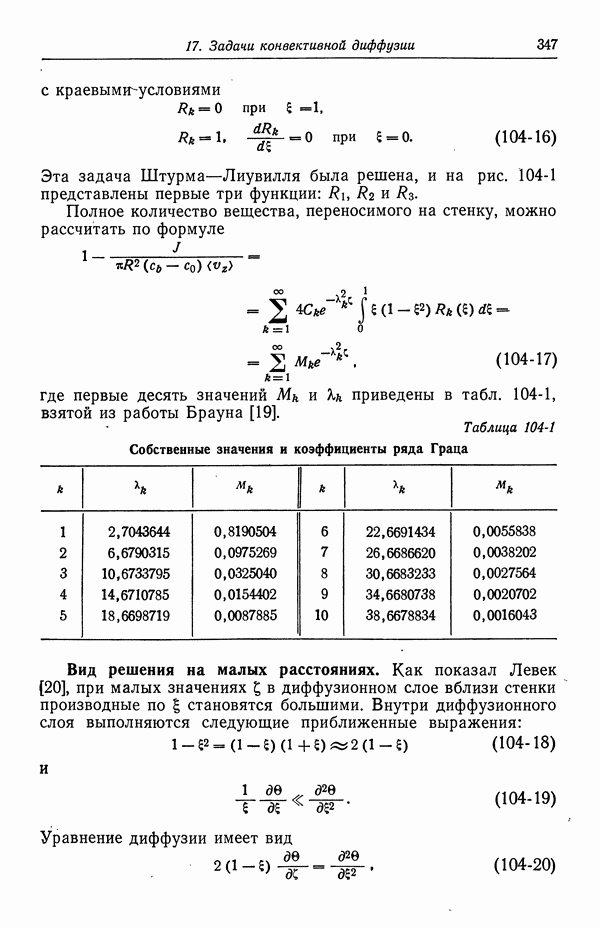
- 104. Задача Граца
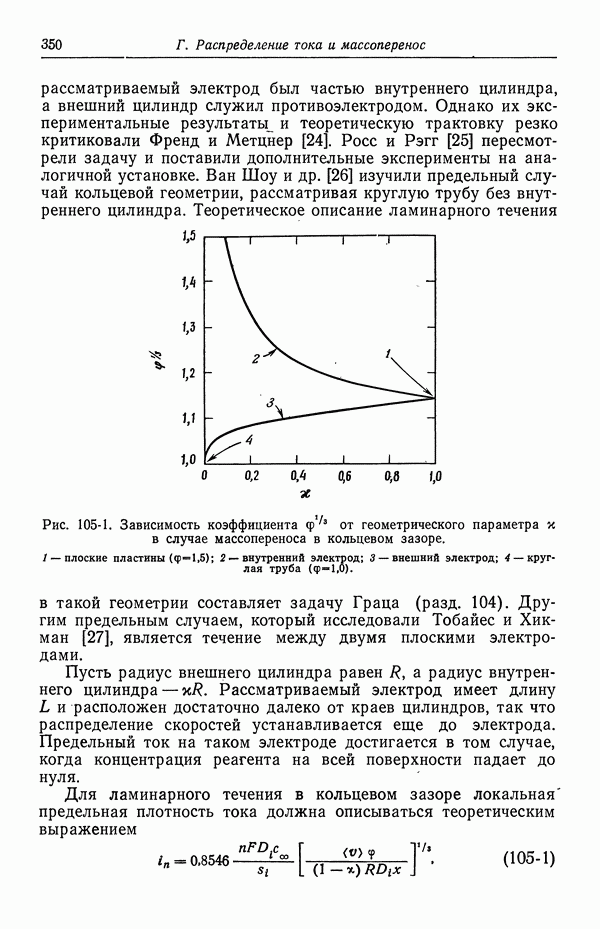
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 111. Свободная конвекция
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
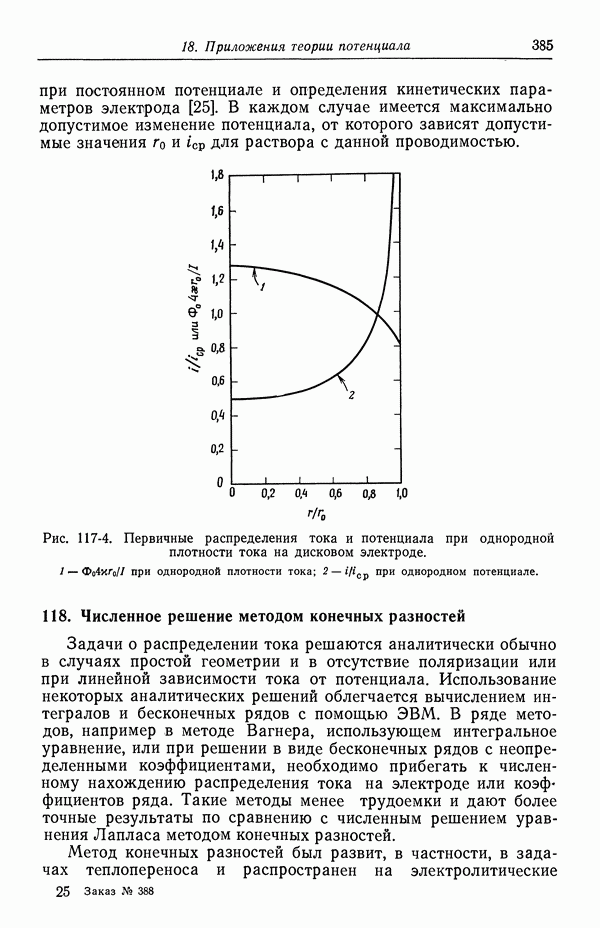
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- СПИСОК ОБОЗНАЧЕНИЙ
- ГЛАВА 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 119. Решение задачи
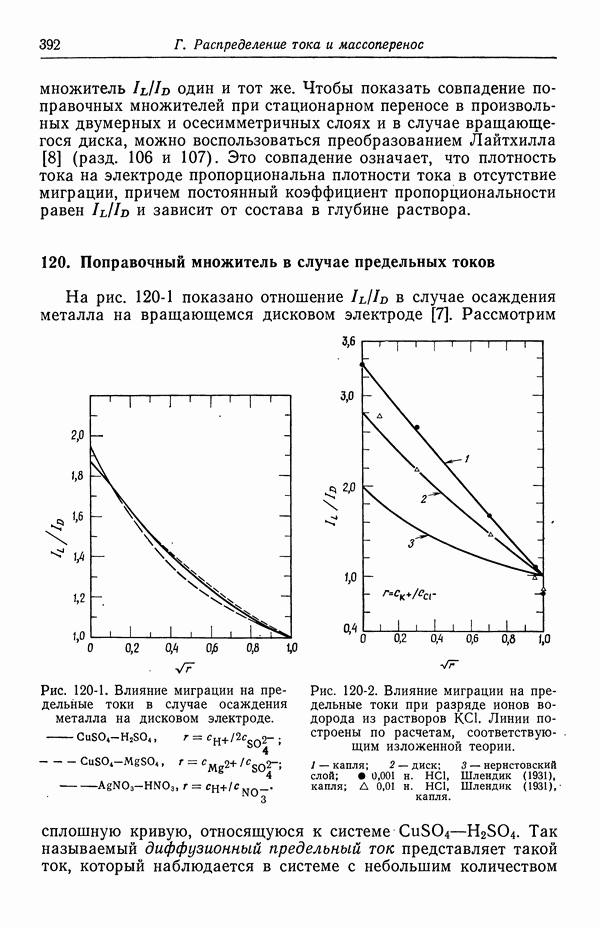
- 120. Поправочный множитель в случае предельных токов
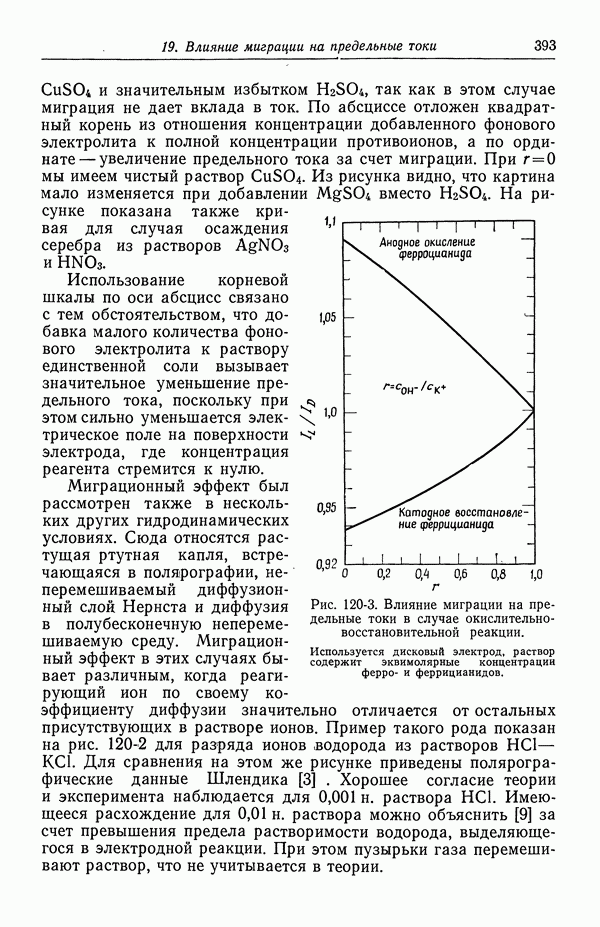
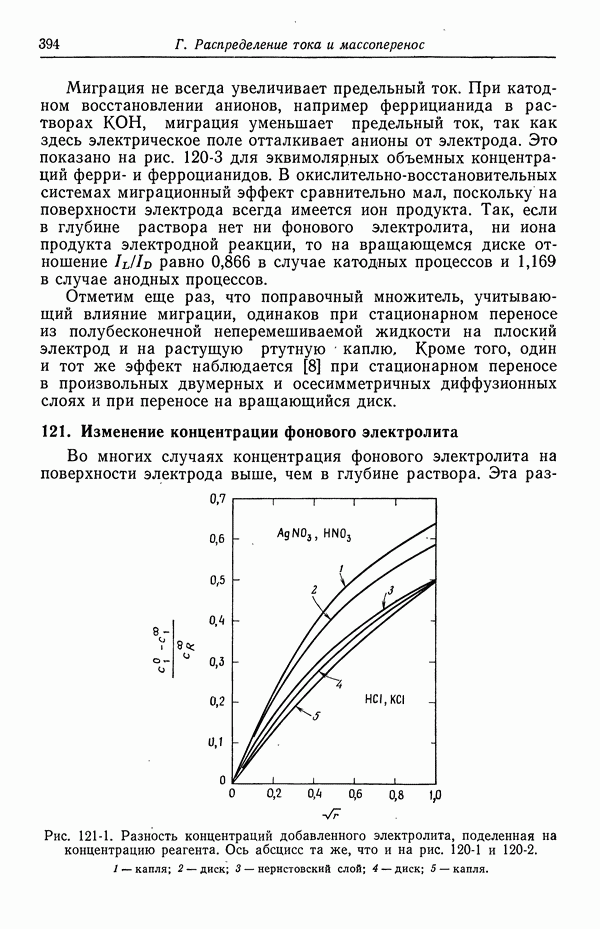
- 121. Изменение концентрации фонового электролита
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ