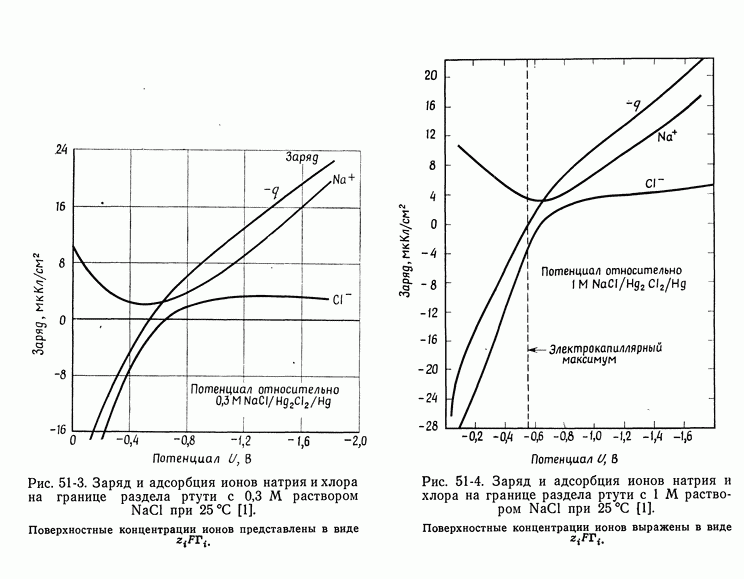
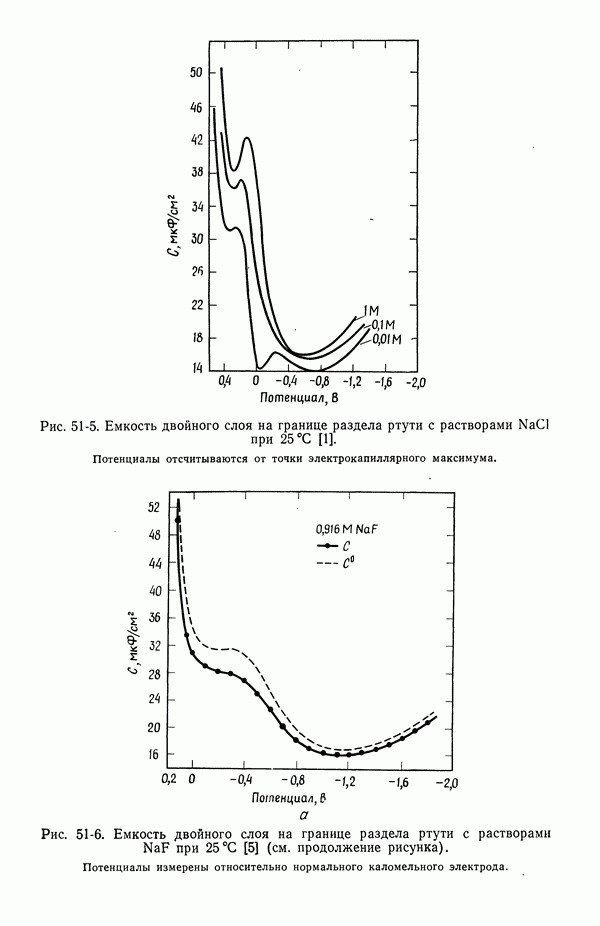
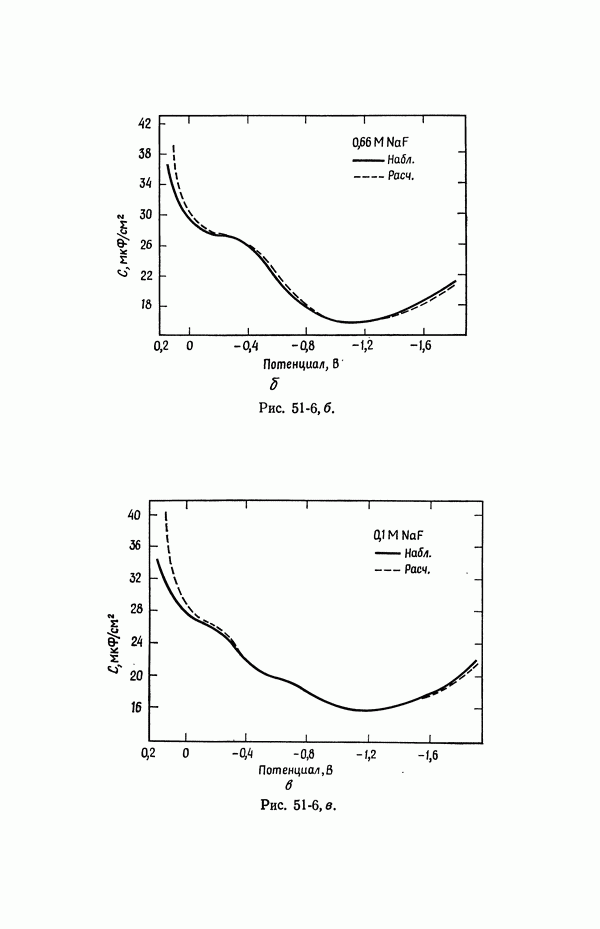
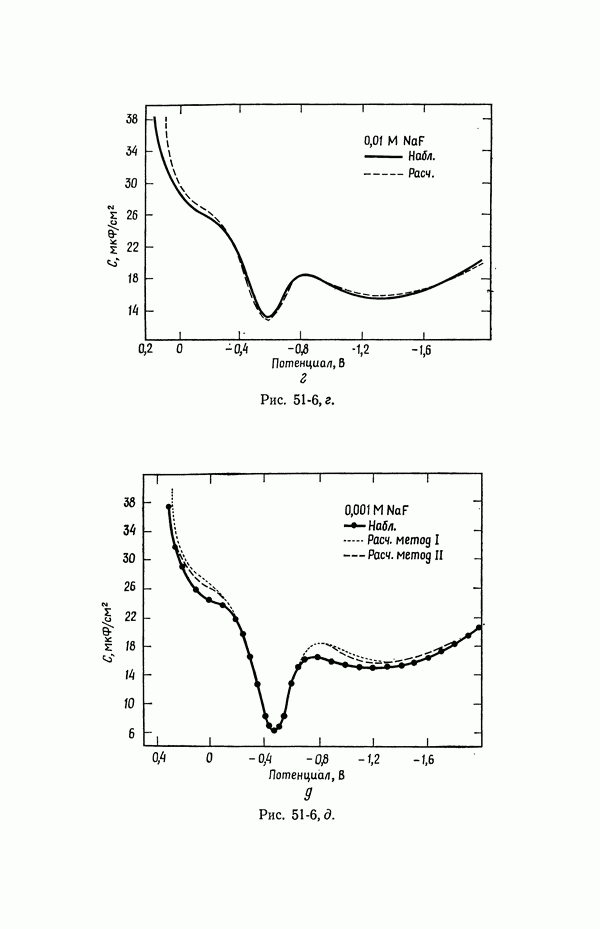
| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Математическое моделирование физических явлений обычно выражается в составлении уравнений в частных производных. Нередко эти уравнения сводятся к обыкновенным дифференциальным либо потому, что имеется всего одна переменная, либо за счет применения специальных методов, таких, как преобразование подобия или метод разделения переменных. Доступность быстродействующих цифровых вычислительных машин и наличие общего метода решения дифференциальных уравнений позволяют рассматривать такого рода задачи без тех грубых упрощений, которые часто приходится допускать, чтобы получить аналитическое решение. Исходные задачи могут быть нелинейными и содержать несколько зависимых переменных. Однако должным образом выполненная линеаризация таких задач часто приводит к ряду сходящихся последовательных приближений, хотя в общем случае сходимость его гарантировать невозможно. Поэтому вначале имеет смысл обсудить метод решения системы линейных дифференциальных уравнений и проиллюстрировать метод линеаризации.
Поскольку в задачах с начальными условиями хорошо работает другой метод (Рунге—Кутта), мы сосредоточим внимание на краевых задачах, в которых обычно задаются условия при  или
или  . Используемый здесь подход оказался полезным в самых разнообразных задачах, так что целесообразно его изложить, чтобы облегчить работу других исследователей [1, 2].
. Используемый здесь подход оказался полезным в самых разнообразных задачах, так что целесообразно его изложить, чтобы облегчить работу других исследователей [1, 2].
Краевые задачи в такой постановке возникают в следующих случаях:
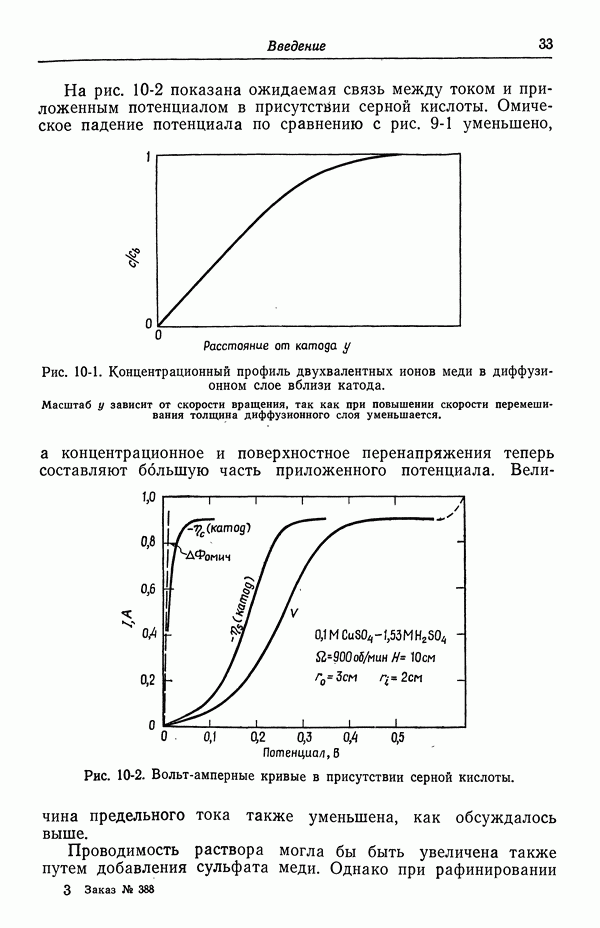
1. Массоперенос в полубесконечной неперемешиваемой среде.
2. Массоперенос в неперемешиваемой пленке или пористой среде, как в случае гетерогенного катализа или пористых электродов.
3. Массоперенос в пограничных слоях, когда профили на разных расстояниях вдоль поверхности подобны. Сюда относится как свободная, так и вынужденная конвекция, а в случае больших чисел Шмидта становится несущественным и гидродинамическое подобие.
4. Распределение скоростей в подобных пограничных слоях (см., например, задачу о течении вблизи вращающегося диска в разд. 96).
5. Распределение заряда и массы в диффузной части электрических двойных слоев.
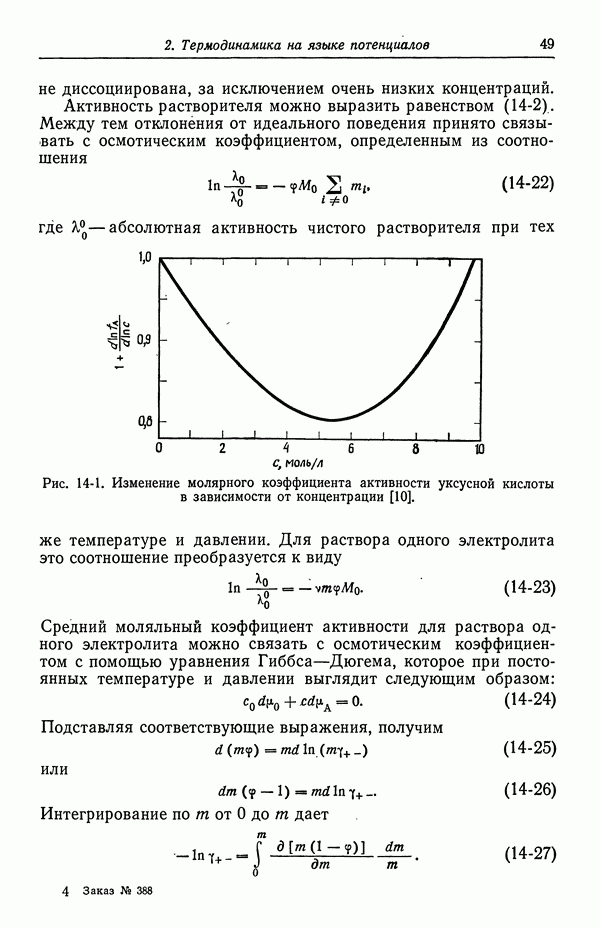
По целому ряду причин на распределение концентрации некоторых компонентов могут влиять распределения других компонентов или поля скоростей и температур. К таким причинам относятся следующие:
1. Коэффициенты диффузии, вязкости и другие физические свойства зависят от состава раствора, температуры и давления.
2. Скорость на поверхности связана со скоростью массопереноса.
3. Компоненты могут быть заряжены и могут взаимодействовать друг с другом через электрический потенциал.
4. Компоненты раствора могут принимать участие в гетерогенных или гомогенных реакциях, как равновесных, так и неравновесных.
5. В случае свободной конвекции движение жидкости обусловлено разностью плотностей, возникающей  счет неоднородности состава или температуры.
счет неоднородности состава или температуры.
Вычислительная процедура вначале была обобщена на случай системы произвольного числа уравнений, описывающих влияние ионной миграции на предельные токи (гл. 19). При этом можно рассматривать произвольное число компонентов в растворе.
Система линейных разностных уравнений
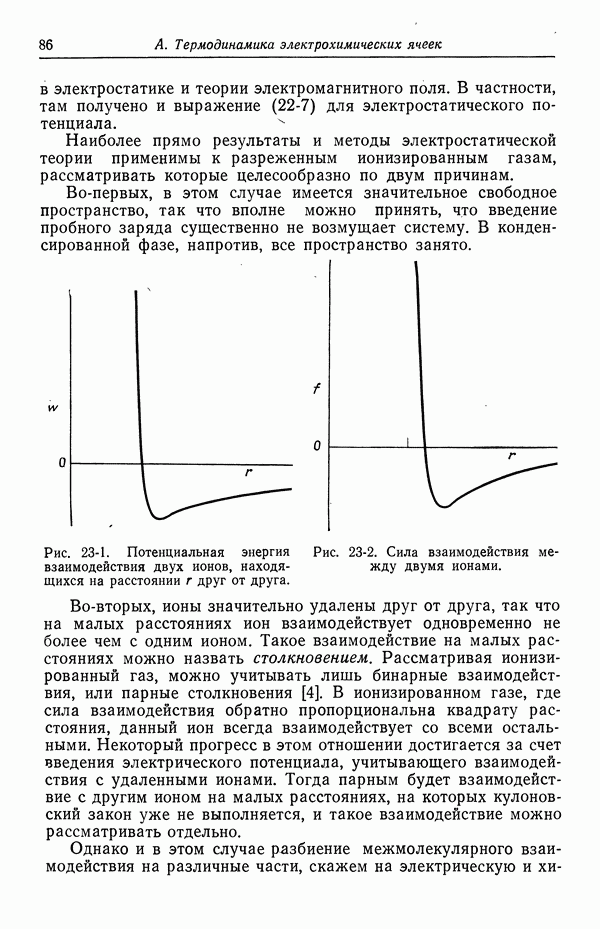
Система  линейных дифференциальных уравнений второго порядка записывается следующим образом:
линейных дифференциальных уравнений второго порядка записывается следующим образом:

где  обозначает n неизвестных функций. Индекс i указывает номер уравнения, причем в каждое уравнение может входить каждая неизвестная
обозначает n неизвестных функций. Индекс i указывает номер уравнения, причем в каждое уравнение может входить каждая неизвестная  . Все уравнения линейны, т. е. коэффициенты
. Все уравнения линейны, т. е. коэффициенты  не зависят от неизвестных величин
не зависят от неизвестных величин 
Заменяя производные конечными разностями по формулам

где h — шаг сетки, получаем следующие разностные уравнения:

Здесь

При  уравнения имеют вид
уравнения имеют вид

Поскольку точки с индексом  нет, коэффициенты
нет, коэффициенты  сюда не входят. Однако, чтобы не потерять возможности рассматривать более сложные краевые условия, в это уравнение был добавлен третий член, в который входят неизвестные величины, соответствующие
сюда не входят. Однако, чтобы не потерять возможности рассматривать более сложные краевые условия, в это уравнение был добавлен третий член, в который входят неизвестные величины, соответствующие  Например, общий вид краевого условия для уравнения
Например, общий вид краевого условия для уравнения  при
при  выглядит так:
выглядит так:

Если мы пользуемся конечно-разностной формой уравнения  , то можно ускорить дело, вводя точку изображение при
, то можно ускорить дело, вводя точку изображение при  находящуюся вне рассматриваемой области (рис. В-1).
находящуюся вне рассматриваемой области (рис. В-1).

Рис. В-l. Воображаемая точка, вводимая при рассмотрении краевых условий, содержащих производные.
Тогда коэффициенты в уравнении  приобретают вид
приобретают вид

Если в краевом условии содержится первая производная, то желательно работать с дифференциальным уравнением в разностном
приближении, записанном для граничной точки  даже если в него входит изображение, расположенное вне рассматриваемой области. Тогда краевые условия в конечноразностной форме записываются как набор дополнительных уравнений, которых должно быть достаточно для исключения неизвестных в точке-изображении. Очевидно, что особых преимуществ в исключении неизвестных в точке-изображении отдельно от решения самих разностных уравнений нет.
даже если в него входит изображение, расположенное вне рассматриваемой области. Тогда краевые условия в конечноразностной форме записываются как набор дополнительных уравнений, которых должно быть достаточно для исключения неизвестных в точке-изображении. Очевидно, что особых преимуществ в исключении неизвестных в точке-изображении отдельно от решения самих разностных уравнений нет.
Если краевые условия не содержат производных  то во введении изображений нет необходимости и
то во введении изображений нет необходимости и  соответствуют
соответствуют 
По тем же причинам при  разностные уравнения записываются в виде
разностные уравнения записываются в виде

где вновь с помощью коэффициентов  учтена возможность более сложных граничных условий на второй границе
учтена возможность более сложных граничных условий на второй границе  рассматриваемой области аналогично коэффициентам
рассматриваемой области аналогично коэффициентам  и при
и при 
Решение системы линейных разностных уравнений
Обратимся теперь к методу решения разностных уравнений  При
При  запишем
запишем  в виде
в виде

После подстановки этого выражения в уравнение  можно видеть, что
можно видеть, что  удовлетворяют уравнениям
удовлетворяют уравнениям

Все три системы уравнений имеют одинаковые матрицы коэффициентов  и легко решаются.
и легко решаются.
Для остальных точек, за исключением  неизвестные
неизвестные  представим следующим образом:
представим следующим образом:

Подставляя уравнение  в уравнение
в уравнение  исключим вначале
исключим вначале  а затем
а затем  после чего положим остающийся коэффициент при
после чего положим остающийся коэффициент при  равным нулю. Это дает систему уравнений для определения и
равным нулю. Это дает систему уравнений для определения и  .
.

где

Эти коэффициенты не следует путать с коэффициентами  в уравнении
в уравнении  Решение выписанных линейных уравнений для каждой точки j очевидно. Отметим лишь, что вначале нужно провести вычисления для точки
Решение выписанных линейных уравнений для каждой точки j очевидно. Отметим лишь, что вначале нужно провести вычисления для точки  поскольку в правой части уравнения
поскольку в правой части уравнения  содержится
содержится  а в матрице коэффициентов
а в матрице коэффициентов  возникает
возникает  Для
Для  уравнения принимают несколько иной вид, так как для исключения
уравнения принимают несколько иной вид, так как для исключения  из уравнения
из уравнения  нужно пользоваться уравнением
нужно пользоваться уравнением  вместо уравнения
вместо уравнения 
Наконец, для точки  имеется уравнение
имеется уравнение  Если с помощью уравнения
Если с помощью уравнения  исключить
исключить  то значения
то значения  можно найти из уравнений
можно найти из уравнений

где

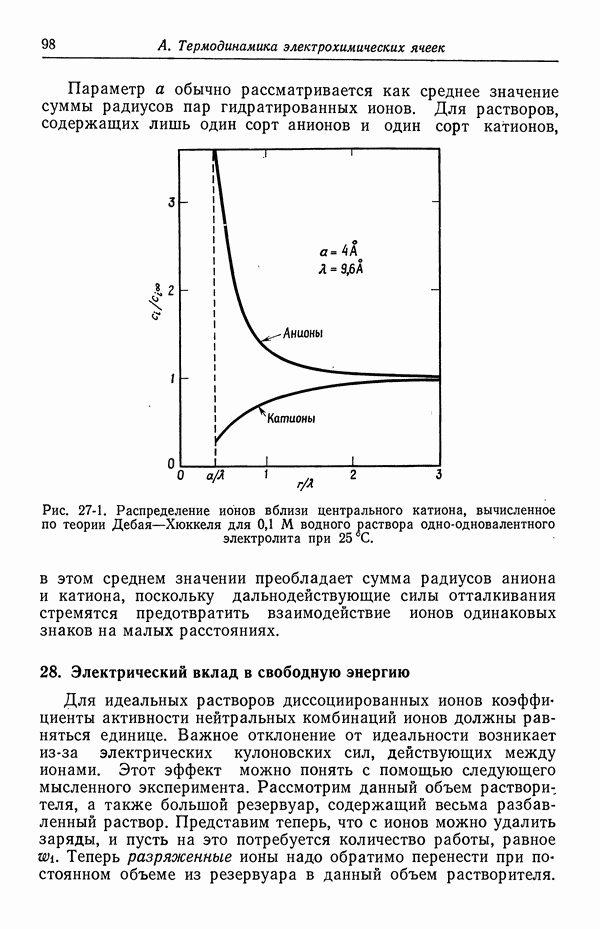
и

Имея значения  теперь можно определить
теперь можно определить  в обратном порядке по j с помощью уравнения
в обратном порядке по j с помощью уравнения  и, наконец, вычислить
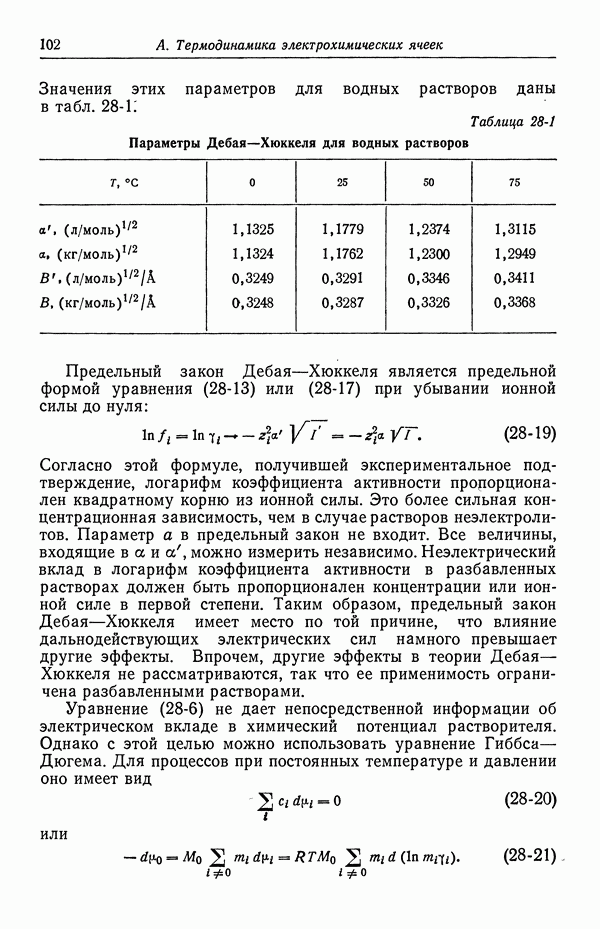
и, наконец, вычислить  по уравнению
по уравнению  Повторные вычисления, которые приходится делать при решении матричных уравнений и при обратных подстановках, конечно, лучше всего про-
Повторные вычисления, которые приходится делать при решении матричных уравнений и при обратных подстановках, конечно, лучше всего про-
водить на больших быстродействующих цифровых машинах.
Поскольку краевые задачи содержат условия как при  так и при
так и при  получить конечные значения неизвестных, начиная с одного из концов, невозможно. Это удается сделать только в задаче с начальными условиями. Вместо однократного прохождения рассматриваемую область проходят дважды в противоположных направлениях. Коэффициенты
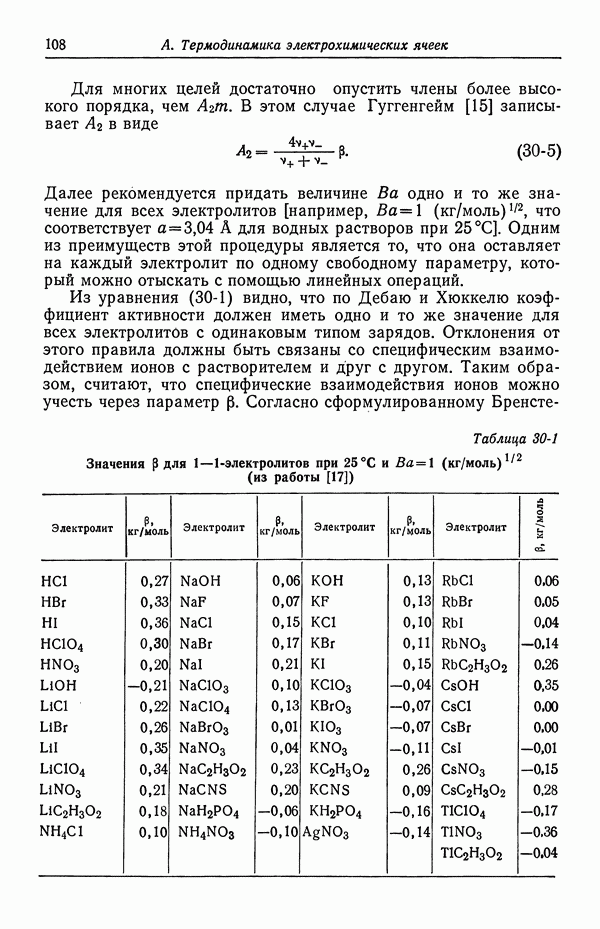
получить конечные значения неизвестных, начиная с одного из концов, невозможно. Это удается сделать только в задаче с начальными условиями. Вместо однократного прохождения рассматриваемую область проходят дважды в противоположных направлениях. Коэффициенты  в уравнении
в уравнении  учитывают то обстоятельство, что краевое условие при
учитывают то обстоятельство, что краевое условие при  должно отражаться на всей рассматриваемой области, причем этот эффект учитывается лишь после проведения обратной подстановки.
должно отражаться на всей рассматриваемой области, причем этот эффект учитывается лишь после проведения обратной подстановки.
Решение нелинейных задач методом линеаризации
Мы рассмотрели метод решения системы линейных разностных уравнений. Однако на практике часто встречаются задачи, сводящиеся к системам нелинейных дифференциальных уравнений. Во многих случаях показано, что решение линеаризованной формы уравнений методом последовательных приближений (или итерациями) дает правильный ответ. Иначе говоря, если линеаризовать уравнения вблизи некоторого пробного решения, то в результате решения линеаризованных уравнений мы приближаемся к решению нелинейной задачи. Найденное решение можно рассматривать как пробное для получения второго приближения, и дальше весь процесс повторяется, пока не будет достигнута нужная точность. Как показывает опыт, сходимость метода не очень чувствительна к выбору первого пробного решения.
Второй закон Фика в одномерном случае, выражающий миграцию и диффузию заряженных компонентов в неперемешиваемой среде (гл. 19), имеет вид

Здесь  концентрация, Ф — электрический потенциал,
концентрация, Ф — электрический потенциал,  коэффициент диффузии,
коэффициент диффузии,  подвижность,
подвижность,  зарядовое число и F — постоянная Фарадея. В этом уравнении нелинейны лишь миграционные члены. Эти члены можно линеаризовать в предположении, что известны почти правильные значения
зарядовое число и F — постоянная Фарадея. В этом уравнении нелинейны лишь миграционные члены. Эти члены можно линеаризовать в предположении, что известны почти правильные значения  , которые можно обозначить
, которые можно обозначить  и что их изменение в одном итерационном цикле сравнительно мало. Тогда можно записать
и что их изменение в одном итерационном цикле сравнительно мало. Тогда можно записать

где мы пренебрегли квадратичными по малым величинам 
и  членами. Заменяя
членами. Заменяя  на
на  на
на  получаем
получаем

Теперь можно привести линеаризованную форму уравнения (В-22):

Таким образом, получена система линейных дифференциальных уравнений. В конечно-разностной форме записи эта система выглядит следующим образом:

Коэффициенты при  , соответствующие
, соответствующие  здесь можно рассматривать как коэффициенты
здесь можно рассматривать как коэффициенты  в уравнении
в уравнении  а потенциал Ф — как одну из неизвестных
а потенциал Ф — как одну из неизвестных  Правая часть уравнения
Правая часть уравнения  соответствует
соответствует 
Еще одно уравнение, относящееся к данной задаче, — условие электронейтральности

Это уравнение уже линейно и не содержит неизвестных при  или
или 
Для пористого электрода дополнительное уравнение может содержать член, соответствующий реакции, в который входят экспоненциальные функции, например

где  безразмерный потенциал, а
безразмерный потенциал, а  концентрация реагента. В линеаризованной форме это уравнение записывается в виде
концентрация реагента. В линеаризованной форме это уравнение записывается в виде

Обсуждение и выводы
Описанная здесь процедура решения системы нелинейных дифференциальных уравнений методом линеаризации и последующих итераций имеет довольно общий характер. Благодаря своей гибкости она оказалась полезной во многих задачах. Конечно, для, конкретных задач иногда можно развить более эффективные методы, однако это достигается за счет потери общности и требует дополнительных усилий.
При решении задач рассматриваемого здесь типа могут быть полезными два других метода. Первый из них сводится к линеаризации и расцеплению уравнений, что достигается путем замены коэффициентов при производных на их выражения через пробное решение, например вместо  пишется
пишется  После этого расцепленные уравнения решаются одно за другим, в результате чего получается новое пробное решение. В общем случае сходимость этого метода несколько хуже сходимости в описанном выше подходе. Тем не менее в некоторых частных случаях, когда перекрестные члены в уравнениях невелики, этот метод работает достаточно хорошо.
После этого расцепленные уравнения решаются одно за другим, в результате чего получается новое пробное решение. В общем случае сходимость этого метода несколько хуже сходимости в описанном выше подходе. Тем не менее в некоторых частных случаях, когда перекрестные члены в уравнениях невелики, этот метод работает достаточно хорошо.
Второй метод состоит в рассмотрении этой задачи как задачи с начальными условиями, которые необходимо искусственно подобрать. Для этого метода не требуется машина с большим объемом памяти, однако выбор дополнительного начального условия, удовлетворяющего краевым условиям при  может оказаться сложным или вообще невозможным.
может оказаться сложным или вообще невозможным.
Ошибки в изложенном методе обусловлены тремя причинами: конечным числом итераций при решении нелинейных задач (эту ошибку можно сделать как угодно малой), разностным приближением дифференциальных уравнений (соответствующая ошибка уменьшается по мере уменьшения шага h) и округлением чисел вычислительной машиной (эта ошибка возрастает при уменьшении шага  ). При резком изменении неизвестных в некоторой области
). При резком изменении неизвестных в некоторой области  сходимость последовательных приближений может нарушаться; в этом случае может оказаться полезным метод сингулярных возмущений.
сходимость последовательных приближений может нарушаться; в этом случае может оказаться полезным метод сингулярных возмущений.
Необходимо сделать замечания относительно уравнений первого и третьего порядков. Если в уравнение входит третья производная, то его можно заменить двумя уравнениями первого и второго порядков. При этом уравнения в конечных разностях по-прежнему содержат точки  Для уравнения первого порядка, возможно, лучше представлять производную с помощью разности значений на краях интервала вместо средней разности, вычисленной для положительного и отрицательного сдвигов относительно рассматриваемого значения аргумента,
Для уравнения первого порядка, возможно, лучше представлять производную с помощью разности значений на краях интервала вместо средней разности, вычисленной для положительного и отрицательного сдвигов относительно рассматриваемого значения аргумента,
как это было принято выше. Если коэффициенту при производной приписывать его среднее значение на рассматриваемом интервале, то ошибка разностного приближения все еще будет порядка  :
:

СПИСОК ЛИТЕРАТУРЫ
1. Newman Ind. Eng. Chem. Fund., 7, 514—517 (1968).
2. Newman Numerical Solution of Coupled, Ordinary Differential Equations, Lawrence Radiation Laboratory, University of California, Berkeley, 1967.
| << Предыдущий параграф |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
- 5. Диффузионный слой
- 6. Концентрационные ячейки
- 7. Концентрационное перенапряжение
- 8. Поверхностное перенапряжение
- 9. Потенциал ячейки
- 10. Фоновый электролит
- 11. Свободная конвекция
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
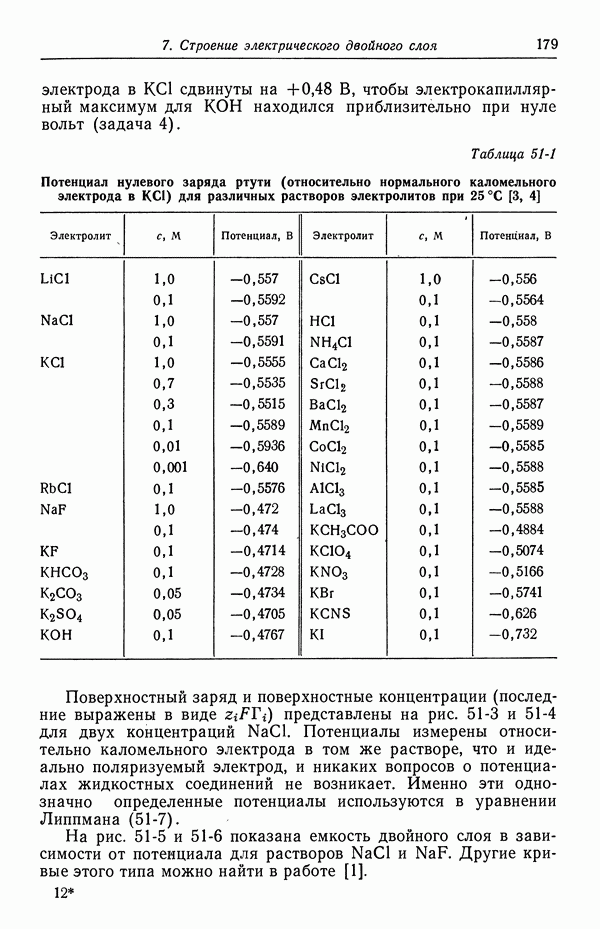
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая—Хюккеля
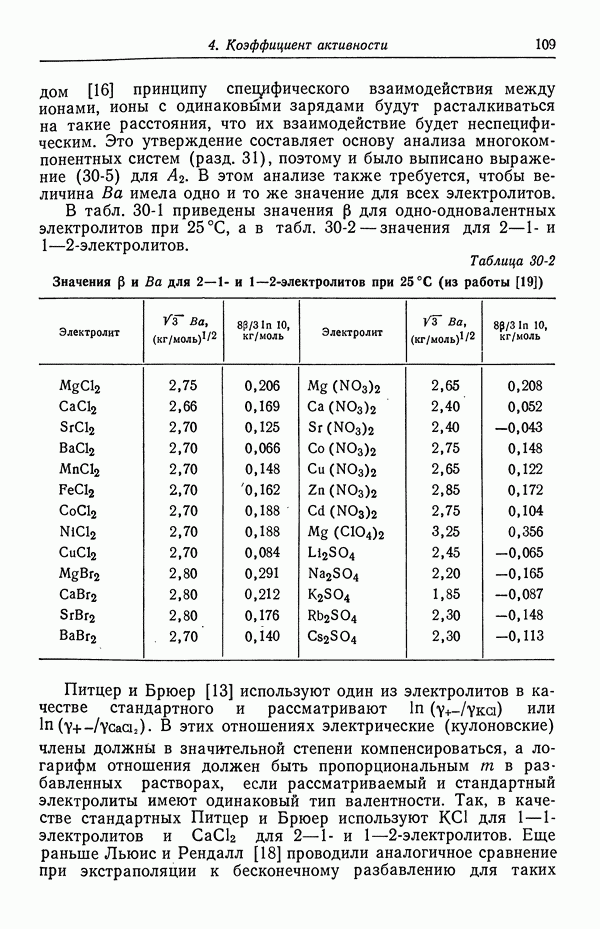
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
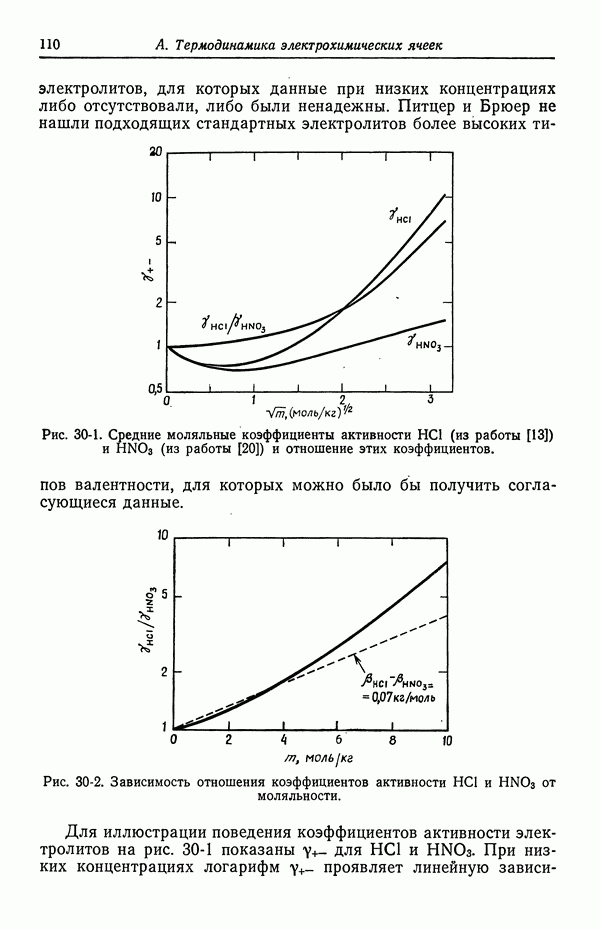
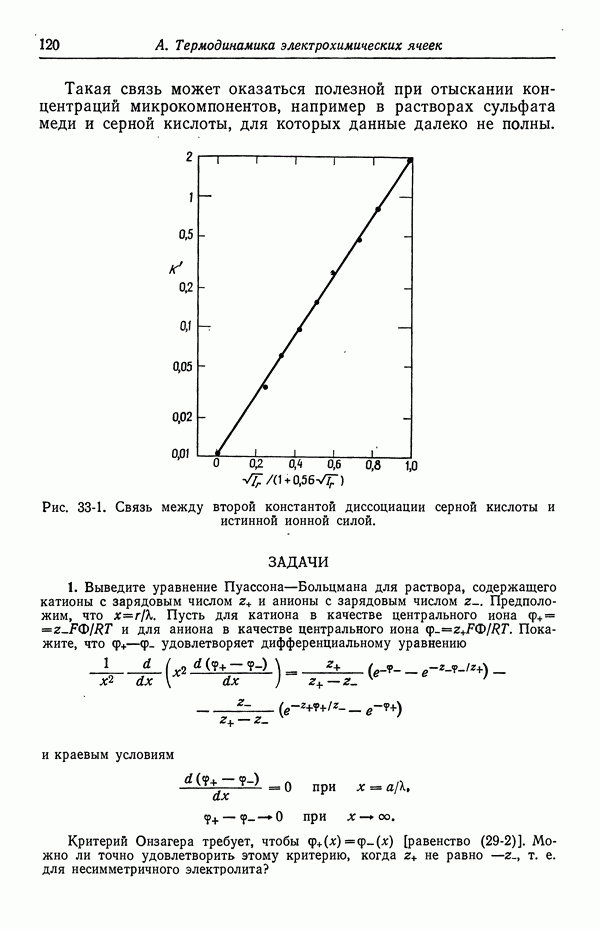
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
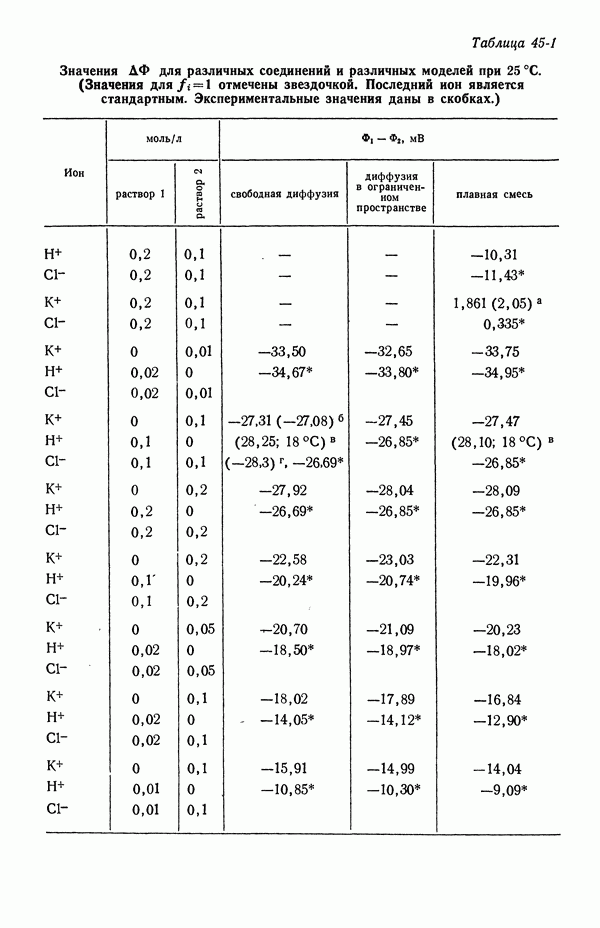
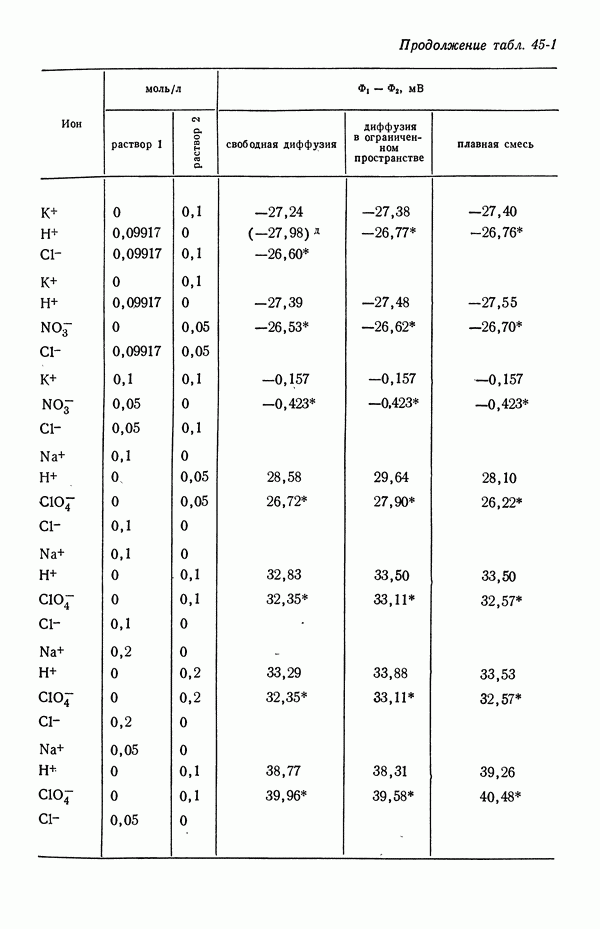
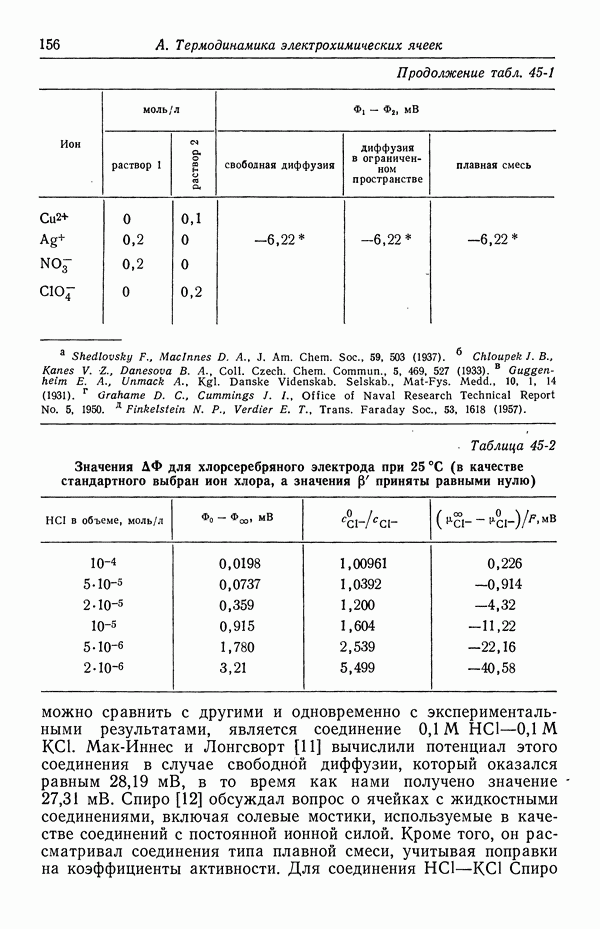
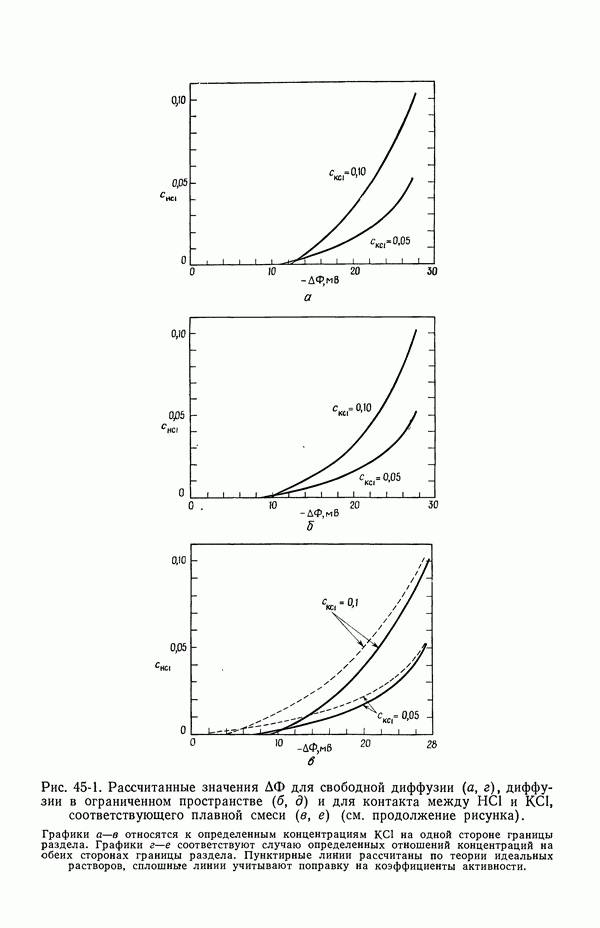
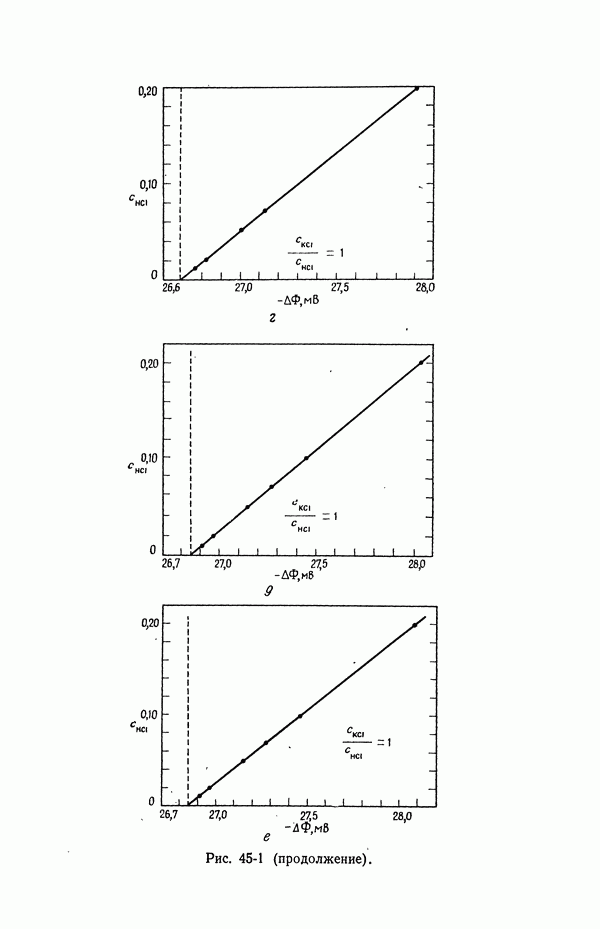
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 49. Качественное описание двойных слоев
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод — раствор
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
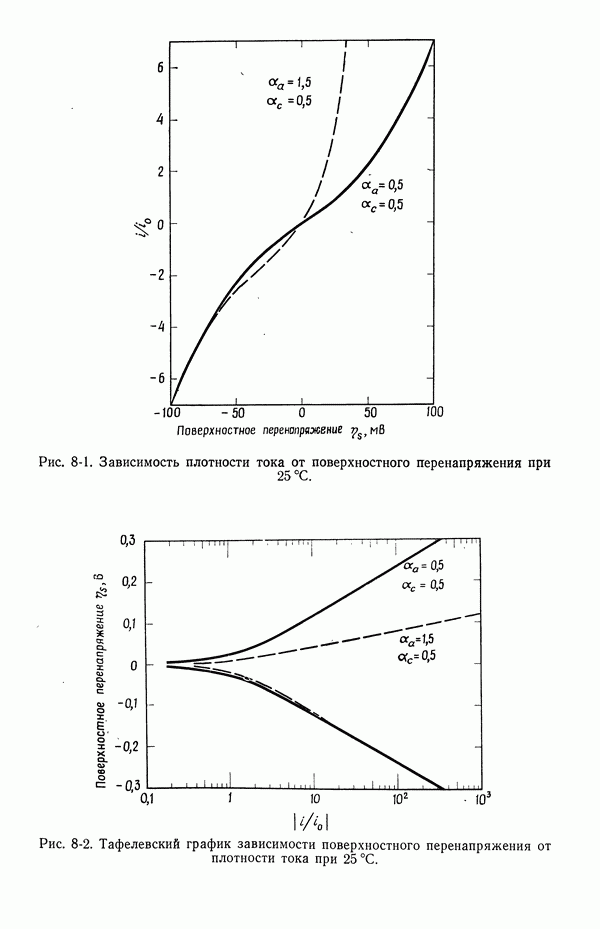
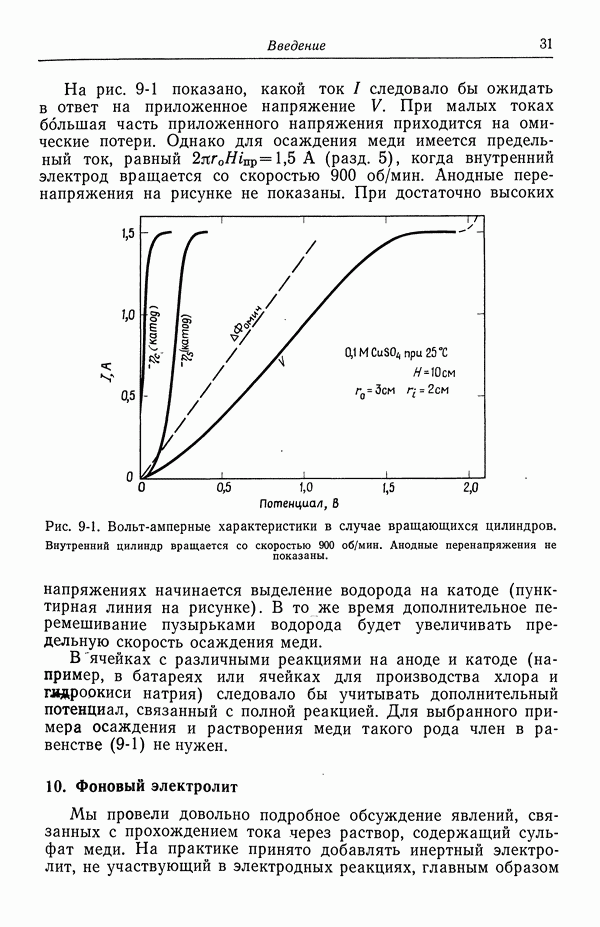
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 66. Динамика границы раздела
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 69. Законы переноса
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 78. Законы переноса
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 92. Интегральные коэффициенты диффузии
- ЗАДАЧА
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 111. Свободная конвекция
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- СПИСОК ОБОЗНАЧЕНИЙ
- ГЛАВА 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 119. Решение задачи
- 120. Поправочный множитель в случае предельных токов
- 121. Изменение концентрации фонового электролита
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ