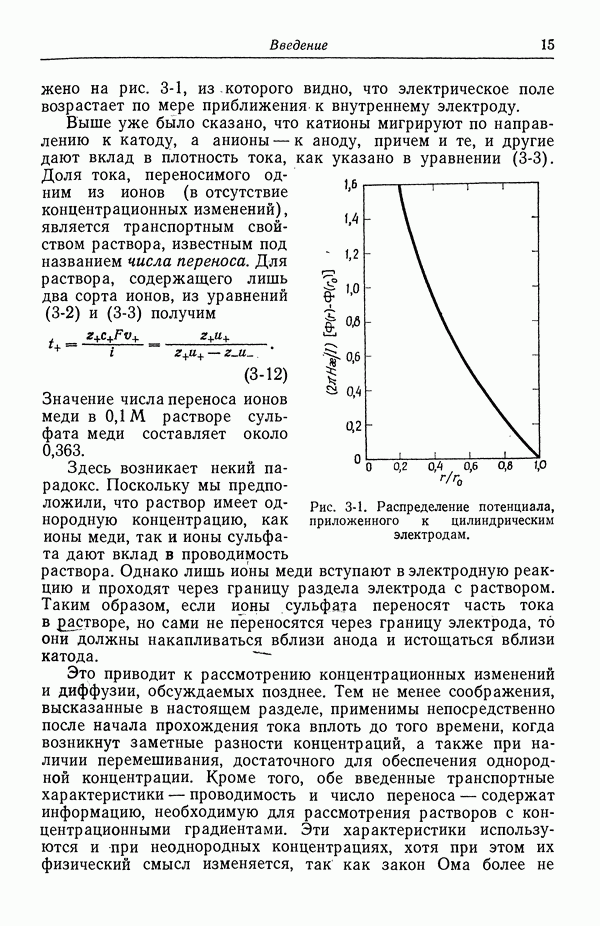
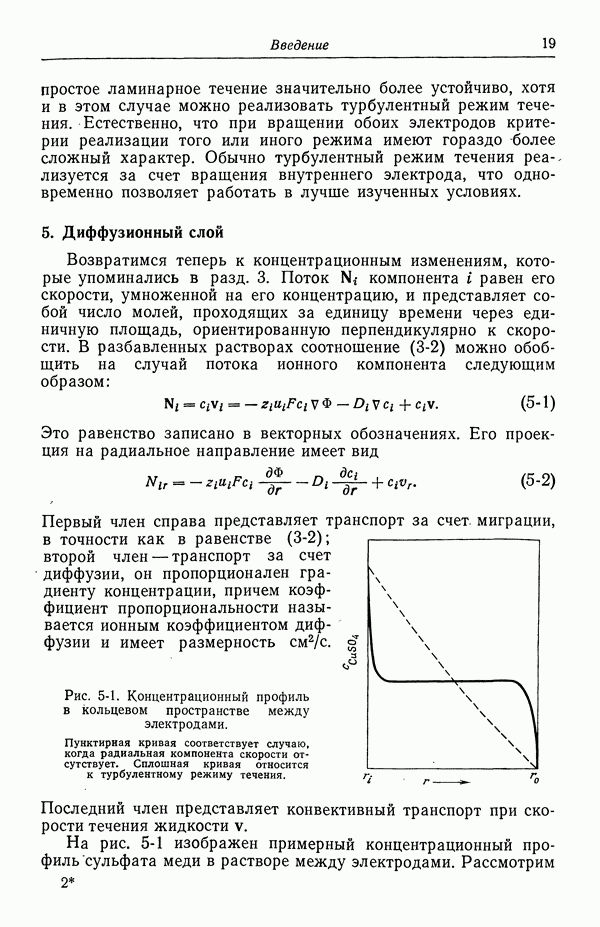
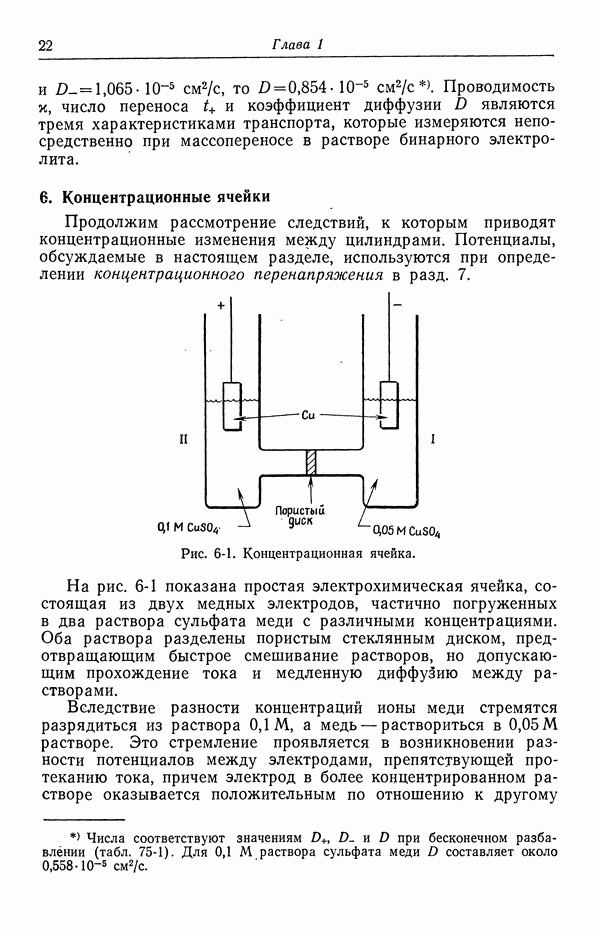
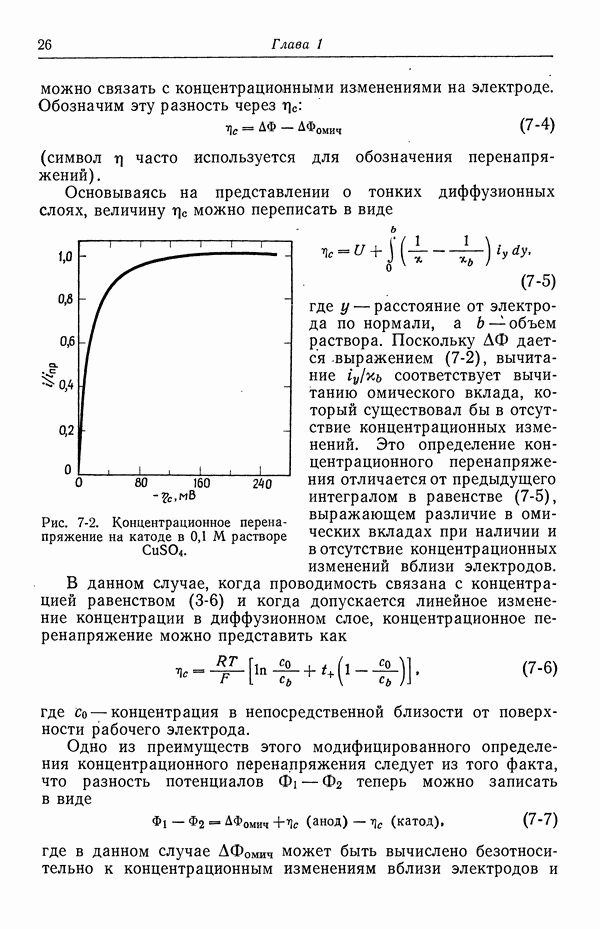
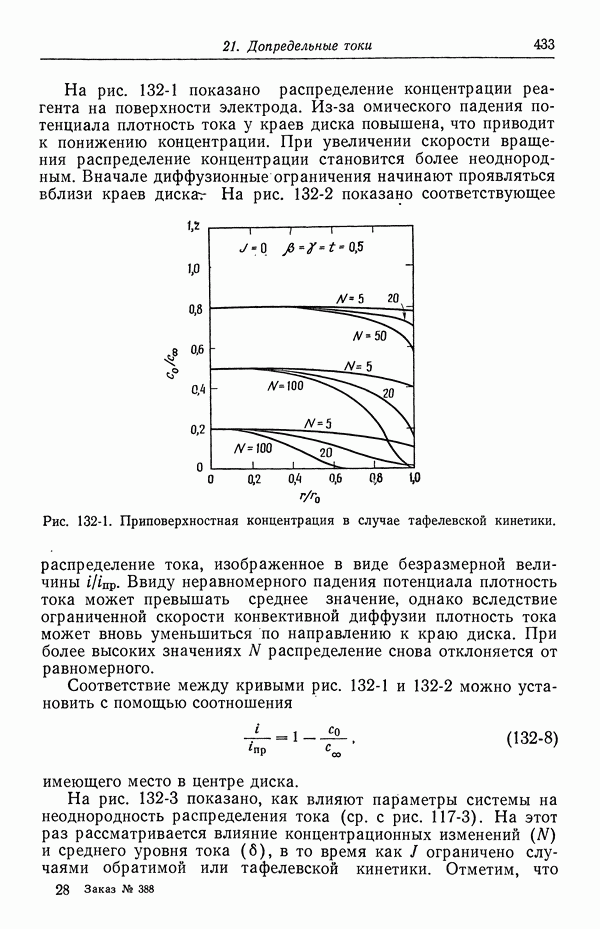
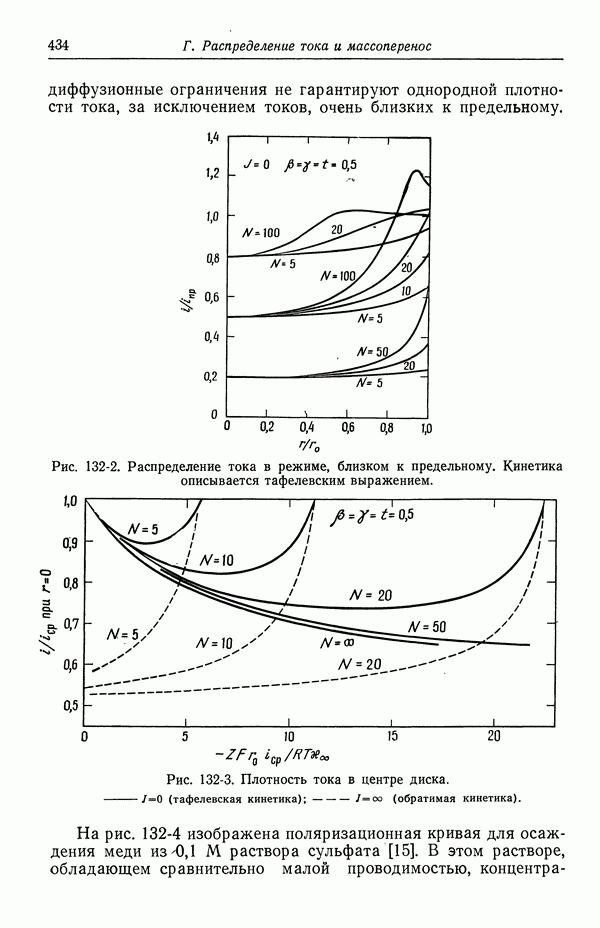
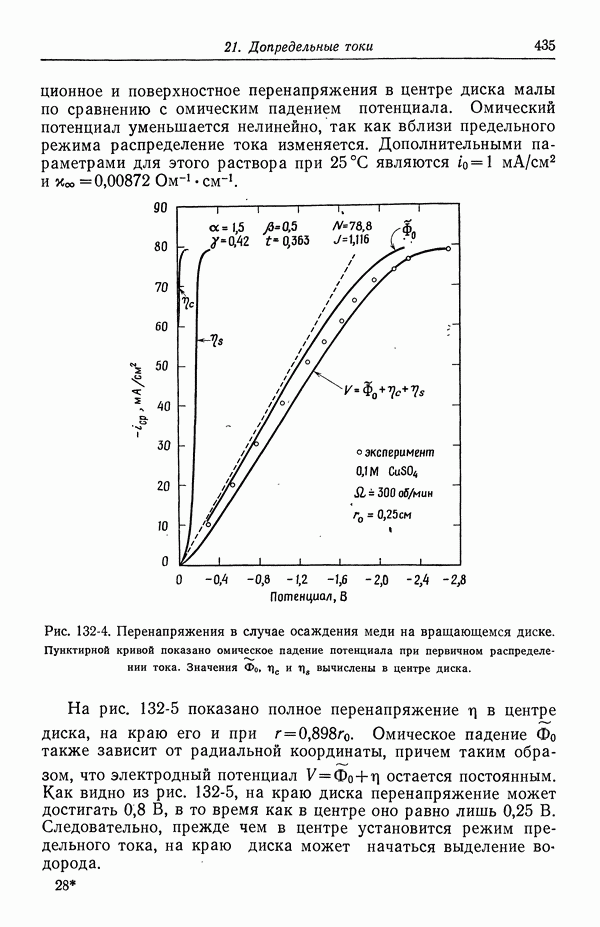
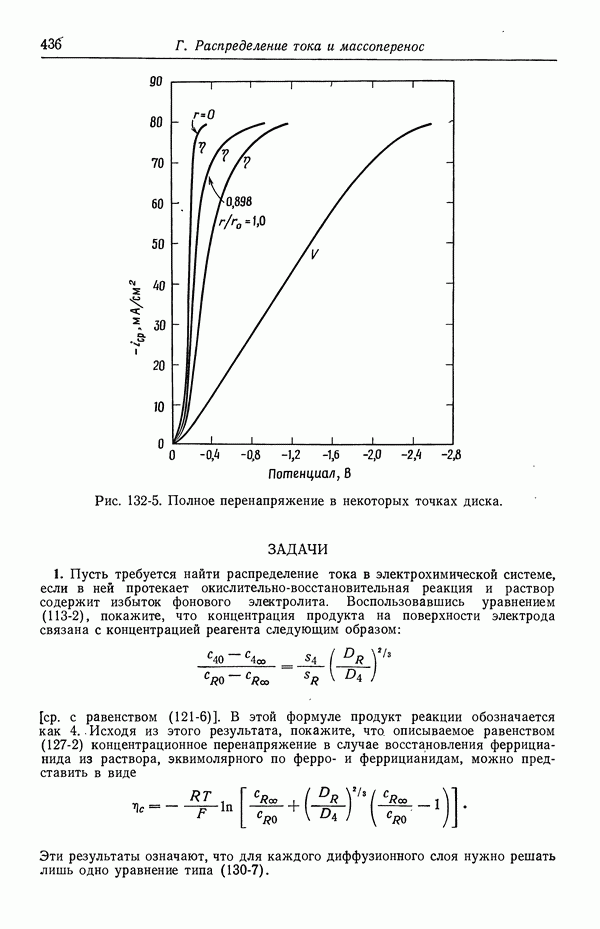
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
57. Модели в кинетике электродных процессов
Мы будем различать простые поверхностные реакции и элементарные стадии поверхностных реакций. Под простой реакцией подразумевается самая простая реакция, которую можно наблюдать с помощью аналитических методов. Это значит, что реагенты и продукты поддаются определению с помощью макроскопического анализа, а промежуточные продукты реакции обнаружить не удается или они полностью неустойчивы. Простая реакция может состоять из одной или более стадий. Элементарная стадия представляет элементарный процесс, через который осуществляется реакция. Так, устойчивый реагент может создавать неустойчивое промежуточное соединение, немедленно вступающее в реакцию в другой элементарной стадии.
Например, реакцию растворения и осаждения меди

можно считать состоящей из двух элементарных стадий, каждая из которых включает перенос электрона:

Согласно Мэттсону и Бокрису [5] по своей природе вторая стадия гораздо медленнее первой. Перенос более одного электрона в элементарной стадии имеет место лишь в исключительных случаях.
Скорости элементарных стадий, входящих в простую реакцию, всегда должны быть пропорциональны друг другу. Например, реакция (57-2) должна пройти каждый раз, когда осуществляется реакция (57-3). Проводить анализ гораздо легче, если реакцию можно рассматривать как простую, поскольку в этом случае скорости элементарных стадий просто связаны друг с другом. Можно ли рассматривать реакцию как простую либо как две или более простые реакции, зависит от того, насколько неустойчиво активное промежуточное соединение, от предела чувствительности наших аналитических методов и от точности, с которой мы хотим описывать систему.
Для реакции с участием меди промежуточные одновалентные ионы не совсем неустойчивы, так что они могут диффундировать от электрода, где они потребляются в ходе реакции диспропорционирования:

Кроме того, имеется различие между анодным и катодным направлениями реакции (57-1). В катодном направлении первой протекает замедленная реакция (57-3). Возникающие при этом одновалентные ионы меди участвуют в реакции (57-2). Таким образом, скорость реакции (57-2) ограничена скоростью подачи одновалентных ионов меди реакцией (57-3) и совпадает со скоростью реакции (57-3). В анодном направлении одновалентные ионы меди образуются в сравнительно быстрой реакции (57-2). Они могут либо диффундировать от электрода, либо участвовать в реакции (57-3). Теперь скорость реакции (57-3) определяется в значительной мере ее собственными кинетическими параметрами, и эта реакция не может протекать так же быстро, как и реакция (57-2). Различие в хкоростях этих реакций соответствует диффузии одновалентных ионов меди от электрода.
Строгое описание анодного процесса требует рассмотрения реакций (57-2) и (57-3) как одновременных (разд. 61), но не как элементарных стадий простой реакции. При этом анализ усложняется необходимостью учета диффузии и конвекции одновалентных ионов меди, для чего следует рассматривать процессы переноса, описанные в части В. С другой стороны, если бы одновалентные ионы меди могли адсорбироваться на электроде, они бы не диффундировали в раствор. Степень покрытия этими ионами увеличилась бы так, чтобы реакции (57-2) и (57-3) вновь протекали с одинаковой скоростью, и тогда реакцию (57-1) можно было бы считать простой.
При дальнейшем рассмотрении реакции с участием меди мы примем, что одновалентные ионы меди не диффундируют от электрода и их концентрация достигает такого значения, что реакции (57-2) и (57-3) протекают с одинаковой скоростью, и потому реакцию (57-1) можно считать простой.
Распределение потенциала в двойном слое (гл. 7) приводит к возникновению разности потенциалов между электродом и раствором, которую мы обозначим через

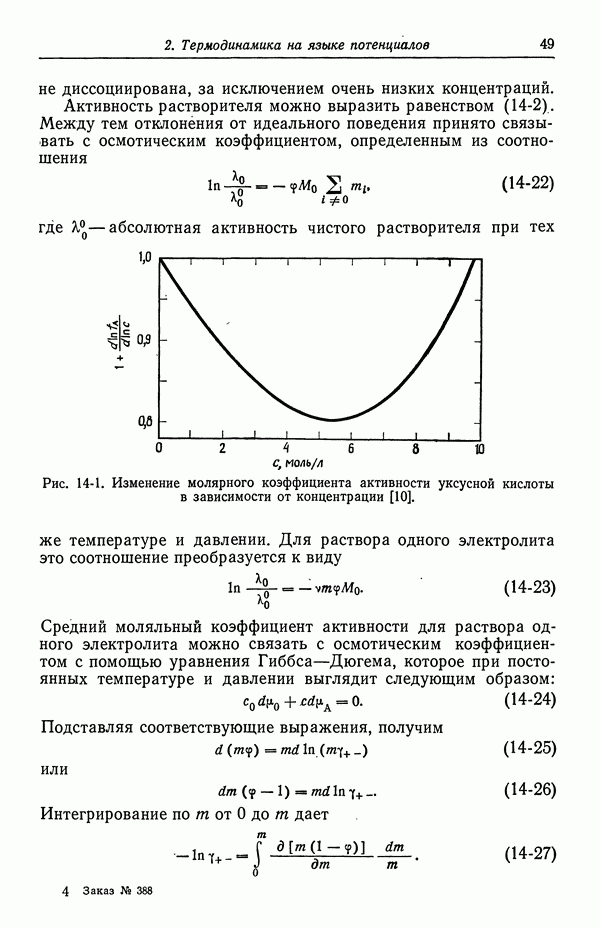
где  — электростатический потенциал электрода, а
— электростатический потенциал электрода, а  — электростатический потенциал раствора непосредственно за двойным слоем. Этот потенциал обычно определен неоднозначно, поэтому V можно считать потенциалом относительно данного электрода (разд. 40).
— электростатический потенциал раствора непосредственно за двойным слоем. Этот потенциал обычно определен неоднозначно, поэтому V можно считать потенциалом относительно данного электрода (разд. 40).
Рассмотрим элементарную стадию, общий вид которой можно представить следующим образом:

Число перенесенных электронов  равно нулю, если в элементарной
равно нулю, если в элементарной
стадии нет переноса заряда, и единице, если перенос имеется. Множественный перенос электронов в элементарной стадии маловероятен. Скорость элементарной стадии можно выразить в виде

Если простая реакция состоит из более чем одной элементарной стадии, то величинам  следует приписать дополнительные индексы, чтобы отличить элементарные стадии друг от друга и от полной реакции.
следует приписать дополнительные индексы, чтобы отличить элементарные стадии друг от друга и от полной реакции.
В уравнении  являются константами скоростей в анодноми катодном направлениях. Можно ожидать, что они будут зависеть от температуры по Аррениусу. Порядки реакции для компонента i в анодном и катодном направлениях равны соответственно
являются константами скоростей в анодноми катодном направлениях. Можно ожидать, что они будут зависеть от температуры по Аррениусу. Порядки реакции для компонента i в анодном и катодном направлениях равны соответственно  и
и  Константы k и экспоненциальные множители вместе представляют аррениусовские константы скоростей с зависящей от потенциала энергией активации, причем
Константы k и экспоненциальные множители вместе представляют аррениусовские константы скоростей с зависящей от потенциала энергией активации, причем  является фактором симметрии, т. е. долей приложенного потенциала У, способствующей катодной реакции. Аналогично
является фактором симметрии, т. е. долей приложенного потенциала У, способствующей катодной реакции. Аналогично  дает долю приложенного потенциала, ускоряющую анодную реакцию. Часто считается, что Р должно равняться
дает долю приложенного потенциала, ускоряющую анодную реакцию. Часто считается, что Р должно равняться  , хотя это и не обосновано строго теоретически.
, хотя это и не обосновано строго теоретически.
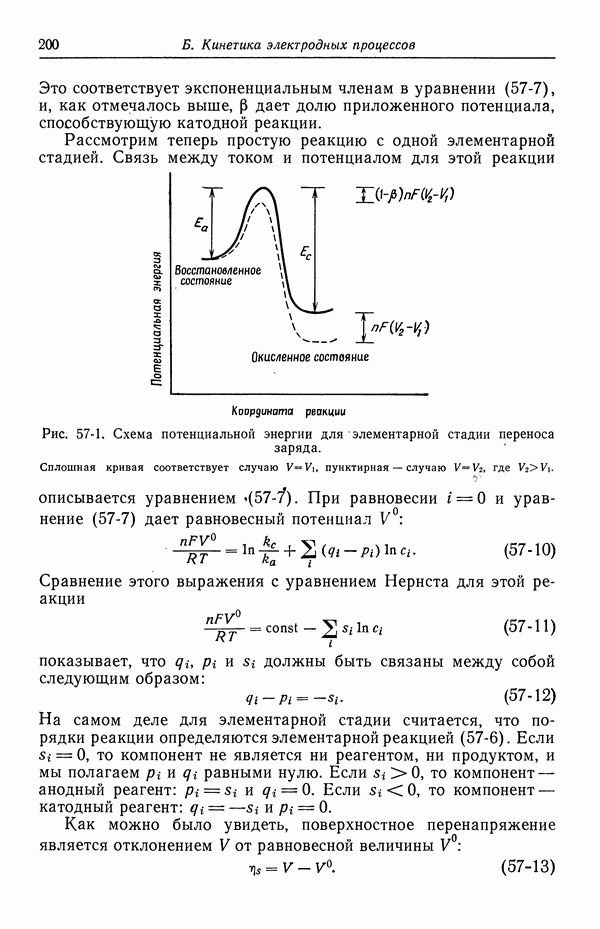
Смысл фактора симметрии  обычно иллюстрируется с помощью схемы потенциальной энергии (рис. 57-1). Кривая потенциальной энергии для приложенного потенциала
обычно иллюстрируется с помощью схемы потенциальной энергии (рис. 57-1). Кривая потенциальной энергии для приложенного потенциала  показана сплошной линией, причем на рисунке указаны энергии активации
показана сплошной линией, причем на рисунке указаны энергии активации  в анодном и катодном направлениях. Изменение приложенного потенциала от
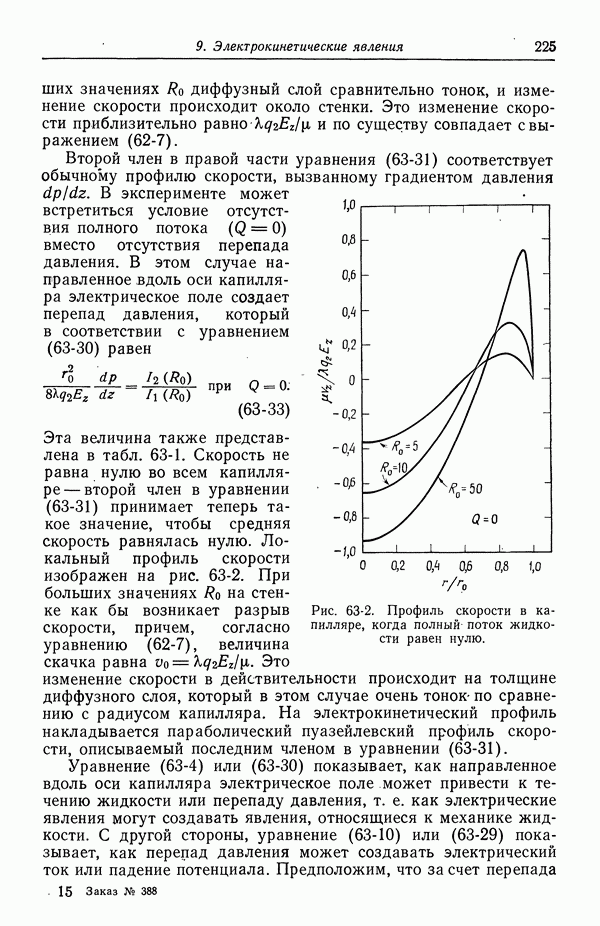
в анодном и катодном направлениях. Изменение приложенного потенциала от  до
до  приводит к изменению энергии восстановленного состояния относительно энергии окисленного состояния на величину
приводит к изменению энергии восстановленного состояния относительно энергии окисленного состояния на величину  что стремится направить реакцию в анодную сторону, если
что стремится направить реакцию в анодную сторону, если 
При  профиль потенциальной энергии изображается пунктирной линией [выбор нуля потенциала здесь несуществен, поэтому восстановленное состояние было изображено при той же энергии; выбор нуля потенциала сказывается на константах скоростей
профиль потенциальной энергии изображается пунктирной линией [выбор нуля потенциала здесь несуществен, поэтому восстановленное состояние было изображено при той же энергии; выбор нуля потенциала сказывается на константах скоростей  в уравнении (57-7)]. Как видно из рис. 57-1, энергия активации в катодном направлении увеличивается на
в уравнении (57-7)]. Как видно из рис. 57-1, энергия активации в катодном направлении увеличивается на  ), а энергия активации в анодном направлении уменьшается на
), а энергия активации в анодном направлении уменьшается на 

Это соответствует экспоненциальным членам в уравнении (57-7), и, как отмечалось выше,  дает долю приложенного потенциала, способствующую катодной реакции.
дает долю приложенного потенциала, способствующую катодной реакции.
Рассмотрим теперь простую реакцию с одной элементарной стадией.

Рис. 57-1. Схема потенциальной энергии для элементарной стадии переноса заряда. Сплошная кривая соответствует случаю  пунктирная — случаю
пунктирная — случаю  где
где 
Связь между током и потенциалом для этой реакции описывается уравнением (57-1). При равновесии  и уравнение (57-7) дает равновесный потенциал
и уравнение (57-7) дает равновесный потенциал  :
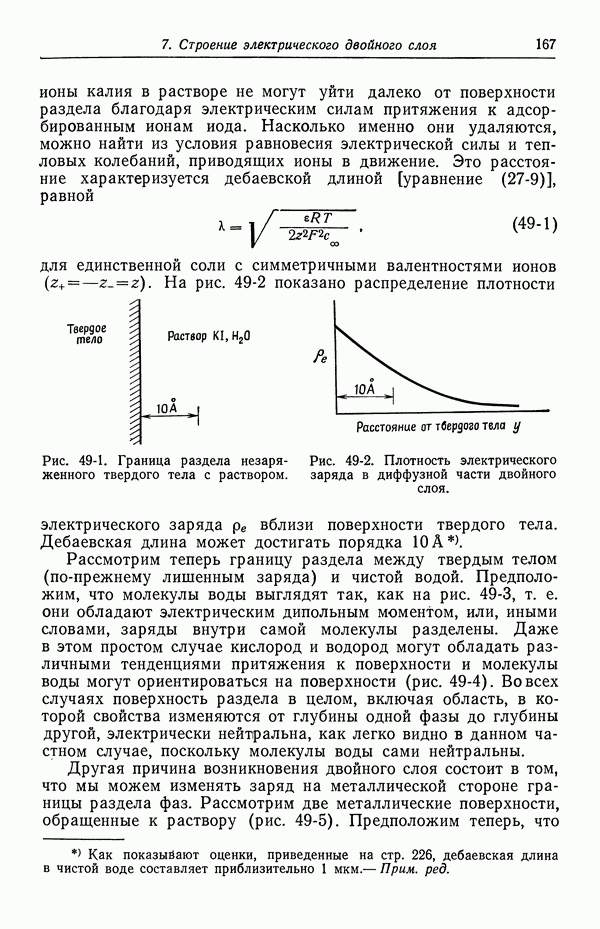
:

Сравнение этого выражения с уравнением Нернста для этой реакции

показывает, что  должны быть связаны между собой следующим образом:
должны быть связаны между собой следующим образом:

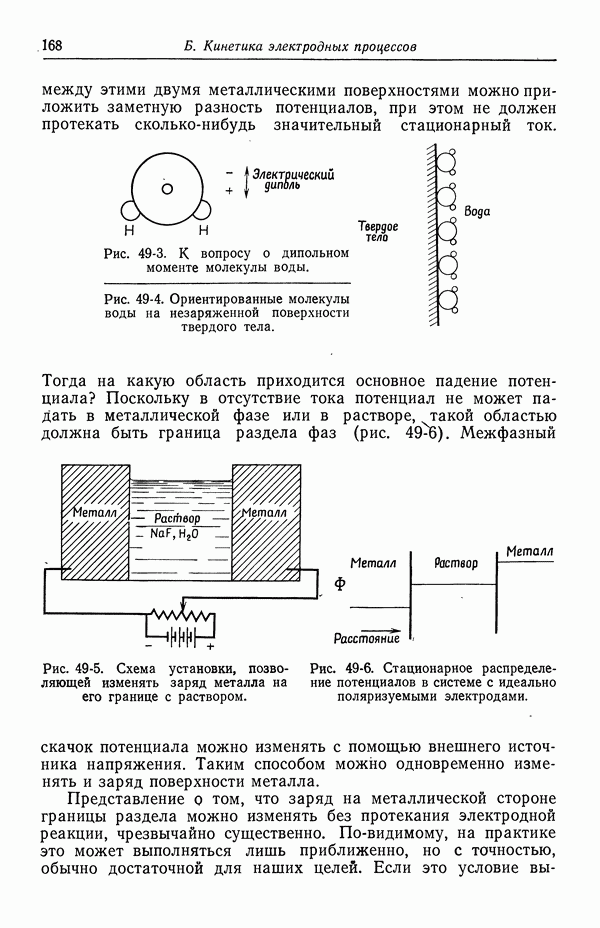
На самом деле для элементарной стадии считается, что порядки реакции определяются элементарной реакцией (57-6). Если  то компонент не является ни реагентом, ни продуктом, и мы полагаем
то компонент не является ни реагентом, ни продуктом, и мы полагаем  равными нулю. Если
равными нулю. Если  то компонент — анодный реагент:
то компонент — анодный реагент:  Если
Если  то компонент — катодный реагент:
то компонент — катодный реагент:  .
.
Как можно было увидеть, поверхностное перенапряжение является отклонением V от равновесной величины 

Это определение  эквивалентно определениям, данным в разд. 8 и 55. Для простой реакции с одной элементарной стадией плотность тока обмена
эквивалентно определениям, данным в разд. 8 и 55. Для простой реакции с одной элементарной стадией плотность тока обмена  равна значению катодного или анодного члена в уравнении (57-7) при равновесии (умноженному на
равна значению катодного или анодного члена в уравнении (57-7) при равновесии (умноженному на  ):
):

С этими определениями  уравнение (57-7) можно переписать в виде
уравнение (57-7) можно переписать в виде

Сравнение этого уравнения с выражением (56-1) показывает, что для единичной элементарной стадии выполняется 
Наконец, используя равенство (57-10) для исключения V0 из уравнения (57-14), получаем

Это выражение дает точную зависимость плотности тока обмена  от концентраций реагентов и продуктов вблизи электрода. Мы видим, что у и
от концентраций реагентов и продуктов вблизи электрода. Мы видим, что у и  в уравнении (56-5) соответствуют
в уравнении (56-5) соответствуют  Поскольку
Поскольку  — дробное число, показатель степени при d в уравнении (57-16) в общем случае является дробным даже при целочисленных
— дробное число, показатель степени при d в уравнении (57-16) в общем случае является дробным даже при целочисленных  . Эта степень положительна, если справедливы изложенные после уравнения (57-12) правила. Таким образом, плотность тока обмена увеличивается при возрастании концентрации как реагентов, так и продуктов.
. Эта степень положительна, если справедливы изложенные после уравнения (57-12) правила. Таким образом, плотность тока обмена увеличивается при возрастании концентрации как реагентов, так и продуктов.
Увеличение концентрации анодного реагента, для которого  приводит к пропорциональному увеличению анодного члена в уравнении (57-7) при постоянном V. Однако величина
приводит к пропорциональному увеличению анодного члена в уравнении (57-7) при постоянном V. Однако величина  связана с этим членом не при постоянном V, а при равновесном потенциале. При увеличении концентрации анодного реагента равновесный потенциал сдвигается таким образом, что оба члена в уравнении (57-7) остаются равными. Поэтому эти члены, а вместе с ними и плотность тока обмена увеличиваются пропорционально дробной степени концентрации анодного реагента.
связана с этим членом не при постоянном V, а при равновесном потенциале. При увеличении концентрации анодного реагента равновесный потенциал сдвигается таким образом, что оба члена в уравнении (57-7) остаются равными. Поэтому эти члены, а вместе с ними и плотность тока обмена увеличиваются пропорционально дробной степени концентрации анодного реагента.
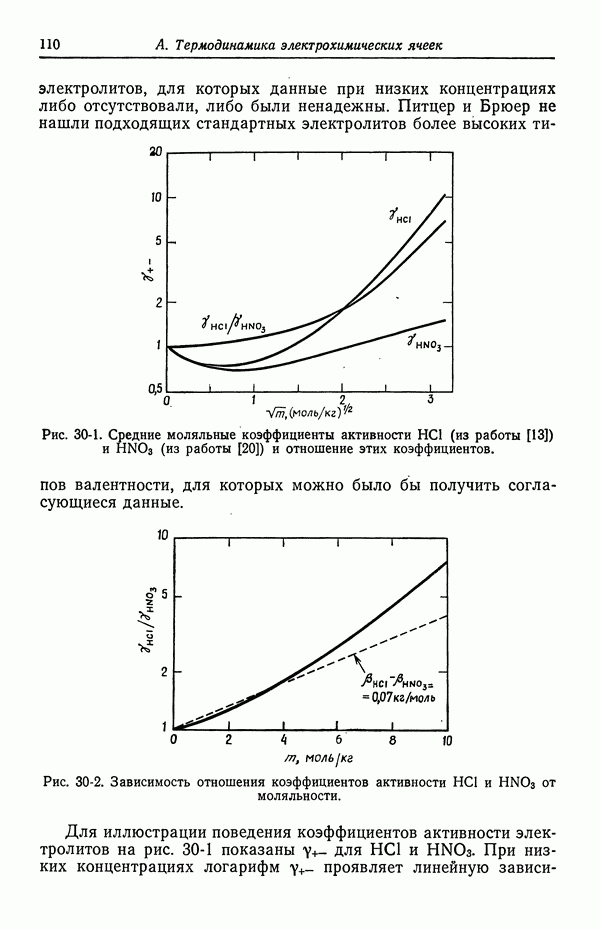
Проиллюстрируем результаты этой модели кинетики электродных процессов на окислительно-восстановительной реакции

где имеется только один реагент и только один продукт,
которые являются растворимыми ионами. Предполагается, что существует лишь одна элементарная стадия, совпадающая с окислительно-восстановительной реакцией (57-17). Следуя правилам для порядков реакции, приведенным после уравнения (57-12), запишем уравнение (57-7) в виде

Здесь подразумевается, что анодная и катодная реакции имеют первый порядок по реагентам, но с зависящими от потенциала константами скоростей.
Равновесный потенциал равен

а плотность тока обмена выражается формулой

[уравнение (57-16)]. Уравнение (57-15) по-прежнему дает связь между током и перенапряжением.
Для более сложных электродных реакций необходимо расписать механизм реакции на элементарные стадии и анализировать кинетику каждой стадии, как уже было проделано для отдельной элементарной стадии. Для элементарных стадий (57-2) и (57-3) реакции на медном электроде уравнение (57-7) можно представить в виде

и

Индексы 2 и 3 соответствуют реакциям (57-2) и (57-3). Концентрация анодного реагента (меди) в реакции (57-2) не была включена в уравнение (57-21), поскольку она постоянна.
Как и ранее, мы будем считать, что реакции (57-2) и (57-3) протекают с одинаковой скоростью. Следовательно,

Введем теперь поверхностное перенапряжение для полной реакции [уравнение (55-4)], а не для отдельных реакций (57-2) и (57-3). Будем также считать, что реакция (57-2) является быстрой и находится в равновесии (более общий случай представлен в задаче 1). Для больших значений  уравнение
уравнение
(57-21) дает зависящую от потенциала равновесную концентрацию одновалентных ионов меди:

Подставляя это выражение в уравнение (57-22), получаем

Отсюда находим равновесный потенциал

и плотность тока обмена

С учетом того, что поверхностное перенапряжение дается равенством (57-13), уравнение (57-25) теперь можно записать в виде

где

и

Из уравнения (57-27) можно выразить концентрационную зависимость плотности тока обмена:

где

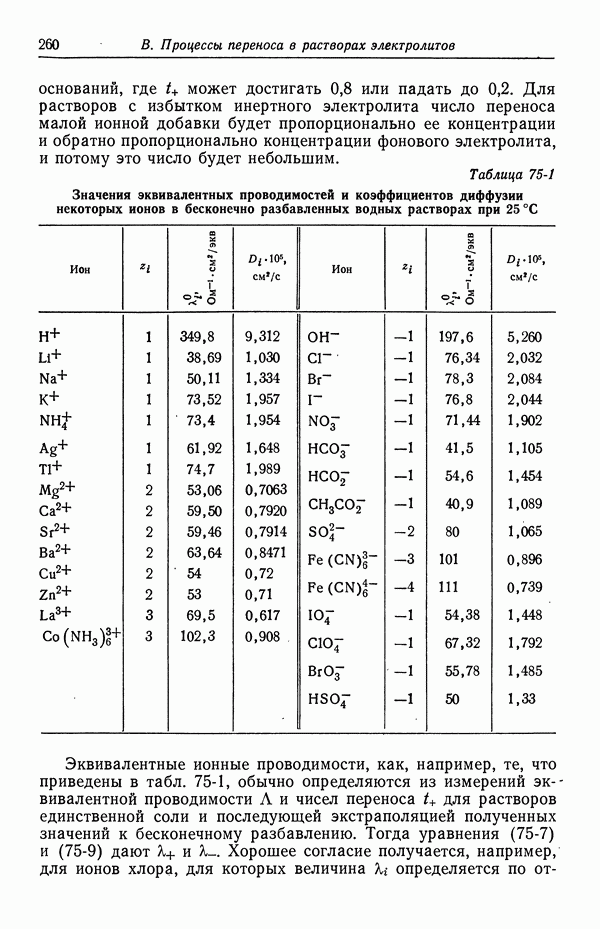
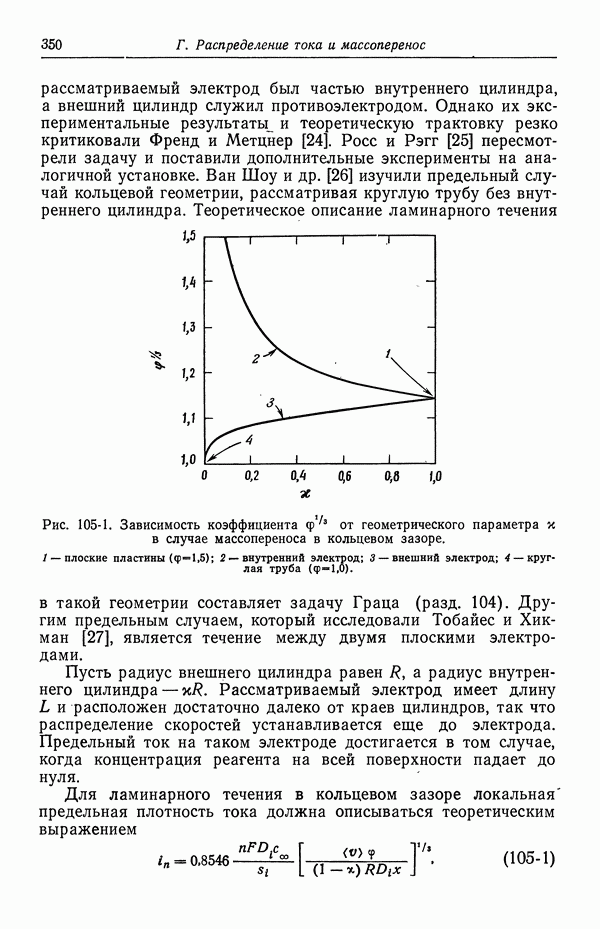
Мэттсон и Бокрис [5] изучали реакцию осаждения и растворения меди в 1 н. серной кислоте с различными концентрациями сульфата меди. Плотность тока обмена может зависеть от концентрации серной кислоты, природы поверхности электрода и концентрации двухвалентных ионов меди. Эти авторы исследовали поверхности, приготовленные охлаждением расплавленной меди в очищениом гелии, а также поверхности, приготовленные электроосаждением меди.
Мэттсон и Бокрис пришли к заключению, что реакции (57-2) присуща гораздо большая скорость, чем реакции (57-3). В пределах воспроизводимости  а это указывает на то, что для реакции (57-3) фактор симметрии
а это указывает на то, что для реакции (57-3) фактор симметрии  равен
равен  -Для у [уравнение (57-31)] получено значение 0,6 в случае электроосажденных электродов и 0,3 в случае приготовленных в гелии электродов. С другой стороны, при
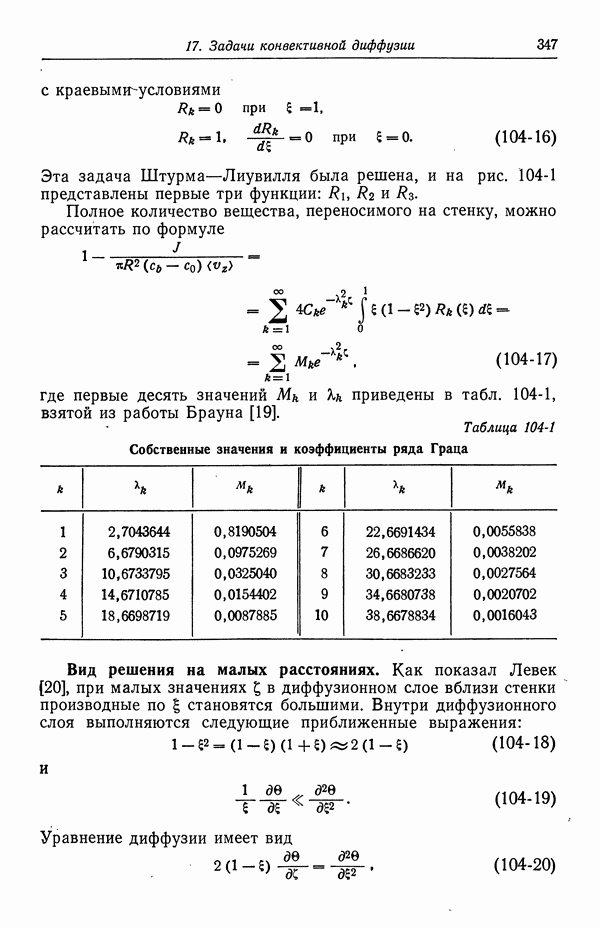
-Для у [уравнение (57-31)] получено значение 0,6 в случае электроосажденных электродов и 0,3 в случае приготовленных в гелии электродов. С другой стороны, при  уравнение (57-32) дает
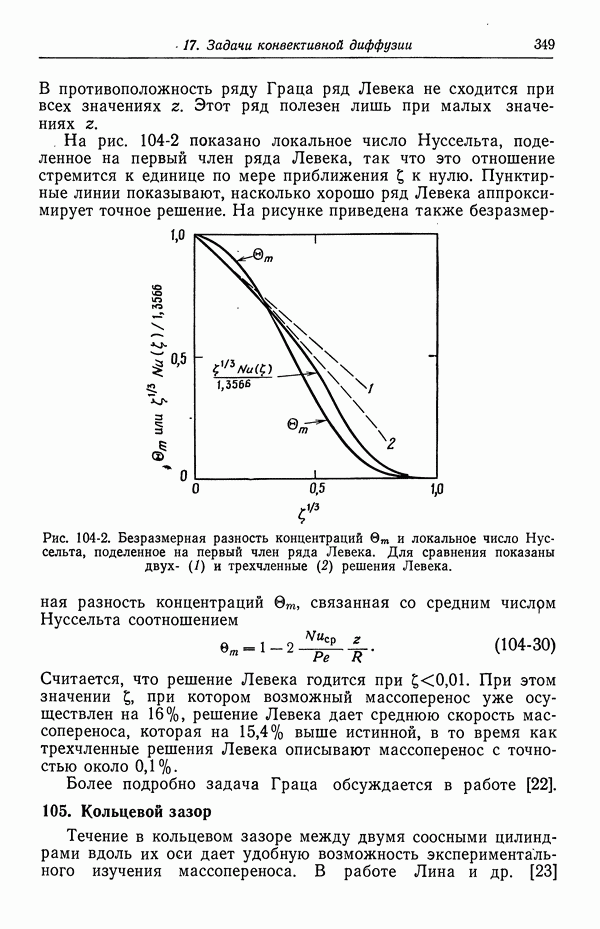
уравнение (57-32) дает 

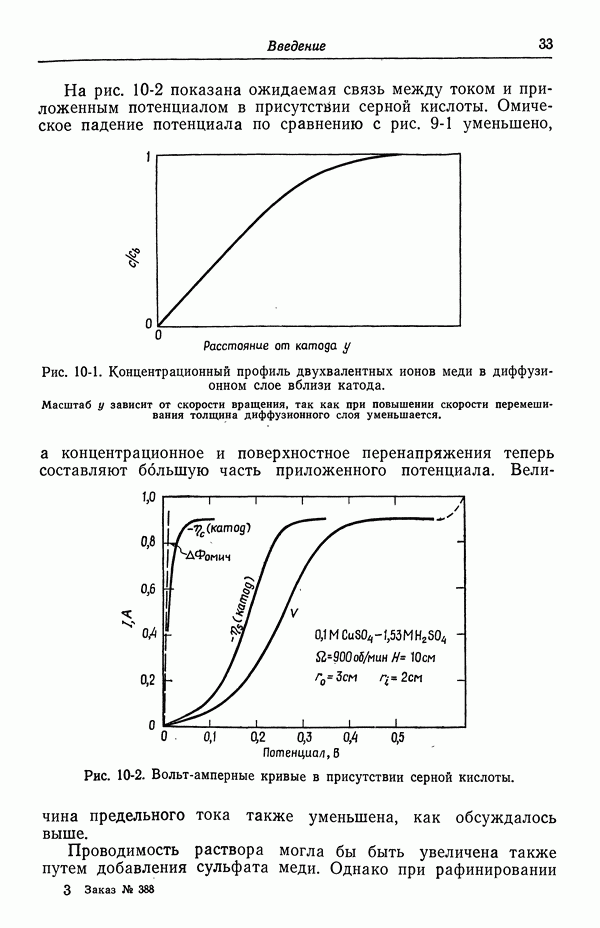
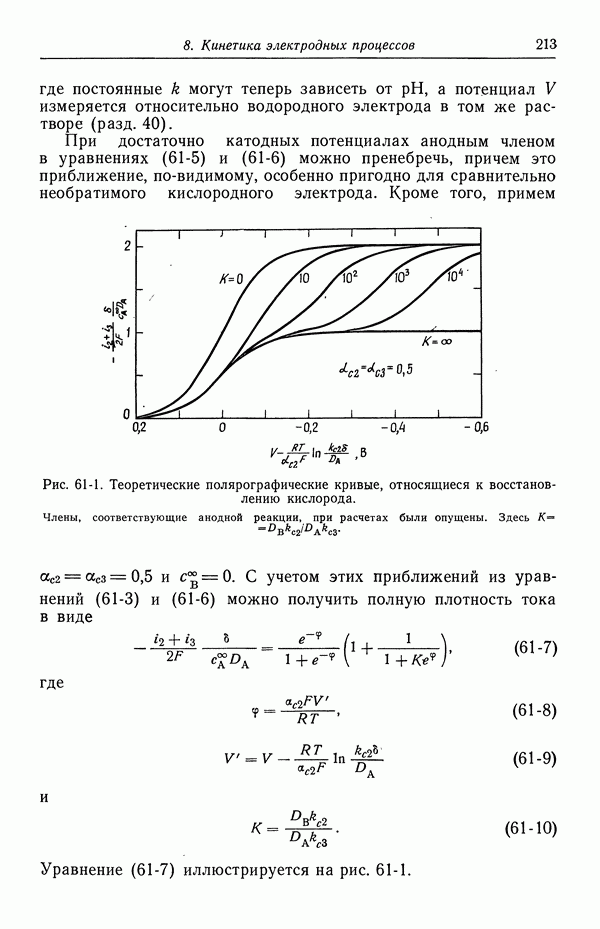
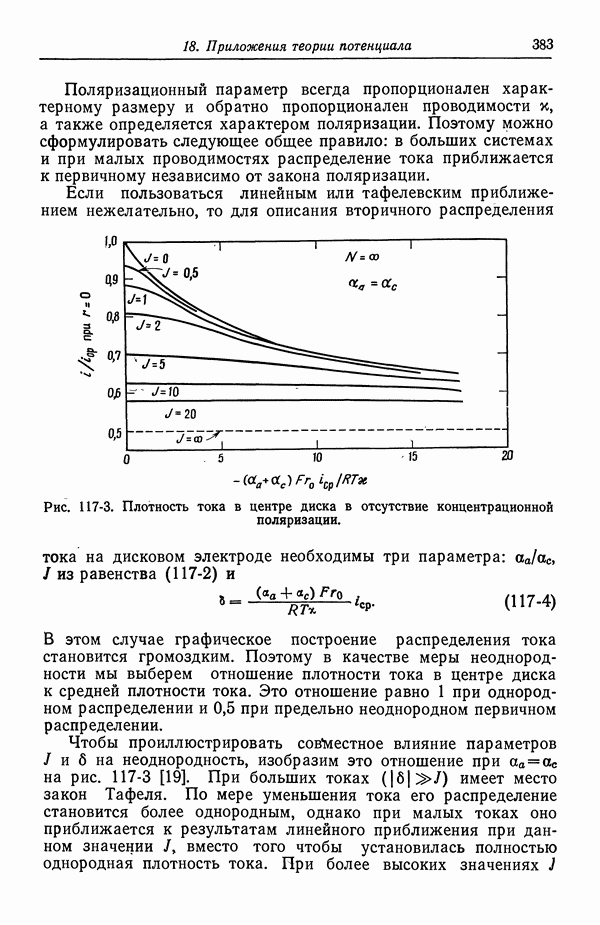
Рис. 57-2. Анодная и катодная составляющие плотности тока, изображенные в зависимости от потенциала, измеренного относительно медного электрода в 1 М растворе CuSO4 (разд. 40).
Плотность тока рассчитана по уравнению (57-25) при  .
.
Наш анализ данных Мэттсона и Бокриса дает для осажденных электродов  . В дальнейших расчетах мы будем использовать это значение у и примем
. В дальнейших расчетах мы будем использовать это значение у и примем  равным
равным  при концентрации двухвалентных ионов меди, равной 0,1 М.
при концентрации двухвалентных ионов меди, равной 0,1 М.
Результаты Мэттсона и Бокриса отклоняются от уравнения (57-28) при низких перенапряжениях. Они отнесли это за счет медленной диффузии адсорбированных ионов и атомов на решеточные центры и от них, утверждая тем самым, что этот процесс не является простым переносом заряда. Вместе с тем фактом, что средний разброс значений тока обмена составляет 10—20%, это служит указанием на то, что кинетику процессов на твердых электродах в общем случае нельзя ни предсказать, ни воспроизвести.
На рис. 57-2 приведены анодный и катодный вклады в плотность тока в соответствии с уравнением (57-25). Это сделано для иллюстрации независимости анодного вклада от концентрации двухвалентных ионов меди, когда этот вклад изображается в зависимости от потенциала, измеренного относительно данного электрода сравнения (см. примечания в конце разд. 40).
Обсуждавшиеся в настоящем разделе модели составляют основу для кинетического уравнения (56-1). Однако эти модели не обладают строгостью термодинамического вывода. Члены в уравнении (57-7) применимы не строго, и в уравнениях (57-10) и (57-11) сравнение делалось с приближенным уравнением Нернста вместо точного термодинамического выражения для равновесного потенциала. Кроме того, потенциал V зависит от выбора электрода сравнения. Различные электроды сравнения приведут, конечно, к различным комбинациям коэффициентов активности ионов.
Уравнение (56-1) содержит однозначно определенный потенциал, поверхностное перенапряжение, и поэтому оно превосходит уравнение (57-7), из которого можно «вывести» уравнение (564). Основываясь на уравнении (56-1), можно лишь сказать, что плотность тока обмена зависит от состава раствора. Модели же дают ясное, хотя и не вполне строгое представление о зависимости плотности тока обмена от состава раствора.
В настоящей главе обсуждается поверхностное перенапряжение само по себе. В гл. 20 изучаются концентрационное и полное перенапряжения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. ВВЕДЕНИЕ
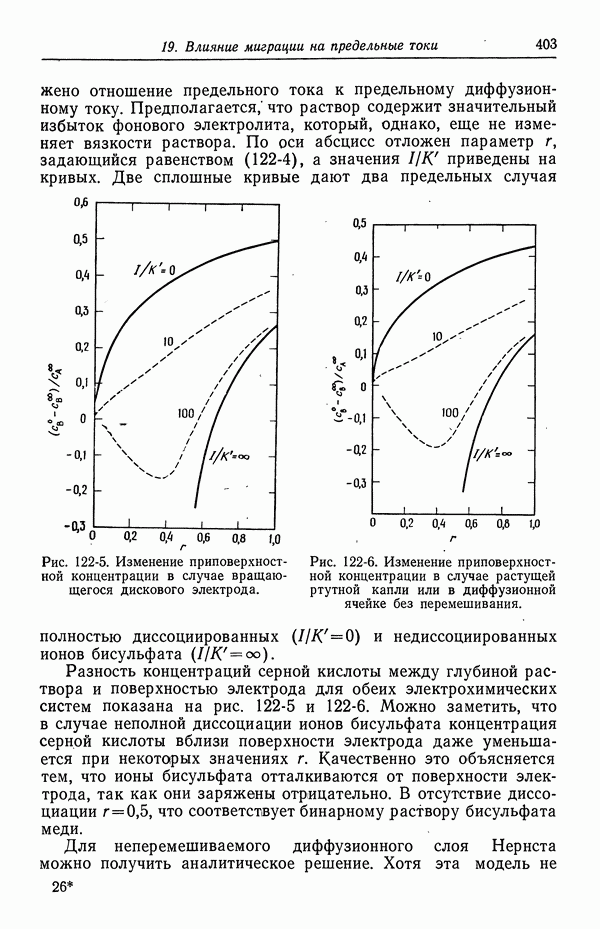
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
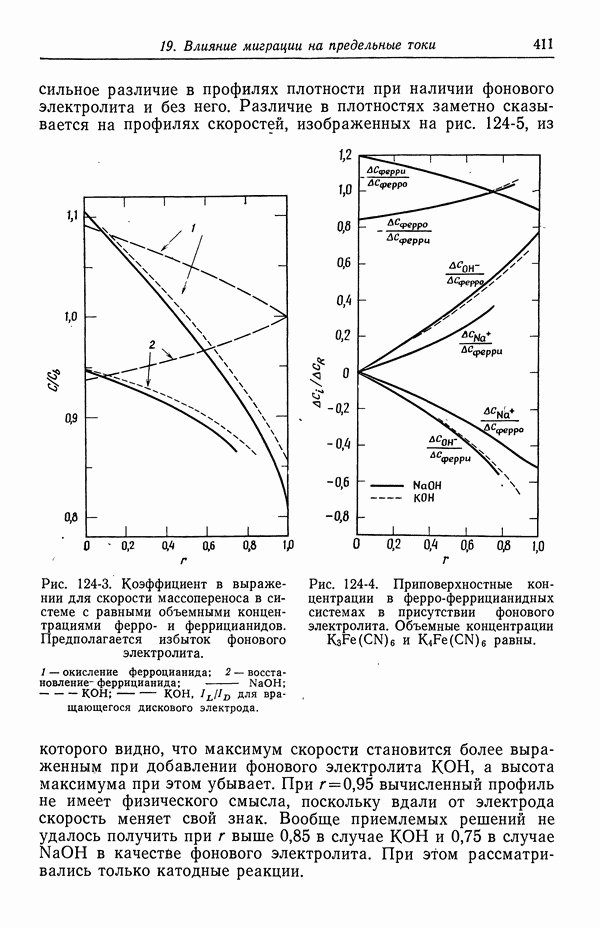
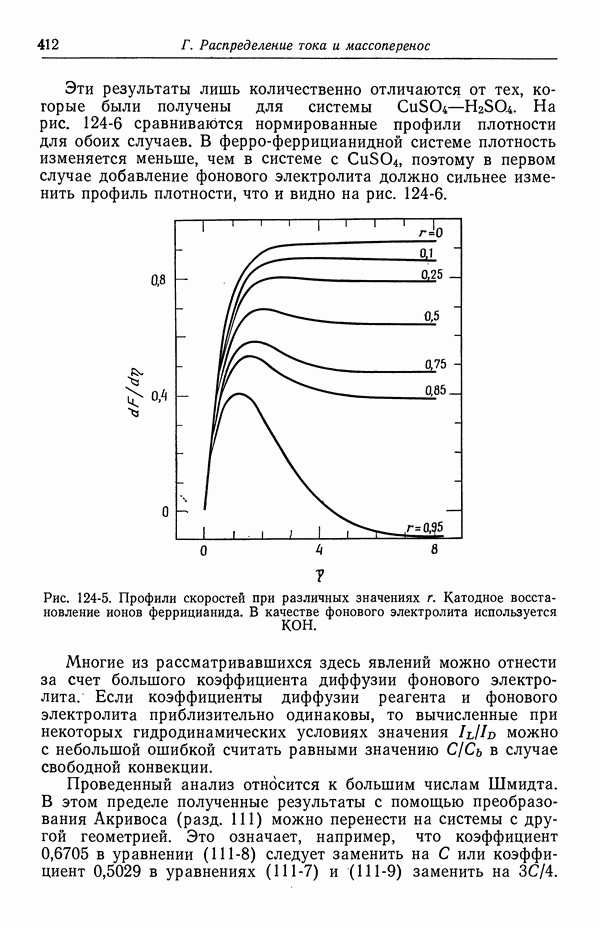
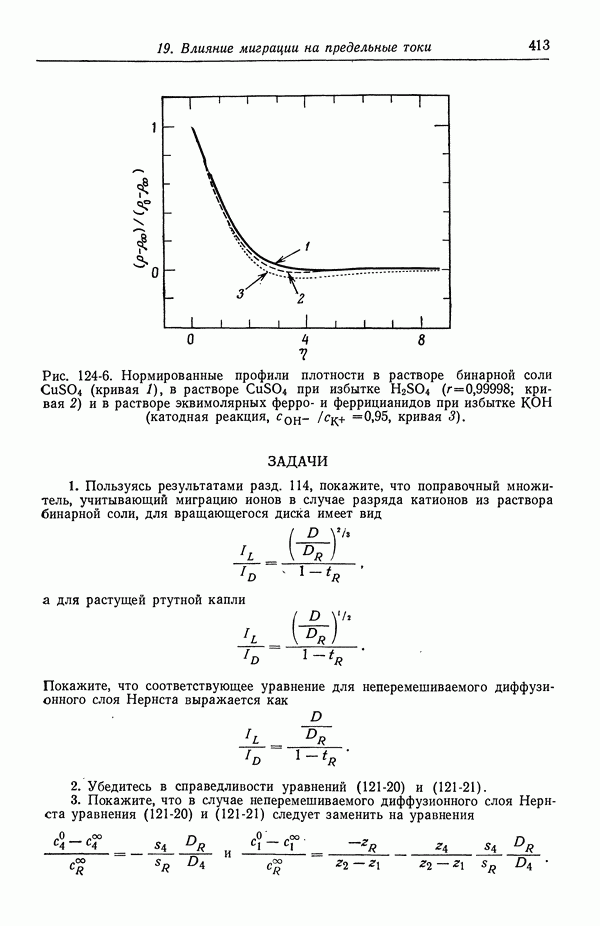
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
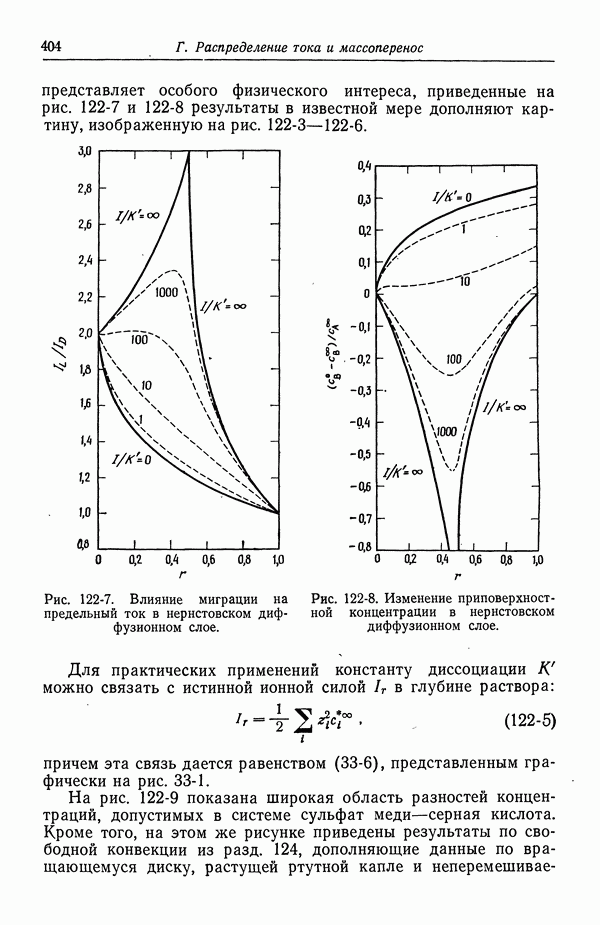
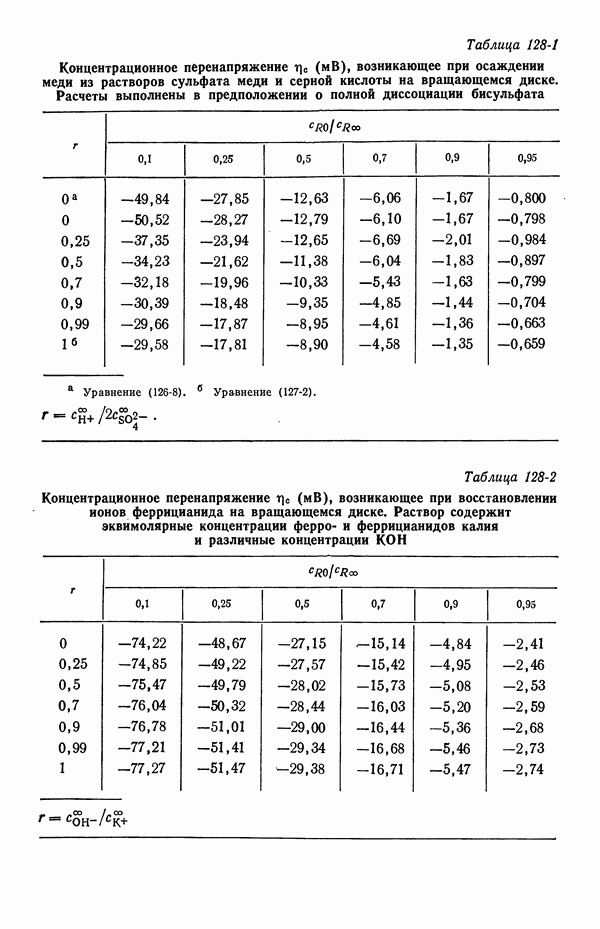
- 5. Диффузионный слой
- 6. Концентрационные ячейки
- 7. Концентрационное перенапряжение
- 8. Поверхностное перенапряжение
- 9. Потенциал ячейки
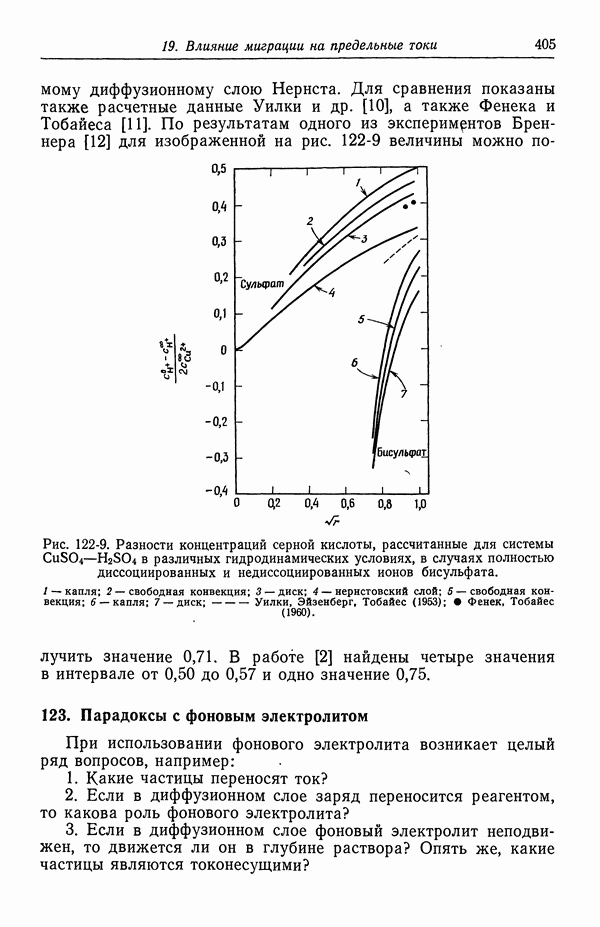
- 10. Фоновый электролит
- 11. Свободная конвекция
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
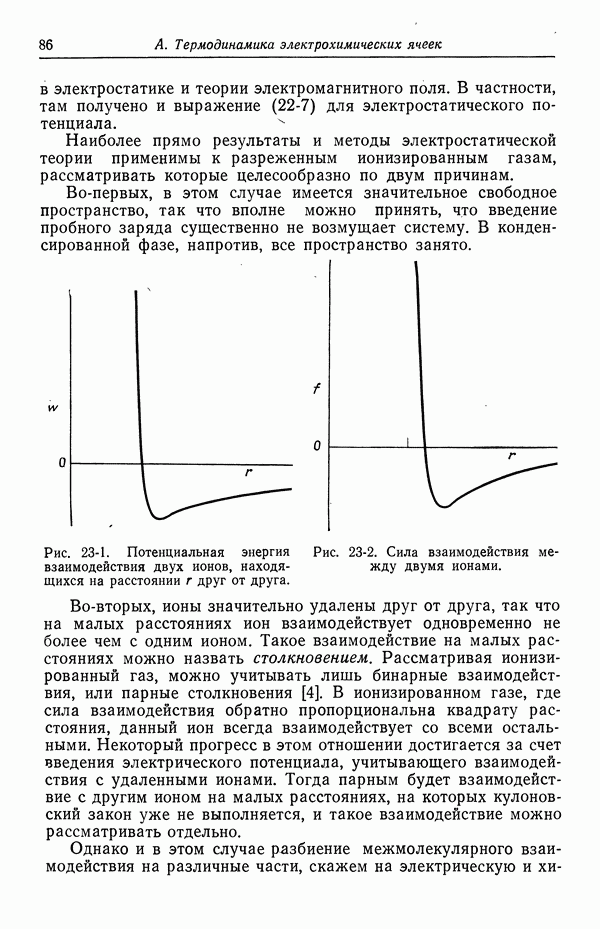
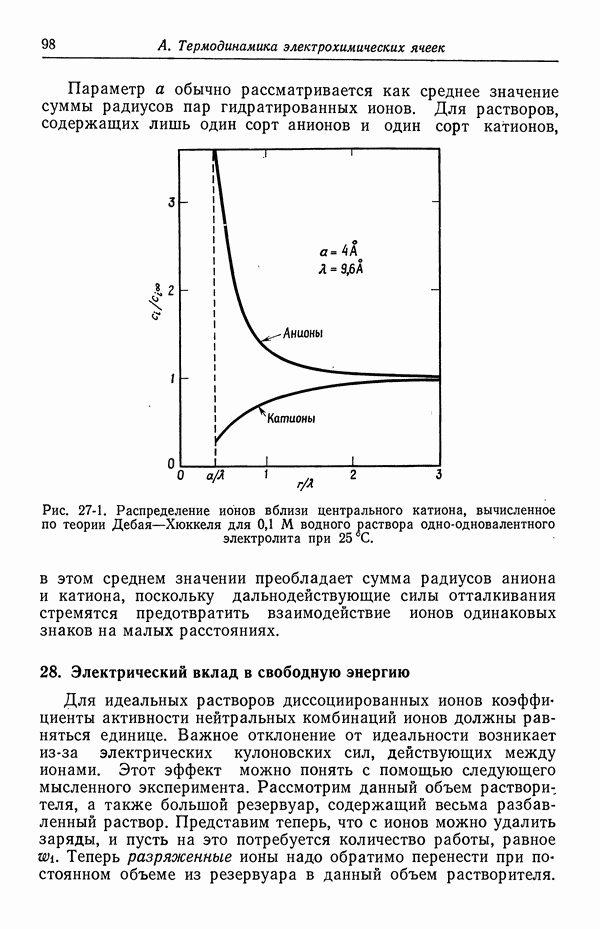
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
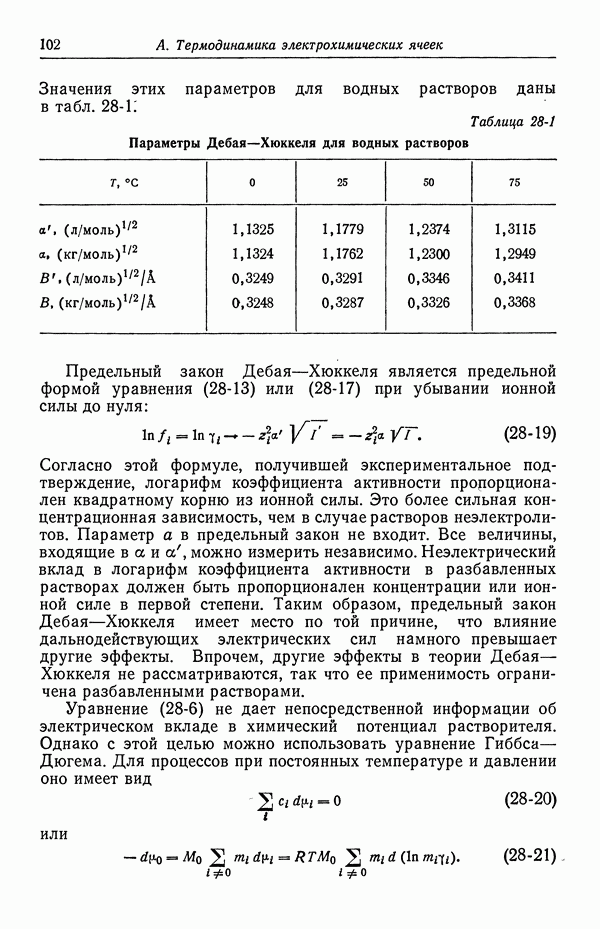
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая—Хюккеля
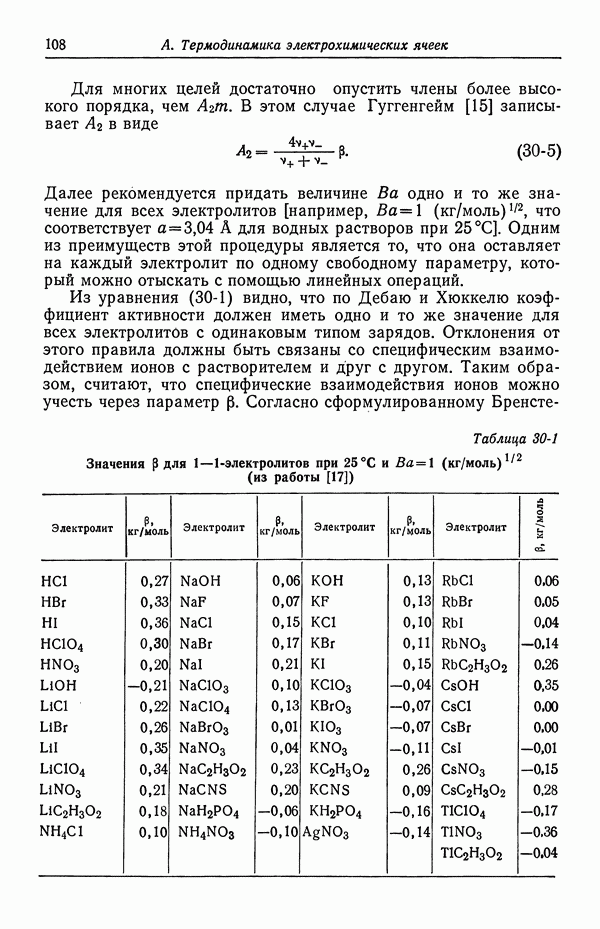
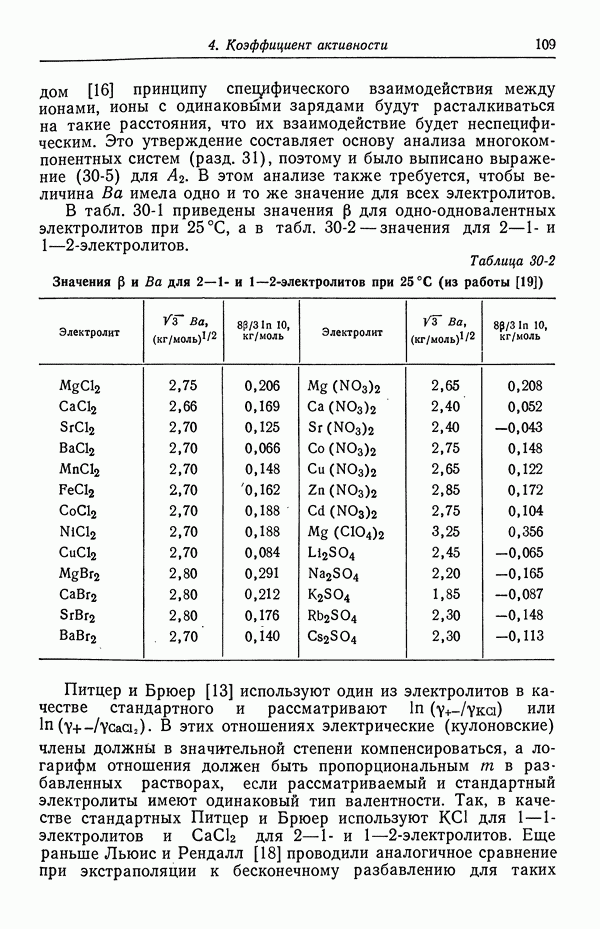
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
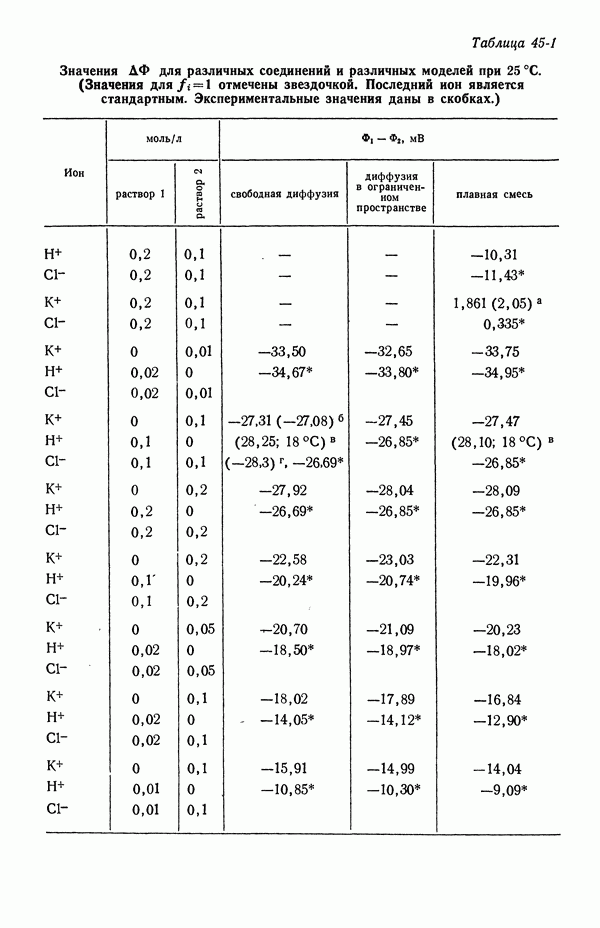
- 40. Потенциалы относительно данного электрода сравнения
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
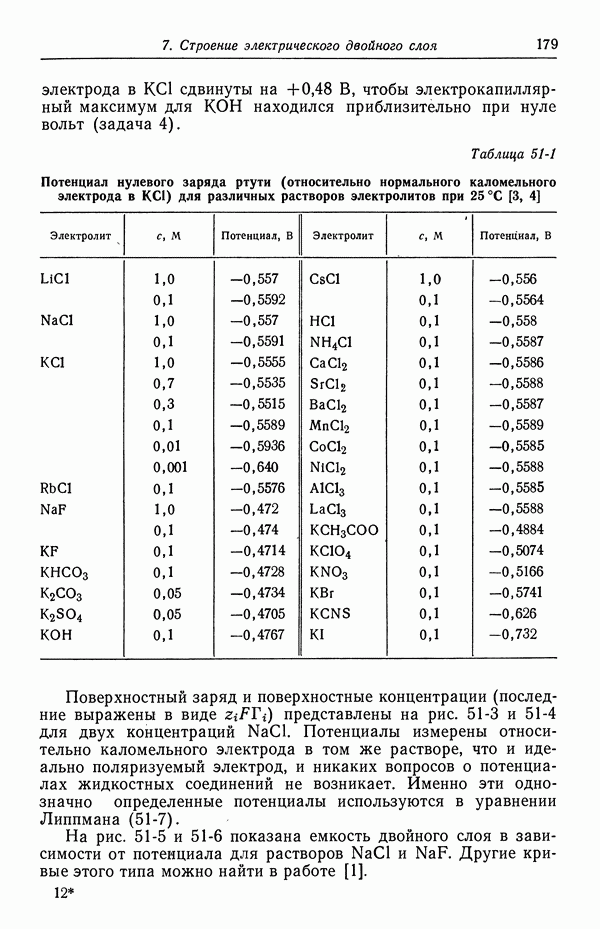
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
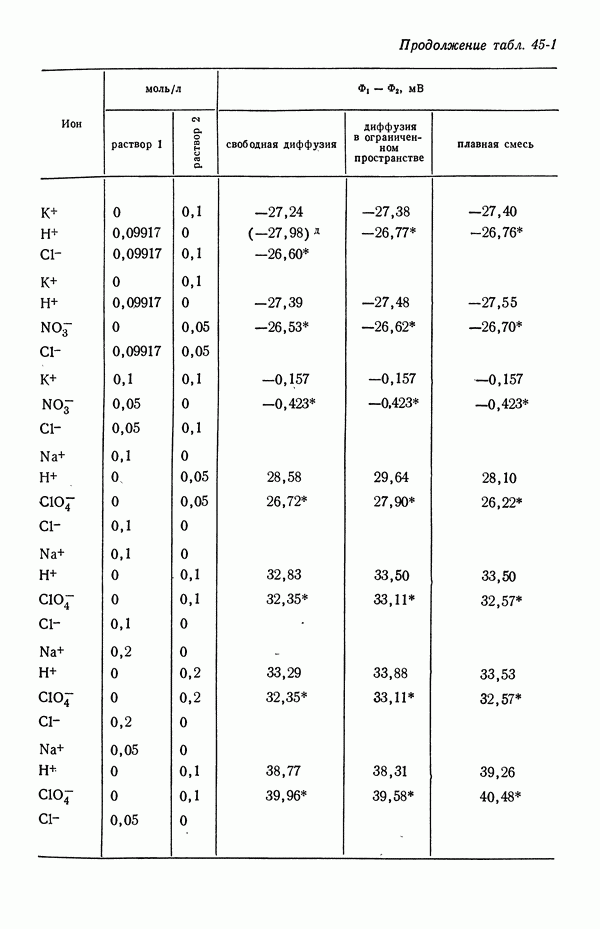
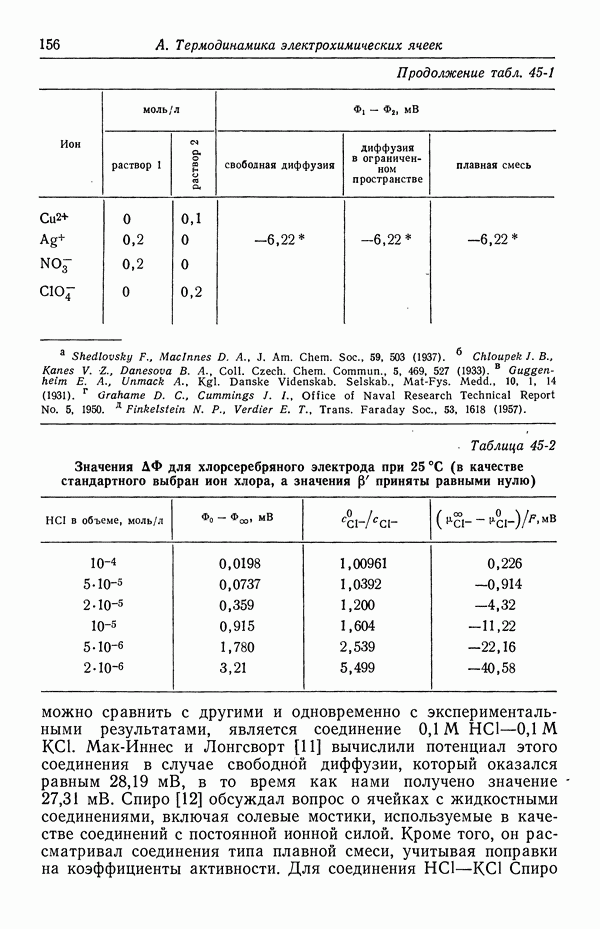
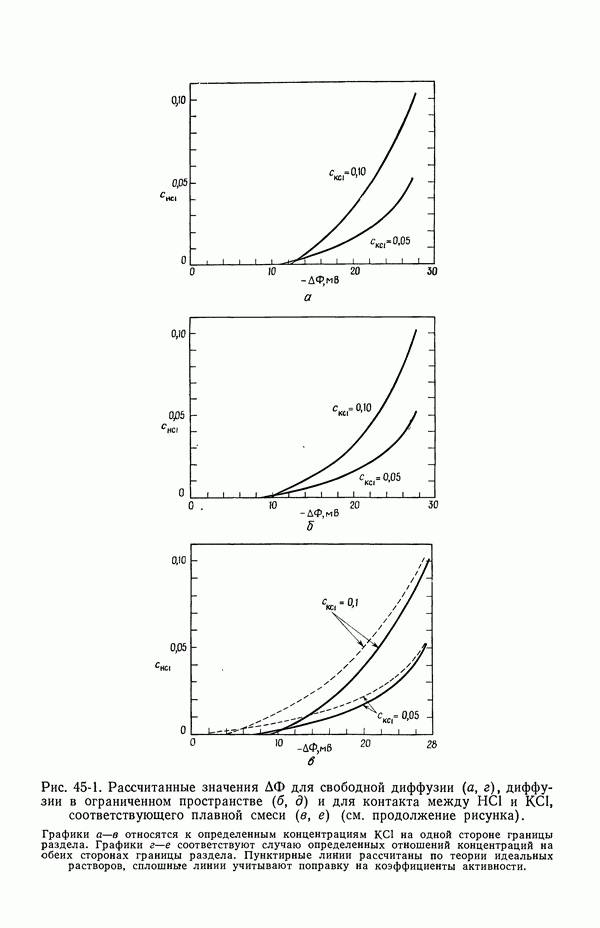
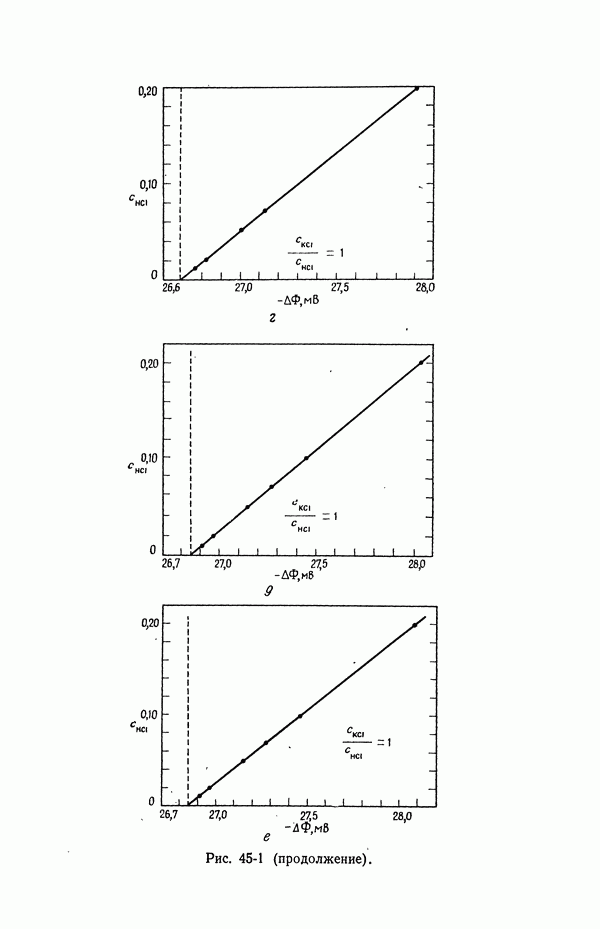
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 49. Качественное описание двойных слоев
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод — раствор
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
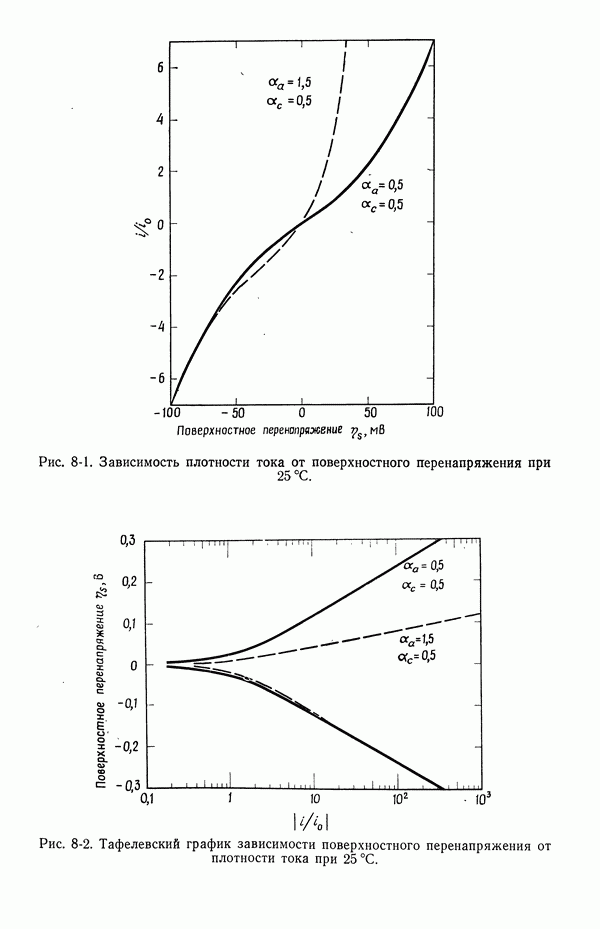
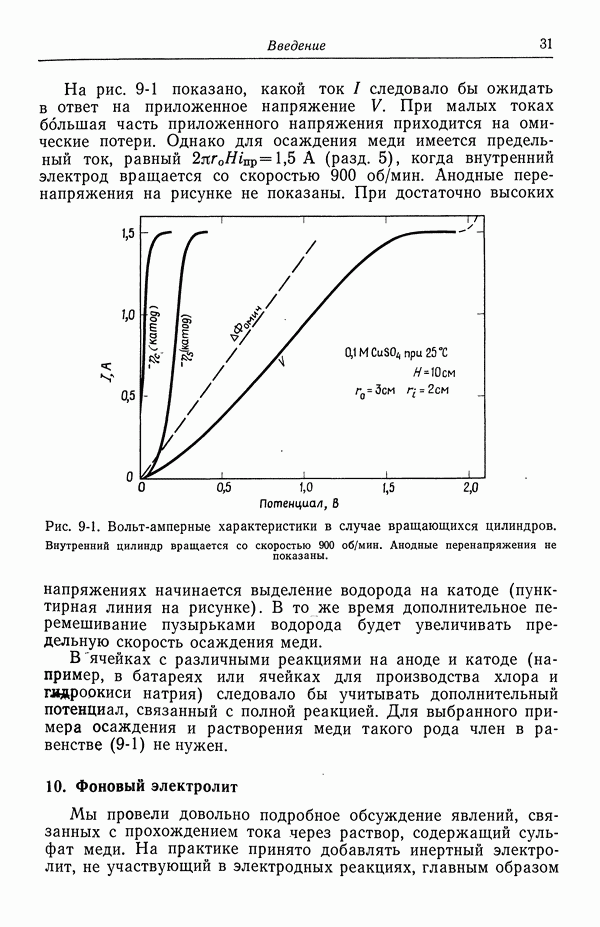
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 66. Динамика границы раздела
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 69. Законы переноса
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 78. Законы переноса
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
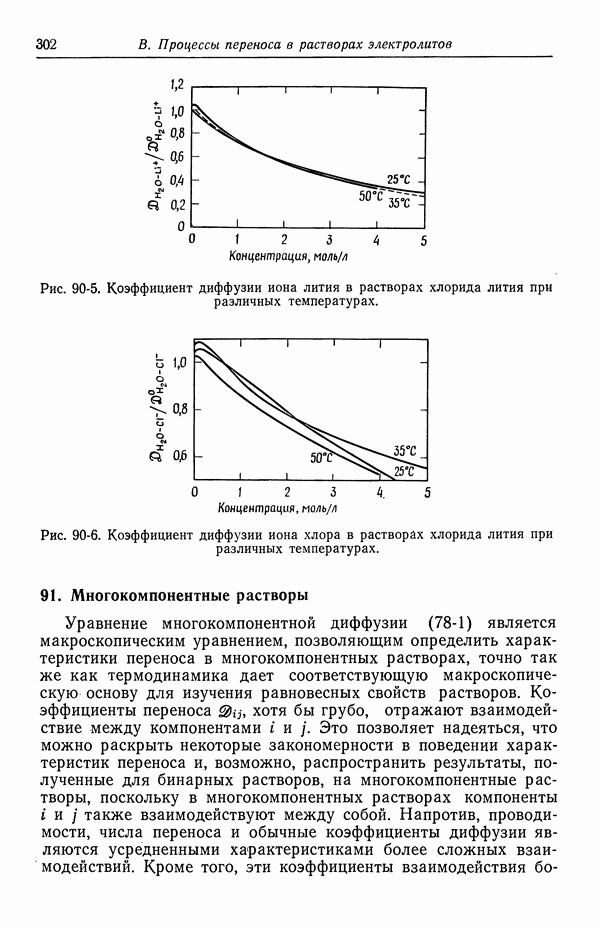
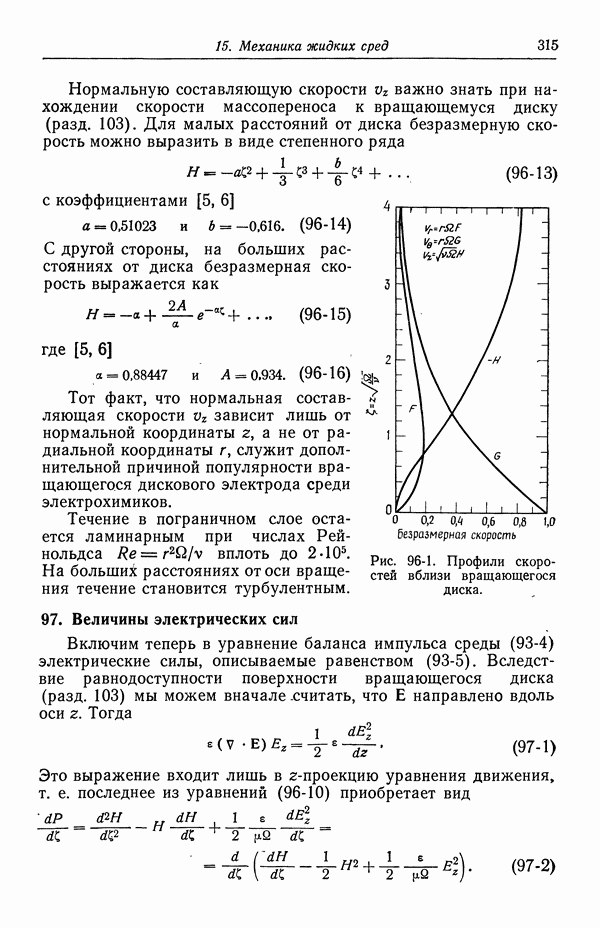
- 90. Растворы, содержащие одну соль
- 92. Интегральные коэффициенты диффузии
- ЗАДАЧА
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
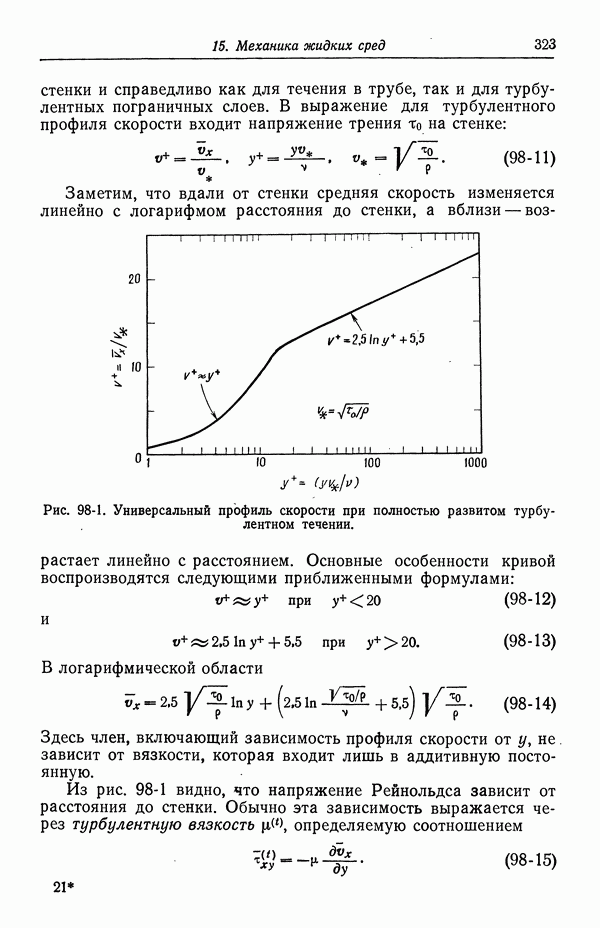
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
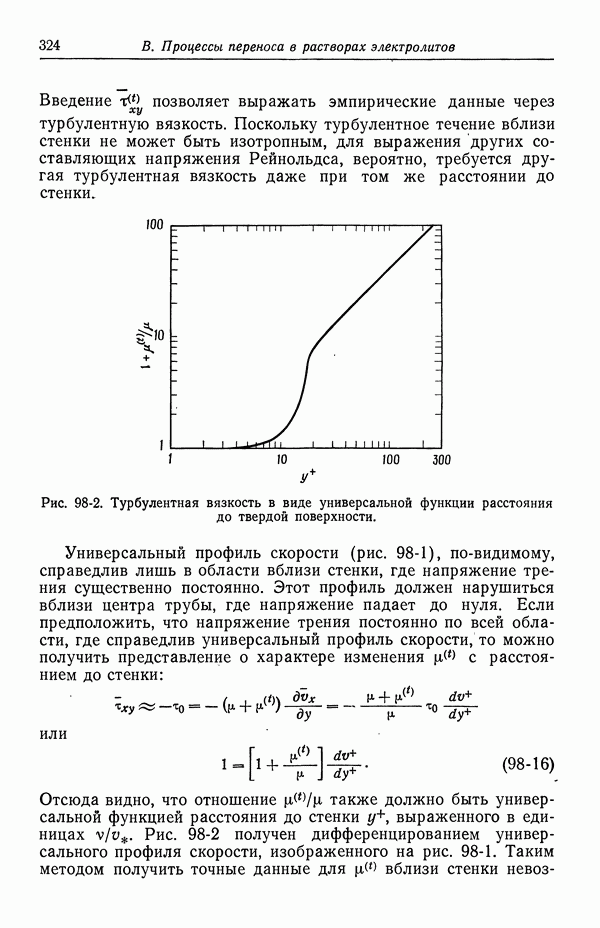
- 98. Турбулентное течение
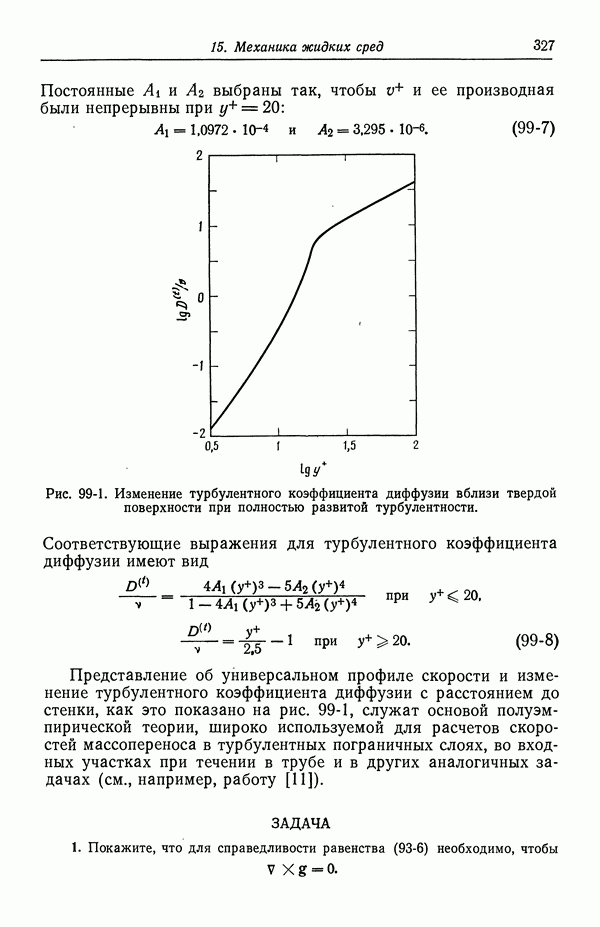
- 99. Массоперенос в турбулентном потоке
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
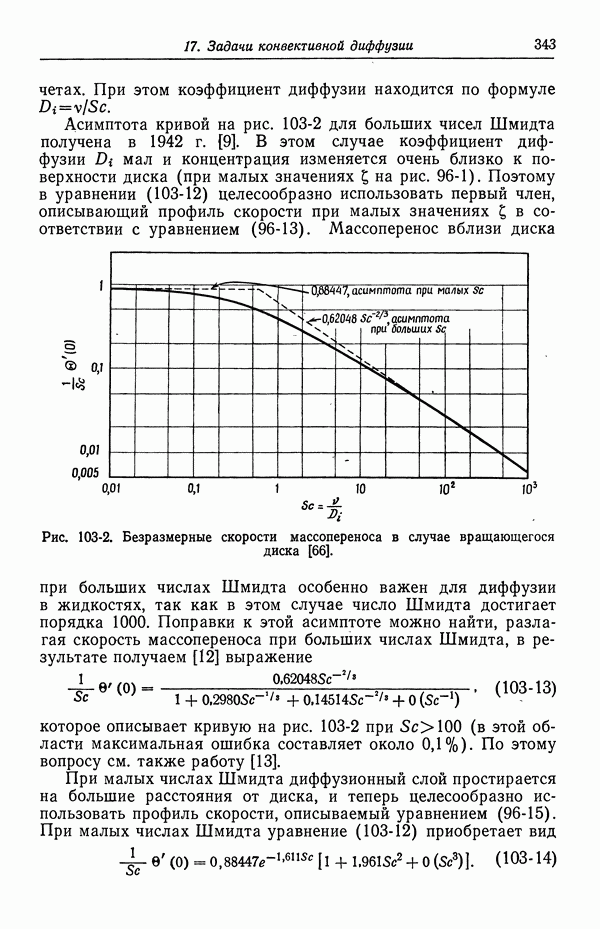
- 103. Вращающийся диск
- 104. Задача Граца
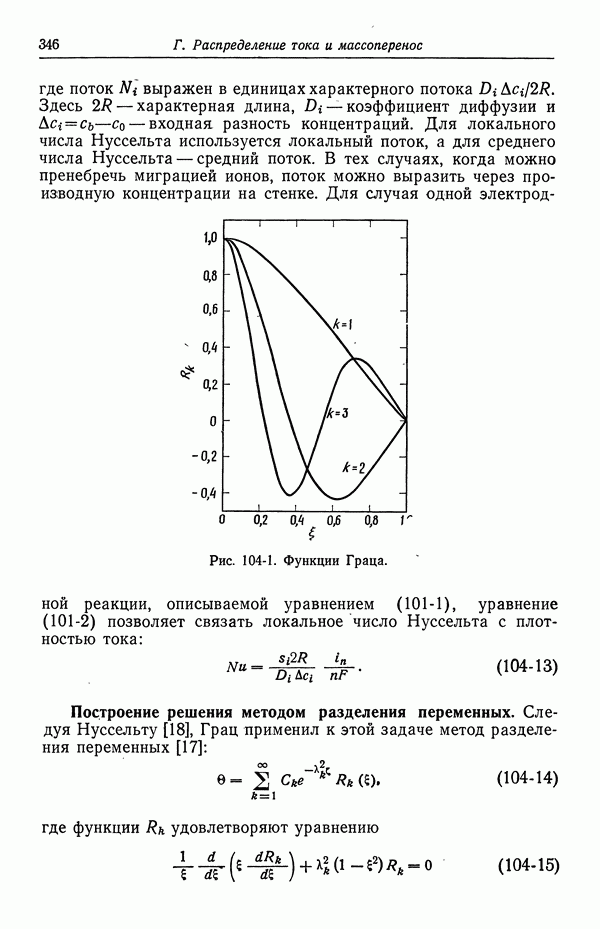
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 111. Свободная конвекция
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
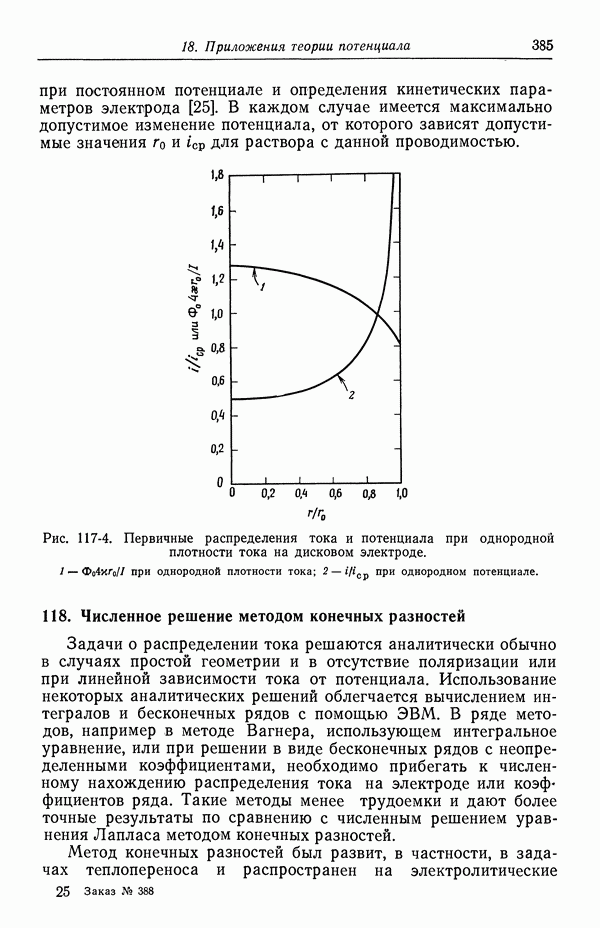
- 116. Первичное распределение тока
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- СПИСОК ОБОЗНАЧЕНИЙ
- ГЛАВА 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 119. Решение задачи
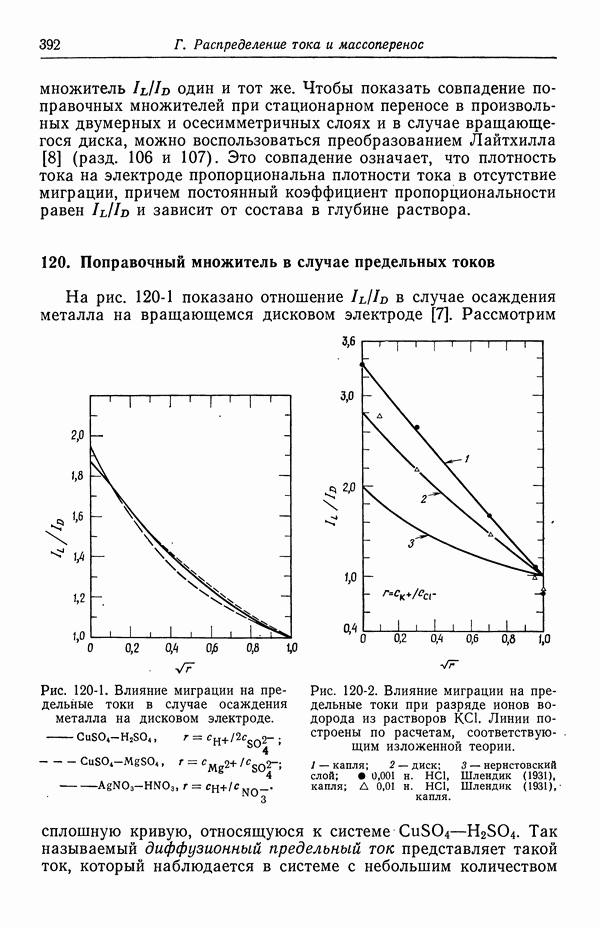
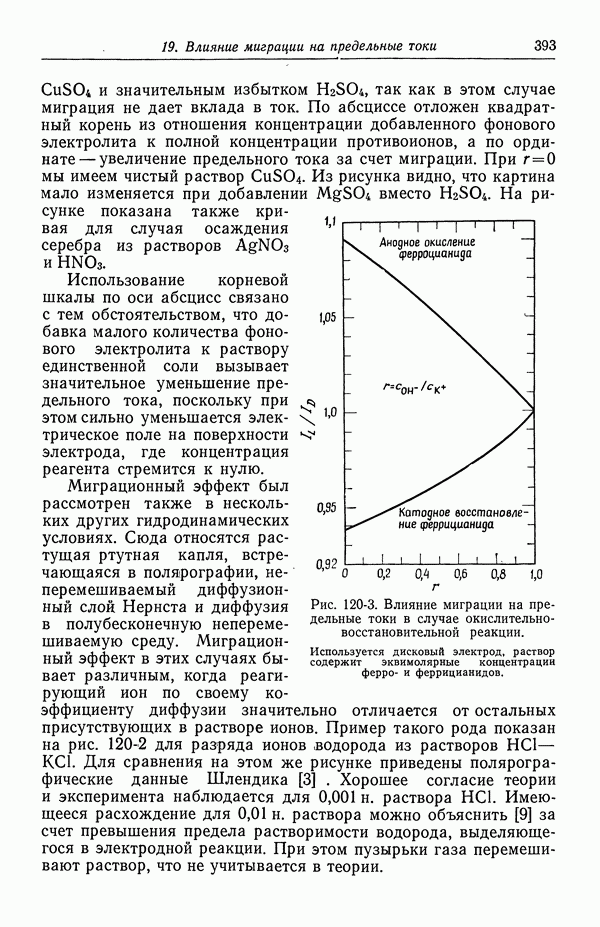
- 120. Поправочный множитель в случае предельных токов
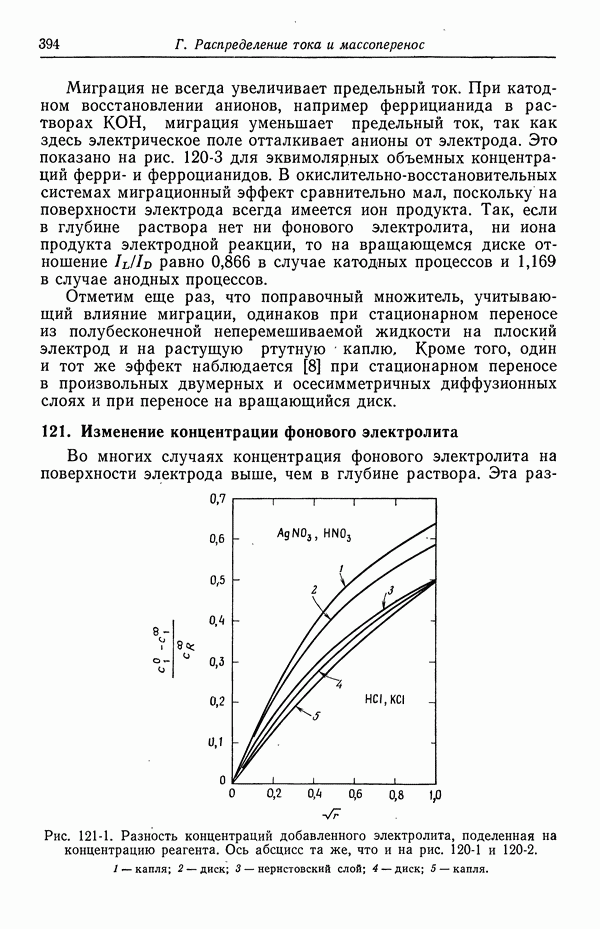
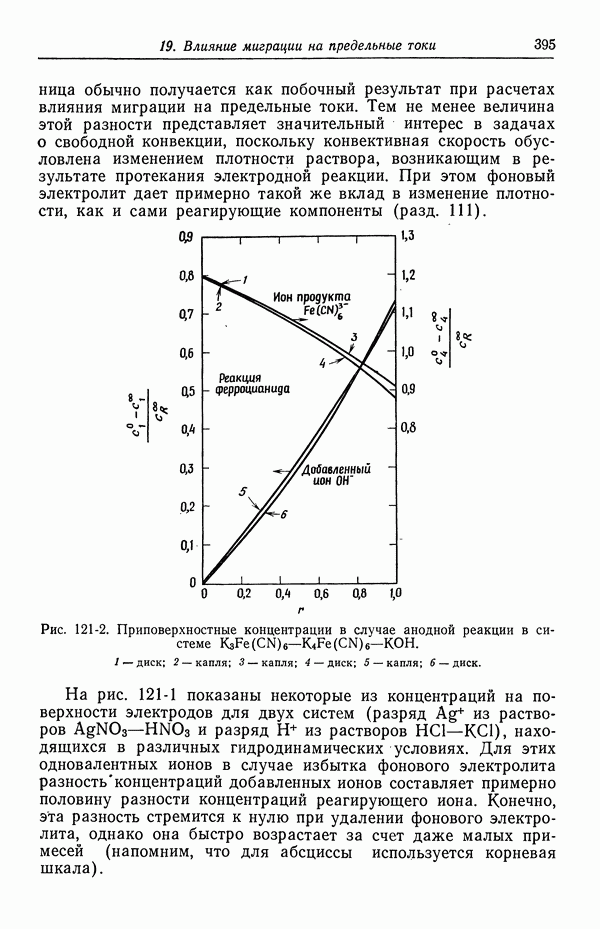
- 121. Изменение концентрации фонового электролита
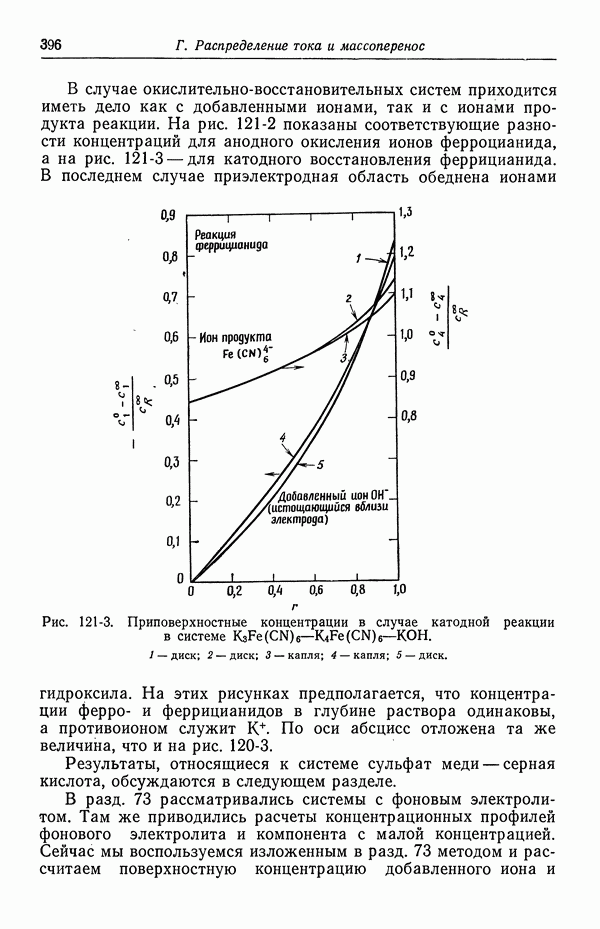
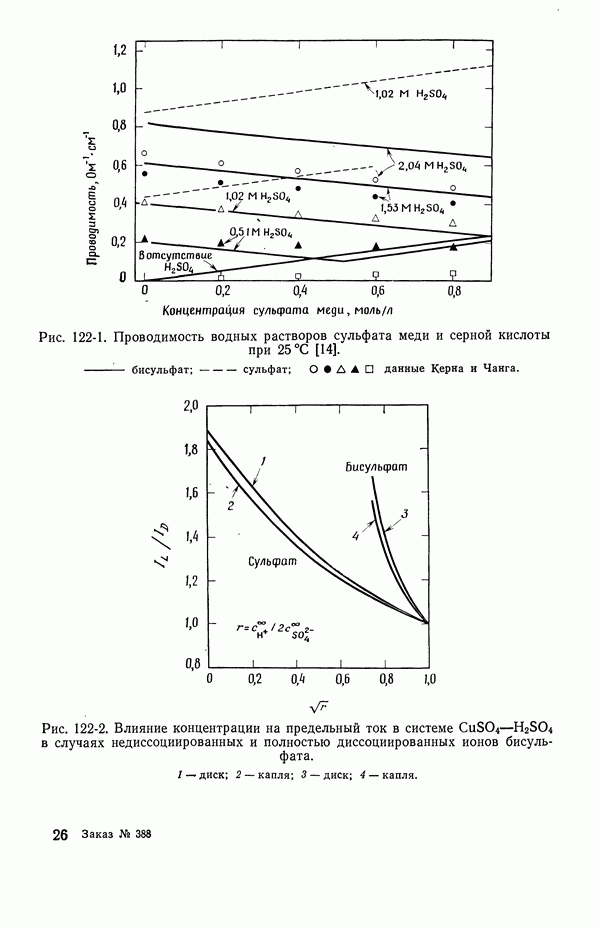
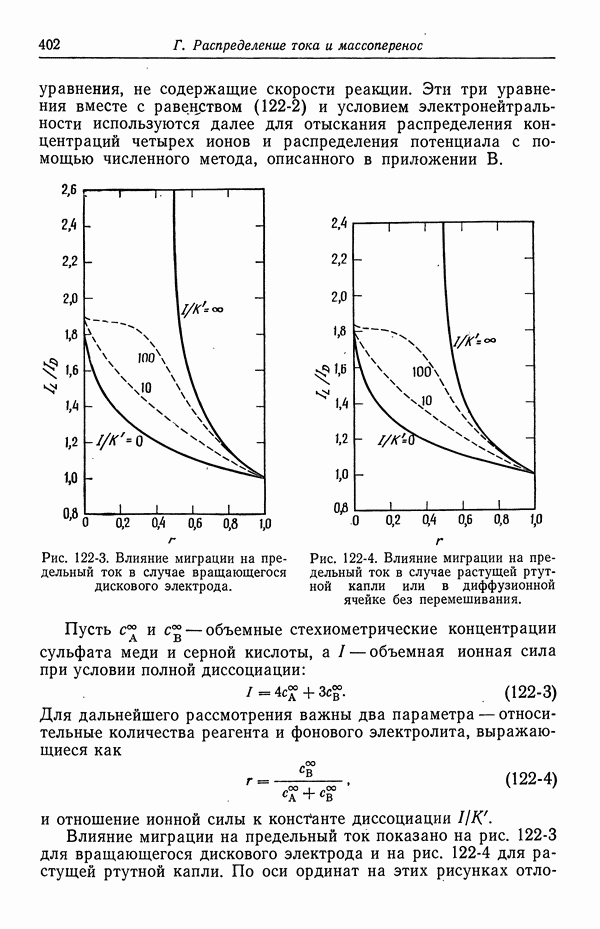
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
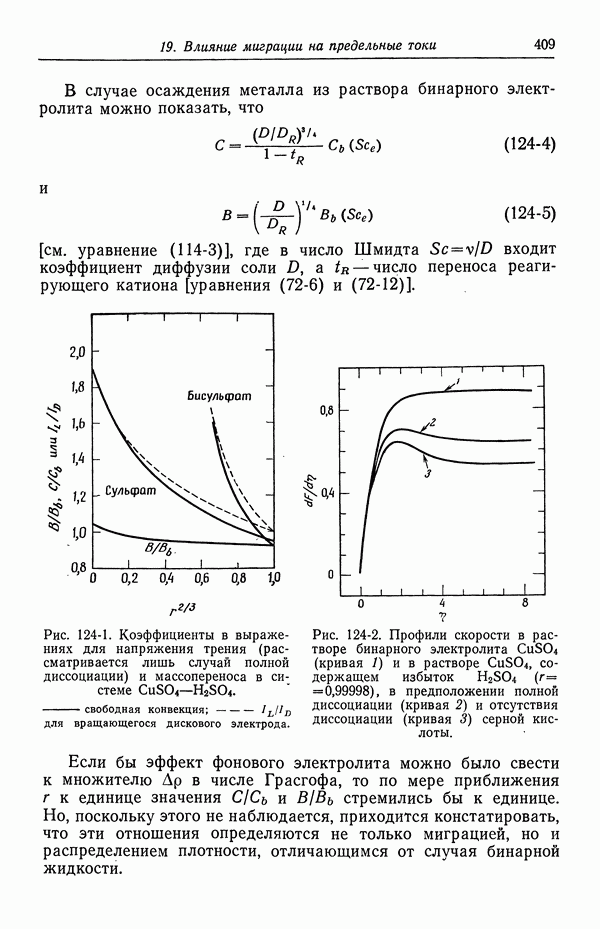
- 124. Предельные токи в случае свободной конвекции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ