| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
122. Роль ионов бисульфата
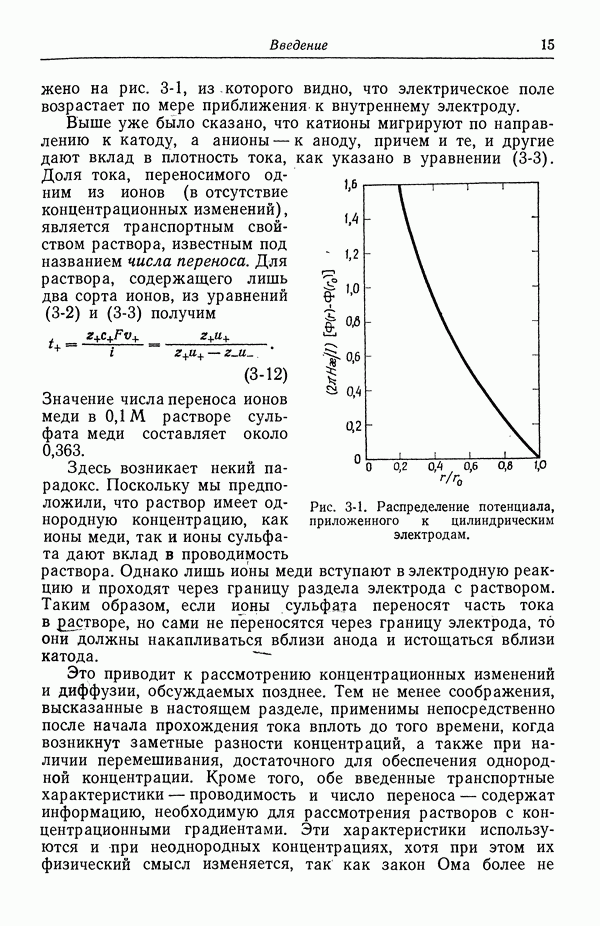
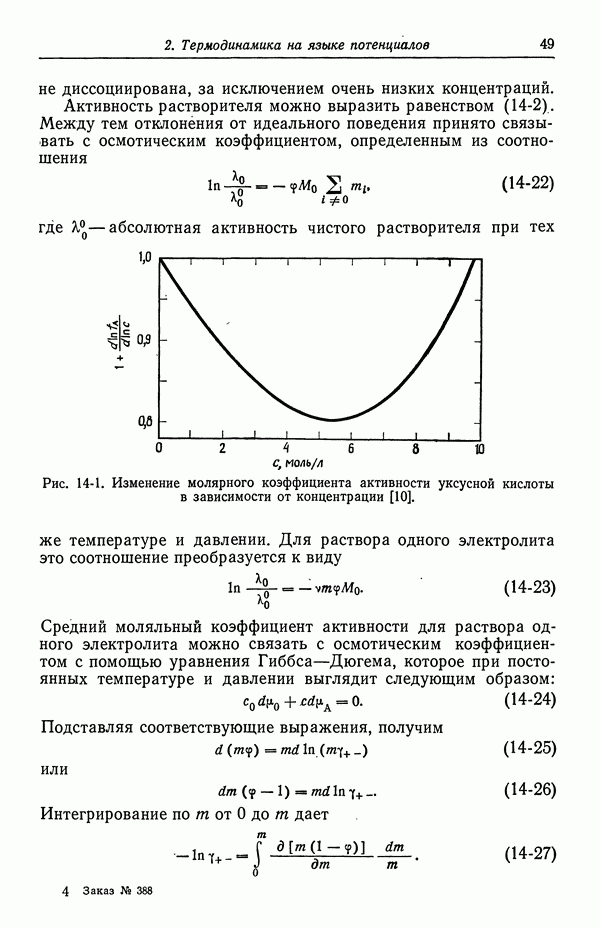
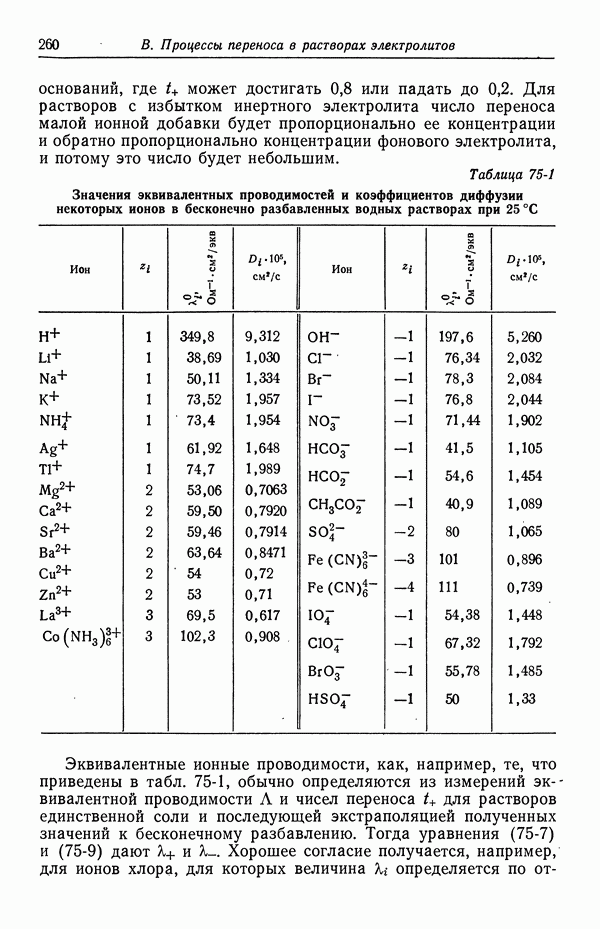
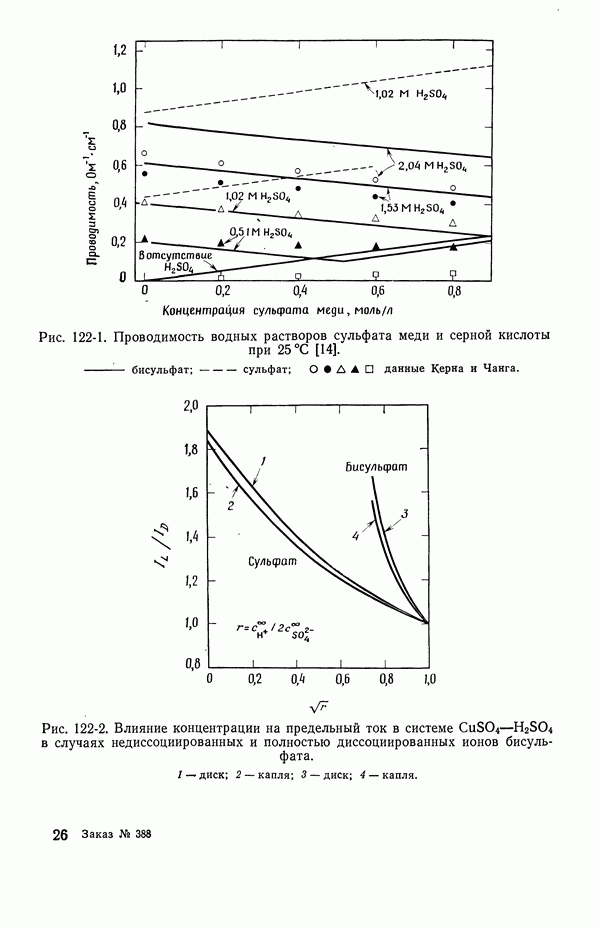
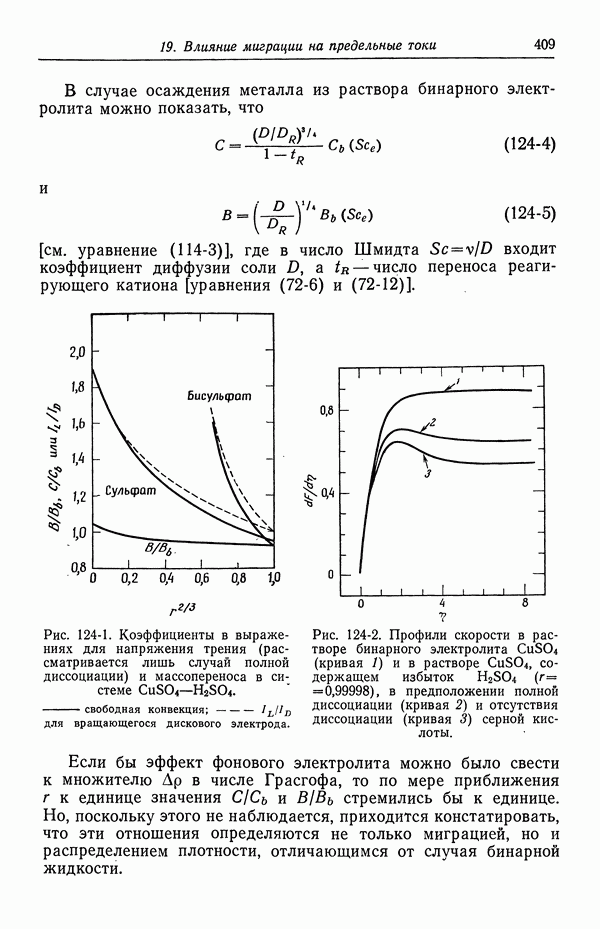
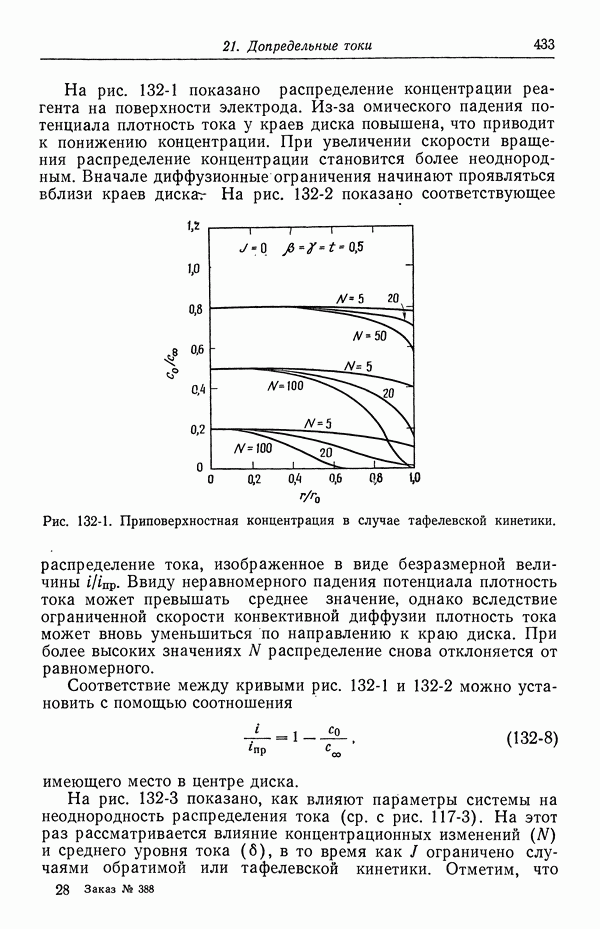
В растворах серной кислоты ионы бисульфата диссоциируют не полностью (разд 33). Простым, но характерным примером может служить рис. 122-1, где показана проводимость растворов сульфата меди и серной кислоты. По мере добавления сульфата меди к раствору серной кислоты проводимость уменьшается. Если вычислять проводимость исходя из предельных ионных подвижностей (табл. 75-1), то результаты вычислений согласуются с экспериментом в предположении, что ионы бисульфата не диссоциируют. С другой стороны, значения, предсказанные на основе рассмотрения ионов сульфата и водорода, количественно и качественно расходятся с наблюдаемыми значениями.
Из неполной диссоциации ионов бисульфата можно также сделать важные заключения относительно влияния миграции на предельные токи. При добавлении сульфата меди в растворы серной кислоты электрическое поле увеличивается не только потому, что возрастает электрический ток, но и вследствие образования ионов бисульфата и падения проводимости. Это показано на рис. 122-2. Отложенный по оси абсцисс параметр  по-прежнему является отношением стехиометрических концентраций серной кислоты и сульфата меди.
по-прежнему является отношением стехиометрических концентраций серной кислоты и сульфата меди.
Можно учесть также частичную диссоциацию ионов бисульфата [2]. Как и в разд. 119, уравнения материального баланса записываются для ионов водорода, сульфата, бисульфата и меди, причем в уравнениях учитывается, когда в этом есть необходимость, скорость гомогенной реакции

[см. уравнение (100-2)]. Будем предполагать реакцию (122-1) быстрой, так что концентрации удовлетворяют соотношению [равенство (33-4)]

где величина К считается не зависящей от координаты. Звездочки в верхнем индексе означают, что раствор состоит из молекул воды и ионов водорода, бисульфата, сульфата и меди. Тогда из уравнений материального баланса получаются три

Рис. 122-1. Проводимость водных растворов сульфата меди и серной кислоты при  данные Керна и Чанга.
данные Керна и Чанга.

Рис. 122-2. Влияние концентрации на предельный ток в системе  в случаях недиссоциированных и полностью диссоциированных ионов бисульфата. 1 - диск; 2 — капля; 3 — диск; 4 — капля.
в случаях недиссоциированных и полностью диссоциированных ионов бисульфата. 1 - диск; 2 — капля; 3 — диск; 4 — капля.
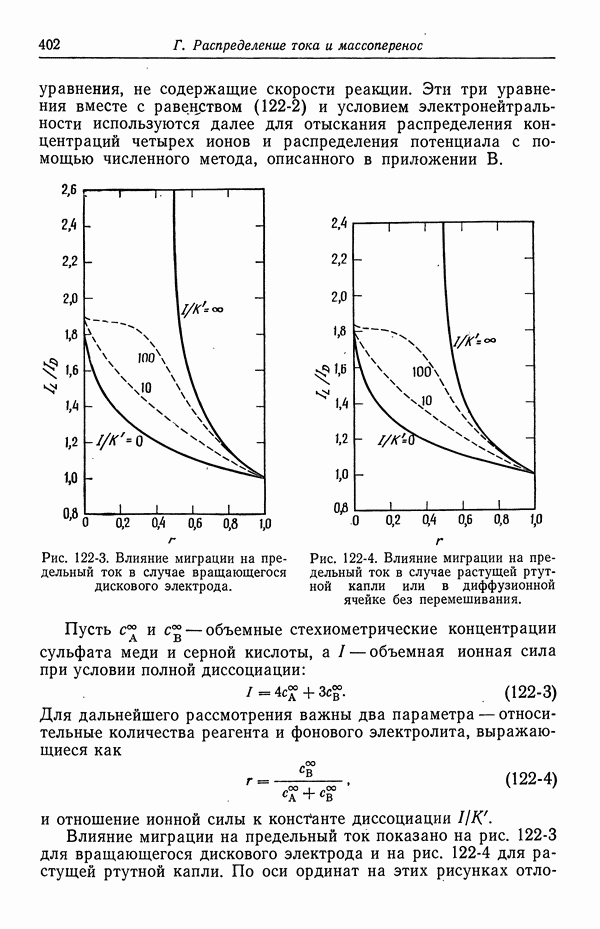
уравнения, не содержащие скорости реакции. Эти три уравнения вместе с равенством (122-2) и условием электронейтральности используются далее для отыскания распределения концентраций четырех ионов и распределения потенциала с помощью численного метода, описанного в приложении В.

Рис. 122-3. Влияние миграции на предельный ток в случае вращающегося дискового электрода.

Рис. 122-4. Влияние миграции на предельный ток в случае растущей ртутной капли или в диффузионной ячейке без перемешивания.
Пусть  — объемные стехиометрические концентрации сульфата меди и серной кислоты,
— объемные стехиометрические концентрации сульфата меди и серной кислоты,  объемная ионная сила при условии полной диссоциации:
объемная ионная сила при условии полной диссоциации:

Для дальнейшего рассмотрения важны два параметра — относительные количества реагента и фонового электролита, выражающиеся как

и отношение ионной силы к константе диссоциации 
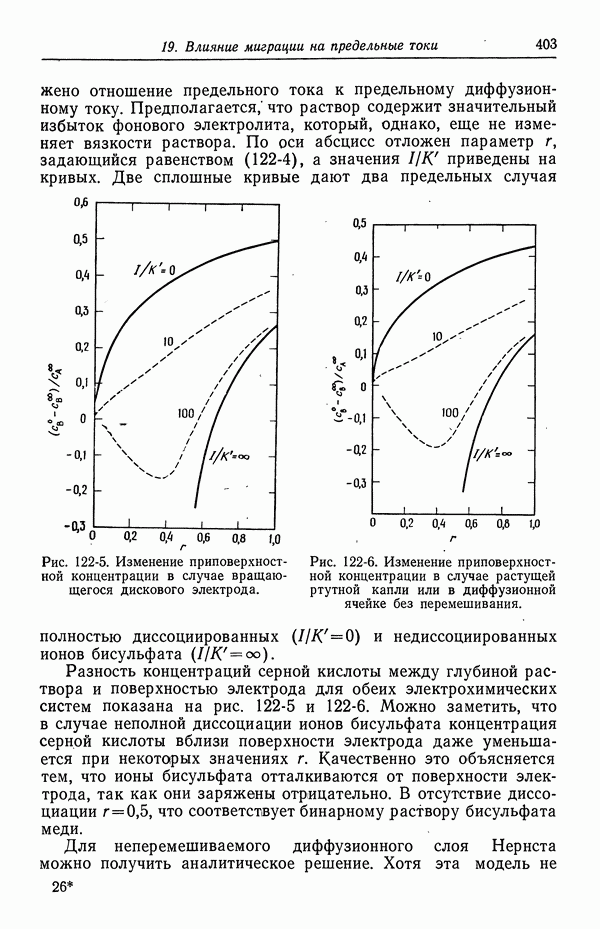
Влияние миграции на предельный ток показано на рис. 122-3 для вращающегося дискового электрода и на рис. 122-4 для растущей ртутной капли. По оси ординат на этих рисунках отложено
отношение предельного тока к предельному диффузионному току. Предполагается, что раствор содержит значительный избыток фонового электролита, который, однако, еще не изменяет вязкости раствора. По оси абсцисс отложен параметр  , задающийся равенством (122-4), а значения
, задающийся равенством (122-4), а значения  приведены на кривых. Две сплошные кривые дают два предельных случая полностью диссоциированных
приведены на кривых. Две сплошные кривые дают два предельных случая полностью диссоциированных  и недиссоциированных ионов бисульфата
и недиссоциированных ионов бисульфата 

Рис. 122-5. Изменение приповерхностной концентрации в случае вращающегося дискового электрода.

Рис. 122-6. Изменение приповерхностной концентрации в случае растущей ртутной капли или в диффузионной ячейке без перемешивания.
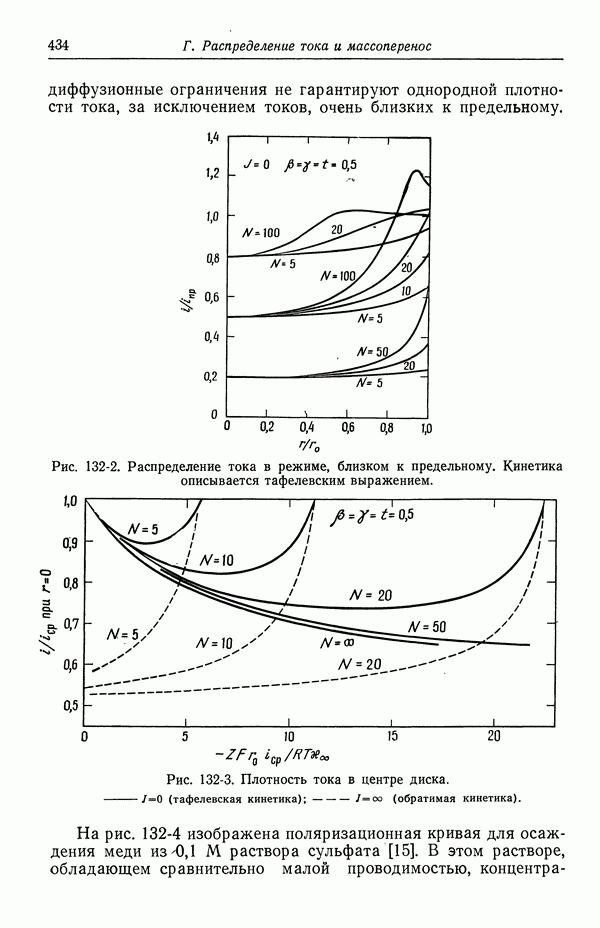
Разность концентраций серной кислоты между глубиной раствора и поверхностью электрода для обеих электрохимических систем показана на рис. 122-5 и 122-6. Можно заметить, что в случае неполной диссоциации ионов бисульфата концентрация серной кислоты вблизи поверхности электрода даже уменьшается при некоторых значениях  . Качественно это объясняется тем, что ионы бисульфата отталкиваются от поверхности электрода, так как они заряжены отрицательно. В отсутствие диссоциации
. Качественно это объясняется тем, что ионы бисульфата отталкиваются от поверхности электрода, так как они заряжены отрицательно. В отсутствие диссоциации  что соответствует бинарному раствору бисульфата меди.
что соответствует бинарному раствору бисульфата меди.
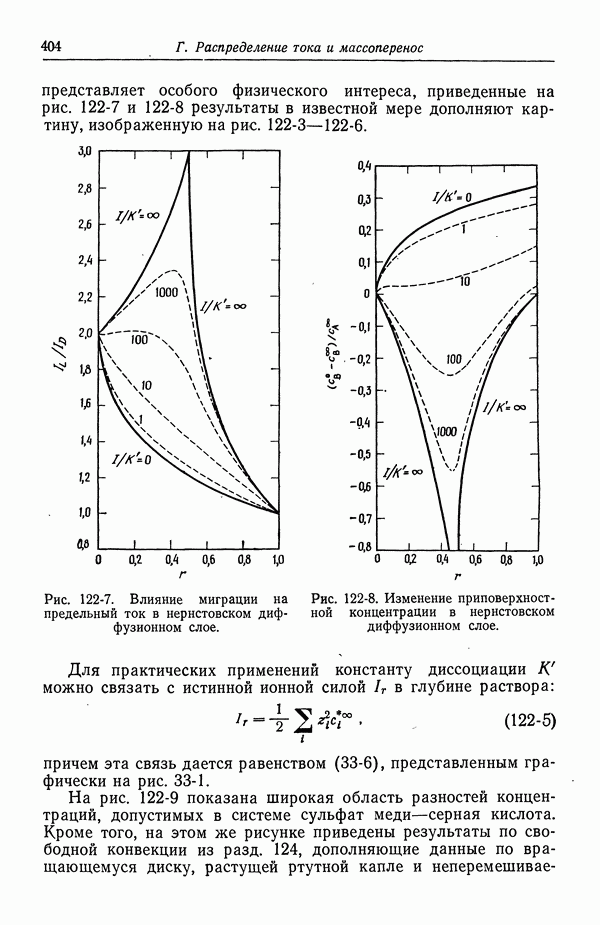
Для неперемешиваемого диффузионного слоя Нернста можно получить аналитическое решение. Хотя эта модель не
представляет особого физического интереса, приведенные на рис. 122-7 и 122-8 результаты в известной мере дополняют картину, изображенную на рис. 122-3 - 122-6.

Рис. 122-7. Влияние миграции на предельный ток в нернстовском диффузионном слое.

Рис. 122-8. Изменение приповерхностной концентрации в нернстовском диффузионном слое.
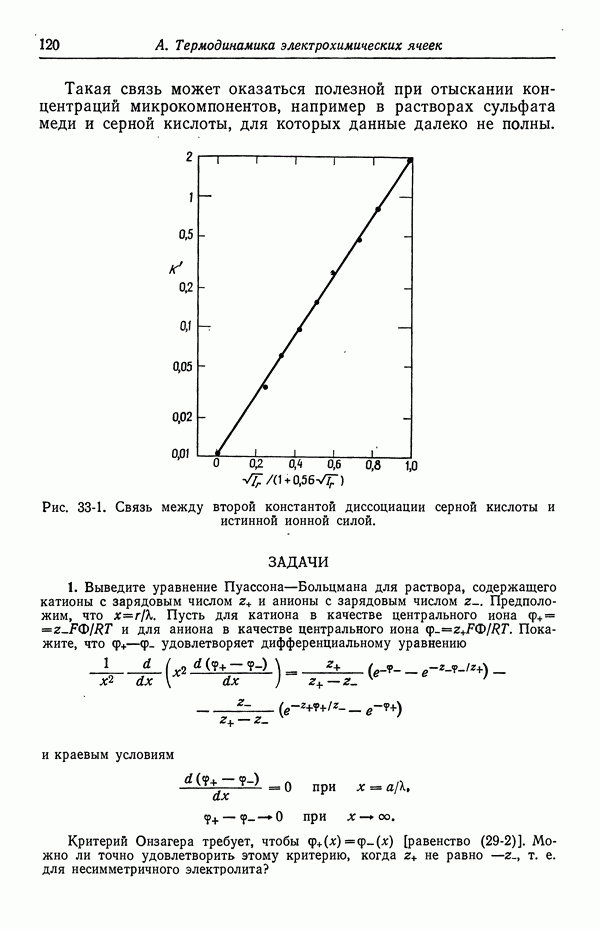
Для практических применений константу диссоциации К можно связать с истинной ионной силой  в глубине раствора:
в глубине раствора:

причем эта связь дается равенством (33-6), представленным графически на рис. 33-1.
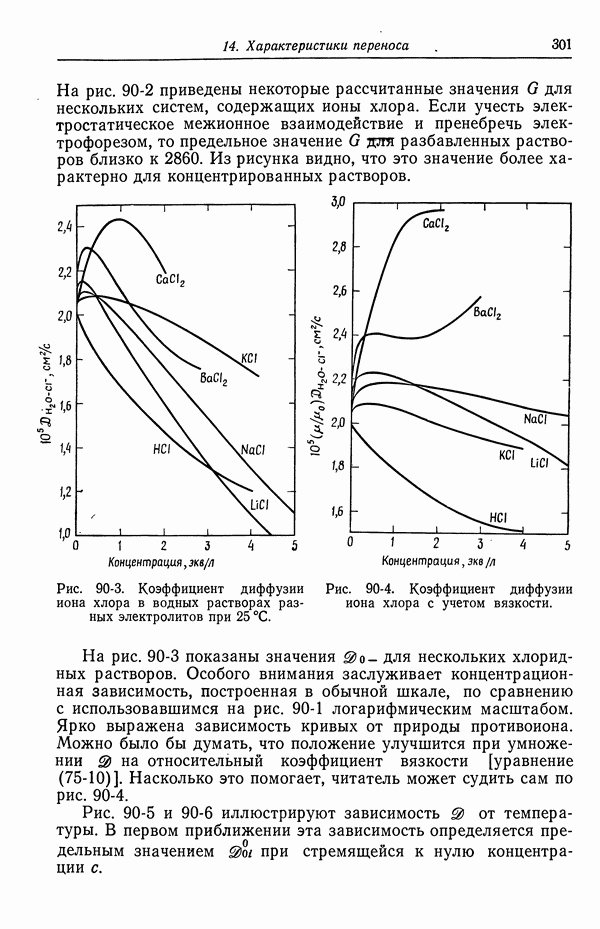
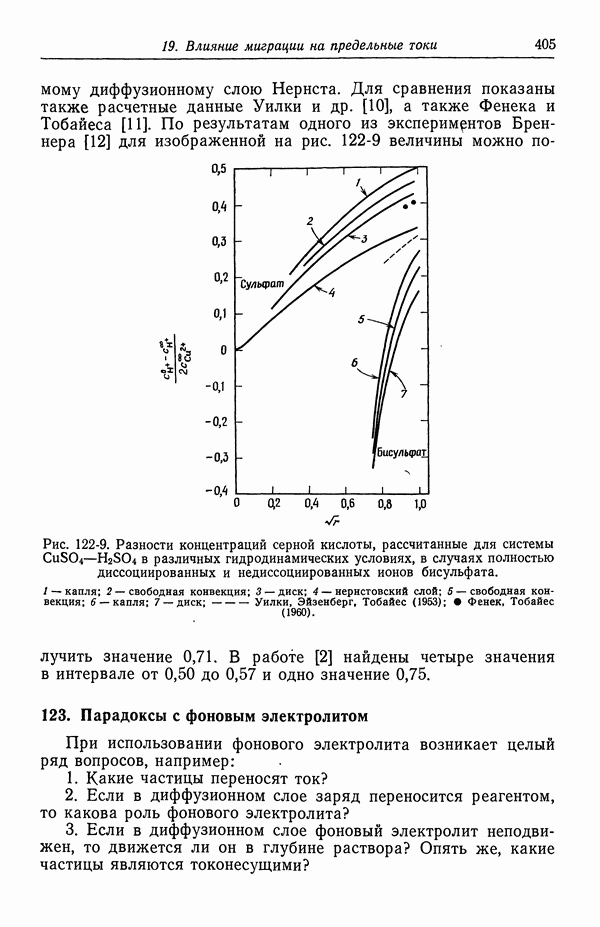
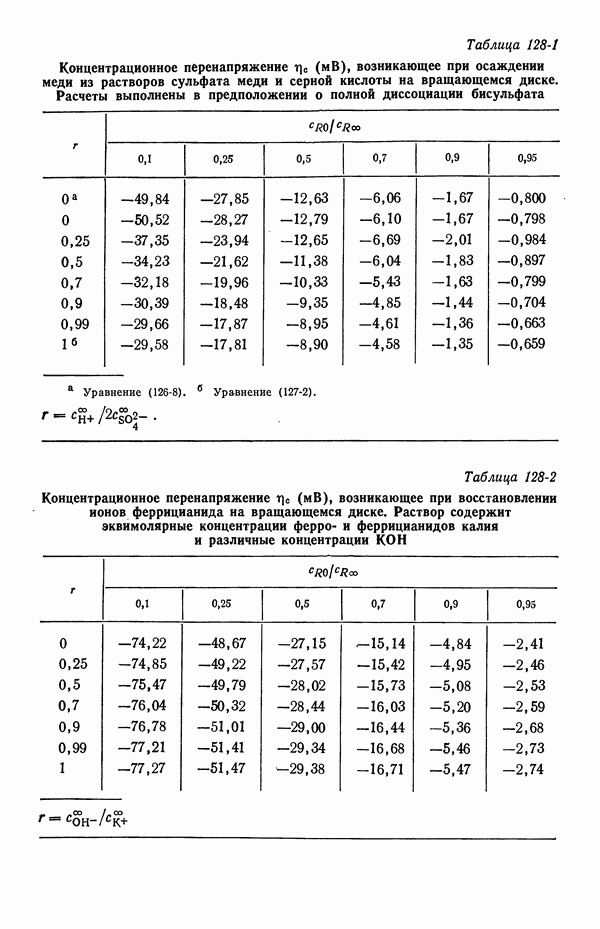
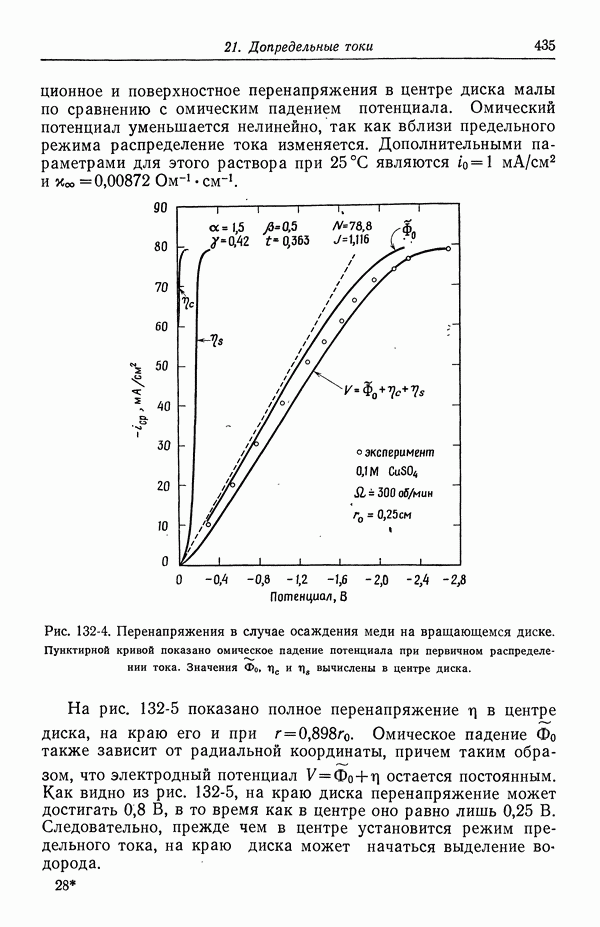
На рис. 122-9 показана широкая область разностей концентраций, допустимых в системе сульфат меди—серная кислота. Кроме того, на этом же рисунке приведены результаты по свободной конвекции из разд. 124, дополняющие данные по вращающемуся диску, растущей ртутной капле и неперемешиваемому
диффузионному слою Нернста. Для сравнения показаны также расчетные данные Уилки и др. [10], а также Фенека и Тобайеса [11]. По результатам одного из экспериментов Бреннера [12] для изображенной на рис. 122-9 величины можно получить значение 0,71.

Рис. 122-9. Разности концентраций серной кислоты, рассчитанные для системы  в различных гидродинамических условиях, в случаях полностью диссоциированных и недиссоциированных ионов бисульфата.
в различных гидродинамических условиях, в случаях полностью диссоциированных и недиссоциированных ионов бисульфата.  капля; 2— свободная конвекция; 3 — диск; 4 — нернстовский слой; 5-свободная конвекция; 6 — капля; 7 - диск;
капля; 2— свободная конвекция; 3 — диск; 4 — нернстовский слой; 5-свободная конвекция; 6 — капля; 7 - диск;  Уилки, Эйзенберг, Тобайес (1953); Фенек, Тобайес
Уилки, Эйзенберг, Тобайес (1953); Фенек, Тобайес 
В работе [2] найдены четыре значения в интервале от 0,50 до 0,57 и одно значение 0,75.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
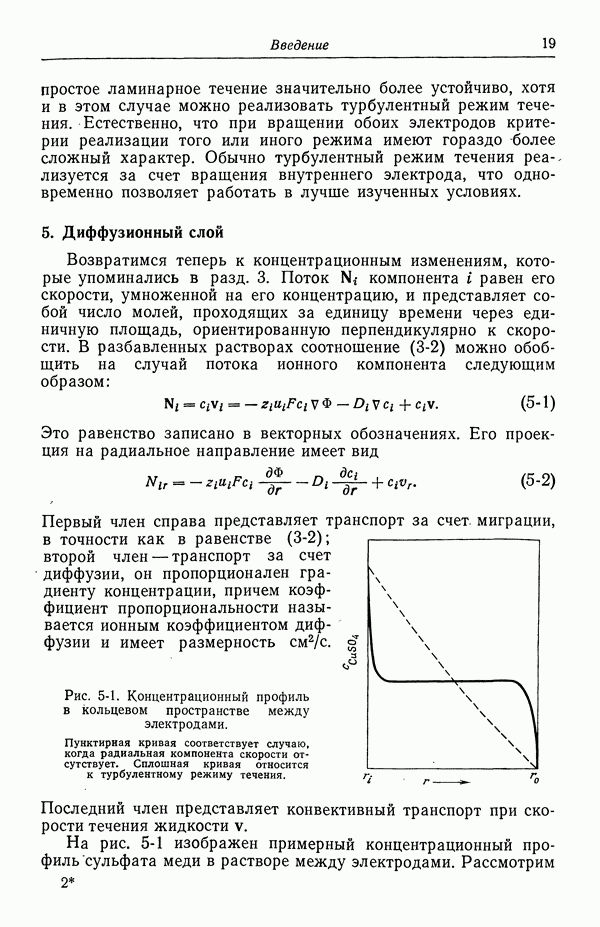
- 5. Диффузионный слой
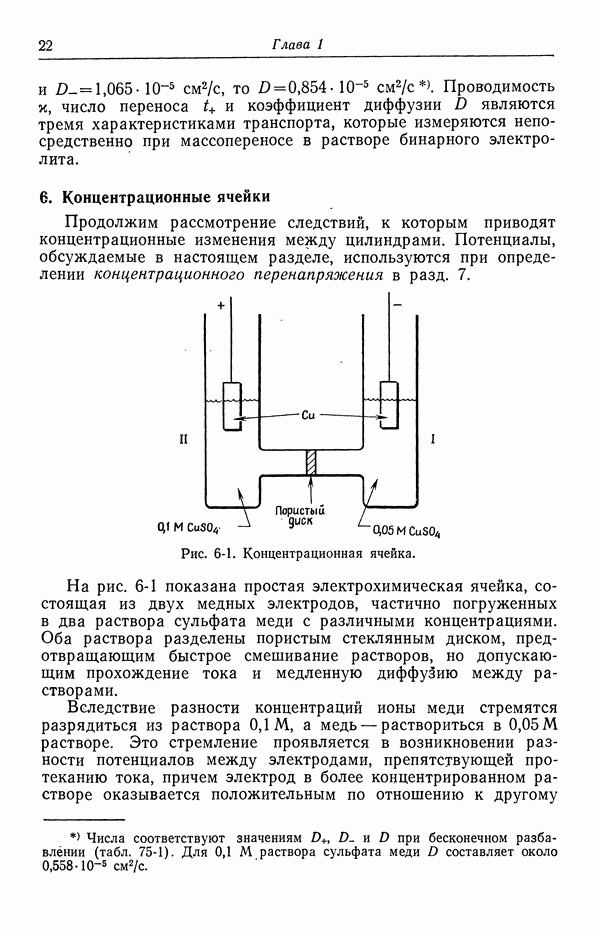
- 6. Концентрационные ячейки
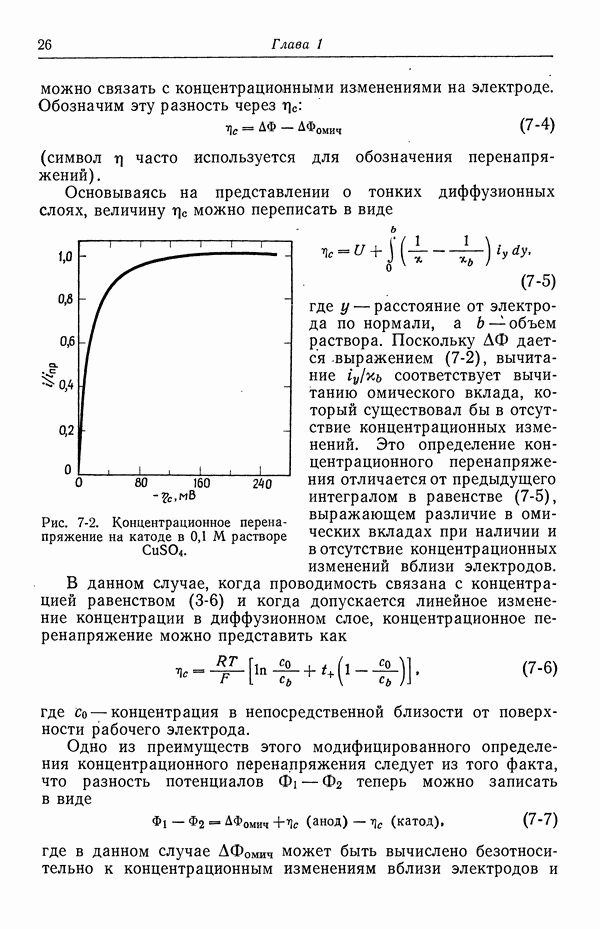
- 7. Концентрационное перенапряжение
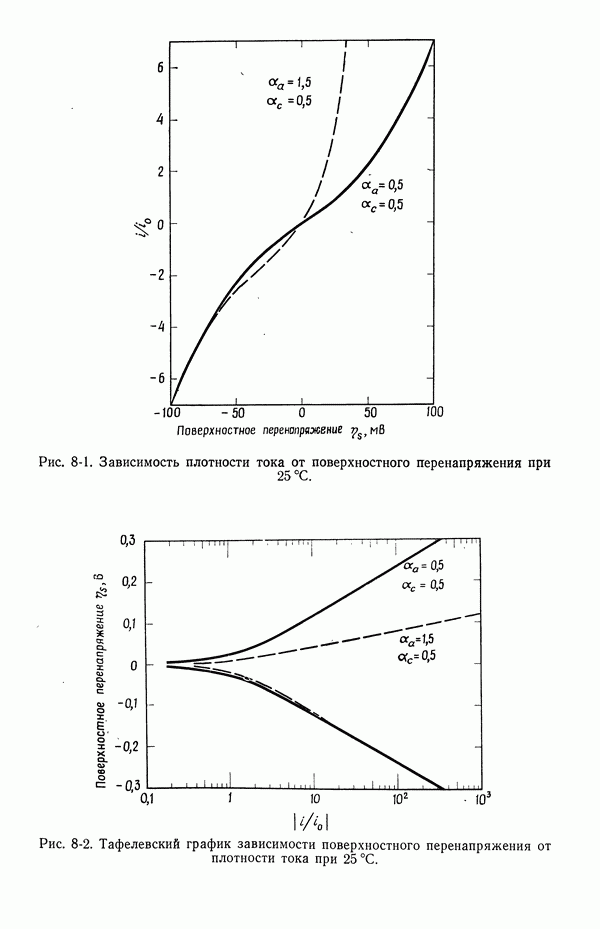
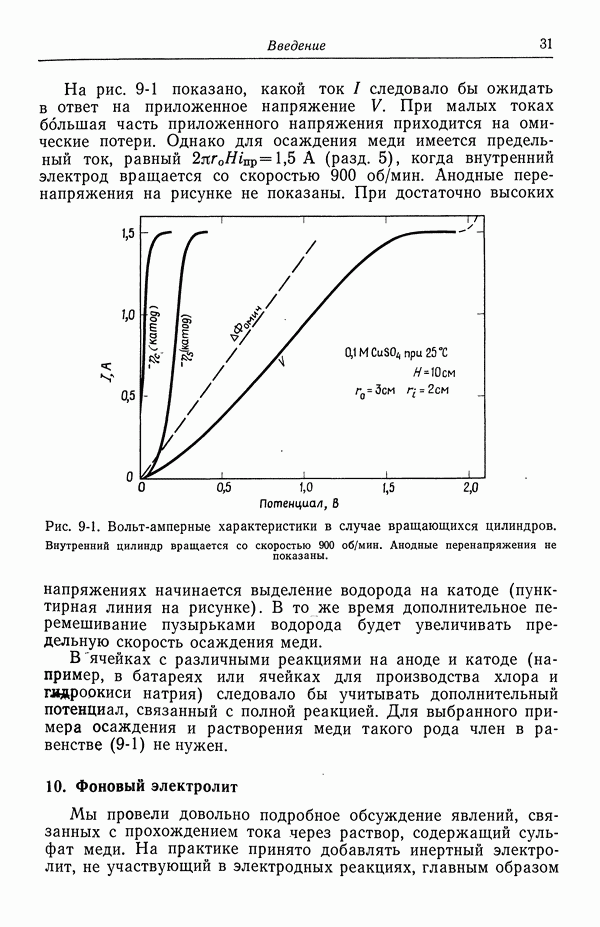
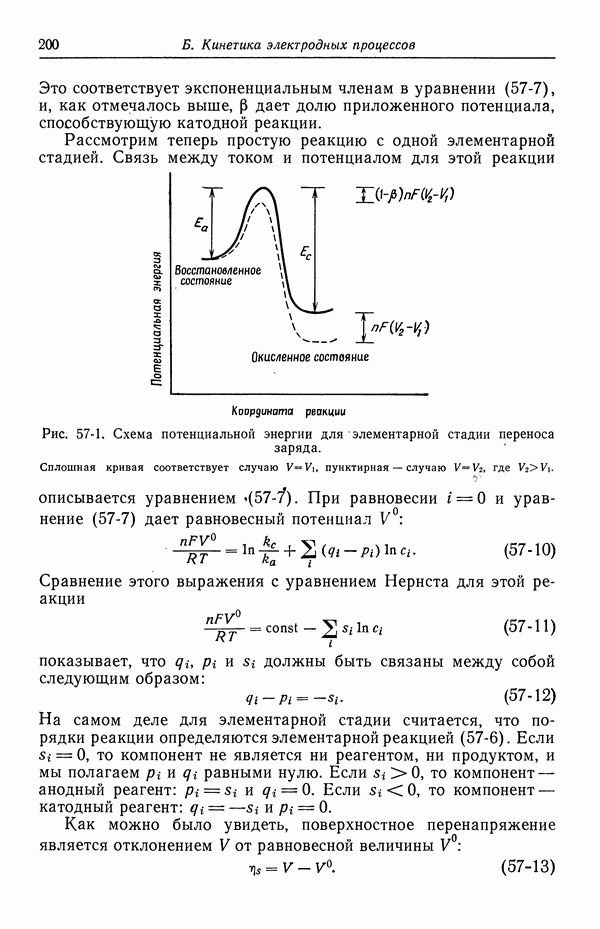
- 8. Поверхностное перенапряжение
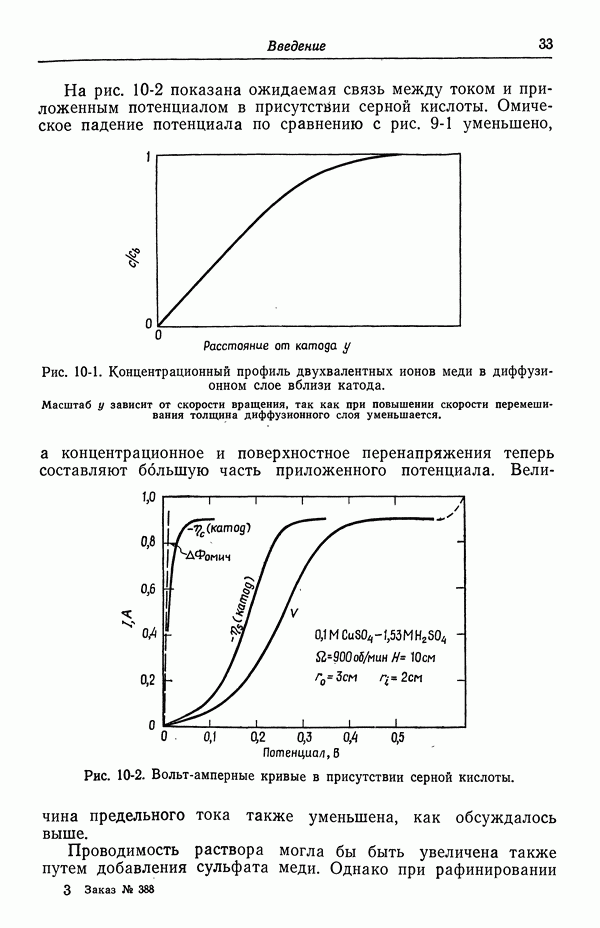
- 9. Потенциал ячейки
- 10. Фоновый электролит
- 11. Свободная конвекция
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
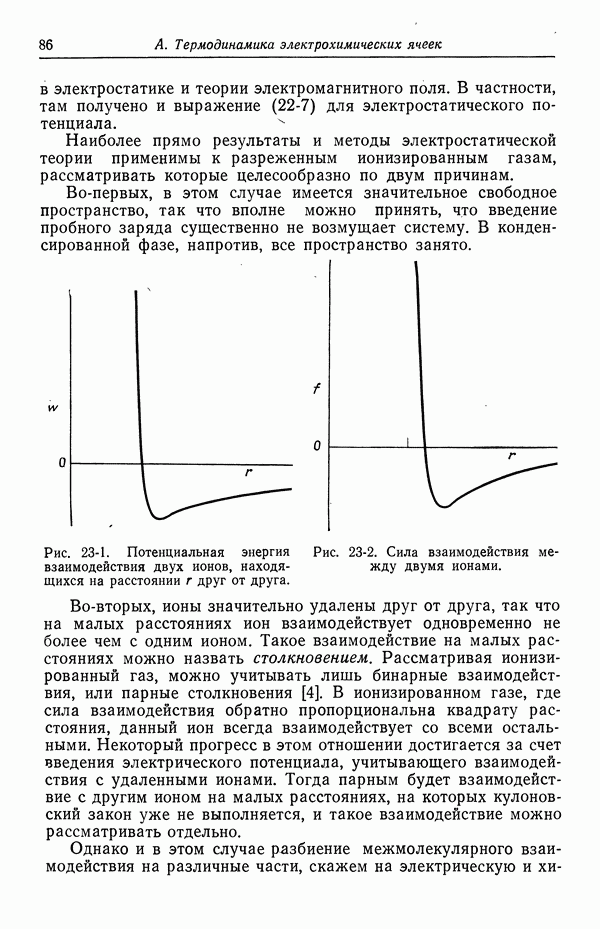
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
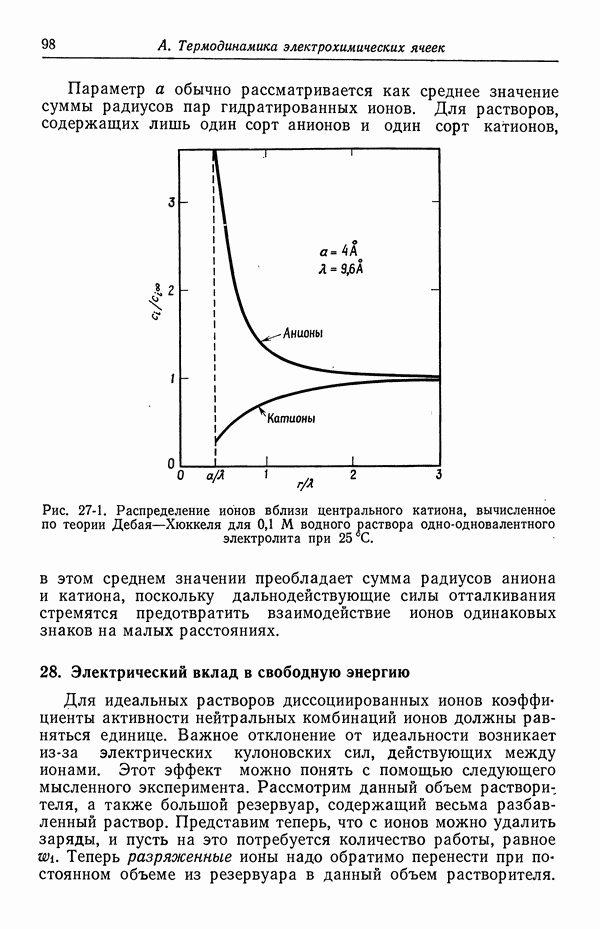
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая—Хюккеля
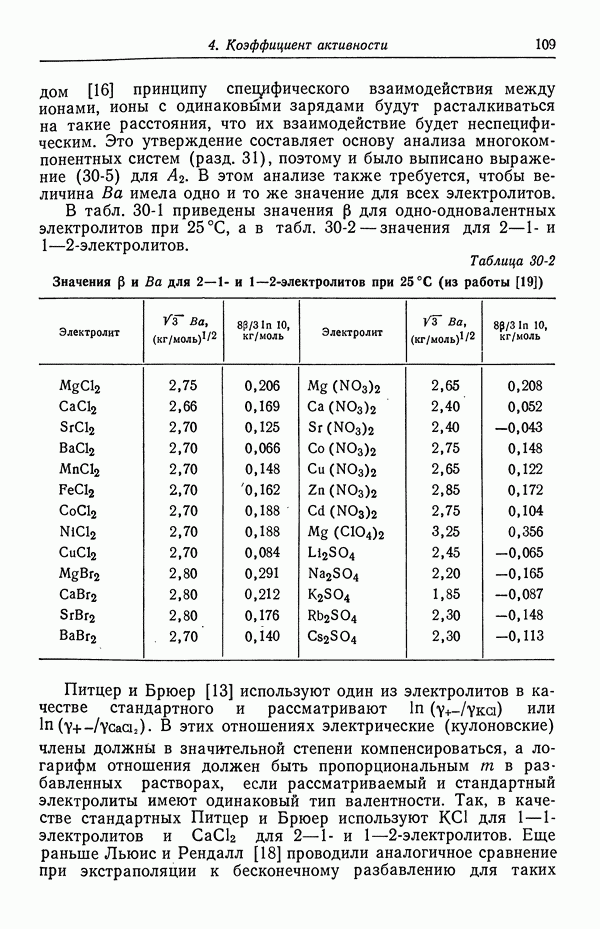
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
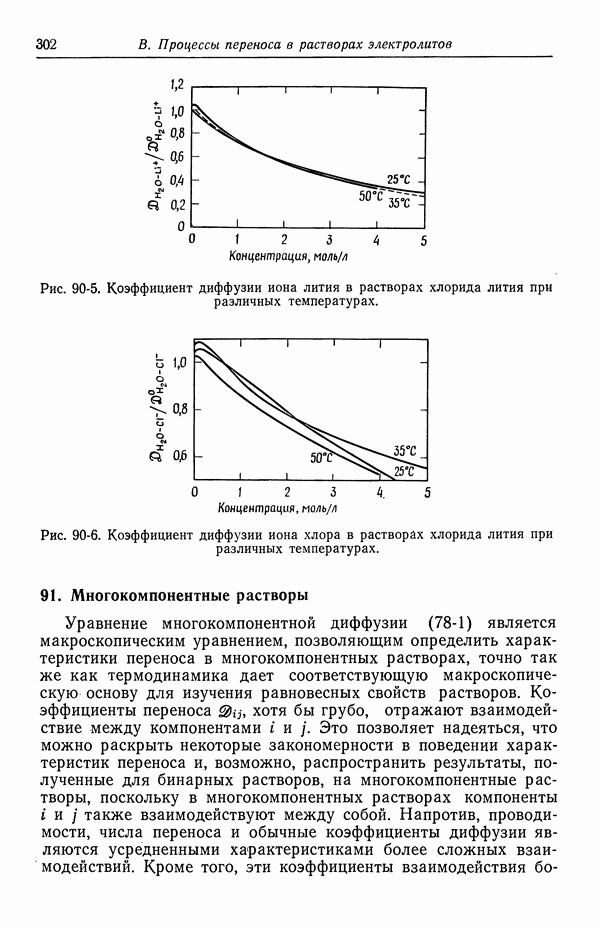
- 32. Измерение коэффициентов активности
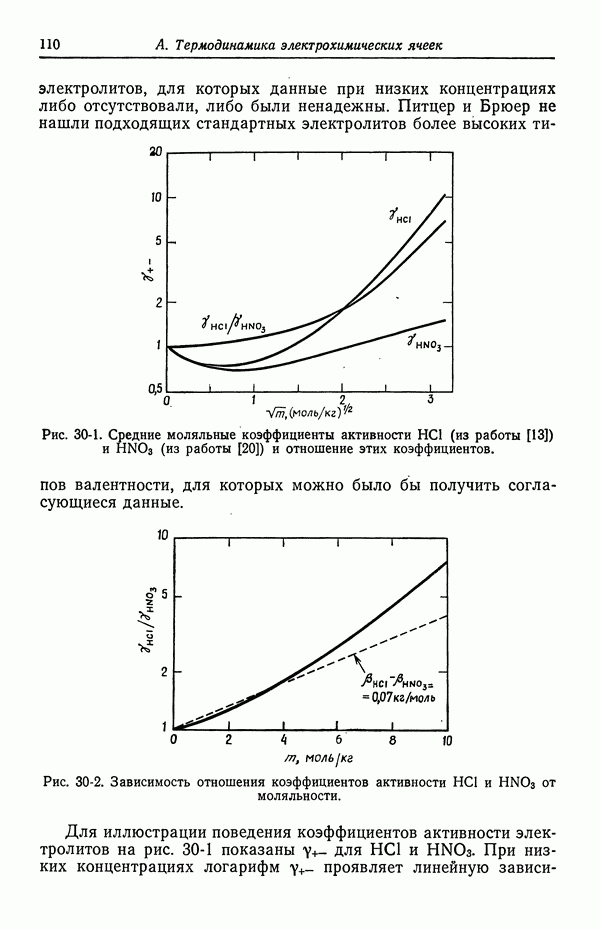
- 33. Слабые электролиты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
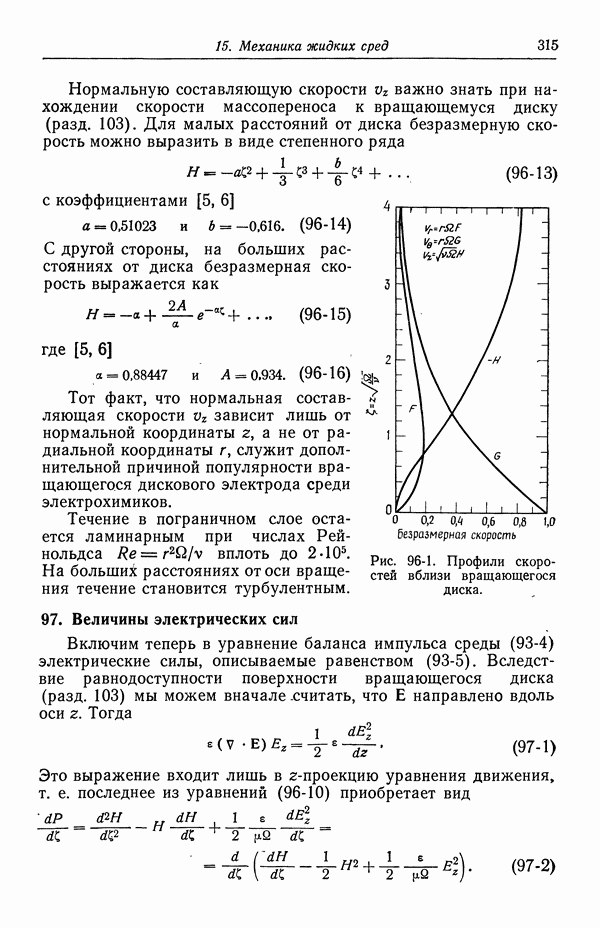
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
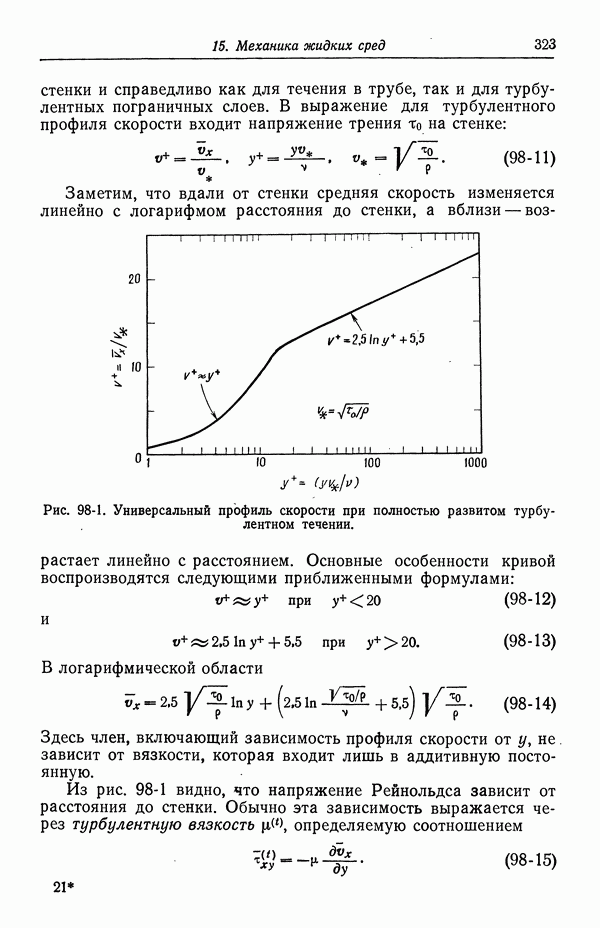
- 36. Водородный электрод
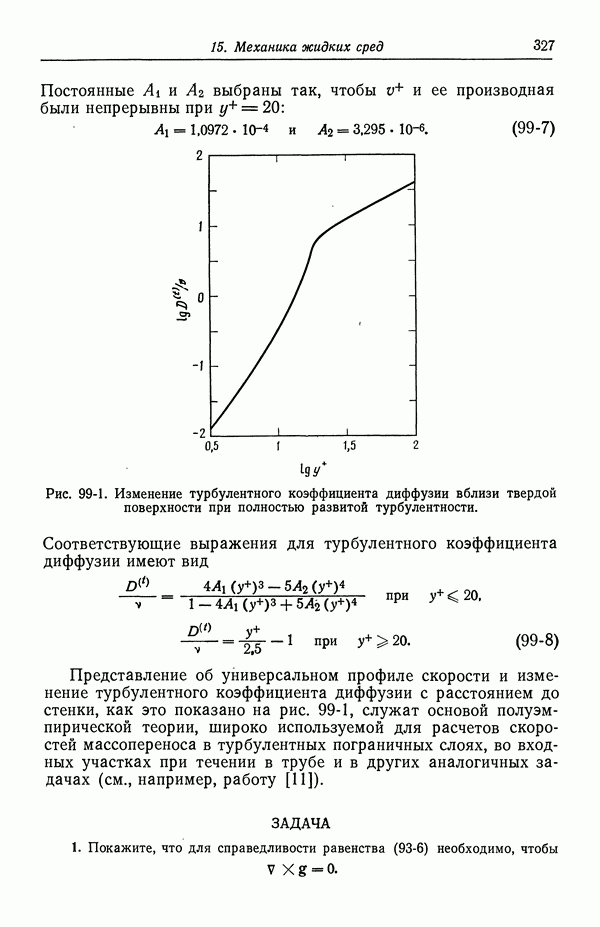
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
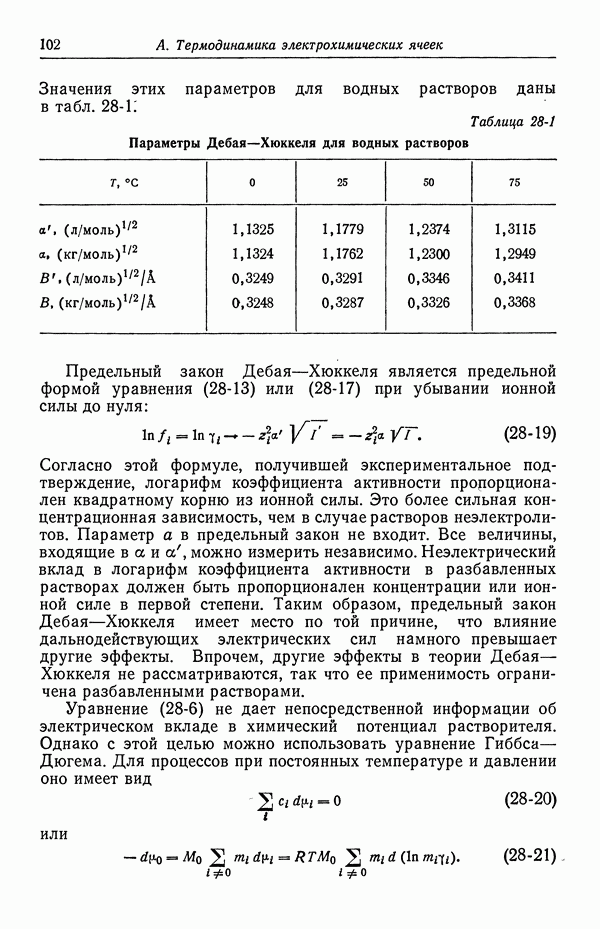
- 40. Потенциалы относительно данного электрода сравнения
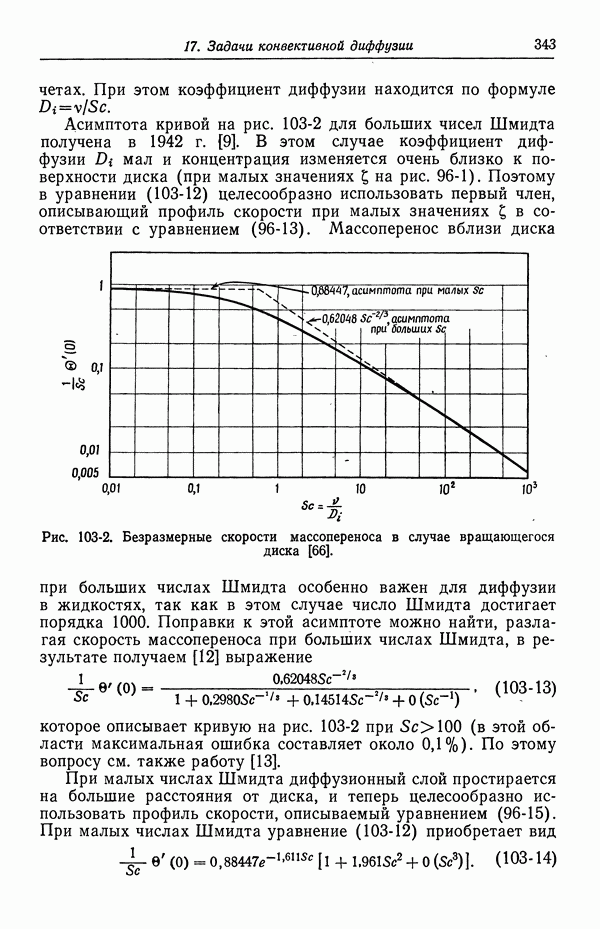
- СПИСОК ОБОЗНАЧЕНИЙ
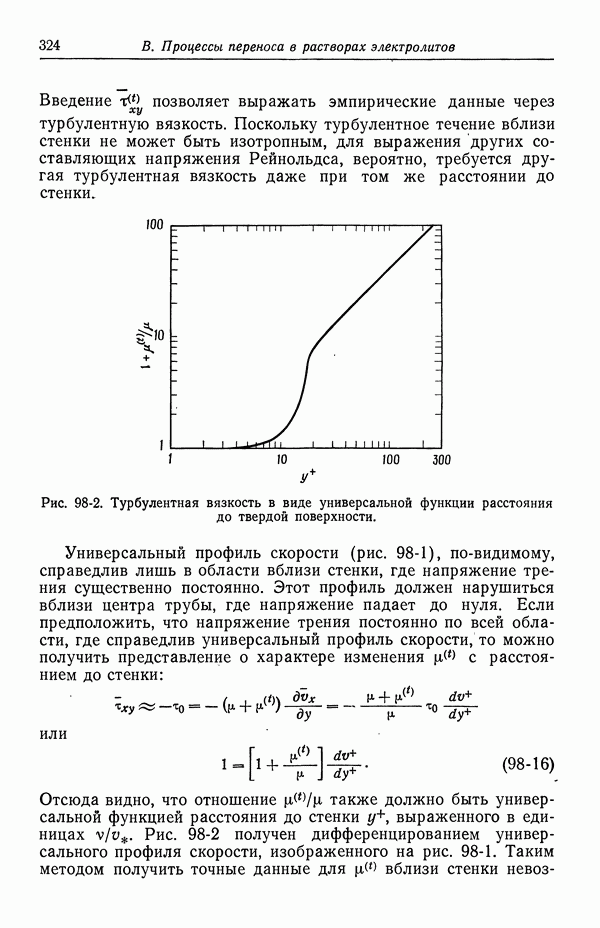
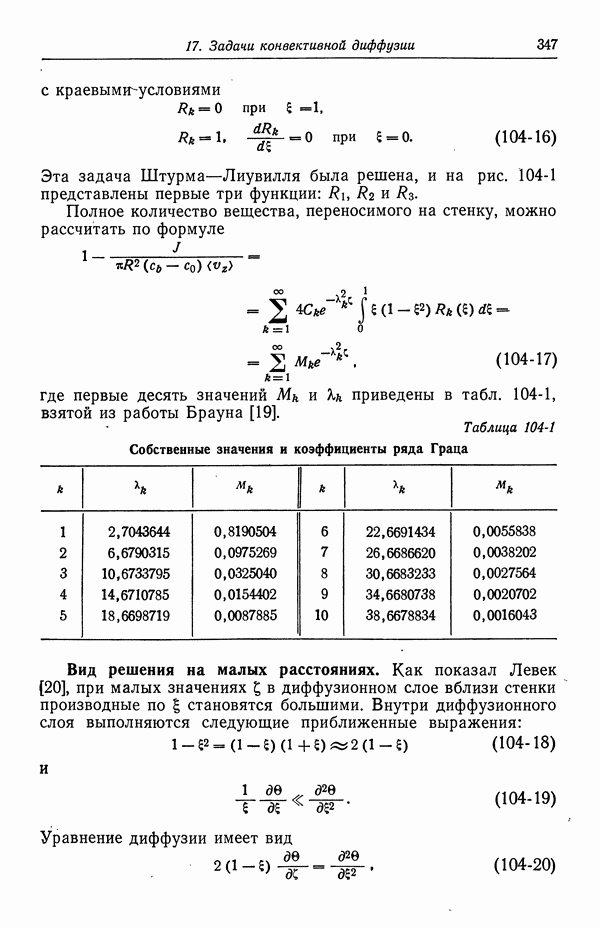
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
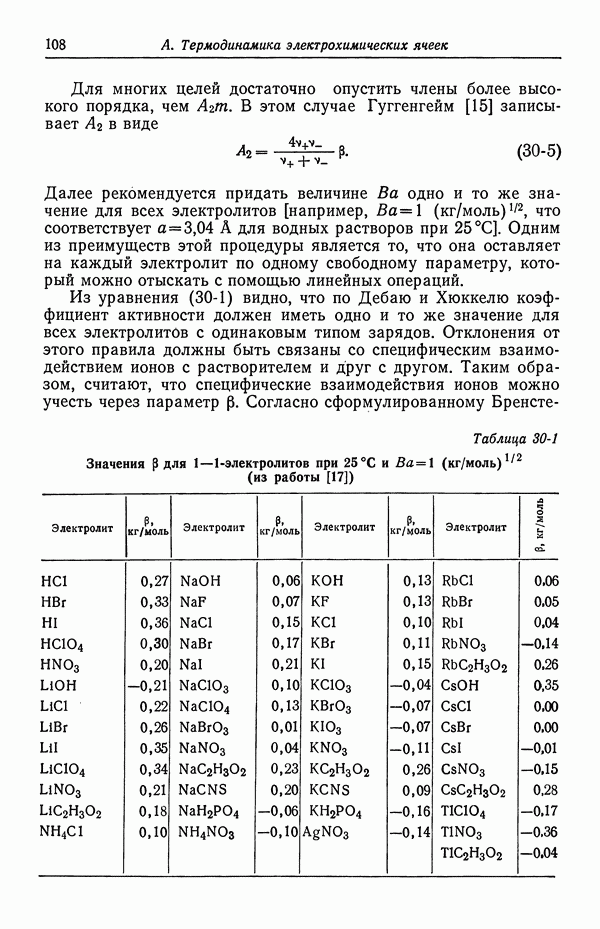
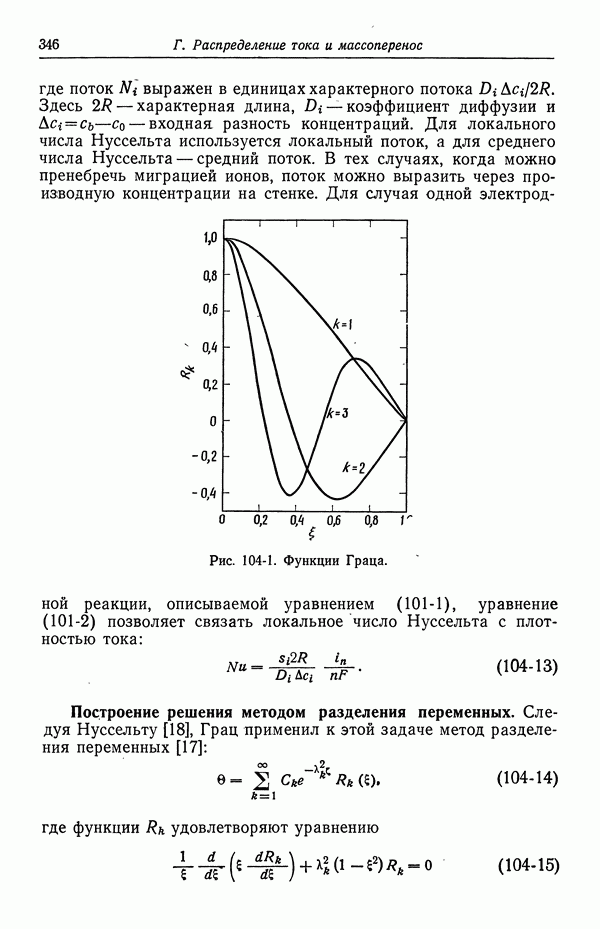
- 44. Определение концентрационных профилей
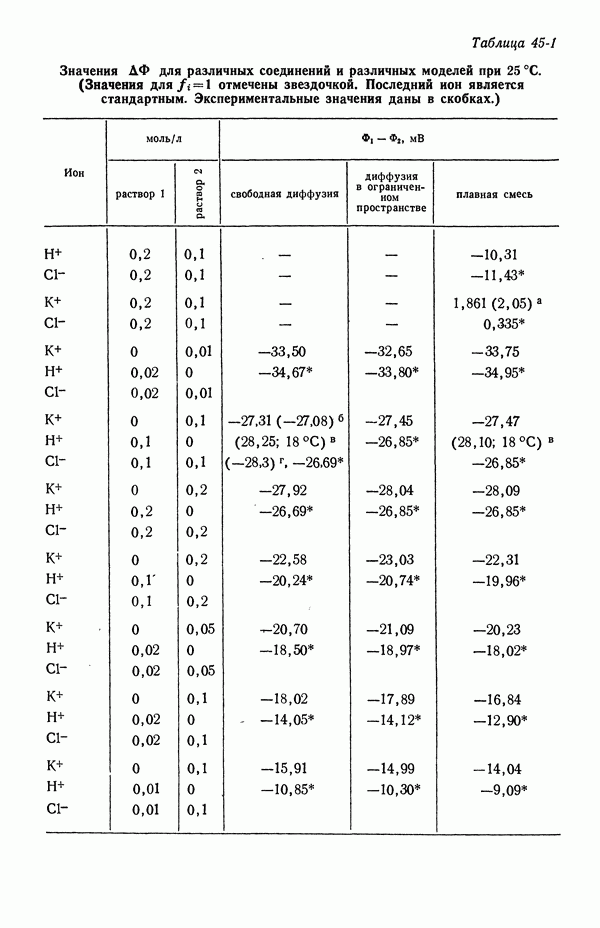
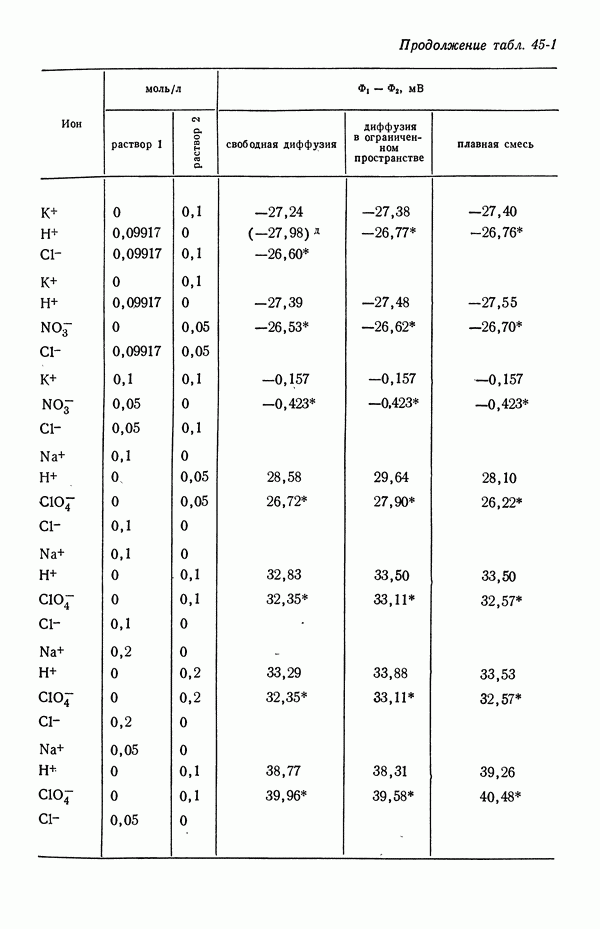
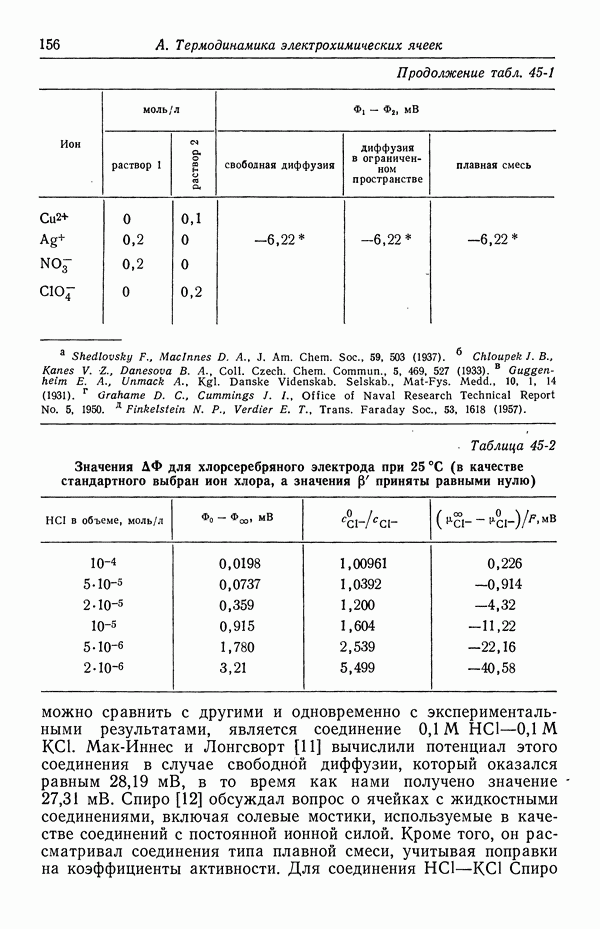
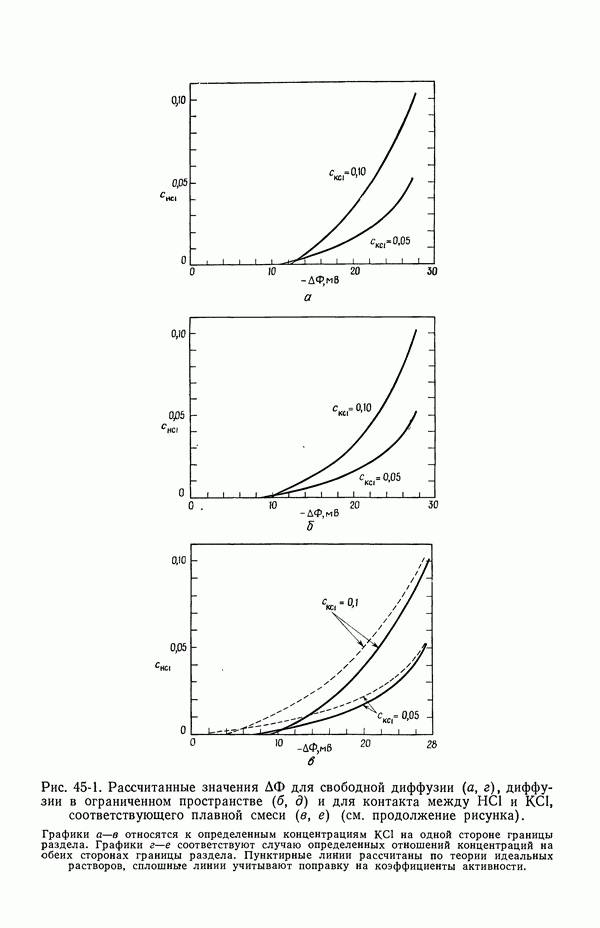
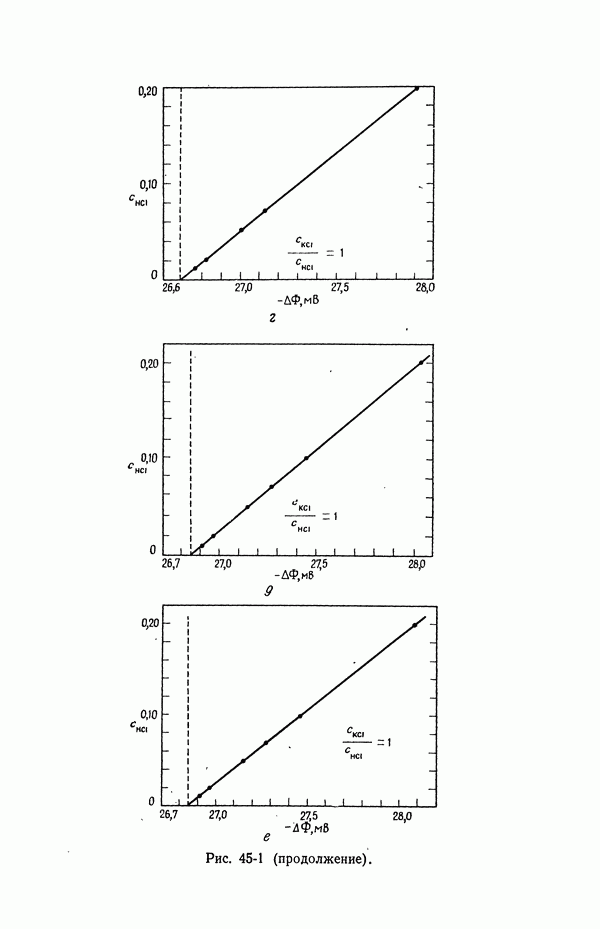
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
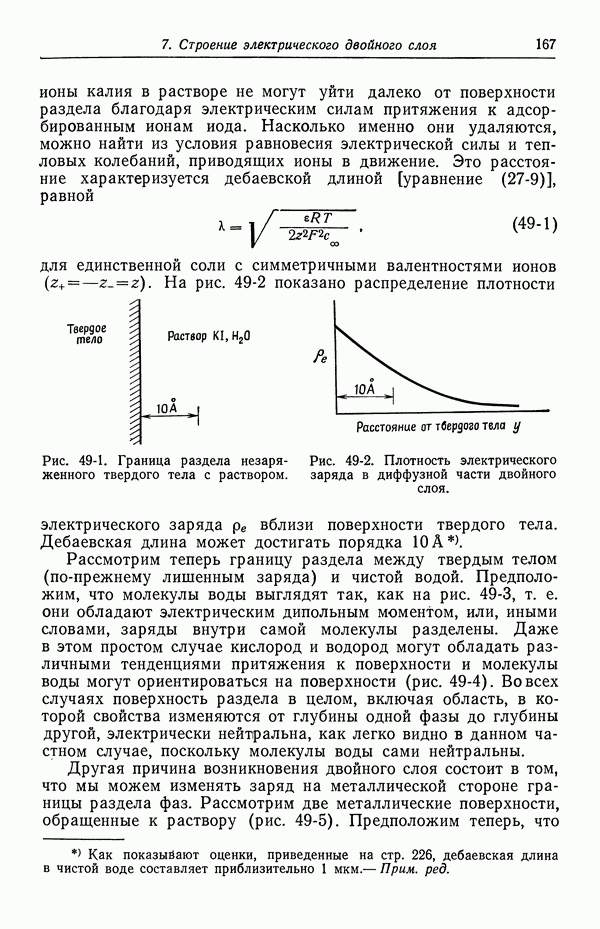
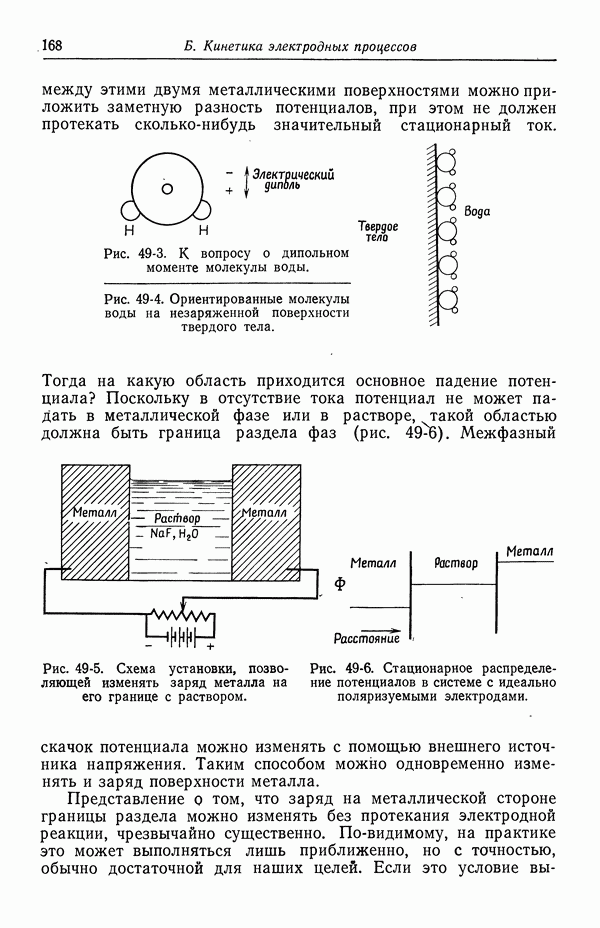
- 49. Качественное описание двойных слоев
- 50. Изотерма адсорбции Гиббса
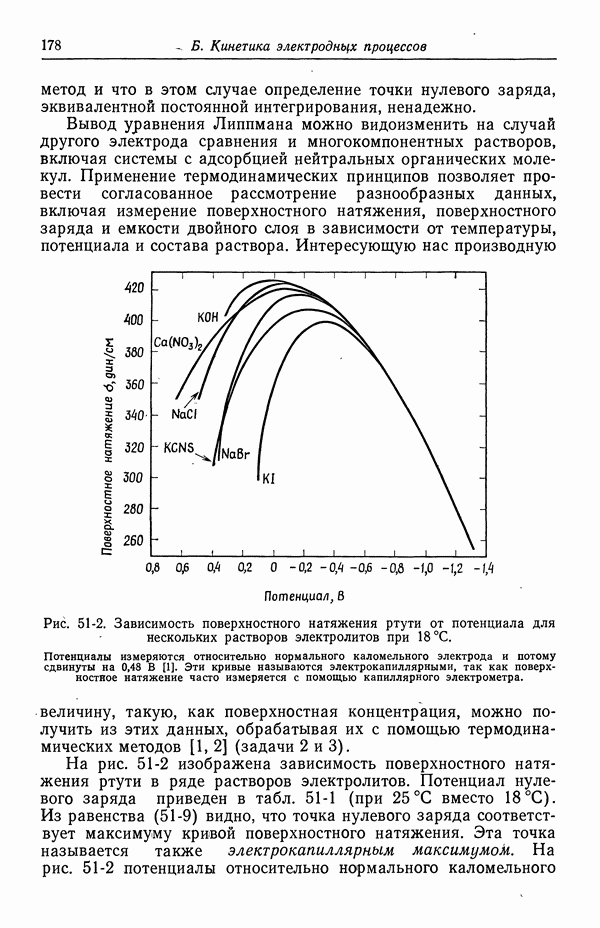
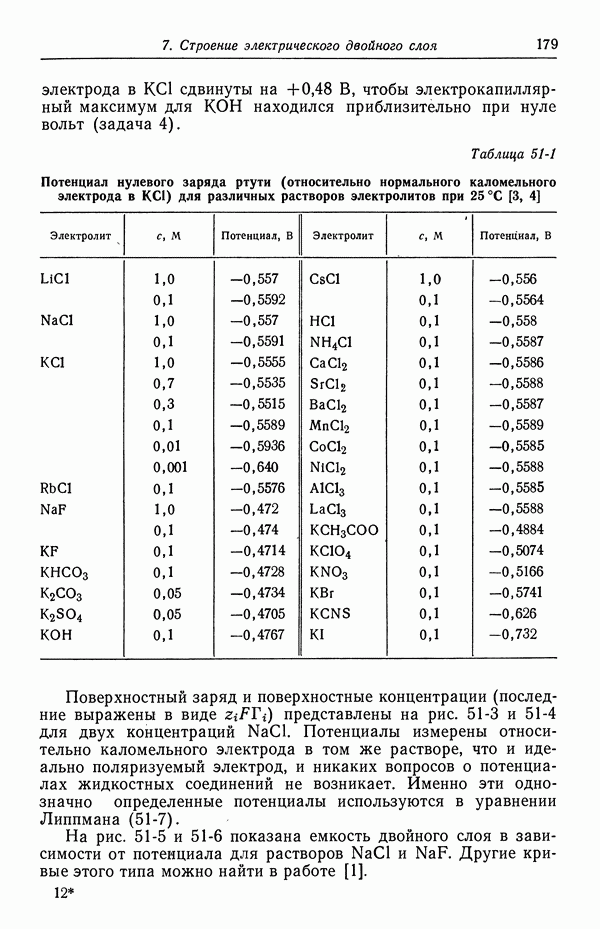
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
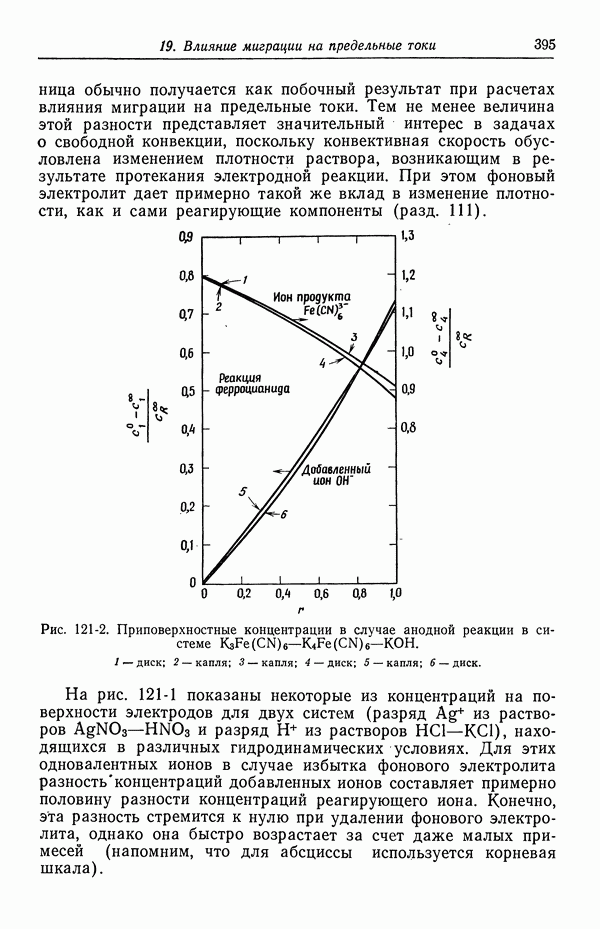
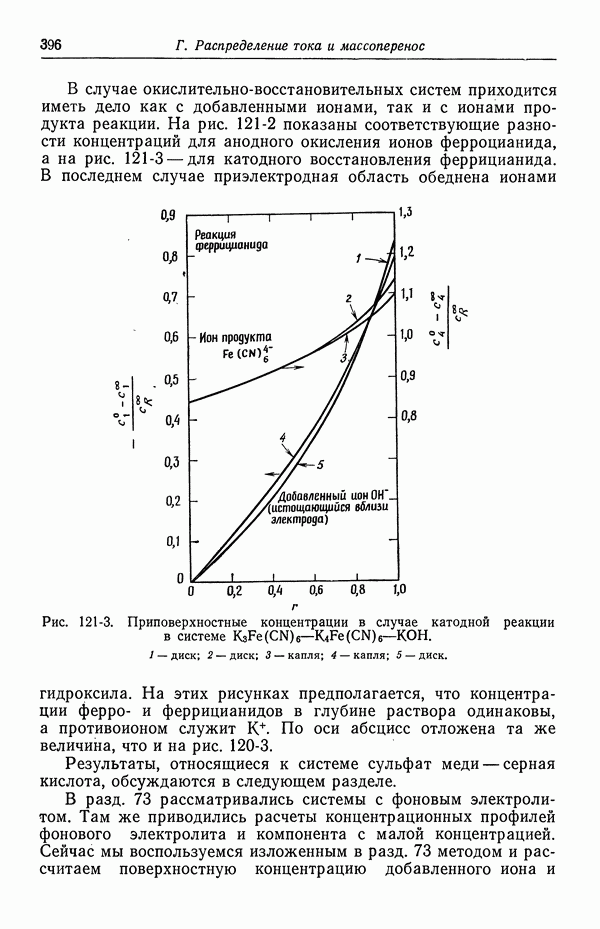
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод — раствор
- ЗАДАЧИ
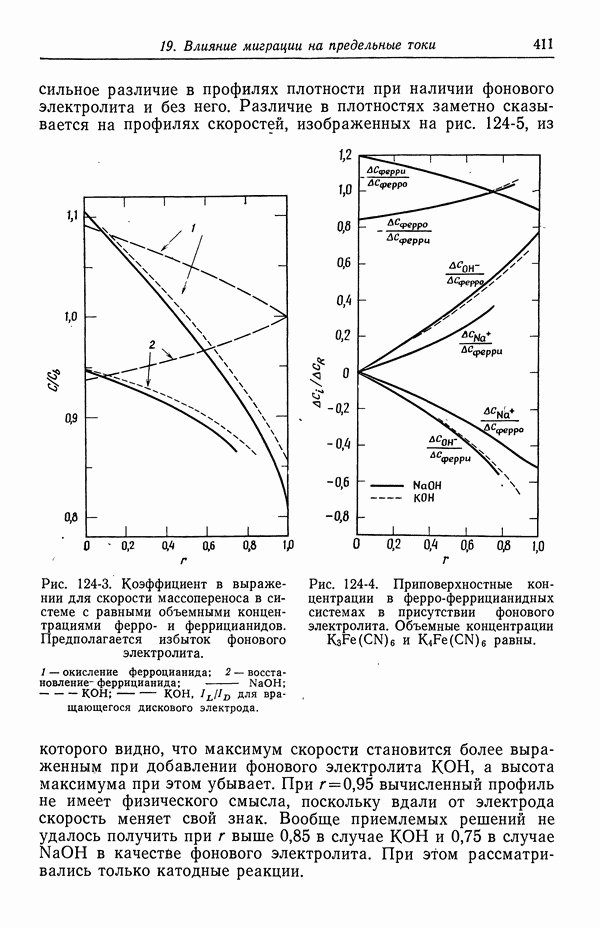
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
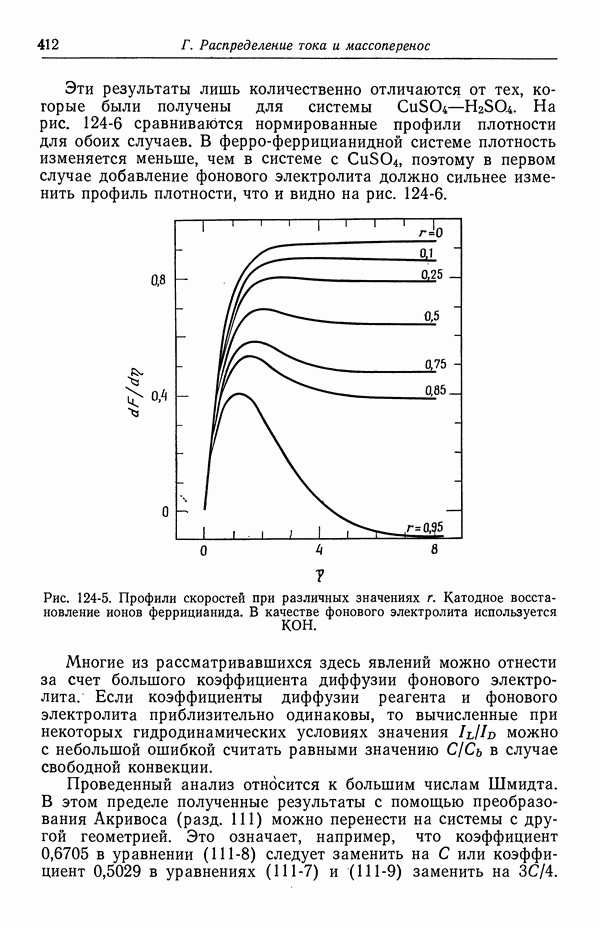
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
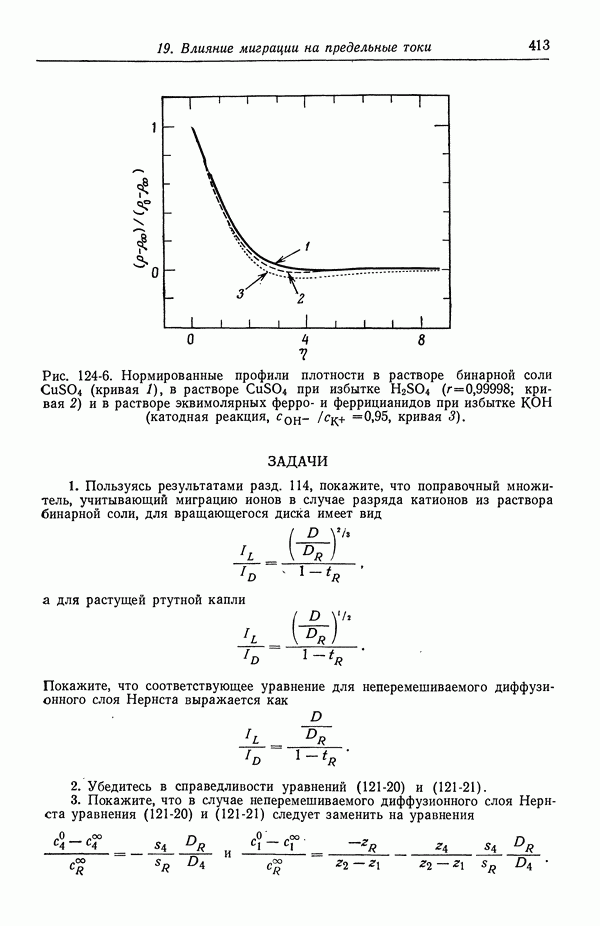
- 60. Методы измерения
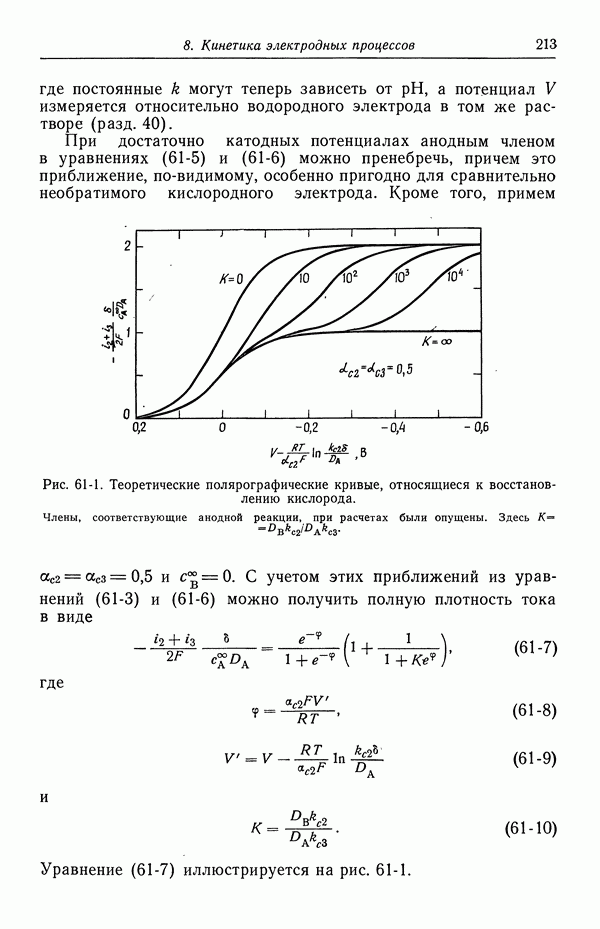
- 61. Одновременно протекающие реакции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
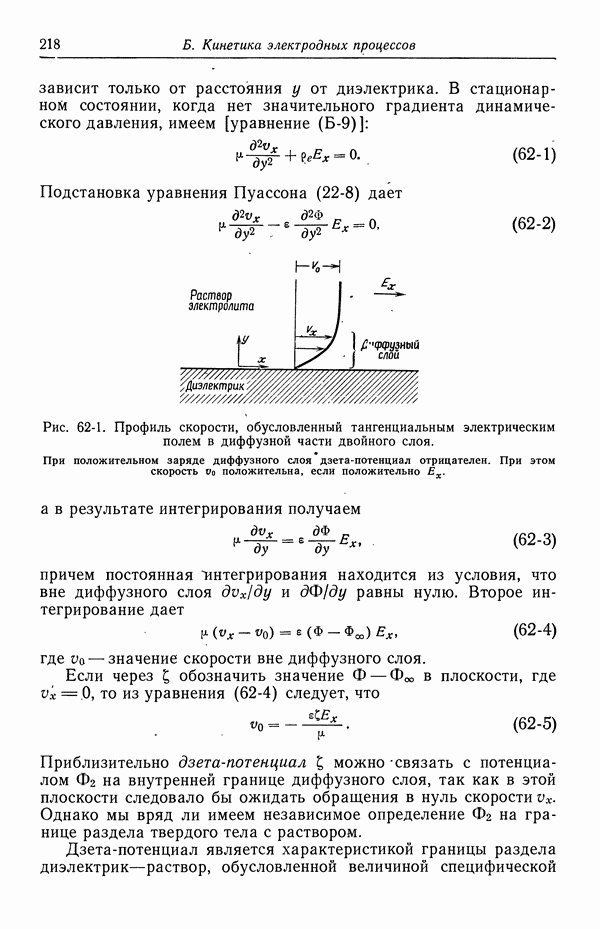
- 62. Разрывная скорость на границе раздела
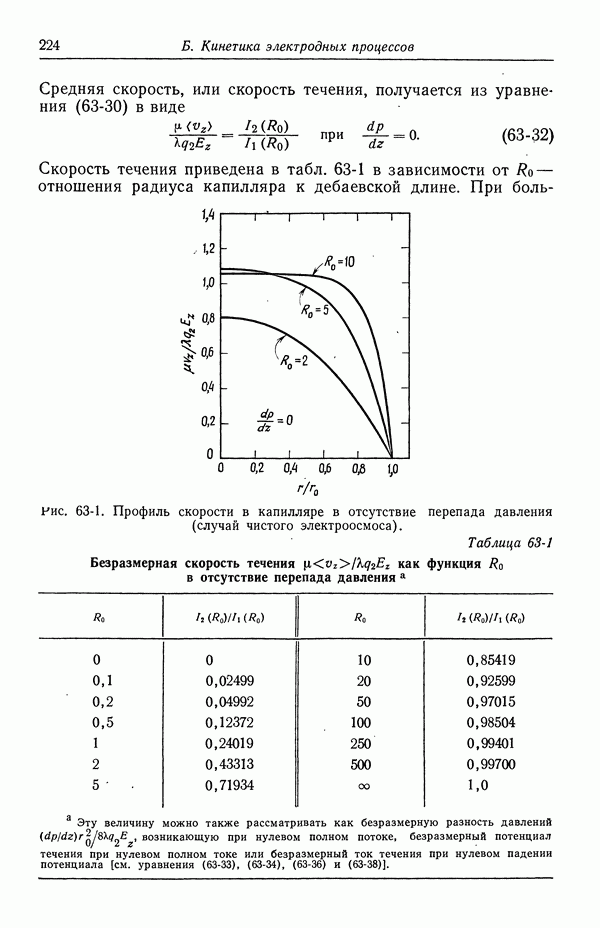
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 66. Динамика границы раздела
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 69. Законы переноса
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 78. Законы переноса
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 92. Интегральные коэффициенты диффузии
- ЗАДАЧА
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- СПИСОК ОБОЗНАЧЕНИЙ
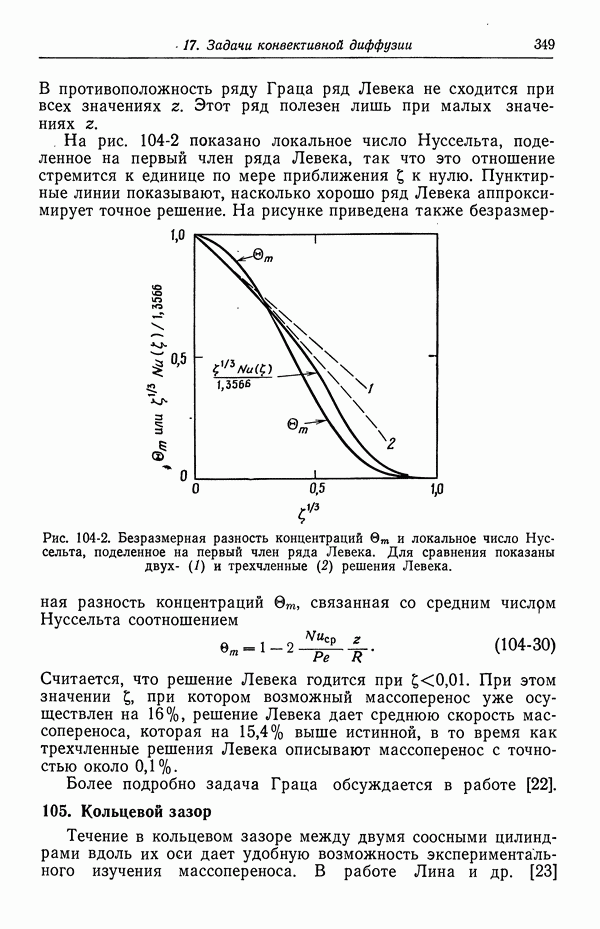
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
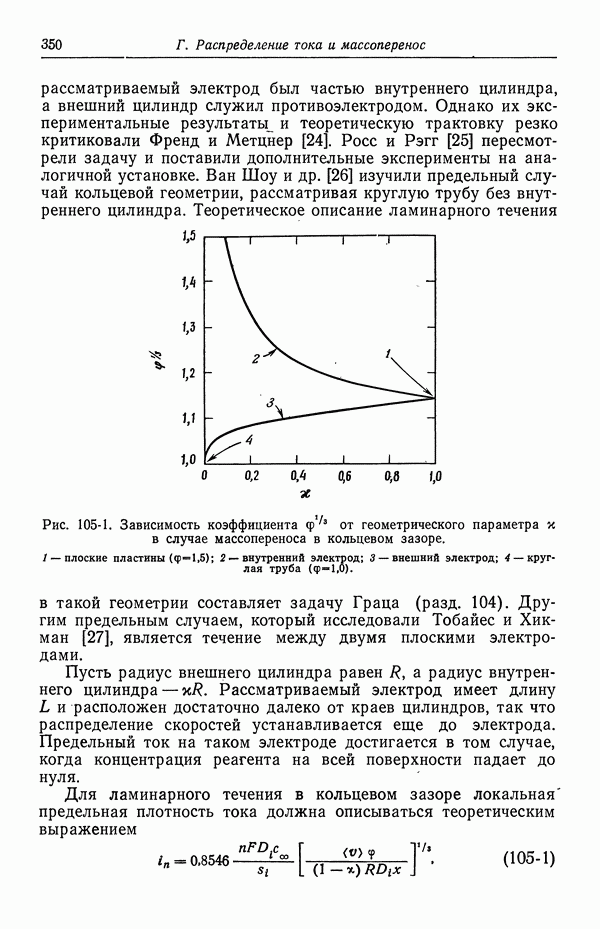
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 111. Свободная конвекция
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
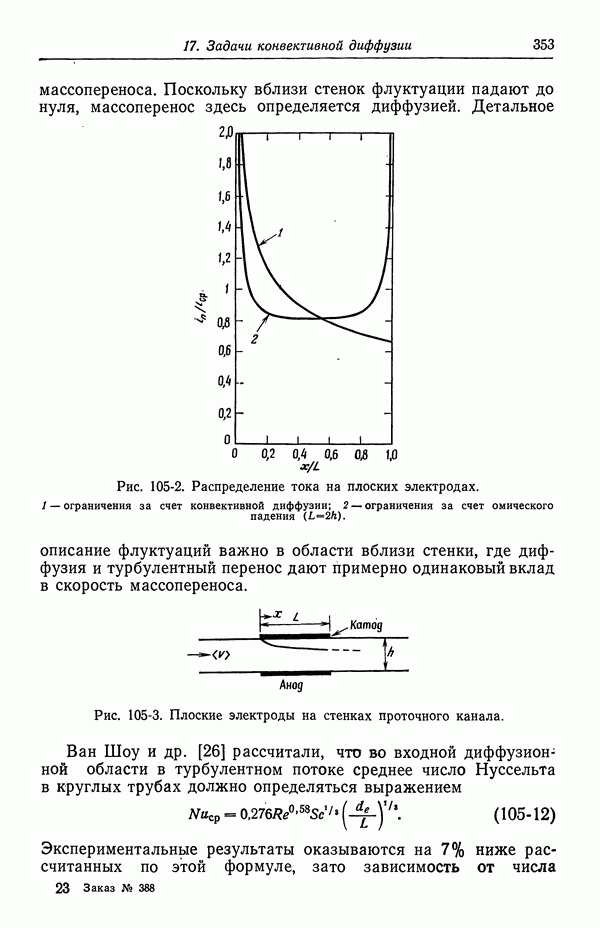
- 114. Бинарные и концентрированные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
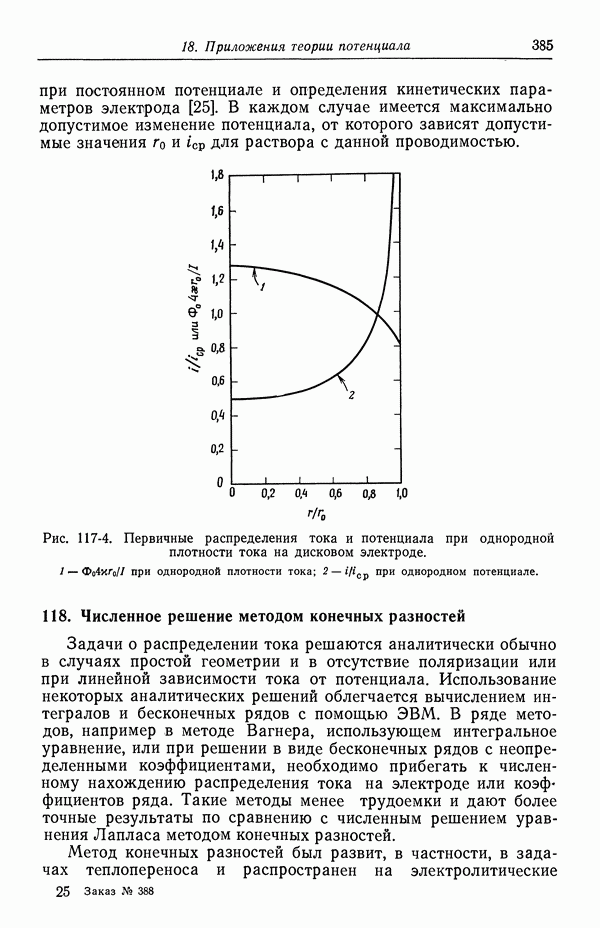
- 116. Первичное распределение тока
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- СПИСОК ОБОЗНАЧЕНИЙ
- ГЛАВА 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 119. Решение задачи
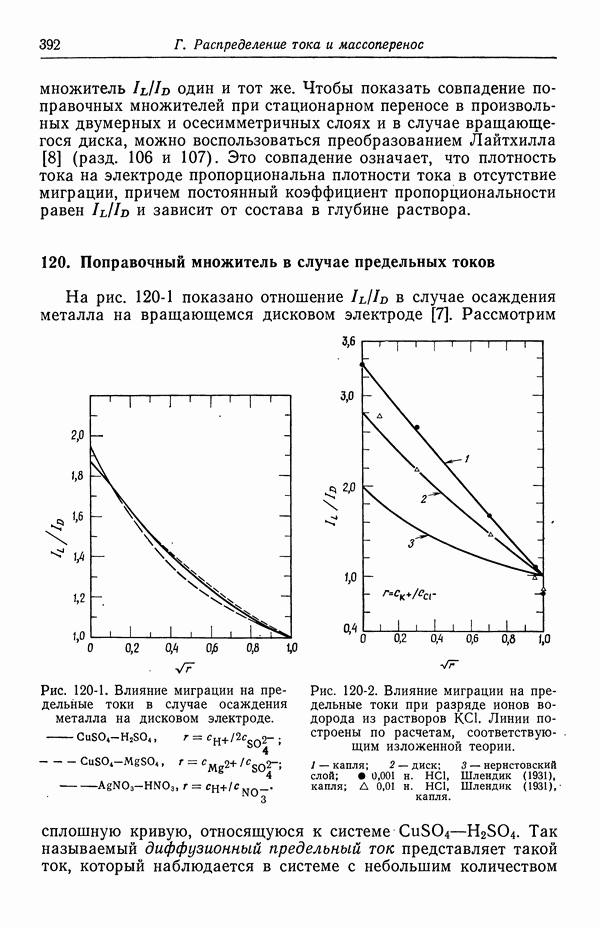
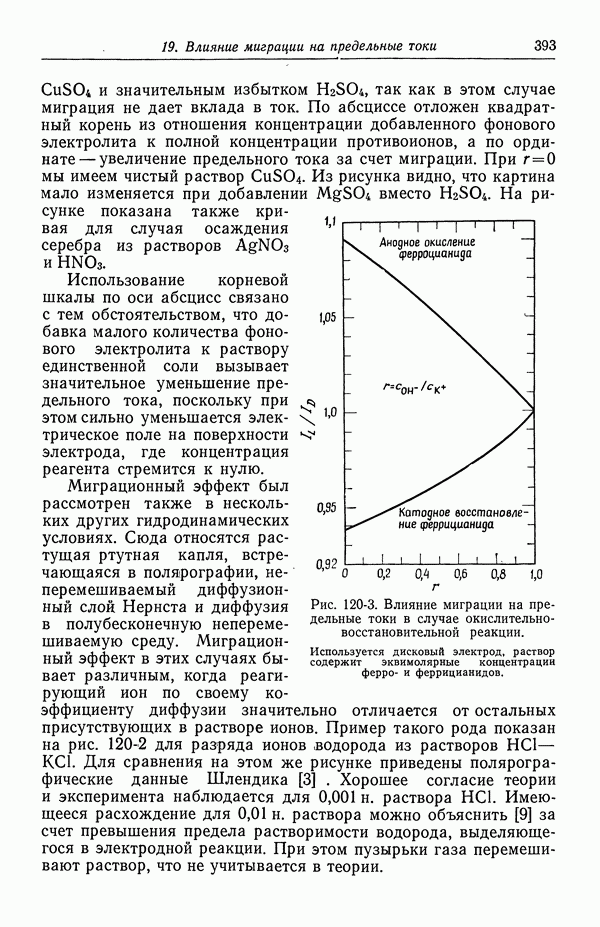
- 120. Поправочный множитель в случае предельных токов
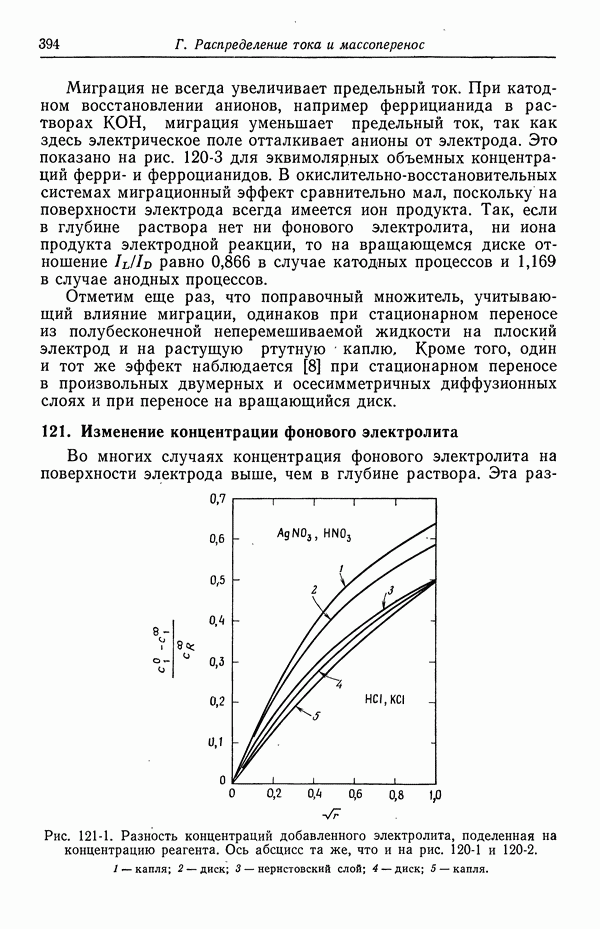
- 121. Изменение концентрации фонового электролита
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ