| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
29. Недостатки модели Дебая—Хюккеля
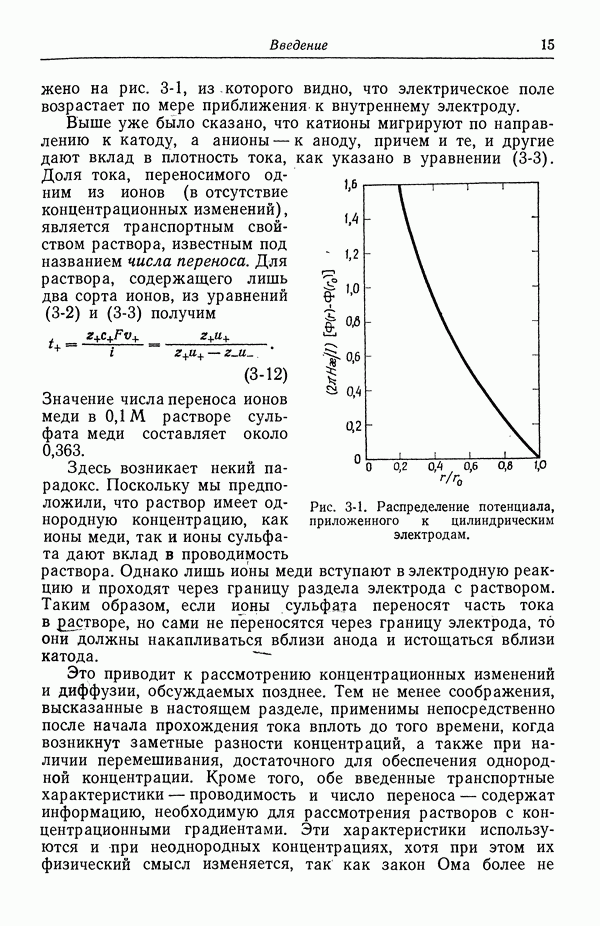
Выражение Дебая—Хюккеля для коэффициентов активности ионных растворов пригодно лишь для разбавленных растворов. Такую ограниченность области применимости можно было бы объяснить неучтенными факторами, которые важны даже для растворов неэлектролитов, допущением о малости потенциала содержащимся в равенстве (27-7), а также неясностью вопроса о правомерности модели с точки зрения статистической механики.
В теории Дебая—Хюккеля рассматривается лишь кулоновское взаимодействие между ионами. Даже при таком узком подходе физическим свойствам типа диэлектрической проницаемости приписываются значения, свойственные чистому растворителю. При более высоких концентрациях становятся важными взаимодействия между ионами и растворителем, а также силы межионного короткодействия. Нельзя также пренебрегать процессами сольватации и ассоциации. Эти эффекты дают вклад в коэффициент активности, пропорциональный концентрации
растворенного вещества даже в растворах неэлектролитов. Следовательно, при концентрациях, при которых такие члены сравнимы с корневым, теория Дебая—Хюккеля не может больше адекватно описывать термодинамические свойства. Выделение электрических вкладов не приносит особой пользы, если только не учитываются эти некулоновские взаимодействия.
Единственное существенное математическое приближение, введенное Дебаем и Хюккелем, содержится в равенстве (27-7). Его пригодность зависит от малости величины  по сравнению с единицей, а это означает, что величина
по сравнению с единицей, а это означает, что величина  должна быть небольшой. Однако для одно-одновалентного электролита в воде это отношение больше единицы, а для электролитов более высоких валентностей и других растворителей положение еще хуже. Кроме того, это отношение не зависит от концентрации, и заранее неочевидно, что такая аппроксимация не вносит ошибки в предельный закон Дебая—Хюккеля.
должна быть небольшой. Однако для одно-одновалентного электролита в воде это отношение больше единицы, а для электролитов более высоких валентностей и других растворителей положение еще хуже. Кроме того, это отношение не зависит от концентрации, и заранее неочевидно, что такая аппроксимация не вносит ошибки в предельный закон Дебая—Хюккеля.
К счастью, предельный закон Дебая—Хюккеля можно обосновать, рассматривая задачу по методу возмущений. В уравнение (28-2) или (28-10) входит потенциал, создаваемый ионным облаком при  Для сильноразбавленных растворов дебаевская длина становится очень большой. Это означает, что большинство ионов, образующих ионное облако, находится от центрального иона на значительном расстоянии, где потенциал, созданный центральным ионом, мал и, следовательно, приближение (27-7) справедливо. Таким образом, для распределения концентрации в области, где находится большая часть заряда облака, получается правильное приближение; это в свою очередь приводит к точному значению потенциала ионного облака при
Для сильноразбавленных растворов дебаевская длина становится очень большой. Это означает, что большинство ионов, образующих ионное облако, находится от центрального иона на значительном расстоянии, где потенциал, созданный центральным ионом, мал и, следовательно, приближение (27-7) справедливо. Таким образом, для распределения концентрации в области, где находится большая часть заряда облака, получается правильное приближение; это в свою очередь приводит к точному значению потенциала ионного облака при  Такой результат получается несмотря на то, что вблизи центрального иона всегда имеется область, где приближение (27-7) не выполняется.
Такой результат получается несмотря на то, что вблизи центрального иона всегда имеется область, где приближение (27-7) не выполняется.
Интересно заметить, что, хотя параметр а и не появляется в предельном законе Дебая—Хюккеля, при нулевом значении а невозможно найти решение нелинейной задачи, за исключением решения в виде ионного облака, сосредоточенного в начале координат.
Уравнение (27-3) известно под названием уравнения Пуассона—Больцмана, и для его решения без приближения (27-7) Дебая—Хюккеля были затрачены большие усилия. Гронвелл
и др. [2], а также Ла Мер и др. [3] получили разложения в ряды при малых значениях параметра  Конечно, это не то же самое, что разложение в ряд при малых значениях концентрации. Позднее Гуггенгейм [4—7] сообщил результаты решения уравнения Пуассона—Больцмана на вычислительной машине. Он пришел к выводу, что разложения Гронвелла не дают заметного улучшения по сравнению с решением Дебая и Хюккеля для водных растворов одно-одновалентного электролита и что учтенные Гронвеллом члены недостаточны для описания электролитов более высоких валентностей. Гуггенгейм выражает некоторую надежду, что из точного решения уравнения Пуассона—Больцмана для больших валентностей можно получить заметные улучшения по сравнению с результатом Дебая и Хюккеля при низких концентрациях, где некулоновские эффекты еще незначительны.
Конечно, это не то же самое, что разложение в ряд при малых значениях концентрации. Позднее Гуггенгейм [4—7] сообщил результаты решения уравнения Пуассона—Больцмана на вычислительной машине. Он пришел к выводу, что разложения Гронвелла не дают заметного улучшения по сравнению с решением Дебая и Хюккеля для водных растворов одно-одновалентного электролита и что учтенные Гронвеллом члены недостаточны для описания электролитов более высоких валентностей. Гуггенгейм выражает некоторую надежду, что из точного решения уравнения Пуассона—Больцмана для больших валентностей можно получить заметные улучшения по сравнению с результатом Дебая и Хюккеля при низких концентрациях, где некулоновские эффекты еще незначительны.
Наконец, следует отметить, что теория Дебая—Хюккеля не является результатом непосредственного применения принципов статистической механики. Можно даже удивляться, что процесс заряжения дает правильное значение электрического вклада в свободную энергию Гельмгольца. Впервые непоследовательность модели Дебая—Хюккеля проявилась, когда уточненные расчеты, согласно процессам заряжения по Дебаю и Гюнтельбергу, привели к различным результатам для  Эти вопросы подробно обсуждены Онзагером [8]. Энергией взаимодействия, которая должна бы войти в больцмановский множитель в уравнении (27-1), является потенциал средней силы, т. е. интеграл от средней силы, связанной с виртуальным перемещением иона, когда рассматриваются все его взаимодействия с растворителем и другими ионами. Такой потенциал не обязательно равен
Эти вопросы подробно обсуждены Онзагером [8]. Энергией взаимодействия, которая должна бы войти в больцмановский множитель в уравнении (27-1), является потенциал средней силы, т. е. интеграл от средней силы, связанной с виртуальным перемещением иона, когда рассматриваются все его взаимодействия с растворителем и другими ионами. Такой потенциал не обязательно равен 
Это противоречие иллюстрируется приведенным Онзагером примером. Обозначим потенциал вокруг центрального иона  через
через  Вероятность найти ион типа
Вероятность найти ион типа  в элементе объема вблизи начала координат пропорциональна
в элементе объема вблизи начала координат пропорциональна  . Согласно модели Дебая—Хюккеля, условная вероятность обнаружить ион типа i в элементе объема на расстоянии
. Согласно модели Дебая—Хюккеля, условная вероятность обнаружить ион типа i в элементе объема на расстоянии  при условии, что в начале координат находится ион типа
при условии, что в начале координат находится ион типа  пропорциональна
пропорциональна  Следовательно, вероятность обнаружить в некоторой точке ион типа
Следовательно, вероятность обнаружить в некоторой точке ион типа  и на расстоянии
и на расстоянии  от него ион типа i пропорциональна
от него ион типа i пропорциональна  Однако эта вероятность не должна зависеть от того, какой из ионов рассматривается в качестве центрального. Таким образом, мы должны иметь
Однако эта вероятность не должна зависеть от того, какой из ионов рассматривается в качестве центрального. Таким образом, мы должны иметь

где член справа — выражение этой вероятности по Дебаю—Хюккелю, когда центральным считается ион типа L Равенство этих выражений требует, чтобы

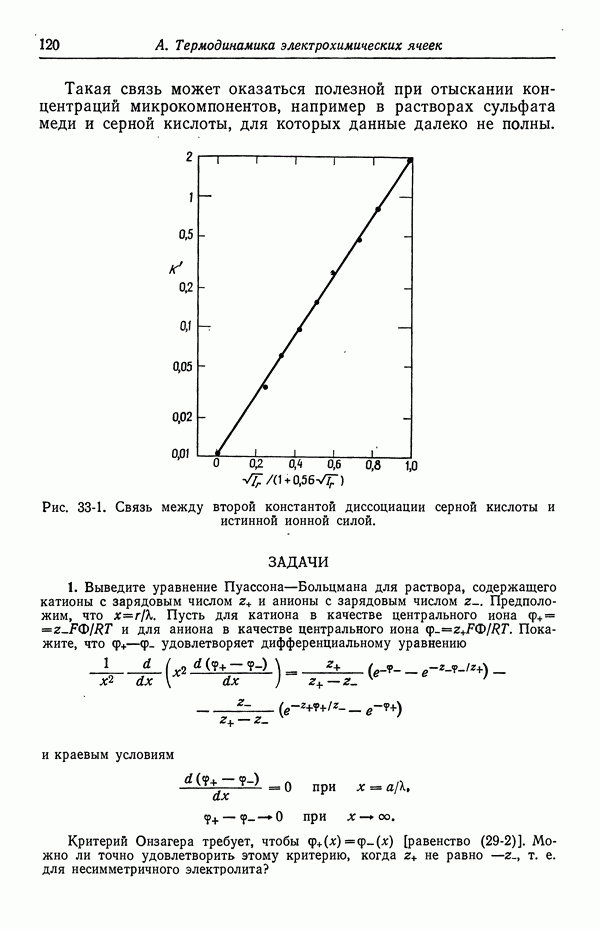
Чтобы завершить пример, нужно показать, что в некотором случае, когда потенциалы  определяются из решения уравнения Пуассона—Больцмана, равенство (29-2) нарушается. Простейшим случаем является несимметричный электролит (задача 1). Для симметричных электролитов равенство (29-2) не нарушается. Между тем это не означает, что в данном случае против основной модели нет возражений. Процессы заряжения по Дебаю и Гюнтельбергу по-прежнему дают различные значения
определяются из решения уравнения Пуассона—Больцмана, равенство (29-2) нарушается. Простейшим случаем является несимметричный электролит (задача 1). Для симметричных электролитов равенство (29-2) не нарушается. Между тем это не означает, что в данном случае против основной модели нет возражений. Процессы заряжения по Дебаю и Гюнтельбергу по-прежнему дают различные значения 
Часто по ошибке утверждает, что модель Дебая—Хюккеля несостоятельна по той причине, что она не удовлетворяет принципу суперпозиции, известному в электростатике. Этот принцип содержится в уравнении Пуассона (27-2): при данном распределении зарядов потенциал удвоится, если удвоить величину всех зарядов, не нарушая их расположения. На самом же деле несостоятельность модели вызвана тем, что ее статистическое рассмотрение не является строгим.
Указанную Онзагером трудность преодолел Майер [9]. Он применил принципы статистической механики к физической модели Дебая—Хюккеля, т. е. к твердым сферическим ионам диаметра а, движущимся в сплошной диэлектрической жидкости. Основные статистические методы, включая конфигурационные интегралы, можно найти в гл. 13 книги Майера и Гепперт-Майер [10], а также в статье Макмиллана и Майера [11]. Эти методы послужили отправной точкой для работы Майера по ионным растворам. Ввиду дальнодействующего характера ку-лоновских сил такое применение статистики оказалось нелегким, да и сам по себе диаграммный метод далеко не прост.
Майеру удается получить предельный закон Дебая—Хюккеля без каких-либо допущений, аналогичных приближению (27-7). Он выписывает также выражение для логарифма коэффициента активности с точностью до членов порядка  и рекомендует вычислять эти члены, не прибегая к разложению при малых с, хотя строгое обоснование того, что при этом точность возрастает, отсутствует.
и рекомендует вычислять эти члены, не прибегая к разложению при малых с, хотя строгое обоснование того, что при этом точность возрастает, отсутствует.
По изложенным в начале данного раздела причинам поправки более высокого порядка к коэффициенту активности получить без учета некулоновских эффектов нельзя, и поэтому мы не будем больше заниматься статистическими методами. Процитируем по этому поводу Резибуа [12]. «Хотя это и малоутешительно,
утешительно, однако следует признать, что строгое подтверждение теории Дебая—Хюккеля представляет собой наиболее значительный прогресс, достигнутый в последние годы в области теории электролитов».
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
- 5. Диффузионный слой
- 6. Концентрационные ячейки
- 7. Концентрационное перенапряжение
- 8. Поверхностное перенапряжение
- 9. Потенциал ячейки
- 10. Фоновый электролит
- 11. Свободная конвекция
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
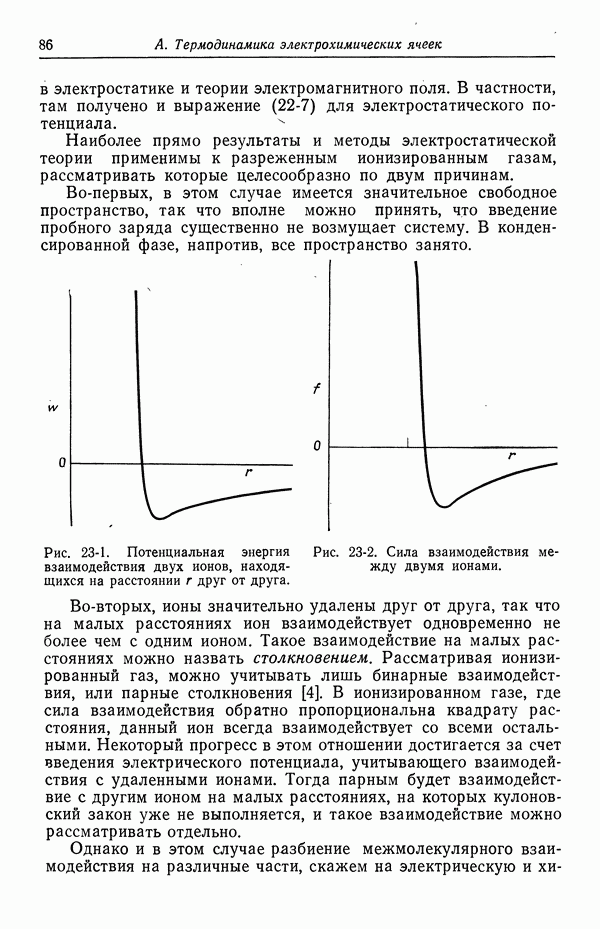
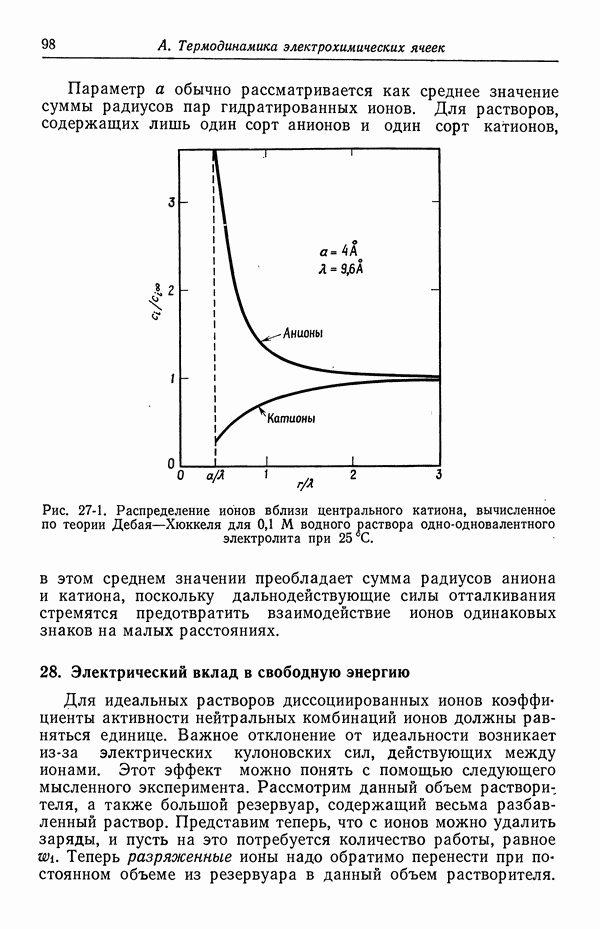
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
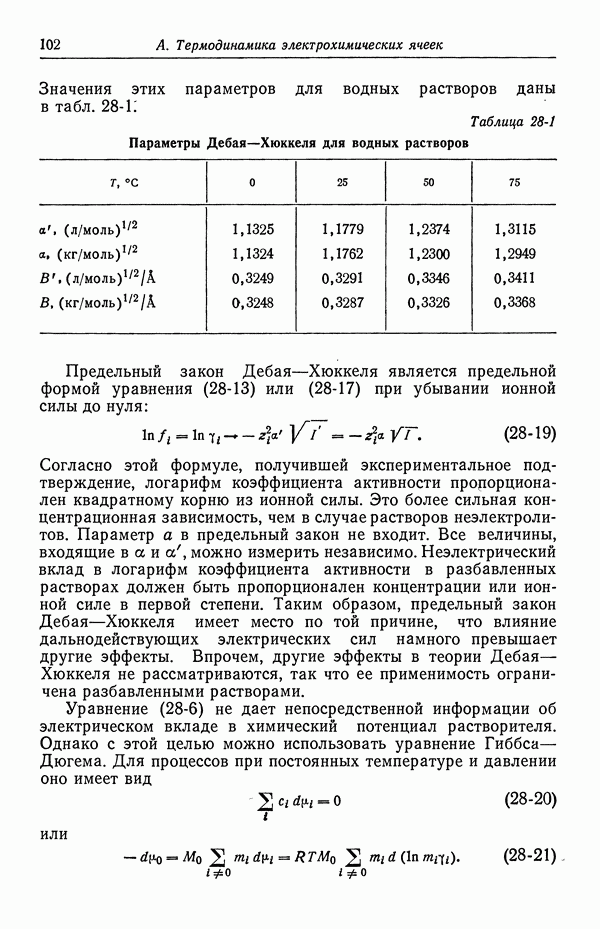
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая—Хюккеля
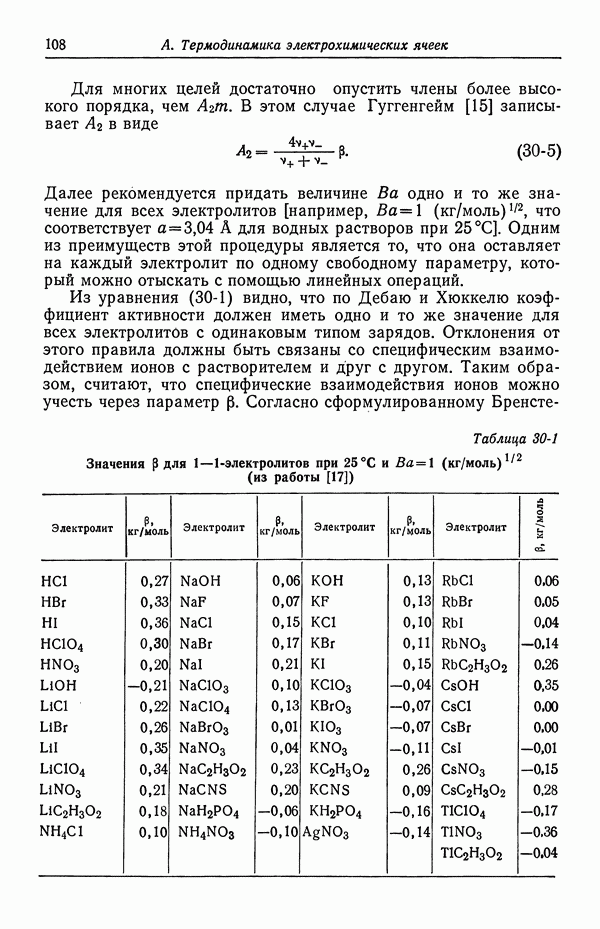
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 49. Качественное описание двойных слоев
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод — раствор
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 66. Динамика границы раздела
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 69. Законы переноса
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 78. Законы переноса
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 92. Интегральные коэффициенты диффузии
- ЗАДАЧА
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 111. Свободная конвекция
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- СПИСОК ОБОЗНАЧЕНИЙ
- ГЛАВА 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 119. Решение задачи
- 120. Поправочный множитель в случае предельных токов
- 121. Изменение концентрации фонового электролита
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ