| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
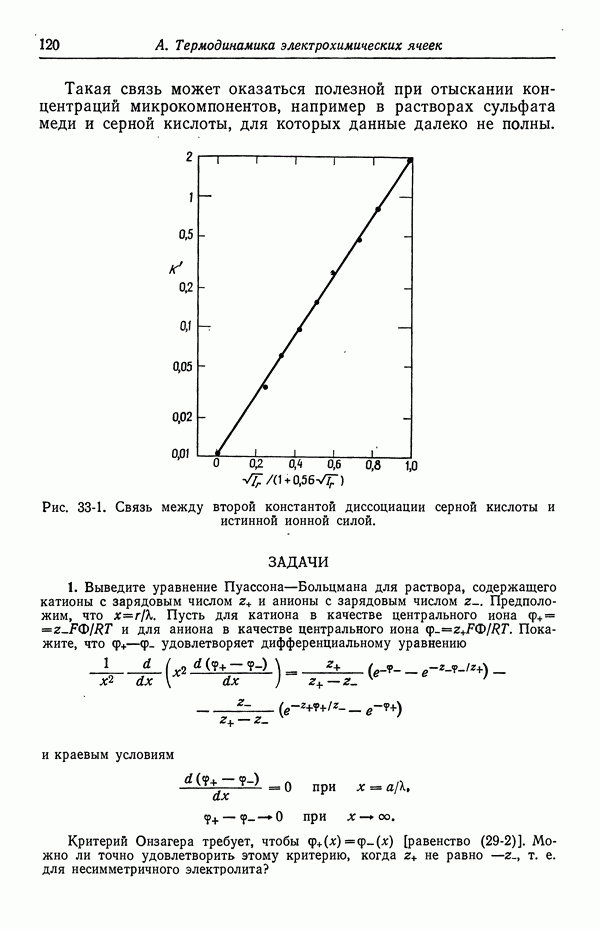
ЗАДАЧИ
1. Выведите уравнение Пуассона—Больцмана для раствора, содержащего катионы с зарядовым числом  и анионы с зарядовым числом
и анионы с зарядовым числом  Предположим, что
Предположим, что  Пусть для катиона в качестве центрального иона
Пусть для катиона в качестве центрального иона  и для аниона в качестве центрального иона
и для аниона в качестве центрального иона  Покажите, что
Покажите, что  удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению

и краевым условиям

Критерий Онзагера требует, чтобы  [равенство (29-2)]. Можно ли точно удовлетворить этому критерию, когда
[равенство (29-2)]. Можно ли точно удовлетворить этому критерию, когда  не равно
не равно  т. е. для несимметричного электролита?
т. е. для несимметричного электролита?
2. Вывести уравнение Пуассона—Больцмана, как в задаче 1. Пусть  так что краевое условие при
так что краевое условие при  принимает вид
принимает вид

Для проверки предельного закона Дебая—Хюккеля решите задачу для небольших значений  , т. е. для низких концентраций.
, т. е. для низких концентраций.
(а) Найдите решение путем разложения в ряд по сингулярным возмущениям, полагая, что внутренняя переменная равна  а внешняя переменная равна
а внешняя переменная равна  работу [28] по применению метода сингулярных возмущений к задачам, представляющим интерес для электрохимии). Во внутренней области потенциал ионного облака пренебрежимо мал (в первом приближении). Во внешней области потенциал мал и экспоненциальный больцмановский член можно линеаризовать.
работу [28] по применению метода сингулярных возмущений к задачам, представляющим интерес для электрохимии). Во внутренней области потенциал ионного облака пренебрежимо мал (в первом приближении). Во внешней области потенциал мал и экспоненциальный больцмановский член можно линеаризовать.
(б) Используйте результат пункта (а) и процесс заряжения по Гюнтельбергу для подтверждения предельного закона Дебая—Хюккеля. По возможности получите следующий член в разложении при малых  .
.
(в) Повторите сказанное в пункте ( ) с дебаевским процессом заряжения.
) с дебаевским процессом заряжения.
3. В разд. 28 использовалась свободная энергия Гельмгольца, в разд. 31 — свободная энергия Гиббса. Рассчитайте разность между А и G и сравните ее с электрическим вкладом в свободную энергию в случае 0,1 моляльного раствора. Получите выражение для разности между производными А по  , вычисленными при постоянных давлении и объеме. Является ли совершенно законным определение химического потенциала растворителя в соответствии с уравнением
, вычисленными при постоянных давлении и объеме. Является ли совершенно законным определение химического потенциала растворителя в соответствии с уравнением  Полностью ли строг вывод уравнения (30-4) из уравнения
Полностью ли строг вывод уравнения (30-4) из уравнения 
4. Смерл и Ньюмен [29] выражают молярные коэффициенты активности растворенных компонентов по существу в виде ср. с уравнением (31-4)]

где суммирование проводится по всем растворенным компонентам,  для пары ионов с одинаковыми зарядами и
для пары ионов с одинаковыми зарядами и 
(а) Согласуется ли это выражение с термодинамическим требованием 
(б) Покажите, что

если выражение Смерла и Ньюмена будет эквивалентным соответствующему выражению для моляльных коэффициентов активности до членов первого порядка по концентрациям растворенных веществ включительно. Здесь  плотность чистого растворителя.
плотность чистого растворителя.
(в) Для раствора одного электролита покажите, что

где  парциальный молярный объем электролита в бесконечно разбавленном растворе. Приняв
парциальный молярный объем электролита в бесконечно разбавленном растворе. Приняв  сравните величину поправочного члена с типичными значениями
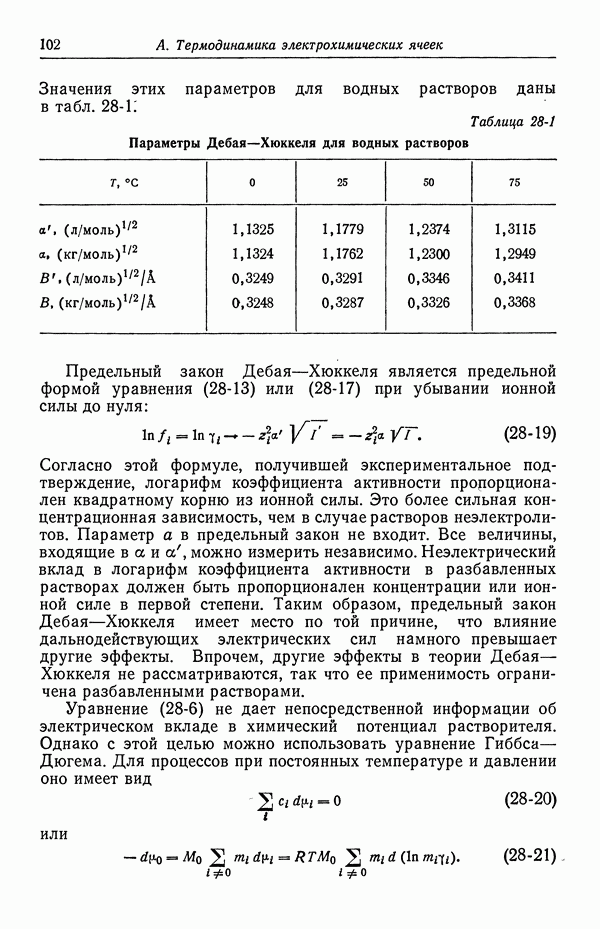
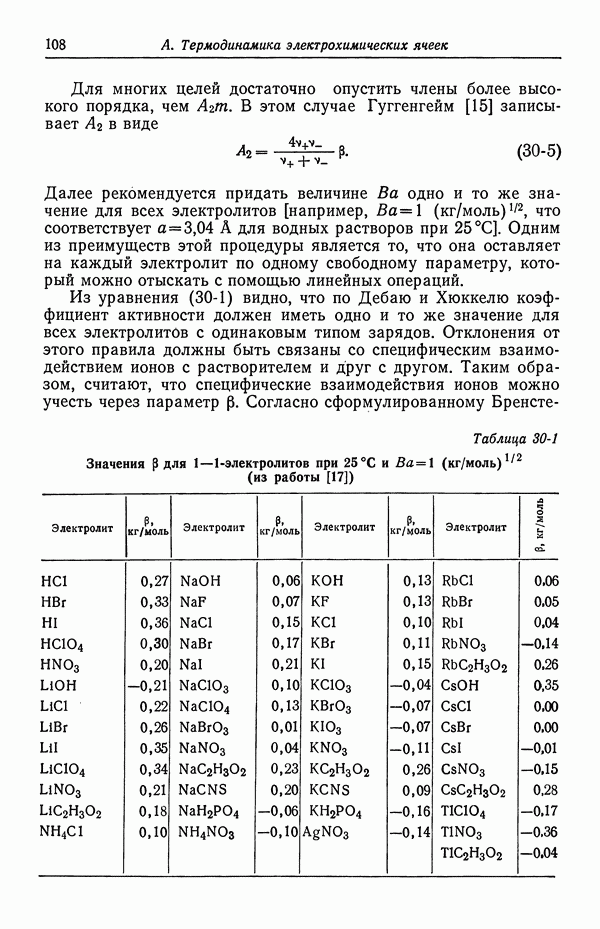
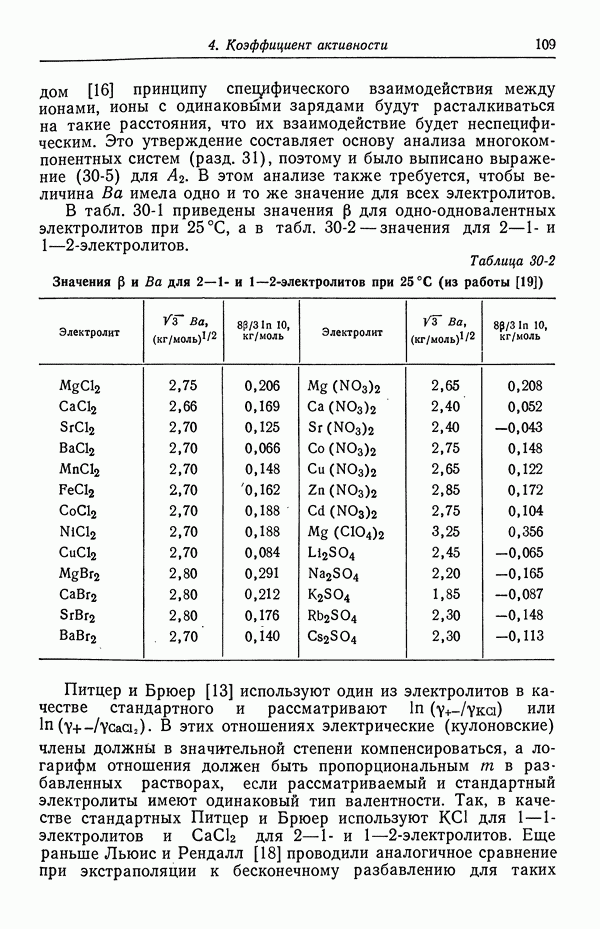
сравните величину поправочного члена с типичными значениями  для одно-одновалентных электролитов из табл. 30-1.
для одно-одновалентных электролитов из табл. 30-1.
5. Примем, что свободная энергия Гиббса для раствора нескольких электролитов может быть выражена в виде

Здесь предполагается, что последние члены, содержащие  , учитывают короткодействие между парами ионов растворенного вещества. Множитель
, учитывают короткодействие между парами ионов растворенного вещества. Множитель  введен исключительно для удобства.
введен исключительно для удобства.
(а) Обсудите, почему это выражение является достаточно общим без включения членов типа  для взаимодействия компонента i с растворителем.
для взаимодействия компонента i с растворителем.
(б) Покажите,  без потери общности можно требовать выполнения условия
без потери общности можно требовать выполнения условия  .
.
(в) Моляльности ионов не являются независимыми, так как они удовлетворяют условию электронейтральности:

Следовательно, поскольку значения  не могут быть найдены по отдельности, определим
не могут быть найдены по отдельности, определим

так чтобы  Покажите, что
Покажите, что

Могут ли быть значения  найдены из эксперимента?
найдены из эксперимента?
(г) Покажите, что для раствора одного электролита выражение для G теперь сводится к

В пункте (в) поясняется, почему для растворов одного электролита члены с  — отсутствуют.
— отсутствуют.
(д) Для смесей, содержащих катионы с одинаковыми зарядовыми числами  и анионы с одинаковыми зарядовыми числами
и анионы с одинаковыми зарядовыми числами  Гуггенгейм [7]
Гуггенгейм [7]
выражает свободную энергию относительно стандартного электролита, для которого  Пусть стандартная свободная энергия
Пусть стандартная свободная энергия  определяется уравнением в пункте
определяется уравнением в пункте  в котором
в котором  заменено на
заменено на  имеют такой смысл:
имеют такой смысл:

где m — полная моляльность раствора. Покажите, что избыток свободной энергии дается выражением

а средний коэффициент активности катиона k и аниона  равен
равен

где  осмотический коэффициент и
осмотический коэффициент и  средний моляльный коэффициент активности стандартного электролита, оба взятые при моляльности,
средний моляльный коэффициент активности стандартного электролита, оба взятые при моляльности,  .
.
(е) Пусть

Покажите, что

и

Заметим, что является стандартным значением для ионов с зарядами противоположных знаков, в то время как аналогичной величины для ионов с одинаковыми зарядами не имеется.
Эти упражнения показывают, что изложенной в разд. 31 теории с ненулевыми  для ионов с противоположными зарядами достаточно для строгого учета коэффициентов активности смесей электролитов до порядка
для ионов с противоположными зарядами достаточно для строгого учета коэффициентов активности смесей электролитов до порядка  включительно.
включительно.
6. (а) Для растворов серной кислоты, рассмотренных в разд. 33, выражайте стехиометрические концентрации ионов водорода и сульфата через микроскопические концентрации ионов водорода, бисульфата и сульфата.
(б) Покажите, что к данной модельной системе при постоянных температуре и давлении применимо уравнение Гиббса—Дюгема

(в) Используя уравнение (33-3), покажите, что по мере приближения ионной силы к нулю

где К пока еще не определена. Принять, что к данной модельной системе применимо уравнение (14-6).
(г) Используя уравнение (14-6) и результат пункта (в), докажите соотношение

(д) Исходя из пунктов  , покажите, что
, покажите, что

где  средний молярный коэффициент активности ионов водорода и сульфата, измеряемый с помощью термодинамических методов.
средний молярный коэффициент активности ионов водорода и сульфата, измеряемый с помощью термодинамических методов.
(е) Если можно измерить  — при одной стехиометрической концентрации, то из приведенного выше результата мы знаем величину
— при одной стехиометрической концентрации, то из приведенного выше результата мы знаем величину  при той же концентрации. Покажите, что
при той же концентрации. Покажите, что

и обсудите, как можно получить величины К и  по отдельности, если концентрация
по отдельности, если концентрация  известна как функция стехиометрической концентрации.
известна как функция стехиометрической концентрации.
Отметим, что в данной задаче мы использовали лишь коэффициенты активности нейтральных комбинаций ионов даже для модельной системы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
- 5. Диффузионный слой
- 6. Концентрационные ячейки
- 7. Концентрационное перенапряжение
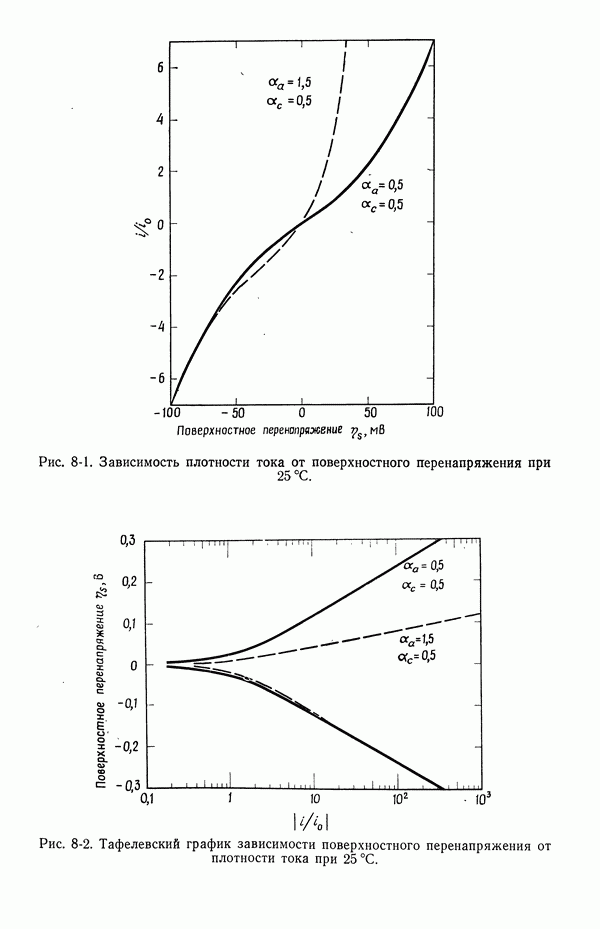
- 8. Поверхностное перенапряжение
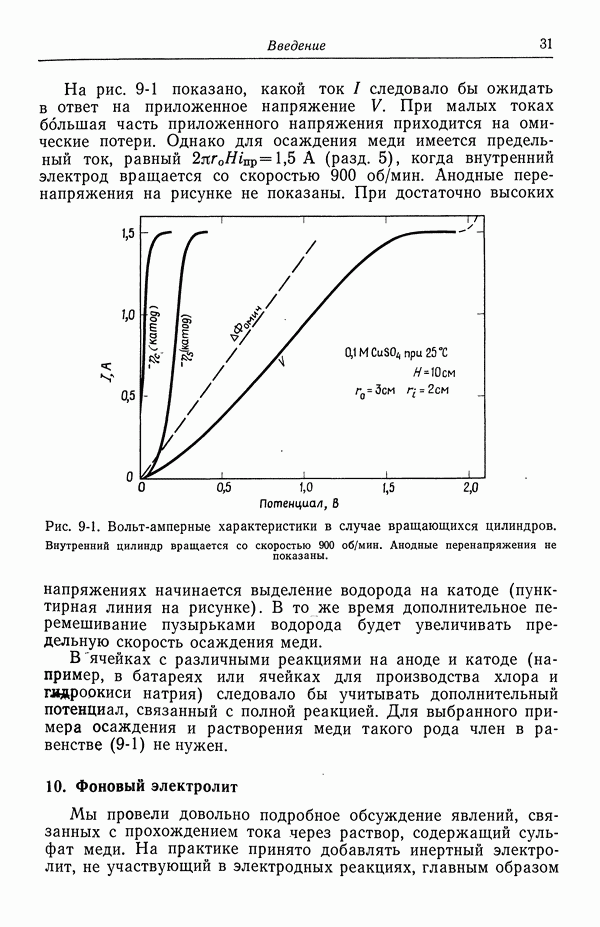
- 9. Потенциал ячейки
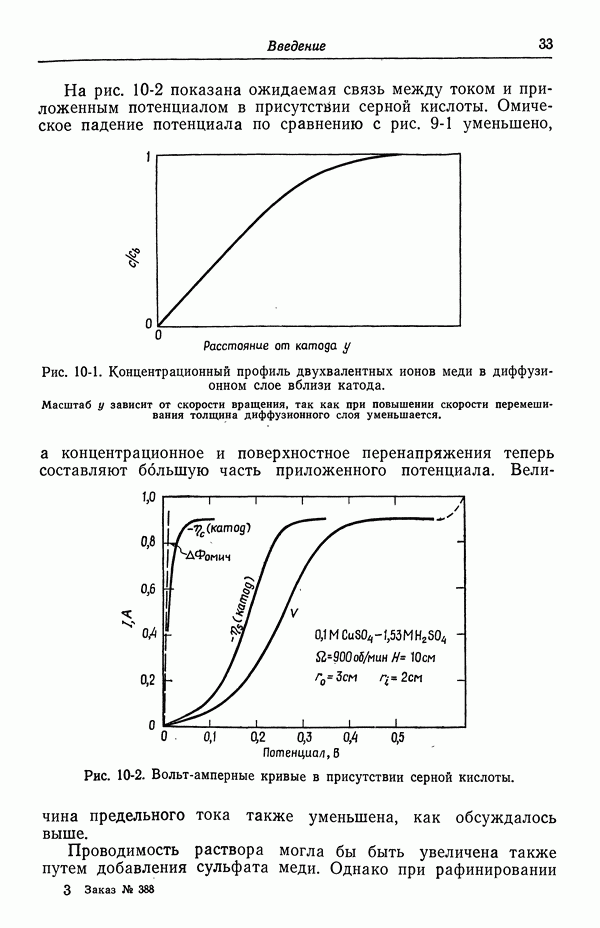
- 10. Фоновый электролит
- 11. Свободная конвекция
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
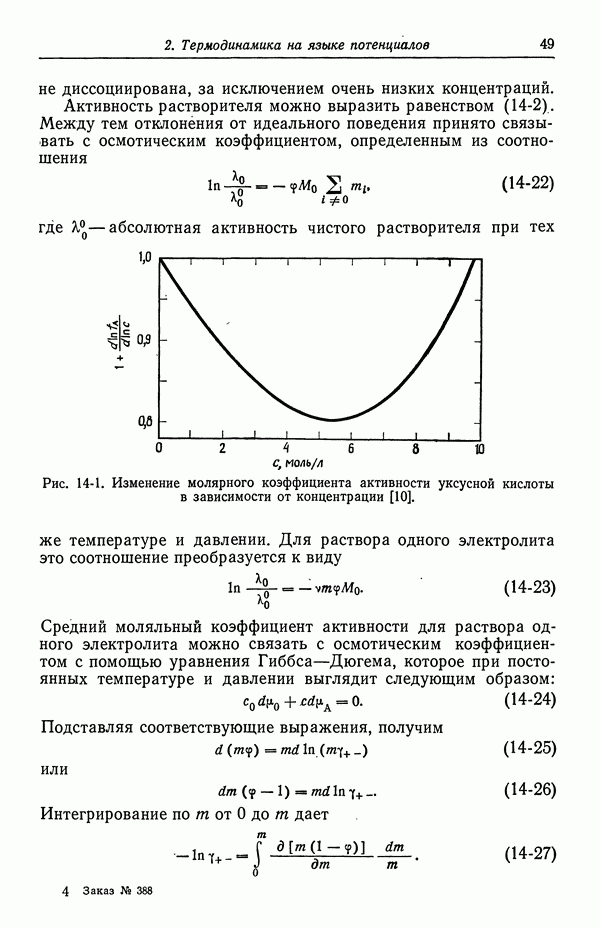
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая—Хюккеля
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 49. Качественное описание двойных слоев
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод — раствор
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 66. Динамика границы раздела
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 69. Законы переноса
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 78. Законы переноса
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 92. Интегральные коэффициенты диффузии
- ЗАДАЧА
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
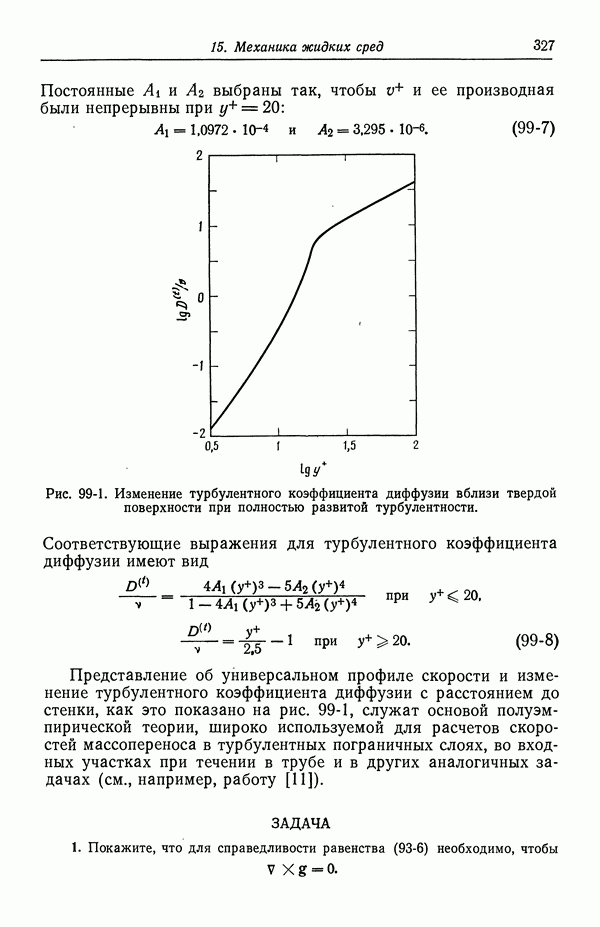
- 99. Массоперенос в турбулентном потоке
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
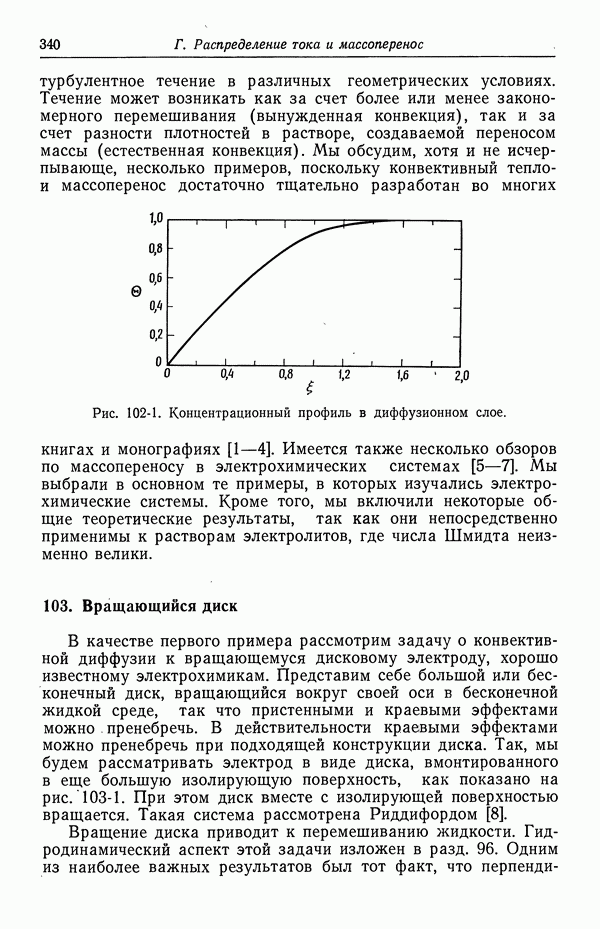
- 102. Упрощенное описание конвективной диффузии
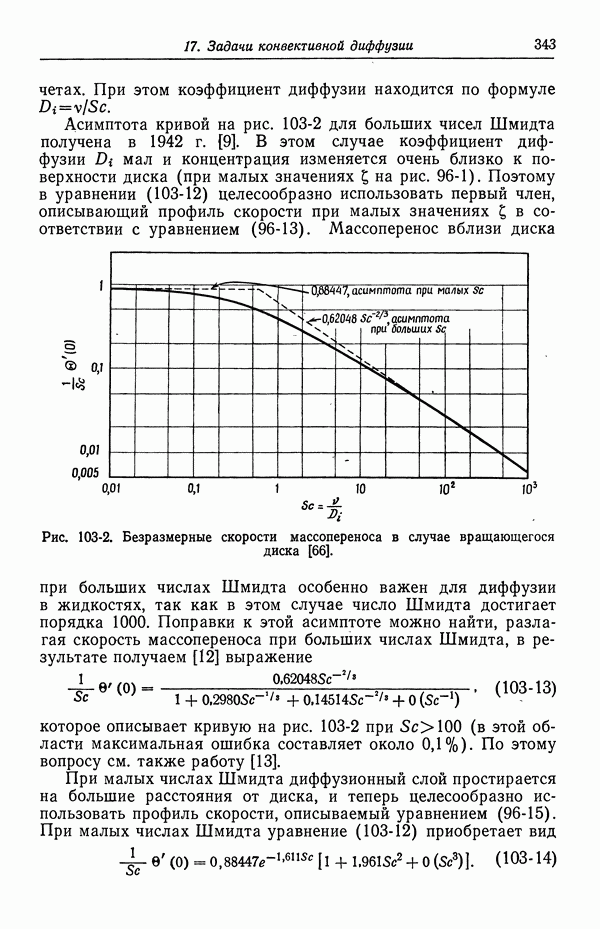
- 103. Вращающийся диск
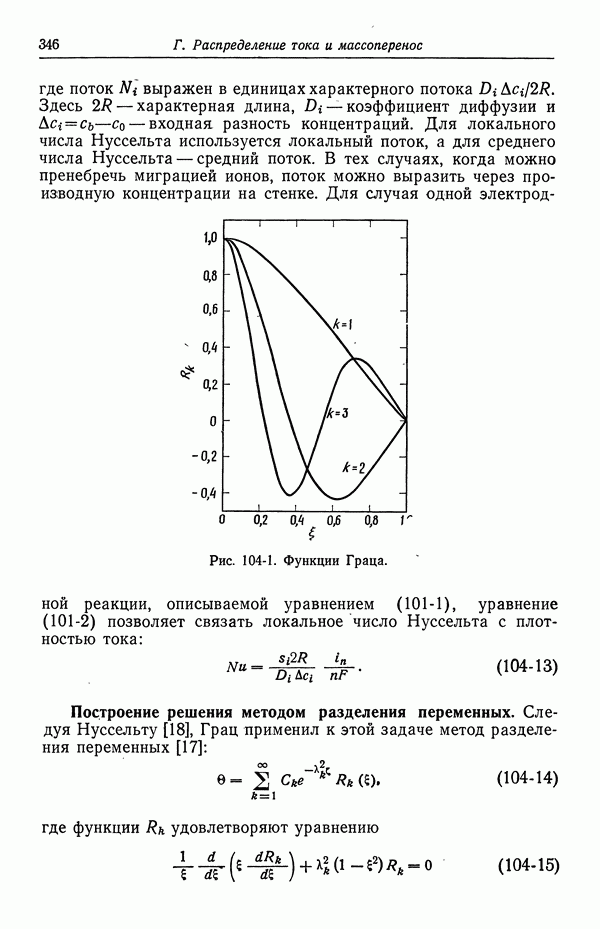
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 111. Свободная конвекция
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- СПИСОК ОБОЗНАЧЕНИЙ
- ГЛАВА 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 119. Решение задачи
- 120. Поправочный множитель в случае предельных токов
- 121. Изменение концентрации фонового электролита
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ