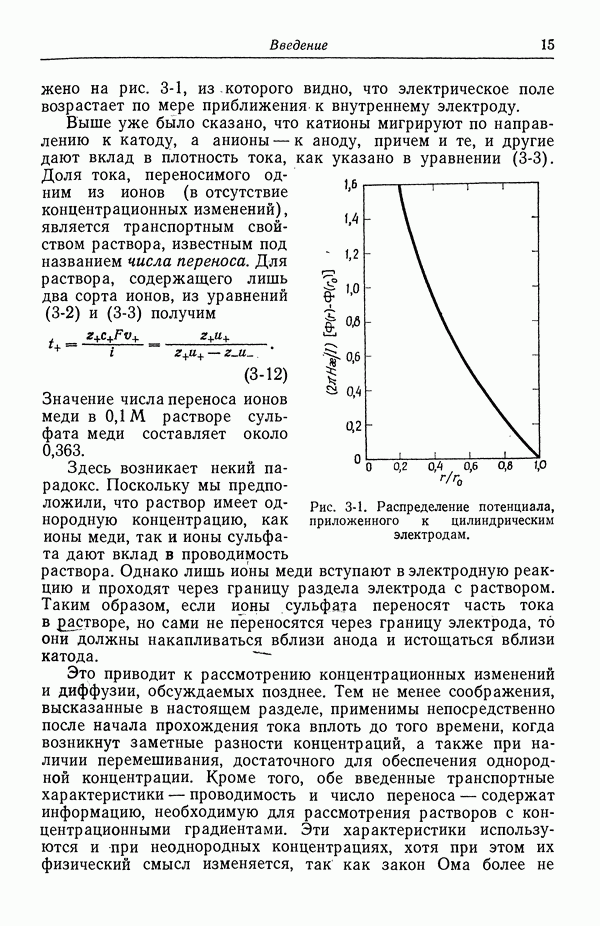
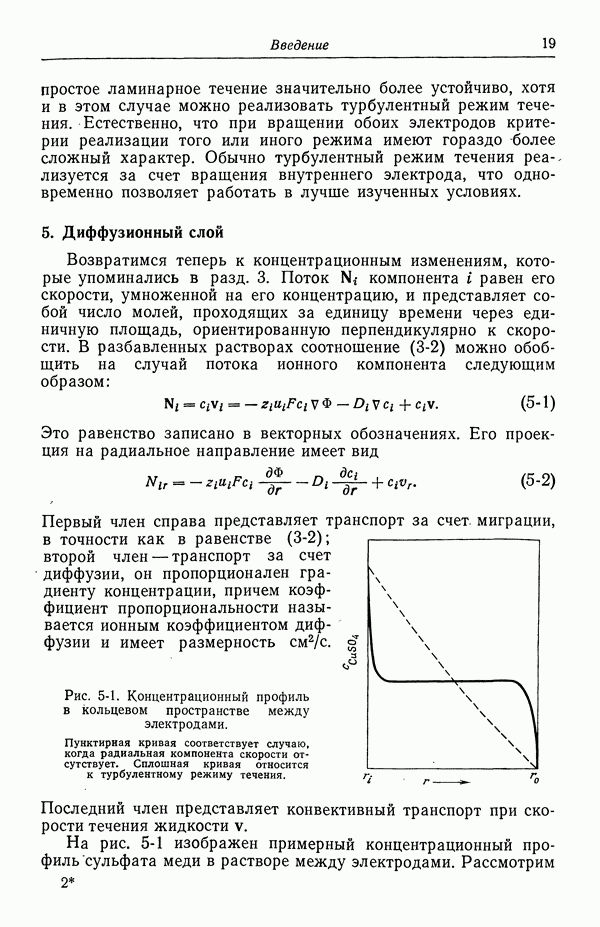
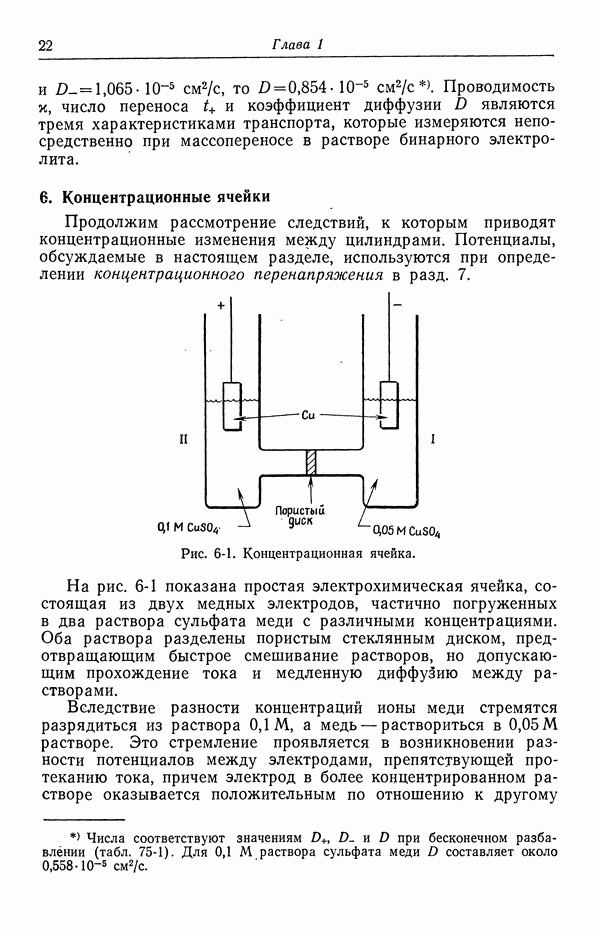
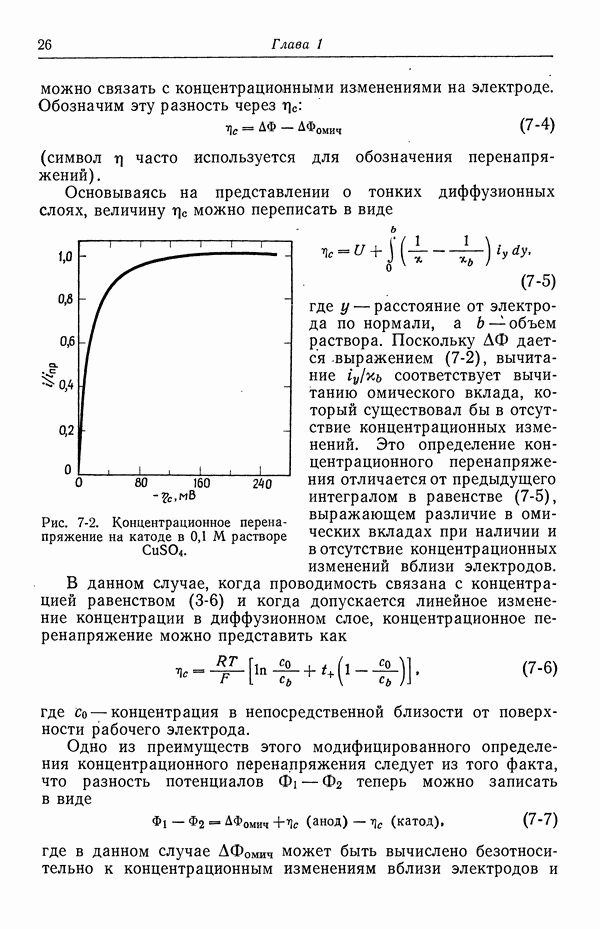
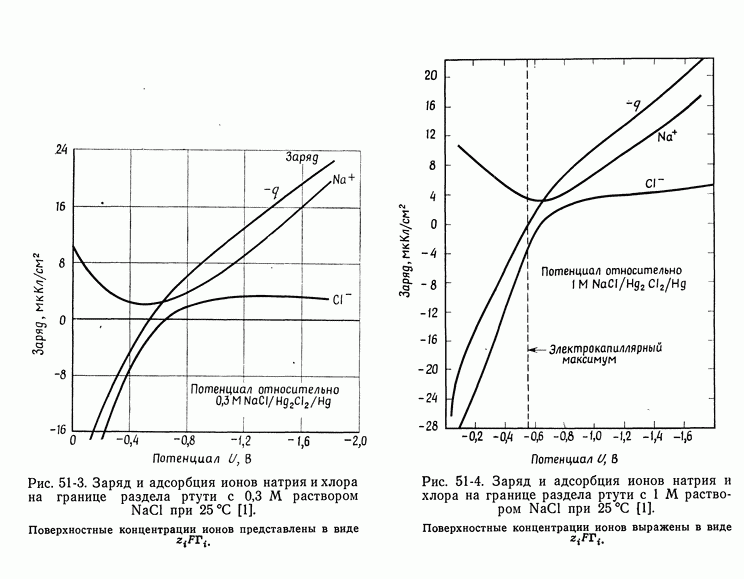
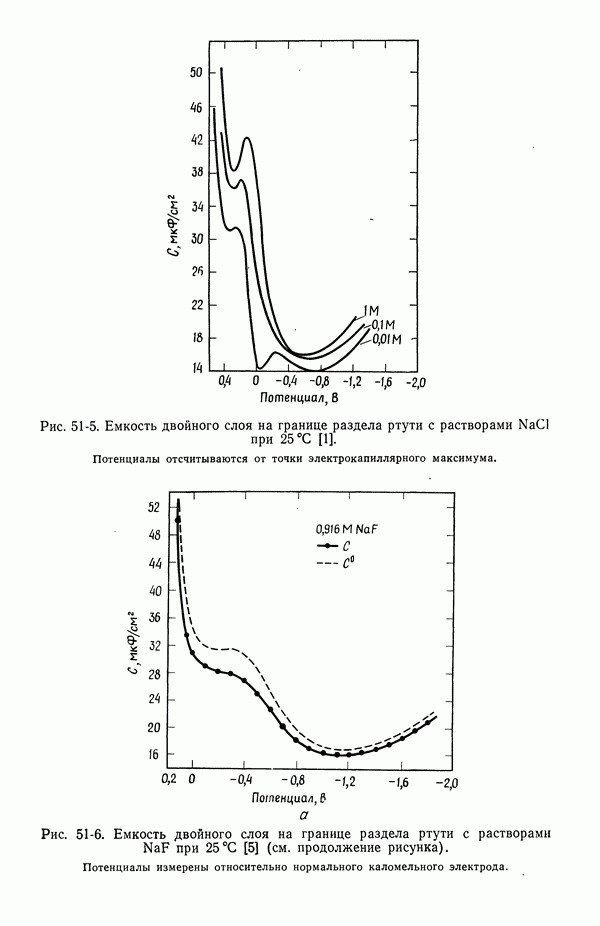
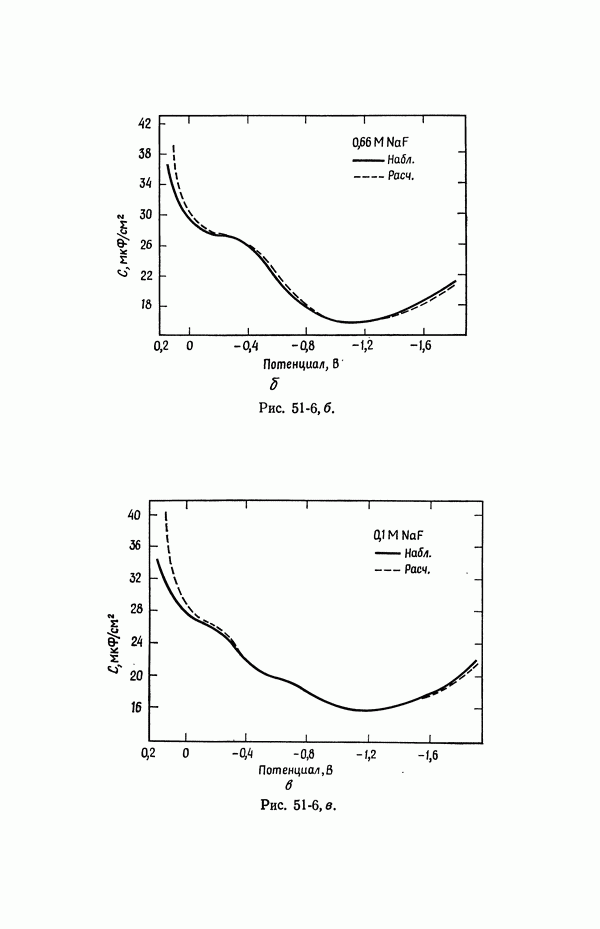
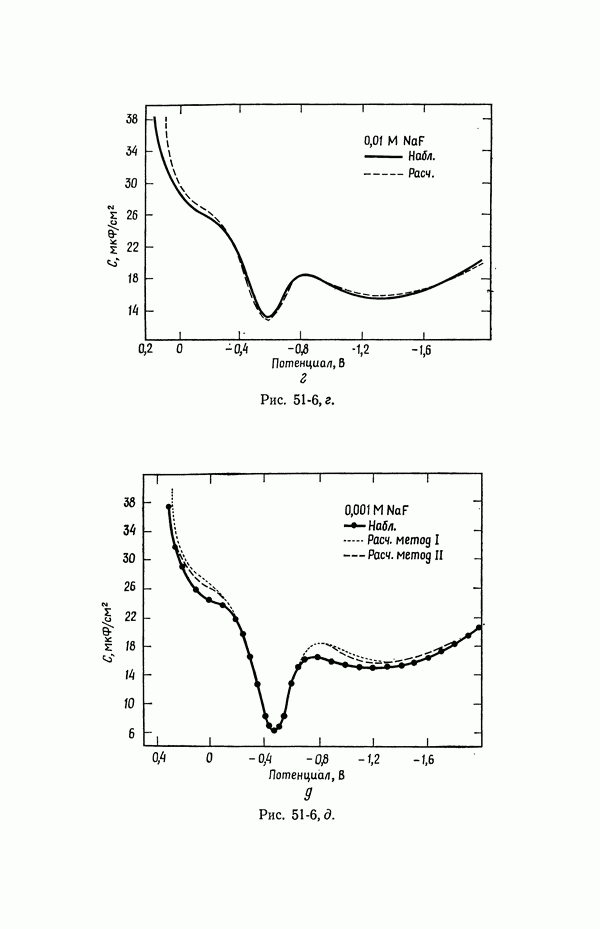
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
31. Многокомпонентные растворы
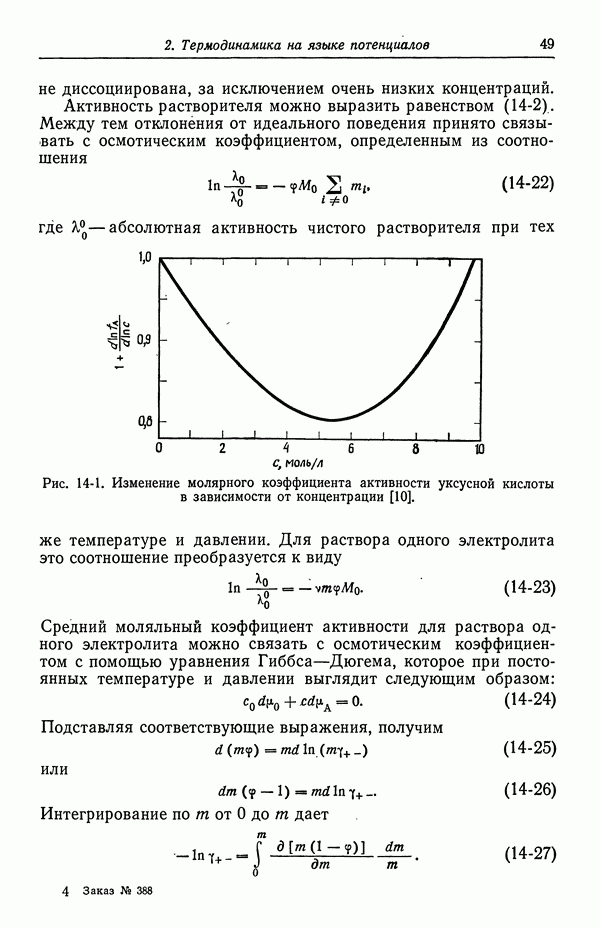
Уравнения (30-3) и (30-4) выражают зависимость коэффициентов активности и осмотических коэффициентов от состава бинарных растворов. Параметры  при данных давлении и температуре приняты постоянными, т. е. не зависящими от концентрации растворенного вещества. Коэффициенты активности и осмотические коэффициенты не являются независимыми: уравнение (30-4) можно получить из уравнения (30-3), применяя соотношение Гиббса—Дюгема при постоянных температуре и давлении. Поскольку химические потенциалы компонентов смеси не независимы, возможные недоразумения легче всего обойти, получая химические потенциалы из выражения для полной свободной энергии. Вместо свободной энергии Гельмгольца используется свободная энергия Гиббса, так что химические потенциалы можно получить дифференцированием при постоянном давлении, а не при постоянном объеме [равенство (13-1)]. При этом соотношение Гиббса—Дюгема легче использовать, если при данном давлении параметры постоянны.
при данных давлении и температуре приняты постоянными, т. е. не зависящими от концентрации растворенного вещества. Коэффициенты активности и осмотические коэффициенты не являются независимыми: уравнение (30-4) можно получить из уравнения (30-3), применяя соотношение Гиббса—Дюгема при постоянных температуре и давлении. Поскольку химические потенциалы компонентов смеси не независимы, возможные недоразумения легче всего обойти, получая химические потенциалы из выражения для полной свободной энергии. Вместо свободной энергии Гельмгольца используется свободная энергия Гиббса, так что химические потенциалы можно получить дифференцированием при постоянном давлении, а не при постоянном объеме [равенство (13-1)]. При этом соотношение Гиббса—Дюгема легче использовать, если при данном давлении параметры постоянны.
Выразим свободную энергию Гиббса для умеренно разбавленных растворов нескольких электролитов в виде [21, 22]

где  — химический потенциал чистого растворителя при тех же температуре и давлении.
— химический потенциал чистого растворителя при тех же температуре и давлении.
Первые два члена в правой части уравнения (31-1) можно рассматривать как идеальный вклад в свободную энергию, однако следует помнить, что это не более чем способ выражения. Идеальный вклад нужно выражать через мольные доли, доли
частиц, объемные доли или концентрации, так как по мере приближения концентрации растворителя к нулю моляльность обращается в бесконечность. Заметим, что комбинация  во втором члене определена однозначно в соответствии с изложенными в разд. 14 правилами, поскольку в целом раствор электронейтрален. Третий член в правой части уравнения (31-1) представляет собой электрический вклад, выражаемый равенством (28-4), поскольку
во втором члене определена однозначно в соответствии с изложенными в разд. 14 правилами, поскольку в целом раствор электронейтрален. Третий член в правой части уравнения (31-1) представляет собой электрический вклад, выражаемый равенством (28-4), поскольку  приближается к
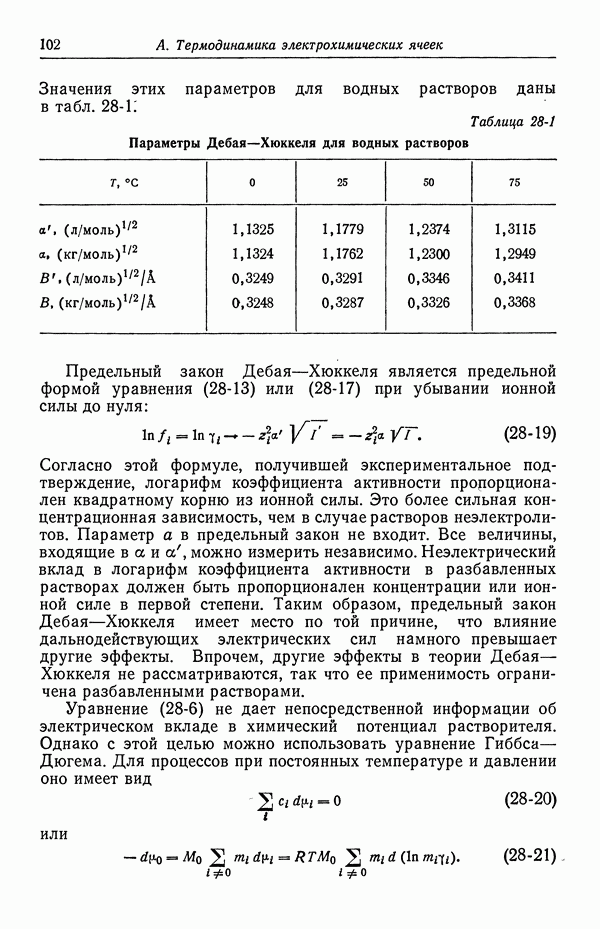
приближается к  по мере стремления ионной силы к нулю. Напомним, что величина а представляет среднее значение суммы радиусов пар гидратированных ионов и что для данного раствора может использоваться лишь одно значение а. Последний член в уравнении (31-1) в первом приближении описывает влияние специфического взаимодействия между парами ионов, и мы примем
по мере стремления ионной силы к нулю. Напомним, что величина а представляет среднее значение суммы радиусов пар гидратированных ионов и что для данного раствора может использоваться лишь одно значение а. Последний член в уравнении (31-1) в первом приближении описывает влияние специфического взаимодействия между парами ионов, и мы примем  (общность при этом не теряется, так как
(общность при этом не теряется, так как  ). В соответствии с бренстедовским принципом специфического взаимодействия ионов
). В соответствии с бренстедовским принципом специфического взаимодействия ионов  положено равным нулю при
положено равным нулю при  , т. е. для пары ионов t и
, т. е. для пары ионов t и  с одинаковыми знаками зарядов.
с одинаковыми знаками зарядов.
В уравнении (31-1) фигурируют моляльности и моляльная ионная сила, поскольку это упрощает дифференцирование и облегчает использование уравнения Гиббса—Дюгема. Кроме того, Скэтчард [22], исходя из теоретических соображений, утверждает, что для выражения электрического вклада в свободную энергию моляльная ионная сила подходит больше всего.
Дифференцирование уравнения (31-1) в соответствии с уравнением (13-1) дает для химического потенциала растворенного компонента

и для химического потенциала растворителя

Поэтому коэффициенты активности растворенных веществ равны

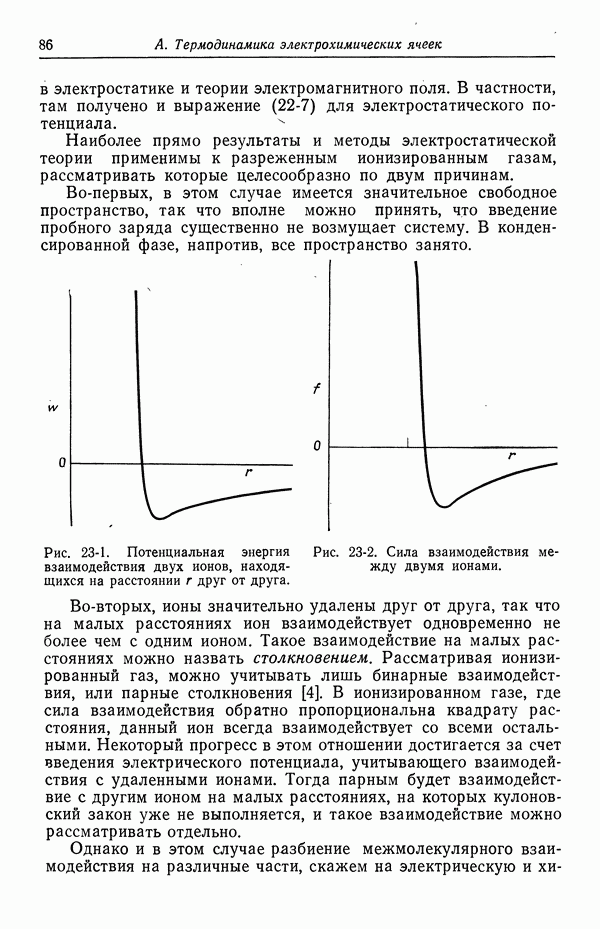
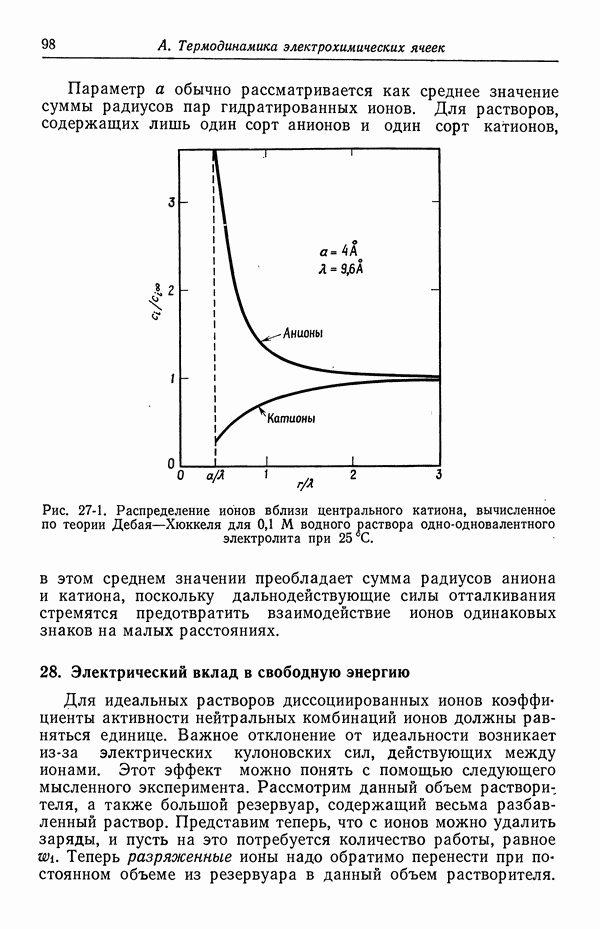
а осмотический коэффициент имеет вид

Хотя равенства (31-2) и (31-4) применяются к отдельным ионам, в них не была включена зависимость от электрического состояния фазы. Следовательно, эти выражения необходимо использовать лишь для электрически нейтральных комбинаций ионов в соответствии с обсуждением, проведенным в разд. 14.
Согласно принципу Бренстеда, относящемуся к специфическому взаимодействию ионов, для пар ионов с одинаковыми зарядами  Это означает, что каждый из коэффициентов
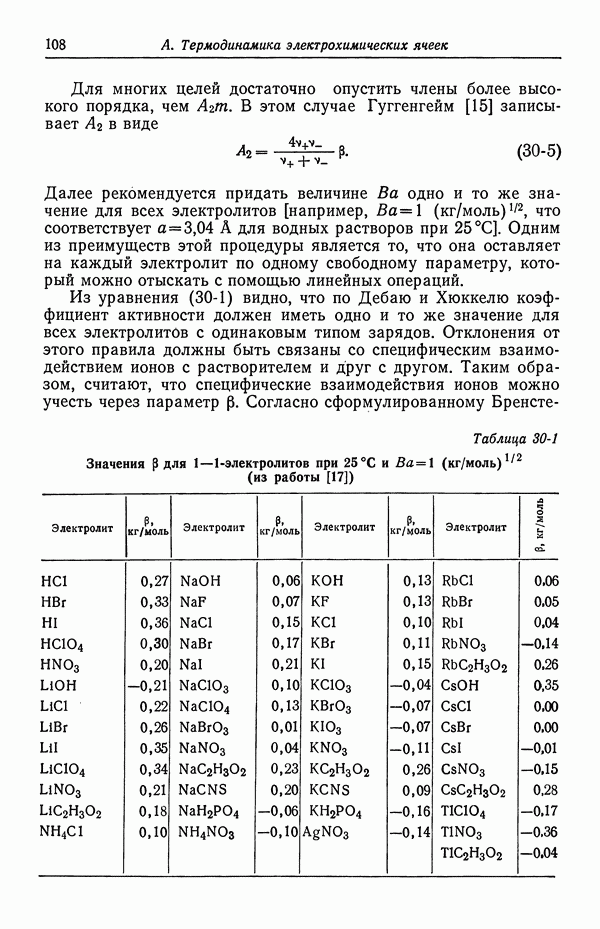
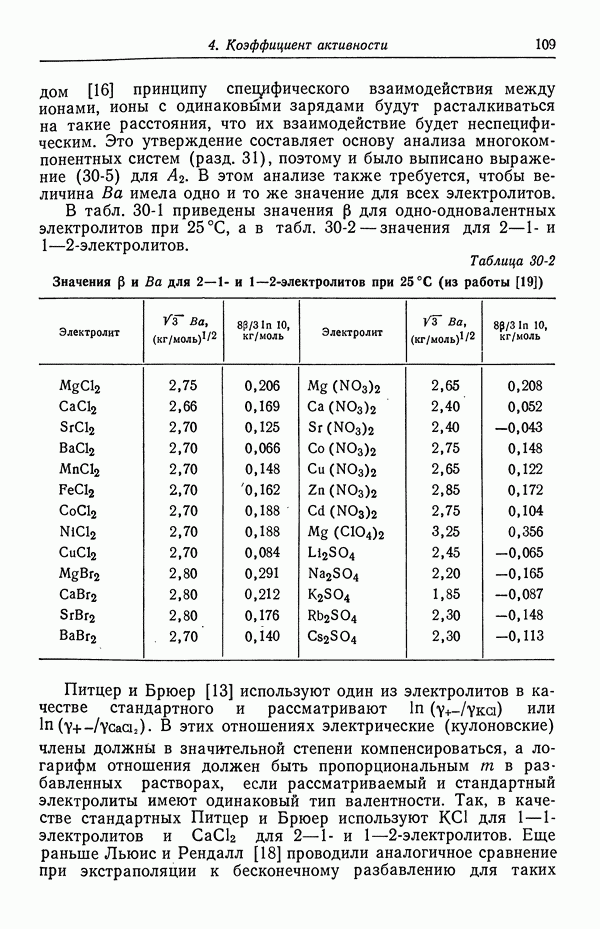
Это означает, что каждый из коэффициентов  , возникающих в этих уравнениях для многокомпонентных растворов, соответствует одному катиону и одному аниону и может быть найден из измерений коэффициентов активности или осмотических коэффициентов в бинарном растворе этого электролита. Такие значения приведены в табл. 30-1 и 30-2. Однако при сравнении с данными для бинарных растворов следует использовать то же самое значение параметра
, возникающих в этих уравнениях для многокомпонентных растворов, соответствует одному катиону и одному аниону и может быть найден из измерений коэффициентов активности или осмотических коэффициентов в бинарном растворе этого электролита. Такие значения приведены в табл. 30-1 и 30-2. Однако при сравнении с данными для бинарных растворов следует использовать то же самое значение параметра  Для систем, фигурирующих в табл. 30-2, нужно выбрать среднее значение
Для систем, фигурирующих в табл. 30-2, нужно выбрать среднее значение  а значения
а значения  вычислить повторно из первоначальных данных. Затем то же значение
вычислить повторно из первоначальных данных. Затем то же значение  необходимо использовать при вычислении значений Р для систем табл. 30-1. В этих расчетах могут помочь таблицы Питцера и Брюера [13], поскольку они дают коэффициенты активности относительно стандартного электролита
необходимо использовать при вычислении значений Р для систем табл. 30-1. В этих расчетах могут помочь таблицы Питцера и Брюера [13], поскольку они дают коэффициенты активности относительно стандартного электролита  или
или 
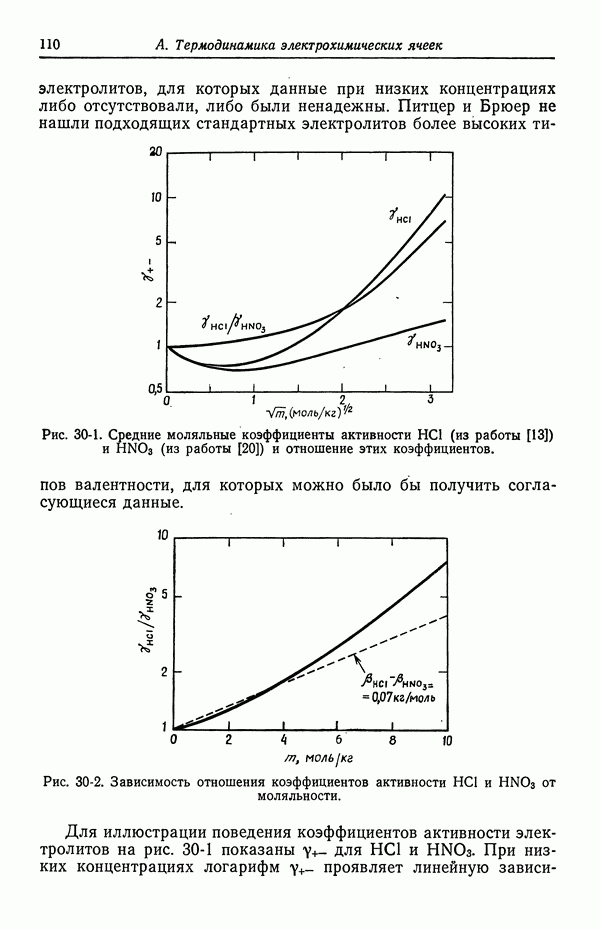
Ценность изложенной выше теории состоит в том, что она позволяет предсказать термодинамические свойства многокомпонентных растворов по измерениям в бинарных растворах. Так, для растворов двух электролитов она предсказывает, что логарифмы коэффициентов активности этих электролитов при постоянной ионной силе изменяются линейно с моляльностью одного из электролитов. Такое поведение коэффициентов активности наблюдается довольно часто.
Если рассмотренный выше подход оказывается недостаточным, то в выражение (31-1) для свободной энергии следует включить дополнительные члены. Для одно-одновалентных электролитов Гуггенгейм [7, 23] расширяет принцип Бренстеда и позволяет коэффициентам  для пар ионов с одинаковыми зарядами отличаться от нуля (при
для пар ионов с одинаковыми зарядами отличаться от нуля (при  значения
значения  по-прежнему равны нулю). Новые значения
по-прежнему равны нулю). Новые значения  (табл. 31-1) не применимы к бинарным растворам и несколько меньше коэффициентов для пар ионов с разными зарядами, что частично согласуется с принципом Бренстеда. Такая модификация не сильно влияет на коэффициенты активности в смешанных электролитах
(табл. 31-1) не применимы к бинарным растворам и несколько меньше коэффициентов для пар ионов с разными зарядами, что частично согласуется с принципом Бренстеда. Такая модификация не сильно влияет на коэффициенты активности в смешанных электролитах
и, по-видимому, более важна при вычислении энтальпий смешения.
Таблица 31-1. Значения  для ионов с одинаковыми зарядами (из работы [7])
для ионов с одинаковыми зарядами (из работы [7])

Кроме членов в уравнении (31-1), Скэтчард [22, 24] обычно приводит члены с моляльностью в третьей и более высоких степенях.
Харнед и Робинсон [25] обобщили данные по равновесным свойствам растворов нескольких электролитов. Они обсуждают поведение коэффициентов активности, соответствующих различным представлениям свободной энергии, и приводят литературу по экспериментальным результатам в различных системах.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
- 5. Диффузионный слой
- 6. Концентрационные ячейки
- 7. Концентрационное перенапряжение
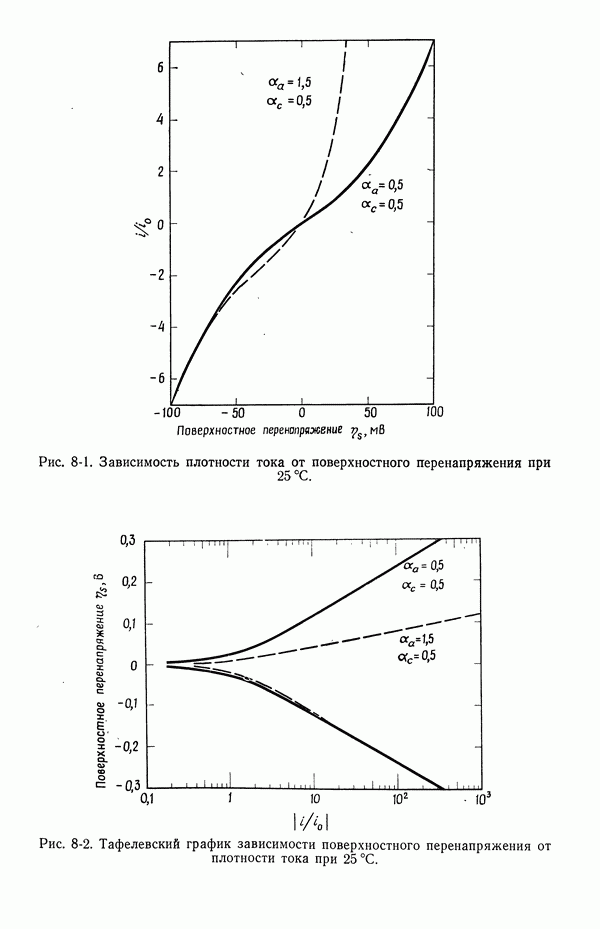
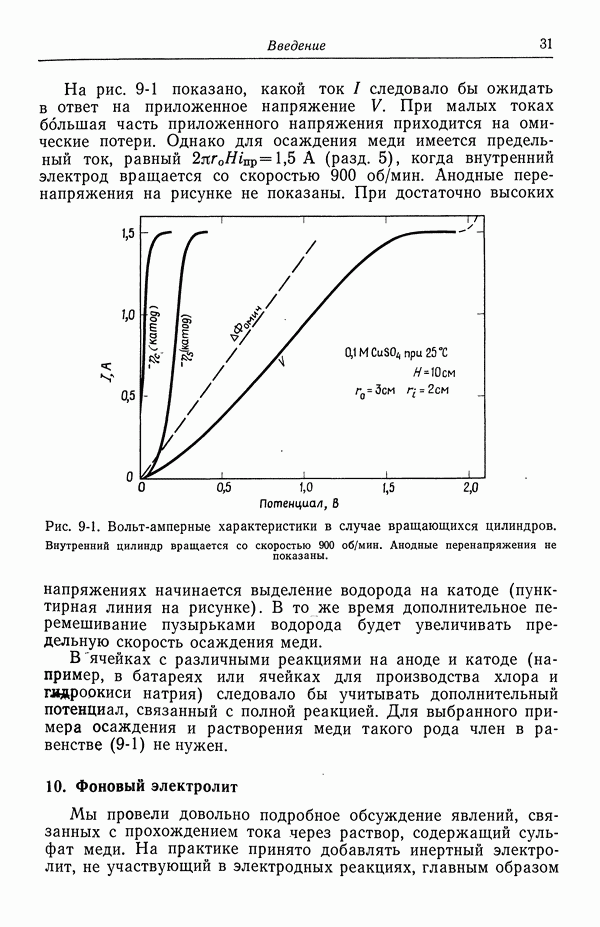
- 8. Поверхностное перенапряжение
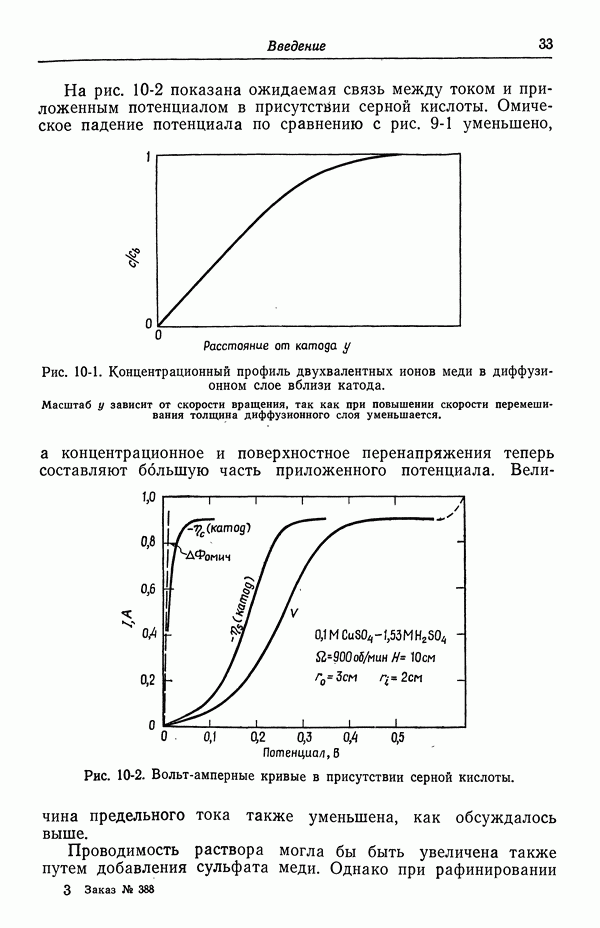
- 9. Потенциал ячейки
- 10. Фоновый электролит
- 11. Свободная конвекция
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая—Хюккеля
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
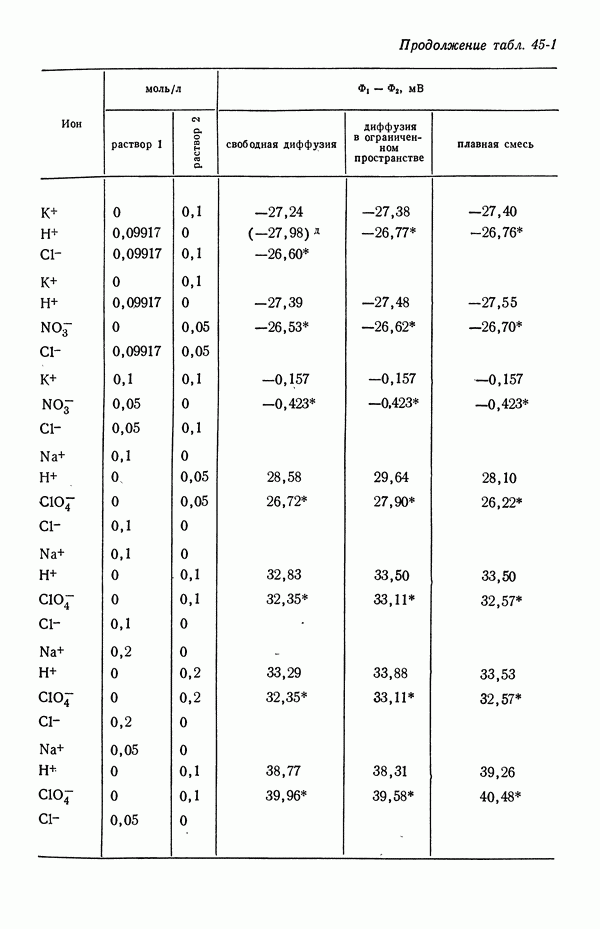
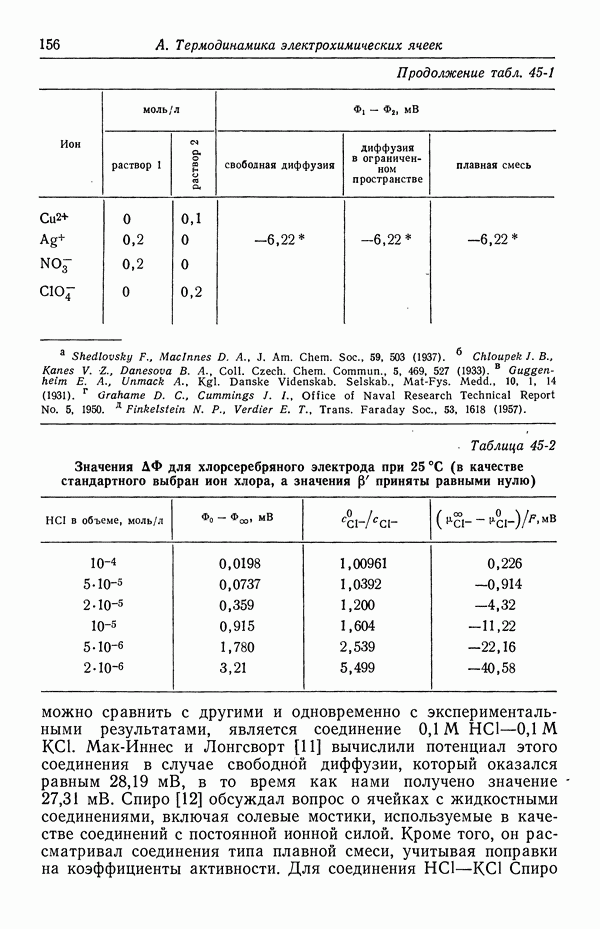
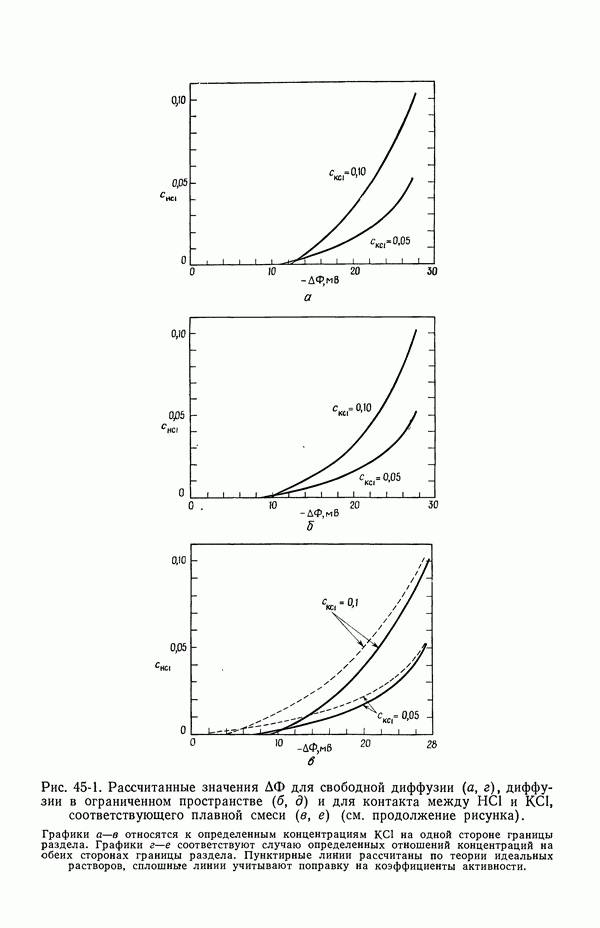
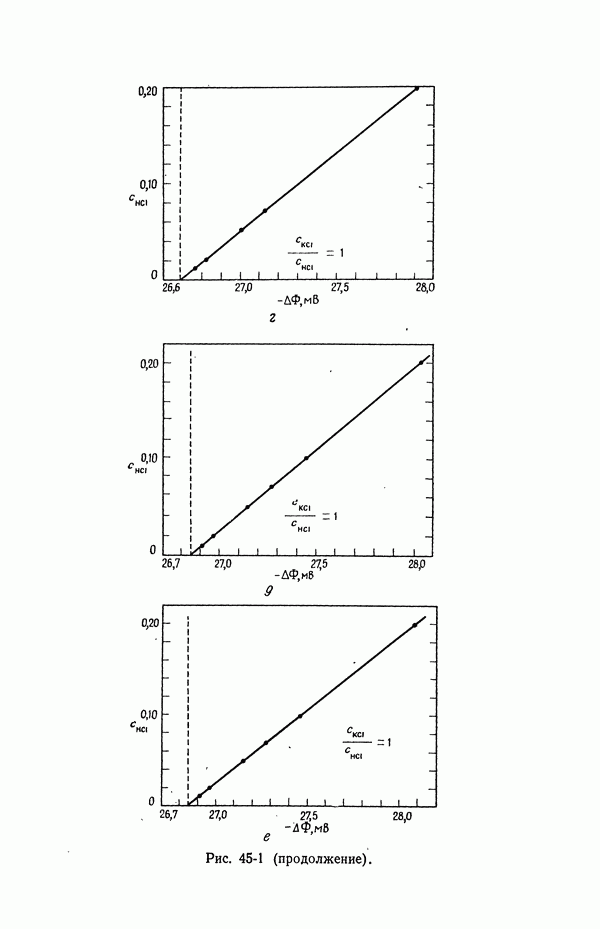
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
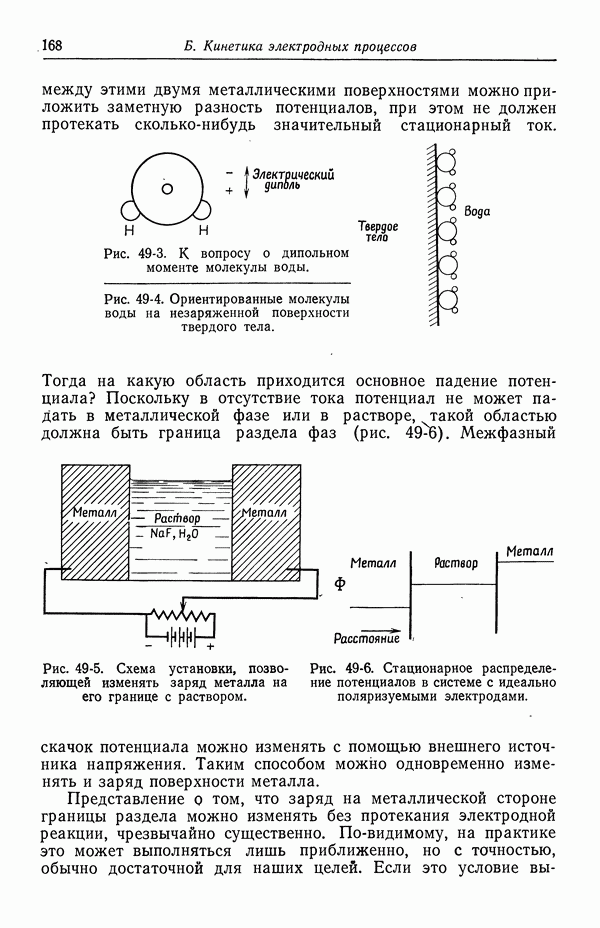
- 49. Качественное описание двойных слоев
- 50. Изотерма адсорбции Гиббса
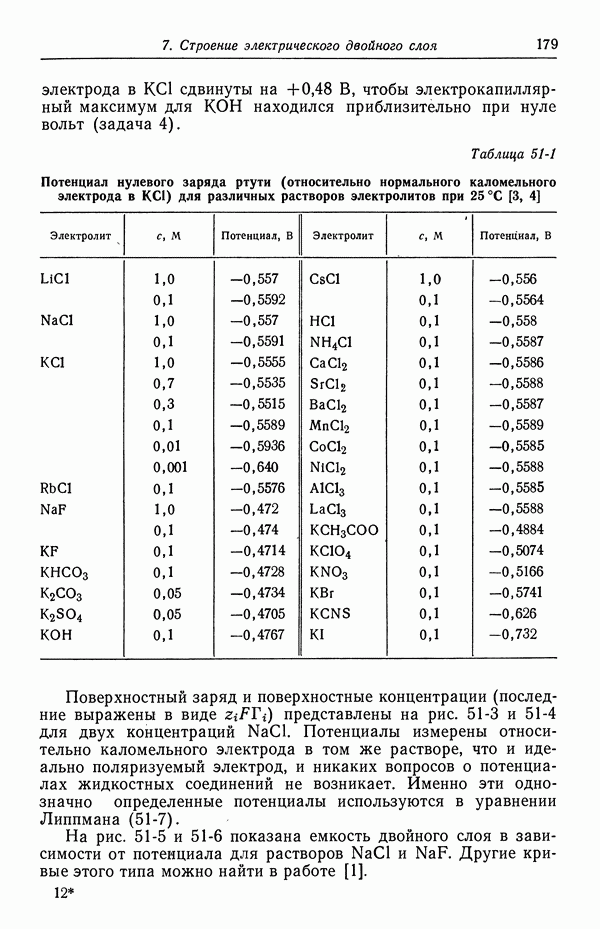
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод — раствор
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 66. Динамика границы раздела
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 69. Законы переноса
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 78. Законы переноса
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 92. Интегральные коэффициенты диффузии
- ЗАДАЧА
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 111. Свободная конвекция
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
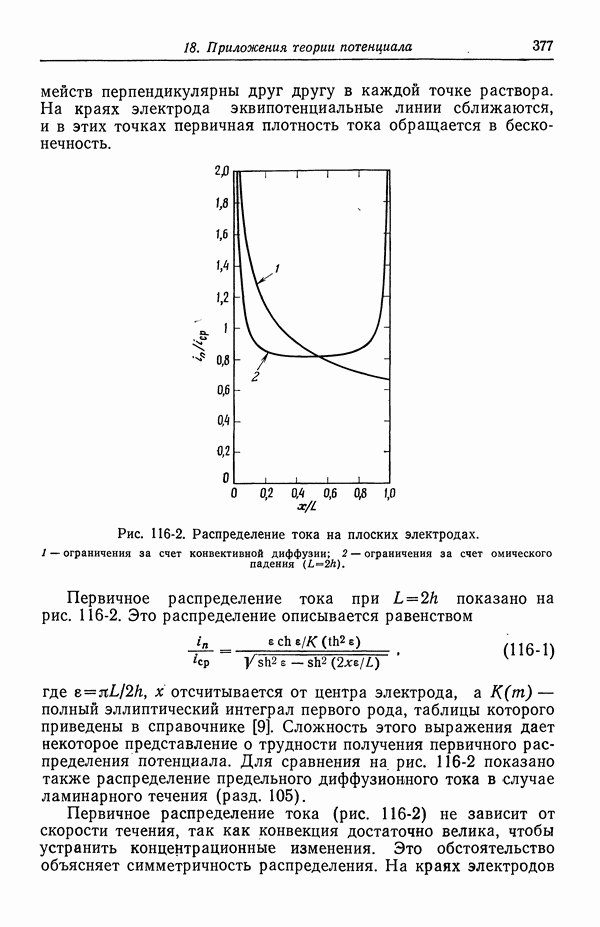
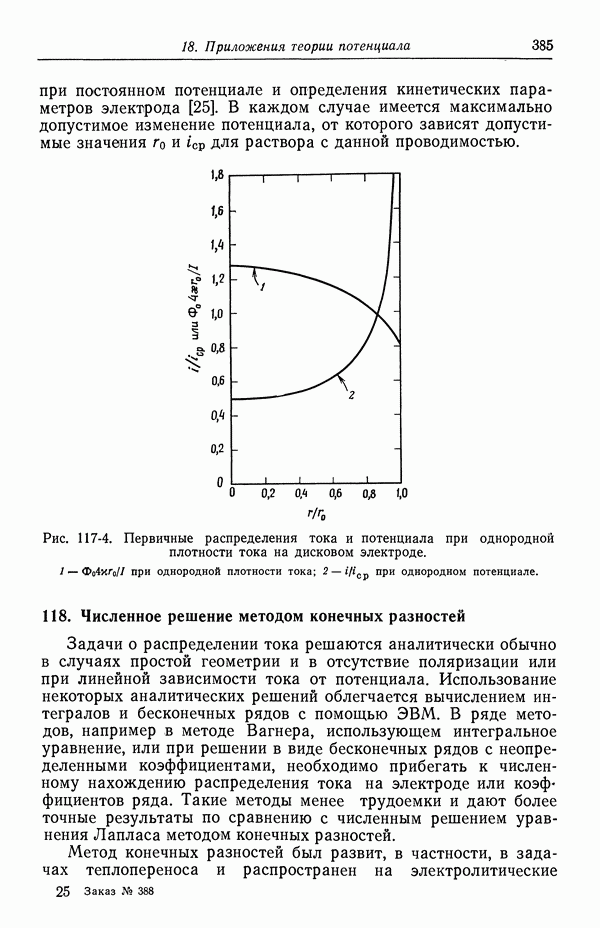
- 116. Первичное распределение тока
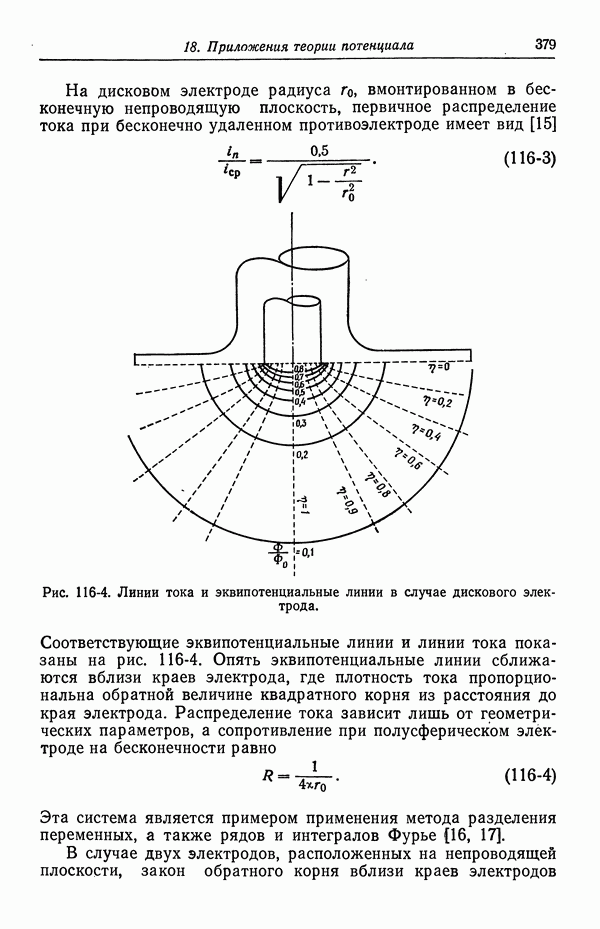
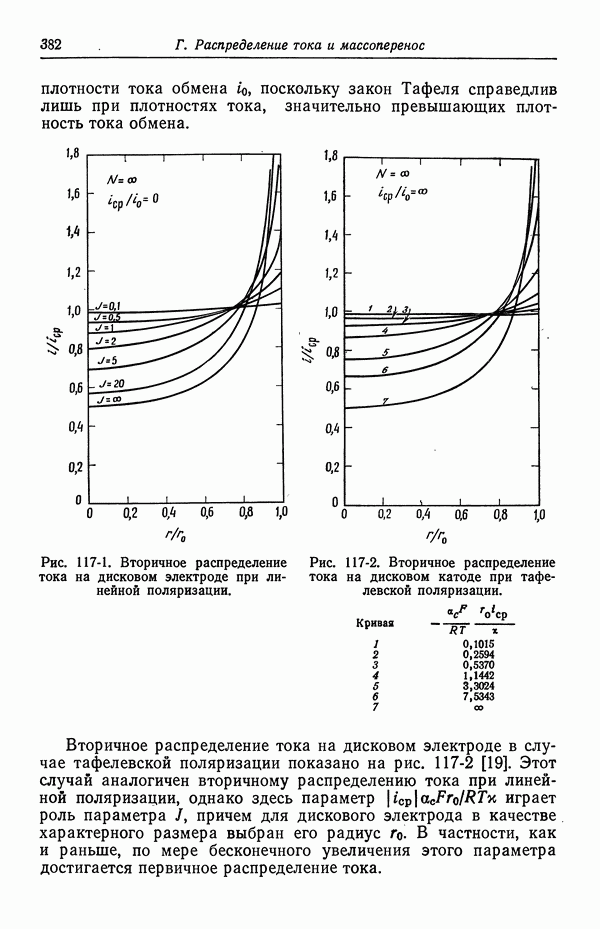
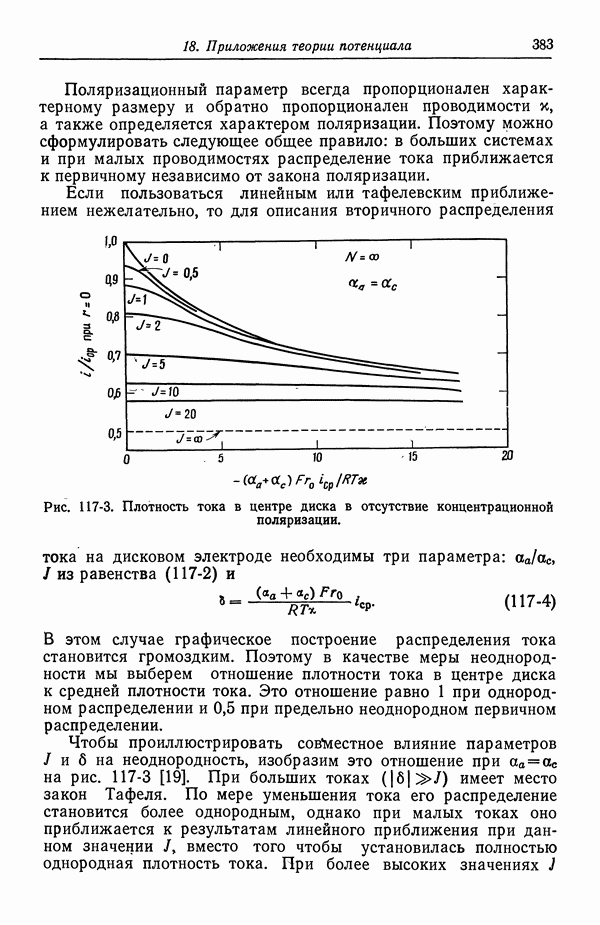
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- СПИСОК ОБОЗНАЧЕНИЙ
- ГЛАВА 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 119. Решение задачи
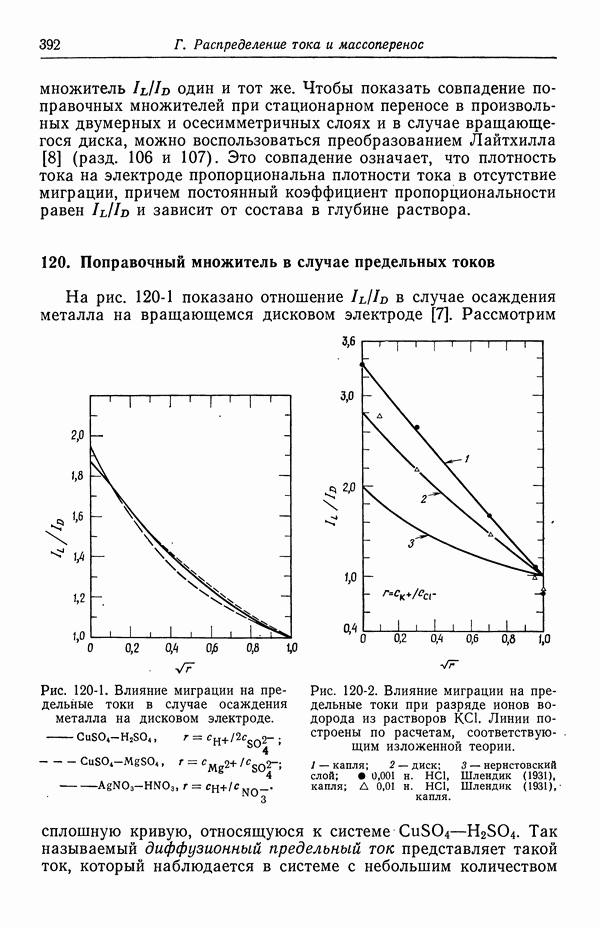
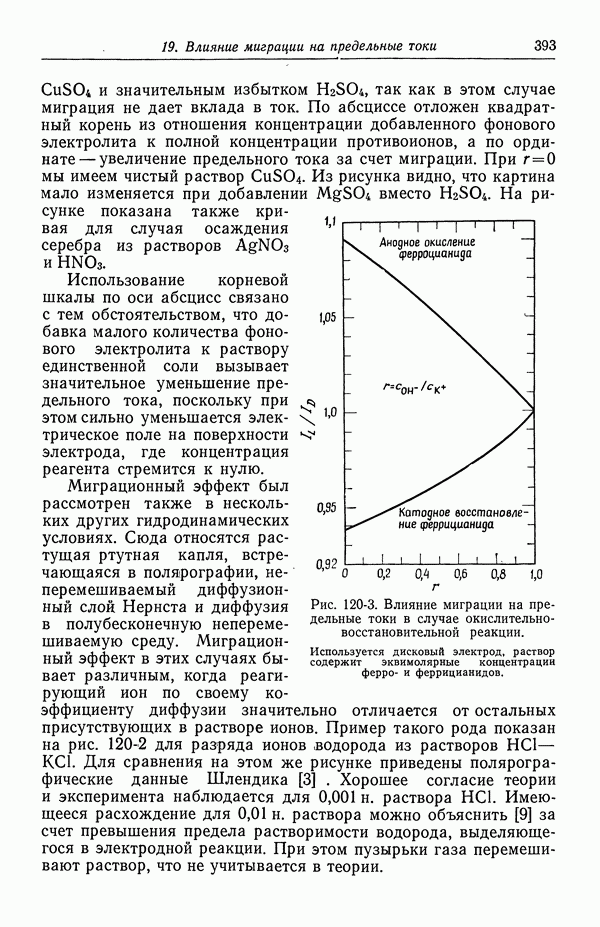
- 120. Поправочный множитель в случае предельных токов
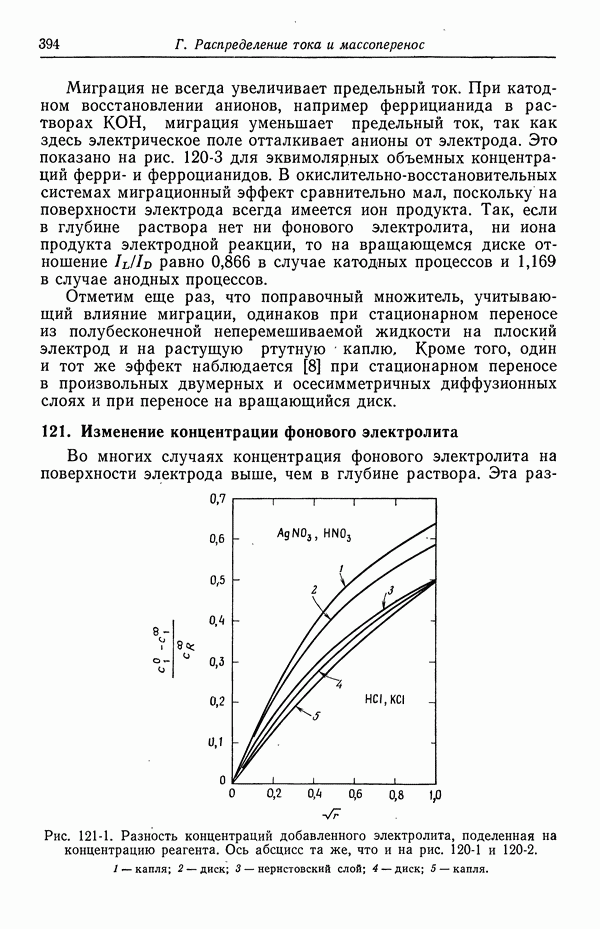
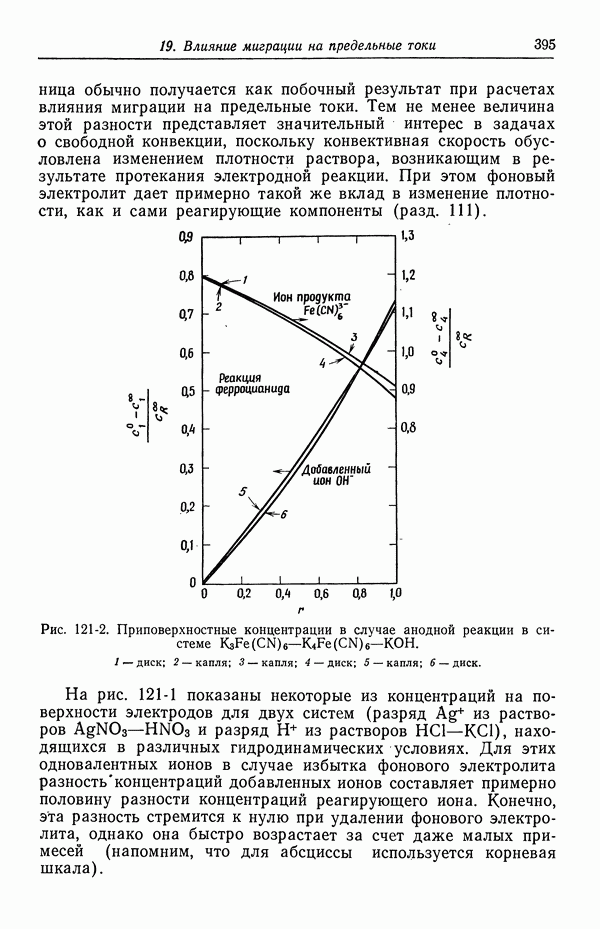
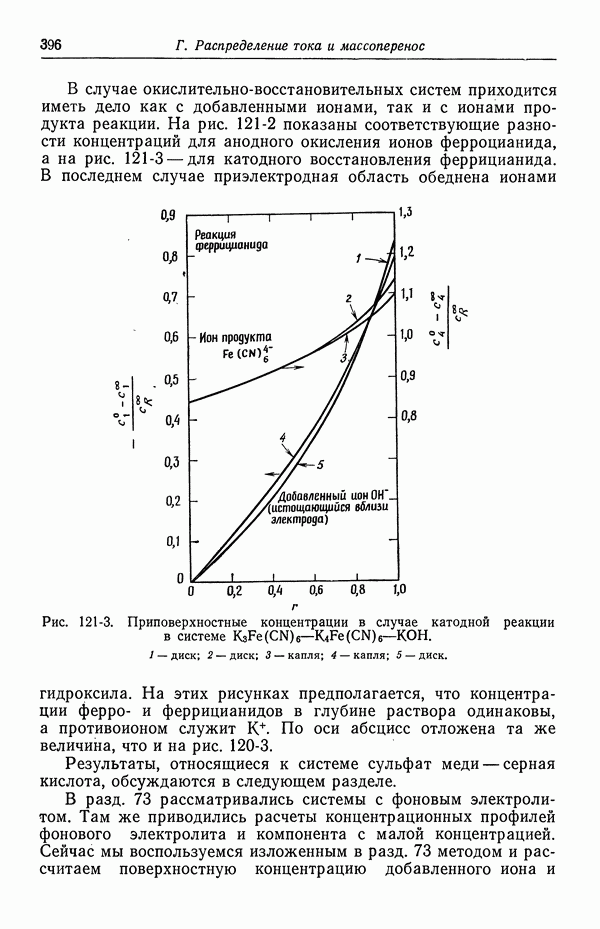
- 121. Изменение концентрации фонового электролита
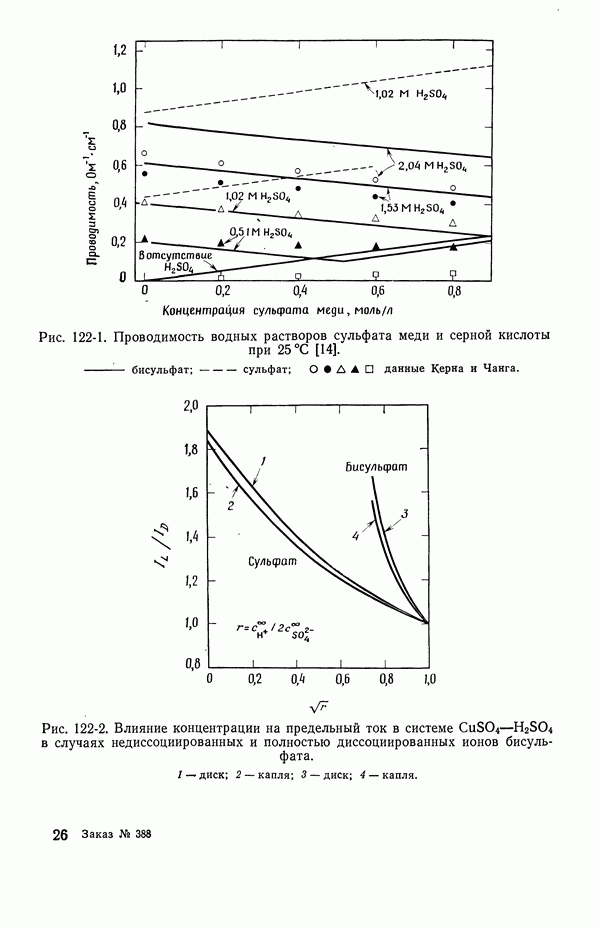
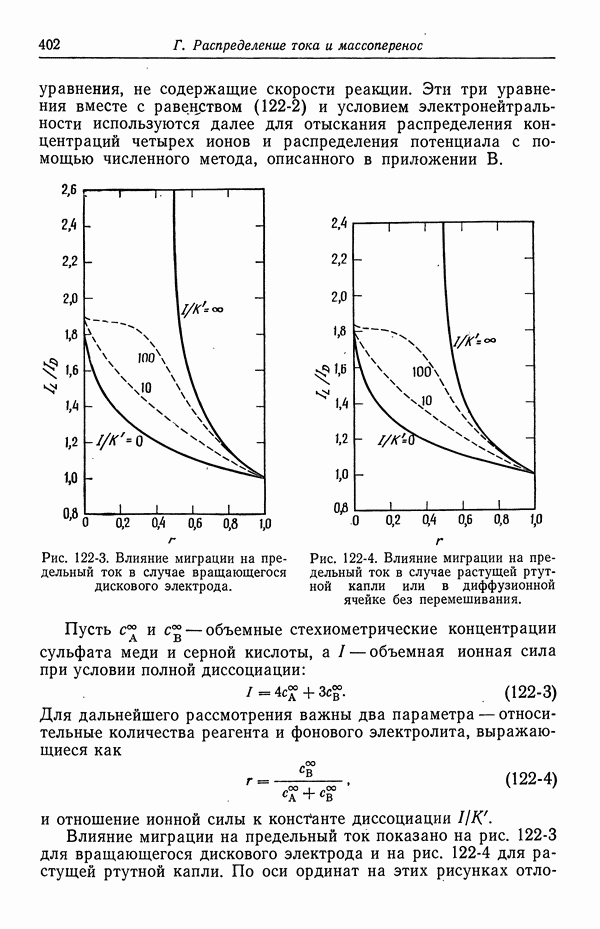
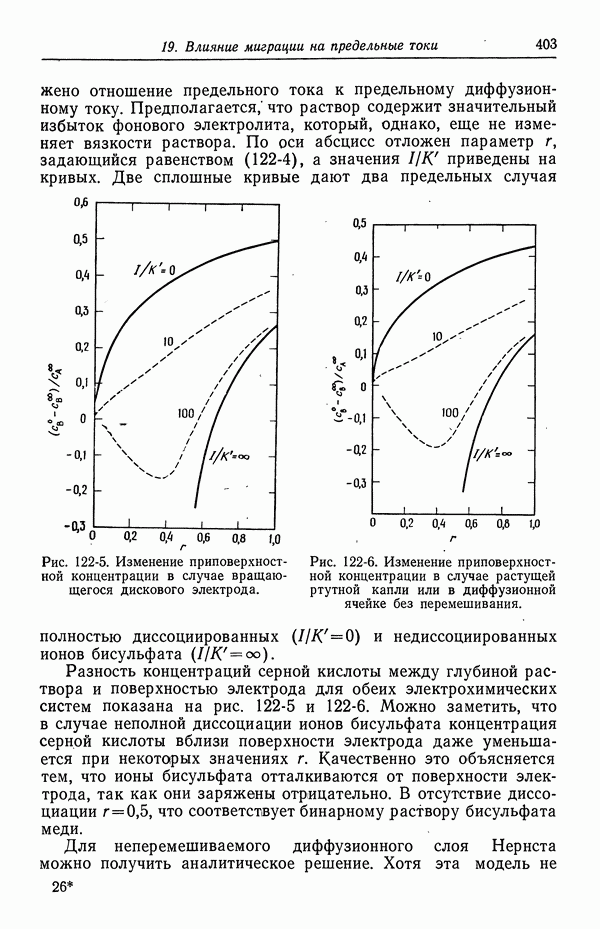
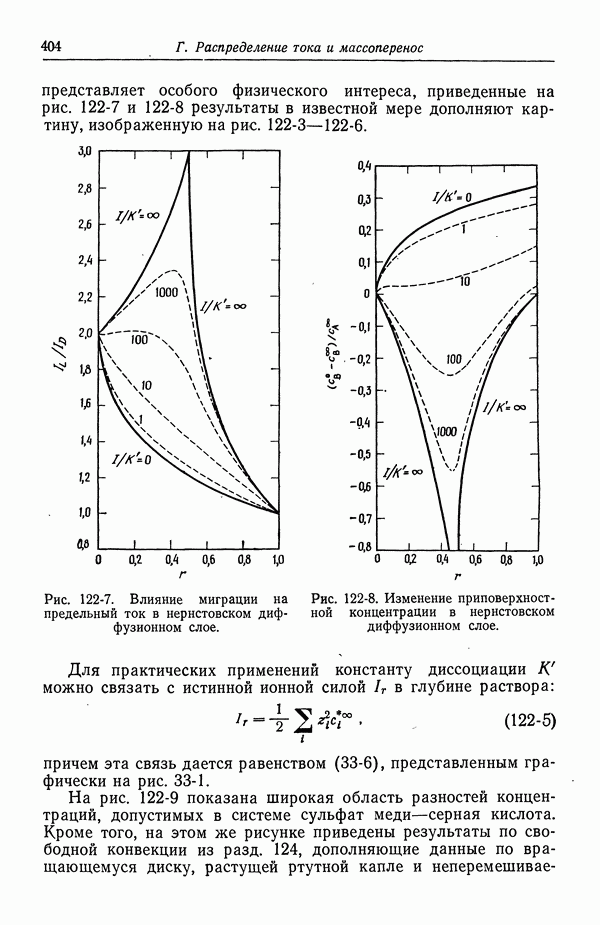
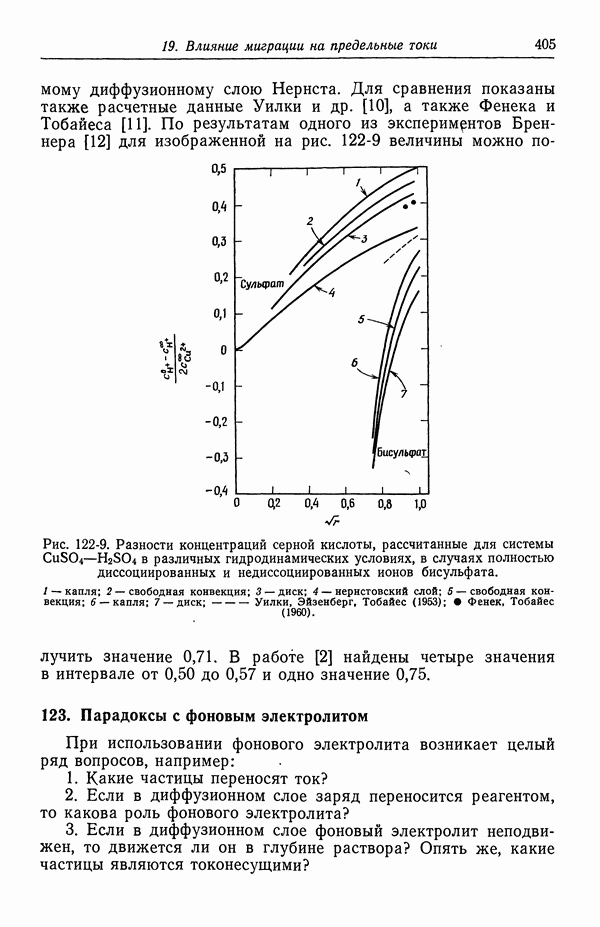
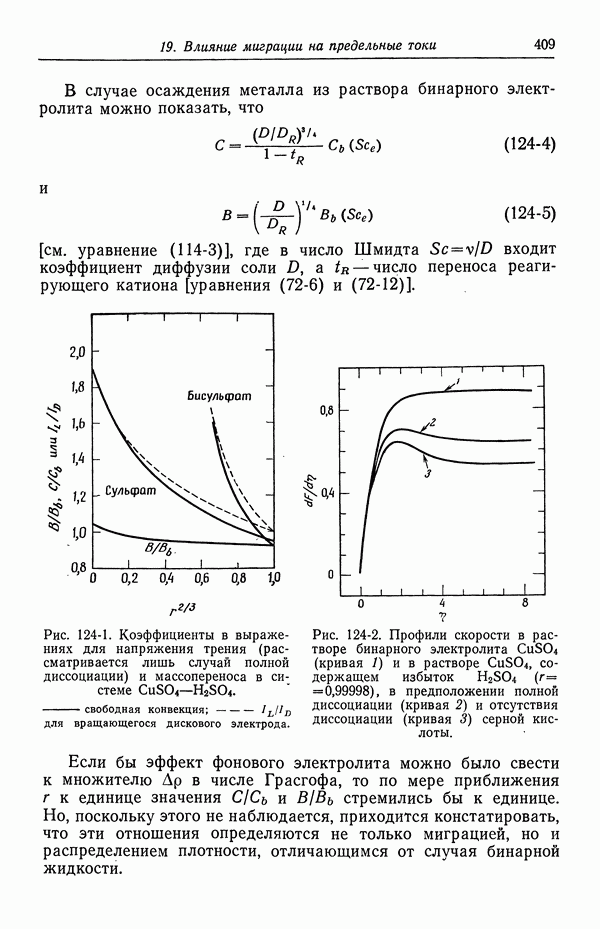
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ