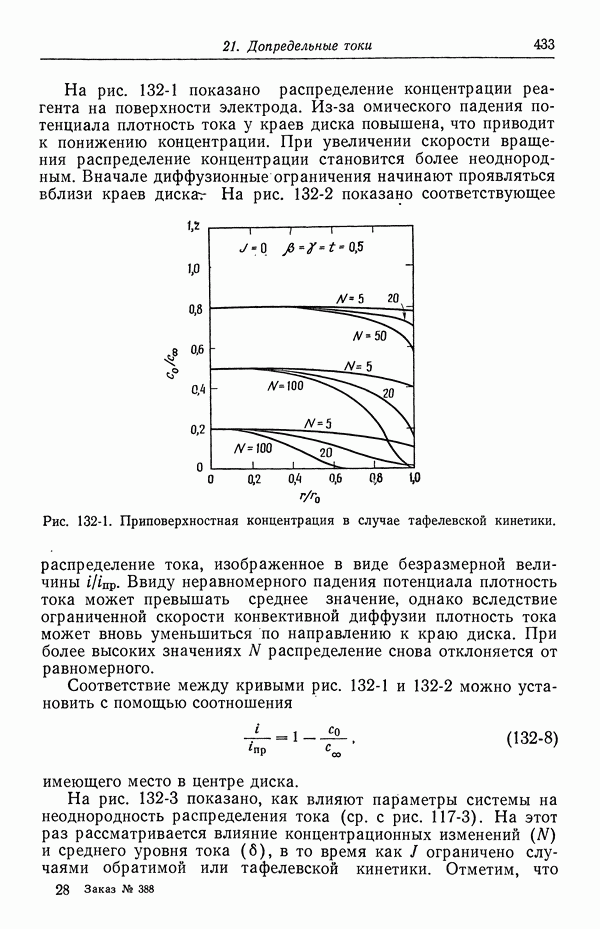
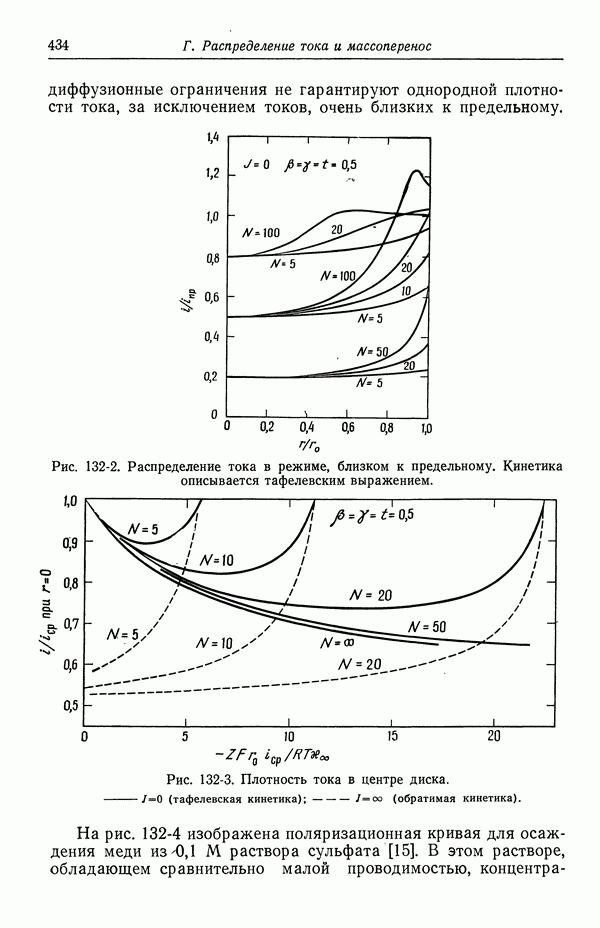
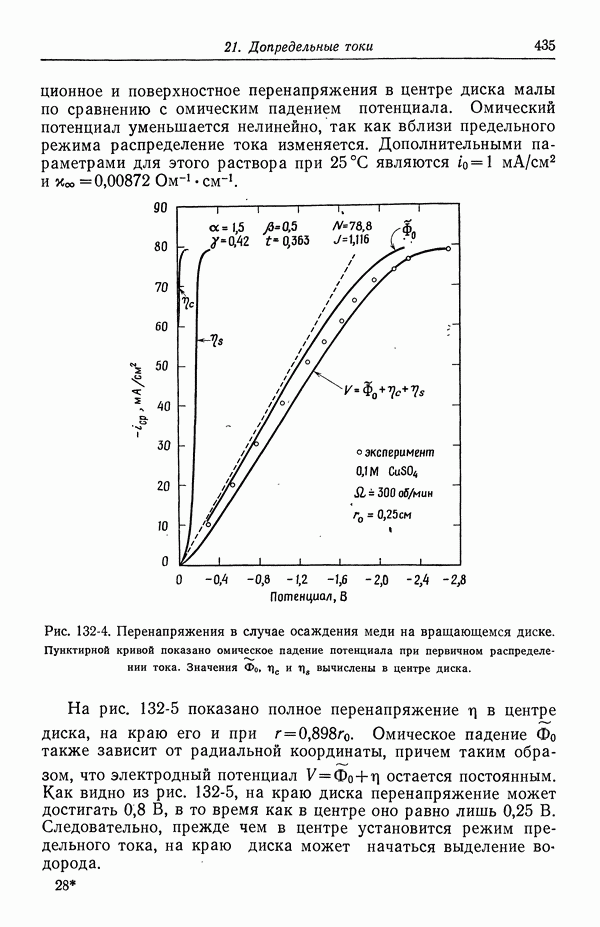
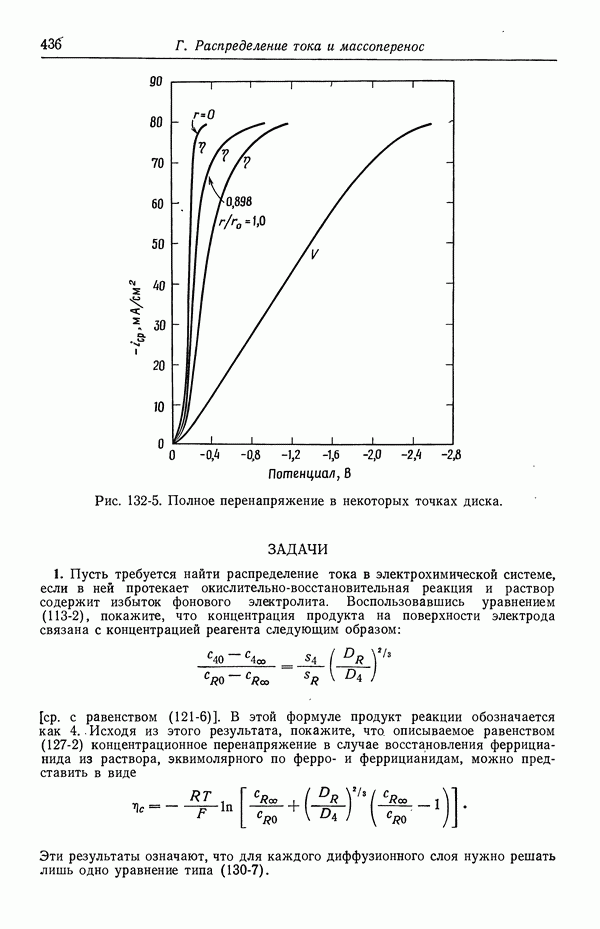
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
23. Межмолекулярные силы
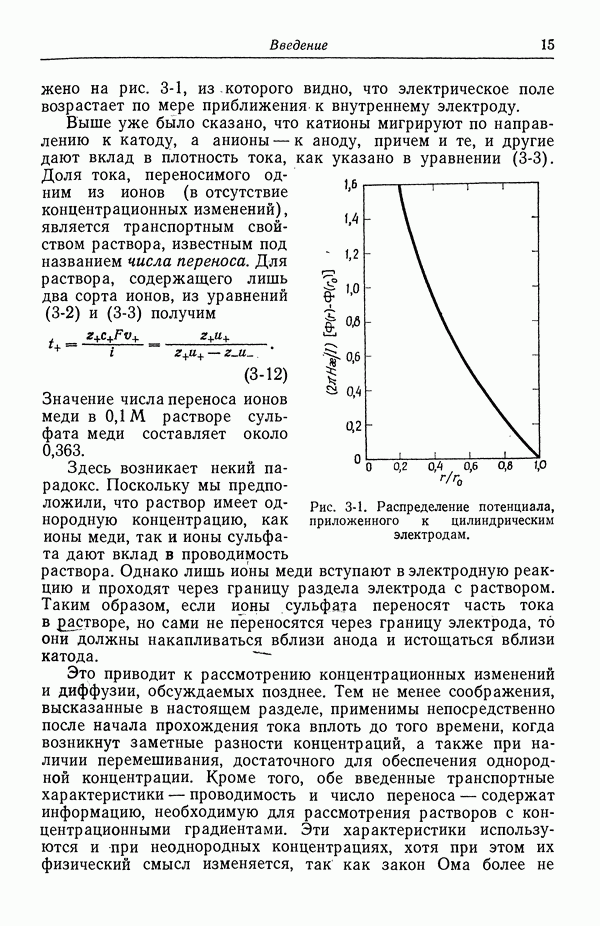
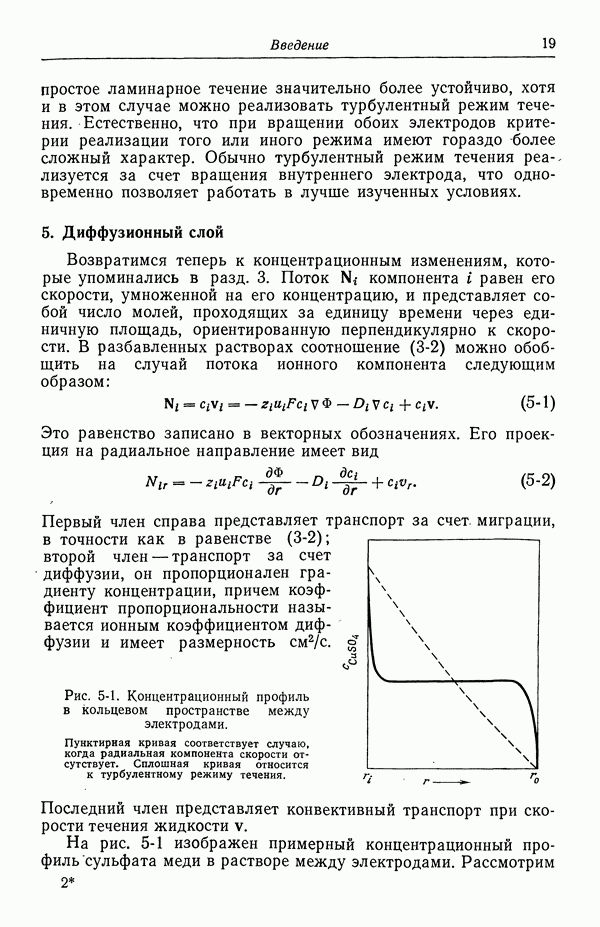
Энергия взаимодействия двух ионов несколько идеализированно представлена на рис. 23-1. Соответствующая сила показана на рис. 23-2. Заслуживающей упоминания особенностью таких взаимодействий является их медленное убывание на больших расстояниях:

Эти частицы называются ионами, так как на больших расстояниях они взаимодействуют согласно закону Кулона, что отличает их от нейтральных неполярных или нейтральных полярных молекул, энергия взаимодействия которых имеет иную асимптотику:

На малых расстояниях силы межионного взаимодействия, изображенные на рис. 23-1 и 23-2, отличаются от описываемых равенствами (23-1). Поскольку это отклонение на малых расстояниях связано со специфической природой данных ионов, его приписывают так называемым специфическим силам коротко - действия. Конечно, разложение кривых рис. 23-1 и 23-2 на кулоновскую и специфическую части является искусственным, так как реально существует единое межмолекулярное взаимодействие и именно оно определяет поведение ионов.
Асимптотическое поведение, выражаемое равенствами (23-1), носит достаточно общий характер и вызывает значительные трудности, заслуживающие специального рассмотрения. Описанию кулоновских взаимодействий отводится заметное место
в электростатике и теории электромагнитного поля. В частности, там получено и выражение (22-7) для электростатического потенциала.
Наиболее прямо результаты и методы электростатической теории применимы к разреженным ионизированным газам, рассматривать которые целесообразно по двум причинам.
Во-первых, в этом случае имеется значительное свободное пространство, так что вполне можно принять, что введение пробного заряда существенно не возмущает систему. В конденсированной фазе, напротив, все пространство занято.

Рис. 23-1. Потенциальная энергия взаимодействия двух ионов, находящихся на расстоянии  друг от друга.
друг от друга.

Рис. 23-2. Сила взаимодействия между двумя ионами.
Во-вторых, ионы значительно удалены друг от друга, так что на малых расстояниях ион взаимодействует одновременно не более чем с одним ионом. Такое взаимодействие на малых расстояниях можно назвать столкновением. Рассматривая ионизированный газ, можно учитывать лишь бинарные взаимодействия, или парные столкновения [4]. В ионизированном газе, где сила взаимодействия обратно пропорциональна квадрату расстояния, данный ион всегда взаимодействует со всеми остальными. Некоторый прогресс в этом отношении достигается за счет введения электрического потенциала, учитывающего взаимодействия с удаленными ионами. Тогда парным будет взаимодействие с другим ионом на малых расстояниях, на которых кулоновский закон уже не выполняется, и такое взаимодействие можно рассматривать отдельно.
Однако и в этом случае разбиение межмолекулярного взаимодействия на различные части, скажем на электрическую и
химическую, не имеет под собой физической основы. Аналогичная трудность возникает при попытках разделить электрохимические потенциалы, использованные в гл. 2, на химические и электрические потенциалы.
Электростатическую теорию можно несколько модифицировать для рассмотрения конденсированных фаз, представляющих собой слабую примесь заряженных частиц в однородной диэлектрической среде. В этом случае электрическое поле заряженных частиц индуцирует в диэлектрической среде диполи или вызывает предпочтительную ориентацию уже имевшихся диполей. Наличие всех этих наведенных в среде зарядов можно учесть введением усредненного электрического поля и усредненного электростатического потенциала. Тогда суммирование в уравнении (22-7) распространяется на все заряженные частицы, кроме зарядов, наведенных в диэлектрической среде. Величины Е и Ф усредняются - по областям пространства, имеющим по меньшей мере молекулярные размеры. При таком усреднении не вошедшие в сумму заряды диполей учитываются путем использования диэлектрической проницаемости среды  вместо проницаемости вакуума
вместо проницаемости вакуума 
Такой подход к рассмотрению конденсированных фаз может быть оправдан лишь при больших расстояниях между заряженными частицами, допускающих применение кулоновского закона, точно так же, как и в случае разреженного ионизированного газа. Кроме того, между заряженными частицами должно быть достаточное количество диэлектрика, чтобы можно было проводить Щднен: Следовательно, и Ф, и  являются макроскопическими величинами, поэтому совершенно бессмысленно обсуждать изменения Ф и
являются макроскопическими величинами, поэтому совершенно бессмысленно обсуждать изменения Ф и  на расстояниях порядка молекулярных размеров. Чтобы вычислить энергию, необходимую для перемещения заряженной частицы из однрй фазы в другую, требуется рассмотреть дополнительно энергию взаимодействия частицы с растворителем и характер распределения заряда вблизи поверхности раздела фаз.
на расстояниях порядка молекулярных размеров. Чтобы вычислить энергию, необходимую для перемещения заряженной частицы из однрй фазы в другую, требуется рассмотреть дополнительно энергию взаимодействия частицы с растворителем и характер распределения заряда вблизи поверхности раздела фаз.
Хотя концентрированные ионные растворы представляют непреодолимые трудности для электростатической теории, кулоновский закон обратного квадрата имеет много важных следствий. Например, кулоновское притяжение между зарядами настолько велико, что отклонения от электронейтральности в растворах электролитов невозможны. Этот вывод справедлив, несмотря на то что на малых расстояниях межионные силы отклоняются от закона Кулона.
Электростатическая модель разбавленной взвеси заряженных частиц в диэлектрической среде была успешно применена в теории Дебая и Хюккеля для вычисления коэффициентов активности крайне разбавленных растворов электролитов. Хотя результаты
и сама модель применимы лишь в пределе бесконечного разбавления, сильные отклонения от поведения идеального раствора можно с уверенностью приписать закону обратного квадрата, управляющего силами между ионами на больших расстояниях. В той же модели можно найти проявление этих сил дальнодействия в других свойствах раствора при больших разбавлениях, что в особенности относится к проводимости.
Силы дальнодействия важны также в электродных процессах. В неравновесном двойном слое на ион могут действовать исключительно большие силы; при этом приходится говорить об очень большом градиенте потенциала в двойном слое вблизи поверхности электрода, хотя строгое определение этого потенциала может быть затруднительным.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. ВВЕДЕНИЕ
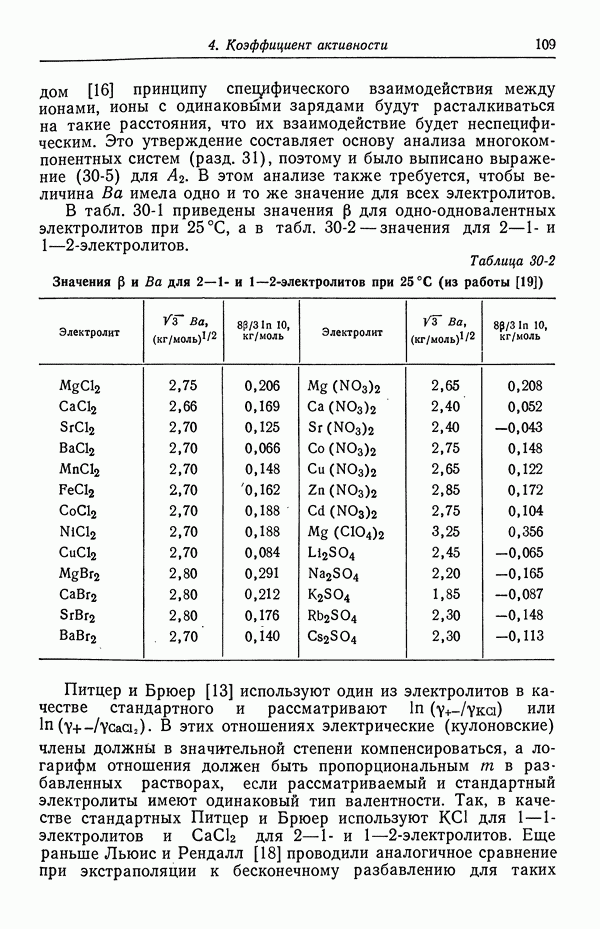
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
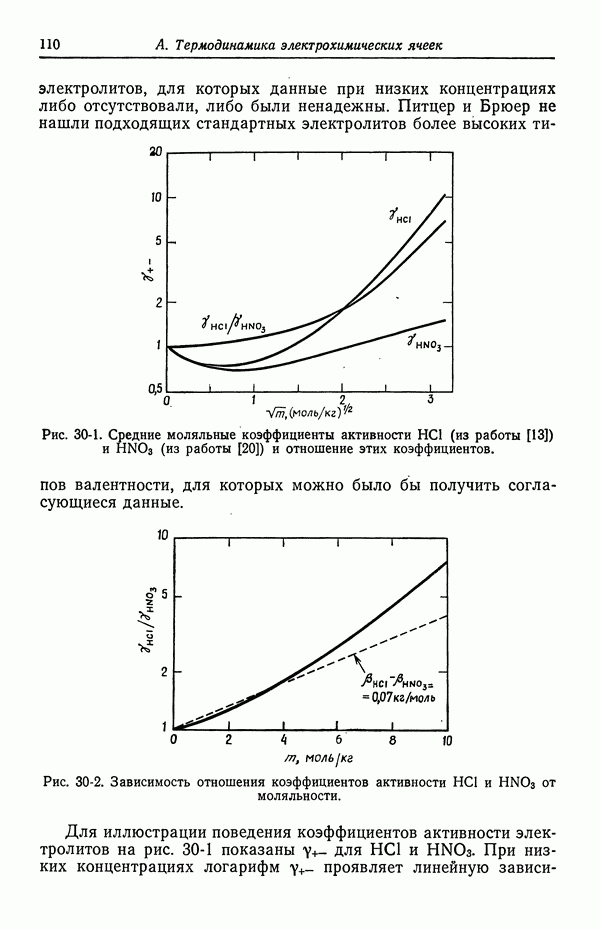
- 4. Течение жидкости
- 5. Диффузионный слой
- 6. Концентрационные ячейки
- 7. Концентрационное перенапряжение
- 8. Поверхностное перенапряжение
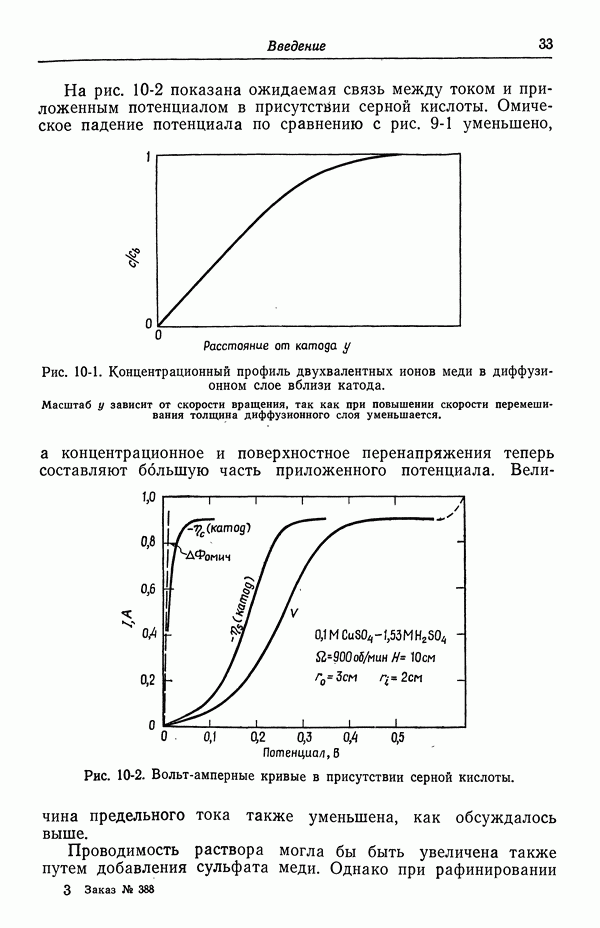
- 9. Потенциал ячейки
- 10. Фоновый электролит
- 11. Свободная конвекция
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
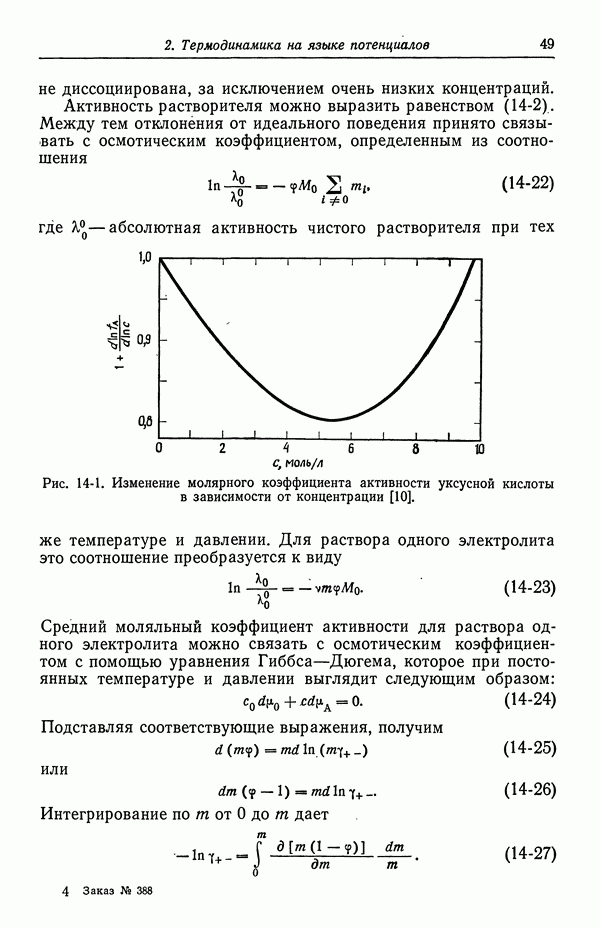
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
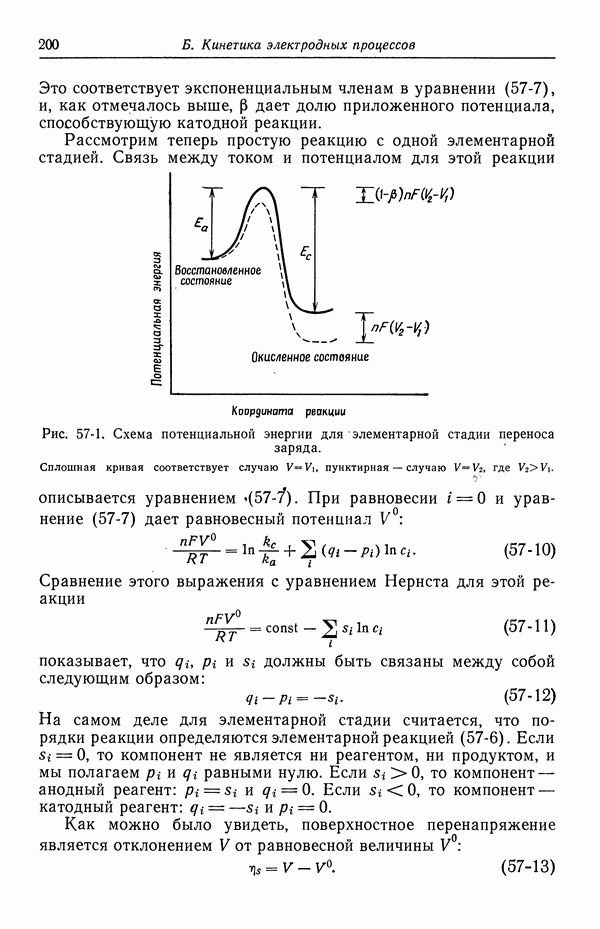
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- СПИСОК ОБОЗНАЧЕНИЙ
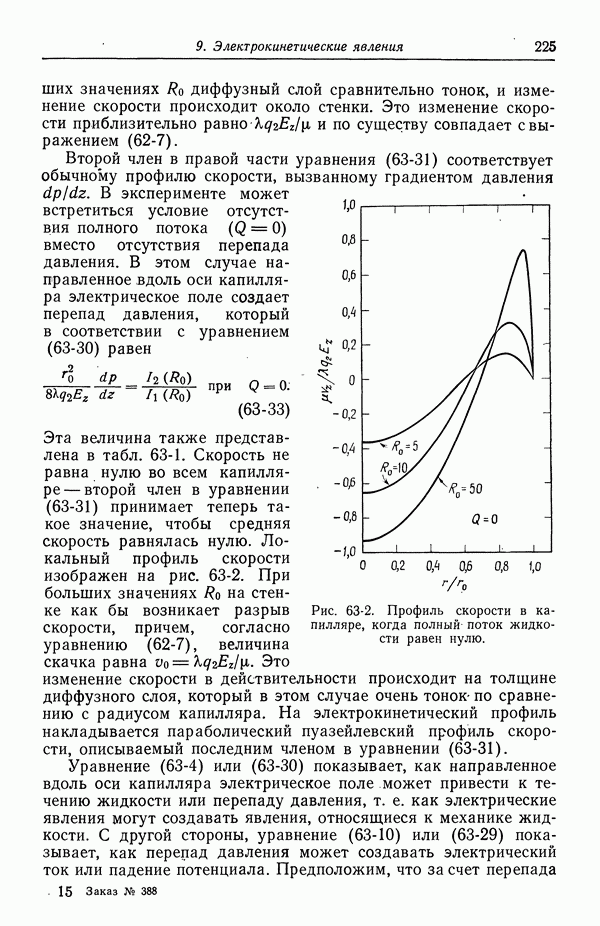
- СПИСОК ЛИТЕРАТУРЫ
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
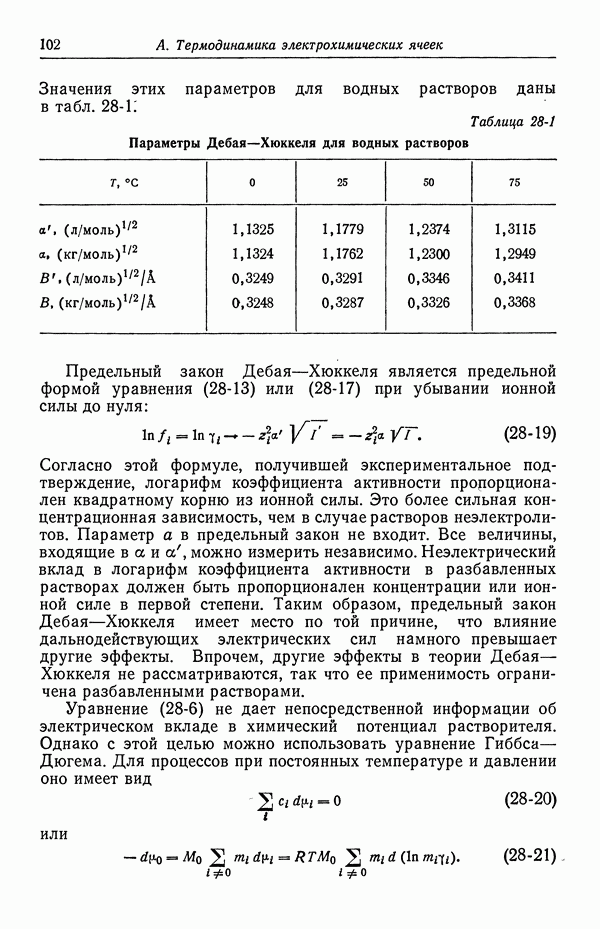
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая—Хюккеля
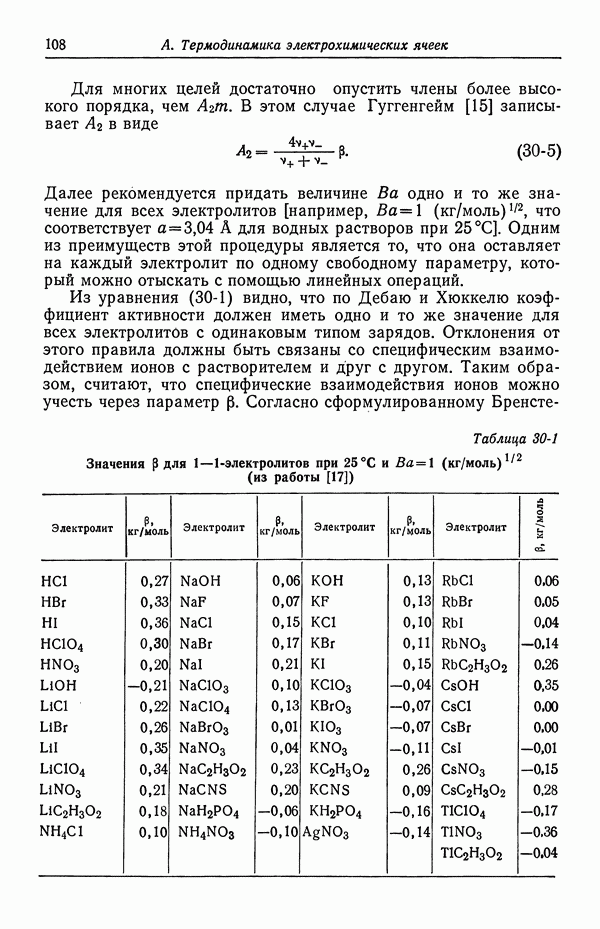
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
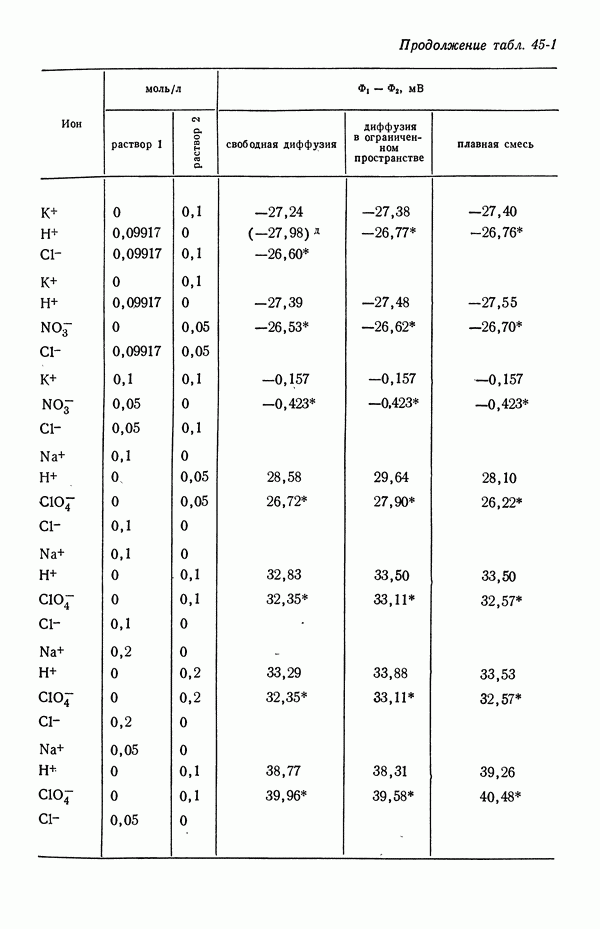
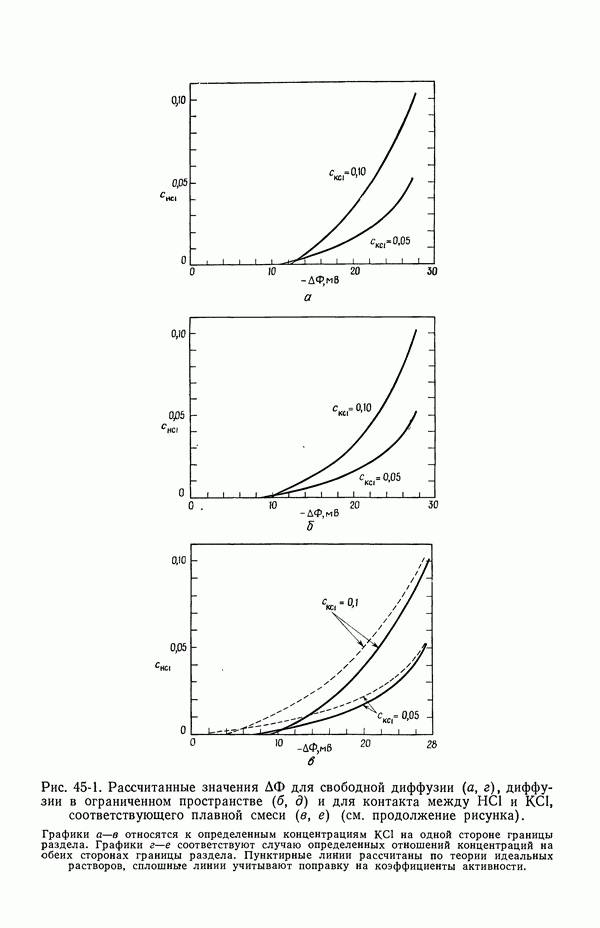
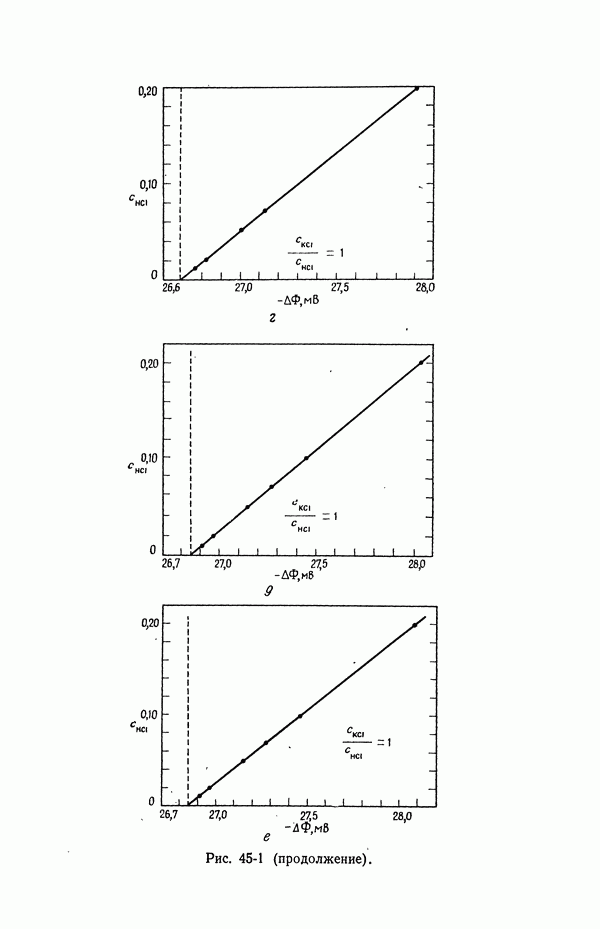
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
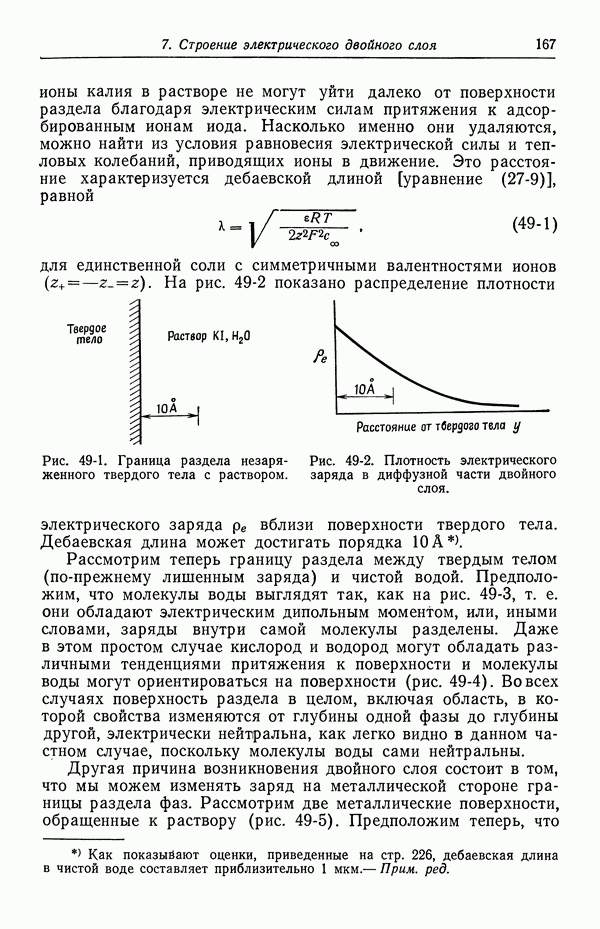
- 49. Качественное описание двойных слоев
- 50. Изотерма адсорбции Гиббса
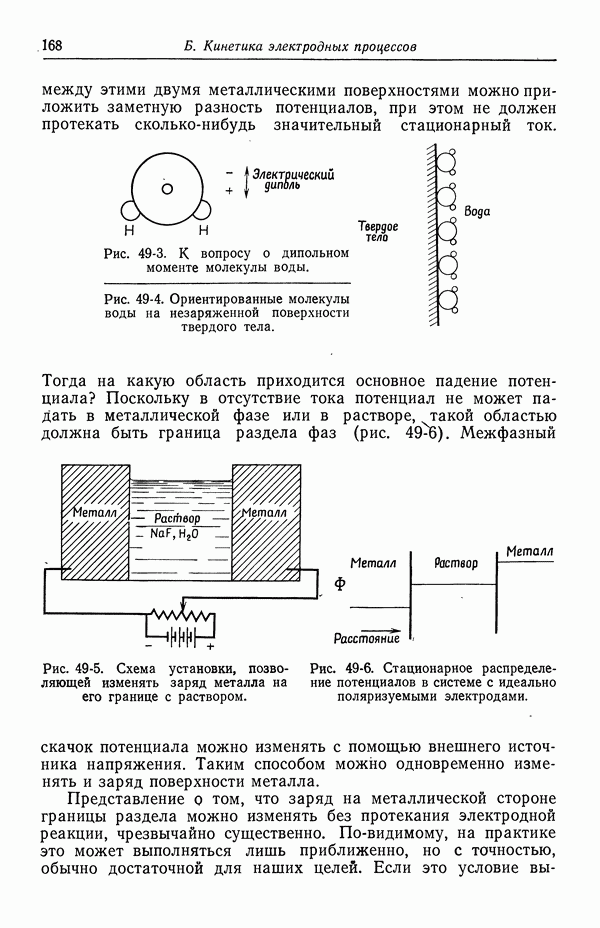
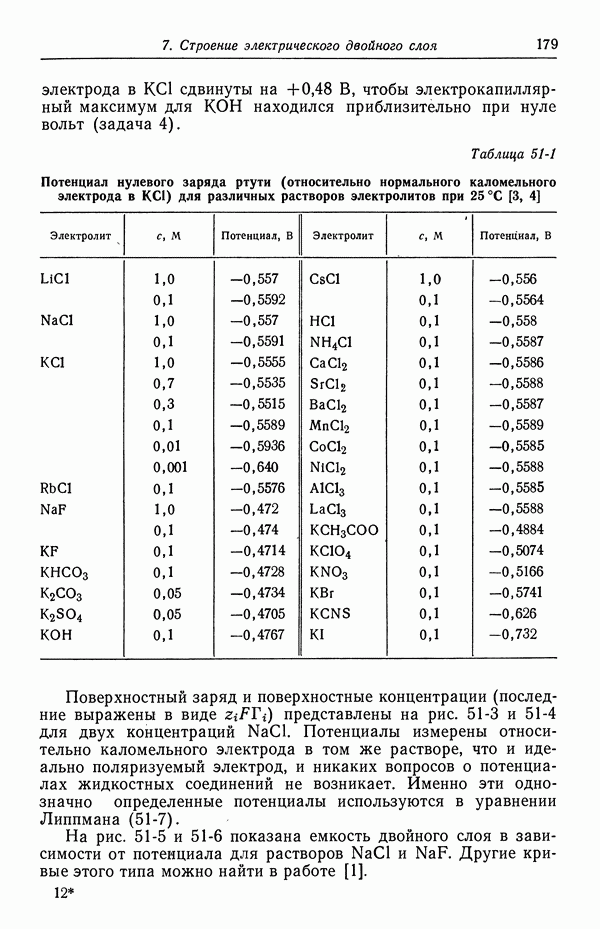
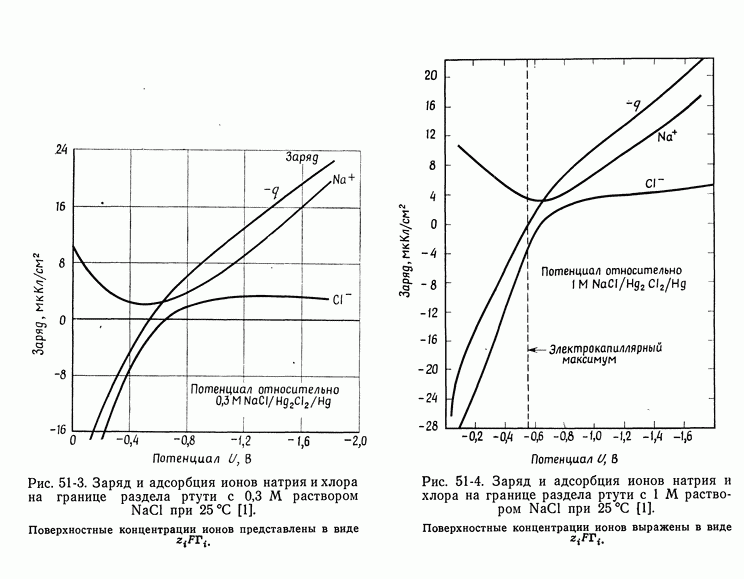
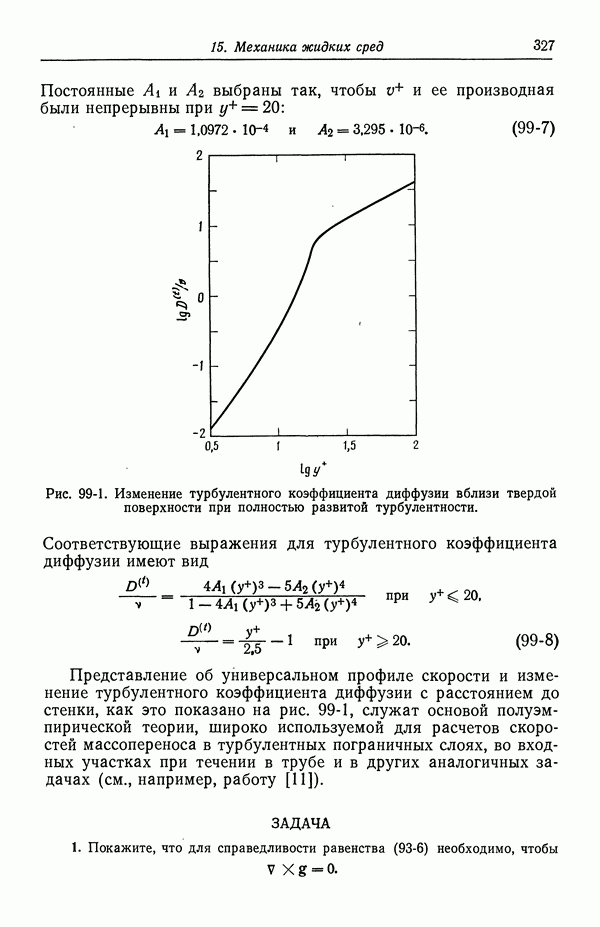
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
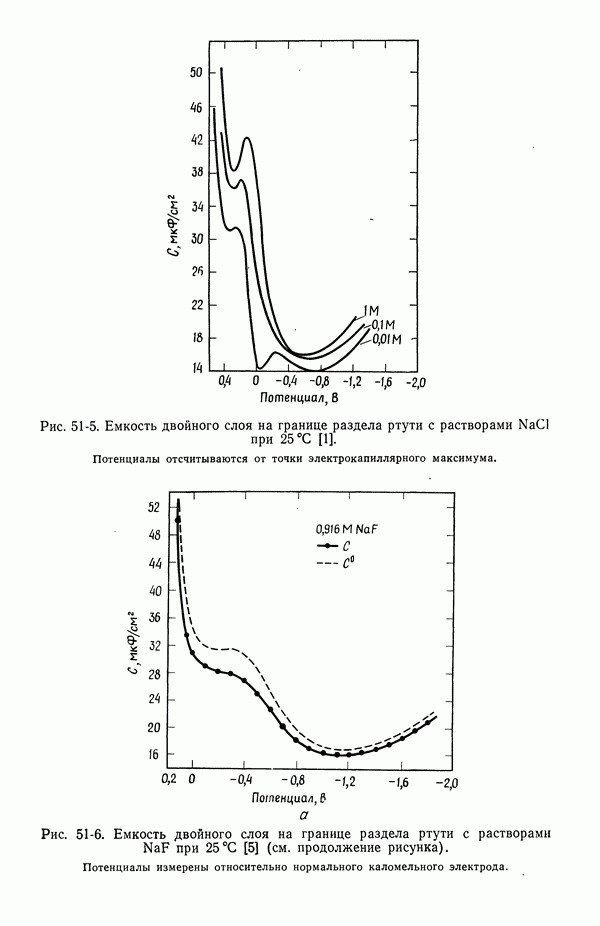
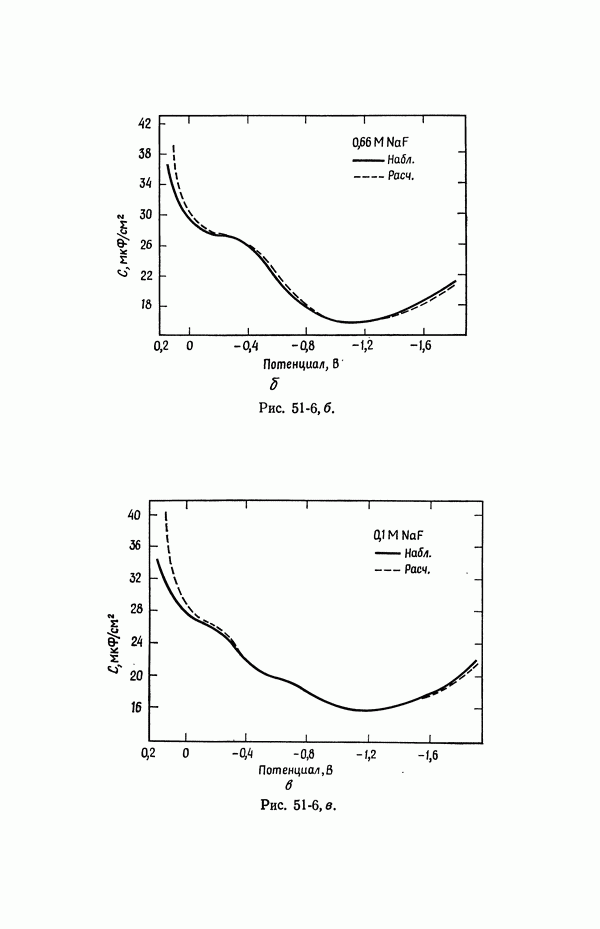
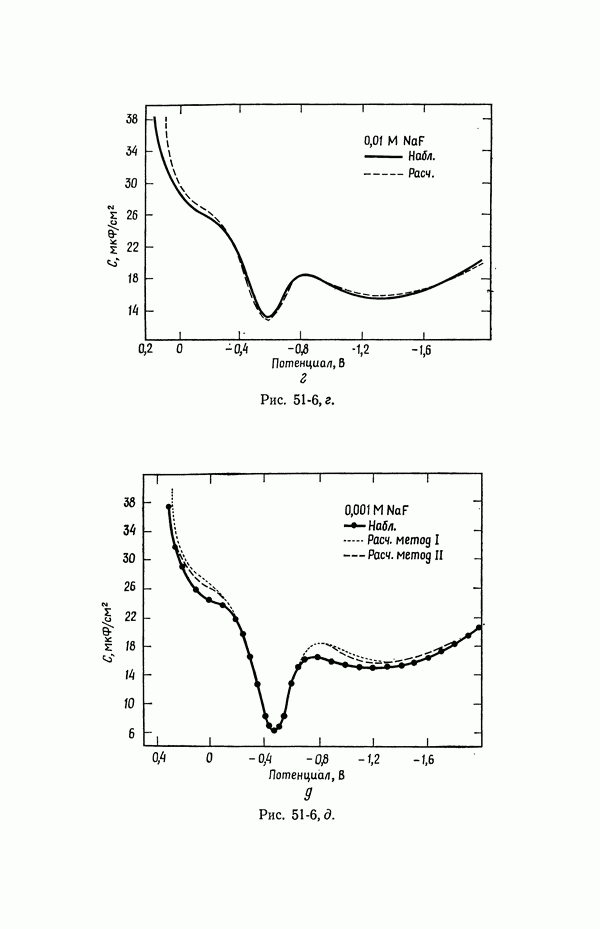
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод — раствор
- ЗАДАЧИ
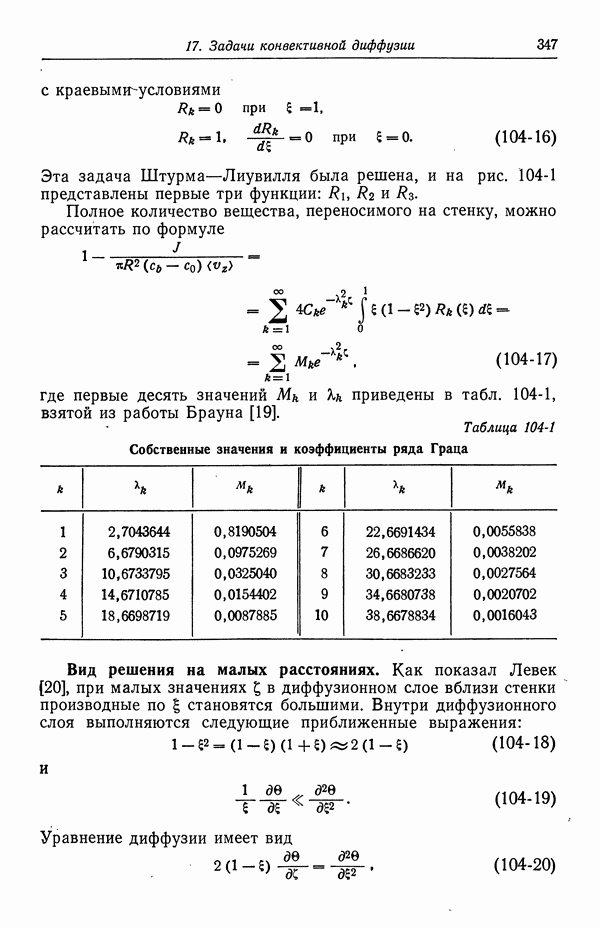
- СПИСОК ОБОЗНАЧЕНИЙ
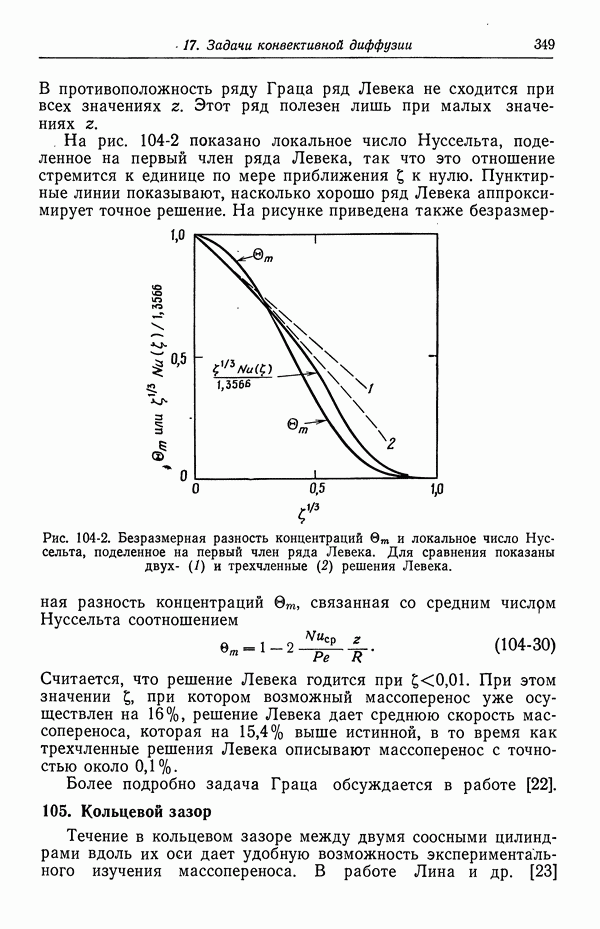
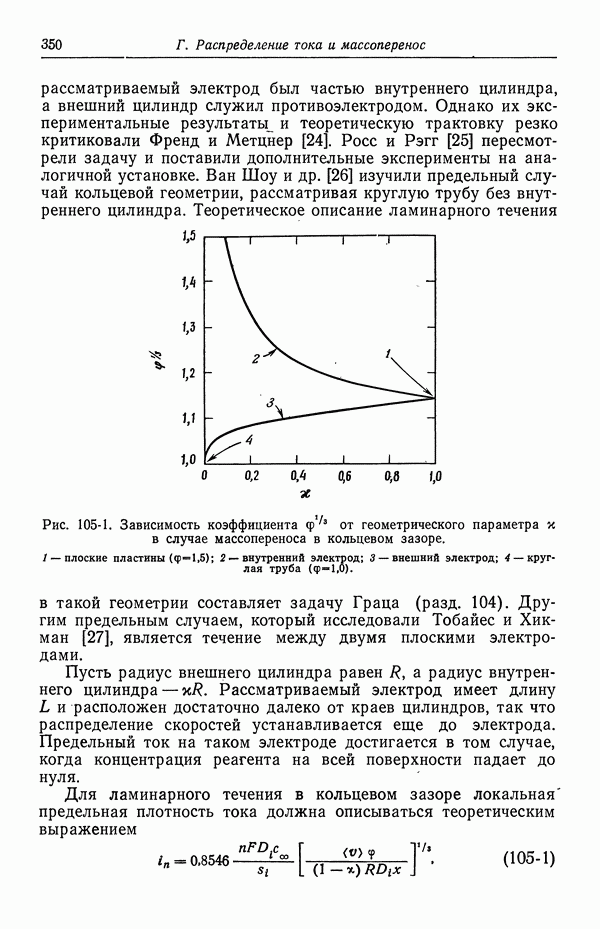
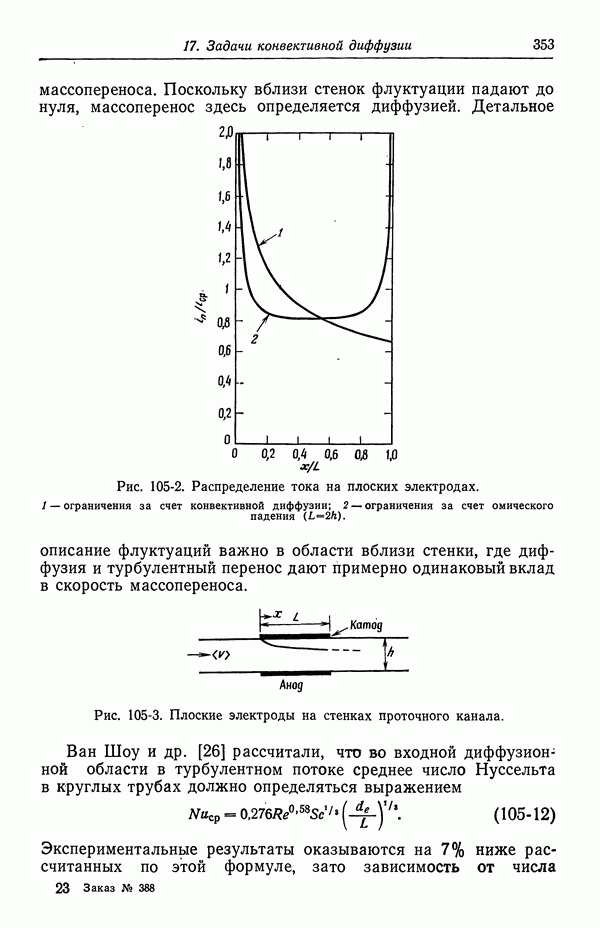
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
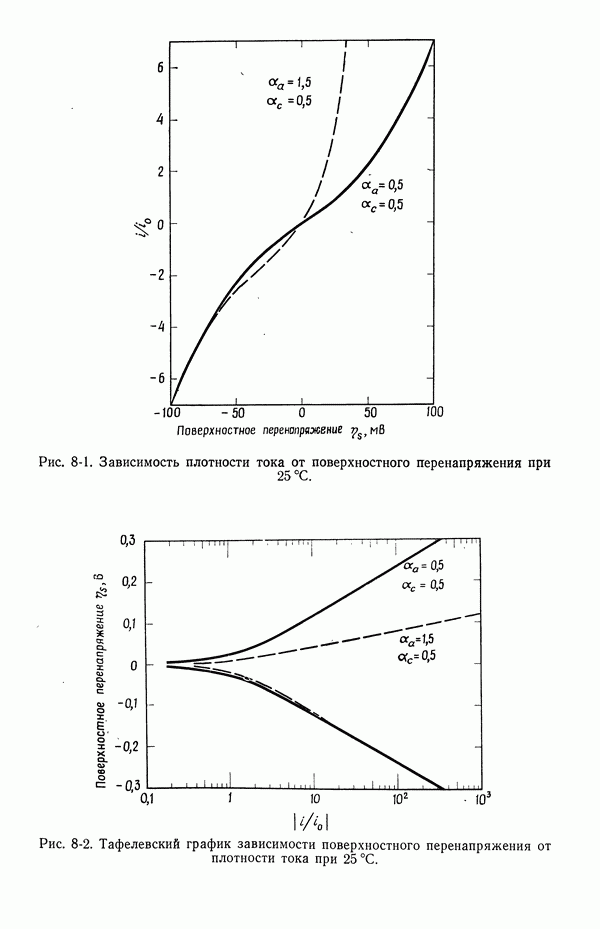
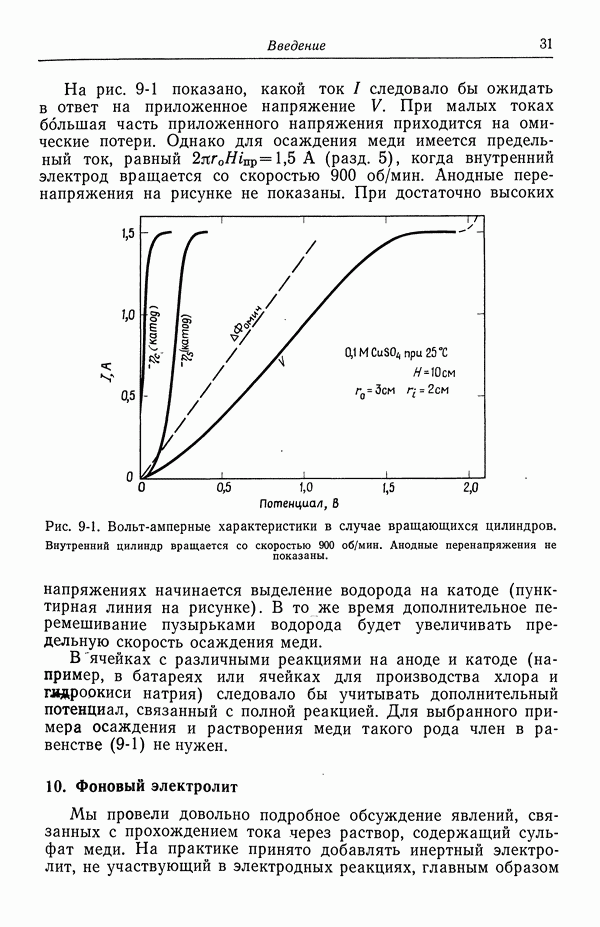
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
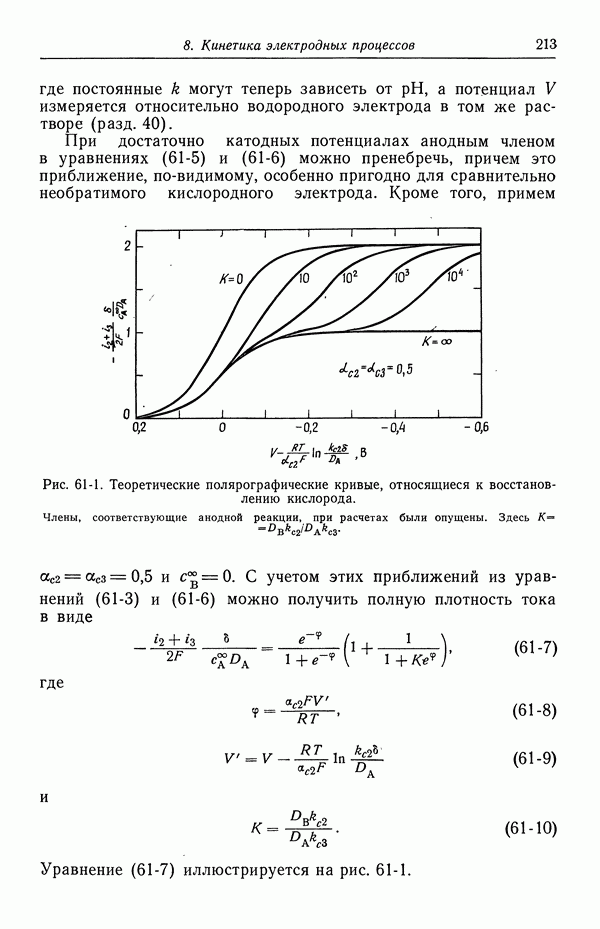
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
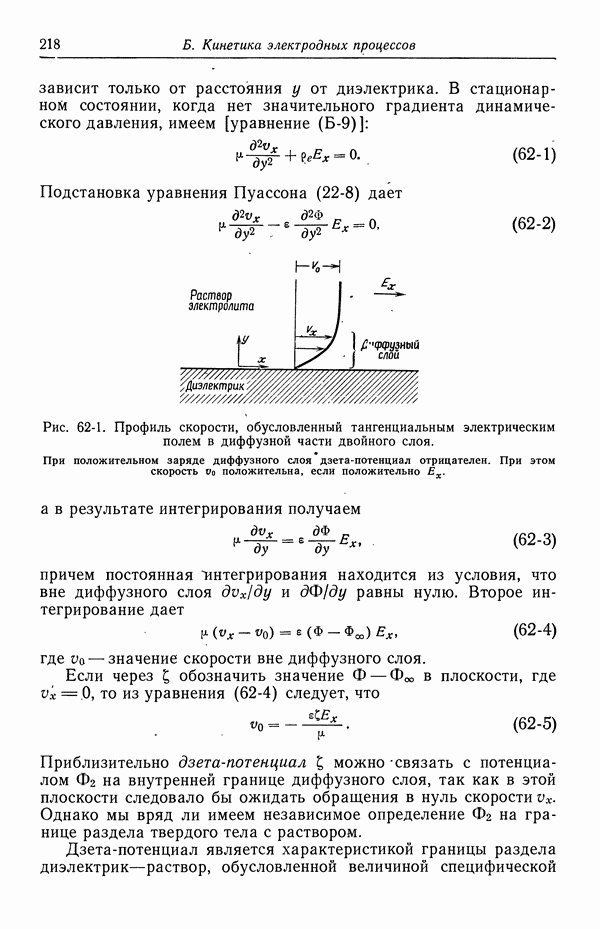
- 62. Разрывная скорость на границе раздела
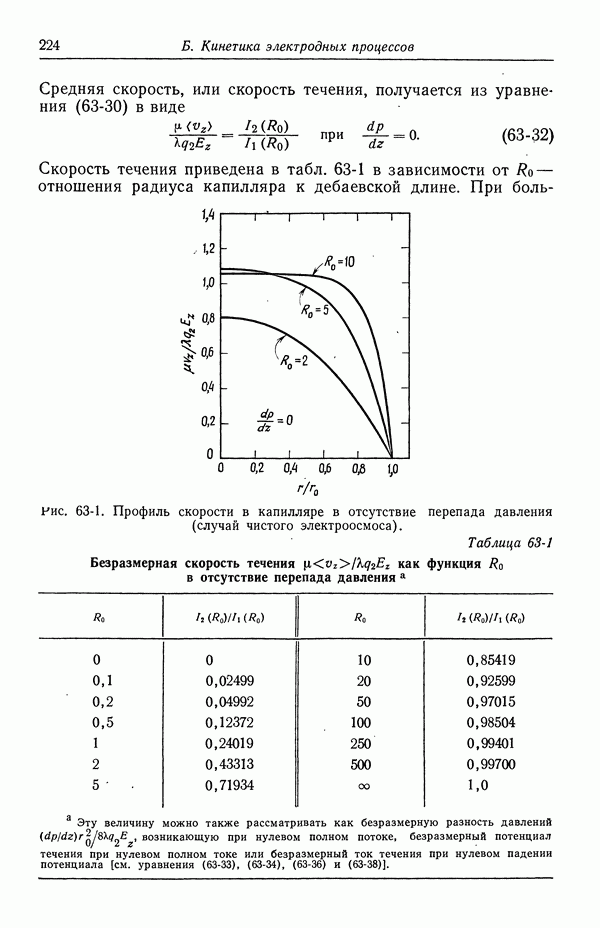
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
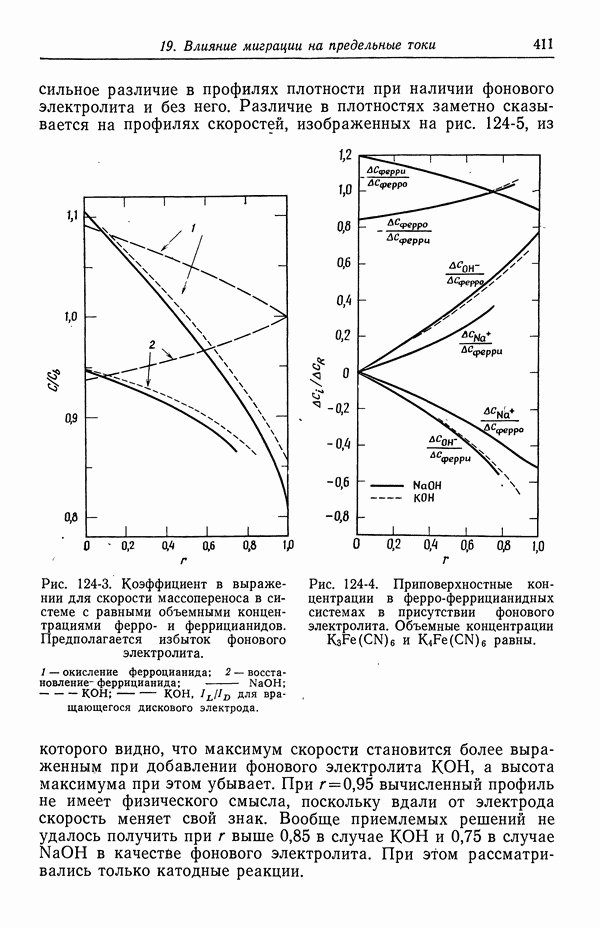
- 66. Динамика границы раздела
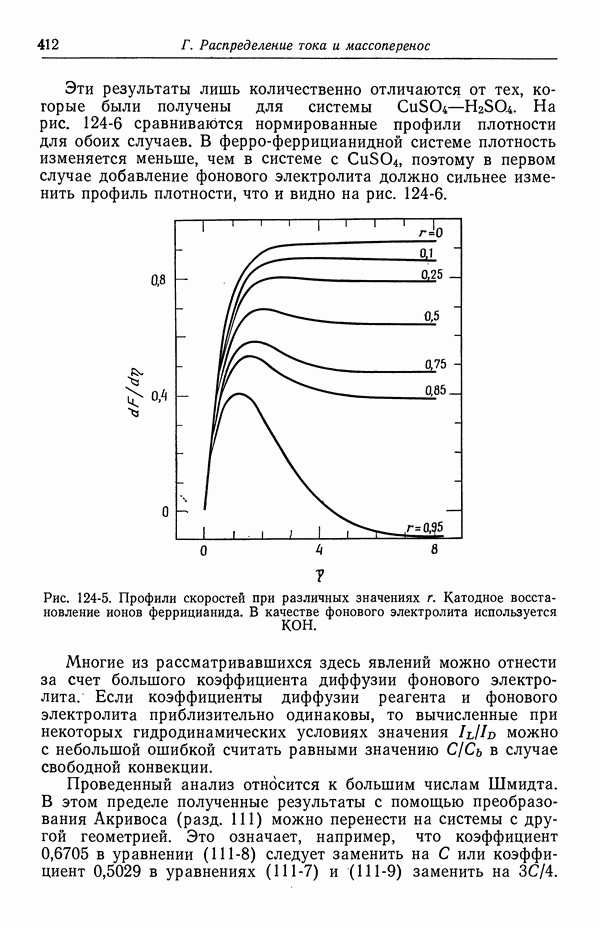
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 69. Законы переноса
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 78. Законы переноса
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 92. Интегральные коэффициенты диффузии
- ЗАДАЧА
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
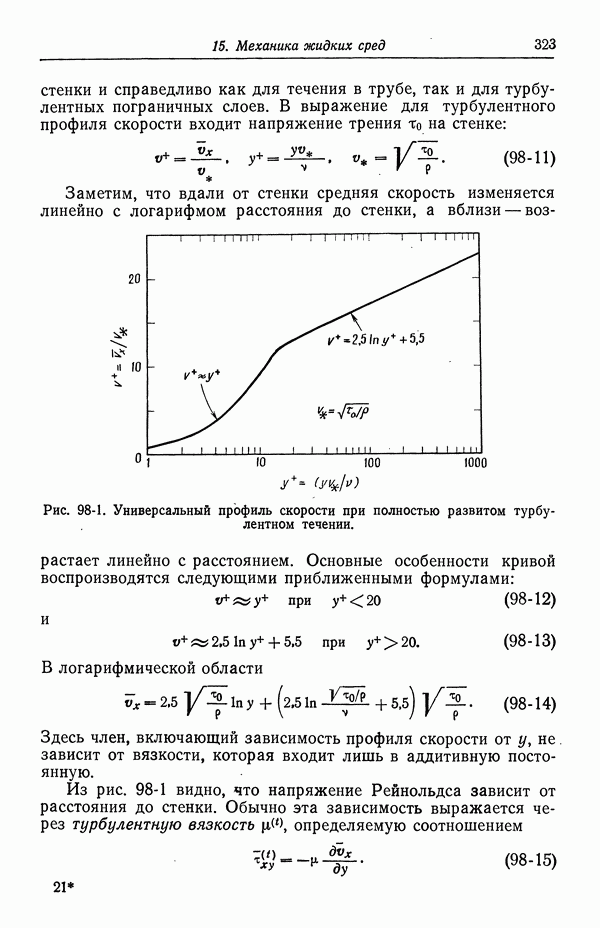
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
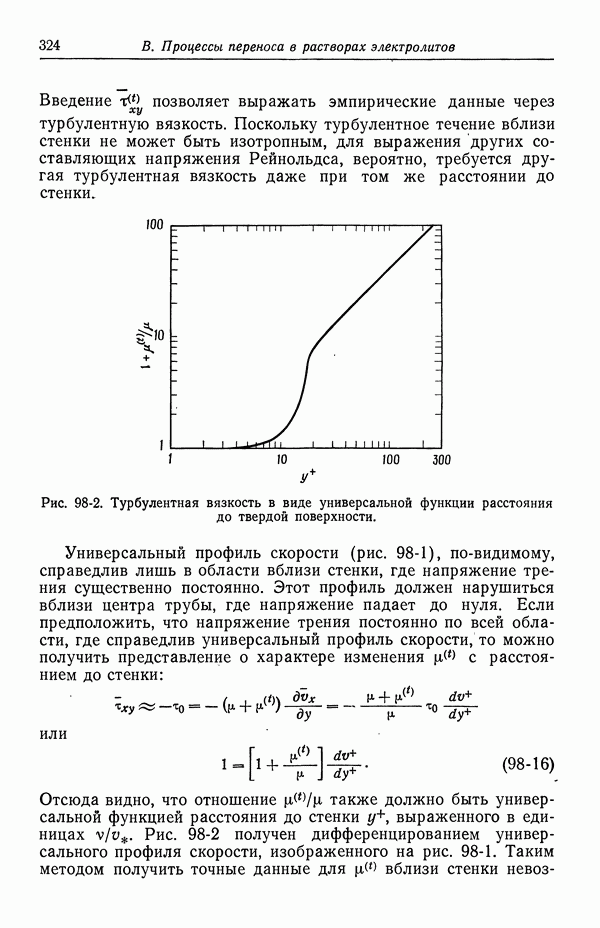
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
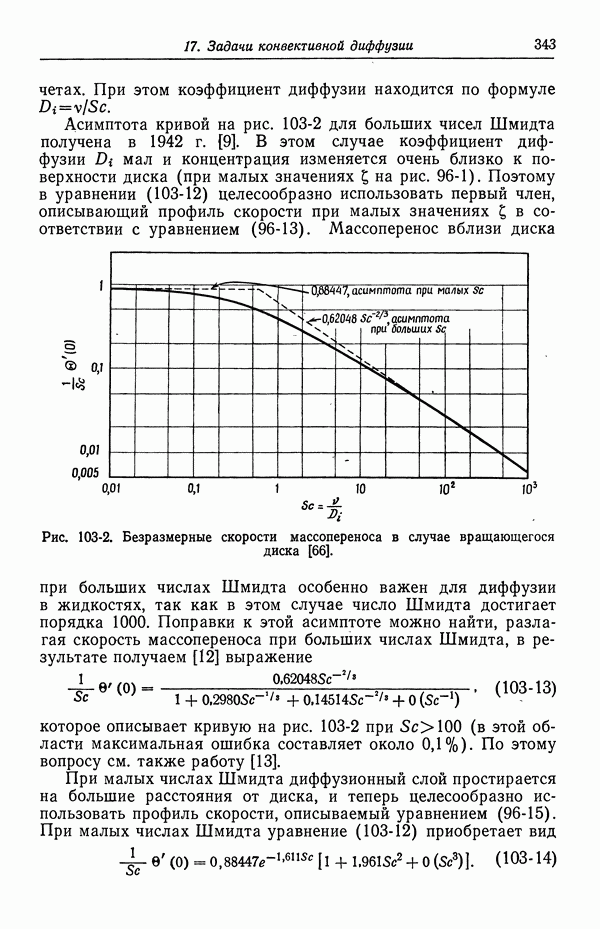
- 103. Вращающийся диск
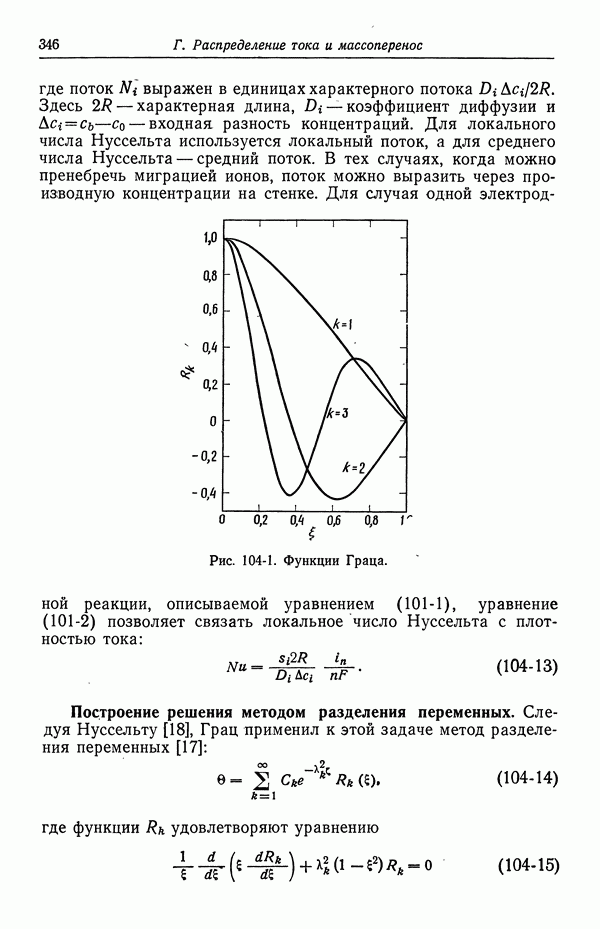
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 111. Свободная конвекция
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
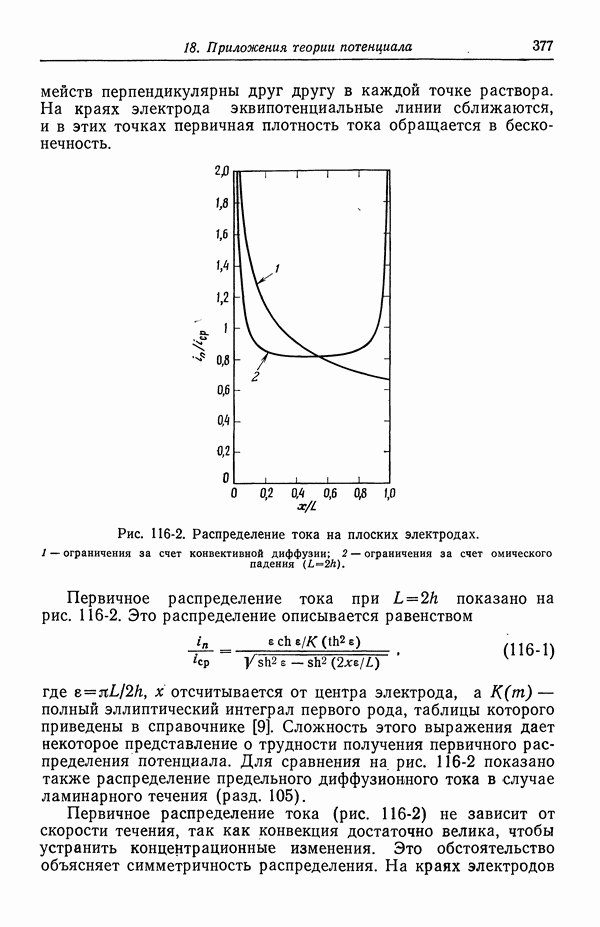
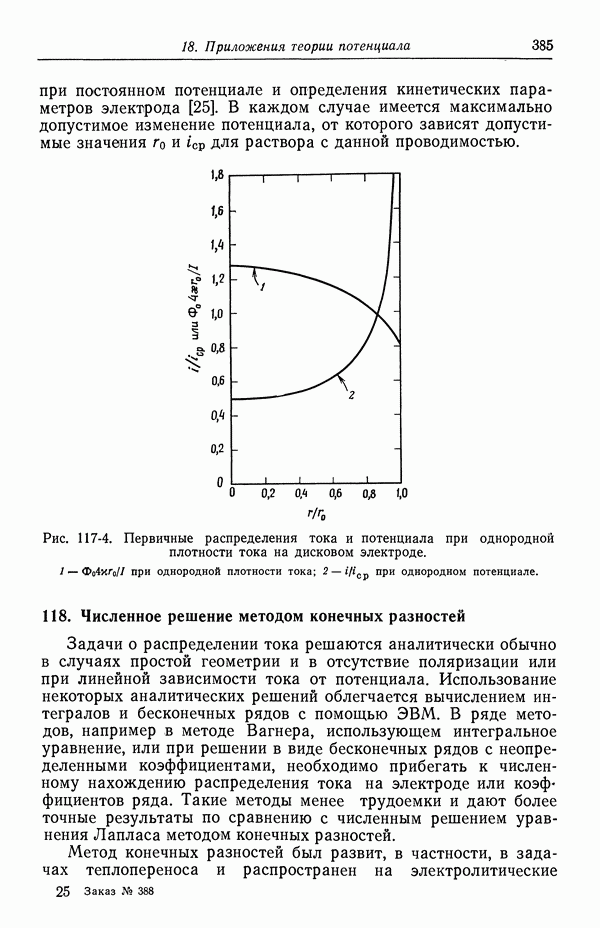
- 116. Первичное распределение тока
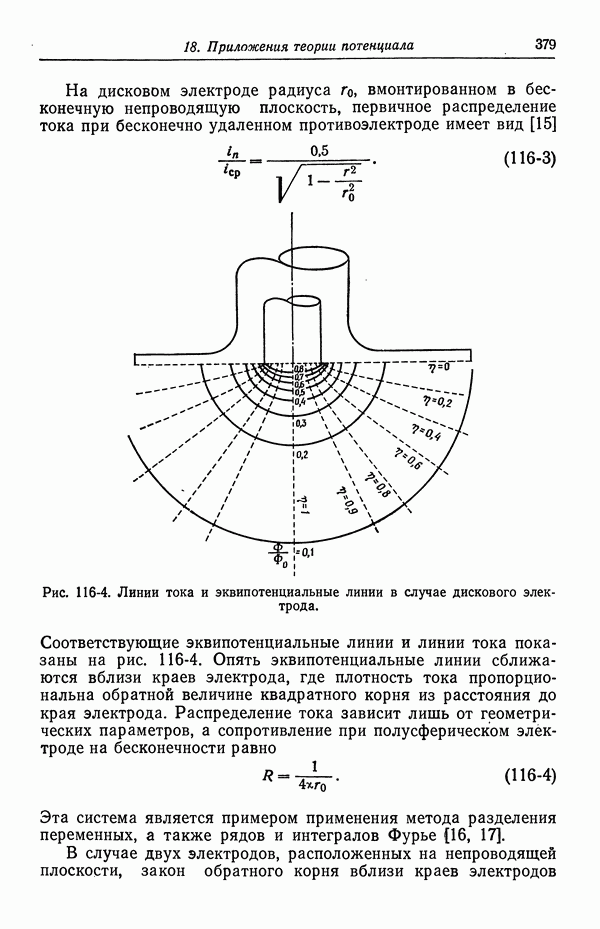
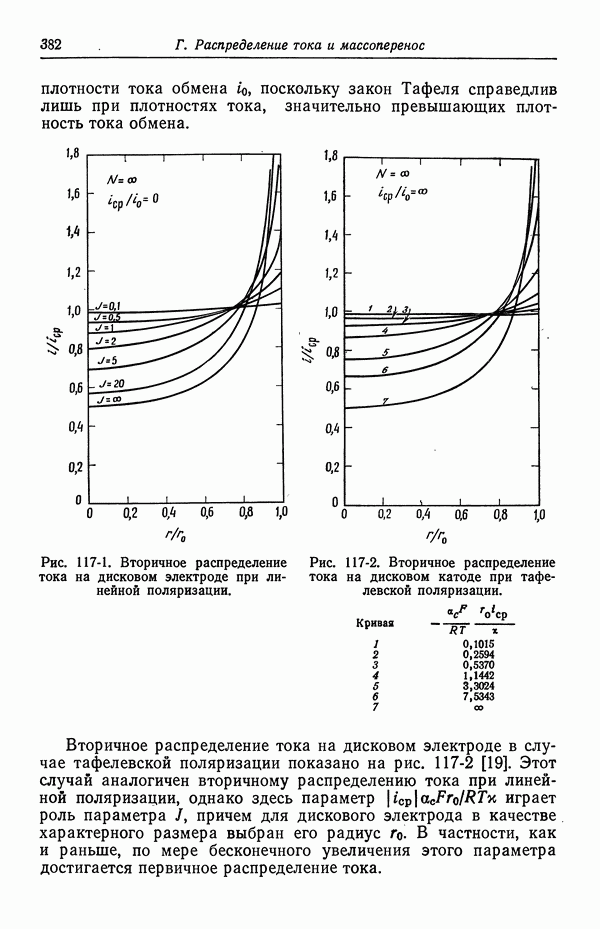
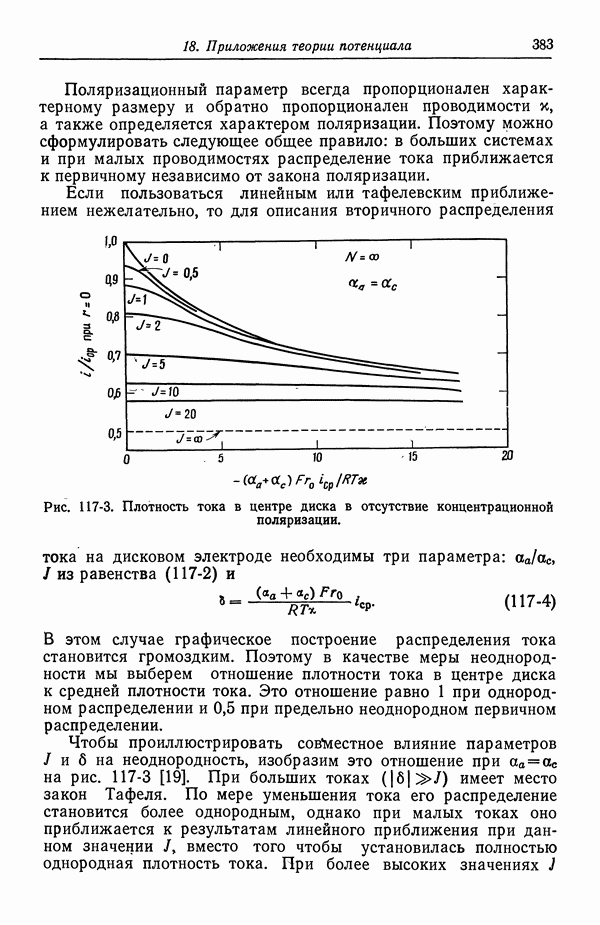
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- СПИСОК ОБОЗНАЧЕНИЙ
- ГЛАВА 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 119. Решение задачи
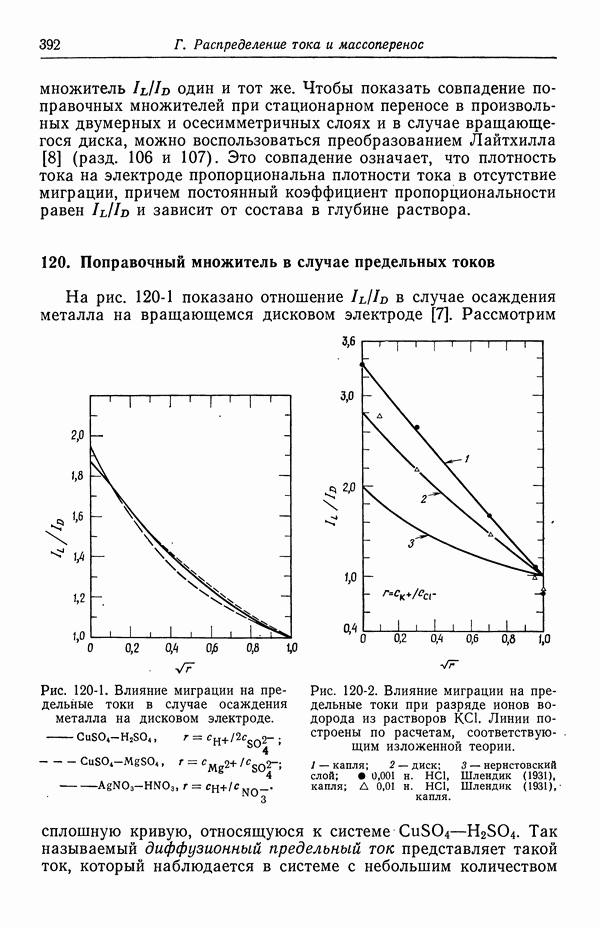
- 120. Поправочный множитель в случае предельных токов
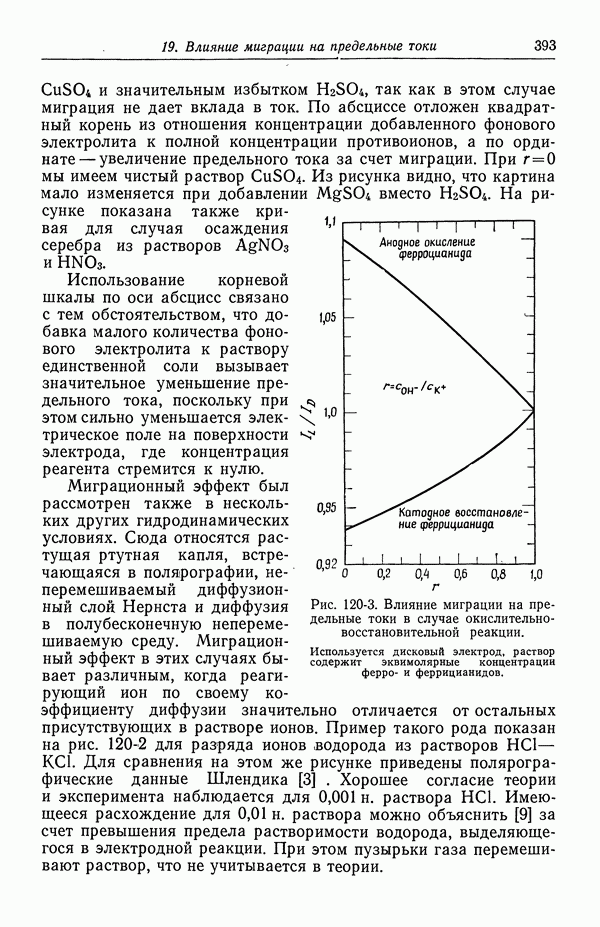
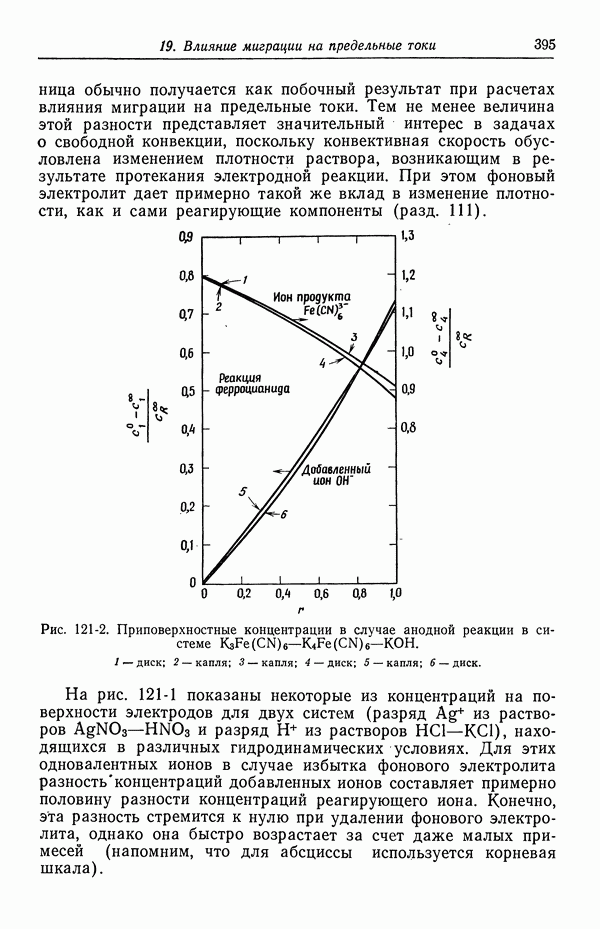
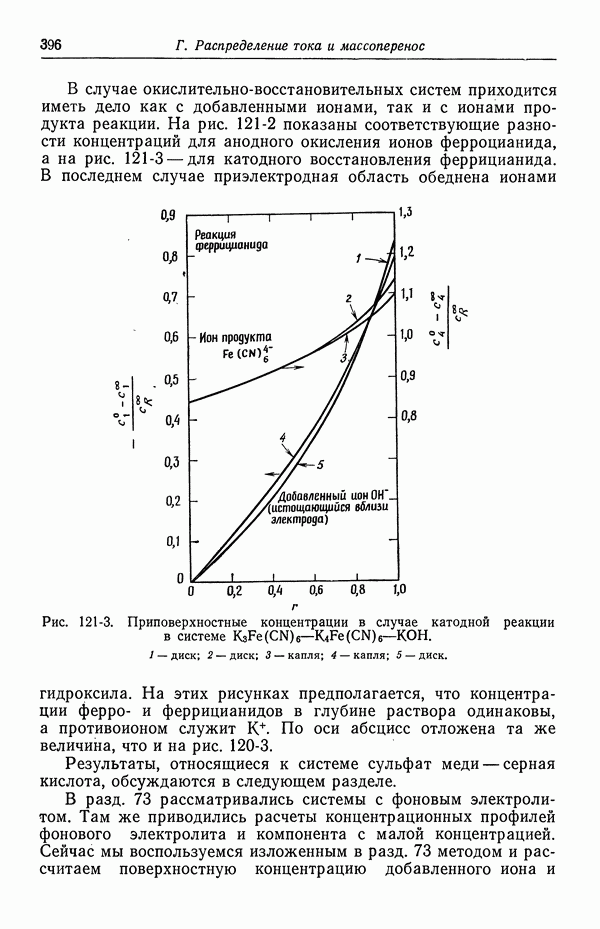
- 121. Изменение концентрации фонового электролита
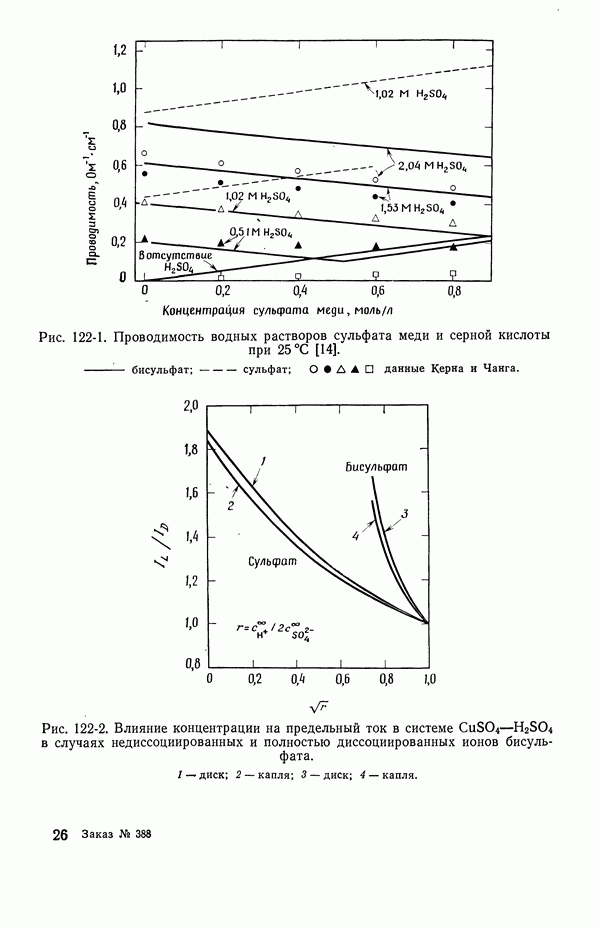
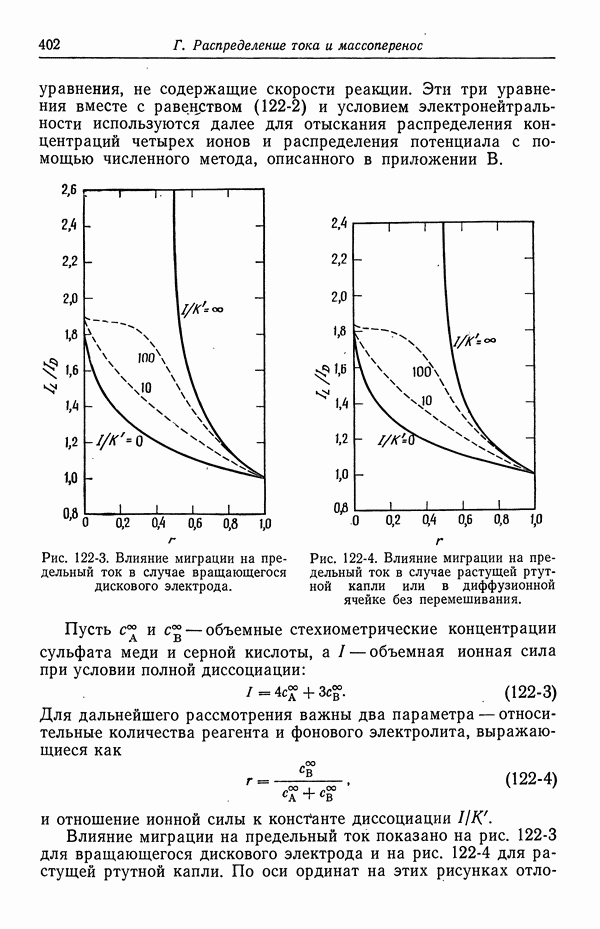
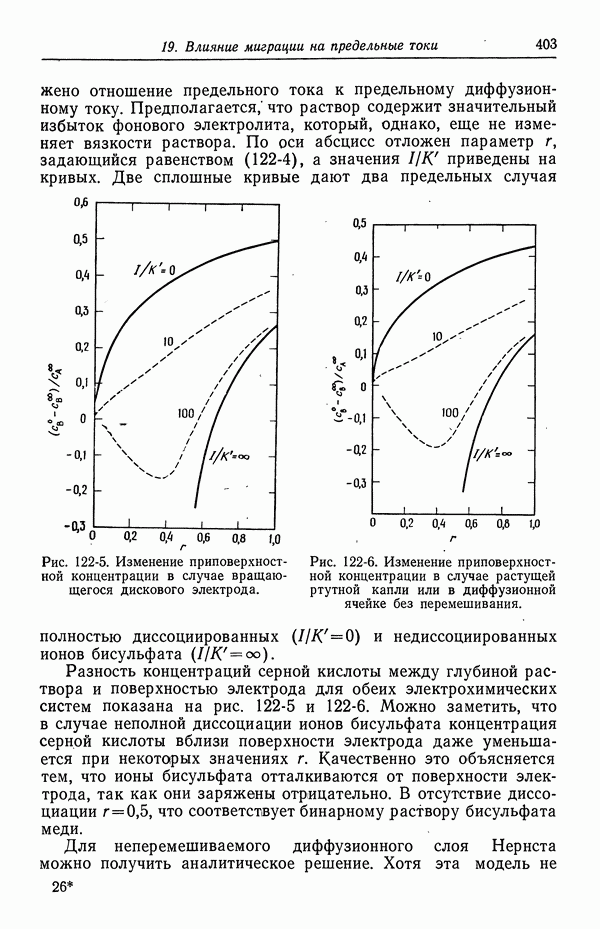
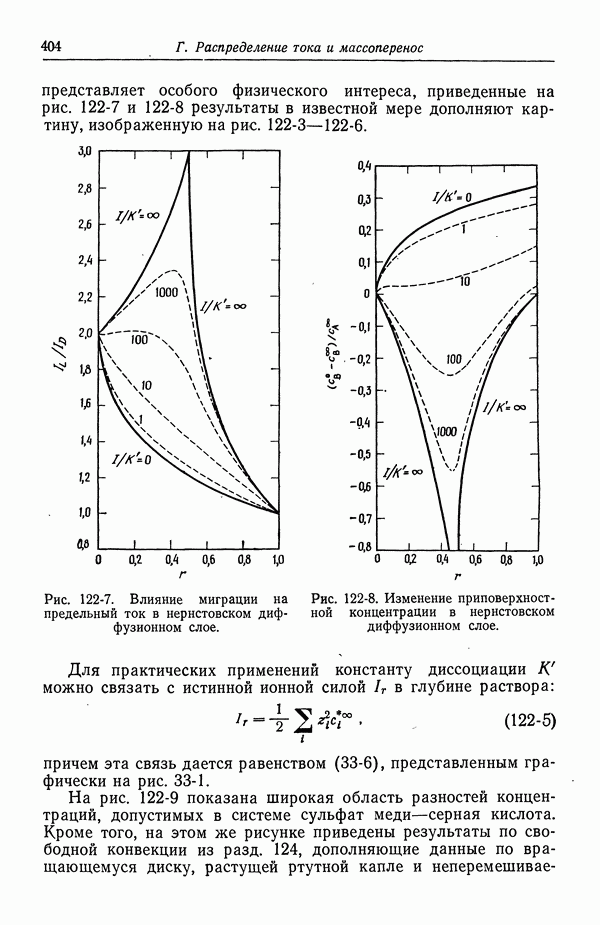
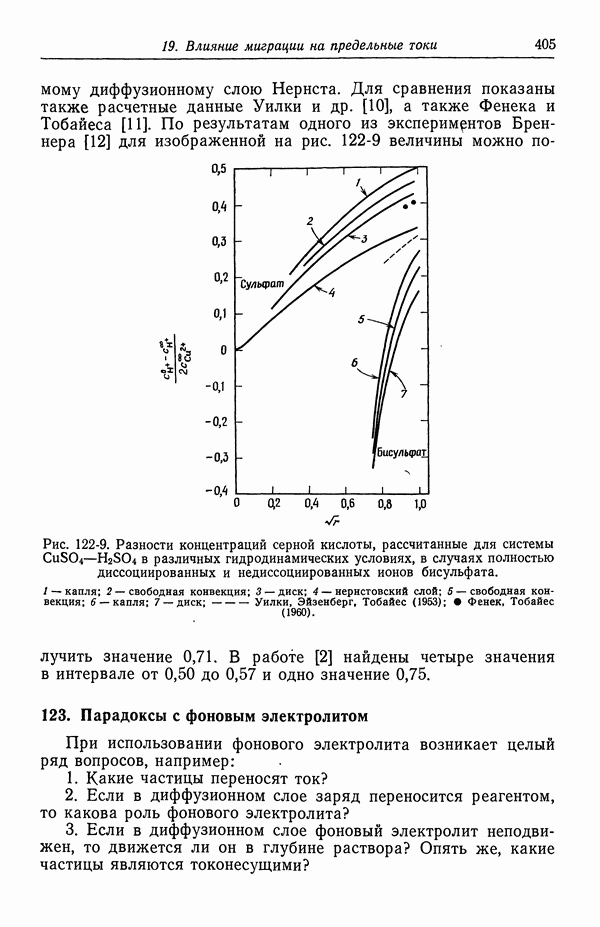
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
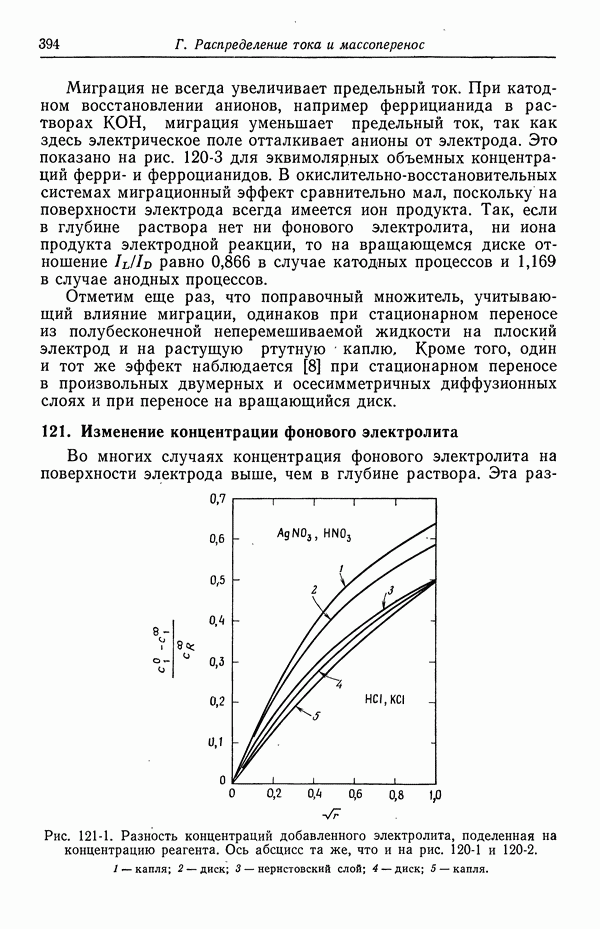
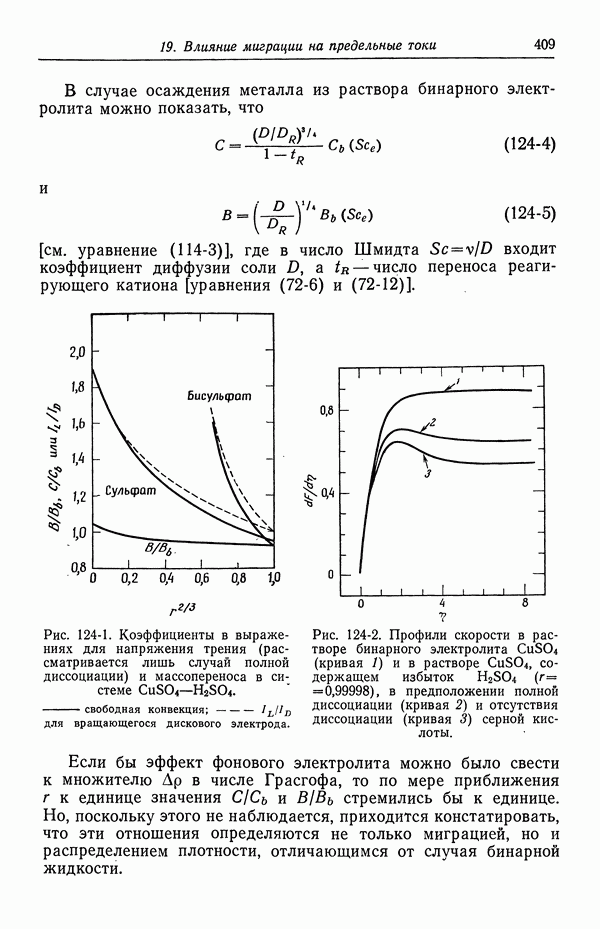
- 124. Предельные токи в случае свободной конвекции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ