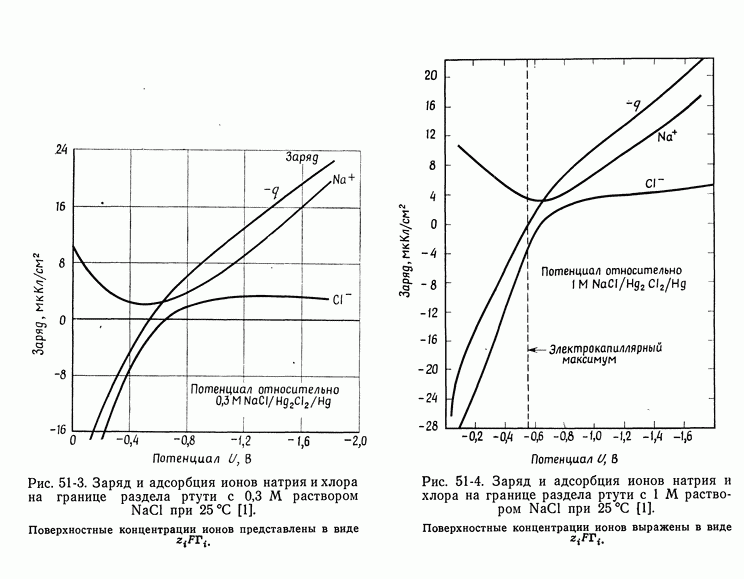
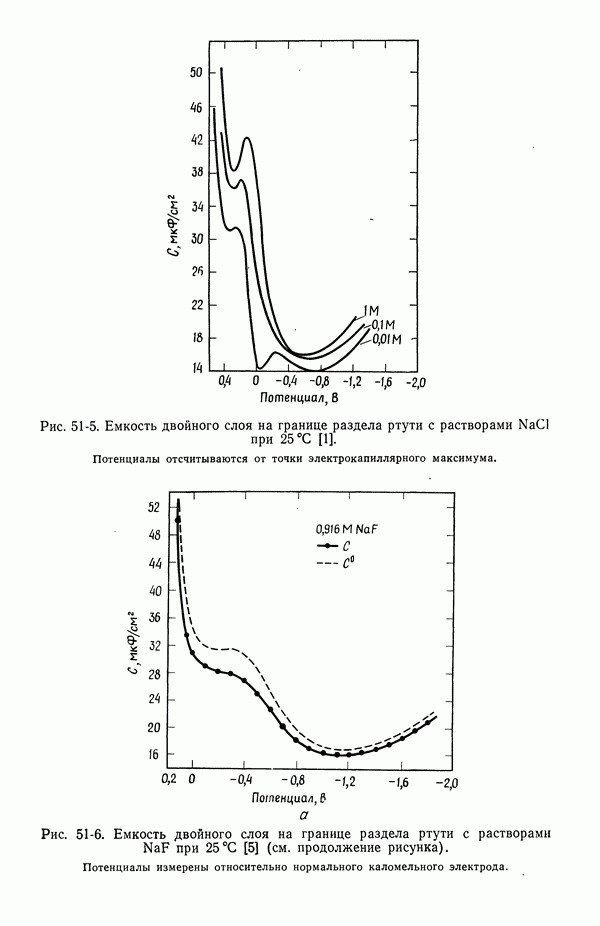
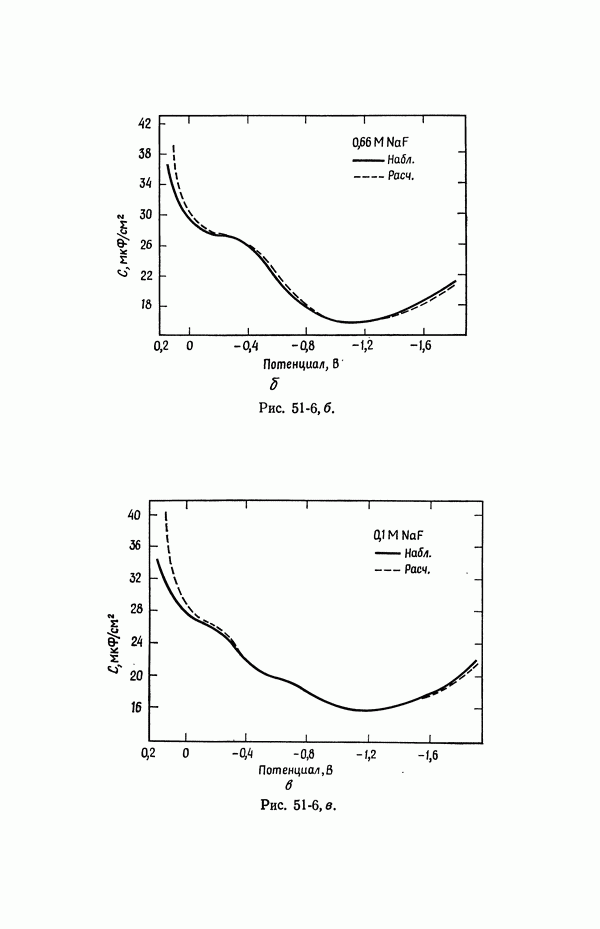
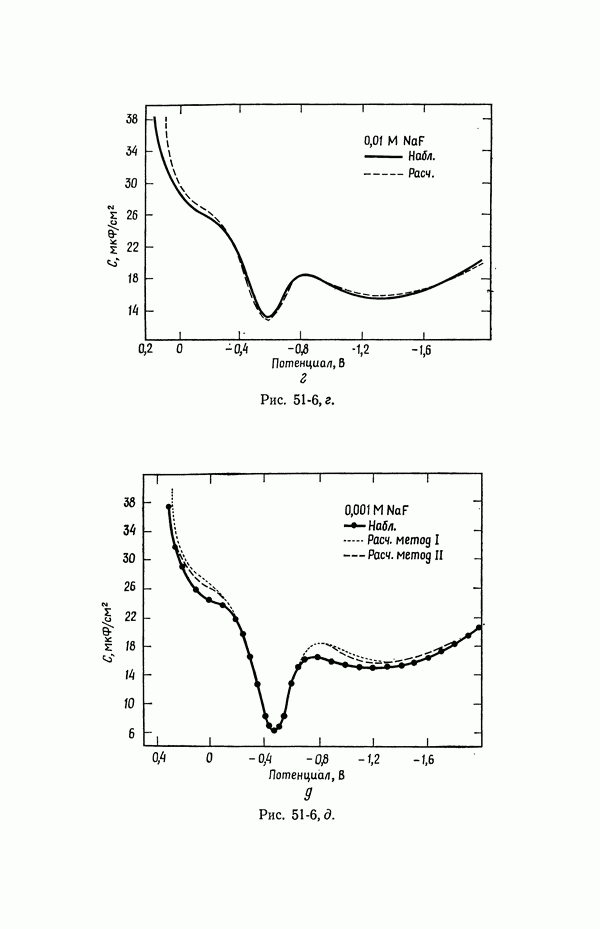
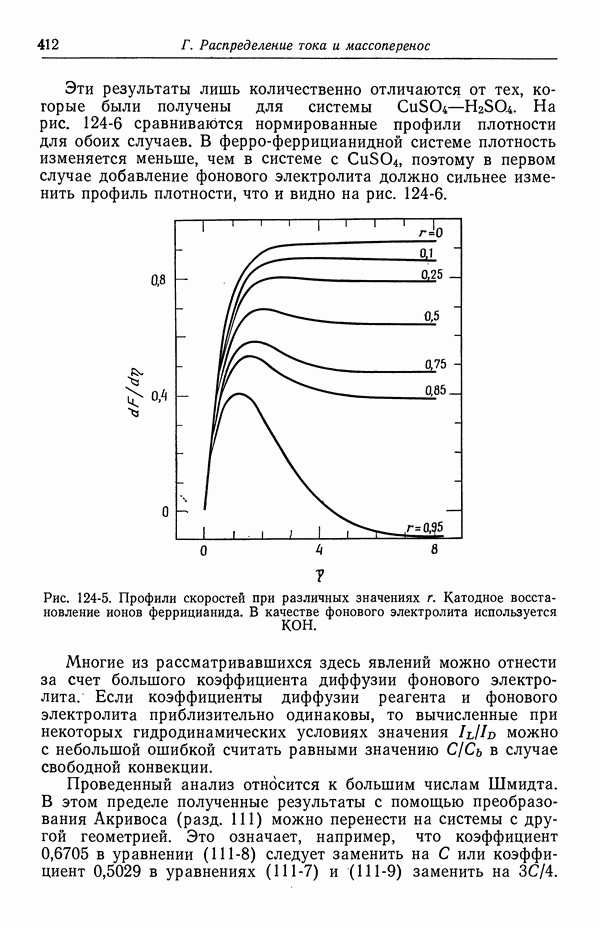
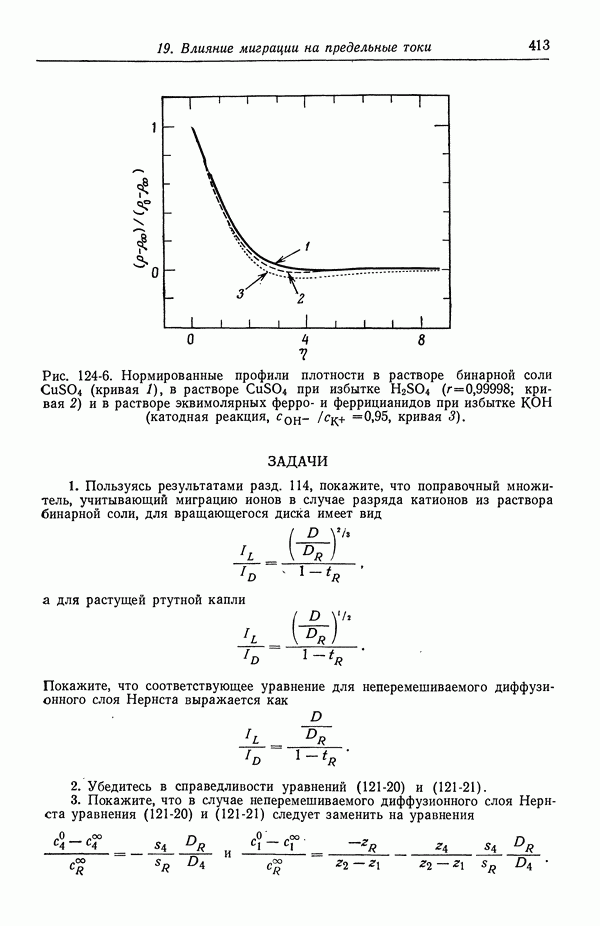
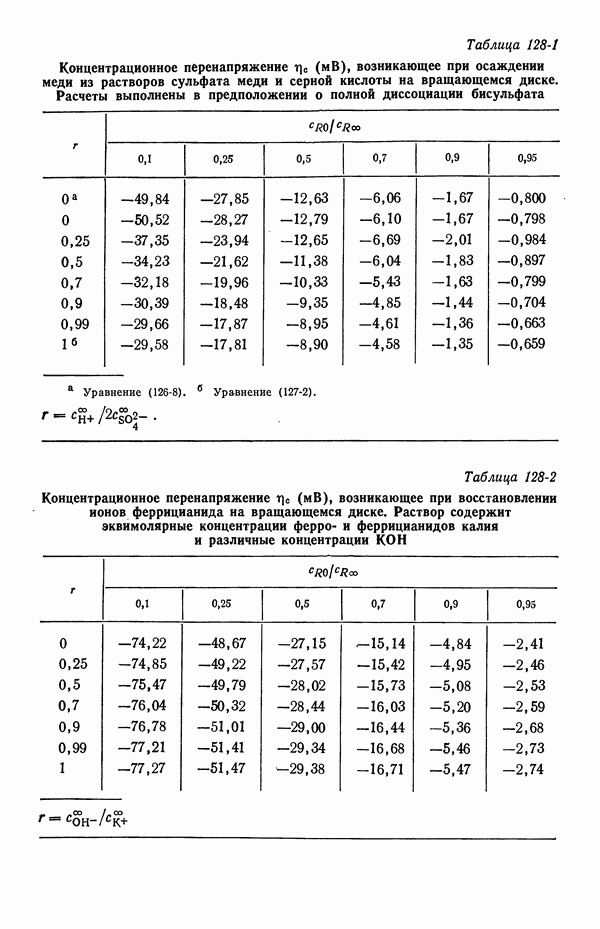
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. Диффузионный слой
Возвратимся теперь к концентрационным изменениям, которые упоминались в разд. 3. Поток  компонента i равен его скорости, умноженной на его концентрацию, и представляет собой число молей, проходящих за единицу времени через единичную площадь, ориентированную перпендикулярно к скорости. В разбавленных растворах соотношение (3-2) можно обобщить на случай потока ионного компонента следующим образом:
компонента i равен его скорости, умноженной на его концентрацию, и представляет собой число молей, проходящих за единицу времени через единичную площадь, ориентированную перпендикулярно к скорости. В разбавленных растворах соотношение (3-2) можно обобщить на случай потока ионного компонента следующим образом:

Это равенство записано в векторных обозначениях. Его проекция на радиальное направление имеет вид

Первый член справа представляет транспорт за счет, миграции, в точности как в равенстве (3-2); второй член — транспорт за счет диффузии, он пропорционален градиенту концентрации, причем коэффициент пропорциональности называется ионным коэффициентом диффузии и имеет размерность см2/с.

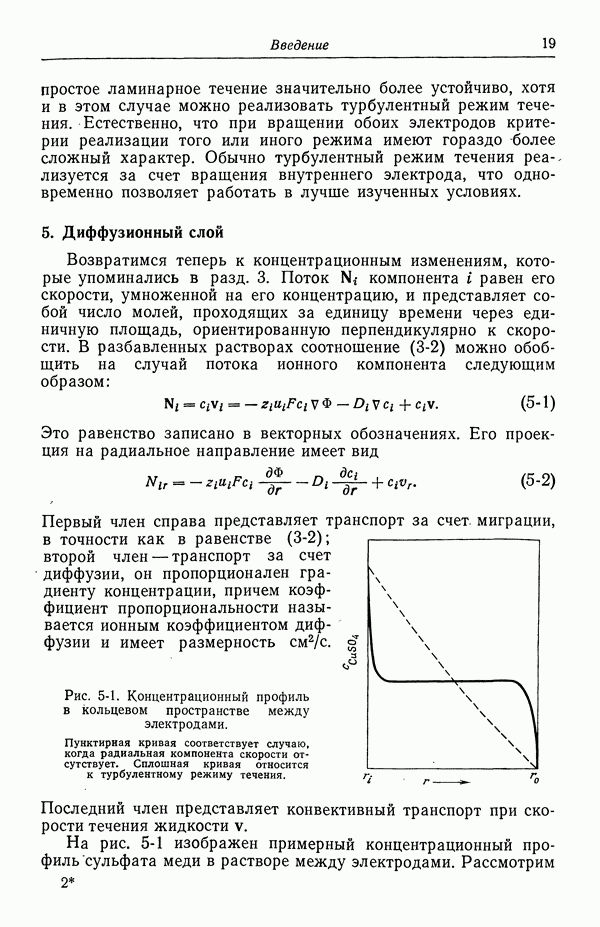
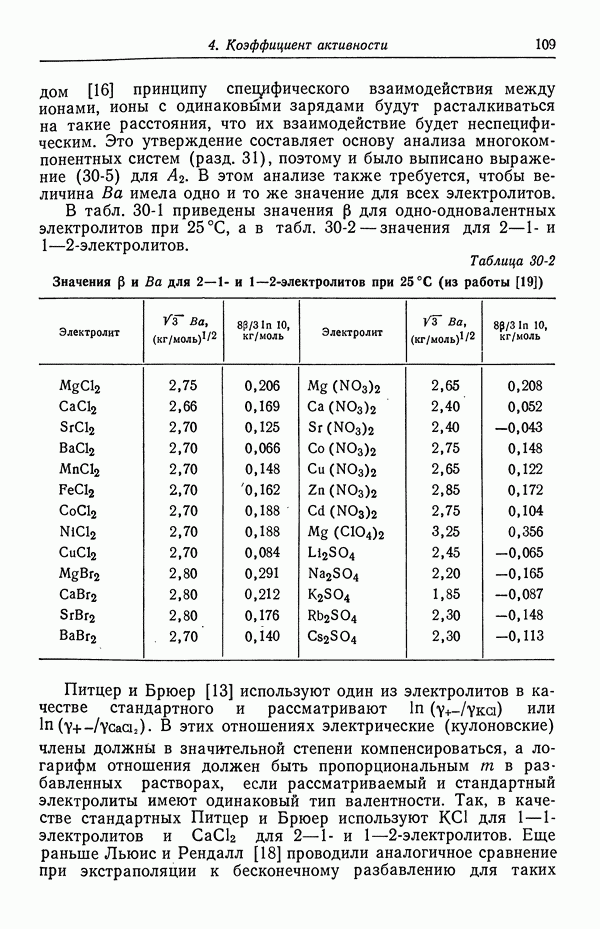
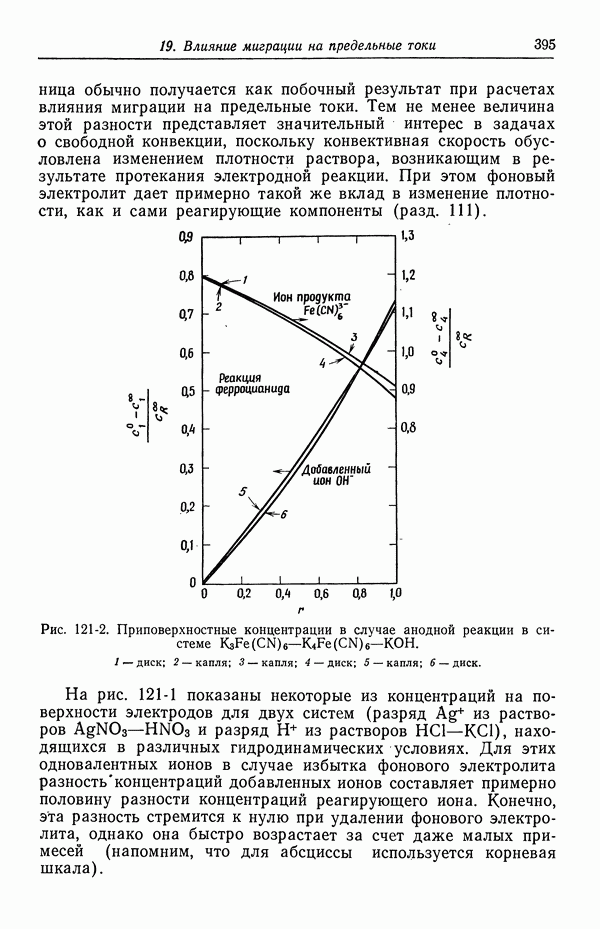
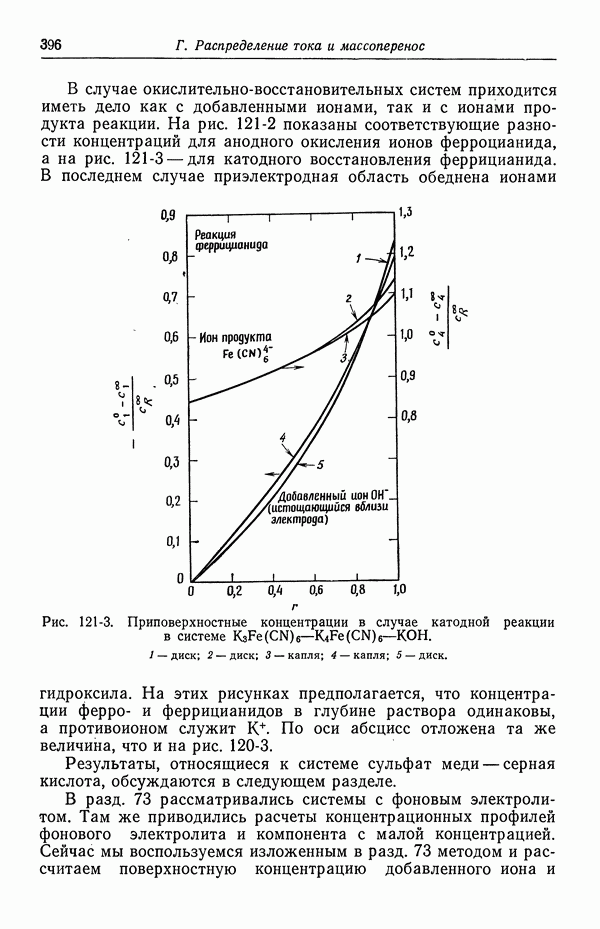
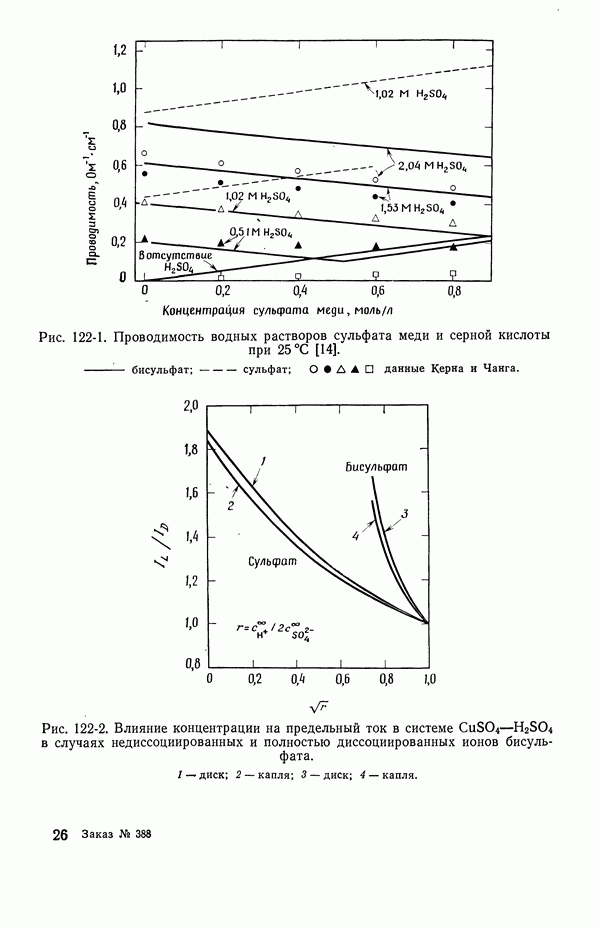
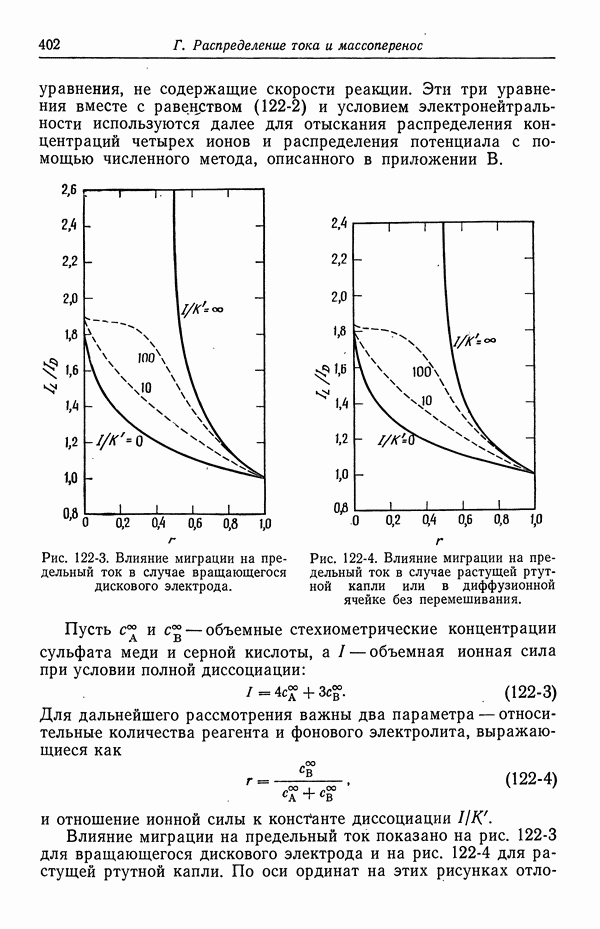
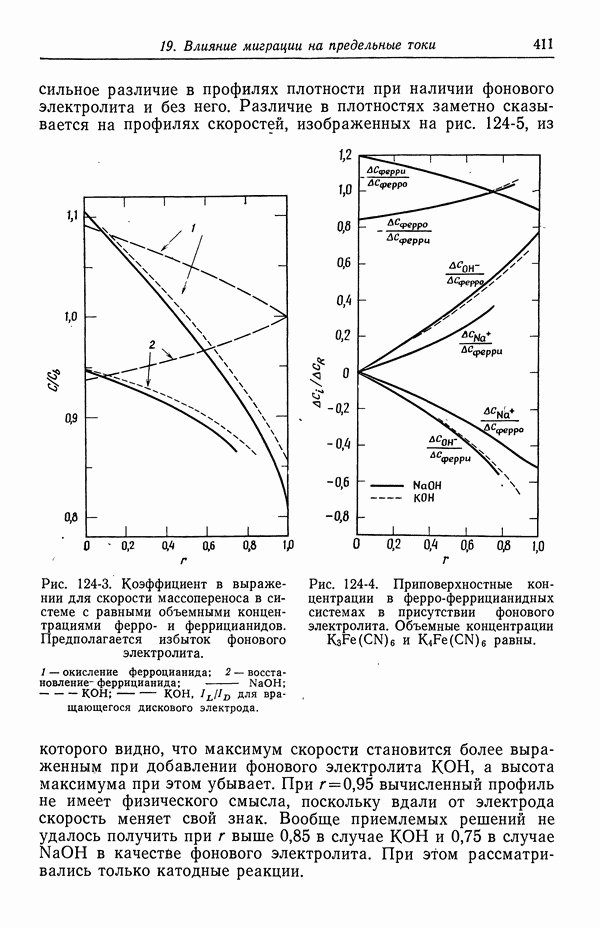
Рис. 5-1. Концентрационный профиль в кольцевом пространстве между электродами.
Пунктирная кривая соответствует случаю, когда радиальная компонента скорости отсутствует. Сплошная кривая относится к турбулентному режиму течения.
Последний член представляет конвективный транспорт при скорости течения жидкости v.
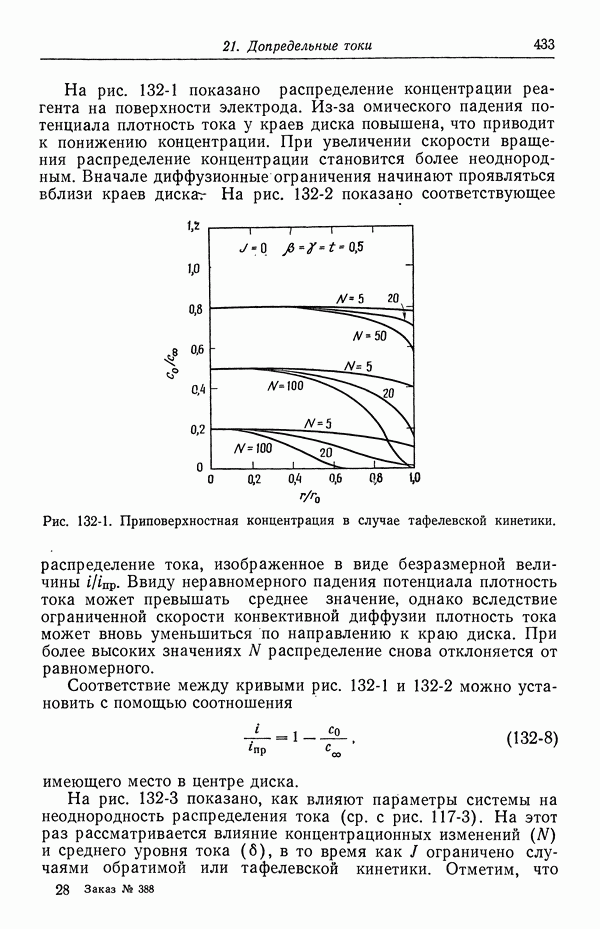
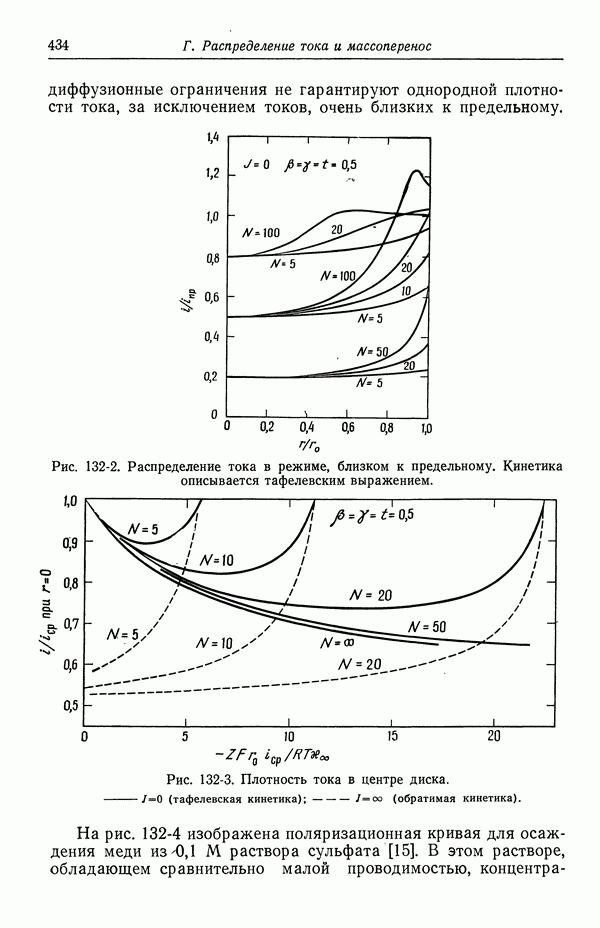
На рис. 5-1 изображен примерный концентрационный профиль сульфата меди в растворе между электродами. Рассмотрим
сначала пунктирную кривую, соответствующую случаю, когда отсутствует радиальная компонента скорости. Примером может служить медленное ламинарное течение с концентрическими линиями тока. В стационарном состоянии нет транспорта ионов сульфата, поскольку на электродах реагируют лишь ионы меди. За счет миграции ионы меди движутся к положительному электроду, т. е. налево на рис. 5-1. Ввиду отсутствия полного потока этих ионов их стремление к миграции компенсировано тенденцией к диффузии направо, в сторону пониженной концентрации. Таким образом, точная форма концентрационного профиля диктуется требованиями баланса между диффузией и миграцией ионов сульфата.
Ионы меди, с другой стороны, движутся за счет миграции направо. Диффундировать они стремятся также направо, помогая этим миграции. Можно сказать, что ионы меди переносят весь ток от анода к катоду.
Сплошная кривая на рис. 5-1 показывает влияние перемешивания раствора при вращении внутреннего цилиндра, создающем турбулентное течение. Конвективный транспорт стремится устранить концентрационные изменения в середине кольцевого пространства. Однако турбулентные флуктуации угасают вблизи поверхности твердых электродов, так что в этих областях миграция и диффузия вновь становятся основными составляющими транспорта. Электродные реакции по-прежнему приводят к истощению раствора вблизи катода и увеличению концентрации вблизи анода.
Таким образом, мы приходим к представлению о том, что при высоких скоростях перемешивания концентрационные изменения заключены в тонких пограничных слоях вблизи электродов. Этот вывод имеет важные следствия при упрощении количественного описания транспорта в электрохимических системах. При возрастании скорости вращения эти диффузионные слои утоньшаются.
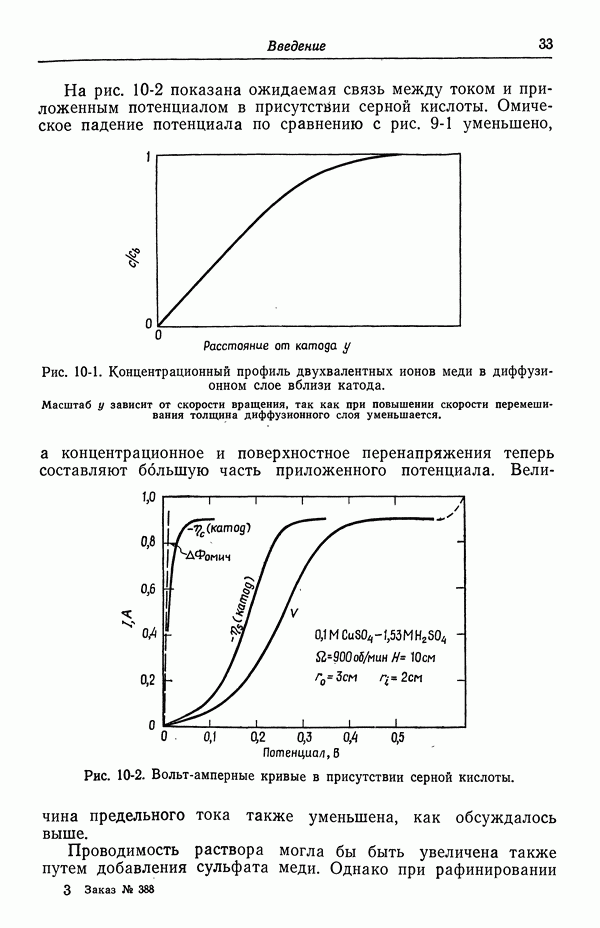
На рис. 5-1 показана концентрация, обращающаяся в нуль на поверхности катода. Это, конечно, предельный случай. При нулевом токе концентрация будет однородной и равной ее среднему значению. По мере увеличения тока отклонения от среднего значения концентрации будут усиливаться в вертикальном направлении, но форма кривой будет аналогична форме одной из кривых, изображенных на рис. 5-1. При предельном токе осаждения меди концентрация на катоде упадет до нуля. Более высокий ток можно пропустить лишь при условии, что начнется другой электродный процесс, в данном случае — выделение водорода.
На поверхностях электродов скорость в радиальном направлении равна нулю и поток ионов сульфата равен нулю. Следовательно,
если уравнение (5-2) написано как для положительного, так и для отрицательного ионов, то из этих двух уравнений можно исключить производную потенциала с помощью условия электронейтральности (3-4). Тогда плотность тока можно связать с производной концентрации на поверхности электрода равенством (3-3), в результате чего получается

где

и

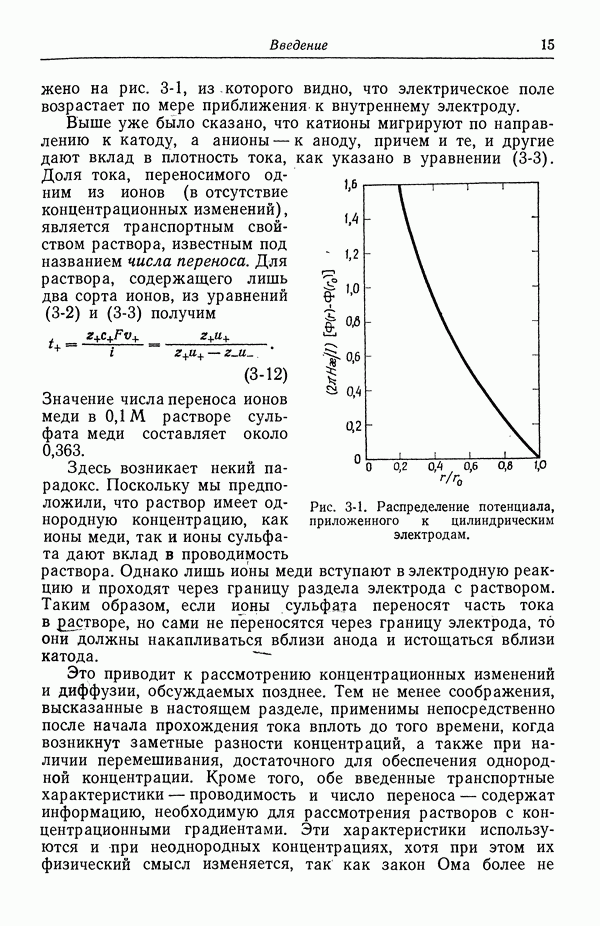
Соотношение (5-3) применимо для токов вплоть до предельного и показывает, что концентрационные градиенты становятся более крутыми по мере увеличения тока. Следовательно, логика построения кривых на рис. 5-1 приводит к выводу, что предельный ток будет гораздо большим при наличии турбулентного течения, чем при простом течении с концентрическими линиями тока. В последнем случае можно оценить предельную плотность тока на катоде, равную  для 0,1 М раствора сульфата меди при
для 0,1 М раствора сульфата меди при  см и
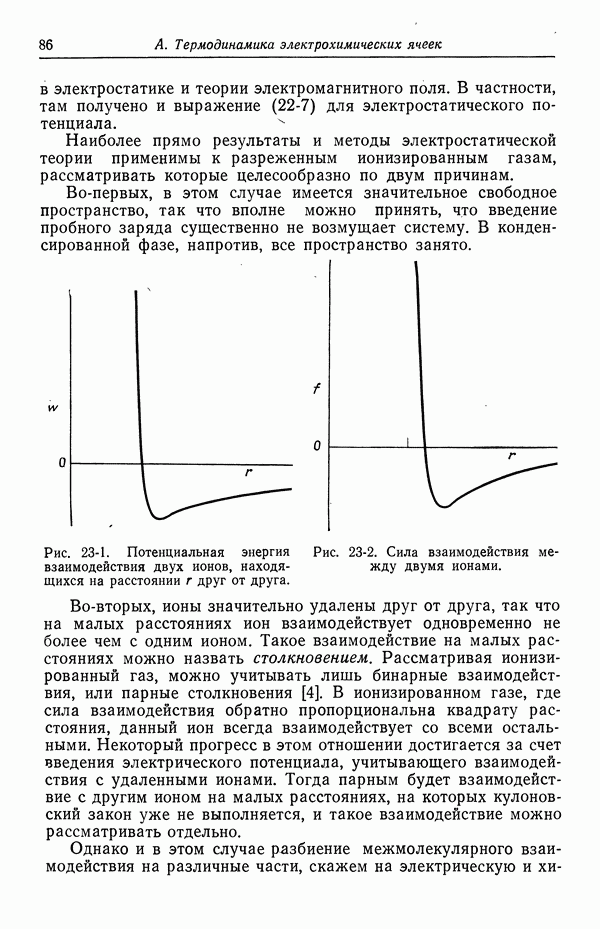
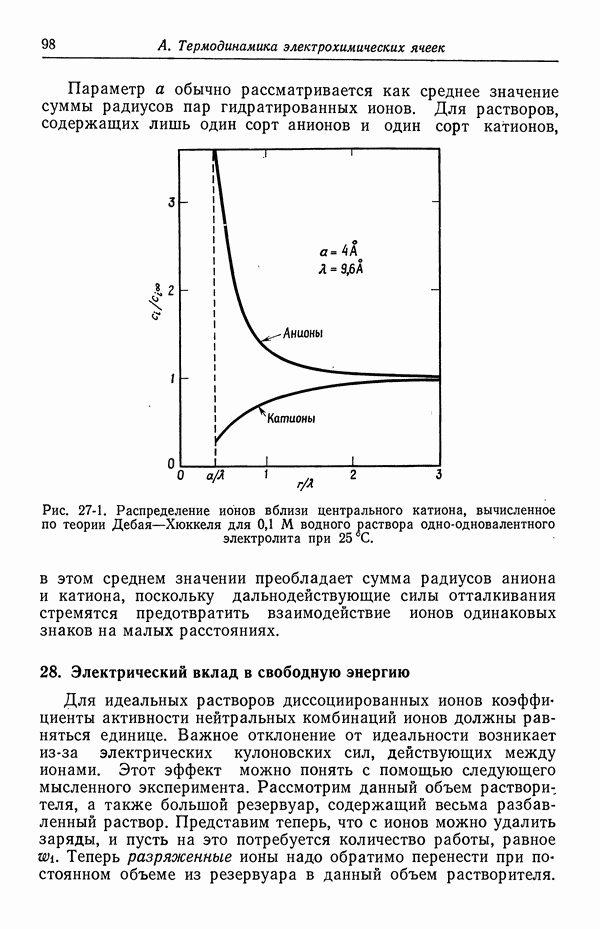
см и  см. Если теперь вращать внутренний цилиндр со скоростью 900 об/мин, что соответствует числу Рейнольдса 20 000, то предельная плотность тока увеличится примерно до
см. Если теперь вращать внутренний цилиндр со скоростью 900 об/мин, что соответствует числу Рейнольдса 20 000, то предельная плотность тока увеличится примерно до  Таким образом, перемешивание раствора оказывает значительное влияние на допустимую величину тока, который можно пропустить через систему.
Таким образом, перемешивание раствора оказывает значительное влияние на допустимую величину тока, который можно пропустить через систему.
Следует отметить, что число переноса  в равенстве (5-3) применяется в области неоднородной концентрации. Оно по-прежнему является фундаментальным свойством транспорта, связанным с подвижностью соотношением (5-4), однако больше не определяет долю тока, переносимую каким-либо ионным компонентом. Из-за наличия диффузии в данном случае ионы меди переносят весь ток. Тем не менее число переноса сохраняет свое численное значение, например
в равенстве (5-3) применяется в области неоднородной концентрации. Оно по-прежнему является фундаментальным свойством транспорта, связанным с подвижностью соотношением (5-4), однако больше не определяет долю тока, переносимую каким-либо ионным компонентом. Из-за наличия диффузии в данном случае ионы меди переносят весь ток. Тем не менее число переноса сохраняет свое численное значение, например  в 0,1 М растворе сульфата меди. Коэффициент D оказывается коэффициентом диффузии сульфата меди, определяющим скорость, с которой сульфат меди диффундировал бы в отсутствие тока. Он имеет промежуточное значение между коэффициентами диффузии ионов меди и сульфата. Например, если
в 0,1 М растворе сульфата меди. Коэффициент D оказывается коэффициентом диффузии сульфата меди, определяющим скорость, с которой сульфат меди диффундировал бы в отсутствие тока. Он имеет промежуточное значение между коэффициентами диффузии ионов меди и сульфата. Например, если 
и  то
то  Проводимость
Проводимость  , число переноса
, число переноса  и коэффициент диффузии D являются тремя характеристиками транспорта, которые измеряются непосредственно при массопереносе в растворе бинарного электролита.
и коэффициент диффузии D являются тремя характеристиками транспорта, которые измеряются непосредственно при массопереносе в растворе бинарного электролита.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
- 5. Диффузионный слой
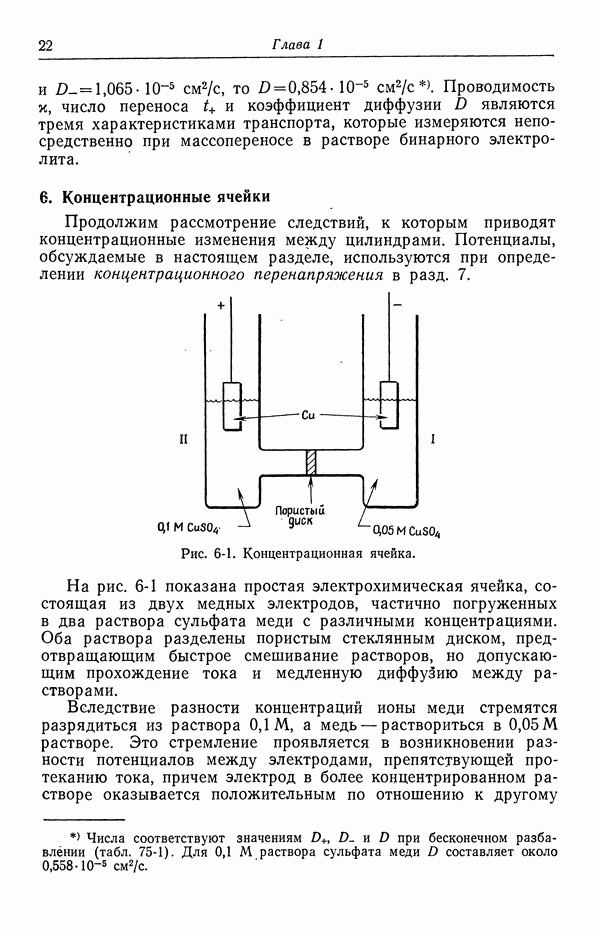
- 6. Концентрационные ячейки
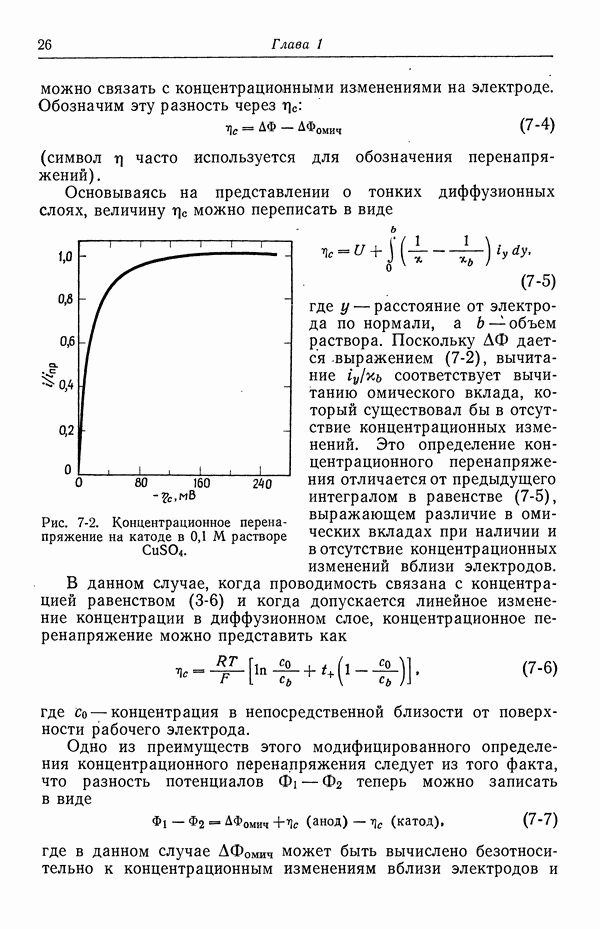
- 7. Концентрационное перенапряжение
- 8. Поверхностное перенапряжение
- 9. Потенциал ячейки
- 10. Фоновый электролит
- 11. Свободная конвекция
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
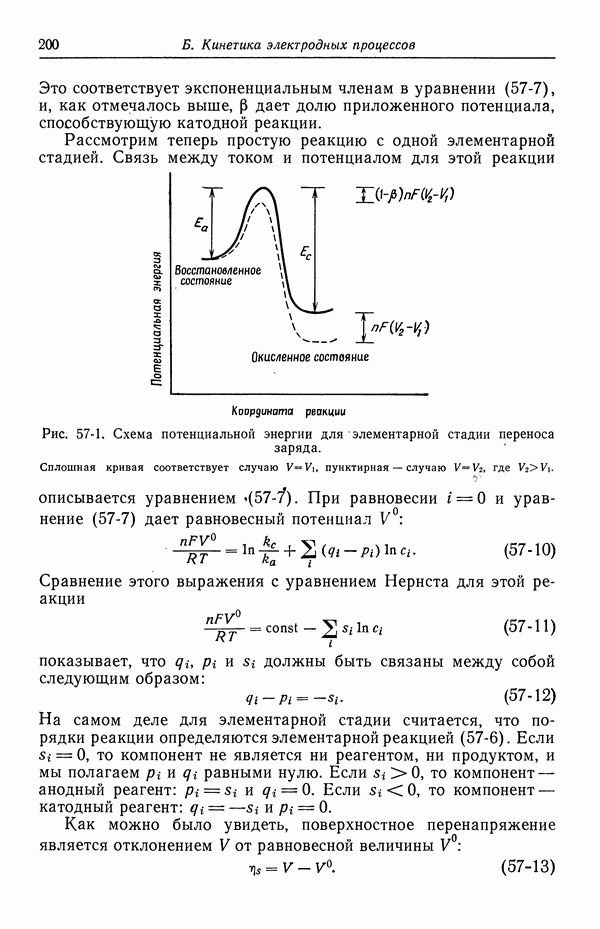
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
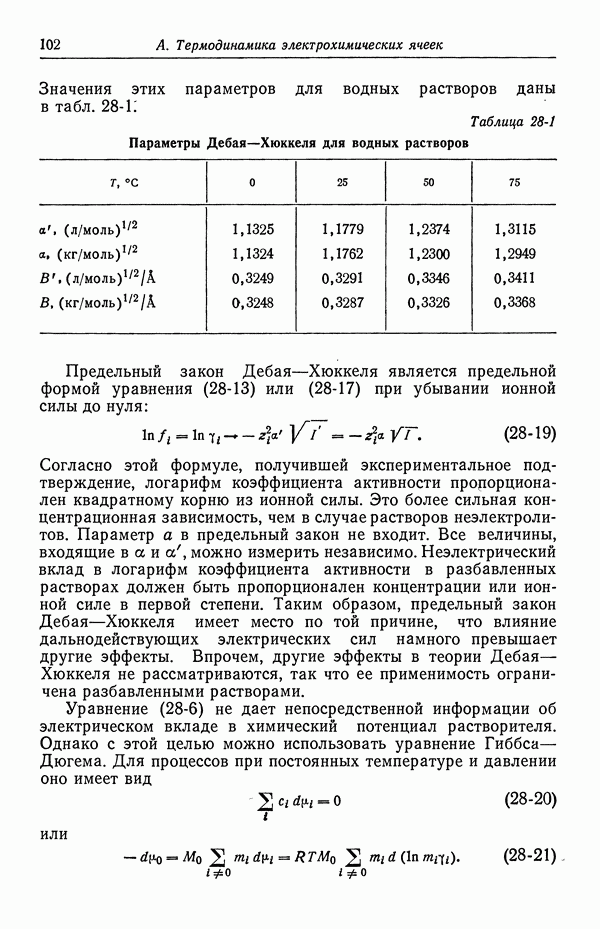
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая—Хюккеля
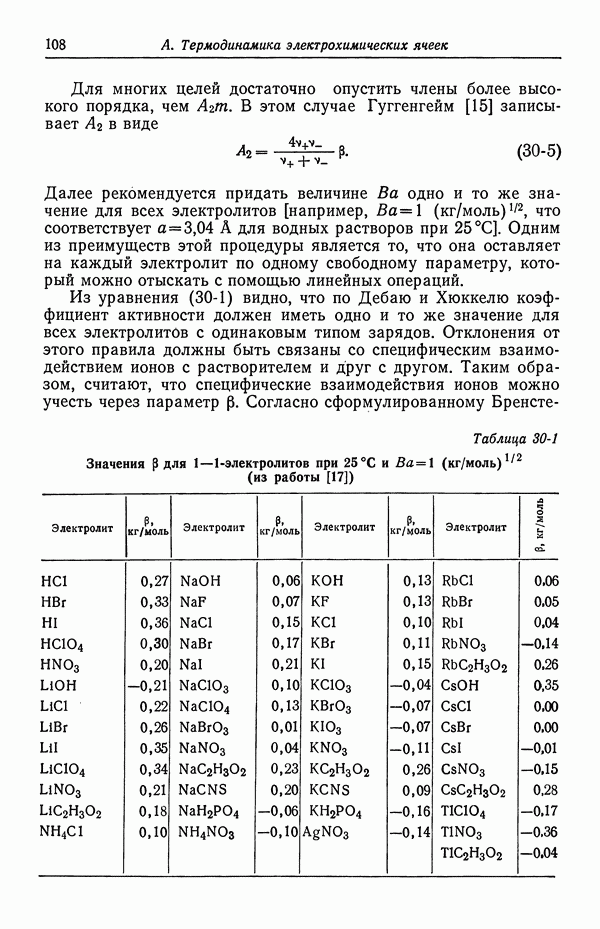
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
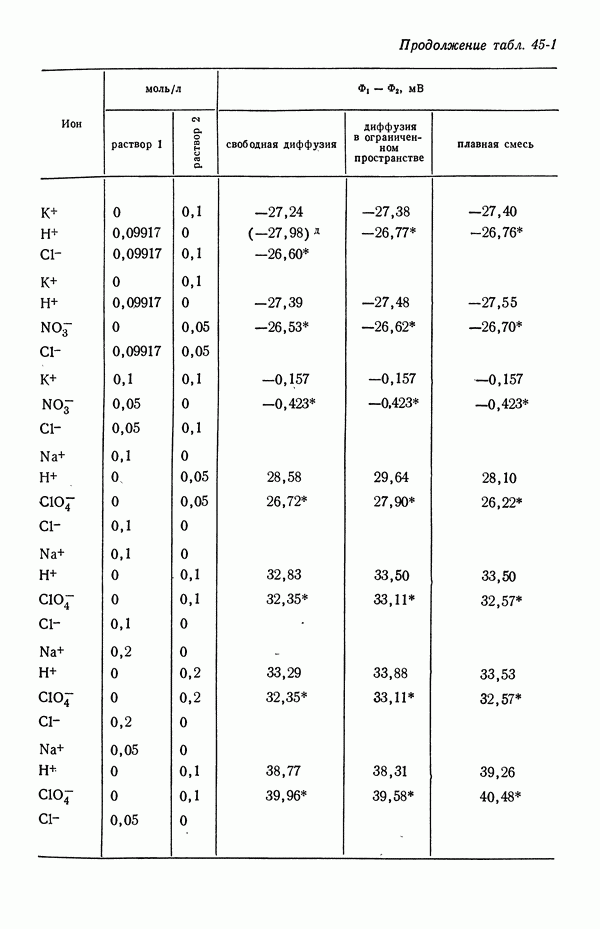
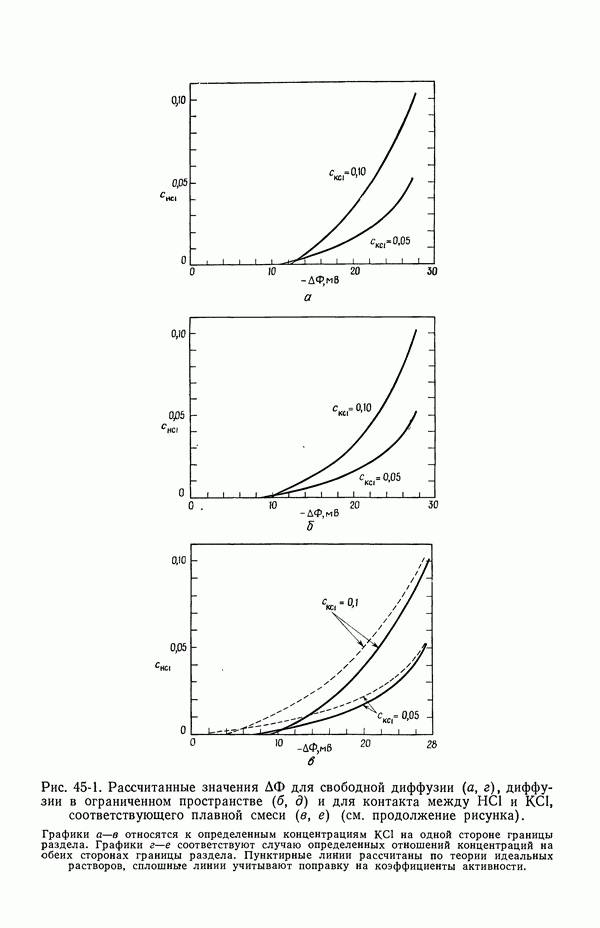
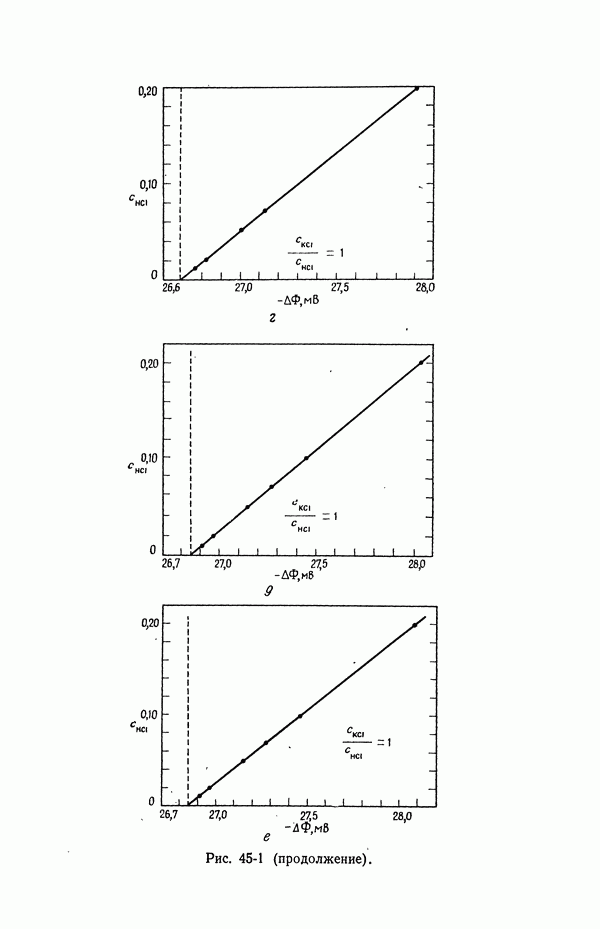
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
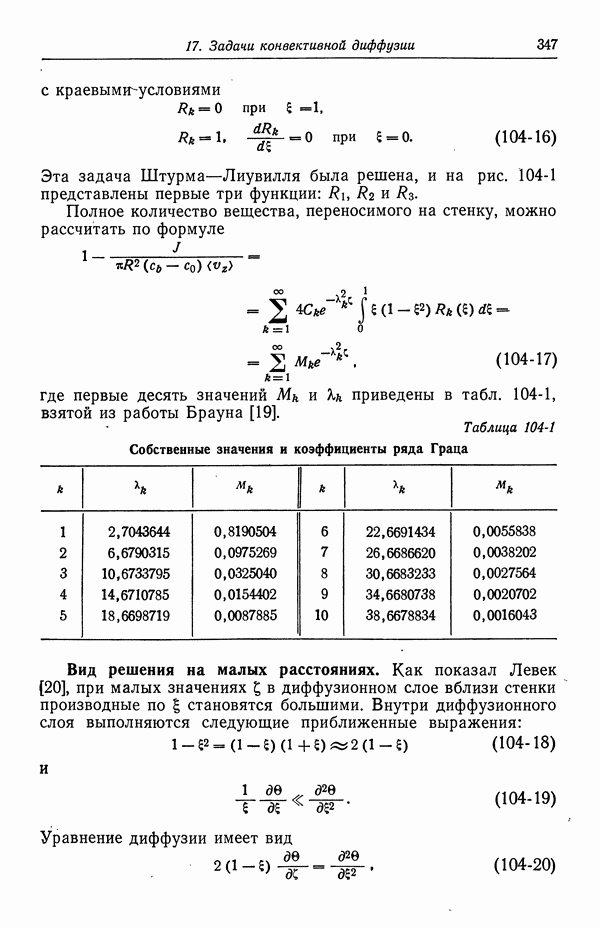
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
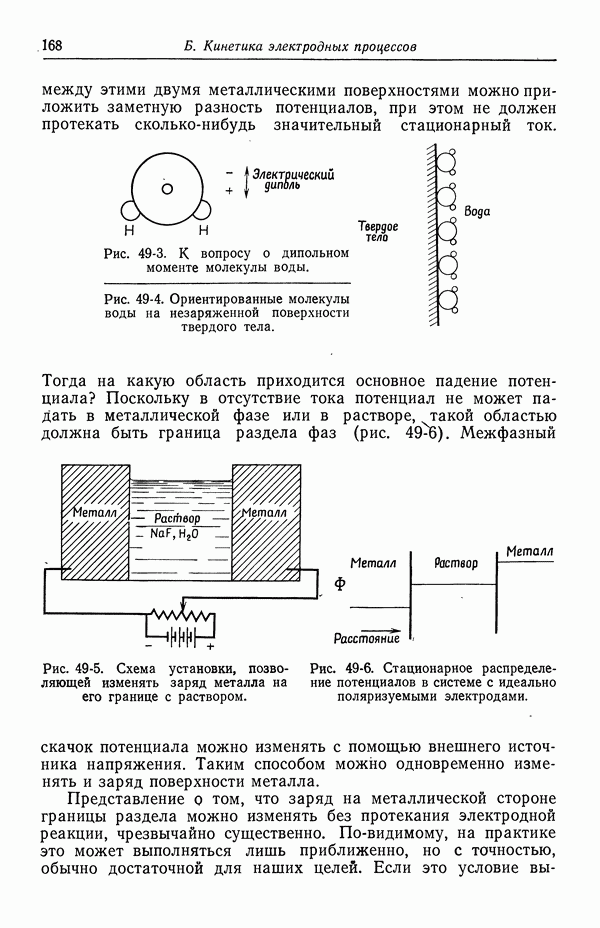
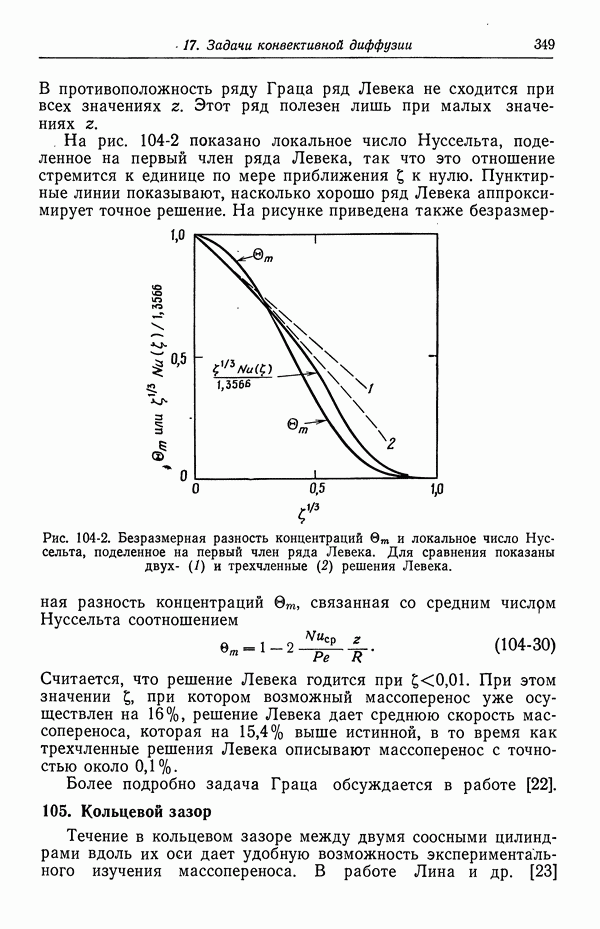
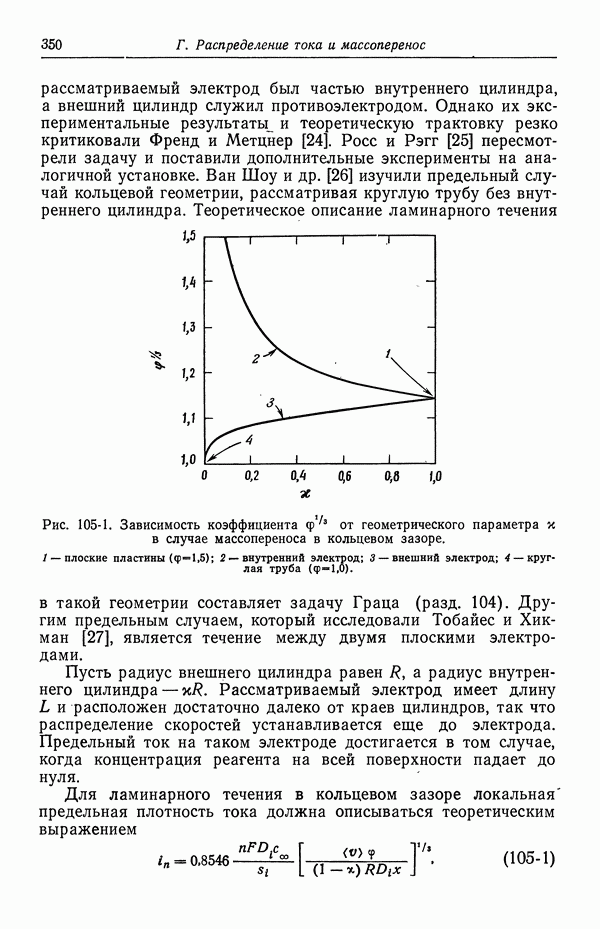
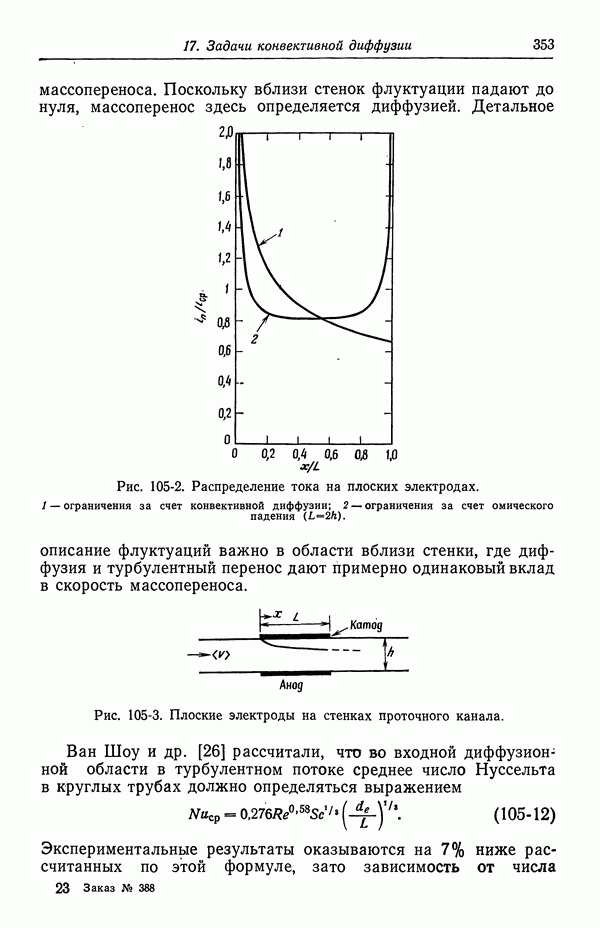
- 49. Качественное описание двойных слоев
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод — раствор
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
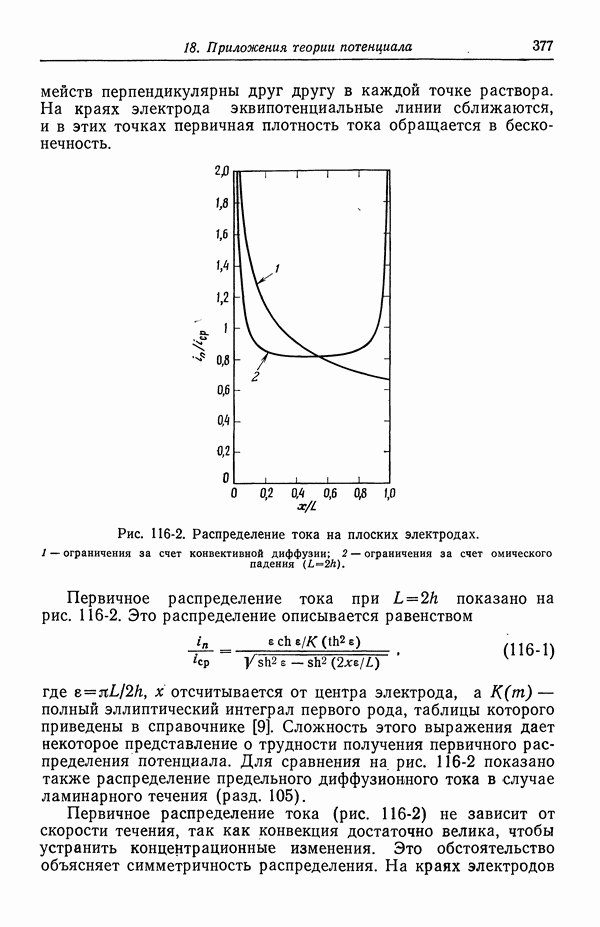
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
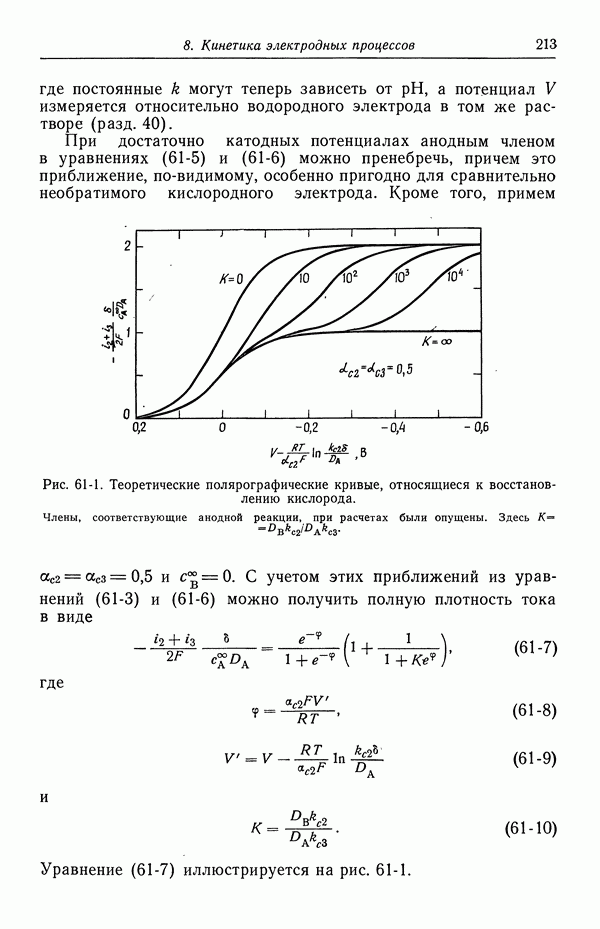
- 61. Одновременно протекающие реакции
- ЗАДАЧИ
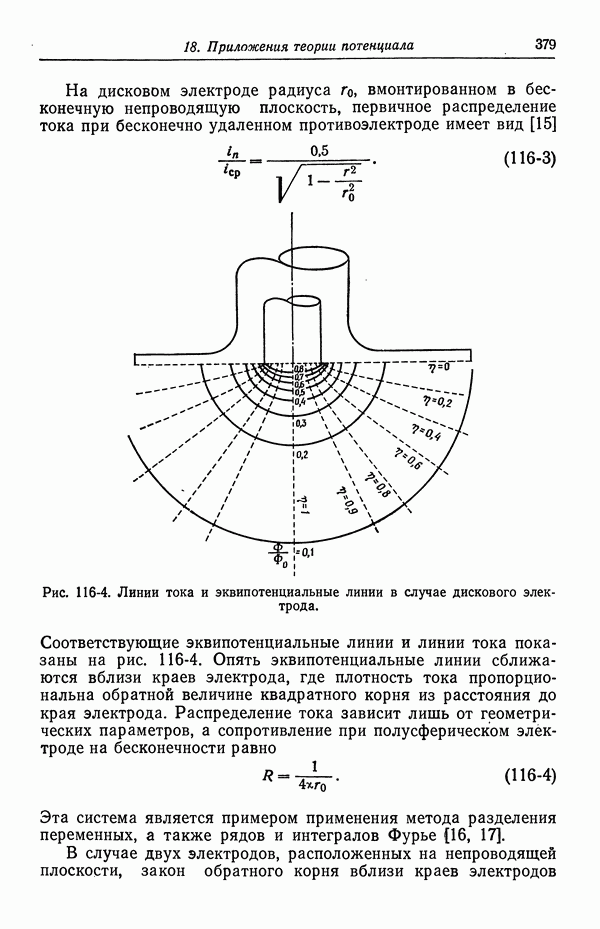
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
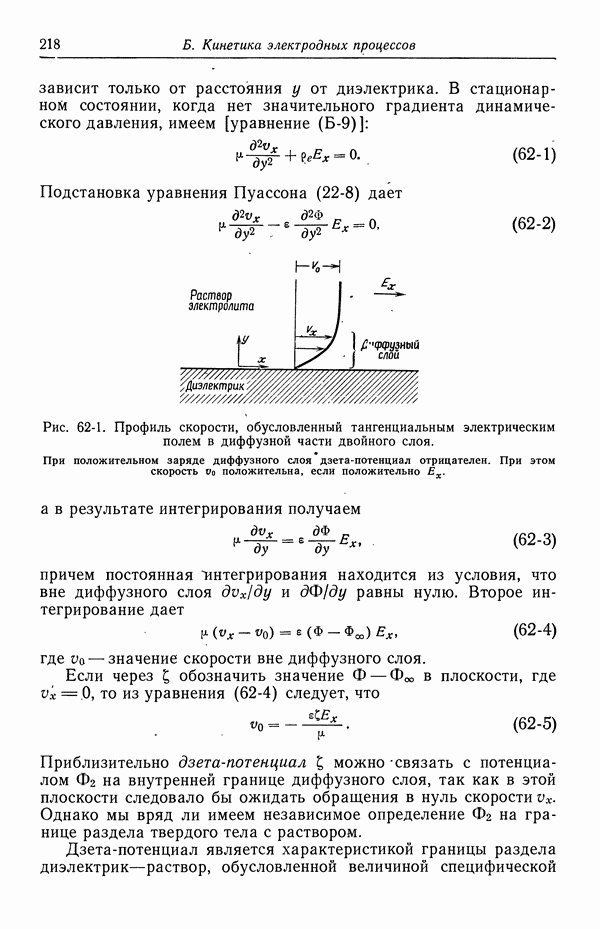
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
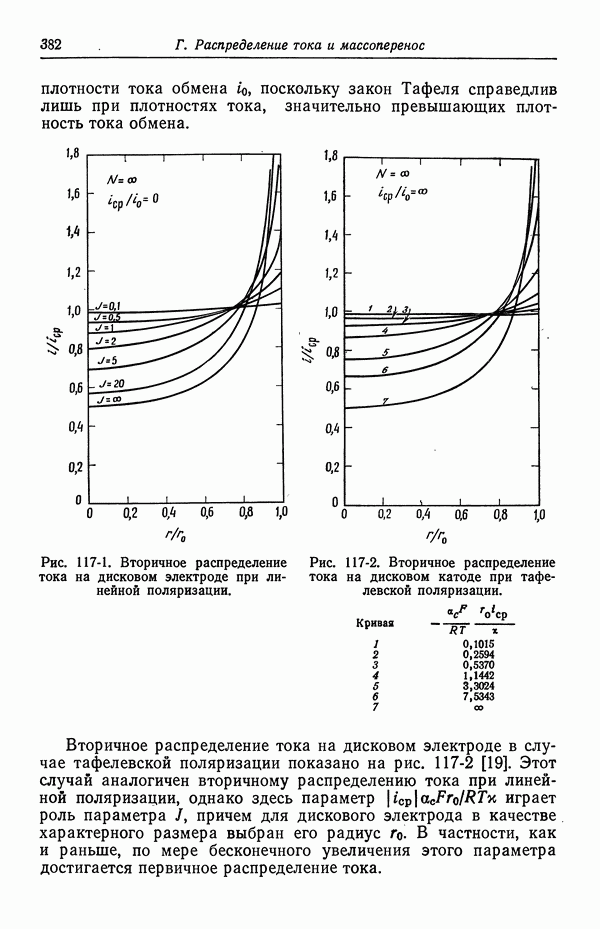
- 64. Электрофорез
- 65. Потенциал осаждения
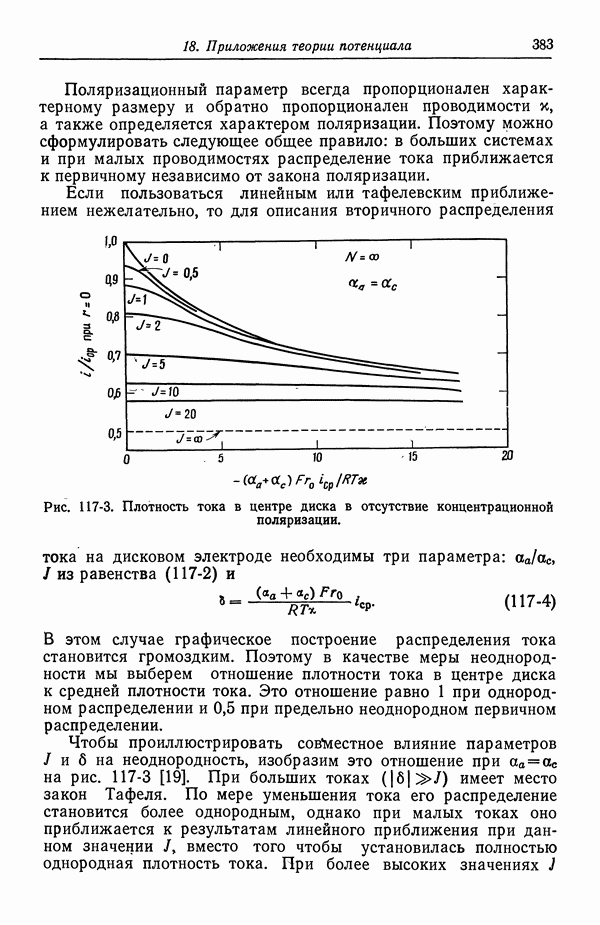
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 66. Динамика границы раздела
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 69. Законы переноса
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 78. Законы переноса
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
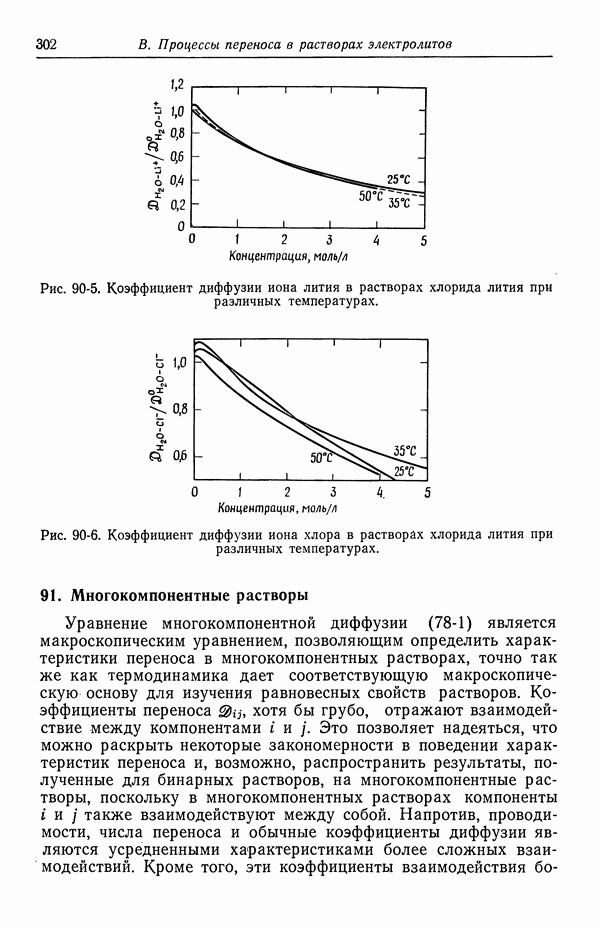
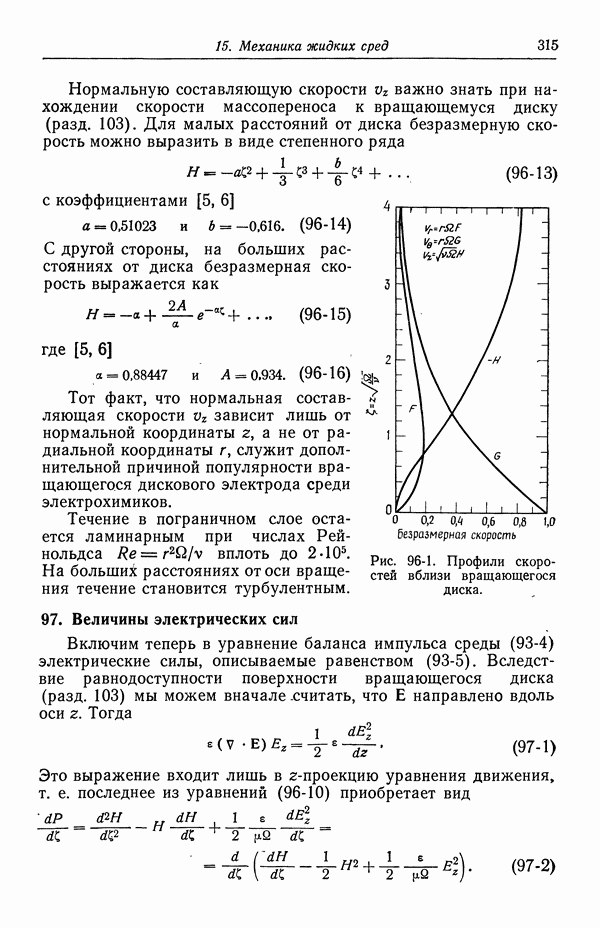
- 90. Растворы, содержащие одну соль
- 92. Интегральные коэффициенты диффузии
- ЗАДАЧА
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
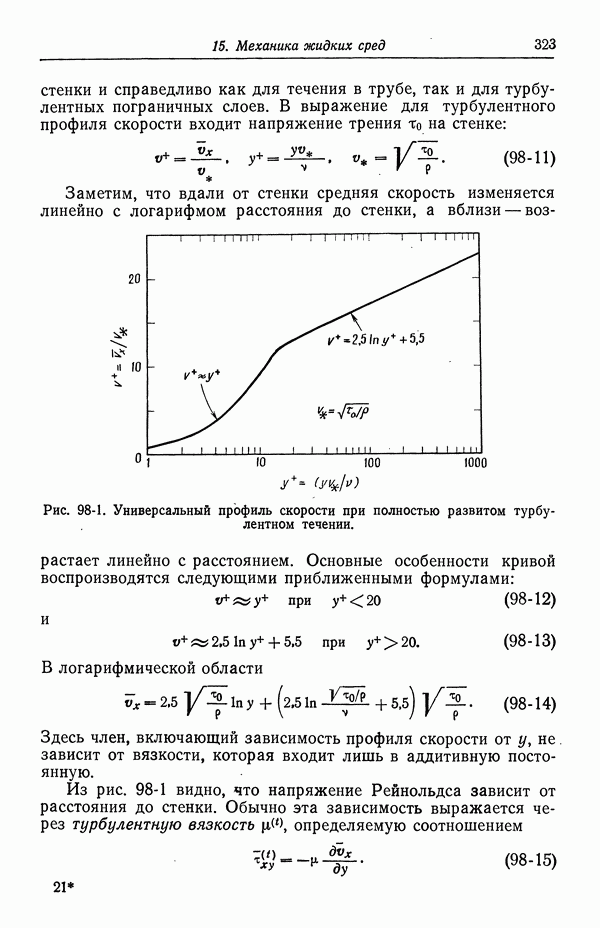
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
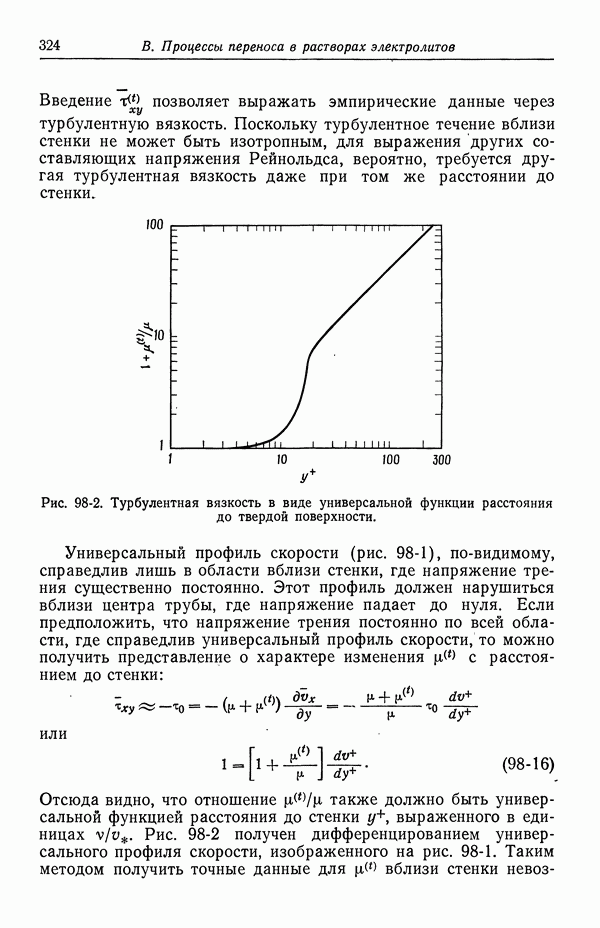
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 111. Свободная конвекция
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
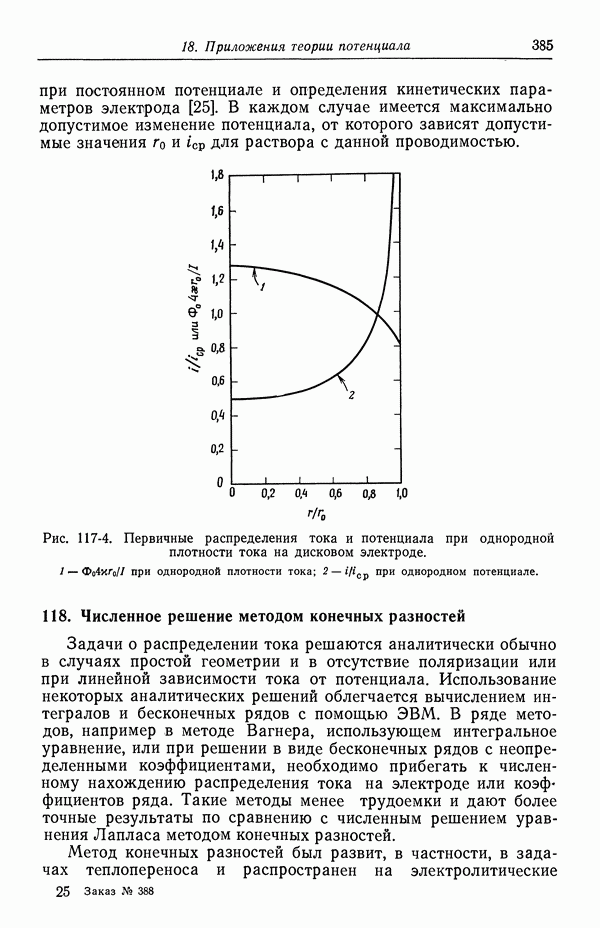
- 116. Первичное распределение тока
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- СПИСОК ОБОЗНАЧЕНИЙ
- ГЛАВА 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 119. Решение задачи
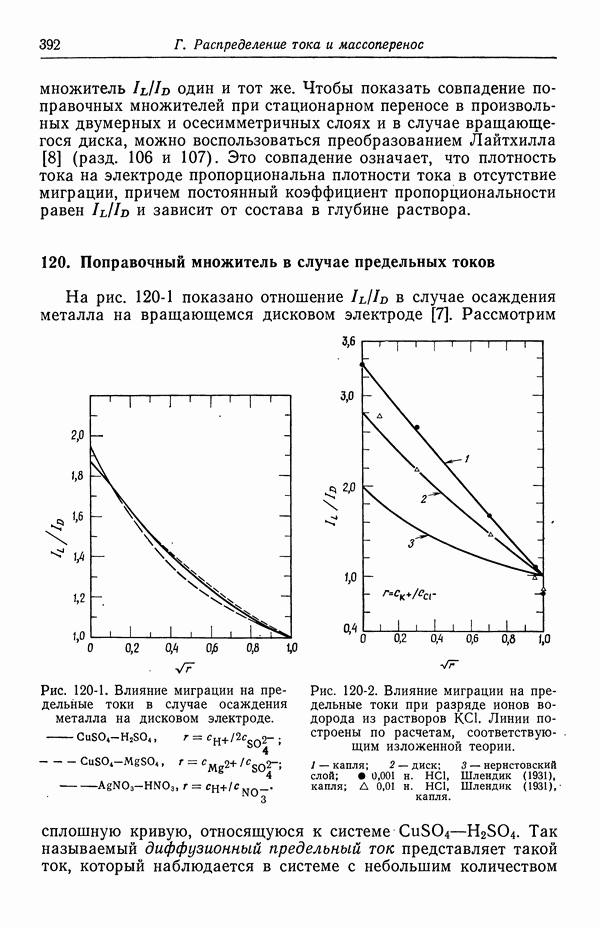
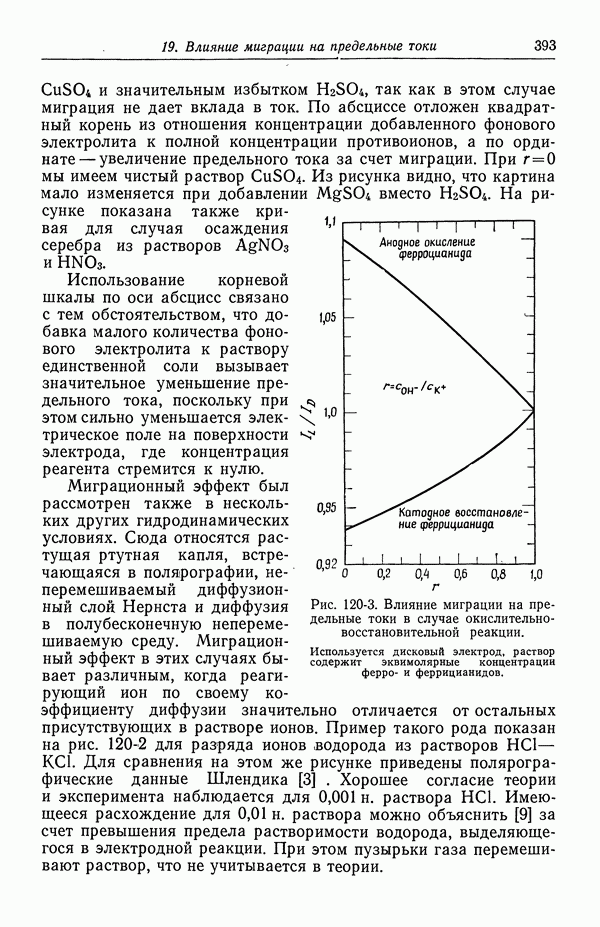
- 120. Поправочный множитель в случае предельных токов
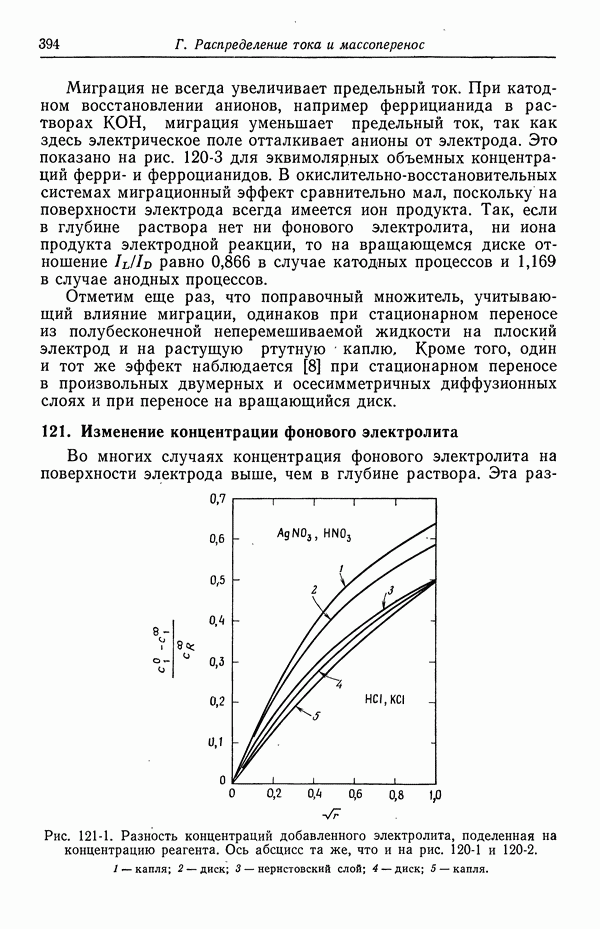
- 121. Изменение концентрации фонового электролита
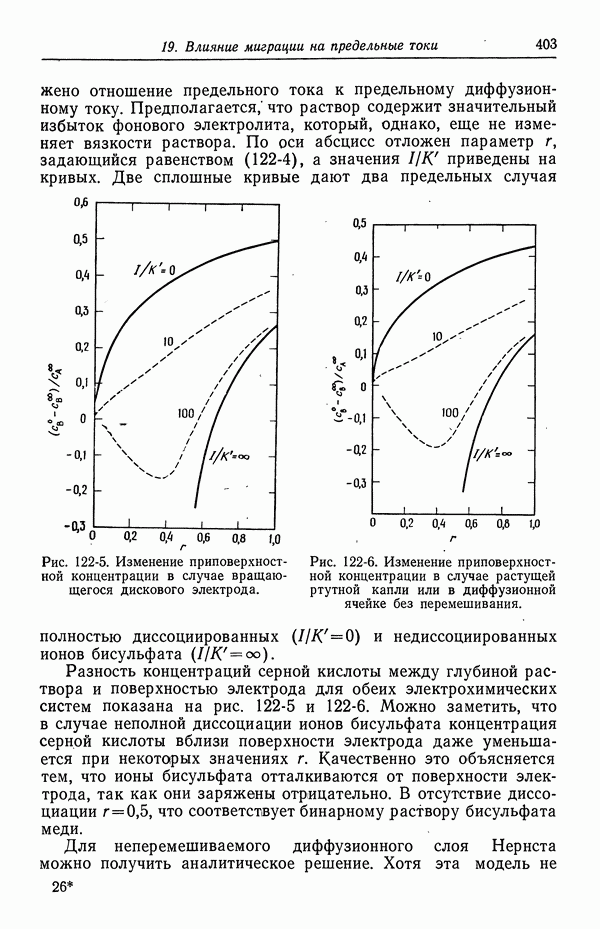
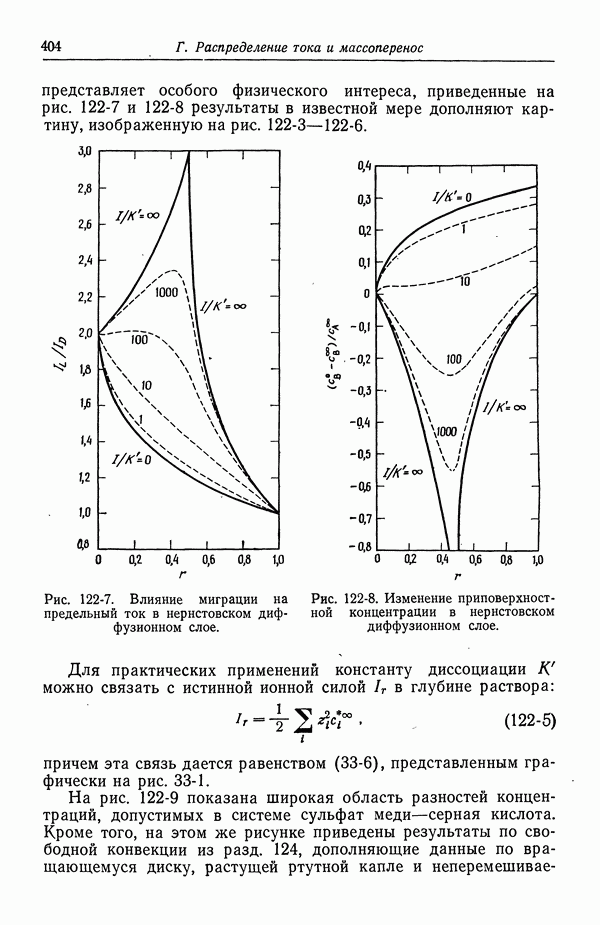
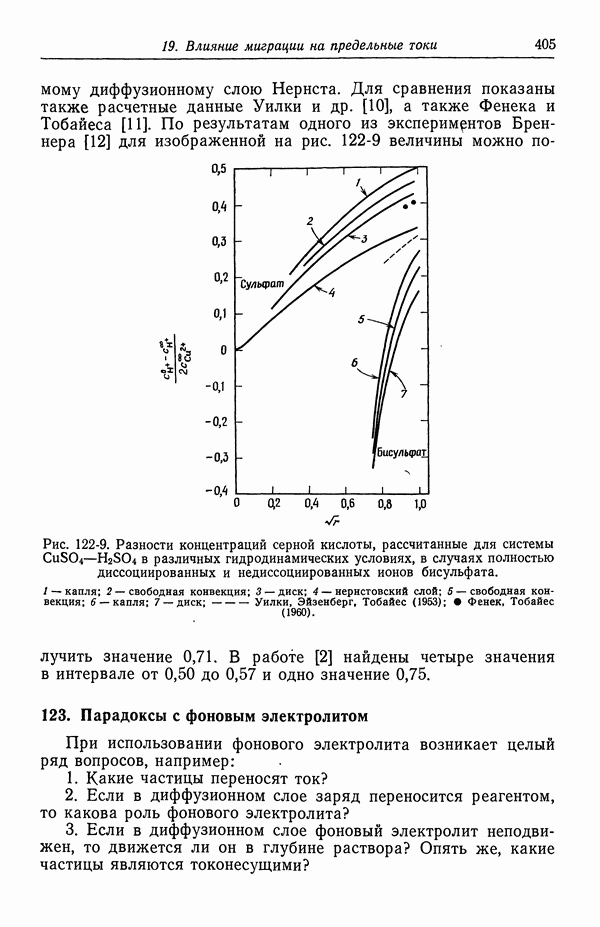
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
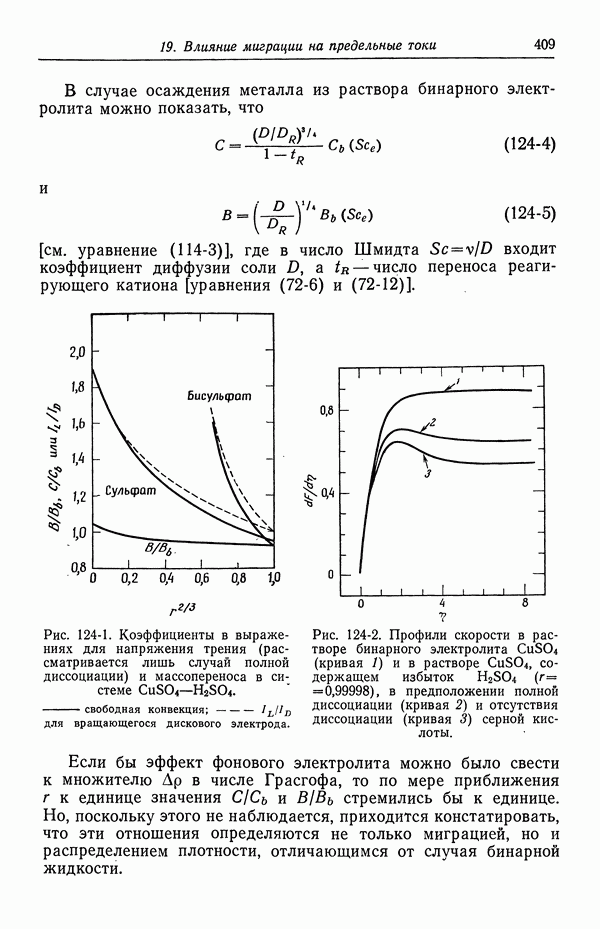
- 124. Предельные токи в случае свободной конвекции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
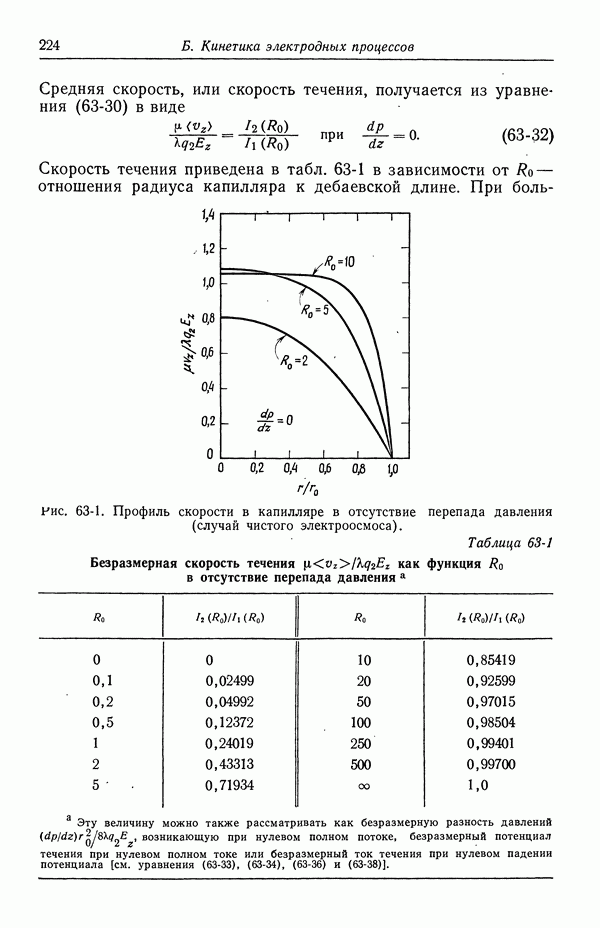
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ