97. Величины электрических сил

Включим теперь в уравнение баланса импульса среды (93-4) электрические силы, описываемые равенством (93-5). Вследствие равнодоступности поверхности вращающегося диска (разд. 103) мы можем вначале считать, что Е направлено вдоль оси . Тогда

Это выражение входит лишь в -проекцию уравнения движения, т. е. последнее из уравнений (96-10) приобретает вид

При Q = 300 об/мин, имеем В/см. Это дает возможность оценить относительную важность электрических сил, поскольку, например, по порядку величины близко к единице. При можно ожидать, что электрическое поле будет порядка В/см. Если бы изменение электрического поля было мало по сравнению с , то электрической силой можно было бы вообще пренебречь.

С учетом уравнения (70-1) электрическое поле можно выразить в виде

а следовательно, плотность электрического заряда равна

Из этих уравнений видно следующее. Плотность электрического заряда отличается от нуля лишь в тонких диффузионных слоях вблизи электродов, так как только в этих областях концентрации и проводимость изменяются. Плотность заряда здесь мала (разд. 76), поскольку мало значение , а вне этих областей она обращается в нуль. Можно также заметить, что электрический эффект будет наибольшим для бинарного электролита, так как в присутствии фонового электролита значение к будет велико по сравнению с изменениями к.

Из уравнения (97-3) видно, что в диффузионных слоях, где отличается от нуля, Е практически перпендикулярно к поверхности электрода. Это означает, что электрическая сила преобладает в уравнении движения, спроектированном на нормальное направление. Электрическая сила влияет на распределение давления, не изменяя профиля скорости. Этот эффект сравнительно несуществен, поскольку именно профиль скорости определяет скорость массопереноса; последнее легко наблюдается в случае вращающегося диска, где, как отмечалось выше, весь электрический эффект может сводиться к изменению динамического давления SP, а профиль скорости не меняется совсем.

Собственно говоря, любую часть которую можно выразить в виде градиента некоторой величины, можно отнести к Такой является часть ротор которой равен нулю:

Ротор Е равен нулю, так как Е — градиент потенциала, взятый с обратным знаком (см. строку 56 в табл. Б-1). Таким образом,

можно заключить, что именно та величина, которая влияет на распределение скоростей, описывается равенством (97-5). Как указывалось выше, отличается от нуля лишь в диффузионных слоях, и поэтому можно ожидать, что Е и почти параллельны друг другу, так что их векторное произведение мало. Это еще раз подтверждает вывод о том, что электрическая сила в основном влияет на давление и мало влияет на скорость.

Далее, при больших числах Шмидта диффузионный слой много тоньше гидродинамического пограничного слоя. Здесь становятся более существенными вязкие силы. Относительно электрических сил можно считать, что они оказывают меньшее влияние по сравнению с тем случаем, когда они приложены вдали от стенки. С другой стороны, скорости здесь гораздо меньше по своей величине и играют существенную роль при определении скорости массопереноса. Следовательно, этот эффект все-таки может быть важным.

Чтобы выяснить влияние электрической силы на профиль скорости, следует применить к уравнению движения (94-4) операцию . Таким образом исключается давление. Допустим, что преобразование фон Кармана (96-9) по-прежнему справедливо, и рассмотрим величину электрической силы, которой раньше мы пренебрегали. Применение операции к уравнению движения дает

а уравнение непрерывности теперь приобретает вид

Правая часть уравнения (97-7) получается из векторного произведения и Е [уравнение (97-5)]. Как отмечалось выше, должны выполняться неравенства Это затрудняет оценку величины этих членов. Чтобы продвинуться дальше, будем считать, что не зависит от , а не зависит от координаты в диффузионном слое и определяется соотношением

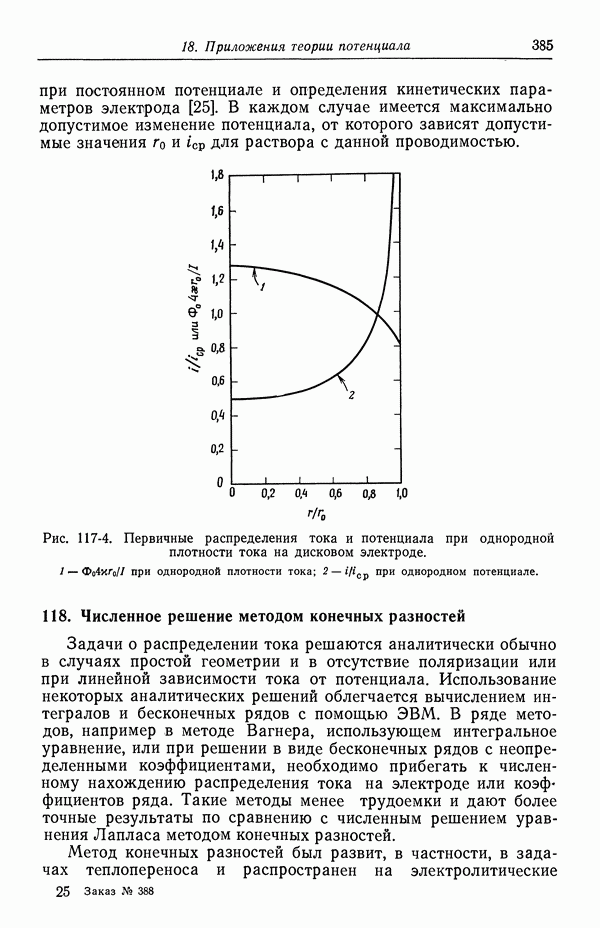
где А приблизительно равно 0,73. Эта формула дает приближенное выражение для зависимости от радиуса тангенциального

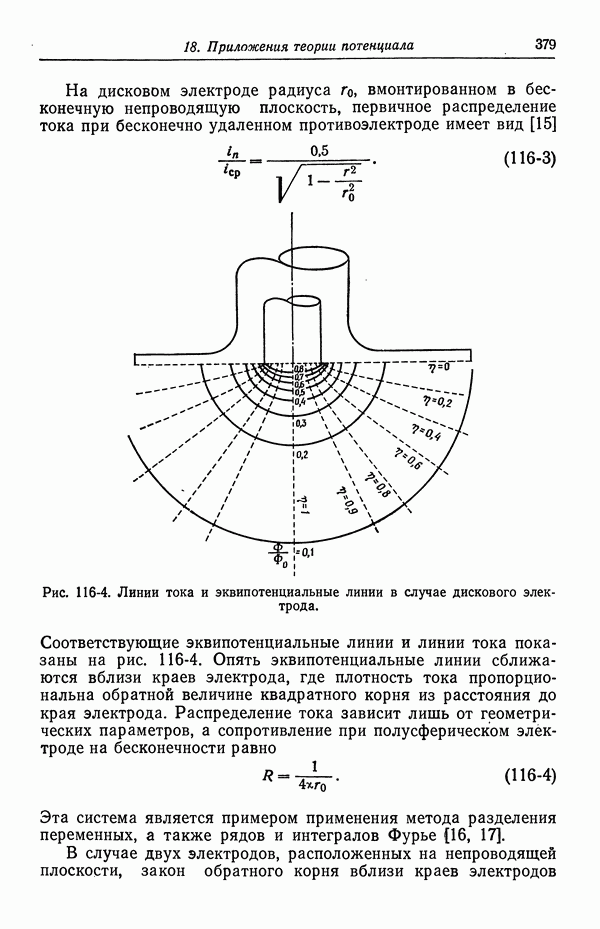
электрического поля сразу за диффузионным слоем, если плотность тока на поверхности диска, вмонтированного в непроводящую плоскость, однородна (рис. 117-4). Положение с тангенциальным электрическим полем здесь аналогично случаю электро-кинетических явлений, рассмотренных в гл. 9.

Теперь, интегрируя уравнение (97-7), получаем

причем постоянная интегрирования равна нулю, так как F, G и стремятся к нулю по мере бесконечного возрастания .

Для бинарного электролита уравнение (97-4) сводится к

где — эквивалентная проводимость [уравнение (75-8)], которая считается постоянной. В качестве решения уравнения конвективной диффузии (72-5) можно принять

где

а значение а дается равенством (96-14). Выражение (97-12) можно получить из уравнения (103-8) при больших числах Шмидта причем со и обозначают концентрации на поверхности электрода и в глубине раствора соответственно. Мы ограничимся реакцией осаждения металла, для которой плотность тока описывается равенством (72-11).

В этих предположениях последний член в уравнении (97-10) принимает вид

Коэффициент в этом выражении оценивается следующим образом:

где, кроме значений, приведенных после уравнения (97-2),

использованы также см для радиуса электрода и для числа Шмидта.

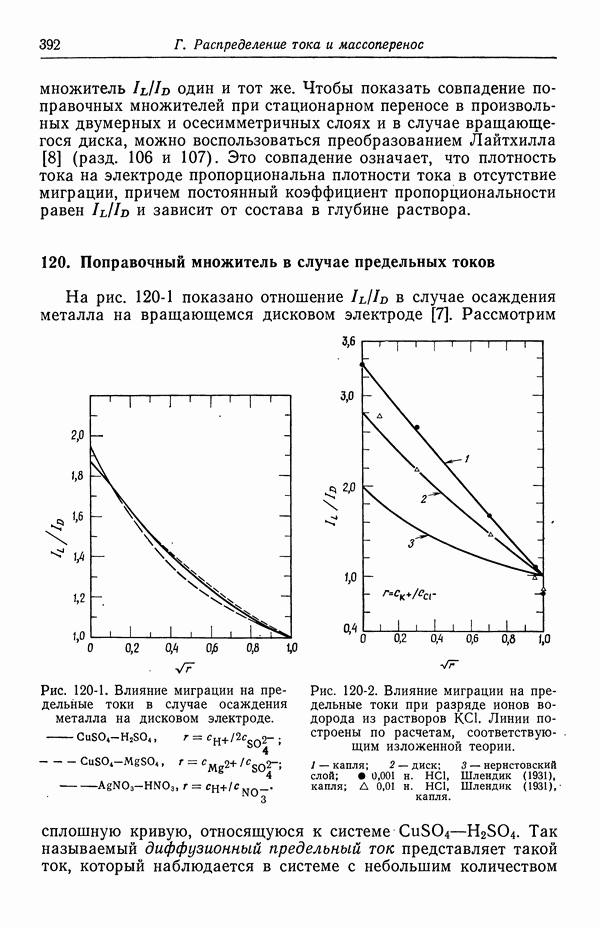
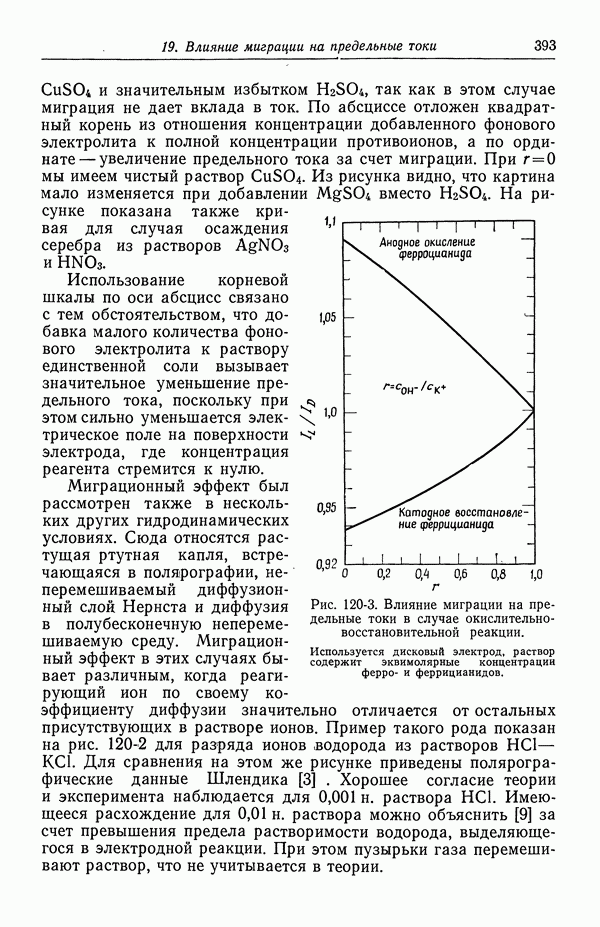
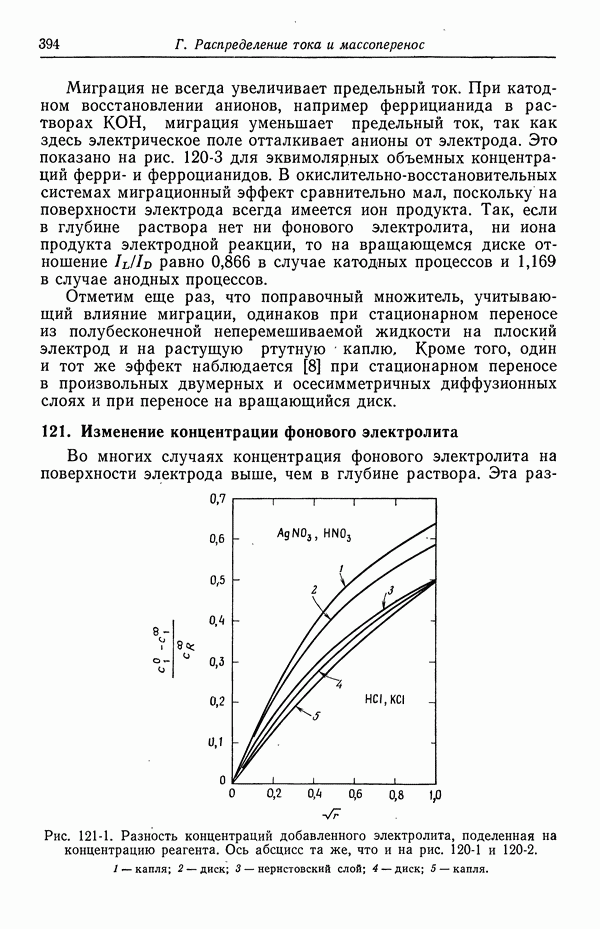
Множитель в уравнении (97-14) или (97-15) учитывает тот факт, что электрическая сила действует лишь внутри диффузионного слоя, который много тоньше гидродинамического пограничного слоя. Коэффициент в уравнении (97-15) показывает, что пренебрегаемая электрическая сила достигает лишь 0,6% от членов, сохранявшихся в уравнении (97-10), которое решалось в разд. 96 (при этом член равен 1 при Множитель, содержащий в уравнении (97-14), показывает, что роль электрического эффекта возрастает при токах, близких к предельному, поскольку в этом случае с на электроде стремится к нулю. Это замечание, конечно, не имеет силы при наличии фонового электролита.