| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
103. Вращающийся диск
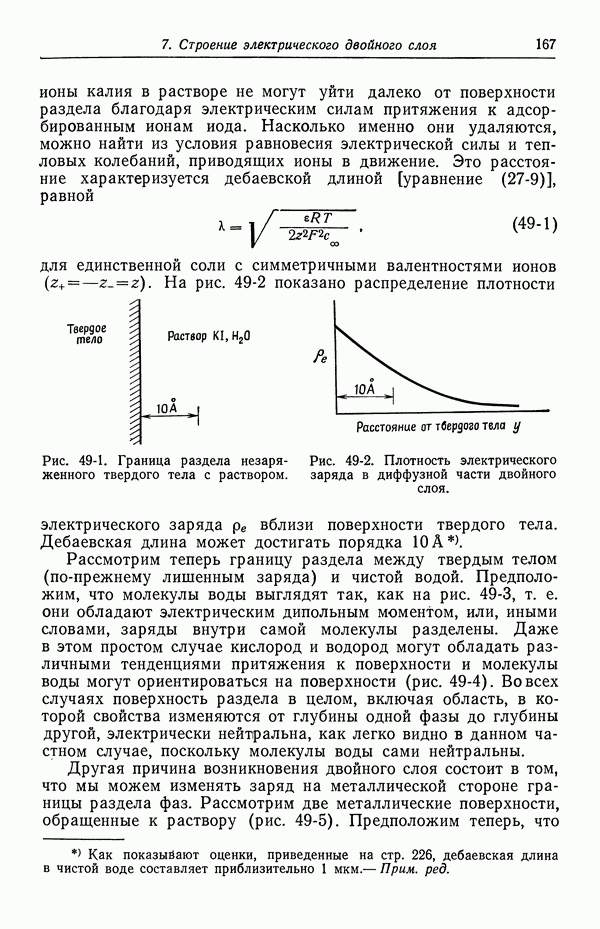
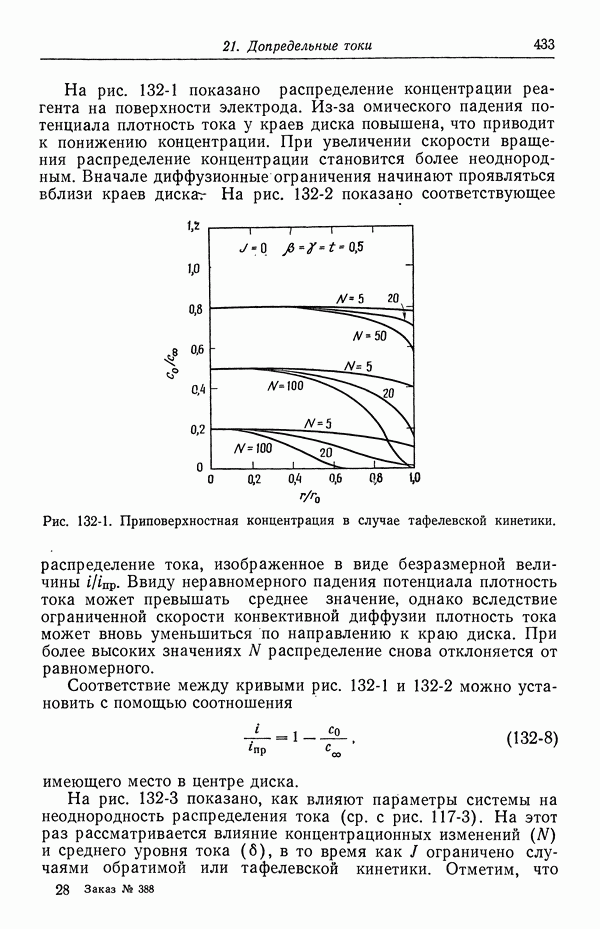
В качестве первого примера рассмотрим задачу о конвективной диффузии к вращающемуся дисковому электроду, хорошо известному электрохимикам. Представим себе большой или бесконечный диск, вращающийся вокруг своей оси в бесконечной жидкой среде, так что пристенными и краевыми эффектами можно пренебречь. В действительности краевыми эффектами можно пренебречь при подходящей конструкции диска. Так, мы будем рассматривать электрод в виде диска, вмонтированного в еще большую изолирующую поверхность, как показано на рис. 103-1. При этом диск вместе с изолирующей поверхностью вращается. Такая система рассмотрена Риддифордом [8].
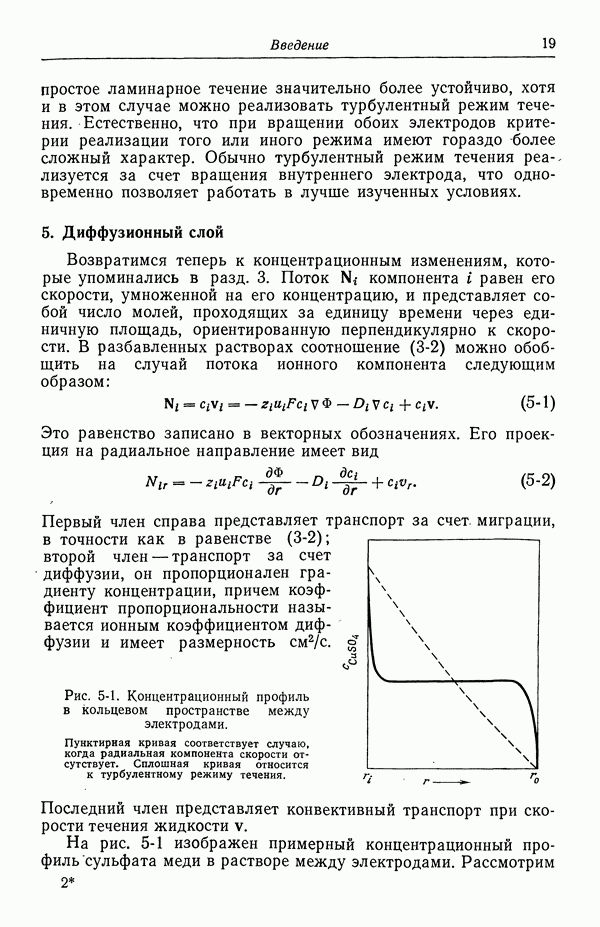
Вращение диска приводит к перемешиванию жидкости. Гидродинамический аспект этой задачи изложен в разд. 96. Одним из наиболее важных результатов был тот факт, что перпендикулярная
к поверхности диска скорость, благодаря которой к диску переносится новый реагент, зависит от z, а не от  :
:

Следовательно, нет причин для того, чтобы концентрация зависела еще от других факторов, кроме расстояния до диска, и уравнение конвективной диффузии (102-2) приобретает вид

с краевыми условиями


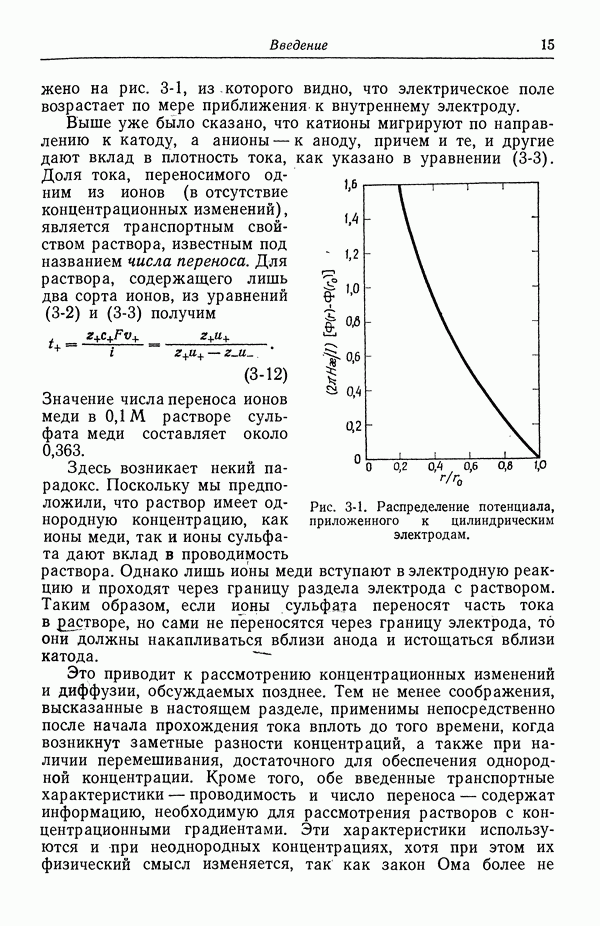
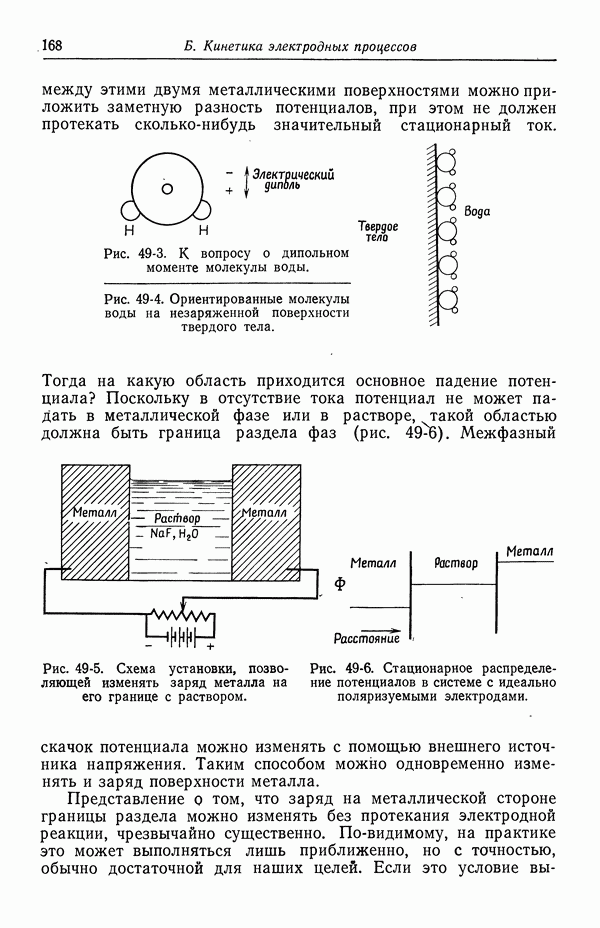
Рис. 103-1. Вращающийся дисковый электрод.
В случае предельного тока  . Таким образом тот факт, что скорость течения, несущего реагент к диску, одинакова на всей поверхности, с математической точки зрения удобен тем, что позволяет свести уравнение конвективной диффузии к обыкновенному дифференциальному уравнению. Практически это обстоятельство выгодно тем, что скорость реакции на электроде будет всюду одинаковой независимо от расстояния до оси вращения.
. Таким образом тот факт, что скорость течения, несущего реагент к диску, одинакова на всей поверхности, с математической точки зрения удобен тем, что позволяет свести уравнение конвективной диффузии к обыкновенному дифференциальному уравнению. Практически это обстоятельство выгодно тем, что скорость реакции на электроде будет всюду одинаковой независимо от расстояния до оси вращения.
В работе [9] проанализирована задача о массопереносе к вращающемуся диску для описанного выше течения. Аналогичная задача о теплопереносе была рассмотрена Вагнером лишь в 1948 г. [10].
Уравнение (103-2) является дифференциальным уравнением первого порядка относительно  Его интегрирование дает
Его интегрирование дает

или

В результате второго интегрирования получаем

Из краевого условия (103-3) теперь можно найти постоянную К:

где последнее выражение получено при использовании равенства (103-1) и числа Шмидта  Тогда решение можно записать в виде
Тогда решение можно записать в виде

Здесь

есть безразмерная концентрация.
Поток на поверхности диска равен

а с помощью уравнения (101-2) плотность тока можно выразить как

где штрих обозначает производную по  и
и

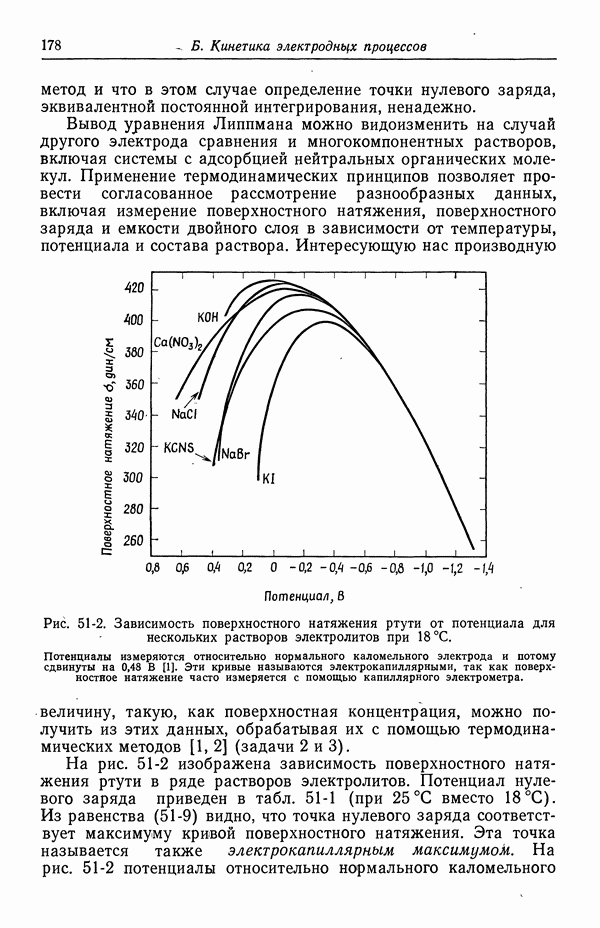
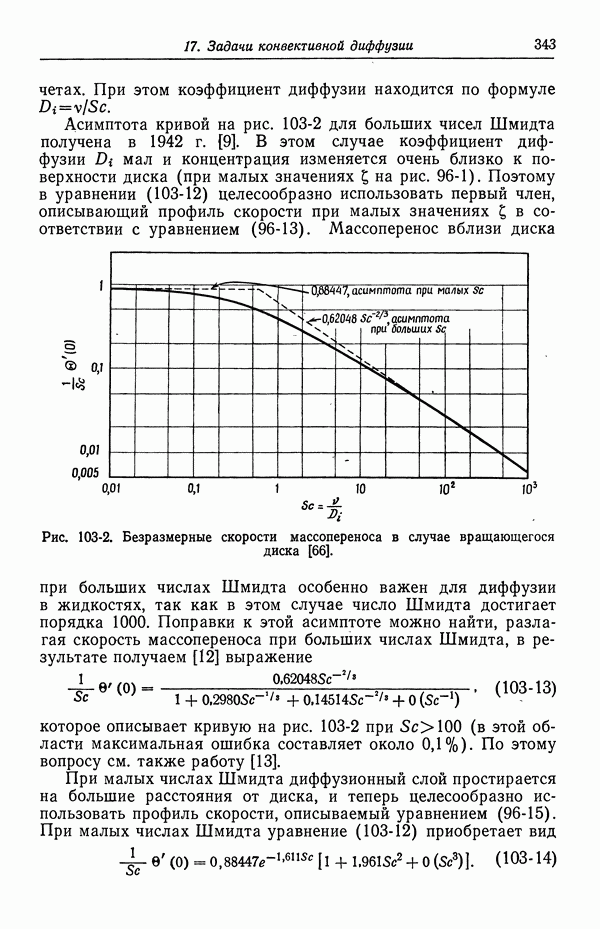
Из равенства (103-12) видно, что безразмерная скорость массопереноса зависит лишь от числа Шмидта  Эта зависимость изображена на рис. 103-2 (см. работу [11]). Если поток массы или плотность тока известны, то ордината не зависит от коэффициента диффузии [равенство (103-11)]. Следовательно, этот графический метод обладает тем преимуществом, что позволяет определять коэффициенты диффузии с помощью вращающегося диска. Ордината вычисляется непосредственно по предельной плотности тока. Тогда число Шмидта можно получить прямо из графика, не прибегая к методу проб и ошибок в
Эта зависимость изображена на рис. 103-2 (см. работу [11]). Если поток массы или плотность тока известны, то ордината не зависит от коэффициента диффузии [равенство (103-11)]. Следовательно, этот графический метод обладает тем преимуществом, что позволяет определять коэффициенты диффузии с помощью вращающегося диска. Ордината вычисляется непосредственно по предельной плотности тока. Тогда число Шмидта можно получить прямо из графика, не прибегая к методу проб и ошибок в
расчетах. При этом коэффициент диффузии находится по формуле 
Асимптота кривой на рис. 103-2 для больших чисел Шмидта получена в 1942 г. [9]. В этом случае коэффициент диффузии  мал и концентрация изменяется очень близко к поверхности диска (при малых значениях
мал и концентрация изменяется очень близко к поверхности диска (при малых значениях  на рис. 96-1). Поэтому в уравнении (103-12) целесообразно использовать первый член, описывающий профиль скорости при малых значениях
на рис. 96-1). Поэтому в уравнении (103-12) целесообразно использовать первый член, описывающий профиль скорости при малых значениях  в соответствии с уравнением (96-13).
в соответствии с уравнением (96-13).

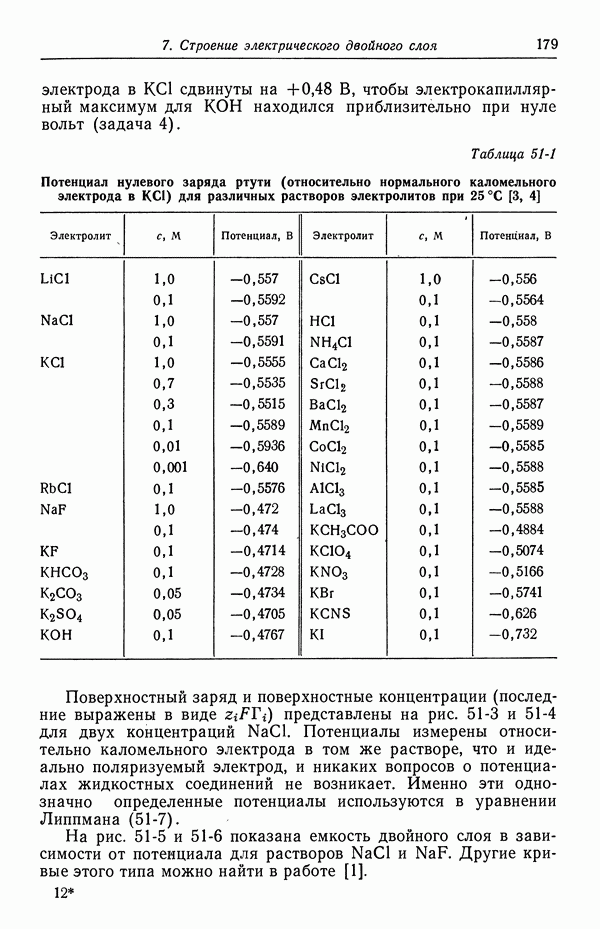
Рис. 103-2. Безразмерные скорости массопереноса в случае вращающегося диска [66].
Массоперенос вблизи диска при больших числах Шмидта особенно важен для диффузии в жидкостях, так как в этом случае число Шмидта достигает порядка 1000. Поправки к этой асимптоте можно найти, разлагая скорость массопереноса при больших числах Шмидта, в результате получаем [12] выражение

которое описывает кривую на рис. 103-2 при  (в этой области максимальная ошибка составляет около
(в этой области максимальная ошибка составляет около  ). По этому вопросу см. также работу [13].
). По этому вопросу см. также работу [13].
При малых числах Шмидта диффузионный слой простирается на большие расстояния от диска, и теперь целесообразно использовать профиль скорости, описываемый уравнением (96-15). При малых числах Шмидта уравнение (103-12) приобретает вид

Первый член этого уравнения показывает, что при очень больших коэффициентах диффузии максимальный поток на диск полностью определяется скоростью конвективного переноса вещества с бесконечности:

Ввиду того что характер течения жидкости вблизи дискового электрода хорошо известен, этот электрод широко использовался для определения коэффициентов диффузии и параметров кинетики электродных процессов. Его можно применять и для количественного (полярографического) анализа в растворах электролитов. Краевой эффект при вращении диска рассмотрен в работе [14].
Широко распространен также вращающийся диск с кольцом, поскольку с помощью кольцевого электрода можно регистрировать активные промежуточные продукты, возникающие на дисковом электроде. Регистрируемые таким образом количества вещества можно сопоставить с теоретическим значением коэффициента эффективности данной системы [15, 16].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
- 5. Диффузионный слой
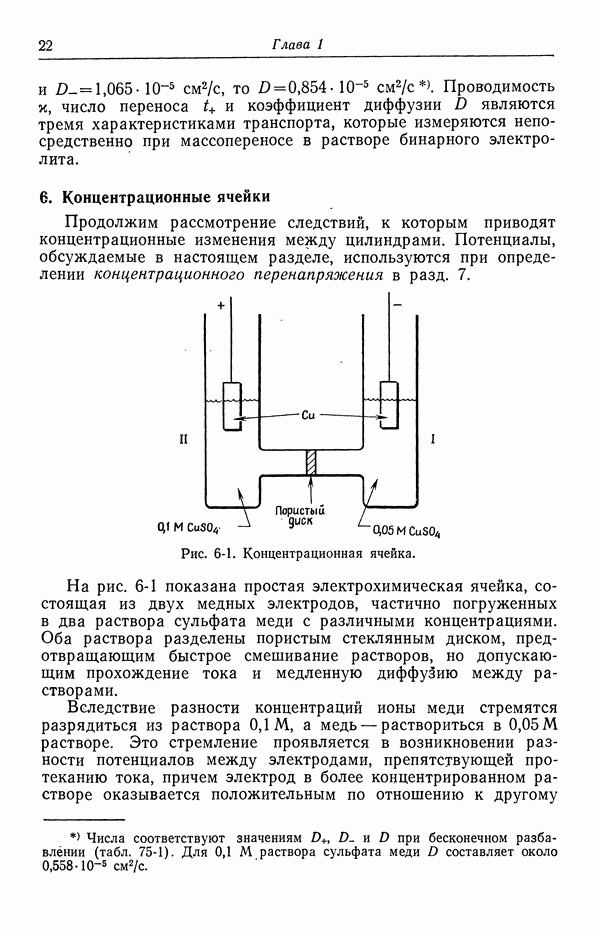
- 6. Концентрационные ячейки
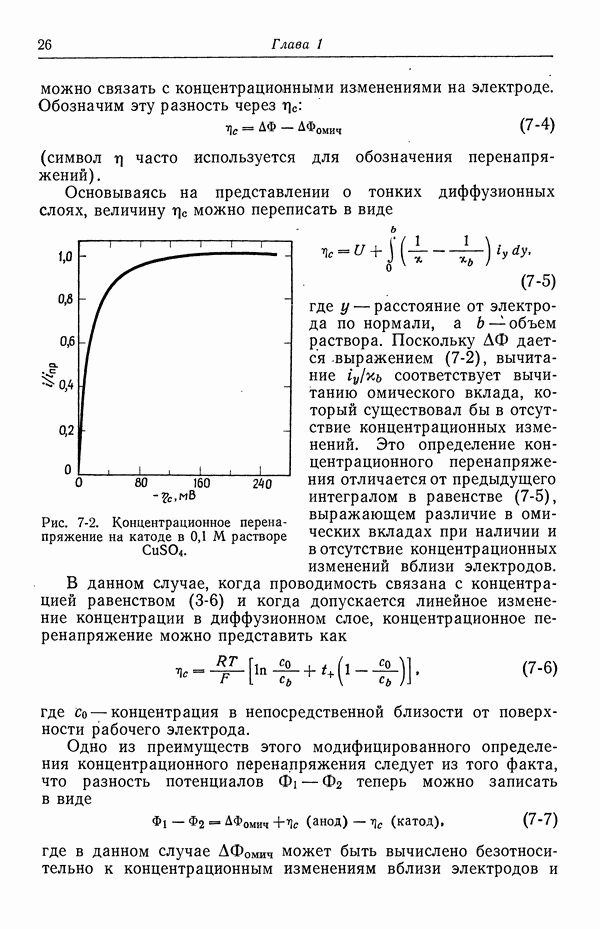
- 7. Концентрационное перенапряжение
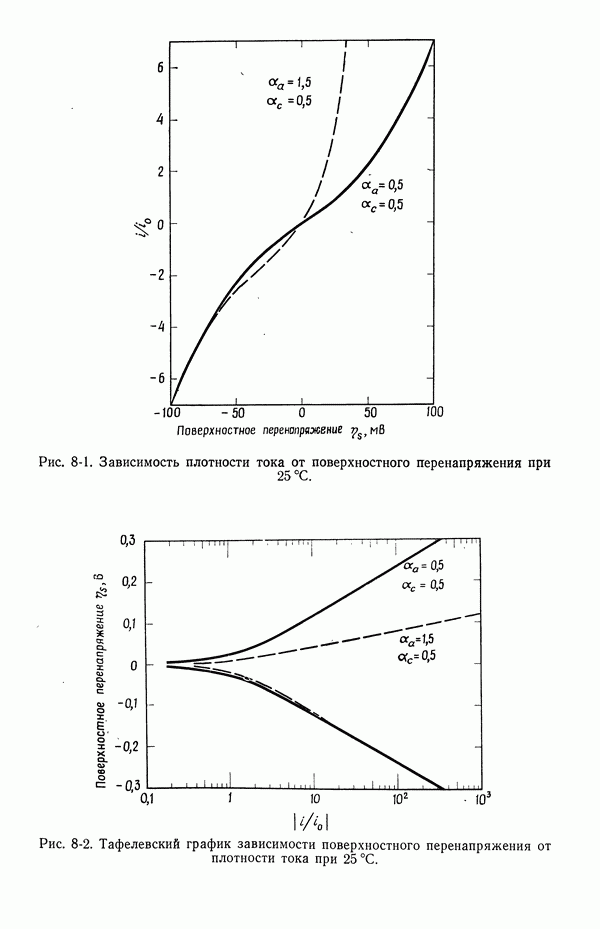
- 8. Поверхностное перенапряжение
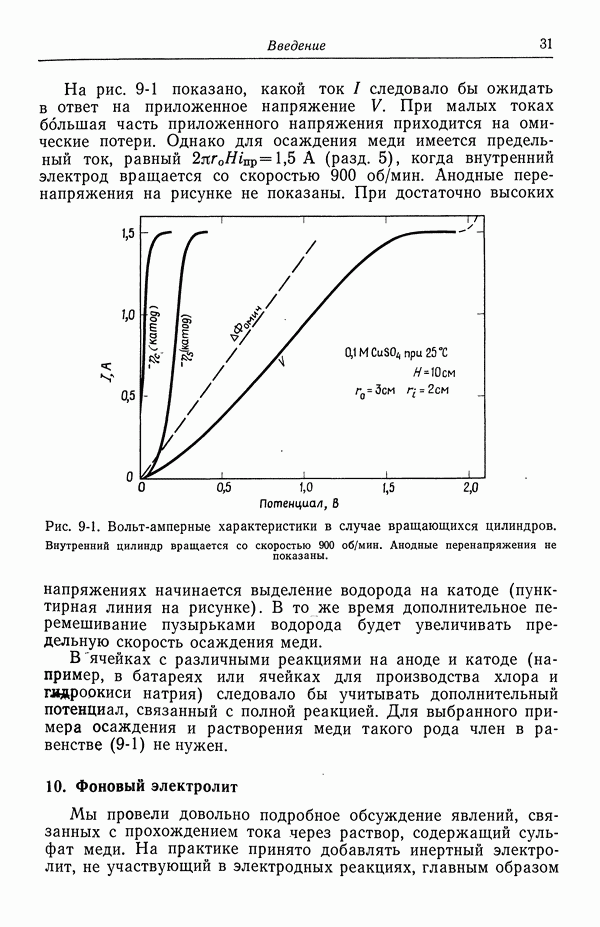
- 9. Потенциал ячейки
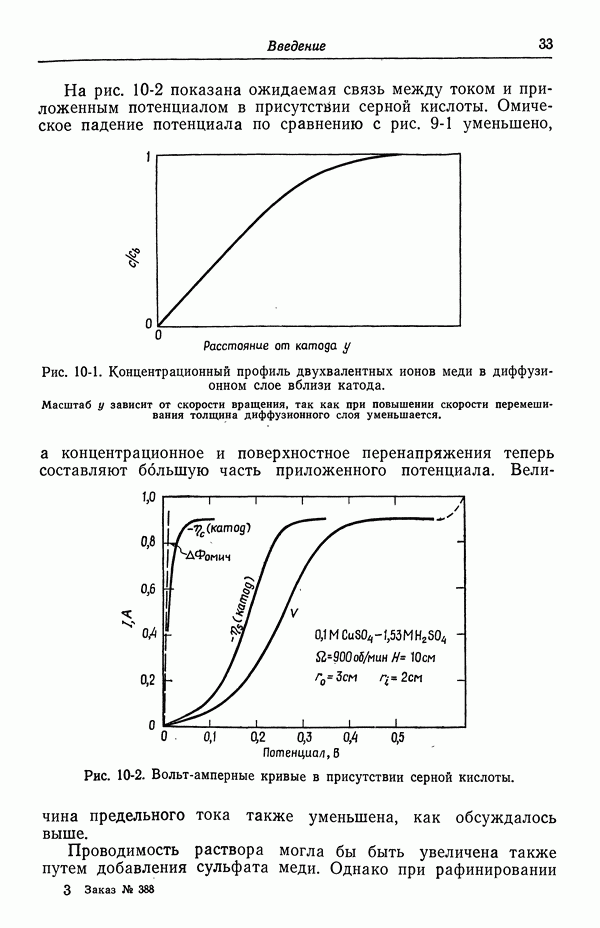
- 10. Фоновый электролит
- 11. Свободная конвекция
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
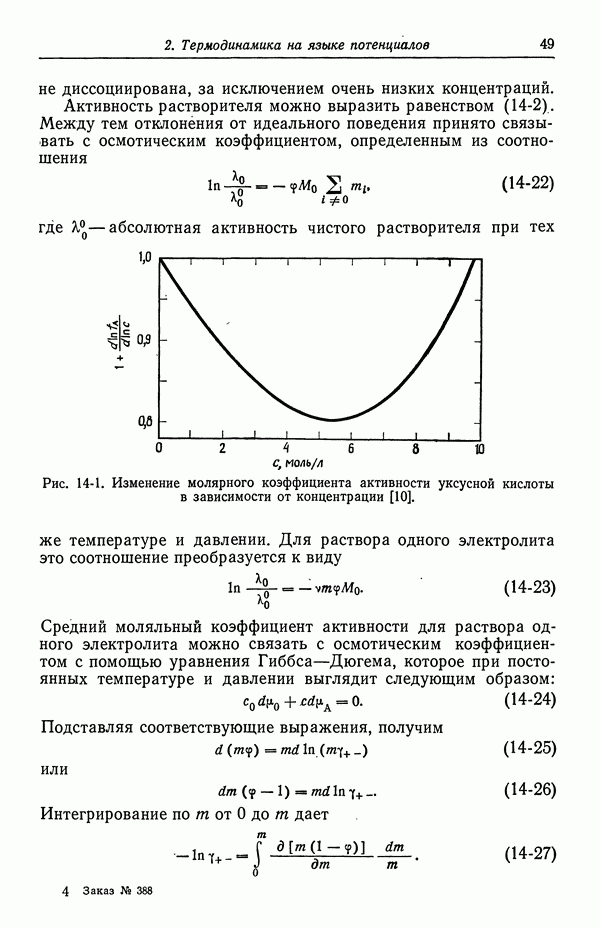
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
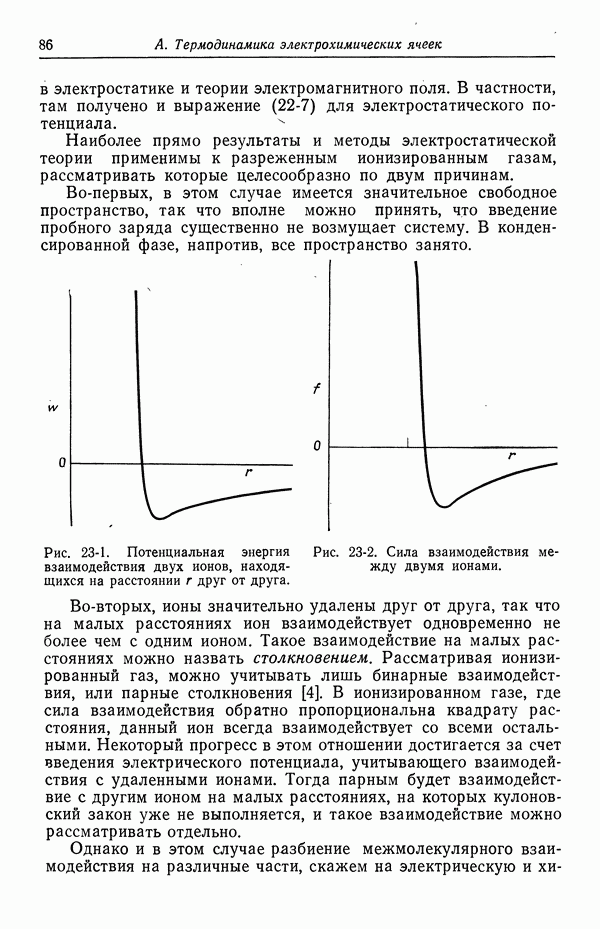
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
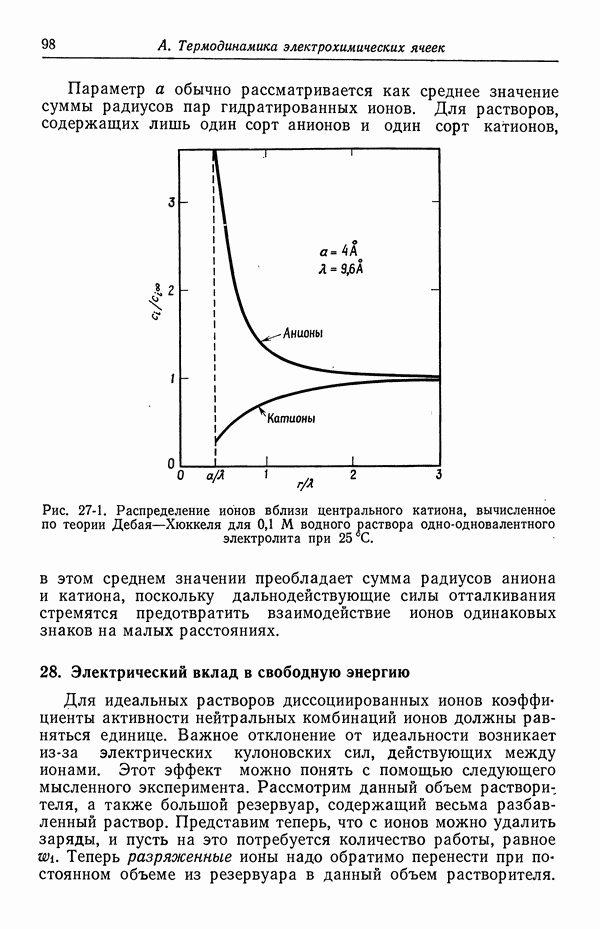
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая—Хюккеля
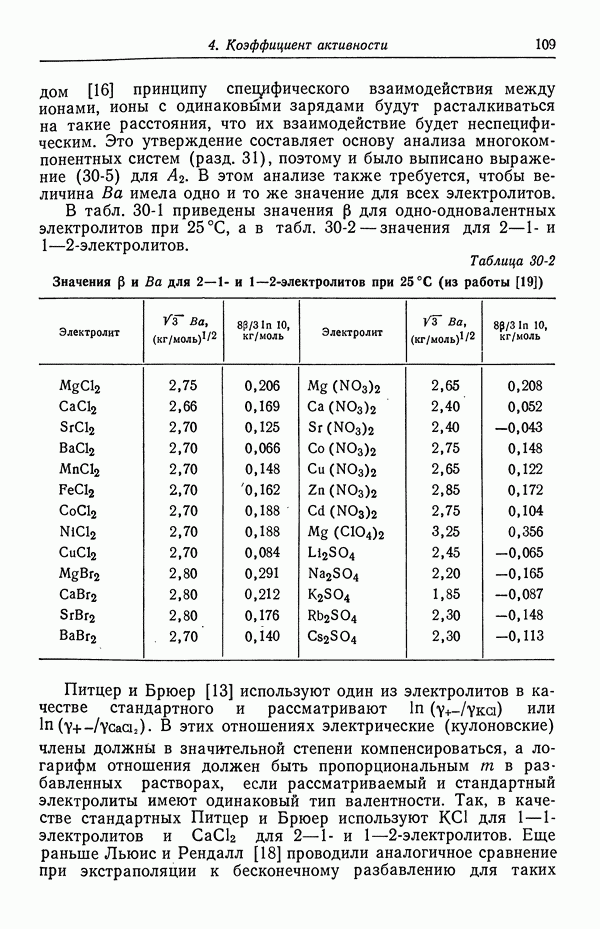
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 49. Качественное описание двойных слоев
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод — раствор
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
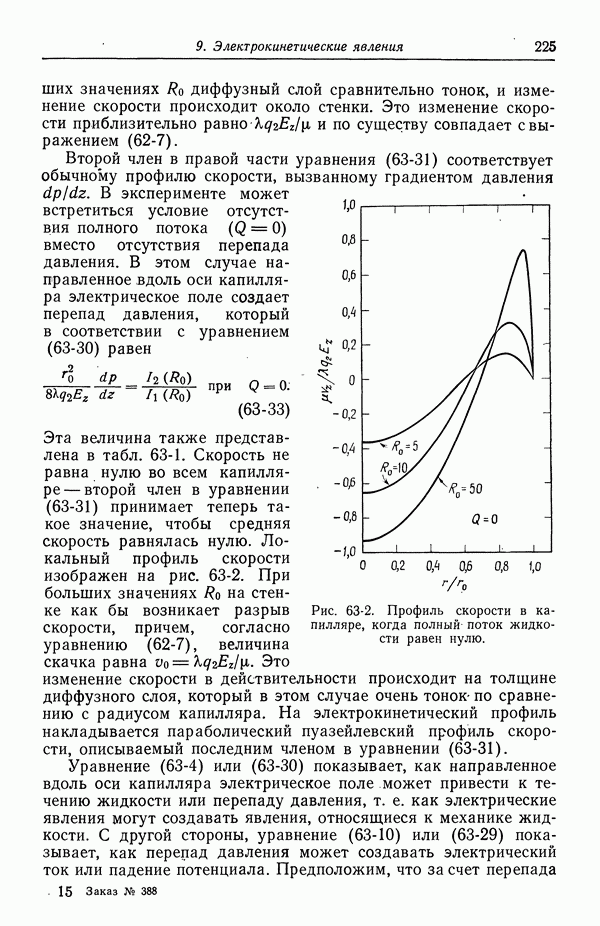
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 66. Динамика границы раздела
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 69. Законы переноса
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
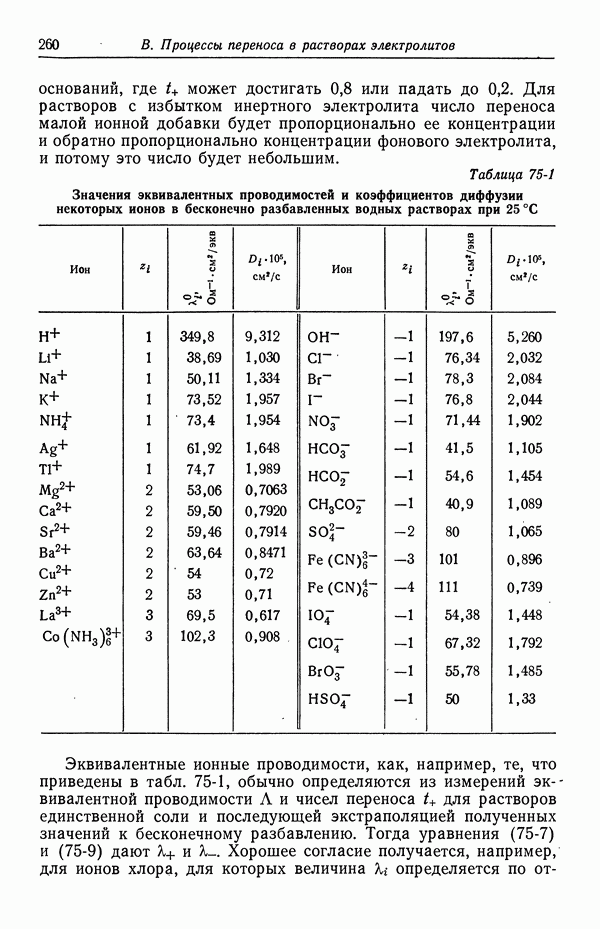
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 78. Законы переноса
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
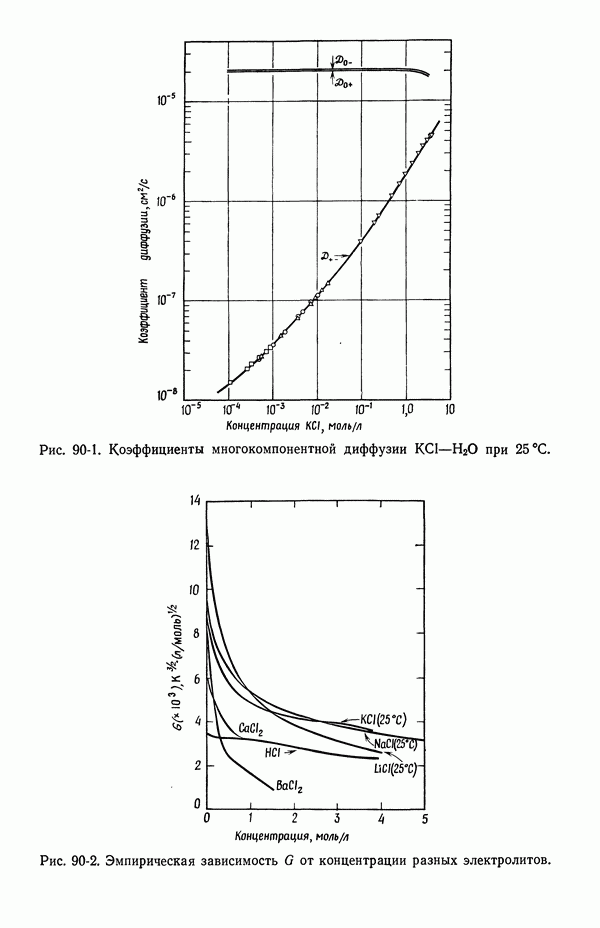
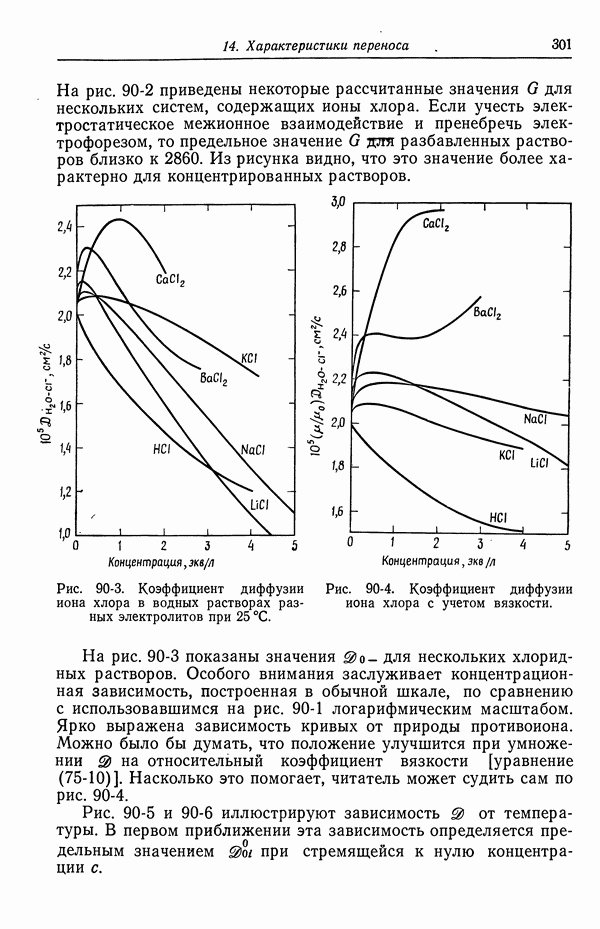
- 90. Растворы, содержащие одну соль
- 92. Интегральные коэффициенты диффузии
- ЗАДАЧА
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
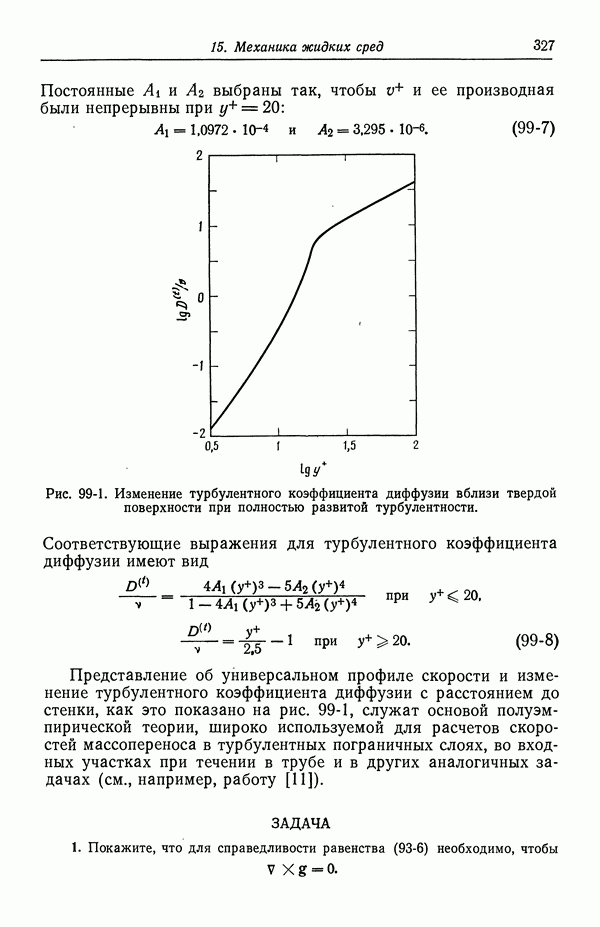
- 99. Массоперенос в турбулентном потоке
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
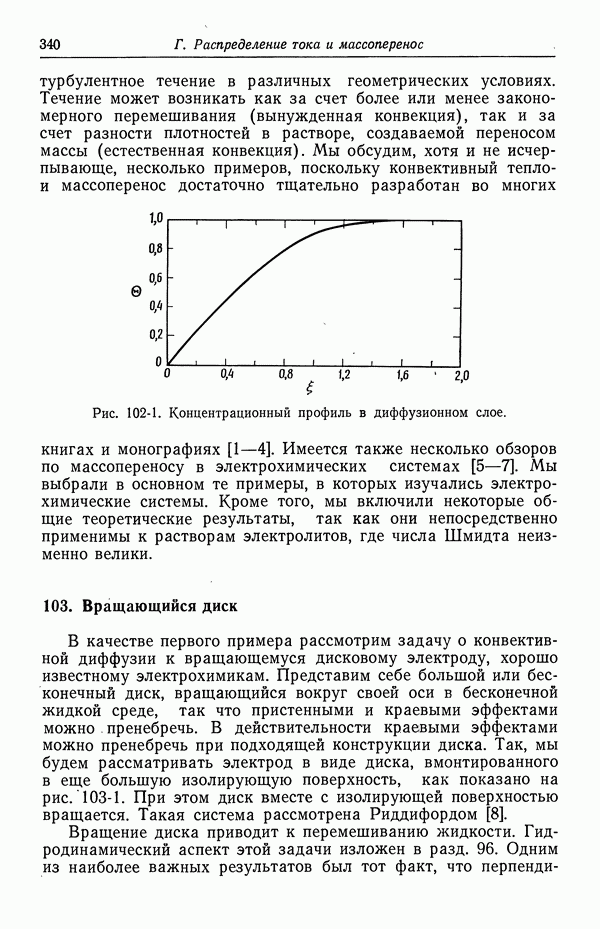
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
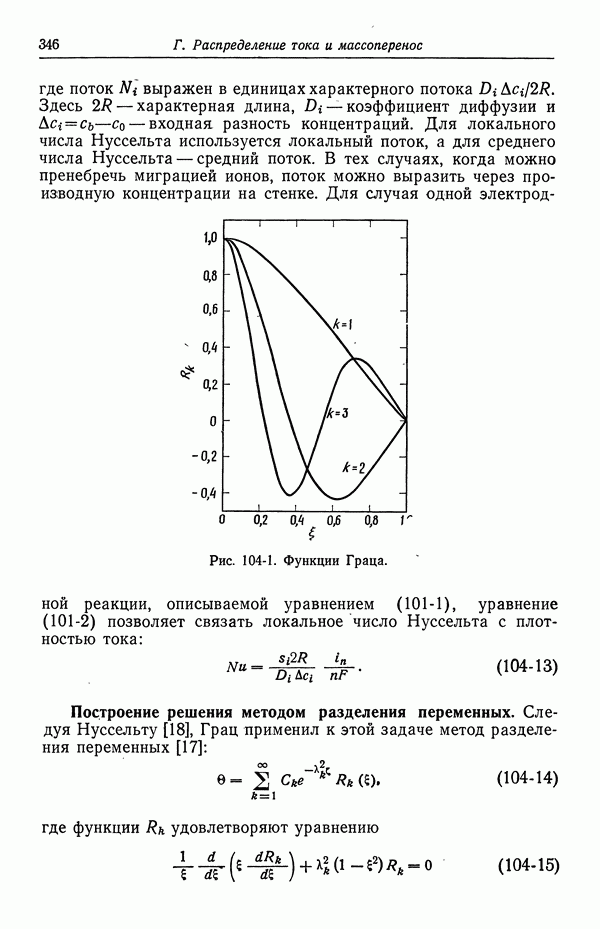
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 111. Свободная конвекция
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
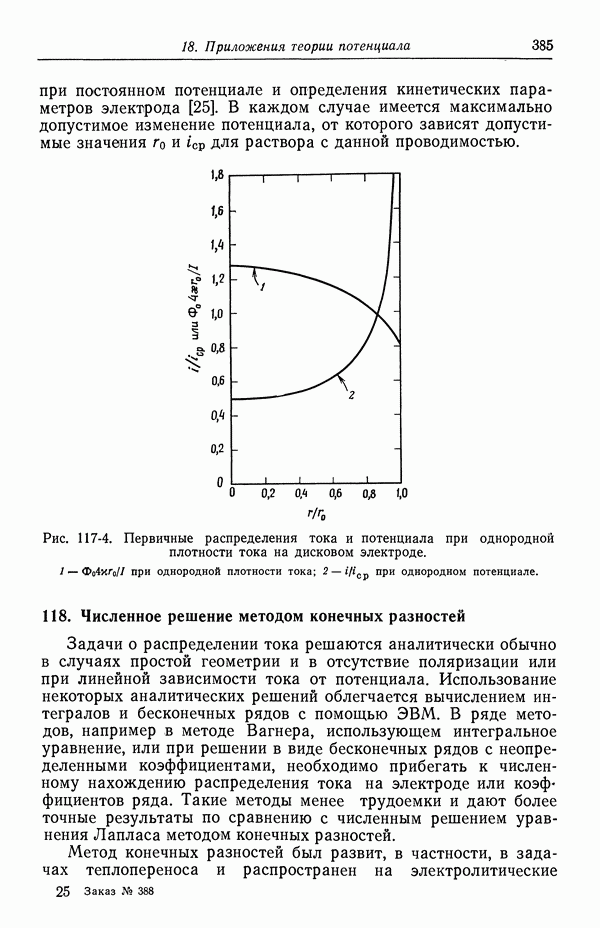
- 116. Первичное распределение тока
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- СПИСОК ОБОЗНАЧЕНИЙ
- ГЛАВА 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 119. Решение задачи
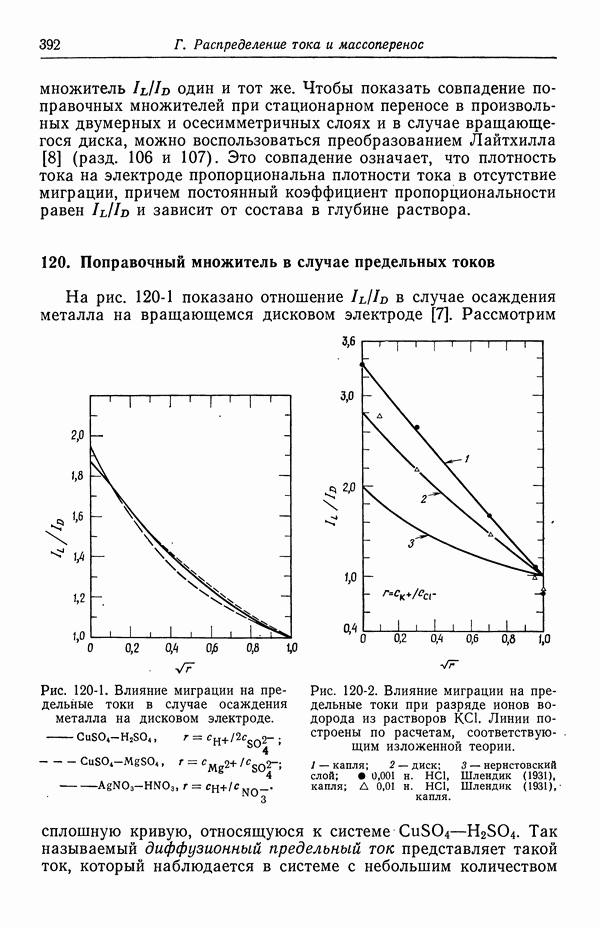
- 120. Поправочный множитель в случае предельных токов
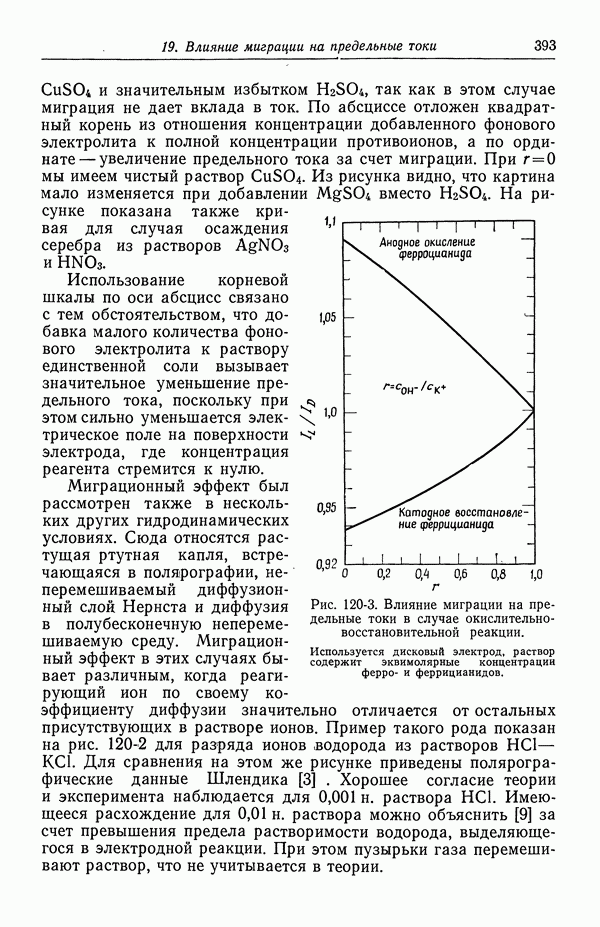
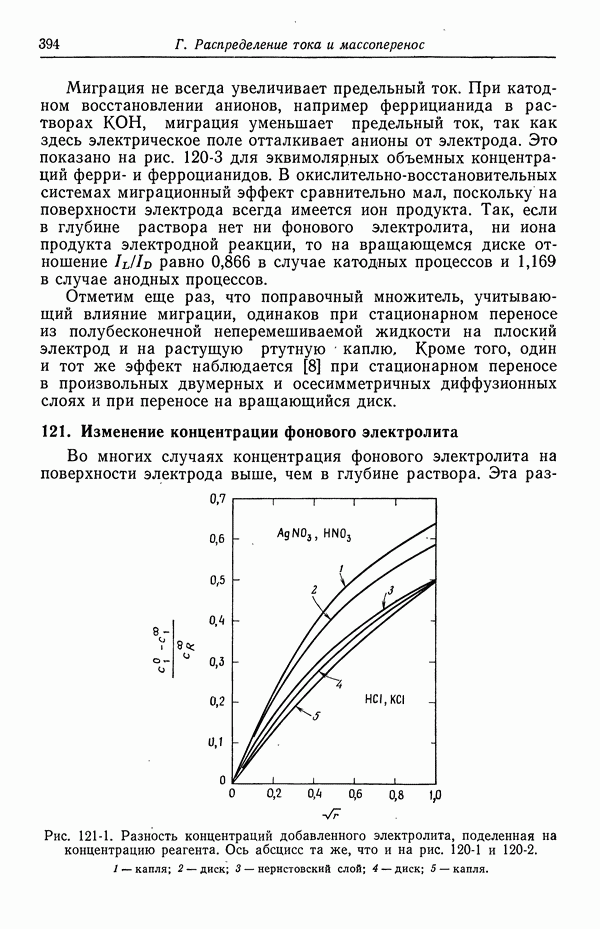
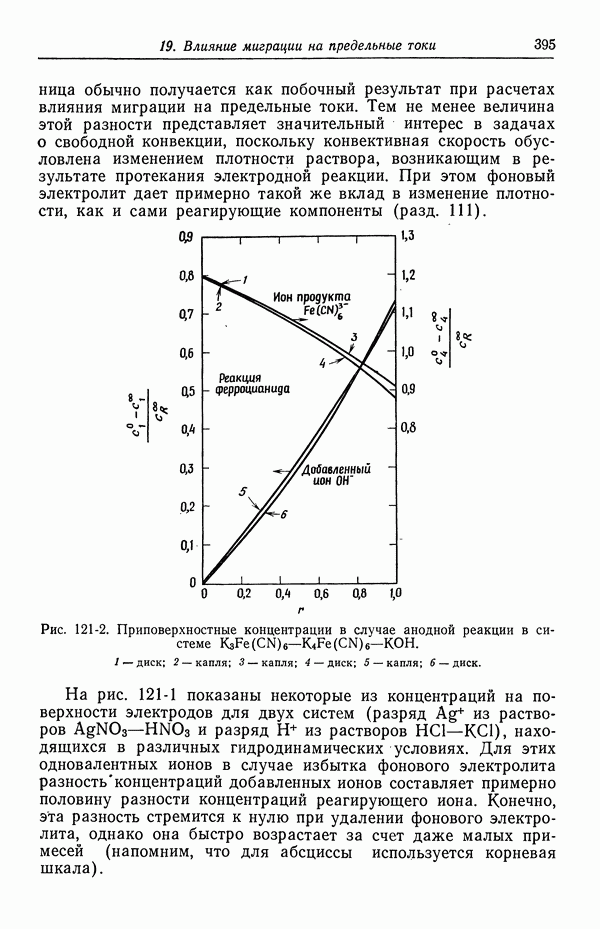
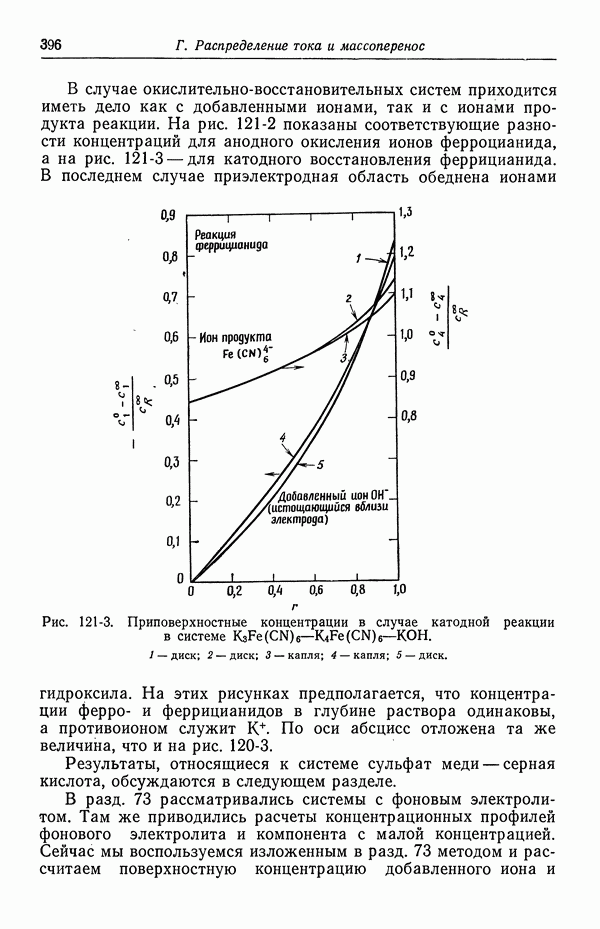
- 121. Изменение концентрации фонового электролита
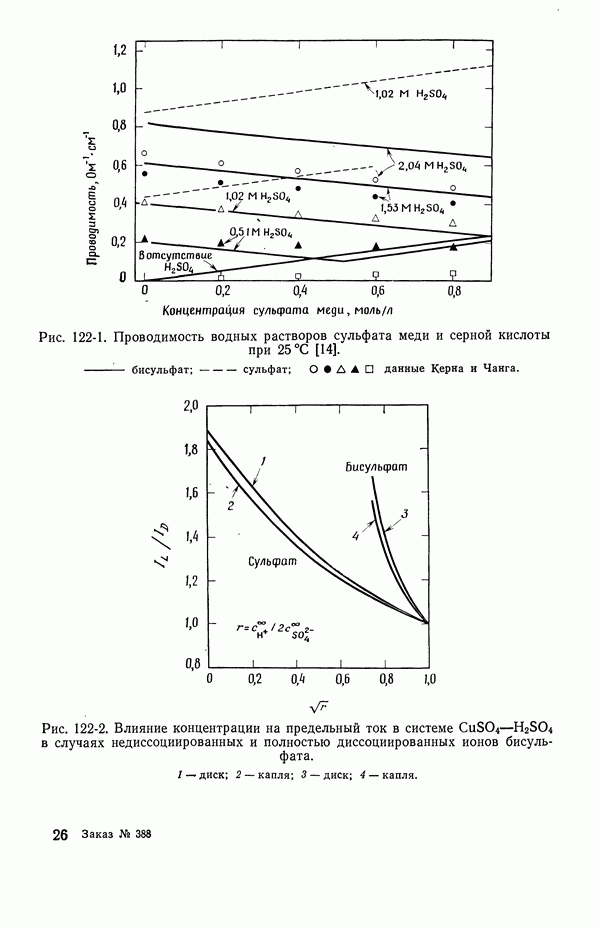
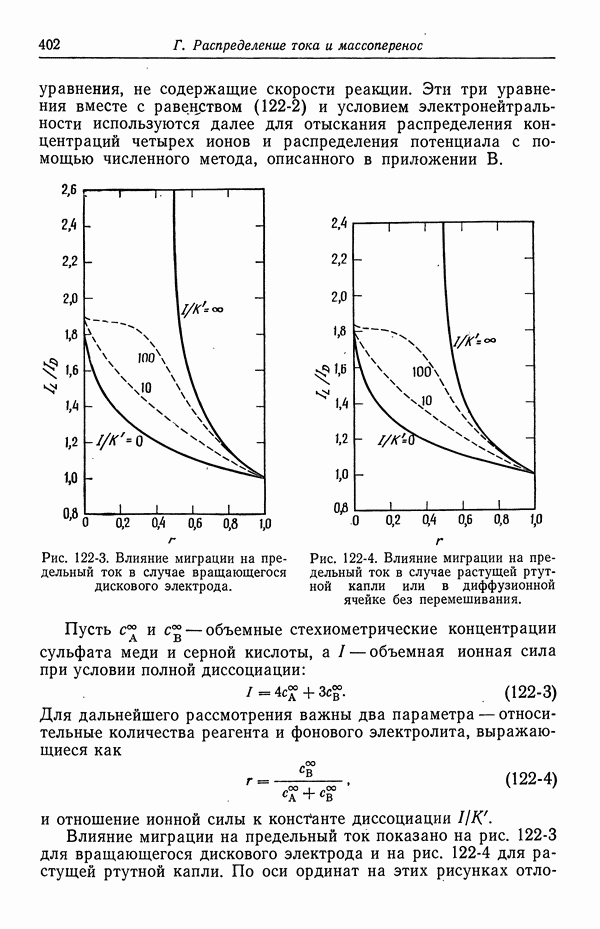
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ