| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
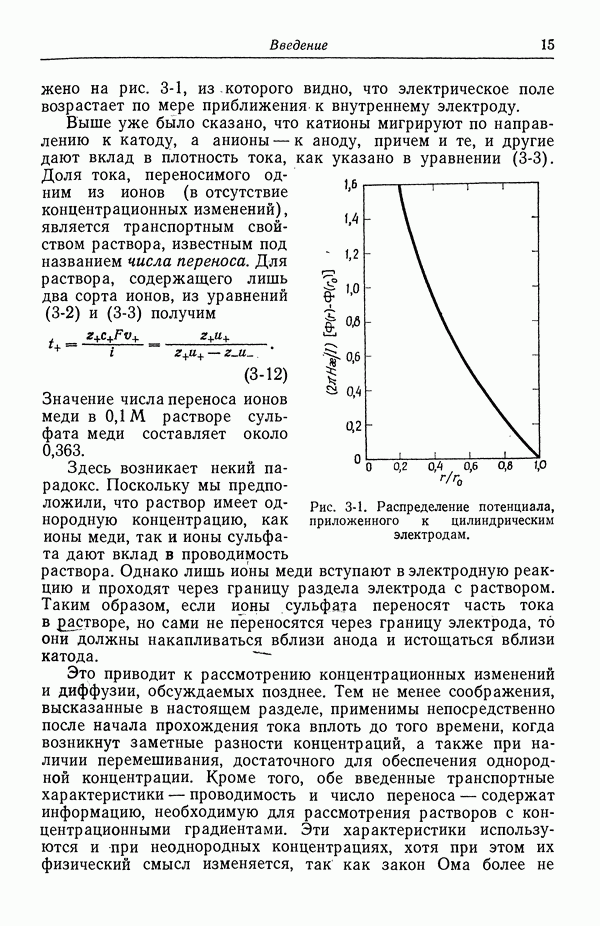
50. Изотерма адсорбции Гиббса
Межфазной границей является область между двумя фазами, которые здесь считаются однородными. На межфазной границе происходит, переход от свойств одной фазы к свойствам другой, причем толщина  межфазной границы может находиться в интервале
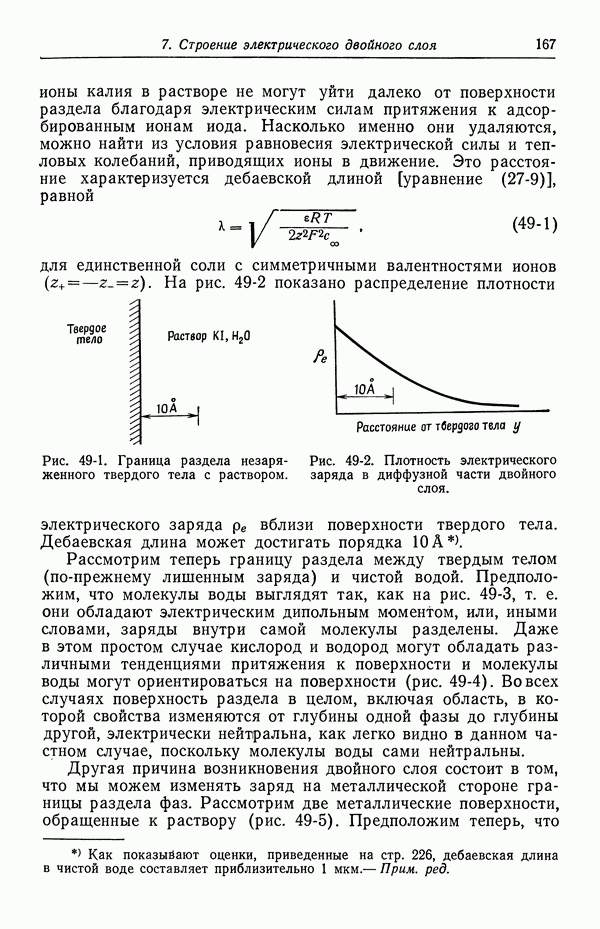
межфазной границы может находиться в интервале  см (рис. 50-1).
см (рис. 50-1).

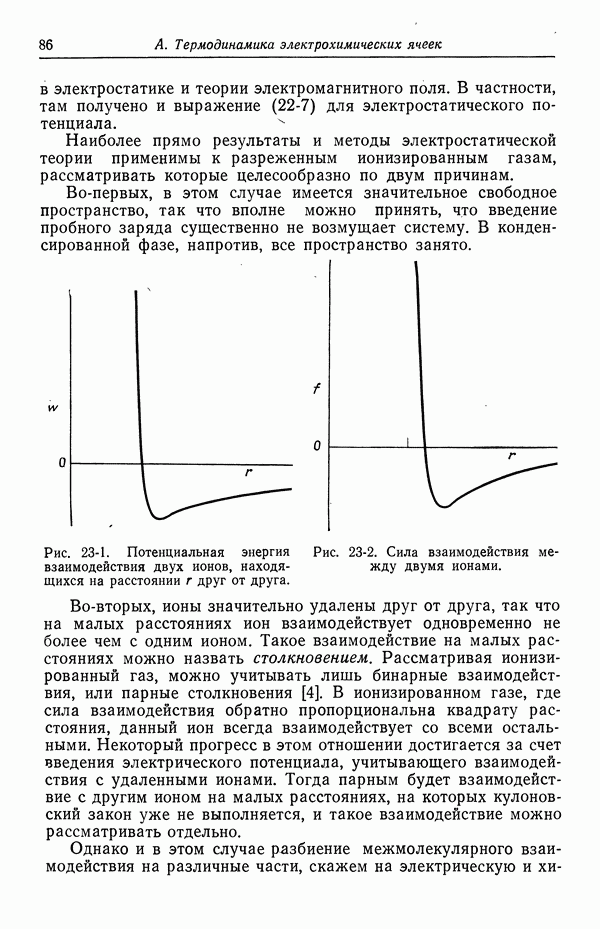
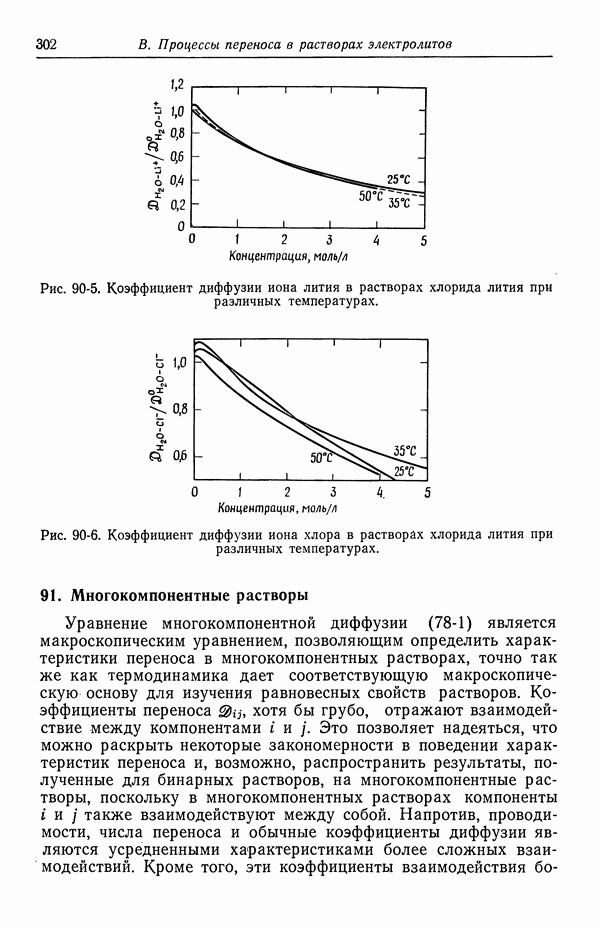
Рис. 50-1. Граница раздела в виде неоднородной области толщиной  между двумя однородными фазами.
между двумя однородными фазами.
Термодинамическое описание поверхности раздела обычно начинается с рассмотрения системы, состоящей из поверхности раздела и двух соседних фаз. Эти три области должны описываться экстенсивными характеристиками. Например, число молей  некоторого компонента системы можно представить в виде
некоторого компонента системы можно представить в виде

Вещество, которое не отнесено ни к одной из однородных фаз, приписывается поверхности раздела. Тогда поверхностная
концентрация  выражаемая обычно в моль/см2, записывается в виде
выражаемая обычно в моль/см2, записывается в виде

где А — площадь поверхности раздела.
Необходимо помнить, что в определении Г имеется некоторая неоднозначность ввиду неопределенности положений поверхностей, ограничивающих границу раздела. Поскольку детальное строение межфазной границы не поддается непосредственному экспериментальному изучению, в своем классическом подходе Гиббс принял толщину межфазной границы равной нулю. Это позволяет свести вопрос к положению только одной поверхности. Пусть она расположена при  (рис. 49-1). Тогда поверхностную концентрацию можно определить как
(рис. 49-1). Тогда поверхностную концентрацию можно определить как

Верхний индекс I при  в этом равенстве служит для того, чтобы подчеркнуть зависимость
в этом равенстве служит для того, чтобы подчеркнуть зависимость  от положения
от положения  поверхности Гиббса. Например, если в качестве такой поверхности выбрать плоскость, расположенную при
поверхности Гиббса. Например, если в качестве такой поверхности выбрать плоскость, расположенную при  то поверхностные концентрации
то поверхностные концентрации  и
и  будут связаны соотношением
будут связаны соотношением

Таким образом, однозначно  определяется лишь в том случае, если концентрации компонента i в обеих соседних однородных фазах одинаковы. Такая ситуация с хорошей точностью возникает для некоторых органических соединений, которые могут адсорбироваться на границе раздела воздух—раствор, но существенно нерастворимы в соседних фазах.
определяется лишь в том случае, если концентрации компонента i в обеих соседних однородных фазах одинаковы. Такая ситуация с хорошей точностью возникает для некоторых органических соединений, которые могут адсорбироваться на границе раздела воздух—раствор, но существенно нерастворимы в соседних фазах.
Определенная выше поверхностная концентрация  может быть и отрицательной. Связанная с выбором положения плоскости Гиббса неоднозначность обычно не опасна, если только ее аккуратно учитывать. Поверхностные концентрации можно сделать определенными, принимая некоторые условия, такие, как равенство
может быть и отрицательной. Связанная с выбором положения плоскости Гиббса неоднозначность обычно не опасна, если только ее аккуратно учитывать. Поверхностные концентрации можно сделать определенными, принимая некоторые условия, такие, как равенство  нулю для данного стандартного компонента, обычно растворителя, или равенство нулю массы поверхности раздела. Иной подход состоит в том, что используются так называемые инварианты Гиббса, которые не зависят от положения поверхности Гиббса. Например, таким инвариантом является величина
нулю для данного стандартного компонента, обычно растворителя, или равенство нулю массы поверхности раздела. Иной подход состоит в том, что используются так называемые инварианты Гиббса, которые не зависят от положения поверхности Гиббса. Например, таким инвариантом является величина

Интенсивные величины можно приписать поверхности раздела в том случае, если они имеют те же значения в соседних однородных фазах. Например, температура и химические потенциалы находящихся в равновесии компонентов имеют смысл и для поверхности.
Поверхностное натяжение а — специфическое интенсивное свойство границы раздела. Оно зависит от температуры и состава соседних фаз. Поверхностное натяжение имеет механический смысл сил, действующих на поверхности, и термодинамический смысл энергии единицы площади поверхности. Например, изменение гиббсовой функции системы, рассмотренной в разд. 49, равно

Интегрирование этого выражения при постоянных температуре, давлении и составе в условиях, когда площадь и число молей могут изменяться от нуля до некоторого ненулевого значения, дает

Если представить это соотношение в виде

то можно показать, что поверхностное натяжение является избытком гиббсовой свободной энергии поверхности (на единицу площади):

Из уравнения (50-6) видно, что поверхностное натяжение является гиббсовым инвариантом, не зависящим от выбора положения поверхности Гиббса.
Дифференцирование уравнения (50-6) и подстановка в уравнение (50-5) дают

С помощью соотношений Гиббса—Дюгема для фаз  например
например

получаем

или

где

Уравнение (50-12) является аналогом соотношения Гиббса— Дюгема для поверхности и известно (при dT=0) под названием изотермы адсорбции Гиббса. Согласно допущению Гиббса, связанный с поверхностью раздела объем равен нулю, так что  можно принять равным нулю. Однако Гуггенгейм предпочитает считать, что граница раздела фаз обладает ненулевой толщиной. В любом случае уравнение (50-12) справедливо независимо от выбора положения поверхности или поверхностей, определяющих границу раздела.
можно принять равным нулю. Однако Гуггенгейм предпочитает считать, что граница раздела фаз обладает ненулевой толщиной. В любом случае уравнение (50-12) справедливо независимо от выбора положения поверхности или поверхностей, определяющих границу раздела.
Адсорбционное уравнение Гиббса полезно при определении поверхностных концентраций  так как точное прямое измерение Г, обычно представляет большие трудности, чем определение изменений поверхностного натяжения и использование уравнения (50-12).
так как точное прямое измерение Г, обычно представляет большие трудности, чем определение изменений поверхностного натяжения и использование уравнения (50-12).
Применяя адсорбционное уравнение Гиббса, нужно помнить, что оно справедливо лишь на границе раздела фаз, находящихся в равновесии. Следовательно, все вариации необходимо проводить с учетом ограничения на фазовое равновесие, что приводит к потере некоторой степени свободы. Для двухкомпонентной системы в качестве независимых переменных можно принять температуру и одну из мольных долей. С учетом уравнений Гиббса—Дюгема для однородных фаз уравнение (50-12) приобретает вид

где  энтропии единицы объема фаз
энтропии единицы объема фаз  Поскольку
Поскольку

окончательно имеем

где

есть энтропия поверхности раздела и поверхностная концентрация компонента 2, вычисленные при таком выборе поверхности Гиббса, что  . Видно, что измерение изменения поверхностного натяжения с
. Видно, что измерение изменения поверхностного натяжения с  при постоянной температуре позволяет определить
при постоянной температуре позволяет определить  Измерение изменения поверхностного натяжения с температурой при постоянном
Измерение изменения поверхностного натяжения с температурой при постоянном  позволяет определить поверхностную энтропию
позволяет определить поверхностную энтропию
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
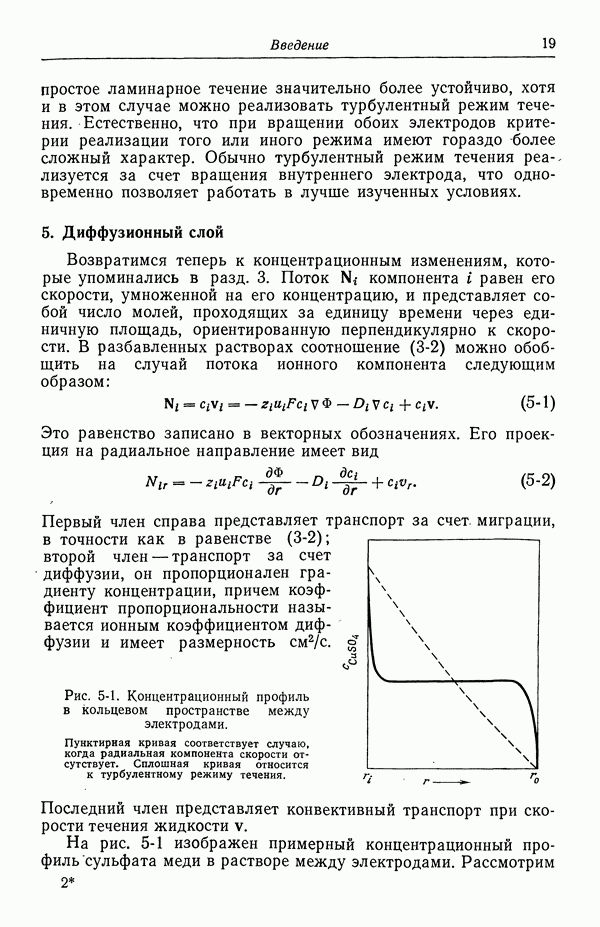
- 4. Течение жидкости
- 5. Диффузионный слой
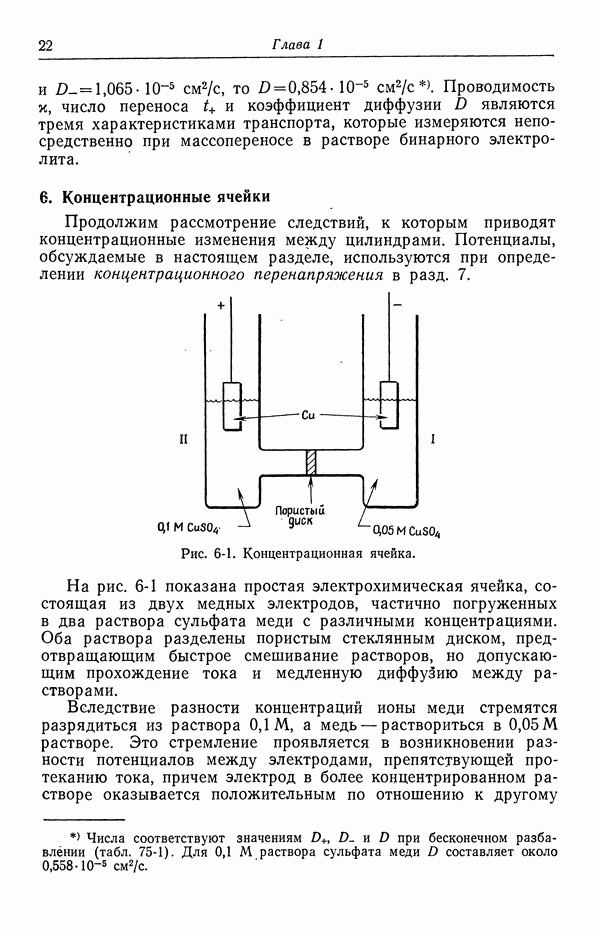
- 6. Концентрационные ячейки
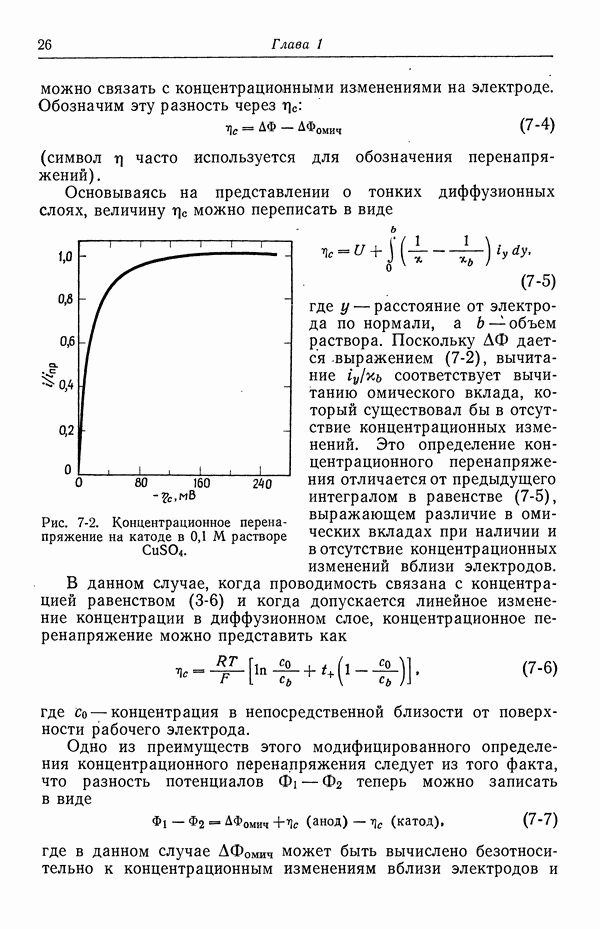
- 7. Концентрационное перенапряжение
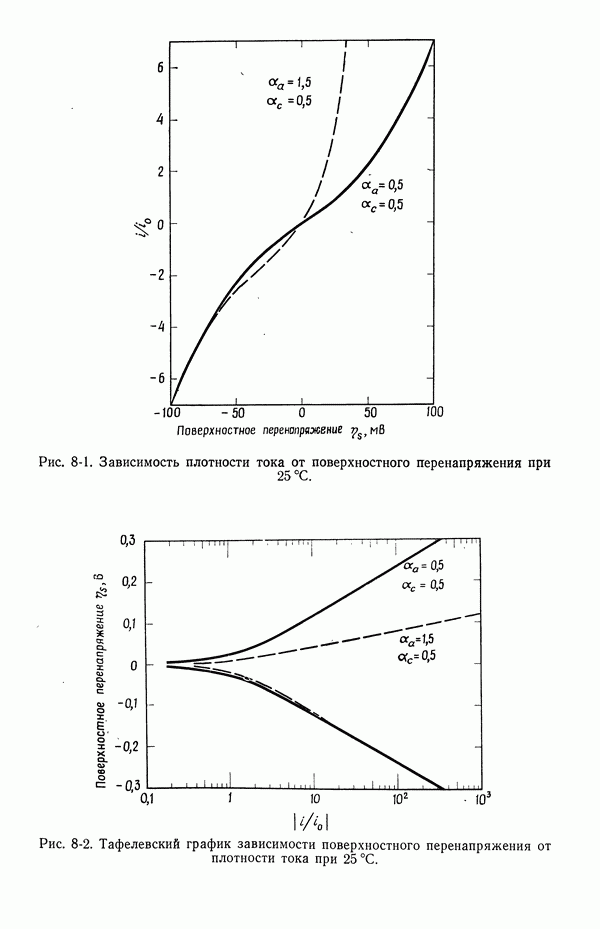
- 8. Поверхностное перенапряжение
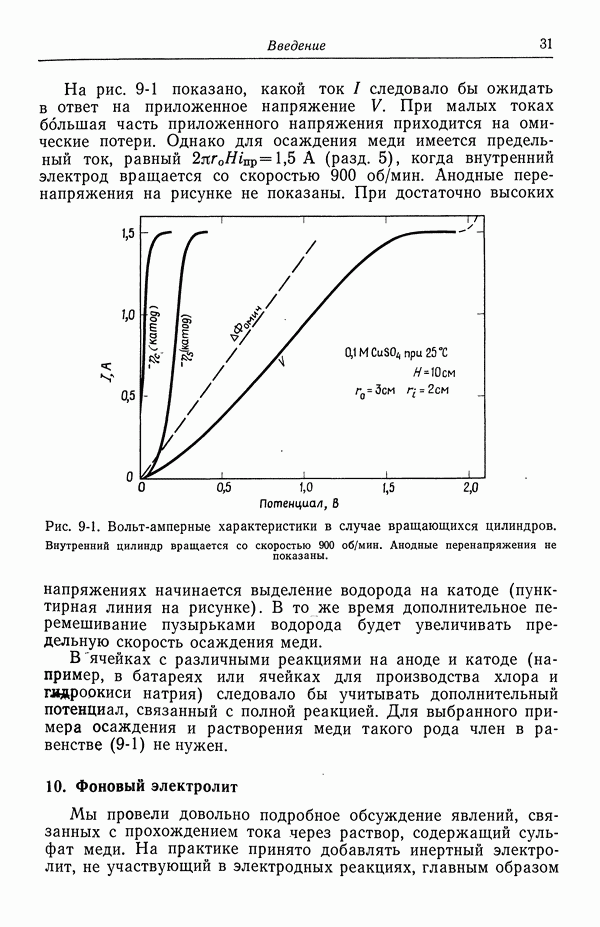
- 9. Потенциал ячейки
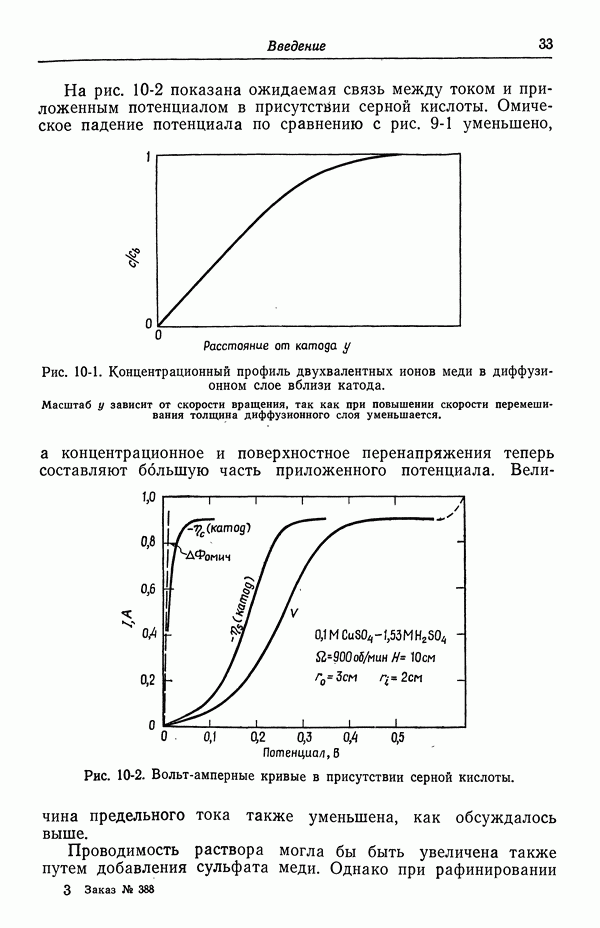
- 10. Фоновый электролит
- 11. Свободная конвекция
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
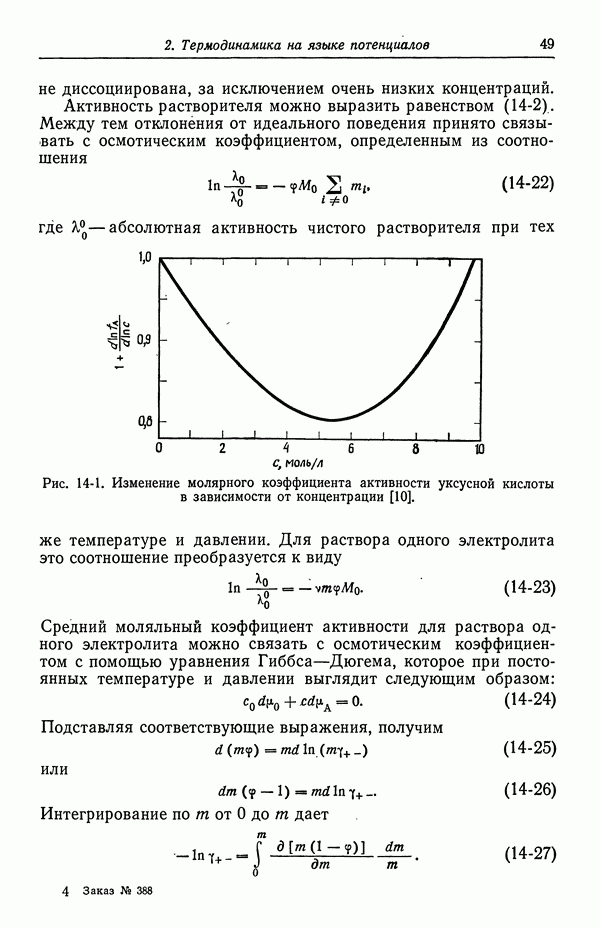
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая—Хюккеля
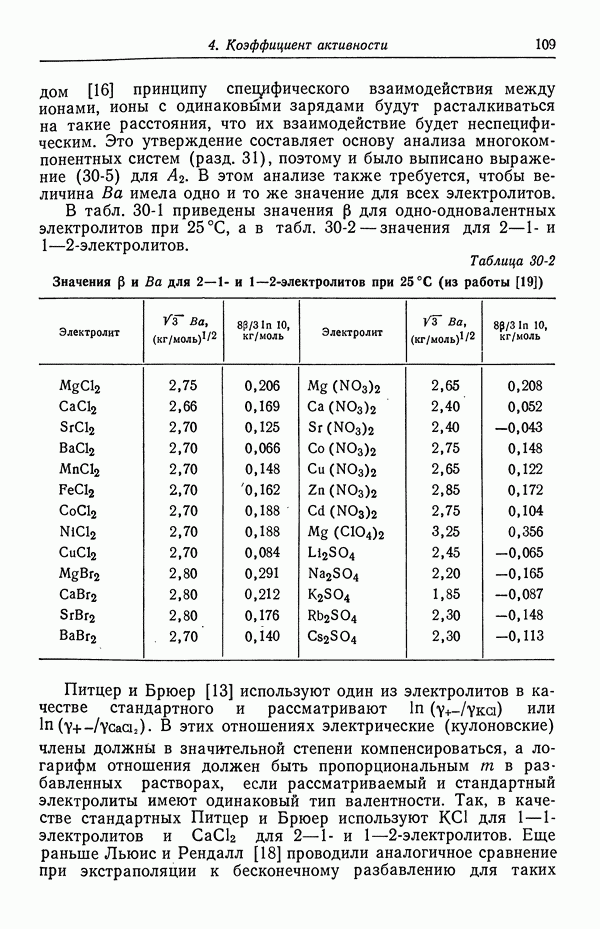
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 49. Качественное описание двойных слоев
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод — раствор
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 66. Динамика границы раздела
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 69. Законы переноса
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 78. Законы переноса
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 92. Интегральные коэффициенты диффузии
- ЗАДАЧА
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
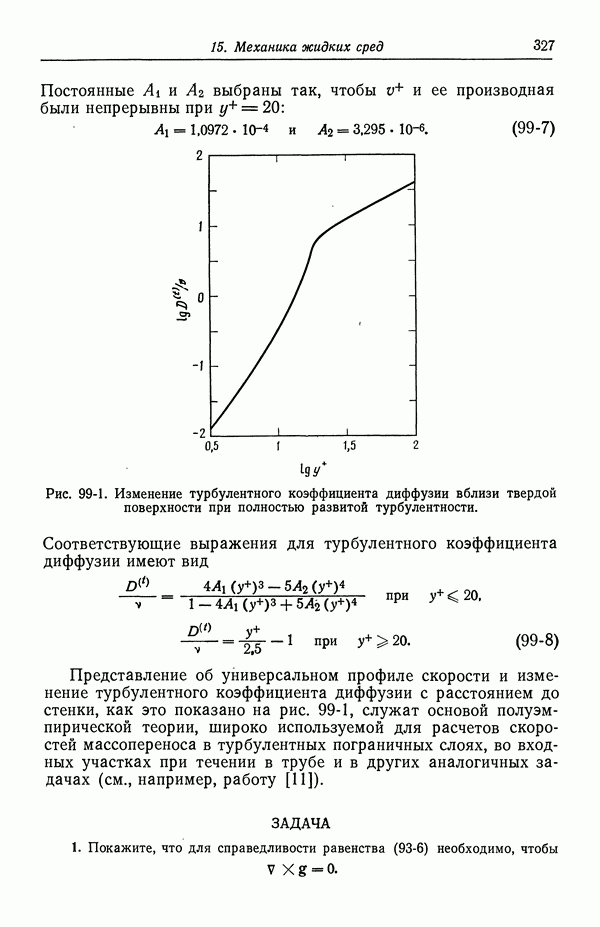
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
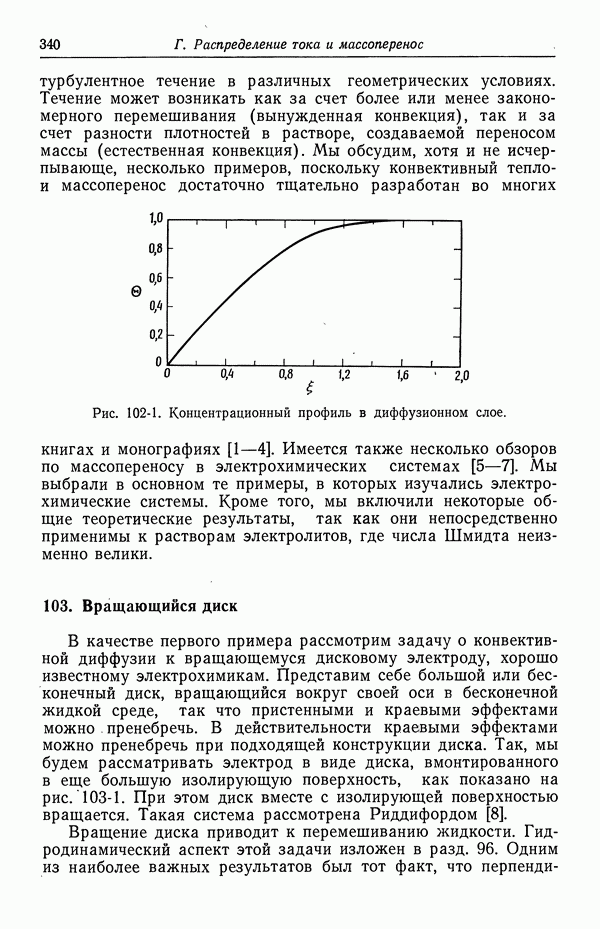
- 102. Упрощенное описание конвективной диффузии
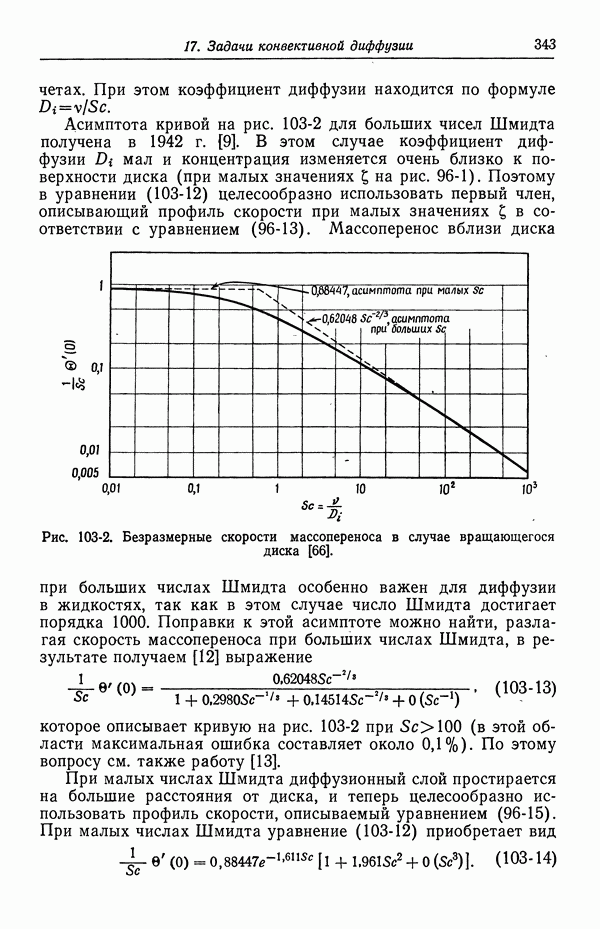
- 103. Вращающийся диск
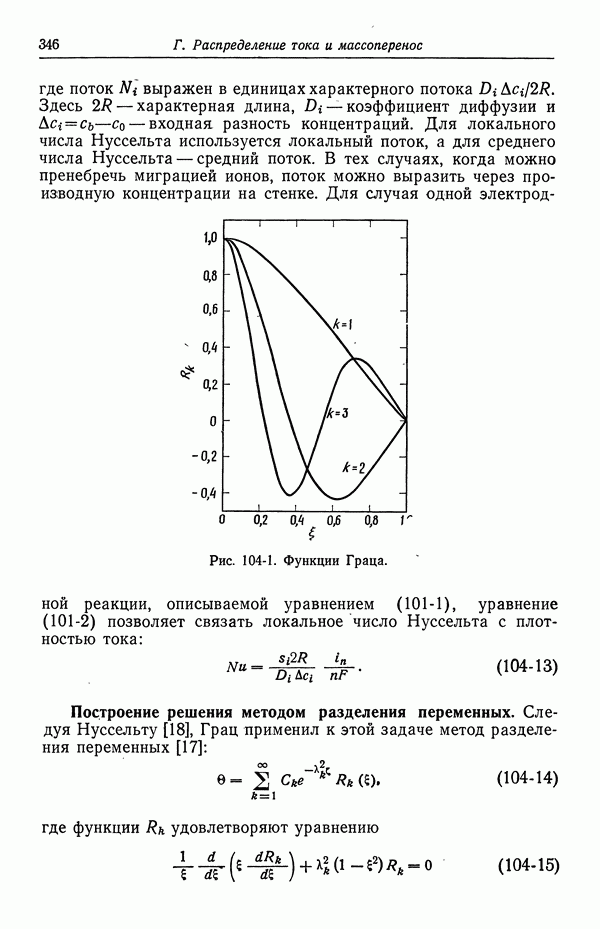
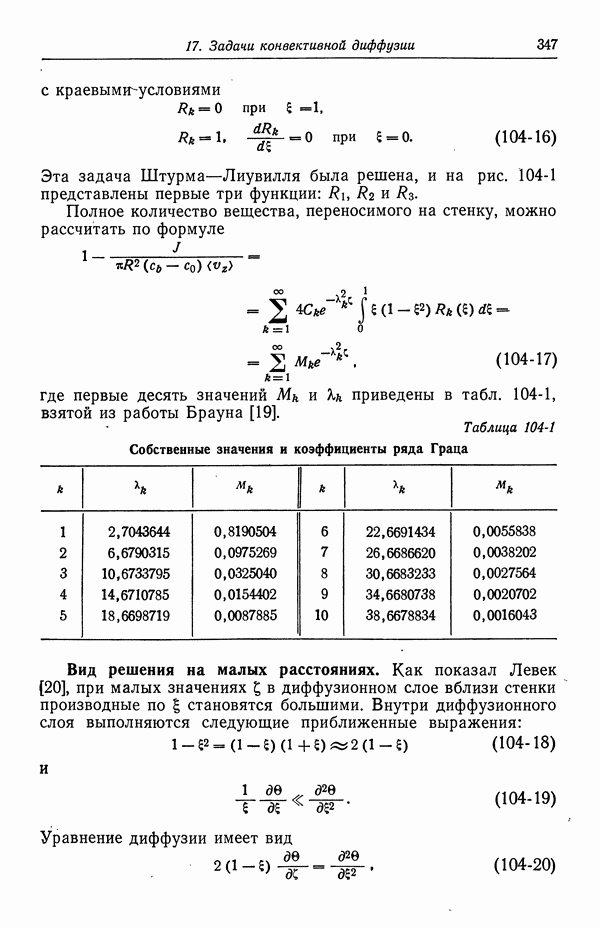
- 104. Задача Граца
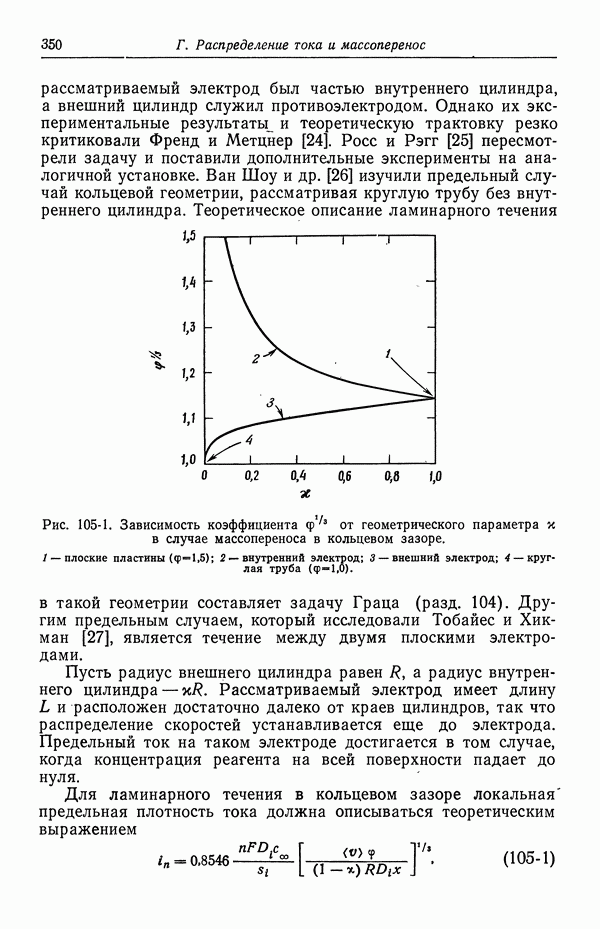
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 111. Свободная конвекция
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
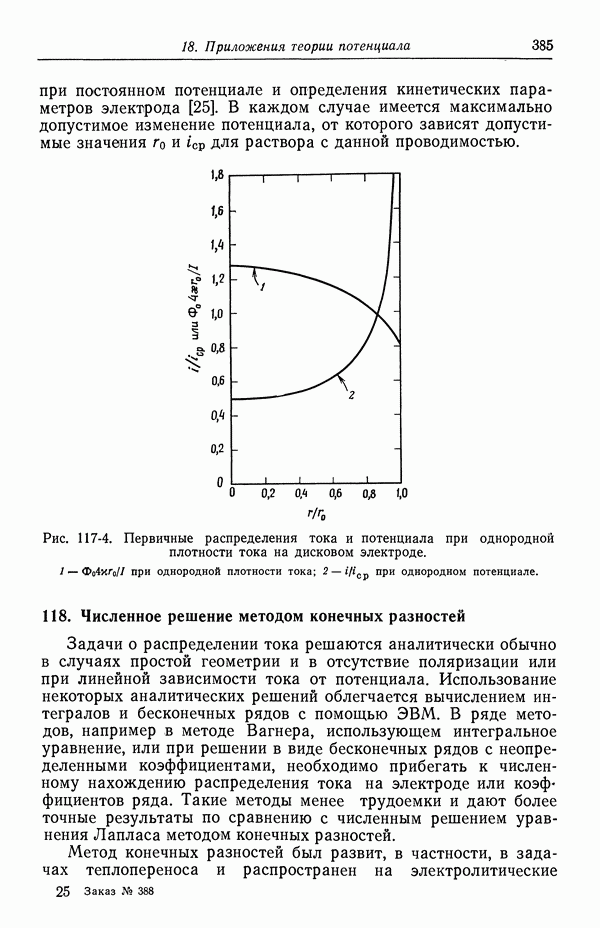
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- СПИСОК ОБОЗНАЧЕНИЙ
- ГЛАВА 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 119. Решение задачи
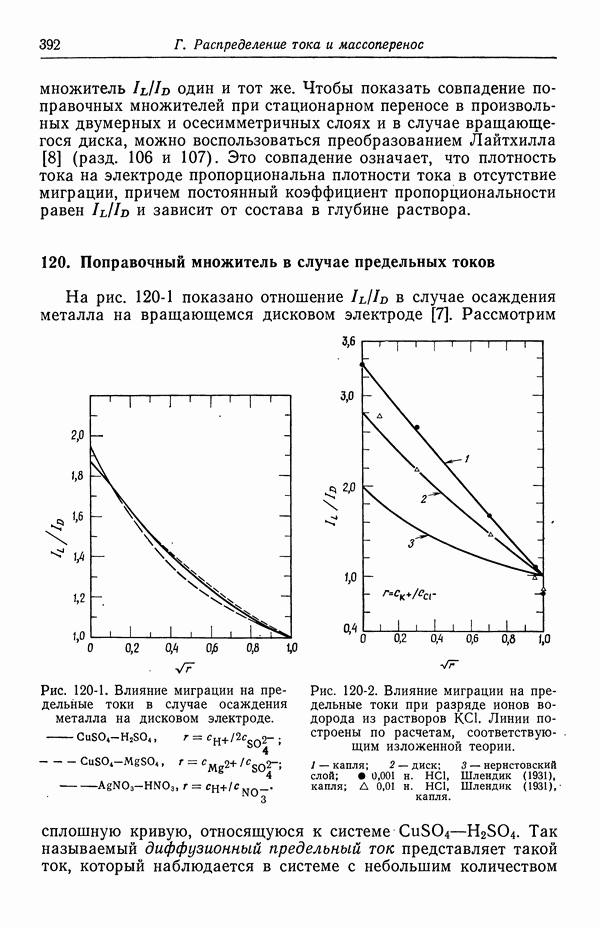
- 120. Поправочный множитель в случае предельных токов
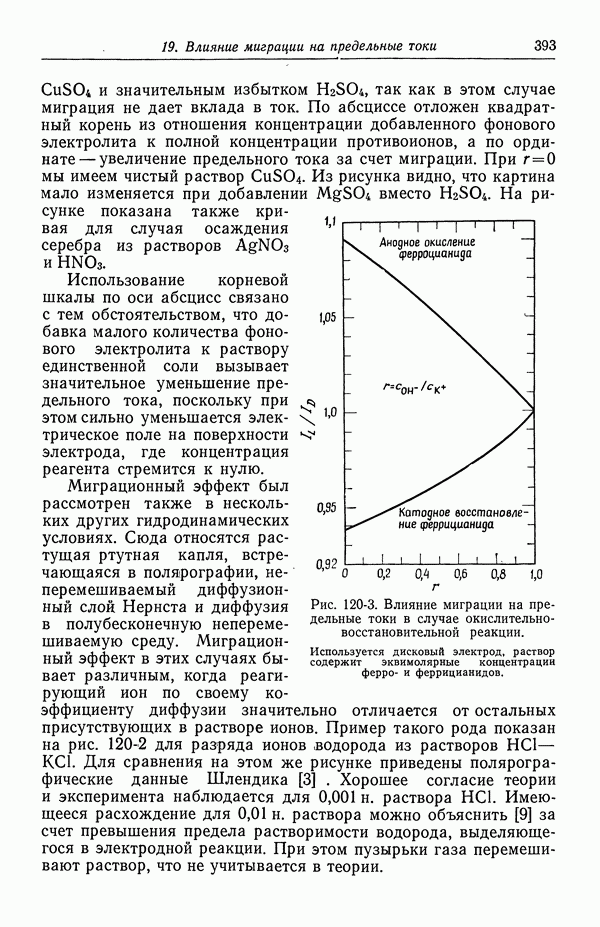
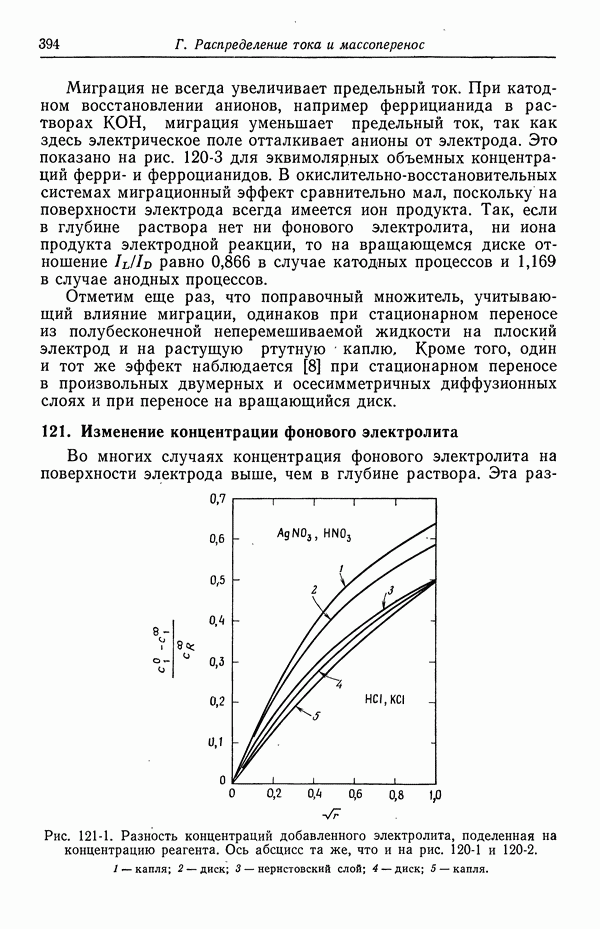
- 121. Изменение концентрации фонового электролита
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ