| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
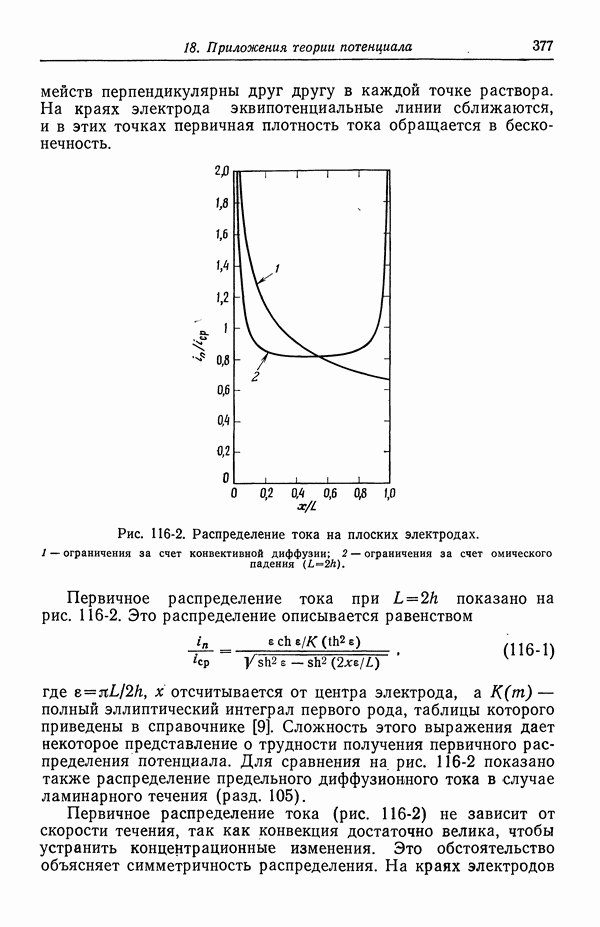
377
378
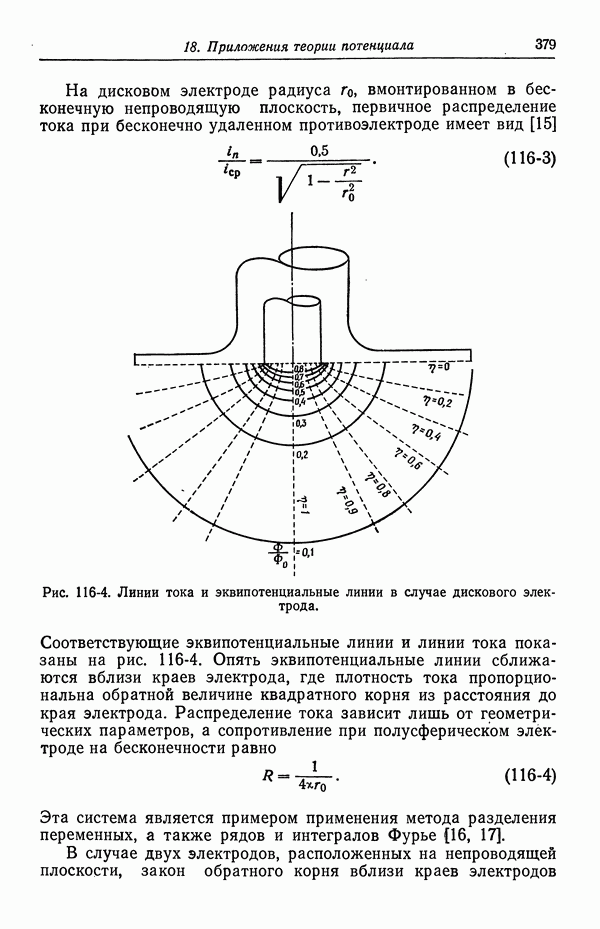
379
380
381
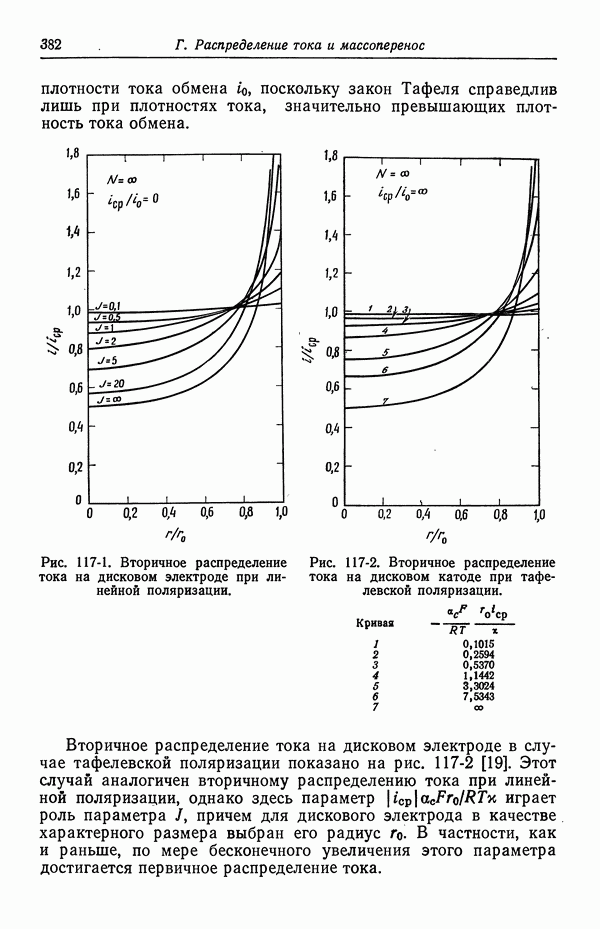
382
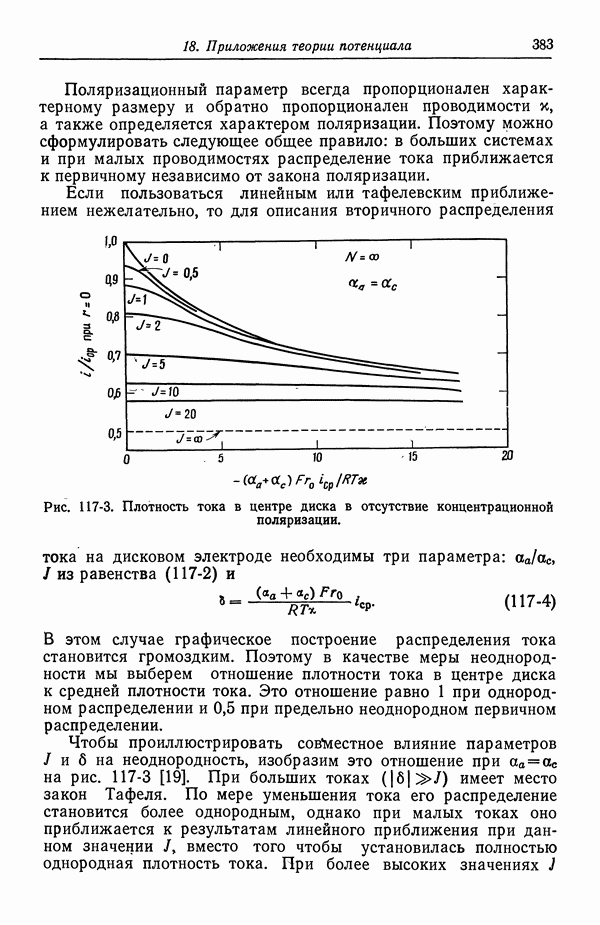
383
384
385
386
387
388
389
390
391
392
393
394
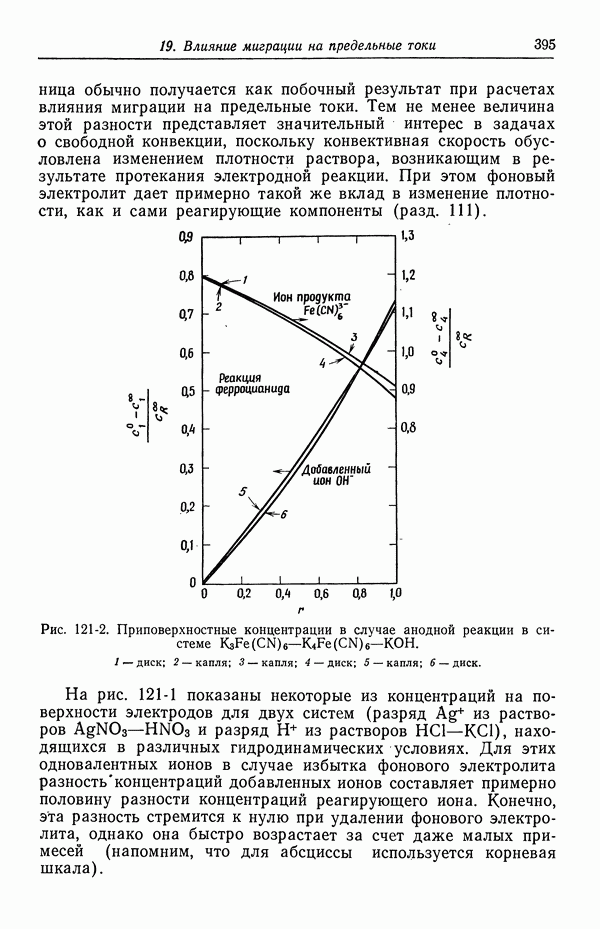
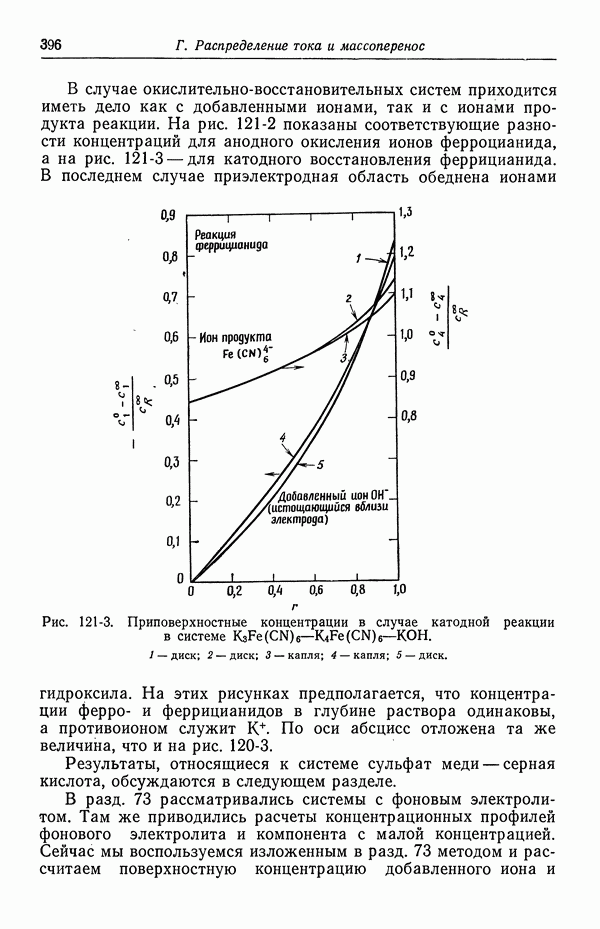
395
396
397
398
399
400
401
402
403
404
405
406
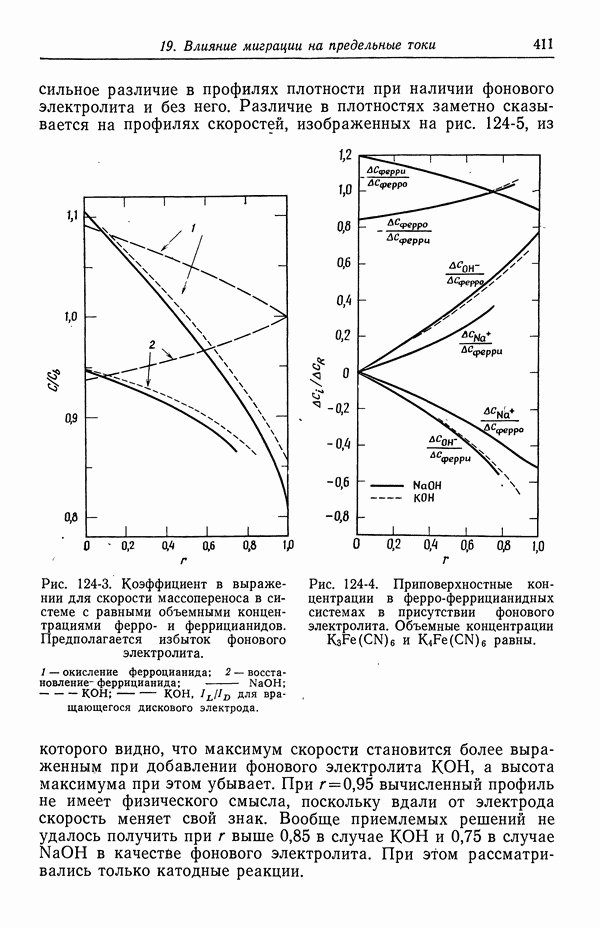
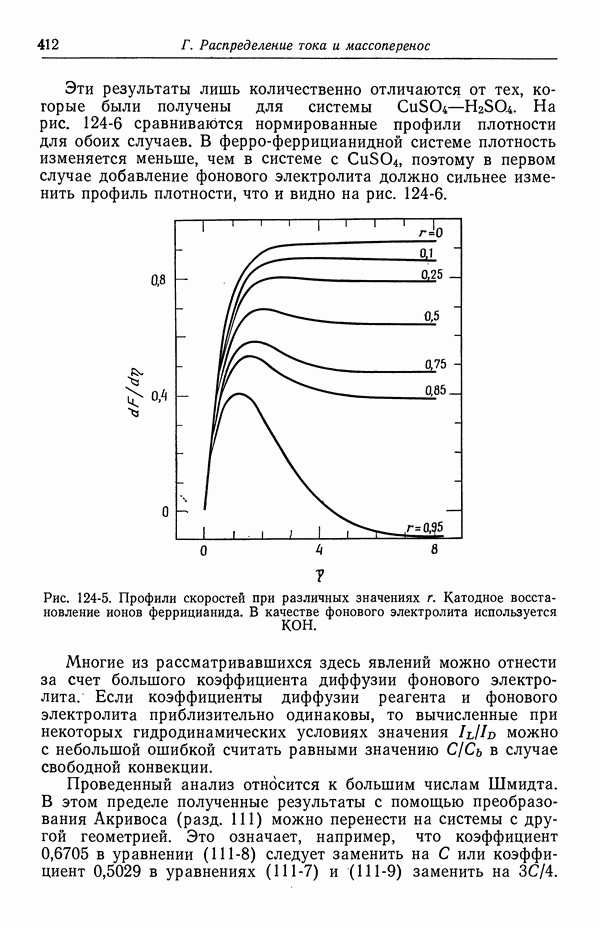
407
408
409
410
411
412
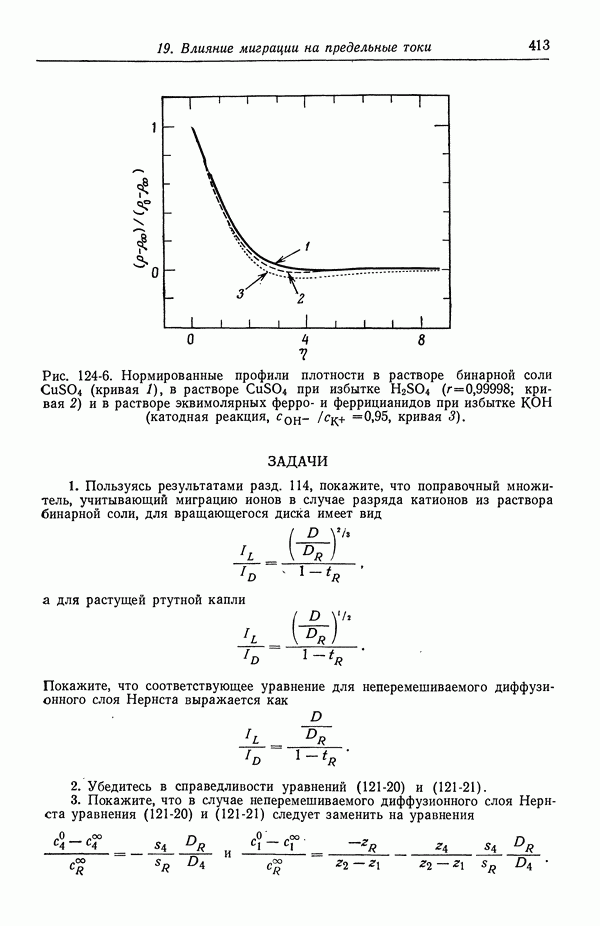
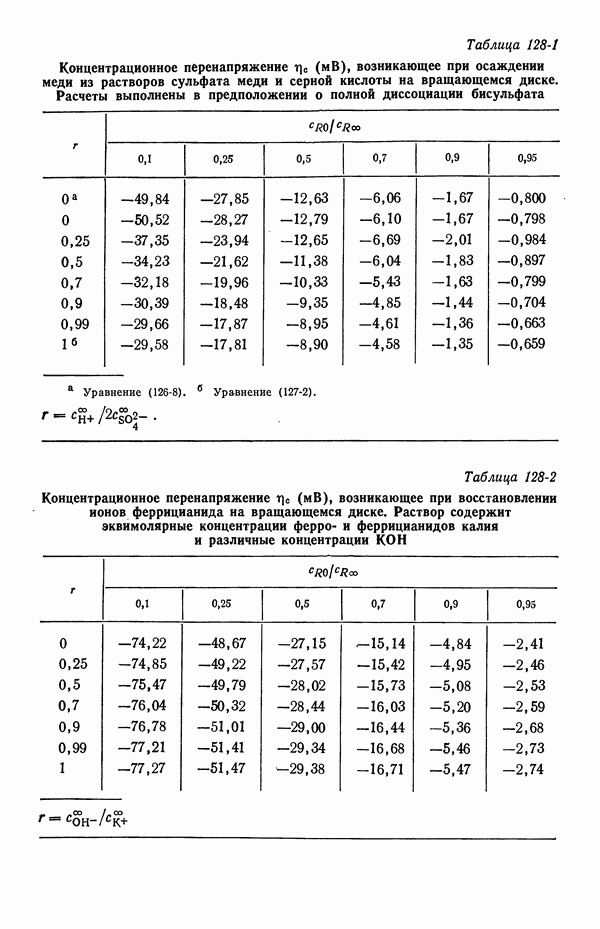
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
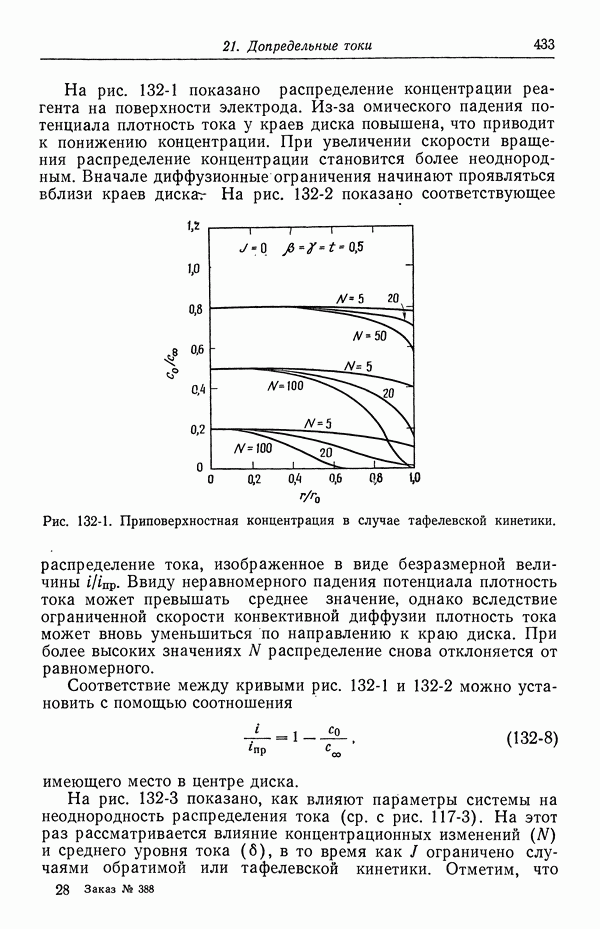
433
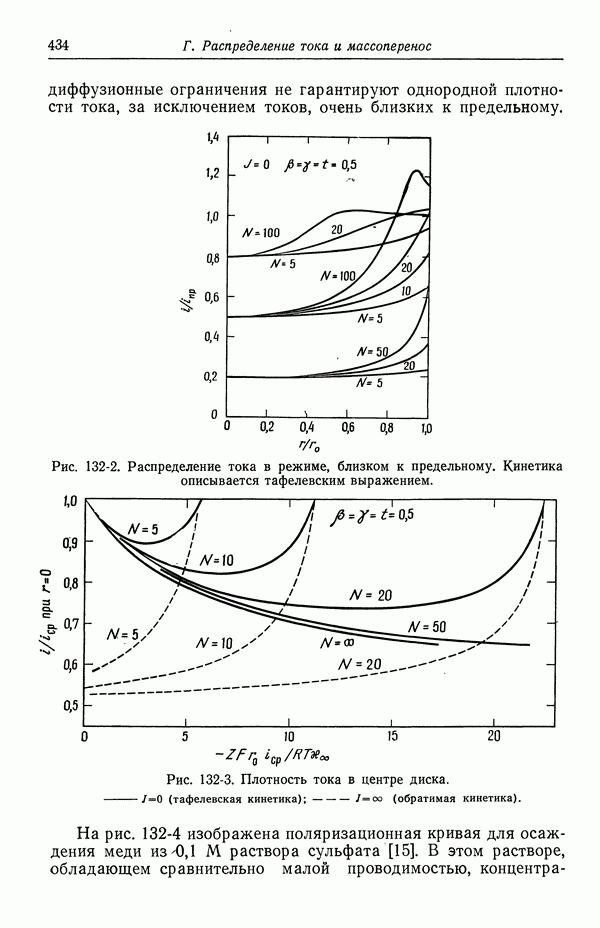
434
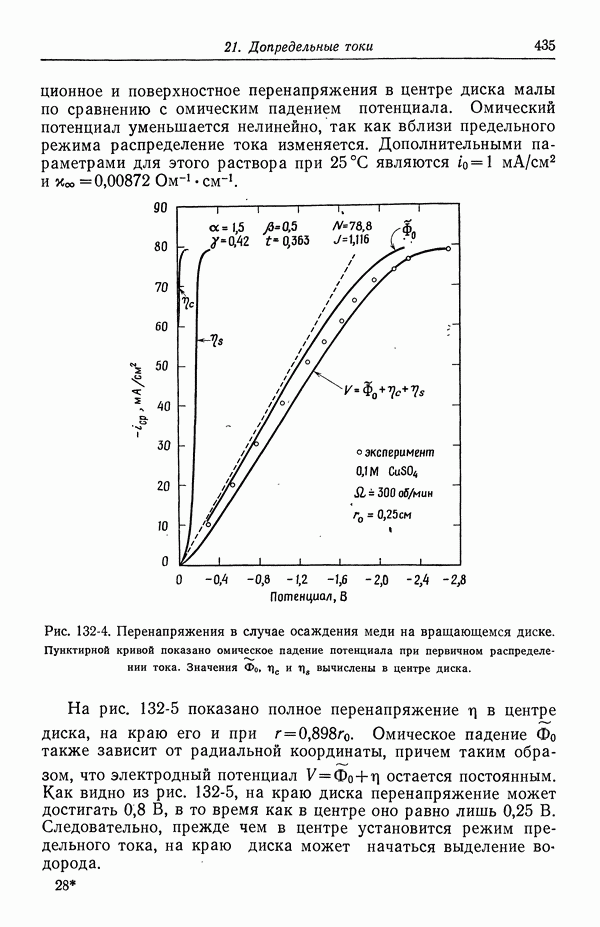
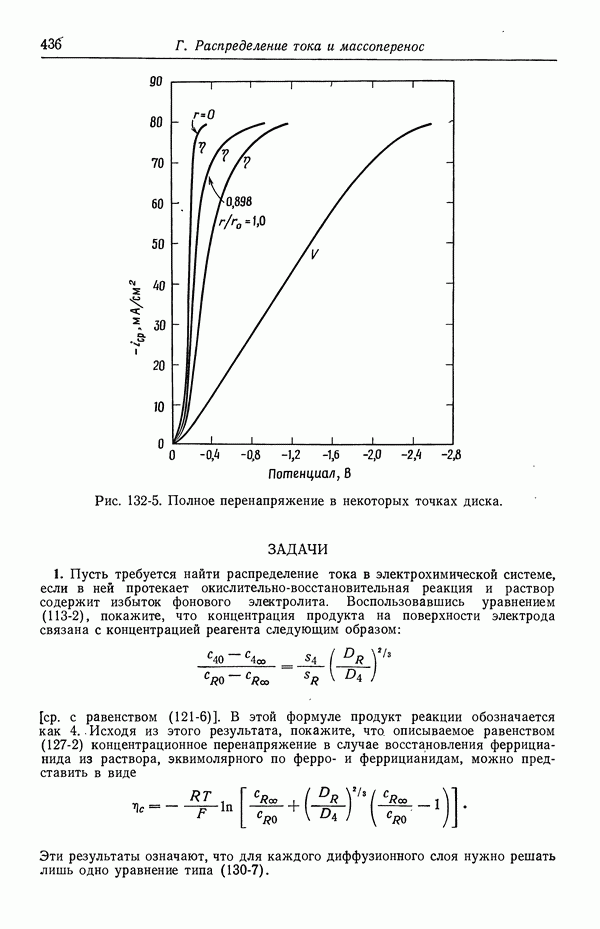
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
Настоящая глава, посвященная термодинамике электрохимических потенциалов, основывается на материале, изложенном в гл. 2. Особое внимание уделяется расчету потенциалов элементов с учетом стандартных электродных потенциалов.
Как показал Тейлор [1], проблемы измерения потенциалов жидкостных соединений и коэффициентов активности отдельных ионов тесно связаны друг с другом. В этом отношении большой интерес представляют также работы [2—4].
41. Уравнение Нернста
Уравнение Нернста введено в конце разд. 18. Здесь мы рассмотрим способы записи этого уравнения для конкретной ячейки. В качестве примера будем использовать ячейку (19-4).
1. Пользуясь химическим и электрохимическим потенциалами, запишем в соответствии с гл. 2 выражение для потенциала ячейки. Для ячейки (19-4) оно дается равенством (19-5):

2. Чтобы выразить электрохимические потенциалы ионов в растворе, используем равенство (26-4). Для газообразных компонентов будем пользоваться летучестью, как отмечалось в задаче 2-14. Для химических потенциалов чистых фаз заменим верхний индекс на 0. Для активности сплавов будем использовать, например, уравнение (20-4). Теперь для ячейки (19-4) имеем

где при использовании равенства (26-4) в качестве компонента  выбран ион хлора.
выбран ион хлора.
3. Пользуясь равенством (14-7), введем стандартный потенциал ячейки. Тогда равенство (41-2) примет вид

где  соответствует строке 7 в табл. 20-1.
соответствует строке 7 в табл. 20-1.
4. Положим все ионные коэффициенты активности равными единице и пренебрежем различием в квазиэлектростатическом потенциале в разных точках раствора. В этом случае равенство (41-3) приобретает вид

Разность потенциалов  в равенствах (41-2) и (41-3) можно назвать потенциалом жидкостного соединения. Входящие в эту разность квазиэлектростатические потенциалы относятся к иону хлора. Ионные коэффициенты активности всегда входят в уравнение таким образом, что произвольный выбор компонента
в равенствах (41-2) и (41-3) можно назвать потенциалом жидкостного соединения. Входящие в эту разность квазиэлектростатические потенциалы относятся к иону хлора. Ионные коэффициенты активности всегда входят в уравнение таким образом, что произвольный выбор компонента  не играет роли. При записи уравнения Нернста пренебрегают как потенциалом жидкостного соединения, так и поправкой на коэффициенты активности. Было бы несколько непоследовательно учитывать только один из этих факторов, так как оба они зависят от выбора компонента п.
не играет роли. При записи уравнения Нернста пренебрегают как потенциалом жидкостного соединения, так и поправкой на коэффициенты активности. Было бы несколько непоследовательно учитывать только один из этих факторов, так как оба они зависят от выбора компонента п.
В последующих разделах настоящей главы будут рассмотрены способы расчета поправок к уравнению Нернста. Сразу же заметим, что для ячеек разд. 17 вместо таких поправок скорее следует искать другие приближения. То же относится и к электролиту с переменной концентрацией.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
- 5. Диффузионный слой
- 6. Концентрационные ячейки
- 7. Концентрационное перенапряжение
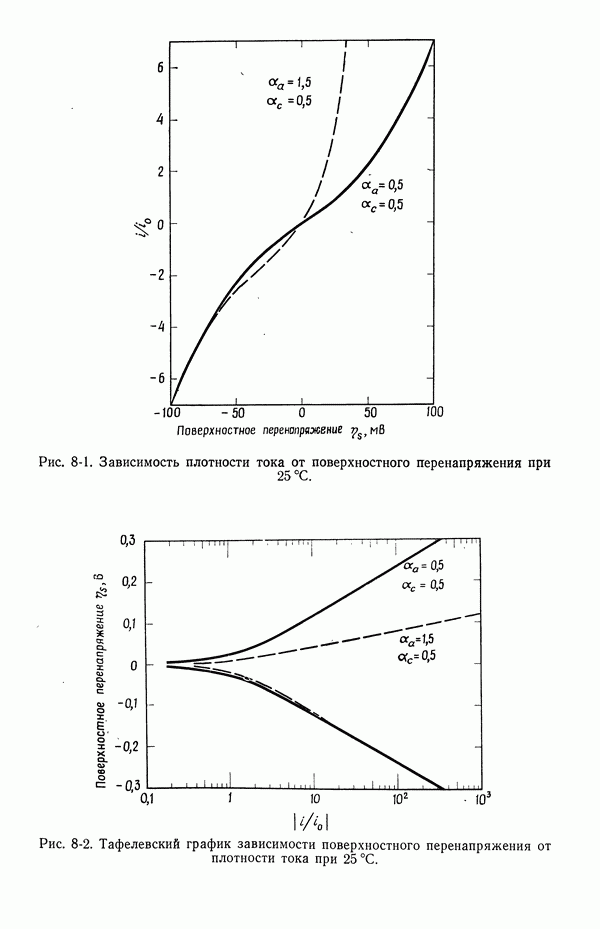
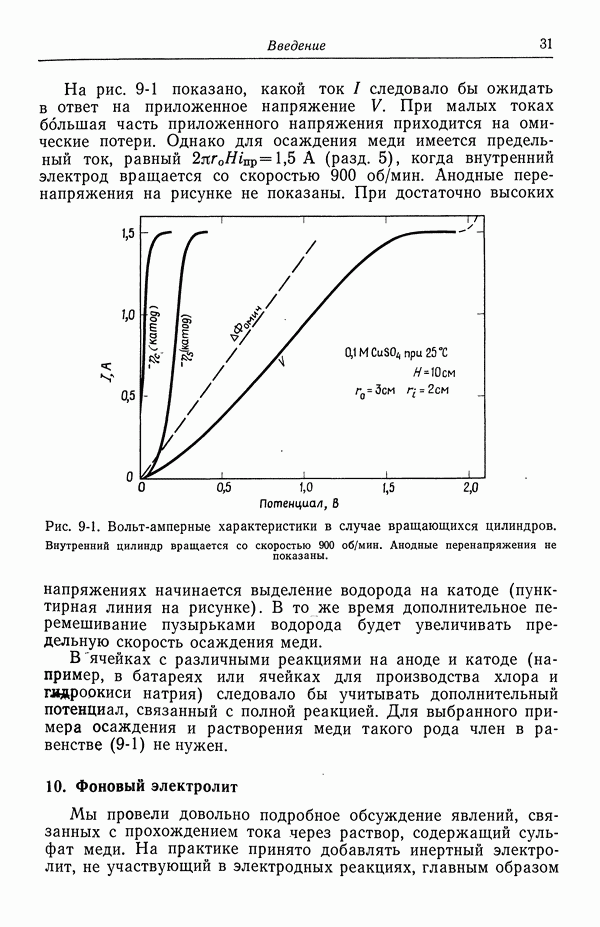
- 8. Поверхностное перенапряжение
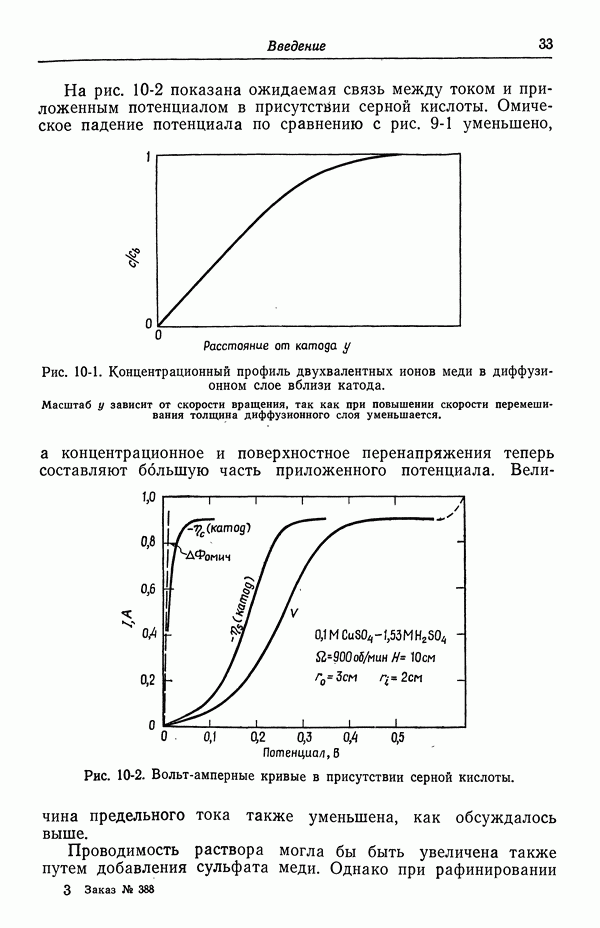
- 9. Потенциал ячейки
- 10. Фоновый электролит
- 11. Свободная конвекция
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
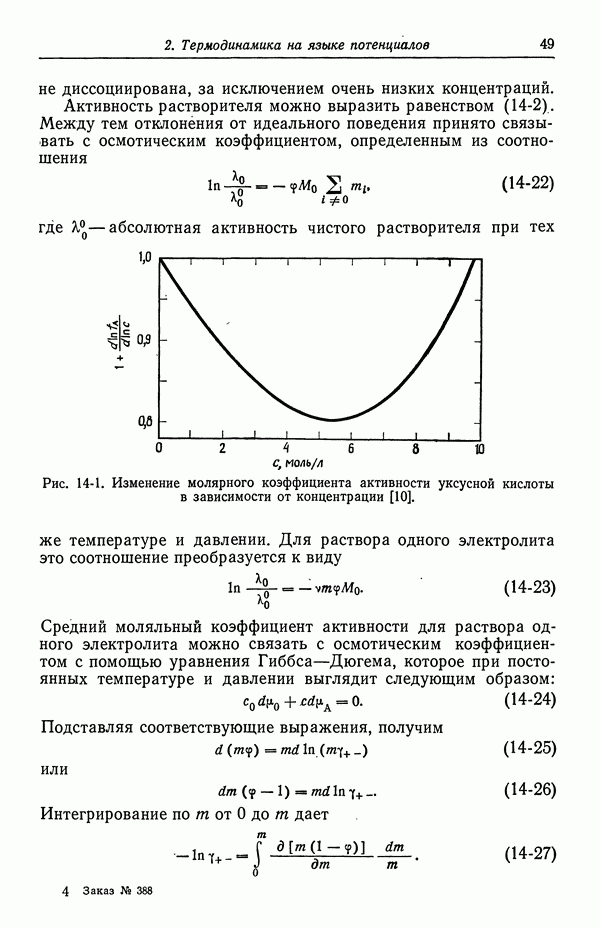
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая—Хюккеля
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 49. Качественное описание двойных слоев
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод — раствор
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 66. Динамика границы раздела
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 69. Законы переноса
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 78. Законы переноса
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 92. Интегральные коэффициенты диффузии
- ЗАДАЧА
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
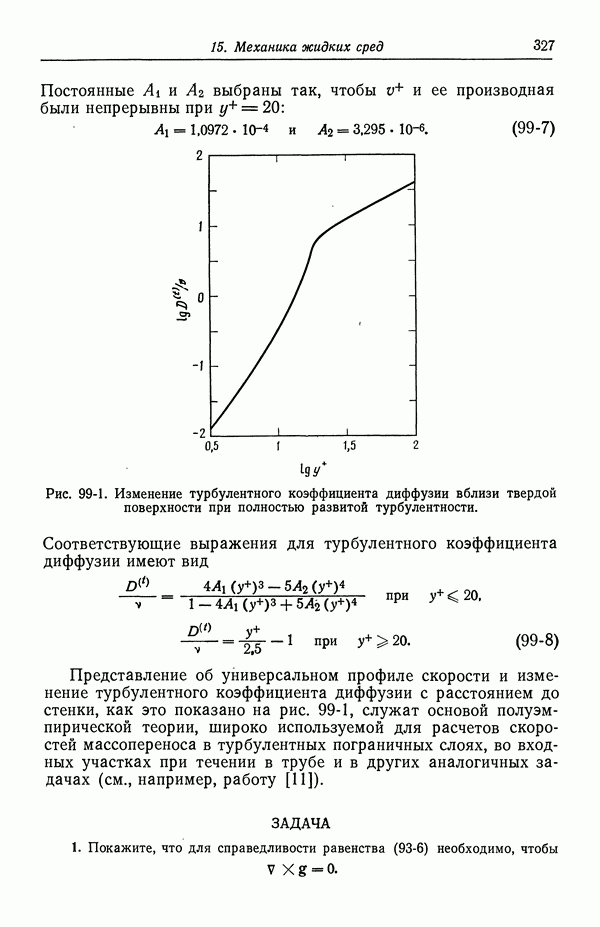
- 99. Массоперенос в турбулентном потоке
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
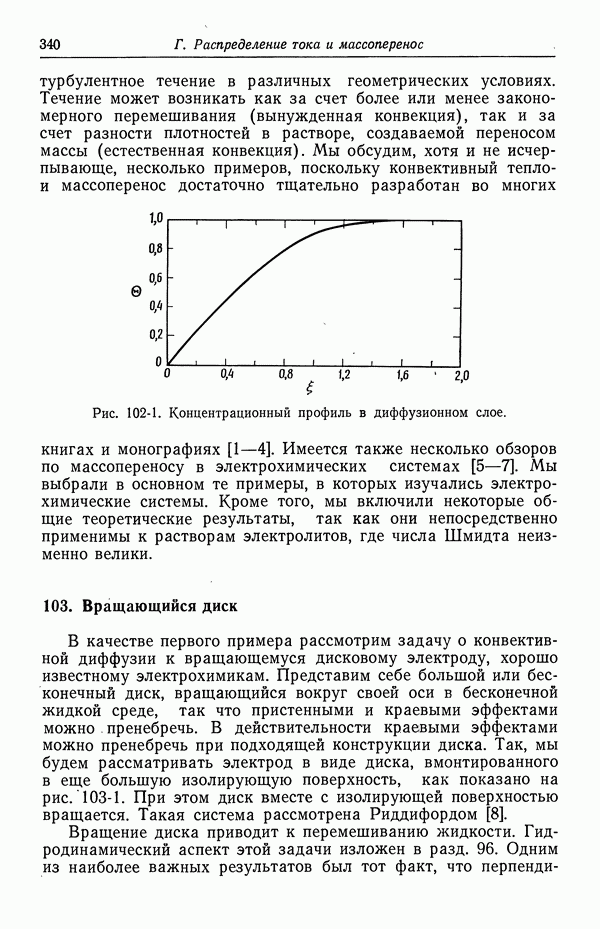
- 102. Упрощенное описание конвективной диффузии
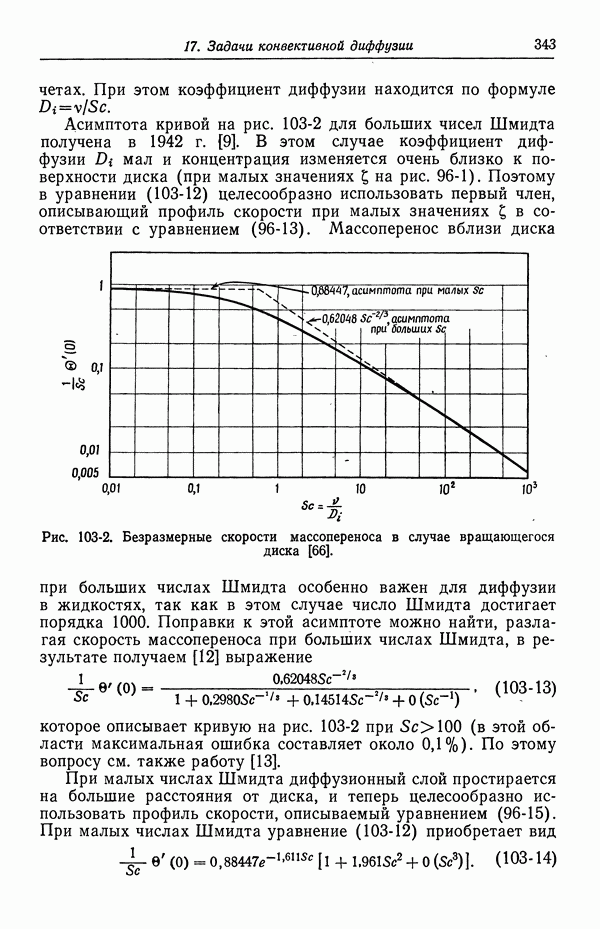
- 103. Вращающийся диск
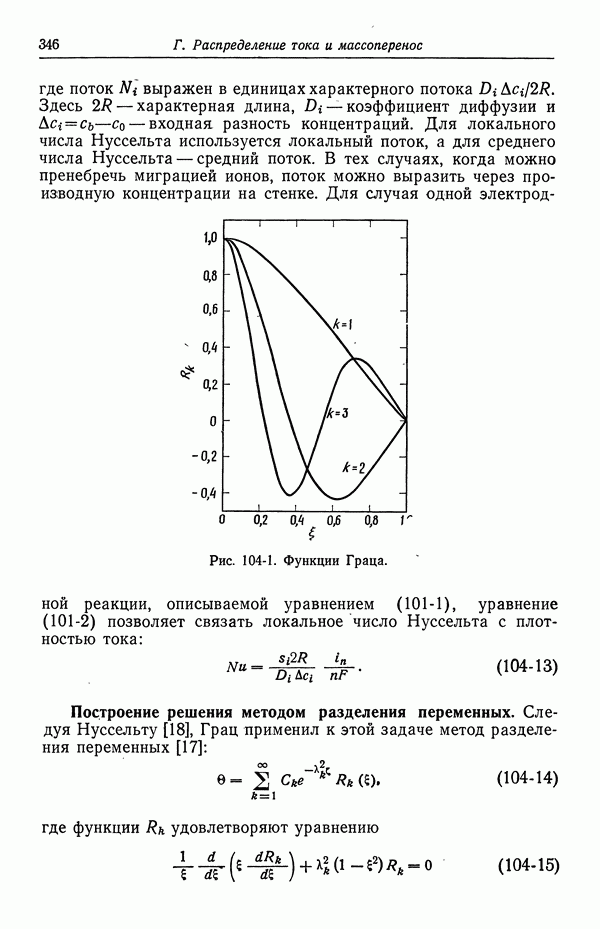
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 111. Свободная конвекция
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
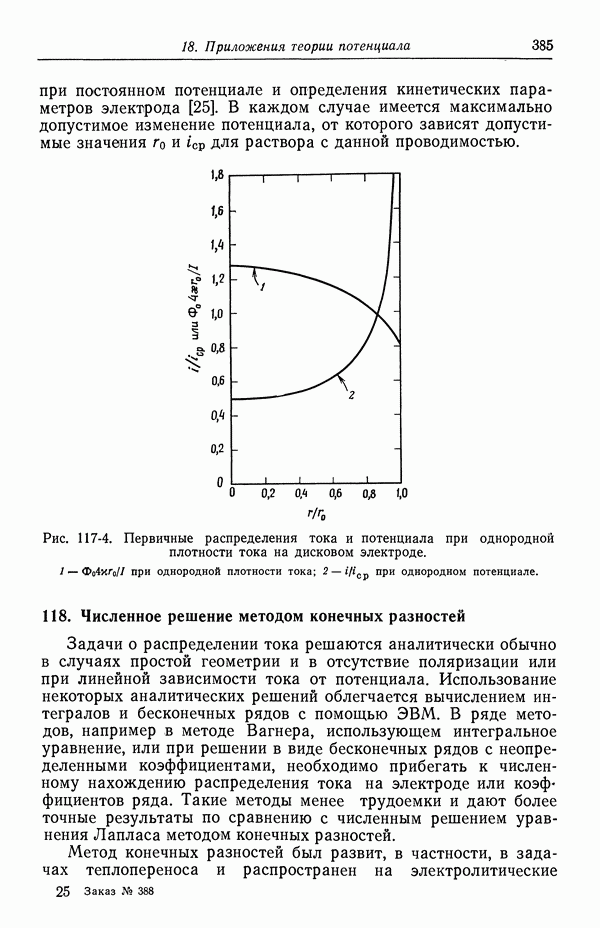
- 116. Первичное распределение тока
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- СПИСОК ОБОЗНАЧЕНИЙ
- ГЛАВА 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 119. Решение задачи
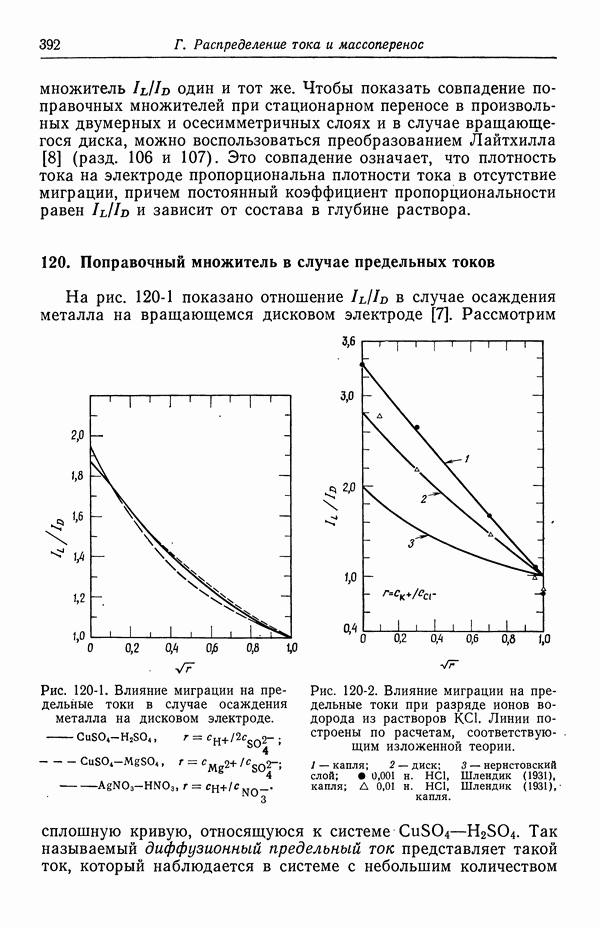
- 120. Поправочный множитель в случае предельных токов
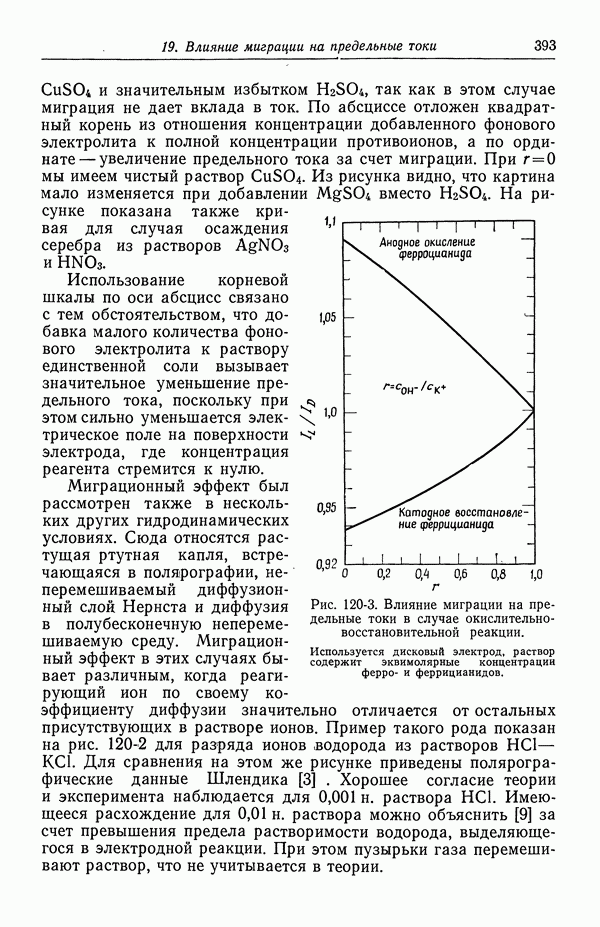
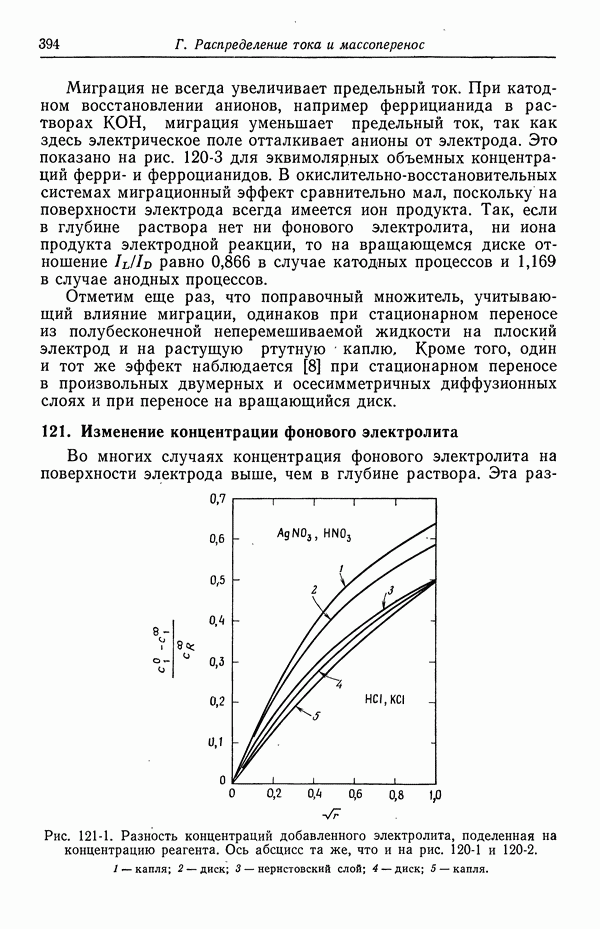
- 121. Изменение концентрации фонового электролита
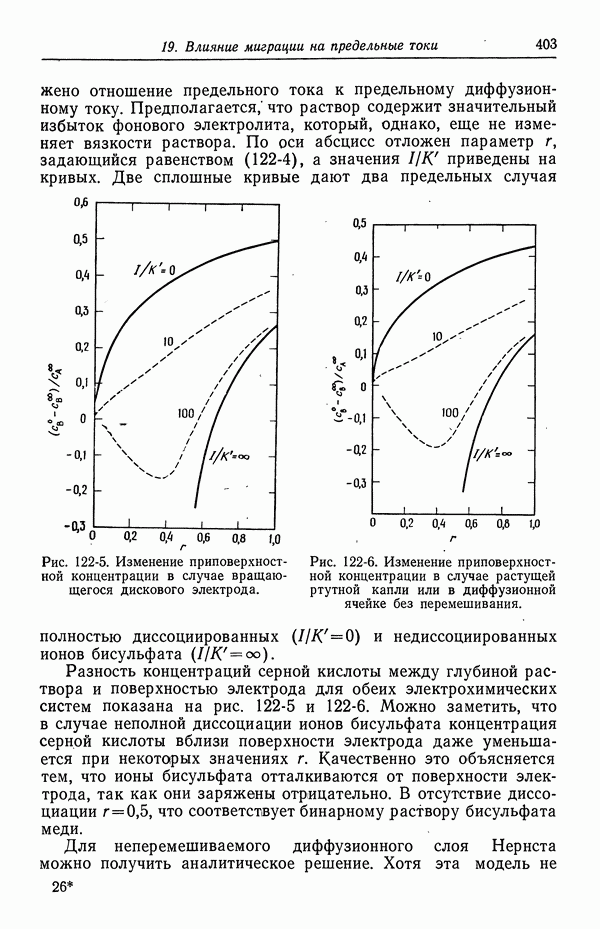
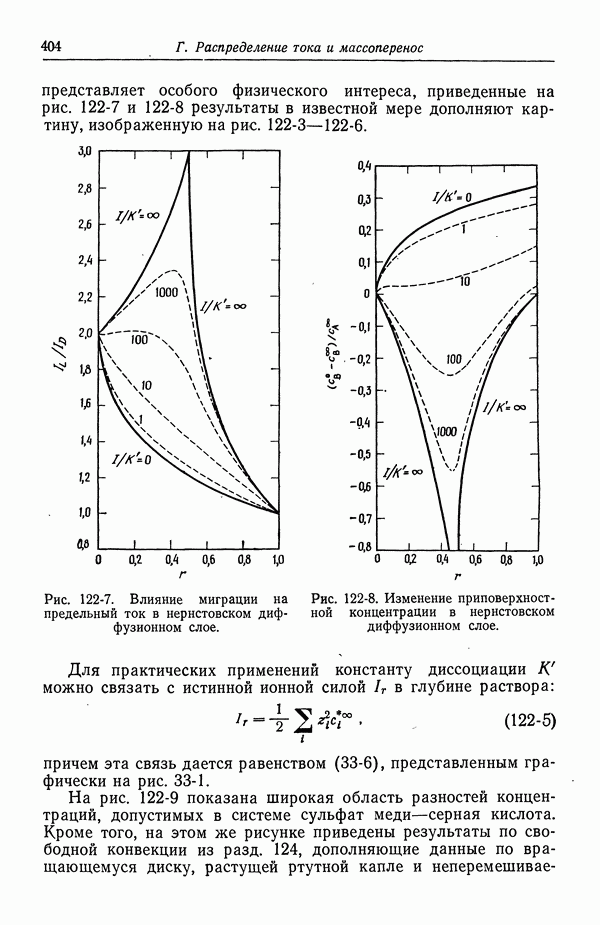
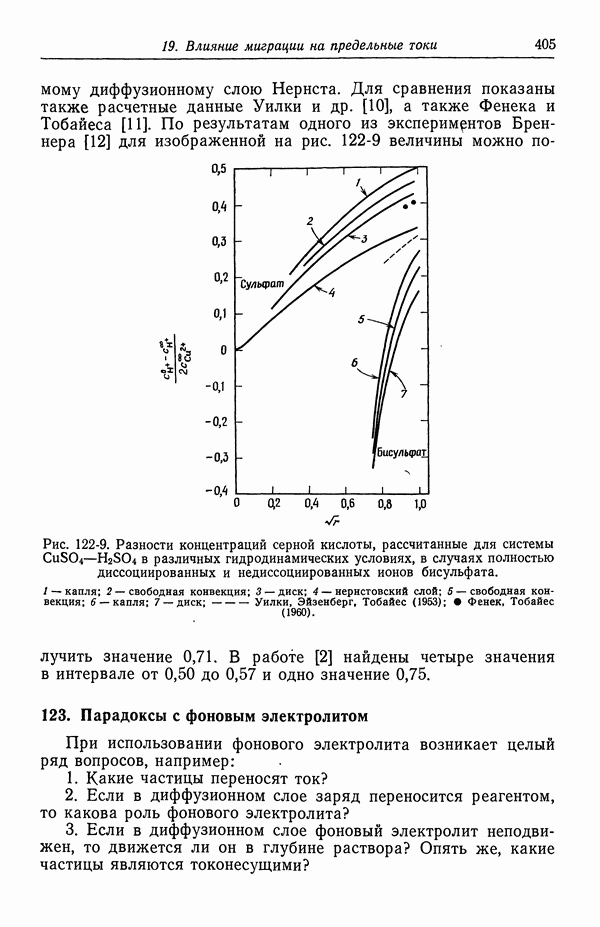
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
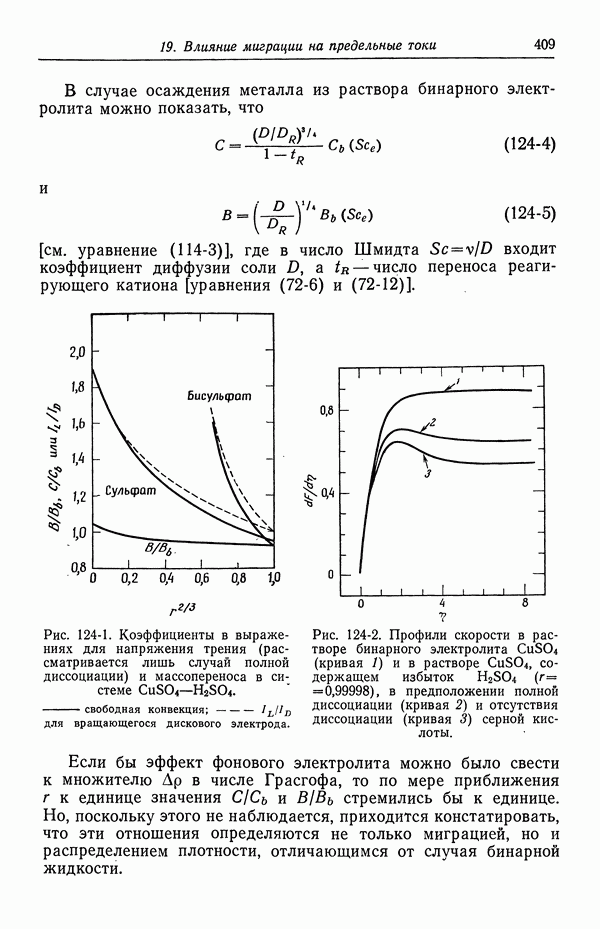
- 124. Предельные токи в случае свободной конвекции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ