| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
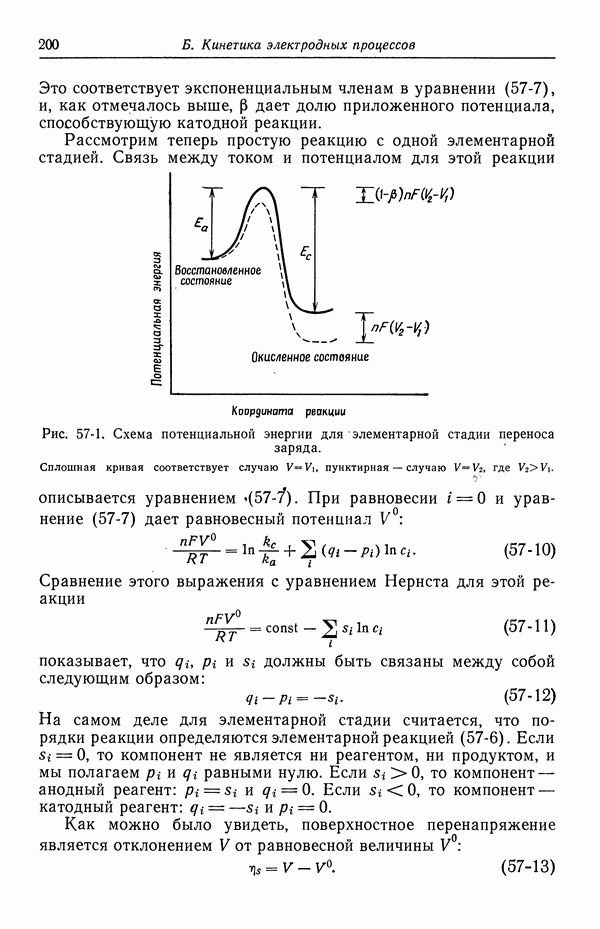
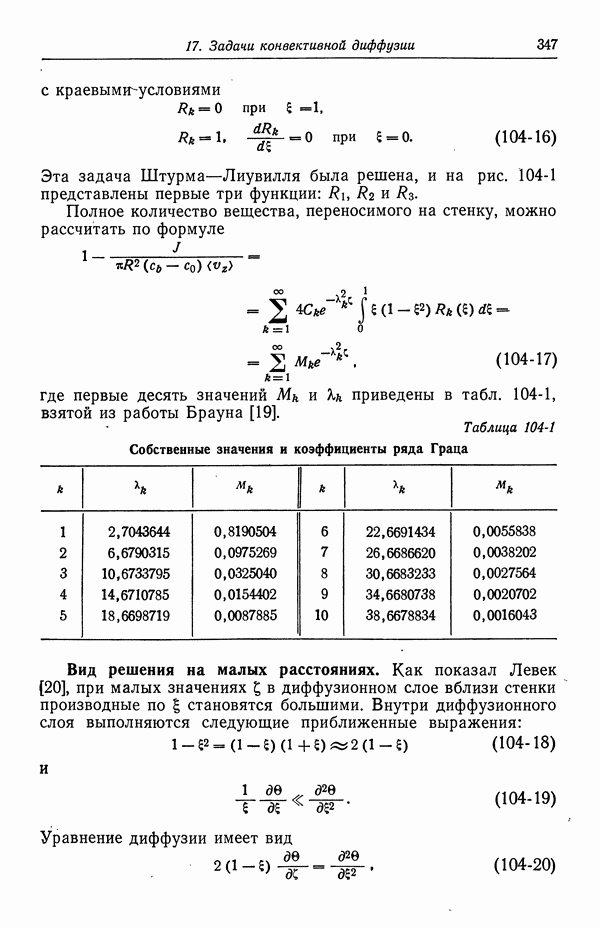
90. Растворы, содержащие одну соль
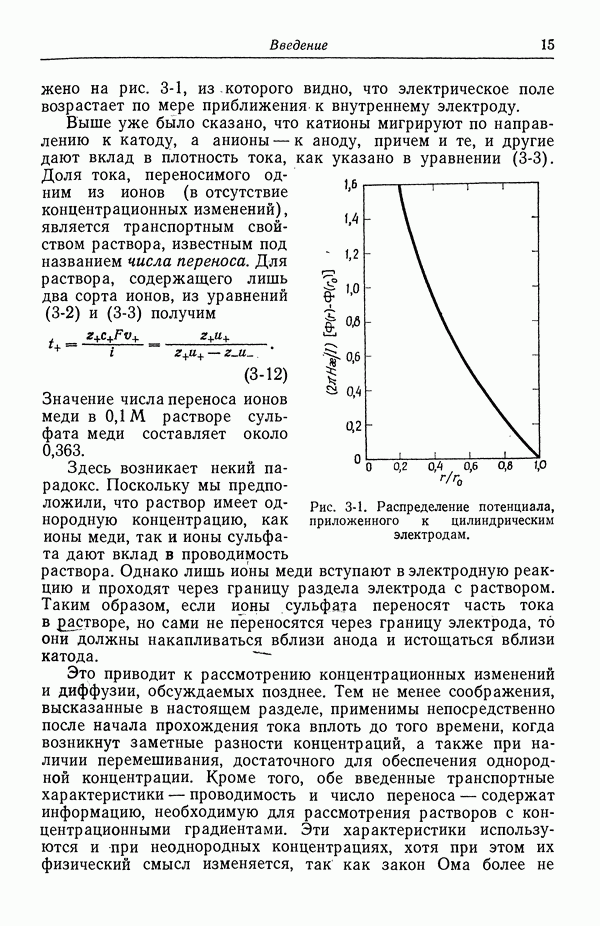
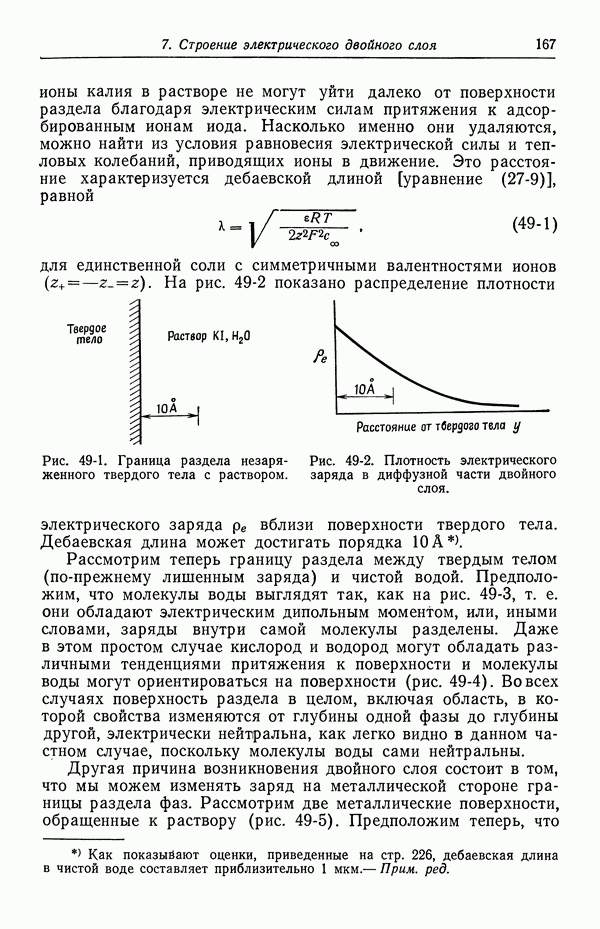
В разд. 79 и 81 указывалось, что растворам единственной соли свойственны три характеристики переноса: проводимость к, коэффициент диффузии D и число переноса t? Эти величины можно измерять как функции концентрации и температуры [1]. Проводимость обычно находится из измерения на переменном токе сопротивления раствора, помещенного между двумя электродами. В методе Гитторфа, сводящемся к измерению чисел переноса, определяют изменения концентрации вблизи анода и катода при прохождении тока. В методе движущейся границы, обычно считающемся более точным, чем метод Гитторфа, измеряют скорость перемещения границы между двумя растворами, например  , при пропускании тока через границу [2]. Коэффициенты диффузии можно измерять путем прослеживания концентрационных изменений поперек пористой стеклянной диафрагмы. Точные результаты можно также получить с помощью оптических измерений концентрационных изменений в области контакта двух растворов с различными концентрациями. Эти измерения можно выполнять либо на малых временах, и тогда начальная граница будет резкой, либо на очень больших временах [3], когда диффузия происходит в ограниченном пространстве протяженностью около 7 см.
, при пропускании тока через границу [2]. Коэффициенты диффузии можно измерять путем прослеживания концентрационных изменений поперек пористой стеклянной диафрагмы. Точные результаты можно также получить с помощью оптических измерений концентрационных изменений в области контакта двух растворов с различными концентрациями. Эти измерения можно выполнять либо на малых временах, и тогда начальная граница будет резкой, либо на очень больших временах [3], когда диффузия происходит в ограниченном пространстве протяженностью около 7 см.
В течение ряда лет множество данных было получено по характеристикам переноса в растворах единственной соли. Хорошим источником данных по проводимости может служить справочник [4]. Каймаков и Варшавская [5] собрали литературу по числам переноса. Робинсон и Стокс [1] привели обзор данных
по коэффициентам диффузии и коэффициентам активности, а Чэпмен и Ньюмен [6] собрали данные для целого ряда систем.
Проводимость, коэффициент диффузии и число переноса представляют собой три совершенно различные характеристики переноса. Имеются основания полагать, что более единообразное описание можно получить, работая с эквивалентными коэффициентами переноса  определенными уравнением (78-1). Эти коэффициенты можно найти по измеренным значениям и, D и
определенными уравнением (78-1). Эти коэффициенты можно найти по измеренным значениям и, D и  решая уравнения (79-5), (79-6) и (81-4):
решая уравнения (79-5), (79-6) и (81-4):

Ясно, что вначале нужно найти 3) по известному значению D в соответствии с уравнением (79-7):

Это уравнение требует, чтобы был известен также коэффициент активности (задача 2-1).
Имеется свыше тридцати бинарных систем [3], информация о которых позволяет рассчитать значения  На рис. 90-1 показаны коэффициенты многокомпонентной диффузии
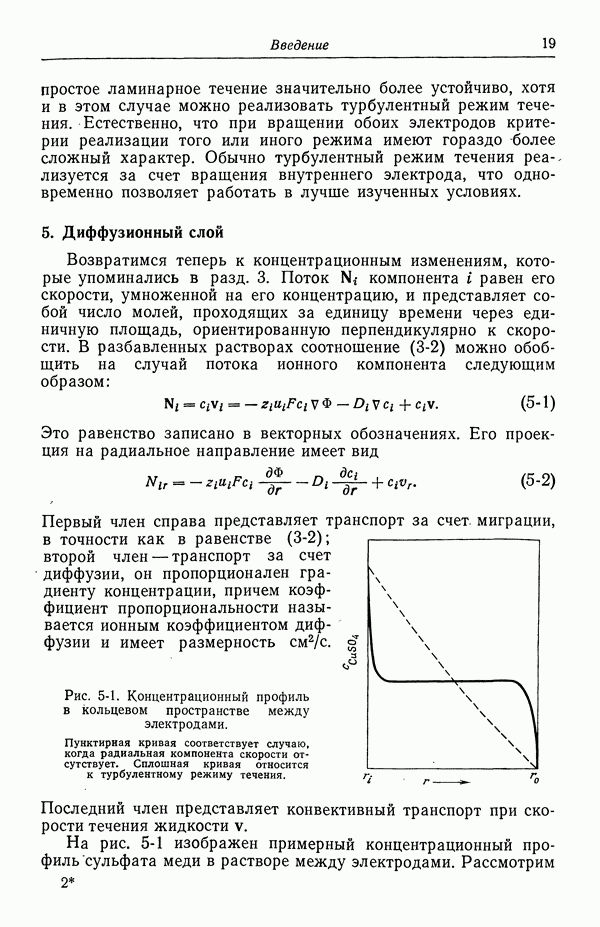
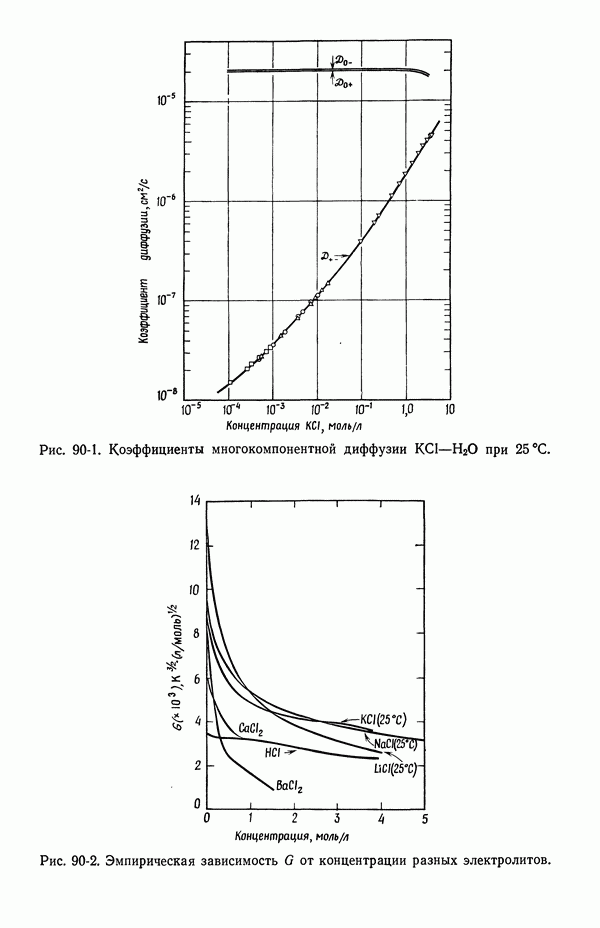
На рис. 90-1 показаны коэффициенты многокомпонентной диффузии  в воде при 25 °С. Можно отметить, что коэффициенты взаимодействия ионов с растворителем практически постоянны, в то время как коэффициенты ион-ионного взаимодействия проявляют зависимость, близкую к корню квадратному из концентрации, что характерно для теории Дебая—Хюккеля—Онзагера, описывающей взаимодействие ионов в разбавленных растворах.
в воде при 25 °С. Можно отметить, что коэффициенты взаимодействия ионов с растворителем практически постоянны, в то время как коэффициенты ион-ионного взаимодействия проявляют зависимость, близкую к корню квадратному из концентрации, что характерно для теории Дебая—Хюккеля—Онзагера, описывающей взаимодействие ионов в разбавленных растворах.
Исходя из этого, определим функцию 

где

и  эквивалентные ионные проводимости при бесконечном разбавлении. По существу значение G равно
эквивалентные ионные проводимости при бесконечном разбавлении. По существу значение G равно  а остальные множители основаны на теории разбавленных растворов.
а остальные множители основаны на теории разбавленных растворов.

Рис. 90-1. Коэффициенты многокомпонентной диффузии  при 25 °С.
при 25 °С.

Рис. 90-2. Эмпирическая зависимость G от концентрации разных электролитов.
На рис. 90-2 приведены некоторые рассчитанные значения G для нескольких систем, содержащих ионы хлора. Если учесть электростатическое межионное взаимодействие и пренебречь электрофорезом, то предельное значение G для разбавленных растворов близко к 2860. Из рисунка видно, что это значение более характерно для концентрированных растворов.

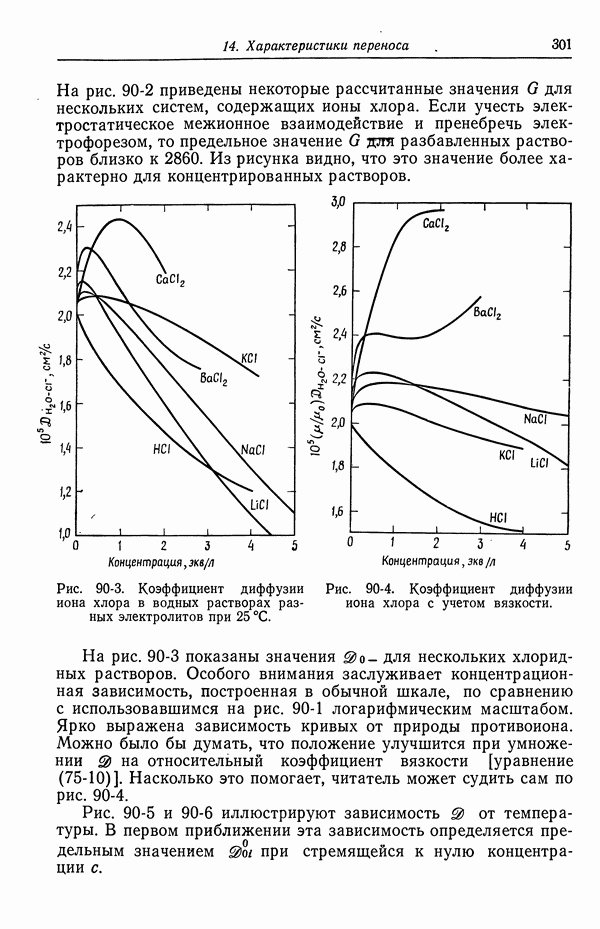
Рис. 90-3. Коэффициент диффузии иона хлора в водных растворах разных электролитов при 25 °С.

Рис. 90-4. Коэффициент диффузии иона хлора с учетом вязкости.
На рис. 90-3 показаны значения  для нескольких хлоридных растворов. Особого внимания заслуживает концентрационная зависимость, построенная в обычной шкале, по сравнению с использовавшимся на рис. 90-1 логарифмическим масштабом. Ярко выражена зависимость кривых от природы противоиона. Можно было бы думать, что положение улучшится при умножении 3 на относительный коэффициент вязкости [уравнение (75-10)]. Насколько это помогает, читатель может судить сам по рис. 90-4.
для нескольких хлоридных растворов. Особого внимания заслуживает концентрационная зависимость, построенная в обычной шкале, по сравнению с использовавшимся на рис. 90-1 логарифмическим масштабом. Ярко выражена зависимость кривых от природы противоиона. Можно было бы думать, что положение улучшится при умножении 3 на относительный коэффициент вязкости [уравнение (75-10)]. Насколько это помогает, читатель может судить сам по рис. 90-4.
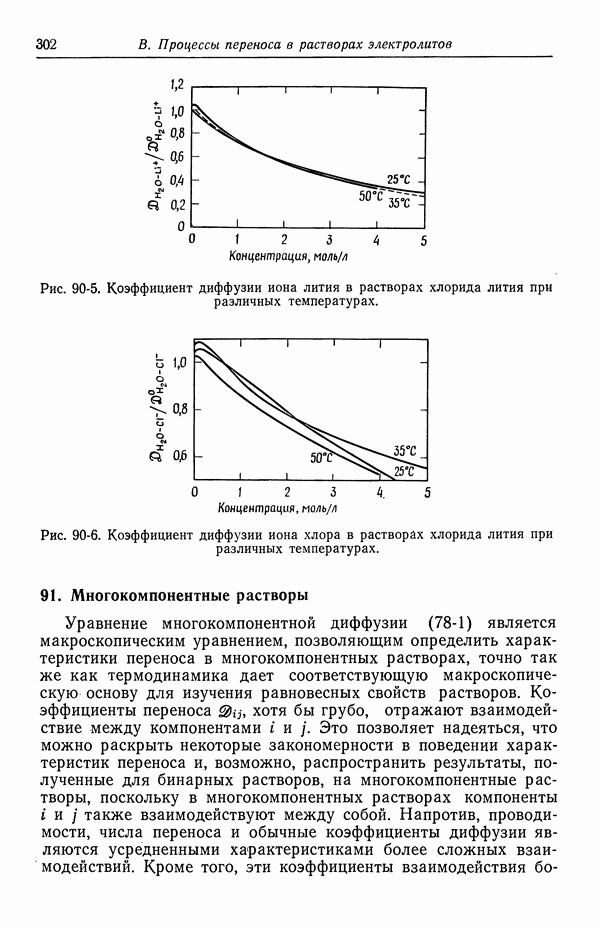
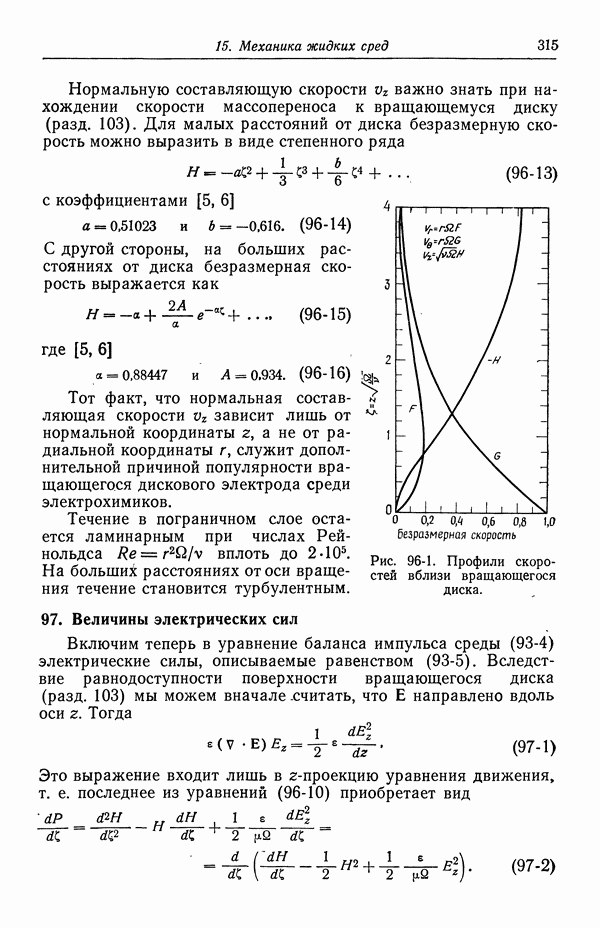
Рис. 90-5 и 90-6 иллюстрируют зависимость 3 от температуры. В первом приближении эта зависимость определяется предельным значением  при стремящейся к нулю концентрации с.
при стремящейся к нулю концентрации с.

Рис. 90-5. Коэффициент диффузии иона лития в растворах хлорида лития при различных температурах.

Рис. 90-6. Коэффициент диффузии иона хлора в растворах хлорида лития при различных температурах.
91. Многокомпонентные растворы
Уравнение многокомпонентной диффузии (78-1) является макроскопическим уравнением, позволяющим определить характеристики переноса в многокомпонентных растворах, точно так же как термодинамика дает соответствующую макроскопическую основу для изучения равновесных свойств растворов. Коэффициенты переноса хотя бы грубо, отражают взаимодействие между компонентами  Это позволяет надеяться, что можно раскрыть некоторые закономерности в поведении характеристик переноса и, возможно, распространить результаты, полученные для бинарных растворов, на многокомпонентные растворы, поскольку в многокомпонентных растворах компоненты
Это позволяет надеяться, что можно раскрыть некоторые закономерности в поведении характеристик переноса и, возможно, распространить результаты, полученные для бинарных растворов, на многокомпонентные растворы, поскольку в многокомпонентных растворах компоненты  также взаимодействуют между собой. Напротив, проводимости, числа переноса и обычные коэффициенты диффузии являются усредненными характеристиками более сложных взаимодействий. Кроме того, эти коэффициенты взаимодействия
также взаимодействуют между собой. Напротив, проводимости, числа переноса и обычные коэффициенты диффузии являются усредненными характеристиками более сложных взаимодействий. Кроме того, эти коэффициенты взаимодействия
более непосредственно связаны с коэффициентами ионной диффузии, применимыми в разбавленных растворах.
Однако в большинстве случаев данные о всех необходимых характеристиках переноса неполны [7]. Для многокомпонентных растворов нельзя использовать метод движущейся границы, и числа переноса приходится получать менее точным методом Гитторфа. Аналогично оптические методы непосредственно не применимы, и коэффициенты диффузии определяют менее точным методом, использующим ячейку с диафрагмой.
Если бы имелись все данные, то в некоторых случаях простой геометрии можно было бы строго применять теорию многокомпонентного переноса. Такое применение сводится к решению обыкновенных дифференциальных уравнений для концентрационных профилей, причем для обращения матрицы переноса, рассмотренного в разд. 83, может использоваться вычислительная машина. В отсутствие таких данных часто приходится возвращаться к теории разбавленных растворов, изложенной в разд. 82 и 77. Однако в некоторых случаях массопереноса удается получить надежные оценки используемых характеристик переноса, как показано в следующем разделе.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
- 5. Диффузионный слой
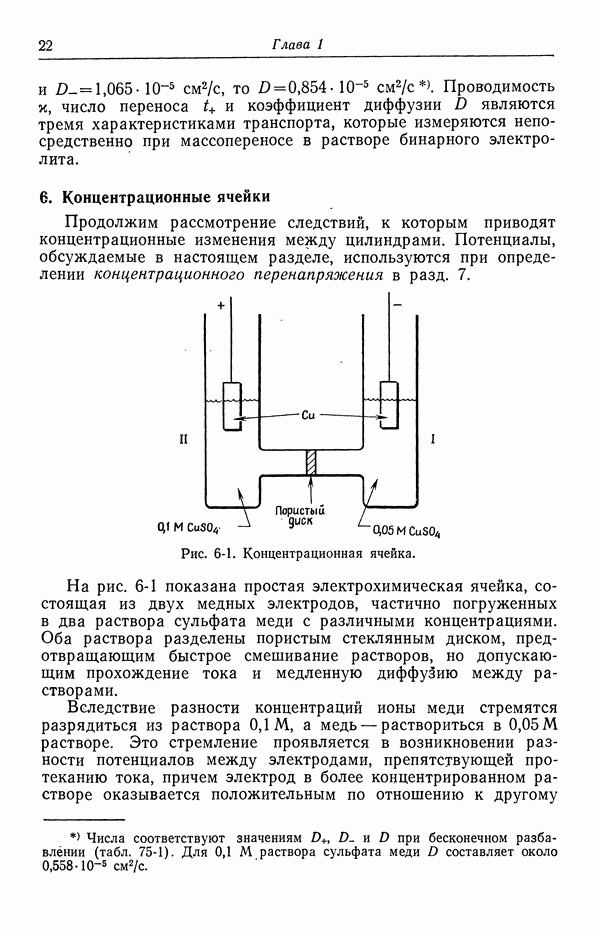
- 6. Концентрационные ячейки
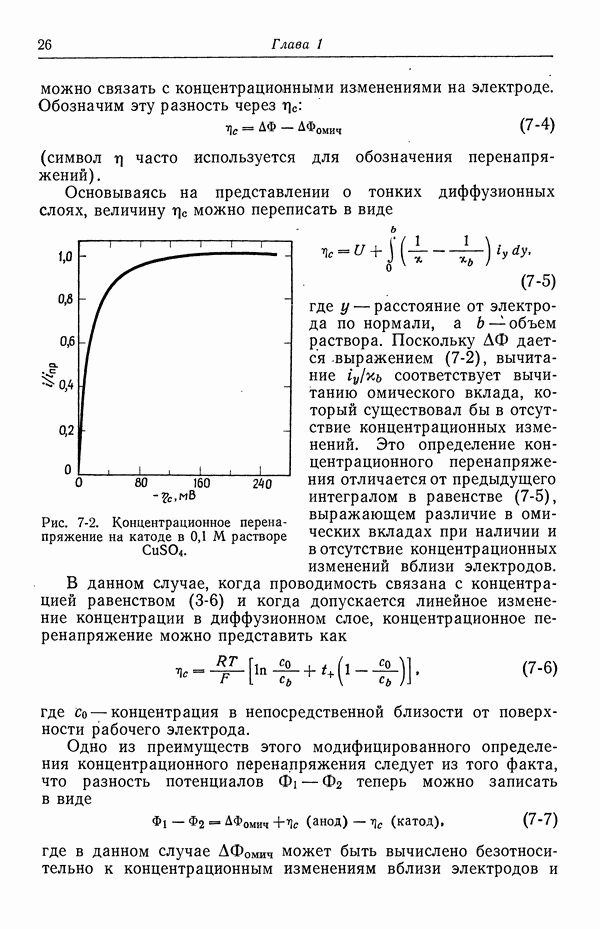
- 7. Концентрационное перенапряжение
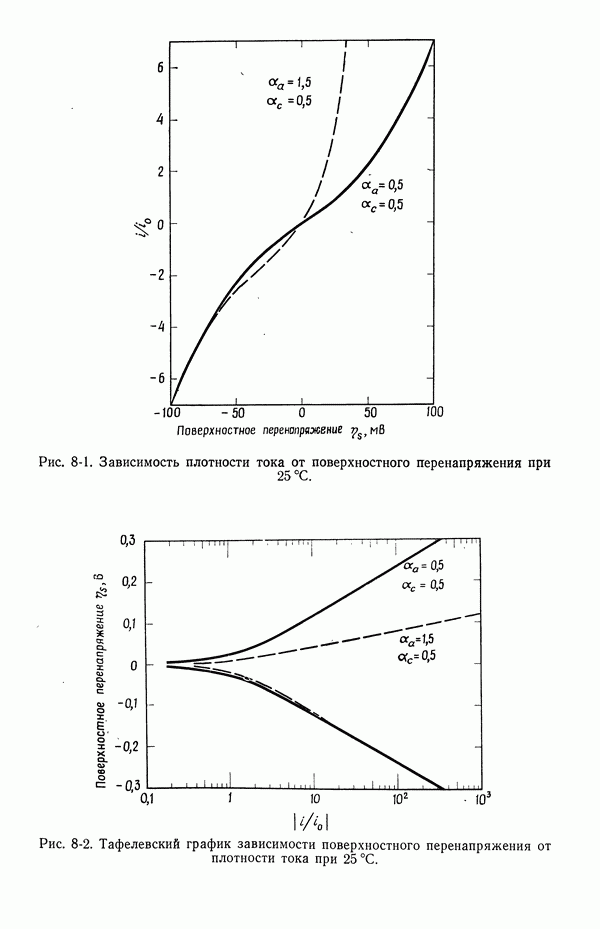
- 8. Поверхностное перенапряжение
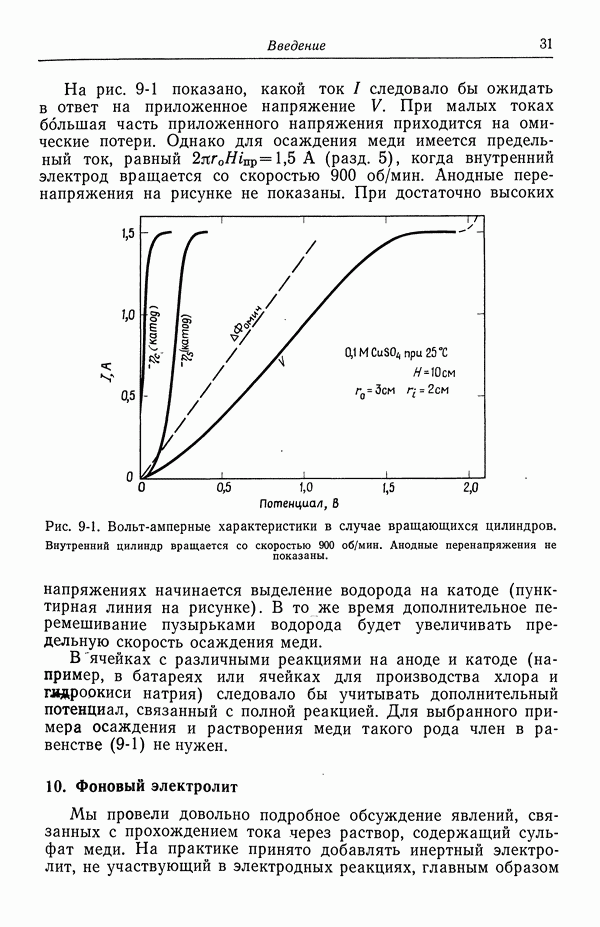
- 9. Потенциал ячейки
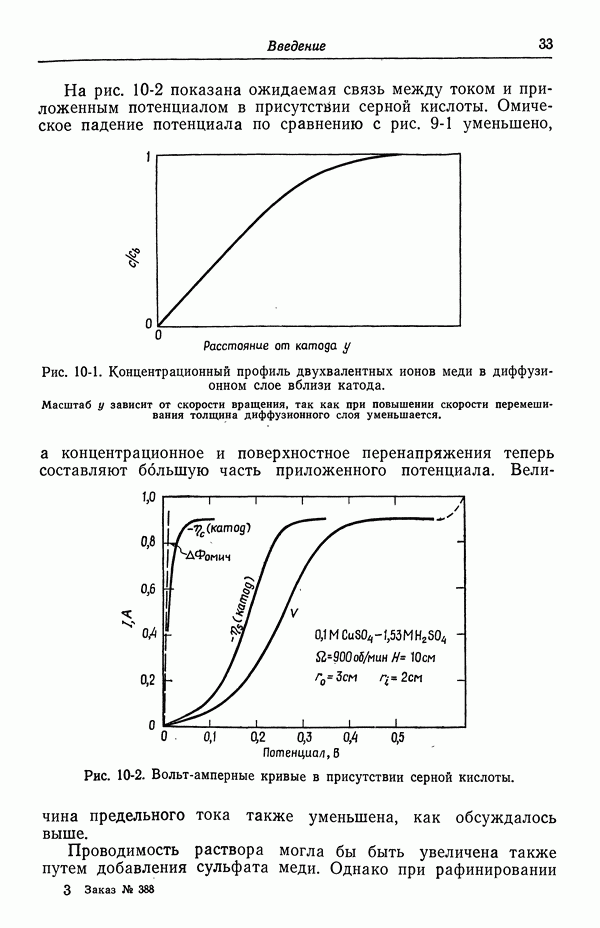
- 10. Фоновый электролит
- 11. Свободная конвекция
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
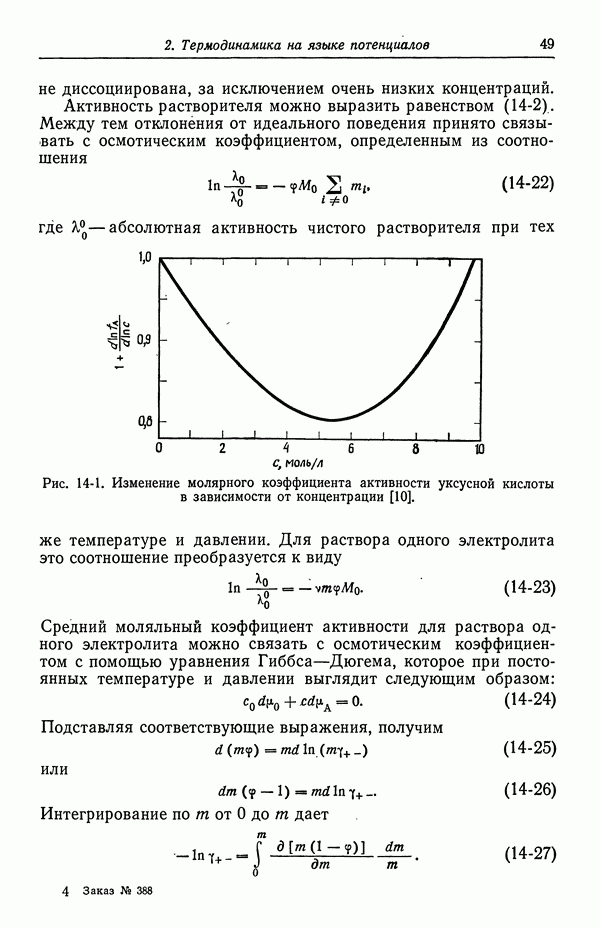
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
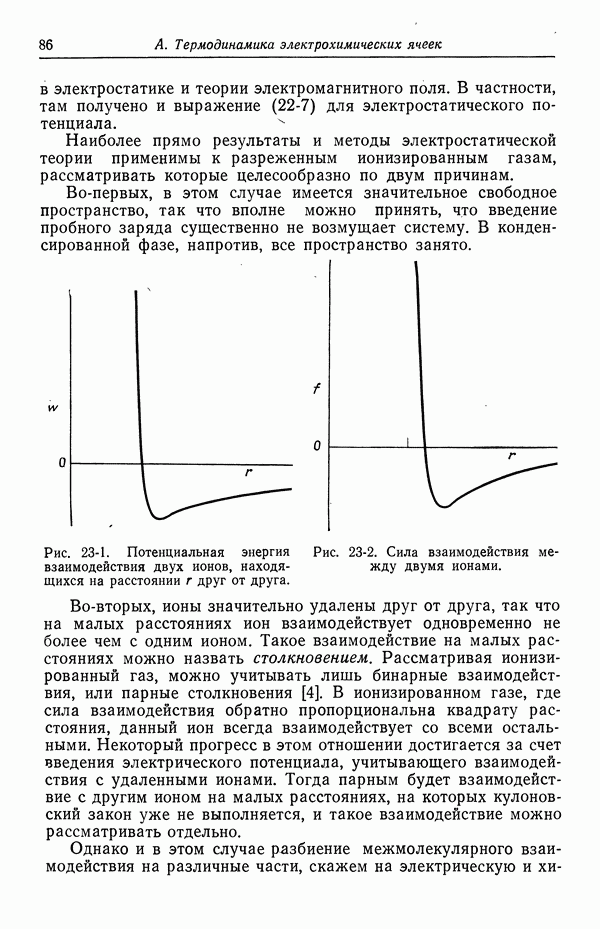
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
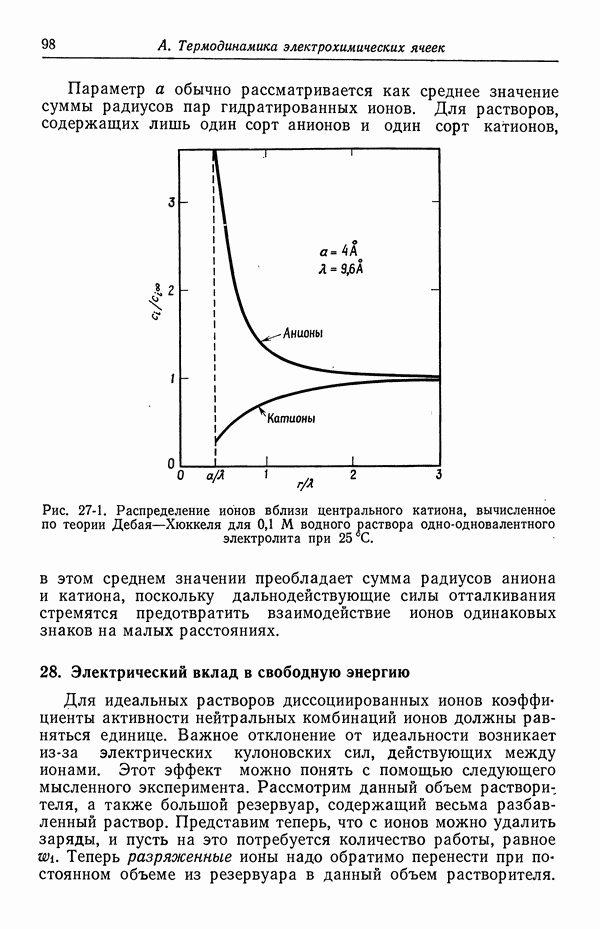
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая—Хюккеля
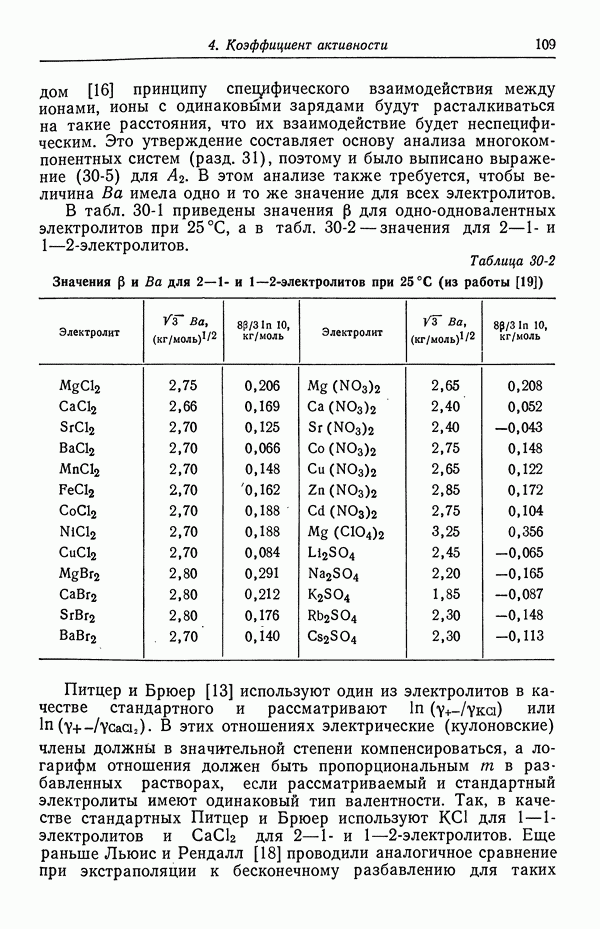
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 49. Качественное описание двойных слоев
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод — раствор
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
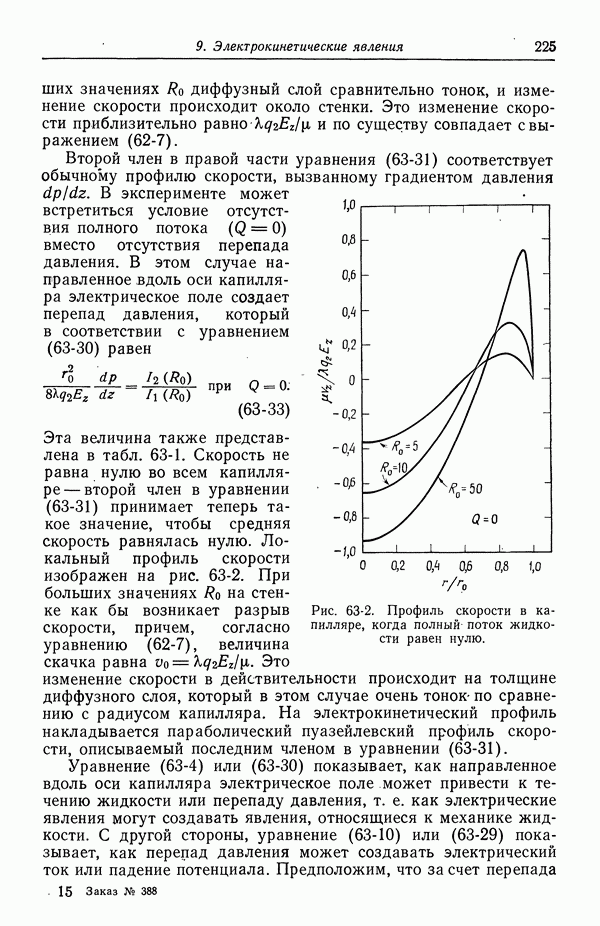
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 66. Динамика границы раздела
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 69. Законы переноса
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 78. Законы переноса
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 92. Интегральные коэффициенты диффузии
- ЗАДАЧА
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 111. Свободная конвекция
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
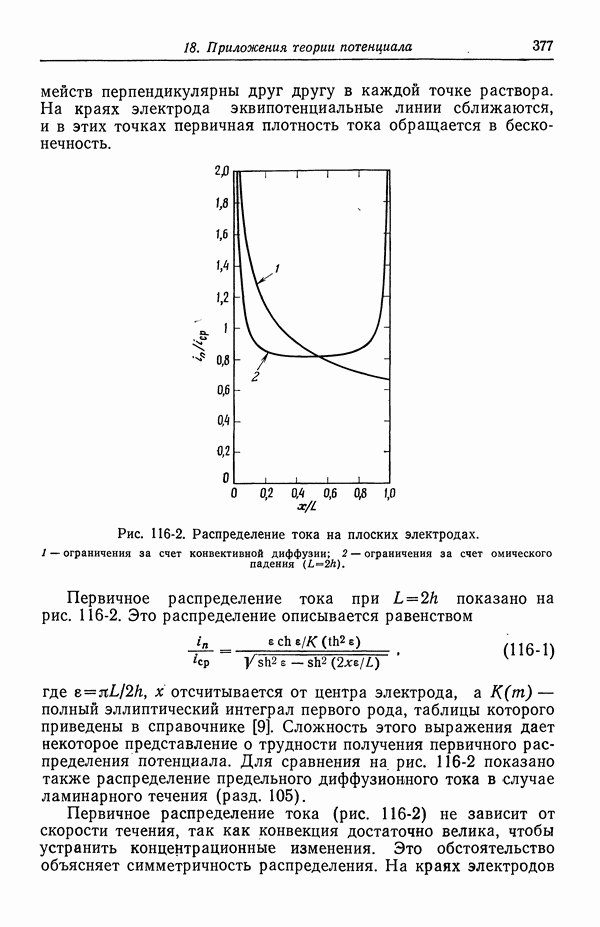
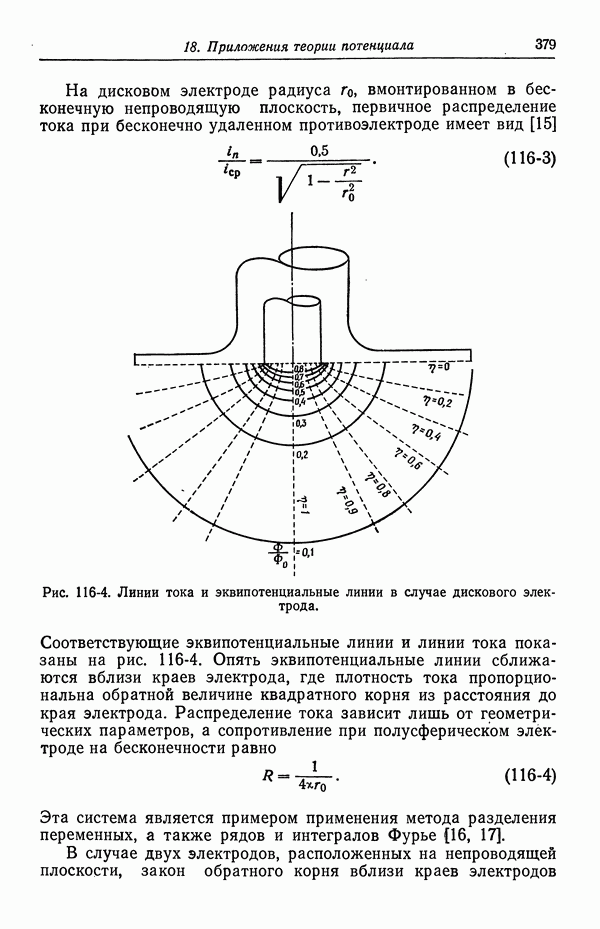
- 116. Первичное распределение тока
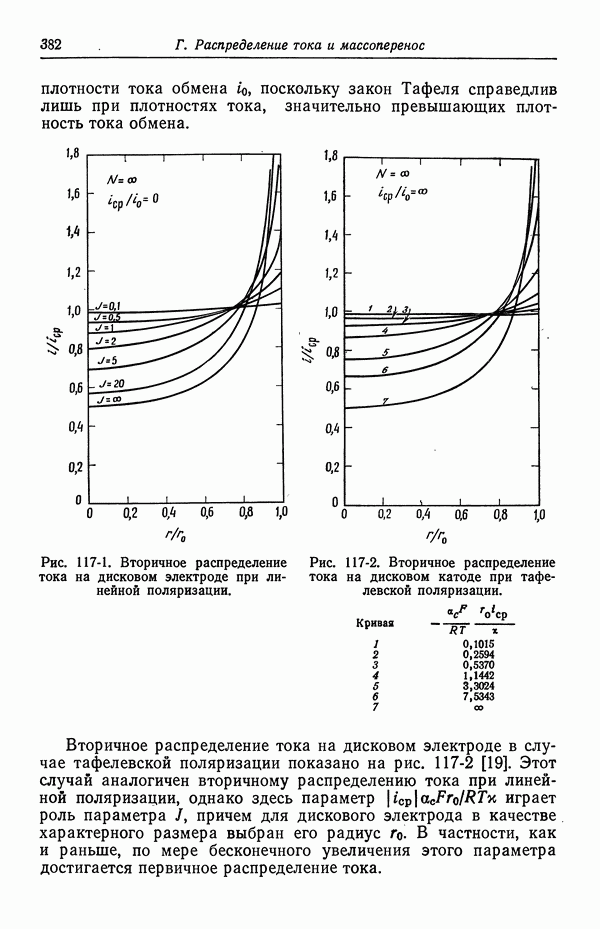
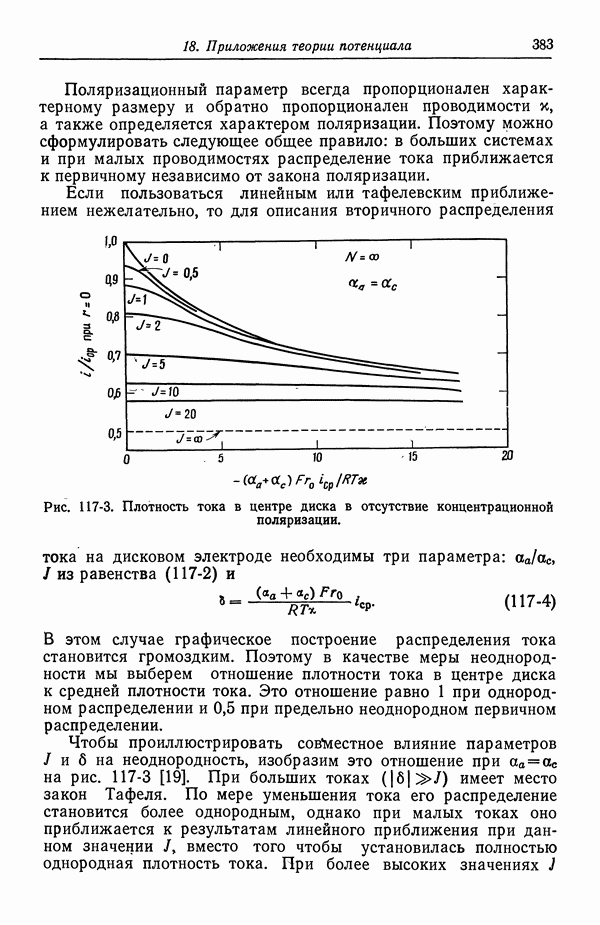
- 117. Вторичное распределение тока
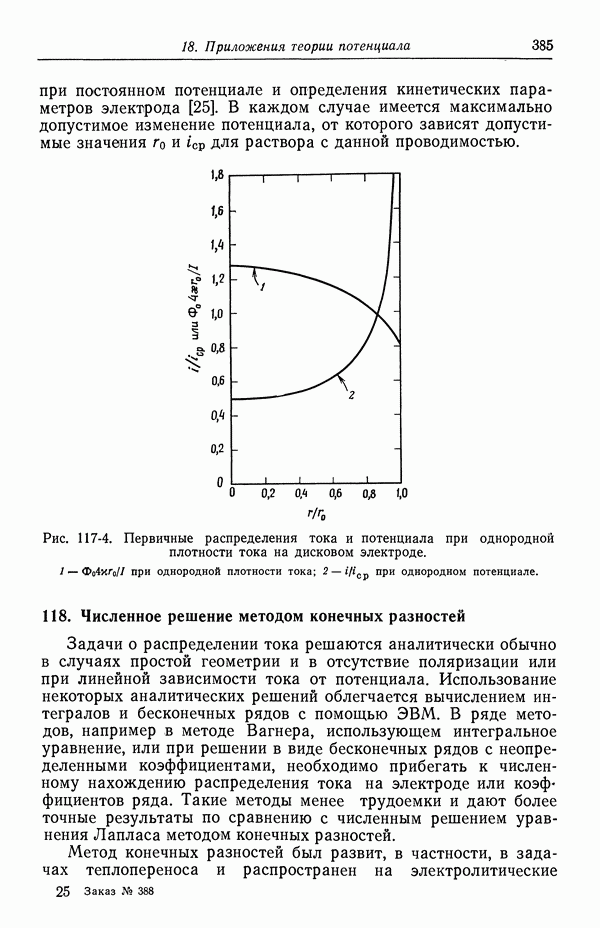
- 118. Численное решение методом конечных разностей
- СПИСОК ОБОЗНАЧЕНИЙ
- ГЛАВА 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 119. Решение задачи
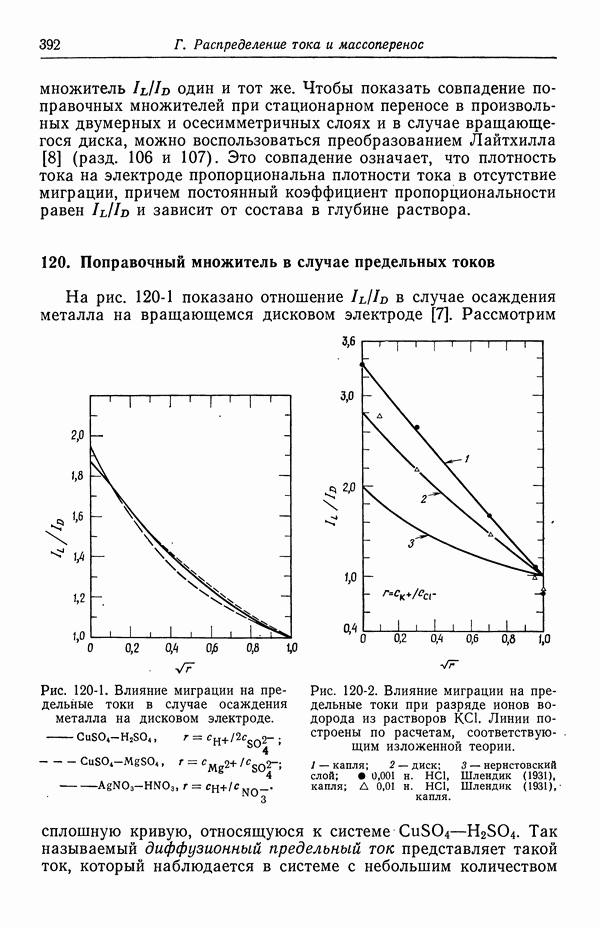
- 120. Поправочный множитель в случае предельных токов
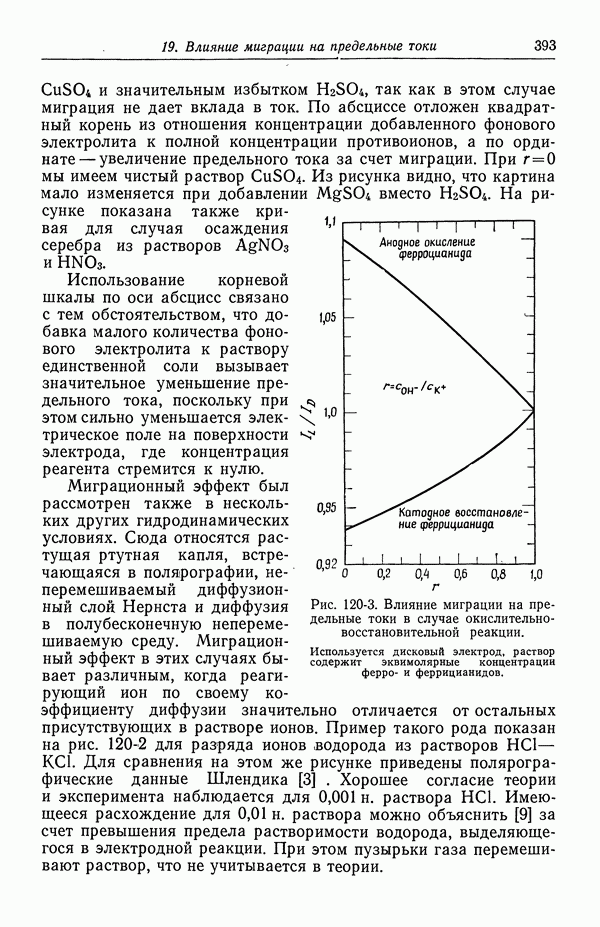
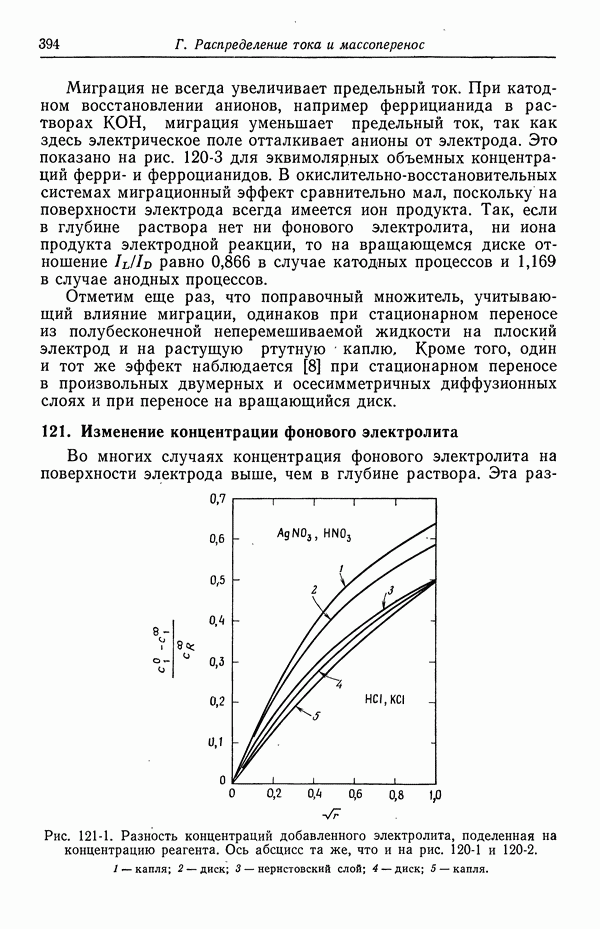
- 121. Изменение концентрации фонового электролита
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ