| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
28. Электрический вклад в свободную энергию
Для идеальных растворов диссоциированных ионов коэффи циенты активности нейтральных комбинаций ионов должны равняться единице. Важное отклонение от идеальности возникает из-за электрических кулоновских сил, действующих между ионами. Этот эффект можно понять с помощью следующего мысленного эксперимента. Рассмотрим данный объем растворителя, а также большой резервуар, содержащий весьма разбавленный раствор. Представим теперь, что с ионов можно удалить заряды, и пусть на это потребуется количество работы, равное  Теперь разряженные ионы надо обратимо перенести при постоянном объеме из резервуара в данный объем растворителя.
Теперь разряженные ионы надо обратимо перенести при постоянном объеме из резервуара в данный объем растворителя.
Затраченная на этот процесс работа является идеальным неэлектрическим вкладом в изменение свободной энергии А Гельмгольца. Средняя концентрация растворенного компонента в новом растворе будет равна с.
Наконец, все ионы нужно одновременно зарядить до начального уровня, на что потребуется затратить работу  . Работа
. Работа  отличается от
отличается от  так как ионы теперь находятся при достаточно высокой концентрации, чтобы экранировать друг друга, и распределение потенциала вокруг центрального иона описывается равенством (27-10). Разность между этими двумя работами рассматривается как электрический вклад в свободную энергию Гельмгольца:
так как ионы теперь находятся при достаточно высокой концентрации, чтобы экранировать друг друга, и распределение потенциала вокруг центрального иона описывается равенством (27-10). Разность между этими двумя работами рассматривается как электрический вклад в свободную энергию Гельмгольца:

Остается лишь расписать это равенство.
Работа, необходимая для переноса элемента заряда  с бесконечности на расстояние
с бесконечности на расстояние  от центрального иона, равна
от центрального иона, равна  Поскольку все ионы должны заряжаться одновременно, через
Поскольку все ионы должны заряжаться одновременно, через  можно обозначить долю заряда иона в процессе заряжения. Тогда заряд иона равен
можно обозначить долю заряда иона в процессе заряжения. Тогда заряд иона равен  причем
причем  изменяется от 0 до 1 в процессе заряжения. Величину
изменяется от 0 до 1 в процессе заряжения. Величину  в уравнении (27-10) нужно представить в виде
в уравнении (27-10) нужно представить в виде  так как X обратно пропорциональна уровню заряда.
так как X обратно пропорциональна уровню заряда.
Следовательно, вклад в  создаваемый заряжением центрального иона валентности
создаваемый заряжением центрального иона валентности  равен
равен

Выражение в скобках является разностью потенциалов в точке  соответствующих процессам заряжения с затратой энергии
соответствующих процессам заряжения с затратой энергии  . Электрический вклад в свободную энергию Гельмгольца равен теперь сумме вкладов от заряжения отдельных ионов:
. Электрический вклад в свободную энергию Гельмгольца равен теперь сумме вкладов от заряжения отдельных ионов:

где  число молей компонента j и L — число Авогадро. Интегрирование этого выражения дает
число молей компонента j и L — число Авогадро. Интегрирование этого выражения дает

где

Химический потенциал компонента можно получить дифференцированием свободной энергии Гельмгольца по соответствующей переменной [равенство (13-1)]:

Из уравнения (28-4) следует

Таким образом, электрический вклад в химический потенциал равен

Второй член возникает вследствие зависимости  от
от  Нужно помнить, что от электрического состояния фазы не зависят лишь нейтральные комбинации этих химических потенциалов. Дифференцируя уравнение (28-8), находим
Нужно помнить, что от электрического состояния фазы не зависят лишь нейтральные комбинации этих химических потенциалов. Дифференцируя уравнение (28-8), находим

Изложенный выше метод получения термодинамических свойств с учетом влияния электрических эффектов известен под названием процесса заряжения по Дебаю. Более непосредственно электрический вклад в химический потенциал можно получить путем так называемого процесса заряжения по Гюнтельбергу. Равенство (28-6) показывает, что химический потенциал компонента равен работе обратимого переноса одного моля компонента в большой объем раствора при постоянных температуре и давлении. Тогда электрический вклад в  обусловлен заряжением одного иона или одного моля ионов в растворе, в котором все другие ионы уже заряжены. Следовательно, в этом процессе
обусловлен заряжением одного иона или одного моля ионов в растворе, в котором все другие ионы уже заряжены. Следовательно, в этом процессе
дебаевская длина  рассматривается как постоянная, так что мы имеем
рассматривается как постоянная, так что мы имеем

Этот результат согласуется с равенством (28-9).
Для разбавленных растворов коэффициент активности теперь можно выразить в виде

Коэффициент активности зависит от состава раствора через дебаевскую длину X. Таким образом, удобно ввести молярную ионную силу раствора

Тогда уравнение (28-11) приобретает вид

где

В приложениях часто используется моляльная концентрация, причем моляльная ионная сила определена соотношением

В разбавленных растворах  приблизительно равно
приблизительно равно  плотности чистого растворителя, так что можно писать
плотности чистого растворителя, так что можно писать  Следовательно, выраженный через моляльную ионную силу коэффициент активности равен
Следовательно, выраженный через моляльную ионную силу коэффициент активности равен

где

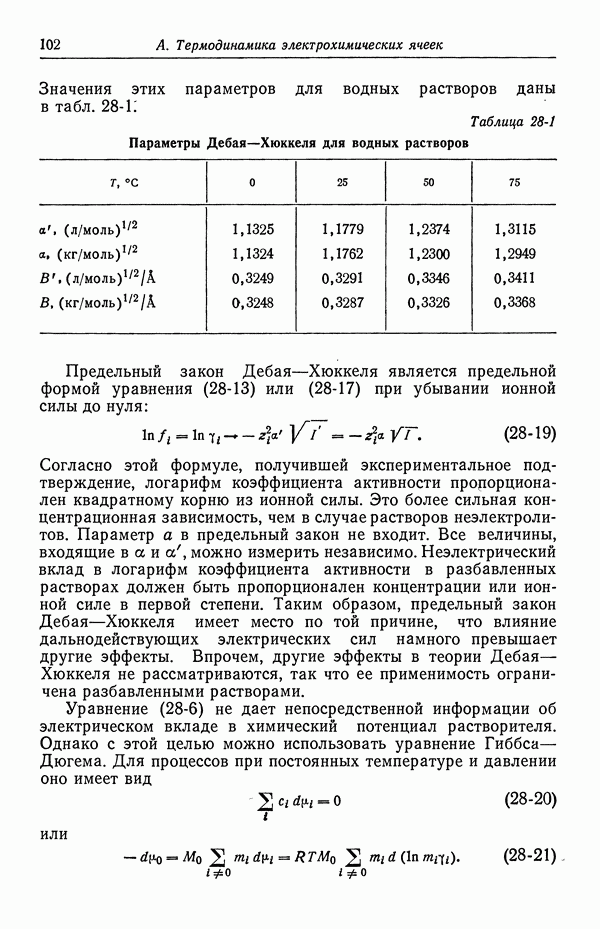
Значения этих параметров для водных растворов даны в табл. 28-1:
Таблица 28-1. Параметры Дебая—Хюккеля для водных растворов

Предельный закон Дебая—Хюккеля является предельной формой уравнения (28-13) или (28-17) при убывании ионной силы до нуля:

Согласно этой формуле, получившей экспериментальное подтверждение, логарифм коэффициента активности пропорционален квадратному корню из ионной силы. Это более сильная концентрационная зависимость, чем в случае растворов неэлектролитов. Параметр а в предельный закон не входит. Все величины, входящие в а и а, можно измерить независимо. Неэлектрический вклад в логарифм коэффициента активности в разбавленных растворах должен быть пропорционален концентрации или ионной силе в первой степени. Таким образом, предельный закон Дебая—Хюккеля имеет место по той причине, что влияние дальнодействующих электрических сил намного превышает другие эффекты. Впрочем, другие эффекты в теории Дебая—Хюккеля не рассматриваются, так что ее применимость ограничена разбавленными растворами.
Уравнение (28-6) не дает непосредственной информации об электрическом вкладе в химический потенциал растворителя. Однако с этой целью можно использовать уравнение Гиббса—Дюгема. Для процессов при постоянных температуре и давлении оно имеет вид

или

Подстановка уравнения (28-17) дает

Интегрируя это соотношение, получаем

где

Сравнение с уравнением (14-22) показывает, что осмотический коэффициент  равен
равен

Поскольку по мере стремления ионной силы к нулю величина а стремится к единице, в разбавленных растворах электролитов разность  пропорциональна квадратному корню из ионной силы.
пропорциональна квадратному корню из ионной силы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
- 5. Диффузионный слой
- 6. Концентрационные ячейки
- 7. Концентрационное перенапряжение
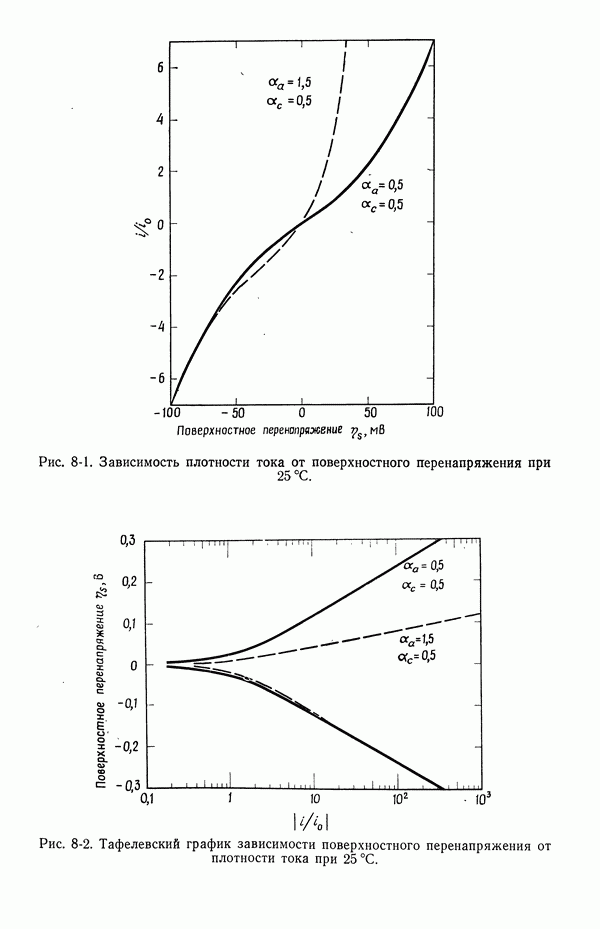
- 8. Поверхностное перенапряжение
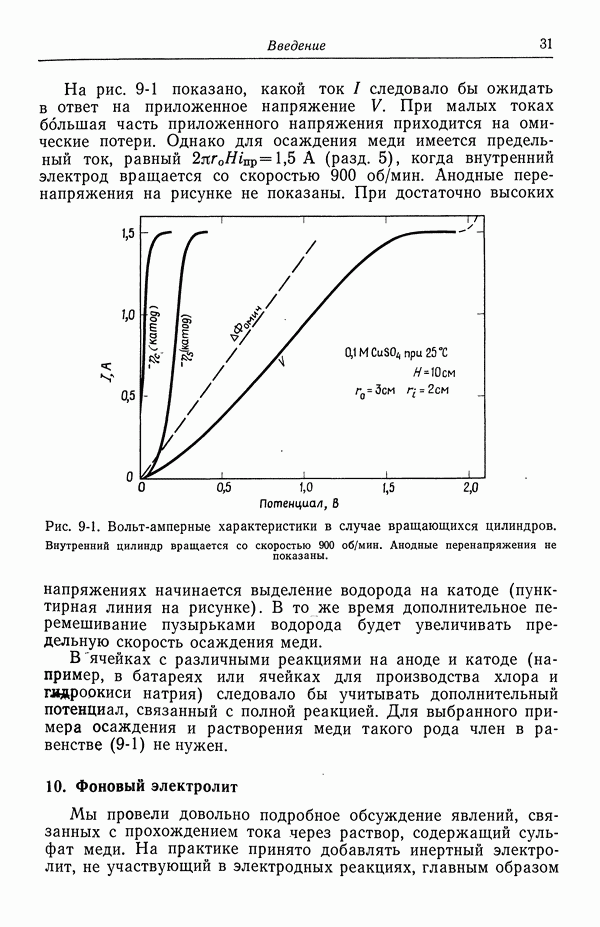
- 9. Потенциал ячейки
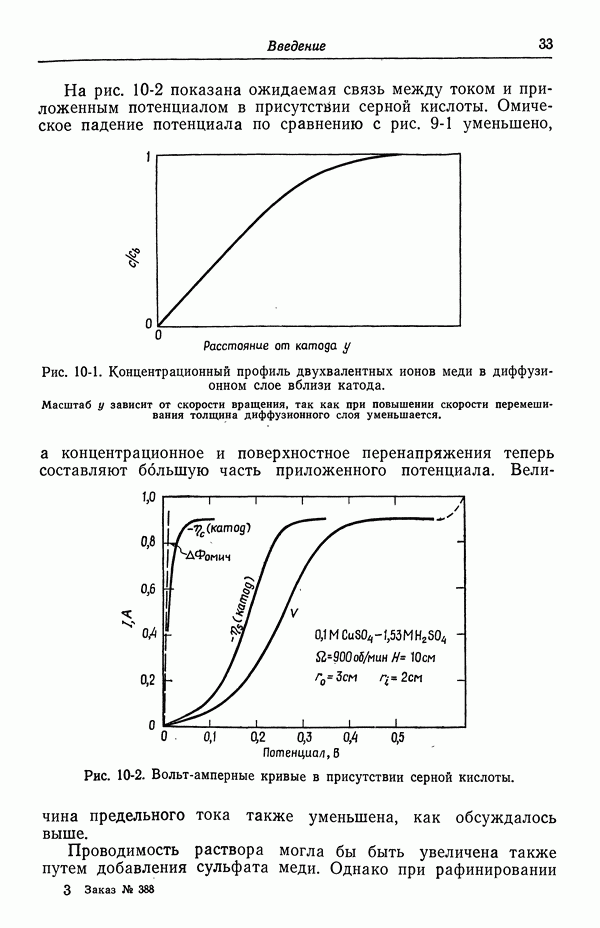
- 10. Фоновый электролит
- 11. Свободная конвекция
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
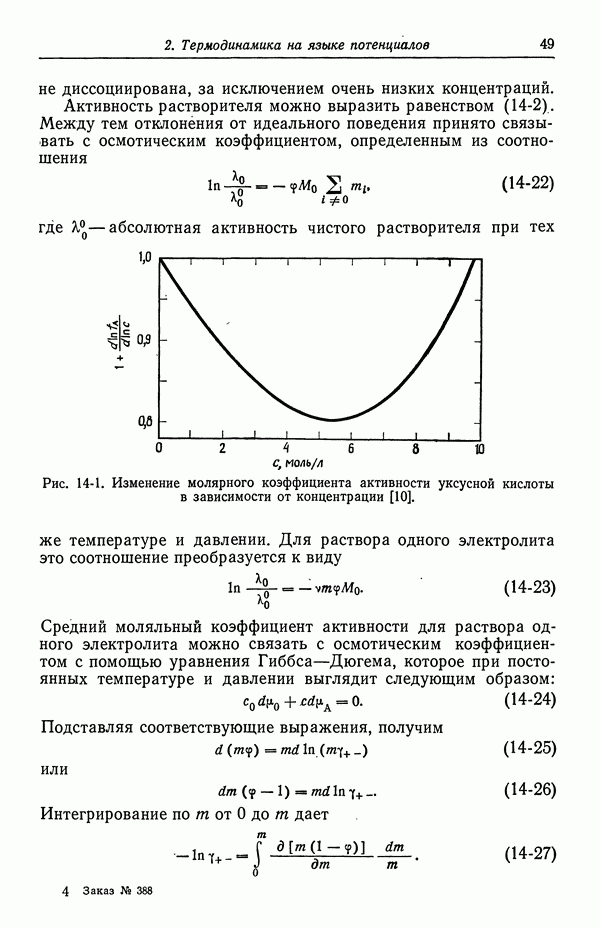
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
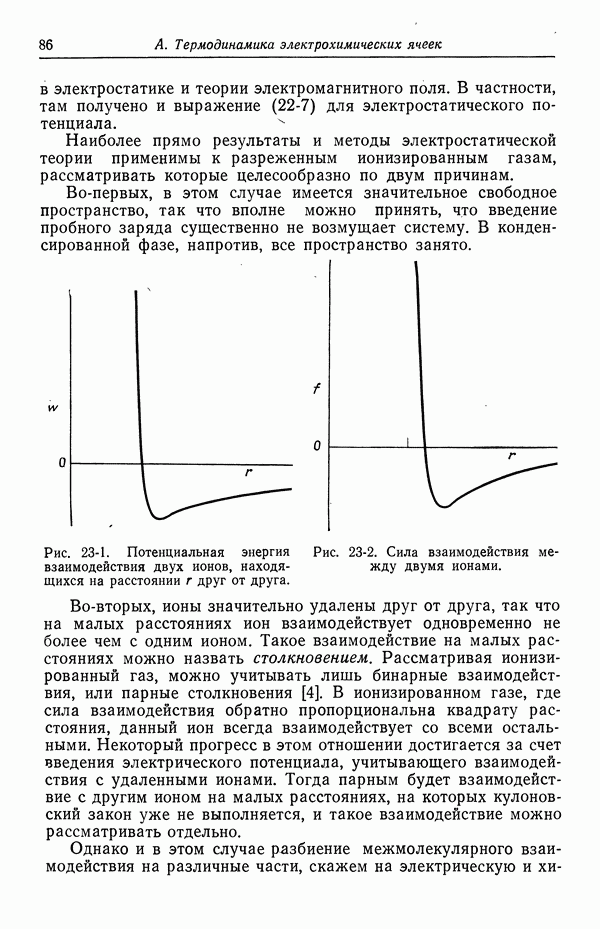
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
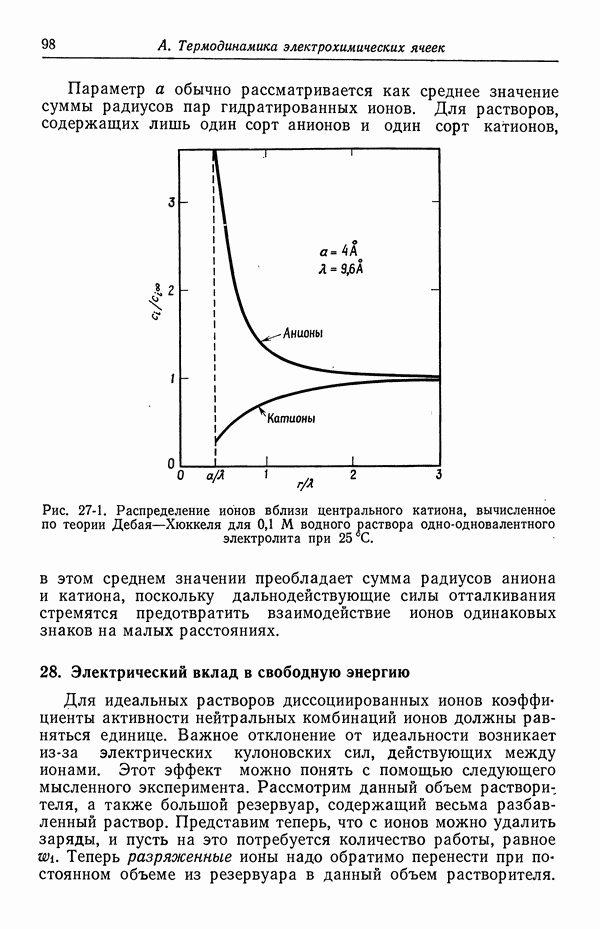
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая—Хюккеля
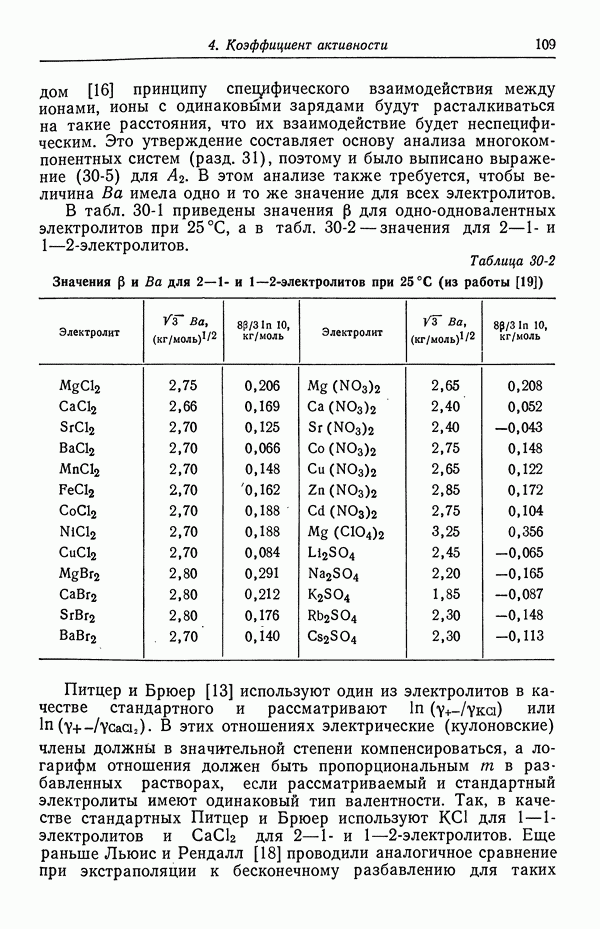
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
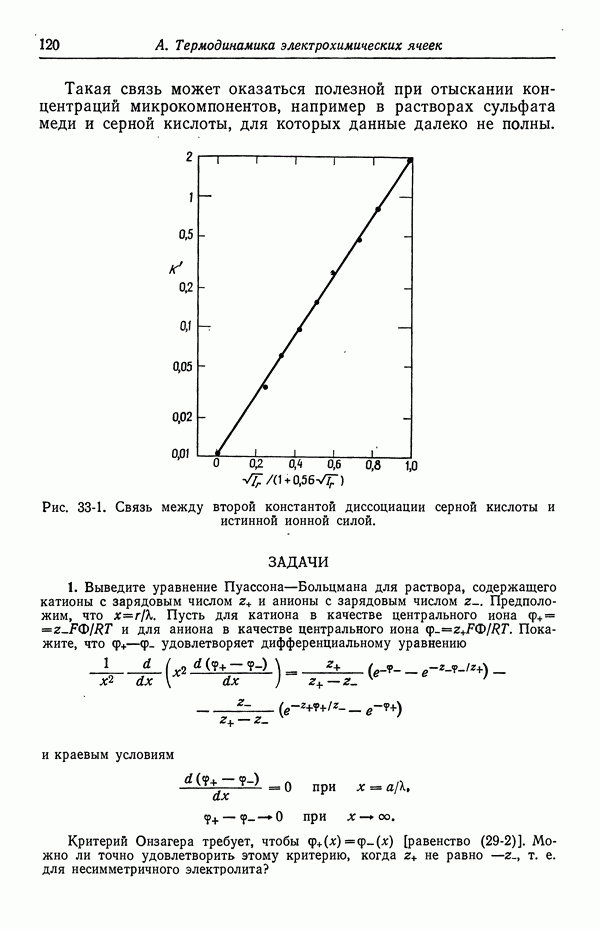
- 33. Слабые электролиты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
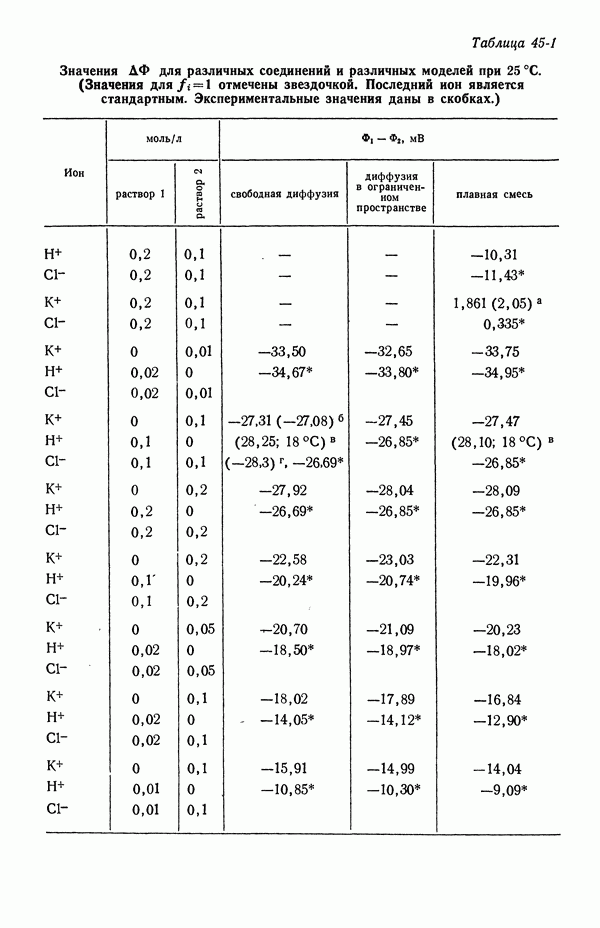
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 49. Качественное описание двойных слоев
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод — раствор
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 66. Динамика границы раздела
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- СПИСОК ОБОЗНАЧЕНИЙ
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 69. Законы переноса
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 78. Законы переноса
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 92. Интегральные коэффициенты диффузии
- ЗАДАЧА
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- СПИСОК ОБОЗНАЧЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 111. Свободная конвекция
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
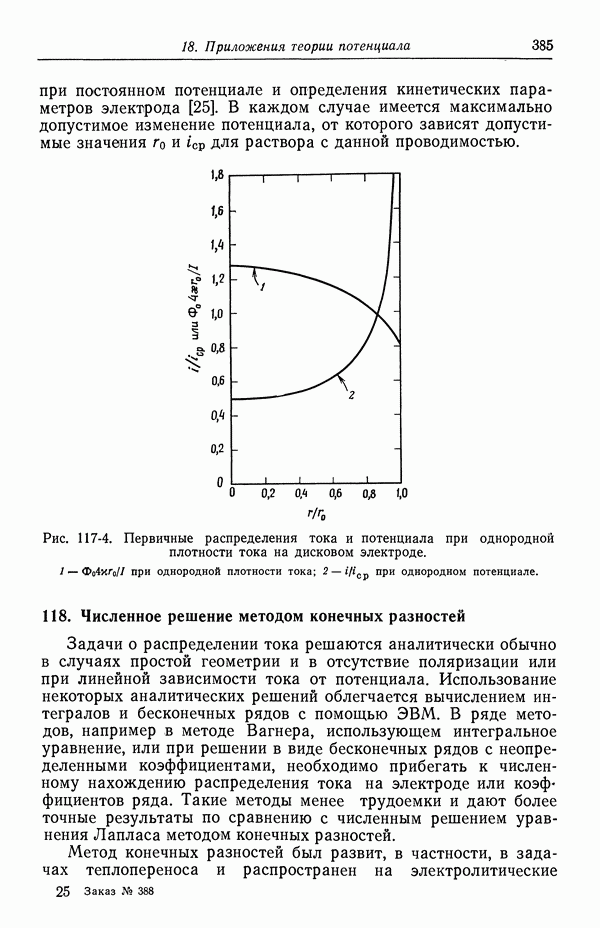
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- СПИСОК ОБОЗНАЧЕНИЙ
- ГЛАВА 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 119. Решение задачи
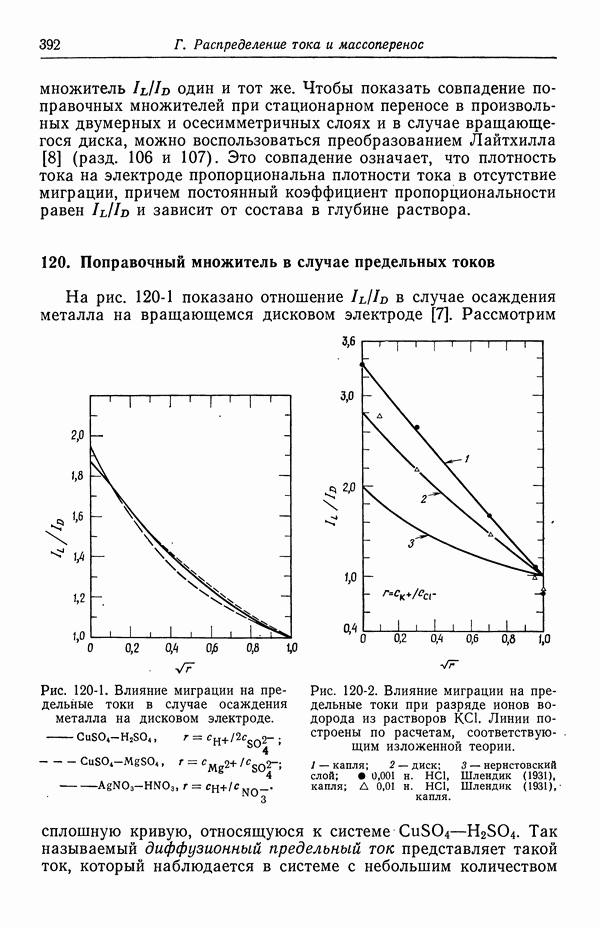
- 120. Поправочный множитель в случае предельных токов
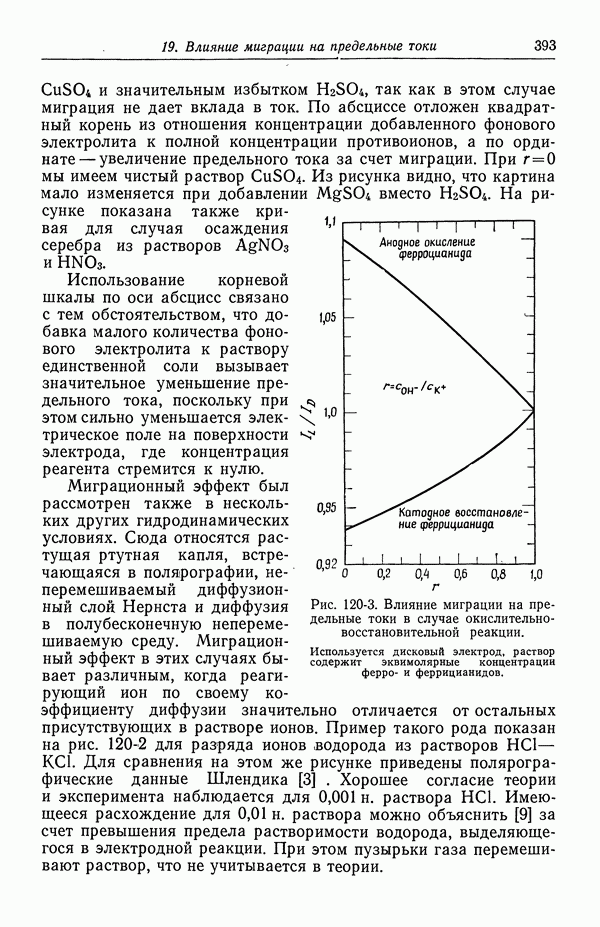
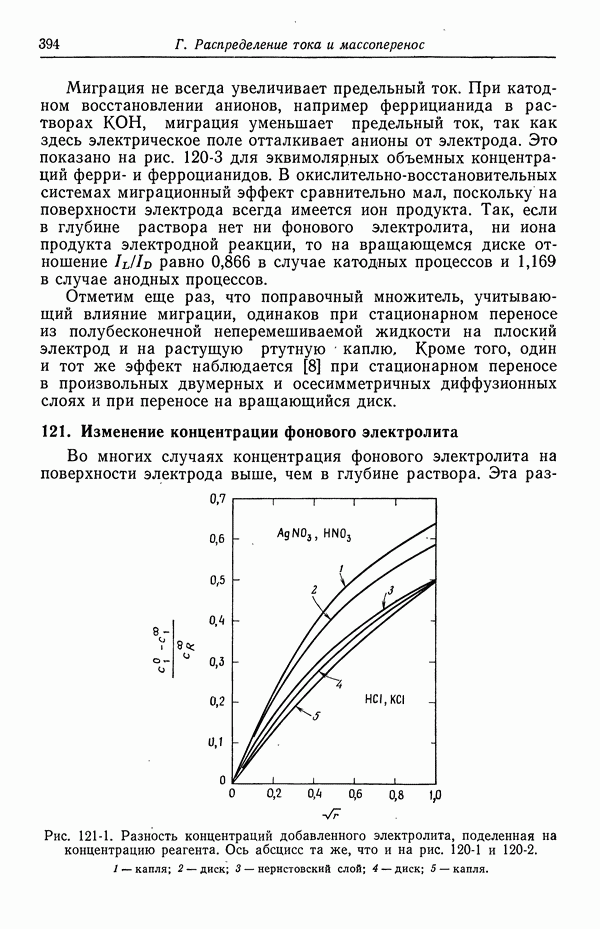
- 121. Изменение концентрации фонового электролита
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- ЗАДАЧИ
- СПИСОК ОБОЗНАЧЕНИЙ
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ