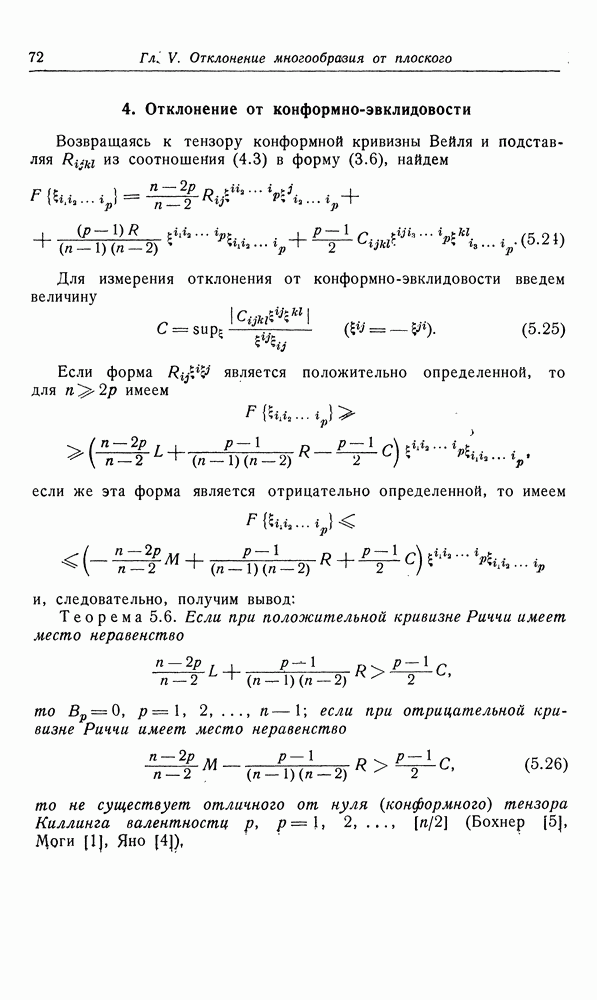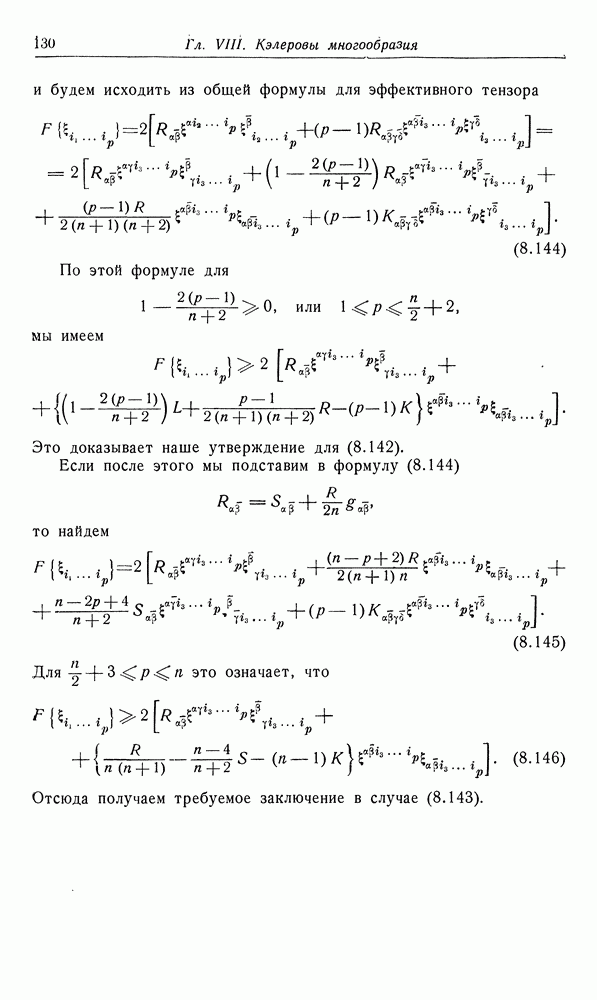| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
7. Теорема о гармоническом векторе и векторе Киллинга
Мы знаем, что если — гармонический вектор, то он удовлетворяет уравнениям

и

если  вектор Киллинга, то он удовлетворяет уравнениям
вектор Киллинга, то он удовлетворяет уравнениям

и

Если мы применим оператор А к скалярному произведению этих двух векторов, то получим

Но, с другой стороны,

поэтому

Применив теперь теорему 2.3, получим

откуда следует
Теорема 2.12. В компактном римановом многообразии  скалярное произведение гармонического вектора и вектора Киллинга есть постоянная величина (Бохнер [8]).
скалярное произведение гармонического вектора и вектора Киллинга есть постоянная величина (Бохнер [8]).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ИЗ ПРЕДИСЛОВИЯ К. ЯНО
- Глава I. РИМАНОВЫ МНОГООБРАЗИЯ
- 1. Римановы многообразия
- 2. Тензорная алгебра
- 3. Тензорный анализ
- 4. Тензоры кривизны
- 5. Кривизна в двумерном направлении
- 6. Параллельное перенесение
- Глава II. ГАРМОНИЧЕСКИЕ ВЕКТОРЫ И ВЕКТОРЫ КИЛЛИНГА
- 2. Теорема Грина
- 3. Некоторые приложения теоремы Хопфа — Бохнера
- 4. Гармонические векторы
- 5. Векторы Киллинга
- 6. Аффинные коллинеации
- 7. Теорема о гармоническом векторе и векторе Киллинга
- 8. Производные Ли
- 9. Производные Ли гармонических тензоров
- 10. Фундаментальная формула
- 11. Некоторые приложения фундаментальной формулы
- 12. Конформные преобразования
- 13. Необходимое и достаточное условие того, чтобы вектор был гармоническим
- 14. Необходимое и достаточное условие того, чтобы вектор был вектором Киллинга
- 15. Движение и аффинные коллинеации
- Глава III. ГАРМОНИЧЕСКИЕ ТЕНЗОРЫ И ТЕНЗОРЫ КИЛЛИНГА
- 1. Некоторые приложения теоремы Хопфа — Бохнера
- 2. Гармонические тензоры
- 3. Тензоры Киллинга
- 4. Фундаментальная формула
- 5. Некоторые приложения фундаментальных формул
- 6. Конформно-киллингов тензор
- 7. Необходимое и достаточное условие того, чтобы антисимметричный тензор был гармоническим или киллинговым
- Глава IV. ГАРМОНИЧЕСКИЕ ТЕНЗОРЫ И ТЕНЗОРЫ КИЛЛИНГА НА ПЛОСКИХ МНОГООБРАЗИЯХ
- 1. Гармонические тензоры и тензоры Киллинга на многообразии постоянной кривизны
- 2. Гармонические тензоры и тензоры Киллинга на конформно-эвклидовом многообразии
- Глава V. ОТКЛОНЕНИЕ МНОГООБРАЗИЯ ОТ ПЛОСКОГО
- 1. Отклонение от постоянства кривизны
- 2. Отклонение от проективно-эвклидовости
- 3. Отклонение от конциркулярно-эвклидовости
- 4. Отклонение от конформно-эвклидовости
- Глава VI. ПРОСТРАНСТВА ПОЛУПРОСТЫХ ГРУПП
- 1. Пространства полупростых групп
- 2. Теорема о кривизне пространства полупростой группы
- 3. Гармонические тензоры в пространстве полупростой группы
- 4. Отклонение группового пространства от плоского
- Глава VII. ПСЕВДОГАРМОНИЧЕСКИЕ И ПСЕВДОКИЛЛИНГОВЫ ТЕНЗОРЫ В МЕТРИЧЕСКИХ МНОГООБРАЗИЯХ С КРУЧЕНИЕМ
- 1. Метрические многообразия с кручением
- 2. Теорема Хопфа — Бохнера и ее приложения
- 3. Псевдогармонические векторы и тензоры
- 4. Псевдокиллинговы векторы и тензоры
- 5. Интегральные формулы
- 6. Необходимые и достаточные условия того, что тензор является псевдогармоническим или псевдокиллинговым
- 7. Обобщение
- Глава VIII. КЭЛЕРОВЫ МНОГООБРАЗИЯ
- 1. Кэлеровы многообразия
- 2. Кривизна в кэлеровом многообразии
- 3. Ковариантные и контравариантные аналитические векторные поля
- 4. Комплексные аналитические многообразия, допускающие транзитивную коммутативную группу преобразований
- 5. Самоприсоединенные векторы, удовлетворяющие соотношениям …
- 6. Аналитические тензоры
- 7. Гармонические векторные поля
- 8. Гармонические тензорные поля
- 9. Поля векторов Киллинга
- 10. Поля тензоров Киллинга
- 11. Тензор hij
- 12. Эффективные гармонические тензоры в плоских многообразиях
- 13. Уклонение многообразия от плоского
- Глава IX. ДОПОЛНЕНИЯ (С. БОХНЕР)
- 1. Симметрические многообразия
- 2. Выпуклость
- 3. Минимальные многообразия
- 4. Комплексное погружение
- 5. Многообразия с достаточным числом векторных или тензорных полей
- 6. Характеристика Эйлера — Пуанкаре
- 7. Некомпактные многообразия и нулевые граничные значения
- 8. Почти автоморфные векторные и тензорные поля