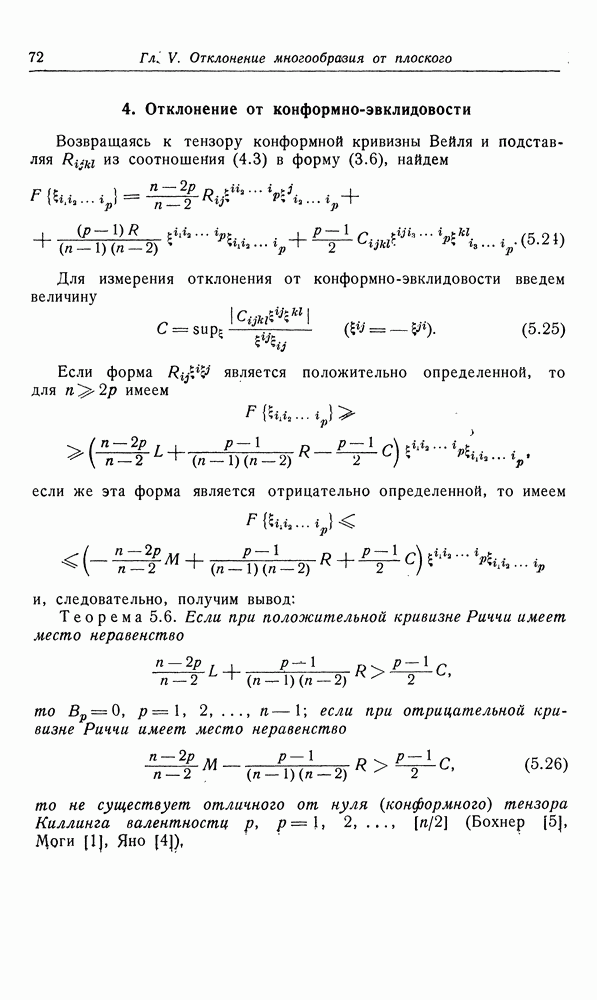| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4. Тензоры кривизны
Для скаляра  ковариантная производная определяется равенствами
ковариантная производная определяется равенствами

Вторая ковариантная производная будет равна

Таким образом, мы видим, что

Однако для векторов и тензоров последовательные ковариантные дифференцирования в общем случае не являются перестановочными. Так, например, для контравариантного вектора  мы получим
мы получим

где величины

являются компонентами смешанного тензора, называемого тензором кривизны Римана-Кристоффеля. Этот тензор, вообще говоря, отличен от нуля.
Аналогичный результат мы получим для ковариантного вектора 

а также для произвольного тензора. Например, для тензора  будем иметь
будем иметь

Формулы (1.43), (1.45) и (1.46) называются формулами Риччи. Из тензора кривизны  свертыванием получим новый тензор
свертыванием получим новый тензор

Умножив этот тензор  на фундаментальный тензор
на фундаментальный тензор  и произведя свертывание, получим скаляр
и произведя свертывание, получим скаляр

Тензор  и скаляр
и скаляр  называются соответственно "тензором Риччи" и "скалярной кривизной".
называются соответственно "тензором Риччи" и "скалярной кривизной".
Из определения (1.44) тензора кривизны легко обнаружить, что компоненты удовлетворяют следующим алгебраическим тождествам:

Следовательно, если положим

то компоненты  будут удовлетворять соотношениям
будут удовлетворять соотношениям

Уравнения (1.50) и (1.53) называются тождествами Бианки первого рода.
Применив формулу Риччи к  получим
получим

откуда

Вычисляя ковариантные компоненты  находим
находим

откуда видно, что

Из тождества (1.50), свертывая по  и применяя (1.49) и (1.54), получим
и применяя (1.49) и (1.54), получим

и уравнения (1.57) показывают, что тензор Риччи  является симметричным тензором. Нужно заметить, что
является симметричным тензором. Нужно заметить, что

т. е.

Для ковариантной производной тензора кривизны  можно вывести соотношение
можно вывести соотношение

которое называется тождеством Бианки второго рода. Из этого тождества свертыванием по  находим
находим

умножив это тождество на  и свернув, получим
и свернув, получим

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ИЗ ПРЕДИСЛОВИЯ К. ЯНО
- Глава I. РИМАНОВЫ МНОГООБРАЗИЯ
- 1. Римановы многообразия
- 2. Тензорная алгебра
- 3. Тензорный анализ
- 4. Тензоры кривизны
- 5. Кривизна в двумерном направлении
- 6. Параллельное перенесение
- Глава II. ГАРМОНИЧЕСКИЕ ВЕКТОРЫ И ВЕКТОРЫ КИЛЛИНГА
- 2. Теорема Грина
- 3. Некоторые приложения теоремы Хопфа — Бохнера
- 4. Гармонические векторы
- 5. Векторы Киллинга
- 6. Аффинные коллинеации
- 7. Теорема о гармоническом векторе и векторе Киллинга
- 8. Производные Ли
- 9. Производные Ли гармонических тензоров
- 10. Фундаментальная формула
- 11. Некоторые приложения фундаментальной формулы
- 12. Конформные преобразования
- 13. Необходимое и достаточное условие того, чтобы вектор был гармоническим
- 14. Необходимое и достаточное условие того, чтобы вектор был вектором Киллинга
- 15. Движение и аффинные коллинеации
- Глава III. ГАРМОНИЧЕСКИЕ ТЕНЗОРЫ И ТЕНЗОРЫ КИЛЛИНГА
- 1. Некоторые приложения теоремы Хопфа — Бохнера
- 2. Гармонические тензоры
- 3. Тензоры Киллинга
- 4. Фундаментальная формула
- 5. Некоторые приложения фундаментальных формул
- 6. Конформно-киллингов тензор
- 7. Необходимое и достаточное условие того, чтобы антисимметричный тензор был гармоническим или киллинговым
- Глава IV. ГАРМОНИЧЕСКИЕ ТЕНЗОРЫ И ТЕНЗОРЫ КИЛЛИНГА НА ПЛОСКИХ МНОГООБРАЗИЯХ
- 1. Гармонические тензоры и тензоры Киллинга на многообразии постоянной кривизны
- 2. Гармонические тензоры и тензоры Киллинга на конформно-эвклидовом многообразии
- Глава V. ОТКЛОНЕНИЕ МНОГООБРАЗИЯ ОТ ПЛОСКОГО
- 1. Отклонение от постоянства кривизны
- 2. Отклонение от проективно-эвклидовости
- 3. Отклонение от конциркулярно-эвклидовости
- 4. Отклонение от конформно-эвклидовости
- Глава VI. ПРОСТРАНСТВА ПОЛУПРОСТЫХ ГРУПП
- 1. Пространства полупростых групп
- 2. Теорема о кривизне пространства полупростой группы
- 3. Гармонические тензоры в пространстве полупростой группы
- 4. Отклонение группового пространства от плоского
- Глава VII. ПСЕВДОГАРМОНИЧЕСКИЕ И ПСЕВДОКИЛЛИНГОВЫ ТЕНЗОРЫ В МЕТРИЧЕСКИХ МНОГООБРАЗИЯХ С КРУЧЕНИЕМ
- 1. Метрические многообразия с кручением
- 2. Теорема Хопфа — Бохнера и ее приложения
- 3. Псевдогармонические векторы и тензоры
- 4. Псевдокиллинговы векторы и тензоры
- 5. Интегральные формулы
- 6. Необходимые и достаточные условия того, что тензор является псевдогармоническим или псевдокиллинговым
- 7. Обобщение
- Глава VIII. КЭЛЕРОВЫ МНОГООБРАЗИЯ
- 1. Кэлеровы многообразия
- 2. Кривизна в кэлеровом многообразии
- 3. Ковариантные и контравариантные аналитические векторные поля
- 4. Комплексные аналитические многообразия, допускающие транзитивную коммутативную группу преобразований
- 5. Самоприсоединенные векторы, удовлетворяющие соотношениям …
- 6. Аналитические тензоры
- 7. Гармонические векторные поля
- 8. Гармонические тензорные поля
- 9. Поля векторов Киллинга
- 10. Поля тензоров Киллинга
- 11. Тензор hij
- 12. Эффективные гармонические тензоры в плоских многообразиях
- 13. Уклонение многообразия от плоского
- Глава IX. ДОПОЛНЕНИЯ (С. БОХНЕР)
- 1. Симметрические многообразия
- 2. Выпуклость
- 3. Минимальные многообразия
- 4. Комплексное погружение
- 5. Многообразия с достаточным числом векторных или тензорных полей
- 6. Характеристика Эйлера — Пуанкаре
- 7. Некомпактные многообразия и нулевые граничные значения
- 8. Почти автоморфные векторные и тензорные поля