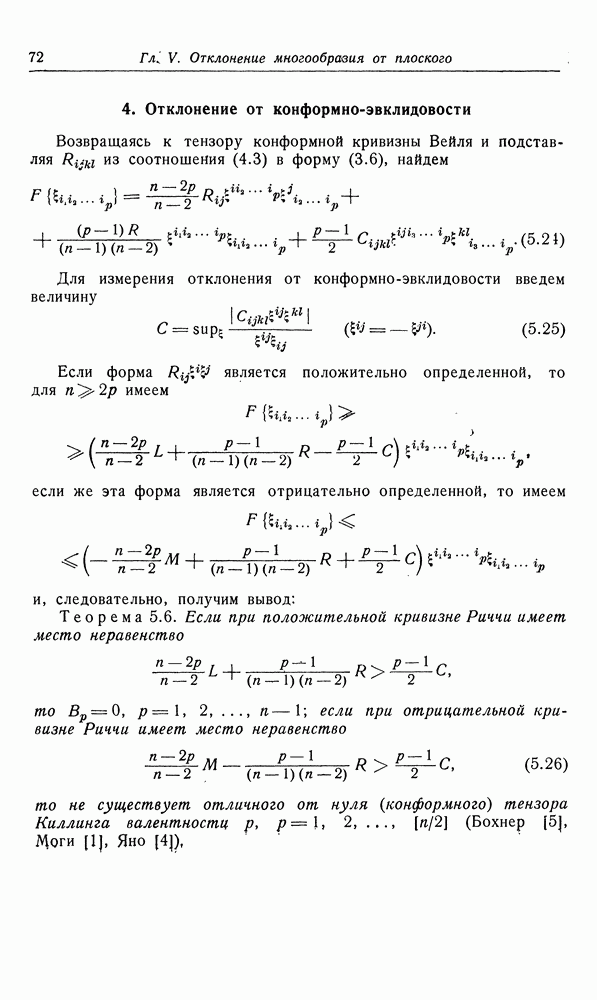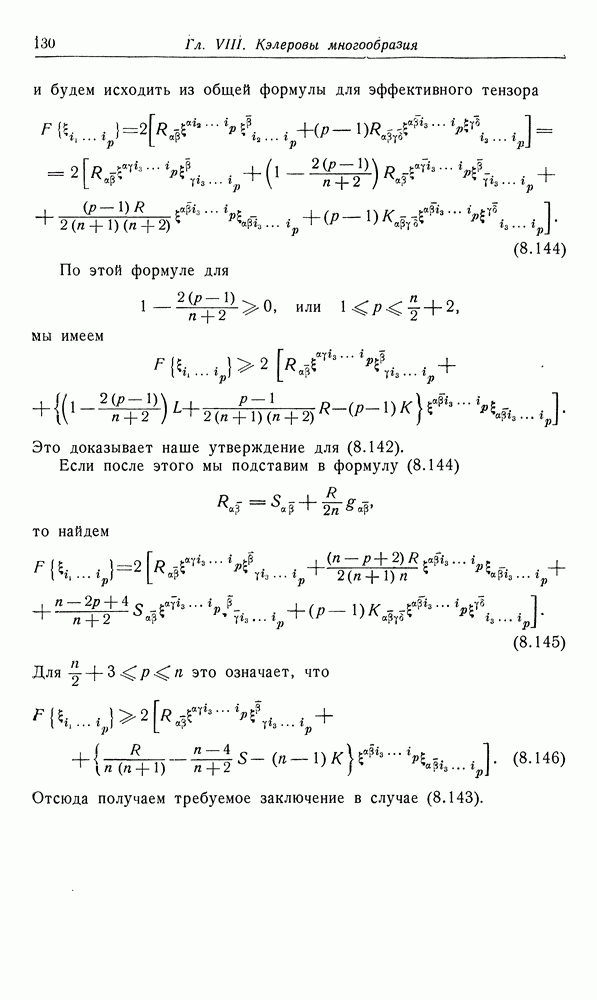| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2. Теорема Грина
Так как дивергенция контравариантного вектора может быть записана в виде

то в компактном ориентируемом римановом многообразии имеет место теорема Грина (см. Бохнер 
Теорема 2.4. В компактном ориентируемом римановом многообразии  для произвольного векторного поля
для произвольного векторного поля  выполняется равенство
выполняется равенство

Чтобы доказать это, заметим сначала, что если ограниченное множество  содержится в координатной окрестности, то
содержится в координатной окрестности, то

Предположим теперь, что  "параллелепипед"
"параллелепипед"  и что вектор X обращается в нуль на границе а. Тогда
и что вектор X обращается в нуль на границе а. Тогда

и, следовательно,

Но так как интеграл от  равен нулю на всяком открытом множестве, на котором вектор X обращается в нуль, то равенство (2.12) показывает, что равенство (2.11) верно, если вектор
равен нулю на всяком открытом множестве, на котором вектор X обращается в нуль, то равенство (2.12) показывает, что равенство (2.11) верно, если вектор  обращается в нуль вне некоторого "параллелепипеда" а.
обращается в нуль вне некоторого "параллелепипеда" а.
Далее, так как многообразие  компактно, то его можно покрыть конечным числом окрестностей
компактно, то его можно покрыть конечным числом окрестностей  замыкания которых будут содержаться в "параллелепипедах"
замыкания которых будут содержаться в "параллелепипедах"  соответственно. Для каждого
соответственно. Для каждого  выберем окрестность
выберем окрестность  промежуточную между
промежуточную между  и неотрицательную скалярную функцию
и неотрицательную скалярную функцию  класса
класса  такую, что
такую, что  вне
вне  Дополняя функцию
Дополняя функцию  нулевыми значениями вне
нулевыми значениями вне  получим всюду на
получим всюду на 

Таким образом, если мы положим

то функция принадлежит классу  причем равна нулю вне параллелепипеда"
причем равна нулю вне параллелепипеда"  и
и

Следовательно, если мы положим

то контравариантное векторное поле  обращается в нуль вне "параллелепипеда"
обращается в нуль вне "параллелепипеда"  . Поэтому мы имеем
. Поэтому мы имеем

Но, с другой стороны,

и, следовательно,

Интегрируя это равенство по всему многообразию, получим

что и доказывает теорему 2.4.
Так как лапласиан  скалярного поля
скалярного поля  может быть записан в виде
может быть записан в виде

то теорема 2.4 приводит к следующей теореме:
Теорема  компактном ориентируемом римановом многообразии
компактном ориентируемом римановом многообразии  для всякого скалярного поля
для всякого скалярного поля  имеет место равенство
имеет место равенство

Если мы применим оператор А к функции  то получим
то получим

следовательно, применение теоремы 2.5 к скалярному полю  дает
дает

Если  всюду в
всюду в  то, как видно из (2.13), мы должны иметь
то, как видно из (2.13), мы должны иметь  всюду в
всюду в  Следовательно, как видно из (2.14), должно выполняться равенство
Следовательно, как видно из (2.14), должно выполняться равенство  т. е.
т. е.  значит,
значит,  Это дает другое доказательство теоремы 2.3 в случае ориентируемого многообразия.
Это дает другое доказательство теоремы 2.3 в случае ориентируемого многообразия.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ИЗ ПРЕДИСЛОВИЯ К. ЯНО
- Глава I. РИМАНОВЫ МНОГООБРАЗИЯ
- 1. Римановы многообразия
- 2. Тензорная алгебра
- 3. Тензорный анализ
- 4. Тензоры кривизны
- 5. Кривизна в двумерном направлении
- 6. Параллельное перенесение
- Глава II. ГАРМОНИЧЕСКИЕ ВЕКТОРЫ И ВЕКТОРЫ КИЛЛИНГА
- 2. Теорема Грина
- 3. Некоторые приложения теоремы Хопфа — Бохнера
- 4. Гармонические векторы
- 5. Векторы Киллинга
- 6. Аффинные коллинеации
- 7. Теорема о гармоническом векторе и векторе Киллинга
- 8. Производные Ли
- 9. Производные Ли гармонических тензоров
- 10. Фундаментальная формула
- 11. Некоторые приложения фундаментальной формулы
- 12. Конформные преобразования
- 13. Необходимое и достаточное условие того, чтобы вектор был гармоническим
- 14. Необходимое и достаточное условие того, чтобы вектор был вектором Киллинга
- 15. Движение и аффинные коллинеации
- Глава III. ГАРМОНИЧЕСКИЕ ТЕНЗОРЫ И ТЕНЗОРЫ КИЛЛИНГА
- 1. Некоторые приложения теоремы Хопфа — Бохнера
- 2. Гармонические тензоры
- 3. Тензоры Киллинга
- 4. Фундаментальная формула
- 5. Некоторые приложения фундаментальных формул
- 6. Конформно-киллингов тензор
- 7. Необходимое и достаточное условие того, чтобы антисимметричный тензор был гармоническим или киллинговым
- Глава IV. ГАРМОНИЧЕСКИЕ ТЕНЗОРЫ И ТЕНЗОРЫ КИЛЛИНГА НА ПЛОСКИХ МНОГООБРАЗИЯХ
- 1. Гармонические тензоры и тензоры Киллинга на многообразии постоянной кривизны
- 2. Гармонические тензоры и тензоры Киллинга на конформно-эвклидовом многообразии
- Глава V. ОТКЛОНЕНИЕ МНОГООБРАЗИЯ ОТ ПЛОСКОГО
- 1. Отклонение от постоянства кривизны
- 2. Отклонение от проективно-эвклидовости
- 3. Отклонение от конциркулярно-эвклидовости
- 4. Отклонение от конформно-эвклидовости
- Глава VI. ПРОСТРАНСТВА ПОЛУПРОСТЫХ ГРУПП
- 1. Пространства полупростых групп
- 2. Теорема о кривизне пространства полупростой группы
- 3. Гармонические тензоры в пространстве полупростой группы
- 4. Отклонение группового пространства от плоского
- Глава VII. ПСЕВДОГАРМОНИЧЕСКИЕ И ПСЕВДОКИЛЛИНГОВЫ ТЕНЗОРЫ В МЕТРИЧЕСКИХ МНОГООБРАЗИЯХ С КРУЧЕНИЕМ
- 1. Метрические многообразия с кручением
- 2. Теорема Хопфа — Бохнера и ее приложения
- 3. Псевдогармонические векторы и тензоры
- 4. Псевдокиллинговы векторы и тензоры
- 5. Интегральные формулы
- 6. Необходимые и достаточные условия того, что тензор является псевдогармоническим или псевдокиллинговым
- 7. Обобщение
- Глава VIII. КЭЛЕРОВЫ МНОГООБРАЗИЯ
- 1. Кэлеровы многообразия
- 2. Кривизна в кэлеровом многообразии
- 3. Ковариантные и контравариантные аналитические векторные поля
- 4. Комплексные аналитические многообразия, допускающие транзитивную коммутативную группу преобразований
- 5. Самоприсоединенные векторы, удовлетворяющие соотношениям …
- 6. Аналитические тензоры
- 7. Гармонические векторные поля
- 8. Гармонические тензорные поля
- 9. Поля векторов Киллинга
- 10. Поля тензоров Киллинга
- 11. Тензор hij
- 12. Эффективные гармонические тензоры в плоских многообразиях
- 13. Уклонение многообразия от плоского
- Глава IX. ДОПОЛНЕНИЯ (С. БОХНЕР)
- 1. Симметрические многообразия
- 2. Выпуклость
- 3. Минимальные многообразия
- 4. Комплексное погружение
- 5. Многообразия с достаточным числом векторных или тензорных полей
- 6. Характеристика Эйлера — Пуанкаре
- 7. Некомпактные многообразия и нулевые граничные значения
- 8. Почти автоморфные векторные и тензорные поля