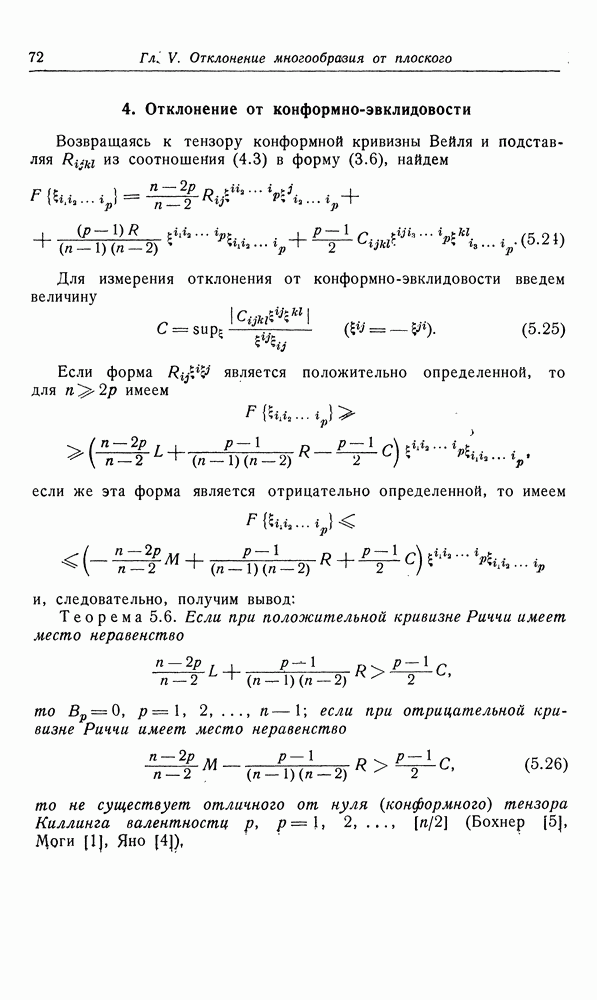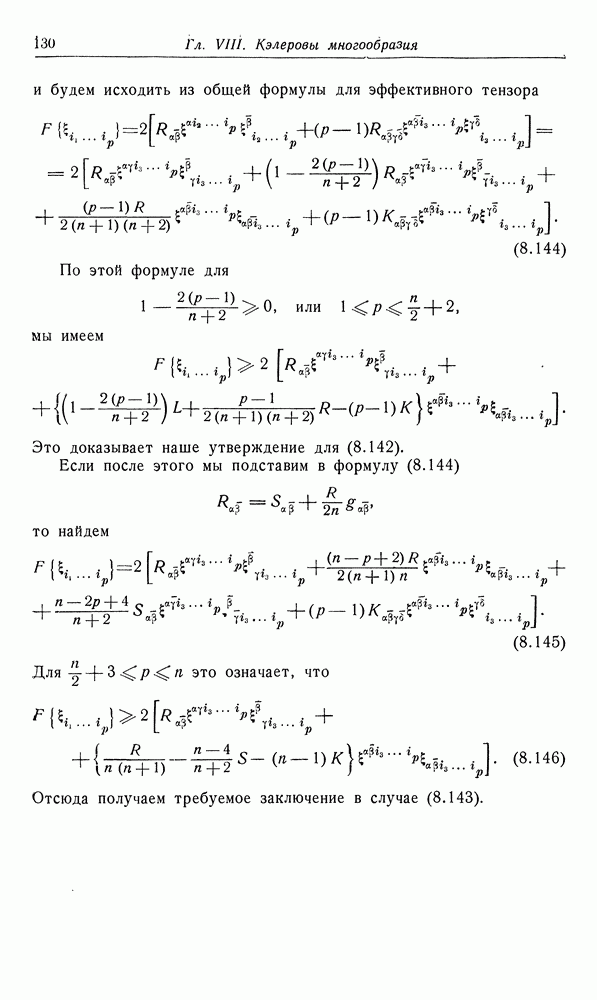| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Тензорная алгебра
Если в некоторой системе координат (я задана форма (1.3) и если в другой системе координат соответственно положим

то мы должны иметь

Вообще если некоторый объект представлен величиной  в системе координат (я и величиной
в системе координат (я и величиной  в какой-либо другой системе координат
в какой-либо другой системе координат  и если
и если

то мы называем этот объект скаляром, а  его компонентами в соответствующих системах координат
его компонентами в соответствующих системах координат  и Таким образом, ds есть компонента скаляра.
и Таким образом, ds есть компонента скаляра. 
Из (1.2) имеем

Вообще если некоторый объект представлен  величинами
величинами  в системе координат
в системе координат  величинами
величинами  в какой-либо другой системе координат
в какой-либо другой системе координат  и если
и если

то мы называем этот объект контравариантным вектором,  его компонентами в соответствующих системах координат
его компонентами в соответствующих системах координат  Таким образом, величины
Таким образом, величины  являются компонентами контравариантного вектора в системе координат
являются компонентами контравариантного вектора в системе координат 
Если некоторый объект определен в каждой точке координатной окрестности  то его компоненты являются функциями от
то его компоненты являются функциями от  Мы говорим, что в таком случае имеется поле объекта. Если мы обозначим через
Мы говорим, что в таком случае имеется поле объекта. Если мы обозначим через  компоненты скалярного поля в соответствующих системах координат
компоненты скалярного поля в соответствующих системах координат  то будем иметь
то будем иметь

откуда, беря частные производные, получим

Вообще если некоторый объект представлен  величинами
величинами  в системе координат
в системе координат  и величинами
и величинами  в какой-либо другой системе координат
в какой-либо другой системе координат  и если
и если

то мы называем этот объект ковариантным вектором,  его компонентами в соответствующих системах координат
его компонентами в соответствующих системах координат  Если
Если  есть компонента скалярного поля, то производные являются компонентами ковариантного вектора. Мы называем такого рода специальный ковариантный вектор градиентом скалярного поля
есть компонента скалярного поля, то производные являются компонентами ковариантного вектора. Мы называем такого рода специальный ковариантный вектор градиентом скалярного поля 
Из условия  имеем
имеем

Вообще если некоторый объект представлен  величинами
величинами

в системе координат 

в какой-либо другой системе координат  и если
и если

то мы называем этот объект смешанным тензором контравариантной валентности  и ковариантной валентности
и ковариантной валентности  а
а

и

— его компонентами в соответствующих системах координат 
Тензор, имеющий только контравариантную валентность, называется контравариантным тензором, а тензор, имеющий только кова-риантную валентность, называется ковариантным тензором. Таким образом,  являются компонентами ковариантного тензорного поля.
являются компонентами ковариантного тензорного поля.
Так как мы предположили, что форма (1.3) положительно определена, то

и, следовательно, мы можем определить величины

Таким образом, имеем

где величины являются известными символами Кронекера.
Легко видеть, что  являются компонентами контравариантного тензора, а суть компоненты смешанного тензора. Мы называем
являются компонентами контравариантного тензора, а суть компоненты смешанного тензора. Мы называем  и соответственно ковариантным, контравариантным и смешанным фундаментальными тензорами.
и соответственно ковариантным, контравариантным и смешанным фундаментальными тензорами.
Если, например, компоненты некоторого тензора удовлетворяют условию

то говорят, что они симметричны относительно  если выполняется условие
если выполняется условие

то говорят, что они антисимметричны относительно 
Легко доказать, что если компоненты тензора симметричны или антисимметричны в какой-либо системе координат, то они являются таковыми же и в любой другой системе координат. Если компоненты контравариантного или ковариантного тензора симметричны (антисимметричны) относительно всех индексов, то мы называем тензор симметричным (антисимметричным) тензором. Так, оба тензора  и являются симметричными.
и являются симметричными.
Определим теперь некоторые алгебраические операции, которые могут быть применены "к тензорам.
I. Сложение и вычитание
Пусть, например,  являются компонентами двух однотипных тензоров, тогда суммы
являются компонентами двух однотипных тензоров, тогда суммы

являются компонентами тензора того же типа, и этот тензор называется суммой двух данных тензоров. Разность двух тензоров определяется аналогичным образом.
II. Умножение
Пусть, например,  являются компонентами двух тензоров каких-либо типов, тогда произведения
являются компонентами двух тензоров каких-либо типов, тогда произведения

являются также компонентами тензора, тип которого определяется положением индексов. Этот тензор называется произведением двух данных тензоров.
III. Свертывание
Пусть, например,  являются компонентами смешанного тензора, тогда величины
являются компонентами смешанного тензора, тогда величины

являются компонентами тензора, имеющего на два индекса меньше, чем исходный тензор. В этом случае мы говорим, что мы свернули тензор  по
по  и I и получили тензор
и I и получили тензор  Поднятие и опускание индексов
Поднятие и опускание индексов
Если  компоненты контравариантного вектора, то
компоненты контравариантного вектора, то  в силу II являются компонентами смешанного тензора и, следовательно,
в силу II являются компонентами смешанного тензора и, следовательно,  являются в силу III компонентами ковариантного вектора. Мы обозначаем его
являются в силу III компонентами ковариантного вектора. Мы обозначаем его  Аналогично, если
Аналогично, если  компоненты ковариантного вектора, то являются, согласно II, компонентами смешанного тензора и, следовательно,
компоненты ковариантного вектора, то являются, согласно II, компонентами смешанного тензора и, следовательно,  являются, согласно III, компонентами контравариантного вектора. Мы обозначаем его
являются, согласно III, компонентами контравариантного вектора. Мы обозначаем его  Очевидно, что если
Очевидно, что если

то

Мы скажем, что  сопряжены друг другу. Таким образом, мы вводим объект, который может быть представлен компонентами
сопряжены друг другу. Таким образом, мы вводим объект, который может быть представлен компонентами  или
или  по нашему выбору. Мы назовем его вектором, а
по нашему выбору. Мы назовем его вектором, а  и
и  -соответственно его контравариантными или ковариантными компонентами.
-соответственно его контравариантными или ковариантными компонентами.
То же самое можно высказать и для компонент некоторого тензора, что иллюстрируется следующими примерами:

Мы говорим, что в первом случае мы опустили индекс а во втором случае подняли индекс  и что при этом мы имеем дело с компонентами одного и того же тензора.
и что при этом мы имеем дело с компонентами одного и того же тензора.
V. Симметрирование и альтернирование
Рассмотрим, например, ковариантный тензор Тк. Образуем сумму всех компонент, полученных из  всевозможными перестановками индексов
всевозможными перестановками индексов  и разделим ее на 3! (число всевозможных перестановок). Обозначим результат через
и разделим ее на 3! (число всевозможных перестановок). Обозначим результат через

и назовем его симметричной частью 
Легко показать, что  являются компонентами симметричного ковариантного тензора; операция перехода от тензора к его симметричной части
являются компонентами симметричного ковариантного тензора; операция перехода от тензора к его симметричной части  называется симметрированием тензора
называется симметрированием тензора  Если исходный тензор симметричен, то имеем
Если исходный тензор симметричен, то имеем 
Рассмотрим снова, например, ковариантный тензор Тк и все компоненты, полученные из  всевозможными перестановками. Поставим теперь знак плюс перед компонентами, полученными из
всевозможными перестановками. Поставим теперь знак плюс перед компонентами, полученными из  четными перестановками индексов, и знак минус — перед компонентами, полученными из
четными перестановками индексов, и знак минус — перед компонентами, полученными из  нечетными перестановками, и образуем алгебраическую сумму этих компонент, деленную на
нечетными перестановками, и образуем алгебраическую сумму этих компонент, деленную на  Обозначим полученный объект
Обозначим полученный объект

и назовем его антисимметричной частью  Легко видеть, что
Легко видеть, что  являются компонентами антисимметричного ковариантного тензора; операция
являются компонентами антисимметричного ковариантного тензора; операция  называется альтернированием
называется альтернированием  Если исходный тензор антисимметричен, то
Если исходный тензор антисимметричен, то 
Можно считать, что формула (1.3) определяет длину  контравариантного вектора
контравариантного вектора  Определим аналогично длину X контравариантного вектора
Определим аналогично длину X контравариантного вектора

Если мы обозначим ковариантные компоненты этого вектора через то написанная выше формула может быть переписана в следующих различных видах:

Вектор, длина которого равна единице, называется единичным вектором. Если и (а — единичные векторы, то:

Отсюда можно доказать, что

Учитывая это, можно определить угол  между двумя единичными векторами
между двумя единичными векторами  и при помощи формулы
и при помощи формулы

а угол  между двумя произвольными векторами
между двумя произвольными векторами  при помощи формулы
при помощи формулы

Уравнение (1.14) дает

Это выражение называется скалярным произведением векторов 
Из формулы (1.14) следует, что два вектора  ортогональны друг другу, если
ортогональны друг другу, если

Далее из закона преобразования 

находим

а с другой стороны, закон преобразования  в
в  -кратном интеграле дает
-кратном интеграле дает

Следовательно, из этих двух уравнений получаем

откуда видно, что

есть скаляр. Мы принимаем  за элементарный объем нашего риманова многообразия.
за элементарный объем нашего риманова многообразия.
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ К. ЯНО
- Глава I. РИМАНОВЫ МНОГООБРАЗИЯ
- 1. Римановы многообразия
- 2. Тензорная алгебра
- 3. Тензорный анализ
- 4. Тензоры кривизны
- 5. Кривизна в двумерном направлении
- 6. Параллельное перенесение
- Глава II. ГАРМОНИЧЕСКИЕ ВЕКТОРЫ И ВЕКТОРЫ КИЛЛИНГА
- 2. Теорема Грина
- 3. Некоторые приложения теоремы Хопфа — Бохнера
- 4. Гармонические векторы
- 5. Векторы Киллинга
- 6. Аффинные коллинеации
- 7. Теорема о гармоническом векторе и векторе Киллинга
- 8. Производные Ли
- 9. Производные Ли гармонических тензоров
- 10. Фундаментальная формула
- 11. Некоторые приложения фундаментальной формулы
- 12. Конформные преобразования
- 13. Необходимое и достаточное условие того, чтобы вектор был гармоническим
- 14. Необходимое и достаточное условие того, чтобы вектор был вектором Киллинга
- 15. Движение и аффинные коллинеации
- Глава III. ГАРМОНИЧЕСКИЕ ТЕНЗОРЫ И ТЕНЗОРЫ КИЛЛИНГА
- 1. Некоторые приложения теоремы Хопфа — Бохнера
- 2. Гармонические тензоры
- 3. Тензоры Киллинга
- 4. Фундаментальная формула
- 5. Некоторые приложения фундаментальных формул
- 6. Конформно-киллингов тензор
- 7. Необходимое и достаточное условие того, чтобы антисимметричный тензор был гармоническим или киллинговым
- Глава IV. ГАРМОНИЧЕСКИЕ ТЕНЗОРЫ И ТЕНЗОРЫ КИЛЛИНГА НА ПЛОСКИХ МНОГООБРАЗИЯХ
- 1. Гармонические тензоры и тензоры Киллинга на многообразии постоянной кривизны
- 2. Гармонические тензоры и тензоры Киллинга на конформно-эвклидовом многообразии
- Глава V. ОТКЛОНЕНИЕ МНОГООБРАЗИЯ ОТ ПЛОСКОГО
- 1. Отклонение от постоянства кривизны
- 2. Отклонение от проективно-эвклидовости
- 3. Отклонение от конциркулярно-эвклидовости
- 4. Отклонение от конформно-эвклидовости
- Глава VI. ПРОСТРАНСТВА ПОЛУПРОСТЫХ ГРУПП
- 1. Пространства полупростых групп
- 2. Теорема о кривизне пространства полупростой группы
- 3. Гармонические тензоры в пространстве полупростой группы
- 4. Отклонение группового пространства от плоского
- Глава VII. ПСЕВДОГАРМОНИЧЕСКИЕ И ПСЕВДОКИЛЛИНГОВЫ ТЕНЗОРЫ В МЕТРИЧЕСКИХ МНОГООБРАЗИЯХ С КРУЧЕНИЕМ
- 1. Метрические многообразия с кручением
- 2. Теорема Хопфа — Бохнера и ее приложения
- 3. Псевдогармонические векторы и тензоры
- 4. Псевдокиллинговы векторы и тензоры
- 5. Интегральные формулы
- 6. Необходимые и достаточные условия того, что тензор является псевдогармоническим или псевдокиллинговым
- 7. Обобщение
- Глава VIII. КЭЛЕРОВЫ МНОГООБРАЗИЯ
- 1. Кэлеровы многообразия
- 2. Кривизна в кэлеровом многообразии
- 3. Ковариантные и контравариантные аналитические векторные поля
- 4. Комплексные аналитические многообразия, допускающие транзитивную коммутативную группу преобразований
- 5. Самоприсоединенные векторы, удовлетворяющие соотношениям …
- 6. Аналитические тензоры
- 7. Гармонические векторные поля
- 8. Гармонические тензорные поля
- 9. Поля векторов Киллинга
- 10. Поля тензоров Киллинга
- 11. Тензор hij
- 12. Эффективные гармонические тензоры в плоских многообразиях
- 13. Уклонение многообразия от плоского
- Глава IX. ДОПОЛНЕНИЯ (С. БОХНЕР)
- 1. Симметрические многообразия
- 2. Выпуклость
- 3. Минимальные многообразия
- 4. Комплексное погружение
- 5. Многообразия с достаточным числом векторных или тензорных полей
- 6. Характеристика Эйлера — Пуанкаре
- 7. Некомпактные многообразия и нулевые граничные значения
- 8. Почти автоморфные векторные и тензорные поля