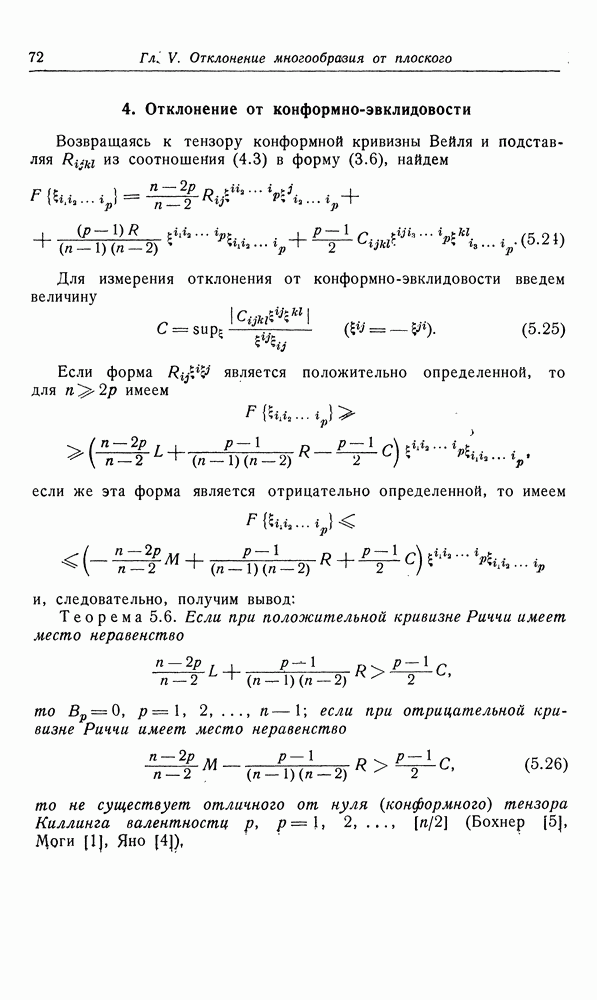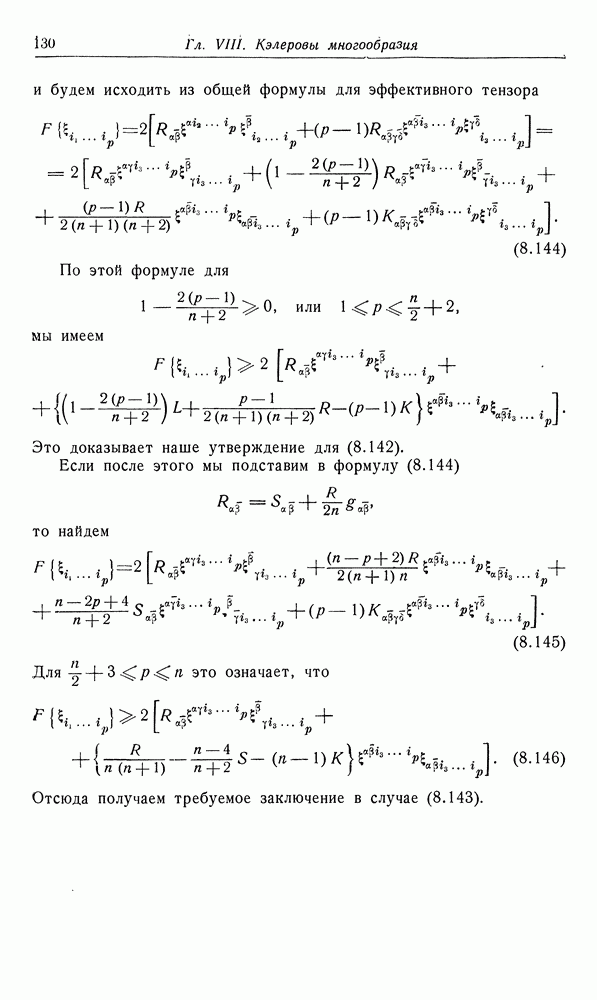| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. Кривизна в двумерном направлении
В двумерном римановом многообразии, фундаментальная квадратичная форма которого имеет вид

единственные ненулевые компоненты тензора Римана — Кристоффеля  будут
будут

Гауссова кривизна К этого многообразия определяется формулой

Рассмотрим теперь в точке  -мерного риманова многообразия два контравариантных вектора
-мерного риманова многообразия два контравариантных вектора  Эти два вектора определяют двумерную плоскость, проходящую через точку
Эти два вектора определяют двумерную плоскость, проходящую через точку  Рассмотрим далее все геодезические, которые проходят через эту точку и касаются двумерной плоскости, натянутой на векторы
Рассмотрим далее все геодезические, которые проходят через эту точку и касаются двумерной плоскости, натянутой на векторы  Эти геодезические образуют двумерную поверхность, которая проходит через точку
Эти геодезические образуют двумерную поверхность, которая проходит через точку  и касается двумерной плоскости, натянутой на векторы
и касается двумерной плоскости, натянутой на векторы 
В силу (1.62) гауссова кривизна К этой поверхности в точке  будет равна
будет равна

или

Эта величина называется кривизной в двумерном направлении, исхрч дящеад из точки  натянутом на векторы
натянутом на векторы 
Если в качестве векторов и мы выберем два единичных взаимно ортогональных вектора, то равенство (1.63) примет вид

Предположим теперь, что в фиксированной точке нашего риманова многообразия кривизна в двумерном направлении не зависит от этого направления. Тогда, как мы можем видеть из (1.63), тензор кривизны  должен иметь вид
должен иметь вид

а тензор 

Если в любой точке многообразия кривизна в двумерном направлении не зависит от направления, проходящего через эту точку, то уравнения (1.65) и (1.66) должны выполняться в каждой точке многообразия и кривизна К оказывается, таким образом, функцией точки.
Из (1.66), свертывая по  получаем
получаем

откуда, умножая на  и свертывая, находим
и свертывая, находим

Далее, уравнение (1.67) может быть переписано также в виде

если мы подставим это выражение в (1.61), то получим

откуда видно, что для 2 производная  следовательно,
следовательно,  и к являются абсолютными константами.
и к являются абсолютными константами.
Итак, если кривизна в двумерном направлении в каждой точке многообразия не зависит от двумерного направления, проходящего через точку, то эта кривизна является абсолютной константой во всем многообразии. Такое риманово многообразие называется многообразием постоянной кривизны.
Если эта постоянная равна нулю, то

В этом случае уравнения

получающиеся из (1.22) при  являются вполне интегрируемыми. Следовательно, существует система координат, в которой
являются вполне интегрируемыми. Следовательно, существует система координат, в которой  стало быть,
стало быть,  Таким образом, всякая координатная окрестность многообразия нулевой кривизны может быть изометрично отображена в некоторую область эвклидова пространства.
Таким образом, всякая координатная окрестность многообразия нулевой кривизны может быть изометрично отображена в некоторую область эвклидова пространства.
Наоборот, если всякая координатная окрестность многообразия может быть изометрично отображена в некоторую область эвклидова пространства, то, очевидно, будет иметь место условие (1.69).
Говорят, что такое риманово многообразие является локально эвклидовым или локально плоским.
Возвращаясь к общему риманову многообразию, рассмотрим в точке  этого многообразия
этого многообразия  контравариантных взаимно ортогональных единичных векторов
контравариантных взаимно ортогональных единичных векторов

Для этих векторов мы имеем

и, следовательно,

Кривизна в двумерном направлении, исходящем из этой точки и определенном двумерной плоскостью, натянутой на векторы будет равна

Следовательно,

или

и

Формула (1.71) показывает, что если мы возьмем единичный контравариантный вектор X и рассмотрим  кривизн в двумерных направлениях, определенных
кривизн в двумерных направлениях, определенных  двумерными плоскостями, натянутыми на вектор
двумерными плоскостями, натянутыми на вектор  и каждый из
и каждый из  единичных векторов, ортогональных к и друг к другу, то сумма этих
единичных векторов, ортогональных к и друг к другу, то сумма этих  кривизн будет равна и не зависит от выбора остальных
кривизн будет равна и не зависит от выбора остальных 
ортогональных единичных векторов. Величину  называют кривизной Риччи в направлении единичного вектора
называют кривизной Риччи в направлении единичного вектора 
Уравнение (1.72) показывает, что сумма  кривизн Риччи в направлении
кривизн Риччи в направлении  взаимно ортогональных единичных векторов равна
взаимно ортогональных единичных векторов равна  и не зависит от выбора этих векторов.
и не зависит от выбора этих векторов.
Рассмотрим далее кривизну Риччи  в направлении некоторого контравариантного вектора
в направлении некоторого контравариантного вектора 

Направление, дающее экстремум величины  определится равенствами
определится равенствами

вообще говоря, существуют  таких взаимно ортогональных направлений. Эти направления называют направлениями Риччи.
таких взаимно ортогональных направлений. Эти направления называют направлениями Риччи.
Многообразие, для которого направления Риччи неопределенны, называется многообразием Эйнштейна. Для такого многообразия имеем

Умножая последнее уравнение на  и свертывая, получим
и свертывая, получим

откуда

Легко видеть из (1.61), что  является абсолютной константой.
является абсолютной константой.
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ К. ЯНО
- Глава I. РИМАНОВЫ МНОГООБРАЗИЯ
- 1. Римановы многообразия
- 2. Тензорная алгебра
- 3. Тензорный анализ
- 4. Тензоры кривизны
- 5. Кривизна в двумерном направлении
- 6. Параллельное перенесение
- Глава II. ГАРМОНИЧЕСКИЕ ВЕКТОРЫ И ВЕКТОРЫ КИЛЛИНГА
- 2. Теорема Грина
- 3. Некоторые приложения теоремы Хопфа — Бохнера
- 4. Гармонические векторы
- 5. Векторы Киллинга
- 6. Аффинные коллинеации
- 7. Теорема о гармоническом векторе и векторе Киллинга
- 8. Производные Ли
- 9. Производные Ли гармонических тензоров
- 10. Фундаментальная формула
- 11. Некоторые приложения фундаментальной формулы
- 12. Конформные преобразования
- 13. Необходимое и достаточное условие того, чтобы вектор был гармоническим
- 14. Необходимое и достаточное условие того, чтобы вектор был вектором Киллинга
- 15. Движение и аффинные коллинеации
- Глава III. ГАРМОНИЧЕСКИЕ ТЕНЗОРЫ И ТЕНЗОРЫ КИЛЛИНГА
- 1. Некоторые приложения теоремы Хопфа — Бохнера
- 2. Гармонические тензоры
- 3. Тензоры Киллинга
- 4. Фундаментальная формула
- 5. Некоторые приложения фундаментальных формул
- 6. Конформно-киллингов тензор
- 7. Необходимое и достаточное условие того, чтобы антисимметричный тензор был гармоническим или киллинговым
- Глава IV. ГАРМОНИЧЕСКИЕ ТЕНЗОРЫ И ТЕНЗОРЫ КИЛЛИНГА НА ПЛОСКИХ МНОГООБРАЗИЯХ
- 1. Гармонические тензоры и тензоры Киллинга на многообразии постоянной кривизны
- 2. Гармонические тензоры и тензоры Киллинга на конформно-эвклидовом многообразии
- Глава V. ОТКЛОНЕНИЕ МНОГООБРАЗИЯ ОТ ПЛОСКОГО
- 1. Отклонение от постоянства кривизны
- 2. Отклонение от проективно-эвклидовости
- 3. Отклонение от конциркулярно-эвклидовости
- 4. Отклонение от конформно-эвклидовости
- Глава VI. ПРОСТРАНСТВА ПОЛУПРОСТЫХ ГРУПП
- 1. Пространства полупростых групп
- 2. Теорема о кривизне пространства полупростой группы
- 3. Гармонические тензоры в пространстве полупростой группы
- 4. Отклонение группового пространства от плоского
- Глава VII. ПСЕВДОГАРМОНИЧЕСКИЕ И ПСЕВДОКИЛЛИНГОВЫ ТЕНЗОРЫ В МЕТРИЧЕСКИХ МНОГООБРАЗИЯХ С КРУЧЕНИЕМ
- 1. Метрические многообразия с кручением
- 2. Теорема Хопфа — Бохнера и ее приложения
- 3. Псевдогармонические векторы и тензоры
- 4. Псевдокиллинговы векторы и тензоры
- 5. Интегральные формулы
- 6. Необходимые и достаточные условия того, что тензор является псевдогармоническим или псевдокиллинговым
- 7. Обобщение
- Глава VIII. КЭЛЕРОВЫ МНОГООБРАЗИЯ
- 1. Кэлеровы многообразия
- 2. Кривизна в кэлеровом многообразии
- 3. Ковариантные и контравариантные аналитические векторные поля
- 4. Комплексные аналитические многообразия, допускающие транзитивную коммутативную группу преобразований
- 5. Самоприсоединенные векторы, удовлетворяющие соотношениям …
- 6. Аналитические тензоры
- 7. Гармонические векторные поля
- 8. Гармонические тензорные поля
- 9. Поля векторов Киллинга
- 10. Поля тензоров Киллинга
- 11. Тензор hij
- 12. Эффективные гармонические тензоры в плоских многообразиях
- 13. Уклонение многообразия от плоского
- Глава IX. ДОПОЛНЕНИЯ (С. БОХНЕР)
- 1. Симметрические многообразия
- 2. Выпуклость
- 3. Минимальные многообразия
- 4. Комплексное погружение
- 5. Многообразия с достаточным числом векторных или тензорных полей
- 6. Характеристика Эйлера — Пуанкаре
- 7. Некомпактные многообразия и нулевые граничные значения
- 8. Почти автоморфные векторные и тензорные поля