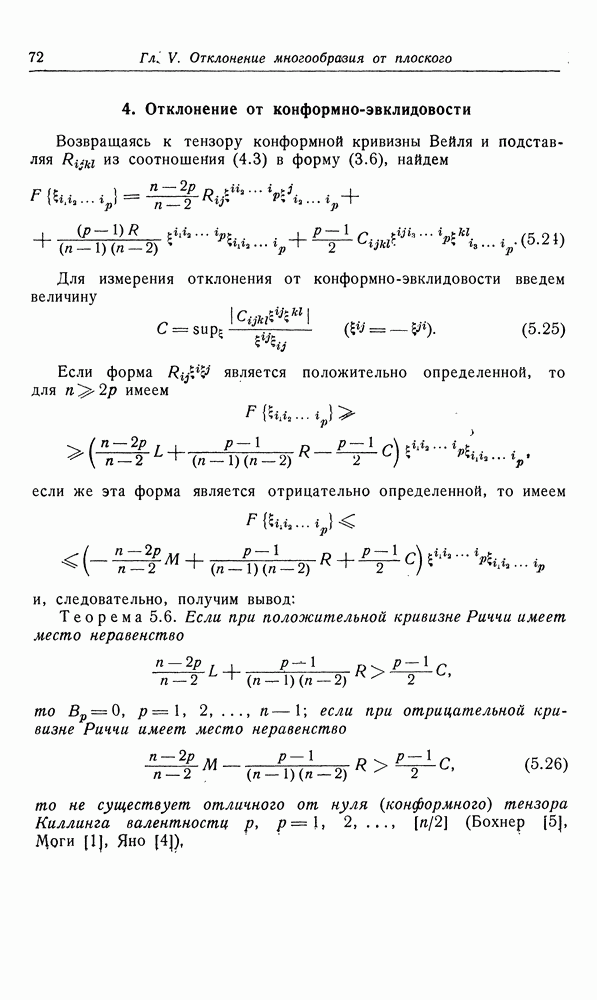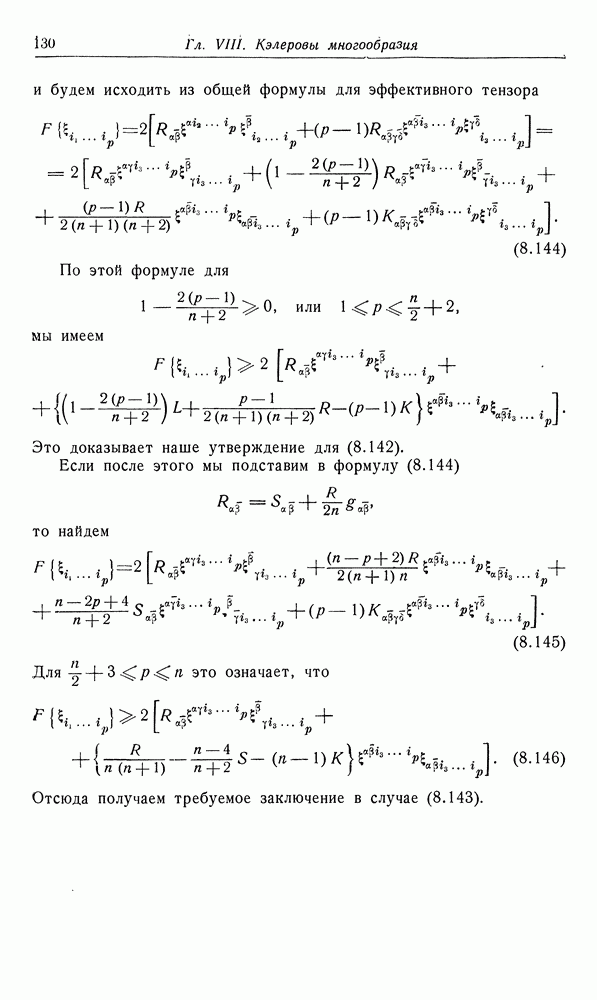| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава I. РИМАНОВЫ МНОГООБРАЗИЯ
1. Римановы многообразия
Рассмотрим хаусдорфово пространство с заданной системой окрестностей  таких, что каждая окрестность
таких, что каждая окрестность  может быть поставлена во взаимно-однозначное непрерывное соответствие с внутренностью гиперсферы
может быть поставлена во взаимно-однозначное непрерывное соответствие с внутренностью гиперсферы

в  -мерном эвклидовом пространстве. Такое пространство будем называть
-мерном эвклидовом пространстве. Такое пространство будем называть  -мерным многообразием. Здесь и в дальнейшем латинские индексы будут пробегать значения
-мерным многообразием. Здесь и в дальнейшем латинские индексы будут пробегать значения 
Это соответствие между точками некоторой окрестности многообразия и точками внутри гиперсферы называется системой координат. Координаты  точки в эвклидовом пространстве, которая соответствует точке
точки в эвклидовом пространстве, которая соответствует точке  многообразия, называются координатами точки
многообразия, называются координатами точки  в этой системе координат. Окрестность, снабженная системой координат, называется координатной окрестностью. Если в окрестности
в этой системе координат. Окрестность, снабженная системой координат, называется координатной окрестностью. Если в окрестности  заданы две системы координат
заданы две системы координат

то существует взаимно-однозначное непрерывное соответствие между этими двумя системами координат, которое может быть выражено уравнениями

или обратно:

Уравнения (1.1) или (1.2) определяют так называемое преобразование координат.
Если  функции класса
функции класса  то есть если они допускают непрерывные частные производные первого, второго,
то есть если они допускают непрерывные частные производные первого, второго,  порядка, и если при 1 якобианы
порядка, и если при 1 якобианы

отличны от нуля для любого преобразования координат в данном многообразии, то мы говорим, что многообразие является многообразием класса 
Очевидно, что если мы имеем в  -мерном многообразии класса
-мерном многообразии класса  функции
функции  удовлетворяющие упомянутым условиям, где
удовлетворяющие упомянутым условиям, где  является начальной системой координат в окрестности
является начальной системой координат в окрестности  то, полагая
то, полагая

мы можем ввести  в качестве новой системы координат в
в качестве новой системы координат в  Мы будем называть такую систему координат допустимой системой координат в
Мы будем называть такую систему координат допустимой системой координат в 
Если многообразие может быть полностью покрыто конечным числом окрестностей  то говорят, что многообразие компактно. Как правило, наши многообразия будут компактны.
то говорят, что многообразие компактно. Как правило, наши многообразия будут компактны.
Иногда мы будем также предполагать ориентируемость многообразия. Если  две допустимые системы координат в координатной окрестности
две допустимые системы координат в координатной окрестности  то якобиан
то якобиан

отличен от нуля всюду в координатной окрестности  следовательно, будучи непрерывной функцией точки в
следовательно, будучи непрерывной функцией точки в  имеет один и тот же знак всюду в
имеет один и тот же знак всюду в  Если этот знак положителен, мы говорим, что эти координатные системы одинаково
Если этот знак положителен, мы говорим, что эти координатные системы одинаково  ориентированы, если знак отрицателен, то они противоположно ориентированы.
ориентированы, если знак отрицателен, то они противоположно ориентированы.
Если существует подмножество множества всех допустимых координатных окрестностей, покрывающее все многообразие, и если любые координатные системы, принадлежащие этому подмножеству и действующие в одной и той же окрестности многообразия, всегда одинаково ориентированы, то говорят, что многообразие ориентируемо.
Предположим теперь, что с каждой координатной окрестностью  в нашем
в нашем  -мерном многообразии класса
-мерном многообразии класса  связана положительно определенная квадратичная дифференциальная форма от дифференциалов
связана положительно определенная квадратичная дифференциальная форма от дифференциалов 

которая не зависит от выбора системы координат и коэффициенты  которой являются функциями класса
которой являются функциями класса  от координат
от координат  В формуле (1.3) по повторяющимся внизу и вверху индексам производится суммирование.
В формуле (1.3) по повторяющимся внизу и вверху индексам производится суммирование.
Геометрически форма (1.3) интерпретируется как квадрат бесконечно малого расстояния  между точками
между точками  Тогда длина дуги кривой
Тогда длина дуги кривой  Дается интегралом
Дается интегралом

Форму (1.3) мы будем называть фундаментальной метрической формой многообразия.
 -мерное многообразие класса
-мерное многообразие класса  в котором задана фундаментальная метрическая форма (1.3), называется
в котором задана фундаментальная метрическая форма (1.3), называется  -мерным римановым многообразием класса
-мерным римановым многообразием класса  Теория таких многообразий называется римановой геометрией (Эйзенхарт [1]),
Теория таких многообразий называется римановой геометрией (Эйзенхарт [1]),
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ К. ЯНО
- Глава I. РИМАНОВЫ МНОГООБРАЗИЯ
- 1. Римановы многообразия
- 2. Тензорная алгебра
- 3. Тензорный анализ
- 4. Тензоры кривизны
- 5. Кривизна в двумерном направлении
- 6. Параллельное перенесение
- Глава II. ГАРМОНИЧЕСКИЕ ВЕКТОРЫ И ВЕКТОРЫ КИЛЛИНГА
- 2. Теорема Грина
- 3. Некоторые приложения теоремы Хопфа — Бохнера
- 4. Гармонические векторы
- 5. Векторы Киллинга
- 6. Аффинные коллинеации
- 7. Теорема о гармоническом векторе и векторе Киллинга
- 8. Производные Ли
- 9. Производные Ли гармонических тензоров
- 10. Фундаментальная формула
- 11. Некоторые приложения фундаментальной формулы
- 12. Конформные преобразования
- 13. Необходимое и достаточное условие того, чтобы вектор был гармоническим
- 14. Необходимое и достаточное условие того, чтобы вектор был вектором Киллинга
- 15. Движение и аффинные коллинеации
- Глава III. ГАРМОНИЧЕСКИЕ ТЕНЗОРЫ И ТЕНЗОРЫ КИЛЛИНГА
- 1. Некоторые приложения теоремы Хопфа — Бохнера
- 2. Гармонические тензоры
- 3. Тензоры Киллинга
- 4. Фундаментальная формула
- 5. Некоторые приложения фундаментальных формул
- 6. Конформно-киллингов тензор
- 7. Необходимое и достаточное условие того, чтобы антисимметричный тензор был гармоническим или киллинговым
- Глава IV. ГАРМОНИЧЕСКИЕ ТЕНЗОРЫ И ТЕНЗОРЫ КИЛЛИНГА НА ПЛОСКИХ МНОГООБРАЗИЯХ
- 1. Гармонические тензоры и тензоры Киллинга на многообразии постоянной кривизны
- 2. Гармонические тензоры и тензоры Киллинга на конформно-эвклидовом многообразии
- Глава V. ОТКЛОНЕНИЕ МНОГООБРАЗИЯ ОТ ПЛОСКОГО
- 1. Отклонение от постоянства кривизны
- 2. Отклонение от проективно-эвклидовости
- 3. Отклонение от конциркулярно-эвклидовости
- 4. Отклонение от конформно-эвклидовости
- Глава VI. ПРОСТРАНСТВА ПОЛУПРОСТЫХ ГРУПП
- 1. Пространства полупростых групп
- 2. Теорема о кривизне пространства полупростой группы
- 3. Гармонические тензоры в пространстве полупростой группы
- 4. Отклонение группового пространства от плоского
- Глава VII. ПСЕВДОГАРМОНИЧЕСКИЕ И ПСЕВДОКИЛЛИНГОВЫ ТЕНЗОРЫ В МЕТРИЧЕСКИХ МНОГООБРАЗИЯХ С КРУЧЕНИЕМ
- 1. Метрические многообразия с кручением
- 2. Теорема Хопфа — Бохнера и ее приложения
- 3. Псевдогармонические векторы и тензоры
- 4. Псевдокиллинговы векторы и тензоры
- 5. Интегральные формулы
- 6. Необходимые и достаточные условия того, что тензор является псевдогармоническим или псевдокиллинговым
- 7. Обобщение
- Глава VIII. КЭЛЕРОВЫ МНОГООБРАЗИЯ
- 1. Кэлеровы многообразия
- 2. Кривизна в кэлеровом многообразии
- 3. Ковариантные и контравариантные аналитические векторные поля
- 4. Комплексные аналитические многообразия, допускающие транзитивную коммутативную группу преобразований
- 5. Самоприсоединенные векторы, удовлетворяющие соотношениям …
- 6. Аналитические тензоры
- 7. Гармонические векторные поля
- 8. Гармонические тензорные поля
- 9. Поля векторов Киллинга
- 10. Поля тензоров Киллинга
- 11. Тензор hij
- 12. Эффективные гармонические тензоры в плоских многообразиях
- 13. Уклонение многообразия от плоского
- Глава IX. ДОПОЛНЕНИЯ (С. БОХНЕР)
- 1. Симметрические многообразия
- 2. Выпуклость
- 3. Минимальные многообразия
- 4. Комплексное погружение
- 5. Многообразия с достаточным числом векторных или тензорных полей
- 6. Характеристика Эйлера — Пуанкаре
- 7. Некомпактные многообразия и нулевые граничные значения
- 8. Почти автоморфные векторные и тензорные поля