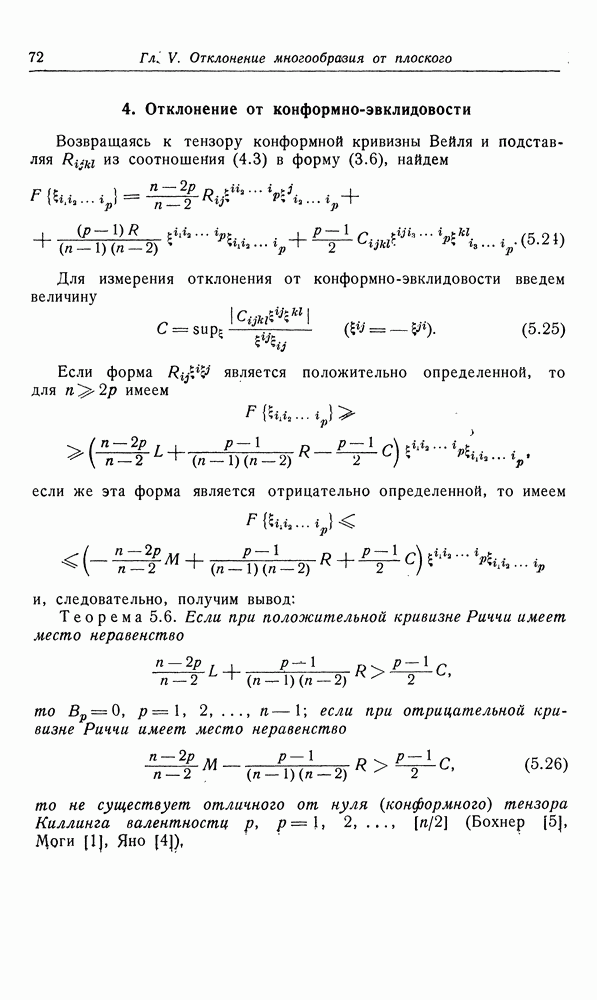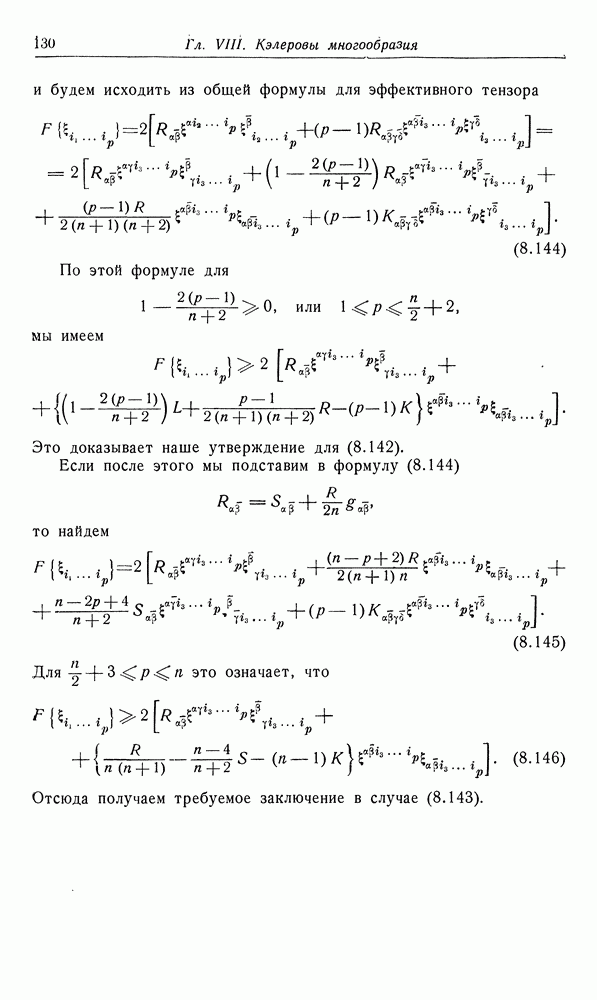| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Тензорный анализ
Рассмотрим кривую  соединяющую две точки
соединяющую две точки  и найдем ее длину
и найдем ее длину

Рассмотрим другую кривую  бесконечно мало), которая проходит через
бесконечно мало), которая проходит через  (следовательно
(следовательно  и является бесконечно близкой к
и является бесконечно близкой к  Первая вариация
Первая вариация  интеграла
интеграла  определяется следующим образом:
определяется следующим образом:

где положено

Мы назовем кривую, для которой  при любых
при любых  геодезической нашего риманова многообразия.
геодезической нашего риманова многообразия.
Вдоль геодезической должны удовлетворяться так называемые дифференциальные уравнения Эйлера

Можно показать, что величины являются ковариантными компонентами вектора.
Возьмем в качестве параметра вдоль геодезической длину дуги  и подсчитаем контравариантные компоненты вектора в результате получим
и подсчитаем контравариантные компоненты вектора в результате получим

где коэффициенты  определяются формулой
определяются формулой

и называются символами Кристоффеля.
Легко проверить, что символы Кристоффеля удовлетворяют следующим тождествам:

Теперь, исходя из того, что в (1.16) являются контравариантными компонентами вектора, мы можем найти следующий закон преобразования символов Кристоффеля при преобразовании координат:

Если  есть компонента скалярного поля, то очевидно, что
есть компонента скалярного поля, то очевидно, что  есть также компонента скаляра,
есть также компонента скаляра,  являются компонентами ковариантного вектора. Мы называем
являются компонентами ковариантного вектора. Мы называем  ковариантным дифференциалом скаляра
ковариантным дифференциалом скаляра  ковариантной производной скаляра
ковариантной производной скаляра  и обозначаем их соответственно
и обозначаем их соответственно

Если  являются компонентами контравариантного векторного поля, то
являются компонентами контравариантного векторного поля, то  не обязательно являются компонентами контравариантного вектора. Но, комбинируя закон преобразования
не обязательно являются компонентами контравариантного вектора. Но, комбинируя закон преобразования  с законом преобразования для
с законом преобразования для  мы можем доказать, что
мы можем доказать, что

являются компонентами контравариантного вектора и

являются компонентами смешанного тензора. Мы называем ковариантным дифференциалом  ковариантной производной
ковариантной производной 
Аналогично, если  являются компонентами ковариантного векторного поля, то
являются компонентами ковариантного векторного поля, то  не обязательно являются компонентами
не обязательно являются компонентами
ковариантного вектора, но мы можем доказать, что

являются компонентами ковариантного вектора и

являются компонентами ковариантного тензора. Мы называем  ковариантным дифференциалом
ковариантным дифференциалом  ковариантной производной
ковариантной производной 
Эта операция ковариантного дифференцирования может быть определена для любого тензора, скажем, для 

Тензор  который имеет тот же тип, что и тензор
который имеет тот же тип, что и тензор  называется ковариантным дифференциалом тензора
называется ковариантным дифференциалом тензора  Тензор
Тензор  имеет на один ковариантный индекс больше, чем тензор
имеет на один ковариантный индекс больше, чем тензор  и называется ковариантной производной тензора
и называется ковариантной производной тензора 
Если мы применим операцию ковариантного дифференцирования к тензорам  и
и  , то получим
, то получим

Таким образом, тензоры  постоянны относительно ковариантного дифференцирования.
постоянны относительно ковариантного дифференцирования.
Легко проверить, что ковариантное дифференцирование подчиняется правилам обычного дифференцирования:

и

Если задано ковариантное векторное поле  то можно образовать антисимметричный тензор
то можно образовать антисимметричный тензор

который не зависит от символов Кристоффеля. Он называется вихрем ковариантного вектора 
Аналогично, если задано антисимметричное тензорное поле  можно образовать антисимметричный тензор
можно образовать антисимметричный тензор

который не зависит от символов Кристоффеля. Он называется вихрем антисимметричного ковариантного тензора

Если задано контравариантное векторное поле  то можно образовать скаляр
то можно образовать скаляр

который зависит только от  Этот скаляр называется дивергенцией контравариантного вектора
Этот скаляр называется дивергенцией контравариантного вектора 
Дивергенция ковариантного вектора  определяется как скаляр
определяется как скаляр

а дивергенция ковариантного тензора  тензор
тензор

Если мы имеем скалярное поле  то мы можем образовать градиент
то мы можем образовать градиент  и вычислить квадрат его длины
и вычислить квадрат его длины

Эта величина называется дифференциальным параметром Бельтрами первого рода скалярного поля 
Мы можем далее вычислить дивергенцию градиента

Эта величина называется дифференциальным параметром Бельтрами второго рода скалярного поля  Она называется также лапласианом от
Она называется также лапласианом от  и обозначается
и обозначается

| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ К. ЯНО
- Глава I. РИМАНОВЫ МНОГООБРАЗИЯ
- 1. Римановы многообразия
- 2. Тензорная алгебра
- 3. Тензорный анализ
- 4. Тензоры кривизны
- 5. Кривизна в двумерном направлении
- 6. Параллельное перенесение
- Глава II. ГАРМОНИЧЕСКИЕ ВЕКТОРЫ И ВЕКТОРЫ КИЛЛИНГА
- 2. Теорема Грина
- 3. Некоторые приложения теоремы Хопфа — Бохнера
- 4. Гармонические векторы
- 5. Векторы Киллинга
- 6. Аффинные коллинеации
- 7. Теорема о гармоническом векторе и векторе Киллинга
- 8. Производные Ли
- 9. Производные Ли гармонических тензоров
- 10. Фундаментальная формула
- 11. Некоторые приложения фундаментальной формулы
- 12. Конформные преобразования
- 13. Необходимое и достаточное условие того, чтобы вектор был гармоническим
- 14. Необходимое и достаточное условие того, чтобы вектор был вектором Киллинга
- 15. Движение и аффинные коллинеации
- Глава III. ГАРМОНИЧЕСКИЕ ТЕНЗОРЫ И ТЕНЗОРЫ КИЛЛИНГА
- 1. Некоторые приложения теоремы Хопфа — Бохнера
- 2. Гармонические тензоры
- 3. Тензоры Киллинга
- 4. Фундаментальная формула
- 5. Некоторые приложения фундаментальных формул
- 6. Конформно-киллингов тензор
- 7. Необходимое и достаточное условие того, чтобы антисимметричный тензор был гармоническим или киллинговым
- Глава IV. ГАРМОНИЧЕСКИЕ ТЕНЗОРЫ И ТЕНЗОРЫ КИЛЛИНГА НА ПЛОСКИХ МНОГООБРАЗИЯХ
- 1. Гармонические тензоры и тензоры Киллинга на многообразии постоянной кривизны
- 2. Гармонические тензоры и тензоры Киллинга на конформно-эвклидовом многообразии
- Глава V. ОТКЛОНЕНИЕ МНОГООБРАЗИЯ ОТ ПЛОСКОГО
- 1. Отклонение от постоянства кривизны
- 2. Отклонение от проективно-эвклидовости
- 3. Отклонение от конциркулярно-эвклидовости
- 4. Отклонение от конформно-эвклидовости
- Глава VI. ПРОСТРАНСТВА ПОЛУПРОСТЫХ ГРУПП
- 1. Пространства полупростых групп
- 2. Теорема о кривизне пространства полупростой группы
- 3. Гармонические тензоры в пространстве полупростой группы
- 4. Отклонение группового пространства от плоского
- Глава VII. ПСЕВДОГАРМОНИЧЕСКИЕ И ПСЕВДОКИЛЛИНГОВЫ ТЕНЗОРЫ В МЕТРИЧЕСКИХ МНОГООБРАЗИЯХ С КРУЧЕНИЕМ
- 1. Метрические многообразия с кручением
- 2. Теорема Хопфа — Бохнера и ее приложения
- 3. Псевдогармонические векторы и тензоры
- 4. Псевдокиллинговы векторы и тензоры
- 5. Интегральные формулы
- 6. Необходимые и достаточные условия того, что тензор является псевдогармоническим или псевдокиллинговым
- 7. Обобщение
- Глава VIII. КЭЛЕРОВЫ МНОГООБРАЗИЯ
- 1. Кэлеровы многообразия
- 2. Кривизна в кэлеровом многообразии
- 3. Ковариантные и контравариантные аналитические векторные поля
- 4. Комплексные аналитические многообразия, допускающие транзитивную коммутативную группу преобразований
- 5. Самоприсоединенные векторы, удовлетворяющие соотношениям …
- 6. Аналитические тензоры
- 7. Гармонические векторные поля
- 8. Гармонические тензорные поля
- 9. Поля векторов Киллинга
- 10. Поля тензоров Киллинга
- 11. Тензор hij
- 12. Эффективные гармонические тензоры в плоских многообразиях
- 13. Уклонение многообразия от плоского
- Глава IX. ДОПОЛНЕНИЯ (С. БОХНЕР)
- 1. Симметрические многообразия
- 2. Выпуклость
- 3. Минимальные многообразия
- 4. Комплексное погружение
- 5. Многообразия с достаточным числом векторных или тензорных полей
- 6. Характеристика Эйлера — Пуанкаре
- 7. Некомпактные многообразия и нулевые граничные значения
- 8. Почти автоморфные векторные и тензорные поля