| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
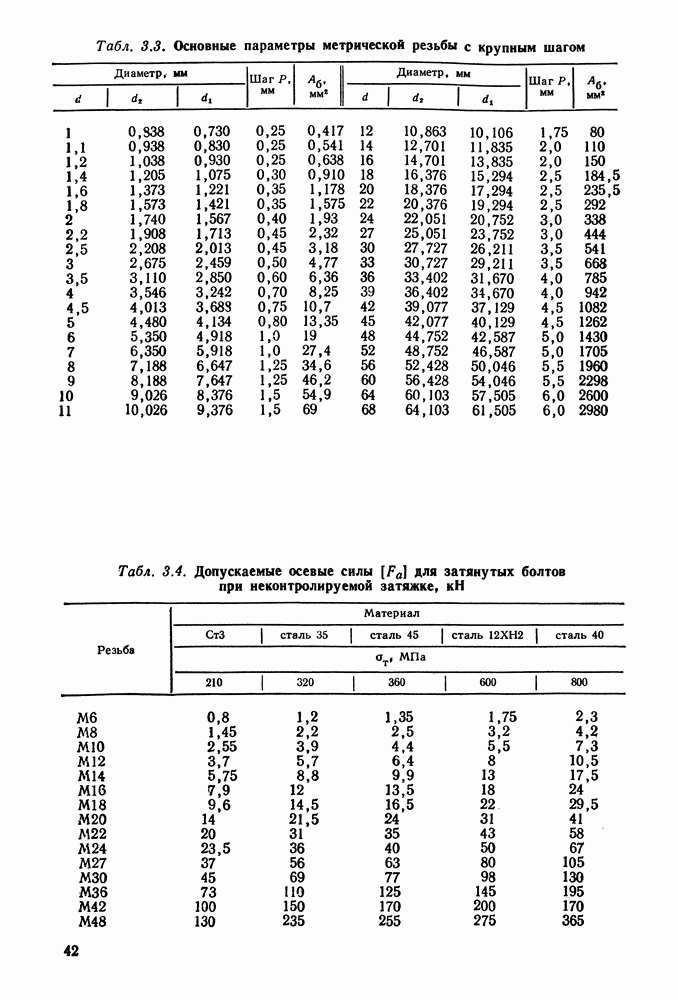
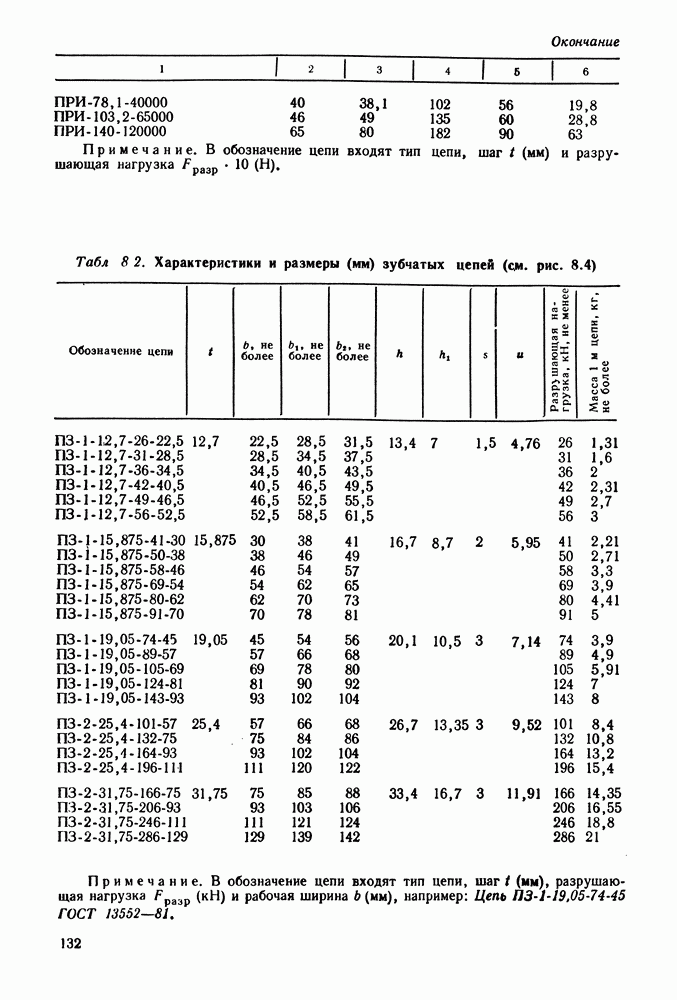
4.5. Примеры расчета
Пример 4.1. Подобрать призматическую шпонку и проверить ее прочность при передаче вращающего момента  от стальной шестерни с шириной ступицы 80 мм к валу диаметром
от стальной шестерни с шириной ступицы 80 мм к валу диаметром  мм.
мм.
Решение. Из табл. 4.1 для заданного диаметра вала выбираем сечение призматической шпонки  мм. Принимаем шпонку на 10 мм короче ступицы шестерни, т. е. расчетная длина шпонки
мм. Принимаем шпонку на 10 мм короче ступицы шестерни, т. е. расчетная длина шпонки  мм.
мм.
Приняв допускаемое напряжение при смятии шпонки  проверим ее прочность:
проверим ее прочность:

что удовлетворительно, так как  (такое значение принято исходя из того, что твердость вала и ступицы будет выше твердости шпонки).
(такое значение принято исходя из того, что твердость вала и ступицы будет выше твердости шпонки).

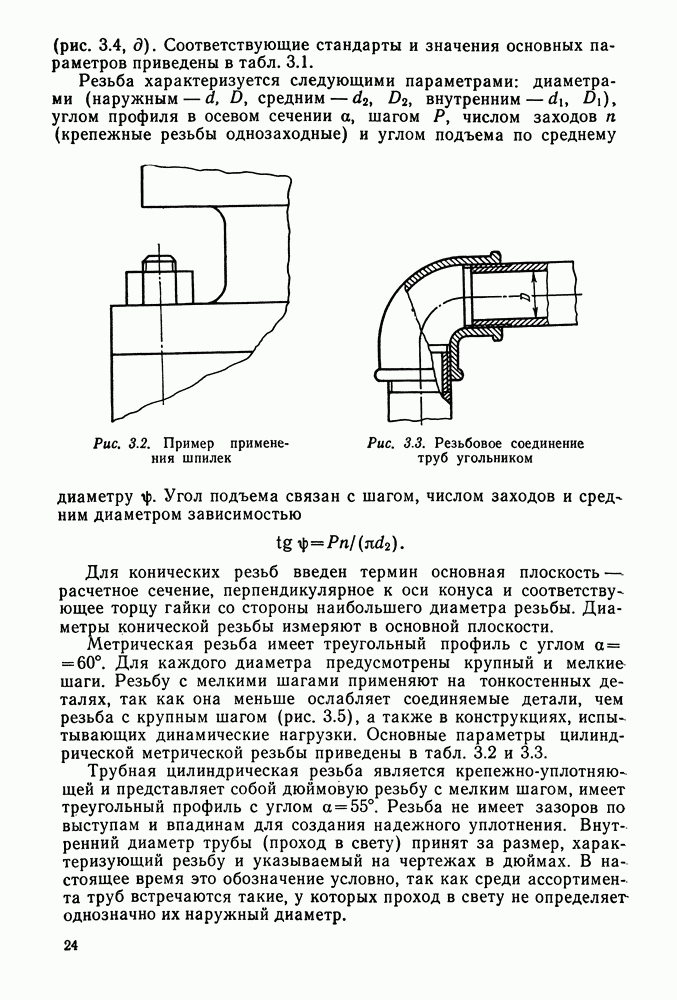
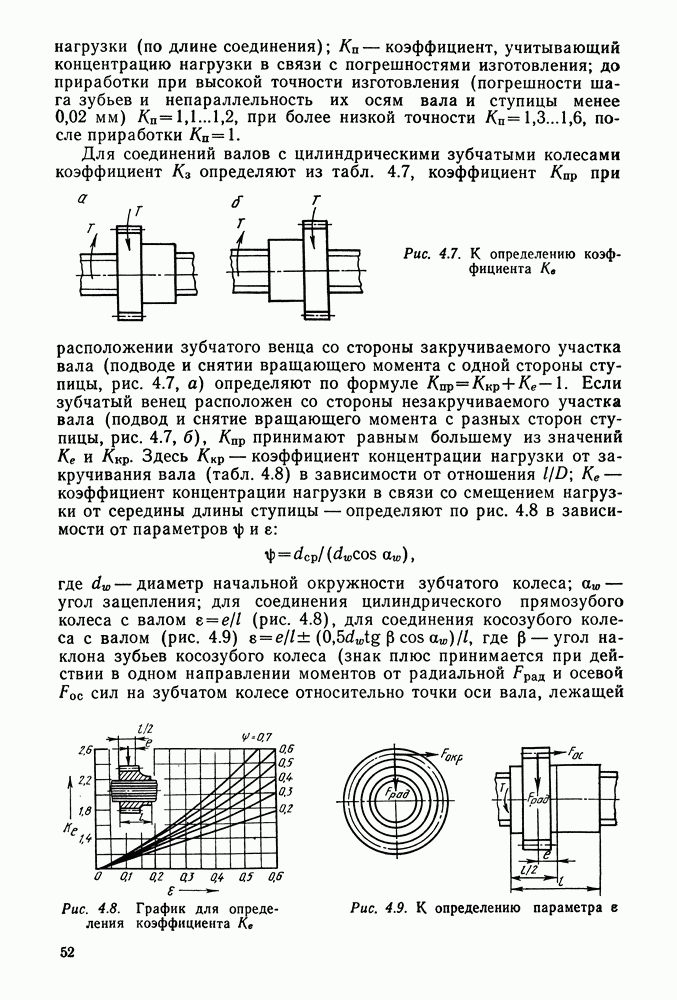
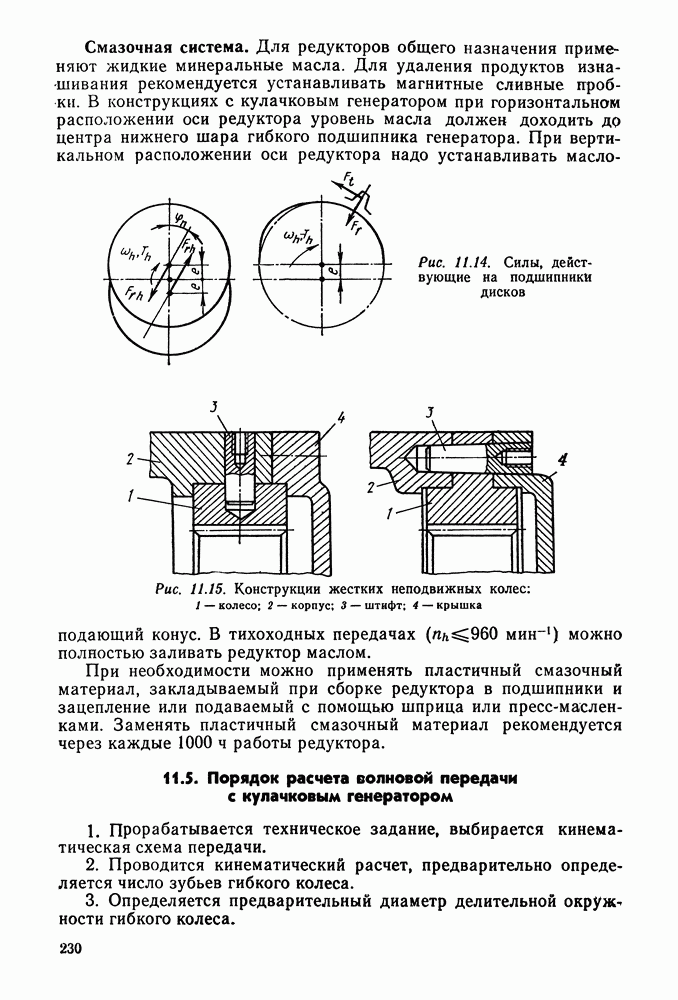
Рис. 4.11. Шлицевое соединение шестерни с валом
Пример 4.2. Проверить зубчатое соединение косозубого колеса диаметром  мм и с углом наклона зубьев
мм и с углом наклона зубьев  с валом (рис. 4.11). Исходные данные: номинальные размеры соединения
с валом (рис. 4.11). Исходные данные: номинальные размеры соединения  передаваемый момент
передаваемый момент  частота вращения вала
частота вращения вала  срок службы
срок службы  материал рабочих поверхностей — сталь
материал рабочих поверхностей — сталь  термообработка — улучшение, твердость
термообработка — улучшение, твердость  условия смазывания средние, режим работы среднеравновероятный (одинаковое время работы со всеми нагрузками), колесо закреплено на валу жестко.
условия смазывания средние, режим работы среднеравновероятный (одинаковое время работы со всеми нагрузками), колесо закреплено на валу жестко.
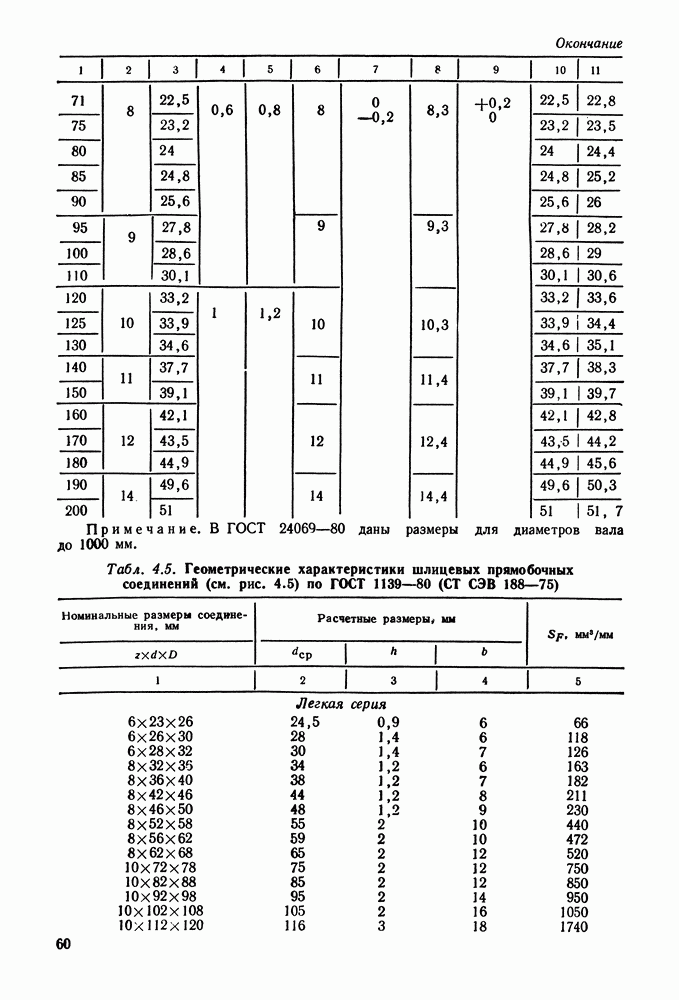
Решение. По табл. 4.5 находим 
Среднее напряжение по формуле (4.2)

Вычисляем соотношения размеров:

В выражении для  принят знак плюс, так как силы
принят знак плюс, так как силы  относительно точки пересечения средней плоскости колеса с его осью создают момент одного знака.
относительно точки пересечения средней плоскости колеса с его осью создают момент одного знака.
Коэффициенты концентрации нагрузки:  (см. табл. 4.8, для наружного диаметра
(см. табл. 4.8, для наружного диаметра  , отношения
, отношения  период после приработки; переменный режим нагрузки);
период после приработки; переменный режим нагрузки);  (см. рис. 4.8, для
(см. рис. 4.8, для  (см. табл. 4.7, для
(см. табл. 4.7, для  (см. табл. 4.7, для
(см. табл. 4.7, для  (так как зубчатый венец расположен со стороны незакручиваемого участка вала, то
(так как зубчатый венец расположен со стороны незакручиваемого участка вала, то  выбирается равным большему из значений
выбирается равным большему из значений  (период после приработки).
(период после приработки).
Общие коэффициенты концентрации по формуле (4.4) и из пояснений к формуле (4.6):

Приняв  определим по формуле (4.3) допускаемое среднее напряжение при смятии:
определим по формуле (4.3) допускаемое среднее напряжение при смятии:

Таким образом, условие (4.2) удовлетворяется, т. е.

По ГОСТ 21425-75 допускается значительная разница между  и
и  в связи с тем, что размеры соединений часто определяются прочностью и жесткостью валов и конструктивными соображениями.
в связи с тем, что размеры соединений часто определяются прочностью и жесткостью валов и конструктивными соображениями.
Число циклов нагружения

Определим коэффициенты [см. пояснения к формуле (4.6)]:
 (табл. 4.11);
(табл. 4.11);  (при среднем смазывании);
(при среднем смазывании);  (при жестком закреплении ступицы на валу);
(при жестком закреплении ступицы на валу); 
Из табл. 4.10 для твердости  находим
находим  Допускаемое среднее напряжение из расчета на износостойкость по формуле (4.6)
Допускаемое среднее напряжение из расчета на износостойкость по формуле (4.6)

т. е. условие (4.5) удовлетворяется, так как

Допускаемое наибольшее напряжение из условия работы без изнашивания для улучшенных зубьев

Условие работы соединения без изнашивания [см. формулу (4.7)]

Пример 4.3. Проверить несущую способность и прочность элементов соединения ступицы с венцом червячного колеса, передающего моменг  Сборка производится прессованием.
Сборка производится прессованием.
Размеры соединения показаны на рис. 4.12. Обод колеса изготовлен из бронзы  по
по  с пределом прочности
с пределом прочности  пределом текучести
пределом текучести  модулем упругости
модулем упругости  Ступица — из чугуна
Ступица — из чугуна  по
по  с
с 
Коэфициенты Пуассона: для чугуна  для бронзы
для бронзы 
Параметры шероховатости посадочных поверхностей  мкм,
мкм,  мкм.
мкм.

Рис. 4. 12. Соединение с натягом венца и ступицы червячного колеса
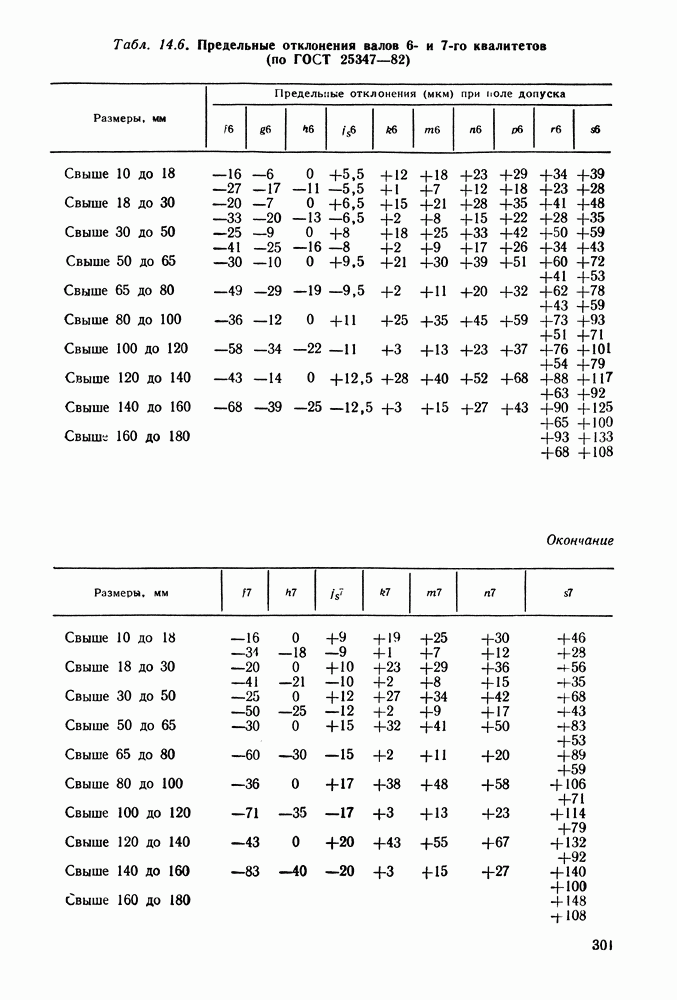
Решение. Из табл. 14.5 и 14.6 находим для заданной посадки  предельные отклонения отверстия: верхнее
предельные отклонения отверстия: верхнее  мкм, нижнее
мкм, нижнее  Предельные отклонения вала: верхнее
Предельные отклонения вала: верхнее  мкм, нижнее
мкм, нижнее  мкм. Наибольший натяг в соединении
мкм. Наибольший натяг в соединении  мкм, наименьший
мкм, наименьший 
Средний натяг  мкм. Допуск диаметра отверстия
мкм. Допуск диаметра отверстия  мкм, допуск диаметра вала
мкм, допуск диаметра вала  мкм. Среднеквадратичное отклонение натяга
мкм. Среднеквадратичное отклонение натяга

Задавшись вероятностью обеспечения натяга в пределах  и
и  равной
равной  (соответственно квантиль нормального распределения натяга
(соответственно квантиль нормального распределения натяга  найдем минимальный и максимальный вероятностный натяги (их абсолютные значения) по формулам (4.8) и (4.12):
найдем минимальный и максимальный вероятностный натяги (их абсолютные значения) по формулам (4.8) и (4.12):

Действительный расчетный натяг для проверки несущей способности соединения находим по формуле (4.9):

Давление на сопряженных поверхностях по формуле (4.10):

Допускаемый вращающий момент находим по формуле (4.11):

что ненамного больше передаваемого момента (т. е. соединение работает на пределе).
Здесь коэффициент трения принят 
Расчетный натяг для проверки прочности элементов соединения находим по формуле (4.13):

Давление при этом натяге по формуле (4.10):

При  условия прочности бронзового венца (4.14) и чугунной ступицы (4.15) соблюдаются
условия прочности бронзового венца (4.14) и чугунной ступицы (4.15) соблюдаются 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Раздел I. СОЕДИНЕНИЯ ДЕТАЛЕЙ МАШИН
- Глава 1. ВАЛЬЦОВОЧНЫЕ СОЕДИНЕНИЯ
- 1.2. Расчет прочных швов
- 1.3. Справочный материал
- 1.4. Примеры расчета
- Глава 2. СВАРНЫЕ, ПАЯНЫЕ И КЛЕЕВЫЕ СОЕДИНЕНИЯ
- 2.1. Общие сведения об основных видах сварных соединений и сварных швов
- 2.2. Расчет прочности сварных швов
- 2.3. Условное изображение сварных швов на чертежах
- 2.4. Паяные соединения
- 2.5. Клеевые соединения
- 2.6. Справочный материал
- 2.7. Примеры расчета
- Глава 3. РЕЗЬБОВЫЕ СОЕДИНЕНИЯ
- 3.2. Определение сил, действующих на один болт
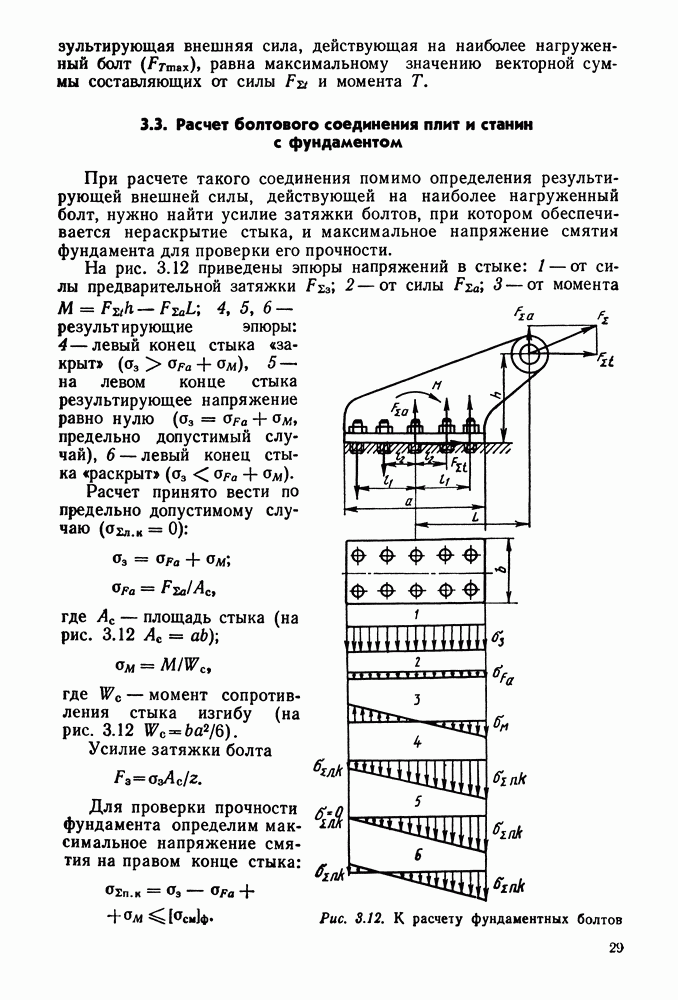
- 3.3. Расчет болтового соединения плит и станин с фундаментом
- 3.4. Расчет стержня болта при постоянных нагрузках
- 3.5. Расчет стержня болта при переменных нагрузках
- 3.6. Расчет витков резьбы на прочность. Определение вращающего момента
- 3.7. Порядок расчета резьбовых соединений
- 3.9. Примеры расчета
- Глава 4. СОЕДИНЕНИЯ ВАЛ — СТУПИЦА (ШПОНОЧНЫЕ, ШЛИЦЕВЫЕ, С НАТЯГОМ)
- 4.2. Шлицевые соединения
- 4.3. Соединения с натягом
- 4.4. Справочный материал
- 4.5. Примеры расчета
- Раздел II. МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ
- Глава 5. КИНЕМАТИЧЕСКИЙ РАСЧЕТ ПРИВОДНЫХ УСТРОЙСТВ И ВЫБОР ЭЛЕКТРОДВИГАТЕЛЯ
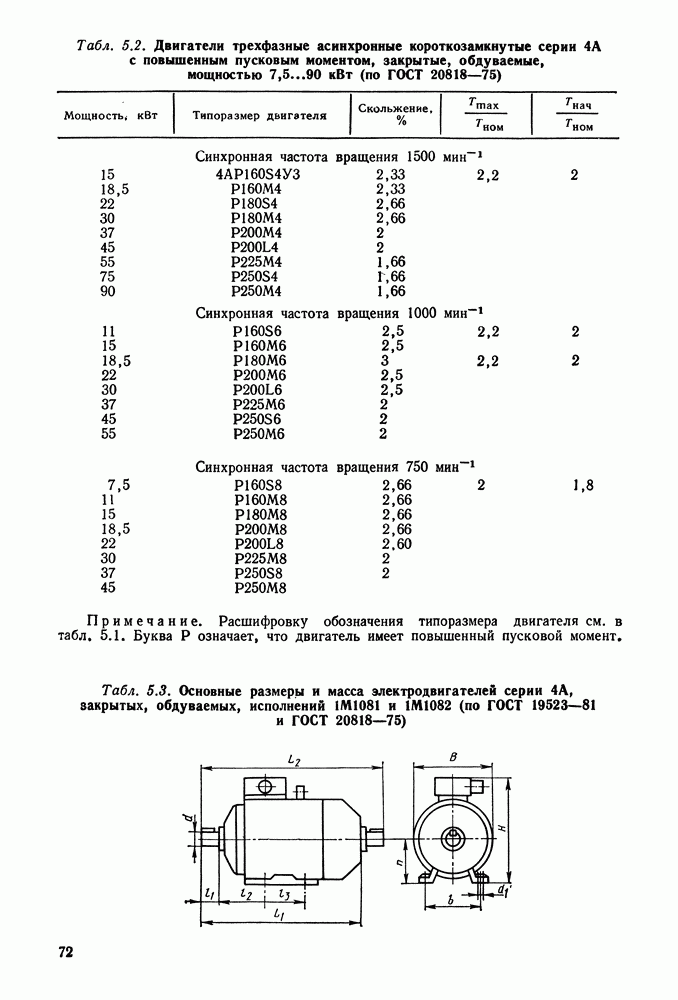
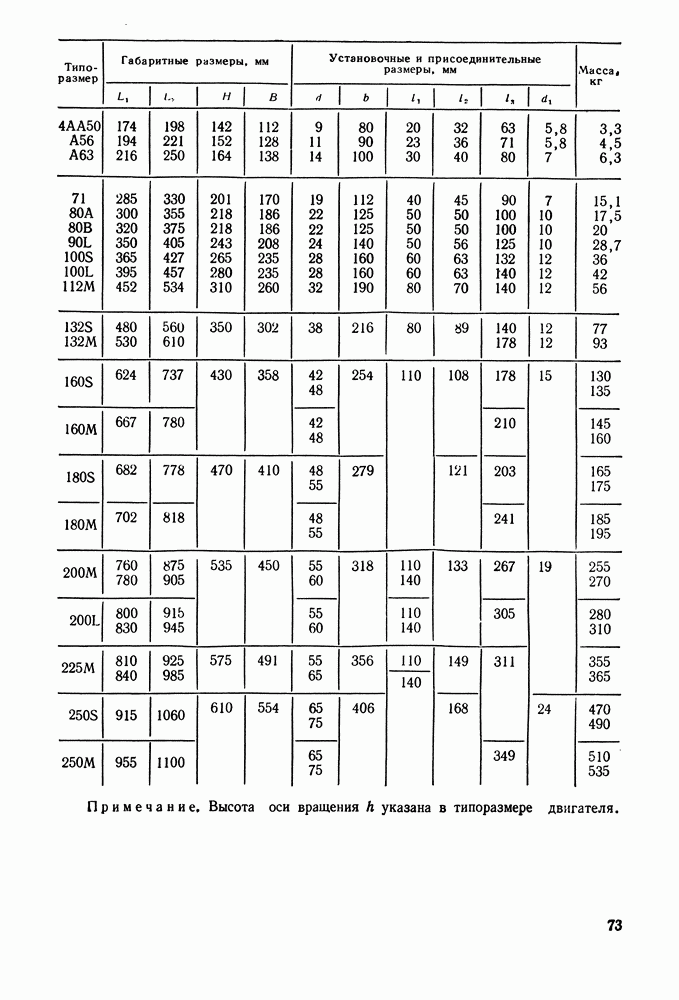
- 5.2. Трехфазные асинхронные электродвигатели
- 5.3. Разбивка общего передаточного числа редуктора по ступеням
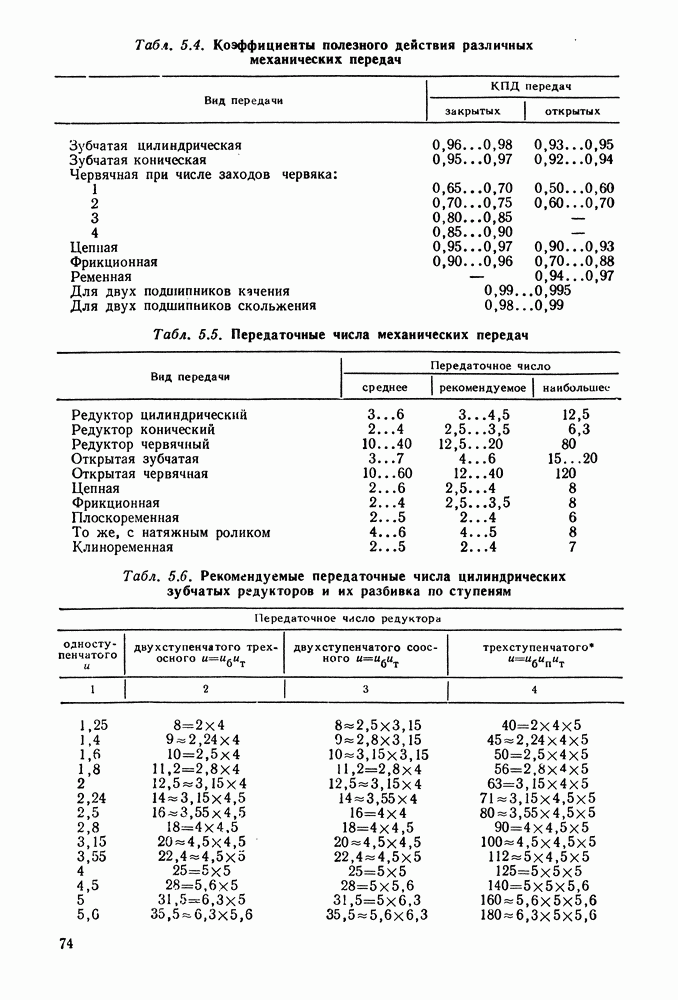
- 5.4. Справочный материал
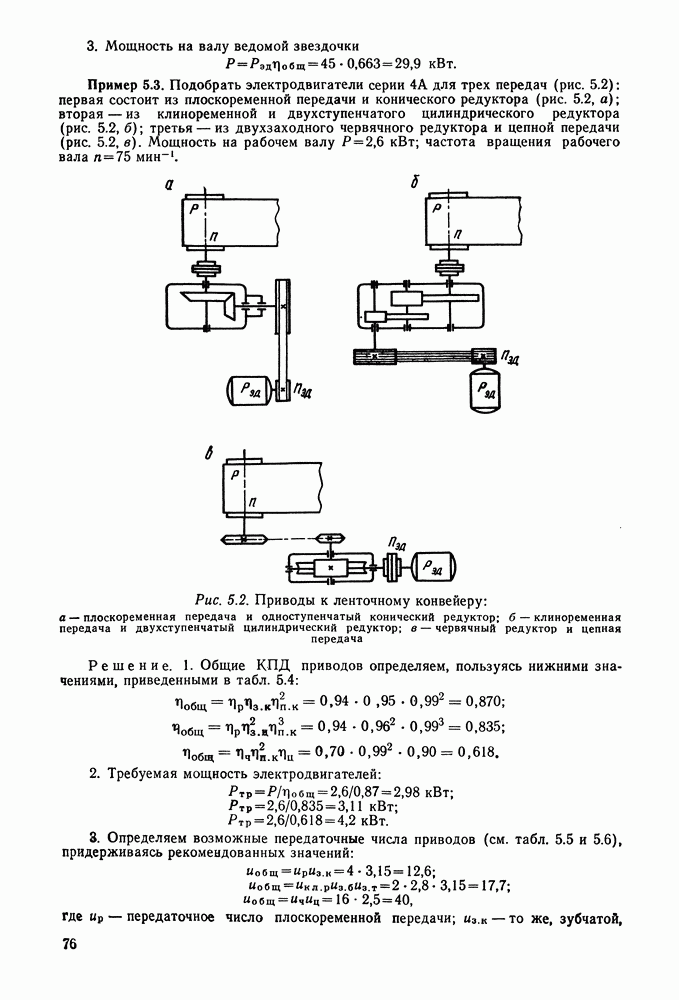
- 5.5. Примеры расчета
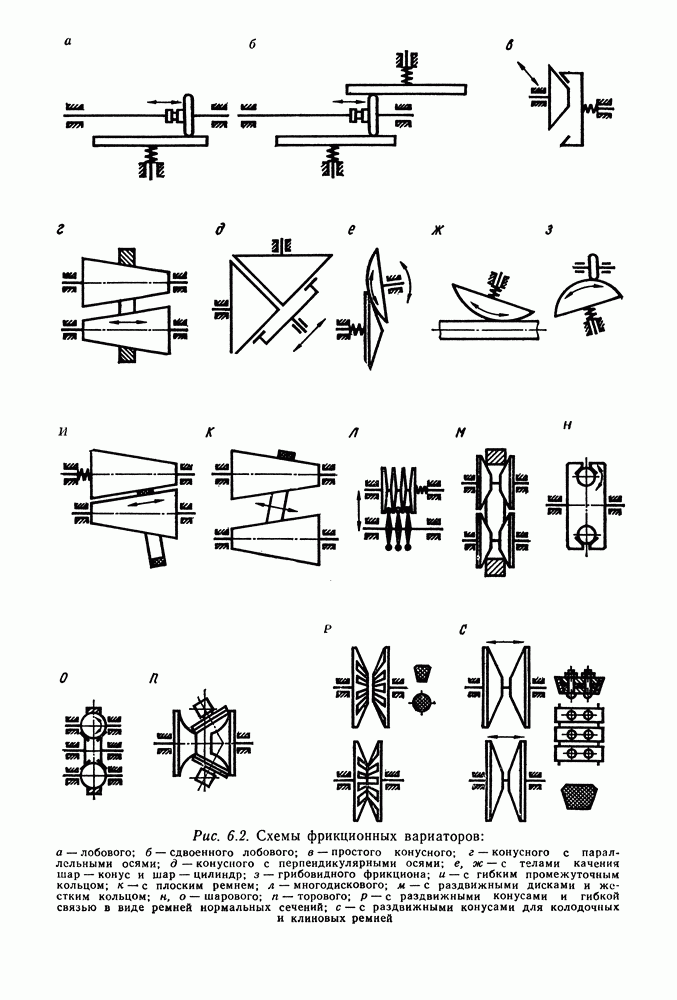
- Глава 6. ФРИКЦИОННЫЕ ПЕРЕДАЧИ И ВАРИАТОРЫ
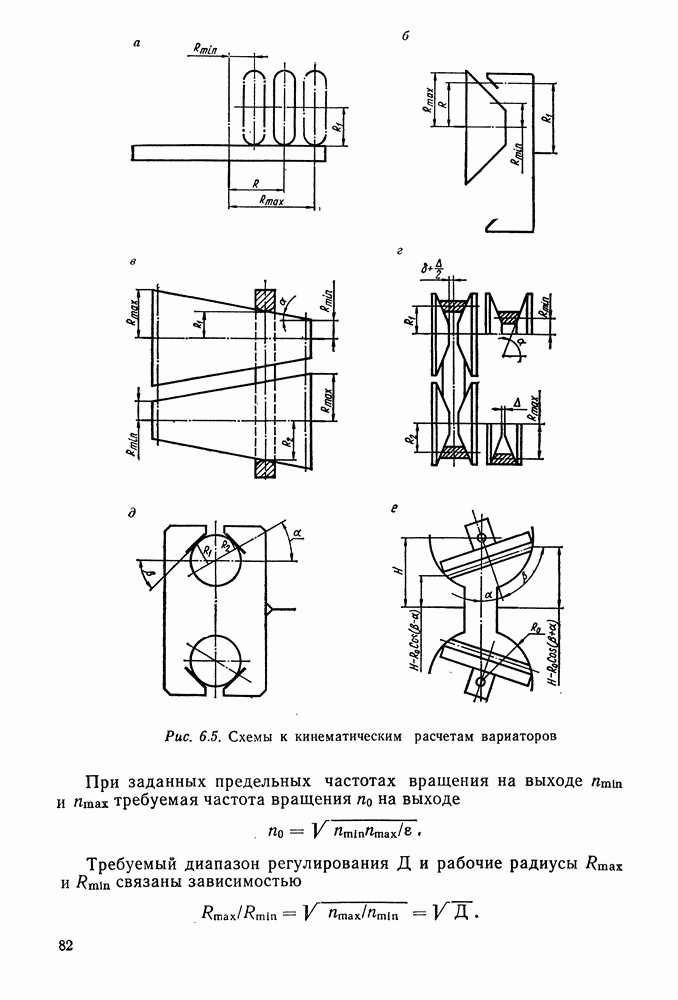
- 6.2. Кинематические расчеты фрикционных передач
- 6.3. Определение сил прижатия фрикционных тел и нагрузки на валы передачи
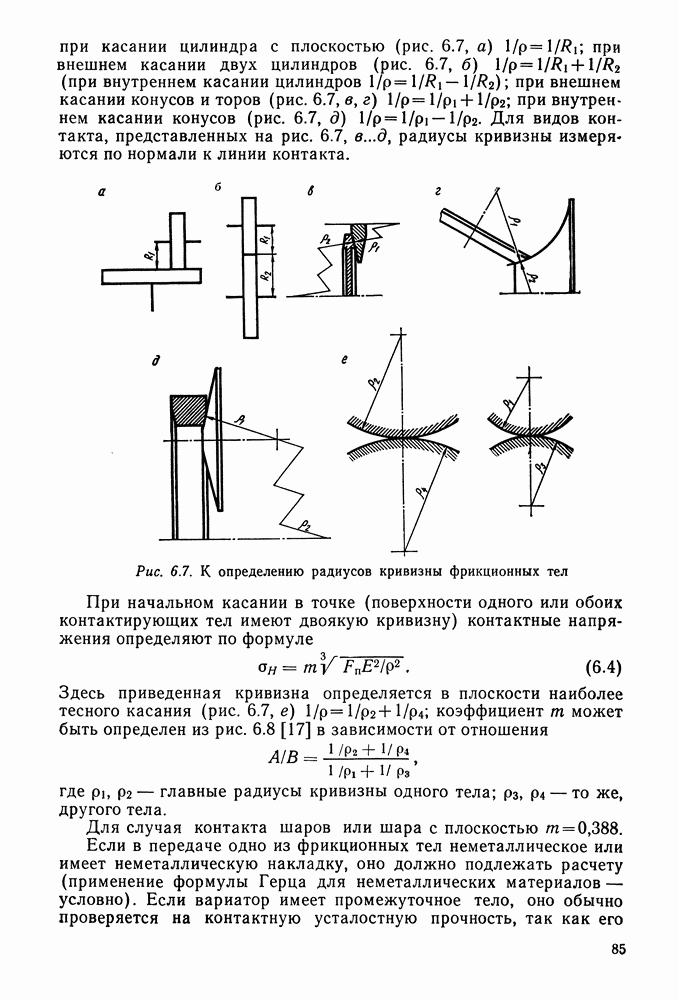
- 6.4. Расчет фрикционных тел на контактную прочность и КПД передач
- 6.5. Справочный материал
- 6.6. Примеры расчета
- Глава 7. РЕМЕННЫЕ ПЕРЕДАЧИ
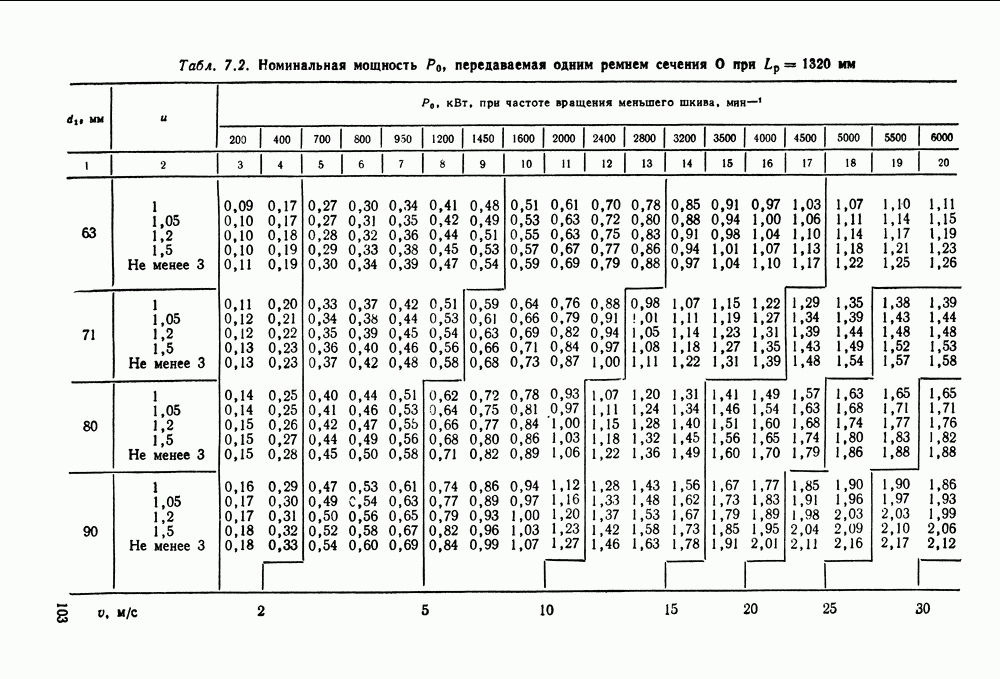
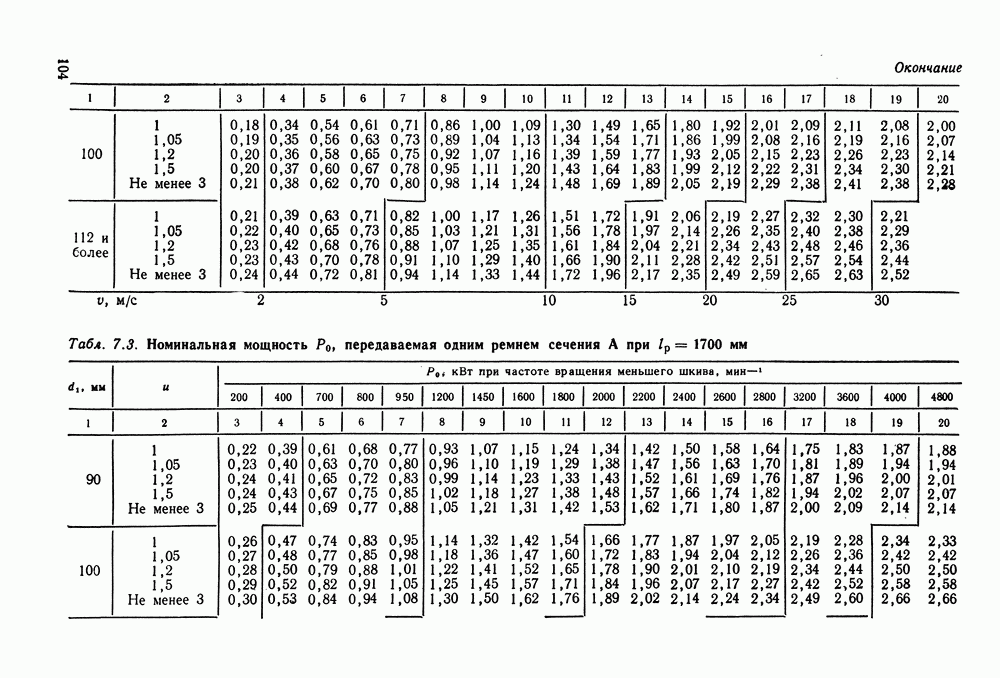
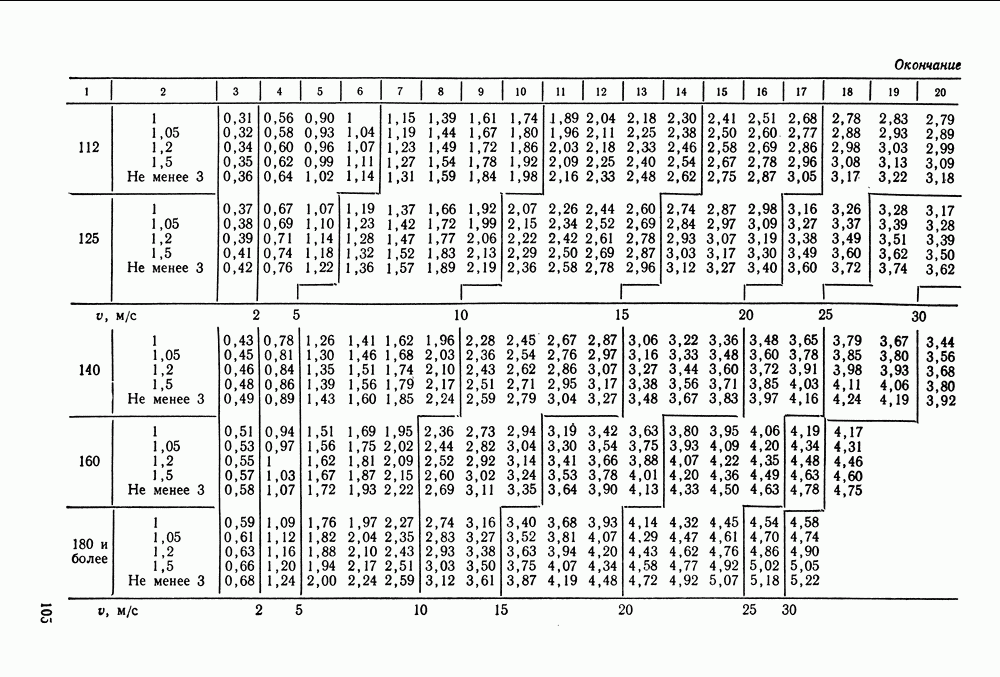
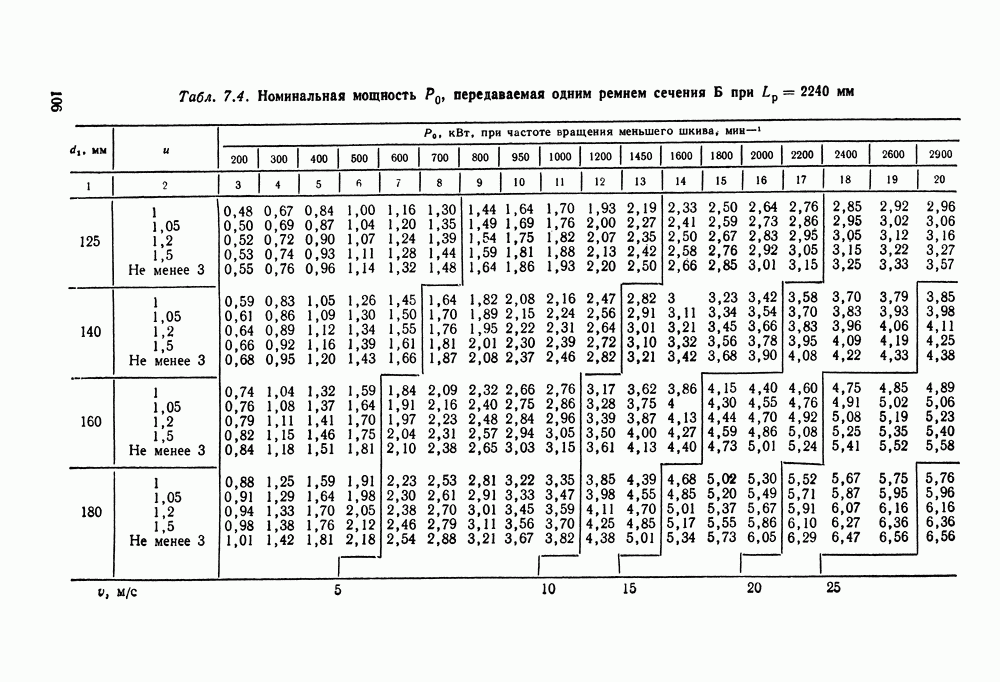
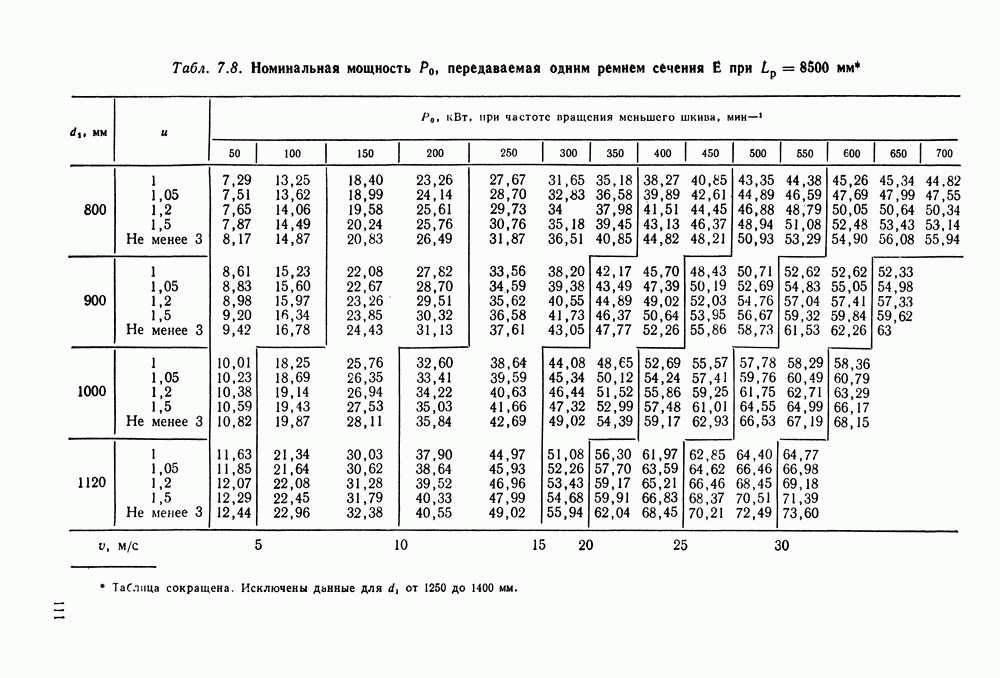
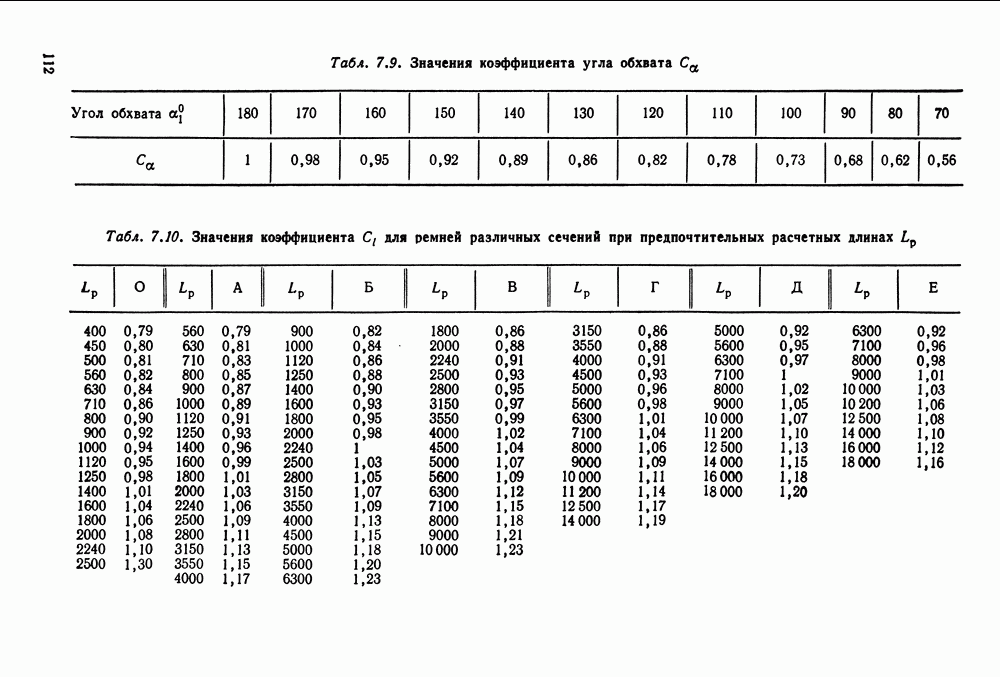
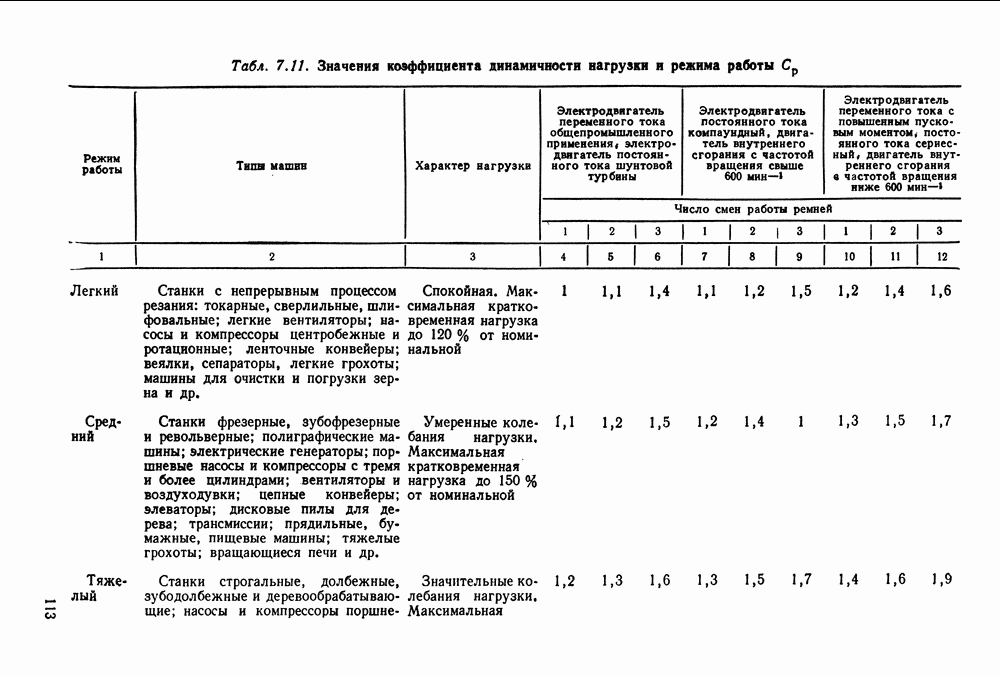
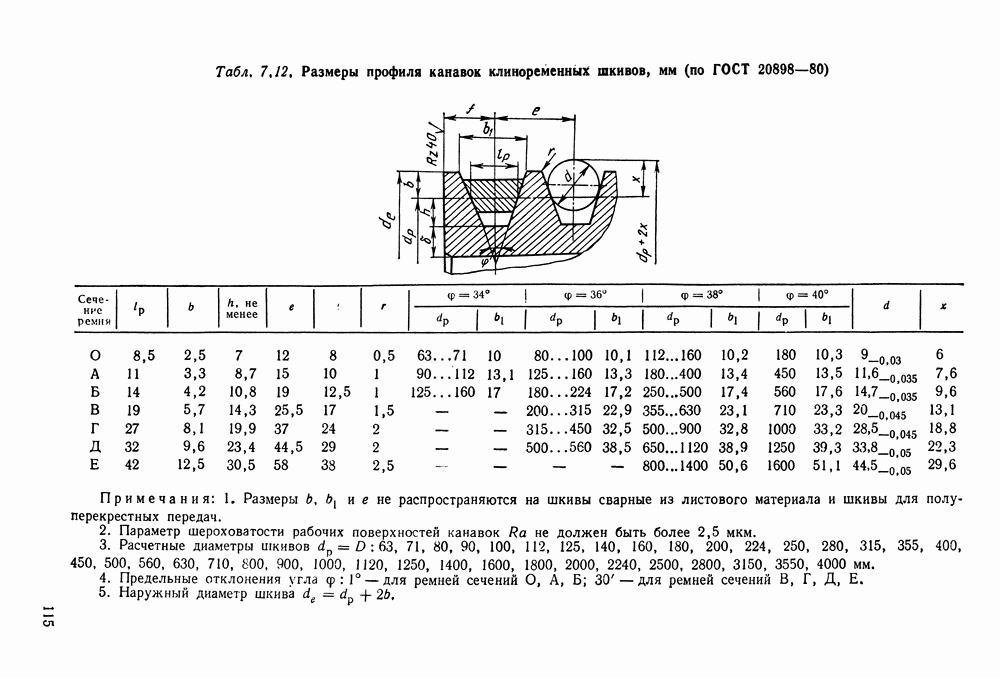
- 7.2. Расчет клиноременных передач
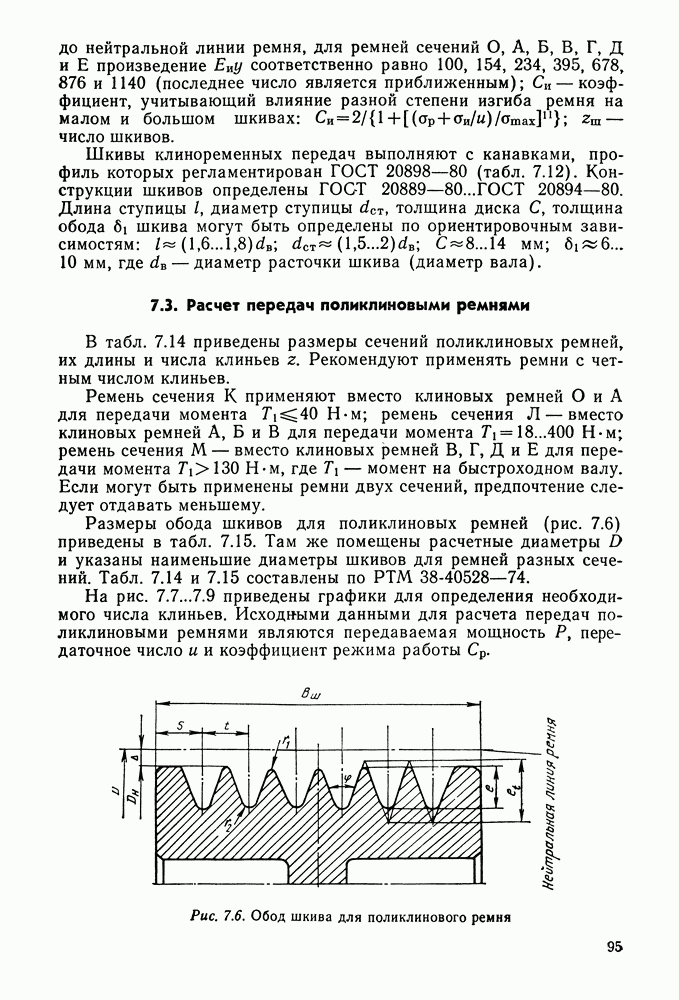
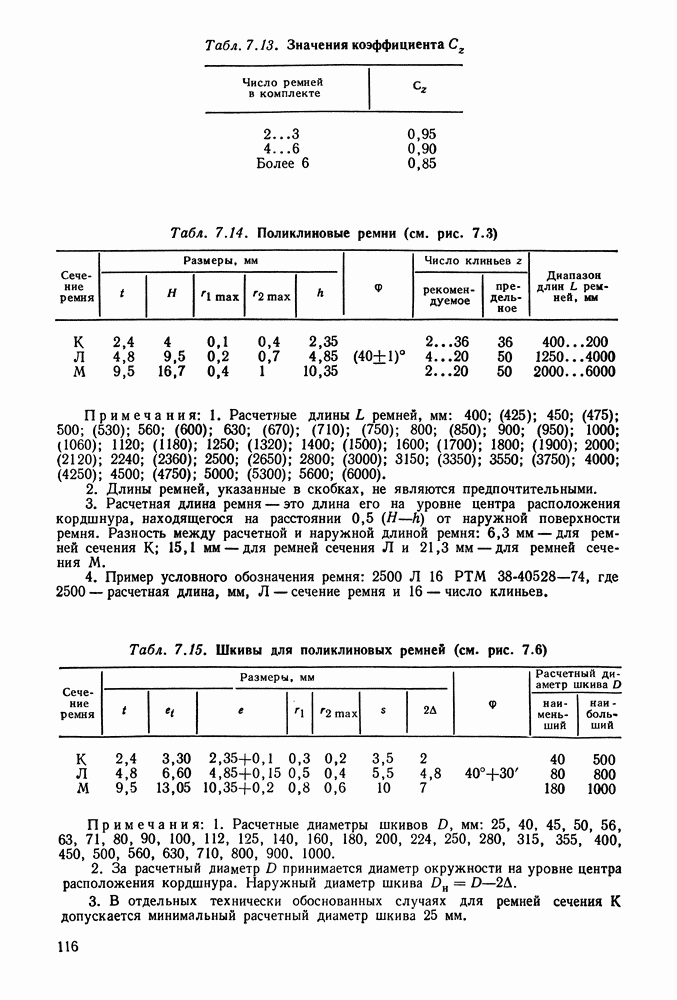
- 7.3. Расчет передач поликлиновыми ремнями
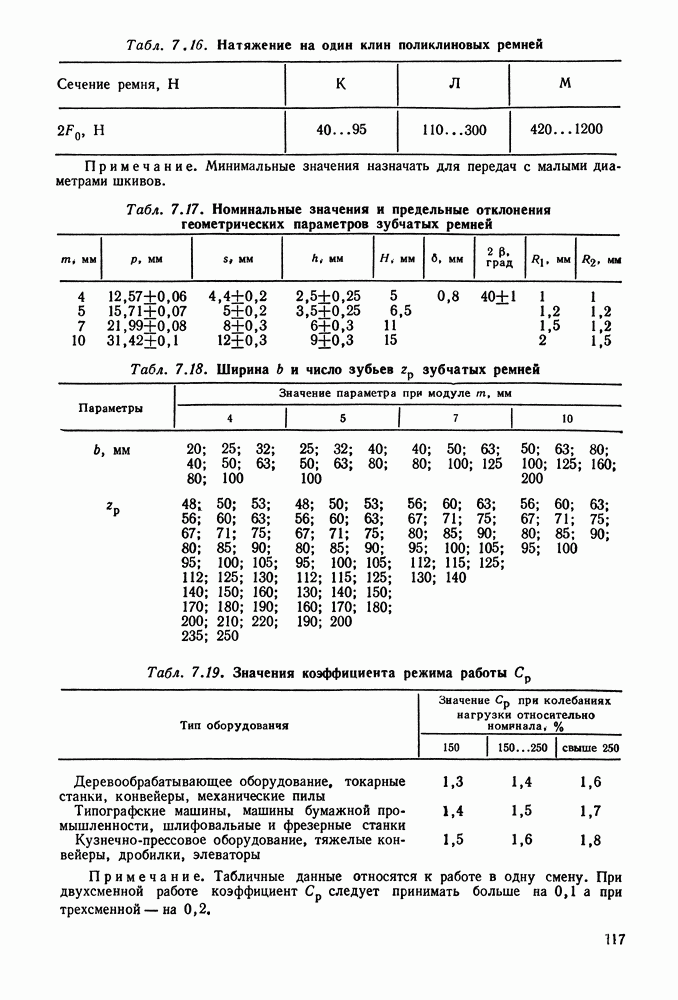
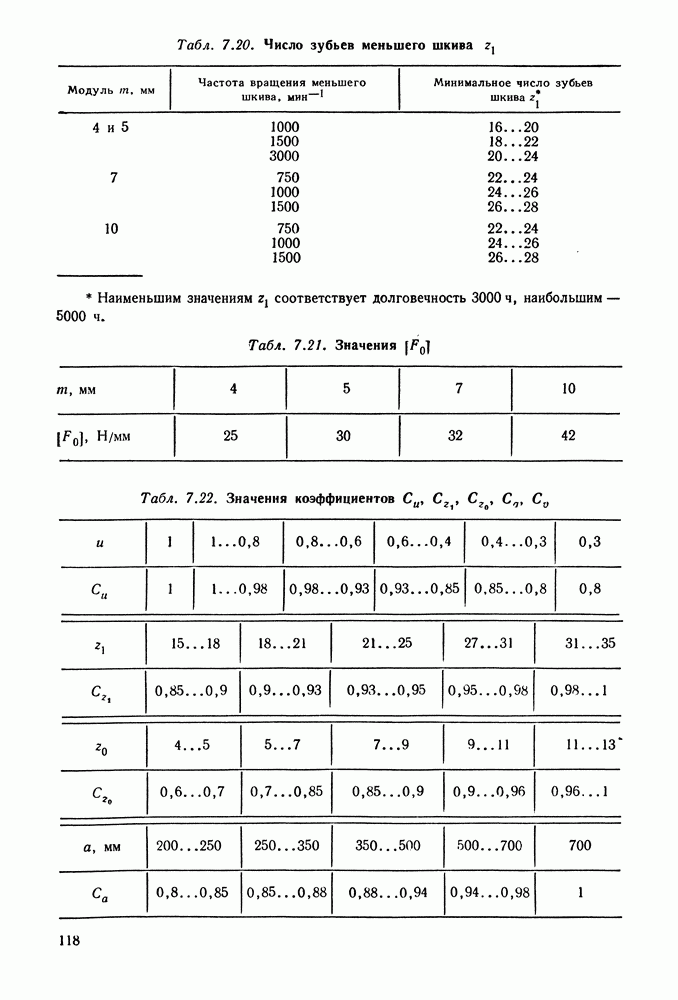
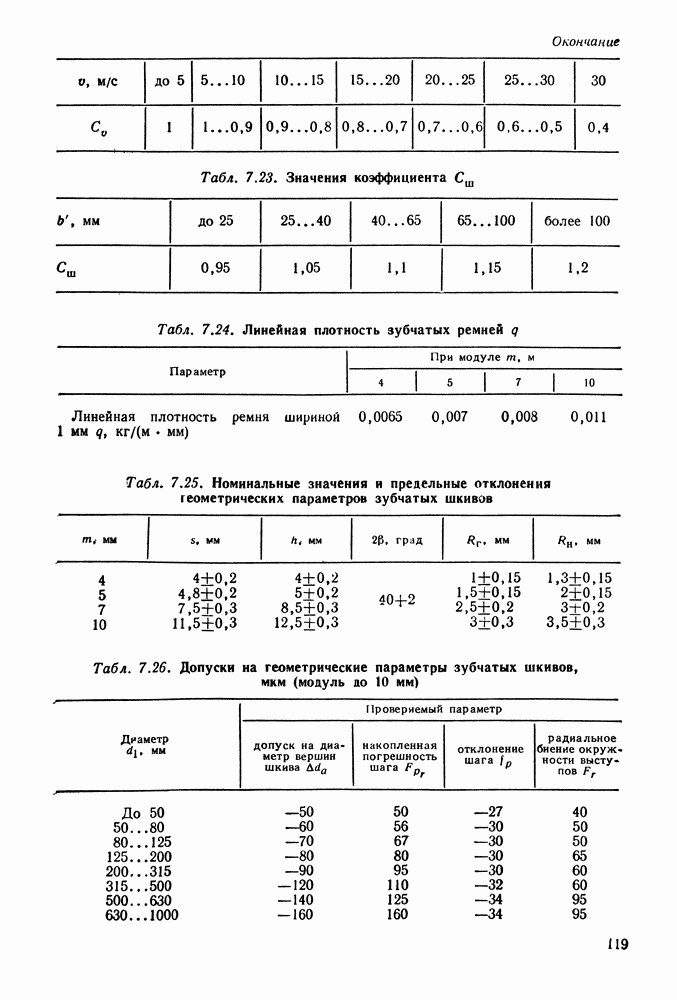
- 7.4. Расчет зубчато-ременных передач
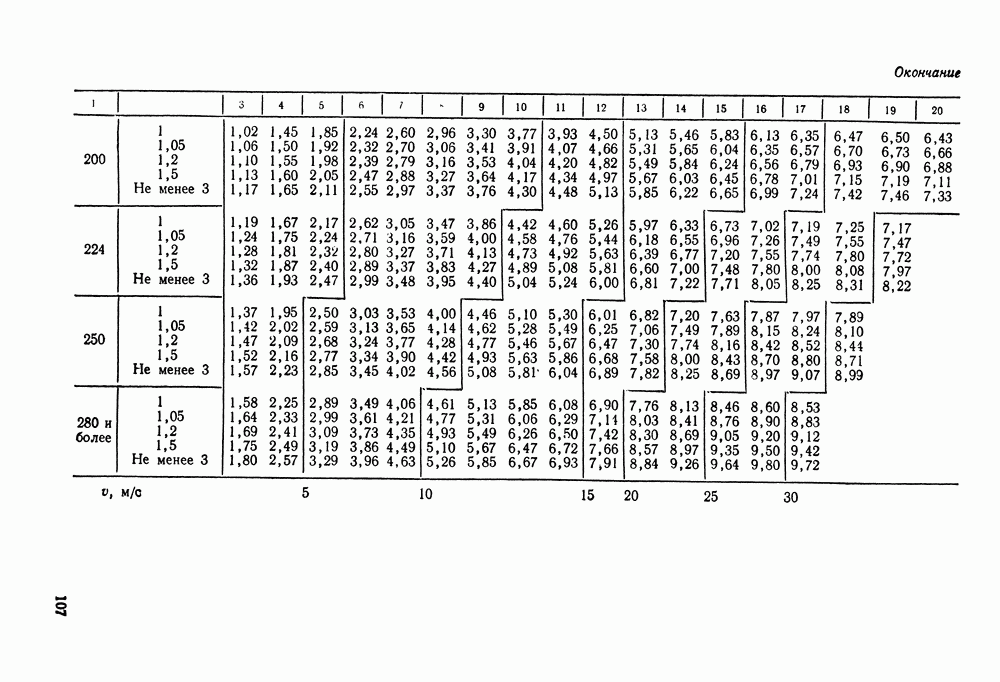
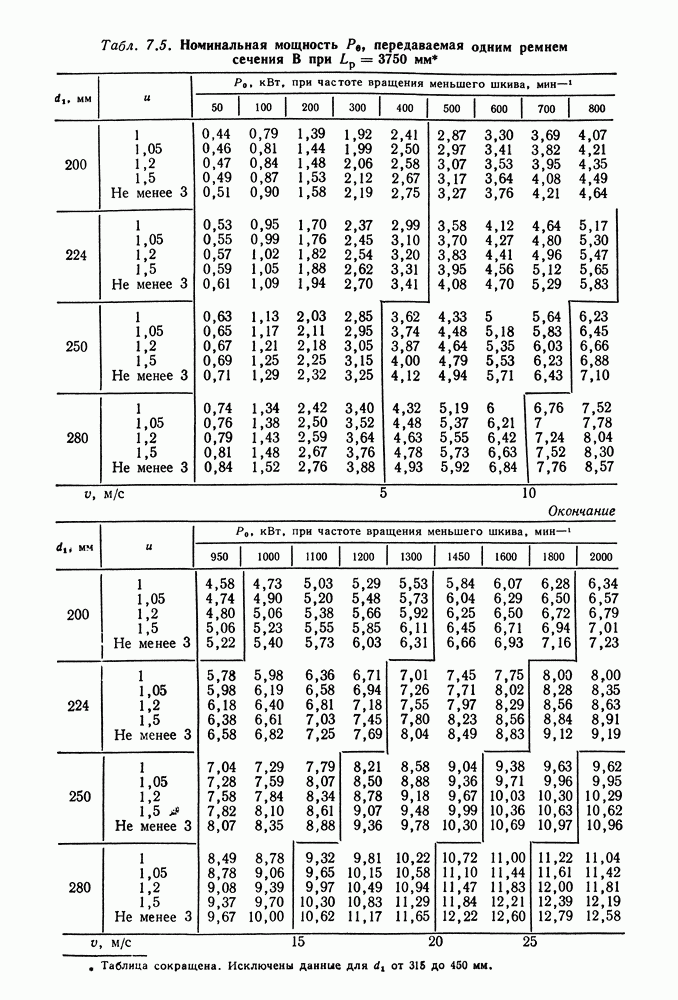
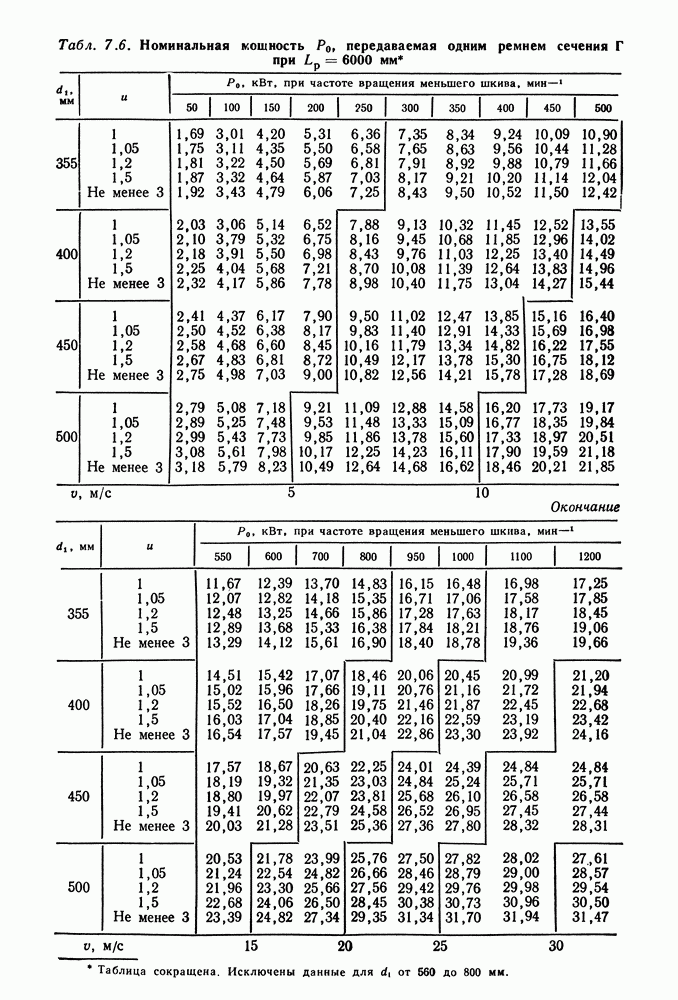
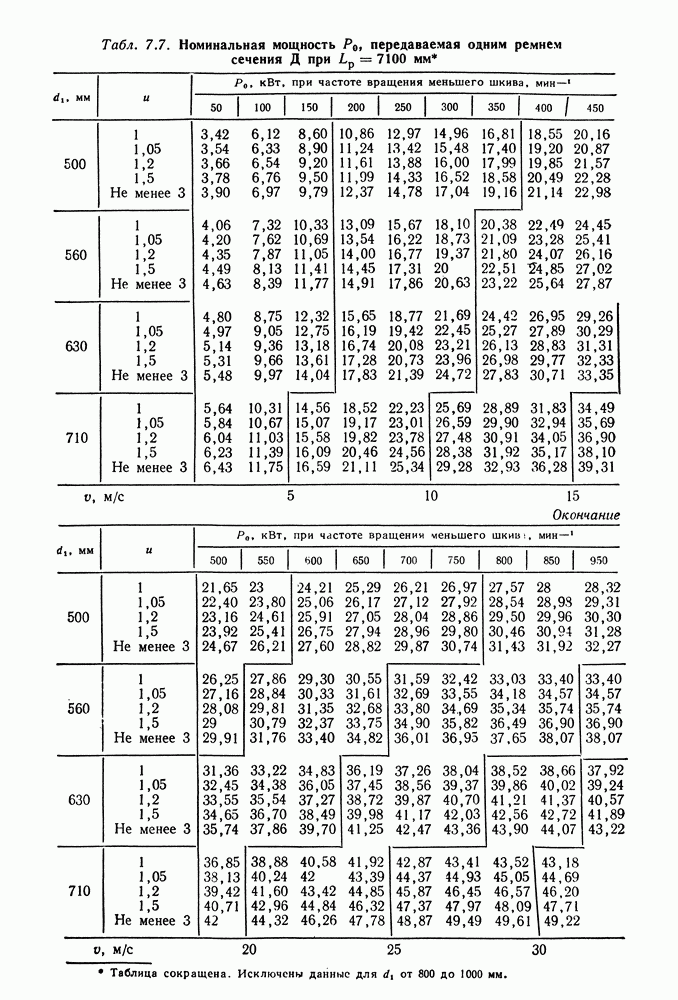
- 7.5. Справочный материал
- 7.6. Примеры расчета
- Глава 8. ЦЕПНЫЕ ПЕРЕДАЧИ
- 8.2. Геометрический, кинематический и силовой расчеты цепных передач
- 8.3. Выбор основных параметров и расчет цепных передач
- 8.4. Справочный материал
- 8.5. Примеры расчета
- Глава 9. ЗУБЧАТЫЕ ПЕРЕДАЧИ
- 9.2. Геометрия и кинематика эвольвентного цилиндрического зацепления
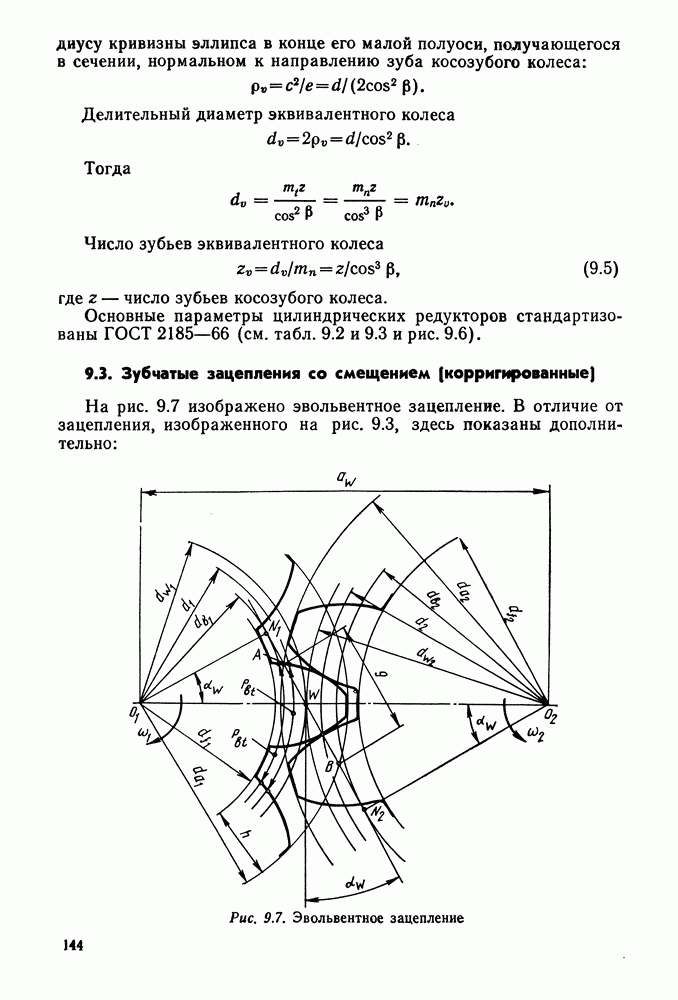
- 9.3. Зубчатые зацепления со смещением (корригированные)
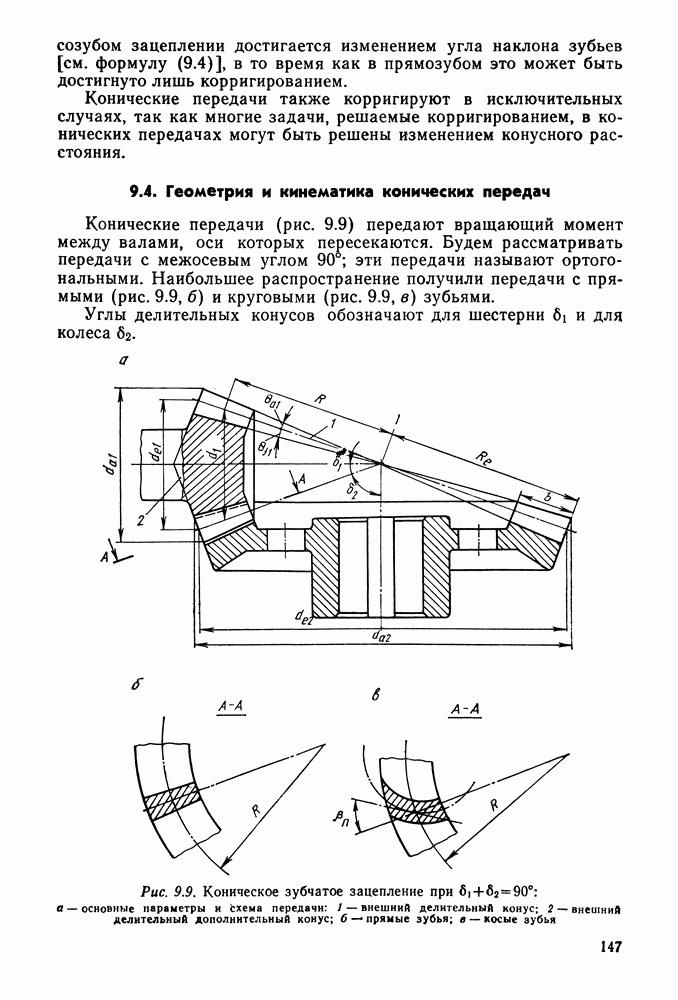
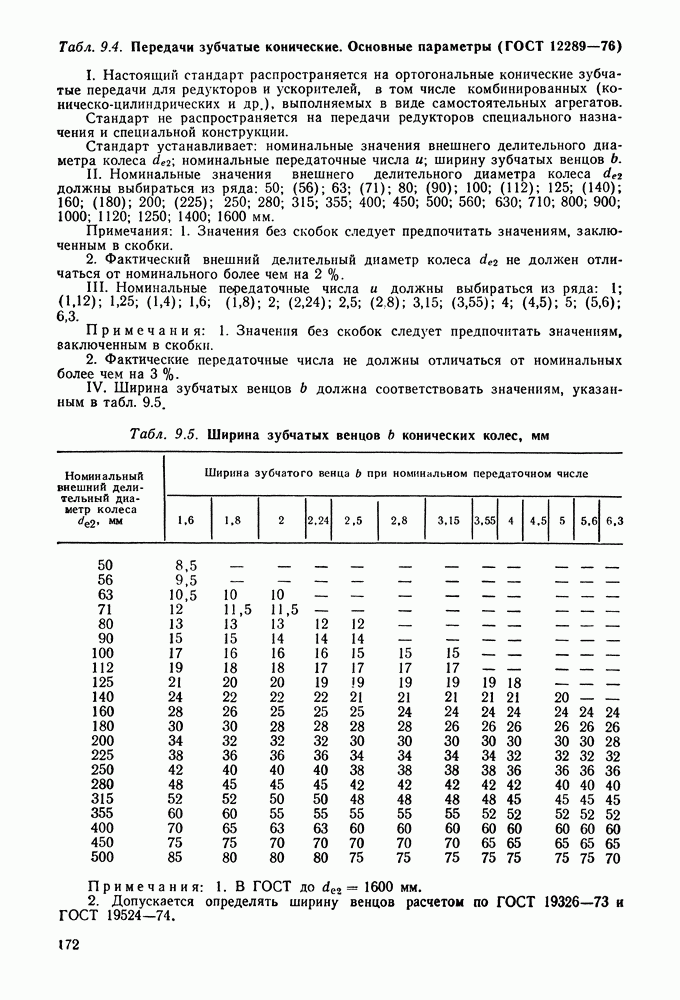
- 9.4. Геометрия и кинематика конических передач
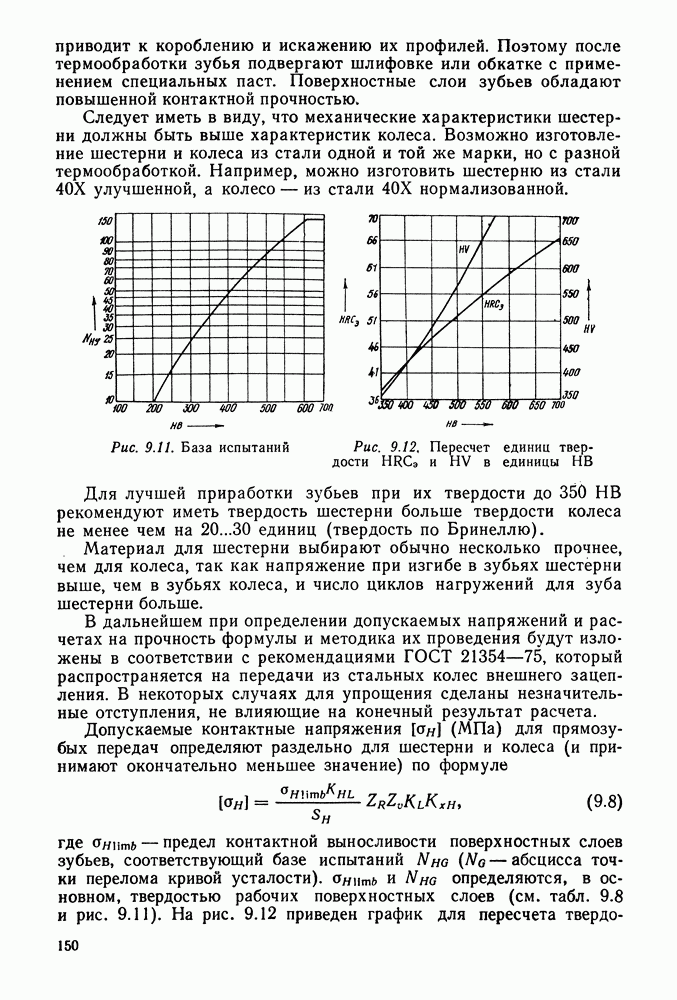
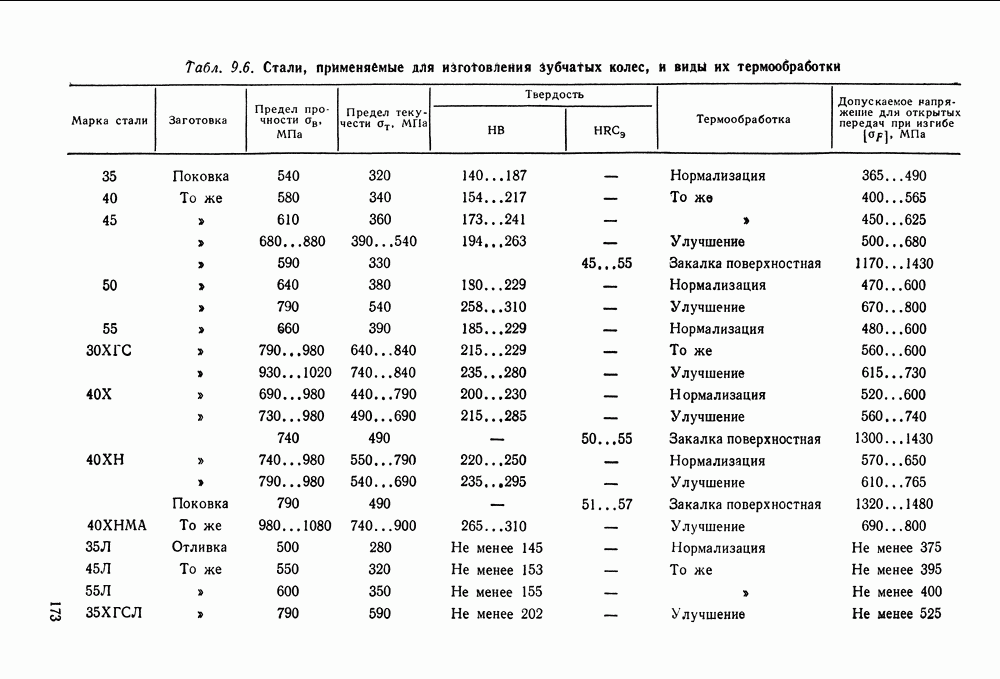
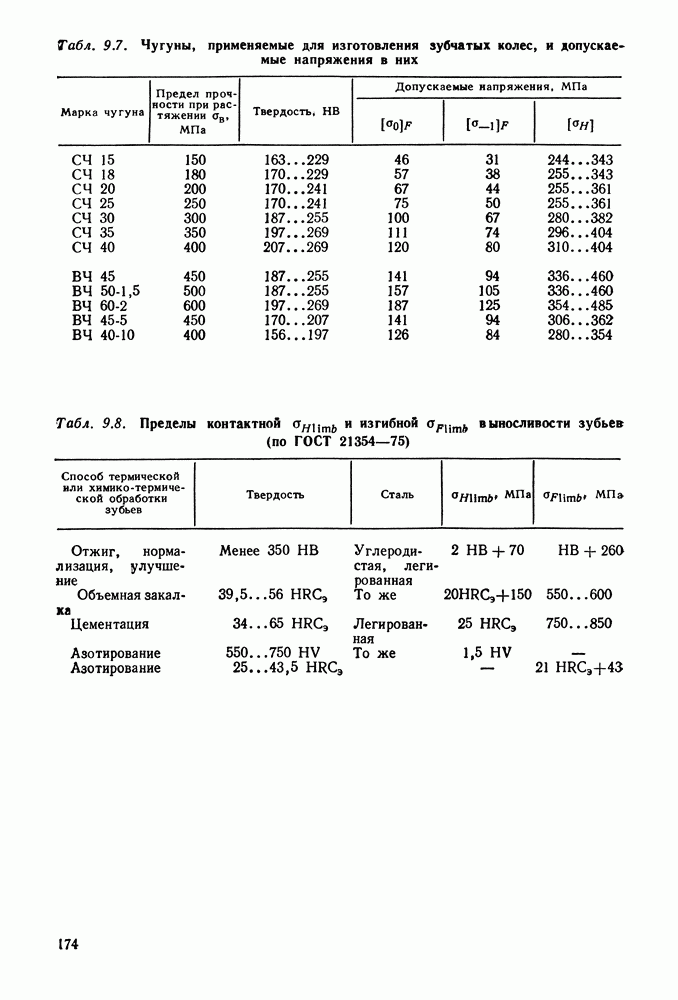
- 9.5. Материалы и допускаемые напряжения
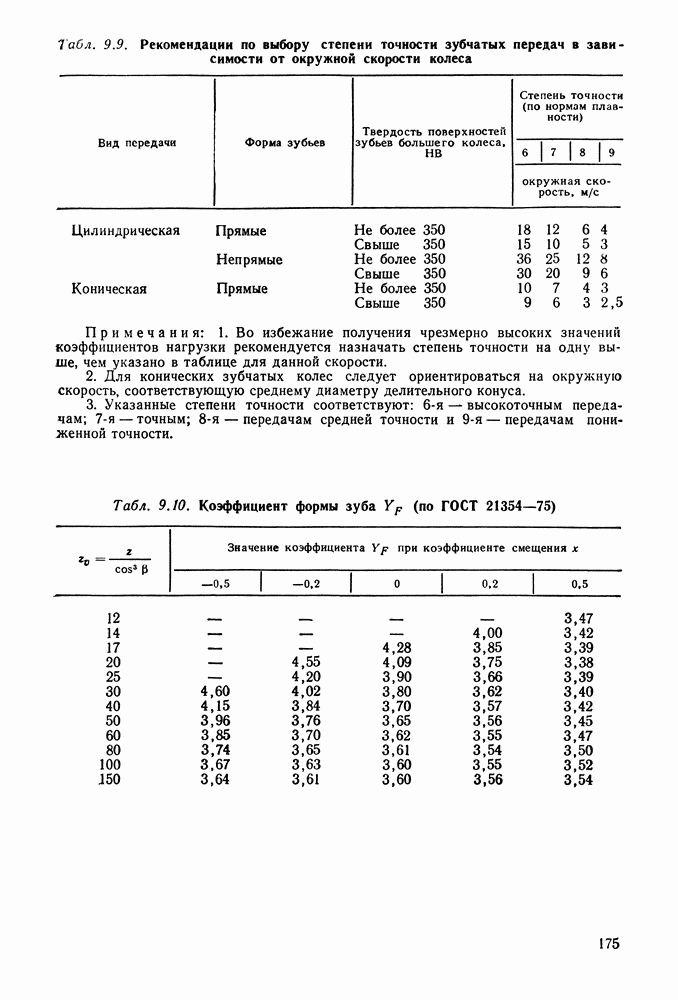
- 9.6. Точность зубчатых передач
- 9.7. Коэффициент нагрузки
- 9.8. Расчет зубчатого зацепления на контактную прочность
- 9.9. Расчет зубьев колес на изгиб
- 9.10. Расчет открытых зубчатых передач
- 9.11. Проверка прочности зубьев колес при перегрузках
- 9.12. Определение размеров стальных зубчатых закрытых передач и проверка их прочности
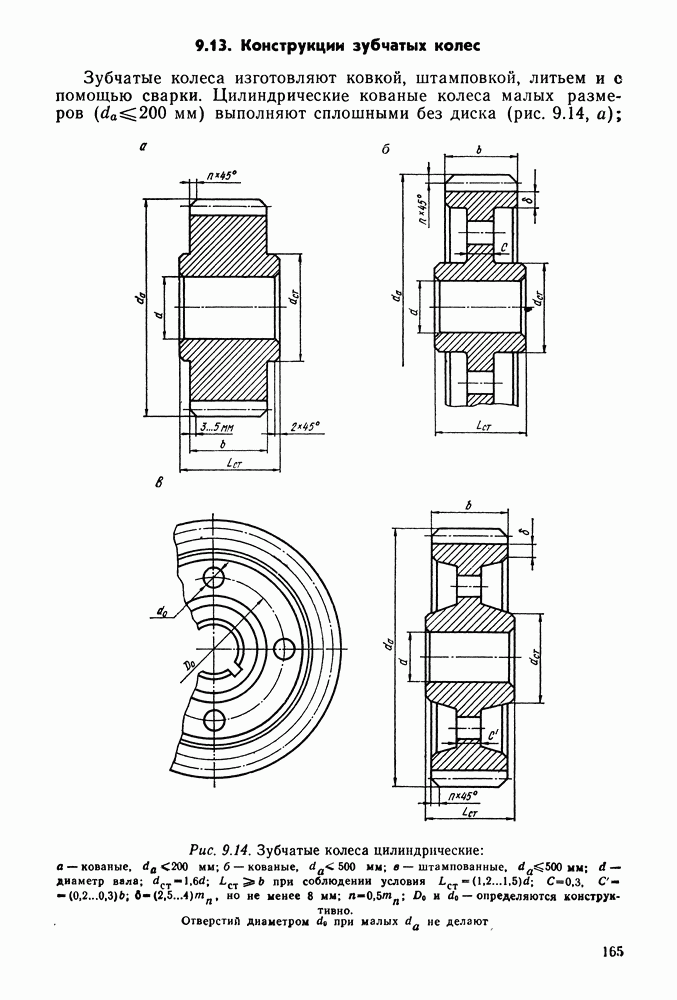
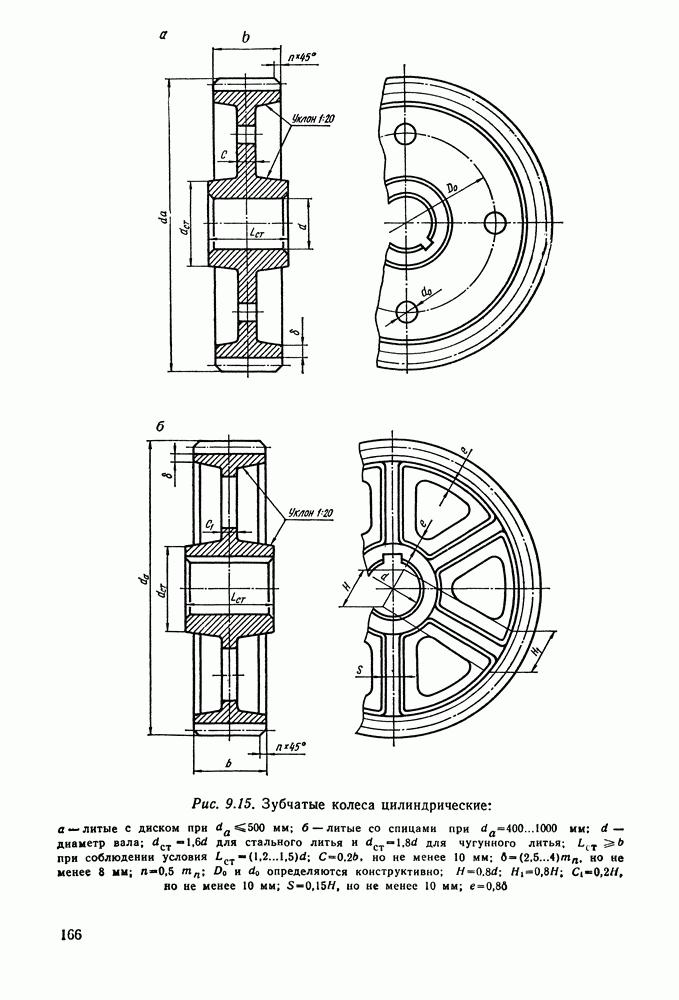
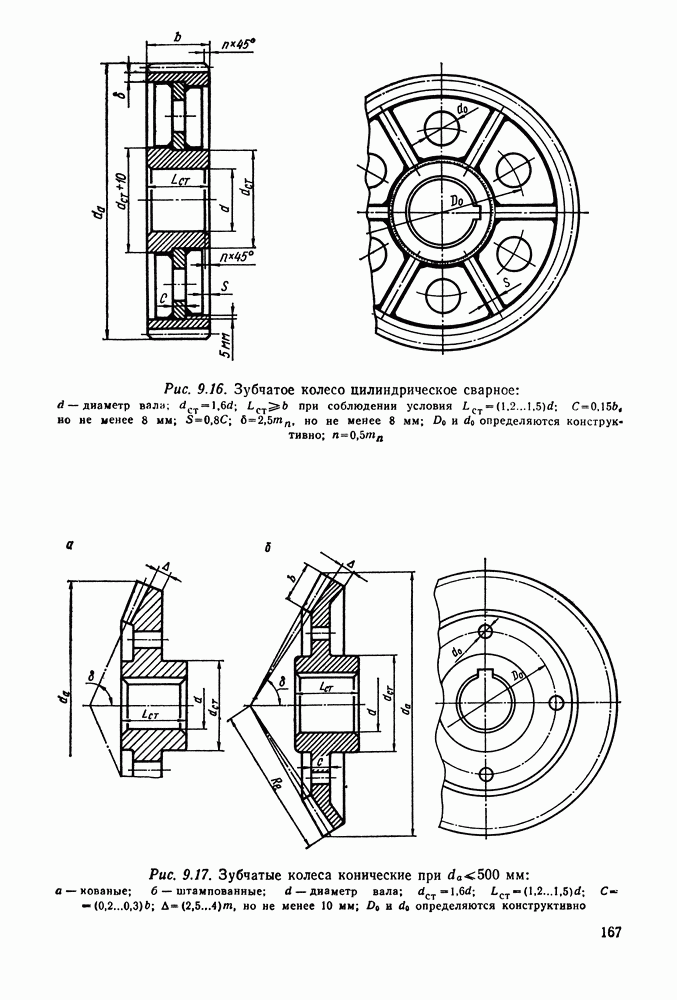
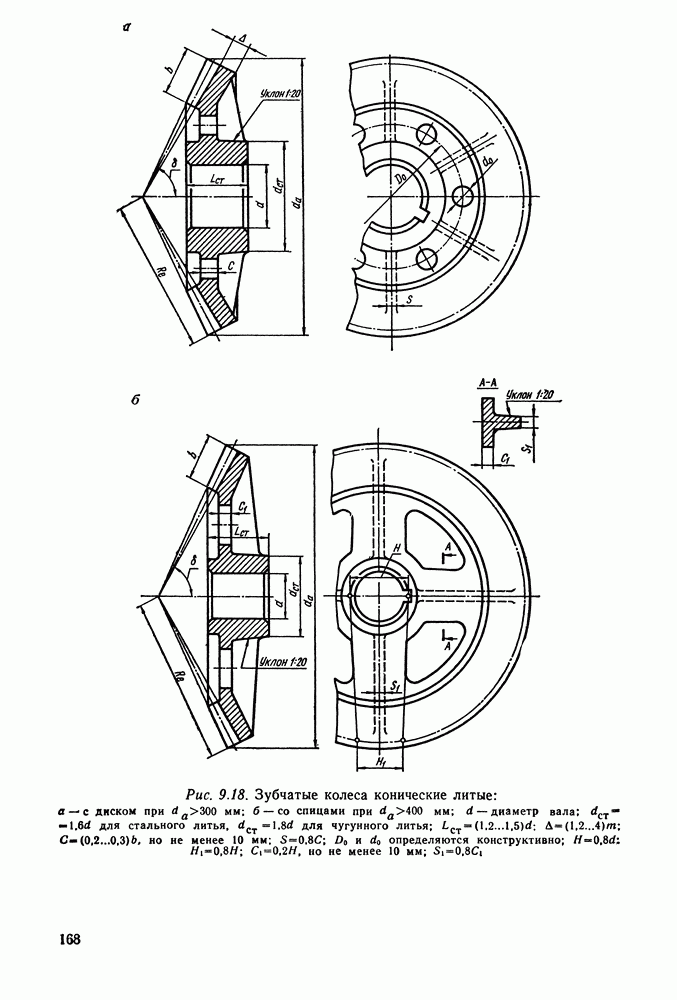
- 9.13. Конструкции зубчатых колес
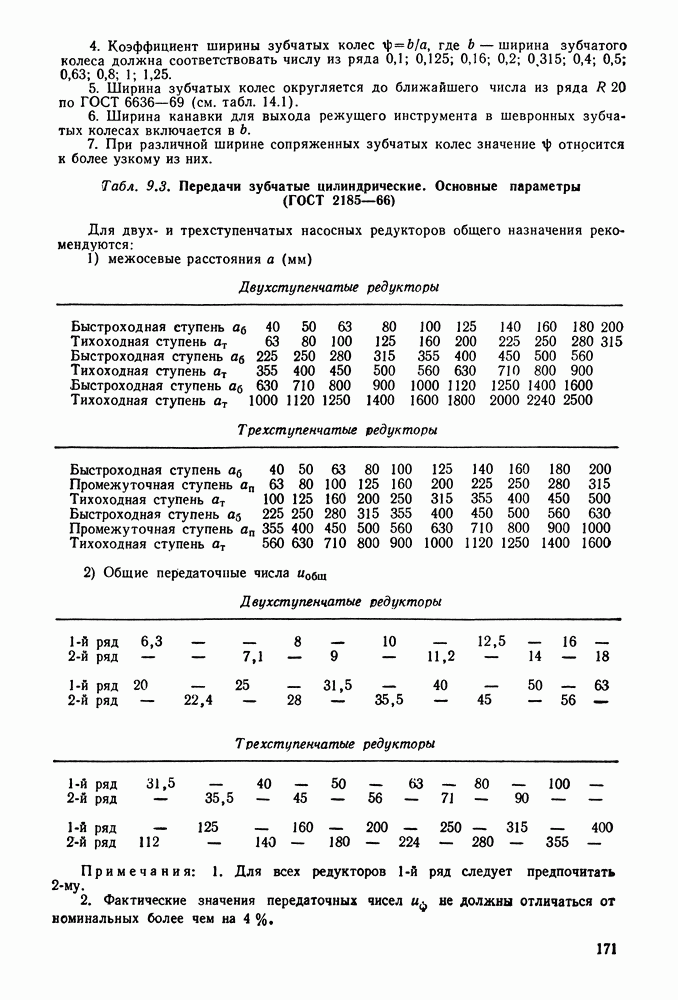
- 9.14. Справочный материал
- 9.15. Примеры расчета
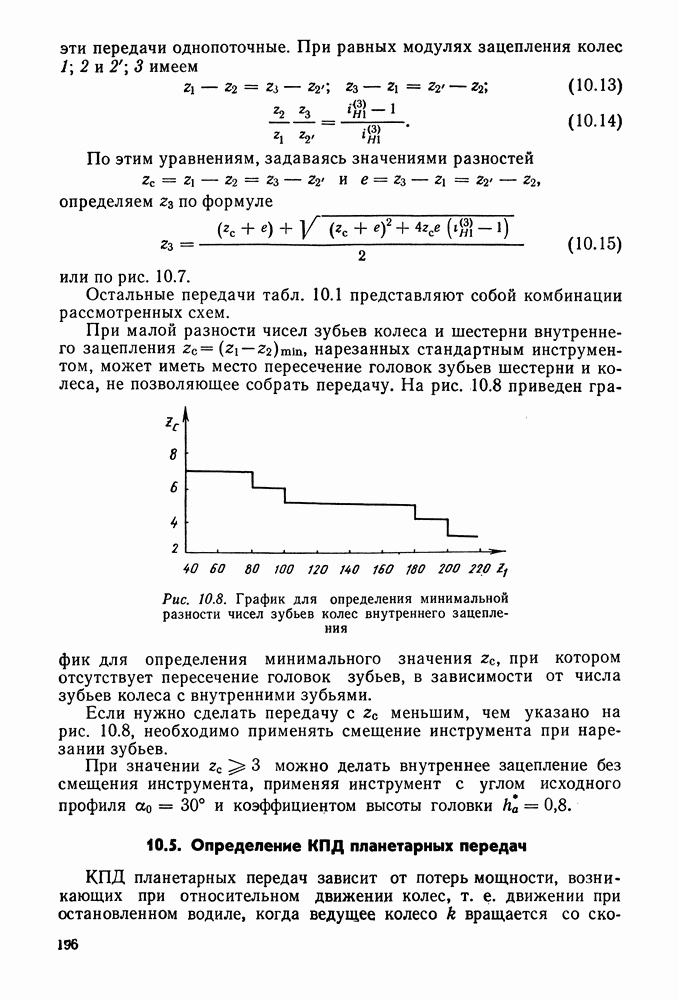
- Глава 10. ПЛАНЕТАРНЫЕ ПЕРЕДАЧИ
- 10.2. Кинематический расчет
- 10.3. Условия собираемости соосных и многопоточных передач
- 10.4. Порядок подбора чисел зубьев при заданном передаточном отношении и числе сателлитов
- 10.5. Определение КПД планетарных передач
- 10.6. Определение сил, действующих в зацеплениях и в опорах осей и валов прямозубых передач
- 10.7. Расчет зубьев планетарных передач на прочность
- 10.8. Конструкция и размеры деталей планетарных передач [14]
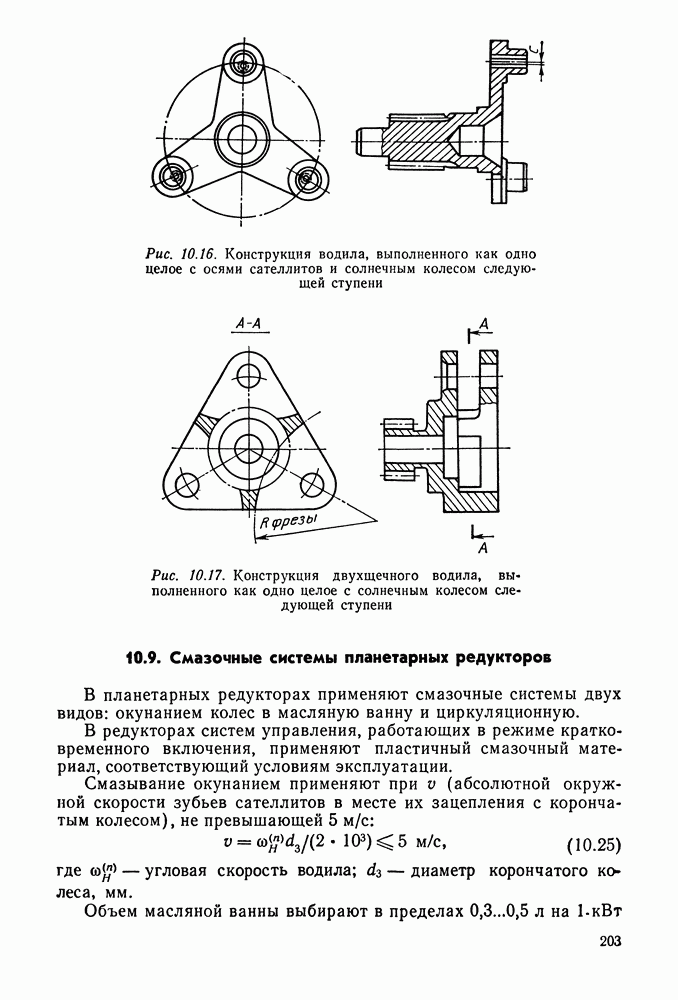
- 10.9. Смазочные системы планетарных редукторов
- 10.10. Порядок проектного расчета планетарного редуктора (схемы 1 и 2 табл. 10.1)
- 10.11. Порядок расчета планетарного мотор-редуктора (схема 1 табл. 10.1)
- 10.12. Справочный материал
- 10.13. Примеры расчета
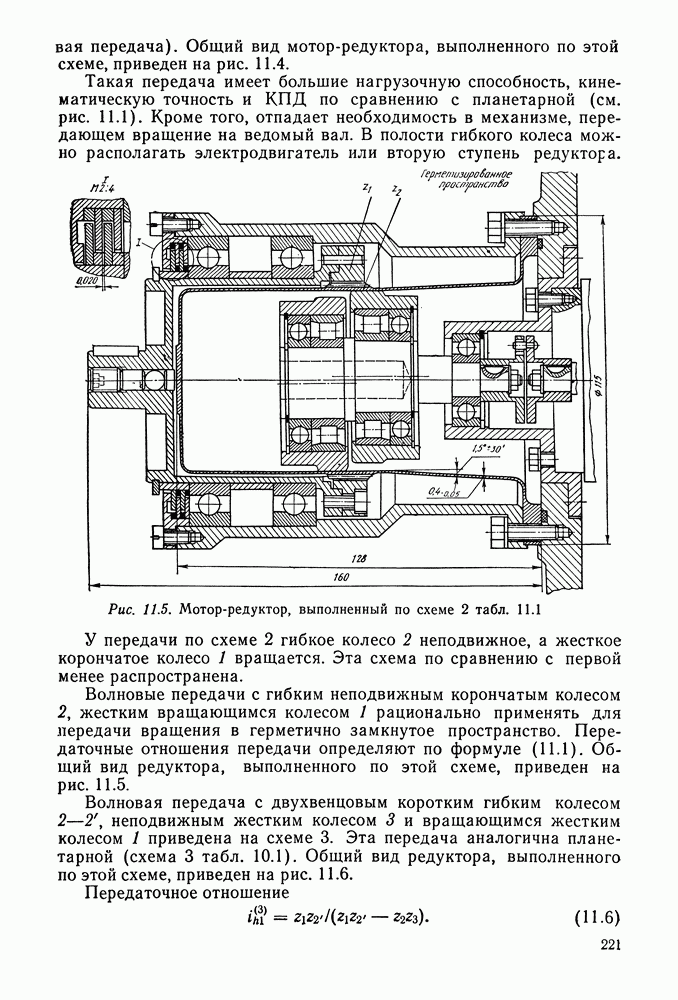
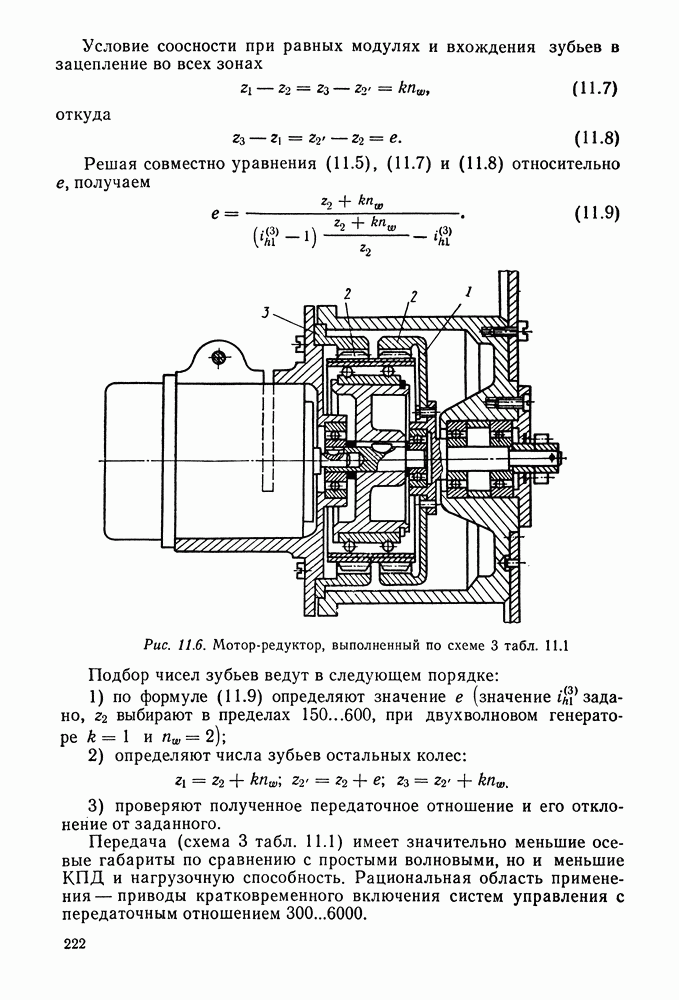
- Глава 11. ВОЛНОВЫЕ ПЕРЕДАЧИ
- 11.2 Основные схемы волновых передач
- 11.3. Проектный расчет волновой зубчатой передачи
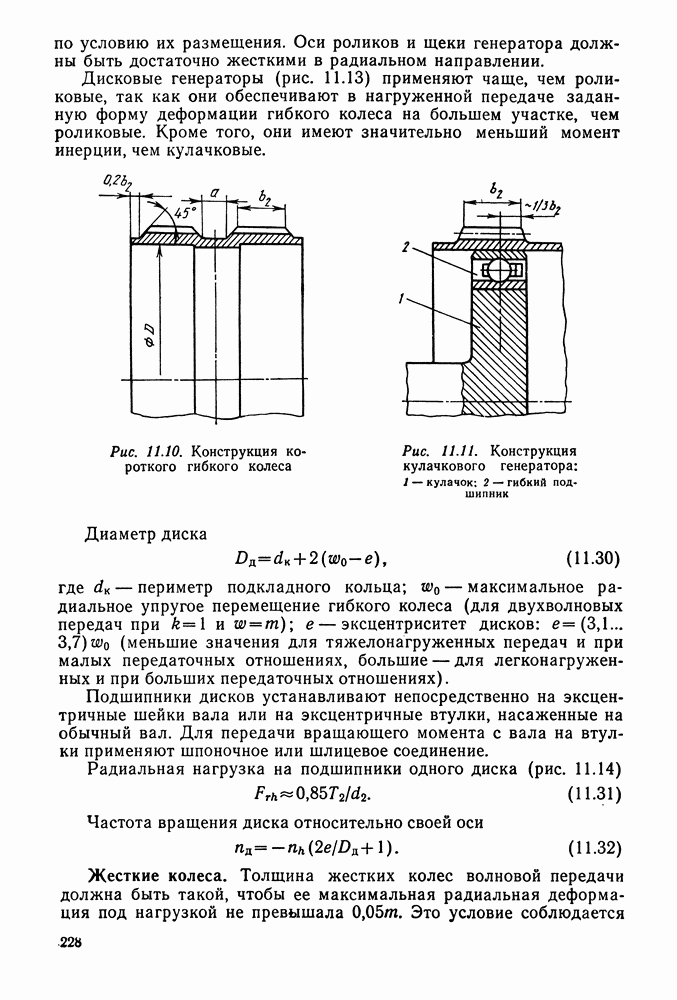
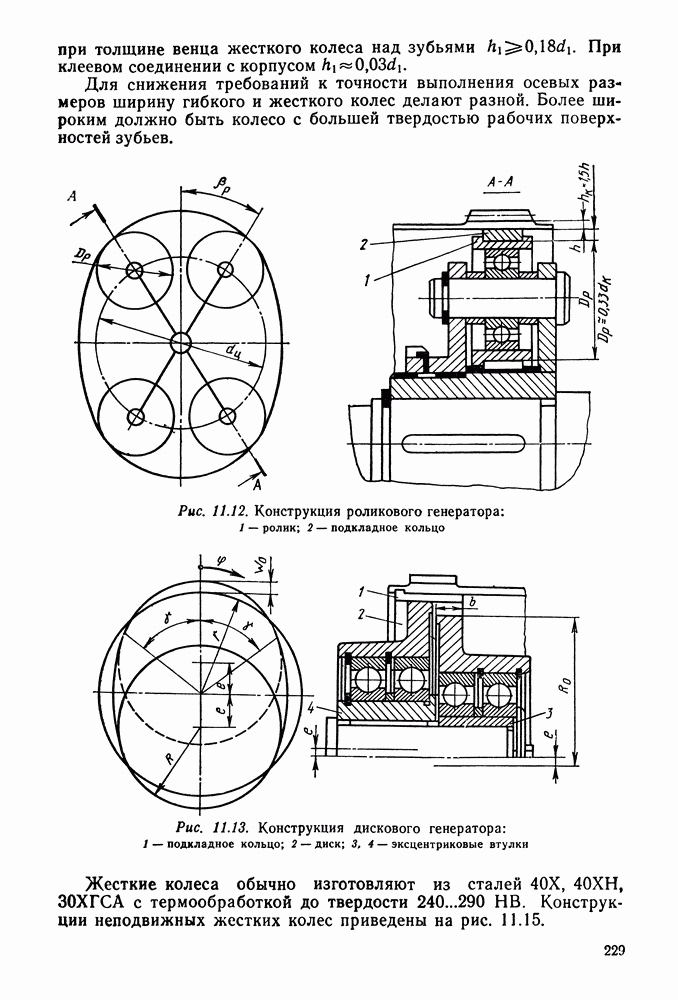
- 11.4. Конструкция и размеры основных деталей волновых передач
- 11.5. Порядок расчета волновой передачи с кулачковым генератором
- 11.6. Справочный материал
- 11.7. Пример расчета
- Глава 12. ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ
- 12.2 Геометрия и кинематика червячного зацепления
- 12.3. Червячные передачи со смещением (корригированные)
- 12.4. Материалы и допускаемые напряжения
- 12.5. Точность червячных передач
- 12.6. Коэффициент нагрузки
- 12.7. Расчет червячного зацепления на контактную прочность
- 12.8. Расчет на изгиб
- 12.9. Расчет открытых червячных передач
- 12.10. Проверка червячных редукторов на нагрев
- 12.11. Конструкция червяков и червячных колес
- 12.12. Справочный материал
- 12.13. Пример расчета
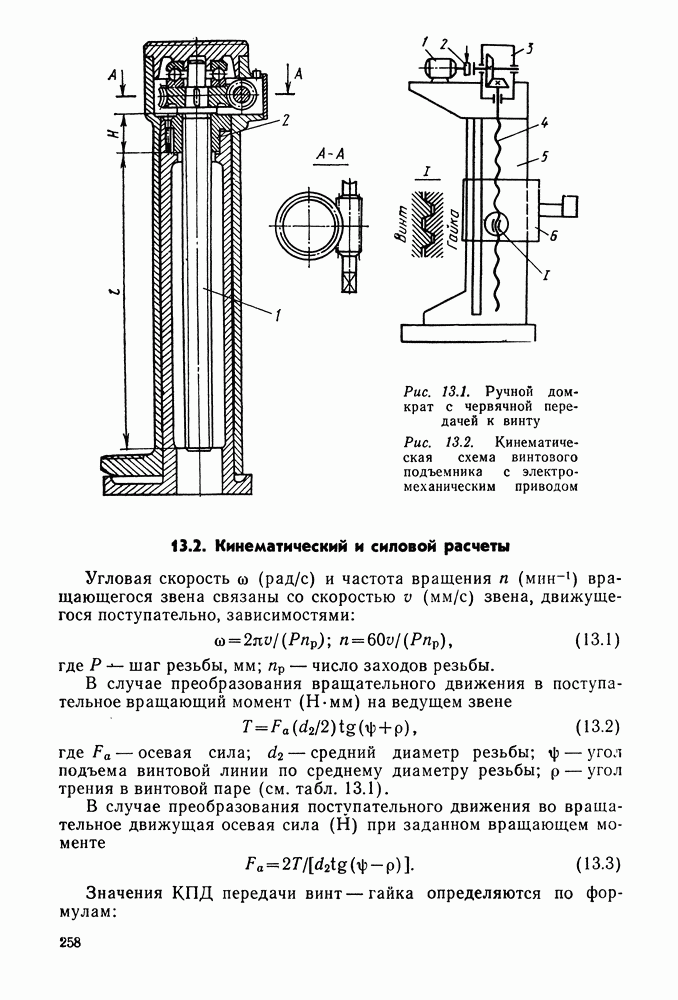
- Глава 13. ПЕРЕДАЧА ВИНТ — ГАЙКА
- 13.2. Кинематический и силовой расчеты
- 13.3. Передача винт—гайка с трением скольжения
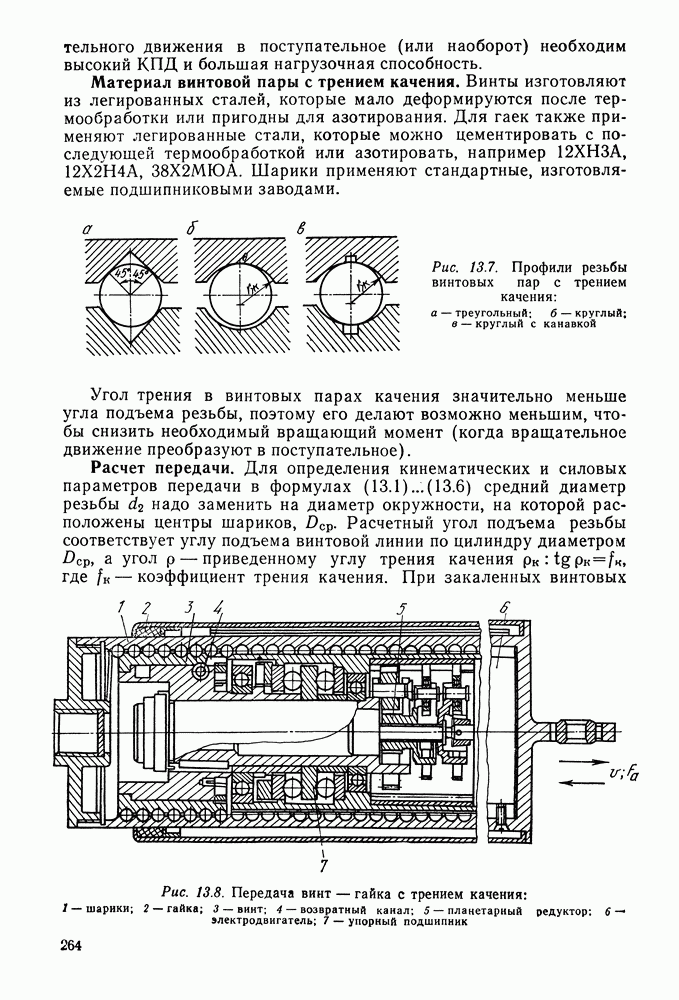
- 13.4. Передача винт — гайка с трением качения
- 13.5. Справочный материал
- 13.6. Пример расчета
- Раздел III. ВАЛЫ, ИХ ОПОРЫ, МУФТЫ, ПРУЖИНЫ
- Глава 14. ВАЛЫ
- 14.2. Некоторые сведения по конструированию валов и выбору материалов
- 14.3. Расчет валов
- 14.4. Посадки основных деталей передач на валы по стандартам СЭВ
- 14.5. Справочный материал
- 14.6. Примеры расчета
- Глава 15. РАДИАЛЬНЫЕ ПОДШИПНИКИ СКОЛЬЖЕНИЯ
- 15.2. Упрощенный расчет подшипников скольжения
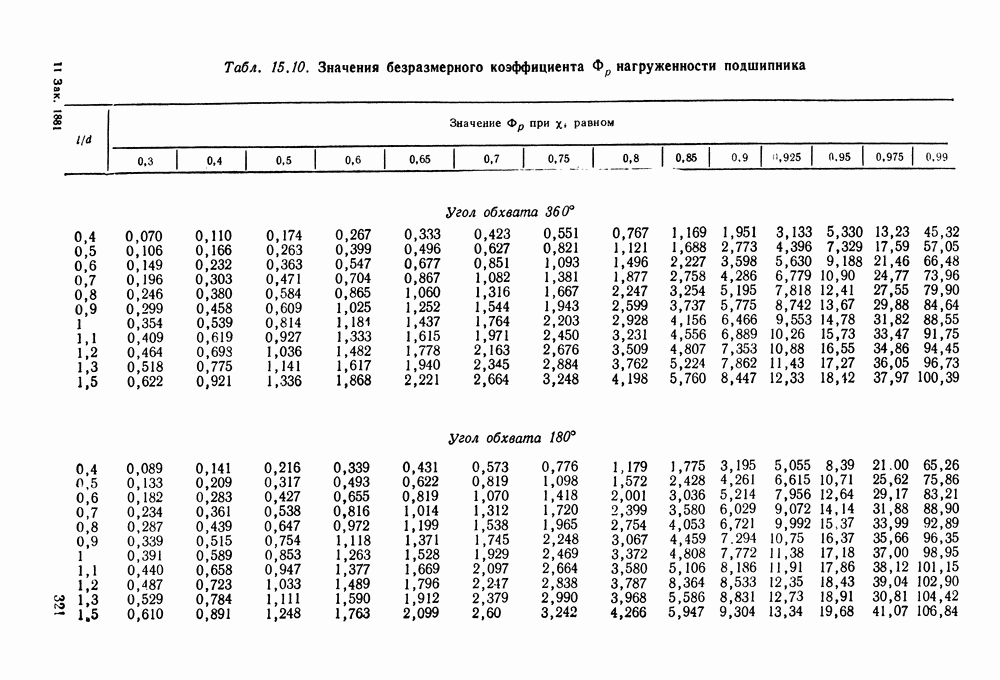
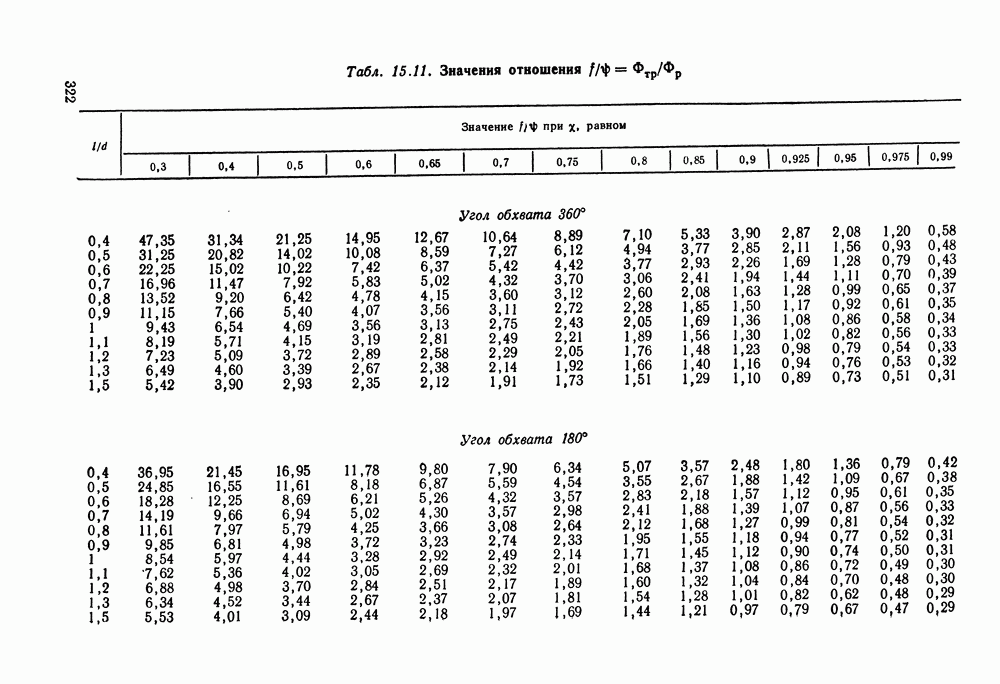
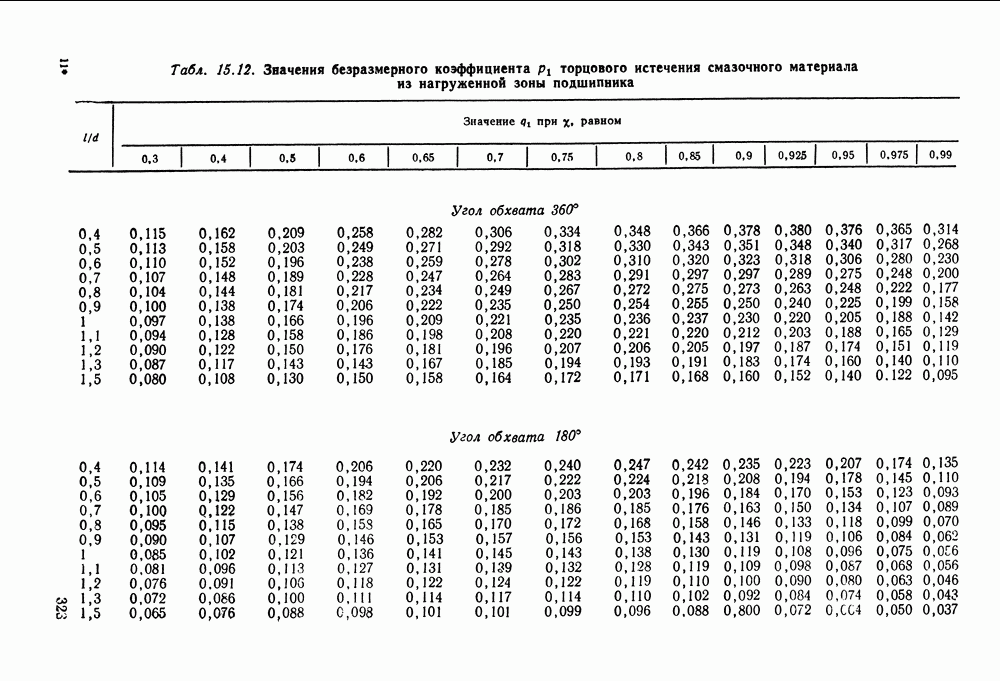
- 15.3. Расчет подшипников жидкостного трения
- 15.4. Сопротивление слоя масла вращению шипа
- 15.5. Тепловой расчет подшипника
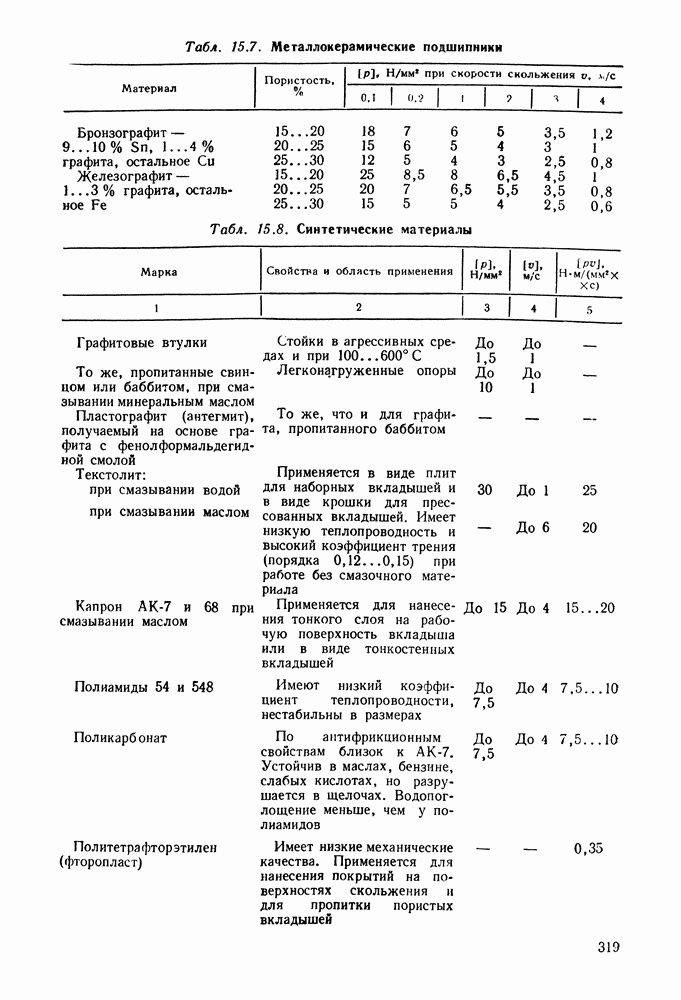
- 15.6. Справочный материал
- 15.7. Примеры расчета
- Глава 16. ПОДШИПНИКИ КАЧЕНИЯ
- 16.2. Условные обозначения и точность подшипников качения
- 16.3. Выбор и проверка подшипников качения по динамической грузоподъемности
- 16.4. Выбор подшипников качения по статической грузоподъемности
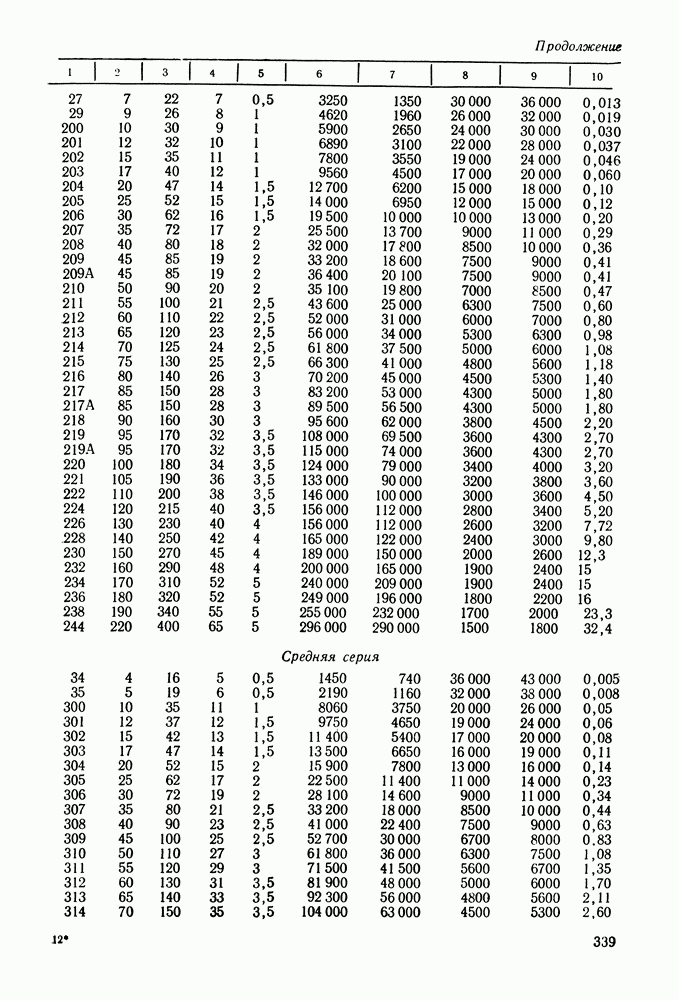
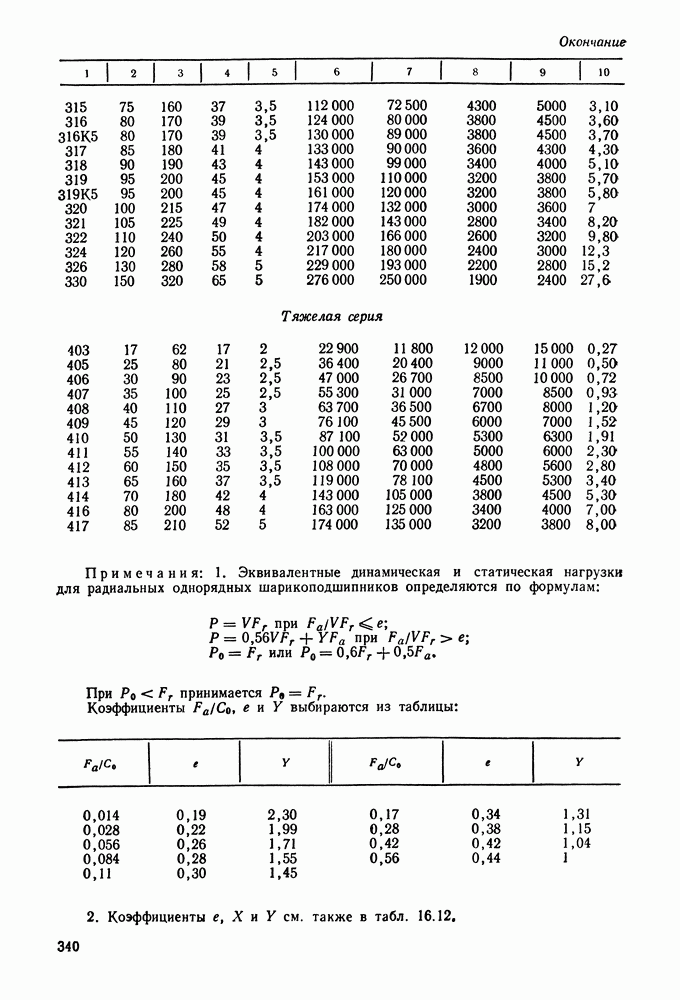
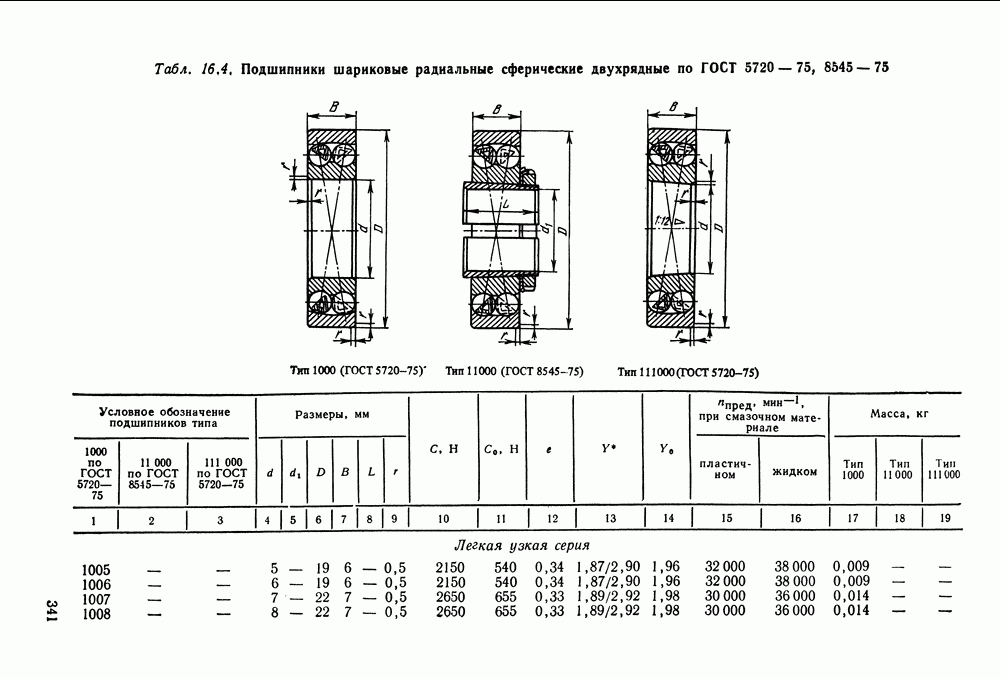
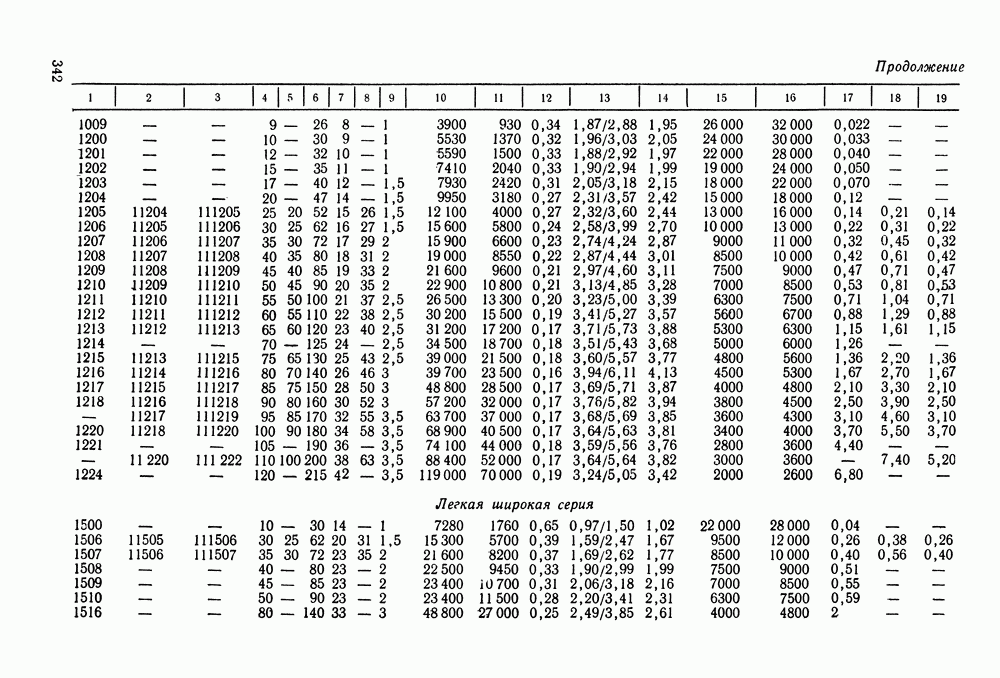
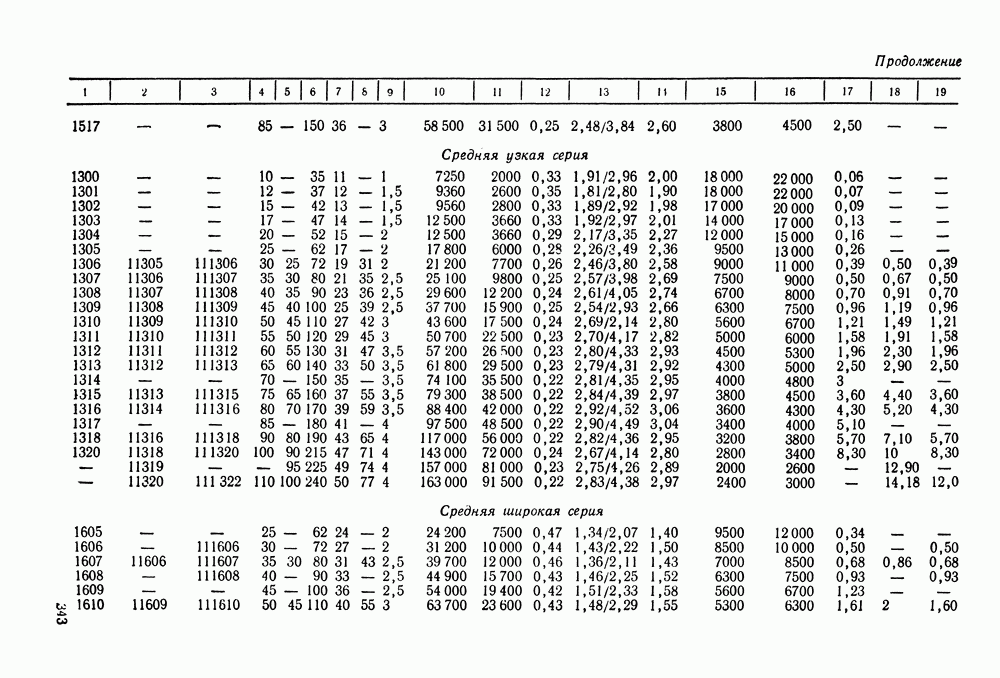
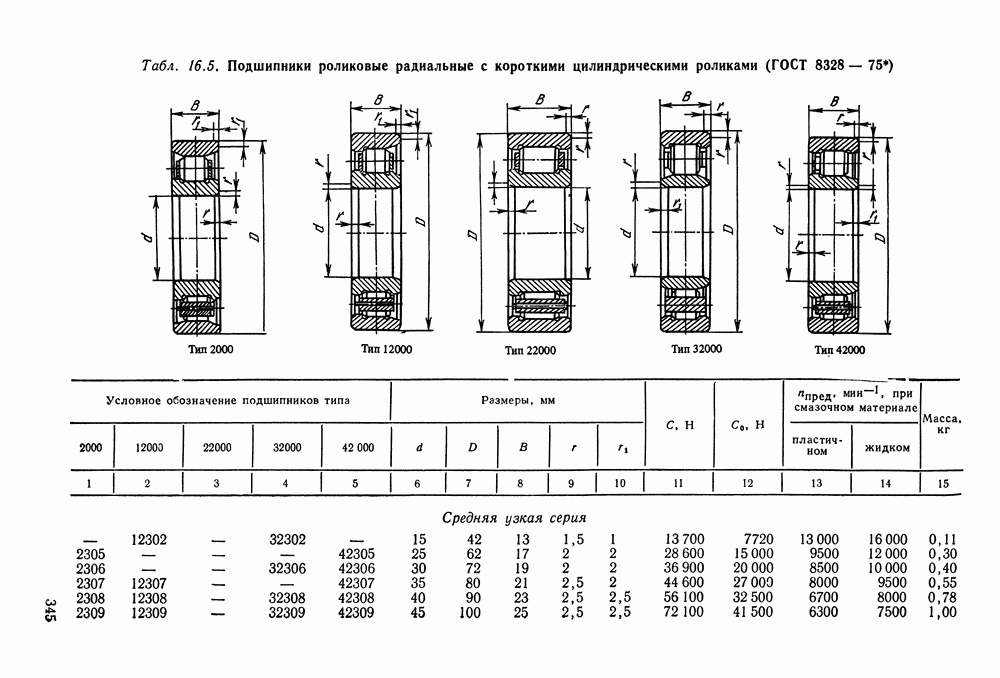
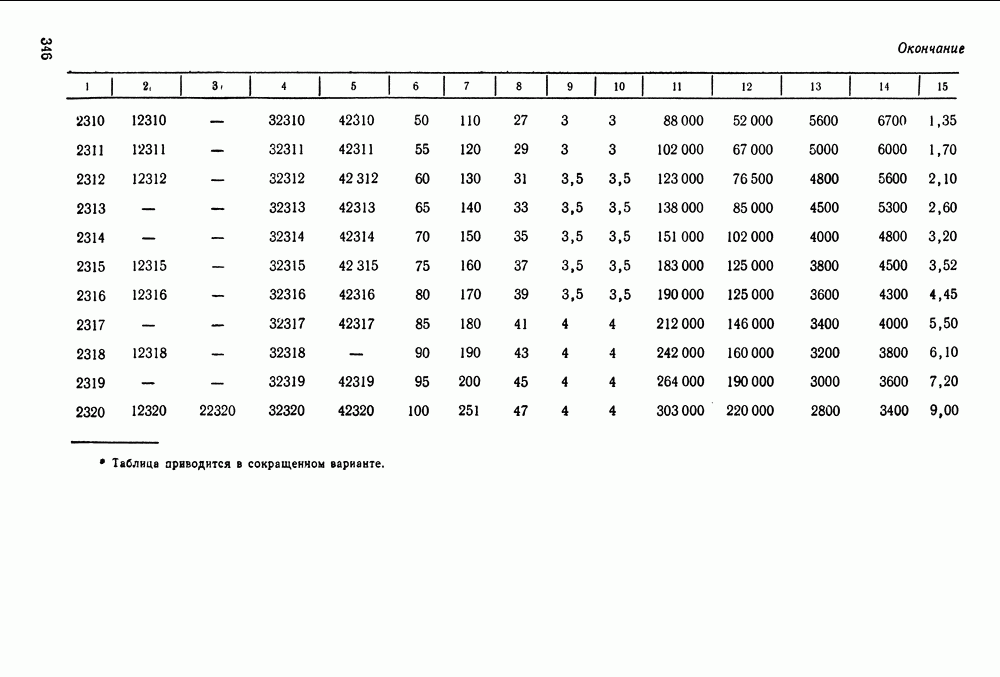
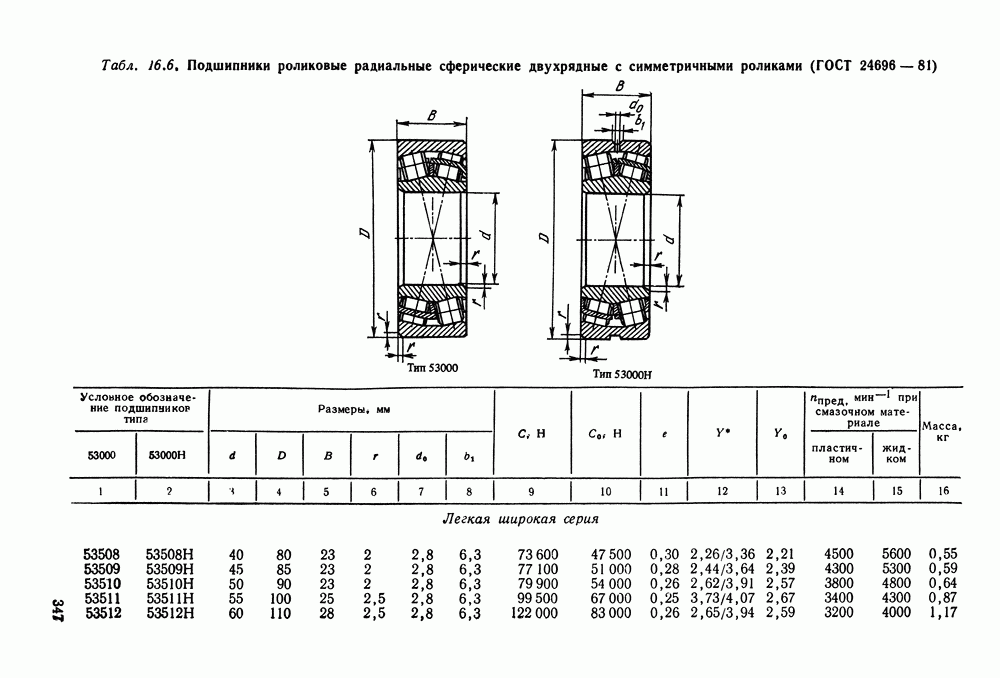
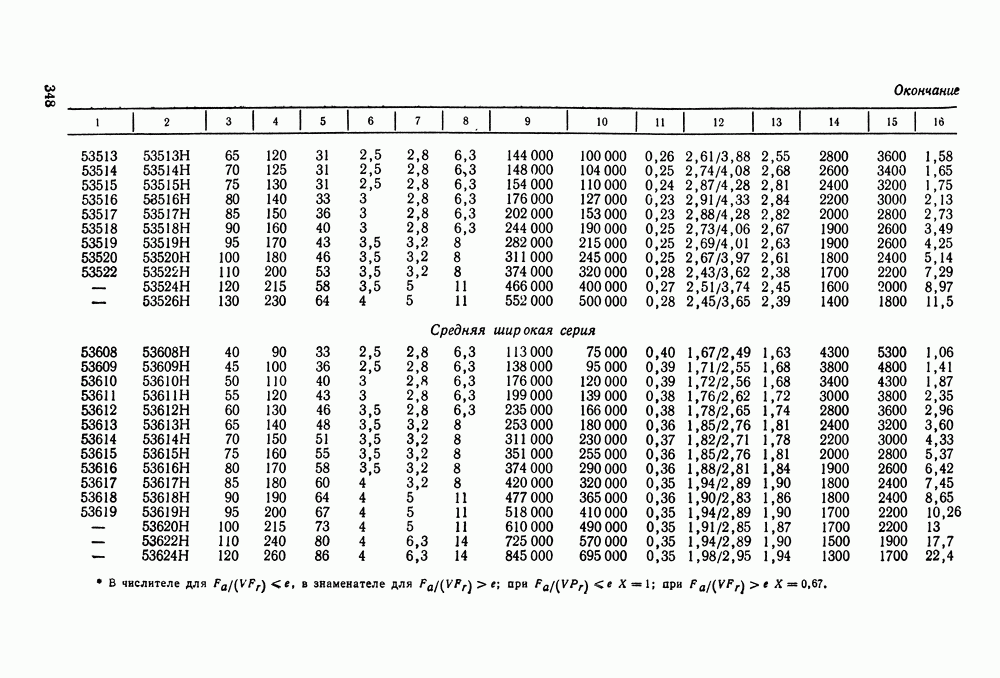
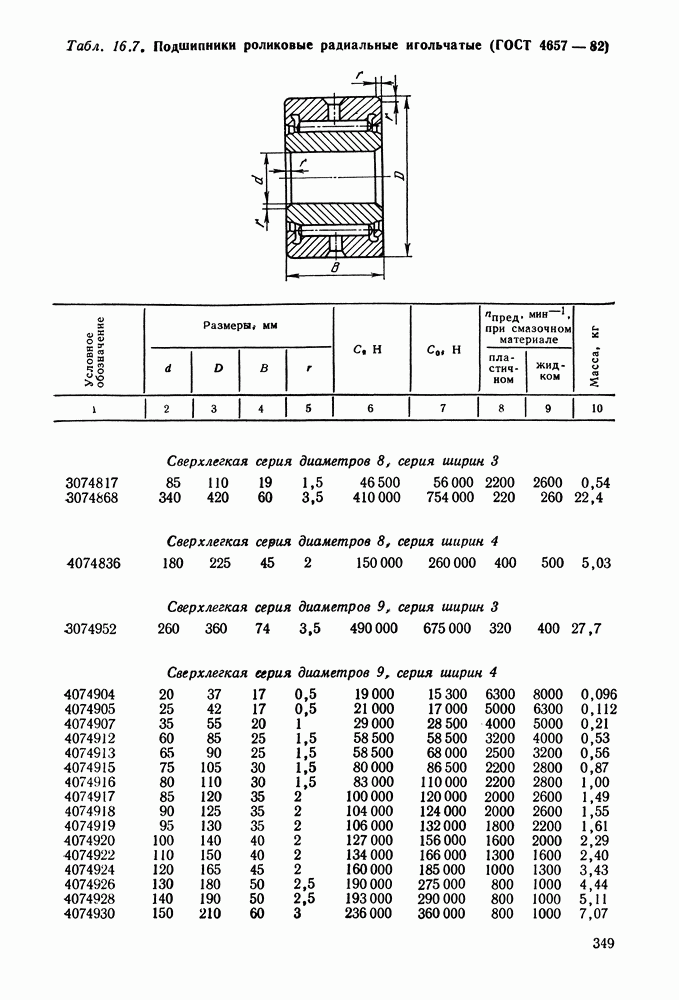
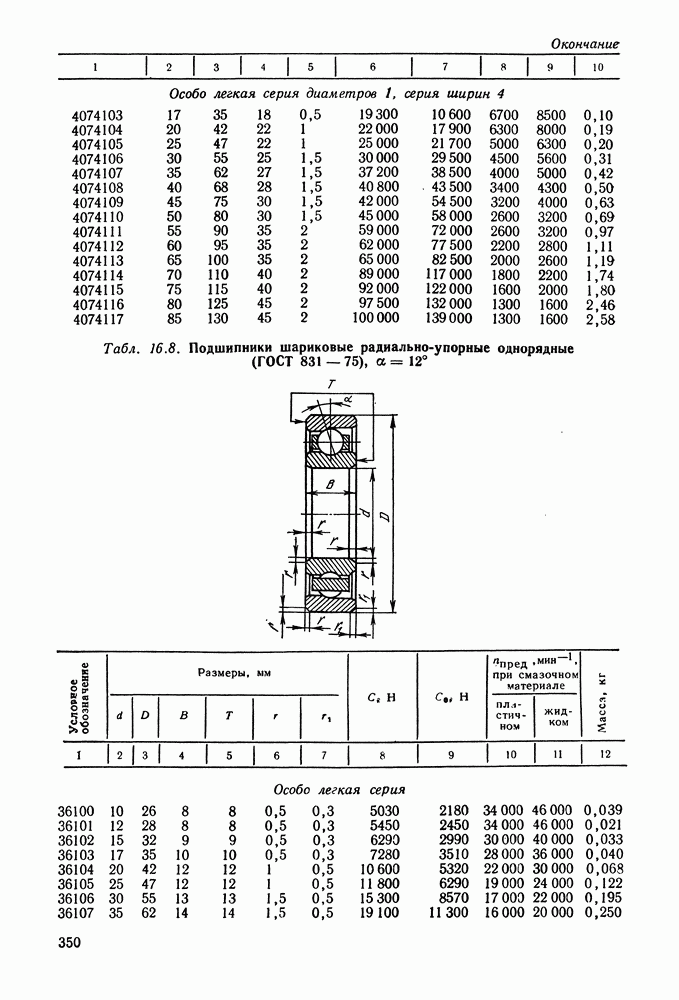
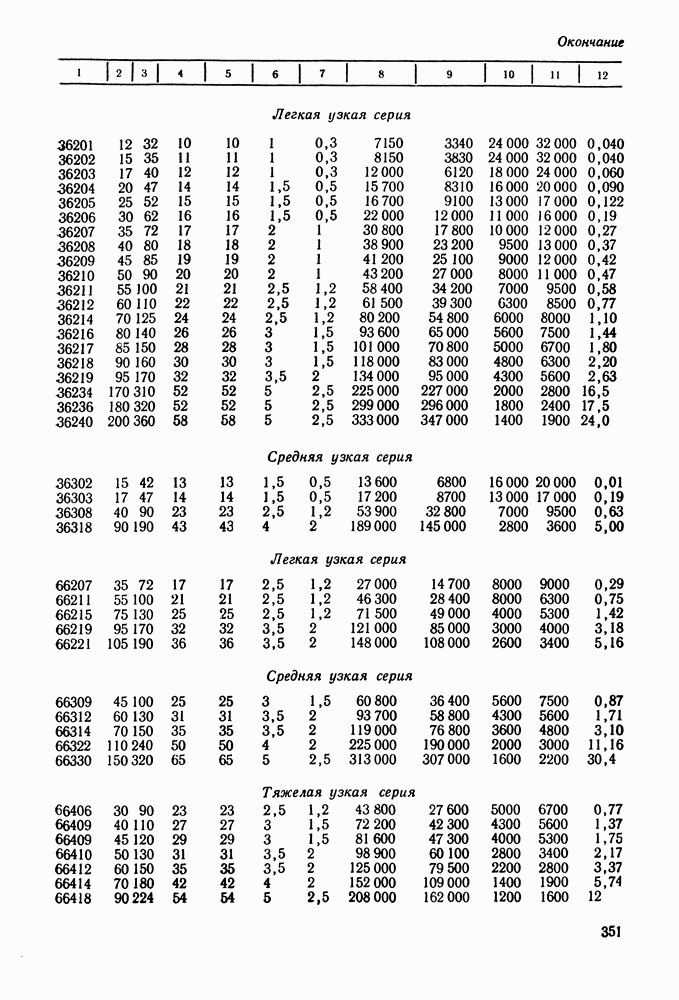
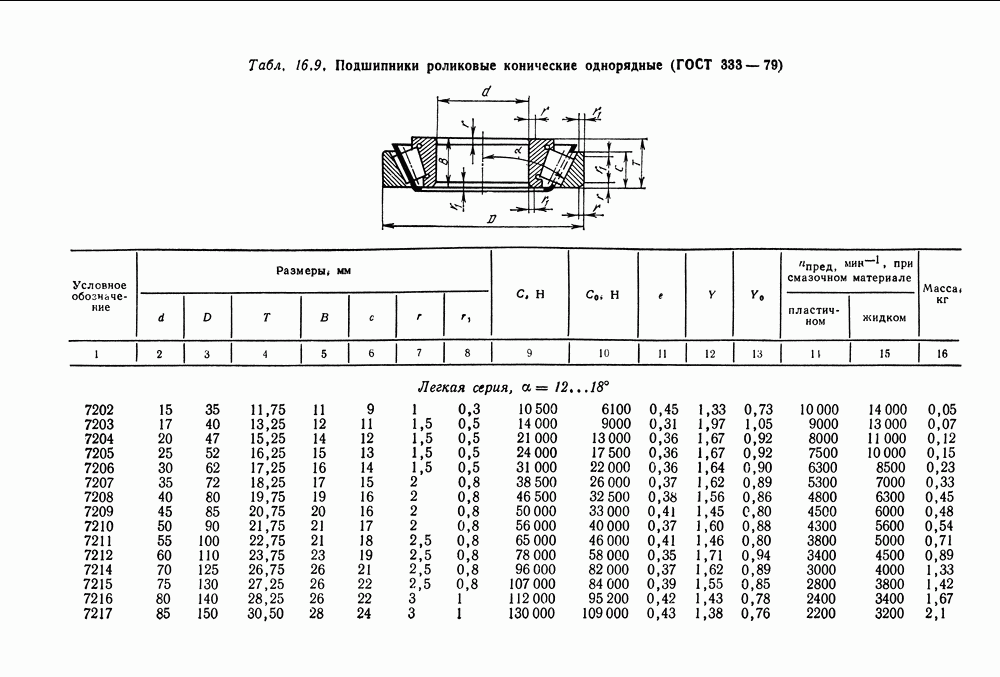
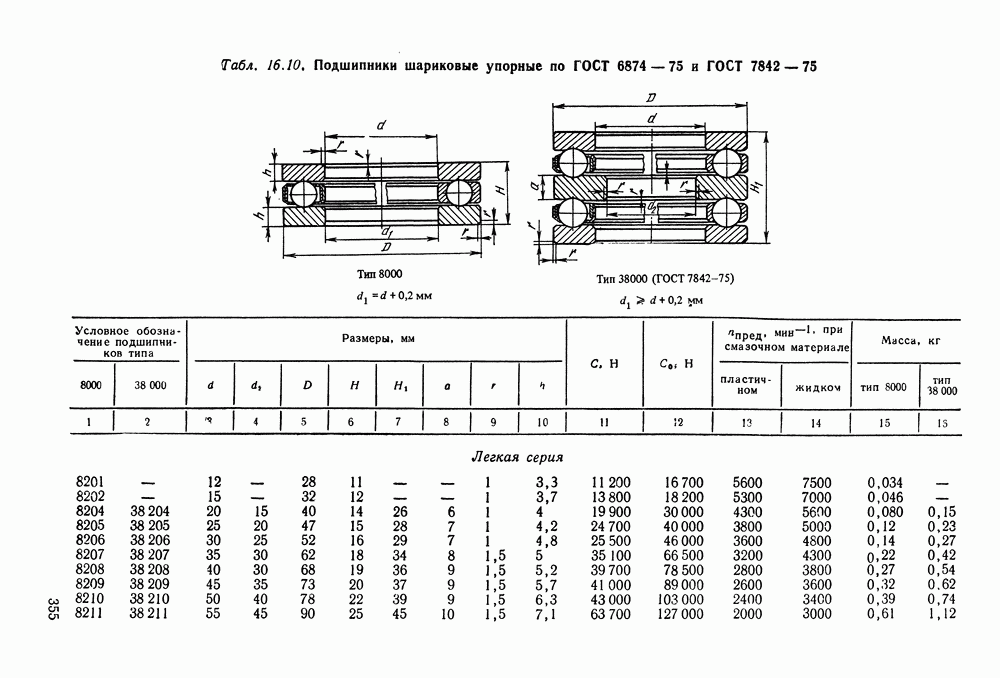
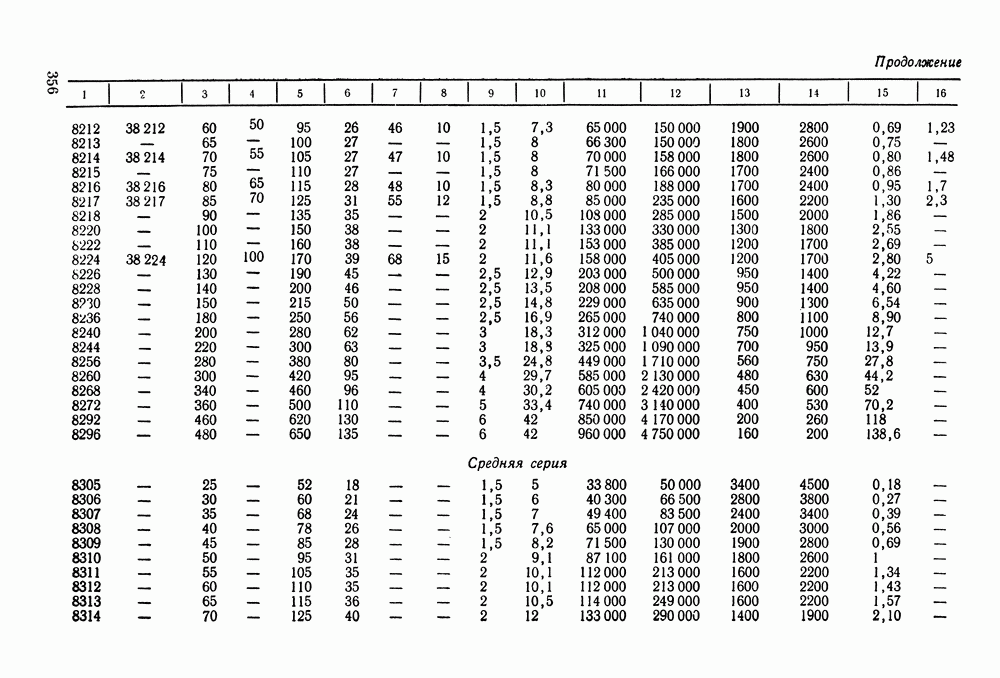
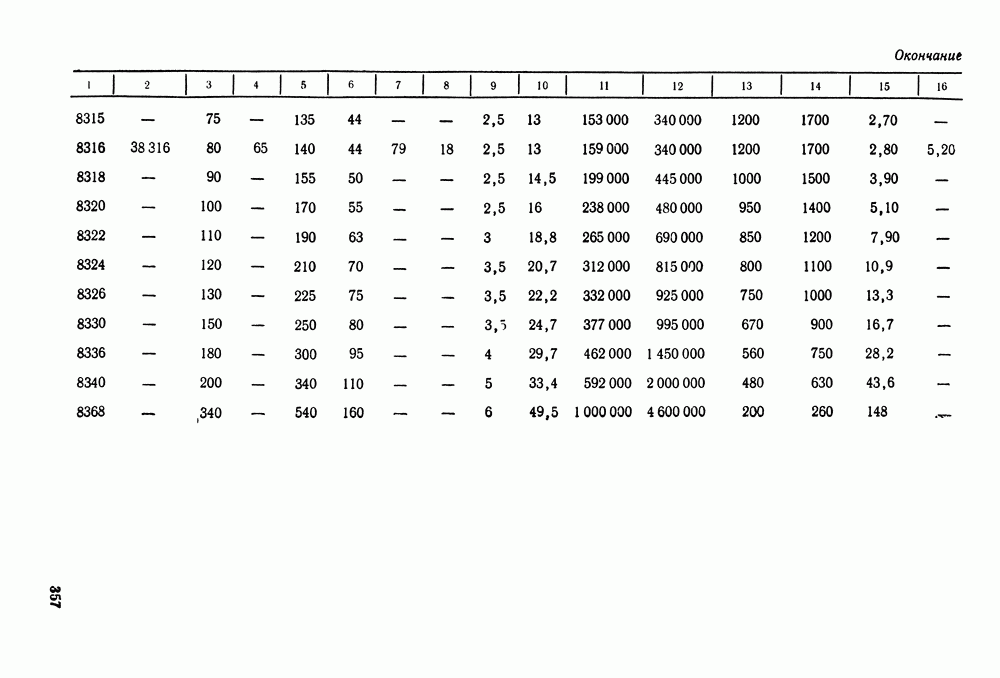
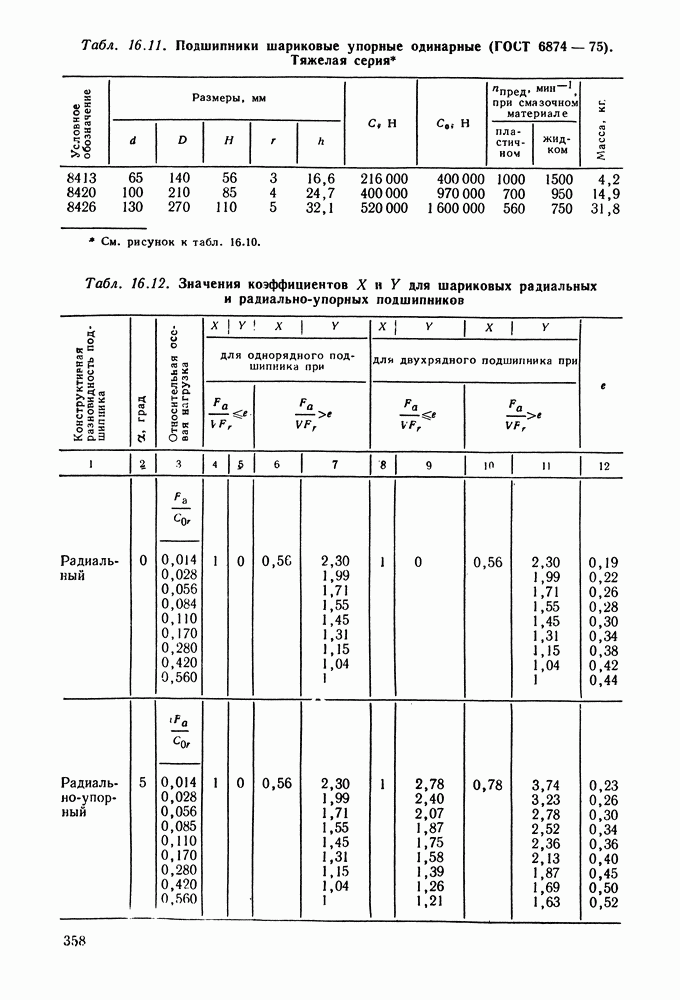
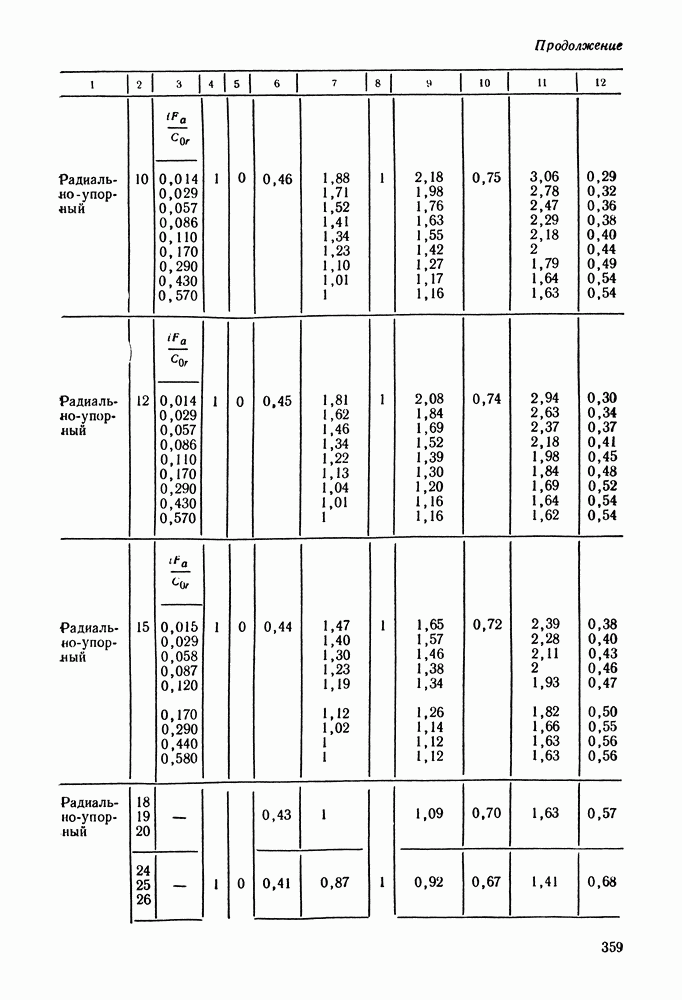
- 16.5. Справочный материал
- 16.6. Пример расчета
- Глава 17. МУФТЫ
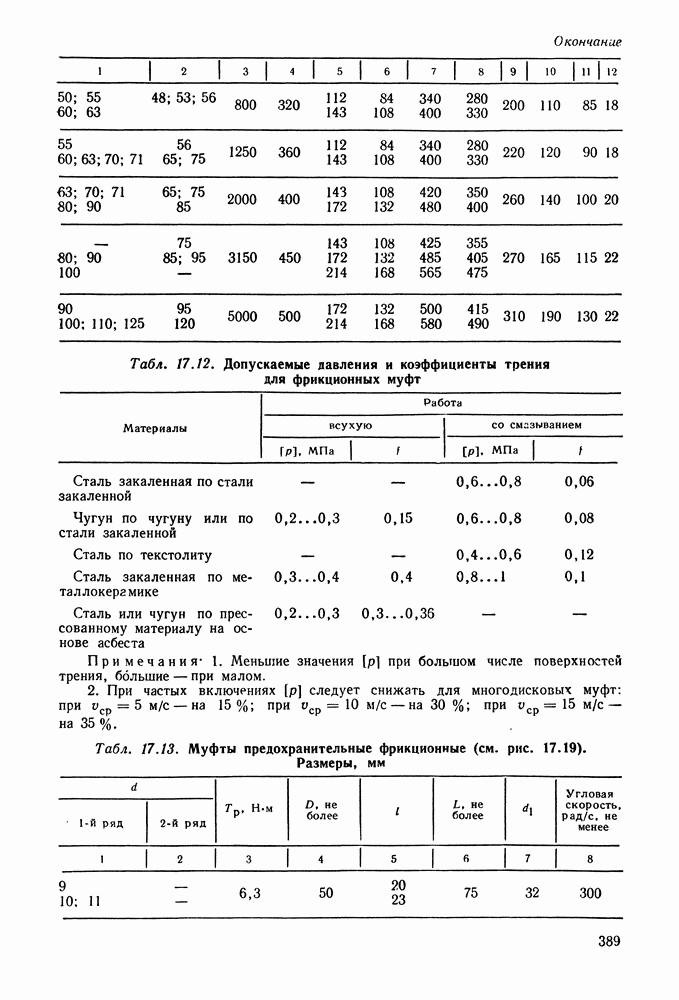
- 17.2. Расчет муфт
- 17.3. Глухие муфты
- 17.4. Компенсирующие муфты
- 17.5. Управляемые (сцепные) муфты
- 17.6. Самоуправляемые муфты
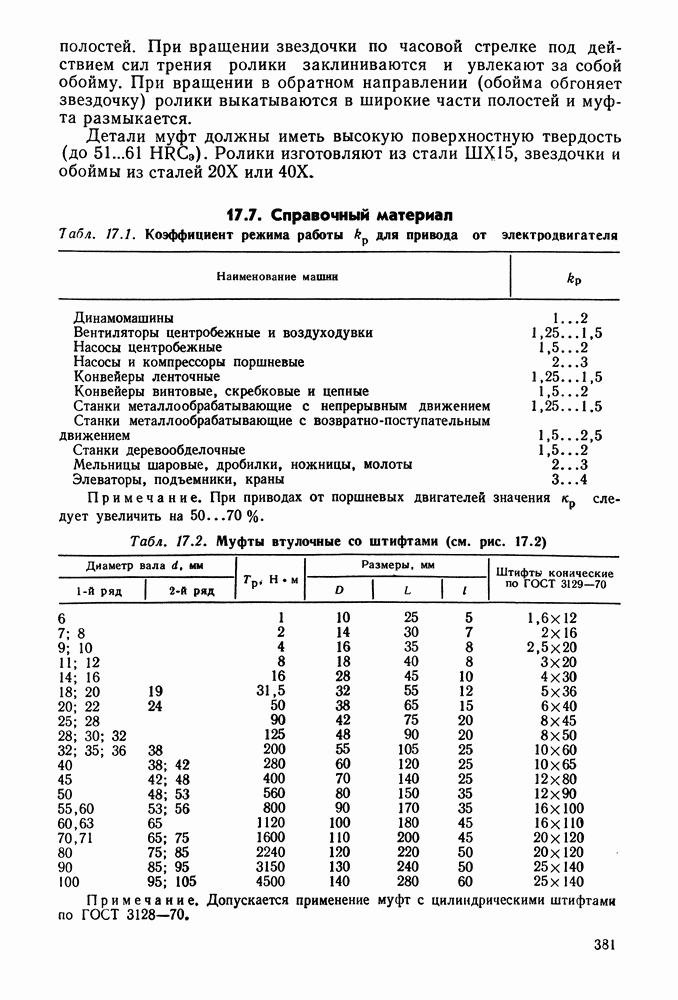
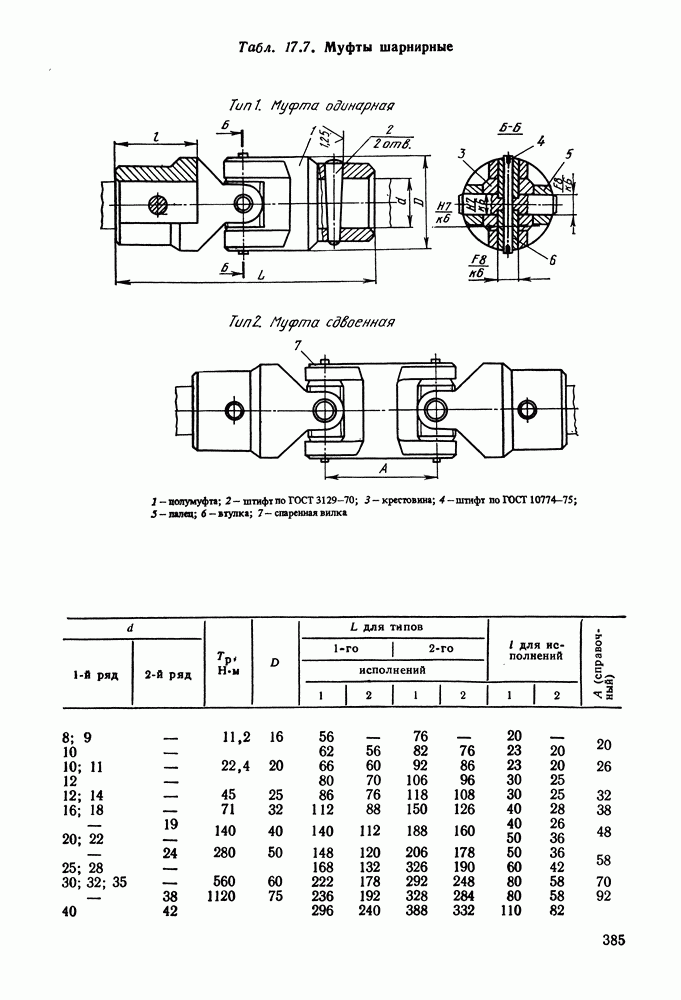
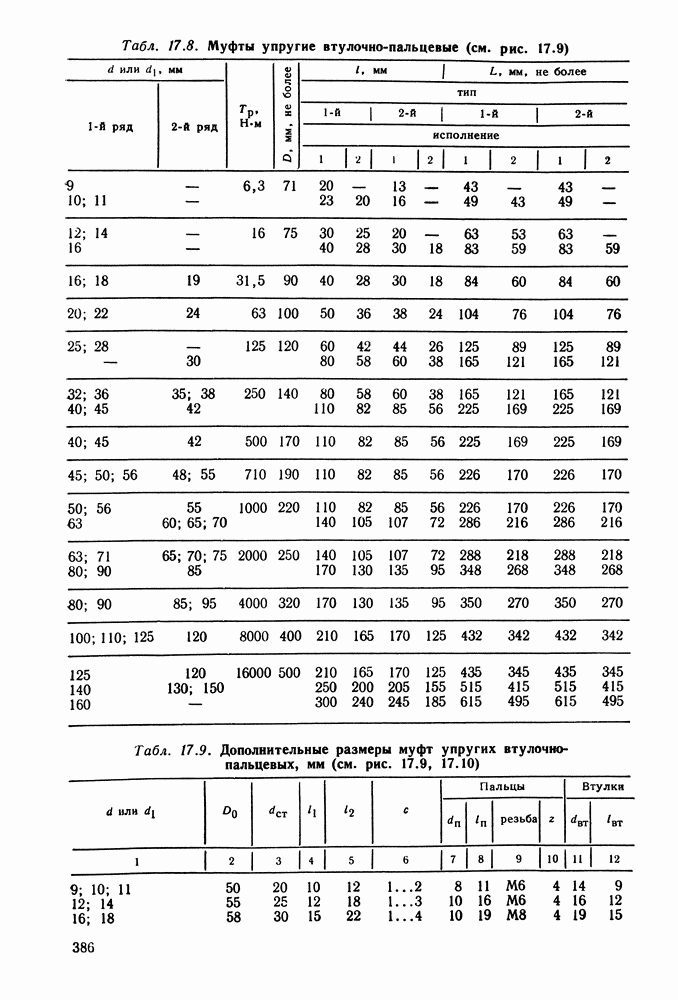
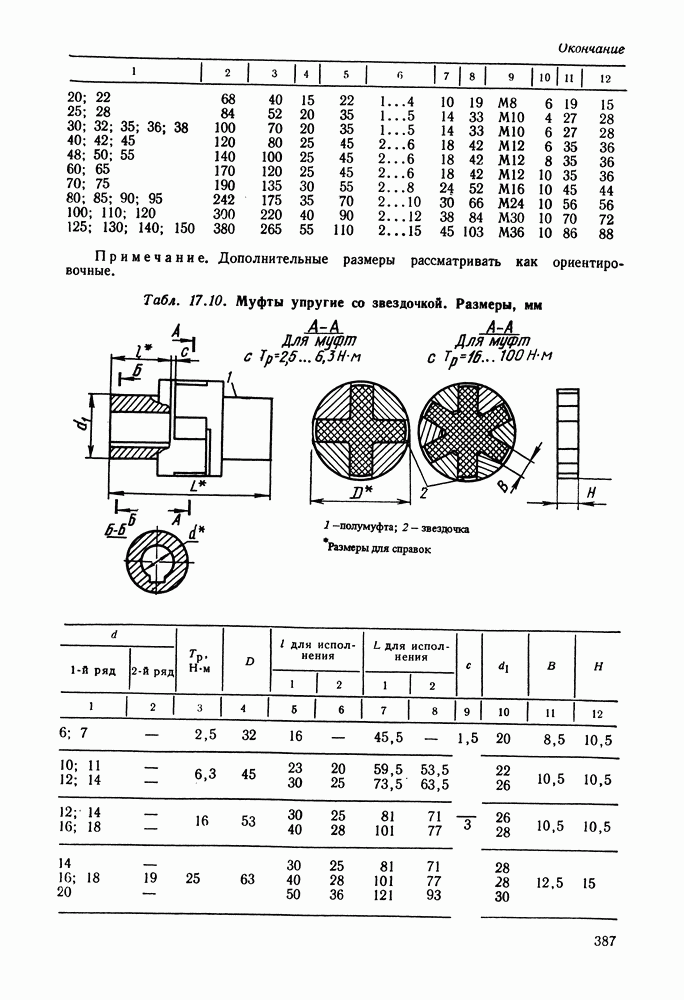
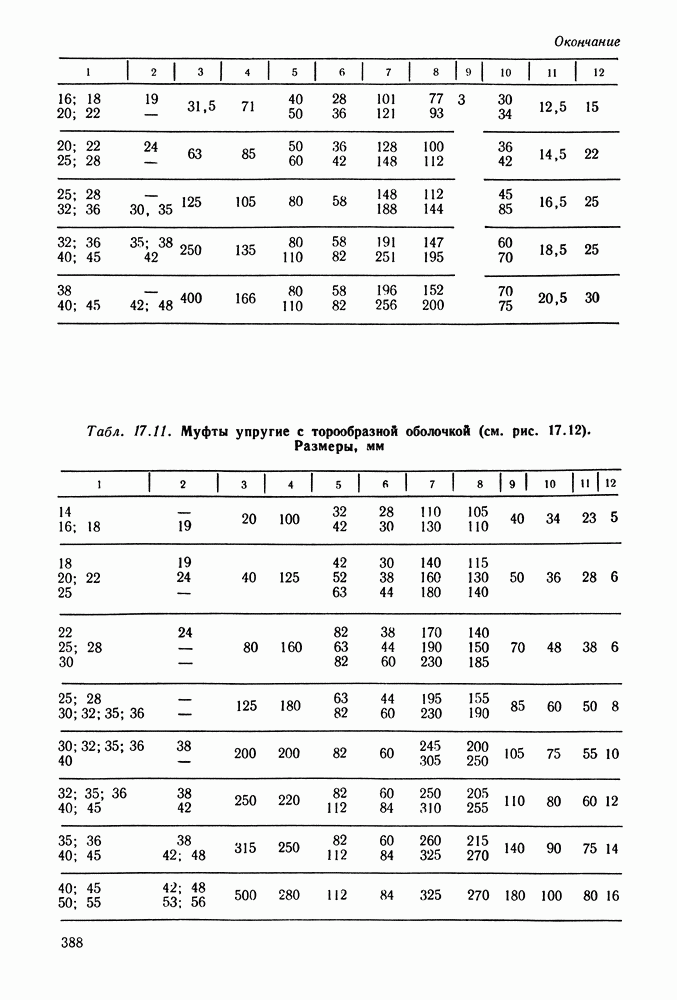
- 17.7. Справочный материал
- 17.8. Примеры расчета
- Глава 18. ПРУЖИНЫ
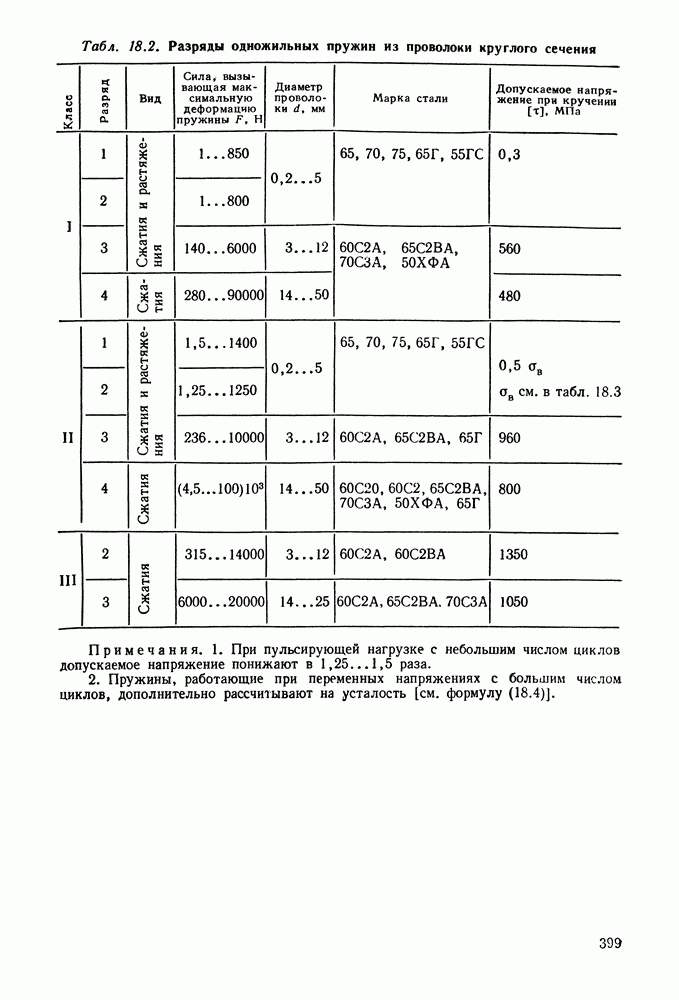
- 18.2. Расчет винтовых пружин на прочность
- 18.3. Расчет винтовых пружин на жесткость
- 18.4. Подбор тарельчатых пружин
- 18.5. Справочный материал
- ЛИТЕРАТУРА