| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9.15. Примеры расчета
Пример 9.1. Закрытая нереверсивная цилиндрическая косозубая передача предназначена для двухсменной работы в течение шести лет. Материал шестерни — сталь  улучшенная, твердостью
улучшенная, твердостью  материал колеса — сталь
материал колеса — сталь  нормализованная, твердостью
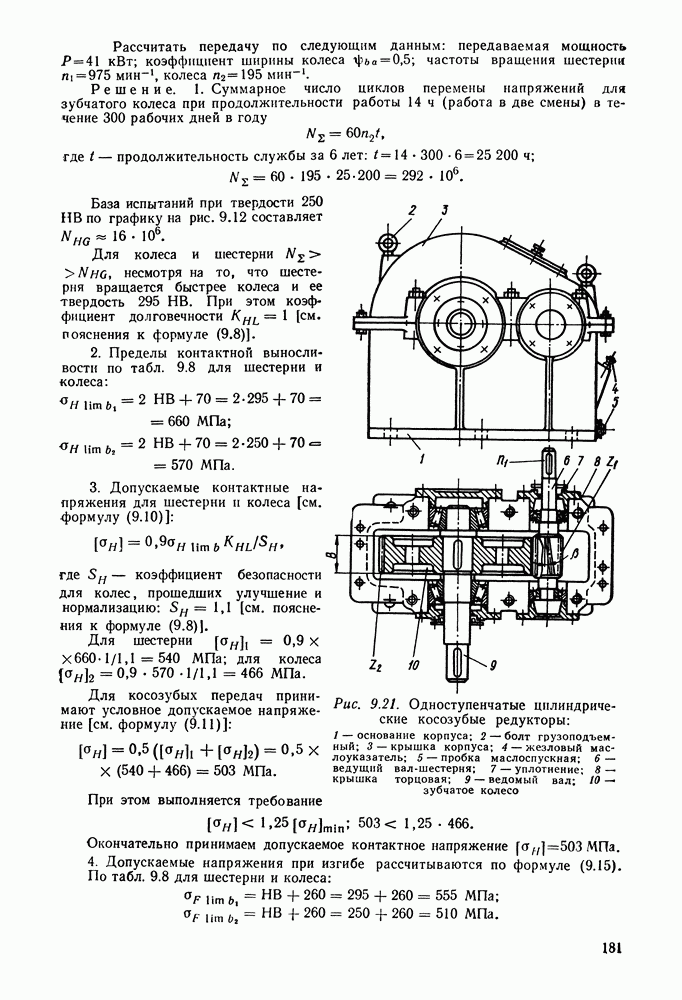
нормализованная, твердостью  . Зубчатые колеса расположены у середины пролета (рис. 9.21).
. Зубчатые колеса расположены у середины пролета (рис. 9.21).
Рассчитать передачу по следующим данным: передаваемая мощность  коэффициент ширины колеса
коэффициент ширины колеса  частоты вращения шестерни
частоты вращения шестерни  колеса
колеса 
Решение. 1. Суммарное число циклов перемены напряжений для зубчатого колеса при продолжительности работы  (работа в две смены) в течение 300 рабочих дней в году
(работа в две смены) в течение 300 рабочих дней в году

где  — продолжительность службы за 6 лет:
— продолжительность службы за 6 лет: 

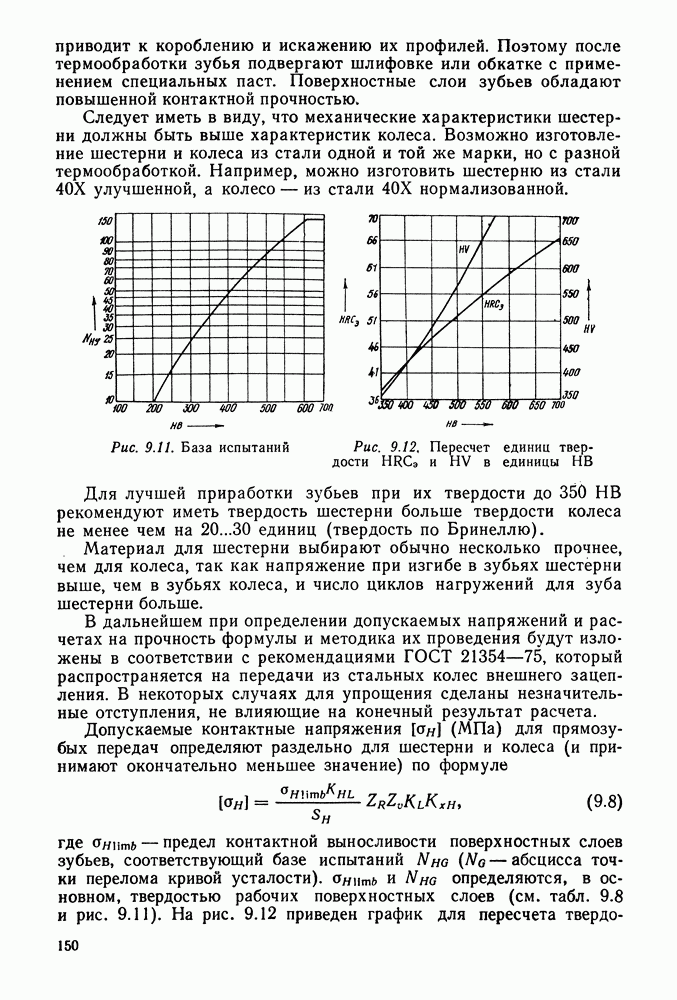
База испытаний при твердости  по графику на рис. 9.12 составляет
по графику на рис. 9.12 составляет 
Для колеса и шестерни  несмотря на то, что шестерня вращается быстрее колеса и ее твердость
несмотря на то, что шестерня вращается быстрее колеса и ее твердость  При этом коэффициент долговечности [см. пояснения к формуле (9.8)].
При этом коэффициент долговечности [см. пояснения к формуле (9.8)].
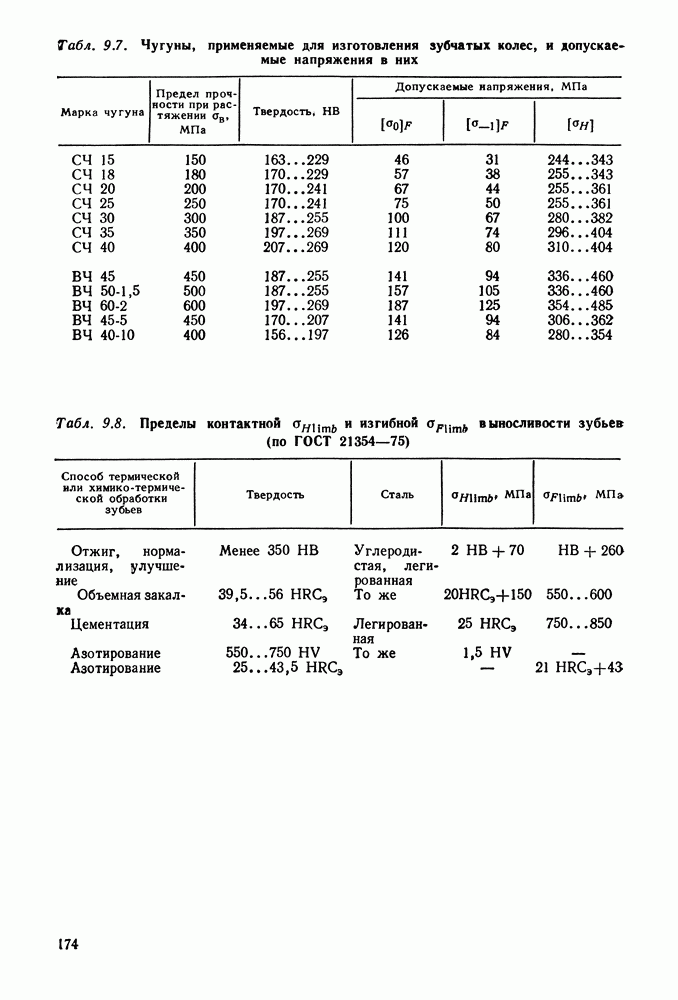
2. Пределы контактной выносливости по табл. 9.8 для шестерни и колеса:


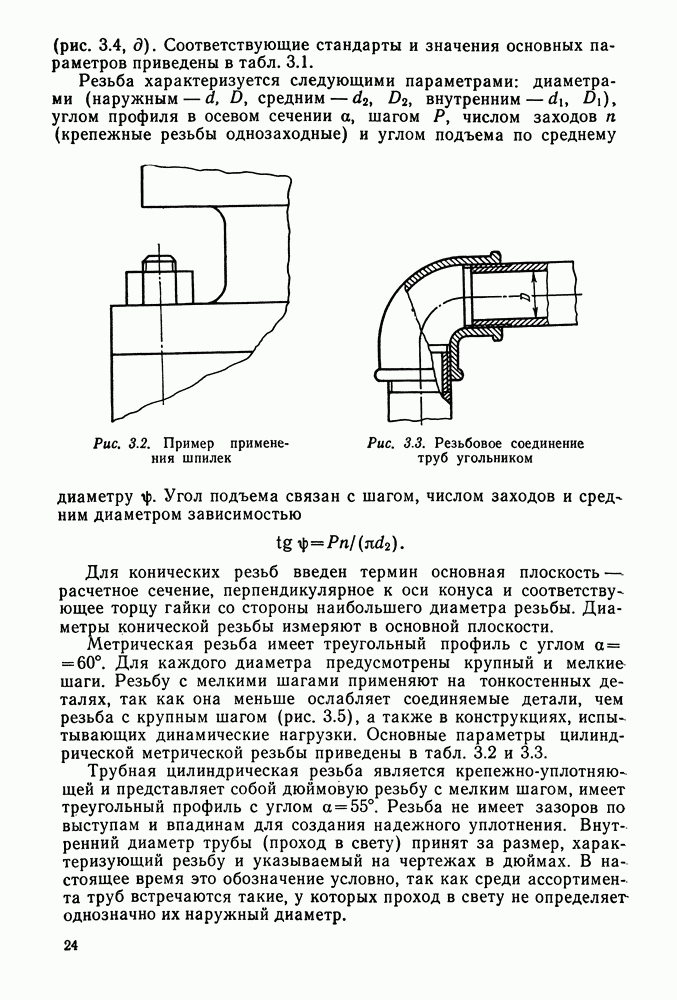
Рис. 9.21. Одноступенчатые цилиндрические косозубые редукторы: 1 — основание корпуса; 2 — болт грузоподъемный; 3 — крышка корпуса; 4 — жезловый маслоуказатель; 5 — пробка маслоспускная; 6 — ведущий вал-шестерня; 7 — уплотнение; 8 — крышка торцовая; 9 — ведомый вал; 10 — зубчатое колесо
3. Допускаемые контактные напряжения для шестерни и колеса [см. формулу (9.10)]:

где  — коэффициент безопасности для колес, прошедших улучшение и нормализацию:
— коэффициент безопасности для колес, прошедших улучшение и нормализацию:  [см. пояснения к формуле (9.8)].
[см. пояснения к формуле (9.8)].
Для шестерни  для колеса
для колеса 
Для косозубых передач принимают условное допускаемое напряжение [см. формулу (9.11)]:

При этом выполняется требование

Окончательно принимаем допускаемое контактное напряжение 
4. Допускаемые напряжения при изгибе рассчитываются по формуле (9.15). По табл. 9.8 для шестерни и колеса:

Коэффициент безопасности принимаем  пояснения к формуле (9.14)]. Принимаем значение коэффициента долговечности при твердости менее
пояснения к формуле (9.14)]. Принимаем значение коэффициента долговечности при твердости менее  и значение коэффициента, учитывающего влияние односторонней нагрузки (редуктор нереверсивный),
и значение коэффициента, учитывающего влияние односторонней нагрузки (редуктор нереверсивный), 
Тогда допускаемые напряжения при изгибе шестерни и колеса:

5. Вращающие моменты на шестерне и на колесе при:

6. Передаточное число 
7. Межосевое расстояние рассчитывается по формуле (9.39):

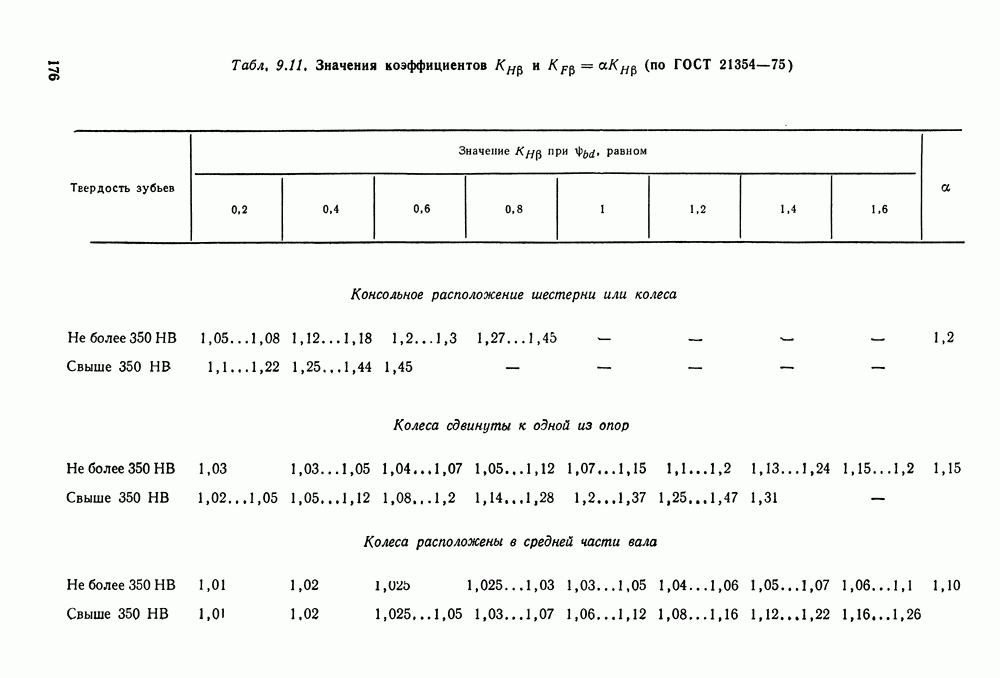
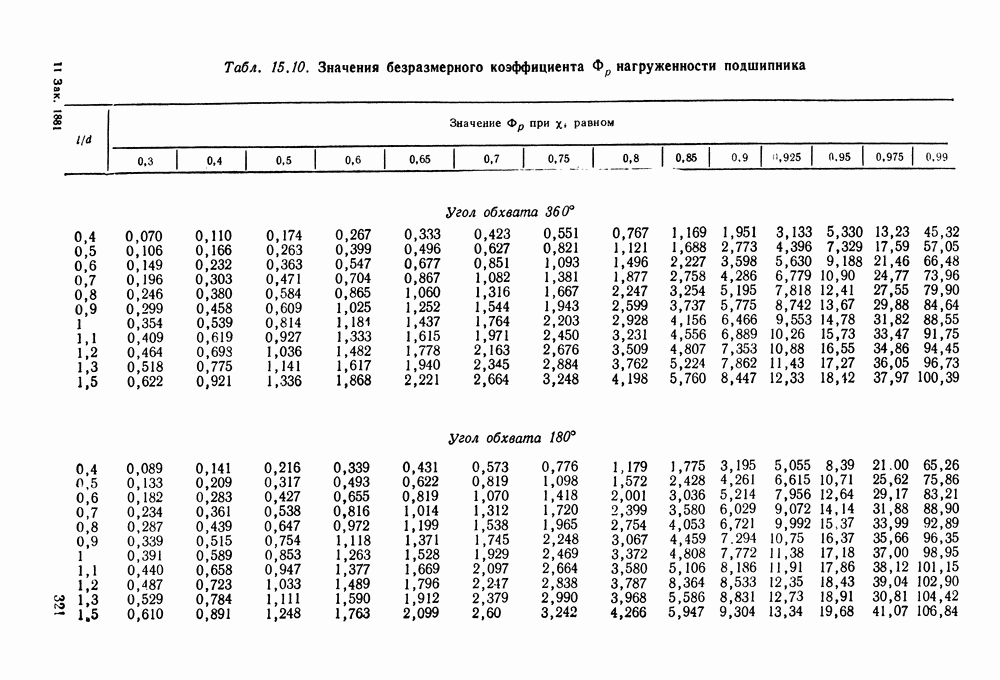
где по табл. 9.11 принимаем 1,08 в соответствии с

Принимаем  мм.
мм.
8. Задаемся числом зубьев шестерни 
9. Тогда число зубьев колеса 
10. Назначаем предварительно угол наклона зубьев  при этом
при этом 
11. Нормальный модуль

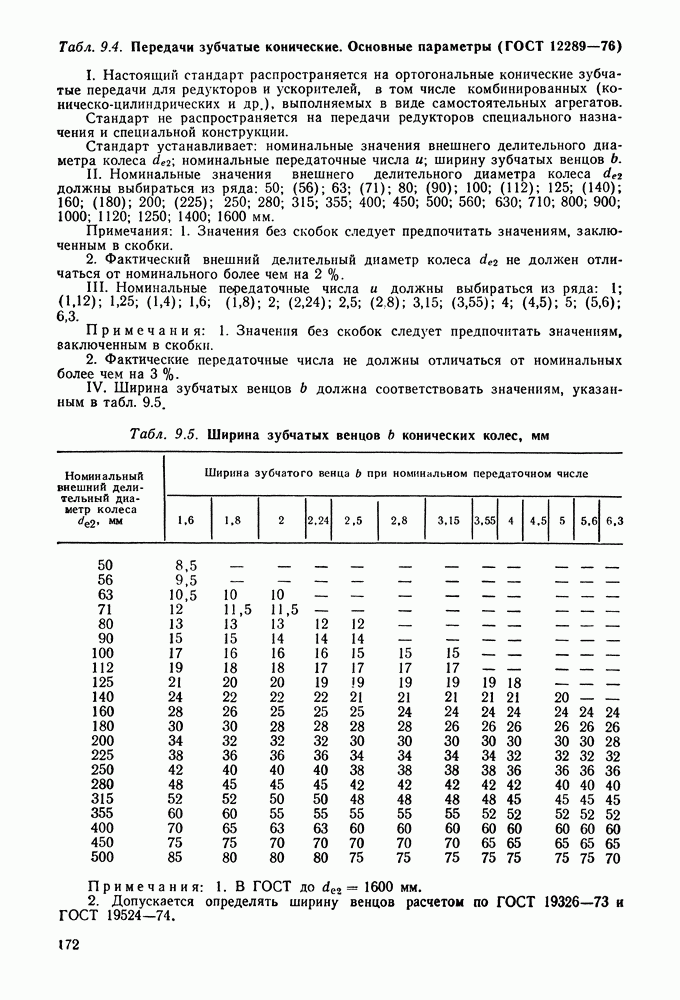
Принимаем по  (см. табл. 9.1) ближайший нормальный модуль
(см. табл. 9.1) ближайший нормальный модуль  мм.
мм.
12. Определяем окончательно угол наклона зубьев:

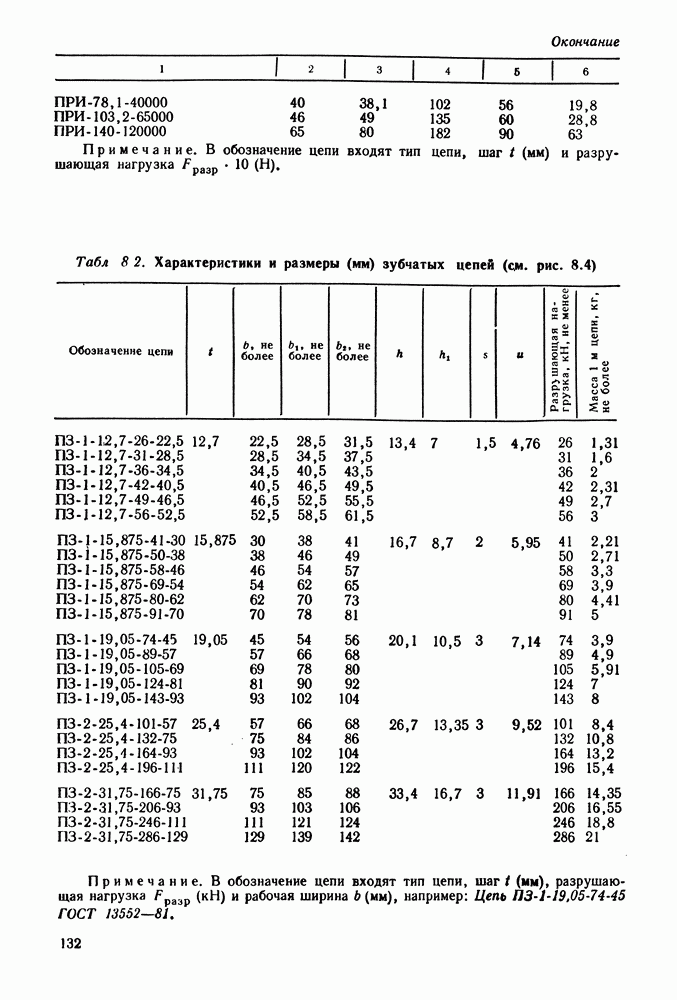
13. Основные размеры шестерни и колеса:

Рабочая ширина колеса  мм; ширина шестерни
мм; ширина шестерни  мм.
мм.
14. Выполняем проверочный расчет на усталость по контактным напряжениям по формуле (9.42).
Определяем окружную скорость:

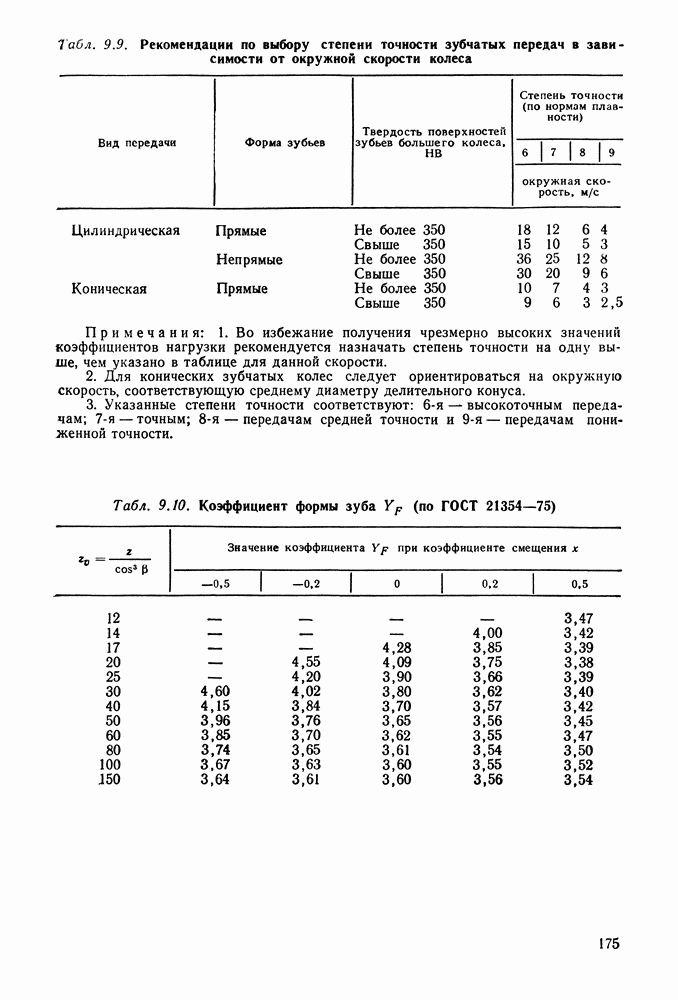
По табл. 9.9 назначаем 8-ю степень точности передачи.
Коэффициенты:

Коэффициент  где
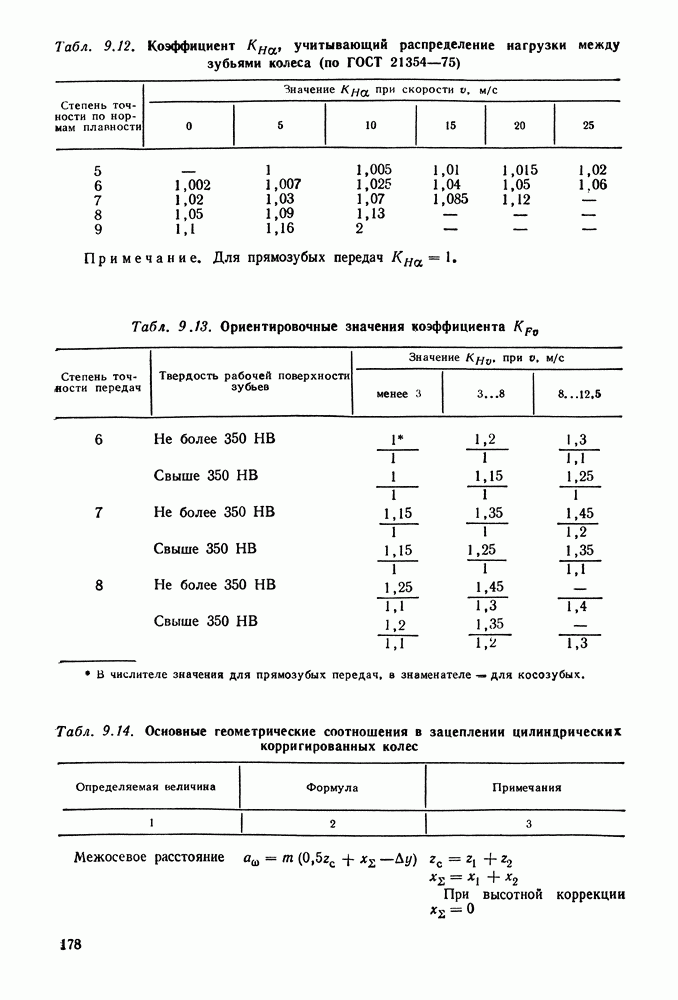
где  по табл. 9.12;
по табл. 9.12;  по табл.
по табл.  (особой точности не требуется):
(особой точности не требуется): 
Контактное напряжение:

т. е. меньше, чем 
Прочность обеспечена.
15. Выполняем проверочный расчет на усталость при изгибе по формуле (9.44). По табл. 9.10 определяем значения коэффициентов  учитывающих форму вуба, в зависимости от эквивалентного числа зубьев при
учитывающих форму вуба, в зависимости от эквивалентного числа зубьев при 

По эквивалентному числу зубьев  и по эквивалентному числу зубьев
и по эквивалентному числу зубьев 
Расчет следует выполнить для того зубчатого колеса, у которого меньше отношение 
В нашем случае:

Расчет проводим по колесу.
Коэффициент  [см. пояснения к формуле (9.44)].
[см. пояснения к формуле (9.44)].
Коэффициент  для косозубых колес:
для косозубых колес:

Коэффициент  где
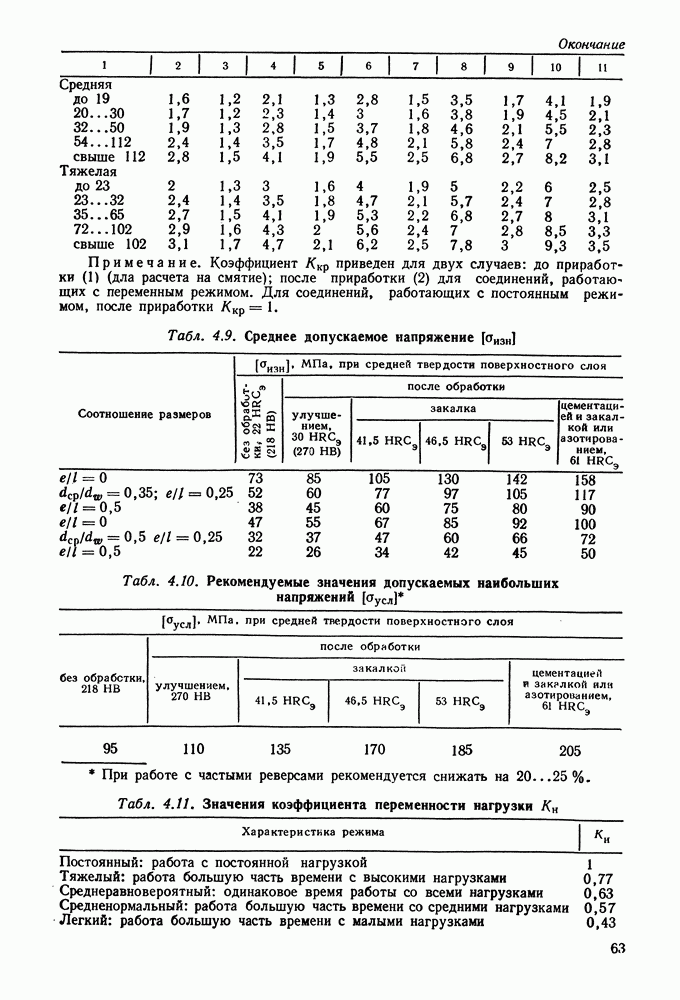
где  — коэффициент, учитывающий распределение нагрузки между зубьями:
— коэффициент, учитывающий распределение нагрузки между зубьями:

Коэффициент  учитывает распределение нагрузки по ширине венца и определяется по табл. 9.11 в зависимости от В нашем случае
учитывает распределение нагрузки по ширине венца и определяется по табл. 9.11 в зависимости от В нашем случае 
Коэффициент  учитывает динамическую нагрузку, возникающую в зацеплении, и определяется по табл.
учитывает динамическую нагрузку, возникающую в зацеплении, и определяется по табл.  Тогда
Тогда 
Напряжение при изгибе

т. е. меньше, чем 
Условие прочности выполнено.
В результате аналогичного расчета закрытой передачи цилиндрическими зубчатыми колесами по тем же исходным данным получаются следующие результаты: межосевое расстояние — 300 мм, модуль — 4 мм, ширина колеса — 150 мм. Таким образом, косозубая передача оказывается выгоднее прямозубой (по габаритам и массе).
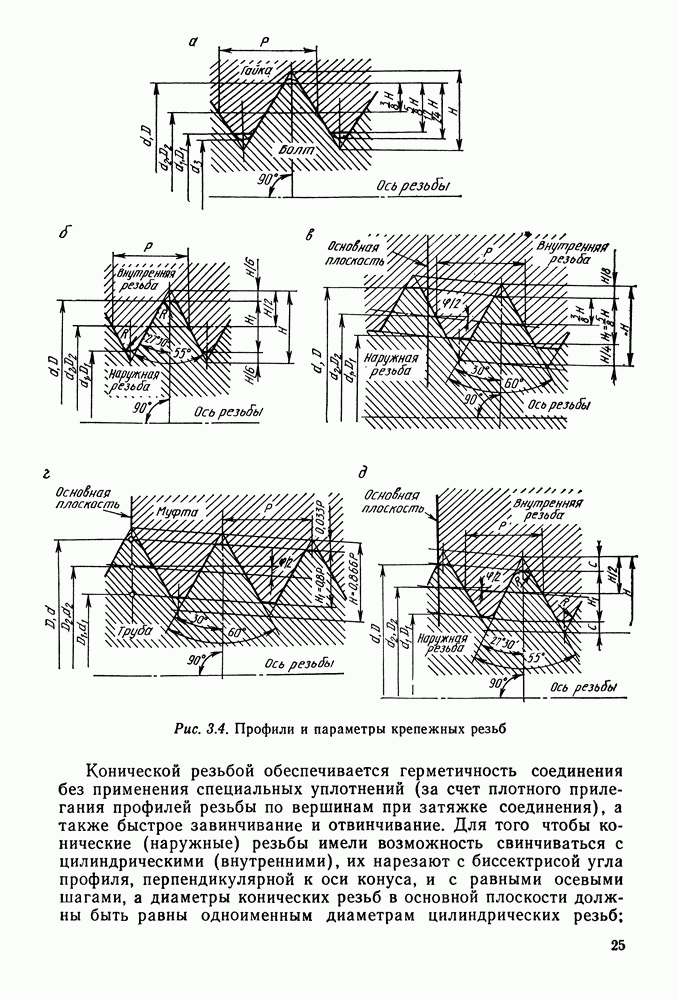
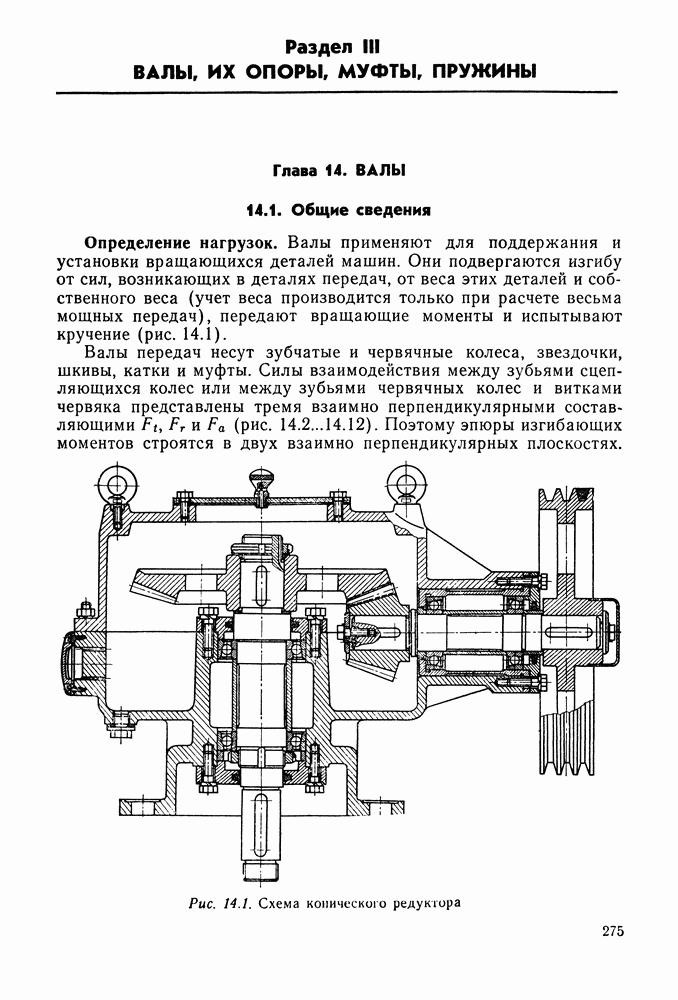
Пример 9.2. Закрытая реверсивная коническая прямозубая передача предназначена для трехсменной работы в течение четырех лет. Шестерня расположена на консоли (рис. 9.22).

Рис. 9.22. Конический редуктор с вертикальным ведущим валом
Рассчитать передачу по следующим данным: момент на зубчатом колесе  мм, коэффициент
мм, коэффициент  частота вращения шестерни
частота вращения шестерни  колеса
колеса 
Параметры передачи должны быть согласованы с ГОСТом.
Сравнить расчетные значения  характеризующие размеры передачи прямозубой и с круговым зубом.
характеризующие размеры передачи прямозубой и с круговым зубом.
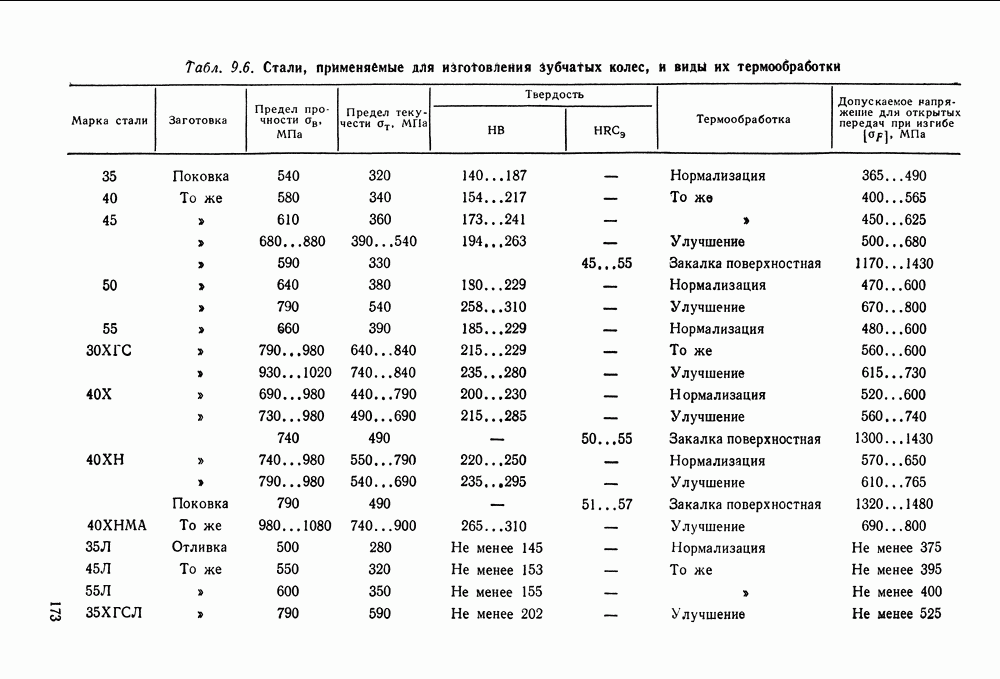
Решение. 1. Так как материалы для шестерни и для колеса не заданы, их следует выбрать по табл. 9.6.
Для шестерни принимаем сталь 45 улучшенную, твердостью примерно  а для колеса — сталь 45 нормализованную, твердостью примерно
а для колеса — сталь 45 нормализованную, твердостью примерно  (принимаем средние значения из приведенных в таблице).
(принимаем средние значения из приведенных в таблице).
2. Суммарное число циклов перемен напряжений для зубчатого колеса при продолжительности работы  в течение 300 рабочих дней в году
в течение 300 рабочих дней в году

Здесь  — срок службы за 4 года.
— срок службы за 4 года.

База испытаний при твердости стали  (см. рис. 9.12) составляет
(см. рис. 9.12) составляет  колеса
колеса  Для
Для  которая вращается быстрее, тем более
которая вращается быстрее, тем более  При этом условии коэффициент долговечности
При этом условии коэффициент долговечности  [см. пояснения к формуле (9.8)].
[см. пояснения к формуле (9.8)].
3. Пределы контактной выносливости по табл. 9.8 для шестерни и для колеса:

4. Допускаемые контактные напряжения для шестерни и для колеса определяются по формуле (9.10), где  (см. пример 9.1).
(см. пример 9.1).
Для шестерни 
Для колеса 
Для прямозубых передач принимают окончательно меньшее значение, т. е. 
Для передач с криволинейными зубьями принимают условное допускаемое напряжение [см. формулу (9.11)]

При этом должно быть выполнено требование 
Поэтому окончательно для колес с криволинейными зубьями (в нашем случае с круговыми зубьями) принимаем допускаемое контактное напряжение

5. Допускаемые напряжения при изгибе [см. формулу (9.14)]

По табл. 9.8 для шестерни и колеса:

Коэффициент безопасности  [см. пояснения к формуле
[см. пояснения к формуле  принимаем значение коэффициента долговечности
принимаем значение коэффициента долговечности  и значение коэффициента, учитывающего влияние реверсивной нагрузки,
и значение коэффициента, учитывающего влияние реверсивной нагрузки, 
Тогда допускаемые напряжения при изгибе для шестерни и колеса:

6. Передаточное число 
7. Внешний делительный диаметр большего конического колеса определяется по формуле (9.40).

Для конических передач с круговыми зубьями  в этом случае
в этом случае

Сравнивая полученные результаты, можно сделать вывод, что коническая передача с круговыми зубьями имеет меньший расчетный параметр  по сравнению с передачей, имеющей прямые зубья. Это уменьшение составляет
по сравнению с передачей, имеющей прямые зубья. Это уменьшение составляет 
Дальнейший расчет проведем для прямозубой передачи.
8. Примем число зубьев шестерни 
9. Число зубьев зубчатого колеса  Принимаем
Принимаем 
10. Внешний окружной модуль

По  (см. табл. 9.1) принимаем
(см. табл. 9.1) принимаем  мм.
мм.
11. Выравниваем параметры редуктора по  (см. табл. 9.4); внешний делительный диаметр большего колеса
(см. табл. 9.4); внешний делительный диаметр большего колеса

передаточное число

В нашем случае и  , и
, и  являются стандартными параметрами, что соответствует требованию к расчету передачи (см. табл. 9.4). Выравнивать значение те до стандартного не обязательно; это следует делать только в тех случаях, когда стандартный модуль те обеспечивает получение стандартного значения
являются стандартными параметрами, что соответствует требованию к расчету передачи (см. табл. 9.4). Выравнивать значение те до стандартного не обязательно; это следует делать только в тех случаях, когда стандартный модуль те обеспечивает получение стандартного значения  и такое фактическое передаточное число
и такое фактическое передаточное число  которое отличается от стандартного не более, чем допустимо. Следует иметь в виду, что в стандартной конической передаче должны соответствовать ГОСТу в первую очередь
которое отличается от стандартного не более, чем допустимо. Следует иметь в виду, что в стандартной конической передаче должны соответствовать ГОСТу в первую очередь  и и, а значение те может соответствовать, но может и не соответствовать ГОСТу.
и и, а значение те может соответствовать, но может и не соответствовать ГОСТу.
12. Проверка частоты вращения  при
при  фактическая частота вращения
фактическая частота вращения

отклонение от заданной  что допустимо.
что допустимо.
13. Конусное расстояние (см. рис. 9.10)

14. Длина зуба или ширина зубчатого венца

По табл.  ) принимаем
) принимаем  мм.
мм.
15. Внешний делительный диаметр шестерни

16. Углы при вершинах начальных конусов

17. Средний делительный диаметр шестерни

18. Средний окружной модуль

19. Средняя скорость

20. По табл. 9.9 при данной скорости для прямых зубьев колес конической передачи при твердости стали менее  можно принять 9-ю степень точности, но для уменьшения динамической нагрузки вместо наинизшей допустимой выбираем 8-ю степень точности (см. примечания к таблице)
можно принять 9-ю степень точности, но для уменьшения динамической нагрузки вместо наинизшей допустимой выбираем 8-ю степень точности (см. примечания к таблице) 
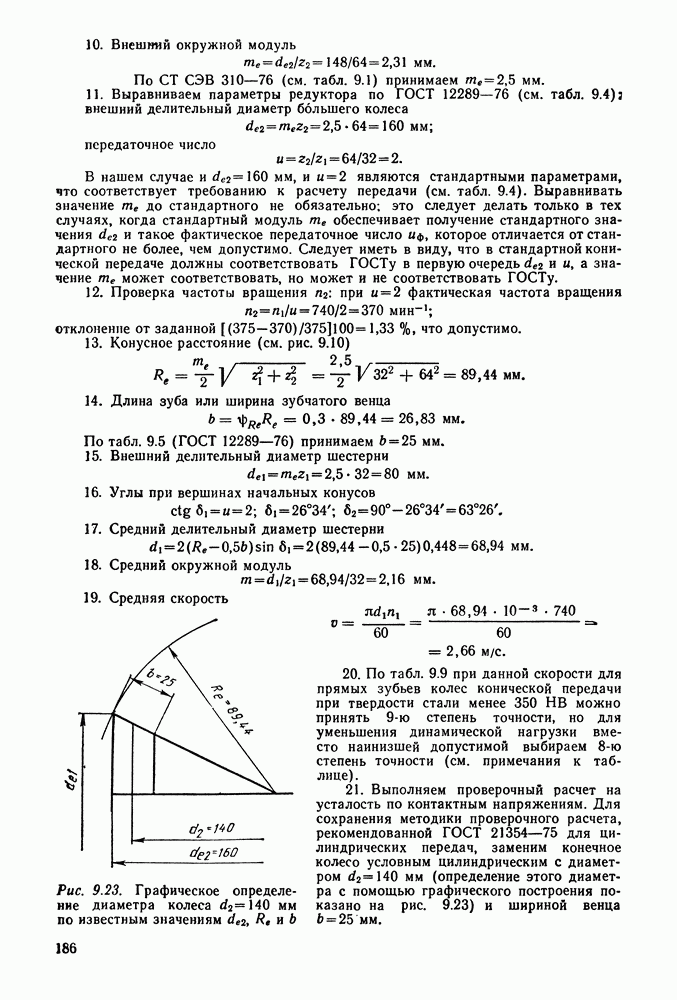
21. Выполняем проверочный расчет на усталость по контактным напряжениям. Для сохранения методики проверочного расчета, рекомендованной  для цилиндрических передач, заменим конечное колесо условным цилиндрическим с диаметром
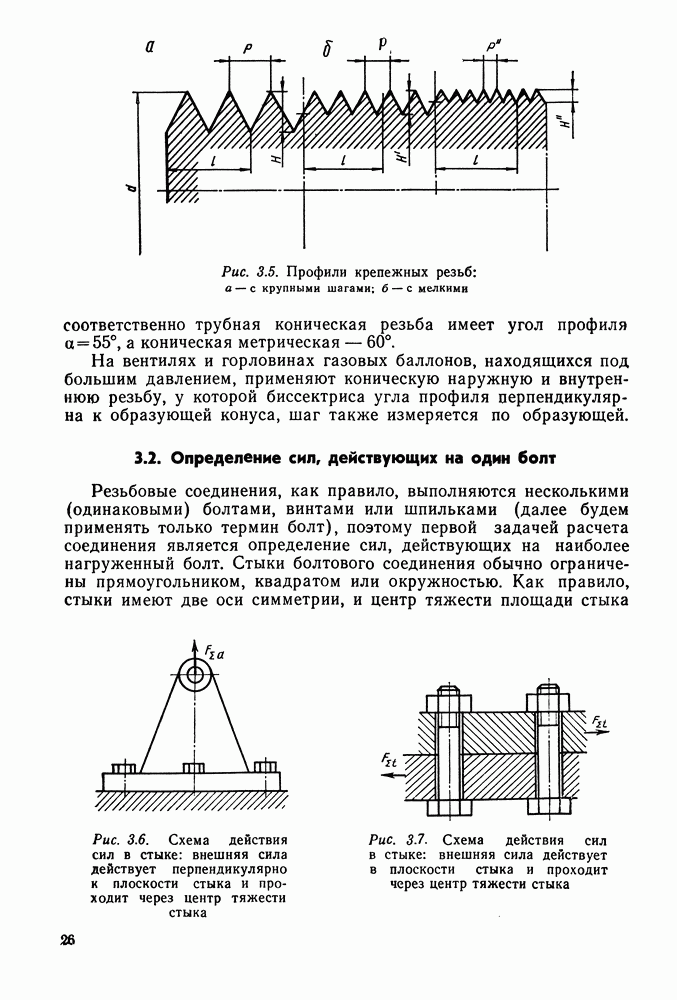
для цилиндрических передач, заменим конечное колесо условным цилиндрическим с диаметром  мм (определение этого диаметра с помощью графического построения показано на рис. 9.23) и шириной венца
мм (определение этого диаметра с помощью графического построения показано на рис. 9.23) и шириной венца  мм.
мм.

Рис. 9.23. Графическое определение диаметра колеса  мм по известным значениям
мм по известным значениям  и
и 

В этой формуле (см. решение примера  по табл. 9.11 в со ответствии
по табл. 9.11 в со ответствии  и консольным расположением одного из колес.
и консольным расположением одного из колес.

т. е. меньше, чем 
Контактная прочность обеспечена.
22. Определяем основные размеры шестерни и колеса. Ранее были определен  мм,
мм,  мм,
мм,  мм.
мм.
Диаметры вершин зубьев (см. рис. 9.10):

Диаметры впадин зубьев:

23. Проверочный расчет на усталость при изгибе ведется по формуле (9.45). Эквивалентные числа зубьев 

По табл. 9.10 выбираем коэффициенты формы зуба  в соответствии с эквивалентными числами зубьев:
в соответствии с эквивалентными числами зубьев:  Дальнейший расчет надо проводить для того колеса, для которого отношение
Дальнейший расчет надо проводить для того колеса, для которого отношение  меньше.
меньше.
Для шестерни  и для колеса
и для колеса  Дальнейший расчет будем проводить по шестерне.
Дальнейший расчет будем проводить по шестерне.
Коэффициент, учитывающий перекрытие зубьев,  для прямозубых колес
для прямозубых колес

Коэффициент, учитывающий наклон зуба, для прямозубых колес  Коэффициент
Коэффициент

где для прямозубых колес  (см. табл. 9.11);
(см. табл. 9.11);  (см. табл. 9.13).
(см. табл. 9.13).
Напряжение при изгибе по формуле (9.45)

т. е. меньше, чем 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Раздел I. СОЕДИНЕНИЯ ДЕТАЛЕЙ МАШИН
- Глава 1. ВАЛЬЦОВОЧНЫЕ СОЕДИНЕНИЯ
- 1.2. Расчет прочных швов
- 1.3. Справочный материал
- 1.4. Примеры расчета
- Глава 2. СВАРНЫЕ, ПАЯНЫЕ И КЛЕЕВЫЕ СОЕДИНЕНИЯ
- 2.1. Общие сведения об основных видах сварных соединений и сварных швов
- 2.2. Расчет прочности сварных швов
- 2.3. Условное изображение сварных швов на чертежах
- 2.4. Паяные соединения
- 2.5. Клеевые соединения
- 2.6. Справочный материал
- 2.7. Примеры расчета
- Глава 3. РЕЗЬБОВЫЕ СОЕДИНЕНИЯ
- 3.2. Определение сил, действующих на один болт
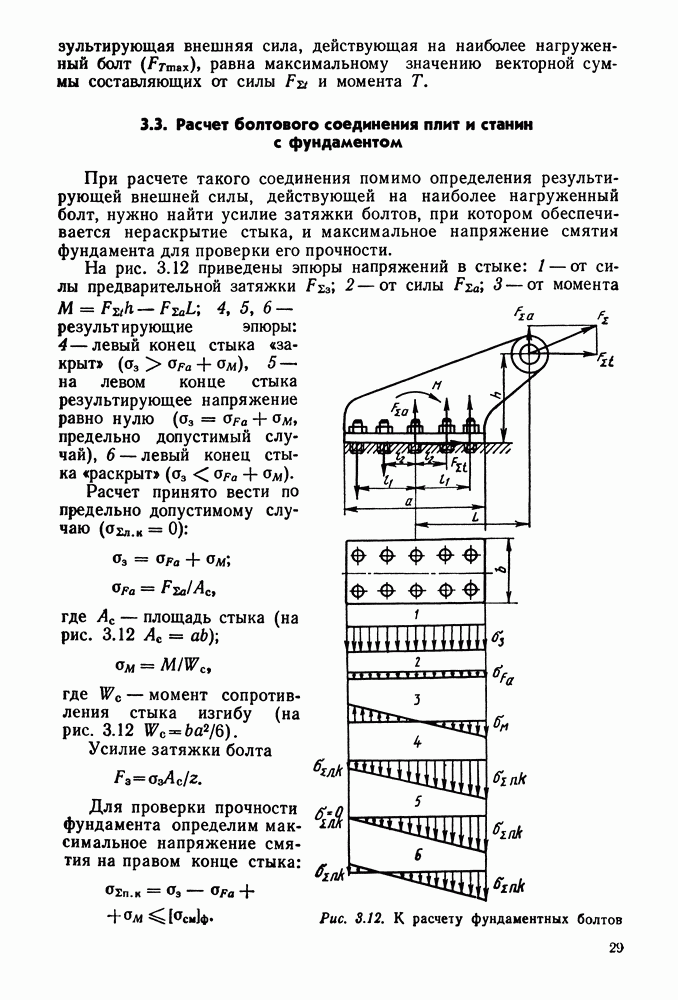
- 3.3. Расчет болтового соединения плит и станин с фундаментом
- 3.4. Расчет стержня болта при постоянных нагрузках
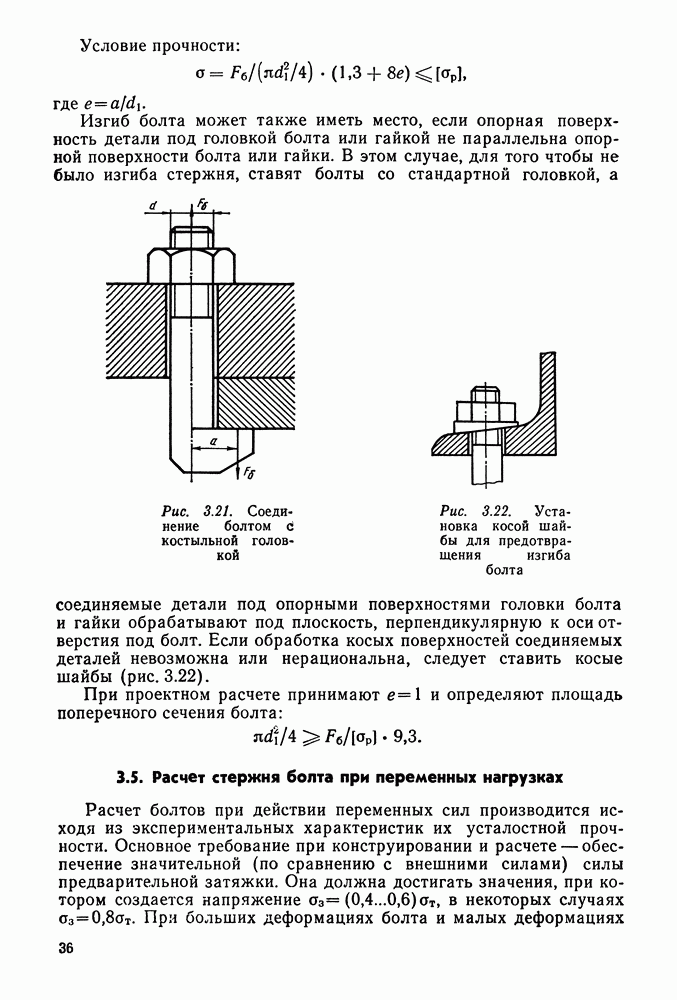
- 3.5. Расчет стержня болта при переменных нагрузках
- 3.6. Расчет витков резьбы на прочность. Определение вращающего момента
- 3.7. Порядок расчета резьбовых соединений
- 3.9. Примеры расчета
- Глава 4. СОЕДИНЕНИЯ ВАЛ — СТУПИЦА (ШПОНОЧНЫЕ, ШЛИЦЕВЫЕ, С НАТЯГОМ)
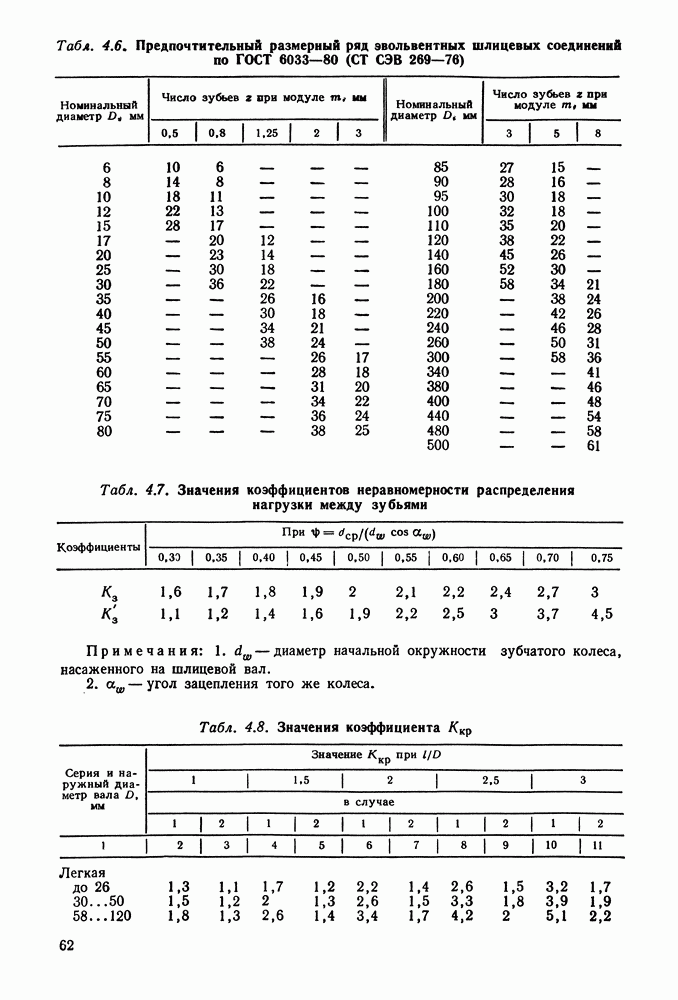
- 4.2. Шлицевые соединения
- 4.3. Соединения с натягом
- 4.4. Справочный материал
- 4.5. Примеры расчета
- Раздел II. МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ
- Глава 5. КИНЕМАТИЧЕСКИЙ РАСЧЕТ ПРИВОДНЫХ УСТРОЙСТВ И ВЫБОР ЭЛЕКТРОДВИГАТЕЛЯ
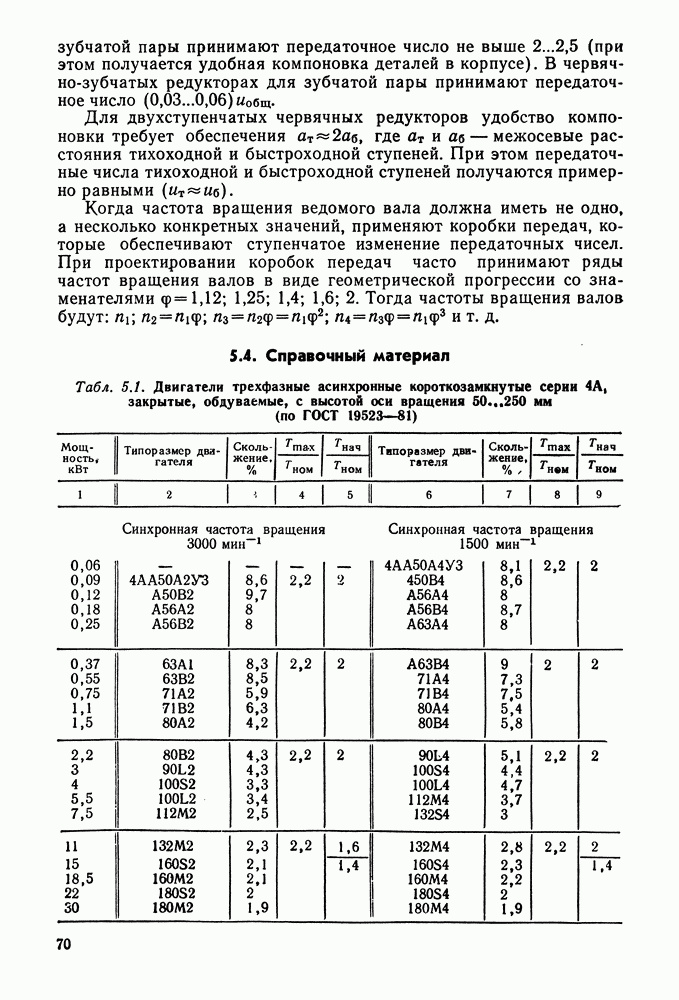
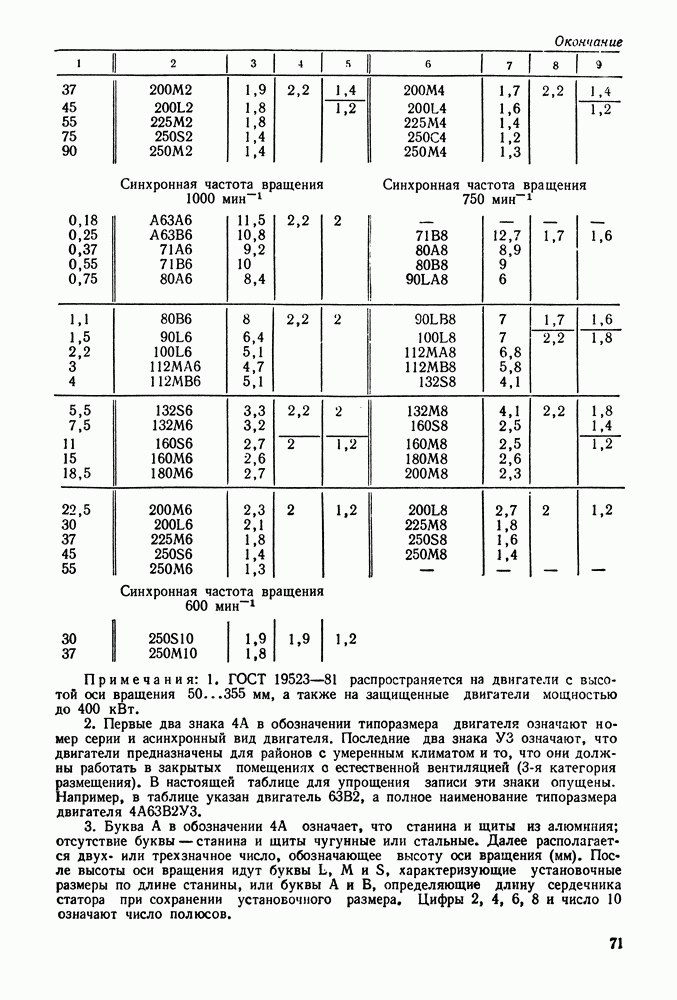
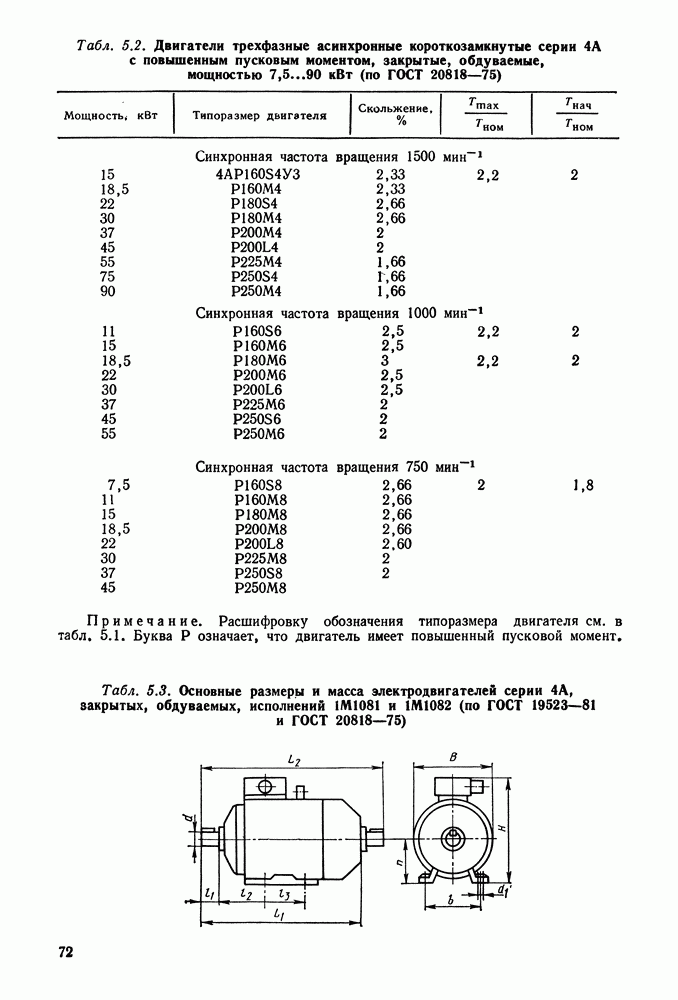
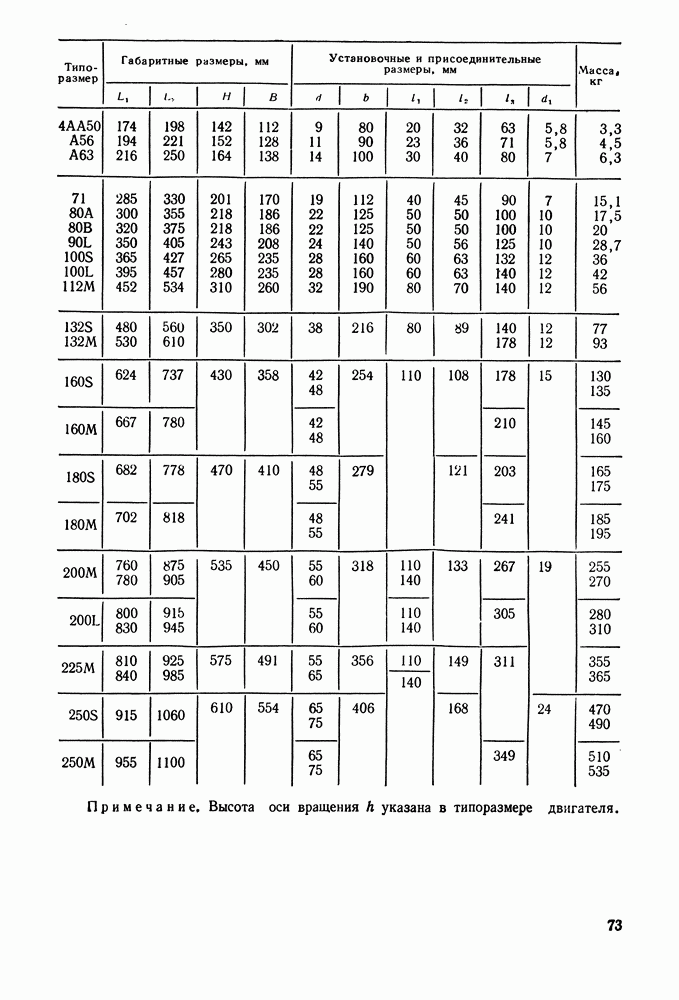
- 5.2. Трехфазные асинхронные электродвигатели
- 5.3. Разбивка общего передаточного числа редуктора по ступеням
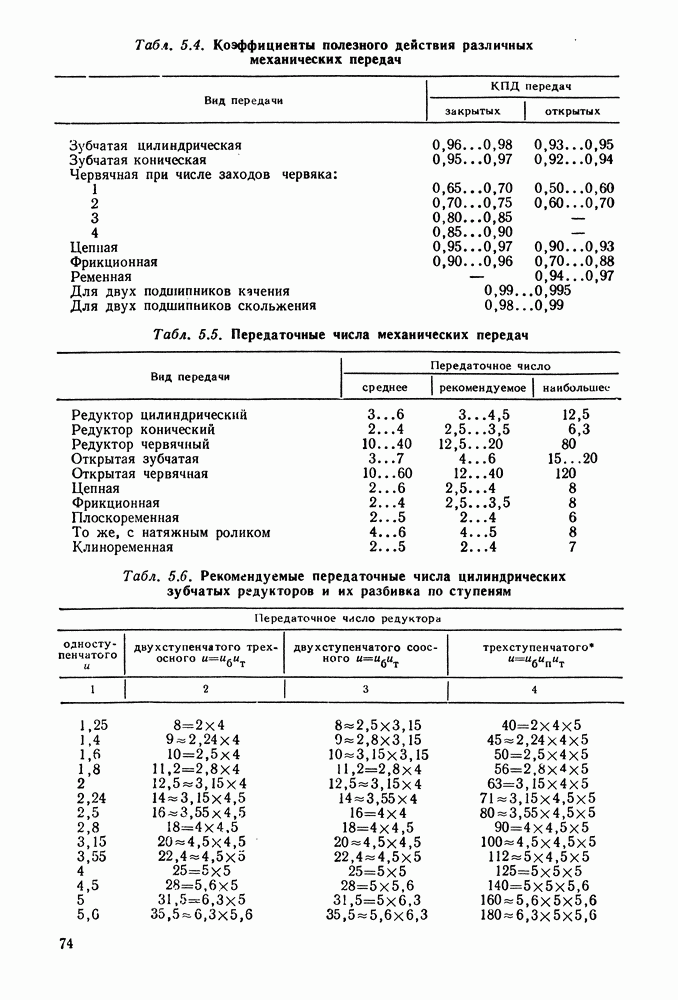
- 5.4. Справочный материал
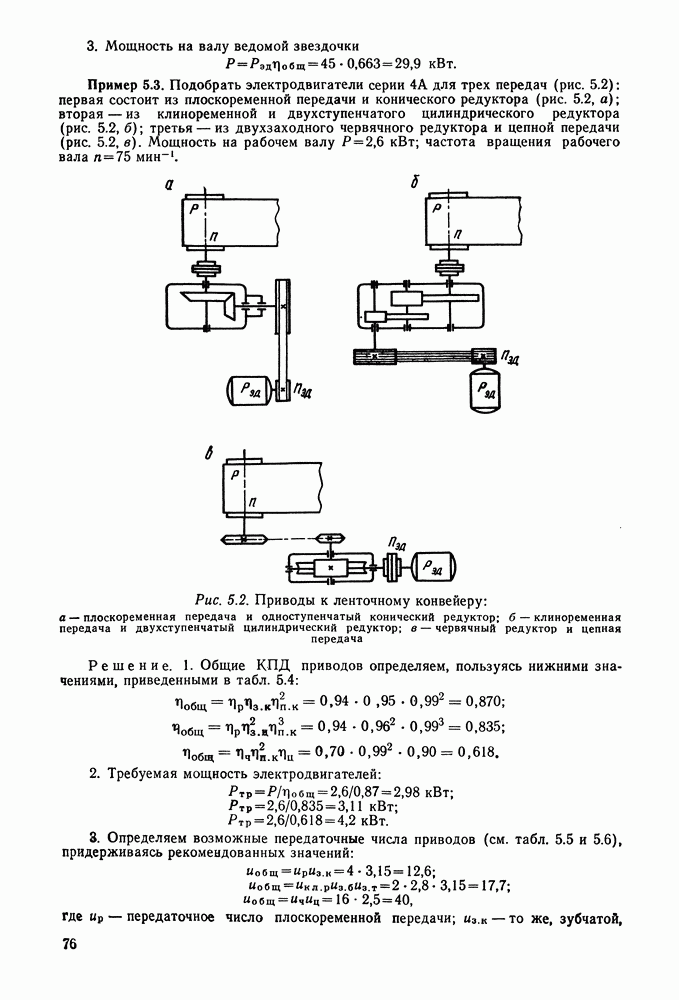
- 5.5. Примеры расчета
- Глава 6. ФРИКЦИОННЫЕ ПЕРЕДАЧИ И ВАРИАТОРЫ
- 6.2. Кинематические расчеты фрикционных передач
- 6.3. Определение сил прижатия фрикционных тел и нагрузки на валы передачи
- 6.4. Расчет фрикционных тел на контактную прочность и КПД передач
- 6.5. Справочный материал
- 6.6. Примеры расчета
- Глава 7. РЕМЕННЫЕ ПЕРЕДАЧИ
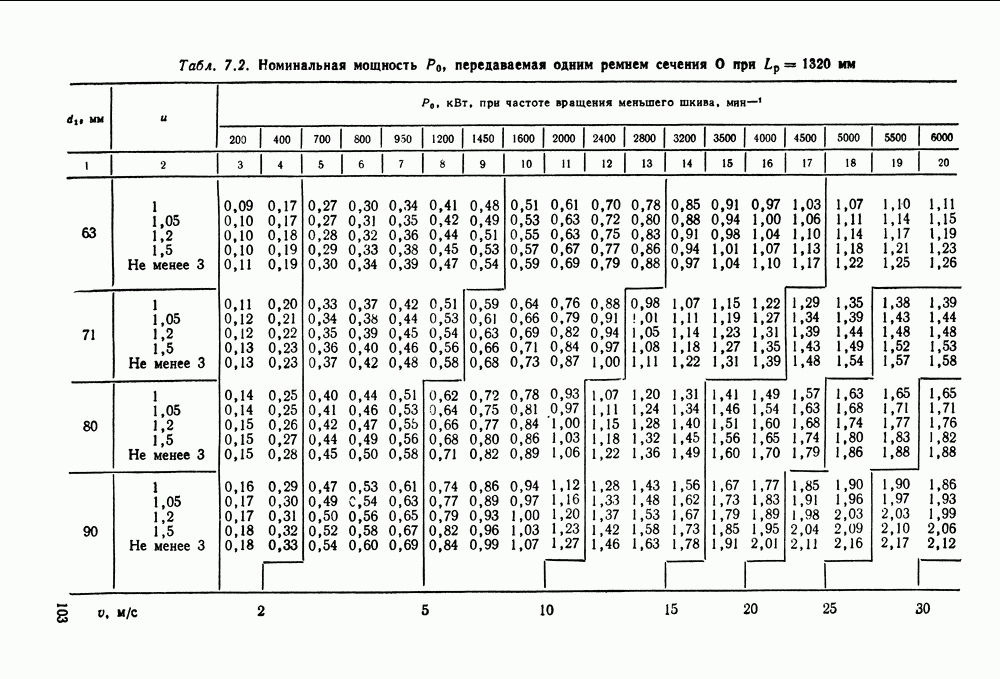
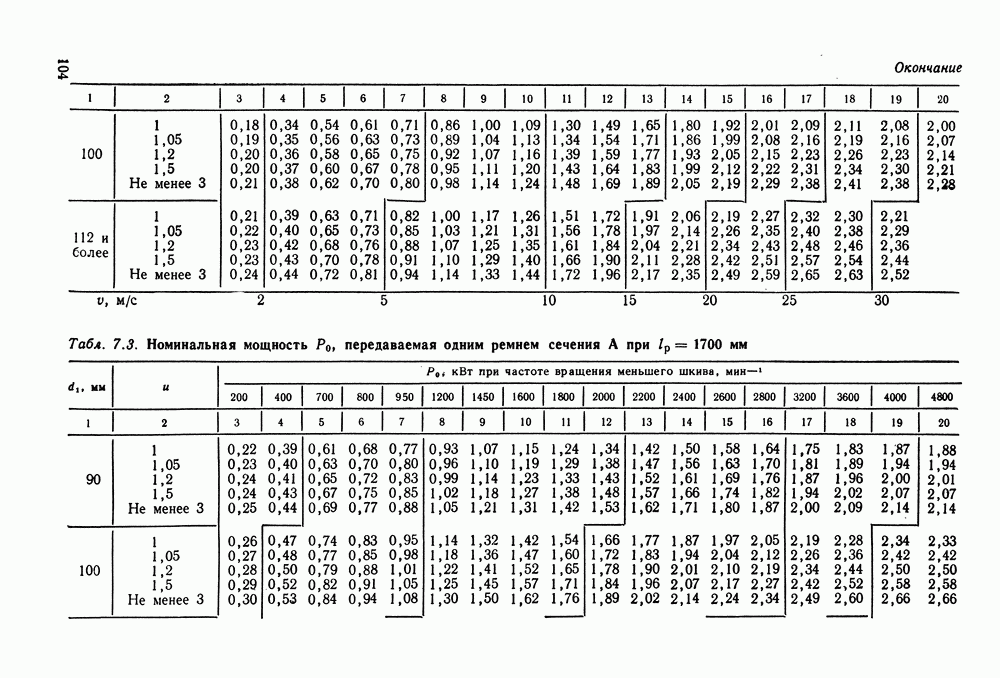
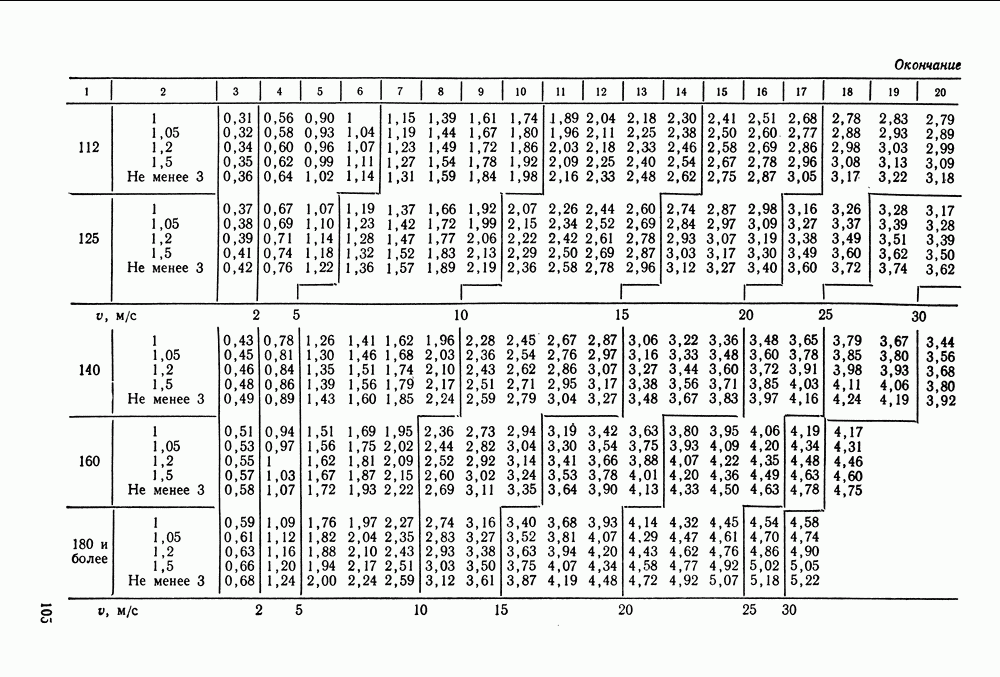
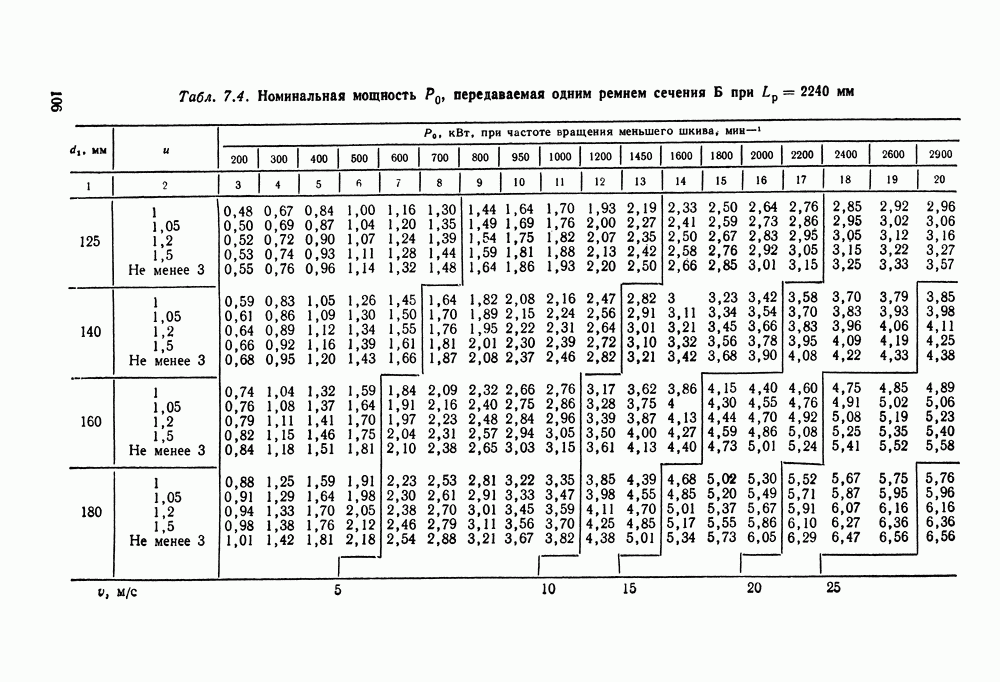
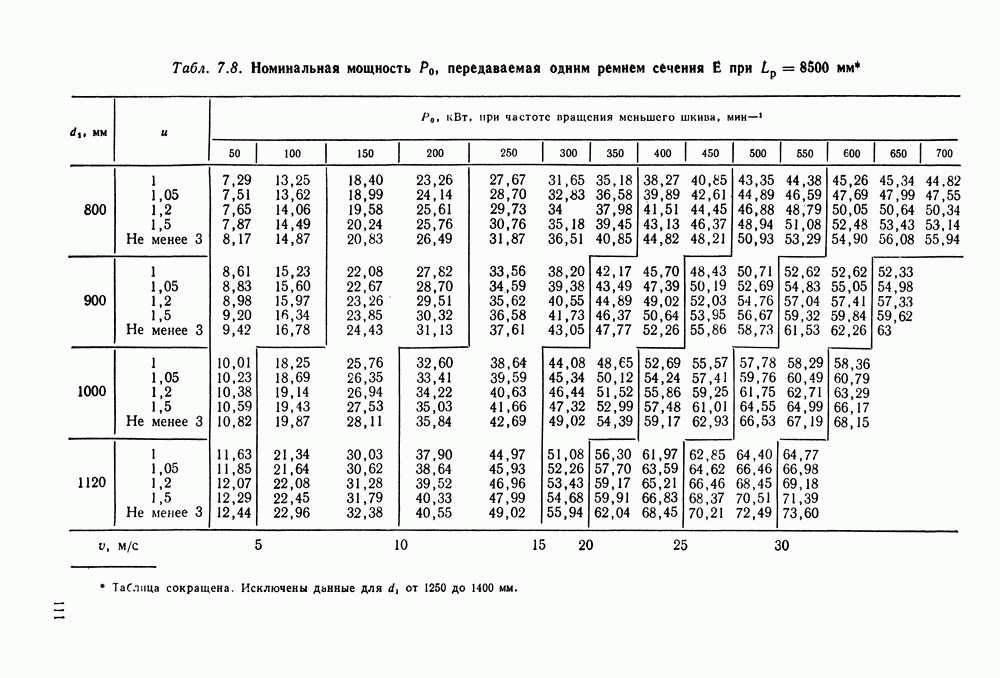
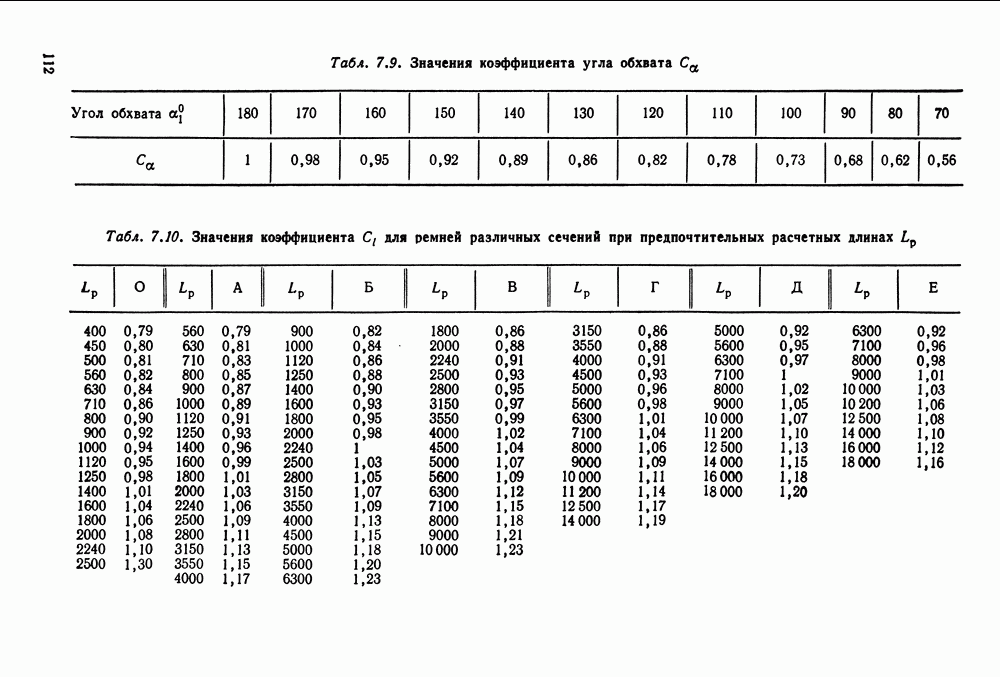
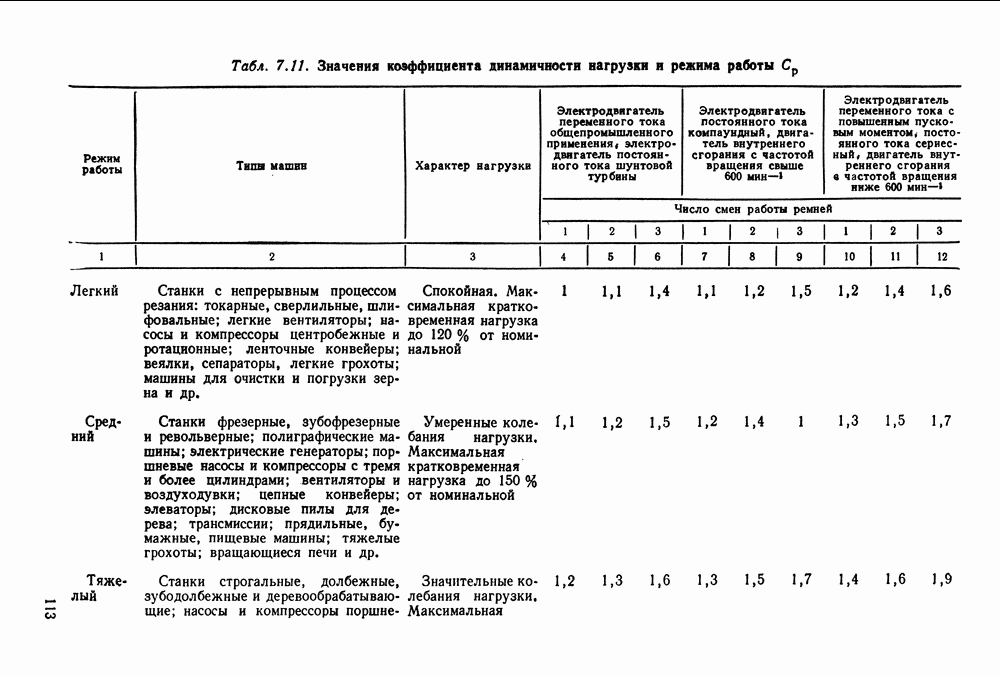
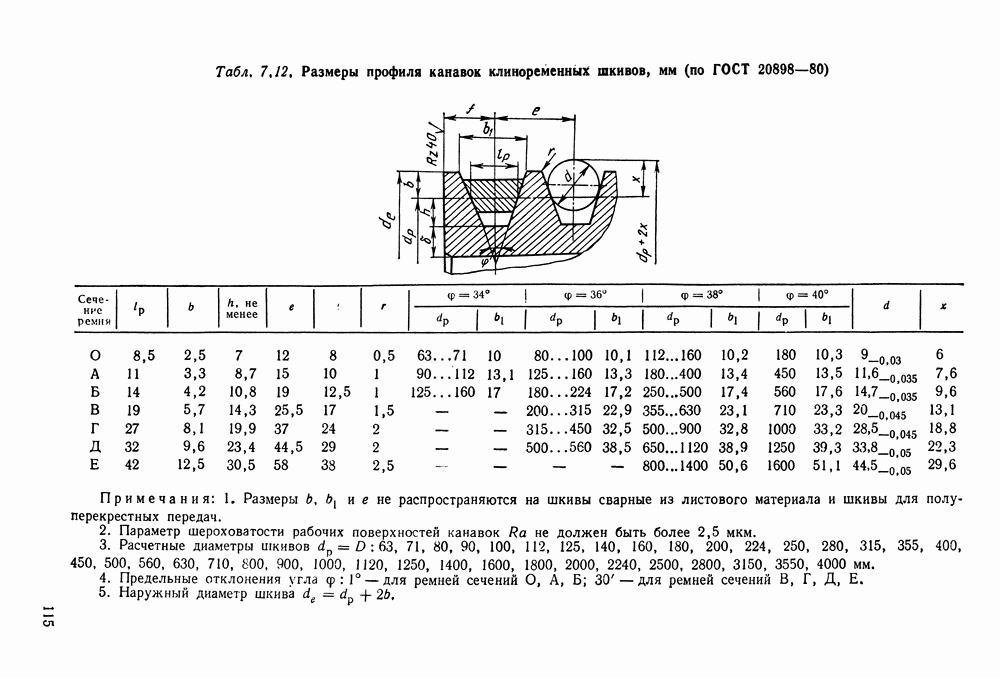
- 7.2. Расчет клиноременных передач
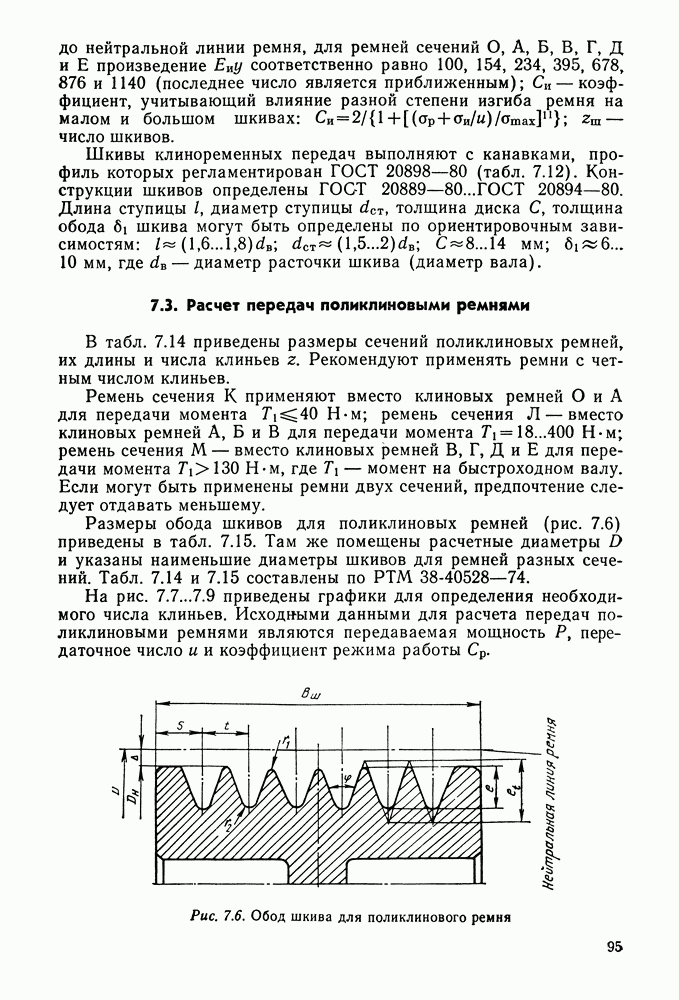
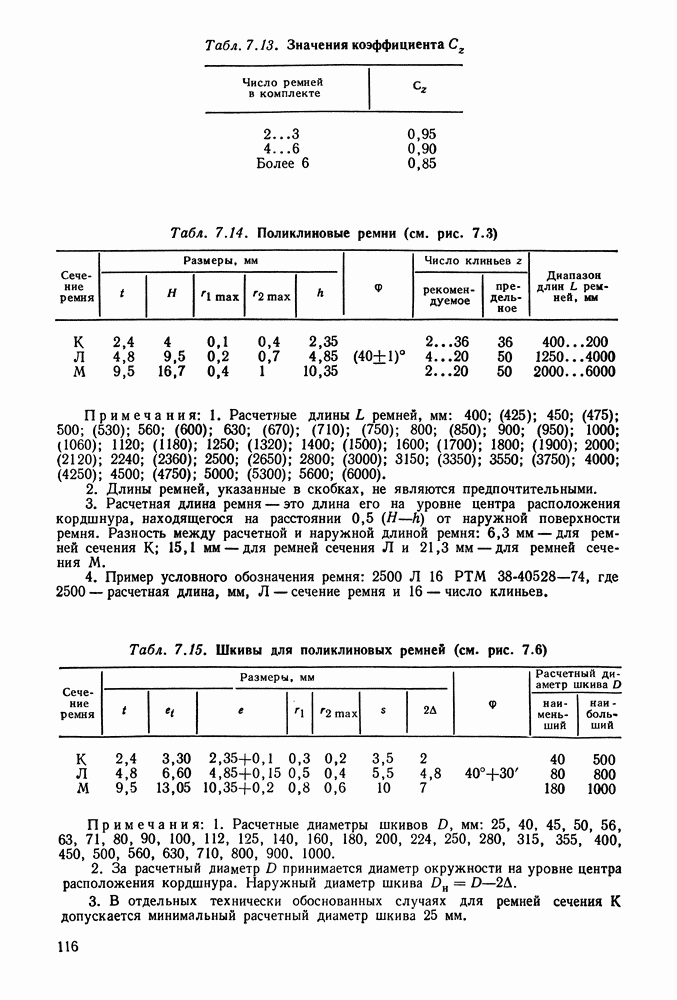
- 7.3. Расчет передач поликлиновыми ремнями
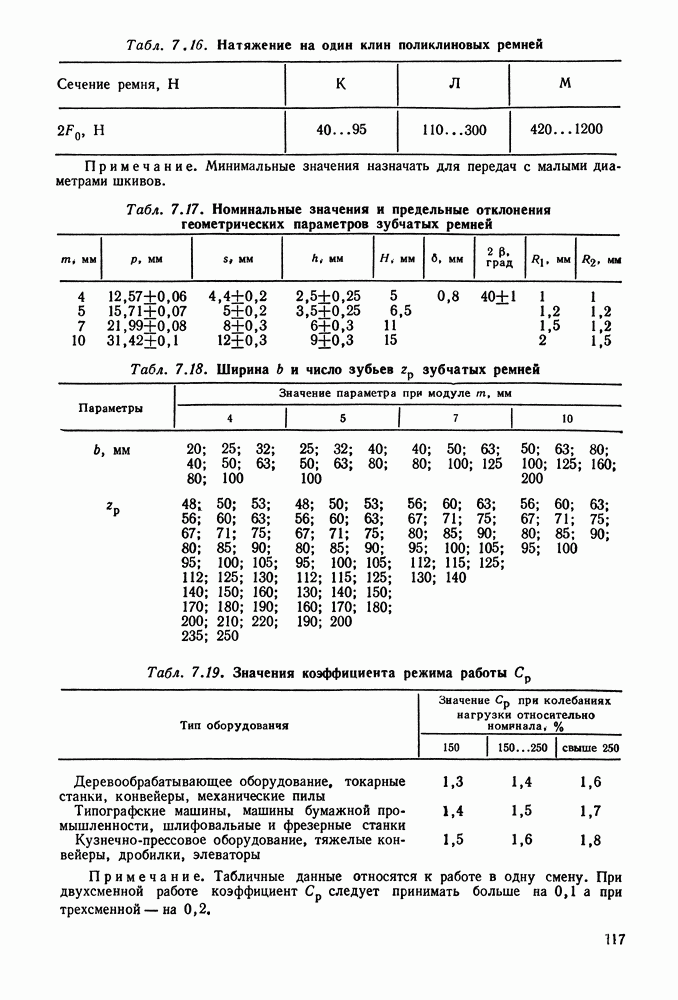
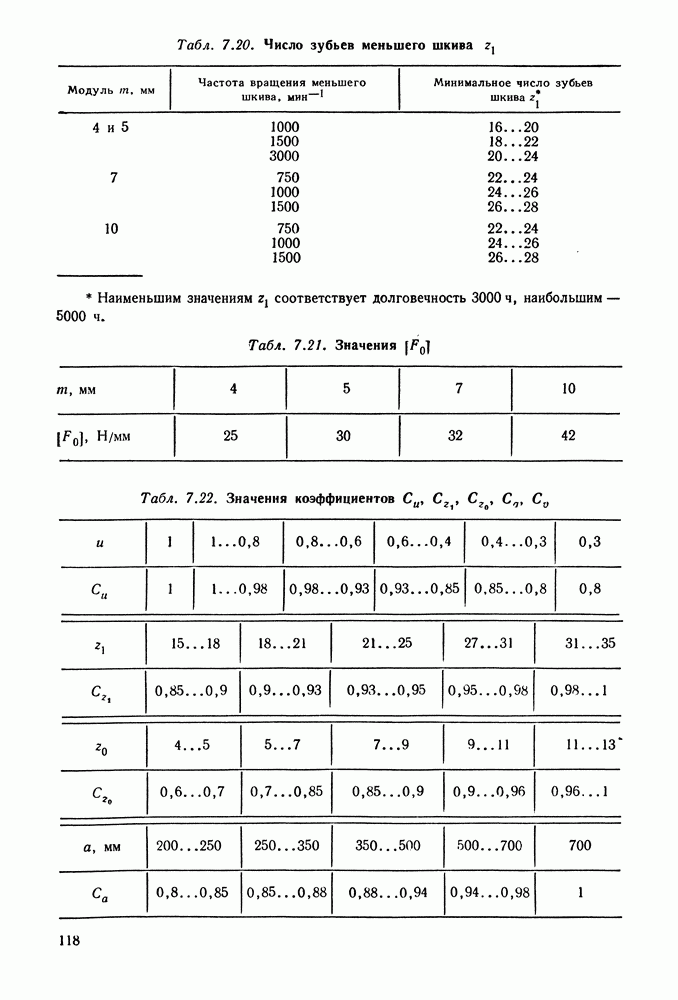
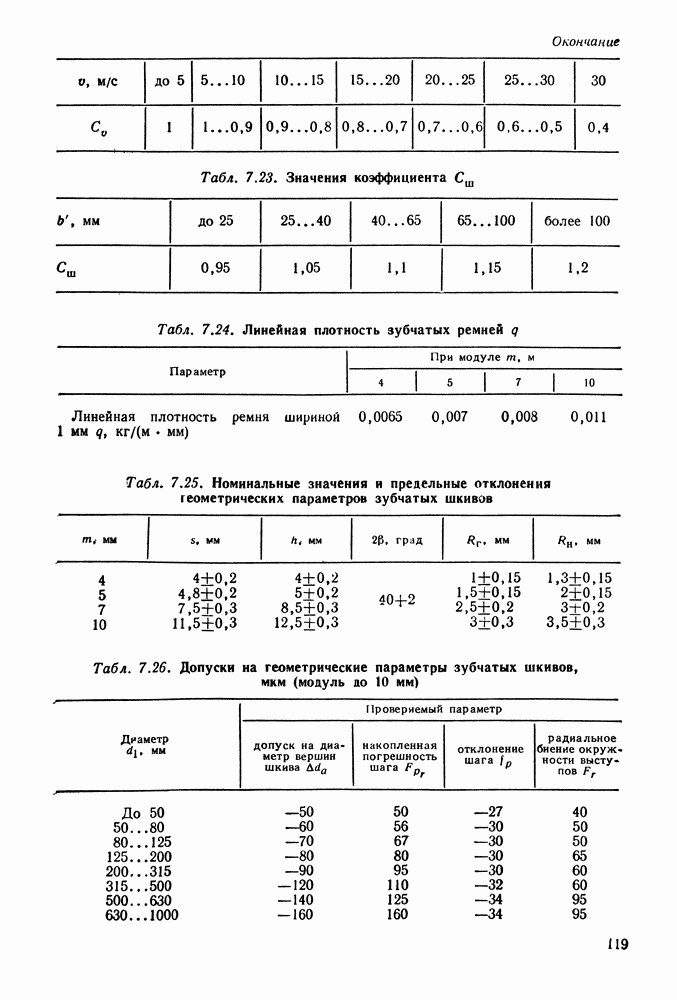
- 7.4. Расчет зубчато-ременных передач
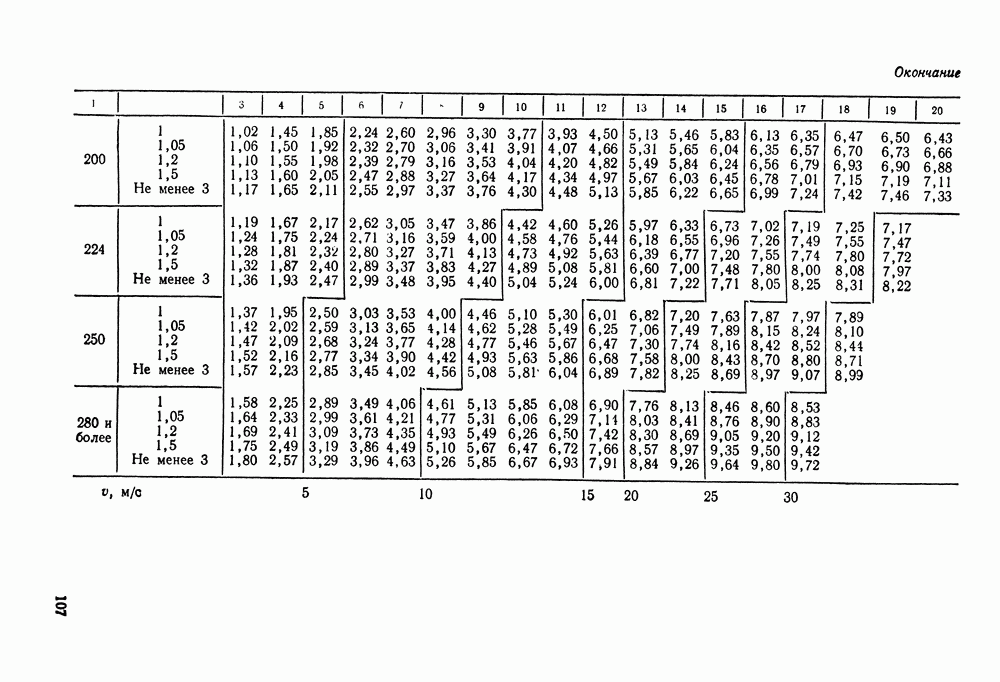
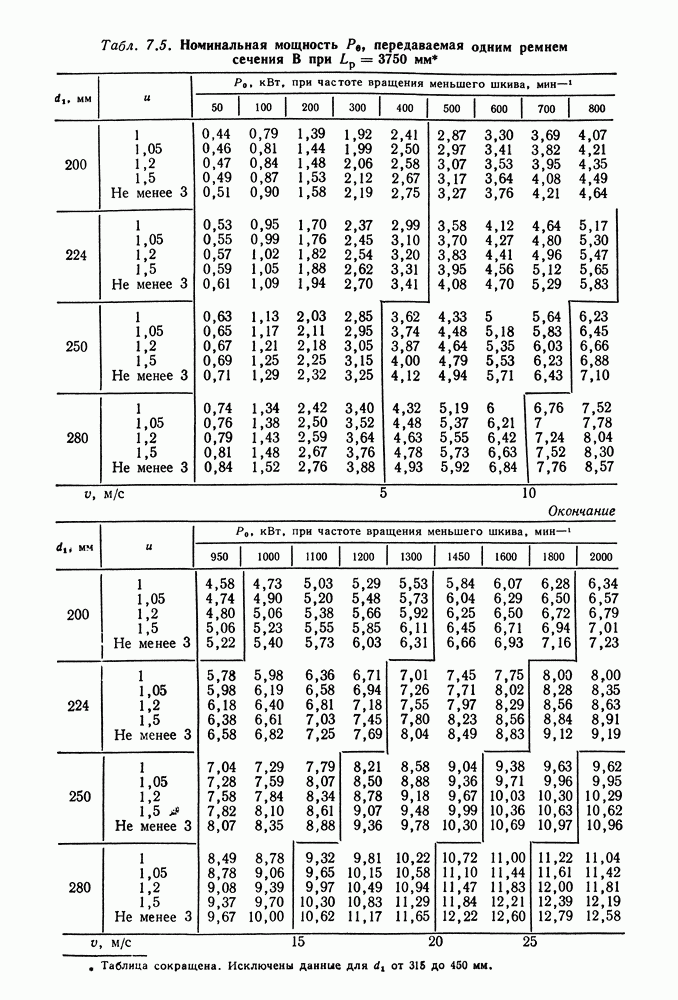
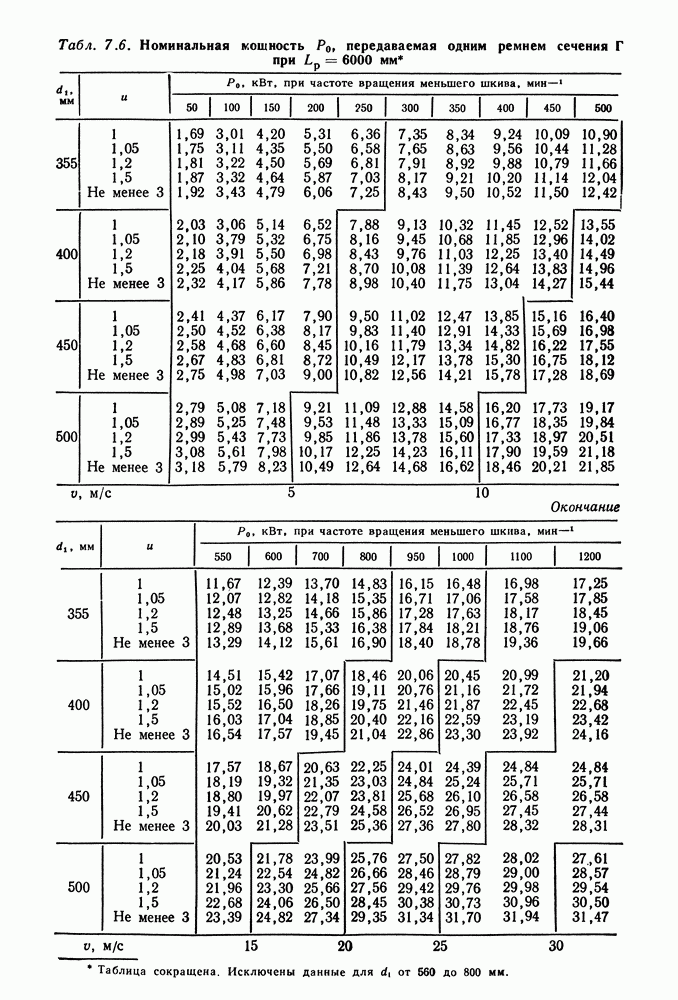
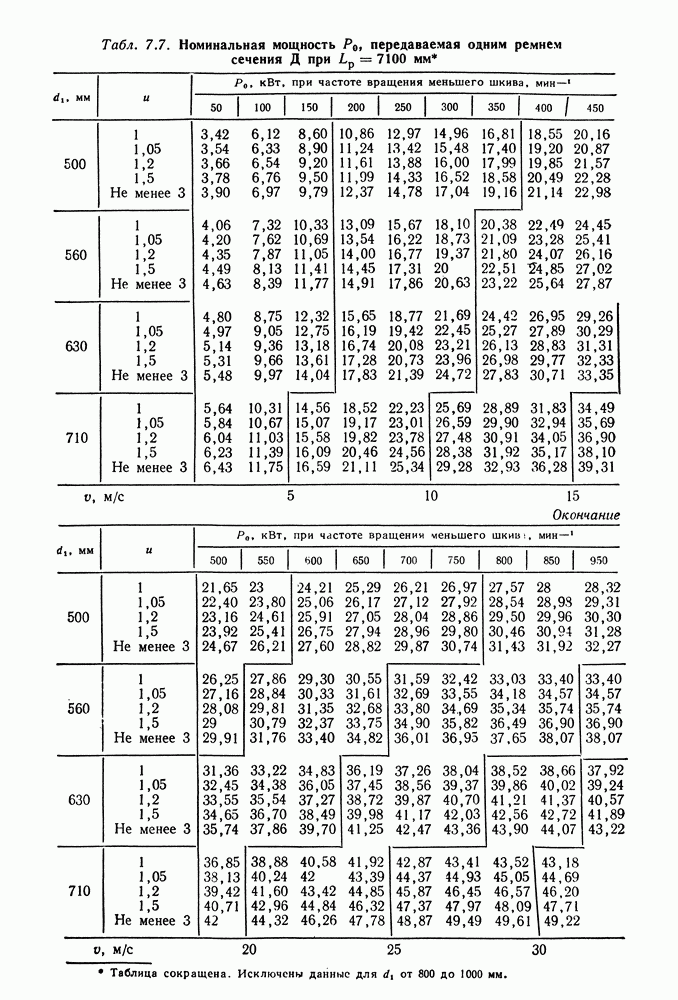
- 7.5. Справочный материал
- 7.6. Примеры расчета
- Глава 8. ЦЕПНЫЕ ПЕРЕДАЧИ
- 8.2. Геометрический, кинематический и силовой расчеты цепных передач
- 8.3. Выбор основных параметров и расчет цепных передач
- 8.4. Справочный материал
- 8.5. Примеры расчета
- Глава 9. ЗУБЧАТЫЕ ПЕРЕДАЧИ
- 9.2. Геометрия и кинематика эвольвентного цилиндрического зацепления
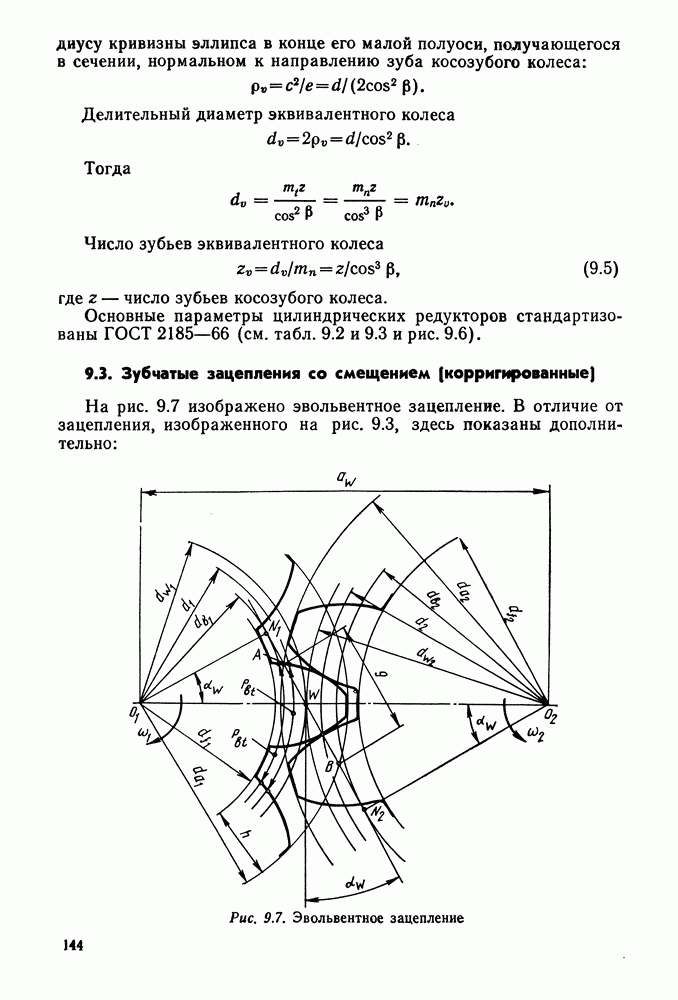
- 9.3. Зубчатые зацепления со смещением (корригированные)
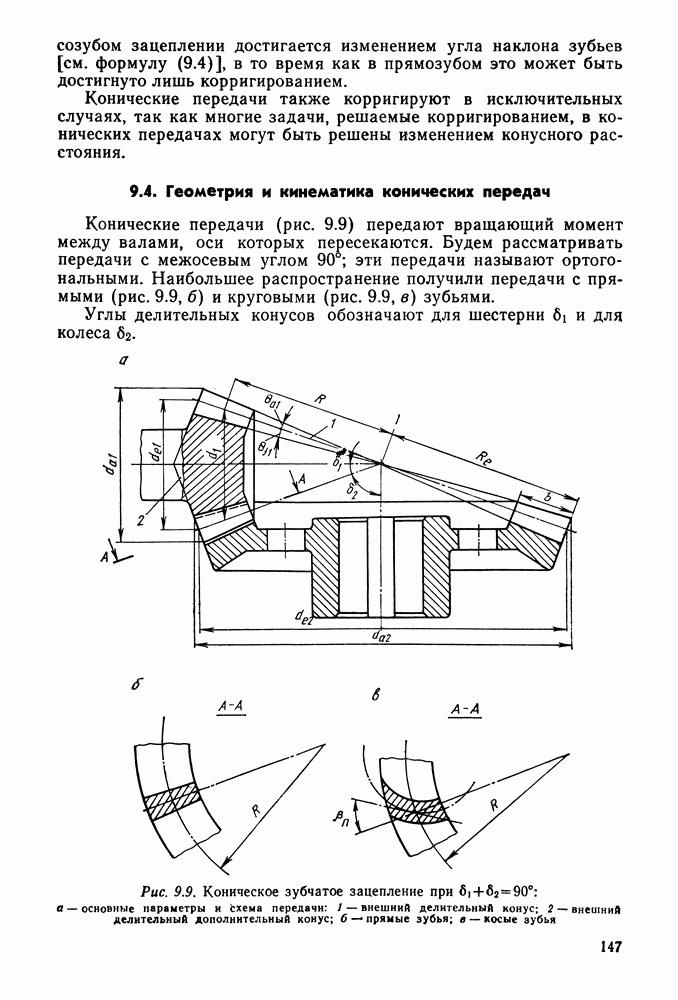
- 9.4. Геометрия и кинематика конических передач
- 9.5. Материалы и допускаемые напряжения
- 9.6. Точность зубчатых передач
- 9.7. Коэффициент нагрузки
- 9.8. Расчет зубчатого зацепления на контактную прочность
- 9.9. Расчет зубьев колес на изгиб
- 9.10. Расчет открытых зубчатых передач
- 9.11. Проверка прочности зубьев колес при перегрузках
- 9.12. Определение размеров стальных зубчатых закрытых передач и проверка их прочности
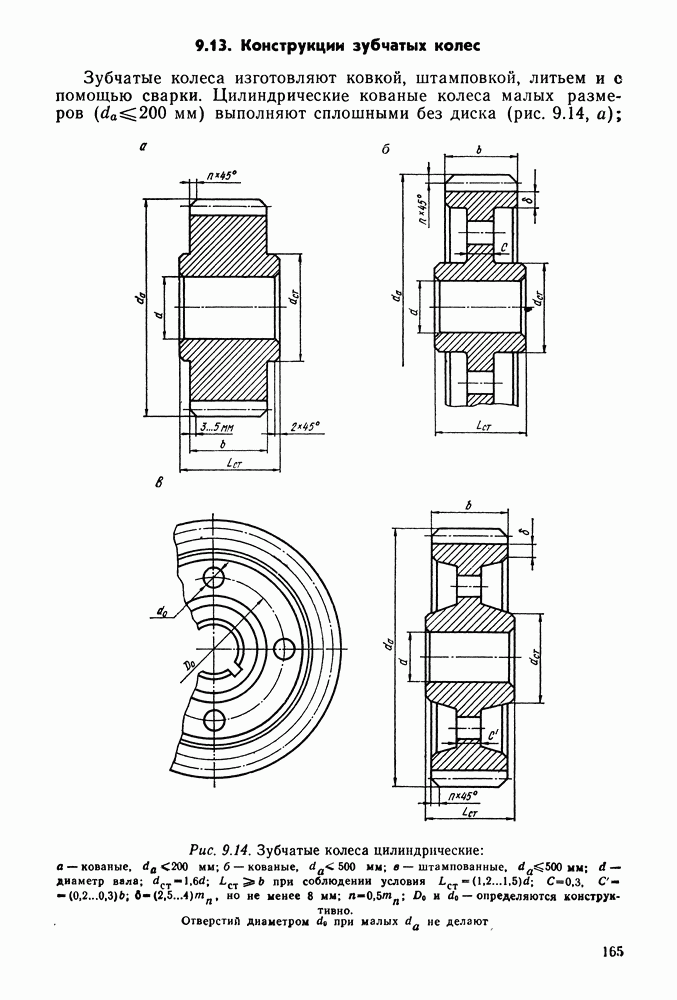
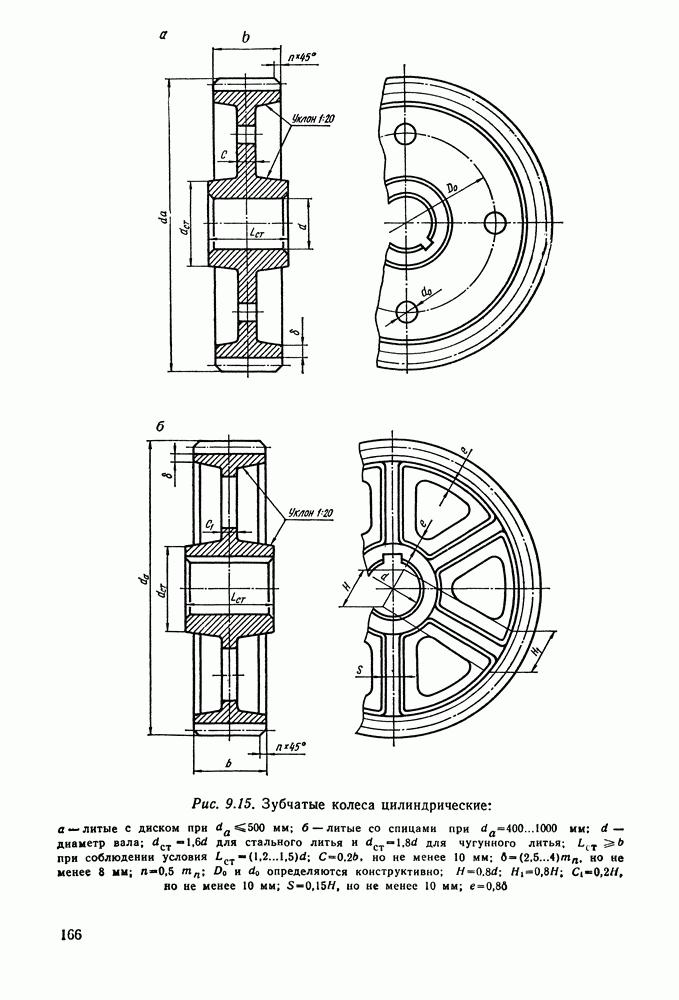
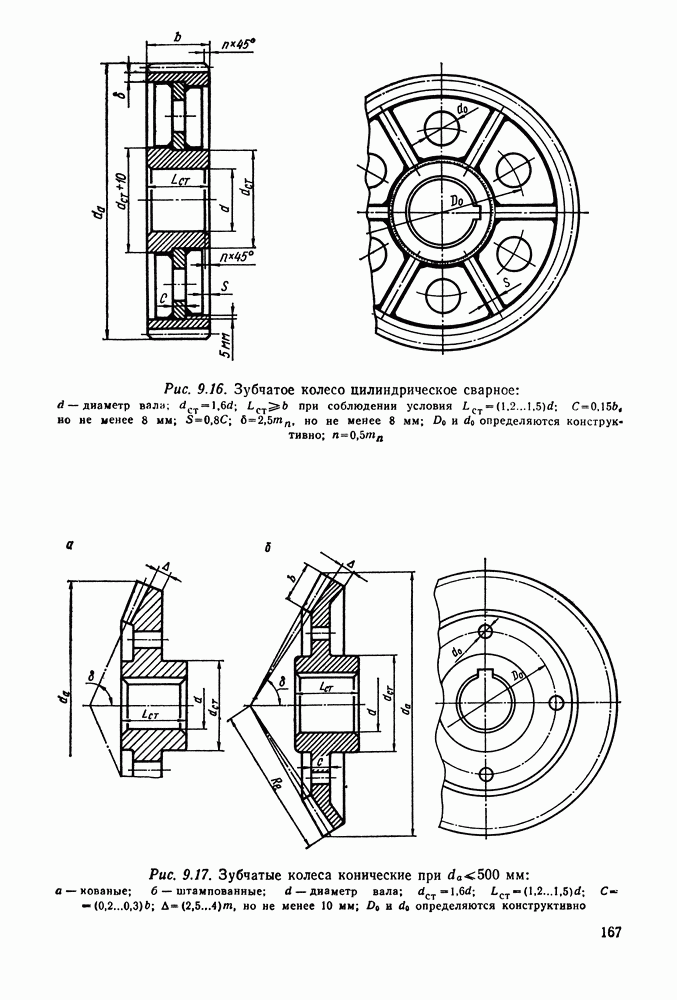
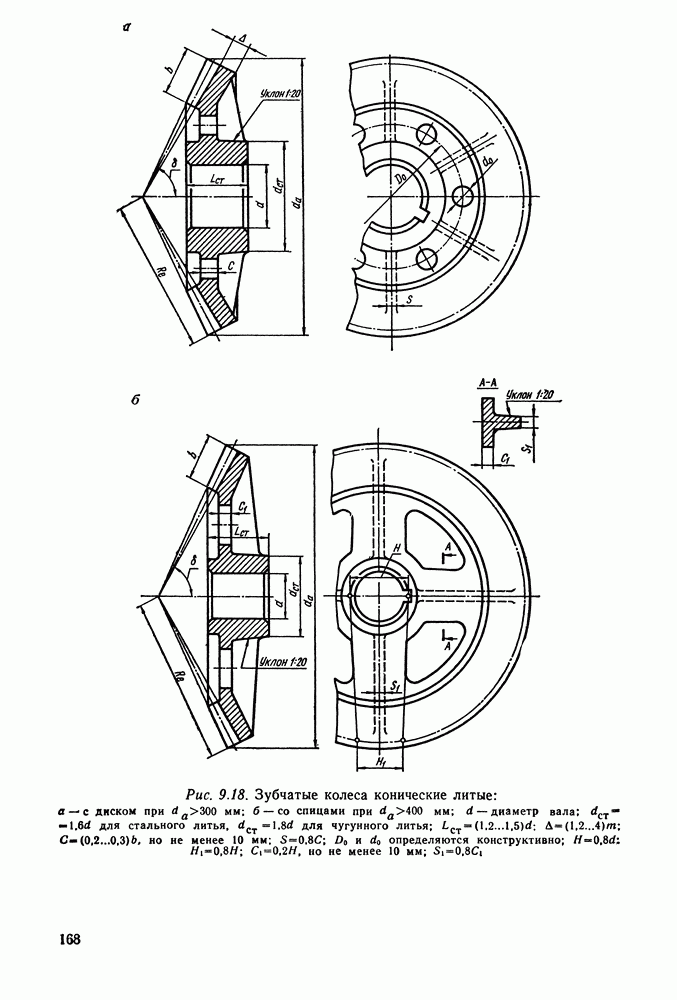
- 9.13. Конструкции зубчатых колес
- 9.14. Справочный материал
- 9.15. Примеры расчета
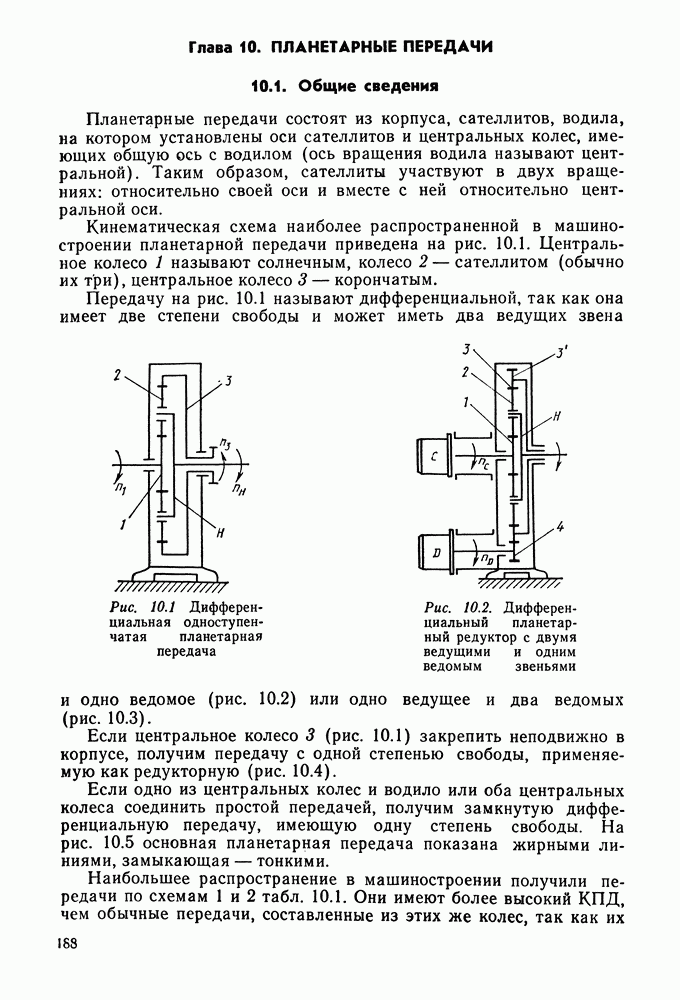
- Глава 10. ПЛАНЕТАРНЫЕ ПЕРЕДАЧИ
- 10.2. Кинематический расчет
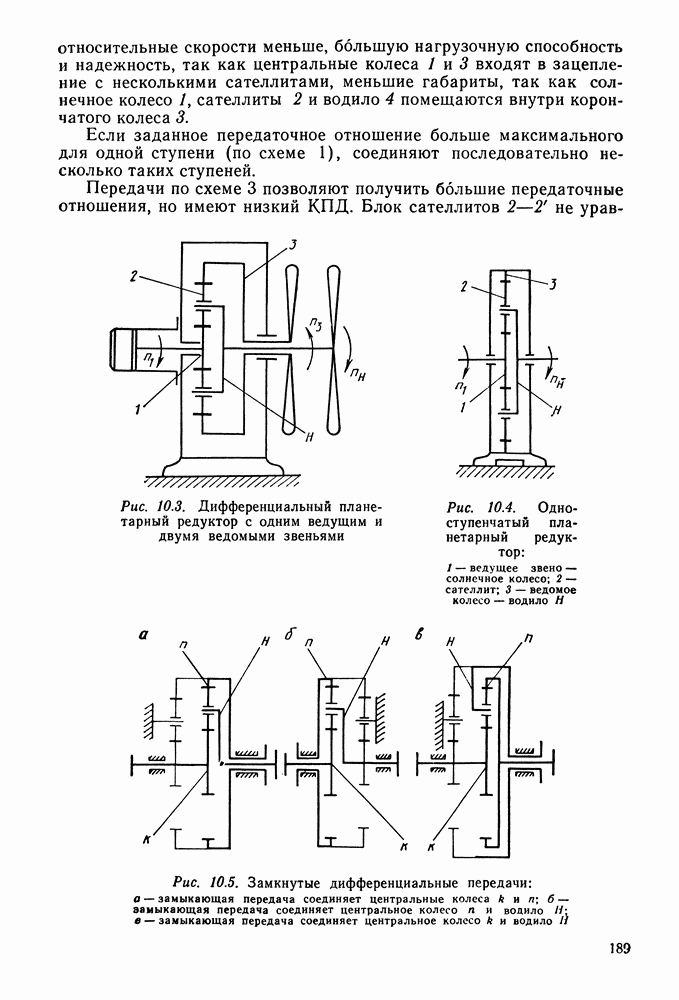
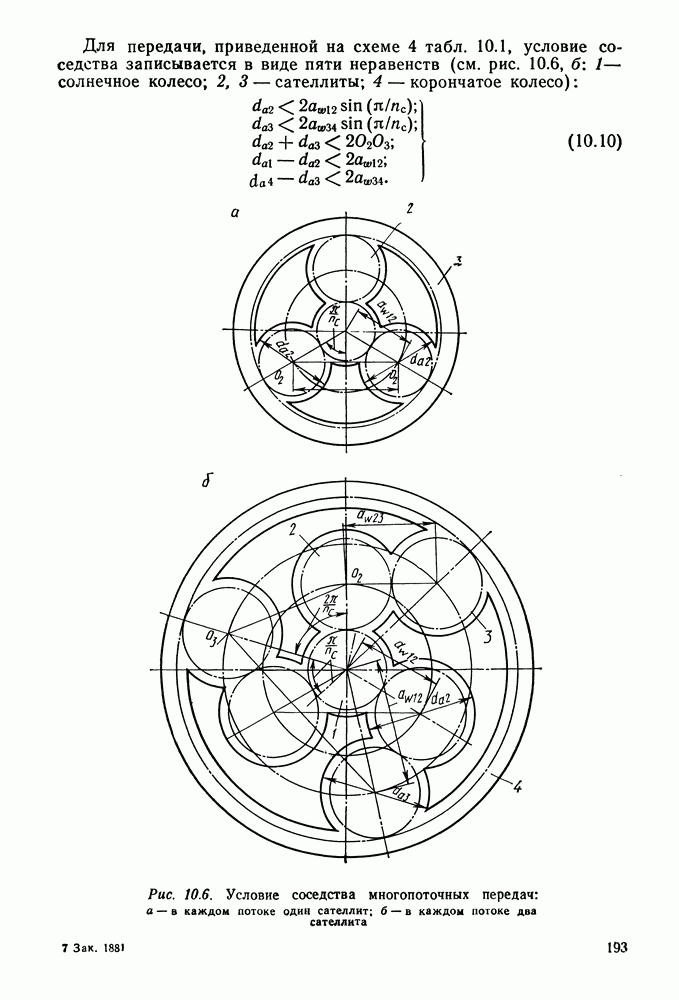
- 10.3. Условия собираемости соосных и многопоточных передач
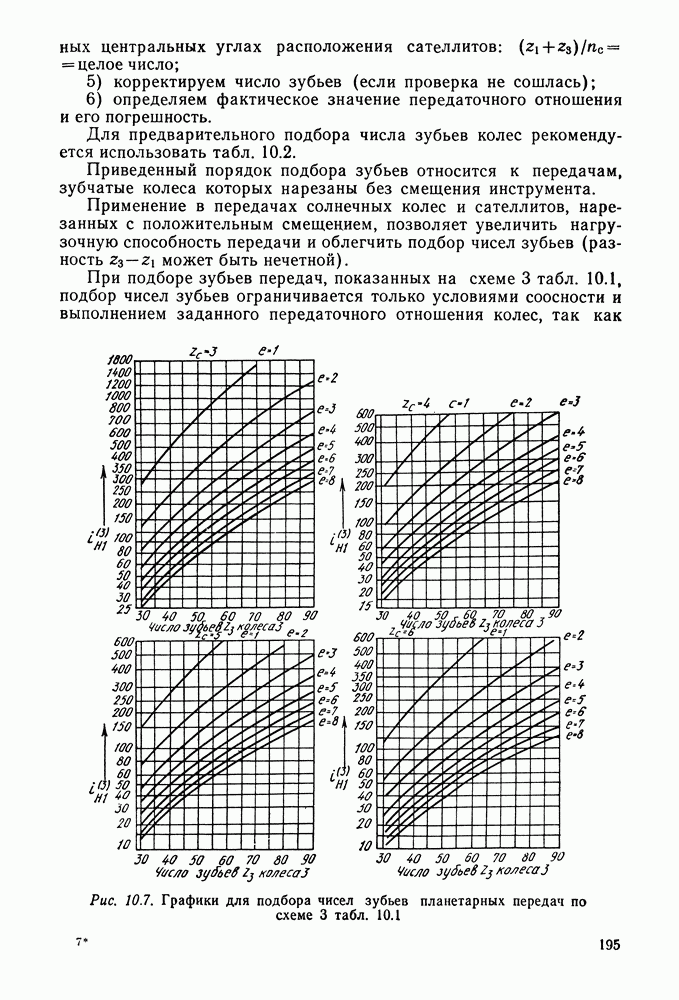
- 10.4. Порядок подбора чисел зубьев при заданном передаточном отношении и числе сателлитов
- 10.5. Определение КПД планетарных передач
- 10.6. Определение сил, действующих в зацеплениях и в опорах осей и валов прямозубых передач
- 10.7. Расчет зубьев планетарных передач на прочность
- 10.8. Конструкция и размеры деталей планетарных передач [14]
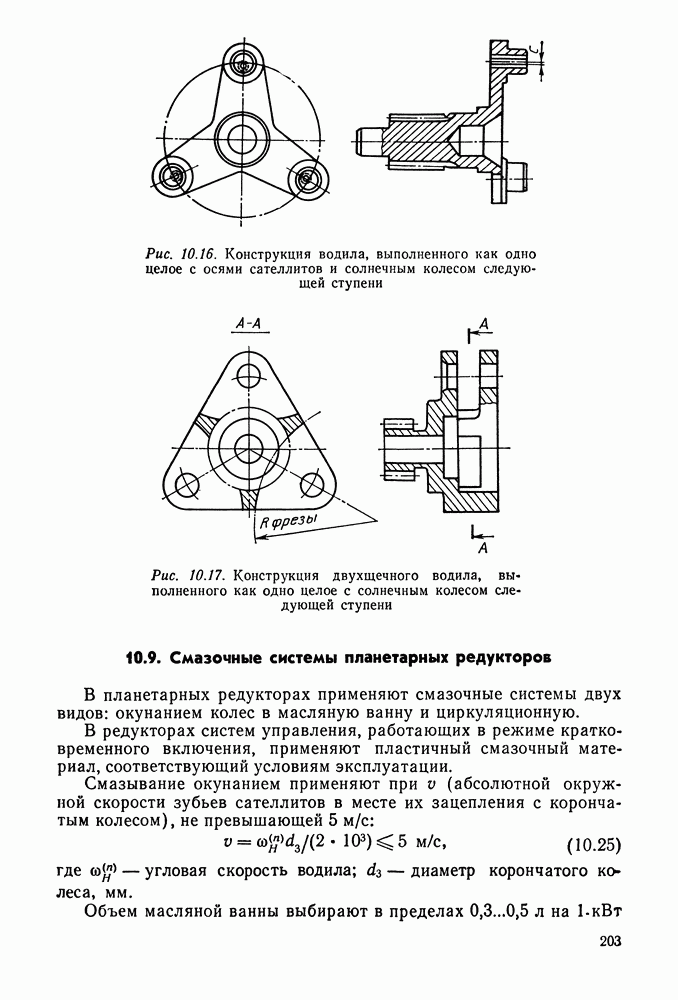
- 10.9. Смазочные системы планетарных редукторов
- 10.10. Порядок проектного расчета планетарного редуктора (схемы 1 и 2 табл. 10.1)
- 10.11. Порядок расчета планетарного мотор-редуктора (схема 1 табл. 10.1)
- 10.12. Справочный материал
- 10.13. Примеры расчета
- Глава 11. ВОЛНОВЫЕ ПЕРЕДАЧИ
- 11.2 Основные схемы волновых передач
- 11.3. Проектный расчет волновой зубчатой передачи
- 11.4. Конструкция и размеры основных деталей волновых передач
- 11.5. Порядок расчета волновой передачи с кулачковым генератором
- 11.6. Справочный материал
- 11.7. Пример расчета
- Глава 12. ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ
- 12.2 Геометрия и кинематика червячного зацепления
- 12.3. Червячные передачи со смещением (корригированные)
- 12.4. Материалы и допускаемые напряжения
- 12.5. Точность червячных передач
- 12.6. Коэффициент нагрузки
- 12.7. Расчет червячного зацепления на контактную прочность
- 12.8. Расчет на изгиб
- 12.9. Расчет открытых червячных передач
- 12.10. Проверка червячных редукторов на нагрев
- 12.11. Конструкция червяков и червячных колес
- 12.12. Справочный материал
- 12.13. Пример расчета
- Глава 13. ПЕРЕДАЧА ВИНТ — ГАЙКА
- 13.2. Кинематический и силовой расчеты
- 13.3. Передача винт—гайка с трением скольжения
- 13.4. Передача винт — гайка с трением качения
- 13.5. Справочный материал
- 13.6. Пример расчета
- Раздел III. ВАЛЫ, ИХ ОПОРЫ, МУФТЫ, ПРУЖИНЫ
- Глава 14. ВАЛЫ
- 14.2. Некоторые сведения по конструированию валов и выбору материалов
- 14.3. Расчет валов
- 14.4. Посадки основных деталей передач на валы по стандартам СЭВ
- 14.5. Справочный материал
- 14.6. Примеры расчета
- Глава 15. РАДИАЛЬНЫЕ ПОДШИПНИКИ СКОЛЬЖЕНИЯ
- 15.2. Упрощенный расчет подшипников скольжения
- 15.3. Расчет подшипников жидкостного трения
- 15.4. Сопротивление слоя масла вращению шипа
- 15.5. Тепловой расчет подшипника
- 15.6. Справочный материал
- 15.7. Примеры расчета
- Глава 16. ПОДШИПНИКИ КАЧЕНИЯ
- 16.2. Условные обозначения и точность подшипников качения
- 16.3. Выбор и проверка подшипников качения по динамической грузоподъемности
- 16.4. Выбор подшипников качения по статической грузоподъемности
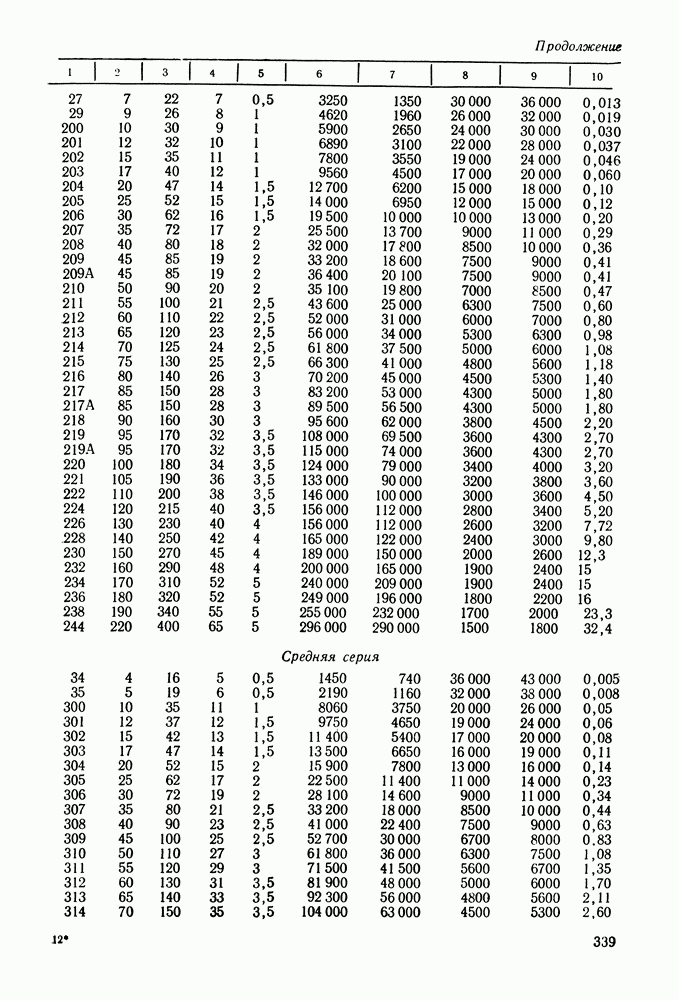
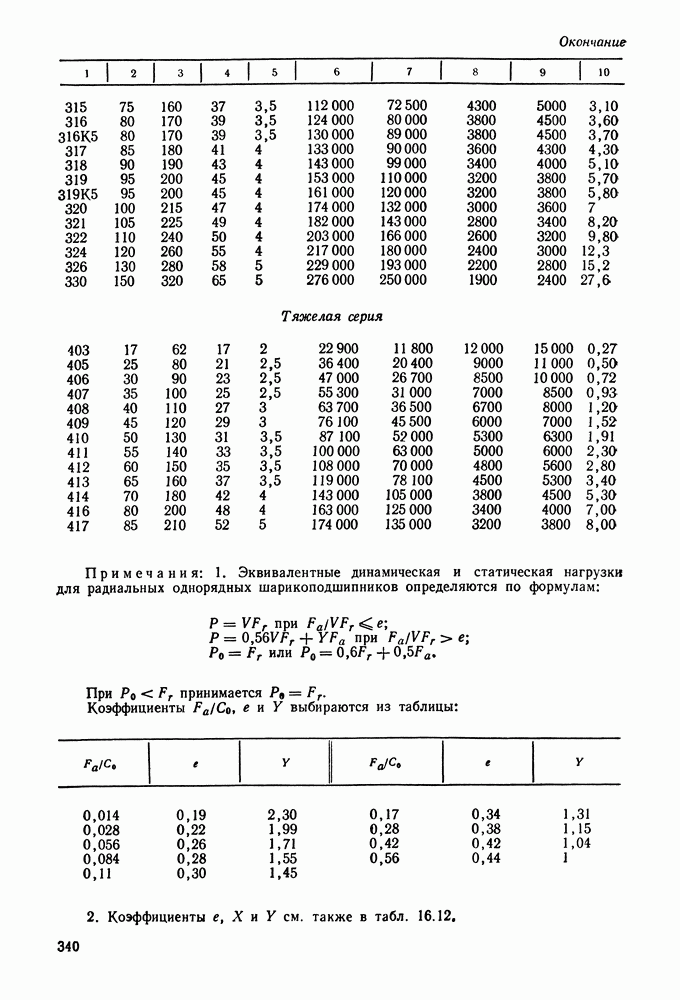
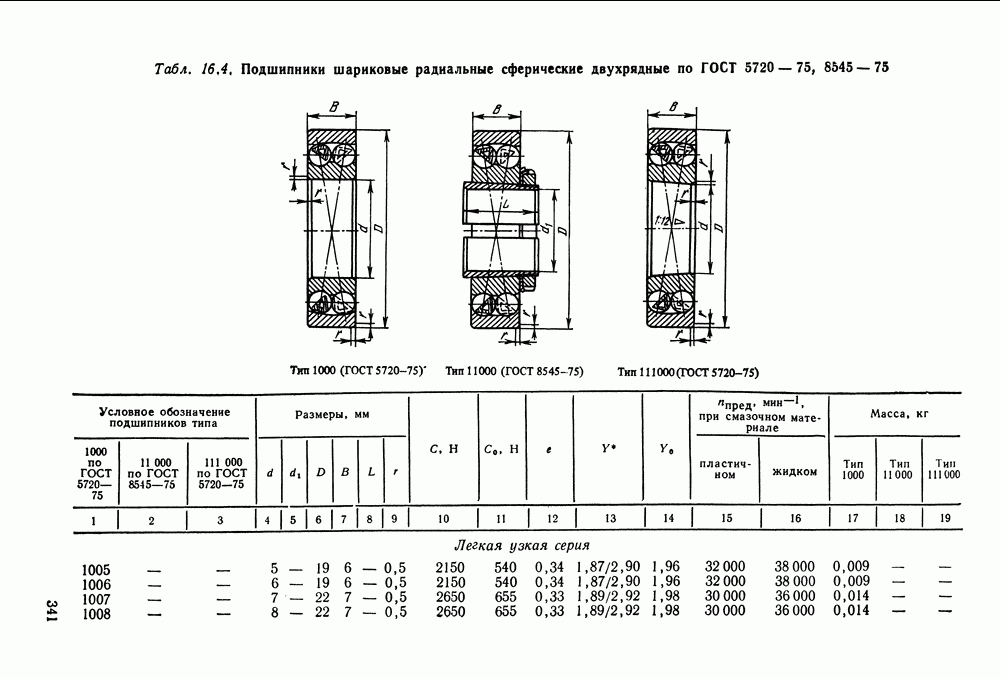
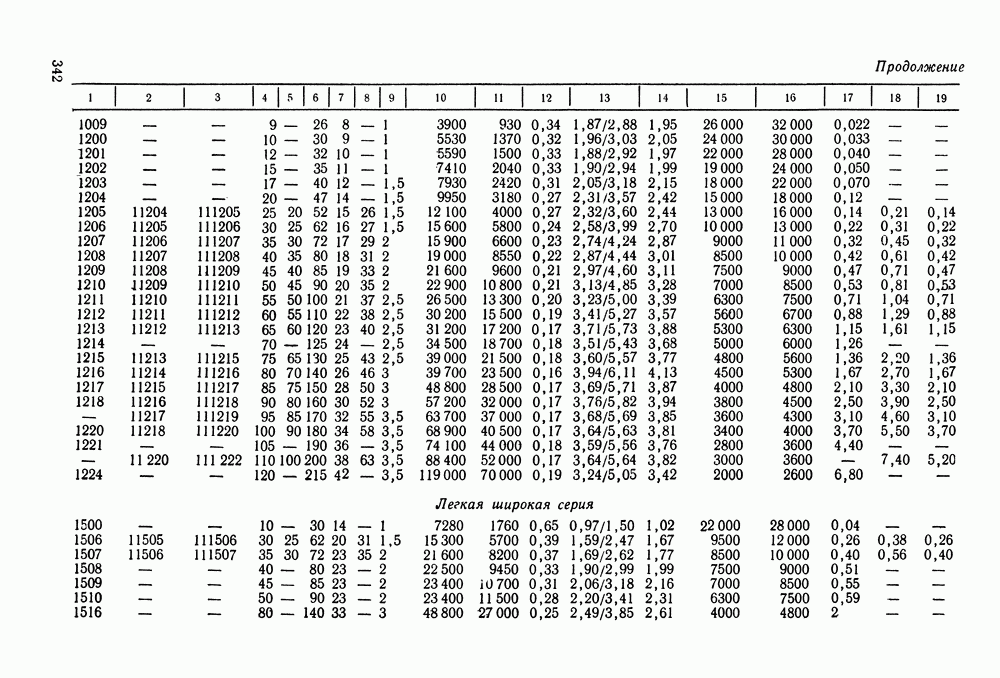
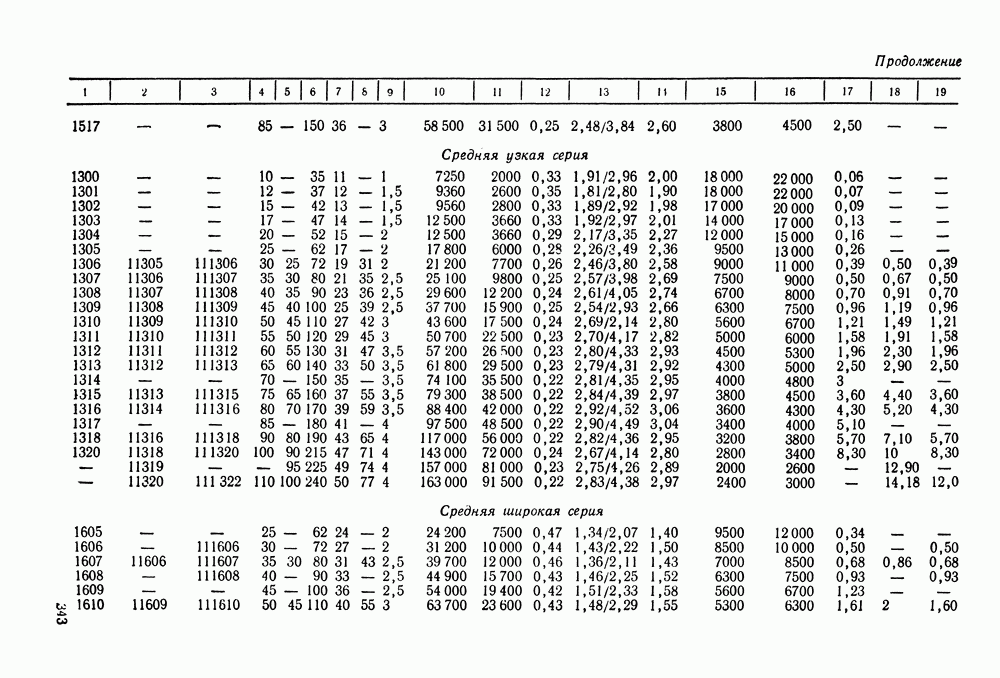
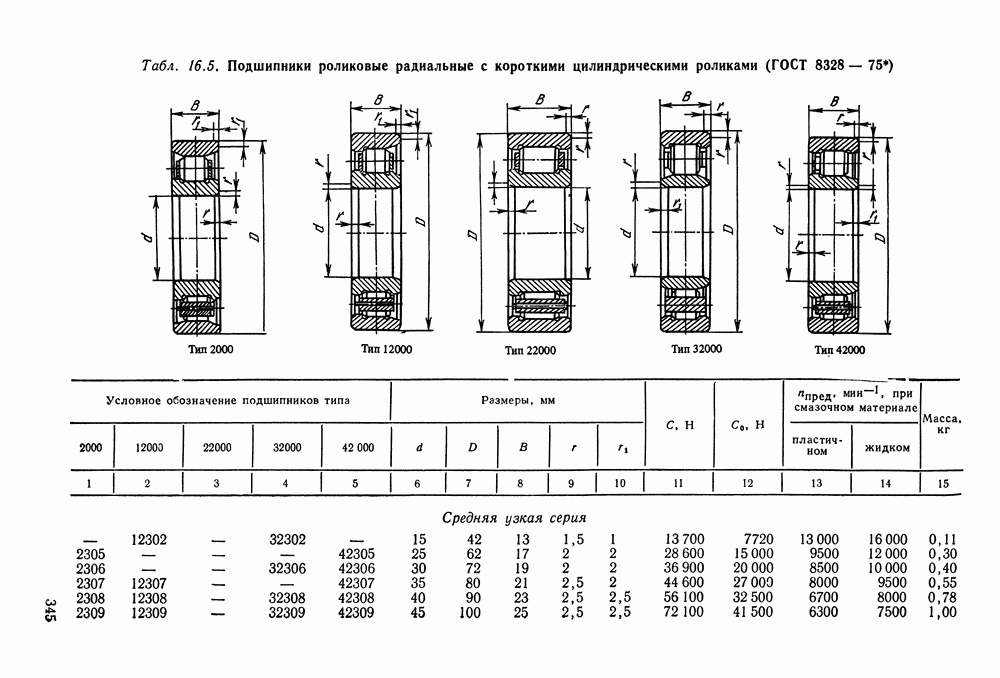
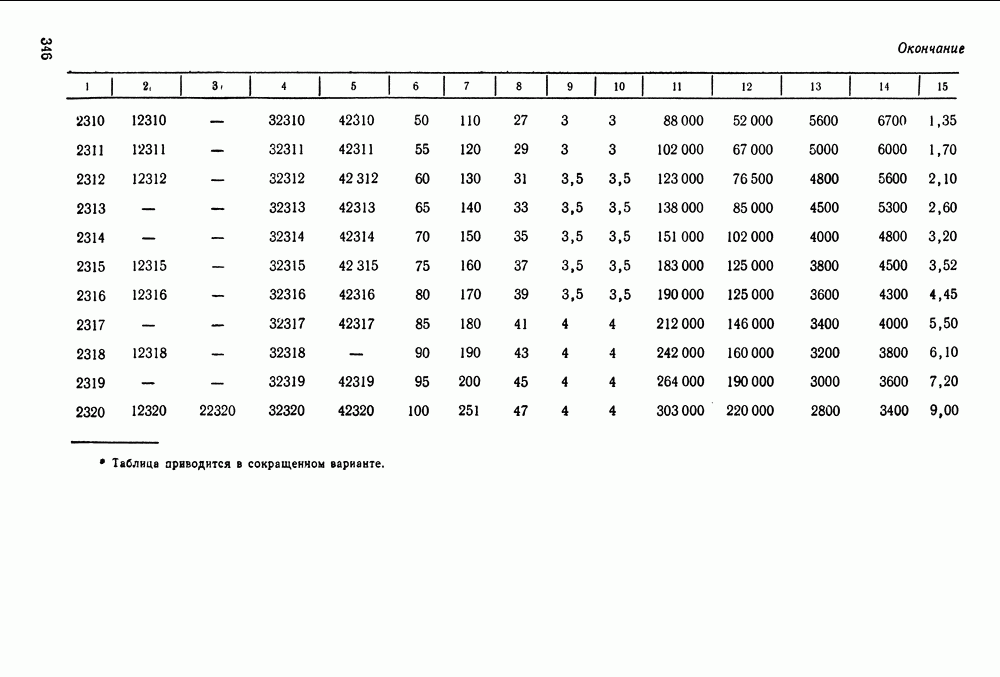
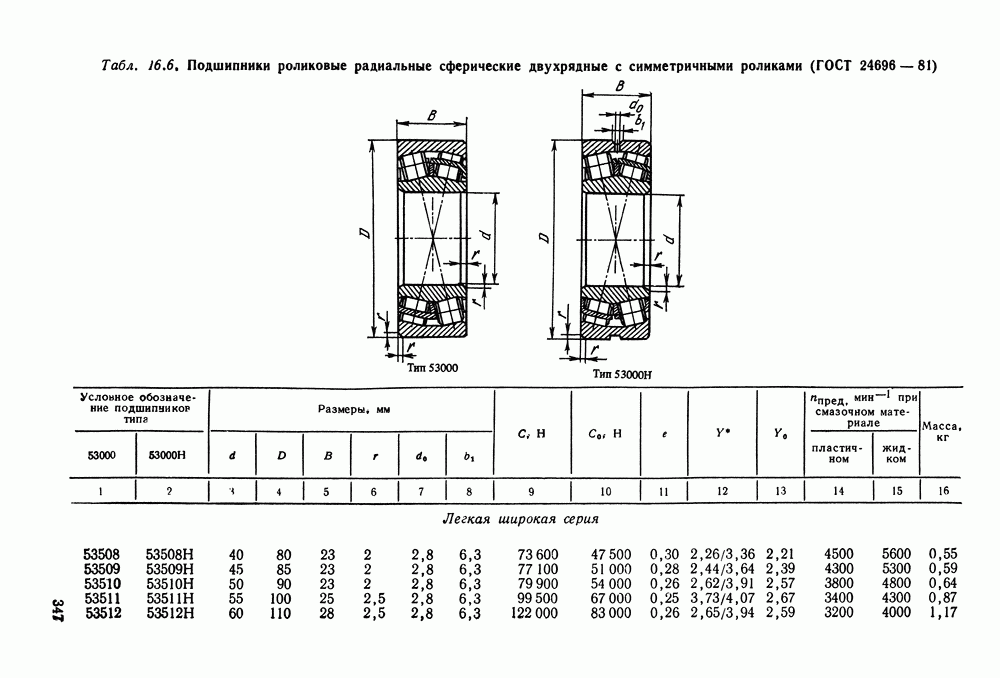
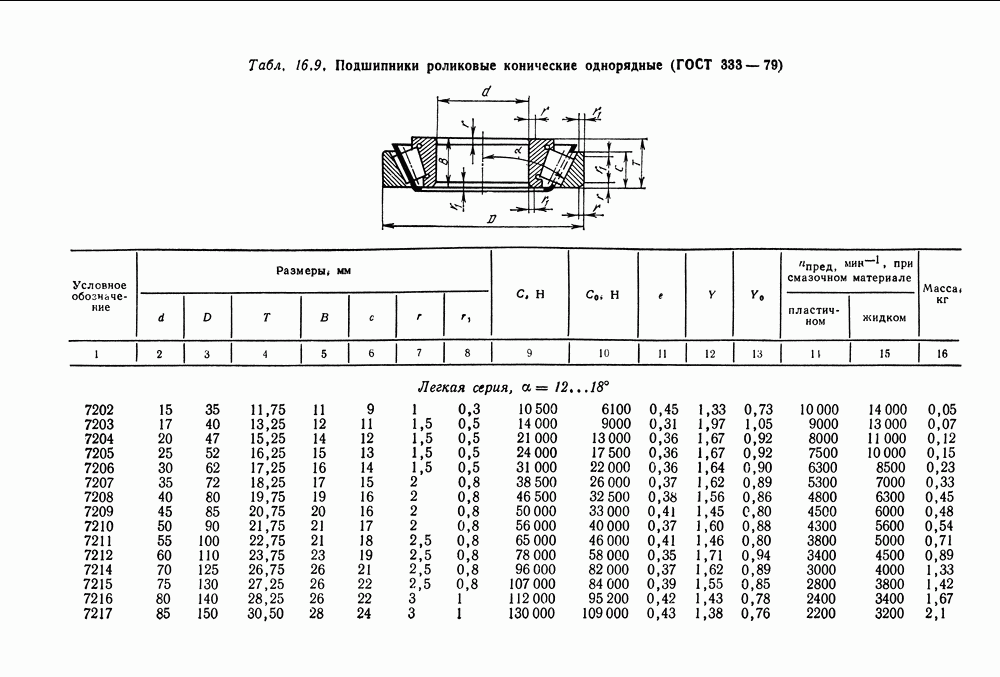
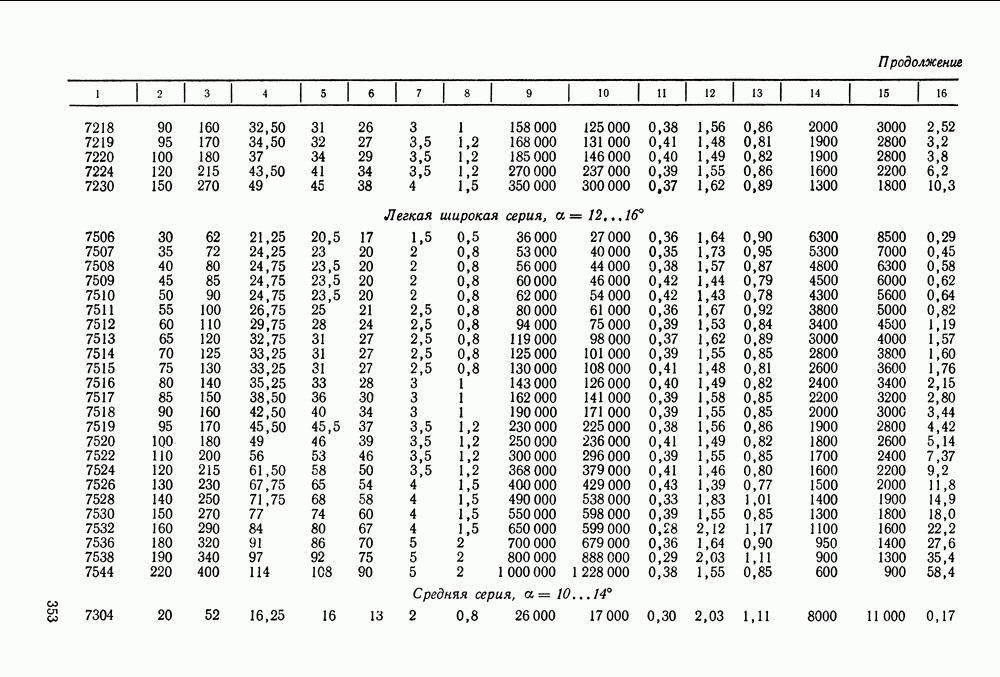
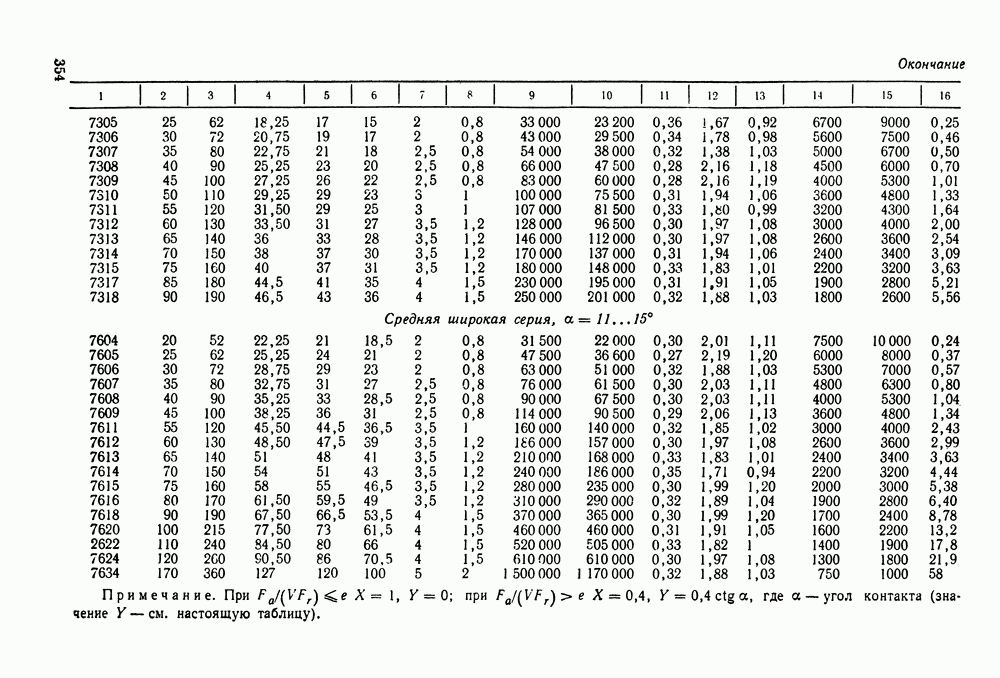
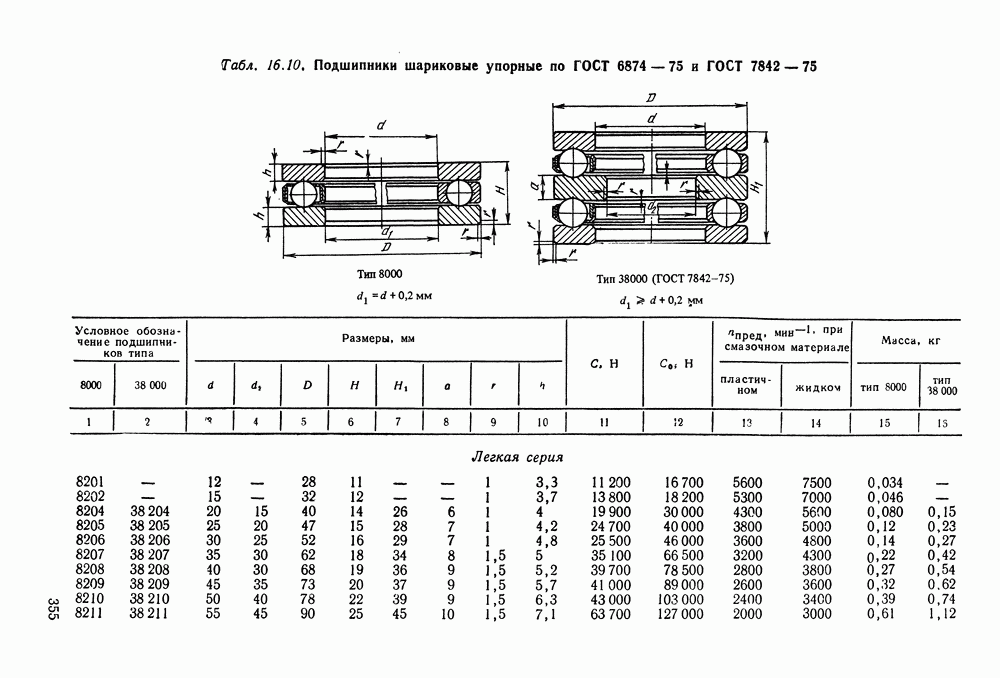
- 16.5. Справочный материал
- 16.6. Пример расчета
- Глава 17. МУФТЫ
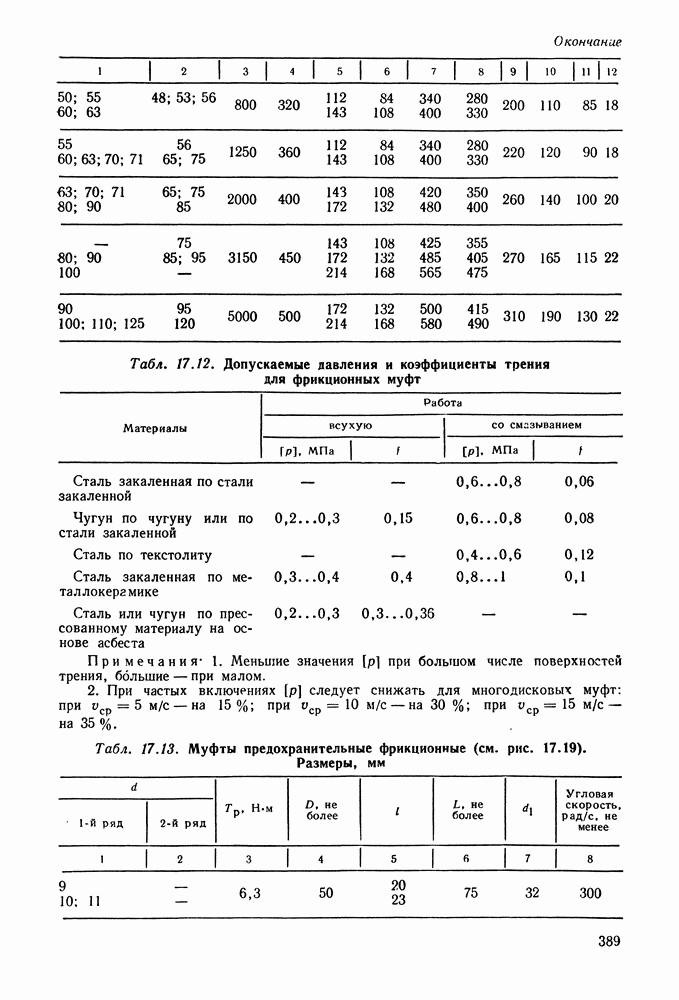
- 17.2. Расчет муфт
- 17.3. Глухие муфты
- 17.4. Компенсирующие муфты
- 17.5. Управляемые (сцепные) муфты
- 17.6. Самоуправляемые муфты
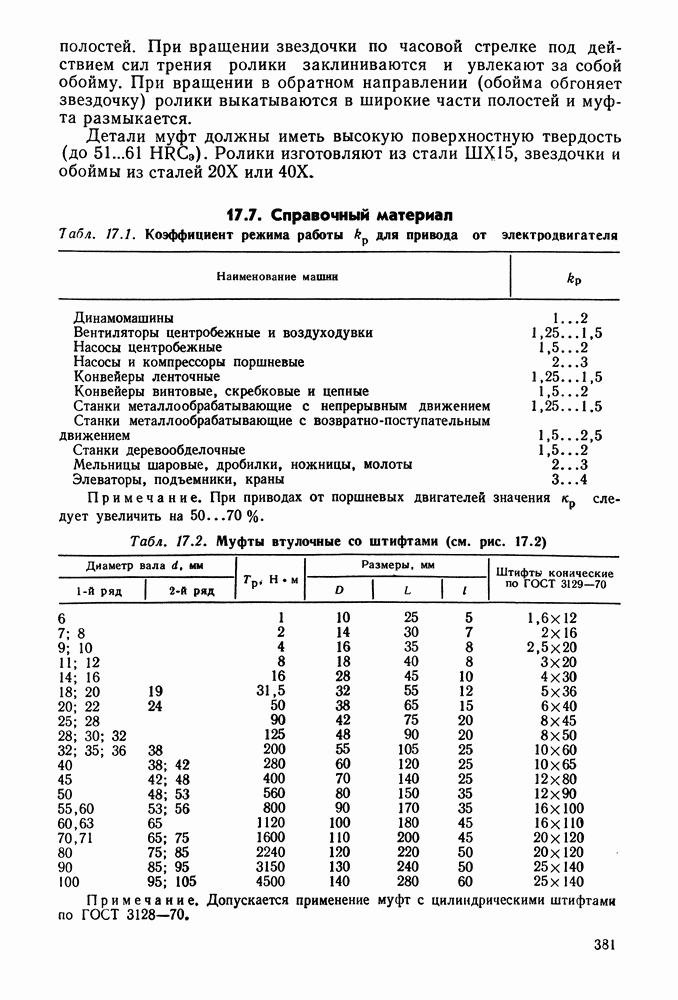
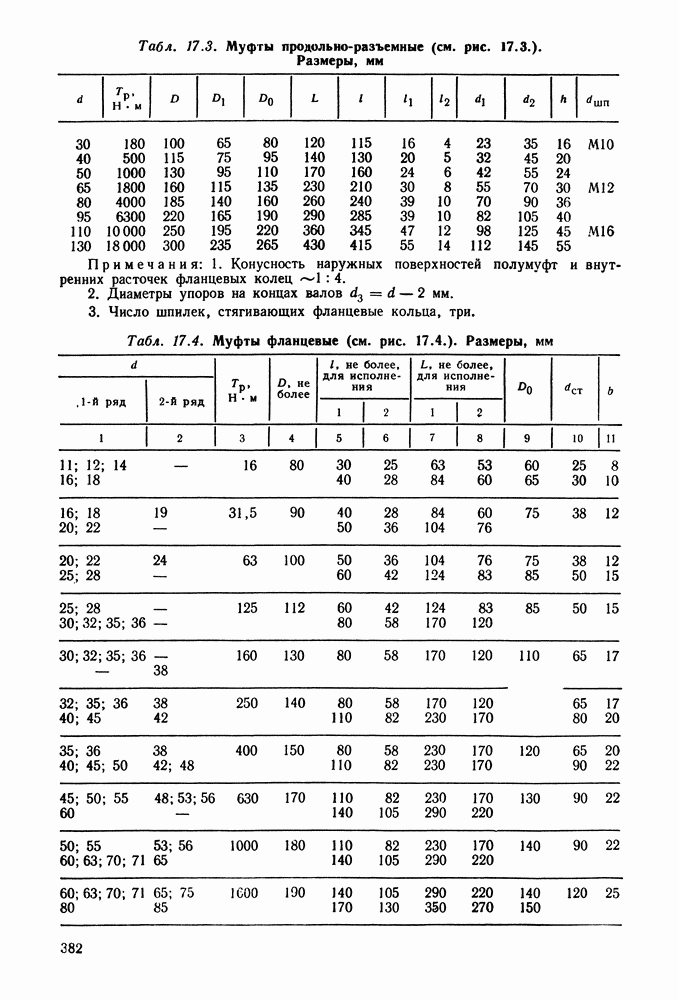
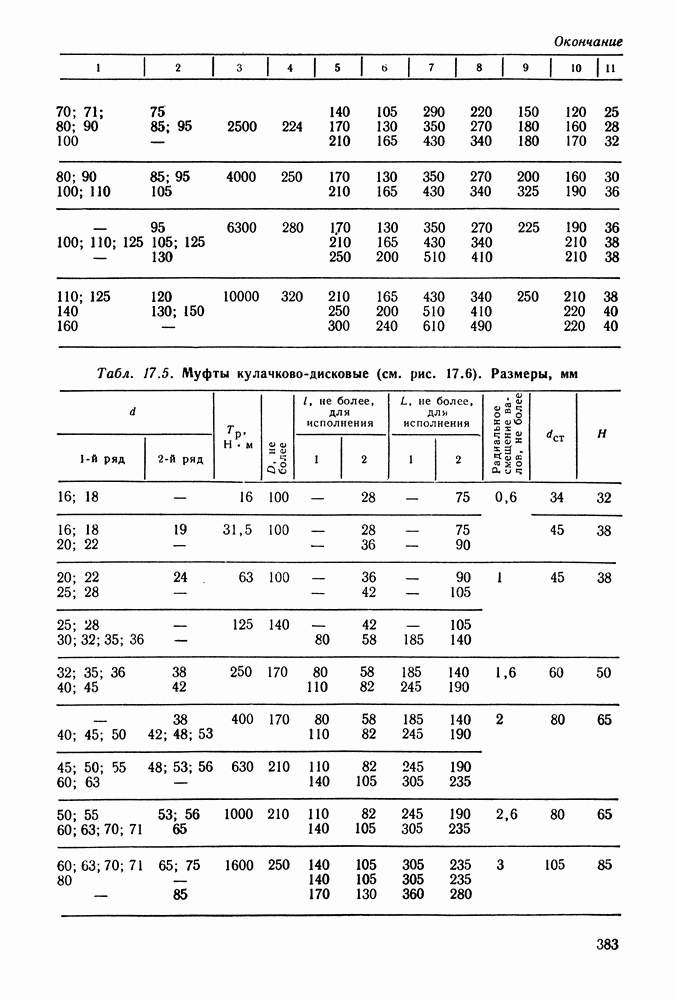
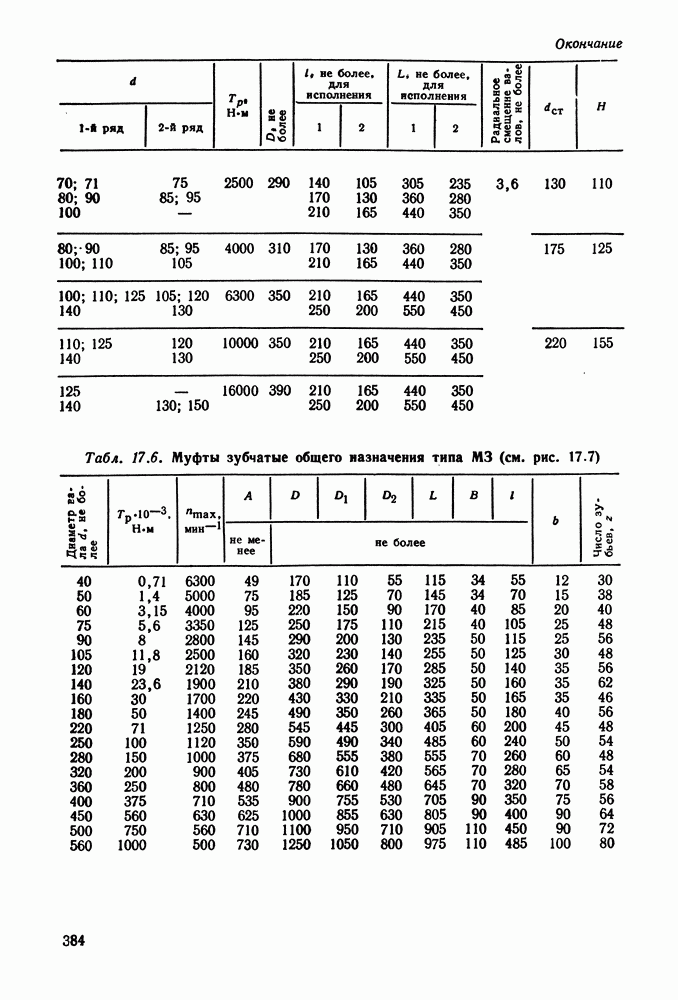
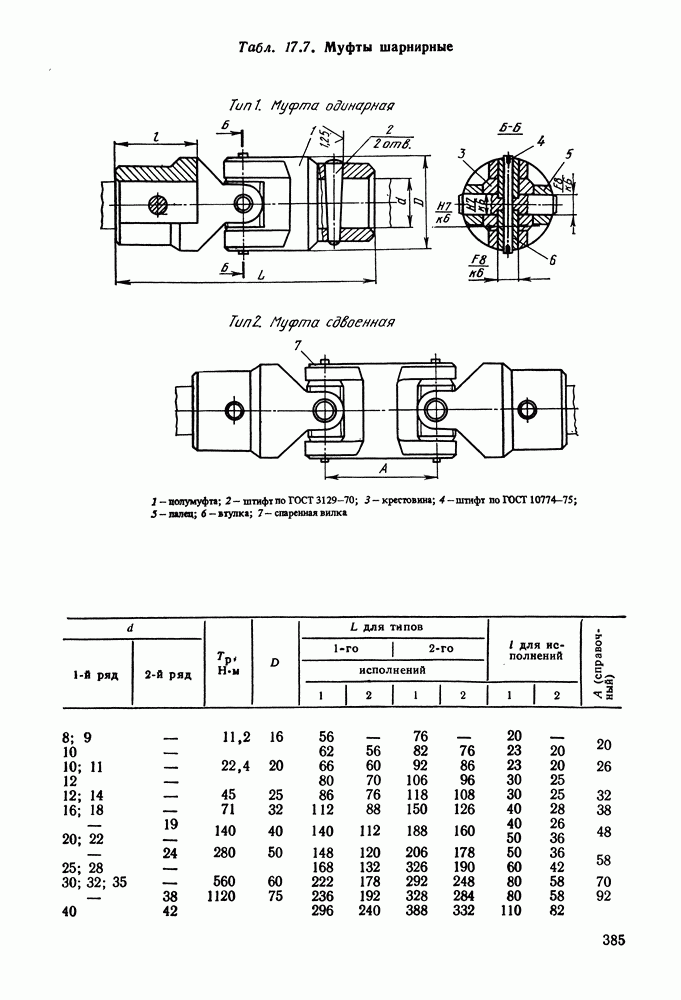
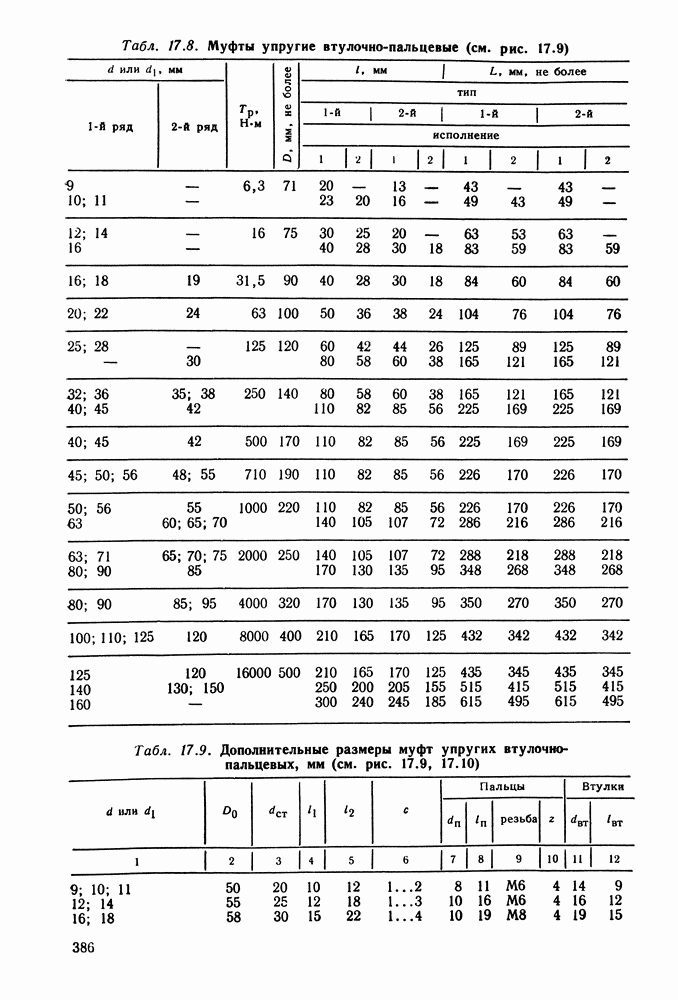
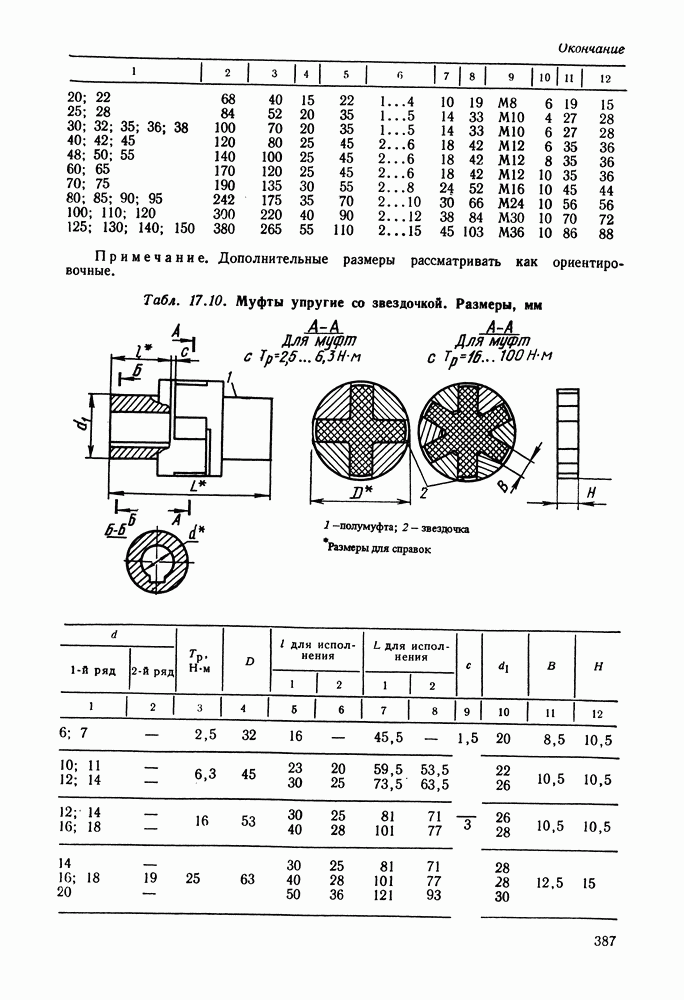
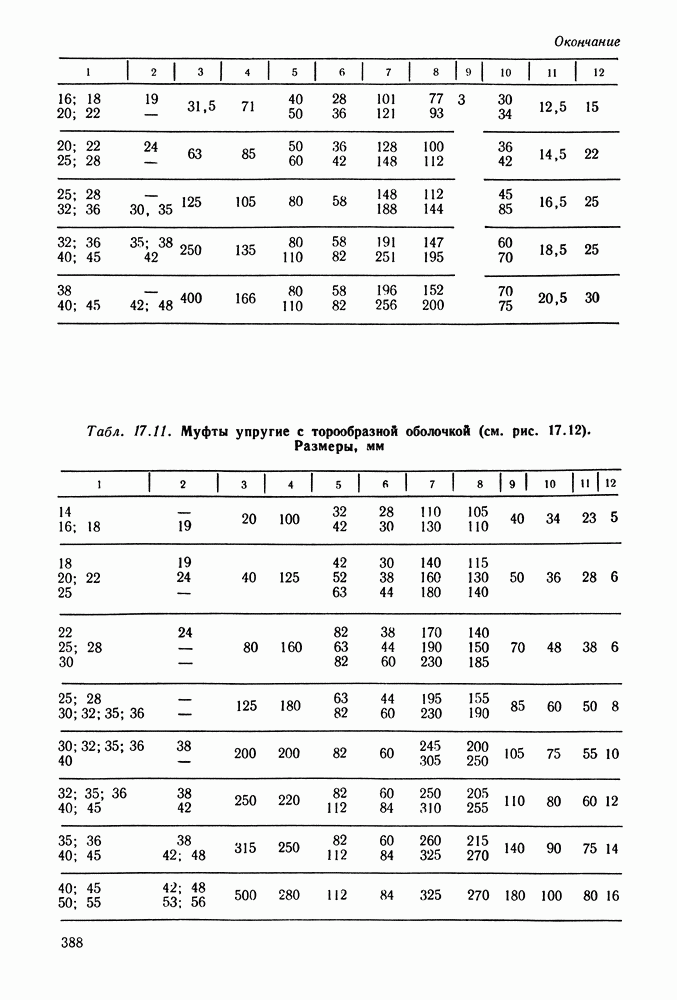
- 17.7. Справочный материал
- 17.8. Примеры расчета
- Глава 18. ПРУЖИНЫ
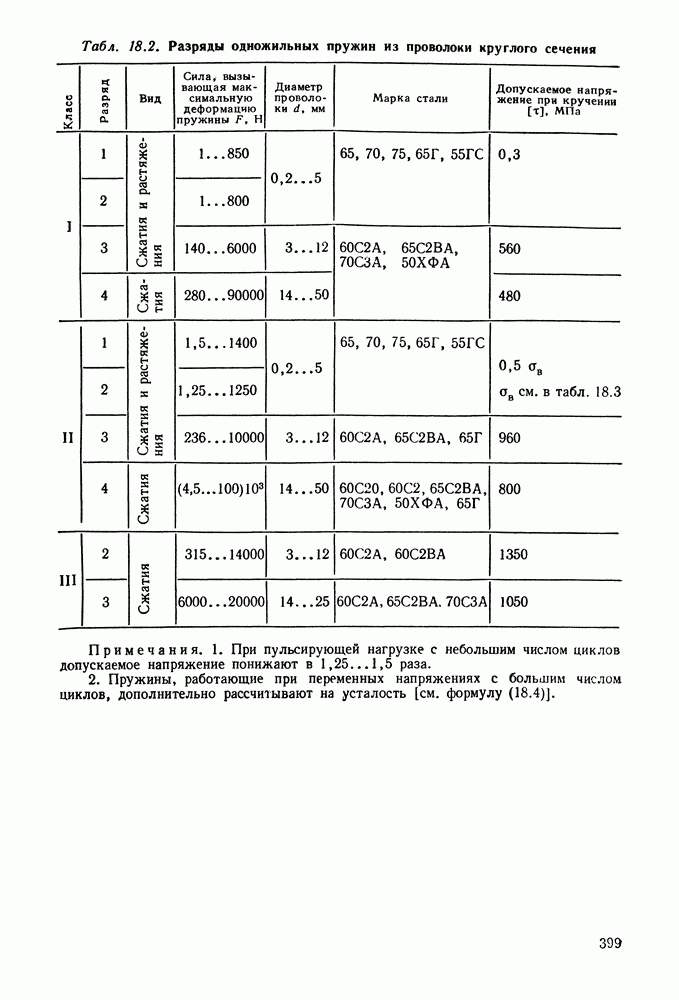
- 18.2. Расчет винтовых пружин на прочность
- 18.3. Расчет винтовых пружин на жесткость
- 18.4. Подбор тарельчатых пружин
- 18.5. Справочный материал
- ЛИТЕРАТУРА