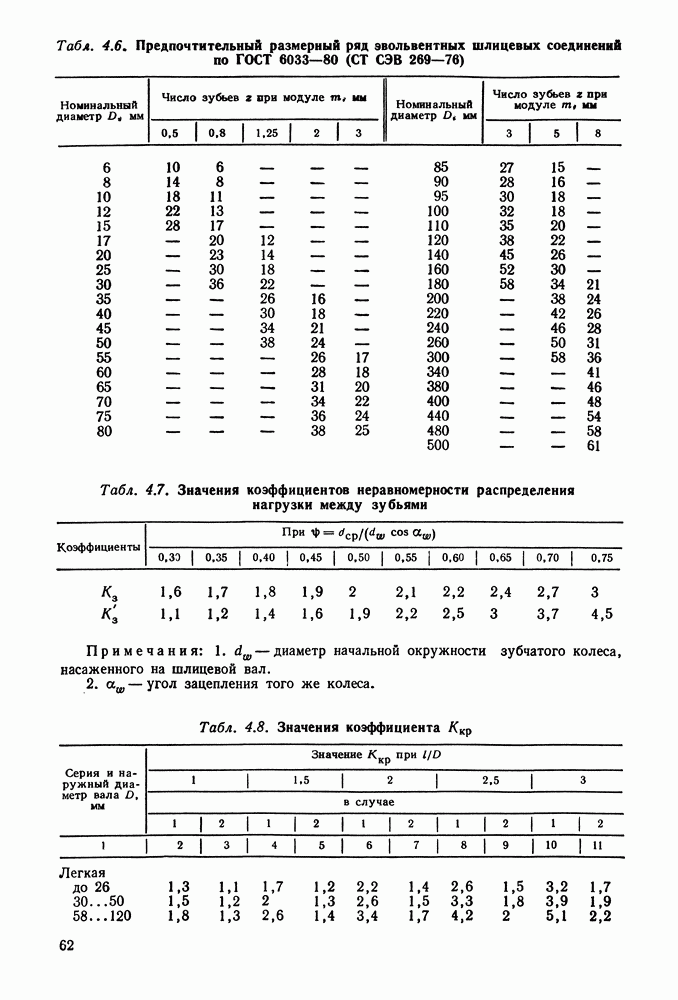
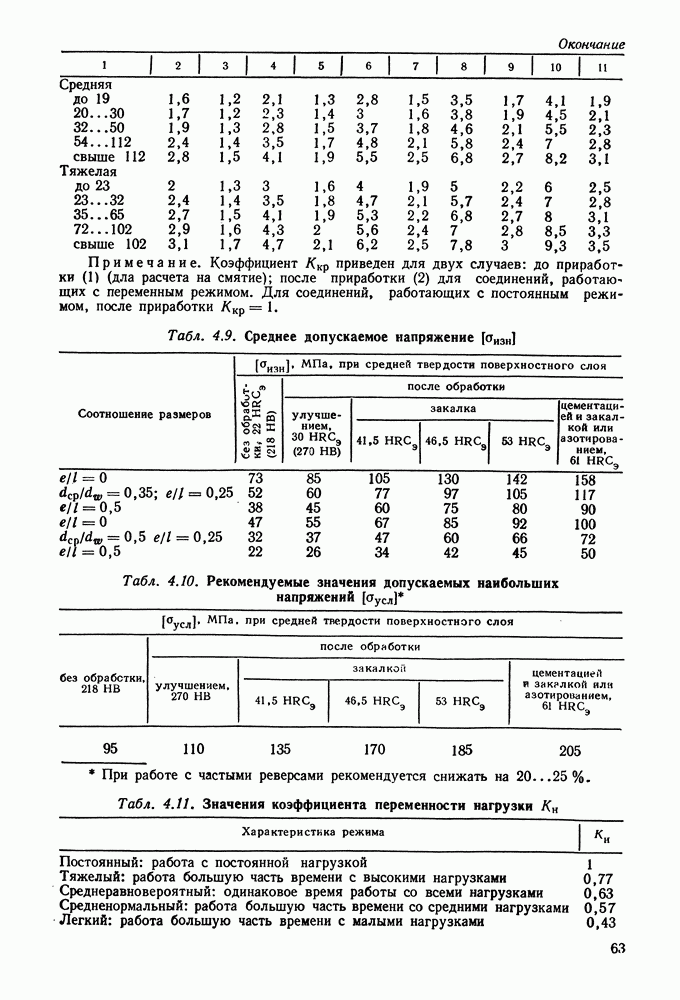
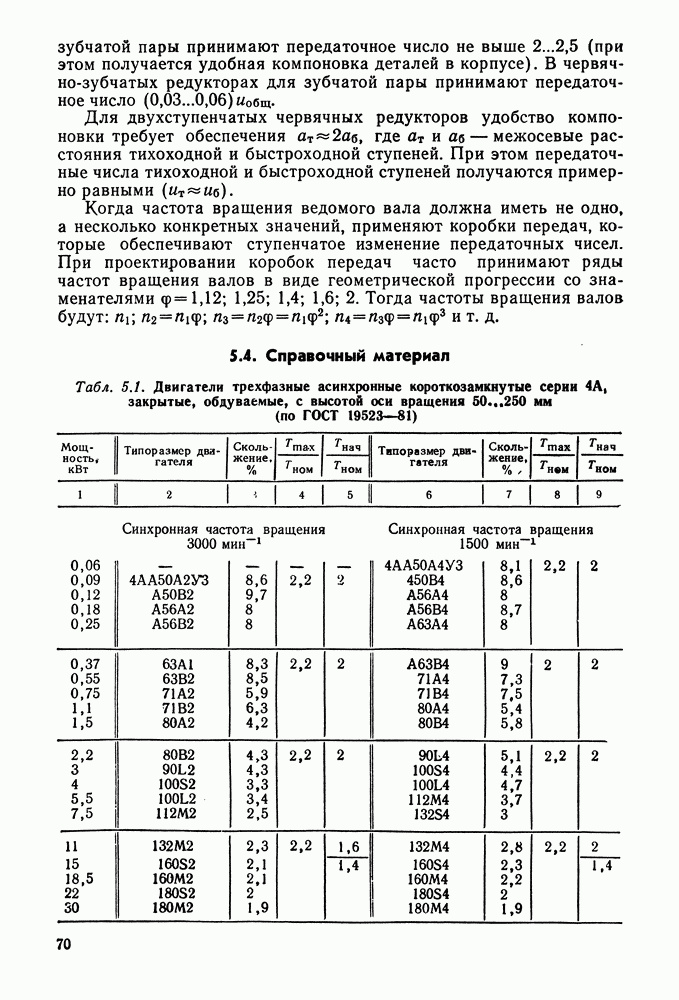
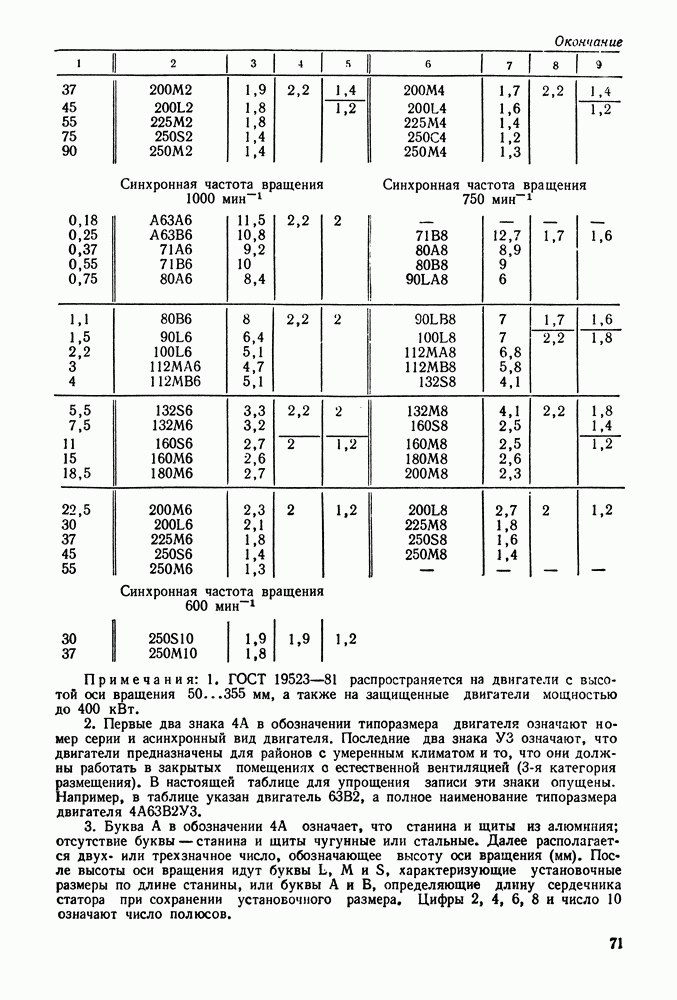
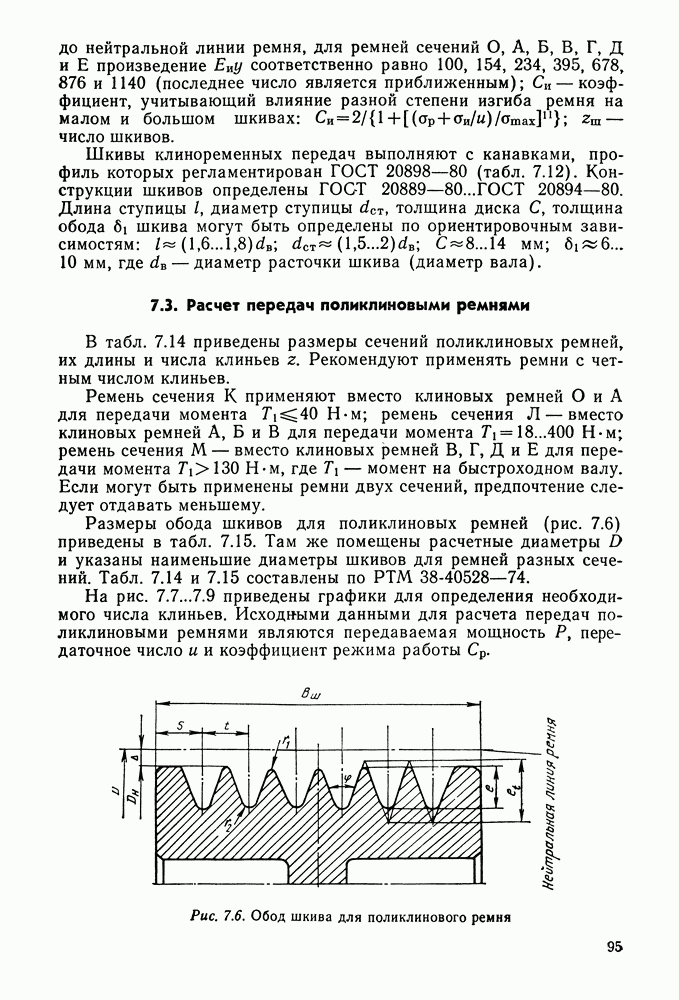
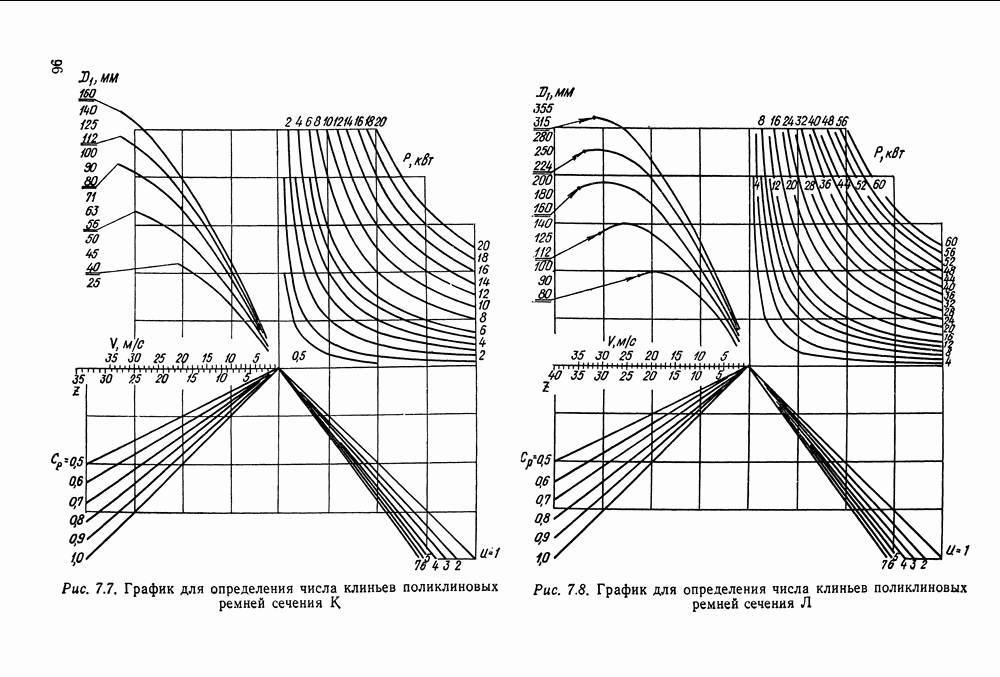
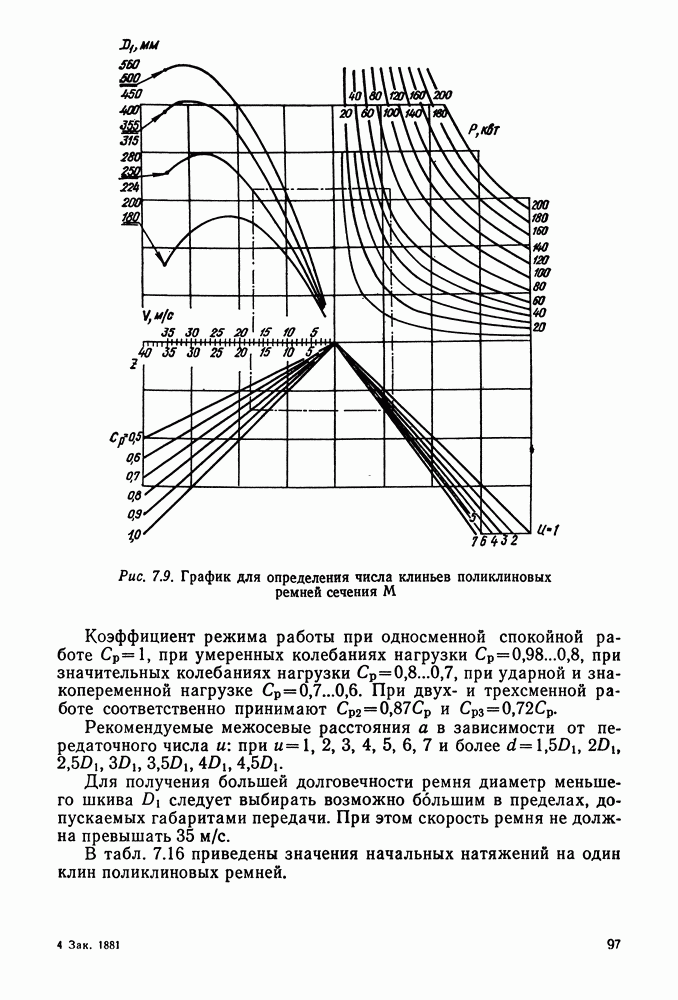
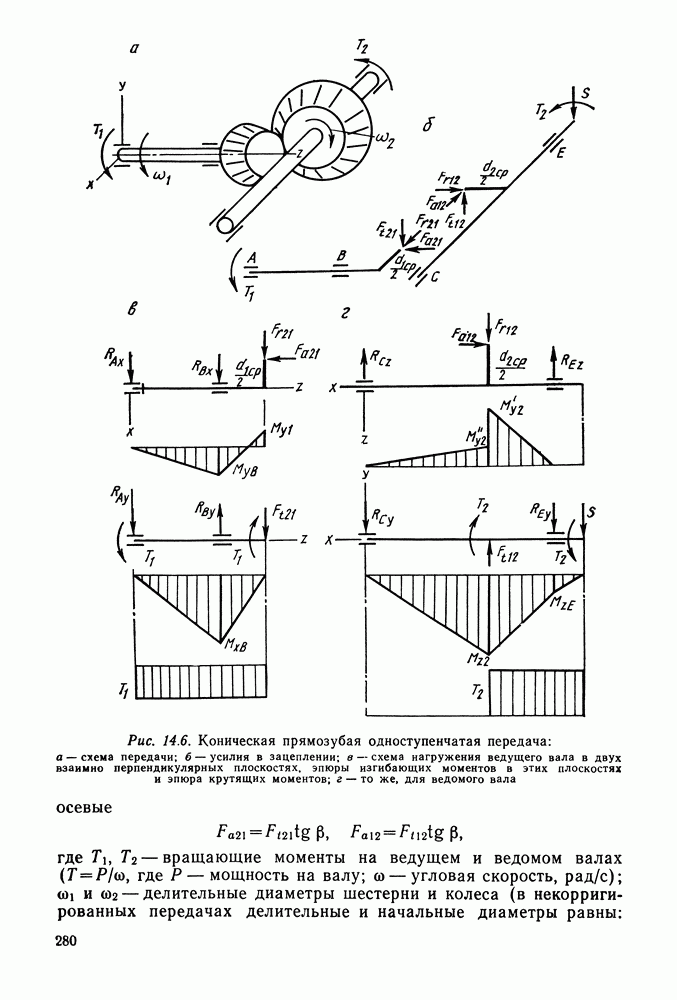
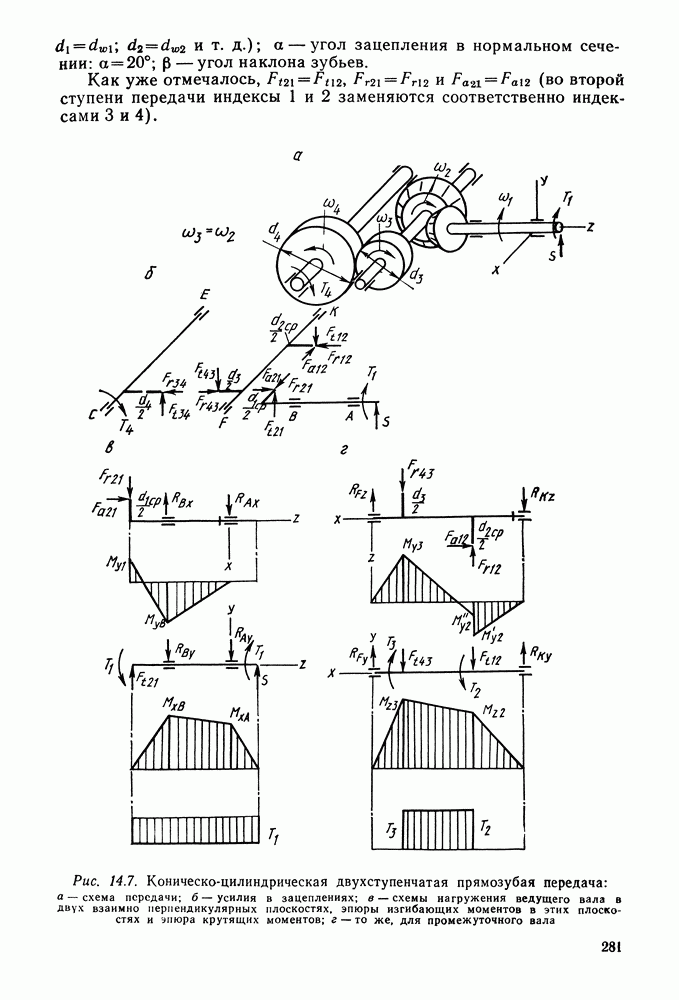
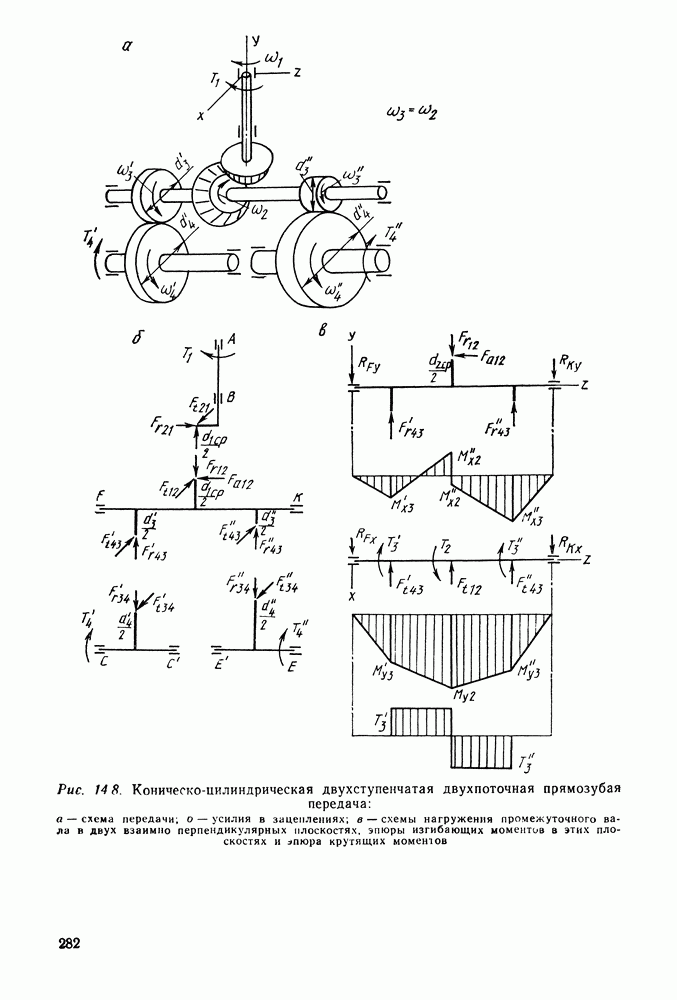
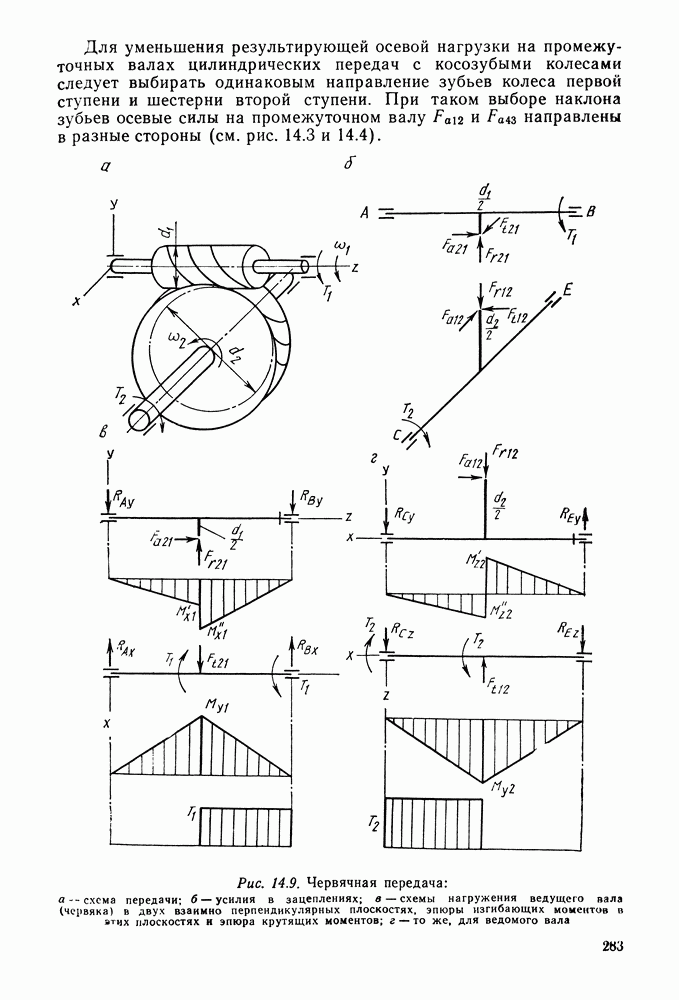
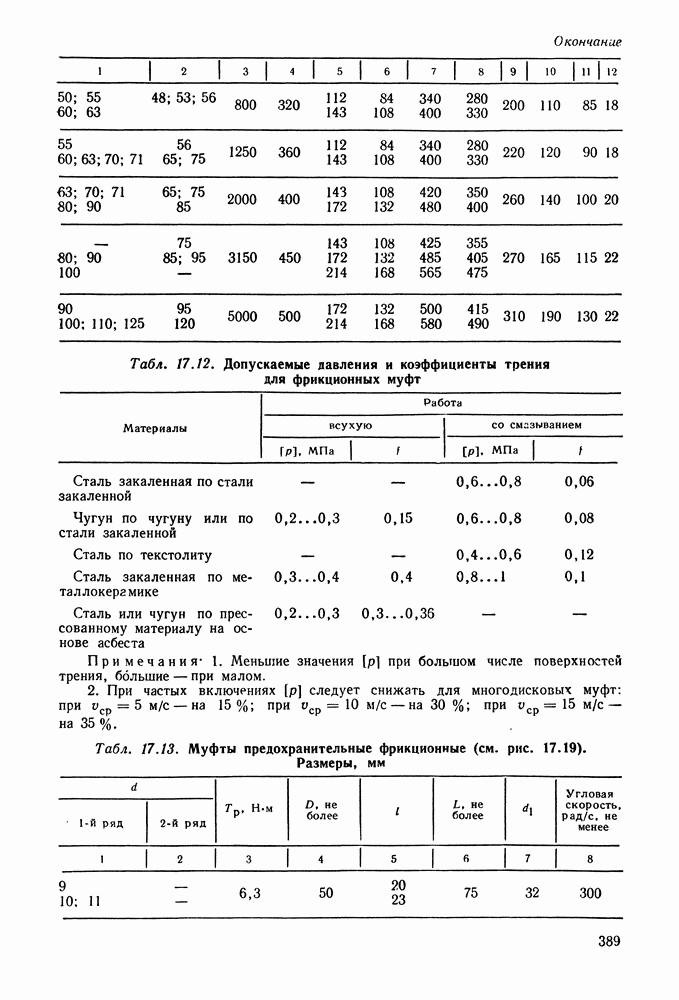
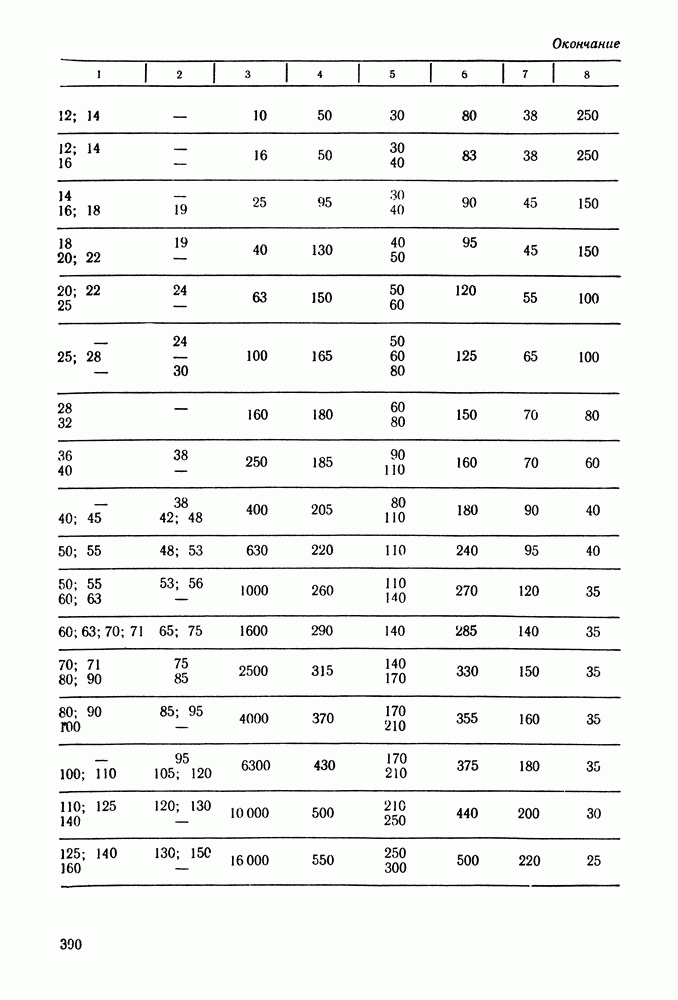
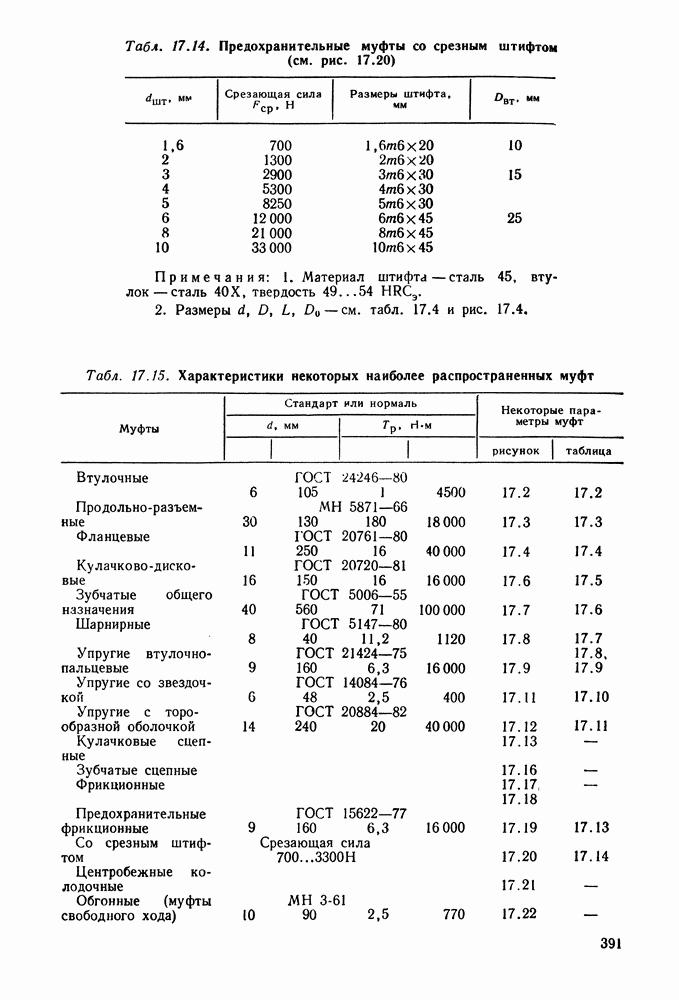
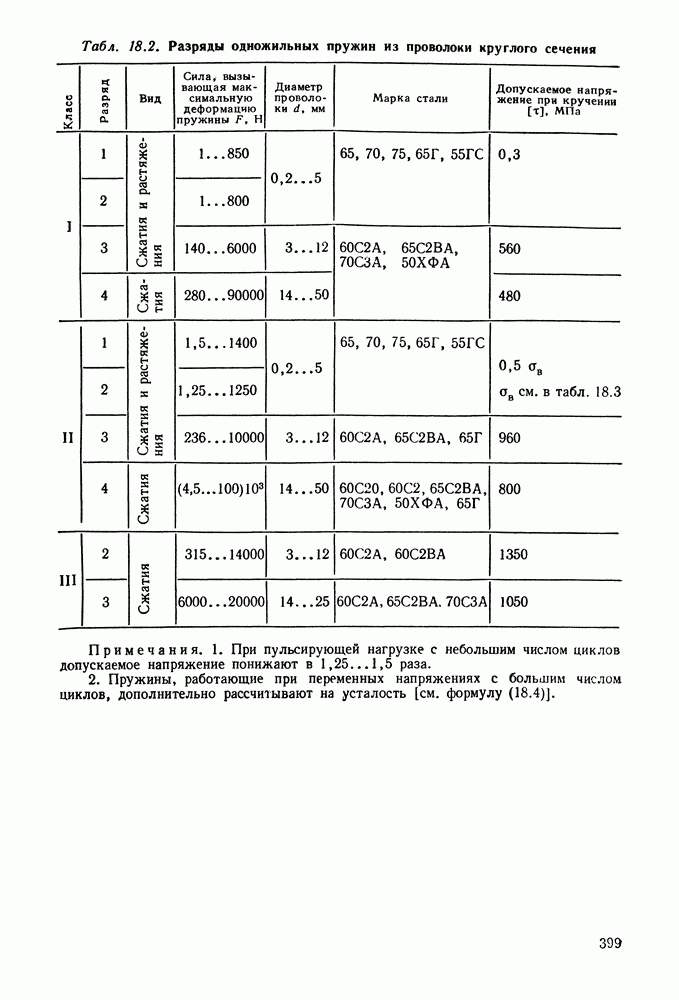
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
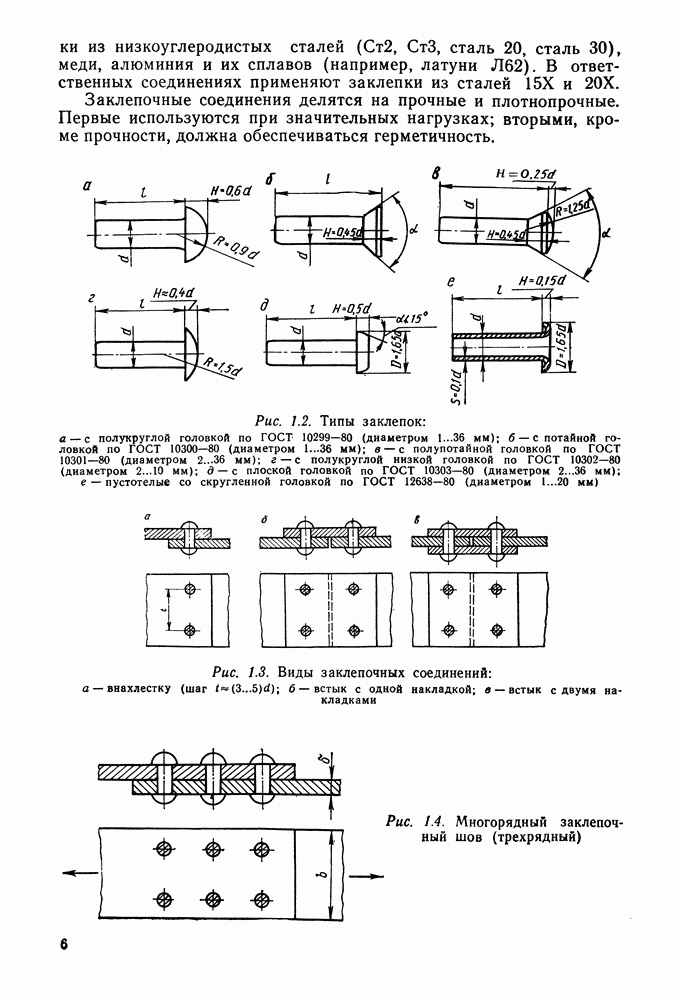
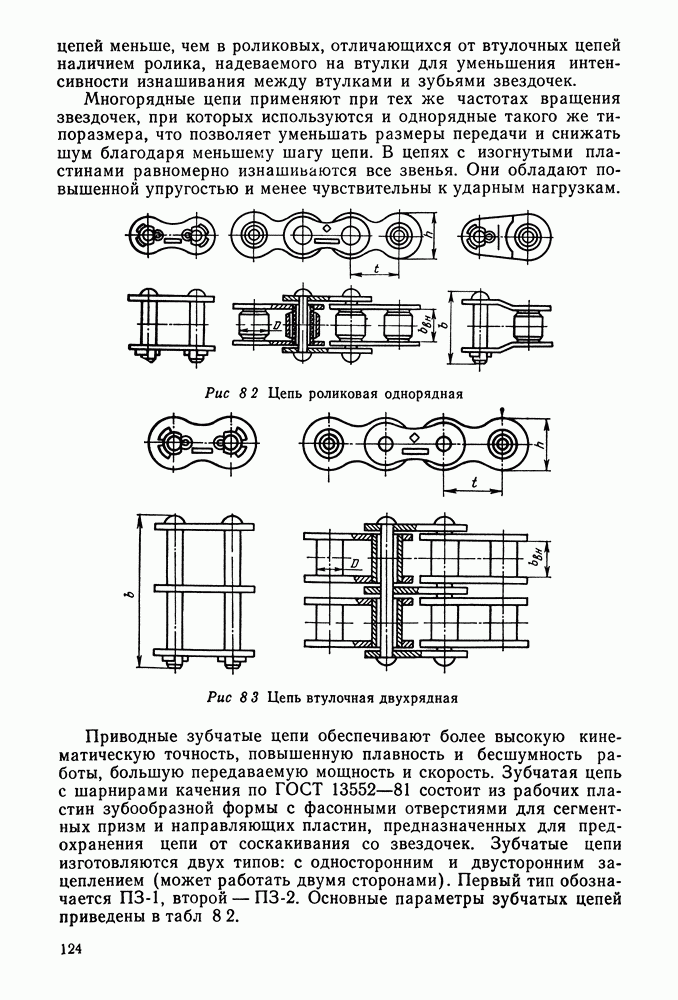
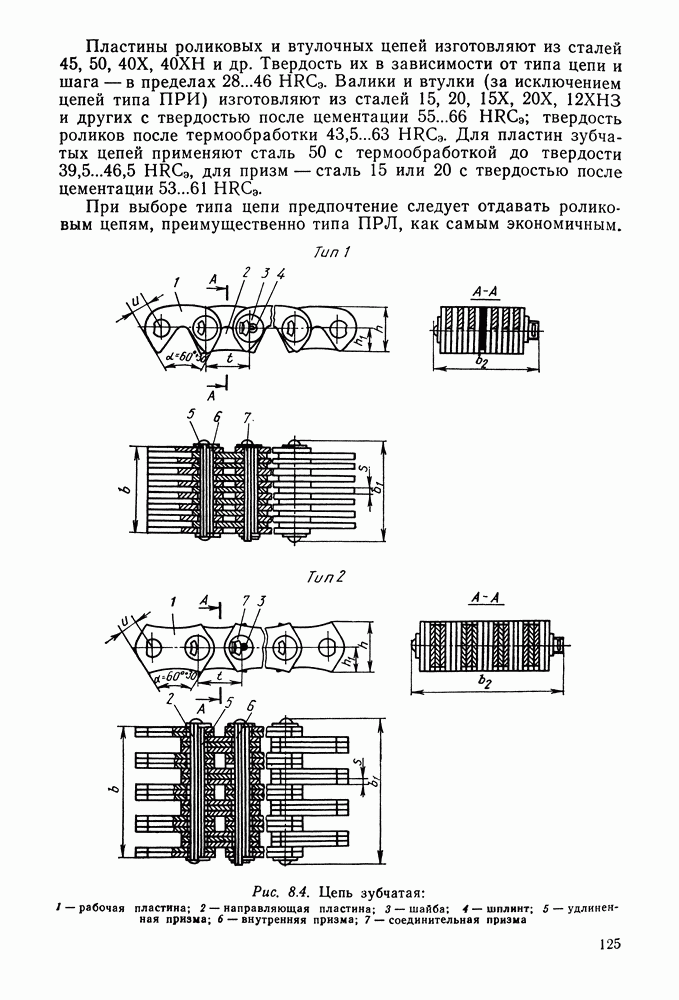
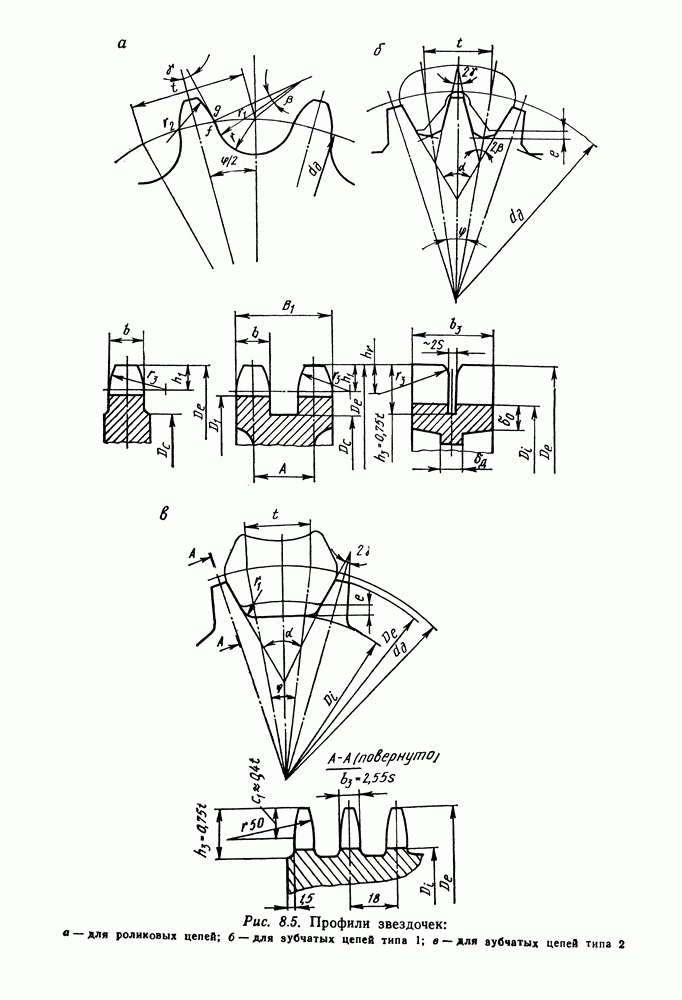
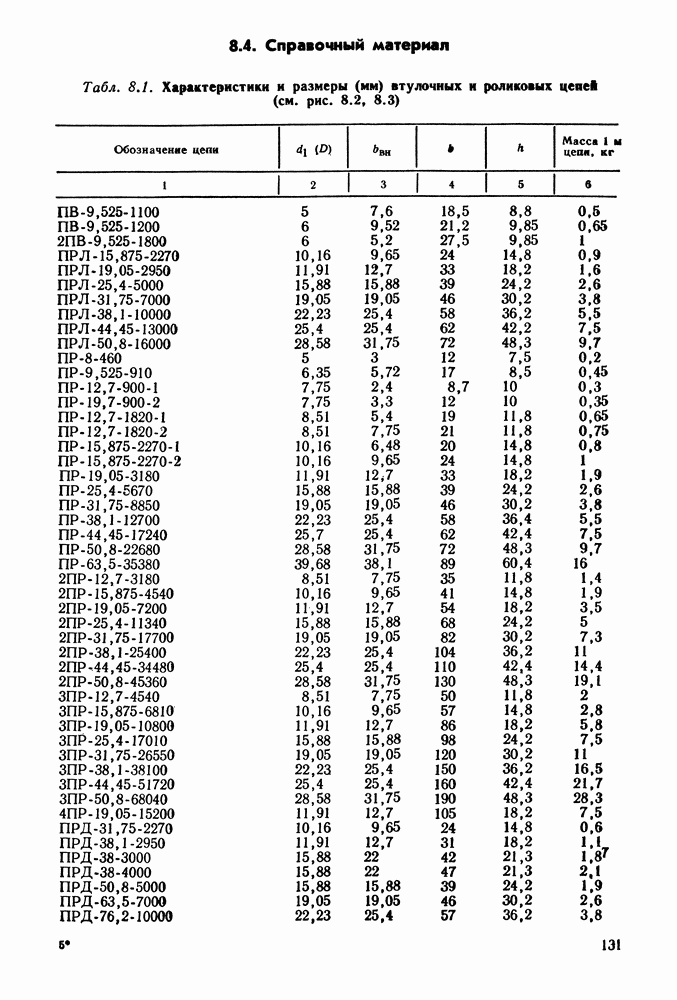
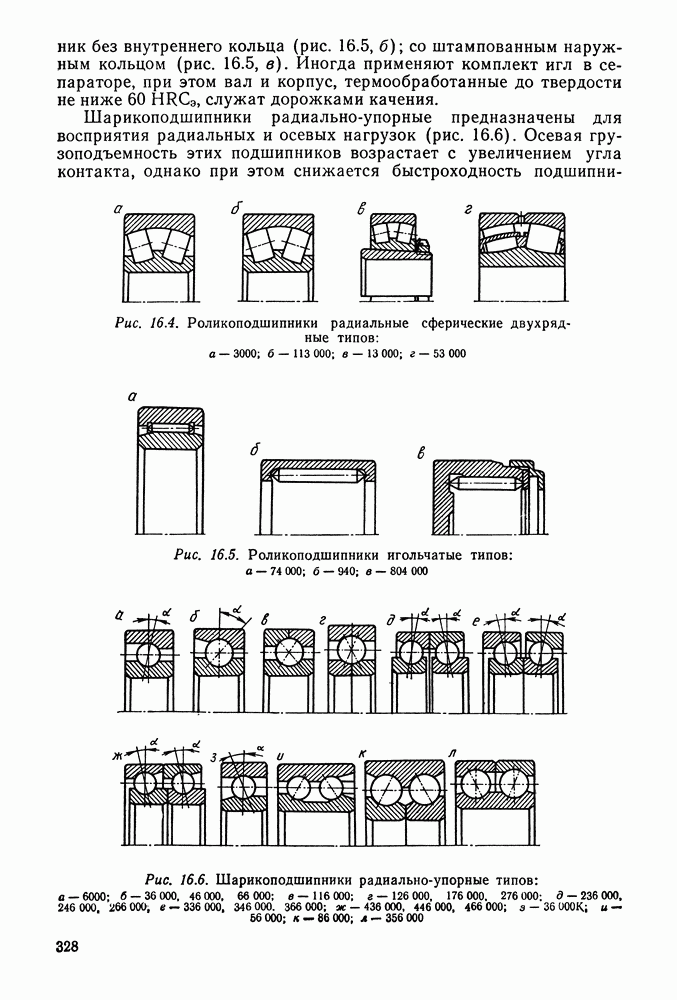
3.9. Примеры расчета
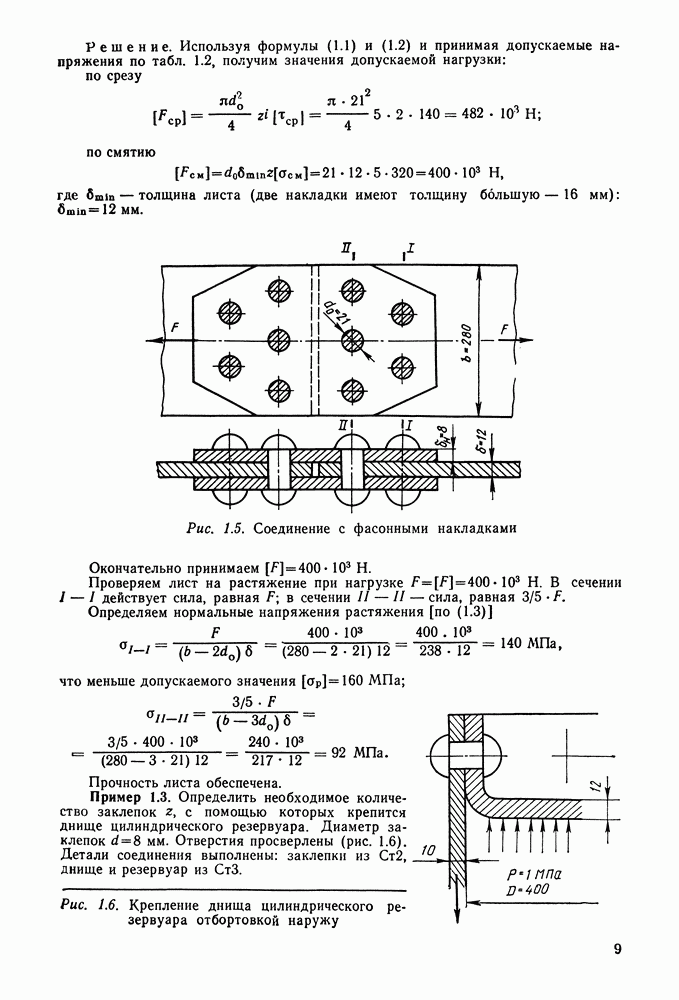
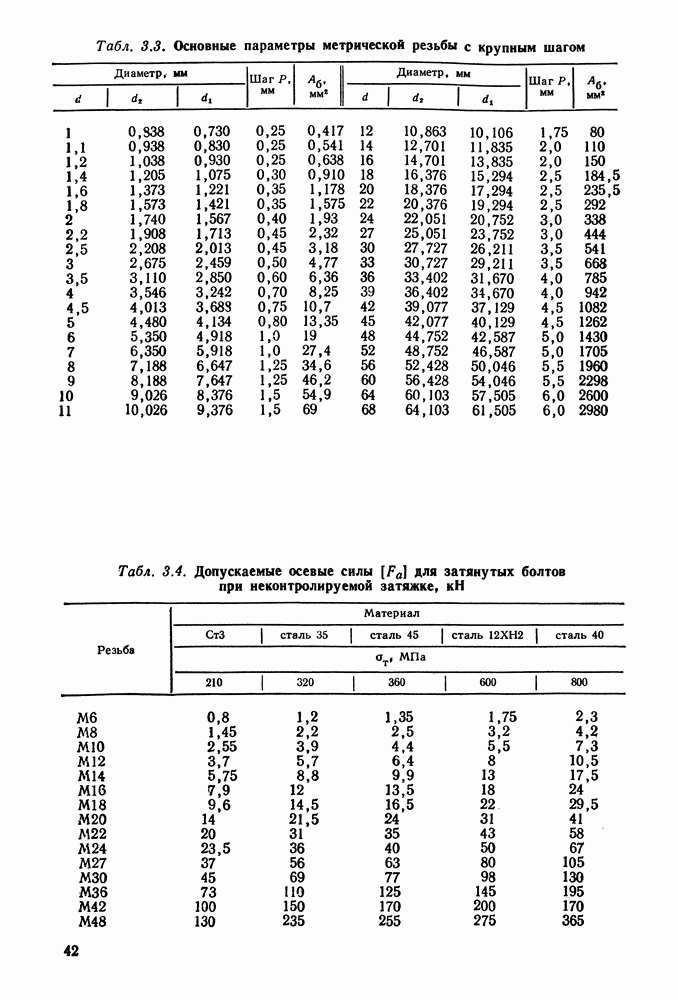
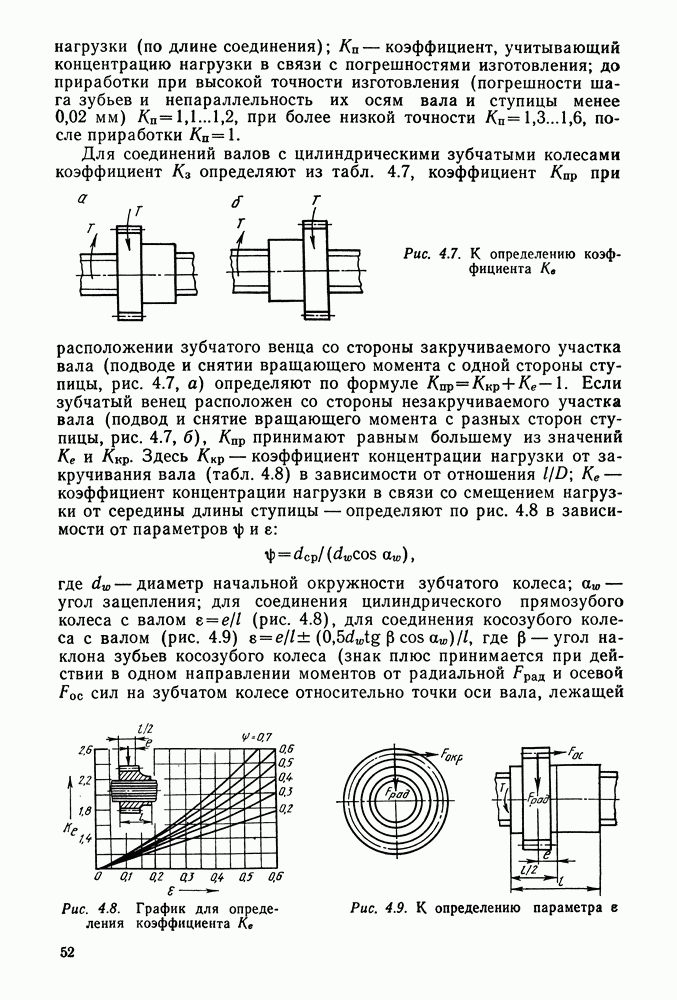
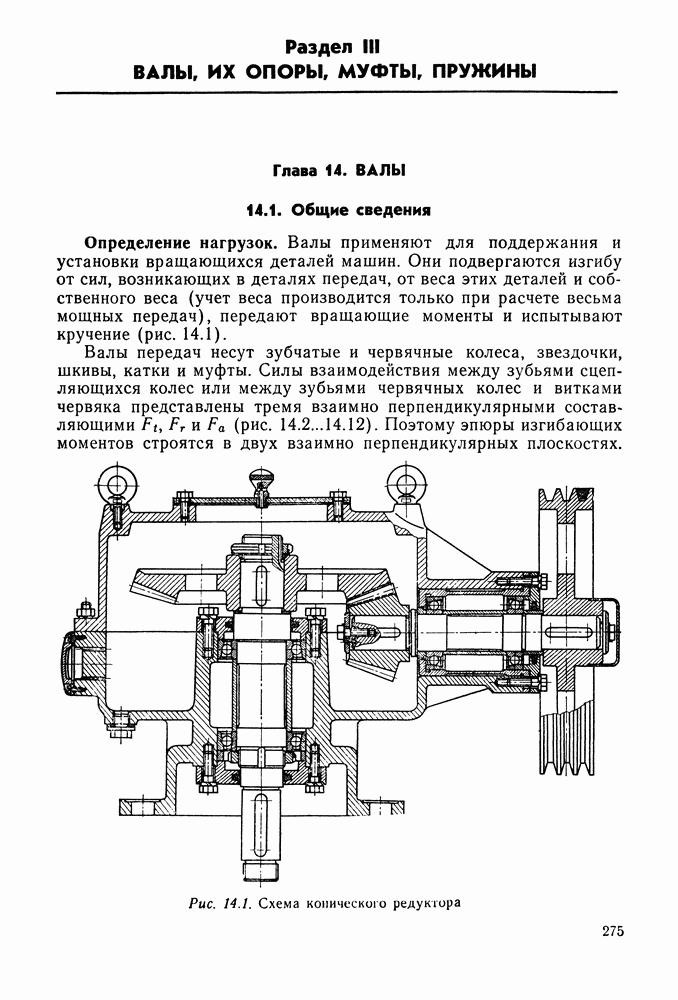
Пример 3.1. Кронштейн, нагруженный силой  , крепится к колонне (рис. 3.25, а) четырьмя болтами, поставленными в отверстия с зазором. Определить диаметр болтов из
, крепится к колонне (рис. 3.25, а) четырьмя болтами, поставленными в отверстия с зазором. Определить диаметр болтов из  при неконтролируемой затяжке.
при неконтролируемой затяжке.
Решение. 1. Определяем силу, действующую на один наиболее нагруженный болт. Приводим силу  к центру тяжести болтового соединения; получаем силу
к центру тяжести болтового соединения; получаем силу  приложенную в центре тяжести, и момент
приложенную в центре тяжести, и момент  мм (рис. 3.25, б). Сила и момент действуют в плоскости стыка и должны быть уравновешены силами трения, вызванными затяжкой болтов. Примем, что точки приложения сил трения совпадают с центрами болтовых отверстий.
мм (рис. 3.25, б). Сила и момент действуют в плоскости стыка и должны быть уравновешены силами трения, вызванными затяжкой болтов. Примем, что точки приложения сил трения совпадают с центрами болтовых отверстий.
Составляющая от силы  (см. формулу (3.2)]:
(см. формулу (3.2)]:

Составляющая от момента Т [см. формулу (3.3), где 

Наибольшая результирующая внешняя нагрузка  (наибольшая геометрическая сумма сил
(наибольшая геометрическая сумма сил  и
и  — для верхнего и нижнего правых болтов (рис. 3.25, в).
— для верхнего и нижнего правых болтов (рис. 3.25, в).

Рис. 3.25. К примеру расчета 3.1
По теореме косинусов

2. Сила затяжки наиболее нагруженного болта [см. формулу (3.4)]

Принимаем 
3. Диаметр болтов определим по табл. 3.4. Для силы затяжки  ближайшее большее значение допускаемой осевой нагрузки
ближайшее большее значение допускаемой осевой нагрузки  , которому соответствует болт
, которому соответствует болт 
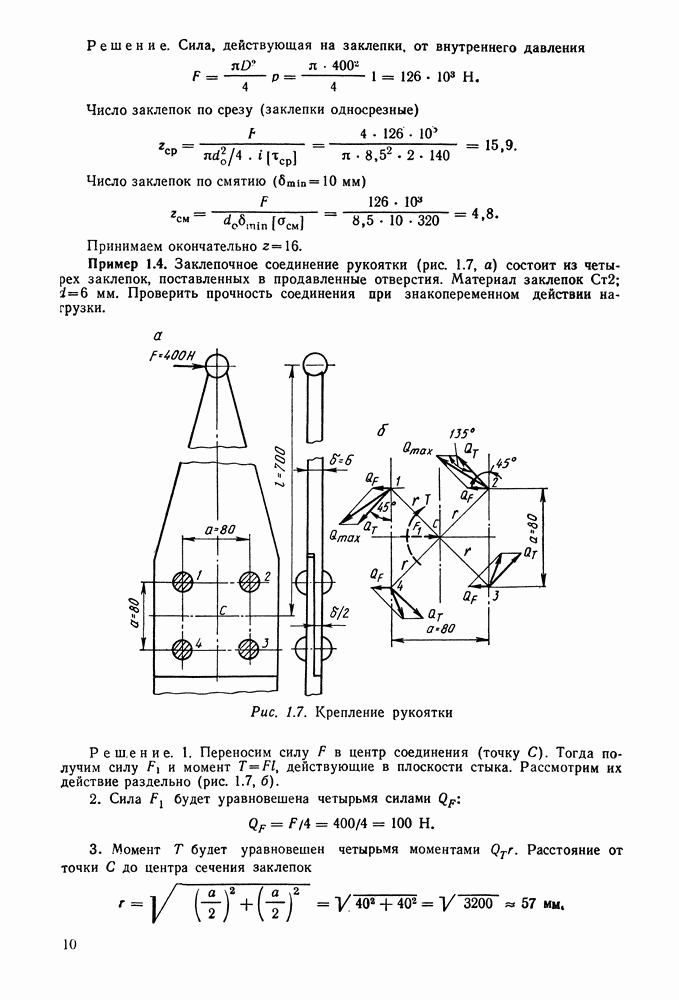
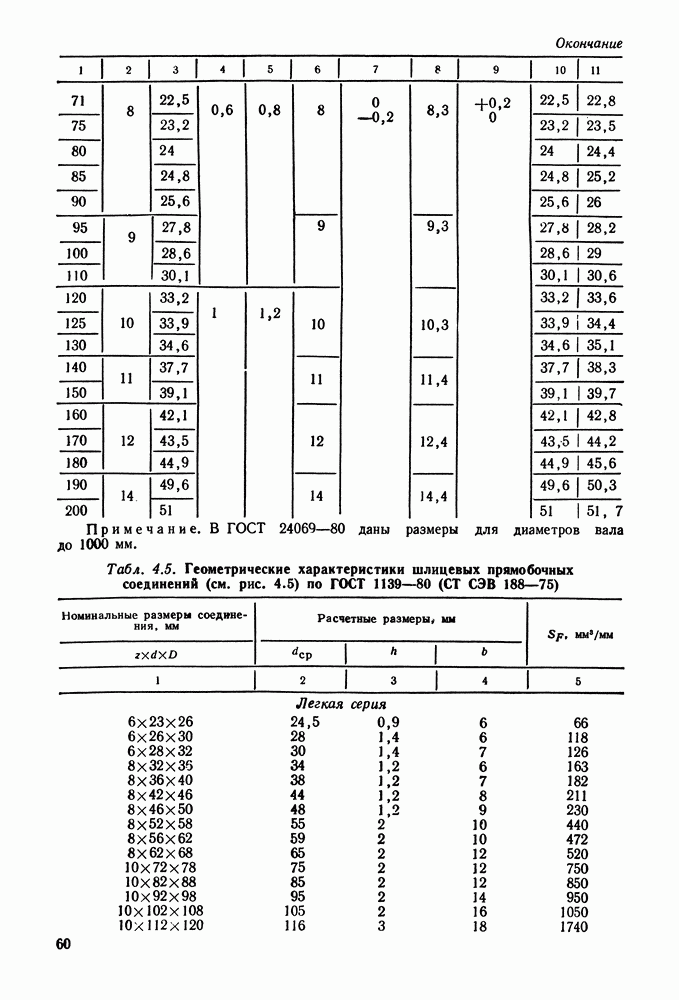
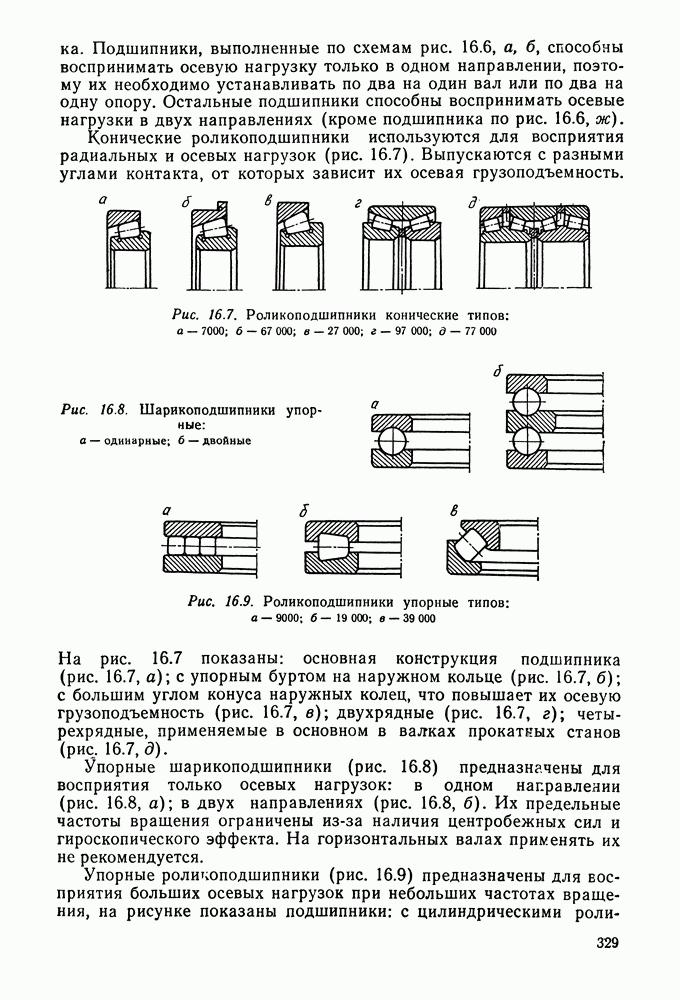
Пример 3.2. Проверить прочность шпилек  (рис. 3.26), крепящих крышку цилиндра поршневого двигателя. Материал шпилек — сталь 45, число шпилек
(рис. 3.26), крепящих крышку цилиндра поршневого двигателя. Материал шпилек — сталь 45, число шпилек
 Давление в цилиндре изменяется от
Давление в цилиндре изменяется от  до
до  по отнулевому циклу. Материал цилиндра и крышки — сталь.
по отнулевому циклу. Материал цилиндра и крышки — сталь.
Решение. 1. Проверка шпилек на статическую прочность. Внешняя сила, действующая на одну шпильку, при наибольшем давлении в камере сжатия [см. формулу (3.1)]

Сила предварительной затяжки шпилек [см. формулы (3.7) и (3.8)]

Коэффициент основной нагрузки [см. формулу (3.9)]


Рис. 3.26. К примеру расчета 3.2
Коэффициент податливости шпильки [см. формулу (3.10)]

где  — соответственно длина и площадь сечения ненарезанной части шпильки:
— соответственно длина и площадь сечения ненарезанной части шпильки: 
— соответственно длина и площадь сечения верхней нарезанной части шпильки, находящейся внутри крышки цилиндра:  соответственно учитываемая длина и площадь поперечного сечения нарезанной части шпильки, ввернутой во фланец цилиндра (обычно принимают 1/3 длины этой части шпильки):
соответственно учитываемая длина и площадь поперечного сечения нарезанной части шпильки, ввернутой во фланец цилиндра (обычно принимают 1/3 длины этой части шпильки): 
Коэффициент податливости стыка [см. формулу 

 (модуль упругости стыка).
(модуль упругости стыка).
Площадь сечения эквивалентной втулки [см. формулу (3.12)]

Расчетная нагрузка шпильки с учетом возможности затяжки под полной нагрузкой [см. формулу (3.13)]

Проверку статической прочности шпилек производим по табл. 3.4.
Для шпильки  из стали 45 допускаемая осевая нагрузка
из стали 45 допускаемая осевая нагрузка  следовательно, статическая прочность шпилек обеспечена.
следовательно, статическая прочность шпилек обеспечена.
2. Проверка прочности шпилек с учетом циклического изменения нагрузкк. Коэффициент запаса прочности по амплитуде [см. формулу (3.14)]

 (см. табл. 3,5 и примечание 2).
(см. табл. 3,5 и примечание 2).
Амплитуда переменных напряжений для отнулевого цикла

где  (см. табл. 3.3).
(см. табл. 3.3).
Полученный коэффициент запаса прочности по амплитуде выше допускаемого  [см. экспликацию к формуле (3.14)].
[см. экспликацию к формуле (3.14)].
Коэффициент запаса прочности по наибольшему напряжению цикла [см. формулу (3.15)]

предел текучести  (см. табл. 3.4), напряжение затяжки
(см. табл. 3.4), напряжение затяжки

Коэффициент запаса прочности по наибольшему напряжению больше допускаемого  [см. экспликацию к формуле (3.15)].
[см. экспликацию к формуле (3.15)].
Прочность шпилек с учетом циклического изменения нагрузки обеспечена, так как оба коэффициента запаса больше допускаемого.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Раздел I. СОЕДИНЕНИЯ ДЕТАЛЕЙ МАШИН
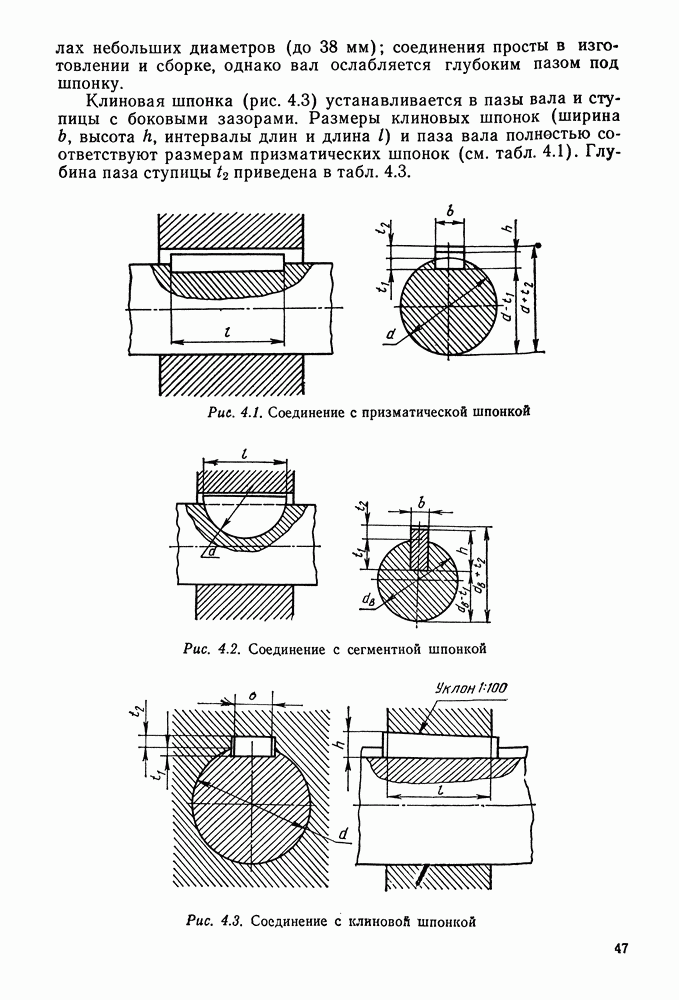
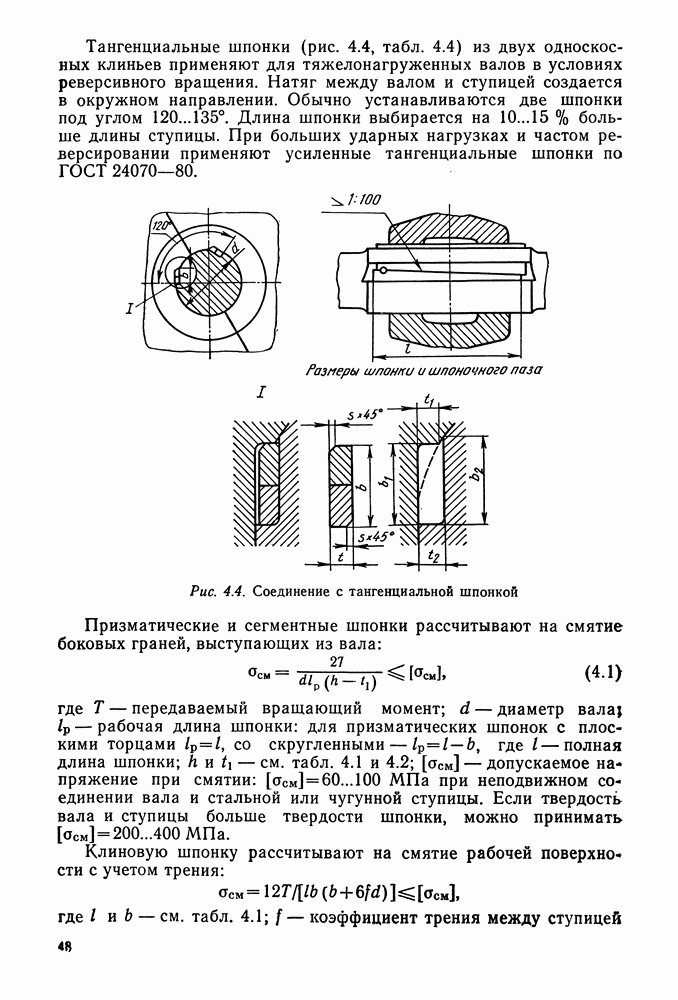
- Глава 1. ВАЛЬЦОВОЧНЫЕ СОЕДИНЕНИЯ
- 1.2. Расчет прочных швов
- 1.3. Справочный материал
- 1.4. Примеры расчета
- Глава 2. СВАРНЫЕ, ПАЯНЫЕ И КЛЕЕВЫЕ СОЕДИНЕНИЯ
- 2.1. Общие сведения об основных видах сварных соединений и сварных швов
- 2.2. Расчет прочности сварных швов
- 2.3. Условное изображение сварных швов на чертежах
- 2.4. Паяные соединения
- 2.5. Клеевые соединения
- 2.6. Справочный материал
- 2.7. Примеры расчета
- Глава 3. РЕЗЬБОВЫЕ СОЕДИНЕНИЯ
- 3.2. Определение сил, действующих на один болт
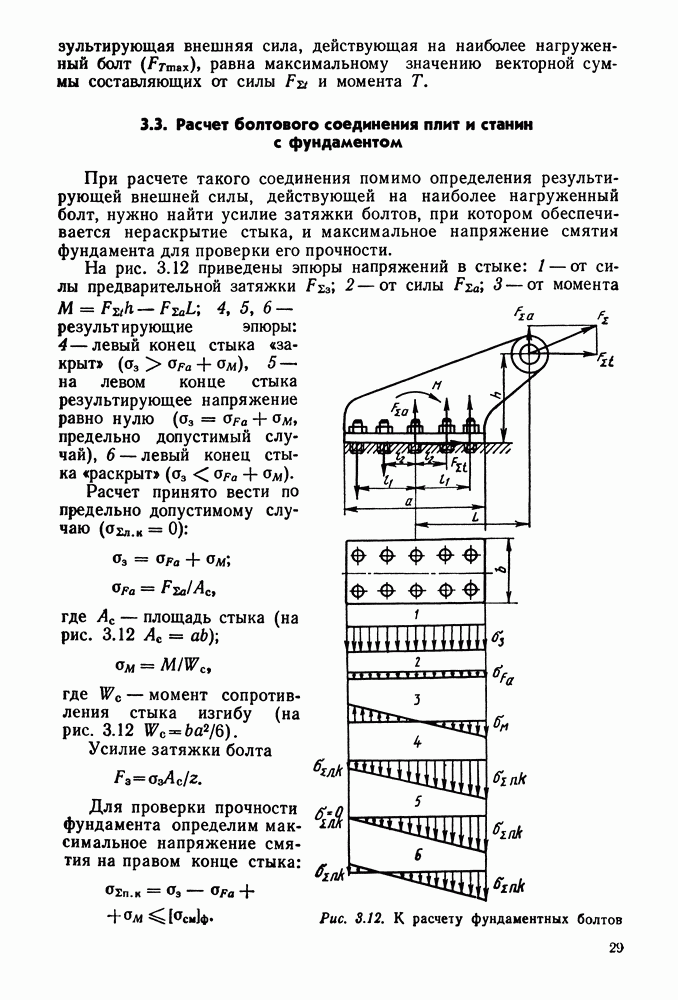
- 3.3. Расчет болтового соединения плит и станин с фундаментом
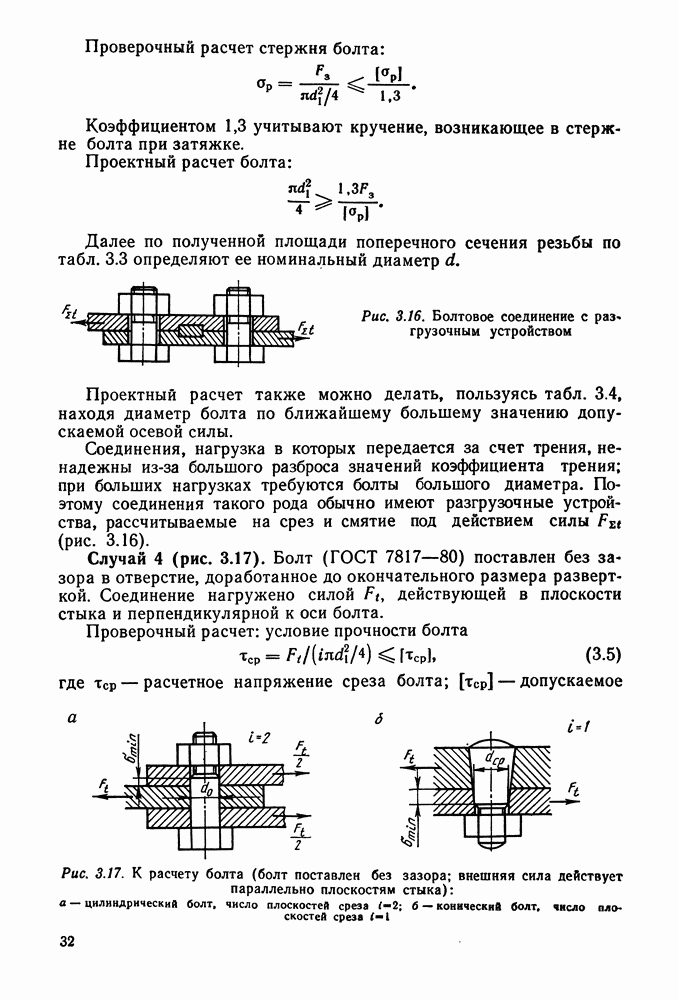
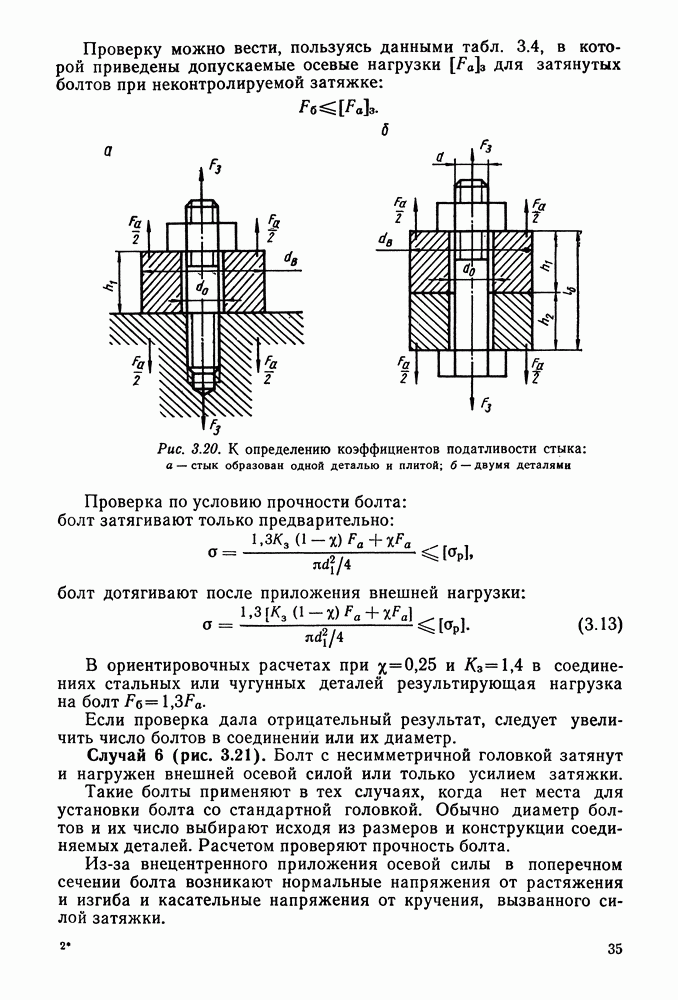
- 3.4. Расчет стержня болта при постоянных нагрузках
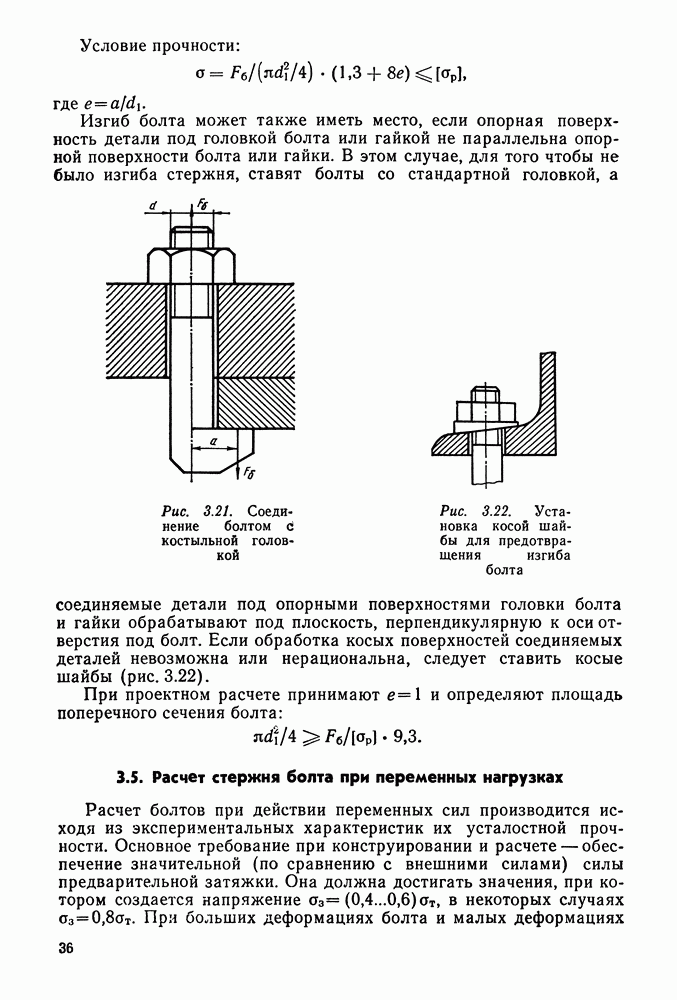
- 3.5. Расчет стержня болта при переменных нагрузках
- 3.6. Расчет витков резьбы на прочность. Определение вращающего момента
- 3.7. Порядок расчета резьбовых соединений
- 3.9. Примеры расчета
- Глава 4. СОЕДИНЕНИЯ ВАЛ — СТУПИЦА (ШПОНОЧНЫЕ, ШЛИЦЕВЫЕ, С НАТЯГОМ)
- 4.2. Шлицевые соединения
- 4.3. Соединения с натягом
- 4.4. Справочный материал
- 4.5. Примеры расчета
- Раздел II. МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ
- Глава 5. КИНЕМАТИЧЕСКИЙ РАСЧЕТ ПРИВОДНЫХ УСТРОЙСТВ И ВЫБОР ЭЛЕКТРОДВИГАТЕЛЯ
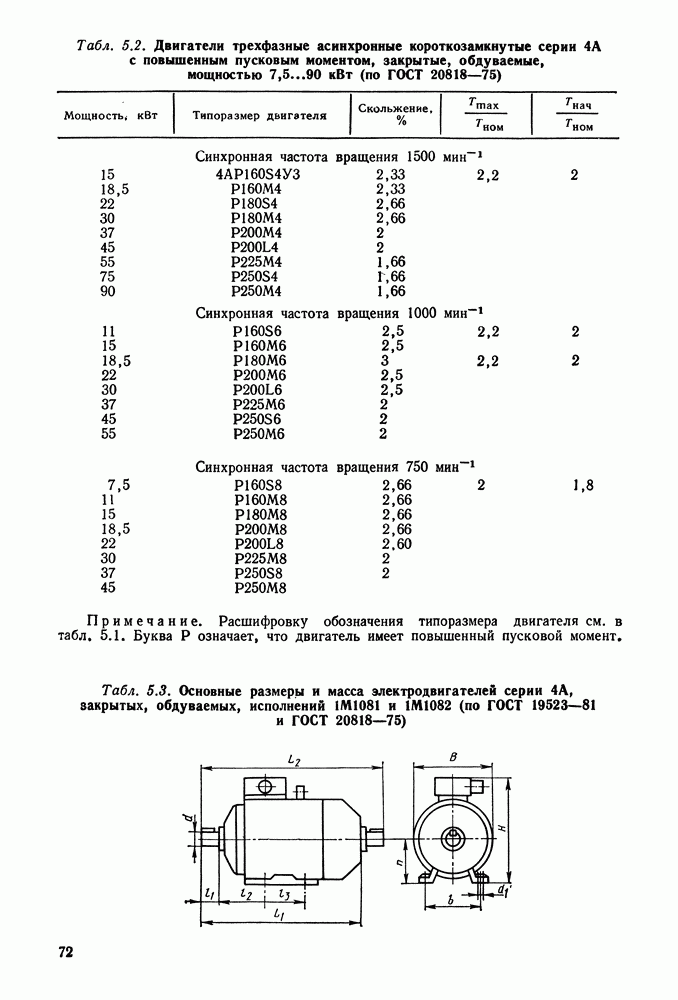
- 5.2. Трехфазные асинхронные электродвигатели
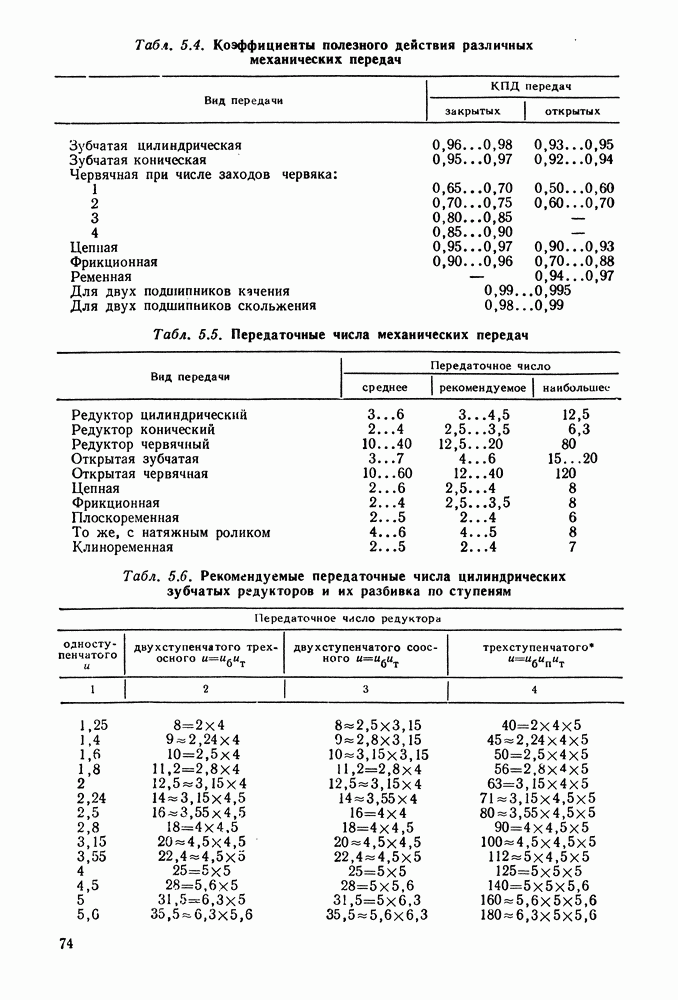
- 5.3. Разбивка общего передаточного числа редуктора по ступеням
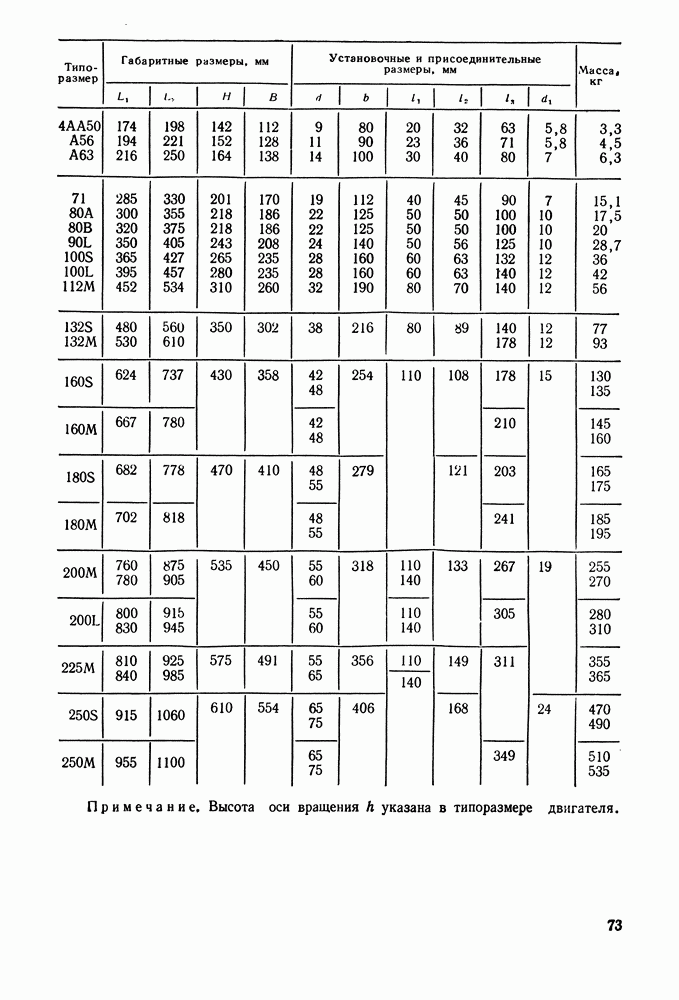
- 5.4. Справочный материал
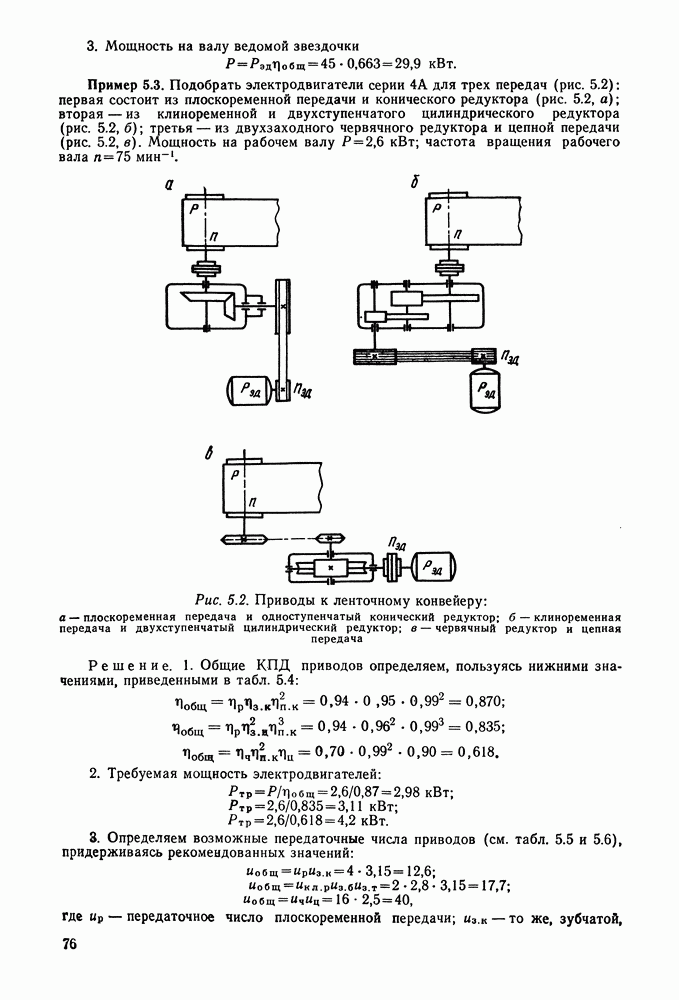
- 5.5. Примеры расчета
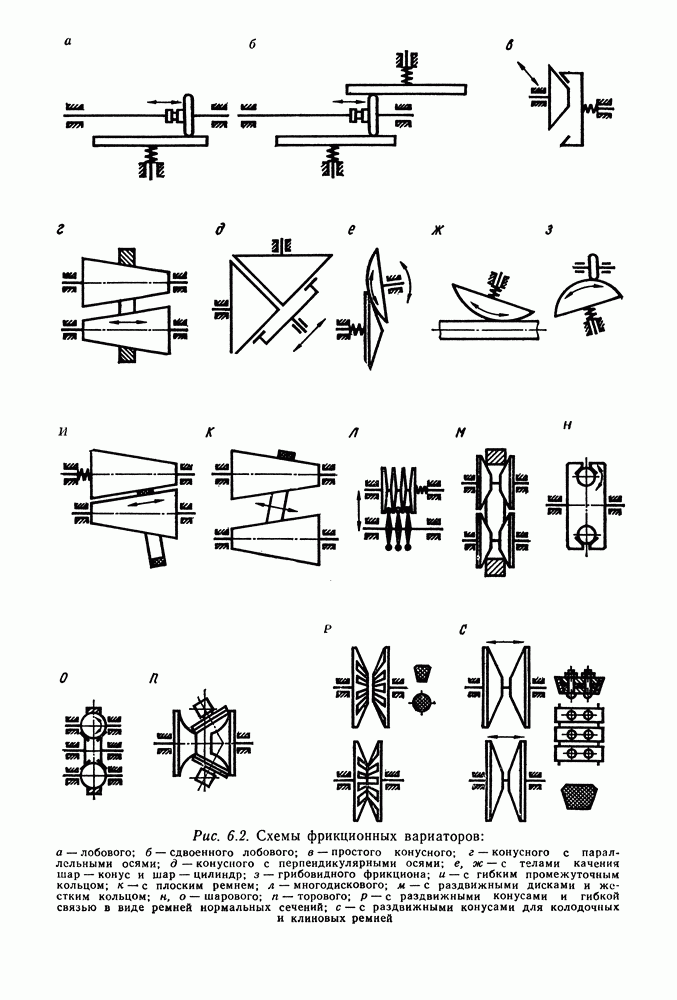
- Глава 6. ФРИКЦИОННЫЕ ПЕРЕДАЧИ И ВАРИАТОРЫ
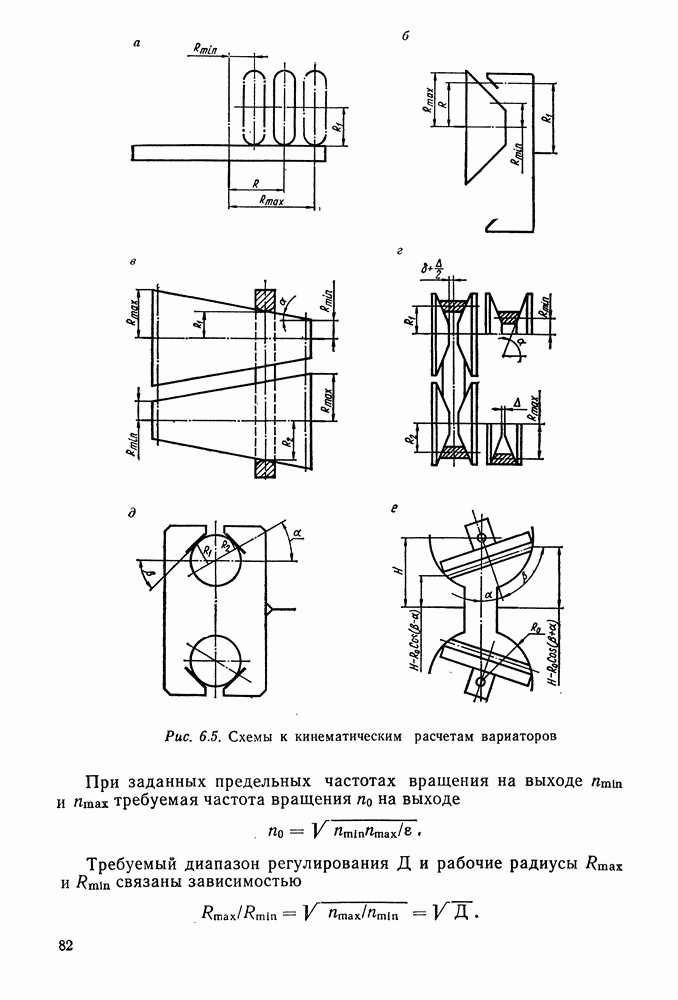
- 6.2. Кинематические расчеты фрикционных передач
- 6.3. Определение сил прижатия фрикционных тел и нагрузки на валы передачи
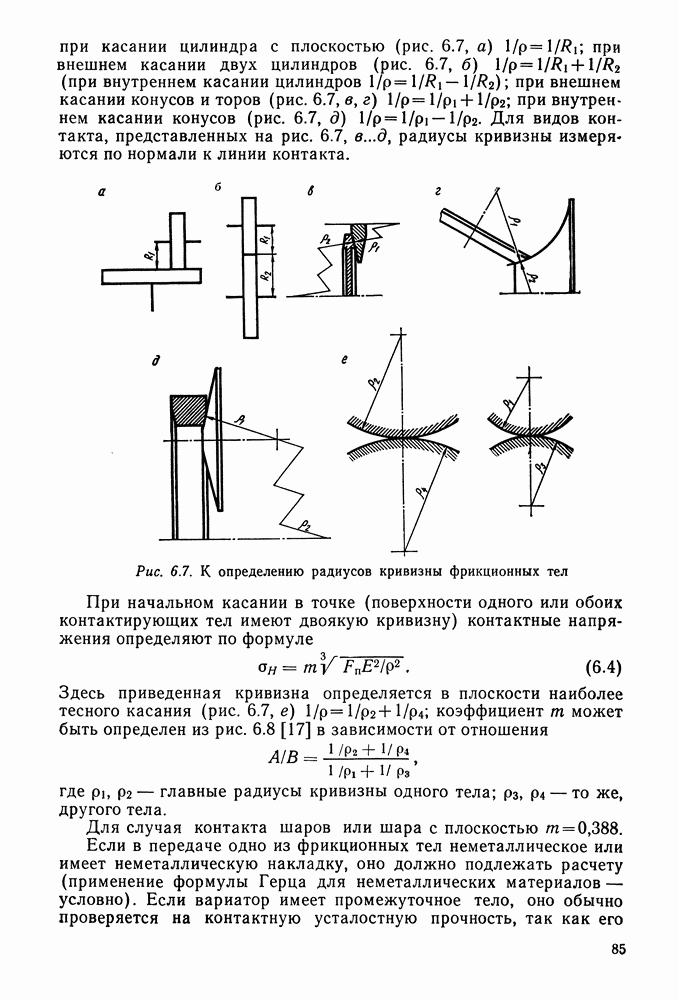
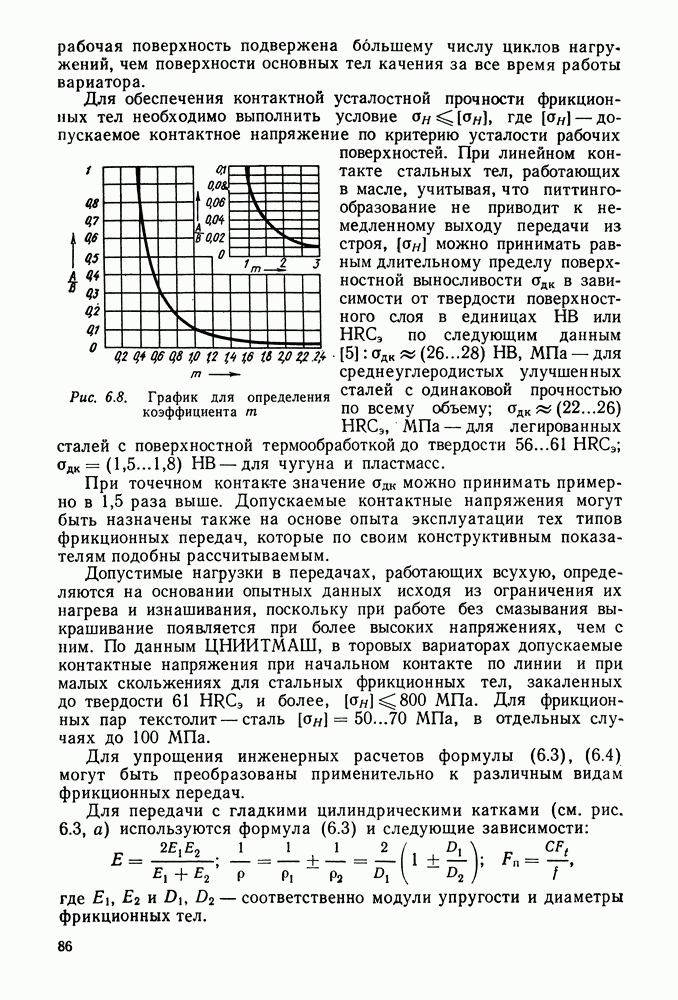
- 6.4. Расчет фрикционных тел на контактную прочность и КПД передач
- 6.5. Справочный материал
- 6.6. Примеры расчета
- Глава 7. РЕМЕННЫЕ ПЕРЕДАЧИ
- 7.2. Расчет клиноременных передач
- 7.3. Расчет передач поликлиновыми ремнями
- 7.4. Расчет зубчато-ременных передач
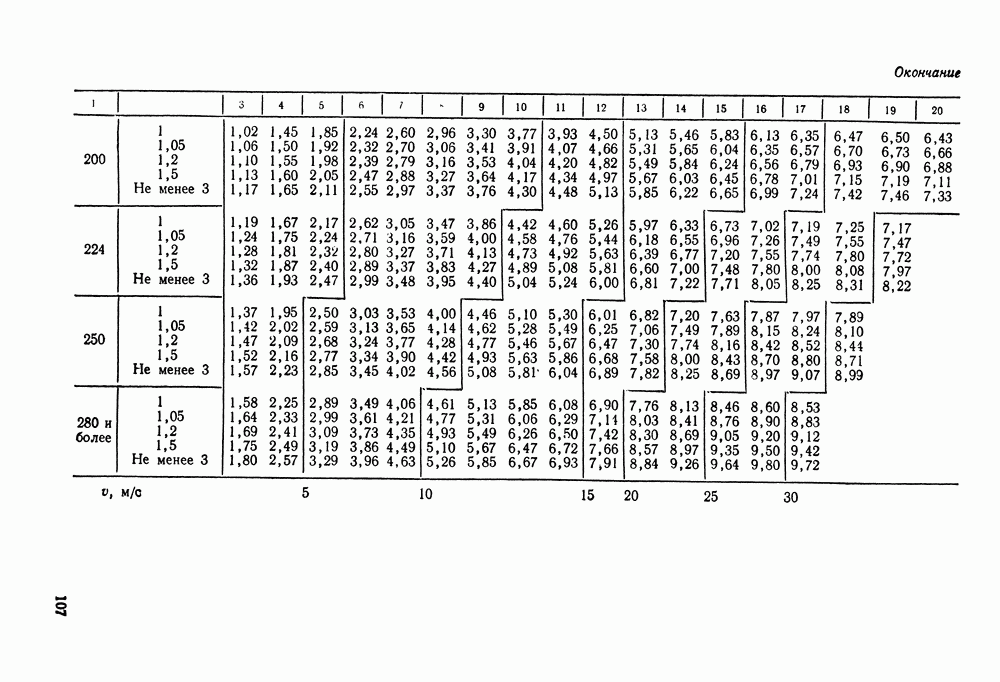
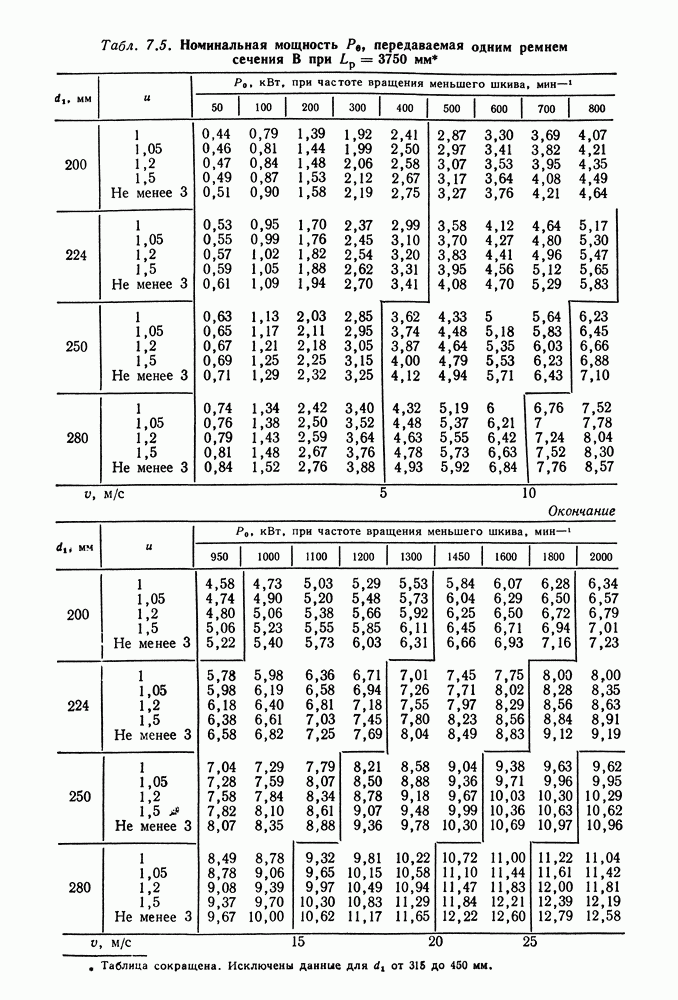
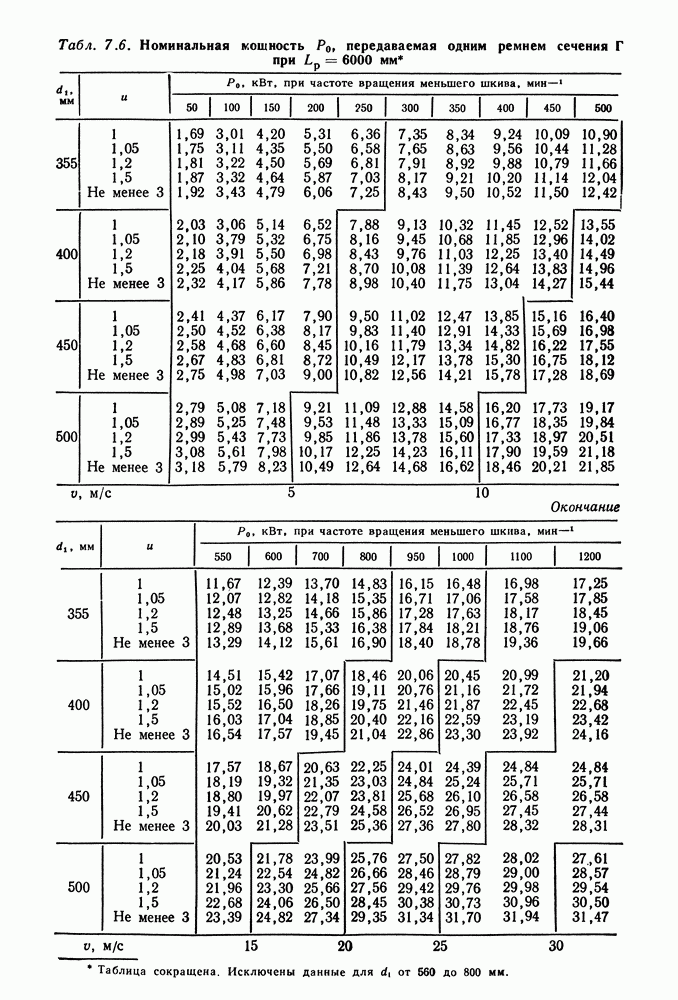
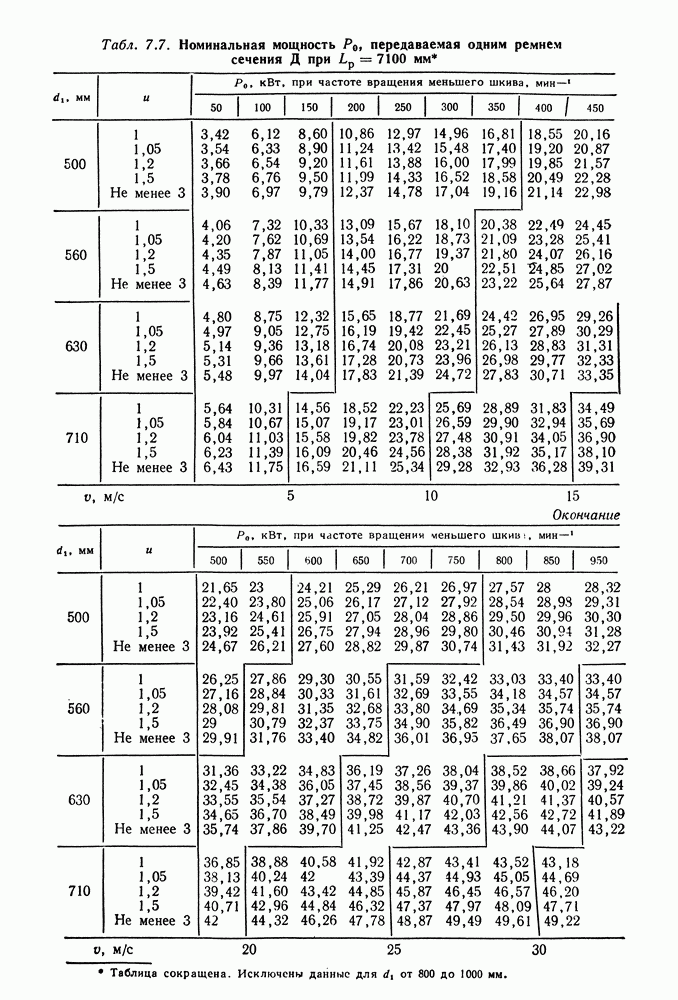
- 7.5. Справочный материал
- 7.6. Примеры расчета
- Глава 8. ЦЕПНЫЕ ПЕРЕДАЧИ
- 8.2. Геометрический, кинематический и силовой расчеты цепных передач
- 8.3. Выбор основных параметров и расчет цепных передач
- 8.4. Справочный материал
- 8.5. Примеры расчета
- Глава 9. ЗУБЧАТЫЕ ПЕРЕДАЧИ
- 9.2. Геометрия и кинематика эвольвентного цилиндрического зацепления
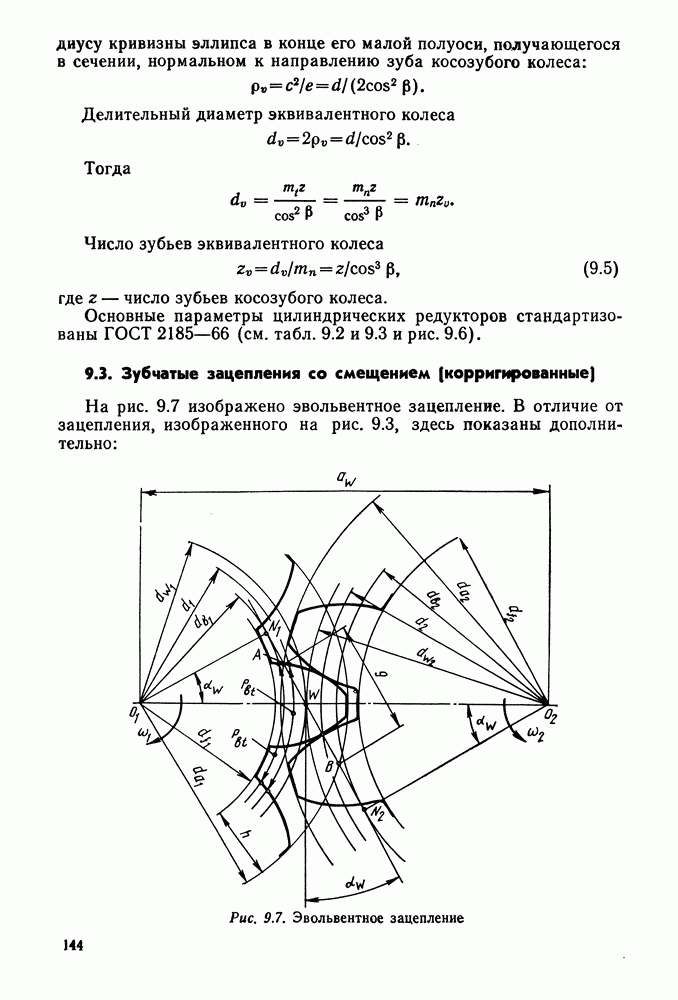
- 9.3. Зубчатые зацепления со смещением (корригированные)
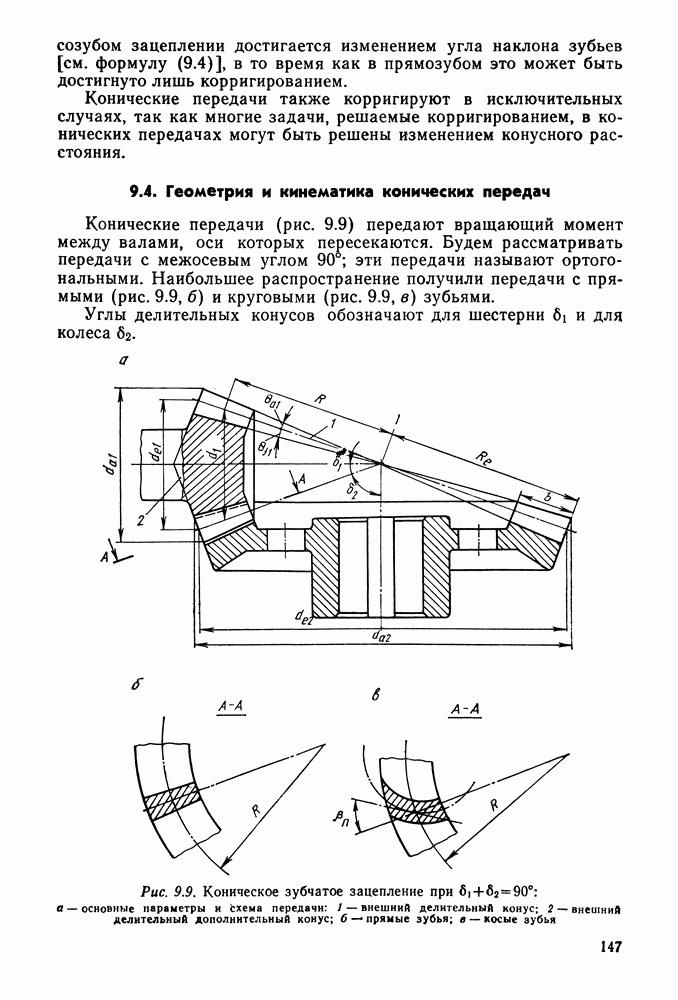
- 9.4. Геометрия и кинематика конических передач
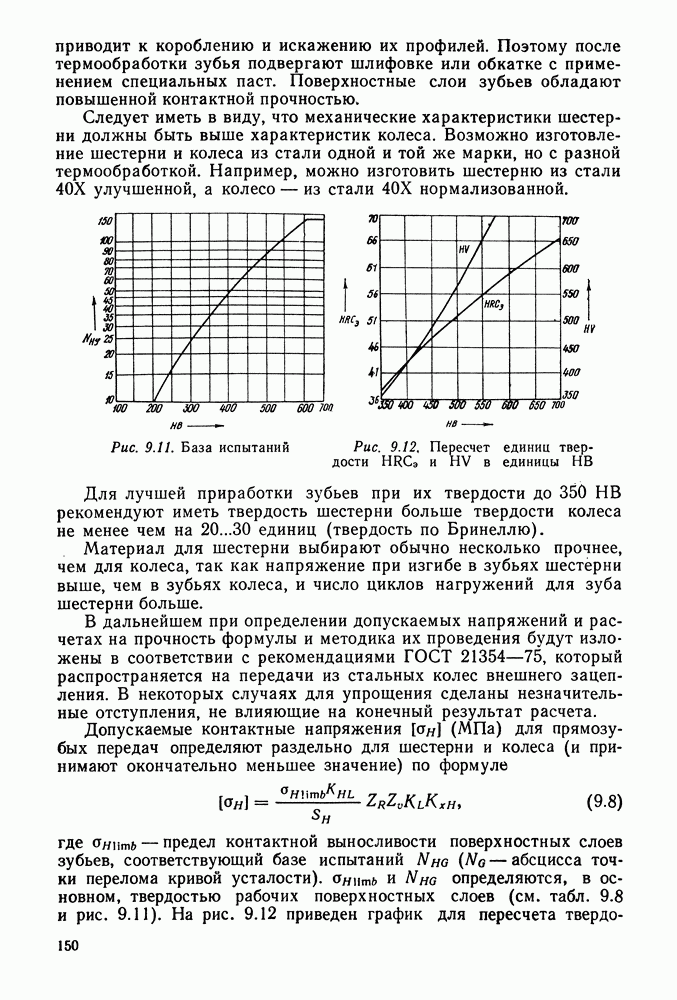
- 9.5. Материалы и допускаемые напряжения
- 9.6. Точность зубчатых передач
- 9.7. Коэффициент нагрузки
- 9.8. Расчет зубчатого зацепления на контактную прочность
- 9.9. Расчет зубьев колес на изгиб
- 9.10. Расчет открытых зубчатых передач
- 9.11. Проверка прочности зубьев колес при перегрузках
- 9.12. Определение размеров стальных зубчатых закрытых передач и проверка их прочности
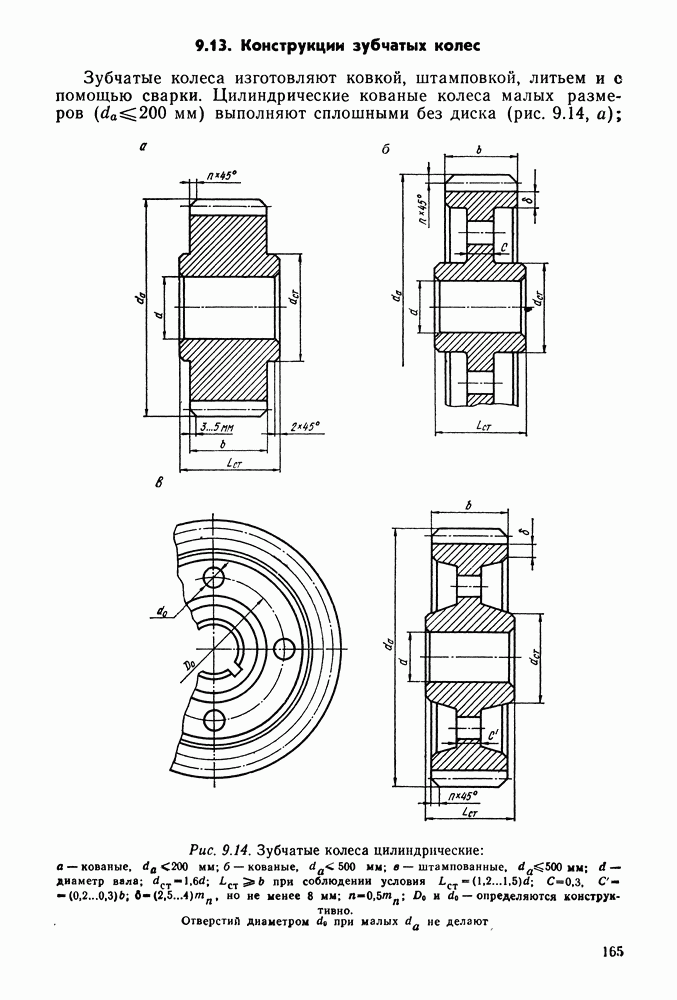
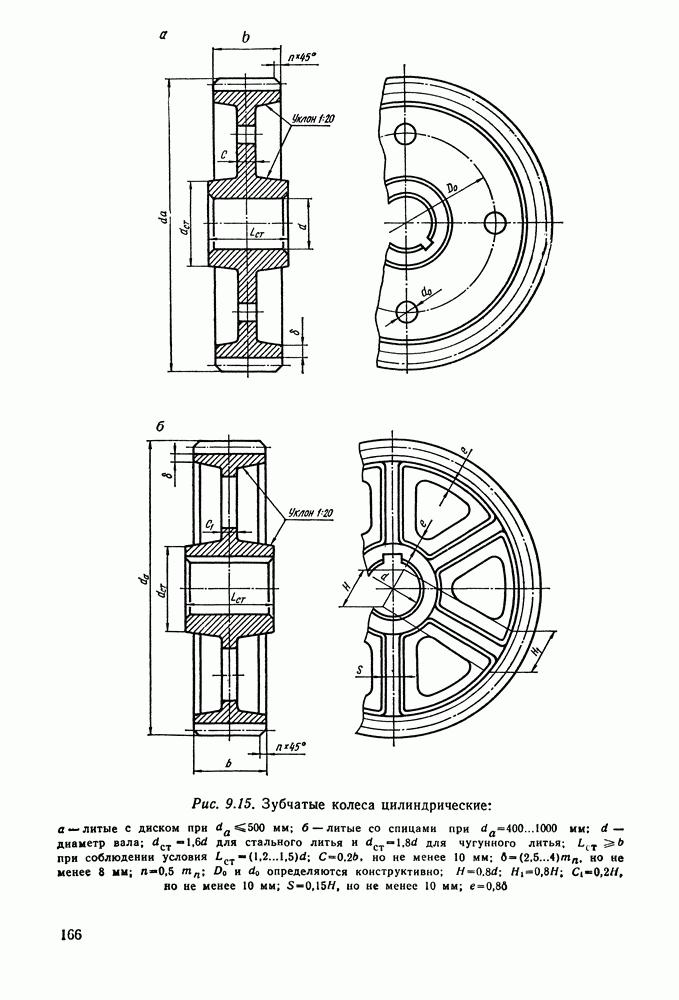
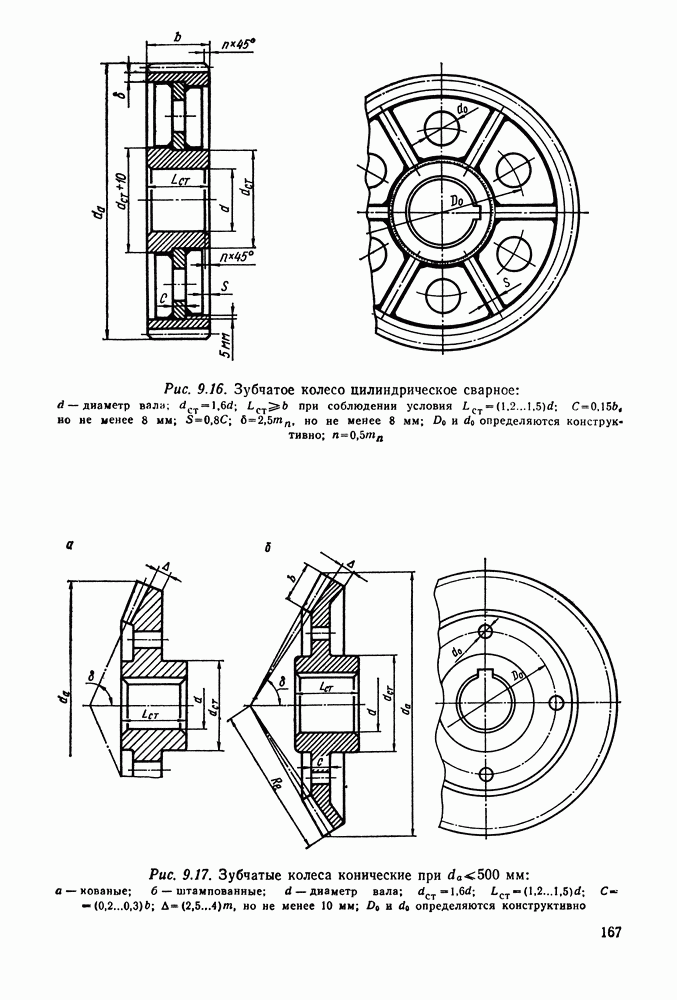
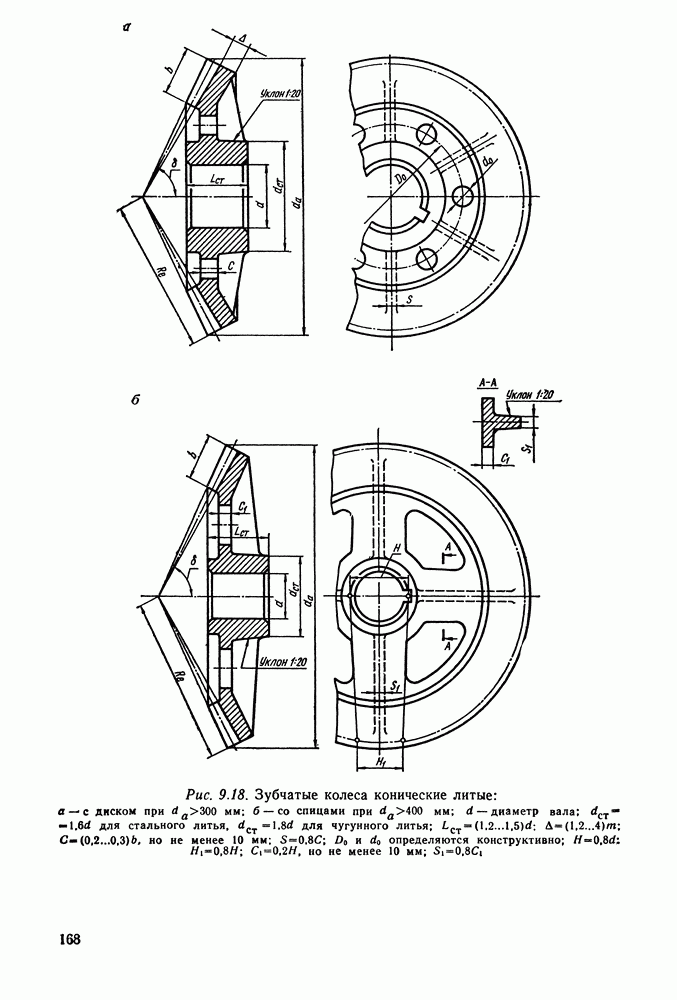
- 9.13. Конструкции зубчатых колес
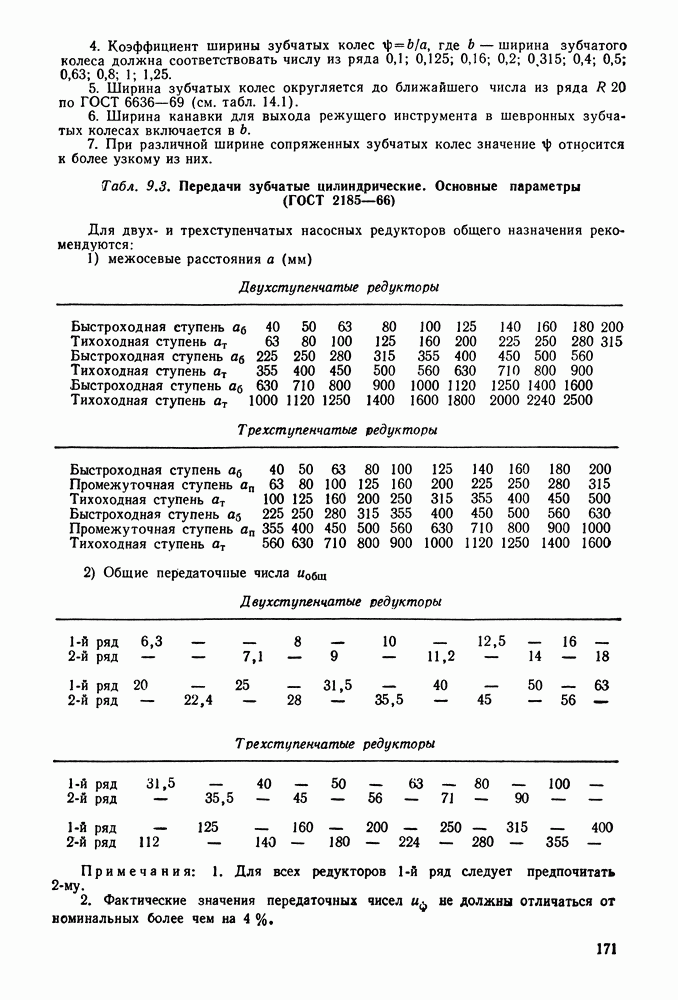
- 9.14. Справочный материал
- 9.15. Примеры расчета
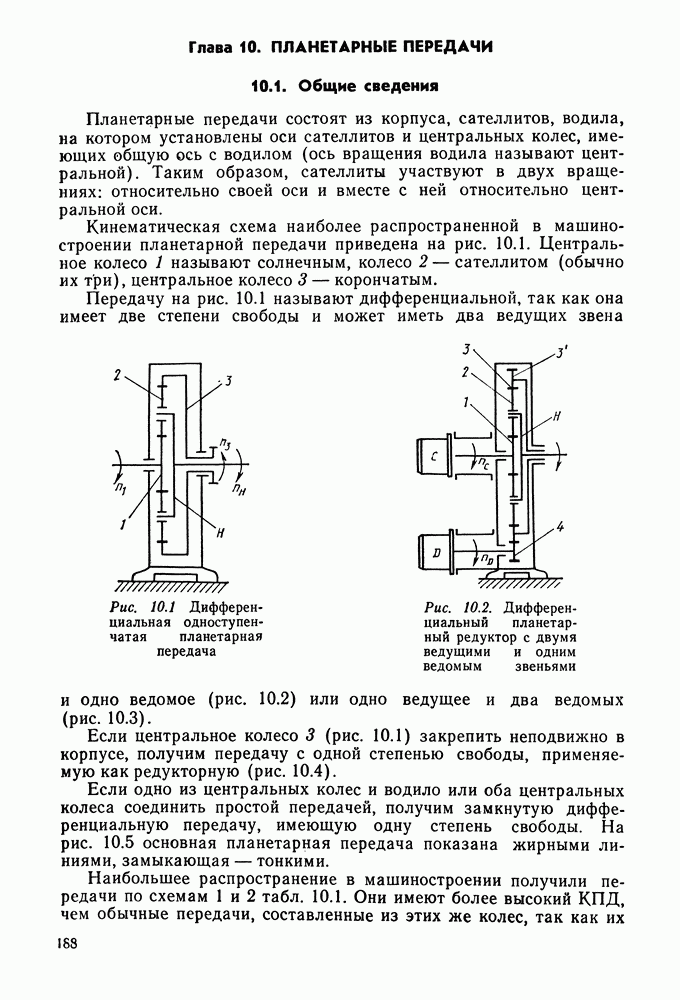
- Глава 10. ПЛАНЕТАРНЫЕ ПЕРЕДАЧИ
- 10.2. Кинематический расчет
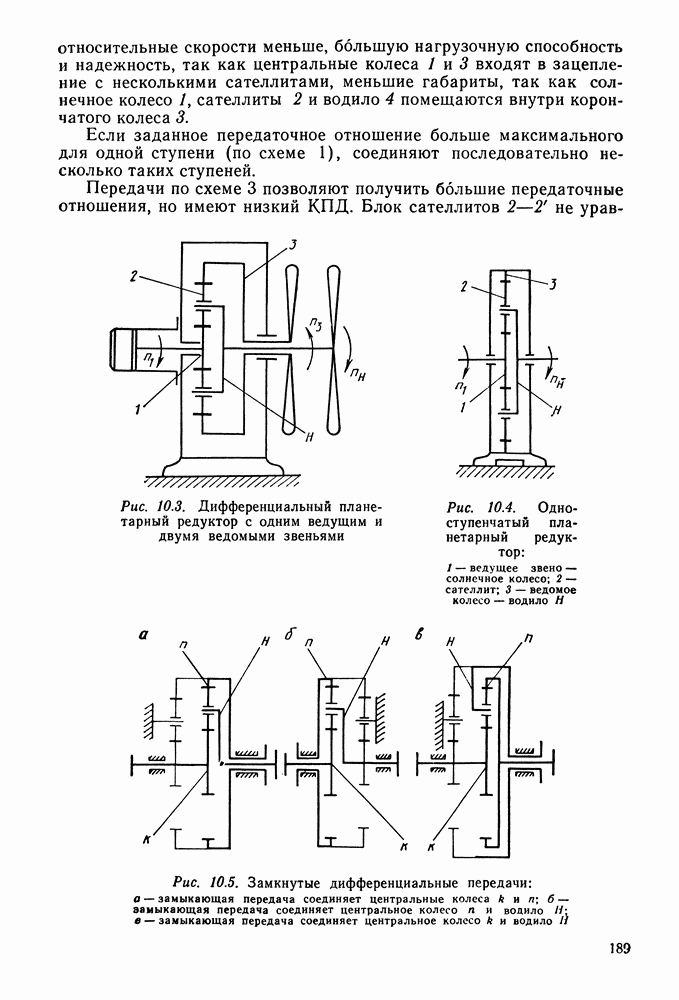
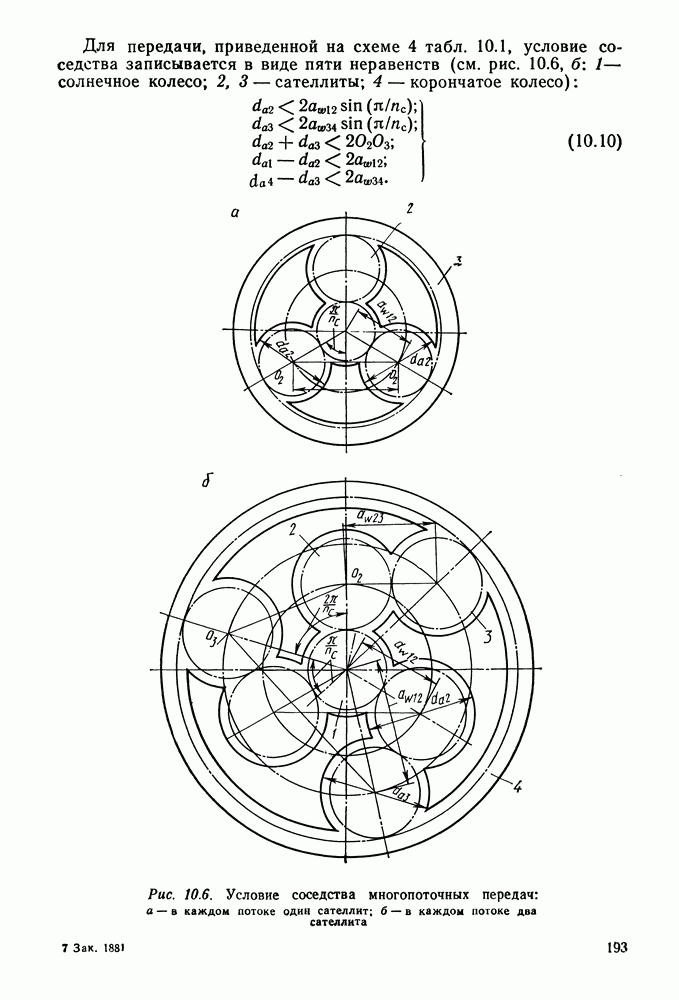
- 10.3. Условия собираемости соосных и многопоточных передач
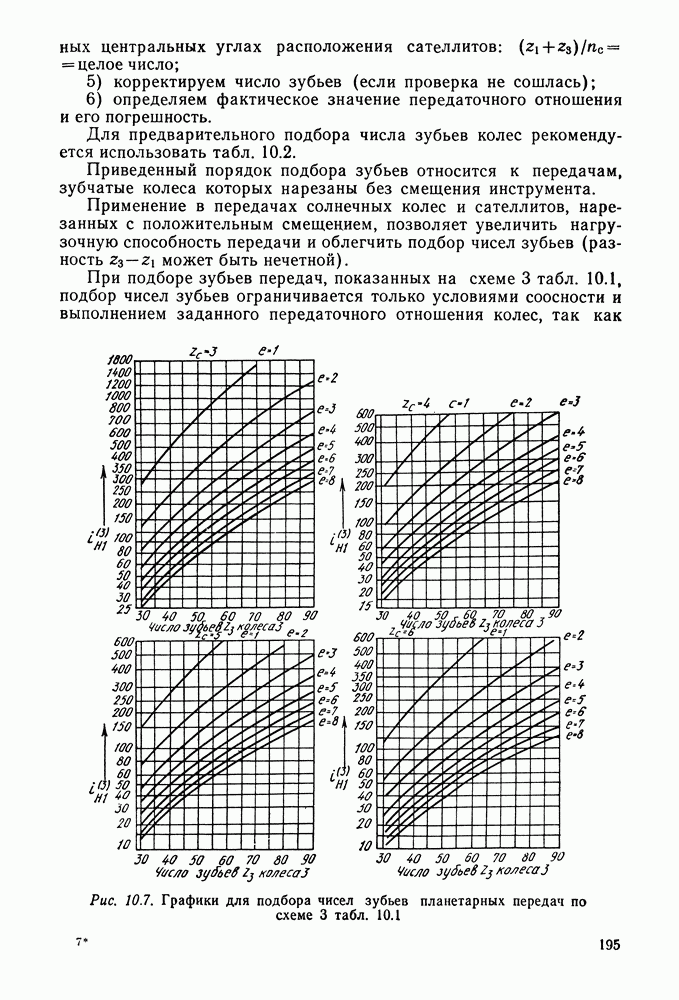
- 10.4. Порядок подбора чисел зубьев при заданном передаточном отношении и числе сателлитов
- 10.5. Определение КПД планетарных передач
- 10.6. Определение сил, действующих в зацеплениях и в опорах осей и валов прямозубых передач
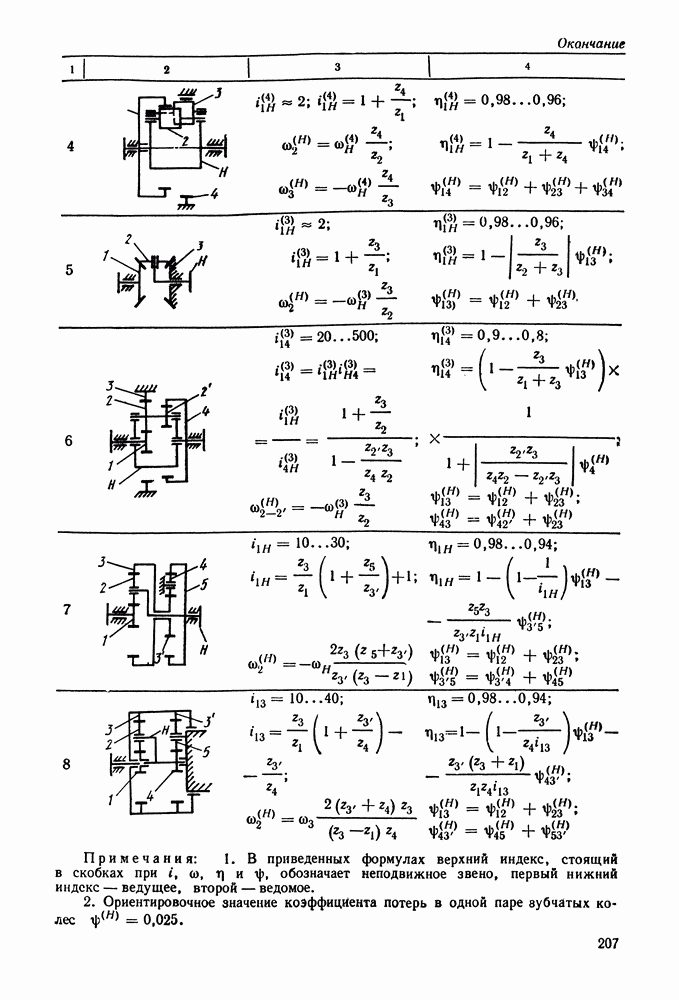
- 10.7. Расчет зубьев планетарных передач на прочность
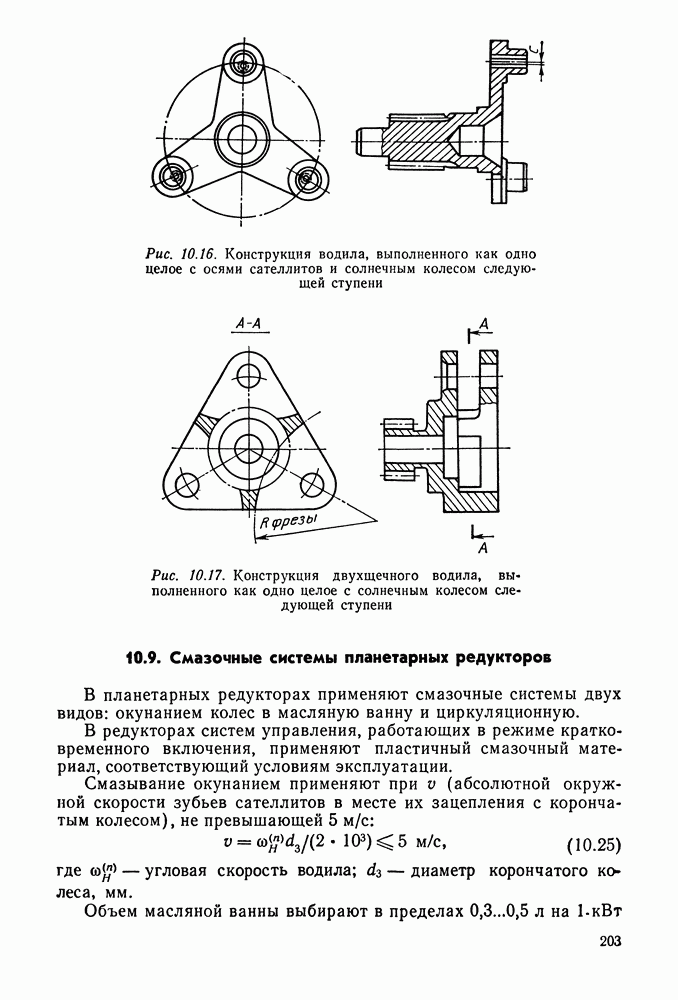
- 10.8. Конструкция и размеры деталей планетарных передач [14]
- 10.9. Смазочные системы планетарных редукторов
- 10.10. Порядок проектного расчета планетарного редуктора (схемы 1 и 2 табл. 10.1)
- 10.11. Порядок расчета планетарного мотор-редуктора (схема 1 табл. 10.1)
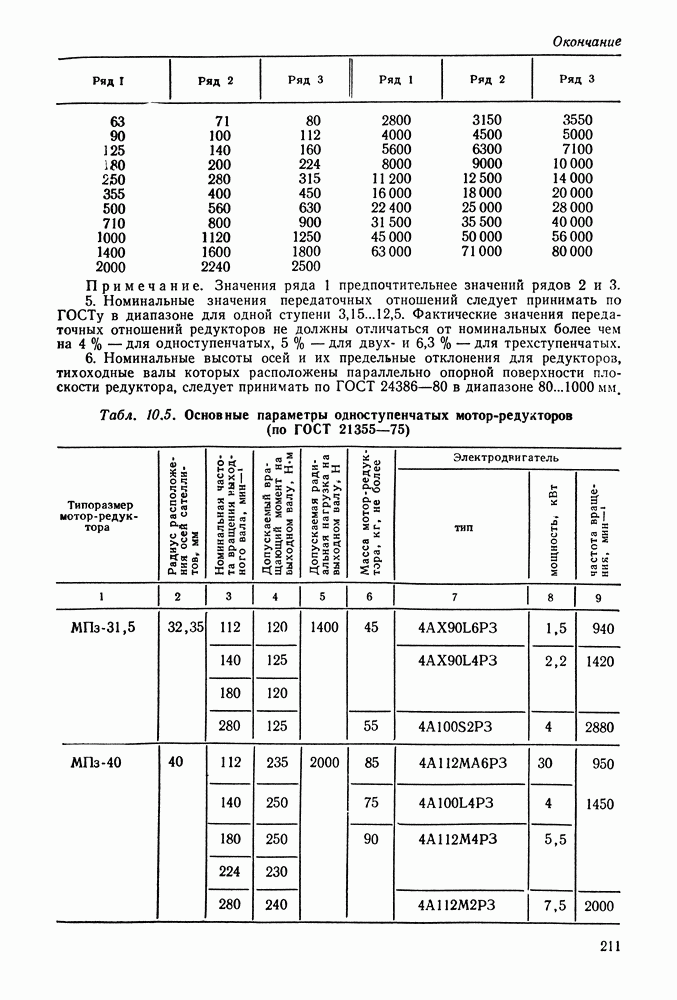
- 10.12. Справочный материал
- 10.13. Примеры расчета
- Глава 11. ВОЛНОВЫЕ ПЕРЕДАЧИ
- 11.2 Основные схемы волновых передач
- 11.3. Проектный расчет волновой зубчатой передачи
- 11.4. Конструкция и размеры основных деталей волновых передач
- 11.5. Порядок расчета волновой передачи с кулачковым генератором
- 11.6. Справочный материал
- 11.7. Пример расчета
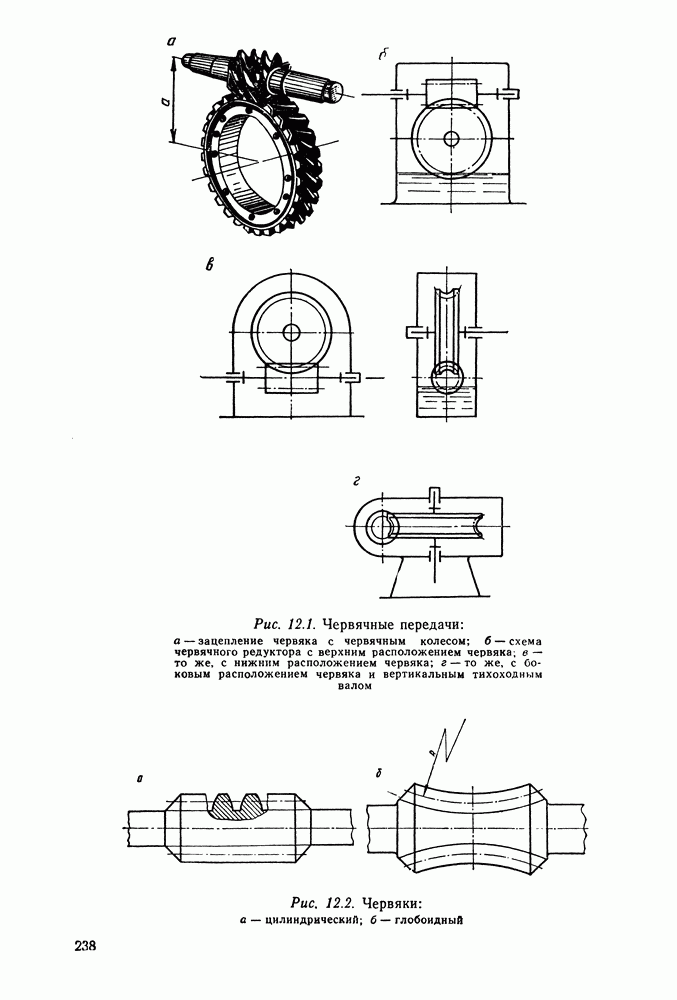
- Глава 12. ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ
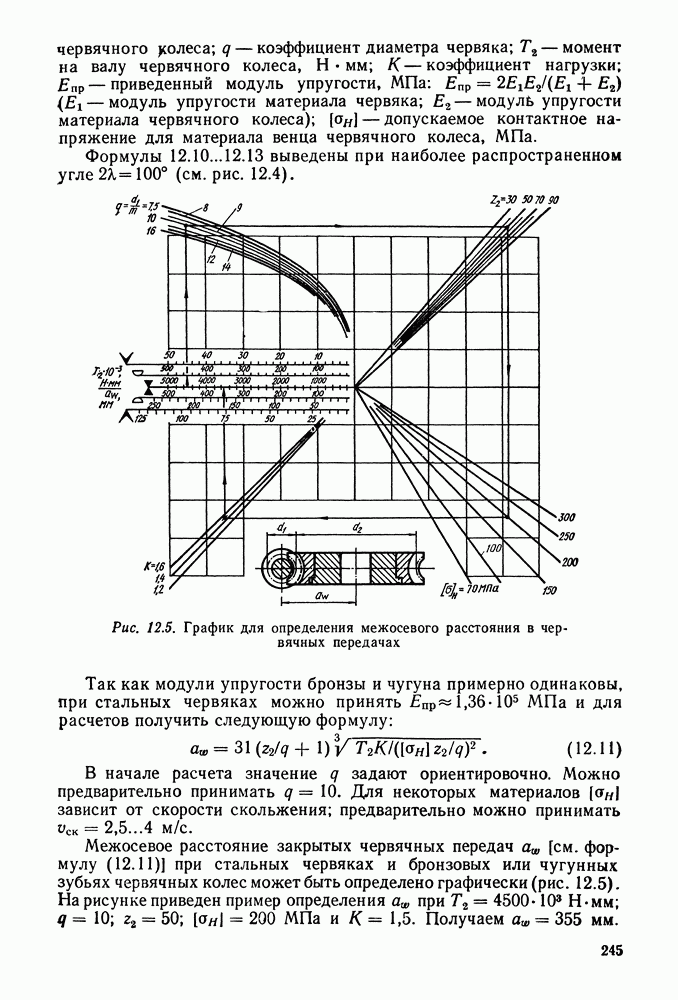
- 12.2 Геометрия и кинематика червячного зацепления
- 12.3. Червячные передачи со смещением (корригированные)
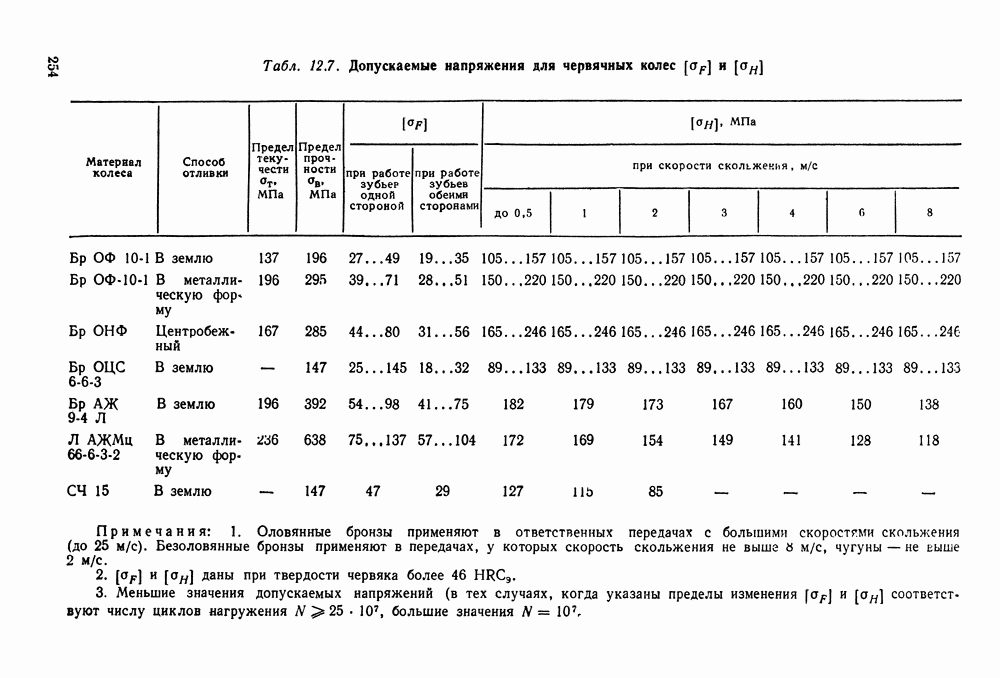
- 12.4. Материалы и допускаемые напряжения
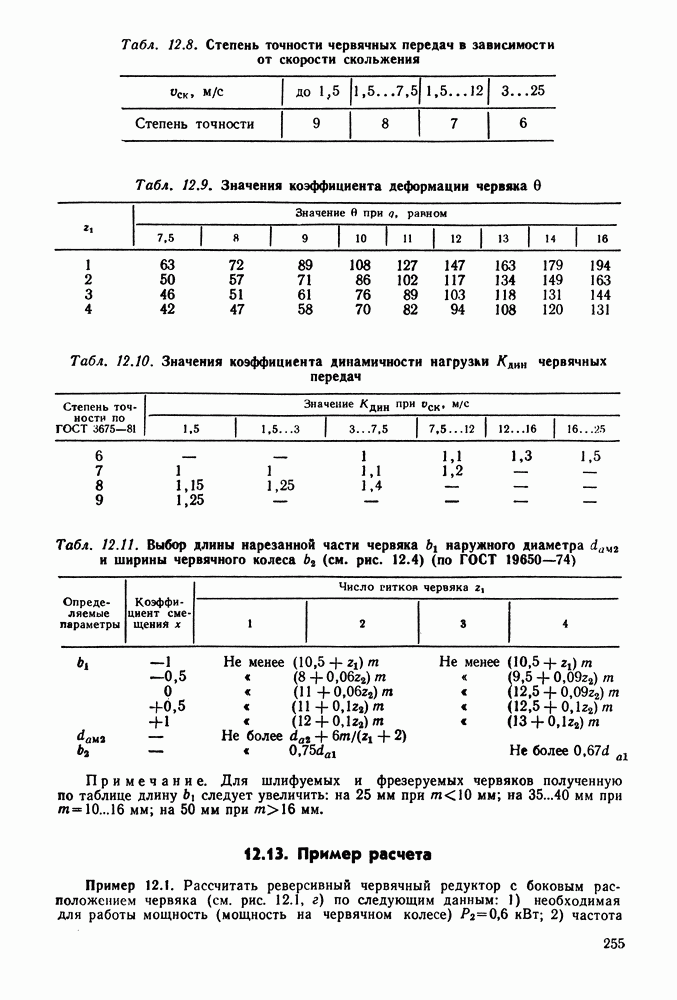
- 12.5. Точность червячных передач
- 12.6. Коэффициент нагрузки
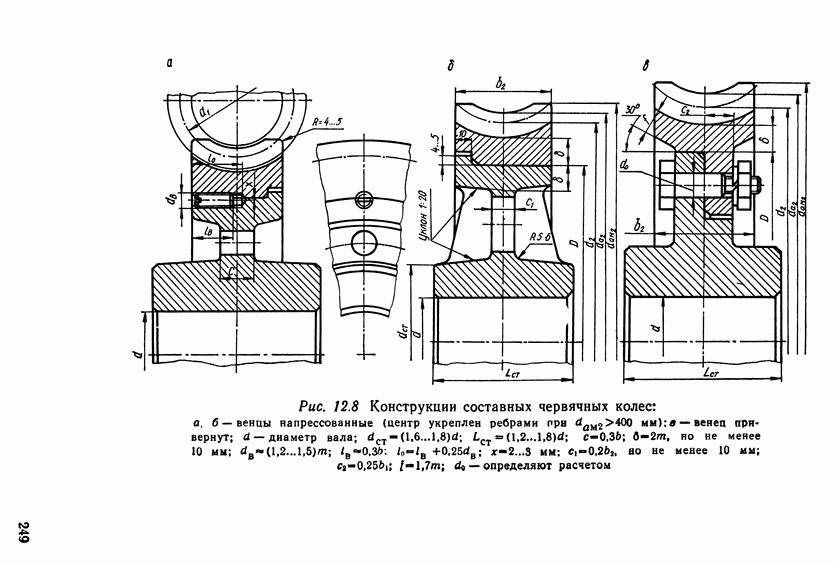
- 12.7. Расчет червячного зацепления на контактную прочность
- 12.8. Расчет на изгиб
- 12.9. Расчет открытых червячных передач
- 12.10. Проверка червячных редукторов на нагрев
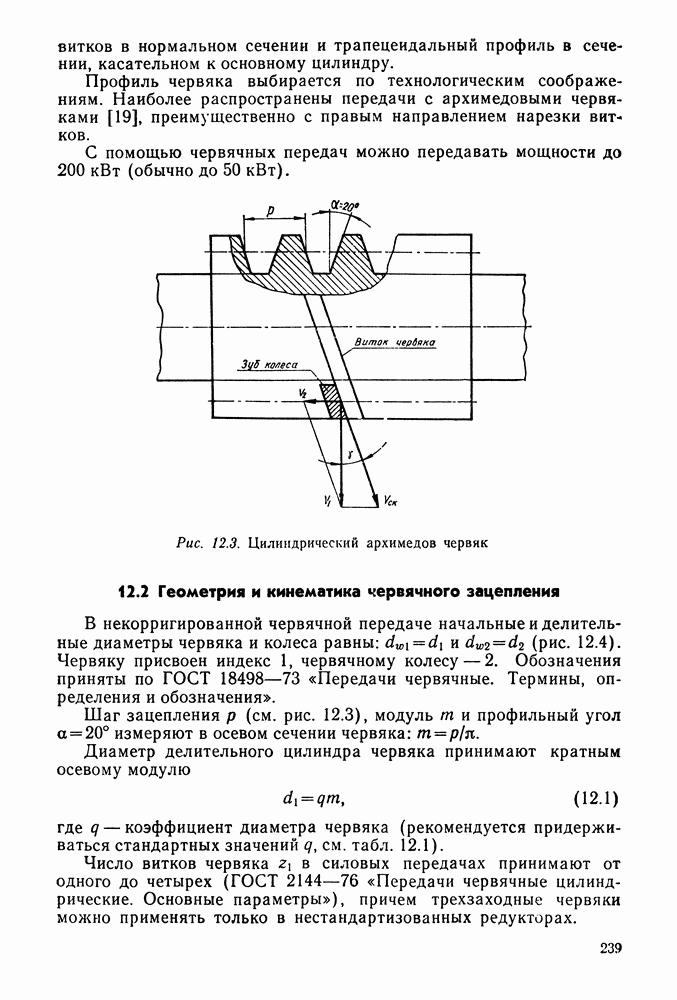
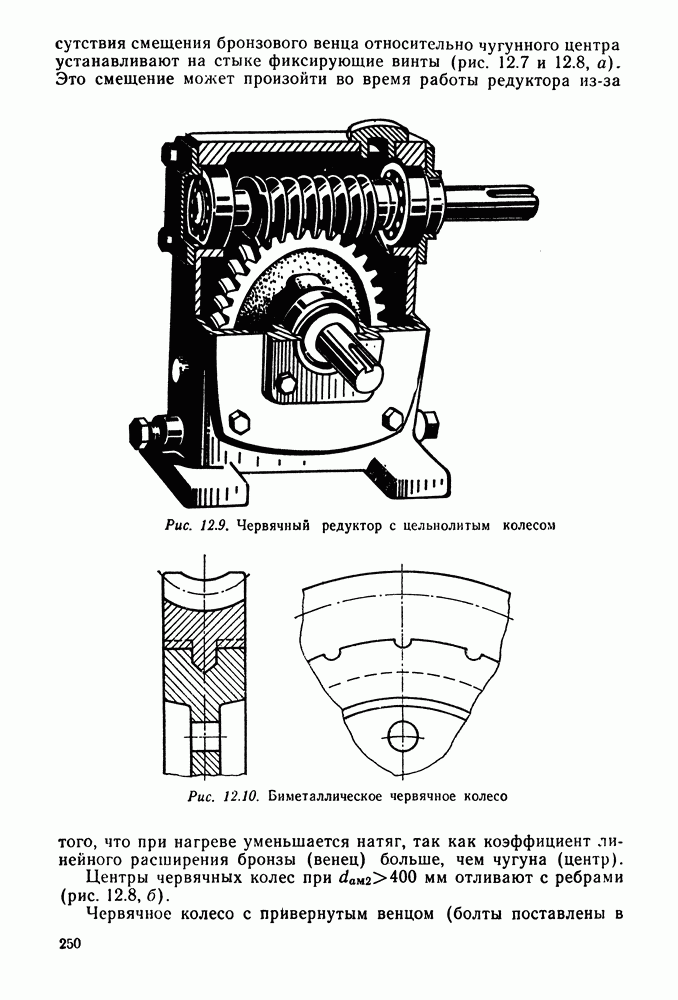
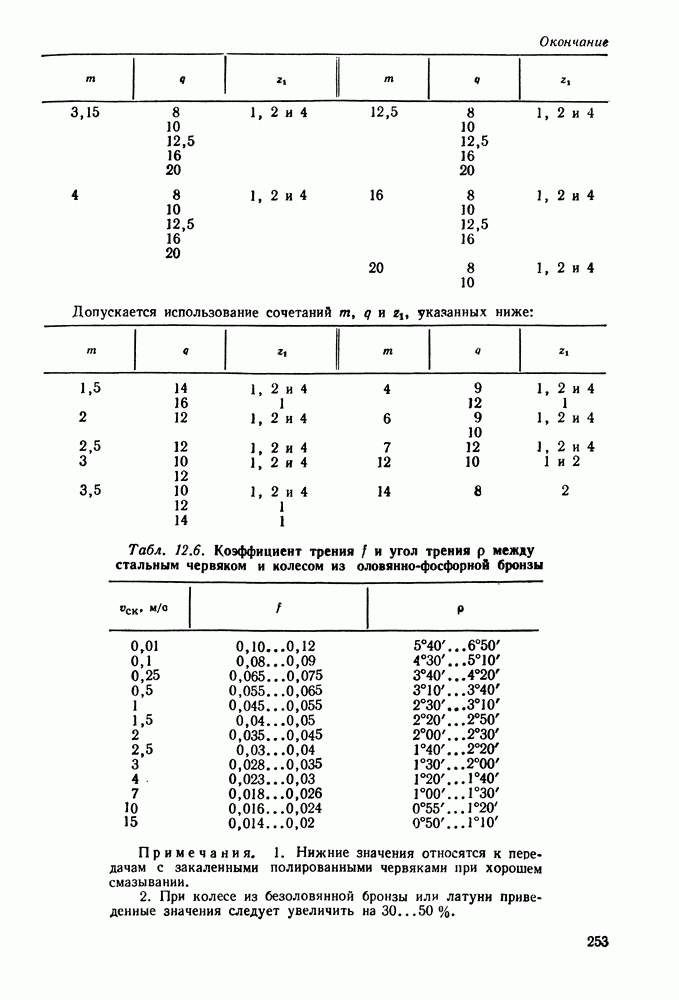
- 12.11. Конструкция червяков и червячных колес
- 12.12. Справочный материал
- 12.13. Пример расчета
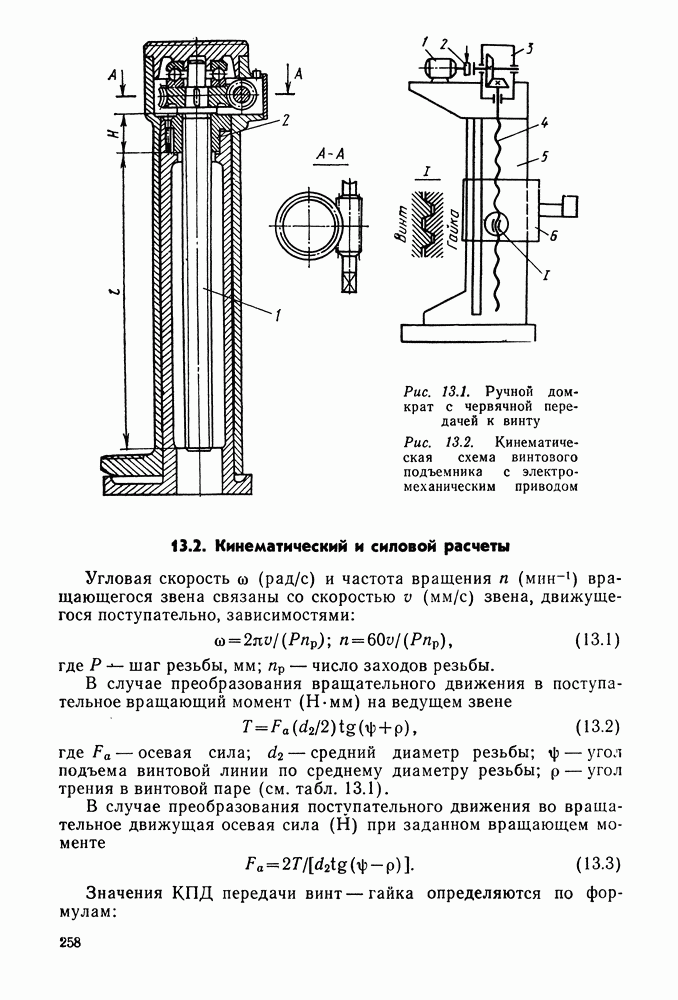
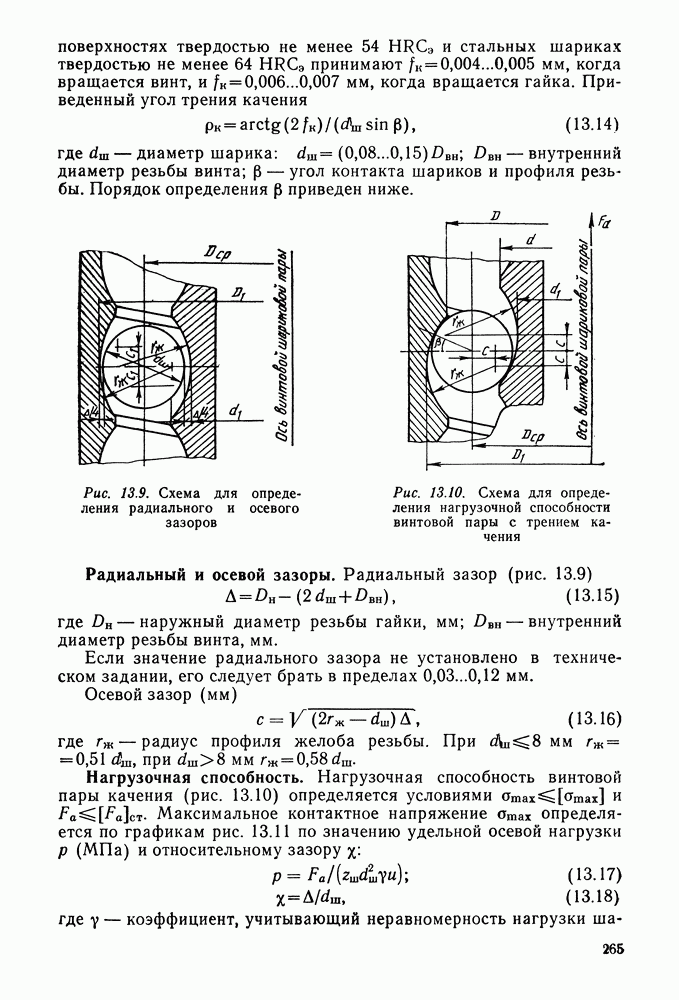
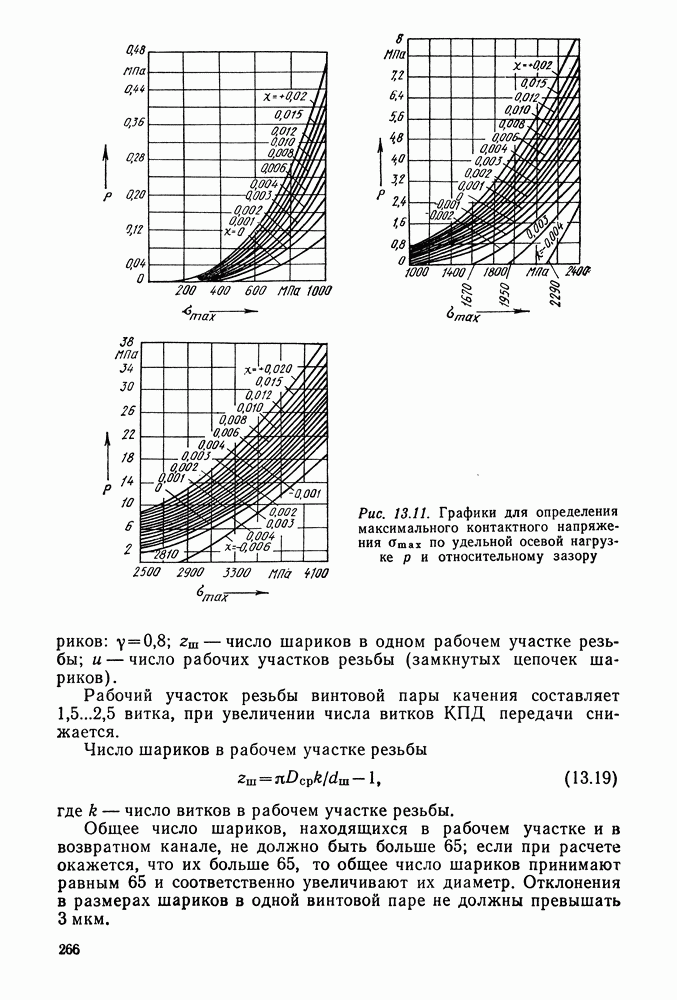
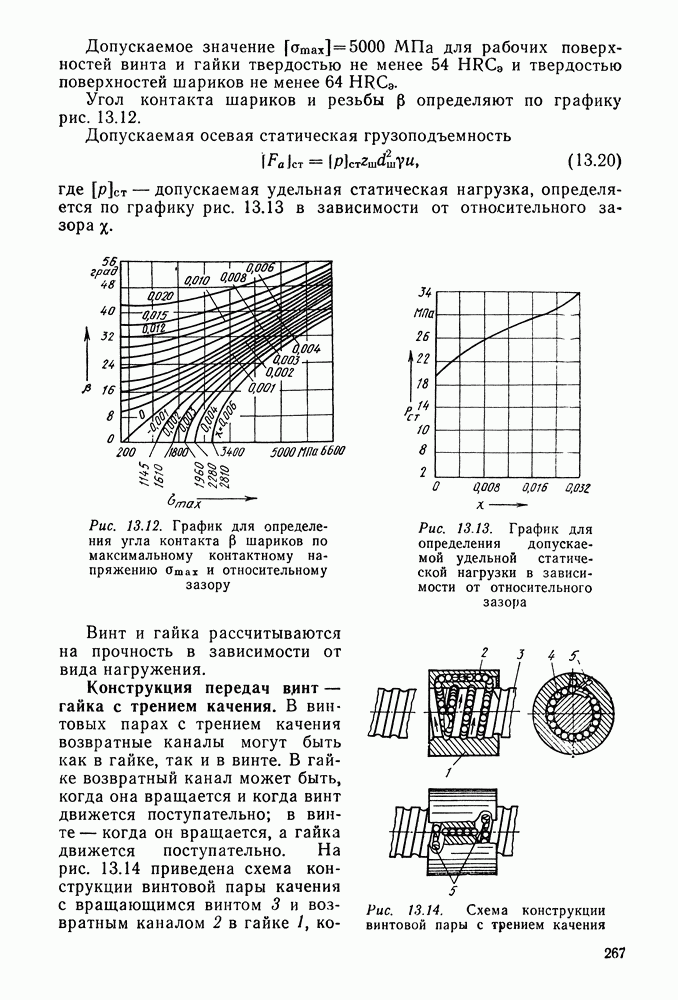
- Глава 13. ПЕРЕДАЧА ВИНТ — ГАЙКА
- 13.2. Кинематический и силовой расчеты
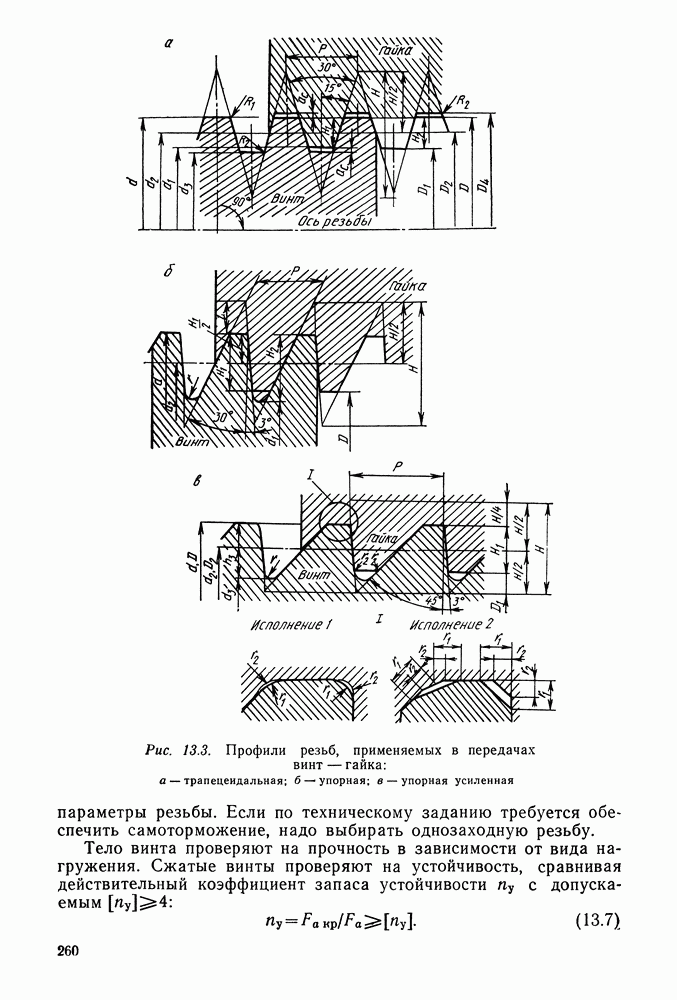
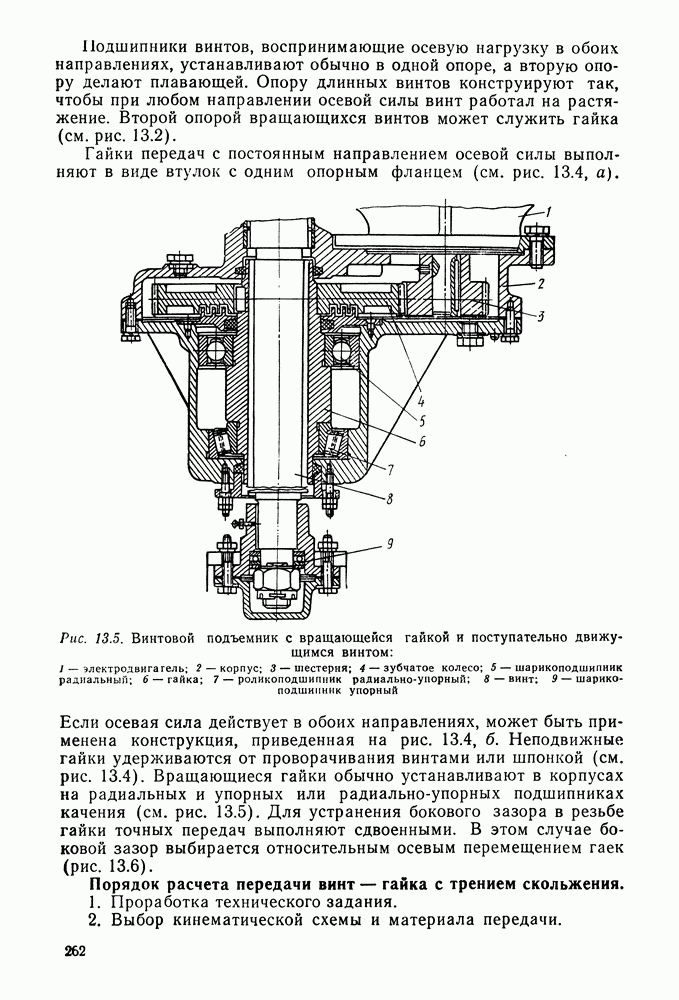
- 13.3. Передача винт—гайка с трением скольжения
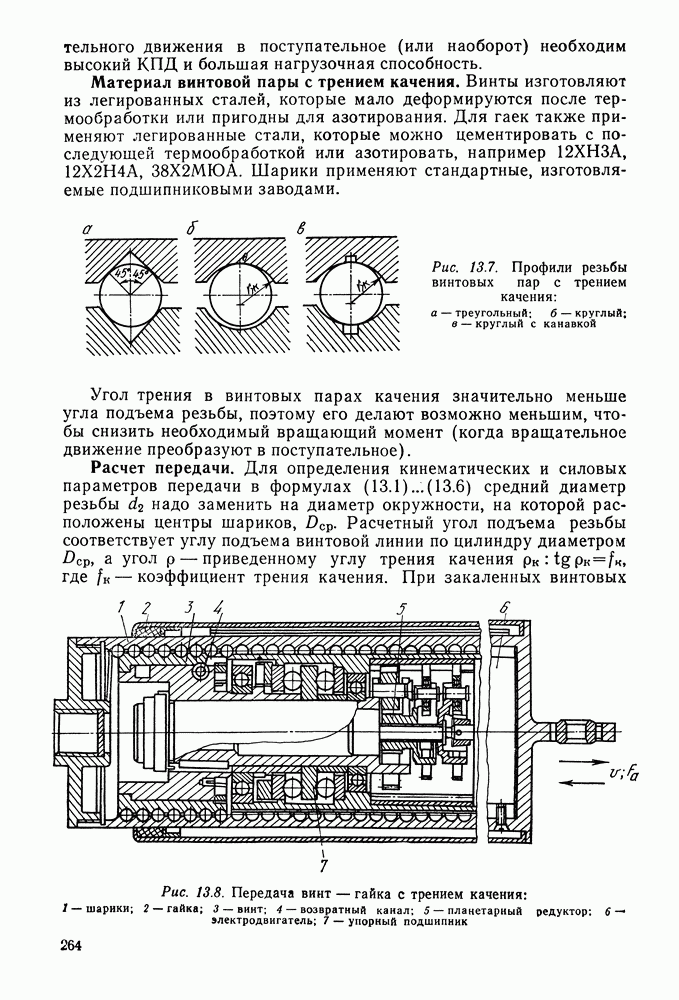
- 13.4. Передача винт — гайка с трением качения
- 13.5. Справочный материал
- 13.6. Пример расчета
- Раздел III. ВАЛЫ, ИХ ОПОРЫ, МУФТЫ, ПРУЖИНЫ
- Глава 14. ВАЛЫ
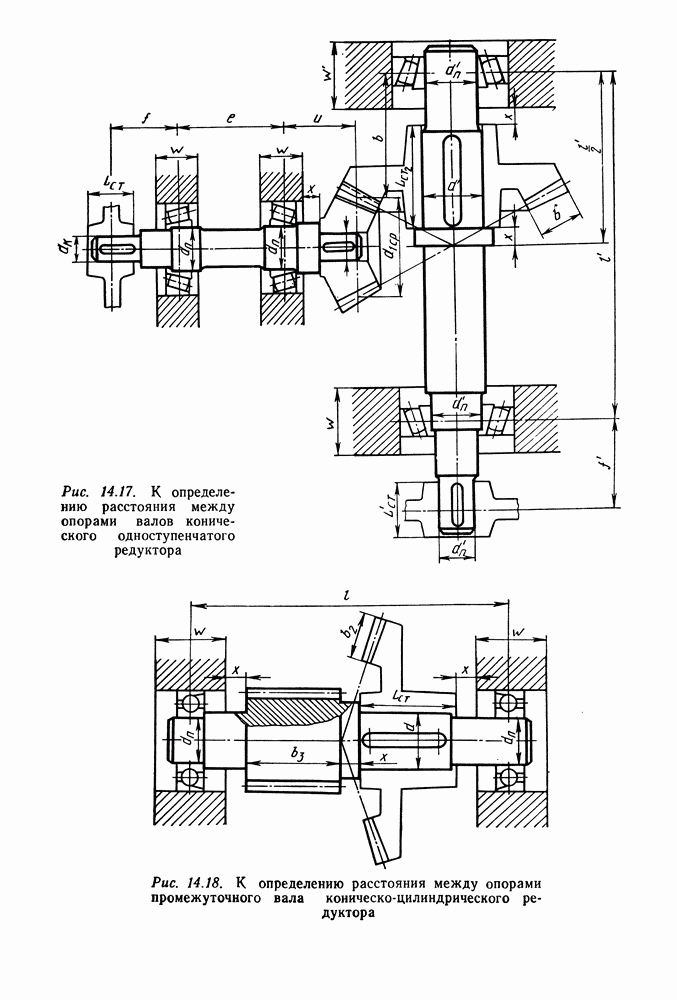
- 14.2. Некоторые сведения по конструированию валов и выбору материалов
- 14.3. Расчет валов
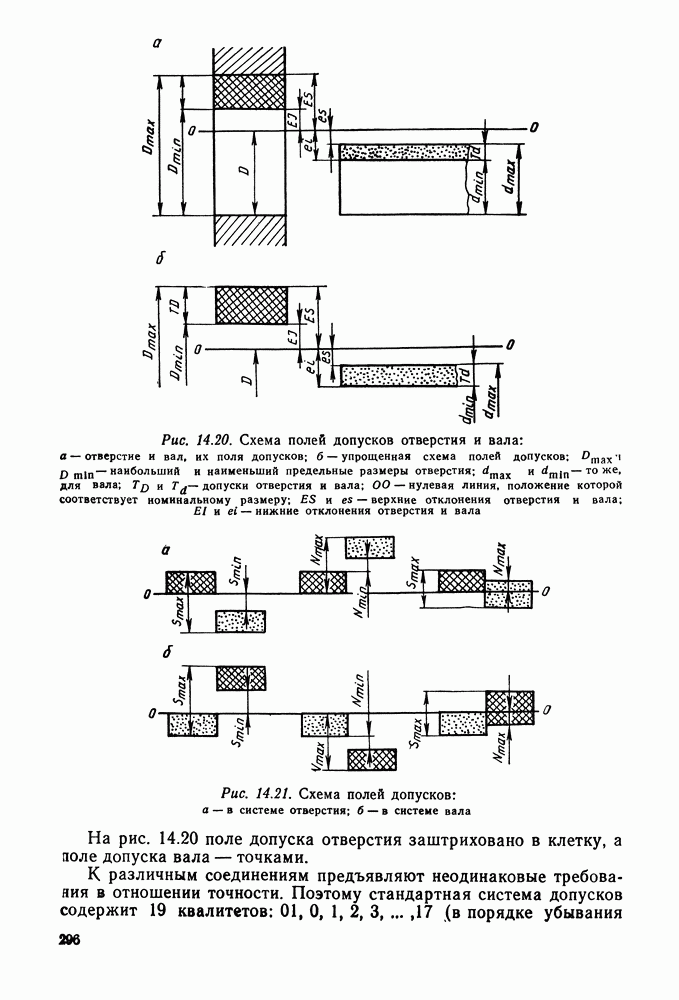
- 14.4. Посадки основных деталей передач на валы по стандартам СЭВ
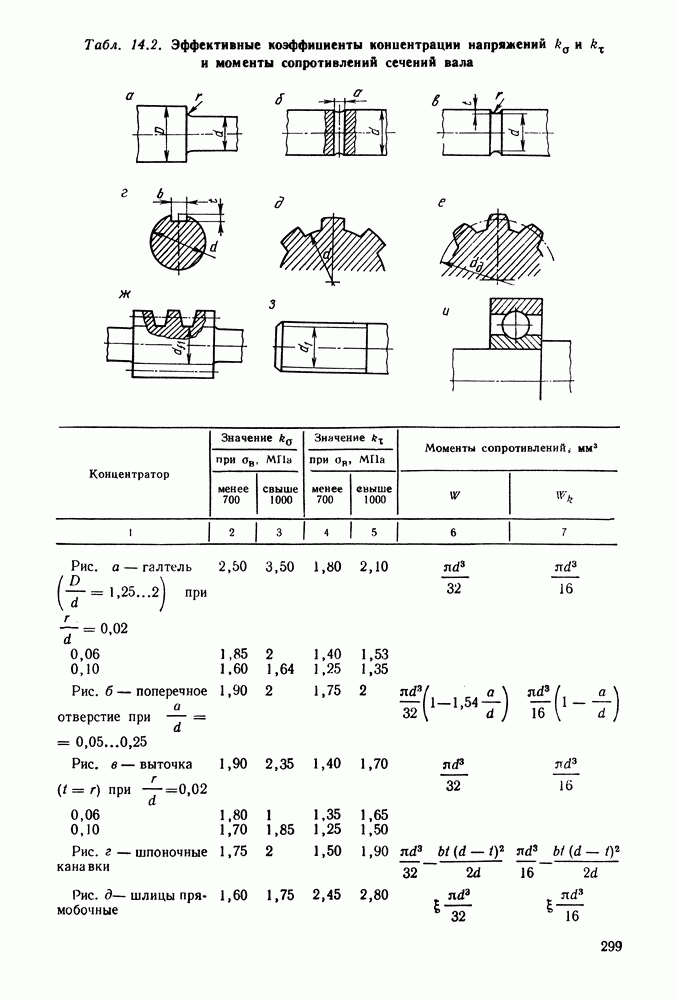
- 14.5. Справочный материал
- 14.6. Примеры расчета
- Глава 15. РАДИАЛЬНЫЕ ПОДШИПНИКИ СКОЛЬЖЕНИЯ
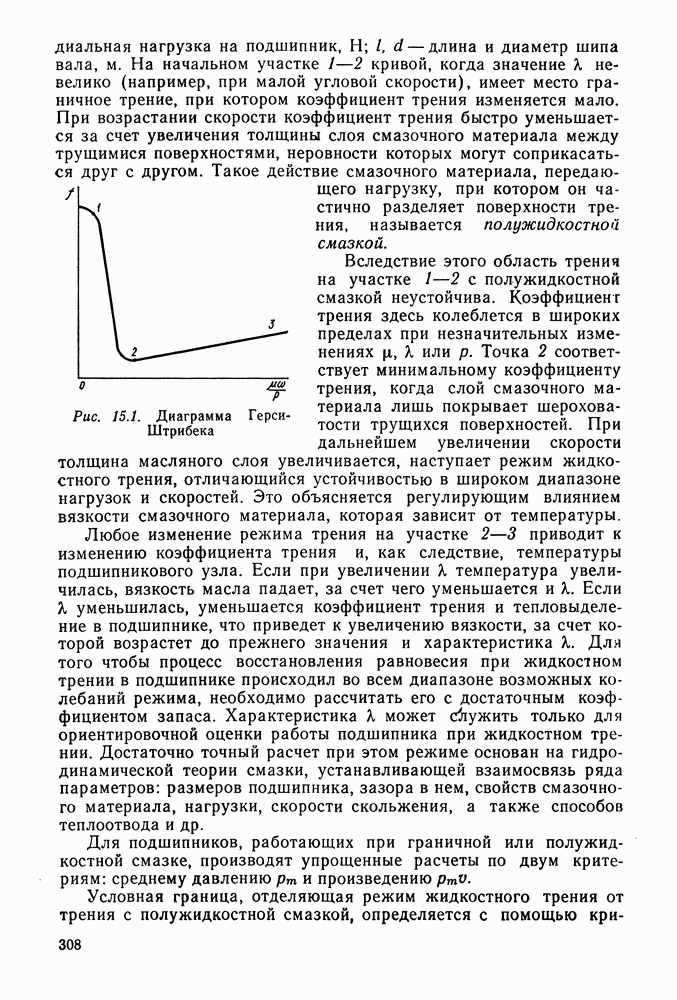
- 15.2. Упрощенный расчет подшипников скольжения
- 15.3. Расчет подшипников жидкостного трения
- 15.4. Сопротивление слоя масла вращению шипа
- 15.5. Тепловой расчет подшипника
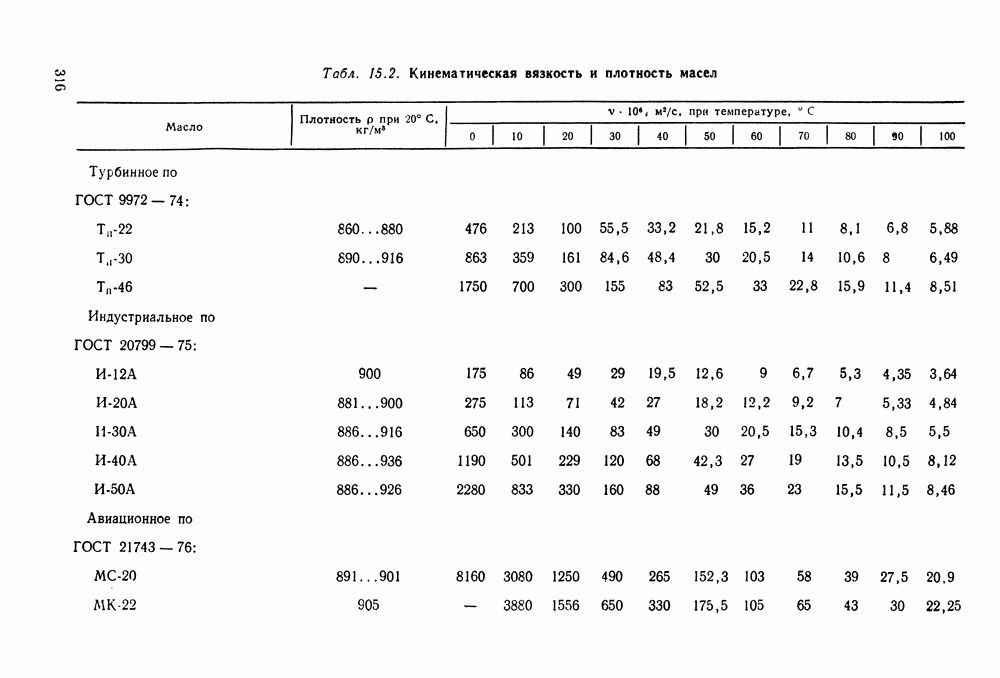
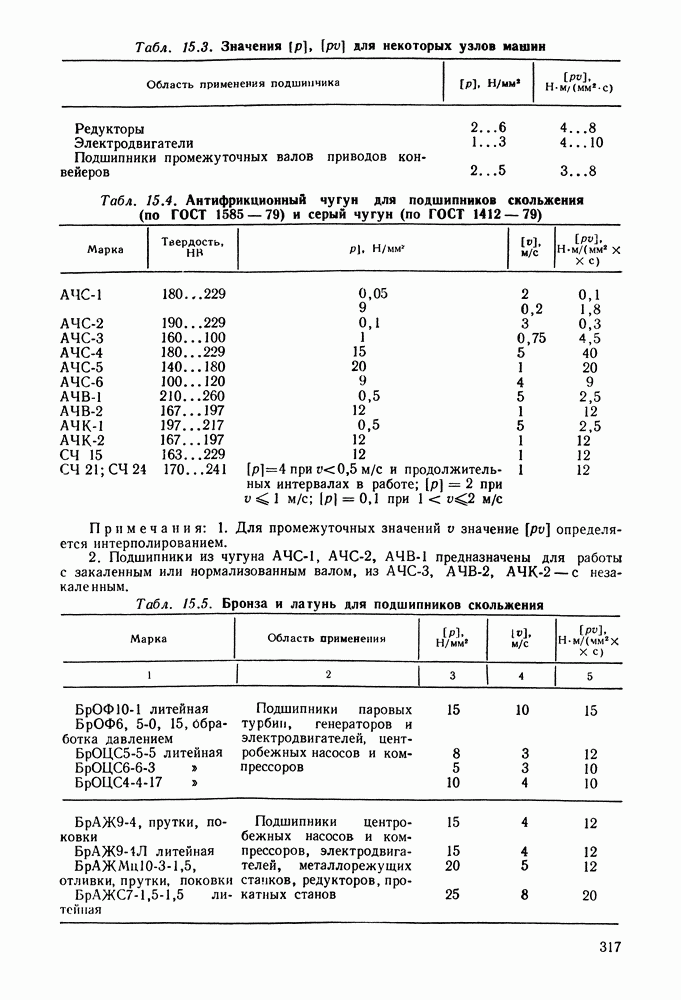
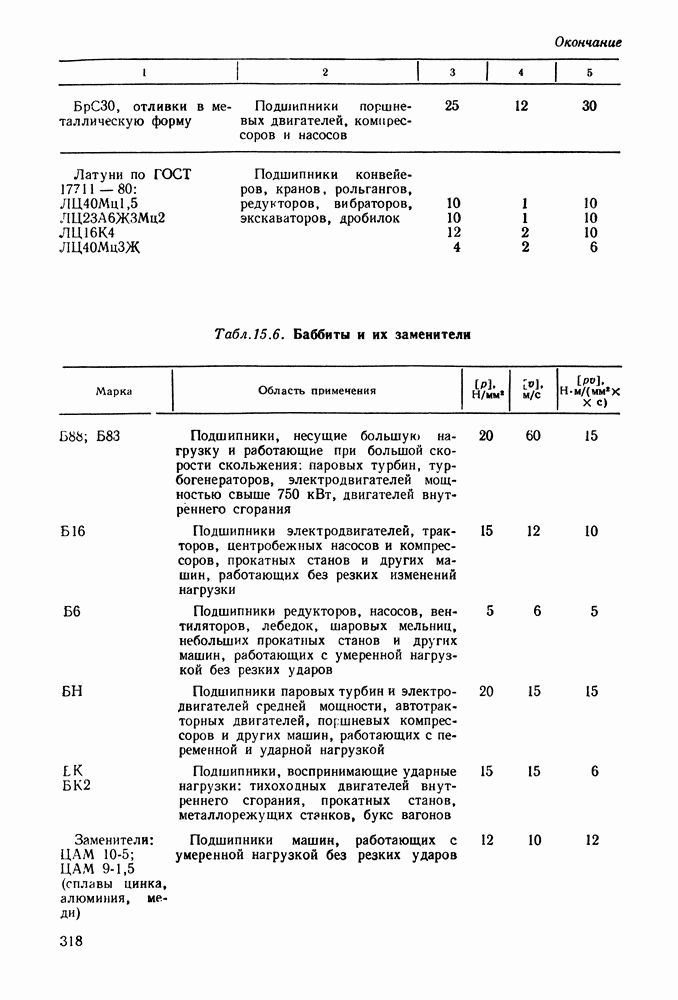
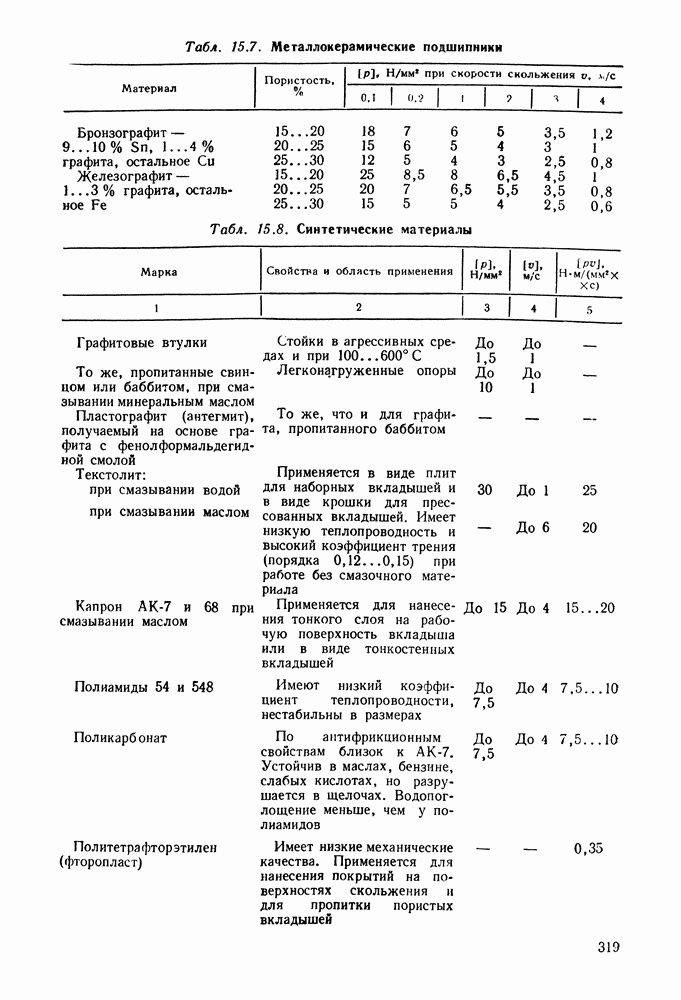
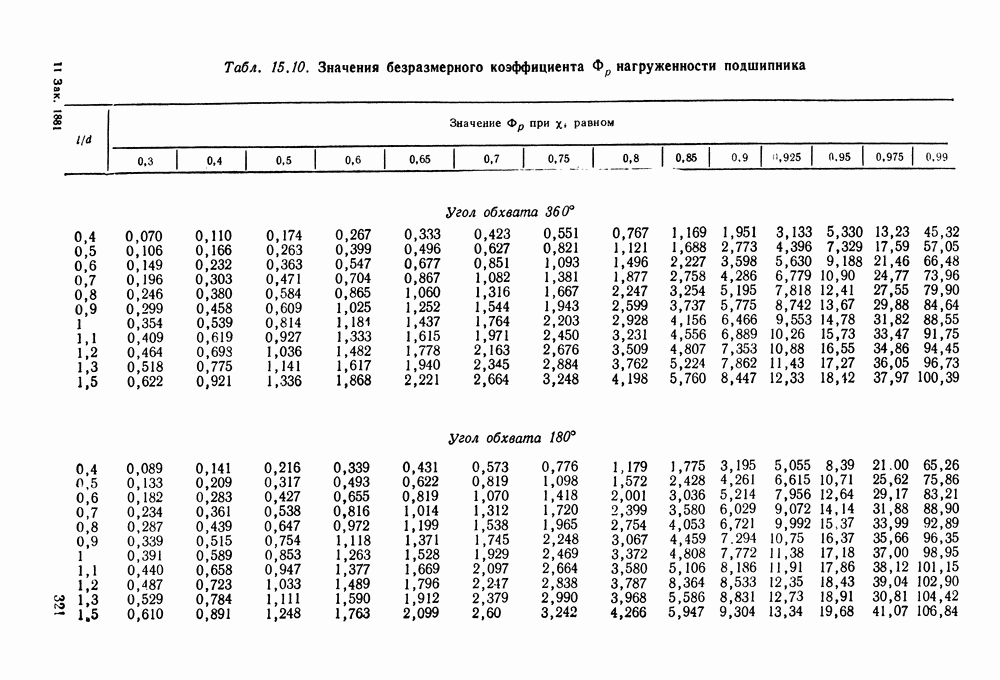
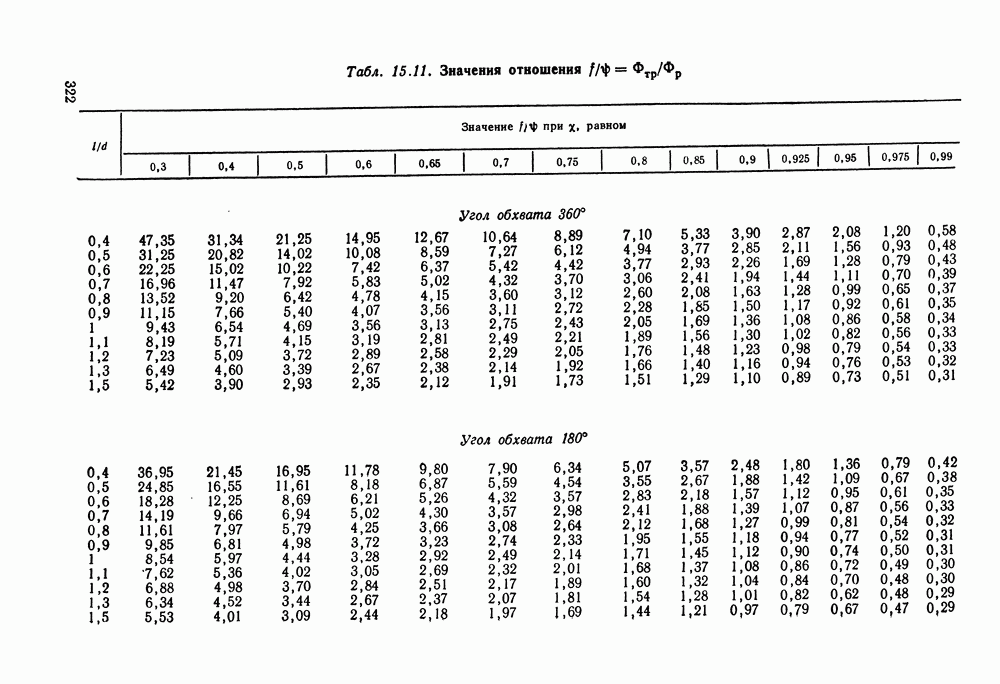
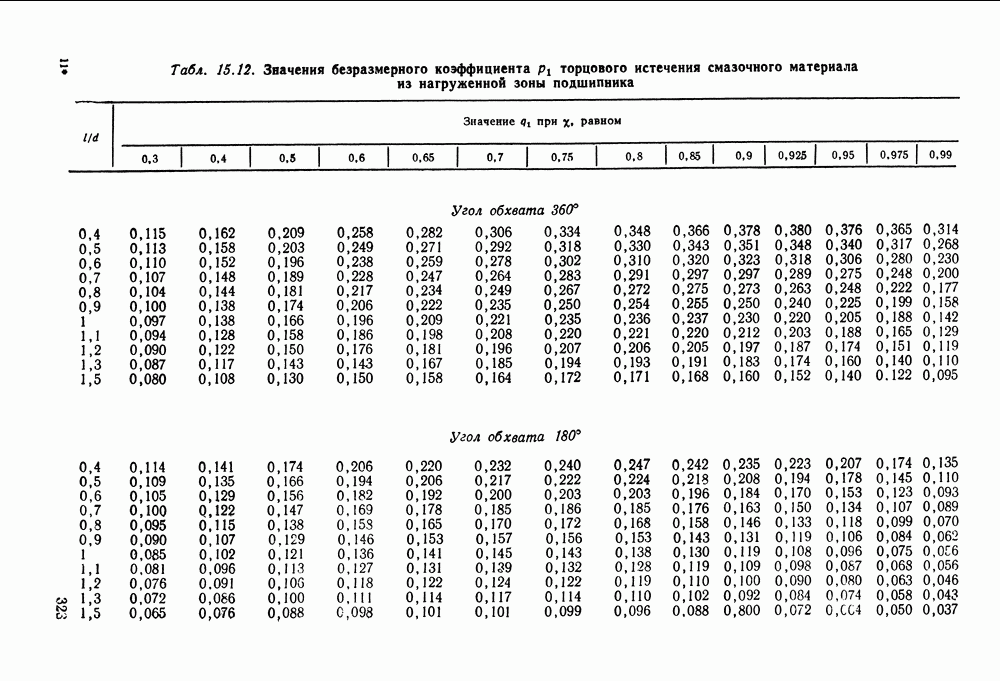
- 15.6. Справочный материал
- 15.7. Примеры расчета
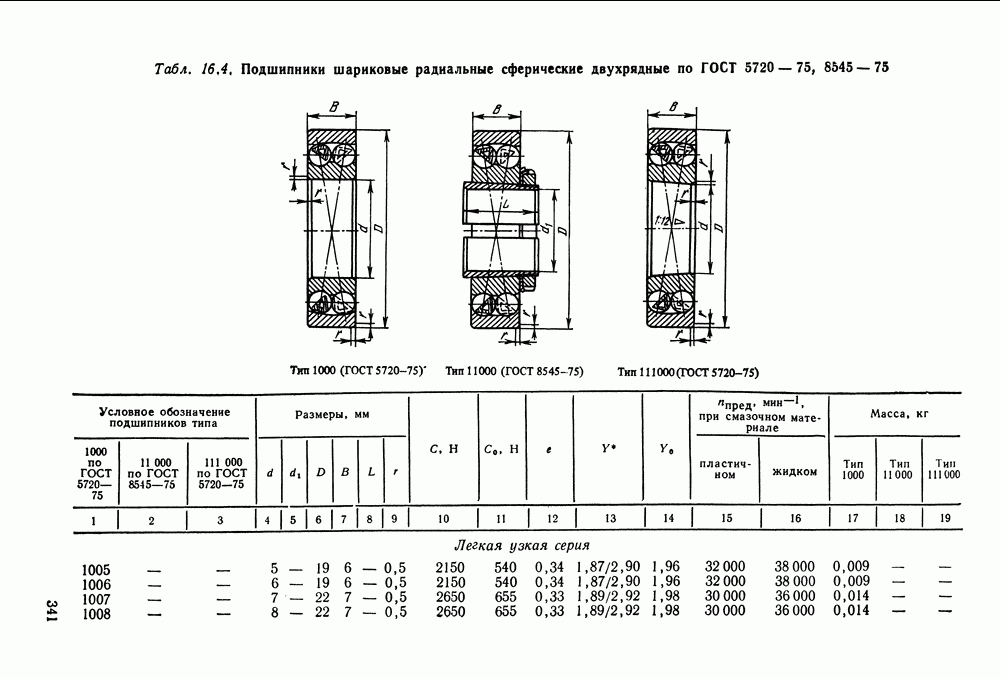
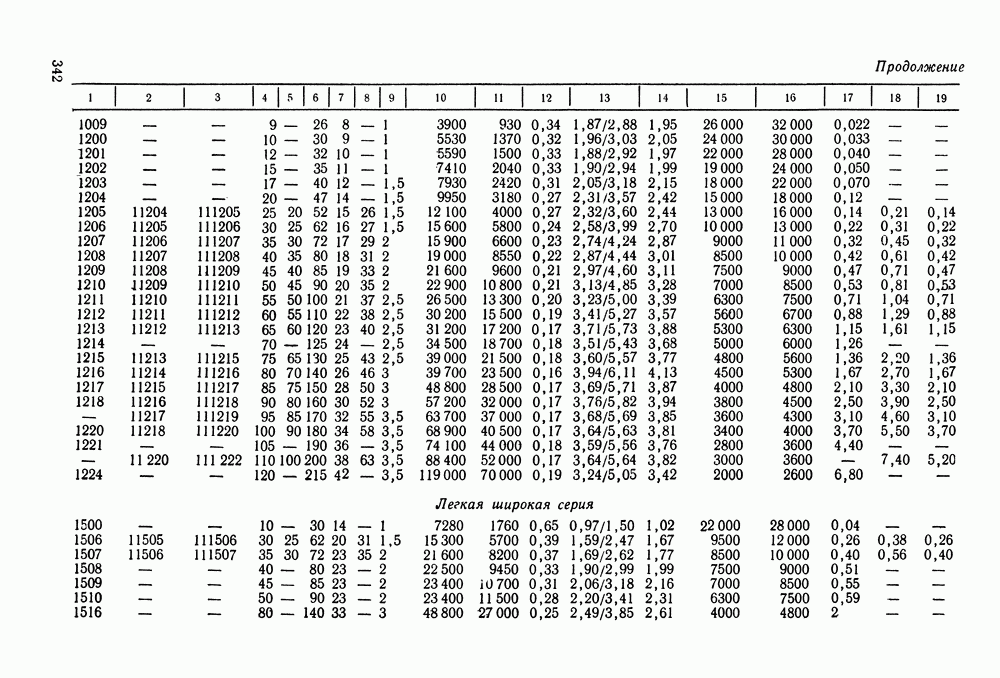
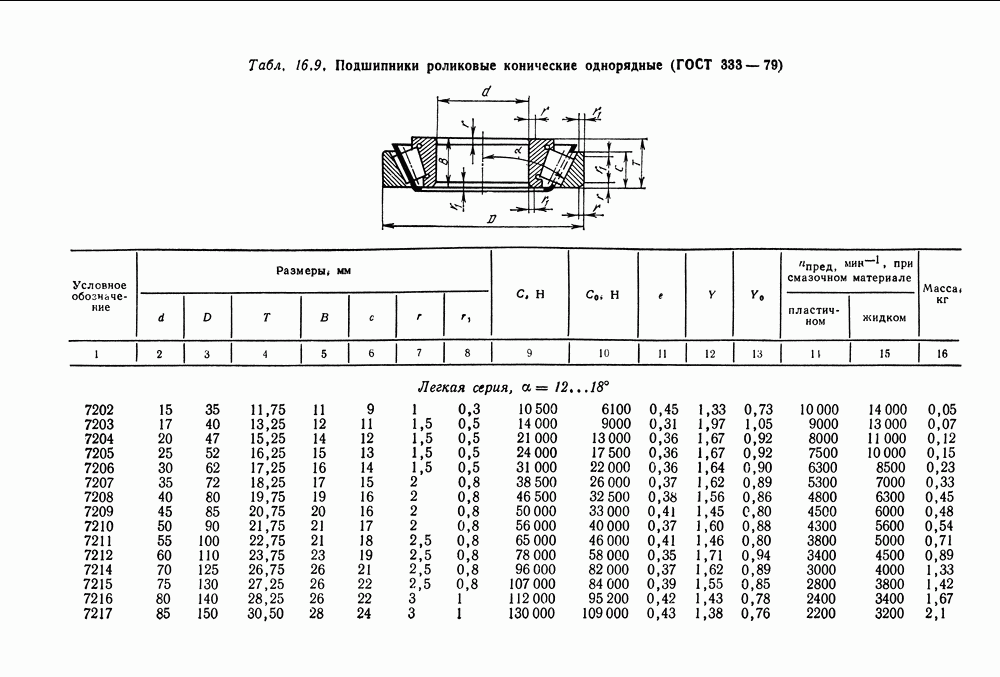
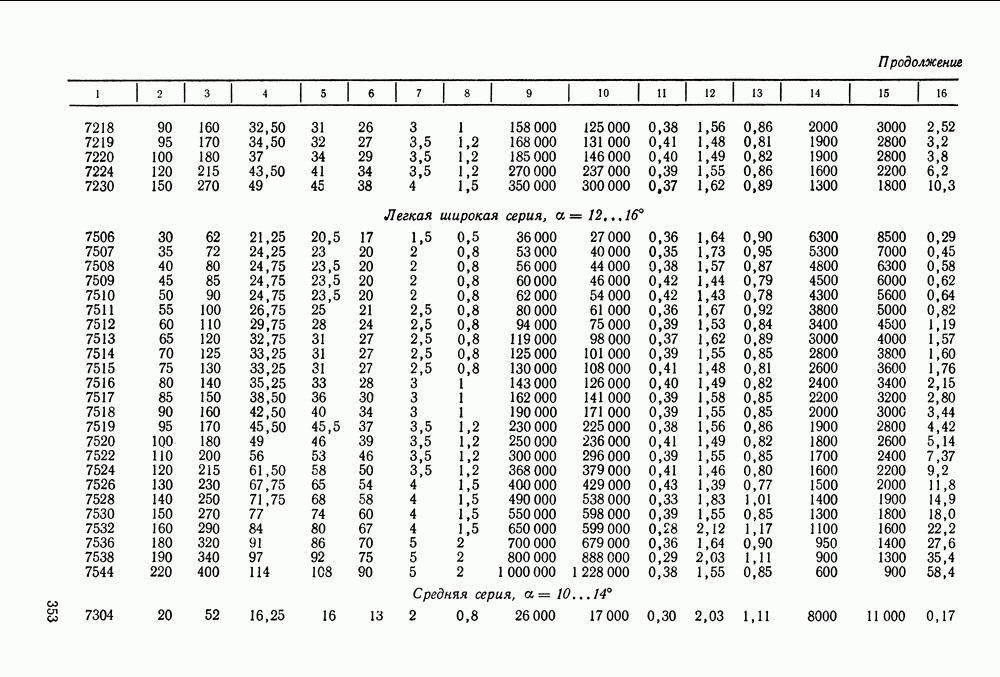
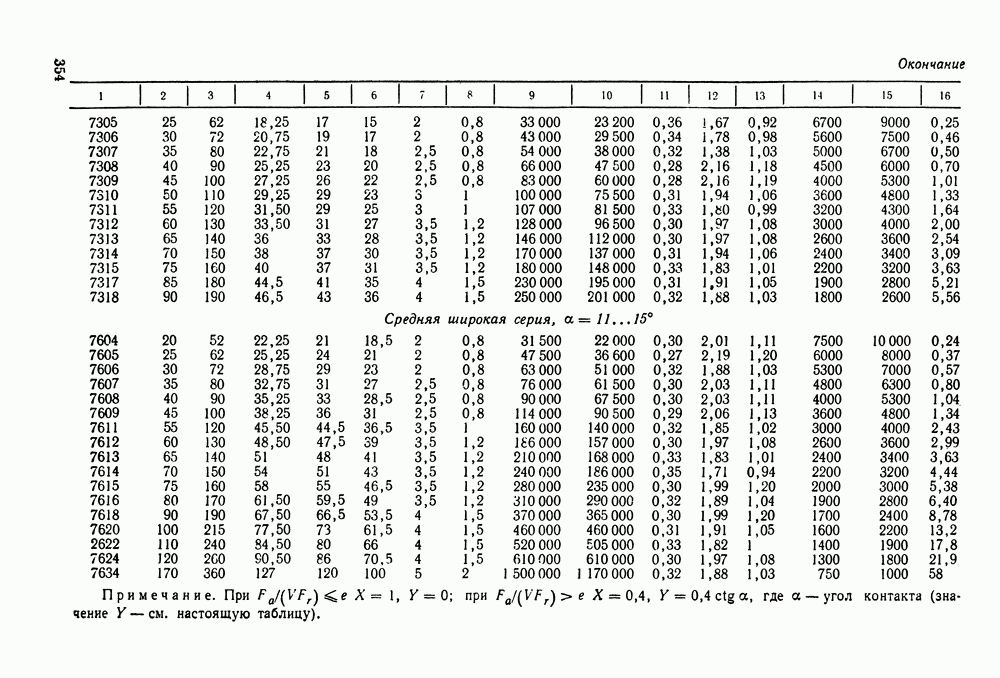
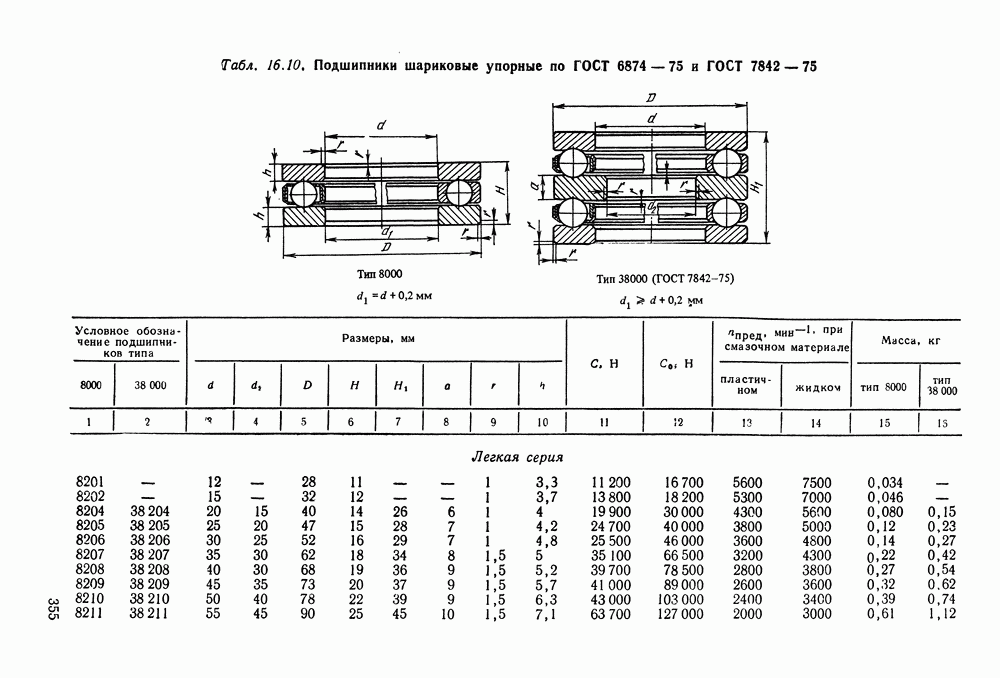
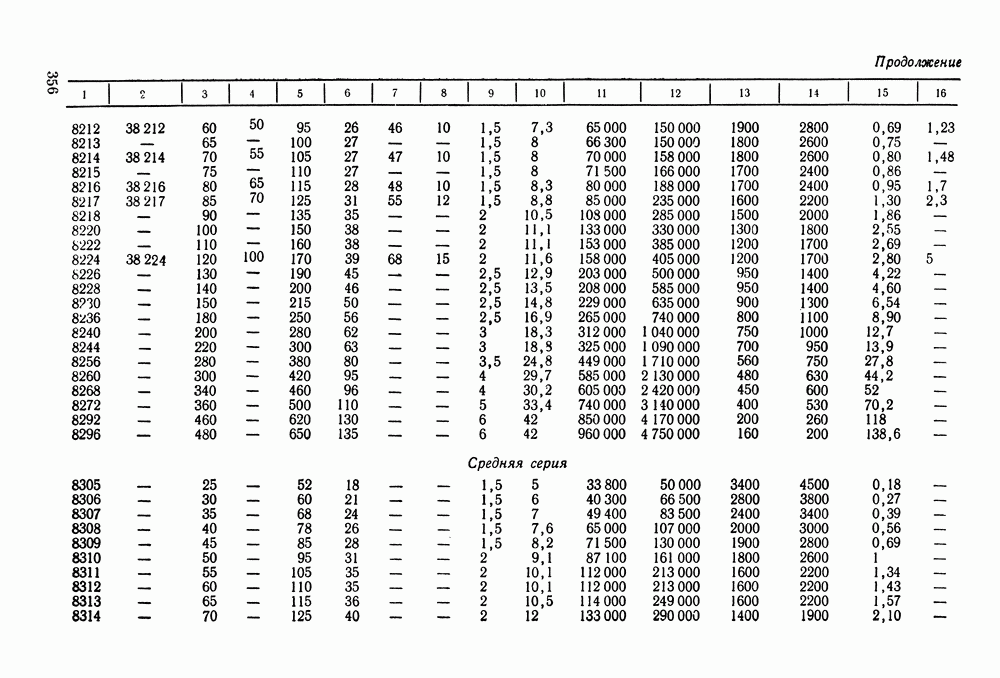
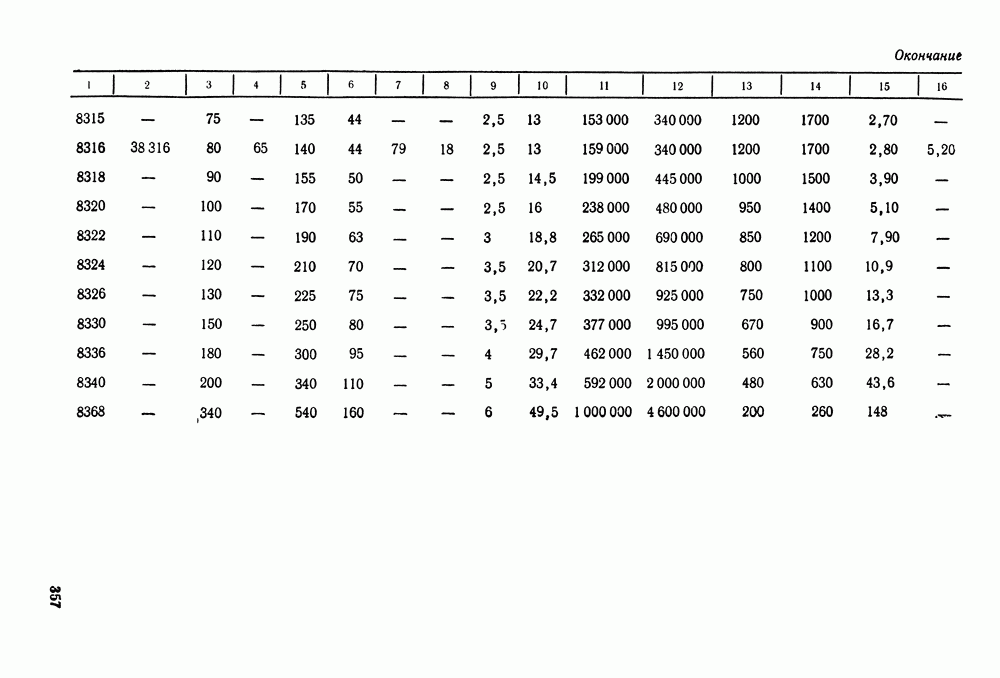
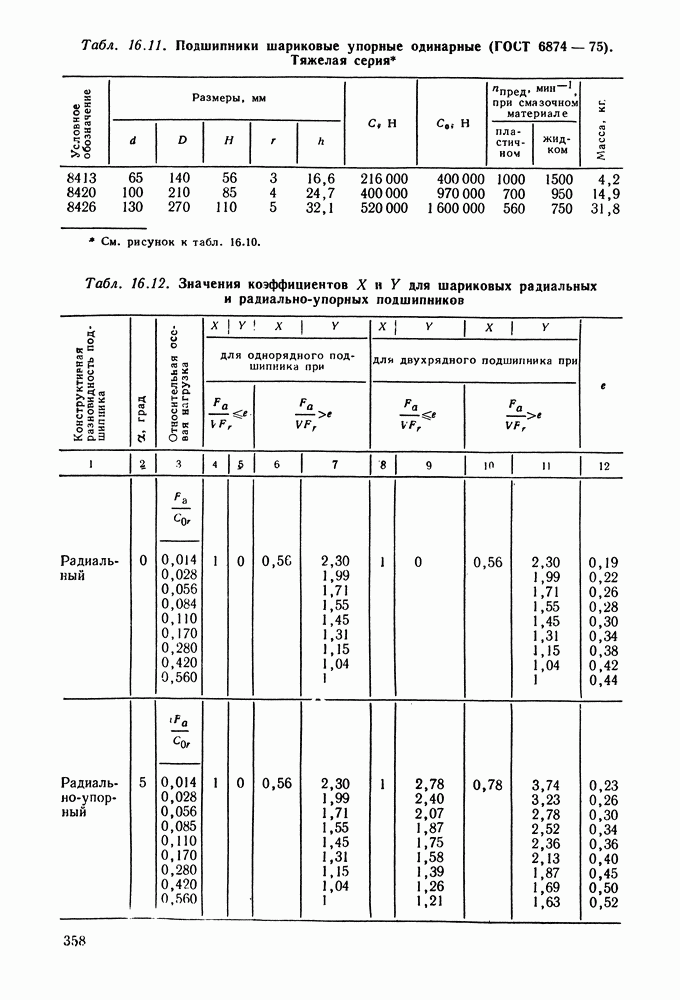
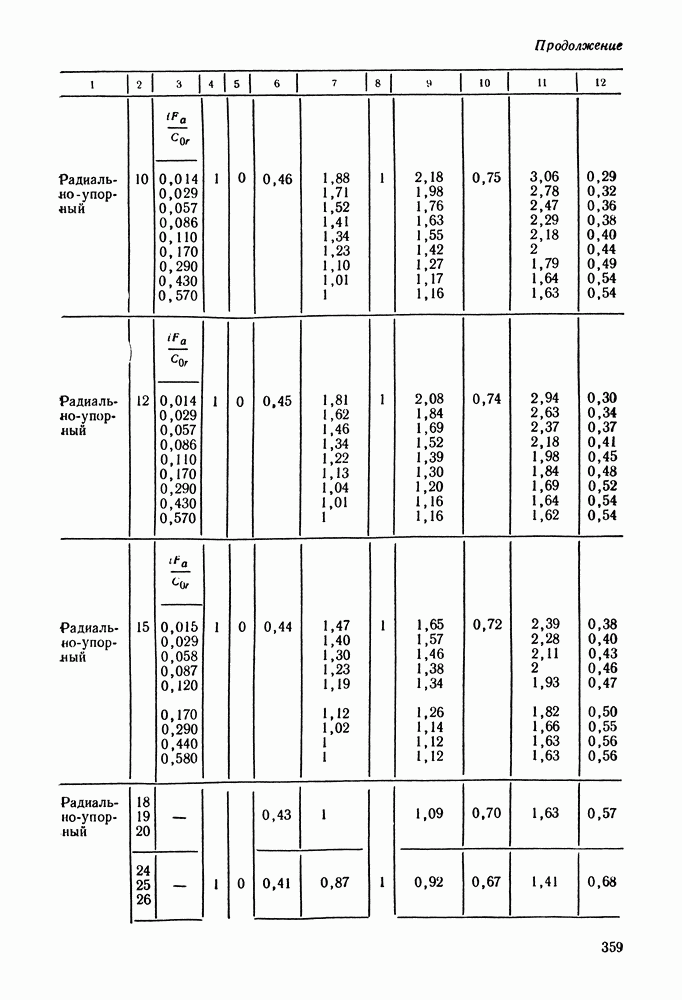
- Глава 16. ПОДШИПНИКИ КАЧЕНИЯ
- 16.2. Условные обозначения и точность подшипников качения
- 16.3. Выбор и проверка подшипников качения по динамической грузоподъемности
- 16.4. Выбор подшипников качения по статической грузоподъемности
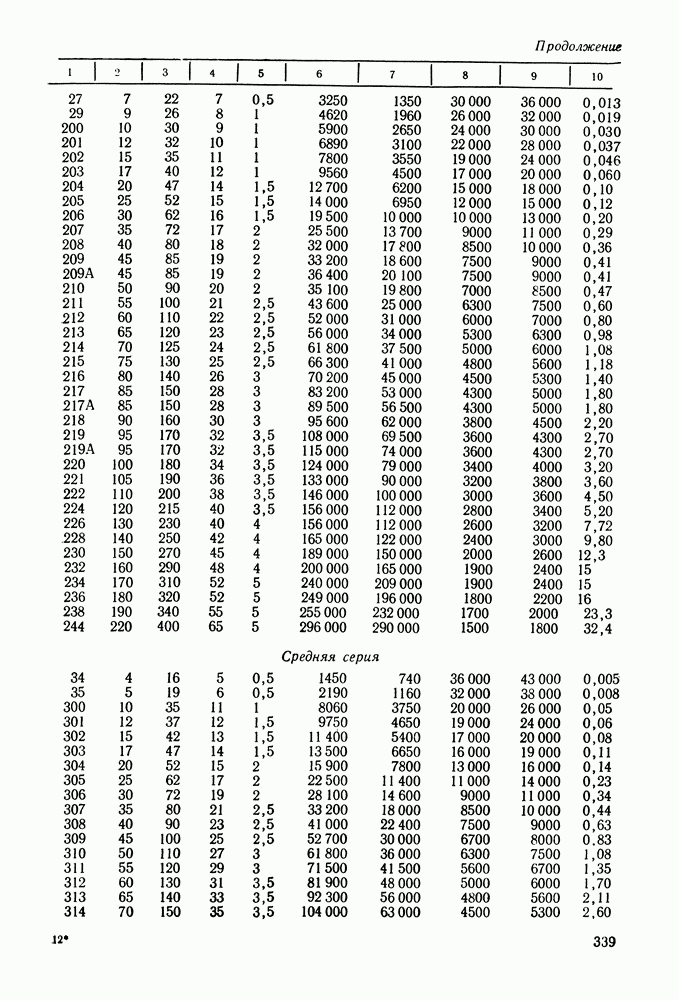
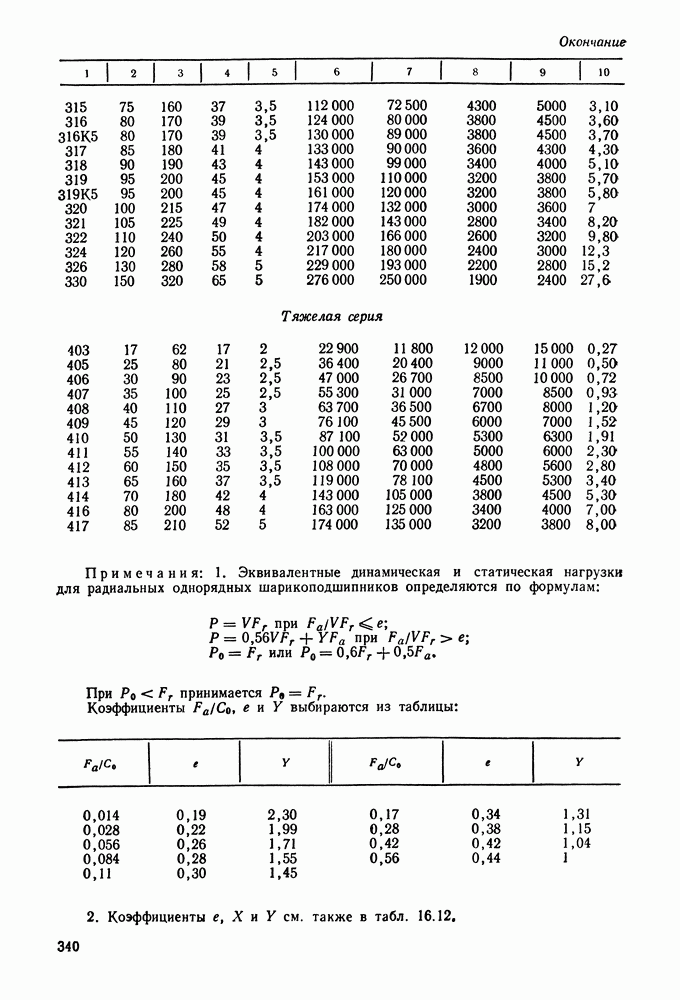
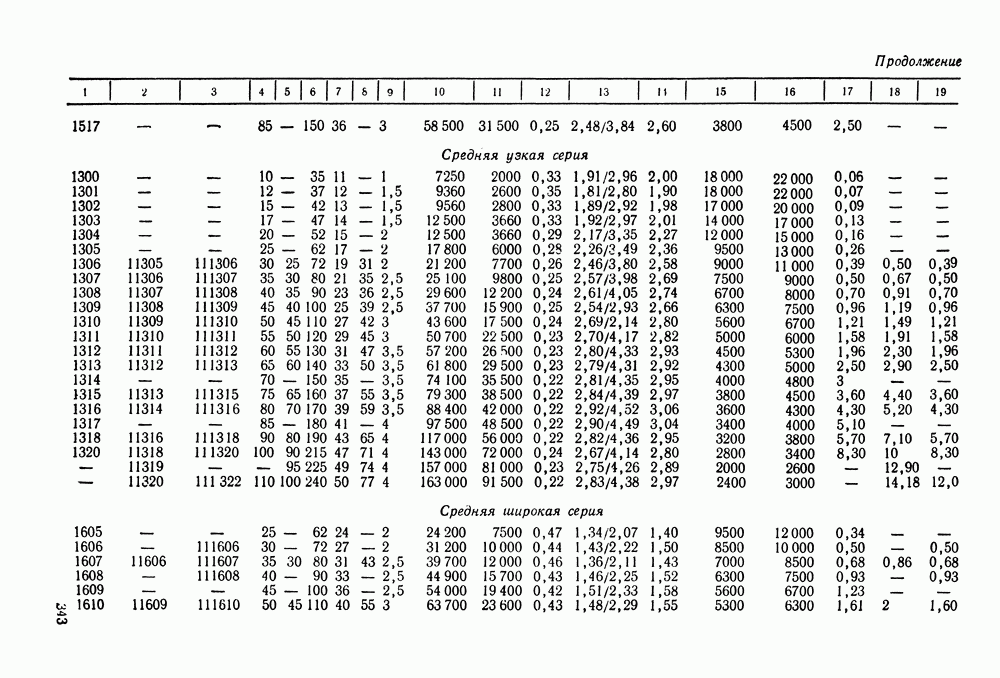
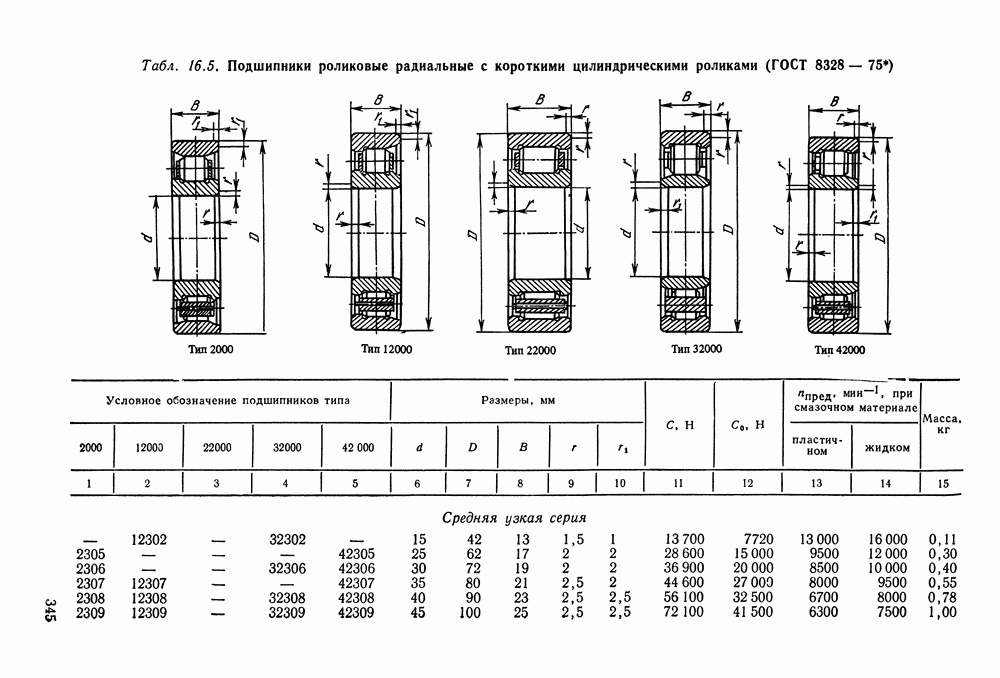
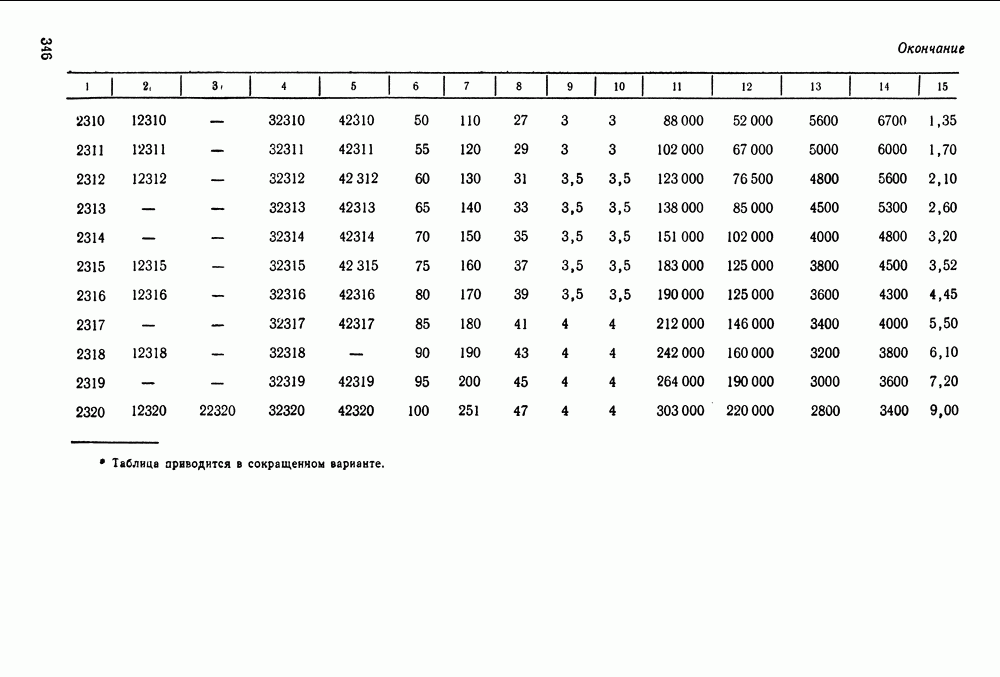
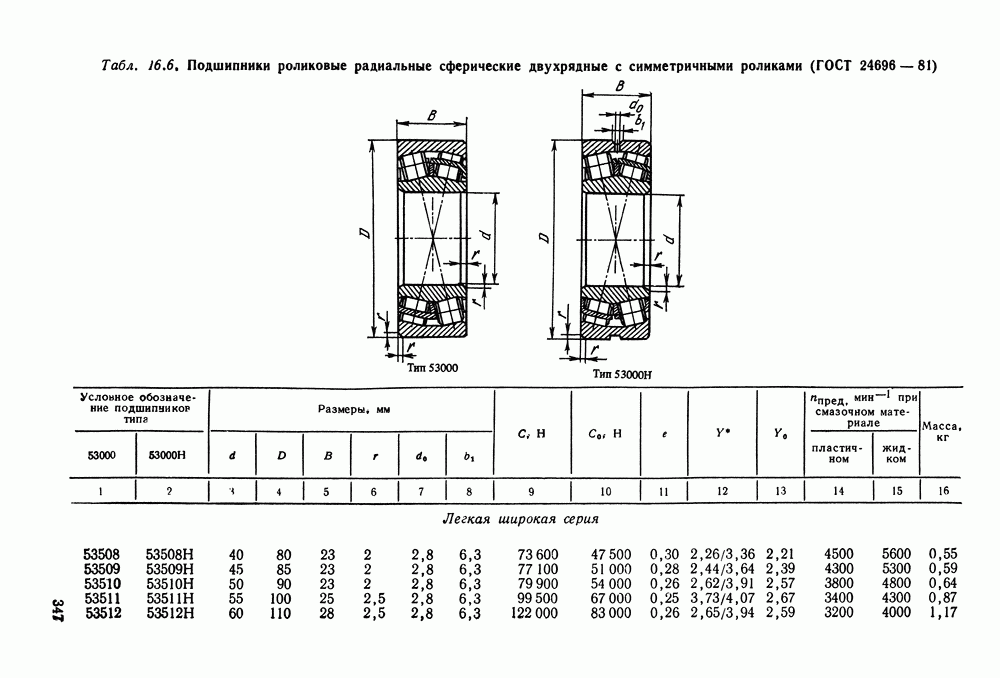
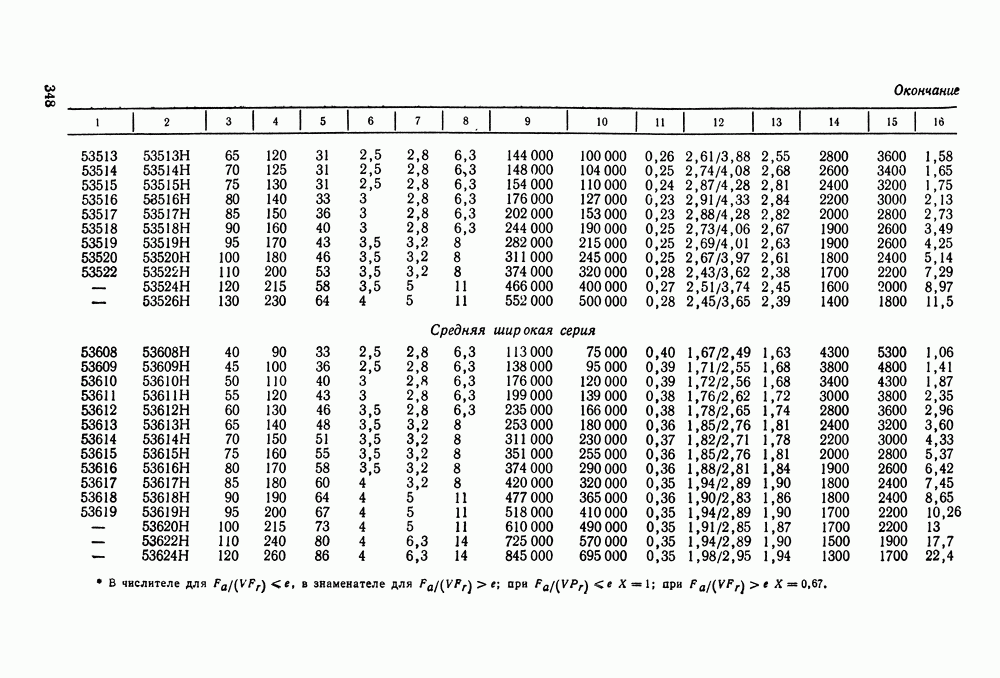
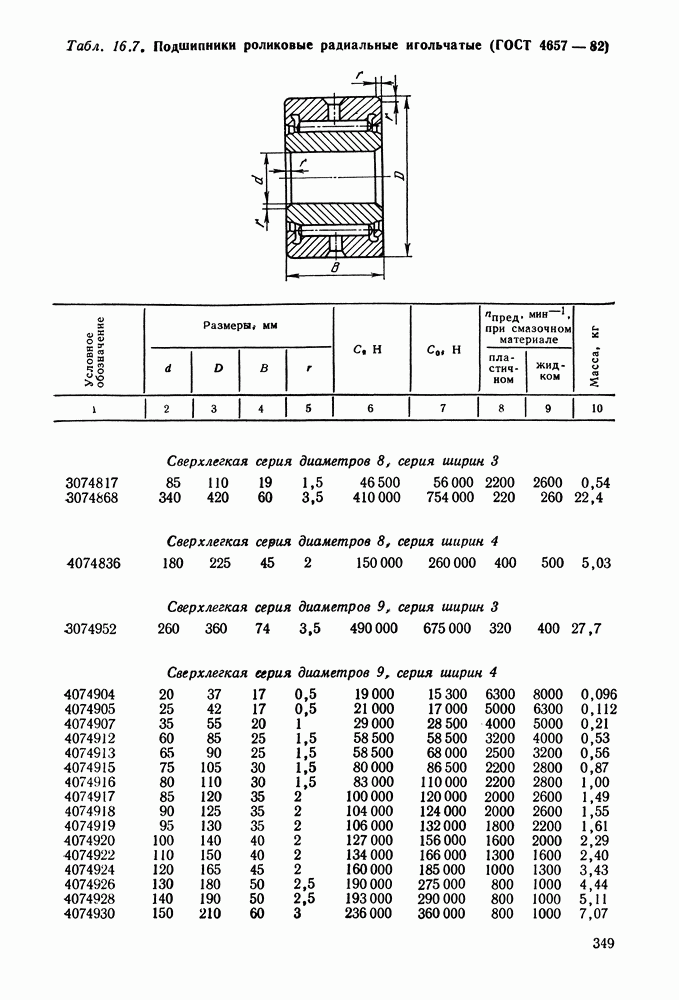
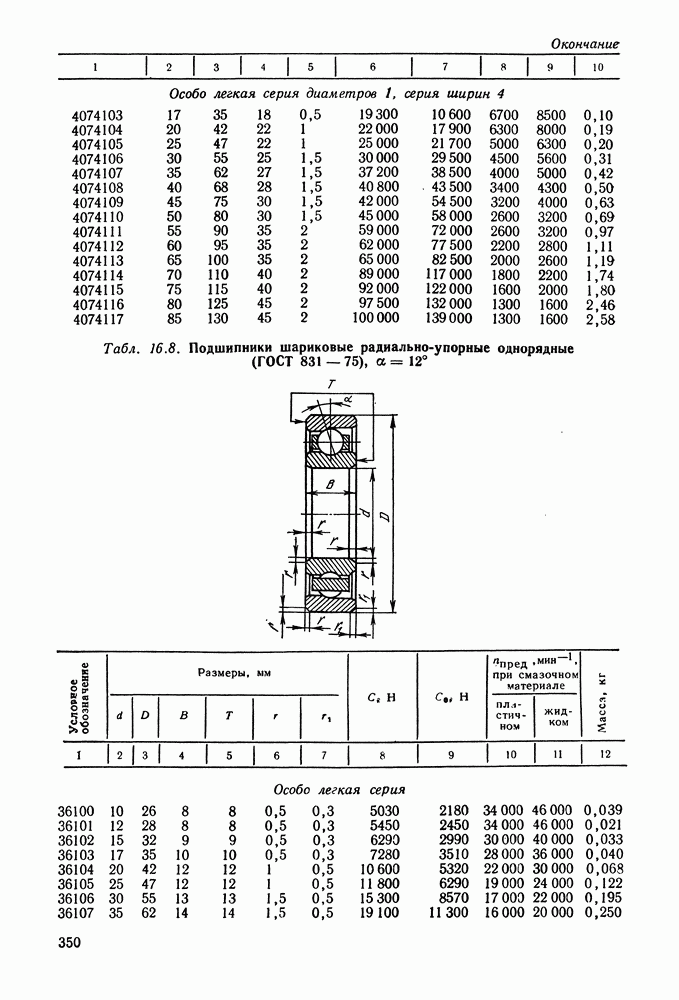
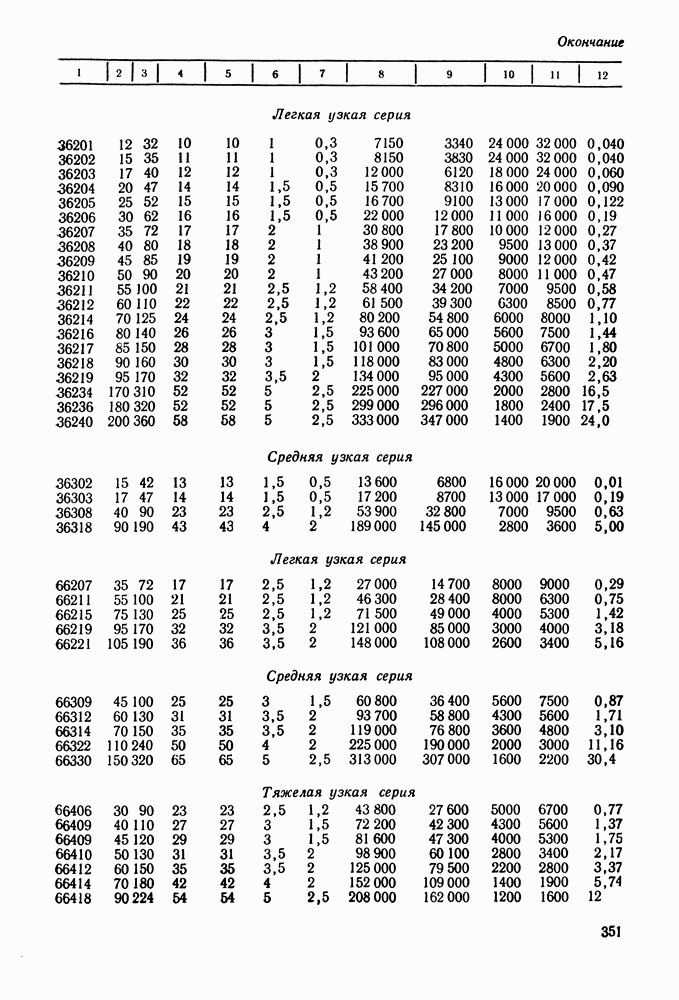
- 16.5. Справочный материал
- 16.6. Пример расчета
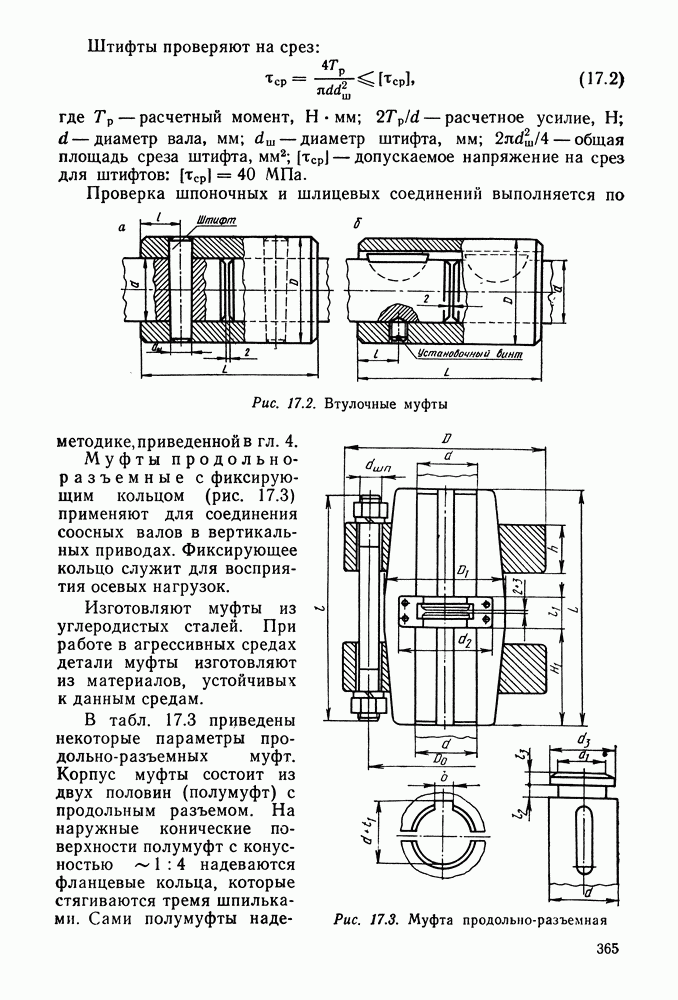
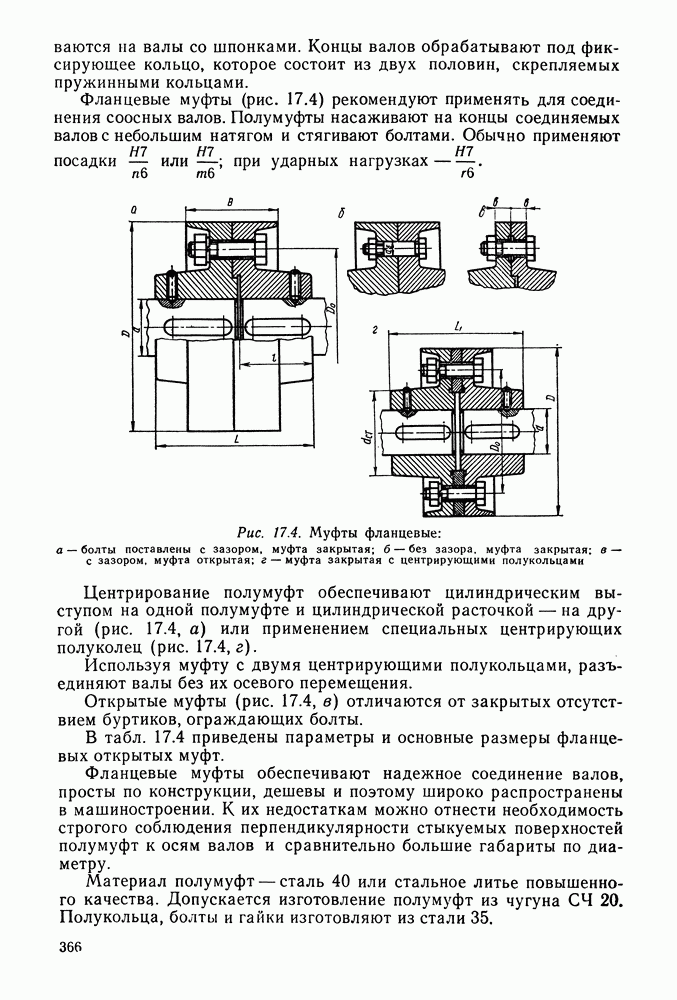
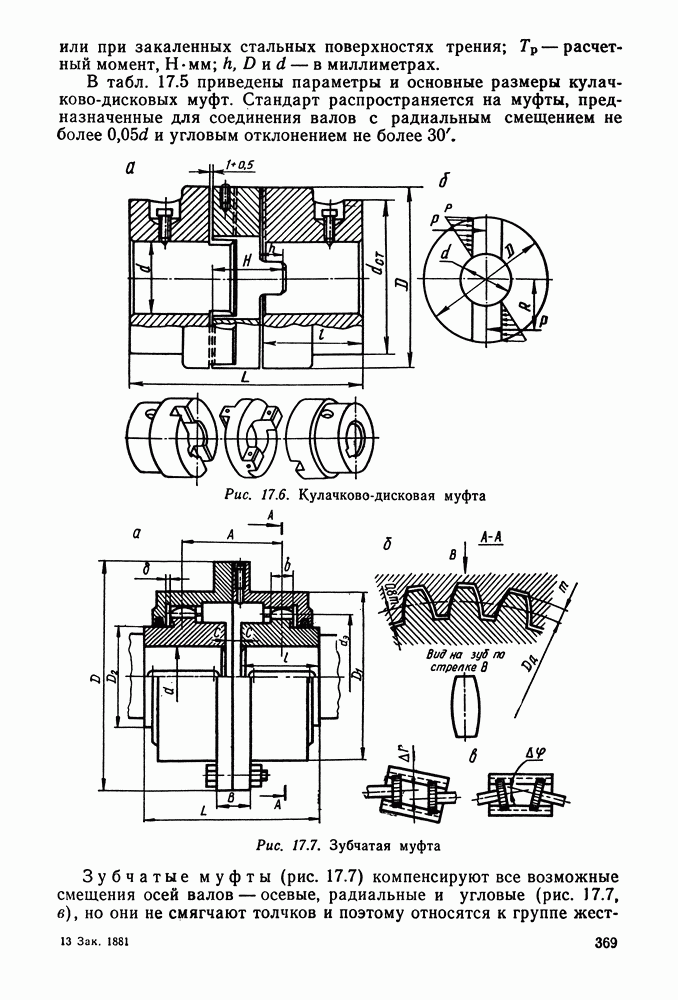
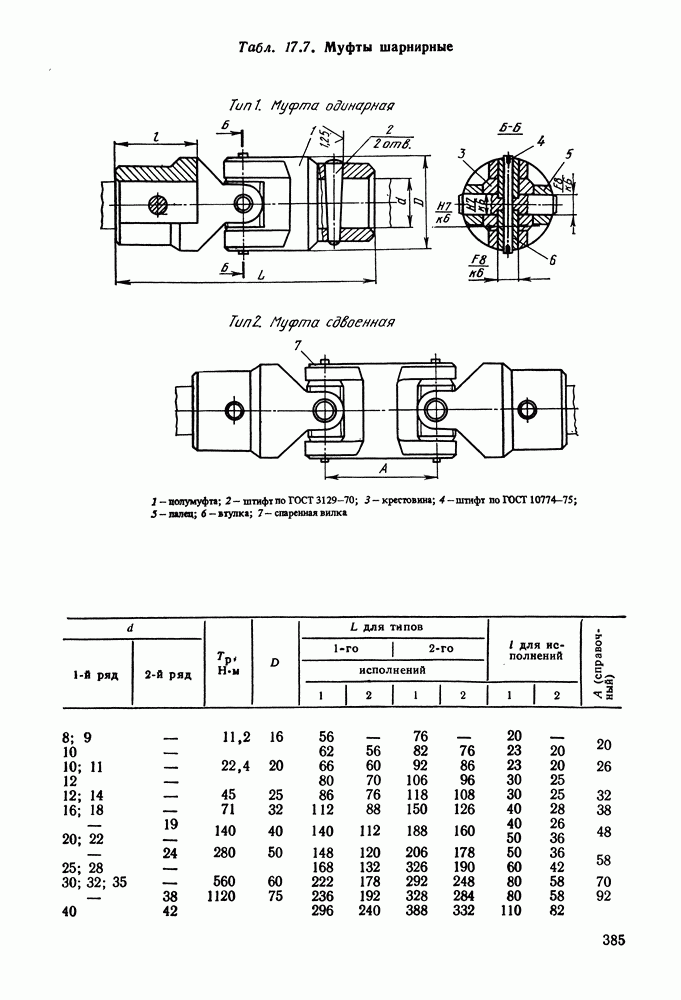
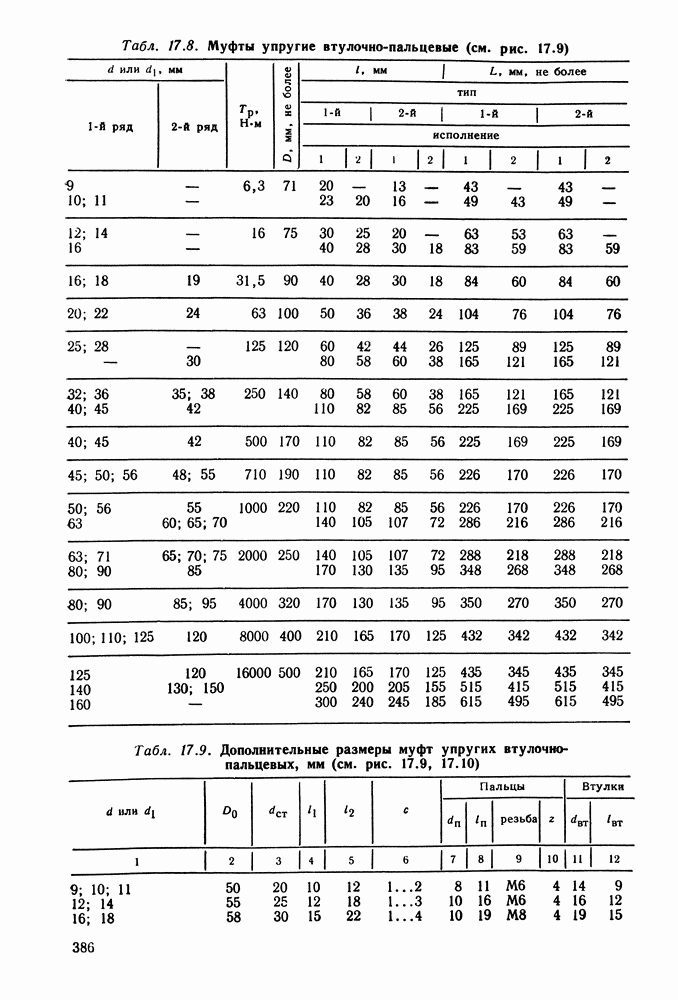
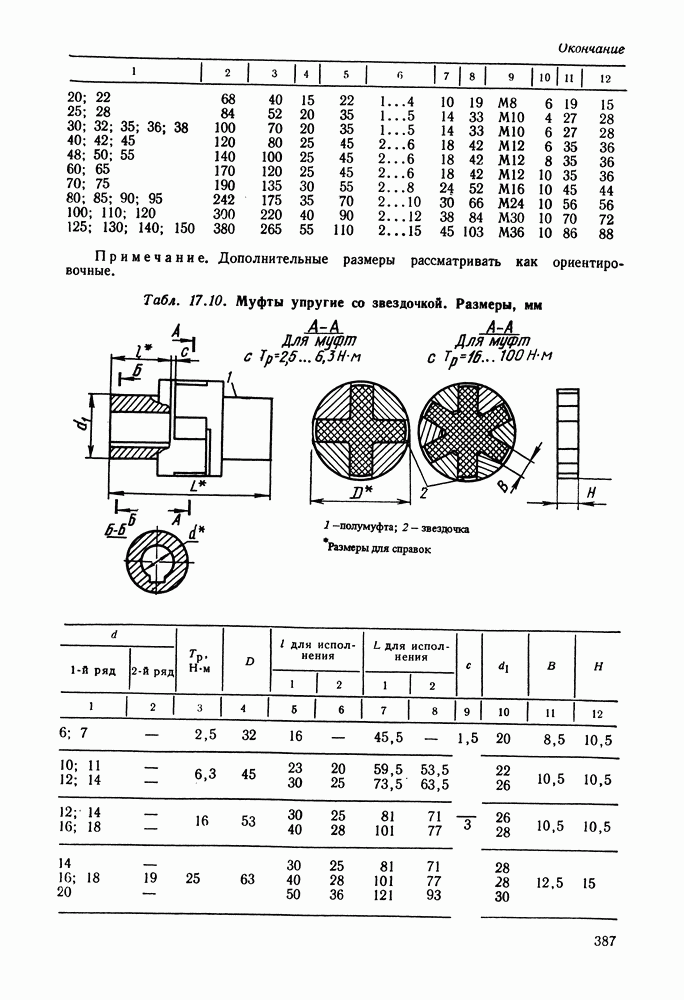
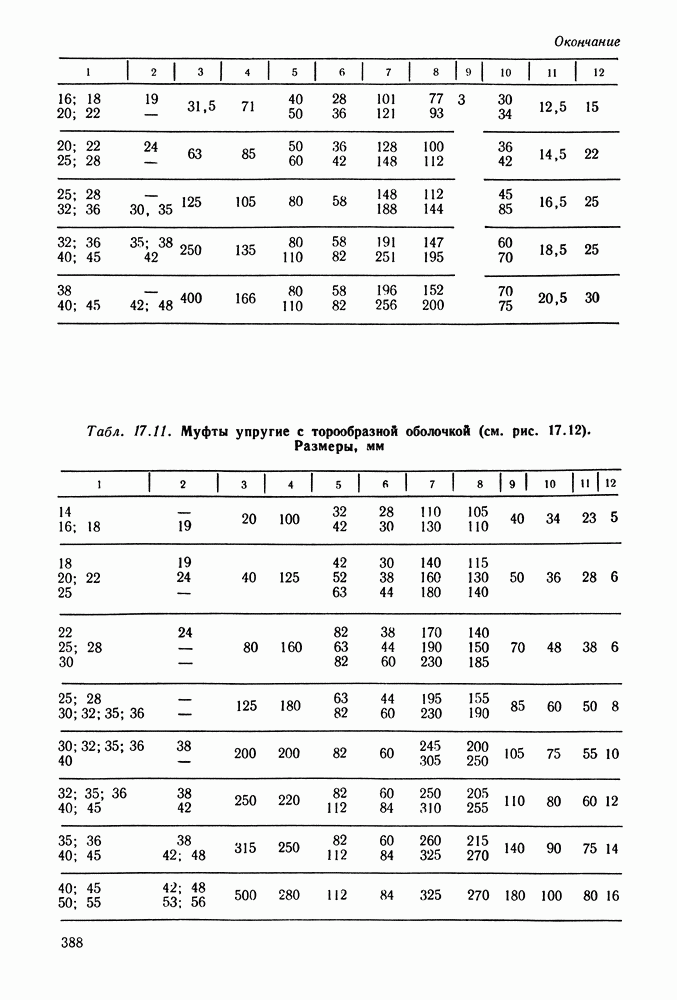
- Глава 17. МУФТЫ
- 17.2. Расчет муфт
- 17.3. Глухие муфты
- 17.4. Компенсирующие муфты
- 17.5. Управляемые (сцепные) муфты
- 17.6. Самоуправляемые муфты
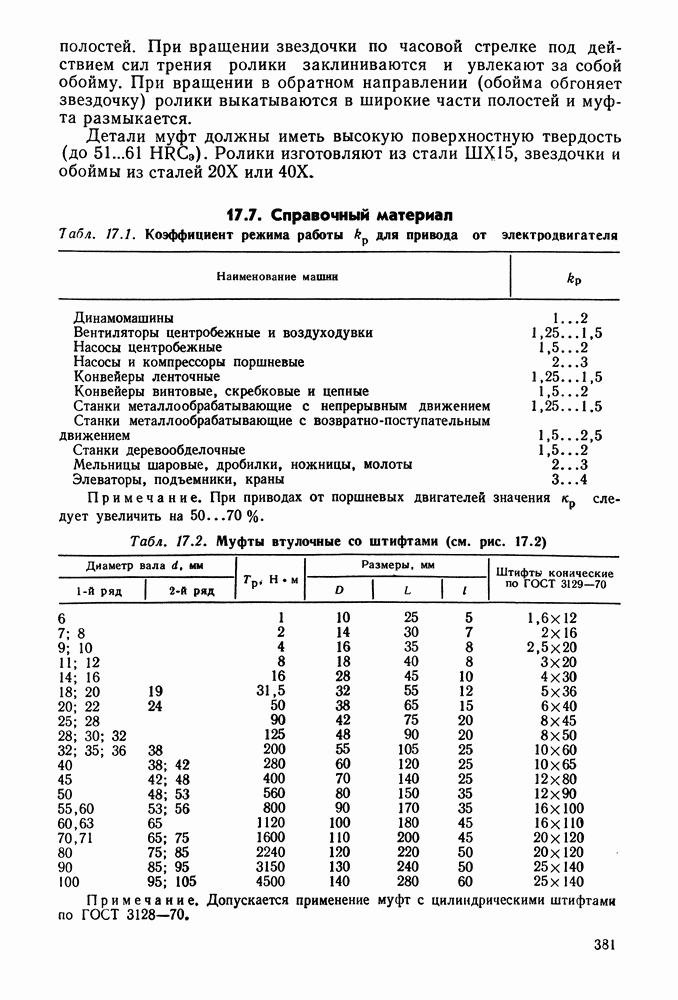
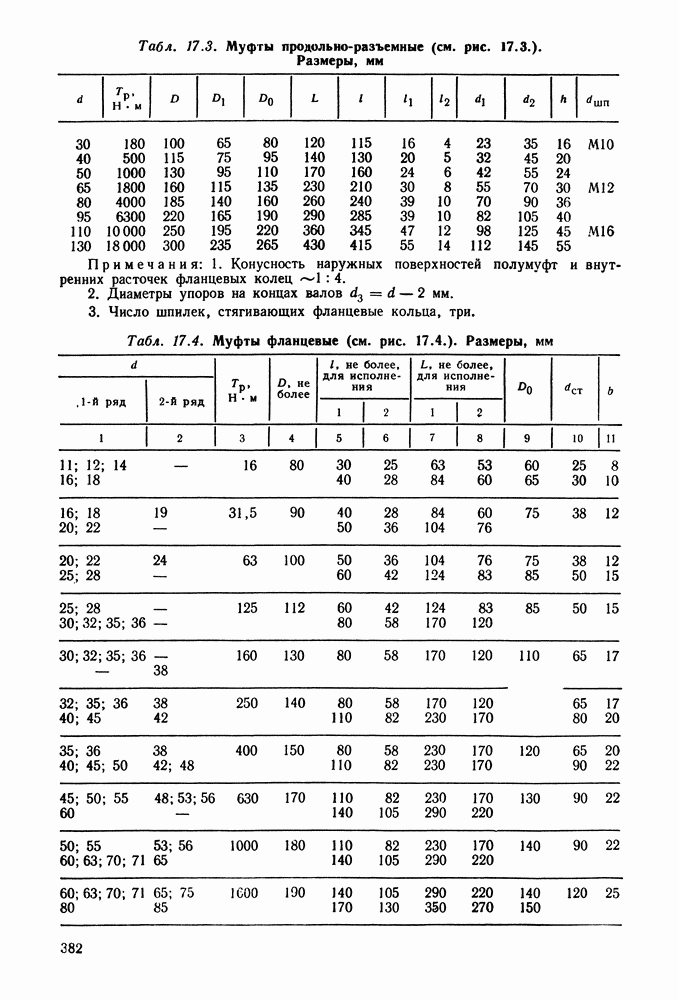
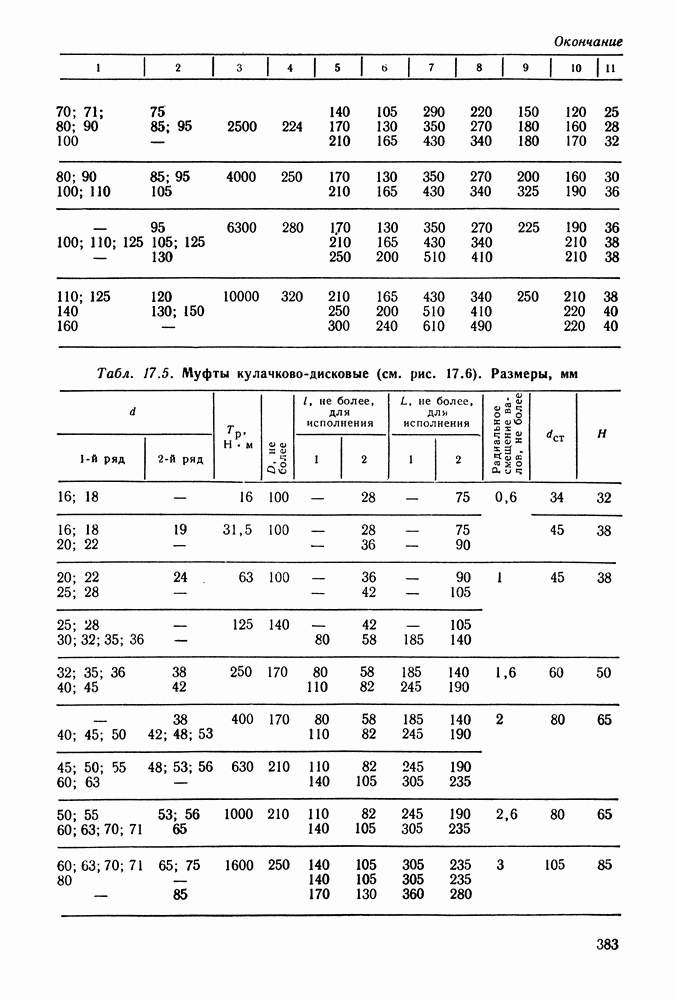
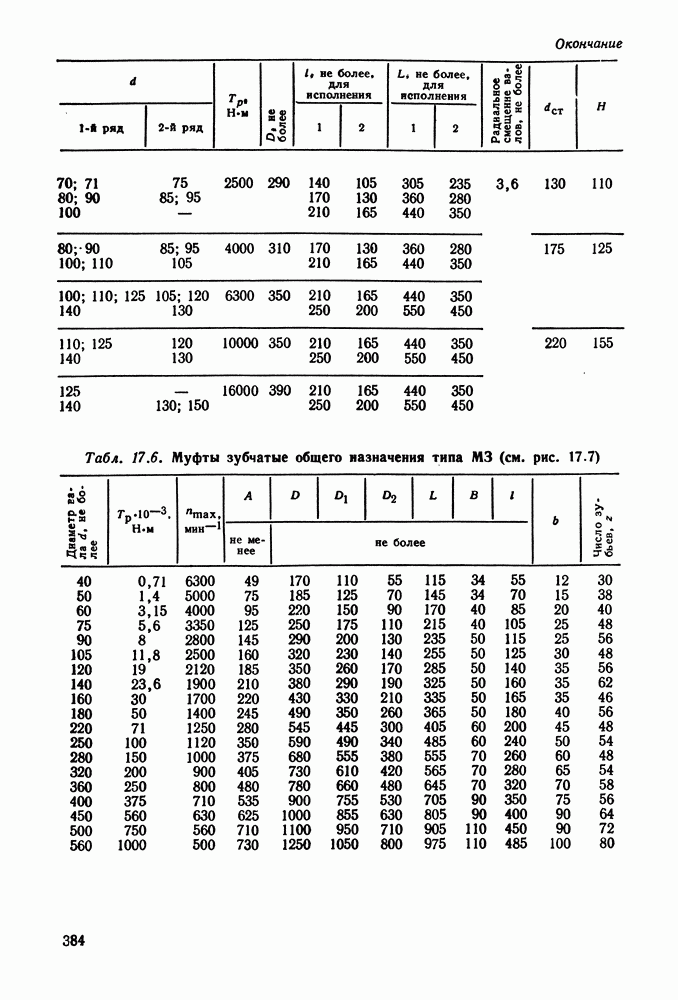
- 17.7. Справочный материал
- 17.8. Примеры расчета
- Глава 18. ПРУЖИНЫ
- 18.2. Расчет винтовых пружин на прочность
- 18.3. Расчет винтовых пружин на жесткость
- 18.4. Подбор тарельчатых пружин
- 18.5. Справочный материал
- ЛИТЕРАТУРА