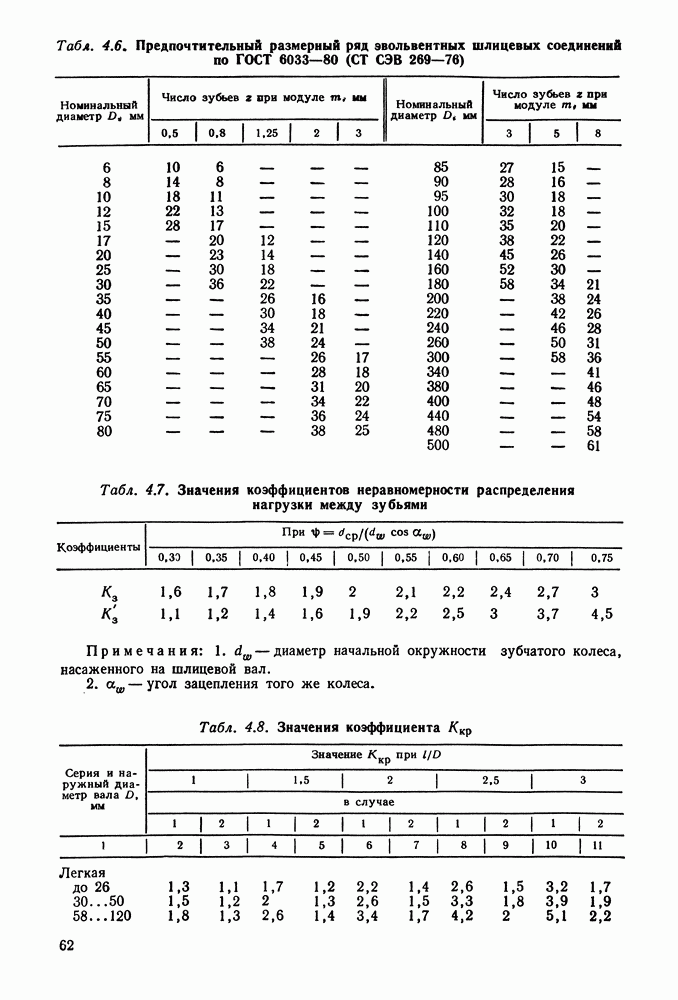
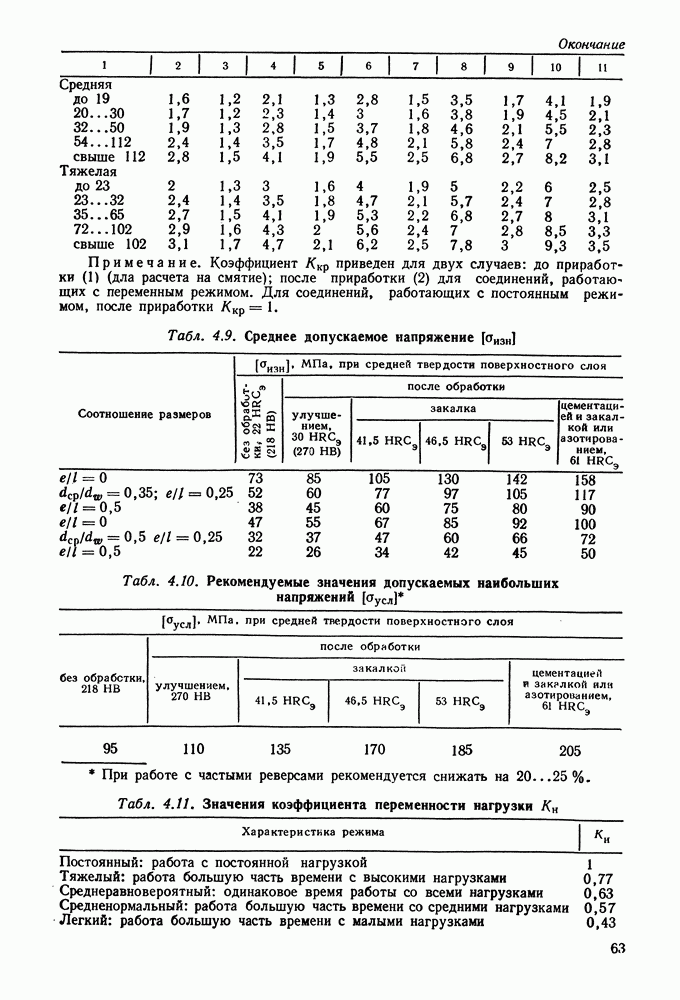
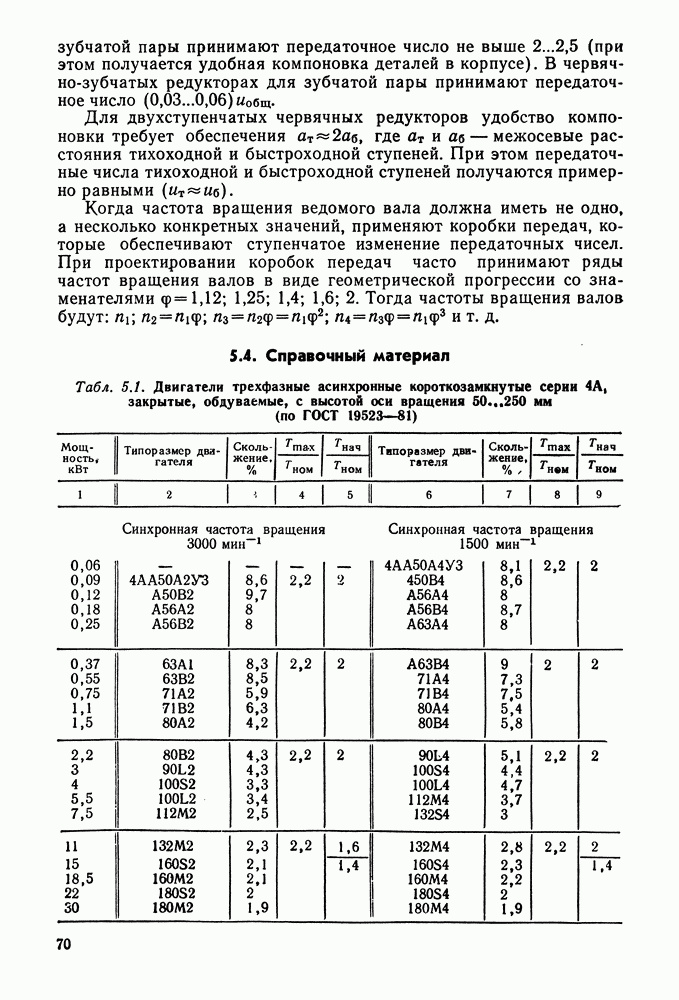
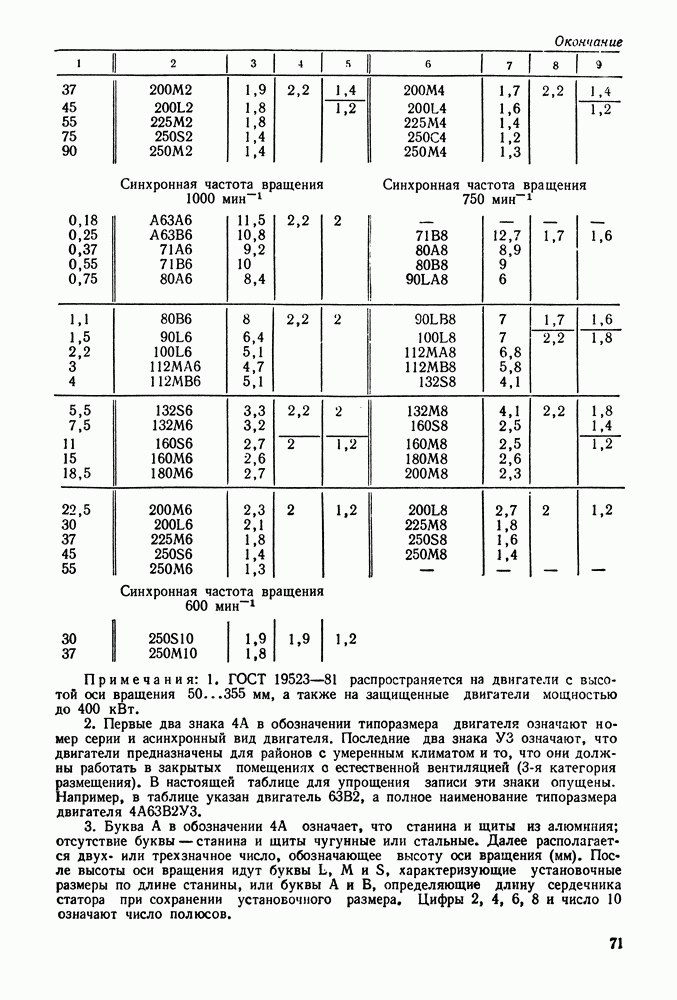
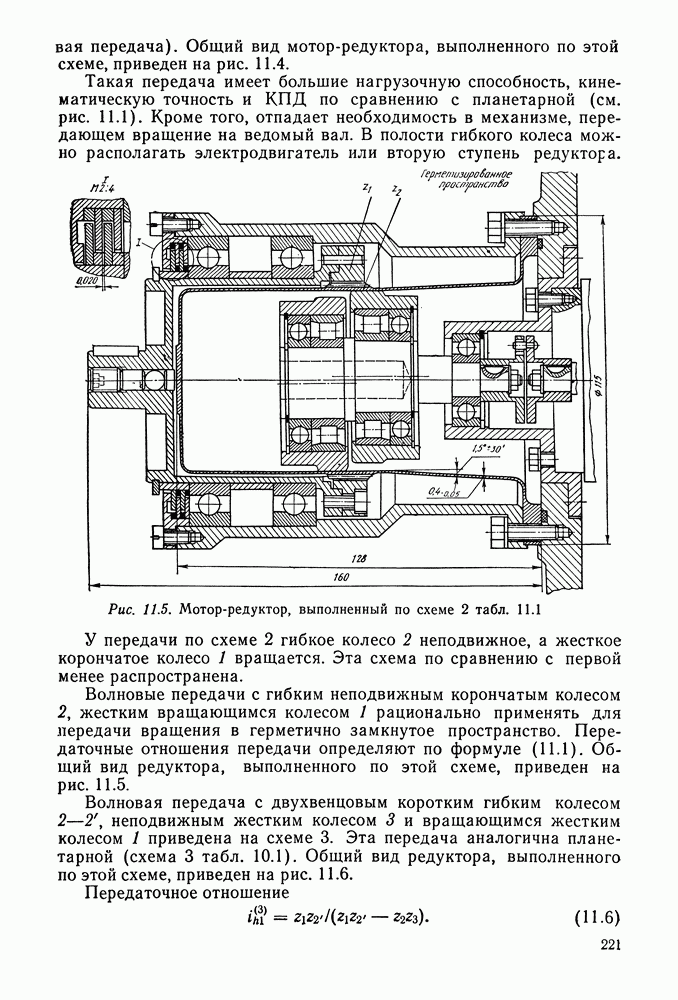
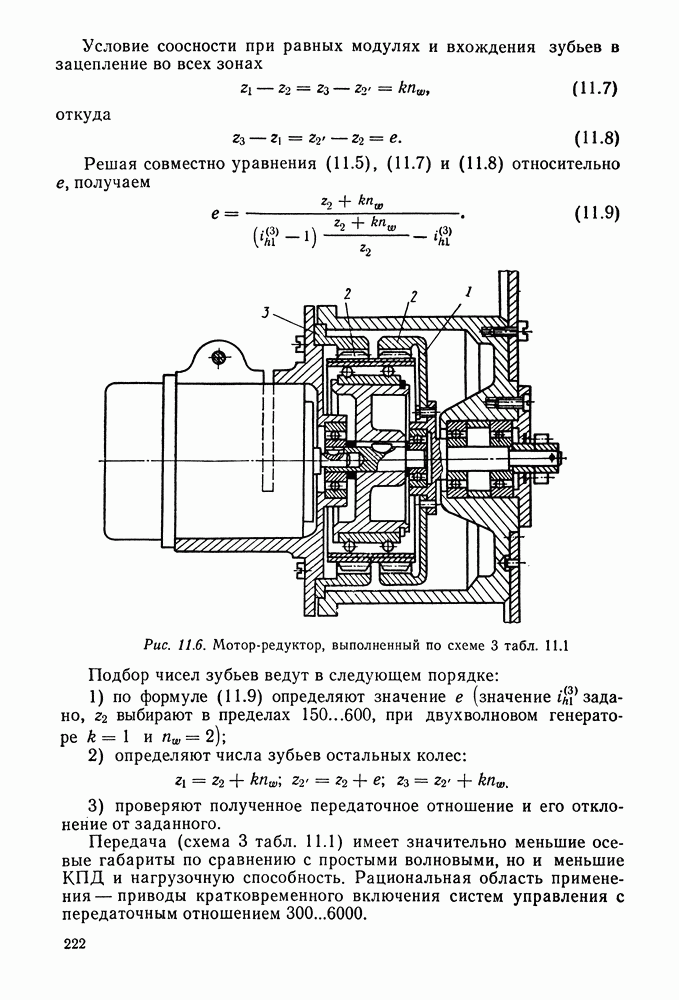
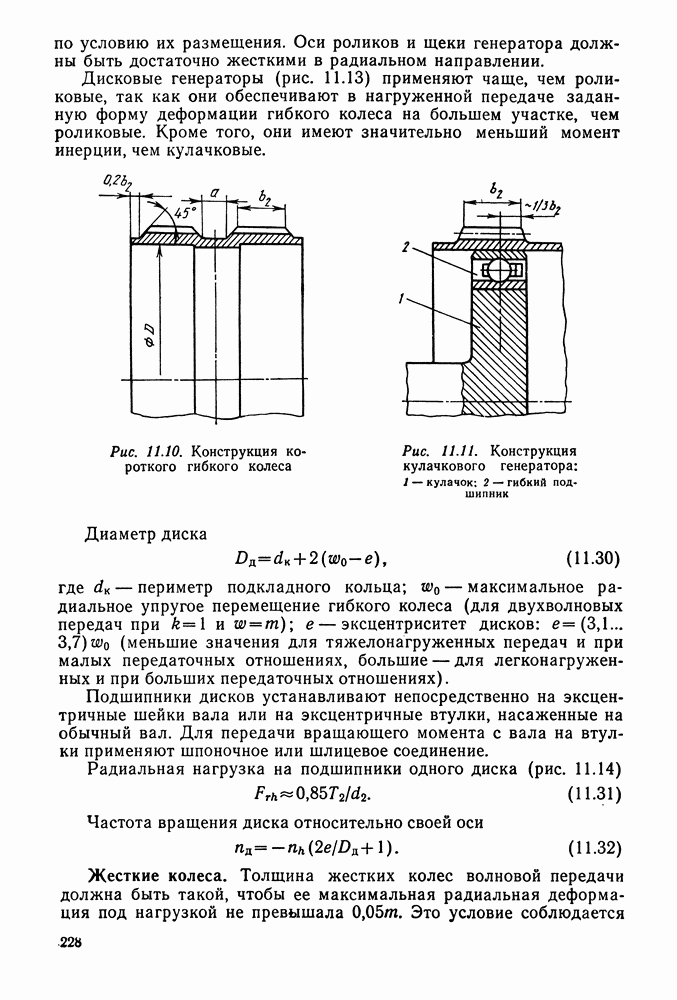
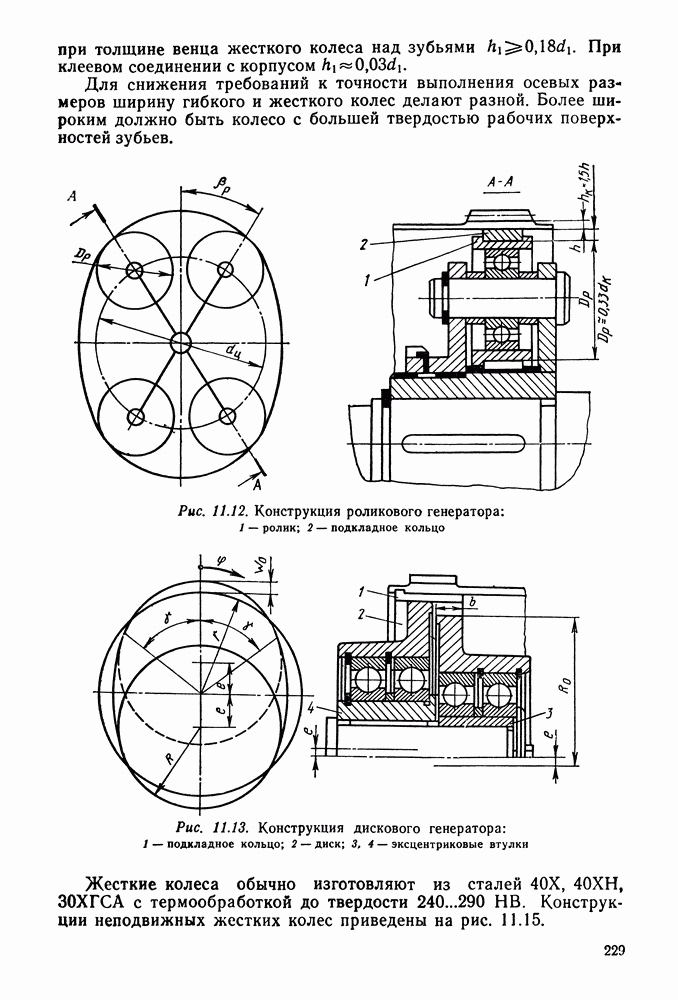
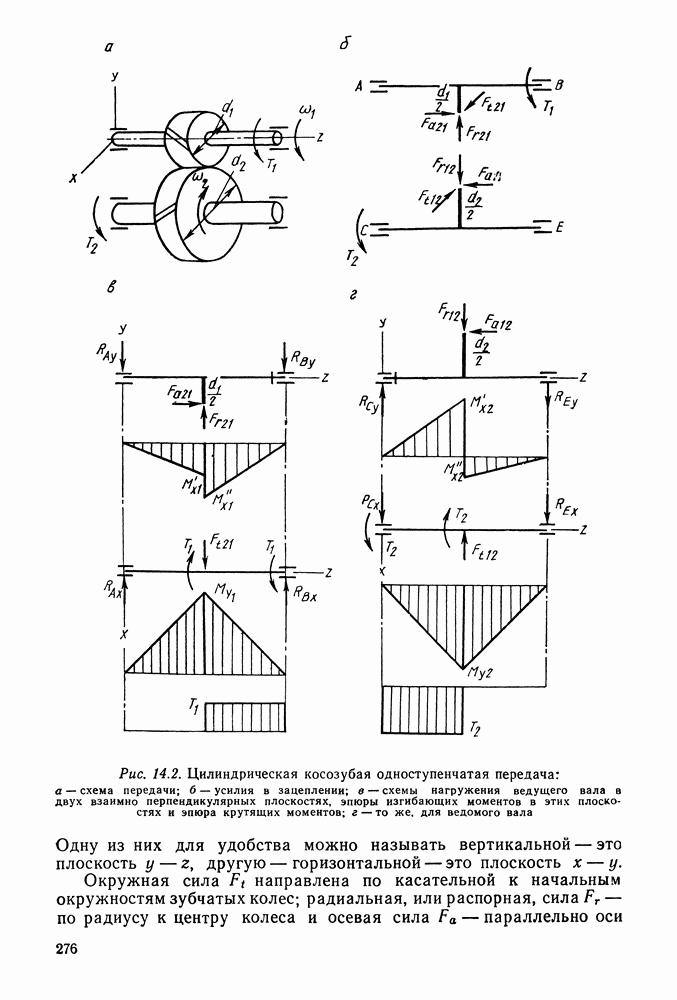
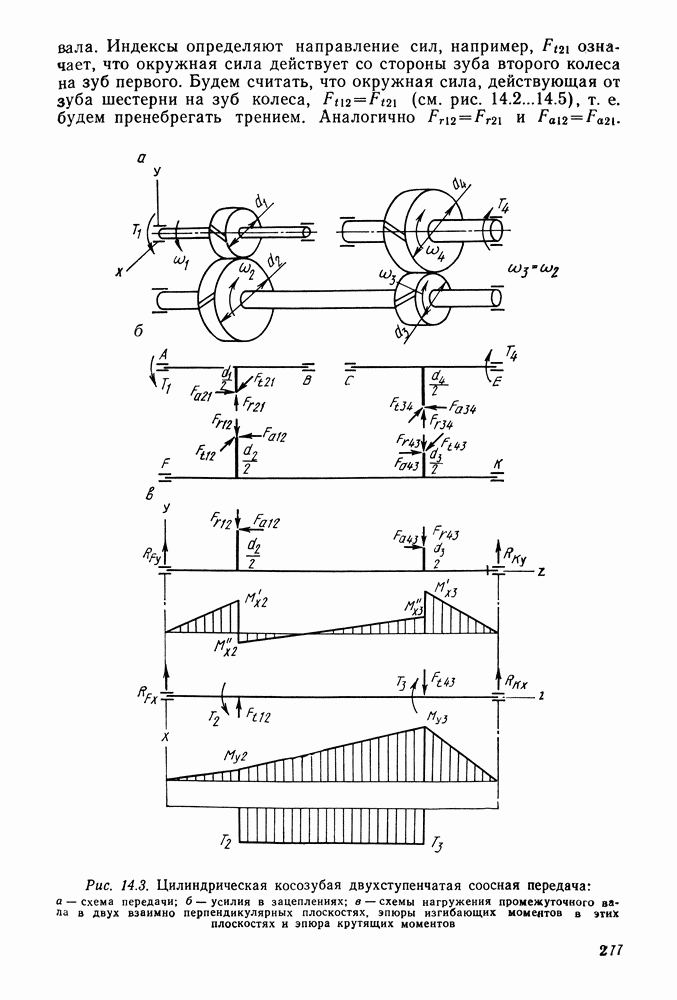
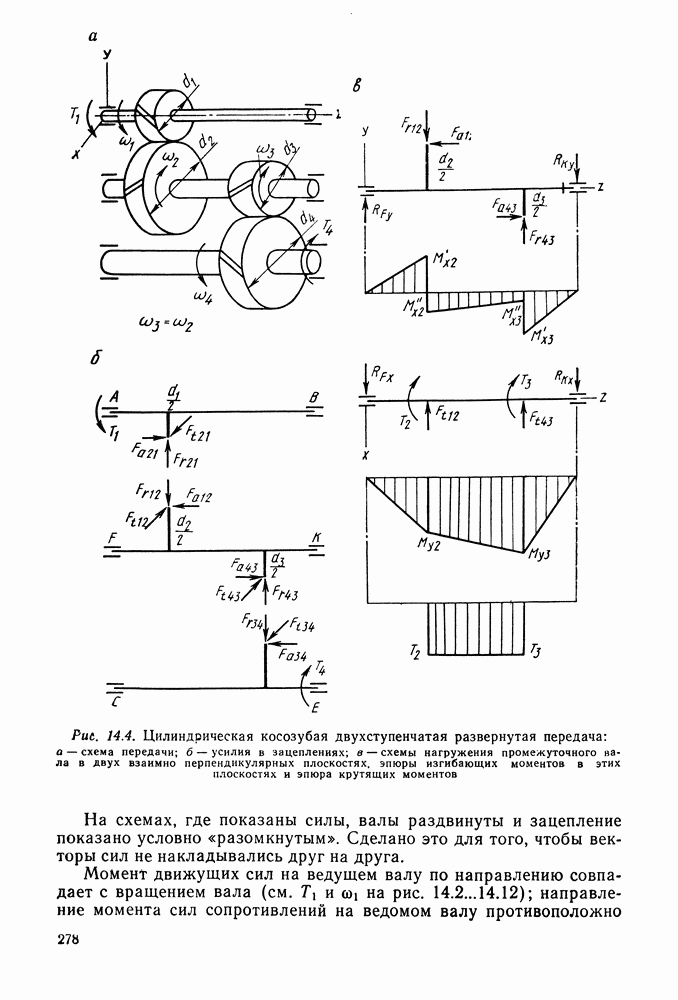
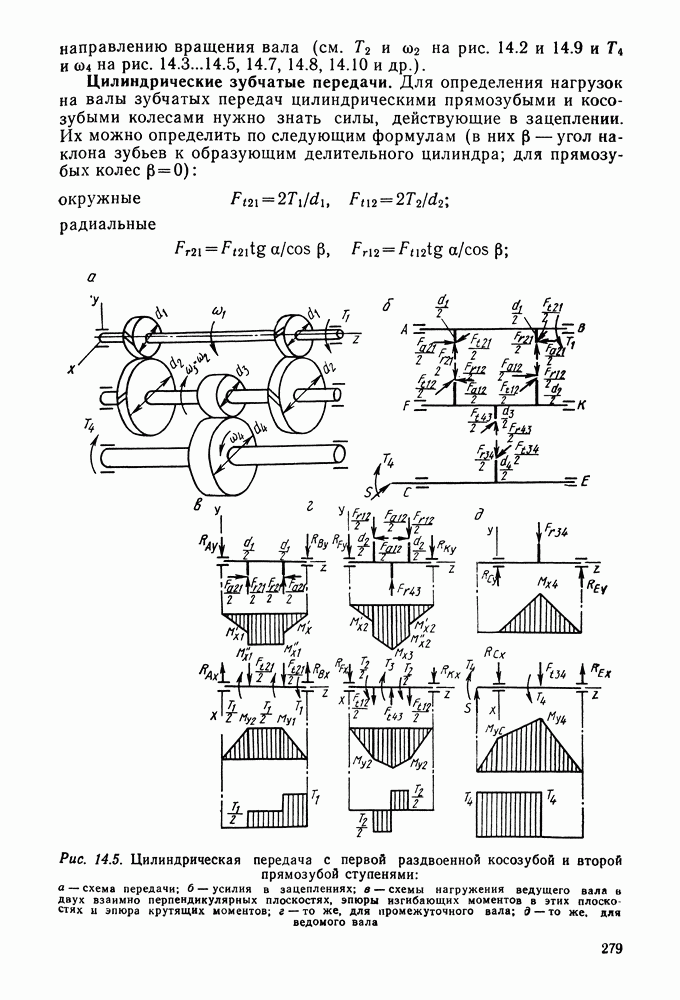
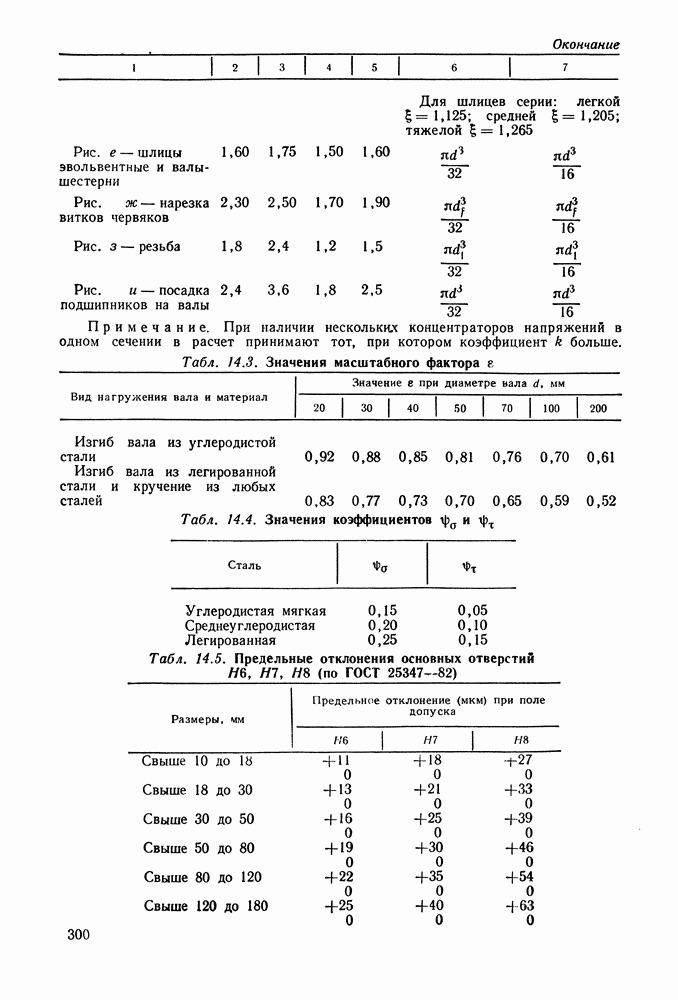
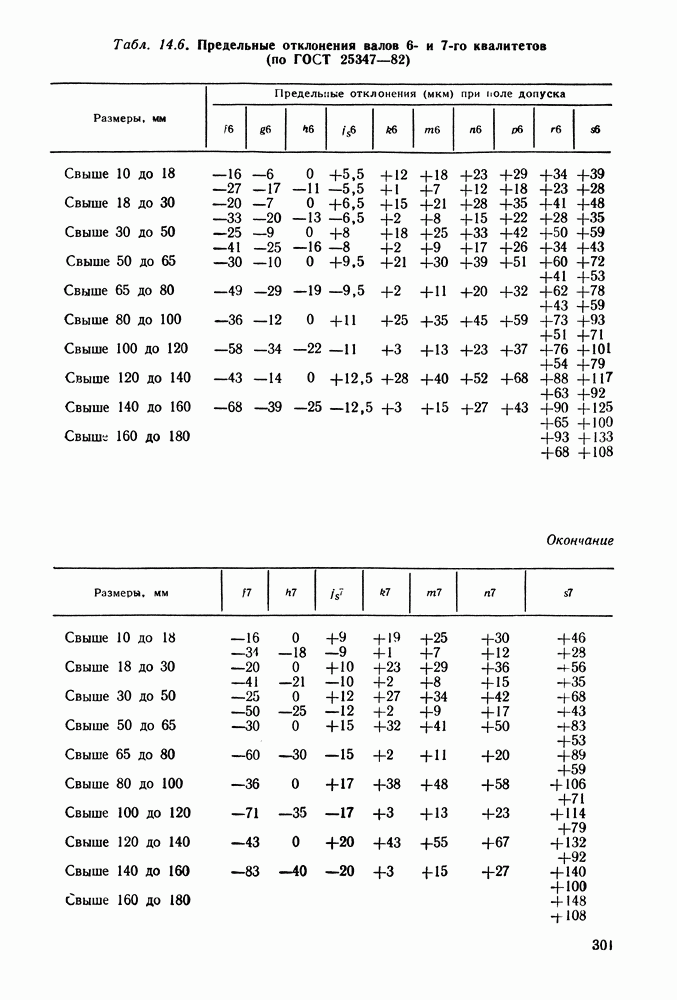
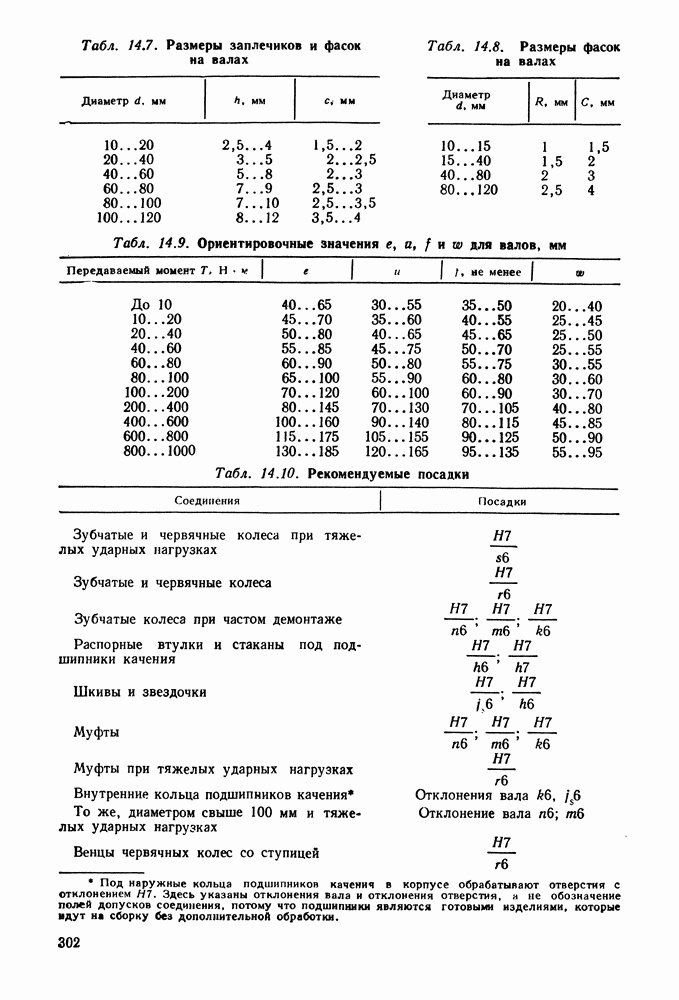
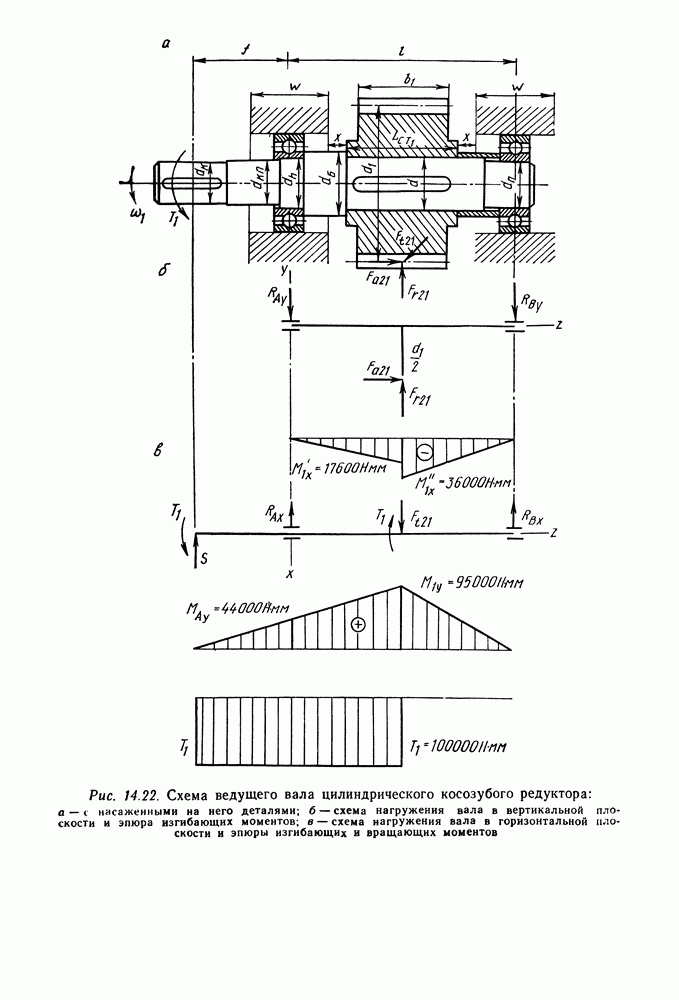
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
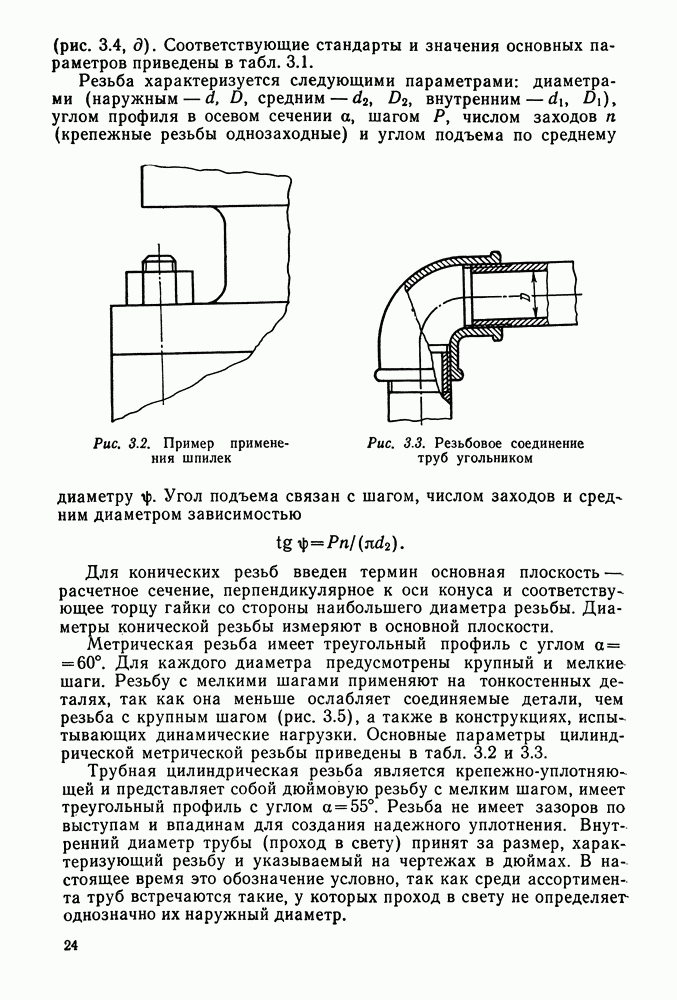
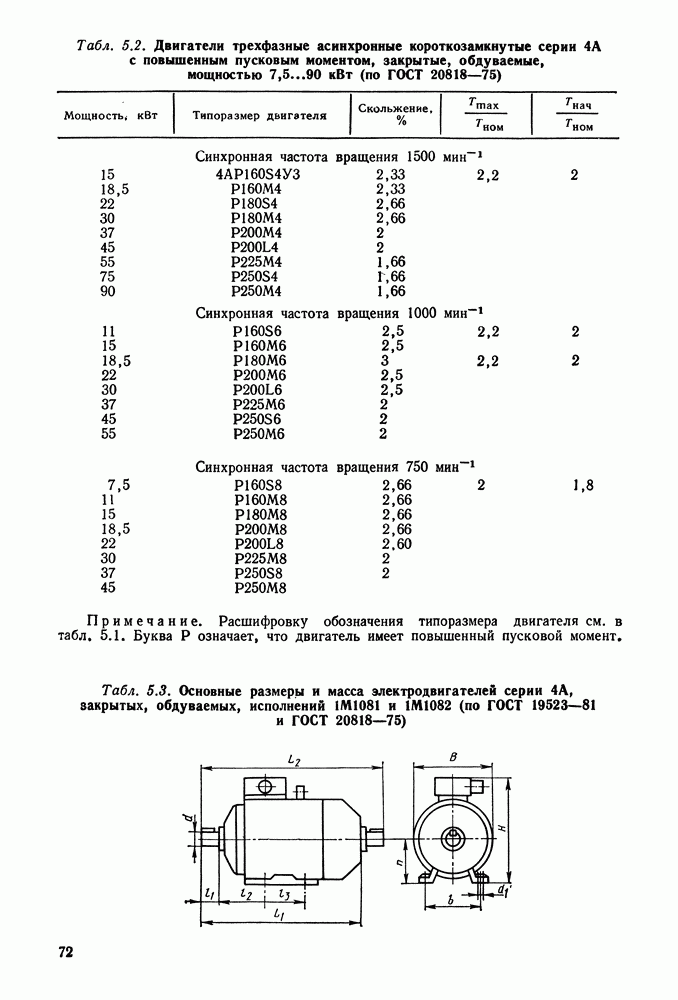
9.2. Геометрия и кинематика эвольвентного цилиндрического зацепления
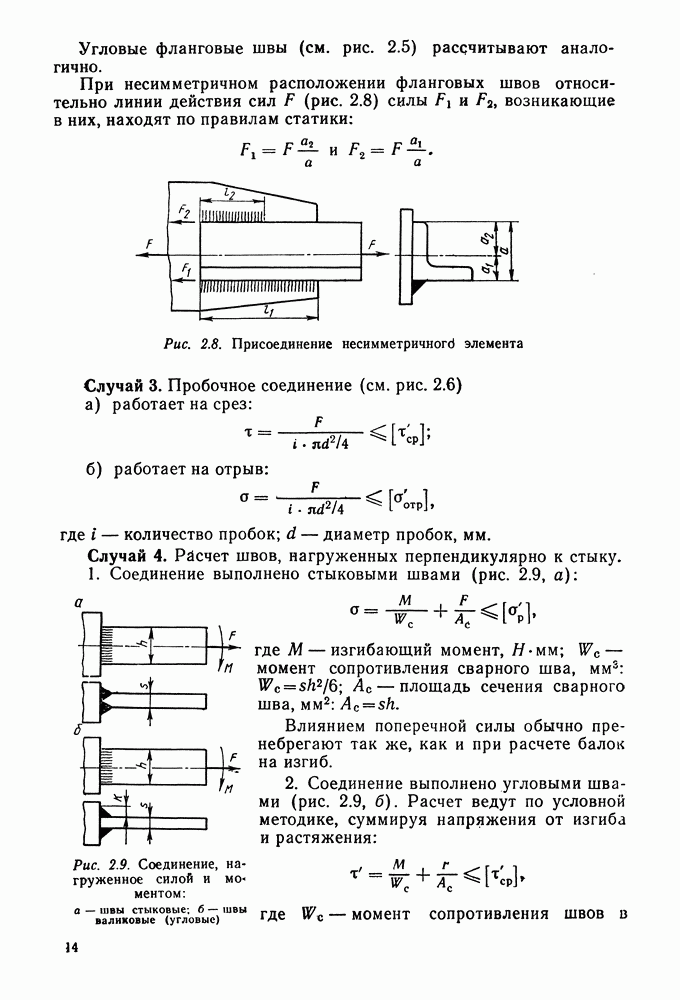
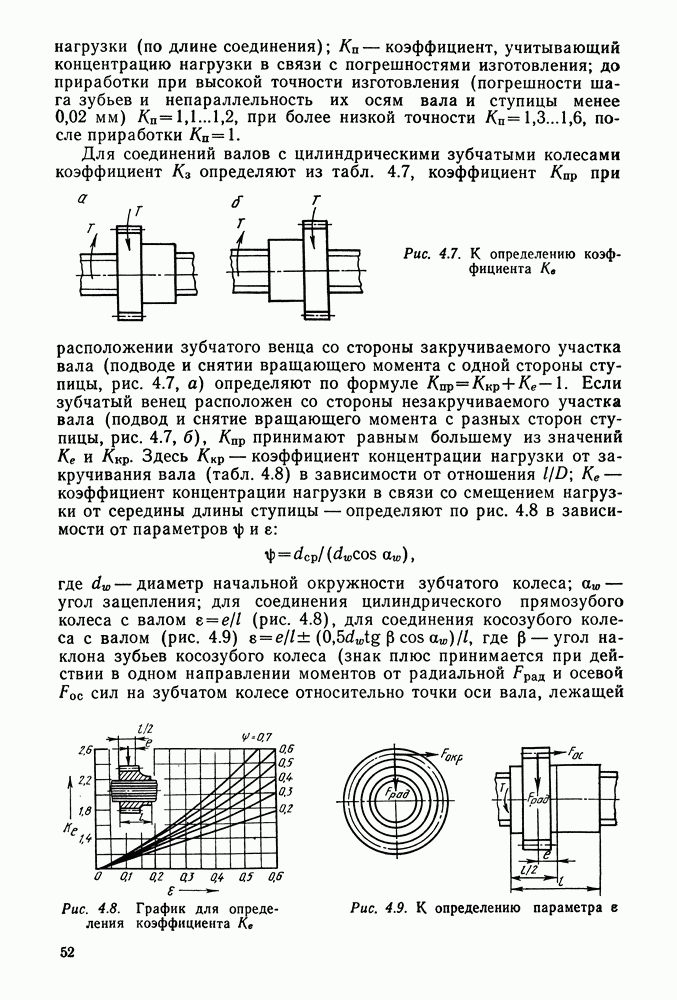
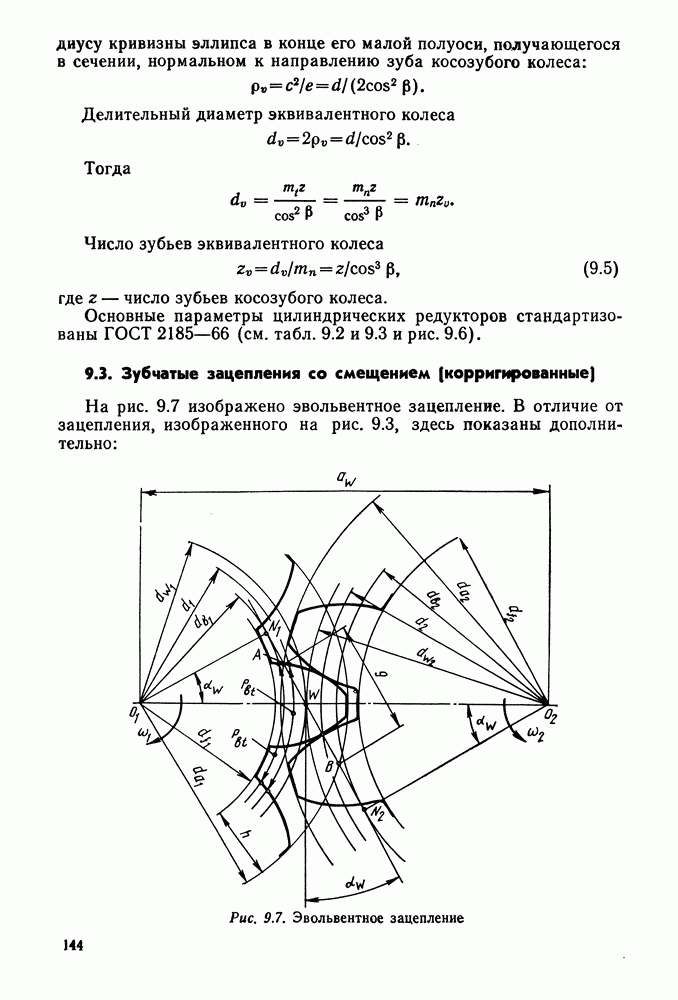
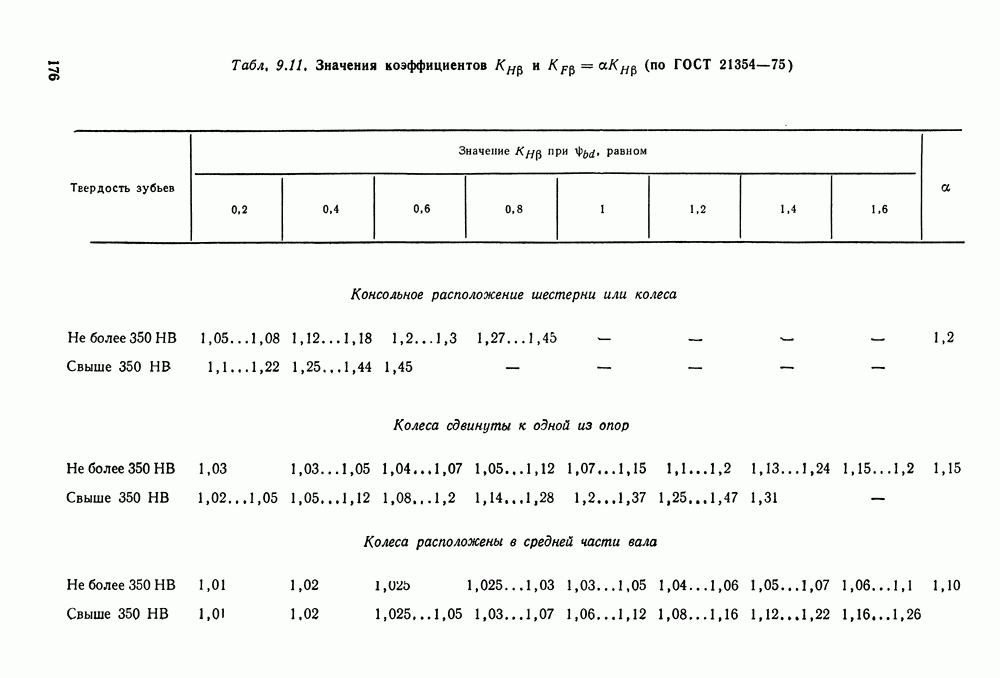
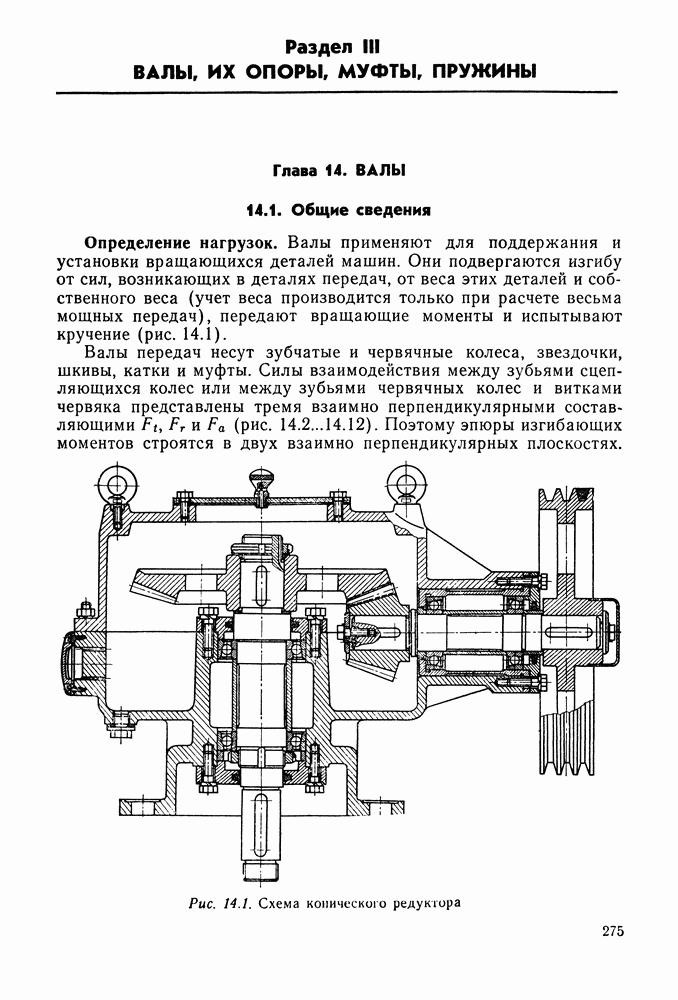
Эвольвентное зацепление пары зубчатых колес (рис. 9.3) характеризуется следующими параметрами.
Начальные окружности (их диаметры  ) — такие окружности, которые в процессе работы передачи перекатываются одна по другой без скольжения. Начальные окружности характерны для зубчатых колес в собранной передаче, а для отдельно взятого колеса понятие начальной окружности отсутствует.
) — такие окружности, которые в процессе работы передачи перекатываются одна по другой без скольжения. Начальные окружности характерны для зубчатых колес в собранной передаче, а для отдельно взятого колеса понятие начальной окружности отсутствует.
Полюс зацепления — точка  касания начальных окружностей.
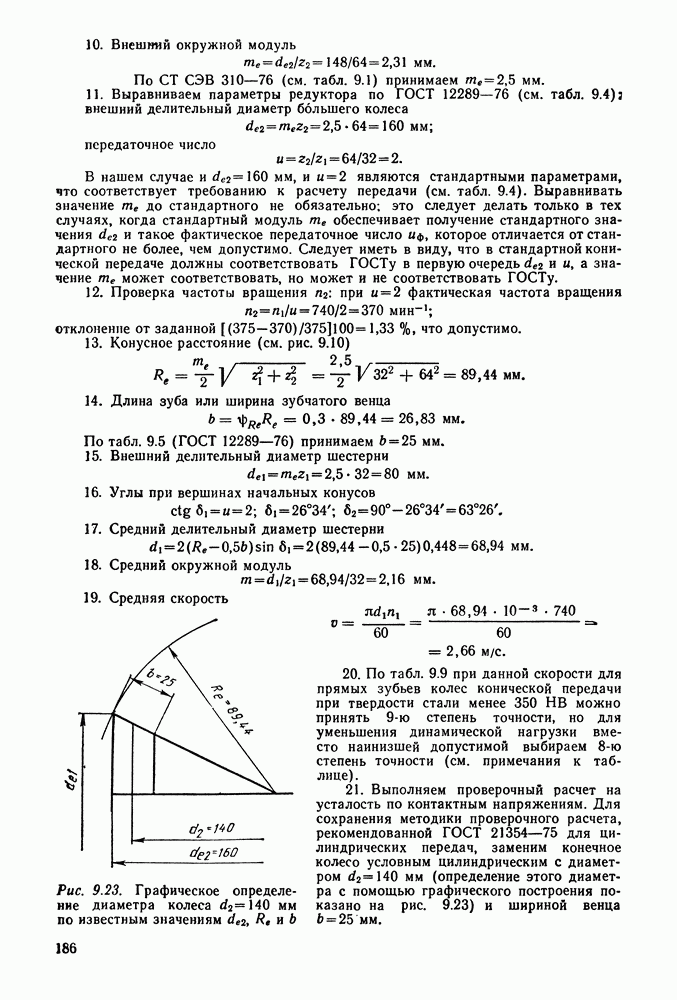
касания начальных окружностей.
Окружной шаг зубьев  — расстояние между одноименными профилями соседних зубьев по дуге концентрической окружности
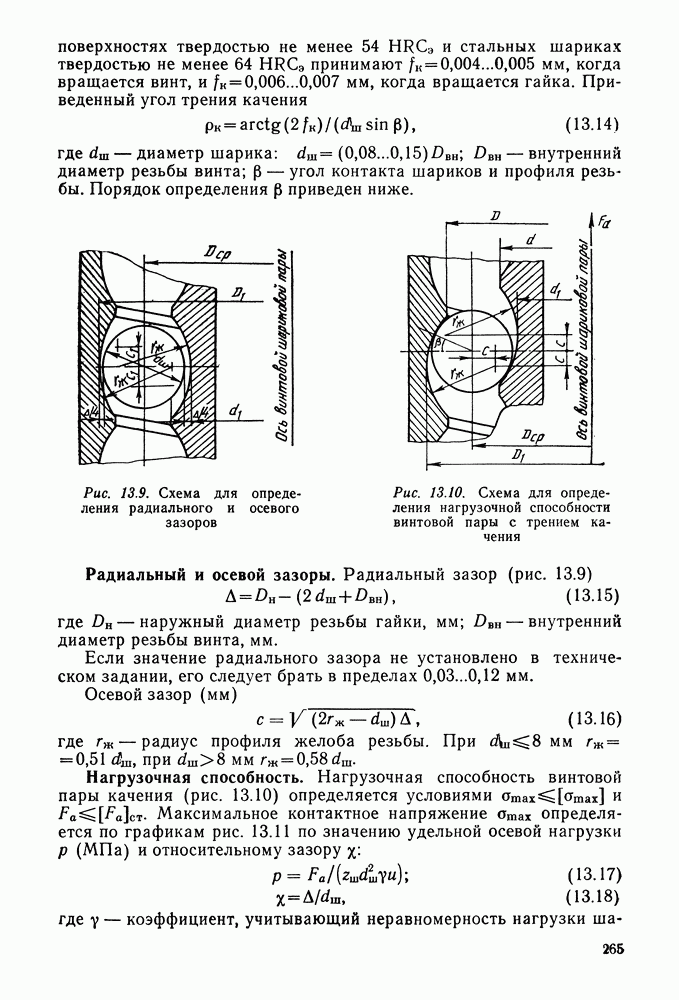
— расстояние между одноименными профилями соседних зубьев по дуге концентрической окружности
зубчатого колеса. Шаг складывается из толщины зуба и ширины впадины между зубьями.
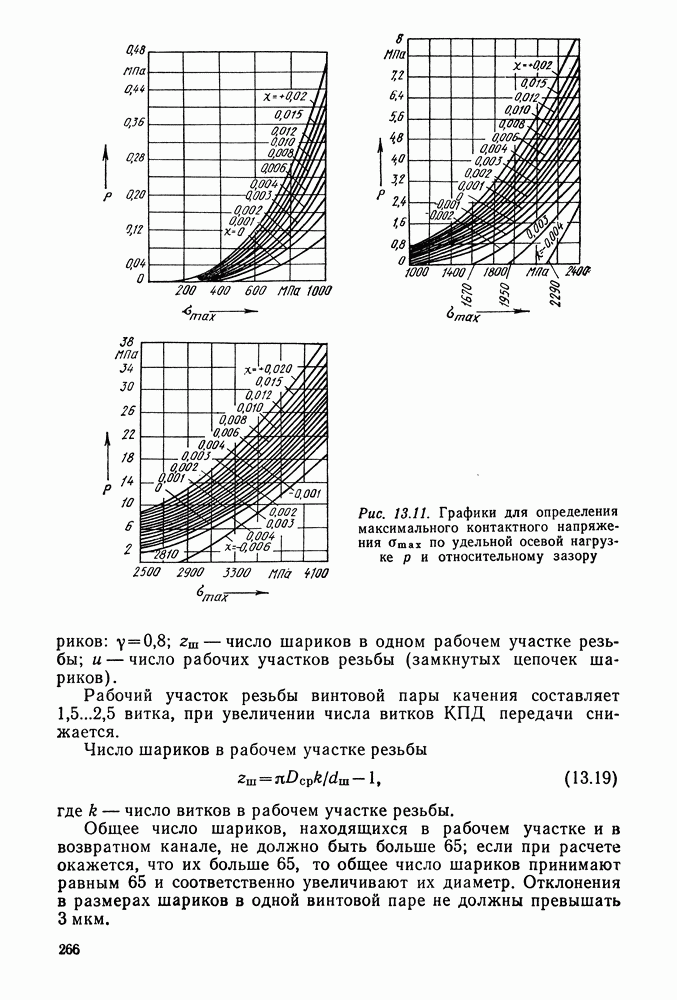
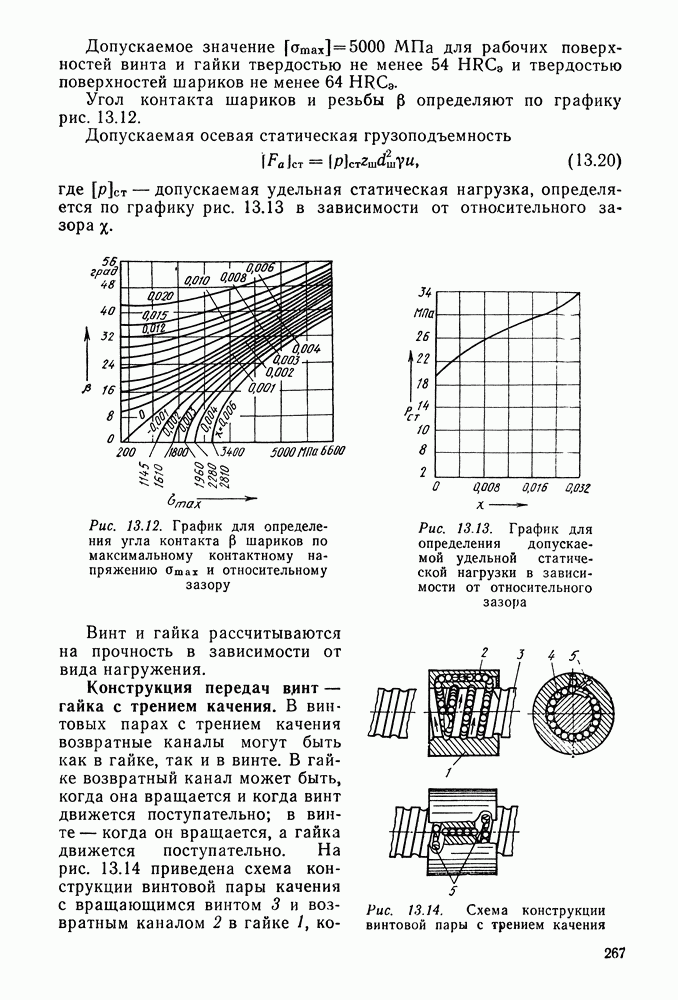
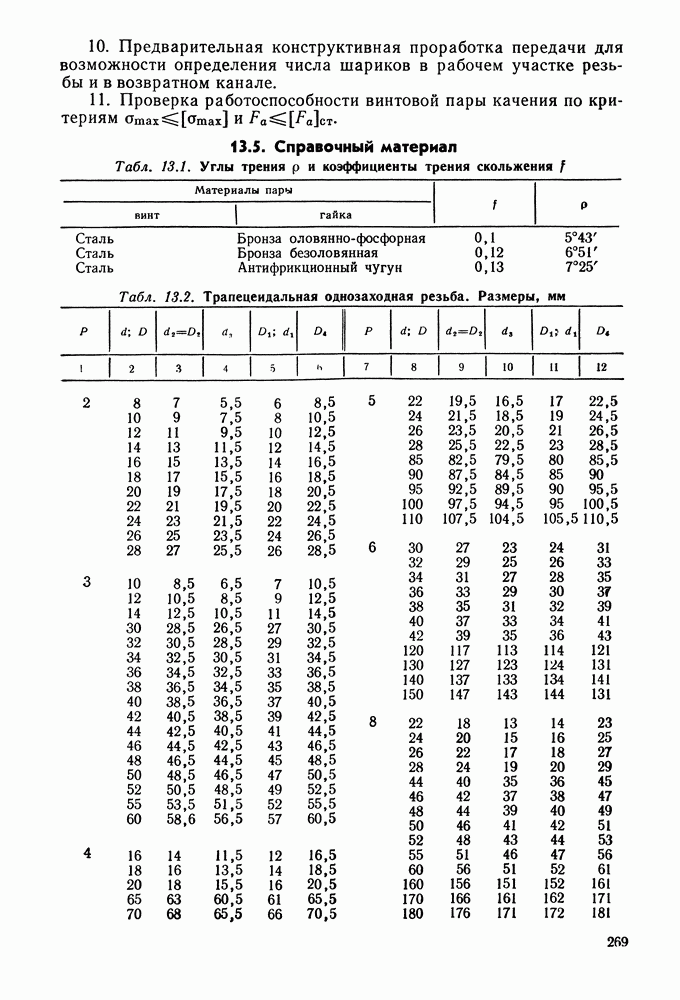
Головка зуба (высоту делительной головки зуба обозначают  — часть зуба между делительной окружностью зубчатого колеса и окружностью вершин зубьев.
— часть зуба между делительной окружностью зубчатого колеса и окружностью вершин зубьев.
Н ожка зуба (высоту делительной ножки зуба обозначают  — часть зуба, расположенная между делительной окружностью и окружностью впадин.
— часть зуба, расположенная между делительной окружностью и окружностью впадин.
Высота зуба 
Окружность вершин зубьев (ее диаметр  ) — окружность, ограничивающая головки зубьев.
) — окружность, ограничивающая головки зубьев.

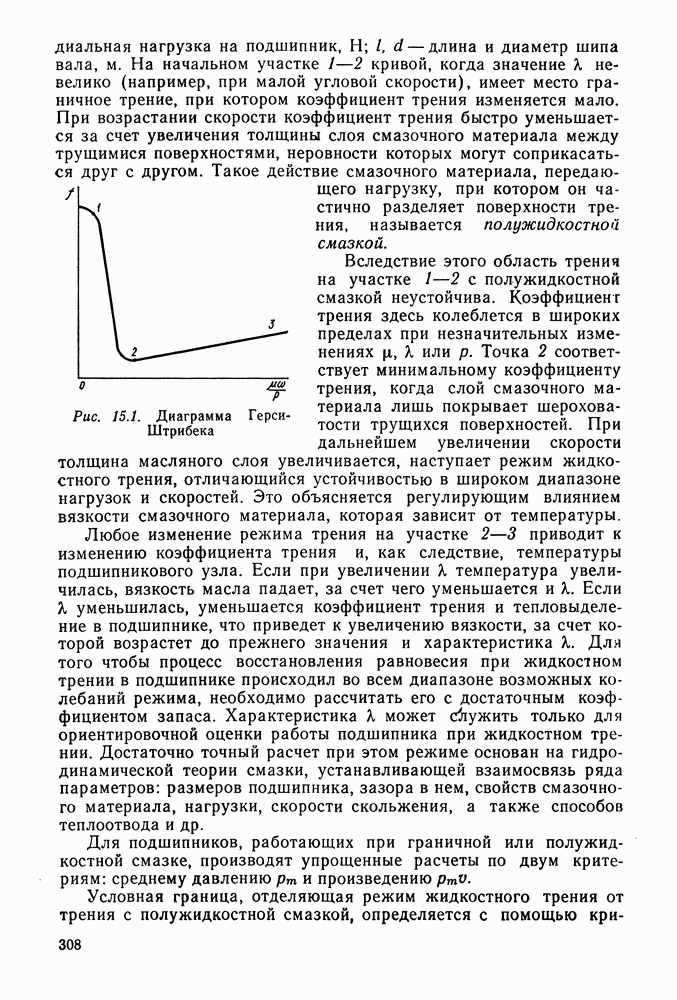
Рис. 9.3. Эвольвентное некорригированное зацепление
Окружность впадин (ее диаметр  — окружность, проходящая через основания впадин зубьев.
— окружность, проходящая через основания впадин зубьев.
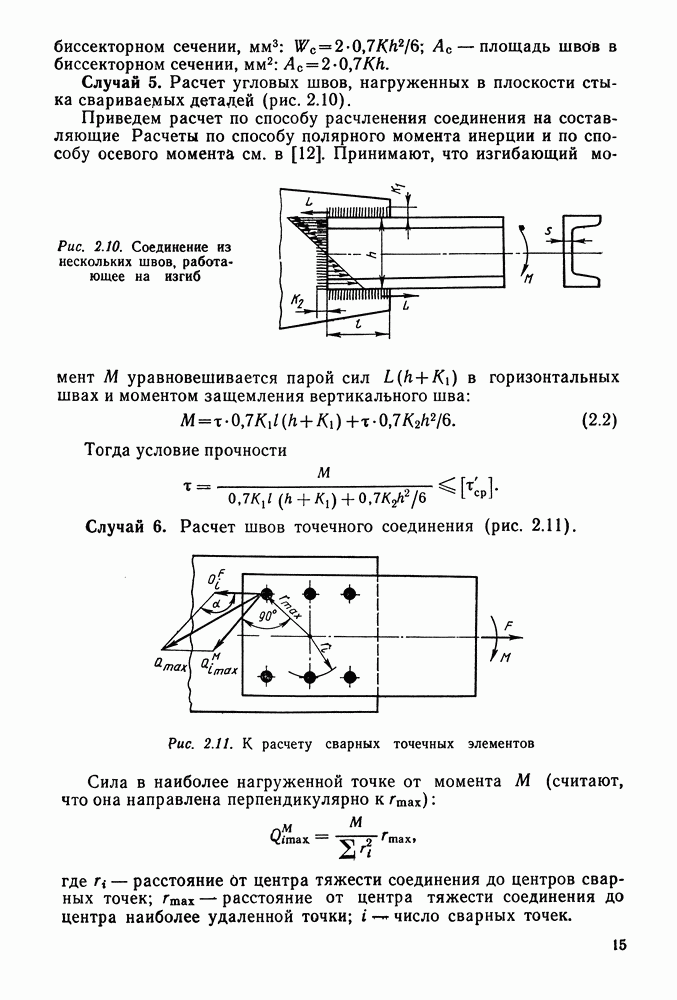
Дуга зацепления  — путь по начальной окружности, проходимый точкой профиля зуба за время зацепления пары сопряженных зубьев.
— путь по начальной окружности, проходимый точкой профиля зуба за время зацепления пары сопряженных зубьев.
Коэффициент перекрытияе — отношение дуги зацепления к шагу: 
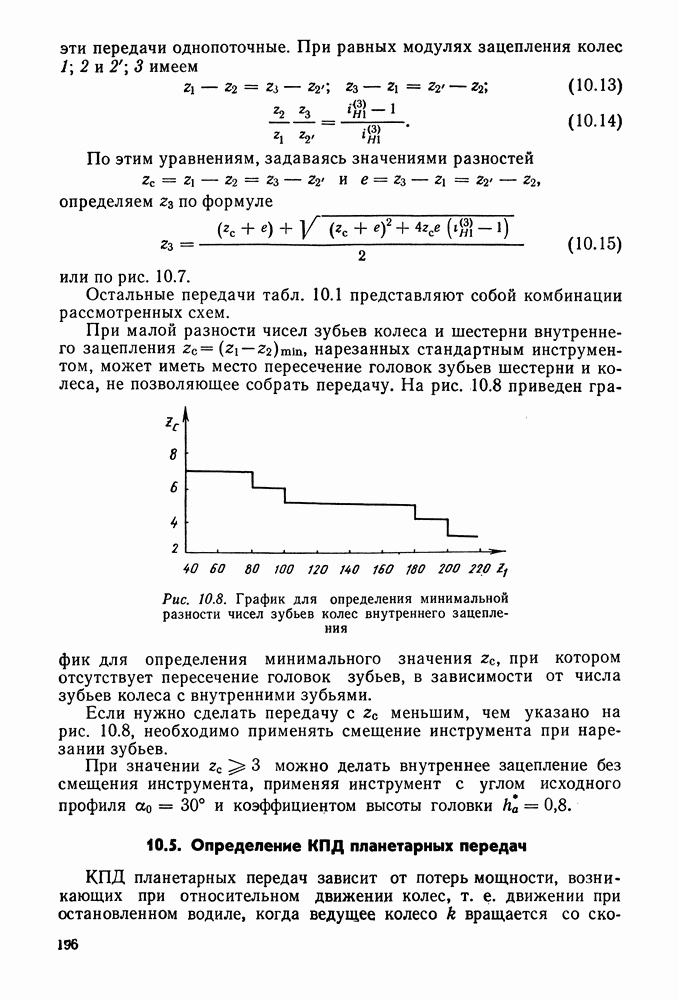
Для непрерывной работы необходимо, чтобы до выхода из зацепления работающей пары зубьев в него вошла еще одна пара. Это произойдет, если дуга зацепления будет больше шага. Чем больше коэффициент перекрытия, тем больше пар зубьев могут одновременно находиться в зацеплении и тем плавнее работает передача. Коэффициент перекрытия показывает, сколько пар зубьев в среднем находится в зацеплении; так, при  в течение
в течение  продолжительности зацепления находятся две пары зубьев, а
продолжительности зацепления находятся две пары зубьев, а  одна.
одна.
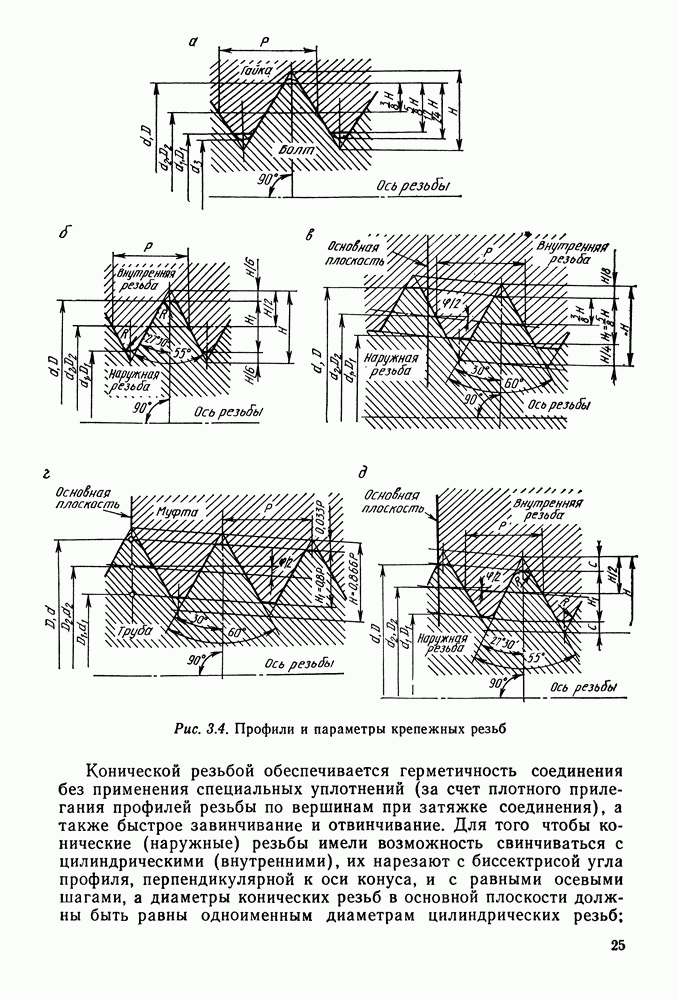
Для непрерывной и плавной работы передачи должно быть  (лучше
(лучше  ).
).
Межосевое расстояние  — сумма радиусов начальных окружностей шестерни и колеса:
— сумма радиусов начальных окружностей шестерни и колеса:

Числа зубьев шестерни и колеса обозначают 
Модуль зацепления — отношение шага к числу  , т. е.
, т. е. 
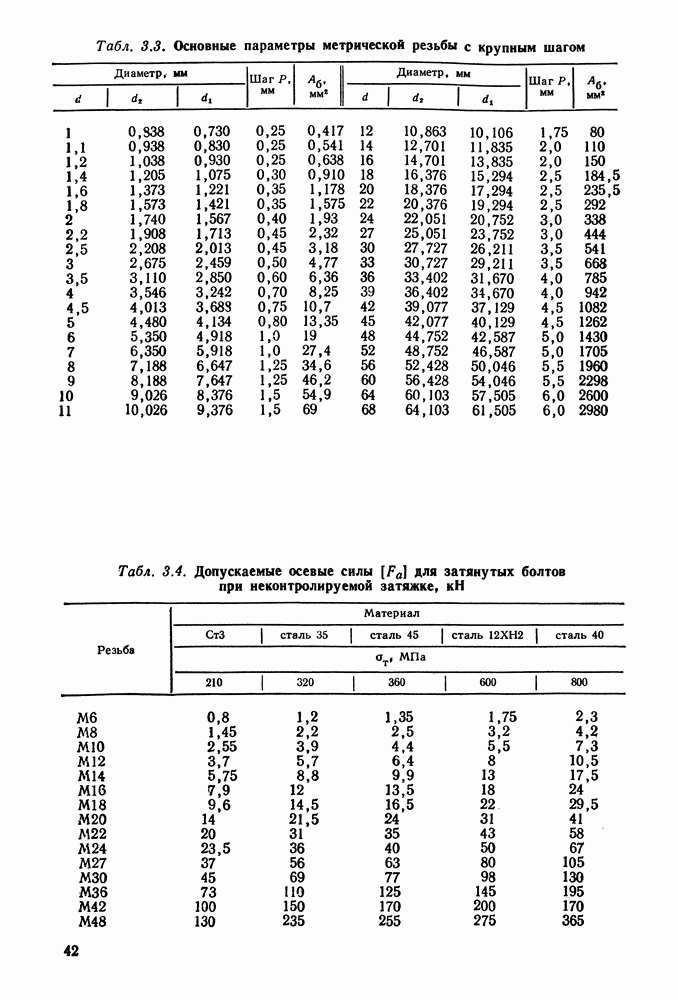
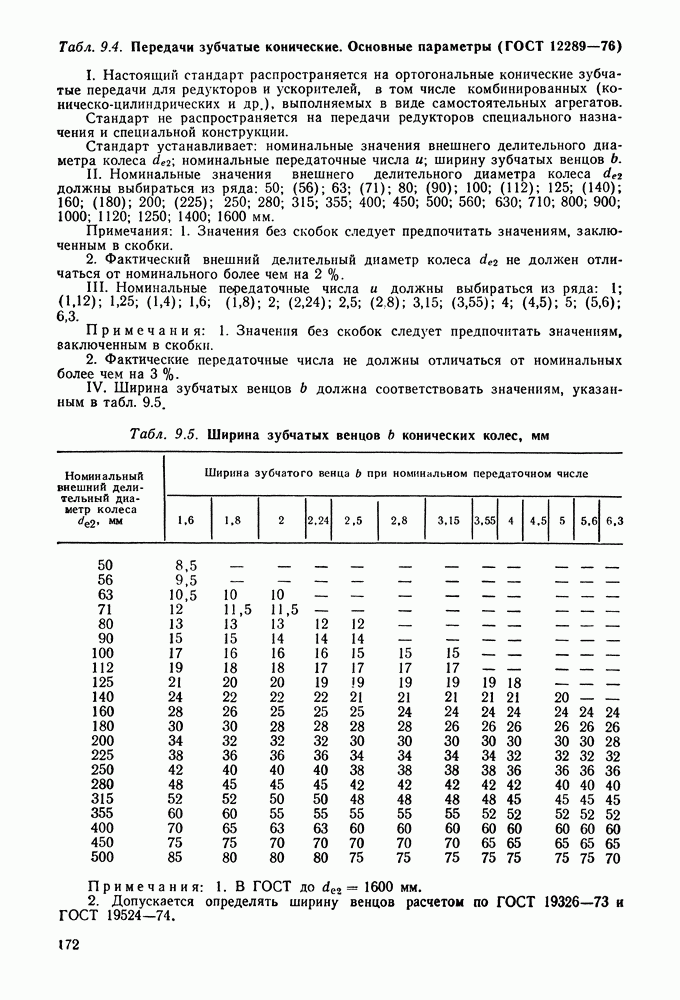
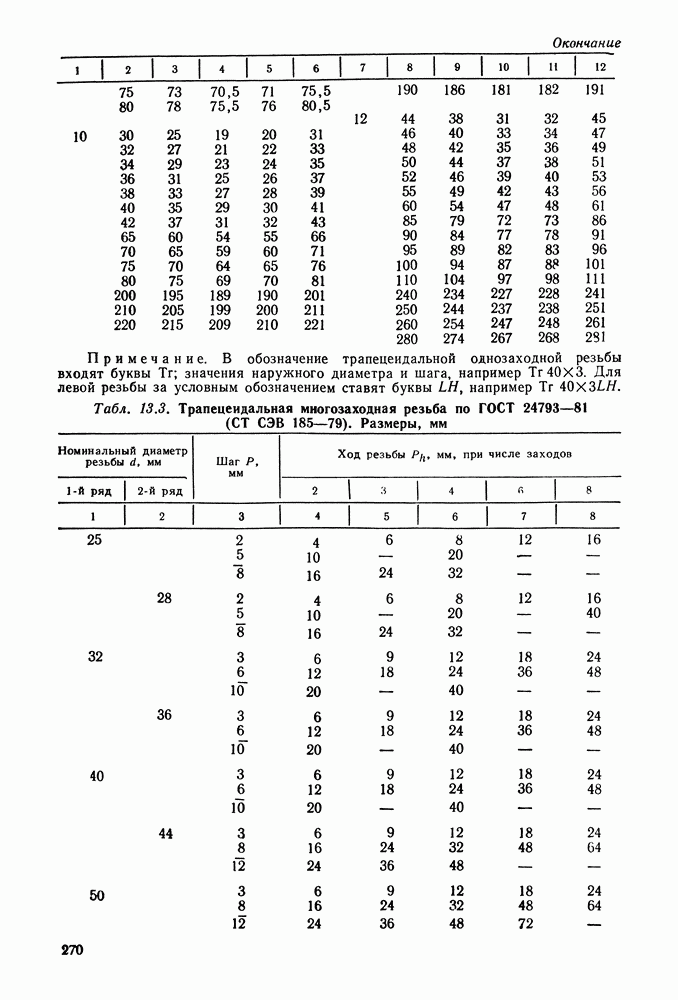
Модули  мм стандартизованы (см. табл. 9.1).
мм стандартизованы (см. табл. 9.1).
Диаметры окружностей:

Межосевое расстояние [см. формулу (9.1)]

где  — суммарное число зубьев:
— суммарное число зубьев: 
Передаточное отношение понижающей передачи равно ее передаточному числу:

где  — угловые скорости,
— угловые скорости,  частота вращения соответственно шестерни и колеса,
частота вращения соответственно шестерни и колеса, 
Передаточное число понижающей передачи 

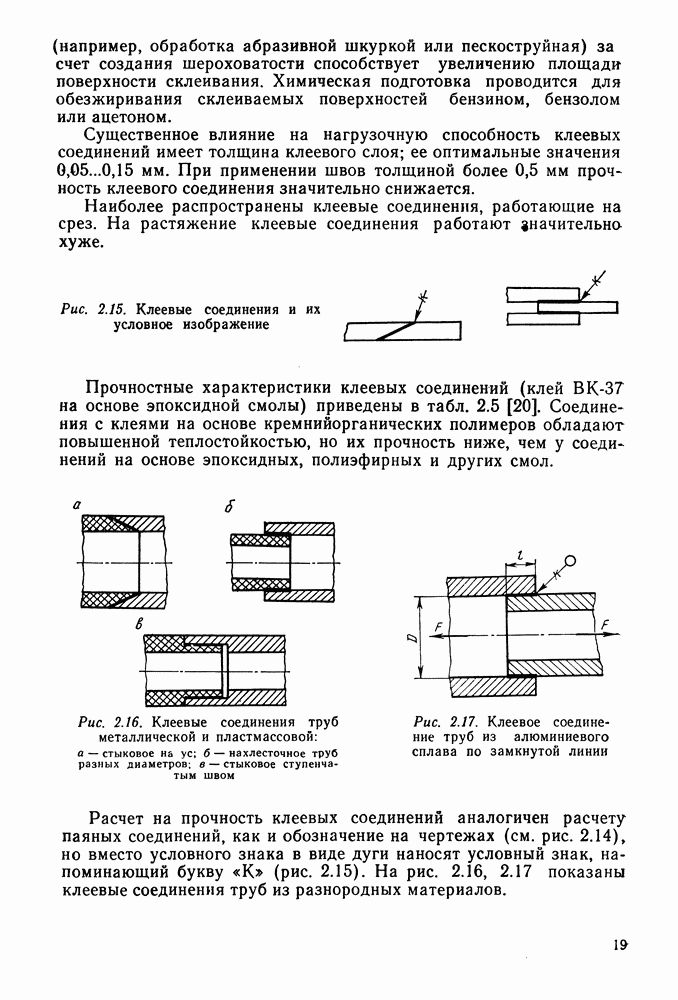
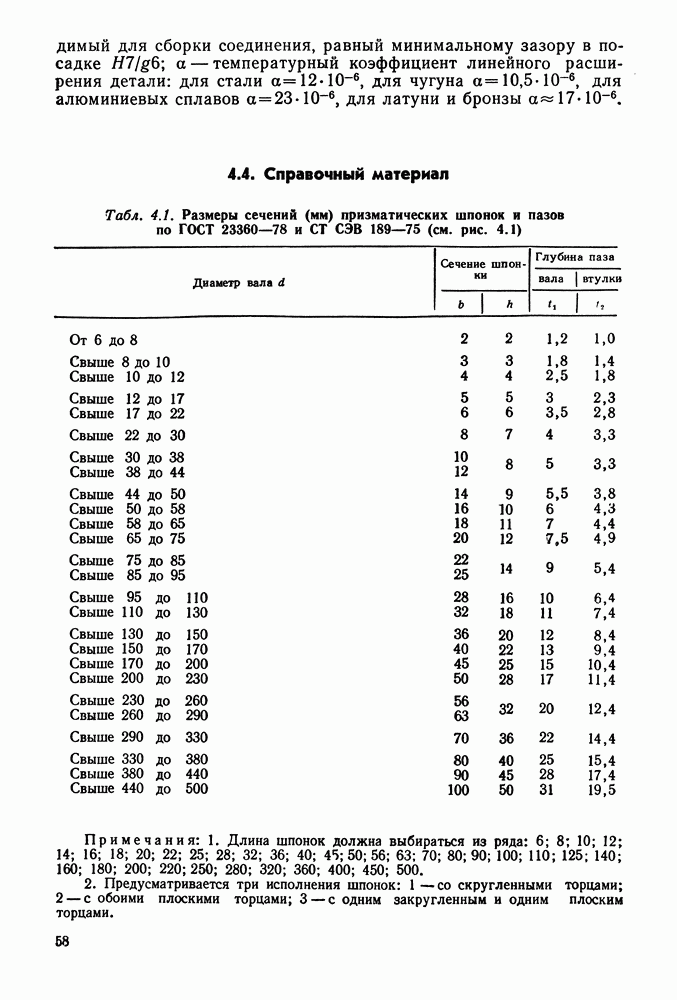
Рис. 9.4. Зависимость формы зубьев от их числа
Передаточные числа одноступенчатой зубчатой передачи в закрытом корпусе могут достигать для цилиндрической пары 10, многоступенчатой — нескольких сот.
При выборе числа зубьев следует иметь в виду, что с уменьшением их числа уменьшается толщина зуба у основания и у вершины (рис. 9.4, а, б), что приводит к понижению его прочности на изгиб. Поэтому не рекомендуют выбирать число зубьев меньше, чем  При числе зубьев
При числе зубьев  происходит подрезание ножки зуба (рис. 9.4, в), что приводит к резкому снижению прочности. При нарезании зубьев инструментом реечного типа
происходит подрезание ножки зуба (рис. 9.4, в), что приводит к резкому снижению прочности. При нарезании зубьев инструментом реечного типа  . В редукторах рекомендуют принимать для первой ступени
. В редукторах рекомендуют принимать для первой ступени  для второй и третьей ступеней
для второй и третьей ступеней  .
.
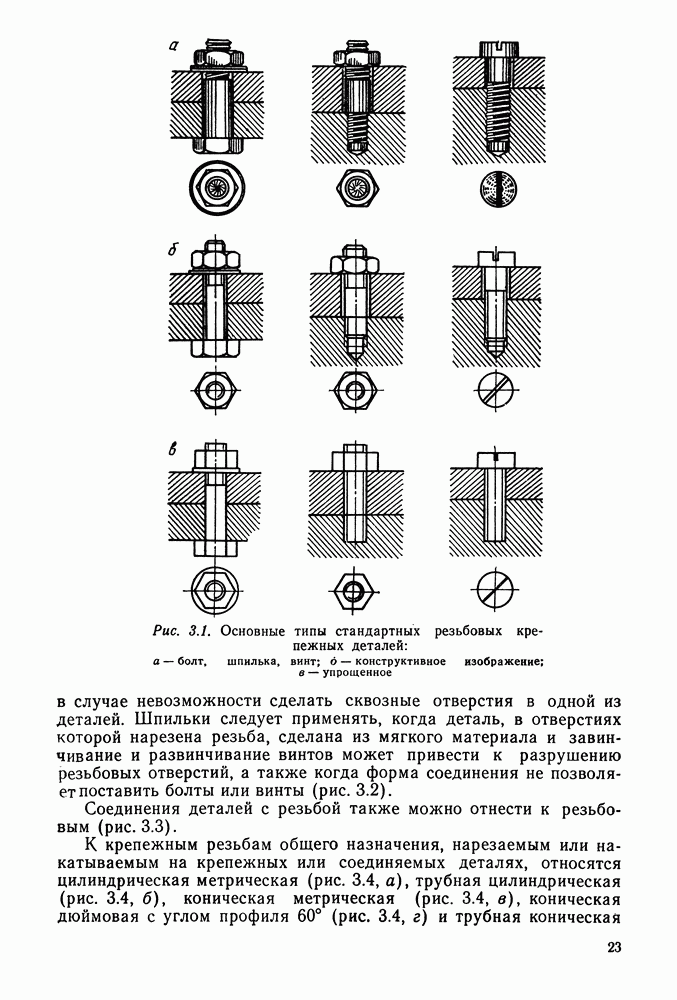
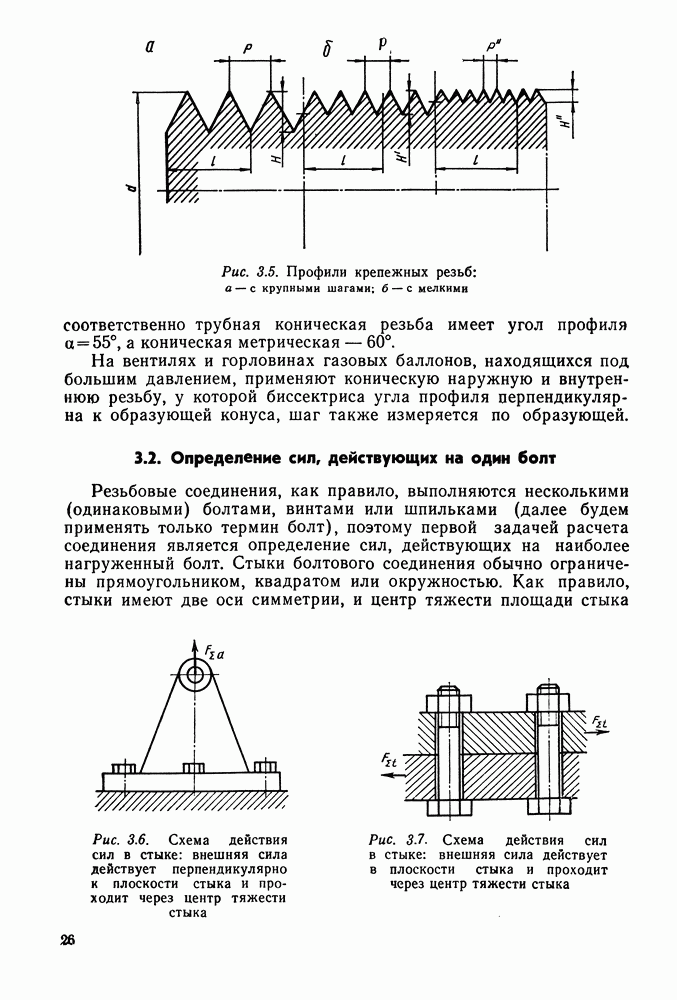
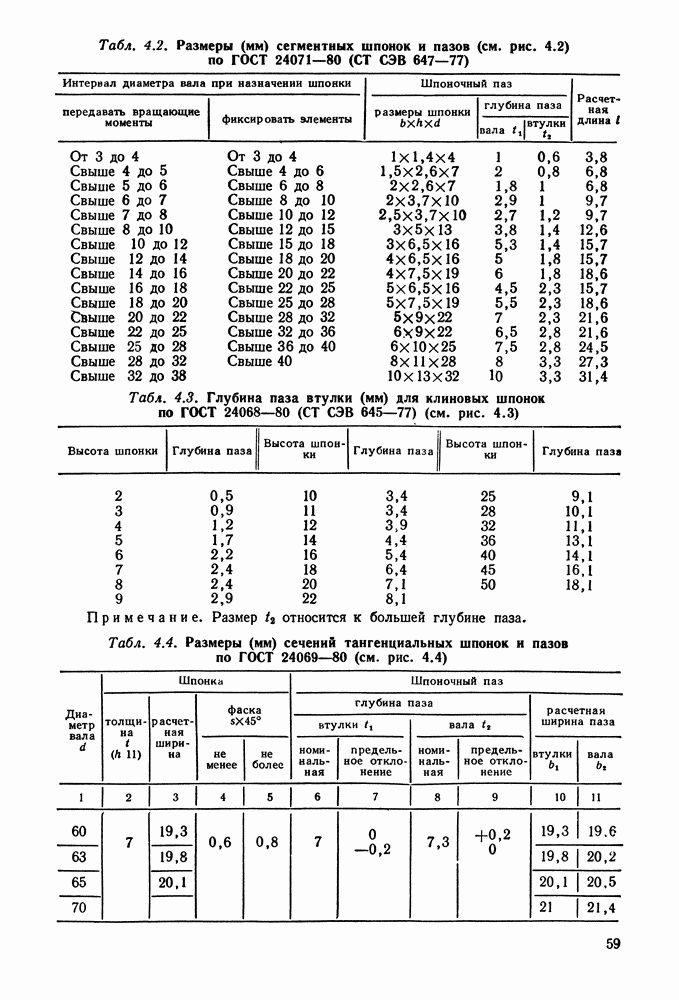
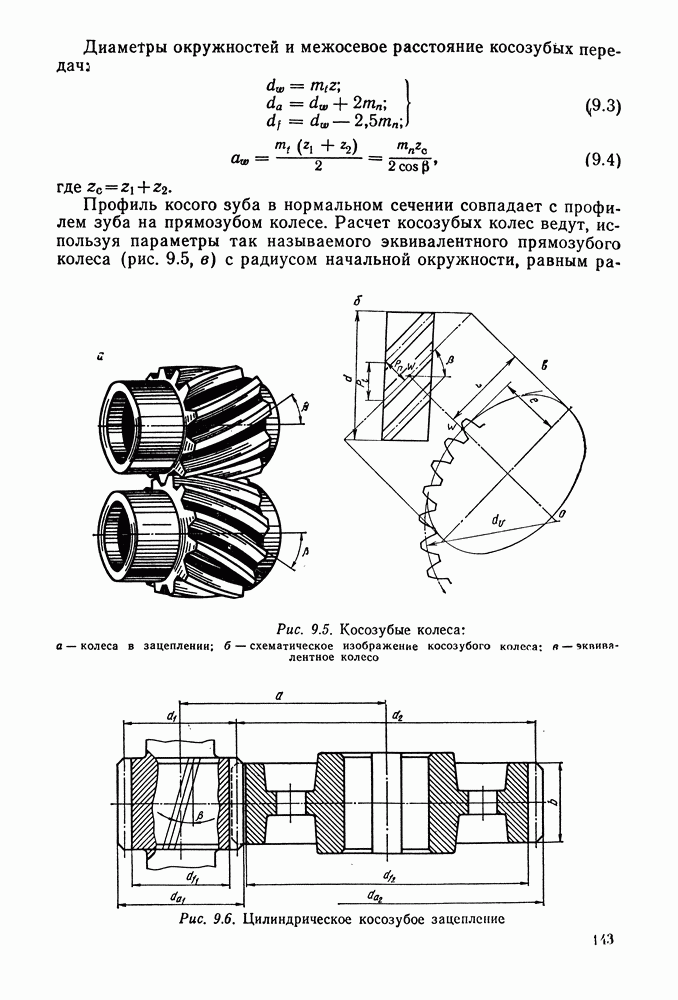
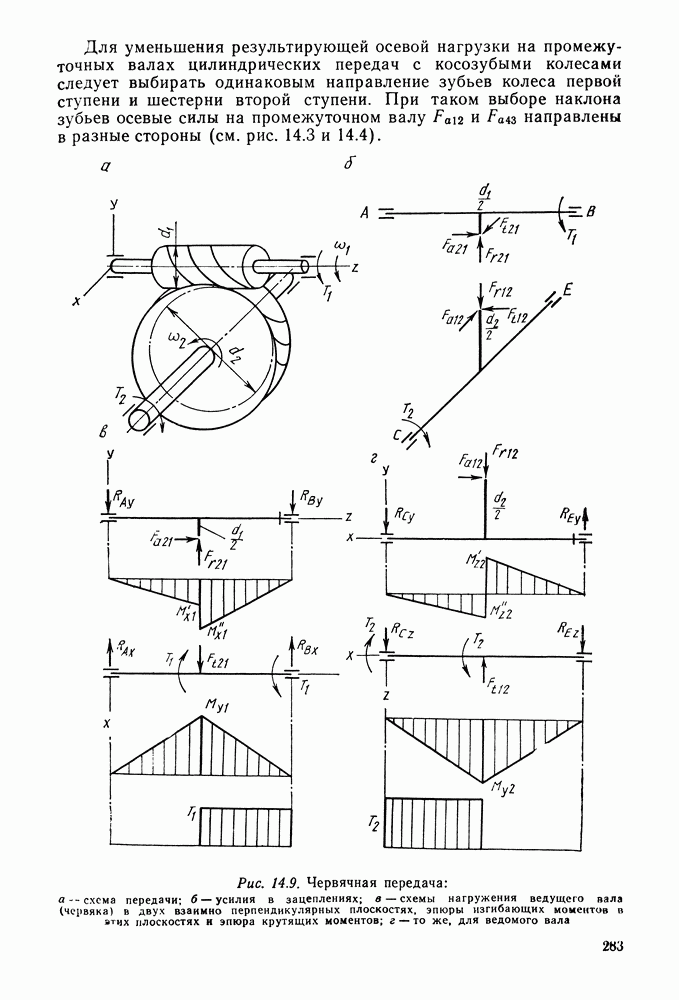
В колесах с косым зубом (рис. 9.5, а) различают окружной шаг  который измеряется параллельно торцу колеса (рис. 9.5, б), и нормальный шаг
который измеряется параллельно торцу колеса (рис. 9.5, б), и нормальный шаг  измеряемый в нормальном к направлению зуба сечении:
измеряемый в нормальном к направлению зуба сечении:

где  — угол наклона зуба. Во избежание больших осевых усилий принимают
— угол наклона зуба. Во избежание больших осевых усилий принимают  (редко до 20°).
(редко до 20°).
Аналогично связаны между собой нормальный  и окружной
и окружной  модули:
модули:

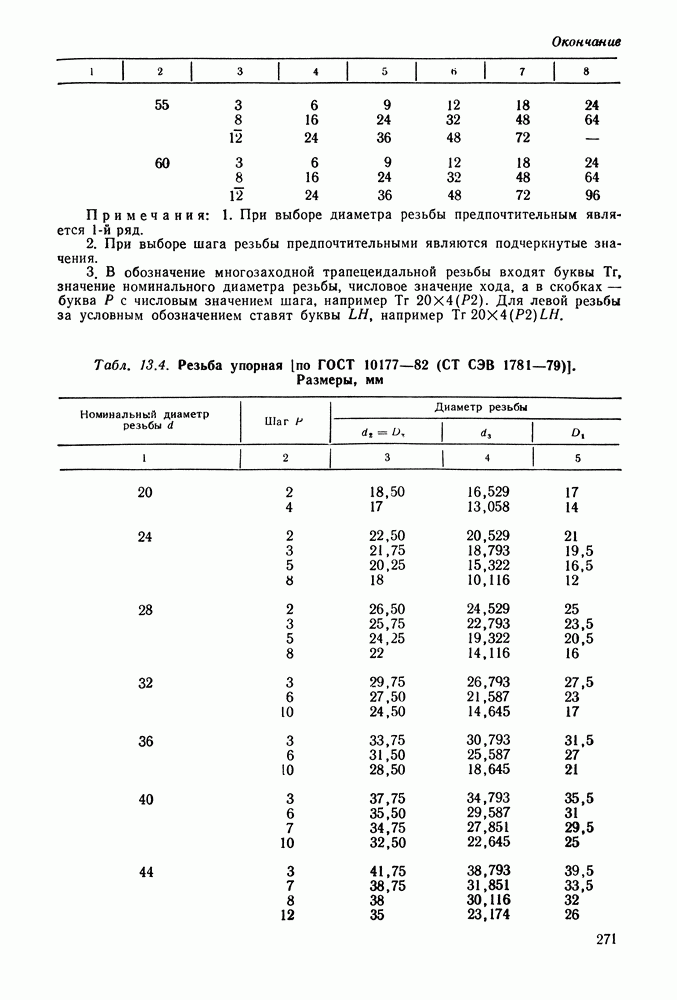
По стандарту выравнивают обычно нормальный модуль (см. табл. 9.1).
Диаметры окружностей и межосевое расстояние косозубых передач;

где
Профиль косого зуба в нормальном сечении совпадает с профилем зуба на прямозубом колесе. Расчет косозубых колес ведут, используя параметры так называемого эквивалентного прямозубого колеса (рис. 9.5, в) с радиусом начальной окружности, равным

Рис. 9.5. Косозубые колеса: а — колеса в зацеплении; б — схематическое изображение косозубого колеса: я — эквивалентное колесо

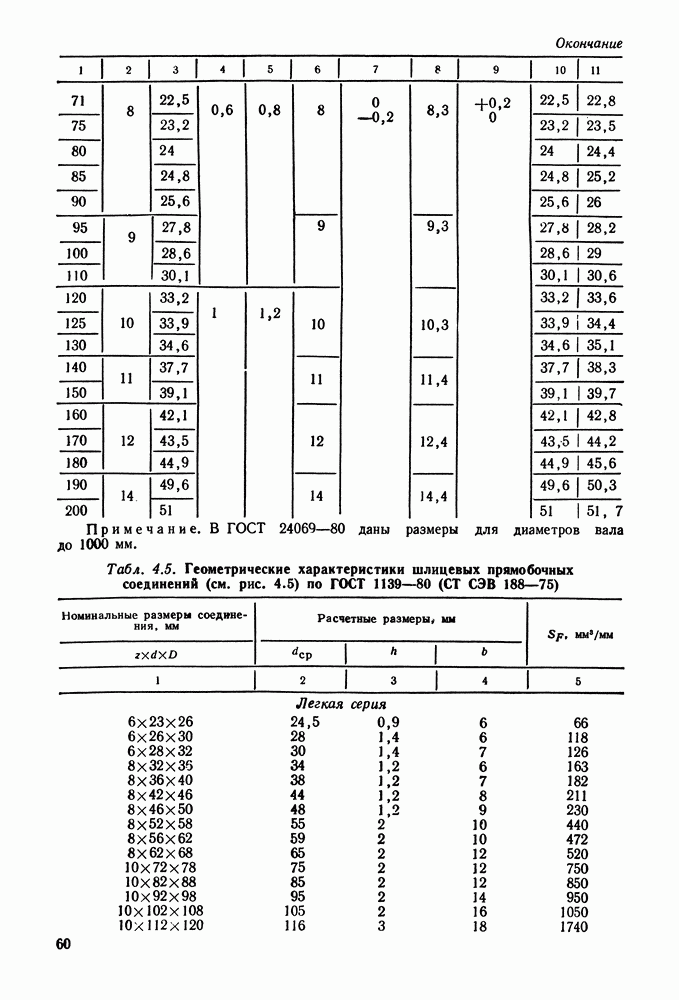
Рис. 9.6. Цилиндрическое косозубое зацепление
радиусу кривизны эллипса в конце его малой полуоси, получающегося в сечении, нормальном к направлению зуба косозубого колеса:

Делительный диаметр эквивалентного колеса

Тогда

Число зубьев эквивалентного колеса

где  — число зубьев косозубого колеса.
— число зубьев косозубого колеса.
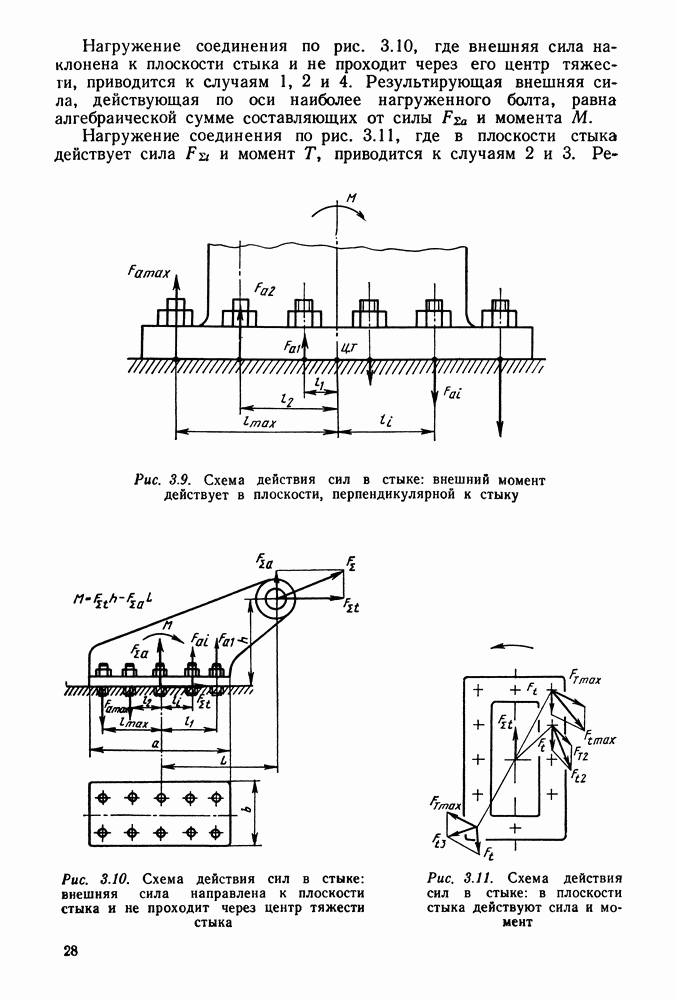
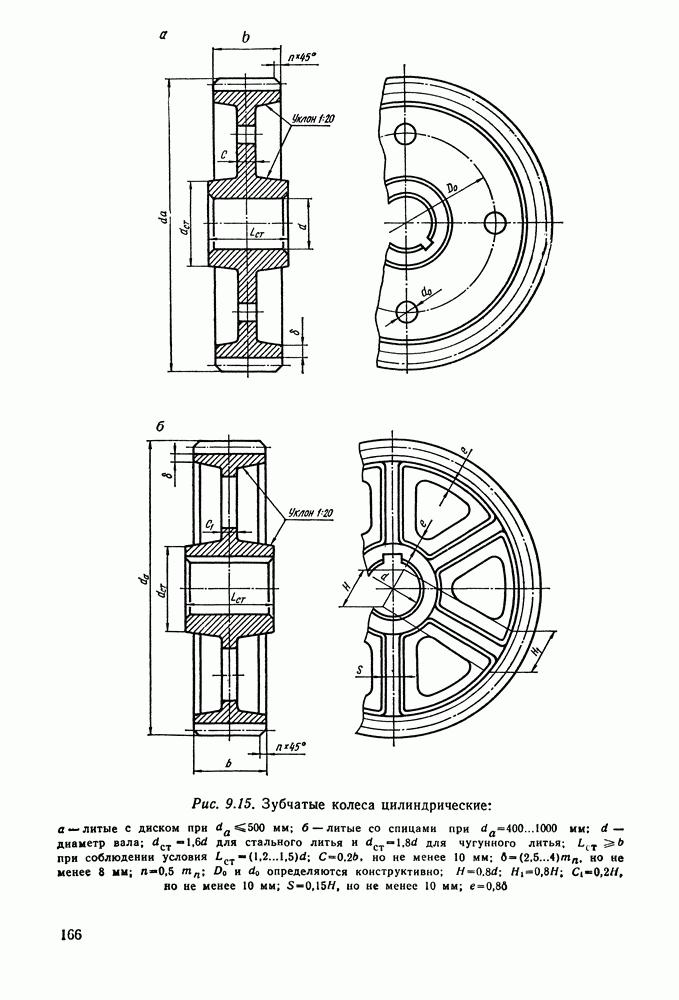
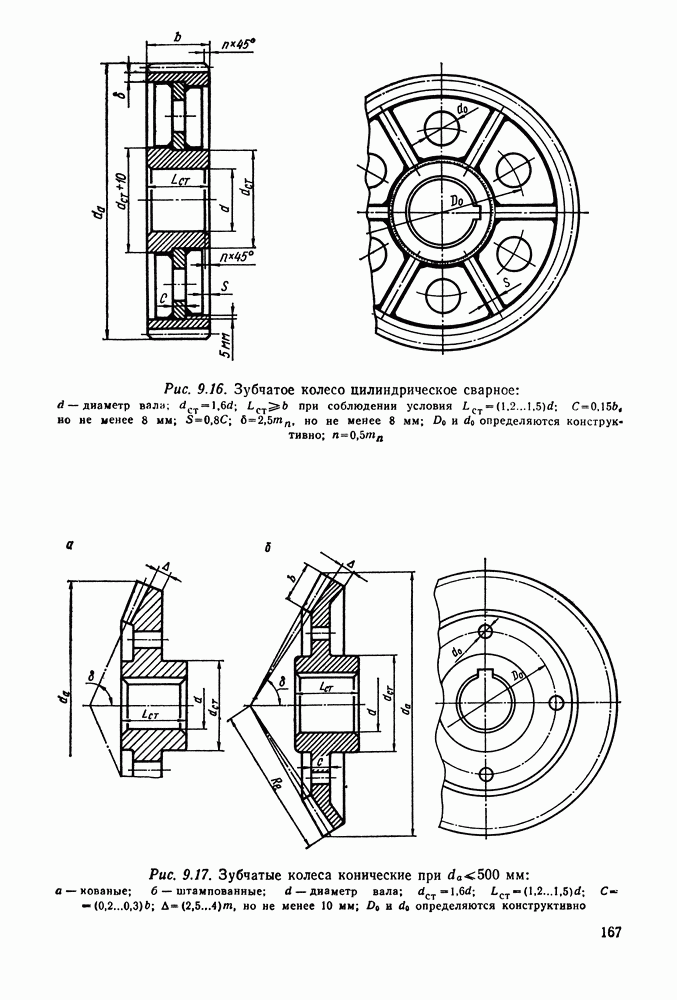
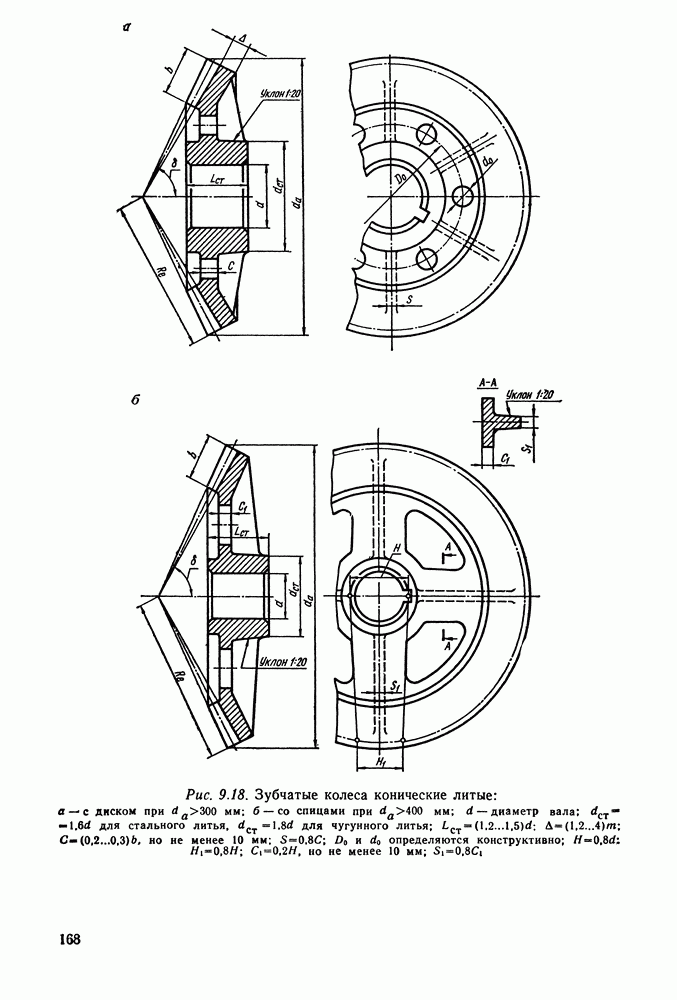
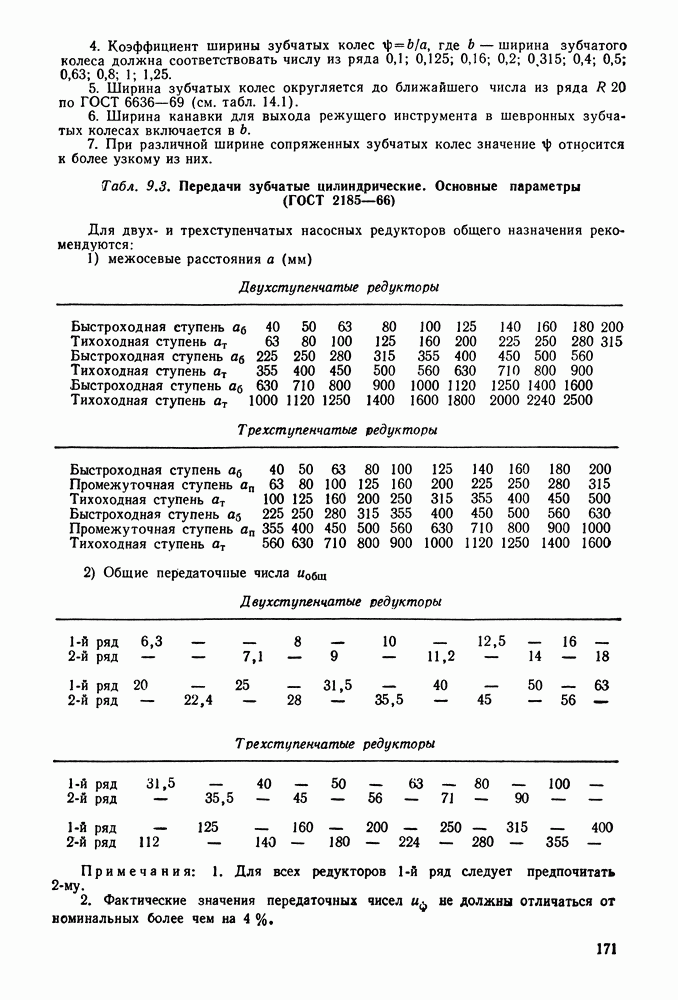
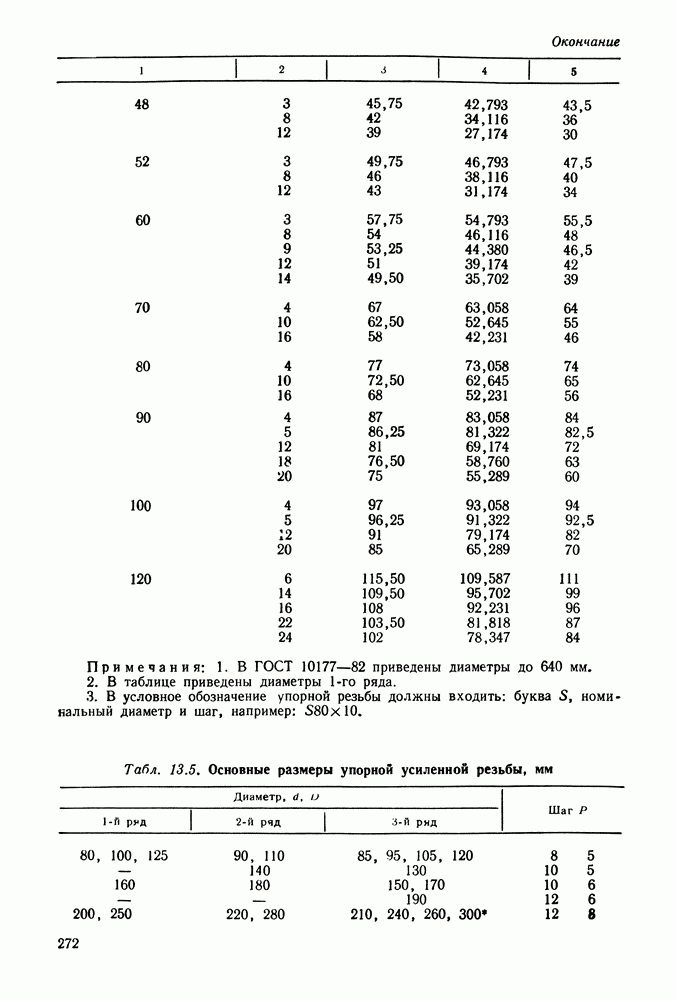
Основные параметры цилиндрических редукторов стандартизованы ГОСТ 2185-66 (см. табл. 9.2 и 9.3 и рис. 9.6).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Раздел I. СОЕДИНЕНИЯ ДЕТАЛЕЙ МАШИН
- Глава 1. ВАЛЬЦОВОЧНЫЕ СОЕДИНЕНИЯ
- 1.2. Расчет прочных швов
- 1.3. Справочный материал
- 1.4. Примеры расчета
- Глава 2. СВАРНЫЕ, ПАЯНЫЕ И КЛЕЕВЫЕ СОЕДИНЕНИЯ
- 2.1. Общие сведения об основных видах сварных соединений и сварных швов
- 2.2. Расчет прочности сварных швов
- 2.3. Условное изображение сварных швов на чертежах
- 2.4. Паяные соединения
- 2.5. Клеевые соединения
- 2.6. Справочный материал
- 2.7. Примеры расчета
- Глава 3. РЕЗЬБОВЫЕ СОЕДИНЕНИЯ
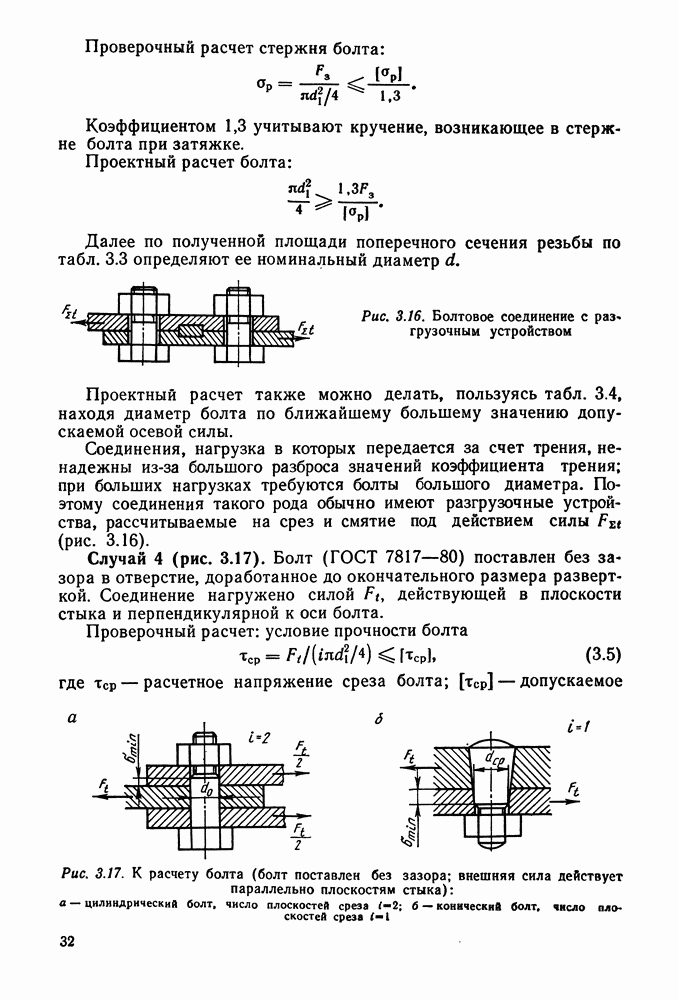
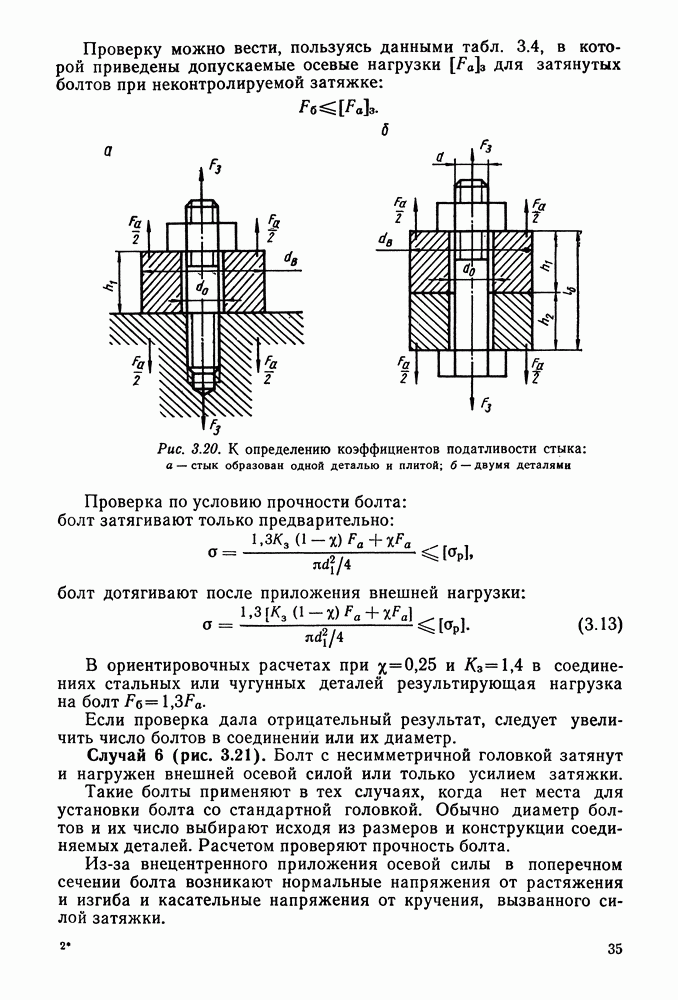
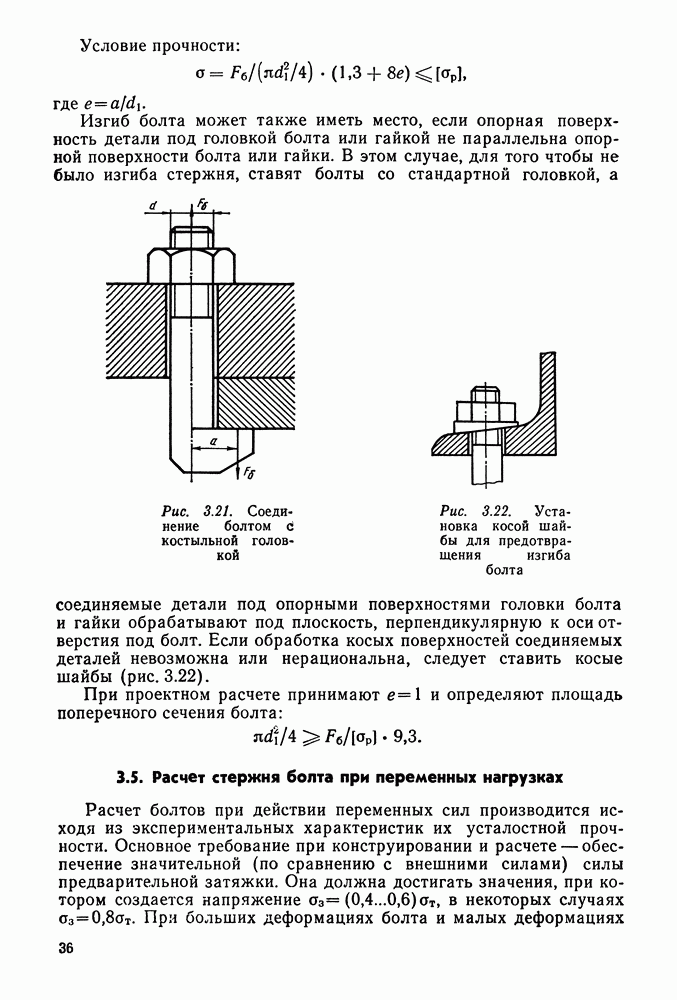
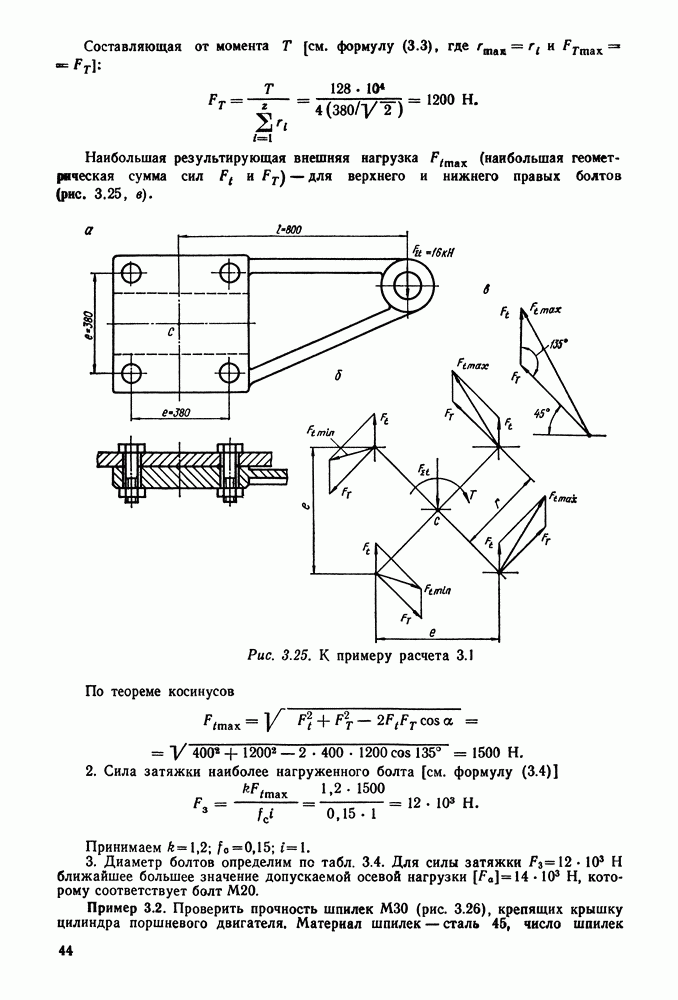
- 3.2. Определение сил, действующих на один болт
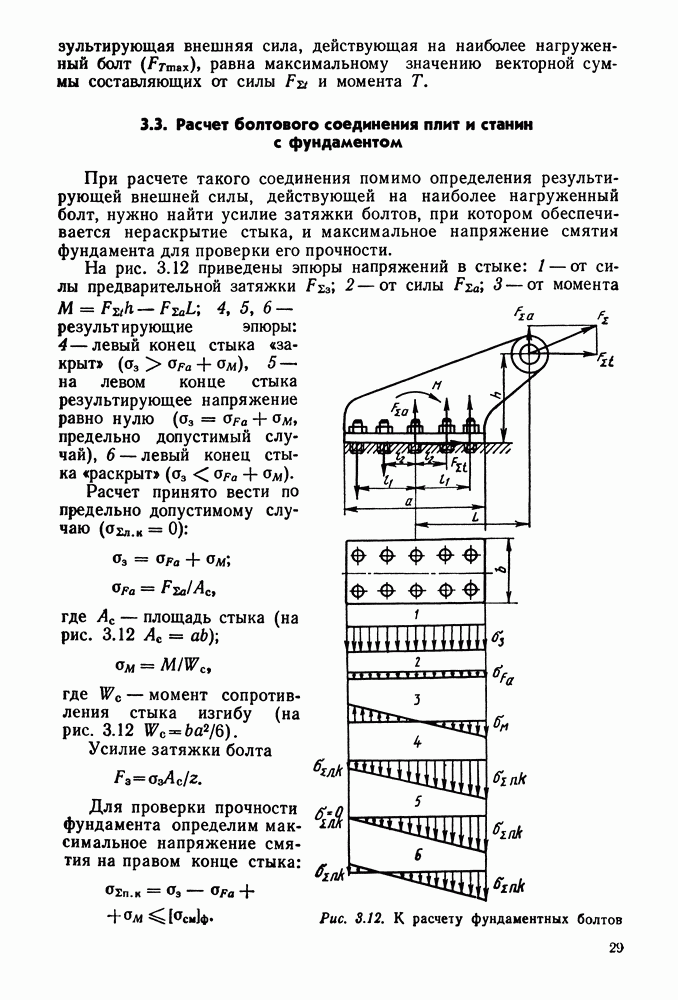
- 3.3. Расчет болтового соединения плит и станин с фундаментом
- 3.4. Расчет стержня болта при постоянных нагрузках
- 3.5. Расчет стержня болта при переменных нагрузках
- 3.6. Расчет витков резьбы на прочность. Определение вращающего момента
- 3.7. Порядок расчета резьбовых соединений
- 3.9. Примеры расчета
- Глава 4. СОЕДИНЕНИЯ ВАЛ — СТУПИЦА (ШПОНОЧНЫЕ, ШЛИЦЕВЫЕ, С НАТЯГОМ)
- 4.2. Шлицевые соединения
- 4.3. Соединения с натягом
- 4.4. Справочный материал
- 4.5. Примеры расчета
- Раздел II. МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ
- Глава 5. КИНЕМАТИЧЕСКИЙ РАСЧЕТ ПРИВОДНЫХ УСТРОЙСТВ И ВЫБОР ЭЛЕКТРОДВИГАТЕЛЯ
- 5.2. Трехфазные асинхронные электродвигатели
- 5.3. Разбивка общего передаточного числа редуктора по ступеням
- 5.4. Справочный материал
- 5.5. Примеры расчета
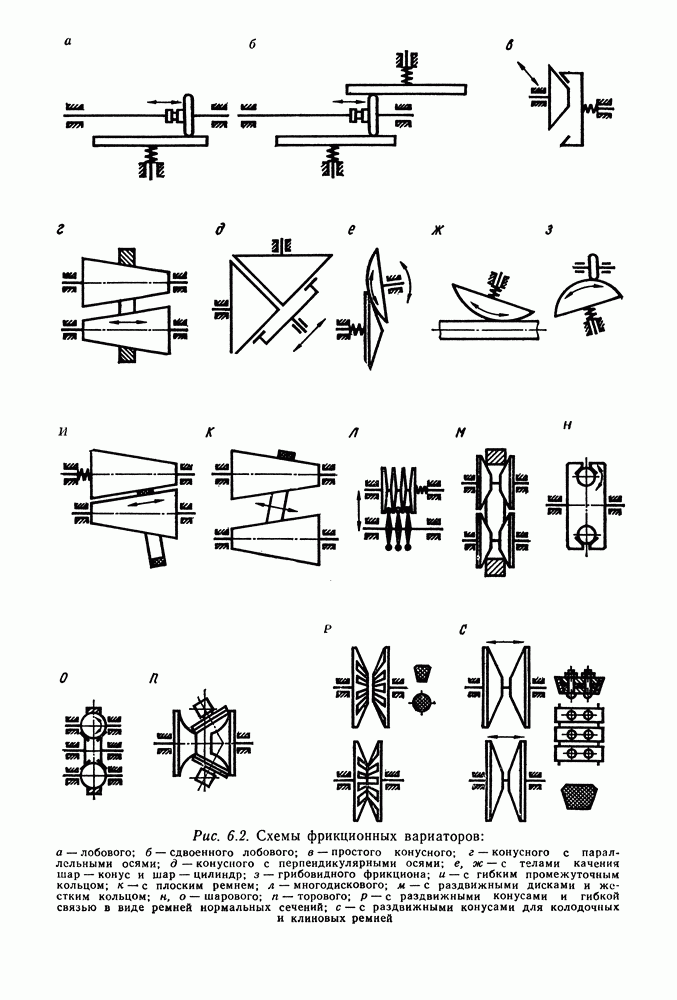
- Глава 6. ФРИКЦИОННЫЕ ПЕРЕДАЧИ И ВАРИАТОРЫ
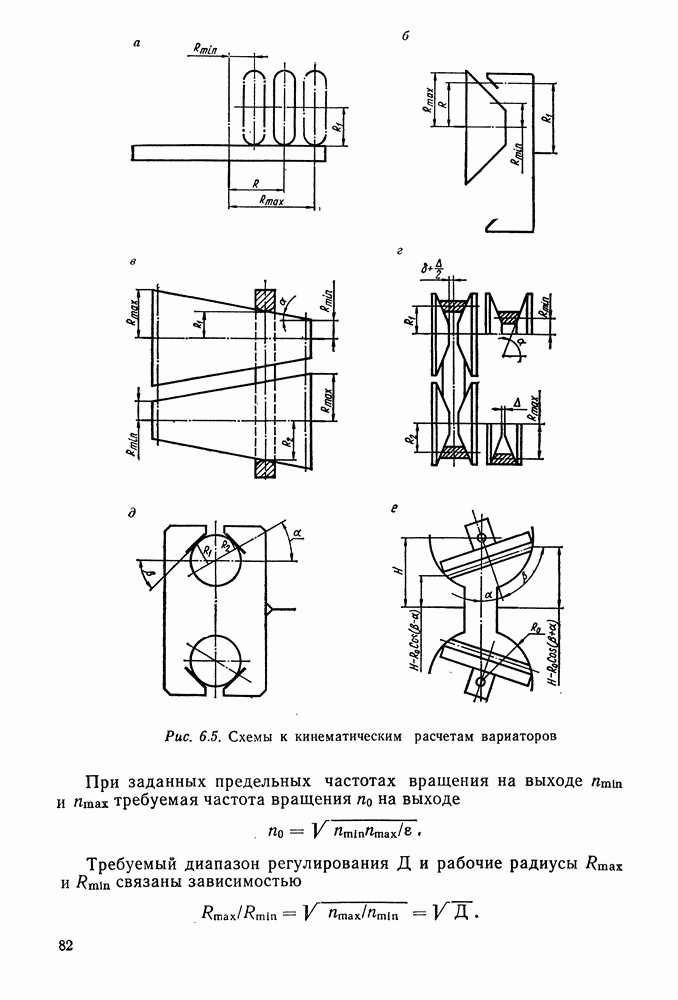
- 6.2. Кинематические расчеты фрикционных передач
- 6.3. Определение сил прижатия фрикционных тел и нагрузки на валы передачи
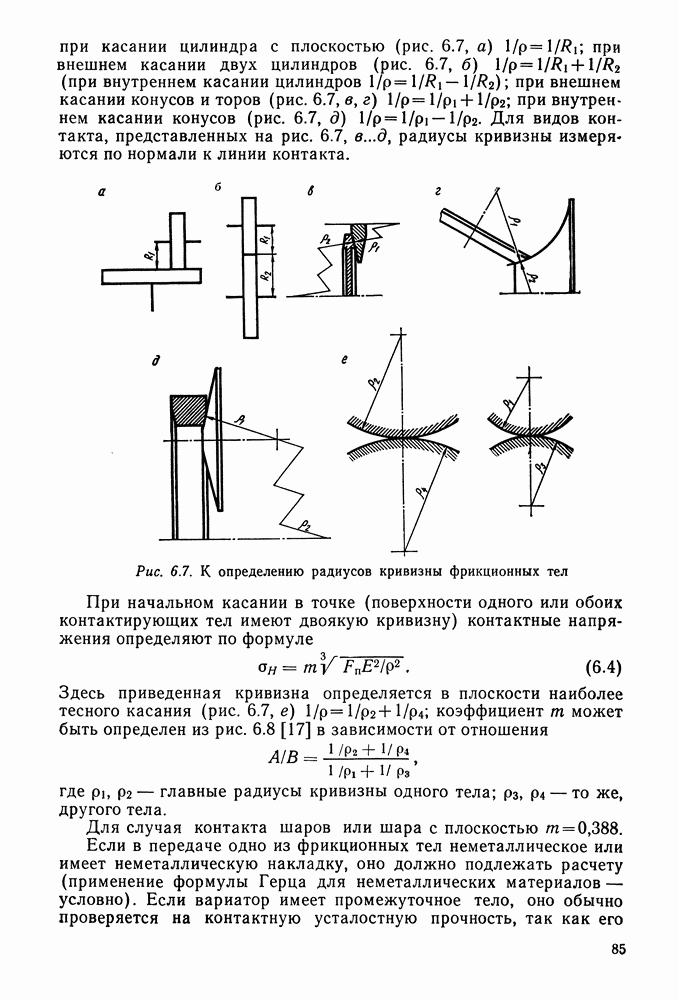
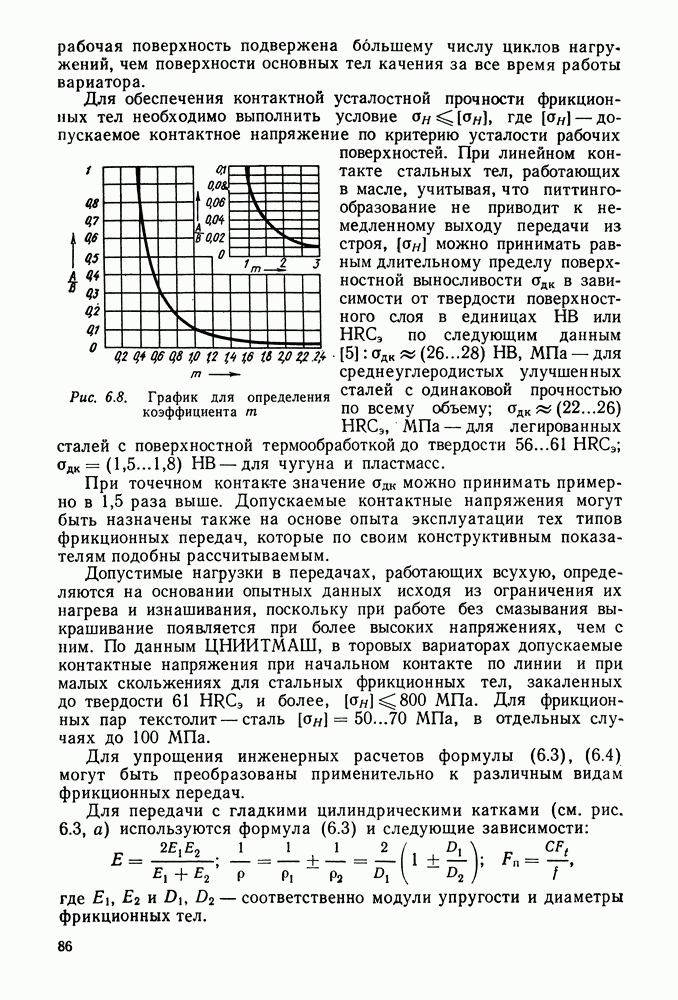
- 6.4. Расчет фрикционных тел на контактную прочность и КПД передач
- 6.5. Справочный материал
- 6.6. Примеры расчета
- Глава 7. РЕМЕННЫЕ ПЕРЕДАЧИ
- 7.2. Расчет клиноременных передач
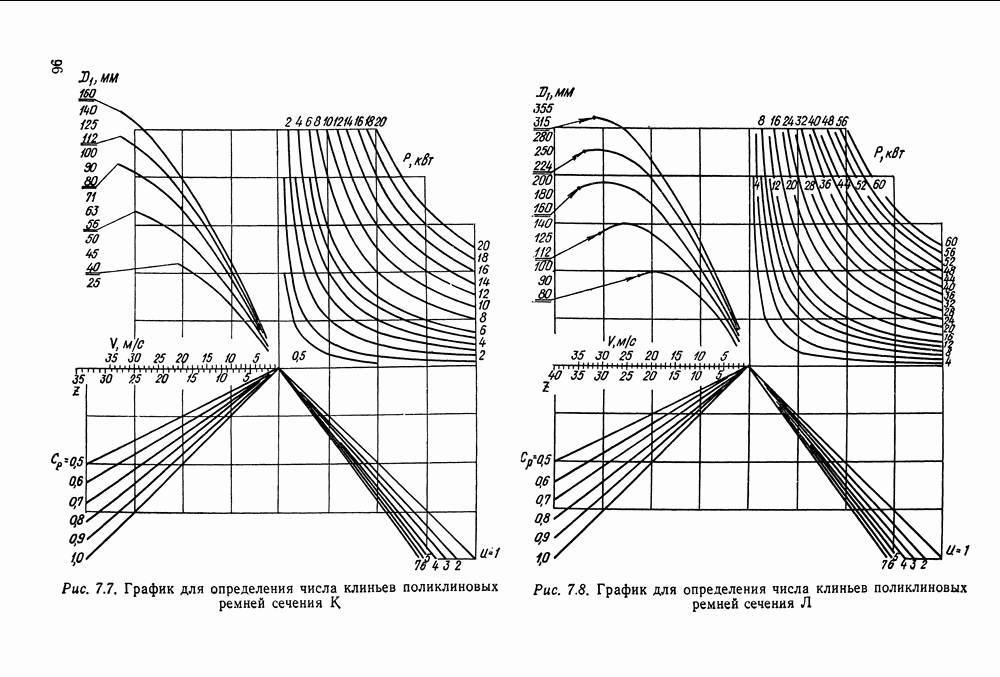
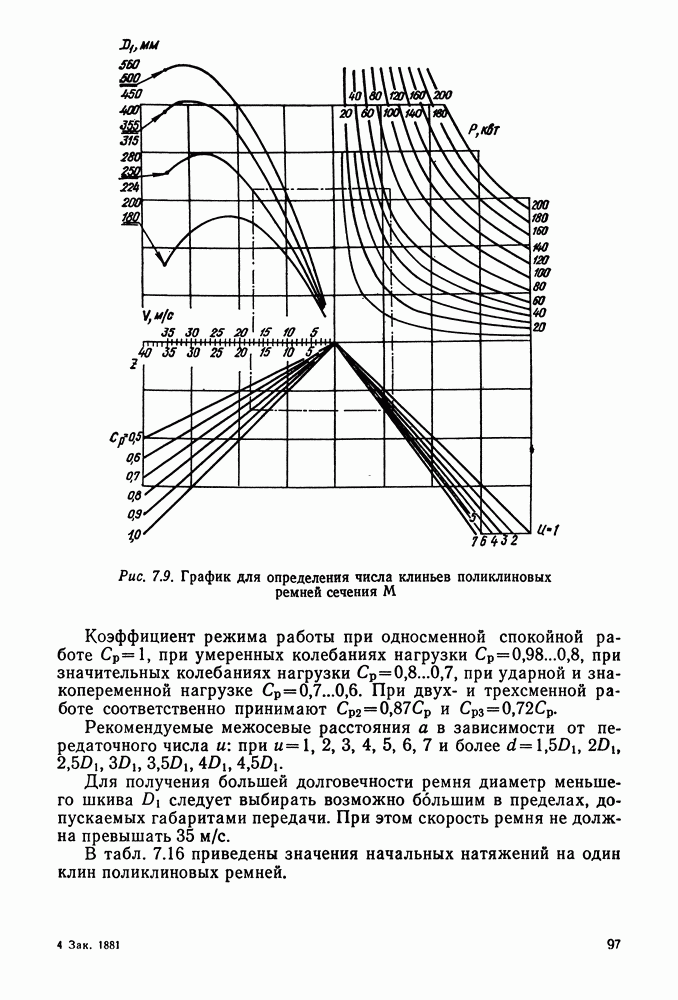
- 7.3. Расчет передач поликлиновыми ремнями
- 7.4. Расчет зубчато-ременных передач
- 7.5. Справочный материал
- 7.6. Примеры расчета
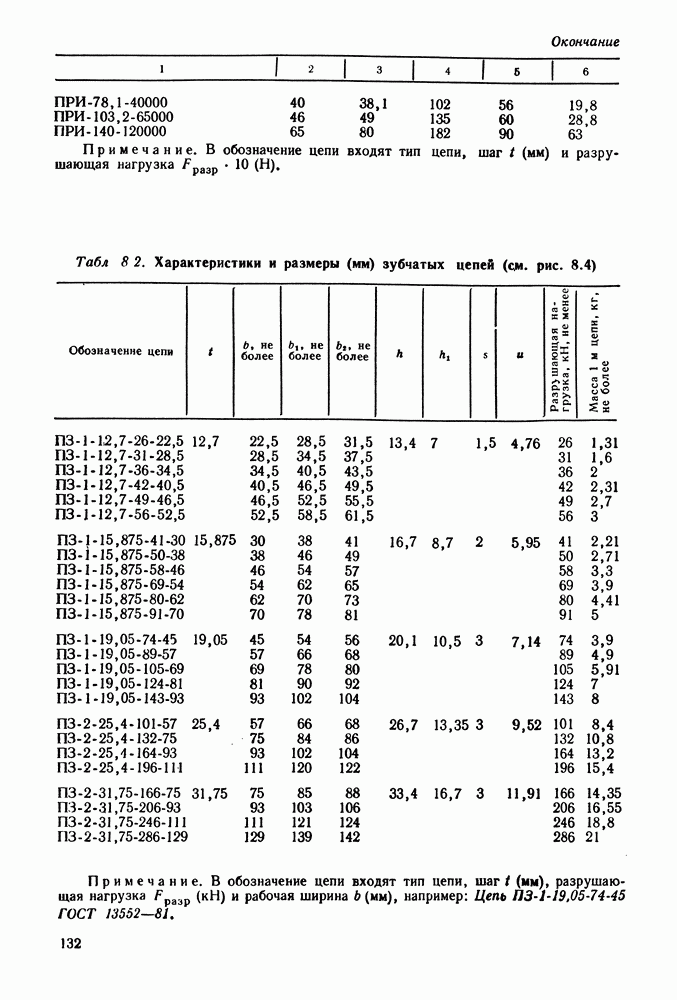
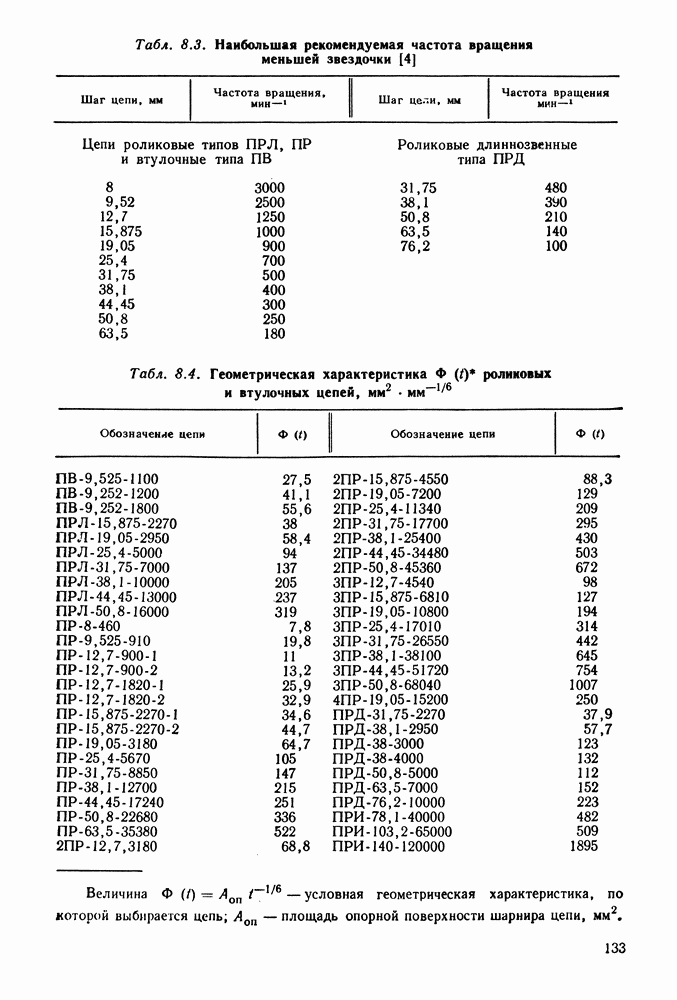
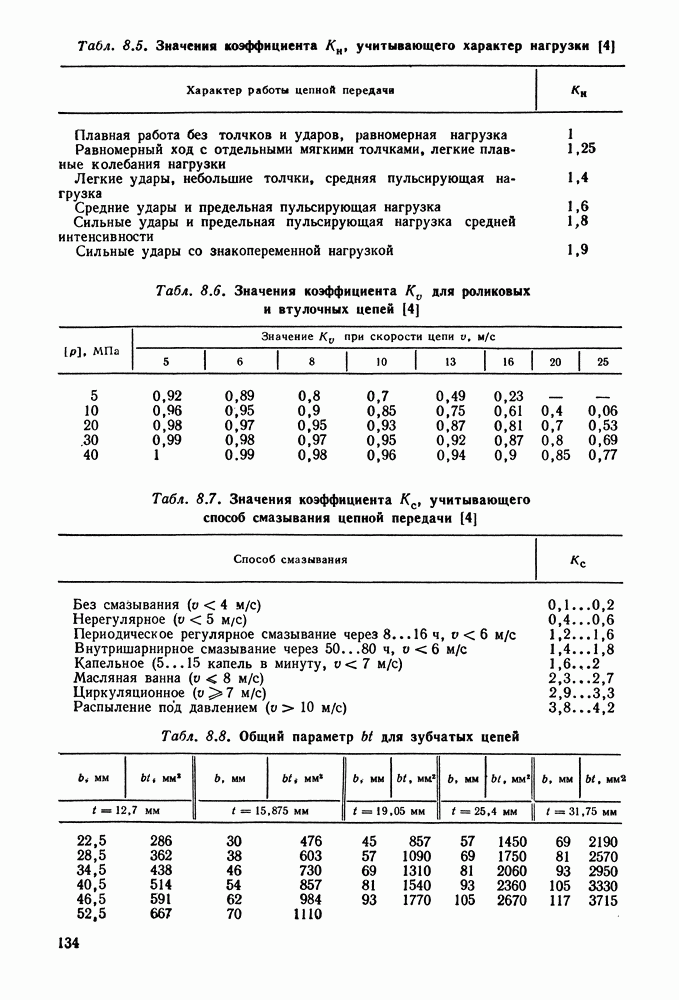
- Глава 8. ЦЕПНЫЕ ПЕРЕДАЧИ
- 8.2. Геометрический, кинематический и силовой расчеты цепных передач
- 8.3. Выбор основных параметров и расчет цепных передач
- 8.4. Справочный материал
- 8.5. Примеры расчета
- Глава 9. ЗУБЧАТЫЕ ПЕРЕДАЧИ
- 9.2. Геометрия и кинематика эвольвентного цилиндрического зацепления
- 9.3. Зубчатые зацепления со смещением (корригированные)
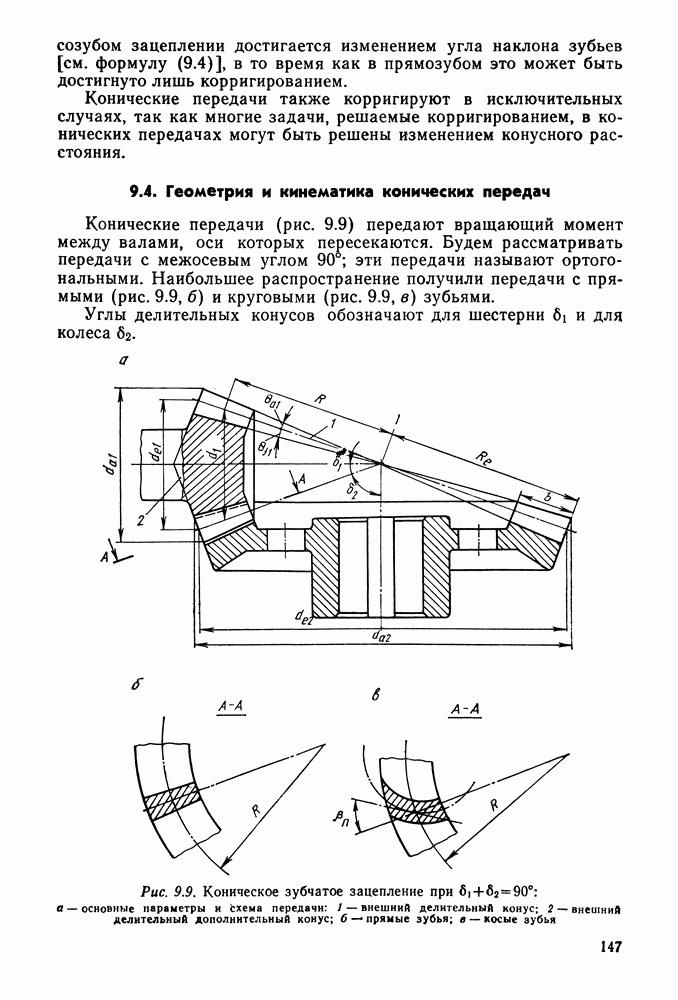
- 9.4. Геометрия и кинематика конических передач
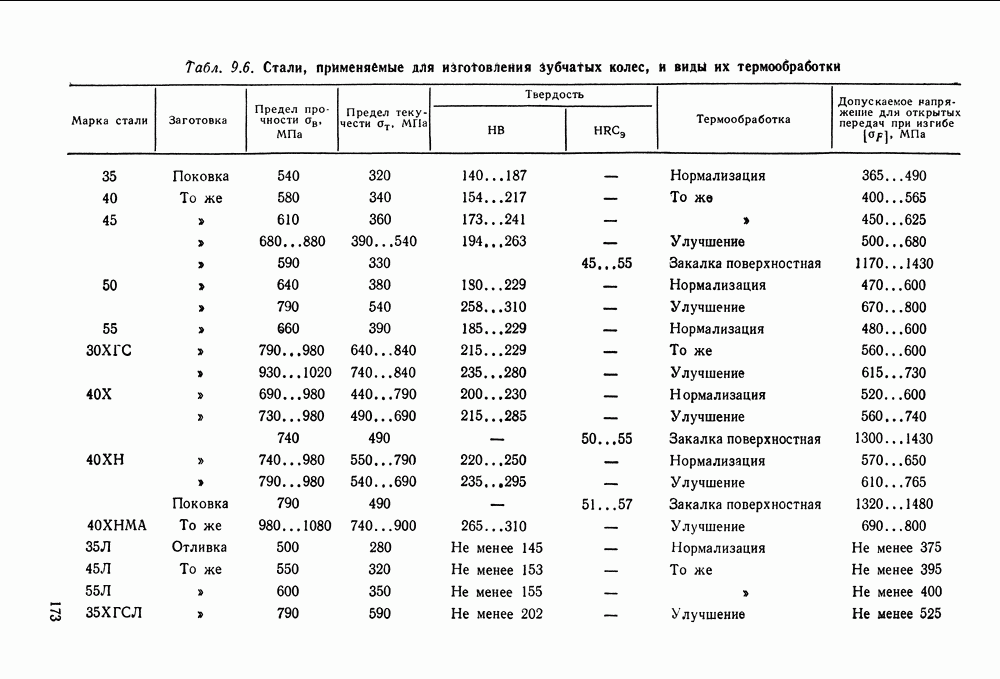
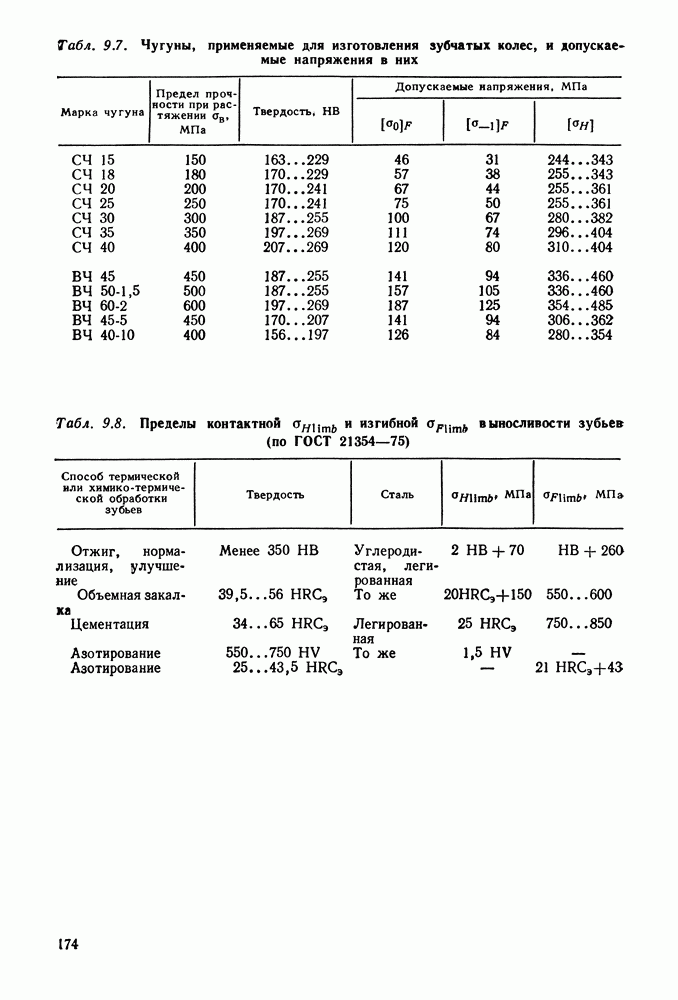
- 9.5. Материалы и допускаемые напряжения
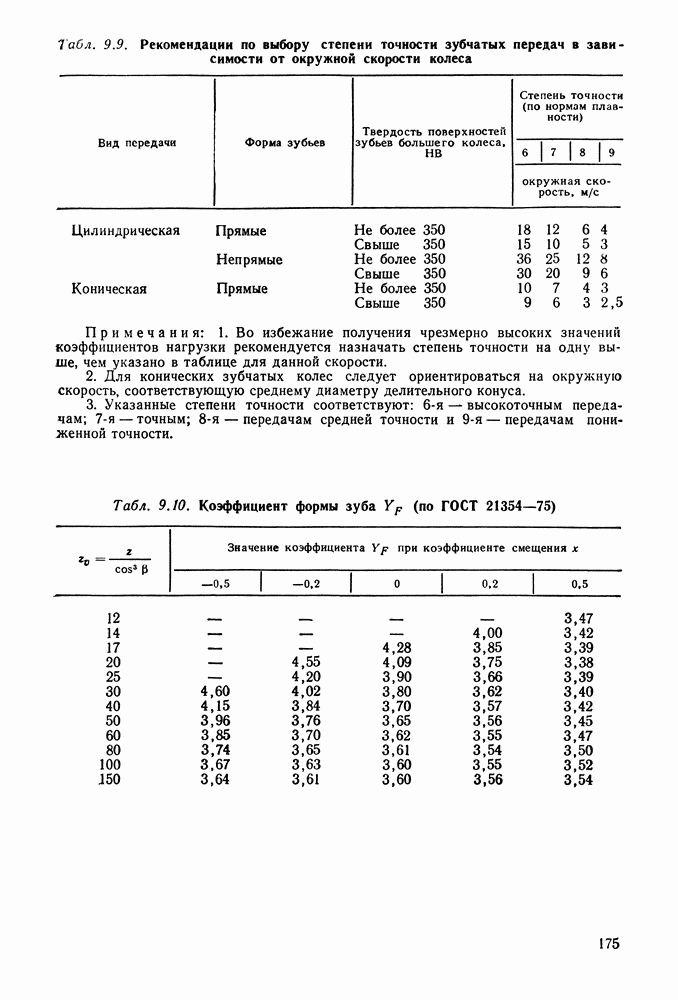
- 9.6. Точность зубчатых передач
- 9.7. Коэффициент нагрузки
- 9.8. Расчет зубчатого зацепления на контактную прочность
- 9.9. Расчет зубьев колес на изгиб
- 9.10. Расчет открытых зубчатых передач
- 9.11. Проверка прочности зубьев колес при перегрузках
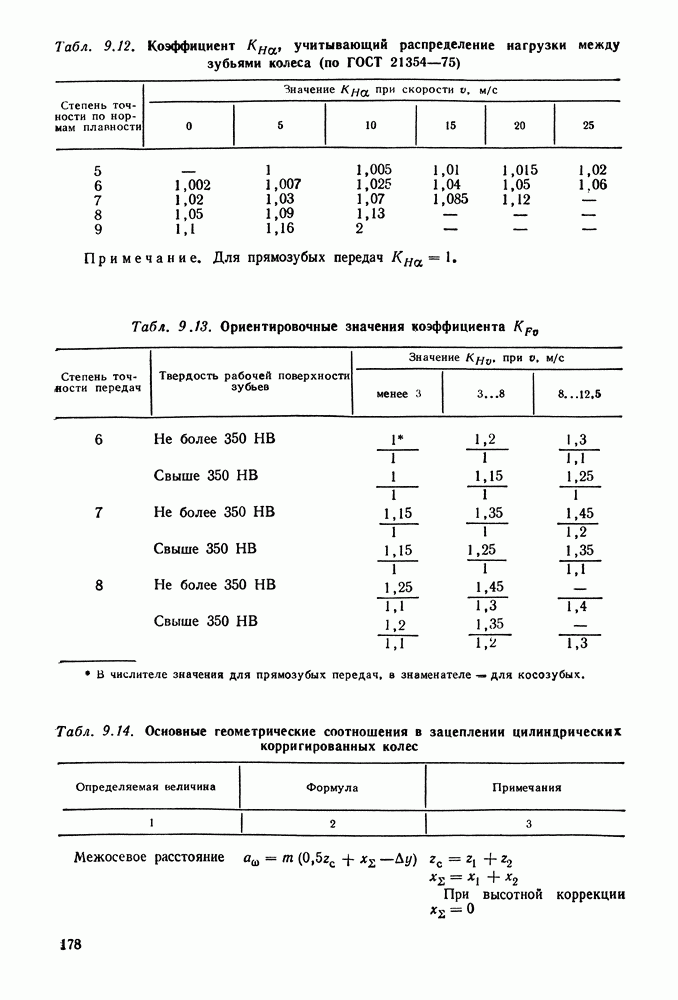
- 9.12. Определение размеров стальных зубчатых закрытых передач и проверка их прочности
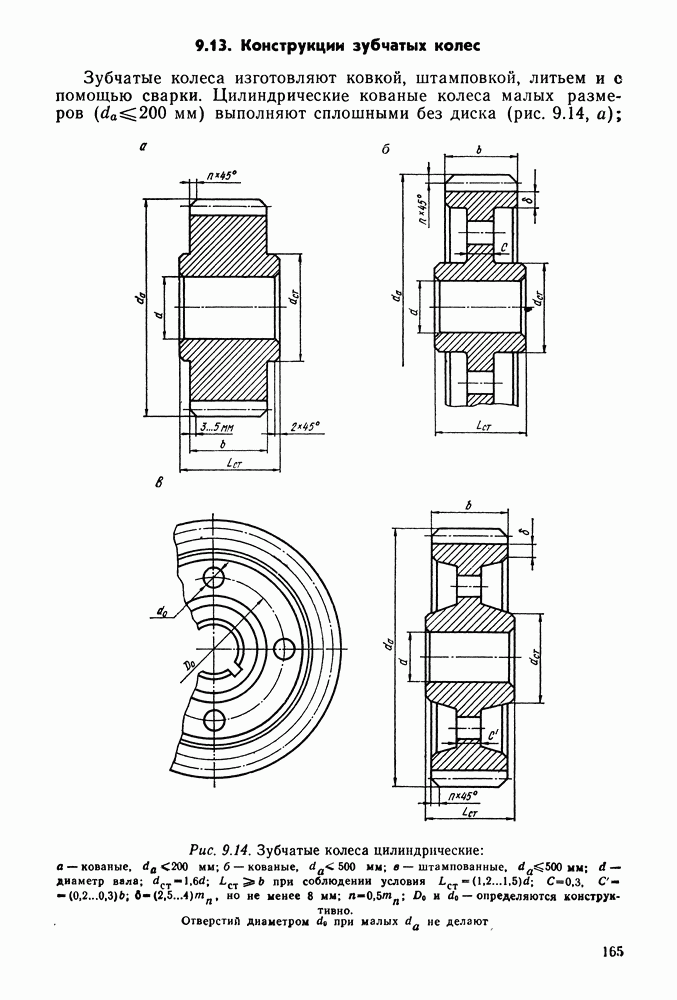
- 9.13. Конструкции зубчатых колес
- 9.14. Справочный материал
- 9.15. Примеры расчета
- Глава 10. ПЛАНЕТАРНЫЕ ПЕРЕДАЧИ
- 10.2. Кинематический расчет
- 10.3. Условия собираемости соосных и многопоточных передач
- 10.4. Порядок подбора чисел зубьев при заданном передаточном отношении и числе сателлитов
- 10.5. Определение КПД планетарных передач
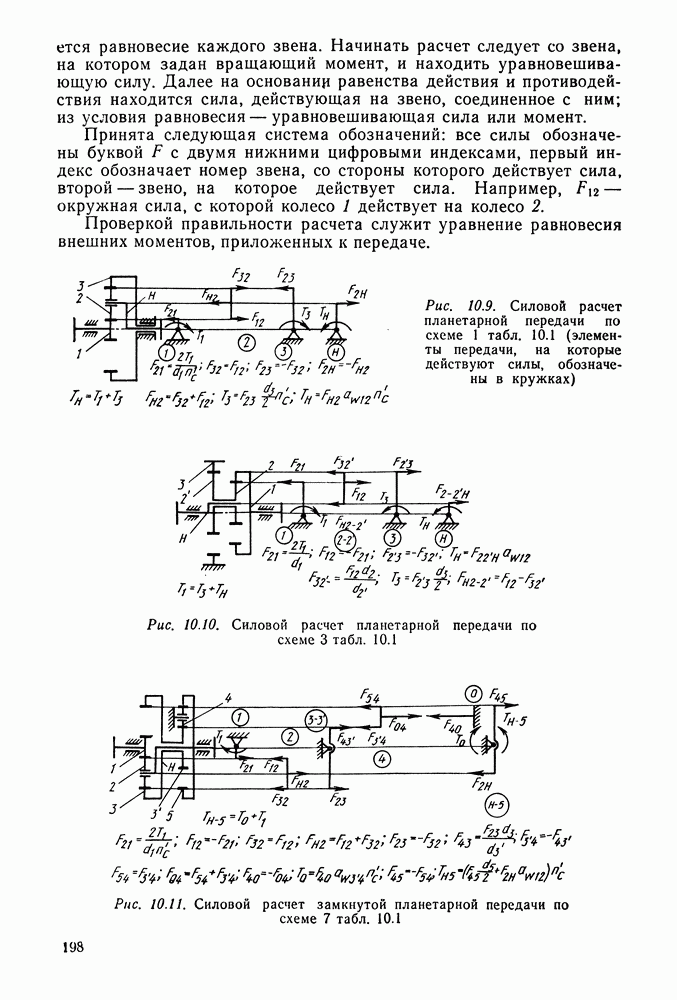
- 10.6. Определение сил, действующих в зацеплениях и в опорах осей и валов прямозубых передач
- 10.7. Расчет зубьев планетарных передач на прочность
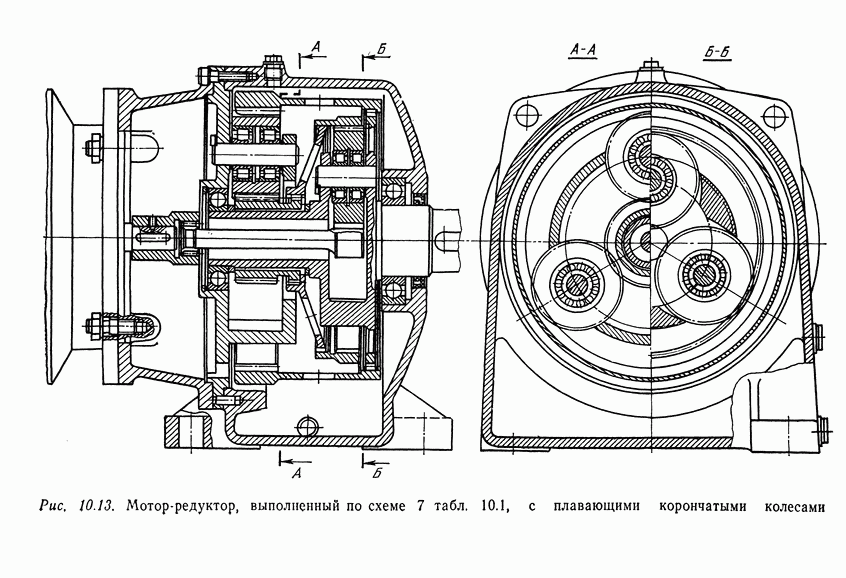
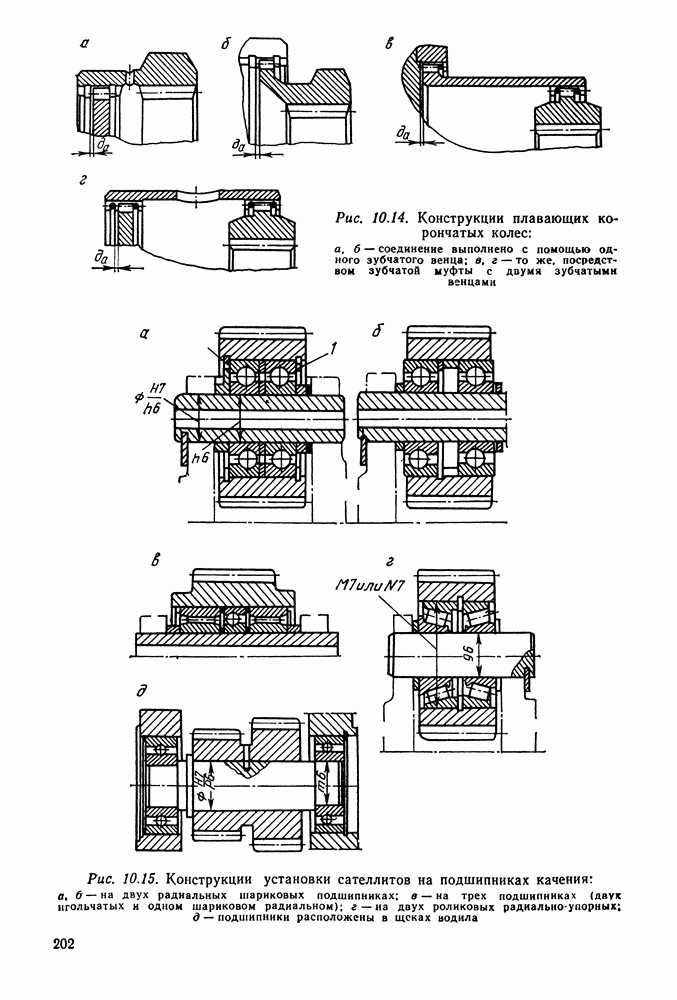
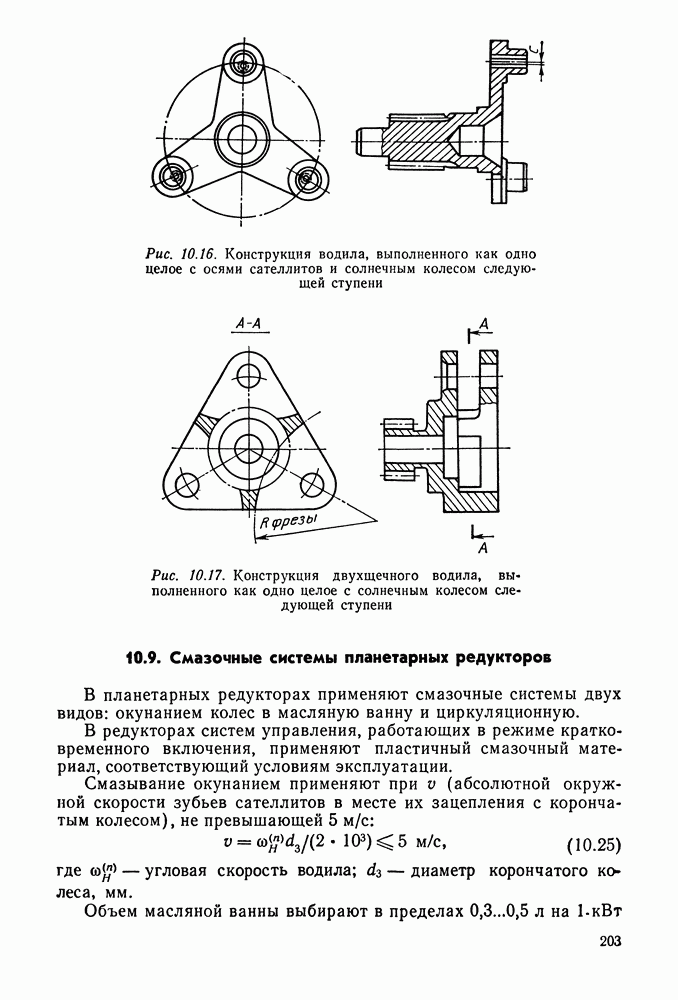
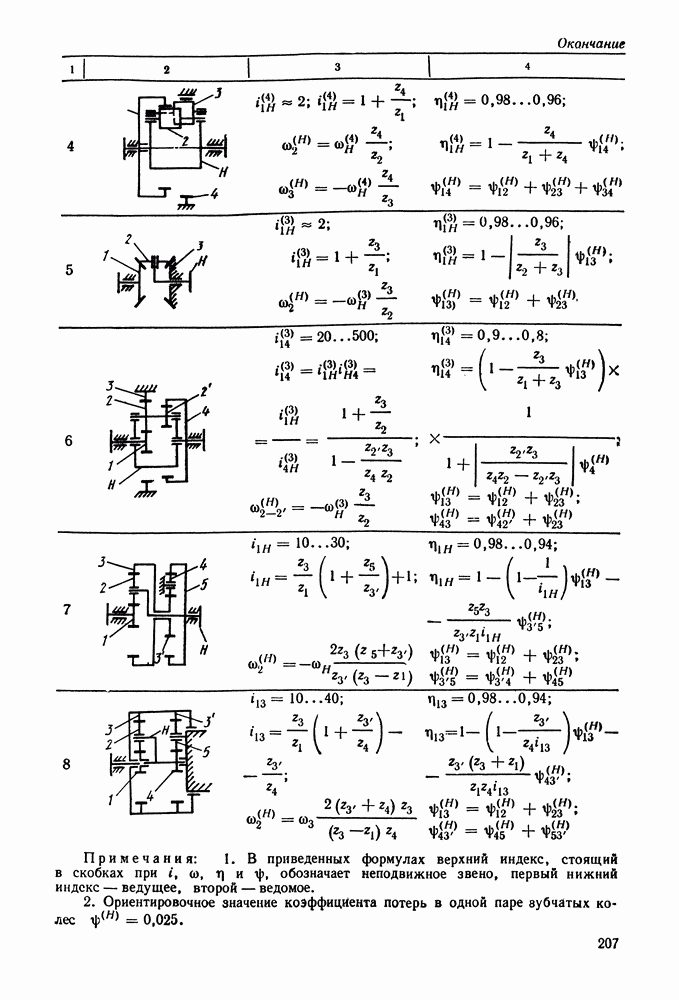
- 10.8. Конструкция и размеры деталей планетарных передач [14]
- 10.9. Смазочные системы планетарных редукторов
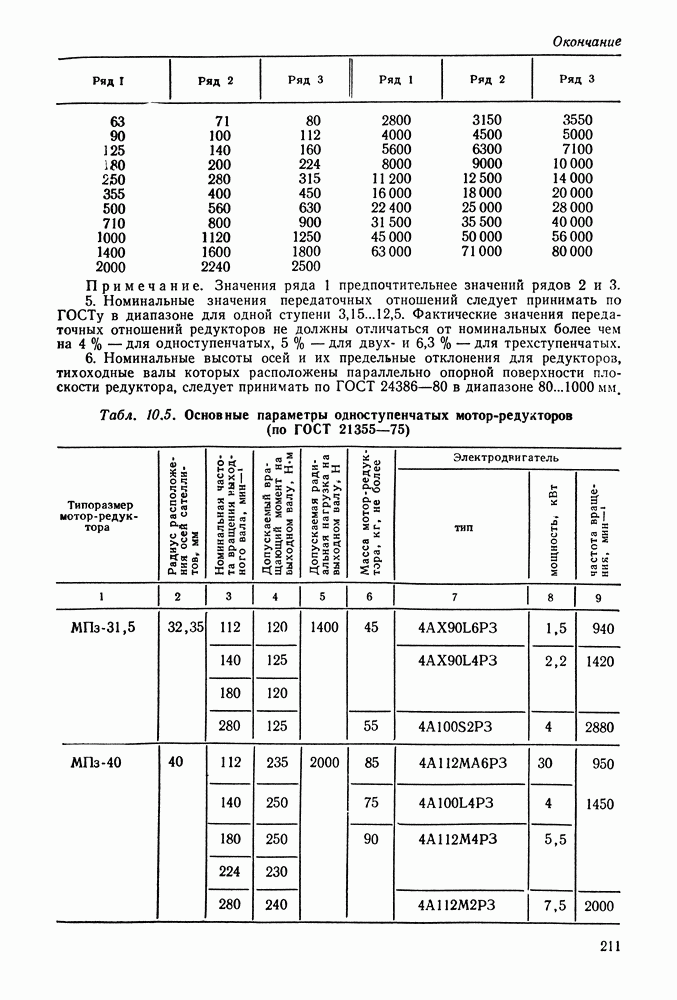
- 10.10. Порядок проектного расчета планетарного редуктора (схемы 1 и 2 табл. 10.1)
- 10.11. Порядок расчета планетарного мотор-редуктора (схема 1 табл. 10.1)
- 10.12. Справочный материал
- 10.13. Примеры расчета
- Глава 11. ВОЛНОВЫЕ ПЕРЕДАЧИ
- 11.2 Основные схемы волновых передач
- 11.3. Проектный расчет волновой зубчатой передачи
- 11.4. Конструкция и размеры основных деталей волновых передач
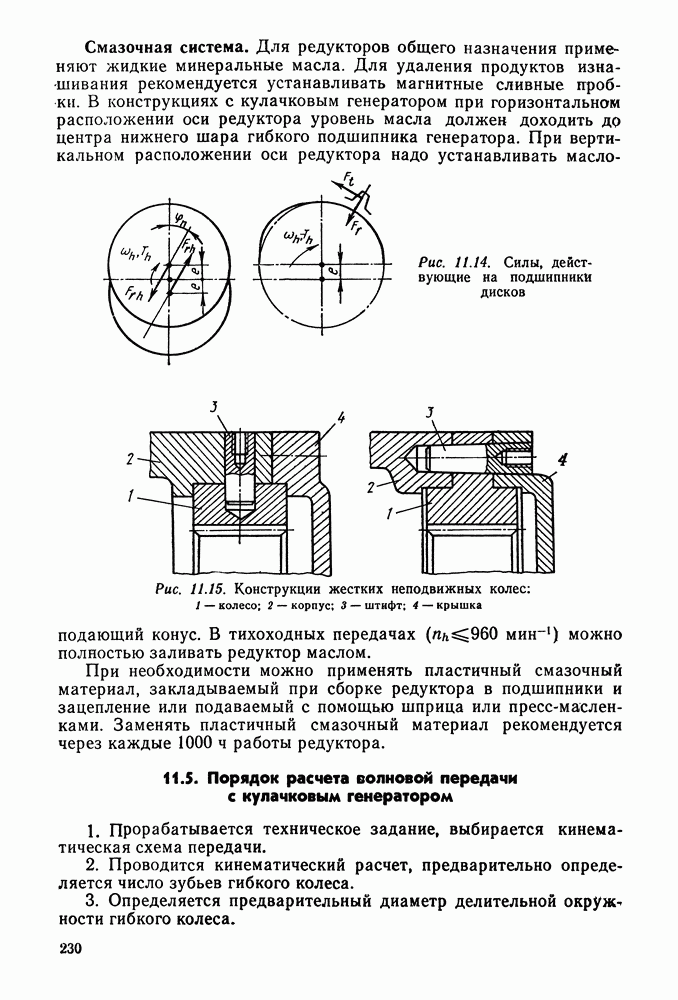
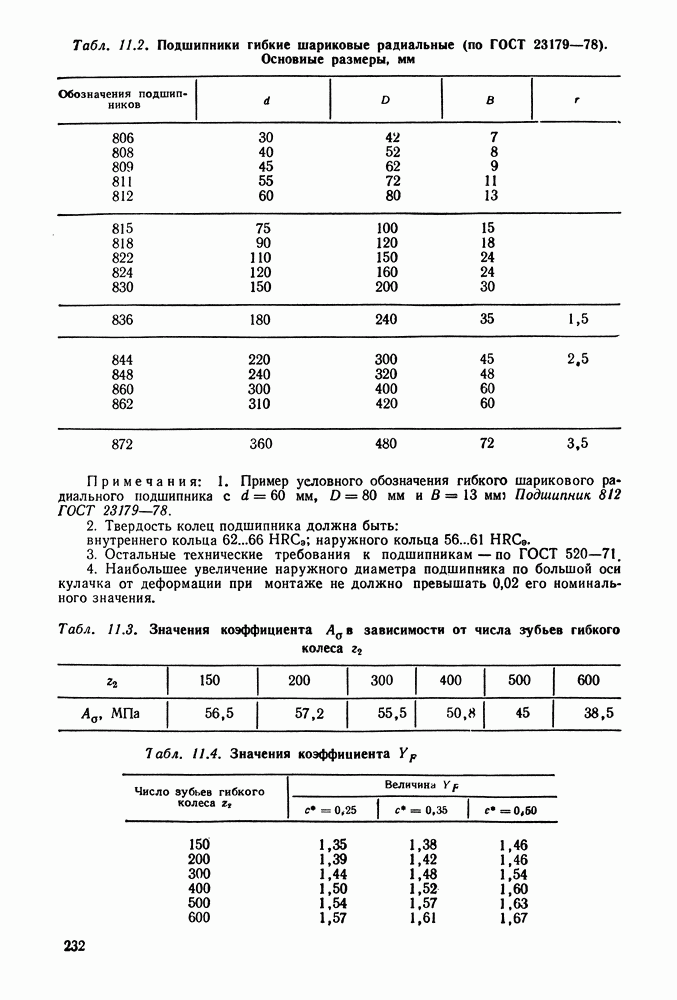
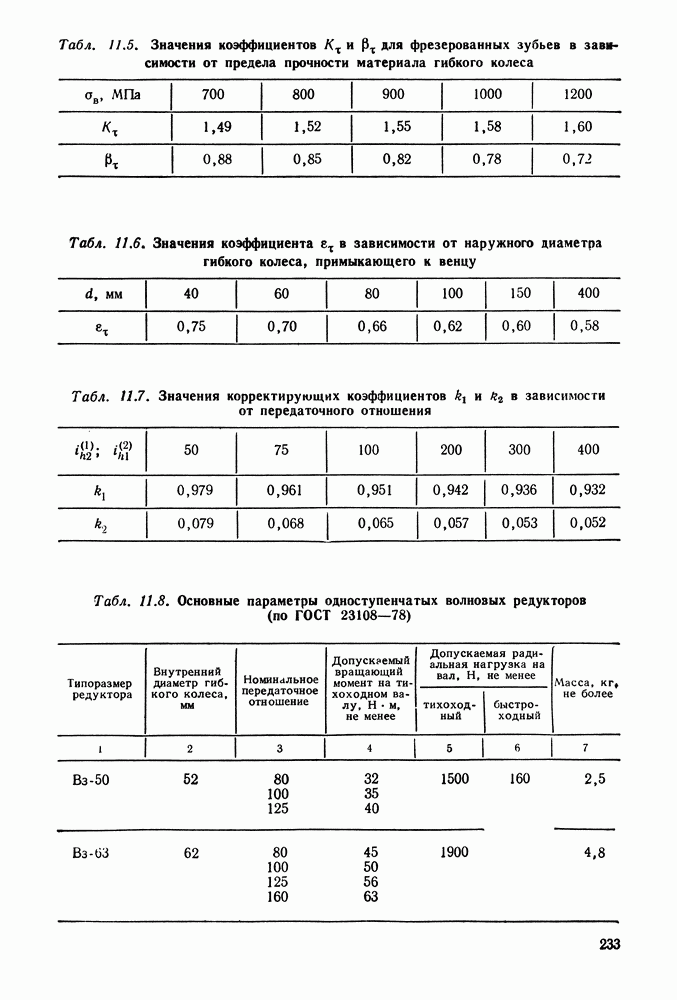
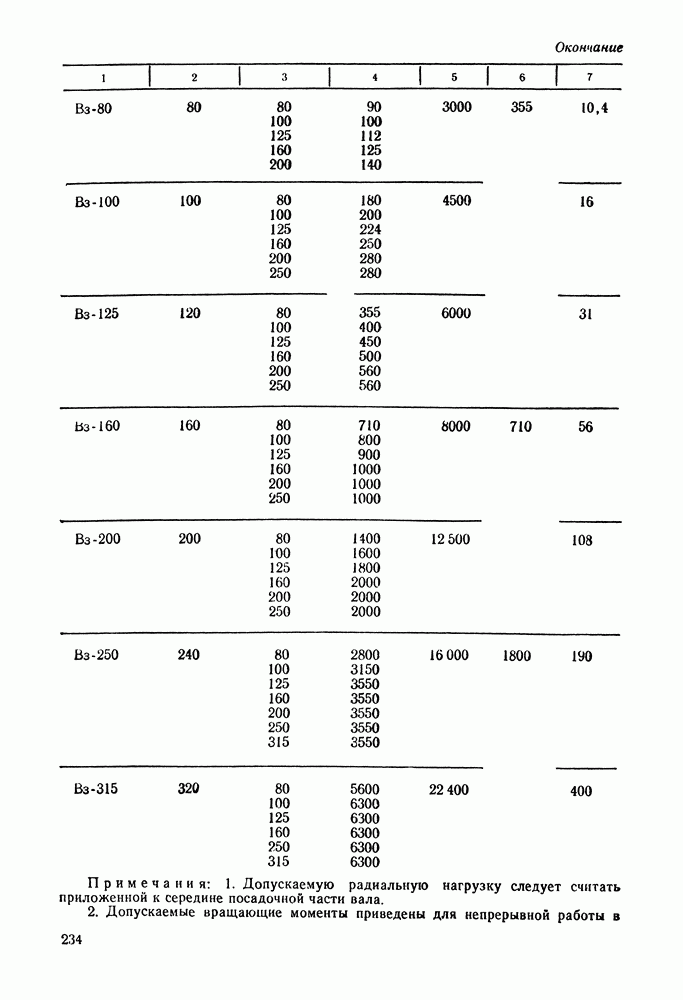
- 11.5. Порядок расчета волновой передачи с кулачковым генератором
- 11.6. Справочный материал
- 11.7. Пример расчета
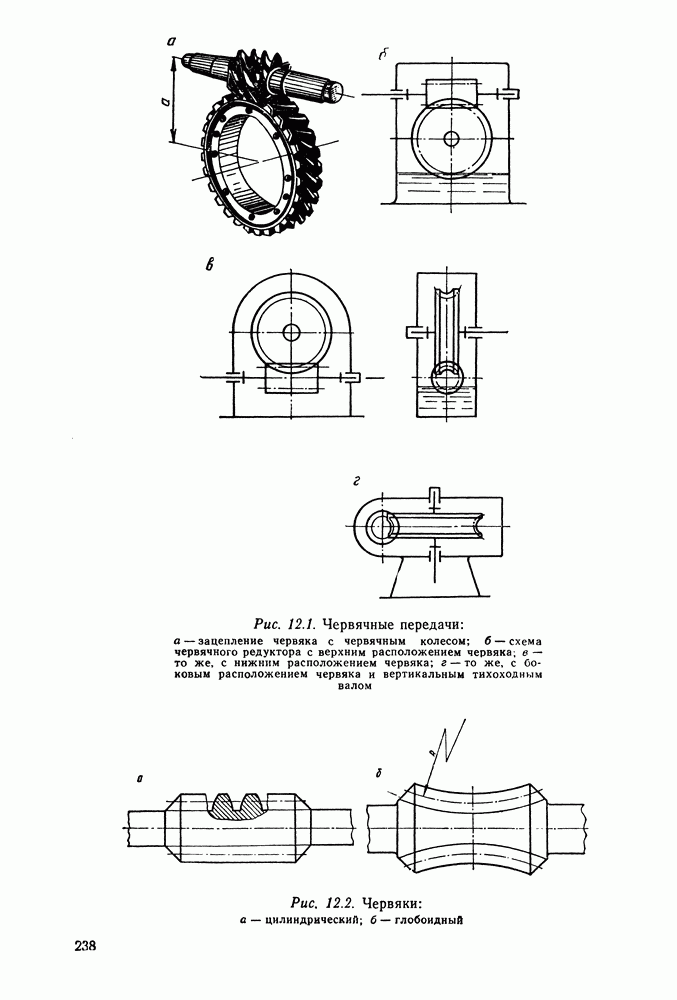
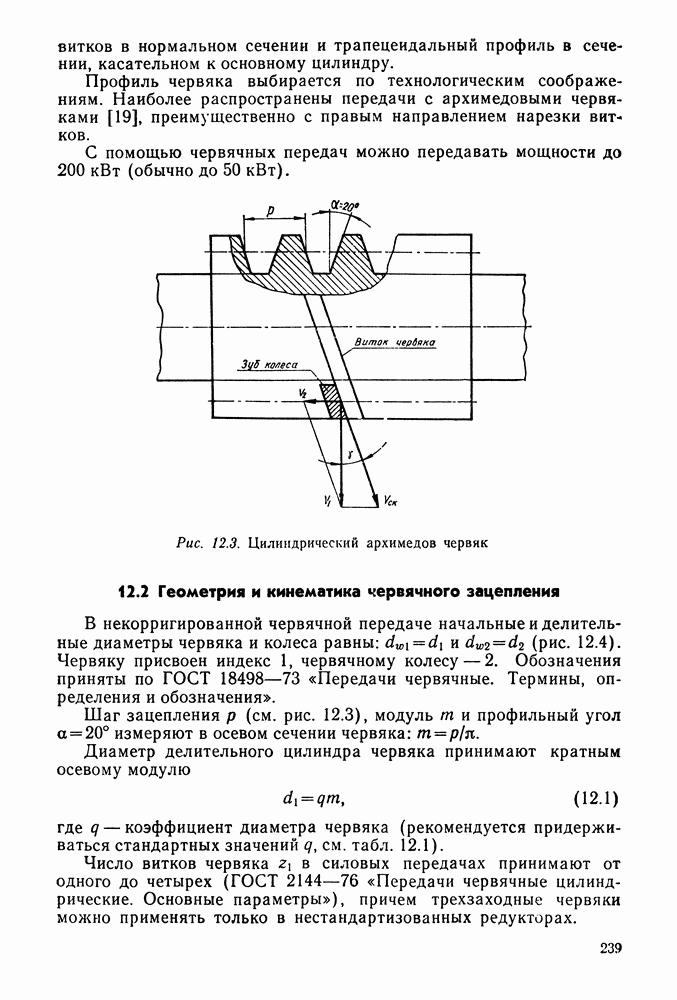
- Глава 12. ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ
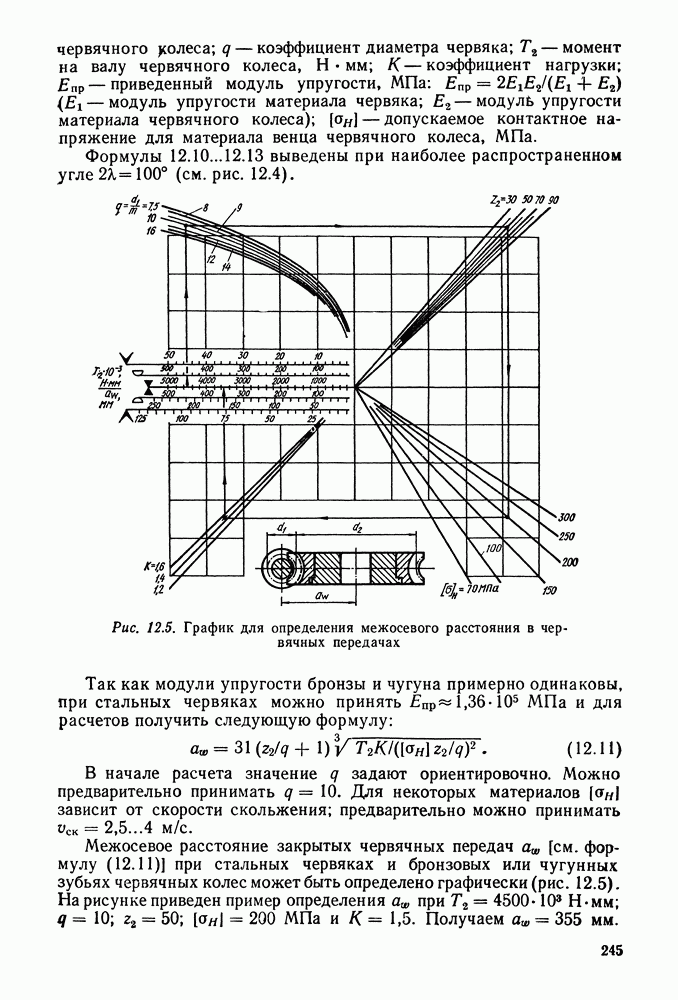
- 12.2 Геометрия и кинематика червячного зацепления
- 12.3. Червячные передачи со смещением (корригированные)
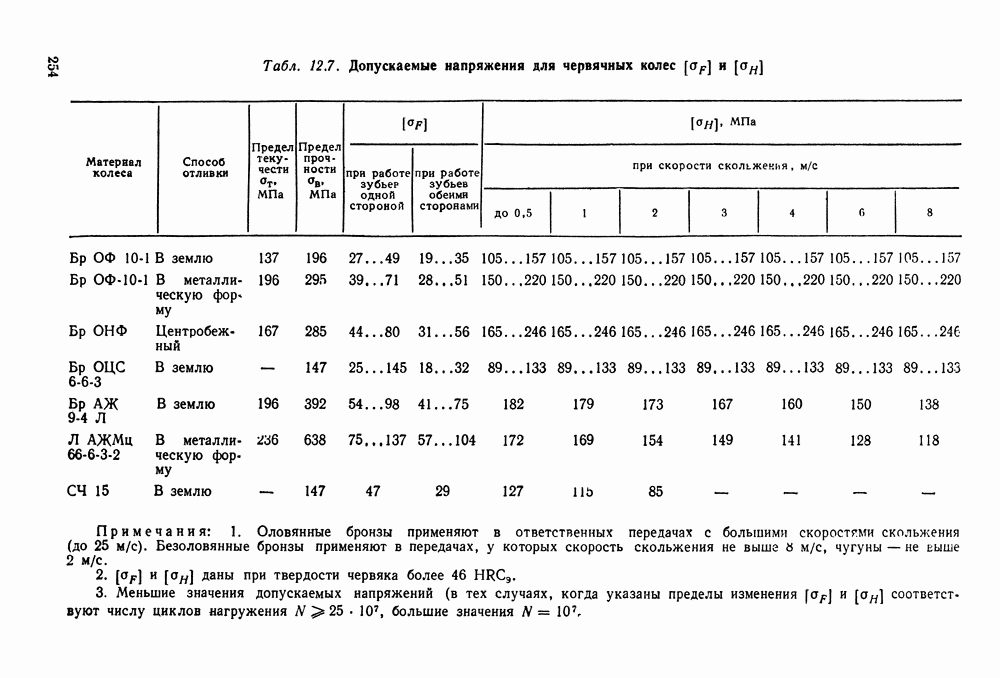
- 12.4. Материалы и допускаемые напряжения
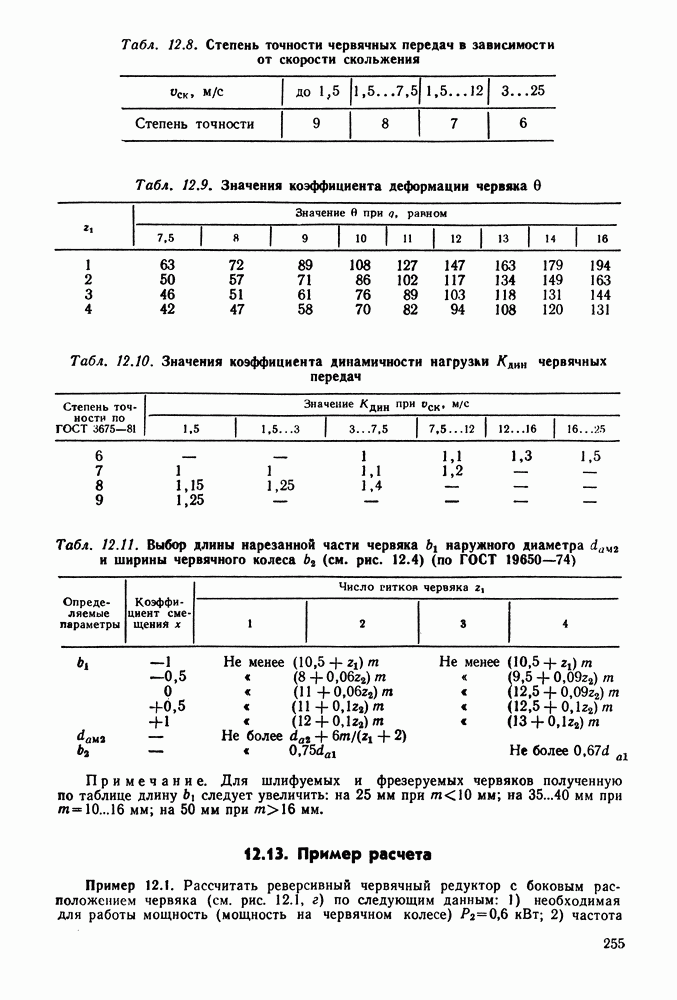
- 12.5. Точность червячных передач
- 12.6. Коэффициент нагрузки
- 12.7. Расчет червячного зацепления на контактную прочность
- 12.8. Расчет на изгиб
- 12.9. Расчет открытых червячных передач
- 12.10. Проверка червячных редукторов на нагрев
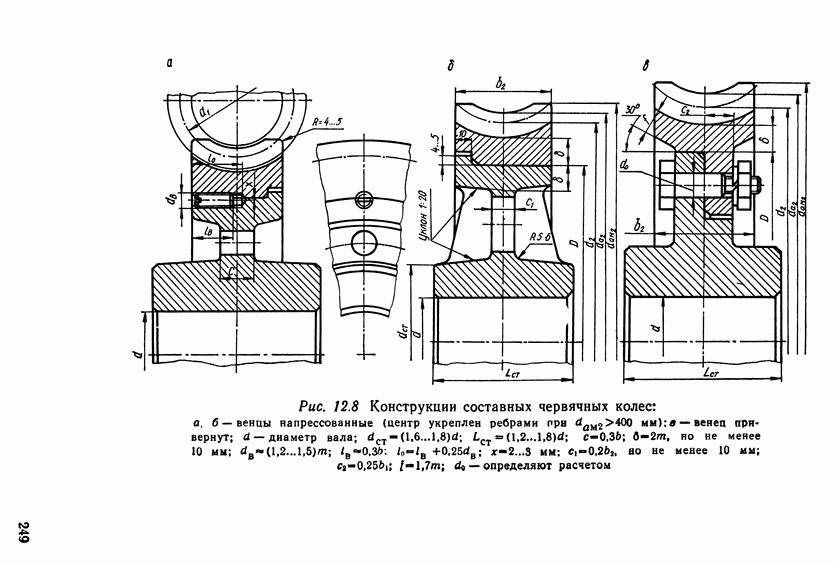
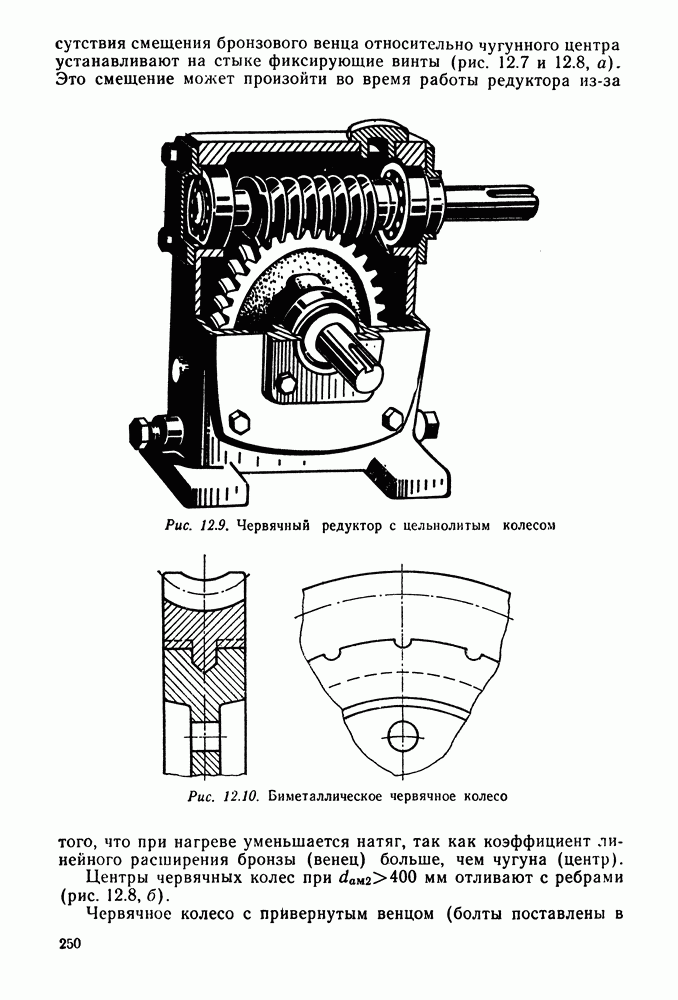
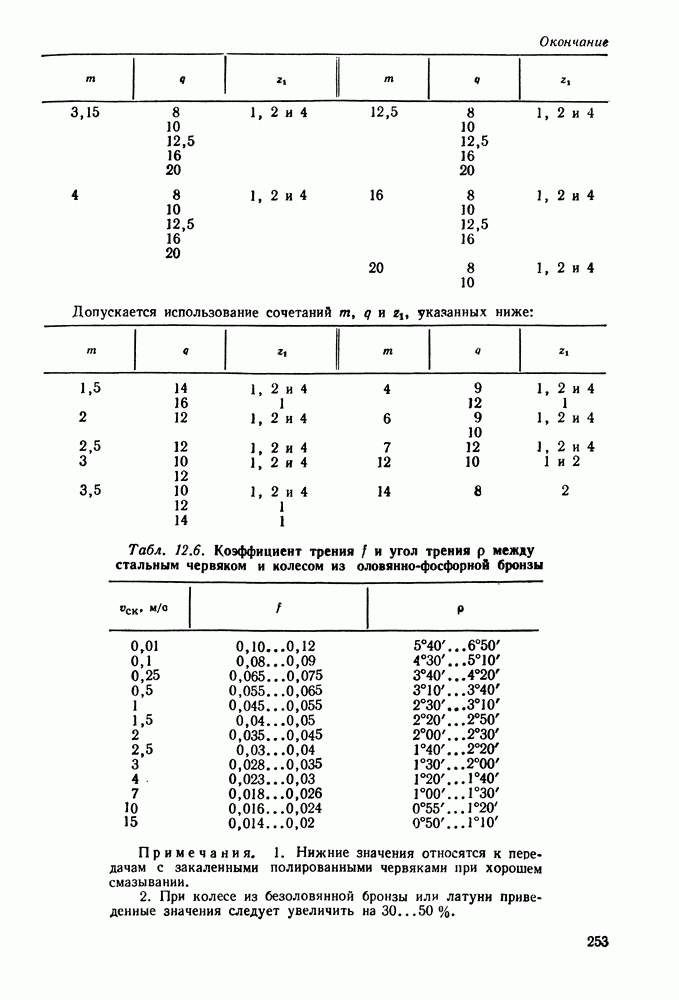
- 12.11. Конструкция червяков и червячных колес
- 12.12. Справочный материал
- 12.13. Пример расчета
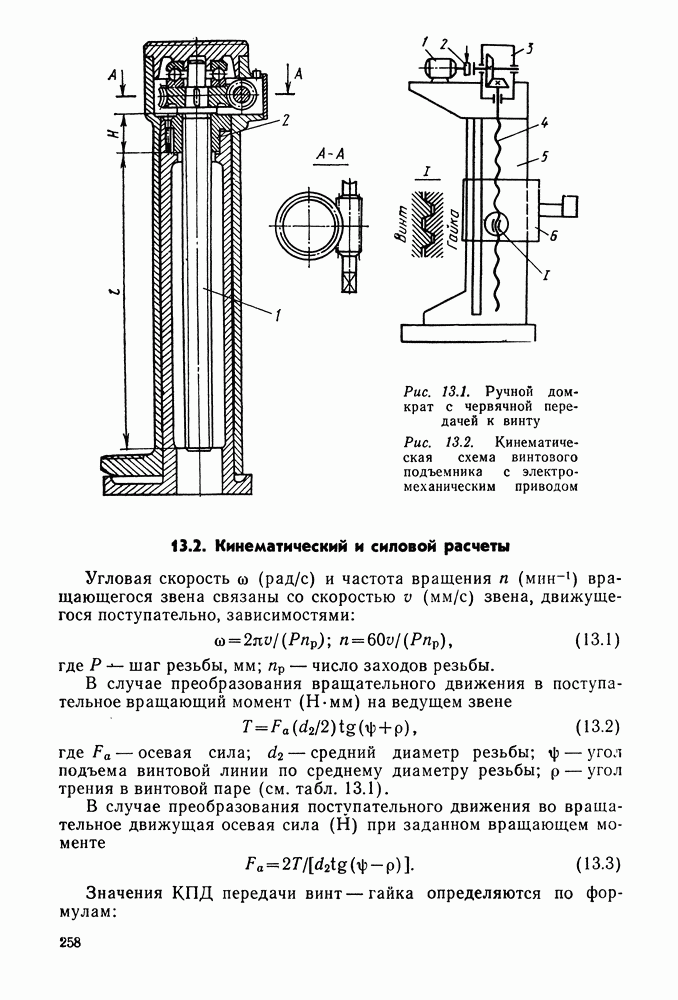
- Глава 13. ПЕРЕДАЧА ВИНТ — ГАЙКА
- 13.2. Кинематический и силовой расчеты
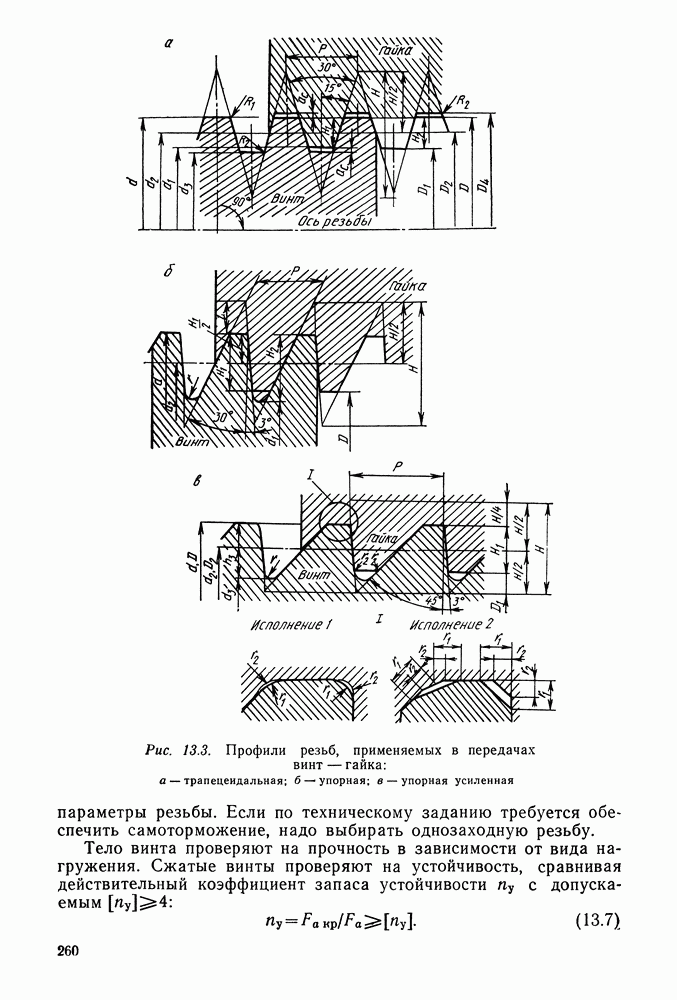
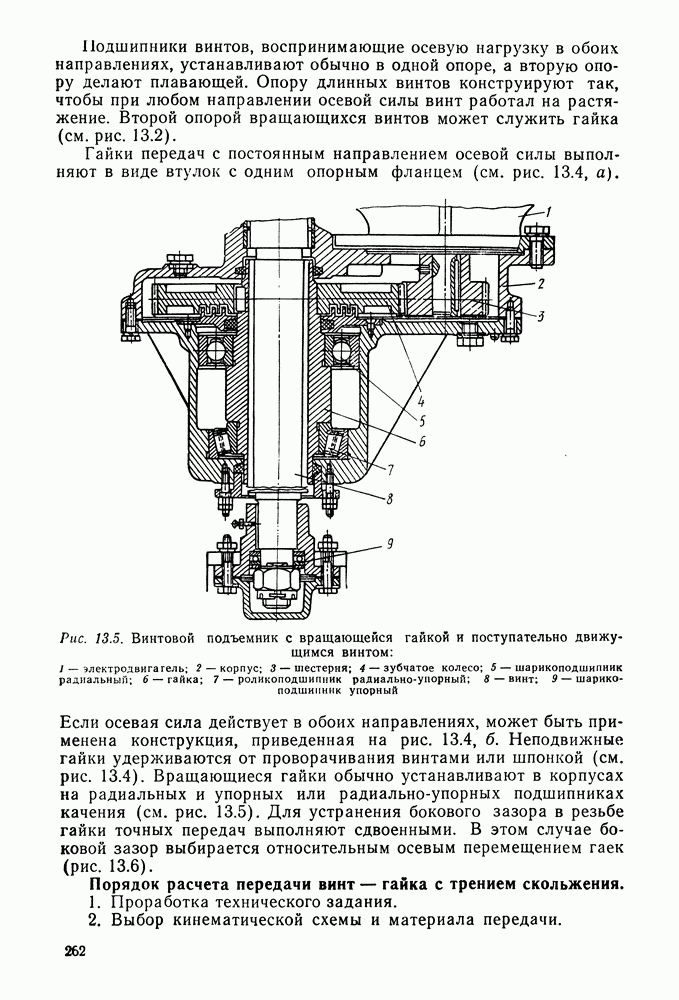
- 13.3. Передача винт—гайка с трением скольжения
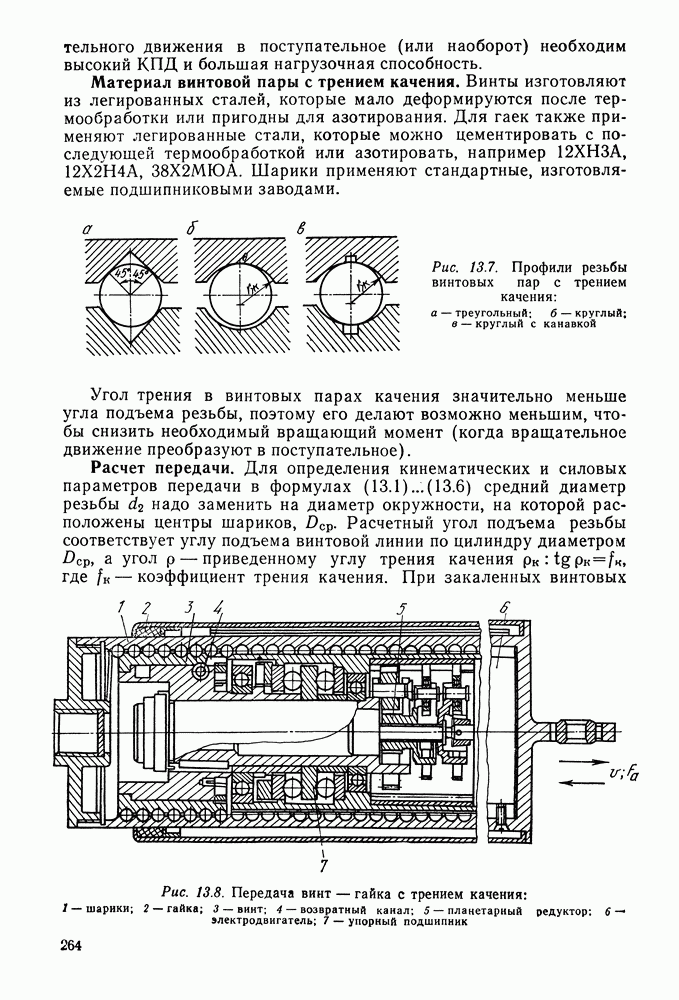
- 13.4. Передача винт — гайка с трением качения
- 13.5. Справочный материал
- 13.6. Пример расчета
- Раздел III. ВАЛЫ, ИХ ОПОРЫ, МУФТЫ, ПРУЖИНЫ
- Глава 14. ВАЛЫ
- 14.2. Некоторые сведения по конструированию валов и выбору материалов
- 14.3. Расчет валов
- 14.4. Посадки основных деталей передач на валы по стандартам СЭВ
- 14.5. Справочный материал
- 14.6. Примеры расчета
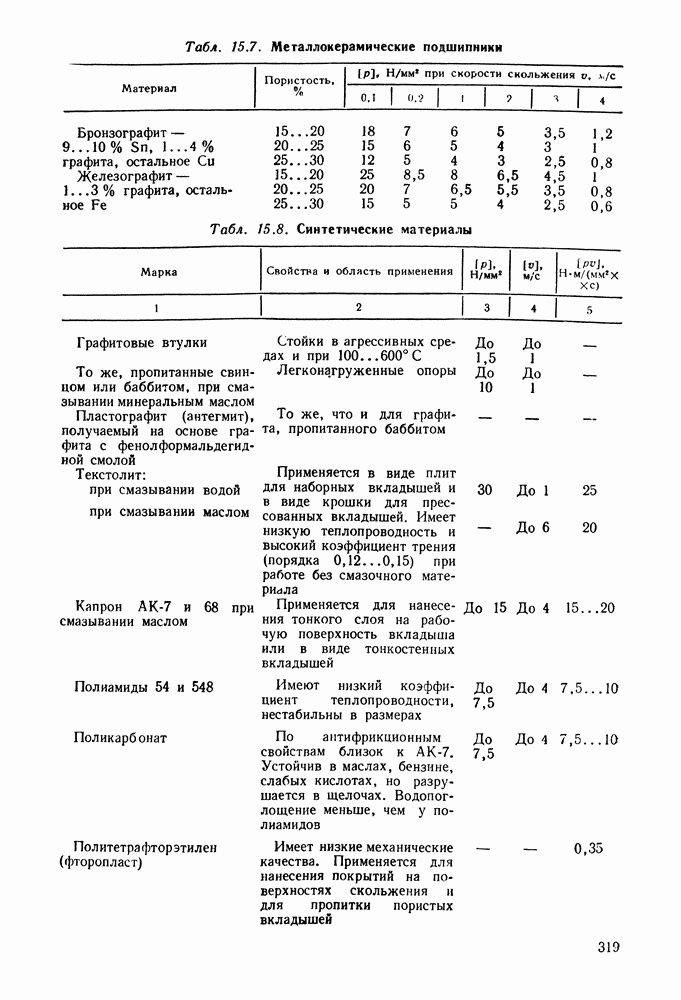
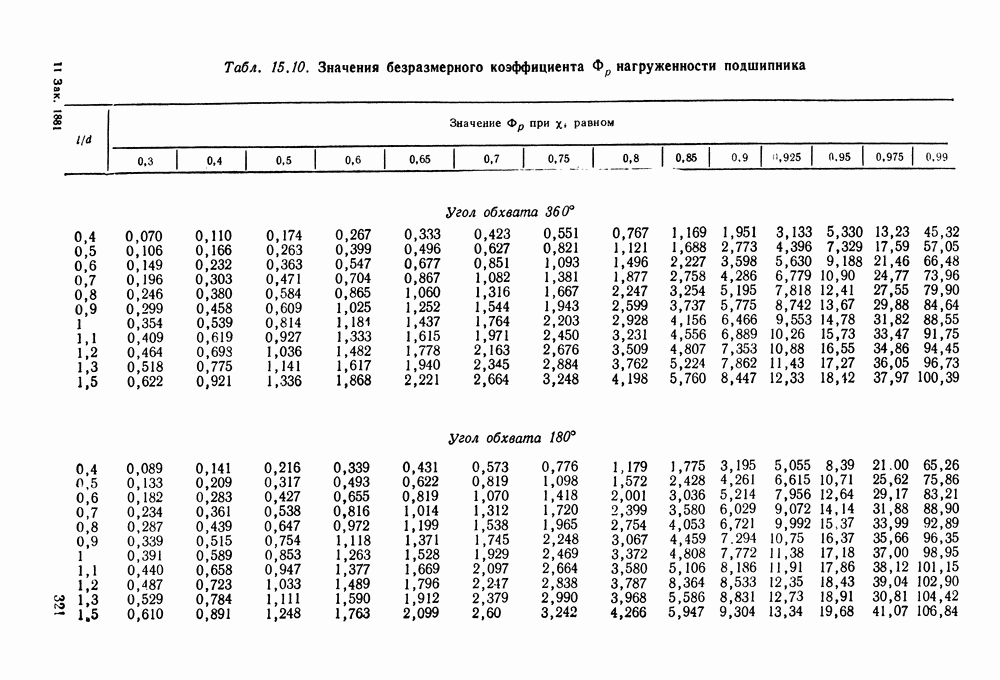
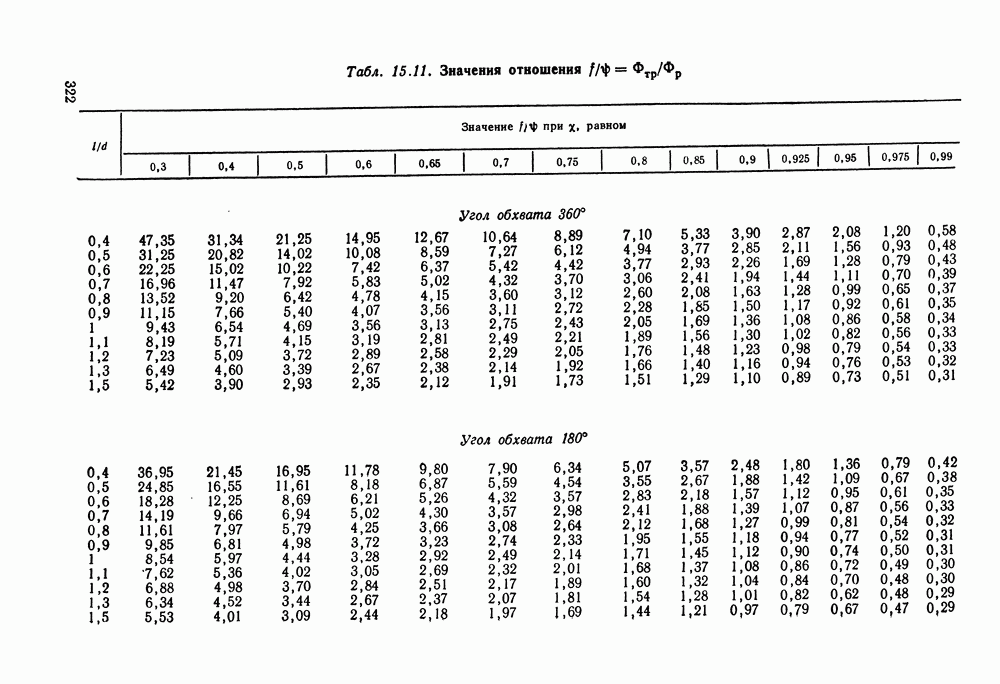
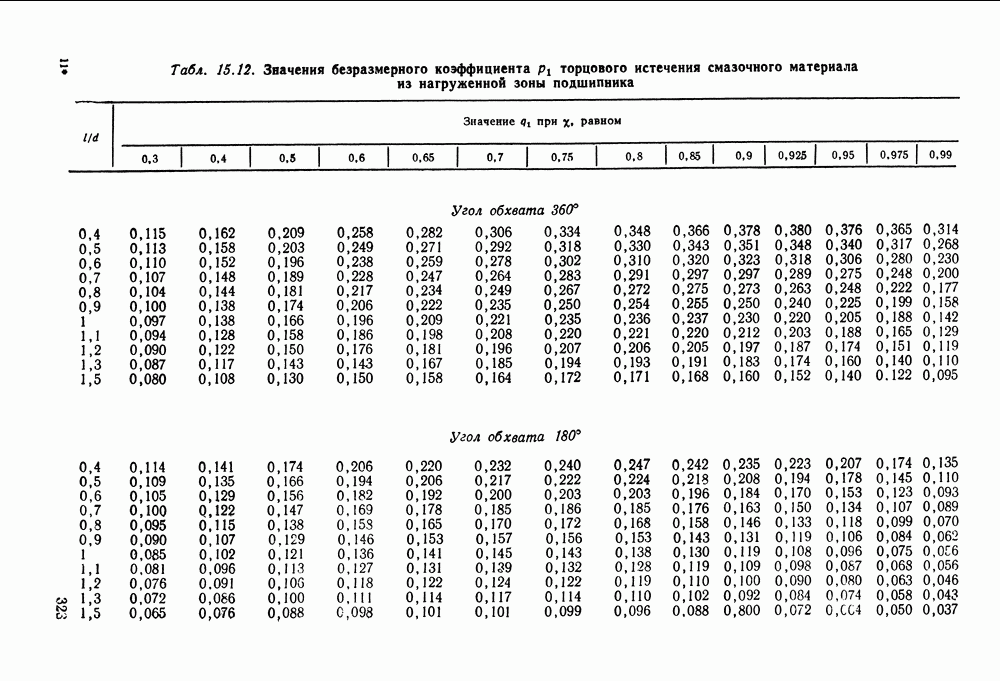
- Глава 15. РАДИАЛЬНЫЕ ПОДШИПНИКИ СКОЛЬЖЕНИЯ
- 15.2. Упрощенный расчет подшипников скольжения
- 15.3. Расчет подшипников жидкостного трения
- 15.4. Сопротивление слоя масла вращению шипа
- 15.5. Тепловой расчет подшипника
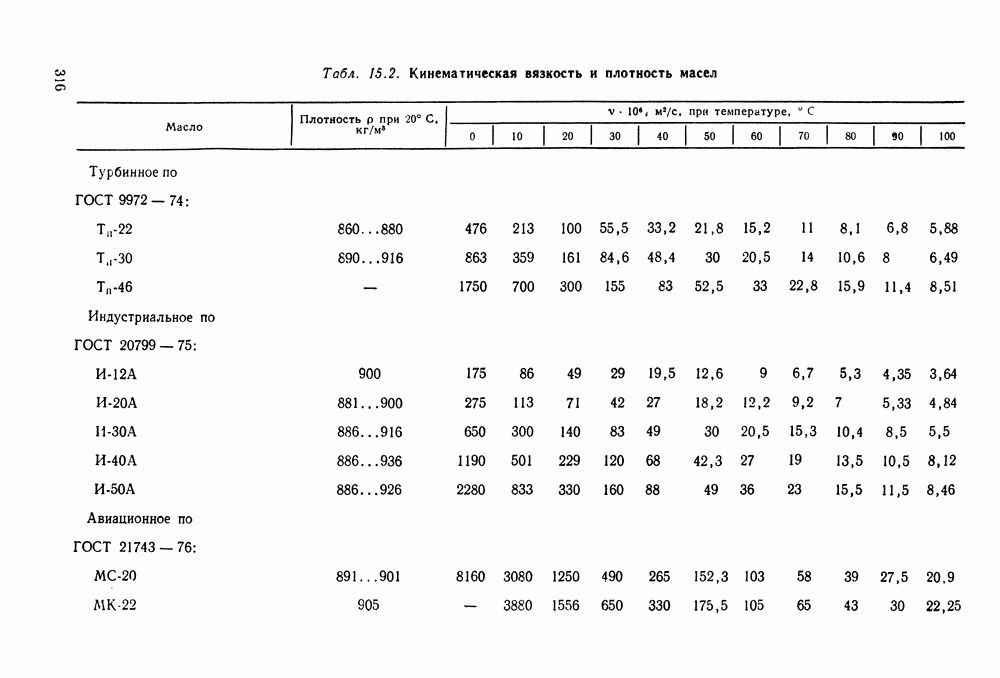
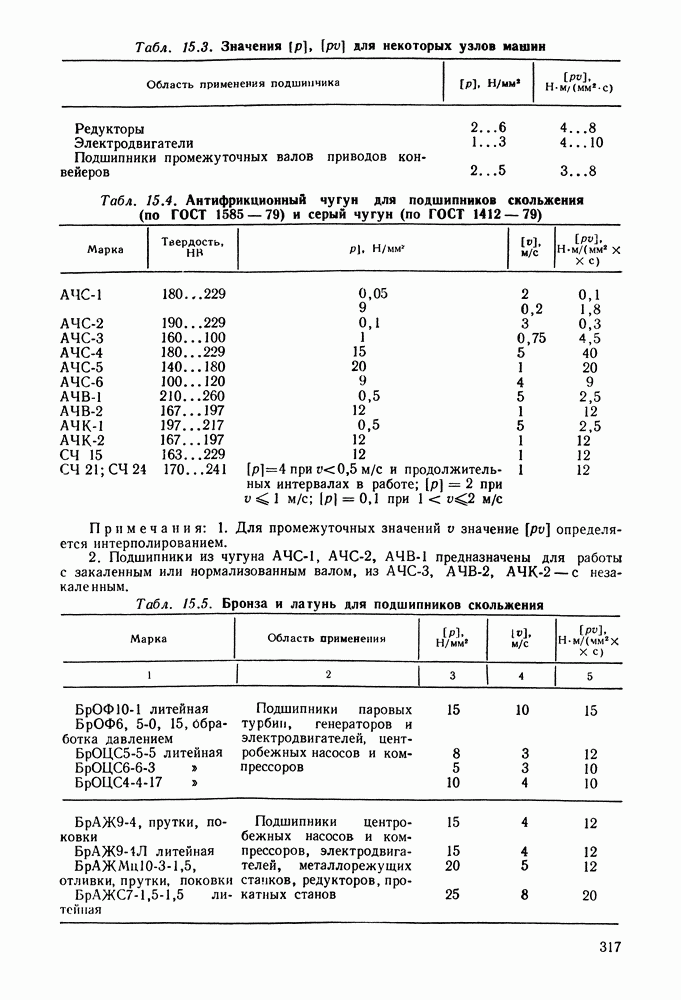
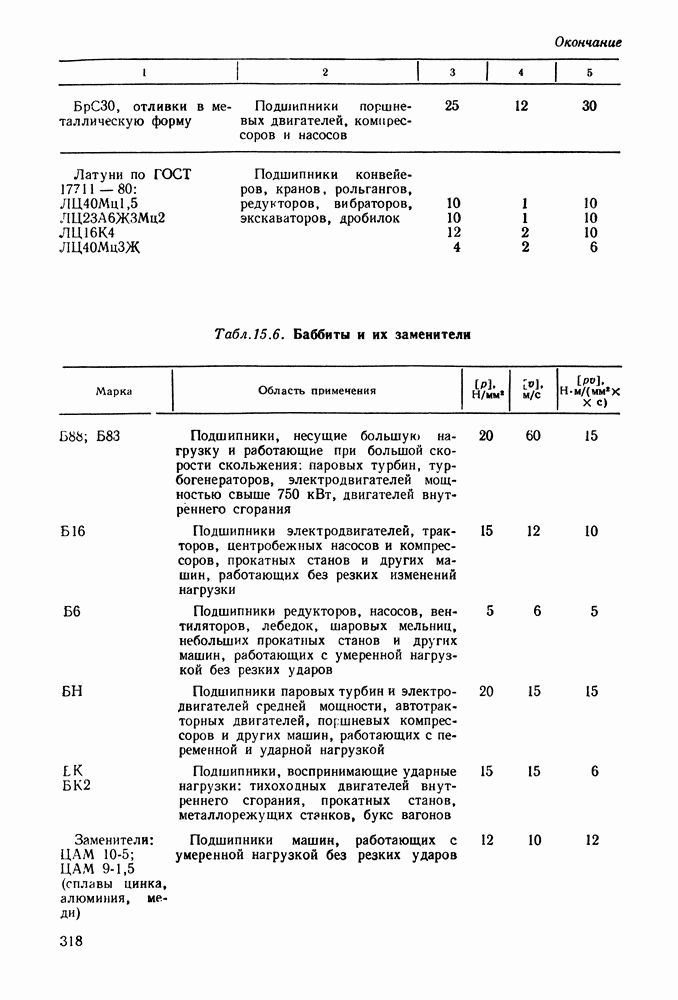
- 15.6. Справочный материал
- 15.7. Примеры расчета
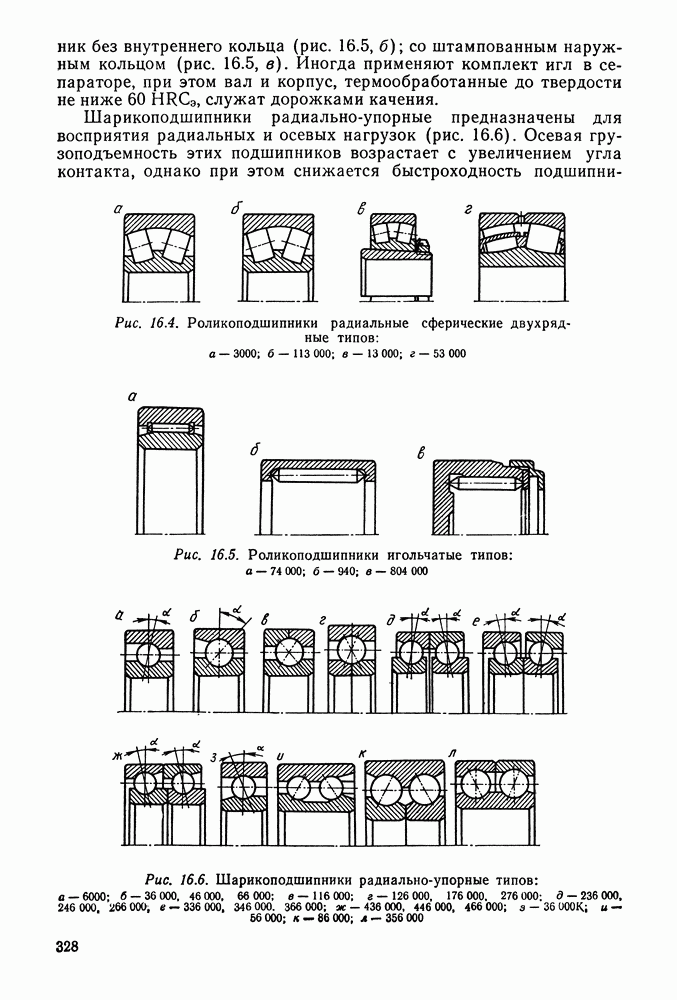
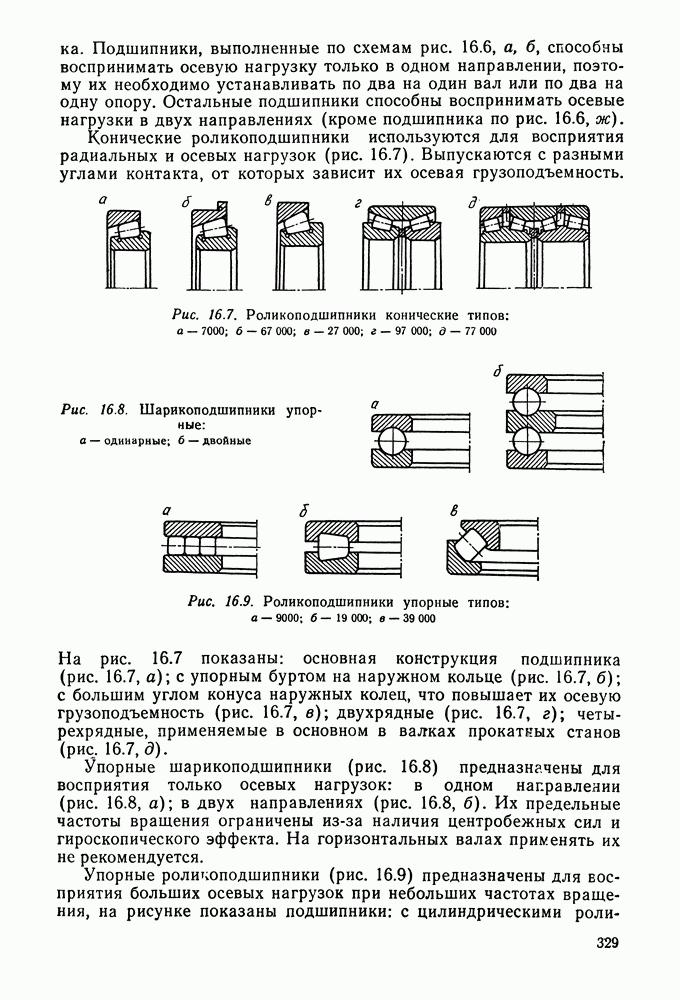
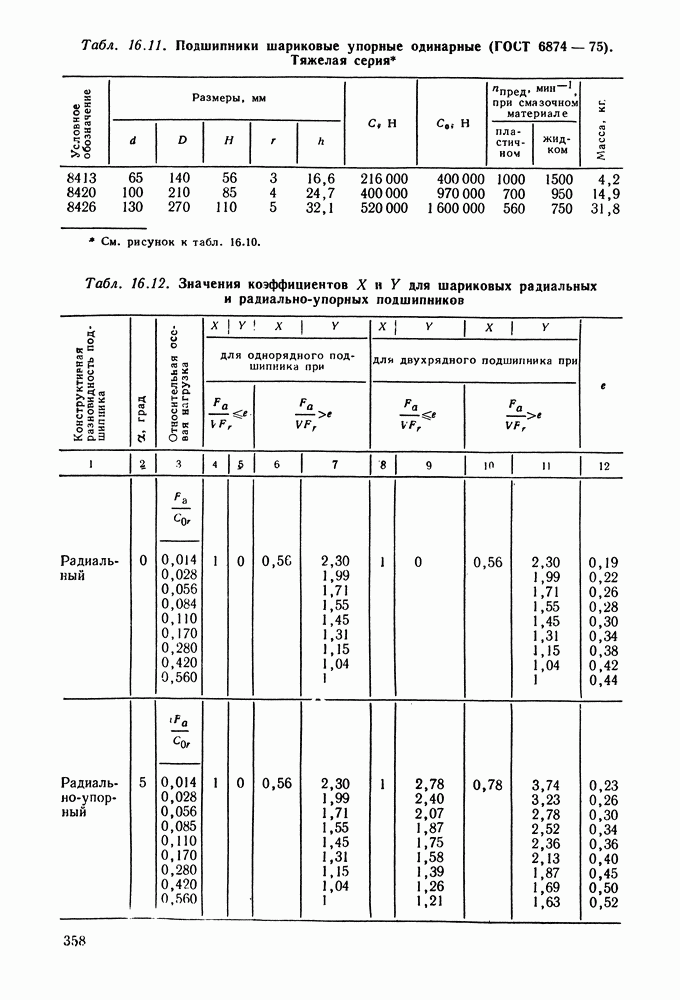
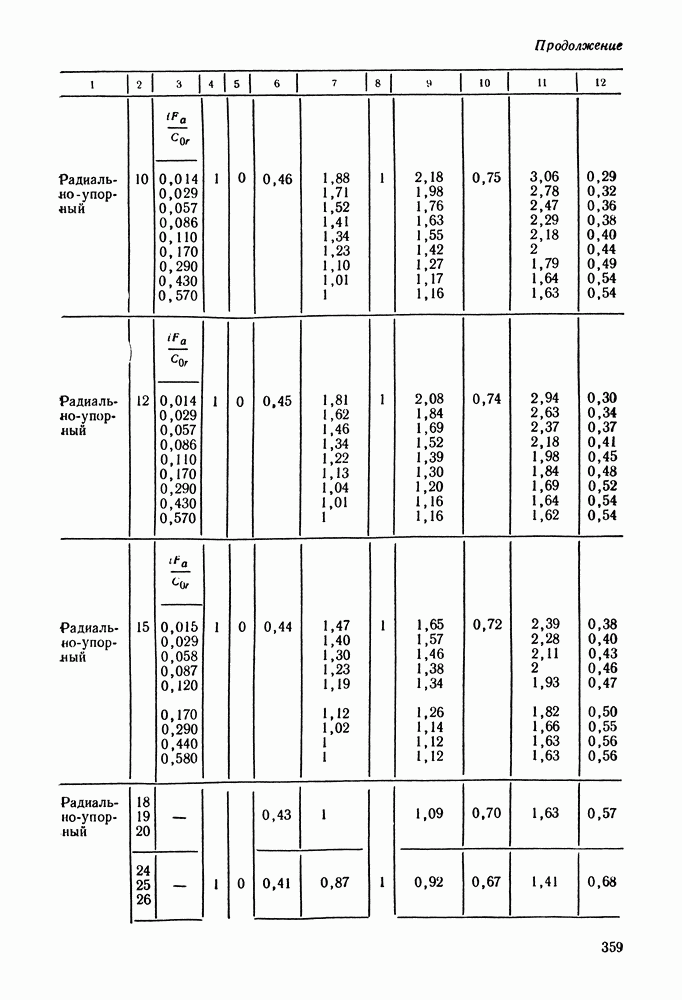
- Глава 16. ПОДШИПНИКИ КАЧЕНИЯ
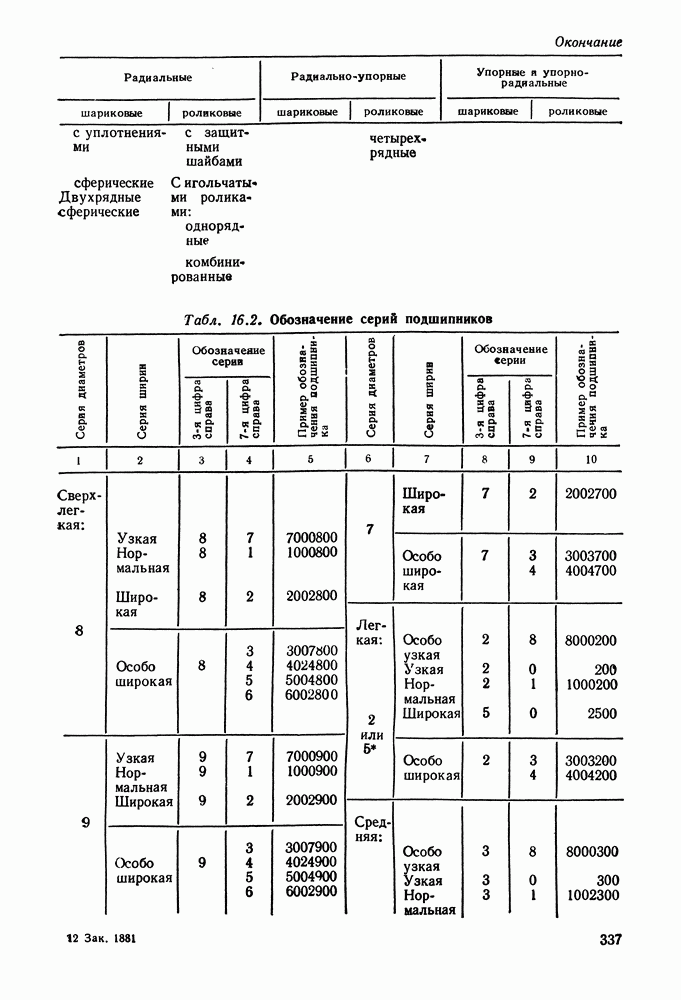
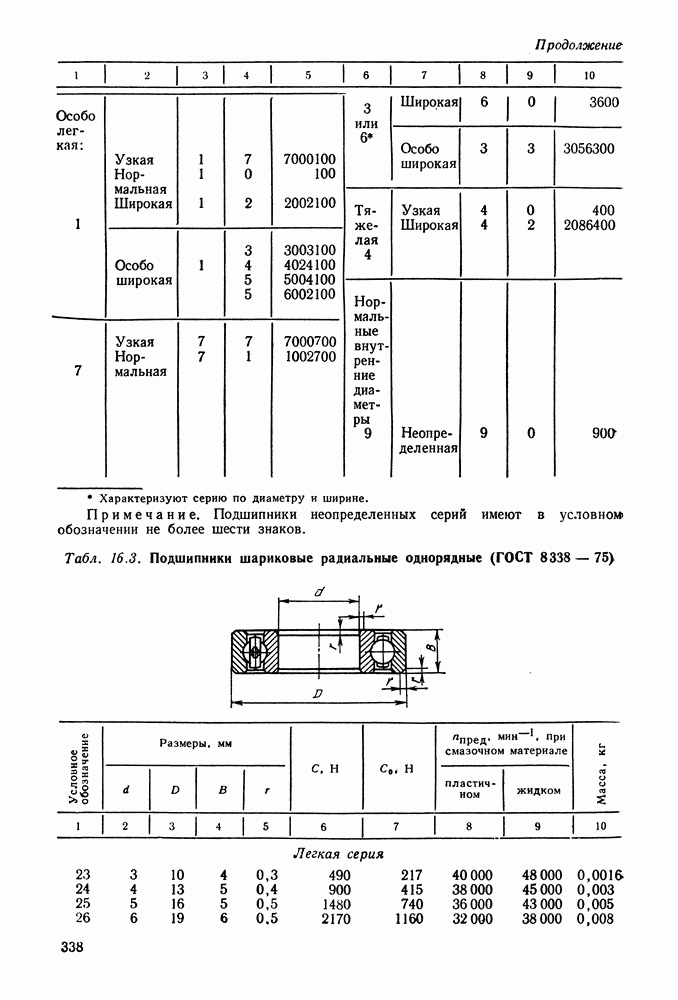
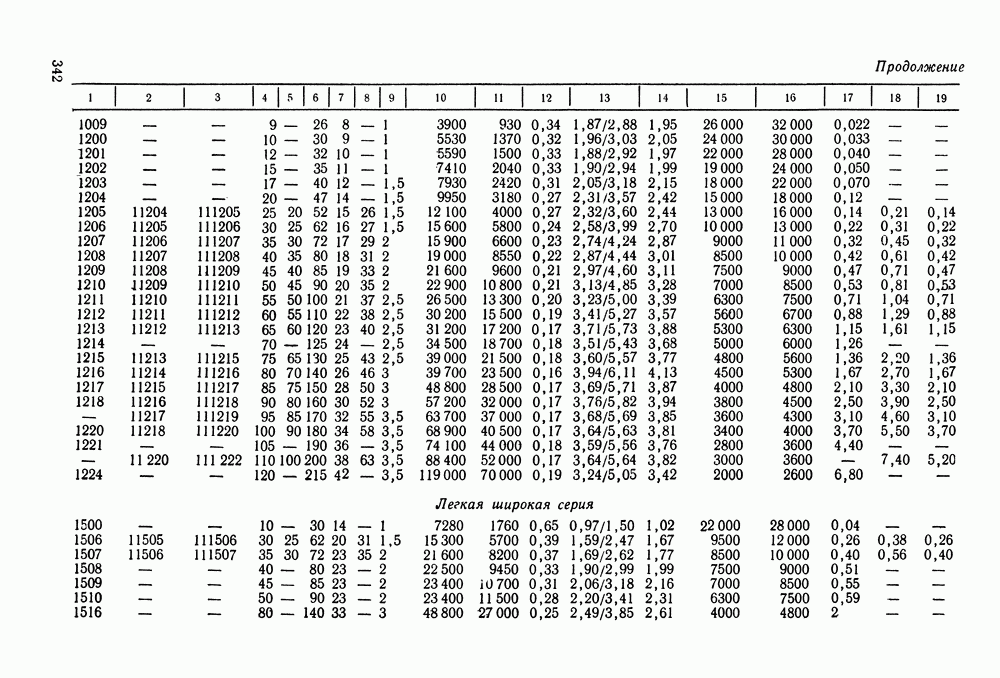
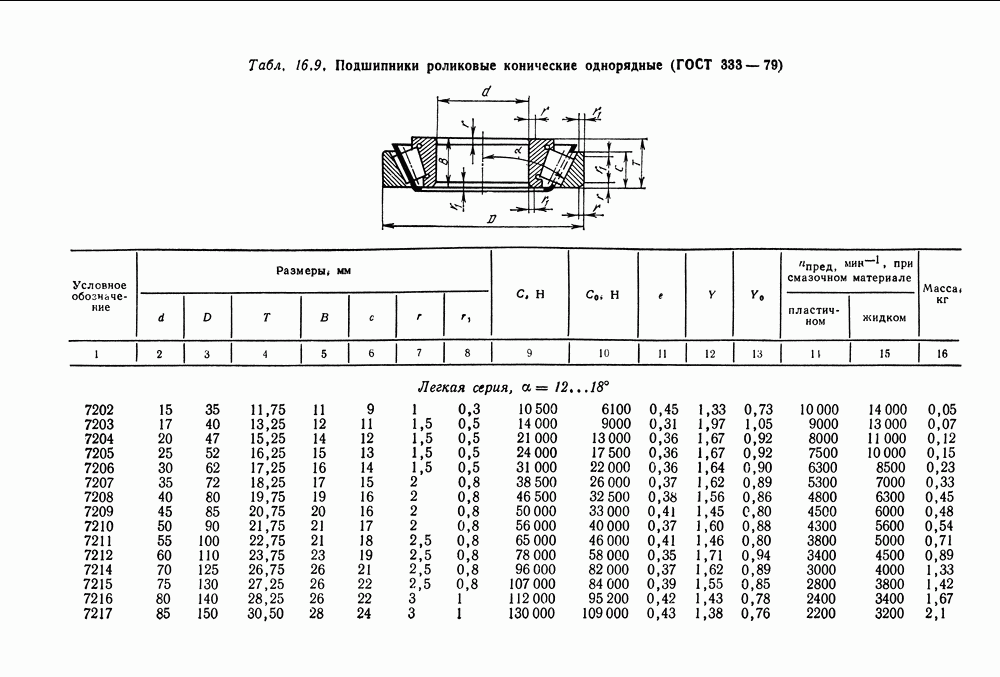
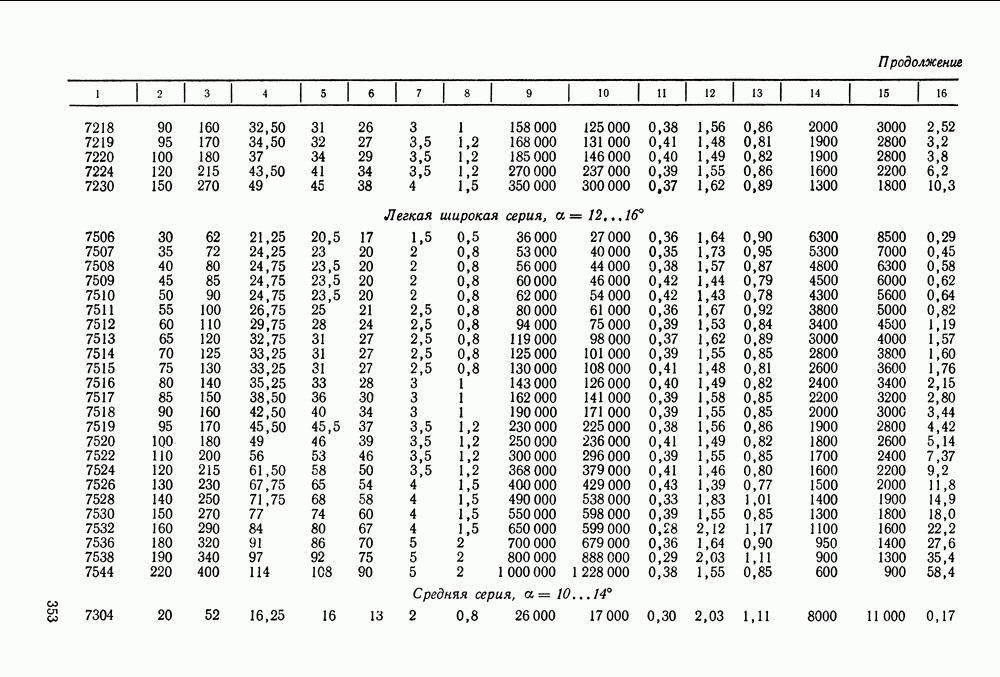
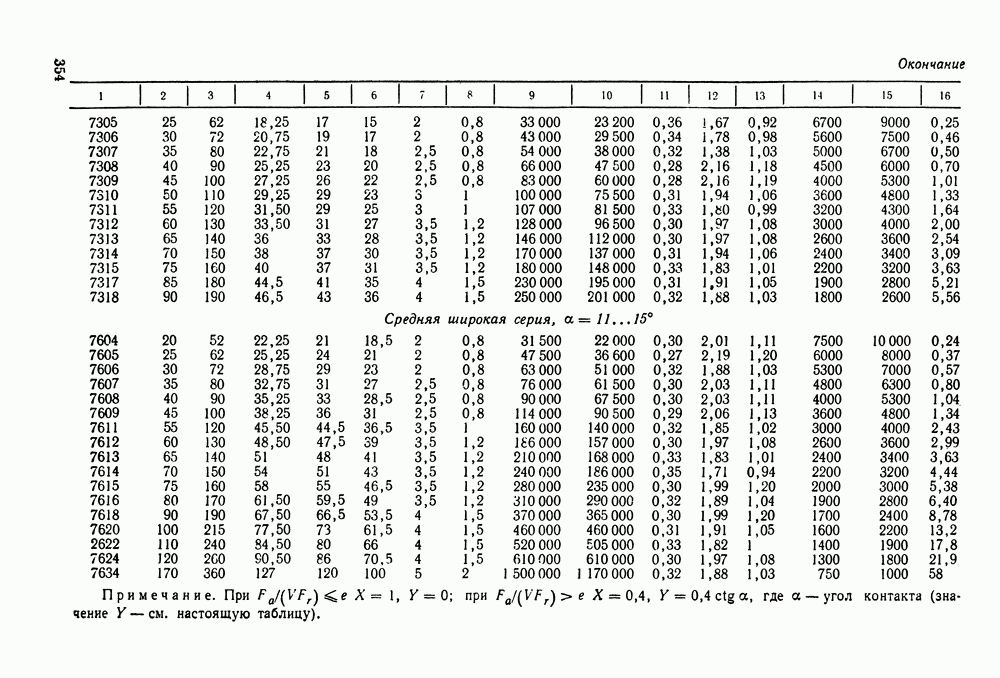
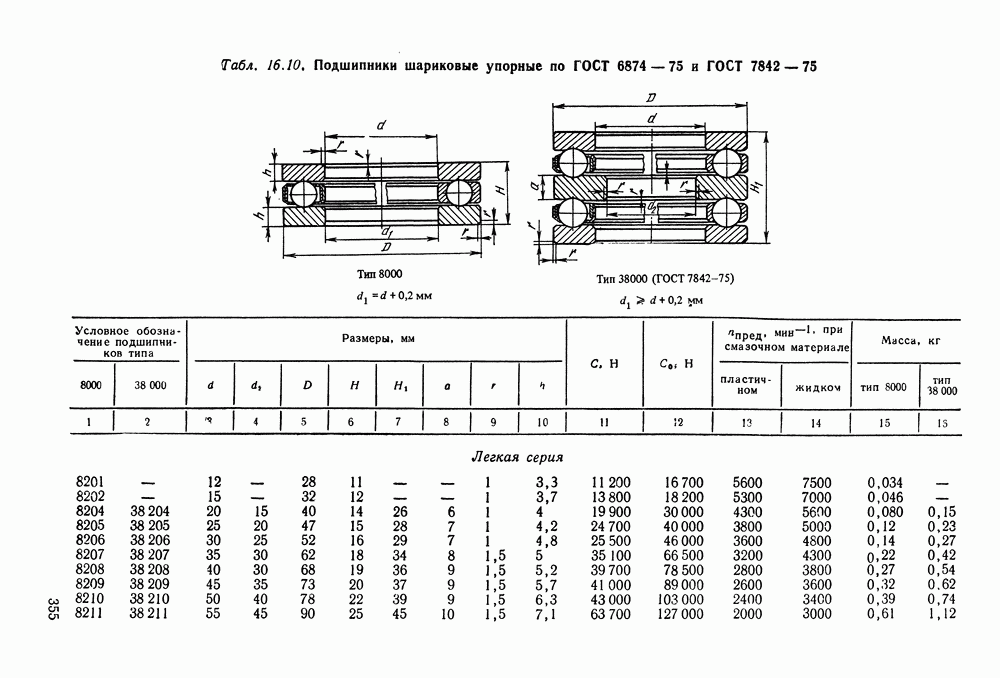
- 16.2. Условные обозначения и точность подшипников качения
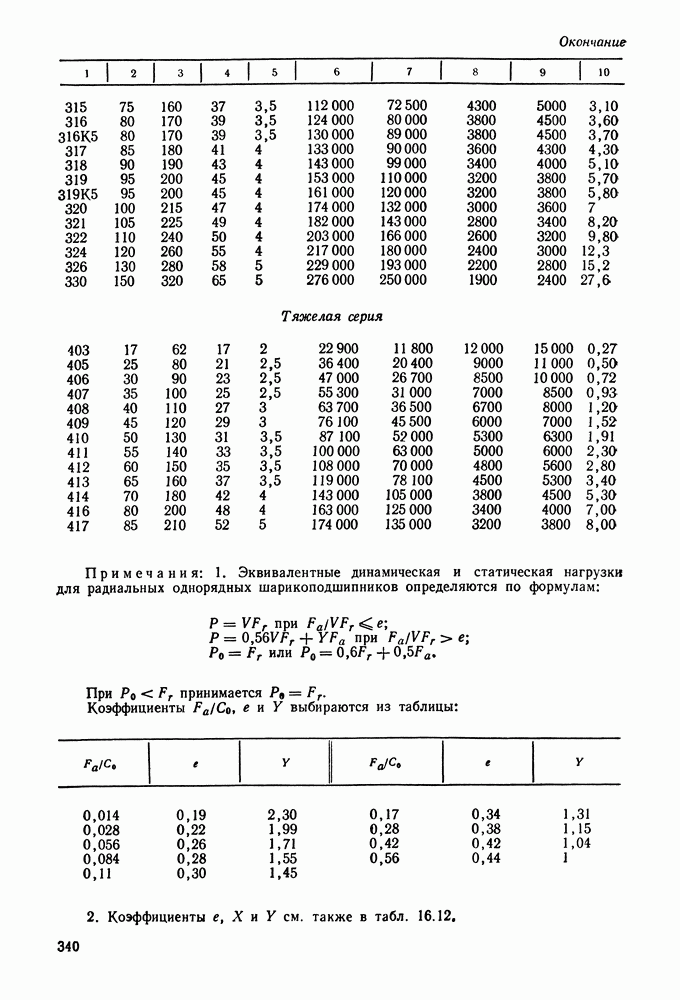
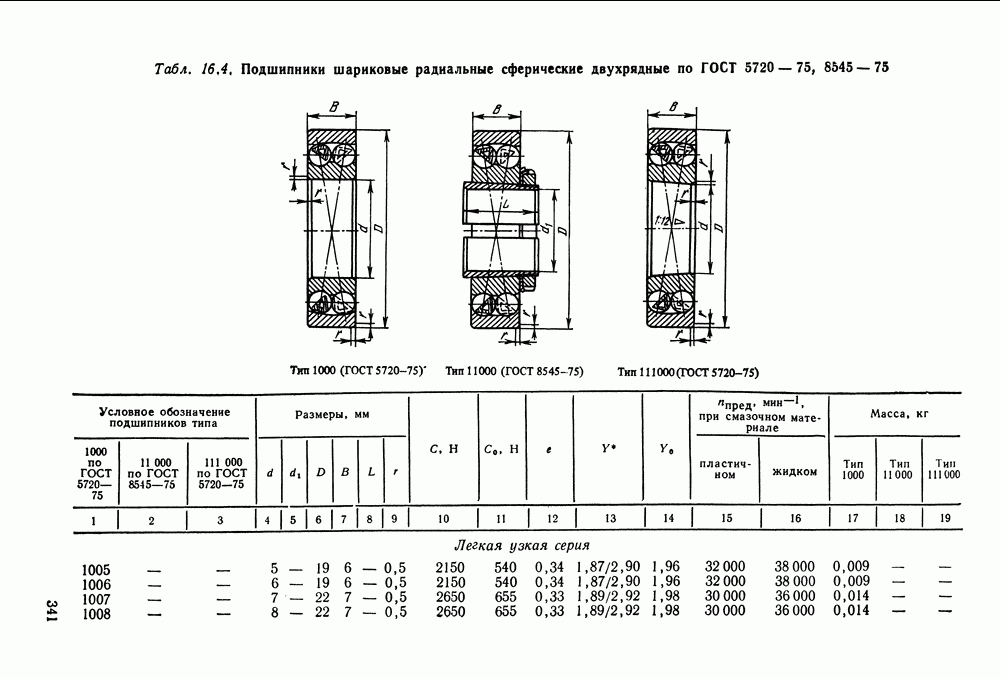
- 16.3. Выбор и проверка подшипников качения по динамической грузоподъемности
- 16.4. Выбор подшипников качения по статической грузоподъемности
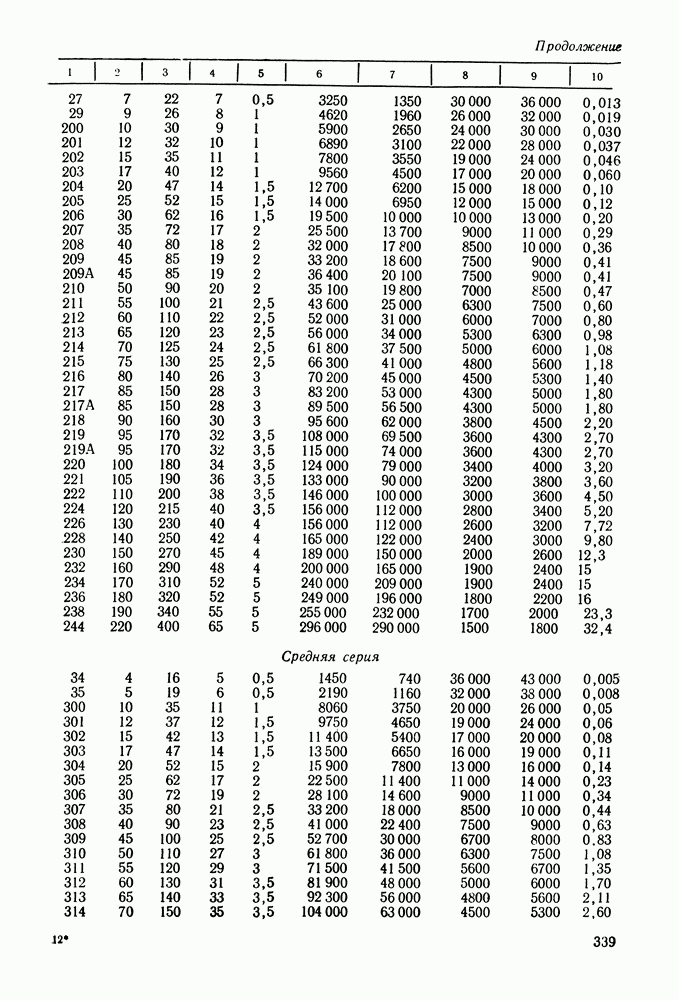
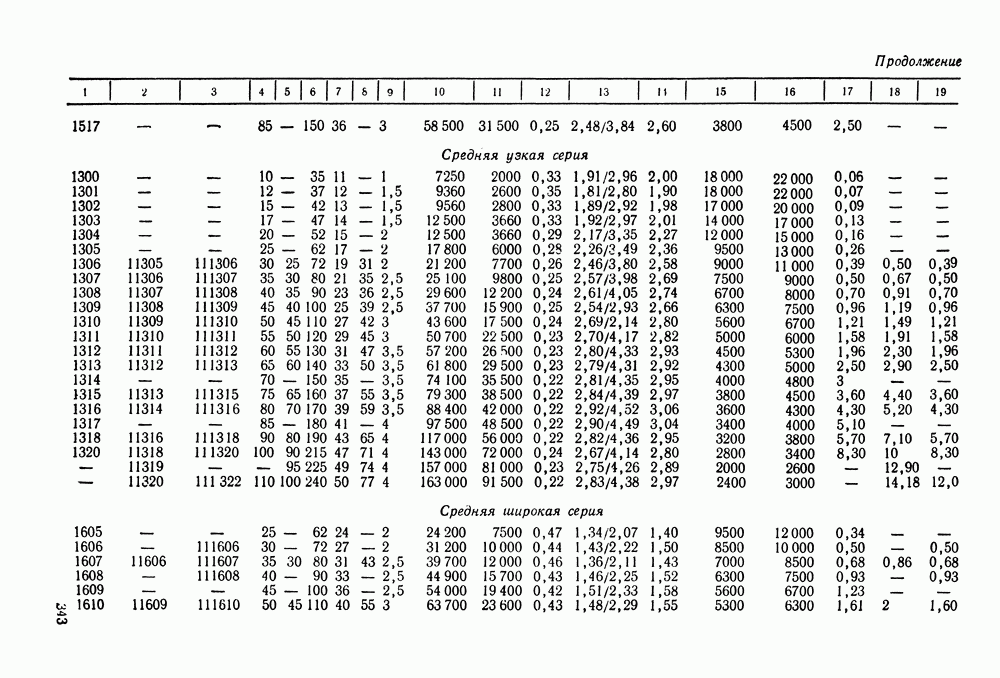
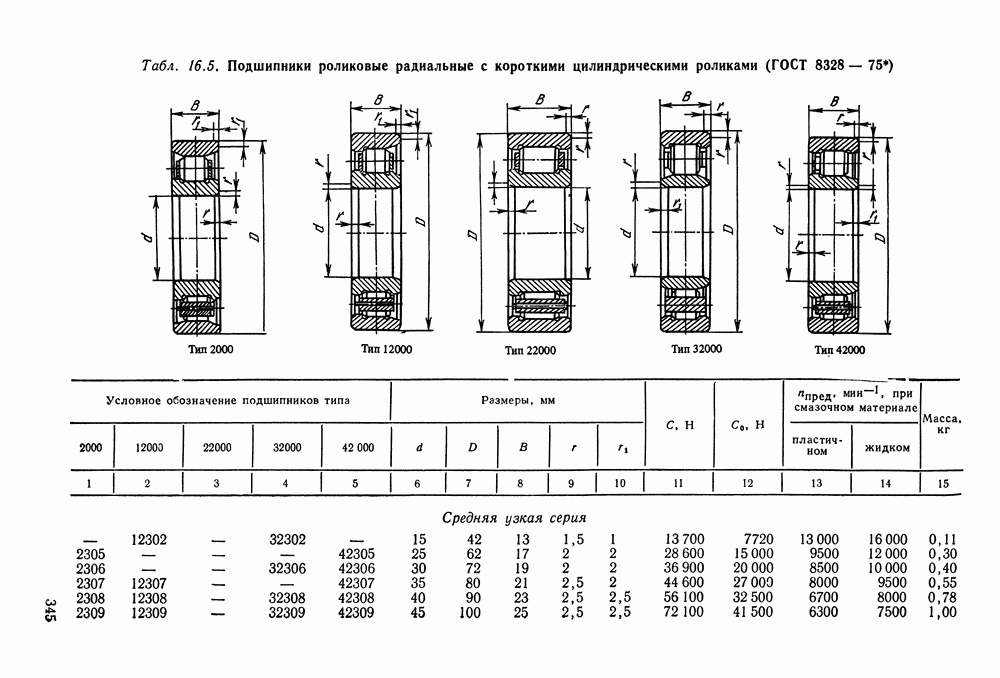
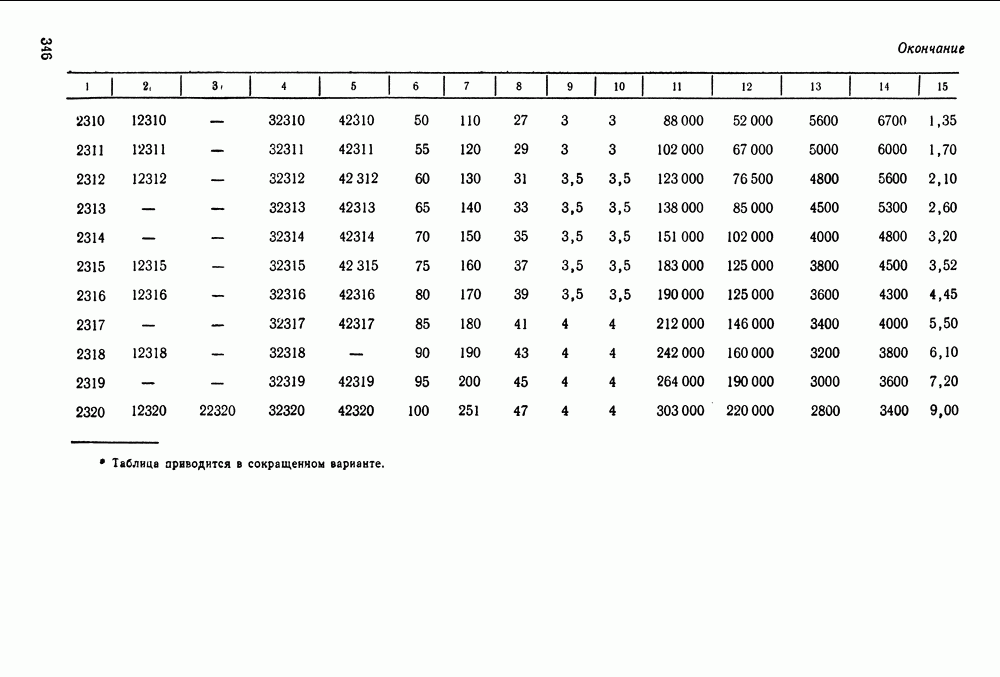
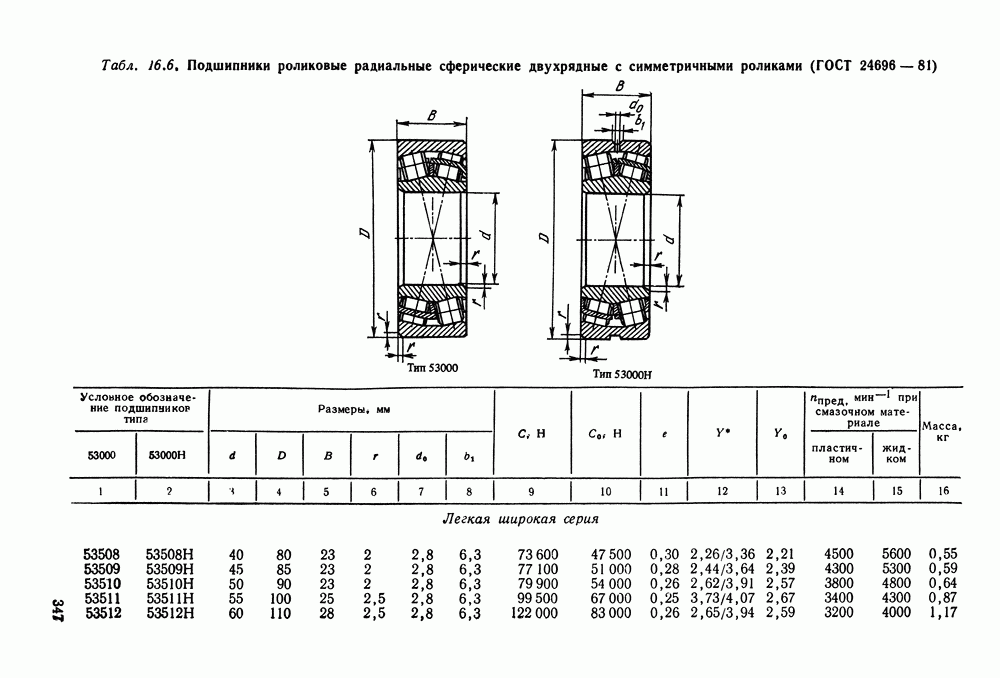
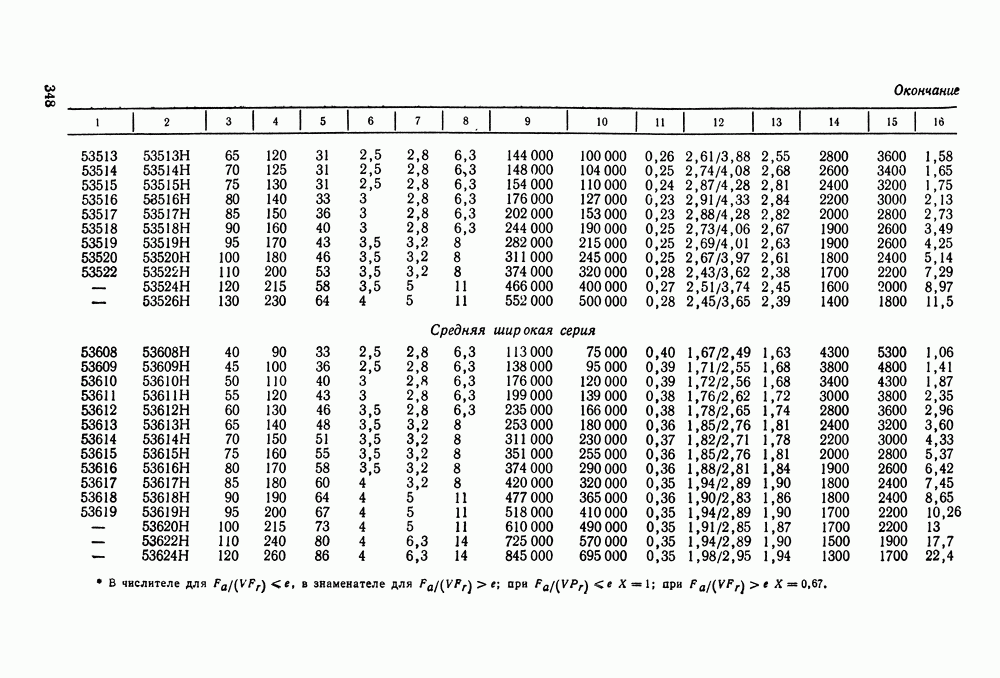
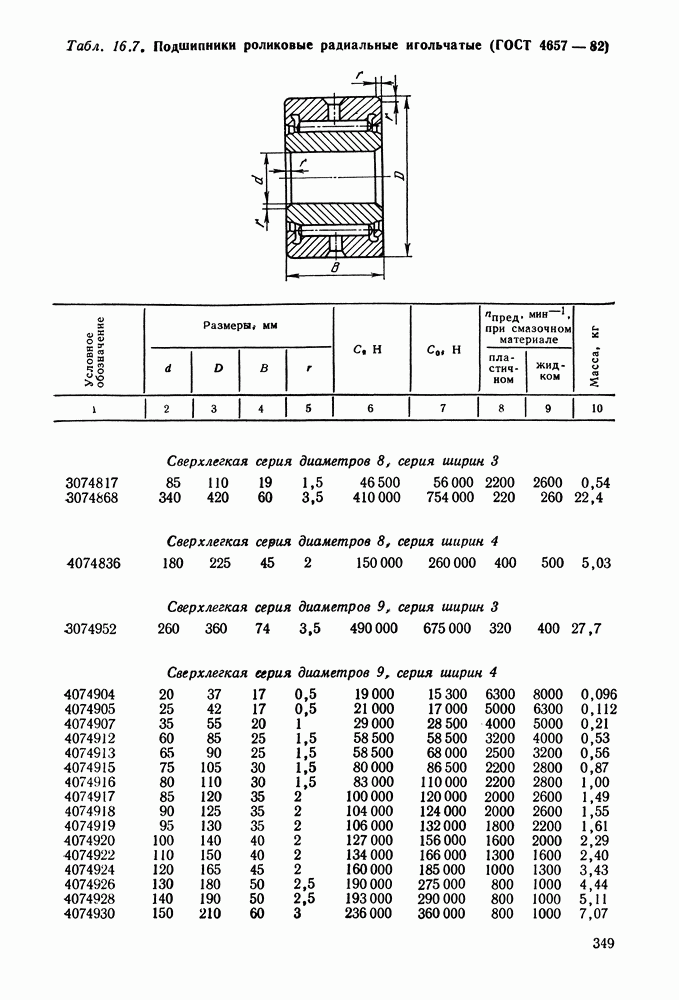
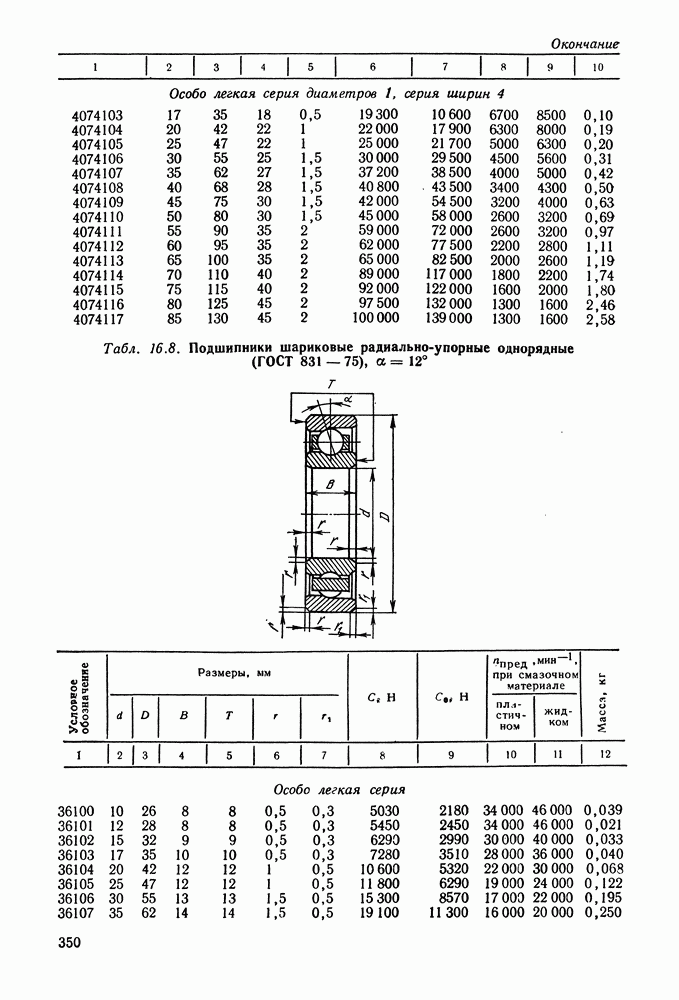
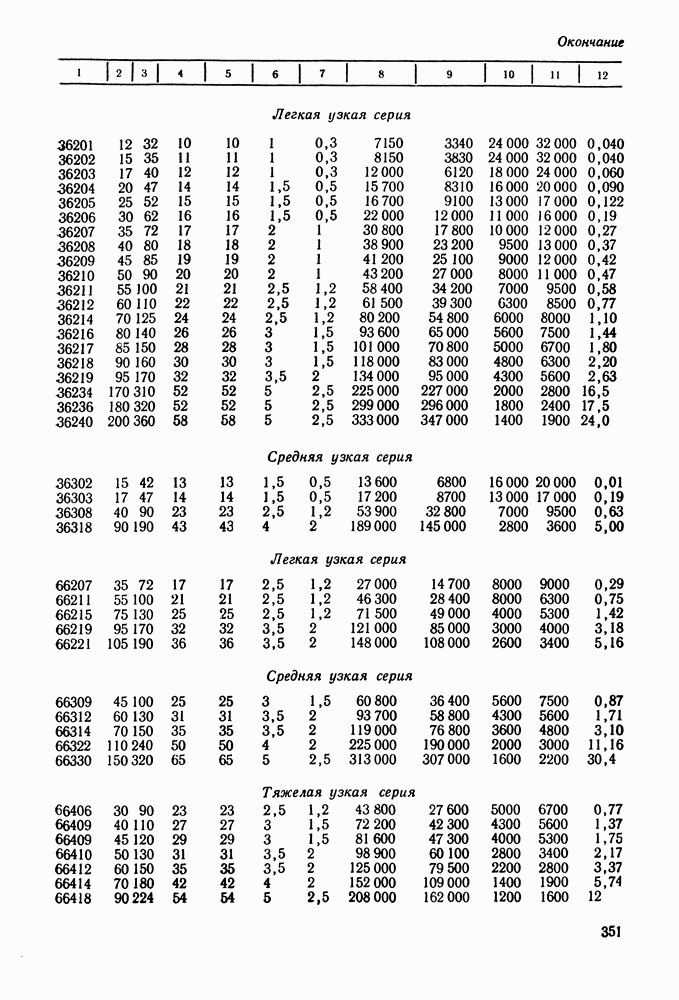
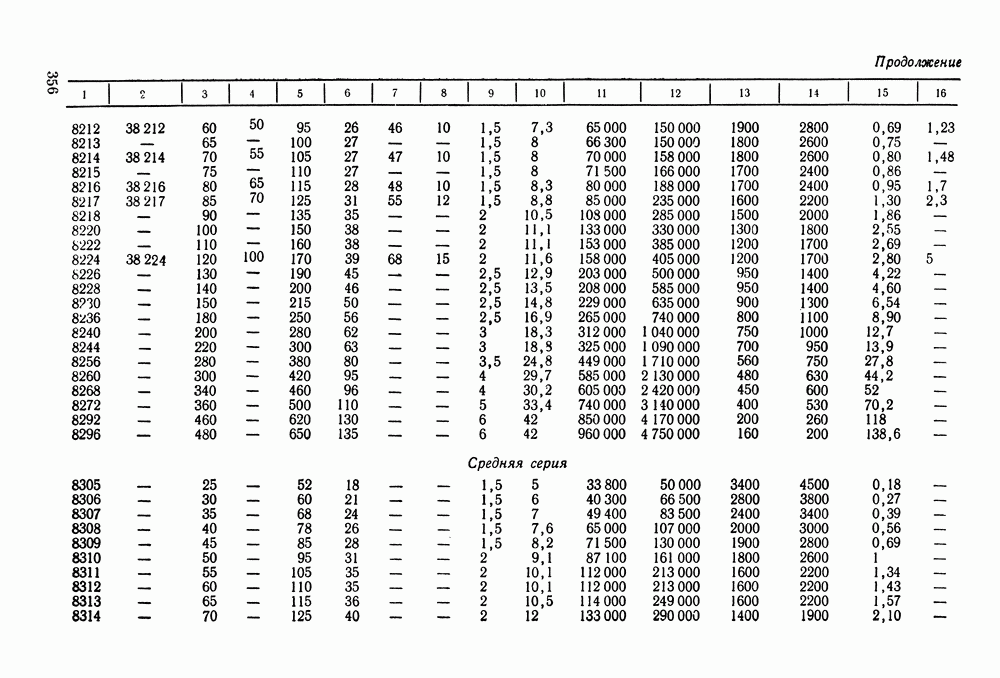
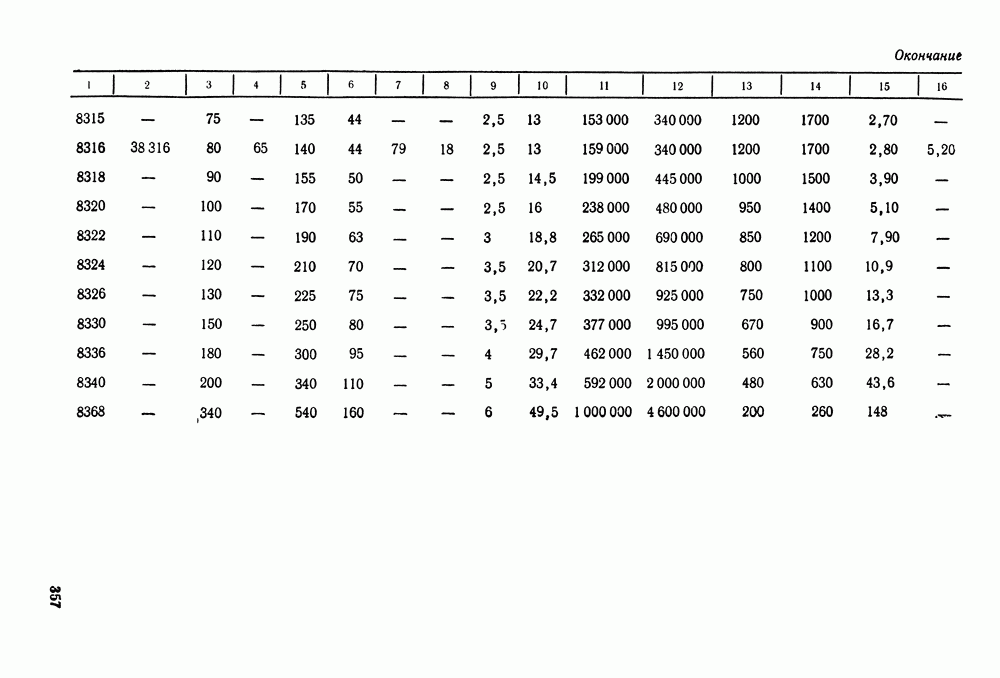
- 16.5. Справочный материал
- 16.6. Пример расчета
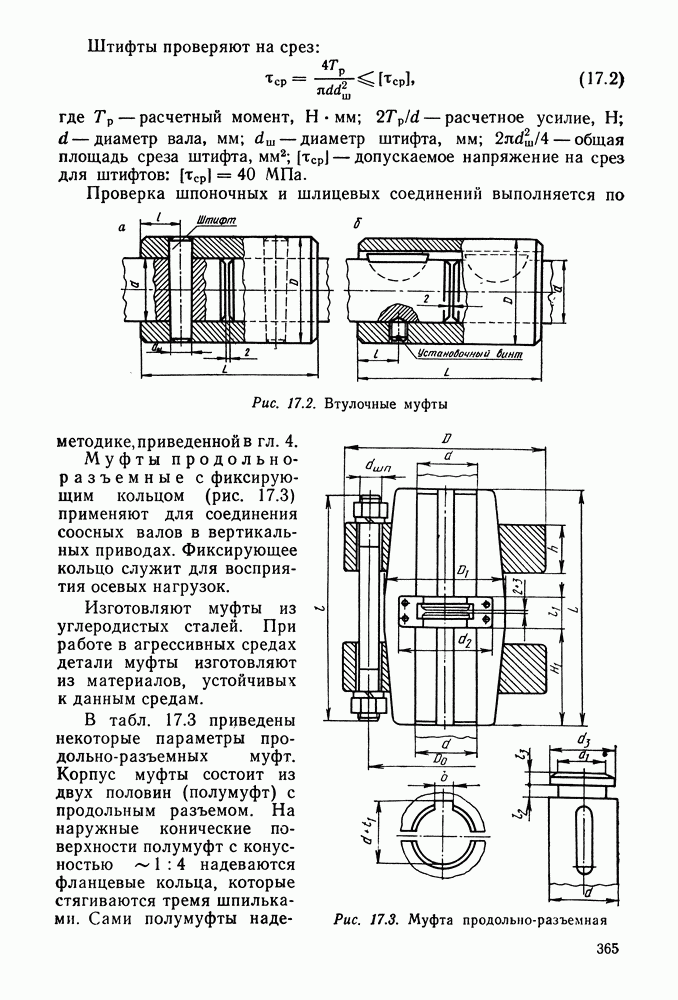
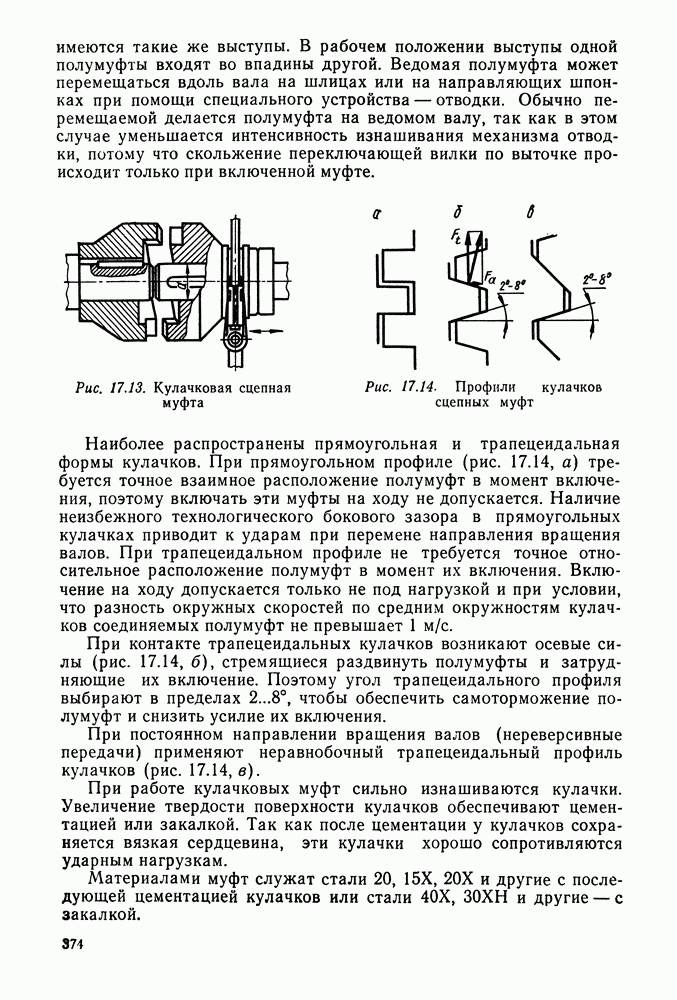
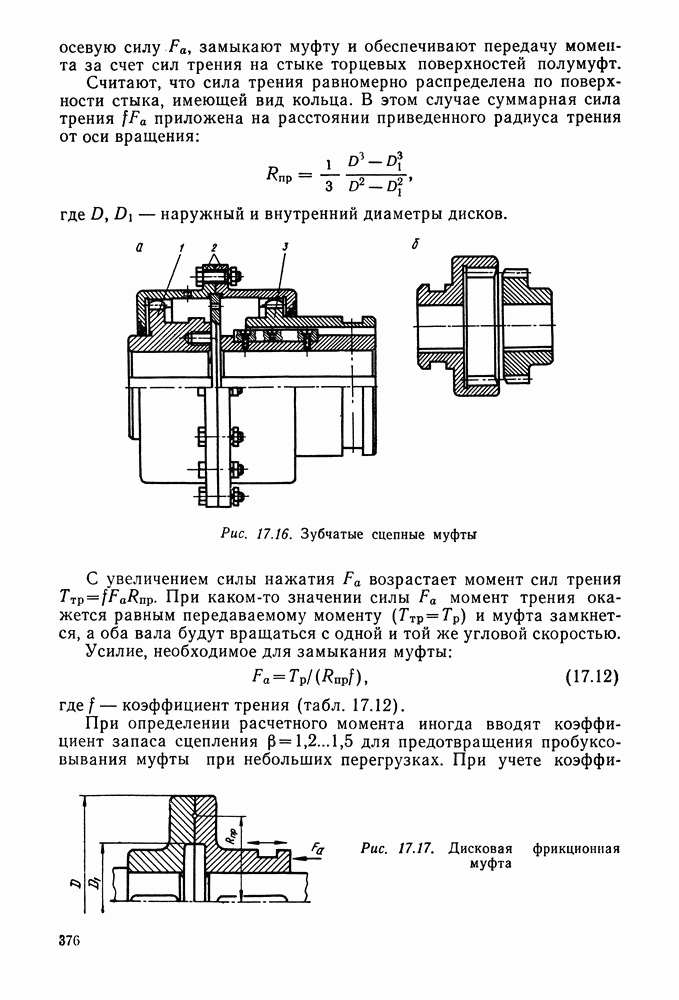
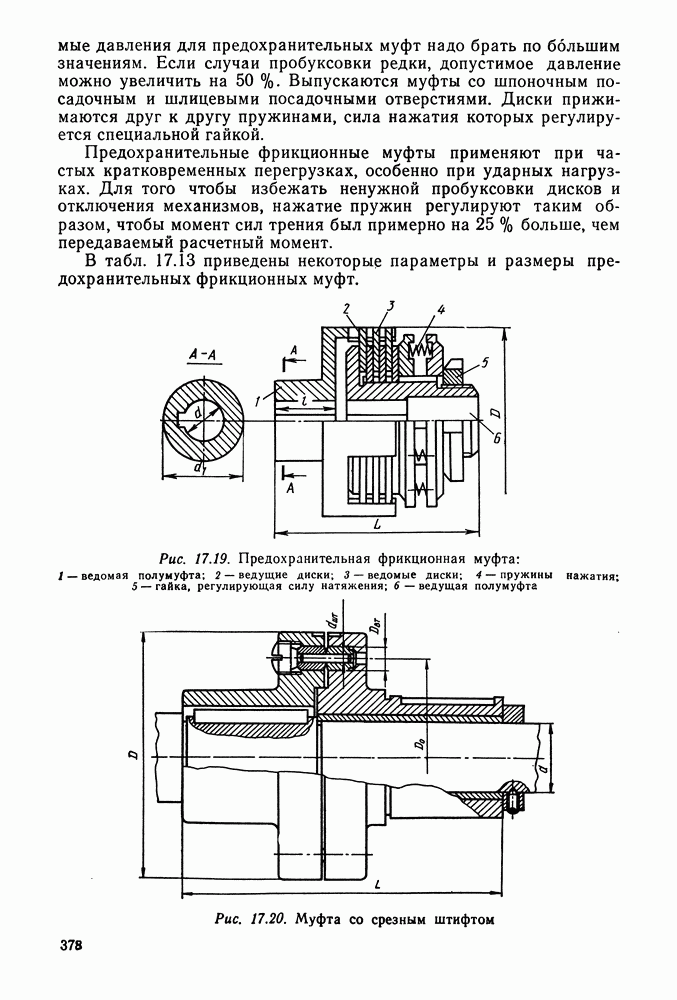
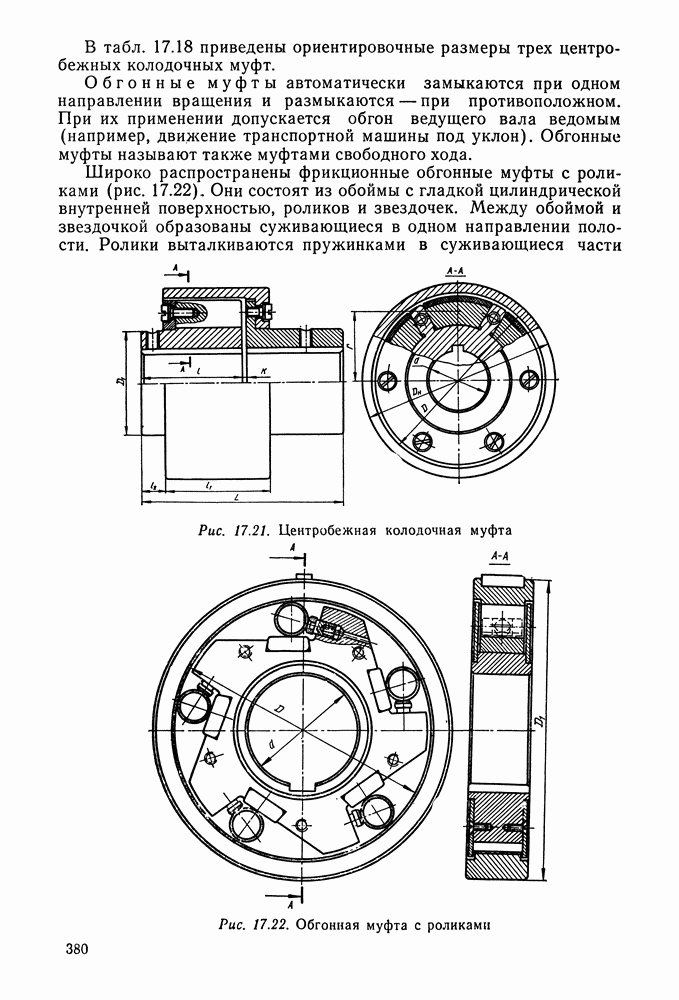
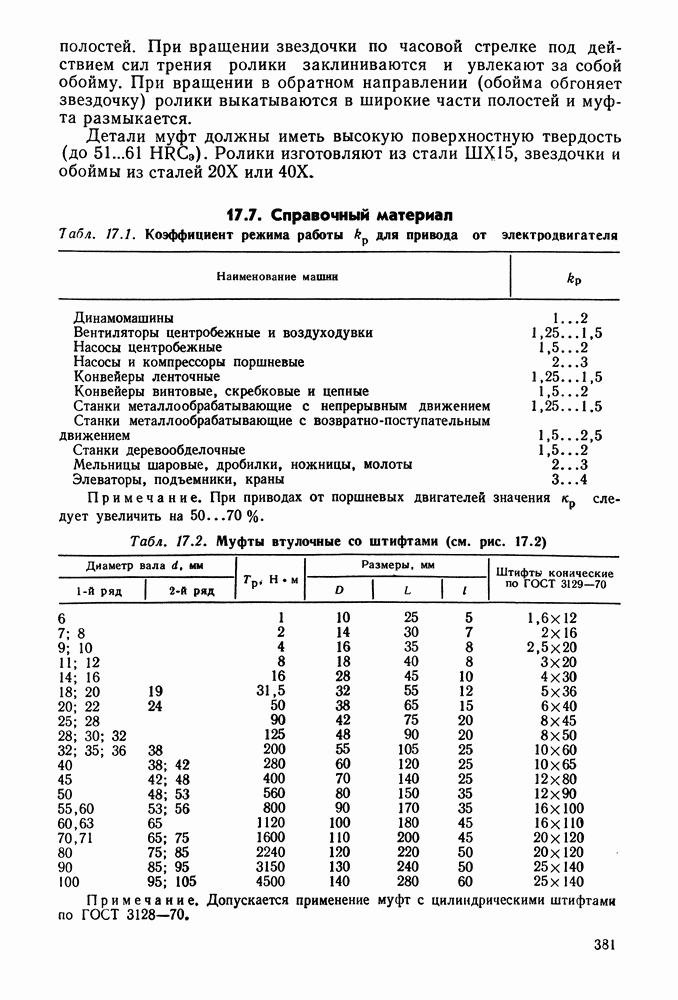
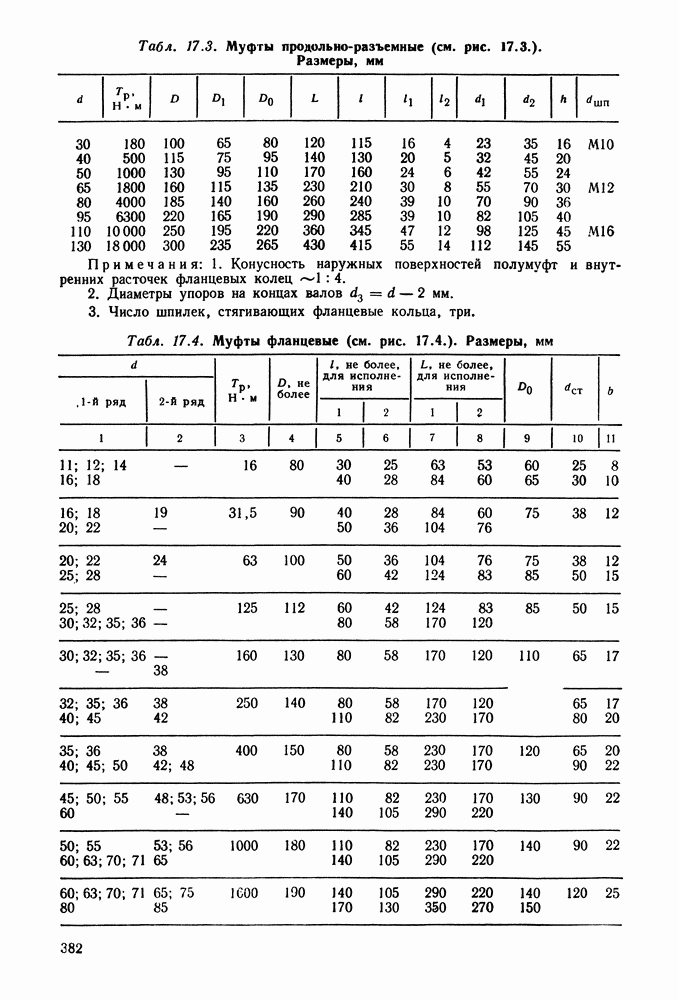
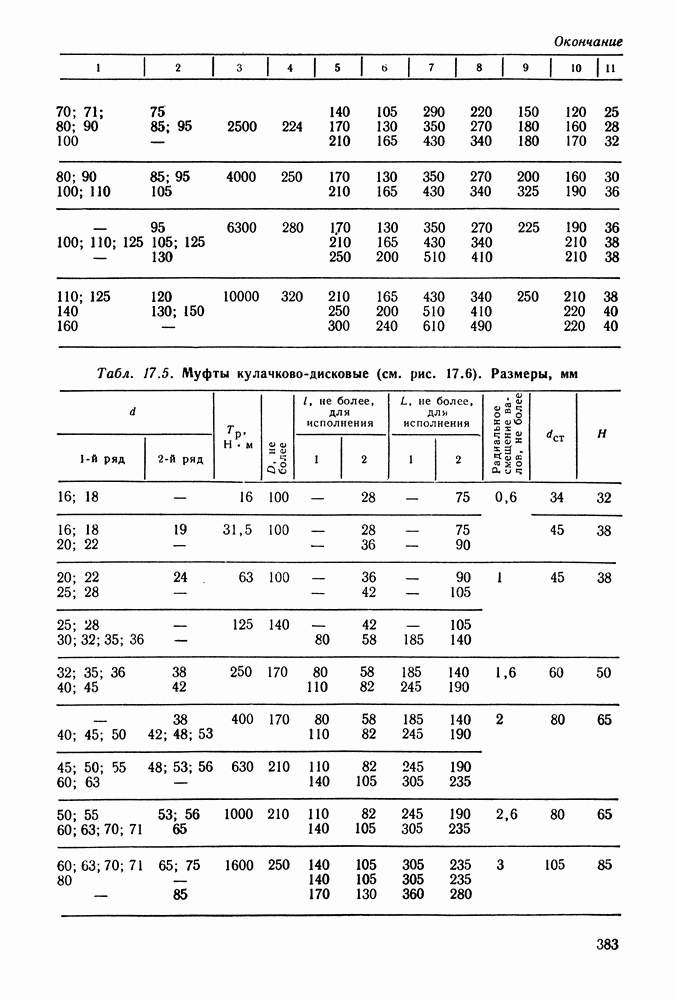
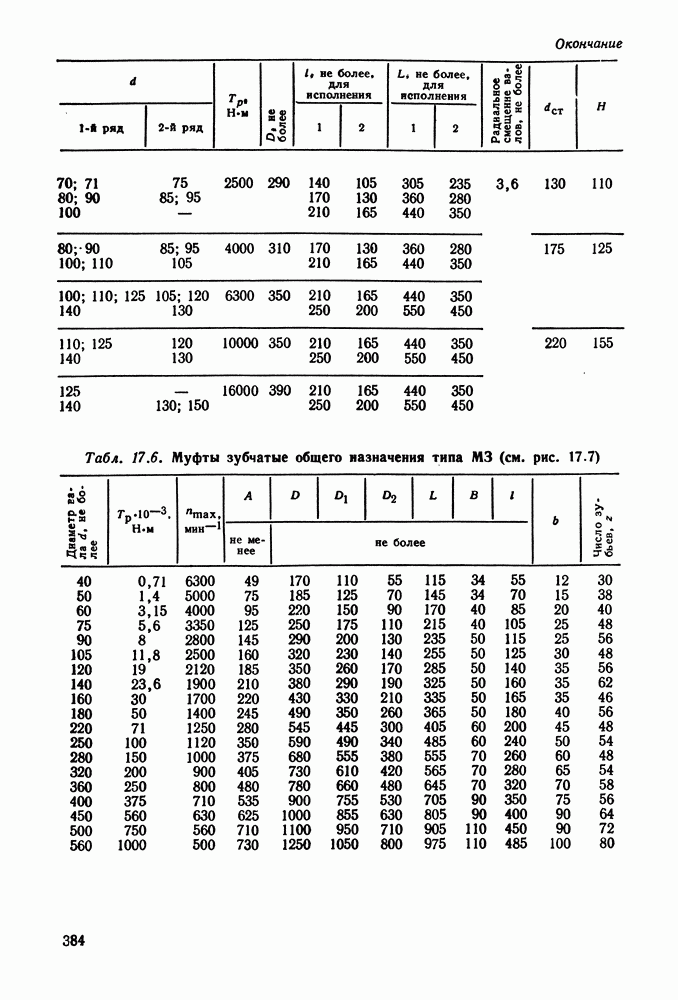
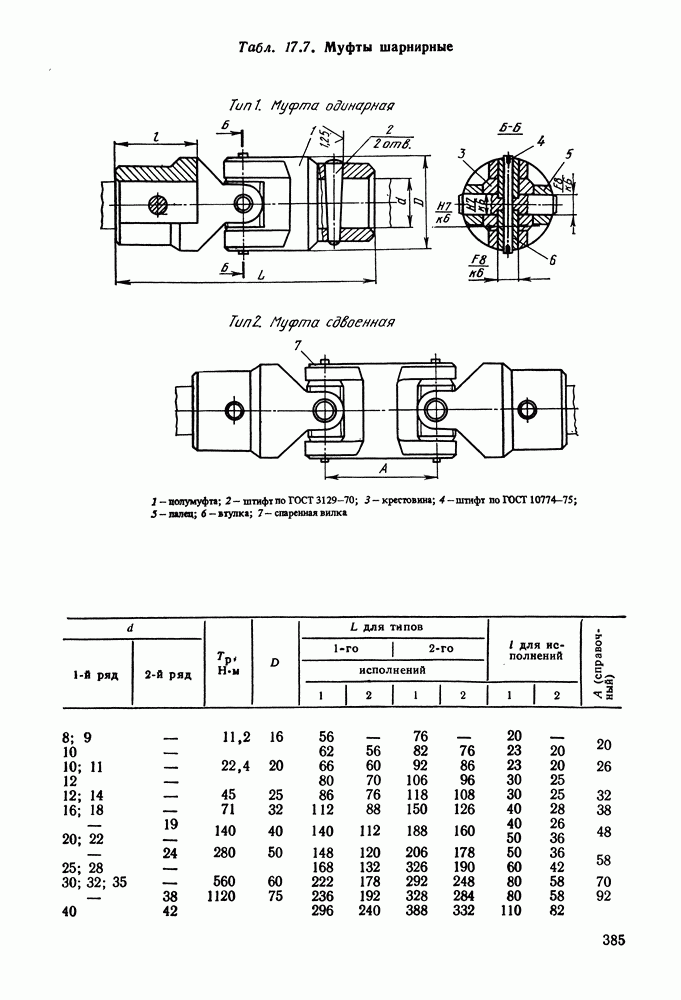
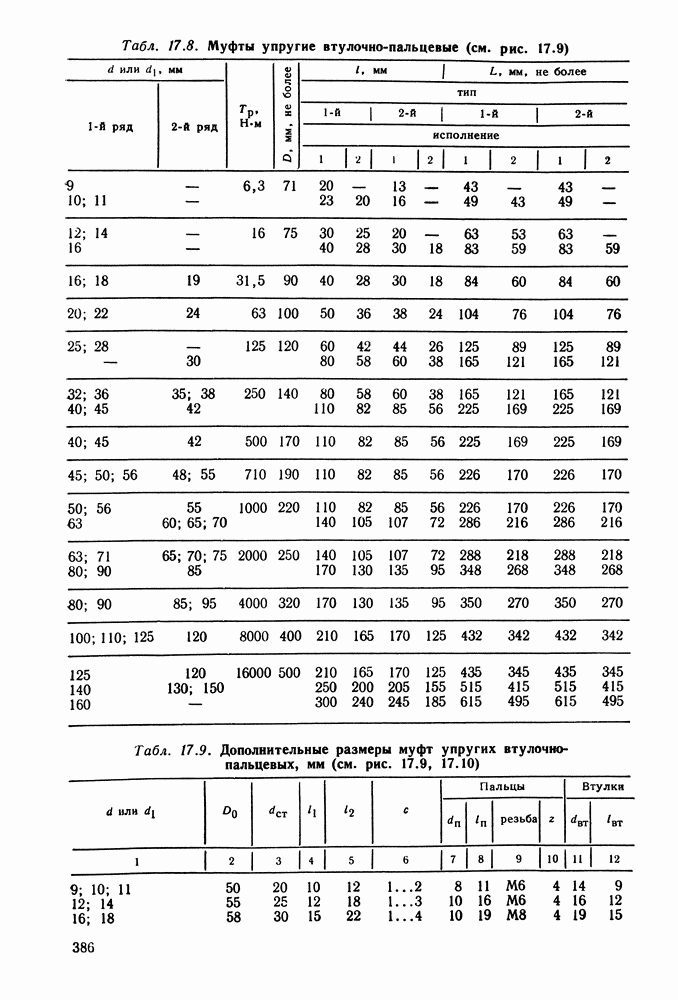
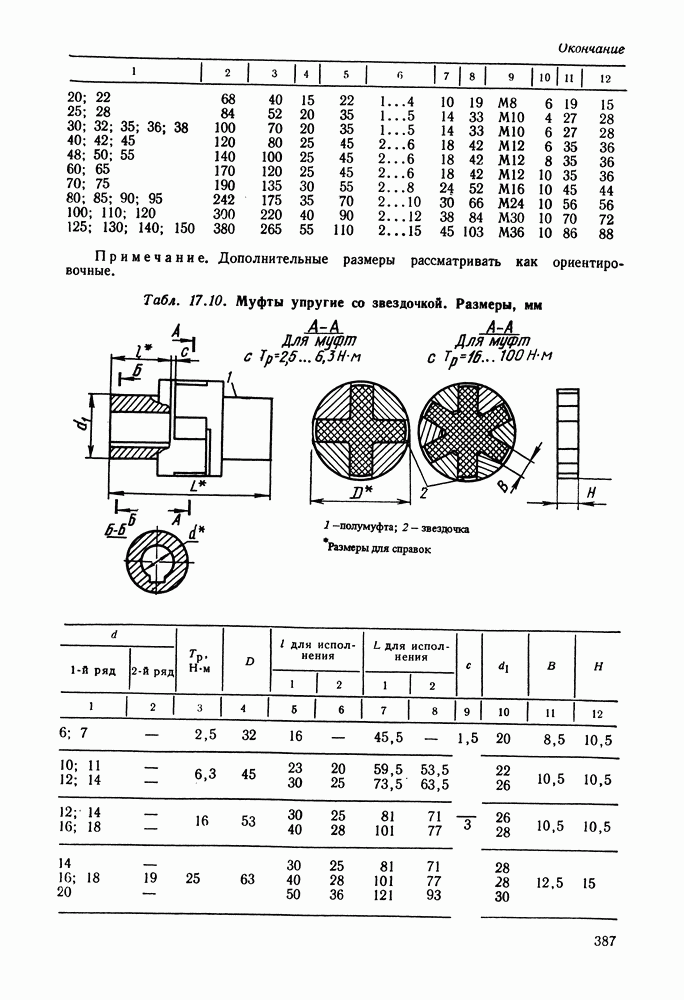
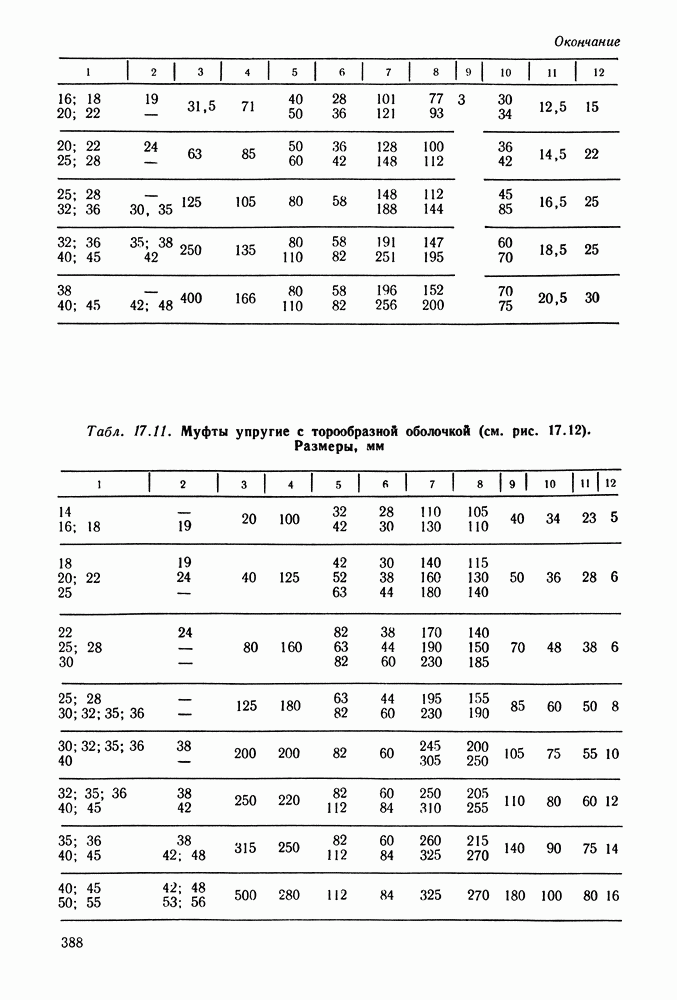
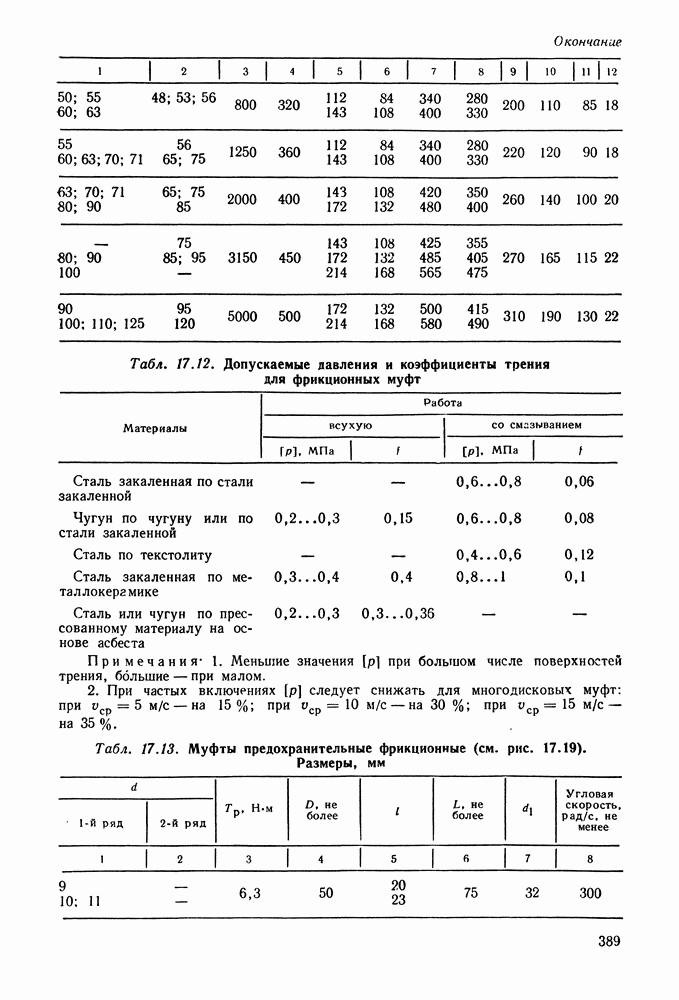
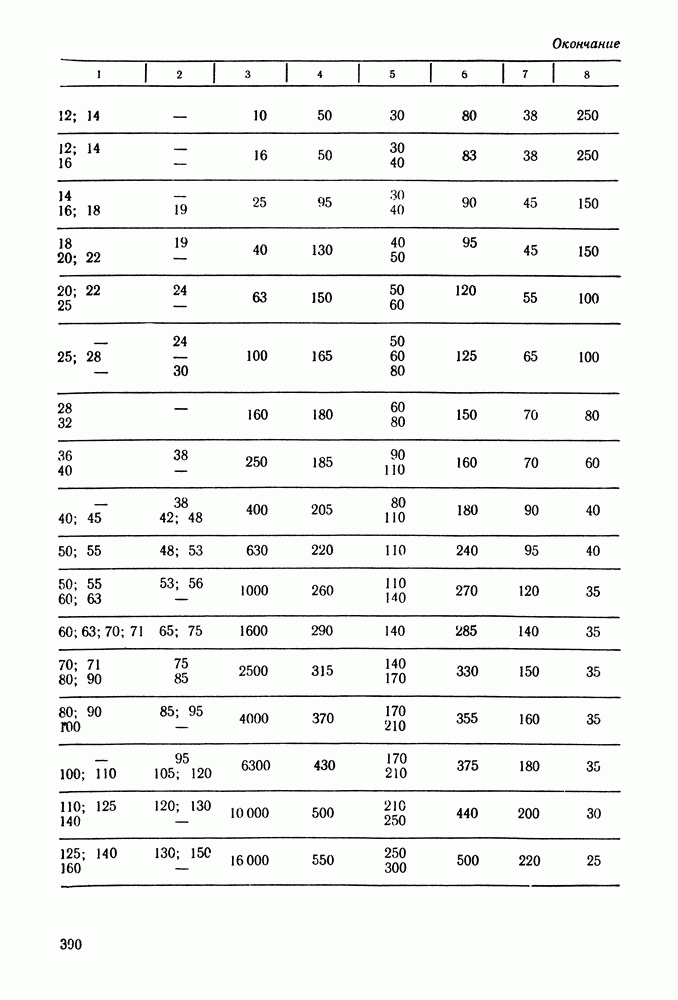
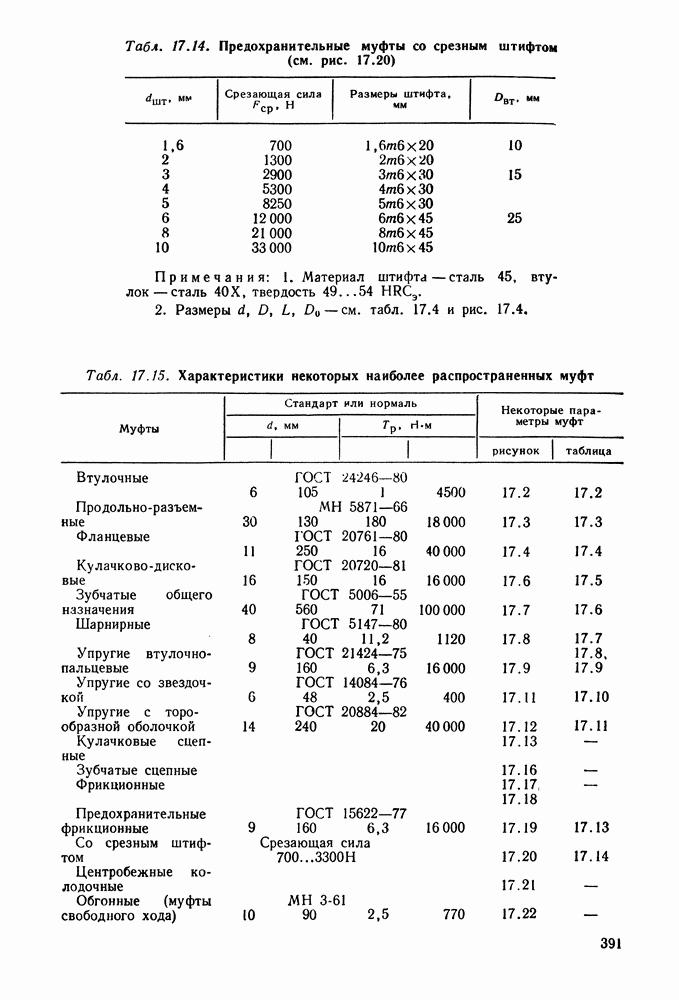
- Глава 17. МУФТЫ
- 17.2. Расчет муфт
- 17.3. Глухие муфты
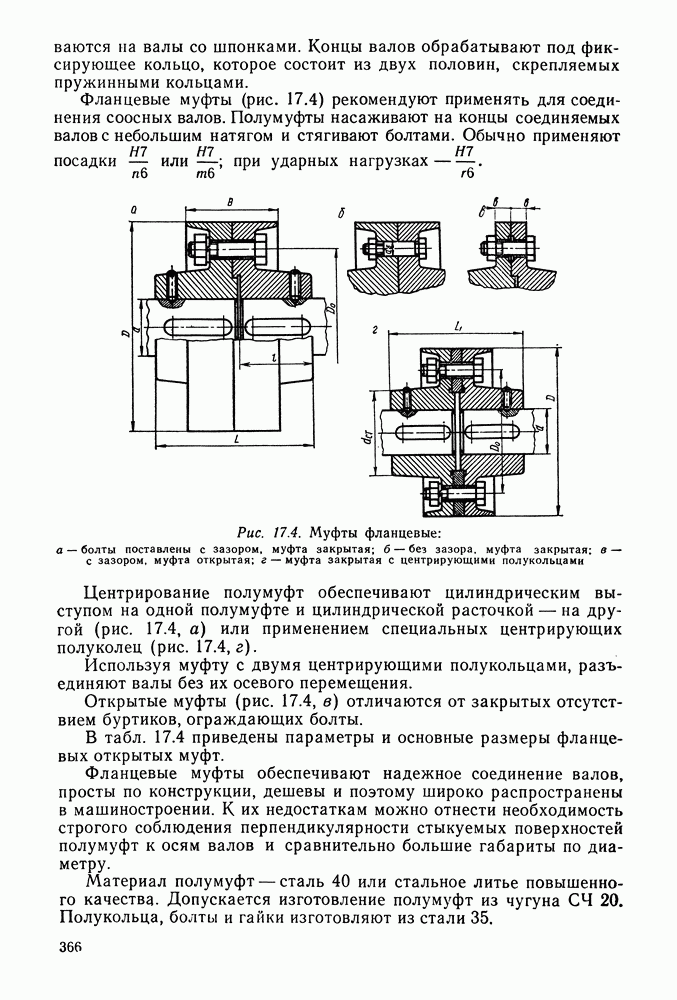
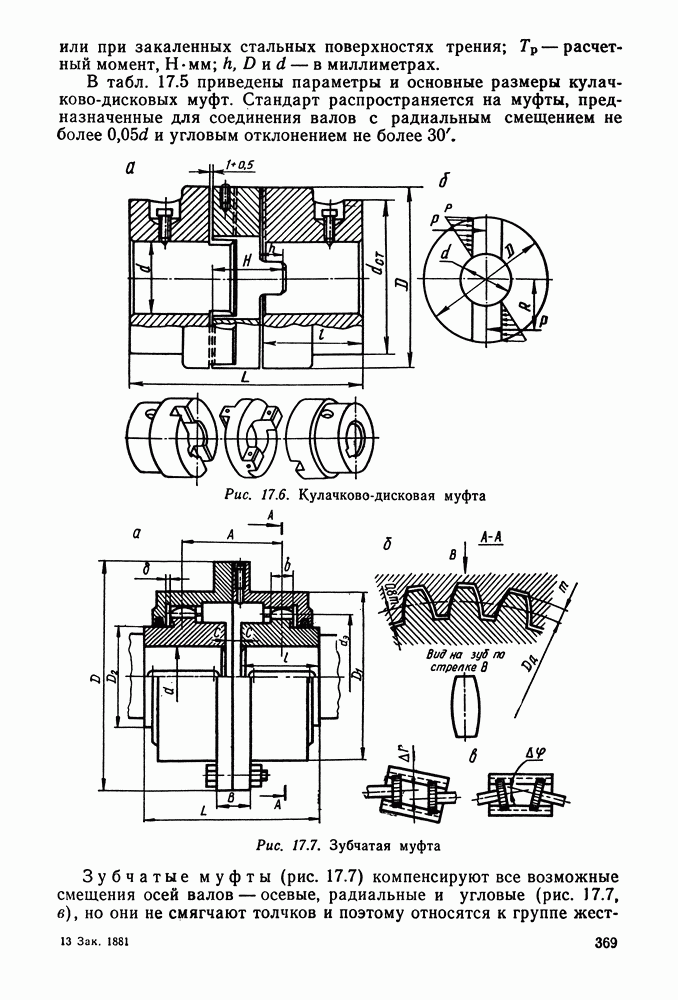
- 17.4. Компенсирующие муфты
- 17.5. Управляемые (сцепные) муфты
- 17.6. Самоуправляемые муфты
- 17.7. Справочный материал
- 17.8. Примеры расчета
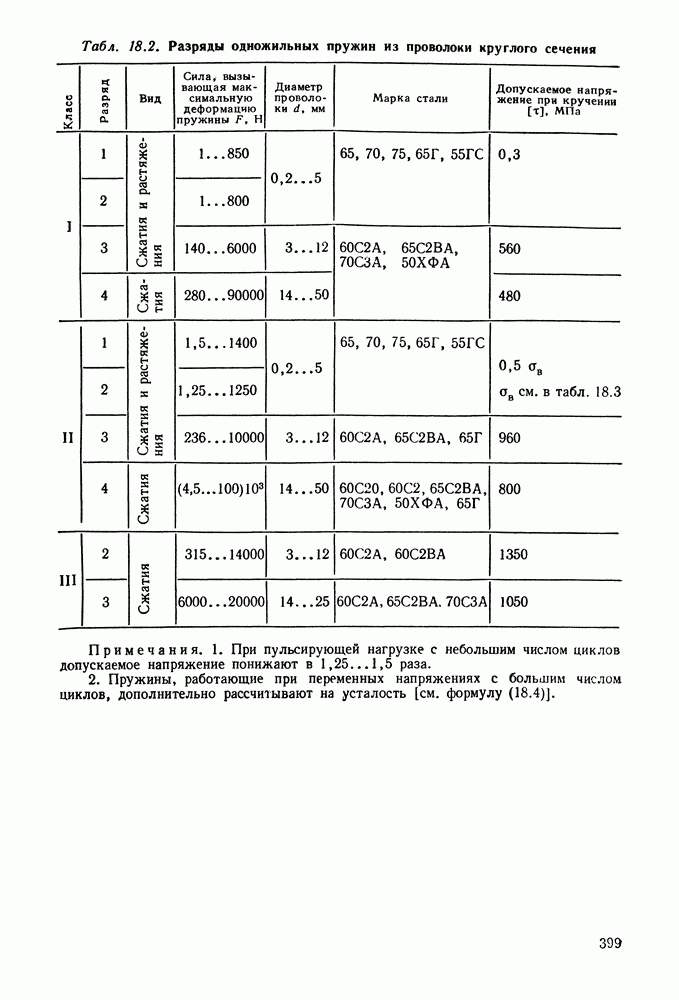
- Глава 18. ПРУЖИНЫ
- 18.2. Расчет винтовых пружин на прочность
- 18.3. Расчет винтовых пружин на жесткость
- 18.4. Подбор тарельчатых пружин
- 18.5. Справочный материал
- ЛИТЕРАТУРА