| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 14. МГНОВЕННАЯ СКОРОСТЬ
Мы сделали попытку свести неравномерное движение к равномерному и для этого ввели среднюю скорость движения. Но это нам не помогло: зная среднюю скорость, нельзя решать самую главную задачу механики — определять положение тела в любой момент времени. Можно ли каким-нибудь другим способом свести неравномерное движение к равномерному?
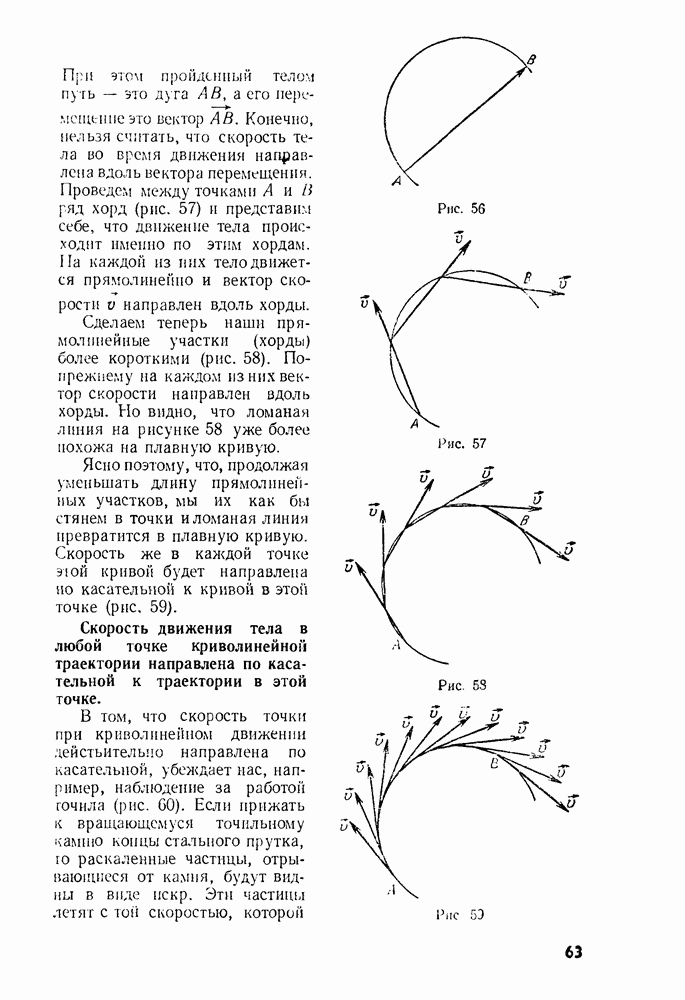
Этого, оказывается, сделать нельзя, потому что механическое движение — это процесс непрерывный. Непрерывность движения состоит в том, что если, например, тело (или точка), двигаясь прямолинейно с возрастающей скоростью, перешло из точки А в точку В, то оно непременно должно побывать во всех промежуточных точках, лежащих между А и В, без всяких пропусков. Но это еще не все. Предположим, что, подходя к точке А, тело двигалось равномерно со скоростью 5 м/сек, а после прохождения точки В оно двигалось тоже равномерно, но со скоростью 30 м/сек. При этом на прохождение участка АВ тело потратило 15 сек. Следовательно, на отрезке АВ скорость тела за 15 сек изменилась на 25 м/сек. Но так же как тело при своем движении не могло миновать ни одну из точек на его пути, его скорость должна была принять все значения скорости между 5 и 30 м/сек. Тоже без всяких пропусков! В этом и состоит непрерывность механического движения: ни координаты тела, ни его скорость не могут изменяться скачками. Отсюда можно сделать очень важный вывод. Различных значений скорости в интервале от 5 до 30 м/сек имеется бесчисленное множество (в математике говорят, бесконечно много значений). Но между точками А и В имеется и бесчисленное множество (бесконечно много!) точек, а 15-секундный интервал времени, в течение которого тело переместилось из точки А в точку В, состоит из бесчисленного множества промежутков времени (время тоже течет без скачков!).
Следовательно, в каждой точке траектории движения и в каждый момент времени тело обладало определенной скоростью.
Скорость, которую имеет тело в данный момент времени и в данной точке траектории, называют мгновенной скоростью.
При равномерном прямолинейном движении скорость тела определяется отношением его перемещения к промежутку времени, за который совершено это перемещение. Что же означает скорость в данной точке или в данный момент времени?
Допустим, что некоторое тело (как всегда, мы в действительности имеем в виду какую-то определенную точку этого тела) движется прямолинейно, но не равномерно. Как вычислить его мгновенную скорость в некоторой точке А его траектории? Выделим небольшом участок  на этой траектории, включающий точку А (рис. 38). Малое перемещение тела на этом участке обозначим через
на этой траектории, включающий точку А (рис. 38). Малое перемещение тела на этом участке обозначим через 

Рис. 38
а малый промежуток времени, в течение которого оно совершено, через  Разделив
Разделив  на
на  мы получим среднюю скорость на этом участке: ведь скорость изменяется непрерывно и в разных местах участка 1 она различна.
мы получим среднюю скорость на этом участке: ведь скорость изменяется непрерывно и в разных местах участка 1 она различна.
Уменьшим теперь длину участка 1. Выберем участок 2 (см. рис. 38), тоже включающий в себя точку А. На этом меньшем участке перемещение равно  и проходит его тело за промежуток времени
и проходит его тело за промежуток времени  Ясно, что на участке 2 скорость тела успевает измениться на меньшую величину. Но отношение
Ясно, что на участке 2 скорость тела успевает измениться на меньшую величину. Но отношение  дает нам и для этого меньшего участка все же среднюю скорость. Еще меньше изменение скорости на протяжении участка 3 (также включающего в себя точку А), меньшего, чем участки 1 и 2, хотя, разделив перемещение
дает нам и для этого меньшего участка все же среднюю скорость. Еще меньше изменение скорости на протяжении участка 3 (также включающего в себя точку А), меньшего, чем участки 1 и 2, хотя, разделив перемещение  на промежуток времени
на промежуток времени  мы опять получим среднюю скорость на этом малом участке траектории. Будем постепенно уменьшать длину участка, а вместе с ним и промежуток времени, за который тело проходит этот участок. В конце концов мы стянем участок траектории, прилегающей к точке А, всамую точку А, а промежуток времени — в момент времени. Тогда-то средняя скорость и станет мгновенной скоростью, потому что на достаточно малом участке изменение скорости будет настолько мало, что его можно не учитывать, значит, можно считать, что скорость не изменяется.
мы опять получим среднюю скорость на этом малом участке траектории. Будем постепенно уменьшать длину участка, а вместе с ним и промежуток времени, за который тело проходит этот участок. В конце концов мы стянем участок траектории, прилегающей к точке А, всамую точку А, а промежуток времени — в момент времени. Тогда-то средняя скорость и станет мгновенной скоростью, потому что на достаточно малом участке изменение скорости будет настолько мало, что его можно не учитывать, значит, можно считать, что скорость не изменяется.
Мгновенная скорость, или скорость в данной точке, равна отношению достаточно малого перемещения на малом участке траектории, прилегающей к этой точке, к малому промежутку времени, в течение которого совершается это перемещение.
Понятно, что скорость равномерного прямолинейного движения — это одновременно его мгновенная и средняя скорость.
Мгновенная скорость — величина векторная. Ее направленна совпадает с направлением перемещения (движения) в данной точка Прием, к которому мы прибегли, чтобы пояснить смысл
мгновенной скорости, состоит, таким образом, в следующем. Участок траектории и время, в течение которого он проходится, мы мысленно постепенно уменьшаем до тех пор, пока участок уже нельзя отличить от точки, промежуток времени — от момента времени, а неравномерное движение — от равномерного. Таким приемом всегда пользуются, когда изучают явления, в которых играют роль какие-нибудь непрерывно изменяющиеся величины.
Нам остается теперь выяснить, что необходимо знать для нахождения мгновенной скорости тела в любой точке траектории и в любой момент времени.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о движении
- § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА
- § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ
- § 3. ПЕРЕМЕЩЕНИЕ
- § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА
- § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ
- § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ
- § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
- § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
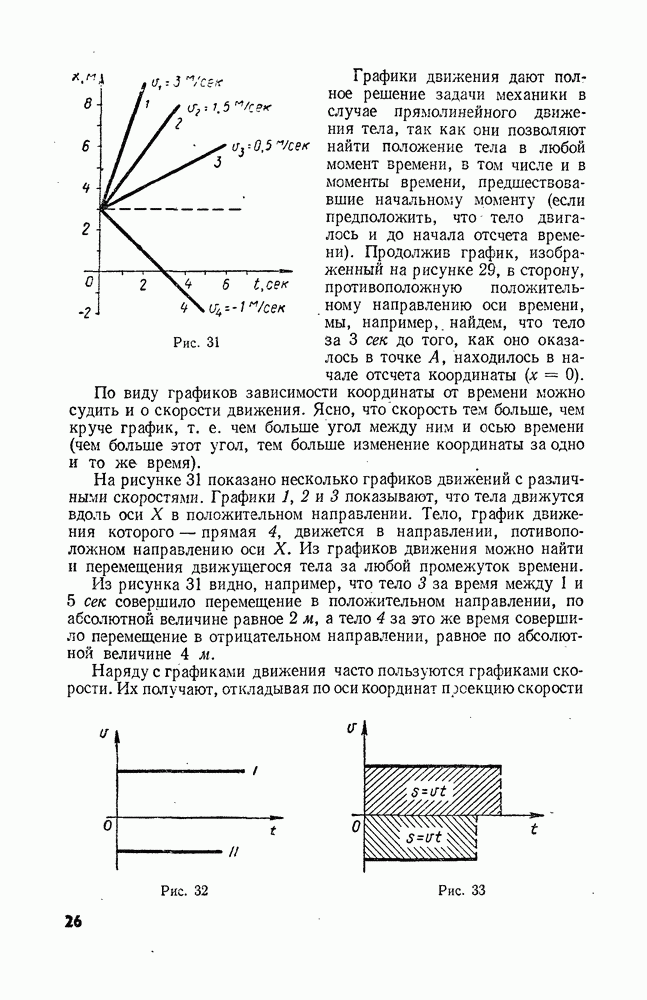
- § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ
- § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
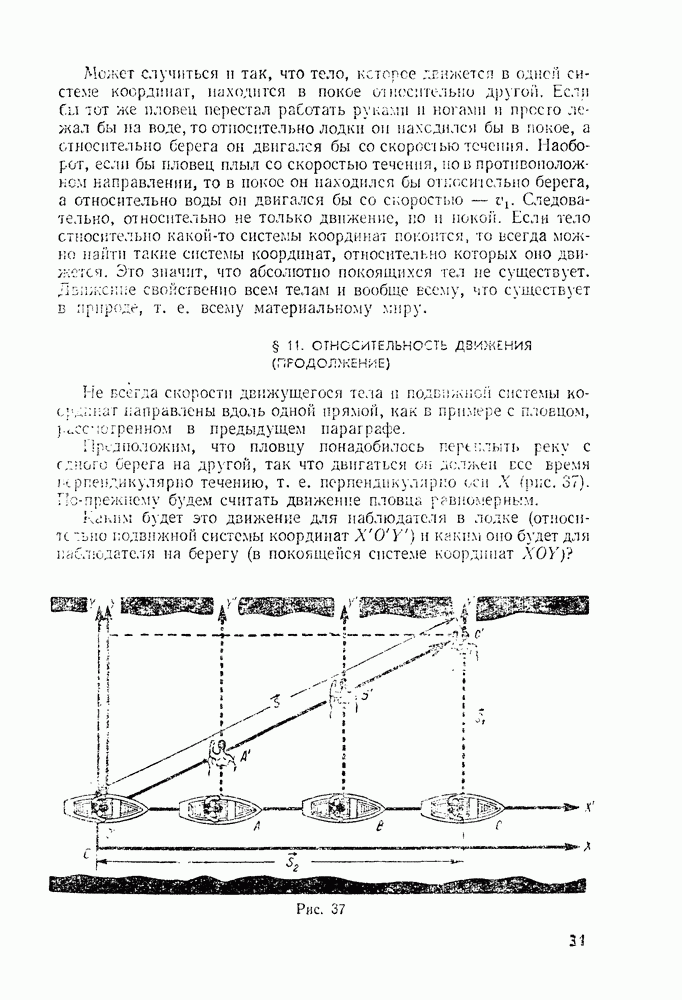
- § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ)
- § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ
- Глава 2. Прямолинейное неравномерное движение
- § 13. СРЕДНЯЯ СКОРОСТЬ
- § 14. МГНОВЕННАЯ СКОРОСТЬ
- § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ
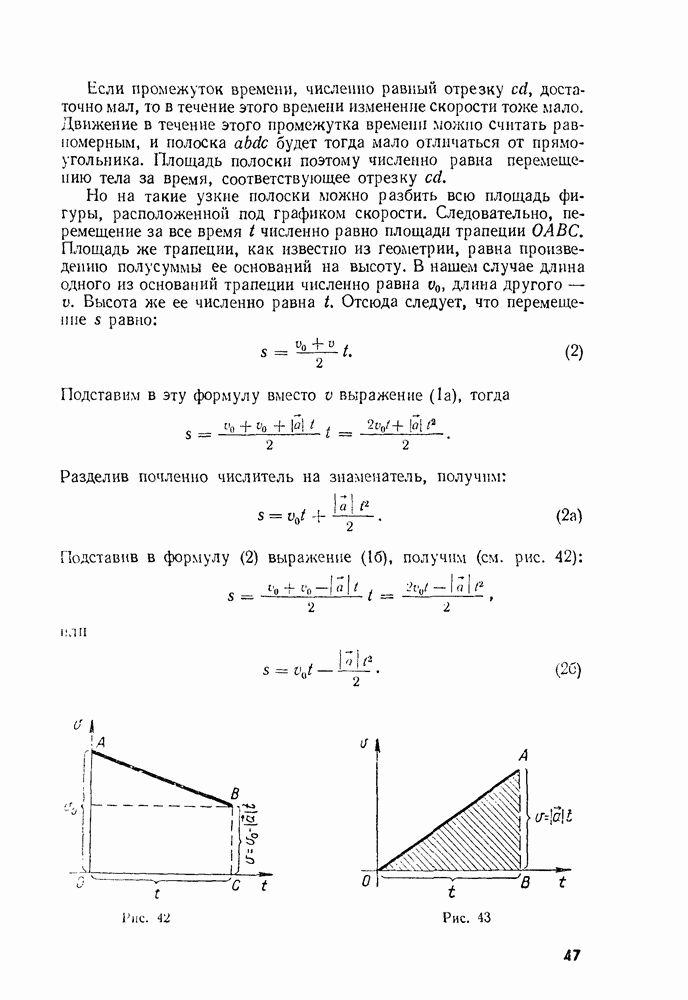
- § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
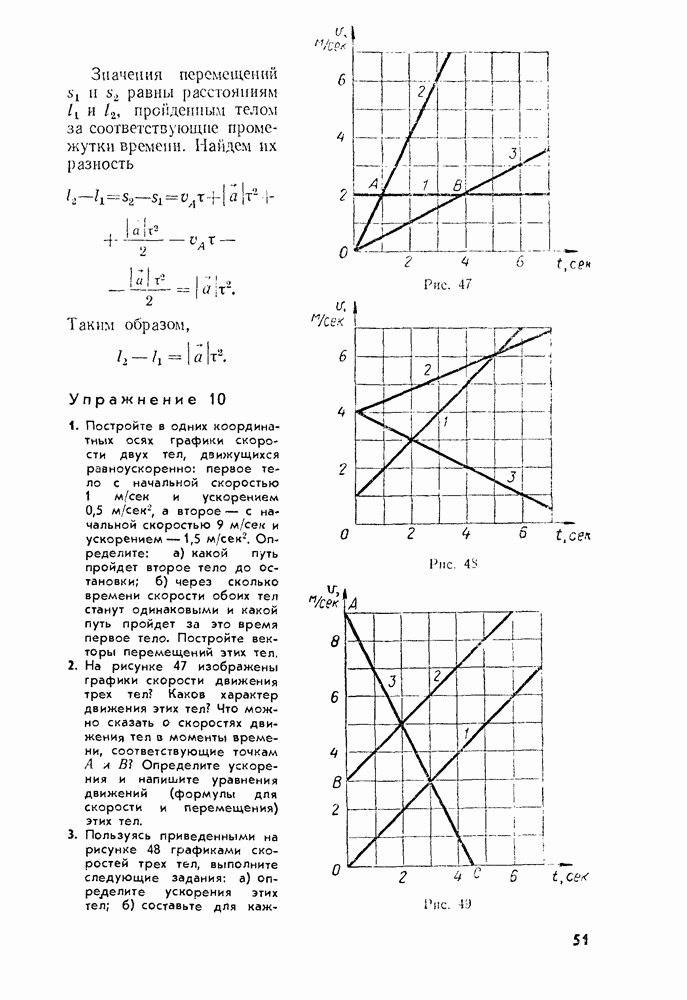
- § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ
- § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ
- § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
- § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
- Глава 3. Криволинейное движение
- § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
- § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ
- § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА
- Динамика
- Глава 4. Законы движения
- § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ
- § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ
- § 31. ИНЕРТНОСТЬ ТЕЛ
- § 32. МАССА ТЕЛ
- § 33. МАССА ЛУНЫ
- § 34. СИЛА
- § 35. ВТОРОЙ ЗАКОН НЬЮТОНА
- § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение)
- § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР
- § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА
- § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА
- Глава 5. Силы природы
- § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ
- § 41. СИЛА УПРУГОСТИ
- § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 44. СИЛА ТЯЖЕСТИ
- § 45. ВЕС ТЕЛ
- § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ
- § 47. МАССА ЗЕМЛИ
- § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ
- § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ
- Глава 6. Применение законов движения
- § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ
- § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ
- § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ
- § 54. НЕВЕСОМОСТЬ
- § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ
- § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО
- § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ
- § 58. ДВИЖЕНИЕ ПЛАНЕТ
- § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ
- § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ
- § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ
- § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ
- § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ
- § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА
- Равновесие тел
- Глава 7. Элементы статики
- § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ
- § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ
- § 67. ПРАВИЛО МОМЕНТОВ
- § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ
- Законы сохранения в механике
- Глава 8. Закон сохранения импульса
- § 70. СИЛА И ИМПУЛЬС
- § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ
- Глава 9. Механическая работа и мощность
- § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ
- § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ
- § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
- § 77. РАБОТА СИЛЫ ТЯЖЕСТИ
- § 78. РАБОТА СИЛЫ УПРУГОСТИ
- § 79. РАБОТА СИЛЫ ТРЕНИЯ
- § 80. МОЩНОСТЬ
- Глава 10. Закон сохранения энергии
- § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА
- § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ
- § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН
- § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
- § 91. СТОЛКНОВЕНИЕ ТЕЛ
- § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ
- § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ
- Заключение
- Лабораторные работы
- 1. Определение ускорения тела при равноускоренном движении
- 2. Определение коэффициента трения скольжения
- 3. Изучение движения тела по параболе
- 4. Выяснение условия равновесия рычага
- 5. Определение центра тяжести плоской пластины
- Ответы к упражнениям