| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
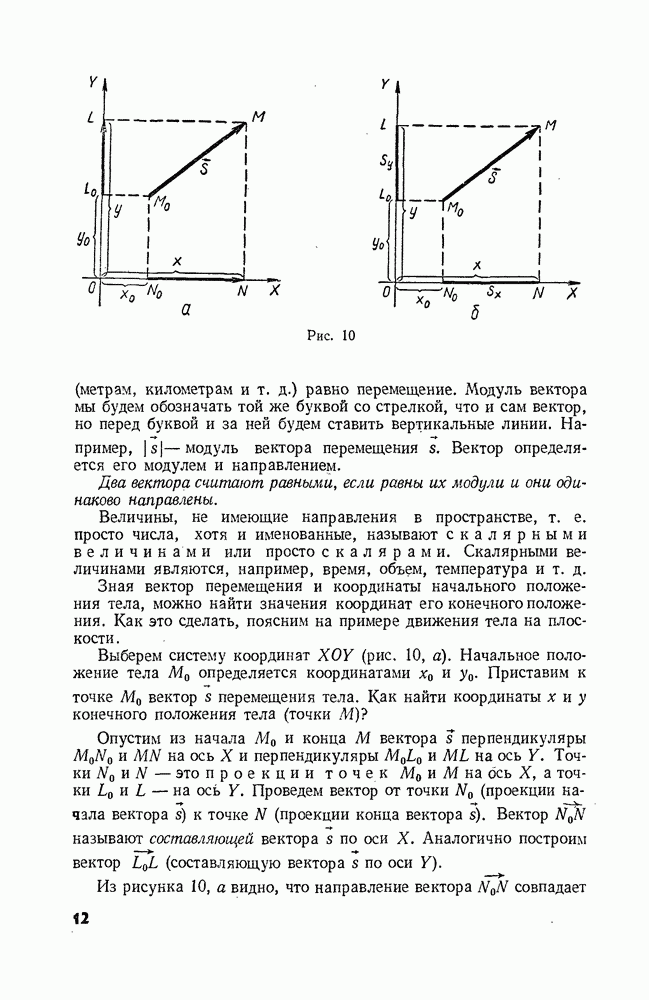
Движение тела по окружности можно описывать тем же способом, которым пользуются при описании прямолинейного движения. Но часто более удобным оказывается другой способ, с которым мы сейчас ознакомимся.
Представим себе, что некоторое тело движется по окружности радиусом  (рис. 65). Проведем из центра О окружности радиус
(рис. 65). Проведем из центра О окружности радиус
к какой-нибудь течке тела А и будем следить не только за самим телом, но  за радиусом, проведенным к нему. Мы увидим, что, по мере того как тело движется, радиус поворачивается. Если, например, тело за промежуток времени
за радиусом, проведенным к нему. Мы увидим, что, по мере того как тело движется, радиус поворачивается. Если, например, тело за промежуток времени  переместилось из точки А в точку В, то за это же время радиус повернулся на угол
переместилось из точки А в точку В, то за это же время радиус повернулся на угол  Этот угол мы будем называть углом поворота радиуса. О движении тела можно, следовательно, сказать, во-первых, что тело за промежуток времени
Этот угол мы будем называть углом поворота радиуса. О движении тела можно, следовательно, сказать, во-первых, что тело за промежуток времени  прешло путь
прешло путь  по дуге
по дуге  окружности, во-вторых, что оно совершило перемещение в, модуль которого равен длине хорды
окружности, во-вторых, что оно совершило перемещение в, модуль которого равен длине хорды  и, в-третьих, что радиус, проведенный к телу, совершил псвсрот на угол
и, в-третьих, что радиус, проведенный к телу, совершил псвсрот на угол 
Если бы тело двигалось по окружности другого радиуса  (см. рис. 65), то длина пройденного пути была бы больше. Большей была бы и длина перемещения
(см. рис. 65), то длина пройденного пути была бы больше. Большей была бы и длина перемещения  Угол же поворота ради
Угол же поворота ради  в обоих случаях остается одним и тем же. Так, конец минутной стрелки маленьких ручных часов за 15 мин проходит путь длиной сколо 1,5 см. За это же время конец минутной стрелки огромных башенных часов (например, часов Спасской башни Кремля) проходит путь длиной в несколько метров. Но минутные стрелки всех часов в мире за четверть часа поворачиваются на один и тот же угол — 50° (рис. 66).
в обоих случаях остается одним и тем же. Так, конец минутной стрелки маленьких ручных часов за 15 мин проходит путь длиной сколо 1,5 см. За это же время конец минутной стрелки огромных башенных часов (например, часов Спасской башни Кремля) проходит путь длиной в несколько метров. Но минутные стрелки всех часов в мире за четверть часа поворачиваются на один и тот же угол — 50° (рис. 66).
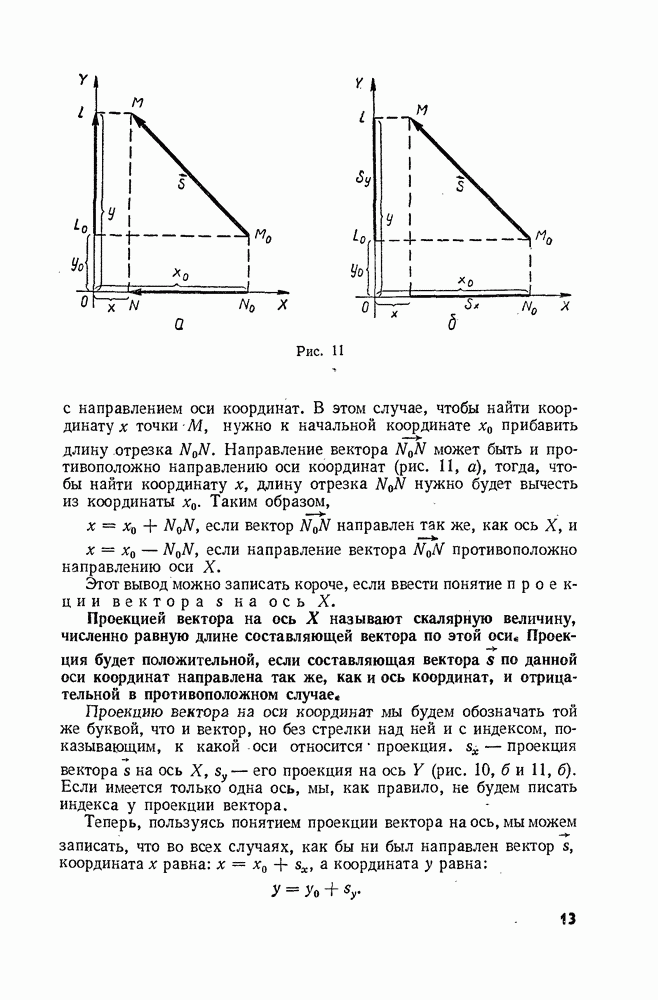
Если мы снова Еернемся к рисунку 65, то увидим, что у тел, движущихся по окружностям с радиусами  равны не только угли псссрсга. В обоих случаях одинаковы и отношения длины дуги к радиусу:
равны не только угли псссрсга. В обоих случаях одинаковы и отношения длины дуги к радиусу:

По какой бы окружности ни двигалось тело, при равных углах поворота радиуса равны и отношения длины дуги к радиусу. Поэтому и сами углы можно измерять величиной этого отношения


Рис. 65

Рис. 66
При таком измерении углов за единицу измерения угла удобно принять не градус, а угол, соответствующий дуге, длина которой I равна радиусу  потому что тогда угол
потому что тогда угол  будет равен единице. Такая единица измерения угла сейчас общепринята в науке, и называют ее радианом (сокращенно рад).
будет равен единице. Такая единица измерения угла сейчас общепринята в науке, и называют ее радианом (сокращенно рад).
Радиан — это угол между двумя радиусами круга, вырезающий на окружности дугу, длина которой равна радиусу.
Легко установить связь между градусом и радианом.
Когда тело (или точка) совершит один полный оборот по окружности радиусом  то длина пройденной дуги будет равна
то длина пройденной дуги будет равна  Поэтому величина угла в радианах равна:
Поэтому величина угла в радианах равна:

Следэзательно, один оборот — это поворот радиуса на угол  рад. В градусной мере этот же угол равен
рад. В градусной мере этот же угол равен  Отсюда
Отсюда

Таким образом, длина дуги, пройденной телом, и угол поворота радиуса, проведенного к нему, связаны формулой

Скорость равномерного движения тела по окружности тоже можно выражать в угловых единицах. Для этого используют понятие угловой скорости.
Под угловой скоростью мы будем понимать отношение угла поворота радиуса, проведенного к телу, к промежутку времени, в течение которого совершен этот поворот. Угловую скорость обозначают греческой буквой со (омега), так что

Так как здесь угол  выражен в радианах, а время
выражен в радианах, а время  в секундах, то угловая скорость со измеряется в радианах в секунду (рад/сек).
в секундах, то угловая скорость со измеряется в радианах в секунду (рад/сек).
В отличие от угловой скорости скорость  измеряемую отношением длины пути
измеряемую отношением длины пути  ко времени
ко времени  и выражаемую в метрах в секунду, называют линейной скоростью. Между угловой скоростью со и линейной скоростью
и выражаемую в метрах в секунду, называют линейной скоростью. Между угловой скоростью со и линейной скоростью  очень простая связь. Если в выражение для угловой скорости подставить вместо
очень простая связь. Если в выражение для угловой скорости подставить вместо  его значение
его значение  то мы получим:
то мы получим: 
Так как в свою очередь  то
то  или
или 
Линейная скорость точки равна произведению угловой скорости на радиус окружности, по которой происходит движение.
Скорость движения тела по окружности часто выражают также числом оборотов в единицу времени. Легко связать угловую скорость с числом оборотов в единицу времени. Действительно, при одном обороте радиус поворачивается на угол в  рад. Значит, совершив в единицу времени, например,
рад. Значит, совершив в единицу времени, например,  оборотов, радиус повернется на угол
оборотов, радиус повернется на угол  рад. Поэтому угловая скорость
рад. Поэтому угловая скорость  и число оборотов в единицу времени
и число оборотов в единицу времени  связаны выражением
связаны выражением

Число оборотов в единицу времени  обычно называют также частотой вращения. Величина, обратная частоте, определяет время, за которое тело делает один оборот. Это время называют периодом вращения и обозначают буквой Т:
обычно называют также частотой вращения. Величина, обратная частоте, определяет время, за которое тело делает один оборот. Это время называют периодом вращения и обозначают буквой Т:

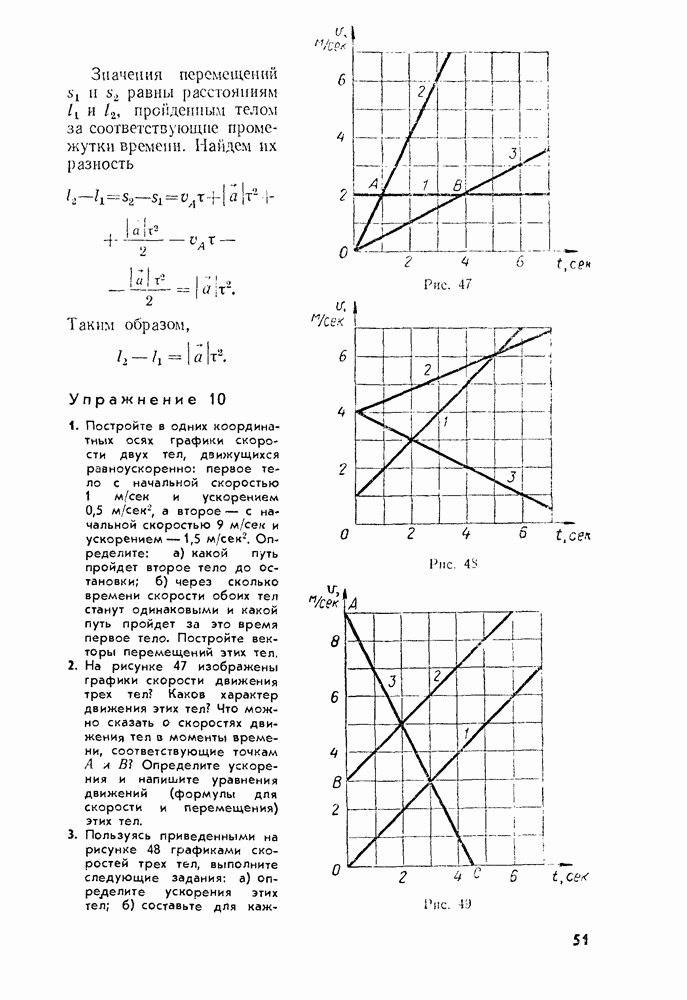
Упражнение 15
1. Что такое угловая скорость? В каких единицах ее измеряют?
2. Как связаны между собой угловая и линейная скорость?
3. Вычислите угловую и линейную скорость движения Земли вокруг Солнца. Радиус орбиты Земли считать равным 150 000.000 км.
4. Какова линейная скорость конца минутной стрелки часов на Спасской башне Московского Кремля, если длина стрелки 3,5 м? Сравните угловую скорость этой стрелки с угловой скоростью минутной стрелки ручных часов.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о движении
- § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА
- § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ
- § 3. ПЕРЕМЕЩЕНИЕ
- § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА
- § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ
- § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ
- § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
- § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
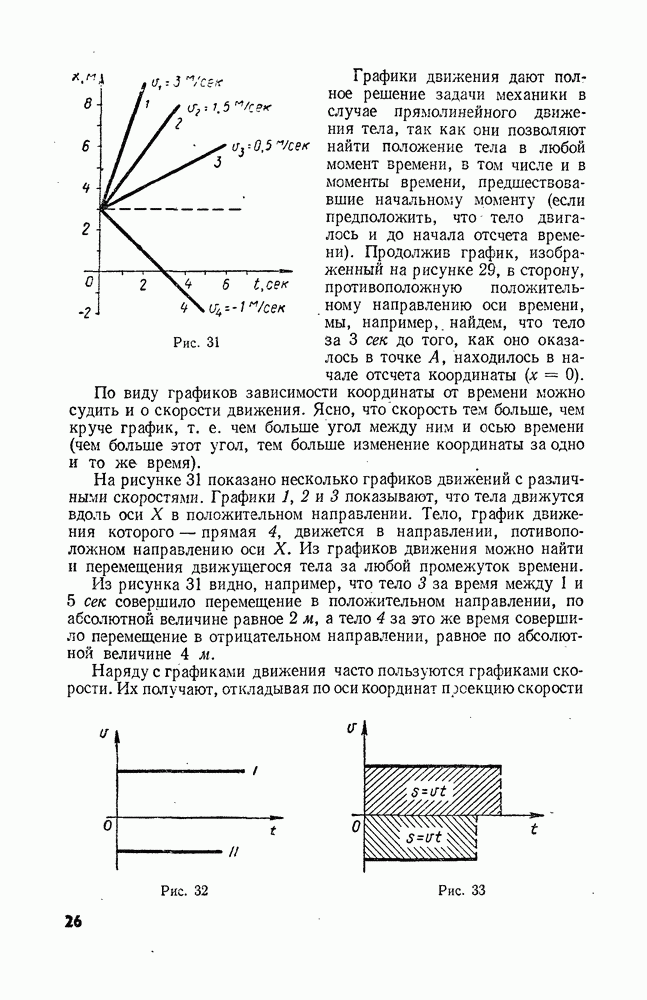
- § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ
- § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
- § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ)
- § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ
- Глава 2. Прямолинейное неравномерное движение
- § 13. СРЕДНЯЯ СКОРОСТЬ
- § 14. МГНОВЕННАЯ СКОРОСТЬ
- § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ
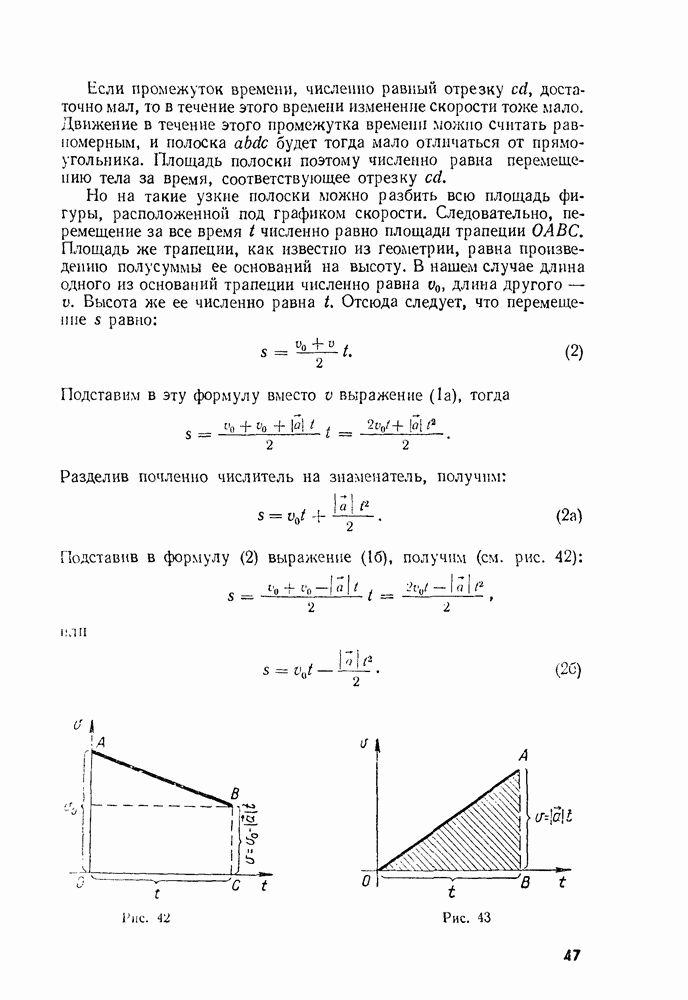
- § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
- § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ
- § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ
- § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
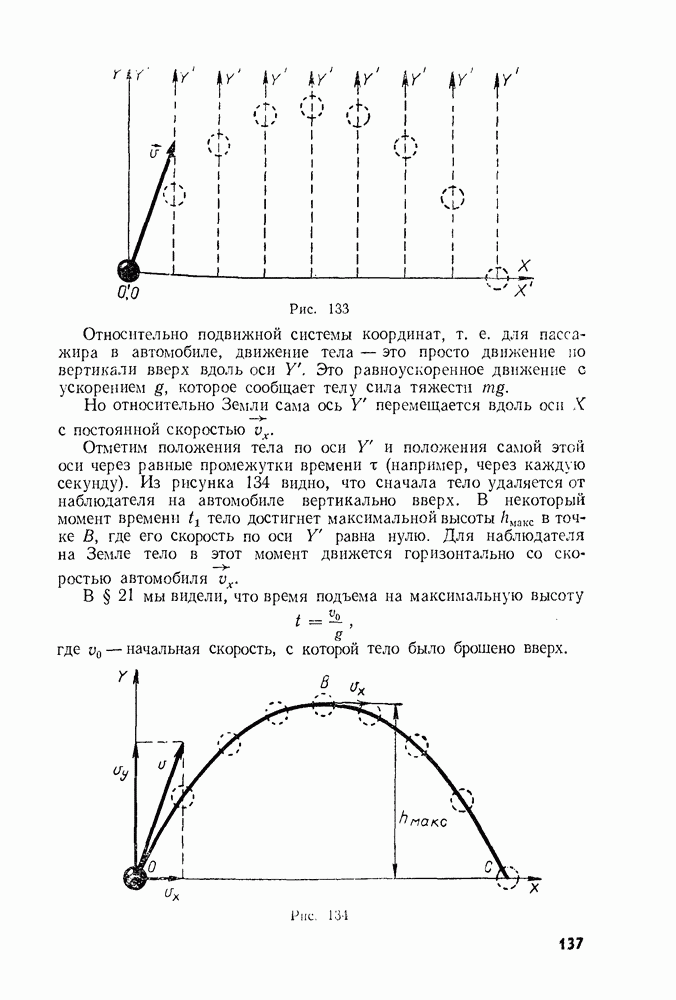
- § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
- Глава 3. Криволинейное движение
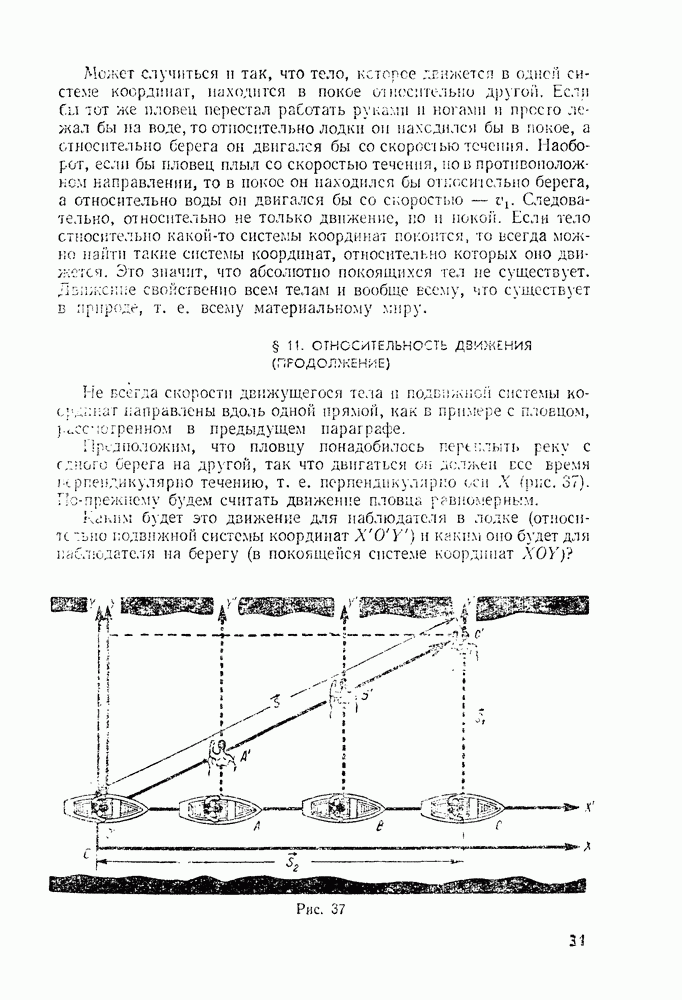
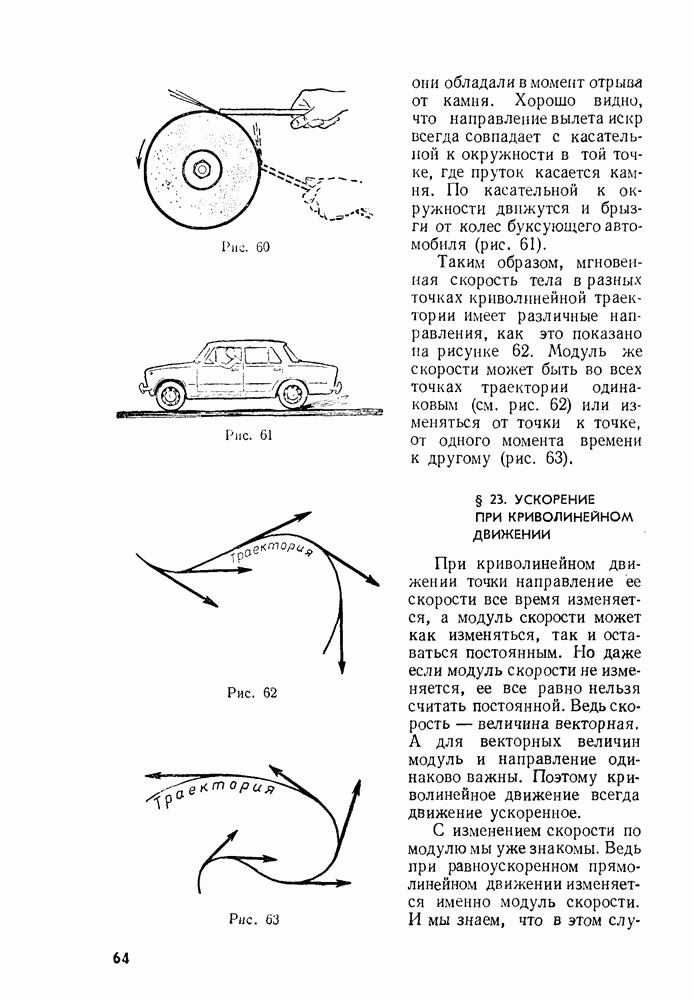
- § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
- § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ
- § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА
- Динамика
- Глава 4. Законы движения
- § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ
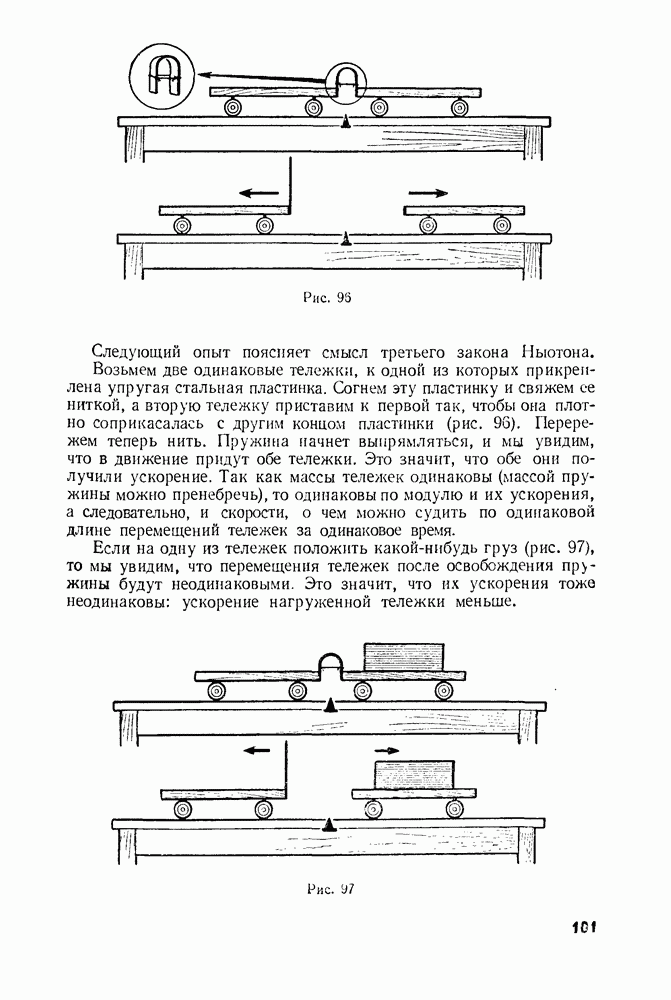
- § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ
- § 31. ИНЕРТНОСТЬ ТЕЛ
- § 32. МАССА ТЕЛ
- § 33. МАССА ЛУНЫ
- § 34. СИЛА
- § 35. ВТОРОЙ ЗАКОН НЬЮТОНА
- § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение)
- § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР
- § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА
- § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА
- Глава 5. Силы природы
- § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ
- § 41. СИЛА УПРУГОСТИ
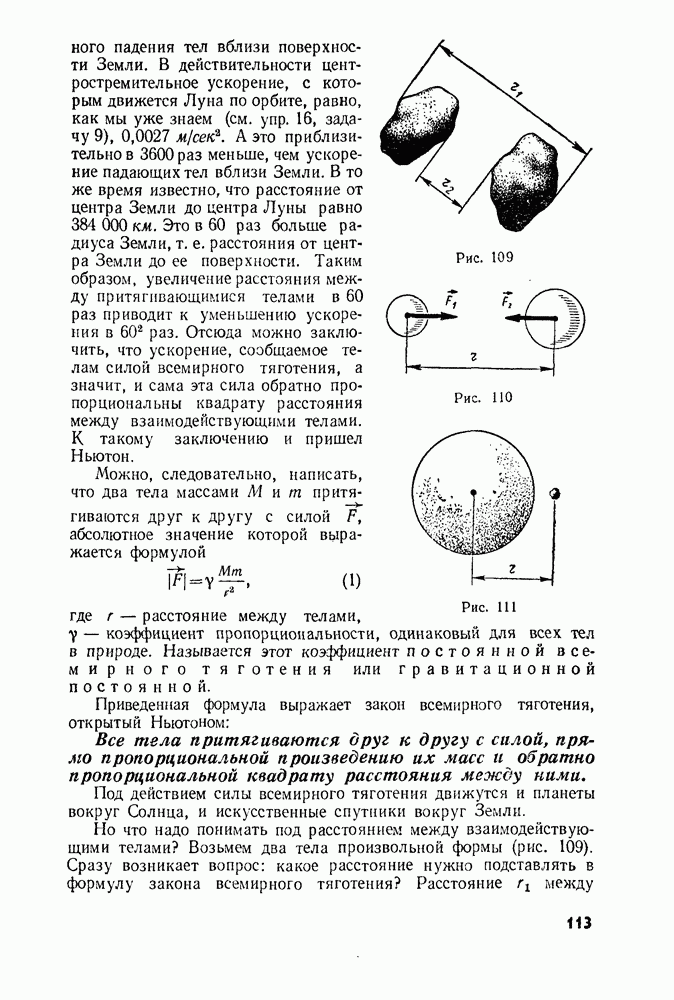
- § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 44. СИЛА ТЯЖЕСТИ
- § 45. ВЕС ТЕЛ
- § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ
- § 47. МАССА ЗЕМЛИ
- § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ
- § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ
- Глава 6. Применение законов движения
- § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ
- § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ
- § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ
- § 54. НЕВЕСОМОСТЬ
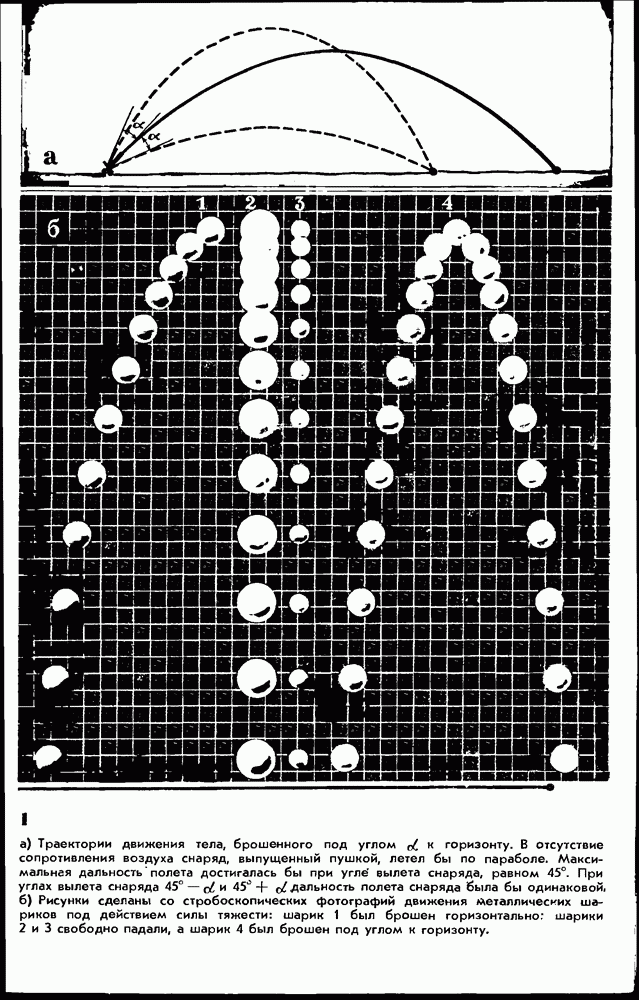
- § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ
- § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО
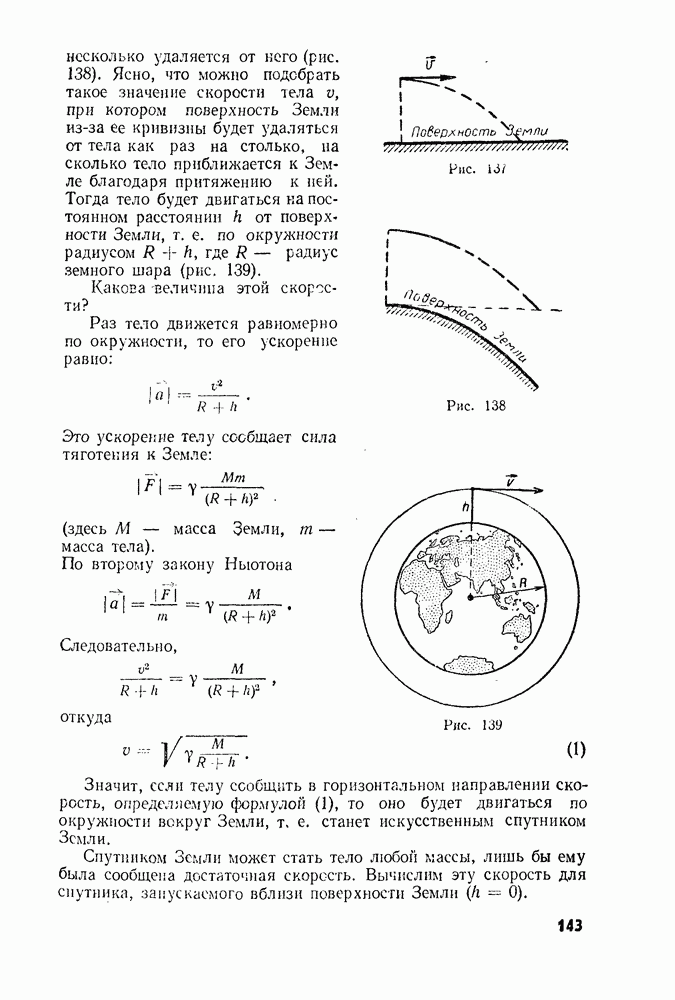
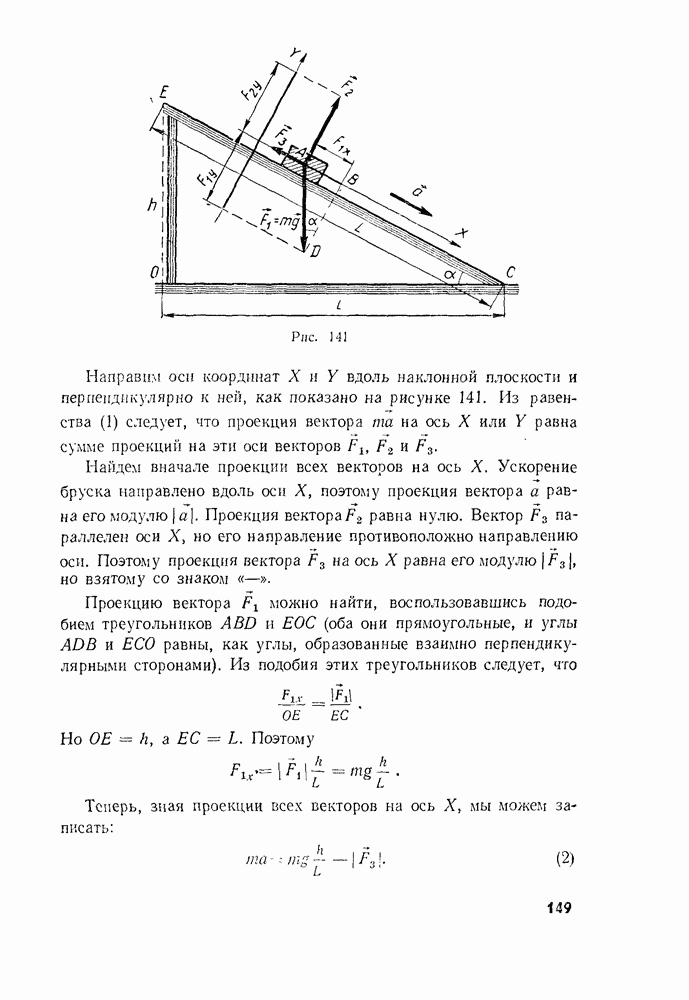
- § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ
- § 58. ДВИЖЕНИЕ ПЛАНЕТ
- § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ
- § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ
- § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ
- § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ
- § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ
- § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА
- Равновесие тел
- Глава 7. Элементы статики
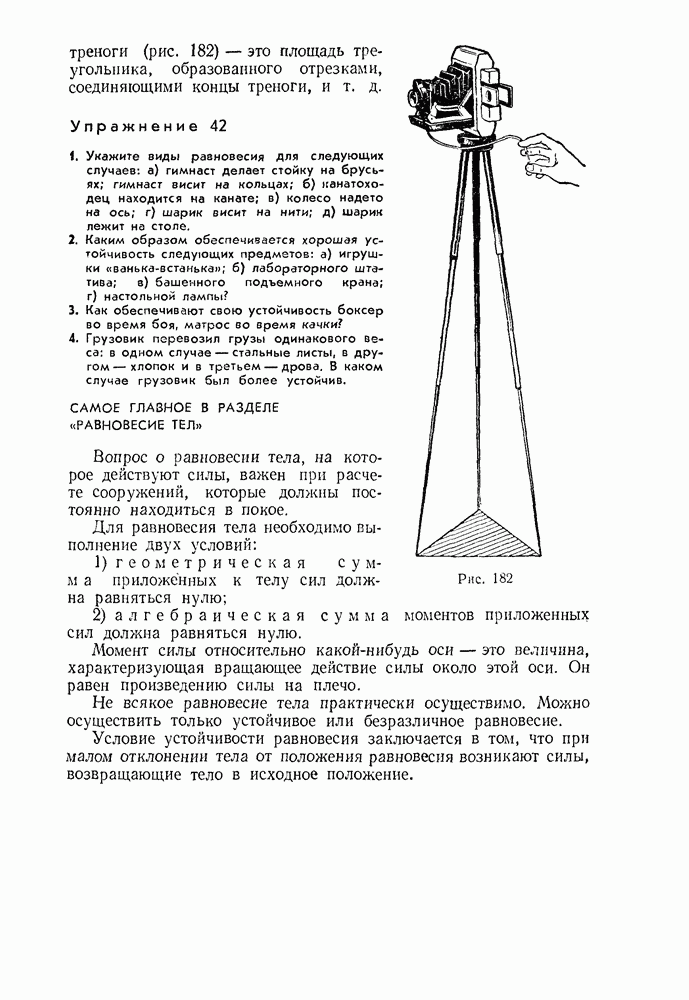
- § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ
- § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ
- § 67. ПРАВИЛО МОМЕНТОВ
- § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ
- Законы сохранения в механике
- Глава 8. Закон сохранения импульса
- § 70. СИЛА И ИМПУЛЬС
- § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ
- Глава 9. Механическая работа и мощность
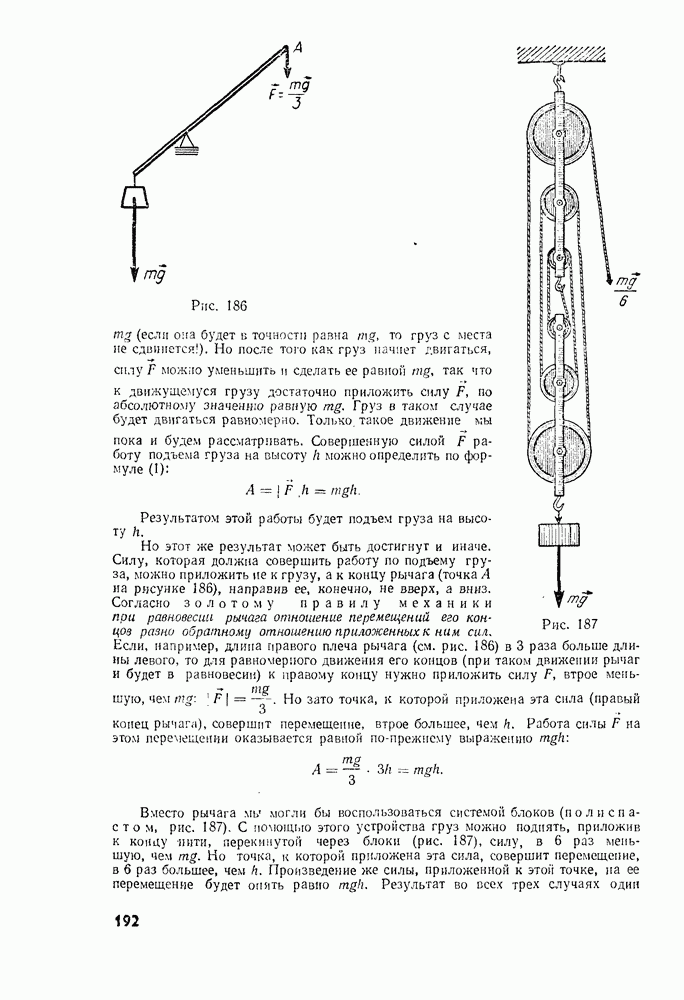
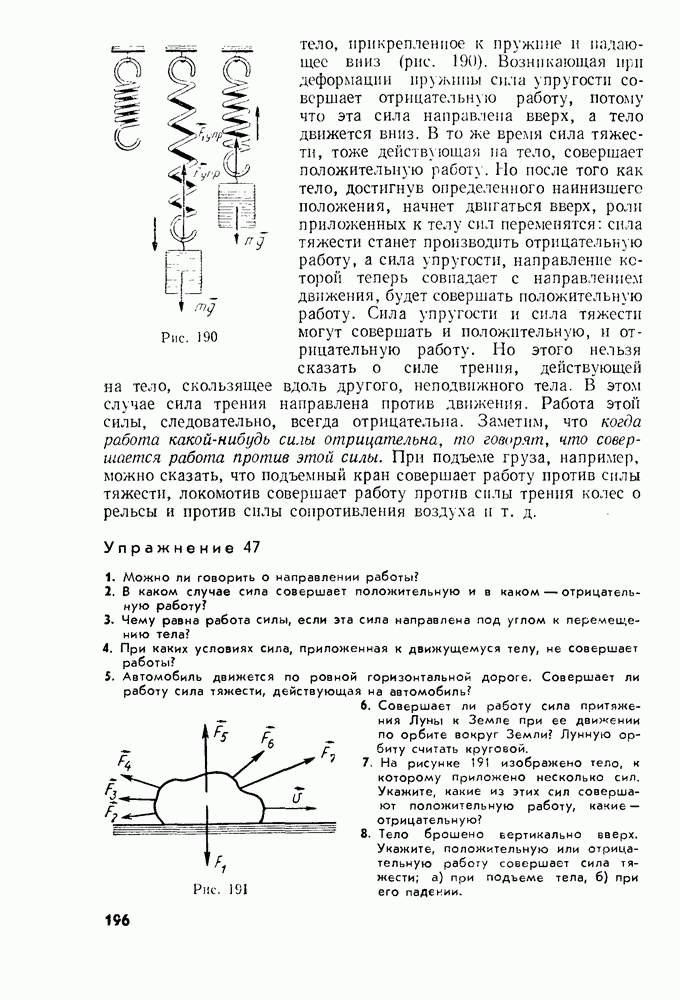
- § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ
- § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ
- § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
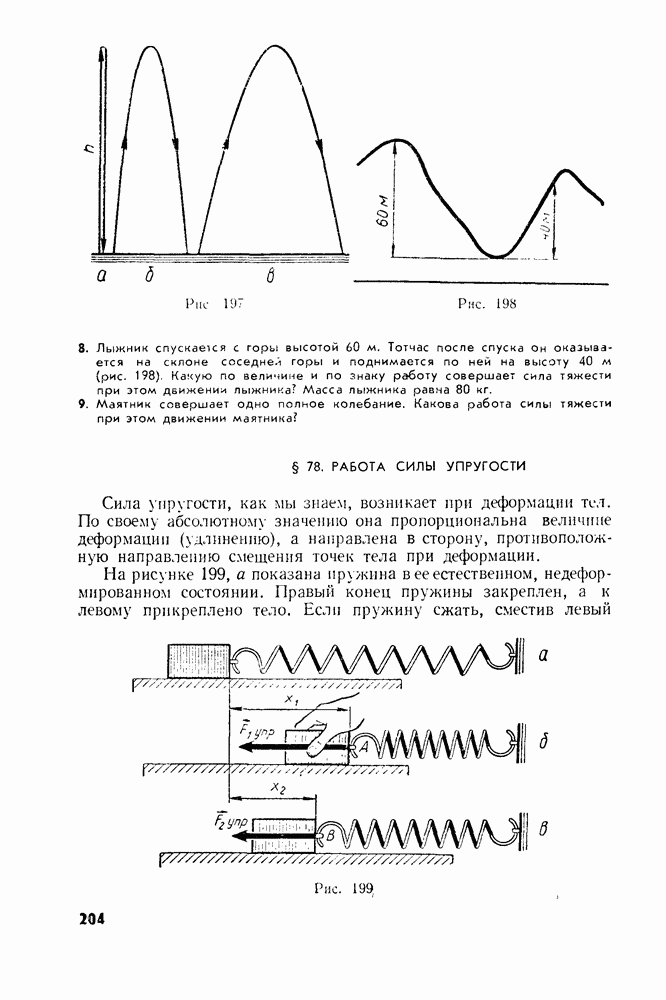
- § 77. РАБОТА СИЛЫ ТЯЖЕСТИ
- § 78. РАБОТА СИЛЫ УПРУГОСТИ
- § 79. РАБОТА СИЛЫ ТРЕНИЯ
- § 80. МОЩНОСТЬ
- Глава 10. Закон сохранения энергии
- § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА
- § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ
- § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН
- § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
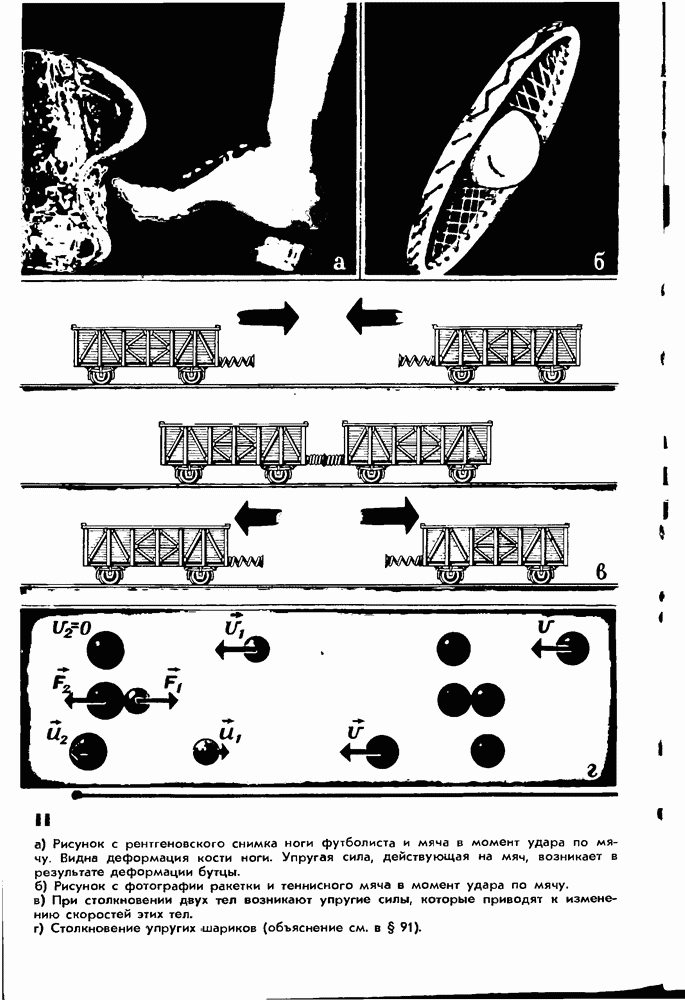
- § 91. СТОЛКНОВЕНИЕ ТЕЛ
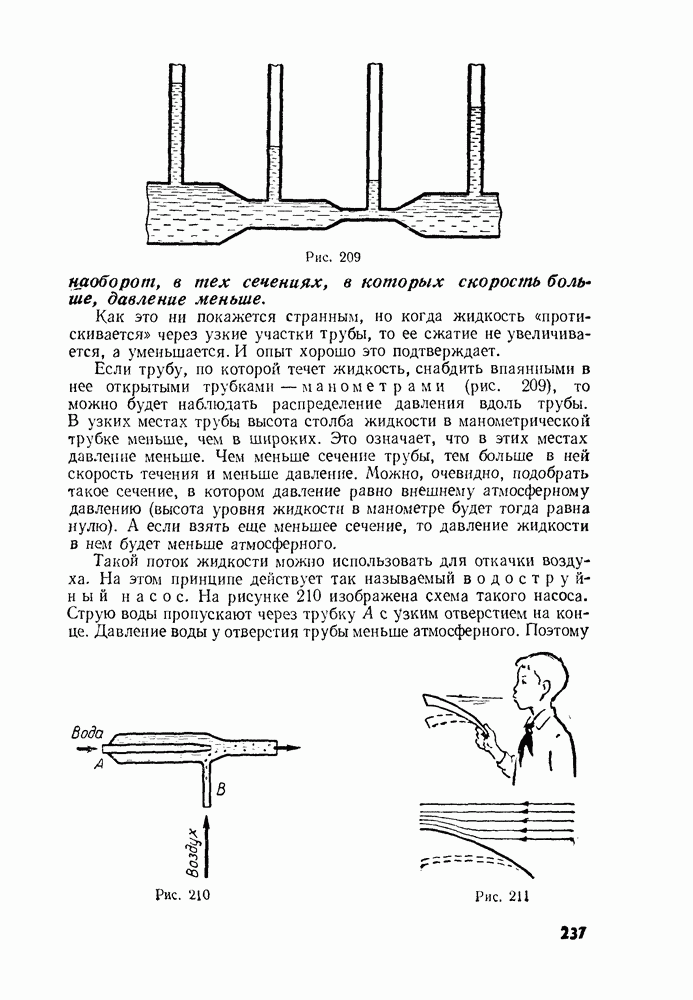
- § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ
- § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ
- Заключение
- Лабораторные работы
- 1. Определение ускорения тела при равноускоренном движении
- 2. Определение коэффициента трения скольжения
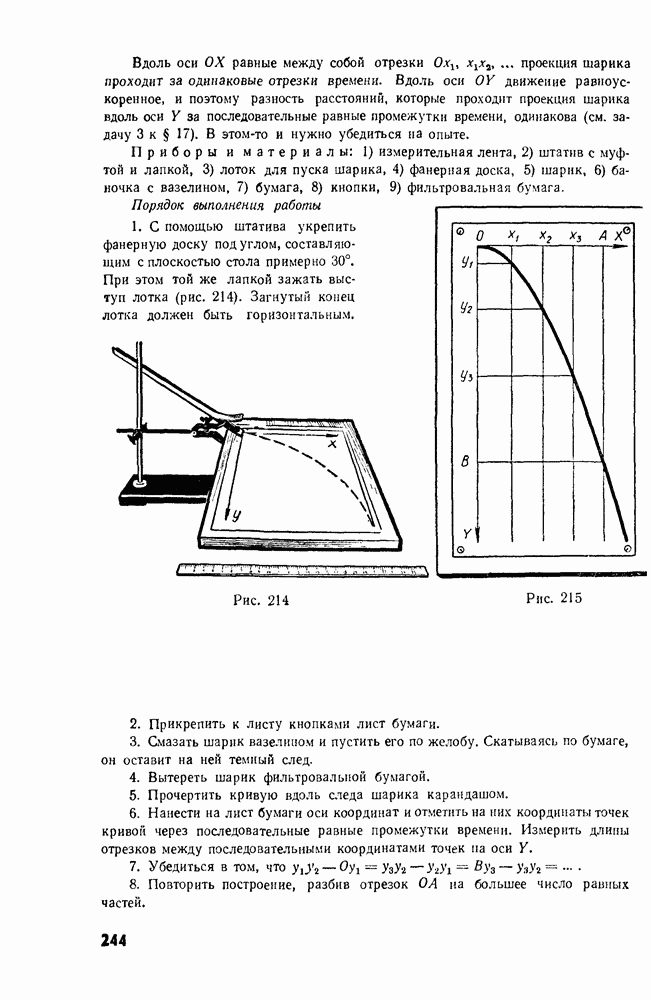
- 3. Изучение движения тела по параболе
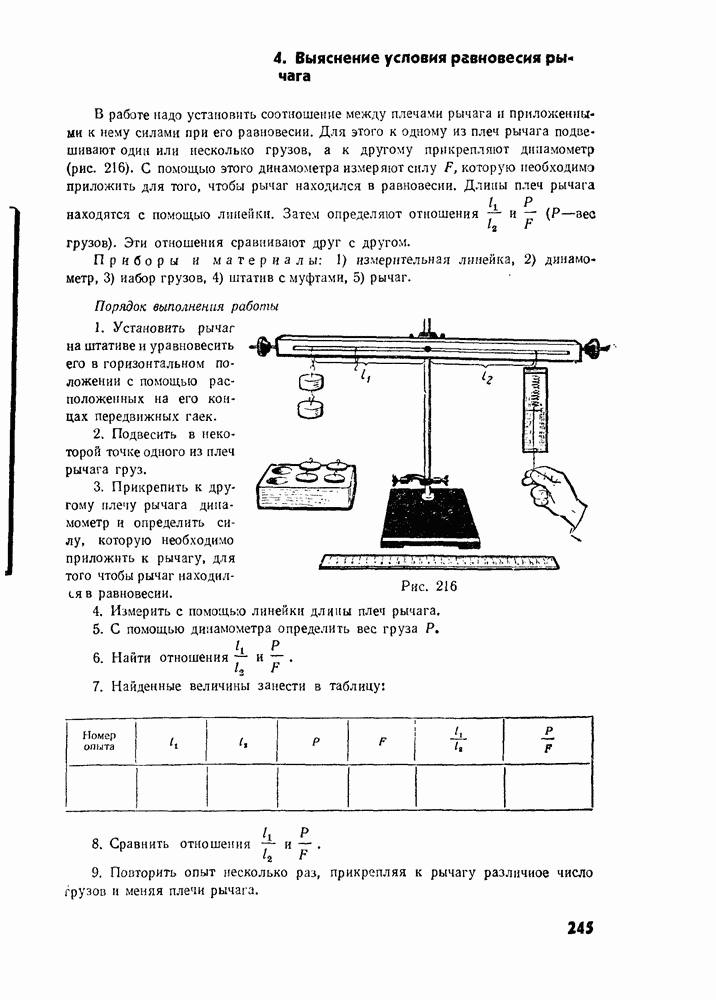
- 4. Выяснение условия равновесия рычага
- 5. Определение центра тяжести плоской пластины
- Ответы к упражнениям