| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ
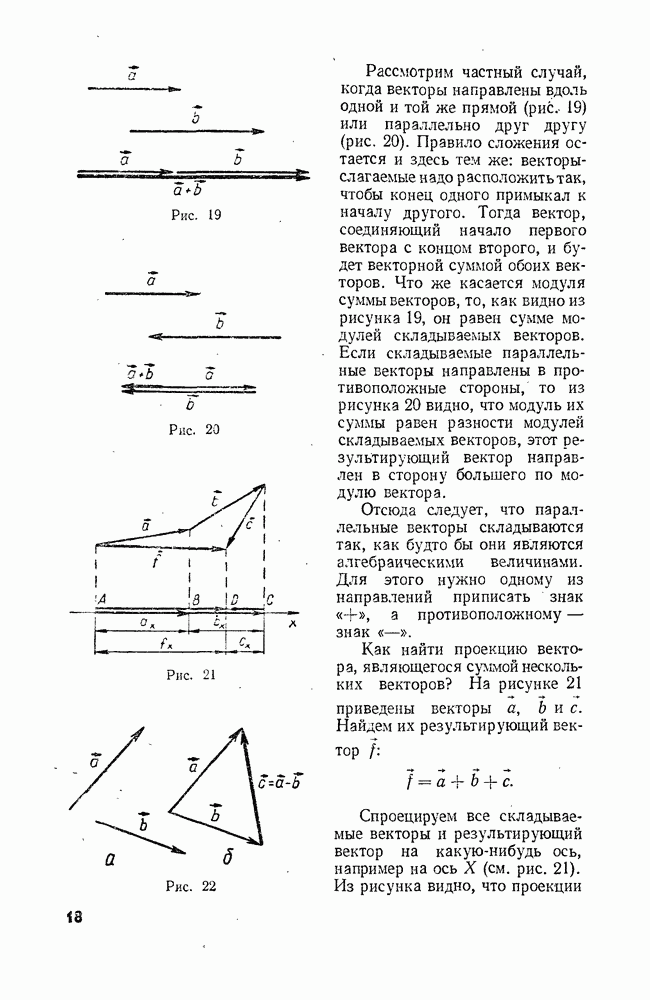
Ознакомимся теперь с тем, как выполняют вычитание векторов. Допустим, что из вектора  надо вычесть вектор
надо вычесть вектор  (рис. 22, а), т. е. найти вектор
(рис. 22, а), т. е. найти вектор  , равный разности
, равный разности 
Когда мы вычитаем одно число из другого, например 5 из 8, мы пишем: 8 - 5 = 3. Но можно написать и так: 8 = 5 + 3. Точно так же равенство  можно заменить равенством
можно заменить равенством  Поэтому, чтобы найти вектор с, равный разности векторов
Поэтому, чтобы найти вектор с, равный разности векторов  нужно найти такой вектор, который в сумме с вычитаемым дает вектор уменьшаемый.
нужно найти такой вектор, который в сумме с вычитаемым дает вектор уменьшаемый.
Сделать это можно следующим простым способом. Расположим векторы  (не меняя их направления) так, чтобы они исходили из одной точки (рис. 22, б). Соединим концы обоих векторов отрезком, направив его от вычитаемого (вектора
(не меняя их направления) так, чтобы они исходили из одной точки (рис. 22, б). Соединим концы обоих векторов отрезком, направив его от вычитаемого (вектора  ) к
) к

Рис. 24

Рис. 25
уменьшаемому (вектору а). Это и есть вектор  Действительно, как это видно из рисунка, вектор а равен сумме векторов
Действительно, как это видно из рисунка, вектор а равен сумме векторов  и с, а это и значит, что
и с, а это и значит, что 
Чтобы найти разность двух векторов а и  нужно расположить их так, чтобы они исходили из одной точки, и соединить концы обоих векторов отрезком, направленным от второго вектора к первому (от вычитаемого к уменьшаемому). Этот направленный отрезок и есть вектор-разность.
нужно расположить их так, чтобы они исходили из одной точки, и соединить концы обоих векторов отрезком, направленным от второго вектора к первому (от вычитаемого к уменьшаемому). Этот направленный отрезок и есть вектор-разность.
По этому же правилу можно вычитать и параллельные векторы (рис.  и рис. 24). Анализ этих рисунков показывает, что параллельные векторы можно вычитать один из другого, как будто бы они являются алгебраическими величинами. Для этого нужно одному из направлений приписать знак
и рис. 24). Анализ этих рисунков показывает, что параллельные векторы можно вычитать один из другого, как будто бы они являются алгебраическими величинами. Для этого нужно одному из направлений приписать знак  а другому — знак
а другому — знак 
Если нам. нужно найти проекцию разности двух векторов, то, так же как и в случае сложения векторов, нет необходимости выполнять геометрические построения.
Действительно, если  то
то  а так как
а так как  то
то 
Следовательно, проекция разности векторов на данную ось равна алгебраической разности их проекций на эту ось.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Глава 1. Общие сведения о движении
- § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА
- § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ
- § 3. ПЕРЕМЕЩЕНИЕ
- § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА
- § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ
- § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ
- § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
- § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
- § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ
- § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
- § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ)
- § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ
- Глава 2. Прямолинейное неравномерное движение
- § 13. СРЕДНЯЯ СКОРОСТЬ
- § 14. МГНОВЕННАЯ СКОРОСТЬ
- § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ
- § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
- § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ
- § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ
- § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
- § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
- Глава 3. Криволинейное движение
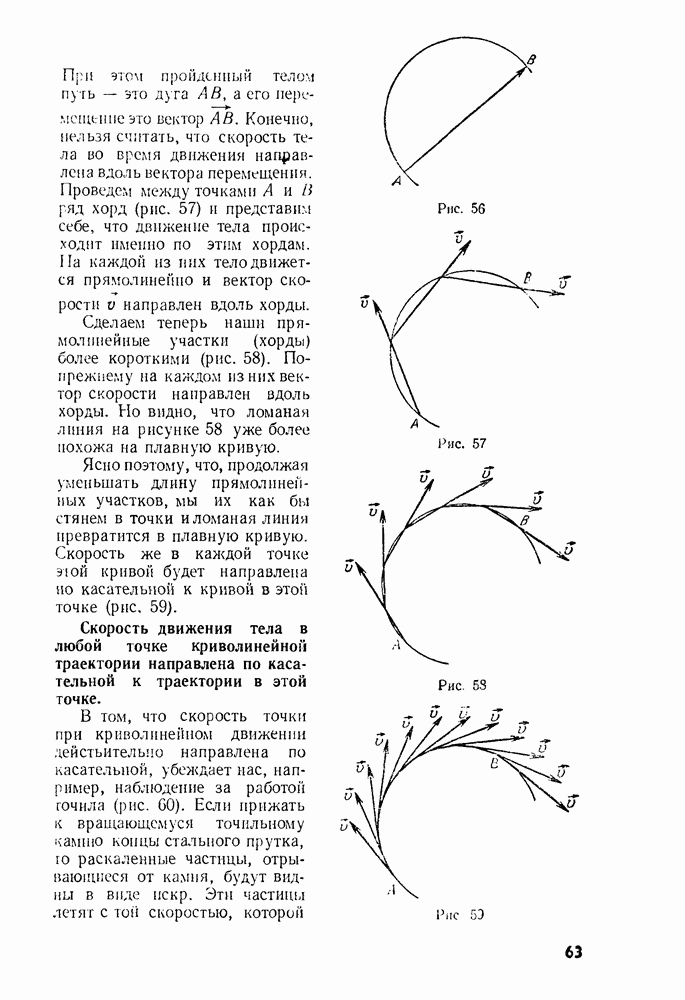
- § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
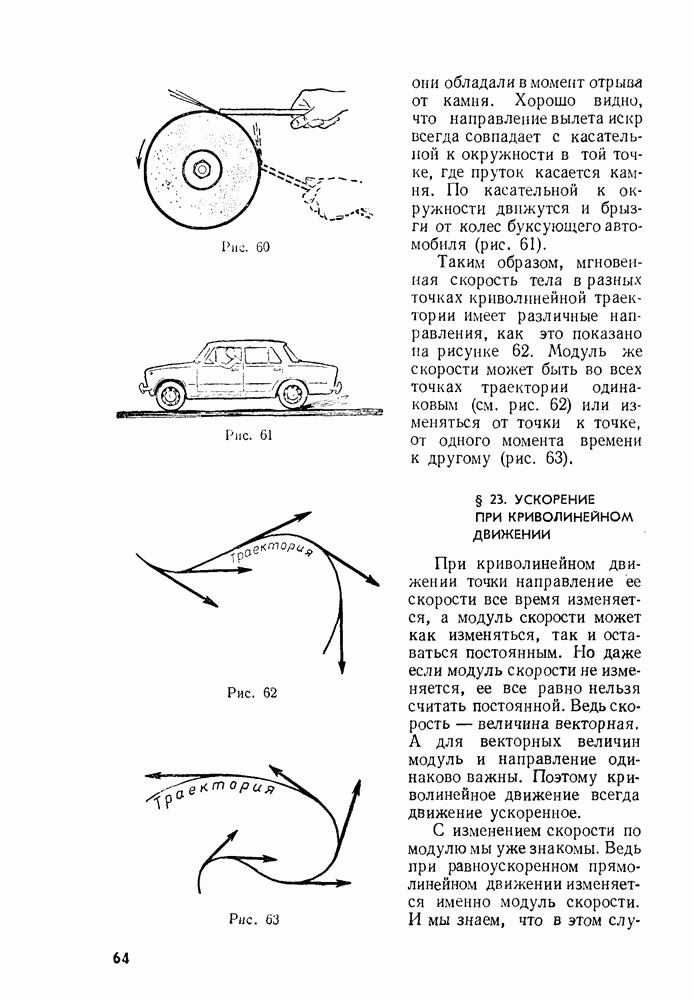
- § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
- § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ
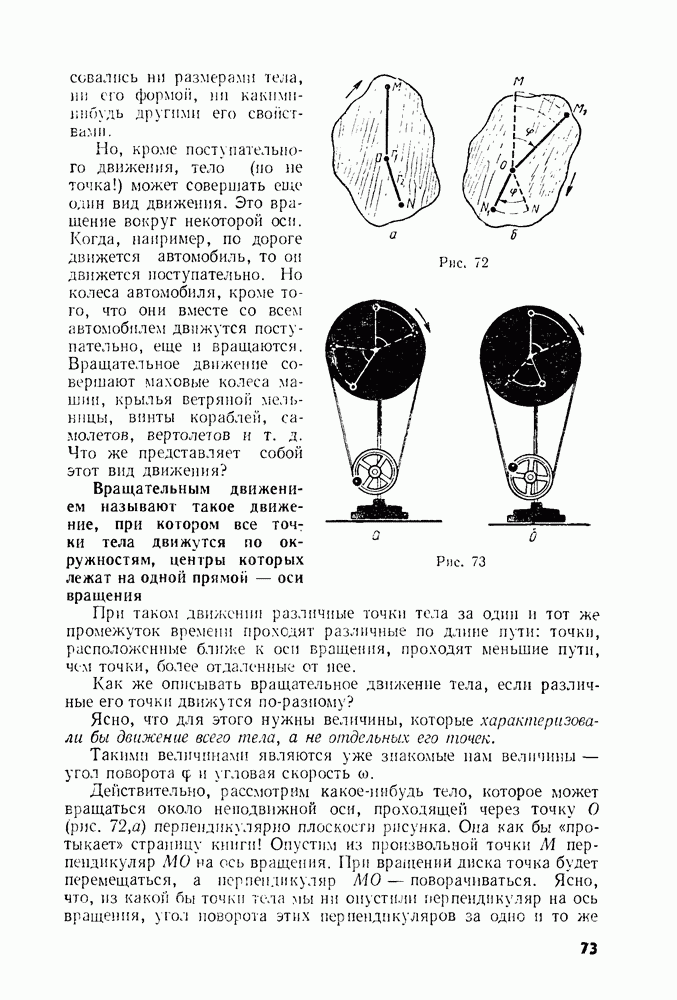
- § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА
- Динамика
- Глава 4. Законы движения
- § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ
- § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ
- § 31. ИНЕРТНОСТЬ ТЕЛ
- § 32. МАССА ТЕЛ
- § 33. МАССА ЛУНЫ
- § 34. СИЛА
- § 35. ВТОРОЙ ЗАКОН НЬЮТОНА
- § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение)
- § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР
- § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА
- § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА
- Глава 5. Силы природы
- § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ
- § 41. СИЛА УПРУГОСТИ
- § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 44. СИЛА ТЯЖЕСТИ
- § 45. ВЕС ТЕЛ
- § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ
- § 47. МАССА ЗЕМЛИ
- § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ
- § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ
- Глава 6. Применение законов движения
- § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ
- § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ
- § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ
- § 54. НЕВЕСОМОСТЬ
- § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ
- § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО
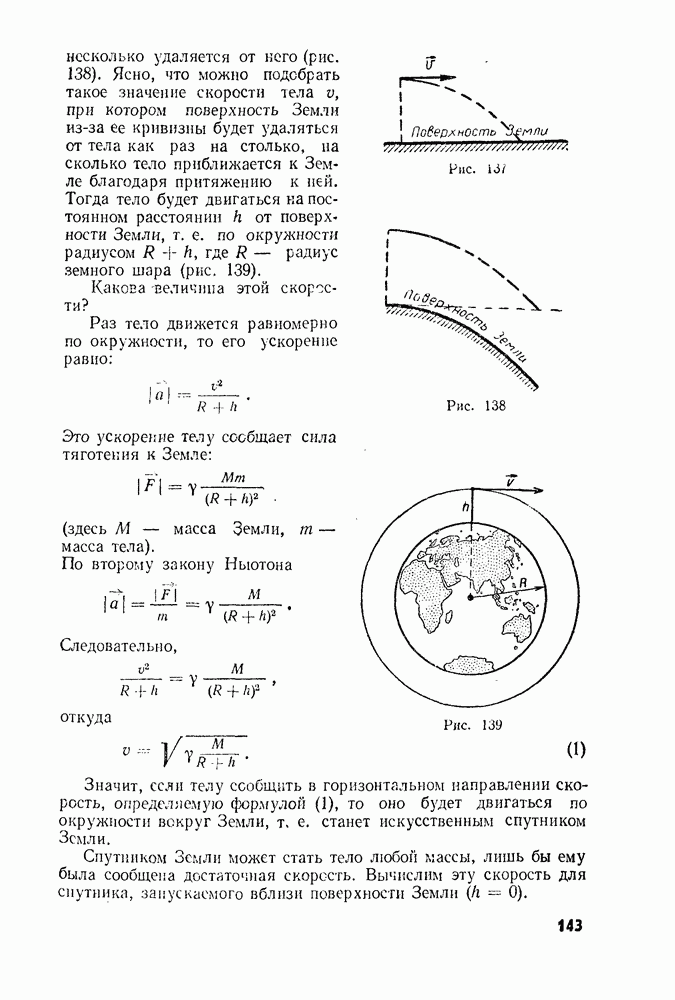
- § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ
- § 58. ДВИЖЕНИЕ ПЛАНЕТ
- § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ
- § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ
- § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ
- § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ
- § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ
- § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА
- Равновесие тел
- Глава 7. Элементы статики
- § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ
- § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ
- § 67. ПРАВИЛО МОМЕНТОВ
- § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ
- Законы сохранения в механике
- Глава 8. Закон сохранения импульса
- § 70. СИЛА И ИМПУЛЬС
- § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ
- Глава 9. Механическая работа и мощность
- § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ
- § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ
- § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
- § 77. РАБОТА СИЛЫ ТЯЖЕСТИ
- § 78. РАБОТА СИЛЫ УПРУГОСТИ
- § 79. РАБОТА СИЛЫ ТРЕНИЯ
- § 80. МОЩНОСТЬ
- Глава 10. Закон сохранения энергии
- § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА
- § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ
- § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН
- § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
- § 91. СТОЛКНОВЕНИЕ ТЕЛ
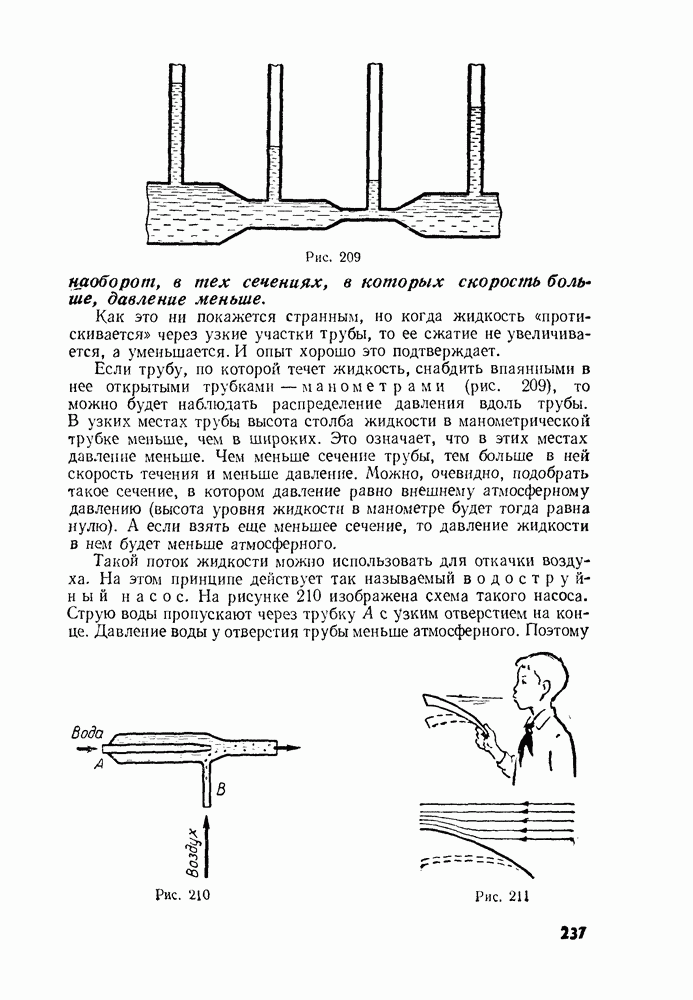
- § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ
- § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ
- Заключение
- Лабораторные работы
- 1. Определение ускорения тела при равноускоренном движении
- 2. Определение коэффициента трения скольжения
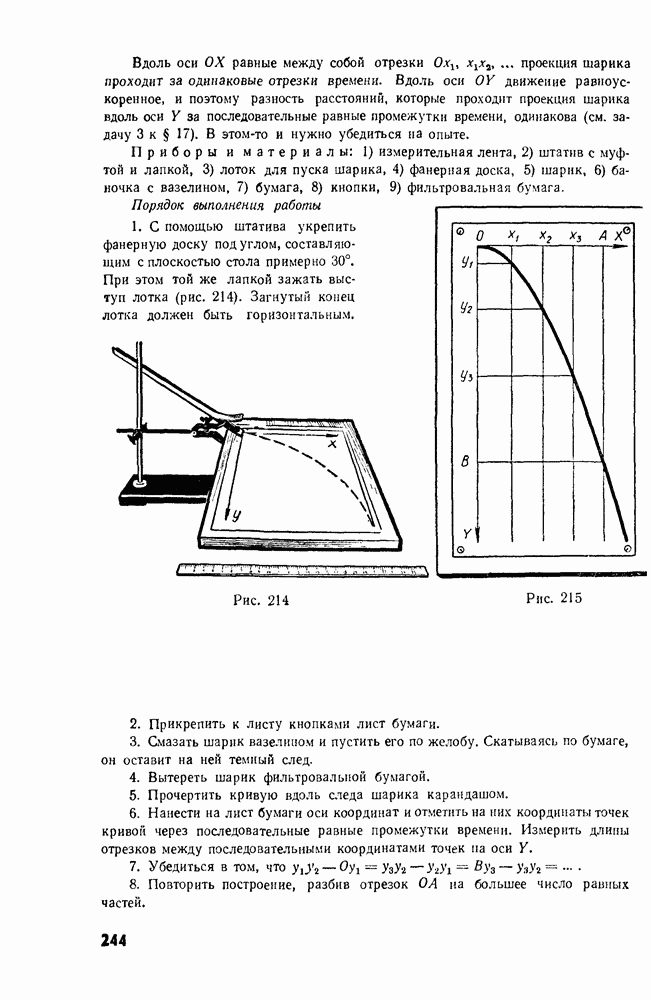
- 3. Изучение движения тела по параболе
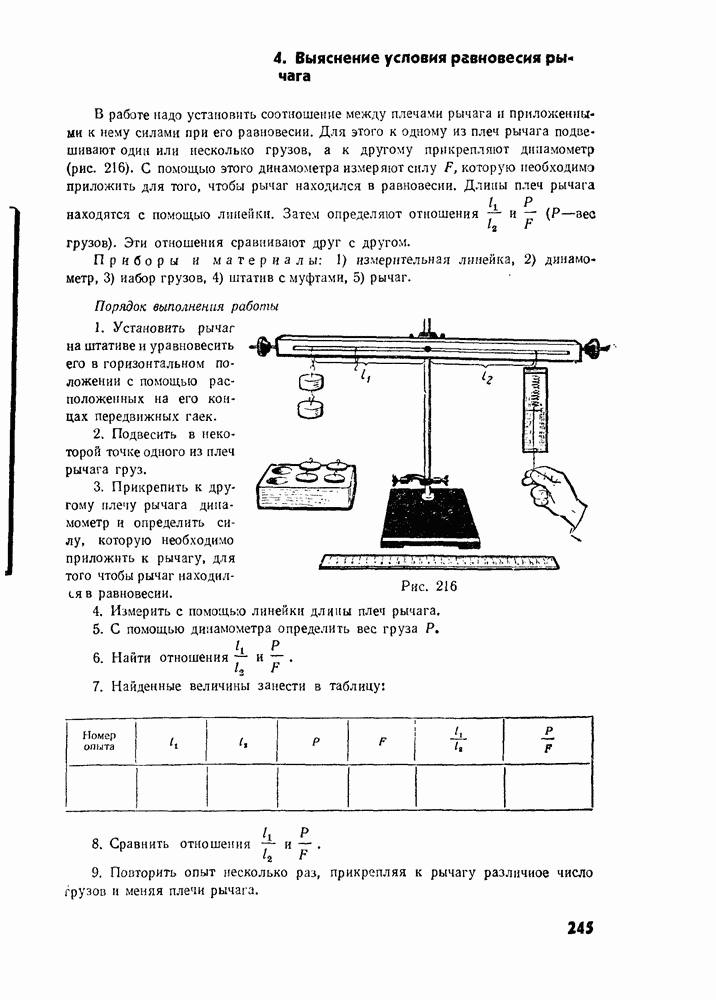
- 4. Выяснение условия равновесия рычага
- 5. Определение центра тяжести плоской пластины
- Ответы к упражнениям