§ 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ

Ознакомившись с новым видом величин — векторами, мы должны теперь узнать, как с ними обращаться, как выполнять над ними математические действия.

Начнем с самой простой из математических операций — со сложения.

Рис. 15

Представим себе пешехода на перекрестке двух улиц, которому надо перейти с угла, обозначенного (рис. 15), на угол Он мог бы направиться непосредственно к этому углу по прямой Тогда мы сказали бы, что перемещение пешехода равно Но на улицах с оживленным движением такой переход запрещен. Поэтому дисциплинированный пешеход перейдет сначала из точки в точку А, а затем из точки А в точку Конечный результат будет таким же, как если бы он прошел по прямой Перемещение достигнуто в результате двух перемещений: Эти перемещения заменили одно. Естественно считать, что перемещение есть сумма двух перемещений

Этот пример ясно показывает, как складываются векторы. На рисунке 15 векторы-слагаемые расположены так, что конец одного из них примыкает к началу другого. А вектор-сумма, или, как говорят, результирующий вектор, — это вектор, соединяющий начало одного из слагаемых с концом другого.

Это общее правило сложения любых векторов, а не только векторов перемещения.

Чтобы сложить два вектора, нужно их расположить так, чтобы конец первого вектора примыкал к началу второго. Вектор, соединяющий начало первого вектора с концом второго, есть сумма обоих векторов.

Рис. 16

Рис. 17.

При выполнении этих построений векторы можно переносить параллельно самим себе (например, векторы на рис. 16, а).

Их можно также менять местами (рис. 16, б). От этого ни модуль, ни направление результирующего вектора не изменяются.

Есть и другой способ сложения двух векторов. Вместо того чтобы располагать складываемые векторы один за другим, как мы только что делали, их располагают так, чтобы они исходили из одной точки (рис. 17). Затем, считая, что расположенные таким образом векторы образуют две сто; роны параллелограмма, достраивают параллелограмм (как показано пунктиром на рис. 17) и проводят диагональ из точки, в которой были совмещены начала складываемых векторов. Эта диагональ и есть результирующий вектор. Приведенное правило сложения векторов называется правилом параллелограмма. Оба способа дают, конечно, один и тот же результат.

Таким образом, в отличие от чисел (скалярных величин) векторы складываются геометрически и результирующий вектор — это геометрическая сумма векторов. Модуль этой суммы векторов (как видно из рассмотренных нами примеров) оказывается меньше суммы модулей этих векторов, так как сумма двух сторон треугольника больше его третьей стороны.

Если складываются не два, а больше векторов, правило сложения остается прежним. Пусть, например, точка совершила последовательно перемещения из О в А, оттуда в В, затем в и Е (рис. 18). Все эти перемещения могут быть заменены одним-единственным перемещением из О в Е по прямой

Перемещение и будет геометрической суммой всех перемещений.

Следовательно, чтобы сложить несколько векторов, надо расположить их так, чтобы конец первого вектора примыкал к началу второго, конец второго — к началу третьего и т. д. Результирующим будет вектор, направленный от начала первого вектора к концу последнего.

Рис. 18.

Рис. 19

Рис. 20

Рис. 21

Рис. 22

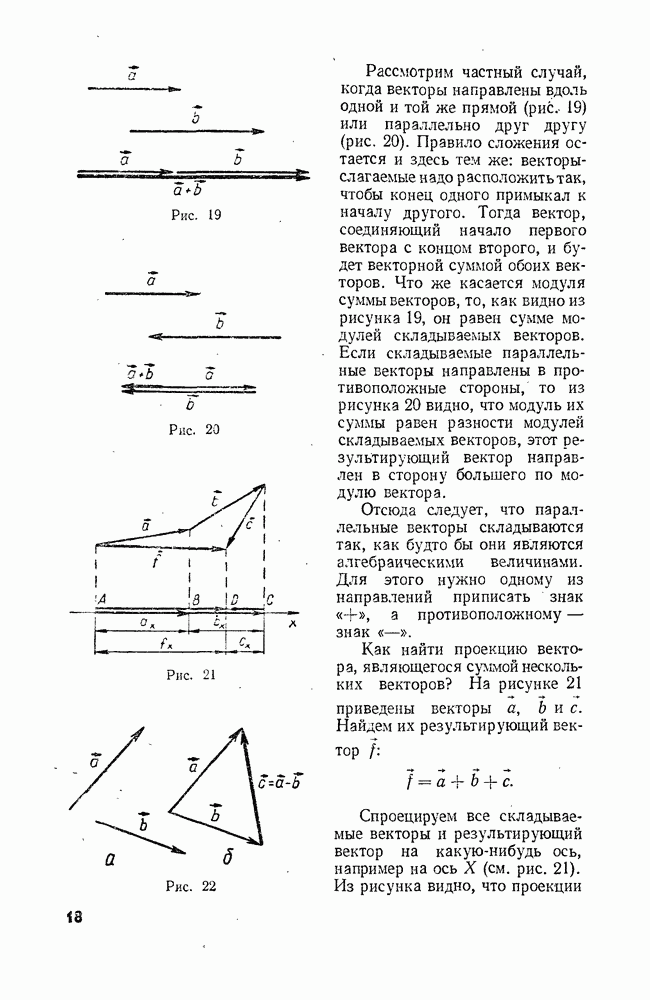
Рассмотрим частный случай, когда векторы направлены вдоль одной и той же прямой (рис. 19) или параллельно друг другу (рис. 20). Правило сложения остается и здесь тем же: векторы-слагаемые надо расположить так, чтобы конец одного примыкал к началу другого. Тогда вектор, соединяющий начало первого вектора с концом второго, и будет векторной суммой обоих векторов. Что же касается модуля суммы векторов, то, как видно из рисунка 19, он равен сумме модулей складываемых векторов. Если складываемые параллельные векторы направлены в противоположные стороны, то из рисунка 20 видно, что модуль их суммы равен разности модулей складываемых векторов, этот результирующий вектор направлен в сторону большего по модулю вектора.

Отсюда следует, что параллельные векторы складываются так, как будто бы они являются алгебраическими величинами. Для этого нужно одному из направлений приписать знак «+», а противоположному — знак «-».

Как найти проекцию вектора, являющегося суммой нескольких векторов? На рисунке 21 приведены векторы Найдем их результирующий вектор

Спроецируем все складываемые векторы и результирующий вектор на какую-нибудь ось, например на ось X (см. рис. 21). Из рисунка видно, что проекции

Рис. 23

векторов а и на ось X положительны, потому что их составляющие по оси и направлены так же, как ось X; проекция же вектора с отрицательна, так как его составляющая по оси направлена против этой оси. Составляющая результирующего вектора — это вектор а проекция этого вектора равна алгебраической сумме проекций Следовательно,

Проекция суммы векторов на данную ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.

Поэтому, для того чтобы найти проекцию суммы векторов, нет необходимости приставлять их друг к другу и находить результирующий вектор. Надо просто сложить проекции всех векторов, учитывая их знаки.