| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ
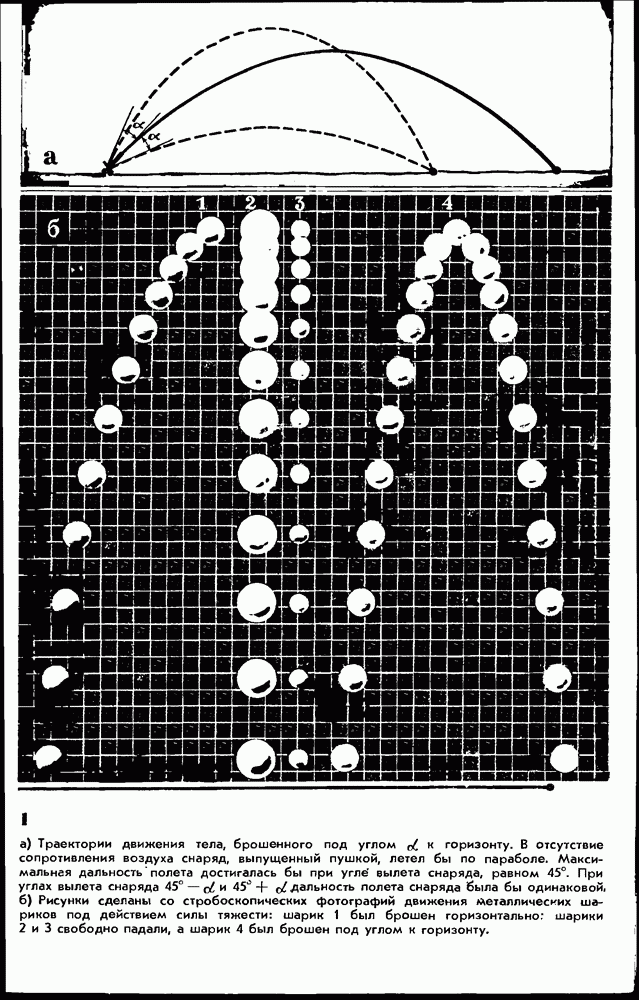
Довольно часто приходится иметь дело с движением тел, получивших начальную скорость не параллельно силе тяжести, а направленную под некоторым углом к ней (или к горизонту). Когда, например, спортсмен толкает ядро, метает диск или копье, он сообщает этим «предметам» именно такую начальную скорость. При артиллерийской стрельбе стволам орудий придается некоторый угол возвышения, так что вылетевший снаряд тоже получает начальную скорость, направленную под углом к горизонту.
Будем считать, что силой сопротивления воздуха можно пренебречь. Как в этом случае движется тело?
Для того чтобы ответить на этот вопрос, рассмотрим следующий несколько искусственный способ бросания тела под углом к горизонту.
Представим себе автомобиль, движущийся равномерно в горизонтальном направлении со скоростью  Пассажир в автомобиле бросает какое-нибудь тело с начальной скоростью
Пассажир в автомобиле бросает какое-нибудь тело с начальной скоростью  вертикально вверх. Это значит, что пассажир видит тело поднимающимся в вертикальном направлении. А как направлена эта скорость относительно Земли?
вертикально вверх. Это значит, что пассажир видит тело поднимающимся в вертикальном направлении. А как направлена эта скорость относительно Земли?
Вспомним, что говорилось в § 11 об относительности движения. Ясно, что автомобиль — это подвижное тело отсчета, а Землю можно считать неподвижным телом отсчета. Тогда скорость тела относительно Земли будет равна векторной сумме скоростей  Из рисунка 132 видно, что относительно Земли начальная скорость
Из рисунка 132 видно, что относительно Земли начальная скорость  направлена к горизонту под некоторым углом а. Следовательно, тело, брошенное с движущегося автомобиля вверх, движется относительно Земли так, как будто бы оно было брошено неподвижным «метателем» под углом а к горизонту.
направлена к горизонту под некоторым углом а. Следовательно, тело, брошенное с движущегося автомобиля вверх, движется относительно Земли так, как будто бы оно было брошено неподвижным «метателем» под углом а к горизонту.
Проследим теперь за дальнейшим движением тела.
Поместим начало неподвижной системы координат в точку, где автомобиль находился в момент броска. Направим ось X вдоль направления движения автомобиля, а ось  по вертикали вверх (именно поэтому мы обозначили скорость по горизонтали через
по вертикали вверх (именно поэтому мы обозначили скорость по горизонтали через  а по вертикали через
а по вертикали через  ). С автомобилем мы свяжем систему координат
). С автомобилем мы свяжем систему координат  направив оси
направив оси  параллельно осям X и Y (рис. 133). Это подвижная система координат.
параллельно осям X и Y (рис. 133). Это подвижная система координат.
Каким будет движение тела относительно каждой из этих систем координат?

Рис. 132

Рис. 133
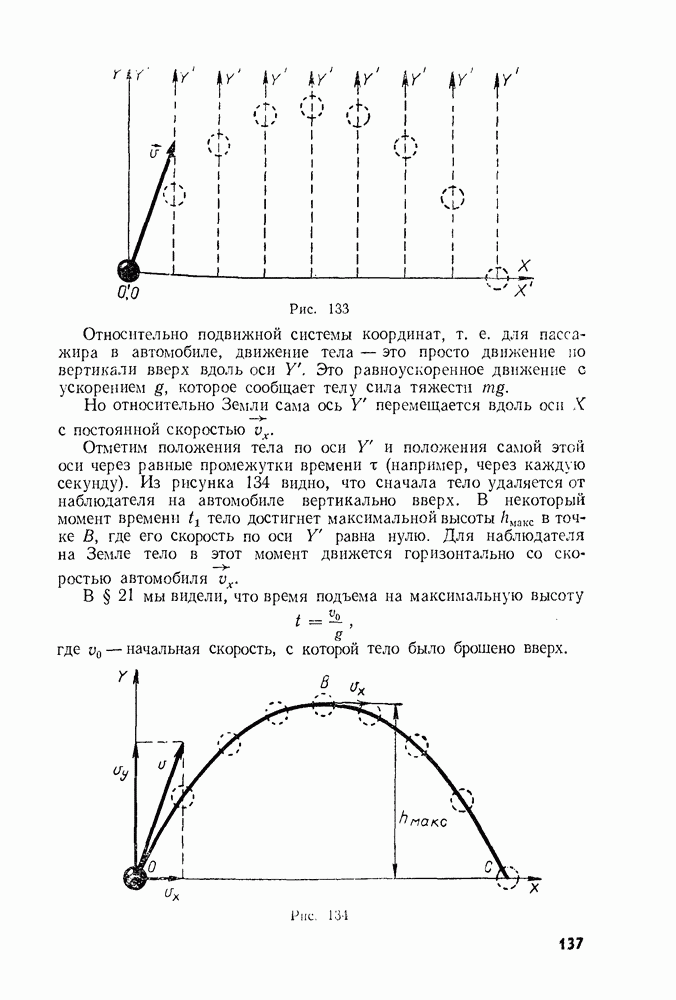
Относительно подвижной системы координат, т. е. для пассажира в автомобиле, движение тела — это просто движение по вертикали вверх вдоль оси  Это равноускоренное движение с ускорением
Это равноускоренное движение с ускорением  которое сообщает телу сила тяжести
которое сообщает телу сила тяжести 
Но относительно Земли сама ось  перемещается вдоль оси X с постоянной скоростью
перемещается вдоль оси X с постоянной скоростью 
Отметим положения тела по оси У и положения самой этой оси через равные промежутки времени  (например, через каждую секунду). Из рисунка 134 видно, что сначала тело удаляется от наблюдателя на автомобиле вертикально вверх. В некоторый момент времени
(например, через каждую секунду). Из рисунка 134 видно, что сначала тело удаляется от наблюдателя на автомобиле вертикально вверх. В некоторый момент времени  тело достигнет максимальной высоты
тело достигнет максимальной высоты  в точке В, где его скорость по оси У равна нулю. Для наблюдателя на Земле тело в этот момент движется горизонтально со скоростью автомобиля
в точке В, где его скорость по оси У равна нулю. Для наблюдателя на Земле тело в этот момент движется горизонтально со скоростью автомобиля 
В § 21 мы видели, что время подъема на максимальную высоту

где  — начальная скорость, с которой тело было брошено вверх.
— начальная скорость, с которой тело было брошено вверх.

Рис. 134
В нашем случае  так что тело достигнет точки В по истечении времени
так что тело достигнет точки В по истечении времени 
Используя полученную в § 21 формулу для максимальной высоты подъема тела, брошенного вертикально вверх  найдем, что в нашем случае
найдем, что в нашем случае 
Начиная с того момента, в который тело достигло точки В, наблюдатель на автомобиле будет видеть, что тело падает вниз все с тем же ускорением  При этом через такие же последовательные промежутки времени
При этом через такие же последовательные промежутки времени  тело будет занимать на оси
тело будет занимать на оси  те же положения, что и при подъеме, но в обратном порядке.
те же положения, что и при подъеме, но в обратном порядке.
В § 21 было показано, что время падения тела равно времени его подъема. Поэтому еще через промежуток времени, тоже равный  тело снова окажется в автомобиле. Значит, полное время движения тела
тело снова окажется в автомобиле. Значит, полное время движения тела

Относительно Земли за этот промежуток времени сама ось  вместе с телом продвинулась вдоль оси X на расстояние
вместе с телом продвинулась вдоль оси X на расстояние  — это дальность полета тела. Обозначим ее через
— это дальность полета тела. Обозначим ее через  .
.
Следовательно, 
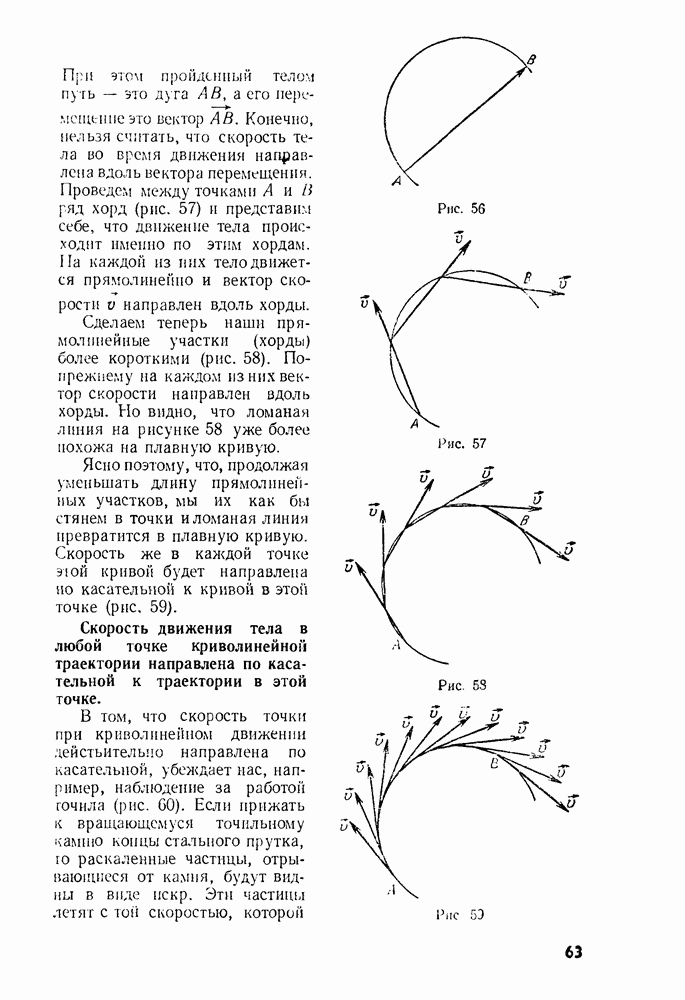
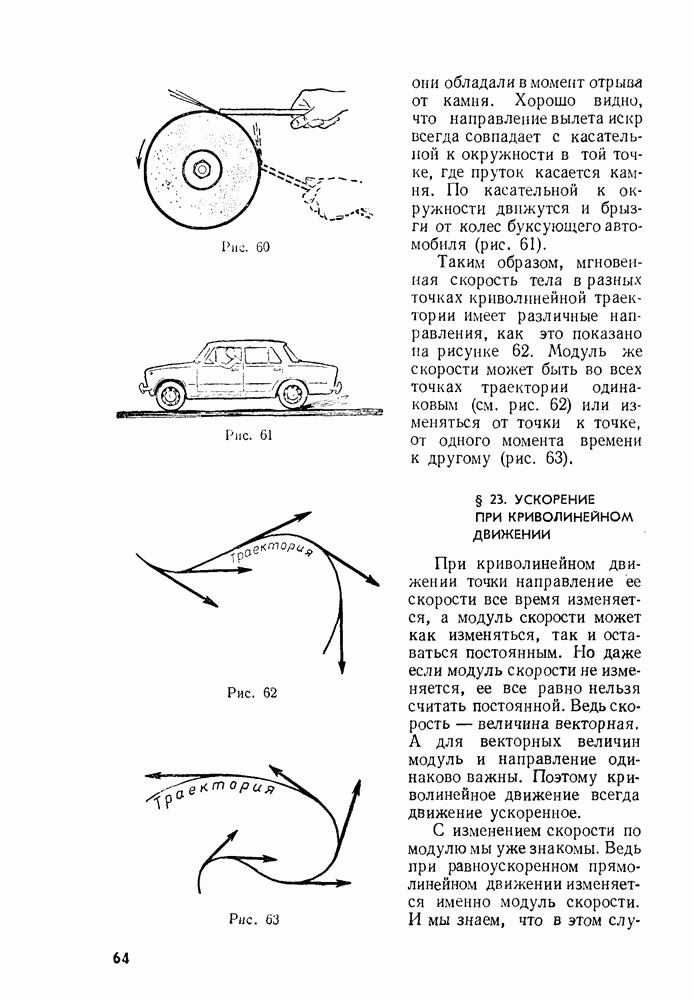
Соединив точки, через которые последовательно проходит тело, плавной кривой, мы получим траекторию движения тела относительно Земли. Эту кривую называют параболой.
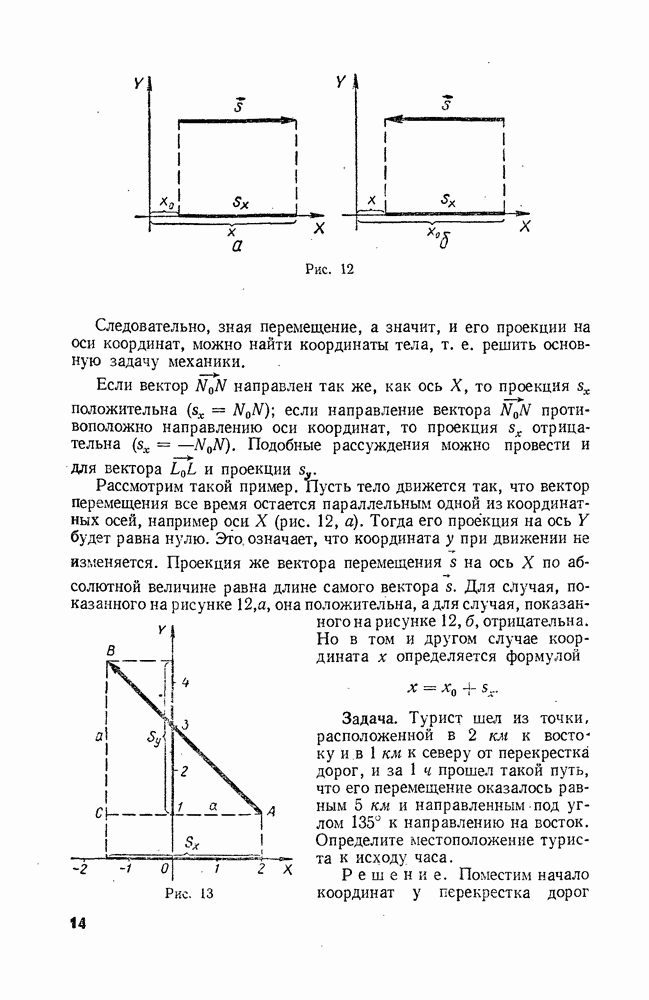
Задача. Самоходная зенитная пушка, установленная на автомашине, во время испытаний запустила вертикально вверх снаряд с начальной скоростью 600 м/сек. В момент выстрела автомашина двигалась со скоростью 21,6 км/ч. После выстрела автомашина остановилась. Как далеко от места выстрела упадет снаряд? До какой высоты он поднимется? Через какое время он упадет на землю?
Считать, что на снаряд действует только сила тяжести (силой сопротивления воздуха пренебречь).
Решение. Дальность полета снаряда можно вычислить по формуле

а максимальную высоту подъема снаряда  по формуле
по формуле

Скорость  это скорость автомобиля. Следовательно,
это скорость автомобиля. Следовательно,  Подставив эти значения в формулы (1) и (2), получим:
Подставив эти значения в формулы (1) и (2), получим:

и

Теперь найдем время полета снаряда. Оно равно:

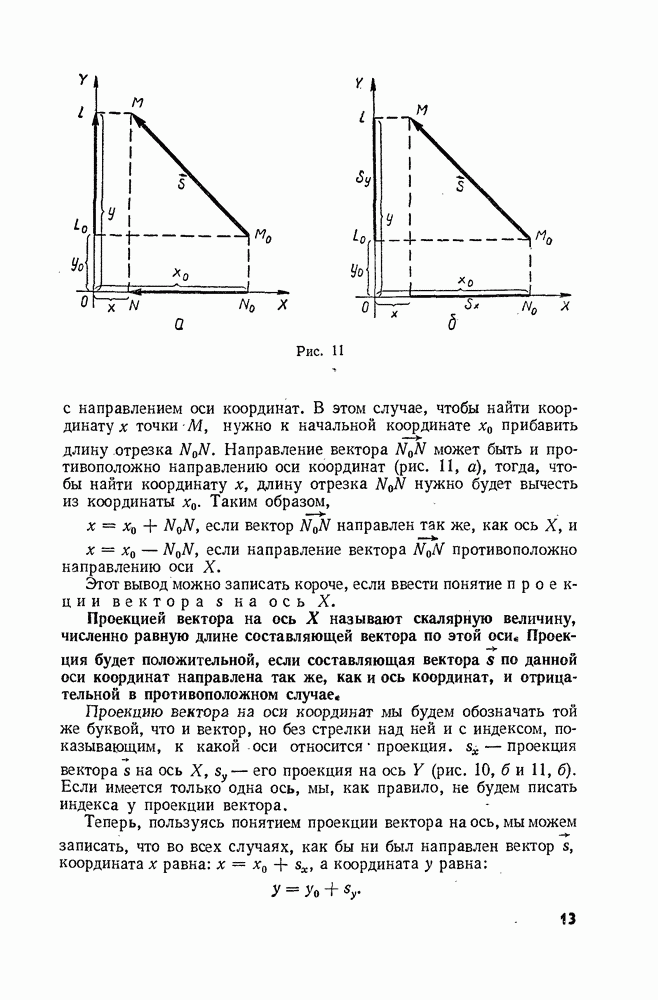
Полученные в этом параграфе формулы для дальности и времени полета тела, брошенного под углом к горизонту, содержат величины  проекции начальной скорости на оси
проекции начальной скорости на оси  . Между тем обычно бывают известны сама начальная скорость
. Между тем обычно бывают известны сама начальная скорость  и угол а, который вектор
и угол а, который вектор  образует с горизонтальной осью X.
образует с горизонтальной осью X.
Из рисунков 132 и 134 видно, что

откуда

Точно так же

и

Пользуясь этими выражениями для  можно формулу для дальности полета написать в таком виде:
можно формулу для дальности полета написать в таком виде:

Максимальную высоту, на которую поднимется тело, можно теперь выразить формулой

Таким образом и дальность, и максимальная высота полета определяются значениями начальной скорости  и угла а, под которым брошено тело.
и угла а, под которым брошено тело.
Из формулы для дальности полета видно, что дальность полета будет наибольшей при заданной начальной скорости у, когда максимально значение произведения  Можно доказать, что это произведение максимально при
Можно доказать, что это произведение максимально при  .
.
Упражнение 32
При ответах на вопросы этого упражнения считать, что трением можно пренебречь.
1. По какой траектории движется тело, брошенное под углом к горизонту?
2. Какая сила действует на тело, брошенное под углом к горизонту, во время его движения?
3. Можно ли движение тела, брошенного под углом к горизонту, считать равноускоренным?
4. С каким ускорением движется тело, брошенное под углом к горизонту? Как направлено ускорение?
5. Постройте траекторию движения тела, брошенного под углом 60° к горизонту. Масштаб чертежа выбрать самостоятельно.
6. Начальная скорость полета спортивного ядра при толкании равна 14 м/сек. На какую наибольшую высоту над поверхностью Земли поднялось ядро, если оно выпущено из точки, находящейся на высоте 2 м? Угол, под которым был сделан толчок, равен 45°.
7. Снаряд, выпущенный из артиллерийского орудия, поразил цель на расстоянии 25 км. Какова начальная скорость снаряда, если известно, что угол возвышения орудия был равен 45°?
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о движении
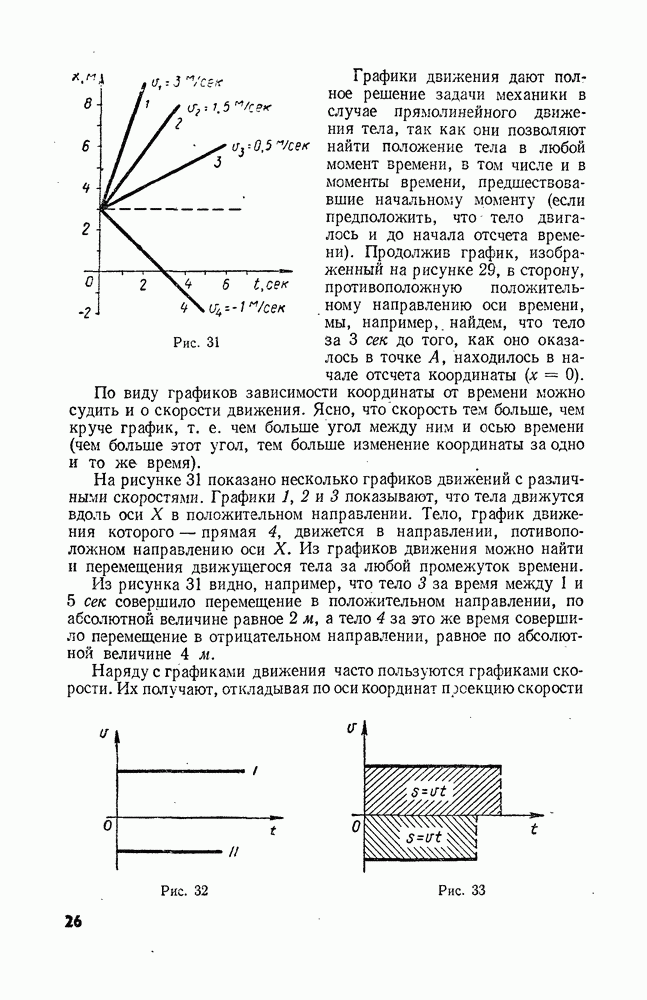
- § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА
- § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ
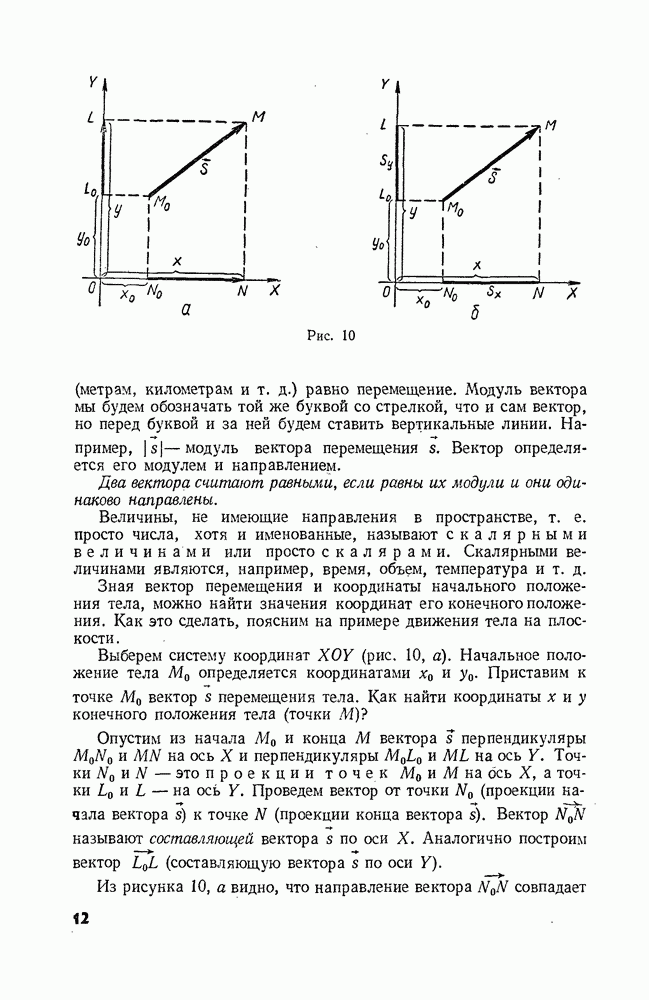
- § 3. ПЕРЕМЕЩЕНИЕ
- § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА
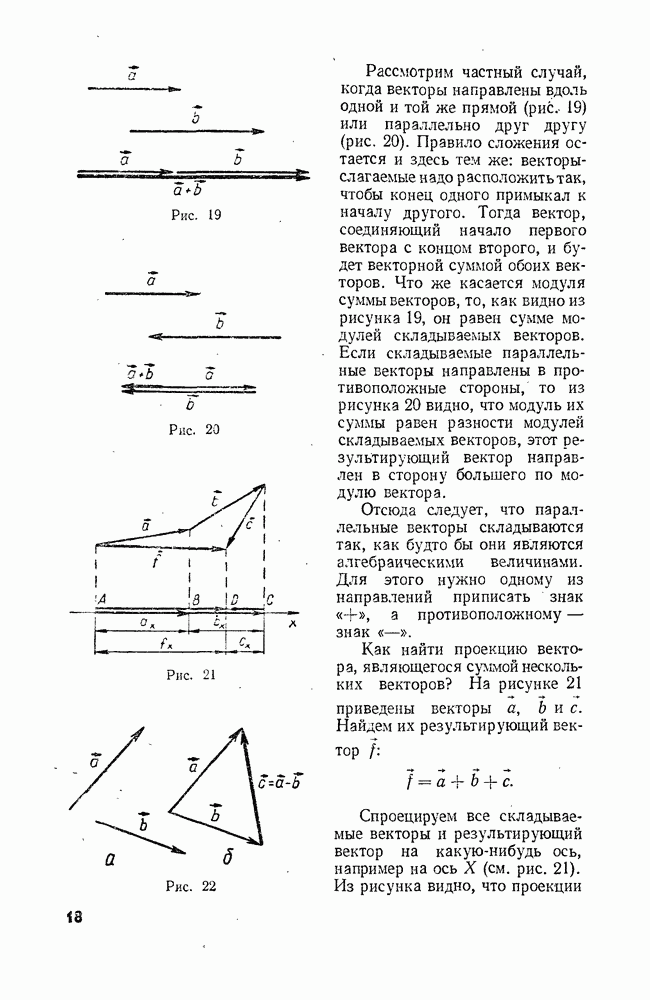
- § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ
- § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ
- § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
- § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
- § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ
- § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
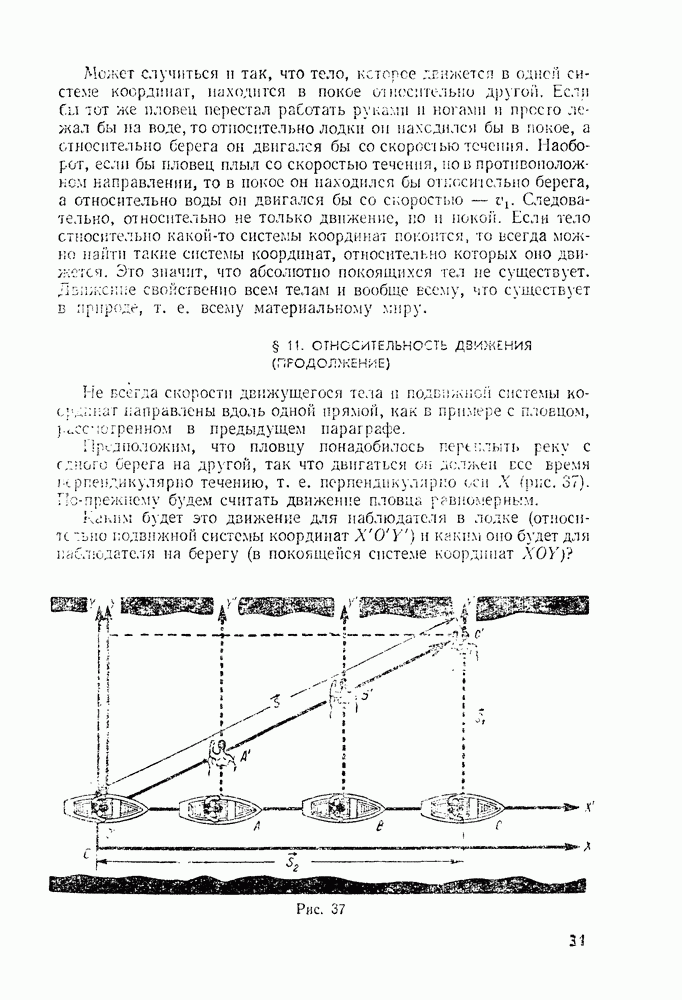
- § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ)
- § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ
- Глава 2. Прямолинейное неравномерное движение
- § 13. СРЕДНЯЯ СКОРОСТЬ
- § 14. МГНОВЕННАЯ СКОРОСТЬ
- § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ
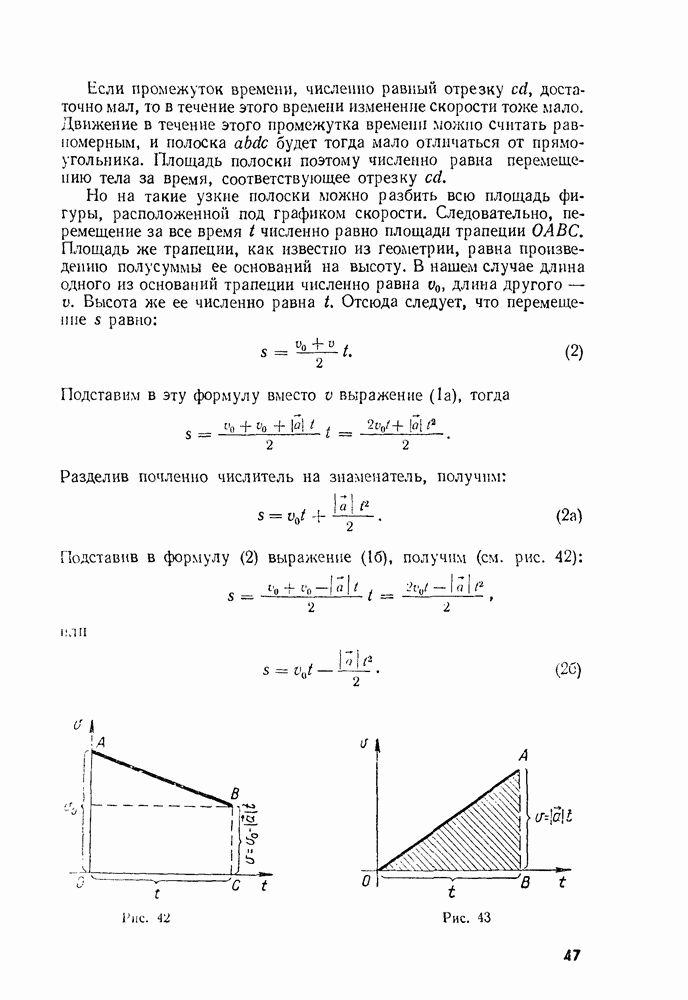
- § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
- § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ
- § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ
- § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
- § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
- Глава 3. Криволинейное движение
- § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
- § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ
- § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА
- Динамика
- Глава 4. Законы движения
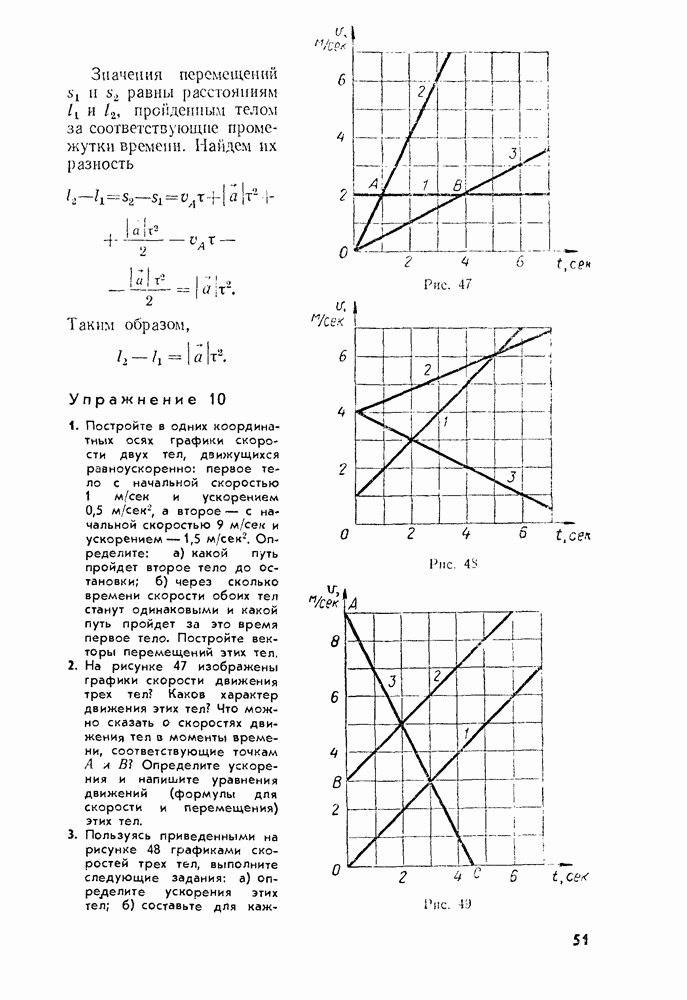
- § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ
- § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ
- § 31. ИНЕРТНОСТЬ ТЕЛ
- § 32. МАССА ТЕЛ
- § 33. МАССА ЛУНЫ
- § 34. СИЛА
- § 35. ВТОРОЙ ЗАКОН НЬЮТОНА
- § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение)
- § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР
- § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА
- § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА
- Глава 5. Силы природы
- § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ
- § 41. СИЛА УПРУГОСТИ
- § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 44. СИЛА ТЯЖЕСТИ
- § 45. ВЕС ТЕЛ
- § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ
- § 47. МАССА ЗЕМЛИ
- § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ
- § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ
- Глава 6. Применение законов движения
- § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ
- § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ
- § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ
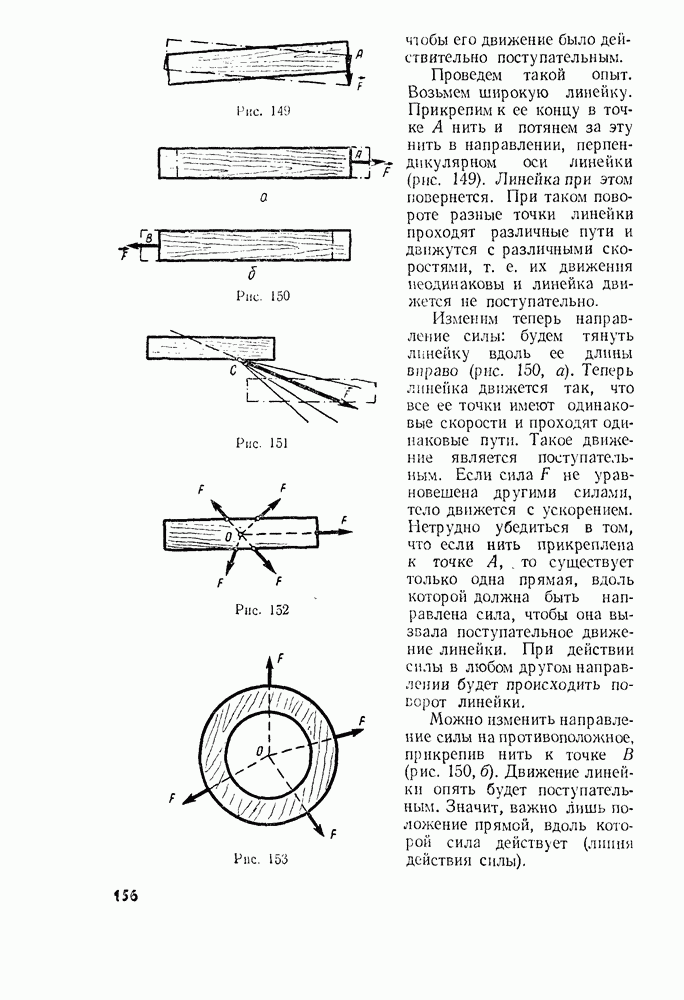
- § 54. НЕВЕСОМОСТЬ
- § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ
- § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО
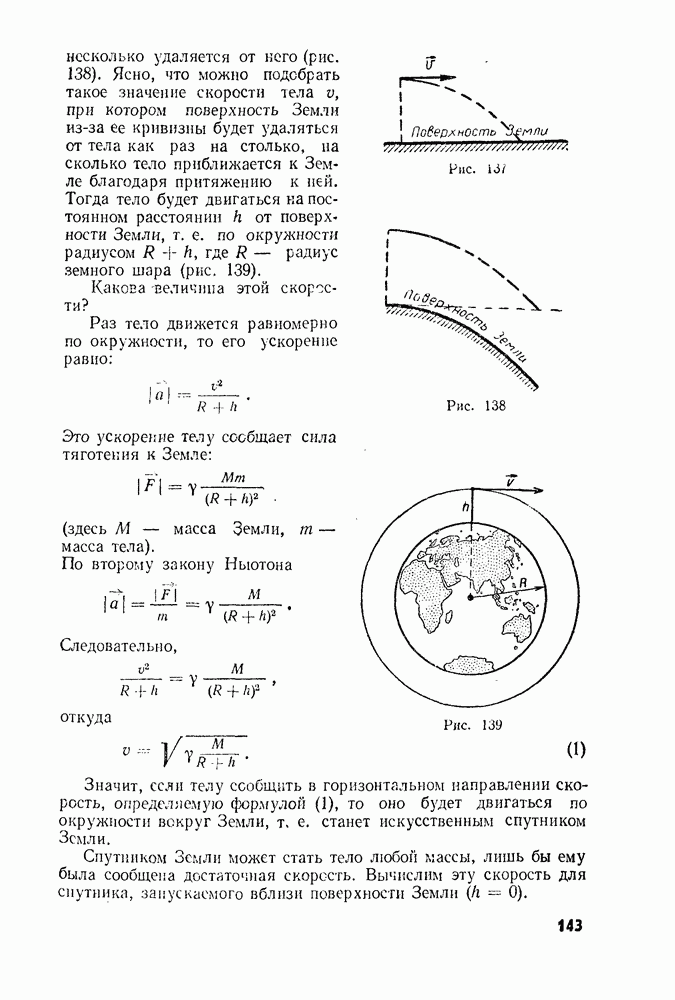
- § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ
- § 58. ДВИЖЕНИЕ ПЛАНЕТ
- § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ
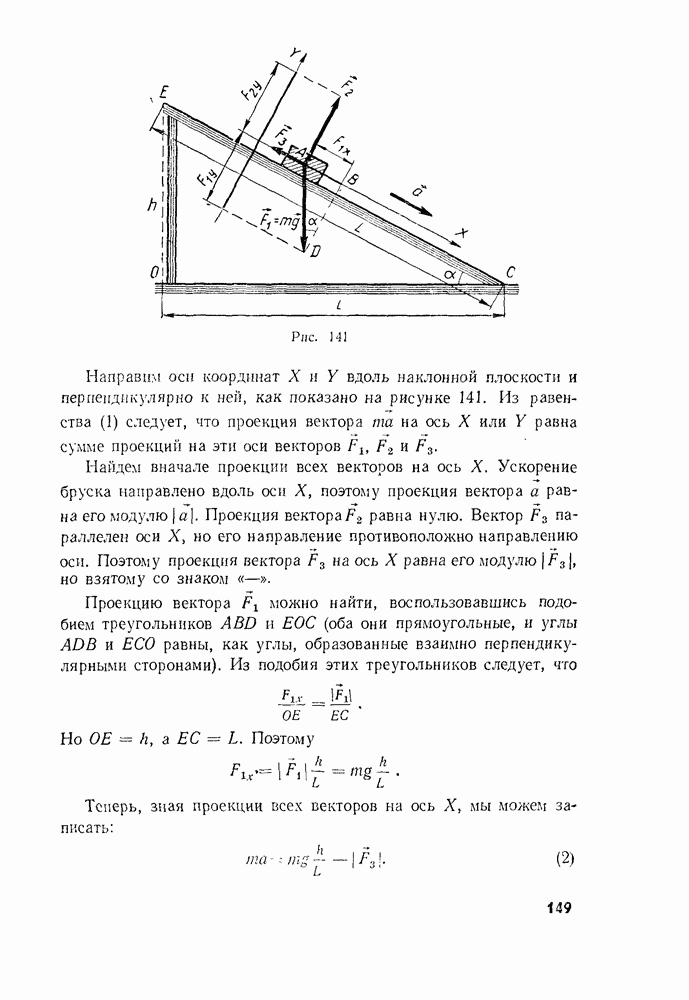
- § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ
- § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ
- § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ
- § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ
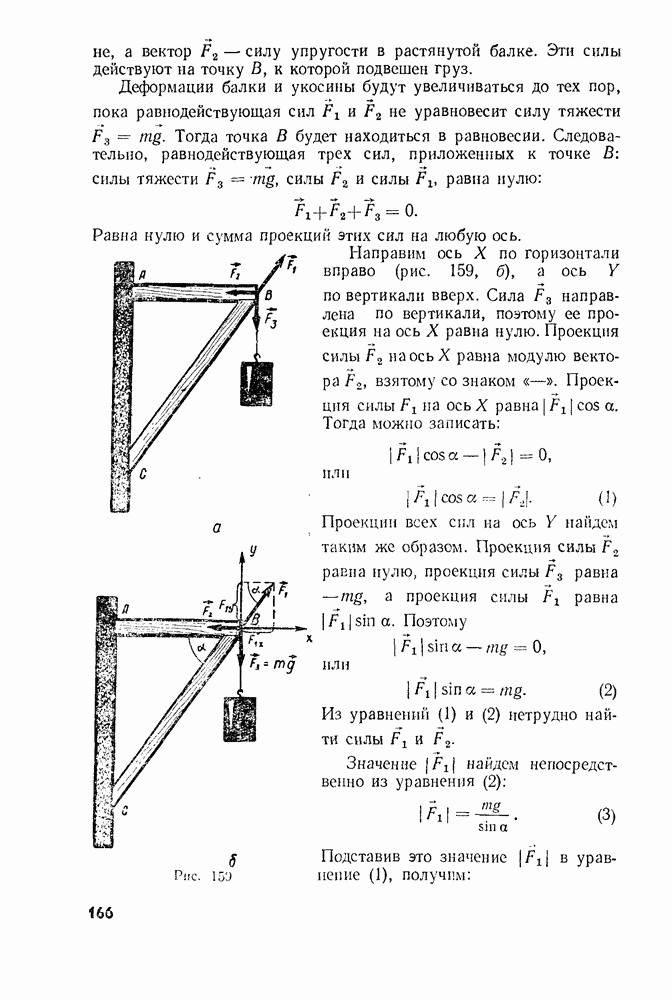
- § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА
- Равновесие тел
- Глава 7. Элементы статики
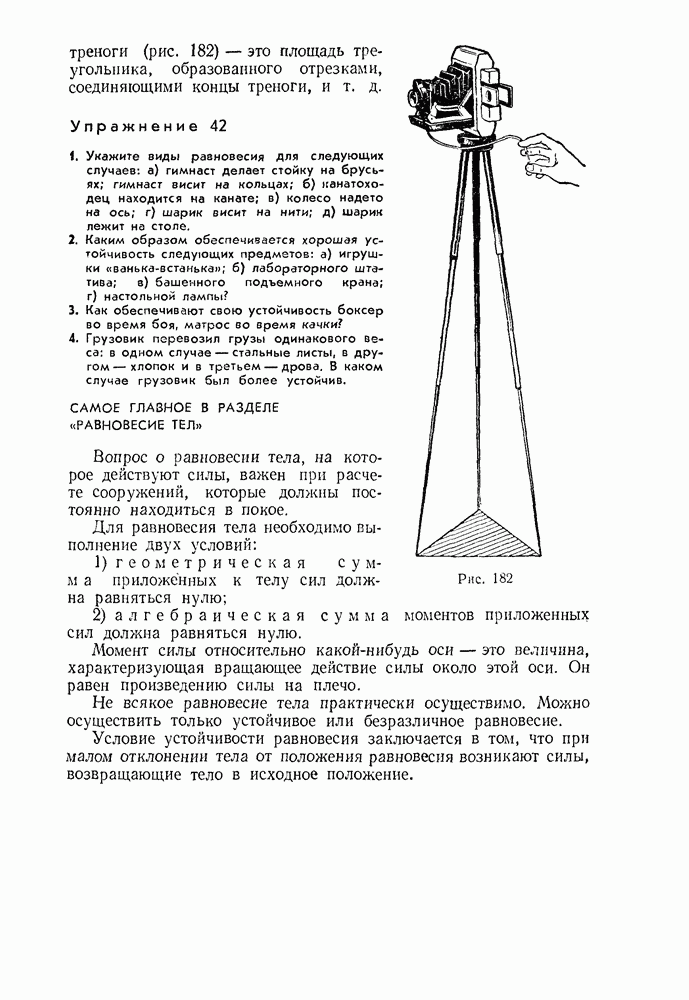
- § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ
- § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ
- § 67. ПРАВИЛО МОМЕНТОВ
- § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ
- Законы сохранения в механике
- Глава 8. Закон сохранения импульса
- § 70. СИЛА И ИМПУЛЬС
- § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ
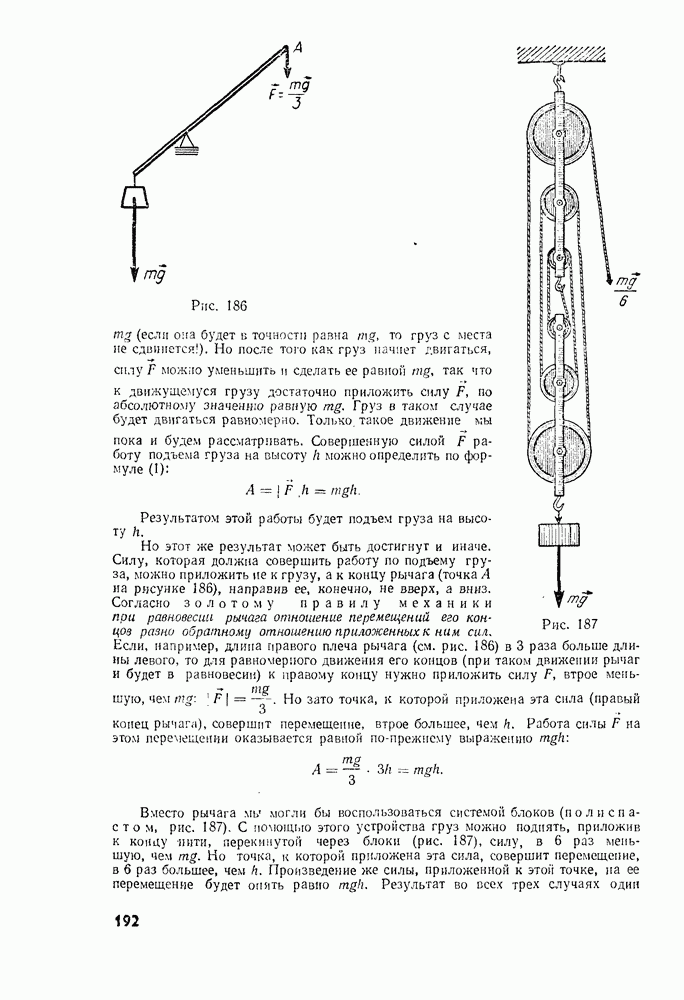
- Глава 9. Механическая работа и мощность
- § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ
- § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ
- § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
- § 77. РАБОТА СИЛЫ ТЯЖЕСТИ
- § 78. РАБОТА СИЛЫ УПРУГОСТИ
- § 79. РАБОТА СИЛЫ ТРЕНИЯ
- § 80. МОЩНОСТЬ
- Глава 10. Закон сохранения энергии
- § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА
- § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ
- § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН
- § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
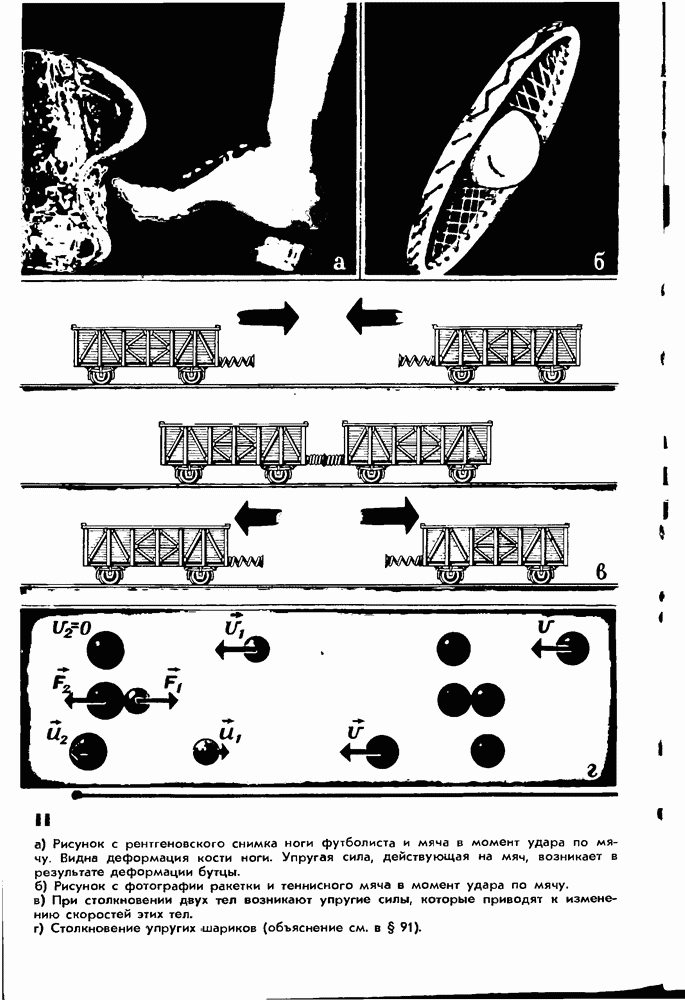
- § 91. СТОЛКНОВЕНИЕ ТЕЛ
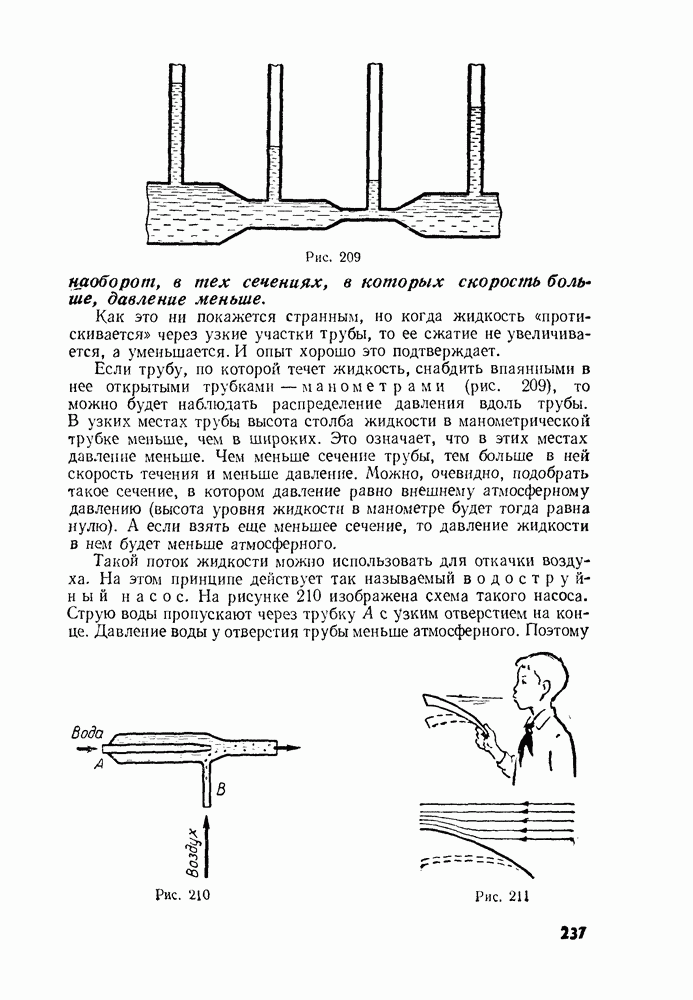
- § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ
- § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ
- Заключение
- Лабораторные работы
- 1. Определение ускорения тела при равноускоренном движении
- 2. Определение коэффициента трения скольжения
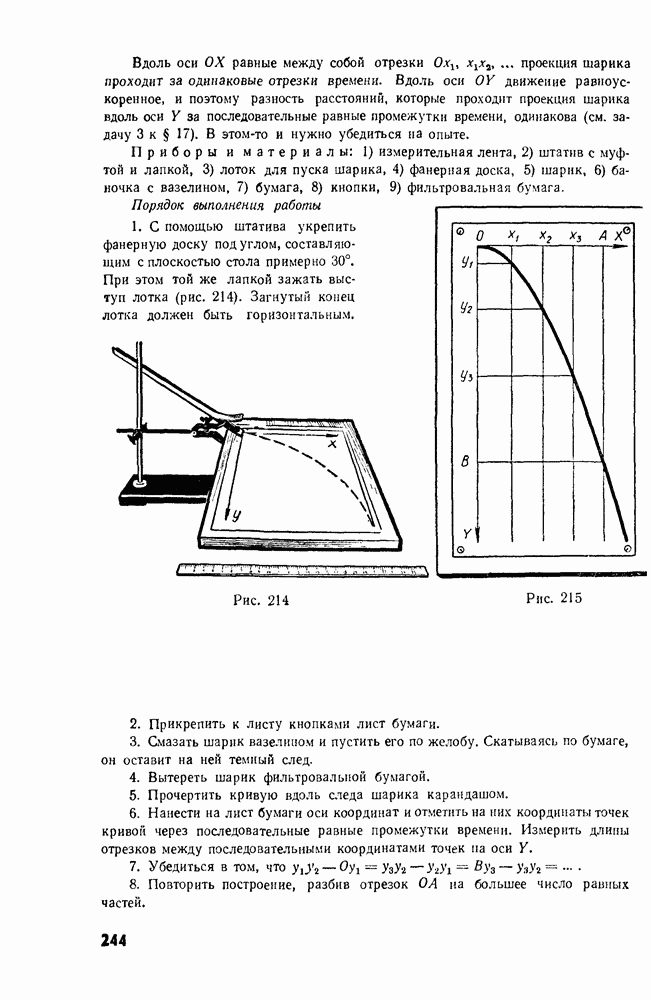
- 3. Изучение движения тела по параболе
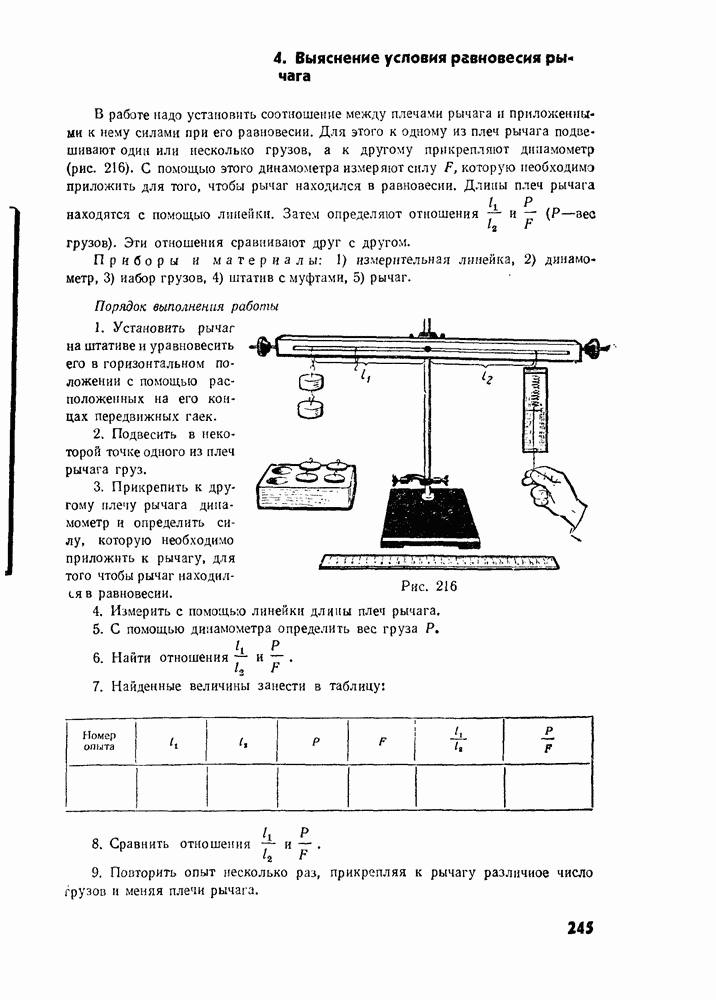
- 4. Выяснение условия равновесия рычага
- 5. Определение центра тяжести плоской пластины
- Ответы к упражнениям