| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ
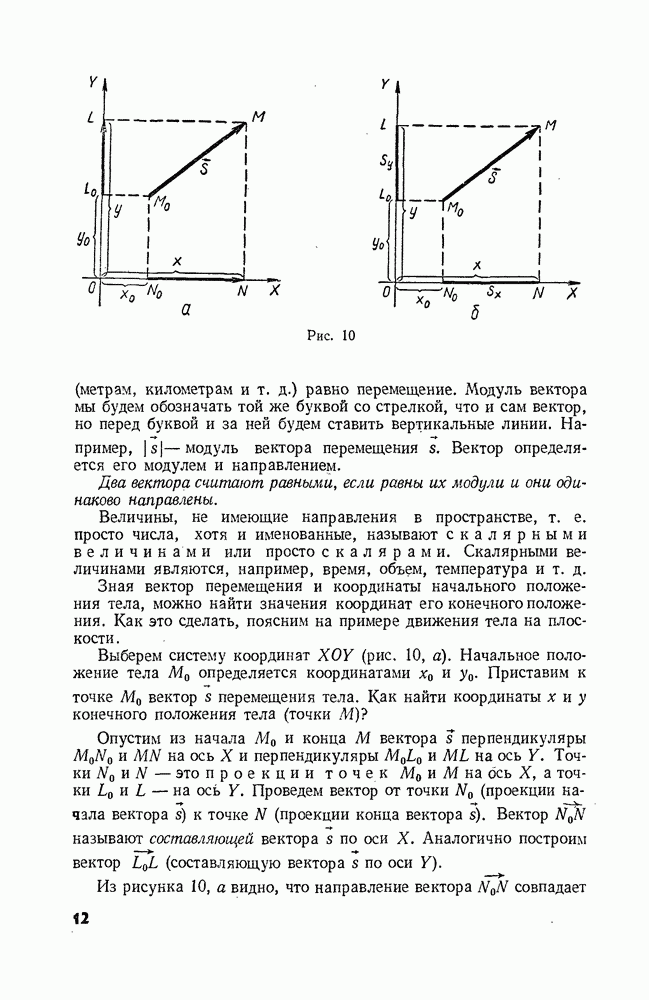
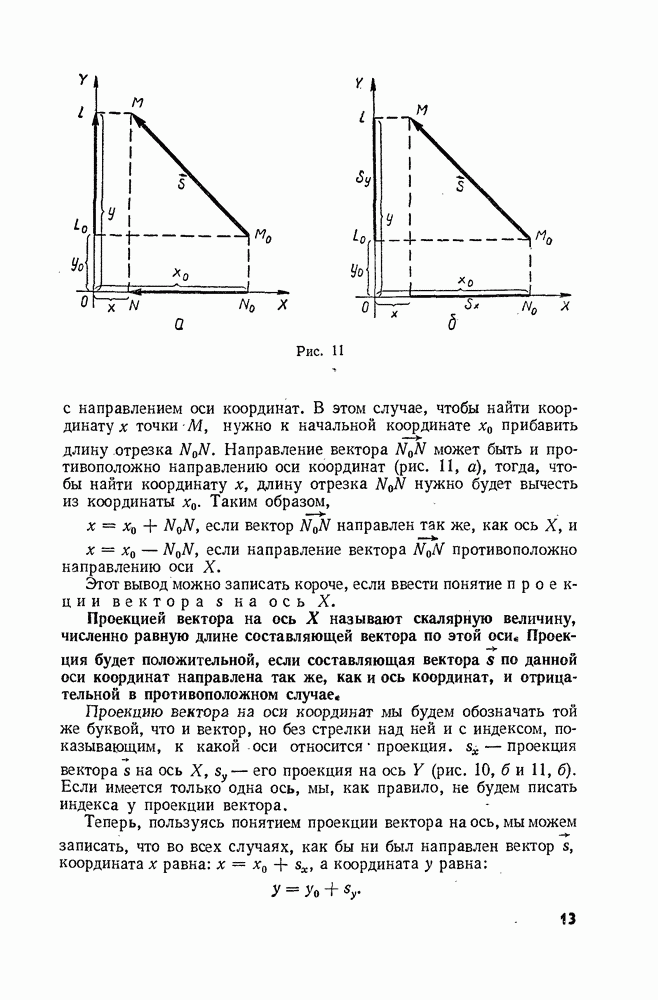
При прямолинейном движении векторы  и
и  направлены вдоль одной прямой, которая является в то же время и траекторией движения. Вдоль этой же прямой в направлении движения телами условились направлять и координатную ось (ось X). В таком случае вектор разности
направлены вдоль одной прямой, которая является в то же время и траекторией движения. Вдоль этой же прямой в направлении движения телами условились направлять и координатную ось (ось X). В таком случае вектор разности  а значит и вектор ускорения а, лежш на той же прямой (см. § 6). Но куда он направлен — в сторону движения (так же как ось X) или против него?
а значит и вектор ускорения а, лежш на той же прямой (см. § 6). Но куда он направлен — в сторону движения (так же как ось X) или против него?
В § 6 мы видели, что проекция разности двух векторов на какую-нибудь ось равна разности их проекций на ту же ось. Следовательно, для проекций векторов  и
и  на ось X можно написать
на ось X можно написать


Рис. 39
Здесь а — проекция вектора а на ось  проекции векторов
проекции векторов  и
и  на ту же ось.
на ту же ось.
Так как все три вектора лежат на одной прямой (оси X), то абсолютные значения их проекций равны абсолютным значениям самих векторов.
Рассмотрим 2 случая ускоренного движения тела.
Первый случай. Скорость тела по абсолютному значению растет (тело «разгоняется»). Это значит, что  Тогда из формулы (1) видно, что проекция ускорения а положительна и равна
Тогда из формулы (1) видно, что проекция ускорения а положительна и равна  Вектор а, следовательно, направлен так же, как ось X, т. е. в сторону движения. Когда, например, бронебойный снаряд движется при выстреле в стволе орудия, его скорость растет и ускорение направлено так же, как и скорость (рис. 39).
Вектор а, следовательно, направлен так же, как ось X, т. е. в сторону движения. Когда, например, бронебойный снаряд движется при выстреле в стволе орудия, его скорость растет и ускорение направлено так же, как и скорость (рис. 39).
Второй случай. Тело тормозится, т. е. абсолютное значение его скорости уменьшается  Из формулы (1) видно, что проекция ускорения а в этом случае отрицательна:
Из формулы (1) видно, что проекция ускорения а в этом случае отрицательна: 
Из формулы (1) можно получить выражение для скорости  :
:

В этой формуле, повторяем,  — проекции векторов
— проекции векторов  на ось X, которые могут быть как положительными, так и отрицательными.
на ось X, которые могут быть как положительными, так и отрицательными.
При решении задач выражение для скорости (2) удобно записывать так, чтобы из него сразу было видно, как направлен вектор ускорения.
Если скорость тела растет (разгон), то  и
и

Когда же скорость тела уменьшается (торможение), 

Понятно, что тело, которое тормозится, должно когда-то остановиться. Это произойдет, как это видно из формулы (26), тогда, когда  станет равным
станет равным  т. е. в момент времени
т. е. в момент времени  Но если ускорение остается постоянным (по модулю и направлению) и после этого момента, то тело, остановившись, начнет двигаться в противоположную сторону. Это видно из того, что при
Но если ускорение остается постоянным (по модулю и направлению) и после этого момента, то тело, остановившись, начнет двигаться в противоположную сторону. Это видно из того, что при  станет больше, чем
станет больше, чем  скорость
скорость  изменит свой знак на обратный. Так
изменит свой знак на обратный. Так
движется, например, тело, брошенное вертикально вверх: долетев до высшей точки траектории, тело начинает движение вниз.
Если  и вектор ускорения направлен так же, как и ось координат, то из формулы (2а) следует, что
и вектор ускорения направлен так же, как и ось координат, то из формулы (2а) следует, что

Если же ось координат выбрана так, что направление вектора ускорения противоположно направлению оси координат, то из формулы (26) следует, что

Знак  в этой формуле означает, что вектор скорости, так же как и вектор ускорения, направлен противоположно направлению оси координат. Модуль скорости, конечно, и в этом случае увеличивается со временем.
в этой формуле означает, что вектор скорости, так же как и вектор ускорения, направлен противоположно направлению оси координат. Модуль скорости, конечно, и в этом случае увеличивается со временем.
Обычно мы называем движение с возрастающей по абсолютной величине скоростью ускоренным движением, а движение с убывающей скоростью  медленным движение
медленным движение  Но в механике любое неравномерное движение является ускоренным движением. Трогается ли автомобиль с места или тормозит, в обоих случаях он движется с ускорением. Ускоренное прямолинейное движение отличается от замедленного только знаком проекции вектора ускорения.
Но в механике любое неравномерное движение является ускоренным движением. Трогается ли автомобиль с места или тормозит, в обоих случаях он движется с ускорением. Ускоренное прямолинейное движение отличается от замедленного только знаком проекции вектора ускорения.
Мы знаем, что и перемещение, и скорость, и траектория движения различны относительно разных тел отсчета, движущихся друг относительно друга.
А ускорение? Относительно ли оно?
Ускорение тела, как мы теперь знаем, определяется векторной разностью двух значений его скорости в различные моменты времени. При переходе от одной системы координат к другой, движущейся относительно первой равномерно и прямолинейно, изменятся оба значения скорости. Но изменятся они на одну и ту же величину. Разность же их останется неизменной. Поэтому и ускорение останется неизменным.
Во всех системах отсчета, движущихся друг относительно друга прямолинейно и равномерно, ускорение тела одинаково.
Но ускорения тела будут различными в системах отсчета, движущихся с ускорением друг относительно друга. В этом случае ускорения складываются так же, как скорости (см. § 10).
Задача. Автомобиль проезжает мимо наблюдателя, двигаясь со скоростью 10 м/сек. В этот момент водитель нажимает на тормоз, и автомобиль начинает двигаться с ускорением  Сколько времени пройдет с того момента, когда водитель нажал на тормоз, до остановки автомобиля?
Сколько времени пройдет с того момента, когда водитель нажал на тормоз, до остановки автомобиля?
Решение. Выберем за начало отсчета то место, в котором находится наблюдатель, и направим координатную ось в сторону движения автомобиля. Тогда проекция скорости автомобиля на эту ось будет положительной. Так как скорость автомобиля
уменьшается, то проекция ускорения отрицательна и мы должны воспользоваться формулой (26):

Откуда

Подставляя в эту формулу численные значения заданных величин, получим:

За положительное направление координатной оси можно принять и направление, противоположное движению. Тогда проекция начальной скорости автомобиля будет отрицательной  а проекция ускорения — положительной, и применять тогда нужно формулу (2а):
а проекция ускорения — положительной, и применять тогда нужно формулу (2а):

Отсюда

Результат получился тот же. Да он и не может зависеть от того, как выбрано направление оси координат!
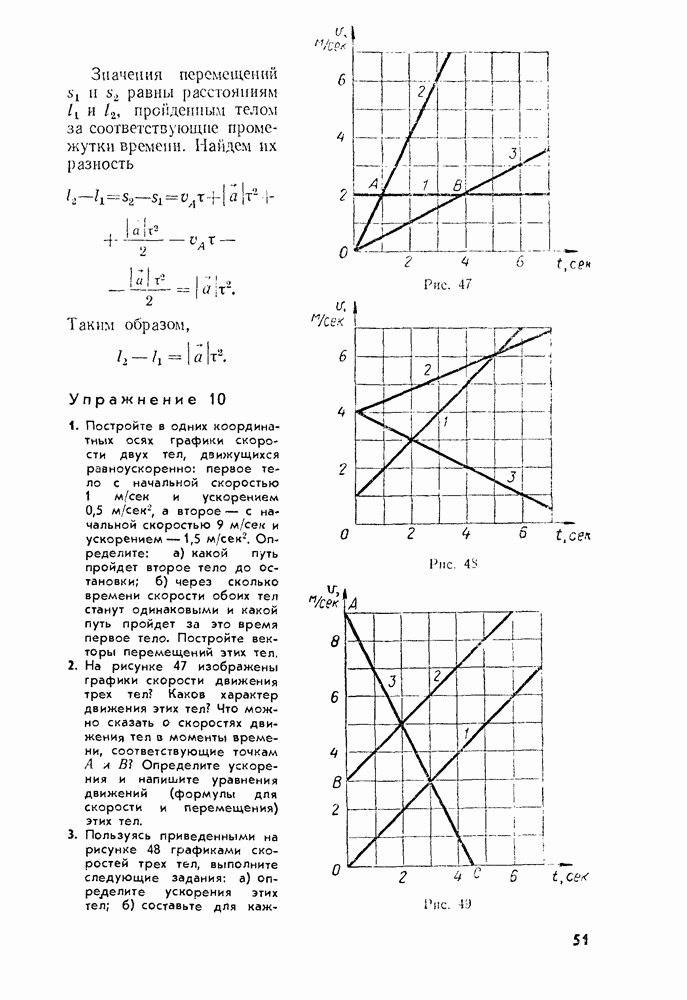
Упражнение 9
1. Что такое ускорение и для чего его нужно знать?
2. При любом неравномерном движении изменяется скорость. Как ускорение характеризует это изменение?
3. Чем отличается замедленное прямолинейное движение от ускоренного?
4. Что такое равноускоренное движение?
5. Троллейбус, трогаясь с места, движется с постоянным ускорением  Через сколько времени он приобретет скорость 54 км/ч?
Через сколько времени он приобретет скорость 54 км/ч?
6. Автомобиль, движущийся со скоростью 36 км/ч, останавливается при торможении в течение 4 сек. С каким ускорением движется автомобиль при торможении?
7. Грузовик, двигаясь с постоянным ускорением, на некотором участке пути увеличил свою скорость с 15 до 25 м/сек. За какое время произошло это увеличение скорости, если ускорение грузовика равно 
8. Какая скорость движения была бы достигнута, если бы тело двигалось прямолинейно с ускорением  в течение 0,5 ч при начальной скорости, равной нулю?
в течение 0,5 ч при начальной скорости, равной нулю?
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о движении
- § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА
- § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ
- § 3. ПЕРЕМЕЩЕНИЕ
- § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА
- § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ
- § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ
- § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
- § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
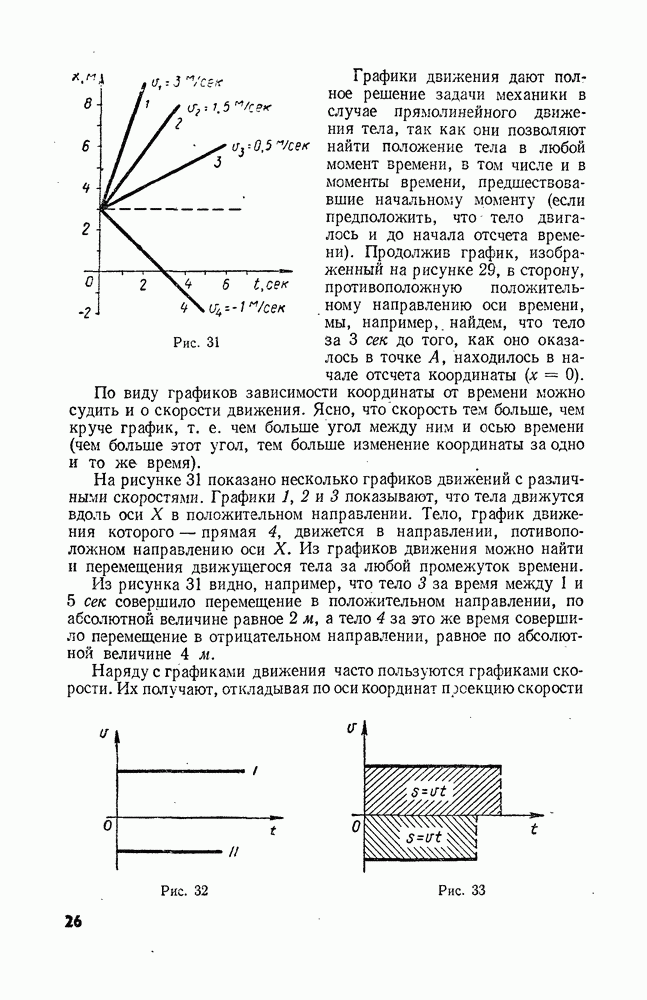
- § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ
- § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
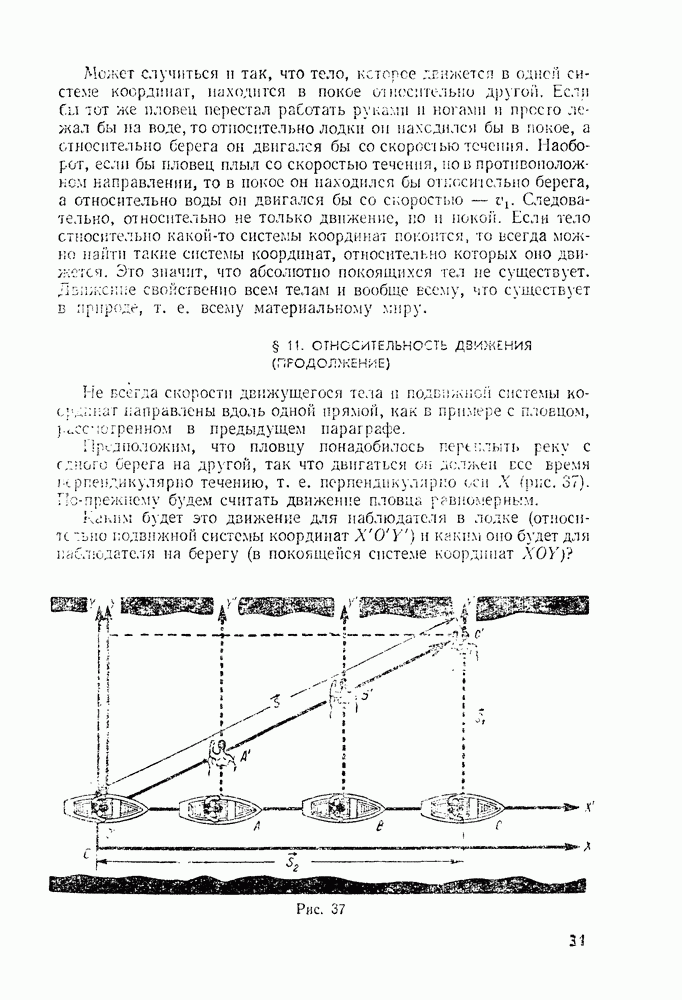
- § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ)
- § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ
- Глава 2. Прямолинейное неравномерное движение
- § 13. СРЕДНЯЯ СКОРОСТЬ
- § 14. МГНОВЕННАЯ СКОРОСТЬ
- § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ
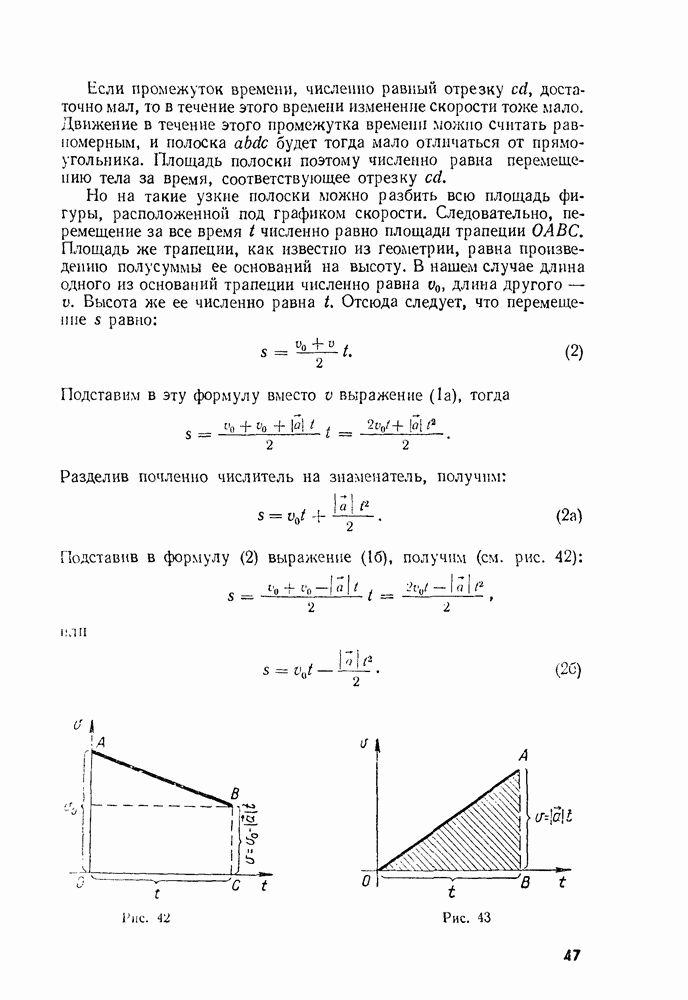
- § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
- § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ
- § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ
- § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
- § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
- Глава 3. Криволинейное движение
- § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
- § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ
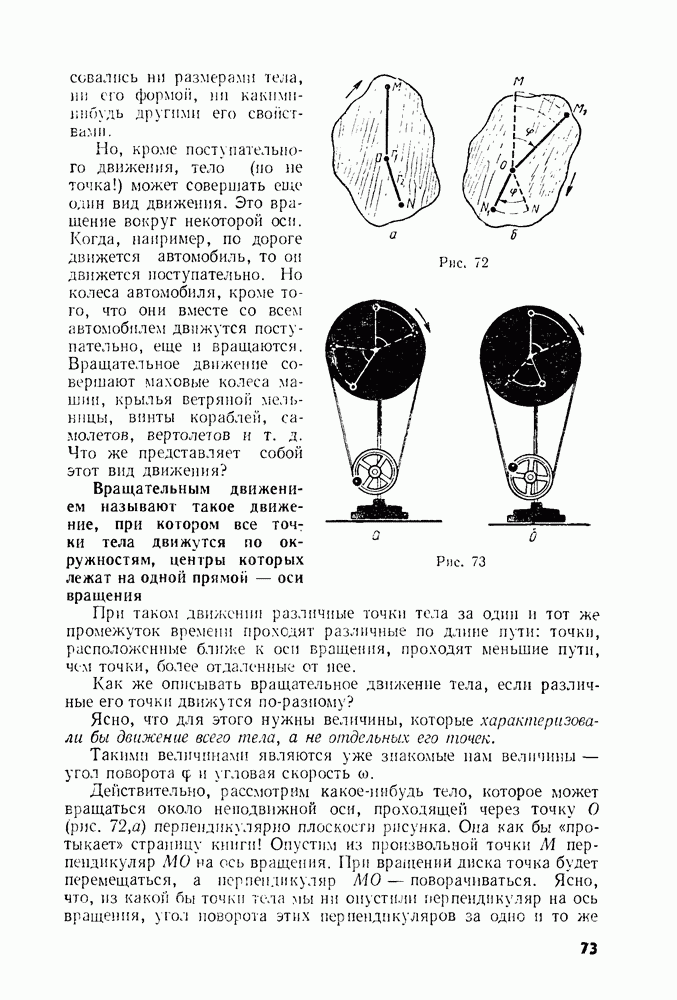
- § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА
- Динамика
- Глава 4. Законы движения
- § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ
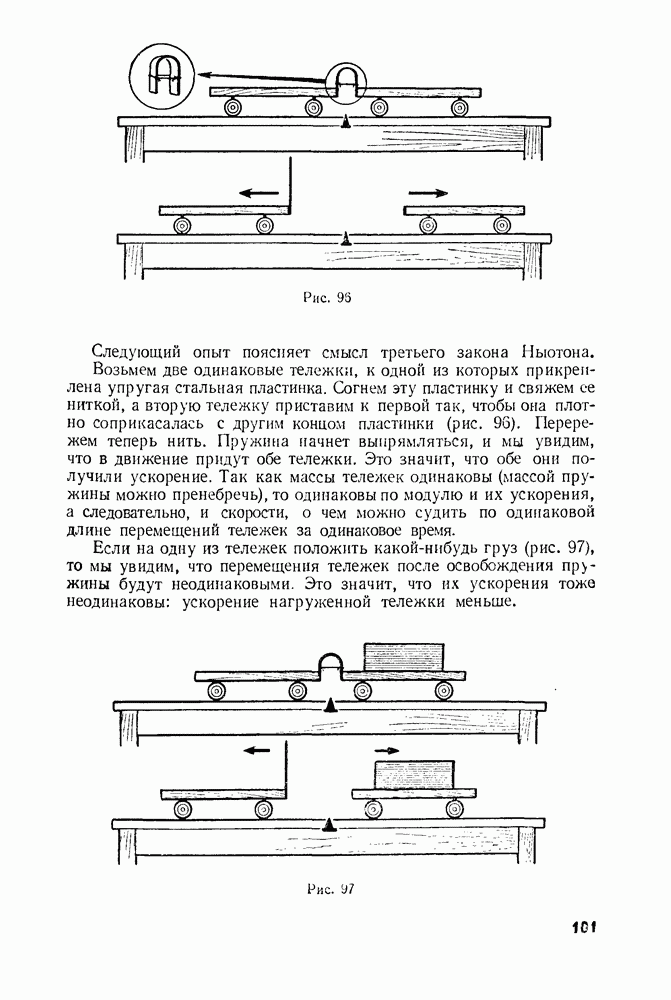
- § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ
- § 31. ИНЕРТНОСТЬ ТЕЛ
- § 32. МАССА ТЕЛ
- § 33. МАССА ЛУНЫ
- § 34. СИЛА
- § 35. ВТОРОЙ ЗАКОН НЬЮТОНА
- § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение)
- § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР
- § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА
- § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА
- Глава 5. Силы природы
- § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ
- § 41. СИЛА УПРУГОСТИ
- § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 44. СИЛА ТЯЖЕСТИ
- § 45. ВЕС ТЕЛ
- § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ
- § 47. МАССА ЗЕМЛИ
- § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ
- § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ
- Глава 6. Применение законов движения
- § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ
- § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ
- § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ
- § 54. НЕВЕСОМОСТЬ
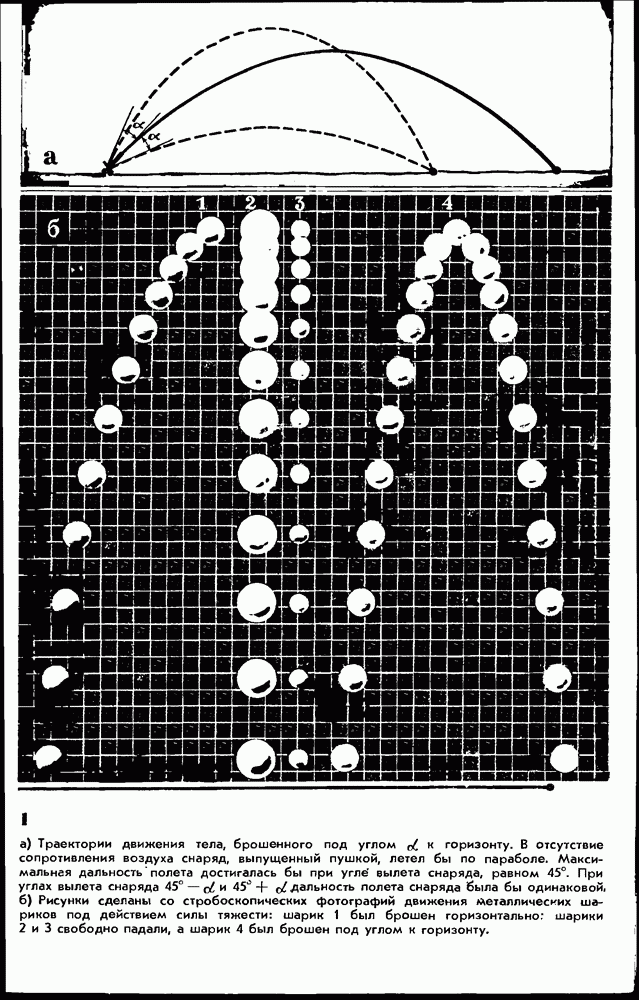
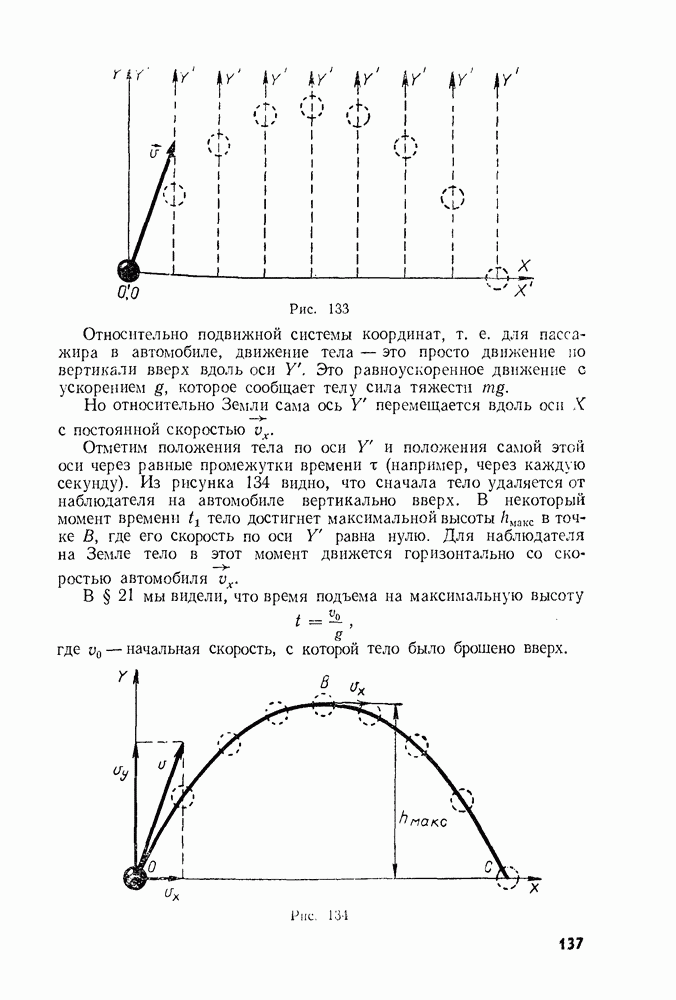
- § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ
- § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО
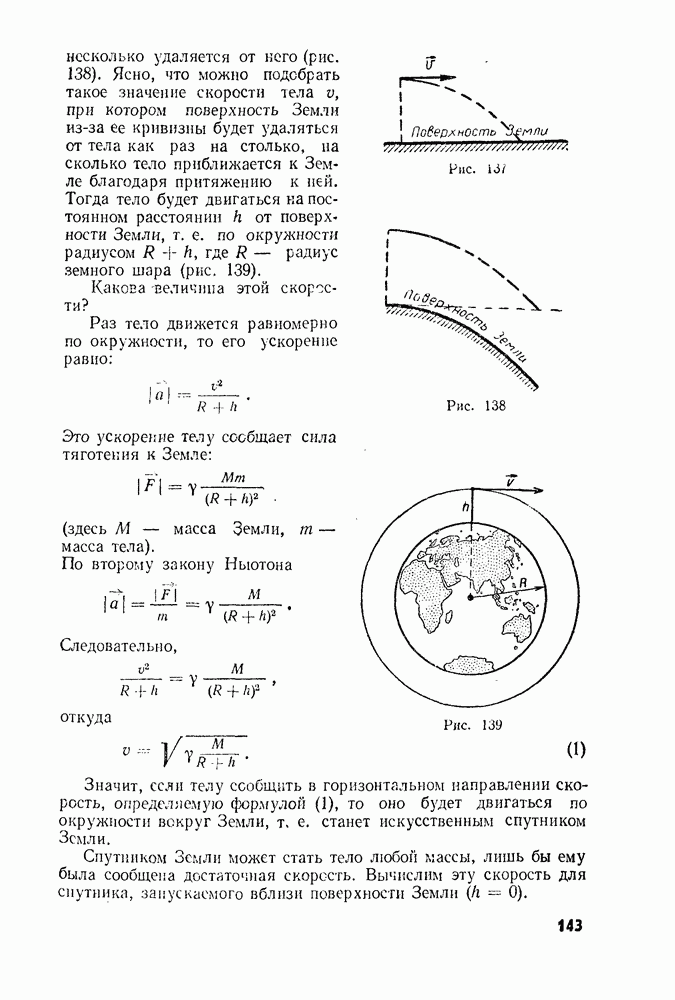
- § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ
- § 58. ДВИЖЕНИЕ ПЛАНЕТ
- § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ
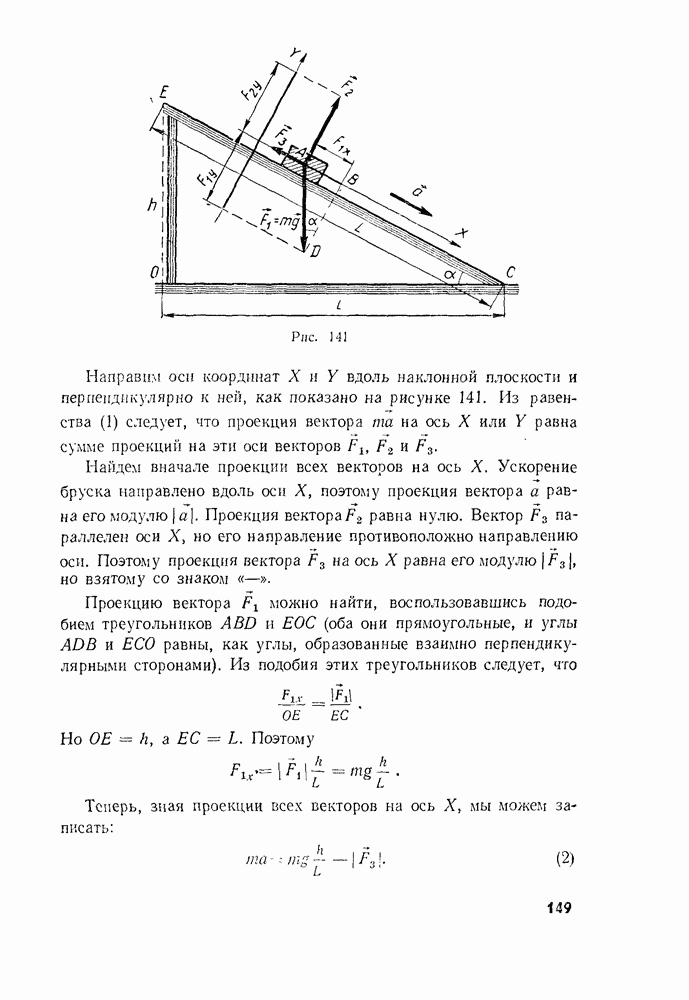
- § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ
- § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ
- § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ
- § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ
- § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА
- Равновесие тел
- Глава 7. Элементы статики
- § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ
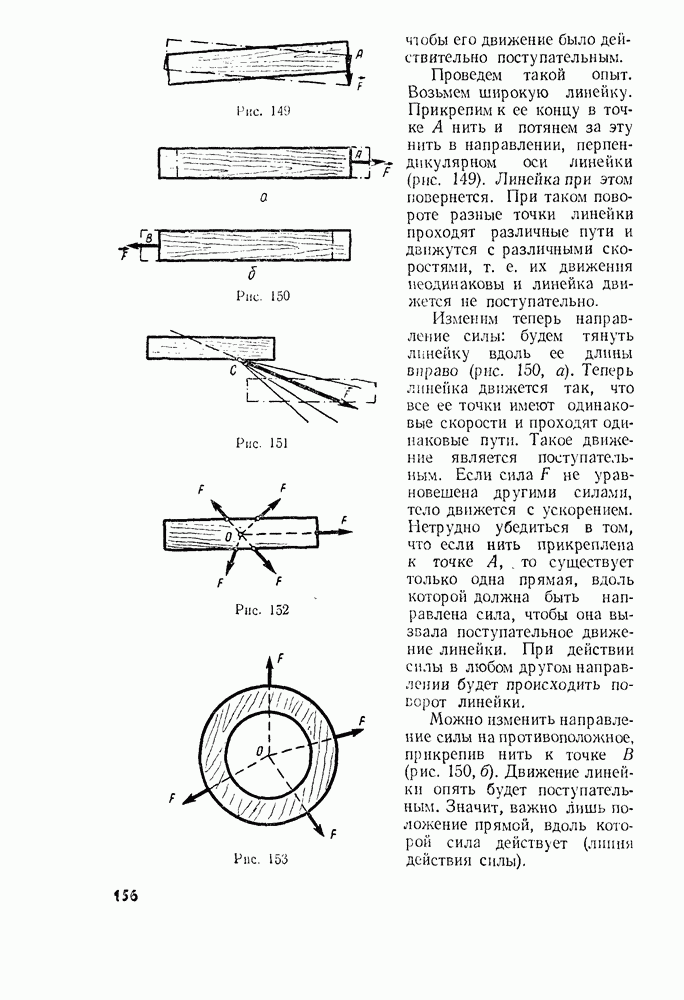
- § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ
- § 67. ПРАВИЛО МОМЕНТОВ
- § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ
- Законы сохранения в механике
- Глава 8. Закон сохранения импульса
- § 70. СИЛА И ИМПУЛЬС
- § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ
- Глава 9. Механическая работа и мощность
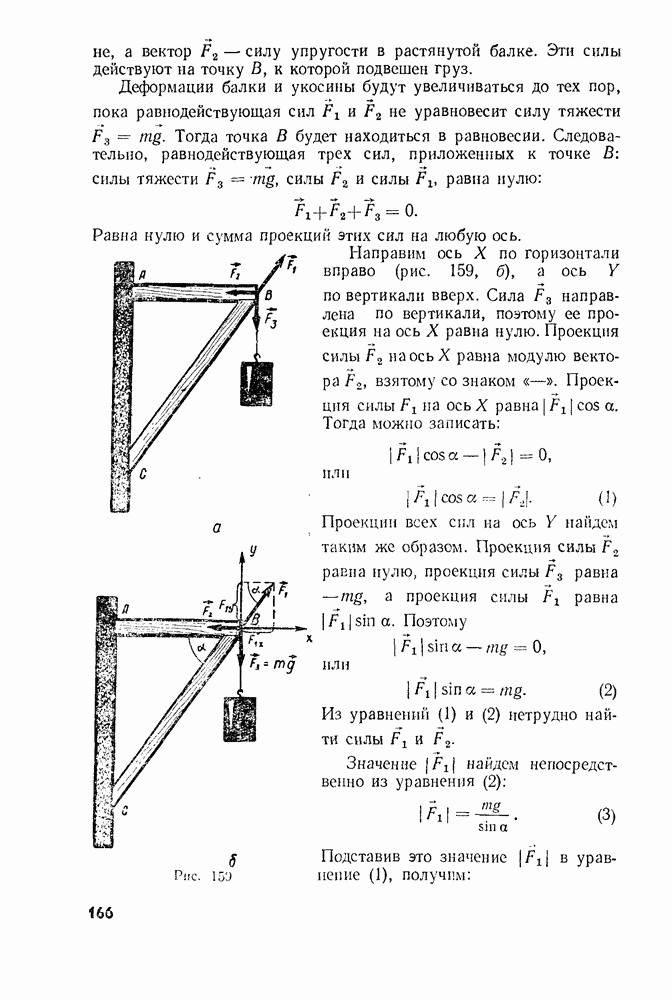
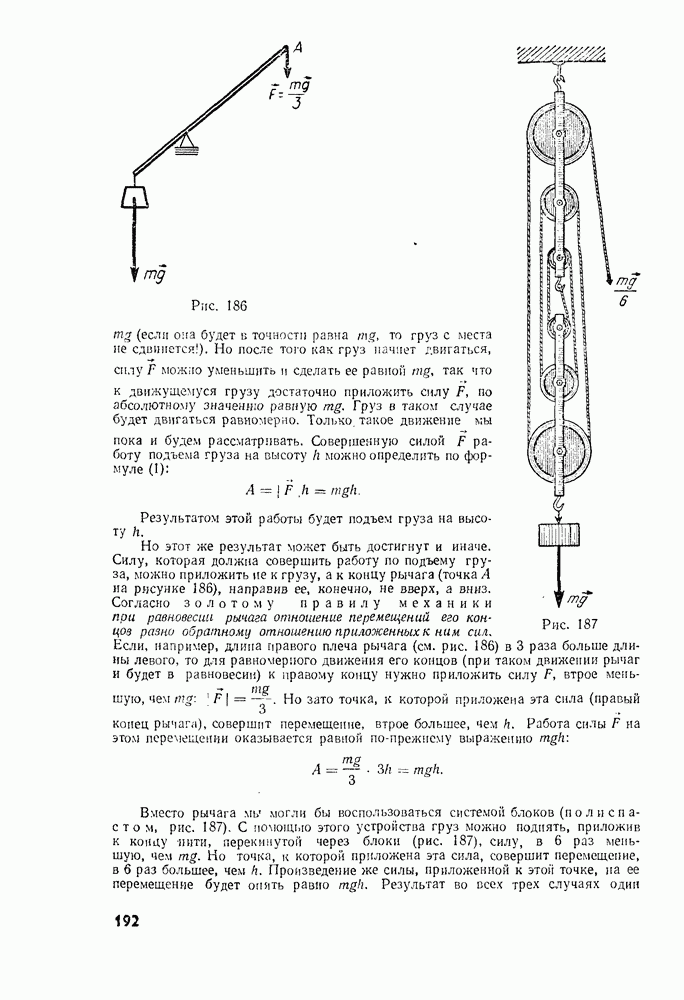
- § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ
- § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ
- § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
- § 77. РАБОТА СИЛЫ ТЯЖЕСТИ
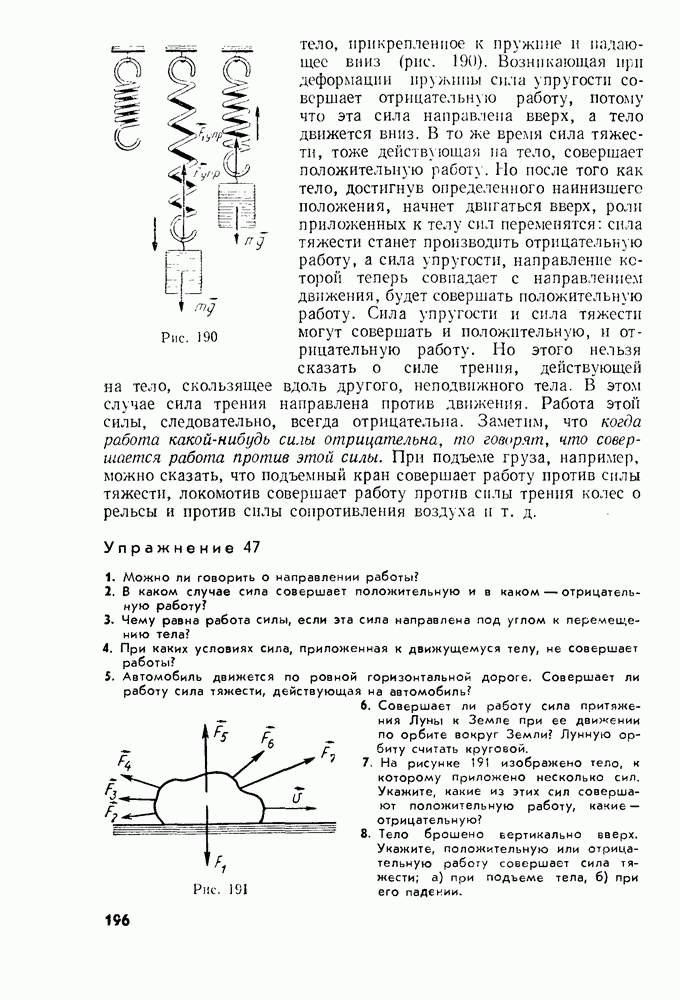
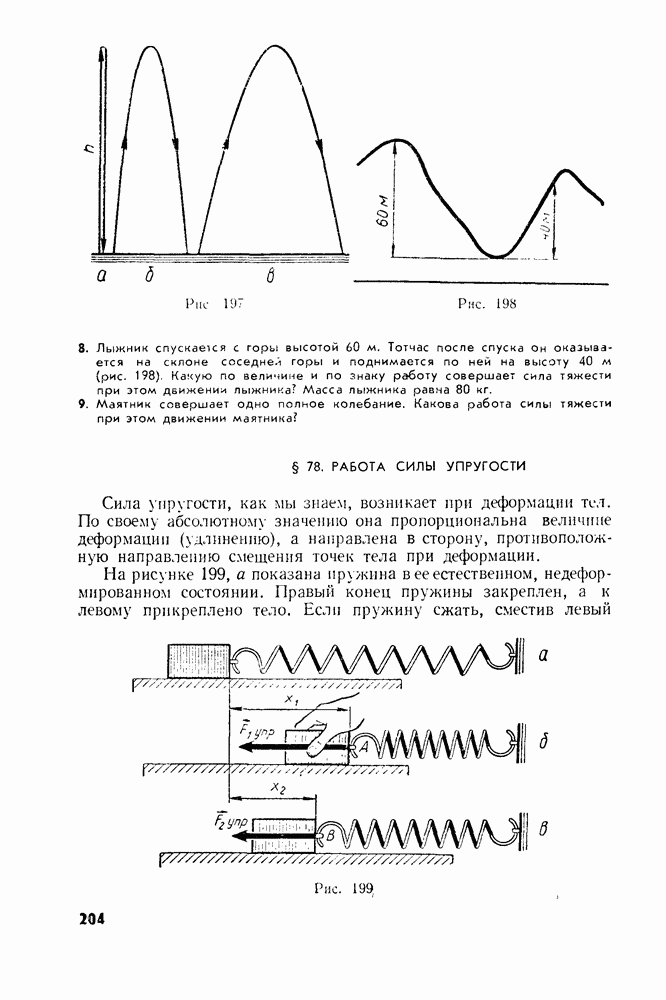
- § 78. РАБОТА СИЛЫ УПРУГОСТИ
- § 79. РАБОТА СИЛЫ ТРЕНИЯ
- § 80. МОЩНОСТЬ
- Глава 10. Закон сохранения энергии
- § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА
- § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ
- § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН
- § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
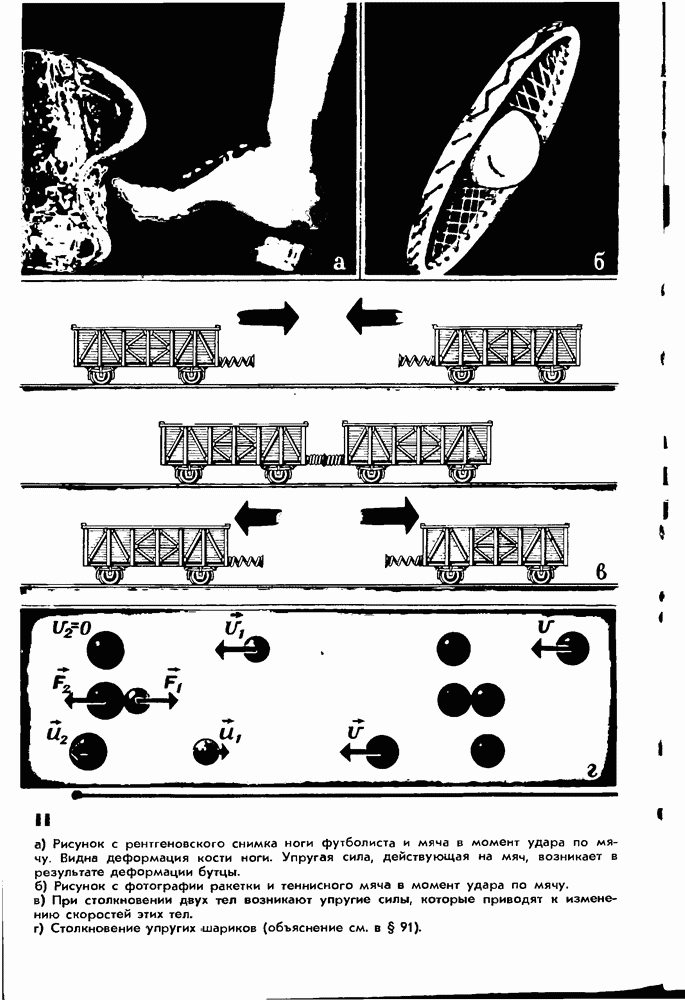
- § 91. СТОЛКНОВЕНИЕ ТЕЛ
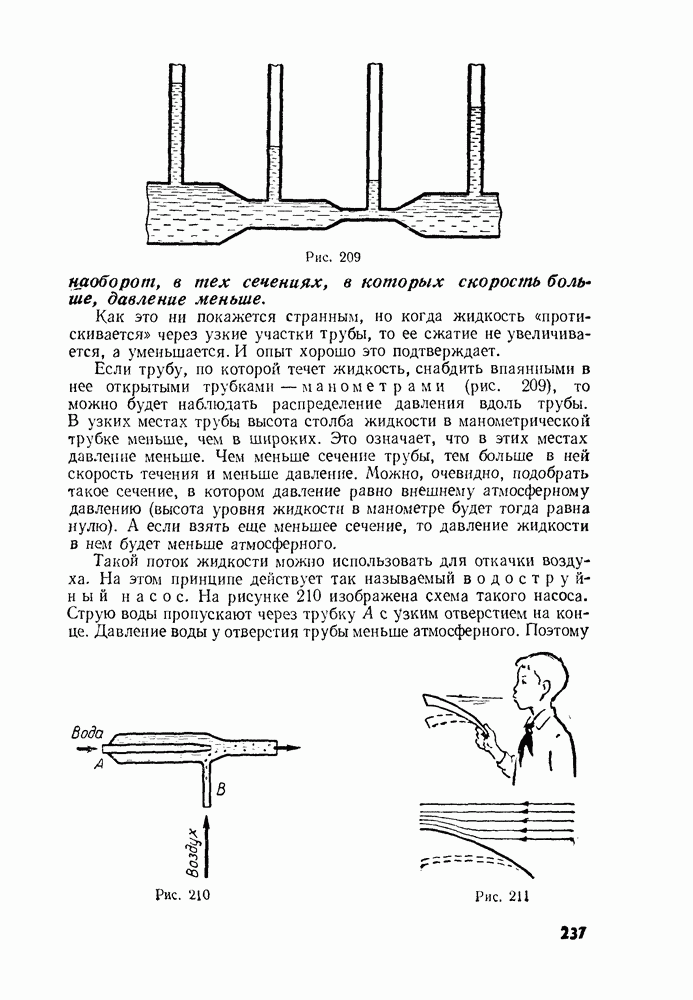
- § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ
- § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ
- Заключение
- Лабораторные работы
- 1. Определение ускорения тела при равноускоренном движении
- 2. Определение коэффициента трения скольжения
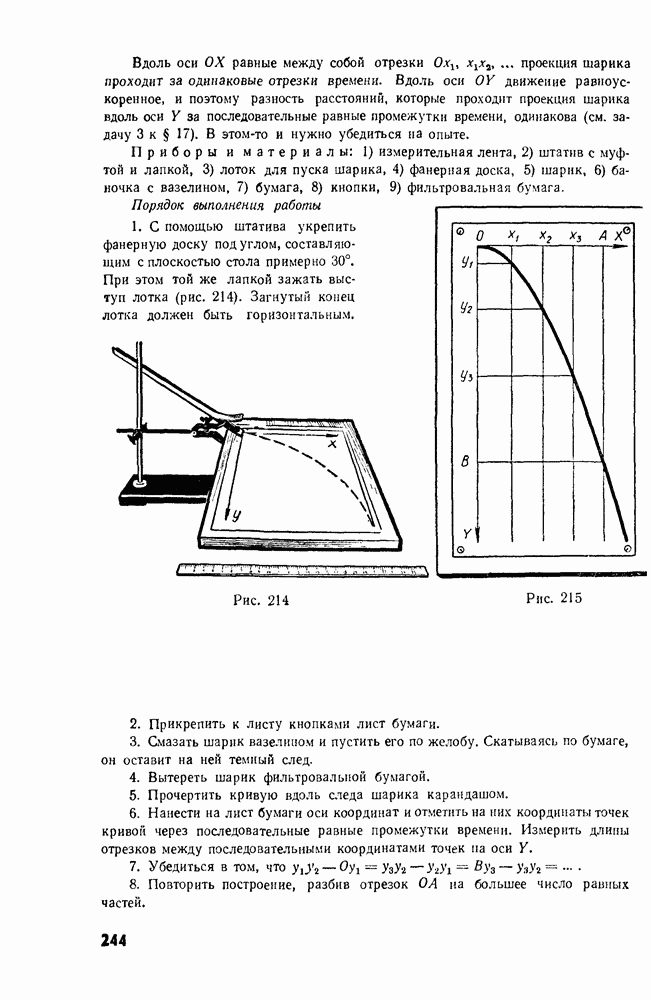
- 3. Изучение движения тела по параболе
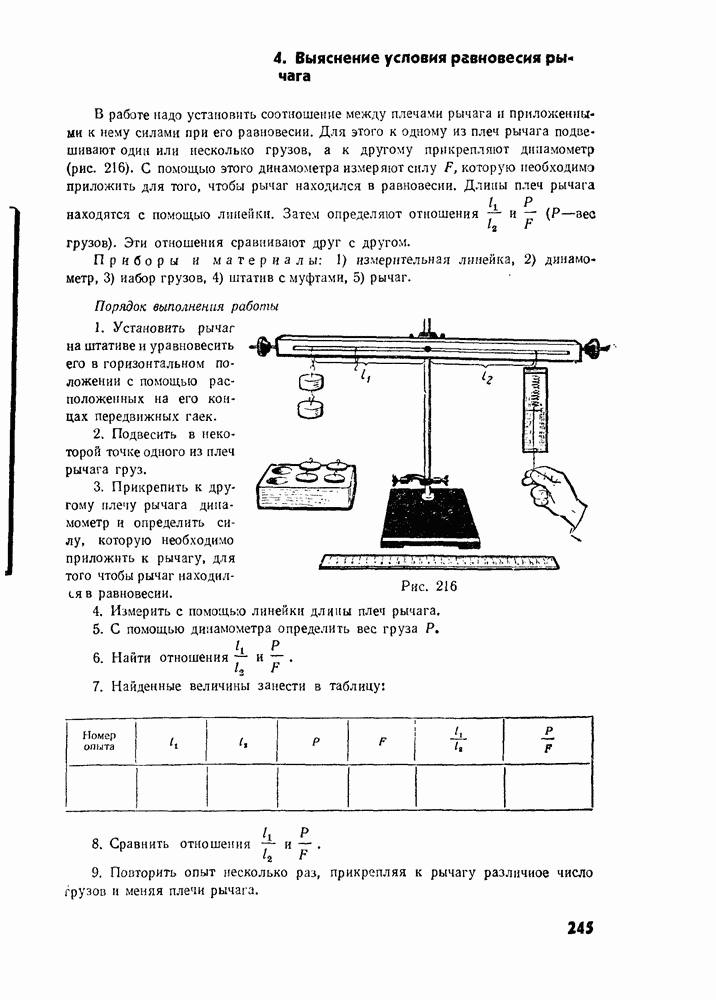
- 4. Выяснение условия равновесия рычага
- 5. Определение центра тяжести плоской пластины
- Ответы к упражнениям