| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ
При поступательном движении все точки тела движутся одинаково. Поэтому такое движение можно рассматривать как движение одной точки тела — его центра масс. При этом мы должны считать, что в центре масс сосредоточена вся масса тела и к нему приложена равнодействующая всех сил, действующих на тело. Из второго закона Ньютона следует, что ускорение этой точки равно нулю, если геометрическая сумма всех приложенных к ней сил — равнодействующая этих сил — равна нулю. Это и есть условие равновесия тела при отсутствии вращения.
Для того чтобы тело при отсутствии вращения находилось в равновесии, необходимо, чтобы равнодействующая сил, приложенных к телу, была равна нулю.
Но если геометрическая сумма сил равна нулю, то и сумма проекций векторов этих сил на любую ось тоже равна нулю. Поэтому условие равновесия тела можно сформулировать и так:
Для того чтобы тело при отсутствии вращения находилось в равновесии, необходимо, чтобы сумма проекций приложенных к телу сил на любую ось была равна нулю.
В равновесии, например, находится тело, к которому, как на рисунке 155, приложены две равные силы, действующие вдоль одной прямой, но направленные в противоположные стороны.
Состояние равновесия — это не обязательно состояние покоя. Согласно второму закону Ньютона при равенстве нулю равнодействующей всех сил, приложенных к телу, оно может двигаться прямолинейно и равномерно. При таком движении тело тоже находится в состоянии равновесия. Например, парашютист, после того как он начал падать с постоянной скоростью, находится в состоянии равновесия.
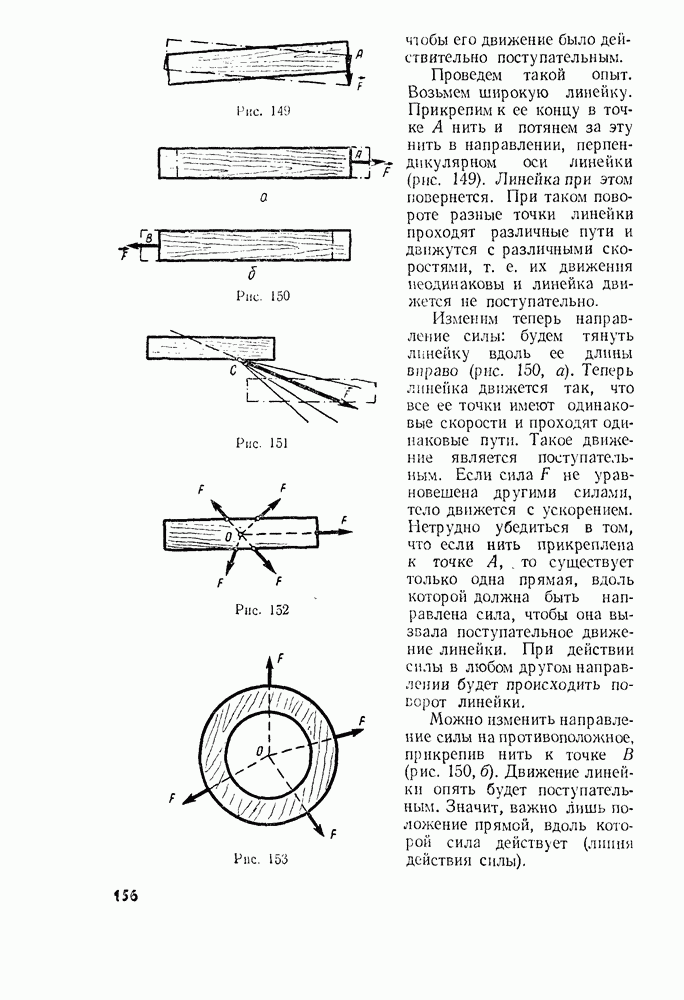
На рисунке 155 силы приложены к телу не в одной точке. Но мы уже видели, что важна не точка приложения силы, а прямая, вдоль которой она действует. Перенос точки приложения силы вдоль линии ее действия ничего не изменяет ни в движении тела, ни в состоянии равновесия. Ясно, например, что ничего не изменится, если, вместо того чтобы тянуть вагонетку, как это показано на рисунке 156, а, еестанут толкать (рис. 156,б).
Если равнодействующая сил, приложенных к телу, не равна нулю, то, для того чтобы тело находилось в состоянии равновесия, к нему должна быть приложена добавочная сила, равная по модулю равнодействующей, но противоположная ей по направлению.
Поясним это на опыте. Прикрепим к двум точкам верхней перекладины рамы ди-

Рис. 155

Рис. 156
нанометры 1 и 2 (рис. 157). При помощи нитей в точке О прикрепим груз. Под действием трех сил  точка О будет находиться в равновесии. Теперь заменим силы, действующие на точку О со стороны двух динамометров, одной силой. Для этого прикрепим к точке О еще один динамометр 3 и потянем его вверх. Когда стрелки динамометров 1 и 2 установятся на нуле шкалы, на точку О будут действовать только две силы. Одна из них — сила упругости пружины динамометра 3, измеряемая этим динамометром, — является равнодействующей сил
точка О будет находиться в равновесии. Теперь заменим силы, действующие на точку О со стороны двух динамометров, одной силой. Для этого прикрепим к точке О еще один динамометр 3 и потянем его вверх. Когда стрелки динамометров 1 и 2 установятся на нуле шкалы, на точку О будут действовать только две силы. Одна из них — сила упругости пружины динамометра 3, измеряемая этим динамометром, — является равнодействующей сил  Сила тяжести груза
Сила тяжести груза  равна этой равнодействующей по абсолютной величине и направлена в противоположную сторону. Поэтому точка О находится в равновесии.
равна этой равнодействующей по абсолютной величине и направлена в противоположную сторону. Поэтому точка О находится в равновесии.
Рассмотрим еще один пример. Как удержать в равновесии лодку, на которую действуют течение реки и ветер, дующий от берега (рис. 158)? Найдем равнодействующую  сил
сил  вызванных ветром и течением воды. Для этого воспользуемся правилом параллелограмма. Диагональ параллелограмма дает величину и
вызванных ветром и течением воды. Для этого воспользуемся правилом параллелограмма. Диагональ параллелограмма дает величину и
Рис. 157 (см. скан)
направление равнодействующей  Для того чтобы лодка была в равновесии, к ней должна быть приложена уравновешивающая сила
Для того чтобы лодка была в равновесии, к ней должна быть приложена уравновешивающая сила  равная этой равнодействующей, но направленная в противоположную сторону. Такой силой, например, может быть сила натяжения каната, прикрепленного одним концом к носу лодки, а другим к берегу. Если, например, сила, с которой текущая вода действует на лодку, равна 150 н, а сила давления ветра равна 100 н, то равнодействующая этих двух взаимно перпендикулярных сил может быть вычислена по теореме Пифагора:
равная этой равнодействующей, но направленная в противоположную сторону. Такой силой, например, может быть сила натяжения каната, прикрепленного одним концом к носу лодки, а другим к берегу. Если, например, сила, с которой текущая вода действует на лодку, равна 150 н, а сила давления ветра равна 100 н, то равнодействующая этих двух взаимно перпендикулярных сил может быть вычислена по теореме Пифагора:

Лодка, следовательно, может быть удержана канатом, способным выдержать натяжение не менее 180 н.
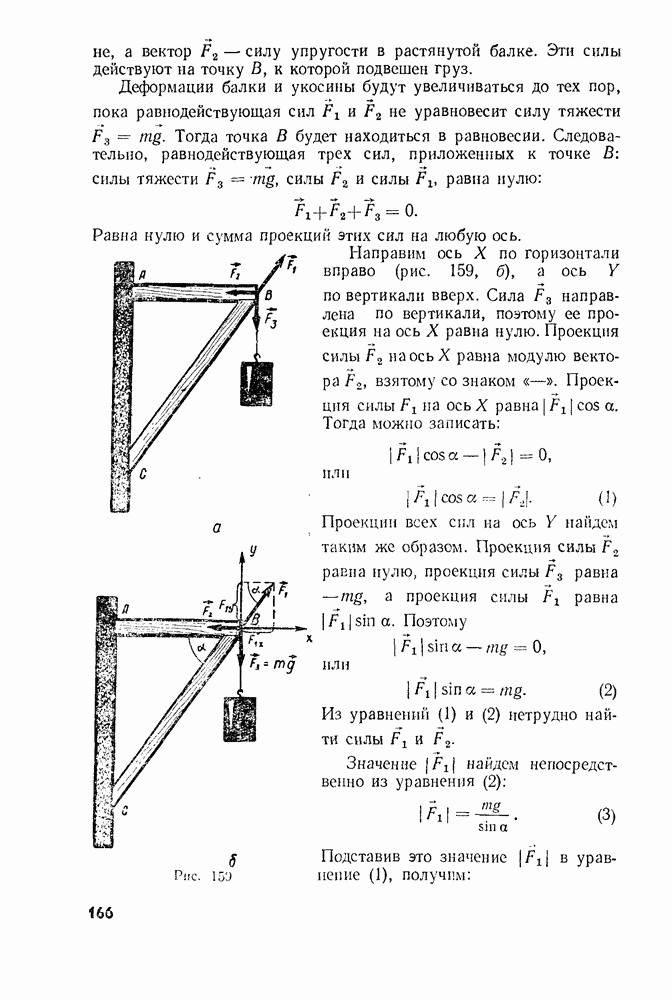
Задача. Груз массой 100 кг подвешен к кронштейну (рис. 159, а), который состоит из поперечной балки  и укосины
и укосины  Определите силы упругости, возникающие в балке и укосине, если
Определите силы упругости, возникающие в балке и укосине, если  .
.
Решение. Прежде всего выясним, каково происхождение сил, действующих на части кронштейна.
Под действием силы тяжести груз начинает падать вертикально вниз. При этом он увлекает за собой конец В балки. Ясно, что балка и укосина вследствие этого деформируются: балка удлиняется, а укосина сжимается (рис. 159, а). В деформированных частях кронштейна возникают силы упругости, направленные в сторону, противоположную деформации. Эти силы и нужно определить. На рисунке 159 вектор  изображает силу упругости в сжатой
изображает силу упругости в сжатой

Рис. 158
укосине, а вектор  силу упругости в растянутой балке. Эти силы действуют на точку В, к которой подвешен груз.
силу упругости в растянутой балке. Эти силы действуют на точку В, к которой подвешен груз.
Деформации балки и укосины будут увеличиваться до тех пор,пока равнодействующая сил и  не уравновесит силу тяжести
не уравновесит силу тяжести  Тогда точка В будет находиться в равновесии. Следовательно, равнодействующая трех сил, приложенных к точке В: силы тяжести
Тогда точка В будет находиться в равновесии. Следовательно, равнодействующая трех сил, приложенных к точке В: силы тяжести  силы
силы  и силы
и силы  равна нулю:
равна нулю:

Равна нулю и сумма проекций этих сил на любую ось.
Направим ось X по горизонтали вправо (рис. 159, б), а ось  по вертикали вверх. Сила
по вертикали вверх. Сила  направлена по вертикали, поэтому ее проекция на ось X равна нулю. Проекция силы
направлена по вертикали, поэтому ее проекция на ось X равна нулю. Проекция силы  на ось X равна модулю вектора
на ось X равна модулю вектора  взятому со знаком
взятому со знаком  Проекция силы
Проекция силы  на ось X равна
на ось X равна  . Тогда можно записать:
. Тогда можно записать:

или

Проекции всех сил на ось  найдем таким же образом. Проекция силы
найдем таким же образом. Проекция силы  равна нулю, проекция силы
равна нулю, проекция силы  равна
равна  а проекция силы равна
а проекция силы равна  Поэтому
Поэтому

или

Из уравнении (1) и (2) нетрудно найти силы и 
Значение  найдем непосредственно из уравнения (2):
найдем непосредственно из уравнения (2):

Подставив это значение  в уравнение (1), получим:
в уравнение (1), получим:

Рис. 159

Из треугольника  видно, что
видно, что

(согласно теореме Пифагора  )
)
Перепишем формулы (3) и (4) с учетом этих соотношений:

Подставив значения  из условия задачи, найдем:
из условия задачи, найдем:

Упражнение 40
1. Груз перемещают с постоянной скоростью по горизонтальной поверхности двумя канатами, к которым прикладывают силы по 500 н. Канаты образуют между собой угол 60°. Определите равнодействующую силу. Как изменяется величина разнодействующей в зависимости от угла между канатами? Рассмотрите случаи, когда угол равен 0, 90, 120 и 180°.
2. На кронштейне подвешен фонарь массой 2 кг (рис. 160). Определите силы упругости, воаникающие в горизонтальной балке АВ и в укосине кронштейна ВС. Угол  равен 30°.
равен 30°.
3. Шар массой 3 кг висит на веревке, прикрепленной к гладкой стене (рис. 161). Определите силу натяжения веревки и силу давления шара на стену. Нить образует со стеной угол 15°,

Рис. 160

Рис. 161

Рис. 162
4. К середине троса длиной 20 м подвешен светильник массой  в следствие чего трос провис на 5 см. Определите силы упругости, возникшие в тросе.
в следствие чего трос провис на 5 см. Определите силы упругости, возникшие в тросе.
5. На наклонной плоскости лежит ящик массой 30 кг. Будет ли ящик соскальзывать вниз, если коэффициент трения ящика о наклонную плоскость равен 0,2? Длина наклонной плоскости 6 м, высота 2 м.
6. Антенная мачта (рис. 162) закреплена оттяжкой АВ, образующей угол 30° с мачтой. Сила, с которой антенна действует на мачту в точке В (натяжение антенны), равна 1000 н. Чему равна сила, сжимающая мачту, и сила, действующая на оттяжку?
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о движении
- § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА
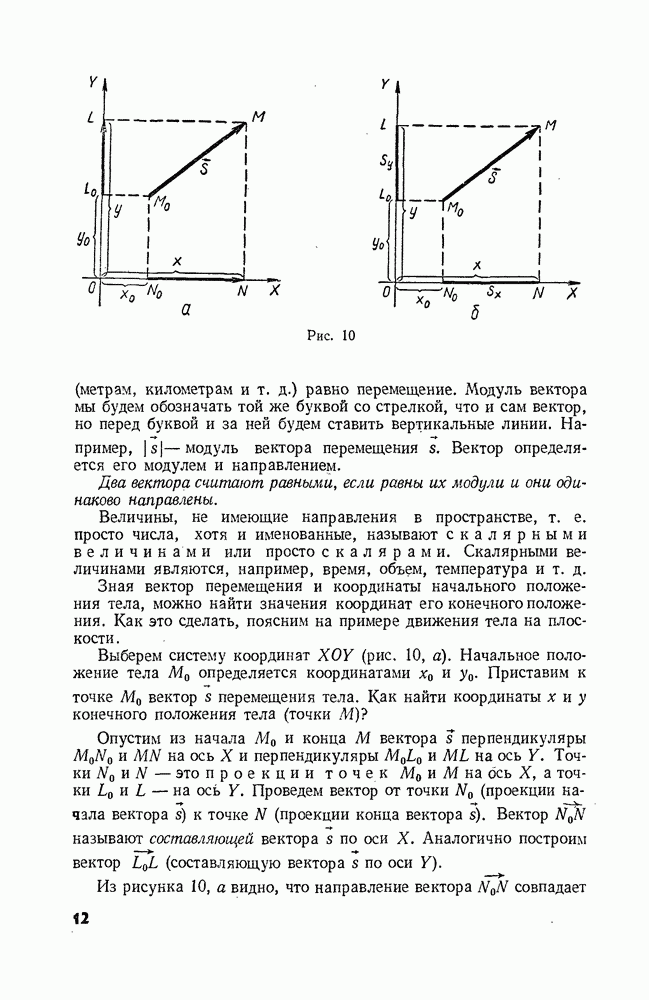
- § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ
- § 3. ПЕРЕМЕЩЕНИЕ
- § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА
- § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ
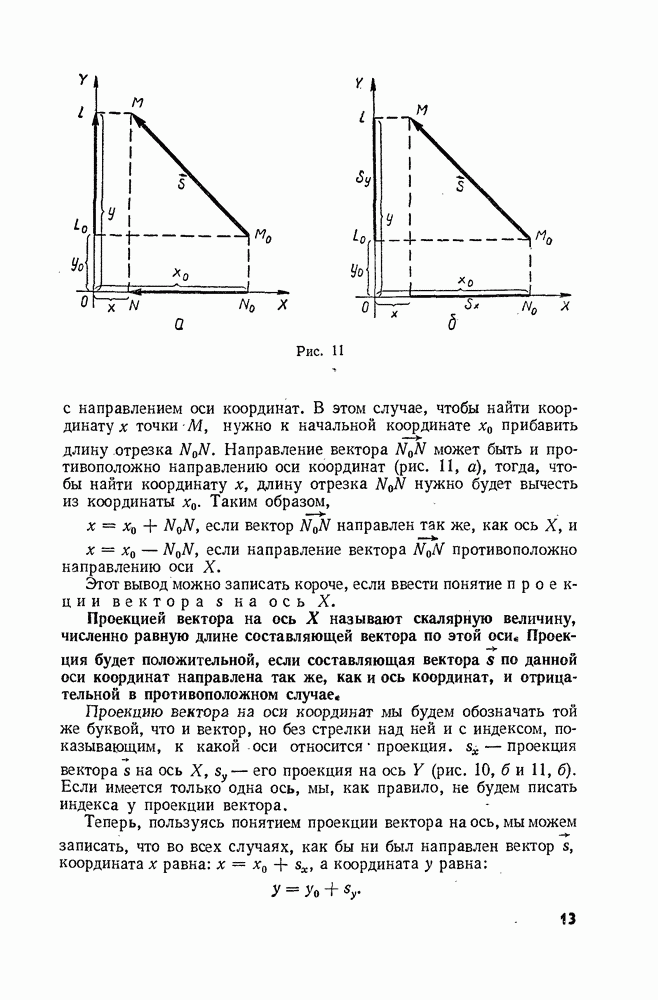
- § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ
- § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
- § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
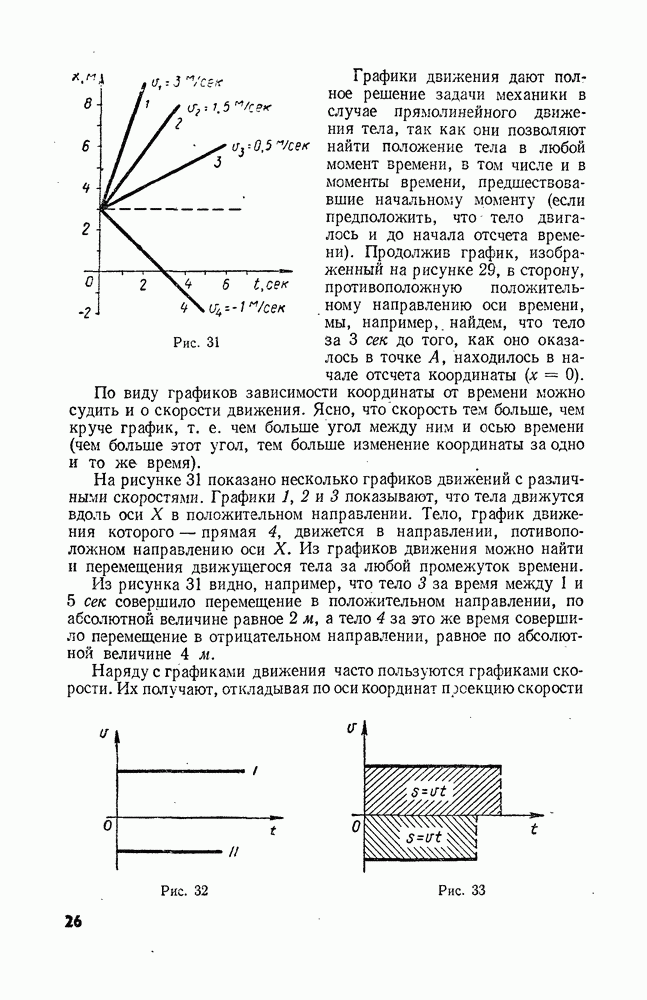
- § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ
- § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
- § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ)
- § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ
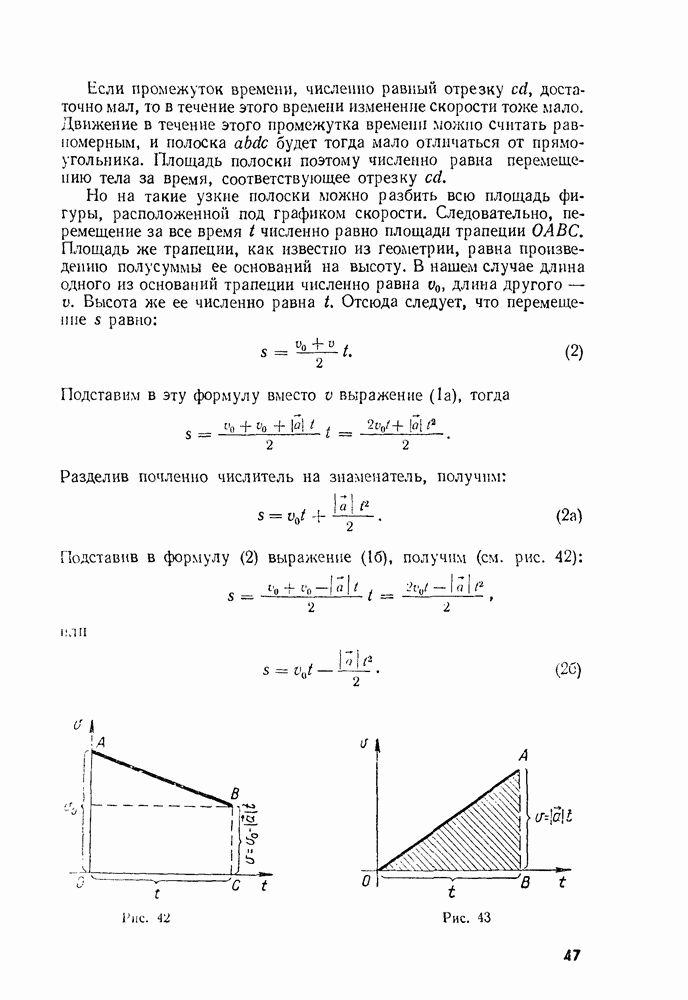
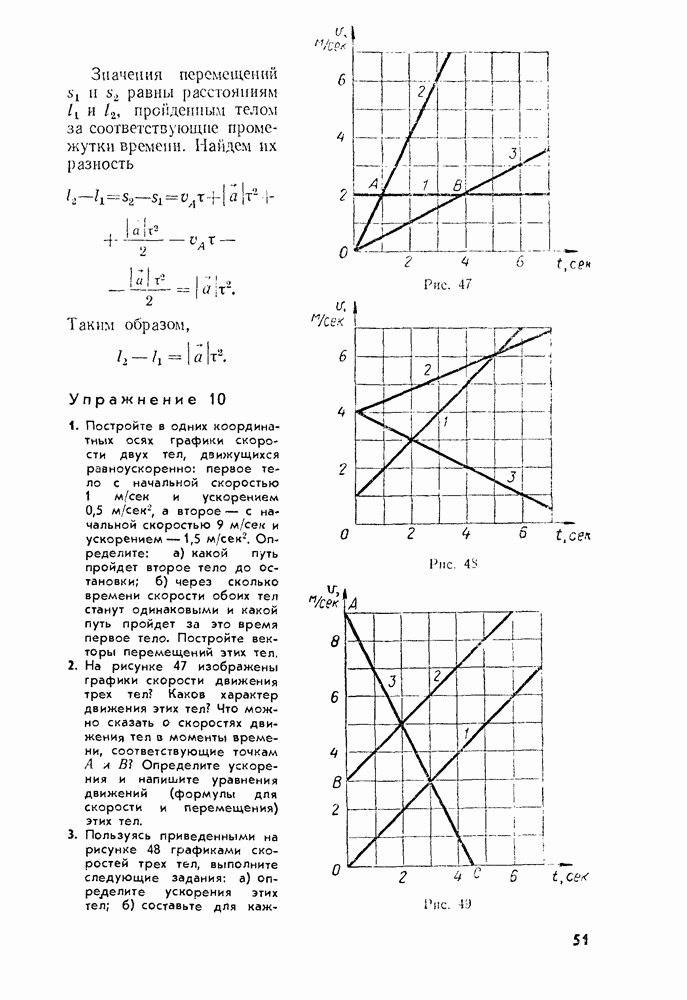
- Глава 2. Прямолинейное неравномерное движение
- § 13. СРЕДНЯЯ СКОРОСТЬ
- § 14. МГНОВЕННАЯ СКОРОСТЬ
- § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ
- § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
- § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ
- § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ
- § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
- § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
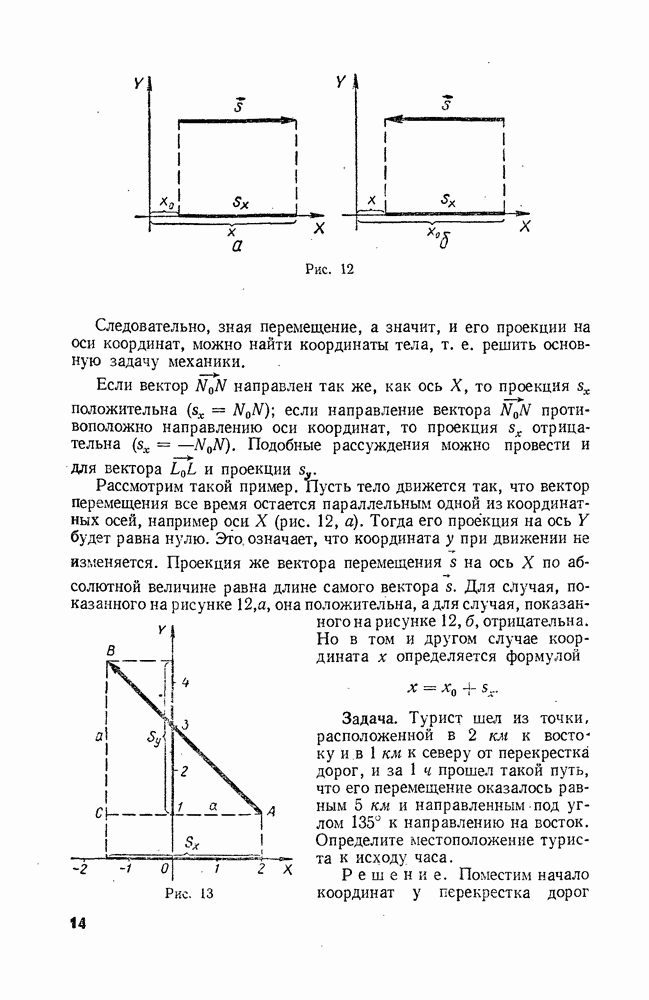
- Глава 3. Криволинейное движение
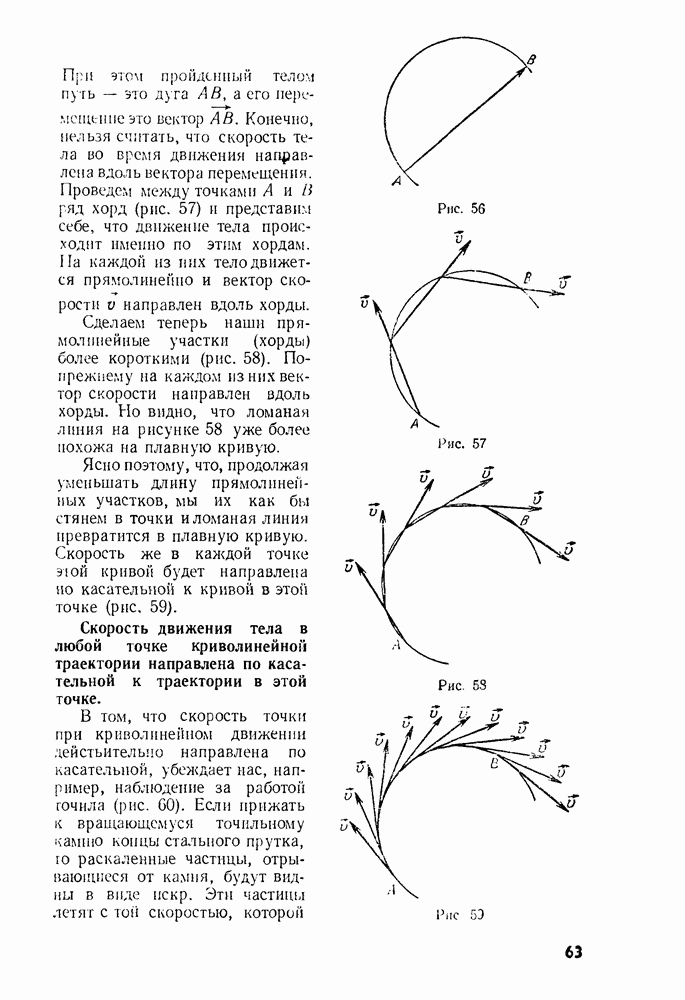
- § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
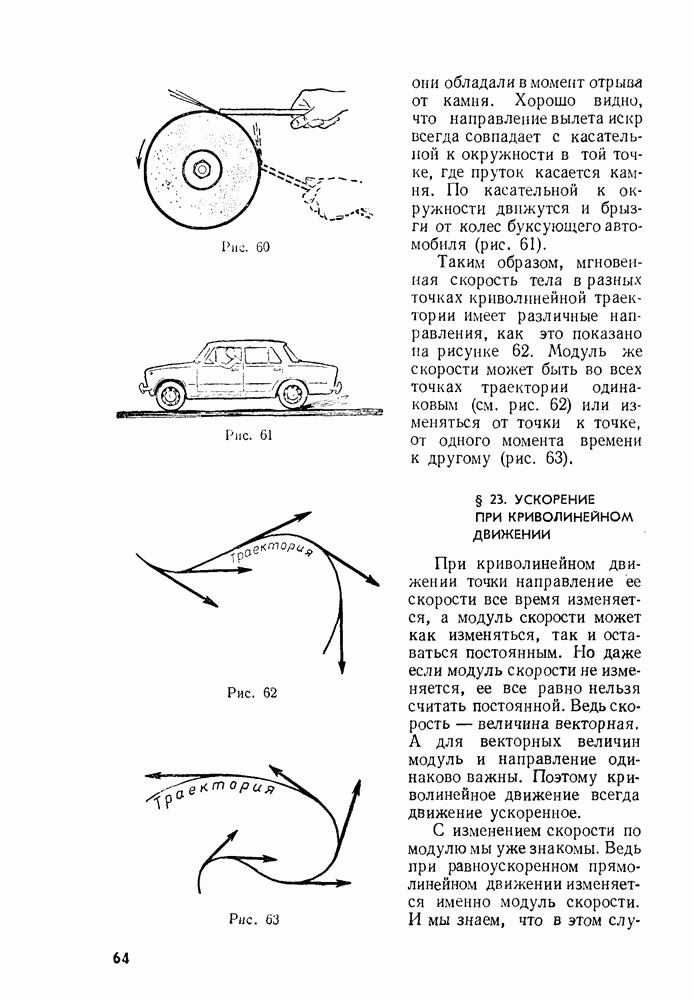
- § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
- § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ
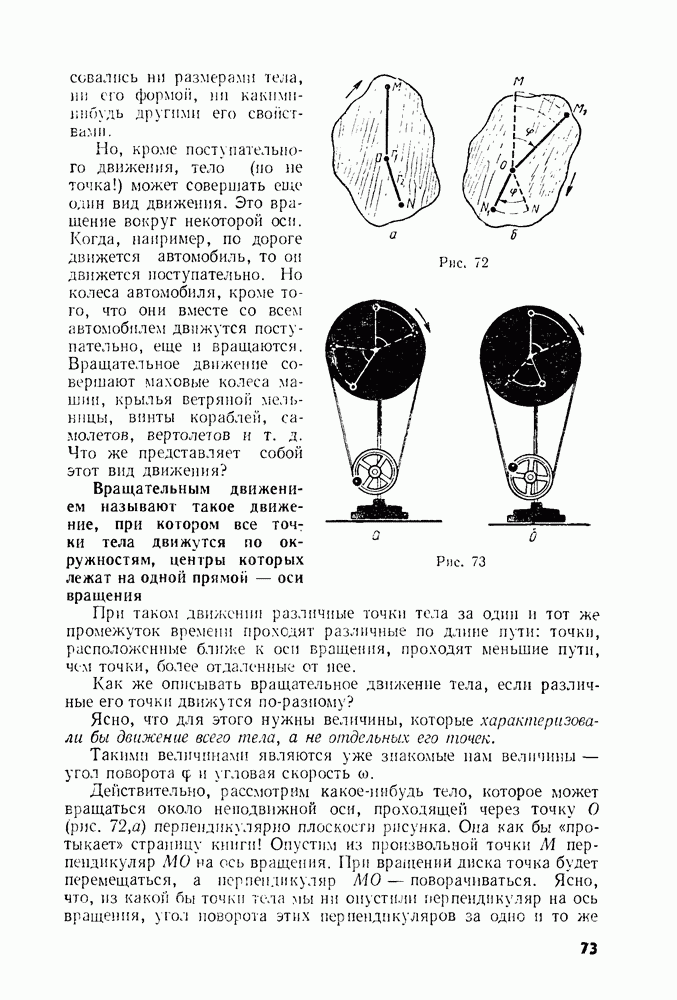
- § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА
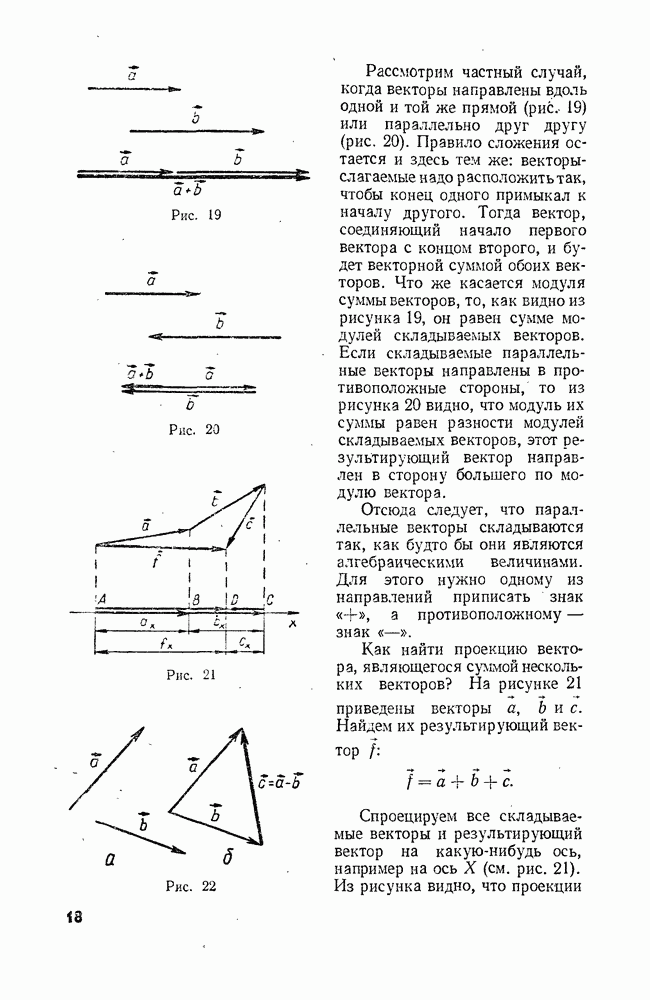
- Динамика
- Глава 4. Законы движения
- § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ
- § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ
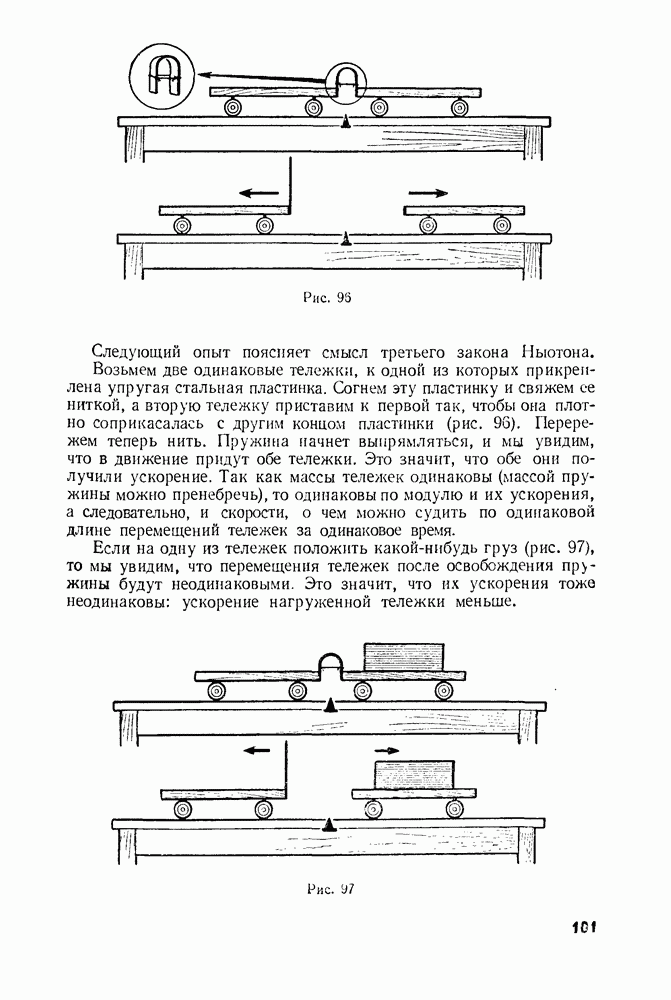
- § 31. ИНЕРТНОСТЬ ТЕЛ
- § 32. МАССА ТЕЛ
- § 33. МАССА ЛУНЫ
- § 34. СИЛА
- § 35. ВТОРОЙ ЗАКОН НЬЮТОНА
- § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение)
- § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР
- § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА
- § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА
- Глава 5. Силы природы
- § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ
- § 41. СИЛА УПРУГОСТИ
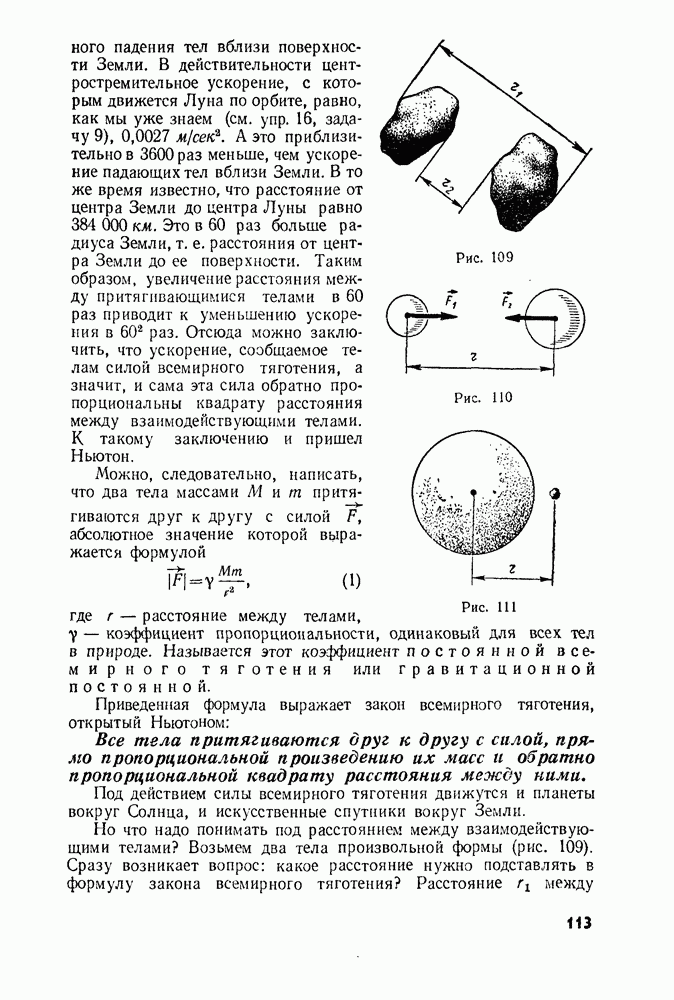
- § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 44. СИЛА ТЯЖЕСТИ
- § 45. ВЕС ТЕЛ
- § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ
- § 47. МАССА ЗЕМЛИ
- § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ
- § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ
- Глава 6. Применение законов движения
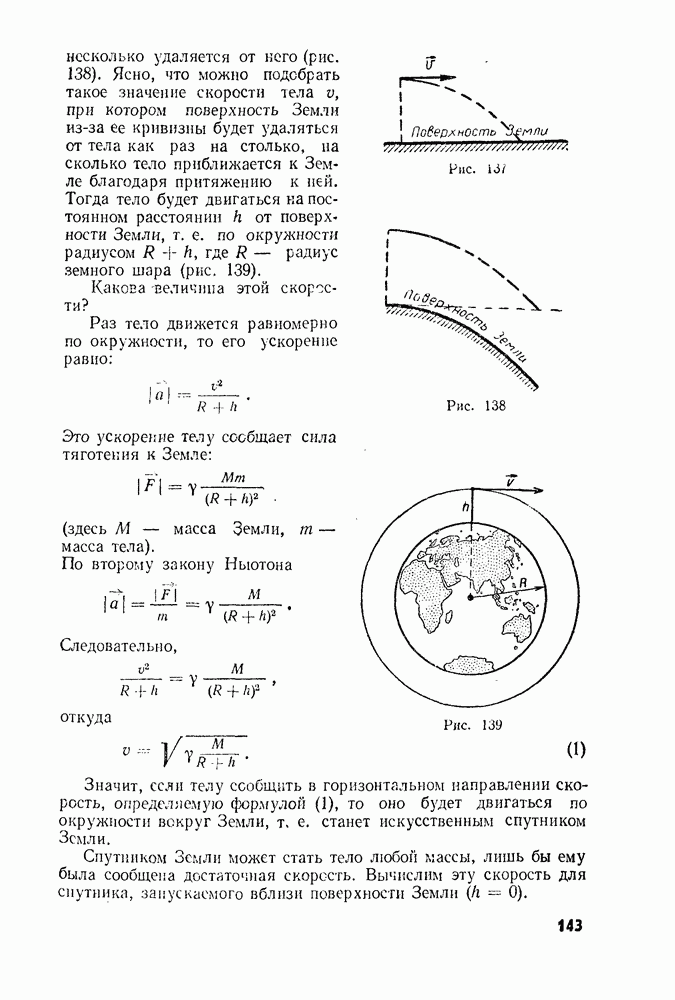
- § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ
- § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ
- § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ
- § 54. НЕВЕСОМОСТЬ
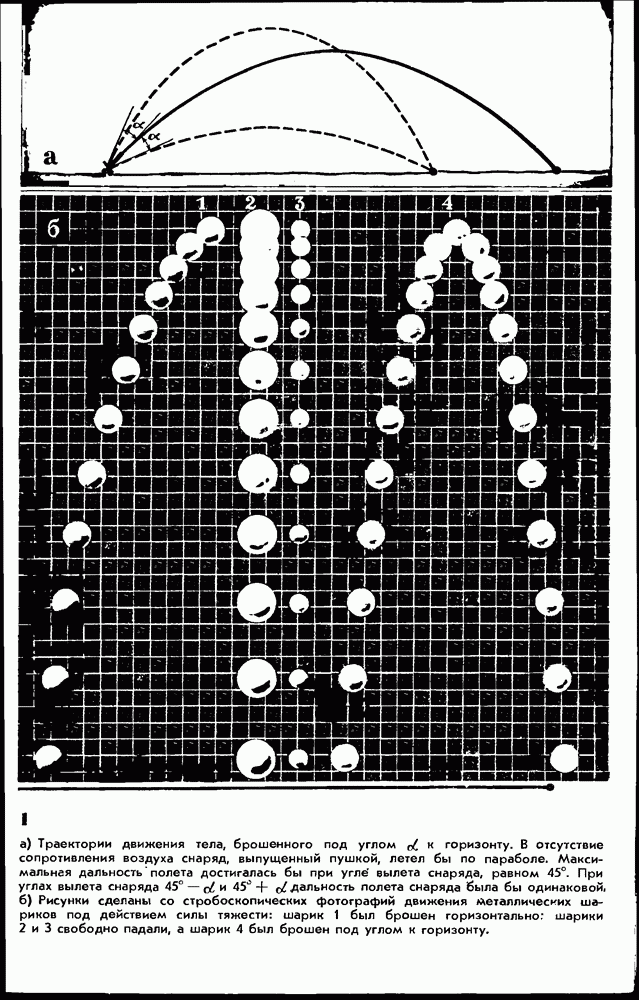
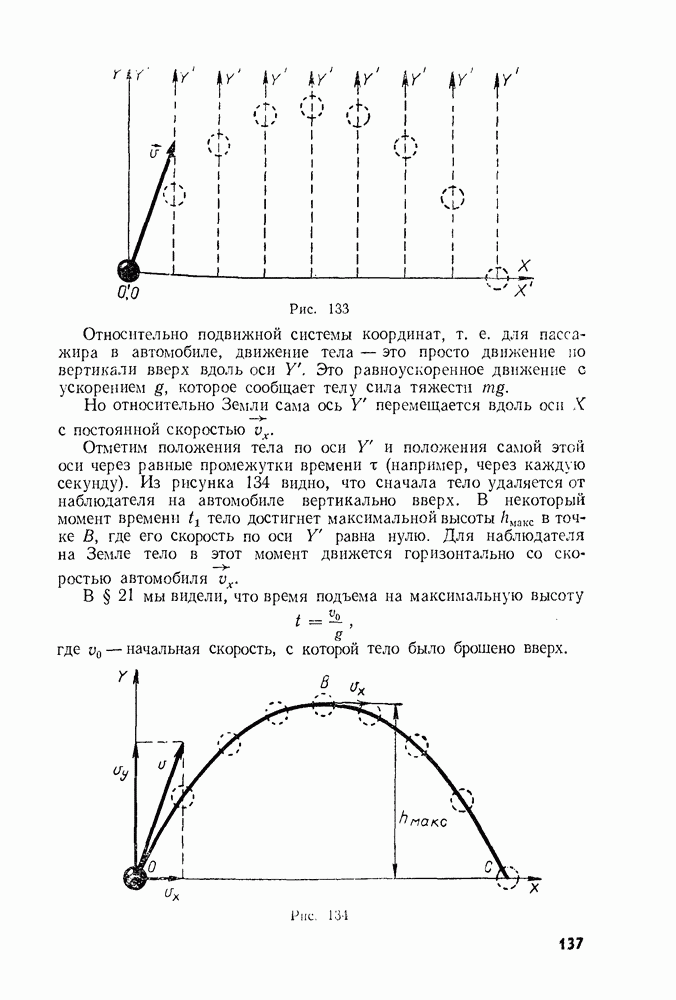
- § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ
- § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО
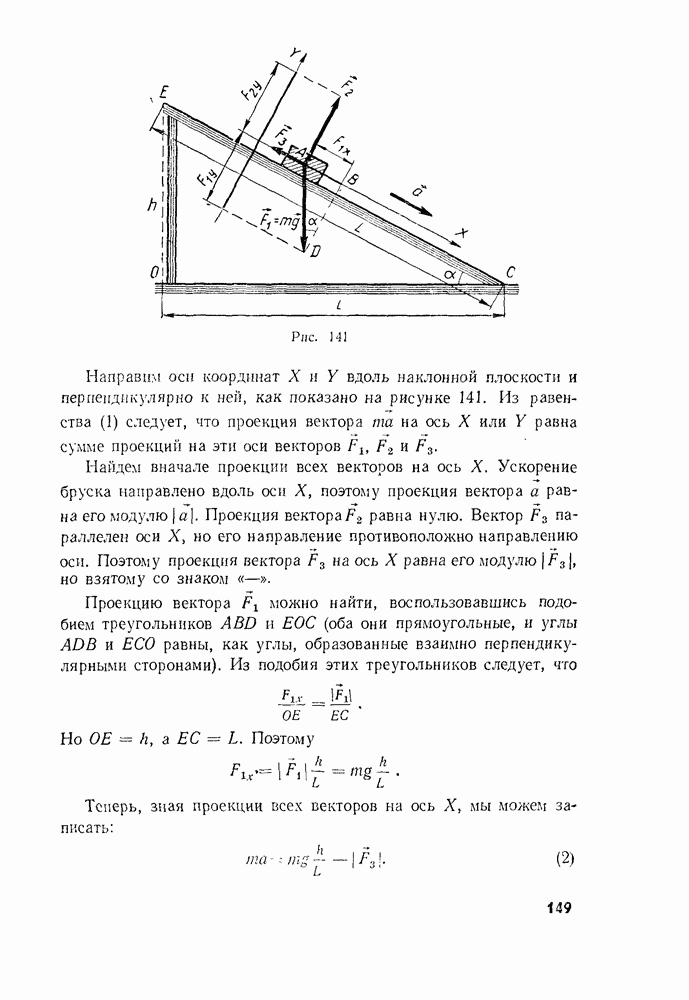
- § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ
- § 58. ДВИЖЕНИЕ ПЛАНЕТ
- § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ
- § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ
- § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ
- § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ
- § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ
- § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА
- Равновесие тел
- Глава 7. Элементы статики
- § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ
- § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ
- § 67. ПРАВИЛО МОМЕНТОВ
- § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ
- Законы сохранения в механике
- Глава 8. Закон сохранения импульса
- § 70. СИЛА И ИМПУЛЬС
- § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ
- Глава 9. Механическая работа и мощность
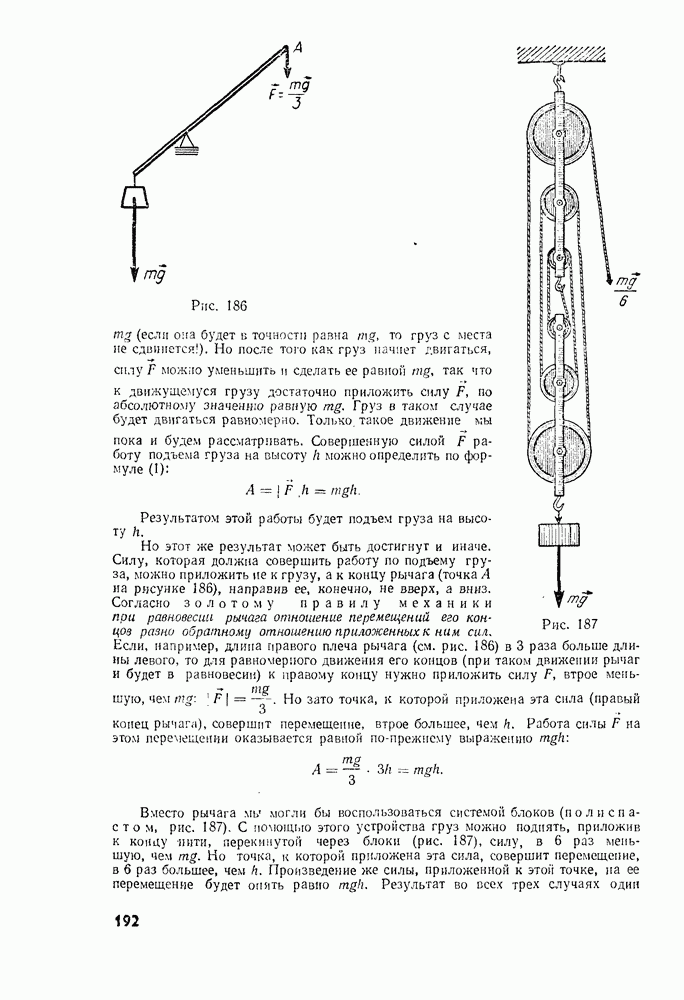
- § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ
- § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ
- § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
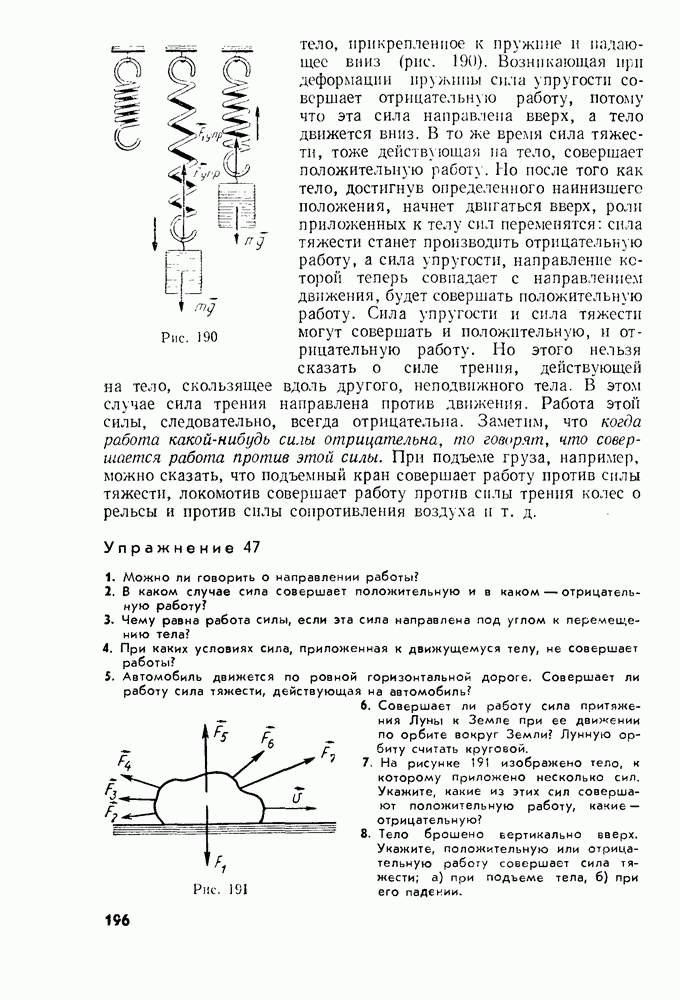
- § 77. РАБОТА СИЛЫ ТЯЖЕСТИ
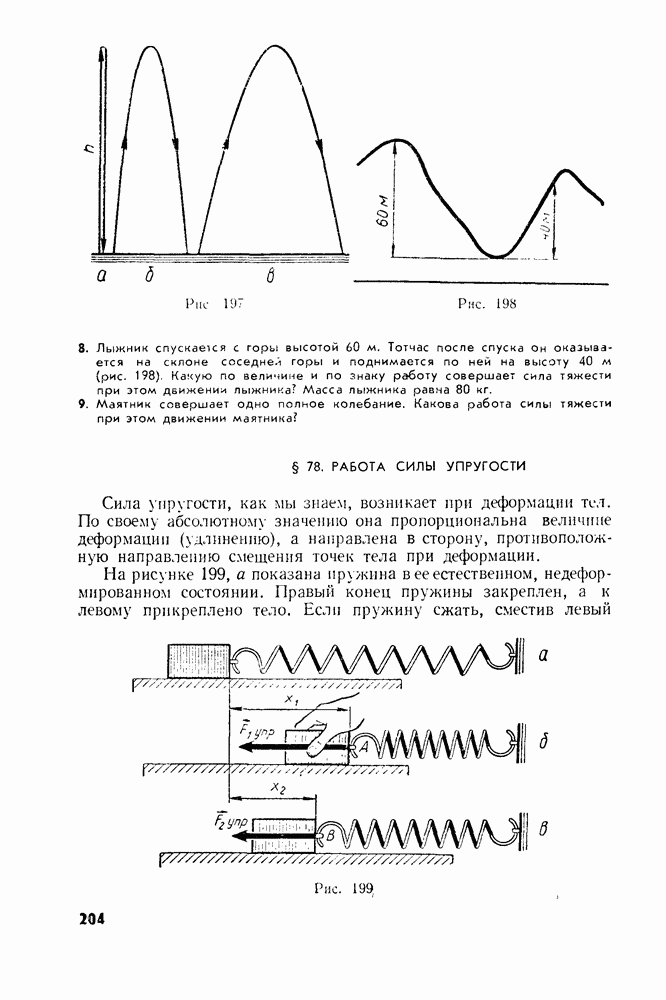
- § 78. РАБОТА СИЛЫ УПРУГОСТИ
- § 79. РАБОТА СИЛЫ ТРЕНИЯ
- § 80. МОЩНОСТЬ
- Глава 10. Закон сохранения энергии
- § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА
- § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ
- § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН
- § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
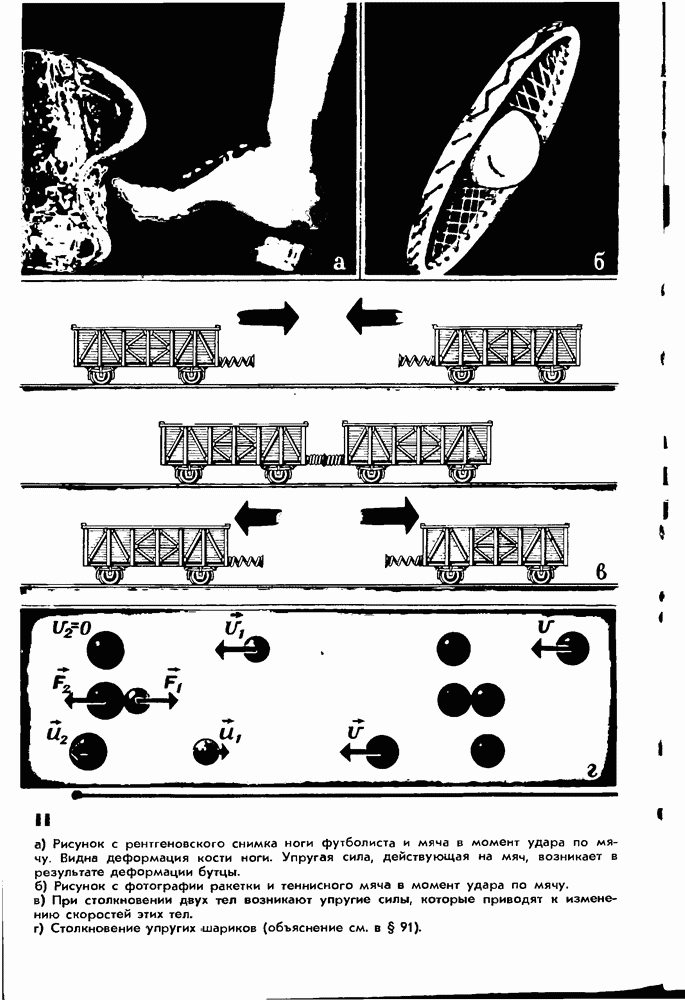
- § 91. СТОЛКНОВЕНИЕ ТЕЛ
- § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ
- § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ
- Заключение
- Лабораторные работы
- 1. Определение ускорения тела при равноускоренном движении
- 2. Определение коэффициента трения скольжения
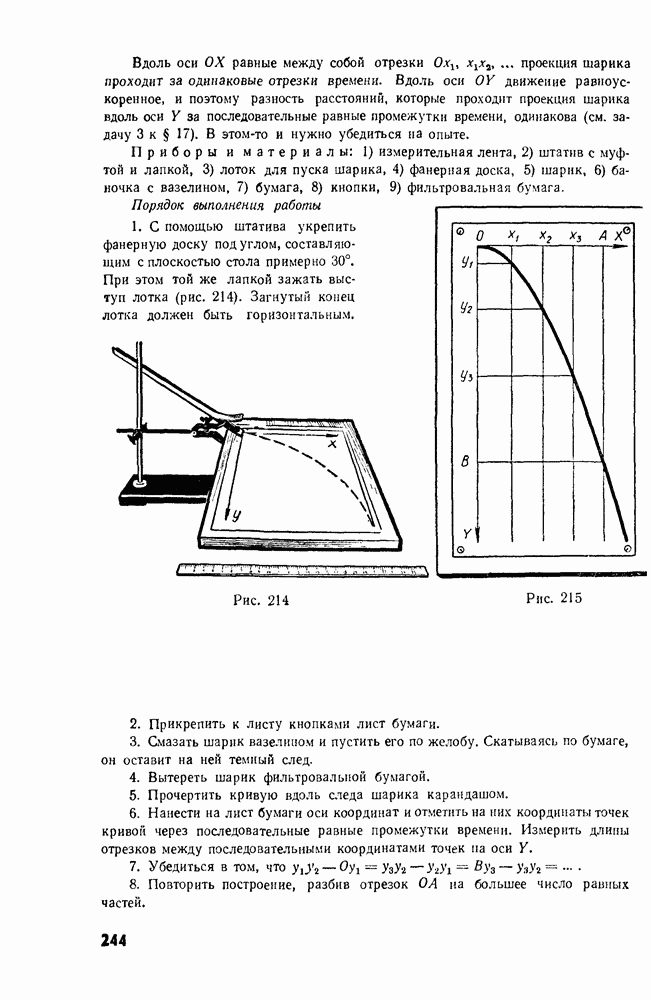
- 3. Изучение движения тела по параболе
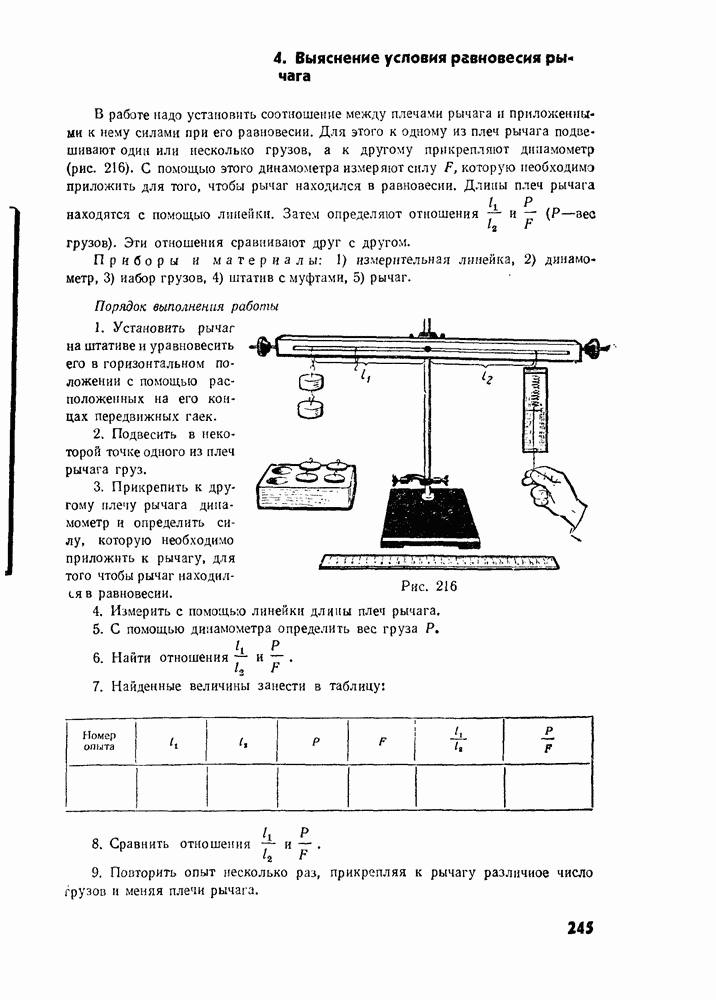
- 4. Выяснение условия равновесия рычага
- 5. Определение центра тяжести плоской пластины
- Ответы к упражнениям