| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 91. СТОЛКНОВЕНИЕ ТЕЛ
Закон сохранения энергии позволяет рецдать механические задачи в тех случаях, когда почему-либо неизвестны действующие на тело хилы. Интересным примером именно такого случая является столкновение двух тел. Этот пример особенно интересен тем, что при его анализе нельзя обойтись одним только законом сохранения энергии. Нужно привлечь еще и закон сохранения импульса (количества движения).
В обыденной жизни и в технике не так уж часто приходится иметь дело со столкновениями тел, но в физике атома и атомных частиц столкновения — очень частое явление.
Для простоты мы сначала рассмотрим столкновение двух шаров массами  из которых второй покоится, а первый движется по направлению ко второму со скоростью
из которых второй покоится, а первый движется по направлению ко второму со скоростью  Будем считать, что движение происходит вдоль линии, соединяющей центры обоих шаров (рис. 205), так что при столкновении шаров имеет место так называемый центральный, или лобовой, удар. Каковы скорости обоих шаров после столкновения?
Будем считать, что движение происходит вдоль линии, соединяющей центры обоих шаров (рис. 205), так что при столкновении шаров имеет место так называемый центральный, или лобовой, удар. Каковы скорости обоих шаров после столкновения?
До столкновения кинетическая энергия второго шара равна нулю, а первого  . Сумма энергий обоих шаров составляет:
. Сумма энергий обоих шаров составляет:


Рис. 205
После столкновения первый шар станет двигаться с некоторой скоростью  Второй шар, скорость которого была равна нулю, также получит какую-то скорость
Второй шар, скорость которого была равна нулю, также получит какую-то скорость  Поэтому после столкновения сумма кинетических энергий двух шаров станет равной
Поэтому после столкновения сумма кинетических энергий двух шаров станет равной

По закону сохранения энергии эта сумма должна быть равна энергии шаров до столкновения:

или

Из этого одного уравнения мы, конечно, не можем найти две неизвестные скорости:  Вот тут-то на помощь и приходит второй закон сохранения — закон сохранения импульса. До столкновения шаров импульс первого шара был равен а импульс второго — нулю. Полный импульс двух шаров был равен:
Вот тут-то на помощь и приходит второй закон сохранения — закон сохранения импульса. До столкновения шаров импульс первого шара был равен а импульс второго — нулю. Полный импульс двух шаров был равен:

После столкновения импульсы обоих шаров изменились и стали равными  а полный импульс стал
а полный импульс стал

По закону сохранения импульса полный импульс при столкновении измениться не может. Поэтому мы должны написать:

Так как движение происходит вдоль прямой, то вместо векторного уравнения можно написать алгебраическое (для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара):

Теперь мы имеем два уравнения:

Такую систему уравнений можно решить и найтн неизвестные скорости их и  шаров после столкновения. Для этого перепишем ее следующим образом:
шаров после столкновения. Для этого перепишем ее следующим образом:

или

Разделив первое уравнение на второе, получим:

Решая теперь это уравнение совместно со вторым уравнением

(проделайте это самостоятельно), найдем, что первый шар после удара будет двигаться со скоростью

а второй — со скоростью

Если оба шара имеют одинаковые массы  то
то  Это значит, что первый шар, столкнувшись со вторым, передал ему свою скорость, а сам остановился (рис. 206).
Это значит, что первый шар, столкнувшись со вторым, передал ему свою скорость, а сам остановился (рис. 206).
Таким образом, пользуясь законами сохранения энергии и импульса, можно, зная скорости тел до столкновения, определить их скорости после столкновения.
А как обстояло дело во время самого столкновения в тот момент, когда центры шаров максимально сблизились?
Очевидно, что в это время они двигались вместе с некоторой скоростью  . При одинаковых массах тел их общая масса равна 2т. По закону сохранения импульса во время совместного движения обоих шаров их импульс должен быть равен общему импульсу до столкновения:
. При одинаковых массах тел их общая масса равна 2т. По закону сохранения импульса во время совместного движения обоих шаров их импульс должен быть равен общему импульсу до столкновения:

Отсюда следует, что

Таким образом, скорость обоих шаров при их совместном движении равна половине

Рис. 206
скорости одного из них до столкновения. Найдем кинетическую энергию обоих шаров для этого момента:

А до столкновения общая энергия обоих шаров была равна

Следовательно, в самый момент столкновения шаров кинетическая энергия уменьшилась вдвое. Куда же пропала половина кинетической энергии? Не происходит ли здесь нарушения закона сохранения энергии?
Энергия, конечно, и во время совместного движения шаров осталась прежней. Дело в том, что во время столкновения оба шара были деформированы и поэтому обладали потенциальной энергией упругого взаимодействия. Именно на величину этой потенциальной энергии и уменьшилась кинетическая энергия шаров.
Задача 1. Шар, имеющий массу  равную 50 г, движется со скоростью
равную 50 г, движется со скоростью  и сталкивается с неподвижным шаром, масса которого
и сталкивается с неподвижным шаром, масса которого  Каковы скорости обоих шаров после столкновения? Столкновение шаров считать центральным.
Каковы скорости обоих шаров после столкновения? Столкновение шаров считать центральным.
Решение. Скорость второго шара вычисляется по формуле

Подставив значения  получим:
получим:

Значение же скорости их первого шара находим по формуле

Знак «минус» показывает, что после столкновения скорость этого шара изменится не только по абсолютному значению, но и по направлению (шар станет двигаться в противоположную сторону).
Задача 2. Шар массой  двигаясь со скоростью
двигаясь со скоростью  сталкивается с неподвижным шаром, масса которого
сталкивается с неподвижным шаром, масса которого  Каковы скорости
Каковы скорости  шаров после столкновения, если столкновение центральное?
шаров после столкновения, если столкновение центральное?
Решение. Скорость  второго шара после столкновения:
второго шара после столкновения:

Скорость  первого шара после столкновения:
первого шара после столкновения:

Теперь знак скорости  такой же, как знак скорости
такой же, как знак скорости  Оба шара, следовательно, после столкновения движутся по одному направлению — так, как двигался первый шар до столкновения.
Оба шара, следовательно, после столкновения движутся по одному направлению — так, как двигался первый шар до столкновения.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о движении
- § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА
- § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ
- § 3. ПЕРЕМЕЩЕНИЕ
- § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА
- § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ
- § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ
- § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
- § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
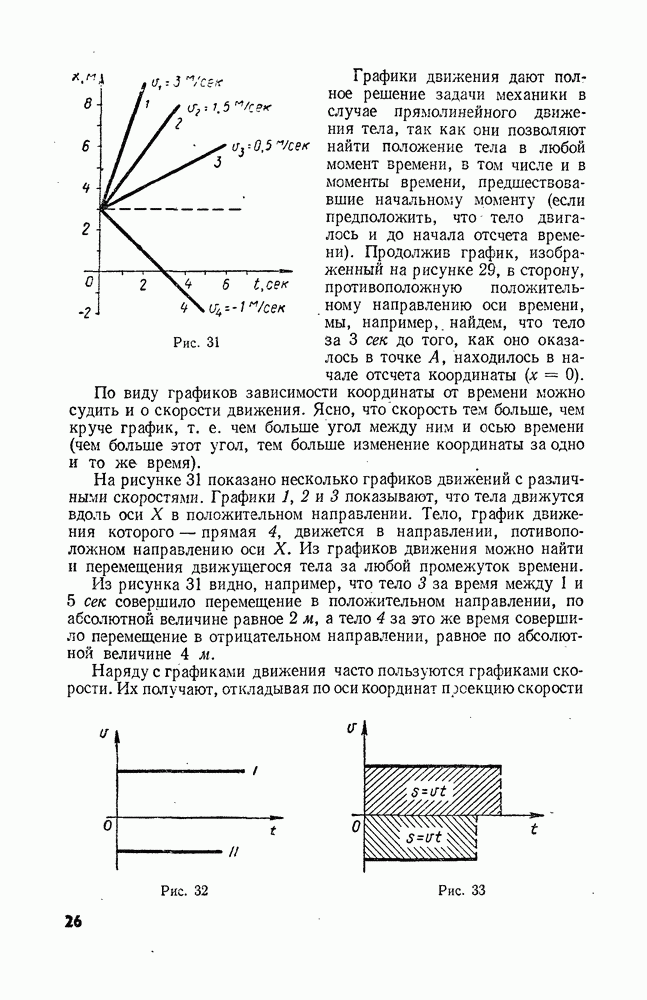
- § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ
- § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
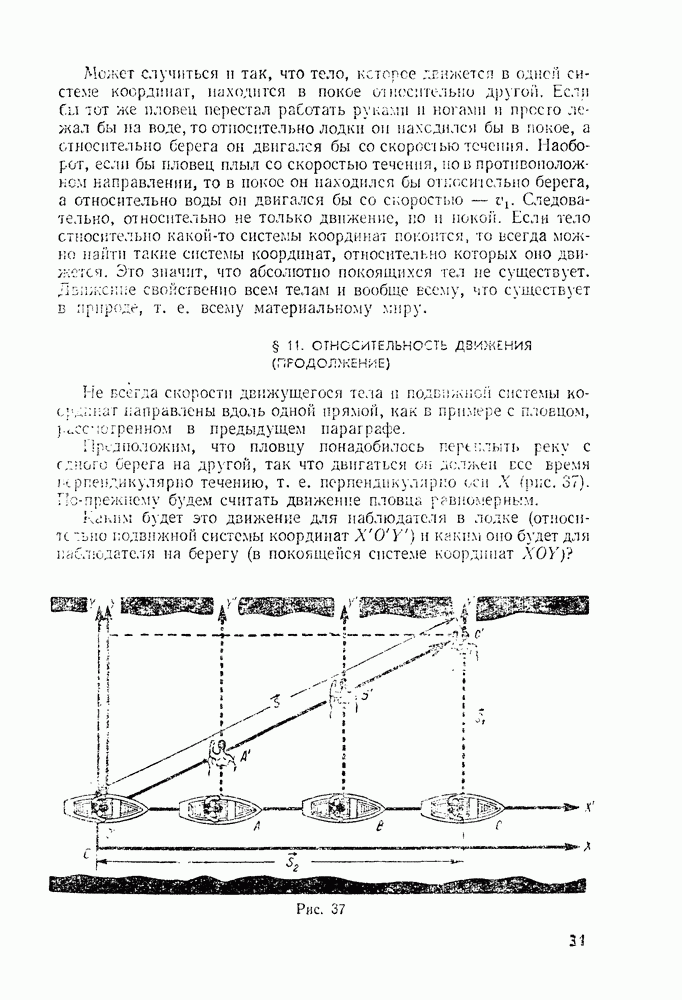
- § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ)
- § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ
- Глава 2. Прямолинейное неравномерное движение
- § 13. СРЕДНЯЯ СКОРОСТЬ
- § 14. МГНОВЕННАЯ СКОРОСТЬ
- § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ
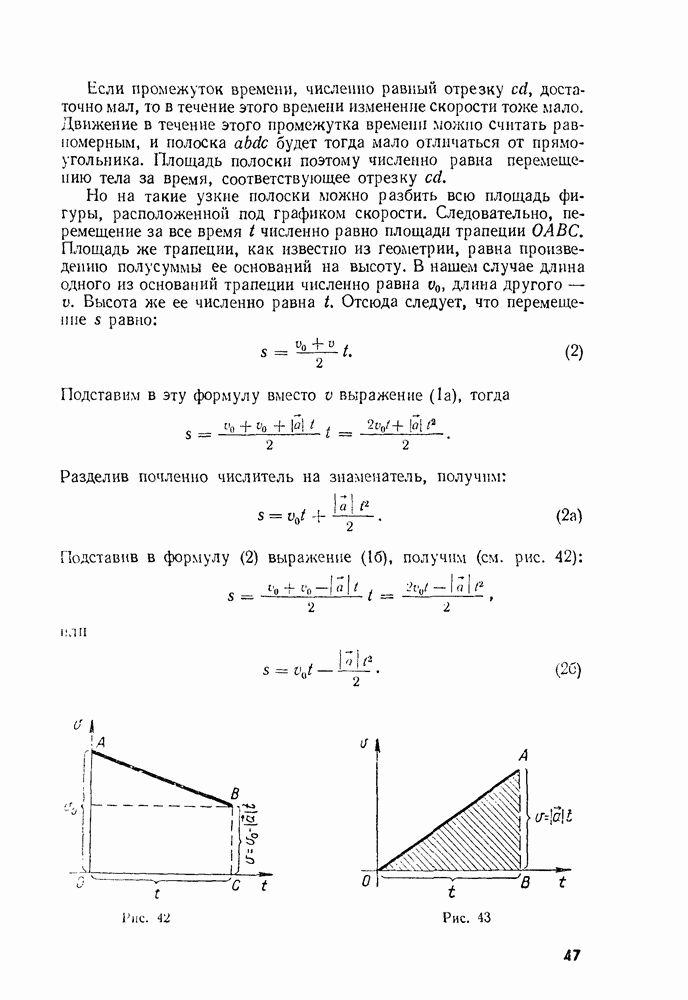
- § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
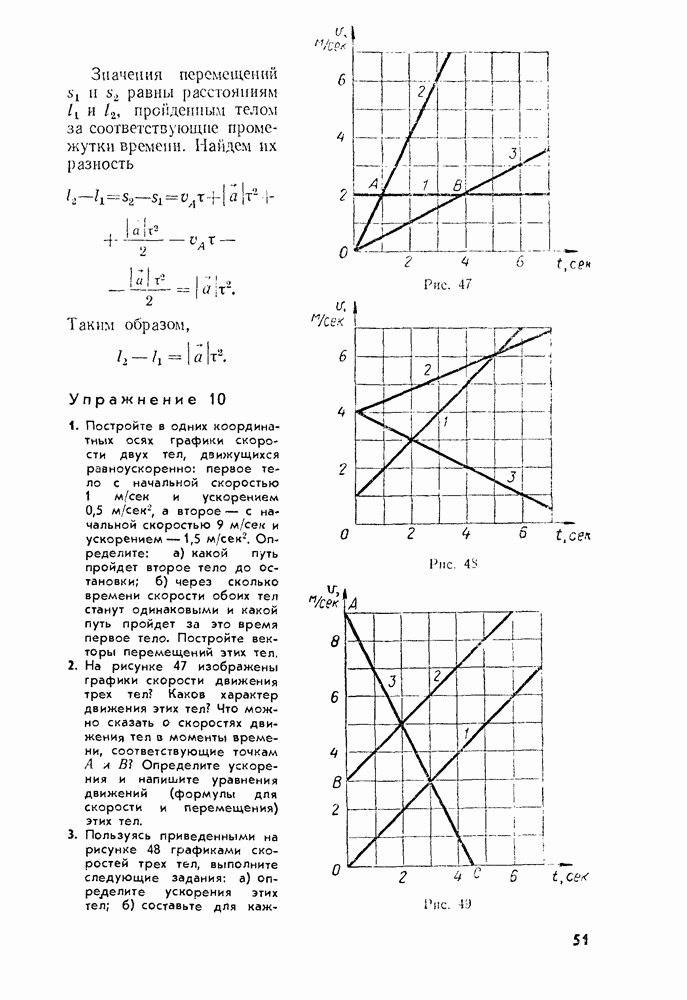
- § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ
- § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ
- § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
- § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
- Глава 3. Криволинейное движение
- § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
- § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ
- § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА
- Динамика
- Глава 4. Законы движения
- § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ
- § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ
- § 31. ИНЕРТНОСТЬ ТЕЛ
- § 32. МАССА ТЕЛ
- § 33. МАССА ЛУНЫ
- § 34. СИЛА
- § 35. ВТОРОЙ ЗАКОН НЬЮТОНА
- § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение)
- § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР
- § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА
- § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА
- Глава 5. Силы природы
- § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ
- § 41. СИЛА УПРУГОСТИ
- § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 44. СИЛА ТЯЖЕСТИ
- § 45. ВЕС ТЕЛ
- § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ
- § 47. МАССА ЗЕМЛИ
- § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ
- § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ
- Глава 6. Применение законов движения
- § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ
- § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ
- § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ
- § 54. НЕВЕСОМОСТЬ
- § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ
- § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО
- § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ
- § 58. ДВИЖЕНИЕ ПЛАНЕТ
- § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ
- § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ
- § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ
- § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ
- § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ
- § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА
- Равновесие тел
- Глава 7. Элементы статики
- § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ
- § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ
- § 67. ПРАВИЛО МОМЕНТОВ
- § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ
- Законы сохранения в механике
- Глава 8. Закон сохранения импульса
- § 70. СИЛА И ИМПУЛЬС
- § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ
- Глава 9. Механическая работа и мощность
- § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ
- § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ
- § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
- § 77. РАБОТА СИЛЫ ТЯЖЕСТИ
- § 78. РАБОТА СИЛЫ УПРУГОСТИ
- § 79. РАБОТА СИЛЫ ТРЕНИЯ
- § 80. МОЩНОСТЬ
- Глава 10. Закон сохранения энергии
- § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА
- § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ
- § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН
- § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
- § 91. СТОЛКНОВЕНИЕ ТЕЛ
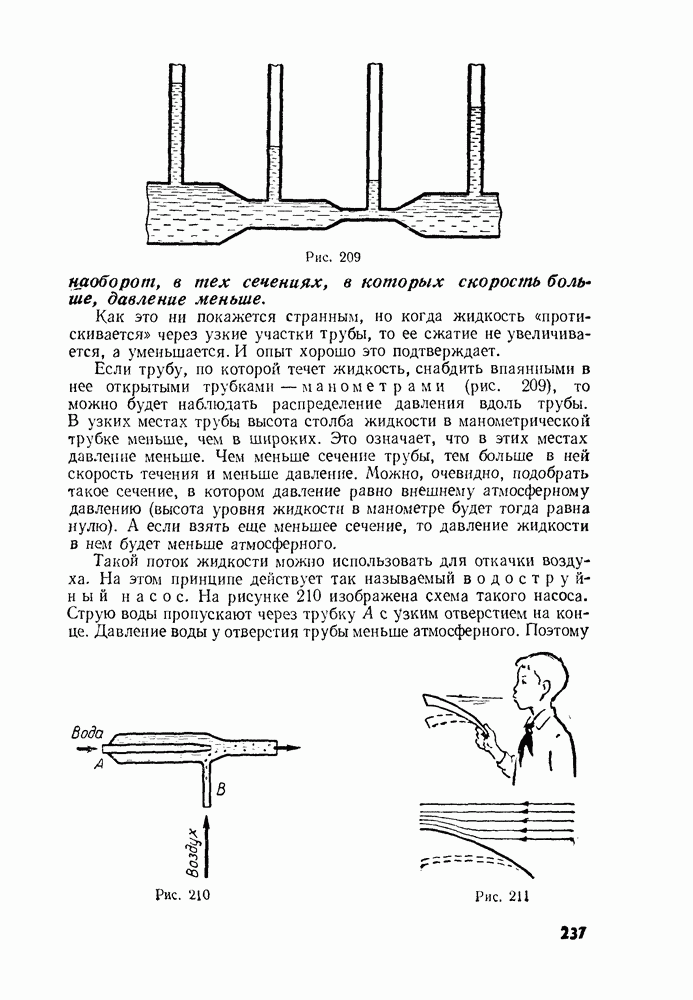
- § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ
- § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ
- Заключение
- Лабораторные работы
- 1. Определение ускорения тела при равноускоренном движении
- 2. Определение коэффициента трения скольжения
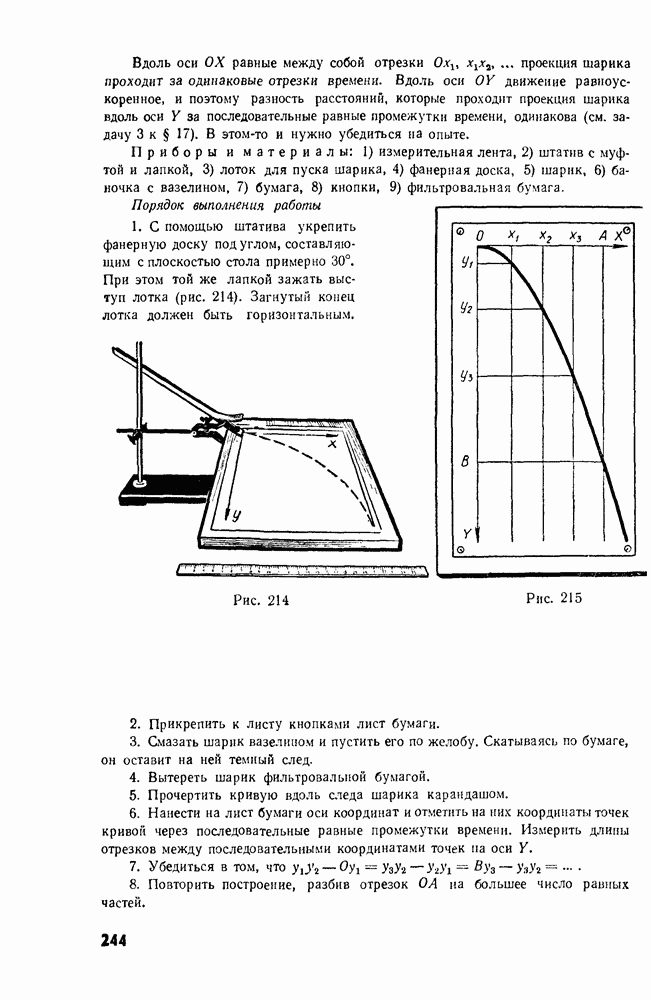
- 3. Изучение движения тела по параболе
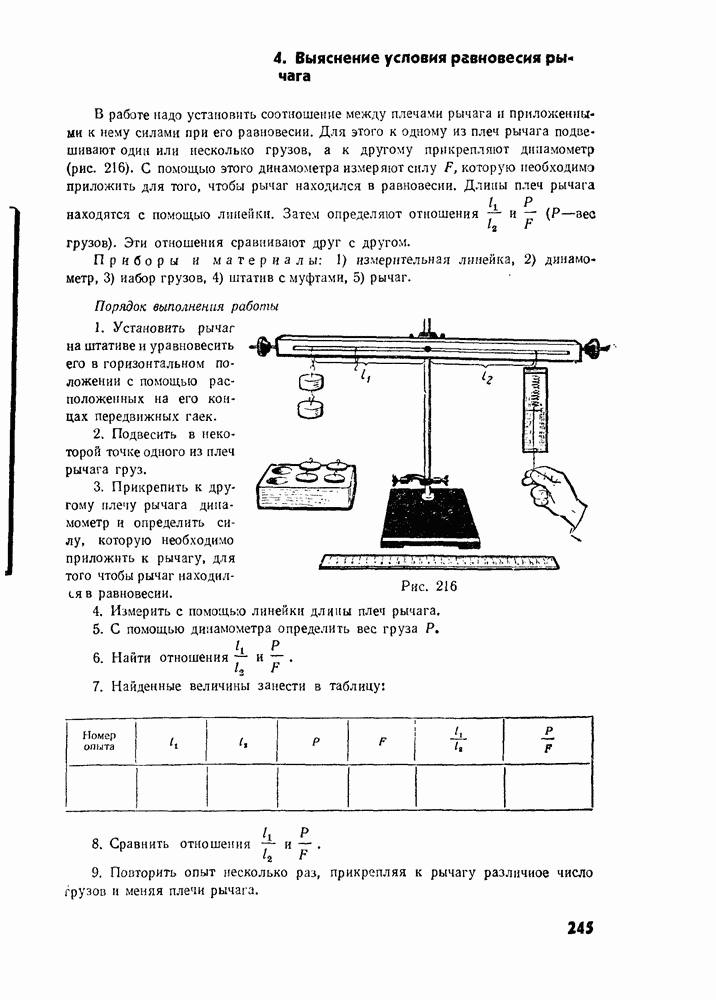
- 4. Выяснение условия равновесия рычага
- 5. Определение центра тяжести плоской пластины
- Ответы к упражнениям