| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ
В предыдущем параграфе были выяснены условия равновесия тела при отсутствии вращения. Но как обеспечивается отсутствие вращения тела, т. е. его равновесие, когда на него действуют силы?
Чтобы ответить на этот вопрос, рассмотрим тело, которое не может совершать поступательного движения, но может поворачиваться или вращаться. Чтобы сделать невозможным поступательное движение тела, его достаточно закрепить в одной точке так, как можно, например, закрепить доску на стене, прибив ее одним гвоздем; поступательное движение такой «пригвожденной» доски становится невозможным, но доска может поворачиваться вокруг гвоздя, который служит ей осью поворота.
Выясним, при каких условиях покоящееся тело с закрепленной осью не будет поворачиваться под действием приложенных к нему сил. Представим себе некоторое тело, к которому в разных точках приложены две силы:  (рис. 163, а). Чтобы найти равнодействующую этих сил, перенесем точки их приложения в точку А (рис. 163, б), в которой пересекаются линии действия обеих сил. Построив параллелограмм на силах
(рис. 163, а). Чтобы найти равнодействующую этих сил, перенесем точки их приложения в точку А (рис. 163, б), в которой пересекаются линии действия обеих сил. Построив параллелограмм на силах  получим их равнодействующую
получим их равнодействующую 
Теперь предположим, что в какой-то точке О на линии, вдоль которой направлена равнодействующая  проходит закрепленная ось, перпендикулярная плоскости чертежа. Мы можем себе, например, представить, что в точке О сквозь тело проходит гвоздь, вбитый в неподвижную стену. Тело в этом случае будет находиться в покое, потому что равнодействующая
проходит закрепленная ось, перпендикулярная плоскости чертежа. Мы можем себе, например, представить, что в точке О сквозь тело проходит гвоздь, вбитый в неподвижную стену. Тело в этом случае будет находиться в покое, потому что равнодействующая  уравновешивается силой реакции (упругости) со стороны закрепленной оси (гвоздя): обе они направлены вдоль одной и той же прямой, равны по абсолютной величине и противоположны по направлению.
уравновешивается силой реакции (упругости) со стороны закрепленной оси (гвоздя): обе они направлены вдоль одной и той же прямой, равны по абсолютной величине и противоположны по направлению.
Предположим теперь, что одна из сил, например  перестала действовать, так что тело подвергается действию только одной силы
перестала действовать, так что тело подвергается действию только одной силы  (рис. 163, в). Из рисунка видно, что эта сила заставит тело вращаться вокруг оси О по часовой стрелке. Если, наоборот, устранить
(рис. 163, в). Из рисунка видно, что эта сила заставит тело вращаться вокруг оси О по часовой стрелке. Если, наоборот, устранить

Рис. 163
силу  то оставшаяся сила
то оставшаяся сила  вызовет вращение против часовой стрелки (рис. 163, г). Значит, каждая из сил
вызовет вращение против часовой стрелки (рис. 163, г). Значит, каждая из сил  обладает вращающим действием, причем эти действия характеризуются противоположными направлениями. Но когда обе силы действуют совместно, их вращающие действия взаимно друг друга компенсируют: вместе они поворота не вызывают. Поэтому следует считать, что, хотя силы
обладает вращающим действием, причем эти действия характеризуются противоположными направлениями. Но когда обе силы действуют совместно, их вращающие действия взаимно друг друга компенсируют: вместе они поворота не вызывают. Поэтому следует считать, что, хотя силы  сами по себе различны как по величине, так и по направлению, их вращающие действия одинаковы, но противоположны по направлению.
сами по себе различны как по величине, так и по направлению, их вращающие действия одинаковы, но противоположны по направлению.
Попытаемся найти величину, которая характеризует вращающее действие силы. Мы пока знаем только, что она должна иметь одинаковые численные значения для обеих сил: 
Обратимся к рисунку  Силы
Силы  неодинаковы по абсолютным значениям:
неодинаковы по абсолютным значениям:  больше
больше  Зато расстояние
Зато расстояние  от точки О (оси) до линии действия силы
от точки О (оси) до линии действия силы  меньше расстояния
меньше расстояния  от оси до линии действия силы
от оси до линии действия силы  Таким образом,
Таким образом,  но
но 
Быть может, равны между собой произведения 
Если это так, то можно будет сказать, что величина, равная произведению силы на длину перпендикуляра, опущенного с закрепленной оси на линию действия силы, как раз и характеризует вращающее действие силы.
Нетрудно доказать, что равенство

действительно выполняется. Для этого проведем на рисунке 163, д вспомогательные прямые ОС и ОВ, параллельные силам  подобия треугольников АВО и
подобия треугольников АВО и  следует, что
следует, что

Отсюда, учитывая, что АВ = ОС, получаем:

Рассмотрим теперь треугольники ОВК и  Эти треугольники подобны, как прямоугольные с равными углами при вершинах С и В (они дополняют равные углы АСО и АВО до 180°). Из их подобия следует, что
Эти треугольники подобны, как прямоугольные с равными углами при вершинах С и В (они дополняют равные углы АСО и АВО до 180°). Из их подобия следует, что

Сравнивая пропорции (1) и (2), получаем:

или

Сделанное выше предположение оправдалось.
Приведенное довольно длинное геометрическое рассуждение позволило нам найти величину, которая одинакова для обеих сил и характеризует вращающее действие силы. Такой величиной является произведение силы на расстояние от линии ее. действия до оси вращения. Величина эта носит несколько странное название — момент силы или вращающий момент относительно оси, проходящей через точку О.
Если обозначить момент силы  буквой М, а расстояние от оси вращения до линии ее действия буквой
буквой М, а расстояние от оси вращения до линии ее действия буквой  то можно написать:
то можно написать:

Заметим, что величина  тоже имеет особое название. Ее называют плечом силы.
тоже имеет особое название. Ее называют плечом силы.
Для новой величины — момента силы — нужно, конечно, найти единицу измерения. Из выражения

видно, что момент силы М равен единице, если и сила  равна единице, и плечо
равна единице, и плечо  равно единице. Значит, за единицу вращающего момента в системе СИ нужно принять момент силы в 1 н, линия действия которой отстоит от оси вращения на 1 м. Эту единицу называют ньютон-метром
равно единице. Значит, за единицу вращающего момента в системе СИ нужно принять момент силы в 1 н, линия действия которой отстоит от оси вращения на 1 м. Эту единицу называют ньютон-метром 

Из курса физики VI класса известно, что в ньютон-метрах выражают работу. Работу, равную  называют джоулем.
называют джоулем.
Момент силы, следовательно, измеряется в таких же единицах, как и работа, но единицу момента силы не принято называть джоулем, с тем чтобы отличать момент силы от работы силы.
В системе СГС единицей момента силы является дина-сантиметр (дин  )
)

| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о движении
- § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА
- § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ
- § 3. ПЕРЕМЕЩЕНИЕ
- § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА
- § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ
- § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ
- § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
- § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
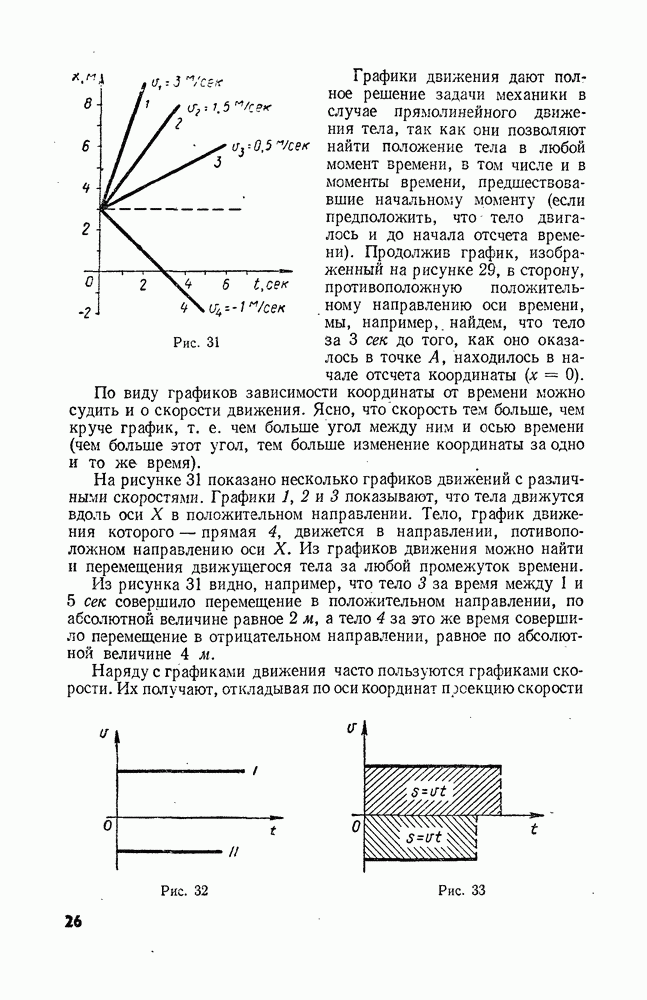
- § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ
- § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
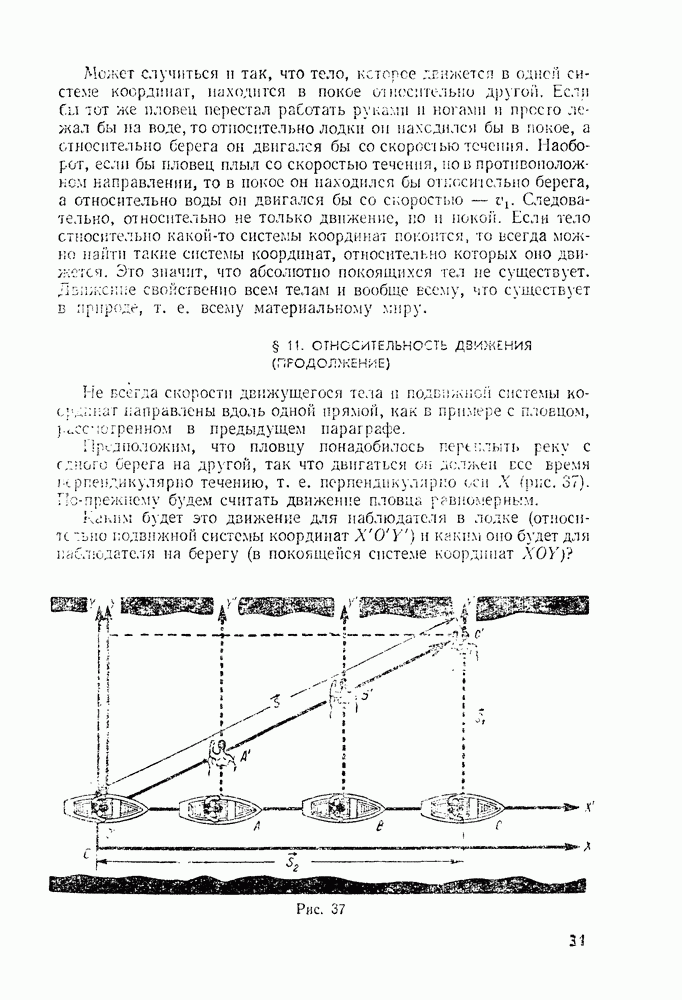
- § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ)
- § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ
- Глава 2. Прямолинейное неравномерное движение
- § 13. СРЕДНЯЯ СКОРОСТЬ
- § 14. МГНОВЕННАЯ СКОРОСТЬ
- § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ
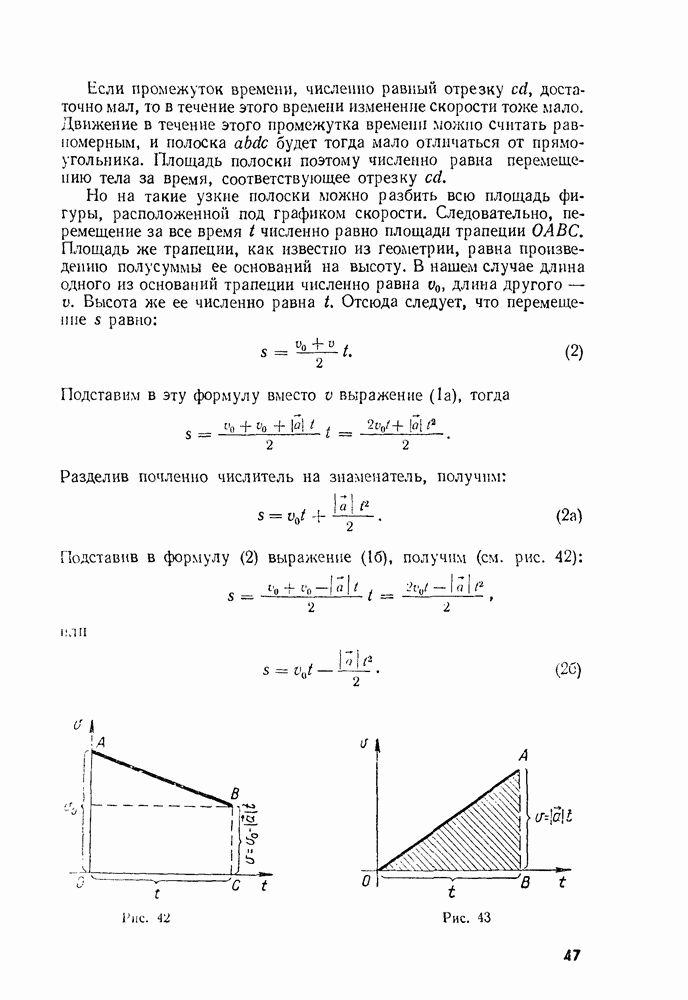
- § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
- § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ
- § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ
- § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
- § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
- Глава 3. Криволинейное движение
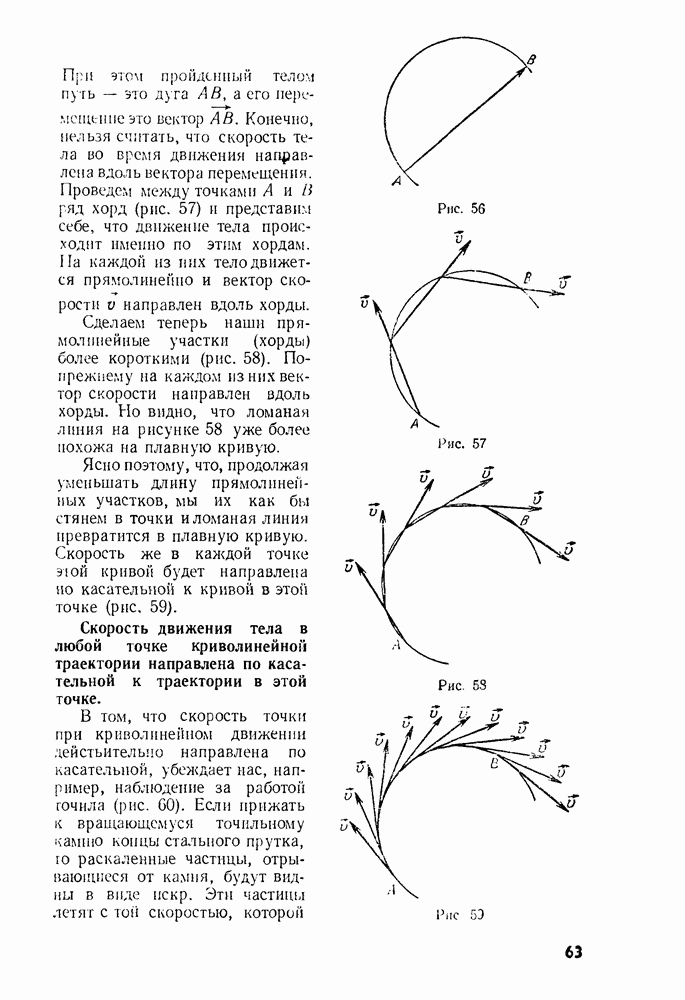
- § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
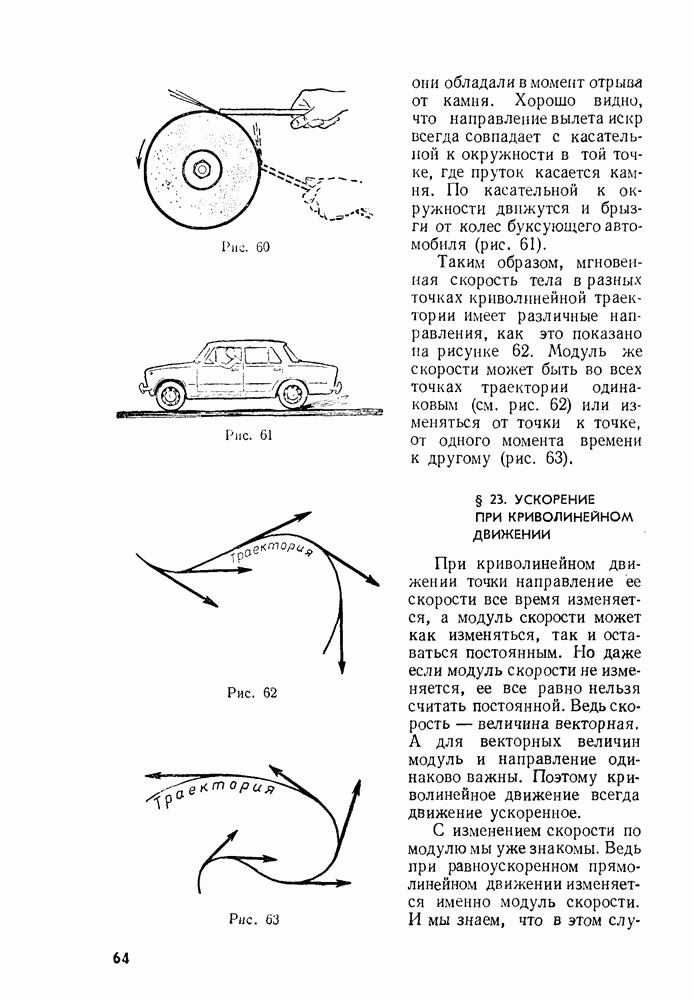
- § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
- § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ
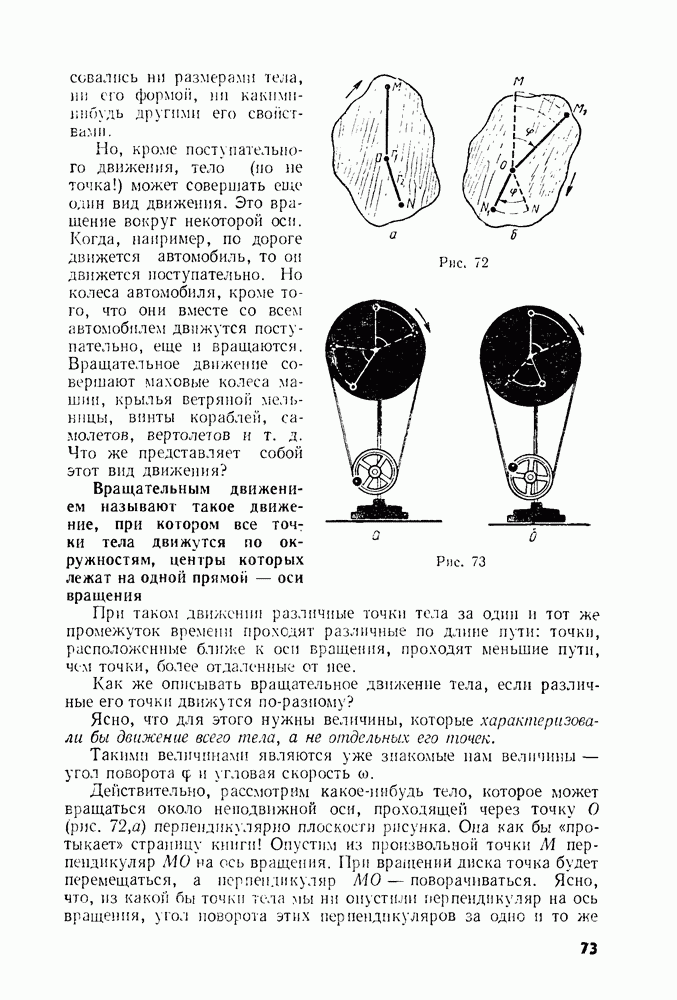
- § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА
- Динамика
- Глава 4. Законы движения
- § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ
- § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ
- § 31. ИНЕРТНОСТЬ ТЕЛ
- § 32. МАССА ТЕЛ
- § 33. МАССА ЛУНЫ
- § 34. СИЛА
- § 35. ВТОРОЙ ЗАКОН НЬЮТОНА
- § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение)
- § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР
- § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА
- § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА
- Глава 5. Силы природы
- § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ
- § 41. СИЛА УПРУГОСТИ
- § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 44. СИЛА ТЯЖЕСТИ
- § 45. ВЕС ТЕЛ
- § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ
- § 47. МАССА ЗЕМЛИ
- § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ
- § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ
- Глава 6. Применение законов движения
- § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ
- § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ
- § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ
- § 54. НЕВЕСОМОСТЬ
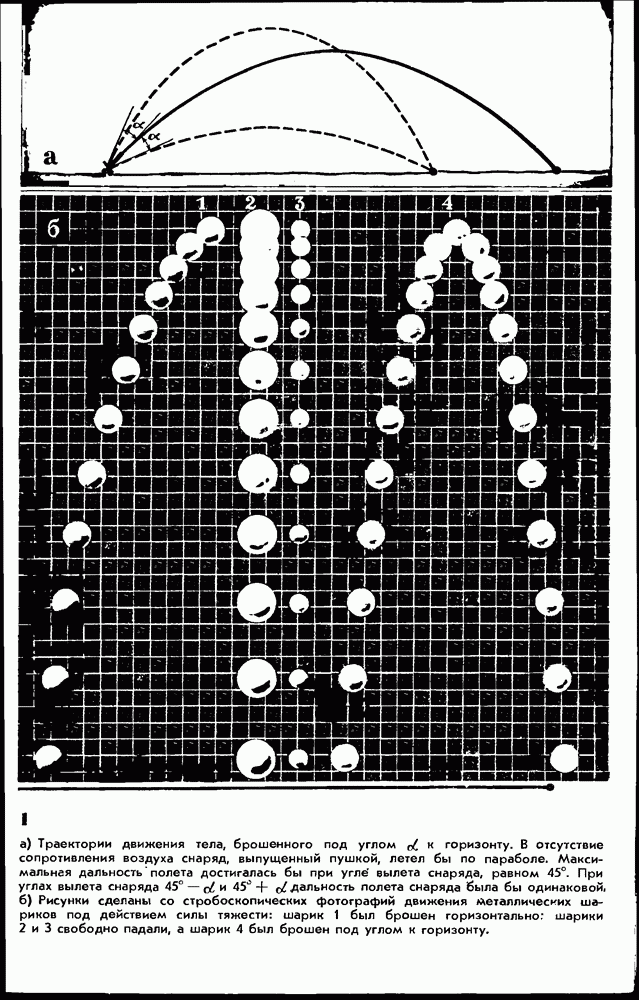
- § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ
- § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО
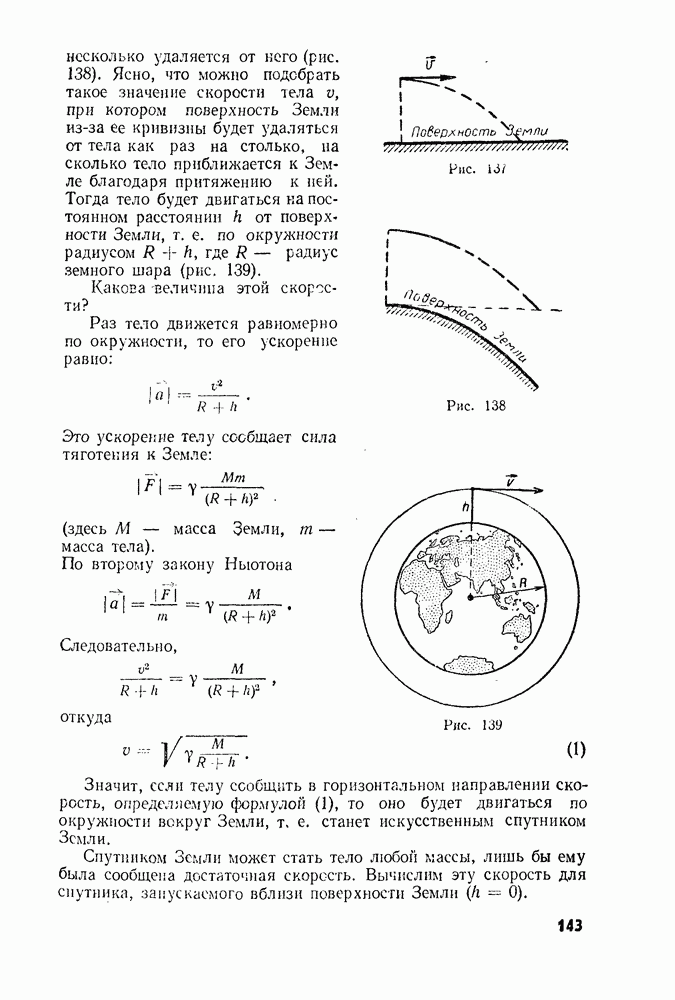
- § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ
- § 58. ДВИЖЕНИЕ ПЛАНЕТ
- § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ
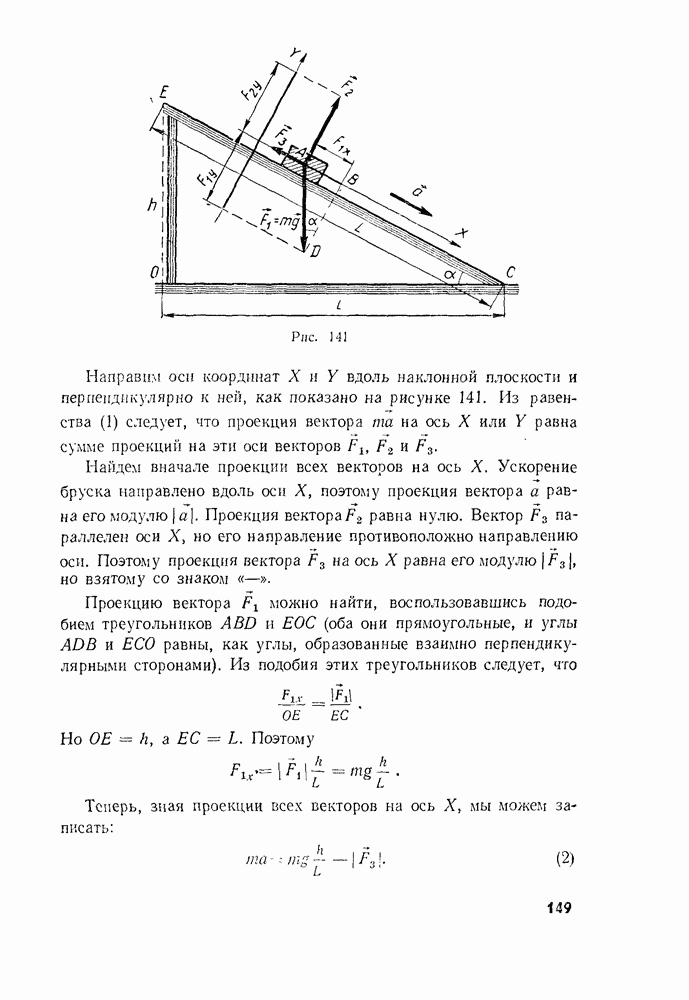
- § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ
- § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ
- § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ
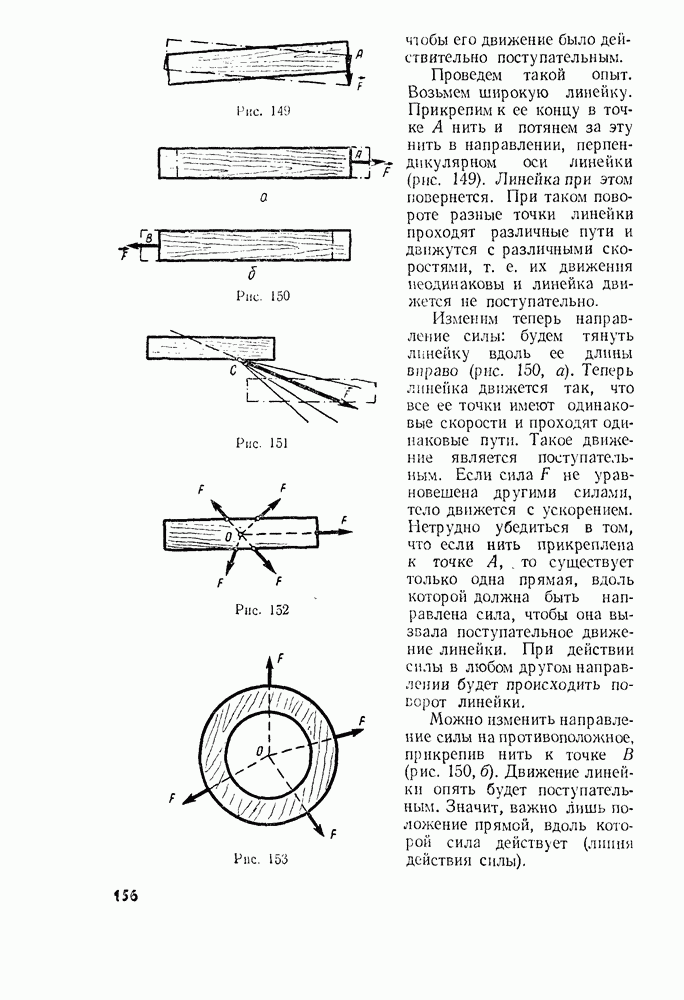
- § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ
- § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА
- Равновесие тел
- Глава 7. Элементы статики
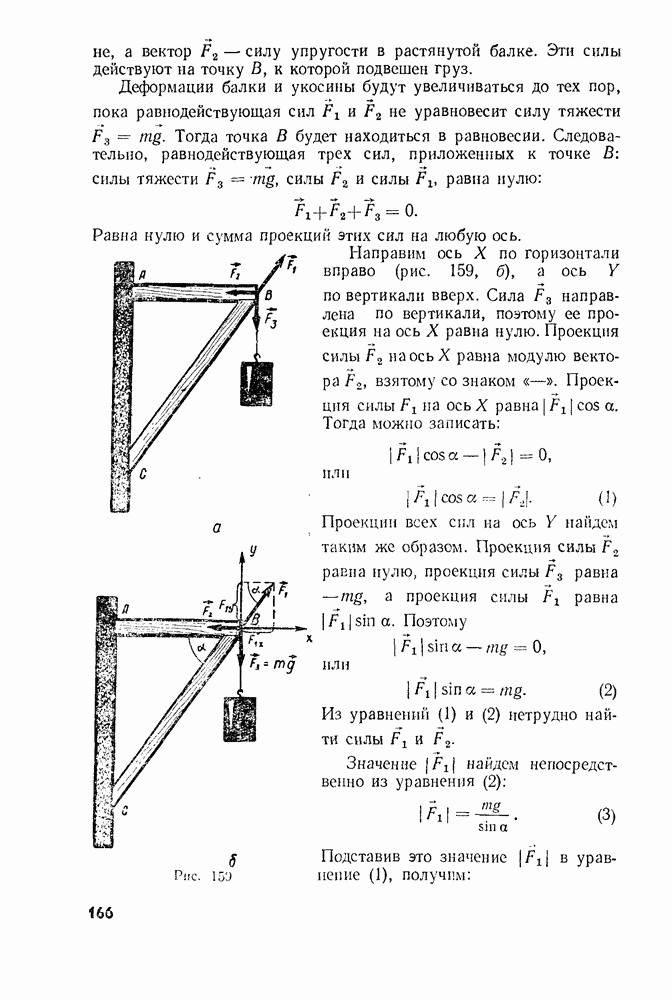
- § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ
- § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ
- § 67. ПРАВИЛО МОМЕНТОВ
- § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ
- Законы сохранения в механике
- Глава 8. Закон сохранения импульса
- § 70. СИЛА И ИМПУЛЬС
- § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ
- Глава 9. Механическая работа и мощность
- § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ
- § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ
- § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
- § 77. РАБОТА СИЛЫ ТЯЖЕСТИ
- § 78. РАБОТА СИЛЫ УПРУГОСТИ
- § 79. РАБОТА СИЛЫ ТРЕНИЯ
- § 80. МОЩНОСТЬ
- Глава 10. Закон сохранения энергии
- § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА
- § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ
- § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН
- § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
- § 91. СТОЛКНОВЕНИЕ ТЕЛ
- § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ
- § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ
- Заключение
- Лабораторные работы
- 1. Определение ускорения тела при равноускоренном движении
- 2. Определение коэффициента трения скольжения
- 3. Изучение движения тела по параболе
- 4. Выяснение условия равновесия рычага
- 5. Определение центра тяжести плоской пластины
- Ответы к упражнениям