| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
Импульсу присуще очень интересное и важное свойство, которым обладают весьма немногие физические величины. Это — свойство сохранения. В чем оно заключается?
Допустим, что два взаимодействующих друг с другом тела, массы которых  движутся относительно какой-то системы отсчета. Обозначим через
движутся относительно какой-то системы отсчета. Обозначим через  их скорости в какой-то момент времени. В результате взаимодействия скорости тел через некоторое время
их скорости в какой-то момент времени. В результате взаимодействия скорости тел через некоторое время  изменятся и станут равными
изменятся и станут равными  Это означает, что на тела при их взаимодействии действовали соответственно силы
Это означает, что на тела при их взаимодействии действовали соответственно силы  равные:
равные:

и

Согласно третьему закону Ньютона силы  равны по абсолютной величине и противоположны по направлению, т. е.
равны по абсолютной величине и противоположны по направлению, т. е.

Следовательно,

или

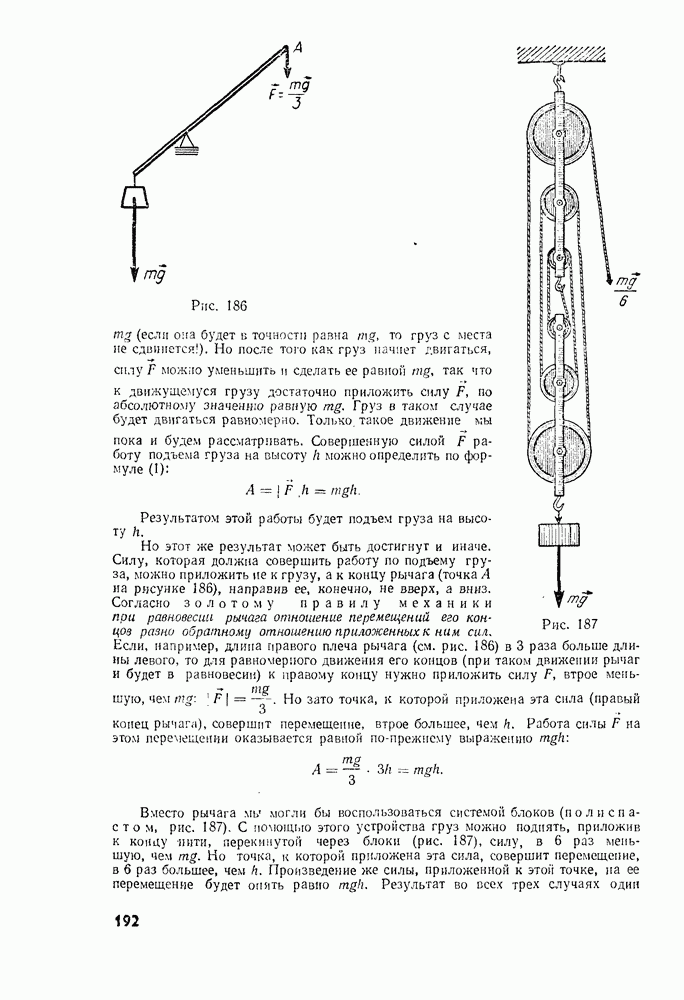
Перепишем последнюю формулу в виде

В левой части этого равенства стоит сумма начальных импульсов двух тел, а в правой — сумма импульсов тех же тел через время  Эти суммы равны между собой. Таким образом, хотя импульс каждого из тел при взаимодействии изменяется, их полный импульс, т. е. сумма импульсов
Эти суммы равны между собой. Таким образом, хотя импульс каждого из тел при взаимодействии изменяется, их полный импульс, т. е. сумма импульсов  тел, остается при этом неизменным. Это и значит, что импульс двух тел при их взаимодействии сохраняется.
тел, остается при этом неизменным. Это и значит, что импульс двух тел при их взаимодействии сохраняется.
Сохранение полного импульса тел при их взаимодействии — один из важнейших законов природы. Можно доказать, и опыт это также подтверждает, что если взаимодействуют не два, а много тел, то геометрическая сумма импульсов всех тел, или, как говорят, системы тел, остается неизменной. Важно только, чтобы эти тела взаимодействовали только друг с другом, чтобы на них не действовали силы со стороны других тел, не входящих в систему (или чтобы эти внешние силы уравновешивались). Такую группу тел, которая не взаимодействует ни с какими другими телами, не входящими в эту группу, называют замкнутой системой. Когда мы до сих пор говорили о взаимодействии двух тел, то тоже имели в виду, что эти тела взаимодействуют только друг с другом, посторонние же тела на них не действуют. Именно для замкнутых систем и справедлив закон сохранения импульса.
Геометрическая сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
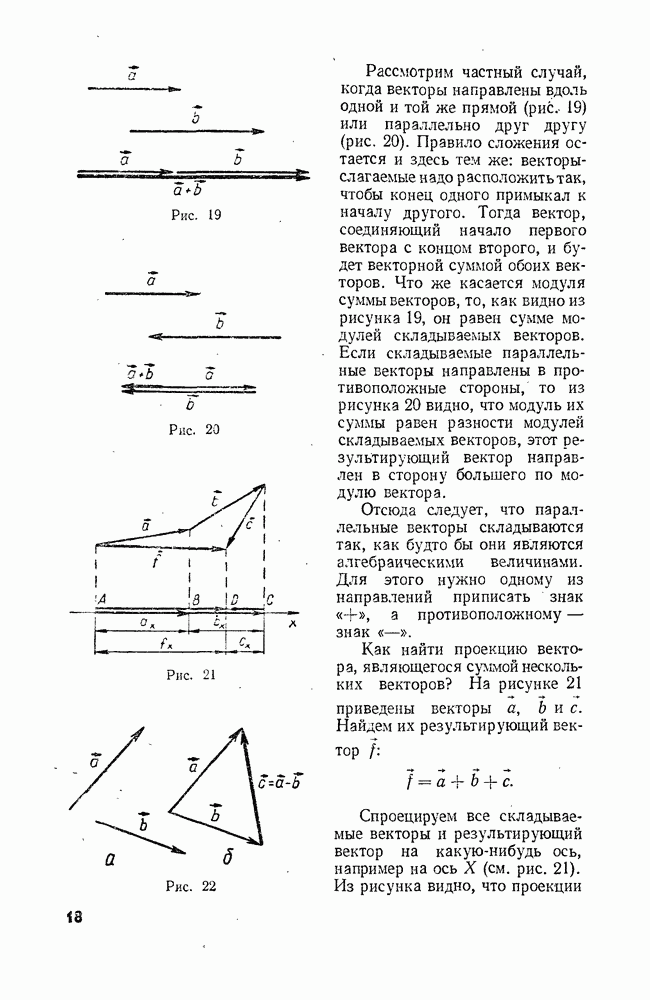
Импульс — это векторная величина. Поэтому если векторная сумма импульсов тел сохраняется постоянной, то и сумма проекций этих импульсов на оси координат также остается постоянной. Вследствие этого геометрическое сложение импульсов можно заменить алгебраическим сложением их проекций.
Следующие опыты поясняют закон сохранения импульса.
1. Поставим на рельсы две тележки одинаковой массы  . К торцу одной тележки прикрепим шарик из пластилина. Пусть тележки движутся навстречу друг другу с одинаковыми по абсолютной величине скоростями
. К торцу одной тележки прикрепим шарик из пластилина. Пусть тележки движутся навстречу друг другу с одинаковыми по абсолютной величине скоростями  (рис. 183). При встрече обе тележки остановятся.
(рис. 183). При встрече обе тележки остановятся.
Объяснить результаты опыта легко. До встречи импульс левой тележки равен  а правой тележки
а правой тележки  (тележки двигались с противоположно направленными скоростями). Значит, до момента встречи тележек их общий импульс был равен нулю:
(тележки двигались с противоположно направленными скоростями). Значит, до момента встречи тележек их общий импульс был равен нулю:

После соударения тележки остановились. Следовательно, и теперь суммарный импульс обеих тележек равен пулю.

Рис. 183

Рис. 184
2. Можно повернуть тележки так, чтобы они были обращены друг к другу пружинными буферами (рис. 184). Тогда, повторив опыт, убедимся в том, что после столкновения обе тележки разъедутся в противоположные стороны. При этом взаимодействии скорости тележек изменят свои направления на противоположные, абсолютные же значения скоростей останутся такими же, какими они были до взаимодействия. Если до встречи импульс левой тележки равен  а правой
а правой  то после встречи импульс левой тележки равен
то после встречи импульс левой тележки равен  а правой
а правой  Поэтому суммарный импульс обеих тележек равен нулю как до, так и после столкновения, как этого и требует закон сохранения импульса.
Поэтому суммарный импульс обеих тележек равен нулю как до, так и после столкновения, как этого и требует закон сохранения импульса.
Задача 1. Тележка массой 150 кг движется по рельсам со скоростью 3,6 км/ч. По дороге бежит человек массой 75 кг. Приблизившись к тележке, он вскакивает на нее и прекращает бег. После этого тележка остановилась. С какой скоростью бежал человек?
Решение. Так как взаимодействие человека и тележки с землей не влияет на их движение в горизонтальном направлении, можно к этой системе применить закон сохранения импульса. Это значит, что суммарный импульс тележки и человека после взаимодействия должен быть таким же, как и до взаимодействия.
Обозначим массу тележки через  и ее скорость до взаимодействия через
и ее скорость до взаимодействия через  массу человека через
массу человека через  и его скорость до взаимодействия через
и его скорость до взаимодействия через  Полный импульс системы до взаимодействия равен
Полный импульс системы до взаимодействия равен

В результате взаимодействия тележка и человек остановились. Следовательно, их общий импульс стал равен нулю. Значит, он был равен нулю и до того, как человек вскочил на тележку:

Тележка и человек движутся по одной прямой. Поэтому можно, направив вдоль этой прямой ось координат, вместо векторной суммы импульсов написать алгебраическую сумму их проекций на эту ось:

Примем направление движения тележки за положительное, тогда

или

Знак «минус» указывает на то, что вектор скорости движения человека был направлен противоположно вектору скорости движения тележки.
Задача 2. Железнодорожный вагон массой 30 т, движущийся со скоростью 1,5 м/сек, сцепляется с неподвижным вагоном, масса которого равна 20 т. Какова скорость вагонов после сцепки? (Вагоны находятся на прямолинейном участке пути.)
Решение. Направим координатную ось вдоль железнодорожного пути. Обозначим массу первого (движущегося) вагона через  массу второго (неподвижного) через
массу второго (неподвижного) через  скорость первого вагона до сцепки через
скорость первого вагона до сцепки через  а общую скорость обоих вагонов после сцепки через
а общую скорость обоих вагонов после сцепки через  . По закону сохранения импульса полный импульс обоих вагонов до и после сцепки должен быть одинаковым. До сцепки полный импульс (его проекция на ось) обоих вагонов был равен
. По закону сохранения импульса полный импульс обоих вагонов до и после сцепки должен быть одинаковым. До сцепки полный импульс (его проекция на ось) обоих вагонов был равен

а после сцепки

Следовательно,

Отсюда

В приведенных задачах мы не знали значений сил взаимодействия между человеком и тележкой или между сцепляющимися вагонами. Но, пользуясь законом сохранения импульса, мы нашли скорости интересующих нас тел. Ясно, что если известны их начальные положения, то, зная их скорости, можно найти положения этих тел в любой момент времени. Вот почему закон сохранения импульса имеет такое большое значение.
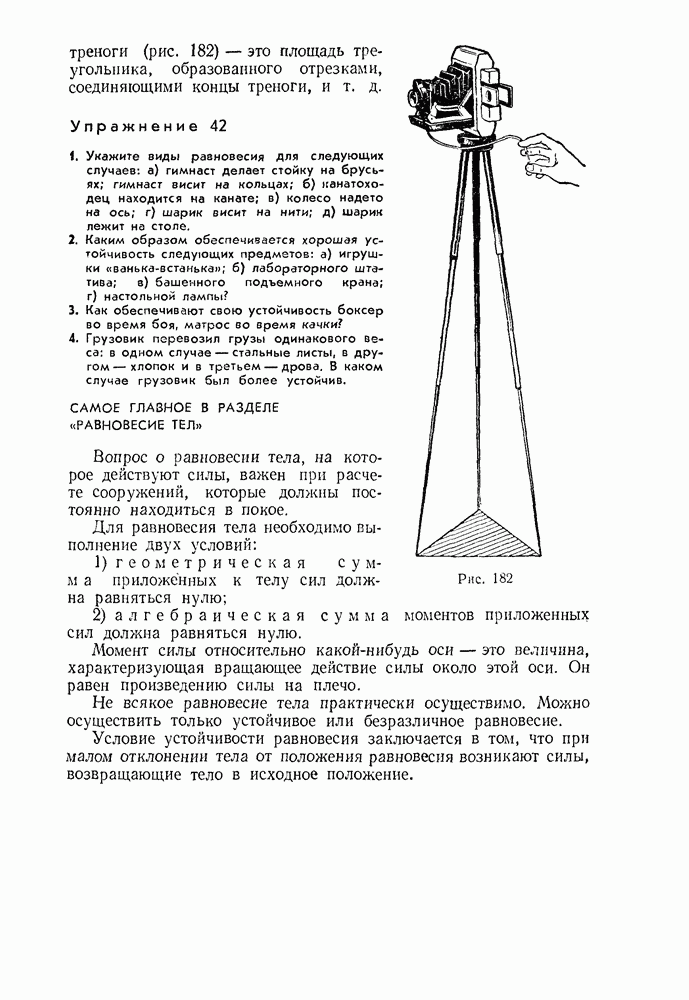
Упражнение 44
1. Человек массой 70 кг, бегущий со скоростью 7 м/сек, догоняет тележку массой 30 кг, движущуюся со скоростью 2 м/сек, и вскакивает на нее. С какой скоростью станет двигаться тележка после этого?
2. При формировании железнодорожного состава три сцепленных между собой вагона, движущиеся со скоростью 0,4 м/сек, сталкиваются с неподвижным вагоном, после чего все вагоны продолжают двигаться в ту же сторону с одинаковой скоростью. Определите эту скорость, если массы всех вагонов одинаковы.
3. Зенитный снаряд взорвался в верхней точке траектории. При этом образовалось Три осколка. Два осколка разлетелись под прямым углом Друг к другу, причем скорость первого осколка массой 9 кг равна 60 м/сек, а скорость второго массой 18 кг равна 40 м/сек. Третий осколок отлетел со скоростью 200 м/сек. Определите графически направление полета Третьего осколка. Какова его масса?
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о движении
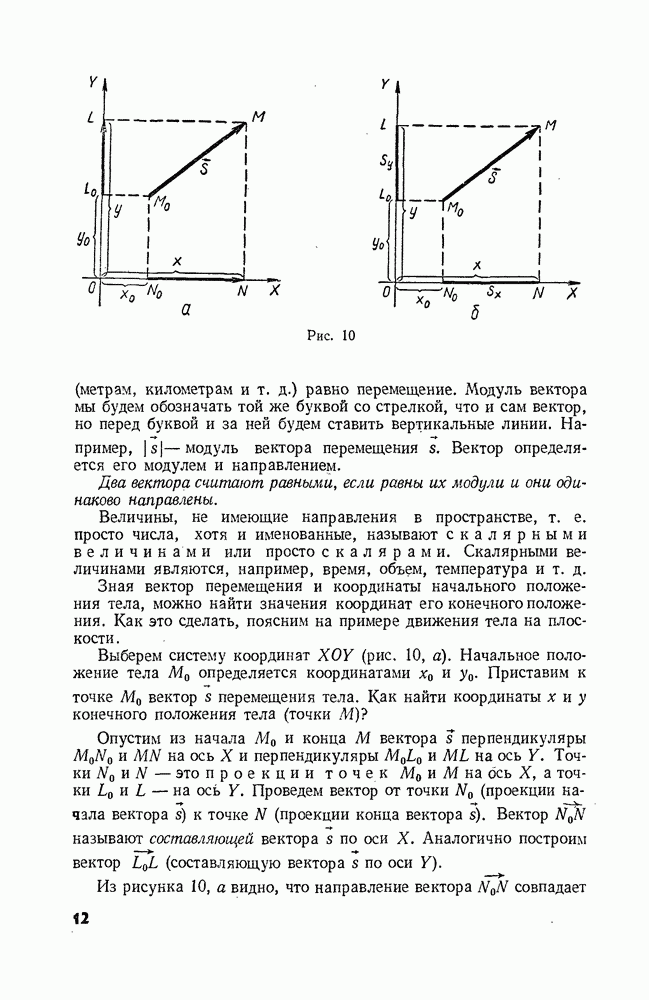
- § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА
- § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ
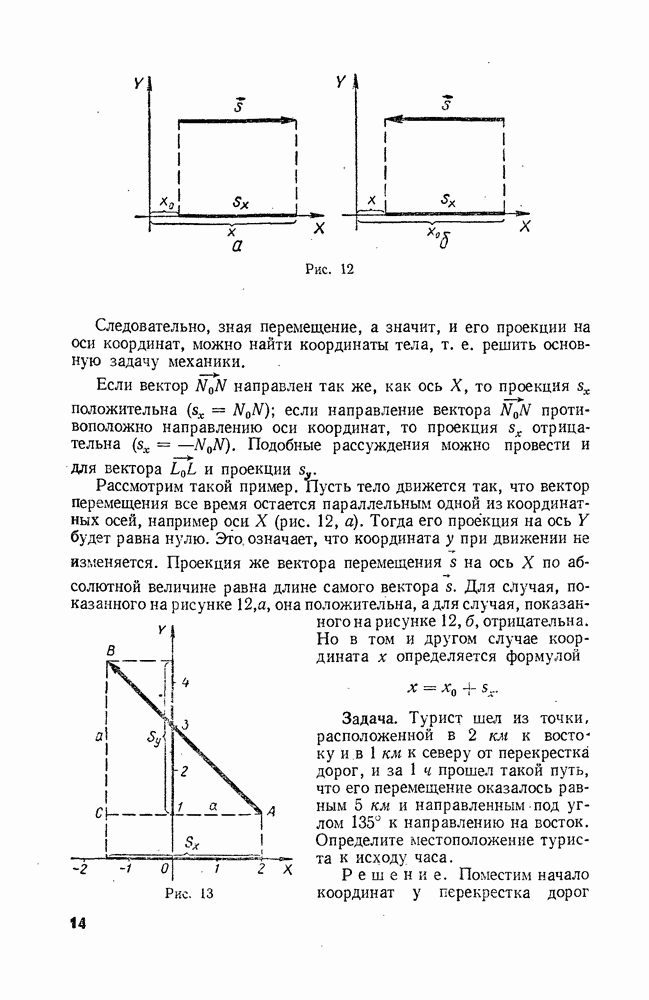
- § 3. ПЕРЕМЕЩЕНИЕ
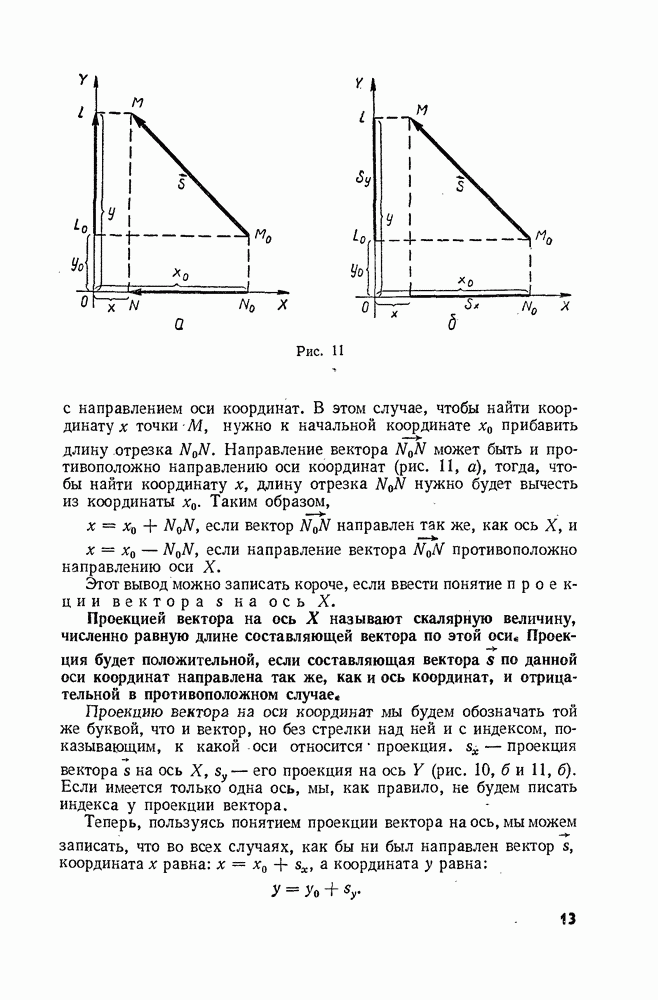
- § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА
- § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ
- § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ
- § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
- § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
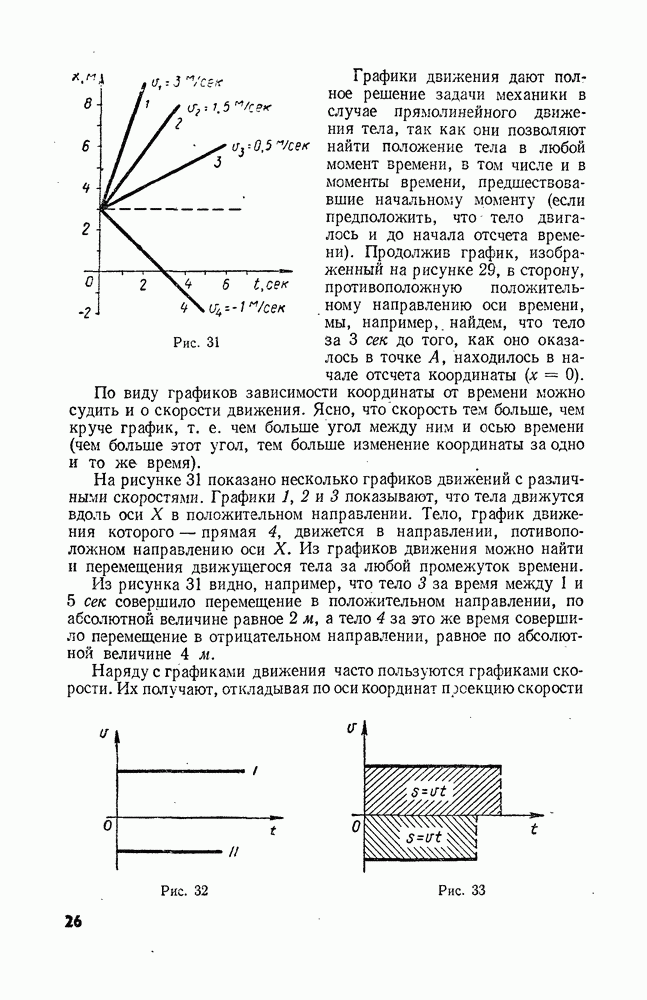
- § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ
- § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
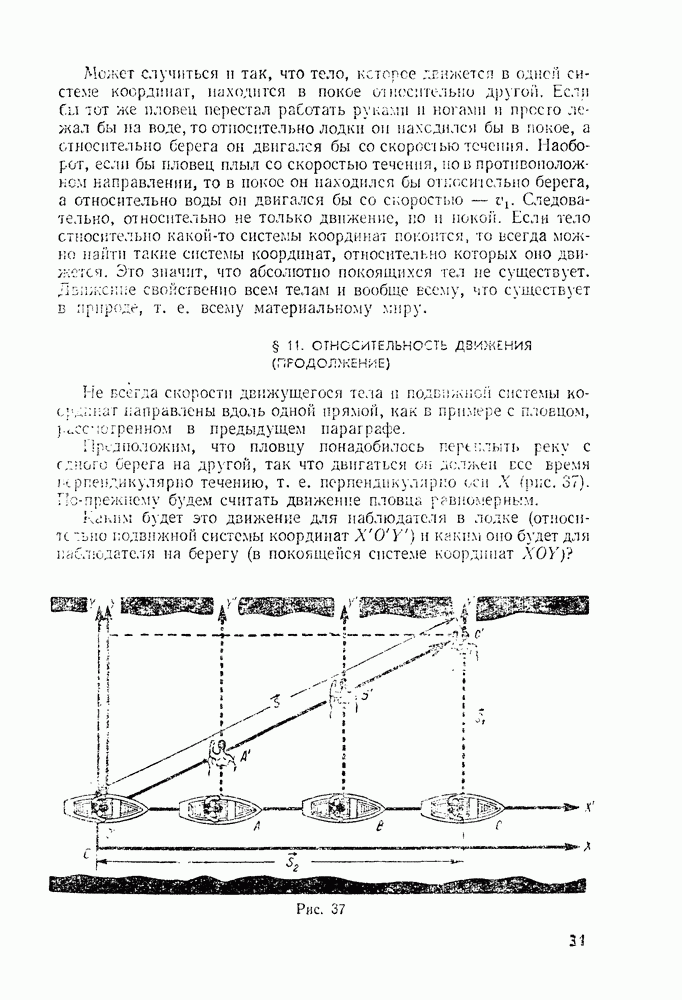
- § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ)
- § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ
- Глава 2. Прямолинейное неравномерное движение
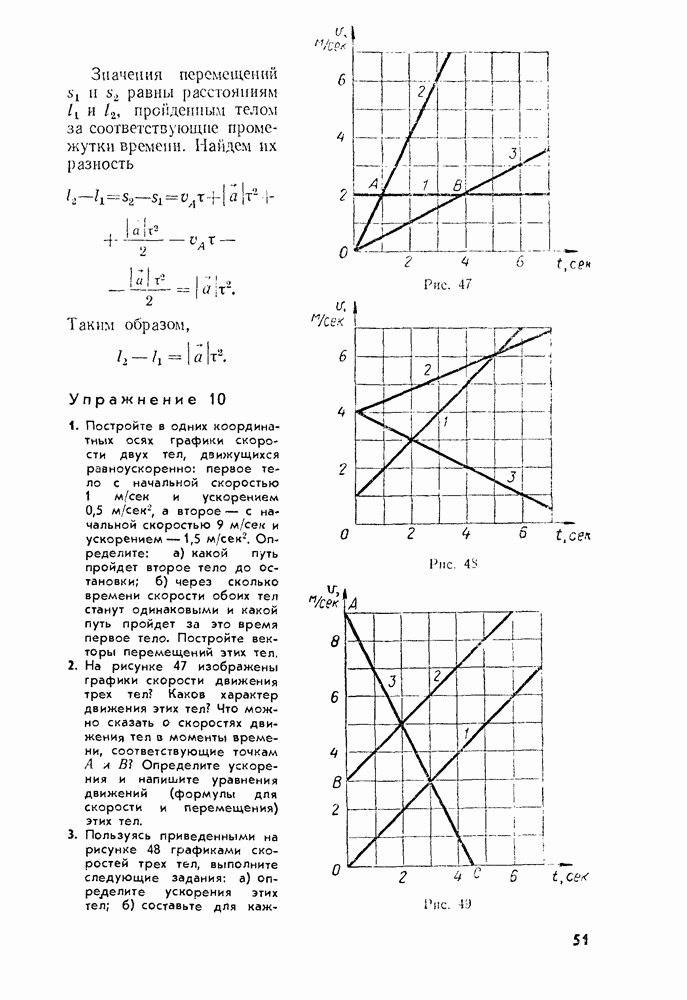
- § 13. СРЕДНЯЯ СКОРОСТЬ
- § 14. МГНОВЕННАЯ СКОРОСТЬ
- § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ
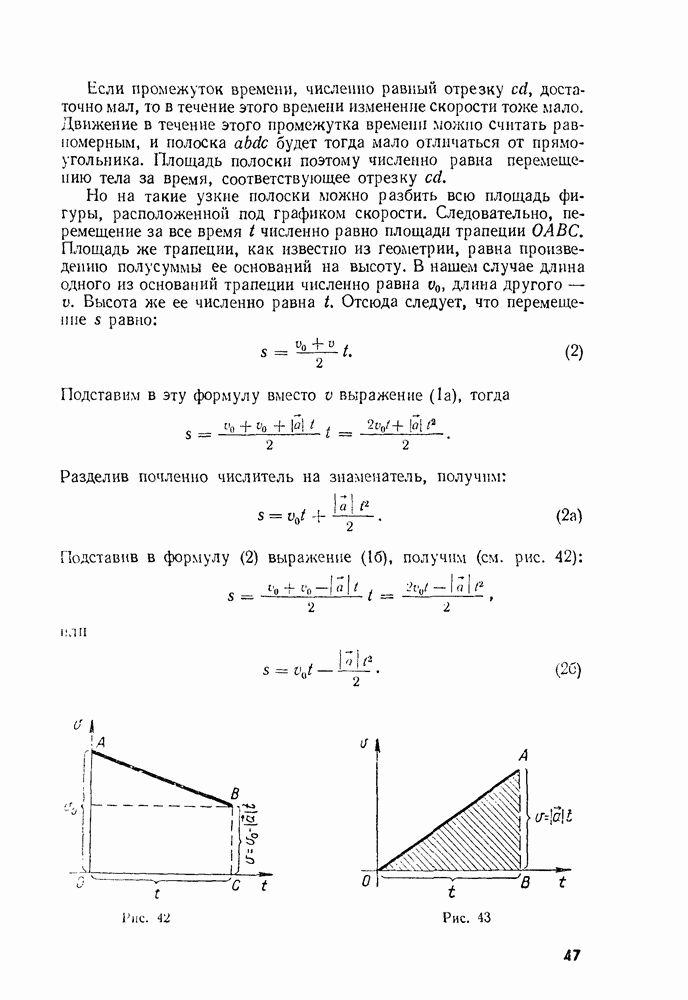
- § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
- § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ
- § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ
- § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
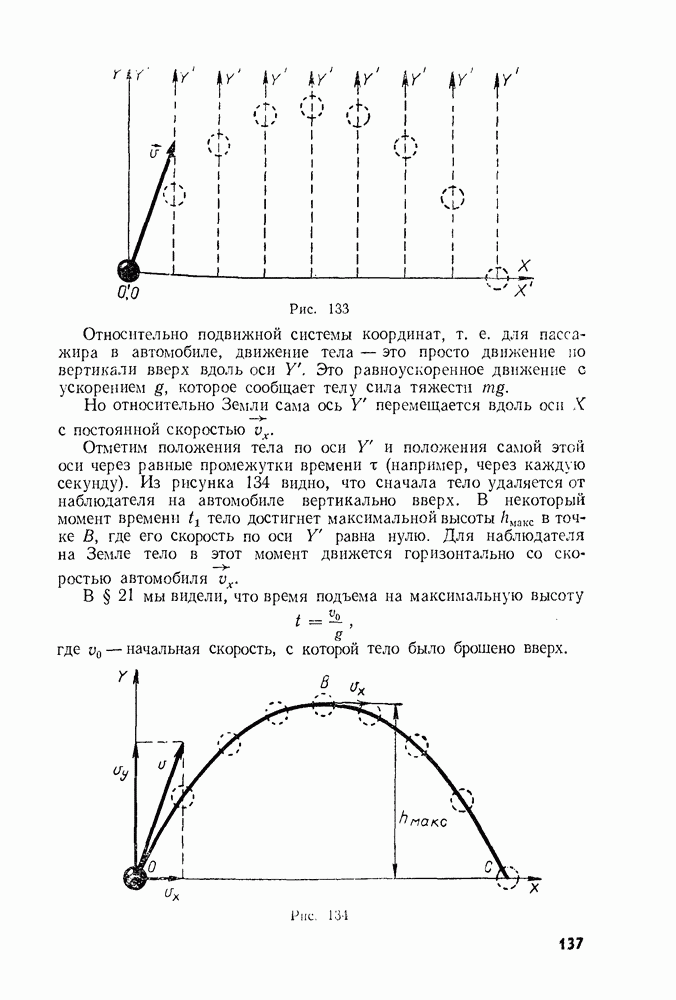
- § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
- Глава 3. Криволинейное движение
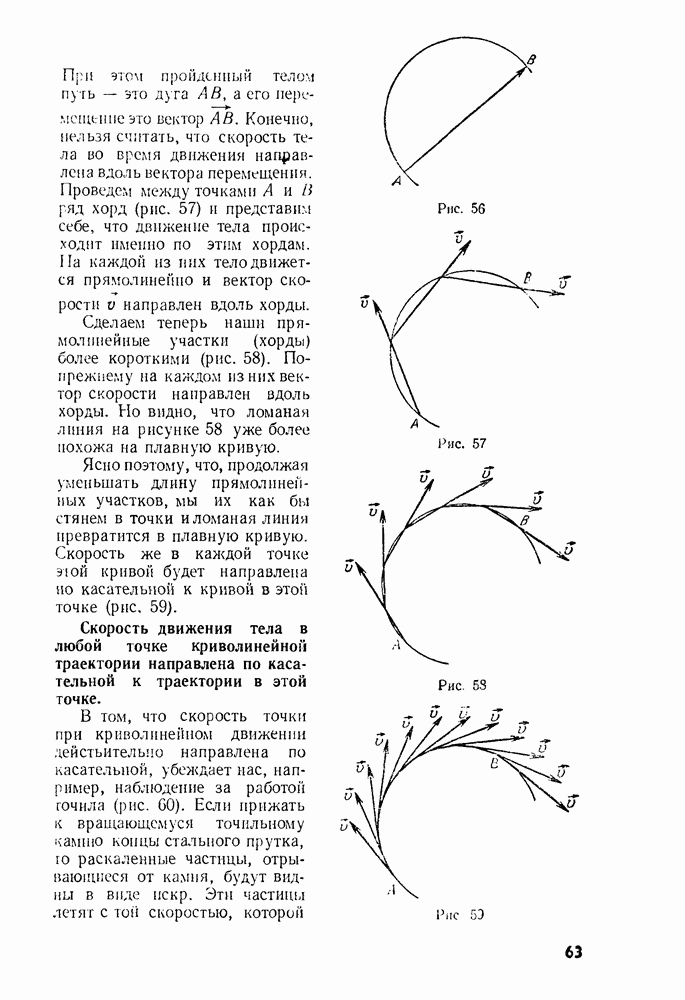
- § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
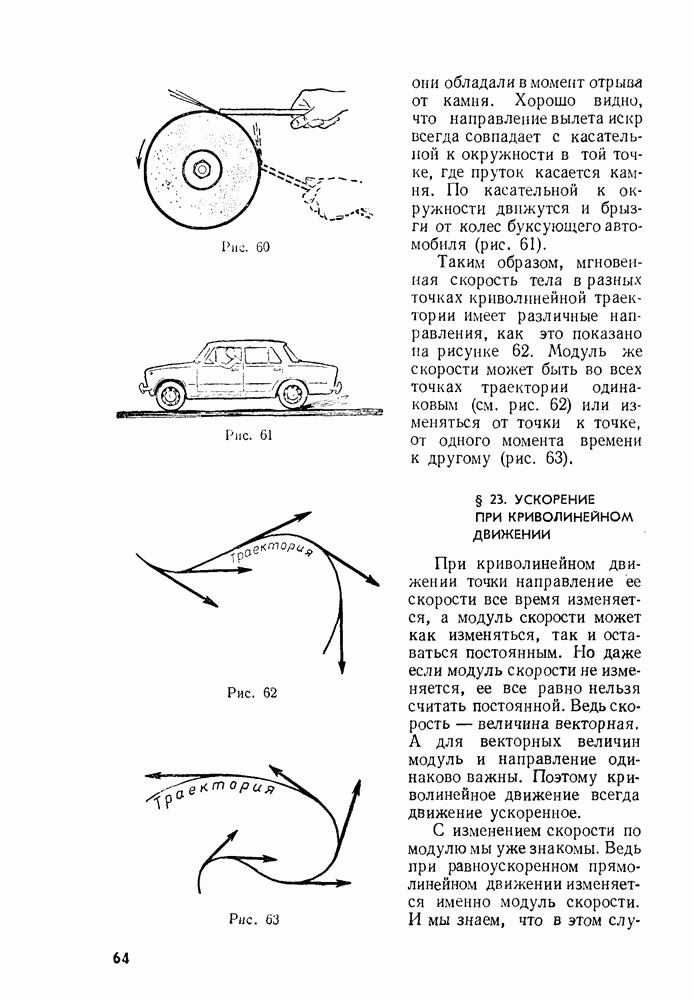
- § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
- § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ
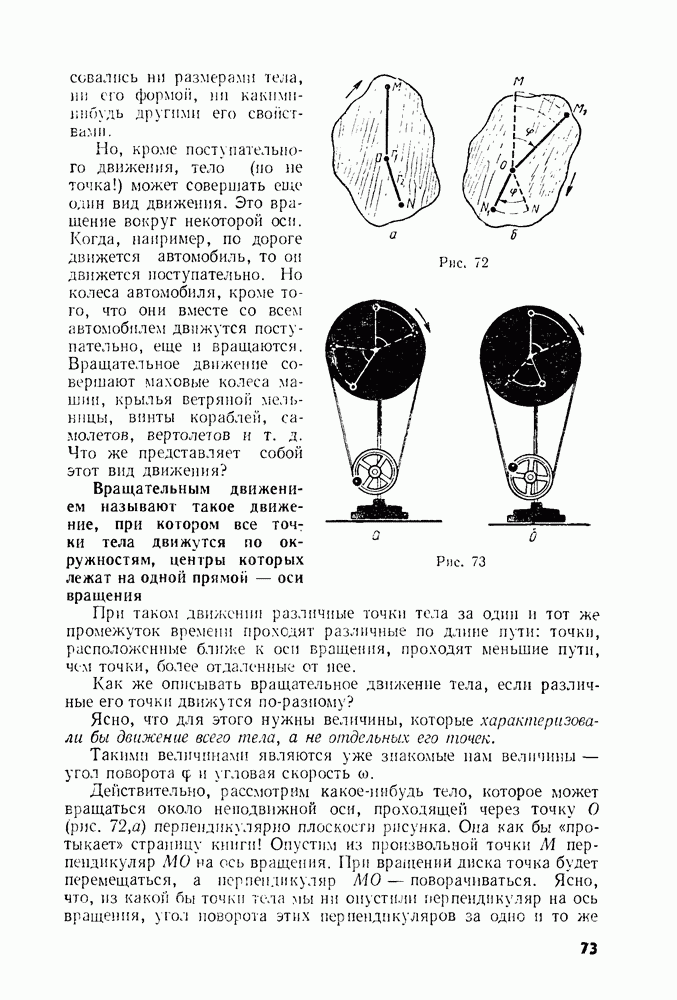
- § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА
- Динамика
- Глава 4. Законы движения
- § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ
- § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ
- § 31. ИНЕРТНОСТЬ ТЕЛ
- § 32. МАССА ТЕЛ
- § 33. МАССА ЛУНЫ
- § 34. СИЛА
- § 35. ВТОРОЙ ЗАКОН НЬЮТОНА
- § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение)
- § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР
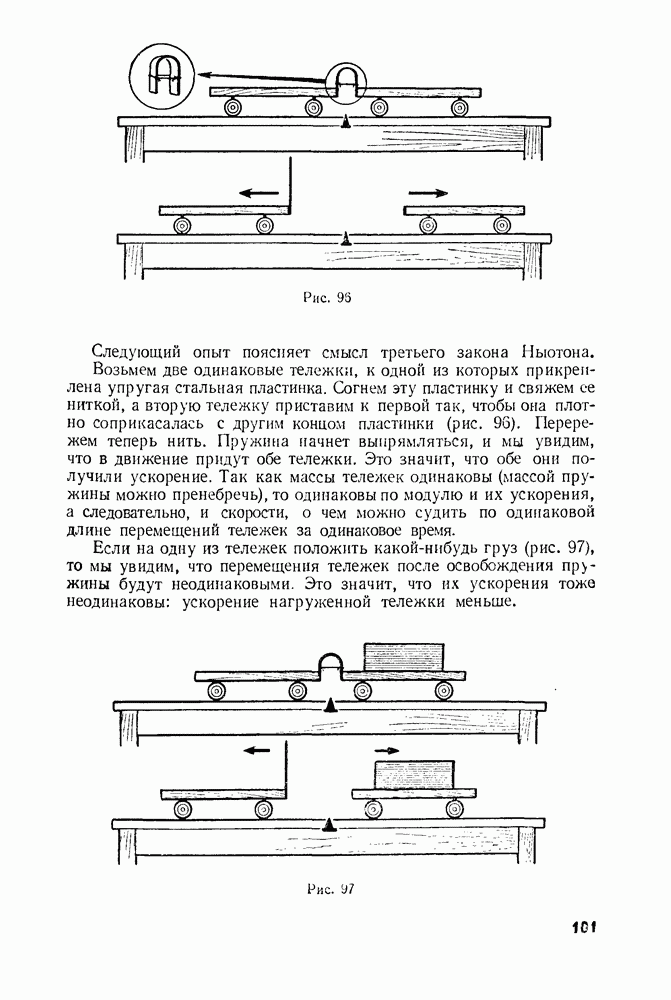
- § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА
- § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА
- Глава 5. Силы природы
- § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ
- § 41. СИЛА УПРУГОСТИ
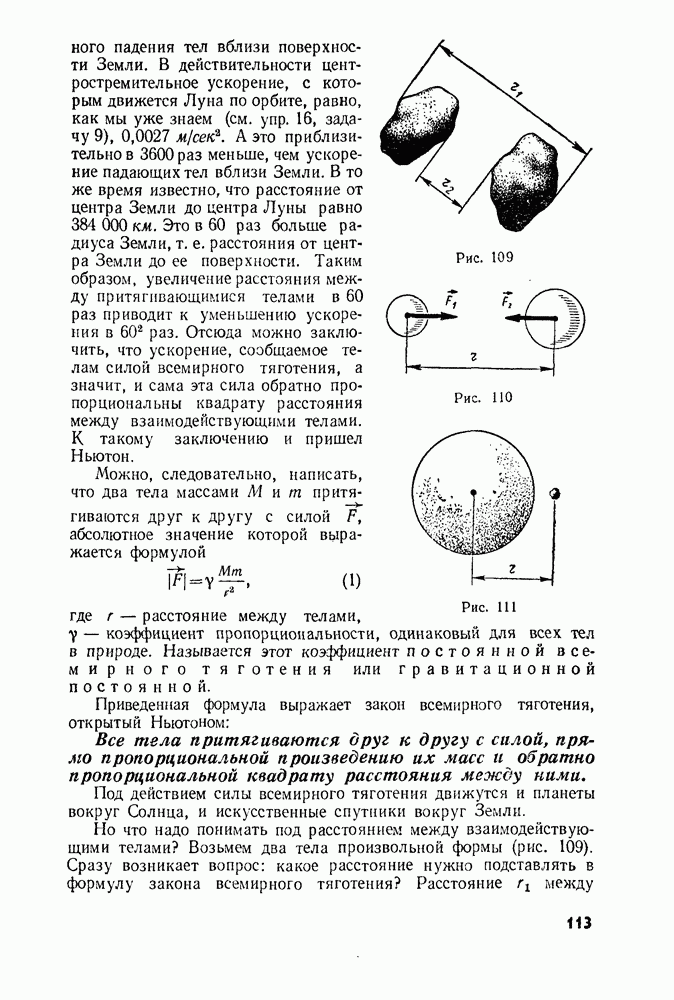
- § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 44. СИЛА ТЯЖЕСТИ
- § 45. ВЕС ТЕЛ
- § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ
- § 47. МАССА ЗЕМЛИ
- § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ
- § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ
- Глава 6. Применение законов движения
- § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ
- § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ
- § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ
- § 54. НЕВЕСОМОСТЬ
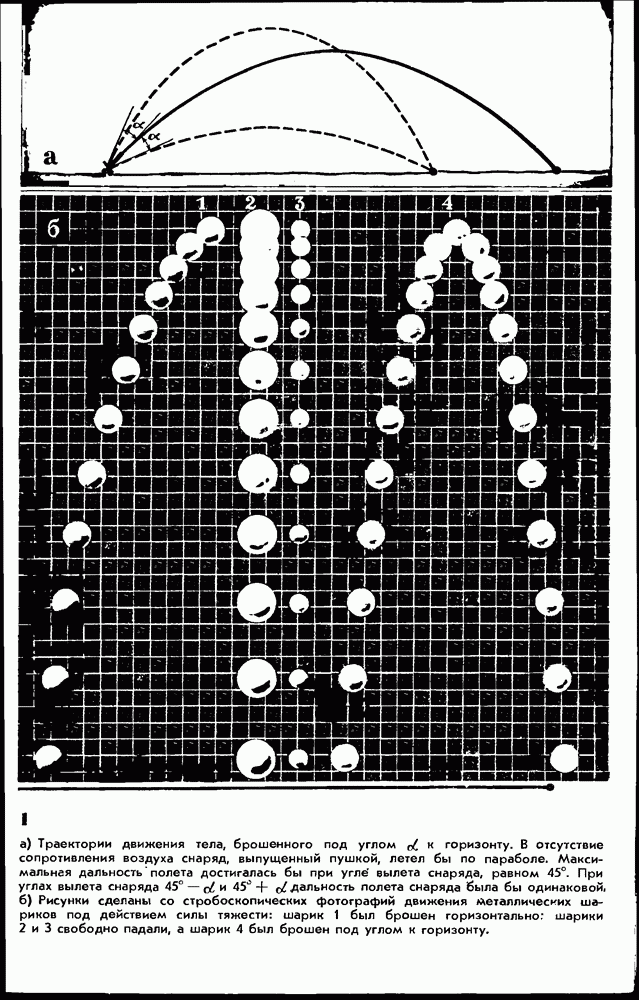
- § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ
- § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО
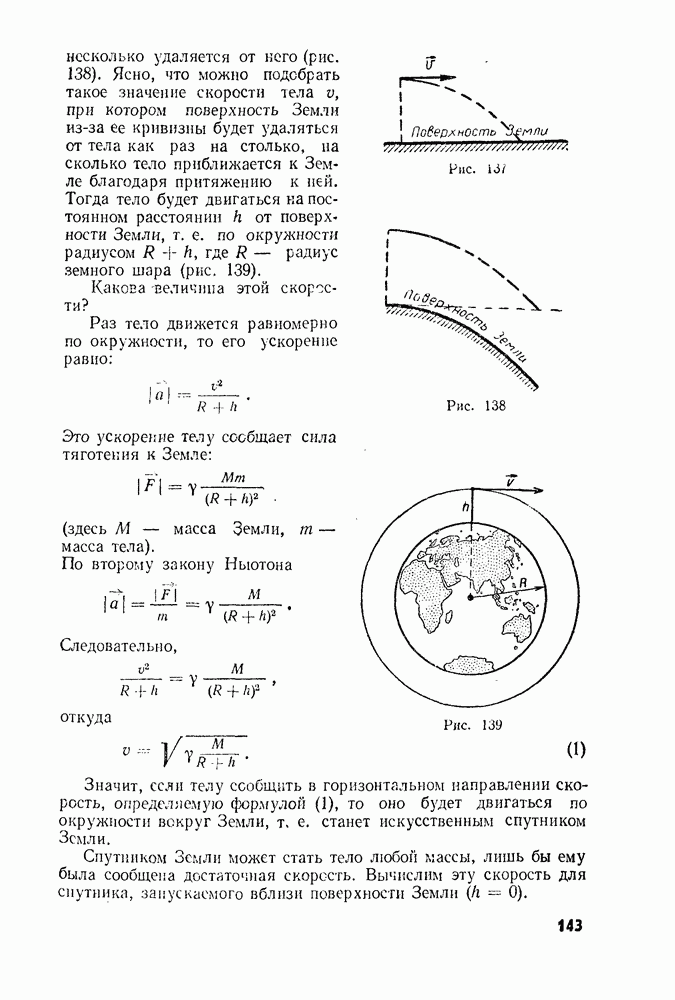
- § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ
- § 58. ДВИЖЕНИЕ ПЛАНЕТ
- § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ
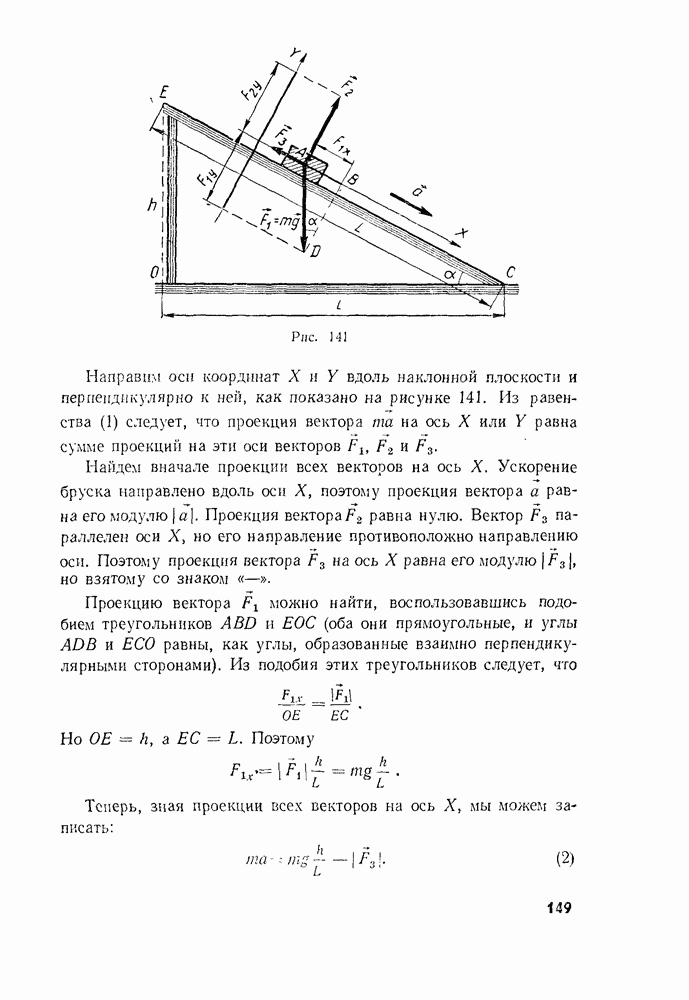
- § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ
- § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ
- § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ
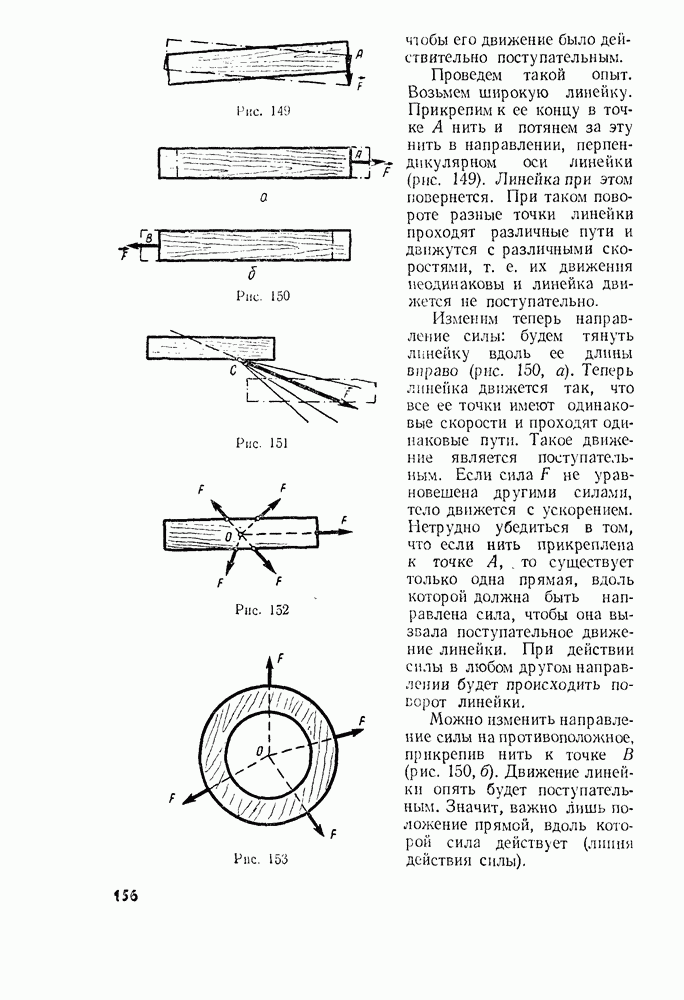
- § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ
- § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА
- Равновесие тел
- Глава 7. Элементы статики
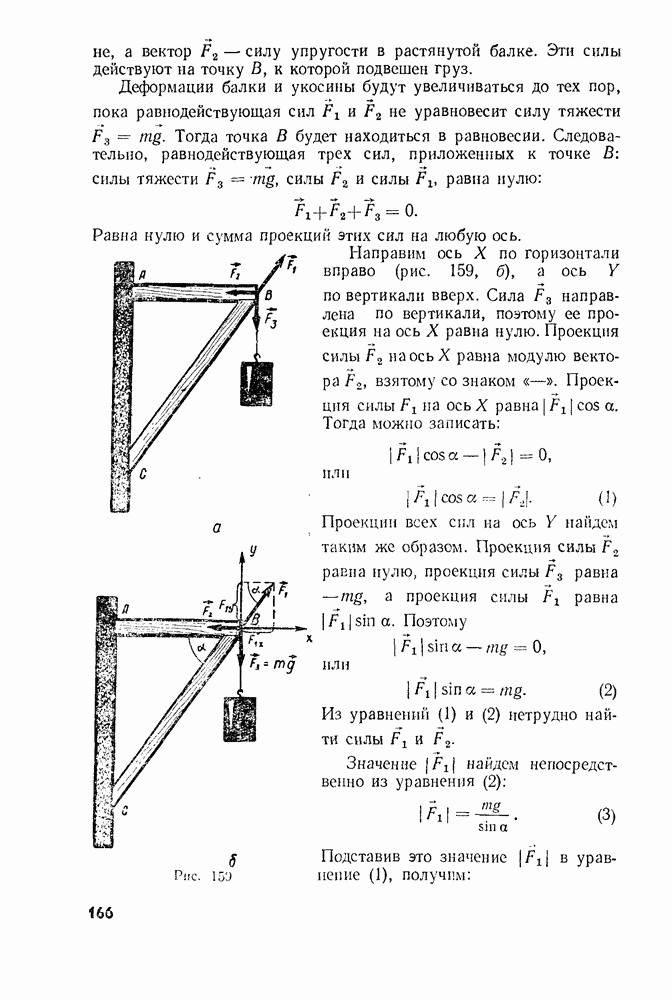
- § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ
- § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ
- § 67. ПРАВИЛО МОМЕНТОВ
- § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ
- Законы сохранения в механике
- Глава 8. Закон сохранения импульса
- § 70. СИЛА И ИМПУЛЬС
- § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ
- Глава 9. Механическая работа и мощность
- § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ
- § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ
- § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
- § 77. РАБОТА СИЛЫ ТЯЖЕСТИ
- § 78. РАБОТА СИЛЫ УПРУГОСТИ
- § 79. РАБОТА СИЛЫ ТРЕНИЯ
- § 80. МОЩНОСТЬ
- Глава 10. Закон сохранения энергии
- § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА
- § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ
- § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН
- § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
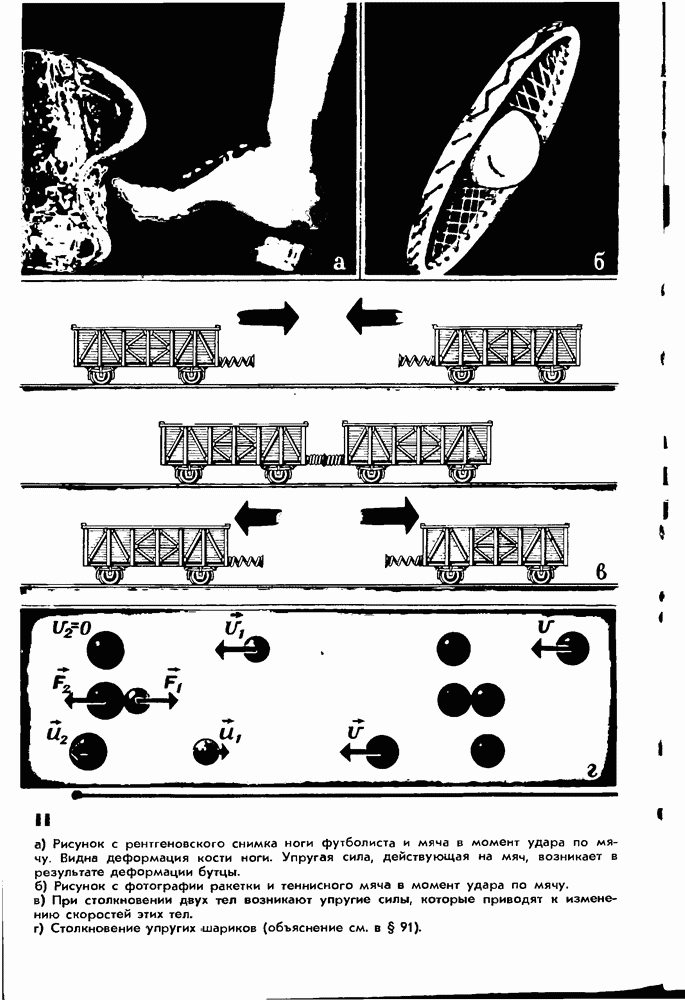
- § 91. СТОЛКНОВЕНИЕ ТЕЛ
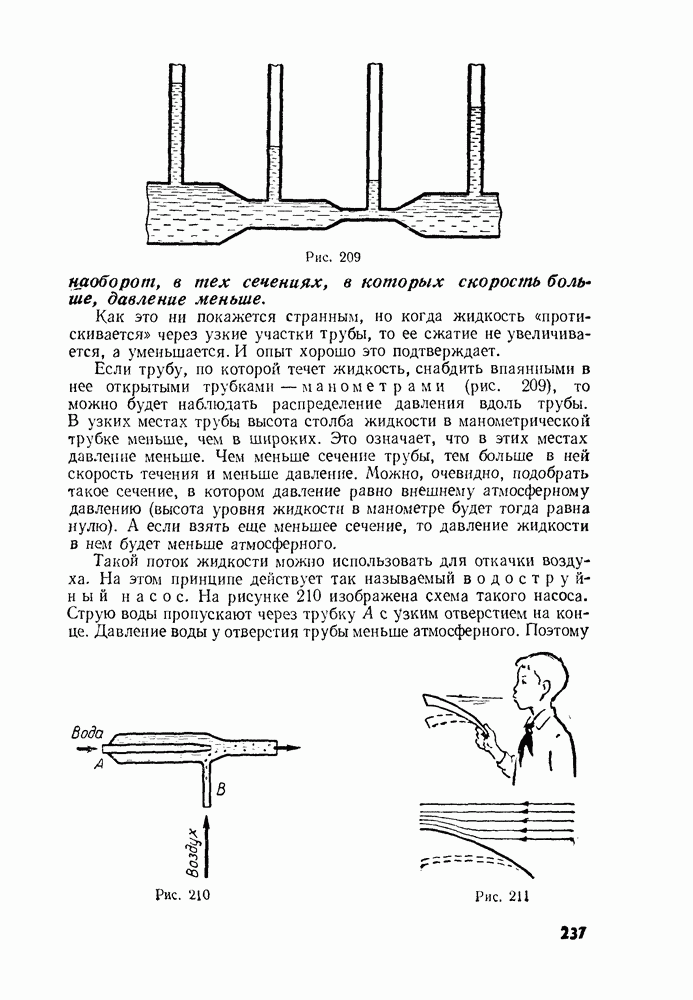
- § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ
- § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ
- Заключение
- Лабораторные работы
- 1. Определение ускорения тела при равноускоренном движении
- 2. Определение коэффициента трения скольжения
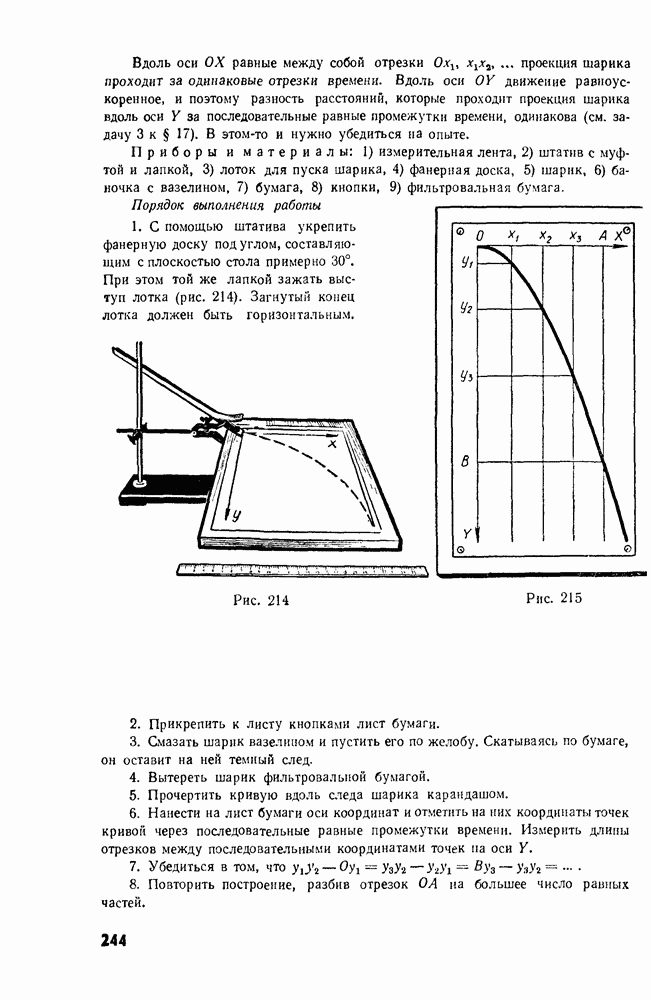
- 3. Изучение движения тела по параболе
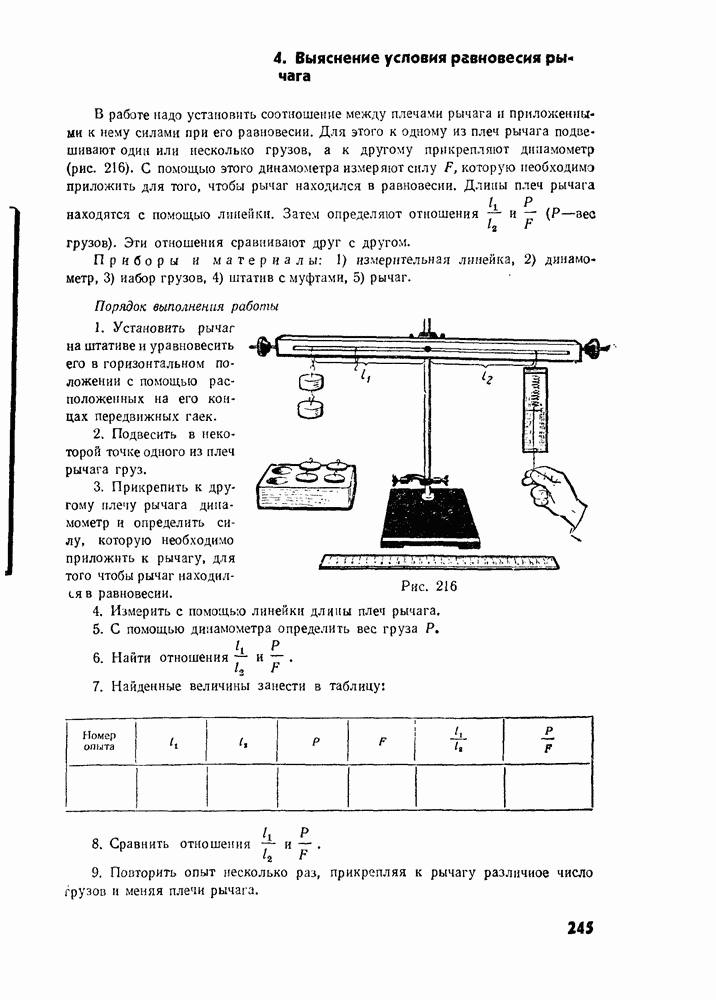
- 4. Выяснение условия равновесия рычага
- 5. Определение центра тяжести плоской пластины
- Ответы к упражнениям