| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
Самое важное для нас — это уметь вычислять перемещение тела, потому что, зная перемещение, можно найти и координаты тела, а это и есть главная задача механики. Как же вычислить перемещение при равноускоренном движении?
Формулу для определения перемещения проще всего получить, если воспользоваться графическим методом.
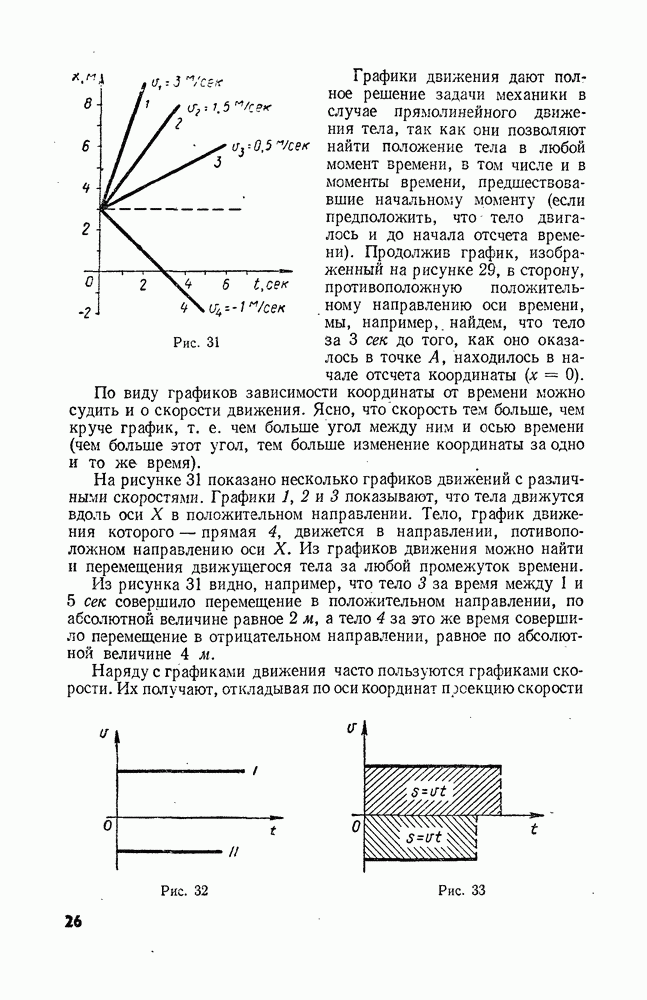
В § 9 мы видели, что при прямолинейном равномерном движении перемещение тела численно равно площади фигуры (прямоугольника), расположенной под графиком скорости. Верно ли это для равноускоренного движения?
При равноускоренном движении тела, происходящем вдоль координатной оси X, скорость с течением времени не остается постоянной, а меняется со временем согласно формулам:

и

Поэтому графики скорости имеют вид, показанный на рисунке 40. Прямая 1 на этом рисунке соответствует движению с «положительным» ускорением (скорость растет), прямая 2 — движению с «отрицательным» ускорением (скорость убывает). Оба графика относятся к случаю, когда в момент времени  тело имело скорость
тело имело скорость 
Выделим на графике скорости равноускоренного движения маленький участок  (рис. 41) и опустим из точек а и
(рис. 41) и опустим из точек а и  перпендикуляры на ось
перпендикуляры на ось  Длина отрезка
Длина отрезка  на оси
на оси  численно равна тому малому промежутку времени, за который скорость изменилась от ее значения в точке а до ее значения в точке
численно равна тому малому промежутку времени, за который скорость изменилась от ее значения в точке а до ее значения в точке  Под участком графика
Под участком графика  получилась узкая полоска
получилась узкая полоска 

Рис. 40

Рис. 41
Нели промежуток времени, численно равный отрезку  достаточно мал, то в течение этого времени изменение скорости тоже мало. Движение в течение этого промежутка времени можно считать равномерным, и полоска
достаточно мал, то в течение этого времени изменение скорости тоже мало. Движение в течение этого промежутка времени можно считать равномерным, и полоска  будет тогда мало отличаться от прямоугольника. Площадь полоски поэтому численно равна перемещению тела за время, соответствующее отрезку
будет тогда мало отличаться от прямоугольника. Площадь полоски поэтому численно равна перемещению тела за время, соответствующее отрезку 
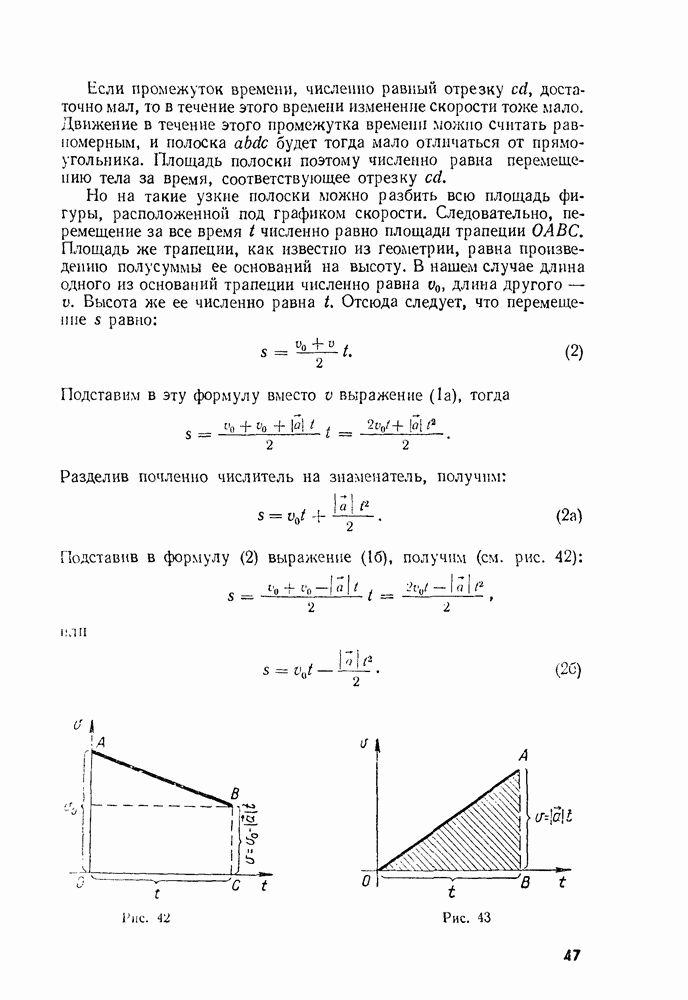
Но на такие узкие полоски можно разбить всю площадь фигуры, расположенной под графиком скорости. Следовательно, перемещение за все время  численно равно площади трапеции
численно равно площади трапеции  Площадь же трапеции, как известно из геометрии, равна произведению полусуммы ее оснований на высоту. В нашем случае длина одного из оснований трапеции численно равна
Площадь же трапеции, как известно из геометрии, равна произведению полусуммы ее оснований на высоту. В нашем случае длина одного из оснований трапеции численно равна  длина другого — V. Высота же ее численно равна
длина другого — V. Высота же ее численно равна  Отсюда следует, что перемещение
Отсюда следует, что перемещение  равно:
равно:

Подставим в эту формулу вместо  выражение (1а), тогда
выражение (1а), тогда

Разделив почленно числитель на знаменатель, получим:

Подставив в формулу (2) выражение (16), получим (см. рис. 42):

или


Рис. 42

Рис. 43
Формулу (2а) применяют в том случае, когда вектор ускорения  направлен так же, как и ось координат, а формулу (26) тогда, когда направление вектора ускорения противоположно направлению этой оси.
направлен так же, как и ось координат, а формулу (26) тогда, когда направление вектора ускорения противоположно направлению этой оси.
Если начальная скорость  равна нулю (рис. 43) и вектор ускорения направлен по оси координат, то из формулы (2а) следует, что
равна нулю (рис. 43) и вектор ускорения направлен по оси координат, то из формулы (2а) следует, что

Если же направление вектора ускорения противоположно направлению оси координат, то из формулы (26) следует, что

(знак «-» здесь означает, что вектор перемещения, так же как и вектор ускорения, направлен противоположно выбранной оси координат).
Напомним, что в формулах (2а) и (26) величины  и
и  могут быть как положительными, так и отрицательными — это проекции векторов
могут быть как положительными, так и отрицательными — это проекции векторов  и
и 
Теперь, когда мы получили формулы для вычисления перемещения, нам легко получить и формулу для вычисления координаты тела. Мы видели (см. § 8), что, для того чтобы найти координату тела  в какой-то момент времени
в какой-то момент времени  надо к начальной координате
надо к начальной координате  прибавить проекцию вектора перемещения тела на ось координат:
прибавить проекцию вектора перемещения тела на ось координат:

Поэтому

 (За) если вектор ускорения направлен так же, как и ось координат, и
(За) если вектор ускорения направлен так же, как и ось координат, и

если направление вектора ускорения противоположно направлению оси координат.
Это и есть формулы, позволяющие находить положение тела в любой момент времени при прямолинейном равноускоренном движении. Для этого нужно знать начальную координату тела  его начальную скорость
его начальную скорость  и ускорение а.
и ускорение а.
Задача 1. Водитель автомобиля, движущегося со скоростью 72 км/ч, увидел красный сигнал светофора и нажал на тормоз. После этого автомобиль начал тормозить, двигаясь с ускорением

Рис. 44
 Какое расстояние пройдет автомобиль за время
Какое расстояние пройдет автомобиль за время  сек после начала торможения? Какое расстояние пройдет автомобиль до полной остановки?
сек после начала торможения? Какое расстояние пройдет автомобиль до полной остановки?
Решение. За начало координат выберем ту точку дороги, в которой автомобиль начал тормозить. Координатную ось направим по направлению движения автомобиля (рис. 44), а начало отсчета времени отнесем к моменту, в который водитель нажал на тормоз. Скорость автомобиля направлена так же, как ось X, а ускорение автомобиля противоположно направлению этой оси. Поэтому проекция скорости на ось X положительна, а проекция ускорения отрицательна и координату автомобиля нужно находить по формуле (36):

Подставляя в эту формулу значения

получим:

Теперь найдем, какое расстояние пройдет автомобиль до полной остановки. Для этого нам нужно знать время движения  . Его можно узнать, воспользовавшись формулой
. Его можно узнать, воспользовавшись формулой 
Так как в тот момент, когда автомобиль останавливается, его скорость  равна нулю, то
равна нулю, то

и

Расстояние, которое пройдет автомобиль до полной остановки, равно координате автомобиля в момент времени 

Задача 2. Определите перемещение тела, график скорости которого показан на рисунке 45. Ускорение тела равно а.
Решение. Так как сначала модуль скорости тела уменьшается со временем, то вектор ускорения направлен противоположно направлению  . Для вычисления перемещения мы можем воспользоваться формулой
. Для вычисления перемещения мы можем воспользоваться формулой

Из графика видно, что  и время движения
и время движения  поэтому:
поэтому:

Полученный ответ показывает, что график, изображенный на рисунке 45, соответствует движению тела сначала в одном направлении, а затем на такое же расстояние в противоположном направлении, в результате чего тело оказывается в исходной точке. Подобный график может, например, относиться к движению тела, брошенного вертикально вверх.
Задача 3. Тело движется вдоль прямой равноускоренно с ускорением а. Найдите разность расстояний, проходимых телом за два следующих один за другим одинаковых промежутка времени т.
Решение. Примем прямую, вдоль которой движется тело, за ось X. Если в точке А (рис. 46) скорость тела была равна  то его перемещение
то его перемещение  за время
за время  равно:
равно:

В точке В тело имело скорость  и его перемещение за следующий промежуток времени
и его перемещение за следующий промежуток времени  равно:
равно:


Рис. 45

Рис. 46

Рис. 47

Рис. 48

Рис. 49
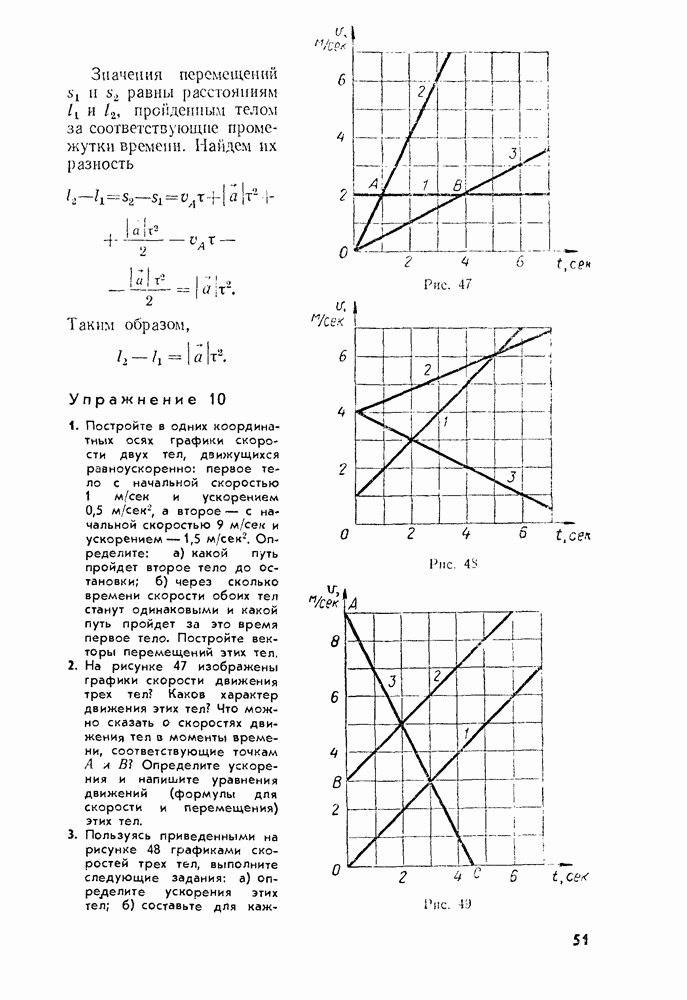
Значения перемещений  равны расстояниям
равны расстояниям  прейденным телом за соответствующие промежутки времени. Найдем их разность
прейденным телом за соответствующие промежутки времени. Найдем их разность

Таким образом,

Упражнение 10
1. Постройте в одних координатных осях графики скорости двух тел, движущихся равноускоренно: первое тело с начальной скоростью 1 м/сек и ускорением  а второе — с начальной скоростью 9 м/сек и ускорением
а второе — с начальной скоростью 9 м/сек и ускорением  Определите: а) какой путь пройдет второе тело до остановки; 6) через сколько времени скорости обоих тел станут одинаковыми и какой путь пройдет за это время первое тело. Постройте векторы перемещений этих тел.
Определите: а) какой путь пройдет второе тело до остановки; 6) через сколько времени скорости обоих тел станут одинаковыми и какой путь пройдет за это время первое тело. Постройте векторы перемещений этих тел.
2. На рисунке 47 изображены графики скорости движения трех тел? Каков характер движения этих тел? Что можно сказать о скоростях движения тел в моменты времени, соответствующие точкам А и В? Определите ускорения и напишите уравнения движений (формулы для скорости и перемещения) этих тел.
3. Пользуясь приведенными на рисунке 48 графиками скоростей трех тел, выполните следующие задания: а) Определите ускорения этих тел; б) составьте для
каждого тела формулу зависимости скорости от времени: в) в чем сходны и чем различаются движения, соответствующие графикам 2 и 3?
4. На рисунке 49 показаны графики скорости движения трех тел. По этим графикам: а) определите, чему соответствуют отрезки ОА, ОВ и ОС на осях координат; 6) найдите ускорения, с которыми движутся тела: в) напишите уравнения движения для каждого тела.
5. Самолет при взлете проходит взлетную полосу за 15 сек и в момент отрыва от зедлли имеет скорость 100 м/сек. С каким ускорением двигался самолет и какова длина взлетной полосы?
6. Автомобиль остановился у светофора. После того как загорелся зеленый сигнал, он начинает двигаться с ускорением  и движется гак до тех пор, пока скорость его не станет равной 16 м/сек, после чего он продолжает движение с постоянной скоростью. На каком расстоянии от светофора окажется автомобиль через 15 сек после появления зеленого сигнала?
и движется гак до тех пор, пока скорость его не станет равной 16 м/сек, после чего он продолжает движение с постоянной скоростью. На каком расстоянии от светофора окажется автомобиль через 15 сек после появления зеленого сигнала?
7. Снаряд, скорость которого равна 1 000 м/сек, пробивает стену блиндажа за  и после этого имеет скорость 200 м/сек. Считая движение снаряда в толще стены равноускоренным, найдите толщину стены.
и после этого имеет скорость 200 м/сек. Считая движение снаряда в толще стены равноускоренным, найдите толщину стены.
8. Ракета движется с ускорением  и к некоторому моменту времени достигает скорости в 900 м/сек. Какой путь она пройдет в следующие
и к некоторому моменту времени достигает скорости в 900 м/сек. Какой путь она пройдет в следующие 
9. На каком расстоянии от Земли оказался бы космический корабль через 30 мин после старта, если бы он все время двигался прямолинейно с ускорением 
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о движении
- § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА
- § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ
- § 3. ПЕРЕМЕЩЕНИЕ
- § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА
- § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ
- § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ
- § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
- § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
- § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ
- § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
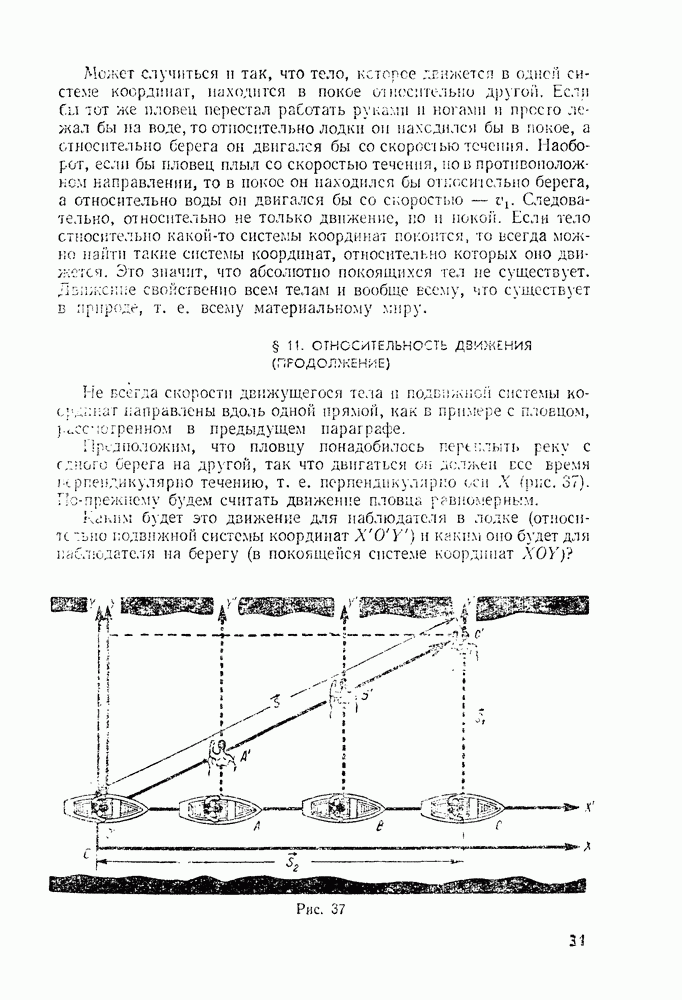
- § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ)
- § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ
- Глава 2. Прямолинейное неравномерное движение
- § 13. СРЕДНЯЯ СКОРОСТЬ
- § 14. МГНОВЕННАЯ СКОРОСТЬ
- § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ
- § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
- § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ
- § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ
- § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
- § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
- Глава 3. Криволинейное движение
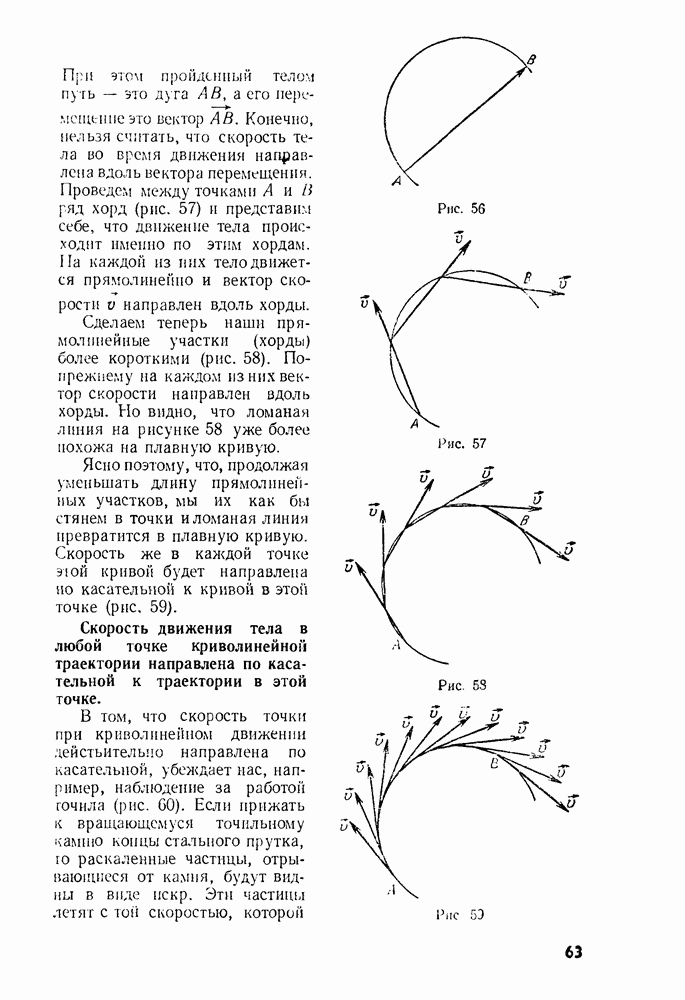
- § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
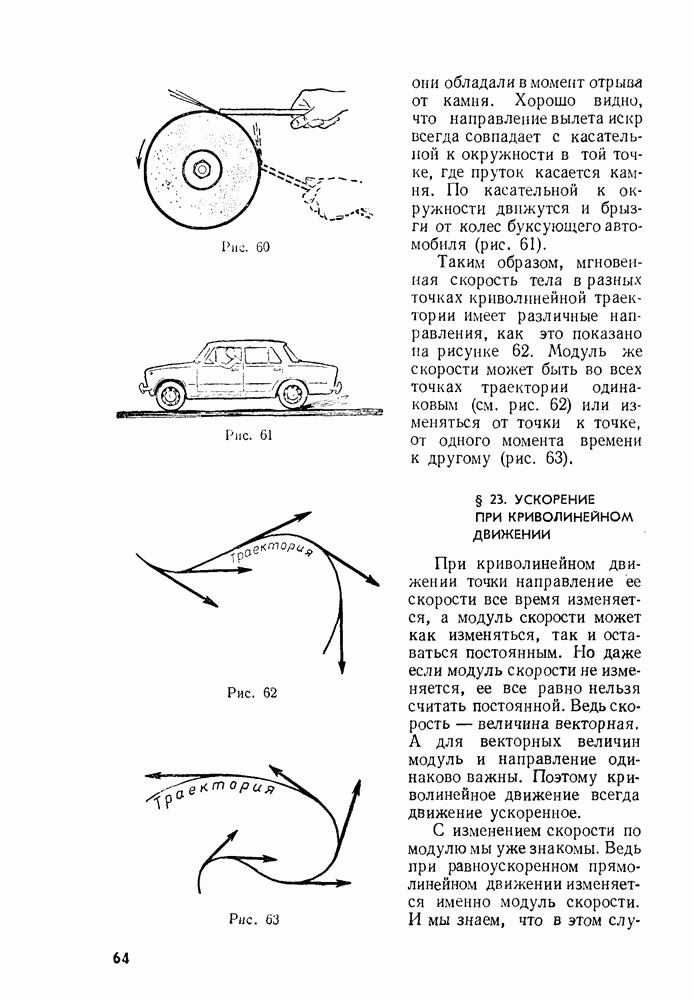
- § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
- § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ
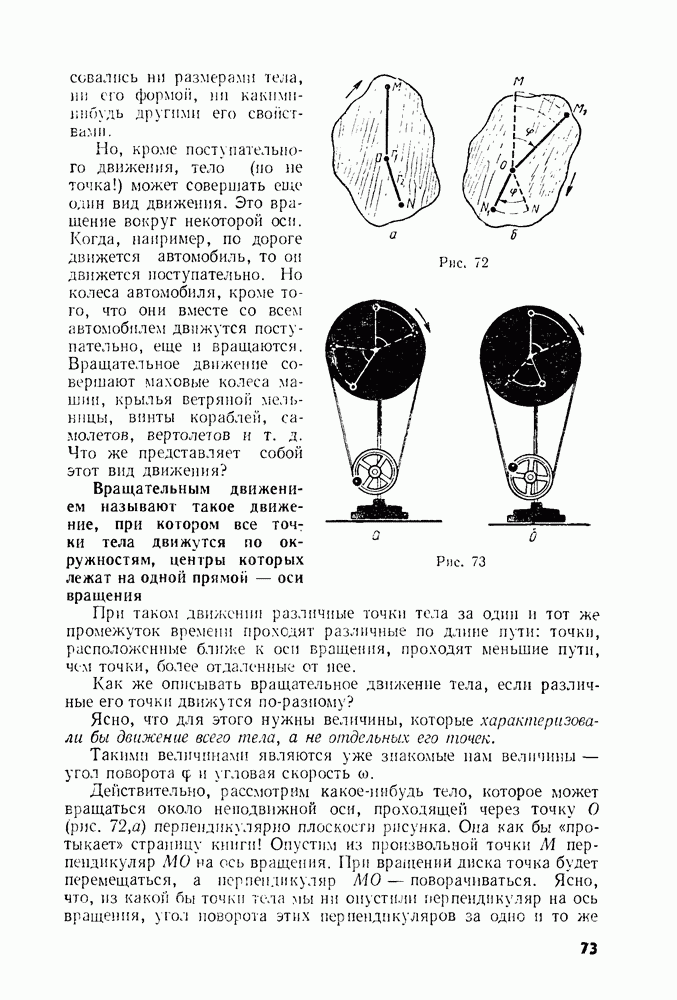
- § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА
- Динамика
- Глава 4. Законы движения
- § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ
- § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ
- § 31. ИНЕРТНОСТЬ ТЕЛ
- § 32. МАССА ТЕЛ
- § 33. МАССА ЛУНЫ
- § 34. СИЛА
- § 35. ВТОРОЙ ЗАКОН НЬЮТОНА
- § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение)
- § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР
- § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА
- § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА
- Глава 5. Силы природы
- § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ
- § 41. СИЛА УПРУГОСТИ
- § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 44. СИЛА ТЯЖЕСТИ
- § 45. ВЕС ТЕЛ
- § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ
- § 47. МАССА ЗЕМЛИ
- § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ
- § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ
- Глава 6. Применение законов движения
- § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ
- § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ
- § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ
- § 54. НЕВЕСОМОСТЬ
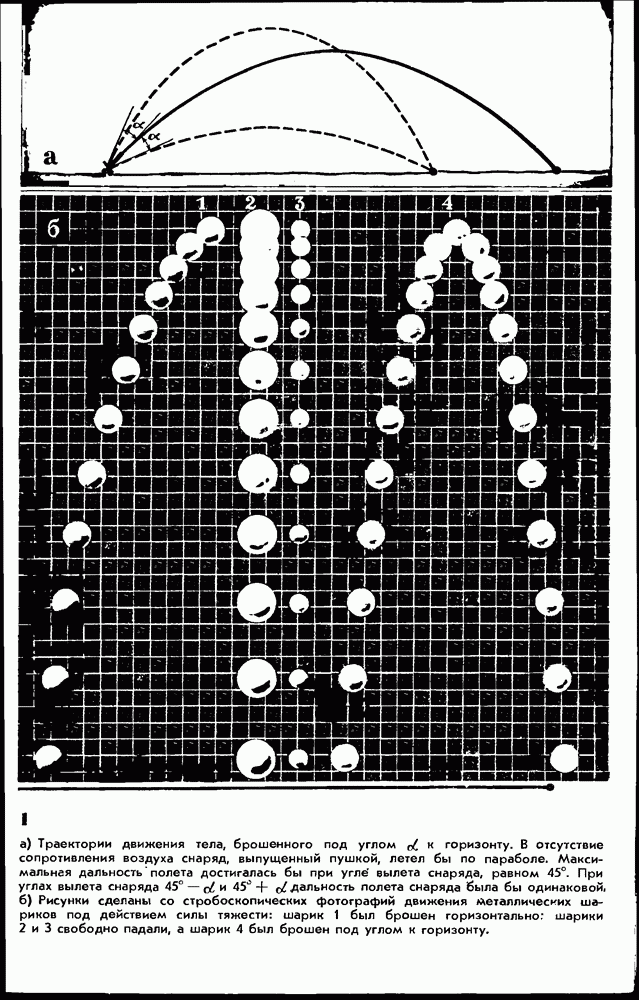
- § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ
- § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО
- § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ
- § 58. ДВИЖЕНИЕ ПЛАНЕТ
- § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ
- § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ
- § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ
- § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ
- § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ
- § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА
- Равновесие тел
- Глава 7. Элементы статики
- § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ
- § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ
- § 67. ПРАВИЛО МОМЕНТОВ
- § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ
- Законы сохранения в механике
- Глава 8. Закон сохранения импульса
- § 70. СИЛА И ИМПУЛЬС
- § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ
- Глава 9. Механическая работа и мощность
- § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ
- § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ
- § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
- § 77. РАБОТА СИЛЫ ТЯЖЕСТИ
- § 78. РАБОТА СИЛЫ УПРУГОСТИ
- § 79. РАБОТА СИЛЫ ТРЕНИЯ
- § 80. МОЩНОСТЬ
- Глава 10. Закон сохранения энергии
- § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА
- § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ
- § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН
- § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
- § 91. СТОЛКНОВЕНИЕ ТЕЛ
- § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ
- § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ
- Заключение
- Лабораторные работы
- 1. Определение ускорения тела при равноускоренном движении
- 2. Определение коэффициента трения скольжения
- 3. Изучение движения тела по параболе
- 4. Выяснение условия равновесия рычага
- 5. Определение центра тяжести плоской пластины
- Ответы к упражнениям