| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ
Вернемся теперь к нашей задаче — найти ускорение, с которым тело движется по окружности с постоянной по модулю скоростью.
Ускорение, как известно, определяется по формуле

где  — скорость тела в некоторый начальный момент времени, а
— скорость тела в некоторый начальный момент времени, а  — его скорость через промежуток времени
— его скорость через промежуток времени  . В нашем случае модули скоростей
. В нашем случае модули скоростей  и
и  равны друг другу.
равны друг другу.
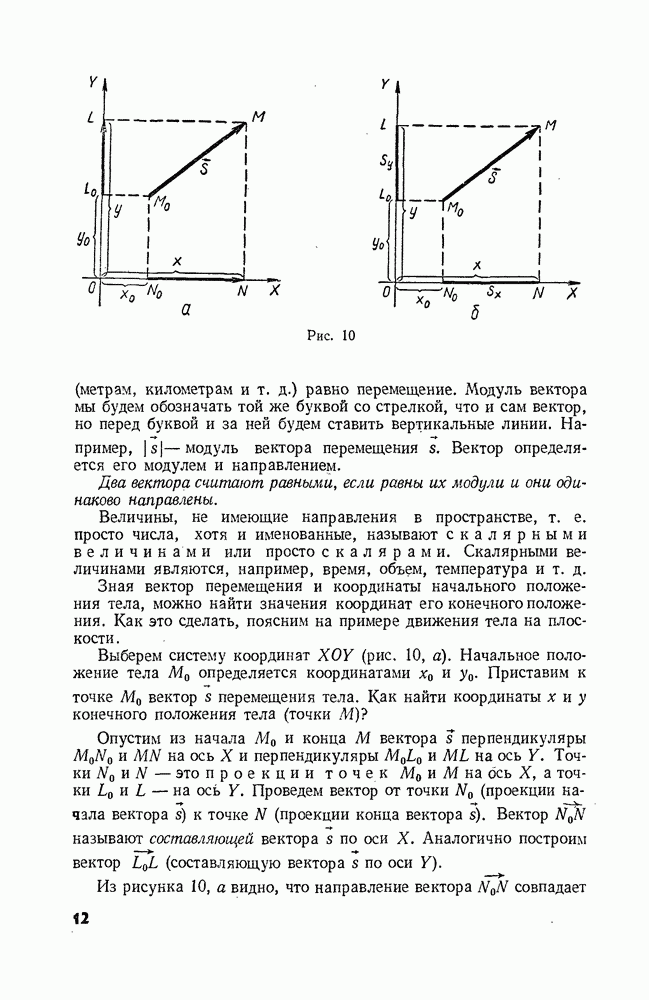
Предположим, что тело движется по окружности радиусом  и что в некоторый момент времени оно находится в точке А (рис. 67).
и что в некоторый момент времени оно находится в точке А (рис. 67).
Чему равно ускорение в этой точке? Скорость  в этой точке направлена по касательной к окружности в точке А. Через
в этой точке направлена по касательной к окружности в точке А. Через  сек тело оказывается в точке В, и скорость его
сек тело оказывается в точке В, и скорость его  теперь
теперь

Рис. 67

Рис. 68
направлена по касательной к окружности в точке В. По модулю скорости  и 10 равны (длины стрелок
и 10 равны (длины стрелок  и
и  одинаковы).
одинаковы).
Мы хотим найти ускорение в точке А окружности (мгновенное ускорение). Поэтому точки А и В мы должны взять близкими друг к другу, настолько близкими, чтобы дуга  как бы стянулась в точку.
как бы стянулась в точку.
Выясним сначала, как направлено это ускорение.
Проведем из центра О окружности радиусы к точкам А и В. Радиус окружности перпендикулярен к касательной в точке касания, следовательно, радиусы  и
и  перпендикулярны векторам
перпендикулярны векторам  и
и  Чтобы узнать направление вектора ускорения, нужно найти вектор, равный разности векторов
Чтобы узнать направление вектора ускорения, нужно найти вектор, равный разности векторов  и
и  Его направление — это и есть направление вектора ускорения. Как производят вычитание векторов, мы уже знаем (см. § 6). Чтобы найти разность
Его направление — это и есть направление вектора ускорения. Как производят вычитание векторов, мы уже знаем (см. § 6). Чтобы найти разность  векторы
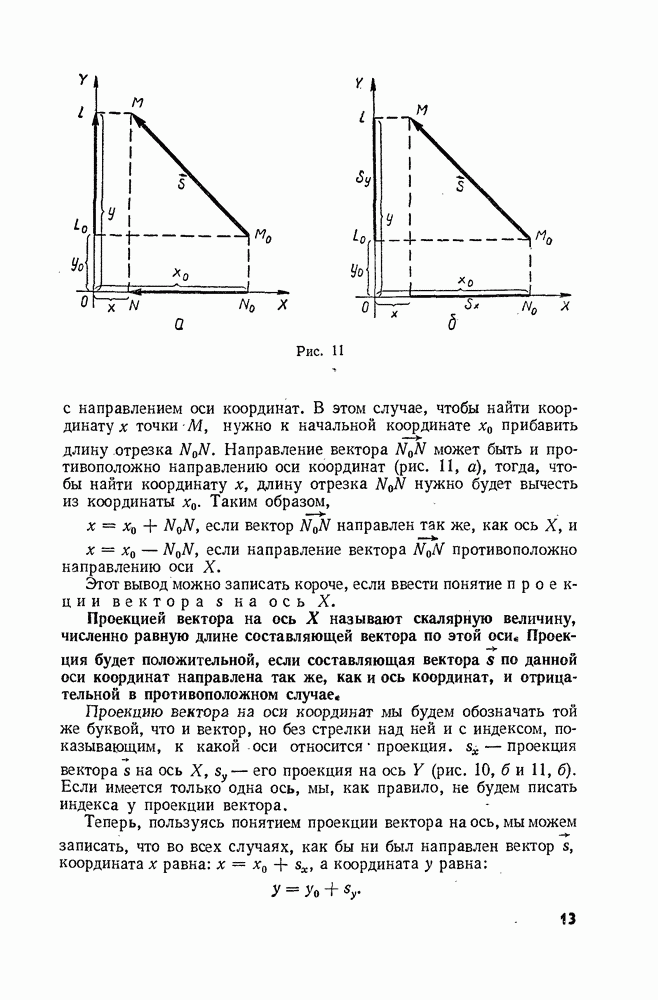
векторы  и расположим так, чтобы они исходили из одной точки (рис. 68), и соединим их концы, направив стрелку от вычитаемого к уменьшаемому (от конца вектора
и расположим так, чтобы они исходили из одной точки (рис. 68), и соединим их концы, направив стрелку от вычитаемого к уменьшаемому (от конца вектора  к концу вектора
к концу вектора  Вектор
Вектор  и есть разность векторов
и есть разность векторов  Следовательно, вдоль вектора
Следовательно, вдоль вектора  направлено ускорение. Что можно сказать об этом направлении?
направлено ускорение. Что можно сказать об этом направлении?
Треугольник  (см. рис. 68) равнобедренный. Угол при вершине А равен углу
(см. рис. 68) равнобедренный. Угол при вершине А равен углу  между радиусами
между радиусами  и
и  (рис. 67), так как они образованы взаимно перпендикулярными сторонами. Точки А и В расположены близко друг к другу, поэтому угол
(рис. 67), так как они образованы взаимно перпендикулярными сторонами. Точки А и В расположены близко друг к другу, поэтому угол  очень мал (близок к нулю). Каждый из углов при основании треугольника
очень мал (близок к нулю). Каждый из углов при основании треугольника  близок к прямому, так как сумма углов треугольника равна двум прямым. Это означает, что вектор
близок к прямому, так как сумма углов треугольника равна двум прямым. Это означает, что вектор 

Рис. 69
перпендикулярно вектору скорости. Значит, и ускорение перпендикулярно скорости. Но скорость направлена по касательной к окружности в точке А, а касательная перпендикулярна радиусу. Значит, и ускорение направлено по радиусу к центру окружности. Его поэтому называют центростремительным ускорением.
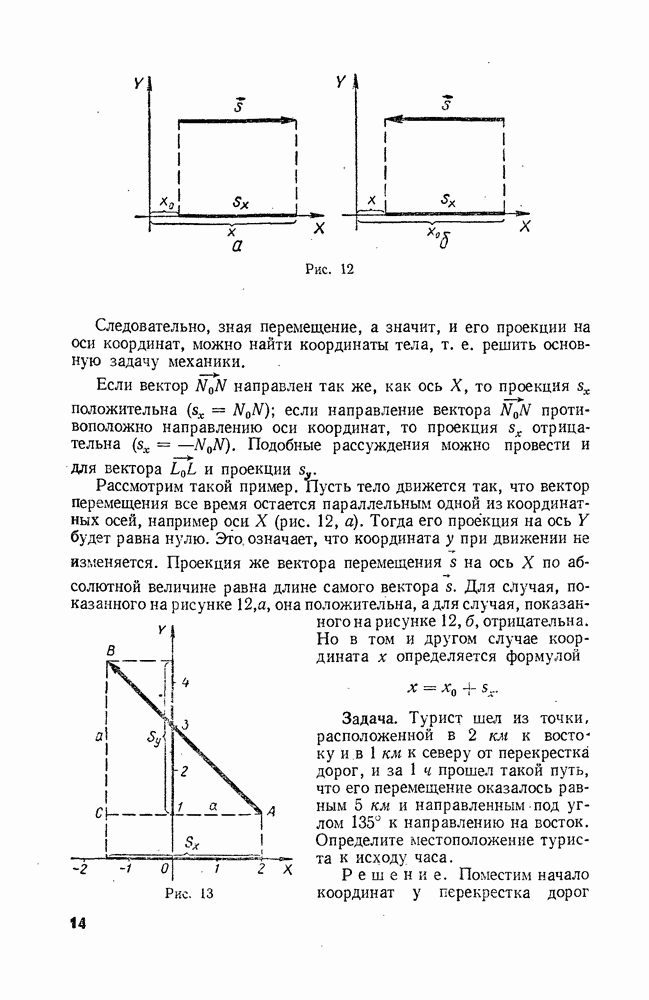
При равномерном движении тела по окружности ускорение в любой ее точке перпендикулярно скорости движения и направлено к центру окружности.
Эта интересная особенность ускорения при движении по окружности с постоянной по модулю скоростью показана на рисунке 69.
Найдем теперь модуль центростремительного ускорения. Для этого нужно найти, чему равно абсолютное значение величины  Из рисунка 68 видно, что модуль разности векторов
Из рисунка 68 видно, что модуль разности векторов  равен длине отрезка
равен длине отрезка  Так как угол
Так как угол  очень мал, то отрезок
очень мал, то отрезок  мало отличается от дуги
мало отличается от дуги  окружности (показанной пунктиром) с центром в точке А. Радиус этой окружности
окружности (показанной пунктиром) с центром в точке А. Радиус этой окружности  численно равен
численно равен  Но, как мы знаем (см. § 24), длина такой дуги равна
Но, как мы знаем (см. § 24), длина такой дуги равна  Следовательно,
Следовательно,  Абсолютное значение ускорения
Абсолютное значение ускорения  равно
равно  . Но
. Но  угловая скорость
угловая скорость  . Поэтому
. Поэтому

Ускорение тела, дсихсущаося по окружности, рлбно произведению его линейной скорости и угловой скорости поворота радиуса, проведенного к телу.
Формулу для центростремительного ускорения удобнее представить в таком виде, чтобы в нее входила величина радиуса окружности, по которой движется тело. Так как угловая и линейная скорости связаны соотношением  (
( — радиус окружности), то, подставив это выражение в формулу
— радиус окружности), то, подставив это выражение в формулу  получим:
получим:

Но  поэтому формулу для центростремительного ускорения можно записать еще и так:
поэтому формулу для центростремительного ускорения можно записать еще и так:

При равномерном движении по окружности тело движется с
ускорением, которое направлено по радиусу к центру окружности и модуль которого определяется выражением 
Следовательно, верно и обратное: если известно, что скорость тела равна  и ускорение тела во всех точках перпендикулярно вектору его скорости и по абсолютному значению равно
и ускорение тела во всех точках перпендикулярно вектору его скорости и по абсолютному значению равно  то можно утверждать, что такое тело движется по окружности, радиус которой
то можно утверждать, что такое тело движется по окружности, радиус которой  определяется формулой
определяется формулой

Значит, если нам известны начальная скорость тела и абсолютное значение его центростремительного ускорения, мы можем изобразить окружность, по которой тело будет двигаться, и найти его положение в любой момент времени (начальное положение тела должно быть, конечно, известно). Тем самым будет решена основная задача механики.
Напомним, что ускорение при равномерном движении по окружности нас интересует потому, что всякое движение по криволинейной траектории представляет собой движение по дугам окружностей различных радиусов.
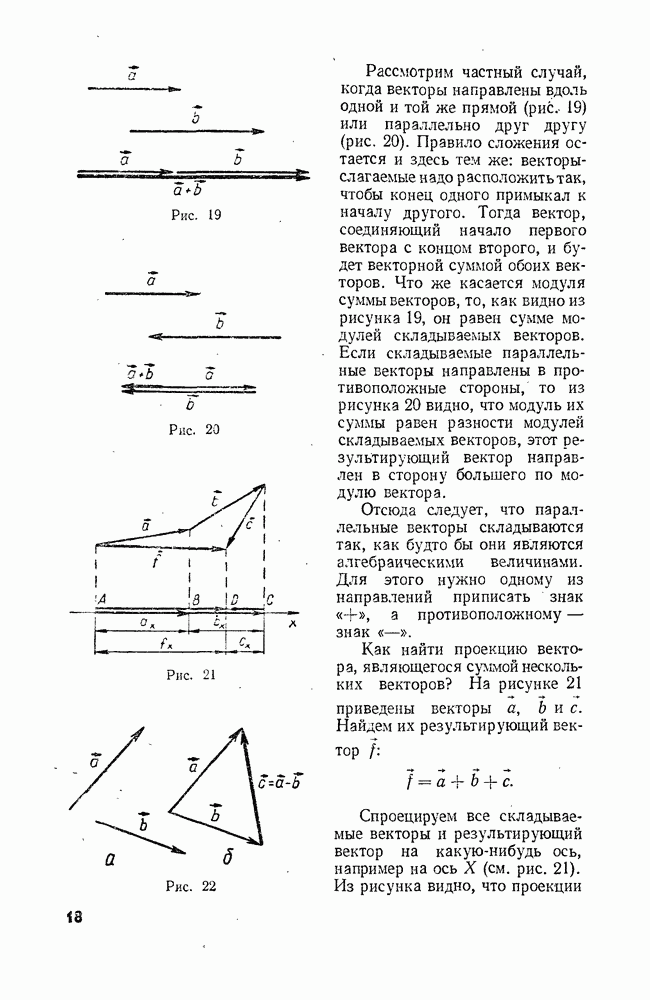
Теперь мы можем сказать, что при равномерном движении в любой точке криволинейной траектории тело движется с ускорением, направленным к центру той окружности, частью которой является данная траектория вблизи этой точки. Численное же значение ускорения зависит от скорости тела в этой точке и от радиуса соответствующей окружности. На рисунке 70 показана некоторая сложная траектория и указаны векторы центростремительного ускорения в различных точках траектории.
Задача. Самолет, выходя из пике, движется по дуге, которая в нижней своей части является дугой окружности радиусом 500 м (рис. 71). Вычислите ускорение самолета в наинизшей точке, если его скорость равна 800 км/ч, и сравните полученное значение с ускорением свободного падения.

Рис. 70

Рис. 71
Решение. Ускорение самолета вычисляем по формуле

Подставив сюда значения

получаем:

Так как

Упражнение 16
1. Как направлено ускорение тела, движущегося по окружности с постоянной по модулю скоростью?
2. Если при движении тела по окружности модуль его скорости изменяется, будет ли ускорение тела направлено к центру окружности?
3. Можно ли считать движение по окружности с постоянным по модулю ускорением равноускоренным движением?
4. Точильный круг, радиус которого равен 10 см, при вращении делает 1 оборот за 0,2 сек. Найдите скорость точек, наиболее удаленных от оси вращения.
5. Автомобиль движется по закруглению дороги радиусом 100 м со скоростью 54 км/ч. Какова величина центростремительного ускорения автомобиля?
6. Период обращения первого корабля-спутника «Восток» вокруг Земли равнялся 90 мин. Среднюю высоту корабля-спутника над Землей можно считать равной 320 км. Радиус Земли равен 6 400 км. Вычислите скорость корабля.
7. Какова скорость движения автомобиля, если его колеса радиусом 30 см делают 10 оборотов в 1 сек?
8. Два шкива, радиусы которых  , соединены бесконечным ремнем. Период вращения шкива меньшего радиуса равен 0,5 сек. Какова скорость перемещения точек ремня? Каков период вращения второго шкива?
, соединены бесконечным ремнем. Период вращения шкива меньшего радиуса равен 0,5 сек. Какова скорость перемещения точек ремня? Каков период вращения второго шкива?
9. Луна движется вокруг Земли на расстоянии 385 000 км от нее, совершая один оборот за 27,3 суток. Вычислите центростремительное ускорение Луны.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о движении
- § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА
- § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ
- § 3. ПЕРЕМЕЩЕНИЕ
- § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА
- § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ
- § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ
- § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
- § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
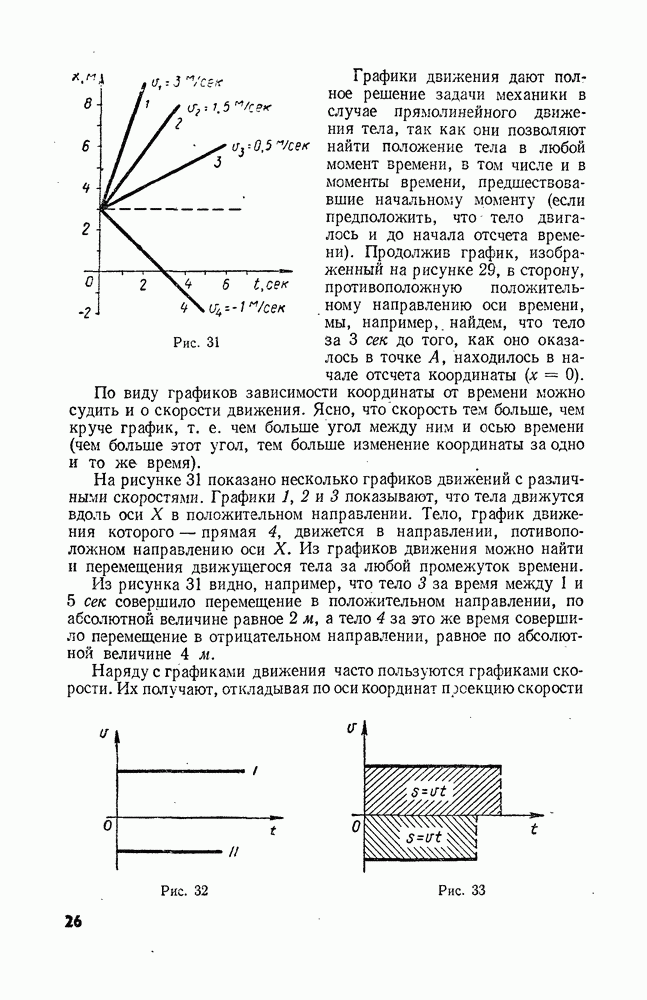
- § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ
- § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
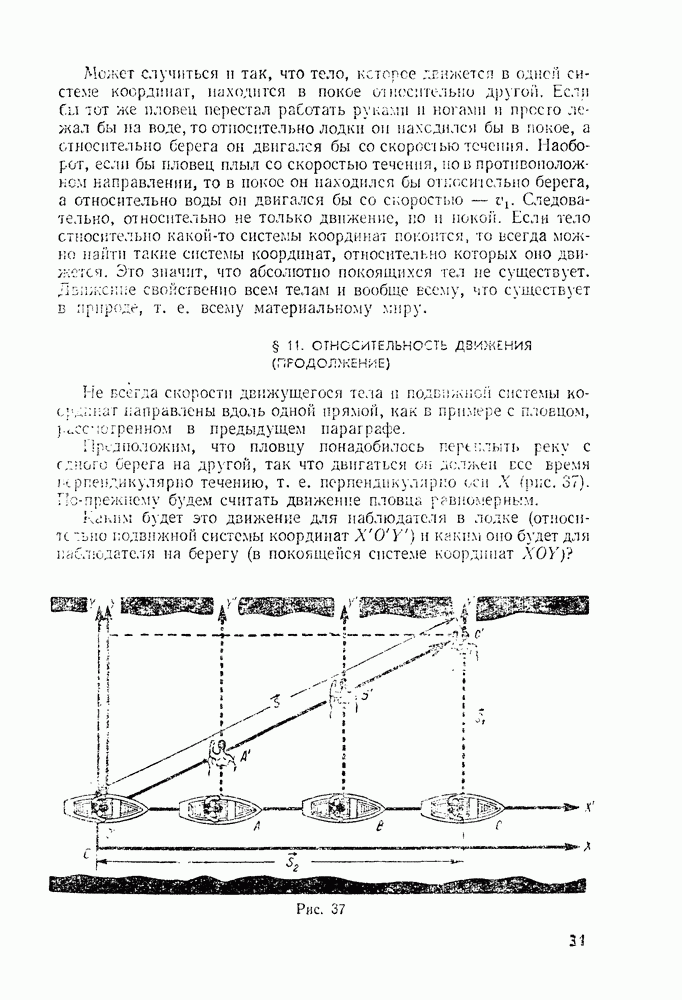
- § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ)
- § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ
- Глава 2. Прямолинейное неравномерное движение
- § 13. СРЕДНЯЯ СКОРОСТЬ
- § 14. МГНОВЕННАЯ СКОРОСТЬ
- § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ
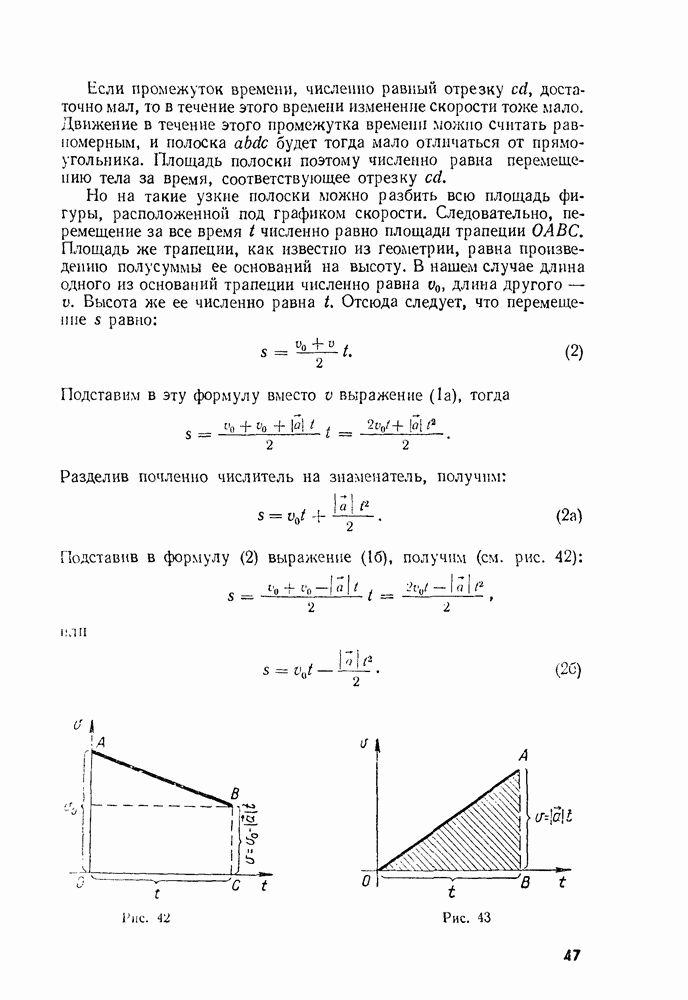
- § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
- § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ
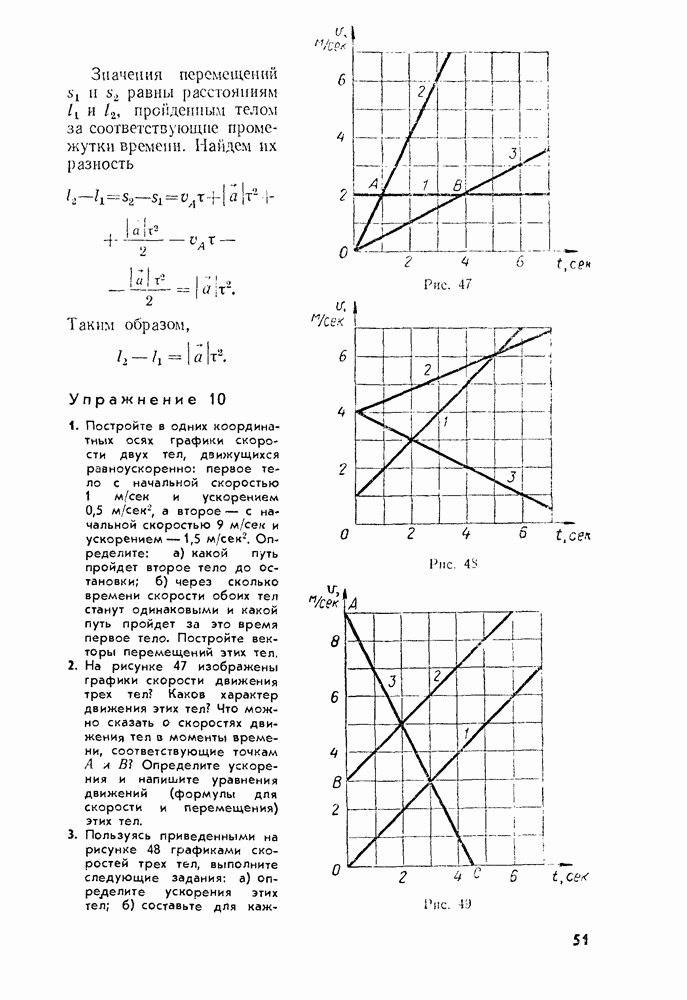
- § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ
- § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
- § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
- Глава 3. Криволинейное движение
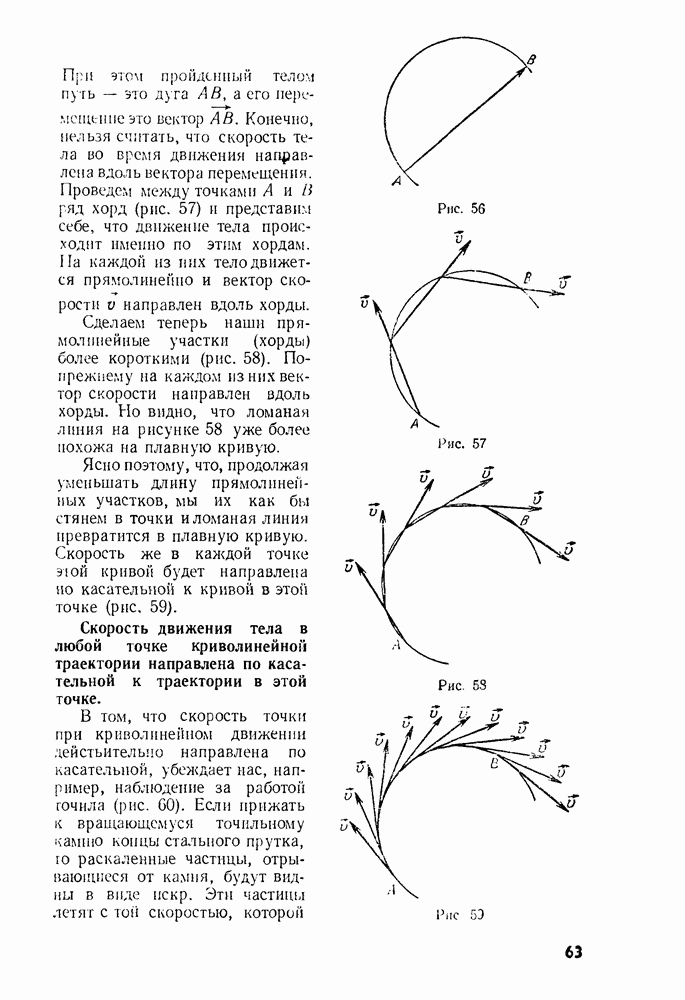
- § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
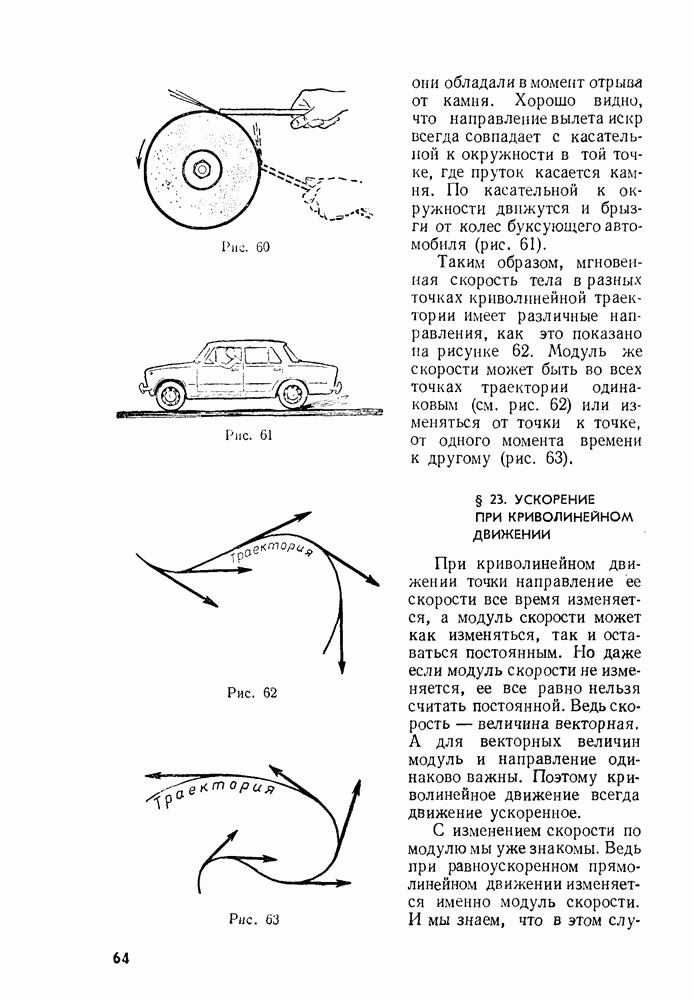
- § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
- § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ
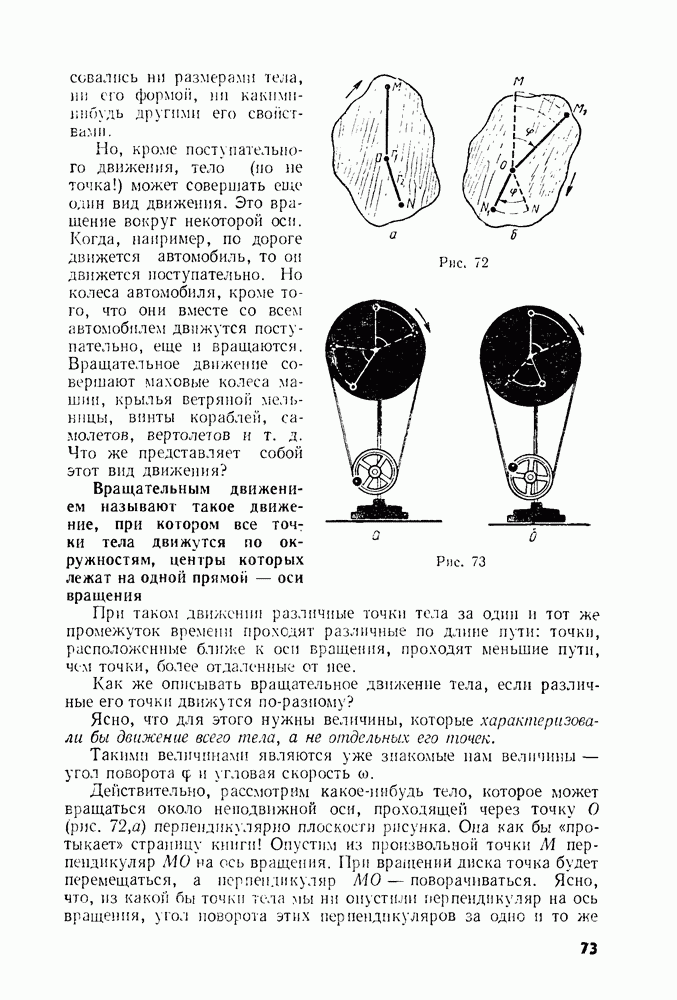
- § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА
- Динамика
- Глава 4. Законы движения
- § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ
- § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ
- § 31. ИНЕРТНОСТЬ ТЕЛ
- § 32. МАССА ТЕЛ
- § 33. МАССА ЛУНЫ
- § 34. СИЛА
- § 35. ВТОРОЙ ЗАКОН НЬЮТОНА
- § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение)
- § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР
- § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА
- § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА
- Глава 5. Силы природы
- § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ
- § 41. СИЛА УПРУГОСТИ
- § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 44. СИЛА ТЯЖЕСТИ
- § 45. ВЕС ТЕЛ
- § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ
- § 47. МАССА ЗЕМЛИ
- § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ
- § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ
- Глава 6. Применение законов движения
- § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ
- § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ
- § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ
- § 54. НЕВЕСОМОСТЬ
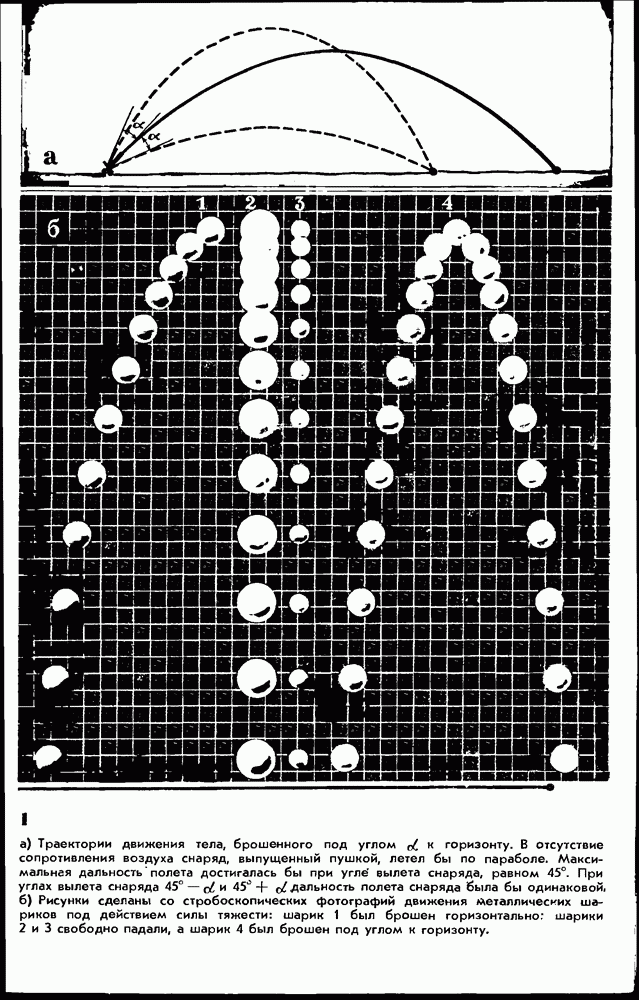
- § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ
- § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО
- § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ
- § 58. ДВИЖЕНИЕ ПЛАНЕТ
- § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ
- § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ
- § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ
- § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ
- § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ
- § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА
- Равновесие тел
- Глава 7. Элементы статики
- § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ
- § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ
- § 67. ПРАВИЛО МОМЕНТОВ
- § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ
- Законы сохранения в механике
- Глава 8. Закон сохранения импульса
- § 70. СИЛА И ИМПУЛЬС
- § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ
- Глава 9. Механическая работа и мощность
- § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ
- § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ
- § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
- § 77. РАБОТА СИЛЫ ТЯЖЕСТИ
- § 78. РАБОТА СИЛЫ УПРУГОСТИ
- § 79. РАБОТА СИЛЫ ТРЕНИЯ
- § 80. МОЩНОСТЬ
- Глава 10. Закон сохранения энергии
- § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА
- § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ
- § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН
- § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
- § 91. СТОЛКНОВЕНИЕ ТЕЛ
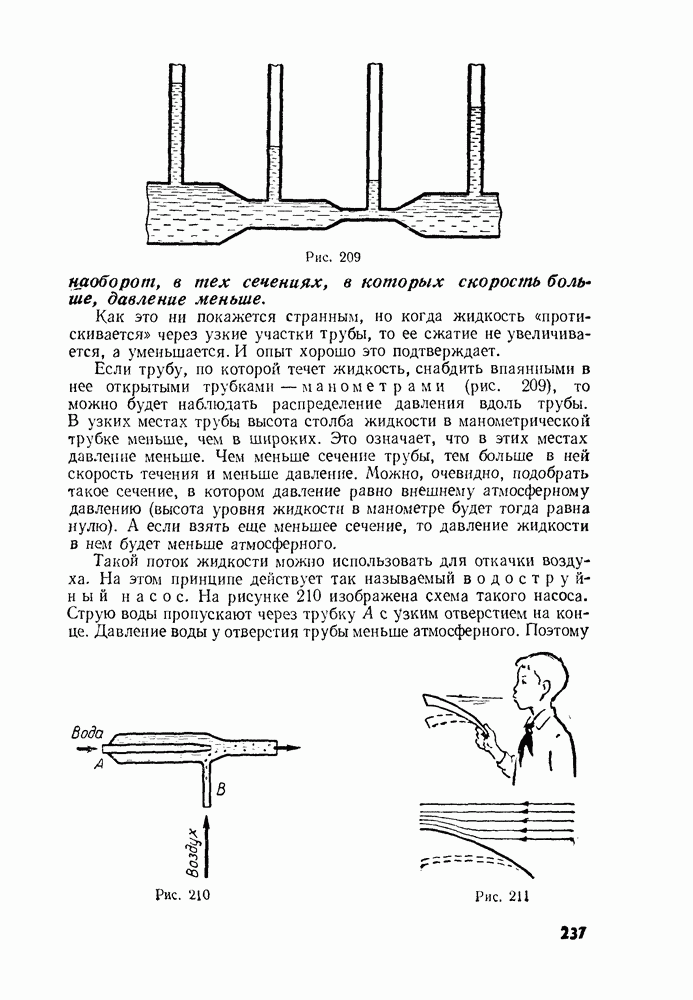
- § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ
- § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ
- Заключение
- Лабораторные работы
- 1. Определение ускорения тела при равноускоренном движении
- 2. Определение коэффициента трения скольжения
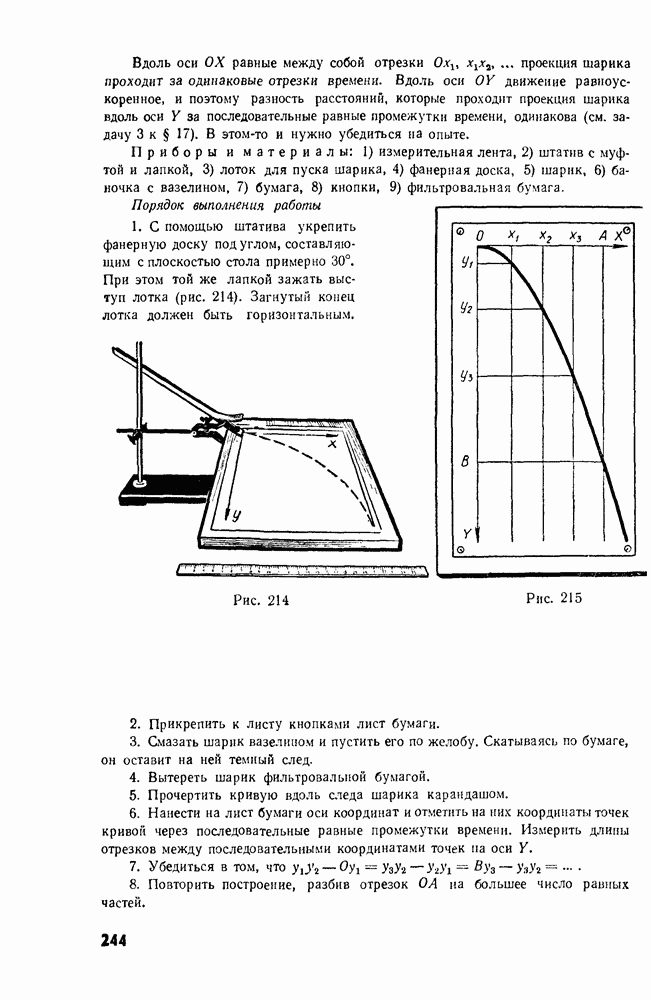
- 3. Изучение движения тела по параболе
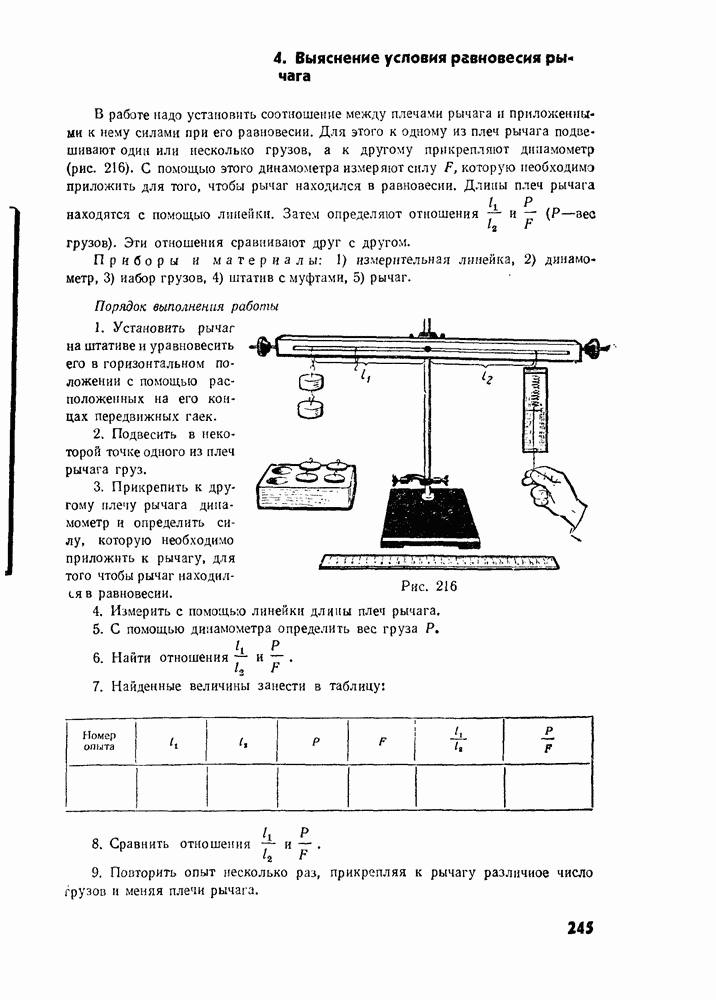
- 4. Выяснение условия равновесия рычага
- 5. Определение центра тяжести плоской пластины
- Ответы к упражнениям