§ 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА

Перемещение — это особая величина. Особая потому, что она задается не только определенным числом, ко и направлением. Таких величин в физике известно много; их называют векторными величинами или просто векторами.

Векторные величины изображают отрезками прямых со стрелками, как это сделано на рисунке 7, а и б. Длина отрезка в определенном масштабе показывает абсолютное значение (модуль) векторной величины, а стрелка указывает ее направление. Векторные величины обозначаются буквами со стрелочкой над ними.

Например, — вектор перемещения. Модуль (или длина) вектора перемещения — число, показывающее, скольким единицам длины

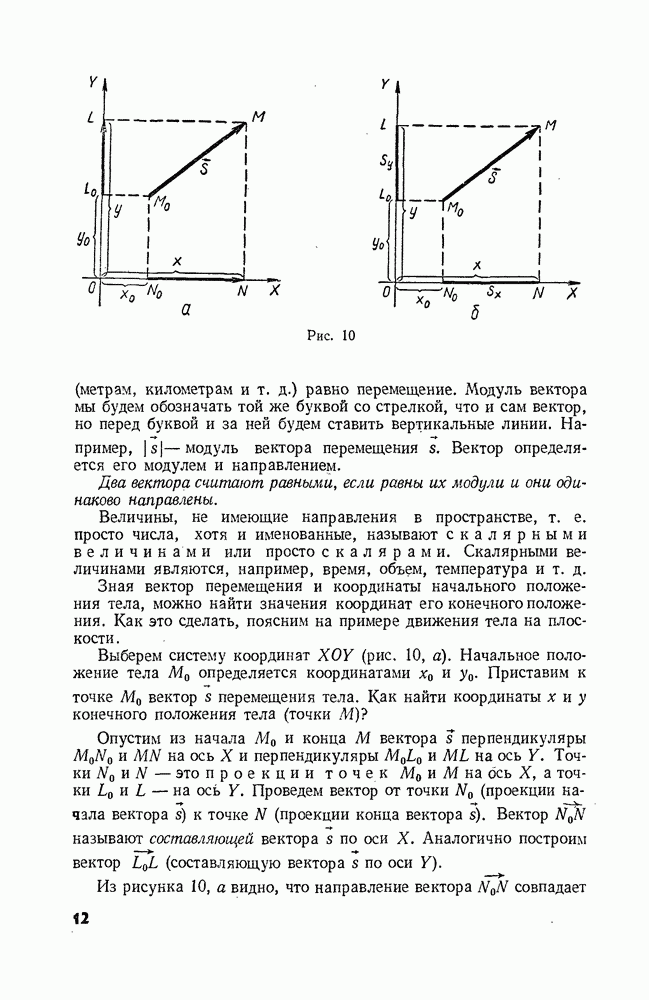
Рис. 10

(метрам, километрам и т. д.) равно перемещение. Модуль вектора мы будем обозначать той же буквой со стрелкой, что и сам вектор, ко перед буквой и за ней будем ставить вертикальные линии. Например, -модуль вектора перемещения Вектор определяется его модулем и направлением.

Два вектора считают равными, если равны их модули и они одинаково направлены.

Величины, не имеющие направления в пространстве, т. е. просто числа, хотя и именованные, называют скалярными величинами или просто скалярами. Скалярными величинами являются, например, время, объем, температура и т. д.

Зная вектор перемещения и координаты начального положения тела, можно найти значения координат его конечного положения. Как это сделать, поясним на примере движения тела на плоскости.

Выберем систему координат (рис. 10, а). Начальное положение тела определяется координатами Приставим к точке вектор перемещения тела. Как найти координаты х и у конечного положения тела (точки М)?

Опустим из качала и конца М вектора перпендикуляры ось X и перпендикуляры на ось Y. Точки — это проекции точек и М на ось X, а точки и L — на ось Y. Проведем вектор от точки (проекции качала вектора ) к точке N (проекции конца вектора ) Вектор называют составляющей вектора по оси X. Аналогично построим вектор (составляющую вектора по оси Y).

Из рисунка 10, а видно, что направление вектора совпадает

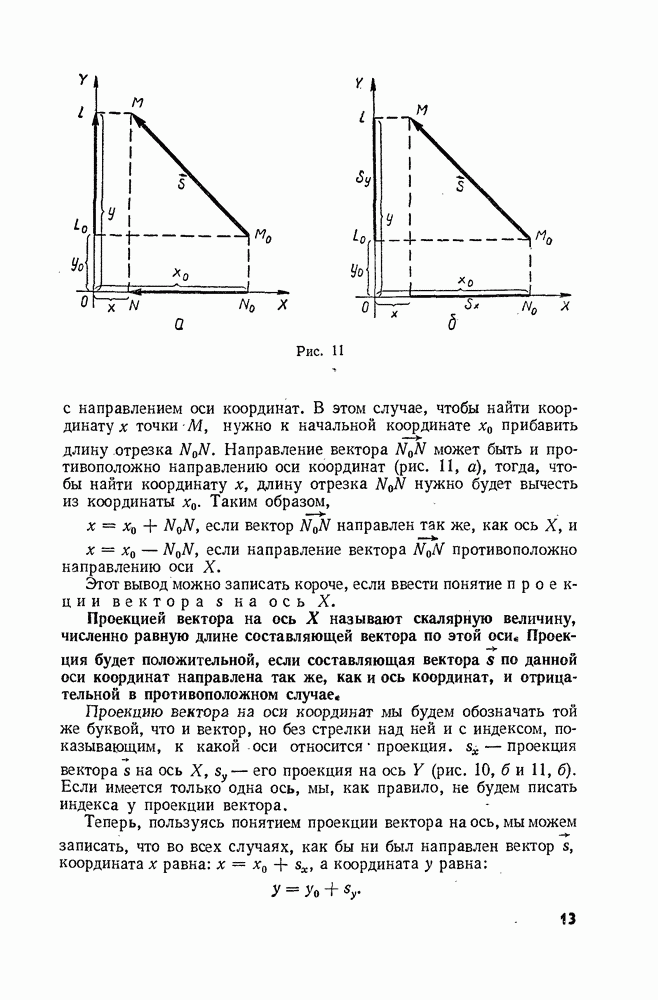
Рис. 11

с направлением оси координат. В этом случае, чтобы найти координату точки М, нужно к начальной координате прибавить длину отрезка Направление вектора может быть и противоположно направлению оси координат (рис. 11, а), тогда, чтобы найти координату длину отрезка нужно будет вычесть из координаты Таким образом,

если вектор направлен так же, как ось X, и если направление вектора противоположно направлению оси X.

Этот вывод можно записать короче, если ввести понятие проекции вектора ось X.

Проекцией вектора на ось X называют скалярную величину, численно равную длине составляющей вектора по этой оси, Проекция будет положительной, если составляющая вектора по данной оси координат направлена так же, как и ось координат, и отрицательной в противоположном случае.

Проекцию вектора оси координат мы будем обозначать той же буквой, что и вектор, но без стрелки над ней и с индексом, показывающим, к какой оси откосится проекция. — проекция вектора на ось его проекция на ось Y (рис. 10, б и 11, б). Если имеется только одна ось, мы, как правило, не будем писать индекса у проекции вектора.

Теперь, пользуясь понятием проекции вектора на ось, мы можем записать, что во всех случаях, как бы ни был направлен вектор координата равна: а координата у равна:

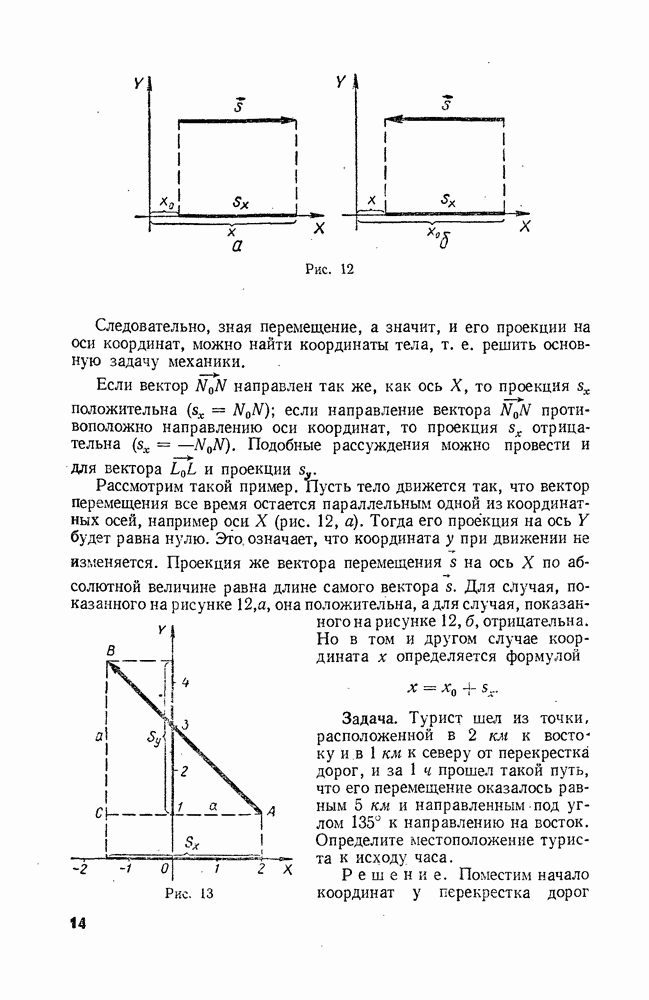
Рис. 12

Следовательно, зная перемещение, а значит, и его проекции на оси координат, можно найти координаты тела, т. е. решить основную задачу механики.

Если вектор направлен так же, как ось X, то проекция положительна если направление вектора противоположно направлению оси координат, то проекция отрицательна Подобные рассуждения можно провести и для вектора и проекции

Рассмотрим такой пример. Пусть тело движется так, что вектор перемещения все время остается параллельным одной из координатных осей, например оси X (рис. 12, а). Тогда его проекция на ось Y будет равна нулю. Это, означает, что координата у при движении не изменяется. Проекция же вектора перемещения на ось X по абсолютной величине равна длине самого вектора Для случая, показанного на рисунке 12,а, она положительна, а для случая, показанного на рисунке 12, б, отрицательна. Но в том и другом случае координата определяется формулой

Задача. Турист шел из точки, расположенной в 2 км к востоку и в 1 км к северу от перекрестка дорог, и за 1 ч прошел такой путь, что его перемещение оказалось равным 5 и и направленным под углом 135° к направлению на восток. Определите местоположение туриста к исходу часа.

Решение. Поместим начало координат у перекрестка дорог

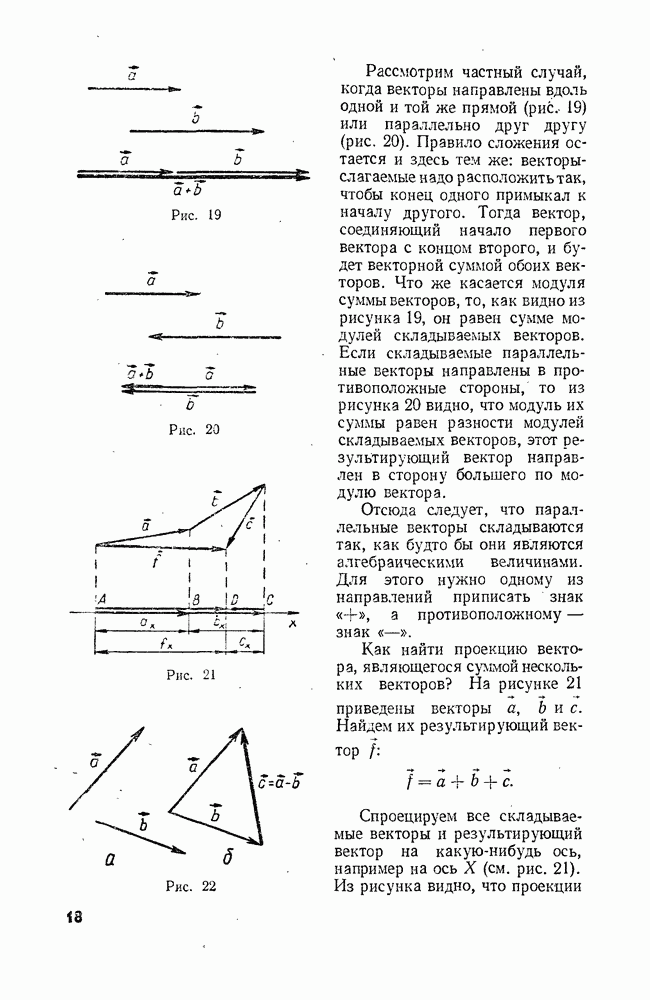
Рис. 13

Рис. 14

и направим оси X и соответственно на восток и на север (рис. 13). Начальное положение туриста (точка А) задано координатами км и км. Из этой точки проведем под углом 135° к оси X вектор перемещения Нам надо найти координаты X и у точки В.

Спроецируем вектор на оси X и Проекции вектора перемещения, как видно из рисунка, равны по абсолютной величине длинам катетов прямоугольного равнобедренного треугольника Обозначим катет треугольника через а, тогда согласно теореме Пифагора

или

Отсюда

Конечные координаты туриста мы найдем по формулам:

Подставив в эти формулы соответствующие значения, получим:

Упражнение 3

1. Пользуясь прямоугольной системой координат, изобразите вектор перемещения, направленный под углом 45° на северо-восток от точки, расположенной в 1 км к востоку и в 2 км к северу от развилки дорог; модуль Еектора перемещения равен 25 км. Найдите координаты конца вектора.

2. Тело переместилось из точки с координатами в точку с координатами Найдите вектор перемещения тела и его проекции на оси координат.

3. Какие векторы называются равными? Что можно сказать о проекциях равных векторов?

4. Как связан вектор перемещения движущегося тела с его координатами?

5. Определите знаки проекций на ось X векторов перемещения, изображенных на рисунке 14.