| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
Если тело находится в равновесии, то это значит, что сумма приложенных к нему сил равна нулю и сумма моментов этих сил относительно оси, вокруг которой тело может вращаться, также равна нулю. Но здесь возникает такой вопрос: а устойчиво ли равновесие?
С первого взгляда видно, например, что положение равновесия шарика на вершине выпуклой подставки (рис. 170) неустойчиво: малейшее отклонение шарика от его равновесного положения приведет к тому, что он скатится вниз. А вот тот же шарик помещен на вогнутой подставке (рис. 171). Его не так-то просто заставить покинуть свое место. Положение шарика можно считать устойчивым. В чем тут дело? Ведь в обоих случаях шарик находится в равновесии: сила тяжести  равна по абсолютной величине противоположно направленной силе упругости (силе реакции)
равна по абсолютной величине противоположно направленной силе упругости (силе реакции)  действующей со стороны опоры (рис. 172 и 173).
действующей со стороны опоры (рис. 172 и 173).
Все дело оказывается именно в том малейшем отклонении, о котором мы упоминали. При самом малом отклонении, которое всегда происходит из-за случайных сотрясений, воздушных течений и других причин, равновесие шарика нарушается. На рисунке 172 видно, что, как только шарик на выпуклой подставке покинул

Рис. 170

Рис. 171
свсе место, сила тяжести  перестает уравновешиваться силой
перестает уравновешиваться силой  со стороны опоры (сила
со стороны опоры (сила  всегда направлена перпендикулярно поверхности соприкосновения шарика и подставки). Геометрическая сумма (равнодействующая) силы тяжести
всегда направлена перпендикулярно поверхности соприкосновения шарика и подставки). Геометрическая сумма (равнодействующая) силы тяжести  и силы реакции
и силы реакции  опоры, т. е. сила
опоры, т. е. сила  направлена так, что шарик еще больше удалится от положения равновесия.
направлена так, что шарик еще больше удалится от положения равновесия.
Иное дело на вогнутой подставке (рис. 173). При малом отклонении от первоначального положения здесь тоже нарушается равновесие. Сила упругости со стороны опоры и здесь уже не будет уравновешивать силу тяжести. Но теперь равнодействующая  направлена так, что тело вернется в прежнее положение. В этом и состоит условие устойчивости равновесия.
направлена так, что тело вернется в прежнее положение. В этом и состоит условие устойчивости равновесия.
Равновесие тела устойчиво, если при малом отклонении от равновесного положения возникает сила, возвращающая тело к положению равновесия.
Равновесие неустойчиво, если при малом отклонении тела от положения равновесия возникает сила, удаляющая тело от этого положения.
Устойчивое и неустойчивое положения равновесия отличаются друг от друга еще и положением центра тяжести тела. Когда шарик находится в положении неустойчивого равновесия, его центр тяжести выше, чем когда он находится в любом соседнем положений. Наоборот, у шарика на вогнутой опоре центр

Рис. 172

Рис. 173

Рис. 174
тяжести в положении устойчивого равновесия ниже, чем в любом из соседних положений. Значит, для устойчивого равновесия центр тяжести тела должен находиться в самом низком из возможных для него положений. Это определение устойчивости и неустойчивости тесно связано с предыдущим.
Возможно и такое положение равновесия, когда малые отклонения от него не приводят к каким-либо изменениям в состоянии тела. Таково, например, положение шарика на плоской опоре (рис. 174). Ясно, что при любом изменении положения шарика оно остается равновесным. Такое равновесие называют безразличным.
Если тело имеет ось вращения, то его устойчивость или неустойчивость зависит от того, возникает ли момент силы, возвращающей тело к положению равновесия или, наоборот, удаляющей тело от этого положения.
В качестве примера рассмотрим обыкновенную линейку, укрепленную на стержне, проходящем через отверстие вблизи ее конца, как показано на рисунке 175, а. В таком положении линейка находится в равновесии, потому что сила тяжести  проходящая через ее центр тяжести, уравновешивается силой реакции
проходящая через ее центр тяжести, уравновешивается силой реакции  (силой упругости) со стороны стержня (опоры). Но если отклонить линейку от вертикального положения (рис. 175, б), то сила тяжести уже не уравновешивается реакцией опоры. Момент
(силой упругости) со стороны стержня (опоры). Но если отклонить линейку от вертикального положения (рис. 175, б), то сила тяжести уже не уравновешивается реакцией опоры. Момент

Рис. 175

Рис. 170

Рис. 177
силы тяжести относительно оси теперь не равен нулю (рис. 175, б). Вследствие этого сила  возвратит линейку (после нескольких колебаний) в исходное положение. Поэтому положение линейки, показанное на рисунке 175, а, устойчиво. Но попытаемся подвесить ту же линейку на стержне так, как это показано на рисунке 176, а. Опыт убедит нас в том, что это сделать невозможно и нетрудно понять почему. Из рисунка 176, а видно, что при вертикальном положении линейки сила тяжести
возвратит линейку (после нескольких колебаний) в исходное положение. Поэтому положение линейки, показанное на рисунке 175, а, устойчиво. Но попытаемся подвесить ту же линейку на стержне так, как это показано на рисунке 176, а. Опыт убедит нас в том, что это сделать невозможно и нетрудно понять почему. Из рисунка 176, а видно, что при вертикальном положении линейки сила тяжести  уравновешивается силой упругости
уравновешивается силой упругости  (реакцией стержня), действующей на линейку со стороны стержня. Линейка должна находиться в равновесии. Но из рисунка 176, б видно, что при любом отклонении линейки от вертикального положения возникает момент силы тяжести. Вследствие этого линейка повернется так, чтобы занять положение, показанное на рисунке 176, в. Значит, равновесие линейки, соответствующее рисунку 176, а, неустойчиво.
(реакцией стержня), действующей на линейку со стороны стержня. Линейка должна находиться в равновесии. Но из рисунка 176, б видно, что при любом отклонении линейки от вертикального положения возникает момент силы тяжести. Вследствие этого линейка повернется так, чтобы занять положение, показанное на рисунке 176, в. Значит, равновесие линейки, соответствующее рисунку 176, а, неустойчиво.
Выходит, что равновесие тела при наличии оси вращения устойчиво, если центр тяжести тела находится ниже оси вращения.
Понятно, что линейка, подвешенная на стержне, проходящем через отверстие в ее центре тяжести, будет находиться в безразличном равновесии (рис. 177). В этом случае при любом положении линейки момент силы тяжести, приложенной к ней, относительно оси вращения равен нулю.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о движении
- § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА
- § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ
- § 3. ПЕРЕМЕЩЕНИЕ
- § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА
- § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ
- § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ
- § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
- § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
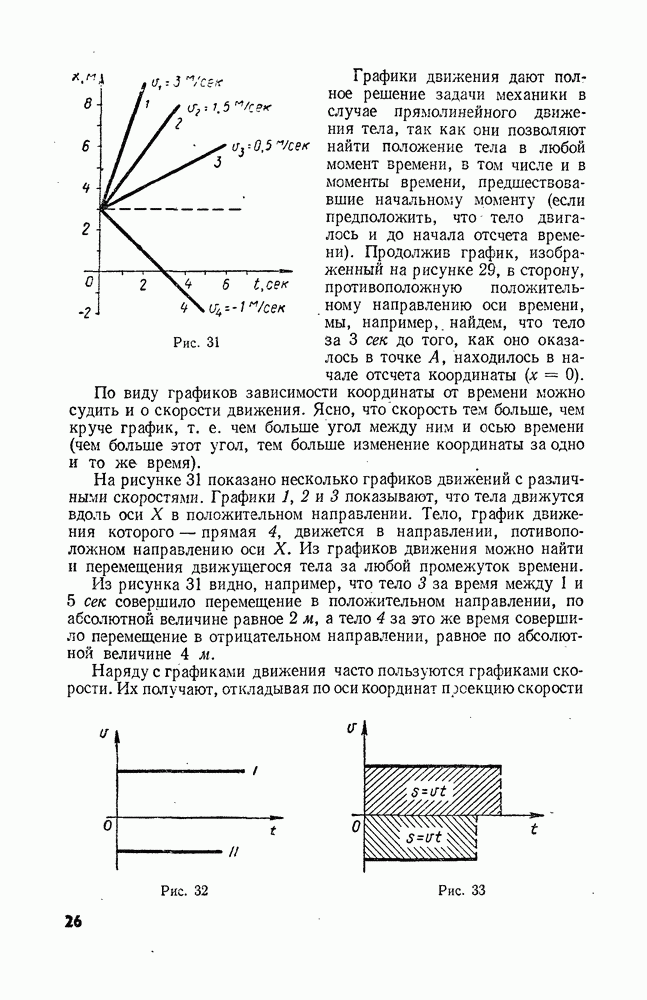
- § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ
- § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
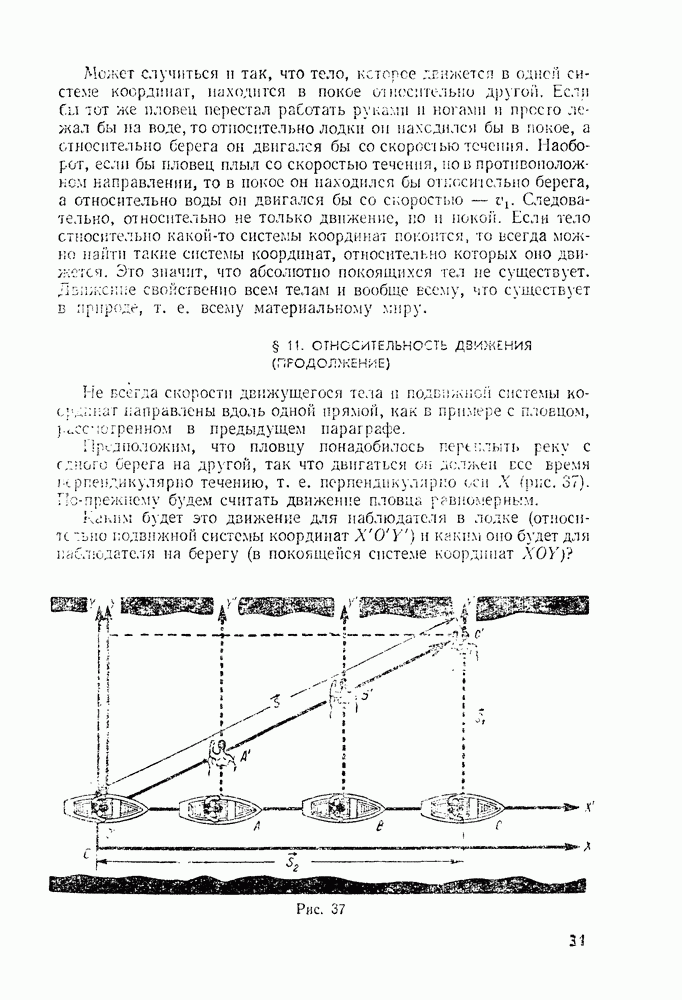
- § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ)
- § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ
- Глава 2. Прямолинейное неравномерное движение
- § 13. СРЕДНЯЯ СКОРОСТЬ
- § 14. МГНОВЕННАЯ СКОРОСТЬ
- § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ
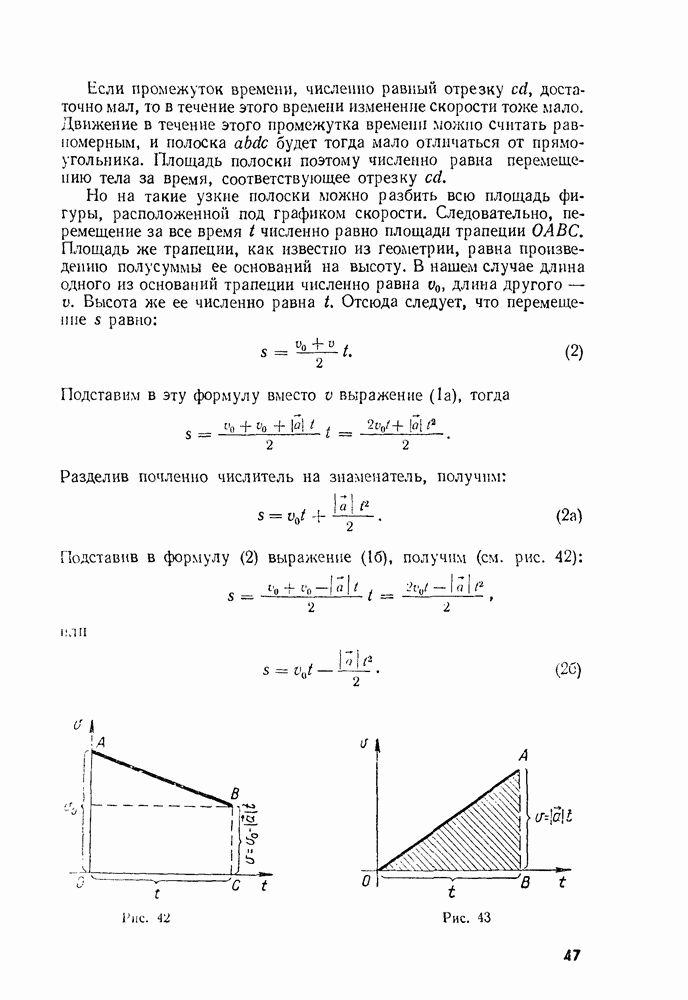
- § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
- § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ
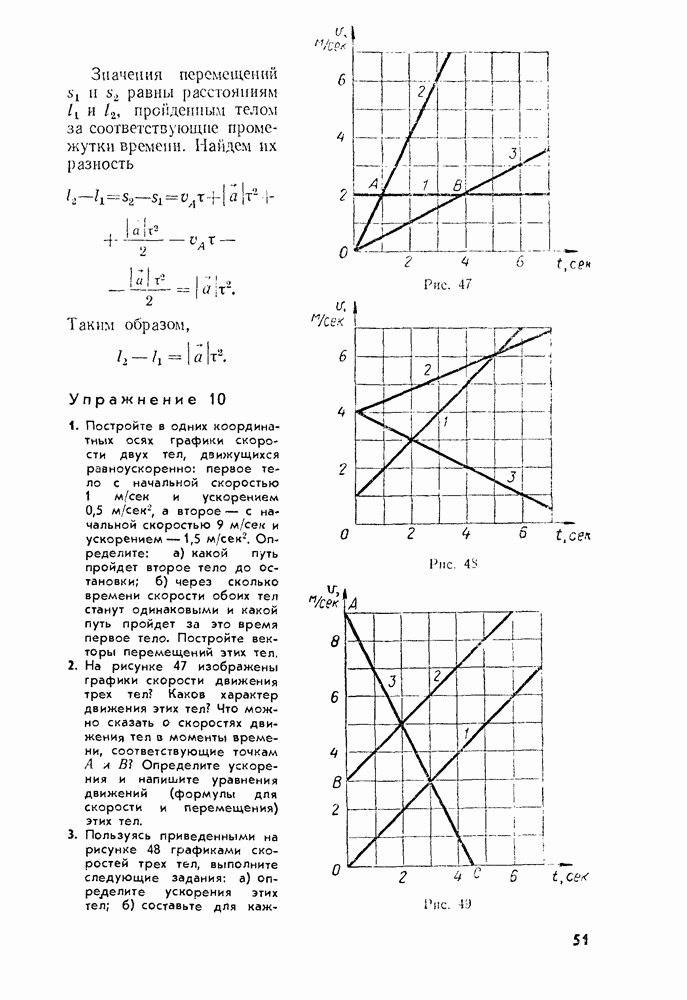
- § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ
- § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
- § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
- Глава 3. Криволинейное движение
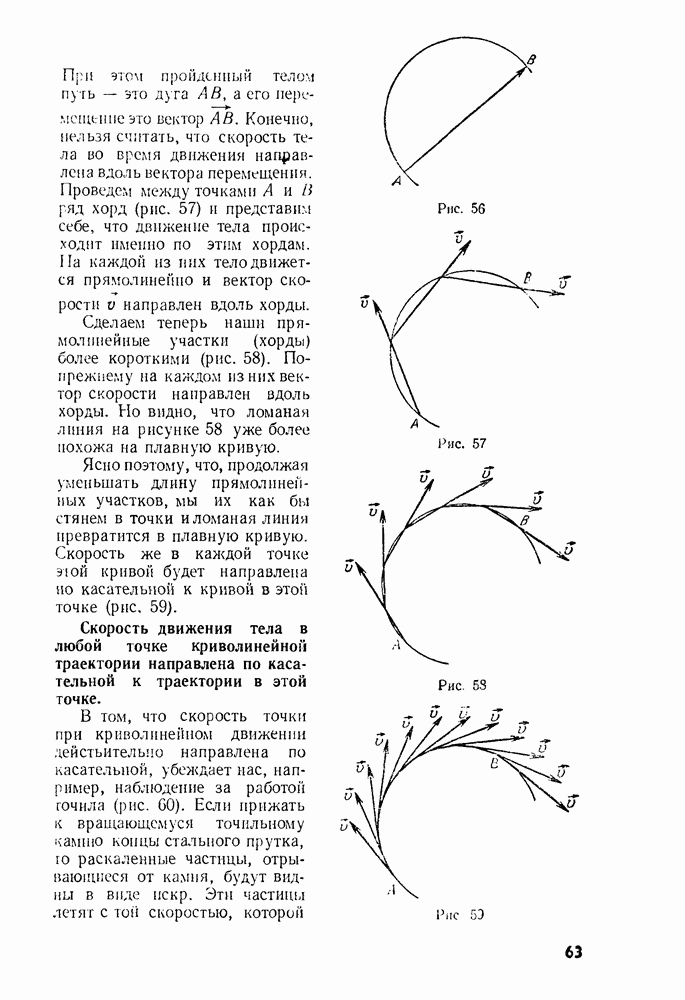
- § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
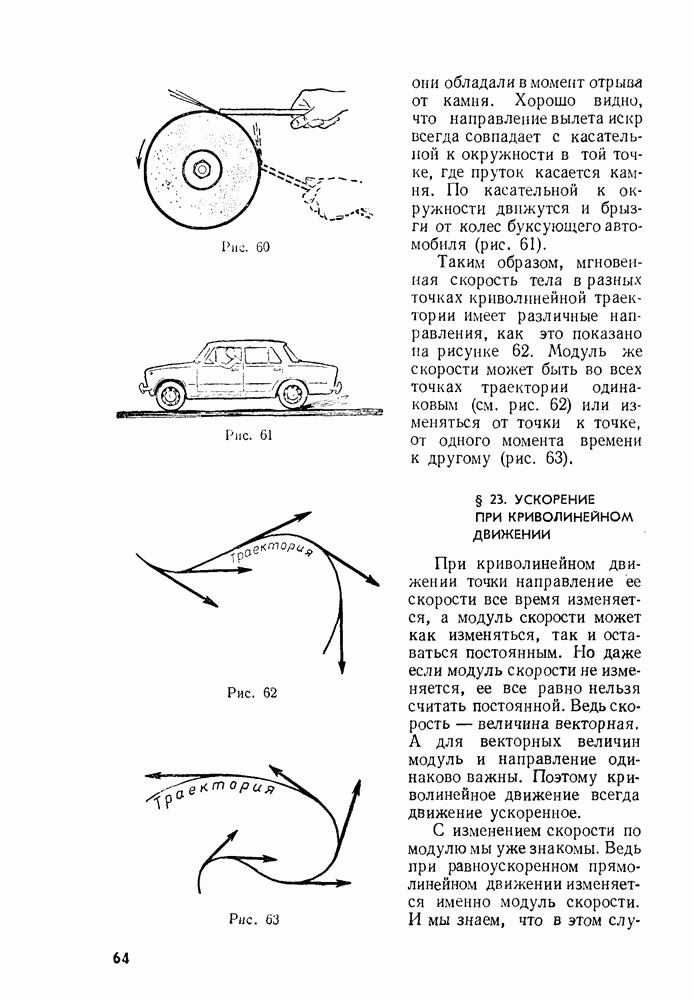
- § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
- § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ
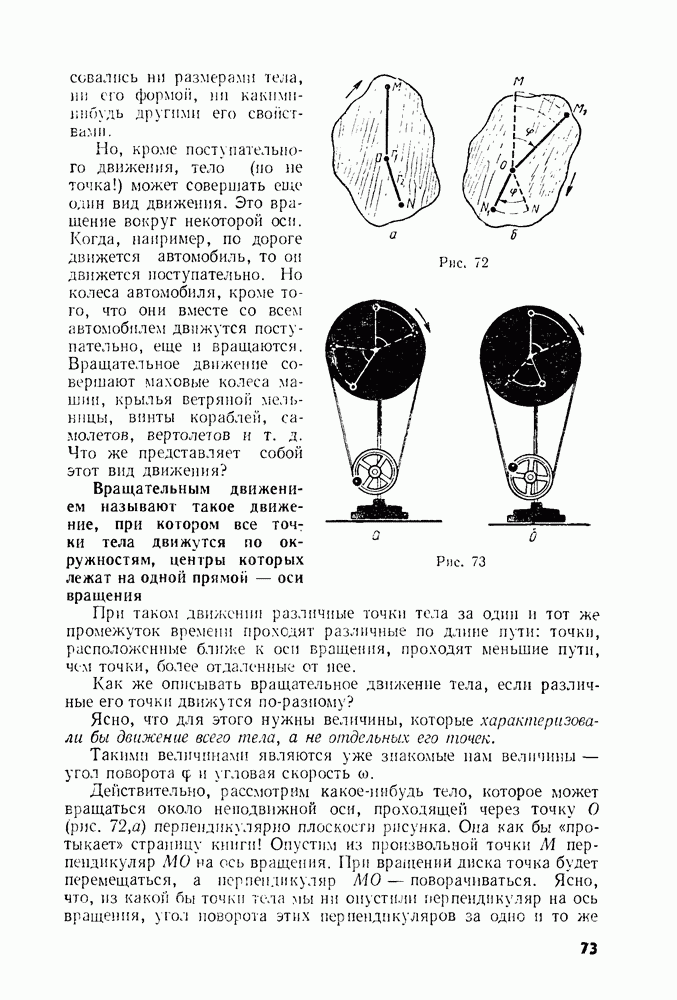
- § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА
- Динамика
- Глава 4. Законы движения
- § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ
- § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ
- § 31. ИНЕРТНОСТЬ ТЕЛ
- § 32. МАССА ТЕЛ
- § 33. МАССА ЛУНЫ
- § 34. СИЛА
- § 35. ВТОРОЙ ЗАКОН НЬЮТОНА
- § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение)
- § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР
- § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА
- § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА
- Глава 5. Силы природы
- § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ
- § 41. СИЛА УПРУГОСТИ
- § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 44. СИЛА ТЯЖЕСТИ
- § 45. ВЕС ТЕЛ
- § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ
- § 47. МАССА ЗЕМЛИ
- § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ
- § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ
- Глава 6. Применение законов движения
- § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ
- § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ
- § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ
- § 54. НЕВЕСОМОСТЬ
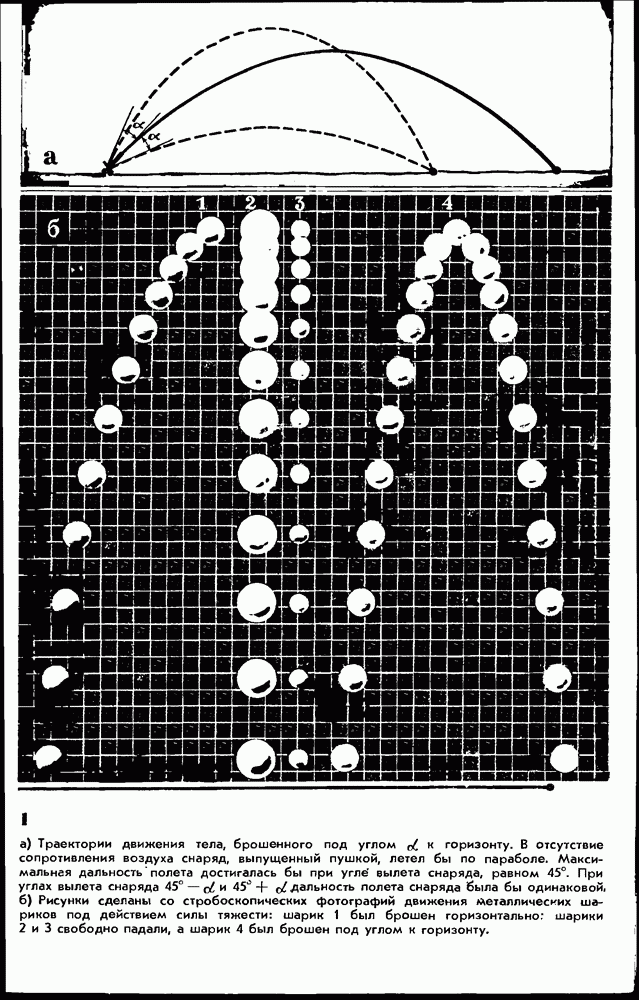
- § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ
- § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО
- § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ
- § 58. ДВИЖЕНИЕ ПЛАНЕТ
- § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ
- § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ
- § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ
- § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ
- § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ
- § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА
- Равновесие тел
- Глава 7. Элементы статики
- § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ
- § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ
- § 67. ПРАВИЛО МОМЕНТОВ
- § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ
- Законы сохранения в механике
- Глава 8. Закон сохранения импульса
- § 70. СИЛА И ИМПУЛЬС
- § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ
- Глава 9. Механическая работа и мощность
- § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ
- § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ
- § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
- § 77. РАБОТА СИЛЫ ТЯЖЕСТИ
- § 78. РАБОТА СИЛЫ УПРУГОСТИ
- § 79. РАБОТА СИЛЫ ТРЕНИЯ
- § 80. МОЩНОСТЬ
- Глава 10. Закон сохранения энергии
- § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА
- § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ
- § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН
- § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
- § 91. СТОЛКНОВЕНИЕ ТЕЛ
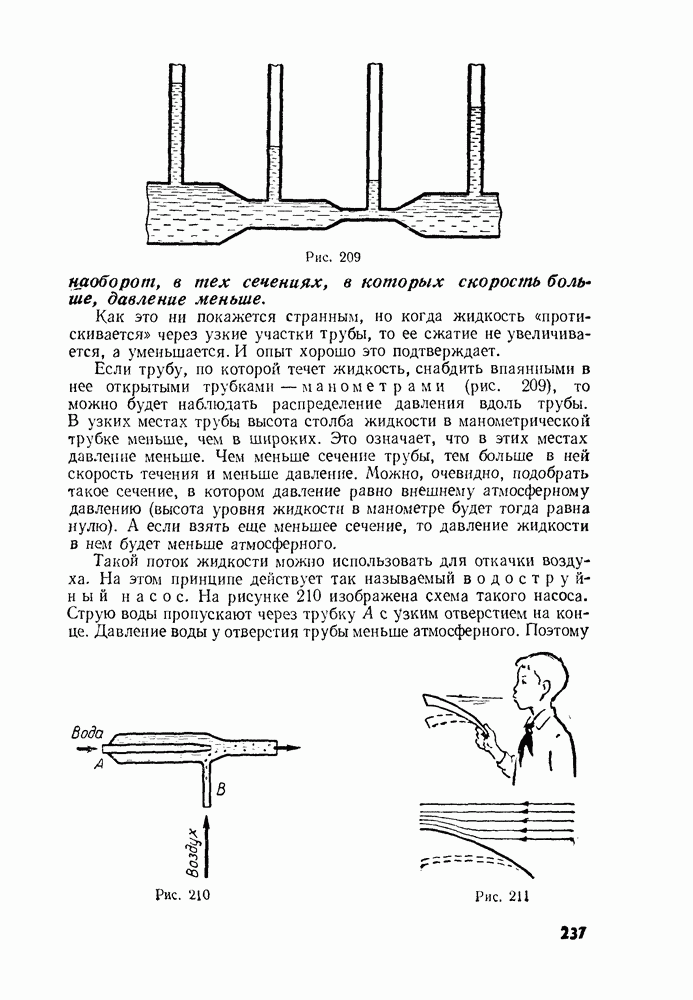
- § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ
- § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ
- Заключение
- Лабораторные работы
- 1. Определение ускорения тела при равноускоренном движении
- 2. Определение коэффициента трения скольжения
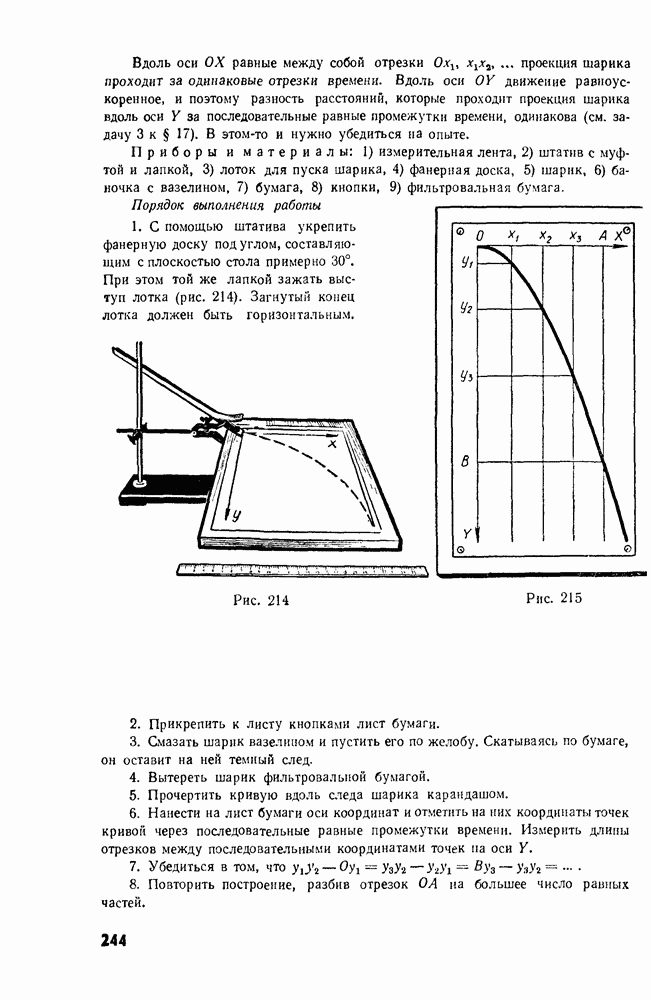
- 3. Изучение движения тела по параболе
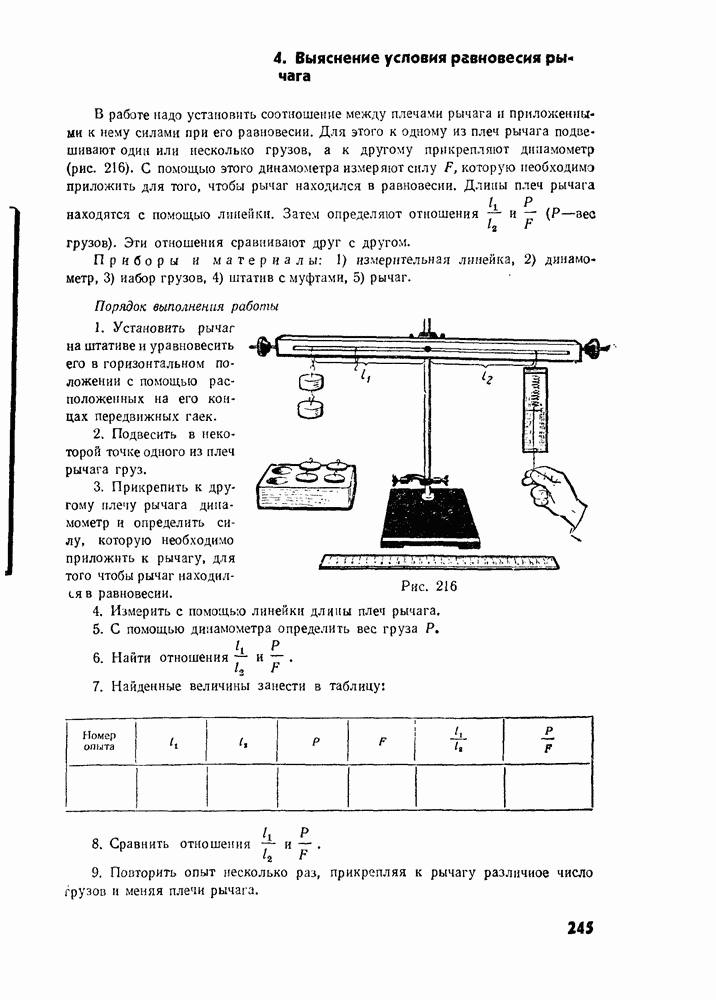
- 4. Выяснение условия равновесия рычага
- 5. Определение центра тяжести плоской пластины
- Ответы к упражнениям