| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 67. ПРАВИЛО МОМЕНТОВ
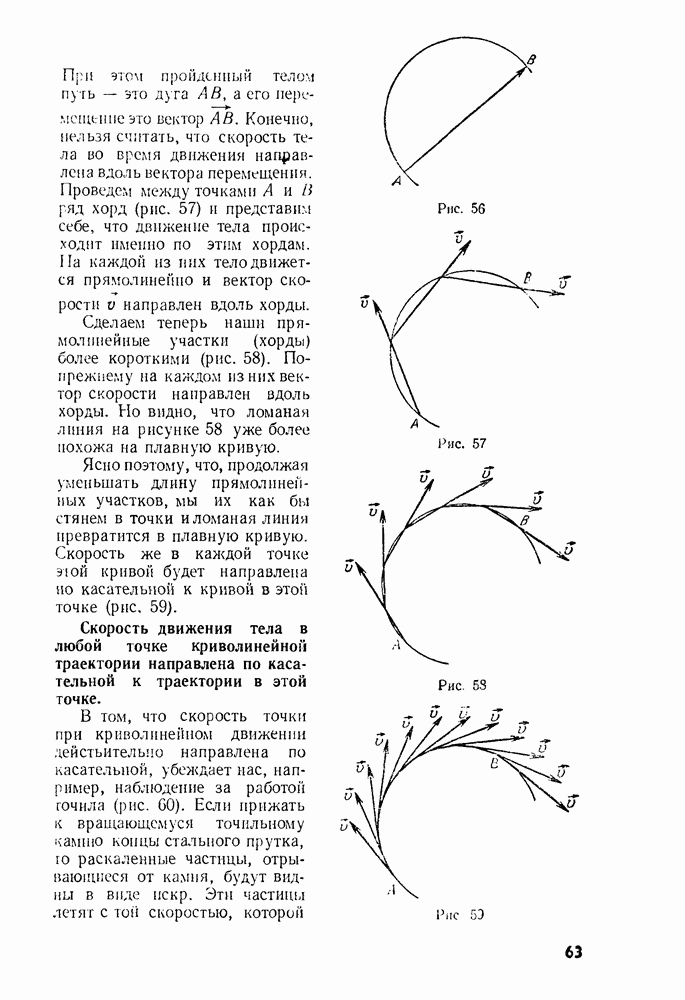
Из того, что было сказано в предыдущем параграфе, становится ясно, почему тело при условиях, показанных на рисунке 163, б, находится в равновесии.
Поступательно тело не может двигаться, потому что ось закреплена. Поворачиваться же оно не может потому, что моменты сил  и
и  равны друг другу по абсолютному значению, но одна сила может повернуть тело по часовой стрелке, а другая — против. И если приписать моментам сил, вращающим это тело в противоположных направлениях, разные знаки, то алгебраическая сумма этих двух моментов окажется равной нулю.
равны друг другу по абсолютному значению, но одна сила может повернуть тело по часовой стрелке, а другая — против. И если приписать моментам сил, вращающим это тело в противоположных направлениях, разные знаки, то алгебраическая сумма этих двух моментов окажется равной нулю.
Тело, способное вращаться вокруг закрепленной оси, находится в равновесии, если сумма моментов сил относительно закрепленной оси, вращающих тело по часовой стрелке, равна сумме моментов сил относительно той же оси, вращающих его против часовой стрелки.
Это и есть правило моментов — условие равновесия тела, имеющего закрепленную ось вращения.
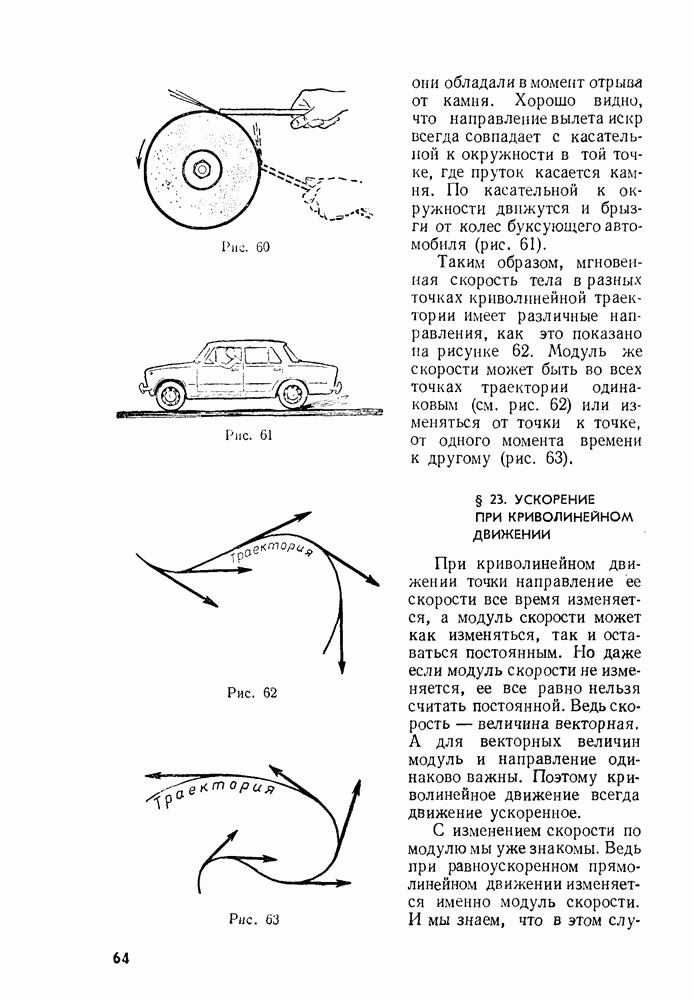
Момент силы зависит от двух величин: от значения самой силы и длины плеча. Один и тот же момент силы может быть создан малой силой, плечо которой велико, и большой силой с малым плечом. Если, например, пытаться закрыть дверь, толкая ее

Рис. 164
поблизости от петель, то этому с успехом сможет противодействовать ребенок, который догадается толкать ее в другую сторону, приложив силу поближе к краю, и дверь останется в покое (рис. 164).
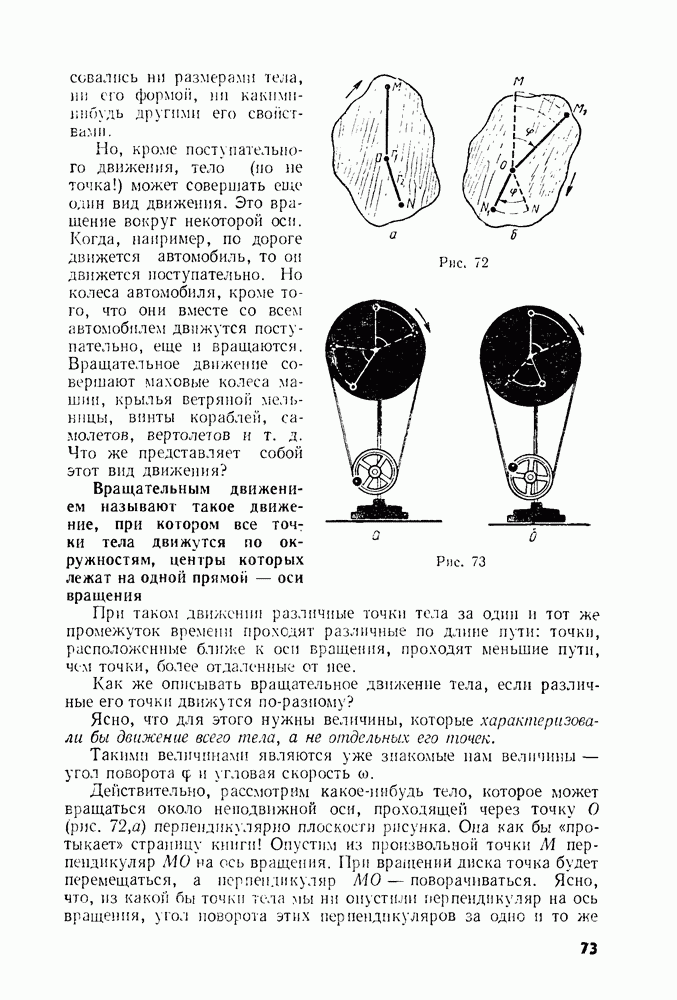
В справедливости правила моментов можно убедиться на опытах, которые проводятся с прибором, изображенным на рисунке 165. Он представляет собой диск А, укрепленный на оси, проходящей через его центр. На диске нанесены окружности, радиусы которых последовательно увеличиваются на 1 см, так что радиус первой, ближайшей к центру окружности равен 1 см, Второй — 2 см и т. д. На окружностях по нескольким диаметрам диска вбиты гвоздики, к которым можно привязывать нити с гирями. Нити переброшены через блоки В и С. Привязывая нити к гвоздикам на разных окружностях и подвешивая к ним различные грузы, создают различные моменты сил, действие которых можно уравновесить моментом силы тяжести третьего груза, подвешенного непосредственно к диску. При этом легко убедиться, что диск находится в равновесии, т. е. не поворачивается, когда алгебраическая сумма моментов всех трех сил равна нулю.
Величина момента силы, с которым действует каждый из грузов, определяется произведением силы тяжести груза на длину перпендикуляра, опущенного из центра диска на нить. Длина же этого перпендикуляра, выраженная в сантиметрах, равна номеру окружности, которой касается нить в точке, куда опущен перпендикуляр.

Рис. 165

Рис. 166

Рис. 167
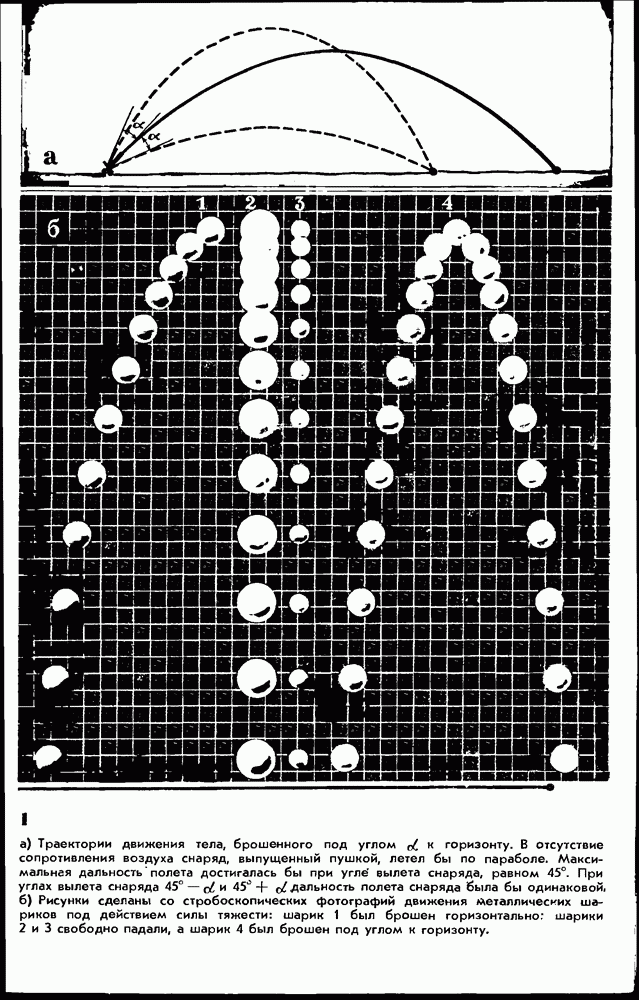
Нетрудно понять, что из правила моментов следует знаменитое правило рычага: рычаг находится в равновесии, когда действующие на него силы обратно пропорциональны плечам. Но это не что иное, как другое выражение правила моментов! Не следует думать, что к рычагу должны быть приложены обязательно параллельные силы. На рисунке 166 показан пример рычага, к которому приложены взаимно перпендикулярные силы 
Теперь мы можем сформулировать общее условие равновесия тела:
Для того, чтобы тело находилось в равновесии, необходимо, чтобы были равны нулю геометрическая сумма приложенных к телу сил и сумма моментов этих сил относительно оси вращения.
Задача. Однородный стержень массой 2 кг прикреплен своим нижним концом к шарниру (рис. 167). К другому его концу подвешен груз массой 2 кг. Стержень удерживается в равновесии горизонтальной оттяжкой, прикрепленной к неподвижной вертикальной стойке. Пользуясь числами, указанными на рисунке, найдите силу натяжения оттяжки.
Решение. На стержень действуют четыре силы: сила тяжести, приложенная к его середине, сила тяжести груза  сила
сила  упругости оттяжки и сила
упругости оттяжки и сила  упругости в шарнире. Осью вращения служит шарнир у нижнего конца стержня. Из перечисленных сил только первые три создают вращающие моменты относительно этой оси. Линия действия силы реакции в шарнире проходит через ось шарнира, и ее момент равен нулю. Из трех указанных сил только одна сила упругости оттяжки поворачивает стержень против часовой стрелки. Две другие вращают его по часовой стрелке. По правилу моментов
упругости в шарнире. Осью вращения служит шарнир у нижнего конца стержня. Из перечисленных сил только первые три создают вращающие моменты относительно этой оси. Линия действия силы реакции в шарнире проходит через ось шарнира, и ее момент равен нулю. Из трех указанных сил только одна сила упругости оттяжки поворачивает стержень против часовой стрелки. Две другие вращают его по часовой стрелке. По правилу моментов

Решая это уравнение, получаем: 

Рис. 168

Рис. 169
Упражнение 41
1. На рисунке 168 изображен однородный стержень, ось вращения которого находится в точке О. На нем в точках А и В подвешены грузы массой
0,2 кг и 0,4 кг соответственно. Какой массы груз должен быть подвешен в точке С, чтобы стержень находился в равновесии?
2. К однородному стержню, который может вращаться вокруг оси О, прикреплен в точке А груз массой 0,8 кг (рис. 169). Какой массы груз нужно прикрепить в точке В, чтобы стержень был в равновесии, если масса стержня 400 г?
3. Приведите примеры практического использования рычага.
4. Покажите, что правило рычага следует из правила моментов.
5. При каком условии рычаг, показанный на рисунке 166, находится в равновесии?
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о движении
- § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА
- § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ
- § 3. ПЕРЕМЕЩЕНИЕ
- § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА
- § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ
- § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ
- § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
- § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
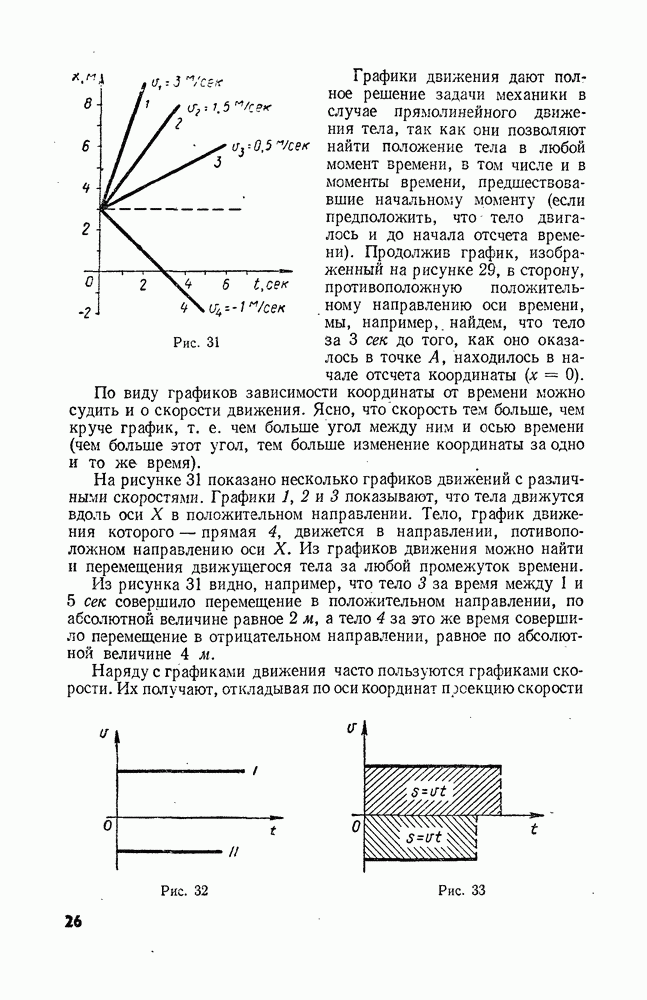
- § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ
- § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
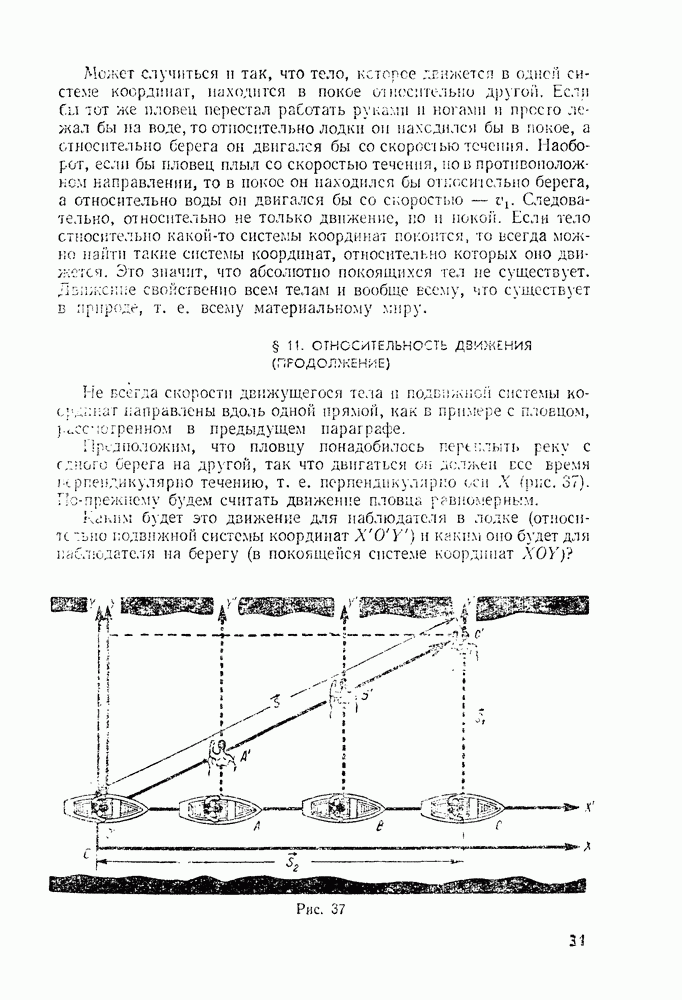
- § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ)
- § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ
- Глава 2. Прямолинейное неравномерное движение
- § 13. СРЕДНЯЯ СКОРОСТЬ
- § 14. МГНОВЕННАЯ СКОРОСТЬ
- § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ
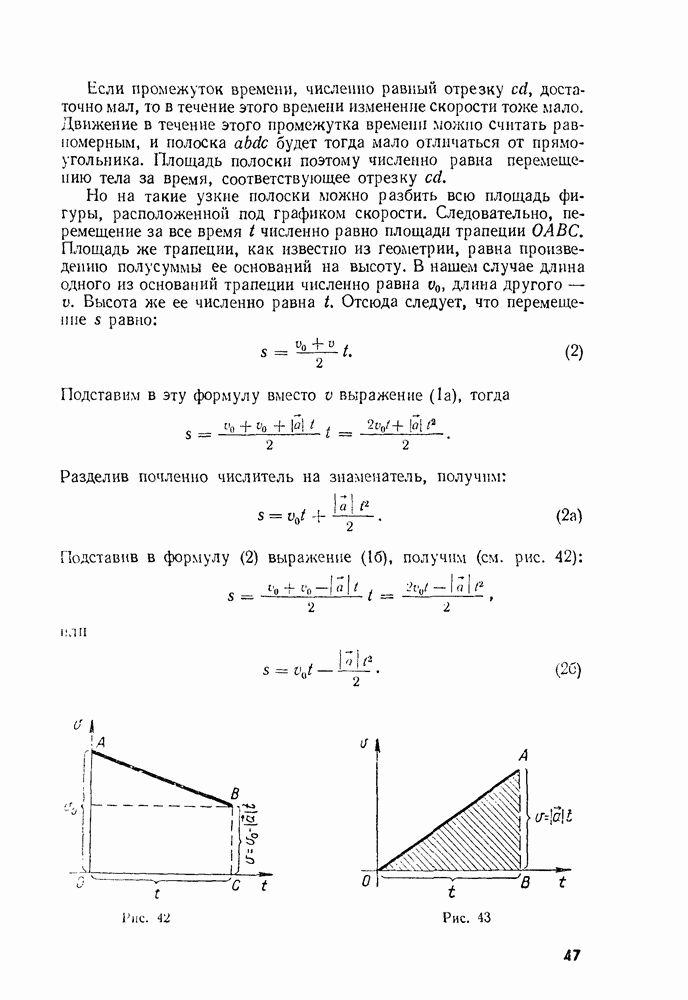
- § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
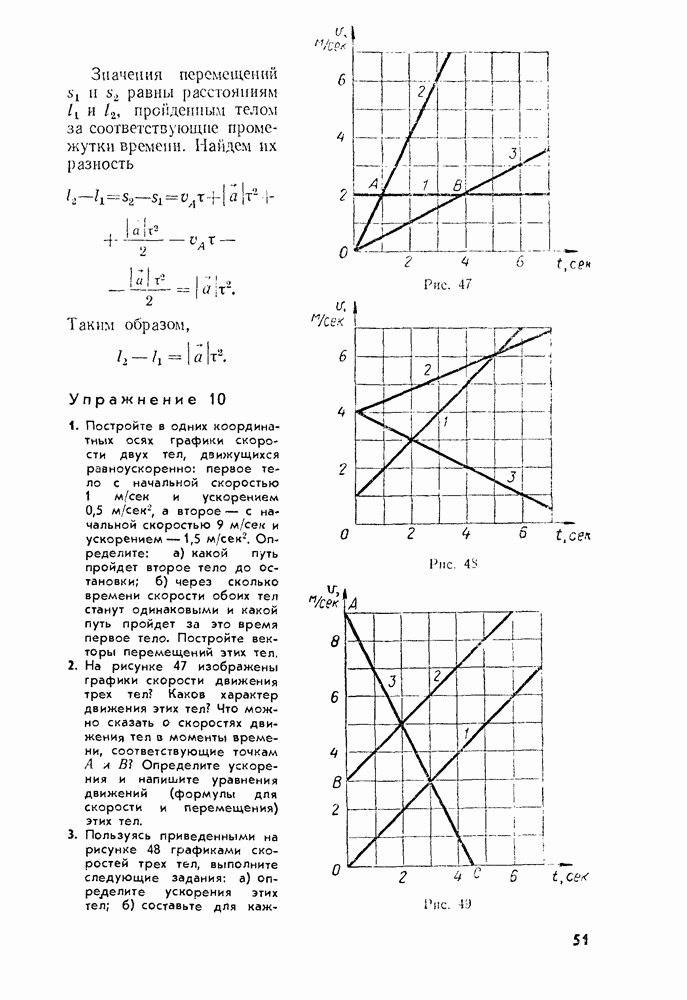
- § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ
- § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ
- § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
- § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
- Глава 3. Криволинейное движение
- § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
- § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ
- § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА
- Динамика
- Глава 4. Законы движения
- § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ
- § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ
- § 31. ИНЕРТНОСТЬ ТЕЛ
- § 32. МАССА ТЕЛ
- § 33. МАССА ЛУНЫ
- § 34. СИЛА
- § 35. ВТОРОЙ ЗАКОН НЬЮТОНА
- § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение)
- § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР
- § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА
- § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА
- Глава 5. Силы природы
- § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ
- § 41. СИЛА УПРУГОСТИ
- § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 44. СИЛА ТЯЖЕСТИ
- § 45. ВЕС ТЕЛ
- § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ
- § 47. МАССА ЗЕМЛИ
- § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ
- § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ
- Глава 6. Применение законов движения
- § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ
- § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ
- § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ
- § 54. НЕВЕСОМОСТЬ
- § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ
- § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО
- § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ
- § 58. ДВИЖЕНИЕ ПЛАНЕТ
- § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ
- § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ
- § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ
- § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ
- § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ
- § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА
- Равновесие тел
- Глава 7. Элементы статики
- § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ
- § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ
- § 67. ПРАВИЛО МОМЕНТОВ
- § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ
- Законы сохранения в механике
- Глава 8. Закон сохранения импульса
- § 70. СИЛА И ИМПУЛЬС
- § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ
- Глава 9. Механическая работа и мощность
- § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ
- § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ
- § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
- § 77. РАБОТА СИЛЫ ТЯЖЕСТИ
- § 78. РАБОТА СИЛЫ УПРУГОСТИ
- § 79. РАБОТА СИЛЫ ТРЕНИЯ
- § 80. МОЩНОСТЬ
- Глава 10. Закон сохранения энергии
- § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА
- § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ
- § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН
- § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
- § 91. СТОЛКНОВЕНИЕ ТЕЛ
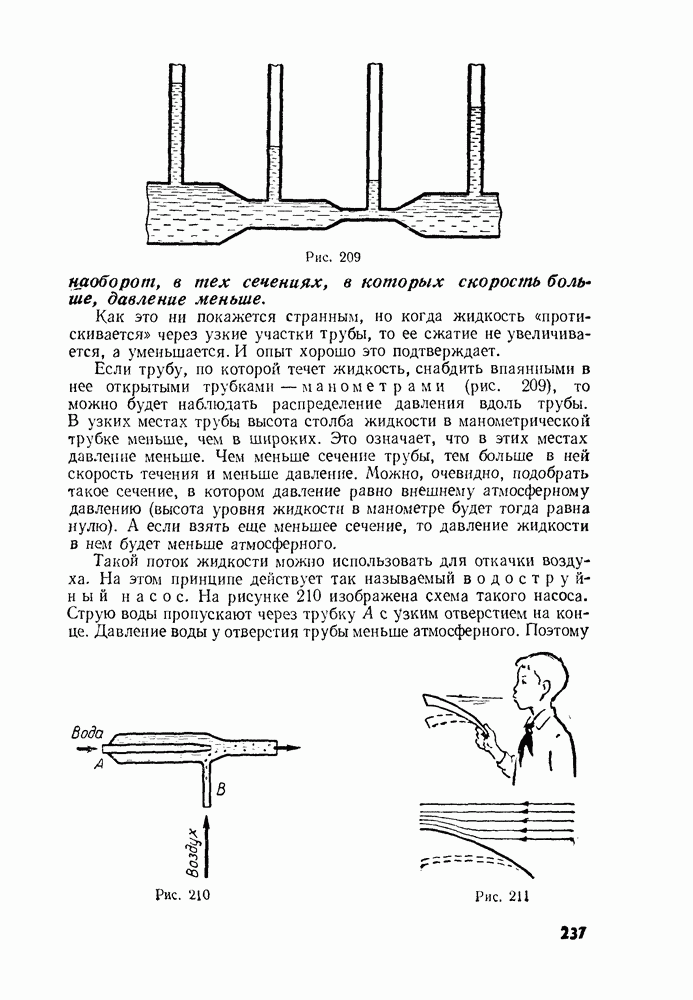
- § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ
- § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ
- Заключение
- Лабораторные работы
- 1. Определение ускорения тела при равноускоренном движении
- 2. Определение коэффициента трения скольжения
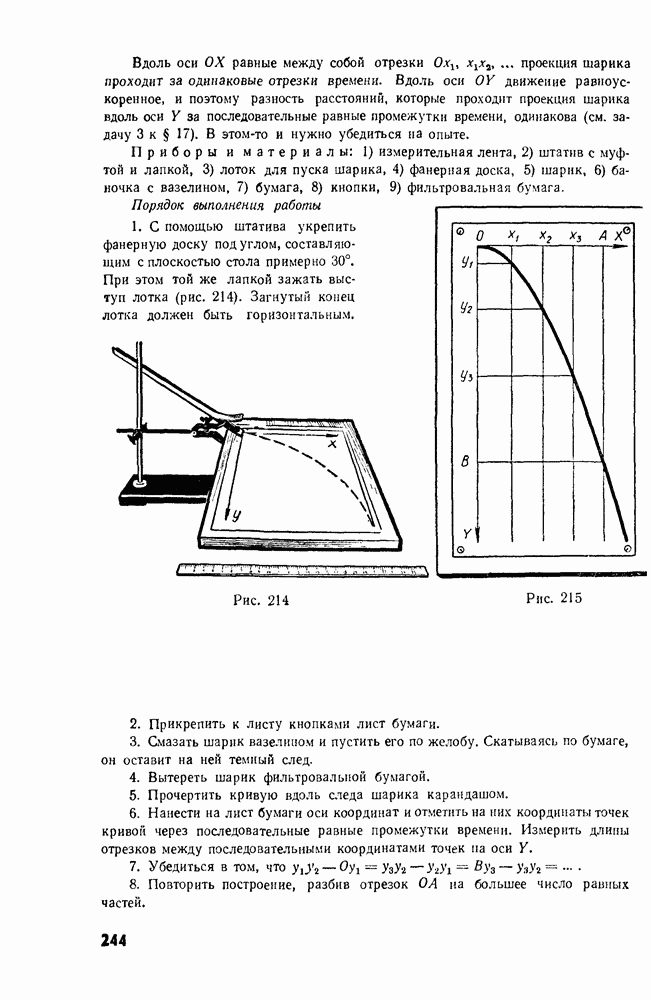
- 3. Изучение движения тела по параболе
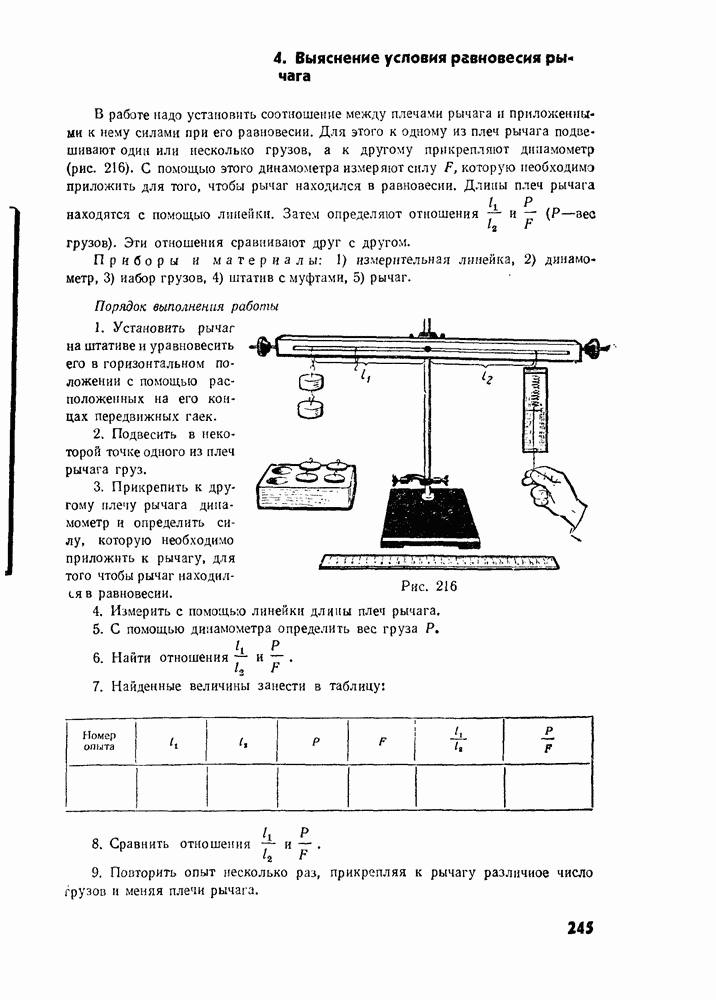
- 4. Выяснение условия равновесия рычага
- 5. Определение центра тяжести плоской пластины
- Ответы к упражнениям