| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ
В предыдущих параграфах этой главы мы выяснили, как движутся тела, если на них действует одна сила — сила упругости, сила тяготения или сила трения. Но в действительности с такими движениями в земных условиях почти никогда не приходится иметь дело. Наряду с силами упругости и тяготения на тело всегда действует и сила трения. Как в таких случаях решать механические задачи?
Напомним прежде всего, что в уравнении, выражающем второй закон Ньютона,

 — это равнодействующая всех сил, приложенных к телу, т. е. геометрическая сумма векторов этих сил. Поэтому, приступая к решению какой-нибудь задачи, нужно сначала выяснить, какие силы действуют на тело, каковы их абсолютные значения и направления. Затем, изобразив на чертеже действующие на тело силы, найти их равнодействующую и, пользуясь законами движения Ньютона, решить задачу.
— это равнодействующая всех сил, приложенных к телу, т. е. геометрическая сумма векторов этих сил. Поэтому, приступая к решению какой-нибудь задачи, нужно сначала выяснить, какие силы действуют на тело, каковы их абсолютные значения и направления. Затем, изобразив на чертеже действующие на тело силы, найти их равнодействующую и, пользуясь законами движения Ньютона, решить задачу.
Но можно и не производить геометрического сложения векторов сил. В § 5 мы узнали, что проекция суммы нескольких векторов на какую-нибудь ось равна сумме проекций этих векторов на ту же ось. Это позволяет нам заменить геометрическое сложение векторов алгебраическим сложением их проекций.
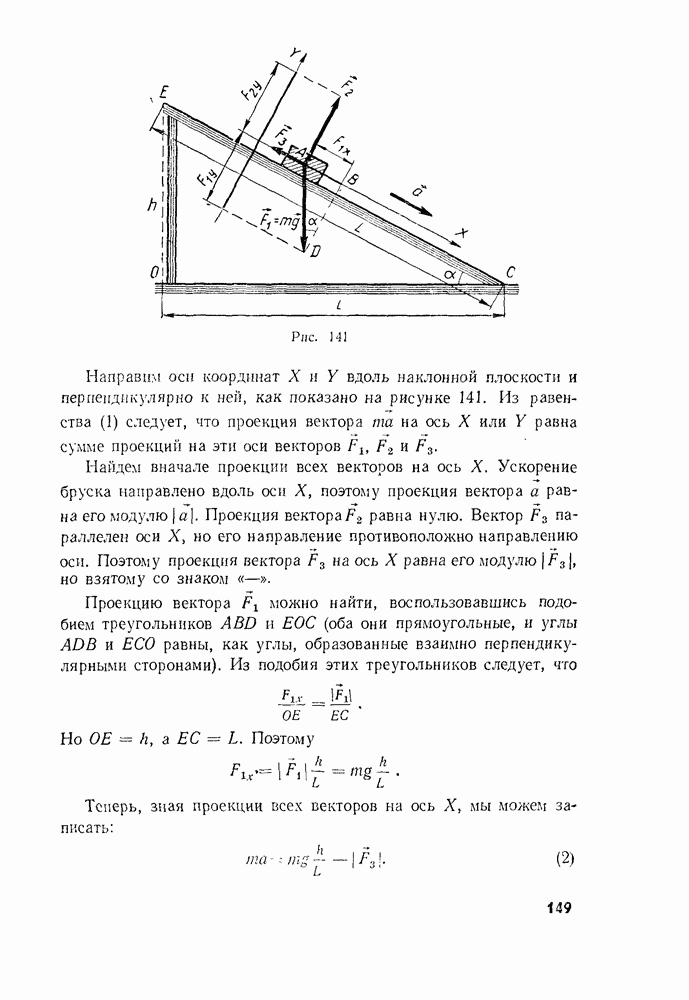
В качестве примера рассмотрим движение тела по наклонной плоскости. Предположим, что по наклонной плоскости с углом наклона а движется брусок массой  (рис. 141). Найдем его ускорение.
(рис. 141). Найдем его ускорение.
На движущийся брусок действуют три силы: сила тяжести  сила реакции опоры (наклонной плоскости)
сила реакции опоры (наклонной плоскости)  перпендикулярная плоскости; сила трения
перпендикулярная плоскости; сила трения  направленная против движения.
направленная против движения.
Ускорение бруска а по условию направлено параллельно наклонной плоскости.
По второму закону Ньютона


Рис. 141
Направим оси координат X и  вдоль наклонной плоскости и перпендикулярно к ней, как показано на рисунке 141. Из равенства (3) следует, что проекция вектора та на ось X или
вдоль наклонной плоскости и перпендикулярно к ней, как показано на рисунке 141. Из равенства (3) следует, что проекция вектора та на ось X или  равна сумме проекций на эти оси векторов
равна сумме проекций на эти оси векторов 
Найдем вначале проекции всех векторов на ось X. Ускорение бруска направлено вдоль оси X, поэтому проекция вектора а равна его модулю  Проекция вектора равна нулю. Вектор
Проекция вектора равна нулю. Вектор  параллелен оси X, но его направление противоположно направлению оси. Поэтому проекция вектора
параллелен оси X, но его направление противоположно направлению оси. Поэтому проекция вектора  на ось X равна его модулю
на ось X равна его модулю  но взятому со знаком
но взятому со знаком 
Проекцию вектора  можно найти, воспользовавшись подобием треугольников
можно найти, воспользовавшись подобием треугольников  (оба они прямоугольные, и углы
(оба они прямоугольные, и углы  равны, как углы, образованные взаимно перпендикулярными сторонами). Из подобия этих треугольников следует, что
равны, как углы, образованные взаимно перпендикулярными сторонами). Из подобия этих треугольников следует, что

Но  Поэтому
Поэтому

Теперь, зная проекции всех векторов на ось X, мы можем записать:

Аналогичное уравнение можно записать и для проекций всех векторов на ось  Проекции векторов а и
Проекции векторов а и  равны нулю, проекция вектора
равны нулю, проекция вектора  по модулю равна
по модулю равна  а проекцию вектора
а проекцию вектора  можно найти из подобия тех же треугольников ABD и ЕОС:
можно найти из подобия тех же треугольников ABD и ЕОС:

Но  (проекция силы
(проекция силы  на ось
на ось  отрицательна),
отрицательна), 
Следовательно,

Отсюда 

Так как проекция ускорения а бруска на ось  равна нулю, то равна нулю и сумма проекций на эту ось всех сил, действующих на брусок. Поэтому
равна нулю, то равна нулю и сумма проекций на эту ось всех сил, действующих на брусок. Поэтому

Рассмотрим вначале случай, когда тело движется без трения (коэффициент трения  ). В этом случае из уравнения (2) найдем, что
). В этом случае из уравнения (2) найдем, что

Отношение  всегда меньше единицы (катет меньше гипотенузы). Значит, по наклонной плоскости тело движется с ускорением меньшим, чем ускорение
всегда меньше единицы (катет меньше гипотенузы). Значит, по наклонной плоскости тело движется с ускорением меньшим, чем ускорение  свободного падения. Чем более полога плоскость, тем меньше отношение
свободного падения. Чем более полога плоскость, тем меньше отношение  и тем меньше ускорение а.
и тем меньше ускорение а.
Но часто силой трения пренебречь нельзя. Найдем поэтому выражение и для величины 
В § 49 было показано, что сила трения пропорциональна модулю силы давления 
Поэтому можно написать, что

В нашем случае сила давления равна, но противоположна по направлению силе реакции опоры  Следовательно, модуль силы
Следовательно, модуль силы  равен просто модулю силы
равен просто модулю силы  Из формулы (3) следует, что
Из формулы (3) следует, что

Отсюда для силы трения  получаем:
получаем:

Подставив значенне  в уравнение (2), мы получим интересующее нас ускорение
в уравнение (2), мы получим интересующее нас ускорение

или (после сокращения на  )
)

Из треугольника  видно, что
видно, что

Поэтому формулу (4) можно переписать в виде

Из этой формулы следует, что когда коэффициент трения равен нулю (т. е. силой трения можно пренебречь),

Упражнение 37
1. Найдите построением геометрическую сумму сил, приложенных к бруску на наклонной плоскости (по рис. 141). Как направлена равнодействующая  этих сил относительно наклонной плоскости?
этих сил относительно наклонной плоскости?
2. С вершины наклонной плоскости высотой 20 см и длиной 1 м соскальзывает брусок. Определите скорость бруска в конце наклонной плоскости. Трение не учитывать.
3. Санки скатываются с горки длиной 10 м за 2 сек. Найдите угол наклона горки. Трение не учитывать.
4. Почему в формулы для ускорения тела на наклонной плоскости не входит масса тела?
5. На наклонной плоскости высотой 5 м и длиной 10 м находится тело массой 50 кг, на которое действует сила  направленная горизонтально и равная 300 н (рис. 142). Определите ускорение тела. (Трением пренебречь.)
направленная горизонтально и равная 300 н (рис. 142). Определите ускорение тела. (Трением пренебречь.)
6. Вычислите ускорение тела, скользящего по наклонной плоскости, если высота и длина ее основания одинаковы, а коэффициент трения тела о наклонную плоскость равен 0,2.
7. Приведите примеры использования наклонной плоскости. В чем ее полезность в этих примерах?
8. Как будет двигаться тело по наклонной плоскости, если проекция силы тяжести на прямую, параллельную наклонной плоскости, численно равна силе трения?

Рис. 142
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о движении
- § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА
- § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ
- § 3. ПЕРЕМЕЩЕНИЕ
- § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА
- § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ
- § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ
- § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
- § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
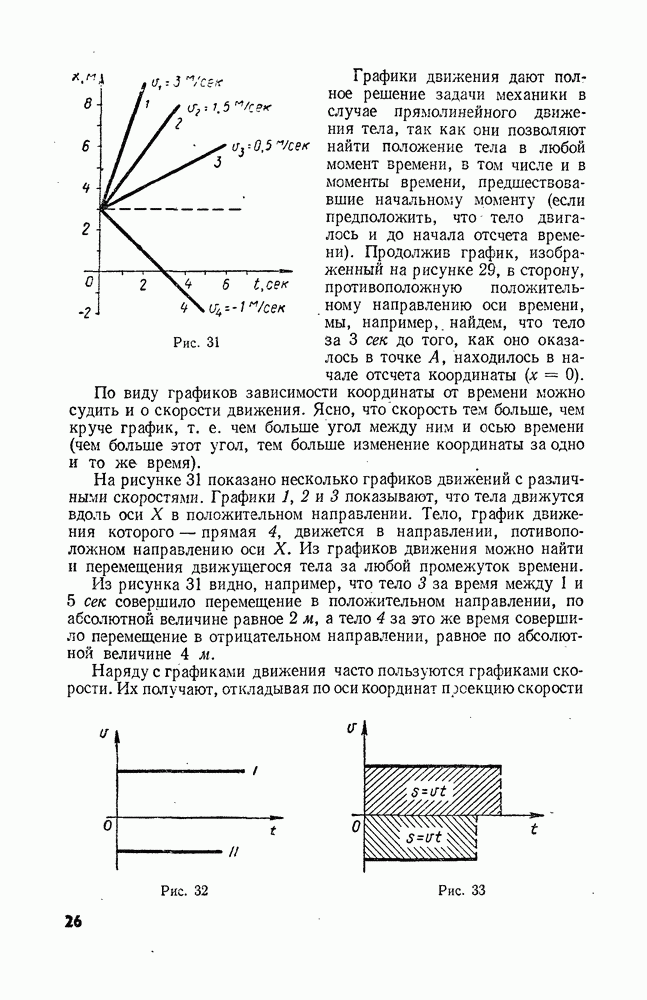
- § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ
- § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
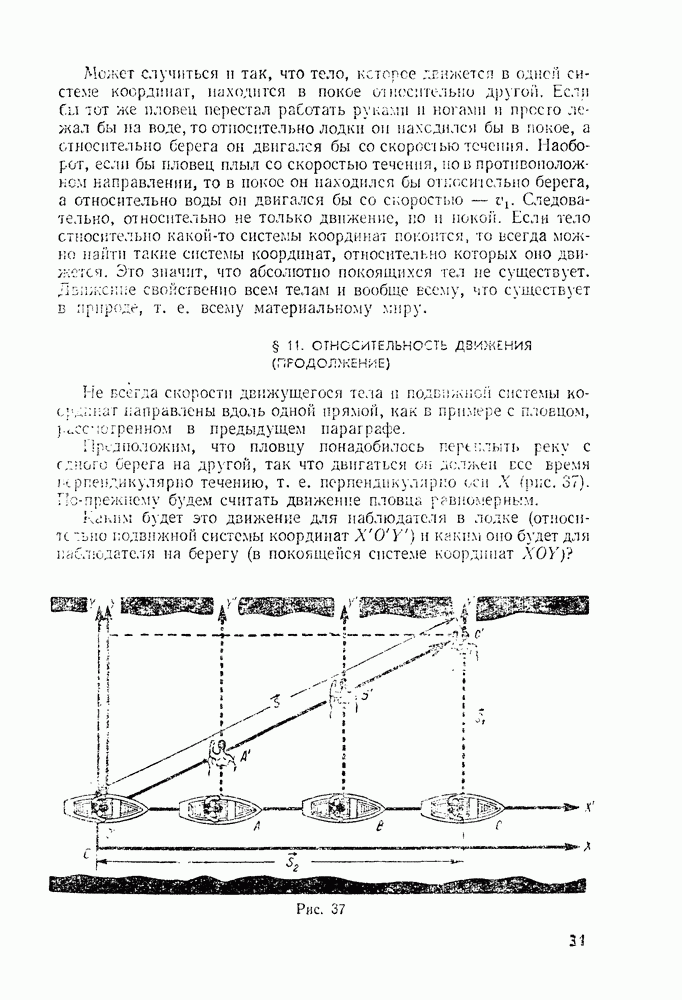
- § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ)
- § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ
- Глава 2. Прямолинейное неравномерное движение
- § 13. СРЕДНЯЯ СКОРОСТЬ
- § 14. МГНОВЕННАЯ СКОРОСТЬ
- § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ
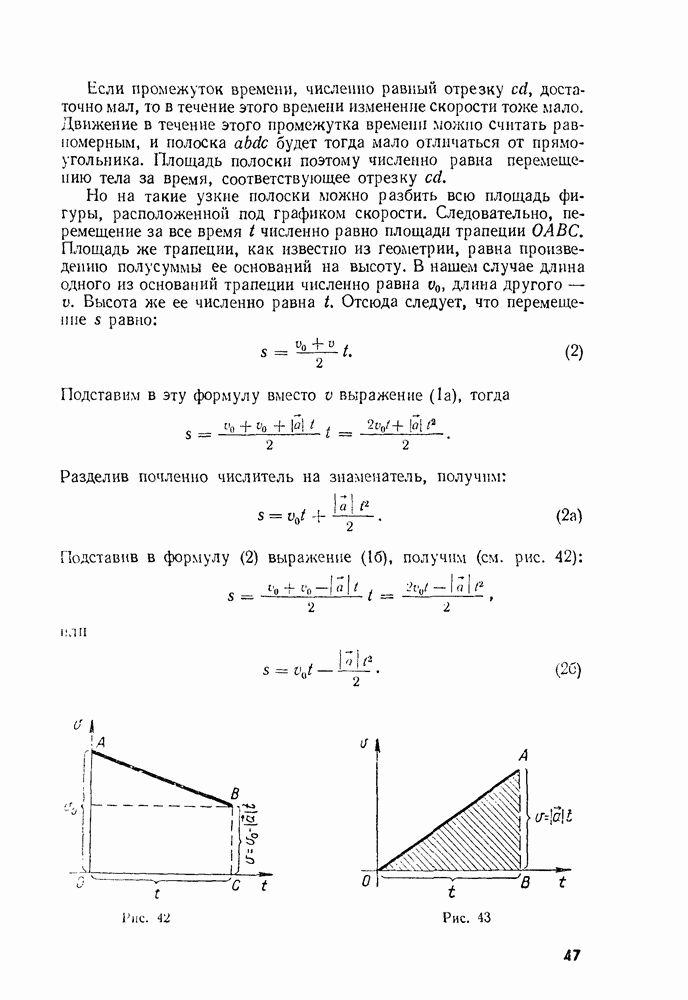
- § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
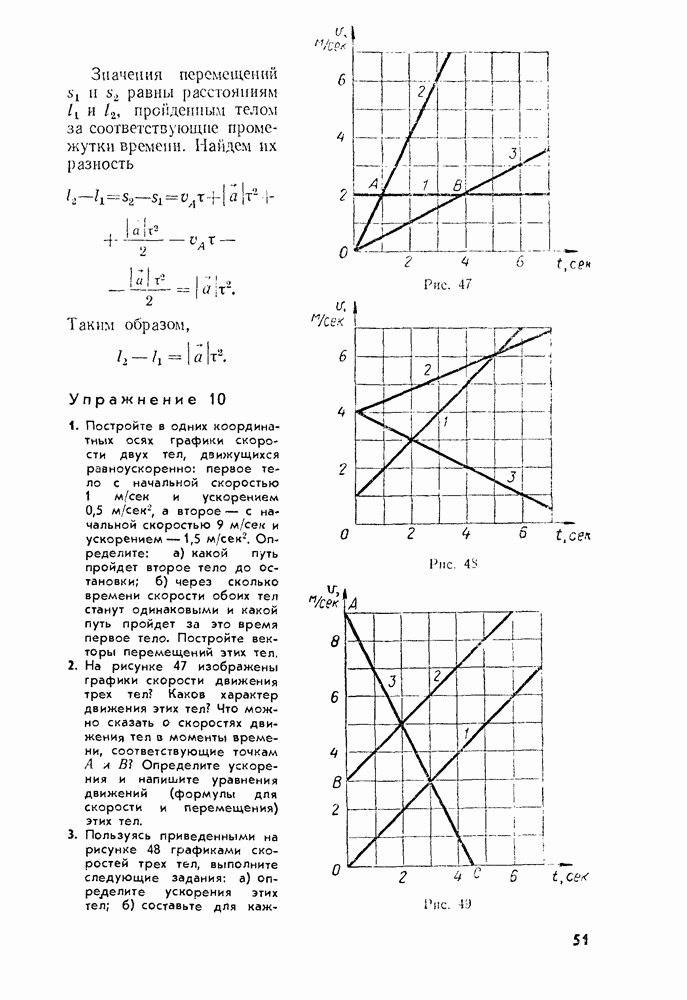
- § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ
- § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ
- § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
- § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
- Глава 3. Криволинейное движение
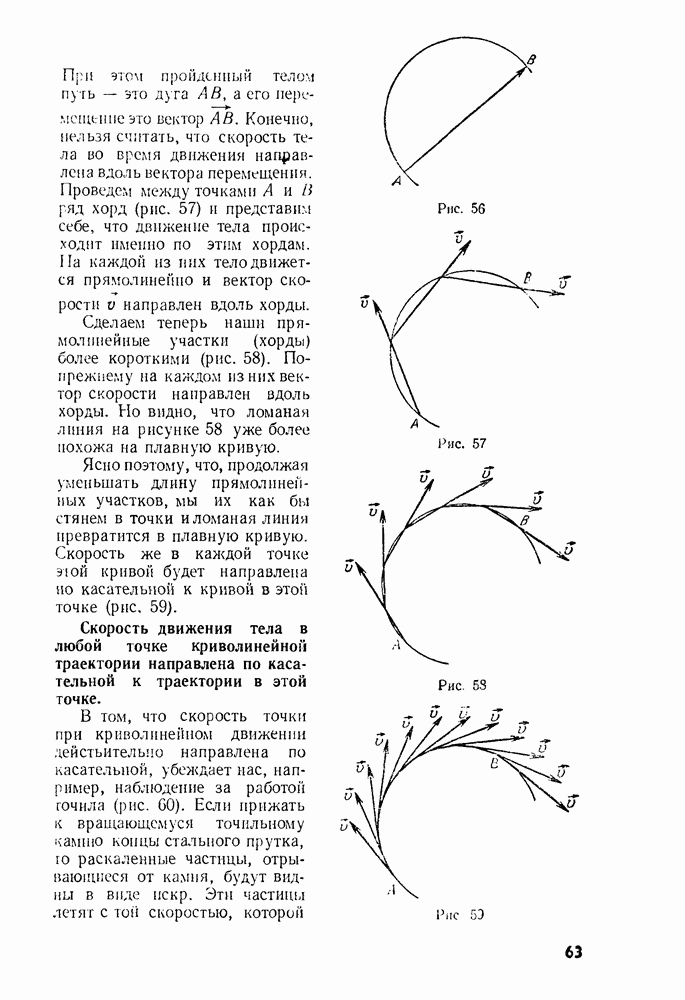
- § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
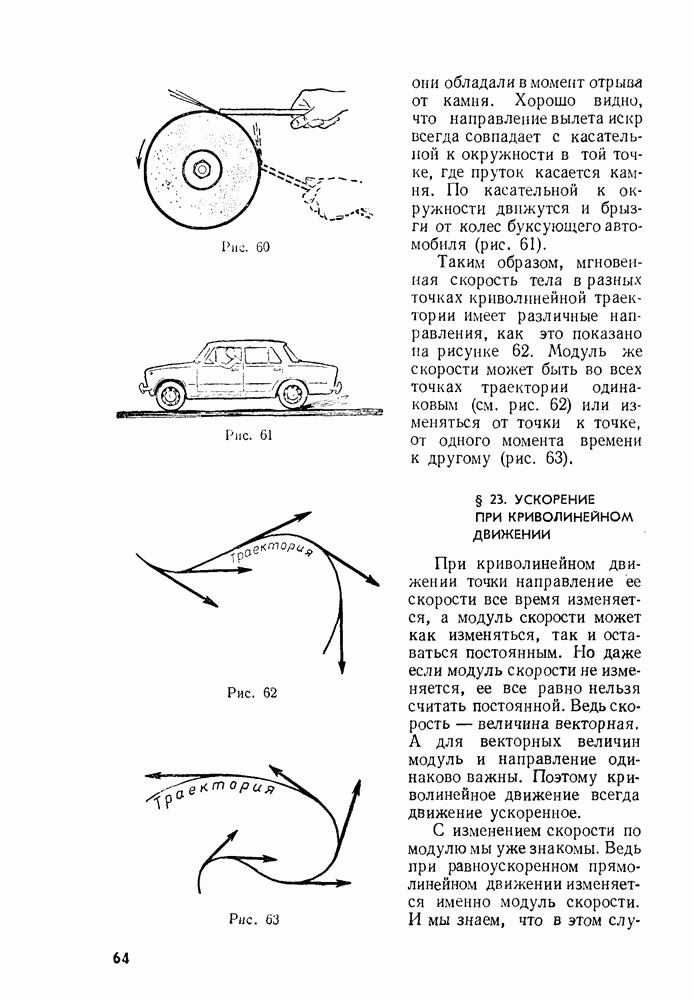
- § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
- § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ
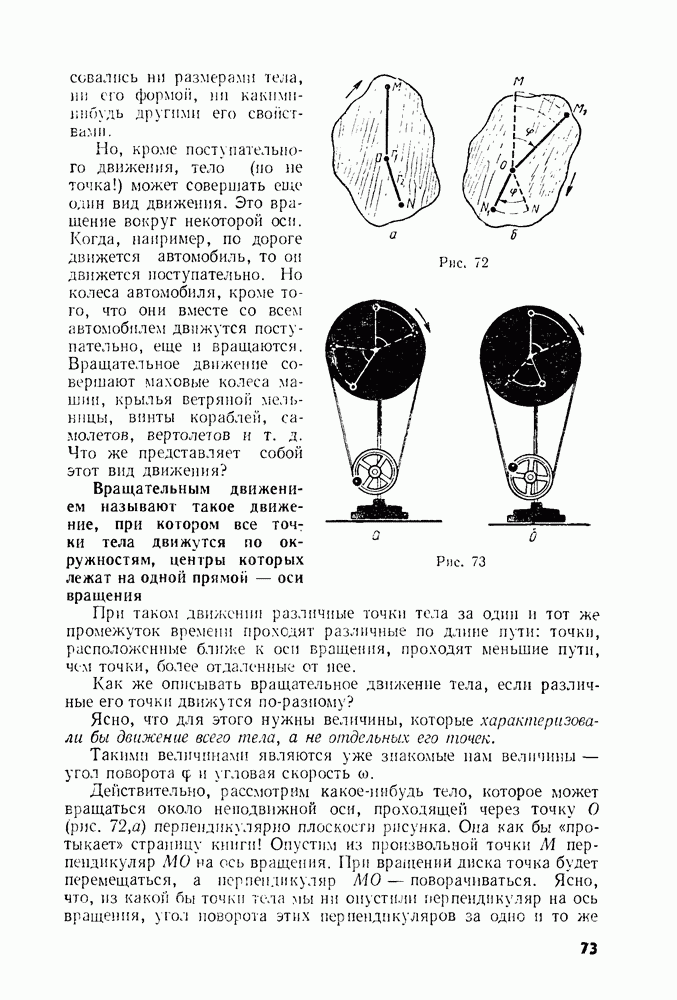
- § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА
- Динамика
- Глава 4. Законы движения
- § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ
- § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ
- § 31. ИНЕРТНОСТЬ ТЕЛ
- § 32. МАССА ТЕЛ
- § 33. МАССА ЛУНЫ
- § 34. СИЛА
- § 35. ВТОРОЙ ЗАКОН НЬЮТОНА
- § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение)
- § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР
- § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА
- § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА
- Глава 5. Силы природы
- § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ
- § 41. СИЛА УПРУГОСТИ
- § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 44. СИЛА ТЯЖЕСТИ
- § 45. ВЕС ТЕЛ
- § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ
- § 47. МАССА ЗЕМЛИ
- § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ
- § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ
- Глава 6. Применение законов движения
- § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ
- § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ
- § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ
- § 54. НЕВЕСОМОСТЬ
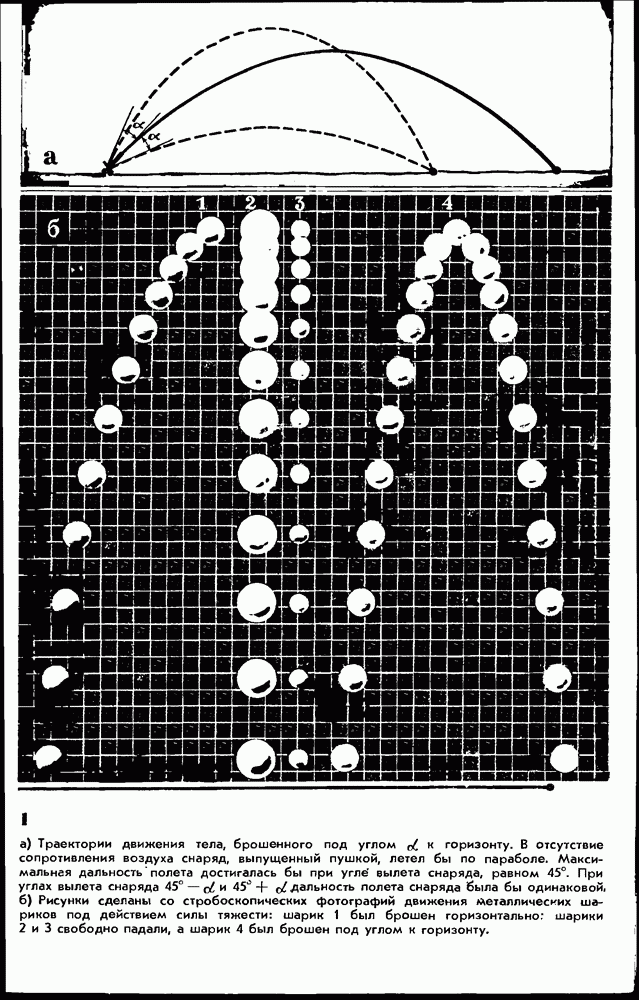
- § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ
- § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО
- § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ
- § 58. ДВИЖЕНИЕ ПЛАНЕТ
- § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ
- § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ
- § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ
- § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ
- § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ
- § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА
- Равновесие тел
- Глава 7. Элементы статики
- § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ
- § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ
- § 67. ПРАВИЛО МОМЕНТОВ
- § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ
- Законы сохранения в механике
- Глава 8. Закон сохранения импульса
- § 70. СИЛА И ИМПУЛЬС
- § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ
- Глава 9. Механическая работа и мощность
- § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ
- § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ
- § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
- § 77. РАБОТА СИЛЫ ТЯЖЕСТИ
- § 78. РАБОТА СИЛЫ УПРУГОСТИ
- § 79. РАБОТА СИЛЫ ТРЕНИЯ
- § 80. МОЩНОСТЬ
- Глава 10. Закон сохранения энергии
- § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА
- § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ
- § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН
- § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
- § 91. СТОЛКНОВЕНИЕ ТЕЛ
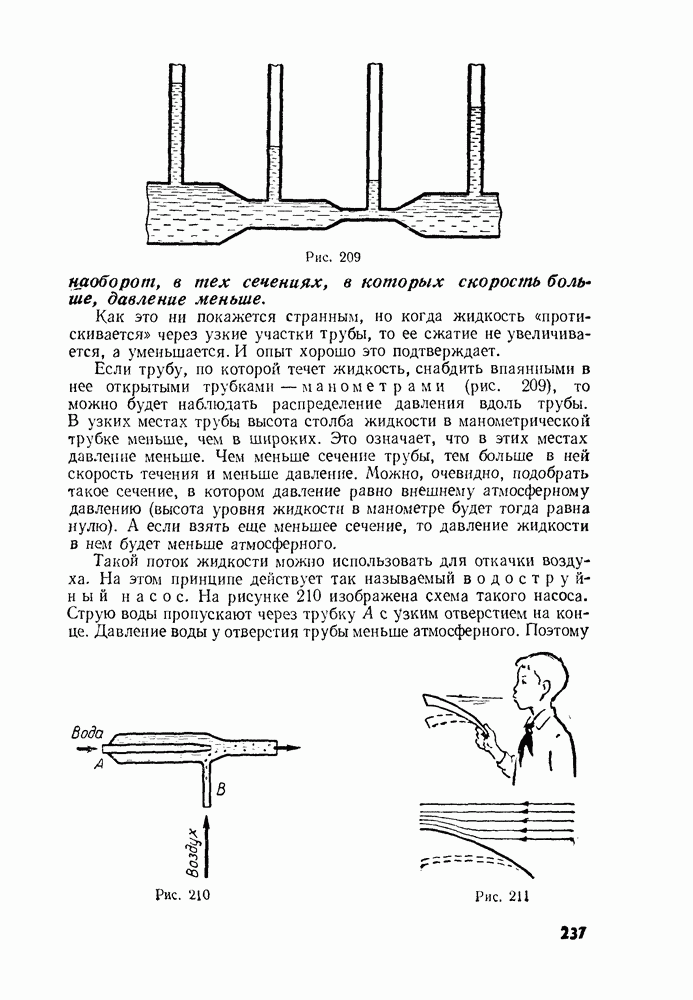
- § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ
- § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ
- Заключение
- Лабораторные работы
- 1. Определение ускорения тела при равноускоренном движении
- 2. Определение коэффициента трения скольжения
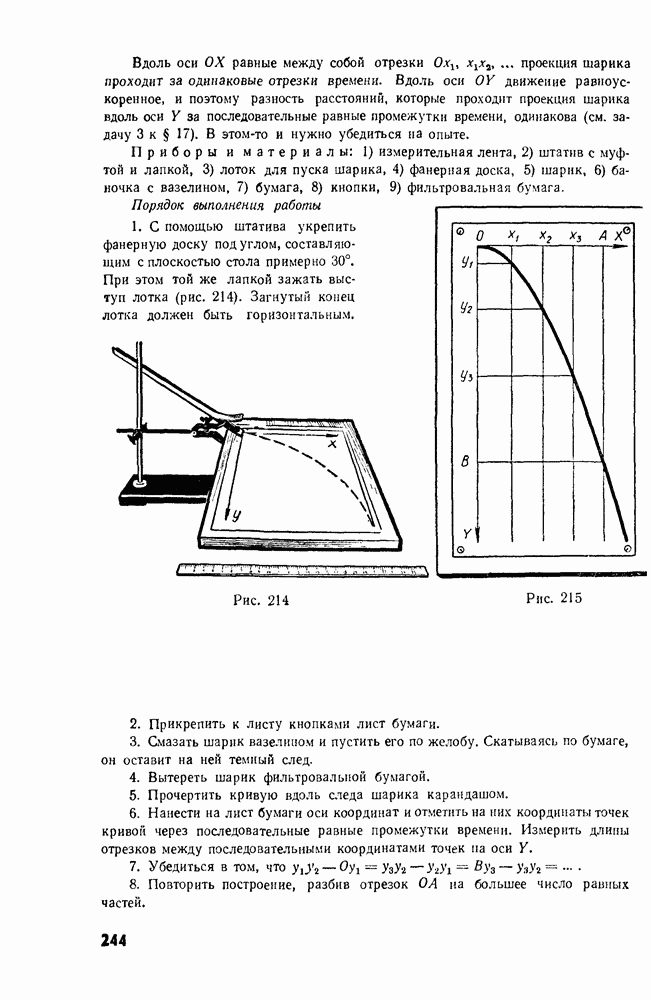
- 3. Изучение движения тела по параболе
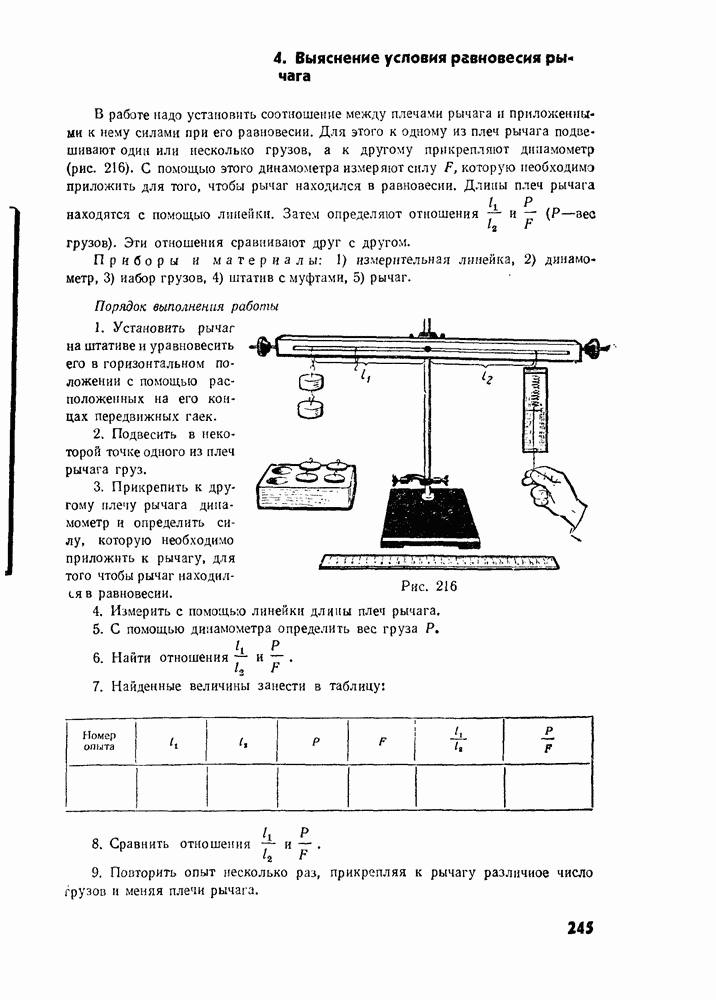
- 4. Выяснение условия равновесия рычага
- 5. Определение центра тяжести плоской пластины
- Ответы к упражнениям